Skip to: [Printable Version (PDF)] [Bibliography] [Footnotes]

Finance and Economics Discussion Series: 2006-42 Screen Reader version ^♣

An Estimate of the Inflation Risk Premium Using a Three-Factor Affine Term Structure Model

J. Benson Durham ^*

Division of Monetary Affairs

Board of Governors of the Federal Reserve System

Washington, DC 20551

(202) 452-2896

[email protected]

Keywords: Affine term structure model, inflation risk premium

Abstract:

This paper decomposes nominal Treasury yields into expected real rates, expected inflation rates, real risk premiums, and inflation risk premiums by separately calibrating a three-factor affine term structure model to the nominal Treasury and TIPS yield curves. Although this particular application seems to produce expected real short rates and inflation rates that are somewhat static, there are theoretical advantages to calibrating the model to nominal and real yields separately. Moreover, the estimates correlate positively with back-of-the-envelope measures of the inflation risk premium. With respect to the current environment, monetary policy uncertainty does not seem to have contributed to the apparent increase in the inflation risk premium since the beginning of 2006. Also, in purely nominal terms, the increase in term premiums thus far this year might be just as much a global as a domestic phenomenon, given that nominal term premiums have also increased in Germany and the United Kingdom.

1. Introduction

This paper outlines an estimate of the inflation risk premium based on a three-factor Gaussian term structure model of both the nominal U.S. Treasury and TIPS yield curves. Model calibration to the nominal and real yield curves separately produces estimates of nominal and real term premiums and, in turn, (zero coupon and forward) inflation risk premiums along the term structure. This particular application of the model produces expected real short rates and inflation rates that are somewhat static, likely because of the very short available sample of TIPS data. Nonetheless, there may be some key theoretical advantages to separate as opposed to joint estimation of the real and nominal curves. Besides, the estimates of the real and inflation risk premiums seem quite sensible. Consistent with similar approaches (Kim and Wright, 2005), these results suggests that term premiums reached very low historical levels during the monetary policy tightening cycle that commenced in June 2004, and even more recently, some of those declines have retraced since the beginning of this year. Also, estimates of the inflation risk premium derived from the model correlate positively with common back-of-the-envelope measures.

This paper also examines whether the inflation risk premium produced by the model correlates with measures of inflation and monetary policy uncertainty. Depending on the particular proxy for those variables, some time-series regressions produce a statistically significant and positive correlation between inflation uncertainty and the inflation risk premium either in levels or first differences. And, at least in levels, there does appear to be a statistically significant and positive relation between Eurodollar implied volatility and the inflation risk premium estimate. Also, the small increase in option-implied monetary policy uncertainty this year has contributed minimally to the apparent increase in the inflation risk premium. Application of a three-factor model to nominal government bond yields in Germany and the United Kingdom also indicates that term premiums have increased in these countries by a similar magnitude, which suggests that the recent rise in term premiums is in part a global rather than a purely domestic phenomenon.

The remainder of the paper is organized as follows. Section 2 briefly reviews the broad literature on inflation risk premiums and outlines the methodology. Section 3 reviews the three-factor (Gaussian) affine term structure used to disentangle expected real rates, expected inflation, the real term premium, and the inflation risk premium from nominal forward and zero-coupon rates, and Section 4 outlines the results in the context of the current environment. Sections 5 and 6 examine the estimates with respect to other measures of the inflation risk premium and to proxies for inflation and monetary policy uncertainty, and Section 7 describes estimates of nominal term premiums in Germany and the United Kingdom vis-à-vis those in the United States. Section 8 concludes.

2. Recovering the Inflation Risk Premium from Term Structure Models

The inflation risk premium is one of many risk premiums that compensate investors for uncertainty, and financial economists have used a wide variety of approaches to estimate that premium. For example, some studies examine ex ante and ex post returns on nominal and inflation-indexed sovereign debt (Kandel et al., 1996), others focus on the covariance of returns on nominal and (hypothetical) indexed government bonds in a traditional CAPM or consumption-based CAPM framework (Campbell and Shiller, 1996; Bodie, 1979), and a few employ a much more behavioral approach (Hammond et al., 1999). More recently, however, inflation risk premium estimates have been obtained from arbitrage-free (affine) term structure models that include both nominal interest rates and inflation (D'Amico et al., 2005).¹ By calibrating a three-factor term structure model to the nominal and real yield curves separately, this paper is most akin to these more recent efforts.

The methodology in this paper abstracts from tax, liquidity, convexity, and other issues. To begin, an instantaneous nominal forward interest rate at some horizon , denoted by , is comprised of the expected future real rate, ; the expected future inflation rate, ; the real forward term premium, ; and the inflation risk premium, , as in

(1)

$$f_t^N =\left( {s_t^R +\pi _t^e } \right)+\left( {p_t^R +p_t^\pi } \right)$$

Or, just in nominal terms, the instantaneous forward rate can be considered the sum of the expected nominal short rate,, and the nominal forward term premium, , as in

(2)

$$f_t^N =s_t^N +p_t^N$$

where

$$s_t^N =s_t^R +\pi _t^e$$

and

$$p_t^N =p_t^R +p_t^\pi$$

As noted in more detail below, one can readily disentangle and fromby fitting a term structure model such as, say, Vasicek (1977) or Cox et al. (1985) to the nominal Treasury curve.² But to obtain an estimate of the inflation risk premium (and thus expected inflation), we also need to model the real yield curve or inflation directly. Similar to (2), the real instantaneous forward rate at some horizon ,, can be decomposed as

(3)

$$f_t^R =s_t^R +p_t^R$$

The key to the approach in this paper is that separate application of an -factor term structure model to real yields produces estimates of the expected real future short rate at time , again , and the real term premium,.

Finally, with and , one can easily recover the (forward) inflation risk premium simply as

(4)

$$p_t^\pi =p_t^N -p_t^R$$

Also, expected future inflation is the difference between the expected future real and nominal rates, derived from the corresponding applications of the model.

3. A Review of a Gaussian Model

To briefly review how to obtainfrom the nominal term structure, assume, just as in Kim and Wright (2005) and similar to Langetieg (1980) and others, that the underlying factors that drive nominal bond prices, denoted by the vector , follow a multivariate (mean-reverting) Ornstein-Uhlenbeck process, as in

(5)

$$dx_t =\kappa \left( {\theta -x_t } \right)dt+\Sigma dw_t$$

where is a three-dimensional Brownian motion, is avector, is a lower triangular matrix, and is a diagonal matrix. Also, (zero coupon) nominal bond yields, , for a given maturity, , at a given time, , are an affine function of , following

(6)

$$y_{n,t} =\frac{A\left( n \right)}{n}+\frac{B\left( n \right)}{n}'x\left( t \right)$$

where the functions and are the solutions to the bond pricing equation, which follows from the assumption that no arbitrage opportunities exist along the yield curve.³ Note that the instantaneous short rate is the limit of (6) as approaches zero and is also therefore a linear function of the model factors. A projection of the factors periods ahead produces the -period-ahead expected short rate,. Also, the instantaneous forward rate, , for a given maturity is also an affine function of and follows

(7)

$$f_{n,t} =\frac{\partial A\left( n \right)}{\partial n}+\frac{\partial B\left( n \right)}{\partial n}'x\left( t \right)$$

The -period ahead instantaneous forward term premium from the model,, is simply the -period ahead instantaneous model-implied forward rate minus the -period-ahead expected short rate.⁴

For and the real curve, I calibrate precisely the same model, where the underlying stochastic processes again follow

(8)

$$d\tilde {x}_t =\tilde {\kappa }\left( {\tilde {\theta }-\tilde {x}_t } \right)dt+\tilde {\Sigma }d\tilde {w}_t$$

and real yields can be expressed as

(9)

$$\tilde {y}_{n,t} =\frac{\tilde {A}\left( n \right)}{n}+\frac{\tilde {B}\left( n \right)}{n}'\tilde {x}\left( t \right)$$

In tandem, (5) and (6) and (8) and (9) produce nominal and real forward, zero-coupon, and instantaneous short rates along the term structure, and therefore one can easily compute (4).⁵

Separate calibration of the model to nominal Treasuries and TIPS obviously implies that the relevant state vectors, and , are formally distinct. They certainly can be positively correlated, as one indeed would expect, but this method imposes no constraints on the latent variables that drive the real and nominal yield curves. The key potential problematic issue with the implementation of (8) and (9) is the very short history of TIPS. Moreover, liquidity was poor during the early period of trading, and therefore any estimate of the real term premium likely includes a sizeable liquidity premium, which in turn biases the inflation risk premium estimate downward.

4. Model Results and the Contemporary Environment

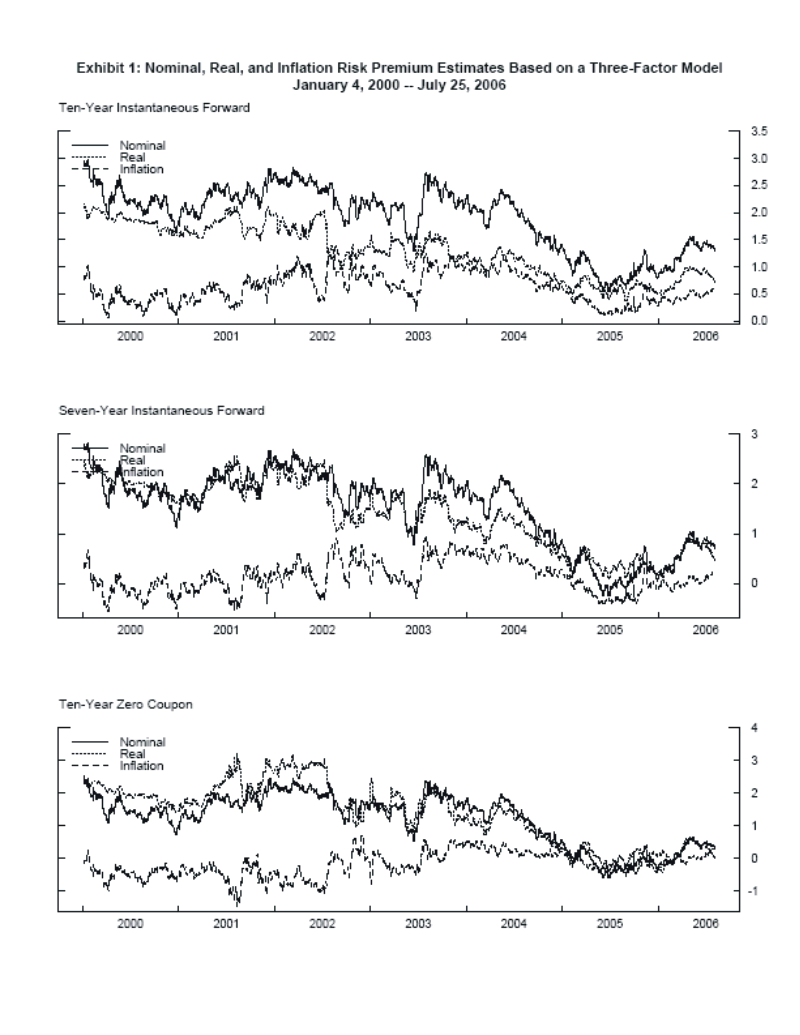
The top panel of Exhibit 1 plots the nominal ten-year instantaneous forward term premium based on the nominal term structure, the real ten-year instantaneous forward term premium based on the TIPS term structure, and the model-implied forward inflation risk premium at that horizon from January 4, 2000 through July 25, 2006. Again, given the relative illiquidity of the TIPS market after the inception of trading, the real term premium likely includes a substantial liquidity premium, and therefore the inflation risk premium is probably understated for the earlier part of the sample. More recently, the inflation risk premium has increased from near sample lows in mid-2005, but it remains at a moderate level--59 basis points, very close to the sample average of 61 basis points.

Table 1 shows the decomposition of ten-year nominal forward rates in more detail for selected dates in the sample. Column 1 indicates that forward rates have fallen 95 basis points from the day before tightening began on June 30, 2004 to the most recent observation on July 25, 2006, and Column 2 shows that the model-implied forward rate has fallen by 69 basis points over this period. The expected real short rate has increased about 14 basis points, while expected inflation is largely unchanged, as noted in Columns 3 and 4, respectively. Also, as indicated in Columns 5 and 6, the decline in the nominal term premium is 45 basis points, and the inflation risk premium is 36 basis points lower since the inception of policy firming.⁶ Regarding developments since the beginning of 2006, the results might be interpreted as consistent with at least a partial unwinding of the "conundrum" of unusually low long-term interest rates, perhaps first identified in early 2005.⁷ In fact, the model attributes virtually all of the increase in forward rates since year-end 2005 to increases in risk premiums, with the increase in the inflation risk premium (32 basis points) a bit more pronounced than the rise in the real term premium (24 basis points).⁸

Returning to the middle panel of Exhibit 1, seven-year instantaneous forward term premiums, perhaps not surprisingly reflect a similar pattern, as they also have rebounded from historic lows. But, some differences are noteworthy. As indicated in Table 2, the increase in the expected real rate since the Federal Open Market Committee (FOMC) began tightening policy is more pronounced than at the ten-year horizon, and the decline in term premiums is comparatively more concentrated in the real as opposed to the inflation risk premium. Also, in general, term premiums over the sample are considerably lower, as the current estimate is 23 basis points, with a sample average of 13 basis points.

Finally, the bottom panel of Exhibit 1 plots the ten-year zero coupon premiums. These estimates are less intuitive, as the inflation risk premium is largely negative from the beginning of the sample through the middle of 2002 and hovers close to zero beyond that point. These results might reflect the fact that fewer TIPS issues are used to fit the shorter end of the curve, which is a less pronounced issue with respect to distant horizon forward rates.

5. Comparisons with Other Measures

Comparisons with other measures of the inflation risk premium are instructive. One back-of-the-envelope proxy refers to the difference between nearly adjacent distant-horizon nominal and real forward rates. For example, the spread between nominal (real) forward rates at two distant horizons is often considered a rough approximation for the nominal (real) term premium, because investors likely expect the nominal (real) short rate to be unchanged far into the future. In turn, one can deduce the inflation risk premium from such estimates. This estimate is based on the assumption that investors' best guess about the trajectory of inflation between, say, nine and ten years ahead is that it will be constant, and therefore the difference between distant forward breakeven rates is the inflation risk premium.

Table 3 summarizes the correlation matrix using daily data from January 4, 2000 through July 25, 2006 between the three-factor model estimate of the ten- and seven-year instantaneous forward inflation risk premiums and two such back-of-the-envelope measures--the forward breakeven inflation spreads between six and seven and between nine and ten years ahead. Consistent with intuition, the ten-year (seven-year) model-based estimate is positively and statistically significantly correlated with the alternative measures, as the coefficients are 0.49 and 0.28 (0.31 and 0.28) vis-à-vis the six- to seven- and nine to ten-year spreads, respectively.⁹ Therefore in general, although the proxies are somewhat crude, these results provide some additional confidence in the model-based estimates.

6. The Inflation Risk Premium and Proxies for Inflation and Policy Uncertainty

Besides alternative measures, another issue is whether the inflation risk premium estimates correlate with other key variables, including various proxies for inflation and monetary policy uncertainty.¹⁰ Toward that end, Table 4 summarizes time-series regressions that generally follow

(10)

$$\bar {p}_t^\pi =\beta _0 +\beta _1 'X_1 +\beta _2 'X_2 +\varepsilon$$

where is either the average level or first difference in the estimate of the inflation risk premium over a given month, is a constant, is a vector of proxies for inflation uncertainty, is a vector of variables related to monetary policy uncertainty, and is an error term. With respect to, the regressions alternatively include the variance and dispersion of near- and long-term inflation forecasts from individual responses from the University of Michigan and Blue Chip surveys, respectively.¹¹ The vector also includes a measure of the dispersion of relative prices in the consumer price index,, in month , following

(11)

$$D_t =\sqrt {\sum\limits_{i=1}^n {w_{i,t} \left( {\pi _{i,t} -\pi _t } \right)^2} }$$

where is the inflation rate of the component of the CPI, is the weight of the component in the index, is the overall CPI inflation rate, and is the number of components.¹² Finally, the surprise component of inflation data releases might be related to inflation uncertainty, as unexpected changes in near term developments might affect inflation uncertainty further ahead. Therefore, the regressions that include monthly changes in the inflation risk premium on the left-hand-side include the squared differences between the released value and the Money Market Services survey median expectation for headline CPI and PPI.¹³

Regarding , the regressions also consider implied Eurodollar volatility, measured at the six-month horizon, as a proxy for uncertainty regarding the path of monetary policy. Of course, uncertainty about policy might be related to uncertainty not only about inflation but also about the real economy and about the reaction function of the Federal Open Market Committee (FOMC). In addition, the regressions include a dummy variable for the period after the transition to the current Chairman on February 1, 2006.

Turning to the results, Regressions 1 and 2 in Table 4 include the monthly average level of the ten-year instantaneous forward inflation risk premium on the left-hand-side. With respect to , two of the crude indicators of inflation uncertainty do not support the hypothesis--somewhat curiously, the variance of the Michigan survey enters Regression 1 negatively and is statistically significant, and the level of relative price changes in the CPI is positive as expected but statistically insignificant in Regressions 1 and 2. However, as Regression 2 indicates, the dispersion in long-run inflation forecasts from Blue Chip enters significantly with the expected positive sign. The coefficient suggests that the range of dispersion in the sample, from 0.6 to 1.1 percent, implies about a 34 basis point increase in the inflation risk premium.

With respect to , the results do suggest that the inflation risk premium correlates significantly and positively with Eurodollar implied volatility. The coefficients from Regressions 1 and 2 imply that a one standard deviation increase in volatility corresponds to just under a 20 basis point increase in the inflation risk premium, which ranged from about 15 to 120 basis points over the sample period. But whatever the economic significance in general, the increase in the inflation risk premium since the beginning of the year, or indeed since the end of the Greenspan era, does not appear to be related to policy uncertainty.¹⁴ In fact, implied volatility has remained historically low so far during 2006,¹⁵ and the coefficient from Regression 1, for example, suggests that only 1 (3) basis point(s) of the 32 (14) basis point increase in the inflation risk premium from December 30, 2005 (January 31, 2006) through July 25, 2006 owes to an increase in uncertainty about the path of short rates, which, it may bear repeating, has been quite small anyway.¹⁶ In addition, the dummy variable for the post January 2006 period is statistically insignificant in both Regressions 1 and 2.

Regressions 3 and 4 examine first differences, and only one of the variables on the right-hand-side enters the model significantly. Monthly changes in the dispersion of long-run inflation forecasts from the Blue Chip survey correlate positively with changes in the premium, although the result is only significant at the 10 percent level.

7. Nominal Term Premium Developments in Germany and the United Kingdom

Again, the increase in inflation risk premiums in the United States since the beginning of the year does not seem to be related to any notable increase in monetary policy uncertainty. Cross-country evidence, albeit suggestive, might also be generally relevant on this score. Briefly, and just in nominal terms, if the recent increase in term premiums in the United States is primarily due either to increased monetary policy uncertainty or idiosyncratic developments related to the central bank, then one might expect smaller relative increases in other countries, all else equal.

Of course, controlling for all relevant variables across cases is impossible, but to consider this issue, I calibrated the same three-factor model used to fit the nominal and real yields curves in the United States, as outlined in (5) - (6),¹⁷ to fitted government bond yield curves for Germany and the United Kingdom.¹⁸ Table 5 summarizes the relevant results, including ten-year instantaneous forward rates, the model-implied ten-year instantaneous forward rates, and nominal forward term premiums for key dates in the sample. Model-implied forward rates in Germany and the United States increased by 60 and 54 basis points, respectively, between July 25, 2006 and year-end 2005, but notably, the comparative increase in the nominal term premium was actually a touch more pronounced in the German than in the American case (70 versus 56 basis points). Also, although the increase in forward rates was smaller in the United Kingdom, the model nonetheless suggests that the back-up in rates so far this year owes primarily to an increase in the nominal term premium. In addition, the share of the drop in forward rates due to declines in term premiums since the inception of Federal Reserve tightening in June 2004 is largely comparable across these three cases. Therefore, although the comparisons are naturally only suggestive and global debt markets are closely interrelated, these results are consistent with the view that the increase in term premiums thus far this year is perhaps just as much a global as a domestic financial phenomenon.

8. Discussion

In summary, this paper decomposes nominal interest rates into expected real rates, expected inflation rates, real risk premiums, and inflation risk premiums by calibrating standard three-factor affine term structure models separately to the nominal Treasury and TIPS yield curves. The key caveats with the procedure regard not the model per se, but the parameter estimation and the short sample on real yields. As noted by Kim and Orphanides (2005), in the absence of survey data, a short sample period biases the estimates of the persistence of the factors downwards, and this effect is especially severe with the TIPS data. In short, this particular application of the model seems comparatively biased toward attributing too much of the movement in forward rates to term premiums. But despite some drawbacks, there may be substantial theoretical advantages in calibrating the model separately to the nominal and real yield curves, as opposed to joint estimation. Joint estimation as conducted by D'Amico et al. (2005) and Kim and Wright (2005) requires that the same three factors drive both the nominal and real term structures, a potentially limiting feature that this estimate avoids.

In addition, the results, both in terms of the current level (at least at more distant horizons) and the time variation of the inflation risk premium, seem broadly consistent with alternative back-of-the-envelope measures and proxies for uncertainty. Also, some tentative inferences regarding the current interest rate environment are noteworthy. Namely, the apparent increase in the inflation risk premium since the beginning of 2006 does not in fact seem to be driven by monetary policy uncertainty, which appears to have remained low this year. More generally and in nominal terms, given similar yield curve developments in Germany and the United Kingdom, the increase in term premiums thus far in 2006 might be more of a global than a primarily domestic financial development.

References

Bodie, Zvi, 1979, "Inflation Risk and Capital Market Equilibrium," NBER Working Paper No. 373 (July).

Campbell, John Y. and Robert J. Shiller, 1996, "A Scorecard for Indexed Government Debt," NBER Working Paper No. 5587 (May).

Cox, J.C., J.E. Ingersoll, and S.A. Ross, 1985, "A Theory of the Term Structure of Interest Rates," Econometrica, Vol. 53, pp. 385-408.

Dai, Q. and K. J. Singleton, 2002, "Expectations Puzzles, Time-Varying Risk Premia, and Dynamic Models of the Term Structure," Journal of Financial Economics, Vol. 63, pp. 415-441.

D'Amico, Stefania, Don Kim, and Min Wei, 2005, "Tips from TIPS: The Informational Content of Treasury Inflation-Protected Security Prices," mimeo.

Das, Sanjiv. R., 2002, "The Surprise Element: Jumps in Interest Rates," Journal of Econometrics, Vol. 106, pp. 27-65.

Durham, J. Benson, 2006, "Additional Analytical Approximations of the Term Structure and Distributional Assumptions for Jump-Diffusion Processes," Journal of Fixed Income, Vol. 15 No. 4 (March), pp. 61-73.

Hammond, P. Brett, Andrew C. Fairbanks, and J. Benson Durham, 1999, "Understanding the Inflation Risk Premium," in John Brynjolfsson, Frank J. Fabozzi, eds., Handbook of Inflation Indexed Bonds. New Hope, PA: Frank J. Fabozzi Associates.

Ho, T. and S. Lee, 1986, "Term Structure Movements and Pricing Interest Rate Contingent Claims," Journal of Finance, Vol. 41, pp. 1011-1029.

Kandel, Shmuel, Aharon R. Ofer, and Oded Sarig, 1996, "Real Interest Rates and Inflation: An Ex-Ante Empirical Analysis, Journal of Finance, Vol. 50 No. 1 (March), pp. 205-225.

Kim, Don and Athanasios Orphanides, 2005, "Term Structure Estimation with Survey Data on Interest Rate Forecasts," Finance and Economics Discussion Series, No. 48.

Kim, Don and Jonathan Wright, 2005, "An Arbitrage-Free Three-Factor Term Structure Model and the Recent Behavior of Long-Term Yields and Distant-Horizon Forward Rates," Finance and Economics Discussion Series, No. 33.

Langetieg, Terrence, 1980, "A Multivariate Model of the Term Structure," Journal of Finance, Vol. 35 No. 1 (March), pp. 71-97.

Piazzesi, M., 2005, "Bond Yields and the Federal Reserve," Journal of Political Economy, Vol. 113 No. 2, pp. 311-344.

Vasicek, O., 1977, "An Equilibrium Characterization of the Term Structure of Interest Rates," Journal of Financial Economics, Vol. 5, pp. 177-188.

Table 1: Decomposition of Ten-year Nominal Instantaneous Forward Treasury Rates

Date	(1) Instantaneous 10-year Forward Rate	(2) Model-implied Instantaneous 10-year Forward Rate	(3) Expected Real Rate	(4) Expected Inflation	(5) Real Term Premium	(6) Inflation Risk Premium
12/29/00	5.90	6.10	1.92	2.34	1.57	0.27
12/28/01	6.72	6.92	1.82	2.39	1.95	0.76
12/31/02	6.28	6.18	1.74	2.39	1.40	0.65
12/31/03	6.38	6.39	1.77	2.38	1.19	1.05
06/29/04	6.42	6.38	1.78	2.42	1.23	0.94
12/30/04	5.82	5.62	1.81	2.44	0.71	0.65
12/30/05	4.86	5.15	1.92	2.42	0.54	0.27
07/25/06	5.47	5.68	1.92	2.40	0.78	0.59
Change to 07/25/06: from 06/29/2004	-0.95	-0.69	0.14	-0.03	-0.45	-0.36
Change to 07/25/06: from 12/30/2005	0.61	0.54	0.00	-0.02	0.24	0.32
Change to 07/20/05: from 06/29/2004	-1.56	-1.35	0.11	0.03	-0.70	-0.79
Kim and Wright (2005)	NA	-1.30	-0.11	-0.14	-0.73	-0.34

Table 2: Decomposition of Seven-year Nominal Instantaneous Forward Treasury Rates

Date	(1) Instantaneous 7-year Forward Rate	(2) Model-implied Instantaneous 7-year Forward Rate	(3) Expected Real Rate	(4) Expected Inflation	(5) Real Term Premium	(6) Inflation Risk Premium
12/29/00	5.61	5.64	1.98	2.26	1.63	-0.23
12/28/01	6.54	6.58	1.70	2.35	2.31	0.22
12/31/02	5.57	5.49	1.50	2.27	1.68	0.04
12/31/03	5.80	5.79	1.58	2.25	1.23	0.73
06/29/04	5.94	5.87	1.60	2.41	1.31	0.55
12/30/04	5.18	5.02	1.69	2.50	0.56	0.26
12/30/05	4.53	4.60	1.98	2.52	0.23	-0.14
07/25/06	5.18	5.22	1.97	2.45	0.57	0.23
Change to 07/25/06 from 06/29/2004	-0.76	-0.65	0.37	0.04	-0.74	-0.32
Change to 07/25/06 from 12/30/2005	0.64	0.63	-0.01	-0.08	0.34	0.37

Table 3: Correlation Matrix of Alternative Inflation Risk Premium Measures
January 4, 2000 - July 25, 2006 (Daily)

	Ten-year Instantaneous Forward Inflation Risk Premium	Seven-year Instantaneous Forward Inflation Risk Premium	Instantaneous Forward Breakeven Spread, 9 to 10 Years	Instantaneous Forward Breakeven Spread, 6 to 7 Years
Ten-year Instantaneous Forward Inflation Risk Premium	1.00
Seven-year Instantaneous Forward Inflation Risk Premium	0.96	1.00
Instantaneous Forward Breakeven Spread, 9 to 10 Years	0.28	0.28	1.00
Instantaneous Forward Breakeven Spread, 6 to 7 Years	0.49	0.31	0.59	1.00

Table 4: Regressions of Ten-year Instantaneous Forward Inflation Risk Premium Estimates on Proxies for Inflation and Monetary Policy Uncertainty
January 2000 - June 2006 (Monthly)

Independent Variables	Dependent Variable: Ten-year Instantaneous Forward Inflation Risk Premium - Level (1)	Dependent Variable: Ten-year Instantaneous Forward Inflation Risk Premium - Level (2)	Dependent Variable: Ten-year Instantaneous Forward Inflation Risk Premium - Change (3)	Dependent Variable: Ten-year Instantaneous Forward Inflation Risk Premium - Change (4)
Michigan Inflation Survey Variance	-0.0144
Michigan Inflation Survey Variance Robust p values	(0.001)**
Michigan Inflation Survey Variance			0.0019
Michigan Inflation Survey Variance Robust p values			(0.574)
Blue Chip Inflation Survey Dispersion		0.6754
Blue Chip Inflation Survey Dispersion Robust p values		(0.000)**
Blue Chip Inflation Survey Dispersion				0.8155
Blue Chip Inflation Survey Dispersion Robust p values				(0.063)+
CPI Relative Price Dispersion	0.5068	-2.1891
CPI Relative Price Dispersion Robust p values	(0.876)	(0.565)
Eurodollar Implied Volatility, 6 Months Ahead	0.0144	0.0140
Eurodollar Implied Volatility, 6 Months Ahead Robust p values	(0.000)**	(0.000)**
Dummy for Post January 2006	0.0403	0.0526	0.0114	0.0304
Dummy for Post January 2006Robust p values	(0.428)	(0.247)	(0.729)	(0.517)
CPI Relative Price Dispersion			-0.1523	0.3298
CPI Relative Price Dispersion Robust p values			(0.949)	(0.894)
Eurodollar Implied Volatility, 6 Months Ahead			0.0065	0.0074
Eurodollar Implied Volatility, 6 Months Ahead Robust p values			(0.394)	(0.318)
Squared CPI Surprise			-0.3352	-0.2383
Squared CPI Surprise Robust p values			(0.415)	(0.587)
Squared PPI Surprise			-0.0067	-0.0146
Squared PPI Surprise Robust p values			(0.783)	(0.599)
Constant	0.4885	-0.3088	0.0033	0.0036
Constant Robust p values	(0.000)**	(0.045)*	(0.906)	(0.896)
Observations	78	75	77	74
R-squared	0.545	0.572	0.043	0.062
Durbin-Watson	0.849	0.802	2.108	2.127

*Robust p values in parentheses (+ significant at 10%; * significant at 5%; ** significant at 1%). Regressions that include Blue Chip data cover January 2000 - March 2006. Return to Table

Table 5: Partial Decomposition of Ten-year Nominal Instantaneous Forward Rates in Germany, the United Kingdom, and the United States

Date	(1) Germany Instantaneous 10-year Forward Rate	(2) Germany Model-implied Instantaneous 10-year Forward Rate	(3) Germany Nominal Forward Term Premium	(4) United Kingdom Instantaneous 10-year Forward Rate	(5) United Kingdom Model-implied Instantaneous 10-year Forward Rate	(6) United Kingdom Nominal Forward Term Premium	(7) United States Instantaneous 10-year Forward Rate	(8) United States Model-implied Instantaneous 10-year Forward Rate	(9) United States Nominal Forward Term Premium
12/29/00	5.64	5.62	2.55	4.15	4.18	-0.02	5.90	6.10	1.83
12/28/01	5.81	5.91	2.85	4.78	4.72	0.40	6.72	6.92	2.70
12/31/02	5.49	5.54	2.46	4.66	4.71	0.50	6.28	6.18	2.04
12/31/03	5.36	5.47	2.36	4.84	4.97	0.74	6.38	6.39	2.24
06/29/04	5.37	5.46	2.34	4.99	5.04	0.80	6.42	6.38	2.18
12/30/04	4.65	4.68	1.45	4.57	4.58	0.42	5.82	5.62	1.37
12/30/05	3.73	3.82	0.43	3.93	3.89	-0.24	4.86	5.15	0.81
07/25/06	4.34	4.43	1.13	4.35	4.38	0.23	5.47	5.68	1.37
Change to 07/25/06: from 06/29/2004	-1.04	-1.03	-1.21	-0.63	-0.65	-0.58	-0.95	-0.69	-0.81
Change to 07/25/06:from 12/30/2005	0.61	0.60	0.70	0.43	0.49	0.46	0.61	0.54	0.56

Footnotes

^* The author thanks Don Kim, Brian Madigan, and Jonathan Wright. Any remaining errors are exclusively his own. The views presented are solely those of the author and do not necessarily represent those of the Federal Reserve Board or its staff. Return to Text

1. This class of so-called "arbitrage-free" models should not be confused with models, such as Ho and Lee (1986), that exactly match a given term structure by fitting a deterministic time trend. Return to Text

2. More precisely, this refers to disentangling the expected future short rate and the forward term premium from the model-implied forward rate, which does not necessarily match the observed forward rate very precisely. Return to Text

3. See Vasicek (1977) and Langetieg (1980) for early derivations of the bond pricing equation in the case of single and multiple factors, respectively. Closed-form solutions for the -factor case can be found in Langetieg (1980), Dai and Singleton (2002), and Kim and Orphanides (2005). Return to Text

4. Also, the -period zero coupon term premium is the model-implied -period zero coupon bond yield minus the average of expected future short rates over the -period horizon. Return to Text

5. In terms of parameter estimation, as outlined in Kim and Wright (2005) and elsewhere, the model can be written in state space form in which the factors are the unobservable state variables, and the observed data are (average) weekly 1.5-, 2-, 3-, 6-, and 10-year zero-coupon rates derived from Svensson-based nominal Treasury and TIPS yield curves. (Some improvement might be made in using spline-based yields as "data" as opposed to the more parameterized Svensson estimates.) The sample for nominal (real) yield curve estimation runs from the week of November 26, 1997 (January 4, 2000) through the week of April 6, 2006 (July 13, 2006). The short sample size is potentially problematic because the mean reversion (and the remaining) parameters are likely to be less reliable if estimated from shorter periods. Return to Text

6. Note that the decomposition of the change from July 20, 2005 from June 24, 2004 using this method and the corresponding decomposition from Kim and Wright (2005) over the same period is largely similar, insofar as the decline in risk premiums accounts for most of the decline in forward rates over the tightening cycle. However, as noted in the last two rows of Table 1, although the declines in real risk premiums are roughly equal, this method produces a notably more pronounced decline in the inflation risk premium over that particular period. Return to Text

7. See Chairman Greenspan's semi-annual February 16, 2005 testimony before the U.S. Senate (http://www.federalreserve.gov/boarddocs/hh/2005/february/testimony.htm). Return to Text

8. In nominal terms and compared to other term structure models that use survey data in the estimation of the parameters, this model seems to attribute comparatively more of the movement in (model-implied) forward rates to movements in the term premium. For example, a variant of the model from Kim and Wright (2005) and Kim and Orphanides (2005) suggests that ten-year instantaneous forward rates increased 68 basis points from year-end 2005 through May 11, 2006, with 37 basis points of the increase due to a rise in the forward term premium. See http://www.federalreserve.gov/pubs/feds/2005/200533/feds200533.xls. In contrast, the application in this paper suggests that nominal forward rates increased 85 basis points, with 69 basis points due to the term premium. Return to Text

9. Also, the correlation between the two alternative measures is 0.59. Return to Text

10. Unfortunately, there are no sufficiently liquid exchange-traded inflation derivatives, such as inflation caps or floors, from which to extract inflation uncertainty over a horizon comparable to the term premium estimates. Return to Text

11. The variance of individual forecasts is effectively a measure of disagreement among respondents. An alternative measure--the central tendency of uncertainty of individual respondents--would likely be a better proxy. (High uncertainty among individual investors could convey little disagreement among market participants.) Unfortunately, indicators of uncertainty for individual survey respondents are not available for either survey. Data on the variance from the Michigan survey are available monthly. Data on the dispersion of long-run CPI inflation forecasts--measured by the difference between the average top ten and average bottom ten forecasts--from the Blue Chip survey are available twice a year in March and October. Regression estimates use linearly interpolated data for missing months. Return to Text

12. Following Kandel et al. (1996), each investor is unlikely to transact in all goods in the CPI basket. Given that market participants observe only a subset of prices, information about inflation is less accurate, and uncertainty is therefore perhaps greater, when relative price changes are large. The six components of the CPI used to estimate are food, energy, non-durables excluding food and energy, durables, rent of shelter, and services excluding energy and shelter. Return to Text

13. Squaring the surprise components both insures that the proxy is positive (Both negative and positive surprises should boost general uncertainty.) and weights larger surprises more heavily. (Larger positive and negative surprises might have a non-linear effect on longer-term uncertainty.) The results reported in Table 4 are no different using core CPI or core PPI. Return to Text

14. This contrasts with some commentary in the contemporary popular press that suggests just such a link. For example, see "Bernanke, Fukui, Trichet Can't Match Greenspan's Rate Clarity," posted on Bloomberg on July 10, 2006, which reported that "(b)y some estimates, confusion over central banks' intentions has raised yields more than 20 basis points above where they would otherwise be" over the course of the year. Return to Text

15. Implied volatility derived from options on Eurodollar futures contracts about six months ahead increased from about 8.73 percent (7.74 percent) to 9.65 percent from December 30, 2006 (January 31, 2006) to July 25, 2006. This historical average of this series from 1994-2005 is about 16.95 percent. Return to Text

16. Also, documenting a relation between recent uncertainty about inflation and the premium is difficult. Although the Blue Chip survey data are somewhat limited, the dispersion of Blue Chip long-run inflation forecasts actually declined from 0.9 to 0.8 percent from October 2005 to March 2006, the latest observation. Return to Text

17. Calibration across markets perhaps particularly raises the issue of alternative restrictions of the Gaussian parameters or even different stochastic processes outside the Gaussian framework. For example, application of Ornstein-Ulhenbeck processes, which potentially permit negative nominal interest rates, might be problematic in cases, such as Japan, in which the zero bound persistently looms during a significant portion of the sample period. For an empirical analysis of affine term structure models, see Dai and Singleton (2000). For alternative stochastic process, such as jump-diffusion, see Das (2002), Piazzesi (2005), or Durham (2006). Return to Text

18. The yields curves for Germany and the United Kingdom are estimated by precisely the same procedure as for nominal and real United States Treasury securities. I estimate the parameters for data on German (United Kingdom) government bond yields using weekly data from November 26, 1997 (January 4, 2000) through April 6, 2006 (April 6, 2006). Return to Text

^♣ This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to Text

Home | Economic Research and Data
Accessibility | Contact us
Last update: November 21, 2006