Expected Stock Returns and
Variance Risk Premia *
Keywords: Return Predictability, Implied Variance, Realized Variance, Equity Risk Premium, Variance Risk Premium, Time-Varying Risk Aversion.
Abstract:
We find that the difference between implied and realized variances, or the variance risk premium, is able to explain more than fifteen percent of the ex-post time series variation in quarterly excess returns on the market portfolio over the 1990 to 2005 sample period, with high (low) premia
predicting high (low) future returns. The magnitude of the return predictability of the variance risk premium easily dominates that afforded by standard predictor variables like the P/E ratio, the dividend yield, the default spread, and the consumption-wealth ratio (CAY). Moreover, combining the
variance risk premium with the P/E ratio results in an ![]() for the quarterly returns of more than twenty-five percent. The results depend crucially on the use of "model-free", as opposed to
standard Black-Scholes, implied variances, and realized variances constructed from high-frequency intraday, as opposed to daily, data. Our findings suggest that temporal variation in risk and risk-aversion both play an important role in determining stock market returns.
for the quarterly returns of more than twenty-five percent. The results depend crucially on the use of "model-free", as opposed to
standard Black-Scholes, implied variances, and realized variances constructed from high-frequency intraday, as opposed to daily, data. Our findings suggest that temporal variation in risk and risk-aversion both play an important role in determining stock market returns.
JEL Classification Numbers: G12, G14.
1 Introduction
Is the return on the stock market predictable? This age-old question arguably still ranks among the most studied and contentious issues in all of economics. Notable recent studies that report evidence in favor of return predictability include Shiller (1984), Keim and Stambaugh (1986), Fama and French (1988a), and Campbell and Shiller (1988) who find that the ratios of price to earning or price to dividend are useful predictors; Campbell (1991) and Hodrick (1992) who report that the de-trended risk-free rate contains forecasting power; the studies of Fama and Schwert (1977), Campbell (1987) and Fama and French (1989) involving different term structure variables; Lamont (1998) who argues that the aggregate dividend payout ratio forecasts excess returns; and Lettau and Ludvigson (2001) who find the consumption-wealth ratio (CAY) to be a good predictor of future stock market performance; see also the general discussions in support of return predictability in Lewellen (2004) and Cochrane (2006). Even though the predictor variables differ across the above cited studies, most suggest that predictability tends to be the strongest over long multi-year horizons. At the same time, there is also evidence that the degree of predictability appears to have diminished somewhat beginning in the mid-to-late 1990s. In lieu of these findings, we show that the difference between "model-free" implied and realized variances, which we term the variance risk premium, provides remarkable accurate and stable forecasts for the quarterly market return over the recent 1990 to 2005 sample period, with high (low) premia predicting high (low) future returns. Moreover, the accuracy of these forecasts easily dominates that afforded by all of the more traditional predictor variables.
The dual variance concepts underlying our variance risk premium are both fairly new. On one the hand, several recent studies have argued for the use of so-called "model-free realized variances" computed by the summation of high-frequency intraday squared returns. As demonstrated in that literature, these types of measures afford much more accurate ex-post observations on the actual return variation than the more traditional sample variances based on daily or coarser frequency return observations (Andersen, Bollerslev, Diebold, and Ebens, 2001; Barndorff-Nielsen and Shephard, 2002; Meddahi, 2002). On the other hand, the recently developed so-called "model-free implied variances" provide ex-ante risk-neutral expectations of the future return variation. Importantly, and in contrast to the standard option-implied variances based on the Black-Scholes pricing formula or some variant thereof, the "model-free implied variances" are computed from option prices without the use of any particular option-pricing model (Carr and Madan, 1998; Jiang and Tian, 2005; Britten-Jones and Neuberger, 2000).
We show that the difference between these new "model-free" implied and realized variances, which we term the variance risk premium, is able to explain more than fifteen percent of the variation in quarterly stock market returns over the 1990 to 2005 period.1 This high degree of predictability clearly dominates that afforded by standard predictor variables like the P/E ratio, the dividend yield, the default spread, the term spread, the risk-free rate, and the consumption-wealth ratio (CAY). Combining the variance risk premium with these other predictor variables, we find that the addition of the P/E ratio results in the greatest overall return predictability of more than twenty-six percent. As explained below, we interpreted this to be consistent with the view that riskiness and risk-aversion are both important for describing the temporal variation in expected stock returns. We further support our empirical results by a number of robustness checks. In this regard we find the use of the "model-free" variance concepts to be crucial, in that the corresponding results based on the traditional Black-Scholes implied variances and realized variances constructed from lower frequency daily data do not support the same strong conclusions.
Why should the difference between implied and realized variances predict stock market returns? Our direct cross-sectional tests offer little support for the idea that the variance risk premium is a systematic risk factor in the usual linear arbitrage pricing (APT) sense. Instead, the variance risk premium may be related (non-linearly) to the coefficient of relative risk aversion within a representative agent setting (Bakshi and Madan, 2006). In a model with time-varying risk aversion, as in, e.g., a model with habit persistence (Campbell and Cochrane, 1999), this therefore provides a direct link for the variance risk premium to explain temporal variation in expected returns. Intuitively, when the variance risk premium is high (low), it generally signals a high (low) degree of risk aversion throughout the economy. Consequently agents tend to simultaneously cut (increase) their consumption and investment expenditures and shift their portfolios from more (less) to less (more) risky assets. This in turn results in a rise (decrease) in expected excess returns and a decrease (increase) in economic growth. In other words, booms and busts follow changes in the market implied risk aversion, as proxied by the difference between the implied and realized variances.
The plan for the rest of the paper is as follows. Section 2 discusses the concepts of "model-free" implied and realized variances used in defining the variance risk premium, along with related practical data issues. Section 3 presents our main results on return predictability and corresponding robustness checks. Section 4 concludes.
2.1 Formal Definitions
In parallel to the standard definition of a forward premium, the variance risk premium is defined as the difference between a current return variation measure and the market's expectation of some future return variation. Formally, let ![]() denote the price of a European call option maturing at time
denote the price of a European call option maturing at time ![]() with strike price
with strike price ![]() , and
, and ![]() denote the price of a time
denote the price of a time ![]() zero-coupon bond maturing at time
zero-coupon bond maturing at time ![]() . As shown by Carr and Madan (1998), Demeterfi, Derman, Kamal, and Zou (1999) and
Britten-Jones and Neuberger (2000), the implied variance or the market's risk-neutral expectation of the total return variation between time
. As shown by Carr and Madan (1998), Demeterfi, Derman, Kamal, and Zou (1999) and
Britten-Jones and Neuberger (2000), the implied variance or the market's risk-neutral expectation of the total return variation between time ![]() and
and ![]() conditional on time
conditional on time ![]() information, say
information, say ![]() , may then be expressed in a "model-free" fashion as the following portfolio of European calls of the underlying futures price,
, may then be expressed in a "model-free" fashion as the following portfolio of European calls of the underlying futures price,
![\displaystyle IV_t \equiv \sum_{i=1}^m \left[{C_t\left(t+1,\frac{K_i}{B(t,t+1)}\right) - C_t\left(t,\frac{K_i}{B(t,t)}\right) \over K_i^2} - {C_t\left(t+1,\frac{K_{i-1}}{B(t,t+1)}\right) - C_t\left(t,\frac{K_{i-1}}{B(t,t)}\right) \over K_{i-1}^2}\right] \Delta K](img12.gif) |
where
In order to define the actual variance, let ![]() denote the logarithmic price of the asset. The realized variation over the discrete
denote the logarithmic price of the asset. The realized variation over the discrete ![]() to
to ![]() time interval is then naturally measured in a "model-free" fashion by
time interval is then naturally measured in a "model-free" fashion by
where the convergence relies on
The variance risk premium underlying our empirical investigations is simply defined as the difference between the ex-ante risk neutral expectation of the future return variation over the ![]() time interval and the ex-post realized return variation over the
time interval and the ex-post realized return variation over the ![]() time interval,
time interval,
| (3) |
Note that
2.2 Data Description
Our empirical analysis is based on data for the aggregate S&P500 composite index from January 1990 through January 2005. We rely on monthly data for the VIX index for quantifying the risk-neutral implied variance measure. The VIX index is based on the highly liquid S&P500 index options
along with the "model-free" approach discussed above explicitly tailored to replicate the risk-neutral variance of a fixed 30-day maturity. The data is obtained directly from the Chicago Board of Options Exchange (CBOE).4 Our monthly realized variance measure is based on the summation of the five-minute squared returns for the S&P500 composite index within the month. The high-frequency data for the S&P500 index is provided by the Institute
of Financial Markets. For a typical month with 22 trading days there are a total of
![]() "five-minute" returns, corresponding to the 78 five-minute
subintervals covering the normal trading hours from 9:30am to 4:00pm along with the close-to-open return.
"five-minute" returns, corresponding to the 78 five-minute
subintervals covering the normal trading hours from 9:30am to 4:00pm along with the close-to-open return.
Even though the monthly realized volatilities and the VIX index are both available on an overlapping daily basis, most of the other variables that we consider in our return predictions are only available monthly or quarterly. Thus, to avoid the dual problems associated with overlapping data samples and missing observations, we will primarily focus on quarterly time series and forecast horizons, appropriately using the values for the last day or the last month in each quarter as the "quarterly" observations.5
To illustrate, Figure 1 plots the time series of implied variances, realized variances, and their differences on a quarterly basis. As immediately evident from the figure, both of the variance measures are somewhat higher during the 1997 to 2002 part of the sample. The few distinct spikes in the measures generally also tend to coincide. Consistent with the earlier empirical evidence cited above, the spread between the implied and realized variances is always positive, indicative of a systematic variance risk premium.
In addition to the variance risk premium, we also consider a set of other more traditional predictor variables. In particular, we obtain monthly P/E ratios and dividend yields for the S&P500 directly from Standard & Poor's. Data on the 3-month T-bill, the default spread (between Moody's BAA and AAA corporate bond spreads), the term spread (between the 10-year T-bond and the 3-month T-bill yields), and the stochastically de-trended risk-free rate (the 1-month T-bill rate minus its backward 12-month moving averages) are taken from the public website of the Federal Reserve Bank of St. Louis. The consumption-wealth ratio (CAY), as defined in Lettau and Ludvigson (2001) and updated until the first quarter of 2005, is downloaded from Lettau and Ludvigson's website. Similar sets of predictor variables for other forecast comparison purposes and sample periods have been used by Lamont (1998), Lettau and Ludvigson (2001), Ang and Bekaert (2006), among many others.
Basic summary statistics for each of the predictor variables are given in Table 1. The mean excess return on the S&P500 over the sample equals 5.97 percent annually. The sample means for the implied and realized variances are 36.30 and 14.90, respectively, corresponding to a variance risk premium of 21.40 (in percentages squared). The numbers for the traditional forecasting variables are all directly in line with those reported in previous studies. In particular, all of the variables are highly persistent with first order autocorrelations ranging from 0.81 to 0.99. In contrast, the serial correlation in the implied and realized quarterly variances are both much less, and the first order autocorrelation for their difference only equals 0.31. As such, this alleviates one of the common concerns related to the use of highly persistent predictor variables and the possibility of spurious or unbalanced regressions.6 Further anticipating the forecasting results discussed next, the traditional predictor variables all correlate fairly weakly with the contemporaneous excess returns with sample correlations ranging from -0.12 to +0.04, while the sample correlations between the returns and the different variance measures are much higher (in an absolute sense) ranging from -0.57 to -0.28.
3 Forecasting Stock Market Returns
All of our forecasts are based on simple linear regressions of the quarterly S&P500 excess returns on the different sets of lagged predictor variables. We focus our comparisons of the accuracy of the different forecasts on the standard adjusted ![]() 's. To allow for serial correlation and heteroskedasticity in the residuals from the estimated regressions we rely on Newey and West (1987) robust
's. To allow for serial correlation and heteroskedasticity in the residuals from the estimated regressions we rely on Newey and West (1987) robust ![]() -statistics based on four lags.
-statistics based on four lags.
3.1 Main Results
Table 2 details our main empirical findings. The regression coefficient for the variance risk premium is estimated to be positive. At an intuitive level, this is consistent with the idea that when the market anticipates high (low) volatility going forward, there is a
discount (premium) built into prices, in turn resulting in high (low) future returns. Moreover, this simple difference between the implied and realized variance is able to explain as much as 15.14 percent of the quarterly variation in the excess returns. This strong degree of predictability is all
the more impressive when compared to the results obtained by regressing the returns on the implied or realized variance in isolation. The corresponding ![]() 's, reported in the next two columns,
indicate that these account for just 6.32 percent and a negative adjusted -1.05 percent of the variation, respectively.7
's, reported in the next two columns,
indicate that these account for just 6.32 percent and a negative adjusted -1.05 percent of the variation, respectively.7
Comparing the regression results for the variance risk premium to the ones for the traditional predictor variables further underscores the significance of the fifteen percent ![]() -square. In
line with the earlier findings of Fama and French (1988a) and Campbell and Shiller (1988), the logarithmic P/E and P/D ratios only explain 6.22 and 2.76 percent of the variation in the quarterly returns, respectively, while the term spread, the
default spread, and the relative risk-free rate all have close to zero or negative
-square. In
line with the earlier findings of Fama and French (1988a) and Campbell and Shiller (1988), the logarithmic P/E and P/D ratios only explain 6.22 and 2.76 percent of the variation in the quarterly returns, respectively, while the term spread, the
default spread, and the relative risk-free rate all have close to zero or negative ![]() 's. Further, the consumption-wealth ratio of Lettau and Ludvigson (2001) accounts
for a modest 4.83 percent of the quarterly return variation, although it still dominates most of the other financial or macroeconomic variables. Looking at the robust
's. Further, the consumption-wealth ratio of Lettau and Ludvigson (2001) accounts
for a modest 4.83 percent of the quarterly return variation, although it still dominates most of the other financial or macroeconomic variables. Looking at the robust ![]() -statistics, the
variance spread also appears highly statistically significant (3.94), while with the possible exception of
-statistics, the
variance spread also appears highly statistically significant (3.94), while with the possible exception of ![]() (-2.81), CAY (2.29) and P/E (-2.08), each of the other predictor variables are
at best marginally significant at conventional levels.
(-2.81), CAY (2.29) and P/E (-2.08), each of the other predictor variables are
at best marginally significant at conventional levels.
A number of the studies cited above have, of course, argued that the degree of predictability afforded by the classic P/E and P/D ratios appear to be the strongest over longer multi-year horizons. Our limited data sample (the VIX index is only available from 1990 and onwards) prevents us from looking at the predictability of the variance risk premium over such horizons. At the same time, several empirical studies also suggest that the evidence in favor of predictability seems to have diminished somewhat during the stock market boom of the mid- to late-1990s. The results for the variance risk premium reported here, thus directly complement these findings by providing strong evidence for quarterly return predictability over the recent 1990 to 2005 sample period.
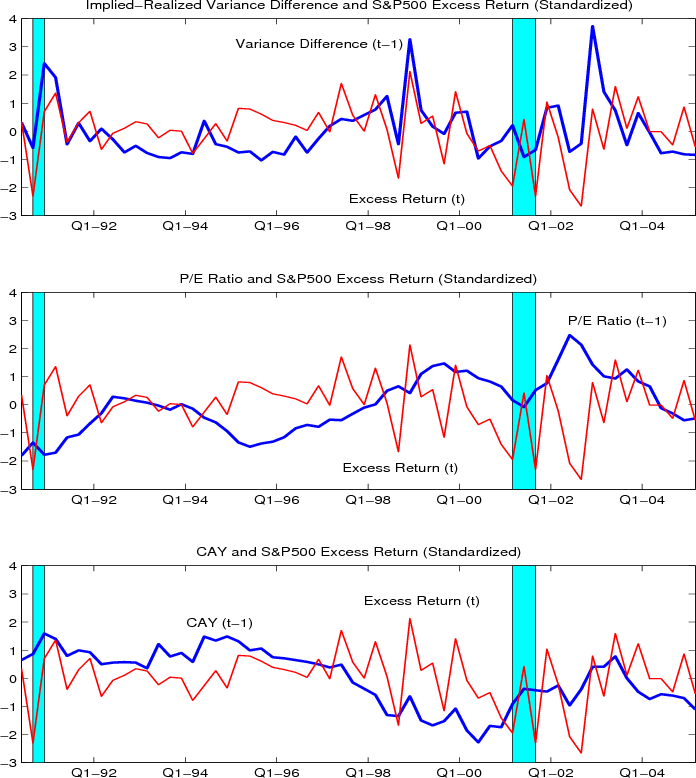
To further illustrate the regression results, we show in Figure 2 the lagged (standardized) time ![]() variance premium, P/E ratio, and CAY, along with the time
variance premium, P/E ratio, and CAY, along with the time
![]() quarterly S&P500 returns. Looking at the lower two panels, the P/E ratio and CAY both seem to capture the longer cycles in the quarterly excess returns, with CAY being slightly more
responsive to short-run fluctuations as well. Meanwhile, the difference between the implied and the realized variances depicted in the top panel not only tracks the longer-run cycles in the excess returns reasonably well, but it also seems to lead the quarter-to-quarter return variation. This
latter pattern may be especially pronounced for the marked spikes associated with the 1991 recession, the 1998 Russian debt and LTCM crises, and the 2002 corporate accounting scandals.
quarterly S&P500 returns. Looking at the lower two panels, the P/E ratio and CAY both seem to capture the longer cycles in the quarterly excess returns, with CAY being slightly more
responsive to short-run fluctuations as well. Meanwhile, the difference between the implied and the realized variances depicted in the top panel not only tracks the longer-run cycles in the excess returns reasonably well, but it also seems to lead the quarter-to-quarter return variation. This
latter pattern may be especially pronounced for the marked spikes associated with the 1991 recession, the 1998 Russian debt and LTCM crises, and the 2002 corporate accounting scandals.
In addition to the simple regressions discussed above, the right panel of Table 2 reports the results from a representative set of multiple regressions. Combining the variance premium with the P/E ratio results in an impressive ![]() of 26.37 percent. Such a high
of 26.37 percent. Such a high ![]() clearly surpasses the forecasting power for quarterly returns previously reported in the
literature with any other forecasting variables. Interestingly, this
clearly surpasses the forecasting power for quarterly returns previously reported in the
literature with any other forecasting variables. Interestingly, this ![]() is also much higher than the sum of the
is also much higher than the sum of the ![]() 's from the two individual forecasting regressions for
's from the two individual forecasting regressions for ![]() and P/E. Intuitively, if expected stock returns are driven by temporal variation in both risk and
risk-aversion, a combination of the P/E ratio and the variance risk premium may effectively account for both. A similar pattern, although to a lessor degree, obtains when including the CAY variable along with the variance premium, which produces an
and P/E. Intuitively, if expected stock returns are driven by temporal variation in both risk and
risk-aversion, a combination of the P/E ratio and the variance risk premium may effectively account for both. A similar pattern, although to a lessor degree, obtains when including the CAY variable along with the variance premium, which produces an ![]() of 20.86 percent. On the other hand, combining the P/E ratio and CAY, the adjusted
of 20.86 percent. On the other hand, combining the P/E ratio and CAY, the adjusted ![]() is merely 5.54 percent, and the robust
is merely 5.54 percent, and the robust
![]() -statistics turn out to be insignificant for both. Also, even though the term spread and the relative short rate are insignificant by themselves, both variables contribute marginally to a
joint predictive regression with the variance premium and the P/E ratio, resulting in the highest overall adjusted
-statistics turn out to be insignificant for both. Also, even though the term spread and the relative short rate are insignificant by themselves, both variables contribute marginally to a
joint predictive regression with the variance premium and the P/E ratio, resulting in the highest overall adjusted ![]() of 27.67 percent.8 Lastly, it is worth noting that the estimated coefficients for the variance risk premium remain remarkably stable, ranging from 0.87 to 1.11 with corresponding
of 27.67 percent.8 Lastly, it is worth noting that the estimated coefficients for the variance risk premium remain remarkably stable, ranging from 0.87 to 1.11 with corresponding ![]() -statistics between 3.85 and 5.27, regardless of the other variables included in the forecast regressions.
-statistics between 3.85 and 5.27, regardless of the other variables included in the forecast regressions.
3.2 Robustness Check
These striking empirical findings naturally raise questions about the robustness and the validity of the results in a wider sense. We next discuss a series of additional regressions and sensitivity checks designed to address these concerns.
3.2.1 Alternative Variance Measures
The "model-free" implied and realized variances are both relatively new concepts. As a first robustness check, we replace the "model-free" variance measures with the standard Black-Scholes implied variance, ![]() , and the realized variance based on low-frequency daily returns,
, and the realized variance based on low-frequency daily returns, ![]() . The regression results for these "old" variance measures are reported in Table
3. The variance risk premium defined by the difference between the Black-Scholes implied variance and the daily return based realized variance still dominates the results based on each of the variance measures in isolation (
. The regression results for these "old" variance measures are reported in Table
3. The variance risk premium defined by the difference between the Black-Scholes implied variance and the daily return based realized variance still dominates the results based on each of the variance measures in isolation (![]() of 3.62 percent versus 3.05 and 0.68 percent, respectively). Meanwhile, replacing the Black-Scholes implied variance with the "model-free" implied variance increases the predictability to 8.08 percent. Similarly, substituting the
realized variance based on daily data with the corresponding high-frequency based measure increases the
of 3.62 percent versus 3.05 and 0.68 percent, respectively). Meanwhile, replacing the Black-Scholes implied variance with the "model-free" implied variance increases the predictability to 8.08 percent. Similarly, substituting the
realized variance based on daily data with the corresponding high-frequency based measure increases the ![]() to 7.30 percent.
to 7.30 percent.
With the exception of P/E and CAY, the ![]() for
for
![]() is still higher than those for all of the other macro-finance variables included in Table 2. However, the
is still higher than those for all of the other macro-finance variables included in Table 2. However, the ![]() for the "model-free" variance premium in Table 2 (15.14 percent) is orders of magnitude greater than the one based on the "old" variance measures (3.62 percent). Combining the "old" variance premium
and the P/E ratio in the same regression results in an
for the "model-free" variance premium in Table 2 (15.14 percent) is orders of magnitude greater than the one based on the "old" variance measures (3.62 percent). Combining the "old" variance premium
and the P/E ratio in the same regression results in an ![]() of 14.35 percent, compared to 26.37 percent for the "model-free" measures. Similarly, mixing the "old" and the "new" variance
measures in the extended regressions results in lower
of 14.35 percent, compared to 26.37 percent for the "model-free" measures. Similarly, mixing the "old" and the "new" variance
measures in the extended regressions results in lower ![]() 's of 20-22 percent and 14-16 percent for
's of 20-22 percent and 14-16 percent for
![]() and
and
![]() , respectively.
, respectively.
All-in-all, comparing the results across Tables 2 and 3, clearly highlight the superior predictive performance afforded by the "model-free" measures and corresponding variance risk premium.
3.2.2 Monthly Return Predictability
As previously noted, for most predictor variables the evidence in favor of return predictability tend to be the strongest over longer multi-year horizons. The limited availability of the "model-free" variance measures prevents us from meaningfully looking beyond a quarter. Instead, as a
further robustness check we report in Table 4 the results from a set of non-overlapping monthly return regressions. Not surprisingly, the degree of predictability afforded by all of the regressions, as measured by the ![]() -square, is in the low single digit. Interestingly, however, with the exception of the P/E ratio, the "model-free" variance risk premium dominates all of the other macro-finance variables, and also has the most significant
-square, is in the low single digit. Interestingly, however, with the exception of the P/E ratio, the "model-free" variance risk premium dominates all of the other macro-finance variables, and also has the most significant ![]() -statistic. Moreover, the
-statistic. Moreover, the ![]() for the difference between the two variance measures (1.24%)
clearly outperforms the implied variance (0.58%) and the realized variance (-0.42%) in isolation. Combining the variance risk premium with the P/E ratio again results in an
for the difference between the two variance measures (1.24%)
clearly outperforms the implied variance (0.58%) and the realized variance (-0.42%) in isolation. Combining the variance risk premium with the P/E ratio again results in an ![]() (3.98%) in
excess of the sum of the two
(3.98%) in
excess of the sum of the two ![]() 's from the individual regressions (1.24% and 2.10%), indirectly pointing to the importance of capturing temporal variation in both risk and risk-aversion. Of
course, assuming that the degree of risk aversion changes only slowly, it is hardly surprising that predictability at the monthly horizon is significantly lower than the previously reported quarterly
's from the individual regressions (1.24% and 2.10%), indirectly pointing to the importance of capturing temporal variation in both risk and risk-aversion. Of
course, assuming that the degree of risk aversion changes only slowly, it is hardly surprising that predictability at the monthly horizon is significantly lower than the previously reported quarterly ![]() 's.
's.
3.2.3 Volatility Risk Premium
The regression results discussed above have all been based on implied and realized variances, and their difference. This mirrors the common use of variance denominated contracts in the over-the-counter swap market (Demeterfi, Derman, Kamal, and Zou, 1999).9 From a theoretical perspective, however, the volatility, or any other nonlinear monotone transformation of the variance, may serve as an alternative, and depending
on the situation more appropriate measure of risk (Merton, 1980). To this end, we report in Table 5 the results obtained by replacing the "model-free" variance measures with their volatility, or standard deviation, counterparts. Interestingly,
including the volatility difference,
![]() , in isolation produces an even higher predictive
, in isolation produces an even higher predictive ![]() of
18.50 percent, compared to the 15.14 percent for the variance premium. Again, including the implied and realized volatility by themselves results in adjusted
of
18.50 percent, compared to the 15.14 percent for the variance premium. Again, including the implied and realized volatility by themselves results in adjusted ![]() 's close to zero. Also, the
coefficient estimates for the volatility difference are very stable and between 4.07 to 4.39, with
's close to zero. Also, the
coefficient estimates for the volatility difference are very stable and between 4.07 to 4.39, with ![]() -statistics around 4.5, in both the simple and multiple regressions. Nonetheless, the
predictive performance in the multiple regressions obtained by including the P/E ratio, CAY, and the term structure variables all fall short of the comparable results for the variance premium in Table 2.
-statistics around 4.5, in both the simple and multiple regressions. Nonetheless, the
predictive performance in the multiple regressions obtained by including the P/E ratio, CAY, and the term structure variables all fall short of the comparable results for the variance premium in Table 2.
3.2.4 Alternative Predictor Variables
The different variables included in the previous tables arguably comprise some of the most commonly advocated predictors. However, several other variables have, of course, been proposed in the literature. While it is literally impossible to investigate all of these suggestions, we report in Table 6 the results for a few additional predictor variables and regressions.
First, a number of studies have argued that returns are subject to mean reversion, or negative serial correlation, although again mostly so over longer multi-year horizons; see, e.g., Fama and French (1988b) and Lo and MacKinlay (1988). The estimates in the first column show that the lagged quarterly excess return has no forecasting power over the present sample period.
Second, Lamont (1998) finds that the corporate payout ratio is useful for predicting quarterly returns. Consistent with the findings in Lettau and Ludvigson (2001), the estimates in the second column indicate that this predictability has completely disappeared over the more recent 1990 to 2005 sample period.
Third, as previously noted, Bollerslev, Gibson, and Zhou (2006) have recently presented forward looking estimates of the volatility risk premium, ![]() ,
within the context of the Heston (1993) one-factor stochastic volatility model, where
,
within the context of the Heston (1993) one-factor stochastic volatility model, where ![]() is allowed to be time-varying and dependent on important
macro-finance variables. The third column reports the regression results using this model-specific parametrically estimated premium. Although the
is allowed to be time-varying and dependent on important
macro-finance variables. The third column reports the regression results using this model-specific parametrically estimated premium. Although the ![]() of 4.47 percent is on par with that of CAY
in the simple regression, the corresponding robust
of 4.47 percent is on par with that of CAY
in the simple regression, the corresponding robust ![]() -statistic of 1.66 is at best marginally significant.10 Moreover, including
-statistic of 1.66 is at best marginally significant.10 Moreover, including ![]() along with the other explanatory variables, completely overturns this significance.
along with the other explanatory variables, completely overturns this significance.
Lastly, we report the results obtained by including the so-called realized quarticity measure
![\displaystyle RQ_t \equiv \sum_{j=1}^{n}\left[p_{t-1+{j\over n}}- p_{t-1+{j-1\over n}(\Delta)}\right]^4.](img53.gif)
Taken as a whole, the results in Table 6 again underscore the robustness and superior predictability of the new "model-free" variance risk premium measure, whether combined with the P/E ratio and some of the other predictor variables, or when used in isolation.
3.3 Economic Interpretation
The striking empirical findings reported above naturally begs the question of why the implied-realized variance difference has the power to forecast returns? The most likely answer is that the premium proxies for time-varying risk aversion. There already exists a large literature concerned with ways in which to extract the market implied risk aversion from options data (see, e.g., Rosenberg and Engle, 2002; Bliss and Panigirtzoglou, 2004; Brandt and Wang, 2003; Gordon and St-Amour, 2004; Jackwerth, 2000; Garcia, Lewis, Pastorello, and Renault, 2006; Aït-Sahalia and Lo, 2000; Balyeat, 2002; Wu, 2005). Most of these studies rely on specific parametric models (like Black-Scholes) for inferring the risk-neutral expectations, while generally also resorting to fairly complex and numerical intensive procedures for estimating the risk-neutral distribution. In contrast, the risk-neutral expected variance used here is based on the idea of replication using a portfolio of European call options sufficiently rich along the strike dimension. The wedge between this "model-free" market-based expectation and the actual return variation thus serves as a measure of the difference between the risk-neutral and objective distributions, or a measure of the market implied risk aversion. The fact that the P/E ratio - as a valuation measure involving both risk and risk aversion - adds more than one-to-one to the degree of predictability relative to the spread alone, also indirectly suggests that the variance premium isn't simply measuring market risk.
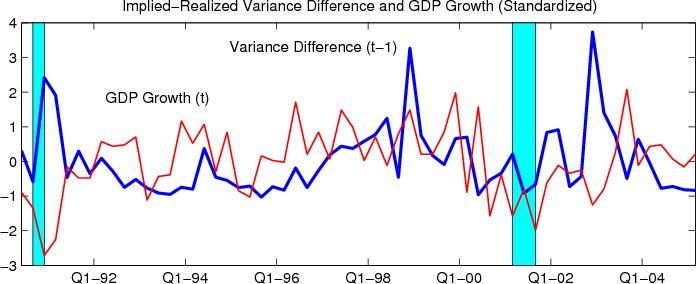
To further appreciate the economics behind the apparent connection between the variance risk premium and returns, Figure 3 plots the lagged premium together with the quarterly growth rate in GDP. As seen from the figure, there is a tendency for the variance risk premium to rise in the quarter before a decline in GDP, while it typically narrows ahead of an increase in GDP. Indeed, the sample correlation between the two series equals -0.16. Thus, not only is the difference between the implied and realized variances positively correlated with expected future returns, it also covaries negatively with the future growth rate in GDP.11 Intuitively, when the variance risk premium is high (low), it generally signals a high (low) degree of risk aversion throughout the economy. Consequently agents tend to simultaneously cut (increase) their consumption and investment expenditures and shift their portfolios from more (less) to less (more) risky assets. This in turn results in a rise (decrease) in expected excess returns and a decrease (increase) in economic growth. In other words, booms and busts are directly associated with changes in the market implied risk aversion, as proxied by the difference between the implied and realized variances.
To further underscore that the variance risk premium is best seen as a proxy for risk aversion as opposed to systematic risk, we complement the time series based evidence with standard cross-sectional asset pricing tests, examining whether the factor loadings for a set of portfolios with different risk characteristics are appropriately dispersed and whether the estimated loadings are actually statistically significant (Lewellen and Nagel, 2006; Burnside, 2006; Daniel and Titman, 2005; Lewellen, Nagel, and Shanken, 2006). More specifically, we begin by running the time-series regressions
4 Conclusion
We provide strong statistical evidence that stock market returns are predictable by the difference between implied and realized variances, or the variance risk premium. The economic magnitude of the documented predictability is large, with the variance risk premium accounting for more than fifteen percent of the quarterly return variation. Combining the variance risk premium with a set of other traditional explanatory variables explains close to thirty percent of the ex-post return variation. The 1990-2005 sample period underlying our empirical investigations experienced quite large return fluctuations. These fluctuations are difficult to justify by variations in economic fundamentals and risk alone. Instead, the variance risk premium may be seen as a "model-free" measure for the aggregate degree of risk aversion in the economy. As such, our results suggest that time-varying risk and risk-aversion are both important for understanding temporal variations in expected stock market returns.
Table 1: Summary Statistics for Key Variables - Summary Statistics
|
|
|
|
|
CAY |
||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Mean | 5.97 | 21.40 | 36.30 | 14.90 | 3.16 | 3.91 | 0.83 | 1.90 | -0.19 | 0.30 |
| Std Dev | 31.44 | 14.86 | 25.78 | 14.92 | 0.26 | 0.36 | 0.22 | 1.11 | 0.74 | 1.92 |
| Skewness | -0.63 | 1.75 | 2.01 | 1.99 | 0.20 | -0.10 | 0.95 | -0.15 | -0.40 | -0.37 |
| Kurtosis | 3.49 | 6.38 | 8.14 | 6.52 | 2.45 | 1.70 | 2.94 | 1.90 | 3.15 | 2.08 |
| AR(1) | -0.07 | 0.31 | 0.41 | 0.44 | 0.91 | 0.96 | 0.83 | 0.88 | 0.81 | 0.90 |
|
|
|
|
|
CAY |
||||||
|---|---|---|---|---|---|---|---|---|---|---|
|
|
1.00 | -0.28 | -0.49 | -0.57 | -0.07 | -0.03 | -0.12 | 0.03 | 0.04 | -0.06 |
|
|
1.00 | 0.86 | 0.50 | 0.17 | 0.09 | 0.35 | -0.17 | -0.21 | -0.01 | |
| 1.00 | 0.87 | 0.37 | 0.35 | 0.35 | -0.28 | -0.24 | -0.22 | |||
| 1.00 | 0.47 | 0.52 | 0.25 | -0.32 | -0.20 | -0.37 | ||||
|
|
1.00 | 0.72 | 0.37 | 0.14 | -0.24 | -0.65 | ||||
|
|
1.00 | -0.00 | -0.37 | 0.08 | -0.89 | |||||
| 1.00 | 0.33 | -0.56 | 0.04 | |||||||
| 1.00 | -0.31 | 0.39 | ||||||||
| 1.00 | -0.12 | |||||||||
| CAY |
1.00 |
Table 2: Forecast Regressions for Quarterly Stock Market Return
Simple, by Regressor; t-stats are in parentheses; data in each column are coincident
The sample period extends from 1990Q1 to 2005Q1. Newey-West robust ![]() -statistics with four lags are reported in parentheses. All variable definitions
are identical to Table 1.
-statistics with four lags are reported in parentheses. All variable definitions
are identical to Table 1.
| Intercept | -12.19 (-1.55) |
-6.13 (-0.83) |
3.89 (0.75) |
113.01 (2.27) |
77.45 (1.84) |
23.00 (1.26) |
7.73 (0.69) |
7.33 (1.70) |
5.06 (1.11) |
| 0.86 (3.94) |
|||||||||
| 0.34 (2.38) |
|||||||||
| 0.17 (0.56) |
|||||||||
|
|
-2.81 (-2.08) |
||||||||
|
|
-1.51 (-1.62) |
||||||||
| -1.67 (-0.87) |
|||||||||
| -0.70 (-0.14) |
|||||||||
| 4.40 (0.91) |
|||||||||
| CAY |
4.16 (2.29) |
||||||||
| Adj. |
15.14 | 6.32 | -1.05 | 6.22 | 2.76 | 0.27 | -1.63 | -0.66 | 4.83 |
| Intercept | 120.85 (1.90) |
-13.89 (-2.18) |
81.50 (1.12) |
107.55 (1.27) |
108.28 (1.72) |
| 0.98 (4.87) |
0.87 (3.85) |
0.97 (4.58) |
1.11 (5.27) |
||
|
|
-3.57 (-2.09) |
-1.99 (-1.04) |
-3.22 (-1.42) |
-3.51 (-2.20) |
|
|
|
|||||
| 4.75 (1.34) |
|||||
| 7.59 (2.29) |
|||||
| CAY |
4.32 (2.58) |
1.98 (0.82) |
0.83 (0.37) |
||
| Adj. |
26.37 | 20.86 | 5.54 | 25.23 | 27.67 |
Table 3: Robustness Check with Alternative Variance Measures
Simple, by Regressor; t-stats are in parentheses; data in each column are coincident
The sample period extends from 1990Q1 to 2005Q1. Newey-West robust
| Constant | -7.11 (-0.97) |
-5.35 (-0.92) |
-3.35 (-0.56) |
-2.75 (-0.42) |
1.57 (0.27) |
|
|
0.50 (2.43) |
||||
|
|
0.74 (3.14) |
||||
|
|
0.46 (1.90) |
||||
| 0.22 (1.72) |
|||||
| 0.23 (1.13) |
|||||
|
|
|||||
| CAY |
|||||
| Adj. |
7.30 | 8.08 | 3.62 | 3.05 | 0.68 |
| Constant | 141.62 (2.27) |
124.46 (1.42) |
134.91 (2.16) |
|
|
0.71 (3.79) |
0.70 (3.53) |
0.84 (3.73) |
|
|
|||
|
|
|||
|
|
-4.06 (-2.39) |
-3.61 (-1.53) |
-4.22 (-2.62) |
| 5.61 (1.22) |
|||
| 6.78 (2.01) |
|||
| CAY |
1.06 (0.41) |
||
| Adj. |
21.04 | 19.89 | 22.39 |
| Constant | 107.74 (1.79) |
95.91 (1.18) |
99.10 (1.67) |
|
|
|||
|
|
0.78 (4.31) |
0.76 (3.52) |
0.82 (4.30) |
|
|
|||
|
|
-2.99 (-1.89) |
-2.68 (-1.24) |
-2.85 (-1.90) |
| 1.85 (0.48) |
|||
| 4.66 (1.45) |
|||
| CAY |
0.75 (0.31) |
||
| Adj. |
15.62 | 14.26 | 13.77 |
| Constant | 129.42 (2.15) |
115.02 (1.35) |
122.71 (2.03) |
|
|
|||
|
|
|||
|
|
0.64 (3.49) |
0.62 (3.05) |
0.71 (3.69) |
|
|
-3.59 (-2.23) |
-3.22 (-1.42) |
-3.59 (-2.32) |
| 3.25 (0.71) |
|||
| 4.76 (1.48) |
|||
| CAY |
0.88 (0.34) |
||
| Adj. |
14.35 | 13.02 | 13.03 |
Table 4: Robustness Check with Monthly Stock Market Return
Simple, by Regressor; t-stats are in parentheses; data in each column are coincident
| Intercept | -1.62 (-0.32) |
-0.79 (-0.14) |
5.07 (1.22) |
103.66 (2.32) |
74.91 (2.00) |
8.95 (0.56) |
8.07 (0.90) |
6.81 (1.91) |
| 0.42 (2.87) |
||||||||
| 0.21 (1.66) |
||||||||
| 0.10 (0.41) |
||||||||
|
|
-2.56 (-2.12) |
|||||||
|
|
-1.45 (-1.75) |
|||||||
| 0.03 (0.15) |
||||||||
| -0.76 (-0.19) |
||||||||
| 1.09 (0.27) |
||||||||
| Adj. |
1.24 | 0.58 | -0.42 | 2.10 | 1.07 | -0.52 | -0.50 | -0.50 |
| Intercept | 105.79 (2.16) |
102.22 (2.11) |
| 0.49 (2.68) |
0.58 (3.03) |
|
|
|
-2.87 (-2.12) |
-2.97 (-2.29) |
|
|
||
| 3.12 (0.85) |
||
| 2.69 (0.75) |
||
| Adj. |
3.98 | 3.37 |
Table 5: Robustness Check with Volatility Risk Premium
Simple, by Regressor; t-stats are in parentheses; data in each column are coincident
| Constant | -27.81 (-2.84) |
-15.82 (-1.17) |
5.20 (0.61) |
|
|
4.42 (4.90) |
||
|
|
1.11 (1.75) |
||
|
|
0.10 (0.13) |
||
|
|
|||
| CAY |
|||
| Adj. |
18.50 | 3.76 | -1.66 |
| Constant | 61.41 (1.03) |
-25.97 (-2.87) |
55.91 (0.73) |
47.63 (0.83) |
|
|
4.15 (4.83) |
4.07 (4.26) |
4.12 (4.44) |
4.39 (5.36) |
|
|
||||
|
|
||||
|
|
-2.29 (-1.45) |
-2.14 (-1.04) |
-2.02 (-1.39) |
|
| 1.48 (0.42) |
||||
| 6.01 (1.66) |
||||
| CAY |
2.72 (1.57) |
0.37 (0.17) |
||
| Adj. |
22.38 | 19.81 | 21.05 | 21.32 |
Table 6: Robustness Check with Alternative Predictor Variables
Simple, by Regressor; t-stats are in parentheses; data in each column are coincident
| Constant | 6.85 (1.41) |
7.66 (0.54) |
-11.32 (-0.90) |
3.74 (0.76) |
|
|
||||
|
|
-0.07 (-0.68) |
|||
|
|
1.68 (0.08) |
|||
| 0.84 (1.66) |
||||
| 0.80 (2.92) |
||||
| Adj. |
-1.17 | -1.68 | 4.47 | 3.28 |
| Constant | 129.03 (2.05) |
132.27 (2.14) |
119.75 (1.96) |
118.26 (1.96) |
| 0.88 (5.02) |
1.01 (4.92) |
1.14 (5.71) |
0.98 (5.78) |
|
|
|
-3.77 (-2.22) |
-3.81 (-2.36) |
-3.76 (-2.53) |
-3.84 (-2.46) |
| 4.91 (1.39) |
6.41 (1.55) |
|||
| 7.29 (2.36) |
9.91 (2.70) |
|||
|
|
||||
|
|
||||
| -0.14 (-0.29) |
-0.14 (-0.30) |
|||
| 0.47 (2.22) |
0.79 (2.33) |
|||
| Adj. |
26.52 | 25.20 | 26.46 | 30.18 |
Table 7: Risk-Factor Test with Fama-French Portfolios
Time-Series: Loading 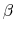
| Market Small |
Market 2 |
Market 3 |
Market 4 |
Market Large |
Small |
2 |
3 |
4 |
Large |
|
|---|---|---|---|---|---|---|---|---|---|---|
| Low | 1.47 | 1.46 | 1.37 | 1.30 | 1.03 | -1.00 | -1.10 | -1.05 | -1.01 | -0.80 |
| 2 | 1.15 | 1.04 | 1.02 | 0.94 | 0.89 | -0.99 | -0.94 | -1.11 | -1.15 | -1.08 |
| 3 | 0.90 | 0.85 | 0.84 | 0.89 | 0.79 | -0.82 | -0.92 | -1.01 | -1.14 | -0.99 |
| 4 | 0.79 | 0.82 | 0.79 | 0.81 | 0.68 | -0.81 | -1.00 | -0.93 | -0.86 | -0.86 |
| High | 0.84 | 0.90 | 0.85 | 0.81 | 0.79 | -0.94 | -0.89 | -0.96 | -0.84 | -1.05 |
| Market Small |
Market 2 |
Market 3 |
Market 4 |
Market Large |
Small |
2 |
3 |
4 |
Large |
|
|---|---|---|---|---|---|---|---|---|---|---|
| Low | 14.43 | 19.50 | 20.47 | 25.54 | 33.98 | -1.38 | -1.70 | -1.76 | -2.05 | -2.21 |
| 2 | 12.21 | 15.30 | 20.29 | 17.56 | 22.52 | -1.67 | -1.76 | -2.47 | -2.71 | -2.93 |
| 3 | 11.97 | 13.14 | 14.20 | 14.08 | 15.78 | -1.62 | -2.08 | -2.33 | -2.74 | -2.64 |
| 4 | 10.66 | 11.57 | 11.85 | 12.84 | 11.22 | -1.72 | -2.23 | -2.31 | -2.29 | -2.78 |
| High | 10.98 | 11.16 | 10.75 | 10.71 | 10.48 | -2.06 | -1.94 | -2.28 | -2.13 | -3.09 |
| Market Small |
Market 2 |
Market 3 |
Market 4 |
Market Large |
Small |
2 |
3 |
4 |
Large |
|
|---|---|---|---|---|---|---|---|---|---|---|
| Low | 49.38 | 64.28 | 67.07 | 77.00 | 88.02 | 1.60 | 2.95 | 3.17 | 3.81 | 4.46 |
| 2 | 44.53 | 63.28 | 73.64 | 76.86 | 78.57 | 2.57 | 4.30 | 7.65 | 10.30 | 10.30 |
| 3 | 48.31 | 59.96 | 67.00 | 66.54 | 67.36 | 3.27 | 6.14 | 8.52 | 9.82 | 9.35 |
| 4 | 45.44 | 55.22 | 55.93 | 64.52 | 50.05 | 3.95 | 7.18 | 6.84 | 6.32 | 6.92 |
| High | 46.25 | 52.60 | 55.12 | 54.06 | 45.92 | 4.94 | 4.25 | 6.16 | 5.02 | 7.16 |
| Market | ||
| Risk Premium |
10.12 | -10.73 |
| 2.45 | -1.54 |
This figure plots the implied variance (top panel, blue line), the realized variance (middle panel, red line), and the difference (bottom panel, black line) for the S&P 500 market index from 1990 Q1 to 2005 Q1. The shaded areas represent NBER recessions. The figure plots the quarterly S&P 500 excess returns (thin red line) together with (lagged) predictor variables (blue lines) from 1990 Q1 to 2005 Q1. The top panel illustrates the variance difference, or variance risk premium, the middle panel graphs the P/E ratio, and the bottom panel depicts the consumption-wealth ratio CAY. The figure plots the GDP growth rates (thin red line) together with the lagged variance differences (blue line), or variance risk premia, from 1990 Q1 to 2005 Q1. Both of the series are standardized to have mean zero and variance one.
Footnotes
![\displaystyle IV_t \equiv 2 \int_0^{\infty}{C_t\left(T_2,\frac{K}{B(t,T_2)}\right) - C_t\left(T_1,\frac{K}{B(t,T_1)}\right) \over K^2} dK = E_t^Q [\mbox{Return Variation }(T_1,T_2)].](img23.gif)
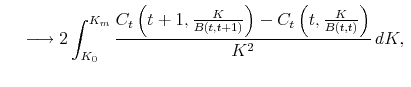
![\displaystyle RV_t \equiv \sum_{j=1}^{n}\left[p_{t-1+{j\over n}}- p_{t-1+{j-1\over n}(\Delta)}\right]^2 \longrightarrow](img29.gif) Return Variation
Return Variation