Estimating the Long-Run User Cost Elasticity for a Small Open Economy: Evidence Using Data from South Africa
Keywords: user cost elasticity, fixed investment, capital accumulation, price of capital, interest rate
Abstract:
JEL classifications: E22, E44, E62, C23
1 Introduction
Understanding the determinants of capital accumulation is essential to understanding business cycles and economic growth, and therefore to effective formulation of economic policy. It is no surprise that estimating the response of capital demand to changes in the user cost of capital (the user cost elasticity) has been one of the most widely researched areas in empirical macroeconomics. Despite the voluminous research on the subject, the results remain somewhat inconclusive. Estimates using aggregate time series data have found an elasticity that is statistically insignificant or, counter-intuitively, positive in sharp contrast to theory based on the neoclassical framework.1
According to the neoclassical theory, both the capital stock and the user cost of capital are determined by demand and supply equilibrium that equates the marginal product of capital services to its marginal opportunity cost. In order to obtain reliable estimates of the user cost elasticity of the capital demand curve, econometricians must be able to isolate exogenous movements in the supply curve for capital. This is particularly challenging in a large open economy like the United States, where the demand and supply of capital services are jointly determined. Estimates that fail to account for this simultaneity are likely to be biased.2 The presence of capital adjustment costs also complicates the estimation process. These costs not only prolong the response of capital to a given change in the user cost, but also cause the magnitude of the response to be closely related to both the size and the anticipated persistence of these shocks (Tevlin and Whelan [2003]). This places an emphasis on obtaining long-run estimates that cut through the noise from transitory changes in investment fundamentals.
This study expands on the insight by Schaller [2006] that in a small open economy, movements in the supply of capital services are more likely to be exogenous because the country is a price taker in the world markets for financial capital and investment goods. We use a quarterly panel of two-digit manufacturing data from South Africa and use a regression technique that accounts for internal adjustment costs by focusing on the long run response of capital. Since South Africa is a small open economy, its domestic demand for capital has a limited effect on interest rates and the price of capital goods, and hence on the user cost, allowing a better estimate of the user cost elasticity.3 Our quarterly panel helps both to emphasize the low frequency movements in the data that are important for capital accumulation and to limit the potential for small-sample bias, which is heightened in this setting due to the serial persistence properties of the data.
We find an estimated user cost elasticity of capital demand in the vicinity of -0.80 that is highly statistically significant and reasonably close the value embedded in the Cobb-Douglas production function that is often assumed by researchers. To our knowledge, the only other studies that have found such a large and significant elasticity are Caballero [1994] and Schaller [2006], who assume a cointegrating relationship between capital, output and the user cost and whose headline estimates of the user cost elasticity use measures of business fixed capital that exclude structures.4 Our study is the first to document such a large elasticity using data for a measure of capital that includes both equipment and structures, and that employs a lagged-difference approach rather than a cointegration technique. We also obtain similar estimates when we use a panel cointegration approach, although our panel cointegration tests suggest that the cointegrating relationship in Caballero [1994] and Schaller [2006] may not be very robust for the South Africa data.
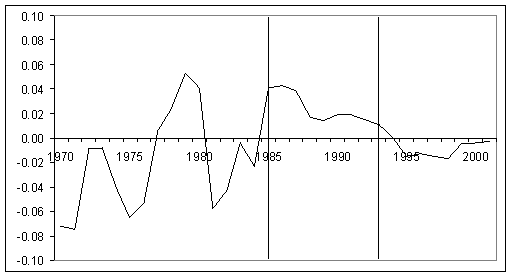
An additional feature of the South African economy exploited in our study is the unique reversion toward autarky that the country experienced beginning around 1985 until early 1994. During this period, the world imposed economic sanctions on South Africa to put pressure on its apartheid regime--a political system that granted different rights to citizens based on race. As a result of the embargo, several foreign public and private entities operating in South Africa decided to disinvest and/or stop making new investments or reinvestments of earnings in the country.5 In addition to these restrictions on capital flows, several countries also restricted or banned trade with South Africa. These restrictions had a meaningful effect on the country's international trade flows. South Africa's trade-to-GDP ratio dropped from an average of 23 percent during the pre-embargo period to an average of 19 percent during the embargo, then rose back to an average of 25 percent after the embargo was lifted. The country's current account balance, shown in Figure 1, also follows a pattern consistent with these restrictions.6 Before 1985, the country registered current account deficits that averaged 2 percent of GDP. However, when economic sanctions intensified between 1985 and 1993, the current account balance swung to a surplus that averaged about 2.4 percent of GDP. After 1993, the current account reversed again to a deficit as the economic sanctions were lifted and the country re-integrated into the world economy.7
South Africa's limited access to world markets when the embargo was in effect suggests that the variables that determine the user cost, such as interest rates and the relative price of capital goods, became much more influenced by domestic factors. We exploit this `natural' experiment to test whether the simultaneity problem has a meaningful effect on our capital elasticity estimates. We find that controlling for the data from the embargo period leads to a statistically significant increase in the absolute value of the user cost elasticity, and that the estimated elasticity during the embargo period is considerably smaller, and, in some cases, close to zero. This finding may help explain why many previous studies that employ data from large economies have had difficulty finding estimates of the capital user cost elasticity that are statistically significant and of the correct sign.
2 Theoretical Framework
We assume that a forward-looking representative firm in each industry chooses a quantity of capital that maximizes its market value in the face of capital adjustment costs. This choice balances the costs of adjustment against the costs associated with departing from the capital that it would hold in a frictionless world. The frictionless capital stock is determined by the neoclassical investment fundamentals, and takes the form:
where ![]() and
and ![]() are the log of output and the log of the user cost for
frictionless capital in industry
are the log of output and the log of the user cost for
frictionless capital in industry ![]() .8 The variable
.8 The variable
![]() is the log of the level of technology, an important fundamental for capital holdings that we assume is known by firms in industry
is the log of the level of technology, an important fundamental for capital holdings that we assume is known by firms in industry ![]() but is not observed by econometricians. The user cost for the frictionless capital stock in each industry is given by:
but is not observed by econometricians. The user cost for the frictionless capital stock in each industry is given by:
where
We follow Hall and Jorgenson [1967] and many others by assuming that firms choose a value for next period's capital stock that minimizes the following quadratic loss function with capital adjustment costs:
where
where
and
so that equation (4) simplifies to the following backward-looking partial-adjustment process:
This shows that the capital stock adjusts in each period towards a target
Tevlin and Whelan [2003] argue that the forward-looking nature of the capital target is crucial for empirical estimation because the response of capital to an unanticipated change in fundamentals will be closely related to the expected persistence of the disturbance. We incorporate this possibility by letting the evolution of the neoclassical fundamentals in each industry be determined by the following reduced-form univariate processes:
Each of the variables
In this expression, each of the long-run responses
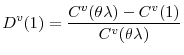 for
for Using equations (4) and (9), the capital stock in each industry can be expressed as
where
The formulation above suggests a number of important implications for the estimation of capital elasticities. First, the long run response of capital to changes in any of the frictionless fundamentals is closely related to the expected persistence of the innovation. The long run response of
capital to a change in any of these fundamentals will only be the same as the frictionless elasticities in equation (1) if the process that describes the evolution of that fundamental contains a unit root. Second, the last term of this equation includes current and lagged
values of the unobserved fundamental ![]() . Since current and lagged values of this factor are likely to be correlated with the observed investment fundamentals, econometricians should be
mindful of the potential for endogeneity when estimating specifications similar to the form in equation (10). In addition, economists often think of technology as an integrated process. If this is true, the cointegration approach, as employed by Caballero [1994] and Schaller [2006], could yield spurious results unless technology shocks do not augment capital.12 A third implication is the potential for small sample bias in the estimates, which is exascerbated in this setting because the term in equation
. Since current and lagged values of this factor are likely to be correlated with the observed investment fundamentals, econometricians should be
mindful of the potential for endogeneity when estimating specifications similar to the form in equation (10). In addition, economists often think of technology as an integrated process. If this is true, the cointegration approach, as employed by Caballero [1994] and Schaller [2006], could yield spurious results unless technology shocks do not augment capital.12 A third implication is the potential for small sample bias in the estimates, which is exascerbated in this setting because the term in equation
![]() involving the unobserved factor
involving the unobserved factor ![]() is likely to be serially correlated.
is likely to be serially correlated.
As in Schaller [2006], our estimation strategy aims to identify the long-run elasticity of capital to the user cost by choosing a sample in which the evolution of the user cost is more likely to be determined by factors outside of the domestic economy. We think that it
is plausible that forecast errors for the user cost (
![]() ) are orthogonal to current and lagged changes in the unobserved productivity factor
) are orthogonal to current and lagged changes in the unobserved productivity factor ![]() because South Africa is a price taker in the international markets.13 Even if this presumption is true, there remains
a possibility that there are some productivity shocks that increase capital demand in all countries, and are therefore correlated to movements in the various factors that compose the user cost of capital. This possibility should be limited to some extent in the South African case because its
economy is relatively isolated from the world's largest economies by geography. We can also at least partially account for this problem by estimating our regression using a panel of industries, where it is more likely that the disturbances stem from idiosyncratic factors, and by controlling for
aggregate shocks that can be identified in the cross-section dimension.
because South Africa is a price taker in the international markets.13 Even if this presumption is true, there remains
a possibility that there are some productivity shocks that increase capital demand in all countries, and are therefore correlated to movements in the various factors that compose the user cost of capital. This possibility should be limited to some extent in the South African case because its
economy is relatively isolated from the world's largest economies by geography. We can also at least partially account for this problem by estimating our regression using a panel of industries, where it is more likely that the disturbances stem from idiosyncratic factors, and by controlling for
aggregate shocks that can be identified in the cross-section dimension.
3.1 Specification and Data
Our primary procedure is to estimate a regression specification of the basic form:
for industries
For all of our regressions, we use a quarterly panel of twenty-four manufacturing industries at the two-digit level that extends from 1970:Q1 to 2001:Q4.16 Industry-level estimates of the capital stock, fixed investment, consumption of fixed capital, price deflators, and output were obtained from South Africa Trade and Industrial Policy Strategies (TIPS). Quarterly data on interest rates, corporate tax rates, tax credits,
capital depreciation allowances, and the aggregate price level are from the South African Reserve Bank. We calculate the user cost of capital in each period and for each industry using equation (2), the components of which were determined as follows. The real borrowing cost
(![]() ) in each quarter is the end-of-quarter nominal prime overdraft rate (a short-term rate charged to commercial banks), to which we add a fixed risk premium and then deduct expected
inflation measured by the realized growth rate in the GDP price deflator over the coming four quarters.17 The price of investment goods (
) in each quarter is the end-of-quarter nominal prime overdraft rate (a short-term rate charged to commercial banks), to which we add a fixed risk premium and then deduct expected
inflation measured by the realized growth rate in the GDP price deflator over the coming four quarters.17 The price of investment goods (
![]() ) is the industry's price deflator net of our estimate of the present value of the tax shields from depreciation allowances.18 The depreciation rate for each industry in each quarter (
) is the industry's price deflator net of our estimate of the present value of the tax shields from depreciation allowances.18 The depreciation rate for each industry in each quarter (
![]() ) is obtained by dividing the industry's consumption of fixed capital by its capital stock at the end of the previous quarter. Finally, we proxy for the anticipated rate of
appreciation in investment goods using the realized rate of appreciation recorded over the following four quarters. Our estimates of the user cost of capital in each quarter differ across industries because of differences in the relative price of capital and the rate of depreciation.
) is obtained by dividing the industry's consumption of fixed capital by its capital stock at the end of the previous quarter. Finally, we proxy for the anticipated rate of
appreciation in investment goods using the realized rate of appreciation recorded over the following four quarters. Our estimates of the user cost of capital in each quarter differ across industries because of differences in the relative price of capital and the rate of depreciation.
It is worth noting that the specification shown above does not include any lagged values of the dependent variable as regressors, unlike the specifications used by Tevlin and Whelan [2003] and others. In principle, the two approaches should be roughly equivalent, since one can recover an autoregressive specification by a simple rearrangement of our structural equation (10).19 Our approach allows the dynamic response of capital to changes in fundamentals to take a general form that, unlike the autoregressive specification, does not impose a geometric rate of decay. In addition, autoregressive specifications may be disadvantageous if the structural error is serially correlated, because the estimated autoregressive parameters would be inconsistent. The autoregressive formulation may also be prone to errors-in-variables problems that could arise if capital growth is measured with error. Measurement error in the rate of capital growth should be relatively innocuous in our specification because it is absorbed by the regression residual. That said, our methodology has the disadvantage that it may miss any portion of the capital response because we can only include a finite number of lags in our regression. In order to limit this possibility, we include an unusually large number of lags in our regression specifications.20
For the reasons explained in the previous section, the long-run elasticities estimated using equation (11) can only be interpreted as the frictionless elasticities in equation (1) when the fundamental in question follows a unit root process. We
consider the unit root issue in Table 1, which shows results of panel unit root tests for each of our variables of interest: capital, the user cost, and output. The table shows results from a number of alternative test procedures that differ in formulation,
robustness, and the maintained null hypothesis. Four of these tests maintain a null that there is a unit root in the series of interest for all industries in the panel: the Levin, Lin and Chu [2002], Im, Pesaran and Shin [2003], Maddala and Wu [1999] and Pesaran [2003] tests. The Im, Pesaran and Shin and Pesaran versions are the most robust of these tests because they allow the possibility that the residuals are correlated in the cross-sectional dimension; the Pesaran test allows
this cross-sectional correlation to take a less restricted form.21 The fifth test, from Hadri, maintains the null that the variable does not follow a unit
root process in any of the industries of the panel. The results for almost all of these tests suggest that the processes for both output and capital contain unit roots. In contrast, the panel tests for the user cost of capital are quite mixed. Nonetheless, the results of the most robust panel tests
seem to offer some limited support for the existence of a unit root in this process. Therefore, even though the evidence for a unit root in the user cost is not overwhelming, these results offer at least some support for interpreting our estimate of the long-run user cost elasticity of capital as
an estimate of the frictionless elasticity parameter ![]() .
.
3.2 Estimates Using the Entire Data Sample
To fix ideas, we begin by reporting results from regression specifications that do not explicitly account for the heightened potential of user cost endogeneity during the embargo portion of the sample period. These results serve as a basis of comparison both to previous studies and for the results we report later that account for the apparent endogeneity of the user cost during the embargo.
Table 2 shows our regression estimates using the difference specification described above. All of these specifications include contemporanous values of the user cost and output, along with 32 lags of each of these variables.22 The regressions also include an embargo fixed effect and a constant (not shown). The results shown in columns (1) to (4) of the table are estimated using pooled OLS, while the results reported in columns (5) to (8) control for industry fixed effects. The standard errors reported for each estimate are robust to the possibility of correlation between the residuals in the cross-sectional dimension. All of these estimates include in the user cost our proxy of anticipated capital gains, but including this term had only a small effect on our estimates.23
Column (1) shows regression results from our baseline OLS specification, while column (5) shows estimates from the same specification with fixed industry effects. Our estimate of the long run user cost elasticity of capital for the baseline case is about -0.66, and is statistically different from zero at significance levels well below one percent. Including industry fixed effects diminishes the absolute magnitude of the user cost elasticity estimate only slightly. The estimates of the long run output elasticity in these two specifications-which are probably inconsistent for the reasons discussed above-are 0.67 for the baseline specification and 0.59 with industry fixed effects. Both of these estimates are statistically distinguishable from zero at standard significance levels, but tests also show that they are well below 1.0 (the neoclassical benchmark) at low levels of significance.
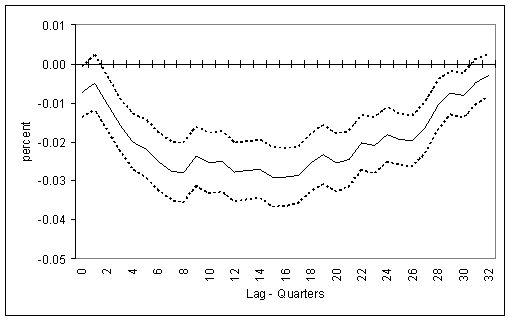
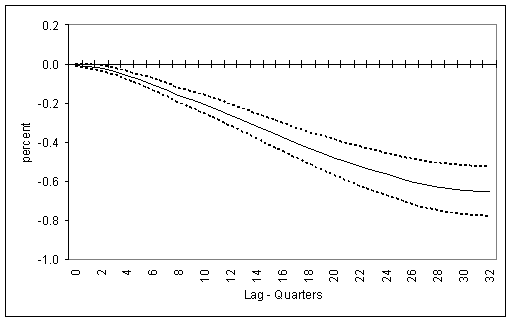
Figure 2 shows the point estimates of the response of capital growth to the user cost at each lag and 95 percent confidence intervals of these estimates, using the OLS benchmark specification reported in column (1). This impulse response function shows a very distinct hump-shape that reaches a rough plateau between the 8th and 17th quarters, and, with the exception of the first and last few lags, the individual responses are very significant. Figure 3 plots these same set of estimates restated as a cumulative response, showing that the total response is quite drawn out. One particularly notable aspect of these estimates is that the marginal response function is not diminishing and concave, as one would expect with convex costs of adjusting the level of capital. Among other things, this characteristic would seem consistent with adjustment costs associated with altering capital growth (the investment rate).
The estimates in the remaining columns of Table 2 use some additional methods to control for endogeneity. Columns (2) and (6) restrict the baseline specification so that the long-run output elasticity is 1.0, as is the case of constant returns to scale. These
estimates should reveal whether the endogeneity of the output term affects the user cost elasticity, as one might expect if our identifying assumption was not valid so that the true residual
![]() is correlated to both output and the user cost. The elasticity estimates from these two specifications are a little larger in absolute magnitude than in the baseline
specification. This suggests that, if our estimates from the baseline specification are inconsistent, they may be too small. However, the point estimates from these restricted regressions are well within any standard confidence interval of the baseline estimates, so the difference is probably not
statistically meaningful. Columns (3) and (7) show estimates that include quarterly dummies that are common across industries, and should therefore control for any remaining "aggregate" component of the true residual that affects capital accumulation in all industries.24 The point estimates of the user cost elasticity obtained using this specification are somewhat smaller in absolute magnitude than those from the baseline
specification, but are well within a standard confidence interval of the baseline estimates. The final set of estimates reported in columns (4) and (8) include both the quarterly dummies and the restriction on the long-run output elasticity. These estimates are roughly in line with the baseline
cases.
is correlated to both output and the user cost. The elasticity estimates from these two specifications are a little larger in absolute magnitude than in the baseline
specification. This suggests that, if our estimates from the baseline specification are inconsistent, they may be too small. However, the point estimates from these restricted regressions are well within any standard confidence interval of the baseline estimates, so the difference is probably not
statistically meaningful. Columns (3) and (7) show estimates that include quarterly dummies that are common across industries, and should therefore control for any remaining "aggregate" component of the true residual that affects capital accumulation in all industries.24 The point estimates of the user cost elasticity obtained using this specification are somewhat smaller in absolute magnitude than those from the baseline
specification, but are well within a standard confidence interval of the baseline estimates. The final set of estimates reported in columns (4) and (8) include both the quarterly dummies and the restriction on the long-run output elasticity. These estimates are roughly in line with the baseline
cases.
To our knowledge, these user cost elasticity estimates are at the high end of those seen in the literature, especially when one takes into account that they include nonresidential structures in the measure of capital. For instance, the cointegration methodology employed by Caballero [1994], using aggregate U.S. data, and Schaller [2006], using aggregate Canadian data, yield estimates of the user cost elasticity that approach or exceed 1.0 in absolute value, but neither of these estimates include nonresidential structures in the measure of capital. When these authors use a measure of capital that includes nonresidential structures, they find that the user cost elasticity is essentially zero. Using a similar specification to our own that is estimated using data from a huge panel of U.S. firms, Chirinko, Fazzari and Meyer [1999] obtain some estimates that are similar in magnitude and precision to our estimates, even though their "preferred" estimates (obtained using an instrumental variables technique) range between -0.5 and 0. However, estimates of this magnitude are far from representative. Usually, empirical estimates of the user cost elasticity are close to zero or have the wrong sign, and are seldom statistically significant.
3.3 Estimates Using a Panel Cointegration Approach
An alternative specification for estimating the long-run elasticities of capital to the user cost and output is to amend equation (10) slightly into a cointegrating specification of the form
where
Assuming that the cointegrating specification is valid, large-sample estimates using this approach should be superior to those from our difference specification. This is because of the well-known property that the structural parameters from a cointegrating regression are super-consistent, even if the presence of endogeneity between the regressors and the residual term. So, in a sufficiently large sample, this method should recover the true structural parameters even if our assumption about the exogeneity of the user cost during the non-embargo period does not hold true. That said, the structural form of our residual suggests that the estimates from this regression may suffer from small sample bias.26 We correct for this possibility by estimating our cointegrating regression by dynamic panel OLS with a large number of leads and lags of the first-difference of the independent variables.27
In order to determine whether the cointegrating specification is valid, we test whether the fitted residual terms ![]() from estimates of equation (12) are
stationary using the same set of tests used in Table 1. As discussed earlier, the panel unit root tests shown in Table 1 provided strong support that there is a unit root in the processes for output and capital, and some partial
support for a unit root in the process for the user cost of the frictionless capital. For robustness in our cointegration tests, we used two separate specifications: The first specification treats the long-run output elasticity
from estimates of equation (12) are
stationary using the same set of tests used in Table 1. As discussed earlier, the panel unit root tests shown in Table 1 provided strong support that there is a unit root in the processes for output and capital, and some partial
support for a unit root in the process for the user cost of the frictionless capital. For robustness in our cointegration tests, we used two separate specifications: The first specification treats the long-run output elasticity ![]() as a free variable and estimates it in the regression, while the second specification is constrained so that this long-run output elasticity is one (as in Caballero [1994] and Schaller [2006]). The
results of these tests are reported in Table 3. As one can see, a handful of the tests do support the null of cointegration, especially for the specifications that restrict the magnitude of the long run output elasticity. However, the large majority of these tests,
including the most robust version of the test from Pesaran [2003], fail to reject the null of no cointegration. Although these results are not conclusive, the weight of the evidence, taken together with the results of the unit root tests described earlier, suggests that the
cointegrating regression approach may not be valid. These findings are also consistent with our priors about the implausibility of a stationary technology factor
as a free variable and estimates it in the regression, while the second specification is constrained so that this long-run output elasticity is one (as in Caballero [1994] and Schaller [2006]). The
results of these tests are reported in Table 3. As one can see, a handful of the tests do support the null of cointegration, especially for the specifications that restrict the magnitude of the long run output elasticity. However, the large majority of these tests,
including the most robust version of the test from Pesaran [2003], fail to reject the null of no cointegration. Although these results are not conclusive, the weight of the evidence, taken together with the results of the unit root tests described earlier, suggests that the
cointegrating regression approach may not be valid. These findings are also consistent with our priors about the implausibility of a stationary technology factor ![]() . That said, our panel
tests may still lack the power needed to reject the null of no cointegration, so we proceed with this approach as a robustness check for our preferred difference specification.
. That said, our panel
tests may still lack the power needed to reject the null of no cointegration, so we proceed with this approach as a robustness check for our preferred difference specification.
Our estimates using this cointegrating specification are reported in Table 4. Columns (1) and (2) of the table report estimates for a specifications that restrict the long-run elasticity of capital to output to be 1. However, the specification in column (1) includes only leads and lags of the change in the user cost as dynamic OLS terms, while column (2) also includes leads and lags of the change in output. The estimates of the user cost elasticity from these specifications are both in the vicinity of -1.0, and are highly significant. The final specification--shown in column (3)--estimates the long run output elasticity of capital as a free variable, and also includes leads and lags of the change in both output and the user cost as dynamic OLS terms. The estimated elasticities from this specification are also highly significant and are somewhat larger in absolute magnitude than our estimates from the difference specification. The user cost elasticity from this specification (-0.94) is a little smaller in absolute magnitude than the constrained estimates in columns (1) and (2) , but is also not statistically distinguishable from -1.0.
3.4 Estimates that Control for the Embargo Period
We now move on to estimates that account for the possibility that the user cost of capital is subject to a heightened degree of endogeneity during the embargo period. To account for this possibility, we augment our original regression specification to include terms that interact the observable explanatory variables with our embargo dummy. Our formulation for this regression is:
| (13) |
so that the embargo affects the entire long run relationship between capital and its fundamentals, but only for observations of these fundamentals that occur within the embargo period. As in our previous difference specification, we estimate this regression using the contemporaneous observations and 32 lags of each the fundamentals (including the interactions with the embargo dummy). Given these estimates, we determine the long-run elasticity of capital with respect to the user cost and output by calculating
Results using this specification are shown in Table 5. The results reported in this table are analogous to those reported in Table 2, with the first four columns showing estimates obtained using a pooled OLS specification, and the second four columns showing estimates that control for industry fixed effects. As in Table 2, columns (1) and (5) use a baseline specification that includes only an embargo fixed effect, while columns (2) to (4) and (6) to (8) include the various controls for endogeneity described earlier. For each of these specifications, the estimate of the long-run user cost during the non-embargo period is larger in absolute magnitude than the corresponding estimates in Table 2 that do not account for embargo interaction effects. All of these estimates are highly significant, and range in magnitude from around -0.71 for the baseline cases in columns (1) and (5) to as high as -0.85 for the estimates in columns (4) and (8) that include quarterly dummies and impose a unit restriction on the long-run output elasticity. In all of our specifications, we found that the embargo period data caused a large and statistically significant drop in the absolute magnitude of the estimated user cost elasticity. These drops were so considerable that the estimated elasticities during the embargo period are quite small, ranging between around -0.05 in column (3) to -0.25 in column (4). In most of these cases, the elasticity during the embargo period is not statistically distinguishable from zero, although the user-cost elasticity is still significant at around five percent or lower in columns (4) and (8)-which control for quarterly dummies and impose the unit restriction on the output elasticity. The table also provides some evidence that the embargo-period data may attenuate our estimate of the output elasticity of capital demand, albeit to a lesser extent than the user cost elasticity. Yet even after accounting for this attenuation, movements in output still had a statistically significant long-run effect on capital accumulation during the embargo period.
These results are consistent with our intuition that the user cost became more endogenous during the embargo period, heightening the degree of inconsistency in our estimates of the user cost elasticity over that period. These findings may help explain why most previous empirical studies of investment using U.S. data tend to find very little role for the user cost in determining the size of the capital stock.28
4 Conclusion
In a closed economy or in a large open economy, both the capital stock and the user cost of capital are jointly determined by domestic demand and supply equilibrium that equates the marginal product and marginal opportunity cost of capital services. This simultaneity introduces inconsistency into estimates of the user cost elasticity. Our study expands on an insight by Schaller [2006] that in a small open economy where the price of investment goods and the interest rate are largely determined by foreign markets, the user cost is less likely to be endogenous, thereby allowing for consistent estimates of the user cost elasticity. Using a quarterly panel of two-digit manufacturing data from South Africa, we obtain estimates of the user cost elasticity that are large and reasonably close to the Cobb-Douglas benchmark. This study is the first to document such a large user cost elasticity for a broad measure of business capital that includes both equipment and structures. Unlike previous studies that obtained large elasticities for just equipment capital, our study does not rely on the existence of a cointegrating relationship between capital, output, and the user cost.
The economic embargo that the world imposed on South Africa between 1985 and early 1994, which forced the economy to behave much more like a closed economy provides another test of Schaller's hypothesis. We find evidence that during the embargo period, the magnitude of the estimated user cost elasticity fell considerably--to magnitudes that are consistent with previous studies in which the user cost was likely endogenous. This finding underscores the importance of identification when forming estimates of the user cost elasticity.
A. Appendix: Omitted Proof
Obtaining the expression in equation (9) boils down to down to calculating:
![\displaystyle \left( 1-\theta\lambda\right) {\displaystyle\sum\limits_{l=0}^{\infty}} (\theta\lambda)^{l}E_{t}\left[ v_{i,t+1+l}^{{}}\right]](img101.gif)
Hansen and Sargent [1980] show that the solution for the bracketed term on the right-hand side of this equality is
Substituting this solution into equation (A1) and distributing through the expectations operator
Now use equation (8) to substitute out the conditional expectation
Equation (9) follows from the equation above by defining:
![\displaystyle D^{v}(L)\equiv\left[ {\displaystyle\sum\limits_{j=1}^{\infty}} c_{j}^{v}L^{j-1}+% {\displaystyle\sum\limits_{j=1}^{\infty}} \left( {\displaystyle\sum\limits_{k=j+1}^{\infty}} \left( \theta\lambda\right) ^{k-j}c_{k}^{v}\right) L^{j-1}\right] .](img110.gif)
Rearranging terms in this equation, it can be shown that
which, once again, can be simplified further using equation (8) to yield
As a final step, note that:
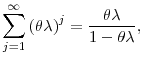
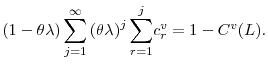
Using these two expressions, one can show that equation (A7) is equivalent to the expression for ![]() in equation (9).
in equation (9).
Figure 3: Estimated Cumulative Marginal Response of Capital to User Cost with 95 percent Confidence Interval
| Test | H |
User Cost | Output | Capital |
|
|---|---|---|---|---|---|
| Levin-Lin-Chu | common unit root | 0.000 | 0.000 | 0.100 | 0.136 |
| Im-Pesaran-Shin | common unit root | 0.003 | 0.772 | 0.963 | 0.448 |
| Maddala-Wu | common unit root | 0.002 | 0704 | 0.945 | 0.048 |
| Pesaran | common unit root | 0.289 | 0.998 | 0.997 | 0.437 |
| Hadri | no unit roots for any group | 0.000 | 0.000 | 0.000 | 0.000 |
| OLS (1) |
OLS (2) |
OLS (3) |
OLS (4) |
FE (5) |
FE (6) |
FE (7) |
FE (8) |
|
|---|---|---|---|---|---|---|---|---|
| Long-Run Output | 0.672 | 1.000 | 0.683 | 1.000 | 0.589 | 1.000 | 0.530 | 1.000 |
| Elasticity | (0.078) | (--) | (0.096) | (--) | (0.089) | (--) | (0.128) | (--) |
| Long-Run User Cost | -0.655 | -0.714 | -0.581 | -0.672 | -0.635 | -0.700 | -0.524 | -0.647 |
| Elasticity | (0.064) | (0.064) | (0.076) | (0.072) | (0.064) | (0.064) | (0.079) | (0.071) |
| Embargo | -0.005 | -0.003 | -0.006 | -0.003 | ||||
| Dummy | (0.001) | (0.004) | (0.001) | (0.001) | ||||
| 0.185 | -- | 0.223 | -- | 0.227 | -- | 0.264 | -- | |
| 1,963 | 1,963 | 1,963 | 1,963 | 1,963 | 1,963 | 1,963 | 1,963 |
| Test | H |
|
|
|---|---|---|---|
| Levin-Lin-Chu | no cointegration | 0.150 | 0.000 |
| Im-Pesaran-Shin | no cointegration | 0.559 | 0.092 |
| Maddala-Wu | no cointegration | 0.000 | 0.000 |
| Pesaran | no cointegration | 0.956 | 0.806 |
| Hadri | cointegration | 0.000 | 0.000 |
| (1) | (2) | (3) | |
|---|---|---|---|
| Long-Run | 1.000 | 1.000 | 0.874 |
| Output Elasticity | (--) | (--) | (0.043) |
| Long-Run | -1.098 | -1.017 | -0.943 |
| User Cost Elasticity | (0.065) | (0.059) | (0.064) |
| 0.277 | 0.538 | 0.648 | |
| 1,469 | 1,469 | 1,469 |
| OLS (1) |
OLS (2) |
OLS (3) |
OLS (4) |
FE (5) |
FE (6) |
FE (7) |
FE (8) |
|
|---|---|---|---|---|---|---|---|---|
| Long-Run Output Elasticity: Non-Embargo | 0.682 | 1.000 | 0.751 | 1.000 | 0.545 | 1.000 | 0.509 | 1.000 |
| Long-Run Output Elasticity: Non-Embargo S.E. | (0.088) | (--) | (0.107) | (--) | (0.095) | (--) | (0.139) | (--) |
| Long-Run Output Elasticity: Embargo Effect | -0.349 | -- | -0.429 | -- | -0.261 | -- | -0.225 | -- |
| Long-Run Output Elasticity: Embargo Effect S.E. | (0.170) | (--) | (0.178) | (--) | 0.204 | (--) | (0.211) | -- |
| Long-Run Output Elasticity: Embargo | 0.333 | 1.000 | 0.322 | 1.000 | 0.284 | 1.000 | 0.284 | 1.000 |
| Long-Run Output Elasticity: Embargo S.E. | (0.148) | (--) | (0.147) | (--) | (0.187) | (--) | (0.193) | (--) |
| Long-Run User Cost Elasticity: Non-Embargo | -0.750 | -0.793 | -0.810 | -0.857 | -0.707 | -0.767 | -0.735 | -0.840 |
| Long-Run User Cost Elasticity: Non-Embargo S.E. | (0.071) | (0.069) | (0.085) | (0.078) | (0.074) | (0.072) | (0.092) | (0.084) |
| Long-Run User Cost Elasticity: Embargo Effect | 0.665 | 0.512 | 0.761 | 0.604 | 0.627 | 0.515 | 0.751 | 0.624 |
| Long-Run User Cost Elasticity: Embargo Effect S.E. | (0.089) | (0.083) | (0.134) | (0.126) | (0.089) | (0.085) | (0.145) | (0.140) |
| Long-Run User Cost Elasticity: Embargo | -0.085 | -0.281 | -0.049 | -0.253 | -0.081 | -0.252 | 0.016 | -0.216 |
| Long-Run User Cost Elasticity: Embargo S.E. | (0.097) | (0.095) | (0.122) | (0.116) | (0.095) | (0.099) | (0.130) | (0.123) |
| Embargo | -0.000 | 0.000 | -0.001 | -0.000 | ||||
| Dummy | (0.002) | (0.001) | (0.002) | (0.001) | ||||
| 0.242 | -- | 0.278 | -- | 0.278 | -- | 0.314 | -- | |
| 1,963 | 1,963 | 1,963 | 1,963 | 1,963 | 1,963 | 1,963 | 1,963 |
Footnotes
![\displaystyle F(A_{i,t},K_{i,t,},L_{i,t})=A_{i,t}\left[ \omega_{i}K_{i,t}^{\frac{\sigma -1}{\sigma}}+(1-\omega_{i})L_{i,t}^{\frac{\sigma-1}{\sigma}}\right] ^{\frac{\sigma}{\sigma-1}}](img8.gif)
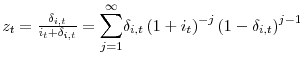 , where
, where ![\displaystyle U_{i,t}=\frac{\overline{p}_{i,t-1}^{k}}{p_{it}(1-\tau_{t})}\left[ r_{t-1}+\zeta+\delta_{i,t}-\frac{E_{t-1}\left[ \Delta\overline{p}_{i,t}% ^{k}\right] }{\overline{p}_{i,t-1}^{k}}\right]%](img14.gif)
![\displaystyle \min_{k_{t+1}}% {\displaystyle\sum\limits_{l=1}^{\infty}} \theta^{l}E_{t}\left[ \gamma\left( \Delta k_{i,t+l}\right) ^{2}+\left( k_{i,t+l}-k_{i,t+l}^{\ast}\right) ^{2}\right]%](img21.gif)
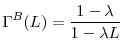 ,
and
,
and 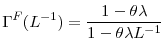 ,
,![\displaystyle k_{i,t+1}^{\ast\ast}=\Gamma^{F}(L^{-1})k_{i,t+1}^{\ast}=\left( 1-\theta \lambda\right) {\displaystyle\sum\limits_{l=0}^{\infty}} (\theta\lambda)^{l}E_{t}\left[ k_{i,t+1+l}^{\ast}\right]](img35.gif) ,
,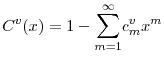 .
.![\displaystyle \left( 1-\theta\lambda\right) {\displaystyle\sum\limits_{l=0}^{\infty}} (\theta\lambda)^{l}E_{t}\left[ v_{i,t+1+l}^{{}}\right] =\left( 1-\theta\lambda\right) E_{t}\left[ {\displaystyle\sum\limits_{l=0}^{\infty}} (\theta\lambda)^{l}E_{t+1}\left( v_{i,t+1+l}\right) \right] ,% %](img104.gif)
![\displaystyle \frac{1}{1-C^{v}(\theta\lambda)}\left[ 1+% {\displaystyle\sum\limits_{j=1}^{\infty}} \left( {\displaystyle\sum\limits_{k=j+1}^{\infty}} \left( \theta\lambda\right) ^{k-j}c_{k}^{v}\right) L^{j}\right] v_{t+1}.%](img105.gif)
![\displaystyle \left( 1-\theta\lambda\right) {\displaystyle\sum\limits_{l=0}^{\infty}} (\theta\lambda)^{l}E_{t}\left[ v_{i,t+1+l}^{{}}\right] =\frac{1-\theta \lambda}{1-C^{v}(\theta\lambda)}\left[ E_{t}v_{t+1}+% {\displaystyle\sum\limits_{j=1}^{\infty}} \left( {\displaystyle\sum\limits_{k=j+1}^{\infty}} \left( \theta\lambda\right) ^{k-j}c_{k}^{v}\right) L^{j}v_{t+1}\right] %](img107.gif)
![\displaystyle \left( 1-\theta\lambda\right) {\displaystyle\sum\limits_{l=0}^{\infty}} (\theta\lambda)^{l}E_{t}\left[ v_{i,t+1+l}^{{}}\right] =\frac{1-\theta \lambda}{1-C^{v}(\theta\lambda)}\left[ {\displaystyle\sum\limits_{j=1}^{\infty}} c_{j}^{v}L^{j-1}+% {\displaystyle\sum\limits_{j=1}^{\infty}} \left( {\displaystyle\sum\limits_{k=j+1}^{\infty}} \left( \theta\lambda\right) ^{k-j}c_{k}^{v}\right) L^{j-1}\right] v_{t},%](img109.gif)
![\displaystyle D^{v}(1)=\frac{1-\theta\lambda}{C^{v}(\theta\lambda)}\left[ 1-C^{v}\left( 1\right) +% {\displaystyle\sum\limits_{j=1}^{\infty}} \left( {\displaystyle\sum\limits_{k=j+1}^{\infty}} \left( \theta\lambda\right) ^{k-j}c_{k}^{v}\right) \right] .% %](img111.gif)
![\displaystyle D^{v}(1)=\frac{1-\theta\lambda}{C^{v}(\theta\lambda)}\left[ 1-C^{v}\left( 1\right) +% {\displaystyle\sum\limits_{j=1}^{\infty}} \left( \theta\lambda\right) ^{j}% {\displaystyle\sum\limits_{k=j+1}^{\infty}} c_{k}^{v}\right] %](img112.gif)
![\displaystyle D^{v}(1)=\frac{1-\theta\lambda}{C^{v}(\theta\lambda)}\left[ 1-C^{v}\left( 1\right) +% {\displaystyle\sum\limits_{j=1}^{\infty}} \left( \theta\lambda\right) ^{j}\left( 1-C^{v}(1)-% {\displaystyle\sum\limits_{r=1}^{j}} c_{r}^{v}\right) \right] .%](img113.gif)