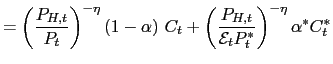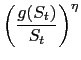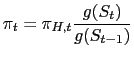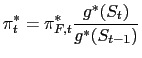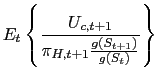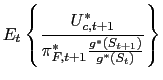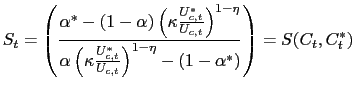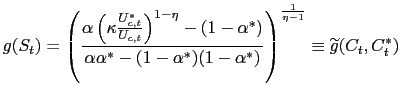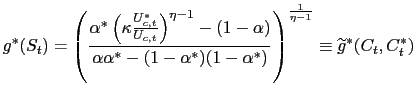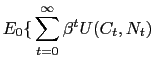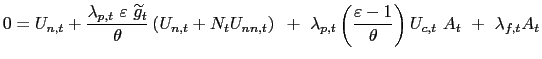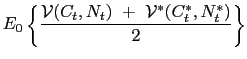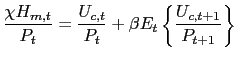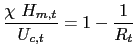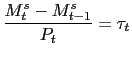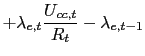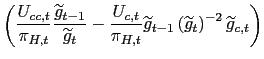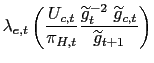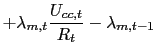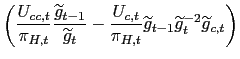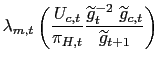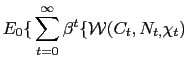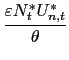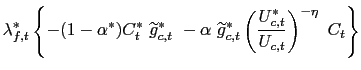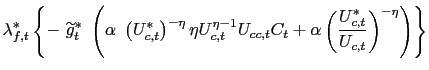Board of Governors of the Federal Reserve System
International Finance Discussion Papers
Number 798, April 2004, Revised Version: late 2004--Screen Reader Version*
This HTML version of this discussion paper is a revised and updated version of the same paper available as a PDF file at http://www.federalreserve.gov/pubs/ifdp/2004/798/ifdp798.pdf.
Ramsey Monetary Policy and International Relative Prices*
International Finance Discussion Papers numbers 797-807 were presented on November 14-15, 2003 at the second conference sponsored by the International Research Forum on Monetary Policy sponsored by the European Central Bank, the Federal Reserve Board, the Center for German and European Studies at Georgetown University, and the Center for Financial Studies at the Goethe University in Frankfurt.
NOTE: International Finance Discussion Papers are preliminary materials circulated to stimulate discussion and critical comment. The views in this paper are solely the responsibility of the author and should not be interpreted as reflecting the views of the Board of Governors of the Federal Reserve System or any other person associated with the Federal Reserve System. References in publications to International Finance Discussion Papers (other than an acknowledgment that the writer has had access to unpublished material) should be cleared with the author or authors. Recent IFDPs are available on the Web at http://www.federalreserve.gov/pubs/ifdp/. This paper can be downloaded without charge from the Social Science Research Network electronic library at http://www.ssrn.com/.
Abstract:
We analyze welfare maximizing monetary policy in a dynamic two-country model with price stickiness and imperfect competition. In this context, a typical terms of trade externality affects policy competition between independent monetary authorities. Unlike the existing literature, we remain consistent to a public finance approach by an explicit consideration of all the distortions that are relevant to the Ramsey planner. This strategy entails two main advantages. First, it allows an exact characterization of optimal policy in an economy that evolves around a steady-state which is not necessarily efficient. Second, it allows to describe a full range of alternative dynamic equilibria when price setters in both countries are forward-looking and households' preferences are not restricted. In this context, and in response to productivity shocks, Nash-competition generally leads to deviations from price stability. The size of this effect is directlly related to parameters indexing openness, such as the elasticity of substitution between domestic and foreign goods and the degree of home bias in consumption.
Keywords: Optimal Monetary Policy, Ramsey planner, Nash equilibrium, Cooperation, Sticky prices, Imperfect competition.
JEL Classification: E52, F41
Non-Technical Summary
In the classic approach to the study of optimal policy in dynamic economies (Ramsey (1927), Atkinson and Stiglitz (1980), Lucas and Stokey (1983), Chari, Christiano and Kehoe (1992)), and in a typical public finance spirit, a social planner maximizes household's welfare subject to a resource constraint, to the constraints describing the equilibrium in the private sector economy, and via an explicit consideration of all the distortions that characterize both the long-run and the cyclical behavior of the economy. In this paper we study welfare maximizing monetary policy in a dynamic two-country model with price stickiness and imperfect competition. In this context, a typical terms of trade externality affects policy competition between independent monetary authorities. Unlike the existing literature, we remain consistent to a public finance spirit by an explicit consideration of all the distortions that are relevant to the Ramsey planner. This strategy entails two main advantages. First, it allows an accurate characterization of optimal policy in an economy that evolves around a steady-state which is not necessarily efficient. Second, it allows to describe a full range of alternative dynamic equilibria when price setters in both countries are completely forward-looking and household's preferences are not restricted. In particular, we study optimal policy both in the long-run and along a dynamic path, and we compare optimal commitment policy under Nash competition and under cooperation. Our analysis can be summarized in terms of three main contributions. First, we show that policy competition in an international setting leads welfare maximizing but independent policymakers to generally deviate from the prescription of price stability. Intuitively, in an open economy, the wedge between the marginal rate of substitution (between consumption and leisure) and the marginal rate of transformation depends not only on the fact that markups are time-varying (due to monopolistic competition coupled with sticky prices), but also on the dynamic behavior of the terms of trade. Hence each country tries to engineer price level movements to try to tilt relative prices in its own favor. It is only when policy is set in a centralized fashion by a world Ramsey planner that the two countries manage to coordinate their policies and thus replicate very closely the equilibrium under flexible prices. Second, and more generally, our approach allows to study optimal policy in dynamic economies that evolve around a steady-state which is not necessarily efficient. In that, it differs crucially from a recurrent strategy in the recent optimal monetary policy New-Keynesian literature that forces another (complementary) policy instrument (e.g., fiscal subsidies) to offset selected sources of distortion (e.g., market power). Third, we argue that, in this framework, welfare gains from cooperation, although positive, are small. To reach this conclusion, once the efficiency conditions of the corresponding optimal policy problem have been characterized, we resort to second order approximation methods (in the neighborhood of the specified Ramsey steadystate). This is required to account for the fact that, when business cycle fluctuations are centered around a distorted steady state, stochastic volatility affects the first moments of those variables that are critical for household's welfare evaluation.
1 Introduction
In the classic approach to the study of optimal policy in dynamic economies (Ramsey (1927), Atkinson and Stiglitz (1976), Lucas and Stokey (1983), Chari, Christiano and Kehoe (1991)), and in a typical public finance spirit, a Ramsey planner maximizes household's welfare subject to a resource constraint, to the constraints describing the equilibrium in the private sector economy, and via an explicit consideration of all the distortions that characterize both the long-run and the cyclical behavior of the economy.
Recently there has been a resurgence of interest for a Ramsey-type approach in dynamic general equilibrium models with nominal rigidities. Khan, King and Wolman (2003) analyze optimal monetary policy in a closed economy where the relevant distortions are imperfect competition, staggered price setting and monetary transaction frictions. Schmitt-Grohe and Uribe (2004), and Siu (2004) focus on the joint optimal determination of monetary and fiscal policy. The robust conclusion of these studies - that optimal policy is associated to the prescription of stable prices - is indeed rooted in the principle that the planner tries to eliminate the distortions induced by fluctuations in the aggregate price level, whether stemming from relative price misalignments or from resource costs of resetting prices.
In this paper we aim at taking this approach to the analysis of policy interdependence in open economies. We characterize welfare maximizing monetary policy in a two-country world where financial markets are complete, policymakers act under commitment and compete in a Nash equilibrium. Both economies are characterized by two main distortions: output is inefficiently low (due to the presence of monopolistic competitive goods markets) and firms face quadratic costs of adjusting prices. However, and relative to a cooperative setting enforced by a world Ramsey planner, openness per se adds a further inefficiency typical of the outcome under a Nash equilibrium. This inefficiency stems from the monopoly power that each country can exert on its own terms of trade, and therefore from an externality that the policy competition motive necessarily entails.1
Relative to the corresponding closed economy literature, a Ramsey-type approach has received much less attention in the study of optimal monetary and exchange rate arrangements for open economies. Cooley and Quadrini (2003) analyze monetary policy interaction in a two-country model with perfectly competitive goods markets, flexible prices and limited financial markets participation. Their model is essentially static in nature and highlights the presence of a systematic inflation bias induced by international policy competition. Our framework differs from theirs in the fact that prices are sticky (so that nominal exchange rate movements exert an effect on international relative prices), goods markets are imperfectly competitive and agents operate in a fully dynamic environment.
A Ramsey-type approach has also been employed in a certain stream of the so-called New Open Economy Macroeconomics literature (which instead typically features nominal rigidities and imperfect competition). This is the case - for instance - in the work of Benigno and Benigno (2003), Corsetti and Pesenti (2003), and Devereux and Engel (2003). In these papers the analysis of optimal policy is simplified by the assumption that prices (or wages) are predetermined one-period. Such an assumption is restrictive, for it typically generates a Lucas-type aggregate supply curve in which the forward-looking nature of inflation is neglected, and along with it the channel through which the anticipation of future policy conduct comes to play a role.2
The present paper differs from the aforementioned contributions in that it employs optimizing producers' price setting decisions that are forward-looking, thereby rendering the corresponding optimal policy problem inherently dynamic. Modelling forward-looking price setting decisions changes the nature of the optimal policy problem in a fundamental way. In practice, it entails that the planner faces a (set of) constraint(s) exhibiting future expectations of control variables. The lack of recursivity which occurs under those circumstances affects the policy program in that future actions `` limit'' the set of feasible actions which are currently available to the planner.3
Our analysis can be summarized in terms of two main contributions. First, we show that policy competition in an international setting leads welfare maximizing but independent policymakers to generally deviate from the prescription of price stability. Intuitively, in an open economy, the wedge between the marginal rate of substitution (between consumption and leisure) and the marginal rate of transformation depends not only on the fact that markups are time-varying (due to monopolistic competition coupled with sticky prices), but also on the dynamic behavior of the terms of trade. Hence either country tries to engineer price level movements to try to tilt relative prices in its own favour, and increase real net income (and consumption) for any given level of disutility of labor. On the other hand, when policy is set in a centralized fashion by a world Ramsey planner, the two countries manage to coordinate their actions in such a way to replicate closely the equilibrium dynamics that would prevail under purely flexible prices (thereby mimicking the outcome of a corresponding world closed economy).
Second, and more generally on a methodological ground, our approach allows to study optimal policy in dynamic open economies that evolve around a steady-state which is not necessarily efficient. In that, it differs crucially from a recurrent approach in the recent New-Keynesian literature that forces another (complementary) policy instrument (e.g., fiscal subsidies) to offset second order effects of stochastic uncertainty on variables' mean levels.4 The same approach resorts to a two-step strategy that involves, at first, taking a log-linear approximation of the competitive equilibrium conditions, and then a quadratic approximation of the correct household's utility function. In particular, resorting to such an approximation method in an open economy requires specific assumptions on preferences, such as log-utility and unitary elasticity of substitution between goods produced in different countries. Yet precisely these assumptions already constrain the form of the optimal policy to coincide, somewhat artificially, with the one that implements the flexible price allocation. Furthermore, if not satisfied, the same conditions do not allow to study each country's policymaker's problem independently, forcing to ignore those equilibria that emerge under policy competition and to restrict the analysis only to the world planner's policy design problem. In fact, relative to the existing literature (e.g., Benigno and Benigno (2003)), a contribution of this paper is precisely in the general characterization of the optimal stabilization policy under Nash competition within a fully dynamic setting and in the presence of uncorrected steady-state distortions.5
The remainder of the paper is organized as follows. Section 2 describes the economic environment and the features of the equilibrium. Section 3 derives the form of the constraints that are relevant to the planner's policy problem. Section 4 analyzes optimal policy under commitment. Section 5 concludes.
2 The Model
The world economy consists of two countries, that we label Home and Foreign. Each economy is populated by infinitely-lived agents, whose total measure is normalized to unity.
2.1 Domestic Households
Let's denote by
![$ C_{t}\equiv\lbrack(1-\alpha)^{\frac{1}{\eta}} C_{H,t}^{\text{ }\frac{\eta-1}{\... ...ha^{\frac{1}{\eta}}C_{F,t}^{\text{ }\frac{\eta-1}{\eta}}]^{\frac{\eta}{\eta-1}}$](img1.gif) a composite consumption index of domestic and imported
bundles of goods, where
a composite consumption index of domestic and imported
bundles of goods, where ![]() is the share of imported goods (i.e., an
inverse measure of home bias in
consumption preferences), and
is the share of imported goods (i.e., an
inverse measure of home bias in
consumption preferences), and ![]() is the elasticity of substitution between
domestic and foreign goods. Each bundle is composed of imperfectly
substitutable varieties (with elasticity of substitution
is the elasticity of substitution between
domestic and foreign goods. Each bundle is composed of imperfectly
substitutable varieties (with elasticity of substitution
![]() ).
Optimal allocation of expenditure within each variety of goods
yields:
).
Optimal allocation of expenditure within each variety of goods
yields:
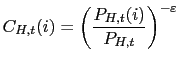
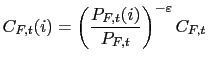
|
(1) |
where
Optimal allocation of expenditure between domestic and foreign bundles yields:
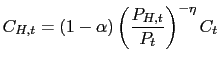 ;
; 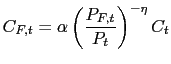
|
(2) |
where
is the CPI index.
We assume, both within and across countries, the existence of
complete markets for state-contingent claims expressed in domestic
units of account.6 Let
![]() denote the history of events
up to date
denote the history of events
up to date ![]() , where
, where
![]() is the event
realization at date
is the event
realization at date ![]() . The
date 0 probability of observing history
. The
date 0 probability of observing history
![]() is given by
is given by
![]() . The
initial state
. The
initial state ![]() is given
so that
is given
so that
![]() .
.
Agents maximize the following expected discounted sum of utilities over possible paths of consumption and labor:7
where
By considering the optimal expenditure conditions (1) and (2), the sequence of budget constraints assumes the following form:
where
For any given state of the world, the following set of efficiency conditions must hold:
where
Taking conditional expectations of equation (7) allows to define a gross nominal interest rate (or return on the corresponding riskless one-period bond) as:
![$\displaystyle =\left[ \beta E_{t}\left\{ \frac{P_{t}}{P_{t+1}}\frac{U_{c,t+1}}{U_{c,t} }\right\} \right] ^{-1}$](img53.gif)
|
which is a familiar consumption Euler equation.
Notice that, following large part of the recent literature, we
do not introduce money explicitly, but rather think of it as
playing the role of nominal unit of account. This modelling choice
has two major consequences. First, it allows us, for the sake of
simplicity, to abstract from an additional distortion stemming from
the presence of transactions frictions. In Appendix A we introduce a more general model in
which real balances enter the utility function as a proxy of the
transaction benefits of holding money. We show that the optimal
policy problem nests our specification in the particular case in
which the weight of real money balances in the utility is
arbitrarily small. Second, it makes natural to think of short-term
nominal interest rates ![]() and
and
![]() as the
underlying instruments of monetary policy.
as the
underlying instruments of monetary policy.
2.2 Law of One Price and Foreign Demand
We assume throughout that the law of one price holds, implying
that
![]() for all
for all
![]() , where
, where
![]() is the
nominal exchange rate, i.e., the price
of foreign currency in terms of home currency, and
is the
nominal exchange rate, i.e., the price
of foreign currency in terms of home currency, and
![]() is
the price of foreign good
is
the price of foreign good ![]() denominated in foreign currency. It is important to
notice that the holding of the law of one price does not necessarily imply that PPP holds, unless we
make the further restrictive assumption of absence of home bias, which entails
denominated in foreign currency. It is important to
notice that the holding of the law of one price does not necessarily imply that PPP holds, unless we
make the further restrictive assumption of absence of home bias, which entails
![]() .10
.10
Let's denote by ![]() foreign households' holdings of the state contingent bond
denominated in domestic units of account. The budget constraint of
the foreign representative household will read (in domestic units
of account):
foreign households' holdings of the state contingent bond
denominated in domestic units of account. The budget constraint of
the foreign representative household will read (in domestic units
of account):
The efficiency condition for bonds' holdings is:
Foreign demand for domestic variety
Taking conditional expectations of (11) and defining
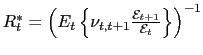 one can write:
one can write:
The remaining efficiency conditions characterizing the foreign economy are then exactly symmetric to the ones of the domestic economy described above.
2.3 Terms of Trade and the Real Exchange Rate
The terms of trade is the relative price of imported goods:
while the real exchange rate is defined as
with
The terms of trade and the real exchange rate are linked through the following expression:
where
with
2.4 Budget Constraints and Risk Sharing
By iterating (5) forward and imposing (8) we can write the infinite sequence of period-by-period budget constraints as a single present value constraint (in domestic units of account ) as follows11:
the price system
Equation (19) states that the sum of initial financial wealth and expected present discounted net income must match the expected present discounted value of consumption.
We proceed in a similar fashion for the Foreign household. The
price system
![]() (expressed in domestic units of account) obtained from the forward
iteration of (11) can be written:
(expressed in domestic units of account) obtained from the forward
iteration of (11) can be written:
Iterating (10) and imposing a corresponding transversality condition we obtain (in domestic units of account)
Equating (19) with (20) yields the following condition linking the real exchange rate to the ratio of the marginal utilities of consumption:
where
An issue concerns the determination of the risk-sharing
parameter ![]() . Below
we argue that the value of
. Below
we argue that the value of ![]() , and in turn the characteristics of the
underlying risk-sharing arrangements, are tied to the initial
distribution of wealth.
, and in turn the characteristics of the
underlying risk-sharing arrangements, are tied to the initial
distribution of wealth.
Consider representative Households in the two countries entering
the initial period zero with predetermined (at time -1) wealth distribution given by a pair
![]() . Below we
clarify how the time -1 risk sharing
arrangement affects the initial distribution of wealth.
. Below we
clarify how the time -1 risk sharing
arrangement affects the initial distribution of wealth.
Definition 1. International risk-sharing requires a time -1 trading of assets such that, as of time zero, households in both countries face the same present value budget constraint.
The above definition amounts to assuming that, for given
equilibrium allocations defining the world competitive equilibrium,
![]() adjusts
endogenously (and residually) to insure that such risk sharing
arrangement is indeed achieved.13 Next
we show that our assumption on risk-sharing allows to pin down the
level of the constant
adjusts
endogenously (and residually) to insure that such risk sharing
arrangement is indeed achieved.13 Next
we show that our assumption on risk-sharing allows to pin down the
level of the constant ![]() in equation (22).
in equation (22).
Lemma 1. If the
risk sharing arrangement is consistent with Definition 1,
then ![]() .
.
Proof. Consider the domestic household maximizing (4) subject to (18). Efficiency requires:
where
By combining (22), (23) and (24) one can write the risk-sharing parameter as:
Thus the requirement that, as of time zero, intertemporal budget
constraints be equalized across households in different countries
implies that the shadow value of nominal wealth be also equalized,
which in turn implies, given (25), that
![]() 14
14
2.5 Domestic Producers
Each monopolistic firm ![]() produces a homogenous good according to:
produces a homogenous good according to:
where
where
Changing output prices is subject to some costs. We follow
Rotemberg (1982) and model the cost of adjusting prices for each
firm ![]() equal to:
equal to:
where the parameter
The cost of price adjustment renders the domestic producer's
pricing problem dynamic. Each producer chooses the price
![]() of variety
of variety
![]() to maximize its total
market value:
to maximize its total
market value:
subject to the constraint
where
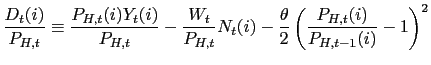
| 0 | 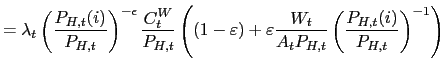
|
(29) |
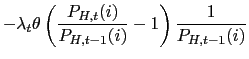
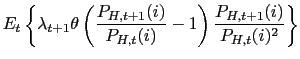
|
where
Let's define
![]() as
the relative price of domestic variety
as
the relative price of domestic variety ![]() and
and
![]() as the gross
aggregate domestic producer inflation
rate. It is useful to see that the above optimal pricing
condition can be rewritten as:
as the gross
aggregate domestic producer inflation
rate. It is useful to see that the above optimal pricing
condition can be rewritten as:
| 0 | 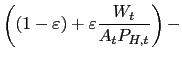
|
(30) |
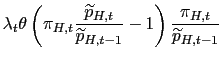
|
||
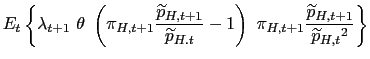
|
3 World Competitive Equilibrium in Primal Form
In this section we show how to derive a compact form of the world competitive equilibrium in terms of a minimal set of relations involving only real allocations in the spirit of the primal approach described in Lucas and Stokey (1983). Khan, King and Wolman (2003) adopt a similar structure to analyze optimal monetary policy in a closed economy with market power, price stickiness and monetary frictions, while Schmitt-Grohe and Uribe (2004) to analyze a problem of joint determination of optimal monetary and fiscal policy.
We focus our attention on a symmetric equilibrium where all domestic producers charge the same price, adopt the same technology and therefore choose the same demand for labor. This implies that:
and corresponding conditions for
In equilibrium state contingent bonds are in zero net supply:
3.1 Pricing and Market Clearing Conditions
In the symmetric equilibrium equation (32) will simplify to:
where
Substituting (6), (15) and (27) we can write:
where in particular the expression for the real marginal cost is:
An analogous condition will hold in Foreign:
Market clearing for domestic variety
for all
Plugging (41) into the definition of
aggregate output
![$ Y_{t} \equiv\left[ \int_{0}^{1}Y(i)^{1-\frac{1}{\varepsilon}}\ di\right] ^{\frac{\varepsilon}{\varepsilon-1}}$](img159.gif) , recalling that
, recalling that
![]() and using
(15) and (16) we can express
market clearing for domestic goods as:
and using
(15) and (16) we can express
market clearing for domestic goods as:
The corresponding market clearing condition for Foreign will read:
The CPI level can be linked to the domestic price level and the terms of trade as follows:
Similarly for CPI inflation in Foreign:
Substituting into (9) and (13) one obtains the following modified expressions for the Euler equations:
At this stage we can propose the following definition of world competitive equilibrium in primal form:
Definition 2. For given interest rate policies
![]() and shock processes
and shock processes
![]() a world (imperfectly) competitive equilibrium
is a set of allocations
a world (imperfectly) competitive equilibrium
is a set of allocations ![]() ,
,
![]() ,
, ![]() ,
,
![]()
![]()
![]() that solves equations (9),
(13), (22), (38), (40), (42), (43).
that solves equations (9),
(13), (22), (38), (40), (42), (43).
Few observations on this form of the competitive equilibrium are
in order. First, nominal interest rates are residual, for they only
show up in equations (9) and (13). This is a typical effect of the cashless
environment adopted here.15 Second,
present value budget constraints (18) and
(21) are not strictly included in the
definition of the competitive equilibrium. In fact, once
equilibrium allocations and policy rules are computed, one can
determine residually the initial distribution of assets
![]() in such a way that
risk-sharing is achieved as in Definition 1.
in such a way that
risk-sharing is achieved as in Definition 1.
The above definition of the equilibrium includes the terms of trade as a part of the competitive allocations. However one can express the terms of trade as a result of the equilibrium consumption allocations. By using (15), (16) and (17) one can write:
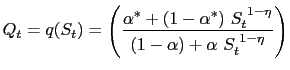
|
(46) |
Notice that if
with
with
In the following, we formulate a proposition that establishes a mapping between the minimal form summarized by conditions (9), (13), (22), (38), (40), (42), (43) expressed above and all remaining real allocations and prices. Establishing such a mapping is a crucial preliminary step for the setup of the optimal policy problem in the section below.
Proposition 1. [Part A]. For given policy
instruments
![]() , equilibrium allocations
, equilibrium allocations ![]() ,
,
![]() ,
,
![]() , prices
, prices
![]() and relative prices
and relative prices
![]() satisfying equations (1), (2), (6), (7), (8), (11), (12), (13), (14), (15), (16),
(17), (18, (21), (22), (27), (37), (42), (43) also satisfy equations
(9) (13), (38), (40), (42), (43). [Part B]. By reverse, using
allocations
satisfying equations (1), (2), (6), (7), (8), (11), (12), (13), (14), (15), (16),
(17), (18, (21), (22), (27), (37), (42), (43) also satisfy equations
(9) (13), (38), (40), (42), (43). [Part B]. By reverse, using
allocations
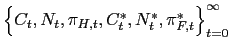 that satisfy equations (9), (13), (38),
(40), (42), (43) it is possible to construct all the remaining
equilibrium (nominal and real) allocations, prices and policy
instruments for Home and Foreign.
that satisfy equations (9), (13), (38),
(40), (42), (43) it is possible to construct all the remaining
equilibrium (nominal and real) allocations, prices and policy
instruments for Home and Foreign.
Proof. See Appendix B
![]()
4 Optimal Monetary Policy
Optimal policy is determined by a monetary authority that maximizes the discounted sum of utility of the representative agent under the constraints that characterize the competitive economy. As in the classical literature on optimal taxation (see Chari, Christiano and Kehoe (1994)) or more recently in the monetary policy closed-economy analysis of Khan et al. (2003), the policy problem takes the form of a constrained allocation problem, in which the government can be thought of choosing directly a feasible allocation subject to those constraints that ensure the existence of instruments and prices which make the same allocation consistent with optimality. In our cashless economy, the minimal set of constraints that are relevant for the Ramsey allocation problem are the ones described in Definition 2. In practice, they consist of an appropriately characterized price implementability constraint (Phillips curve) and of an appropriately characterized resource constraint.16
A distinctive feature of the Ramsey-type analysis undertaken
here is that we allow the relevant distortions characterizing the
private sector economy to remain explicit. The private sector world
economy is characterized by three
distortions. The first two, market power and price
stickiness, are common to both the closed and the open economy
version of our model. The price stickiness distortion, summarized
by the quadratic term in inflation in the resource constraint, is
obviously minimized at zero net inflation (i.e.,
![]() for all
for all ![]() . On the other hand, the presence
of market power renders the steady-state level of output and
employment inefficiently low.
. On the other hand, the presence
of market power renders the steady-state level of output and
employment inefficiently low.
As also emphasized in Corsetti and Pesenti (2001), what in general distinguishes the analysis of an open economy is the presence of an additional inefficiency, that we label international relative price distortion. This stems from the possibility for each country, in the presence of rigid nominal prices, of strategically affecting the terms of trade, and in turn of reducing the (expected) disutility of labor effort for any given level of consumption. This externality creates per se room for policy competition. The interesting aspect concerns the extent to which such policy competition motive may lead each policymaker to try to deviate from the prescription of price stability that would typically characterize optimal policy in the closed economy version of our model.
Below we solve the optimal allocation problem under the assumption that commitment is feasible.17 We study two international policy arrangements. In the first, policymakers in the two countries conduct policy in a competitive fashion by choosing allocations independently. Relative to the existing literature, it is of particular interest to characterize a Nash-equilibrium under policy competition and within the context of general consumption preferences, forward-looking price setting and uncorrected steady-state distortions.18 In the second policy regime, a world social planner forces the two policymakers to coordinate their actions to maximize global welfare.
4.1 Optimal Policy under Nash Competition
We begin with the analysis of policy competition. We have the following definition of a Nash-Ramsey allocation problem (from Home's perspective):
Definition 3.
Let
![]() represent sequences of Lagrange
multipliers on the constraints (38) and
(42) respectively. For any given
allocation
represent sequences of Lagrange
multipliers on the constraints (38) and
(42) respectively. For any given
allocation
![]() and stochastic processes
and stochastic processes ![]() ,
,
![]() ,
plans for the control variables
,
plans for the control variables ![]()
![]()
![]() and for the costate variables
and for the costate variables
![]()
![]() represent a Nash-constrained allocation if they solve the
following maximization problem:
represent a Nash-constrained allocation if they solve the
following maximization problem:
![$\displaystyle \left[ U_{c,t}\pi_{H,t}(\pi_{H,t}-1)-\beta E_{t}\left\{ U_{c,t+1}... ...detilde{g}_{t}}{U_{c,t}A_{t}}+\frac{\varepsilon -1}{\varepsilon}\right) \right]$](img219.gif)
|
||
![$\displaystyle \left[ A_{t}N_{t}-\widetilde{g}_{t}^{\text{ }\eta}\left[ (1-\alph... ...ight] \text{ }-\frac{\theta}{2}\left( \pi_{H,t}-1\right) ^{2}\right] {\LARGE\}}$](img221.gif)
|
where
Notice that the distinctive feature of the commitment problem
under Nash competition is that the Home policymaker does not internalize that the relative price
![]() depends also on the level of consumption in Foreign (see equation
(50) above), and that, symmetrically, the
relative price
depends also on the level of consumption in Foreign (see equation
(50) above), and that, symmetrically, the
relative price
![]() is affected by its own
consumption choice. It is clear that the externality works via
foreign consumption affecting international relative prices and in
turn domestic real marginal cost. For any given level of foreign
consumption, a fall (rise) in domestic
consumption leads to an appreciation (depreciation) of the terms of
trade and therefore to a fall (rise) in labor effort and real
marginal cost (see equation (39)).
is affected by its own
consumption choice. It is clear that the externality works via
foreign consumption affecting international relative prices and in
turn domestic real marginal cost. For any given level of foreign
consumption, a fall (rise) in domestic
consumption leads to an appreciation (depreciation) of the terms of
trade and therefore to a fall (rise) in labor effort and real
marginal cost (see equation (39)).
4.1.1 Non-recursivity and Initial Conditions
As a result of the constraint (38)
exhibiting future expectations of control variables, the
maximization problem as spelled out in (42) is
intrinsically non-recursive.19 As
first emphasized in Kydland and Prescott (1980), and then developed
in Marcet and Marimon (1999), a formal way to rewrite the same
problem in a recursive stationary form is to enlarge the planner's
state space with additional (pseudo) costate variables. Such
variables, that we denote ![]() and
and
![]() respectively for Home and Foreign, bear the crucial meaning of
tracking, along the dynamics, the value to the planner of
committing to the pre-announced policy plan.
respectively for Home and Foreign, bear the crucial meaning of
tracking, along the dynamics, the value to the planner of
committing to the pre-announced policy plan.
A related aspect concerns the specification of the law of motion of these Lagrange multipliers. For in our case the forward-looking Phillips curve constraint features a simple one-period expectation, the same costate variables have to obey the laws of motion:20
A further point concerns the definition of the appropriate
initial conditions for ![]() and
and
![]() .
Marcet and Marimon (1999) show that for the modified (recursive)
Lagrangian to generate a global optimum under time zero commitment
it must hold:
.
Marcet and Marimon (1999) show that for the modified (recursive)
Lagrangian to generate a global optimum under time zero commitment
it must hold:
The above condition states that there is no value to the policy planner, in either country and as of time zero, attached to prior commitments.
In Appendix C we show how to
reformulate the optimal plan in an equivalent recursive stationary
form. First order conditions for time ![]() for the choice of
for the choice of ![]() ,
, ![]() and
and ![]() imply respectively:
imply respectively:
| 0 | 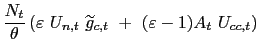
|
(53) |
![$\displaystyle \left( \eta\text{ }\widetilde{g}_{t}^{\text{ }\eta -1}\text{ }\wi... ...\ast}}{U_{c,t}}\right) ^{\eta}\alpha^{\ast}\text{ }C_{t} ^{\ast}\right] \right)$](img242.gif)
|
||
where
The system of efficiency conditions in Home is completed by the law of motion (53), the initial condition (54) and by the constraints (38) and (42) holding with equality.21
Once defined a completely symmetric problem for the policy maker in Foreign, we can state the following definition of a Nash equilibrium:
Definition 4. (Nash equilibrium under
commitment). The set of
processes
![]()
![]()
![]()
![]() ,
, ![]()
![]()
![]()
![]() fully describe a Nash equilibrium
under commitment if they solve the system of equations (55) - (57), equations
(38), (42) holding with
equality, along with a symmetric set of conditions jointly holding
for Foreign.
fully describe a Nash equilibrium
under commitment if they solve the system of equations (55) - (57), equations
(38), (42) holding with
equality, along with a symmetric set of conditions jointly holding
for Foreign.
4.1.2 Nash-Optimal Inflation Rate in the Long-Run
To determine the long-run optimal inflation rate associated to the Nash-game described above, one needs to solve the steady-state version of the set of efficiency conditions (55)-(57), (38 ), (42). To develop an analogy with the Ramsey-Cass-Koopmans model, this amounts to computing the modified golden rule steady state. This per se contrasts with the golden rule inflation rate, which would correspond to the one that maximizes households' instantaneous utility under the requirement that the planner is constrained to choose only among constant allocations. It is well known that in dynamic economies with discounted utility the two concepts of long-run optimal policy do not coincide.22
The following Lemma establishes what is the average optimal inflation rate under Nash-competition.
Lemma 2. The (net) producer inflation rate associated to the steady-state of the Nash-Ramsey policy problem is zero.
Proof. To see this consider the steady-state version of equation (57). In that case it holds:
| (56) |
Given that
Under the assumption
![]() ,
the solution to the steady-state of the Nash game is symmetric and
features
,
the solution to the steady-state of the Nash game is symmetric and
features
![]() ,
,
![]() ,
,
![]()
![]() . As a
corollary of Lemma 2 and of the fact that in the symmetric steady
state
. As a
corollary of Lemma 2 and of the fact that in the symmetric steady
state
![]() ,
we also have that the CPI (net) rate of
inflation is zero, i.e.,
,
we also have that the CPI (net) rate of
inflation is zero, i.e.,
![]() .
.
Hence the steady state of the solution to the Nash-optimal
policy indicates that, if unconstrained, both policymakers would choose to set the economy
along a path that would lead to a long-run net inflation rate of
zero. The intuition for this result is simple. One can view the
modified golden rule as the long-run state of the economy when the
discount rate ![]() converges to
converges to ![]() . In this
case the steady-state version of the Phillips curve relation
(38) is vertical, and the policymaker of
either country cannot exert any effect on markups by setting
inflation rates different from zero. Hence a second-best policy
requires to choose the rate of inflation that minimizes the price
adjustment cost distortion. It is intuitive to see that this
constitutes the only long-run Nash equilibrium.
. In this
case the steady-state version of the Phillips curve relation
(38) is vertical, and the policymaker of
either country cannot exert any effect on markups by setting
inflation rates different from zero. Hence a second-best policy
requires to choose the rate of inflation that minimizes the price
adjustment cost distortion. It is intuitive to see that this
constitutes the only long-run Nash equilibrium.
Notice that the result that the optimal average inflation rate (under Nash competition) is zero is obtained endogenously despite the fact that the underlying steady-state distortions remain fully specified. In that it contrasts with the typical approach in the New Keynesian optimal policy literature, pioneered by Rotemberg and Woodford (1997), which assumes that fiscal subsidies are in place to correct for the market power distortion, thereby having artificially the zero-inflation steady state coincide with the efficient one.23
4.1.3 Optimal Stabilization Policy around the Long-Run Steady-State
We are now in the position to analyze the dynamic features of the optimal commitment policy under Nash competition. In this section we interpret optimal policy in the sense of optimal stabilization in response to shocks. The motivation driving our analysis is to explore the extent to which, in response to shocks, Nash competition among policymakers generates deviations from price stability, which we have already shown above to be the average optimal policy outcome.
To this end, we proceed in the following way. First, we compute (for both countries) the stationary allocations that characterize the deterministic steady state of the first order conditions (55)-(57) (and symmetric ones for Foreign). We then compute a log-linear approximation of the respective policy functions in the neighborhood of the same steady state.
The spirit of this exercise deserves some further comments. In concentrating on (log-linear) dynamics in the neighborhood of the steady state associated to the efficiency conditions, we deviate from the initial condition (54) in the fact that we set the initial value of the lagged Lagrange multipliers equal to their deterministic steady state values, i.e.,:
where
It is important to understand that this strategy corresponds to focussing on a particular dimension. Namely, optimal stabilization policy in response to bounded shocks that hit in the neighborhood of the long-run steady state. This amounts to implicitly assuming that the economy has been evolving and policy been conducted around such a steady already for a long period of time.25, 26
4.1.4 Parameterization
In conducting our simulations we employ the following form of
the period utility:
![]() . The time unit is meant to be quarters. The discount factor
. The time unit is meant to be quarters. The discount factor
![]() is equal to
is equal to
![]() . The degree of
risk aversion
. The degree of
risk aversion ![]() is
is
![]() (which implies
log-utility and in turn consistence with a balanced growth path),
the inverse elasticity of labor supply
(which implies
log-utility and in turn consistence with a balanced growth path),
the inverse elasticity of labor supply ![]() is equal to
is equal to ![]() , which is a common value in the
real business cycle literature. As a benchmark, we set the
elasticity of substitution between domestic and foreign goods
, which is a common value in the
real business cycle literature. As a benchmark, we set the
elasticity of substitution between domestic and foreign goods
![]() equal to
equal to
![]() (see below for a
discussion). As in Bergin and Tchakarov (2003), and consistent with
estimates by Ireland (2001), we set the price stickiness parameter
(see below for a
discussion). As in Bergin and Tchakarov (2003), and consistent with
estimates by Ireland (2001), we set the price stickiness parameter
![]() equal to
equal to
![]() . The elasticity
. The elasticity
![]() between
varieties produced by the monopolistic sector is
between
varieties produced by the monopolistic sector is ![]() , implying a steady-state markup of
, implying a steady-state markup of
![]() percent.
percent.
The (inverse) degree of home bias ![]() , identified by the share of foreign imported
goods in the domestic consumption basket, is set to a default value
of
, identified by the share of foreign imported
goods in the domestic consumption basket, is set to a default value
of ![]() . This implies the
existence of a mild home bias, which is
assumed to be symmetric across countries (
. This implies the
existence of a mild home bias, which is
assumed to be symmetric across countries (
![]() ).
Finally (log) productivity in both countries is assumed to follow
an autoregressive process:
).
Finally (log) productivity in both countries is assumed to follow
an autoregressive process:
4.1.5 Response to Asymmetric Productivity Shocks
Figure 1 displays impulse responses of selected Home and Foreign variables to a one percent rise in Home productivity in the case of Nash-commitment.
Since productivity is higher in Home, the adjustment to the
equilibrium requires an increase in the demand of domestic goods
relative to foreign goods. This is achieved by means of a terms of
trade depreciation, captured by a rise in the CPI to PPI ratio
![]() .
.
Hence we see that price (markup) stability is not the Nash equilibrium of the underlying policy game in response to an asymmetric shock. Consumption rises both in Home and Foreign as a result of higher productivity and risk-sharing. However the rise in Home consumption exceeds the one in Foreign in order to achieve the necessary real exchange rate depreciation. The only equilibrium is one in which the same real (terms of trade) depreciation is achieved via an increase in prices in both countries. In fact, and due to risk sharing, both countries face the incentive to increase prices to tilt the terms of trade in their own favor, thereby achieving a relatively higher real income for any given level of labor effort.
The intuition for why the policymaker will not find it optimal
to replicate the flexible price allocation is simple, and is best
understood in the case of logarithmic utility. In that case, in
fact, and in response to a rise in productivity, real income
![]() will exceed
(fall short of) consumption depending on whether
will exceed
(fall short of) consumption depending on whether ![]() or
or ![]() . To see this, notice that by
combining (22) with (41)
one obtains, in the case
. To see this, notice that by
combining (22) with (41)
one obtains, in the case ![]() ,
,
![]() , or, in different terms ,
, or, in different terms ,
![]()
![]() for all
for all ![]() . This is the knife-edge case of continuously
balanced trade analyzed in Corsetti and Pesenti (2001).
. This is the knife-edge case of continuously
balanced trade analyzed in Corsetti and Pesenti (2001).
More generally, if ![]()
![]() , at the margin and
relative to the flexible price allocation, the planner can
make the consumer better off by contracting (expanding) employment
and output below their natural levels (i.e., appreciate the terms
of trade relative to its natural level) in response to a rise
(fall) in real income above (below) consumption (i.e., in response
to a trade surplus (deficit)). However, in a Nash-game where policy
objectives collide, neither country succeeds in manipulating the
terms of trade beyond the adjustment that is necessary in response
to the asymmetric productivity shock. The resulting effect is an
inefficient level of consumption. In general the marginal welfare
gain of appreciating the terms of trade (relative to the
equilibrium response under purely flexible price) rises with the
elasticity of substitution
, at the margin and
relative to the flexible price allocation, the planner can
make the consumer better off by contracting (expanding) employment
and output below their natural levels (i.e., appreciate the terms
of trade relative to its natural level) in response to a rise
(fall) in real income above (below) consumption (i.e., in response
to a trade surplus (deficit)). However, in a Nash-game where policy
objectives collide, neither country succeeds in manipulating the
terms of trade beyond the adjustment that is necessary in response
to the asymmetric productivity shock. The resulting effect is an
inefficient level of consumption. In general the marginal welfare
gain of appreciating the terms of trade (relative to the
equilibrium response under purely flexible price) rises with the
elasticity of substitution ![]() .
.
It is also interesting to notice that policy competition generates a dynamic behavior of the price level that resembles the one in response to a cost-push shock. The novel aspect of this result is that the same dynamics are obtained in response to a productivity shock, which is not aimed per se (like in many recent New Keynesian studies of optimal monetary policy) to induce the artificial effect of exogenously drifting the economy away from the efficient allocation. The fact that productivity shocks are a source of price variability under the optimal policy is here an endogenous outcome of the competition on international relative prices.28
4.1.6 Sensitivity Analysis
While the result above suggests that markup variability is an
equilibrium outcome of policy competition (unless, with log
utility, ![]() ,
deviations from a price stability policy appears quantitatively
small. Figure 2 illustrates how the
incentive to generate price movements vary with the critical
elasticity parameter, namely
,
deviations from a price stability policy appears quantitatively
small. Figure 2 illustrates how the
incentive to generate price movements vary with the critical
elasticity parameter, namely ![]() .
.
The figure displays impulse responses (under Nash-commitment) of
the same selected variables to a productivity shock for alternative
values of ![]()
![]()
![]() . The first case corresponds to the
benchmark one of Cobb-Douglas preferences typically employed in the
linear-quadratic approach to the study of optimal policy for open
economies. The literature lacks a consensus on the value of this
parameter. Collard and Dellas (2002) derive an estimated value of
. The first case corresponds to the
benchmark one of Cobb-Douglas preferences typically employed in the
linear-quadratic approach to the study of optimal policy for open
economies. The literature lacks a consensus on the value of this
parameter. Collard and Dellas (2002) derive an estimated value of
![]() . In their
quantitative (theoretical) study, Backus, Kehoe and Kydland (1995)
explore a range of
. In their
quantitative (theoretical) study, Backus, Kehoe and Kydland (1995)
explore a range of ![]() between 0 and
between 0 and ![]() . Chari et al. (2002) set
. Chari et al. (2002) set
![]() , while Bergin
and Tchakarov (2004) set
, while Bergin
and Tchakarov (2004) set ![]() . Anderson and Van Wincoop (2004) argue for much
larger values, in the order of
. Anderson and Van Wincoop (2004) argue for much
larger values, in the order of ![]() to
to ![]() .
Overall, there seems to exist both empirical and theoretical
support for the hypothesis that the value of
.
Overall, there seems to exist both empirical and theoretical
support for the hypothesis that the value of ![]() lies well above unity.
lies well above unity.
Thus the figure highlights the coincidence of the Nash-optimal
response with a close-to-price stability strategy only in the
particular case of ![]()
![]()
![]() . In this knife-edge case, the
income effect of the required terms of trade depreciation (given
the relatively higher productivity in Home) balances the incentive
to switch expenditure towards Home goods.29 In general, the higher the elasticity
of substitution, the larger the deviations from price
stability.
. In this knife-edge case, the
income effect of the required terms of trade depreciation (given
the relatively higher productivity in Home) balances the incentive
to switch expenditure towards Home goods.29 In general, the higher the elasticity
of substitution, the larger the deviations from price
stability.
Figure 3 conducts a sensitivity
analysis to illustrate how Nash-optimal inflation volatility varies
with both parameters that index openness in our economy, namely the
(inverse of) home bias ![]() and the elasticity
and the elasticity ![]() .
.
In conducting this experiment we keep our assumption of
symmetric degree of home bias, i.e.,
![]() .
In this case we allow
.
In this case we allow ![]() to assume values ranging from the benchmark case
of
to assume values ranging from the benchmark case
of ![]() to the extreme value
of
to the extreme value
of ![]() suggested by the
recent survey of Anderson and Van Wincoop (2004). Hence we see that
Nash-optimal producer inflation volatility is increasing in both
the degree of trade openness (inverse of home bias) and the
elasticity of substitution. One may notice, though, that with
values of
suggested by the
recent survey of Anderson and Van Wincoop (2004). Hence we see that
Nash-optimal producer inflation volatility is increasing in both
the degree of trade openness (inverse of home bias) and the
elasticity of substitution. One may notice, though, that with
values of ![]() beyond
beyond
![]() and reaching the
extreme values suggested by the recent literature inflation
volatility tends to level off. To gather an intuition of why
optimal inflation volatility is increasing in the (inverse of) home
bias, recall that the terms of trade affects the real marginal cost
(thereby activating the externality in our setting) via the
relative price
and reaching the
extreme values suggested by the recent literature inflation
volatility tends to level off. To gather an intuition of why
optimal inflation volatility is increasing in the (inverse of) home
bias, recall that the terms of trade affects the real marginal cost
(thereby activating the externality in our setting) via the
relative price ![]() . Log-linearizing equation (15) we have:
. Log-linearizing equation (15) we have:
![]() . Hence the
larger
. Hence the
larger ![]() the
larger the variation in
the
larger the variation in
![]() necessary to achieve any required equilibrium variation in
necessary to achieve any required equilibrium variation in
![]() , and
hence the larger the expenditure switching effect that generates
the externality in our setting.
, and
hence the larger the expenditure switching effect that generates
the externality in our setting.
4.2 Optimal Policy under Cooperation
So far we have analyzed optimal policy conduct under the
assumption that the policymakers in the two countries act in a
competitive fashion. Under cooperation, a social planner explicitly
recognizes the channel of interdependence that works through the
relative prices
![]() and
and
![]() . Below we define the
world Ramsey planner problem, under the assumption that the same
planner aims at maximizing the average
level of utility of the two countries. We also assume that both
countries receive equal weight in the planner's objective
function.
. Below we define the
world Ramsey planner problem, under the assumption that the same
planner aims at maximizing the average
level of utility of the two countries. We also assume that both
countries receive equal weight in the planner's objective
function.
Let's define the world Ramsey period
utility objective as
![]() , where
, where
![]() and
and
![]() . Then the Ramsey maximization problem can be defined as
follows:
. Then the Ramsey maximization problem can be defined as
follows:
Definition 5. Let
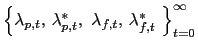 represent sequences of Lagrange
multipliers on the constraints (38), (40), (42) and (43) respectively. For any given stochastic
processes
represent sequences of Lagrange
multipliers on the constraints (38), (40), (42) and (43) respectively. For any given stochastic
processes ![]()
![]() ,
plans for the control variables
,
plans for the control variables ![]()
![]()
![]()
![]()
![]()
![]() , and for the
costate variables
, and for the
costate variables
![]()
![]()
![]()
![]() represent a first-best constrained allocation if they
solve the following maximization problem:
represent a first-best constrained allocation if they
solve the following maximization problem:
![$\displaystyle \lambda_{p,t}\left[ U_{c,t}\pi_{H,t}(\pi_{H,t}-1)-\beta E_{t}\lef... ...detilde{g}_{t}}{U_{c,t}A_{t}}+\frac{\varepsilon -1}{\varepsilon}\right) \right]$](img334.gif)
|
||
![$\displaystyle \lambda_{f,t}\left[ A_{t}N_{t}-\widetilde{g}_{t}^{\text{ }\eta}\l... ...t}^{\ast}\right] \text{ }-\frac{\theta}{2}\left( \pi_{H,t}-1\right) ^{2}\right]$](img335.gif)
|
||
![$\displaystyle \lambda_{p,t}^{\ast}\left[ U_{c,t}^{\ast}\text{ } \pi_{F,t}^{\ast... ...}{U_{c,t}^{\ast}A_{t}^{\ast}}+\frac{\varepsilon-1}{\varepsilon }\right) \right]$](img336.gif)
|
||
![$\displaystyle \lambda_{f,t}^{\ast}\left[ A_{t}^{\ast}N\ast _{t}-\widetilde{g}_{... ...t}\right] \text{ }-\frac{\theta}{2}\left( \pi_{F,t}^{\ast}-1\right) ^{2}\right]$](img337.gif)
|
We defer to Appendix D the
description of the first order conditions corresponding to this
plan. The discussion on the non-recursivity structure of the
problem follows exactly the logic applied above to the
re-definition of the Nash-commitment policy setup. In practice,
this will entail specifying an equivalent recursive stationary
program in the new world planner's state space defined by
![]() .
.
4.2.1 Ramsey Steady-State
A deterministic Ramsey steady state is a set of allocations
![]() that solves the steady-state version of the efficiency
conditions associated to the program under Definition 5. This
steady state has a symmetric solution in which
that solves the steady-state version of the efficiency
conditions associated to the program under Definition 5. This
steady state has a symmetric solution in which
![]() . Hence, and exactly like in
the steady-state version of the efficiency conditions of the Nash
problem analyzed above, the unconstrained long run optimal
inflation policy is associated with price stability in both
countries. It follows that the deterministic steady states under
the two policy regimes, Nash and Cooperation, differ crucially in
the implied values for the Lagrange multipliers
. Hence, and exactly like in
the steady-state version of the efficiency conditions of the Nash
problem analyzed above, the unconstrained long run optimal
inflation policy is associated with price stability in both
countries. It follows that the deterministic steady states under
the two policy regimes, Nash and Cooperation, differ crucially in
the implied values for the Lagrange multipliers
![]()
![]()
![]()
![]() .
.
4.2.2 Optimal Response to Shocks around the Ramsey Steady-State: Nash vs. Cooperation
Figure 4 displays impulse responses to a normalized one percent increase in home productivity and compares selected variables under Nash versus Cooperation.
Under policy cooperation, the planner coordinates the responses of both policy makers to achieve the required terms of trade depreciation only by means of a nominal exchange rate depreciation. In other words, it is optimal for the Ramsey planner to have both countries targeting very closely the flexible price allocation. This results in a dampened dynamic of the terms of trade under cooperation. The crucial aspect is that this is now compatible with a smooth path of the price level (the response of the price level, measured in percent deviation from steady state, barely deviates from zero) and with a smoother response of employment, for any given variation in consumption. The reason why perfect price stability is not the equilibrium outcome under cooperation is due to the underlying asymmetric nature of the shock. In fact, while it is globally optimal for the world planner to minimize the underlying relative price distortion, it remains efficient, at the margin, to have the country experiencing the positive rise in productivity to slightly deviate from price stability and appreciate the terms of trade (relative to the strictly flexible price policy).
5 Conclusions
We have laid out a typical public finance framework for the analysis of welfare maximizing monetary policy within a world economy characterized by three distortions: market power, rigidity in the adjustment of producer prices and international terms of trade externality.
The main novelty of our approach is methodological. In fact, and relative to the existing literature, it allows to characterize optimal policy in a multi-country setting where the same relevant distortions remain uncorrected. Thus in our setting, and unlike most of the existing literature, the presence of forward-looking price setting decisions as well as of a general form of household's preferences over the consumption of domestic and foreign goods do not represent a constraint for the exact characterization of optimal monetary policy under commitment.
Despite the generality of the approach, our modelling framework remains restrictive in three main dimensions. First, in assuming that the law of one price for traded goods holds continually. Second, in allowing households to obtain full risk sharing via international financial markets. Third, in not allowing households to invest in physical capital. Amending on all these features should aim at generating less trivial dynamics of the current account than the ones generated here via the only movements in the trade balance. Such dynamics may be of first order importance, for instance, for the welfare evaluation of alternative (exchange rate) policies along two dimensions. First, they would more critically affect the transition from the time of policy implementation to the long-run steady state of the new policy. Second, they would impinge on the transition from one policy regime to another. For instance from Nash-competition to cooperation, or from the optimal commitment policy to a fixed exchange rate arrangement. We are currently investigating all these issues in our ongoing work.
A General Model with Monetary Friction
In this section we briefly lay out a model in which money entering the utility function is justified by the presence of transactions frictions. We show that if real balances enter the utility function separably it is possible to nest the Nash-Ramsey allocation problem specified in (52) as a particular case. Agents maximize the following expected discounted sum of utilities over possible paths of consumption, money balances and labor:
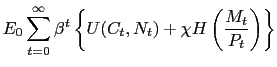
The sequence of budget constraints assumes the following form:
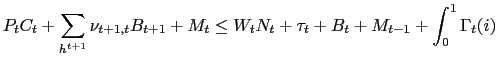
By combining (61) and (9) one can typically derive a money demand equation:
The government budget constraint reads:
where
| (62) | ||
 |
| (63) | ||
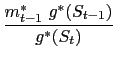
|
The Nash-Ramsey problem differs from the one in the cashless
economy in the fact that the set of feasible allocations must
include both the nominal interest rates
![]() and the
choice of real money balances
and the
choice of real money balances
![]() . This
requires extending the number of constraints to include equations
(9) and (62), with the
equivalent expressions for Foreign. In practice the Nash-Ramsey allocation problem in the model with
monetary frictions can be defined as follows (in the representative
case of Home):
. This
requires extending the number of constraints to include equations
(9) and (62), with the
equivalent expressions for Foreign. In practice the Nash-Ramsey allocation problem in the model with
monetary frictions can be defined as follows (in the representative
case of Home):
Choose
![]() and
and ![]()
![]()
![]()
![]()
![]()
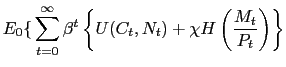
![$\displaystyle +\beta^{t}\lambda_{e,t}\left[ \frac{U_{c,t}}{R_{t}}-\beta\text{ }... ...+1}}{\pi_{H,t+1}\frac{\widetilde{g}_{t+1} }{\widetilde{g}_{t}}}\right\} \right]$](img372.gif)
|
||
![$\displaystyle +\beta^{t}\lambda_{m,t}\left[ \frac{\chi\text{ }H_{m,t}}{U_{c,t}}-\left( 1-\frac{1}{R_{t}}\right) \right]$](img373.gif)
|
||
![$\displaystyle \left[ U_{c,t}\pi_{H,t}(\pi_{H,t}-1)-\beta E_{t}\left\{ U_{c,t+1}... ...detilde{g}_{t}}{U_{c,t}A_{t}}+\frac{\varepsilon -1}{\varepsilon}\right) \right]$](img219.gif)
|
||
![$\displaystyle \left[ A_{t}N_{t}-\widetilde{g}_{t}^{\text{ }\eta}\left[ (1-\alph... ...ight] \text{ }-\frac{\theta}{2}\left( \pi_{H,t}-1\right) ^{2}\right] {\LARGE\}}$](img221.gif)
|
where
The set of first order conditions reads as follows:
| eq. |
(65) |
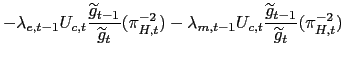
|
(66) |
Lemma 3. If the
weight ![]() on real money balances in the utility function
approaches zero, then the first order conditions of the Nash-Ramsey
problem in the model with transaction frictions coincide with those
of the Nash-Ramsey problem in the cashless model.
on real money balances in the utility function
approaches zero, then the first order conditions of the Nash-Ramsey
problem in the model with transaction frictions coincide with those
of the Nash-Ramsey problem in the cashless model.
Proof. To see this one needs to
notice that, for
![]() ,
(69) implies
,
(69) implies
![]() . Substituting this into
(66), (68) and
(70) one obtains that such conditions
coincide with (55)-(57 )
. Substituting this into
(66), (68) and
(70) one obtains that such conditions
coincide with (55)-(57 )
![]()
B Proof of Proposition 1
The proof of part A follows from the
equation manipulations presented in Section 3. As for part B, given
![]() from the
Ramsey problem, obtain
from the
Ramsey problem, obtain ![]() and
and
![]() respectively from (50) and (51). Then derive
respectively from (50) and (51). Then derive ![]() from (49). Then obtain
from (49). Then obtain
![]() ,
, ![]() ,
,
![]() ,
,
![]() by
using (2). Given
by
using (2). Given ![]() and
and
![]() obtain
obtain
![]() and
and
![]() from
allocations
from
allocations
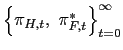 . Using the fact that the law of one price holds, and given
. Using the fact that the law of one price holds, and given
![]()
![]() and
and
![]() , pin down the
nominal exchange rate by using the definition of the terms of
trade:
, pin down the
nominal exchange rate by using the definition of the terms of
trade:
![]() .
Next, obtain
.
Next, obtain ![]() from
(22). To obtain
from
(22). To obtain ![]() and
and
![]() use
(3) and the symmetric expression for Foreign.
Given
use
(3) and the symmetric expression for Foreign.
Given
![]()
![]() ,
,
![]() and
and
![]() , use
(44) and (45) to obtain
, use
(44) and (45) to obtain
![]() and
and
![]() . To
derive
. To
derive ![]() and
and
![]() use
(39) and the symmetric expression in Foreign.
Next, use (27) and the symmetric
expression in Foreign to obtain
use
(39) and the symmetric expression in Foreign.
Next, use (27) and the symmetric
expression in Foreign to obtain ![]() and
and ![]() . Finally use (7)
. Finally use (7)![]() to
obtain
to
obtain ![]() ,
(9) and (13) to obtain
,
(9) and (13) to obtain
![]() and
and
![]() .
.
C The Stationary Policy Problem
Below we derive the stationary form of the policy problem under Nash commitment. We illustrate the argument only for the Home policymaker's problem, since the problem in Foreign is exactly symmetric. Let's consider the optimal plan as formulated in equation (52) in the text. By applying the law of iterated expectations and by grouping expectations and multipliers that share the same date one obtains:
![$\displaystyle +\lambda_{p,0}\left[ U_{c,0}\text{ }\pi_{H,0}\text{ }(\pi_{H,0} -... ...detilde{g}_{0}}{U_{c,0}A_{0}}+\frac{\varepsilon-1} {\varepsilon}\right) \right]$](img420.gif)
|
||
![$\displaystyle +\lambda_{f,0}\left[ A_{0}N_{0}-(1-\alpha)C_{0}\widetilde{g}_{0}^... ...alpha^{\ast}C_{0}^{\ast}-\frac{\theta}{2}\left( \pi _{H,0}-1\right) ^{2}\right]$](img421.gif)
|
||
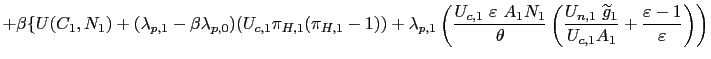
|
||
![$\displaystyle +\lambda_{f,1}\left[ A_{1}N_{1}-(1-\alpha)C_{1}\text{ }\widetilde... ...-\frac{\theta}{2}\left( \pi_{H,1}-1\right) ^{2}\right] +...{\LARGE\}\}}\text{ }$](img423.gif)
|
Notice that this problem is not
time-invariant due to the fact that the constraints at time
zero lack the term
![]() .
For this reason we amplify the state space to introduce a new
(pseudo) costate variable
.
For this reason we amplify the state space to introduce a new
(pseudo) costate variable ![]() and define a new policy functional
and define a new policy functional
![]() . We then write the optimal policy plan in the following
form:
. We then write the optimal policy plan in the following
form:
Choose
![]() and
and
![]()
![]()
![]() to
to
![$\displaystyle +\lambda_{p,t}\left[ U_{c,t}\text{ }\pi_{H,t}\text{ }(\pi_{H,t} -... ...detilde{g}_{t}}{U_{c,t}A_{t}}+\frac{\varepsilon -1}{\varepsilon}\right) \right]$](img428.gif)
|
||
![$\displaystyle +\lambda_{f,t}\left[ A_{t}N_{t}-(1-\alpha)\ C_{t}\widetilde{g}_{t... ...C_{t}^{\ast}-\frac{\theta}{2}\left( \pi_{H,t}-1\right) ^{2}\right] {\LARGE\}\}}$](img429.gif)
|
with law of motion for the new costate
D First Order Conditions of the Cooperation-Commitment Problem
First order conditions for the choice of ![]() ,
, ![]() ,
, ![]() for the Ramsey problem under Cooperation at
time
for the Ramsey problem under Cooperation at
time ![]() read:
read:
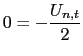 |
(74) |
| (75) |
This system is completed by symmetric conditions on
Bibliography
Adao, B., Correia, I., P. Teles, (2003), `` Gaps and Triangles'', Review of Economic Studies, 60, 4.
Anderson J. and E. Van Wincoop (2004), "Trade Costs", forthcoming Journal of Economic Literature.
Atkinson, A. B. and J. Stiglitz, (1976), `` The Design of Tax Structure: Direct Versus Indirect Taxation'', Journal of Public Economics, 6, 1-2, 55-75.
Backus, D., P.K Kehoe and F. E. Kydland (1995), '' International Business Cycles: Theory and Evidence'', in Frontiers of Business Cycle Research, Edited by Thomas F. Cooley, Princeton University Press.
Benigno, P. and G. Benigno, (2003), `` Price Stability Open Economies'', Review of Economic Studies, 60,4.
Benigno, P. and G. Benigno, (2004), `` Implementing Monetary Cooperation Through Inflation Targeting'', unpublished, New York University and London School of Economics.
Benigno, P. and M. Woodford (2004), "Inflation Stabilization and Welfare: The Case of a Distorted Steady State", Mimeo Princeton University.
Bergin P. and I. Tchakarov (2004), "Does Exchange Rate Variability Matter for Welfare? A Quantitative Investigation", Mimeo U.C. Davis.
Calvo G. (1978), "On the Time Consistency of Optimal Policy in a Monetary Economy", Econometrica, vol. 46, issue 6, pages 1411-28
Canzoneri, M. and D. Henderson, (1991), `` Monetary Policy in Interdepenent Economies: A Game Theoretic Approach'', Cambridge: MIT Press.
Chari, V.V. and P.J. Kehoe, (1990), `` International Coordination of Fiscal Policy in Limiting Economies'', Journal of Political Economy, June.
Chari, V.V. and P.J. Kehoe, (1998), `` Optimal Fiscal and Monetary Policy'', in Handbook of Macroeconomics, M. Woodford and J. Taylor Eds, North Holland.
Chari, V.V., P.J. Kehoe, and E. McGrattan (2002): `` Can Sticky Price Models Generate Volatile and Persistent Real Exhange Rates?,'' Review of Economic Studies 69, 533-563.
Chari, V.V., L. J. Christiano and P.J. Kehoe (1991), `` Optimal Fiscal and Monetary Policy: Some Recent Results'', Journal of Money, Credit and Banking, 23:519 539.
Chari V. V. , L. J. Christiano and P.J. Kehoe, (1994), `` Optimal Fiscal Policy in A Business Cycle Model'', Journal of Political Economy, 102:617 652.
Clarida, R, J. Galí, and M. Gertler (1999): `` The Science of Monetary Policy: A New Keynesian Perspective,'' Journal of Economic Literature, vol. 37, 1661-1707.
Clarida, R., J. Galí, and M. Gertler (2002): `` A Simple Framework for International Monetary Policy Analysis,'' Journal of Monetary Economics, vol. 49, no. 5, 879-904.
Collard F. and H. Dellas (2002), `` Exchange rate systems and macroeconomic stability", Journal of Monetary Economics, 49(3), pp. 571-599.
Cooley T. and V. Quadrini (2003), "Common Currencies vs. Monetary Independence", Review of Economic Studies, 60, 4.
Corsetti, G. and P. Pesenti (2001): `` Welfare and Macroeconomic Interdependence,'' Quarterly Journal of Economics vol. CXVI,issue 2, 421-446.
Corsetti, G. and P. Pesenti (2003): '' International Dimensions of Optimal Monetary Policy'', forthcoming Journal of Monetary Economics.
Devereux, M. and C. Engel, (2003), `` Monetary Policy in the Open Economy Revisited: Exchange Rate Flexibility and Price Setting Behavior,'' Review of Economic Studies, 60, 765-783.
Friedman, M. (1959), `` The Optimum Quantity of Money'', in The Optimum Quantity of Money, and Other Essays, Aldine Publishing Company, Chicago.
Galí, J. and T. Monacelli, (2004), `` Monetary Policy and Exchange Rate Volatility in A Small Open Economy'', Mimeo.
Goodfriend, M. and R. King, (2000), `` The Case for Price Stability'', European Central Bank Conference on '' Price Stability''.
Henderson D. and J. Kim, (2002), `` Exact Utilities under Alternative Monetary Rules in a Simple Macro Model with Optimizing Agents'', Mimeo.
Ireland, P. N., (1996), `` The Role of Countercyclical. Monetary Policy'', Journal of Political Economy, 104, 704-723.
Ireland (2001), "Sticky-Price Models of the Business Cycle: Specification and Stability", Journal of Monetary Economics, November.
Johnson, Harry G., (1954), `` Optimum Tariffs and Retaliation,'' Review of Economic Studies, 1. 2, 142-53.
Kehoe, P. J. and F. Perri, (2000), `` International Business Cycles With Endogenous Incomplete Markets'', NBER w.p. 7870.
Khan, A., R. King and A.L. Wolman, (2003), `` Optimal Monetary Policy'', Review of Economic Studies, 60,4.
Kim J. and S. Kim, (2002), `` Spurious Welfare Reversals in International Business Cycle Models'', forthcoming Journal of International Economics.
King, R. and A. L. Wolman, (1999), `` What Should the Monetary Authority Do When Prices Are Sticky?'', in Taylor, J. B., ed., Monetary Policy Rules, Chicago: university of Chicago Press, 349-398.
Kollmann R., (2003), `` Monetary Policy Rules in an Interdependent World'', Mimeo.
Kydland, F. and E. C. Prescott, (1977), "Rules Rather Than Discretion: The Inconsistency of Optimal Plans", Journal of Political Economy, 1977, vol. 85, issue 3, pages 473-91.
Kydland, F. and E. C. Prescott, (1980), `` Dynamic Optimal Taxation, Rational Expectations and Optimal Control'' , Journal of Economic Dynamics and Control, 2:79-91.
Lucas, R. E. and N. Stokey, (1983), `` Optimal Fiscal and Monetary Policy in an Economy Without Capital'', Journal of Monetary Economics, 12:55-93.
Marcet, A. and R. Marimon, (1999), `` Recursive Contracts'', mimeo, Universitat Pompeu Fabra and European University Institute.
Klein, P. and J.V. Rios-Rull, (1999), `` Time-Consistent Optimal Fiscal Policy'', mimeo, Institute for International Economic Studies and University of Pennsylvania.
Pappa, E., (2004), `` Do the ECB and the Fed really need to Cooperate? Optimal Monetary Policy in a Two-Country World'', Journal of Monetary Economics.
Persson, T. and G. Tabellini (1995), "Double-Edged Incentives: Institutions and Policy Coordination", Handbook of International Economics, G. Grossman and K. Rogoff Eds., Vol 3.
Ramsey, F. P., (1927), `` A contribution to the Theory of Taxation'', Economic Journal, 37:47-61.
Rotemberg, J. and M. Woodford (1997), `` An Optimizing Based Econometric Framework for the Evaluation of Monetary Policy'', in B. Bernanke and J. Rotemberg, eds., NBER Macroeconomics Annual, Cambridge, MA, MIT Press.
Schmitt-Grohe, S. and M. Uribe (2004), `` Optimal Fiscal and Monetary Policy under Sticky Prices'', Journal of Economic Theory, 114,198-230.
Siu, H. (2004) "Optimal Fiscal and Monetary Policy with Sticky Prices", Journal of Monetary Economics 51(3), April.
Sutherland, A. (2002), `` International Monetary Policy Coordination and Financial Market Integration'' CEPR Discussion Paper No 4251.
Woodford, M. (2003), `` Interest & Prices'', Princeton University Press.
Yun, T., (1996), `` Nominal Price Rigidity, Money Supply Endogeneity, and Business Cycle'', Journal of Monetary Economics, 37: 345-370.
Footnotes
* First draft October 2003. We thank Gianluca Benigno, Albert Marcet and Pedro Teles for useful discussions. We also thank Luca Dedola, Fiorella de Fiore, Jordi Gali, Stephanie Schmitt-Grohe, Alan Sutherland, Jaume Ventura and seminar participants at AUEB, Bonn University, European Central Bank, European University Institute, Lisbon University Nova, Riksbank, Universitat Pompeu Fabra, the Federal Reserve Board/ECB International Research Forum on Monetary Policy, the CEPR/INSEAD conference on Monetary Policy Effectiveness: Theory, Evidence and Challenges, and the Society for Economic Dynamics conference 2004 for comments. Ester Faia gratefully acknowledges support from the DSGE grant. All errors are our own responsibility. Return to text
†. Correspondence to Universitat Pompeu Fabra, Ramon Trias Fargas 25, Barcelona, Spain. E-mail: [email protected], homepage: http://www.econ.upf.es/~faia/. Return to text
‡. Correspondence to IGIER Universita' Bocconi, Via Salasco 3/5, 20136 Milan, Italy. Email: [email protected], Tel: +39-02-58363330, Fax: +39-02-58363332, Web page: www.igier.uni-bocconi.it/monacelli. Return to text
1. The idea that terms of trade spillovers generate an externality and therefore room for international (monetary and/or fiscal) policy coordination is already discussed (although within ad-hoc models) in Canzoneri and Henderson (1991), Persson and Tabellini (1995) and dates back in the trade literature at least to Johnson (1954). Chari and Kehoe (1990) discuss the specific role of terms of trade distortions for optimal fiscal policy in a two-country general equilibrium model. More recently, see Corsetti and Pesenti (2001), Benigno and Benigno (2003), Sutherland (2002). Return to text
2. It is by now well understood that this entails a major consequence in that it neglects the sense in which (time consistent) discretionary policies are suboptimal in dynamic environments with forward-looking price (and/or wage) decisions (Woodford, 2003). Return to text
3. The main consequence of this is that the set of equilibria that obtains in the case of an optimal policy constrained by predetermined price setting decisions differs from the one obtained in the presence of forward-looking price setting. See Marcet and Marimon (1999). Return to text
4. See, for instance, Rotemberg and Woodford (1997), Woodford (2003), Benigno and Benigno (2003), Clarida, Gali and Gertler (2002). Return to text
5. More recently, Benigno and Woodford (2004) show (within a closed economy model) how to preserve a quadratic approximation of the household's welfare objective in the case in which the economy fluctuates around a non-efficient steady-state. This per se requires taking a second order approximation also of (some of) the underlying equilibrium conditions. Benigno and Benigno (2004) and Pappa (2004) apply this approximation method to a two-country optimal policy dynamic model. The key difference of the approach employed in this paper is that, while maintaining general features such uncorrected steady-state distortions and forward-looking price setting decisions, we are able to describe the optimal policy problem in its exact form, without resorting to approximation methods. Return to text
6. Given that, in our setting, the law of one price holds continually, the unit of denomination of the payoffs of state-contingent assets is not strictly relevant. Alternatively, e.g., in the case in which deviations from the law of one price are due to consumer currency pricing, as in Devereux and Engel (2003), the distinction between nominal and real payoffs would be relevant for the specification of the equilibrium. Return to text
7. Asset market completeness at the national level allows to express the household maximization program in terms of a representative consumer. The underlying idea is that the initial holdings of financial wealth adjust as a residual endogenous variable in such a way that, as of time zero, each national household faces, in the presence of aggregate shocks, the same present value budget constraint (and therefore chooses the same consumption stream). See Woodford (2003). Return to text
8. Hence the expression for lifetime utility is equivalent to writing
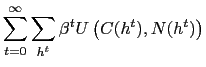
9. Each domestic household owns an equal share of the domestic monopolistic firms. We abstract from international trade in shares. Return to text
10. This differs, e.g., from Benigno
and Benigno (2003) and Devereux and Engel (2003) for which PPP
holds at all times. One can easily verify that PPP holds in our
case only in the absence of home bias by manipulating the CPI
expression and substituting conditions
![]() and
and
![]() , which are
implied by the fact that the law of one price holds. Return to text
, which are
implied by the fact that the law of one price holds. Return to text
11. This requires also that the
implicit government budget constraint be satisfied. Given the
absence of government purchases, this simply reads
![]() . Return to
text
. Return to
text
12. As a consequence of complete markets whether the same trading is undertaken at time zero or sequentially is irrelevant for the specification of the equilibrium. Return to text
13. An alternative specification would be to consider the case where the initial risk-sharing trading of assets takes place in a competitive fashion. We leave to a companion paper the analysis of optimal policy in which the initial distribution of wealth is determined endogenously. Return to text
14. This is the normalization
adopted in Chari et al. (2002). The difference here is that we show
that ![]() must
endogenously assume a unitary value under the risk-sharing
arrangement described above. Return to
text
must
endogenously assume a unitary value under the risk-sharing
arrangement described above. Return to
text
15. One may notice that this is the parallel in the cashless economy of the real money balances being residual in the competitive equilibrium with transaction frictions when utility is separable in consumption and real balances. See Appendix A. Return to text
16. In Appendix A we show how this set of constraints needs to be extended in a more general economy featuring monetary transactions frictions. Return to text
17. This allows to abstract from any incentive of policymakers to resort to surprise deflation as in the work of Corsetti and Pesenti (2001). Return to text
18. Benigno and Benigno (2003), for instance, focus on policy competition in a model with one-period predetermined prices, and limit their analysis only to Nash equilibria conditional on one particular strategy (i.e., price stability). Return to text
19. See Kydland and Prescott (1977), Calvo (1978). As such the system does not satisfy per se the principle of optimality, according to which the optimal decision at time t is a time invariant function only of a small set of state variables. Return to text
20. The law of motion of the additional costate variables would take a more general form if the expectations horizon in the forward-looking constraint(s) featured a more complicated structure. See Marcet and Marimon (1999). Return to text
21. As a consequence of the
underlying time consistency problem the system of first order
conditions takes a different form at time ![]() . One can easily obtain that
system by considering that, at
. One can easily obtain that
system by considering that, at ![]() , equation (54) must
hold. Return to text
, equation (54) must
hold. Return to text
22. See King and Wolman (1999) and Khan et al. (2003) for a closed-economy analysis on this point. Return to text
23. See Woodford (2003) for a similar result in a closed economy model where a linear quadratic approach is applied to the study of optimal policy in the presence of uncorrected steady state distortions. Return to text
24. See Khan et al. (2003) for an application of this strategy to an optimal monetary policy problem in a closed economy. Return to text
25. From a methodological point view, it is also of independent interest to notice that we reverse the logic of the so-called linear-quadratic approach to the optimal policy problem. In fact, we employ standard log-linear approximation methods to describe the policy function only when the exact optimal Ramsey allocation has been already characterized. Return to text
26. Technically speaking, one should
add the following further clarification. Assuming initial
conditions as (59) renders the approximation
valid only if
![]() and
and
![]() lie in the neighborhood of
a stochastic steady state which includes the values
lie in the neighborhood of
a stochastic steady state which includes the values
![]() This is most likely the
case in the presence of bounded shocks of the size employed in this
paper. Return to text
This is most likely the
case in the presence of bounded shocks of the size employed in this
paper. Return to text
27. See Khan et al. (2003). However, and more generally, Adao et al (2003) and Khan et al. (2003) show that in the presence of (real) demand shocks, e.g., exogenous variations in government purchases, strict price stability ceases to correspond to the optimal policy even in the prototype sticky price model with imperfect competition. Return to text
28. For an analysis of the optimal policy setting in response to cost-push shocks see Woodford (2003) and Clarida et al. (1999). For open economy models with one-period predetermined prices see Sutherland (2002). Return to text
29. Another way of seeing this is to
notice that in the case ![]() it holds that
it holds that
![]()
![]() at all times.
Substituting this into equation (39) one can
see that the domestic real marginal cost ceases to depend on any
foreign variable, thereby shutting down any policy competition
motive on the terms of trade.
at all times.
Substituting this into equation (39) one can
see that the domestic real marginal cost ceases to depend on any
foreign variable, thereby shutting down any policy competition
motive on the terms of trade.
Table 1: Volatility and Welfare under Alernative Policy Regimes
High Home Bias Nash |
High Home Bias Cooperation |
Low Home Bias Nash |
Low Home Bias Cooperation |
Low Elasticity Nash |
Low Elasticity Cooperation |
|
| Consumption | 1.553 | 1.443 | 1.834 | 1.695 | 1.561 | 1.491 |
| labor | 0.227 | 0.196 | 0.184 | 0.100 | 0.155 | 0.142 |
| PPI Inflation | 0.053 | 0.005 | 0.072 | 0.006 | 0.041 | 0.009 |
| CPI / PPI Ratio | 0.698 | 0.699 | 0.240 | 0.237 | 1.552 | 1.541 |
| Welfare cost (delta) | 0.0122 | 0.0113 | 0.0157 | 0.0146 | 0.0118 | 0.0118 |
Note: Standard deviations are in %. The welfare cost (in %) is the propostional upwaard shift in the consumption process that would make the representative household indifferent between its random consumption allocation and a nonrandom consumption allocation with the same mean.
Figure 1: Impulse Responses to a Positive Home Productivity Shock: Nash-Optimal vs. Inflation Targeting
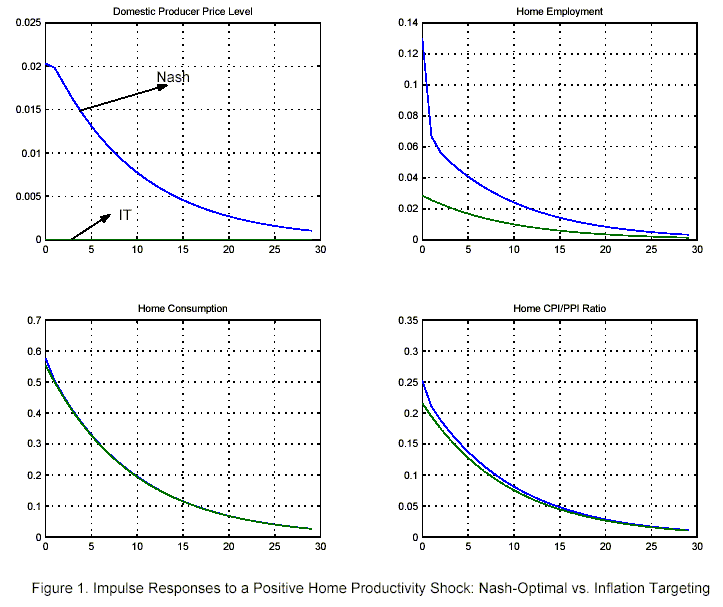
Figure 2: Response to a Productivity Shock under Nash-Optimal: Effect of varying the Elasticity of Substitution
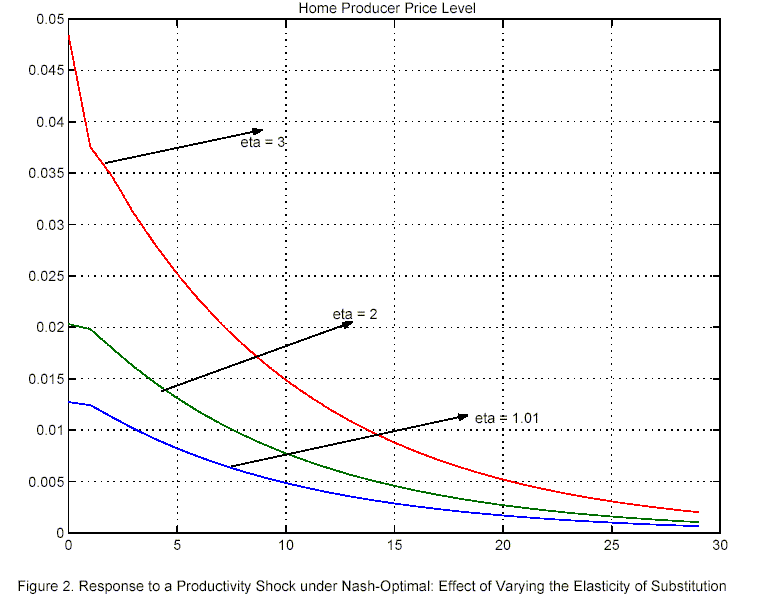
Figure 3: Impulse Responses to a Home Productivity Shock: Nash vs. Cooperation
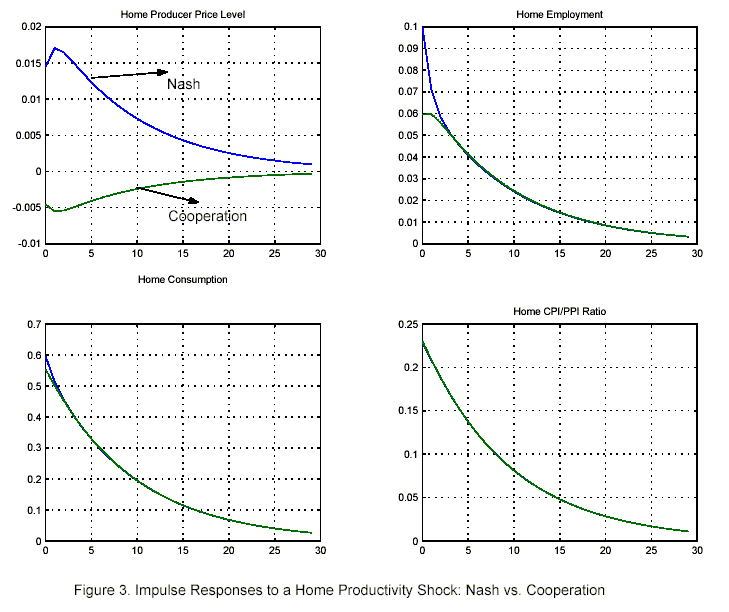
Figure 4: Effect of Varying Openness on the Golden Rule Steady-State under Nash Competition
Figure 5: Effect of Varying Openness on the Golden Rule Steady-State Inflation Rate.
This version is optimized for use by screen readers. A printable pdf version is available.
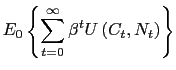
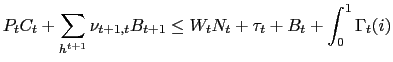
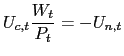
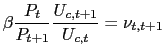
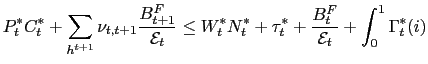
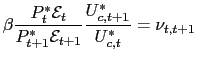
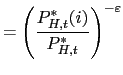
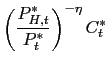
![$\displaystyle R_{t}^{\ast}=\left[ \beta\text{ }E_{t}\left\{ \frac{P_{t}^{\ast}} {P_{t+1}^{\ast}}\frac{U_{c,t+1}^{\ast}}{U_{c,t}^{\ast}}\right\} \right] ^{-1}$](img72.gif)
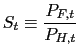
![$\displaystyle \frac{P_{t}}{P_{H,t}}=[(1-\alpha)+\alpha S_{t}^{\text{ }1-\eta}]^{\frac {1}{1-\eta}}\equiv g(S_{t})$](img75.gif)
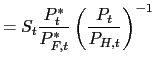
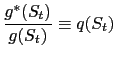
![$\displaystyle \frac{P_{t}^{\ast}\text{ }}{P_{F,t}^{\ast}}=[(1-\alpha^{\ast})+\alpha^{\ast }S_{t}^{\text{ }\eta-1}]^{\frac{1}{1-\eta}}\equiv g^{\ast}(S_{t})$](img81.gif)
![$\displaystyle B_{0}+\sum_{t=0}^{\infty}\left( \sum_{h^{t}}\nu_{0,t}\right) \lef... ...t}(i)\right] =\sum_{t=0}^{\infty}\left( \sum_{h^{t}}\nu_{0,t}\right) P_{t}C_{t}$](img85.gif)
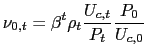
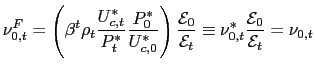
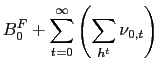
![$\displaystyle \left[ W_{t}^{\ast}N_{t}^{\ast}+\Gamma_{t}^{\ast }\right] =\sum_{t=0}^{\infty}\left( \sum_{h^{t}}\nu_{0,t}\right)$](img92.gif)
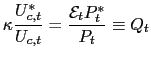
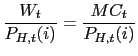
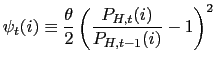
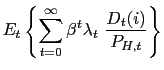
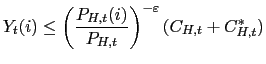
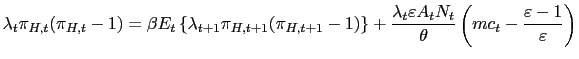
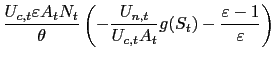
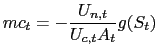
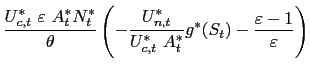
![$\displaystyle =\left( \frac{P_{H,t}(i)}{P_{H,t}}\right) ^{-\varepsilon}\left[ \... ...t}}{P_{t}^{\ast}}\right) ^{-\eta}\alpha^{\ast}C_{t}^{\ast }\right] +\psi_{t}(i)$](img158.gif)