
Board of Governors of the Federal Reserve System
International Finance Discussion Papers
Number 1075, March 2013 --- Screen Reader
Version*
Asymmetric Information and the Death of ABS CDOs
NOTE: International Finance Discussion Papers are preliminary materials circulated to stimulate discussion and critical comment. References in publications to International Finance Discussion Papers (other than an acknowledgment that the writer has had access to unpublished material) should be cleared with the author or authors. Recent IFDPs are available on the Web at http://www.federalreserve.gov/pubs/ifdp/. This paper can be downloaded without charge from the Social Science Research Network electronic library at http://www.ssrn.com/.
Abstract:
A key feature of the 2007 financial crisis is that for some classes of securities trade has practically ceased. And where trade has occurred, it appears that market prices are well below their intrinsic values. This seems especially true for those securities where the payoff streams are particularly complex, for example, structured finance ABS CDOs. One explanation for this is that information about these securities' intrinsic values since the crisis has been asymmetric, with current holders having better information than potential buyers. We first characterize the information asymmetries that were present in the structured finance ABS CDO market. Because many of the CDO dealers had partially or fully integrated the pipeline from mortgage originations through CDO issuance, they had informational advantages over potential buyers that could well have disrupted trading in CDOs as the crisis took hold in August of 2007. Using a "workhorse" model for pricing securities under asymmetric information and a novel dataset for the intrinsic values of ABS CDOs, we show how the resulting adverse selection problem could explain why the bulk of these securities either trade at significant discounts to their intrinsic values or do not trade at all.
Keywords: CDO, securitization, asymmetric, lemons
JEL classification: C63, D82, D43
1 Introduction
Collateralized debt obligations (CDOs) were at the heart of the 2007-2008 financial crisis. By January 2009, global banks, insurers, and asset managers had written down $218 billion in losses from their holdings of CDOs of asset backed securities (ABS), or 42 percent of their crisis-related losses (see Table 1). They had also taken $84 billion of losses on residential mortgage backed securities (RMBS), mostly from private label U.S. subprime mortgages. These firms were being penalized by markets for having these "toxic" assets on their balance sheets, and would have probably sold them at prices close to the fair liquidation value of the underlying collateral if they could have. But secondary market prices were well below intrinsic values, and selling in this distressed market would have crystallized losses and eroded their capital position even further. When CDO markets froze, many large financial institutions had no choice but to keep these securities on their books. The uncertainty surrounding the size and location of these CDO-related losses contributed to heightened counterparty risk, which in turn led to the collapse of interbank funding markets, setting off the Panic of 2007 (Gorton (2009)).
Interlinkages between ABS prices and liquidity provision through the the shadow banking system likely amplified the collapse of ABS markets in the second half of 2007. Krishnamurthy (2010), Allen and Carletti (2008), and Bolton, Santos, and Scheinkman (2011) analyze how the inability of investors to raise funds to purchase these securities could have impaired normal market functioning and dislodged prices from fundamentals. Similarly, Gorton and Metrick (2012) and Caballero and Simsek (2009) discuss how concerns about the liquidity of asset-backed securities used as collateral in repo transactions, combined with increased counterparty risk led to a run in the repo market, which in turn impeded funding for ABS CDOs.3 Further contributing to the downward spiral in asset prices was the deleveraging cycle that took place as a result of procyclical active balance sheet management (Adrian and Shin (2010)). These factors certainly played a destabilizing role in the market for ABS CDOs. The contribution of this paper is to show that, even absent these factors, asymmetric information between buyers and sellers regarding the quality of ABS CDOs would have sufficed to shutter this market.
Gorton (2009) argues that this asymmetric information stemmed from a loss of information about the quality of the underlying loans that occurred as a result of the long chain of structures inherent in the subprime securitization process.4 We expand this argument by documenting how vertical integration in the securitization of subprime mortgages provided the CDO dealers informational advantages over potential buyers. We then assess the extent to which this asymmetric information could have contributed to the sudden evaporation of liquidity for structured finance ABS CDOs during the crisis, and the dislodging of secondary market prices of these securities from their intrinsic values.
Because the analysis proceeds in parts which are only joined together at the end, we provide the following roadmap: In the next section section we summarize how subprime mortgages were securitized into ABS CDOs, and how this market collapsed in the second half of 2007, resulting in the sudden evaporation of liquidity and the dislodging of prices from intrinsic values. Having established the facts that we are trying to explain with asymmetric information, in Section 3 we describe the nature of the asymmetric information between sellers and potential buyers of ABS CDOs. In Sections 4 and 5, we lay out a "workhorse" model for pricing securities under asymmetric information, and describe a novel dataset for the intrinsic values of ABS CDOs. More details on the computation of these intrinsic values, which capture the fair liquidation value of the underlying collateral, can be found in Appendix A. In Section 6, we take these data directly to the model and show how asymmetric information between sellers and potential buyers could explain both the evaporation of liquidity and the dislodging of prices from intrinsic values. The last section concludes.
2 Securitization from Mortgage Loans to CDOs and the Onset of the Financial Crisis
The residential mortgage market experienced tremendous growth in securitization over the last decade. We focus on the securitization of private label securities, in particular structured finance ABS CDOs. These CDOs are backed, in part, by mortgages that do not conform to the criteria for purchase by Fannie Mae and Freddie Mac, which establish limits on debt-to-income ratio, documentation requirements, and maximum loan amount.
The securitization chain begins with the pooling of prime, Alt-A, subprime, and junior-lien mortgages into residential mortgage-backed securities (RMBS). These RMBS securities are tranched based on seniority, with senior note holders having priority over the principal and interest payments collected from the underlying loans. This senior-subordinate structure is often referred to as the "waterfall." The most senior notes are rated AAA because they are the last to incur losses stemming from loan defaults. Generally, the AAA-, AA-, and A-rated RMBS are purchased by so-called "High Grade" ABS CDOs, whereas the BBB-, and BB-rated RMBS are purchased by "Mezzanine" ABS CDOs. These CDOs are also issued with senior/subordinate structure. Finally, both High Grade and Mezzanine ABS CDOs are purchased by other CDOs, which are often referred to as CDO-squareds because they are primarily backed by CDOs.5
Even before the crisis, there were only moderate levels of secondary market activity for ABS-CDOs. This was so for several reasons. First, the lower-rated tranches of these CDOs were largely recycled into other CDOs or hedged through "correlation trades".6 Second, several of the largest CDO dealers retained many of the AAA CDO bonds they issued (Financial Crisis Inquiry Commission (2011), Chapter 8). Finally, the remaining AAA bonds sold in the market were designed as buy-and-hold investments and, for the most part, were privately traded over-the-counter among institutional investors such as banks, hedge funds, mutual funds, pension funds, insurance companies, endowments, and local governments (IOSCO (2009)). Even so, secondary market activity for CDOs increased notably between 2003 and 2005, as spreads for seasoned CDOs tightened relative to those of new-issue CDOs (Lucas, Goodman, and Fabozzi (2006)).
On July 10, 2007, both Moody's and S&P downgraded hundreds of subprime RMBS that had been issued in the fourth quarter of 2005 and in 2006, and placed others on watch citing higher than anticipated rates of early payment defaults, aggressive underwriting of mortgages, fraud, and slowing home price appreciation (Moody's Investor Service (2007) and Standard & Poor's (2007a)). Furthermore, S&P announced that they were changing their assumptions on house prices going forward, projecting that house prices would decline 8 percent nationwide between 2006 and 2008, bottoming out in the first quarter of 2008.
On July 10, the effect of these negative rating actions on the ratings and expected performance of CDOs was much more uncertain- it was unclear how many of these RMBS were placed into the CDOs, and how these downgrades would affect the underlying assumptions of the copula models used by the ratings agencies (and many investors). For example, in a conference call with investors (Standard & Poor's (2007b)), S&P surveillance director Enestine Warner stated that "For CDO squareds – we are very much analyzing those. The difficulty with trying to include them on an exposure list is that they're more opaque and not as linear to analyze." Regarding the model-based methodologies for rating CDOs, S&P managing director Pat Jordan stated that "As far as correlations in CDOs within our stress models, you know, we do have an assumption for correlations. We are studying the actual experience now and over time it will determine whether that should result in any kind of change to either the correlation or any other component of our stress models for CDOs." It was only over the ensuing weeks that S&P would discover that most of the publicly traded ABS CDOs contained the downgraded BBB bonds. Investors learned that there were lemons in the market for CDOs, but figuring out which CDOs were the lemons would prove to be tricky.
Rating agencies and many other market participants relied on copula models to estimate expected collateral losses on ABS CDOs, similar to the ones used to value corporate CDOs. However, unlike the models used for RMBS securities which capture the sensitivity of the performance of the underlying mortgage loans to changes in house prices and other economic fundamentals, the copula models relied instead on correlations among bonds in the CDOs to estimate losses. The probability of default and expected losses produced by these models are extremely sensitive to model parameters based on historical performance of the underlying bonds, which, prior to 2007, was exceptionally good (Heitfield (2010)). Crucially, these models were not designed to directly capture the sensitivity of the performance of the underlying assets to systemic changes in house prices or changes in attributes that affect mortgage loan performance.7
Issuance and secondary-market trading of ABS CDOs declined considerably by August 2007. On August 9, BNP Paribas froze subscriptions and redemptions to several of its funds, and suspended computation of their net asset values because of "the complete evaporation of liquidity in certain market segments of the U.S. securitisation market," which "has made it impossible to value certain assets fairly regardless of their quality or credit rating."(New York Times (2007)) A survey of industry participants and market authorities by the International Organization of Securities Commissions (IOSCO) found that "secondary market trading in SFPs [structured finance products] appears to have declined significantly since the onset of the credit crisis."(IOSCO (2009), p.10) As Ross Heller, an executive director at J.P. Morgan Securities Inc., put it: "We're definitely in a period of very low liquidity at the moment." (Bloomberg (2008))
And where trades did occur, it appeared that market prices were well below what one might have believed to be the intrinsic value for that class of security. The above-mentioned IOSCO survey of industry participants noted that:
"Respondents observe that, although there are some potential buyers in the market currently, most holders of SFPs [structured finance products] are reluctant to sell. Respondents noted that this could be ascribed to a general belief that the hold-to-maturity value of many SFPs exceeds the value that could be attained in the current secondary market." (IOSCO (2009), p.10)
Similarly, in a White Paper accompanying the March 23, 2009 press release announcing the details of the Public-Private Investment Program to purchase troubled assets, the Treasury stated that "while fundamentals have surely deteriorated over the past 18-24 months, there is evidence that current prices for some legacy assets embed substantial liquidity discounts." (U.S. Department of the Treasury (2009)) In sum, the secondary market for ABS CDOs virtually disappeared, and where trades did occur, secondary market prices dislodged from fundamentals.
By the end of 2007, Citigroup and Merrill Lynch reported spectacular losses of $24 billion and $25 billion, respectively, largely from their extensive CDO businesses (Financial Crisis Inquiry Commission (2011)). Billions more in CDO-related losses were reported by other large financial institutions such as Bank of America, Morgan Stanley, J.P. Morgan, Bear Stearns, as well as by insurance companies and hedge funds. Had these institutions been able to sell these CDOs at prices close to their intrinsic values, they likely would have done so because market participants began discriminating between firms with "toxic" assets on their balance sheets and those without. But, as confirmed by a survey of market participants, "selling into the current market would crystallize losses and could potentially erode the sellers' capital position." (IOSCO (2009), p.10)
3 Information asymmetries in the market for CDOs
Starting in summer of 2007, sellers (i.e. all the dealers and some of the largest financial firms around the world) wanted to sell their CDOs to avoid mark-to-market losses and the uncertainty that these assets were generating on their balance sheets. But when ABS CDOs began to suffer downgrades in July 2007, potential buyers could no longer trust the ratings or the copula models that broke down. Also, it soon became apparent that RMBS and CDO ratings were grossly inflated. Because rating agencies were only paid if they were selected to rate the deal, they were incentivized to inflate ratings in order to participate in more deals and increase their market share.8 As demonstrated by Cordell, Huang, and Williams (2012) (hereafter CHW), the only way to correctly value a CDO was by digging deep into its collateral and valuing it using loan-level data. But most investors either relied on rating agency ratings or used the standard copula models to value the CDOs. Others did not have the expertise, the resources, or the time to compute the intrinsic values of these securities. The sellers, on the other hand, having originated many of these CDOs, had large warehouse lines of subprime loans as well as many newly issued subprime securities, and were better equipped to value these securities because they had better knowledge of their underlying risks.
This superior knowledge of the underlying risks derives mainly from the fact that the largest CDO dealers were also in the business of originating the underlying RMBS (Table 2). But the vertical integration in the securitization process went even further than that. As shown in Table 3, most CDO dealers also entered the business of originating and servicing mortgages by acquiring large subprime originators and servicers. Most were either fully integrated (doing originations, issuance of RMBS, issuance of CDOs, and, finally, servicing the mortgages) or were partially integrated by engaging in some part of the mortgage chain. By owning an originator, CDO dealers would have information on the quality of the originations. By owning a servicer, they could see firsthand the early payment defaults (EPDs) and rise in delinquencies that started after house prices peaked in late 2005.
Further complicating the investor's ability to penetrate the CDO's portfolio is the fact that a CDO portfolio is not static; the CDO manager may purchase new assets, with constraints, to replace securities that pay down or mature. For example, when the financial crisis deepened and it became difficult to issue new CDOs, Citigroup and other large underwriters were holding large "warehouses" of RMBS intended to serve as collateral for future CDO issuances. To avoid losses on these RMBS, CDO underwriters began selling them into existing CDOs (Financial Crisis Inquiry Commission (2011), p. 197), essentially transferring the credit risk of these warehouse bonds to previous CDO noteholders.
This informational asymmetry could have been further amplified by the fact that CDOs are extremely complex, making it difficult for the average investor to forecast how a specific level of subprime losses would impact a CDO (Goodman, Li, Lucas, Zimmerman, and Fabozzi (2008) and Brunnermeier (2009)). For example, the existence of triggers and other complicated cash flow mechanics make it difficult to determine which bonds will be written down even if one knows the amount of collateral losses a deal will suffer.9 Goodman, Li, Lucas, Zimmerman, and Fabozzi (2008) state that "Calculating expected bond losses on mezzanine CDOs is a complex, highly data-intensive task that requires access to a large database and a large amount of computing power, as well as knowledgeable analysts. Hence it is difficult for the average investor to forecast how a specific level of subprime losses will impact a mezzanine CDO." (p.317)
In addition, the relative returns of the various tranches could be manipulated by the CDO manager to favor those tranches he held. For example, Lucas, Goodman, and Fabozzi (2006) describe how a CDO manager is able to manipulate the overcollateralization ratio over time to disguise par-building trades in an attempt to continue to redirect cash flows to the lower tranches. Also, the CDO manager may have financial ties with some note-holders that could result in a conflict of interest or outright fraud (Tavakoli (2003)). There are now many lawsuits underway in which CDO investors allege that the CDO issuers committed fraud by: (1) not disclosing conflicts of interest such as the short positions of other investors who helped pick the assets that went into the CDO, or (2) selectively placing risky assets into the CDOs in order to offload them from their own balance sheets, or (3) misinforming the investors about the true quality of the assets underlying the CDO, or (4) improperly obtaining millions of dollars in advisory fees and undisclosed profits at the expense of clients and investors.
Having established the sudden evaporation in liquidity in the market for ABS CDOs, and the informational advantage that sellers had over potential buyers, we now turn to our model of asymmetric information.
4 The model
In a straightforward generalization of the Akerlof (1970) lemon's model, we start with a set of existing
securities
![]() where
where ![]() denotes a particular security. The quantity of security
denotes a particular security. The quantity of security ![]() is given by
is given by ![]() . The intrinsic value of
security
. The intrinsic value of
security ![]() , defined as the fair liquidation value of
the underlying collateral, is
, defined as the fair liquidation value of
the underlying collateral, is ![]() ,
,
![]() . Importantly, this intrinsic
value of the security does not depend on who holds the security.
There may be several types of securities holders, which we index by
. Importantly, this intrinsic
value of the security does not depend on who holds the security.
There may be several types of securities holders, which we index by
![]() . An individual's portfolio is denoted
. An individual's portfolio is denoted
![]() and
and
![]() . The total intrinsic
value of agent
. The total intrinsic
value of agent ![]() 's portfolio is
's portfolio is
![$\displaystyle TT[\mathbf{A}(i)]=\sum_{t}a(i,t)\cdot T(t).$](img12.gif) |
(1) |
Agents are risk neutral and have preferences over the money they
have on hand (![]() ) and the intrinsic value of the
securities they hold. Their utility functions have the form
) and the intrinsic value of the
securities they hold. Their utility functions have the form
| (2) |
where ![]() ,
,
![]() ,
,
![]() is an agent-specific
discount factor. This discount factor reflects the fact that some
agents are willing to sell their securities at a discount to their
intrinsic value.
is an agent-specific
discount factor. This discount factor reflects the fact that some
agents are willing to sell their securities at a discount to their
intrinsic value.
For now we assume the
![]() and
and ![]() are known
to everyone. It will be handy to also have
are known
to everyone. It will be handy to also have
![]() represent
the set of intrinsic values and
represent
the set of intrinsic values and
![]() represent the set of possible
prices for these securities.
represent the set of possible
prices for these securities.
4.1 No disclosure and delayed revelation
To keep the model simple, we assume it is impossible for the current holder of a security to credibly reveal its intrinsic value to a potential buyer. In addition, we assume that after a security trades there is a significant delay before the intrinsic value is revealed to the buyer. This assures that in a single period a given security only changes hands once. In Section 6, we argue that our results would still hold under the more realistic assumption that buyers attach some weight to the possibility that sellers are better informed. Also, when we take the model to the data, we will give the potential buyers the benefit of the doubt by endowing them with information on the vintage, seniority, and CDO type, as well as information on the distribution of the CDO intrinsic values.
The sellers
Utility maximization implies that the minimum price that a current
holder would require to relinquish a security with true payoff
![]() is
is
![]()
which we refer to as the value to the seller. Note that
![]() maps a true payoff into a price,
maps a true payoff into a price,
![]() .
.
Because
![]() is monotonic, we can we can define
is monotonic, we can we can define
![]() as the
maximal value of
as the
maximal value of ![]() that seller
that seller ![]() will offer when given the opportunity to sell securities for price
will offer when given the opportunity to sell securities for price
![]() .
.
Define
![]() . This is the set of securities that seller
. This is the set of securities that seller ![]() will
offer at price
will
offer at price ![]() . The total set of securities that
will be offered by all sellers at price
. The total set of securities that
will be offered by all sellers at price ![]() is
is
![]() .
Note that
.
Note that
![]() maps
maps
![]() . We call the total
set of securities offered at price
. We call the total
set of securities offered at price ![]() the 'fruit
bowl'; it is our basic supply relationship.
the 'fruit
bowl'; it is our basic supply relationship.
We can now define the average intrinsic value of the securities offered at a given price as
![$\displaystyle AT[\mathbf{S}[p]]=E[T(t):t\in \mathbf{S}[p]]=\frac{\sum_{t\in \mathbf{S} [p]}a(t)\cdot T(t)}{\sum_{t\in \mathbf{S}[p]}a(t)}.$](img39.gif)
|
(3) |
The buyer(s)
Like the sellers, the representative buyer only cares about the
average, or total, true payoff of the portfolio he acquires.
However, the buyer may require that the price he pays for the
securities represent a discount, ![]() , to their true
payoff. Thus, when offered a set of securities
, to their true
payoff. Thus, when offered a set of securities
![]() , he will value a draw from it at
some fraction,
, he will value a draw from it at
some fraction, ![]() , of the elements' expected true
payoff.10
, of the elements' expected true
payoff.10
![$\displaystyle V_{b}[\mathbf{Z}]=x_{b}\cdot E[T(t):t\in \mathbf{Z}]=\frac{x_{b}\cdot \sum_{t\in \mathbf{Z}}a(t)\cdot T(t)}{\sum_{t\in \mathbf{Z}}a(t)}=x_{b}\cdot AT[\mathbf{Z}].$](img43.gif)
|
(4) |
![]() is the maximal per-unit price the buyer
is willing to pay for the securities in
is the maximal per-unit price the buyer
is willing to pay for the securities in
![]() . We assume there are enough buyers
so that in principle the entire set of securities could trade
hands.
. We assume there are enough buyers
so that in principle the entire set of securities could trade
hands.
4.1.1 The equilibrium
We assume that sellers cannot coordinate with each other and that
prices are determined in an exchange following a Dutch
auction.11 The auction begins with an
auctioneer calling out the highest price, which results in the
sellers throwing all their securities into the fruit bowl. Assuming
some dispersion in the initial intrinsic values, the average value
of the fruit bowl is less than the maximum price called, so there
will be no trade at this price. As the auctioneer lowers the price,
some informed sellers withdraw their higher valued securities from
the fruit bowl, causing the average intrinsic value (
![]() ) of the securities in the
fruit bowl to fall. One can think of this as a race. As the price
is lowered it comes closer to the average value of what is in the
fruit bowl. At the same time the value of the bowl is declining and
moving away from the price as the better securities are removed.
Eventually, the price called out will be such that buyers value a
draw from the fruit bowl at the same price that elicited the fruit
bowl to be filled. That is, the equilibrium is the
) of the securities in the
fruit bowl to fall. One can think of this as a race. As the price
is lowered it comes closer to the average value of what is in the
fruit bowl. At the same time the value of the bowl is declining and
moving away from the price as the better securities are removed.
Eventually, the price called out will be such that buyers value a
draw from the fruit bowl at the same price that elicited the fruit
bowl to be filled. That is, the equilibrium is the
![]() pair such
that
pair such
that
| (5) |
Buyers know that they will be "overpaying" for some low-value
securities and "underpaying" for some high-value securities in
the fruit bowl they purchase, but in the end they pay exactly what
the bowl is worth to them, and all utility gains from trade go to
the sellers. There will always be at least one equilibrium,
although it may be trivial in that only the securities with the
lowest value trade at a price equal to ![]() , which may be
zero. For now we admit these 'niggling' equilibria and trades,
although they can be eliminated by introducing a small transaction
cost. It is easy to show that: (1) If
, which may be
zero. For now we admit these 'niggling' equilibria and trades,
although they can be eliminated by introducing a small transaction
cost. It is easy to show that: (1) If ![]() and
and
![]() for any
for any
![]() , then there will be
non-trivial trades. And (2), if
, then there will be
non-trivial trades. And (2), if
![]() for all
for all
![]() then all securities will be
traded at a price
then all securities will be
traded at a price
![]() . Also, there may
be more than one pair
. Also, there may
be more than one pair
![]() and the
Dutch auction implies that the equilibrium with the highest price
will be chosen. At the equilibrium price
and the
Dutch auction implies that the equilibrium with the highest price
will be chosen. At the equilibrium price ![]() ,
we denote the maximal value of
,
we denote the maximal value of ![]() offered by any
seller by
offered by any
seller by
![]() .
.
If all sellers have the same discount factor, ![]() , and all buyers have the same discount factor,
, and all buyers have the same discount factor,
![]() , then the set of securities traded in
equilibrium is determined by the ratio
, then the set of securities traded in
equilibrium is determined by the ratio ![]() . That
is, by combining equations 4 and 5 and the fact
that in equilibrium,
. That
is, by combining equations 4 and 5 and the fact
that in equilibrium,
![]() , we get that
, we get that
![$\displaystyle \frac{\sum_{t\in \mathbf{S}[p*]}a(t)\cdot T(t)}{\sum_{t\in \mathbf{S}[p*]}a(t)T^{\max^{\ast }}}=\frac{x_s}{x_b}.$](img64.gif)
|
(6) |
The left-hand side of equation 6 measures the
"junkiness" of the fruit bowl at the equilibrium price
![]() - the numerator is the total value of
the securities in the fruit bowl, and the denominator is maximum
possible value of the securities in the fruit bowl if they were all
valued at
- the numerator is the total value of
the securities in the fruit bowl, and the denominator is maximum
possible value of the securities in the fruit bowl if they were all
valued at
![]() . Equation 6 therefore
implies that the junkier the securities offered into the fruit
bowl, the larger the discount that sellers would have to accept
(lower
. Equation 6 therefore
implies that the junkier the securities offered into the fruit
bowl, the larger the discount that sellers would have to accept
(lower ![]() ) for trade to occur. Thus, the ratio
) for trade to occur. Thus, the ratio
![]() uniquely determines which securities
trade in equilibrium, but the equilibrium price
uniquely determines which securities
trade in equilibrium, but the equilibrium price ![]() will depend on the level of either
will depend on the level of either ![]() or
or ![]() .
.
Graphical illustration of the equilibrium
We demonstrate the equilibrium conditions graphically using the
examples illustrated in Figures 1 through 3. The top part of
each panel shows how the equilibrium price (![]() )
is determined. The bottom part shows the distribution of securities
in the market, and those that are traded at the equilibrium price.
)
is determined. The bottom part shows the distribution of securities
in the market, and those that are traded at the equilibrium price.
Turning to the top portion of each panel, on the horizontal axis
we plot the intrinsic value of the securities, ![]() .
On the vertical axis we plot the average price of a set of
securities or the value of some set of securities to the holders.
It will be handy to have a
.
On the vertical axis we plot the average price of a set of
securities or the value of some set of securities to the holders.
It will be handy to have a ![]() line
(
line
(![]() ) which maps any security with intrinsic
value
) which maps any security with intrinsic
value ![]() into a price equal to
into a price equal to ![]() .
When the buyer's discount
.
When the buyer's discount ![]() , the
equilibria are the
, the
equilibria are the
![]() pairs such
that
pairs such
that
![]() . On the
graph, the equilibria occur when the
. On the
graph, the equilibria occur when the
![]() line touches the
line touches the
![]() line. Without regard to the distribution
of securities we can also plot
line. Without regard to the distribution
of securities we can also plot ![]() , which gives
the minimum price that the seller would require to relinquish a
security with payoff
, which gives
the minimum price that the seller would require to relinquish a
security with payoff ![]() . If all sellers have the
same discount factor, call it
. If all sellers have the
same discount factor, call it ![]() , then
, then
![]() is just a ray from the origin
with slope
is just a ray from the origin
with slope ![]() , which is less than one. At the
equilibrium price
, which is less than one. At the
equilibrium price ![]() , the corresponding
, the corresponding
![]() is given by
is given by
![]() , and all securities
with payoffs
, and all securities
with payoffs
![]() will be offered into
the fruit bowl and traded at that price.
will be offered into
the fruit bowl and traded at that price.
Examples with a uniform distribution
To plot
![]() we need to know the
distribution of the intrinsic values of the securities. To keep
this first example simple, we will assume a uniform distribution on
we need to know the
distribution of the intrinsic values of the securities. To keep
this first example simple, we will assume a uniform distribution on
![]() with lower and upper bounds
with lower and upper bounds ![]() and
and ![]() . That is
. That is
![]() . In this
case
. In this
case
![$\displaystyle AT[\mathbf{S}[p]]=E[T:L<T(t)<T^{\max }]=\frac{\sum_{t\in \mathbf{S} [p]}a(t)\cdot T(t)}{\sum_{t\in \mathbf{S}[p]}a(t)}=\frac{(L+T^{\max }[p])}{2} =\frac{(L+p/x_{s})}{2}, $](img97.gif)
and the resulting equilibrium price is
![]() .
.
The left panel of Figure 1 illustrates the
uniform case when ![]() . The equilibrium is
such that some of the securities--those valued at
. The equilibrium is
such that some of the securities--those valued at
![]() or less
--trade at a price (
or less
--trade at a price (![]() ) equal to the
average intrinsic value of all securities in the fruit bowl.
) equal to the
average intrinsic value of all securities in the fruit bowl.
So far, we assumed that it takes a long time for the new buyer
of a security to ascertain its intrinsic value. We clearly need
something like this to keep the new buyers from aggravating the
adverse selection problem. To see this, consider the same example
shown on the left panel of Figure 1. What happens to
the market after the securities with payoffs
![]() change hands?
change hands?
Suppose all of these first-round trades have taken place and we
now allow those who purchased securities to learn the intrinsic
value of the securities they acquired. In the second round of
trading, the potential sellers comprise all security holders: those
who bought securities in the first-round and those who had
securities in the first round but never sold them. These two groups
of potential sellers have different discount factors. Those who
bought securities in the first round when they had a discount
factor of ![]() , have the same discount factor
of 1 in the second round because they are not
liquidity constrained. That is, they have no incentive to sell
their securities at a price that is less than their intrinsic
values. As such, their
, have the same discount factor
of 1 in the second round because they are not
liquidity constrained. That is, they have no incentive to sell
their securities at a price that is less than their intrinsic
values. As such, their ![]() schedule will be the
schedule will be the
![]() line between
line between ![]() and
and
![]() , shown by the green line in
the right panel of Figure 1. For the other
sellers who never sold their securities in the first round, their
, shown by the green line in
the right panel of Figure 1. For the other
sellers who never sold their securities in the first round, their
![]() schedule (shown in red) remains
schedule (shown in red) remains
![]() (where
(where ![]() ).
The blue
).
The blue
![]() line representing the
average intrinsic value of the basket of securities offered at a
given price
line representing the
average intrinsic value of the basket of securities offered at a
given price ![]() is now above the
is now above the ![]() line for all
line for all ![]() . That is, only
securities with
. That is, only
securities with ![]() would possibly trade in the
second round.12
would possibly trade in the
second round.12
Figure 2 illustrates
the two uniform cases when ![]() . In the left
panel of Figure 2,
. In the left
panel of Figure 2,
![]() and no securities are traded
(except maybe those worth zero). In the right panel,
and no securities are traded
(except maybe those worth zero). In the right panel, ![]() and all securities are traded at an indeterminate
price somewhere between
and all securities are traded at an indeterminate
price somewhere between ![]() and
and ![]() .
.
Examples with a more general distribution
If the payoffs are uniformly distributed with ![]() , trade is limited to cases where the sellers' discount is
large (
, trade is limited to cases where the sellers' discount is
large (![]() ). For more general
distributions, this is not the case. The left panel of Figure 3 illustrates an
example where the distribution of securities has a small mass
between
). For more general
distributions, this is not the case. The left panel of Figure 3 illustrates an
example where the distribution of securities has a small mass
between ![]() and
and ![]() , the seller's
discount is not too small (
, the seller's
discount is not too small (
![]() ) and yet there are no
(non-trivial) trades in equilibrium. This example shows how a few
lemons can ruin the market.
) and yet there are no
(non-trivial) trades in equilibrium. This example shows how a few
lemons can ruin the market.
The right panel of Figure 3 illustrates
multiple equilibria. The Dutch auction results in trades at the
equilibrium with the highest price (![]() ).
However, one could easily impose alternative rules on the bidding
process.
).
However, one could easily impose alternative rules on the bidding
process.
5 Data
We use data on the intrinsic values of 4,865 individual CDO securities (from 672 CDO deals), computed as of March 2011 by CHW. Appendix A provides more details on how these intrinsic values are computed. The original CHW sample comprises 727 CDO deals, but we exclude 213 deals from the 2000-2005 vintages that were liquidated as of March 2011 because they were likely liquidated before the financial crisis erupted in 2007. To compute these intrinsic values, CHW use the Intex engine which covers the universe of publicly traded private-label RMBS and ABS CDO deals in the United States. The Intex engine not only warehouses data on the underlying collateral backing each CDO, it also programs into its cash-flow engine the structural features of each deal, such as loss allocations among the tranches, triggers, prepayment penalty allocations, and interest rate hedges. This allows buyers and sellers a common set of tools to generate their own valuations. For each CDO deal, the securities are tranched based on their seniority. At the tranche level, there are 4,865 individual CDO securities in our sample: 734 Senior AAA, 1,009 Junior AAA, 1,387 AA and A, 828 BBB, 252 BB/B, and 655 NR (not rated, equity, or "first-loss" tranche). Mezzanine CDOs make up about two-thirds of the CDOs in our sample; the rest are High Grade CDOs.
Roughly three-quarters of the 4,865 CDO bonds in the CHW data were originated between the second half of 2005 and the end of 2007. These CDOs experienced higher losses than those issued in earlier years because they are primarily backed by subprime securities and other ABS CDOs. As described above, underwriting standards for subprime mortgages deteriorated significantly in the second half of 2005, and further in 2006 and 2007, as can be seen by the dramatic upward shift in the cumulative default rate curves for subprime loans starting in 2005 (Figure 4). CHW and Goodman, Li, Lucas, Zimmerman, and Fabozzi (2008) find that CDO losses increase by year of origination. Also, during the first half of 2005 ISDA published a template for executing credit default swaps of ABS on a Pay-As-You-Go basis, which made it easier to invest CDO collateral synthetically and brought about an explosion in synthetic CDO issuance starting in the second half of the year (see Figure 5). We therefore take CDO vintage into account when we examine how these securities trade under asymmetric information. To this end, we label CDOs that were issued on or before June 30, 2005 as the "early" vintage, and those issued after this date as the "late" vintage.
Table 4 summarizes the distributions of intrinsic values for the various CDO categories in our sample. Only the most senior tranches of the early vintage CDOs have average intrinsic values greater than 50. All CDO categories with seniority AA/A and below, and all of the late vintage CDOs experienced heavy losses, as can be seen by the low means and medians for their intrinsic values. Furthermore, the high standard deviations of the intrinsic values indicate that they are highly dispersed between 0 and 100.
6 Trading CDOs under asymmetric information
We now examine how these 4,865 CDOs would trade when potential buyers cannot penetrate a CDO's portfolio to determine its intrinsic value, only the sellers can. Even so, to give the buyers the benefit of the doubt, we assume that they are equipped with some valuable information. That is, when considering the purchase of a CDO tranche they know its seniority, its vintage, and whether it is a High Grade or Mezzanine CDO. But more importantly, we assume that each buyer knows the true distribution of intrinsic values for the type of CDO he is considering to buy. One can think of each CDO as having a label (much like the label on a bottle of wine) with three stamps on it: a High Grade or Mezzanine stamp, a Seniority stamp (e.g. Sr-AAA), and a vintage stamp (early or late). For example, a CDO's label may read "High Grade, Jr-AAA, early vintage." Another CDO's label may read "Mezzanine, BBB, late vintage." We will consider trading in markets for CDOs that have the same label. Sellers are assumed to know the intrinsic value of a CDO, but cannot credibly reveal this to the buyer. Referring back to the model in Section 4, buyers value a draw from the fruit bowl at the same price that elicited the fruit bowl to be filled. Assuming that prices are called following a Dutch auction, we compute the resulting trading equilibria for the various CDO markets. For a given CDO market, it will be useful to define 'meaningful' trades as those involving securities other than the ones with the lowest intrinsic value.
For simplicity, we set the buyers discount factor (![]() ) to 0.9. That is, a buyer is willing to pay at most 90
for a CDO with
) to 0.9. That is, a buyer is willing to pay at most 90
for a CDO with ![]() . This normalization is not
important for our results because, as we showed earlier, it is the
ratio between the sellers' and buyer's discounts (
. This normalization is not
important for our results because, as we showed earlier, it is the
ratio between the sellers' and buyer's discounts (![]() ) that uniquely determines which securities trade in
equilibrium. The junkier the securities offered into the fruit
bowl, the more desperate sellers would have to be (relative to the
buyers) in order for trade to occur. To determine the price at
which they trade, we would still need knowledge of, or an
assumption about, one of the discount factors. Instead of
arbitrarily fixing
) that uniquely determines which securities trade in
equilibrium. The junkier the securities offered into the fruit
bowl, the more desperate sellers would have to be (relative to the
buyers) in order for trade to occur. To determine the price at
which they trade, we would still need knowledge of, or an
assumption about, one of the discount factors. Instead of
arbitrarily fixing ![]() and examining the
resulting equilibria, we ask the following question: given the
distribution of intrinsic values in our data, how desperate do the
sellers have to be in order for there to be trade under asymmetric
information? More specifically, we will search for
and examining the
resulting equilibria, we ask the following question: given the
distribution of intrinsic values in our data, how desperate do the
sellers have to be in order for there to be trade under asymmetric
information? More specifically, we will search for ![]() , which is the maximum value of
, which is the maximum value of ![]() at which meaningful trades occur. The minimum haircut
that sellers would be willing to take on the intrinsic value of
their securities for meaningful trades to occur is therefore
at which meaningful trades occur. The minimum haircut
that sellers would be willing to take on the intrinsic value of
their securities for meaningful trades to occur is therefore
![]() .
.
We first consider trading under asymmetric information in the
high grade, senior-AAA, early vintage CDOs, which were regarded as
relatively safe before July 2007. For these securities, our model
implies that they will only trade if the sellers' discount factor
is 0.64 or less, which is a hair-cut of at least 36 percent on the
intrinsic values of their securities. The left panel of Figure 6 illustrates
the graphical interpretation of the equilibrium when
![]() (the buyers discount is
fixed at
(the buyers discount is
fixed at ![]() ). At the equilibrium price
). At the equilibrium price ![]() the maximum value of
the maximum value of ![]() that sellers
will offer into the fruit bowl is
that sellers
will offer into the fruit bowl is
![]() . As indicated by the
grey-shaded bars in the bottom part of the panel, those securities
having intrinsic values greater than 70 will not trade. Holders who
did not sell would rightfully feel aggrieved if the market assigns
a value of 45 to their securities which are all worth more than
70.
. As indicated by the
grey-shaded bars in the bottom part of the panel, those securities
having intrinsic values greater than 70 will not trade. Holders who
did not sell would rightfully feel aggrieved if the market assigns
a value of 45 to their securities which are all worth more than
70.
The mezzanine, senior-AAA, early vintage CDOs in our sample
experienced the lowest losses of all categories. The average
intrinsic value for this group is 84.5. For these CDOs, trade can
occur under asymmetric information as long as the sellers discount
factor is no higher than 0.87, which implies a minimum haircut of
13 percent. The resulting equilibrium when
![]() is shown in the right
panel of Figure 6. Although this
equilibrium results in some meaningful trade, only 4 of the 126
securities trade. If
is shown in the right
panel of Figure 6. Although this
equilibrium results in some meaningful trade, only 4 of the 126
securities trade. If
![]() , that is, if the sellers
were willing to incur a haircut of 24 percent, then all securities
would trade at an equilibrium price of
, that is, if the sellers
were willing to incur a haircut of 24 percent, then all securities
would trade at an equilibrium price of ![]() .
.
There are many more absolute lemons in the market for late
vintage CDOs- which puts more mass in the far left tail of the
distribution of values and imparts more "damaging" dispersion to
the distribution. This implies that sellers would have to be more
desperate to sell these securities (lower ![]() ) in
order for there to be meaningful trades. For example, meaningful
trades only occur for the high-grade, senior-AAA, late vintage CDOs
when the sellers' discount factor is 0.42 or less, which would
imply a haircut of at least 58 percent. The resulting equilibrium
with
) in
order for there to be meaningful trades. For example, meaningful
trades only occur for the high-grade, senior-AAA, late vintage CDOs
when the sellers' discount factor is 0.42 or less, which would
imply a haircut of at least 58 percent. The resulting equilibrium
with
![]() is shown in the left
panel of Figure 7. Only securities
with
is shown in the left
panel of Figure 7. Only securities
with ![]() are offered into the fruit bowl and
traded, at a price
are offered into the fruit bowl and
traded, at a price ![]() . For the mezzanine,
senior-AAA, late vintage CDOs, there are so many lemons that
meaningful trades only occur when the sellers' discount is 0.29 or
smaller (a haircut of at least 71 percent). As shown in the right
panel of Figure 7, the resulting
equilibrium with
. For the mezzanine,
senior-AAA, late vintage CDOs, there are so many lemons that
meaningful trades only occur when the sellers' discount is 0.29 or
smaller (a haircut of at least 71 percent). As shown in the right
panel of Figure 7, the resulting
equilibrium with
![]() is such that everything
trades. This is a knife-edge equilibrium in the sense that raising
the sellers discount by a smidgen would result in no trades.
is such that everything
trades. This is a knife-edge equilibrium in the sense that raising
the sellers discount by a smidgen would result in no trades.
Table 5 shows
the maximum sellers' discount at which meaningful trades occur
(![]() ) for each of the CDO categories.
) for each of the CDO categories.
![]() is only above 0.50 for the high
grade and mezzanine, Sr-AAA, early vintage categories. For all
other categories,
is only above 0.50 for the high
grade and mezzanine, Sr-AAA, early vintage categories. For all
other categories, ![]() is below 0.5,
implying that trading in these securities would only occur if
sellers would be willing to accept a haircut of at least 50
percent.
is below 0.5,
implying that trading in these securities would only occur if
sellers would be willing to accept a haircut of at least 50
percent.
All told, given the distribution of intrinsic values of CDOs, our model implies that unless the sellers were extremely desperate to rid themselves of these securities, only the highest rated, early vintage CDOs would trade under asymmetric information. If trading did take place for the late vintage and less senior securities, our model would predict that these securities would have traded at prices well below their intrinsic values. Both of these findings are consistent with the sharp decline in secondary market activity for ABS CDOs that took place in the second half of 2007, and the earlier-cited IOSCO survey response that "the hold-to-maturity value of many structured finance products exceeds the value that could be attained in the current secondary market." In our view, the downgrades of hundreds of subprime mortgage backed securities on July 10, 2007 by Moody's and S&P was a wake-up call to investors who learned that there were potentially many lemons among the CDOs. The sudden realization about the presence of lemons in the CDO market came at a time when neither the ratings nor the copula models being used to value CDOs could be trusted. Buyers and sellers learned that the only way to accurately value a CDO was by building machinery to value its underlying assets using loan-level data, in much the same way it was done for the underlying RMBS bonds themselves. Because sellers had underwritten many of these CDOs, they had better knowledge of the underlying loans and recently issued RMBS bonds, and thus better understood their inherent risks. This introduced asymmetric information between buyers and sellers, which in turn, would explain why the market for ABS CDOs shut down. The severe losses suffered in the market combined with the way it was concentrated in the largest financial firms explain how this information, once revealed, could set off the Panic of 2007.
Before concluding, we should emphasize that it is not
necessarily the lack of information about the CDOs' intrinsic
values that shutter these markets; rather, it is the asymmetric
distribution of this information. For example, suppose the sellers
are as poorly informed as the buyers: They know the distribution of
intrinsic values within any label, but they do not know the
intrinsic values of the individual securities, including the ones
they hold. For now we also assume the buyers know the extent of the
sellers' ignorance, and that ![]() . In
this case, the risk neutral seller would value his securities at
the average intrinsic value of all securities within the label. As
such, any price at or above
. In
this case, the risk neutral seller would value his securities at
the average intrinsic value of all securities within the label. As
such, any price at or above
![]() will elicit all
securities for that label to be supplied to the fruit bowl. Since
buyers would be willing to pay anything less than
will elicit all
securities for that label to be supplied to the fruit bowl. Since
buyers would be willing to pay anything less than
![]() , which is above
, which is above
![]() , the entire stock of
securities would trade. Thus it is not the lack of information that
shutters the market, but the asymmetric distribution of that
information.
, the entire stock of
securities would trade. Thus it is not the lack of information that
shutters the market, but the asymmetric distribution of that
information.
Finally, we note that the possibility that the sellers are better informed than buyers is sufficient to shutter the market even if sellers are not actually better informed. Developing this fully is beyond the scope of this paper, but the argument is straightforward: If buyers fear (or place some probability on the possibility) that sellers know the intrinsic value of their individual securities, then the buyers will value a draw from the fruit bowl at some weighted average of (1) the average intrinsic value of all the securities for a given label-assuming sellers are ignorant of individual securities' values, and (2) the lower average value of what informed sellers would offer to the fruit bowl for a given price. Thus, if the weight attached to the possibility (2) that sellers are informed is high enough, the market will collapse, even if few or no sellers are in fact well informed.
7 Conclusion
The 2007-2008 financial crisis led to a freezing of CDO markets and a disconnect between market prices (for the few trades that did occur) and fundamentals. Home mortgages were securitized through a long chain of financial intermediaries, which culminated in the creation of CDOs. Many of the largest CDO dealers were fully integrated (doing originations, issuance of RMBS, issuance of CDOs, and, finally, servicing the mortgages), which gave them an informational advantage over potential buyers. Also, the complexity and opaqueness of these securities made it easy for asymmetric information to arise between current holders and potential buyers. We show how vertical integration, opacity, and complexity in the securitization process and the resulting asymmetric information between buyers and sellers could have amplified the stresses already present in CDO markets, by making these markets illiquid and dislodging prices from intrinsic values.
Using a novel dataset on the distribution of intrinsic values of structured finance ABS CDOs, we examine which securities would trade under asymmetric information. The likelihood of trade depends not only on the distribution of intrinsic values of the CDOs but also on the ratio between the sellers’ and buyers' discount factor. For the 4,865 CDOs in our sample, we find that the informational problems were so severe that most of the CDOs would not trade unless the sellers were willing to sell their securities at a very steep discount to their intrinsic values.
We take this as evidence that asymmetric information about the intrinsic values of the CDOs was sufficient to cause CDOs to stop trading and their prices to be well below what most holders valued them at. This is not to imply that asymmetric information was the only factor leading to the market's breakdown. Indeed there were likely many factors, the question we ask is if asymmetric information alone would be sufficient to cause this. The experiment is to give the potential buyers less information than current holders and determine the conditions under which there would be significant trade. Because we give the buyers perfect information about the distribution of the intrinsic values within relative narrow groups of securities, the experiment is rigged to favor a negative answer. That is, it is rigged to find that asymmetric information alone is not sufficient to shutter these markets. However, given the distribution of the CDO intrinsic values, we find that asymmetric information would be sufficient to close the markets. For a couple of labels we find trade even when sellers are not massively desperate for cash; their discount factors are greater than 0.5. But in these two cases only the junkiest of the securities trade. We therefore conclude that the information asymmetries were sufficient to shut down the CDO market. These securities are still not trading in any meaningful way and, if one buys our results, they may never.
Appendix A
This appendix summarizes the methodology used by CHW to value ABS CDOs. These CDO values are the intrinsic values used in our analysis. They are calculated as the liquidation value of the underlying ABS (mostly RMBS) collateral- the value that a CDO bondholder would receive if the CDO manager sold all the underlying ABS bonds and allocated the proceeds according to the CDO bondholders' positions in the waterfall structure. Valuing the 213 CDOs that were already liquidated as of March 2011 is fairly straightforward, since this involves simply summing up the actual principal payments made to the CDO bondholders as reported in the trustee's final liquidation report provided to Intex (or from other sources if it was not). Table 7 in CHW shows that the 213 liquidated SF CDO deals experienced losses of $162 billion, a loss rate of 78 percent.
For the 514 non-liquidated, or active, CDOs (as of March 2011), the idea is to compute the expected fair liquidation values of the still-active underlying ABS (mostly RMBS) collateral, and then feed these as recovery amounts into the CDO waterfall. The fair liquidation values of the underlying RMBS are, in turn, computed using realized and expected write-downs on the underlying mortgage loans and securities, computed from models described below. First, CHW determine that, of the original $432.6 billion original balance of CDO collateral, $75.9 billion in principal had already been paid back to the CDO bondholders, while $134.4 billion had already been written down as losses as of March 2011. This leaves $222.3 billion in ABS collateral backing the 514 still active CDOs.
The next step is to determine the fair liquidation value of this remaining $222.3 billion of CDO collateral by estimating expected losses, and then feeding these recovery values into the CDO waterfall to determine how much each ABS CDO bond recovers, and ultimately loses. Table 8 in CHW describes the methodologies used for valuing the 23,147 unique securities underlying these active CDOs. Roughly two-thirds are RMBS, which are backed by subprime, Alt-A and prime mortgages. These RMBS were valued using the proprietary prepayment, default, and loss models of Andrew Davidson & Company, a leading market modeling vendor, which is seamlessly integrated with the Intex cash flow engine for valuation and loss estimation.13 Each ABS collateral asset (or loan) contributes its fair value liquidation proceeds to the ABS deal, with the aggregate recovery amounts allocated in the Intex software to the various tranches of the ABS CDO deals according to the CDO waterfall.14 All told, CHW estimated $123 billion in expected write-downs stemming from these ABS bonds underlying the still active CDOs (on top of the $134.4 billion that had already been written down).
As of March 2011 the actual write downs of $162 billion for the 213 liquidated SF CDOs combined with $134 billion actual and $123 billion expected write-downs for the 514 still active SF CDOs sum up to a grand write-down total of $420 billion, 65 percent of the $641 billion of ABS of CDO issuance (Table 10 in CHW). While different valuation methods can be used to estimate ABS CDO losses, it is noteworthy that as of March 2011, 71 percent of the write-downs had already been realized. Of the remaining 29 percent of estimated write-downs ($123 billion), most came from still-active BBB- and A-rated subprime and alt-A RMBS securities that were trading at values at or new zero. Based on this, loss estimates will not likely vary much by the valuation method chosen.
References
Adrian, T., and H. S. Shin (2010): "Liquidity and leverage," Journal of Financial Intermediation, 19(3), 418-437.
Akerlof, G. A. (1970): "The Market for 'Lemons': Quality Uncertainty and the Market Mechanism," The Quarterly Journal of Economics, 84(3), 488-500.
Allen, F., and E. Carletti (2008): "The Role of Liquidity in Financial Crises," Working paper 08-33, Wharton Financial Institutions Center, University of Pennsylvania.
Arora, S., B. Barak, M. Brunnermeier, and R. Ge (2009): "Computational Complexity and Information Asymmetry in Financial Products," Working paper, Princeton University.
Bloomberg (2008): "CDO Market is Almost Frozen, J.P. Morgan, Merrill say," Feb.5, 2008, http://www. bloomberg.com/apps/news?sid=aCk0Qr1f2Eew&pid=newsarchive.
Bolton, P., T. Santos, and J. A. Scheinkman (2011): "Outside and Inside Liquidity," The Quarterly Journal of Economics, 126(1), 259-321.
Brunnermeier, M. K. (2009): "Deciphering the Liquidity and Credit Crunch 2007-2008," Journal of Economic Perspectives, 23(1), 77-100.
Caballero, R. J., and A. Simsek (2009): "Fire Sales in a Model of Complexity," NBER Working Papers 15479, National Bureau of Economic Research, Inc.
Calomiris, C. W. (2008): "The Subprime Turmoil: What's Old, What's New, and What's Next," Working paper, Columbia Business School.
Cordell, L., Y. Huang, and M. Williams (2012): "Collateral damage: Sizing and assessing the subprime CDO crisis," Working Papers 11-30, Federal Reserve Bank of Philadelphia.
Creditflux Ltd. (2009): "Creditflux tally of credit write-downs as of January 26, 2009," http://www.creditflux.com/Assets/Documents/Creditfluxwritedowns.xls.
DeMarzo, P., and D. Duffie (1999): "A Liquidity-Based Model of Security Design," Econometrica, 67(1), 65-100.
DeMarzo, P. M. (2005): "The Pooling and Tranching of Securities: A Model of Informed Intermediation," Review of Financial Studies, 18(1), 1-35.
Duffie, D., and N. Garleanu (2001): "Risk and valuation of collateralized debt obligations," Financial Analysts Journal, 57(1), 41-59.
Elizalde, A. (2006): "Credit Risk Models IV: Understanding and Pricing CDOs," Working Papers 2006-0608, CEMFI.
Financial Crisis Inquiry Commission (2011): "The Financial Crisis Inquiry Report," Public Affairs, New York, http://www.gpo.gov/fdsys/pkg/GPO-FCIC/pdf/GPO-FCIC.pdf.
Goodman, L. S., S. Li, D. J. Lucas, T. A. Zimmerman, and F. J. Fabozzi (2008): Subprime Mortgage Credit Derivatives. John Wiley & Sons, Inc.
Gorton, G. (2009): "Information, Liquidity, and the (Ongoing) Panic of 2007," American Economic Review, 99(2), 567-72.
Gorton, G., and A. Metrick (2012): "Securitized banking and the run on repo," Journal of Financial Economics, 104(3), 425-451.
Heitfield, E. (2010): "Lessons from the Crisis in Mortgage-Backed Structured Securities: Where Did Credit Ratings Go Wrong?," in Rethinking Risk Measurement and Reporting, ed. by K. Blocker, vol. 1. Risk Books, London.
IOSCO (2009): "Transparency of Structured Finance Products," Consultation report, International Organization of Securities Commissions.
Krishnamurthy, A. (2010): "How Debt Markets Have Malfunctioned in the Crisis," Journal of Economic Perspectives, 24(1), 3-28.
Lucas, D. J., L. S. Goodman, and F. J. Fabozzi (2006): Collateralized Debt Obligations, Structures and Analysis. John Wiley & Sons, Inc., second edn.
Moody's Investor Service (2000): "Moody's Approach to Rating Multisector CDOs," September 15, 2000; http://fcic-static.law.stanford.edu/cdn_media/fcic-docs/2000-09-15Moody'sApproachtoRatingMultisectorCDOs(Moody'sSpecialReport).pdf.
Moody's Investor Service (2007): "Moody's downgrades subprime first-lien RMBS," Jul 10, 2007.
New York Times (2007): "BNP Paribas suspends funds because of subprime problems," August 9, 2007, http://www.nytimes.com/2007/08/09/business/worldbusiness/09iht-09bnp.7054054.html.
Standard & Poor's (2007a): "612 U.S. Subprime RMBS Classes Put on NegativeWatch; Methodology Revisions Announced," Ratings Announcement: July 10, 2007.
Standard & Poor's (2007b): "Transcript from Standard & Poor's Structured Finance Call on July 10, 2007.," http://avenue-s.us/resources/StandardandPoor'sStructuredFinance.pdf.
Tavakoli, J. M. (2003): Collateralized Debt Obligations and Structured Finance, New Developments in Cash & Synthetic Securitization. John Wiley & Sons, Inc.
U.S. Department of Justice (2013): "United States of America, Plaintiff, v. McGraw-Hill Companies, Inc. and Standard & Poor's Financial Services LLC, Defendants. Case number CV13-00779.," http://www.justice.gov/iso/opa/resources/849201325104924250796.PDF.
U.S. Department of the Treasury (2009): "Public-Private Investment Program," March 23, 2009 White Paper.
Tables
Table 1
| Firm Type | ABS CDOs | Corp. Credit | RMBS | Other or Undefined | Total Write- downs |
|---|---|---|---|---|---|
| Insurers/asset managers | 61,074 | 6,320 | 10,386 | 3,8347 | 116,126 |
| North American banks | 84,319 | 23,702 | 42,272 | 59,011 | 209,305 |
| European banks | 63,464 | 18,579 | 26,423 | 62,634 | 171,100 |
| Asia/emerging market banks | 9,358 | 4,724 | 5,728 | 3,743 | 23,553 |
| Totals | 218,216 | 53,324 | 84,810 | 163,735 | 520,084 |
| Share of total writedowns | 42% | 10% | 16% | 32% | 100% |
Table 1: Crisis-Related ABS CDO writedowns through January 26, 2009 (in millions of dollars). Source: Creditflux Ltd. (2009). Based on publicly disclosed company information compiled by Creditflux Ltd. According to Creditflux, ABS CDO writedowns were no longer reported separately after February 2008. By this time, most rms had substantially written down their holdings.
Table 2
| CDO Dealers | Subprime RMBS Issuance | ABS CDO Issuance |
|---|---|---|
| Merrill Lynch | 76,747 | 91,767 |
| Citigroup | 54,032 | 70,552 |
| UBS Warburg | 20,024 | 65,409 |
| Goldman, Sachs & Co. | 52,727 | 59,103 |
| Credit Suisse First Boston | 99,081 | 38,209 |
| Deutsche Bank Securities | 59,635 | 37,362 |
| Wachovia Securities | 12,528 | 25,033 |
| RBS Greenwich Capital | 31,643 | 23,869 |
| Calyon Securities | 0 | 22,825 |
| Banc of America Securities | 28,524 | 22,617 |
| Barclays Capital | 33,812 | 21,424 |
| Lehman Brothers | 170,342 | 19,116 |
| Bear Stearns | 61,698 | 19,111 |
| Morgan Stanley | 121,289 | 14,237 |
| WestLB Securities | 0 | 12,125 |
| SG Corporate & Inv. Banking | 4,796 | 11,609 |
| Dresdner Kleinwort Wasserstein | 0 | 9,875 |
| JP Morgan | 53,628 | 7,584 |
| Totals | 880,507 | 57,1826 |
Table 2: CDO Dealers' Issuance of Subprime RMBS and ABS CDOs (in millions of dollars). Source: Intex Solutions, Inc.
Table 3
| CDO Dealers | Originators | Services | RMBS Shelves | Level of Integration |
|---|---|---|---|---|
| Merrill | First Franklin (2006, Ownit (2005) | Wilsire Credit, First Franklin (2006) | SURF, MLHEL, MLMI, MLFF, MLFF in 2007 | Full |
| Citigroup | CitiFinancial (2000), Argent (2007) | CitiMortgage, AMC Mtge. Services (2007) | Citigroup Mtge. Trust, Salomon Brother Mtge., Citifinancial Mtge., Citicorp Res. | Full |
| UBS | -- | -- | MASTR | Partial |
| Goldman Sachs | Southern Pacific (1999), Senderra Funding (2007) | Litton Servicing (2007) | GSABS, GSAMP | Partial |
| Credit Suisse | DLJ Mtge. (2000) | SPS (2004) | ABSHE, HEAT, HEMT, CSFB Mtge | Full |
| Deutsche Bank | Chapel Funding (2006), MortgageIT (2006) | Chapel Funding (2006) | ACE | Full |
| Wachovia | -- | -- | Wachovia Asset Securitization | Partial |
| RBS | -- | -- | SVHE | Partial |
| Calyon | -- | -- | -- | None |
| Bank of America | Countrywide (2008) | Countrywide (2008) | BAFC | Partial |
| Barclays | Equifirst (2007) | HomeEq(2006) | SABR, EquiFirst Loan Sec. Trust | Full |
| Lehman Brothers | BNC (2003), Aurora (2003), Finance America (2004), SIB Mtge. (2004), Preferred Mtge. (2004) | Aurora (2003) | SAIL, ARC, SASCO, SASC, BNC Mtge. Loan Trust, Finance America Mtge. Loan Trust | Full |
| Bear Stearns | Encore Credit (2007) | EMC | BSABS, EMC Mtge. Loan Trust, Encore Credit | Full |
| Morgan Stanley | Saxon (2006), CityMortgage (2006) | Saxon | MSAB, MSHE, MSDW, MS Mtge. Loan Trust | Full |
| WestLB | -- | -- | -- | None |
| SG Corporate | -- | -- | SG Mtge. Securities Trust | Partial |
| Dresdner | -- | -- | -- | None |
| JP Morgan | Chase Home Finance, WAMu (2008) | Chase Home Finance, WaMu (2008) | JPM Mtge. Acquisition Trust, CFLAT, CFAB | Full |
Table 3: CDO Dealer Vertical Integration of Subprime Securitization. Notes: The table shows the acquisition of subprime originators and servicers (along with dates where available), and lists names of RMBS issuance shelves run by each dealer. Sources: Intex for issuance volume, numerous industry sources for other data.
Table 4
| CDO category | N | Mean | Median | Max | Min | Std. Dev. |
|---|---|---|---|---|---|---|
| HG, Sr-AAA, early vintage | 56 | 66.3 | 67.8 | 100 | 0 | 25 |
| HG, Jr-AAA, early vintage | 67 | 28.9 | 0.8 | 100 | 0 | 38.4 |
| HG, AA/A, early vintage | 79 | 4.5 | 0 | 100 | 0 | 15.2 |
| HG, BBB, early vintage | 44 | 8.3 | 0.4 | 58.6 | 0 | 14 |
| HG, BB/B, early vintage | 9 | 0 | 0 | 0 | 0 | 0 |
| HG, NR, early vintage | 41 | 2.4 | 0 | 98.6 | 0 | 15.4 |
| HG, Sr-AAA, late vintage | 236 | 34.5 | 33.8 | 100 | 0 | 26.2 |
| HG, Jr-AAA, late vintage | 349 | 8.6 | 0 | 100 | 0 | 20.6 |
| HG, AA/A, late vintage | 412 | 1.7 | 0 | 100 | 0 | 9.2 |
| HG, BBB, late vintage | 178 | 1.8 | 0 | 100 | 0 | 10.7 |
| HG, BB/B, late vintage | 61 | 1.2 | 0 | 15.7 | 0 | 3.2 |
| HG, NR, late vintage | 185 | 1 | 0 | 100 | 0 | 8.7 |
| Mez, Sr-AAA, early vintage | 126 | 84.5 | 88.4 | 100 | 42.1 | 16.3 |
| Mez, Jr-AAA, early vintage | 184 | 55.2 | 68.2 | 100 | 0 | 42.8 |
| Mez, AA/A, early vintage | 254 | 18.4 | 0 | 100 | 0 | 34.6 |
| Mez, BBB, early vintage | 208 | 13.8 | 0 | 100 | 0 | 25.8 |
| Mez, BB/B, early vintage | 49 | 1.9 | 0 | 66.2 | 0 | 9.8 |
| Mez, NR, early vintage | 142 | 2.2 | 0 | 100 | 0 | 14 |
| Mez, Sr-AAA, late vintage | 316 | 32.4 | 19.1 | 100 | 0 | 34.1 |
| Mez, Jr-AAA, late vintage | 409 | 7.7 | 0 | 100 | 0 | 21.4 |
| Mez, AA/A, late vintage | 642 | 3.2 | 0 | 100 | 0 | 14.7 |
| Mez, BBB, late vintage | 398 | 4.1 | 0.2 | 100 | 0 | 12.8 |
| Mez, BB/B, late vintage | 133 | 4.4 | 0 | 100 | 0 | 12.2 |
| Mez, NR, late vintage | 287 | 1.5 | 0 | 100 | 0 | 11.8 |
Table 4: Summary statistics for distribution of intrinsic values by CDO type and vintage.
Table 5
| CDO category | Tmax | # of Secs with T > 0 | # of Secs with T > 0 Traded | P*/AT[A] | |
|---|---|---|---|---|---|
| HG, Sr-AAA, early vintage | 0.64 | 71 | 55 | 31 | 0.68 |
| HG, Jr-AAA, early vintage | 0.25 | 100 | 33 | 33 | 0.90 |
| HG, AA/A, early vintage | 0.10 | 22 | 15 | 13 | 0.51 |
| HG, BBB, early vintage | 0.22 | 15 | 21 | 15 | 0.42 |
| HG, BB/B, early vintage | 0 | 0 | 0 | 0 | n.a. |
| HG, NR, early vintage | 0.02 | 99 | 1 | 1 | 0.90 |
| HG, Sr-AAA, late vintage | 0.42 | 59 | 206 | 175 | 0.71 |
| HG, Jr-AAA, late vintage | 0.08 | 68 | 107 | 99 | 0.70 |
| HG, AA/A, late vintage | 0.03 | 41 | 57 | 54 | 0.71 |
| HG, BBB, late vintage | 0.01 | 100 | 26 | 26 | 0.90 |
| HG, BB/B, late vintage | 0.10 | 11 | 9 | 8 | 0.92 |
| HG, NR, late vintage | 0.01 | 100 | 3 | 3 | 0.90 |
| Mez, Sr-AAA, early vintage | 0.87 | 48 | 126 | 4 | 0.49 |
| Mez, Jr-AAA, early vintage | 0.50 | 100 | 137 | 137 | 0.90 |
| Mez, AA/A, early vintage | 0.16 | 100 | 82 | 82 | 0.90 |
| Mez, BBB, early vintage | 0.15 | 31 | 98 | 72 | 0.35 |
| Mez, BB/B, early vintage | 0.02 | 67 | 5 | 5 | 0.90 |
| Mez, NR, early vintage | 0.02 | 100 | 6 | 6 | 0.90 |
| Mez, Sr-AAA, late vintage | 0.29 | 100 | 251 | 251 | 0.90 |
| Mez, Jr-AAA, late vintage | 0.07 | 100 | 115 | 115 | 0.90 |
| Mez, AA/A, late vintage | 0.03 | 100 | 106 | 106 | 0.90 |
| Mez, BBB, late vintage | 0.06 | 36 | 167 | 161 | 0.63 |
| Mez, BB/B, late vintage | 0.06 | 56 | 48 | 47 | 0.80 |
| Mez, NR, late vintage | 0.01 | 100 | 7 | 7 | 0.90 |
Trading under asymmetric
information with ![]() .
. ![]() is
the maximum value of
is
the maximum value of ![]() for which meaningful
trades occur.
for which meaningful
trades occur. ![]() is the maximal value of
is the maximal value of
![]() that sellers will offer when given the
opportunity to sell securities at the equilibrium price
that sellers will offer when given the
opportunity to sell securities at the equilibrium price ![]() .
.
Figures
Figure 1
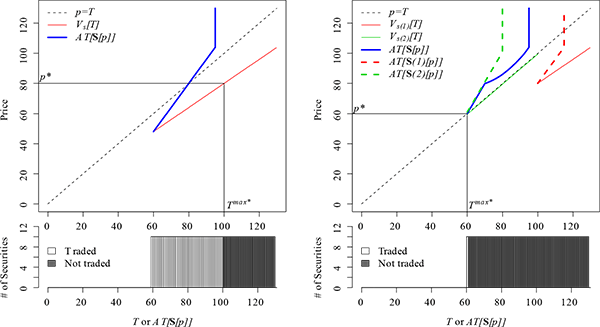
Figure 1: Trading when
securities are uniformly distributed between ![]() and
and ![]() . Left panel: Seller's discount
(
. Left panel: Seller's discount
(![]() ) is set to 0.8, and only some securities
will trade. Right panel: Second round of trading.
) is set to 0.8, and only some securities
will trade. Right panel: Second round of trading.
Figure 2
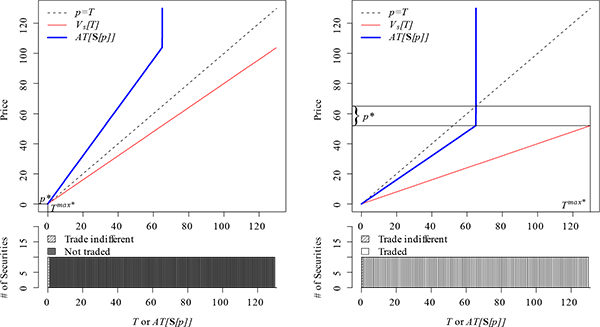
Figure 2: Trading when
securities are uniformly distributed between ![]() and
and ![]() . Left panel: Seller's discount
(
. Left panel: Seller's discount
(![]() ) is set to 0.8, and only securities with
) is set to 0.8, and only securities with
![]() will trade. Right panel:
will trade. Right panel: ![]() and all securities trade.
and all securities trade.
Figure 3
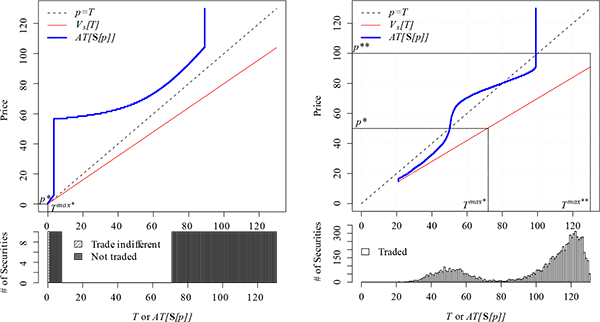
Figure 3: Left panel: A significant mass of payoffs close to zero can preclude all trade. Right panel: Multiple equilibria.
Figure 4
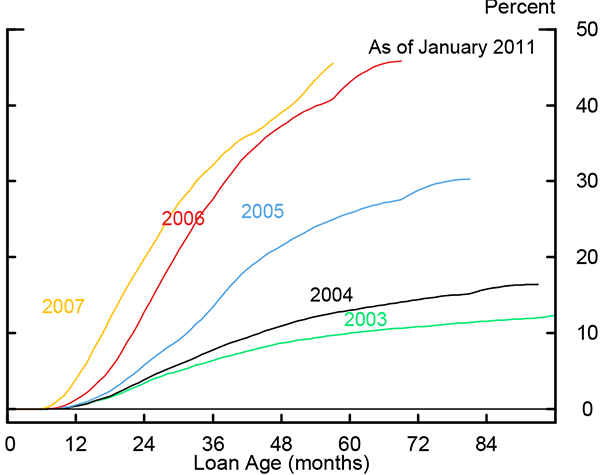
Figure 4: Cumulative defaults on subprime loans. Source: Federal Reserve Board calculations using CoreLogic data.
Figure 5
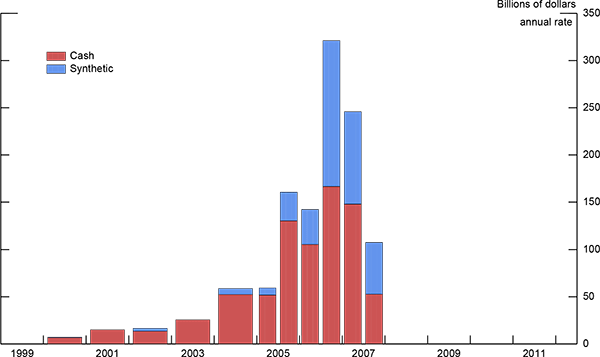
Figure 5: Issuance of publicly traded SF ABS CDOs. Source: Cordell, Huang, and Williams (2012).
Data for Figure 5: Issuance of publicly traded SF ABS CDOs
(Billions of dollars, annual rate)
| Year | Cash | Synthetic | Total |
|---|---|---|---|
| 1999 | 0 | - | 0 |
| 2000 | 6 | 1 | 7 |
| 2001 | 15 | - | 15 |
| 2002 | 13 | 3 | 16 |
| 2003 | 25 | - | 25 |
| 2004 | 52 | 6 | 59 |
| 2005H1 | 52 | 8 | 59 |
| 2005H2 | 130 | 31 | 161 |
| 2006H1 | 105 | 37 | 142 |
| 2006H2 | 167 | 155 | 321 |
| 2007H1 | 148 | 98 | 246 |
| 2007H2 | 52 | 55 | 107 |
| Total | 440 | 201 | 641 |
Figure 6
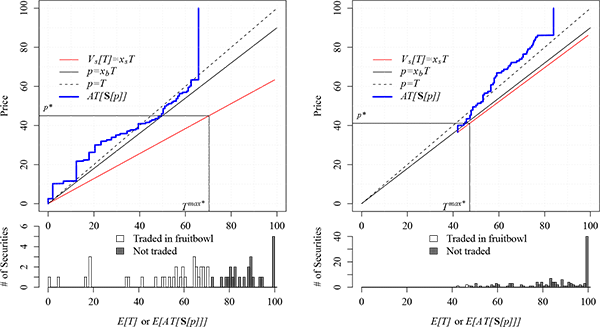
Figure 6: Trading of early
vintage Sr-AAA rated CDOs. Left panel: High grade CDOs, with
![]() . Right panel: Mezzanine CDOs, with
. Right panel: Mezzanine CDOs, with
![]()
Figure 7
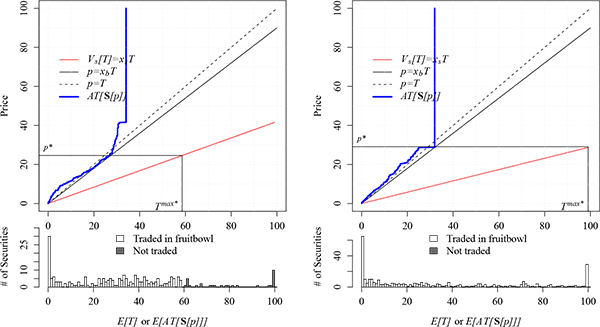
Figure 7: Trading of late
vintage Sr-AAA rated CDOs. Left panel: High grade CDOs, with
![]() . Right panel: Mezzanine CDOs, with
. Right panel: Mezzanine CDOs, with
![]()
Footnotes
1. Address for correspondence: 20th
and C St. NW, Mail Stop 42, Washington, DC 20551.
E-mail: [email protected]. Phone: +1(202)452-2244. FAX:
+1(202)263-4852. Return to
text
2. We thank Meredith Williams and Yilin Huang for providing us with crucial data, and Ronel Elul for discussing an earlier version of this paper at the Global Financial Crisis research workshop held at the Federal Reserve Board. We are also indebted to Gene Phillips, Gregory Feldberg, John Ammer, Neil Ericsson, and participants of the 2010 International Risk Management Conference in Florence, Italy, and International Atlantic Economic Society conference participants in Canada for their helpful comments. Michelle Welch, Grant Long, and Zachary Kurtz provided excellent research assistance. The views in this paper are solely the responsibility of the authors and should not be interpreted as reflecting the views of the Board of Governors of the Federal Reserve System or of any other person associated with the Federal Reserve System. Return to text
3. Counterparty risk could have been further intensified by the asymmetry of informationabout the true financial positions of borrowers (Calomiris (2008)). Return to text
4. In theory, securitization could ameliorate the effects of asymmetric information when the seller signals his private information regarding the quality of the assets underlying a CDO to the buyer by retaining the riskier junior tranche (DeMarzo (2005) and DeMarzo and Duffie (1999)). But in practice, CDO issuers typically retained the most senior tranche. And even if the issuer retained the junior tranche, there is no guarantee that he would not sell it later on, or keep it but short the tranche above it so that he actually profits when the CDO loses value, as happened with the correlation trades. Also, signaling would not fully ameliorate the lemon's problem when computational complexity makes it difficult to calculate a CDO's intrinsic value (Arora, Barak, Brunnermeier, and Ge (2009)) Return to text
5. 628 of the 727 CDOs in the Cordell, Huang, and Williams (2012) data had at least some CDOs as collateral, so they define a CDO-squared as having at least 50 percent of the total deal collateral as CDOs. Return to text
6. As shown in Table 5 of Cordell, Huang, and Williams (2012), two-thirds of BBB- and AA-rated CDO tranches were recycled into other CDOs and CDO-squareds. The correlation trade was executed by buying the equity tranche of a CDO and hedging it by shorting other tranches, mainly the lower-rated tranches of the CDOs. See Financial Crisis Inquiry Commission (2011), p. 192 for a discussion. Return to text
7. For a discussion of the copula framework used by the rating agencies and others, see Duffie and Garleanu (2001), Moody's Investor Service (2000), and Elizalde (2006). Return to text
8. On Feb. 4, 2013, the U.S. Department of Justice filed a law suit against S&P alleging that S&P "devised, participated in, and executed a scheme to defraud investors in RMBS and CDO tranches... to obtain money from these investors by means of material false and fraudulent pretenses, representations, and promises, and the concealment of material facts." U.S. Department of Justice (2013) Return to text
9. Most subprime RMBS deals use an excess spread/overcollateralization (ES/OC) structure to protect investors against losses on the underlying loans. Excess spread (ES) is the difference between the average rate on the loans securitized in the deal and the rate on the RMBS bonds issued from the securitization. Overcollateralization (OC) provides an additional buffer against losses. The lower-rated tranches will begin incurring losses only after the ES and OC are exhausted. At three years, a trigger test is performed to evaluate if the deal is performing well. If the deal passes this trigger test, some of the OC can be released to pay down principal. Return to text
10. We will stick with tradition and frame this in terms of expectations. However, in the current setup there will be no uncertainty about the securities traded, so it is just as natural to think of this as the mean or average value of the securities traded rather than the expected value of a draw from the portfolio. Return to text
11. Although buyers do not know the intrinsic values of the individual securities, there is no winner's curse in our setup because all buyers value the bundle of securities offered into the fruit bowl equally, based on their perfect knowledge of the distribution of the intrinsic values and their knowledge of the sellers' discount factor. Return to text
12. Since all the securities with a value
of ![]() were traded in the first round, and they
are now held by agents with identical discount factor
were traded in the first round, and they
are now held by agents with identical discount factor ![]() , there are no gains to be had for these holders to trade
the securities among themselves. Return
to text
, there are no gains to be had for these holders to trade
the securities among themselves. Return
to text
13. See http://www.ad-co.com/ .The advantage of using a leading market vendor is that their fair values are good representations of what investors will pay in the market for these RMBS securities. Return to text
14. For CDOs that have other CDOs as collateral, CHW first compute the fair liquidation values of the underlying CDOs, and then feed these values together with those of all other assets in the CDO's portfolio into the CDO's waterfall to determine the tranche payoffs. Return to text
This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to text