
Board of Governors of the Federal Reserve System
International Finance Discussion Papers
Number 897, June 2007--- Screen Reader
Version*
Oil Shocks and External Adjustment
NOTE: International Finance Discussion Papers are preliminary materials circulated to stimulate discussion and critical comment. References in publications to International Finance Discussion Papers (other than an acknowledgment that the writer has had access to unpublished material) should be cleared with the author or authors. Recent IFDPs are available on the Web at http://www.federalreserve.gov/pubs/ifdp/. This paper can be downloaded without charge from the Social Science Research Network electronic library at http://www.ssrn.com/.
Abstract:
This paper investigates how oil price shocks affect the trade balance and terms of trade in a two country DSGE model. We show that the response of the external sector depends critically on the structure of financial market risk-sharing. Under incomplete markets, higher oil prices reduce the relative wealth of an oil-importing country, and induce its nonoil terms of trade to deteriorate, and its nonoil trade balance to improve. The magnitude of the nonoil terms of trade response hinges on structural parameters that affect the divergence in wealth effects across oil importers and exporters, including the elasticity of substitution between oil and other inputs in production, and the discount factor. By contrast, cross-country wealth differences effectively disappear under complete markets, with the implication that oil shocks have essentially no effect on the nonoil terms of trade or the nonoil trade balance.
Keywords:oil-price shocks, trade, DSGE models
JEL classification:F32, F41
1 Introduction
The tripling of world oil prices over the past few years has stimulated renewed interest in the macroeconomic consequences of oil price shocks. Understandably, much attention has focused on the implications of oil price changes for domestic output and prices.1 However, from an open economy perspective, it is also of interest to identify the channels through which oil price shocks affect trade and the real exchange rate. Such questions seem particularly relevant in recent years, as oil prices have escalated against the backdrop of a large and persistent U.S. trade deficit.2
An additional reason for analyzing oil price shocks is that they may generate large shifts in purchasing power between oil-exporting and oil-importing countries. Because the magnitude of such wealth effects depends on the availability of risk-sharing arrangements across countries, studying oil shocks is useful in assessing how alternative financial market structures may influence macroeconomic outcomes. While this has been an important issue in the academic literature since the influential work of [Cole and Obstfeld 1991], the literature is somewhat ambiguous about whether differences in financial market structure have pronounced effects. This ambiguity may reflect a nearly exclusive focus on technology shocks, which may generate smaller wealth differences across countries than plausibly-calibrated oil price shocks.3
In this paper, we investigate how a rise in oil prices affects trade and the real exchange rate in the context of a two country DSGE model. In the spirit of a large empirical and theoretical literature, our simulations focus on a permanent rise in the relative price of oil that is induced by an adverse supply shock in the oil-exporting country; however, our key conclusions about trade and the exchange rate are not sensitive to this particular characterization of the oil supply shock, and in fact continue to hold even for a price hike generated by a rise in foreign oil demand (i.e, an oil-specific demand shock in our model).4 Our general equilibrium framework is useful in identifying structural features of the economy that influence the response of trade and the exchange rate to the oil shock. Moreover, it provides a natural framework for assessing the implications of the two alternative financial market structures of complete and incomplete markets that are often contrasted in the literature.
Our modeling framework builds on the open economy DSGE model of [Backus and Crucini 1998]. In our model, each country produces a distinct tradable output good which is used as an input into the production of consumption and investment goods both at home and abroad. Oil serves as an input into the production of the domestic tradable good, and also enters directly into the household consumption bundle (with each production function having a constant elasticity of substitution form). One country is an oil-importer, reflecting its relatively low endowment of energy, while the other is an oil-exporter.
We generalize the Backus and Crucini model by allowing for convex costs of adjusting the share of oil used in production and consumption. Adjustment costs provide a tractable way of capturing the putty-clay nature of oil demand (see [Atkeson and Kehoe 1999] and [Wei 2003]), and allow our model to account for the substantial wedge between the short and long-run elasticity of oil demand that appears to be a robust finding of the empirical literature. Finally, we depart from the complete markets framework of Backus and Crucini insofar as we assume that financial markets are incomplete across national borders in our benchmark specification.5
With incomplete financial markets, we find that the effects of the permanent oil price hike on the nonoil terms of trade and the overall trade balance depend on the divergence in wealth effects between the oil-importing and oil-exporting country blocks. Under our benchmark calibration, the oil importing country experiences a highly persistent deterioration in the oil component of its trade balance. The only way for the oil-importer to satisfy its intertemporal trade balance condition is for its nonoil component to improve by a sufficient amount, which requires some initial worsening of its nonoil terms of trade (or real exchange rate, as the latter adjusts proportionately).
Several structural factors play a key role in determining the relative wealth effects across countries by influencing the magnitude of transfers from oil-importers to exporters, their persistence, and how they are discounted. Notably, a low time-path of the oil price elasticity of demand implies that the oil importer runs more persistent deficits on the oil component of its trade balance, while the oil-exporter experiences a more persistent revenue windfall. This magnifies the difference in wealth effects across countries, and hence requires a much larger depreciation of the oil-importer's nonoil terms of trade in order to satisfy the intertemporal current account balance condition. Moreover, we show that the depreciation is larger when the steady state real interest rate is higher, and the oil importer has a smaller oil endowment.
We proceed to show that the responses of the trade balance and nonoil terms of trade are dramatically different under complete markets. In response to an oil price hike, the oil importer receives an insurance transfer that enables it to satisfy its intertemporal current account balance constraint without having to run an eventual nonoil trade surplus. Thus, oil shocks have essentially no effect on the nonoil terms of trade or nonoil trade balance. In addition, the structural parameters identified above as markedly affecting cross-country wealth effects under incomplete markets have basically no impact on the nonoil terms of trade or the nonoil balance.
We conclude by conducting sensitivity analysis to the particular type of oil price shock assumed, and to our benchmark assumption that wages and prices are fully flexible. While our benchmark model assumes that the adverse supply shock pushes up the oil price permanently - under the assumption that the foreign exporter reduces supply enough to support the higher price - our conclusions are unchanged under the assumption that the oil price rises endogenously in response to an exogenous contraction in foreign oil supply. Moreover, a taste-driven rise in foreign oil demand that induces a comparable rise in the oil price as the adverse supply shock has similar effects on the trade responses of the home country (as well as on other variables). Thus, our analysis suggests that only the path of the oil price is relevant to the home country, provided that the oil price hike is generated by a foreign supply or demand disturbance that is specific to the oil market. Finally, we show that although nominal rigidities in prices and wages affect the path of domestic absorption in the short-run, their inclusion has little consequence for the trade and nonoil terms of trade responses that are our principal focus.
The remainder of the paper is organized as follows. Section 2 describes our benchmark model, and Section 3 the calibration. Section 4 provides simulation results for our benchmark model under incomplete markets, while Section 5 considers complete markets. Section 6 assesses the sensitivity of our results to alternative types of oil price shocks, and Section 7 to the inclusion of nominal rigidities. Section 8 concludes.
2 Model Description
2.1 Model Overview
Our model is comprised of two countries, a home country (calibrated based on U.S. data) and a foreign country (rest-of-the-world). The structure of each country block is symmetric, although our calibration allows for differences in population size and in the per capita oil endowment. Each country specializes in the production of a final good that is an imperfect substitute for the final good produced in the other country. Production requires capital, labor, and oil. The consumption bundle entering the household utility function depends on consumption of the domestically-produced good, on imports of the foreign good, and oil. However, it is convenient for expositional purposes to assume that this composite consumption bundle is simply produced by a competitive distribution sector (with a productive structure that mirrors household preferences over the three goods). While asset markets are complete at the country level, we assume that asset markets are incomplete internationally. Finally, both the United States and foreign country are endowed with a non-storable flow supply of oil each period.
2.2 Households
The utility functional of a typical member of household
![]() is
is
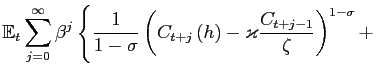
|
||
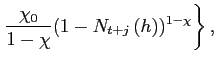
|
(1) |
where the discount factor
Each member of household ![]() faces a flow budget
constraint in period
faces a flow budget
constraint in period ![]() which states that his
combined expenditure on goods and on the net accumulation of
financial assets must equal his disposable income:
which states that his
combined expenditure on goods and on the net accumulation of
financial assets must equal his disposable income:
![\begin{displaymath}\begin{array}[c]{c} P_{Ct}C_{t}\left( h\right) +P_{It}I_{t}\left( h\right) + \frac{e_{t} P_{Bt}^{\ast}B_{Ft+1}(h)}{\phi_{Bt}}-e_{t}B_{Ft}(h)\\ =W_{t}\left( h\right) N_{t}\left( h\right) + R_{Kt}K_{t}(h) +\Gamma _{t}\left( h\right) +T_{t}\left( h\right) -P_{Dt}\phi_{It}(h). \end{array}\end{displaymath}](img19.gif)
|
(2) |
Final consumption goods are purchased at the price ![]() and final investment goods at the price
and final investment goods at the price ![]() Investment in physical capital augments the per
capita capital stock
Investment in physical capital augments the per
capita capital stock
![]() according to a linear transition
law of the form:
according to a linear transition
law of the form:
| (3) |
where ![]() is the depreciation rate of capital.
is the depreciation rate of capital.
Households accumulate financial assets by purchasing
state-contingent domestic bonds, and a non state-contingent foreign
bond (given the representative agent structure, we omit terms
involving the former from the household's budget constraint). Thus,
the term
![]() in the budget constraint
represents the quantity of the non-state contingent bond purchased
by a typical member of household
in the budget constraint
represents the quantity of the non-state contingent bond purchased
by a typical member of household ![]() at time
at time ![]() that pays one unit of the foreign unit of account in the
subsequent period,
that pays one unit of the foreign unit of account in the
subsequent period,
![]() is the price of the bond in the
foreign unit of account, and
is the price of the bond in the
foreign unit of account, and ![]() is the exchange
rate expressed in terms of the home unit of account relative to the
foreign unit of account. To ensure that net foreign assets are
stationary, we follow [Turnovsky 1985] and assume there is an
intermediation cost
is the exchange
rate expressed in terms of the home unit of account relative to the
foreign unit of account. To ensure that net foreign assets are
stationary, we follow [Turnovsky 1985] and assume there is an
intermediation cost ![]() paid by households
in the home country for purchases of foreign bonds. Specifically,
the intermediation cost depends on the ratio of economy-wide
holdings of net foreign assets to nominal output and is given
by:
paid by households
in the home country for purchases of foreign bonds. Specifically,
the intermediation cost depends on the ratio of economy-wide
holdings of net foreign assets to nominal output and is given
by:
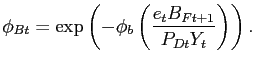
|
(4) |
If the home economy has an overall net lender position internationally, then a household will earn a lower return on any holdings of foreign bonds. By contrast, if the economy has a net debtor position, a household will pay a higher return on any foreign debt.
Each member of household ![]() earns labor income
earns labor income
![]() and capital income
and capital income
![]() . Each member also receives an
aliquot share
. Each member also receives an
aliquot share
![]() of firm profits,
and receives net transfers of
of firm profits,
and receives net transfers of ![]() . Finally, as
in [Christiano et al. 2005], it is costly to change the level
of gross investment from the previous period, so that the
acceleration in the capital stock is penalized:
. Finally, as
in [Christiano et al. 2005], it is costly to change the level
of gross investment from the previous period, so that the
acceleration in the capital stock is penalized:
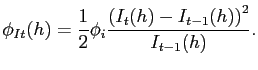
|
(5) |
Because this cost is measured in units of the domestically-produced good
In every period ![]() , household
, household ![]() maximizes the utility functional (1) with respect to its consumption, labor
supply, investment, (end-of-period) capital stock, and holdings of
foreign bonds, subject to its budget constraint (2), and the transition equation for capital
(3). In doing so, a household takes as
given prices, wages, net transfers, and aggregate quantities such
as lagged aggregate consumption.
maximizes the utility functional (1) with respect to its consumption, labor
supply, investment, (end-of-period) capital stock, and holdings of
foreign bonds, subject to its budget constraint (2), and the transition equation for capital
(3). In doing so, a household takes as
given prices, wages, net transfers, and aggregate quantities such
as lagged aggregate consumption.
2.3 Firms and Production
Each country produces a single distinct nonoil output good. Focusing on the home country, this output good is produced by perfectly competitive firms according to a constant-returns-to-scale technology. The representative firm's technology can be characterized as a nested constant-elasticity of substitution (CES) specification of the form:
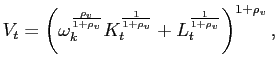
|
(6) |
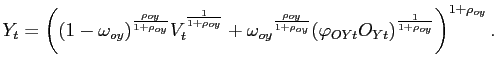
|
(7) |
Each producer utilizes capital and labor services, ![]() and
and ![]() , to make a ``value-added" input
, to make a ``value-added" input
![]() . This composite input is combined with
oil
. This composite input is combined with
oil ![]() to produce the domestic output good
to produce the domestic output good
![]() . The factor
. The factor
![]() reflects costs of adjusting the
oil intensity of the final output good, and is assumed to take the
following quadratic form:
reflects costs of adjusting the
oil intensity of the final output good, and is assumed to take the
following quadratic form:
![$\displaystyle \varphi_{OYt}=\left[ 1-\frac{\varphi_{oy}}{2} \left( \frac{\frac{O_{Yt} }{V_{t}}}{\frac{O^{A}_{Yt-1}}{V^{A}_{t-1}}}-1\right) ^{2}\right] ,$](img49.gif)
|
(8) |
where
![]() and
and
![]() denote oil inputs and value added
aggregated over all firms. From an aggregate perspective, this
specification allows for oil use to respond quickly to gross
domestic output, while potentially allowing for very slow
adjustment to relative price changes.6
denote oil inputs and value added
aggregated over all firms. From an aggregate perspective, this
specification allows for oil use to respond quickly to gross
domestic output, while potentially allowing for very slow
adjustment to relative price changes.6
Given the presence of adjustment costs, the representative
producer can be regarded as choosing a contingency plan for
![]() ,
, ![]() , and
, and
![]() that minimizes the discounted expected
cost of producing the domestic output good subject to equations
(6)-(8). In solving
this problem, the producer takes as given the rental price of
capital
that minimizes the discounted expected
cost of producing the domestic output good subject to equations
(6)-(8). In solving
this problem, the producer takes as given the rental price of
capital ![]() , the wage
, the wage ![]() , and the
after-tax price of oil
, and the
after-tax price of oil
![]() . The relation between the
after-tax oil price and pre-tax price
. The relation between the
after-tax oil price and pre-tax price ![]() can be
expressed:
can be
expressed:
| (9) |
where
Production of Consumption and Investment Goods
The consumption basket ![]() that enters the
household's budget constraint can be regarded as produced by
perfectly competitive consumption distributors. These distributors
purchase a nonoil consumption good
that enters the
household's budget constraint can be regarded as produced by
perfectly competitive consumption distributors. These distributors
purchase a nonoil consumption good ![]() (described below) and oil
(described below) and oil ![]() as inputs in
perfectly competitive input markets, and produce the composite
consumption good according to a CES production function:
as inputs in
perfectly competitive input markets, and produce the composite
consumption good according to a CES production function:
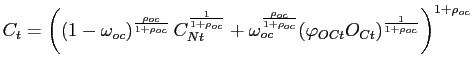
|
(10) |
where the quasi-share parameter
![]() determines the importance of oil
purchases in the household's composite consumption bundle, and the
parameter
determines the importance of oil
purchases in the household's composite consumption bundle, and the
parameter ![]() determines the long-run price
elasticity of demand for oil. The form of the production function
mirrors the preferences of households over consumption of nonoil
goods and oil. The term
determines the long-run price
elasticity of demand for oil. The form of the production function
mirrors the preferences of households over consumption of nonoil
goods and oil. The term
![]() captures costs of adjusting oil
consumption (at the household level), and is assumed to have the
quadratic form:
captures costs of adjusting oil
consumption (at the household level), and is assumed to have the
quadratic form:
![$\displaystyle \varphi_{OCt}=\left[ 1-\frac{\varphi_{oc}}{2}\left( \frac{\frac{O_{Ct} }{C_{Nt}}}{\frac{O^{A}_{Ct-1}}{C^{A}_{Nt-1}}}-1\right) ^{2}\right] ,$](img71.gif)
|
(11) |
where
Thus, households are similar to firms in that they adjust their
oil demand slowly in response to changes in the relative price of
oil. As in the case of firms, the presence of adjustment costs
implies that the consumption distributors must solve a dynamic
problem of choosing a contingency path for their inputs ![]() and
and ![]() so as to minimize their
discounted expected costs of producing the consumption bundle,
taking as given (after-tax) input prices
so as to minimize their
discounted expected costs of producing the consumption bundle,
taking as given (after-tax) input prices ![]() and
and
![]() , respectively (n.b., the
after-tax price of oil is assumed to be the same for households and
firms). The Lagrangian multiplier from this cost-minimization
problem determines the price of the consumption bundle they charge
to households, i.e.,
, respectively (n.b., the
after-tax price of oil is assumed to be the same for households and
firms). The Lagrangian multiplier from this cost-minimization
problem determines the price of the consumption bundle they charge
to households, i.e., ![]() in the household's
budget constraint given in equation (2).
in the household's
budget constraint given in equation (2).
Similarly, it is also convenient to regard the nonoil
consumption good ![]() and investment good
and investment good
![]() as produced by perfectly competitive
distributors. Both the domestically-produced good and the foreign
(nonoil) good are utilized as inputs, though we allow for the
proportion of each input to differ between nonoil consumption and
investment goods. Thus, the production function for the nonoil
consumption good
as produced by perfectly competitive
distributors. Both the domestically-produced good and the foreign
(nonoil) good are utilized as inputs, though we allow for the
proportion of each input to differ between nonoil consumption and
investment goods. Thus, the production function for the nonoil
consumption good ![]() is given by:
is given by:
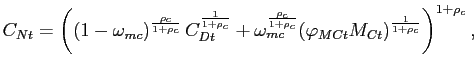
|
(12) |
where ![]() denotes the quantity of
domestically-produced goods used as inputs by the representative
nonoil consumption distributor (purchased at a price of
denotes the quantity of
domestically-produced goods used as inputs by the representative
nonoil consumption distributor (purchased at a price of ![]() ),
), ![]() denotes imports of the foreign
good (purchased at a price of
denotes imports of the foreign
good (purchased at a price of ![]() ), and
), and
![]() represents a cost of adjusting
imports. This adjustment cost takes a quadratic form:
represents a cost of adjusting
imports. This adjustment cost takes a quadratic form:
![$\displaystyle \varphi_{MCt}=\left[ 1-\frac{\varphi_{mc}}{2}\left( \frac{\frac{M_{Ct} }{C_{Dt}}}{\frac{M^{A}_{Ct-1}}{C^{A}_{Dt-1}}}-1\right) ^{2}\right] ,$](img88.gif)
|
(13) |
where
![]() and
and
![]() denote (nonoil) goods
consumption imports and domestic consumption inputs aggregated over
all households. The Lagrangian multiplier from the
cost-minimization problem for the distributors determines the price
of the nonoil consumption good
denote (nonoil) goods
consumption imports and domestic consumption inputs aggregated over
all households. The Lagrangian multiplier from the
cost-minimization problem for the distributors determines the price
of the nonoil consumption good ![]() .
.
The adjustment cost specification in equation (13) allows the level of imports to jump costlessly in response to changes in overall consumption or investment demand but makes the import share of either consumption or investment goods less responsive in the short-run than in the long run to changes in the relative price of imports. As a result, movements in the relative price of imports that are induced by oil price innovations will affect the nonoil goods demand only gradually. Nevertheless, our calibration will imply a faster reaction of goods trade relative to the oil trade.
Finally, the production function for investment goods is
isomorphic to that given in equation (12),
though allowing for possible differences in the import intensity of
investment goods (determined by
![]() , akin to
, akin to
![]() in equation (12)), the degree of substitutibility between nonoil
imports and domestically-produced goods in producing investment
goods (determined by
in equation (12)), the degree of substitutibility between nonoil
imports and domestically-produced goods in producing investment
goods (determined by ![]() ), and the parameter
determining import adjustment costs
), and the parameter
determining import adjustment costs
![]() . As expected, the presence of
adjustment costs means that nonoil consumption and investment goods
distributors must solve a dynamic cost minimization problem (with
the Lagrangian from the problem facing investment distributors
determining the price of new investment goods
. As expected, the presence of
adjustment costs means that nonoil consumption and investment goods
distributors must solve a dynamic cost minimization problem (with
the Lagrangian from the problem facing investment distributors
determining the price of new investment goods ![]() that appears in the household's budget
constraint).7
that appears in the household's budget
constraint).7
2.4 The Oil Market
We assume that the home country is simply endowed with an
exogenous flow supply of oil each period of ![]() . In
our benchmark model, we assume that the pre-tax price of oil
relative to the domestic output good
. In
our benchmark model, we assume that the pre-tax price of oil
relative to the domestic output good ![]() is
determined by an exogenous stochastic process. With both domestic
oil supply and the oil price determined exogenously, foreign oil
production
is
determined by an exogenous stochastic process. With both domestic
oil supply and the oil price determined exogenously, foreign oil
production
![]() must adjust endogenously to clear
the world oil market:
must adjust endogenously to clear
the world oil market:
| (14) |
Thus, the sum of the home and foreign oil production equals the sum of home and foreign consumption (by firms and households). The relative price of oil is assumed to follow a simple AR(1) of the form:
| (15) |
The persistence parameter ![]() is set
arbitrarily close to one, so that the log of the relative price of
oil effectively follows a random walk.
is set
arbitrarily close to one, so that the log of the relative price of
oil effectively follows a random walk.
In Section 6, we conduct sensitivity analysis in an alternative
framework in which the oil price is determined endogenously to
equate supply and demand in the world oil market. In this case, the
foreign production level
![]() in equation (14) is assumed to follow an exogenous
stochastic process (as discussed below, an AR(1) in the growth
rate).
in equation (14) is assumed to follow an exogenous
stochastic process (as discussed below, an AR(1) in the growth
rate).
2.5 Fiscal Policy
We assume that a fixed share ![]() of the domestic
output good
of the domestic
output good ![]() is purchased by the government
(n.b., the import content of government purchases is zero). These
government purchases
is purchased by the government
(n.b., the import content of government purchases is zero). These
government purchases ![]() have no direct effect
on household utility. Given the Ricardian structure of our model,
we assume that net lump-sum transfers
have no direct effect
on household utility. Given the Ricardian structure of our model,
we assume that net lump-sum transfers ![]() are
adjusted each period to balance the government receipts and
revenues, so that:
are
adjusted each period to balance the government receipts and
revenues, so that:
| (16) |
2.6 Resource Constraints for Nonoil Goods, and Net Foreign Assets
The resource constraint for the nonoil goods sector of the home economy can be written as:
| (17) |
recalling that ![]() denotes the home country's
exports, and
denotes the home country's
exports, and ![]() resources that are lost due to
costs of adjusting investment.
resources that are lost due to
costs of adjusting investment.
The evolution of net foreign assets can be expressed as:
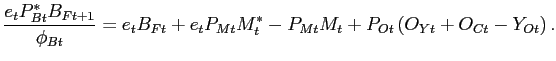
|
(18) |
This expression can be derived from the budget constraint of the households after imposing the government budget constraint and the definition of firm profits.
3 Solution Method and Calibration
We solve the model by log-linearizing the equations around the model's steady state. To obtain the reduced-form solution of the model, we use the numerical algorithm of [Anderson and Moore 1985], which provides an efficient implementation of the method proposed by [Blanchard and Kahn 1980] (see also [Anderson 1997]).8
The model is calibrated at a quarterly frequency. The parameter values for the home economy under our benchmark calibration are listed in Table 1; parameters for the foreign economy are identical except for the trade share parameters (which are determined by balanced trade given relative population sizes).
The discount factor ![]() is 0.99. The parameter
is 0.99. The parameter
![]() in the subutility function over
consumption is set equal to 1 (implying a logarithmic form). The
parameter determining the degree of habit persistence in
consumption
in the subutility function over
consumption is set equal to 1 (implying a logarithmic form). The
parameter determining the degree of habit persistence in
consumption ![]() is set to 0.8. We set
is set to 0.8. We set
![]() , implying a Frisch elasticity of
labor supply of 0.2, which is considerably lower than if
preferences were logarithmic in leisure, but well within the range
of most empirical estimates. The utility parameter
, implying a Frisch elasticity of
labor supply of 0.2, which is considerably lower than if
preferences were logarithmic in leisure, but well within the range
of most empirical estimates. The utility parameter ![]() is set so that employment comprises one-third of the
household's time endowment. The population size parameter
is set so that employment comprises one-third of the
household's time endowment. The population size parameter
![]() is set so that U.S. nonoil output
comprises one fourth of world nonoil output.
is set so that U.S. nonoil output
comprises one fourth of world nonoil output.
The production function parameter ![]() is
set to -2, implying an elasticity of substitution between capital
and labor of 0.5. We set the parameter for the cost of adjusting
investment,
is
set to -2, implying an elasticity of substitution between capital
and labor of 0.5. We set the parameter for the cost of adjusting
investment,
![]() , close to the value used by
[Christiano et al. 2005]. The depreciation rate of capital
, close to the value used by
[Christiano et al. 2005]. The depreciation rate of capital
![]() is consistent with an annual
depreciation rate of 10 percent. We set the government share of
output to 18 percent, and the quasi-capital share parameter
is consistent with an annual
depreciation rate of 10 percent. We set the government share of
output to 18 percent, and the quasi-capital share parameter
![]() to 1.61, so that the investment
share of output equals an empirically-realistic value of 20
percent.
to 1.61, so that the investment
share of output equals an empirically-realistic value of 20
percent.
Our calibration of
![]() and
and
![]() is determined by the overall oil
share of output, the end-use ratios of oil in consumption and
production, and the level of oil taxes. Based on data from the
Energy Information Administration of the U.S. Department of Energy,
the overall oil share of the domestic economy is set to 3 percent,
with one-third of total oil usage accounted for by households, and
two-thirds by firms.9 The level of oil imports for the home
country is set at 50% of total demand (this determines the local
production share of oil in the steady state). This estimate is
based on 2003 data for the United States obtained from British
Petroleum (and include oil and natural gas). Using U.S. data
obtained from the International Energy Agency, the ad-valorem tax
on oil (
is determined by the overall oil
share of output, the end-use ratios of oil in consumption and
production, and the level of oil taxes. Based on data from the
Energy Information Administration of the U.S. Department of Energy,
the overall oil share of the domestic economy is set to 3 percent,
with one-third of total oil usage accounted for by households, and
two-thirds by firms.9 The level of oil imports for the home
country is set at 50% of total demand (this determines the local
production share of oil in the steady state). This estimate is
based on 2003 data for the United States obtained from British
Petroleum (and include oil and natural gas). Using U.S. data
obtained from the International Energy Agency, the ad-valorem tax
on oil (![]() ) is set at 10 percent, while the
specific oil tax (
) is set at 10 percent, while the
specific oil tax (![]() ) is set at 20
percent.
) is set at 20
percent.
Our choices for the parameters that determine the short- and
long-run elasticity of substitution for oil (![]() ,
, ![]() ,
,
![]() and
and
![]() ) are motivated by the
regression results described in Appendix A. Based on our regression
estimates, the parameter
) are motivated by the
regression results described in Appendix A. Based on our regression
estimates, the parameter ![]() is set to imply a
long-run elasticity of substitution between oil and the other
factors of production of 0.5, while the the adjustment cost
parameter
is set to imply a
long-run elasticity of substitution between oil and the other
factors of production of 0.5, while the the adjustment cost
parameter
![]() implies that the half life of
the response of oil demand to a permanent rise in the oil price is
10 years. Thus, as in most other studies, we find that the
short-run elasticity of oil demand is very small relative to the
long-run elasticity. Moreover, the implied time path of the price
elasticity of demand for oil is within the wide range of estimates
for energy own price elasticities reported in surveys such as [Dahl
and Sterner 1991] or [Atkins and Jazayeri 2004], which range
between 0 to 0.11 (in absolute value) for the short-run elasticity,
and between 0 and 3.44 for the long-run elasticity.10 Our
regression analysis constrains the time path of the elasticity of
oil demand to be the same for households as for firms (so
implies that the half life of
the response of oil demand to a permanent rise in the oil price is
10 years. Thus, as in most other studies, we find that the
short-run elasticity of oil demand is very small relative to the
long-run elasticity. Moreover, the implied time path of the price
elasticity of demand for oil is within the wide range of estimates
for energy own price elasticities reported in surveys such as [Dahl
and Sterner 1991] or [Atkins and Jazayeri 2004], which range
between 0 to 0.11 (in absolute value) for the short-run elasticity,
and between 0 and 3.44 for the long-run elasticity.10 Our
regression analysis constrains the time path of the elasticity of
oil demand to be the same for households as for firms (so
![]() =
= ![]() and
and
![]() =
=
![]() ).
).
Turning to the parameters determining trade flows, the parameter
![]() is chosen to match the estimated
average share of imports in total U.S. consumption of about 6
percent (using NIPA data), while the parameter
is chosen to match the estimated
average share of imports in total U.S. consumption of about 6
percent (using NIPA data), while the parameter
![]() is chosen to match the average
share of imports in total U.S. investment of about 43 percent. This
calibration implies a nonoil-goods import-to-GDP ratio for the home
country of about 12 percent. Given that trade is balanced in steady
state, and that the oil import share for the home country is 1.5
percent of GDP, the goods export share is 13.5 percent of GDP.
is chosen to match the average
share of imports in total U.S. investment of about 43 percent. This
calibration implies a nonoil-goods import-to-GDP ratio for the home
country of about 12 percent. Given that trade is balanced in steady
state, and that the oil import share for the home country is 1.5
percent of GDP, the goods export share is 13.5 percent of GDP.
We assume that
![]() , consistent with a
long-run price elasticity of demand for imported consumption and
investment goods of 1.5.11 We set the adjustment cost
parameters
, consistent with a
long-run price elasticity of demand for imported consumption and
investment goods of 1.5.11 We set the adjustment cost
parameters
![]() =
=
![]() = 10, so that the half life of
the response to a permanent terms of trade change is 2-1/2 years.
Thus, while we allow for some lag in the adjustment of nonoil goods
trade to terms of trade changes, this adjustment process is much
more rapid than for oil.12 We choose a small value (0.0001) for
the financial intermediation cost
= 10, so that the half life of
the response to a permanent terms of trade change is 2-1/2 years.
Thus, while we allow for some lag in the adjustment of nonoil goods
trade to terms of trade changes, this adjustment process is much
more rapid than for oil.12 We choose a small value (0.0001) for
the financial intermediation cost ![]() (a
positive value of this parameter ensures that the model has a
unique steady state).
(a
positive value of this parameter ensures that the model has a
unique steady state).
4 Model Simulations
4.1 Benchmark Calibration
Figure 1 shows responses of the home country (the United States) to a 50 percent permanent rise in the relative price of oil under our benchmark calibration. While this is a substantial rise, [Blanchard and Galí 2007] have documented how the oil price rose over 100 percent in logarithmic percentage terms on four occasions since the first OPEC shock in 1973.
The oil price shock induces a progressive fall in U.S. oil demand as both households and firms substitute away from this more costly input (upper left panel). With a pre-tax oil elasticity of demand of one half and roughly 80 percent passthrough of the pretax oil price to the aftertax price, oil demand drops roughly 20 percent in the long run.13 As noted above, our calibration implies that the half-life of the adjustment to this new long-run level is about 10 years.
The progressive decline in oil use has effects on output, the expenditure components, and the real interest rate that are qualitatively similar to those of a persistent decline in productivity growth. Thus, gross output declines gradually in response to lower oil use and a falling capital stock, while consumption contracts due to a reduction in household permanent income (however, in contrast to the case of a productivity shock, the long-run consumption decline exceeds that of gross output, since energy imports rise when expressed in units of the domestic good). Investment spending falls, reflecting that a lower path of oil usage pushes down the current and future marginal product of capital. The decline in the marginal productivity of capital induces a modest fall in domestic real interest rates (notwithstanding a transient initial rise due to habit persistence in consumption).
Turning to the implications for the external sector, the rise in oil prices causes a sharp and immediate deterioration of the overall (nominal) trade balance equal to about 1-1/4 percentage points of GDP. In the short run, this shift in the overall balance mainly reflects a deterioration in the oil component due to higher oil prices (as the volume of oil imports is nearly fixed). In the longer term, the overall trade deficit narrows and even shifts into surplus roughly fifteen years after the occurrence of the shock.
Several forces provide a catalyst for eventual trade balance improvement. First, oil import volumes gradually decline. Importantly, because the United States produces half of its oil demand in the pre-shock steady state and U.S. oil supply is assumed to be price inelastic, the decline in oil imports is much larger than the fall in total oil demand in percentage terms: thus, while oil demand falls around 20 percent in the long run, oil imports fall about 40 percent. Second, a decline in the nonoil terms of trade spurs an improvement in U.S. real nonoil exports, while retarding nonoil imports (as the relative price of imports rises, and exports fall). We provide an extensive discussion of the factors affecting the direction and magnitude of this nonoil terms of trade effect below. Finally, the fall in domestic consumption and investment also compresses real nonoil imports (although the effect on net exports is somewhat muted due to a decline in foreign investment spending).
From an accounting perspective, adjustments in both the oil and nonoil components of the nominal trade balance play a quantitatively important role in contributing to the eventual improvement in the overall balance. As indicated by Figure 1, the overall trade balance improves about 1-1/2 percentage points of GDP between the immediate aftermath of the shock and the end of the thirty year horizon shown, and more than half of this improvement is attributable to the oil balance. Nevertheless, given our benchmark calibration of the elasticity of oil demand of 1/2, the oil balance remains in substantial deficit even in the long run. Thus, intertemporal balance requires that adjustment in the nonoil balance also play a sizeable role, which is achieved largely through the worsening of the nonoil terms of trade.14
4.2 The Oil Elasticity of Substitution and the Discount Factor
The magnitude of the effects of the oil price shock on the nonoil terms of trade and on the composition of trade adjustment depends critically on the elasticity of substitution between oil and other factor inputs. To illustrate this sensitivity, Figure 2 contrasts responses under our benchmark calibration to the 50 percent oil price hike with responses derived under two alternative calibrations of this long-run elasticity. One alternative imposes a long-run elasticity of unity, consistent with a Cobb-Douglas production function over the factor inputs. A second alternative imposes a long-run elasticity of 0.05, much lower than our benchmark, and close to a Leontief specification. In each case, the adjustment cost parameter on oil is changed so that the half life of adjustment to a permanent shock remains 10 years (while other parameters are unchanged).
The upper left panel compares the response of total oil demand under the three specifications. Unsurprisingly, oil demand eventually shows a much larger decline under the Cobb-Douglas specification than under the benchmark. With a pre-tax oil elasticity of demand of unity (and again, roughly 80 percent passthrough of the pre-tax oil price to the after-tax price), oil demand drops roughly 40 percent in the long run. Under the near-Leontief specification, oil demand shows a fairly small contraction, even in the long run. Conversely, the contractionary effects on domestic demand are larger when it is difficult to substitute away from oil, reflecting the larger reduction in permanent income, and a greater decline in investment (since the marginal product of capital falls by a more substantial magnitude).
Turning to the implications for the trade balance, the responses under the near-Leontief case are qualitatively the same as under our benchmark. However, from a quantitative perspective, the much smaller decline in oil use translates into a smaller fall in oil imports, accounting for the much larger deterioration of the nominal oil balance apparent in Figure 2. Given the requirement of intertemporal balance, the permanent deterioration of the oil component of the trade balance in turn requires a larger offsetting improvement of the nonoil component than under our benchmark calibration; thus, the nonoil balance improves 1-1/2 percentage point of GDP after 30 years, roughly twice as much as under the benchmark. This greater improvement of the nonoil balance is brought about by a decline of the nonoil terms of trade that is twice as large as under the benchmark. In our general equilibrium framework, the larger nonoil terms of trade decline reflects the interplay of the greater shortfall on the domestic oil balance, and the correspondingly greater wealth effect abroad.
The responses under the Cobb-Douglas specification exhibit some striking differences from specifications with lower long-run oil elasticities. The 40 percent fall in oil demand in the long run produces a much larger percentage decline in oil imports (since the United States meets a substantial fraction of its oil demand with domestic production), implying an eventual improvement in the nominal oil balance. This in turn allows the nonoil balance and terms of trade to remain essentially unchanged. Clearly, the high ability to substitute away from oil mitigates the negative wealth effect on the United States, and implies a smaller positive wealth effect abroad.
In Figure 3, we examine the sensitivity of our results to
alternative parameterizations of the discount factor ![]() . The discount factor affects the responses through two
related channels. First, it affects the cost of U.S. external
borrowing, which is relevant given that the shock induces an
initial trade deficit that is highly persistent. Thus, a low value
of the discount factor implies a high steady state real interest
rate, which by increasing the debt-servicing costs has a depressing
effect on U.S. wealth and consumption (and conversely for a high
discount factor). Second, it determines how the foreign economy
discounts current and future oil receipts, and thus influences the
wealth effects of the shock abroad. Given that foreign oil revenues
decline through time as the U.S. substitutes away from oil, a low
value of the discount factor magnifies the wealth effects on the
foreign country. Thus, as seen in the figure, the U.S. nonoil
balance under the low discount factor of
. The discount factor affects the responses through two
related channels. First, it affects the cost of U.S. external
borrowing, which is relevant given that the shock induces an
initial trade deficit that is highly persistent. Thus, a low value
of the discount factor implies a high steady state real interest
rate, which by increasing the debt-servicing costs has a depressing
effect on U.S. wealth and consumption (and conversely for a high
discount factor). Second, it determines how the foreign economy
discounts current and future oil receipts, and thus influences the
wealth effects of the shock abroad. Given that foreign oil revenues
decline through time as the U.S. substitutes away from oil, a low
value of the discount factor magnifies the wealth effects on the
foreign country. Thus, as seen in the figure, the U.S. nonoil
balance under the low discount factor of ![]() =
0.975 improves by more than twice as much as under the benchmark
calibration, while the deterioration of the U.S. terms of trade is
about 50 percent larger. Conversely, the nonoil terms of trade and
nonoil balance exhibit smaller movements than under the benchmark
when the discount factor rises to
=
0.975 improves by more than twice as much as under the benchmark
calibration, while the deterioration of the U.S. terms of trade is
about 50 percent larger. Conversely, the nonoil terms of trade and
nonoil balance exhibit smaller movements than under the benchmark
when the discount factor rises to ![]() =
0.995.
=
0.995.
Our foregoing results indicate that the effects of an oil price hike on nonoil terms of trade and the nonoil trade balance can vary substantially depending on the elasticity of substitution between oil and other inputs, and on the discount factor. Given parameter uncertainty, it is useful to identify regions of a two dimensional space in these parameters that tend to imply a substantial nonoil terms of trade worsening and associated improvement in the nonoil balance, from regions that generate a nonoil terms of trade improvement and deterioration of the nonoil balance.
We perform this exercise in the contour plot shown in Figure 4.
Each of the isoquants identifies pairs of the parameters that imply
the same magnitude of deterioration in the nonoil terms of trade,
with the magnitude labeled next to the relevant isoquant (the terms
of trade response is an average over the first two years following
the 50 percent oil shock). Because the nonoil terms of trade
response turns out to be closely aligned with a response of the
nonoil trade balance of the opposite sign, we focus exclusively on
the former. Thus, to the northeast of the ``0" isoquant, the nonoil
terms of trade actually improve in response to the price hike, and
there is a corresponding deterioration of the nonoil trade balance
(not shown). This region corresponds to a high long-run degree of
substitutibility between oil and other factors, and a high value of
the discount factor. Under these conditions, U.S. oil imports
eventually fall enough that the oil component of the U.S. trade
balance moves into surplus (relative to its initial steady state),
so that foreign oil revenues fall in the long-run. Given that the
U.S. faces low borrowing costs, and that foreign wealth effects are
small or negative (reflecting a long horizon for discounting the
future, and the expectation of an eventual fall in revenue), the
nonoil balance runs small but persistent deficits, and the nonoil
terms of trade show the slight improvement implied by Figure 4. By
contrast, the nonoil terms of trade deteriorate progressively as
the two key parameters are varied in a southwesterly direction. For
example, given that the vertical axis corresponds to a long-run
elasticity of .05, the point on the vertical axis corresponding to
a discount factor of
![]() yields the near-Leontief case
shown in Figure 2. In this region of the parameter space, the large
and persistent increase in the oil deficit requires the nonoil
balance to eventually shift into a substantial surplus, which is
accomplished through a nonoil terms of trade deterioration
exceeding 5 percent. With the same low elasticity but a lower
discount factor, higher U.S. borrowing costs and a larger foreign
wealth effect would amplify the required depreciation in the nonoil
terms of trade.
yields the near-Leontief case
shown in Figure 2. In this region of the parameter space, the large
and persistent increase in the oil deficit requires the nonoil
balance to eventually shift into a substantial surplus, which is
accomplished through a nonoil terms of trade deterioration
exceeding 5 percent. With the same low elasticity but a lower
discount factor, higher U.S. borrowing costs and a larger foreign
wealth effect would amplify the required depreciation in the nonoil
terms of trade.
4.3 The Role of Domestic Oil Production
In our benchmark calibration, the United States meets nearly one half of its oil demand through domestic production in the pre-shock steady state. Figure 5 considers an alternative in which U.S. production is fixed at zero, while other features of our calibration remain unchanged. In addition to highlighting the implications of domestic production for our results, this alternative is useful for assessing how a higher degree of reliance on imported oil - similar to that of Japan or the euro area - might affect the response of trade flows and the nonoil terms of trade.15
Two features of Figure 5 are especially noteworthy. First, the deterioration of the nonoil terms of trade under this alternative calibration is more than twice as large as in the benchmark; and second, the nonoil trade balance moves into a much larger surplus. These differences reflect that the oil price hike induces a much smaller percentage decline in real oil imports in the case in which domestic production is zero (as oil imports simply fall by the same percentage as oil demand), so that there is a much larger deterioration of the oil component of the nominal trade balance. Because intertemporal current account balance in turn requires a bigger improvement in the nonoil balance, the nonoil terms of trade must deteriorate by a larger amount.
Thus, our analysis suggests that the fact that the U.S. produces a sizeable fraction of the oil it consumes may help partly insulate the nonoil terms of trade from the effects of oil price shocks. By contrast, a region such as the euro area that produces much less of its own oil might experience considerably more pressure on its nonoil terms of trade.16
4.4 Specific Taxes on Energy
Figure 6 investigates the implications of varying the specific
tax rate on oil from its benchmark value of
![]() . In particular, we consider
an alternative in which the specific tax rate is set to 0.4, and
another case in which it is set equal to zero. A higher tax rate
induces a larger depreciation in the terms of trade, and
correspondingly, a somewhat larger improvement of the nonoil trade
balance.
. In particular, we consider
an alternative in which the specific tax rate is set to 0.4, and
another case in which it is set equal to zero. A higher tax rate
induces a larger depreciation in the terms of trade, and
correspondingly, a somewhat larger improvement of the nonoil trade
balance.
These effects reflect that the higher specific oil tax damps the long-run elasticity of oil demand with respect to the pre-tax oil price. To see this, note that this elasticity can be expressed as:
![$\displaystyle \rho_{oy} \left[ \frac{1+\tau_{ov}}{1+\tau_{ov}+\tau_{os}}\right]$](img148.gif)
|
(19) |
where ![]() is the elasticity of oil demand
with respect to the after-tax price (for firms and households), and
the remaining ratio is the percentage response of the after-tax oil
price to a change in the pre-tax price. Thus, as the specific tax
on oil rises, the pre-tax elasticity of oil demand is lower for any
given value of the after-tax elasticity, so that oil imports fall
by less in response to an oil price hike. Accordingly,
intertemporal current account balance requires a bigger improvement
in the nonoil balance in the case with the higher tax rate, and
correspondingly, a larger decline in the nonoil terms of trade. The
effects in the case of a lower tax rate can be understood by a
symmetric argument.
is the elasticity of oil demand
with respect to the after-tax price (for firms and households), and
the remaining ratio is the percentage response of the after-tax oil
price to a change in the pre-tax price. Thus, as the specific tax
on oil rises, the pre-tax elasticity of oil demand is lower for any
given value of the after-tax elasticity, so that oil imports fall
by less in response to an oil price hike. Accordingly,
intertemporal current account balance requires a bigger improvement
in the nonoil balance in the case with the higher tax rate, and
correspondingly, a larger decline in the nonoil terms of trade. The
effects in the case of a lower tax rate can be understood by a
symmetric argument.
Nevertheless, as suggested by the equation above, the wedge introduced by specific taxes can only change the level of the pre-tax elasticity noticeably if the after-tax elasticity is fairly high. Thus, the effect is quite small quantitatively even for an after-tax oil price elasticity in the range of our benchmark value of 0.5. This analysis suggests that empirically relevant differences in specific tax rates between the United States and the euro area - with the latter close to the 40 percent rate considered in our alternative - probably play little role in contributing to different effects of oil shocks on the nonoil terms of trade or external balance across the two regions.
5 Complete vs. Incomplete Markets
In our benchmark model with incomplete markets, oil price shocks have substantial wealth effects that diverge across countries. It is helpful to contrast these results with an alternative financial structure of complete markets in order to emphasize the pivotal role that such cross-country changes in the distribution of wealth play in driving the dynamics of the terms of trade and nonoil trade balance.
Figure 7 contrasts responses to the permanent oil price shock in our benchmark model with incomplete markets to responses derived from a variant that allows for complete financial markets. The results are strikingly different: in particular, the nonoil terms of trade remain unchanged from baseline under complete markets, and the nonoil trade balance is essentially unaffected.
These disparities reflect that ownership of the profit flow associated with oil production is effectively shared across countries in the complete markets case through insurance transfers. Although oil price hikes still have a contractionary effect on consumption - reflecting that the higher factor price lowers productivity - there is no added hit to an oil importer associated with a transfer of wealth across countries. With symmetric wealth effects and labor supply responses across countries, the nonoil terms of trade remain essentially unchanged. Even though the oil-importing country runs an overall trade deficit under complete markets, it receives insurance payments that offset the higher nominal oil expenditures: these transfers allow it to avoid having to accrue a surplus on its nonoil balance (as was necessary to achieve intertemporal current account balance in the incomplete markets case).
As a corollary, the structural factors highlighted in Section 4 as influencing the magnitude of the nonoil terms of trade and nonoil trade balance responses operate on these variables only insofar as the shock has differential wealth effects across countries. But this hinges on the incomplete market structure. Hence, with these differential wealth effects (virtually) eliminated under complete markets, variations in these structural factors - including the elasticity of substitution between oil and other inputs, the steady state real interest rate, and the magnitude of domestic oil production of the oil importer - have essentially no effect on the nonoil terms of trade or nonoil balance. This is illustrated in Figure 7, which also shows the complete markets response for the case of an extremely low long-run substitution elasticity between oil and other inputs of 0.05, compared with 0.5 in our benchmark. Under complete markets, the response of the nonoil terms of trade and the nonoil trade balance are indistinguishable for these very different substitution elasticities; this contrasts sharply with the large divergence in the incomplete markets case that was highlighted in our discussion of Figure 2.
6 An Endogenous Oil Price
We have thus far assumed the relative price of oil to be determined exogenously, and assessed the effects of permanent oil price shocks. This approach has a long precedent in the literature, as it appeared to capture key features of the dramatic OPEC-driven oil price hikes of the 1970s. However, our analysis of the effects of oil shocks on the external balance does not hinge on specifying the relative price of oil as an exogenous process. In this section, we show that similar results obtain in a framework in which the oil price responds endogenously to shocks either to the quantity of oil supplied by the foreign sector, or to foreign oil demand in response to a taste-shock.
Figure 8 shows responses to an adverse supply shock that induces
a gradual reduction in the foreign flow endowment of oil
![]() . In this framework, the foreign
endowment is assumed to follow an AR(1) in the growth rate with an
autoregressive parameter of 0.9, and the innovation is scaled so
that the relative price of oil rises 50 percent above baseline at
its peak under our benchmark calibration. Although the peak effect
is identical to that analyzed earlier, the figure shows that the
oil price declines considerably over the long simulation horizon.
The gradual decline in the oil price is due to falling world oil
demand as households and firms substitute away from oil.
. In this framework, the foreign
endowment is assumed to follow an AR(1) in the growth rate with an
autoregressive parameter of 0.9, and the innovation is scaled so
that the relative price of oil rises 50 percent above baseline at
its peak under our benchmark calibration. Although the peak effect
is identical to that analyzed earlier, the figure shows that the
oil price declines considerably over the long simulation horizon.
The gradual decline in the oil price is due to falling world oil
demand as households and firms substitute away from oil.
Focusing on our benchmark calibration, it is clear from Figure 8 that the qualitative effects of the oil supply shock are identical to those derived under an exogenous shock to the oil price (recalling Figure 1). Thus, the higher oil price shifts the trade balance of the oil-importer into persistent deficit. This deficit must be offset by an improvement in the nonoil balance, which is achieved through a deterioration in the nonoil terms of trade. The notable difference between the responses in Figure 8 and those in Figure 1 is that the former are quantitatively smaller. This simply reflects that the oil price hike is less persistent, and the wealth transfer to the oil-importer correspondingly smaller.
Our results showing how key structural parameters affect the response of the nonoil terms of trade and the trade balance (Figures 2-5) continue to obtain in the case of an endogenous price response. In fact, the divergence in responses across alternative calibrations of the elasticity of substitution parameter and the domestic production share parameter tends to be even larger than in simulations with an exogenous oil price. To illustrate this, Figure 8 compares the effects of the oil quantity shock under our benchmark calibration in which the oil elasticity of demand is set to 0.5 with alternatives in which the elasticity is set equal to unity and 0.05 (the same alternatives considered in Figure 2). Given that the fall in world oil supply is identical across simulations, the oil price shows a larger and more persistent increase as the long-run oil price elasticity of substitution declines. Accordingly, the terms of trade deteriorate by more (and the nonoil balance improves by more) if the oil price elasticity of demand is low, which mirrors the qualitative pattern in Figure 2. However, because the oil price response is now much larger under the low-elasticity calibration, the magnitude of the nonoil terms of trade deterioration and nonoil trade balance response is greatly amplified. By comparison, under a high elasticity of substitution the oil price remains only slightly above its pre-shock baseline in the long-run, so that the terms of trade and nonoil balance remain nearly unchanged.
We next compare the effects of an oil price rise generated by
the supply shock with a similar-sized price increase induced by a
demand shock that is specific to the oil market. To model the
latter in our framework, we modify the foreign consumption demand
equation to allow for a preference shock
![]() to the foreign demand for
oil:
to the foreign demand for
oil:
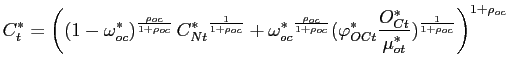
|
(20) |
Thus, a rise in
![]() raises the marginal
productivity of oil abroad, and hence raises household oil demand
at constant relative prices.17 As in the case of the supply
shock, we assume that the demand shock follows an autoregressive
process in the growth rate (the autoregressive parameter is 0.88).
raises the marginal
productivity of oil abroad, and hence raises household oil demand
at constant relative prices.17 As in the case of the supply
shock, we assume that the demand shock follows an autoregressive
process in the growth rate (the autoregressive parameter is 0.88).
Figure 9 compares the responses of the home country to the supply and demand shock in the oil market. The latter is scaled so that the peak response of the oil price is roughly the same as for the supply shock. The two shocks affect the home country through similar channels, and have comparable effects on the trade balance and nonoil terms of trade, as well as on other domestic variables (such as absorption). Thus, either shock causes the oil component of the trade balance to shift into persistent deficit, which in turn induces the nonoil terms of trade to depreciate.
Our results suggest that only the path of the oil price is relevant to the home country, provided that the oil price hike is generated by a foreign supply or demand disturbance that is specific to the oil market. From a practical perspective, it is immaterial to the United States whether oil prices rise because of a supply contraction in the Middle East, or because of cold weather in China, so long as the oil price responds commensurately.
But in interpreting our results, two important caveats are important. First, insofar as we designed our comparison to elicit similar oil price paths, our analysis should not be taken to imply that reasonably calibrated oil-specific demand and supply shocks generate similar oil price responses. Clearly, these shocks may have different effects on the dynamic response of the oil price, depending on the size of underlying innovations, and on the time path of the elasticities of the supply and demand for oil.18 The second caveat is that there are many other types of shocks that affect world oil demand primarily through their effects on aggregate expenditure. For example, a rise in foreign productivity growth raises oil demand through its stimulative effect on foreign absorption. The effects on the home country of a given-sized oil price hike induced by this latter type of foreign demand shock could diverge markedly from that caused by an oil supply shock, reflecting the different channels through which the shock would affect the foreign economy; roughly speaking, the differences arise through channels that would remain operative even if the oil share of the world economy declined toward zero. As there are a myriad of different shocks that affect aggregate demand, oil price increases associated with different underlying shocks (e.g., productivity growth vs. consumption taste shock) could be associated with quite different responses of the home economy.
7 Allowing for Nominal Rigidities
This section examines the sensitivity of our results to the
inclusion of nominal rigidities in both price- and wage-setting. In
particular, we consider an alternative version of our model that
modifies our flexible price framework along several dimensions that
have become standard in the literature on dynamic New-Keynesian
models. First, we account for stickiness in the aggregate price of
the domestically produced nonoil good ![]() by
assuming that it is produced by a continuum of
monopolistically-competitive firms that set prices for an extended
duration in overlapping staggered contracts. In this framework, the
domestically produced nonoil good in equation (7) effectively serves as the factor input to the
monopolistic producers (thus, all producers have the same marginal
cost). These monopolistically-competitive firms set prices in their
domestic currency in Calvo-style contracts (so that there is
``producer currency pricing" in the export market), with a mean
contract duration of four quarters, and full indexation to past
prices (as in the model of Christiano, Eichenbaum, and Evans 2005).
Second, we allow for nominal wage stickiness by assuming that wages
are set in staggered contracts by a continuum of households with
differentiated labor inputs. Wages are also set in Calvo-style
staggered contracts with a mean duration of four quarters, with
full indexation (to past wage inflation in our case). Finally, we
assume that monetary policy is determined by an estimated interest
rate reaction function of the form:
by
assuming that it is produced by a continuum of
monopolistically-competitive firms that set prices for an extended
duration in overlapping staggered contracts. In this framework, the
domestically produced nonoil good in equation (7) effectively serves as the factor input to the
monopolistic producers (thus, all producers have the same marginal
cost). These monopolistically-competitive firms set prices in their
domestic currency in Calvo-style contracts (so that there is
``producer currency pricing" in the export market), with a mean
contract duration of four quarters, and full indexation to past
prices (as in the model of Christiano, Eichenbaum, and Evans 2005).
Second, we allow for nominal wage stickiness by assuming that wages
are set in staggered contracts by a continuum of households with
differentiated labor inputs. Wages are also set in Calvo-style
staggered contracts with a mean duration of four quarters, with
full indexation (to past wage inflation in our case). Finally, we
assume that monetary policy is determined by an estimated interest
rate reaction function of the form:
| (21) |
In the above, ![]() is the annualized nominal interest
rate,
is the annualized nominal interest
rate,
![]() is the four-quarter inflation
rate of the aggregate output deflator (i.e.,
is the four-quarter inflation
rate of the aggregate output deflator (i.e.,
![]() ),
),
![]() and
and ![]() are
the steady-state real interest rate and the central bank's constant
inflation target, respectively (both expressed at annual rate), and
are
the steady-state real interest rate and the central bank's constant
inflation target, respectively (both expressed at annual rate), and
![]() is the (annualized) quarterly
growth rate of aggregate output. We estimated the parameters of the
monetary policy rule using U.S. data from 1983:1-2003:4.19 Our
estimates implied
is the (annualized) quarterly
growth rate of aggregate output. We estimated the parameters of the
monetary policy rule using U.S. data from 1983:1-2003:4.19 Our
estimates implied
![]() ,
,
![]() , and
, and
![]() .
.
As seen in Figure 10, the response of the trade balance and its components in the model with nominal rigidities is virtually identical to that in the model with flexible prices and wages, and the response of the nonoil terms of trade is also very similar. This similarity reflects that the response of oil demand is mainly driven by the large change in the relative price of energy. Thus, given a similar response of the oil component of the trade balance across the two models, the required adjustment in the nonoil balance and nonoil terms of trade turns out to be similar. Importantly, the requisite nonoil terms of trade adjustment can occur even in the model with nominal rigidities because the exchange rate is flexible to adjust. As Figure 10 shows an alternative monetary policy that responds to inflation only would yield only minor differences in the responses of the oil and nonoil trade balance relative to our estimated policy rule.20
8 Conclusion
This paper has investigated how a rise in oil prices affects the U.S. trade balance and the nonoil terms of trade. We have shown that because oil shocks potentially generate large wealth transfers between oil-importing and exporting countries, the nature of financial market risk-sharing can have major implications for the response of the external sector. Under incomplete markets, a rise in the oil price generates a depreciation of the nonoil terms of trade, which induces the nonoil trade balance to improve enough to eventually correct the trade deficit. By contrast, given that insurance transfers erase these wealth effects under complete markets, oil shocks have essentially no effect on the nonoil terms of trade or the nonoil trade balance.
In future work, it would be desirable to apply our modeling framework to account for cross-country differences in the response of the external sector to oil price shocks, and to assess the role that various factors (e.g., size of domestic oil production) might have played in generating such disparities. Toward this end, we would like to estimate our model using full information methods, drawing on cross-country data. In a related context, it would also be interesting to estimate the impact of alternative types of demand and supply shocks using the restrictions of a theoretical model, including shocks that are specific to the oil market, and other shocks that affect oil prices through their influence on aggregate demand. Such analysis would provide a model-based complement to recent empirical work by [Kilian et al. 2007] conducted in a SVAR framework.
Bibliography
Anderson, G. (1997). A Reliable and Computationally Efficient Algorithm for Imposing the Saddle Point Property in Dynamic Models. Federal Reserve Board, Occasional Staff's Studies 4.
Anderson, G. and G. Moore (1985). A Linear Algebraic Procedure for Solving Linear Perfect Foresight Models. Economic Letters 17, 247-52.
Atkeson, A. and P. J. Kehoe (1999). Models of Energy Use: Putty-Putty versus Putty-Clay. American Economic Review 89(4), 1028-1043.
Atkins, F. J. and S. T. Jazayeri (2004). A Literature Review of Demand Studies in World Oil Markets. Manuscript, University of Calgary.
Backus, D. and M. Crucini (1998). Oil Prices and the Terms of Trade. Journal of International Economics 50, 185-213.
Baxter, M. and M. Crucini (1995). Business Cycles and the Asset Structure of Foreign Trade. International Economic Review 36(4), 821-854.
Bernanke, B., M. Gertler, and M. Watson (1997). Systematic Monetary Policy and the Effects of Oil Price Shocks. Brookings Papers on Economics Activity (1), 91-142.
Blanchard, O. and J. Galí (2007). The Macroeconomic Effects of Oil Price Shocks: Why are the 2000s so Different from the 1970s? Manuscript, MIT.
Blanchard, O. J. and C. M. Kahn (1980). The Solution of Linear Difference Models under Rational Expectations. Econometrica 48(5), 1305-1312.
Cavallo, M. and T. Wu (2006). Measuring Oil-Price Shocks Using Market-Based Information. Federal Reserve Bank of San Francisco, Working Paper 2006-28.
Christiano, L. J., M. Eichenbaum, and C. L. Evans (2005). Nominal Rigidities and the Dynamic Effects of a Shock to Monetary Policy. Journal of Political Economy 113(1), 1-45.
Cole, H. L. and M. Obstfeld (1991). Commodity Trade and International Risk Sharing: How Much Do Financial Markets Matter. Journal of Monetary Economics 28, 3-24.
Cooper, J. C. (2003). Price Elasticity of Demand for Crude Oil: Estimates for 23 Countries. Opec Review 27, 1-8.
Corsetti, G., L. Dedola, and S. Leduc (2004). International Risk Sharing and the Transmission of Productivity Shocks. CEPR Discussion Papers No. 4746.
Dahl, C. and T. Sterner (1991). Analysing Gasoline Demand Elasticities: a survey. Energy Economics 13(3), 203-210.
Erceg, C., L. Guerrieri, and C. Gust (2006). Trade Adjustment and the Composition of Trade. FRB International Finance Discussion Papers No. 859.
Erceg, C., C. Gust, and D. López-Salido (2007). The Transmission of Domestic Shocks in Open Economies. Manuscript, Federal Reserve Board.
Finn, M. (2000). Perfect Competition and the Effects of Energy Price Increases on Economic Activity. Journal of Money, Credit, and Banking 32(3), 400-416.
Fuhrer, J. C. and G. R. Moore (1995, February). Inflation Persistence. Quarterly Journal of Economics (440), 127-159.
Gallaway, M. P., C. A. McDaniel, and S. A. Rivera (2003). Short-Run and Long-Run Industry-Level Estimates of U.S. Armington Elasticities. North American Journal of Economics and Finance 14, 49-68.
Golub, S. S. (1983). Oil Prices and Exchange Rates. The Economic Journal 93(371), 576-593.
Hamilton, J. (1983). Oil and the Macroeconomy since World War II. Journal of Political Economy 91(2), 228-48.
Hamilton, J. (2003). What Is an Oil Shock. Journal of Econometrics 113, 363-98.
Hamilton, J. and C. Herrera (2004). Oil Shocks and Aggregate Macroeconomic Behavior: The Role of Monetary Policy: Comment. Journal of Money, Credit, Banking 36(2), 265-86.
Hooper, P., K. Johnson, and J. Marquez (2000). Trade Elasticities for the G-7 Countries. Princeton Studies in International Economics.
Kilian, L. (2006). Exogenous Oil Supply Shocks: How Big Are They and How Much Do They Matter for the U.S. Economy? Forthcoming, Review of Economics and Statistics.
Kilian, L., A. Rebucci, and N. Spatafora (2007). Oil Shocks and External Balances. Manuscript, University of Michigan.
Kim, I.-M. and P. Loungani (1992). The Role of Energy in Real Business Cycle Models. Journal of Monetary Economics 29(2), 173-189.
Laffer, A. B. and T. Agmon (1978). Trade, Payments and Adjustment: the Case of the Oil Price Rise. Kyklos 31, 68-85.
Leduc, S. and K. Sill (2004). A Quantitative Analysis of Oil-Price Shocks, Systematic Monetary Policy, and Economic Downturns. Journal of Monetary Economics 51, 781-808.
Rotemberg, J. and M. Woodford (1996). Imperfect Competition and the Effects of Energy Price Increases on Economic Activity. Journal of Money, Credit, and Banking 28(4), 549-577.
Schmitt-Grohe, S. and M. Uribe (2003). Closing Small Open Economy Models. Journal of International Economics 61(1), 163-185.
Smets, F. and R. Wouters (2003). An Estimated Dynamic Stochastic General Equilibrium Model of the Euro Area. Journal of the European Economic Association 1(5), 1124-1175.
Turnovsky, S. J. (1985). Domestic and Foreign Disturbances in an Optimizing Model of Exchange-Rate Determination. Journal of International Money and Finance 4(1), 151-71.
Wei, C. (2003). Energy, the Stock Market, and the Putty-Clay Investment Models. American Economic Review 93(1), 311-23.
Table 1. Calibration of Baseline Model: Panel 1 - Parameters Governing Households' Behavior
Parameter | Used to Determine | Parameter | Used to Determine |
|---|---|---|---|
| | discount factor | labor supply elasticity | |
| intertemporal consumption elasticity | | consumption habits | |
| | investment adjustment cost | | financial intermediation cost |
| | oil elasticity in consumption (0.5) | | oil adj. costs in consumption |
| | specific oil tax | | ad valorem oil tax |
| | weight of oil in consumption |
Table 1. Calibration of Baseline Model: Panel 2 - Parameters Governing Firms' Behavior
| Parameter | Used to Determine | Parameter | Used to Determine |
|---|---|---|---|
| | depreciation rate of capital | | K-L sub. elasticity (0.5) |
| | parameter on K in value added | | weight of oil in production |
| | value-added oil sub. elasticity (0.5) | | oil adj. costs in production |
Table 1. Calibration of Baseline Model: Panel 3 - Parameters Governing International Trade
| Parameter | Used to Determine | Parameter | Used to Determine |
|---|---|---|---|
| | consumption import sub. elasticity (1.5) | | weight of imports in nonoil consumption |
| | investment import sub. elasticity (1.5) | | weight of imports in investment |
| | consumption import adj. costs | | investment import adj. costs |
![]() The Frisch elasticity is
The Frisch elasticity is ![]() .
.
Figure 1. A 50% Increase in the Price of Oil
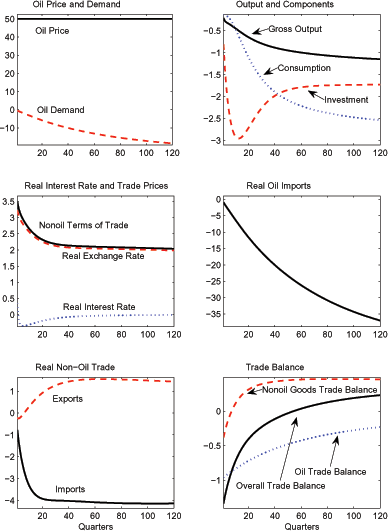
Data for Figure 1, Panel 1 - A 50% Increase in the Price of Oil
| Period | Oil price and demand: oil price |
Output and components: gross output |
Real interest rate and trade prices: nonoil terms of trade |
Real oil imports |
Real nonoil trade: imports |
Trade balance: overall trade balance |
Oil price and demand: oil demand |
Output and components: investment |
|---|---|---|---|---|---|---|---|---|
| 1 | 50 | -0.21 |
3.50 |
-0.94 |
-0.77 |
-1.34 |
-0.47 |
-0.81 |
| 2 | 50 | -0.28 |
3.28 |
-1.60 |
-1.30 |
-1.23 |
-0.80 |
-1.35 |
| 3 | 50 | -0.31 |
3.15 |
-2.19 |
-1.71 |
-1.15 |
-1.10 |
-1.75 |
| 4 | 50 | -0.33 |
3.05 |
-2.77 |
-2.06 |
-1.07 |
-1.39 |
-2.06 |
| 5 | 50 | -0.34 |
2.97 |
-3.35 |
-2.36 |
-1.00 |
-1.68 |
-2.31 |
| 6 | 50 | -0.36 |
2.89 |
-3.93 |
-2.62 |
-0.94 |
-1.97 |
-2.51 |
| 7 | 50 | -0.38 |
2.83 |
-4.51 |
-2.84 |
-0.88 |
-2.25 |
-2.66 |
| 8 | 50 | -0.40 |
2.76 |
-5.09 |
-3.03 |
-0.82 |
-2.54 |
-2.77 |
| 9 | 50 | -0.42 |
2.71 |
-5.66 |
-3.19 |
-0.77 |
-2.83 |
-2.86 |
| 10 | 50 | -0.45 |
2.65 |
-6.24 |
-3.33 |
-0.72 |
-3.12 |
-2.91 |
| 11 | 50 | -0.47 |
2.61 |
-6.80 |
-3.44 |
-0.68 |
-3.40 |
-2.94 |
| 12 | 50 | -0.49 |
2.56 |
-7.37 |
-3.54 |
-0.64 |
-3.68 |
-2.96 |
| 13 | 50 | -0.51 |
2.52 |
-7.92 |
-3.62 |
-0.60 |
-3.96 |
-2.95 |
| 14 | 50 | -0.53 |
2.48 |
-8.47 |
-3.69 |
-0.57 |
-4.24 |
-2.94 |
| 15 | 50 | -0.55 |
2.45 |
-9.01 |
-3.75 |
-0.53 |
-4.51 |
-2.92 |
| 16 | 50 | -0.57 |
2.42 |
-9.55 |
-3.80 |
-0.50 |
-4.77 |
-2.88 |
| 17 | 50 | -0.59 |
2.39 |
-10.07 |
-3.84 |
-0.48 |
-5.04 |
-2.85 |
| 18 | 50 | -0.61 |
2.36 |
-10.59 |
-3.87 |
-0.45 |
-5.30 |
-2.80 |
| 19 | 50 | -0.63 |
2.34 |
-11.10 |
-3.90 |
-0.42 |
-5.55 |
-2.76 |
| 20 | 50 | -0.65 |
2.32 |
-11.60 |
-3.92 |
-0.40 |
-5.80 |
-2.71 |
| 21 | 50 | -0.67 |
2.30 |
-12.09 |
-3.94 |
-0.38 |
-6.05 |
-2.66 |
| 22 | 50 | -0.68 |
2.28 |
-12.58 |
-3.95 |
-0.36 |
-6.29 |
-2.61 |
| 23 | 50 | -0.70 |
2.26 |
-13.06 |
-3.96 |
-0.34 |
-6.53 |
-2.57 |
| 24 | 50 | -0.71 |
2.25 |
-13.53 |
-3.97 |
-0.32 |
-6.76 |
-2.52 |
| 25 | 50 | -0.73 |
2.23 |
-13.99 |
-3.98 |
-0.30 |
-6.99 |
-2.47 |
| 26 | 50 | -0.74 |
2.22 |
-14.44 |
-3.99 |
-0.29 |
-7.22 |
-2.42 |
| 27 | 50 | -0.76 |
2.21 |
-14.89 |
-3.99 |
-0.27 |
-7.44 |
-2.38 |
| 28 | 50 | -0.77 |
2.20 |
-15.32 |
-4.00 |
-0.25 |
-7.66 |
-2.34 |
| 29 | 50 | -0.78 |
2.19 |
-15.76 |
-4.00 |
-0.24 |
-7.88 |
-2.30 |
| 30 | 50 | -0.79 |
2.18 |
-16.18 |
-4.00 |
-0.23 |
-8.09 |
-2.26 |
| 31 | 50 | -0.80 |
2.18 |
-16.60 |
-4.00 |
-0.21 |
-8.30 |
-2.22 |
| 32 | 50 | -0.81 |
2.17 |
-17.01 |
-4.00 |
-0.20 |
-8.50 |
-2.19 |
| 33 | 50 | -0.83 |
2.16 |
-17.41 |
-4.01 |
-0.19 |
-8.70 |
-2.16 |
| 34 | 50 | -0.83 |
2.16 |
-17.81 |
-4.01 |
-0.18 |
-8.90 |
-2.13 |
| 35 | 50 | -0.84 |
2.15 |
-18.20 |
-4.01 |
-0.16 |
-9.10 |
-2.10 |
| 36 | 50 | -0.85 |
2.15 |
-18.58 |
-4.01 |
-0.15 |
-9.29 |
-2.07 |
| 37 | 50 | -0.86 |
2.14 |
-18.96 |
-4.01 |
-0.14 |
-9.48 |
-2.05 |
| 38 | 50 | -0.87 |
2.14 |
-19.33 |
-4.02 |
-0.13 |
-9.66 |
-2.02 |
| 39 | 50 | -0.88 |
2.14 |
-19.69 |
-4.02 |
-0.12 |
-9.85 |
-2.00 |
| 40 | 50 | -0.89 |
2.13 |
-20.05 |
-4.02 |
-0.11 |
-10.03 |
-1.98 |
| 41 | 50 | -0.89 |
2.13 |
-20.41 |
-4.02 |
-0.10 |
-10.20 |
-1.96 |
| 42 | 50 | -0.90 |
2.13 |
-20.76 |
-4.03 |
-0.09 |
-10.38 |
-1.95 |
| 43 | 50 | -0.91 |
2.13 |
-21.10 |
-4.03 |
-0.08 |
-10.55 |
-1.93 |
| 44 | 50 | -0.91 |
2.12 |
-21.44 |
-4.03 |
-0.07 |
-10.72 |
-1.92 |
| 45 | 50 | -0.92 |
2.12 |
-21.77 |
-4.03 |
-0.07 |
-10.89 |
-1.90 |
| 46 | 50 | -0.93 |
2.12 |
-22.10 |
-4.04 |
-0.06 |
-11.05 |
-1.89 |
| 47 | 50 | -0.93 |
2.12 |
-22.42 |
-4.04 |
-0.05 |
-11.21 |
-1.88 |
| 48 | 50 | -0.94 |
2.12 |
-22.74 |
-4.04 |
-0.04 |
-11.37 |
-1.87 |
| 49 | 50 | -0.95 |
2.11 |
-23.05 |
-4.05 |
-0.03 |
-11.53 |
-1.86 |
| 50 | 50 | -0.95 |
2.11 |
-23.36 |
-4.05 |
-0.03 |
-11.68 |
-1.85 |
| 51 | 50 | -0.96 |
2.11 |
-23.67 |
-4.05 |
-0.02 |
-11.83 |
-1.84 |
| 52 | 50 | -0.96 |
2.11 |
-23.97 |
-4.06 |
-0.01 |
-11.98 |
-1.83 |
| 53 | 50 | -0.97 |
2.11 |
-24.26 |
-4.06 |
-0.01 |
-12.13 |
-1.82 |
| 54 | 50 | -0.97 |
2.11 |
-24.55 |
-4.06 |
0.00 |
-12.28 |
-1.82 |
| 55 | 50 | -0.98 |
2.11 |
-24.84 |
-4.07 |
0.01 |
-12.42 |
-1.81 |
| 56 | 50 | -0.98 |
2.10 |
-25.12 |
-4.07 |
0.01 |
-12.56 |
-1.81 |
| 57 | 50 | -0.99 |
2.10 |
-25.40 |
-4.07 |
0.02 |
-12.70 |
-1.80 |
| 58 | 50 | -0.99 |
2.10 |
-25.67 |
-4.08 |
0.03 |
-12.84 |
-1.80 |
| 59 | 50 | -0.99 |
2.10 |
-25.95 |
-4.08 |
0.03 |
-12.97 |
-1.79 |
| 60 | 50 | -1.00 |
2.10 |
-26.21 |
-4.08 |
0.04 |
-13.11 |
-1.79 |
| 61 | 50 | -1.00 |
2.10 |
-26.48 |
-4.08 |
0.04 |
-13.24 |
-1.78 |
| 62 | 50 | -1.01 |
2.10 |
-26.73 |
-4.09 |
0.05 |
-13.37 |
-1.78 |
| 63 | 50 | -1.01 |
2.10 |
-26.99 |
-4.09 |
0.05 |
-13.50 |
-1.78 |
| 64 | 50 | -1.01 |
2.09 |
-27.24 |
-4.09 |
0.06 |
-13.62 |
-1.77 |
| 65 | 50 | -1.02 |
2.09 |
-27.49 |
-4.10 |
0.07 |
-13.75 |
-1.77 |
| 66 | 50 | -1.02 |
2.09 |
-27.74 |
-4.10 |
0.07 |
-13.87 |
-1.77 |
| 67 | 50 | -1.03 |
2.09 |
-27.98 |
-4.10 |
0.08 |
-13.99 |
-1.77 |
| 68 | 50 | -1.03 |
2.09 |
-28.22 |
-4.10 |
0.08 |
-14.11 |
-1.76 |
| 69 | 50 | -1.03 |
2.09 |
-28.45 |
-4.11 |
0.09 |
-14.23 |
-1.76 |
| 70 | 50 | -1.04 |
2.09 |
-28.68 |
-4.11 |
0.09 |
-14.34 |
-1.76 |
| 71 | 50 | -1.04 |
2.09 |
-28.91 |
-4.11 |
0.09 |
-14.46 |
-1.76 |
| 72 | 50 | -1.04 |
2.09 |
-29.14 |
-4.11 |
0.10 |
-14.57 |
-1.76 |
| 73 | 50 | -1.05 |
2.09 |
-29.36 |
-4.11 |
0.10 |
-14.68 |
-1.75 |
| 74 | 50 | -1.05 |
2.08 |
-29.58 |
-4.12 |
0.11 |
-14.79 |
-1.75 |
| 75 | 50 | -1.05 |
2.08 |
-29.79 |
-4.12 |
0.11 |
-14.90 |
-1.75 |
| 76 | 50 | -1.05 |
2.08 |
-30.01 |
-4.12 |
0.12 |
-15.00 |
-1.75 |
| 77 | 50 | -1.06 |
2.08 |
-30.22 |
-4.12 |
0.12 |
-15.11 |
-1.75 |
| 78 | 50 | -1.06 |
2.08 |
-30.42 |
-4.12 |
0.12 |
-15.21 |
-1.75 |
| 79 | 50 | -1.06 |
2.08 |
-30.63 |
-4.12 |
0.13 |
-15.31 |
-1.75 |
| 80 | 50 | -1.07 |
2.08 |
-30.83 |
-4.13 |
0.13 |
-15.41 |
-1.75 |
| 81 | 50 | -1.07 |
2.08 |
-31.03 |
-4.13 |
0.13 |
-15.51 |
-1.74 |
| 82 | 50 | -1.07 |
2.08 |
-31.22 |
-4.13 |
0.14 |
-15.61 |
-1.74 |
| 83 | 50 | -1.07 |
2.07 |
-31.42 |
-4.13 |
0.14 |
-15.71 |
-1.74 |
| 84 | 50 | -1.08 |
2.07 |
-31.61 |
-4.13 |
0.15 |
-15.80 |
-1.74 |
| 85 | 50 | -1.08 |
2.07 |
-31.79 |
-4.13 |
0.15 |
-15.90 |
-1.74 |
| 86 | 50 | -1.08 |
2.07 |
-31.98 |
-4.13 |
0.15 |
-15.99 |
-1.74 |
| 87 | 50 | -1.08 |
2.07 |
-32.16 |
-4.13 |
0.16 |
-16.08 |
-1.74 |
| 88 | 50 | -1.09 |
2.07 |
-32.34 |
-4.13 |
0.16 |
-16.17 |
-1.74 |
| 89 | 50 | -1.09 |
2.07 |
-32.52 |
-4.14 |
0.16 |
-16.26 |
-1.74 |
| 90 | 50 | -1.09 |
2.07 |
-32.69 |
-4.14 |
0.16 |
-16.35 |
-1.74 |
| 91 | 50 | -1.09 |
2.07 |
-32.87 |
-4.14 |
0.17 |
-16.43 |
-1.74 |
| 92 | 50 | -1.10 |
2.07 |
-33.04 |
-4.14 |
0.17 |
-16.52 |
-1.74 |
| 93 | 50 | -1.10 |
2.06 |
-33.21 |
-4.14 |
0.17 |
-16.60 |
-1.74 |
| 94 | 50 | -1.10 |
2.06 |
-33.37 |
-4.14 |
0.18 |
-16.69 |
-1.74 |
| 95 | 50 | -1.10 |
2.06 |
-33.54 |
-4.14 |
0.18 |
-16.77 |
-1.74 |
| 96 | 50 | -1.11 |
2.06 |
-33.70 |
-4.14 |
0.18 |
-16.85 |
-1.73 |
| 97 | 50 | -1.11 |
2.06 |
-33.86 |
-4.14 |
0.18 |
-16.93 |
-1.73 |
| 98 | 50 | -1.11 |
2.06 |
-34.01 |
-4.14 |
0.19 |
-17.01 |
-1.73 |
| 99 | 50 | -1.11 |
2.06 |
-34.17 |
-4.14 |
0.19 |
-17.08 |
-1.73 |
| 100 | 50 | -1.11 |
2.06 |
-34.32 |
-4.14 |
0.19 |
-17.16 |
-1.73 |
| 101 | 50 | -1.12 |
2.06 |
-34.47 |
-4.14 |
0.19 |
-17.24 |
-1.73 |
| 102 | 50 | -1.12 |
2.05 |
-34.62 |
-4.14 |
0.20 |
-17.31 |
-1.73 |
| 103 | 50 | -1.12 |
2.05 |
-34.77 |
-4.14 |
0.20 |
-17.38 |
-1.73 |
| 104 | 50 | -1.12 |
2.05 |
-34.91 |
-4.14 |
0.20 |
-17.46 |
-1.73 |
| 105 | 50 | -1.12 |
2.05 |
-35.05 |
-4.14 |
0.20 |
-17.53 |
-1.73 |
| 106 | 50 | -1.13 |
2.05 |
-35.19 |
-4.14 |
0.21 |
-17.60 |
-1.73 |
| 107 | 50 | -1.13 |
2.05 |
-35.33 |
-4.14 |
0.21 |
-17.67 |
-1.73 |
| 108 | 50 | -1.13 |
2.05 |
-35.47 |
-4.14 |
0.21 |
-17.73 |
-1.73 |
| 109 | 50 | -1.13 |
2.05 |
-35.60 |
-4.14 |
0.21 |
-17.80 |
-1.73 |
| 110 | 50 | -1.13 |
2.05 |
-35.74 |
-4.14 |
0.21 |
-17.87 |
-1.73 |
| 111 | 50 | -1.13 |
2.04 |
-35.87 |
-4.14 |
0.22 |
-17.93 |
-1.73 |
| 112 | 50 | -1.14 |
2.04 |
-36.00 |
-4.14 |
0.22 |
-18.00 |
-1.73 |
| 113 | 50 | -1.14 |
2.04 |
-36.13 |
-4.14 |
0.22 |
-18.06 |
-1.73 |
| 114 | 50 | -1.14 |
2.04 |
-36.25 |
-4.14 |
0.22 |
-18.13 |
-1.73 |
| 115 | 50 | -1.14 |
2.04 |
-36.38 |
-4.14 |
0.22 |
-18.19 |
-1.73 |
| 116 | 50 | -1.14 |
2.04 |
-36.50 |
-4.14 |
0.23 |
-18.25 |
-1.73 |
| 117 | 50 | -1.14 |
2.04 |
-36.62 |
-4.14 |
0.23 |
-18.31 |
-1.73 |
| 118 | 50 | -1.15 |
2.04 |
-36.74 |
-4.14 |
0.23 |
-18.37 |
-1.73 |
| 119 | 50 | -1.15 |
2.04 |
-36.86 |
-4.14 |
0.23 |
-18.43 |
-1.73 |
| 120 | 50 | -1.15 |
2.03 |
-36.97 |
-4.14 |
0.23 |
-18.49 |
-1.73 |
Data for Figure 1, Panel 2 - A 50% Increase in the Price of Oil
| Period | Oil price and demand: oil price |
Real interest rate and trade prices: real exchange rate |
Real nonoil trade: exports |
Trade balance: nonoil goods trade balance |
Output and components: consumption |
Real interest rate and trade prices: real interest rate |
Trade balance: oil trade balance |
|---|---|---|---|---|---|---|---|
| 1 | 50 | 3.23 |
-0.22 |
-0.38 |
-0.13 |
0.35 |
-0.96 |
| 2 | 50 | 3.06 |
-0.25 |
-0.29 |
-0.16 |
-0.17 |
-0.94 |
| 3 | 50 | 2.96 |
-0.22 |
-0.22 |
-0.16 |
-0.31 |
-0.93 |
| 4 | 50 | 2.88 |
-0.16 |
-0.16 |
-0.17 |
-0.35 |
-0.91 |
| 5 | 50 | 2.81 |
-0.09 |
-0.10 |
-0.20 |
-0.35 |
-0.90 |
| 6 | 50 | 2.76 |
-0.01 |
-0.05 |
-0.24 |
-0.35 |
-0.89 |
| 7 | 50 | 2.70 |
0.07 |
0.00 |
-0.28 |
-0.34 |
-0.87 |
| 8 | 50 | 2.65 |
0.14 |
0.04 |
-0.33 |
-0.33 |
-0.86 |
| 9 | 50 | 2.60 |
0.22 |
0.08 |
-0.39 |
-0.32 |
-0.85 |
| 10 | 50 | 2.56 |
0.30 |
0.11 |
-0.46 |
-0.31 |
-0.83 |
| 11 | 50 | 2.52 |
0.37 |
0.14 |
-0.52 |
-0.30 |
-0.82 |
| 12 | 50 | 2.48 |
0.45 |
0.17 |
-0.59 |
-0.29 |
-0.81 |
| 13 | 50 | 2.44 |
0.51 |
0.19 |
-0.65 |
-0.27 |
-0.80 |
| 14 | 50 | 2.41 |
0.58 |
0.22 |
-0.72 |
-0.26 |
-0.78 |
| 15 | 50 | 2.37 |
0.65 |
0.24 |
-0.79 |
-0.25 |
-0.77 |
| 16 | 50 | 2.35 |
0.71 |
0.26 |
-0.86 |
-0.24 |
-0.76 |
| 17 | 50 | 2.32 |
0.76 |
0.27 |
-0.92 |
-0.23 |
-0.75 |
| 18 | 50 | 2.29 |
0.82 |
0.29 |
-0.99 |
-0.22 |
-0.74 |
| 19 | 50 | 2.27 |
0.87 |
0.30 |
-1.05 |
-0.20 |
-0.73 |
| 20 | 50 | 2.25 |
0.92 |
0.32 |
-1.11 |
-0.19 |
-0.72 |
| 21 | 50 | 2.23 |
0.96 |
0.33 |
-1.17 |
-0.18 |
-0.71 |
| 22 | 50 | 2.22 |
1.01 |
0.34 |
-1.22 |
-0.18 |
-0.70 |
| 23 | 50 | 2.20 |
1.05 |
0.35 |
-1.28 |
-0.17 |
-0.69 |
| 24 | 50 | 2.19 |
1.08 |
0.36 |
-1.33 |
-0.16 |
-0.68 |
| 25 | 50 | 2.17 |
1.12 |
0.36 |
-1.38 |
-0.15 |
-0.67 |
| 26 | 50 | 2.16 |
1.15 |
0.37 |
-1.42 |
-0.14 |
-0.66 |
| 27 | 50 | 2.15 |
1.18 |
0.38 |
-1.47 |
-0.13 |
-0.65 |
| 28 | 50 | 2.14 |
1.21 |
0.38 |
-1.51 |
-0.13 |
-0.64 |
| 29 | 50 | 2.13 |
1.24 |
0.39 |
-1.55 |
-0.12 |
-0.63 |
| 30 | 50 | 2.12 |
1.27 |
0.39 |
-1.59 |
-0.12 |
-0.62 |
| 31 | 50 | 2.12 |
1.29 |
0.40 |
-1.63 |
-0.11 |
-0.61 |
| 32 | 50 | 2.11 |
1.31 |
0.40 |
-1.67 |
-0.10 |
-0.60 |
| 33 | 50 | 2.10 |
1.33 |
0.41 |
-1.70 |
-0.10 |
-0.60 |
| 34 | 50 | 2.10 |
1.35 |
0.41 |
-1.73 |
-0.09 |
-0.59 |
| 35 | 50 | 2.09 |
1.37 |
0.42 |
-1.76 |
-0.09 |
-0.58 |
| 36 | 50 | 2.09 |
1.38 |
0.42 |
-1.79 |
-0.09 |
-0.57 |
| 37 | 50 | 2.08 |
1.40 |
0.42 |
-1.82 |
-0.08 |
-0.56 |
| 38 | 50 | 2.08 |
1.41 |
0.42 |
-1.85 |
-0.08 |
-0.56 |
| 39 | 50 | 2.08 |
1.43 |
0.43 |
-1.87 |
-0.08 |
-0.55 |
| 40 | 50 | 2.07 |
1.44 |
0.43 |
-1.90 |
-0.07 |
-0.54 |
| 41 | 50 | 2.07 |
1.45 |
0.43 |
-1.92 |
-0.07 |
-0.53 |
| 42 | 50 | 2.07 |
1.46 |
0.44 |
-1.94 |
-0.07 |
-0.53 |
| 43 | 50 | 2.07 |
1.47 |
0.44 |
-1.96 |
-0.06 |
-0.52 |
| 44 | 50 | 2.06 |
1.48 |
0.44 |
-1.98 |
-0.06 |
-0.51 |
| 45 | 50 | 2.06 |
1.49 |
0.44 |
-2.00 |
-0.06 |
-0.51 |
| 46 | 50 | 2.06 |
1.50 |
0.44 |
-2.02 |
-0.06 |
-0.50 |
| 47 | 50 | 2.06 |
1.50 |
0.44 |
-2.04 |
-0.05 |
-0.49 |
| 48 | 50 | 2.06 |
1.51 |
0.45 |
-2.05 |
-0.05 |
-0.49 |
| 49 | 50 | 2.06 |
1.52 |
0.45 |
-2.07 |
-0.05 |
-0.48 |
| 50 | 50 | 2.05 |
1.52 |
0.45 |
-2.09 |
-0.05 |
-0.48 |
| 51 | 50 | 2.05 |
1.53 |
0.45 |
-2.10 |
-0.05 |
-0.47 |
| 52 | 50 | 2.05 |
1.53 |
0.45 |
-2.12 |
-0.05 |
-0.46 |
| 53 | 50 | 2.05 |
1.53 |
0.45 |
-2.13 |
-0.04 |
-0.46 |
| 54 | 50 | 2.05 |
1.54 |
0.45 |
-2.14 |
-0.04 |
-0.45 |
| 55 | 50 | 2.05 |
1.54 |
0.46 |
-2.16 |
-0.04 |
-0.45 |
| 56 | 50 | 2.05 |
1.54 |
0.46 |
-2.17 |
-0.04 |
-0.44 |
| 57 | 50 | 2.05 |
1.55 |
0.46 |
-2.18 |
-0.04 |
-0.44 |
| 58 | 50 | 2.04 |
1.55 |
0.46 |
-2.19 |
-0.04 |
-0.43 |
| 59 | 50 | 2.04 |
1.55 |
0.46 |
-2.20 |
-0.04 |
-0.43 |
| 60 | 50 | 2.04 |
1.55 |
0.46 |
-2.21 |
-0.04 |
-0.42 |
| 61 | 50 | 2.04 |
1.55 |
0.46 |
-2.22 |
-0.03 |
-0.42 |
| 62 | 50 | 2.04 |
1.55 |
0.46 |
-2.23 |
-0.03 |
-0.41 |
| 63 | 50 | 2.04 |
1.55 |
0.46 |
-2.24 |
-0.03 |
-0.41 |
| 64 | 50 | 2.04 |
1.55 |
0.46 |
-2.25 |
-0.03 |
-0.40 |
| 65 | 50 | 2.04 |
1.55 |
0.46 |
-2.26 |
-0.03 |
-0.40 |
| 66 | 50 | 2.04 |
1.55 |
0.46 |
-2.27 |
-0.03 |
-0.39 |
| 67 | 50 | 2.04 |
1.55 |
0.46 |
-2.28 |
-0.03 |
-0.39 |
| 68 | 50 | 2.03 |
1.55 |
0.46 |
-2.29 |
-0.03 |
-0.38 |
| 69 | 50 | 2.03 |
1.55 |
0.47 |
-2.30 |
-0.03 |
-0.38 |
| 70 | 50 | 2.03 |
1.55 |
0.47 |
-2.30 |
-0.03 |
-0.38 |
| 71 | 50 | 2.03 |
1.55 |
0.47 |
-2.31 |
-0.03 |
-0.37 |
| 72 | 50 | 2.03 |
1.55 |
0.47 |
-2.32 |
-0.03 |
-0.37 |
| 73 | 50 | 2.03 |
1.55 |
0.47 |
-2.33 |
-0.03 |
-0.36 |
| 74 | 50 | 2.03 |
1.55 |
0.47 |
-2.33 |
-0.02 |
-0.36 |
| 75 | 50 | 2.03 |
1.54 |
0.47 |
-2.34 |
-0.02 |
-0.36 |
| 76 | 50 | 2.03 |
1.54 |
0.47 |
-2.35 |
-0.02 |
-0.35 |
| 77 | 50 | 2.03 |
1.54 |
0.47 |
-2.36 |
-0.02 |
-0.35 |
| 78 | 50 | 2.03 |
1.54 |
0.47 |
-2.36 |
-0.02 |
-0.34 |
| 79 | 50 | 2.02 |
1.54 |
0.47 |
-2.37 |
-0.02 |
-0.34 |
| 80 | 50 | 2.02 |
1.54 |
0.47 |
-2.37 |
-0.02 |
-0.34 |
| 81 | 50 | 2.02 |
1.53 |
0.47 |
-2.38 |
-0.02 |
-0.33 |
| 82 | 50 | 2.02 |
1.53 |
0.47 |
-2.39 |
-0.02 |
-0.33 |
| 83 | 50 | 2.02 |
1.53 |
0.47 |
-2.39 |
-0.02 |
-0.33 |
| 84 | 50 | 2.02 |
1.53 |
0.47 |
-2.40 |
-0.02 |
-0.32 |
| 85 | 50 | 2.02 |
1.53 |
0.47 |
-2.40 |
-0.02 |
-0.32 |
| 86 | 50 | 2.02 |
1.52 |
0.47 |
-2.41 |
-0.02 |
-0.32 |
| 87 | 50 | 2.02 |
1.52 |
0.47 |
-2.41 |
-0.02 |
-0.31 |
| 88 | 50 | 2.02 |
1.52 |
0.47 |
-2.42 |
-0.02 |
-0.31 |
| 89 | 50 | 2.02 |
1.52 |
0.47 |
-2.42 |
-0.02 |
-0.31 |
| 90 | 50 | 2.01 |
1.51 |
0.47 |
-2.43 |
-0.02 |
-0.30 |
| 91 | 50 | 2.01 |
1.51 |
0.47 |
-2.43 |
-0.02 |
-0.30 |
| 92 | 50 | 2.01 |
1.51 |
0.47 |
-2.44 |
-0.02 |
-0.30 |
| 93 | 50 | 2.01 |
1.51 |
0.47 |
-2.44 |
-0.02 |
-0.29 |
| 94 | 50 | 2.01 |
1.50 |
0.47 |
-2.45 |
-0.02 |
-0.29 |
| 95 | 50 | 2.01 |
1.50 |
0.47 |
-2.45 |
-0.02 |
-0.29 |
| 96 | 50 | 2.01 |
1.50 |
0.47 |
-2.46 |
-0.02 |
-0.29 |
| 97 | 50 | 2.01 |
1.50 |
0.47 |
-2.46 |
-0.02 |
-0.28 |
| 98 | 50 | 2.01 |
1.49 |
0.47 |
-2.46 |
-0.01 |
-0.28 |
| 99 | 50 | 2.01 |
1.49 |
0.47 |
-2.47 |
-0.01 |
-0.28 |
| 100 | 50 | 2.00 |
1.49 |
0.47 |
-2.47 |
-0.01 |
-0.27 |
| 101 | 50 | 2.00 |
1.49 |
0.47 |
-2.48 |
-0.01 |
-0.27 |
| 102 | 50 | 2.00 |
1.48 |
0.47 |
-2.48 |
-0.01 |
-0.27 |
| 103 | 50 | 2.00 |
1.48 |
0.47 |
-2.48 |
-0.01 |
-0.27 |
| 104 | 50 | 2.00 |
1.48 |
0.47 |
-2.49 |
-0.01 |
-0.26 |
| 105 | 50 | 2.00 |
1.48 |
0.47 |
-2.49 |
-0.01 |
-0.26 |
| 106 | 50 | 2.00 |
1.47 |
0.47 |
-2.49 |
-0.01 |
-0.26 |
| 107 | 50 | 2.00 |
1.47 |
0.47 |
-2.50 |
-0.01 |
-0.26 |
| 108 | 50 | 2.00 |
1.47 |
0.46 |
-2.50 |
-0.01 |
-0.25 |
| 109 | 50 | 1.99 |
1.47 |
0.46 |
-2.50 |
-0.01 |
-0.25 |
| 110 | 50 | 1.99 |
1.46 |
0.46 |
-2.51 |
-0.01 |
-0.25 |
| 111 | 50 | 1.99 |
1.46 |
0.46 |
-2.51 |
-0.01 |
-0.25 |
| 112 | 50 | 1.99 |
1.46 |
0.46 |
-2.51 |
-0.01 |
-0.25 |
| 113 | 50 | 1.99 |
1.45 |
0.46 |
-2.52 |
-0.01 |
-0.24 |
| 114 | 50 | 1.99 |
1.45 |
0.46 |
-2.52 |
-0.01 |
-0.24 |
| 115 | 50 | 1.99 |
1.45 |
0.46 |
-2.52 |
-0.01 |
-0.24 |
| 116 | 50 | 1.99 |
1.45 |
0.46 |
-2.53 |
-0.01 |
-0.24 |
| 117 | 50 | 1.99 |
1.44 |
0.46 |
-2.53 |
-0.01 |
-0.23 |
| 118 | 50 | 1.98 |
1.44 |
0.46 |
-2.53 |
-0.01 |
-0.23 |
| 119 | 50 | 1.98 |
1.44 |
0.46 |
-2.53 |
-0.01 |
-0.23 |
| 120 | 50 | 1.98 |
1.44 |
0.46 |
-2.54 |
-0.01 |
-0.23 |
Figure 2. A 50% Rise in the Oil Price: Alternative Price Elasticities of Oil Demand
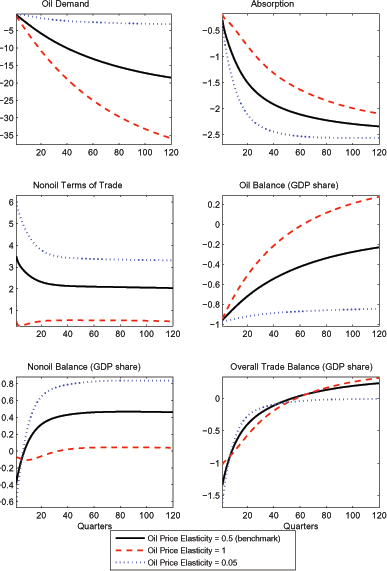
Data for Figure 2, Panel 1 - A 50% Rise in the Oil Price: Alternative Price Elasticities of Oil Demand
| Period | Oil demand: oil price elasticity = 0.5 (bench-mark) |
Absorption: oil price elasticity = 0.5 (bench-mark) |
Nonoil terms of trade: oil price elasticity = 0.5 (bench-mark) |
Oil balance: GDP share: oil price elasticity = 0.5 (bench-mark) |
Nonoil balance: GDP share: oil price elasticity = 0.5 (bench-mark) |
Overall trade balance: GDP share: oil price elasticity = 0.5 (bench-mark) |
Oil demand: oil price elasticity = 1 |
Absorption: oil price elasticity = 1 |
Nonoil terms of trade: oil price elasticity = 1 |
|---|---|---|---|---|---|---|---|---|---|
| 1 | -0.47 |
-0.30 |
3.50 |
-0.96 |
-0.38 |
-1.34 |
-0.75 |
-0.19 |
0.49 |
| 2 | -0.80 |
-0.44 |
3.28 |
-0.94 |
-0.29 |
-1.23 |
-1.37 |
-0.25 |
0.34 |
| 3 | -1.10 |
-0.55 |
3.15 |
-0.93 |
-0.22 |
-1.15 |
-1.95 |
-0.28 |
0.30 |
| 4 | -1.39 |
-0.63 |
3.05 |
-0.91 |
-0.16 |
-1.07 |
-2.51 |
-0.30 |
0.29 |
| 5 | -1.68 |
-0.71 |
2.97 |
-0.90 |
-0.10 |
-1.00 |
-3.07 |
-0.32 |
0.30 |
| 6 | -1.97 |
-0.79 |
2.89 |
-0.89 |
-0.05 |
-0.94 |
-3.62 |
-0.35 |
0.32 |
| 7 | -2.25 |
-0.86 |
2.83 |
-0.87 |
0.00 |
-0.88 |
-4.17 |
-0.37 |
0.34 |
| 8 | -2.54 |
-0.92 |
2.76 |
-0.86 |
0.04 |
-0.82 |
-4.71 |
-0.40 |
0.35 |
| 9 | -2.83 |
-0.99 |
2.71 |
-0.85 |
0.08 |
-0.77 |
-5.25 |
-0.43 |
0.37 |
| 10 | -3.12 |
-1.05 |
2.65 |
-0.83 |
0.11 |
-0.72 |
-5.78 |
-0.46 |
0.39 |
| 11 | -3.40 |
-1.11 |
2.61 |
-0.82 |
0.14 |
-0.68 |
-6.30 |
-0.50 |
0.40 |
| 12 | -3.68 |
-1.16 |
2.56 |
-0.81 |
0.17 |
-0.64 |
-6.82 |
-0.53 |
0.42 |
| 13 | -3.96 |
-1.21 |
2.52 |
-0.80 |
0.19 |
-0.60 |
-7.34 |
-0.56 |
0.43 |
| 14 | -4.24 |
-1.26 |
2.48 |
-0.78 |
0.22 |
-0.57 |
-7.84 |
-0.60 |
0.45 |
| 15 | -4.51 |
-1.30 |
2.45 |
-0.77 |
0.24 |
-0.53 |
-8.34 |
-0.63 |
0.46 |
| 16 | -4.77 |
-1.35 |
2.42 |
-0.76 |
0.26 |
-0.50 |
-8.84 |
-0.66 |
0.47 |
| 17 | -5.04 |
-1.39 |
2.39 |
-0.75 |
0.27 |
-0.48 |
-9.32 |
-0.70 |
0.48 |
| 18 | -5.30 |
-1.43 |
2.36 |
-0.74 |
0.29 |
-0.45 |
-9.80 |
-0.73 |
0.49 |
| 19 | -5.55 |
-1.46 |
2.34 |
-0.73 |
0.30 |
-0.42 |
-10.28 |
-0.76 |
0.50 |
| 20 | -5.80 |
-1.50 |
2.32 |
-0.72 |
0.32 |
-0.40 |
-10.75 |
-0.80 |
0.50 |
| 21 | -6.05 |
-1.53 |
2.30 |
-0.71 |
0.33 |
-0.38 |
-11.21 |
-0.83 |
0.51 |
| 22 | -6.29 |
-1.56 |
2.28 |
-0.70 |
0.34 |
-0.36 |
-11.66 |
-0.86 |
0.52 |
| 23 | -6.53 |
-1.59 |
2.26 |
-0.69 |
0.35 |
-0.34 |
-12.11 |
-0.89 |
0.52 |
| 24 | -6.76 |
-1.62 |
2.25 |
-0.68 |
0.36 |
-0.32 |
-12.56 |
-0.92 |
0.53 |
| 25 | -6.99 |
-1.64 |
2.23 |
-0.67 |
0.36 |
-0.30 |
-12.99 |
-0.95 |
0.53 |
| 26 | -7.22 |
-1.67 |
2.22 |
-0.66 |
0.37 |
-0.29 |
-13.43 |
-0.98 |
0.53 |
| 27 | -7.44 |
-1.69 |
2.21 |
-0.65 |
0.38 |
-0.27 |
-13.85 |
-1.01 |
0.54 |
| 28 | -7.66 |
-1.71 |
2.20 |
-0.64 |
0.38 |
-0.25 |
-14.27 |
-1.04 |
0.54 |
| 29 | -7.88 |
-1.73 |
2.19 |
-0.63 |
0.39 |
-0.24 |
-14.68 |
-1.06 |
0.54 |
| 30 | -8.09 |
-1.75 |
2.18 |
-0.62 |
0.39 |
-0.23 |
-15.09 |
-1.09 |
0.54 |
| 31 | -8.30 |
-1.77 |
2.18 |
-0.61 |
0.40 |
-0.21 |
-15.50 |
-1.12 |
0.55 |
| 32 | -8.50 |
-1.79 |
2.17 |
-0.60 |
0.40 |
-0.20 |
-15.89 |
-1.14 |
0.55 |
| 33 | -8.70 |
-1.81 |
2.16 |
-0.60 |
0.41 |
-0.19 |
-16.28 |
-1.17 |
0.55 |
| 34 | -8.90 |
-1.83 |
2.16 |
-0.59 |
0.41 |
-0.18 |
-16.67 |
-1.19 |
0.55 |
| 35 | -9.10 |
-1.84 |
2.15 |
-0.58 |
0.42 |
-0.16 |
-17.05 |
-1.21 |
0.55 |
| 36 | -9.29 |
-1.86 |
2.15 |
-0.57 |
0.42 |
-0.15 |
-17.43 |
-1.23 |
0.55 |
| 37 | -9.48 |
-1.87 |
2.14 |
-0.56 |
0.42 |
-0.14 |
-17.80 |
-1.26 |
0.55 |
| 38 | -9.66 |
-1.89 |
2.14 |
-0.56 |
0.42 |
-0.13 |
-18.16 |
-1.28 |
0.55 |
| 39 | -9.85 |
-1.90 |
2.14 |
-0.55 |
0.43 |
-0.12 |
-18.52 |
-1.30 |
0.55 |
| 40 | -10.03 |
-1.92 |
2.13 |
-0.54 |
0.43 |
-0.11 |
-18.87 |
-1.32 |
0.55 |
| 41 | -10.20 |
-1.93 |
2.13 |
-0.53 |
0.43 |
-0.10 |
-19.22 |
-1.34 |
0.55 |
| 42 | -10.38 |
-1.94 |
2.13 |
-0.53 |
0.44 |
-0.09 |
-19.57 |
-1.36 |
0.55 |
| 43 | -10.55 |
-1.95 |
2.13 |
-0.52 |
0.44 |
-0.08 |
-19.91 |
-1.38 |
0.55 |
| 44 | -10.72 |
-1.97 |
2.12 |
-0.51 |
0.44 |
-0.07 |
-20.24 |
-1.39 |
0.55 |
| 45 | -10.89 |
-1.98 |
2.12 |
-0.51 |
0.44 |
-0.07 |
-20.57 |
-1.41 |
0.55 |
| 46 | -11.05 |
-1.99 |
2.12 |
-0.50 |
0.44 |
-0.06 |
-20.90 |
-1.43 |
0.55 |
| 47 | -11.21 |
-2.00 |
2.12 |
-0.49 |
0.44 |
-0.05 |
-21.22 |
-1.45 |
0.55 |
| 48 | -11.37 |
-2.01 |
2.12 |
-0.49 |
0.45 |
-0.04 |
-21.54 |
-1.46 |
0.55 |
| 49 | -11.53 |
-2.02 |
2.11 |
-0.48 |
0.45 |
-0.03 |
-21.85 |
-1.48 |
0.55 |
| 50 | -11.68 |
-2.03 |
2.11 |
-0.48 |
0.45 |
-0.03 |
-22.16 |
-1.49 |
0.55 |
| 51 | -11.83 |
-2.04 |
2.11 |
-0.47 |
0.45 |
-0.02 |
-22.46 |
-1.51 |
0.55 |
| 52 | -11.98 |
-2.05 |
2.11 |
-0.46 |
0.45 |
-0.01 |
-22.76 |
-1.52 |
0.55 |
| 53 | -12.13 |
-2.05 |
2.11 |
-0.46 |
0.45 |
-0.01 |
-23.06 |
-1.54 |
0.55 |
| 54 | -12.28 |
-2.06 |
2.11 |
-0.45 |
0.45 |
0.00 |
-23.35 |
-1.55 |
0.55 |
| 55 | -12.42 |
-2.07 |
2.11 |
-0.45 |
0.46 |
0.01 |
-23.64 |
-1.57 |
0.55 |
| 56 | -12.56 |
-2.08 |
2.10 |
-0.44 |
0.46 |
0.01 |
-23.92 |
-1.58 |
0.55 |
| 57 | -12.70 |
-2.09 |
2.10 |
-0.44 |
0.46 |
0.02 |
-24.20 |
-1.59 |
0.55 |
| 58 | -12.84 |
-2.09 |
2.10 |
-0.43 |
0.46 |
0.03 |
-24.47 |
-1.61 |
0.55 |
| 59 | -12.97 |
-2.10 |
2.10 |
-0.43 |
0.46 |
0.03 |
-24.75 |
-1.62 |
0.55 |
| 60 | -13.11 |
-2.11 |
2.10 |
-0.42 |
0.46 |
0.04 |
-25.01 |
-1.63 |
0.55 |
| 61 | -13.24 |
-2.12 |
2.10 |
-0.42 |
0.46 |
0.04 |
-25.28 |
-1.65 |
0.55 |
| 62 | -13.37 |
-2.12 |
2.10 |
-0.41 |
0.46 |
0.05 |
-25.54 |
-1.66 |
0.55 |
| 63 | -13.50 |
-2.13 |
2.10 |
-0.41 |
0.46 |
0.05 |
-25.80 |
-1.67 |
0.55 |
| 64 | -13.62 |
-2.14 |
2.09 |
-0.40 |
0.46 |
0.06 |
-26.05 |
-1.68 |
0.55 |
| 65 | -13.75 |
-2.14 |
2.09 |
-0.40 |
0.46 |
0.07 |
-26.30 |
-1.69 |
0.55 |
| 66 | -13.87 |
-2.15 |
2.09 |
-0.39 |
0.46 |
0.07 |
-26.55 |
-1.70 |
0.55 |
| 67 | -13.99 |
-2.15 |
2.09 |
-0.39 |
0.46 |
0.08 |
-26.79 |
-1.72 |
0.55 |
| 68 | -14.11 |
-2.16 |
2.09 |
-0.38 |
0.46 |
0.08 |
-27.03 |
-1.73 |
0.55 |
| 69 | -14.23 |
-2.17 |
2.09 |
-0.38 |
0.47 |
0.09 |
-27.26 |
-1.74 |
0.55 |
| 70 | -14.34 |
-2.17 |
2.09 |
-0.38 |
0.47 |
0.09 |
-27.50 |
-1.75 |
0.55 |
| 71 | -14.46 |
-2.18 |
2.09 |
-0.37 |
0.47 |
0.09 |
-27.73 |
-1.76 |
0.55 |
| 72 | -14.57 |
-2.18 |
2.09 |
-0.37 |
0.47 |
0.10 |
-27.95 |
-1.77 |
0.55 |
| 73 | -14.68 |
-2.19 |
2.09 |
-0.36 |
0.47 |
0.10 |
-28.18 |
-1.78 |
0.55 |
| 74 | -14.79 |
-2.19 |
2.08 |
-0.36 |
0.47 |
0.11 |
-28.40 |
-1.79 |
0.55 |
| 75 | -14.90 |
-2.20 |
2.08 |
-0.36 |
0.47 |
0.11 |
-28.62 |
-1.80 |
0.55 |
| 76 | -15.00 |
-2.20 |
2.08 |
-0.35 |
0.47 |
0.12 |
-28.83 |
-1.81 |
0.55 |
| 77 | -15.11 |
-2.21 |
2.08 |
-0.35 |
0.47 |
0.12 |
-29.04 |
-1.82 |
0.55 |
| 78 | -15.21 |
-2.21 |
2.08 |
-0.34 |
0.47 |
0.12 |
-29.25 |
-1.82 |
0.54 |
| 79 | -15.31 |
-2.22 |
2.08 |
-0.34 |
0.47 |
0.13 |
-29.46 |
-1.83 |
0.54 |
| 80 | -15.41 |
-2.22 |
2.08 |
-0.34 |
0.47 |
0.13 |
-29.66 |
-1.84 |
0.54 |
| 81 | -15.51 |
-2.22 |
2.08 |
-0.33 |
0.47 |
0.13 |
-29.86 |
-1.85 |
0.54 |
| 82 | -15.61 |
-2.23 |
2.08 |
-0.33 |
0.47 |
0.14 |
-30.06 |
-1.86 |
0.54 |
| 83 | -15.71 |
-2.23 |
2.07 |
-0.33 |
0.47 |
0.14 |
-30.25 |
-1.87 |
0.54 |
| 84 | -15.80 |
-2.24 |
2.07 |
-0.32 |
0.47 |
0.15 |
-30.45 |
-1.88 |
0.54 |
| 85 | -15.90 |
-2.24 |
2.07 |
-0.32 |
0.47 |
0.15 |
-30.64 |
-1.88 |
0.54 |
| 86 | -15.99 |
-2.24 |
2.07 |
-0.32 |
0.47 |
0.15 |
-30.82 |
-1.89 |
0.54 |
| 87 | -16.08 |
-2.25 |
2.07 |
-0.31 |
0.47 |
0.16 |
-31.01 |
-1.90 |
0.54 |
| 88 | -16.17 |
-2.25 |
2.07 |
-0.31 |
0.47 |
0.16 |
-31.19 |
-1.91 |
0.54 |
| 89 | -16.26 |
-2.26 |
2.07 |
-0.31 |
0.47 |
0.16 |
-31.37 |
-1.92 |
0.54 |
| 90 | -16.35 |
-2.26 |
2.07 |
-0.30 |
0.47 |
0.16 |
-31.55 |
-1.92 |
0.54 |
| 91 | -16.43 |
-2.26 |
2.07 |
-0.30 |
0.47 |
0.17 |
-31.72 |
-1.93 |
0.54 |
| 92 | -16.52 |
-2.27 |
2.07 |
-0.30 |
0.47 |
0.17 |
-31.89 |
-1.94 |
0.53 |
| 93 | -16.60 |
-2.27 |
2.06 |
-0.29 |
0.47 |
0.17 |
-32.06 |
-1.94 |
0.53 |
| 94 | -16.69 |
-2.27 |
2.06 |
-0.29 |
0.47 |
0.18 |
-32.23 |
-1.95 |
0.53 |
| 95 | -16.77 |
-2.28 |
2.06 |
-0.29 |
0.47 |
0.18 |
-32.40 |
-1.96 |
0.53 |
| 96 | -16.85 |
-2.28 |
2.06 |
-0.29 |
0.47 |
0.18 |
-32.56 |
-1.96 |
0.53 |
| 97 | -16.93 |
-2.28 |
2.06 |
-0.28 |
0.47 |
0.18 |
-32.72 |
-1.97 |
0.53 |
| 98 | -17.01 |
-2.29 |
2.06 |
-0.28 |
0.47 |
0.19 |
-32.88 |
-1.98 |
0.53 |
| 99 | -17.08 |
-2.29 |
2.06 |
-0.28 |
0.47 |
0.19 |
-33.04 |
-1.98 |
0.53 |
| 100 | -17.16 |
-2.29 |
2.06 |
-0.27 |
0.47 |
0.19 |
-33.19 |
-1.99 |
0.53 |
| 101 | -17.24 |
-2.29 |
2.06 |
-0.27 |
0.47 |
0.19 |
-33.34 |
-2.00 |
0.52 |
| 102 | -17.31 |
-2.30 |
2.05 |
-0.27 |
0.47 |
0.20 |
-33.49 |
-2.00 |
0.52 |
| 103 | -17.38 |
-2.30 |
2.05 |
-0.27 |
0.47 |
0.20 |
-33.64 |
-2.01 |
0.52 |
| 104 | -17.46 |
-2.30 |
2.05 |
-0.26 |
0.47 |
0.20 |
-33.79 |
-2.01 |
0.52 |
| 105 | -17.53 |
-2.31 |
2.05 |
-0.26 |
0.47 |
0.20 |
-33.93 |
-2.02 |
0.52 |
| 106 | -17.60 |
-2.31 |
2.05 |
-0.26 |
0.47 |
0.21 |
-34.07 |
-2.02 |
0.52 |
| 107 | -17.67 |
-2.31 |
2.05 |
-0.26 |
0.47 |
0.21 |
-34.21 |
-2.03 |
0.52 |
| 108 | -17.73 |
-2.31 |
2.05 |
-0.25 |
0.46 |
0.21 |
-34.35 |
-2.04 |
0.52 |
| 109 | -17.80 |
-2.31 |
2.05 |
-0.25 |
0.46 |
0.21 |
-34.49 |
-2.04 |
0.51 |
| 110 | -17.87 |
-2.32 |
2.05 |
-0.25 |
0.46 |
0.21 |
-34.62 |
-2.05 |
0.51 |
| 111 | -17.93 |
-2.32 |
2.04 |
-0.25 |
0.46 |
0.22 |
-34.76 |
-2.05 |
0.51 |
| 112 | -18.00 |
-2.32 |
2.04 |
-0.25 |
0.46 |
0.22 |
-34.89 |
-2.06 |
0.51 |
| 113 | -18.06 |
-2.32 |
2.04 |
-0.24 |
0.46 |
0.22 |
-35.02 |
-2.06 |
0.51 |
| 114 | -18.13 |
-2.33 |
2.04 |
-0.24 |
0.46 |
0.22 |
-35.14 |
-2.07 |
0.51 |
| 115 | -18.19 |
-2.33 |
2.04 |
-0.24 |
0.46 |
0.22 |
-35.27 |
-2.07 |
0.51 |
| 116 | -18.25 |
-2.33 |
2.04 |
-0.24 |
0.46 |
0.23 |
-35.39 |
-2.08 |
0.50 |
| 117 | -18.31 |
-2.33 |
2.04 |
-0.23 |
0.46 |
0.23 |
-35.52 |
-2.08 |
0.50 |
| 118 | -18.37 |
-2.33 |
2.04 |
-0.23 |
0.46 |
0.23 |
-35.64 |
-2.08 |
0.50 |
| 119 | -18.43 |
-2.34 |
2.04 |
-0.23 |
0.46 |
0.23 |
-35.76 |
-2.09 |
0.50 |
| 120 | -18.49 |
-2.34 |
2.03 |
-0.23 |
0.46 |
0.23 |
-35.87 |
-2.09 |
0.50 |
Data for Figure 2, Panel 2 - A 50% Rise in the Oil Price: Alternative Price Elasticities of Oil Demand
| Period | Oil balance: GDP share: oil price elasticity = 1 |
Nonoil balance: GDP share: oil price elasticity = 1 |
Overall trade balance: GDP share: oil price elasticity = 1 |
Oil demand: oil price elasticity = 0.05 |
Absorption: oil price elasticity = 0.05 |
Nonoil terms of trade: oil price elasticity = 0.05 |
Oil balance: GDP share: oil price elasticity = 0.05 |
Nonoil balance: GDP share: oil price elasticity = 0.05 |
Overall trade balance: GDP share: oil price elasticity = 0.05 |
|---|---|---|---|---|---|---|---|---|---|
| 1 | -0.94 |
-0.08 |
-1.02 |
-0.22 |
-0.39 |
6.01 |
-0.97 |
-0.64 |
-1.61 |
| 2 | -0.91 |
-0.08 |
-0.99 |
-0.30 |
-0.61 |
5.73 |
-0.97 |
-0.48 |
-1.44 |
| 3 | -0.89 |
-0.08 |
-0.97 |
-0.35 |
-0.78 |
5.51 |
-0.96 |
-0.34 |
-1.30 |
| 4 | -0.86 |
-0.09 |
-0.95 |
-0.40 |
-0.92 |
5.33 |
-0.96 |
-0.22 |
-1.18 |
| 5 | -0.83 |
-0.09 |
-0.93 |
-0.45 |
-1.05 |
5.16 |
-0.96 |
-0.10 |
-1.06 |
| 6 | -0.81 |
-0.10 |
-0.91 |
-0.51 |
-1.17 |
5.00 |
-0.96 |
0.00 |
-0.96 |
| 7 | -0.78 |
-0.10 |
-0.89 |
-0.57 |
-1.28 |
4.86 |
-0.95 |
0.08 |
-0.87 |
| 8 | -0.76 |
-0.11 |
-0.87 |
-0.64 |
-1.38 |
4.73 |
-0.95 |
0.16 |
-0.79 |
| 9 | -0.74 |
-0.11 |
-0.84 |
-0.71 |
-1.48 |
4.61 |
-0.95 |
0.24 |
-0.71 |
| 10 | -0.71 |
-0.11 |
-0.82 |
-0.78 |
-1.56 |
4.50 |
-0.95 |
0.30 |
-0.65 |
| 11 | -0.69 |
-0.10 |
-0.79 |
-0.85 |
-1.64 |
4.39 |
-0.94 |
0.35 |
-0.59 |
| 12 | -0.67 |
-0.10 |
-0.77 |
-0.92 |
-1.71 |
4.30 |
-0.94 |
0.40 |
-0.53 |
| 13 | -0.65 |
-0.10 |
-0.74 |
-0.99 |
-1.78 |
4.21 |
-0.94 |
0.45 |
-0.49 |
| 14 | -0.63 |
-0.09 |
-0.72 |
-1.06 |
-1.84 |
4.13 |
-0.93 |
0.49 |
-0.45 |
| 15 | -0.60 |
-0.09 |
-0.69 |
-1.13 |
-1.90 |
4.06 |
-0.93 |
0.52 |
-0.41 |
| 16 | -0.58 |
-0.08 |
-0.67 |
-1.20 |
-1.95 |
4.00 |
-0.93 |
0.55 |
-0.37 |
| 17 | -0.56 |
-0.08 |
-0.64 |
-1.26 |
-2.00 |
3.94 |
-0.93 |
0.58 |
-0.34 |
| 18 | -0.54 |
-0.07 |
-0.62 |
-1.32 |
-2.04 |
3.88 |
-0.92 |
0.61 |
-0.32 |
| 19 | -0.53 |
-0.07 |
-0.59 |
-1.39 |
-2.08 |
3.83 |
-0.92 |
0.63 |
-0.29 |
| 20 | -0.51 |
-0.06 |
-0.57 |
-1.44 |
-2.11 |
3.79 |
-0.92 |
0.65 |
-0.27 |
| 21 | -0.49 |
-0.06 |
-0.54 |
-1.50 |
-2.14 |
3.75 |
-0.92 |
0.66 |
-0.25 |
| 22 | -0.47 |
-0.05 |
-0.52 |
-1.56 |
-2.17 |
3.71 |
-0.91 |
0.68 |
-0.24 |
| 23 | -0.45 |
-0.04 |
-0.50 |
-1.61 |
-2.20 |
3.68 |
-0.91 |
0.69 |
-0.22 |
| 24 | -0.44 |
-0.04 |
-0.48 |
-1.66 |
-2.23 |
3.65 |
-0.91 |
0.70 |
-0.21 |
| 25 | -0.42 |
-0.03 |
-0.45 |
-1.71 |
-2.25 |
3.62 |
-0.91 |
0.71 |
-0.20 |
| 26 | -0.40 |
-0.03 |
-0.43 |
-1.75 |
-2.27 |
3.60 |
-0.91 |
0.72 |
-0.19 |
| 27 | -0.39 |
-0.02 |
-0.41 |
-1.80 |
-2.29 |
3.58 |
-0.90 |
0.73 |
-0.18 |
| 28 | -0.37 |
-0.02 |
-0.39 |
-1.84 |
-2.31 |
3.56 |
-0.90 |
0.74 |
-0.17 |
| 29 | -0.36 |
-0.01 |
-0.37 |
-1.88 |
-2.32 |
3.54 |
-0.90 |
0.74 |
-0.16 |
| 30 | -0.34 |
-0.01 |
-0.35 |
-1.92 |
-2.34 |
3.53 |
-0.90 |
0.75 |
-0.15 |
| 31 | -0.33 |
-0.01 |
-0.33 |
-1.96 |
-2.35 |
3.51 |
-0.90 |
0.75 |
-0.14 |
| 32 | -0.31 |
0.00 |
-0.32 |
-1.99 |
-2.36 |
3.50 |
-0.90 |
0.76 |
-0.14 |
| 33 | -0.30 |
0.00 |
-0.30 |
-2.03 |
-2.38 |
3.49 |
-0.89 |
0.76 |
-0.13 |
| 34 | -0.29 |
0.00 |
-0.28 |
-2.06 |
-2.39 |
3.48 |
-0.89 |
0.77 |
-0.13 |
| 35 | -0.27 |
0.01 |
-0.27 |
-2.09 |
-2.40 |
3.47 |
-0.89 |
0.77 |
-0.12 |
| 36 | -0.26 |
0.01 |
-0.25 |
-2.12 |
-2.41 |
3.46 |
-0.89 |
0.78 |
-0.11 |
| 37 | -0.25 |
0.01 |
-0.23 |
-2.15 |
-2.42 |
3.45 |
-0.89 |
0.78 |
-0.11 |
| 38 | -0.24 |
0.02 |
-0.22 |
-2.18 |
-2.43 |
3.45 |
-0.89 |
0.78 |
-0.11 |
| 39 | -0.22 |
0.02 |
-0.20 |
-2.21 |
-2.43 |
3.44 |
-0.89 |
0.79 |
-0.10 |
| 40 | -0.21 |
0.02 |
-0.19 |
-2.23 |
-2.44 |
3.44 |
-0.89 |
0.79 |
-0.10 |
| 41 | -0.20 |
0.02 |
-0.18 |
-2.26 |
-2.45 |
3.43 |
-0.88 |
0.79 |
-0.09 |
| 42 | -0.19 |
0.02 |
-0.16 |
-2.28 |
-2.45 |
3.43 |
-0.88 |
0.79 |
-0.09 |
| 43 | -0.18 |
0.03 |
-0.15 |
-2.30 |
-2.46 |
3.42 |
-0.88 |
0.80 |
-0.09 |
| 44 | -0.17 |
0.03 |
-0.14 |
-2.33 |
-2.47 |
3.42 |
-0.88 |
0.80 |
-0.08 |
| 45 | -0.15 |
0.03 |
-0.13 |
-2.35 |
-2.47 |
3.41 |
-0.88 |
0.80 |
-0.08 |
| 46 | -0.14 |
0.03 |
-0.11 |
-2.37 |
-2.48 |
3.41 |
-0.88 |
0.80 |
-0.08 |
| 47 | -0.13 |
0.03 |
-0.10 |
-2.39 |
-2.48 |
3.41 |
-0.88 |
0.81 |
-0.07 |
| 48 | -0.12 |
0.03 |
-0.09 |
-2.41 |
-2.49 |
3.40 |
-0.88 |
0.81 |
-0.07 |
| 49 | -0.11 |
0.03 |
-0.08 |
-2.43 |
-2.49 |
3.40 |
-0.88 |
0.81 |
-0.07 |
| 50 | -0.10 |
0.04 |
-0.07 |
-2.45 |
-2.50 |
3.40 |
-0.88 |
0.81 |
-0.06 |
| 51 | -0.09 |
0.04 |
-0.06 |
-2.47 |
-2.50 |
3.40 |
-0.87 |
0.81 |
-0.06 |
| 52 | -0.09 |
0.04 |
-0.05 |
-2.49 |
-2.50 |
3.39 |
-0.87 |
0.82 |
-0.06 |
| 53 | -0.08 |
0.04 |
-0.04 |
-2.50 |
-2.51 |
3.39 |
-0.87 |
0.82 |
-0.06 |
| 54 | -0.07 |
0.04 |
-0.03 |
-2.52 |
-2.51 |
3.39 |
-0.87 |
0.82 |
-0.05 |
| 55 | -0.06 |
0.04 |
-0.02 |
-2.54 |
-2.51 |
3.39 |
-0.87 |
0.82 |
-0.05 |
| 56 | -0.05 |
0.04 |
-0.01 |
-2.55 |
-2.52 |
3.39 |
-0.87 |
0.82 |
-0.05 |
| 57 | -0.04 |
0.04 |
0.00 |
-2.57 |
-2.52 |
3.38 |
-0.87 |
0.82 |
-0.05 |
| 58 | -0.03 |
0.04 |
0.01 |
-2.59 |
-2.52 |
3.38 |
-0.87 |
0.82 |
-0.05 |
| 59 | -0.02 |
0.04 |
0.02 |
-2.60 |
-2.53 |
3.38 |
-0.87 |
0.83 |
-0.04 |
| 60 | -0.02 |
0.04 |
0.03 |
-2.62 |
-2.53 |
3.38 |
-0.87 |
0.83 |
-0.04 |
| 61 | -0.01 |
0.04 |
0.03 |
-2.63 |
-2.53 |
3.38 |
-0.87 |
0.83 |
-0.04 |
| 62 | 0.00 |
0.04 |
0.04 |
-2.64 |
-2.53 |
3.37 |
-0.87 |
0.83 |
-0.04 |
| 63 | 0.01 |
0.04 |
0.05 |
-2.66 |
-2.53 |
3.37 |
-0.87 |
0.83 |
-0.04 |
| 64 | 0.01 |
0.04 |
0.06 |
-2.67 |
-2.54 |
3.37 |
-0.87 |
0.83 |
-0.04 |
| 65 | 0.02 |
0.04 |
0.07 |
-2.69 |
-2.54 |
3.37 |
-0.87 |
0.83 |
-0.03 |
| 66 | 0.03 |
0.04 |
0.07 |
-2.70 |
-2.54 |
3.37 |
-0.86 |
0.83 |
-0.03 |
| 67 | 0.04 |
0.04 |
0.08 |
-2.71 |
-2.54 |
3.37 |
-0.86 |
0.83 |
-0.03 |
| 68 | 0.04 |
0.04 |
0.09 |
-2.73 |
-2.54 |
3.36 |
-0.86 |
0.83 |
-0.03 |
| 69 | 0.05 |
0.04 |
0.09 |
-2.74 |
-2.54 |
3.36 |
-0.86 |
0.83 |
-0.03 |
| 70 | 0.06 |
0.04 |
0.10 |
-2.75 |
-2.55 |
3.36 |
-0.86 |
0.83 |
-0.03 |
| 71 | 0.06 |
0.04 |
0.11 |
-2.76 |
-2.55 |
3.36 |
-0.86 |
0.83 |
-0.03 |
| 72 | 0.07 |
0.05 |
0.11 |
-2.77 |
-2.55 |
3.36 |
-0.86 |
0.83 |
-0.03 |
| 73 | 0.08 |
0.05 |
0.12 |
-2.79 |
-2.55 |
3.36 |
-0.86 |
0.84 |
-0.03 |
| 74 | 0.08 |
0.05 |
0.13 |
-2.80 |
-2.55 |
3.36 |
-0.86 |
0.84 |
-0.02 |
| 75 | 0.09 |
0.05 |
0.13 |
-2.81 |
-2.55 |
3.35 |
-0.86 |
0.84 |
-0.02 |
| 76 | 0.09 |
0.05 |
0.14 |
-2.82 |
-2.55 |
3.35 |
-0.86 |
0.84 |
-0.02 |
| 77 | 0.10 |
0.05 |
0.15 |
-2.83 |
-2.55 |
3.35 |
-0.86 |
0.84 |
-0.02 |
| 78 | 0.11 |
0.05 |
0.15 |
-2.84 |
-2.55 |
3.35 |
-0.86 |
0.84 |
-0.02 |
| 79 | 0.11 |
0.05 |
0.16 |
-2.85 |
-2.55 |
3.35 |
-0.86 |
0.84 |
-0.02 |
| 80 | 0.12 |
0.05 |
0.16 |
-2.86 |
-2.55 |
3.35 |
-0.86 |
0.84 |
-0.02 |
| 81 | 0.12 |
0.05 |
0.17 |
-2.87 |
-2.55 |
3.35 |
-0.86 |
0.84 |
-0.02 |
| 82 | 0.13 |
0.05 |
0.17 |
-2.88 |
-2.56 |
3.35 |
-0.86 |
0.84 |
-0.02 |
| 83 | 0.13 |
0.05 |
0.18 |
-2.89 |
-2.56 |
3.34 |
-0.86 |
0.84 |
-0.02 |
| 84 | 0.14 |
0.05 |
0.18 |
-2.90 |
-2.56 |
3.34 |
-0.86 |
0.84 |
-0.02 |
| 85 | 0.14 |
0.05 |
0.19 |
-2.91 |
-2.56 |
3.34 |
-0.85 |
0.84 |
-0.02 |
| 86 | 0.15 |
0.05 |
0.19 |
-2.92 |
-2.56 |
3.34 |
-0.85 |
0.84 |
-0.02 |
| 87 | 0.15 |
0.05 |
0.20 |
-2.93 |
-2.56 |
3.34 |
-0.85 |
0.84 |
-0.02 |
| 88 | 0.16 |
0.05 |
0.20 |
-2.94 |
-2.56 |
3.34 |
-0.85 |
0.84 |
-0.02 |
| 89 | 0.16 |
0.05 |
0.21 |
-2.95 |
-2.56 |
3.34 |
-0.85 |
0.84 |
-0.02 |
| 90 | 0.17 |
0.05 |
0.21 |
-2.96 |
-2.56 |
3.34 |
-0.85 |
0.84 |
-0.01 |
| 91 | 0.17 |
0.05 |
0.22 |
-2.97 |
-2.56 |
3.34 |
-0.85 |
0.84 |
-0.01 |
| 92 | 0.18 |
0.05 |
0.22 |
-2.97 |
-2.56 |
3.33 |
-0.85 |
0.84 |
-0.01 |
| 93 | 0.18 |
0.05 |
0.23 |
-2.98 |
-2.56 |
3.33 |
-0.85 |
0.84 |
-0.01 |
| 94 | 0.18 |
0.05 |
0.23 |
-2.99 |
-2.56 |
3.33 |
-0.85 |
0.84 |
-0.01 |
| 95 | 0.19 |
0.04 |
0.23 |
-3.00 |
-2.56 |
3.33 |
-0.85 |
0.84 |
-0.01 |
| 96 | 0.19 |
0.04 |
0.24 |
-3.01 |
-2.56 |
3.33 |
-0.85 |
0.84 |
-0.01 |
| 97 | 0.20 |
0.04 |
0.24 |
-3.02 |
-2.56 |
3.33 |
-0.85 |
0.84 |
-0.01 |
| 98 | 0.20 |
0.04 |
0.25 |
-3.02 |
-2.56 |
3.33 |
-0.85 |
0.84 |
-0.01 |
| 99 | 0.21 |
0.04 |
0.25 |
-3.03 |
-2.56 |
3.33 |
-0.85 |
0.84 |
-0.01 |
| 100 | 0.21 |
0.04 |
0.25 |
-3.04 |
-2.56 |
3.33 |
-0.85 |
0.84 |
-0.01 |
| 101 | 0.21 |
0.04 |
0.26 |
-3.05 |
-2.56 |
3.33 |
-0.85 |
0.84 |
-0.01 |
| 102 | 0.22 |
0.04 |
0.26 |
-3.05 |
-2.56 |
3.33 |
-0.85 |
0.84 |
-0.01 |
| 103 | 0.22 |
0.04 |
0.26 |
-3.06 |
-2.56 |
3.32 |
-0.85 |
0.84 |
-0.01 |
| 104 | 0.22 |
0.04 |
0.27 |
-3.07 |
-2.56 |
3.32 |
-0.85 |
0.84 |
-0.01 |
| 105 | 0.23 |
0.04 |
0.27 |
-3.07 |
-2.56 |
3.32 |
-0.85 |
0.84 |
-0.01 |
| 106 | 0.23 |
0.04 |
0.27 |
-3.08 |
-2.56 |
3.32 |
-0.85 |
0.84 |
-0.01 |
| 107 | 0.24 |
0.04 |
0.28 |
-3.09 |
-2.56 |
3.32 |
-0.85 |
0.84 |
-0.01 |
| 108 | 0.24 |
0.04 |
0.28 |
-3.10 |
-2.56 |
3.32 |
-0.85 |
0.84 |
-0.01 |
| 109 | 0.24 |
0.04 |
0.28 |
-3.10 |
-2.56 |
3.32 |
-0.85 |
0.84 |
-0.01 |
| 110 | 0.25 |
0.04 |
0.29 |
-3.11 |
-2.56 |
3.32 |
-0.85 |
0.84 |
-0.01 |
| 111 | 0.25 |
0.04 |
0.29 |
-3.11 |
-2.56 |
3.32 |
-0.85 |
0.84 |
-0.01 |
| 112 | 0.25 |
0.04 |
0.29 |
-3.12 |
-2.56 |
3.32 |
-0.84 |
0.84 |
-0.01 |
| 113 | 0.26 |
0.04 |
0.30 |
-3.13 |
-2.56 |
3.32 |
-0.84 |
0.84 |
-0.01 |
| 114 | 0.26 |
0.04 |
0.30 |
-3.13 |
-2.56 |
3.31 |
-0.84 |
0.84 |
-0.01 |
| 115 | 0.26 |
0.04 |
0.30 |
-3.14 |
-2.56 |
3.31 |
-0.84 |
0.83 |
-0.01 |
| 116 | 0.26 |
0.04 |
0.30 |
-3.15 |
-2.56 |
3.31 |
-0.84 |
0.83 |
-0.01 |
| 117 | 0.27 |
0.04 |
0.31 |
-3.15 |
-2.56 |
3.31 |
-0.84 |
0.83 |
-0.01 |
| 118 | 0.27 |
0.04 |
0.31 |
-3.16 |
-2.56 |
3.31 |
-0.84 |
0.83 |
-0.01 |
| 119 | 0.27 |
0.04 |
0.31 |
-3.16 |
-2.56 |
3.31 |
-0.84 |
0.83 |
-0.01 |
| 120 | 0.28 |
0.04 |
0.31 |
-3.17 |
-2.56 |
3.31 |
-0.84 |
0.83 |
-0.01 |
Figure 3. 50% Rise in the Oil Price: Alternative Discount Factors
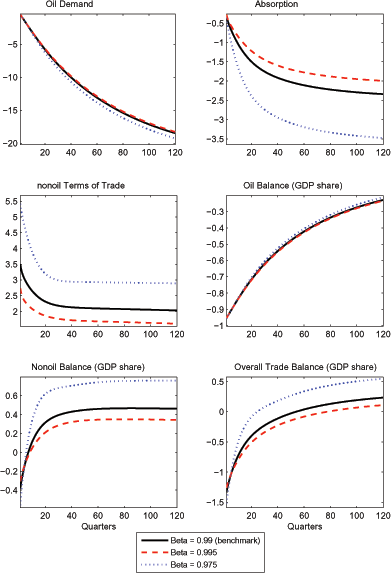
Data for Figure 3, Panel 1 - 50% Rise in the Oil Price: Alternative Discount Factors
| Period | Oil demand: beta = 0.99 (bench-mark) |
Absorption: beta = 0.99 (bench-mark) |
Nonoil terms of trade: beta = 0.99 (bench-mark) |
Oil balance: GDP share: beta = 0.99 (bench-mark) |
Nonoil balance: GDP share: beta = 0.99 (bench-mark) |
Overall trade balance: GDP share: beta = 0.99 (bench-mark) |
Oil demand: beta = 0.995 |
Absorption: beta = 0.995 |
Nonoil terms of trade: beta = 0.995 |
|---|---|---|---|---|---|---|---|---|---|
| 1 | -0.47 |
-0.30 |
3.50 |
-0.96 |
-0.38 |
-1.34 |
-0.48 |
-0.28 |
2.73 |
| 2 | -0.80 |
-0.44 |
3.28 |
-0.94 |
-0.29 |
-1.23 |
-0.81 |
-0.40 |
2.53 |
| 3 | -1.10 |
-0.55 |
3.15 |
-0.93 |
-0.22 |
-1.15 |
-1.11 |
-0.48 |
2.42 |
| 4 | -1.39 |
-0.63 |
3.05 |
-0.91 |
-0.16 |
-1.07 |
-1.39 |
-0.54 |
2.35 |
| 5 | -1.68 |
-0.71 |
2.97 |
-0.90 |
-0.10 |
-1.00 |
-1.68 |
-0.60 |
2.29 |
| 6 | -1.97 |
-0.79 |
2.89 |
-0.89 |
-0.05 |
-0.94 |
-1.96 |
-0.65 |
2.24 |
| 7 | -2.25 |
-0.86 |
2.83 |
-0.87 |
0.00 |
-0.88 |
-2.24 |
-0.71 |
2.20 |
| 8 | -2.54 |
-0.92 |
2.76 |
-0.86 |
0.04 |
-0.82 |
-2.52 |
-0.76 |
2.16 |
| 9 | -2.83 |
-0.99 |
2.71 |
-0.85 |
0.08 |
-0.77 |
-2.80 |
-0.81 |
2.12 |
| 10 | -3.12 |
-1.05 |
2.65 |
-0.83 |
0.11 |
-0.72 |
-3.08 |
-0.85 |
2.09 |
| 11 | -3.40 |
-1.11 |
2.61 |
-0.82 |
0.14 |
-0.68 |
-3.35 |
-0.90 |
2.06 |
| 12 | -3.68 |
-1.16 |
2.56 |
-0.81 |
0.17 |
-0.64 |
-3.63 |
-0.94 |
2.03 |
| 13 | -3.96 |
-1.21 |
2.52 |
-0.80 |
0.19 |
-0.60 |
-3.90 |
-0.98 |
2.00 |
| 14 | -4.24 |
-1.26 |
2.48 |
-0.78 |
0.22 |
-0.57 |
-4.16 |
-1.02 |
1.98 |
| 15 | -4.51 |
-1.30 |
2.45 |
-0.77 |
0.24 |
-0.53 |
-4.42 |
-1.06 |
1.95 |
| 16 | -4.77 |
-1.35 |
2.42 |
-0.76 |
0.26 |
-0.50 |
-4.68 |
-1.09 |
1.93 |
| 17 | -5.04 |
-1.39 |
2.39 |
-0.75 |
0.27 |
-0.48 |
-4.94 |
-1.13 |
1.91 |
| 18 | -5.30 |
-1.43 |
2.36 |
-0.74 |
0.29 |
-0.45 |
-5.19 |
-1.16 |
1.90 |
| 19 | -5.55 |
-1.46 |
2.34 |
-0.73 |
0.30 |
-0.42 |
-5.44 |
-1.19 |
1.88 |
| 20 | -5.80 |
-1.50 |
2.32 |
-0.72 |
0.32 |
-0.40 |
-5.68 |
-1.22 |
1.87 |
| 21 | -6.05 |
-1.53 |
2.30 |
-0.71 |
0.33 |
-0.38 |
-5.92 |
-1.25 |
1.85 |
| 22 | -6.29 |
-1.56 |
2.28 |
-0.70 |
0.34 |
-0.36 |
-6.16 |
-1.27 |
1.84 |
| 23 | -6.53 |
-1.59 |
2.26 |
-0.69 |
0.35 |
-0.34 |
-6.39 |
-1.30 |
1.83 |
| 24 | -6.76 |
-1.62 |
2.25 |
-0.68 |
0.36 |
-0.32 |
-6.62 |
-1.32 |
1.82 |
| 25 | -6.99 |
-1.64 |
2.23 |
-0.67 |
0.36 |
-0.30 |
-6.85 |
-1.35 |
1.81 |
| 26 | -7.22 |
-1.67 |
2.22 |
-0.66 |
0.37 |
-0.29 |
-7.07 |
-1.37 |
1.80 |
| 27 | -7.44 |
-1.69 |
2.21 |
-0.65 |
0.38 |
-0.27 |
-7.29 |
-1.39 |
1.79 |
| 28 | -7.66 |
-1.71 |
2.20 |
-0.64 |
0.38 |
-0.25 |
-7.51 |
-1.41 |
1.78 |
| 29 | -7.88 |
-1.73 |
2.19 |
-0.63 |
0.39 |
-0.24 |
-7.72 |
-1.43 |
1.78 |
| 30 | -8.09 |
-1.75 |
2.18 |
-0.62 |
0.39 |
-0.23 |
-7.93 |
-1.45 |
1.77 |
| 31 | -8.30 |
-1.77 |
2.18 |
-0.61 |
0.40 |
-0.21 |
-8.13 |
-1.47 |
1.76 |
| 32 | -8.50 |
-1.79 |
2.17 |
-0.60 |
0.40 |
-0.20 |
-8.33 |
-1.48 |
1.76 |
| 33 | -8.70 |
-1.81 |
2.16 |
-0.60 |
0.41 |
-0.19 |
-8.53 |
-1.50 |
1.75 |
| 34 | -8.90 |
-1.83 |
2.16 |
-0.59 |
0.41 |
-0.18 |
-8.73 |
-1.52 |
1.75 |
| 35 | -9.10 |
-1.84 |
2.15 |
-0.58 |
0.42 |
-0.16 |
-8.92 |
-1.53 |
1.74 |
| 36 | -9.29 |
-1.86 |
2.15 |
-0.57 |
0.42 |
-0.15 |
-9.11 |
-1.55 |
1.74 |
| 37 | -9.48 |
-1.87 |
2.14 |
-0.56 |
0.42 |
-0.14 |
-9.30 |
-1.56 |
1.73 |
| 38 | -9.66 |
-1.89 |
2.14 |
-0.56 |
0.42 |
-0.13 |
-9.48 |
-1.57 |
1.73 |
| 39 | -9.85 |
-1.90 |
2.14 |
-0.55 |
0.43 |
-0.12 |
-9.67 |
-1.59 |
1.73 |
| 40 | -10.03 |
-1.92 |
2.13 |
-0.54 |
0.43 |
-0.11 |
-9.84 |
-1.60 |
1.72 |
| 41 | -10.20 |
-1.93 |
2.13 |
-0.53 |
0.43 |
-0.10 |
-10.02 |
-1.61 |
1.72 |
| 42 | -10.38 |
-1.94 |
2.13 |
-0.53 |
0.44 |
-0.09 |
-10.19 |
-1.62 |
1.72 |
| 43 | -10.55 |
-1.95 |
2.13 |
-0.52 |
0.44 |
-0.08 |
-10.36 |
-1.63 |
1.72 |
| 44 | -10.72 |
-1.97 |
2.12 |
-0.51 |
0.44 |
-0.07 |
-10.53 |
-1.64 |
1.71 |
| 45 | -10.89 |
-1.98 |
2.12 |
-0.51 |
0.44 |
-0.07 |
-10.70 |
-1.65 |
1.71 |
| 46 | -11.05 |
-1.99 |
2.12 |
-0.50 |
0.44 |
-0.06 |
-10.86 |
-1.66 |
1.71 |
| 47 | -11.21 |
-2.00 |
2.12 |
-0.49 |
0.44 |
-0.05 |
-11.02 |
-1.67 |
1.71 |
| 48 | -11.37 |
-2.01 |
2.12 |
-0.49 |
0.45 |
-0.04 |
-11.18 |
-1.68 |
1.71 |
| 49 | -11.53 |
-2.02 |
2.11 |
-0.48 |
0.45 |
-0.03 |
-11.34 |
-1.69 |
1.70 |
| 50 | -11.68 |
-2.03 |
2.11 |
-0.48 |
0.45 |
-0.03 |
-11.49 |
-1.70 |
1.70 |
| 51 | -11.83 |
-2.04 |
2.11 |
-0.47 |
0.45 |
-0.02 |
-11.64 |
-1.71 |
1.70 |
| 52 | -11.98 |
-2.05 |
2.11 |
-0.46 |
0.45 |
-0.01 |
-11.79 |
-1.72 |
1.70 |
| 53 | -12.13 |
-2.05 |
2.11 |
-0.46 |
0.45 |
-0.01 |
-11.94 |
-1.73 |
1.70 |
| 54 | -12.28 |
-2.06 |
2.11 |
-0.45 |
0.45 |
0.00 |
-12.08 |
-1.73 |
1.70 |
| 55 | -12.42 |
-2.07 |
2.11 |
-0.45 |
0.46 |
0.01 |
-12.23 |
-1.74 |
1.69 |
| 56 | -12.56 |
-2.08 |
2.10 |
-0.44 |
0.46 |
0.01 |
-12.37 |
-1.75 |
1.69 |
| 57 | -12.70 |
-2.09 |
2.10 |
-0.44 |
0.46 |
0.02 |
-12.51 |
-1.76 |
1.69 |
| 58 | -12.84 |
-2.09 |
2.10 |
-0.43 |
0.46 |
0.03 |
-12.64 |
-1.76 |
1.69 |
| 59 | -12.97 |
-2.10 |
2.10 |
-0.43 |
0.46 |
0.03 |
-12.78 |
-1.77 |
1.69 |
| 60 | -13.11 |
-2.11 |
2.10 |
-0.42 |
0.46 |
0.04 |
-12.91 |
-1.78 |
1.69 |
| 61 | -13.24 |
-2.12 |
2.10 |
-0.42 |
0.46 |
0.04 |
-13.04 |
-1.78 |
1.69 |
| 62 | -13.37 |
-2.12 |
2.10 |
-0.41 |
0.46 |
0.05 |
-13.17 |
-1.79 |
1.69 |
| 63 | -13.50 |
-2.13 |
2.10 |
-0.41 |
0.46 |
0.05 |
-13.30 |
-1.80 |
1.68 |
| 64 | -13.62 |
-2.14 |
2.09 |
-0.40 |
0.46 |
0.06 |
-13.42 |
-1.80 |
1.68 |
| 65 | -13.75 |
-2.14 |
2.09 |
-0.40 |
0.46 |
0.07 |
-13.55 |
-1.81 |
1.68 |
| 66 | -13.87 |
-2.15 |
2.09 |
-0.39 |
0.46 |
0.07 |
-13.67 |
-1.81 |
1.68 |
| 67 | -13.99 |
-2.15 |
2.09 |
-0.39 |
0.46 |
0.08 |
-13.79 |
-1.82 |
1.68 |
| 68 | -14.11 |
-2.16 |
2.09 |
-0.38 |
0.46 |
0.08 |
-13.91 |
-1.82 |
1.68 |
| 69 | -14.23 |
-2.17 |
2.09 |
-0.38 |
0.47 |
0.09 |
-14.03 |
-1.83 |
1.68 |
| 70 | -14.34 |
-2.17 |
2.09 |
-0.38 |
0.47 |
0.09 |
-14.14 |
-1.84 |
1.68 |
| 71 | -14.46 |
-2.18 |
2.09 |
-0.37 |
0.47 |
0.09 |
-14.26 |
-1.84 |
1.67 |
| 72 | -14.57 |
-2.18 |
2.09 |
-0.37 |
0.47 |
0.10 |
-14.37 |
-1.85 |
1.67 |
| 73 | -14.68 |
-2.19 |
2.09 |
-0.36 |
0.47 |
0.10 |
-14.48 |
-1.85 |
1.67 |
| 74 | -14.79 |
-2.19 |
2.08 |
-0.36 |
0.47 |
0.11 |
-14.59 |
-1.85 |
1.67 |
| 75 | -14.90 |
-2.20 |
2.08 |
-0.36 |
0.47 |
0.11 |
-14.70 |
-1.86 |
1.67 |
| 76 | -15.00 |
-2.20 |
2.08 |
-0.35 |
0.47 |
0.12 |
-14.80 |
-1.86 |
1.67 |
| 77 | -15.11 |
-2.21 |
2.08 |
-0.35 |
0.47 |
0.12 |
-14.91 |
-1.87 |
1.67 |
| 78 | -15.21 |
-2.21 |
2.08 |
-0.34 |
0.47 |
0.12 |
-15.01 |
-1.87 |
1.67 |
| 79 | -15.31 |
-2.22 |
2.08 |
-0.34 |
0.47 |
0.13 |
-15.11 |
-1.88 |
1.67 |
| 80 | -15.41 |
-2.22 |
2.08 |
-0.34 |
0.47 |
0.13 |
-15.21 |
-1.88 |
1.66 |
| 81 | -15.51 |
-2.22 |
2.08 |
-0.33 |
0.47 |
0.13 |
-15.31 |
-1.89 |
1.66 |
| 82 | -15.61 |
-2.23 |
2.08 |
-0.33 |
0.47 |
0.14 |
-15.41 |
-1.89 |
1.66 |
| 83 | -15.71 |
-2.23 |
2.07 |
-0.33 |
0.47 |
0.14 |
-15.51 |
-1.89 |
1.66 |
| 84 | -15.80 |
-2.24 |
2.07 |
-0.32 |
0.47 |
0.15 |
-15.60 |
-1.90 |
1.66 |
| 85 | -15.90 |
-2.24 |
2.07 |
-0.32 |
0.47 |
0.15 |
-15.70 |
-1.90 |
1.66 |
| 86 | -15.99 |
-2.24 |
2.07 |
-0.32 |
0.47 |
0.15 |
-15.79 |
-1.90 |
1.66 |
| 87 | -16.08 |
-2.25 |
2.07 |
-0.31 |
0.47 |
0.16 |
-15.88 |
-1.91 |
1.66 |
| 88 | -16.17 |
-2.25 |
2.07 |
-0.31 |
0.47 |
0.16 |
-15.97 |
-1.91 |
1.66 |
| 89 | -16.26 |
-2.26 |
2.07 |
-0.31 |
0.47 |
0.16 |
-16.06 |
-1.92 |
1.65 |
| 90 | -16.35 |
-2.26 |
2.07 |
-0.30 |
0.47 |
0.16 |
-16.15 |
-1.92 |
1.65 |
| 91 | -16.43 |
-2.26 |
2.07 |
-0.30 |
0.47 |
0.17 |
-16.23 |
-1.92 |
1.65 |
| 92 | -16.52 |
-2.27 |
2.07 |
-0.30 |
0.47 |
0.17 |
-16.32 |
-1.93 |
1.65 |
| 93 | -16.60 |
-2.27 |
2.06 |
-0.29 |
0.47 |
0.17 |
-16.40 |
-1.93 |
1.65 |
| 94 | -16.69 |
-2.27 |
2.06 |
-0.29 |
0.47 |
0.18 |
-16.49 |
-1.93 |
1.65 |
| 95 | -16.77 |
-2.28 |
2.06 |
-0.29 |
0.47 |
0.18 |
-16.57 |
-1.93 |
1.65 |
| 96 | -16.85 |
-2.28 |
2.06 |
-0.29 |
0.47 |
0.18 |
-16.65 |
-1.94 |
1.65 |
| 97 | -16.93 |
-2.28 |
2.06 |
-0.28 |
0.47 |
0.18 |
-16.73 |
-1.94 |
1.64 |
| 98 | -17.01 |
-2.29 |
2.06 |
-0.28 |
0.47 |
0.19 |
-16.81 |
-1.94 |
1.64 |
| 99 | -17.08 |
-2.29 |
2.06 |
-0.28 |
0.47 |
0.19 |
-16.88 |
-1.95 |
1.64 |
| 100 | -17.16 |
-2.29 |
2.06 |
-0.27 |
0.47 |
0.19 |
-16.96 |
-1.95 |
1.64 |
| 101 | -17.24 |
-2.29 |
2.06 |
-0.27 |
0.47 |
0.19 |
-17.03 |
-1.95 |
1.64 |
| 102 | -17.31 |
-2.30 |
2.05 |
-0.27 |
0.47 |
0.20 |
-17.11 |
-1.95 |
1.64 |
| 103 | -17.38 |
-2.30 |
2.05 |
-0.27 |
0.47 |
0.20 |
-17.18 |
-1.96 |
1.64 |
| 104 | -17.46 |
-2.30 |
2.05 |
-0.26 |
0.47 |
0.20 |
-17.25 |
-1.96 |
1.64 |
| 105 | -17.53 |
-2.31 |
2.05 |
-0.26 |
0.47 |
0.20 |
-17.33 |
-1.96 |
1.63 |
| 106 | -17.60 |
-2.31 |
2.05 |
-0.26 |
0.47 |
0.21 |
-17.40 |
-1.96 |
1.63 |
| 107 | -17.67 |
-2.31 |
2.05 |
-0.26 |
0.47 |
0.21 |
-17.47 |
-1.97 |
1.63 |
| 108 | -17.73 |
-2.31 |
2.05 |
-0.25 |
0.46 |
0.21 |
-17.53 |
-1.97 |
1.63 |
| 109 | -17.80 |
-2.31 |
2.05 |
-0.25 |
0.46 |
0.21 |
-17.60 |
-1.97 |
1.63 |
| 110 | -17.87 |
-2.32 |
2.05 |
-0.25 |
0.46 |
0.21 |
-17.67 |
-1.97 |
1.63 |
| 111 | -17.93 |
-2.32 |
2.04 |
-0.25 |
0.46 |
0.22 |
-17.73 |
-1.98 |
1.63 |
| 112 | -18.00 |
-2.32 |
2.04 |
-0.25 |
0.46 |
0.22 |
-17.80 |
-1.98 |
1.63 |
| 113 | -18.06 |
-2.32 |
2.04 |
-0.24 |
0.46 |
0.22 |
-17.86 |
-1.98 |
1.62 |
| 114 | -18.13 |
-2.33 |
2.04 |
-0.24 |
0.46 |
0.22 |
-17.92 |
-1.98 |
1.62 |
| 115 | -18.19 |
-2.33 |
2.04 |
-0.24 |
0.46 |
0.22 |
-17.99 |
-1.98 |
1.62 |
| 116 | -18.25 |
-2.33 |
2.04 |
-0.24 |
0.46 |
0.23 |
-18.05 |
-1.99 |
1.62 |
| 117 | -18.31 |
-2.33 |
2.04 |
-0.23 |
0.46 |
0.23 |
-18.11 |
-1.99 |
1.62 |
| 118 | -18.37 |
-2.33 |
2.04 |
-0.23 |
0.46 |
0.23 |
-18.17 |
-1.99 |
1.62 |
| 119 | -18.43 |
-2.34 |
2.04 |
-0.23 |
0.46 |
0.23 |
-18.23 |
-1.99 |
1.62 |
| 120 | -18.49 |
-2.34 |
2.03 |
-0.23 |
0.46 |
0.23 |
-18.28 |
-1.99 |
1.61 |
Data for Figure 3, Panel 2 - 50% Rise in the Oil Price: Alternative Discount Factors
| Period | Oil balance: GDP share: beta = 0.995 |
Nonoil balance: GDP share: beta = 0.995 |
Overall trade balance: GDP share: beta = 0.995 |
Oil demand: beta = 0.975 |
Absorption: beta = 0.975 |
Nonoil terms of trade: beta = 0.975 |
Oil balance: GDP share: beta = 0.975 |
Nonoil balance: GDP share: beta = 0.975 |
Overall trade balance: GDP share: beta = 0.975 |
|---|---|---|---|---|---|---|---|---|---|
| 1 | -0.96 |
-0.31 |
-1.26 |
-0.44 |
-0.36 |
5.41 |
-0.96 |
-0.56 |
-1.52 |
| 2 | -0.94 |
-0.24 |
-1.18 |
-0.76 |
-0.58 |
5.15 |
-0.94 |
-0.40 |
-1.35 |
| 3 | -0.93 |
-0.19 |
-1.12 |
-1.07 |
-0.75 |
4.94 |
-0.93 |
-0.27 |
-1.20 |
| 4 | -0.91 |
-0.15 |
-1.06 |
-1.37 |
-0.91 |
4.75 |
-0.91 |
-0.15 |
-1.06 |
| 5 | -0.90 |
-0.11 |
-1.01 |
-1.68 |
-1.05 |
4.58 |
-0.90 |
-0.04 |
-0.94 |
| 6 | -0.89 |
-0.07 |
-0.96 |
-2.00 |
-1.19 |
4.42 |
-0.89 |
0.05 |
-0.83 |
| 7 | -0.87 |
-0.04 |
-0.91 |
-2.32 |
-1.32 |
4.27 |
-0.87 |
0.14 |
-0.73 |
| 8 | -0.86 |
-0.01 |
-0.87 |
-2.64 |
-1.44 |
4.14 |
-0.86 |
0.21 |
-0.65 |
| 9 | -0.85 |
0.02 |
-0.83 |
-2.96 |
-1.56 |
4.01 |
-0.84 |
0.28 |
-0.57 |
| 10 | -0.84 |
0.04 |
-0.79 |
-3.28 |
-1.66 |
3.90 |
-0.83 |
0.33 |
-0.50 |
| 11 | -0.82 |
0.07 |
-0.76 |
-3.60 |
-1.76 |
3.79 |
-0.82 |
0.38 |
-0.43 |
| 12 | -0.81 |
0.09 |
-0.72 |
-3.91 |
-1.85 |
3.70 |
-0.80 |
0.43 |
-0.38 |
| 13 | -0.80 |
0.11 |
-0.69 |
-4.22 |
-1.94 |
3.61 |
-0.79 |
0.46 |
-0.32 |
| 14 | -0.79 |
0.13 |
-0.66 |
-4.53 |
-2.02 |
3.53 |
-0.78 |
0.50 |
-0.28 |
| 15 | -0.78 |
0.14 |
-0.63 |
-4.83 |
-2.09 |
3.46 |
-0.76 |
0.53 |
-0.24 |
| 16 | -0.76 |
0.16 |
-0.60 |
-5.13 |
-2.16 |
3.40 |
-0.75 |
0.55 |
-0.20 |
| 17 | -0.75 |
0.17 |
-0.58 |
-5.42 |
-2.22 |
3.34 |
-0.74 |
0.57 |
-0.17 |
| 18 | -0.74 |
0.19 |
-0.55 |
-5.70 |
-2.28 |
3.29 |
-0.73 |
0.59 |
-0.14 |
| 19 | -0.73 |
0.20 |
-0.53 |
-5.98 |
-2.33 |
3.24 |
-0.72 |
0.61 |
-0.11 |
| 20 | -0.72 |
0.21 |
-0.51 |
-6.26 |
-2.38 |
3.20 |
-0.70 |
0.62 |
-0.09 |
| 21 | -0.71 |
0.22 |
-0.49 |
-6.53 |
-2.43 |
3.17 |
-0.69 |
0.63 |
-0.06 |
| 22 | -0.70 |
0.23 |
-0.47 |
-6.79 |
-2.48 |
3.13 |
-0.68 |
0.64 |
-0.04 |
| 23 | -0.69 |
0.24 |
-0.45 |
-7.05 |
-2.52 |
3.11 |
-0.67 |
0.65 |
-0.02 |
| 24 | -0.68 |
0.25 |
-0.43 |
-7.30 |
-2.55 |
3.08 |
-0.66 |
0.65 |
-0.01 |
| 25 | -0.67 |
0.26 |
-0.41 |
-7.55 |
-2.59 |
3.06 |
-0.65 |
0.66 |
0.01 |
| 26 | -0.66 |
0.26 |
-0.40 |
-7.79 |
-2.62 |
3.04 |
-0.64 |
0.67 |
0.02 |
| 27 | -0.65 |
0.27 |
-0.38 |
-8.03 |
-2.66 |
3.02 |
-0.63 |
0.67 |
0.04 |
| 28 | -0.64 |
0.28 |
-0.37 |
-8.26 |
-2.69 |
3.01 |
-0.62 |
0.67 |
0.05 |
| 29 | -0.63 |
0.28 |
-0.35 |
-8.49 |
-2.71 |
3.00 |
-0.61 |
0.68 |
0.07 |
| 30 | -0.63 |
0.29 |
-0.34 |
-8.71 |
-2.74 |
2.99 |
-0.60 |
0.68 |
0.08 |
| 31 | -0.62 |
0.29 |
-0.33 |
-8.93 |
-2.77 |
2.98 |
-0.60 |
0.68 |
0.09 |
| 32 | -0.61 |
0.30 |
-0.31 |
-9.15 |
-2.79 |
2.97 |
-0.59 |
0.69 |
0.10 |
| 33 | -0.60 |
0.30 |
-0.30 |
-9.36 |
-2.81 |
2.97 |
-0.58 |
0.69 |
0.11 |
| 34 | -0.59 |
0.30 |
-0.29 |
-9.56 |
-2.83 |
2.96 |
-0.57 |
0.69 |
0.12 |
| 35 | -0.58 |
0.31 |
-0.28 |
-9.76 |
-2.85 |
2.96 |
-0.56 |
0.70 |
0.13 |
| 36 | -0.58 |
0.31 |
-0.27 |
-9.96 |
-2.87 |
2.95 |
-0.55 |
0.70 |
0.14 |
| 37 | -0.57 |
0.31 |
-0.26 |
-10.16 |
-2.89 |
2.95 |
-0.55 |
0.70 |
0.15 |
| 38 | -0.56 |
0.32 |
-0.25 |
-10.35 |
-2.91 |
2.95 |
-0.54 |
0.70 |
0.16 |
| 39 | -0.55 |
0.32 |
-0.24 |
-10.54 |
-2.93 |
2.95 |
-0.53 |
0.70 |
0.17 |
| 40 | -0.55 |
0.32 |
-0.23 |
-10.72 |
-2.95 |
2.94 |
-0.52 |
0.71 |
0.18 |
| 41 | -0.54 |
0.32 |
-0.22 |
-10.90 |
-2.96 |
2.94 |
-0.52 |
0.71 |
0.19 |
| 42 | -0.53 |
0.33 |
-0.21 |
-11.08 |
-2.98 |
2.94 |
-0.51 |
0.71 |
0.20 |
| 43 | -0.53 |
0.33 |
-0.20 |
-11.26 |
-2.99 |
2.94 |
-0.50 |
0.71 |
0.21 |
| 44 | -0.52 |
0.33 |
-0.19 |
-11.43 |
-3.01 |
2.94 |
-0.50 |
0.71 |
0.22 |
| 45 | -0.51 |
0.33 |
-0.18 |
-11.60 |
-3.02 |
2.94 |
-0.49 |
0.72 |
0.23 |
| 46 | -0.51 |
0.33 |
-0.17 |
-11.77 |
-3.04 |
2.94 |
-0.48 |
0.72 |
0.24 |
| 47 | -0.50 |
0.33 |
-0.17 |
-11.93 |
-3.05 |
2.94 |
-0.48 |
0.72 |
0.24 |
| 48 | -0.49 |
0.34 |
-0.16 |
-12.09 |
-3.06 |
2.94 |
-0.47 |
0.72 |
0.25 |
| 49 | -0.49 |
0.34 |
-0.15 |
-12.25 |
-3.08 |
2.94 |
-0.46 |
0.72 |
0.26 |
| 50 | -0.48 |
0.34 |
-0.14 |
-12.41 |
-3.09 |
2.94 |
-0.46 |
0.73 |
0.27 |
| 51 | -0.48 |
0.34 |
-0.14 |
-12.57 |
-3.10 |
2.94 |
-0.45 |
0.73 |
0.28 |
| 52 | -0.47 |
0.34 |
-0.13 |
-12.72 |
-3.11 |
2.94 |
-0.45 |
0.73 |
0.28 |
| 53 | -0.46 |
0.34 |
-0.12 |
-12.87 |
-3.12 |
2.93 |
-0.44 |
0.73 |
0.29 |
| 54 | -0.46 |
0.34 |
-0.12 |
-13.01 |
-3.13 |
2.93 |
-0.44 |
0.73 |
0.30 |
| 55 | -0.45 |
0.34 |
-0.11 |
-13.16 |
-3.15 |
2.93 |
-0.43 |
0.73 |
0.30 |
| 56 | -0.45 |
0.34 |
-0.10 |
-13.30 |
-3.16 |
2.93 |
-0.42 |
0.74 |
0.31 |
| 57 | -0.44 |
0.34 |
-0.10 |
-13.44 |
-3.17 |
2.93 |
-0.42 |
0.74 |
0.32 |
| 58 | -0.44 |
0.35 |
-0.09 |
-13.58 |
-3.18 |
2.93 |
-0.41 |
0.74 |
0.32 |
| 59 | -0.43 |
0.35 |
-0.09 |
-13.72 |
-3.18 |
2.93 |
-0.41 |
0.74 |
0.33 |
| 60 | -0.43 |
0.35 |
-0.08 |
-13.86 |
-3.19 |
2.93 |
-0.40 |
0.74 |
0.34 |
| 61 | -0.42 |
0.35 |
-0.08 |
-13.99 |
-3.20 |
2.93 |
-0.40 |
0.74 |
0.34 |
| 62 | -0.42 |
0.35 |
-0.07 |
-14.12 |
-3.21 |
2.93 |
-0.39 |
0.74 |
0.35 |
| 63 | -0.41 |
0.35 |
-0.06 |
-14.25 |
-3.22 |
2.93 |
-0.39 |
0.75 |
0.36 |
| 64 | -0.41 |
0.35 |
-0.06 |
-14.38 |
-3.23 |
2.93 |
-0.38 |
0.75 |
0.36 |
| 65 | -0.40 |
0.35 |
-0.05 |
-14.50 |
-3.24 |
2.93 |
-0.38 |
0.75 |
0.37 |
| 66 | -0.40 |
0.35 |
-0.05 |
-14.63 |
-3.24 |
2.93 |
-0.38 |
0.75 |
0.37 |
| 67 | -0.39 |
0.35 |
-0.04 |
-14.75 |
-3.25 |
2.93 |
-0.37 |
0.75 |
0.38 |
| 68 | -0.39 |
0.35 |
-0.04 |
-14.87 |
-3.26 |
2.93 |
-0.37 |
0.75 |
0.38 |
| 69 | -0.39 |
0.35 |
-0.04 |
-14.99 |
-3.27 |
2.92 |
-0.36 |
0.75 |
0.39 |
| 70 | -0.38 |
0.35 |
-0.03 |
-15.10 |
-3.27 |
2.92 |
-0.36 |
0.75 |
0.39 |
| 71 | -0.38 |
0.35 |
-0.03 |
-15.22 |
-3.28 |
2.92 |
-0.35 |
0.75 |
0.40 |
| 72 | -0.37 |
0.35 |
-0.02 |
-15.33 |
-3.29 |
2.92 |
-0.35 |
0.75 |
0.40 |
| 73 | -0.37 |
0.35 |
-0.02 |
-15.44 |
-3.29 |
2.92 |
-0.35 |
0.75 |
0.41 |
| 74 | -0.36 |
0.35 |
-0.01 |
-15.55 |
-3.30 |
2.92 |
-0.34 |
0.75 |
0.41 |
| 75 | -0.36 |
0.35 |
-0.01 |
-15.66 |
-3.30 |
2.92 |
-0.34 |
0.76 |
0.42 |
| 76 | -0.36 |
0.35 |
-0.01 |
-15.77 |
-3.31 |
2.92 |
-0.33 |
0.76 |
0.42 |
| 77 | -0.35 |
0.35 |
0.00 |
-15.88 |
-3.32 |
2.92 |
-0.33 |
0.76 |
0.43 |
| 78 | -0.35 |
0.35 |
0.00 |
-15.98 |
-3.32 |
2.92 |
-0.33 |
0.76 |
0.43 |
| 79 | -0.35 |
0.35 |
0.01 |
-16.08 |
-3.33 |
2.92 |
-0.32 |
0.76 |
0.43 |
| 80 | -0.34 |
0.35 |
0.01 |
-16.18 |
-3.33 |
2.92 |
-0.32 |
0.76 |
0.44 |
| 81 | -0.34 |
0.35 |
0.01 |
-16.28 |
-3.34 |
2.92 |
-0.32 |
0.76 |
0.44 |
| 82 | -0.33 |
0.35 |
0.02 |
-16.38 |
-3.34 |
2.92 |
-0.31 |
0.76 |
0.45 |
| 83 | -0.33 |
0.35 |
0.02 |
-16.48 |
-3.35 |
2.92 |
-0.31 |
0.76 |
0.45 |
| 84 | -0.33 |
0.35 |
0.02 |
-16.58 |
-3.35 |
2.91 |
-0.31 |
0.76 |
0.45 |
| 85 | -0.32 |
0.35 |
0.03 |
-16.67 |
-3.36 |
2.91 |
-0.30 |
0.76 |
0.46 |
| 86 | -0.32 |
0.35 |
0.03 |
-16.76 |
-3.36 |
2.91 |
-0.30 |
0.76 |
0.46 |
| 87 | -0.32 |
0.35 |
0.03 |
-16.86 |
-3.37 |
2.91 |
-0.30 |
0.76 |
0.46 |
| 88 | -0.31 |
0.35 |
0.04 |
-16.95 |
-3.37 |
2.91 |
-0.29 |
0.76 |
0.47 |
| 89 | -0.31 |
0.35 |
0.04 |
-17.04 |
-3.38 |
2.91 |
-0.29 |
0.76 |
0.47 |
| 90 | -0.31 |
0.35 |
0.04 |
-17.12 |
-3.38 |
2.91 |
-0.29 |
0.76 |
0.47 |
| 91 | -0.30 |
0.35 |
0.04 |
-17.21 |
-3.38 |
2.91 |
-0.28 |
0.76 |
0.48 |
| 92 | -0.30 |
0.35 |
0.05 |
-17.30 |
-3.39 |
2.91 |
-0.28 |
0.76 |
0.48 |
| 93 | -0.30 |
0.35 |
0.05 |
-17.38 |
-3.39 |
2.91 |
-0.28 |
0.76 |
0.48 |
| 94 | -0.30 |
0.35 |
0.05 |
-17.46 |
-3.40 |
2.91 |
-0.27 |
0.76 |
0.49 |
| 95 | -0.29 |
0.35 |
0.06 |
-17.55 |
-3.40 |
2.91 |
-0.27 |
0.76 |
0.49 |
| 96 | -0.29 |
0.35 |
0.06 |
-17.63 |
-3.40 |
2.91 |
-0.27 |
0.76 |
0.49 |
| 97 | -0.29 |
0.35 |
0.06 |
-17.71 |
-3.41 |
2.91 |
-0.27 |
0.76 |
0.49 |
| 98 | -0.28 |
0.35 |
0.06 |
-17.79 |
-3.41 |
2.91 |
-0.26 |
0.76 |
0.50 |
| 99 | -0.28 |
0.35 |
0.07 |
-17.86 |
-3.41 |
2.91 |
-0.26 |
0.76 |
0.50 |
| 100 | -0.28 |
0.35 |
0.07 |
-17.94 |
-3.42 |
2.91 |
-0.26 |
0.76 |
0.50 |
| 101 | -0.28 |
0.35 |
0.07 |
-18.02 |
-3.42 |
2.90 |
-0.25 |
0.76 |
0.51 |
| 102 | -0.27 |
0.35 |
0.07 |
-18.09 |
-3.43 |
2.90 |
-0.25 |
0.76 |
0.51 |
| 103 | -0.27 |
0.35 |
0.08 |
-18.16 |
-3.43 |
2.90 |
-0.25 |
0.76 |
0.51 |
| 104 | -0.27 |
0.35 |
0.08 |
-18.24 |
-3.43 |
2.90 |
-0.25 |
0.76 |
0.51 |
| 105 | -0.27 |
0.35 |
0.08 |
-18.31 |
-3.43 |
2.90 |
-0.24 |
0.76 |
0.52 |
| 106 | -0.26 |
0.35 |
0.08 |
-18.38 |
-3.44 |
2.90 |
-0.24 |
0.76 |
0.52 |
| 107 | -0.26 |
0.35 |
0.08 |
-18.45 |
-3.44 |
2.90 |
-0.24 |
0.76 |
0.52 |
| 108 | -0.26 |
0.35 |
0.09 |
-18.52 |
-3.44 |
2.90 |
-0.24 |
0.76 |
0.52 |
| 109 | -0.26 |
0.35 |
0.09 |
-18.59 |
-3.45 |
2.90 |
-0.24 |
0.76 |
0.52 |
| 110 | -0.25 |
0.35 |
0.09 |
-18.65 |
-3.45 |
2.90 |
-0.23 |
0.76 |
0.53 |
| 111 | -0.25 |
0.35 |
0.09 |
-18.72 |
-3.45 |
2.90 |
-0.23 |
0.76 |
0.53 |
| 112 | -0.25 |
0.35 |
0.10 |
-18.78 |
-3.46 |
2.90 |
-0.23 |
0.76 |
0.53 |
| 113 | -0.25 |
0.34 |
0.10 |
-18.85 |
-3.46 |
2.90 |
-0.23 |
0.76 |
0.53 |
| 114 | -0.25 |
0.34 |
0.10 |
-18.91 |
-3.46 |
2.90 |
-0.22 |
0.76 |
0.54 |
| 115 | -0.24 |
0.34 |
0.10 |
-18.97 |
-3.46 |
2.90 |
-0.22 |
0.76 |
0.54 |
| 116 | -0.24 |
0.34 |
0.10 |
-19.03 |
-3.47 |
2.90 |
-0.22 |
0.76 |
0.54 |
| 117 | -0.24 |
0.34 |
0.10 |
-19.10 |
-3.47 |
2.90 |
-0.22 |
0.76 |
0.54 |
| 118 | -0.24 |
0.34 |
0.11 |
-19.15 |
-3.47 |
2.90 |
-0.22 |
0.76 |
0.54 |
| 119 | -0.24 |
0.34 |
0.11 |
-19.21 |
-3.47 |
2.89 |
-0.21 |
0.76 |
0.55 |
| 120 | -0.23 |
0.34 |
0.11 |
-19.27 |
-3.48 |
2.89 |
-0.21 |
0.76 |
0.55 |
Figure 4. Contours of the 2-Year Average Response of the Terms of Trade to a 50% Permanent Increase in the Price of Oil (baseline calibration)
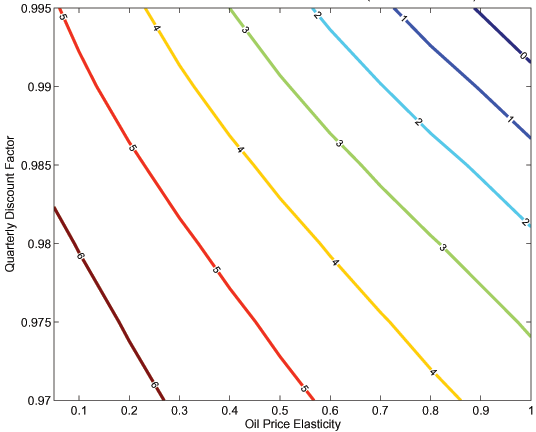
Figure 5. 50% Rise in the Oil Price: Alternative Levels of Domestic Oil Production
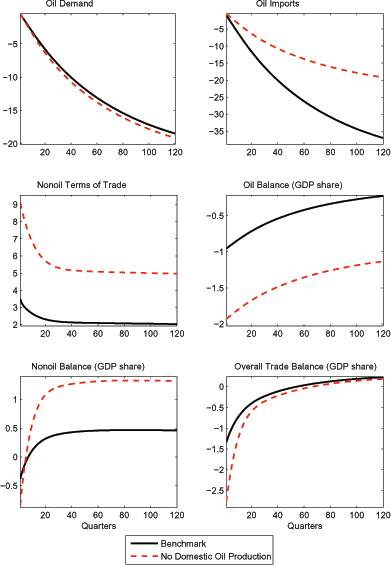
Data for Figure 5, Panel 1 - 50% Rise in the Oil Price: Alternative Levels of Domestic Oil Production
| Period | Oil demand: benchmark |
Oil imports: benchmark |
Nonoil terms of trade: benchmark |
Oil balance: GDP share: benchmark |
Nonoil balance: GDP share: benchmark |
Overall trade balance: GDP share: benchmark |
|---|---|---|---|---|---|---|
| 1 | -0.47 |
-0.94 |
3.50 |
-0.96 |
-0.38 |
-1.34 |
| 2 | -0.80 |
-1.60 |
3.28 |
-0.94 |
-0.29 |
-1.23 |
| 3 | -1.10 |
-2.19 |
3.15 |
-0.93 |
-0.22 |
-1.15 |
| 4 | -1.39 |
-2.77 |
3.05 |
-0.91 |
-0.16 |
-1.07 |
| 5 | -1.68 |
-3.35 |
2.97 |
-0.90 |
-0.10 |
-1.00 |
| 6 | -1.97 |
-3.93 |
2.89 |
-0.89 |
-0.05 |
-0.94 |
| 7 | -2.25 |
-4.51 |
2.83 |
-0.87 |
0.00 |
-0.88 |
| 8 | -2.54 |
-5.09 |
2.76 |
-0.86 |
0.04 |
-0.82 |
| 9 | -2.83 |
-5.66 |
2.71 |
-0.85 |
0.08 |
-0.77 |
| 10 | -3.12 |
-6.24 |
2.65 |
-0.83 |
0.11 |
-0.72 |
| 11 | -3.40 |
-6.80 |
2.61 |
-0.82 |
0.14 |
-0.68 |
| 12 | -3.68 |
-7.37 |
2.56 |
-0.81 |
0.17 |
-0.64 |
| 13 | -3.96 |
-7.92 |
2.52 |
-0.80 |
0.19 |
-0.60 |
| 14 | -4.24 |
-8.47 |
2.48 |
-0.78 |
0.22 |
-0.57 |
| 15 | -4.51 |
-9.01 |
2.45 |
-0.77 |
0.24 |
-0.53 |
| 16 | -4.77 |
-9.55 |
2.42 |
-0.76 |
0.26 |
-0.50 |
| 17 | -5.04 |
-10.07 |
2.39 |
-0.75 |
0.27 |
-0.48 |
| 18 | -5.30 |
-10.59 |
2.36 |
-0.74 |
0.29 |
-0.45 |
| 19 | -5.55 |
-11.10 |
2.34 |
-0.73 |
0.30 |
-0.42 |
| 20 | -5.80 |
-11.60 |
2.32 |
-0.72 |
0.32 |
-0.40 |
| 21 | -6.05 |
-12.09 |
2.30 |
-0.71 |
0.33 |
-0.38 |
| 22 | -6.29 |
-12.58 |
2.28 |
-0.70 |
0.34 |
-0.36 |
| 23 | -6.53 |
-13.06 |
2.26 |
-0.69 |
0.35 |
-0.34 |
| 24 | -6.76 |
-13.53 |
2.25 |
-0.68 |
0.36 |
-0.32 |
| 25 | -6.99 |
-13.99 |
2.23 |
-0.67 |
0.36 |
-0.30 |
| 26 | -7.22 |
-14.44 |
2.22 |
-0.66 |
0.37 |
-0.29 |
| 27 | -7.44 |
-14.89 |
2.21 |
-0.65 |
0.38 |
-0.27 |
| 28 | -7.66 |
-15.32 |
2.20 |
-0.64 |
0.38 |
-0.25 |
| 29 | -7.88 |
-15.76 |
2.19 |
-0.63 |
0.39 |
-0.24 |
| 30 | -8.09 |
-16.18 |
2.18 |
-0.62 |
0.39 |
-0.23 |
| 31 | -8.30 |
-16.60 |
2.18 |
-0.61 |
0.40 |
-0.21 |
| 32 | -8.50 |
-17.01 |
2.17 |
-0.60 |
0.40 |
-0.20 |
| 33 | -8.70 |
-17.41 |
2.16 |
-0.60 |
0.41 |
-0.19 |
| 34 | -8.90 |
-17.81 |
2.16 |
-0.59 |
0.41 |
-0.18 |
| 35 | -9.10 |
-18.20 |
2.15 |
-0.58 |
0.42 |
-0.16 |
| 36 | -9.29 |
-18.58 |
2.15 |
-0.57 |
0.42 |
-0.15 |
| 37 | -9.48 |
-18.96 |
2.14 |
-0.56 |
0.42 |
-0.14 |
| 38 | -9.66 |
-19.33 |
2.14 |
-0.56 |
0.42 |
-0.13 |
| 39 | -9.85 |
-19.69 |
2.14 |
-0.55 |
0.43 |
-0.12 |
| 40 | -10.03 |
-20.05 |
2.13 |
-0.54 |
0.43 |
-0.11 |
| 41 | -10.20 |
-20.41 |
2.13 |
-0.53 |
0.43 |
-0.10 |
| 42 | -10.38 |
-20.76 |
2.13 |
-0.53 |
0.44 |
-0.09 |
| 43 | -10.55 |
-21.10 |
2.13 |
-0.52 |
0.44 |
-0.08 |
| 44 | -10.72 |
-21.44 |
2.12 |
-0.51 |
0.44 |
-0.07 |
| 45 | -10.89 |
-21.77 |
2.12 |
-0.51 |
0.44 |
-0.07 |
| 46 | -11.05 |
-22.10 |
2.12 |
-0.50 |
0.44 |
-0.06 |
| 47 | -11.21 |
-22.42 |
2.12 |
-0.49 |
0.44 |
-0.05 |
| 48 | -11.37 |
-22.74 |
2.12 |
-0.49 |
0.45 |
-0.04 |
| 49 | -11.53 |
-23.05 |
2.11 |
-0.48 |
0.45 |
-0.03 |
| 50 | -11.68 |
-23.36 |
2.11 |
-0.48 |
0.45 |
-0.03 |
| 51 | -11.83 |
-23.67 |
2.11 |
-0.47 |
0.45 |
-0.02 |
| 52 | -11.98 |
-23.97 |
2.11 |
-0.46 |
0.45 |
-0.01 |
| 53 | -12.13 |
-24.26 |
2.11 |
-0.46 |
0.45 |
-0.01 |
| 54 | -12.28 |
-24.55 |
2.11 |
-0.45 |
0.45 |
0.00 |
| 55 | -12.42 |
-24.84 |
2.11 |
-0.45 |
0.46 |
0.01 |
| 56 | -12.56 |
-25.12 |
2.10 |
-0.44 |
0.46 |
0.01 |
| 57 | -12.70 |
-25.40 |
2.10 |
-0.44 |
0.46 |
0.02 |
| 58 | -12.84 |
-25.67 |
2.10 |
-0.43 |
0.46 |
0.03 |
| 59 | -12.97 |
-25.95 |
2.10 |
-0.43 |
0.46 |
0.03 |
| 60 | -13.11 |
-26.21 |
2.10 |
-0.42 |
0.46 |
0.04 |
| 61 | -13.24 |
-26.48 |
2.10 |
-0.42 |
0.46 |
0.04 |
| 62 | -13.37 |
-26.73 |
2.10 |
-0.41 |
0.46 |
0.05 |
| 63 | -13.50 |
-26.99 |
2.10 |
-0.41 |
0.46 |
0.05 |
| 64 | -13.62 |
-27.24 |
2.09 |
-0.40 |
0.46 |
0.06 |
| 65 | -13.75 |
-27.49 |
2.09 |
-0.40 |
0.46 |
0.07 |
| 66 | -13.87 |
-27.74 |
2.09 |
-0.39 |
0.46 |
0.07 |
| 67 | -13.99 |
-27.98 |
2.09 |
-0.39 |
0.46 |
0.08 |
| 68 | -14.11 |
-28.22 |
2.09 |
-0.38 |
0.46 |
0.08 |
| 69 | -14.23 |
-28.45 |
2.09 |
-0.38 |
0.47 |
0.09 |
| 70 | -14.34 |
-28.68 |
2.09 |
-0.38 |
0.47 |
0.09 |
| 71 | -14.46 |
-28.91 |
2.09 |
-0.37 |
0.47 |
0.09 |
| 72 | -14.57 |
-29.14 |
2.09 |
-0.37 |
0.47 |
0.10 |
| 73 | -14.68 |
-29.36 |
2.09 |
-0.36 |
0.47 |
0.10 |
| 74 | -14.79 |
-29.58 |
2.08 |
-0.36 |
0.47 |
0.11 |
| 75 | -14.90 |
-29.79 |
2.08 |
-0.36 |
0.47 |
0.11 |
| 76 | -15.00 |
-30.01 |
2.08 |
-0.35 |
0.47 |
0.12 |
| 77 | -15.11 |
-30.22 |
2.08 |
-0.35 |
0.47 |
0.12 |
| 78 | -15.21 |
-30.42 |
2.08 |
-0.34 |
0.47 |
0.12 |
| 79 | -15.31 |
-30.63 |
2.08 |
-0.34 |
0.47 |
0.13 |
| 80 | -15.41 |
-30.83 |
2.08 |
-0.34 |
0.47 |
0.13 |
| 81 | -15.51 |
-31.03 |
2.08 |
-0.33 |
0.47 |
0.13 |
| 82 | -15.61 |
-31.22 |
2.08 |
-0.33 |
0.47 |
0.14 |
| 83 | -15.71 |
-31.42 |
2.07 |
-0.33 |
0.47 |
0.14 |
| 84 | -15.80 |
-31.61 |
2.07 |
-0.32 |
0.47 |
0.15 |
| 85 | -15.90 |
-31.79 |
2.07 |
-0.32 |
0.47 |
0.15 |
| 86 | -15.99 |
-31.98 |
2.07 |
-0.32 |
0.47 |
0.15 |
| 87 | -16.08 |
-32.16 |
2.07 |
-0.31 |
0.47 |
0.16 |
| 88 | -16.17 |
-32.34 |
2.07 |
-0.31 |
0.47 |
0.16 |
| 89 | -16.26 |
-32.52 |
2.07 |
-0.31 |
0.47 |
0.16 |
| 90 | -16.35 |
-32.69 |
2.07 |
-0.30 |
0.47 |
0.16 |
| 91 | -16.43 |
-32.87 |
2.07 |
-0.30 |
0.47 |
0.17 |
| 92 | -16.52 |
-33.04 |
2.07 |
-0.30 |
0.47 |
0.17 |
| 93 | -16.60 |
-33.21 |
2.06 |
-0.29 |
0.47 |
0.17 |
| 94 | -16.69 |
-33.37 |
2.06 |
-0.29 |
0.47 |
0.18 |
| 95 | -16.77 |
-33.54 |
2.06 |
-0.29 |
0.47 |
0.18 |
| 96 | -16.85 |
-33.70 |
2.06 |
-0.29 |
0.47 |
0.18 |
| 97 | -16.93 |
-33.86 |
2.06 |
-0.28 |
0.47 |
0.18 |
| 98 | -17.01 |
-34.01 |
2.06 |
-0.28 |
0.47 |
0.19 |
| 99 | -17.08 |
-34.17 |
2.06 |
-0.28 |
0.47 |
0.19 |
| 100 | -17.16 |
-34.32 |
2.06 |
-0.27 |
0.47 |
0.19 |
| 101 | -17.24 |
-34.47 |
2.06 |
-0.27 |
0.47 |
0.19 |
| 102 | -17.31 |
-34.62 |
2.05 |
-0.27 |
0.47 |
0.20 |
| 103 | -17.38 |
-34.77 |
2.05 |
-0.27 |
0.47 |
0.20 |
| 104 | -17.46 |
-34.91 |
2.05 |
-0.26 |
0.47 |
0.20 |
| 105 | -17.53 |
-35.05 |
2.05 |
-0.26 |
0.47 |
0.20 |
| 106 | -17.60 |
-35.19 |
2.05 |
-0.26 |
0.47 |
0.21 |
| 107 | -17.67 |
-35.33 |
2.05 |
-0.26 |
0.47 |
0.21 |
| 108 | -17.73 |
-35.47 |
2.05 |
-0.25 |
0.46 |
0.21 |
| 109 | -17.80 |
-35.60 |
2.05 |
-0.25 |
0.46 |
0.21 |
| 110 | -17.87 |
-35.74 |
2.05 |
-0.25 |
0.46 |
0.21 |
| 111 | -17.93 |
-35.87 |
2.04 |
-0.25 |
0.46 |
0.22 |
| 112 | -18.00 |
-36.00 |
2.04 |
-0.25 |
0.46 |
0.22 |
| 113 | -18.06 |
-36.13 |
2.04 |
-0.24 |
0.46 |
0.22 |
| 114 | -18.13 |
-36.25 |
2.04 |
-0.24 |
0.46 |
0.22 |
| 115 | -18.19 |
-36.38 |
2.04 |
-0.24 |
0.46 |
0.22 |
| 116 | -18.25 |
-36.50 |
2.04 |
-0.24 |
0.46 |
0.23 |
| 117 | -18.31 |
-36.62 |
2.04 |
-0.23 |
0.46 |
0.23 |
| 118 | -18.37 |
-36.74 |
2.04 |
-0.23 |
0.46 |
0.23 |
| 119 | -18.43 |
-36.86 |
2.04 |
-0.23 |
0.46 |
0.23 |
| 120 | -18.49 |
-36.97 |
2.03 |
-0.23 |
0.46 |
0.23 |
Data for Figure 5, Panel 2 - 50% Rise in the Oil Price: Alternative Levels of Domestic Oil Production
| Period | Oil demand: no domestic oil production |
Oil imports: no domestic oil production |
Nonoil terms of trade: no domestic oil production |
Oil balance: GDP share: no domestic oil production |
Nonoil balance: GDP share: no domestic oil production |
Overall trade balance: GDP share: no domestic oil production |
|---|---|---|---|---|---|---|
| 1 | -0.48 |
-0.48 |
9.09 |
-1.93 |
-0.84 |
-2.77 |
| 2 | -0.84 |
-0.84 |
8.74 |
-1.91 |
-0.61 |
-2.52 |
| 3 | -1.16 |
-1.16 |
8.43 |
-1.90 |
-0.40 |
-2.30 |
| 4 | -1.48 |
-1.48 |
8.15 |
-1.89 |
-0.21 |
-2.10 |
| 5 | -1.80 |
-1.80 |
7.89 |
-1.87 |
-0.05 |
-1.92 |
| 6 | -2.12 |
-2.13 |
7.65 |
-1.86 |
0.10 |
-1.75 |
| 7 | -2.45 |
-2.45 |
7.42 |
-1.84 |
0.24 |
-1.60 |
| 8 | -2.77 |
-2.77 |
7.21 |
-1.83 |
0.36 |
-1.47 |
| 9 | -3.09 |
-3.09 |
7.02 |
-1.81 |
0.47 |
-1.35 |
| 10 | -3.41 |
-3.41 |
6.84 |
-1.80 |
0.56 |
-1.24 |
| 11 | -3.72 |
-3.72 |
6.68 |
-1.79 |
0.65 |
-1.14 |
| 12 | -4.03 |
-4.04 |
6.53 |
-1.77 |
0.72 |
-1.05 |
| 13 | -4.34 |
-4.34 |
6.39 |
-1.76 |
0.79 |
-0.97 |
| 14 | -4.64 |
-4.64 |
6.27 |
-1.75 |
0.85 |
-0.90 |
| 15 | -4.94 |
-4.94 |
6.16 |
-1.73 |
0.90 |
-0.83 |
| 16 | -5.23 |
-5.23 |
6.05 |
-1.72 |
0.95 |
-0.77 |
| 17 | -5.51 |
-5.52 |
5.96 |
-1.71 |
0.99 |
-0.72 |
| 18 | -5.79 |
-5.80 |
5.87 |
-1.70 |
1.02 |
-0.68 |
| 19 | -6.07 |
-6.07 |
5.79 |
-1.69 |
1.05 |
-0.63 |
| 20 | -6.34 |
-6.34 |
5.72 |
-1.67 |
1.08 |
-0.59 |
| 21 | -6.60 |
-6.61 |
5.66 |
-1.66 |
1.10 |
-0.56 |
| 22 | -6.86 |
-6.87 |
5.60 |
-1.65 |
1.12 |
-0.53 |
| 23 | -7.11 |
-7.12 |
5.55 |
-1.64 |
1.14 |
-0.50 |
| 24 | -7.36 |
-7.37 |
5.50 |
-1.63 |
1.16 |
-0.47 |
| 25 | -7.60 |
-7.61 |
5.46 |
-1.62 |
1.17 |
-0.45 |
| 26 | -7.84 |
-7.85 |
5.42 |
-1.61 |
1.19 |
-0.42 |
| 27 | -8.07 |
-8.08 |
5.39 |
-1.60 |
1.20 |
-0.40 |
| 28 | -8.30 |
-8.31 |
5.36 |
-1.59 |
1.21 |
-0.38 |
| 29 | -8.52 |
-8.53 |
5.33 |
-1.58 |
1.21 |
-0.37 |
| 30 | -8.74 |
-8.75 |
5.31 |
-1.57 |
1.22 |
-0.35 |
| 31 | -8.95 |
-8.96 |
5.29 |
-1.56 |
1.23 |
-0.33 |
| 32 | -9.16 |
-9.17 |
5.27 |
-1.55 |
1.24 |
-0.32 |
| 33 | -9.37 |
-9.38 |
5.25 |
-1.54 |
1.24 |
-0.30 |
| 34 | -9.57 |
-9.58 |
5.24 |
-1.54 |
1.25 |
-0.29 |
| 35 | -9.77 |
-9.78 |
5.22 |
-1.53 |
1.25 |
-0.28 |
| 36 | -9.96 |
-9.97 |
5.21 |
-1.52 |
1.26 |
-0.26 |
| 37 | -10.15 |
-10.16 |
5.20 |
-1.51 |
1.26 |
-0.25 |
| 38 | -10.34 |
-10.35 |
5.19 |
-1.50 |
1.26 |
-0.24 |
| 39 | -10.53 |
-10.54 |
5.18 |
-1.49 |
1.27 |
-0.23 |
| 40 | -10.71 |
-10.72 |
5.17 |
-1.49 |
1.27 |
-0.21 |
| 41 | -10.89 |
-10.90 |
5.16 |
-1.48 |
1.28 |
-0.20 |
| 42 | -11.06 |
-11.07 |
5.16 |
-1.47 |
1.28 |
-0.19 |
| 43 | -11.23 |
-11.24 |
5.15 |
-1.46 |
1.28 |
-0.18 |
| 44 | -11.40 |
-11.41 |
5.15 |
-1.46 |
1.28 |
-0.17 |
| 45 | -11.57 |
-11.58 |
5.14 |
-1.45 |
1.29 |
-0.16 |
| 46 | -11.73 |
-11.74 |
5.13 |
-1.44 |
1.29 |
-0.15 |
| 47 | -11.89 |
-11.91 |
5.13 |
-1.44 |
1.29 |
-0.14 |
| 48 | -12.05 |
-12.06 |
5.13 |
-1.43 |
1.29 |
-0.13 |
| 49 | -12.21 |
-12.22 |
5.12 |
-1.42 |
1.30 |
-0.12 |
| 50 | -12.36 |
-12.38 |
5.12 |
-1.42 |
1.30 |
-0.12 |
| 51 | -12.51 |
-12.53 |
5.11 |
-1.41 |
1.30 |
-0.11 |
| 52 | -12.66 |
-12.68 |
5.11 |
-1.40 |
1.30 |
-0.10 |
| 53 | -12.81 |
-12.82 |
5.11 |
-1.40 |
1.31 |
-0.09 |
| 54 | -12.96 |
-12.97 |
5.10 |
-1.39 |
1.31 |
-0.08 |
| 55 | -13.10 |
-13.11 |
5.10 |
-1.38 |
1.31 |
-0.07 |
| 56 | -13.24 |
-13.25 |
5.10 |
-1.38 |
1.31 |
-0.07 |
| 57 | -13.38 |
-13.39 |
5.10 |
-1.37 |
1.31 |
-0.06 |
| 58 | -13.52 |
-13.53 |
5.09 |
-1.37 |
1.32 |
-0.05 |
| 59 | -13.65 |
-13.66 |
5.09 |
-1.36 |
1.32 |
-0.04 |
| 60 | -13.78 |
-13.80 |
5.09 |
-1.36 |
1.32 |
-0.04 |
| 61 | -13.91 |
-13.93 |
5.08 |
-1.35 |
1.32 |
-0.03 |
| 62 | -14.04 |
-14.06 |
5.08 |
-1.34 |
1.32 |
-0.02 |
| 63 | -14.17 |
-14.19 |
5.08 |
-1.34 |
1.32 |
-0.02 |
| 64 | -14.30 |
-14.31 |
5.08 |
-1.33 |
1.32 |
-0.01 |
| 65 | -14.42 |
-14.43 |
5.07 |
-1.33 |
1.32 |
0.00 |
| 66 | -14.54 |
-14.56 |
5.07 |
-1.32 |
1.33 |
0.00 |
| 67 | -14.66 |
-14.68 |
5.07 |
-1.32 |
1.33 |
0.01 |
| 68 | -14.78 |
-14.80 |
5.07 |
-1.31 |
1.33 |
0.01 |
| 69 | -14.90 |
-14.91 |
5.06 |
-1.31 |
1.33 |
0.02 |
| 70 | -15.01 |
-15.03 |
5.06 |
-1.30 |
1.33 |
0.03 |
| 71 | -15.13 |
-15.14 |
5.06 |
-1.30 |
1.33 |
0.03 |
| 72 | -15.24 |
-15.26 |
5.06 |
-1.29 |
1.33 |
0.04 |
| 73 | -15.35 |
-15.37 |
5.06 |
-1.29 |
1.33 |
0.04 |
| 74 | -15.46 |
-15.48 |
5.05 |
-1.28 |
1.33 |
0.05 |
| 75 | -15.57 |
-15.58 |
5.05 |
-1.28 |
1.33 |
0.05 |
| 76 | -15.67 |
-15.69 |
5.05 |
-1.28 |
1.33 |
0.06 |
| 77 | -15.78 |
-15.79 |
5.05 |
-1.27 |
1.33 |
0.06 |
| 78 | -15.88 |
-15.90 |
5.05 |
-1.27 |
1.33 |
0.07 |
| 79 | -15.98 |
-16.00 |
5.04 |
-1.26 |
1.33 |
0.07 |
| 80 | -16.08 |
-16.10 |
5.04 |
-1.26 |
1.33 |
0.07 |
| 81 | -16.18 |
-16.20 |
5.04 |
-1.25 |
1.33 |
0.08 |
| 82 | -16.28 |
-16.30 |
5.04 |
-1.25 |
1.33 |
0.08 |
| 83 | -16.38 |
-16.39 |
5.04 |
-1.25 |
1.33 |
0.09 |
| 84 | -16.47 |
-16.49 |
5.03 |
-1.24 |
1.33 |
0.09 |
| 85 | -16.57 |
-16.58 |
5.03 |
-1.24 |
1.33 |
0.09 |
| 86 | -16.66 |
-16.67 |
5.03 |
-1.23 |
1.33 |
0.10 |
| 87 | -16.75 |
-16.77 |
5.03 |
-1.23 |
1.33 |
0.10 |
| 88 | -16.84 |
-16.86 |
5.03 |
-1.23 |
1.33 |
0.11 |
| 89 | -16.93 |
-16.94 |
5.02 |
-1.22 |
1.33 |
0.11 |
| 90 | -17.02 |
-17.03 |
5.02 |
-1.22 |
1.33 |
0.11 |
| 91 | -17.10 |
-17.12 |
5.02 |
-1.22 |
1.33 |
0.12 |
| 92 | -17.19 |
-17.20 |
5.02 |
-1.21 |
1.33 |
0.12 |
| 93 | -17.27 |
-17.29 |
5.02 |
-1.21 |
1.33 |
0.12 |
| 94 | -17.35 |
-17.37 |
5.01 |
-1.21 |
1.33 |
0.13 |
| 95 | -17.43 |
-17.45 |
5.01 |
-1.20 |
1.33 |
0.13 |
| 96 | -17.51 |
-17.53 |
5.01 |
-1.20 |
1.33 |
0.13 |
| 97 | -17.59 |
-17.61 |
5.01 |
-1.20 |
1.33 |
0.14 |
| 98 | -17.67 |
-17.69 |
5.01 |
-1.19 |
1.33 |
0.14 |
| 99 | -17.75 |
-17.77 |
5.01 |
-1.19 |
1.33 |
0.14 |
| 100 | -17.83 |
-17.84 |
5.00 |
-1.19 |
1.33 |
0.14 |
| 101 | -17.90 |
-17.92 |
5.00 |
-1.18 |
1.33 |
0.15 |
| 102 | -17.97 |
-17.99 |
5.00 |
-1.18 |
1.33 |
0.15 |
| 103 | -18.05 |
-18.07 |
5.00 |
-1.18 |
1.33 |
0.15 |
| 104 | -18.12 |
-18.14 |
5.00 |
-1.18 |
1.33 |
0.15 |
| 105 | -18.19 |
-18.21 |
5.00 |
-1.17 |
1.33 |
0.16 |
| 106 | -18.26 |
-18.28 |
4.99 |
-1.17 |
1.33 |
0.16 |
| 107 | -18.33 |
-18.35 |
4.99 |
-1.17 |
1.33 |
0.16 |
| 108 | -18.40 |
-18.42 |
4.99 |
-1.16 |
1.33 |
0.16 |
| 109 | -18.47 |
-18.48 |
4.99 |
-1.16 |
1.33 |
0.17 |
| 110 | -18.53 |
-18.55 |
4.99 |
-1.16 |
1.33 |
0.17 |
| 111 | -18.60 |
-18.62 |
4.99 |
-1.16 |
1.33 |
0.17 |
| 112 | -18.66 |
-18.68 |
4.98 |
-1.15 |
1.33 |
0.17 |
| 113 | -18.73 |
-18.74 |
4.98 |
-1.15 |
1.33 |
0.18 |
| 114 | -18.79 |
-18.81 |
4.98 |
-1.15 |
1.33 |
0.18 |
| 115 | -18.85 |
-18.87 |
4.98 |
-1.15 |
1.33 |
0.18 |
| 116 | -18.91 |
-18.93 |
4.98 |
-1.14 |
1.33 |
0.18 |
| 117 | -18.97 |
-18.99 |
4.98 |
-1.14 |
1.33 |
0.18 |
| 118 | -19.03 |
-19.05 |
4.97 |
-1.14 |
1.32 |
0.19 |
| 119 | -19.09 |
-19.11 |
4.97 |
-1.14 |
1.32 |
0.19 |
| 120 | -19.15 |
-19.17 |
4.97 |
-1.13 |
1.32 |
0.19 |
Figure 6. 50% Rise in the Oil Price: Alternative Levels of Specific Oil Taxes
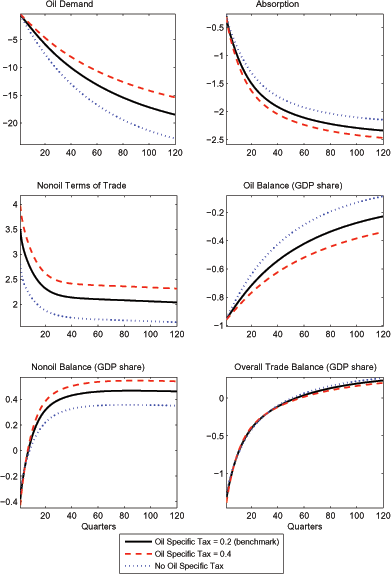
Data for Figure 6, Panel 1: 50% Rise in the Oil Price: Alternative Levels of Specific Oil Taxes
| Period | Oil demand: oil specific tax = 0.2 (bench-mark) |
Absorption: oil specific tax = 0.2 (bench-mark) |
Nonoil terms of trade: oil specific tax = 0.2 (bench-mark) |
Oil balance: GDP share: oil specific tax = 0.2 (bench-mark) |
Nonoil balance: GDP share: oil specific tax = 0.2 (bench-mark) |
Overall trade balance: GDP share: oil specific tax = 0.2 (bench-mark) |
Oil demand: oil specific tax = 0.4 |
Absorption: oil specific tax = 0.4 |
Nonoil terms of trade: oil specific tax = 0.4 |
|---|---|---|---|---|---|---|---|---|---|
| 1 | -0.47 |
-0.30 |
3.50 |
-0.96 |
-0.38 |
-1.34 |
-0.40 |
-0.32 |
3.97 |
| 2 | -0.80 |
-0.44 |
3.28 |
-0.94 |
-0.29 |
-1.23 |
-0.66 |
-0.48 |
3.75 |
| 3 | -1.10 |
-0.55 |
3.15 |
-0.93 |
-0.22 |
-1.15 |
-0.89 |
-0.59 |
3.61 |
| 4 | -1.39 |
-0.63 |
3.05 |
-0.91 |
-0.16 |
-1.07 |
-1.11 |
-0.69 |
3.50 |
| 5 | -1.68 |
-0.71 |
2.97 |
-0.90 |
-0.10 |
-1.00 |
-1.34 |
-0.78 |
3.40 |
| 6 | -1.97 |
-0.79 |
2.89 |
-0.89 |
-0.05 |
-0.94 |
-1.57 |
-0.86 |
3.31 |
| 7 | -2.25 |
-0.86 |
2.83 |
-0.87 |
0.00 |
-0.88 |
-1.79 |
-0.94 |
3.23 |
| 8 | -2.54 |
-0.92 |
2.76 |
-0.86 |
0.04 |
-0.82 |
-2.02 |
-1.02 |
3.16 |
| 9 | -2.83 |
-0.99 |
2.71 |
-0.85 |
0.08 |
-0.77 |
-2.25 |
-1.09 |
3.09 |
| 10 | -3.12 |
-1.05 |
2.65 |
-0.83 |
0.11 |
-0.72 |
-2.48 |
-1.16 |
3.02 |
| 11 | -3.40 |
-1.11 |
2.61 |
-0.82 |
0.14 |
-0.68 |
-2.71 |
-1.22 |
2.97 |
| 12 | -3.68 |
-1.16 |
2.56 |
-0.81 |
0.17 |
-0.64 |
-2.93 |
-1.28 |
2.91 |
| 13 | -3.96 |
-1.21 |
2.52 |
-0.80 |
0.19 |
-0.60 |
-3.16 |
-1.33 |
2.86 |
| 14 | -4.24 |
-1.26 |
2.48 |
-0.78 |
0.22 |
-0.57 |
-3.38 |
-1.38 |
2.82 |
| 15 | -4.51 |
-1.30 |
2.45 |
-0.77 |
0.24 |
-0.53 |
-3.60 |
-1.43 |
2.78 |
| 16 | -4.77 |
-1.35 |
2.42 |
-0.76 |
0.26 |
-0.50 |
-3.81 |
-1.48 |
2.74 |
| 17 | -5.04 |
-1.39 |
2.39 |
-0.75 |
0.27 |
-0.48 |
-4.03 |
-1.52 |
2.70 |
| 18 | -5.30 |
-1.43 |
2.36 |
-0.74 |
0.29 |
-0.45 |
-4.23 |
-1.56 |
2.67 |
| 19 | -5.55 |
-1.46 |
2.34 |
-0.73 |
0.30 |
-0.42 |
-4.44 |
-1.59 |
2.64 |
| 20 | -5.80 |
-1.50 |
2.32 |
-0.72 |
0.32 |
-0.40 |
-4.64 |
-1.63 |
2.62 |
| 21 | -6.05 |
-1.53 |
2.30 |
-0.71 |
0.33 |
-0.38 |
-4.84 |
-1.66 |
2.60 |
| 22 | -6.29 |
-1.56 |
2.28 |
-0.70 |
0.34 |
-0.36 |
-5.04 |
-1.69 |
2.57 |
| 23 | -6.53 |
-1.59 |
2.26 |
-0.69 |
0.35 |
-0.34 |
-5.23 |
-1.72 |
2.55 |
| 24 | -6.76 |
-1.62 |
2.25 |
-0.68 |
0.36 |
-0.32 |
-5.42 |
-1.75 |
2.54 |
| 25 | -6.99 |
-1.64 |
2.23 |
-0.67 |
0.36 |
-0.30 |
-5.61 |
-1.78 |
2.52 |
| 26 | -7.22 |
-1.67 |
2.22 |
-0.66 |
0.37 |
-0.29 |
-5.79 |
-1.80 |
2.51 |
| 27 | -7.44 |
-1.69 |
2.21 |
-0.65 |
0.38 |
-0.27 |
-5.97 |
-1.83 |
2.50 |
| 28 | -7.66 |
-1.71 |
2.20 |
-0.64 |
0.38 |
-0.25 |
-6.15 |
-1.85 |
2.48 |
| 29 | -7.88 |
-1.73 |
2.19 |
-0.63 |
0.39 |
-0.24 |
-6.33 |
-1.87 |
2.47 |
| 30 | -8.09 |
-1.75 |
2.18 |
-0.62 |
0.39 |
-0.23 |
-6.50 |
-1.89 |
2.46 |
| 31 | -8.30 |
-1.77 |
2.18 |
-0.61 |
0.40 |
-0.21 |
-6.67 |
-1.91 |
2.46 |
| 32 | -8.50 |
-1.79 |
2.17 |
-0.60 |
0.40 |
-0.20 |
-6.83 |
-1.93 |
2.45 |
| 33 | -8.70 |
-1.81 |
2.16 |
-0.60 |
0.41 |
-0.19 |
-7.00 |
-1.94 |
2.44 |
| 34 | -8.90 |
-1.83 |
2.16 |
-0.59 |
0.41 |
-0.18 |
-7.16 |
-1.96 |
2.44 |
| 35 | -9.10 |
-1.84 |
2.15 |
-0.58 |
0.42 |
-0.16 |
-7.32 |
-1.98 |
2.43 |
| 36 | -9.29 |
-1.86 |
2.15 |
-0.57 |
0.42 |
-0.15 |
-7.47 |
-1.99 |
2.43 |
| 37 | -9.48 |
-1.87 |
2.14 |
-0.56 |
0.42 |
-0.14 |
-7.63 |
-2.01 |
2.42 |
| 38 | -9.66 |
-1.89 |
2.14 |
-0.56 |
0.42 |
-0.13 |
-7.78 |
-2.02 |
2.42 |
| 39 | -9.85 |
-1.90 |
2.14 |
-0.55 |
0.43 |
-0.12 |
-7.93 |
-2.03 |
2.41 |
| 40 | -10.03 |
-1.92 |
2.13 |
-0.54 |
0.43 |
-0.11 |
-8.08 |
-2.05 |
2.41 |
| 41 | -10.20 |
-1.93 |
2.13 |
-0.53 |
0.43 |
-0.10 |
-8.22 |
-2.06 |
2.41 |
| 42 | -10.38 |
-1.94 |
2.13 |
-0.53 |
0.44 |
-0.09 |
-8.36 |
-2.07 |
2.41 |
| 43 | -10.55 |
-1.95 |
2.13 |
-0.52 |
0.44 |
-0.08 |
-8.51 |
-2.08 |
2.40 |
| 44 | -10.72 |
-1.97 |
2.12 |
-0.51 |
0.44 |
-0.07 |
-8.64 |
-2.09 |
2.40 |
| 45 | -10.89 |
-1.98 |
2.12 |
-0.51 |
0.44 |
-0.07 |
-8.78 |
-2.11 |
2.40 |
| 46 | -11.05 |
-1.99 |
2.12 |
-0.50 |
0.44 |
-0.06 |
-8.92 |
-2.12 |
2.40 |
| 47 | -11.21 |
-2.00 |
2.12 |
-0.49 |
0.44 |
-0.05 |
-9.05 |
-2.13 |
2.40 |
| 48 | -11.37 |
-2.01 |
2.12 |
-0.49 |
0.45 |
-0.04 |
-9.18 |
-2.14 |
2.39 |
| 49 | -11.53 |
-2.02 |
2.11 |
-0.48 |
0.45 |
-0.03 |
-9.31 |
-2.15 |
2.39 |
| 50 | -11.68 |
-2.03 |
2.11 |
-0.48 |
0.45 |
-0.03 |
-9.44 |
-2.16 |
2.39 |
| 51 | -11.83 |
-2.04 |
2.11 |
-0.47 |
0.45 |
-0.02 |
-9.56 |
-2.16 |
2.39 |
| 52 | -11.98 |
-2.05 |
2.11 |
-0.46 |
0.45 |
-0.01 |
-9.69 |
-2.17 |
2.39 |
| 53 | -12.13 |
-2.05 |
2.11 |
-0.46 |
0.45 |
-0.01 |
-9.81 |
-2.18 |
2.39 |
| 54 | -12.28 |
-2.06 |
2.11 |
-0.45 |
0.45 |
0.00 |
-9.93 |
-2.19 |
2.38 |
| 55 | -12.42 |
-2.07 |
2.11 |
-0.45 |
0.46 |
0.01 |
-10.05 |
-2.20 |
2.38 |
| 56 | -12.56 |
-2.08 |
2.10 |
-0.44 |
0.46 |
0.01 |
-10.17 |
-2.21 |
2.38 |
| 57 | -12.70 |
-2.09 |
2.10 |
-0.44 |
0.46 |
0.02 |
-10.29 |
-2.21 |
2.38 |
| 58 | -12.84 |
-2.09 |
2.10 |
-0.43 |
0.46 |
0.03 |
-10.40 |
-2.22 |
2.38 |
| 59 | -12.97 |
-2.10 |
2.10 |
-0.43 |
0.46 |
0.03 |
-10.52 |
-2.23 |
2.38 |
| 60 | -13.11 |
-2.11 |
2.10 |
-0.42 |
0.46 |
0.04 |
-10.63 |
-2.24 |
2.38 |
| 61 | -13.24 |
-2.12 |
2.10 |
-0.42 |
0.46 |
0.04 |
-10.74 |
-2.24 |
2.38 |
| 62 | -13.37 |
-2.12 |
2.10 |
-0.41 |
0.46 |
0.05 |
-10.85 |
-2.25 |
2.38 |
| 63 | -13.50 |
-2.13 |
2.10 |
-0.41 |
0.46 |
0.05 |
-10.96 |
-2.26 |
2.37 |
| 64 | -13.62 |
-2.14 |
2.09 |
-0.40 |
0.46 |
0.06 |
-11.06 |
-2.26 |
2.37 |
| 65 | -13.75 |
-2.14 |
2.09 |
-0.40 |
0.46 |
0.07 |
-11.17 |
-2.27 |
2.37 |
| 66 | -13.87 |
-2.15 |
2.09 |
-0.39 |
0.46 |
0.07 |
-11.27 |
-2.28 |
2.37 |
| 67 | -13.99 |
-2.15 |
2.09 |
-0.39 |
0.46 |
0.08 |
-11.38 |
-2.28 |
2.37 |
| 68 | -14.11 |
-2.16 |
2.09 |
-0.38 |
0.46 |
0.08 |
-11.48 |
-2.29 |
2.37 |
| 69 | -14.23 |
-2.17 |
2.09 |
-0.38 |
0.47 |
0.09 |
-11.58 |
-2.29 |
2.37 |
| 70 | -14.34 |
-2.17 |
2.09 |
-0.38 |
0.47 |
0.09 |
-11.68 |
-2.30 |
2.37 |
| 71 | -14.46 |
-2.18 |
2.09 |
-0.37 |
0.47 |
0.09 |
-11.78 |
-2.30 |
2.37 |
| 72 | -14.57 |
-2.18 |
2.09 |
-0.37 |
0.47 |
0.10 |
-11.87 |
-2.31 |
2.36 |
| 73 | -14.68 |
-2.19 |
2.09 |
-0.36 |
0.47 |
0.10 |
-11.97 |
-2.31 |
2.36 |
| 74 | -14.79 |
-2.19 |
2.08 |
-0.36 |
0.47 |
0.11 |
-12.06 |
-2.32 |
2.36 |
| 75 | -14.90 |
-2.20 |
2.08 |
-0.36 |
0.47 |
0.11 |
-12.16 |
-2.32 |
2.36 |
| 76 | -15.00 |
-2.20 |
2.08 |
-0.35 |
0.47 |
0.12 |
-12.25 |
-2.33 |
2.36 |
| 77 | -15.11 |
-2.21 |
2.08 |
-0.35 |
0.47 |
0.12 |
-12.34 |
-2.33 |
2.36 |
| 78 | -15.21 |
-2.21 |
2.08 |
-0.34 |
0.47 |
0.12 |
-12.43 |
-2.34 |
2.36 |
| 79 | -15.31 |
-2.22 |
2.08 |
-0.34 |
0.47 |
0.13 |
-12.52 |
-2.34 |
2.36 |
| 80 | -15.41 |
-2.22 |
2.08 |
-0.34 |
0.47 |
0.13 |
-12.61 |
-2.35 |
2.36 |
| 81 | -15.51 |
-2.22 |
2.08 |
-0.33 |
0.47 |
0.13 |
-12.69 |
-2.35 |
2.36 |
| 82 | -15.61 |
-2.23 |
2.08 |
-0.33 |
0.47 |
0.14 |
-12.78 |
-2.36 |
2.35 |
| 83 | -15.71 |
-2.23 |
2.07 |
-0.33 |
0.47 |
0.14 |
-12.86 |
-2.36 |
2.35 |
| 84 | -15.80 |
-2.24 |
2.07 |
-0.32 |
0.47 |
0.15 |
-12.95 |
-2.36 |
2.35 |
| 85 | -15.90 |
-2.24 |
2.07 |
-0.32 |
0.47 |
0.15 |
-13.03 |
-2.37 |
2.35 |
| 86 | -15.99 |
-2.24 |
2.07 |
-0.32 |
0.47 |
0.15 |
-13.11 |
-2.37 |
2.35 |
| 87 | -16.08 |
-2.25 |
2.07 |
-0.31 |
0.47 |
0.16 |
-13.19 |
-2.38 |
2.35 |
| 88 | -16.17 |
-2.25 |
2.07 |
-0.31 |
0.47 |
0.16 |
-13.27 |
-2.38 |
2.35 |
| 89 | -16.26 |
-2.26 |
2.07 |
-0.31 |
0.47 |
0.16 |
-13.35 |
-2.38 |
2.35 |
| 90 | -16.35 |
-2.26 |
2.07 |
-0.30 |
0.47 |
0.16 |
-13.43 |
-2.39 |
2.35 |
| 91 | -16.43 |
-2.26 |
2.07 |
-0.30 |
0.47 |
0.17 |
-13.50 |
-2.39 |
2.34 |
| 92 | -16.52 |
-2.27 |
2.07 |
-0.30 |
0.47 |
0.17 |
-13.58 |
-2.39 |
2.34 |
| 93 | -16.60 |
-2.27 |
2.06 |
-0.29 |
0.47 |
0.17 |
-13.65 |
-2.40 |
2.34 |
| 94 | -16.69 |
-2.27 |
2.06 |
-0.29 |
0.47 |
0.18 |
-13.73 |
-2.40 |
2.34 |
| 95 | -16.77 |
-2.28 |
2.06 |
-0.29 |
0.47 |
0.18 |
-13.80 |
-2.40 |
2.34 |
| 96 | -16.85 |
-2.28 |
2.06 |
-0.29 |
0.47 |
0.18 |
-13.87 |
-2.41 |
2.34 |
| 97 | -16.93 |
-2.28 |
2.06 |
-0.28 |
0.47 |
0.18 |
-13.95 |
-2.41 |
2.34 |
| 98 | -17.01 |
-2.29 |
2.06 |
-0.28 |
0.47 |
0.19 |
-14.02 |
-2.41 |
2.34 |
| 99 | -17.08 |
-2.29 |
2.06 |
-0.28 |
0.47 |
0.19 |
-14.09 |
-2.42 |
2.34 |
| 100 | -17.16 |
-2.29 |
2.06 |
-0.27 |
0.47 |
0.19 |
-14.16 |
-2.42 |
2.33 |
| 101 | -17.24 |
-2.29 |
2.06 |
-0.27 |
0.47 |
0.19 |
-14.22 |
-2.42 |
2.33 |
| 102 | -17.31 |
-2.30 |
2.05 |
-0.27 |
0.47 |
0.20 |
-14.29 |
-2.43 |
2.33 |
| 103 | -17.38 |
-2.30 |
2.05 |
-0.27 |
0.47 |
0.20 |
-14.36 |
-2.43 |
2.33 |
| 104 | -17.46 |
-2.30 |
2.05 |
-0.26 |
0.47 |
0.20 |
-14.42 |
-2.43 |
2.33 |
| 105 | -17.53 |
-2.31 |
2.05 |
-0.26 |
0.47 |
0.20 |
-14.49 |
-2.43 |
2.33 |
| 106 | -17.60 |
-2.31 |
2.05 |
-0.26 |
0.47 |
0.21 |
-14.55 |
-2.44 |
2.33 |
| 107 | -17.67 |
-2.31 |
2.05 |
-0.26 |
0.47 |
0.21 |
-14.62 |
-2.44 |
2.33 |
| 108 | -17.73 |
-2.31 |
2.05 |
-0.25 |
0.46 |
0.21 |
-14.68 |
-2.44 |
2.33 |
| 109 | -17.80 |
-2.31 |
2.05 |
-0.25 |
0.46 |
0.21 |
-14.74 |
-2.44 |
2.32 |
| 110 | -17.87 |
-2.32 |
2.05 |
-0.25 |
0.46 |
0.21 |
-14.80 |
-2.45 |
2.32 |
| 111 | -17.93 |
-2.32 |
2.04 |
-0.25 |
0.46 |
0.22 |
-14.86 |
-2.45 |
2.32 |
| 112 | -18.00 |
-2.32 |
2.04 |
-0.25 |
0.46 |
0.22 |
-14.92 |
-2.45 |
2.32 |
| 113 | -18.06 |
-2.32 |
2.04 |
-0.24 |
0.46 |
0.22 |
-14.98 |
-2.45 |
2.32 |
| 114 | -18.13 |
-2.33 |
2.04 |
-0.24 |
0.46 |
0.22 |
-15.04 |
-2.46 |
2.32 |
| 115 | -18.19 |
-2.33 |
2.04 |
-0.24 |
0.46 |
0.22 |
-15.10 |
-2.46 |
2.32 |
| 116 | -18.25 |
-2.33 |
2.04 |
-0.24 |
0.46 |
0.23 |
-15.15 |
-2.46 |
2.32 |
| 117 | -18.31 |
-2.33 |
2.04 |
-0.23 |
0.46 |
0.23 |
-15.21 |
-2.46 |
2.31 |
| 118 | -18.37 |
-2.33 |
2.04 |
-0.23 |
0.46 |
0.23 |
-15.27 |
-2.47 |
2.31 |
| 119 | -18.43 |
-2.34 |
2.04 |
-0.23 |
0.46 |
0.23 |
-15.32 |
-2.47 |
2.31 |
| 120 | -18.49 |
-2.34 |
2.03 |
-0.23 |
0.46 |
0.23 |
-15.38 |
-2.47 |
2.31 |
Data for Figure 6, Panel 2 - 50% Rise in the Oil Price: Alternative Levels of Specific Oil Taxes
| Period | Oil balance: GDP share: oil specific tax = 0.4 |
Nonoil balance: GDP share: oil specific tax = 0.4 |
Overall trade balance: oil specific tax = 0.4 |
Oil demand: no oil specific tax |
Absorption: no oil specific tax |
Nonoil terms of trade: no oil specific tax |
Oil balance: GDP share: no oil specific tax |
Nonoil balance: GDP share: no oil specific tax |
Overall trade balance: GDP share: no oil specific tax |
|---|---|---|---|---|---|---|---|---|---|
| 1 | -0.96 |
-0.43 |
-1.39 |
-0.58 |
-0.27 |
2.80 |
-0.95 |
-0.31 |
-1.26 |
| 2 | -0.95 |
-0.33 |
-1.27 |
-1.02 |
-0.40 |
2.59 |
-0.93 |
-0.24 |
-1.17 |
| 3 | -0.94 |
-0.24 |
-1.18 |
-1.43 |
-0.48 |
2.48 |
-0.91 |
-0.19 |
-1.10 |
| 4 | -0.93 |
-0.16 |
-1.09 |
-1.82 |
-0.55 |
2.40 |
-0.89 |
-0.15 |
-1.04 |
| 5 | -0.92 |
-0.10 |
-1.01 |
-2.21 |
-0.61 |
2.34 |
-0.87 |
-0.10 |
-0.98 |
| 6 | -0.91 |
-0.04 |
-0.94 |
-2.60 |
-0.67 |
2.29 |
-0.86 |
-0.07 |
-0.92 |
| 7 | -0.89 |
0.02 |
-0.88 |
-2.98 |
-0.73 |
2.24 |
-0.84 |
-0.03 |
-0.87 |
| 8 | -0.88 |
0.07 |
-0.82 |
-3.37 |
-0.79 |
2.19 |
-0.82 |
0.00 |
-0.82 |
| 9 | -0.87 |
0.11 |
-0.76 |
-3.75 |
-0.84 |
2.15 |
-0.80 |
0.02 |
-0.78 |
| 10 | -0.86 |
0.15 |
-0.71 |
-4.12 |
-0.90 |
2.11 |
-0.79 |
0.05 |
-0.74 |
| 11 | -0.85 |
0.19 |
-0.67 |
-4.49 |
-0.95 |
2.08 |
-0.77 |
0.07 |
-0.70 |
| 12 | -0.84 |
0.22 |
-0.62 |
-4.86 |
-0.99 |
2.05 |
-0.76 |
0.10 |
-0.66 |
| 13 | -0.83 |
0.25 |
-0.59 |
-5.22 |
-1.04 |
2.02 |
-0.74 |
0.12 |
-0.62 |
| 14 | -0.82 |
0.27 |
-0.55 |
-5.58 |
-1.08 |
1.99 |
-0.72 |
0.13 |
-0.59 |
| 15 | -0.81 |
0.30 |
-0.52 |
-5.93 |
-1.13 |
1.97 |
-0.71 |
0.15 |
-0.56 |
| 16 | -0.80 |
0.32 |
-0.49 |
-6.27 |
-1.17 |
1.95 |
-0.69 |
0.17 |
-0.53 |
| 17 | -0.80 |
0.34 |
-0.46 |
-6.61 |
-1.20 |
1.93 |
-0.68 |
0.18 |
-0.50 |
| 18 | -0.79 |
0.35 |
-0.43 |
-6.94 |
-1.24 |
1.91 |
-0.67 |
0.19 |
-0.47 |
| 19 | -0.78 |
0.37 |
-0.41 |
-7.27 |
-1.27 |
1.89 |
-0.65 |
0.21 |
-0.45 |
| 20 | -0.77 |
0.38 |
-0.38 |
-7.59 |
-1.31 |
1.87 |
-0.64 |
0.22 |
-0.42 |
| 21 | -0.76 |
0.40 |
-0.36 |
-7.91 |
-1.34 |
1.86 |
-0.63 |
0.23 |
-0.40 |
| 22 | -0.75 |
0.41 |
-0.34 |
-8.22 |
-1.37 |
1.85 |
-0.61 |
0.24 |
-0.38 |
| 23 | -0.74 |
0.42 |
-0.33 |
-8.53 |
-1.40 |
1.83 |
-0.60 |
0.25 |
-0.35 |
| 24 | -0.73 |
0.43 |
-0.31 |
-8.83 |
-1.42 |
1.82 |
-0.59 |
0.25 |
-0.33 |
| 25 | -0.73 |
0.44 |
-0.29 |
-9.12 |
-1.45 |
1.81 |
-0.58 |
0.26 |
-0.31 |
| 26 | -0.72 |
0.44 |
-0.28 |
-9.41 |
-1.48 |
1.80 |
-0.56 |
0.27 |
-0.30 |
| 27 | -0.71 |
0.45 |
-0.26 |
-9.69 |
-1.50 |
1.80 |
-0.55 |
0.27 |
-0.28 |
| 28 | -0.70 |
0.46 |
-0.25 |
-9.97 |
-1.52 |
1.79 |
-0.54 |
0.28 |
-0.26 |
| 29 | -0.70 |
0.46 |
-0.23 |
-10.25 |
-1.54 |
1.78 |
-0.53 |
0.29 |
-0.24 |
| 30 | -0.69 |
0.47 |
-0.22 |
-10.52 |
-1.56 |
1.77 |
-0.52 |
0.29 |
-0.23 |
| 31 | -0.68 |
0.47 |
-0.21 |
-10.78 |
-1.58 |
1.77 |
-0.51 |
0.30 |
-0.21 |
| 32 | -0.67 |
0.48 |
-0.20 |
-11.04 |
-1.60 |
1.76 |
-0.50 |
0.30 |
-0.20 |
| 33 | -0.67 |
0.48 |
-0.19 |
-11.30 |
-1.62 |
1.76 |
-0.49 |
0.30 |
-0.19 |
| 34 | -0.66 |
0.48 |
-0.18 |
-11.55 |
-1.64 |
1.75 |
-0.48 |
0.31 |
-0.17 |
| 35 | -0.65 |
0.49 |
-0.17 |
-11.79 |
-1.66 |
1.75 |
-0.47 |
0.31 |
-0.16 |
| 36 | -0.65 |
0.49 |
-0.16 |
-12.03 |
-1.67 |
1.74 |
-0.46 |
0.31 |
-0.15 |
| 37 | -0.64 |
0.50 |
-0.15 |
-12.27 |
-1.69 |
1.74 |
-0.45 |
0.32 |
-0.13 |
| 38 | -0.64 |
0.50 |
-0.14 |
-12.50 |
-1.70 |
1.74 |
-0.44 |
0.32 |
-0.12 |
| 39 | -0.63 |
0.50 |
-0.13 |
-12.73 |
-1.72 |
1.73 |
-0.43 |
0.32 |
-0.11 |
| 40 | -0.62 |
0.50 |
-0.12 |
-12.96 |
-1.73 |
1.73 |
-0.43 |
0.33 |
-0.10 |
| 41 | -0.62 |
0.51 |
-0.11 |
-13.18 |
-1.74 |
1.73 |
-0.42 |
0.33 |
-0.09 |
| 42 | -0.61 |
0.51 |
-0.10 |
-13.40 |
-1.76 |
1.72 |
-0.41 |
0.33 |
-0.08 |
| 43 | -0.61 |
0.51 |
-0.09 |
-13.61 |
-1.77 |
1.72 |
-0.40 |
0.33 |
-0.07 |
| 44 | -0.60 |
0.51 |
-0.09 |
-13.82 |
-1.78 |
1.72 |
-0.39 |
0.33 |
-0.06 |
| 45 | -0.59 |
0.52 |
-0.08 |
-14.03 |
-1.79 |
1.72 |
-0.39 |
0.34 |
-0.05 |
| 46 | -0.59 |
0.52 |
-0.07 |
-14.23 |
-1.80 |
1.72 |
-0.38 |
0.34 |
-0.04 |
| 47 | -0.58 |
0.52 |
-0.06 |
-14.43 |
-1.81 |
1.71 |
-0.37 |
0.34 |
-0.03 |
| 48 | -0.58 |
0.52 |
-0.06 |
-14.62 |
-1.82 |
1.71 |
-0.36 |
0.34 |
-0.02 |
| 49 | -0.57 |
0.52 |
-0.05 |
-14.82 |
-1.83 |
1.71 |
-0.36 |
0.34 |
-0.01 |
| 50 | -0.57 |
0.52 |
-0.04 |
-15.01 |
-1.84 |
1.71 |
-0.35 |
0.34 |
-0.01 |
| 51 | -0.56 |
0.53 |
-0.04 |
-15.19 |
-1.85 |
1.71 |
-0.34 |
0.34 |
0.00 |
| 52 | -0.56 |
0.53 |
-0.03 |
-15.37 |
-1.86 |
1.71 |
-0.34 |
0.35 |
0.01 |
| 53 | -0.55 |
0.53 |
-0.02 |
-15.55 |
-1.87 |
1.70 |
-0.33 |
0.35 |
0.02 |
| 54 | -0.55 |
0.53 |
-0.02 |
-15.73 |
-1.88 |
1.70 |
-0.32 |
0.35 |
0.02 |
| 55 | -0.54 |
0.53 |
-0.01 |
-15.91 |
-1.89 |
1.70 |
-0.32 |
0.35 |
0.03 |
| 56 | -0.54 |
0.53 |
-0.01 |
-16.08 |
-1.90 |
1.70 |
-0.31 |
0.35 |
0.04 |
| 57 | -0.53 |
0.53 |
0.00 |
-16.24 |
-1.90 |
1.70 |
-0.30 |
0.35 |
0.04 |
| 58 | -0.53 |
0.53 |
0.01 |
-16.41 |
-1.91 |
1.70 |
-0.30 |
0.35 |
0.05 |
| 59 | -0.52 |
0.54 |
0.01 |
-16.57 |
-1.92 |
1.70 |
-0.29 |
0.35 |
0.06 |
| 60 | -0.52 |
0.54 |
0.02 |
-16.73 |
-1.93 |
1.70 |
-0.29 |
0.35 |
0.06 |
| 61 | -0.52 |
0.54 |
0.02 |
-16.89 |
-1.93 |
1.69 |
-0.28 |
0.35 |
0.07 |
| 62 | -0.51 |
0.54 |
0.03 |
-17.04 |
-1.94 |
1.69 |
-0.28 |
0.35 |
0.08 |
| 63 | -0.51 |
0.54 |
0.03 |
-17.20 |
-1.95 |
1.69 |
-0.27 |
0.35 |
0.08 |
| 64 | -0.50 |
0.54 |
0.04 |
-17.35 |
-1.95 |
1.69 |
-0.27 |
0.35 |
0.09 |
| 65 | -0.50 |
0.54 |
0.04 |
-17.49 |
-1.96 |
1.69 |
-0.26 |
0.35 |
0.09 |
| 66 | -0.49 |
0.54 |
0.05 |
-17.64 |
-1.96 |
1.69 |
-0.26 |
0.35 |
0.10 |
| 67 | -0.49 |
0.54 |
0.05 |
-17.78 |
-1.97 |
1.69 |
-0.25 |
0.35 |
0.10 |
| 68 | -0.49 |
0.54 |
0.06 |
-17.92 |
-1.98 |
1.69 |
-0.25 |
0.35 |
0.11 |
| 69 | -0.48 |
0.54 |
0.06 |
-18.06 |
-1.98 |
1.69 |
-0.24 |
0.36 |
0.11 |
| 70 | -0.48 |
0.54 |
0.06 |
-18.19 |
-1.99 |
1.69 |
-0.24 |
0.36 |
0.12 |
| 71 | -0.47 |
0.54 |
0.07 |
-18.33 |
-1.99 |
1.68 |
-0.23 |
0.36 |
0.12 |
| 72 | -0.47 |
0.54 |
0.07 |
-18.46 |
-2.00 |
1.68 |
-0.23 |
0.36 |
0.13 |
| 73 | -0.47 |
0.54 |
0.08 |
-18.59 |
-2.00 |
1.68 |
-0.22 |
0.36 |
0.13 |
| 74 | -0.46 |
0.54 |
0.08 |
-18.71 |
-2.01 |
1.68 |
-0.22 |
0.36 |
0.14 |
| 75 | -0.46 |
0.54 |
0.08 |
-18.84 |
-2.01 |
1.68 |
-0.21 |
0.36 |
0.14 |
| 76 | -0.46 |
0.54 |
0.09 |
-18.96 |
-2.02 |
1.68 |
-0.21 |
0.36 |
0.15 |
| 77 | -0.45 |
0.54 |
0.09 |
-19.08 |
-2.02 |
1.68 |
-0.21 |
0.36 |
0.15 |
| 78 | -0.45 |
0.55 |
0.10 |
-19.20 |
-2.03 |
1.68 |
-0.20 |
0.36 |
0.15 |
| 79 | -0.45 |
0.55 |
0.10 |
-19.32 |
-2.03 |
1.68 |
-0.20 |
0.36 |
0.16 |
| 80 | -0.44 |
0.55 |
0.10 |
-19.43 |
-2.03 |
1.68 |
-0.19 |
0.36 |
0.16 |
| 81 | -0.44 |
0.55 |
0.11 |
-19.54 |
-2.04 |
1.68 |
-0.19 |
0.36 |
0.17 |
| 82 | -0.44 |
0.55 |
0.11 |
-19.66 |
-2.04 |
1.67 |
-0.19 |
0.36 |
0.17 |
| 83 | -0.43 |
0.55 |
0.11 |
-19.77 |
-2.05 |
1.67 |
-0.18 |
0.36 |
0.17 |
| 84 | -0.43 |
0.55 |
0.12 |
-19.87 |
-2.05 |
1.67 |
-0.18 |
0.36 |
0.18 |
| 85 | -0.43 |
0.55 |
0.12 |
-19.98 |
-2.05 |
1.67 |
-0.18 |
0.36 |
0.18 |
| 86 | -0.42 |
0.55 |
0.12 |
-20.08 |
-2.06 |
1.67 |
-0.17 |
0.36 |
0.18 |
| 87 | -0.42 |
0.55 |
0.13 |
-20.19 |
-2.06 |
1.67 |
-0.17 |
0.36 |
0.19 |
| 88 | -0.42 |
0.55 |
0.13 |
-20.29 |
-2.07 |
1.67 |
-0.17 |
0.36 |
0.19 |
| 89 | -0.41 |
0.55 |
0.13 |
-20.39 |
-2.07 |
1.67 |
-0.16 |
0.36 |
0.19 |
| 90 | -0.41 |
0.55 |
0.13 |
-20.48 |
-2.07 |
1.67 |
-0.16 |
0.36 |
0.20 |
| 91 | -0.41 |
0.55 |
0.14 |
-20.58 |
-2.08 |
1.67 |
-0.16 |
0.36 |
0.20 |
| 92 | -0.41 |
0.55 |
0.14 |
-20.67 |
-2.08 |
1.67 |
-0.15 |
0.36 |
0.20 |
| 93 | -0.40 |
0.55 |
0.14 |
-20.77 |
-2.08 |
1.66 |
-0.15 |
0.36 |
0.21 |
| 94 | -0.40 |
0.55 |
0.15 |
-20.86 |
-2.09 |
1.66 |
-0.15 |
0.36 |
0.21 |
| 95 | -0.40 |
0.55 |
0.15 |
-20.95 |
-2.09 |
1.66 |
-0.14 |
0.36 |
0.21 |
| 96 | -0.39 |
0.55 |
0.15 |
-21.04 |
-2.09 |
1.66 |
-0.14 |
0.36 |
0.21 |
| 97 | -0.39 |
0.55 |
0.15 |
-21.12 |
-2.09 |
1.66 |
-0.14 |
0.36 |
0.22 |
| 98 | -0.39 |
0.55 |
0.16 |
-21.21 |
-2.10 |
1.66 |
-0.14 |
0.36 |
0.22 |
| 99 | -0.39 |
0.55 |
0.16 |
-21.29 |
-2.10 |
1.66 |
-0.13 |
0.35 |
0.22 |
| 100 | -0.38 |
0.55 |
0.16 |
-21.38 |
-2.10 |
1.66 |
-0.13 |
0.35 |
0.22 |
| 101 | -0.38 |
0.55 |
0.16 |
-21.46 |
-2.11 |
1.66 |
-0.13 |
0.35 |
0.23 |
| 102 | -0.38 |
0.54 |
0.17 |
-21.54 |
-2.11 |
1.66 |
-0.13 |
0.35 |
0.23 |
| 103 | -0.38 |
0.54 |
0.17 |
-21.62 |
-2.11 |
1.65 |
-0.12 |
0.35 |
0.23 |
| 104 | -0.37 |
0.54 |
0.17 |
-21.69 |
-2.11 |
1.65 |
-0.12 |
0.35 |
0.23 |
| 105 | -0.37 |
0.54 |
0.17 |
-21.77 |
-2.12 |
1.65 |
-0.12 |
0.35 |
0.24 |
| 106 | -0.37 |
0.54 |
0.17 |
-21.85 |
-2.12 |
1.65 |
-0.12 |
0.35 |
0.24 |
| 107 | -0.37 |
0.54 |
0.18 |
-21.92 |
-2.12 |
1.65 |
-0.11 |
0.35 |
0.24 |
| 108 | -0.36 |
0.54 |
0.18 |
-21.99 |
-2.12 |
1.65 |
-0.11 |
0.35 |
0.24 |
| 109 | -0.36 |
0.54 |
0.18 |
-22.07 |
-2.12 |
1.65 |
-0.11 |
0.35 |
0.24 |
| 110 | -0.36 |
0.54 |
0.18 |
-22.14 |
-2.13 |
1.65 |
-0.11 |
0.35 |
0.25 |
| 111 | -0.36 |
0.54 |
0.19 |
-22.20 |
-2.13 |
1.65 |
-0.10 |
0.35 |
0.25 |
| 112 | -0.36 |
0.54 |
0.19 |
-22.27 |
-2.13 |
1.65 |
-0.10 |
0.35 |
0.25 |
| 113 | -0.35 |
0.54 |
0.19 |
-22.34 |
-2.13 |
1.64 |
-0.10 |
0.35 |
0.25 |
| 114 | -0.35 |
0.54 |
0.19 |
-22.41 |
-2.14 |
1.64 |
-0.10 |
0.35 |
0.25 |
| 115 | -0.35 |
0.54 |
0.19 |
-22.47 |
-2.14 |
1.64 |
-0.10 |
0.35 |
0.26 |
| 116 | -0.35 |
0.54 |
0.19 |
-22.54 |
-2.14 |
1.64 |
-0.09 |
0.35 |
0.26 |
| 117 | -0.35 |
0.54 |
0.20 |
-22.60 |
-2.14 |
1.64 |
-0.09 |
0.35 |
0.26 |
| 118 | -0.34 |
0.54 |
0.20 |
-22.66 |
-2.14 |
1.64 |
-0.09 |
0.35 |
0.26 |
| 119 | -0.34 |
0.54 |
0.20 |
-22.72 |
-2.14 |
1.64 |
-0.09 |
0.35 |
0.26 |
| 120 | -0.34 |
0.54 |
0.20 |
-22.78 |
-2.15 |
1.64 |
-0.09 |
0.35 |
0.26 |
Figure 7. 50% Rise in the Oil Price: Complete and Incomplete Markets
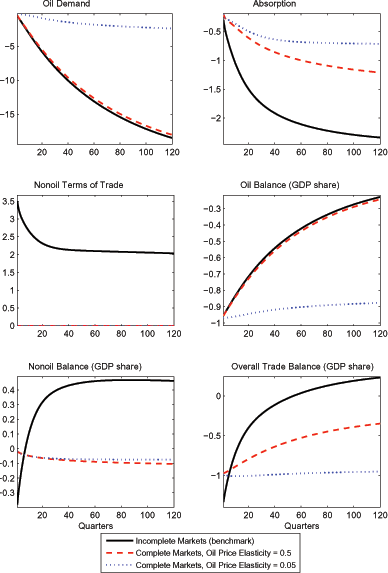
Data for Figure 7, Panel 1 - 50% Rise in the Oil Price: Complete and Incomplete Markets
| Period | Oil demand: incomplete markets (bench-mark) |
Absorption: incomplete markets (bench-mark) |
Nonoil terms of trade: incomplete markets (bench-mark) |
Oil balance: GDP share: incomplete markets (bench-mark) |
Nonoil balance: GDP share: incomplete markets (bench-mark) |
Overall trade balance: GDP share: incomplete markets (bench-mark) |
Oil demand: complete markets, oil price elasticity = 0.5 |
Absorption: complete markets, oil price elasticity = 0.5 |
Nonoil terms of trade: complete markets, oil price elasticity = 0.5 |
|---|---|---|---|---|---|---|---|---|---|
| 1 | -0.47 |
-0.30 |
3.50 |
-0.96 |
-0.38 |
-1.34 |
-0.46 |
-0.20 |
0.00 |
| 2 | -0.80 |
-0.44 |
3.28 |
-0.94 |
-0.29 |
-1.23 |
-0.77 |
-0.26 |
0.00 |
| 3 | -1.10 |
-0.55 |
3.15 |
-0.93 |
-0.22 |
-1.15 |
-1.06 |
-0.29 |
0.00 |
| 4 | -1.39 |
-0.63 |
3.05 |
-0.91 |
-0.16 |
-1.07 |
-1.33 |
-0.31 |
0.00 |
| 5 | -1.68 |
-0.71 |
2.97 |
-0.90 |
-0.10 |
-1.00 |
-1.60 |
-0.33 |
0.00 |
| 6 | -1.97 |
-0.79 |
2.89 |
-0.89 |
-0.05 |
-0.94 |
-1.88 |
-0.34 |
0.00 |
| 7 | -2.25 |
-0.86 |
2.83 |
-0.87 |
0.00 |
-0.88 |
-2.15 |
-0.36 |
0.00 |
| 8 | -2.54 |
-0.92 |
2.76 |
-0.86 |
0.04 |
-0.82 |
-2.42 |
-0.38 |
0.00 |
| 9 | -2.83 |
-0.99 |
2.71 |
-0.85 |
0.08 |
-0.77 |
-2.69 |
-0.40 |
0.00 |
| 10 | -3.12 |
-1.05 |
2.65 |
-0.83 |
0.11 |
-0.72 |
-2.96 |
-0.42 |
0.00 |
| 11 | -3.40 |
-1.11 |
2.61 |
-0.82 |
0.14 |
-0.68 |
-3.23 |
-0.44 |
0.00 |
| 12 | -3.68 |
-1.16 |
2.56 |
-0.81 |
0.17 |
-0.64 |
-3.49 |
-0.46 |
0.00 |
| 13 | -3.96 |
-1.21 |
2.52 |
-0.80 |
0.19 |
-0.60 |
-3.75 |
-0.48 |
0.00 |
| 14 | -4.24 |
-1.26 |
2.48 |
-0.78 |
0.22 |
-0.57 |
-4.01 |
-0.50 |
0.00 |
| 15 | -4.51 |
-1.30 |
2.45 |
-0.77 |
0.24 |
-0.53 |
-4.27 |
-0.52 |
0.00 |
| 16 | -4.77 |
-1.35 |
2.42 |
-0.76 |
0.26 |
-0.50 |
-4.52 |
-0.54 |
0.00 |
| 17 | -5.04 |
-1.39 |
2.39 |
-0.75 |
0.27 |
-0.48 |
-4.77 |
-0.56 |
0.00 |
| 18 | -5.30 |
-1.43 |
2.36 |
-0.74 |
0.29 |
-0.45 |
-5.01 |
-0.58 |
0.00 |
| 19 | -5.55 |
-1.46 |
2.34 |
-0.73 |
0.30 |
-0.42 |
-5.26 |
-0.59 |
0.00 |
| 20 | -5.80 |
-1.50 |
2.32 |
-0.72 |
0.32 |
-0.40 |
-5.50 |
-0.61 |
0.00 |
| 21 | -6.05 |
-1.53 |
2.30 |
-0.71 |
0.33 |
-0.38 |
-5.73 |
-0.63 |
0.00 |
| 22 | -6.29 |
-1.56 |
2.28 |
-0.70 |
0.34 |
-0.36 |
-5.96 |
-0.64 |
0.00 |
| 23 | -6.53 |
-1.59 |
2.26 |
-0.69 |
0.35 |
-0.34 |
-6.19 |
-0.66 |
0.00 |
| 24 | -6.76 |
-1.62 |
2.25 |
-0.68 |
0.36 |
-0.32 |
-6.42 |
-0.67 |
0.00 |
| 25 | -6.99 |
-1.64 |
2.23 |
-0.67 |
0.36 |
-0.30 |
-6.64 |
-0.69 |
0.00 |
| 26 | -7.22 |
-1.67 |
2.22 |
-0.66 |
0.37 |
-0.29 |
-6.86 |
-0.70 |
0.00 |
| 27 | -7.44 |
-1.69 |
2.21 |
-0.65 |
0.38 |
-0.27 |
-7.08 |
-0.72 |
0.00 |
| 28 | -7.66 |
-1.71 |
2.20 |
-0.64 |
0.38 |
-0.25 |
-7.29 |
-0.73 |
0.00 |
| 29 | -7.88 |
-1.73 |
2.19 |
-0.63 |
0.39 |
-0.24 |
-7.50 |
-0.74 |
0.00 |
| 30 | -8.09 |
-1.75 |
2.18 |
-0.62 |
0.39 |
-0.23 |
-7.70 |
-0.75 |
0.00 |
| 31 | -8.30 |
-1.77 |
2.18 |
-0.61 |
0.40 |
-0.21 |
-7.91 |
-0.77 |
0.00 |
| 32 | -8.50 |
-1.79 |
2.17 |
-0.60 |
0.40 |
-0.20 |
-8.11 |
-0.78 |
0.00 |
| 33 | -8.70 |
-1.81 |
2.16 |
-0.60 |
0.41 |
-0.19 |
-8.30 |
-0.79 |
0.00 |
| 34 | -8.90 |
-1.83 |
2.16 |
-0.59 |
0.41 |
-0.18 |
-8.50 |
-0.80 |
0.00 |
| 35 | -9.10 |
-1.84 |
2.15 |
-0.58 |
0.42 |
-0.16 |
-8.69 |
-0.81 |
0.00 |
| 36 | -9.29 |
-1.86 |
2.15 |
-0.57 |
0.42 |
-0.15 |
-8.88 |
-0.82 |
0.00 |
| 37 | -9.48 |
-1.87 |
2.14 |
-0.56 |
0.42 |
-0.14 |
-9.06 |
-0.83 |
0.00 |
| 38 | -9.66 |
-1.89 |
2.14 |
-0.56 |
0.42 |
-0.13 |
-9.24 |
-0.84 |
0.00 |
| 39 | -9.85 |
-1.90 |
2.14 |
-0.55 |
0.43 |
-0.12 |
-9.42 |
-0.85 |
0.00 |
| 40 | -10.03 |
-1.92 |
2.13 |
-0.54 |
0.43 |
-0.11 |
-9.60 |
-0.86 |
0.00 |
| 41 | -10.20 |
-1.93 |
2.13 |
-0.53 |
0.43 |
-0.10 |
-9.77 |
-0.87 |
0.00 |
| 42 | -10.38 |
-1.94 |
2.13 |
-0.53 |
0.44 |
-0.09 |
-9.95 |
-0.88 |
0.00 |
| 43 | -10.55 |
-1.95 |
2.13 |
-0.52 |
0.44 |
-0.08 |
-10.12 |
-0.88 |
0.00 |
| 44 | -10.72 |
-1.97 |
2.12 |
-0.51 |
0.44 |
-0.07 |
-10.28 |
-0.89 |
0.00 |
| 45 | -10.89 |
-1.98 |
2.12 |
-0.51 |
0.44 |
-0.07 |
-10.45 |
-0.90 |
0.00 |
| 46 | -11.05 |
-1.99 |
2.12 |
-0.50 |
0.44 |
-0.06 |
-10.61 |
-0.91 |
0.00 |
| 47 | -11.21 |
-2.00 |
2.12 |
-0.49 |
0.44 |
-0.05 |
-10.77 |
-0.92 |
0.00 |
| 48 | -11.37 |
-2.01 |
2.12 |
-0.49 |
0.45 |
-0.04 |
-10.93 |
-0.92 |
0.00 |
| 49 | -11.53 |
-2.02 |
2.11 |
-0.48 |
0.45 |
-0.03 |
-11.08 |
-0.93 |
0.00 |
| 50 | -11.68 |
-2.03 |
2.11 |
-0.48 |
0.45 |
-0.03 |
-11.23 |
-0.94 |
0.00 |
| 51 | -11.83 |
-2.04 |
2.11 |
-0.47 |
0.45 |
-0.02 |
-11.39 |
-0.94 |
0.00 |
| 52 | -11.98 |
-2.05 |
2.11 |
-0.46 |
0.45 |
-0.01 |
-11.53 |
-0.95 |
0.00 |
| 53 | -12.13 |
-2.05 |
2.11 |
-0.46 |
0.45 |
-0.01 |
-11.68 |
-0.96 |
0.00 |
| 54 | -12.28 |
-2.06 |
2.11 |
-0.45 |
0.45 |
0.00 |
-11.83 |
-0.96 |
0.00 |
| 55 | -12.42 |
-2.07 |
2.11 |
-0.45 |
0.46 |
0.01 |
-11.97 |
-0.97 |
0.00 |
| 56 | -12.56 |
-2.08 |
2.10 |
-0.44 |
0.46 |
0.01 |
-12.11 |
-0.98 |
0.00 |
| 57 | -12.70 |
-2.09 |
2.10 |
-0.44 |
0.46 |
0.02 |
-12.25 |
-0.98 |
0.00 |
| 58 | -12.84 |
-2.09 |
2.10 |
-0.43 |
0.46 |
0.03 |
-12.38 |
-0.99 |
0.00 |
| 59 | -12.97 |
-2.10 |
2.10 |
-0.43 |
0.46 |
0.03 |
-12.52 |
-0.99 |
0.00 |
| 60 | -13.11 |
-2.11 |
2.10 |
-0.42 |
0.46 |
0.04 |
-12.65 |
-1.00 |
0.00 |
| 61 | -13.24 |
-2.12 |
2.10 |
-0.42 |
0.46 |
0.04 |
-12.78 |
-1.01 |
0.00 |
| 62 | -13.37 |
-2.12 |
2.10 |
-0.41 |
0.46 |
0.05 |
-12.91 |
-1.01 |
0.00 |
| 63 | -13.50 |
-2.13 |
2.10 |
-0.41 |
0.46 |
0.05 |
-13.04 |
-1.02 |
0.00 |
| 64 | -13.62 |
-2.14 |
2.09 |
-0.40 |
0.46 |
0.06 |
-13.16 |
-1.02 |
0.00 |
| 65 | -13.75 |
-2.14 |
2.09 |
-0.40 |
0.46 |
0.07 |
-13.29 |
-1.03 |
0.00 |
| 66 | -13.87 |
-2.15 |
2.09 |
-0.39 |
0.46 |
0.07 |
-13.41 |
-1.03 |
0.00 |
| 67 | -13.99 |
-2.15 |
2.09 |
-0.39 |
0.46 |
0.08 |
-13.53 |
-1.04 |
0.00 |
| 68 | -14.11 |
-2.16 |
2.09 |
-0.38 |
0.46 |
0.08 |
-13.65 |
-1.04 |
0.00 |
| 69 | -14.23 |
-2.17 |
2.09 |
-0.38 |
0.47 |
0.09 |
-13.76 |
-1.05 |
0.00 |
| 70 | -14.34 |
-2.17 |
2.09 |
-0.38 |
0.47 |
0.09 |
-13.88 |
-1.05 |
0.00 |
| 71 | -14.46 |
-2.18 |
2.09 |
-0.37 |
0.47 |
0.09 |
-13.99 |
-1.06 |
0.00 |
| 72 | -14.57 |
-2.18 |
2.09 |
-0.37 |
0.47 |
0.10 |
-14.11 |
-1.06 |
0.00 |
| 73 | -14.68 |
-2.19 |
2.09 |
-0.36 |
0.47 |
0.10 |
-14.22 |
-1.06 |
0.00 |
| 74 | -14.79 |
-2.19 |
2.08 |
-0.36 |
0.47 |
0.11 |
-14.33 |
-1.07 |
0.00 |
| 75 | -14.90 |
-2.20 |
2.08 |
-0.36 |
0.47 |
0.11 |
-14.43 |
-1.07 |
0.00 |
| 76 | -15.00 |
-2.20 |
2.08 |
-0.35 |
0.47 |
0.12 |
-14.54 |
-1.08 |
0.00 |
| 77 | -15.11 |
-2.21 |
2.08 |
-0.35 |
0.47 |
0.12 |
-14.64 |
-1.08 |
0.00 |
| 78 | -15.21 |
-2.21 |
2.08 |
-0.34 |
0.47 |
0.12 |
-14.75 |
-1.09 |
0.00 |
| 79 | -15.31 |
-2.22 |
2.08 |
-0.34 |
0.47 |
0.13 |
-14.85 |
-1.09 |
0.00 |
| 80 | -15.41 |
-2.22 |
2.08 |
-0.34 |
0.47 |
0.13 |
-14.95 |
-1.09 |
0.00 |
| 81 | -15.51 |
-2.22 |
2.08 |
-0.33 |
0.47 |
0.13 |
-15.05 |
-1.10 |
0.00 |
| 82 | -15.61 |
-2.23 |
2.08 |
-0.33 |
0.47 |
0.14 |
-15.15 |
-1.10 |
0.00 |
| 83 | -15.71 |
-2.23 |
2.07 |
-0.33 |
0.47 |
0.14 |
-15.24 |
-1.10 |
0.00 |
| 84 | -15.80 |
-2.24 |
2.07 |
-0.32 |
0.47 |
0.15 |
-15.34 |
-1.11 |
0.00 |
| 85 | -15.90 |
-2.24 |
2.07 |
-0.32 |
0.47 |
0.15 |
-15.43 |
-1.11 |
0.00 |
| 86 | -15.99 |
-2.24 |
2.07 |
-0.32 |
0.47 |
0.15 |
-15.52 |
-1.12 |
0.00 |
| 87 | -16.08 |
-2.25 |
2.07 |
-0.31 |
0.47 |
0.16 |
-15.62 |
-1.12 |
0.00 |
| 88 | -16.17 |
-2.25 |
2.07 |
-0.31 |
0.47 |
0.16 |
-15.71 |
-1.12 |
0.00 |
| 89 | -16.26 |
-2.26 |
2.07 |
-0.31 |
0.47 |
0.16 |
-15.79 |
-1.13 |
0.00 |
| 90 | -16.35 |
-2.26 |
2.07 |
-0.30 |
0.47 |
0.16 |
-15.88 |
-1.13 |
0.00 |
| 91 | -16.43 |
-2.26 |
2.07 |
-0.30 |
0.47 |
0.17 |
-15.97 |
-1.13 |
0.00 |
| 92 | -16.52 |
-2.27 |
2.07 |
-0.30 |
0.47 |
0.17 |
-16.05 |
-1.14 |
0.00 |
| 93 | -16.60 |
-2.27 |
2.06 |
-0.29 |
0.47 |
0.17 |
-16.14 |
-1.14 |
0.00 |
| 94 | -16.69 |
-2.27 |
2.06 |
-0.29 |
0.47 |
0.18 |
-16.22 |
-1.14 |
0.00 |
| 95 | -16.77 |
-2.28 |
2.06 |
-0.29 |
0.47 |
0.18 |
-16.30 |
-1.15 |
0.00 |
| 96 | -16.85 |
-2.28 |
2.06 |
-0.29 |
0.47 |
0.18 |
-16.38 |
-1.15 |
0.00 |
| 97 | -16.93 |
-2.28 |
2.06 |
-0.28 |
0.47 |
0.18 |
-16.46 |
-1.15 |
0.00 |
| 98 | -17.01 |
-2.29 |
2.06 |
-0.28 |
0.47 |
0.19 |
-16.54 |
-1.16 |
0.00 |
| 99 | -17.08 |
-2.29 |
2.06 |
-0.28 |
0.47 |
0.19 |
-16.62 |
-1.16 |
0.00 |
| 100 | -17.16 |
-2.29 |
2.06 |
-0.27 |
0.47 |
0.19 |
-16.70 |
-1.16 |
0.00 |
| 101 | -17.24 |
-2.29 |
2.06 |
-0.27 |
0.47 |
0.19 |
-16.77 |
-1.16 |
0.00 |
| 102 | -17.31 |
-2.30 |
2.05 |
-0.27 |
0.47 |
0.20 |
-16.84 |
-1.17 |
0.00 |
| 103 | -17.38 |
-2.30 |
2.05 |
-0.27 |
0.47 |
0.20 |
-16.92 |
-1.17 |
0.00 |
| 104 | -17.46 |
-2.30 |
2.05 |
-0.26 |
0.47 |
0.20 |
-16.99 |
-1.17 |
0.00 |
| 105 | -17.53 |
-2.31 |
2.05 |
-0.26 |
0.47 |
0.20 |
-17.06 |
-1.18 |
0.00 |
| 106 | -17.60 |
-2.31 |
2.05 |
-0.26 |
0.47 |
0.21 |
-17.13 |
-1.18 |
0.00 |
| 107 | -17.67 |
-2.31 |
2.05 |
-0.26 |
0.47 |
0.21 |
-17.20 |
-1.18 |
0.00 |
| 108 | -17.73 |
-2.31 |
2.05 |
-0.25 |
0.46 |
0.21 |
-17.27 |
-1.18 |
0.00 |
| 109 | -17.80 |
-2.31 |
2.05 |
-0.25 |
0.46 |
0.21 |
-17.34 |
-1.19 |
0.00 |
| 110 | -17.87 |
-2.32 |
2.05 |
-0.25 |
0.46 |
0.21 |
-17.40 |
-1.19 |
0.00 |
| 111 | -17.93 |
-2.32 |
2.04 |
-0.25 |
0.46 |
0.22 |
-17.47 |
-1.19 |
0.00 |
| 112 | -18.00 |
-2.32 |
2.04 |
-0.25 |
0.46 |
0.22 |
-17.53 |
-1.19 |
0.00 |
| 113 | -18.06 |
-2.32 |
2.04 |
-0.24 |
0.46 |
0.22 |
-17.60 |
-1.20 |
0.00 |
| 114 | -18.13 |
-2.33 |
2.04 |
-0.24 |
0.46 |
0.22 |
-17.66 |
-1.20 |
0.00 |
| 115 | -18.19 |
-2.33 |
2.04 |
-0.24 |
0.46 |
0.22 |
-17.72 |
-1.20 |
0.00 |
| 116 | -18.25 |
-2.33 |
2.04 |
-0.24 |
0.46 |
0.23 |
-17.79 |
-1.20 |
0.00 |
| 117 | -18.31 |
-2.33 |
2.04 |
-0.23 |
0.46 |
0.23 |
-17.85 |
-1.21 |
0.00 |
| 118 | -18.37 |
-2.33 |
2.04 |
-0.23 |
0.46 |
0.23 |
-17.91 |
-1.21 |
0.00 |
| 119 | -18.43 |
-2.34 |
2.04 |
-0.23 |
0.46 |
0.23 |
-17.96 |
-1.21 |
0.00 |
| 120 | -18.49 |
-2.34 |
2.03 |
-0.23 |
0.46 |
0.23 |
-18.02 |
-1.21 |
0.00 |
Data for Figure 7, Panel 2 - 50% Rise in the Oil Price: Complete and Incomplete Markets
| Period | Oil balance: GDP share: complete markets, oil price elasticity = 0.5 |
Nonoil balance: GDP share: complete markets, oil price elasticity = 0.5 |
Overall trade balance: GDP share: complete markets, oil price elasticity = 0.5 |
Oil demand: complete markets, oil price elasticity = 0.05 |
Absorption: complete markets, oil price elasticity = 0.05 |
Nonoil terms of trade: complete markets, oil price elasticity = 0.05 |
Oil balance: GDP share: complete markets, oil price elasticity = 0.05 |
Nonoil balance: GDP share: complete markets, oil price elasticity = 0.05 |
Overall trade balance: GDP share: complete markets, oil price elasticity = 0.05 |
|---|---|---|---|---|---|---|---|---|---|
| 1 | -0.96 |
-0.02 |
-0.97 |
-0.20 |
-0.20 |
0.00 |
-0.97 |
-0.02 |
-0.99 |
| 2 | -0.94 |
-0.02 |
-0.97 |
-0.25 |
-0.26 |
0.00 |
-0.97 |
-0.03 |
-0.99 |
| 3 | -0.93 |
-0.03 |
-0.96 |
-0.27 |
-0.28 |
0.00 |
-0.97 |
-0.03 |
-1.00 |
| 4 | -0.92 |
-0.03 |
-0.95 |
-0.29 |
-0.29 |
0.00 |
-0.97 |
-0.04 |
-1.00 |
| 5 | -0.90 |
-0.04 |
-0.94 |
-0.31 |
-0.30 |
0.00 |
-0.97 |
-0.04 |
-1.00 |
| 6 | -0.89 |
-0.04 |
-0.93 |
-0.34 |
-0.31 |
0.00 |
-0.97 |
-0.04 |
-1.01 |
| 7 | -0.88 |
-0.04 |
-0.92 |
-0.37 |
-0.32 |
0.00 |
-0.96 |
-0.04 |
-1.01 |
| 8 | -0.87 |
-0.04 |
-0.91 |
-0.40 |
-0.34 |
0.00 |
-0.96 |
-0.05 |
-1.01 |
| 9 | -0.85 |
-0.05 |
-0.90 |
-0.43 |
-0.35 |
0.00 |
-0.96 |
-0.05 |
-1.01 |
| 10 | -0.84 |
-0.05 |
-0.89 |
-0.47 |
-0.37 |
0.00 |
-0.96 |
-0.05 |
-1.01 |
| 11 | -0.83 |
-0.05 |
-0.88 |
-0.51 |
-0.38 |
0.00 |
-0.96 |
-0.05 |
-1.01 |
| 12 | -0.82 |
-0.05 |
-0.87 |
-0.55 |
-0.39 |
0.00 |
-0.96 |
-0.05 |
-1.01 |
| 13 | -0.81 |
-0.05 |
-0.86 |
-0.59 |
-0.41 |
0.00 |
-0.96 |
-0.05 |
-1.01 |
| 14 | -0.79 |
-0.06 |
-0.85 |
-0.63 |
-0.42 |
0.00 |
-0.95 |
-0.06 |
-1.01 |
| 15 | -0.78 |
-0.06 |
-0.84 |
-0.67 |
-0.43 |
0.00 |
-0.95 |
-0.06 |
-1.01 |
| 16 | -0.77 |
-0.06 |
-0.83 |
-0.71 |
-0.45 |
0.00 |
-0.95 |
-0.06 |
-1.01 |
| 17 | -0.76 |
-0.06 |
-0.82 |
-0.75 |
-0.46 |
0.00 |
-0.95 |
-0.06 |
-1.01 |
| 18 | -0.75 |
-0.06 |
-0.81 |
-0.79 |
-0.47 |
0.00 |
-0.95 |
-0.06 |
-1.01 |
| 19 | -0.74 |
-0.06 |
-0.80 |
-0.83 |
-0.49 |
0.00 |
-0.95 |
-0.06 |
-1.01 |
| 20 | -0.73 |
-0.06 |
-0.79 |
-0.87 |
-0.50 |
0.00 |
-0.94 |
-0.06 |
-1.01 |
| 21 | -0.72 |
-0.06 |
-0.78 |
-0.91 |
-0.51 |
0.00 |
-0.94 |
-0.06 |
-1.01 |
| 22 | -0.71 |
-0.07 |
-0.77 |
-0.94 |
-0.52 |
0.00 |
-0.94 |
-0.06 |
-1.00 |
| 23 | -0.70 |
-0.07 |
-0.77 |
-0.98 |
-0.53 |
0.00 |
-0.94 |
-0.06 |
-1.00 |
| 24 | -0.69 |
-0.07 |
-0.76 |
-1.01 |
-0.54 |
0.00 |
-0.94 |
-0.06 |
-1.00 |
| 25 | -0.68 |
-0.07 |
-0.75 |
-1.05 |
-0.55 |
0.00 |
-0.94 |
-0.06 |
-1.00 |
| 26 | -0.67 |
-0.07 |
-0.74 |
-1.08 |
-0.56 |
0.00 |
-0.94 |
-0.07 |
-1.00 |
| 27 | -0.66 |
-0.07 |
-0.73 |
-1.11 |
-0.56 |
0.00 |
-0.93 |
-0.07 |
-1.00 |
| 28 | -0.65 |
-0.07 |
-0.72 |
-1.15 |
-0.57 |
0.00 |
-0.93 |
-0.07 |
-1.00 |
| 29 | -0.64 |
-0.07 |
-0.72 |
-1.18 |
-0.58 |
0.00 |
-0.93 |
-0.07 |
-1.00 |
| 30 | -0.64 |
-0.07 |
-0.71 |
-1.21 |
-0.59 |
0.00 |
-0.93 |
-0.07 |
-1.00 |
| 31 | -0.63 |
-0.07 |
-0.70 |
-1.24 |
-0.59 |
0.00 |
-0.93 |
-0.07 |
-1.00 |
| 32 | -0.62 |
-0.07 |
-0.69 |
-1.26 |
-0.60 |
0.00 |
-0.93 |
-0.07 |
-1.00 |
| 33 | -0.61 |
-0.08 |
-0.69 |
-1.29 |
-0.60 |
0.00 |
-0.93 |
-0.07 |
-0.99 |
| 34 | -0.60 |
-0.08 |
-0.68 |
-1.32 |
-0.61 |
0.00 |
-0.93 |
-0.07 |
-0.99 |
| 35 | -0.59 |
-0.08 |
-0.67 |
-1.35 |
-0.62 |
0.00 |
-0.92 |
-0.07 |
-0.99 |
| 36 | -0.59 |
-0.08 |
-0.66 |
-1.37 |
-0.62 |
0.00 |
-0.92 |
-0.07 |
-0.99 |
| 37 | -0.58 |
-0.08 |
-0.66 |
-1.40 |
-0.63 |
0.00 |
-0.92 |
-0.07 |
-0.99 |
| 38 | -0.57 |
-0.08 |
-0.65 |
-1.42 |
-0.63 |
0.00 |
-0.92 |
-0.07 |
-0.99 |
| 39 | -0.56 |
-0.08 |
-0.64 |
-1.44 |
-0.63 |
0.00 |
-0.92 |
-0.07 |
-0.99 |
| 40 | -0.56 |
-0.08 |
-0.64 |
-1.47 |
-0.64 |
0.00 |
-0.92 |
-0.07 |
-0.99 |
| 41 | -0.55 |
-0.08 |
-0.63 |
-1.49 |
-0.64 |
0.00 |
-0.92 |
-0.07 |
-0.99 |
| 42 | -0.54 |
-0.08 |
-0.62 |
-1.51 |
-0.64 |
0.00 |
-0.92 |
-0.07 |
-0.99 |
| 43 | -0.54 |
-0.08 |
-0.62 |
-1.53 |
-0.65 |
0.00 |
-0.92 |
-0.07 |
-0.99 |
| 44 | -0.53 |
-0.08 |
-0.61 |
-1.55 |
-0.65 |
0.00 |
-0.92 |
-0.07 |
-0.99 |
| 45 | -0.52 |
-0.08 |
-0.61 |
-1.57 |
-0.65 |
0.00 |
-0.91 |
-0.07 |
-0.99 |
| 46 | -0.52 |
-0.08 |
-0.60 |
-1.59 |
-0.66 |
0.00 |
-0.91 |
-0.07 |
-0.98 |
| 47 | -0.51 |
-0.08 |
-0.59 |
-1.61 |
-0.66 |
0.00 |
-0.91 |
-0.07 |
-0.98 |
| 48 | -0.50 |
-0.08 |
-0.59 |
-1.63 |
-0.66 |
0.00 |
-0.91 |
-0.07 |
-0.98 |
| 49 | -0.50 |
-0.08 |
-0.58 |
-1.65 |
-0.66 |
0.00 |
-0.91 |
-0.07 |
-0.98 |
| 50 | -0.49 |
-0.08 |
-0.58 |
-1.66 |
-0.67 |
0.00 |
-0.91 |
-0.07 |
-0.98 |
| 51 | -0.49 |
-0.09 |
-0.57 |
-1.68 |
-0.67 |
0.00 |
-0.91 |
-0.07 |
-0.98 |
| 52 | -0.48 |
-0.09 |
-0.57 |
-1.70 |
-0.67 |
0.00 |
-0.91 |
-0.07 |
-0.98 |
| 53 | -0.48 |
-0.09 |
-0.56 |
-1.72 |
-0.67 |
0.00 |
-0.91 |
-0.07 |
-0.98 |
| 54 | -0.47 |
-0.09 |
-0.56 |
-1.73 |
-0.67 |
0.00 |
-0.91 |
-0.07 |
-0.98 |
| 55 | -0.46 |
-0.09 |
-0.55 |
-1.75 |
-0.68 |
0.00 |
-0.91 |
-0.07 |
-0.98 |
| 56 | -0.46 |
-0.09 |
-0.55 |
-1.76 |
-0.68 |
0.00 |
-0.91 |
-0.07 |
-0.98 |
| 57 | -0.45 |
-0.09 |
-0.54 |
-1.78 |
-0.68 |
0.00 |
-0.90 |
-0.07 |
-0.98 |
| 58 | -0.45 |
-0.09 |
-0.54 |
-1.80 |
-0.68 |
0.00 |
-0.90 |
-0.07 |
-0.98 |
| 59 | -0.44 |
-0.09 |
-0.53 |
-1.81 |
-0.68 |
0.00 |
-0.90 |
-0.07 |
-0.98 |
| 60 | -0.44 |
-0.09 |
-0.53 |
-1.82 |
-0.68 |
0.00 |
-0.90 |
-0.07 |
-0.98 |
| 61 | -0.43 |
-0.09 |
-0.52 |
-1.84 |
-0.68 |
0.00 |
-0.90 |
-0.07 |
-0.97 |
| 62 | -0.43 |
-0.09 |
-0.52 |
-1.85 |
-0.69 |
0.00 |
-0.90 |
-0.07 |
-0.97 |
| 63 | -0.42 |
-0.09 |
-0.51 |
-1.87 |
-0.69 |
0.00 |
-0.90 |
-0.07 |
-0.97 |
| 64 | -0.42 |
-0.09 |
-0.51 |
-1.88 |
-0.69 |
0.00 |
-0.90 |
-0.07 |
-0.97 |
| 65 | -0.41 |
-0.09 |
-0.50 |
-1.89 |
-0.69 |
0.00 |
-0.90 |
-0.07 |
-0.97 |
| 66 | -0.41 |
-0.09 |
-0.50 |
-1.91 |
-0.69 |
0.00 |
-0.90 |
-0.07 |
-0.97 |
| 67 | -0.40 |
-0.09 |
-0.50 |
-1.92 |
-0.69 |
0.00 |
-0.90 |
-0.07 |
-0.97 |
| 68 | -0.40 |
-0.09 |
-0.49 |
-1.93 |
-0.69 |
0.00 |
-0.90 |
-0.07 |
-0.97 |
| 69 | -0.40 |
-0.09 |
-0.49 |
-1.94 |
-0.69 |
0.00 |
-0.90 |
-0.07 |
-0.97 |
| 70 | -0.39 |
-0.09 |
-0.48 |
-1.96 |
-0.69 |
0.00 |
-0.90 |
-0.07 |
-0.97 |
| 71 | -0.39 |
-0.09 |
-0.48 |
-1.97 |
-0.69 |
0.00 |
-0.90 |
-0.07 |
-0.97 |
| 72 | -0.38 |
-0.09 |
-0.48 |
-1.98 |
-0.69 |
0.00 |
-0.90 |
-0.07 |
-0.97 |
| 73 | -0.38 |
-0.09 |
-0.47 |
-1.99 |
-0.70 |
0.00 |
-0.89 |
-0.07 |
-0.97 |
| 74 | -0.38 |
-0.09 |
-0.47 |
-2.00 |
-0.70 |
0.00 |
-0.89 |
-0.07 |
-0.97 |
| 75 | -0.37 |
-0.09 |
-0.46 |
-2.01 |
-0.70 |
0.00 |
-0.89 |
-0.07 |
-0.97 |
| 76 | -0.37 |
-0.09 |
-0.46 |
-2.03 |
-0.70 |
0.00 |
-0.89 |
-0.07 |
-0.97 |
| 77 | -0.36 |
-0.09 |
-0.46 |
-2.04 |
-0.70 |
0.00 |
-0.89 |
-0.07 |
-0.97 |
| 78 | -0.36 |
-0.09 |
-0.45 |
-2.05 |
-0.70 |
0.00 |
-0.89 |
-0.07 |
-0.97 |
| 79 | -0.36 |
-0.09 |
-0.45 |
-2.06 |
-0.70 |
0.00 |
-0.89 |
-0.07 |
-0.97 |
| 80 | -0.35 |
-0.10 |
-0.45 |
-2.07 |
-0.70 |
0.00 |
-0.89 |
-0.07 |
-0.96 |
| 81 | -0.35 |
-0.10 |
-0.44 |
-2.08 |
-0.70 |
0.00 |
-0.89 |
-0.07 |
-0.96 |
| 82 | -0.34 |
-0.10 |
-0.44 |
-2.09 |
-0.70 |
0.00 |
-0.89 |
-0.07 |
-0.96 |
| 83 | -0.34 |
-0.10 |
-0.44 |
-2.10 |
-0.70 |
0.00 |
-0.89 |
-0.07 |
-0.96 |
| 84 | -0.34 |
-0.10 |
-0.43 |
-2.11 |
-0.70 |
0.00 |
-0.89 |
-0.07 |
-0.96 |
| 85 | -0.33 |
-0.10 |
-0.43 |
-2.12 |
-0.70 |
0.00 |
-0.89 |
-0.07 |
-0.96 |
| 86 | -0.33 |
-0.10 |
-0.43 |
-2.13 |
-0.70 |
0.00 |
-0.89 |
-0.07 |
-0.96 |
| 87 | -0.33 |
-0.10 |
-0.42 |
-2.14 |
-0.70 |
0.00 |
-0.89 |
-0.07 |
-0.96 |
| 88 | -0.32 |
-0.10 |
-0.42 |
-2.14 |
-0.70 |
0.00 |
-0.89 |
-0.07 |
-0.96 |
| 89 | -0.32 |
-0.10 |
-0.42 |
-2.15 |
-0.70 |
0.00 |
-0.89 |
-0.07 |
-0.96 |
| 90 | -0.32 |
-0.10 |
-0.42 |
-2.16 |
-0.70 |
0.00 |
-0.89 |
-0.07 |
-0.96 |
| 91 | -0.32 |
-0.10 |
-0.41 |
-2.17 |
-0.71 |
0.00 |
-0.89 |
-0.07 |
-0.96 |
| 92 | -0.31 |
-0.10 |
-0.41 |
-2.18 |
-0.71 |
0.00 |
-0.89 |
-0.07 |
-0.96 |
| 93 | -0.31 |
-0.10 |
-0.41 |
-2.19 |
-0.71 |
0.00 |
-0.89 |
-0.07 |
-0.96 |
| 94 | -0.31 |
-0.10 |
-0.40 |
-2.20 |
-0.71 |
0.00 |
-0.89 |
-0.07 |
-0.96 |
| 95 | -0.30 |
-0.10 |
-0.40 |
-2.21 |
-0.71 |
0.00 |
-0.88 |
-0.07 |
-0.96 |
| 96 | -0.30 |
-0.10 |
-0.40 |
-2.21 |
-0.71 |
0.00 |
-0.88 |
-0.07 |
-0.96 |
| 97 | -0.30 |
-0.10 |
-0.40 |
-2.22 |
-0.71 |
0.00 |
-0.88 |
-0.07 |
-0.96 |
| 98 | -0.29 |
-0.10 |
-0.39 |
-2.23 |
-0.71 |
0.00 |
-0.88 |
-0.07 |
-0.96 |
| 99 | -0.29 |
-0.10 |
-0.39 |
-2.24 |
-0.71 |
0.00 |
-0.88 |
-0.07 |
-0.96 |
| 100 | -0.29 |
-0.10 |
-0.39 |
-2.25 |
-0.71 |
0.00 |
-0.88 |
-0.07 |
-0.96 |
| 101 | -0.29 |
-0.10 |
-0.39 |
-2.25 |
-0.71 |
0.00 |
-0.88 |
-0.07 |
-0.96 |
| 102 | -0.28 |
-0.10 |
-0.38 |
-2.26 |
-0.71 |
0.00 |
-0.88 |
-0.07 |
-0.96 |
| 103 | -0.28 |
-0.10 |
-0.38 |
-2.27 |
-0.71 |
0.00 |
-0.88 |
-0.07 |
-0.96 |
| 104 | -0.28 |
-0.10 |
-0.38 |
-2.27 |
-0.71 |
0.00 |
-0.88 |
-0.07 |
-0.96 |
| 105 | -0.28 |
-0.10 |
-0.38 |
-2.28 |
-0.71 |
0.00 |
-0.88 |
-0.07 |
-0.96 |
| 106 | -0.27 |
-0.10 |
-0.38 |
-2.29 |
-0.71 |
0.00 |
-0.88 |
-0.07 |
-0.96 |
| 107 | -0.27 |
-0.10 |
-0.37 |
-2.30 |
-0.71 |
0.00 |
-0.88 |
-0.07 |
-0.95 |
| 108 | -0.27 |
-0.10 |
-0.37 |
-2.30 |
-0.71 |
0.00 |
-0.88 |
-0.07 |
-0.95 |
| 109 | -0.27 |
-0.10 |
-0.37 |
-2.31 |
-0.71 |
0.00 |
-0.88 |
-0.07 |
-0.95 |
| 110 | -0.26 |
-0.10 |
-0.37 |
-2.32 |
-0.71 |
0.00 |
-0.88 |
-0.07 |
-0.95 |
| 111 | -0.26 |
-0.10 |
-0.36 |
-2.32 |
-0.71 |
0.00 |
-0.88 |
-0.07 |
-0.95 |
| 112 | -0.26 |
-0.10 |
-0.36 |
-2.33 |
-0.71 |
0.00 |
-0.88 |
-0.07 |
-0.95 |
| 113 | -0.26 |
-0.10 |
-0.36 |
-2.34 |
-0.71 |
0.00 |
-0.88 |
-0.07 |
-0.95 |
| 114 | -0.26 |
-0.10 |
-0.36 |
-2.34 |
-0.71 |
0.00 |
-0.88 |
-0.07 |
-0.95 |
| 115 | -0.25 |
-0.10 |
-0.36 |
-2.35 |
-0.71 |
0.00 |
-0.88 |
-0.07 |
-0.95 |
| 116 | -0.25 |
-0.10 |
-0.35 |
-2.35 |
-0.71 |
0.00 |
-0.88 |
-0.07 |
-0.95 |
| 117 | -0.25 |
-0.10 |
-0.35 |
-2.36 |
-0.71 |
0.00 |
-0.88 |
-0.07 |
-0.95 |
| 118 | -0.25 |
-0.10 |
-0.35 |
-2.37 |
-0.71 |
0.00 |
-0.88 |
-0.07 |
-0.95 |
| 119 | -0.25 |
-0.10 |
-0.35 |
-2.37 |
-0.71 |
0.00 |
-0.88 |
-0.07 |
-0.95 |
| 120 | -0.24 |
-0.10 |
-0.35 |
-2.38 |
-0.71 |
0.00 |
-0.88 |
-0.07 |
-0.95 |
Figure 8. Contraction in Foreign Oil Supply
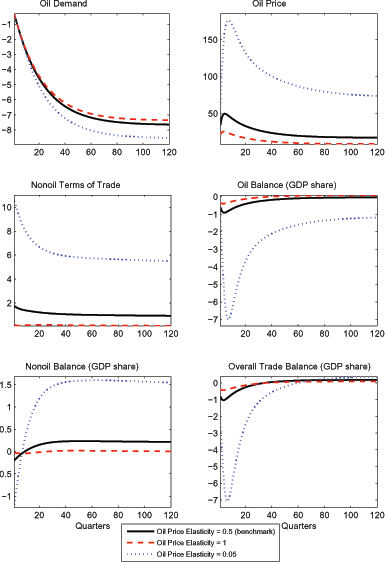
Data for Figure 8, Panel 1 - Contraction in Foreign Oil Supply
| Period | Oil demand: oil price elasticity = 0.5 (bench-mark) |
Oil price: oil price elasticity = 0.5 (bench-mark) |
Nonoil terms of trade: oil price elasticity = 0.5 (bench-mark) |
Oil balance: GDP share: oil price elasticity = 0.5 (bench-mark) |
Nonoil balance: GDP share: oil price elasticity = 0.5 (bench-mark) |
Overall trade balance: GDP share: oil price elasticity = 0.5 (bench-mark) |
Oil demand: oil price elasticity = 1 |
Oil price: oil price elasticity = 1 |
Nonoil terms of trade: oil price elasticity = 1 |
|---|---|---|---|---|---|---|---|---|---|
| 1 | -0.32 |
34.21 |
1.73 |
-0.60 |
-0.20 |
-0.80 |
-0.32 |
21.25 |
0.17 |
| 2 | -0.63 |
44.22 |
1.67 |
-0.81 |
-0.17 |
-0.98 |
-0.63 |
24.45 |
0.12 |
| 3 | -0.94 |
48.36 |
1.60 |
-0.89 |
-0.14 |
-1.03 |
-0.93 |
25.30 |
0.11 |
| 4 | -1.23 |
49.54 |
1.54 |
-0.91 |
-0.11 |
-1.02 |
-1.22 |
25.18 |
0.10 |
| 5 | -1.52 |
49.25 |
1.50 |
-0.89 |
-0.08 |
-0.97 |
-1.50 |
24.66 |
0.10 |
| 6 | -1.79 |
48.26 |
1.47 |
-0.85 |
-0.06 |
-0.91 |
-1.76 |
24.00 |
0.11 |
| 7 | -2.05 |
46.98 |
1.44 |
-0.81 |
-0.04 |
-0.85 |
-2.01 |
23.31 |
0.11 |
| 8 | -2.30 |
45.59 |
1.41 |
-0.77 |
-0.02 |
-0.78 |
-2.25 |
22.62 |
0.12 |
| 9 | -2.54 |
44.20 |
1.39 |
-0.73 |
0.00 |
-0.72 |
-2.48 |
21.96 |
0.13 |
| 10 | -2.77 |
42.85 |
1.37 |
-0.69 |
0.02 |
-0.66 |
-2.70 |
21.32 |
0.13 |
| 11 | -2.99 |
41.56 |
1.35 |
-0.65 |
0.04 |
-0.61 |
-2.91 |
20.72 |
0.14 |
| 12 | -3.20 |
40.34 |
1.33 |
-0.61 |
0.05 |
-0.56 |
-3.11 |
20.15 |
0.14 |
| 13 | -3.40 |
39.19 |
1.31 |
-0.58 |
0.07 |
-0.51 |
-3.30 |
19.60 |
0.15 |
| 14 | -3.59 |
38.11 |
1.29 |
-0.55 |
0.08 |
-0.47 |
-3.49 |
19.08 |
0.15 |
| 15 | -3.77 |
37.09 |
1.28 |
-0.52 |
0.10 |
-0.43 |
-3.66 |
18.59 |
0.16 |
| 16 | -3.94 |
36.13 |
1.26 |
-0.50 |
0.11 |
-0.39 |
-3.83 |
18.12 |
0.16 |
| 17 | -4.11 |
35.23 |
1.25 |
-0.47 |
0.12 |
-0.35 |
-3.99 |
17.68 |
0.16 |
| 18 | -4.27 |
34.37 |
1.23 |
-0.45 |
0.13 |
-0.32 |
-4.14 |
17.25 |
0.16 |
| 19 | -4.42 |
33.57 |
1.22 |
-0.43 |
0.14 |
-0.29 |
-4.28 |
16.85 |
0.16 |
| 20 | -4.57 |
32.80 |
1.21 |
-0.41 |
0.15 |
-0.26 |
-4.42 |
16.46 |
0.17 |
| 21 | -4.71 |
32.08 |
1.20 |
-0.39 |
0.16 |
-0.23 |
-4.56 |
16.09 |
0.17 |
| 22 | -4.84 |
31.39 |
1.18 |
-0.37 |
0.17 |
-0.20 |
-4.68 |
15.74 |
0.17 |
| 23 | -4.97 |
30.74 |
1.17 |
-0.35 |
0.17 |
-0.18 |
-4.81 |
15.41 |
0.17 |
| 24 | -5.09 |
30.12 |
1.16 |
-0.34 |
0.18 |
-0.16 |
-4.92 |
15.09 |
0.16 |
| 25 | -5.20 |
29.53 |
1.15 |
-0.32 |
0.19 |
-0.14 |
-5.03 |
14.78 |
0.16 |
| 26 | -5.31 |
28.97 |
1.14 |
-0.31 |
0.19 |
-0.12 |
-5.14 |
14.49 |
0.16 |
| 27 | -5.42 |
28.44 |
1.13 |
-0.30 |
0.20 |
-0.10 |
-5.24 |
14.22 |
0.16 |
| 28 | -5.52 |
27.93 |
1.12 |
-0.28 |
0.20 |
-0.08 |
-5.34 |
13.95 |
0.16 |
| 29 | -5.62 |
27.45 |
1.12 |
-0.27 |
0.20 |
-0.07 |
-5.43 |
13.70 |
0.16 |
| 30 | -5.71 |
26.99 |
1.11 |
-0.26 |
0.21 |
-0.05 |
-5.52 |
13.46 |
0.16 |
| 31 | -5.80 |
26.55 |
1.10 |
-0.25 |
0.21 |
-0.04 |
-5.60 |
13.23 |
0.15 |
| 32 | -5.88 |
26.13 |
1.09 |
-0.24 |
0.21 |
-0.02 |
-5.68 |
13.01 |
0.15 |
| 33 | -5.96 |
25.73 |
1.09 |
-0.23 |
0.22 |
-0.01 |
-5.76 |
12.80 |
0.15 |
| 34 | -6.04 |
25.34 |
1.08 |
-0.22 |
0.22 |
0.00 |
-5.83 |
12.60 |
0.15 |
| 35 | -6.11 |
24.98 |
1.08 |
-0.21 |
0.22 |
0.01 |
-5.91 |
12.41 |
0.15 |
| 36 | -6.18 |
24.63 |
1.07 |
-0.20 |
0.22 |
0.02 |
-5.97 |
12.22 |
0.15 |
| 37 | -6.25 |
24.29 |
1.06 |
-0.20 |
0.23 |
0.03 |
-6.04 |
12.05 |
0.14 |
| 38 | -6.31 |
23.97 |
1.06 |
-0.19 |
0.23 |
0.04 |
-6.10 |
11.88 |
0.14 |
| 39 | -6.37 |
23.67 |
1.05 |
-0.18 |
0.23 |
0.05 |
-6.16 |
11.72 |
0.14 |
| 40 | -6.43 |
23.37 |
1.05 |
-0.17 |
0.23 |
0.06 |
-6.21 |
11.57 |
0.14 |
| 41 | -6.49 |
23.09 |
1.05 |
-0.17 |
0.23 |
0.06 |
-6.27 |
11.42 |
0.14 |
| 42 | -6.54 |
22.82 |
1.04 |
-0.16 |
0.23 |
0.07 |
-6.32 |
11.28 |
0.14 |
| 43 | -6.59 |
22.57 |
1.04 |
-0.15 |
0.23 |
0.08 |
-6.37 |
11.15 |
0.13 |
| 44 | -6.64 |
22.32 |
1.03 |
-0.15 |
0.23 |
0.08 |
-6.41 |
11.02 |
0.13 |
| 45 | -6.69 |
22.08 |
1.03 |
-0.14 |
0.23 |
0.09 |
-6.46 |
10.90 |
0.13 |
| 46 | -6.73 |
21.86 |
1.03 |
-0.14 |
0.23 |
0.09 |
-6.50 |
10.79 |
0.13 |
| 47 | -6.77 |
21.64 |
1.02 |
-0.13 |
0.23 |
0.10 |
-6.54 |
10.68 |
0.13 |
| 48 | -6.81 |
21.44 |
1.02 |
-0.13 |
0.23 |
0.10 |
-6.58 |
10.57 |
0.13 |
| 49 | -6.85 |
21.24 |
1.02 |
-0.12 |
0.23 |
0.11 |
-6.62 |
10.47 |
0.13 |
| 50 | -6.89 |
21.05 |
1.01 |
-0.12 |
0.23 |
0.11 |
-6.65 |
10.37 |
0.12 |
| 51 | -6.93 |
20.87 |
1.01 |
-0.12 |
0.23 |
0.12 |
-6.68 |
10.28 |
0.12 |
| 52 | -6.96 |
20.69 |
1.01 |
-0.11 |
0.23 |
0.12 |
-6.72 |
10.19 |
0.12 |
| 53 | -6.99 |
20.53 |
1.01 |
-0.11 |
0.23 |
0.13 |
-6.75 |
10.11 |
0.12 |
| 54 | -7.02 |
20.37 |
1.00 |
-0.11 |
0.23 |
0.13 |
-6.78 |
10.02 |
0.12 |
| 55 | -7.05 |
20.21 |
1.00 |
-0.10 |
0.23 |
0.13 |
-6.80 |
9.95 |
0.12 |
| 56 | -7.08 |
20.07 |
1.00 |
-0.10 |
0.23 |
0.13 |
-6.83 |
9.87 |
0.12 |
| 57 | -7.10 |
19.93 |
1.00 |
-0.10 |
0.23 |
0.14 |
-6.86 |
9.80 |
0.12 |
| 58 | -7.13 |
19.79 |
1.00 |
-0.09 |
0.23 |
0.14 |
-6.88 |
9.74 |
0.12 |
| 59 | -7.15 |
19.66 |
0.99 |
-0.09 |
0.23 |
0.14 |
-6.90 |
9.67 |
0.12 |
| 60 | -7.18 |
19.54 |
0.99 |
-0.09 |
0.23 |
0.15 |
-6.93 |
9.61 |
0.11 |
| 61 | -7.20 |
19.42 |
0.99 |
-0.08 |
0.23 |
0.15 |
-6.95 |
9.55 |
0.11 |
| 62 | -7.22 |
19.31 |
0.99 |
-0.08 |
0.23 |
0.15 |
-6.97 |
9.49 |
0.11 |
| 63 | -7.24 |
19.20 |
0.99 |
-0.08 |
0.23 |
0.15 |
-6.99 |
9.44 |
0.11 |
| 64 | -7.26 |
19.10 |
0.99 |
-0.08 |
0.23 |
0.15 |
-7.00 |
9.39 |
0.11 |
| 65 | -7.28 |
19.00 |
0.98 |
-0.08 |
0.23 |
0.16 |
-7.02 |
9.34 |
0.11 |
| 66 | -7.30 |
18.90 |
0.98 |
-0.07 |
0.23 |
0.16 |
-7.04 |
9.29 |
0.11 |
| 67 | -7.31 |
18.81 |
0.98 |
-0.07 |
0.23 |
0.16 |
-7.05 |
9.25 |
0.11 |
| 68 | -7.33 |
18.73 |
0.98 |
-0.07 |
0.23 |
0.16 |
-7.07 |
9.21 |
0.11 |
| 69 | -7.35 |
18.64 |
0.98 |
-0.07 |
0.23 |
0.16 |
-7.08 |
9.16 |
0.11 |
| 70 | -7.36 |
18.56 |
0.98 |
-0.07 |
0.23 |
0.16 |
-7.10 |
9.12 |
0.11 |
| 71 | -7.37 |
18.49 |
0.97 |
-0.06 |
0.23 |
0.17 |
-7.11 |
9.09 |
0.11 |
| 72 | -7.39 |
18.41 |
0.97 |
-0.06 |
0.23 |
0.17 |
-7.12 |
9.05 |
0.11 |
| 73 | -7.40 |
18.34 |
0.97 |
-0.06 |
0.23 |
0.17 |
-7.13 |
9.02 |
0.11 |
| 74 | -7.41 |
18.27 |
0.97 |
-0.06 |
0.23 |
0.17 |
-7.15 |
8.98 |
0.10 |
| 75 | -7.42 |
18.21 |
0.97 |
-0.06 |
0.23 |
0.17 |
-7.16 |
8.95 |
0.10 |
| 76 | -7.43 |
18.15 |
0.97 |
-0.06 |
0.23 |
0.17 |
-7.17 |
8.92 |
0.10 |
| 77 | -7.45 |
18.09 |
0.97 |
-0.06 |
0.23 |
0.17 |
-7.18 |
8.89 |
0.10 |
| 78 | -7.46 |
18.03 |
0.97 |
-0.05 |
0.23 |
0.17 |
-7.19 |
8.87 |
0.10 |
| 79 | -7.47 |
17.98 |
0.96 |
-0.05 |
0.23 |
0.17 |
-7.20 |
8.84 |
0.10 |
| 80 | -7.47 |
17.93 |
0.96 |
-0.05 |
0.23 |
0.17 |
-7.20 |
8.82 |
0.10 |
| 81 | -7.48 |
17.88 |
0.96 |
-0.05 |
0.23 |
0.18 |
-7.21 |
8.79 |
0.10 |
| 82 | -7.49 |
17.83 |
0.96 |
-0.05 |
0.23 |
0.18 |
-7.22 |
8.77 |
0.10 |
| 83 | -7.50 |
17.78 |
0.96 |
-0.05 |
0.23 |
0.18 |
-7.23 |
8.75 |
0.10 |
| 84 | -7.51 |
17.74 |
0.96 |
-0.05 |
0.23 |
0.18 |
-7.23 |
8.73 |
0.10 |
| 85 | -7.51 |
17.70 |
0.96 |
-0.05 |
0.22 |
0.18 |
-7.24 |
8.71 |
0.10 |
| 86 | -7.52 |
17.66 |
0.96 |
-0.05 |
0.22 |
0.18 |
-7.25 |
8.69 |
0.10 |
| 87 | -7.53 |
17.62 |
0.95 |
-0.05 |
0.22 |
0.18 |
-7.25 |
8.67 |
0.10 |
| 88 | -7.53 |
17.58 |
0.95 |
-0.04 |
0.22 |
0.18 |
-7.26 |
8.65 |
0.10 |
| 89 | -7.54 |
17.55 |
0.95 |
-0.04 |
0.22 |
0.18 |
-7.26 |
8.63 |
0.10 |
| 90 | -7.55 |
17.52 |
0.95 |
-0.04 |
0.22 |
0.18 |
-7.27 |
8.62 |
0.10 |
| 91 | -7.55 |
17.48 |
0.95 |
-0.04 |
0.22 |
0.18 |
-7.27 |
8.60 |
0.09 |
| 92 | -7.56 |
17.45 |
0.95 |
-0.04 |
0.22 |
0.18 |
-7.28 |
8.59 |
0.09 |
| 93 | -7.56 |
17.42 |
0.95 |
-0.04 |
0.22 |
0.18 |
-7.28 |
8.57 |
0.09 |
| 94 | -7.57 |
17.40 |
0.95 |
-0.04 |
0.22 |
0.18 |
-7.29 |
8.56 |
0.09 |
| 95 | -7.57 |
17.37 |
0.94 |
-0.04 |
0.22 |
0.18 |
-7.29 |
8.55 |
0.09 |
| 96 | -7.58 |
17.34 |
0.94 |
-0.04 |
0.22 |
0.18 |
-7.30 |
8.54 |
0.09 |
| 97 | -7.58 |
17.32 |
0.94 |
-0.04 |
0.22 |
0.18 |
-7.30 |
8.52 |
0.09 |
| 98 | -7.58 |
17.30 |
0.94 |
-0.04 |
0.22 |
0.18 |
-7.30 |
8.51 |
0.09 |
| 99 | -7.59 |
17.27 |
0.94 |
-0.04 |
0.22 |
0.18 |
-7.31 |
8.50 |
0.09 |
| 100 | -7.59 |
17.25 |
0.94 |
-0.04 |
0.22 |
0.18 |
-7.31 |
8.49 |
0.09 |
| 101 | -7.60 |
17.23 |
0.94 |
-0.04 |
0.22 |
0.18 |
-7.31 |
8.48 |
0.09 |
| 102 | -7.60 |
17.21 |
0.94 |
-0.04 |
0.22 |
0.18 |
-7.32 |
8.47 |
0.09 |
| 103 | -7.60 |
17.19 |
0.94 |
-0.04 |
0.22 |
0.18 |
-7.32 |
8.46 |
0.09 |
| 104 | -7.61 |
17.17 |
0.93 |
-0.04 |
0.22 |
0.18 |
-7.32 |
8.46 |
0.09 |
| 105 | -7.61 |
17.16 |
0.93 |
-0.04 |
0.22 |
0.18 |
-7.32 |
8.45 |
0.09 |
| 106 | -7.61 |
17.14 |
0.93 |
-0.04 |
0.22 |
0.18 |
-7.33 |
8.44 |
0.09 |
| 107 | -7.61 |
17.12 |
0.93 |
-0.04 |
0.22 |
0.18 |
-7.33 |
8.43 |
0.09 |
| 108 | -7.62 |
17.11 |
0.93 |
-0.04 |
0.22 |
0.18 |
-7.33 |
8.43 |
0.09 |
| 109 | -7.62 |
17.09 |
0.93 |
-0.03 |
0.22 |
0.18 |
-7.33 |
8.42 |
0.08 |
| 110 | -7.62 |
17.08 |
0.93 |
-0.03 |
0.22 |
0.18 |
-7.33 |
8.41 |
0.08 |
| 111 | -7.62 |
17.07 |
0.93 |
-0.03 |
0.22 |
0.18 |
-7.33 |
8.41 |
0.08 |
| 112 | -7.62 |
17.05 |
0.93 |
-0.03 |
0.22 |
0.18 |
-7.34 |
8.40 |
0.08 |
| 113 | -7.63 |
17.04 |
0.93 |
-0.03 |
0.22 |
0.18 |
-7.34 |
8.39 |
0.08 |
| 114 | -7.63 |
17.03 |
0.92 |
-0.03 |
0.22 |
0.18 |
-7.34 |
8.39 |
0.08 |
| 115 | -7.63 |
17.02 |
0.92 |
-0.03 |
0.22 |
0.18 |
-7.34 |
8.38 |
0.08 |
| 116 | -7.63 |
17.01 |
0.92 |
-0.03 |
0.22 |
0.18 |
-7.34 |
8.38 |
0.08 |
| 117 | -7.63 |
17.00 |
0.92 |
-0.03 |
0.22 |
0.18 |
-7.34 |
8.37 |
0.08 |
| 118 | -7.64 |
16.99 |
0.92 |
-0.03 |
0.21 |
0.18 |
-7.34 |
8.37 |
0.08 |
| 119 | -7.64 |
16.98 |
0.92 |
-0.03 |
0.21 |
0.18 |
-7.35 |
8.36 |
0.08 |
| 120 | -7.64 |
16.97 |
0.92 |
-0.03 |
0.21 |
0.18 |
-7.35 |
8.36 |
0.08 |
Data for Figure 8, Panel 2 - Contraction in Foreign Oil Supply
| Period | Oil balance: GDP share: oil price elasticity = 1 |
Nonoil balance: GDP share: oil price elasticity = 1 |
Overall trade balance:GDP share: oil price elasticity = 1 |
Oil demand: oil price elasticity = 0.05 |
Oil price: oil price elasticity = 0.05 |
Nonoil terms of trade: oil price elasticity = 0.05 |
Oil balance: GDP share: oil price elasticity = 0.05 |
Nonoil balance: GDP share: oil price elasticity = 0.05 |
Overall trade balance: GDP share: oil price elasticity = 0.05 |
|---|---|---|---|---|---|---|---|---|---|
| 1 | -0.34 |
-0.03 |
-0.37 |
-0.33 |
59.31 |
10.49 |
-1.21 |
-1.19 |
-2.40 |
| 2 | -0.39 |
-0.03 |
-0.43 |
-0.63 |
107.54 |
10.24 |
-2.87 |
-0.98 |
-3.85 |
| 3 | -0.40 |
-0.03 |
-0.43 |
-0.94 |
138.83 |
9.87 |
-4.45 |
-0.76 |
-5.21 |
| 4 | -0.39 |
-0.04 |
-0.42 |
-1.24 |
158.27 |
9.50 |
-5.69 |
-0.55 |
-6.24 |
| 5 | -0.37 |
-0.04 |
-0.40 |
-1.54 |
169.48 |
9.15 |
-6.50 |
-0.36 |
-6.86 |
| 6 | -0.34 |
-0.04 |
-0.38 |
-1.84 |
175.04 |
8.85 |
-6.92 |
-0.18 |
-7.09 |
| 7 | -0.32 |
-0.04 |
-0.36 |
-2.13 |
176.79 |
8.58 |
-7.02 |
-0.01 |
-7.03 |
| 8 | -0.30 |
-0.04 |
-0.34 |
-2.42 |
176.01 |
8.33 |
-6.91 |
0.14 |
-6.77 |
| 9 | -0.28 |
-0.04 |
-0.32 |
-2.69 |
173.61 |
8.11 |
-6.67 |
0.28 |
-6.39 |
| 10 | -0.26 |
-0.04 |
-0.30 |
-2.96 |
170.22 |
7.92 |
-6.36 |
0.41 |
-5.95 |
| 11 | -0.24 |
-0.04 |
-0.28 |
-3.22 |
166.28 |
7.74 |
-6.02 |
0.52 |
-5.49 |
| 12 | -0.23 |
-0.04 |
-0.26 |
-3.46 |
162.08 |
7.58 |
-5.67 |
0.63 |
-5.05 |
| 13 | -0.21 |
-0.03 |
-0.25 |
-3.70 |
157.82 |
7.43 |
-5.34 |
0.72 |
-4.62 |
| 14 | -0.20 |
-0.03 |
-0.23 |
-3.93 |
153.62 |
7.29 |
-5.03 |
0.81 |
-4.22 |
| 15 | -0.18 |
-0.03 |
-0.21 |
-4.14 |
149.58 |
7.17 |
-4.75 |
0.89 |
-3.86 |
| 16 | -0.17 |
-0.03 |
-0.19 |
-4.35 |
145.73 |
7.05 |
-4.49 |
0.96 |
-3.53 |
| 17 | -0.16 |
-0.02 |
-0.18 |
-4.55 |
142.09 |
6.95 |
-4.25 |
1.03 |
-3.23 |
| 18 | -0.14 |
-0.02 |
-0.16 |
-4.73 |
138.69 |
6.85 |
-4.04 |
1.08 |
-2.96 |
| 19 | -0.13 |
-0.02 |
-0.15 |
-4.91 |
135.50 |
6.77 |
-3.85 |
1.14 |
-2.71 |
| 20 | -0.12 |
-0.01 |
-0.14 |
-5.08 |
132.54 |
6.68 |
-3.68 |
1.19 |
-2.49 |
| 21 | -0.11 |
-0.01 |
-0.12 |
-5.25 |
129.79 |
6.61 |
-3.52 |
1.23 |
-2.29 |
| 22 | -0.10 |
-0.01 |
-0.11 |
-5.40 |
127.22 |
6.54 |
-3.38 |
1.27 |
-2.11 |
| 23 | -0.09 |
-0.01 |
-0.10 |
-5.55 |
124.84 |
6.48 |
-3.25 |
1.30 |
-1.95 |
| 24 | -0.08 |
0.00 |
-0.09 |
-5.69 |
122.62 |
6.42 |
-3.13 |
1.33 |
-1.80 |
| 25 | -0.08 |
0.00 |
-0.08 |
-5.83 |
120.55 |
6.37 |
-3.03 |
1.36 |
-1.67 |
| 26 | -0.07 |
0.00 |
-0.07 |
-5.96 |
118.62 |
6.32 |
-2.93 |
1.39 |
-1.54 |
| 27 | -0.06 |
0.00 |
-0.06 |
-6.08 |
116.80 |
6.27 |
-2.84 |
1.41 |
-1.43 |
| 28 | -0.05 |
0.00 |
-0.05 |
-6.19 |
115.11 |
6.23 |
-2.76 |
1.43 |
-1.33 |
| 29 | -0.05 |
0.01 |
-0.04 |
-6.30 |
113.51 |
6.19 |
-2.68 |
1.45 |
-1.24 |
| 30 | -0.04 |
0.01 |
-0.03 |
-6.41 |
112.00 |
6.16 |
-2.61 |
1.46 |
-1.15 |
| 31 | -0.03 |
0.01 |
-0.02 |
-6.51 |
110.58 |
6.12 |
-2.54 |
1.48 |
-1.07 |
| 32 | -0.03 |
0.01 |
-0.02 |
-6.61 |
109.23 |
6.10 |
-2.48 |
1.49 |
-0.99 |
| 33 | -0.02 |
0.01 |
-0.01 |
-6.70 |
107.95 |
6.07 |
-2.43 |
1.50 |
-0.92 |
| 34 | -0.02 |
0.01 |
0.00 |
-6.78 |
106.73 |
6.04 |
-2.37 |
1.51 |
-0.86 |
| 35 | -0.01 |
0.01 |
0.00 |
-6.86 |
105.57 |
6.02 |
-2.32 |
1.52 |
-0.80 |
| 36 | -0.01 |
0.01 |
0.01 |
-6.94 |
104.46 |
6.00 |
-2.27 |
1.53 |
-0.74 |
| 37 | 0.00 |
0.02 |
0.01 |
-7.02 |
103.40 |
5.98 |
-2.23 |
1.54 |
-0.69 |
| 38 | 0.00 |
0.02 |
0.02 |
-7.09 |
102.38 |
5.96 |
-2.18 |
1.54 |
-0.64 |
| 39 | 0.01 |
0.02 |
0.02 |
-7.16 |
101.40 |
5.94 |
-2.14 |
1.55 |
-0.59 |
| 40 | 0.01 |
0.02 |
0.03 |
-7.22 |
100.46 |
5.93 |
-2.11 |
1.56 |
-0.55 |
| 41 | 0.01 |
0.02 |
0.03 |
-7.28 |
99.55 |
5.91 |
-2.07 |
1.56 |
-0.51 |
| 42 | 0.02 |
0.02 |
0.03 |
-7.34 |
98.68 |
5.90 |
-2.03 |
1.57 |
-0.47 |
| 43 | 0.02 |
0.02 |
0.04 |
-7.40 |
97.83 |
5.88 |
-2.00 |
1.57 |
-0.43 |
| 44 | 0.02 |
0.02 |
0.04 |
-7.45 |
97.02 |
5.87 |
-1.97 |
1.57 |
-0.39 |
| 45 | 0.03 |
0.02 |
0.04 |
-7.50 |
96.23 |
5.86 |
-1.94 |
1.58 |
-0.36 |
| 46 | 0.03 |
0.02 |
0.05 |
-7.55 |
95.46 |
5.85 |
-1.91 |
1.58 |
-0.33 |
| 47 | 0.03 |
0.02 |
0.05 |
-7.59 |
94.72 |
5.84 |
-1.88 |
1.58 |
-0.30 |
| 48 | 0.03 |
0.02 |
0.05 |
-7.64 |
94.00 |
5.83 |
-1.85 |
1.58 |
-0.27 |
| 49 | 0.04 |
0.02 |
0.06 |
-7.68 |
93.30 |
5.82 |
-1.83 |
1.59 |
-0.24 |
| 50 | 0.04 |
0.02 |
0.06 |
-7.72 |
92.63 |
5.81 |
-1.80 |
1.59 |
-0.21 |
| 51 | 0.04 |
0.02 |
0.06 |
-7.76 |
91.97 |
5.80 |
-1.78 |
1.59 |
-0.19 |
| 52 | 0.04 |
0.02 |
0.06 |
-7.79 |
91.33 |
5.80 |
-1.75 |
1.59 |
-0.16 |
| 53 | 0.05 |
0.02 |
0.06 |
-7.83 |
90.72 |
5.79 |
-1.73 |
1.59 |
-0.14 |
| 54 | 0.05 |
0.02 |
0.07 |
-7.86 |
90.11 |
5.78 |
-1.71 |
1.59 |
-0.11 |
| 55 | 0.05 |
0.02 |
0.07 |
-7.89 |
89.53 |
5.77 |
-1.69 |
1.60 |
-0.09 |
| 56 | 0.05 |
0.02 |
0.07 |
-7.92 |
88.96 |
5.77 |
-1.67 |
1.60 |
-0.07 |
| 57 | 0.05 |
0.02 |
0.07 |
-7.95 |
88.41 |
5.76 |
-1.65 |
1.60 |
-0.05 |
| 58 | 0.06 |
0.02 |
0.07 |
-7.98 |
87.88 |
5.75 |
-1.63 |
1.60 |
-0.03 |
| 59 | 0.06 |
0.02 |
0.07 |
-8.00 |
87.36 |
5.75 |
-1.61 |
1.60 |
-0.01 |
| 60 | 0.06 |
0.02 |
0.08 |
-8.03 |
86.86 |
5.74 |
-1.59 |
1.60 |
0.00 |
| 61 | 0.06 |
0.02 |
0.08 |
-8.05 |
86.37 |
5.73 |
-1.58 |
1.60 |
0.02 |
| 62 | 0.06 |
0.02 |
0.08 |
-8.07 |
85.89 |
5.73 |
-1.56 |
1.60 |
0.04 |
| 63 | 0.06 |
0.02 |
0.08 |
-8.10 |
85.43 |
5.72 |
-1.55 |
1.60 |
0.05 |
| 64 | 0.06 |
0.02 |
0.08 |
-8.12 |
84.98 |
5.72 |
-1.53 |
1.60 |
0.07 |
| 65 | 0.07 |
0.02 |
0.08 |
-8.14 |
84.55 |
5.71 |
-1.52 |
1.60 |
0.08 |
| 66 | 0.07 |
0.02 |
0.08 |
-8.16 |
84.13 |
5.70 |
-1.50 |
1.60 |
0.10 |
| 67 | 0.07 |
0.02 |
0.08 |
-8.17 |
83.72 |
5.70 |
-1.49 |
1.60 |
0.11 |
| 68 | 0.07 |
0.01 |
0.08 |
-8.19 |
83.32 |
5.69 |
-1.48 |
1.60 |
0.12 |
| 69 | 0.07 |
0.01 |
0.08 |
-8.21 |
82.94 |
5.69 |
-1.46 |
1.60 |
0.13 |
| 70 | 0.07 |
0.01 |
0.08 |
-8.22 |
82.57 |
5.68 |
-1.45 |
1.60 |
0.14 |
| 71 | 0.07 |
0.01 |
0.09 |
-8.24 |
82.20 |
5.68 |
-1.44 |
1.60 |
0.16 |
| 72 | 0.07 |
0.01 |
0.09 |
-8.25 |
81.85 |
5.67 |
-1.43 |
1.60 |
0.17 |
| 73 | 0.07 |
0.01 |
0.09 |
-8.27 |
81.52 |
5.67 |
-1.42 |
1.60 |
0.18 |
| 74 | 0.07 |
0.01 |
0.09 |
-8.28 |
81.19 |
5.66 |
-1.41 |
1.59 |
0.19 |
| 75 | 0.07 |
0.01 |
0.09 |
-8.29 |
80.87 |
5.66 |
-1.40 |
1.59 |
0.20 |
| 76 | 0.08 |
0.01 |
0.09 |
-8.30 |
80.56 |
5.66 |
-1.39 |
1.59 |
0.20 |
| 77 | 0.08 |
0.01 |
0.09 |
-8.32 |
80.26 |
5.65 |
-1.38 |
1.59 |
0.21 |
| 78 | 0.08 |
0.01 |
0.09 |
-8.33 |
79.98 |
5.65 |
-1.37 |
1.59 |
0.22 |
| 79 | 0.08 |
0.01 |
0.09 |
-8.34 |
79.70 |
5.64 |
-1.36 |
1.59 |
0.23 |
| 80 | 0.08 |
0.01 |
0.09 |
-8.35 |
79.43 |
5.64 |
-1.35 |
1.59 |
0.24 |
| 81 | 0.08 |
0.01 |
0.09 |
-8.36 |
79.17 |
5.63 |
-1.34 |
1.59 |
0.24 |
| 82 | 0.08 |
0.01 |
0.09 |
-8.37 |
78.91 |
5.63 |
-1.34 |
1.59 |
0.25 |
| 83 | 0.08 |
0.01 |
0.09 |
-8.37 |
78.67 |
5.62 |
-1.33 |
1.59 |
0.26 |
| 84 | 0.08 |
0.01 |
0.09 |
-8.38 |
78.43 |
5.62 |
-1.32 |
1.59 |
0.26 |
| 85 | 0.08 |
0.01 |
0.09 |
-8.39 |
78.20 |
5.62 |
-1.32 |
1.58 |
0.27 |
| 86 | 0.08 |
0.01 |
0.09 |
-8.40 |
77.98 |
5.61 |
-1.31 |
1.58 |
0.27 |
| 87 | 0.08 |
0.01 |
0.09 |
-8.41 |
77.77 |
5.61 |
-1.30 |
1.58 |
0.28 |
| 88 | 0.08 |
0.01 |
0.09 |
-8.41 |
77.57 |
5.61 |
-1.30 |
1.58 |
0.29 |
| 89 | 0.08 |
0.01 |
0.09 |
-8.42 |
77.37 |
5.60 |
-1.29 |
1.58 |
0.29 |
| 90 | 0.08 |
0.01 |
0.09 |
-8.42 |
77.17 |
5.60 |
-1.28 |
1.58 |
0.29 |
| 91 | 0.08 |
0.01 |
0.09 |
-8.43 |
76.99 |
5.59 |
-1.28 |
1.58 |
0.30 |
| 92 | 0.08 |
0.01 |
0.09 |
-8.44 |
76.81 |
5.59 |
-1.27 |
1.58 |
0.30 |
| 93 | 0.08 |
0.01 |
0.09 |
-8.44 |
76.64 |
5.59 |
-1.27 |
1.58 |
0.31 |
| 94 | 0.08 |
0.01 |
0.09 |
-8.45 |
76.47 |
5.58 |
-1.26 |
1.57 |
0.31 |
| 95 | 0.08 |
0.01 |
0.09 |
-8.45 |
76.31 |
5.58 |
-1.26 |
1.57 |
0.31 |
| 96 | 0.08 |
0.01 |
0.09 |
-8.46 |
76.15 |
5.58 |
-1.25 |
1.57 |
0.32 |
| 97 | 0.08 |
0.01 |
0.09 |
-8.46 |
76.00 |
5.57 |
-1.25 |
1.57 |
0.32 |
| 98 | 0.08 |
0.01 |
0.09 |
-8.47 |
75.86 |
5.57 |
-1.25 |
1.57 |
0.32 |
| 99 | 0.09 |
0.01 |
0.09 |
-8.47 |
75.72 |
5.57 |
-1.24 |
1.57 |
0.33 |
| 100 | 0.09 |
0.01 |
0.09 |
-8.47 |
75.59 |
5.56 |
-1.24 |
1.57 |
0.33 |
| 101 | 0.09 |
0.01 |
0.09 |
-8.48 |
75.46 |
5.56 |
-1.23 |
1.57 |
0.33 |
| 102 | 0.09 |
0.01 |
0.09 |
-8.48 |
75.33 |
5.56 |
-1.23 |
1.57 |
0.34 |
| 103 | 0.09 |
0.01 |
0.09 |
-8.48 |
75.21 |
5.55 |
-1.23 |
1.56 |
0.34 |
| 104 | 0.09 |
0.01 |
0.09 |
-8.49 |
75.09 |
5.55 |
-1.22 |
1.56 |
0.34 |
| 105 | 0.09 |
0.01 |
0.09 |
-8.49 |
74.98 |
5.55 |
-1.22 |
1.56 |
0.34 |
| 106 | 0.09 |
0.01 |
0.09 |
-8.49 |
74.87 |
5.54 |
-1.22 |
1.56 |
0.34 |
| 107 | 0.09 |
0.01 |
0.09 |
-8.49 |
74.77 |
5.54 |
-1.21 |
1.56 |
0.35 |
| 108 | 0.09 |
0.01 |
0.09 |
-8.50 |
74.67 |
5.54 |
-1.21 |
1.56 |
0.35 |
| 109 | 0.09 |
0.01 |
0.09 |
-8.50 |
74.57 |
5.53 |
-1.21 |
1.56 |
0.35 |
| 110 | 0.09 |
0.01 |
0.09 |
-8.50 |
74.48 |
5.53 |
-1.21 |
1.56 |
0.35 |
| 111 | 0.09 |
0.01 |
0.09 |
-8.50 |
74.39 |
5.53 |
-1.20 |
1.55 |
0.35 |
| 112 | 0.09 |
0.01 |
0.09 |
-8.51 |
74.30 |
5.52 |
-1.20 |
1.55 |
0.35 |
| 113 | 0.09 |
0.01 |
0.09 |
-8.51 |
74.22 |
5.52 |
-1.20 |
1.55 |
0.35 |
| 114 | 0.09 |
0.01 |
0.09 |
-8.51 |
74.14 |
5.52 |
-1.20 |
1.55 |
0.36 |
| 115 | 0.09 |
0.01 |
0.09 |
-8.51 |
74.06 |
5.51 |
-1.19 |
1.55 |
0.36 |
| 116 | 0.09 |
0.01 |
0.09 |
-8.51 |
73.99 |
5.51 |
-1.19 |
1.55 |
0.36 |
| 117 | 0.09 |
0.01 |
0.09 |
-8.51 |
73.92 |
5.51 |
-1.19 |
1.55 |
0.36 |
| 118 | 0.09 |
0.01 |
0.09 |
-8.52 |
73.85 |
5.51 |
-1.19 |
1.55 |
0.36 |
| 119 | 0.09 |
0.01 |
0.09 |
-8.52 |
73.78 |
5.50 |
-1.19 |
1.55 |
0.36 |
| 120 | 0.09 |
0.01 |
0.09 |
-8.52 |
73.72 |
5.50 |
-1.18 |
1.54 |
0.36 |
Figure 9. Comparing a Contraction in Foreign Oil Supply with an Expansion in Foreign Oil Demand
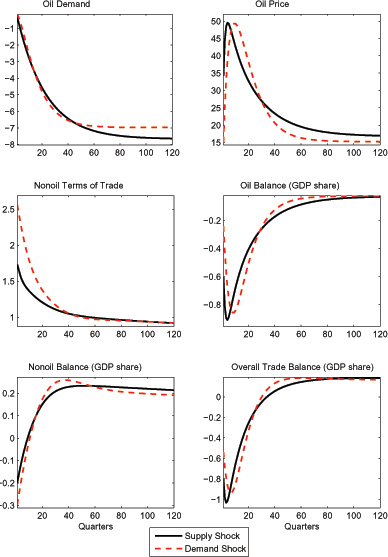
Data for Figure 9, Panel 1 - Comparing a Contraction in Foreign Oil Supply with an Expansion in Foreign Oil Demand
| Period | Oil price: supply shock |
Absorption: supply shock |
Nonoil terms of trade: supply shock |
Oil balance: GDP share: supply shock |
Nonoil balance: GDP share: supply shock |
Overall trade balance: GDP share: supply shock |
|---|---|---|---|---|---|---|
| 1 | 34.21 |
-0.18 |
1.73 |
-0.60 |
-0.20 |
-0.80 |
| 2 | 44.22 |
-0.28 |
1.67 |
-0.81 |
-0.17 |
-0.98 |
| 3 | 48.36 |
-0.35 |
1.60 |
-0.89 |
-0.14 |
-1.03 |
| 4 | 49.54 |
-0.40 |
1.54 |
-0.91 |
-0.11 |
-1.02 |
| 5 | 49.25 |
-0.44 |
1.50 |
-0.89 |
-0.08 |
-0.97 |
| 6 | 48.26 |
-0.48 |
1.47 |
-0.85 |
-0.06 |
-0.91 |
| 7 | 46.98 |
-0.52 |
1.44 |
-0.81 |
-0.04 |
-0.85 |
| 8 | 45.59 |
-0.55 |
1.41 |
-0.77 |
-0.02 |
-0.78 |
| 9 | 44.20 |
-0.58 |
1.39 |
-0.73 |
0.00 |
-0.72 |
| 10 | 42.85 |
-0.61 |
1.37 |
-0.69 |
0.02 |
-0.66 |
| 11 | 41.56 |
-0.63 |
1.35 |
-0.65 |
0.04 |
-0.61 |
| 12 | 40.34 |
-0.66 |
1.33 |
-0.61 |
0.05 |
-0.56 |
| 13 | 39.19 |
-0.69 |
1.31 |
-0.58 |
0.07 |
-0.51 |
| 14 | 38.11 |
-0.71 |
1.29 |
-0.55 |
0.08 |
-0.47 |
| 15 | 37.09 |
-0.73 |
1.28 |
-0.52 |
0.10 |
-0.43 |
| 16 | 36.13 |
-0.75 |
1.26 |
-0.50 |
0.11 |
-0.39 |
| 17 | 35.23 |
-0.77 |
1.25 |
-0.47 |
0.12 |
-0.35 |
| 18 | 34.37 |
-0.79 |
1.23 |
-0.45 |
0.13 |
-0.32 |
| 19 | 33.57 |
-0.81 |
1.22 |
-0.43 |
0.14 |
-0.29 |
| 20 | 32.80 |
-0.82 |
1.21 |
-0.41 |
0.15 |
-0.26 |
| 21 | 32.08 |
-0.84 |
1.20 |
-0.39 |
0.16 |
-0.23 |
| 22 | 31.39 |
-0.85 |
1.18 |
-0.37 |
0.17 |
-0.20 |
| 23 | 30.74 |
-0.87 |
1.17 |
-0.35 |
0.17 |
-0.18 |
| 24 | 30.12 |
-0.88 |
1.16 |
-0.34 |
0.18 |
-0.16 |
| 25 | 29.53 |
-0.89 |
1.15 |
-0.32 |
0.19 |
-0.14 |
| 26 | 28.97 |
-0.90 |
1.14 |
-0.31 |
0.19 |
-0.12 |
| 27 | 28.44 |
-0.91 |
1.13 |
-0.30 |
0.20 |
-0.10 |
| 28 | 27.93 |
-0.92 |
1.12 |
-0.28 |
0.20 |
-0.08 |
| 29 | 27.45 |
-0.93 |
1.12 |
-0.27 |
0.20 |
-0.07 |
| 30 | 26.99 |
-0.94 |
1.11 |
-0.26 |
0.21 |
-0.05 |
| 31 | 26.55 |
-0.94 |
1.10 |
-0.25 |
0.21 |
-0.04 |
| 32 | 26.13 |
-0.95 |
1.09 |
-0.24 |
0.21 |
-0.02 |
| 33 | 25.73 |
-0.96 |
1.09 |
-0.23 |
0.22 |
-0.01 |
| 34 | 25.34 |
-0.96 |
1.08 |
-0.22 |
0.22 |
0.00 |
| 35 | 24.98 |
-0.96 |
1.08 |
-0.21 |
0.22 |
0.01 |
| 36 | 24.63 |
-0.97 |
1.07 |
-0.20 |
0.22 |
0.02 |
| 37 | 24.29 |
-0.97 |
1.06 |
-0.20 |
0.23 |
0.03 |
| 38 | 23.97 |
-0.98 |
1.06 |
-0.19 |
0.23 |
0.04 |
| 39 | 23.67 |
-0.98 |
1.05 |
-0.18 |
0.23 |
0.05 |
| 40 | 23.37 |
-0.98 |
1.05 |
-0.17 |
0.23 |
0.06 |
| 41 | 23.09 |
-0.98 |
1.05 |
-0.17 |
0.23 |
0.06 |
| 42 | 22.82 |
-0.99 |
1.04 |
-0.16 |
0.23 |
0.07 |
| 43 | 22.57 |
-0.99 |
1.04 |
-0.15 |
0.23 |
0.08 |
| 44 | 22.32 |
-0.99 |
1.03 |
-0.15 |
0.23 |
0.08 |
| 45 | 22.08 |
-0.99 |
1.03 |
-0.14 |
0.23 |
0.09 |
| 46 | 21.86 |
-0.99 |
1.03 |
-0.14 |
0.23 |
0.09 |
| 47 | 21.64 |
-0.99 |
1.02 |
-0.13 |
0.23 |
0.10 |
| 48 | 21.44 |
-0.99 |
1.02 |
-0.13 |
0.23 |
0.10 |
| 49 | 21.24 |
-1.00 |
1.02 |
-0.12 |
0.23 |
0.11 |
| 50 | 21.05 |
-1.00 |
1.01 |
-0.12 |
0.23 |
0.11 |
| 51 | 20.87 |
-1.00 |
1.01 |
-0.12 |
0.23 |
0.12 |
| 52 | 20.69 |
-1.00 |
1.01 |
-0.11 |
0.23 |
0.12 |
| 53 | 20.53 |
-1.00 |
1.01 |
-0.11 |
0.23 |
0.13 |
| 54 | 20.37 |
-1.00 |
1.00 |
-0.11 |
0.23 |
0.13 |
| 55 | 20.21 |
-1.00 |
1.00 |
-0.10 |
0.23 |
0.13 |
| 56 | 20.07 |
-1.00 |
1.00 |
-0.10 |
0.23 |
0.13 |
| 57 | 19.93 |
-1.00 |
1.00 |
-0.10 |
0.23 |
0.14 |
| 58 | 19.79 |
-1.00 |
1.00 |
-0.09 |
0.23 |
0.14 |
| 59 | 19.66 |
-1.00 |
0.99 |
-0.09 |
0.23 |
0.14 |
| 60 | 19.54 |
-1.00 |
0.99 |
-0.09 |
0.23 |
0.15 |
| 61 | 19.42 |
-1.00 |
0.99 |
-0.08 |
0.23 |
0.15 |
| 62 | 19.31 |
-1.00 |
0.99 |
-0.08 |
0.23 |
0.15 |
| 63 | 19.20 |
-1.00 |
0.99 |
-0.08 |
0.23 |
0.15 |
| 64 | 19.10 |
-0.99 |
0.99 |
-0.08 |
0.23 |
0.15 |
| 65 | 19.00 |
-0.99 |
0.98 |
-0.08 |
0.23 |
0.16 |
| 66 | 18.90 |
-0.99 |
0.98 |
-0.07 |
0.23 |
0.16 |
| 67 | 18.81 |
-0.99 |
0.98 |
-0.07 |
0.23 |
0.16 |
| 68 | 18.73 |
-0.99 |
0.98 |
-0.07 |
0.23 |
0.16 |
| 69 | 18.64 |
-0.99 |
0.98 |
-0.07 |
0.23 |
0.16 |
| 70 | 18.56 |
-0.99 |
0.98 |
-0.07 |
0.23 |
0.16 |
| 71 | 18.49 |
-0.99 |
0.97 |
-0.06 |
0.23 |
0.17 |
| 72 | 18.41 |
-0.99 |
0.97 |
-0.06 |
0.23 |
0.17 |
| 73 | 18.34 |
-0.99 |
0.97 |
-0.06 |
0.23 |
0.17 |
| 74 | 18.27 |
-0.99 |
0.97 |
-0.06 |
0.23 |
0.17 |
| 75 | 18.21 |
-0.99 |
0.97 |
-0.06 |
0.23 |
0.17 |
| 76 | 18.15 |
-0.99 |
0.97 |
-0.06 |
0.23 |
0.17 |
| 77 | 18.09 |
-0.99 |
0.97 |
-0.06 |
0.23 |
0.17 |
| 78 | 18.03 |
-0.99 |
0.97 |
-0.05 |
0.23 |
0.17 |
| 79 | 17.98 |
-0.99 |
0.96 |
-0.05 |
0.23 |
0.17 |
| 80 | 17.93 |
-0.98 |
0.96 |
-0.05 |
0.23 |
0.17 |
| 81 | 17.88 |
-0.98 |
0.96 |
-0.05 |
0.23 |
0.18 |
| 82 | 17.83 |
-0.98 |
0.96 |
-0.05 |
0.23 |
0.18 |
| 83 | 17.78 |
-0.98 |
0.96 |
-0.05 |
0.23 |
0.18 |
| 84 | 17.74 |
-0.98 |
0.96 |
-0.05 |
0.23 |
0.18 |
| 85 | 17.70 |
-0.98 |
0.96 |
-0.05 |
0.22 |
0.18 |
| 86 | 17.66 |
-0.98 |
0.96 |
-0.05 |
0.22 |
0.18 |
| 87 | 17.62 |
-0.98 |
0.95 |
-0.05 |
0.22 |
0.18 |
| 88 | 17.58 |
-0.98 |
0.95 |
-0.04 |
0.22 |
0.18 |
| 89 | 17.55 |
-0.98 |
0.95 |
-0.04 |
0.22 |
0.18 |
| 90 | 17.52 |
-0.98 |
0.95 |
-0.04 |
0.22 |
0.18 |
| 91 | 17.48 |
-0.98 |
0.95 |
-0.04 |
0.22 |
0.18 |
| 92 | 17.45 |
-0.98 |
0.95 |
-0.04 |
0.22 |
0.18 |
| 93 | 17.42 |
-0.98 |
0.95 |
-0.04 |
0.22 |
0.18 |
| 94 | 17.40 |
-0.98 |
0.95 |
-0.04 |
0.22 |
0.18 |
| 95 | 17.37 |
-0.97 |
0.94 |
-0.04 |
0.22 |
0.18 |
| 96 | 17.34 |
-0.97 |
0.94 |
-0.04 |
0.22 |
0.18 |
| 97 | 17.32 |
-0.97 |
0.94 |
-0.04 |
0.22 |
0.18 |
| 98 | 17.30 |
-0.97 |
0.94 |
-0.04 |
0.22 |
0.18 |
| 99 | 17.27 |
-0.97 |
0.94 |
-0.04 |
0.22 |
0.18 |
| 100 | 17.25 |
-0.97 |
0.94 |
-0.04 |
0.22 |
0.18 |
| 101 | 17.23 |
-0.97 |
0.94 |
-0.04 |
0.22 |
0.18 |
| 102 | 17.21 |
-0.97 |
0.94 |
-0.04 |
0.22 |
0.18 |
| 103 | 17.19 |
-0.97 |
0.94 |
-0.04 |
0.22 |
0.18 |
| 104 | 17.17 |
-0.97 |
0.93 |
-0.04 |
0.22 |
0.18 |
| 105 | 17.16 |
-0.97 |
0.93 |
-0.04 |
0.22 |
0.18 |
| 106 | 17.14 |
-0.97 |
0.93 |
-0.04 |
0.22 |
0.18 |
| 107 | 17.12 |
-0.97 |
0.93 |
-0.04 |
0.22 |
0.18 |
| 108 | 17.11 |
-0.97 |
0.93 |
-0.04 |
0.22 |
0.18 |
| 109 | 17.09 |
-0.97 |
0.93 |
-0.03 |
0.22 |
0.18 |
| 110 | 17.08 |
-0.96 |
0.93 |
-0.03 |
0.22 |
0.18 |
| 111 | 17.07 |
-0.96 |
0.93 |
-0.03 |
0.22 |
0.18 |
| 112 | 17.05 |
-0.96 |
0.93 |
-0.03 |
0.22 |
0.18 |
| 113 | 17.04 |
-0.96 |
0.93 |
-0.03 |
0.22 |
0.18 |
| 114 | 17.03 |
-0.96 |
0.92 |
-0.03 |
0.22 |
0.18 |
| 115 | 17.02 |
-0.96 |
0.92 |
-0.03 |
0.22 |
0.18 |
| 116 | 17.01 |
-0.96 |
0.92 |
-0.03 |
0.22 |
0.18 |
| 117 | 17.00 |
-0.96 |
0.92 |
-0.03 |
0.22 |
0.18 |
| 118 | 16.99 |
-0.96 |
0.92 |
-0.03 |
0.21 |
0.18 |
| 119 | 16.98 |
-0.96 |
0.92 |
-0.03 |
0.21 |
0.18 |
| 120 | 16.97 |
-0.96 |
0.92 |
-0.03 |
0.21 |
0.18 |
Data for Figure 9, Panel 2 - Comparing a Contraction in Foreign Oil Supply with an Expansion in Foreign Oil Demand
| Period | Oil price: demand shock |
Absorption: demand shock |
Nonoil terms of trade: demand shock |
Oil balance: GDP share: demand shock |
Nonoil balance: GDP share: demand shock |
Overall trade balance: GDP share: demand shock |
|---|---|---|---|---|---|---|
| 1 | 15.09 |
-0.14 |
2.56 |
-0.24 |
-0.30 |
-0.54 |
| 2 | 24.93 |
-0.24 |
2.46 |
-0.42 |
-0.26 |
-0.68 |
| 3 | 32.52 |
-0.32 |
2.35 |
-0.56 |
-0.22 |
-0.78 |
| 4 | 38.26 |
-0.40 |
2.26 |
-0.67 |
-0.19 |
-0.86 |
| 5 | 42.49 |
-0.47 |
2.16 |
-0.75 |
-0.16 |
-0.91 |
| 6 | 45.49 |
-0.53 |
2.08 |
-0.81 |
-0.12 |
-0.93 |
| 7 | 47.49 |
-0.58 |
2.00 |
-0.84 |
-0.09 |
-0.94 |
| 8 | 48.69 |
-0.63 |
1.92 |
-0.86 |
-0.07 |
-0.92 |
| 9 | 49.25 |
-0.67 |
1.86 |
-0.86 |
-0.04 |
-0.89 |
| 10 | 49.29 |
-0.71 |
1.79 |
-0.84 |
-0.01 |
-0.86 |
| 11 | 48.93 |
-0.74 |
1.73 |
-0.82 |
0.01 |
-0.81 |
| 12 | 48.26 |
-0.77 |
1.68 |
-0.79 |
0.04 |
-0.76 |
| 13 | 47.35 |
-0.80 |
1.63 |
-0.76 |
0.06 |
-0.71 |
| 14 | 46.27 |
-0.83 |
1.59 |
-0.73 |
0.08 |
-0.65 |
| 15 | 45.05 |
-0.85 |
1.55 |
-0.69 |
0.10 |
-0.59 |
| 16 | 43.75 |
-0.87 |
1.51 |
-0.65 |
0.11 |
-0.54 |
| 17 | 42.40 |
-0.89 |
1.47 |
-0.61 |
0.13 |
-0.48 |
| 18 | 41.02 |
-0.91 |
1.44 |
-0.58 |
0.15 |
-0.43 |
| 19 | 39.64 |
-0.92 |
1.41 |
-0.54 |
0.16 |
-0.38 |
| 20 | 38.27 |
-0.94 |
1.38 |
-0.51 |
0.17 |
-0.33 |
| 21 | 36.92 |
-0.95 |
1.35 |
-0.47 |
0.18 |
-0.29 |
| 22 | 35.61 |
-0.96 |
1.33 |
-0.44 |
0.20 |
-0.25 |
| 23 | 34.34 |
-0.97 |
1.30 |
-0.41 |
0.20 |
-0.21 |
| 24 | 33.12 |
-0.98 |
1.28 |
-0.38 |
0.21 |
-0.17 |
| 25 | 31.95 |
-0.99 |
1.26 |
-0.36 |
0.22 |
-0.14 |
| 26 | 30.83 |
-0.99 |
1.24 |
-0.33 |
0.23 |
-0.10 |
| 27 | 29.77 |
-1.00 |
1.22 |
-0.31 |
0.23 |
-0.08 |
| 28 | 28.77 |
-1.00 |
1.20 |
-0.29 |
0.24 |
-0.05 |
| 29 | 27.82 |
-1.00 |
1.19 |
-0.27 |
0.24 |
-0.02 |
| 30 | 26.93 |
-1.01 |
1.17 |
-0.25 |
0.25 |
0.00 |
| 31 | 26.09 |
-1.01 |
1.15 |
-0.23 |
0.25 |
0.02 |
| 32 | 25.31 |
-1.01 |
1.14 |
-0.22 |
0.25 |
0.04 |
| 33 | 24.57 |
-1.01 |
1.13 |
-0.20 |
0.26 |
0.05 |
| 34 | 23.88 |
-1.01 |
1.12 |
-0.19 |
0.26 |
0.07 |
| 35 | 23.24 |
-1.01 |
1.10 |
-0.17 |
0.26 |
0.08 |
| 36 | 22.64 |
-1.01 |
1.09 |
-0.16 |
0.26 |
0.10 |
| 37 | 22.09 |
-1.01 |
1.08 |
-0.15 |
0.26 |
0.11 |
| 38 | 21.57 |
-1.01 |
1.07 |
-0.14 |
0.26 |
0.12 |
| 39 | 21.09 |
-1.01 |
1.06 |
-0.13 |
0.26 |
0.13 |
| 40 | 20.64 |
-1.01 |
1.05 |
-0.12 |
0.26 |
0.13 |
| 41 | 20.23 |
-1.00 |
1.05 |
-0.12 |
0.26 |
0.14 |
| 42 | 19.85 |
-1.00 |
1.04 |
-0.11 |
0.26 |
0.15 |
| 43 | 19.49 |
-1.00 |
1.03 |
-0.10 |
0.26 |
0.15 |
| 44 | 19.16 |
-1.00 |
1.03 |
-0.10 |
0.25 |
0.16 |
| 45 | 18.86 |
-0.99 |
1.02 |
-0.09 |
0.25 |
0.16 |
| 46 | 18.58 |
-0.99 |
1.02 |
-0.09 |
0.25 |
0.17 |
| 47 | 18.32 |
-0.99 |
1.01 |
-0.08 |
0.25 |
0.17 |
| 48 | 18.08 |
-0.99 |
1.01 |
-0.08 |
0.25 |
0.17 |
| 49 | 17.86 |
-0.98 |
1.00 |
-0.07 |
0.25 |
0.17 |
| 50 | 17.66 |
-0.98 |
1.00 |
-0.07 |
0.24 |
0.18 |
| 51 | 17.47 |
-0.98 |
0.99 |
-0.07 |
0.24 |
0.18 |
| 52 | 17.30 |
-0.97 |
0.99 |
-0.06 |
0.24 |
0.18 |
| 53 | 17.14 |
-0.97 |
0.99 |
-0.06 |
0.24 |
0.18 |
| 54 | 16.99 |
-0.97 |
0.98 |
-0.06 |
0.24 |
0.18 |
| 55 | 16.86 |
-0.97 |
0.98 |
-0.05 |
0.24 |
0.18 |
| 56 | 16.73 |
-0.96 |
0.98 |
-0.05 |
0.23 |
0.18 |
| 57 | 16.62 |
-0.96 |
0.98 |
-0.05 |
0.23 |
0.18 |
| 58 | 16.51 |
-0.96 |
0.98 |
-0.05 |
0.23 |
0.18 |
| 59 | 16.42 |
-0.96 |
0.97 |
-0.05 |
0.23 |
0.18 |
| 60 | 16.33 |
-0.95 |
0.97 |
-0.04 |
0.23 |
0.18 |
| 61 | 16.24 |
-0.95 |
0.97 |
-0.04 |
0.23 |
0.18 |
| 62 | 16.17 |
-0.95 |
0.97 |
-0.04 |
0.23 |
0.18 |
| 63 | 16.10 |
-0.95 |
0.97 |
-0.04 |
0.22 |
0.18 |
| 64 | 16.03 |
-0.94 |
0.97 |
-0.04 |
0.22 |
0.18 |
| 65 | 15.97 |
-0.94 |
0.97 |
-0.04 |
0.22 |
0.18 |
| 66 | 15.92 |
-0.94 |
0.96 |
-0.04 |
0.22 |
0.18 |
| 67 | 15.87 |
-0.94 |
0.96 |
-0.04 |
0.22 |
0.18 |
| 68 | 15.82 |
-0.94 |
0.96 |
-0.04 |
0.22 |
0.18 |
| 69 | 15.78 |
-0.94 |
0.96 |
-0.04 |
0.22 |
0.18 |
| 70 | 15.74 |
-0.93 |
0.96 |
-0.03 |
0.22 |
0.18 |
| 71 | 15.70 |
-0.93 |
0.96 |
-0.03 |
0.21 |
0.18 |
| 72 | 15.67 |
-0.93 |
0.96 |
-0.03 |
0.21 |
0.18 |
| 73 | 15.64 |
-0.93 |
0.96 |
-0.03 |
0.21 |
0.18 |
| 74 | 15.61 |
-0.93 |
0.96 |
-0.03 |
0.21 |
0.18 |
| 75 | 15.58 |
-0.93 |
0.96 |
-0.03 |
0.21 |
0.18 |
| 76 | 15.55 |
-0.92 |
0.96 |
-0.03 |
0.21 |
0.18 |
| 77 | 15.53 |
-0.92 |
0.96 |
-0.03 |
0.21 |
0.18 |
| 78 | 15.51 |
-0.92 |
0.95 |
-0.03 |
0.21 |
0.18 |
| 79 | 15.49 |
-0.92 |
0.95 |
-0.03 |
0.21 |
0.18 |
| 80 | 15.47 |
-0.92 |
0.95 |
-0.03 |
0.21 |
0.18 |
| 81 | 15.46 |
-0.92 |
0.95 |
-0.03 |
0.21 |
0.18 |
| 82 | 15.44 |
-0.92 |
0.95 |
-0.03 |
0.21 |
0.18 |
| 83 | 15.43 |
-0.92 |
0.95 |
-0.03 |
0.21 |
0.18 |
| 84 | 15.41 |
-0.92 |
0.95 |
-0.03 |
0.20 |
0.18 |
| 85 | 15.40 |
-0.91 |
0.95 |
-0.03 |
0.20 |
0.18 |
| 86 | 15.39 |
-0.91 |
0.95 |
-0.03 |
0.20 |
0.18 |
| 87 | 15.38 |
-0.91 |
0.95 |
-0.03 |
0.20 |
0.18 |
| 88 | 15.37 |
-0.91 |
0.95 |
-0.03 |
0.20 |
0.17 |
| 89 | 15.36 |
-0.91 |
0.95 |
-0.03 |
0.20 |
0.17 |
| 90 | 15.35 |
-0.91 |
0.95 |
-0.03 |
0.20 |
0.17 |
| 91 | 15.34 |
-0.91 |
0.95 |
-0.03 |
0.20 |
0.17 |
| 92 | 15.33 |
-0.91 |
0.94 |
-0.03 |
0.20 |
0.17 |
| 93 | 15.32 |
-0.91 |
0.94 |
-0.03 |
0.20 |
0.17 |
| 94 | 15.32 |
-0.91 |
0.94 |
-0.03 |
0.20 |
0.17 |
| 95 | 15.31 |
-0.91 |
0.94 |
-0.03 |
0.20 |
0.17 |
| 96 | 15.31 |
-0.90 |
0.94 |
-0.03 |
0.20 |
0.17 |
| 97 | 15.30 |
-0.90 |
0.94 |
-0.03 |
0.20 |
0.17 |
| 98 | 15.30 |
-0.90 |
0.94 |
-0.03 |
0.20 |
0.17 |
| 99 | 15.29 |
-0.90 |
0.94 |
-0.03 |
0.20 |
0.17 |
| 100 | 15.29 |
-0.90 |
0.94 |
-0.03 |
0.20 |
0.17 |
| 101 | 15.28 |
-0.90 |
0.94 |
-0.03 |
0.20 |
0.17 |
| 102 | 15.28 |
-0.90 |
0.94 |
-0.03 |
0.20 |
0.17 |
| 103 | 15.27 |
-0.90 |
0.94 |
-0.03 |
0.20 |
0.17 |
| 104 | 15.27 |
-0.90 |
0.93 |
-0.03 |
0.20 |
0.17 |
| 105 | 15.27 |
-0.90 |
0.93 |
-0.03 |
0.20 |
0.17 |
| 106 | 15.26 |
-0.90 |
0.93 |
-0.03 |
0.20 |
0.17 |
| 107 | 15.26 |
-0.90 |
0.93 |
-0.03 |
0.20 |
0.17 |
| 108 | 15.26 |
-0.90 |
0.93 |
-0.03 |
0.20 |
0.17 |
| 109 | 15.25 |
-0.90 |
0.93 |
-0.03 |
0.20 |
0.17 |
| 110 | 15.25 |
-0.90 |
0.93 |
-0.03 |
0.19 |
0.17 |
| 111 | 15.25 |
-0.90 |
0.93 |
-0.03 |
0.19 |
0.17 |
| 112 | 15.25 |
-0.89 |
0.93 |
-0.03 |
0.19 |
0.17 |
| 113 | 15.24 |
-0.89 |
0.93 |
-0.03 |
0.19 |
0.17 |
| 114 | 15.24 |
-0.89 |
0.93 |
-0.03 |
0.19 |
0.17 |
| 115 | 15.24 |
-0.89 |
0.93 |
-0.03 |
0.19 |
0.17 |
| 116 | 15.24 |
-0.89 |
0.92 |
-0.03 |
0.19 |
0.17 |
| 117 | 15.24 |
-0.89 |
0.92 |
-0.03 |
0.19 |
0.17 |
| 118 | 15.23 |
-0.89 |
0.92 |
-0.03 |
0.19 |
0.17 |
| 119 | 15.23 |
-0.89 |
0.92 |
-0.03 |
0.19 |
0.17 |
| 120 | 15.23 |
-0.89 |
0.92 |
-0.03 |
0.19 |
0.17 |
Figure 10. 50% Rise in the Oil Price: Flexible vs. Sticky Prices
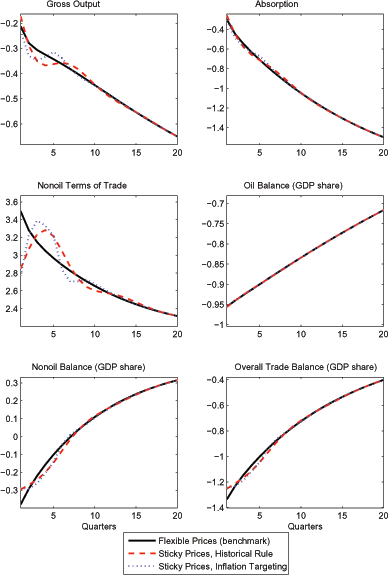
Data for Figure 10, Panel 1 - 50% Rise in the Oil Price: Flexible vs. Sticky Prices
| Period | Gross output: flexible prices (bench-mark) |
Absorption: flexible prices (bench-mark) |
Nonoil terms of trade: flexible prices (bench-mark) |
Oil balance: GDP share: flexible prices (bench-mark) |
Nonoil balance: GDP share: flexible prices (bench-mark) |
Overall trade balance: GDP share: flexible prices (bench-mark) |
Gross output: sticky prices, historical rule |
Absorption: sticky prices, historical rule |
Nonoil terms of trade: sticky prices, historical rule |
|---|---|---|---|---|---|---|---|---|---|
| 1 | -0.21 |
-0.30 |
3.50 |
-0.96 |
-0.38 |
-1.34 |
-0.17 |
-0.26 |
2.85 |
| 2 | -0.28 |
-0.44 |
3.28 |
-0.94 |
-0.29 |
-1.23 |
-0.29 |
-0.45 |
3.07 |
| 3 | -0.31 |
-0.55 |
3.15 |
-0.93 |
-0.22 |
-1.15 |
-0.35 |
-0.58 |
3.24 |
| 4 | -0.33 |
-0.63 |
3.05 |
-0.91 |
-0.16 |
-1.07 |
-0.37 |
-0.66 |
3.28 |
| 5 | -0.34 |
-0.71 |
2.97 |
-0.90 |
-0.10 |
-1.00 |
-0.36 |
-0.71 |
3.21 |
| 6 | -0.36 |
-0.79 |
2.89 |
-0.89 |
-0.05 |
-0.94 |
-0.36 |
-0.77 |
3.05 |
| 7 | -0.38 |
-0.86 |
2.83 |
-0.87 |
0.00 |
-0.88 |
-0.36 |
-0.83 |
2.87 |
| 8 | -0.40 |
-0.92 |
2.76 |
-0.86 |
0.04 |
-0.82 |
-0.38 |
-0.90 |
2.73 |
| 9 | -0.42 |
-0.99 |
2.71 |
-0.85 |
0.08 |
-0.77 |
-0.41 |
-0.97 |
2.64 |
| 10 | -0.45 |
-1.05 |
2.65 |
-0.83 |
0.11 |
-0.72 |
-0.44 |
-1.04 |
2.60 |
| 11 | -0.47 |
-1.11 |
2.61 |
-0.82 |
0.14 |
-0.68 |
-0.47 |
-1.11 |
2.58 |
| 12 | -0.49 |
-1.16 |
2.56 |
-0.81 |
0.17 |
-0.64 |
-0.50 |
-1.17 |
2.57 |
| 13 | -0.51 |
-1.21 |
2.52 |
-0.80 |
0.19 |
-0.60 |
-0.52 |
-1.22 |
2.54 |
| 14 | -0.53 |
-1.26 |
2.48 |
-0.78 |
0.22 |
-0.57 |
-0.53 |
-1.26 |
2.51 |
| 15 | -0.55 |
-1.30 |
2.45 |
-0.77 |
0.24 |
-0.53 |
-0.55 |
-1.30 |
2.47 |
| 16 | -0.57 |
-1.35 |
2.42 |
-0.76 |
0.26 |
-0.50 |
-0.57 |
-1.35 |
2.43 |
| 17 | -0.59 |
-1.39 |
2.39 |
-0.75 |
0.27 |
-0.48 |
-0.59 |
-1.39 |
2.40 |
| 18 | -0.61 |
-1.43 |
2.36 |
-0.74 |
0.29 |
-0.45 |
-0.61 |
-1.43 |
2.36 |
| 19 | -0.63 |
-1.46 |
2.34 |
-0.73 |
0.30 |
-0.42 |
-0.63 |
-1.46 |
2.34 |
| 20 | -0.65 |
-1.50 |
2.32 |
-0.72 |
0.32 |
-0.40 |
-0.65 |
-1.50 |
2.32 |
| 21 | -0.67 |
-1.53 |
2.30 |
-0.71 |
0.33 |
-0.38 |
-0.67 |
-1.53 |
2.30 |
| 22 | -0.68 |
-1.56 |
2.28 |
-0.70 |
0.34 |
-0.36 |
-0.68 |
-1.56 |
2.28 |
| 23 | -0.70 |
-1.59 |
2.26 |
-0.69 |
0.35 |
-0.34 |
-0.70 |
-1.59 |
2.27 |
| 24 | -0.71 |
-1.62 |
2.25 |
-0.68 |
0.36 |
-0.32 |
-0.71 |
-1.62 |
2.25 |
| 25 | -0.73 |
-1.64 |
2.23 |
-0.67 |
0.36 |
-0.30 |
-0.73 |
-1.64 |
2.24 |
| 26 | -0.74 |
-1.67 |
2.22 |
-0.66 |
0.37 |
-0.29 |
-0.74 |
-1.67 |
2.23 |
| 27 | -0.76 |
-1.69 |
2.21 |
-0.65 |
0.38 |
-0.27 |
-0.76 |
-1.69 |
2.21 |
| 28 | -0.77 |
-1.71 |
2.20 |
-0.64 |
0.38 |
-0.25 |
-0.77 |
-1.72 |
2.20 |
| 29 | -0.78 |
-1.73 |
2.19 |
-0.63 |
0.39 |
-0.24 |
-0.78 |
-1.74 |
2.19 |
| 30 | -0.79 |
-1.75 |
2.18 |
-0.62 |
0.39 |
-0.23 |
-0.79 |
-1.76 |
2.19 |
| 31 | -0.80 |
-1.77 |
2.18 |
-0.61 |
0.40 |
-0.21 |
-0.80 |
-1.78 |
2.18 |
| 32 | -0.81 |
-1.79 |
2.17 |
-0.60 |
0.40 |
-0.20 |
-0.82 |
-1.80 |
2.17 |
| 33 | -0.83 |
-1.81 |
2.16 |
-0.60 |
0.41 |
-0.19 |
-0.83 |
-1.81 |
2.17 |
| 34 | -0.83 |
-1.83 |
2.16 |
-0.59 |
0.41 |
-0.18 |
-0.84 |
-1.83 |
2.16 |
| 35 | -0.84 |
-1.84 |
2.15 |
-0.58 |
0.42 |
-0.16 |
-0.84 |
-1.85 |
2.16 |
| 36 | -0.85 |
-1.86 |
2.15 |
-0.57 |
0.42 |
-0.15 |
-0.85 |
-1.86 |
2.15 |
| 37 | -0.86 |
-1.87 |
2.14 |
-0.56 |
0.42 |
-0.14 |
-0.86 |
-1.88 |
2.15 |
| 38 | -0.87 |
-1.89 |
2.14 |
-0.56 |
0.42 |
-0.13 |
-0.87 |
-1.89 |
2.14 |
| 39 | -0.88 |
-1.90 |
2.14 |
-0.55 |
0.43 |
-0.12 |
-0.88 |
-1.90 |
2.14 |
| 40 | -0.89 |
-1.92 |
2.13 |
-0.54 |
0.43 |
-0.11 |
-0.89 |
-1.92 |
2.14 |
| 41 | -0.89 |
-1.93 |
2.13 |
-0.53 |
0.43 |
-0.10 |
-0.89 |
-1.93 |
2.13 |
| 42 | -0.90 |
-1.94 |
2.13 |
-0.53 |
0.44 |
-0.09 |
-0.90 |
-1.94 |
2.13 |
| 43 | -0.91 |
-1.95 |
2.13 |
-0.52 |
0.44 |
-0.08 |
-0.91 |
-1.96 |
2.13 |
| 44 | -0.91 |
-1.97 |
2.12 |
-0.51 |
0.44 |
-0.07 |
-0.92 |
-1.97 |
2.13 |
| 45 | -0.92 |
-1.98 |
2.12 |
-0.51 |
0.44 |
-0.07 |
-0.92 |
-1.98 |
2.12 |
| 46 | -0.93 |
-1.99 |
2.12 |
-0.50 |
0.44 |
-0.06 |
-0.93 |
-1.99 |
2.12 |
| 47 | -0.93 |
-2.00 |
2.12 |
-0.49 |
0.44 |
-0.05 |
-0.93 |
-2.00 |
2.12 |
| 48 | -0.94 |
-2.01 |
2.12 |
-0.49 |
0.45 |
-0.04 |
-0.94 |
-2.01 |
2.12 |
| 49 | -0.95 |
-2.02 |
2.11 |
-0.48 |
0.45 |
-0.03 |
-0.95 |
-2.02 |
2.12 |
| 50 | -0.95 |
-2.03 |
2.11 |
-0.48 |
0.45 |
-0.03 |
-0.95 |
-2.03 |
2.11 |
| 51 | -0.96 |
-2.04 |
2.11 |
-0.47 |
0.45 |
-0.02 |
-0.96 |
-2.04 |
2.11 |
| 52 | -0.96 |
-2.05 |
2.11 |
-0.46 |
0.45 |
-0.01 |
-0.96 |
-2.05 |
2.11 |
| 53 | -0.97 |
-2.05 |
2.11 |
-0.46 |
0.45 |
-0.01 |
-0.97 |
-2.06 |
2.11 |
| 54 | -0.97 |
-2.06 |
2.11 |
-0.45 |
0.45 |
0.00 |
-0.97 |
-2.06 |
2.11 |
| 55 | -0.98 |
-2.07 |
2.11 |
-0.45 |
0.46 |
0.01 |
-0.98 |
-2.07 |
2.11 |
| 56 | -0.98 |
-2.08 |
2.10 |
-0.44 |
0.46 |
0.01 |
-0.98 |
-2.08 |
2.11 |
| 57 | -0.99 |
-2.09 |
2.10 |
-0.44 |
0.46 |
0.02 |
-0.99 |
-2.09 |
2.10 |
| 58 | -0.99 |
-2.09 |
2.10 |
-0.43 |
0.46 |
0.03 |
-0.99 |
-2.10 |
2.10 |
| 59 | -0.99 |
-2.10 |
2.10 |
-0.43 |
0.46 |
0.03 |
-0.99 |
-2.10 |
2.10 |
| 60 | -1.00 |
-2.11 |
2.10 |
-0.42 |
0.46 |
0.04 |
-1.00 |
-2.11 |
2.10 |
| 61 | -1.00 |
-2.12 |
2.10 |
-0.42 |
0.46 |
0.04 |
-1.00 |
-2.12 |
2.10 |
| 62 | -1.01 |
-2.12 |
2.10 |
-0.41 |
0.46 |
0.05 |
-1.01 |
-2.12 |
2.10 |
| 63 | -1.01 |
-2.13 |
2.10 |
-0.41 |
0.46 |
0.05 |
-1.01 |
-2.13 |
2.10 |
| 64 | -1.01 |
-2.14 |
2.09 |
-0.40 |
0.46 |
0.06 |
-1.01 |
-2.14 |
2.10 |
| 65 | -1.02 |
-2.14 |
2.09 |
-0.40 |
0.46 |
0.07 |
-1.02 |
-2.14 |
2.09 |
| 66 | -1.02 |
-2.15 |
2.09 |
-0.39 |
0.46 |
0.07 |
-1.02 |
-2.15 |
2.09 |
| 67 | -1.03 |
-2.15 |
2.09 |
-0.39 |
0.46 |
0.08 |
-1.03 |
-2.16 |
2.09 |
| 68 | -1.03 |
-2.16 |
2.09 |
-0.38 |
0.46 |
0.08 |
-1.03 |
-2.16 |
2.09 |
| 69 | -1.03 |
-2.17 |
2.09 |
-0.38 |
0.47 |
0.09 |
-1.03 |
-2.17 |
2.09 |
| 70 | -1.04 |
-2.17 |
2.09 |
-0.38 |
0.47 |
0.09 |
-1.04 |
-2.17 |
2.09 |
| 71 | -1.04 |
-2.18 |
2.09 |
-0.37 |
0.47 |
0.09 |
-1.04 |
-2.18 |
2.09 |
| 72 | -1.04 |
-2.18 |
2.09 |
-0.37 |
0.47 |
0.10 |
-1.04 |
-2.18 |
2.09 |
| 73 | -1.05 |
-2.19 |
2.09 |
-0.36 |
0.47 |
0.10 |
-1.05 |
-2.19 |
2.09 |
| 74 | -1.05 |
-2.19 |
2.08 |
-0.36 |
0.47 |
0.11 |
-1.05 |
-2.19 |
2.09 |
| 75 | -1.05 |
-2.20 |
2.08 |
-0.36 |
0.47 |
0.11 |
-1.05 |
-2.20 |
2.08 |
| 76 | -1.05 |
-2.20 |
2.08 |
-0.35 |
0.47 |
0.12 |
-1.05 |
-2.20 |
2.08 |
| 77 | -1.06 |
-2.21 |
2.08 |
-0.35 |
0.47 |
0.12 |
-1.06 |
-2.21 |
2.08 |
| 78 | -1.06 |
-2.21 |
2.08 |
-0.34 |
0.47 |
0.12 |
-1.06 |
-2.21 |
2.08 |
| 79 | -1.06 |
-2.22 |
2.08 |
-0.34 |
0.47 |
0.13 |
-1.06 |
-2.22 |
2.08 |
| 80 | -1.07 |
-2.22 |
2.08 |
-0.34 |
0.47 |
0.13 |
-1.07 |
-2.22 |
2.08 |
| 81 | -1.07 |
-2.22 |
2.08 |
-0.33 |
0.47 |
0.13 |
-1.07 |
-2.23 |
2.08 |
| 82 | -1.07 |
-2.23 |
2.08 |
-0.33 |
0.47 |
0.14 |
-1.07 |
-2.23 |
2.08 |
| 83 | -1.07 |
-2.23 |
2.07 |
-0.33 |
0.47 |
0.14 |
-1.07 |
-2.23 |
2.08 |
| 84 | -1.08 |
-2.24 |
2.07 |
-0.32 |
0.47 |
0.15 |
-1.08 |
-2.24 |
2.08 |
| 85 | -1.08 |
-2.24 |
2.07 |
-0.32 |
0.47 |
0.15 |
-1.08 |
-2.24 |
2.07 |
| 86 | -1.08 |
-2.24 |
2.07 |
-0.32 |
0.47 |
0.15 |
-1.08 |
-2.25 |
2.07 |
| 87 | -1.08 |
-2.25 |
2.07 |
-0.31 |
0.47 |
0.16 |
-1.09 |
-2.25 |
2.07 |
| 88 | -1.09 |
-2.25 |
2.07 |
-0.31 |
0.47 |
0.16 |
-1.09 |
-2.25 |
2.07 |
| 89 | -1.09 |
-2.26 |
2.07 |
-0.31 |
0.47 |
0.16 |
-1.09 |
-2.26 |
2.07 |
| 90 | -1.09 |
-2.26 |
2.07 |
-0.30 |
0.47 |
0.16 |
-1.09 |
-2.26 |
2.07 |
| 91 | -1.09 |
-2.26 |
2.07 |
-0.30 |
0.47 |
0.17 |
-1.09 |
-2.26 |
2.07 |
| 92 | -1.10 |
-2.27 |
2.07 |
-0.30 |
0.47 |
0.17 |
-1.10 |
-2.27 |
2.07 |
| 93 | -1.10 |
-2.27 |
2.06 |
-0.29 |
0.47 |
0.17 |
-1.10 |
-2.27 |
2.07 |
| 94 | -1.10 |
-2.27 |
2.06 |
-0.29 |
0.47 |
0.18 |
-1.10 |
-2.27 |
2.06 |
| 95 | -1.10 |
-2.28 |
2.06 |
-0.29 |
0.47 |
0.18 |
-1.10 |
-2.28 |
2.06 |
| 96 | -1.11 |
-2.28 |
2.06 |
-0.29 |
0.47 |
0.18 |
-1.11 |
-2.28 |
2.06 |
| 97 | -1.11 |
-2.28 |
2.06 |
-0.28 |
0.47 |
0.18 |
-1.11 |
-2.28 |
2.06 |
| 98 | -1.11 |
-2.29 |
2.06 |
-0.28 |
0.47 |
0.19 |
-1.11 |
-2.29 |
2.06 |
| 99 | -1.11 |
-2.29 |
2.06 |
-0.28 |
0.47 |
0.19 |
-1.11 |
-2.29 |
2.06 |
| 100 | -1.11 |
-2.29 |
2.06 |
-0.27 |
0.47 |
0.19 |
-1.11 |
-2.29 |
2.06 |
| 101 | -1.12 |
-2.29 |
2.06 |
-0.27 |
0.47 |
0.19 |
-1.12 |
-2.30 |
2.06 |
| 102 | -1.12 |
-2.30 |
2.05 |
-0.27 |
0.47 |
0.20 |
-1.12 |
-2.30 |
2.06 |
| 103 | -1.12 |
-2.30 |
2.05 |
-0.27 |
0.47 |
0.20 |
-1.12 |
-2.30 |
2.06 |
| 104 | -1.12 |
-2.30 |
2.05 |
-0.26 |
0.47 |
0.20 |
-1.12 |
-2.30 |
2.05 |
| 105 | -1.12 |
-2.31 |
2.05 |
-0.26 |
0.47 |
0.20 |
-1.12 |
-2.31 |
2.05 |
| 106 | -1.13 |
-2.31 |
2.05 |
-0.26 |
0.47 |
0.21 |
-1.13 |
-2.31 |
2.05 |
| 107 | -1.13 |
-2.31 |
2.05 |
-0.26 |
0.47 |
0.21 |
-1.13 |
-2.31 |
2.05 |
| 108 | -1.13 |
-2.31 |
2.05 |
-0.25 |
0.46 |
0.21 |
-1.13 |
-2.31 |
2.05 |
| 109 | -1.13 |
-2.31 |
2.05 |
-0.25 |
0.46 |
0.21 |
-1.13 |
-2.32 |
2.05 |
| 110 | -1.13 |
-2.32 |
2.05 |
-0.25 |
0.46 |
0.21 |
-1.13 |
-2.32 |
2.05 |
| 111 | -1.13 |
-2.32 |
2.04 |
-0.25 |
0.46 |
0.22 |
-1.13 |
-2.32 |
2.05 |
| 112 | -1.14 |
-2.32 |
2.04 |
-0.25 |
0.46 |
0.22 |
-1.14 |
-2.32 |
2.04 |
| 113 | -1.14 |
-2.32 |
2.04 |
-0.24 |
0.46 |
0.22 |
-1.14 |
-2.32 |
2.04 |
| 114 | -1.14 |
-2.33 |
2.04 |
-0.24 |
0.46 |
0.22 |
-1.14 |
-2.33 |
2.04 |
| 115 | -1.14 |
-2.33 |
2.04 |
-0.24 |
0.46 |
0.22 |
-1.14 |
-2.33 |
2.04 |
| 116 | -1.14 |
-2.33 |
2.04 |
-0.24 |
0.46 |
0.23 |
-1.14 |
-2.33 |
2.04 |
| 117 | -1.14 |
-2.33 |
2.04 |
-0.23 |
0.46 |
0.23 |
-1.14 |
-2.33 |
2.04 |
| 118 | -1.15 |
-2.33 |
2.04 |
-0.23 |
0.46 |
0.23 |
-1.15 |
-2.34 |
2.04 |
| 119 | -1.15 |
-2.34 |
2.04 |
-0.23 |
0.46 |
0.23 |
-1.15 |
-2.34 |
2.04 |
| 120 | -1.15 |
-2.34 |
2.03 |
-0.23 |
0.46 |
0.23 |
-1.15 |
-2.34 |
2.04 |
Data for Figure 10, Panel 2 - 50% Rise in the Oil Price: Flexible vs. Sticky Prices
| Period | Oil balance: GDP share: sticky prices, historical rule |
Nonoil balance: GDP share: sticky prices, historical rule |
Overall trade balance: GDP share: sticky prices, historical rule |
Gross output: sticky prices, inflation targeting |
Absorption: sticky prices, inflation targeting |
Nonoil terms of trade: sticky prices, inflation targeting |
Oil balance: GDP share: sticky prices, inflation targeting |
Nonoil balance: GDP share: sticky price, inflation targeting |
Overall trade balance: GDP share: sticky prices, inflation targeting |
|---|---|---|---|---|---|---|---|---|---|
| 1 | -0.96 | -0.30 | -1.25 | -0.23 | -0.31 | 2.77 | -0.95 | -0.29 | -1.24 |
| 2 | -0.94 | -0.27 | -1.21 | -0.33 | -0.49 | 3.23 | -0.94 | -0.29 | -1.23 |
| 3 | -0.93 | -0.24 | -1.17 | -0.35 | -0.58 | 3.39 | -0.93 | -0.26 | -1.19 |
| 4 | -0.91 | -0.20 | -1.11 | -0.33 | -0.63 | 3.33 | -0.91 | -0.20 | -1.12 |
| 5 | -0.90 | -0.15 | -1.05 | -0.31 | -0.67 | 3.22 | -0.90 | -0.14 | -1.04 |
| 6 | -0.89 | -0.08 | -0.97 | -0.34 | -0.76 | 2.84 | -0.89 | -0.05 | -0.94 |
| 7 | -0.87 | -0.02 | -0.89 | -0.38 | -0.85 | 2.70 | -0.87 | 0.01 | -0.86 |
| 8 | -0.86 | 0.04 | -0.82 | -0.41 | -0.93 | 2.71 | -0.86 | 0.04 | -0.82 |
| 9 | -0.85 | 0.08 | -0.77 | -0.43 | -0.99 | 2.73 | -0.85 | 0.07 | -0.78 |
| 10 | -0.83 | 0.12 | -0.72 | -0.45 | -1.05 | 2.67 | -0.83 | 0.11 | -0.73 |
| 11 | -0.82 | 0.14 | -0.68 | -0.47 | -1.10 | 2.62 | -0.82 | 0.14 | -0.68 |
| 12 | -0.81 | 0.17 | -0.64 | -0.49 | -1.16 | 2.58 | -0.81 | 0.17 | -0.64 |
| 13 | -0.80 | 0.19 | -0.61 | -0.51 | -1.21 | 2.53 | -0.80 | 0.19 | -0.60 |
| 14 | -0.78 | 0.21 | -0.57 | -0.53 | -1.26 | 2.48 | -0.78 | 0.22 | -0.57 |
| 15 | -0.77 | 0.23 | -0.54 | -0.55 | -1.30 | 2.45 | -0.77 | 0.24 | -0.53 |
| 16 | -0.76 | 0.25 | -0.51 | -0.57 | -1.35 | 2.42 | -0.76 | 0.26 | -0.50 |
| 17 | -0.75 | 0.27 | -0.48 | -0.59 | -1.39 | 2.39 | -0.75 | 0.27 | -0.48 |
| 18 | -0.74 | 0.29 | -0.45 | -0.61 | -1.43 | 2.37 | -0.74 | 0.29 | -0.45 |
| 19 | -0.73 | 0.30 | -0.42 | -0.63 | -1.46 | 2.34 | -0.73 | 0.30 | -0.42 |
| 20 | -0.72 | 0.32 | -0.40 | -0.65 | -1.50 | 2.32 | -0.72 | 0.32 | -0.40 |
| 21 | -0.71 | 0.33 | -0.38 | -0.67 | -1.53 | 2.30 | -0.71 | 0.33 | -0.38 |
| 22 | -0.70 | 0.34 | -0.36 | -0.68 | -1.56 | 2.28 | -0.70 | 0.34 | -0.36 |
| 23 | -0.69 | 0.35 | -0.34 | -0.70 | -1.59 | 2.27 | -0.69 | 0.35 | -0.34 |
| 24 | -0.68 | 0.36 | -0.32 | -0.71 | -1.62 | 2.25 | -0.68 | 0.36 | -0.32 |
| 25 | -0.67 | 0.36 | -0.30 | -0.73 | -1.64 | 2.24 | -0.67 | 0.36 | -0.30 |
| 26 | -0.66 | 0.37 | -0.28 | -0.74 | -1.67 | 2.22 | -0.66 | 0.37 | -0.28 |
| 27 | -0.65 | 0.38 | -0.27 | -0.76 | -1.69 | 2.21 | -0.65 | 0.38 | -0.27 |
| 28 | -0.64 | 0.38 | -0.25 | -0.77 | -1.71 | 2.20 | -0.64 | 0.38 | -0.25 |
| 29 | -0.63 | 0.39 | -0.24 | -0.78 | -1.74 | 2.19 | -0.63 | 0.39 | -0.24 |
| 30 | -0.62 | 0.40 | -0.22 | -0.79 | -1.76 | 2.19 | -0.62 | 0.40 | -0.23 |
| 31 | -0.61 | 0.40 | -0.21 | -0.80 | -1.78 | 2.18 | -0.61 | 0.40 | -0.21 |
| 32 | -0.60 | 0.40 | -0.20 | -0.82 | -1.79 | 2.17 | -0.60 | 0.40 | -0.20 |
| 33 | -0.60 | 0.41 | -0.19 | -0.83 | -1.81 | 2.17 | -0.60 | 0.41 | -0.19 |
| 34 | -0.59 | 0.41 | -0.17 | -0.84 | -1.83 | 2.16 | -0.59 | 0.41 | -0.17 |
| 35 | -0.58 | 0.42 | -0.16 | -0.84 | -1.85 | 2.15 | -0.58 | 0.42 | -0.16 |
| 36 | -0.57 | 0.42 | -0.15 | -0.85 | -1.86 | 2.15 | -0.57 | 0.42 | -0.15 |
| 37 | -0.56 | 0.42 | -0.14 | -0.86 | -1.88 | 2.15 | -0.56 | 0.42 | -0.14 |
| 38 | -0.56 | 0.43 | -0.13 | -0.87 | -1.89 | 2.14 | -0.56 | 0.43 | -0.13 |
| 39 | -0.55 | 0.43 | -0.12 | -0.88 | -1.90 | 2.14 | -0.55 | 0.43 | -0.12 |
| 40 | -0.54 | 0.43 | -0.11 | -0.89 | -1.92 | 2.14 | -0.54 | 0.43 | -0.11 |
| 41 | -0.53 | 0.43 | -0.10 | -0.89 | -1.93 | 2.13 | -0.53 | 0.43 | -0.10 |
| 42 | -0.53 | 0.44 | -0.09 | -0.90 | -1.94 | 2.13 | -0.53 | 0.44 | -0.09 |
| 43 | -0.52 | 0.44 | -0.08 | -0.91 | -1.95 | 2.13 | -0.52 | 0.44 | -0.08 |
| 44 | -0.51 | 0.44 | -0.07 | -0.91 | -1.97 | 2.12 | -0.51 | 0.44 | -0.07 |
| 45 | -0.51 | 0.44 | -0.07 | -0.92 | -1.98 | 2.12 | -0.51 | 0.44 | -0.07 |
| 46 | -0.50 | 0.44 | -0.06 | -0.93 | -1.99 | 2.12 | -0.50 | 0.44 | -0.06 |
| 47 | -0.49 | 0.45 | -0.05 | -0.93 | -2.00 | 2.12 | -0.49 | 0.45 | -0.05 |
| 48 | -0.49 | 0.45 | -0.04 | -0.94 | -2.01 | 2.12 | -0.49 | 0.45 | -0.04 |
| 49 | -0.48 | 0.45 | -0.03 | -0.95 | -2.02 | 2.12 | -0.48 | 0.45 | -0.03 |
| 50 | -0.48 | 0.45 | -0.03 | -0.95 | -2.03 | 2.11 | -0.48 | 0.45 | -0.03 |
| 51 | -0.47 | 0.45 | -0.02 | -0.96 | -2.04 | 2.11 | -0.47 | 0.45 | -0.02 |
| 52 | -0.46 | 0.45 | -0.01 | -0.96 | -2.05 | 2.11 | -0.46 | 0.45 | -0.01 |
| 53 | -0.46 | 0.45 | -0.01 | -0.97 | -2.06 | 2.11 | -0.46 | 0.45 | -0.01 |
| 54 | -0.45 | 0.46 | 0.00 | -0.97 | -2.06 | 2.11 | -0.45 | 0.45 | 0.00 |
| 55 | -0.45 | 0.46 | 0.01 | -0.98 | -2.07 | 2.11 | -0.45 | 0.46 | 0.01 |
| 56 | -0.44 | 0.46 | 0.01 | -0.98 | -2.08 | 2.10 | -0.44 | 0.46 | 0.01 |
| 57 | -0.44 | 0.46 | 0.02 | -0.99 | -2.09 | 2.10 | -0.44 | 0.46 | 0.02 |
| 58 | -0.43 | 0.46 | 0.03 | -0.99 | -2.10 | 2.10 | -0.43 | 0.46 | 0.03 |
| 59 | -0.43 | 0.46 | 0.03 | -0.99 | -2.10 | 2.10 | -0.43 | 0.46 | 0.03 |
| 60 | -0.42 | 0.46 | 0.04 | -1.00 | -2.11 | 2.10 | -0.42 | 0.46 | 0.04 |
| 61 | -0.42 | 0.46 | 0.04 | -1.00 | -2.12 | 2.10 | -0.42 | 0.46 | 0.04 |
| 62 | -0.41 | 0.46 | 0.05 | -1.01 | -2.12 | 2.10 | -0.41 | 0.46 | 0.05 |
| 63 | -0.41 | 0.46 | 0.06 | -1.01 | -2.13 | 2.10 | -0.41 | 0.46 | 0.06 |
| 64 | -0.40 | 0.46 | 0.06 | -1.01 | -2.14 | 2.10 | -0.40 | 0.46 | 0.06 |
| 65 | -0.40 | 0.46 | 0.07 | -1.02 | -2.14 | 2.09 | -0.40 | 0.46 | 0.07 |
| 66 | -0.39 | 0.46 | 0.07 | -1.02 | -2.15 | 2.09 | -0.39 | 0.46 | 0.07 |
| 67 | -0.39 | 0.46 | 0.08 | -1.03 | -2.16 | 2.09 | -0.39 | 0.46 | 0.08 |
| 68 | -0.38 | 0.47 | 0.08 | -1.03 | -2.16 | 2.09 | -0.38 | 0.46 | 0.08 |
| 69 | -0.38 | 0.47 | 0.09 | -1.03 | -2.17 | 2.09 | -0.38 | 0.47 | 0.09 |
| 70 | -0.38 | 0.47 | 0.09 | -1.04 | -2.17 | 2.09 | -0.38 | 0.47 | 0.09 |
| 71 | -0.37 | 0.47 | 0.09 | -1.04 | -2.18 | 2.09 | -0.37 | 0.47 | 0.09 |
| 72 | -0.37 | 0.47 | 0.10 | -1.04 | -2.18 | 2.09 | -0.37 | 0.47 | 0.10 |
| 73 | -0.36 | 0.47 | 0.10 | -1.05 | -2.19 | 2.09 | -0.36 | 0.47 | 0.10 |
| 74 | -0.36 | 0.47 | 0.11 | -1.05 | -2.19 | 2.08 | -0.36 | 0.47 | 0.11 |
| 75 | -0.36 | 0.47 | 0.11 | -1.05 | -2.20 | 2.08 | -0.36 | 0.47 | 0.11 |
| 76 | -0.35 | 0.47 | 0.12 | -1.05 | -2.20 | 2.08 | -0.35 | 0.47 | 0.12 |
| 77 | -0.35 | 0.47 | 0.12 | -1.06 | -2.21 | 2.08 | -0.35 | 0.47 | 0.12 |
| 78 | -0.34 | 0.47 | 0.12 | -1.06 | -2.21 | 2.08 | -0.34 | 0.47 | 0.12 |
| 79 | -0.34 | 0.47 | 0.13 | -1.06 | -2.22 | 2.08 | -0.34 | 0.47 | 0.13 |
| 80 | -0.34 | 0.47 | 0.13 | -1.07 | -2.22 | 2.08 | -0.34 | 0.47 | 0.13 |
| 81 | -0.33 | 0.47 | 0.14 | -1.07 | -2.23 | 2.08 | -0.33 | 0.47 | 0.13 |
| 82 | -0.33 | 0.47 | 0.14 | -1.07 | -2.23 | 2.08 | -0.33 | 0.47 | 0.14 |
| 83 | -0.33 | 0.47 | 0.14 | -1.07 | -2.23 | 2.08 | -0.33 | 0.47 | 0.14 |
| 84 | -0.32 | 0.47 | 0.15 | -1.08 | -2.24 | 2.07 | -0.32 | 0.47 | 0.15 |
| 85 | -0.32 | 0.47 | 0.15 | -1.08 | -2.24 | 2.07 | -0.32 | 0.47 | 0.15 |
| 86 | -0.32 | 0.47 | 0.15 | -1.08 | -2.25 | 2.07 | -0.32 | 0.47 | 0.15 |
| 87 | -0.31 | 0.47 | 0.16 | -1.09 | -2.25 | 2.07 | -0.31 | 0.47 | 0.16 |
| 88 | -0.31 | 0.47 | 0.16 | -1.09 | -2.25 | 2.07 | -0.31 | 0.47 | 0.16 |
| 89 | -0.31 | 0.47 | 0.16 | -1.09 | -2.26 | 2.07 | -0.31 | 0.47 | 0.16 |
| 90 | -0.30 | 0.47 | 0.16 | -1.09 | -2.26 | 2.07 | -0.30 | 0.47 | 0.16 |
| 91 | -0.30 | 0.47 | 0.17 | -1.09 | -2.26 | 2.07 | -0.30 | 0.47 | 0.17 |
| 92 | -0.30 | 0.47 | 0.17 | -1.10 | -2.27 | 2.07 | -0.30 | 0.47 | 0.17 |
| 93 | -0.29 | 0.47 | 0.17 | -1.10 | -2.27 | 2.07 | -0.29 | 0.47 | 0.17 |
| 94 | -0.29 | 0.47 | 0.18 | -1.10 | -2.27 | 2.06 | -0.29 | 0.47 | 0.18 |
| 95 | -0.29 | 0.47 | 0.18 | -1.10 | -2.28 | 2.06 | -0.29 | 0.47 | 0.18 |
| 96 | -0.29 | 0.47 | 0.18 | -1.11 | -2.28 | 2.06 | -0.29 | 0.47 | 0.18 |
| 97 | -0.28 | 0.47 | 0.18 | -1.11 | -2.28 | 2.06 | -0.28 | 0.47 | 0.18 |
| 98 | -0.28 | 0.47 | 0.19 | -1.11 | -2.29 | 2.06 | -0.28 | 0.47 | 0.19 |
| 99 | -0.28 | 0.47 | 0.19 | -1.11 | -2.29 | 2.06 | -0.28 | 0.47 | 0.19 |
| 100 | -0.27 | 0.47 | 0.19 | -1.11 | -2.29 | 2.06 | -0.27 | 0.47 | 0.19 |
| 101 | -0.27 | 0.47 | 0.19 | -1.12 | -2.29 | 2.06 | -0.27 | 0.47 | 0.19 |
| 102 | -0.27 | 0.47 | 0.20 | -1.12 | -2.30 | 2.06 | -0.27 | 0.47 | 0.20 |
| 103 | -0.27 | 0.47 | 0.20 | -1.12 | -2.30 | 2.05 | -0.27 | 0.47 | 0.20 |
| 104 | -0.26 | 0.47 | 0.20 | -1.12 | -2.30 | 2.05 | -0.26 | 0.47 | 0.20 |
| 105 | -0.26 | 0.47 | 0.20 | -1.12 | -2.31 | 2.05 | -0.26 | 0.47 | 0.20 |
| 106 | -0.26 | 0.47 | 0.21 | -1.13 | -2.31 | 2.05 | -0.26 | 0.47 | 0.21 |
| 107 | -0.26 | 0.47 | 0.21 | -1.13 | -2.31 | 2.05 | -0.26 | 0.47 | 0.21 |
| 108 | -0.25 | 0.47 | 0.21 | -1.13 | -2.31 | 2.05 | -0.25 | 0.47 | 0.21 |
| 109 | -0.25 | 0.47 | 0.21 | -1.13 | -2.32 | 2.05 | -0.25 | 0.46 | 0.21 |
| 110 | -0.25 | 0.46 | 0.22 | -1.13 | -2.32 | 2.05 | -0.25 | 0.46 | 0.22 |
| 111 | -0.25 | 0.46 | 0.22 | -1.13 | -2.32 | 2.05 | -0.25 | 0.46 | 0.22 |
| 112 | -0.25 | 0.46 | 0.22 | -1.14 | -2.32 | 2.04 | -0.25 | 0.46 | 0.22 |
| 113 | -0.24 | 0.46 | 0.22 | -1.14 | -2.32 | 2.04 | -0.24 | 0.46 | 0.22 |
| 114 | -0.24 | 0.46 | 0.22 | -1.14 | -2.33 | 2.04 | -0.24 | 0.46 | 0.22 |
| 115 | -0.24 | 0.46 | 0.23 | -1.14 | -2.33 | 2.04 | -0.24 | 0.46 | 0.22 |
| 116 | -0.24 | 0.46 | 0.23 | -1.14 | -2.33 | 2.04 | -0.24 | 0.46 | 0.23 |
| 117 | -0.23 | 0.46 | 0.23 | -1.14 | -2.33 | 2.04 | -0.23 | 0.46 | 0.23 |
| 118 | -0.23 | 0.46 | 0.23 | -1.15 | -2.34 | 2.04 | -0.23 | 0.46 | 0.23 |
| 119 | -0.23 | 0.46 | 0.23 | -1.15 | -2.34 | 2.04 | -0.23 | 0.46 | 0.23 |
| 120 | -0.23 | 0.46 | 0.23 | -1.15 | -2.34 | 2.04 | -0.23 | 0.46 | 0.23 |
A. Appendix: Estimation of the Oil Demand Equation
Abstracting from taxes, the log-linearized behavioral equation determining aggregate oil demand can be expressed as:
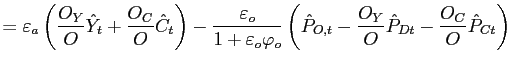
|
||
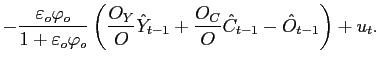
|
(22) |
In equation (22), a "hat" denotes a
variable's percentage deviation from its steady state value. Steady
state values are distinguished by the omission of a time subscript.
To derive the equation above, we imposed the restrictions
![]() and
and
![]() ,
by which the price elasticity of oil demand is equalized across the
two end uses in our model at each point in time. The parameter
,
by which the price elasticity of oil demand is equalized across the
two end uses in our model at each point in time. The parameter
![]() is the absolute value of the
long-run price elasticity of oil demand. The variable
is the absolute value of the
long-run price elasticity of oil demand. The variable ![]() reflects a stochastic shock to oil demand, as discussed
in Section 6. Our model imposes that the coefficient
reflects a stochastic shock to oil demand, as discussed
in Section 6. Our model imposes that the coefficient
![]() on contemporaneous activity
on contemporaneous activity
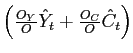 equals one, but we estimate it as a free parameter as a test of
our specification.
equals one, but we estimate it as a free parameter as a test of
our specification.
To control for endogeneity, our econometric approach follows [Fuhrer and Moore 1995]. As a statistical model, we use a three equation VAR(4) that includes oil demand, the activity measure, and the relative price measure.21 The demand equation (22) replaces the oil equation in that VAR system. We estimate this system using maximum likelihood.
As a measure of oil, demand we take total petroleum consumption (product supplied) from the Energy Information Administration. We construct the activity measure as a weighted average of consumption and GDP from the National Income and Product Accounts (NIPA).22For the relative price measure, we use the crude oil producer price index series from the Bureau of Labor Statistics, and the consumption and GDP deflators from NIPA. We run all regression equations using log linearly detrended quarterly data. The estimation sample covers the period from the second quarter of 1948 to the fourth quarter of 2005.
The regression results for the oil demand equation are
summarized in Table 2. The
estimated elasticity for the activity measure is not significantly
different from 1, which is the value imposed by our theoretical
model. The oil price elasticity is estimated at 0.28. Our baseline
calibration value of 0.5 is within one standard deviation. The
estimated adjustment cost parameter
![]() is 139.2, which implies a half
life of 7 years for the response of oil demand to a permanent price
increase. Our baseline half life of 10 years lies within one
standard deviation of the estimate of
is 139.2, which implies a half
life of 7 years for the response of oil demand to a permanent price
increase. Our baseline half life of 10 years lies within one
standard deviation of the estimate of
![]() .
.
The Durbin Watson statistics suggests serial correlation in the regression residuals of the oil demand equation. To address the potential mispecification, we modify the adjustment cost function for oil demand in production (equations 8) as follows:
![$\displaystyle \varphi_{OYt}=\left[ 1-\frac{\varphi_{oy1}}{2} \left( \frac{\frac{O_{Yt} }{V_{t}}}{\frac{O^{A}_{Yt-1}}{V^{A}_{t-1}}}-1\right) ^{2}-\frac{\varphi _{oy2}}{2} \left( \frac{\frac{O_{Yt-1}}{V_{t-1}}}{\frac{O^{A}_{Yt-2}} {V^{A}_{t-2}}}-1\right) ^{2}\right] .$](img211.gif)
|
(23) |
We change the adjustment cost function for oil demand in consumption (equation 11) analogously.
Upon log-linearizing, the aggregate oil demand equation now takes the form:
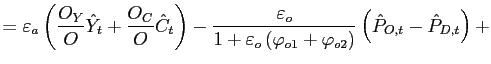
|
(24) | |
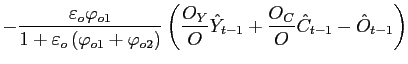
|
||
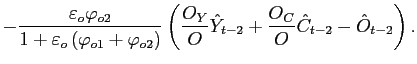
|
(25) |
Following the same estimation procedure as described above we obtain estimates summarized in Table 3.
This alternative regression specification reduces the residual
autocorrelation, as indicated by a lower Durbin-Watson statistic.
The coefficient estimates
![]() and
and
![]() are not significantly
different from those in the simpler specification. Again, we fail
to reject the restriction imposed by our theoretical model that
are not significantly
different from those in the simpler specification. Again, we fail
to reject the restriction imposed by our theoretical model that
![]() is 1. The estimates for the
adjustment cost parameters
is 1. The estimates for the
adjustment cost parameters
![]() and
and
![]() imply a half life of 10 years
for the response of oil demand to a permanent price increase, as in
our baseline calibration. Given the short length of the time series
and the slow adjustment of oil demand, it is difficult to estimate
the long-run elasticity precisely. Nonetheless, the regression does
very well at capturing the variation in oil demand, as suggested by
the high
imply a half life of 10 years
for the response of oil demand to a permanent price increase, as in
our baseline calibration. Given the short length of the time series
and the slow adjustment of oil demand, it is difficult to estimate
the long-run elasticity precisely. Nonetheless, the regression does
very well at capturing the variation in oil demand, as suggested by
the high ![]() statistic.
statistic.
Table 2. Regression Results for Baseline Oil Demand Equation*
Coefficient | Std. Error | Prob. | |
|---|---|---|---|
| | 1.05 | 0.05 | 0.00 |
| | 0.28 | 0.27 | 0.30 |
| | 139.2 | 95.0 | 0.14 |
![]() =0.98
=0.98
Durbin-Watson stat. = 2.40
* See equation (22).
Table 3. Regression Results for Augmented Oil Demand Equation*
Coefficient | Std. Error | Prob. | |
|---|---|---|---|
| | 1.04 | 0.05 | 0.00 |
| | 0.45 | 0.42 | 0.29 |
| | 81.9 | 40.3 | 0.04 |
| | 21.3 | 11.6 | 0.07 |
![]() =0.98
=0.98
Durbin-Watson stat. = 2.05
* See equation (24).
Footnotes
** Corresponding author is Luca Guerrieri, Telephone (202) 452 2550, E-mail [email protected]. The authors thank Roc Armenter, Brett Berger, Chris Carroll, Don Coletti, Joe Gagnon, Lutz Kilian, Enrique Mendoza, Trevor Reeve, and seminar participants at the Bank of Canada, the IMF, the Federal Reserve Board, the Federal Reserve Banks of Atlanta and New York, and Johns Hopkins University. We are particularly grateful to Christopher Gust and Eric Swanson for many insightful comments, and to Hilary Croke for excellent research assistance. The views expressed in this paper are solely the responsibility of the authors and should not be interpreted as reflecting the views of the Board of Governors of the Federal Reserve System or of any other person associated with the Federal Reserve System. Return to text
1. A large body of empirical research has attempted to identify the effects of energy supply disruptions on real output and prices; examples include [Hamilton 1983], [Hamilton 2003], [Kilian 2006], and [Cavallo and Wu 2006]. [Bernanke et al. 1997] argued that the economy's reaction to oil shocks could be heavily influenced by the reaction of monetary policy (see also [Hamilton and Herrera 2004]). Return to text
2. In a recent working paper [Kilian et al. 2007] used a structural VAR to analyze the reaction of the oil and nonoil trade balance to both oil supply and demand shocks. Return to text
3. In line with the analysis of [Cole and Obstfeld 1991], the literature suggests that complete and incomplete markets imply very similar macroeconomic responses to a technology shock when the trade price elasticity is around unity, e.g., [Erceg et al. 2007]. However, a high trade price elasticity can generate substantial divergence across these alternative financial market structures under certain conditions on labor supply (different preferences over labor supply appear to account for why [Baxter and Crucini 1995] found significant disparities, while [Schmitt-Grohe and Uribe 2003] did not). Finally, [Corsetti et al. 2004] showed that very low trade price elasticities can also imply pronounced differences across financial market structures. Return to text
4. The assumption that oil price innovations are driven by exogenous changes in supply is typical in the empirical literature, e.g., [Hamilton 1983], [Hamilton 2003], and [Bernanke et al. 1997], and also has a long tradition in DSGE modeling. Notable examples of the latter include [Kim and Loungani 1992], [Rotemberg and Woodford 1996], [Finn 2000], [Leduc and Sill 2004] and [Blanchard and Galí 2007]. However, recent empirical analysis by [Kilian 2006] has challenged the traditional view. In particular, Kilian used structural VAR analysis to argue that demand shocks - both specific to the oil market and for industrial commodities generally - have played a much larger role in driving oil price fluctuations than acknowledged in most of the literature. Hence, while our benchmark model follows the usual approach of assuming a supply-driven hike in the oil price, we also consider the implications of one type of demand-driven oil price increase. Return to text
5. Backus and Crucini used their model to explain instability in the time series correlation between output and the terms of trade that they attributed to changes in the relative importance of oil and technology shocks. Given this focus, their results would seem likely to hold under either financial market structure. Return to text
6. This form of adjustment cost implies a time-varying elasticity of substitution for oil, an important feature of putty-clay models such as in [Atkeson and Kehoe 1999] and [Wei 2003]. In their setting, a large variety of types of capital goods are combined with energy in different fixed proportions. Thus the short-run elasticity of substitution for oil is low. In the long run, the elasticity is higher, as firms can invest in capital goods with different fixed energy intensities. Return to text
7. As discussed in [Erceg et al. 2006], our trade specification implies that the activity variable driving (nonoil) import and export demand can be regarded as a weighted average of consumption and investment, with the latter receiving a large weight (consistent with the high weight of investment in U.S. trade). The paper also provides empirical support in favor of this specification over a more standard specification in which the real activity variable driving trade is total absorption. Return to text
8. The steady state around which we linearize depends on the relative level of technology in each country, which we initialize to unity. We evaluated the robustness of our solution procedure by using a nonlinear Newton-Raphson algorithm that does not rely on linearization around an initial steady state, and found that the results were nearly identical to those reported. Return to text
9. In calibrating our model, we adopt a more inclusive interpretation of the oil sector that also incorporates natural gas. Our inclusion of natural gas reflects the close substitutability between oil and natural gas as energy inputs, and the high correlation between movements in oil prices and natural gas prices. Over the period 1970-2005, the correlation between crude oil prices and natural gas prices was 0.9 (using data from NYMEX). Return to text
10. Some of the variation in the elasticity estimates depends on the specific energy aggregate being used. [Cooper 2003] estimated the long-run price elasticity of the demand for crude oil - the same energy aggregate we examine - and found a very similar value of 0.45. Return to text
11. [Hooper et al. 2000] estimated trade price elasticities using aggregate data for G-7 countries. They reported a long-run export price elasticity of 1.5 for the United States. Return to text
12. The analysis of [Hooper et al. 2000] found that the long-run export price elasticity for U.S. goods and services was several times larger than the short-run elasticity; [Gallaway et al. 2003] found a similar disparity between long- and short-run trade price elasticities using industry-level data. Return to text
13. While the fall in energy demand due to the direct effect of higher prices is amplified by an endogenous decline in output and consumption, the latter effect is small. Return to text
14. [Laffer and Agmon 1978] observed that the overall trade balance of oil importing countries rebounded relatively quickly following the first oil crisis of the 1970s, with the nonoil component playing a prominent role in reducing the overall trade gap. Return to text
15. [Golub 1983] provides an early example of a model linking the exchange rate response to an oil shock with the level of oil imports. Return to text
16. Interestingly, the empirical analysis of [Kilian 2006] seems consistent with these implications. In particular, Kilian found that an exogenous oil price increase would lead to a depreciation relative to the dollar for Italy, France, Germany, and Japan, all countries whose level of per capita domestic oil production is lower than for the United States. Moreover, he found the Canadian dollar appreciated, which is also in line with our model given that Canada is a major energy exporter. Return to text
17. The increase in the marginal product reflects that oil and nonoil consumption goods are complements in the household consumption bundle under our baseline calibration. Return to text
18. Thus, even if only the path of the oil price response matters for oil-market specific shocks, it is still of interest to understand the transmission process from various oil demand and supply shocks to oil prices. For example, colder weather in China would presumably have smaller and shorter-lived effects on oil prices than a rise in oil demand associated with a greater use of motorized vehicles. Return to text
19. We estimated the rule using instrumental variables with lags of inflation and output growth as instruments. Return to text
20. [Leduc and Sill 2004] emphasized that alternative monetary policy rules can lead to markedly different responses of output to oil price increases. In our setup, increasing the long-run elasticity would increase the differences brought about by alternative monetary rules for the response of output and absorption. However, varying the policy rule has a negligible impact on the oil and nonoil trade balance response, because of offsetting movements in the nonoil terms of trade. Return to text
21. We chose a lag length of 4 to avoid serial correlation in the residual. Return to text
22. The weights reflect the share of total oil usage devoted to consumption and production under our baseline calibration (of 1/3 and 2/3, respectively. Gross output is the theoretically preferred production measure implied by our model. However, because deriving a gross output measure requires estimating the share of oil imports directed towards production, we used GDP in our benchmark specification. As a robustness check, we constructed an alternative proxy for gross output, and found little difference from the results reported below. Return to text
This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to text