Systemic Risk from Real Estate and Macro-prudential Regulation1
Abstract:
There is considerable evidence that boom and bust cycles in real estate are the primary cause of financial crises. This paper develops a model of real estate pricing based on rational behavior with two regimes. In "normal times" prices of housing units are determined by the consumers who live in them and are equal to the discounted stream of housing services. In "boom and bust times" speculators find it profitable to borrow from banks and enter the market. There is an agency problem because banks are unable to fully assess the risk that the speculators are taking and this leads to risk shifting and asset substitution. The result is a bubble in real estate prices in that they are higher than the discounted stream of housing services during the boom phase. This model is then used as the basis for analyzing macro-prudential polices designed to prevent the occurrence of such bubbles. These measures include monetary policy, fiscal tools such as real estate transfer taxes, and annual real estate taxes and banking regulation such as restrictions on loan-to-value ratios, countercyclical capital requirements and loan provisions.
1 Introduction
Banking regulation failed to prevent the crisis that started in the summer of 2007. One reason is that it was based on a micro-prudential approach. This involved regulating the risk taken by individual banks. The idea was that if the risk taken by each individual bank was limited then the risk in the financial system as a whole would be limited as well. The problem is that this approach ignores systemic risk. This is the risk faced by the financial system as a whole.
Systemic risk is a complex phenomenon and our understanding of it is still limited. However, there are at least four types of systemic risk. The first is banking panics. These are self-fulfilling multiple equilibria as modeled by Bryant (1980) and Diamond and Dybvig (1983). The work of Friedman and Schwartz (1963) suggested that this was the most important systemic risk. The second is asset price falls that lead to banking crises. There can be many reasons for asset price falls, including business cycle downturns as emphasized by Gorton (1988), the bursting of real estate bubbles, and sovereign default. The last two appear to be particularly important in the current crisis. The third type of systemic risk is contagion in the banking system (Allen and Gale (2000a)) or in the payments system (Freixas, Parigi, and Rochet (2000)) that can lead to the collapse of the financial system. The fourth is foreign exchange mismatches in the banking system. These appear to have been at the heart of the 1997 Asian financial crisis.
Herring and Wachter (1999), Reinhart and Rogoff (2009), and Crowe, Dell'Ariccia, Igan, and Rabanal (2011) have provided evidence that the most important source of systemic risk is the collapse of real estate prices. This has been true both historically and in the current crisis. Our focus is on this type of systemic risk and how it can be countered using macro-prudential policies. Section 2 considers the importance of real estate booms and busts for financial crises, including the current one. Four features are focused on in this context. The first is the positive serial correlation of real estate prices, the second is the regional variation in real estate prices, the third is the role of low interest rates in setting off booms, and the fourth is the availability of credit.
Most of the analysis of real estate prices in the literature is done using standard valuation principles. Poterba (1984) models real estate prices as determined by the discounted stream of rental payments or housing services and this approach is widely used. While this theory has proved very useful in many circumstances, it does not appear to be consistent with the boom-bust cycles or bubbles that play such an important role as a cause of financial crises. In many cases, real estate prices appear to rise dramatically in the space of a few years and then quickly collapse. We argue that any policy analysis of how to prevent financial crises that arise as a result of real estate booms and busts must be based on models that are consistent with this kind of phenomenon. Section 3 of the paper reviews theories of bubbles that can potentially explain these events. These can be divided into four categories: (i) bubbles based on infinite horizon OLG models, (ii) asymmetric information bubbles, (iii) agency theories, and (iv) behavioral theories. We argue that agency theories provide the best foundation for developing a theory of real estate bubbles.
Building on Allen and Gale (2000b) and Allen and Carletti (2010a), Section 4 develops a model of real estate pricing. The model has two regimes. In the first, which we refer to as "normal times," real estate prices are driven by consumer preferences for housing services and reflect these fundamentals. The model works in a similar way to standard real estate pricing models like Poterba (1984). In the basic model there are two periods and three dates, t = 0, 1 and 2. Real estate consumers are risk neutral and consume housing services in the first period between dates 0 and 1 and in the second period between dates 1 and 2. There is an aggregate downward sloping demand curve for housing services that determines their price at each date. The supply at date 0 is fixed. At date 1 there is a random supply shock that makes the price of housing services at that date random. If the supply is large the price is low, while if it is small the price is high. In normal times it is only consumers that buy or rent houses. The rental price is just the value of housing services at that date. The price of houses is the discounted stream of housing services, or equivalently rents.
In the second pricing regime, which we term "boom and bust," speculators enter the real estate market. Unlike consumers who have knowledge of the real estate market because they live there, the speculators need to pay a participation cost to acquire information. This cost depends on the liquidity of the particular market and the geographical features so it varies across regions. If interest rates are sufficiently low and credit is plentiful enough then it will be possible to cover the participation cost in some regions and speculators will enter the market. They invest partly with their own money and borrow the rest. The speculators have limited liability. This means that they can default without penalty. As a result there is a standard risk shifting problem. They will invest in risky real estate and will be prepared to pay more than the fundamental because they keep the upside while the lender bears the cost of default. This is why the price can rise above the fundamental and there can be a bubble.
In this paper we do not focus on the lender's decision. For simplicity, we assume that the government guarantees the debt issued by the bank. Allen and Gale (2003) explain that this government guarantee is not a necessary condition for a bubble to occur. If asymmetric information allows the risky borrowers to pool with safe borrowers then it can be rational for the banks to lend even without government guarantees.
An important feature of the model is that bubbles are regional. Even though interest rates and many features of the credit market are common, the different participation costs for speculators mean that some markets will be in a boom bust regime while others are not. Other parameters such as loan-to-value ratios and underwriting standards may vary across regions as well but for simplicity we focus on varying participation costs.
When the supply of housing at date 2 is large, then the price of housing will fall and in the boom and bust regime there will be a banking crisis. The speculators will default and the government will have to rescue the banks. In the case where the supply of housing is small, the price will be high and the speculators will make large profits.
The size of the bubble will depend on the amount of credit available. We take this as exogenous. As discussed in Section 2, the justification for this is that after the 1997 Asian Crisis, Asian central banks and governments acquired large amounts of foreign exchange reserves. The apparent reason for this was to self-insure rather than be forced to go to the IMF if a similar set of circumstances occurred again. These funds by their nature needed to be invested primarily in dollars or euros. Much of the funds invested in the U.S. appear to have ended up in the real estate market. Some of this was through direct investment in securitized mortgages. Other funds were invested short term and were used to finance special investment vehicles holding securitized mortgages. Another channel was that they were placed in banks on short term deposit and the banks held mortgages. These flows may have been direct or indirect by displacing other funds that were eventually used to fund real estate investment.
As documented in Section 2, over the 2000's the amount of credit available grew because the Asian central banks expanded their holdings of dollar assets. We develop a three period version of the model where the supply of credit is random in the last-but-one period. This also creates a risk shifting problem and accentuates the bubble. The growing credit ensures that the real estate prices are positively serially correlated.
Section 5 discusses macro-prudential policies to prevent real estate bubbles and the associated financial crises in the context of the model. We divide these policies into three categories: (i) monetary policy, (ii) fiscal tools, and (iii) regulation of banks. The section also discusses the limited empirical evidence concerning macro-prudential policies. There are a number of puzzles in this evidence that the model can shed light on due to the threshold effects it captures. The empirical effects of policies will depend very much on the regime an economy is in.
There has been a large literature discussing whether or not it is a good idea for central banks to use monetary policy to "lean against the wind" by raising interest rates to prick asset price bubbles. The conventional wisdom before the crisis, often described as the "Greenspan orthodoxy" was that since it was difficult to identify asset price bubbles it was better to let them burst and clean up the mess afterwards. The current crisis has called into question this orthodoxy. There is also the issue of how much interest rates would have to be raised to prick bubbles. A number of papers, which are discussed in Section 5, suggest that interest rates would need to be raised a large amount to achieve this aim. Particularly in large economies such as the U.S., Eurozone, or China the regions without bubbles would be adversely affected by such raises in interest rates. The existence of the threshold in our model suggests a different policy orientation. The key issue in this case is how to avoid entering the speculative regime. If a country is already experiencing a bubble the policy issue is how to have the speculators leave the market and this may be much more difficult if a bubble is underway. The existence of the threshold also has important implications for empirical work since not distinguishing between the two regimes may lead to incorrect conclusions.
A number of fiscal policy tools can be used in normal times to avoid the market becoming speculative or to encourage the elimination of speculation if the real estate market has already taken off. The first is a tax on real estate transfers. This will make speculation less profitable. Other kinds of taxes, such as property taxes, will have the same effect. Tax breaks on owning houses such as interest deductibility should also be curbed. The evidence on the effectiveness of tax policies is mixed. Again we argue this may be because of threshold effects.
The final category of policy is banking regulation. The first set of instruments is regulations on loan-to-value ratios. We discuss these in the context of the model. The empirical evidence from several Asian countries is that these are effective for a short period of time but then people appear to be able to find ways around them and their effectiveness does not last. The second is regulation of banks' capital and loss reserves. The idea here is to strengthen the banks so that even though there may be a boom-bust cycle the banks will be able to withstand the bust without failing. One tool is countercyclical capital requirements and risk weights. The notion is that banks should strengthen their capital buffers during good times and then run them down in the event of a bust. Another tool is dynamic provisioning. Banks' loan loss provisions can be made countercyclical so that they are increased in the upswing phase of the cycle and reduced in the downswing phase.
Finally, Section 6 contains concluding remarks.
2 Real Estate Prices and Financial Crises
There is extensive evidence that the most important cause of banking crises is real estate booms and busts. Herring and Wachter (1999) document a wide range of boom and bust real estate cycles and their effect on banks. These episodes include Boston in the 1970's and 1980's, Sweden in the 1980's and 1990's, the Japanese bubble of the same period, and Thailand in the 1990's.
Reinhart and Rogoff (2009, Chapter 13) provide a broad range of episodes where real estate played an important role in causing banking crises. These include the Big 5 in advanced Economies: Spain in the 1970's, Norway in the 1980's, Sweden, Finland and Japan in the 1990's; the Big 6 in the Asian Crisis in 1997: Hong Kong, Indonesia, Malaysia, the Philippines, South Korea, and Thailand. Other examples from emerging countries are Colombia in 1998 and Argentina in 2001. Two interesting historical episodes are Norway in 1898 and the US in the Great Depression. In Chapter 16 they provide evidence of the important role real estate played in many countries during the Great Depression.
Finally, Crowe et al. (2011, Text Table 1, p. 5) give data on the relationship between real estate boom and bust cycles, banking crises, credit crunches and macroeconomic performance using a sample of 40 countries. For example, more than two thirds of the 46 systemic banking crises for which house price data are available were preceded by boom and bust episodes. In addition, 35 out of 51 boom and bust episodes were followed by a banking crisis.
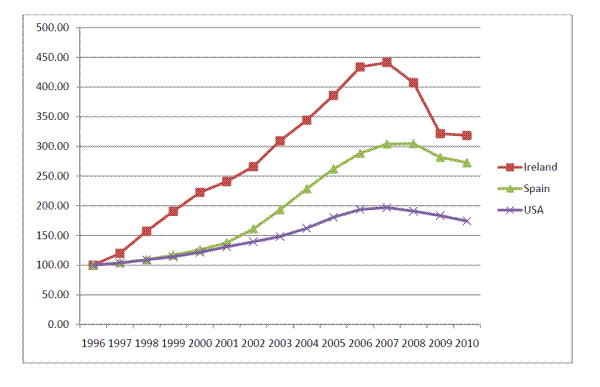
Real estate clearly played an important role in the current crisis. Figure 1 plots nominal housing prices in Ireland, Spain and the U.S. It can be seen that the boom and bust in Ireland was particularly large. This was the cause of their massive banking crisis. Because the state guaranteed the banks' debt the boom bust cycle has also caused a sovereign debt crisis. This led to the bail-out by other Eurozone and European Union governments. Spain also had a large run up in real estate prices. So far they have not fallen nearly as much as in Ireland. However, as Taylor (2008) points out, Spain had the biggest housing boom as measured by the change in housing investment as a share of stocktickerGDP. This is why their unemployment rate has been so high during the bust phase of the cycle.
The plots in Figure 1 suggest that there might be positive serial correlation in housing returns. Case and Shiller (1989), Englund, Quigley and Redfearn (1998) and Glaeser and Gyourko (2007) have investigated this issue on a range of different data sets. They do indeed find evidence of positive serial correlation. For example, Glaeser and Gyourko (2007) find that a $1 increase in real estate prices one year will on average be followed by a $0.71 increase the following year. Thus once a real estate boom has started it is likely that it will persist for some time. Similarly for a bust, once real estate prices have started to fall this is likely to continue. This feature of real estate prices is very different from stock prices where there is extensive evidence that stock returns are (at least to a first approximation) a random walk. The serial correlation in real estate returns is an important phenomenon that is not well understood.
A striking feature of Figure 1 is that the U.S. boom and bust cycle was much less extreme than in Ireland and Spain. However, this is misleading because the figures are for the country as a whole. There was a very wide range of experiences in different parts of the country. Figure 2 shows the experiences of the 10 cities that make up the Case-Shiller 10 City Index. Two things stand out from the figure. The first is that from the mid 1990's until the early 2000's the prices in all ten cities move together. But for the next few years they had widely different experiences. Miami and Los Angeles had massive booms and busts while Denver had a relatively small change in prices, with the other cities somewhere in between. However, in all these cities the interest rates and many other features of the credit market were common. It is not well understood why the experiences were so similar and then so different.
One of the major debates about the boom and bust episodes in the current crisis is the extent to which the real estate bubble in these countries was the result of loose monetary policy and global imbalances that led to excessive credit availability. Central banks, in particular the Federal Reserve in the U.S., set very low interest rates during the early 2000's to avoid a recession after the bursting of the tech bubble in 2000 and the 9/11 terrorist attacks in 2001. As argued by Taylor (2008) these levels of interest rates were much lower than in previous U.S. recessions relative to the economic indicators at the time captured by the "Taylor rule".
Although the ECB did not set as low absolute rates as the Federal Reserve, the different countries had very different economic conditions. As Figure 1 shows, Spain and Ireland also had very large run ups in property prices. For them the ECB's policy was very loose. Other countries in the Eurozone, such as Germany, did not have a housing boom. Their inflation rates and other economic indicators were such that for them the European Central Bank's interest rates did not correspond to a loose monetary policy.
Taylor's position has been quite controversial. For example, Bernanke (2010) has argued that the Taylor rule is sensitive to the choice of inflation measure and to whether actual or forecasted inflation and output gaps are used. Once changes in these measures are introduced, it is no longer clear whether interest rates were unusually low given the state of the economy or whether house prices were unusually high given interest rates and the state of the economy. Bernanke (2010) concludes that Taylor`s claim is not persuasive enough. He suggests that what seems to have played a crucial role in setting the stage for the crisis is financial innovation in the form of mortgage contracts and securitization. Rather than interest rates being set too low, the implications of financial innovation for monetary policy transmission were not understood by monetary policy makers. This failure together with weak financial regulation and supervision set the stage for the crisis.
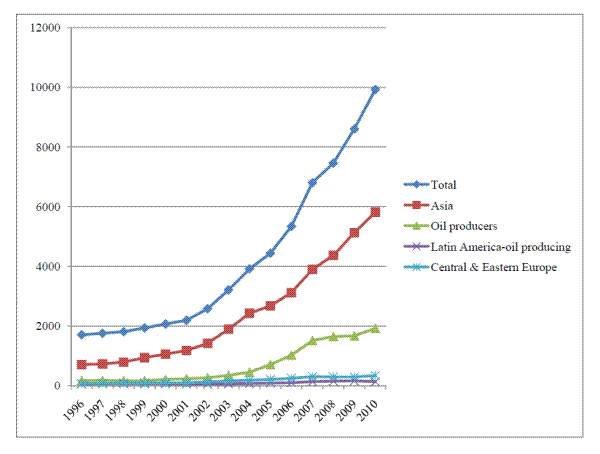
As Allen and Gale (2000b, 2003, 2004, and 2007) have argued, asset price bubbles are also caused by growth in credit. During the recent crisis, credit expanded rapidly in the countries with low interest rates due to the presence of global imbalances. Several Asian countries started accumulating large amounts of reserves in the late 1990s and these grew to high levels. Figure 3 illustrates that this acquisition of reserves was primarily an Asian phenomenon. Oil producers also accumulated reserves when oil prices rose but primarily it was the Asian countries and particularly the East Asian countries. In Latin America and Central and Eastern European countries reserves did not increase significantly. Why did Asian countries increase their reserves so much? Allen and Carletti (2010b) and Allen and Hong (2011) argue that the Asian countries affected by the crisis of 1997 started accumulating reserves in response to the tough conditions that the International Monetary Fund imposed on them in exchange for financial assistance. The motivations for the reserve accumulation of China, which is the largest holder, are more complex than this. Beside the precautionary reason, China started accumulating reserves to avoid allowing its currency to strengthen and damage its exports as well as to increase its political power. It gradually found that the U.S. and Eurozone were much more accommodating and less critical of its policies when it held large amounts of their debt.
The Asian countries invested these huge reserves mostly in PersonNamedebt instruments as they experienced difficulties in buying equities. An example was the blocked acquisition by the Chinese state oil company CNOOC of the American Unocal. The country-regionplaceU.S. authorities blocked the transaction on the grounds that Unocal was a strategic firm. As a consequence, Asian countries turned to PersonNamedebt instruments, in particular Treasuries, Fannie and Freddie mortgage-backed securities, and many other types.
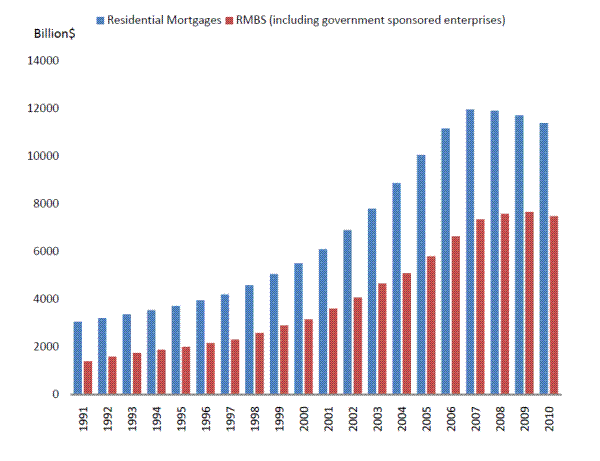
Figure 4 shows the total amount of residential mortgages and residential mortgage backed securities (RMBS) in the U.S. in the 1990's and 2000's. It can be seen that in the early 2000's total mortgages were about $6 trillion. By 2006 they had doubled to about $12 trillion. This growth in mortgages roughly corresponded to the growth in foreign exchange reserves. The Chinese, for example, directly bought many Fannie Mae and Freddie Mac securitized mortgages. They also bought many Treasury securities. This freed up funds of other investors to invest in mortgages. In addition to long term securities, much of the foreign exchange reserves were invested short term. Since many of the mortgages were funded by short term investments, this part of the increase in reserves ultimately helped fund mortgages. To the extent the reserves were invested in banks, they also contributed to the ability of these banks to fund mortgages held on their balance sheets. Thus overall, the increase in reserves enabled a large increase in the amount of mortgage credit available.
In summary, we have focused on four features of the real estate and mortgage markets. The first is the positive serial correlation of real estate prices that has been documented. The second is the wide regional variation in real estate prices in the U.S. The experience in the Eurozone is similar. Countries like Ireland and Spain had large booms and busts, while Germany's real estate prices were fairly constant, despite the fact that all of them were part of the same monetary union. The third issue we discussed was debate about the role of low interest rates in setting off real estate booms. Finally, we documented the large rise in foreign exchange reserves, particularly those held by Asian countries and the significant expansion in the availability of mortgage credit that occurred at the same time.
3 Theories of Bubbles
Arguably the most important reform to prevent future financial crises is to design policies that ensure that real estate boom and bust episodes, or in other words bubbles, are minimized. In order to do this we need tractable models of bubbles that can be used as a basis for policy analysis. Developing such theories has so far proved a difficult task.
Much of the early theoretical literature was concerned with showing that bubbles do not arise in standard models. Tirole (1982) argued that with a finite horizon or a finite number of agents, bubbles in which asset prices deviate from fundamentals are not consistent with rational behavior. Santos and Woodford (1997) have argued that the conditions under which bubbles arise in standard general equilibrium frameworks are very special.
Building on the overlapping generations model of Samuelson (1958), Tirole (1985) showed that bubbles could exist in infinite horizon models in which all agents are rational. A literature based on developments of this model has developed. Recent contributions include Caballero and Krishnamurthy (2006), and Farhi and Tirole (2010). An important issue with these models is the extent to which the OLG framework is consistent with the kind of bubbles in real estate and stock markets that are documented in Kaminsky and Reinhart (1999), Reinhart and Rogoff (2009) and elsewhere where bank credit appears to play an important role and the bubbles grow very quickly before bursting.
A second branch of the bubbles literature builds on asymmetric information models where everybody rationally believes that they may be able to sell the asset at a higher price even though it is above its fundamental. Allen, Morris and Postlewaite (1993) developed a discrete-time, finite-horizon model where the absence of common knowledge led to bubbles in asset prices. However, the model is not very robust. Conlon (2004) and Dobles-Madrid (2010) develop more appealing versions of this kind of model that are more robust.
A third branch develops agency theories of bubbles. Allen and Gorton (1993) constructed a model with continuous time and a finite horizon in which an agency problem between investors and portfolio managers could produce bubbles even though all participants were rational. Allen and Gale (2000) develop a model with an agency problem in discrete time where bubbles arise as a result of an expansion in credit. Barlevy (2009) extends this kind of model to allow for more general debt contracts and dynamic considerations. Allen and Gale (2003, 2004, 2007) and Adrian and Shin (2008) explicitly focus on the relationship between lending and asset price bubbles.
The difficulty in reconciling bubbles with rational behavior resulted in many authors such as De Long, Shleifer, Summers and Waldmann (1990) developing a fourth type of asset pricing model based on irrational behavior. Herring and Wachter (1999) provide a behavioral theory based on "disaster myopia". Recent contributions in this strand of the literature, which involve slight deviations from rationality and provide appealing models of bubbles, include Abreu and Brunnermeier (2003) and Scheinkman and Xiong (2003).
Perhaps the most promising theory of bubbles to analyze real estate bubbles is agency theories. Allen and Gale (2000, 2003, 2004, and 2007) show how a risk shifting problem in the banking system can lead to asset price bubbles. However, their model does not explain why the real estate market in many countries operates without bubbles for long periods of time. An important extension is to understand why there appear to be two regimes, one where fundamentals drive real estate prices and one where speculators enter the market and there is a bubble. It is also important that such a theory should be consistent with the positive serial correlation in housing prices and the wide regional variations in bubbles that are observed in areas with the same interest rates and monetary regimes. The next section develops such a model.
4 A Theory Real Estate Pricing
The Model
We start by considering the case where there are two periods and three dates t = 0, 1, 2. At date 0 there is an existing stock of housing that supplies ![]() units of housing. We assume
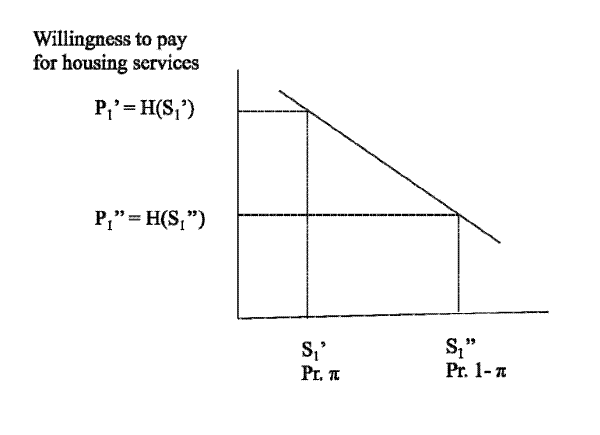
there is a representative consumer that has a willingness to pay for S units of housing per period of H(S) where H'(S) < 0, as shown in Figure 5. It is possible to rent housing each period. The rent is paid at the beginning of the period so
units of housing. We assume
there is a representative consumer that has a willingness to pay for S units of housing per period of H(S) where H'(S) < 0, as shown in Figure 5. It is possible to rent housing each period. The rent is paid at the beginning of the period so ![]() is paid at date t for the period between date t and date t+1. When there is a fixed supply
is paid at date t for the period between date t and date t+1. When there is a fixed supply ![]() of housing in period t the rate
paid is
of housing in period t the rate
paid is ![]() =
= ![]() . The opportunity cost of capital per period of the consumers
is
. The opportunity cost of capital per period of the consumers
is ![]() and they are risk neutral.
and they are risk neutral.
Pricing in Normal Times
In addition to a rental market there is a market for buying houses at price P![]() . For the moment we assume the only people in this market are consumers. The amount the consumers are
willing to pay is the flow of housing services they receive or equivalently, the rent they would pay. At date t = 1 there is one period remaining so the purchase price and the rental rate are the same
. For the moment we assume the only people in this market are consumers. The amount the consumers are
willing to pay is the flow of housing services they receive or equivalently, the rent they would pay. At date t = 1 there is one period remaining so the purchase price and the rental rate are the same
At date t = 0 the supply of housing at date 1 is random. It is low at ![]() with probability
with probability ![]() in which case
in which case
It is high at ![]() with probability
with probability ![]() in which case
in which case
Since
![]() , we have
, we have
![]() , as shown in Figure 5.
, as shown in Figure 5.
At date 0 with supply ![]() we have the rental price
we have the rental price
The price of the house at date 0 is ![]() , given consumers' risk neutrality and their opportunity cost of capital is
, given consumers' risk neutrality and their opportunity cost of capital is ![]() is
is
In this case it can be seen that real estate prices are driven by the fundamentals of the expected flow of housing services. We refer to the case where the pricing equation is (1) as "normal times".
We have not modeled where consumers obtain the funds to purchase houses. For simplicity we assume that they use their own funds. It is equivalent if they borrow to buy and do not default either because the transaction costs of doing so are too high or because it is not legally possible. We could introduce another group of consumers that borrows with limited liability but this would complicate the analysis without changing the results significantly.
The Role of Speculators
We next introduce speculators who have wealth W to the model. They are risk neutral and their opportunity cost is ![]() . They earn this return by investing in alternative investments.
Another possibility is for them to borrow and invest in real estate. Their cost of participating in the real estate market is
. They earn this return by investing in alternative investments.
Another possibility is for them to borrow and invest in real estate. Their cost of participating in the real estate market is ![]() . Unlike consumers who live in their houses and hence have
knowledge about their local housing market, speculators do not. They must expend the cost
. Unlike consumers who live in their houses and hence have
knowledge about their local housing market, speculators do not. They must expend the cost ![]() to investigate its characteristics. This cost varies by region. In places where the market is
liquid and there are many more transactions, it is easier to deduce the market characteristics. Also in places where housing is denser, it will also be cheaper to acquire the necessary information. Hence
to investigate its characteristics. This cost varies by region. In places where the market is
liquid and there are many more transactions, it is easier to deduce the market characteristics. Also in places where housing is denser, it will also be cheaper to acquire the necessary information. Hence ![]() will be lower in liquid and dense housing markets than in illiquid and sparsely populated housing markets.
will be lower in liquid and dense housing markets than in illiquid and sparsely populated housing markets.
If speculators borrow their loan to value ratio is ![]() so that if they buy x units of housing at price
so that if they buy x units of housing at price ![]() then
then
or
At date 0 they can borrow
![]() at
at ![]() and invest in real estate. They have limited liability, so
they receive
and invest in real estate. They have limited liability, so
they receive
| Max |
Given the random supply at date 1 and the resulting random price, there may be default. We focus on the case where there is no default when the price is high but there is when it is low so
and
There is thus default with probability ![]() so that the speculators' expected profits are
so that the speculators' expected profits are
![]() . Speculators will be unwilling to enter the real estate market provided
. Speculators will be unwilling to enter the real estate market provided
The left hand side is the expected profits at date 1 less the participation cost paid at date 0. The right hand side is the amount earned by speculators in their alternative investment. In this case there will be normal times and real estate will be priced as in (1).
Pricing in Boom and Bust Times
However, if the inequality (3) is reversed then speculators will be willing to invest in real estate. In this case borrowing to buy housing is more profitable than the speculators' alternative opportunity. As a result they will compete to buy properties and since at
date 0 real estate is in fixed supply, the purchase price of housing ![]() will be bid up above its fundamental
will be bid up above its fundamental ![]() until speculators no longer have an incentive to enter. This will occur when
until speculators no longer have an incentive to enter. This will occur when ![]() and
and
Substituting for W using (2) and solving for the price gives
A bubble occurs when
One special case of particular interest is where
![]() ,
,
![]() and
and ![]() =
= ![]() =
= ![]() =
= ![]() .
Here
.
Here
since
![]() . Hence in this case there is a bubble. The inequality (6) illustrates why. For the speculators who are investing with borrowed money and have
limited liability, what matters is the return distribution where they do not default. For the consumers, it is the whole return distribution that matters. We have modeled speculators and consumers as different to bring out the differences between buying with your own money and investing with
borrowed money and limited liability. As mentioned above we could introduce a third group of consumers who borrow with limited liability but this would not change the results qualitatively.
. Hence in this case there is a bubble. The inequality (6) illustrates why. For the speculators who are investing with borrowed money and have
limited liability, what matters is the return distribution where they do not default. For the consumers, it is the whole return distribution that matters. We have modeled speculators and consumers as different to bring out the differences between buying with your own money and investing with
borrowed money and limited liability. As mentioned above we could introduce a third group of consumers who borrow with limited liability but this would not change the results qualitatively.
If the supply of real estate at date 1 turns out to be high and prices are low then there will be a default at date 1 and this may cause a financial crisis if speculators make up a significant proportion of banks' borrowers.
The special case illustrates that bubbles can occur as a result of speculation. However, this is not the only situation where bubbles will occur. There are a wide range of parameter values where the inequality in (3) will be reversed and speculators will enter. The lower is the interest rate that speculators can borrow at relative to their opportunity cost of capital the more likely speculation will occur. Similarly, the higher the loan-to-value ratio and the lower is the participation cost, the more likely speculation will occur.
Since the participation cost ![]() varies across regions, it is straightforward to see that speculation may occur in some regions while not in others. Given our justification for
varies across regions, it is straightforward to see that speculation may occur in some regions while not in others. Given our justification for
![]() , speculation is more likely to occur when it is low and this will happen in liquid markets with high density. We have used this as a modeling device. There are many other parameters
that could vary regionally. For example, bankruptcy laws and as a result underwriting standards and loan-to-value ratios may differ. For these reasons we may see normal pricing in some regions while there are boom and bust times in other regions.
, speculation is more likely to occur when it is low and this will happen in liquid markets with high density. We have used this as a modeling device. There are many other parameters
that could vary regionally. For example, bankruptcy laws and as a result underwriting standards and loan-to-value ratios may differ. For these reasons we may see normal pricing in some regions while there are boom and bust times in other regions.
So far we have not discussed the lending decision of the bank. As discussed in Allen and Gale (2003, 2004, 2007) there are a number of ways to explain why banks are willing to rationally lend to speculators. The first is that government guarantees such as deposit insurance mean that it is the government rather than the bank that ultimately bears the downside of the speculation. Another possibility is that speculators are able to pool with other borrowers who effectively subsidize their losses. In this case in a competitive banking system it is ultimately depositors that bear the costs of speculation.
We have taken supply as fixed in the short run and with a random supply response in the long term. The randomness can be thought of as due to the uncertain supply response. In practice supply responses can be large if the bubble is long lasting and big. It is large supply responses that can potentially be so damaging when the bubble bursts. The high unemployment in Spain and Ireland are examples of this.
Endogenous Loan-to-Value Ratios
We have so far taken the loan-to-value ratio ![]() as exogenous. Given our justification for the supply of funds as being driven by self-insurance motives of Asian countries, the supply
is likely to be quite inelastic. Since central banks control at least short term interest rates, it may well be that loan-to-value ratios adjust to clear the market. The increase in subprime mortgages in the U.S. in the early 2000's is consistent with this. We next develop a version of the model
where this happens.
as exogenous. Given our justification for the supply of funds as being driven by self-insurance motives of Asian countries, the supply
is likely to be quite inelastic. Since central banks control at least short term interest rates, it may well be that loan-to-value ratios adjust to clear the market. The increase in subprime mortgages in the U.S. in the early 2000's is consistent with this. We next develop a version of the model
where this happens.
Suppose there are N speculators and the aggregate amount of credit at date t is X![]() . Then when speculators' demand is equal to supply so
. Then when speculators' demand is equal to supply so ![]()
For simplicity we focus on the case where ![]() ,
, ![]() ,
, ![]() and
and ![]() =
= ![]() =
= ![]() =
= ![]() . Here
. Here
It can be seen from (8) that the price is not only driven by the payoffs in the good state but also by the aggregate amount of credit in the market. The higher the amount of credit available, the higher the price will be.
A Three-Period Model
We have focused on the two-period case so far. We next consider the case where there are three periods by adding the date t = -1 before date 0. In the case where consumers determine the price, similarly to (1), at date t = -1 the price would be
where ![]() =
= ![]() . This assumes that supply is fixed at
. This assumes that supply is fixed at ![]() at date t = -1.
at date t = -1.
Next consider the case with speculators. Suppose that at date t = -1 the level of credit at date 0, ![]() , is perceived to be random. With probability
, is perceived to be random. With probability ![]() the aggregate amount of credit is
the aggregate amount of credit is ![]() and with probability
and with probability
![]() it is
it is ![]() where
where
![]() . Considering the same special case as in the previous section we can see that the price will be high (low) when aggregate credit is high (low) so
. Considering the same special case as in the previous section we can see that the price will be high (low) when aggregate credit is high (low) so
![$\displaystyle P_{0}^{B}' =\pi \left[H_{0} +\frac{P_{1}'}{(1+r)} \right] + (1-\pi )X'_{0} > P_{0}^{B}](img55.gif) |
Assuming that bankruptcy occurs only when prices are low, as before, we can show
![\displaystyle P_{-1}^{B} = \pi _{0} \left[H_{-1} +\pi \left[\frac{H_{0} }{1+r} + \frac{P_{1}'}{(1+r)^{2} } \right] + \frac{(1-\pi )X'_{0} }{1+r} \right] + (1-\pi )X_{-1} .](img56.gif) |
If we keep lengthening the horizon the size of the bubble will grow because what is relevant for pricing with speculation is the upper part of the distribution of returns not the whole distribution as in normal times. There is a whole sequence of discounted upper parts of the distribution and so the bubble is larger. What's more the greater the uncertainty, the higher the price of the asset.
As discussed in Section 2, one of the interesting features of real estate prices is that in contrast to stocks, returns are positively serially correlated. The theory presented provides a possible explanation of this. A bubble will continue as long as prices have good outcomes and this will occur as long as credit keeps growing and there is no supply response. During the period of growing credit, returns will be positively serially correlated in regions where there is a boom bust cycle. This would correspond to the period from the early 2000's until 2006 when credit grew rapidly in the U.S. as shown in Figure 4.
5 Macro-prudential Policies
The previous sections have highlighted systemic risk arising from bubbles in real estate prices. This section discusses the policies that might be put in place to deal with this source of systemic risk. We start with the role of monetary policy and in particular of interest rate policy, then consider the role of fiscal tools such as transfer taxes. Finally, we consider the role of banking regulation.
Interest Rate Policy
There has been much discussion about the extent to which interest rates should be adjusted in response to changes in asset prices. Very few central banks have taken the approach of targeting real estate prices. Cecchetti (2005) and Cagliarini, Kent and Stevens (2010) give the examples of Australia and Sweden. In Australia in 2003 an increase in interest rates that was partially justified to the public by developments in the housing markets led to a softening of the real estate market and a fall in nominal house prices in a number of areas of the country. Sweden's central bank, the Riksbank, has for some time considered property prices when making interest rate decisions. Ingves (2007) gives the example of February 23, 2006 when the Executive Board of the Riksbank voted to raise the interest rate by 0.25% because of house price increases. The question is whether this is a good idea.
In an important early paper, Borio and Lowe (2002) suggest that while it is difficult to predict asset price bubbles and in particular property bubbles, it is not impossible. They provide evidence that rapid credit growth combined with large increases in real estate prices can lead to financial instability. In low inflation environments they suggest that inflationary pressures can first appear in asset prices rather than in the prices of goods and services. They argue that in such cases it may be appropriate to use monetary policy by raising interest rates to prick asset bubbles and to preserve financial and monetary stability.
Assenmacher-Wesche and Gerlach (2008, 2010) have argued that it is extremely costly in terms of reductions in GDP to use monetary policy to deal with real estate bubbles. They use a vector autoregression methodology to study the relationships between inflation, economic activity, credit, monetary policy and property and equity prices in 17 OECD countries using quarterly data from 1986-2006. Among other things they find that to offset a 15 percent rise in residential property prices the central bank might have to depress real GDP by 5 percent. This suggests that monetary policy should not be used to prick real estate bubbles as it is simply too costly.
Assenmacher-Wesche and Gerlach do not use a theory of bubbles in their analysis. An important issue is that much of the time, as discussed above, real estate markets do not have bubbles. For example, it seems that in the U.S. property prices were much of the time determined by fundamentals from the 1930's through to the 1990's. There were no sudden run-ups and collapses in prices. This suggests that there are important threshold effects. Much of the time when prices are driven by fundamentals large rises in interest rates will be required to reduce property prices even a few percent as their results suggest. It is important to distinguish between the two regimes in empirical work. The effect may be different in bubble times.
The theory above suggests that the key issue is to prevent a change of regime. Once a bubble is started it may be quite difficult to break it as aggregate credit may drive the dynamics and this may be difficult to counteract. Focusing on the special case where ![]() =
= ![]() =
= ![]() =
= ![]() and simplifying (1) and (4) we have
and simplifying (1) and (4) we have
and
Provided
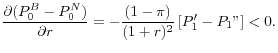 |
Hence cutting interest rates can trigger a bubble if the loan to value ratio is high enough. This model thus provides a rationale for why low interest rates may be undesirable.
Fiscal Tools
Perhaps the most obvious example of a fiscal tool that may help prevent a real estate bubble is a transfer tax T when a property changes hands. In this case the condition (3) to prevent the entry of speculators is changed to
By making the transfer tax large enough it should be possible to prevent bubbles.
Crowe et al. (2011) point out that Belgium has large transfer taxes and has had very little property price booms and busts. On the other hand, Japan also has had a high transfer tax but has had a massive boom and bust episode. The theory presented here throws some light on this. A high transfer tax will help prevent a bubble. But once a bubble is triggered it is aggregate credit dynamics that drive the bubble and these can overwhelm the effect of the transfer tax.
Another kind of tax that has been suggested as having a role to pay in this context is annual property taxes. These can also be incorporated in (3) and it can be seen they reduce the likelihood of a bubble.
Bank Regulation
One of the widely recommended macro-prudential policy for controlling boom and bust cycles is to put restrictions on loan-to-value ratios. In the context of the model presented it can straightforwardly be seen that this will have the desired effect in a bubble. Using (11) it can be seen that
![\displaystyle \frac{\partial P_{0}^{B} }{\partial \lambda } = \frac{(1-\pi )}{\left[1-(1-\pi )\lambda \right]} P_{0}^{B} >0.](img64.gif) |
Hence lowering loan-to-value ratios through regulation will lead to a reduction in real estate prices in a boom in the context of the model.
However, in practice this does not seem to occur. Crowe et al. (2011) survey the literature on the effects of these types of macroprudential measures to eliminate real estate booms. They have been tried in several Asian countries including, Hong Kong, Korea, and Singapore. The regulations appear to be effective in the short term but not in the medium and long term. It seems that people are able to fairly quickly work out how to circumvent the regulations.
Other types of banking regulation that have been suggested such as countercyclical capital ratios or loan loss provisions are different in terms of their purpose. They are designed to allow banks to withstand shocks if a real estate bubble should burst. These are desirable to implement provided they are not too costly.
6 Concluding Remarks
Most of the existing literature on real estate valuation uses a model like Poterba (1984) where prices are equal to discounted payoff streams. These kinds of models are difficult to reconcile with boom and bust cycles of the kind that are often observed. This paper develops a model of real estate bubbles to analyze to understand when such situations can arise. The model is then used to analyze macroprudential regulations to prevent boom and bust cycles.
Abreu, D. and M. Brunnermeier (2003). "Bubbles and Crashes," Econometrica 71, 173-204.
Adrian, T. and H. Shin (2008). "Financial Intermediaries, Financial Stability and Monetary Policy," 2008 Jackson Hole Conference Proceedings, Federal Reserve Bank of Kansas City, 287-334.
Allen, F. and E. Carletti (2010a). "What Should Central Banks do About Real Estate Prices?" Working Paper 11-29, Wharton Financial Institutions Center, University of Pennsylvania.
Allen, F. and E. Carletti (2010b). "An Overview of the Crisis: Causes, Consequences and Solutions," International Review of Finance 10, 1-27.
Allen, F. and D. Gale (2000a). "Financial Contagion," Journal of Political Economy 108, 1-33.
Allen, F. and D. Gale (2000b). "Bubbles and Crises," Economic Journal 110, 236-255.
Allen, F. and D. Gale (2003). "Asset Price Bubbles and Stock Market Interlinkages" in Asset Price Bubbles: The Implications for Monetary, Regulatory, and International Policies edited by William C. Hunter, George G. Kaufman, and Michael Pomerleano, Cambridge: MIT Press, 323-336.
Allen, F. and D. Gale (2004). "Asset Price Bubbles and Monetary Policy" (with D. Gale) in Global Governance and Financial Crises, edited by M. Desai and Y. Said, New York and London: Routledge, Chapter 3, 19-42.
Allen, F. and D. Gale (2007). UnPersonNamederstanding Financial Crises, Clarendon Lecture Series in Finance, Oxford: Oxford University Press.
Allen, F. and G. Gorton (1993). "Churning Bubbles," Review of Economic Studies 60, 813-836.
Allen, F. and J. Hong (2011). "Why are there Global Imbalances? The Case of South Korea," Working Paper 11-32, Wharton Financial Institutions Center, University of Pennsylvania.
Allen, F., S. Morris, and A. Postlewaite (1993). "Finite Bubbles with Short Sale Constraints and Asymmetric Information," Journal of Economic Theory 61, 206-229.
Assenmacher-Wesche, K. and S. Gerlach (2008). "Monetary Policy, Asset Prices and Macroeconomic Conditions: A Panel-VAR Study," working paper, Institute for Monetary and Financial Stability, University of Frankfurt.
Assenmacher-Wesche, K. and S. Gerlach (2010). "Financial Structure and the Impact of Monetary Policy on Property Prices," working paper, Institute for Monetary and Financial Stability, University of Frankfurt.
Barlevy, G. (2009). "A Leverage-based Model of Speculative Bubbles," working paper, Federal Reserve Bank of Chicago.
Bernanke, B. (2010). "Monetary Policy and the Housing Bubble," Speech to the Annual Meeting of the American Economic Association, Atlanta, Georgia, http://www.federalreserve.gov/newsevents/speech/bernanke20100103a.htm.
Borio, C. and P. Lowe (2002). "Asset Prices, Financial and Monetary Stability: Exploring the Nexus," BIS Working Paper 114, Basel, Switzerland.
Bryant, J. (1980). "A Model of Reserves, Bank Runs, and Deposit Insurance," Journal of Banking and Finance 4, 335-344.
Caballero, R., and A. Krishnamurthy (2006). "Bubbles and Capital Flow Volatility: Causes and Risk Management," Journal of Monetary Economics 53, 35-53.
Cagliarini, A., C. Kent, and G. Stevens (2010). "Fifty Years of Monetary Policy: What Have we Learned?", working paper, Reserve Bank of Australia.
Case, K. and R. Shiller (1989). "The Efficiency of the Market for Single-Family Homes," American Economic Review 79, 125-137.
Cecchetti, S. (2005). "The Brave New World of Central Banking: The Policy Challenges Posed by Asset Price Booms and Busts," Czech National Bank, Working Paper Series No. 14.
Conlon, J. (2004). "Simple Finite Horizon Bubbles Robust to Higher Order Knowledge," Econometrica 72, 927-36.
Crowe, C., G. Dell'Ariccia, D. Igan, Rabanal (2011). "How to Deal with Real Estate Booms: Lessons from Country Experiences," IMF Working Paper 11/91.
De Long, B., A. Shleifer, L. Summers, and R. Waldmann, (1990). "Positive Feedback Investment Strategies and Destabilizing Rational Speculation," Journal of Finance 45, 379-395.
Diamond, D. and P. Dybvig (1983). "Bank Runs, Deposit Insurance, and Liquidity," Journal of Political Economy 91, 401-419.
Dobles-Madrid, A. (2009). "A Robust Model of Bubbles with Multidimesional Uncertainty," working paper, Michigan State University.
Englund, P., J. Quigley and C. Redfearn (1998). "Improved Price Indexes for Real Estate: Measuring the Course of Swedish Housing Prices," Journal of Urban Economics 44, 171-196.
Farhi, E. and J. Tirole (2010). "Bubbly Liquidity," Review of Economic Studies, forthcoming.
Freixas, X., B. Parigi, and J. Rochet (2000). "Systemic Risk, Interbank Relations and Liquidity Provision by the Central Bank," Journal of Money, Credit & Banking 32, 611-38.
Friedman, M. and A. Schwartz (1963). A Monetary History of the United States, 1867-1960, Princeton University Press, Princeton, NJ.
Giovazzi, F. and F. Mishkin (2006). "An Evaluation of Swedish Monetary Policy 1995-2005," Reports from the Riksdag 2006/07:RFR 1, Committee on Finance.
Glaeser, E. and J. Gyourko (2007). "Housing Dynamics," working paper, Wharton School, University of Pennsylvania.
Gorton, G. (1988). "Banking Panics and Business Cycles," CityplaceOxford Economic Papers 40, 751-781.
Herring, R. and S. Wachter (1999). Real Estate Booms and Banking Busts: An International Perspective, Wharton Financial Institutions Center Working Paper 99-27, University of Pennsylvania.
Ingves, S. (2007). "Housing and Monetary Policy: A View from an Inflation-Targeting Central Bank," 2007 Federal Reserve Bank of Kansas City Conference Volume on Housing, Housing Finance, and Monetary Policy, 433-443.
Kaminsky, G. and C. Reinhart (1999). "The Twin Crises: The Causes of Banking and Balance-of-Payments Problems," American Economic Review 89, 473-500.
Poterba, J. (1984). "Tax Subsidies to Owner-Occupied Housing: An Asset-Market Approach," Quarterly Journal of Economics 99, 729-752.
Reinhart, C., and K. Rogoff (2009). This Time is Different: Eight Centuries of Financial Folly, CityOxford and placePrinceton: Princeton University Press.
Samuelson, P. (1958). "An Exact Consumption-Loan Model of Interest with or without the Social Contrivance of Money," Journal of Political Economy 66, 467-482.
Santos, M. and M. Woodford (1997). "Rational Asset Pricing Bubbles," Econometrica 65, 19-57.
Scheinkman, J., and W. Xiong (2003). "Overconfidence and Speculative Bubbles," Journal of Political Economy 111, 1183-1220.
Taylor, J. (2008). "The Financial Crisis and the Policy Responses: An Empirical Analysis of What Went Wrong," working paper, Stanford University.
Tirole, J. (1982). "On the Possibility of Speculation under Rational Expectations," Econometrica 50, 1163-1181.
Tirole, J. (1985). "Asset Bubbles and Overlapping Generations," Econometrica 53, 1499-1528.
Sources: Irish Dep. of the Environment, Banco de España, FHFA, OECD.
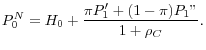
![\displaystyle P_{0}^{B} =\frac{\pi }{\pi \lambda + (1 - \lambda )(1 + \rho _{S} )/(1+r_{0} )} \left[H_{0} \frac{(1+\rho _{S} )}{(1+r_{0} )} + \frac{P_{1}'}{(1+r_{0})} - \frac{2\phi }{\pi S_{0} } \frac{(1+\rho _{S} )}{(1+r_{0} )} \right].](img35.gif)
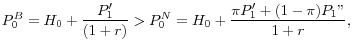
![\displaystyle P_{0}^{B} =\pi \left[H_{0} +\frac{P_{1}'}{(1+r)} \right]+(1-\pi )X_{0} .](img45.gif)
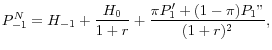
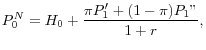
![\displaystyle P_{0}^{B} =\frac{\pi }{1-(1-\pi )\lambda } \left[H_{0} +\frac{P_{1}'}{(1+r)} - \frac{2\phi }{\pi S_{0} } \right].](img58.gif)