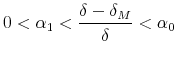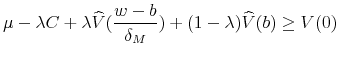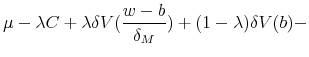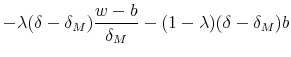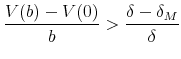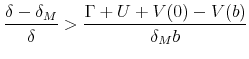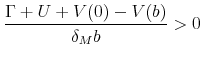TAMING SIFIS*
Abstract:
1 INTRODUCTION
One of the main lessons that can be drawn from the subprime crisis of 2007-09 is probably the threat posed by "Systemically Important Financial Institutions" (SIFIs) to the stability of the financial sectors of most developed countries. Even if the Too Big To Fail (TBTF) issue has long been recognized as of major importance1, the way the subprime crisis has been managed by public authorities in many countries does not leave any ambiguity: it is now clear that any large financial institution that encounters financial problems can expect to be rescued out by public authorities on the grounds that it is TBTF or Too Interconnected To Fail. The turmoil that followed the failure of Lehman Brothers in September 2008 has indeed led governments to commit to an unconditional support of any troubled financial institution whose failure might create major disruptions. Of course this support can take several forms, ranging from a straight bail-out, where the government does not require any control rights in exchange for its financial support, to a temporary nationalization involving firing managers without indemnities and expropriating shareholders. These different modes of intervention have obviously very different consequences in terms of moral hazard.
The impact of such decisions on market discipline can also be significant, as illustrated by the situation that emerged after the Continental Illinois bail-out in 1984. At the time, it took more than five years2 for market discipline to be somewhat restored . But this bail-out was a single event, and the Comptroller of the Currency of the time tried to maintain, as much as he could, some ambiguity on which banks were really TBTF . This time all ambiguity has been resolved in a dramatic way: all large financial institutions will always be rescued. Unless resolute reforms are undertaken, it will probably take a very long time to restore market discipline again3.
The Dodd-Franck Bill passed by the U.S. Congress in July 2010 rightly identifies this issue as a priority, and endows the Fed with special regulatory powers vis a vis these SIFIs, including non-banks. A new institution is created, the "Financial Stability Oversight Council" in charge of identifying, monitoring and addressing systemic risks posed by large and complex financial firms and making recommendations to regulators so as to avoid that these firms threaten the financial stability of the United States. In the same spirit, the European Systemic Risk Board set-up by the European Commission has received a similar mission. However in both cases, the regulatory instruments that need to be used for this purpose have not been specified explicitly by legislators.
The objective of this paper is to explore what can be done for "taming SIFIs". For this purpose we develop a simple model of a TBTF institution, i.e. an institution that cannot be closed down (either because it is "vital" for the proper functioning of the financial system, or because its closure would generate large negative externalities) but than can be subject to huge losses (an event that we call a "crisis")that shareholders cannot be forced to cover. The other important ingredient of our model is endogenous risk taking: we assume that, at each date, the manager can modify the level of risk taken by the SIFI. This choice is unobservable by third parties, thus potentially generating moral hazard. Taking a high level of risk generates private benefits for the manager, who is protected by limited liability. The manager's risk choice depend on the structure of the compensation package that shareholders offer him. This compensation package in turn depends on the resolution procedure used by supervisors when there is a crisis. Our paper is thus related to two strands of the academic literature.
The first of these strands studies bank resolution procedures. Two recent contributions to this literature are Shim(2006), and Kocherlakota and Shim(2007), who consider the impact of different modes of regulatory intervention on the incentives of bank managers, and look at the social cost of the liquidation of banks' assets. By contrast, our model is specific to SIFIs, in the sense that we do not allow any asset liquidation, even partial: the SIFI must continue operating at full scale. Other papers study how different types of regulatory sanctions or restrictions that can be imposed as a bank becomes more and more undercapitalized, in line with the US regulation of Prompt Corrective Action (Shim, 2006; Freixas and Parigi, 2009). These papers assume that banks' shareholders are able to perfectly monitor bank managers, thus assuming away the potential agency problem between bank managers and shareholders. This assumption is not suitable for SIFIs, which are large and complex organizations, typically held by a diffuse shareholder basis. This is why our paper models the conflict of interest between managers and shareholders.
The second strand of the literature connected to our work is the theory of multiperiod contracts under moral hazard. The methodology developed by Spear and Srivastava (1987) and Thomas and Worral (1990) has recently been applied to corporate finance models as in DeMarzo and Fishman (2007), and Biais, Mariotti, Plantin and Rochet (2007). The discussion paper version of this last paper (BMPR 2004 in the sequel) contains developments that are closely related to the present paper. Other recent contributions to this field use continuous time models, in particular Sannikov (2003), DeMarzo, Fishman, He and Wang (2008), or Biais, Mariotti, Rochet and Villeneuve (2007). Myerson (2009) uses a very similar framework for modeling corruption and delegation of local government.
Another specificity of our SIFI is that it is exposed to risks characterized by a very small probability and a very large loss (extreme events). If this loss materializes, its size is such that shareholders are not willing to recapitalize the bank. For the same reason, a private insurance solution is not possible, since the size of the loss exceeds the capacity of private insurers. This is why some form of public intervention is needed. We examine the impact of different resolution procedures and show that moral hazard can only be avoided if the SIFI is supervised by a strong and independent institution, which we call the Systemic Risk Authority (SRA). We show that, in conformity with the recommendations of many experts, this SRA should be endowed with special resolution powers for SIFIs and that a systemic tax should be levied with the objective to fund the cost of these future resolutions. However, we go further and suggest that the SRA should also have a say on the compensation packages of the managers of the SIFIs. The control of managers remunerations during bank restructuring episodes might be a necessary complement to classical regulatory instruments. 4
The paper is organized as follows. The model is developed in Section 2. Then Section 3 studies the situation without ex-ante regulation, and shows that in this case moral hazard is inevitable. However moral hazard can be avoided if a special resolution procedure for SIFIs can be credibly announced in advance. The section also provides conditions under which it is optimal to be tough, i.e. expropriating shareholders and removing managers every time a crisis occurs. Finally, we suggest a way to reduce the cost of these restructuring episodes by offering a grace period to new managers. In Section 4 we show that this contract is optimal when the probability of crises is small enough. However, if the compensation package of the manager is not controlled by the SRA, the shareholders of the SIFI choose a remuneration that does not depend on the performance of the bank. To avoid excessive risk taking during the grace period, it is thus necessary to let the SRA have a say on the pay of the bank's manager, at least during the period immediately following the restructuring.
2 THE MODEL
There is a single Systematically Important bank, or more generally Financial Institution, that we call a SIFI. The term "systematically important" refers to the fact that public authorities cannot let it disappear. There can be several reasons for this, such as the size or "interconnectedness" of the SIFI, but there are not modeled explicitly. We content ourselves with assuming that the closure of the SIFI would inflict too large externalities on the rest of the economy. Clearly, this opens the door to possibilities of exploitation of this situation by the shareholders of the SIFI, to the detriment of taxpayers. The main objective of the paper is to examine what can be done to limit these possibilities, which constitute the core of the "Too Big to Fail" syndrome.
The SIFI has a fixed size5, and its activities generate at each period
![]() a positive cash flow
a positive cash flow ![]() The possibility of a "systemic crisis"
is modeled by a (small) probability
The possibility of a "systemic crisis"
is modeled by a (small) probability ![]() that the bank experiences (large) losses
that the bank experiences (large) losses ![]() We offer two alternative interpretations of this technology:
We offer two alternative interpretations of this technology:
- derivative products like CDSs: the SIFI sells protection and receives at each period a premium
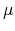 , but it may be obliged to cover big losses
, but it may be obliged to cover big losses 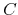 if a credit event occurs (crisis). The case of AIG, which was bailed out by U.S. authorities in 2009, fits this interpretation.
if a credit event occurs (crisis). The case of AIG, which was bailed out by U.S. authorities in 2009, fits this interpretation. - transformation of a volume
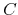 of insured deposits into risky investments. The cash flow
of insured deposits into risky investments. The cash flow 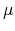 is then interpreted as the (per period) net return on investment, after interest has been paid to depositors. If a crisis occurs, all investment is lost, and depositors must be repaid in full. The large commercial banks that invested massively into AAA tranches of CDOs or other
highly speculative products fit well this interpretation.
is then interpreted as the (per period) net return on investment, after interest has been paid to depositors. If a crisis occurs, all investment is lost, and depositors must be repaid in full. The large commercial banks that invested massively into AAA tranches of CDOs or other
highly speculative products fit well this interpretation.
The SIFI (from now on, we call it the "bank") has to be run by a manager. This manager can be selected among a pool of potential candidates who are all identical: they are risk neutral and discount the future at rate
![]() . They do not have any initial wealth that could be pledged. A potential manager accepts to manage the bank if and only if he is promised expected payments that have an expected
present value of at least
. They do not have any initial wealth that could be pledged. A potential manager accepts to manage the bank if and only if he is promised expected payments that have an expected
present value of at least ![]() corresponding for example to the utility equivalent of the training cost that has to be incurred (once and for all) so as to be able to manage the bank.
corresponding for example to the utility equivalent of the training cost that has to be incurred (once and for all) so as to be able to manage the bank.
![]() also represents the social cost of replacing an incumbent manager.
also represents the social cost of replacing an incumbent manager.
The bank is owned by private investors (the bank's shareholders), who are risk neutral, and have a discount factor
![]() Note that managers are more impatient than shareholders. We assume that the bank is profitable: if it operates forever, its activity generates a net expected value
Note that managers are more impatient than shareholders. We assume that the bank is profitable: if it operates forever, its activity generates a net expected value
![]() that exceeds the training cost
that exceeds the training cost ![]() . In this
first best situation, the bank's ex ante shareholder value would be
. In this
first best situation, the bank's ex ante shareholder value would be
![]() However, we also assume that
However, we also assume that
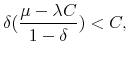 |
(1) |
which means that the bank's shareholders prefer to default in the advent of a crisis: the losses are higher than the discounted continuation value of the bank. In this case, when a crisis occurs, shareholders refuse to inject the capital needed to cover the losses. In the absence on public intervention, the bank would be closed after the first crisis, and its ex ante shareholder value would be:
| (2) |
However, we assume that the negative externalities inflicted on the rest of the economy by the closure of the bank would be too large (and in particular bigger than the losses ![]() ) so that
public authorities are obliged to intervene: this is precisely why the bank is called "systematically important".
) so that
public authorities are obliged to intervene: this is precisely why the bank is called "systematically important".
Note that assumption (1) above implies that the bail-out cost ![]() is quite large. To be consistent with our previous assumption (that
is quite large. To be consistent with our previous assumption (that ![]() ) this requires that
) this requires that ![]() be quite small. Thus the crisis events studied in our model are characterized by large losses
be quite small. Thus the crisis events studied in our model are characterized by large losses
![]() occurring with a small probability
occurring with a small probability ![]() .
.
Social welfare would be increased if the bank could buy private insurance. Suppose indeed that the losses of the bank could be covered by a private insurer in exchange for a fair premium
![]() paid at each period. Then the bank could continue forever, generating the first best social surplus
paid at each period. Then the bank could continue forever, generating the first best social surplus
![]() Note however that such insurance would have to be compulsory, since shareholder value is higher without insurance: our assumption that
Note however that such insurance would have to be compulsory, since shareholder value is higher without insurance: our assumption that
![]() implies indeed that
implies indeed that
![]() is smaller than
is smaller than
![]() .
.
However the private insurance solution is made impossible by the size ![]() of potential losses: it is assumed to exceed the capacity of any private insurer. Thus insurance against crises can
only be provided by public authorities, which may have extended resolution powers, like firing the managers and expropriating the shareholders in the advent of a crisis. This decision, which we call "restructuring" the bank, has a positive cost
of potential losses: it is assumed to exceed the capacity of any private insurer. Thus insurance against crises can
only be provided by public authorities, which may have extended resolution powers, like firing the managers and expropriating the shareholders in the advent of a crisis. This decision, which we call "restructuring" the bank, has a positive cost ![]() (that must be borne in addition to
(that must be borne in addition to ![]() and
and ![]() ) and it is therefore ex post inefficient. We have already seen that, since potential managers are identical to the incumbent manager, it is never ex post optimal to replace the latter (remember the presence of a training cost
) and it is therefore ex post inefficient. We have already seen that, since potential managers are identical to the incumbent manager, it is never ex post optimal to replace the latter (remember the presence of a training cost ![]() . Similarly, the presence of the restructuring cost
. Similarly, the presence of the restructuring cost ![]() implies that it is never ex
post optimal for public authorities to expropriate shareholders. It would always be ex post more efficient to let the bank continue without changing its management and ownership.
implies that it is never ex
post optimal for public authorities to expropriate shareholders. It would always be ex post more efficient to let the bank continue without changing its management and ownership.
The second important feature of our model is moral hazard, captured here by an asset substitution problem. The manager has, in each period, the possibility to select (without being detected) an alternative investment that is more risky than the optimal investment (it
has a higher probability of losses
![]() but provides him with a private benefit
but provides him with a private benefit ![]() per period. We assume that high risk taking is socially inefficient: private benefits are less than the expected cost of the increase in risk:
per period. We assume that high risk taking is socially inefficient: private benefits are less than the expected cost of the increase in risk:
As explained below, an important consequence of moral hazard is that public authorities might be forced to commit to restructure the bank after a crisis (even if it is ex post inefficient), in order to ensure that shareholders provide the bank manager with proper incentives for limited risk taking. A SRA is precisely meant to constitute a commitment device for public authorities.
3 RESOLUTION PROCEDURES FOR SIFIS
This section first studies the situation without ex ante resolution procedure for SIFIs. In that situation moral hazard is inevitable. Moral hazard can only be avoided if a strong and independent systemic risk authority is put in place ex ante, which serves as a commitment device for public authorities. A special resolution procedure for SIFIs can be credibly announced in advance. We provide conditions under which it is optimal to be tough, i.e. expropriating shareholders and removing managers every time a crisis occurs. Then we suggest a way to reduce the cost of these restructuring episodes by offering a grace period to new managers.
3.1 No ex-ante resolution procedure
Consider first a situation in which there is no ex-ante resolution procedure for SIFIs. In case of a crisis, shareholders are not willing to recapitalize the bank and public authorities are obliged to intervene ex post. Then there is no point in restructuring the bank, because this would be costly and it is obviously too late to change the risk decisions previously made by the manager. In this situation, shareholders anticipate that they will not be penalized in the event of a crisis, and therefore they have no incentives to design a compensation contract that would lead the manager to take a low level of risk. indeed, by letting the manager shirk, shareholders can offer him a lower expected payment. Moreover, given that the manager is more impatient than the shareholders, it is more efficient for the shareholders to frontload these payments, through what we call a "golden hand shake". i.e.a lump-sum payment at the signature of the contract6
The fact that the manager's compensation is independent of his performance leads to excessive risk taking. Moreover taxpayers incur the cost of bailing out the bank in case of crisis. The expected present value of the cost for taxpayers is thus
![]() This cost could be ex ante transferred to shareholders by requiring the bank to pay a systemic tax7
This cost could be ex ante transferred to shareholders by requiring the bank to pay a systemic tax7
![]() in each period. This would prevent subsidization of the bank by taxpayers but it would not curb its excessive risk taking. To do this, one needs to go further,
and create ex ante a systemic risk authority that is endowed with special resolution powers. We now examine what precise agenda should be given to this systemic risk authority.
in each period. This would prevent subsidization of the bank by taxpayers but it would not curb its excessive risk taking. To do this, one needs to go further,
and create ex ante a systemic risk authority that is endowed with special resolution powers. We now examine what precise agenda should be given to this systemic risk authority.
3.2 A Strong and Independent Systemic Risk Authority
We have just seen that excessive risk taking would not be curbed by a simple insurance system, even if this system is fully financed ex ante by fair premiums. The reason is moral hazard: insurance premiums cannot be conditioned on risk taking decisions, because these decisions are unobservable. Of course there is a large academic literature that analyzes the tools designed by the insurance industry for dealing with this problem: bonus/penalty systems (also called experience ratings), deductibles, tort systems and the like. But these tools would be insufficient here, as we are studying an extreme configuration, with very big losses that occur very infrequently.
This particular situation requires the intervention of a special institution, that we call a systemic risk authority (SRA). This special institution must benefit from the backing of the Treasury (in order to be able to cover the huge losses associated with a crisis) but at the same time must be independent from political powers, so as to resist the temptation of a bail-out, which is always the ex post efficient solution to a crisis. The SRA should also be strong, in the sense that it should be endowed with special resolution powers allowing to fire the manager and expropriate the shareholders in case of a crisis. These powers are needed to force shareholders to choose remuneration schemes that induce managers to limit their risk taking. At the end of the paper, we discuss the possibility for the SRA to control directly the remuneration packages of managers.
Consider thus a situation where such a strong and independent SRA has been put in place. In the advent of a crisis, this authority is committed to restructure the bank, i.e. expropriating initial shareholders and removing the managers. Immediately after restructuring has taken place, the
authority sells off the shares of the bank to new shareholders for a price ![]() An equivalent interpretation is that the SRA has the power to force existing shareholders to inject and amount
An equivalent interpretation is that the SRA has the power to force existing shareholders to inject and amount
![]() . By convention, the restructuring cost
. By convention, the restructuring cost ![]() includes the cost of organizing of
this new equity issue. New shareholders then offer a contract to a new manager, specifying an initial payment
includes the cost of organizing of
this new equity issue. New shareholders then offer a contract to a new manager, specifying an initial payment ![]() (the golden hand shake) and a salary (or bonus)
(the golden hand shake) and a salary (or bonus) ![]() that is paid to the manager at each period, until a crisis happens. The expected continuation pay-off of the manager, denoted
that is paid to the manager at each period, until a crisis happens. The expected continuation pay-off of the manager, denoted ![]() , is thus given by:
, is thus given by:
| (3) |
By solving this equation we obtain:
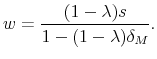 |
(4) |
The associate golden handshake is then
| (5) |
The condition ensuring that the manager does not take excessive risk( the Incentive Compatibility Condition or ICC) is simply:
| (6) |
which is equivalent to:
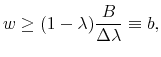 |
(7) |
or:
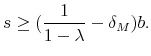 |
(8) |
Finally, the Government levies a systemic tax
| (9) |
The term between brackets corresponds to the net present value of the cash inflow that the government needs to inject in case of a crisis: an immediate payment
Shareholder value ![]() is determined by a simple recursive equation:
is determined by a simple recursive equation:
| (10) |
where
| (11) |
Solving these three equations in ![]() and
and ![]() we obtain:
we obtain:
Proposition 1: The optimal combinations9 of systemic tax ![]() , golden handshake
, golden handshake ![]() and managerial bonus
and managerial bonus ![]() that preserve the manager's incentive compatibility condition and participation constraint, together with the expected budget constraint of the SRA, give rise to the following
level of social surplus:
that preserve the manager's incentive compatibility condition and participation constraint, together with the expected budget constraint of the SRA, give rise to the following
level of social surplus:
![\displaystyle V=\frac{\mu -\lambda \lbrack C+\delta (\Gamma +U)]-(1-\lambda )(\delta -\delta _{M})b}{1-\delta },](img48.gif) |
(12) |
Maximum10 shareholder value is:
![\displaystyle S=V-b=\frac{\mu -\lambda \lbrack C+\delta (\Gamma +U)]-[1-(1-\lambda )\delta _{M}-\lambda \delta ]b}{1-\delta }](img49.gif) |
(13) |
The social surplus formula obtained in Proposition 1 has a natural interpretation. In each period the bank generates a cash flow ![]() With probability
With probability ![]() there is a crisis, in which case the cost
there is a crisis, in which case the cost ![]() is incurred immediately and the additional costs
is incurred immediately and the additional costs ![]() (restructuring) and
(restructuring) and ![]() (training a new manager) have to be incurred at the next
period11. With probability (
(training a new manager) have to be incurred at the next
period11. With probability (
![]() there is no crisis and the only social cost is associated with the back loading of the payments to the manager. This is needed to provide him with the incentives to select the
correct level of risk: instead of receiving upfront his full training cost
there is no crisis and the only social cost is associated with the back loading of the payments to the manager. This is needed to provide him with the incentives to select the
correct level of risk: instead of receiving upfront his full training cost ![]() the manager only receives
the manager only receives ![]() and is promised for the future a salary
and is promised for the future a salary ![]() as long as there is no crisis. Since the manager is more impatient than the shareholders, this back loading is socially
costly.
as long as there is no crisis. Since the manager is more impatient than the shareholders, this back loading is socially
costly.
Thus preventing moral hazard is costly. It requires setting up a strong an independent SRA with special resolution powers. The credible threat of expropriating shareholders functions as a deductible in an insurance contract. This deductible is set at the maximum level that is compatible with
shareholders limited liability, i.e. the value ![]() of the shares. As we comment below, this might not be enough to ensure that managers are given correct incentives for limited risk taking.
Indeed, when B is large enough compared with S, shareholders prefer to let managers shirk even when they face the risk of expropriation in case of a crisis. In that case, the SRA must be given also some control on the remuneration of managers.
We come back to this crucial issue below. For examine how the previous contract can be improved by granting a grace period to each newly hired manager.
of the shares. As we comment below, this might not be enough to ensure that managers are given correct incentives for limited risk taking.
Indeed, when B is large enough compared with S, shareholders prefer to let managers shirk even when they face the risk of expropriation in case of a crisis. In that case, the SRA must be given also some control on the remuneration of managers.
We come back to this crucial issue below. For examine how the previous contract can be improved by granting a grace period to each newly hired manager.
3.3 Introducing a grace period for the manager
Suppose that the SRA considers offering a "grace period" to the new manager. This means that if a crisis occurs during the first period of the manager's mandate, the systemic risk authorities promise to inject the amount needed to continue operating the bank, but do not restructure it. They let
the manager (and the shareholders) continue independently of the outcome: the manager is guaranteed to keep his job for at least one period. After this "grace period" the previous contract is implemented, comprising the restructuring of the bank in case of a crisis, a systemic tax ![]() and a managerial bonus
and a managerial bonus ![]() as above. For the moment we only consider a one shot deviation from
the previous contract: the grace period is only offered to the new manager. In the next section, we look at the stationary situation where, in the future also,every newly hired manager also benefits from such a grace period.
as above. For the moment we only consider a one shot deviation from
the previous contract: the grace period is only offered to the new manager. In the next section, we look at the stationary situation where, in the future also,every newly hired manager also benefits from such a grace period.
The benefit generated by the grace period is associated with avoiding a costly restructuring, should a second crisis occur immediately after the bank has been restructured. Thus the systemic tax is smaller during the grace period:
![]() The cost associated with the grace period is that the manager must be promised a higher bonus
The cost associated with the grace period is that the manager must be promised a higher bonus ![]() in case of success, because the manager knows that he will not be fired if a crisis occurs. The minimum bonus that is needed to provide the appropriate incentives for risk taking during the grace period is:
in case of success, because the manager knows that he will not be fired if a crisis occurs. The minimum bonus that is needed to provide the appropriate incentives for risk taking during the grace period is:
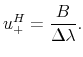 |
(14) |
Recall that the bonus needed to provide incentives in subsequent periods is only
![\displaystyle s=[1-\delta _{M}(1-\lambda )]\frac{B}{\Delta \lambda }.](img56.gif) |
(15) |
This is smaller than
Thanks to the grace period, the golden hand shake can be reduced to:
| (16) |
provided this term is positive. This corresponds to the situation where the cost
In both cases, the overall surplus generated by offering a grace period to the new manager is given by:
| (17) |
Indeed, after the grace period, the previous contract is implemented, leading to a continuation value
Now if we compare with the surplus generated by the previous contract, we obtain:
Proposition 2: Whenever
![]() , guaranteeing a grace period (immediately after a restructuring episode) to a newly hired manager is socially beneficial.
, guaranteeing a grace period (immediately after a restructuring episode) to a newly hired manager is socially beneficial.
Proof: It results from a simple comparison between the two equations that characterize ![]() and
and
![]()
| (18) |
and:
| (19) |
It is easy to see that
![]() if and only if
if and only if
![]() ,which is implied by our assumption that
,which is implied by our assumption that
![]()
The role of the grace period is to affect the initial division of surplus between investors and managers. Indeed, we have here a classical trade-off between incentives, which are improved by backloading managers'payments and efficiency, which push towards frontloading these payments, given that managers are more impatient than investors. When managers' reservation utility U is high enough, it turns out to be efficient for the investors to offer such a grace period , because this reduces substantially the golden handshake that is needed to attract new managers. This is reminiscent of the results of Opp (2010), who studies the dynamics of firms' investment in countries with poor legal enforcement. Like us, Opp uses a stationary dynamic model with moral hazard. He shows that initial investment distortions may be Pareto superior to persistent investment at the static optimum. In other words, in spite of the stationarity of the model, the optimal dynamic contract may be non stationary in the sense that it distinguishes the initial period where a new agent is hired from the rest of the periods. Interestingly, it is never optimal to extend the grace period to more than one period.
One may also wonder whether more complex compensation schemes might be welfare improving. The following section shows that this is not the case: when the probability of a crisis is small enough, the contract characterized in Proposition 2 is indeed the socially optimal contract.
4 THE SOCIALLY OPTIMAL CONTRACT
So far we have only considered simple contracts, in the spirit of Shapiro and Stiglitz 13 (1984): the manager receives a constant wage (independently of his seniority), and he is fired whenever there is a crisis. In this section we consider the most general set-up and allow any kind of dynamic contracts, where wages and firing decisions can
be history dependent. Following the classical methodology developed by Spear and Srivastava (1987) and Thomas and Worral (1990), we adopt the recursive method used for solving such repeated moral hazard problems. In this method, the decisions specified in a contract are parameterized by the
continuation pay-off of the bank manager (the agent). This continuation pay-off is denoted ![]() . Our analysis is closely related with BMPR (2004). The main difference is that, because of our Too
Big To Fail situation, the bank is never closed nor downsized. However the regulator has the power to restructure the bank, i.e. expropriate the shareholders and replace the manager.
. Our analysis is closely related with BMPR (2004). The main difference is that, because of our Too
Big To Fail situation, the bank is never closed nor downsized. However the regulator has the power to restructure the bank, i.e. expropriate the shareholders and replace the manager.
At the beginning of each period, the contract specifies (as a function of the current manager's continuation pay-off ![]() ) the probability
) the probability ![]() that the bank is restructured, With the complement probability
that the bank is restructured, With the complement probability ![]() , the manager continues and the contract
specifies:
, the manager continues and the contract
specifies:
- the current payments to the agent,
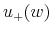 and
and 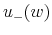 conditionally on its
performance (the two outcomes are denoted +, when there is no crisis, and - when a crisis occurs),
conditionally on its
performance (the two outcomes are denoted +, when there is no crisis, and - when a crisis occurs), - the continuation payoffs
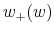 and
and 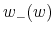 promised to the agent after the
current period. They are also conditional on cumulated performance
promised to the agent after the
current period. They are also conditional on cumulated performance 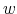 .
.
We restrict attention to the case where excessive risk taking is so costly that it is always socially optimal (even in the second best contract) to prevent this behavior by giving appropriate incentives to the agent.
The socially optimal (second best) regulatory contract is parameterized by the continuation pay-off ![]() of the agent. It is characterized by a social surplus function
of the agent. It is characterized by a social surplus function ![]() that satisfies the following Bellman equation:
that satisfies the following Bellman equation:
under the constraints
where
The incentives for the manager to take a low level of risk depend upon its compensation package. He has the choice between an expected return of
![]() when taking a low level of risk and an expected return equal to
when taking a low level of risk and an expected return equal to
![]() when taking a high level of risk (and obtaining the private benefit
when taking a high level of risk (and obtaining the private benefit ![]() . The incentive compatibility condition is satisfied if and only if
. The incentive compatibility condition is satisfied if and only if
The compensation packages that maximize managerial incentives correspond to
Since we constrain the systemic risk authority to balance its expected budget in each period, it must be that
![]() We can thus eliminate
We can thus eliminate ![]() from the Bellman equation, and express
everything as a function of
from the Bellman equation, and express
everything as a function of ![]() .
.
Note also that the objective function does not depend on current payments ![]() and
and ![]() The above program can thus be dramatically simplified by eliminating these variables in the constraints. For the general method we refer to BMPR (2004).
The above program can thus be dramatically simplified by eliminating these variables in the constraints. For the general method we refer to BMPR (2004).![]() We just need to
note here that when (
We just need to
note here that when (
![]() holds with equality and
holds with equality and ![]() one can explicitly solve for
one can explicitly solve for ![]() and
and ![]() :
:
![]() and
and
![]() The positivity constraints are then equivalent to
The positivity constraints are then equivalent to
![]() and
and
![]() respectively, where
respectively, where ![]() is defined by
is defined by
![]() Before stating the simplified problem, it is useful to introduce the following auxiliary function:
Before stating the simplified problem, it is useful to introduce the following auxiliary function:
![]()
Thanks to this simplification, the optimal contract can be equivalently associated with the Bellman function ![]() that solves for all
that solves for all ![]() the simpler problem:
the simpler problem:
under the constraints
The last thing to be remarked is that restructuring must occur with probability one when ![]() (this is the only possible way to provide the agent, who has limited liability, with a zero
continuation value. Therefore:
(this is the only possible way to provide the agent, who has limited liability, with a zero
continuation value. Therefore:
![]() It is easy to establish existence and uniqueness of the solution
It is easy to establish existence and uniqueness of the solution ![]()
Lemma 1:When the bank is Too Big to Fail14 (so that it is socially optimal to let the bank continue
forever), there exists a unique continuous bounded solution to (23) under the constraints (24)(25)(26) that satisfies
![]()
Proof: This is an easy consequence of Blackwell's fixed point theorem (see Stokey and Lucas 1989).
A direct adaptation of BMPR (2004) then gives a characterization of this solution when ![]() is small enough:
is small enough:
Proposition 3 When
![]() and
and ![]() is small enough, the optimal contract can be described as follows:
is small enough, the optimal contract can be described as follows:
- when a new manager is hired (this is what we call the grace period; it includes the initial period where the bank is started), he is guaranteed to keep his job for one period and is promised a continuation utility
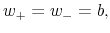 irrespectively of its current performance. He receives a high bonus
irrespectively of its current performance. He receives a high bonus
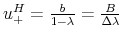 in case of success and nothing in case of a crisis;
in case of success and nothing in case of a crisis; - in all other periods, the manager receives a (lower) bonus
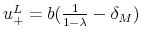 in case of success and is fired (with no indemnity) in case of a crisis.
in case of success and is fired (with no indemnity) in case of a crisis.
Proof: see Appendix.
When the probability of crises ![]() is larger, it can be shown that the optimal contract still involves a grace period. However, it is less tough in the following sense: after the
grace period, the consequence of a single loss is just to suppress the bonus to the manager. It takes several consecutive losses to provoke the restructuring of the bank.
is larger, it can be shown that the optimal contract still involves a grace period. However, it is less tough in the following sense: after the
grace period, the consequence of a single loss is just to suppress the bonus to the manager. It takes several consecutive losses to provoke the restructuring of the bank.
5 IS REGULATORY CONTROL OF BANKERS' REMUNERATIONS NECESSARY?
Proposition 3 clarifies the role of the SRA: restructuring the bank after a crisis, and levying the systemic tax that is needed to cover the expected cost of crisis resolution. However the grace period introduces a peculiarity: if a crisis occurs during this period (that is, immediately after a
restructuring episode), the SRA should bail out the bank without firing the managers nor expropriating the shareholders. If shareholders are free to choose the remuneration package of the manager (as it should be in general), they will prefer, during the grace period, to pay him a low bonus
![]() irrespectively of his performance rather than paying him a high bonus
irrespectively of his performance rather than paying him a high bonus
![]() only in case of success. This reduces the expected cost of the compensation paid by shareholders (who are thus strictly
better-off) to the manager, but the manager obtains the same expected pay-off (because he takes excessive risk and gets the associated private benefit
only in case of success. This reduces the expected cost of the compensation paid by shareholders (who are thus strictly
better-off) to the manager, but the manager obtains the same expected pay-off (because he takes excessive risk and gets the associated private benefit ![]() .
.
However this is socially harmful: excessive risk is always taken by newly hired managers, with the consent of shareholders. Avoiding this necessitates some form of intrusion of the SRA during the grace period, for example by forbidding that bonuses be paid in case of losses.
Proposition 4: We make the same assumptions as in proposition 3. If the SRA does not control the compensation of the manager during the restructuring period, the new shareholders find it optimal to pay the manager irrespectively of its performance. As a result the manager chooses an excessive level of risk during the first period.
Proposition 4 can be extended to the case where the probability of crises is higher and the optimal contract is as described in the comments after Proposition 3. Thus the result that bankers remunerations should be controlled by the Systemic Risk Authority during crisis periods is robust.
The result that the control by the SRA of managers' remunerations might be necessary to avoid moral hazard does not rely on the existence of the grace period. Even when the reservation utility of the banker is lower, so that no golden handshake and thus no grace period is necessary, it might still be the case that shareholders are willing to let managers shirk. This happens when the savings B in the managers'expected compensation obtained by letting him shirk are greater than the increase in the expected loss of shareholders due to shirking. This constitutes a strong argument in favor of letting regulators have a say on bankers'pay, as advocated for example by Bebchuck ans Spamann (2009).
6 Appendix
Proof of Proposition 3:
We show that when
![]() and
and ![]() small enough:
small enough:
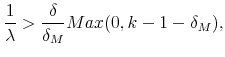 |
the optimal contract is the one described in Proposition 3. It is easily checked that in this case, the associated social surplus function
Where we use the notation
The auxiliary function
![]() is defined by:
is defined by:
Where
![]() for
for ![]() and
and
![]() The optimality of our contract requires that
The optimality of our contract requires that ![]() be concave, with a maximum for
be concave, with a maximum for
![]() and that
and that
![]() be maximum for
be maximum for ![]() This is guaranteed if
This is guaranteed if
Notice that the above formulas imply that ![]() is continuous and concave.
is continuous and concave.
Case 1: Consider first the case where neither constraint (25), nor (26) binds. In this case,
![]() and
and ![]() is optimal if:
is optimal if:
Moreover we have to check that for
![]() neither (25) nor (26) are violated, which is equivalent to
neither (25) nor (26) are violated, which is equivalent to
From this we are able to compute the associated payments to the agent in both states:
Case 2: Second, consider the case where only the constraint (25) is binding15.
In this case, ![]() solves the maximization problem, again provided that the function between brackets is an increasing function of
solves the maximization problem, again provided that the function between brackets is an increasing function of ![]() . Consequently, (25) only will be binding, thus implying
. Consequently, (25) only will be binding, thus implying ![]() and
and
![]() while
while ![]() and
and
![]() are as in Case 1.
are as in Case 1.
Then the condition for the function between brackets to be increasing is:
Note that, as
![]() reaches its maximum for
reaches its maximum for ![]()
![]() and consequently, condition (31) implies (29).
and consequently, condition (31) implies (29).
Since the couple (
![]() ) is supposed to violate constraint (25), it must be that
) is supposed to violate constraint (25), it must be that
![]() . Simultaneously, the non-negativity of
. Simultaneously, the non-negativity of
![]() implies
implies ![]() Thus:
Thus:
Finally, ![]() satisfies (26) whenever
satisfies (26) whenever ![]()
Case 3: Third, consider the case where (25) is binding and ![]() Then,
Then,
![]() and
and
![]() Then we have
Then we have ![]() and
and
![]() The necessary condition for ((25)) to be binding at
The necessary condition for ((25)) to be binding at ![]() is then:
is then:
Again, (26) will be satisfied as
Note that conditions (30), (32) and (33) cover all possible cases and are mutually exclusive.
We now determine the expression of ![]() that is given by the above solution. We have to distinguish three different cases.
that is given by the above solution. We have to distinguish three different cases.
- First, for
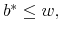 using
using
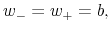 and
and 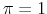 we obtain
we obtain
- Secondly, going to the other extreme, assume
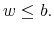 Using the expression of the solution for case 3 we obtain
Using the expression of the solution for case 3 we obtain
So that
![\alpha _{0}=\frac{1}{b}\left[ \mu -\lambda C+\lambda \delta V(0))+(1-\lambda )\delta V(b)-(1-\lambda )(\delta -\delta _{M})b-V(0)\right]](img187.gif) and
and
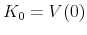
- Third , assume
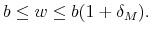 Using the expression of the solution for case 2 we obtain:
Using the expression of the solution for case 2 we obtain:
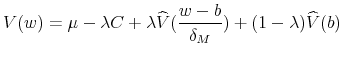
Since
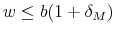 implies
implies
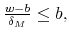
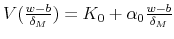
and
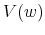
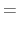
![\displaystyle \mu -\lambda C+\lambda \delta \left[ K_{0}+\alpha _{0}\frac{w-b}{% \delta _{M}}\right] +(1-\lambda )\delta V(b)-](img196.gif)
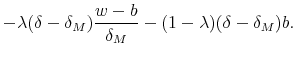
Therefore
![\alpha _{1}=\frac{\lambda }{\delta _{M}}\left[ \delta \alpha _{0}-(\delta -\delta _{M})\right]](img198.gif) and
and
![]() that
is,
that
is,
It is easy to check that ![]() is a continuous function.Moreover when
is a continuous function.Moreover when ![]() we
have:
we
have:
Thus we can solve for the values of
Replacing
so that
![\displaystyle V(b)=\frac{(1+\lambda \delta )(\mu -\lambda C)-\lambda \delta (\Gamma +U)-% \left[ (1-\lambda +\lambda \delta )(\delta -\delta _{M})b\right] }{1-\lambda \delta ^{2}-(1-\lambda )\delta }.](img207.gif) |
Using
![\displaystyle V(b)=\frac{1}{1-\delta }\left[ \mu -\lambda C-(\delta -\delta _{M})b-\frac{% \lambda \delta (\Gamma +U)-\lambda (\delta -\delta _{M})b}{1+\lambda \delta }% \right]](img209.gif) |
This allows us to compute
![\displaystyle V(b^{\ast })=\frac{1}{1-\delta }\left[ \mu -\lambda C-(\delta -\delta _{M})b-% \frac{\lambda \delta ^{2}(\Gamma +U)-\lambda \delta (\delta -\delta _{M})b}{% 1+\lambda \delta }\right],](img210.gif) |
or, equivalently
![\displaystyle V(b^{\ast })=\frac{1}{1-\delta }\left[ \mu -\lambda C-\frac{\lambda \delta ^{2}(\Gamma +U)+(\delta -\delta _{M})b}{1+\lambda \delta }\right].](img211.gif) |
Using
![\displaystyle V(0)=\frac{1}{1-\delta }\left[ \mu -\lambda C-\frac{(1-\lambda\delta+\lambda\delta^{2} )(\Gamma +U)+(\delta -\delta _{M})b}{1+\lambda \delta }\right]](img213.gif) |
From these expressions we can compute
![]()
Simplifying by
![]() and rearranging terms yields:
and rearranging terms yields:
![\displaystyle V(b)-V(0)=\frac{1}{(1+\lambda \delta )}\left[ \Gamma +U+\lambda (\delta -\delta _{M})b\right]](img216.gif) |
Remember that
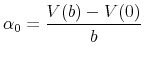 |
and
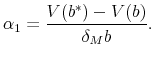 |
We need to check that
![]()
![]() , which can be rewritten as:
, which can be rewritten as:
Consider first condition (37) . Using the value of ![]() given above yields
given above yields
This is equivalent to our assumption that
Regarding (38):
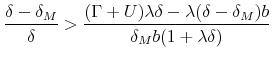 |
it is equivalent to:
which is itself equivalent to:
When
![]() this is always satisfied. Otherwise, this is true when
this is always satisfied. Otherwise, this is true when
![\displaystyle \frac{b(\delta -\delta _{M})\delta _{M}}{\delta \lbrack \delta (\Gamma +U)-(\delta -\delta _{M})b\{1+\delta _{M}\}]}>\lambda,](img231.gif) |
which is exactly what we have assumed.
7 References
Acharya,V., L. Pedersen, T. and M.Richardson (2009)"A Tax on Systemic Risk", in Restoring Financial Stability: How to Repair a Failed System Viral Acharya (Editor), Matthew Richardson (Editor), New York University Stern School of Business
Bebchuck, L. and H. Spamann(2009) "Regulating Bankers' Pay," John M. Olin Center for Law, Economics, and Business Discussion Paper No. 641, 6/2009.
Biais, B. T. Mariotti, G.Plantin,and J.-C. Rochet, (2004) "Dynamic Security Design" CEPR discussion paper 4753.
Biais, B. T. Mariotti, G.Plantin,and J.-C. Rochet, (2007) "Dynamic Security Design:Convergence to Continuous Time and Asset Pricing Implications". Review of Economic Studies 74, 345-390.
Biais, B., T. Mariotti, J.-C. Rochet, and S. Villeneuve (2010): "Large risks, limited liability, and dynamic moral hazard," Econometrica, 78, 73-118.
Cheng, I., H. Hong and J. Scheinkman, (2009)"Yesterday's Heroes: Compensation and Creative Risk-Taking" mimeo, Princeton University.
Chesney,M., J.Stromberg and A.F.Wagner (2010): "Risk-taking incentives, governance, and losses in the financial crisis" discussion paper, University of Zurich
DeMarzo, P.M. and M.J. Fishman (2007), " Agency and Optimal Investment Dynamics " Review of Financial Studies 2007 20(1):151-188.
DeMarzo, P., M. Fishman, Z. He and N. Wang. "Dynamic agency and the theory of investment" Working Pap., Columbia University, 2008.
DeMarzo, P.M. and Y. Sannikov (2006), "Optimal Security Design and Dynamic Capital Structure in a Continuous-Time Agency Model", Journal of Finance, 61(6) : 2681-2724.
Fahlenbrach, R., and R. Stulz (2010), "Bank CEO incentives and the credit crisis", Journal of Financial Economics, forthcoming.
Kashyap, A., R. Rajan and J. Stein (2008![]() ""Rethinking Capital Regulation", Kansas City Symposium on Financial Stability.
""Rethinking Capital Regulation", Kansas City Symposium on Financial Stability.
Kocherlakota, N. and I. Shim (2007) "Forbearance and prompt corrective action", Journal of Money Credit and Banking 39, 1107-1129.
Kose,J.,H. Mehran, and Y. Qian, (2008) "Outside monitoring and CEO compensation in the banking industry" Mimeo.
Morgan, D. and K. Stiroh (2005). "Too big to fail after all these years", Federal Reserve Bank of New York Staff Reports (220), 1-23.
Mülbert, P. (2010) "Corporate Governance of Banks after the Financial Crisis - Theory, Evidence, Reforms" Mimeo,ECGI.
Myerson, R. (2008) "Leadership, Trust, And Power: Dynamic Moral Hazard In High Office" WP Chicago University, http://home.uchicago.edu/~rmyerson/research/power.pdf.
O'Hara, M. and W. Shaw (1990). "Deposit Insurance and Wealth Effects: The Value of Being Too-Big-to-Fail", Journal of Finance 45, 1587-1600.
Opp, M.M. (2010) "Expropriation Risk and Technology", discussion paper, Chicago GSB.
Sannikov, Y. (2003), "A Continuous-Time Version of the Principal-Agent Problem" (Mimeo, Stanford University).
Shim, I. (2006) "Dynamic Prudential Regulation: Is Prompt Corrective Action Optimal?" BIS WP.
Shapiro, C. and J. Stiglitz (1984): "Equilibrium Unemployment as a Worker Disciplinary Device", American Economic Review 74:433-444.
Spear, S.E., and S. Srivastava (1987): "On Repeated Moral Hazard with Discounting," Review of Economic Studies, 54, 599-617.
Stern,G.H., and R.J. Feldman (2004): "Too Big To Fail,"Brookings, Washington,D.C.
Stokey,N. R. Lucas and E. C. Prescott, (1989), "Recursive methods in economic dynamics"Harvard College, Cambridge.
Thomas, J. and T. Worrall (1990): "Income Fluctuation and Asymmetric Information: An Example of a Repeated Principal-Agent Problem," Journal of Economic Theory, 51, 367-390.
Völz, M. and M. Wedow: "Does banks' size distort market prices? Evidence for too-big-to-fail in the CDS market" Deutsche Bundesbank Discussion Paper Series 2: Banking and Financial Studies No 06/2009.