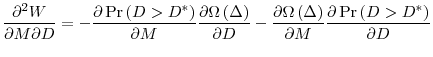The Seeds of a Crisis: A Theory of Bank Liquidity and Risk-Taking over the Business Cycle*
Keywords: Bubbles, flight to quality, Greenspan put, leaning against liquidity, leaning against the wind, monetary policy, moral hazard
Abstract:
"For too long, the debate has got sidetracked. Into whether we can rely on monetary policy `mopping up' after bubbles burst. Or into whether monetary policy could be used to control asset prices as well as doing its orthodox job of steering nominal trends in the economy..." - Paul Tucker, Executive Director for Markets and Monetary Policy Committee (MPC) member at the Bank of England.1
1 Introduction
It is clear that in the period leading up to the global financial crisis of 2007-2009, credit and asset prices were growing at a ferocious pace.2 In the United States, for example, in the five-year period from 2002 to 2007, the ratio of debt to national income went up from 3.75 to one, to 4.75 to one. It had taken the prior full decade to accomplish this feat, and fifteen years prior to that. During this same period, house prices grew at an unprecedented rate of 11% per year while there was no evidence of appreciating borrower quality over this period. The credit growth was across board, in mortgages, especially sub-prime ones, in financing of leveraged buy-out transactions (LBOs), and through increasing issuance of low-rated bonds. This rapid rise in asset volume and prices met with a precipitous fall. For instance, the median house price divided by rent in the United States3 over the 1975 to 2003 period varied within a relatively tight band around its long-run mean. Yet starting in late 2003, this ratio increased at an alarming rate. In mid 2006, however, the ratio flattened and kept falling sharply until 2009 (See Figure 1).
The Figure graphs the demeaned value of the ratio of the Office of Federal Housing Enterprise Oversight (OFHEO) repeat-sale house price index to the Bureau of Labor Statistics (BLS) shelter index (i.e., gross rent plus utilities components of the CPI). Because of demeaning, the average value of this ratio is zero.What caused this tremendous asset growth and the subsequent puncture is likely to intrigue economists for years. Some have argued that the global economy was in a relatively benign low-volatility environment in the decade leading up to the ongoing crisis (the so-called "Great Moderation", see Stock and Watson, 2002). In departure from this view, we argue that it is likely not a coincidence that the phase of remarkable asset growth described above started at the turn of the global recession of 2001-2002. In fact, in response to the unprecedented rate of corporate defaults and heightened macroeconomic risk during that recession, the Federal Reserve lowered interest rates to 1%, the lowest level since 1958. A period of abundant availability of liquidity to the financial sector ensued, bank balance-sheets grew two-fold within four years, and when the "bubble burst", a number of agency problems within banks in those years came to the fore. Such problems were primarily concentrated in centers that were in charge of undertaking large risks and took the form of risk-takers being paid out huge bonuses based on the volume of assets they created rather than on (long-term) profits they generated.4
In this paper, we develop a theoretical model that combines these ingredients and explains why access to abundant liquidity aggravates the risk-taking moral hazard at banks, giving rise to asset price bubbles. Somewhat perversely, the seeds of crisis are sown when the macroeconomic risk is high and investors in the economy switch from investments to savings in the form of bank deposits. We argue that these bubbles can be counteracted by Central Banks with a contractionary monetary policy in such times, and conversely can in fact be exacerbated by expansionary monetary policy in such times. Expansionary monetary policy may be tempting to persist with when macroeconomic risk is high, but this may flush banks with (even more) liquidity, fueling credit booms and asset price bubbles and sowing seeds of the next crisis.
We first develop a benchmark model in Section 2.1 wherein the representative bank collects deposits from investors and then allocates a fraction of these deposits to investment projects. The bank faces random deposit withdrawals and in case of liquidity shortfalls suffers a penalty cost. The penalty cost could be interpreted as the cost of fire sales or alternatively the cost of raising external finance from markets. In order to avoid such costs the bank has an incentive to set aside some reserves (cash and marketable assets or other forms of ready liquidity). The rest of the deposits are invested in projects (e.g. houses) depending on the demand for loans (e.g. mortgages). The bank chooses the optimal lending rate that maximizes its expected profits subject to the depositors' participation constraint. We show in this benchmark model that the bank lending rate appropriately reflects the underlying risk of the project.
In Section 2.2 we enrich the model to study how agency problems within the bank affect the pricing of loans. In practice, bankers and loan officers ("bank managers") often have incentives to give out excessive loans since their payoffs are proportional not only to the realized profits and losses on loans but also to the amount of loans advanced.5 We show that such incentives can arise as part of an optimal contracting outcome of a principal-agent problem when managerial action or effort is unobservable. Further, under the optimal contract, bank managers may have an incentive to underprice the risk of the investments. However, we show that such mispricing of risk only occurs when the bank is awash with liquidity (deposits). This is because in presence of excessive liquidity the manager attaches too little weight to the scenario where the bank might later face liquidity shortfalls. In other words, excessive liquidity encourages managers to disregard downside risk, increase loan volume and underprice the risks of projects.
We then show in Section 2.2.3 that such behavior ultimately has an impact on asset prices. We assume that the demand for loans arises from investments by the household or corporate sector in underlying assets of the economy. To show how asset price " bubbles" are formed we first define the " fundamental" asset prices as those that arise in the absence of any agency frictions within banks. We construct the optimal demand function for assets by bank borrowers and then solve for the underlying asset price given the market clearing condition that the aggregate demand for assets should equal their finite supply. If the bank lending rate underprices risks, then there is an increase in aggregate borrowing from banks. This in turn fuels an excessive demand for assets in the real sector which leads to prices rising above their fundamental values. We interpret this asset price inflation as a " bubble". Importantly, such bubbles are formed only when bank liquidity is high enough as only then do bank managers underprice risk.
Next, in Section 3 we study when are asset price bubbles most likely to be formed. We show that this is the case when the macroeconomic risk in the economy is high. When macroeconomic risk increases, depositors avoid direct entrepreneurial investments and prefer to save their money in bank deposits which are perceived to be safer. Gatev and Strahan (2006) offer direct empirical evidence consistent with this effect. In our model, such "flight to quality" results in excessive bank liquidity and induces bubble formation in line with our earlier results.
Finally, we study the implications of the results for optimal monetary policy. We show that if the Central Bank adopts a contractionary monetary policy in times of excessive bank liquidity, then it can counter the flight to quality by drawing out the increases in bank liquidity and avoiding the emergence of bubbles. On the contrary, if the Central Bank adopts an expansionary monetary policy then this accentuates the formation of bubbles. Intuitively, an increase in the money supply only serves to increase bank liquidity further when there is already a flight to quality of deposits. Our model can thus explain how lax monetary policy by the Scandinavian Central Banks in 1980's, Bank of Japan during 1986-1987, and the Federal Reserve in the United States during most of the Greenspan era culminated in housing and real estate bubbles in these countries. In contrast, in times of scarce bank liquidity, banks raise lending rates which adversely affects aggregate investment. We show that during these times if the Central Bank adopts an expansionary monetary policy then it can boost aggregate investment by effectively injecting liquidity into the banking system. We thus argue in Section 4 that the optimal monetary policy involves a "leaning against liquidity" approach, which recognizes that "leaning against macroeconomic risk" is not necessarily the desirable policy.
Proponents of the `Greenspan camp' argue that monetary policy should not be geared towards avoiding the emergence of bubbles and should focus instead on targeting the natural interest rate and the natural rate of employment as has traditionally been the case. This is justified on the basis that central banks cannot pinpoint an asset price bubble. Nevertheless, we prove that targeting bank liquidity is optimal even if central banks are not aware of where the economy is in the business cycle. Since the asset price bubble is intuitively tied to bank liquidity, we believe that the central banks' task in identifying times for employing a contractionary policy is not as onerous as is often suggested since its task is to track the extent of liquidity of the banking (more broadly, financial intermediation) sector.6
While Jensen and Meckling (1976) showed that leverage induces equityholders to prefer excessive risk, our point is concerned with risk-taking incentives inside banks as a function of liquidity. On this front, the mechanics of our model are similar to Myers and Rajan (1998) wherein access to liquidity allows financial firms to switch to riskier assets, and the anticipation of such behavior, renders them illiquid ex ante. The channel in our model is somewhat different in that when banks are flush with liquidity, managers are hedged from the downside risks they undertake, and this induces risk-taking incentives.
Allen and Gale (2000) show in a model of risk-shifting that uncertainty in monetary policy acts to exacerbate the risk-taking incentives ex ante and fosters an asset price bubble. Diamond and Rajan (2008) show that lowering interest rates ex post may be desirable for a central bank in order to avoid bank runs and fire sales, but that this can induce moral hazard and incentivize banks to hold more illiquid assets. It may thus be desirable for the Central Bank to commit to raising interest rates when they are low. In our model, the focus is also on the ex-ante effects of central bank intervention. The difference arises from the fact that our model embeds the principal-agent problem between dispersed shareholders of banks and the loan officers or the risk takers. The severity of the agency problem is affected by the availability of liquidity, and thus by central bank interventions. Importantly, in the absence of bank-level agency problems, there is no excess in credit growth and central bank interventions do not distort credit outcomes.
In another related paper Farhi and Tirole (2009) study how monetary policy has an affect on the collective behavior of banks. They argue that banks have an incentive to correlate their risk exposures because if everyone engages in maturity transformation (for example), authorities have little choice ex post other than facilitating refinancing. They thus argue that the optimal monetary policy is inherently time inconsistent. Acharya and Yorulmazer (2007) also study the incentives for banks to correlate their risks when regulatory forbearance (bailout policy) suffers from a time-consistency problem. In a model with two banks they show that banks have an incentive to reduce their correlations given the possibility that one bank may acquire the other. However, if the rents obtained from such an acquisition are outweighed by the bailout guarantee when both banks fail, then banks herd and seek to maximize their correlation. In contrast to these papers, our paper studies whether or not monetary policy should target asset prices given the agency problems inherent in banks.
In a recent paper, Agur and Demertzis (2010) also argue that monetary policy concerned with financial stability may have to be conservative and set higher rates on average, but in reaction to negative shocks, be more aggressive, i.e. engage in deeper but shorter-lived cuts (compared to traditional monetary policy concerned only with inflation or output) when there are negative macroeconomic shocks.
Thakor (2005) argues that bank over-lending is due to banks permitting higher loan commitments and not invoking the MAC clause during booms given reputational concerns.7 The alternative view provided by our paper is that over-lending occurs mainly due to higher spot lending by banks subsequent to a deposit influx.
2.1 Base case
We consider a three-period model of a bank wherein the bank at ![]() receives deposits
receives deposits ![]() from risk-neutral investors. Each investor deposits 1 unit of his endowment in the bank. The reservation utility of depositors is given by
from risk-neutral investors. Each investor deposits 1 unit of his endowment in the bank. The reservation utility of depositors is given by ![]() . Hence in order to secure deposits the bank needs to set the rate of return on deposits,
. Hence in order to secure deposits the bank needs to set the rate of return on deposits, ![]() , such that the
depositors earn an expected payoff of at least
, such that the
depositors earn an expected payoff of at least ![]() .
.
The bank subsequently makes investments in projects while holding a fraction of the deposits as liquid reserves, ![]() . The bank-funded projects either succeed or fail at
. The bank-funded projects either succeed or fail at ![]() . The probability of success of bank projects is given by
. The probability of success of bank projects is given by ![]() and in the event the project
is successful it pays off at
and in the event the project
is successful it pays off at ![]() . The project is illiquid in the sense that if it were to be liquidated prematurely at
. The project is illiquid in the sense that if it were to be liquidated prematurely at ![]() the bank faces a penalty or a liquidation cost. The bank observes
the bank faces a penalty or a liquidation cost. The bank observes ![]() and sets
and sets ![]() which is the (gross) rate of return on loans. When choosing the lending rate, the bank takes into account the demand function for loans (say, by the corporate sector) which is given by
which is the (gross) rate of return on loans. When choosing the lending rate, the bank takes into account the demand function for loans (say, by the corporate sector) which is given by
![]() where
where
![]() . Bank reserves are thus given by:
. Bank reserves are thus given by:
The bank may experience withdrawals at ![]() and for simplicity we assume that the fraction of depositors who experience a liquidity shock is a random variable given by
and for simplicity we assume that the fraction of depositors who experience a liquidity shock is a random variable given by ![]() , where
, where
![]() .8 The cumulative
distribution function of
.8 The cumulative
distribution function of ![]() is given by
is given by
![]() while the probability distribution function is denoted by
while the probability distribution function is denoted by
![]() . Each depositor who withdraws early receives 1 unit of his
endowment back at
. Each depositor who withdraws early receives 1 unit of his
endowment back at ![]() . Thus the total amount of withdrawals at
. Thus the total amount of withdrawals at ![]() is given by
is given by
![]() . If the realization of
. If the realization of
![]() is greater than
is greater than ![]() , then the bank faces a liquidity shortage, and it
incurs a penalty cost, given by
, then the bank faces a liquidity shortage, and it
incurs a penalty cost, given by
![]() , which is proportional to the liquidity shortage, where
, which is proportional to the liquidity shortage, where
![]() .
.
The penalty cost can be justified in a number of ways. The bank may be forced to cover the shortfall in a costly manner by selling some of its assets prematurely at fire-sale prices. This is particularly likely when firms in other industries are also facing difficulties.9 Alternatively the bank can raise external financing via capital markets. However, this is also costly because raising equity leads to dilution of existing shareholders due to the debt overhang problem (Myers, 1977). Furthermore, raising external finance entails a price impact due to the adverse selection problem a la Myers and Majluf (1984). Capital-raising can also entail costs related to monitoring that the new financier must undertake. Finally, if the bank attempts to cover the shortfall by emergency borrowing from the central bank, this can also be costly as the central bank may charge a penalty rate. Finally, apart from pecuniary costs, the bank may also suffer non-pecuniary costs such as a reputational cost, e.g., the stigma associated with borrowing from the central bank's emergency facilities.
If the projects financed by bank borrowings are successful, then the bank is solvent and is able to repay the patient depositors the promised rate of return of ![]() at
at ![]() , whilst the equityholders consume the residual returns from bank investments after these depositors have been paid off. However, in case of the failure of bank-funded projects, the surplus reserves,
, whilst the equityholders consume the residual returns from bank investments after these depositors have been paid off. However, in case of the failure of bank-funded projects, the surplus reserves,
![]() , if any, are divided amongst the patient depositors whilst the equityholders consume zero. The sequence of events is summarized in the timeline depicted in Figure 2.
, if any, are divided amongst the patient depositors whilst the equityholders consume zero. The sequence of events is summarized in the timeline depicted in Figure 2.
Given this setup the risk neutral bank's problem is as follows:
subject to
where
The above program says that the bank chooses deposit and lending rates as well as the level of bank reserves so as to maximize its expected profits,
Note that for simplicity we have considered a setup with a given penalty cost. In the appendix we consider a setup wherein the penalty costs are explicitly calculated in an environment where the bank finances the shortfall by selling its assets at fire-sale prices. We show that in this
three-period environment, the objective function of the bank is analogous to equation (1) and is given by ![]() minus a cost term which is proportional to the bank's
liquidity shortfall. Hence our qualitative results are unchanged and thus we use the simpler setup given its parsimony and tractability.
minus a cost term which is proportional to the bank's
liquidity shortfall. Hence our qualitative results are unchanged and thus we use the simpler setup given its parsimony and tractability.
We next solve the bank's optimization problem and derive the first-best lending and deposit rates and the optimal level of bank reserves. Subsequently we study how the riskiness of bank projects as well as bank liquidity affects the loan rate offered by the bank. The results are summarized in Proposition 1.
- The optimal gross lending rate is given by
where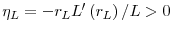 is the elasticity of the demand for loans. The optimal gross deposit rate is given by
is the elasticity of the demand for loans. The optimal gross deposit rate is given by
And, the optimal level of reserves is given by:
- (Risk effect)
 , i.e., an increase in risk (
, i.e., an increase in risk (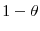 ), ceteris paribus, increases the equilibrium lending rate.
), ceteris paribus, increases the equilibrium lending rate. - (Liquidity effect)
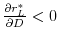 , i.e., an increase in bank liquidity, ceteris paribus, decreases the equilibrium lending rate.
, i.e., an increase in bank liquidity, ceteris paribus, decreases the equilibrium lending rate.
It is interesting to note that as the elasticity of demand for loans decreases, the lending rate increases and hence the spread between the loan rate and deposit rate increases. This result is consistent with the Monti-Klein (Klein, 1971 and Monti, 1972) model. As expected, the greater the market power of the bank, the higher will be the lending rate that it can charge and vice versa.
The second and third parts of the proposition are also intuitive. The lending rate prices both risk and liquidity. An increase in liquidity lowers the expected cost of liquidity shortage and the bank passes some of this benefit to the borrowers via a lower loan rate.
2.2.1 Setting of the problem
So far we have abstracted from any agency issues between the bank equityholders and the bank manager. Let us now consider a setting where such issues are relevant.
A study by OCC (1988) found that "Management-driven weaknesses played a significant role in the decline of 90 percent of the failed and problem banks the OCC evaluated... directors' or managements' overly aggressive behavior resulted in imprudent lending practices and excessive loan growth." They also found that 73% of the failed banks had indulged in over-lending. This indicates that principal-agent problems within banks have been one of the key reasons for bank failures and that bank managers tend to engage in `overly aggressive risk-taking behavior'.10 Perhaps even more striking evidence is presented by the financial crisis of 2007-2009 which has revealed that in the period preceding the crisis, traders and large profit/risk centers at a large number of financial institutions were paying themselves bonuses based on the size of their risky positions rather than their long-run profitability. Moreover, in many cases, it was a conscious choice of senior management to silence the risk management groups that had spotted weaknesses in the portfolio of building risks.11
To study how such managerial agency problems can have an effect on bank policies, we model the agency problem within banks explicitly. Let ![]() denote the unobservable effort level of the
manager, such that
denote the unobservable effort level of the
manager, such that
![]() , where
, where
![]() . We assume that although the loans are affected by effort, they are not fully determined by it. The stochastic relationship is necessary to ensure that effort level remains
unobservable. We assume that the distribution of loan demand
. We assume that although the loans are affected by effort, they are not fully determined by it. The stochastic relationship is necessary to ensure that effort level remains
unobservable. We assume that the distribution of loan demand
![]() conditional on
conditional on ![]() first-order stochastically dominates the
distribution conditional on
first-order stochastically dominates the
distribution conditional on ![]() . In other words, for a given level of lending rate, the manager on average makes a higher volume of loans when he exerts high effort relative to the case
where he exerts lower effort, i.e.
. In other words, for a given level of lending rate, the manager on average makes a higher volume of loans when he exerts high effort relative to the case
where he exerts lower effort, i.e.
![]() . In addition to
. In addition to
![]() , both the principal and the agent can observe the realization of bank's net profit,
, both the principal and the agent can observe the realization of bank's net profit, ![]() .
.
The manager is risk averse and his utility is increasing in wages, ![]() , but decreasing in effort. Furthermore, we suppose that
, but decreasing in effort. Furthermore, we suppose that
![]() . This means that the incremental increase in the expected profit
from implementing a high effort is greater than the increase in the expected wage costs from implementing the high effort. In other words the principal has an incentive to implement the high effort level since the gains from doing so are greater than the associated costs.
. This means that the incremental increase in the expected profit
from implementing a high effort is greater than the increase in the expected wage costs from implementing the high effort. In other words the principal has an incentive to implement the high effort level since the gains from doing so are greater than the associated costs.
We assume that bank liquidity is non-verifiable. This is plausible given that liquidity is not even well-defined as it can take several forms. Furthermore, bank liquidity may be lent out to other banks via the interbank market or conversely it may be the excess liquidity of other banks that makes it way to the bank in question. It is also particularly difficult to verify off-balance sheet liquidity which may take the form of unused loan commitments.
The time line is as follows: At ![]() the bank raises deposits, the principal offers a contract to the manager (such that
the bank raises deposits, the principal offers a contract to the manager (such that ![]() is chosen) and the manager chooses
is chosen) and the manager chooses ![]() . At
. At ![]() , for a given level of
, for a given level of ![]() the volume of loans will be realized. As before, at
the volume of loans will be realized. As before, at ![]() there may be early withdrawals and finally at
there may be early withdrawals and finally at ![]() the payoffs are realized and divided between the parties given the contractual terms. The timeline is depicted in Figure 3.
the payoffs are realized and divided between the parties given the contractual terms. The timeline is depicted in Figure 3.
In the presence of symmetric information, there is no agency problem and the bank's problem is analogous to that of Section 2.1 with the bank maximizing
subject to the following participation constraint
where
The first-best lending rate analogous to equation (4) is given by
where
Next, we introduce the agency problem. We assume that the manager can observe the quality of the project (![]() and distribution of depositor withdrawals or its liquidity needs (
and distribution of depositor withdrawals or its liquidity needs (
![]() ) but this information is not observable to the principal and hence the principal cannot infer the first-best loan rate.12 Consequently, the principal will be unable to enforce the first-best rate and there will be a deviation from the first-best even if the principal is able to implement
) but this information is not observable to the principal and hence the principal cannot infer the first-best loan rate.12 Consequently, the principal will be unable to enforce the first-best rate and there will be a deviation from the first-best even if the principal is able to implement ![]() via the incentive compatibility condition. We assume, however, that the risk premium required on deposits (defined as
via the incentive compatibility condition. We assume, however, that the risk premium required on deposits (defined as
![]() ) is public information and hence the participation constraint (7) still needs to be satisfied.13
) is public information and hence the participation constraint (7) still needs to be satisfied.13
Given this setup with asymmetric information, we prove in the appendix the following important proposition on the manager's compensation contract.14
Such contracts are ubiquitous in practice whereby the bonuses of managers are increasing in the volume of loans and profits. For simplicity we limit the analysis to linear contracts such that the manager's payoff is a proportion ![]() of loans and a proportion
of loans and a proportion ![]() of profits net of penalty costs.15
of profits net of penalty costs.15
Hence the bank manager maximizes the following:
subject to the participation constraint (7) and where
The intuition behind the above proposition is straightforward. The bank manager has an additional incentive to lower lending rates as this allows him to make more loans and his payoff is increasing in the amount of lending.
2.2.2 Liquidity-induced agency problem
The intuition as to why the optimal contract in the preceding section depends on both the volume of loans and net profit is as follows: Managerial compensation solely dependent on profits would be suboptimal from a risk-sharing standpoint since profits are affected not just by loans but also by random withdrawals by depositors. In other words, net profit is not a sufficient statistic for loans with respect to effort. On the other hand, if managerial compensation only depends on the volume of loans, then the manager will be incentivized to lower lending rates as much as possible because he will not be penalized when low lending rates adversely impact net profits. In this case, the volume of loans will be excessive, reserves will be too low and hence liquidity shortages very likely. Hence the optimal contract is a function of both loans and net profits which are observable to the principal.
Ideally the principal would want the manager to exert high effort as well as set the first-best lending rate. But given asymmetric information the manager cannot be explicitly penalized for setting a lending rate lower than the first-best. Now let us suppose the principal can conduct a costly
audit which verifies whether or not the manager acted overly aggressively. In particular, the audit reveals the quality of the project (![]() ) and the distribution of liquidity needs (
) and the distribution of liquidity needs (
![]() ). This enables the principal to infer the first-best loan rate, as given by (9), and thus the principal is able to infer whether or not the
manager had acted aggressively by setting a lending rate below the first-best. More specifically the contracting problem involves the following stages: The principal offers a contract to the manager. The manager optimizes his payoff under this contract by choosing the effort level and setting the
lending rate. The principal conducts an audit following a liquidity shortfall and if it is inferred that the manager had acted overly aggressively by setting a lending rate below the first-best then the manager is penalized a proportion
). This enables the principal to infer the first-best loan rate, as given by (9), and thus the principal is able to infer whether or not the
manager had acted aggressively by setting a lending rate below the first-best. More specifically the contracting problem involves the following stages: The principal offers a contract to the manager. The manager optimizes his payoff under this contract by choosing the effort level and setting the
lending rate. The principal conducts an audit following a liquidity shortfall and if it is inferred that the manager had acted overly aggressively by setting a lending rate below the first-best then the manager is penalized a proportion ![]() of the penalty costs, where
of the penalty costs, where
![]() .16 It is assumed
that the manager has limited liability and hence there is an upper bound on the punishment that can be imposed. Given that
.16 It is assumed
that the manager has limited liability and hence there is an upper bound on the punishment that can be imposed. Given that
![]() , this implies that at most the manager incurs the entire penalty costs.
, this implies that at most the manager incurs the entire penalty costs.
Optimal risk sharing now dictates that the manager's payoff only be a function of loan volume as long as there is no liquidity shortfall. This is because in the absence of an audit, the manager's payoff is conditioned on bank profits so as to constrain his risk-taking appetite. However, in the presence of an audit, conditioning on bank profits is superfluous since managerial behavior can be constrained directly by imposing a penalty on the manager following a liquidity shortfall if it is inferred that he had set a lending rate below the first-best. Hence the manager's payoff will be a function of loan volume as long as there are no liquidity shortfalls but he will be penalized in the event of a liquidity shortfall if it is inferred that he had acted over-aggressively. The manager now faces a trade-off. If he behaves overly aggressively, his utility is higher as long as there are no liquidity shortfalls and subsequently no penalties. However, if a liquidity shortfall is realized then the manager is penalized and would be worse off. We can then prove the following proposition.
The above proposition says that for high enough bank liquidity the manager has an incentive to engage in overly-aggressive behavior by mispricing in the loan rate the underlying risk of loans. It should be noted that the agency problem is only actuated when bank liquidity is high enough. This is because even though the manager bears a proportion of the penalty costs, in the presence of excessive liquidity, the probability of experiencing a liquidity shortage is low and this encourages the manager to indulge in excessive lending. Because of this `insurance effect' of liquidity, the manager's compensation becomes more sensitive to loan volume. The manager will thus indulge in excessive lending as long as his payoffs from doing so exceed his payoffs in the first-best world. On the other hand, for low enough liquidity the agency problem is immaterial since in this case the manager's expected payoff in the first-best world exceeds his expected compensation from acting over-aggressively. Hence for low enough liquidity the manager does not sanction excessive loans for the fear of incurring a penalty in the event of a liquidity shortfall.
2.2.3 Asset pricing
Next we consider the asset pricing implications of our model. We define the fundamental asset price as the price that holds in the absence of any distortions created by agency problems. We then compare the fundamental asset price with the actual asset price which may or may not be distorted
depending on whether or not agency problems have been actuated within the banking system. To facilitate this comparison we first model the asset demand by bank borrowers which was so far taken as given. We assume that there exists a continuum, ![]() , of risk-neutral borrowers who have no wealth and hence need to borrow in order to finance investments. Since there is a continuum of borrowers and loans cannot be conditioned on their size, they can borrow as much as they like at the going
rate of interest.
, of risk-neutral borrowers who have no wealth and hence need to borrow in order to finance investments. Since there is a continuum of borrowers and loans cannot be conditioned on their size, they can borrow as much as they like at the going
rate of interest.
Although there is a continuum of borrowers, we shall analyze the behavior of a representative borrower. This implies that the equilibrium is symmetric and that all borrowers choose the same portfolio. The fact that all borrowers are identical ex post means that the bank cannot discriminate between borrowers by conditioning the terms of the loan on the amount borrowed or any other characteristic.
Let ![]() denote the number of units of the asset demanded by the representative borrower and
denote the number of units of the asset demanded by the representative borrower and ![]() denote the total supply of the risky asset. We assume for simplicity that the supply of the asset is finite and fixed. The asset returns a cash flow of
denote the total supply of the risky asset. We assume for simplicity that the supply of the asset is finite and fixed. The asset returns a cash flow of ![]() per unit with a
probability of
per unit with a
probability of ![]() . Let
. Let ![]() denote the price of one unit of the asset.
denote the price of one unit of the asset.
As in Allen and Gale (2000) we assume the borrowers face a non-pecuniary cost of investing in the risky asset
![]() such that it satisfies the usual neoclassical properties:
such that it satisfies the usual neoclassical properties:
![]() ,
,
![]() and
and
![]() for all
for all ![]() . The purpose of the
investment cost is to restrict the size of the individual portfolios and to ensure the concavity of the borrower's objective function.
. The purpose of the
investment cost is to restrict the size of the individual portfolios and to ensure the concavity of the borrower's objective function.
The optimization problem faced by the representative borrower is to choose the amount of borrowing so as to maximize expected profits. That is
Note that the borrower has to pay an interest of
The first-order condition of the above problem is as follows:
Setting
As expected, the asset price is the discounted value of the expected cash flows net of the investment cost. It is also clear that there is a one-to-one mapping from the (gross) lending rate, ![]() , to the asset price,
, to the asset price, ![]() . Let
. Let ![]() denote the fundamental
(gross) lending rate which is the rate obtained in the absence of any distortions such as agency problems. Recall that
denote the fundamental
(gross) lending rate which is the rate obtained in the absence of any distortions such as agency problems. Recall that ![]() is the rate which maximizes the equity value of the bank.
Since depositors always earn
is the rate which maximizes the equity value of the bank.
Since depositors always earn ![]() on average,
on average,
![]() is also the rate which maximizes the value of the bank. Hence
is also the rate which maximizes the value of the bank. Hence
![]() is given by expression (9). Then the fundamental asset price is given by:
is given by expression (9). Then the fundamental asset price is given by:
Since the total amount of loans for a given ![]() is
is
![]() and the amount borrowed by an individual borrower is
and the amount borrowed by an individual borrower is ![]() ,
it has to be the case that
,
it has to be the case that
![]() . Hence, using the market-clearing condition (12) the asset price can also be written as:
. Hence, using the market-clearing condition (12) the asset price can also be written as:
Using the above formulation it is again clear that there is a one-to-one mapping from the lending rate to the asset price.17 Thus the fundamental asset price can also be rewritten as:
Having derived the fundamental asset price we can next define an asset price bubble. An asset price bubble is formed whenever ![]() since the asset is
overpriced. Note that
since the asset is
overpriced. Note that ![]() as long as
as long as
![]() . Intuitively, a lending rate lower than the fundamental rate creates a high demand for the asset which in turn leads to an increase in asset prices over and above the fundamental values.
. Intuitively, a lending rate lower than the fundamental rate creates a high demand for the asset which in turn leads to an increase in asset prices over and above the fundamental values.
From Proposition 3 we know that the loan rate in the presence of an agency problem is lower than the fundamental rate. Furthermore, from Proposition 4 we know that this agency problem is actuated for high enough bank liquidity. Given that the asset price is given by expression (13) and the fundamental asset price is defined by (14) we immediately have the following corollary to Propositions 3 and 4.
Corollary 1:
To better understand the mechanics behind the formation of a bubble, the four-quadrant diagram in figure 4 is useful. Quadrant I in the figure depicts the relationship between the risk of project failure,
![]() , and the loan rate,
, and the loan rate, ![]() , charged by the bank. In general
the higher the riskiness the higher would be the equilibrium lending rate as is captured by the line
, charged by the bank. In general
the higher the riskiness the higher would be the equilibrium lending rate as is captured by the line ![]() . The loan rate in turn determines the demand for loans and the volume of credit in the
economy. For any given lending rate, the amount of bank loans is given by
. The loan rate in turn determines the demand for loans and the volume of credit in the
economy. For any given lending rate, the amount of bank loans is given by
![]() . Since
. Since
![]() we know that the lower the loan rate the higher is the amount of investment in the economy as is captured by the line
we know that the lower the loan rate the higher is the amount of investment in the economy as is captured by the line ![]() in quadrant II. From the expression derived in equation (15) we know that the market clearing condition is
in quadrant II. From the expression derived in equation (15) we know that the market clearing condition is ![]() . In other words, the price of the assets multiplied by the supply of the asset has to be equal to the total demand for the asset. Hence the demand for the asset determines the asset price and this relationship is captured by the line
. In other words, the price of the assets multiplied by the supply of the asset has to be equal to the total demand for the asset. Hence the demand for the asset determines the asset price and this relationship is captured by the line ![]() in quadrant III. Notice that the higher the demand for the asset, the higher is its price. Finally quadrant IV derives the relationship between the asset price and risk. In general, the higher is the underlying risk the lower will be the asset price as is depicted by the line
in quadrant III. Notice that the higher the demand for the asset, the higher is its price. Finally quadrant IV derives the relationship between the asset price and risk. In general, the higher is the underlying risk the lower will be the asset price as is depicted by the line ![]() . The equilibrium relationship between asset price and risk is derived by tracing the effect of risk on the loan rate, which in turn has an effect on the amount of investment which subsequently determines the asset price.
. The equilibrium relationship between asset price and risk is derived by tracing the effect of risk on the loan rate, which in turn has an effect on the amount of investment which subsequently determines the asset price.
Let the line ![]() represent the fundamental relationship between risk and the bank loan rate, i.e. the relationship that would be obtained in the absence of agency issues. Then for any given level of risk, the fundamental asset price would be represented by the line
represent the fundamental relationship between risk and the bank loan rate, i.e. the relationship that would be obtained in the absence of agency issues. Then for any given level of risk, the fundamental asset price would be represented by the line ![]() . However, as we showed in Proposition 4 an agency problem is actuated for sufficiently high bank liquidity levels where the bank loan rate is lower for any given level of risk. This in turn shifts the
. However, as we showed in Proposition 4 an agency problem is actuated for sufficiently high bank liquidity levels where the bank loan rate is lower for any given level of risk. This in turn shifts the ![]() line to
line to ![]() . From quadrant II we know that the volume of credit in the economy increases following lower loan rates. Consequently asset prices increase as a result of market-clearing as is shown in quadrant III. The final relationship between asset prices and risk is shown in quadrant IV and it is obvious that the actuation of the principal-agent problem shifts the
. From quadrant II we know that the volume of credit in the economy increases following lower loan rates. Consequently asset prices increase as a result of market-clearing as is shown in quadrant III. The final relationship between asset prices and risk is shown in quadrant IV and it is obvious that the actuation of the principal-agent problem shifts the ![]() line to
line to ![]() . In the end we see that the asset price is higher for the same level of risk leading to the formation of a bubble.
. In the end we see that the asset price is higher for the same level of risk leading to the formation of a bubble.
It is also interesting to note that our model implies that the size of the bubble is monotonic in the leverage of bank borrowers. This is because bank borrowers in the model borrow more the lower the lending rates offered by the banks. The greater the severity of the agency problems, the lower are the lending rates, which encourages excessive bank borrowing. This increase in leverage in turn increases asset demand which pushes up asset prices.
Our model helps explain how agency problems in the banking sector can induce the formation of asset price bubbles. In terms of the four-quadrant diagram we would be reducing our attention to quadrant IV alone if we fail to consider the role of the banking sector. Embedding of the banking sector in a pricing framework gives us a fuller picture of how the banking sector contributes to equilibrium asset or investment demand in the economy and to the formation of asset price bubbles.
3.1 High macroeconomic risk
We have established so far that asset price bubbles are formed when bank liquidity is substantially high. So the question that arises is when are banks most likely to be flushed with liquidity. In an empirical study, Gatev and Strahan (2006) find that as spreads in the commercial paper market increase, bank deposits increase while bank asset (loan) growth also increases. The spreads on commercial paper are a measure of the investors' perception of risk in the real economy. Intuitively, when investors are apprehensive of the risk in the entrepreneurial sector they are more likely to deposit their investments in banks rather than make direct investments.18
To formalize the above intuition we integrate with the model the entrepreneurial sector, endogenize the quantity of deposits in the economy and show that bank deposits will increase at a time when the underlying risk increases. Consider an economy where entrepreneurs have access to projects that
yield a terminal cash flow ![]() if it succeeds and 0 otherwise. The probability of success depends partly on the realization of the state variable,
if it succeeds and 0 otherwise. The probability of success depends partly on the realization of the state variable,
![]() , and partly on the entrepreneurs' effort decision,
, and partly on the entrepreneurs' effort decision, ![]() , which
identifies whether the entrepreneur is diligent (
, which
identifies whether the entrepreneur is diligent (![]() ) or shirks (
) or shirks (![]() ) in which
case, entrepreneurs extract a private benefit of
) in which
case, entrepreneurs extract a private benefit of ![]() . If the entrepreneur is diligent, the probability of success is
. If the entrepreneur is diligent, the probability of success is ![]() but in the presence of shirking the probability of success is
but in the presence of shirking the probability of success is
![]() , where
, where
![]() . The realization of the state variable
. The realization of the state variable ![]() is
observable to the entrepreneurs.
is
observable to the entrepreneurs.
Entrepreneurs promise to pay the risk-neutral investors who invest directly in their projects a face value of ![]() . Thus the expected payoff of the risk-neutral entrepreneurs whose projects
are financed by direct investment is given by:
. Thus the expected payoff of the risk-neutral entrepreneurs whose projects
are financed by direct investment is given by:
One can then prove the following proposition.
The above proposition says that entrepreneurs are more likely to shirk when macroeconomic risk is high. Intuitively, an increase in macroeconomic risk lowers the success probability of entrepreneurial projects which encourages entrepreneurs to shirk so as to consume their private benefits.
We know that investors on average earn ![]() from bank investment. Let
from bank investment. Let
![]() denote the expected utility of the investor from entrepreneurial investment. We assume there exists
denote the expected utility of the investor from entrepreneurial investment. We assume there exists
![]() such that:
such that:
That is, the expected utility of investors from direct investment will be higher than that from bank investment as long as
If investors perfectly observe ![]() before deciding whether to invest directly in projects or in banks, all investments will either be channeled directly into projects or into banks
depending on the realization of
before deciding whether to invest directly in projects or in banks, all investments will either be channeled directly into projects or into banks
depending on the realization of ![]() . Hence in order to make a more realistic distribution of investments between entrepreneurs and deposits we assume that depositors do not observe
. Hence in order to make a more realistic distribution of investments between entrepreneurs and deposits we assume that depositors do not observe
![]() but each depositor receives an imperfect signal,
but each depositor receives an imperfect signal, ![]() , on the basis of
which they decide whether to allocate their endowments to direct entrepreneurial investment or bank deposits. A signal
, on the basis of
which they decide whether to allocate their endowments to direct entrepreneurial investment or bank deposits. A signal ![]() received by investor
received by investor ![]() is a good signal which implies that
is a good signal which implies that
![]() but a signal
but a signal ![]() is a bad signal which would be
an indication to the investor that
is a bad signal which would be
an indication to the investor that
![]() . Thus an investor allocates his capital to entrepreneurial projects only if he receives a good signal.19
. Thus an investor allocates his capital to entrepreneurial projects only if he receives a good signal.19
The probability distribution of the signals is assumed to be identical and independent across depositors and given as:
![]() and
and
![]() , where
, where
![]() . Investors only observe their own signals and are not aware of the probability distribution of the signals. The simple formulation of the probability distribution
implies that a proportion
. Investors only observe their own signals and are not aware of the probability distribution of the signals. The simple formulation of the probability distribution
implies that a proportion
![]() of the investors will allocate their endowments to entrepreneurial projects while a proportion
of the investors will allocate their endowments to entrepreneurial projects while a proportion
![]() will allocate their endowments to bank deposits. This formulation implies that the better the macroeconomic state
will allocate their endowments to bank deposits. This formulation implies that the better the macroeconomic state ![]() , the higher would be the amount of direct investments. However a low realization of
, the higher would be the amount of direct investments. However a low realization of ![]() would imply that a larger amount of
endowments will be tunneled to bank deposits. Hence, bank deposits are given by
would imply that a larger amount of
endowments will be tunneled to bank deposits. Hence, bank deposits are given by
![]() assuming that there are a total of
assuming that there are a total of ![]() risk
neutral investors.
risk
neutral investors.
It is clear from the formulation of ![]() that bank liquidity increases when the underlying macroeconomic risk is high. This is consistent with the findings of Gatev and Strahan (2006) cited
earlier. However, we hypothesize that for extremely high macroeconomic risk (very low
that bank liquidity increases when the underlying macroeconomic risk is high. This is consistent with the findings of Gatev and Strahan (2006) cited
earlier. However, we hypothesize that for extremely high macroeconomic risk (very low ![]() ) bank liquidity may be adversely affected. This is because casual observation of crises suggests
that once macroeconomic risk crosses a certain threshold the bubble bursts subsequently, adversely affecting banks' liquidity. Nevertheless since this paper focuses on the formation of bubbles rather than the burst of bubbles we do not model this phenomenon but simply capture this by assuming that
) bank liquidity may be adversely affected. This is because casual observation of crises suggests
that once macroeconomic risk crosses a certain threshold the bubble bursts subsequently, adversely affecting banks' liquidity. Nevertheless since this paper focuses on the formation of bubbles rather than the burst of bubbles we do not model this phenomenon but simply capture this by assuming that
![]()
![]() where
where
![]() is the threshold below which bank liquidity decreases as
is the threshold below which bank liquidity decreases as ![]() decreases.
decreases.
We can then prove the following proposition.
As macroeconomic risk increases, there is a flight to quality whereby investors prefer to invest in bank deposits rather than engage in direct lending. Subsequently, banks find themselves flushed with liquidity during times when spreads in the commercial paper market (i.e. the direct funding costs of entrepreneurs by investors) are high. Excessive liquidity encourages bank managers to increase the volume of credit in the economy by mispricing of underlying risk. This in turn fuels a bubble in asset prices.
3.2 Loose monetary policy
Before we turn to the implications for central bank's monetary policy, we briefly discuss how monetary policy has a direct effect on bank's liquidity. When embarking on an expansionary monetary policy via open market operations, central banks buy government securities from primary dealers who have accounts with depository institutions. The way this transaction works in practice is that the central bank directly credits the reserves which commercial banks have with the central bank, hence effectively increasing the deposit base of the bank. On the other hand, in order to implement a contractionary monetary policy, the central banks sell government securities to primary dealers and at the same time debit their accounts which effectively reduces the deposit base of banks. Hence bank deposits are a function of both macroeconomic risk (![]() ) as well as monetary policy (
) as well as monetary policy (![]() ):
):
The above relationship is depicted in Figure 5. As discussed in the previous section, as macroeconomic risk increases there is a flight to quality whereby bank deposits increase and this continues until risk crosses the threshold
In the figure, ![]() is the liquidity threshold above which asset price bubbles are formed. When macroeconomic risk increases above
is the liquidity threshold above which asset price bubbles are formed. When macroeconomic risk increases above ![]() to say
to say ![]() , bank liquidity crosses the threshold
, bank liquidity crosses the threshold ![]() to
to ![]() leading to the formation of a bubble. However the central bank can offset this effect via a contractionary monetary policy which will shift the
leading to the formation of a bubble. However the central bank can offset this effect via a contractionary monetary policy which will shift the ![]() line downwards. The magnitude of the contractionary monetary policy should be such that the
line downwards. The magnitude of the contractionary monetary policy should be such that the ![]() line moves downwards to at
least
line moves downwards to at
least
![]() . As can be seen from the figure this is the minimum shift that is required to ensure that for the new level of risk
. As can be seen from the figure this is the minimum shift that is required to ensure that for the new level of risk
![]() , bank liquidity is at or below
, bank liquidity is at or below ![]() .
.
It is interesting to note from Figure 5 that even if the macroeconomic risk level is below
![]() , central banks can fuel asset price bubbles by adopting loose monetary policies thereby shifting the
, central banks can fuel asset price bubbles by adopting loose monetary policies thereby shifting the ![]() line upwards such that the liquidity level crosses the threshold
line upwards such that the liquidity level crosses the threshold
![]() . Indeed Kindleberger (2005) in his study on the history of financial crises notes that: "Speculative manias gather speed through expansion of money and credit."
. Indeed Kindleberger (2005) in his study on the history of financial crises notes that: "Speculative manias gather speed through expansion of money and credit."
4 Optimal monetary policy
We next formalize the argument in Section 3.2 and study implications for optimal monetary policy in the presence of the following trade-off faced by the central bank: An increase in money supply increases aggregate investment, but an increase in money supply also increases
bank liquidity and we know from our earlier results that excessive bank liquidity can induce bubbles in asset prices. As discussed formally in the extension (section A.2 of the Appendix) bubbles are costly given that aggressive behavior of managers and underpriced loan rates result in a
deterioration in the quality of bank investments which in turn increases the average default risk and hence the expected default costs. Let the expected cost of the bubble, conditional on ![]() , be denoted by
, be denoted by
![]() , where
, where
![]() denotes the expected size of the bubble. We make the plausible assumption that the cost of the bubble increases with the
size of the bubble, i.e.
denotes the expected size of the bubble. We make the plausible assumption that the cost of the bubble increases with the
size of the bubble, i.e.
![]() . (This is also shown formally in extension A.2 of the Appendix).
. (This is also shown formally in extension A.2 of the Appendix).
The trade-off faced by the central bank can be expressed by the following expected welfare (objective) function:
where
Taking the derivative of (19) with respect to ![]() we get the first-order condition:
we get the first-order condition:
where
We assume that the SOC is satisfied, namely:
![]() . This will be the case if there exist diminishing returns on investment and if the marginal cost of a bubble is a
non-decreasing function of the money supply. The assumption of diminishing returns to investment implies that as money supply increases, the marginal benefits (in terms of higher investment) increase but at a decreasing rate. As discussed in section A.2 of the appendix, managers progressively make
worse quality loans, which can also explain the diminishing returns on investment. The assumption that the marginal cost of a bubble is a non-decreasing function of money supply implies that as bank liquidity and subsequently the expected size of the bubble increases, the incremental cost of the
bubble does not decrease. This is also plausible because if anything we expect the marginal cost of a bubble to be an increasing function of the size of the bubble.
. This will be the case if there exist diminishing returns on investment and if the marginal cost of a bubble is a
non-decreasing function of the money supply. The assumption of diminishing returns to investment implies that as money supply increases, the marginal benefits (in terms of higher investment) increase but at a decreasing rate. As discussed in section A.2 of the appendix, managers progressively make
worse quality loans, which can also explain the diminishing returns on investment. The assumption that the marginal cost of a bubble is a non-decreasing function of money supply implies that as bank liquidity and subsequently the expected size of the bubble increases, the incremental cost of the
bubble does not decrease. This is also plausible because if anything we expect the marginal cost of a bubble to be an increasing function of the size of the bubble.
We can now prove the following proposition.
However, if the size of the bubble is decreasing in macroeconomic risk, i.e., ![]() , then the optimal monetary policy dictates that the central bank increase the money supply as macroeconomic risk increases. More formally,
, then the optimal monetary policy dictates that the central bank increase the money supply as macroeconomic risk increases. More formally,
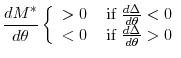 . . |
The intuition behind the above proposition is as follows: If the expected size of the bubble is increasing in macroeconomic risk, i.e.
![]() , say for instance due to a flight to quality effect which increases bank liquidity, then this raises the cost of bubbles. The central bank can counter this
effect by decreasing the money supply and hence draining out liquidity from the banking system. If, on the other hand, bank liquidity is decreasing in macroeconomic risk and consequently the expected size of the bubble decreases as the underlying risk increases, i.e.
, say for instance due to a flight to quality effect which increases bank liquidity, then this raises the cost of bubbles. The central bank can counter this
effect by decreasing the money supply and hence draining out liquidity from the banking system. If, on the other hand, bank liquidity is decreasing in macroeconomic risk and consequently the expected size of the bubble decreases as the underlying risk increases, i.e.
![]() , say for instance, due to investors' loss of confidence in times of a crisis, then the central bank can offset this effect by increasing the money supply. In
other words, the central bank should lean against macroeconomic risk as long as the expected cost of a bubble is increasing with risk, but should lean with macroeconomic risk as long as the expected cost of a bubble is decreasing with risk.
, say for instance, due to investors' loss of confidence in times of a crisis, then the central bank can offset this effect by increasing the money supply. In
other words, the central bank should lean against macroeconomic risk as long as the expected cost of a bubble is increasing with risk, but should lean with macroeconomic risk as long as the expected cost of a bubble is decreasing with risk.
Proponents of the Greenspan camp may argue that the central bank may not be aware where we are in the business cycle and hence whether bank liquidity is increasing or decreasing in macroeconomic risk. Nevertheless, it can be shown that a much simpler policy recommendation is to lean against bank liquidity regardless of where we are in the business cycle. The optimality of this policy is stated in the following proposition.
The above proposition is intuitive. In times of excessive bank liquidity, bubbles are likely to be formed and the central bank can avoid the formation of bubbles by tightening monetary policy. On the other hand, in times of scarce liquidity, banks raise loan rates and hence aggregate investment is adversely affected. The central bank can prevent the fall in investment by loosening monetary policy.
We thus argue that the `Greenspan put' should be employed in times of falling bank liquidity. However, in times when banks are flush with liquidity, a loose monetary policy only enhances the liquidity insurance enjoyed by banks, and thus aggravates their risk-taking incentives. This in turn increases the likelihood of bubbles in asset prices.
4.1 Discussion
Traditionally, as suggested by the Taylor rule, monetary policy has targeted interest rates and employment. However, in the light of our results, we argue that monetary policy should also target asset prices. Our results suggest that asset prices can be targeted if the monetary authorities adopt a "leaning against liquidity" approach. In fact we showed that a "leaning against liquidity" policy performs a twofold purpose: In times of abundant liquidity it counters the surge in asset prices, whilst in times of scarce liquidity it performs the role of quantitative easing and subsequently encourages investment.
Allen and Gale in their book "Understanding financial crises" document the following: "In Finland an expansionary budget in 1987 resulted in massive credit expansion. The ratio of bank loans to nominal GDP increased from 55 percent in 1984 to 90 percent in 1990. Housing prices rose by a total of 68 percent in 1987 and 1988... In Sweden a steady credit expansion through the late 1980's led to a property boom." These observations are perfectly in line with our model. Loose monetary policies can potentially lead to excessive liquidity in the banking system which in turn encourages bank mangers to underprice the underlying risk and thereby increase the volume of credit in the economy. This in turn creates an asset price bubble.
Our model can also explain how lax monetary policy in Japan during the mid 1980s led to asset price inflation. Bank of Japan (BOJ) reduced the official discount rate five times between January, 1986 and February, 1987, leaving it finally at 2.5 percent. It is widely accepted that the easy credit policies adopted by BOJ created excess liquidity in the Japanese economy, as also acknowledged by Goyal and Yamada (2004). The sequence of events started with the Plaza Accord (1985), in which the G5 countries agreed on a stronger yen so as to lower the U.S. trade deficit. However, BOJ's intervention in foreign exchange markets appreciated the yen rapidly. Responding to the strengthening yen and seeking to avert deflationary effects in the domestic economy, Bank of Japan lowered interest rates and consequently increased liquidity in the economy. In the subsequent years a large real estate bubble was formed.
One of the causes of the current subprime crisis has been suggested to be the loose monetary policy adopted by the Federal Reserve in the United States. In 2003, the Fed lowered the federal funds rate to 1% - a level that was last seen only in 1958. Subsequently banks mispriced risk and indulged in over-lending which finally culminated in the subprime crisis. In fact the world was awash with liquidity prior to the crisis. We would thus argue that this excess of liquidity contributed significantly in causing the crisis.
The issue of when a central bank should tighten monetary policy following a crisis has resurfaced in the aftermath of the rescue packages administered to recover from the crisis of 2007-09. For instance, the Federal Reserve in the United States has discussed raising the interest paid to banks on their reserves holdings and selling its inventory of mortgage-backed assets as potential tools. The Federal Reserve Chairman Bernanke has however assessed that "The economy continues to require the support of accommodative monetary policies. However, we have been working to ensure that we have the tools to reverse, at the appropriate time, the currently very high degree of monetary stimulus" (Financial Times, February 11 2010). Broadly though, Chairman Bernanke has stated a preference for "leaving rates low for an extended period."
In contrast, some other countries have already started the monetary tightening process. China, in particular, has "ordered its commercial banks to increase the reserves (by 50 basis points from February 25) they hold, as an effort to control rapid lending, rather than significantly tighten monetary policy" (Financial Times, February 13 2010). The Chinese economy expanded by 10.7 per cent in the fourth quarter of 2009 and Chinese banks issued a record Rmb9,600bn in new loans in 2009, about double the amount from the previous year, which fueled a rapid increase in asset prices, especially in Chinese stock markets. House prices in China had increased by 7.8 per cent in December 2009 from the same month a year earlier (Financial Times, January 14 2010). Not surprisingly, given the results of our model, the liquidity of Chinese banks also soared during this period. In fact, household and corporate deposits in the Chinese banking system are now equivalent to a record 150 per cent of gross domestic product (Financial Times, March 3 2010).
Both of these examples get at the heart of our policy discussion. Our mode highlights that the key parameter to examine is the extent of bank lending in the economy, as in the discussion about Chinese lending and asset prices above, and that the risk of the Federal Reserve not tightening monetary policy sufficiently soon is precisely that lending may take off by several multiples given the high levels of bank liquidity (reserves) and force the central bank to either tighten excessively ex post or be mopping up after the asset prices have been inflated too high.
Finally, Naqvi (2007) shows that the central bank's lender of last resort operations need to be complemented ex ante by an efficient supervisory framework so as to avoid the moral hazard repercussions of bail-outs. What we learn from our paper is that such supervision is even more essential during times when the banking system is flushed with liquidity. This is because during such times bank managers are more likely to under-price risk and hence over-invest. Thus adequate supervision in times of abundant liquidity might be another possible tool to mitigate the risk-taking appetite of banks.
5 Conclusion
We develop a theory of bank lending explaining how the seeds of a crisis may be sown when banks are flush with liquidity. The main empirical implication of our model is that excessive liquidity induces risk-taking behavior on the part of bank managers. In summary, we obtain the following results: (a) bank managers will behave in an overly-aggressive manner by mispricing risk when bank liquidity is sufficiently high; (b) asset price bubbles are formed for high enough bank liquidity; (c) bubbles are more likely to be formed when the underlying macroeconomic risk is high as it induces investors to save with banks rather than make direct entrepreneurial investments; and, finally (d) bubbles are more likely to be formed following loose monetary policies adopted by the central bank.
We also show that the optimal monetary policy involves a " leaning against liquidity" approach, i.e. a central bank should adopt a contractionary monetary policy at times when banks are awash with liquidity so as to draw out their reserves; and it should adopt an expansionary monetary policy at times when banks have scarce liquidity so as to boost investment.
Some, most notably Alan Greenspan, have argued that "we are never certain where we are in the cycle"20 and hence monetary policy should not be used to target asset prices. Nevertheless, our model showed that even if this is the case a "leaning against liquidity" policy can be rationalized. Thus we argue that monetary policy should target not just interest rates and employment but also asset prices as they are reflections of the risk appetite of the financial intermediation sector.
Appendix
A.1 Extension: Bank's objective function in the presence of fire-sale prices for assets liquidated prematurely. In this appendix we will derive the bank's objective function in a setup where instead of taking the penalty cost term as exogenous we derive the term in an environment where the bank can finance the liquidity shortfall by liquidating assets at fire-sale prices. We show that the objective function in this setup has the same generic form as that in the main body of the paper and hence the qualitative results are unaffected.
The timing of the game is as follows. At time ![]() the bank receives deposits and then invests a fraction of these deposits in investment projects via loans to entrepreneurs. A proportion of the total loans, £, are of very good quality such that they repay early with probability 1 at
the bank receives deposits and then invests a fraction of these deposits in investment projects via loans to entrepreneurs. A proportion of the total loans, £, are of very good quality such that they repay early with probability 1 at ![]() . These loans are indexed by
. These loans are indexed by ![]() and the rate of return on these loans is
and the rate of return on these loans is ![]() . However such investments are scarce so the bank cannot make its entire investments in such assets. The rest of the investments are made in assets which repay at
. However such investments are scarce so the bank cannot make its entire investments in such assets. The rest of the investments are made in assets which repay at ![]() with a probability of
with a probability of ![]() . These investments are indexed by
. These investments are indexed by ![]() and the rate of return on these investments is given by
and the rate of return on these investments is given by ![]() . Thus the total investment is given by £
. Thus the total investment is given by £ ![]() . The rest of the deposits are retained as reserves,
. The rest of the deposits are retained as reserves, ![]() .
.
At time ![]() the bank distributes a fraction of its `early returns',
the bank distributes a fraction of its `early returns',
![]() , to its equityholders in the form of dividends where the dividend payout ratio is given by
, to its equityholders in the form of dividends where the dividend payout ratio is given by ![]() . For simplicity we normalize
. For simplicity we normalize ![]() , which implies that the early returns are accrued by the equityholders. Furthermore, at
, which implies that the early returns are accrued by the equityholders. Furthermore, at ![]() the bank experiences a random liquidity shock such that there are withdrawals of
the bank experiences a random liquidity shock such that there are withdrawals of
![]() . If the bank reserves at
. If the bank reserves at ![]() are insufficient to service these
withdrawals then the bank will have to inefficiently liquidate a fraction,
are insufficient to service these
withdrawals then the bank will have to inefficiently liquidate a fraction, ![]() , of its portfolio. The value of the bank's portfolio at
, of its portfolio. The value of the bank's portfolio at ![]() is given by
is given by
![]() . However, the fire-sale value of the portfolio is
. However, the fire-sale value of the portfolio is
![]() , where
, where
![]() . Thus the fraction of premature liquidation is given by
. Thus the fraction of premature liquidation is given by
![]() . We assume for simplicity that the value of the bank's portfolio is high enough so that it can
service its withdrawals without going bankrupt. This is just for simplicity and allowing for bankruptcy does not change the results.
. We assume for simplicity that the value of the bank's portfolio is high enough so that it can
service its withdrawals without going bankrupt. This is just for simplicity and allowing for bankruptcy does not change the results.
Finally at time ![]() the returns from bank investments, if any, are divided amongst the depositors and the bank equityholders. With probability
the returns from bank investments, if any, are divided amongst the depositors and the bank equityholders. With probability ![]() , the return from the `late' projects will be realized and the equityholders will consume
, the return from the `late' projects will be realized and the equityholders will consume
![]() where
where
![]() if
if
![]() and 0 otherwise. Also note that the equityholders need to make the promised payment
and 0 otherwise. Also note that the equityholders need to make the promised payment ![]() to the patient depositors. With probability
to the patient depositors. With probability ![]() the late projects fail and the value of reserves is divided amongst the depositors.
In this case the equityholders only consume their dividends at
the late projects fail and the value of reserves is divided amongst the depositors.
In this case the equityholders only consume their dividends at ![]() .
.
Given this setup the expected profits of the bank's equityholders is given by:
Since
![]() and
and
![]() we can rewrite the above as follows:
we can rewrite the above as follows:
where
To show the qualitative equivalence of the above dynamic setup with that of the static setup, we first note that
![]() as defined in equation (3) given that
as defined in equation (3) given that
![]() . Thus,
. Thus,
Note that
Also note that
A.2 Extension: Cost of a bubble
Suppose that bank borrowers have an outside option given by
![]() . In other words, if they do not borrow from banks to invest in projects they can consume their outside option. Furthermore, bank borrowers are heterogenous in the sense that the
project of borrower
. In other words, if they do not borrow from banks to invest in projects they can consume their outside option. Furthermore, bank borrowers are heterogenous in the sense that the
project of borrower ![]() succeeds with probability
succeeds with probability
![]() . Banks cannot observe the success probability of individual entrepreneurs and hence under a pooling equilibrium they set a loan rate which cannot be conditioned on the individual
. Banks cannot observe the success probability of individual entrepreneurs and hence under a pooling equilibrium they set a loan rate which cannot be conditioned on the individual
![]() 's but is based on the average risk of the participating entrepreneurs. The projects require a capital of
's but is based on the average risk of the participating entrepreneurs. The projects require a capital of ![]() and if the project succeeds it generates a cash flow
and if the project succeeds it generates a cash flow ![]() , where
, where ![]() . For simplicity we assume that borrowers have limited wealth and hence need to borrow
. For simplicity we assume that borrowers have limited wealth and hence need to borrow ![]() from banks in order to become entrepreneurs. Given limited liability and a
loan rate,
from banks in order to become entrepreneurs. Given limited liability and a
loan rate, ![]() , charged by banks, borrower
, charged by banks, borrower ![]() will invest in his project and
hence borrow from the bank if and only if
will invest in his project and
hence borrow from the bank if and only if
or if and only if
 . . |
Hence as long as
Suppose that there are many entrepreneurs each with a unique success probability
![]() such that
such that ![]() is uniformly distributed between
is uniformly distributed between
![]() . As long as there are no agency problems between bank equityholders and bank managers, the loan rate is given by
. As long as there are no agency problems between bank equityholders and bank managers, the loan rate is given by
![]() . Thus in the no-agency world, all entrepreneurs with
. Thus in the no-agency world, all entrepreneurs with
![]() will invest whilst the infra-marginal entrepreneur will be indifferent between investing and consuming his outside option. Thus the marginal entrepreneur's
success probability, denoted by
will invest whilst the infra-marginal entrepreneur will be indifferent between investing and consuming his outside option. Thus the marginal entrepreneur's
success probability, denoted by
![]() , satisfies the following:
, satisfies the following:
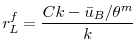 |
or
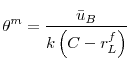 . . |
Hence the average success probability of the active entrepreneurs in the no-agency world is given by:
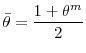 . . |
Next we introduce a cost of default in the economy denoted by ![]() . If the projects of the (active) entrepreneurs fail then a default occurs and the economy suffers a cost
. If the projects of the (active) entrepreneurs fail then a default occurs and the economy suffers a cost ![]() . This cost can take several forms. It could be a cost suffered by the taxpayers who eventually foot the bill for bank bailouts. It could be a cost suffered by the banking system: if banks are not
bailed out it would be the cost of bank failures; it can represent a reputational cost for banks; banks can also face a cost in terms of tougher regulations (for instance limits on the size of banks, limits on proprietary trading and/or higher regulatory taxes). Finally it could represent a
political cost borne by regulators. Hence in the absence of agency problems, the average default cost of an active entrepreneur is given by
. This cost can take several forms. It could be a cost suffered by the taxpayers who eventually foot the bill for bank bailouts. It could be a cost suffered by the banking system: if banks are not
bailed out it would be the cost of bank failures; it can represent a reputational cost for banks; banks can also face a cost in terms of tougher regulations (for instance limits on the size of banks, limits on proprietary trading and/or higher regulatory taxes). Finally it could represent a
political cost borne by regulators. Hence in the absence of agency problems, the average default cost of an active entrepreneur is given by
We have shown that in the presence of an agency problem, bank managers act over-aggressively and set a loan rate, ![]() , such that
, such that
![]() . When the loan rate is lowered, this encourages over-investment and some agents who were previously consuming their outside options will have an incentive to indulge
in bank borrowing. In the presence of an agency problem, the marginal entrepreneur's success probability is given by:
. When the loan rate is lowered, this encourages over-investment and some agents who were previously consuming their outside options will have an incentive to indulge
in bank borrowing. In the presence of an agency problem, the marginal entrepreneur's success probability is given by:
where
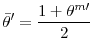 . . |
It is clear that the average success probability of projects falls in the presence of an agency problem. In other words, the average quality of loans deteriorates when managers behave over-aggressively. The average default cost is now given by
where
Intuitively when managers act over-aggressively they set a loan rate which encourages excessive borrowing. This leads to a deterioration of the average quality of loans and hence increases the economy's cost of default. Thus in bubble periods there is over-investment due to a worsening of the quality of loans. This in turn is conducive to higher default costs on average.
Thus the cost of the bubble can be defined as
Let
A.3 Proofs
Proof of Proposition 1. The participation constraint of the bank will be binding because otherwise the bank can increase its expected profits by slightly reducing ![]() . Thus,
. Thus,
![]() is given by the solution to the following:
is given by the solution to the following:
![\displaystyle E\left( \tilde{x}\right) +\left( 1-E\left( \tilde{x}\right) \right) \left[ \theta r_{D}+\left( 1-\theta \right) \frac{E\left[ \max \left( R-\tilde{x}% D,0\right) \right] }{D}\right] =\bar{u}](img246.gif) |
where
We can then substitute
![]() in the bank's objective function and hence
in the bank's objective function and hence
![]() will be the solution to the following unconstrained maximization problem:
will be the solution to the following unconstrained maximization problem:
Assuming that
![\displaystyle \frac{\partial \Pi }{\partial r_{L}}=\theta L\left( r_{L}\right) -\theta \Pr % \left[ \tilde{x}D<R\right] L^{\prime }\left( r_{L}\right) +\theta r_{L}L^{\prime }\left( r_{L}\right)](img253.gif) |
Noting that
From the FOC (22), if we solve for
![]() directly without exploiting the definition of
directly without exploiting the definition of ![]() we get the
following expression for the return on loans:
we get the
following expression for the return on loans:
Taking the partial derivative of the above expression w.r.t.
since
Next note that
![]() , i.e. an increase in bank liquidity (deposits) lowers the probability of liquidity shortfalls since
, i.e. an increase in bank liquidity (deposits) lowers the probability of liquidity shortfalls since ![]() . Then taking the partial derivative of (23) w.r.t.
. Then taking the partial derivative of (23) w.r.t.
![]() we get:
we get:
Hence
Proof of Proposition 2. Both the principal and the agent can observe the realized amount of loans and the bank's net profit. The joint density of loans and net profits conditional on ![]() is given by
is given by ![]() whilst the distribution function is given by
whilst the distribution function is given by ![]() , where
, where ![]() is the realized value of net profits.
is the realized value of net profits.
In our setup ![]() is not a sufficient statistic for
is not a sufficient statistic for ![]() w.r.t. effort and vice versa. Hence given the results of Holmstrom (1979) the optimal compensation schedule should be a function of both
w.r.t. effort and vice versa. Hence given the results of Holmstrom (1979) the optimal compensation schedule should be a function of both ![]() and
and ![]() .
.
The manager is an expected utility maximizer with a Bernoulli utility function ![]() over his payoffs or wage
over his payoffs or wage ![]() and effort
and effort ![]() . The utility function satisfies
. The utility function satisfies ![]() ,
, ![]() and
and ![]() (where the subscripts denote the partial derivatives). This implies that the manager prefers more wealth to less, he is risk averse and dislikes high effort.
More specifically we assume that the utility function is given by
(where the subscripts denote the partial derivatives). This implies that the manager prefers more wealth to less, he is risk averse and dislikes high effort.
More specifically we assume that the utility function is given by ![]() , where
, where ![]() and
and ![]() .
.
We can now write down the optimal contract. Since bank profits are decreasing in managerial wages, the optimal compensation scheme solves the following:
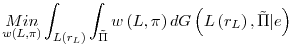 |
subject to
where
Letting ![]() and
and ![]() denote the multipliers for constraints (26) and (27) respectively, then optimization of the Lagrangian yields the following characterization for the optimal compensation schedule:
denote the multipliers for constraints (26) and (27) respectively, then optimization of the Lagrangian yields the following characterization for the optimal compensation schedule:
![\displaystyle \frac{1}{v^{\prime }\left( w\left( L,\pi \right) \right) }=\mu _{1}+\mu _{2}% \left[ 1-\frac{g\left( L\left( r_{L}\right) ,\tilde{\Pi}\vert e_{L}\right) }{% g\left( L\left( r_{L}\right) ,\tilde{\Pi}\vert e_{H}\right) }\right]](img282.gif) |
We know from standard contract theory that in any solution to the optimization problem with ![]() , both
, both ![]() and
and ![]() must be strictly positive. (See for instance, Holmstrom (1979)). This implies that both constraints (26) and (27) are binding. Hence unlike the first best solution, the optimal compensation scheme is not a constant but varies with
must be strictly positive. (See for instance, Holmstrom (1979)). This implies that both constraints (26) and (27) are binding. Hence unlike the first best solution, the optimal compensation scheme is not a constant but varies with ![]() and
and
![]() .
.
As is common in the literature, we then invoke the monotone likelihood ratio property (MLRP), i.e.
![]() is decreasing in
is decreasing in ![]() and
and
![]() . In words, this means that as bank loans and bank profits increase, the likelihood of getting a given level of loans and profits if effort is
. In words, this means that as bank loans and bank profits increase, the likelihood of getting a given level of loans and profits if effort is ![]() , relative to the likelihood if effort is
, relative to the likelihood if effort is ![]() must increase. Given that
must increase. Given that
![]() , this implies that the manager's wages are monotonically increasing in
, this implies that the manager's wages are monotonically increasing in ![]() and
and
![]() . Q.E.D.
. Q.E.D.
Proof of Proposition 3. The proof is along the same lines as the proof to Proposition (1). Define
![]() . Thus maximizing (10) is equivalent to maximizing the following objective function:
. Thus maximizing (10) is equivalent to maximizing the following objective function:
Let
![\displaystyle -r_{p}\Pr \left[ \left( \tilde{x}D\geq R\right) \vert e=e_{H}\right] \bar{L}% _{H}^{\prime }-\theta D\left( 1-E\left( \tilde{x}\right) \right) \frac{% \partial r_{D}^{\ast }}{\partial r_{L}}=0\text{.}](img293.gif) |
The participation constraint is given by (7) and as before it holds with equality. Solving for
where
Proof of Proposition 4. If the manager engages in overly-aggressive behavior, his expected payoff is given by the following expression:
where
However, in the absence of agency problems, the expected loan volume is given by
![]() which denotes the expected loan volume in the first best world conditional on the manager exerting high effort. Thus the expected payoff of
the manager in the absence of agency problem is simply given by
which denotes the expected loan volume in the first best world conditional on the manager exerting high effort. Thus the expected payoff of
the manager in the absence of agency problem is simply given by
![]() . Since the manager can always earn this expected payoff in the absence of agency problems,
. Since the manager can always earn this expected payoff in the absence of agency problems,
![]() can be treated as an opportunity cost in the agency world. In other words, the manager has to earn at least
can be treated as an opportunity cost in the agency world. In other words, the manager has to earn at least
![]() in the agency world as otherwise the manager would be better off by not acting over-aggressively.
in the agency world as otherwise the manager would be better off by not acting over-aggressively.
Thus the problem of the manager is to maximize
The first order condition is given by:
We assume that the second order condition is satisfied, i.e.
![\displaystyle \frac{\partial ^{2}E\left[ \max \left( \tilde{x}D-R^{a},0\right) \vert e=e_{H}% \right] }{\partial \bar{L}_{H}^{a2}}<0.](img308.gif) |
Differentiating the total derivative of the FOC wrt
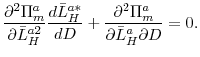 |
where
Since
![]() given the SOC, it follows that
given the SOC, it follows that
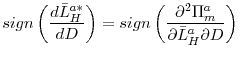 |
Thus one needs to prove that
![]() as this would imply that an increase in deposits would increase the equilibrium loan volume (in expected terms)
and hence overall the manager would be better off.
as this would imply that an increase in deposits would increase the equilibrium loan volume (in expected terms)
and hence overall the manager would be better off.
Taking the partial derivative of (30) wrt ![]() we obtain:
we obtain:
where
Hence as deposits increase, managers have an incentive to act over-aggressively and increase the expected loan volume (via setting a lower lending rate) and they will indulge in this practice as long as their payoffs from doing so increase their payoffs in the default first best world (i.e. their opportunity cost). Conversely, for low enough liquidity there will be no agency problems as in this case the manager would be better off by setting the first best lending rate. Q.E.D.
Proof of Proposition 5. We know from (17) that entrepreneurs will choose ![]() if and only if
if and only if
![]() . This implies that entrepreneurs will shirk if and only if
. This implies that entrepreneurs will shirk if and only if
![]() . Q.E.D.
. Q.E.D.
Proof of Proposition 6. Comparing (13) with (14) we know that ![]() if and only if
if and only if
![]() . From the proof to Proposition 4 we know that
. From the proof to Proposition 4 we know that
![]() for sufficiently high
for sufficiently high ![]() . Let
. Let ![]() denote the threshold below which
denote the threshold below which
![]() and assume the plausible that the number of investors
and assume the plausible that the number of investors ![]() is
big enough so that
is
big enough so that ![]() exists. Hence all we need to show is that
exists. Hence all we need to show is that
![]()
![]() . Since
. Since
![]()
![]() it follows that
it follows that
![]()
![]() . Since
. Since ![]() is
monotonically decreasing in
is
monotonically decreasing in ![]() for all
for all
![]() it follows that there exists a threshold
it follows that there exists a threshold
![]() below which
below which
![]() and hence
and hence ![]() , where
, where
![]() is such that it solves
is such that it solves
![]() . Q.E.D.
. Q.E.D.
Proof of Proposition 7. Differentiating the total derivative of the FOC (20) wrt ![]() we get:
we get:
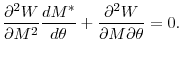 |
Since
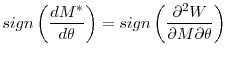 . . |
Taking the partial derivative of (20) wrt
We know that
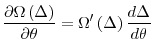 |
Given that
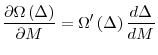 |
where
Next note that
![]() is a necessary condition for
is a necessary condition for
![]() since the expected size of the bubble increases as liquidity increases. Conversely,
since the expected size of the bubble increases as liquidity increases. Conversely,
![]() is a necessary condition for
is a necessary condition for
![]() . It follows that,
. It follows that,
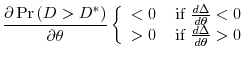 |
Thus, the second term in (32) is positive if
Proof of Proposition 8. Differentiating the total derivative of the FOC (20) wrt ![]() we get:
we get:
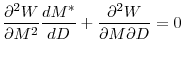 . . |
Since
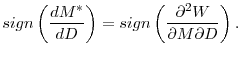 |
Taking the partial derivative of (20) wrt
We know that
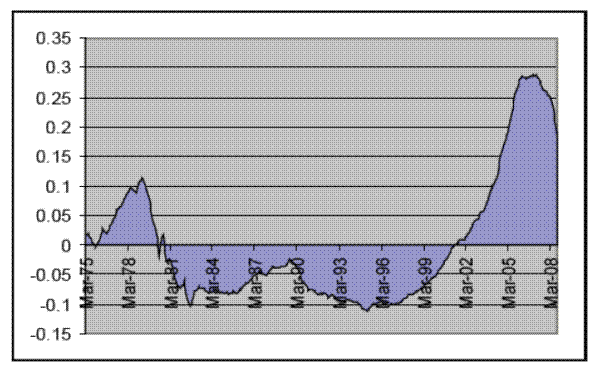
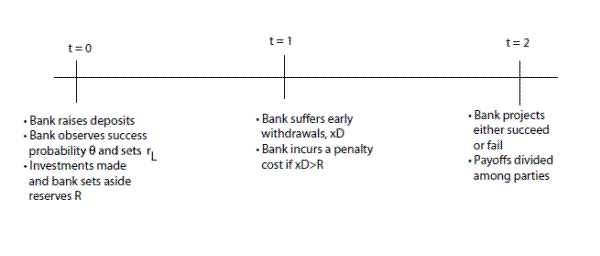
![\displaystyle E\left( \tilde{x}\right) +\left( 1-E\left( \tilde{x}\right) \right) \left[ \theta r_{D}+\left( 1-\theta \right) \frac{E\left[ \max \left( R-\tilde{x}% D,0\right) \right] }{\left( 1-E\left( \tilde{x}\right) \right) D}\right] \geq \bar{u}](img25.gif)
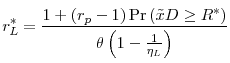
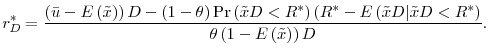
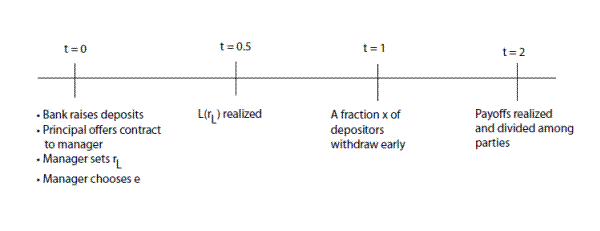
![\displaystyle E\left( \tilde{x}\right) +\left( 1-E\left( \tilde{x}\right) \right) \left[ \theta r_{D}+\left( 1-\theta \right) \frac{E\left[ \max \left( R-\tilde{x}% D,0\right) \vert e=e_{H}\right] }{\left( 1-E\left( \tilde{x}\right) \right) D}% \right] \geq \bar{u}](img54.gif)
![\displaystyle r_{L}^{f}=\frac{1+\left( r_{p}-1\right) \Pr \left[ \left( \tilde{x}D\geq \bar{R}_{f}\right) \vert e=e_{H}\right] }{\theta \left( 1-\frac{1}{\bar{\eta}_{L}}% \right) }](img56.gif)
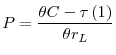 .
.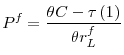 .
.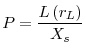 .
.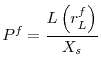 .
.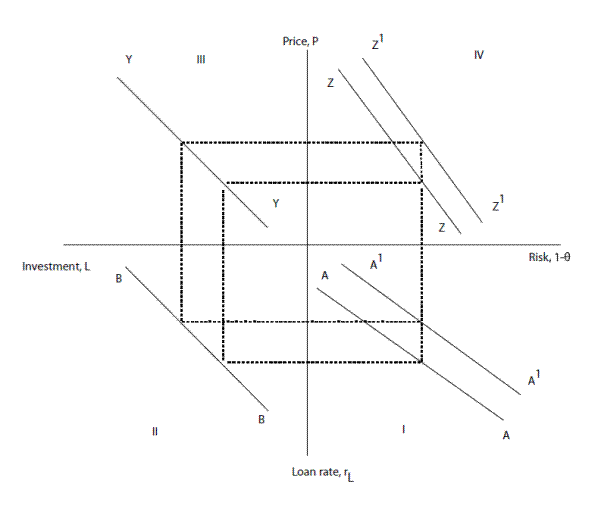
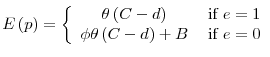 .
.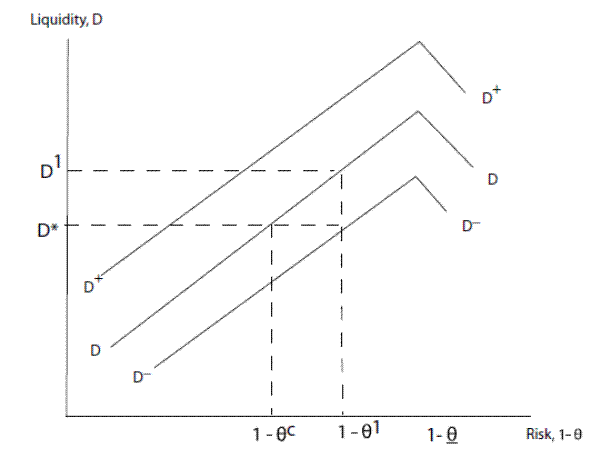
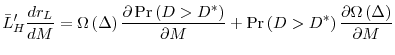
![\displaystyle -r_{p}\Pr \left[ \tilde{x}D\geq R\right] L^{\prime }\left( r_{L}\right) -\theta D\left( 1-E\left( \tilde{x}\right) \right) \frac{\partial r_{D}^{\ast }}{\partial r_{L}}=0](img254.gif) .
.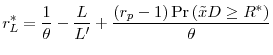
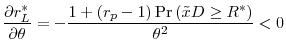
![\displaystyle \frac{\partial r_{L}^{\ast }}{\partial \left[ 1-F\left( R\right) \right] }=% \frac{r_{p}-1}{\theta }>0](img263.gif)
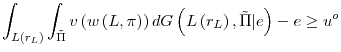
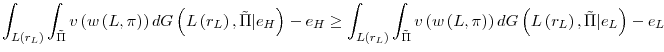
![\displaystyle r_{L}^{\ast a}=\frac{1-\alpha +\left( r_{p}-1\right) \Pr \left[ \left( \tilde{x}D\geq R\right) \vert e=e_{H}\right] }{\theta \left( 1-\frac{1}{\bar{\eta}% _{L}}\right) }](img296.gif)
![\displaystyle \beta -\gamma r_{p}\frac{\partial E\left[ \max \left( \tilde{x}% D-R^{a},0\right) \vert e=e_{H}\right] }{\partial \bar{L}_{H}^{a}}](img307.gif)
![\displaystyle -\gamma r_{p}\frac{\partial E\left[ \max \left( \tilde{x}D-R^{a},0\right) \vert e=e_{H}\right] }{\partial \bar{L}_{H}^{a}\partial D}](img314.gif)
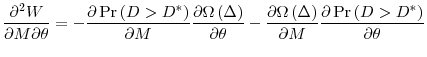 .
.