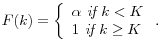Skip to: [Printable Version (PDF)] [Bibliography] [Footnotes]

Key Developments in Monetary Economics: Screen Reader version ^♣

The mechanism design approach to monetary theory*

Neil Wallace

1 Introduction

The mechanism design approach to monetary theory is the search for fruitful settings or environments in which something that resembles monetary trade actually accomplishes something--or, in Hahn's [7] terminology, in which money is essential. Fruitfulness means that the settings provide new insights about puzzling observations and policy questions.

The search for settings in which money is essential is hardly new. Suggestions about absence-of-double-coincidence diffculties go back at least to Roman times (see Monroe [14]). However, despite being repeated over and over again ever since, those statements are incomplete. After all, if they were regarded as satisfactory, then the search would long ago have been regarded as over. If it were over, then the problem of integrating price theory and monetary theory would not have been one of the big unsolved problems in economics throughout the 20th century--as evidenced, for example, by the opening remark in a 1996 paper by Banerjee and Maskin [2]: "Money is something of an embarrassment to economic theory."

Monetary trade accomplishes something if monetary trade is necessary for the achievement of some desirable allocations. To establish such necessity, it must be shown that there is no other way to achieve those allocations. That, in turn, requires that all other ways be considered. Mechanism design is the tool that can be used to consider all other ways. Needless to say, models with cash-in-advance constraints--or, more generally, models with asset-specific transaction costs--and models with real balances as arguments of utility or production functions are not among the candidates for settings in which monetary trade is essential. The former is ruled out because its structure does not permit us to ask about other ways of achieving allocations and the latter is ruled out because it is at best an implicit version of the former.

So what kinds of settings lend themselves to a mechanism design analysis and are fruitful? My general suggestion is that we study environments with three sorts of frictions: imperfect monitoring, costly connections among people, and imperfect recognizability of assets. After I briefly discuss those frictions, I will turn to a specific illustrative model and use it to consider how close we can get to explaining as an optimum the following features of actual economies: currency is a uniform object; currency is (usually) dominated in rate of return; some transactions are accomplished using currency and others are accomplished in other ways.

2 Some frictions

If money is to be essential, then we need to stay away from the Arrow-Debreu model and its second welfare theorem. That's easy enough to do: competitive trade is not a mechanism and the Arrow-Debreu model assumes that people can commit to future actions. I assume that trade is accomplished through a mechanism and that people cannot commit to future actions. We also need to stay away from folk-theorem results. That is accomplished by assuming sufficient discounting, a sufficiently large number of agents, and imperfect monitoring.

2.1 Imperfect monitoring

The ancient absence-of-double-coincidence suggestion is incomplete in at least one important sense. Does it apply if the two people are part of a small isolated community--a small kubbitz, a small Amish community, or a family? It seems as if the two people are meant to be strangers in some sense. One of the first discussions of the sense they are strangers is in Ostroy [16]. He suggests that money is a substitute for knowledge of previous actions. The modern term for describing what is known about previous actions is monitoring: perfect monitoring means common knowledge of all previous actions; imperfect knowledge means anything else. Townsend [19] uses imperfect monitoring to motivate the use of money in an explicit intertemporal model, and Kocherlakota [9] combines it with no commitment. Given no commitment, which I maintain throughout, the crucial proposition implicit in this work is that imperfect monitoring is necessary for money to be essential.

A proof of such necessity would proceed by contradiction. Suppose there is perfect monitoring and that there is an implementable allocation that makes use of fiat money, an intrinsically useless object. Perfect monitoring means that previous actions are common knowledge. So suppose that some initial condition, which includes the distribution of money holdings, and previous actions determine the evolution of actions and holdings of money. In other words, there is a composite mapping from previous actons to current actions, composite in the sense that an intermediate stage involves money holdings and transfers of money among people. Now, consider the implied direct mapping from previous actions to current actions without the use of money. The claim is that implementability of the actions implied by the composite mapping implies implementability of the same actions using the direct mapping. Hence, money is not essential.

The above sketch of a proof uses fiat money rather than commodity money. Fiat money is convenient because the alternative mechanism that uses the direct mapping can simply ignore the fiat money--can treat it as worthless. That could not be done with commodity money. And with commodity money, it is more delicate to distinguish between monetary trade and nonmonetary trade. Indeed, the advantage of using fiat money in the argument is similar to the advantage of using it in the quantity theory of money and its neutrality proposition--something that was done by Hume and others even when actual money was a commodity.

The above claim is supposed to apply to any model and, in particular, to models with private information about types. And, there is no assumption about discounting. No commitment and discounting help determine the conditions for implementability, which can always be stated in terms of actions that do not involve fiat money.

Why might money help if there is imperfect monitoring? If those a person will meet in the future do not directly observe what is done today, then it may help for the person to collect some evidence that can subsequently be shown. That is, acquiring money today can weaken future truth-telling constraints about today's actions. If we think of fiat money as a physical and durable object like currency, then, counterfeiting aside, it can serve that role. Others can say "show me" if the person tries to overstate holdings of it.

The above claim implies that better and better monitoring is one route to a cashless economy. Of course, it need not be the only route to a cashless economy. More generally, while the claim asserts that imperfect monitoring is necessary for monetary trade to be essential, it says nothing about sufficient conditions. It does suggest that no monitoring at all--each person's previous actions are private information to the person--offers the best shot at making money essential. However, if we want a setting in which some form of credit exists, then no monitoring is too extreme.

Credit of any sort requires some monitoring in the sense in which we are using that term. Therefore, if we want both monetary trade and credit in the same model, we need something between perfect monitorting and no monitoring. As in other areas of economics--for example, transport costs in international-trade theory--extreme versions are both easy to describe and, often, easy to analyze. The challenge is to specify and analyze intermediate situations.

2.2 Costly connections among people

Absence-of-double-coincidence has almost always been described in terms of meetings between two people. That has led to a large literature in which people meet in pairs. Any such model should interpreted as one in which connections among people are costly. Models of pairwise meetings in discrete time assume that one pairwise meeting per period is free and that all others are infinitely costly. Pairwise meetings at random, which I will use below, assume that the free meeting is determined randomly. Of course, any such model is very different from having everyone together or at least connected as in the Arrow-Debreu model.

It is evident that pairwise meetings were originally invoked as a way to limit the role of quid pro quo or spot trade in commodities. However, pairwise meetings are not necessary in order that there be a role for intertemporal trade. All we need is a potential role for credit and frictions that inhibit credit.

So why bother with models of pairwise meetings? One reason for studying models with pairwise meetings is that such meetings can provide a rationale for imperfect monitoring. In a large economy, if people meet in pairs and, therefore, know only what they have experienced or what they have been told by people they meet, then imperfect monitoring emerges as an implication. This point of view is explored in Kocherlakota [9] and Araujo [1]. Also, models of pairwise meetings are attractive settings for exploring issues like counterfeiting, imperfect divisibility of money, and float.

Models of pairwise meetings, however, also come with complications. One is the wide range of equilibrium concepts used to answer the old question: What do a pair who meet to trade do? One approach taken in the literature is descriptive--e.g., the buyer and seller make alternating offers, buyers make take-it-or-leave-it offers, or sellers commit to posted prices. Another approach explores all implementable outcomes subject either to individual defection or such defection and cooperative defection by the pair in the meeting. In keeping with the spirit of mechansim design analysis, I will, for the most part, adopt the second approach.

2.3 Imperfect recognizability

Recognizability has often appeared in lists, along with divisibility and portability, as a desirable property of a medium of exchange. Settings with imperfect recognizability generally give rise to asymmetric information in which the current holder of an object knows more about its qualities than a potential acquirer of it. I will sugggest that such asymmetric information is one explanation for our seeming preference for uniform currency. However, because my discussion of imperfect recognizability is far from complete, I start by assuming perfect recognizability.

3 An illustrative model with perfect recognizability

Central banks in the U.K., the U.S., and several other countries emerged as legally mandated monopoly issuers of banknotes from systems in which there were many private banks issuing banknotes. In an attempt to model and compare the latter (which I call an inside- or private-money system) to the former (which I call an outside-money system), Cavalcanti and Wallace [4] use a model with an extreme form of imperfect monitoring: an exogenous fraction of people are perfectly monitored (the potential issuers of private money) and the rest are not monitored at all. Indeed, the rest are assumed to be anonymous. Here I set out that model more generally than has been done and prove some simple results about implementable allocations in it.

3.1 The model

The background environment is an elaboration of that in Shi [17] and Trejos and Wright [20]. Time is discrete. There is a nonatomic and unit measure of infinitely lived people. Preferences are additively separable over dates, and people maximize expected discounted utility with discount factor $\delta\in (0,1)$ . Period utility is , where $x\in \mathbb{R}_{+}$ is consumption and $y\in \mathbb{R}% _{+}$ is production. The functions and are strictly increasing and differentiable with strictly concave, convex, , and, there exists $\tilde{y}>0$ such that $c(\tilde{y})=u(\tilde{y})$ . In addition, production is perishable.

The set of people is partitioned initially and permanently in an exogenous way into two sets: the fraction $\alpha$ are monitored ( people) and the fraction $1-\alpha$ are not ( people), where $\alpha$ should be interpreted as the economy's monitoring capacity. The history of each person is common knowledge, while that of each person is private to the person. (It is as if each person wears a computer chip that transmits everything about the person to everyone else.) The only thing known about an person is that the person is not an person.

In order to allow for a discussion of inside money, each person has a printing press capable of turning out identical, divisible, and durable objects. Those turned out by the printing press of any one person are, however, distinguishable from those turned out by other peoples' printing presses. This is the perfect recognizability assumption.

There are two stages at each date. Stage 1 has pairwise meetings at random: a person is a producer (seller) at each date with probability $\theta$ , a consumer (buyer) with probability $\theta$ , and is neither (meets no one) with probability $1-2\theta$ , where $\theta \leq 1/2$ . Any production and consumption necessarily occurs at stage 1 and no one ever both consumes and produces at a the same date.¹ Stage 2 has a centralized meeting which can be used for transfers of money among agents. It is intended to be the model's analogue of a clearing house, a federal funds market, or a commercial paper market. Because there are no goods at stage 2, there are no separate stage-2 preferences.

One benchmark allocation in the above model is production (and consumption) equal to $\arg \max_{x}[u(x)-c(x)]$ , denoted $x^{\ast }$ , in every (single-coincidence) meeting. According to a representative-agent welfare criterion that views people as identical before being assigned type, or , initial money holdings, and histories, that allocation is the first-best allocation--first-best in the sense of best subject only to the pairwise structure.

One convenient feature of the above setting is this simple description of the first best. Notice that first-best actions are the same at every date: produce $x^{\ast }$ whenever you are a producer in a meeting and consume $% x^{\ast }$ whenever you are a consumer in a meeting. As might be expected, the difficulty is getting the producer to produce $x^{\ast }$ . One possible difficulty arises solely from discounting and is present even if everyone is an person. But, as noted above, money cannot help if everyone is an person. The presence of people gives money a role. However, as we will see, money is necessarily accompanied by history-dependent actions, and, hence, a departure from the first best.

3.2 A class of allocations

Although richer classes of allocations could be considered, I limit allocations to ones in which all monies issued by people who have not defected (and any initial money) and money issued by the planner are treated as perfect substitutes and all monies issued by people are worthless. (Hence, I simply assume that people do not issue money.) Therefore, a person's state at the beginning of date prior to pairwise meetings is an element in the set $\mathbb{S}_{t}=(\mathbb{I\times }H^{t-1}\times \mathbb{R}% _{+}\mathbb{)}$ , where $\mathbb{I}=\{m,n\}$ is the person's type, and $% H^{t-1}$ is the set of possible histories starting from the initial date, , up through date . A history for a person describes who was met in the past in pairwise meetings and includes the state of each meeting partner. A generic element of $\mathbb{S}_{t}$ is denoted $% s_{t}=(i,h^{t-1},z)$ , where is holdings of money issued by others (other monitored people or the planner). If , then $s_{t}$ is common knowledge. If not, then $(h^{t-1},z)$ is private information. In particular, an person can hide money. The post-meeting state of a person is the same kind of object except that it includes what happened at stage 1.

Given a starting distribution of people over states, an allocation is a sequence that describes what happens in meetings at stage 1 and at stage 2 as a function of the states of people. The state of a date- pairwise meeting is $(s_{t}^{p},s_{t}^{c})\in \mathbb{S}_{t}^{2}$ , where the first component describes the producer and the second the consumer as they enter the meeting. In a pairwise meeting, the actions are some amount of production and consumption and state transitions for the two people. At stage 2, the only action is a state transition. At both stages, it is convenient to allow for randomization so that there can be a distribution of actions at stage 1 at a given date for the same kind of meeting.

An allocation describes what happens in the economy in the following sense. Given the initial distribution over $\mathbb{S}_{0}$ and the assumption that meetings occur at random, the date-0 actions imply a date- 1 distribution over $\mathbb{S}_{1}$ , and so on.

3.3 Incentive-feasible (IC) allocations

There are two kinds of constraints on allocations: physical feasibility restrictions and incentive constraints. As regards physical constraints, the updating of histories must be consistent in the sense that if a person has history $h^{t}$ at the start of period , then $h^{t+1}$ for this person must be a continuation of $h^{t}$ . Also, actions must be feasible. For example, in a meeting between two people, people who by assumption do not issue money, total end-of-trade money holdings cannot exceed total pre-trade money holdings. The transitions at stage 2 permit transfers of money to and from the planner.

As regards incentive constraints, we allow for two kinds of Nash implementation: one requires that the allocation be immune to individual defection and the other requires that it be immune to both individual and cooperative pairwise defection of those in a pariwise meeting. Nash means that each person or pair takes as given no-defection by everyone else. Common to both notions are the following assumed punishments. Defection by an person has no future consequences for the person except those implied by the current trade to which the person defects. Defection by an person is common knowledge and is assumed to be punished by permanent expulsion from the set of people to the set of people starting at the next stage.²

Such exclusion may seem like a weak punishment. One alternative would be economy-wide reversion to autarky as a response to a defection. That would not be best if there were a small probability of errors in actions. And, even without such errors, it would not be time-consistent for the society. If economy-wide or even positive measure punishments are not imposed, then the assumed punishment can be justified by assuming that there is free exit at any time from the set of people to the set of people. Even if that were not assumed, it would be delicate to impose stronger individual punishments. Even if an person is a known defector, people would in general want to trade with that person.

Given the structure of the model, an individual defection is always to no trade at the current stage: in a pairwise meeting, it is zero production and consumption and an unchanged holding of money; at stage 2, it is no transfer of money. If the defector is an person, then there are no further consequences. If the defector is an person, then that person begins the next stage as an person with the money held and with a useless printing press--useless because the defection is assumed to make that person's money worthless.

As regards cooperative defections in pairwise meetings, there are three kinds of meetings. In a meeting between two people, there is no private information. Any cooperative defection has both people becoming people at the next date with both monies issued by those people worthless. Hence, in any defection their total money holdings are limited by the money holdings they bring into the meeting and two people cannot make each other rich by issuing money to each other. The restriction implied by the possibility of cooperative defection is that their payoffs (the profile of the current utility payoff plus the discounted continuation value for the producer and the consumer) must be weakly outside the payoff frontier of a meeting between two people with the same profile of money holdings. In a meeting between an person and an person, there is one-sided asymmetric information. Again, any cooperative defection has the person becoming an person at the next date. Both for those meetings and for meetings between two people, a full analysis requires that some notion of the core under asymmetric information must be adopted. (When two people meet, there is two-sided asymmetric information if only because both the producer and the consumer can hide money.)

The results presented below, which are not existence results, do not depend on which notion is adopted. In particular, the arguments take as given the trades and payoffs of people.

3.4 Results

There are three simple results about the set of IC allocations. The first is that more monitoring is better.

Claim 1 In terms of production and consumption, the set of IC allocations is weakly increasing in fraction who are monitored..

Proof. Consider two economies, economy 1 and economy 2, that are identical except for $\alpha$ : let $\alpha _{2}>\alpha _{1}$ . If the allocation $A_{1}$ is IC for economy 1, then there exists $A_{2}$ that is IC for economy 2 and has the same production and consumption. The allocation $A_{2}$ is constructed by having the additional monitored people behave exactly as do the nonmonitored people under $A_{1}$ that they " replace." In other words, in economy 2, select at random a fraction $(\alpha _{2}-\alpha _{1})/\alpha _{2}$ of the

people and give them a special starting history, a label, and have them behave exactly as

people do in $A_{1}$ . Have everyone else behave as they do in $A_{1}$ . Then because $A_{1}$ is IC in economy 1, it follows that $A_{2}$ is IC in economy 2. In other words, having an

person behave like an

person is always IC because defection of any sort is always to

status. $\qedsymbol$

The next claim says that allocations can be limited to those in which people enter stage 1 without money--with only their printing presses. In general, people acquire money in pairwise meetings when they produce for people. Therefore, such an allocation calls for them to immediately destroy any money received or, equivalently, turn it in to the planner at the next stage 2.³ A consequence is that any spending by an person in a meeting involves the issue of that person's money. This result uses the restriction that only allocations in which all monies issued by monitored nondefectors are perfect substitutes are considered.

Claim 2 If an allocation is IC, then there is another allocation with the same production and consumption in which monitored people enter stage 1 without money.

Proof. Consider an arbitrary IC allocation in which some

person enters a pairwise meeting with some money at some date. Consider an alternative that is identical except that this person has turned in that money at the previous stage 2, but keeps spending unchanged by issuing the person's own money instead of spending the money issued by others. Because all monies are perfect substitutes, trading partners are not affected, and, therefore, no-defection payoffs are not affected. What about defection payoffs? A consequence of the ability of

people to hide money is that the discounted utility of an

person is weakly increasing in money holdings. That implies that the defection payoffs implied by the alternative are no larger than those of the given arbitrary allocation. Hence, the alternative is also IC. $\qedsymbol$

Notice that the converse of this claim does not hold. Start with an allocation in which people hold no money and consider an alternative which differs only in that at some date an person has not turned in the money received earlier. Does willingness to turn in the money imply that the alternative is IC? It does not. The money is turned in prior to the next meeting (before the next trade realization is revealed). It is based on an expected value over such realizations and the defection realizations. But that implied inequality does not imply no defection in each subsequent trade realization.

Why have money transferred to an person in a pairwise meeting if the person will simply turn it in? If the person making the transfer is an person, then the transfer provides an additional inducement for that person to have acquired money in the past. Also, if an allocation is to have people issue money when they are consumers in meetings with people, then unless they collect money from people when they are producers in meetings with people, holdings of money by people would be growing. That would produce the model's analogue of inflation.

If the person making the transfer is another person, then the transfer plays no role and can be eliminated. If it is eliminated, then an outside observer will see production and consumption occur without any transfer of money. That is the model's version of a credit transaction. It follows, in accord with the necessity of imperfect monitoring, that if everyone is monitored, then money is not needed. It also follows that any production by an person--whether for another person or for an person--is supported entirely by threatened expulsion from the set of people.

Claim 3 If not everyone is monitored, then the first-best is not IC.

Proof. Suppose it is IC and consider two mutually exhaustive possibilities. Either the support of the distribution of money holdings across

people at some date prior to stage 1 contains two different holdings, $m_{1}$ and $m_{2}$ , with $m_{2}>m_{1}$ , and money is valuable in the sense that the discounted value of the holding $m_{2}$ exceeds that of the holding $m_{1}$ or not. The former--a nondegenerate distribution and valuable money-- contradicts the first-best because the first-best implies that everyone has the same discounted utility prior to pairwise meetings at every date. If the latter, then discounted utilities are degenerate at every date either because there is a degenerate distribution of money holdings or because all holdings in the support have equal discounted value. However, if this holds at some date, then the first-best actions imply that it does not hold at the next date. In particular, those

people who are supposed to produce $x^{\ast }$ in a pairwise meeting must see a future reward from doing so or they defect to no trade. But that future reward can only take the form of higher money holdings prior to stage 1 at the next date to which are attached higher discounted utility. Hence, the degeneracy and first-best actions cannot hold at every date. $\qedsymbol$

Before I go on to discuss the consequences of imperfect recognizability, several comments about the above model should be made. First, the assumption that people do not issue money seems innocuous because I permit the planner to make positive transfers of money at stage 2 to people. Such transfers--perhaps, sprinkled in a random way among people--would seem to be a good substitute for making the money issued by a subset of the people acceptable.

Second, no mention has been made of a commonly studied intervention in models of money: the use of taxes to finance the payment of interest on money--either explicitly or through deflation. A special case is real interest that exactly offsets discounting, what is called the Friedman rule. Such schemes do not have to be considered separately because they are included in the class of allocations set out above. For example, a deflation can be produced by having money in the hands of people decline over time. Although that cannot be achieved by an explicit tax on people, it can be achieved in other ways: one way is by having people issue less money when they are consumers in meetings with people than they collect and destroy when they are producers in meetings with people; another is having people consume less per unit of money transferred in meetings with people than they produce per unit of money received in meetings with people.

Whether such schemes are IC and optimal cannot be addressed without imposing additional structure on the model. However, even at this level of generality, any such analysis seems very different from the analysis of deflation or paying interest on money in representative-agent models. The financing of any such scheme has to come from taxes on people. And because those people can defect, such taxation is scarce. And although this model is very extreme in its monitoring assumptions, a case can be made that it better represents how credit and currency are used in modern economies than does a representative-agent model.

Finally, although the model was introduced in order to contrast inside and outside money, so far nothing has been said about that contrast. Outside money is the special case in which no one but the planner issues money. The restriction that no one issue money is IC because if money-issue is a defection, then that money becomes worthless at the next date and, therefore, is worthless when issued. However, because outside money is a special case with additional restrictions, imposing it in the above setting cannot help.

Does it hurt? Without imposing additional structure, I cannot demonstrate that it hurts. But I can describe why it might hurt. Under outside money, the spending of people seems to be tied to their individual histories (as it necessarily is for people). However, the introduction of stage 2 goes some way toward removing that dependence. In particular, stage 2 can be used for transfers among the people (something like borrowing and lending among themselves or, more precisely, insurance among them) and there can be transfers to and from the planner--all of which are subject to defection constraints. Those defection constraints, though, tend to be tighter under outside money because the result in claim 2 is lost--namely, that people enter pairwise meetings without money. According to the model, that is why imposing outside money might hurt.

4 Imperfect recognizability and uniform currency

Despite the benefit of private currencies just identified, we almost always observe uniform currencies. There are many possible reasons. One concerns recognizability problems with many distinct currencies. Such problems could take a variety of forms. Here, I consider the threat of counterfeiting.

In the context of the model above, suppose some people have a costly counterfeiting technology of the following sort. At any stage 2, they can produce counterfeits subject to a positive fixed cost and a constant marginal cost. In stage 1 meetings, suppose producers cannot distinguish between genuine currency and counterfeits until after they acquire the currency. Then they learn whether they have acquired genuine currency or counterfeits.

There are two conceivable kinds of allocations in these circumstances. In one, counterfeits are produced and known counterfeits and genuine currency are perfect substitutes. Even if this kind of allocation is implementable, it has obvious shortcomings from the point of welfare. It is identical to one without counterfeiting, but in which the genuine currencies of the potential counterfeiters are treated as perfect substitutes with other currencies. In such an allocation, those people never produce and issue currency period after period.

The other kind of allocation is one in which known counterfeits are less valuable than genuine currency. Here, there is asymmetric information between the producer and the consumer in a pairwise meeting: the consumer knows whether he or she has genuine or counterfeit currency and the producer does not. Any such allocation is either a pooling allocationm or a separating allocation. A separating allocation hardly fits our notion of counterfeiting, because producers end up accepting known counterfeits. Hence, most analyses focus on pooling allocations.

In part, because there is no standard notion of the core under asymmetric information, all existing analyses adopt a particular game form in these situations. Nosal and Wallace [15] study counterfeiting in a context of a signalling game formulation and impose the Cho-Kreps intuitive criterion as a refinement. The implication is that there is no pooling equilibrium. The deviating offer that destroys a pooling equilibrium is that the consumer with genuine currency offers a smaller trade: he offers less currency for less output and the producer infers from this offer that it is coming from a consumer with genuine currency.

Nosal and Wallace assume that known counterfeits are worthless and, therefore, that there is no separating equilibrium. That and their conclusion about the absence of a pooling equilibrium implies that there is no equilibrium in which counterfeiting occurs. But an equilibrium in which genuine currency is valuable and no counterfeiting occurs exists only if counterfeiting is sufficiently costly. Otherwise, the only equilibrium is autarky. Put differently, they conclude that counterfeiting is a threat to existence of an equilibrium in which genuine currency is valuable. An implication of their analysis is that there should be sufficient enforcement to prevent counterfeiting.

That implication takes us in the direction of a single uniform currency if we assume, as seems plausible, that the prevention of counterfeiting is much easier with a single uniform currency than with many private currencies.⁴

5 Optima under a uniform outside currency

As suggested above, under outside money, stage 2 in the prototype model takes on added importance. First, it could be desirable for there to be transfers of currrency among people--transfers that accomplish insurance. In particular, it may be desirable and incentive feasible to have those people who recently earned outside money make transfers to those who recently spent such money. Second, the planner who controls outside money might participate in the transfer scheme. To get a sense about what optima might look like under outside money, Deviatov and Wallace [5] study an example of the prototype model in which there is an exogenous two-date periodic productivity process--a deterministic seasonal.

In their example, the discount factor is .95, the utiltiy of consuming is $% 2x^{1/2}$ , and the disutility of producing when is odd (low productivity dates) and when is even (high productivity dates). Therefore, $(.8)^{2}$ is the first-best output at low productivity dates and $(1.2)^{2}$ at high productivity dates. Each person is a producer with probability and is a consumer with probability , and monitored people are one-quarter of the population. Aside from the discount factor being sufficiently high in a sense to be described, this specification is not the result of a search.

For this example, Deviatov and Wallace compute the maximum of ex ante representative-agent utility--prior to the assignment into types, monitored or nonmonitored, and prior to the assignment of initial currency holdings, the distribution of which is treated as among the choice variables of the planner. The constraints are individual defection at both stages, and, in addition, pairwise cooperative defection at stage 1 pairwise meetings. They simplify the problem in three important respects. First, they search only over two-date periodic allocations. Second, currency is indivisible and holdings prior to stage 1 are restricted to be in $\{0,1\}$ . Third, while lotteries are allowed (and play a role), randomization is not allowed. They study and compare two versions of this problem: in one, called no-intervention, the quantity of currency is constrained to be constant; in the other, it, like everything else, is permitted to be two-date periodic.

Constraining currency holdings to $\{0,1\}$ is an extreme assumption, but is not misleading. As noted above, the economic problem in this model is to free current actions from previous realizations. The $\{0,1\}$ money holdings exaccerbate this problem, but is not misleading. As regards the discount factor, it is high in two senses, each related to providing simple benchmark allocations. First, it is high enough so that if everyone were monitored, then the first-best allocation, one with first-best outputs in every meeting, would be implementable. Second, the discount factor is high enough so that the best allocation subject to treating everyone like an person, which is an implementable allocation, has half the agents with a unit of currency and has first best outputs in one-quarter of the meetings. Moreover, in that allocation, the intervention and nonintervention versions are identical. Ex ante utility for that allocation is equal to one-quarter of the upper bound, one quarter because trade in a pairwise meeting requires that the potential consumer have money and that the potential producer not have money.

Some features of the optimum are common whether or not there is intervention. First, the discounted utility of an person is roughly 2/3 of the upper bound, while that of an person prior to the assignment of money is roughly 1/3 of the upper bound. Second, there are no transfers of currency to people. Third, all people enter stage 1 with a unit of currency and the constraint that they not defect when called on to produce is binding in many meetings. It follows that production by people is supported entirely by threatened expulsion from the set of people, as happens generally under inside money. Of course, as noted above, the threatened punishment under inside money would be greater, and that would allow better allocations to be achieved under perfect recognizability.

Intervention in the example looks like the granting of 0 interest loans to the aggregate of people at stage 2 following pairwise meetings at the high-productivity date, with repayment at stage 2 following the next low productivity meetings. In terms of outputs, intervention shows up mainly in meetings between and people. Intervention frees the distribution of money holdings between and people from the constraint that net currency trades between the two groups are zero at every date. A consequence is intervention has smoother outputs in those meetings, smoother relative to the respective first-best outputs. Perhaps, the simplest way to describe the role of intervention is that loans at stage 2 after the high productivity date restore the currency holdings of people and, thereby, permit higher spending by them in the pairwise meetings with people at the high productivity date. Obviously, the distinction between and and people and the fact that they interact are crucial features of the example.

6 Extensions of the prototype model

The protoype model is extreme in many respects. Here I comment on some directions in which it could be generalized.

6.1 Capital

A seemingly troublesome feature of the prototype model is the absence of forms of wealth other than currency. Indeed, in the inside-money version, people hold no wealth, while people have some wealth but all of it is in the form of currency. Here I describe a way to remedy that troublesome feature by introducing into the model putty-clay capital.

In the version above, the production technology in pairwise meetings has a single input, labor or effort. As has been recognized by others, that could amended so that output produced in a meeting is a function of the producer's labor and capital, say , where is the person's effort and is the person's capital at a date, and where, could be assumed to be standard--say, linear homogeneous and strictly quasi-concave. As in the model without capital, the period utility for a person is , where denotes consumption.

The crucial assumptions concern the law of motion for a person's capital. One specification is that a person's gross investment good and consumption good are the same object. If so, then in a meeting with a producer at a date, the usual putty restriction on consumption and gross investment would hold: the sum of the two, both nonnegative, is bounded above by the output acquired from the producer in the meeting. The clay aspect of capital is that existing capital cannot be transferred to another person.

How does this structure of production in pairwise meetings influence what is traded in those meetings and in stage 2? If there were only people, then the model would be unchanged except that the state space would be richer. Now each person would be characterized by a portfolio, money and capital--although the latter could not be traded. If there were only people, the implication that money is not needed is unaffected. Even with a mixture of and people, the only difference is the richer state space. Whether under inside money or outside money, there is, perhaps, a greater potential role for insurance. But people are no better able to participate, while people have essentially the same defection constraints on their participation as they have in the version without capital. In particular, the existence of capital of the above sort would not seem to enlarge the risk-sharing possibilities for either type of person.

One plausible conjecture about this version is that an optimum would display less dispersion in capital holdings across people than among people. That is, one would guess that capital is more efficiently distributed among people than among people.

6.2 Endogenous monitored status

The prototype model has an exogenous fraction who are perfectly monitored ( people). That exogeneity assumption can be reconciled with one-time free entry into status if each person makes such a choice subject to a one-time, additively separable utility cost that is idstributed in a very special way. Let $F:R_{+}\rightarrow \lbrack 0,1]$ , where is the fraction of people who can become permanently monitored with a one-time additively separable utility cost no greater than . For the prototype model, takes the special form:

$\displaystyle F(k)=\left\{ \begin{array}{l} \alpha \textit{ if }k<K \\ 1\textit{ if }k\geq K\end{array}% \right. .$

(1)

Here, $F(0)=\alpha$ and 0 is a normalized lower bound on discounted utility, the value of autarky. Also, it is easy enough to choose a large enough

so that a person with cost

would never choose to be an

person for any incentive-feasible allocation.

To allow for initial free entry into status, the sequence of actions at the initial date is as follows. People are ex ante identical. Then the planner announces an allocation, including initial distributions of money dependent on or status. Then, in accord with the distribution function , each person privately learns his cost of becoming an person and chooses whether to become an person. Then, initial money holdings are distributed. If the allocation satisfies the incentive constraints, which include the restriction that those with low enough utility-cost of becoming an person choose status and that the rest do not, then trades are undertaken in accord with the planner's suggestion.

Let $v_{t}^{j}(x)$ be the discounted expected utility of a type $j\in \{m,n\}$ at the beginning of date of someone who holds amount of money, the only asset. The free-exit assumption implies that one of the constraints on the planner is $v_{t}^{m}(x)\geq v_{t}^{n}(x)$ for all . This, in turn, implies $v_{0}^{m}\geq v_{0}^{n}$ , where $% v_{0}^{j}=E_{x}v_{0}^{j}(x)$ and $E_{x}$ denotes expectation taken over the relevant initial distribution of money. For the above model in which is given by (1), the restriction that people choose status as intended by the planner is nothing more than $K\geq v_{0}^{m}\geq v_{0}^{n}\geq 0$ --that is, nothing more than is implied by free exit from status at any time. Notice that initial free-entry into status is consistent with $v_{0}^{m}>v_{0}^{n}$ , which is almost certainly a robust feature of an optimum in the model.

However, initial free-entry imposes an additional constraint if is continuous and strictly increasing and if a person's realization from is private information. (For the in (1), private information about the realization plays no role.) Under such assumptions, (i) initial money holdings can be assigned based only on whether the person chooses to become monitored; and (ii) $v_{0}^{m}-v_{0}^{n}=\hat{k}$ , where $F(\hat{k})$ is the fraction who choose status.

In such a version, the shape of will play a role in determining the optimum allocation. That is, the planner will, in effect, be concerned about how the allocation affects the fraction who choose to become monitored.

6.3 Other information structures and other financial instruments

When compared to the actual economy, the prototype model is deficient in terms of the limited financial instruments that appear in it. Indeed, whether under inside money or outside money, the only financial instrument seems to be something like a uniform currency. Mainly because of the extreme monitoring assumptions, instruments like checking accounts, debit cards, credit cards, cell-phone money, and bills of exchange are either not feasible or not needed.

All such instruments are supported by an informational network. By assumption, people cannot be part of any such network. As for people, they are part of a perfect and costless network that reveals their actions to everyone. Hence, other financial instruments which potentially convey information about people are not needed. There is however, a caveat. I have imposed that currency, whether inside or outside, is treated as a uniform object in equilibrium. Conceivably, there might be a role for distinct objects to be held by people.

The set of implementable allocations could conceivably be enriched by having different assets with different rates of return available to people. In Bryant and Wallace [3], people are faced with non-linear and increasing returns on saving among which they self-select and that can enrich in a beneficial way the set of implementable allocations. In Kocherlakota [10], facing people with some assets that can be traded for goods and others with higher returns that can only be saved enlarges the set of implementable allocations in a beneficial way. But those analyses are silent about what allows non-linear returns to be implementable? Thus, for example, Kocherlakota simply assumes that his higher reutrn assets, called bonds, cannot be traded for goods directly. In Bryant and Wallace, the bonds are explicitly indivisible and large, but little is said about why they cannot be shared or intermediated.

The prototype model can help in that regard. To fix ideas, suppose the planner at stage 2 sells high-denomination, one period, payable-to-the-bearer bonds intended to be bought by some people. Their high denomination limits their use in trade in pairwise meetings among people. (Independent of denomination, the planner could have people not accept them at stage 1.) However, if the bonds dominate currency in rate of return across stage 2 at adjoining dates, then they give rise to a profitable arbitrage opportunity: hold the bonds as assets and issue small-denomination, one-period, payable-to-the-bearer claims. But who could engage in such intermediation? It involves promises, which, in the prototype model, can only be made by people. But the actions of people are public. Hence, if the planner wants to prevent such intermediation, then he can. Put somewhat differently, a legal restriction against such intermediation is easy to enforce in the prototype model. Indeed, for closely related reasons, it would seem to be easy to enforce in the actual economy.

Thus, the prtoype model is one example in which assumptions about the information structure have implications about the kinds of financial instruments that might exist and that might play a beneficial role.

6.4 Production and consumption at stage 2

There is a substantial literature that resembles the prototype model but has production and consumption at stage 2 when everyone is together. Most of it follows Lagos Wright [12] and has identical and quasi-linear preferences at stage 2. A general version with production and consumption at stage 2 would qualitatively resemble the prototype model, but the version with identical and quasi-linear preferences at stage 2 does not.

The essential features of the Lagos Wright model are most easily seen in a version with identical and linear preferences at stage 2: there is a stage 2 perishable good for which there are identical and additively separable preferences (additively separable from stage-1 preferences) for everyone that are given by the identity function. Positive consumption of this good interpreted as consumption and negative consumption is interpreted as production of it. Trade at stage 2 is modeled as competitive price-taking trade. (If in a mechansim design version, group defection is permitted, then such trade is without loss of generality because it is equivalent to the static core at stage 2.) The insight of Lagos and Wright is that the outcome of such trade absorbs all wealth differences among people entering stage 2 through differences in consumption of that good. It follows that the distribution of wealth entering stage 2 is not a state of the economy going forward from the end of stage 2. A similar role is played by the large-family in Shi [18]. ⁵ In each case, the economy starts anew with an essentially exogenous distribution of money at each date.⁶

While there is a huge gain in terms of tractability from the Lagos Wright specification or Shi's large family model, insufficient attention has been paid to what is lost from those specifications. Put differently, insufficient attention has been paid to studying the robustness of conclusions to what is a very special preference specification in Lagos Wright and a very special notion of decision making in Shi's large-family model. One thing lost is the result that the first best is not implementable if there are people (see HKW [8]). That result depends on a relationship, possibly the identity relationship, between the distribution of money across people at the begiining of of stage 1 at one date and that distribution at the end of previous stage 1. That is not present in either the Lagis-Wright formulation of the Shi large family model. Another thing lost is the risk-sharing role of monetary transfers among people at stage 2. All such risk-sharing is accomplished through trade in the linear good. More generally, I suspect that the differences between outcomes according to monitored status are lost in such models. That seems to be a high price to pay for tractability.

7 Concluding remarks

I began by defining the mechansim-design approach to monetary economics and then turned immediately to a discussion of a particular model. The model builds on the pioneering work on matching models of Kiyotaki and Wright [11], Trejos and Wright [20] and Shi [17] who were the first to formulate coherent intertemporal models of trade in which people meet in pairs and use money. It also builds on the ideas about the connection between imperfect monitoring and monetary trade of Ostroy [16], Townsend [19], and Kocherlakota [9].

The goal of the discussion is to explain as an optimum three features of most actual economies: currency is a uniform object; currency is (usually) dominated in rate of return; some transactions are accomplished using currency and others are accomplished in other ways. Toward that end, I first described how private money would work and its advantages under the assumption of perfect recognizability. Then, in what I regard as the weakest part of the discussion, I invoked imperfect recognizability as a disadvantage of private money. Finally, to explain why currrency is dominated in return, I invoked a connection between the main feature of the model that gives currency a role, the imperfect monitoring, and who can and who cannot be taxed. I suggested that the implied restrictions on taxation will in many settings imply that the optimum does not have currency earning the Friedman-rule rate of return.

The models I have described seem both special and complicated. Is that inevitable? Maybe it is. First, models with imperfect monitoring, costly connections among people, and imperfect recognizability are unlikely to be simple. Second, monetary trade is a descriptive or positive feature of an economy. It will not be an implication of every environment we can imagine.

Although this may seem discouraging, I wonder whether that is warranted. First, by its very nature, the mechanism design approach to monetary economics accomplishes the long-standing goal of integrating moneyary economics with the rest of economics. However, it is not the integration that seemed to be the goal a century or more ago; namely, integration with the then current version of the Arrow-Debreu model. Part of the progress we have made is to understand why that is not the right goal. Instead, the goal should be integration with the rest of economics that deals with frictions. Second, although I am far from a neutral observer, I see considerable progress in the last 20 years.

Among the issues addressed in recent work are private versus government currency, the issue focussed on above, the long-standing puzzle concerning profitability of private currency systems in the 19th century (see Wallace and Zhu [21]), the denomination structure of currency (see [13]), and the analysis of counterfeiting (see [15]). While these are not strictly mechanism-design analyses because they assume particular trading protocols in pairwise meetings, they are closely related in that they use models with the same kinds of frictions. In that sense, they illustrate the fruitfulness of studying issues in monetary economics against the background of models in which something that resembles monetary trade is the best way to achieve good outcomes.

Bibliography

Araujo, L.,

Social norms and money. J. of Monetary Economics 51, 2004, 241-256.

Banerjee, A and E. Maskin,

A Walrasian theory of money and barter, Quarterly Journal of Economics, 111, (1996), 955-1005.

Bryant, J. and N. Wallace,

A price discrimination analysis of monetary policy, Review of Economic Studies, 51, 1984, 279-288.

Cavalcanti, R. and N. Wallace,

Inside and outside money as alternative media of exchange. J. of Money, Banking, and Credit, 31, (1999, part 2), 443-57.

Deviatov, A. and N. Wallace,

A model in which monetary policy is about money. J. of Monetary Economics, 56, (2009),283-88.

Galenianos, M. and P. Kircher,

A model of money with mutlilateral matching. J. of Monetary Economics, 2008, 55, 1054-1066.

Hahn, F.,

On the foundations of monetary theory, Chapter 13 in Essays in Modern Economics, edited by Michael Parkin with A.R. Nobay, New York, Barnes and Noble, 1973.

Hu, T.W, J. Kennan, N. Wallace,

Coaltion-proof trade and the Friedman rule in the Lagos-Wright model, J. of Political Economy, 117, (2009),116-37

Kocherlakota, N.

Money is memory. J. of Economic Theory 81, 1998, 232-51.

Kocherlakota, N.,

Societal benefit of illiquid bonds, J. of Economic Theory, 108, (2003), 179-193.

Kiyotaki, N. and Wright, R.

On money as a medium of exchange. J. of Political Economy 97, 1989, 927-54.

Lagos, R. and Wright, R.,

A unified framework for monetary theory and policy analysis. J. of Political Economy 113, 2005, 463-484.

Lee, M., Wallace, N., and Zhu, T.,

Modeling denomination structures. Econometrica 73, 2005, 949-960.

Monroe, A. E.,

Monetary Theory Before Adam Smith. New York: Kelley., 1966.

Nosal, E and N. Wallace,

A model of (the threat of) counterfeiting, J. of Monetary Economics, 54, (2007), 994-1001.

Ostroy, J.,

The informational efficiency of monetary exchange, American Economic Review, 63:, (1973), 597-610.

Shi, S.,

Money and prices: a model of search and bargaining. J. of Economic Theory, 67, (1995), 467-98.

Shi, S.,

A divisible search model of money. Econometrica 65, 1997, 75-102.

Townsend, R.M., 1989.

Currency and credit in a private information economy. J. of Political Economy 97, 1323-44.

Trejos, A. and R. Wright,

Search, bargaining, money and prices. J. of Political Economy 103, (1995), 118-41.

Wallace, N and T. Zhu,

Float on a note, J. of Monetary Economics, 54, (2007), 229-246.

Zhu, T.,

Equilibrium concepts in the large household model, Theoretical Economics, 3, 2008, 257-81.

Footnotes

* This is a preliminary version. Please do not cite without permission of the author. Return to Text

1. As is well-known, one underlying setting is a

-good,

- type setting in which there is an equal measure of each type. A type-

person consumes only type-

good and produces only type-

good for $k\in \{1,2,...,K\}$ , where addition is modulo

. If

, then we get the model in the text with $\theta =1/K$ . Return to Text

2. Throughout, I take for granted that the set of incentive-feasible allocations is the set of weakly implementable allocations. See Zhu [22] for an explicit definition of implementability that can be adapted to this setting. Return to Text

3. Of course, if money were costly to produce, then it would be wasteful to destroy it. In that case, stage 2 could be used as a kind of clearing stage during which

people turn in other issuer's notes and receive their own notes for subsequent use. Return to Text

4. Does counterfeiting exist? In the U.S., it is estimated that one in ten thousand dollars are counterfeits (see ????). That is close enough to zero be treated as zero in the sense that it would not be worthwhile to think about a deviating offer in a pooling equilibrium with that proportion of counterfeits. Return to Text

5. On the modeling of the large family model, see Zhu [22]) Return to Text

6. Often, this distribution is degenerate, but not in every model. (See Galenianos and ??? for a model in which the starting anew property holds, but in which there is a nondegenerate distribution at the end of stage 2.) Return to Text

^♣ This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to Text