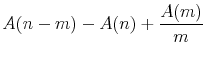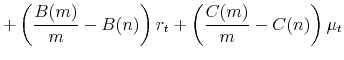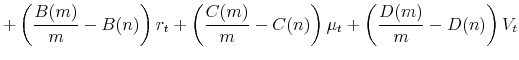Skip to: [Printable Version (PDF)] [Bibliography] [Footnotes]

Finance and Economics Discussion Series: 2007-22 Screen Reader version ^♣

Bond Risk Premia and Realized
Jump Volatility*

Jonathan Wright* and Hao Zhou*

First Draft: November 2006
This Draft: March 2007

Keywords: Unspanned Stochastic Volatility, Expected Excess Bond Returns, Expectations Hypothesis, Countercyclical Risk Premia, Realized Jump Volatility, Bi-Power Variation

Abstract:

We find that adding a measure of market jump volatility risk to a regression of excess bond returns on the term structure of forward rates nearly doubles the R^2 of the regression. Our market jump volatility measure is based on the realized jumps identified from high-frequency stock market returns using the bi-power variation technique. The significant enhancement of bond return predictability is robust to different forecasting horizons, to using non-overlapping returns and to the choice of different window sizes in computing the jump volatility. This market jump volatility factor also crowds out the price-dividend ratio in explaining much of the countercyclical movement in bond risk premia. We argue that this finding provides support for the unspanned stochastic volatility hypothesis according to which the conditional distribution of excess bond returns is affected by state variables that are not in the span of the term structure of yields and forward rates.

JEL Classification Numbers: G12, G14, E43, C22.

1 Introduction

The Expectations Hypothesis (EH) is well known to be a miserable failure, with bond risk premia being large and time-varying_ A regression of yield changes on yield spreads produces a negative slope coefficient instead of unity, as would be implied by the Expectations Hypothesis (Campbell and Shiller, 1991), and forward rates can predict future excess bond returns (Fama and Bliss, 1987). Indeed Cochrane and Piazzesi (2005) recently showed that using multiple forward rates to predict bond excess returns generates a very high degree of predictability, with values of around 30-40 percent. Authors have also used the ARCH in mean (ARCH-M) model to relate excess bond returns to the conditional volatility of those excess returns including Engle, Lilien, and Robins (1987). They found that both conditional variance and the term structure variables had explanatory power for excess bond returns.

The ARCH-M model is a useful tool for considering the relationship between volatility and excess bond returns. But in the last few years, much progress has been made in using high-frequency data to obtain realized volatility estimates. Further, if we observe high-frequency data on the price of an asset, and assume that jumps in the price of this asset are both rare and large, then Barndorff-Nielsen and Shephard (2004), Andersen, Bollerslev, and Diebold (2006), and Huang and Tauchen (2005) show how to detect the days on which jumps occur and how to estimate the magnitude of these jumps. These estimates all have the advantage of being model-free--it has to be assumed that asset prices follow a jump diffusion process, but no specific parametric model needs to be estimated. It then seems natural to try to relate realized volatility and the distribution of jumps to bond risk premia (Tauchen and Zhou, 2006).

Ideally, we would like to study the relationship between risk premia for holding a bond over a given holding period and investors' ex-ante forecasts of volatility and the jump density over that same period. Unfortunately these forecasts are not observed. But, we can easily construct backward-looking rolling estimates of realized volatility, jump intensity, jump mean and jump volatility. Then, treating these as proxies for forecasts of realized volatility, jump intensity, jump mean and jump volatility over the holding period, we can ask whether these risk measures are priced. With this motivation, this paper augments some standard regressions for excess bond returns with measures of realized volatility, jump intensity, jump mean and jump volatility constructed from five-minute S&P500 intraday returns. We also consider using realized jump risk measures constructed from five-minute bond returns, although the theoretical motivation for using the S&P500 returns to construct the jump measure seems strongest, because this is the usual proxy for the market returns of investors.

Our key finding is that augmenting regressions of excess bond returns on forward rates with realized stock market jump volatility greatly increases the predictability of excess bond returns, with $R^{2}$ values nearly doubling from 24-29 percent to 48-52 percent (our sample is shorter than that used by Cochrane and Piazzesi (2005) and yields a somewhat smaller $R^{2}$ than they obtained). This result is consistent with Tauchen and Zhou (2006), who find that this jump volatility measure can predict the credit spreads better than interest rate factors and volatility factors including option-implied volatility. In contrast, inclusion of other high-frequency jump measures--jump intensity and jump mean--in the equation for predicting excess bond returns raises the $R^{2}$ by at most a couple of percentage points. And, if we augment the regression of excess bond returns on forward rates with realized volatility (instead of any of these jump risk measures), the coefficient on realized volatility is significantly positive, but the $R^{2}$ goes up only to 35-40 percent.

We relate this finding to the recent literature on unspanned stochastic volatility (USV). USV is the hypothesis that bond markets are incomplete and that there is at least one state variable that drives innovations in bond derivatives prices but not innovations in bond yields. As pointed out by Collin-Dufresne and Goldstein (2002), if the bond market is complete, then bond yields can be written as an invertible function of the state variables and so the state variables lie in the span of the term structure of yields. On the other hand, under the USV hypothesis, the state variables do not lie in the span of the term structure of yields. Since expected excess bond returns are a function of the state variables, we argue that this gives a direct test of the USV hypothesis. Similar reasoning is used by Almeida, Graveline, and Joslin (2006) and Joslin (2007). If the USV hypothesis is false, then expected excess bond returns should be spanned by the term structure of yields and so in a regression of excess bond returns on term structure variables and any other predictors, the inclusion of enough term structure control variables should always cause the other predictors to become insignificant. On the other hand, if the USV hypothesis is correct, then the other predictors may be significant as long as they are correlated with the unspanned state variable that does not drive innovations in bond yields but affects the conditional mean of bond yields.

Thus, we interpret our finding that jump volatility is a highly significant predictor of excess bond returns even after controlling for the term structure of forward rates as strong evidence for the USV hypothesis. The USV interpretation is also consistent with the earlier ARCH-M evidence that controlling for the term structure does not eliminate the return-risk trade-off effect on government bond market. Recent work by Ludvigson and Ng (2006) finds that some extracted macroeconomic factors have additional forecasting power for expected bond returns in addition to the information in forward rates and by the same token this is also evidence for the USV hypothesis. Jump volatility however produces a larger improvement in predictive power than these macroeconomic factors and as such represents stronger evidence for USV.

We perform a number of robustness checks, including shortening the holding period, changing the size of the rolling window used to construct the jump measures, using only non-overlapping data, and continue to find an important role for market jump risk in forecasting excess bond returns. The information content of jump volatility seems to complement that of forward rates, such that the $R^{2}$ of the regression on both jump volatility and forward rates is a good bit larger than the from the regression on either variable alone.

Our measure of jump volatility is highly correlated with the price-dividend ratio. We find that in a regression of excess equity returns on jump volatility and the price-dividend ratio, the two predictors are jointly significant but neither is individually significant. In contrast, augmenting our excess bond return forecasting equations with the price-dividend ratio does little to change the significance of jump volatility. In this sense, although both jump volatility and the price-dividend ratio are informative about the cash flow risk, it is the jump volatility that contains more information about discount rate risk.

Standard affine models can explain the violation of the EH only with quite unusual model specifications that may be inconsistent with the second moments of interest rates (Bansal, Tauchen, and Zhou, 2004; Roberds and Whiteman, 1999; Dai and Singleton, 2000). However, much progress has been made recently in constructing models that may explain some of the predictability patterns in excess bond returns. These include models with richer specifications of the market prices of risk or preferences (Dai and Singleton, 2002; Duarte, 2004; Duffee, 2002; Wachter, 2006) and models with regime shifts. For example, Bansal and Zhou (2002), Ang and Bekaert (2002), Evans (2003), and Dai, Singleton, and Yang (2006) use regime-switching models of the term structure to identify the effect of economic expansions and recessions on bond risk premia. Such nonlinear regime-shifts models and the unspanned stochastic volatility hypothesis may be almost observationally equivalent.

The rest of the paper is organized as follows: the next section discusses the jump identification mechanism based on high-frequency intraday data, then Section 3 contains the empirical work on using realized jump volatility to forecast excess bond returns, Section 4 discusses the relationship with the literature on unspanned stochastic volatility in more detail, and Section 5 concludes.

2 Econometric Estimation of Jump Volatility Risk

In this section, we discuss our econometric method for constructing market jump risk measures, which may potentially constitute unspanned volatility factors in predicting excess returns above and beyond those obtained from current yields or forward rates.

Assuming that the stock market price follows a jump-diffusion process (, ), this paper takes a direct approach to identify realized jumps based on the seminal work by Barndorff-Nielsen and Shephard (2006,2004). This approach uses high-frequency data to disentangle realized volatility into separate continuous and jump components (see, Andersen, Bollerslev, and Diebold, 2006; Huang and Tauchen, 2005, as well) and hence to detect days on which jumps occur and to estimate the magnitude of these jumps. The methodology for filtering jumps from bi-power variation is by now fairly standard, but we review it briefly, to keep the paper self-contained.

Let $s_t=\log(S_t)$ denote the time logarithmic price of an asset, which evolves in continuous time as a jump diffusion process:

$\displaystyle ds_t=\alpha_tdt+\sigma_t dW_t +J_t dq_t$

(1)

where $\alpha_t$ and $\sigma_t$ are the instantaneous drift and diffusion functions that are completely general and may be stochastic (subject to the regularity conditions),

is the standard Brownian motion,

is a Poisson jump process with intensity $\lambda_{J_t}$ , and

refers to the corresponding (log) jump size distributed as Normal $(\mu_{J_t}, \sigma_{J_t})$ . Note that the jump intensity, mean and volatility are all allowed to be time-varying in a completely unrestricted way. Time is measured in daily units and the intra-daily returns are defined as follows:

$\displaystyle r^s_{t,j} \equiv s_{t,j\cdot \Delta}-s_{t,(j-1)\cdot \Delta}$

(2)

where $r^s_{t,j}$ refers to the $j^{th}$ within-day return on day

, and $% \Delta$ is the sampling frequency within each day.

Barndorff-Nielsen and Shephard (2004) propose two general measures for the quadratic variation process--realized variance and realized bi-power variation--which converge uniformly (as $\Delta \rightarrow 0$ or $m=1/\Delta \rightarrow \infty$ ) to different functionals of the underlying jump-diffusion process,

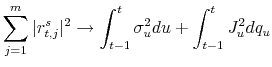$\displaystyle RV_t$	$\displaystyle \equiv$	$\displaystyle \sum_{j=1}^{m} \vert r^s_{t,j}\vert^2 \rightarrow\int_{t-1}^{t}\sigma^2_udu+ \int_{t-1}^{t} J_u^2 dq_u$	(3)
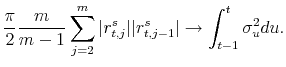$\displaystyle BV_t$	$\displaystyle \equiv$	$\displaystyle \frac{\pi}{2}\frac{m}{m-1} \sum_{j=2}^{m} \vert r^s_{t,j}\vert \vert r^s_{t,j-1}\vert \rightarrow \int_{t-1}^{t} \sigma^2_udu.$	(4)

Therefore the difference between the realized variance and bi-power variation is zero when there is no jump and strictly positive when there is a jump (asymptotically). This is the basis of the method for identifying jumps.

A variety of specific jump detection techniques are proposed and studied by Barndorff-Nielsen and Shephard (2004), Andersen, Bollerslev, and Diebold (2006), and Huang and Tauchen (2005). Here we adopted the ratio statistics favored by their findings,

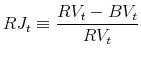$\displaystyle RJ_t \equiv \frac{RV_t - BV_t}{RV_t}$

(5)

which converges to a standard normal distribution with appropriate scaling

$\displaystyle ZJ_t \equiv \frac{RJ_t}{\sqrt{[(\frac{\pi}{2})^2+\pi-5] \frac{1}{m}\max(1,% \frac{TP_t}{BV_t^2})}} \overset{d}{\longrightarrow} \mathcal{N} (0, 1)$

(6)

This test has excellent size and power properties and is quite accurate in detecting jumps as documented in Monte Carlo work (Huang and Tauchen, 2005).¹

Following Tauchen and Zhou (2006), we further assume that there is at most one jump per day and that the jump size dominates the return when a jump occurs. These assumptions allow us to filter out the daily realized jumps as

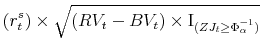$\displaystyle \hat J_t=$ sign $\displaystyle (r^s_t)\times\sqrt{(RV_t-BV_t) \times\mbox{I}% _{(ZJ_t\ge\Phi^{-1}_{\alpha})}}$

(8)

where $\Phi$ is the cumulative distribution function of a standard Normal, $% \alpha$ is the significance level of the

-test, and I $% _{(ZJ_t\ge\Phi^{-1}_{\alpha})}$ is the resulting indicator function that is one if and only if there is a jump during that day.

Once the jumps have been identified, we can then estimate the jump intensity, mean and variance as,

$\displaystyle {JI_{t}}$	$\displaystyle =$	$\displaystyle \frac{\mbox{Number of Realized Jump Days}} {% \mbox{Number of Total Trading Days}} \notag$
$\displaystyle {JM_{t}}$	$\displaystyle =$	$\displaystyle \mbox {Mean of Realized Jumps} \notag$
$\displaystyle {JV_{t}}$	$\displaystyle =$	$\displaystyle \mbox {Standard Deviation of Realized Jumps} \notag$

with appropriate formulas for the standard error estimates.

These "realized" jump risk measures can greatly facilitate our effort of estimating various risk premia of interest. The reason is that jump parameters are generally very hard to pin down even with both underlying and derivative assets prices, due to the fact that jumps are latent in daily return data and are rare events in financial markets.². Direct identification of realized jumps and the characterization of time-varying jump risk measures have important implications for interpreting financial market risk premia.

3 Predicting Excess Bond Returns

If jump risk were priced, then the risk premium on any asset over a given holding period should be related to the forecast of the jump density over that holding period. In particular, excess returns on longer term bonds over those on shorter maturity bonds should be related to the forecast of the jump density. The methodology that we described in the previous section allows us to identify and estimate jumps and to construct backward-looking rolling estimates of jump mean, jump intensity and jump volatility. These may in turn be good proxies for the forecasts of future jump mean, jump intensity and jump volatility, and they have the important advantage of being completely model-free--no model has to be specified or estimated to construct them. Accordingly, these rolling jump risk measures may be correlated with risk premia, and may be useful for predicting excess bond returns. Investigating this possibility empirically is the focus of the remainder of this section.

3.1 Variable Definitions and Empirical Strategy

Our measures of realized volatility, jump mean, jump intensity and jump volatility are based on data on the S&P500 index at the five-minute frequency from January 1986 to December 2005, provided by the Institute of Financial Markets. The data cover the period from 9:30am to 4:00pm New York time each day, for a total of 78 observations per day and can be used to construct continuously compounded returns as the log difference in price index quotes. Using these data and the methods described in the previous section, we constructed the realized volatility at the daily frequency, tested for jumps on each day, and estimated the magnitude of the jumps on those days when jumps were detected. Let $D_{t}^{DAILY}$ denote the dummy that is 1 if and only if a jump is detected on day and recall that $\hat J_t$ denotes the estimated magnitude of the jump on day . For our empirical work, let the -month rolling average realized volatility, jump intensity, jump mean, and jump volatility be defined as, respectively,

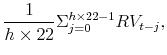$\displaystyle RV_{t}^{h}$	$\displaystyle =$	$\displaystyle \frac{1}{h\times22}\Sigma_{j=0}^{h\times22-1}RV_{t-j}, \notag$
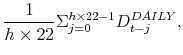$\displaystyle JI_{t}^{h}$	$\displaystyle =$	$\displaystyle \frac{1}{h\times22}\Sigma _{j=0}^{h\times22-1}D_{t-j}^{DAILY}, \notag$
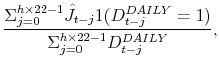$\displaystyle JM_{t}^{h}$	$\displaystyle =$	$\displaystyle \frac{\Sigma _{j=0}^{h\times22-1} \hat J_{t-j} 1(D_{t-j}^{DAILY}=1)} {\Sigma _{j=0}^{h\times22-1}D_{t-j}^{DAILY}}, \notag$
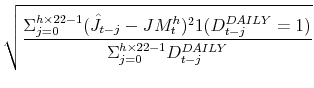$\displaystyle JV_{t}^{h}$	$\displaystyle =$	$\displaystyle \sqrt{\frac{\Sigma_{j=0}^{h\times22-1}( \hat J_{t-j} -JM_{t}^{h})^{2}1(D_{t-j}^{DAILY} =1)}{\Sigma_{j=0}^{h\times22-1}D_{t-j}^{DAILY}}} \notag$

where the means and volatilities are calculated only over days where jumps are detected. Realized volatility can be estimated arbitrarily accurately with a fixed span of sufficiently high-frequency data (abstracting from issues of market microstructure noise), whereas this is not true for jump intensity, mean or volatility. For this reason, while we use a relatively short rolling window for estimating realized volatility (

equal to one month), we use much longer rolling windows for measuring jump intensity, jump mean and jump volatility, setting the parameter

to 24 months or 12 months. The tradeoff in selecting

is, of course, that a shorter window gives a more noisy, but more timely, measure of agents' perceptions of jump risk. Figure 1 shows plots of the 24-month rolling jump intensity, jump mean and jump volatility, respectively. This measure of jump volatility rose during the recession of the early 1990s, and rose more sharply in the most recent recession, but has been drifting down since late 2001.

Tauchen and Zhou (2006) use these realized jump risk measures to forecast corporate bond spreads, and find that the realized jump volatility measure can predict these spreads better than interest rate factors and volatility factors including option-implied volatility. In this paper, we use these realized jump risk measures to forecast excess bond returns. The excess return on holding an -month bond over the return on holding an -month bond for a holding period of months is given by $% ex_{t+m}^{m,n}=p_{t+m}^{n-m}-p_{t}^{n}-(m/12)y_{t}^{m}$ where $y_{t}^{j}$ denotes the annual continuously compounded yield on a -month zero coupon bond and $p_{t}^{j}=-(j/12)y_{t}$ is the log price of this bond. We used end-of-month data on zero-coupon yields and the three-month risk-free rate from the CRSP Fama-Bliss data, and hence constructed these excess returns.

All the regressions for excess bond returns that we consider in this paper are nested within the specification

$\displaystyle ex_{t+m}^{m,n}=\beta _{0}+\beta _{1}f_{t}^{12}+\beta _{2}f_{t}^{36}+\beta _{3}f_{t}^{60}+\beta _{4}RV_{t}^{1}+\beta _{5}JM_{t}^{h}+\beta _{6}JI_{t}^{h}+\beta _{7}JV_{t}^{h}+\varepsilon _{t+m}$

(9)

where $f_{t}^{j}=p_{t}^{j-12}-p_{t}^{j}$ denotes the

-year forward rate with a 12-months period and $RV_{t}^{1}$ , $JM_{t}^{h}$ , $\;JI_{t}^{h}$ and $% JV_{t}^{h}$ denote the realized volatility and jump measures in rolling windows ending on the last day of month

, constructed from high-frequency equity data as defined earlier. Using just the forward rates gives the regression of Cochrane and Piazzesi (2005), except that, following Bansal, Tauchen, and Zhou (2004), we use three forward rates instead of five, to minimize the near-perfect collinearity problem. But we also consider the predictive power of rolling realized volatility and jump risk variables.

Some summary statistics for these variables are given in Table 1. Realized equity volatility is about 11.5 percentage points (expressed in annualized terms) with a standard deviation of about 5 percentage points. The means of our jump intensity, jump mean and jump volatility measures are 13 percent, 0.06 percentage points and 0.50 percentage points, respectively. Turning to the correlation structure, the excess returns and forward rates are highly collinear. Realized volatility and jump volatility are positively correlated with excess returns. Jump volatility has a strong negative correlation with forward rates (-0.67 to -0.63). The correlation between realized volatility and jump volatility is 0.63, which is not surprising since jump volatility is a component of realized volatility. Now we turn to the main empirical finding in this paper.

3.2 The Main Result

Table 2 shows coefficient estimates, associated t-statistics and $R^{2}$ values for several specifications setting (one-year holding period) and (two-year rolling windows in constructing jump risk measures) where the maturity of the longer-term bond is set to 24, 36, 48 and 60 months. Forward rates are included in all specifications in this table. The forward rates show the familiar "tent-shaped" pattern, are often individually significant, and always jointly overwhelmingly significant, with an $R^{2}$ in the range 24-29 percent, which is considerable, although somewhat lower than reported for a different sample period by Cochrane and Piazzesi (2005). But if we add jump volatility to the regression of excess returns on forward rates, the coefficient on jump volatility is positive and statistically significant for each and the $R^{2}$ rises to 48-52 percent. All else equal, higher jump volatility is estimated to lead investors to demand higher future excess returns on longer-maturity bonds. Adding realized volatility to the regression of excess returns on forward rates also improves the fit notably (Table 2), and the coefficient on realized volatility is statistically significant, which is to be expected since jump volatility is a component of realized volatility. However, the significance and magnitude of the improvement in is quite a bit weaker. Meanwhile jump mean and jump intensity have no significant predictive power for excess bond returns. This is true for all choices of the maturity of the longer-term bond, .

Table 3 shows the same regressions as Table 2, except omitting the forward rates. If we do not control for the term structure of forward rates, jump volatility remains positively related to future excess returns, but not significantly so. Jump volatility is clearly not the only variable with predictive power for future excess returns, but it seems to add predictive power over and above the term structure of forward rates that is both statistically and economically significant. And, the information content of jump volatility seems to complement that of forward rates, in that the $R^{2}$ of the regression on both jump volatility and forward rates is larger than the on either of the variables separately. Controlling for jump volatility does not change the coefficients on the forward rates greatly, suggesting that the term structure of forward rates and jump volatility are measuring different components of bond risk premia. This result is completely in line with the hypothesis of unspanned stochastic volatility (see Section 4), in that the jump volatility risk factor is not spanned by the current term structure but can forecast bond excess returns above and beyond those achieved by current forward rates.

The ex-post excess returns on holding long term bonds (Figure 2, top panel) averaged around zero during the expansion during the mid and late 1990s, with positive excess returns at some times being offset by negative excess returns as the Federal Open Market Committee (FOMC) was tightening monetary policy during 1994 and around the time of the 1998 Long-Term Capital Management (LTCM) crisis. On the other hand, the excess returns were large and positive during and immediately after the 1990 and 2001 recessions. The predicted excess returns using only the forward rate term structure (middle panel) shows some of this countercyclical variation, but are positive for nearly all of the 1990s and so, on average, overpredict excess returns during these years, while underpredicting excess returns during and immediately after the most recent recession. However, adding the market jump volatility risk measure (bottom panel), the model correctly predicts an average risk premium around zero during most of the 1990s, including negative excess returns in 1994 and 1998, and it is also more successful in predicting high returns during and immediately after the most recent recession. Jump volatility has declined since the last recession, and this may indeed help explain some of the recent decline in longer maturity yields that was referred to by former Federal Reserve Chairman Greenspan as a "conundrum" (discussed further in Kim and Wright, 2005), although jump volatility in 24-month windows ending at the end of our sample is still not especially low by historical standards.

3.3 Robustness Checks

It is well known that severe small-sample size distortions may arise in return prediction regressions with highly persistent regressors and overlapping returns.³ To mitigate this problem, we re-ran our regressions using non-overlapping data. Table 4 shows the results from the same regressions as in Table 2 (i.e. setting and and various values of ), but using only the forward rates of each December, so that the holding periods do not overlap. The results are very similar to those in Table 2, and the jump volatility measure is highly significant, though realized volatility is not. The overall predictability increases from 20-26 percent when using only forward rates to 42-45 percent when jump volatility is included.

Tables 2-4 follow Cochrane and Piazzesi (2005) in considering a one-year holding period (). But, since we have only 18 non-overlapping periods in our sample, giving a quite small effective sample size, it also seems appropriate to consider results with a one-quarter holding period (), for which there are four times as many non-overlapping periods.⁴ These results are shown in Table 5. The $R^{2}$ values are lower at this shorter horizon, but jump volatility is again consistently positively and significantly related to future excess bond returns, once we control for the forward rates. Realized volatility is significant at the 5 percent level for two of the four maturities. The other realized jump measures have no significant association with future excess returns.

For the parameter (rolling window size for jump risk measures), we want to pick a value that is large enough not to give noisy estimates, but small enough to give timely measures of agents' perceptions of jump risk. A range of reasonable choices might be from 6 to 24 months, and our results are not very sensitive to varying over this range. For example, Table 6 shows the results with overlapping data at the one-year horizon () and choosing a shorter rolling window for estimating jump statistics . These results are very similar to those in Table 2, in that the total predictability of bond risk premia is nearly doubled with jump volatility included. The slope coefficient for jump volatility remains positive and highly significant.

3.4 Realized Volatility and Jump Measures Using Bond Data

We also investigated regressing excess returns on the term structure of forward rates and realized volatility and jump measures as in Table 2, except using 30-year Treasury bond futures to construct the realized volatility and jump measures rather than stock price data. We obtained five-minute data on Treasury bond futures from RC Research using the same sample period as before, to make the results comparable.

The results are shown in Table 7. Neither bond realized volatility nor bond jump volatility is statistically significant as a predictor of bond excess returns and the improvement in from including these variables is very slight. This is consistent with the finding in Andersen and Benzoni (2006) that bond realized volatility is not spanned by the bond yields, although our approach is different in that we are predicting excess bond returns.

The inclusion of bond jump intensity does not help predict bond excess returns either. However, the bond jump mean is significantly negative as a predictor of excess bond returns implying that downward jumps in bond prices are followed by large positive excess returns. Indeed, adding the bond jump mean to the regression of excess bond returns on forward rates can nearly double the . This suggests that the bond jump mean may act as an unspanned stochastic mean factor that cannot be hedged with the current yields but can forecast bond excess returns, which is again consistent with the multi-factor model of incomplete fixed-income market examined by Collin-Dufresne, Goldstein, and Jones (2006a).

3.5 Forecasting Excess Stock Returns

The empirical link between the equity risk premium and macro-finance state variables has been well established (see, e.g., Campbell and Shiller, 1988b,a; , ; Fama and French, 1988), but it seems interesting to examine whether the jump variables that help predict excess bond returns might also have some incremental predictive power for excess stock returns. To investigate this, we augmented the usual dividend-yield regression for predicting excess stock returns with our measures of realized volatility and market jump risk. The three-month excess returns on the stock market are given by $ex_{t+3}=r_{t+3}-r_{ft}$ , where $r_{t+3}$ is the return on the S&P500 dividend-inclusive index from the end of month to the end of month and $r_{ft}$ is the three-month risk-free rate from the CRSP Fama-Bliss data at the end of month . The regressions for excess stock returns that we consider are nested within the specification

$\displaystyle ex_{t+3}=\beta _{0}+\beta _{1}\log(P/D)_{t}+\beta _{2}RV_{t}^{1}+\beta _{3}JM_{t}^{24}+\beta _{4}JI_{t}^{24}+\beta _{5}JV_{t}^{24}+\varepsilon _{t+1}$

(10)

where $\log(P/D)_{t}$ denotes the log price-dividend ratio for month

and $RV_{t}^{1}$ , $JM_{t}^{24}$ , $\;JI_{t}^{24}$ and $JV_{t}^{24}$ denote the realized volatility and jump measures in rolling windows ending on the last day of month

The results are reported in Table 8. Consistent with the existing literature, the price-dividend ratio can predict a small share of return variation (4 percent), and is just statistically significant. On the other hand, none of the high-frequency based risk measures has any detectable predictive power, except for the jump volatility which on its own gives an of 7 percent and is statistically significant. Using both the price-dividend ratio and realized jump volatility as predictors, neither is statistically significant separately (though they are jointly significant), and the remains at about 7 percent, suggesting that the dividend yield and jump volatility contain similar information about cash flow risk. Note that the sign of the slope coefficient on the jump volatility variable is negative, meaning that higher jump volatility is associated with lower equity risk premia. This is puzzling, but many papers have found the relationship between equity risk and return to be unstable and possibly even to have the wrong sign (see, for example Chou, Engle, and Kane, 1992; Bollerslev and Zhou, 2006; Glosten, Jagannathan, and Runkle, 1993; Campbell, 1987; Turner, Startz, and Nelson, 1989; Lettau and Ludvigson, 2003; Breen, Glosten, and Jagannathan, 1989, among others). A re-examination of this puzzle may be fruitful along the line of Guo and Whitelaw (2006).

The price-dividend ratio covaries positively with jump volatility (with a correlation coefficient of 0.67), consistent with the finding that adding the price-dividend ratio to a regression of excess stock returns on jump volatility leaves the about unchanged. This positive correlation can be seen in Figure 3, which shows the time series of both the price-dividend ratio and jump volatility. Both variables appear countercyclical and reflect the aggregate cash flow risk embedded in stock excess returns. Motivated by this, and the fact that some researchers including Fama and French (1989) have found that the dividend yield helps predict excess bond returns as well as excess stock returns, we investigated augmenting the regressions for excess bond returns shown in Table 2 with the stock price-dividend ratio. As seen in Table 9, in these regressions the jump volatility remains statistically significant, while the coefficient on the price-dividend ratio is not significantly different from zero. Thus, although both jump volatility and the price-dividend ratio are informative about the cash flow risk in equity returns, it is the jump volatility that contains more information about the discount rate risk in bond returns.

4 Economic Interpretation under Incomplete Markets

In this section, we discuss in more detail the interpretation of regressions of excess bond returns on term structure control variables and other predictors under the incomplete market setting with unspanned stochastic volatility. Under incomplete markets with affine factor dynamics (Collin-Dufresne and Goldstein, 2002), bond yields alone cannot hedge the unspanned volatility risk. However, an important feature of the USV model is that the unspanned risk factor affects the conditional mean and volatility functions of other spanned risk factors (see, Singleton, 2006, pages 322-325). Therefore expected excess bond returns depend not only on the bond yields through the spanned risk factors, but also on the unspanned risk factor. This link provides an explanation for the earlier finding of the ARCH-in-mean effect in bond market (Engle, Lilien, and Robins, 1987), even after controlling for the term structure of yields.

4.1 Unspanned Stochastic Volatility

Recent empirical tests find strong evidence for the existence of unspanned stochastic volatility (see, , ; Casassus, Collin-Dufresne, and Goldstein, 2005; Heidari and Wu, 2003; Collin-Dufresne, Goldstein, and Jones, 2006a; Li and Zhao, 2005; Andersen and Benzoni, 2006, among others).⁵ The regression of options-implied or estimated volatilities on bond yields is a valid test for the existence of USV, subject to the proper controls for specification error and measurement error in extracting these volatility measures. However, an alternative way is to test the USV implication that the unspanned volatility must predict the bond excess returns above and beyond what can be predicted by the current yields or forward rates.

We illustrate the idea with an specification (Dai and Singleton, 2000)--which is a three factor affine model with one square-root volatility factor. Following Collin-Dufresne and Goldstein (2002), all three factor affine models can be rotated such that the state vectors are the spot rate , the drift of spot rate $\mu_t=(1/dt)E^Q [dr_t]$ and the variance of spot rate . The risk-neutral factor dynamics $X_t^{\prime}=[r_t,\mu_t,V_t]$ is given by

$\displaystyle d X_t = (a^Q+b^Q X_t) dt + \sqrt{\Omega_0+\Omega_V (V_t-\underline{V})} dW^Q$

(11)

where

is a three-dimensional vector of independent Brownian motions under the risk-neutral measure, $\underline{V}$ is a non-negative lower bound, and $\Omega_0+\Omega_V (V_t-\underline{V})$ is positive definite. Also, the drift and volatility parameters are restricted in the following form

$\begin{displaymath}a^Q=\left[% \begin{array}{c} 0 \\ a_{\mu}^Q \\ a_{V}^Q\end{array}% \right],\ b^Q=\left[% \begin{array}{ccc} 0 & 1 & 0 \\ b_{\mu r}^Q & b_{\mu\mu}^Q & b_{\mu V}^Q \\ 0 & 0 & b_{VV}^Q\end{array}% \right],\ \Omega_0=\left[% \begin{array}{ccc} \underline{V} & \underline{c}_{r\mu} & 0 \\ \underline{c}_{r\mu} & \underline{\sigma}_{\mu} & 0 \\ 0 & 0 & 0\end{array}% \right],\ \Omega_V=\left[% \begin{array}{ccc} 1 & c_{r\mu} & c_{rV} \\ c_{r\mu} & \sigma_{\mu} & c_{\mu V} \\ c_{r V} & c_{\mu V} & \sigma_V \end{array}% \right]\end{displaymath}$

The model is maximal, as defined in Dai and Singleton (2000), in that all the parameters are identifiable regardless of the data availability (, ).

Then under complete markets, all trivariate affine models have bond prices of the following form

$\displaystyle P(t,T;r_t,\mu_t,V_t) = e^{A(T-t)+B(T-t)r_t+C(T-t)\mu_t+D(T-t)V_t},$

(12)

where

, and

are solutions to a system of ordinary differential equations (Duffie and Kan, 1996). However, under incomplete markets, Collin-Dufresne and Goldstein (2002) show that bond prices can be reduced to

$\displaystyle P(t,T;r_t,\mu_t,V_t) \equiv P(t,T;r_t,\mu_t) = e^{A(T-t)+B(T-t)r_t+C(T-t)\mu_t},$

(13)

In other words, bond prices do not depend on the unspanned volatility. This condition further restricts the drift and volatility parameter in the

model as

$\displaystyle b_{\mu r}^Q=-2c_{r\mu}^2,\ b_{\mu\mu}^Q=3c_{r\mu},\ b_{\mu V}^Q=1\$ and $\displaystyle \ \ \sigma_{\mu}=c_{r\mu}^2$

(14)

In particular, the restriction $b_{\mu V}^Q=1\ne0$ makes the conditional expectation $E_t^Q[\mu_{T}]$ linearly depend on

; and the (1, 2) entry of

matrix $b^Q_{r\mu}=1\ne0$ makes the conditional expectation $E_t^Q[r_{T}]$ linearly depend on

through $E_t^Q[\mu_{T}]$ recursively. This feature mirrors an important stochastic volatility model in the equity option literature (Heston, 1993), where the unspanned equity volatility also affects the conditional distribution of the state vector.

4.2 Predicting Excess Bond Returns

The fact that unspanned stochastic volatility affects the conditional mean of the state vector has important implications for predicting excess bond returns. Letting the market price of risk process be $\Lambda_t = \lambda \sqrt{\Omega_0+\Omega_V (V_t-\underline{V})}$ with $\lambda \in R^{1\times3}$ , we can transform to the objective dynamics

$\displaystyle d X_t = (a+b X_t) dt + \sqrt{\Omega_0+\Omega_V (V_t-\underline{V})} dW$

(15)

which governs the time-series evolution of the state vector.⁶ Aside from some special cases, the instantaneous drift under the physical measure

has the same form as under the risk-neutral measure

. Hence the conditional means $E_t[\mu_{T}]$ and $E_t[r_{T}]$ are also linear functions of stochastic volatility

Under incomplete markets, with the bond pricing solution given in eq. (13), the expected excess returns for holding an -period bond over the returns on holding a - period bond for a holding period of periods can be written as

$\displaystyle E_t[ex_{t+m}^{m,n}]$	$\displaystyle =$	$\displaystyle A(n-m)-A(n)+\frac{A(m)}{m} \notag$
		$\displaystyle +\left({\frac{B(m)}{m}}-B(n)\right)r_{t}+\left({\frac{C(m)}{m}}% -C(n)\right)\mu_{t} \notag$
		$\displaystyle +B(n-m)E_t[r_{t+m}]+C(n-m)E_t[\mu_{t+m}]$	(16)

where the conditional means $E_t[r_{t+m}]$ and $E_t[\mu_{t+m}]$ are linear functions of

, which is not in the span of yields. In contrast, under complete markets, the bond pricing solution given in eq. (12) implies that the expected excess bond return can be written as

$\displaystyle E_t[ex_{t+m}^{m,n}]$	$\displaystyle =$	$\displaystyle A(n-m)-A(n)+\frac{A(m)}{m} \notag$
		$\displaystyle +\left({\frac{B(m)}{m}}-B(n)\right)r_{t}+\left({\frac{C(m)}{m}}% -C(n)\right)\mu_{t}+\left(\frac{D(m)}{m}-D(n)\right)V_{t} \notag$
		$\displaystyle +B(n-m)E_t[r_{t+m}]+C(n-m)E_t[\mu_{t+m}]+D(n-m)E_t[V_{t+m}]$	(17)

and all the terms in eq. (17) are in the span of yields.

Thus, if the bond market is complete, then there should exist no macroeconomic or financial variable that can improve the population forecastability of excess bond returns once we control for the term structure of bond yields. However, if markets are incomplete, then any variable that is correlated with this unspanned volatility factor may add to the predictability of excess bond returns. Of course the challenge is how to find such a proxy for unspanned stochastic volatility. The current methods include implied volatility from fixed-income derivatives markets (e.g., Collin-Dufresne and Goldstein, 2002) and realized volatility from intraday bond prices (Andersen and Benzoni, 2006). Indeed, Almeida, Graveline, and Joslin (2006) and Joslin (2007) find that an unspanned stochastic volatility factor constructed from fixed income options markets is important for predicting bond excess returns. We instead adopt a measure of jump volatility from the equity market, which has an orthogonal innovation relative to the term structure, and find that this also has substantial forecasting power for bond excess returns.

5 Conclusion

There is considerable evidence of predictability in excess returns on a range of assets, but it is especially strong for longer maturity bonds, perhaps because their pricing is not complicated by uncertain cash flows. Part of the predictability may owe to time-variation in the distribution of jump risk, but empirical work on this has been hampered until recently by econometricians' difficulties in identifying jumps. Recently studies (Andersen, Bollerslev, and Diebold, 2006; Tauchen and Zhou, 2006; Huang and Tauchen, 2005; Barndorff-Nielsen and Shephard, 2004) have shown how high-frequency data can be used reliably to detect jumps and to estimate their size, under the assumption that jumps are large and rare, and these methods can then easily be used to construct rolling estimates of jump intensity, jump mean and jump volatility.

A simple implication of jump risk being priced is that these measures should have some predictive power for future excess returns. In this paper, we have found evidence that they do. Augmenting a standard regression of excess bond returns on forward rates with realized jump volatility constructed from high-frequency stock price data, we find that the coefficient on jump volatility is both economically and statistically significant. The predictability of bond risk premia can nearly be doubled by including the jump volatility risk measure. Jump volatility also dominates other risk measures constructed from high-frequency data--namely jump intensity, jump mean, and realized volatility. Although both jump volatility and the price-dividend ratio are informative about the cash flow risk in equity returns, it is the jump volatility that contains more information about the discount rate risk in bond returns.

Jump volatility appears countercyclical--peaking around the 1990 and especially the 2001 recessions. In a number of important episodes, predicted excess returns constructed using both jump volatility and the term structure of forward rates track the actual ex-post excess returns more closely than predicted excess returns constructed using forward rates alone, including during the period in 1994 when the FOMC was tightening monetary policy, the 1998 LTCM crisis, and in the most recent recession. A decline in jump volatility may also account for part of the decline in long-term yields since the FOMC began tightening monetary policy in the middle of 2004. Our result is robust to shortening the holding period, changing the size of the rolling window used to construct the jump measures and using only non-overlapping data. The tent-shape pattern of regression coefficients on the forward term structure however exists regardless whether of whether or not we control for jump volatility.

The existing literature has used implied volatility from fixed-income derivatives (e.g., Collin-Dufresne and Goldstein, 2002) and realized volatility from intraday bond prices (Andersen and Benzoni, 2006) to test the unspanned stochastic volatility hypothesis. Our finding that stock market jump volatility has significant forecasting power for excess bond returns above and beyond that obtained from forward rates alone, is also consistent with this hypothesis.

Bibliography

Aït-Sahalia, Yacine, (2004)

"Disentangling Diffusion from Jumps"
Journal of Financial Economics, 74, 487-528.

Almeida, Caio, Jeremy J. Graveline, and Scott Joslin, (2006)

"Do Interest Rate Options Contain Information About Excess Returns."
Working Paper.
Standford University GSB.

Andersen, Torben G_ and Luca Benzoni, (2006)

"Can Bonds Hedge Volatility Risk in the U.S. Treasury Market? A Specification Test for Affine Term Structure Models."
Working Paper.
Carlson School of Management, University of Minnesota.

Andersen, Torben G., Luca Benzoni, and Jesper Lund, (2002)

"An Empirical Investigation of Continuous-Time Equity Return Models."
Journal of Finance, 57, 1239-1284.

Andersen, Torben G., Tim Bollerslev, and Francis X. Diebold, (2006)

"Roughing It Up: Including Jump Components in the Measurement, Modeling and Forecasting of Return Volatility."
Review of Economics and Statistics.
forthcoming.

Ang, Andrew and Geert Bekaert, (2002)

"Regime Switches in Interest Rates."
Journal of Business and Economic Statistics, 20, 163-182.

Bansal, Ravi, George Tauchen, and Hao Zhou, (2004)

"Regime Shifts, Risk Premiums in the Term Structure, and the Business Cycle."
Journal of Business and Economic Statistics, 22, 396-409.

Bansal, Ravi and Hao Zhou, (2002)

"Term Structure of Interest Rates with Regime Shifts"
Journal of Finance, 57, 1997-2043.

Barndorff-Nielsen, Ole and Neil Shephard, (2004)

"Power and Bipower Variation with Stochastic Volatility and Jumps."
Journal of Financial Econometrics, 2, 1-48.

Barndorff-Nielsen, Ole and Neil Shephard, (2006)

"Econometrics of Testing for Jumps in Financial Economics Using Bipower Variation."
Journal of Financial Econometrics, 4, 1-30.

Bates, David S., (2000)

"Post-'87 Crash Fears in the S&P 500 Futures Option Market."
Journal of Econometrics, 94, 181-238.

Bikbov, Ruslan and Mikhail Chernov, (2004)

"Term Structure and Volatility: Lessons from the Eurodollar Markets."
Working Paper.
Columbia University GSB.

Bollerslev, Tim and Hao Zhou, (2006)

"Volatility Puzzles: A Simple Framework for Gauging Return-Volatility Regressions."
Journal of Econometrics, 131, 123-150.

Boudoukh, Jacob, Matthew Richardson, and Robert F. Whitelaw, (2006)

"The Myth of Long-Horizon Predictability."
NBER Working Paper No.11841.

Breen, William, Lawrence R. Glosten, and Ravi Jagannathan, (1989)

"Economic Significance of Predictable Variations in Stock Index Returns."
Journal of Finance, 44, 1177-1189.

Campbell, John Y., (1987)

"Stock Returns and the Term Structure.
Journal of Financial Economics, 18, 373-399.

Campbell, John Y. and Robert J. Shiller (1988a).

"The Dividend-Price Ratio and Expectations of Future Dividends and Discount Factors."
Review of Financial Studies, 1, 195-228.

Campbell, John Y. and Robert J. Shiller (1988b).

"Stock Prices, Earnings, and Expected Dividends."
Journal of Finance, 43, 661-676.

Campbell, John Y. and Robert J. Shiller, (1991)

"Yield Spreads and Interest Rate Movements: A Bird's Eye View."
Review of Economic Studies, 58, 495-514.

Campbell, John Y. and Motohiro Yogo, (2006)

"Efficient Tests of Stock Return Predictability."
Journal of Financial Economics, 81, 27-60.

Casassus, Jaime, Pierre Collin-Dufresne, and Robert S. Goldstein, (2005)

"Unspanned Stochastic Volatility and Fixed Income Derivatives Pricing."
Journal of Banking and Finance, 29, 2723-2749.

Chernov, Mikhail, A. Ronald Gallant, Eric Ghysels, and George Tauchen, (2003)

"Alternative Models for Stock Price Dynamics."
Journal of Econometrics, 116, 225-258.

Chou, Ray Y., Robert F. Engle, and Alex Kane, (1992)

"Measuring Risk Aversion from Excess Returns on a Stock Index."
Journal of Econometrics, 52, 201-224.

Cochrane, John H. and Monika Piazzesi, (2005)

"Bond Risk Premia."
American Economic Review, 95, 138-160.

Collin-Dufresne, Pierre and Robert S. Goldstein, (2002)

"Do Bonds Span the Fixed Income Markets? Theory and Evidence for Unspanned Stochastic Volatility."
Journal of Finance, 57, 1685-1730.

Collin-Dufresne, Pierre, Robert S. Goldstein, and Christopher S. Jones (2006a).

"Can Interest Rate Volatility be Extracted from the Cross Section of Bond Yields? An Investigation of Unspanned Stochastic Volatility."
Working Paper.
Marshall School of Business, University of Southern California.

Collin-Dufresne, Pierre, Robert S. Goldstein, and Christopher S. Jones (2006b).

"Identification of Maximal Affine Term Structure Models."
Forthcoming.

Dai, Qiang and Kenneth J. Singleton, (2000)

"Specification Analysis of Affine Term Structure Models."
Journal of Finance, 55, 1943-1978.

Dai, Qiang and Kenneth J. Singleton, (2002)

"Expectation Puzzles, Time-varying Risk Premia, and Dynamic Models of the Term Structure_"
Journal of Financial Economics, 63, 415-441.

Dai, Qiang, Kenneth J. Singleton, and Wei Yang, (2006)

"Regime Shifts in a Dynamic Term Structure Model of the U.S. Treasury Yields."
Review of Financial Studies.
forthcoming.

Duarte, Jefferson, (2004)

"Evaluating An Alternative Risk Preference in Affine Term Structure Models."
Review of Financial Studies, 17, 379-404.

Duffee, Gregory, (2002)

"Term Premia and Interest Rate Forecasts in Affine Models."
Journal of Finance, 57, 405-443.

Duffie, Darrell and Rui Kan, (1996)

"A Yield-Factor Model of Interest Rates."
Mathematical Finance, 6, 379-406.

Engle, Robert F., David M. Lilien, and Russell P. Robins, (1987)

"Estimating Time Varying Risk Premia in the Term Structure: The ARCH-M Model."
Econometrica, 55, 391-407.

Eraker, Bjørn, Michael Johannes, and Nicholas Polson, (2003)

"The Impact of Jumps in Equity Index Volatility and Returns."
Journal of Finance, 53, 1269-1300.

Evans, Martin D. D., (2003)

"Real Risk, Inflation Risk, and the Term Structure."
Economic Journal, 113, 345-389.

Fama, Eugene F. and Robert T. Bliss, (1987)

"The Information in Long-Maturity Forward Rates."
American Economic Review, 77, 680-692.

Fama, Eugene F. and Kenneth R. French, (1988)

"Dividend Yields and Expected Stock Returns."
Journal of Financial Economics, 22, 3-25.

Fama, Eugene F. and Kenneth R. French, (1989)

"Business Conditions and Expected Returns on Stocks and Bonds."
Journal of Financial Economics, 25, 23-49.

Fan, Rong, Anurag Gupta, and Peter Ritchken, (2003)

"Hedging in the Possible Presence of Unspanned Stochastic Volatility: Evidence from Swaption Markets."
Journal of Finance, 58, 2219-2248.

Ferson, Wayne E., Sergei Sarkissian, and Timothy T. Simin, (2003)

"Spurious Regressions in Financial Economics?"
Journal of Finance, 1393-1414.

Glosten, Larry R., Ravi Jagannathan, and David Runkle, (1993)

"On the Relation between the Expected Value and the Volatility of the Nominal Excess Return on Stocks."
Journal of Finance, 48, 1779-1801.

Guo, Hui and Robert F. Whitelaw, (2006)

"Uncovering the Risk-Return Relation in the Stock Market."
Journal of Finance, 61, 1433-1463.

Heidari, Massoud and Liuren Wu, (2003)

"Are Interest Rate Derivatives Spanned by the Term Structure of Interest Rates?"
Journal of Fixed Income, 13, 75-86.

Heston, Steven, (1993)

"A Closed-Form Solution for Options with Stochastic Volatility with Applications to Bond and Currency Options."
Review of Financial Studies, 6, 327-343.

Huang, Xin and George Tauchen, (2005)

"The Relative Contribution of Jumps to Total Price Variance."
Journal of Financial Econometrics, 3, 456-499.

Joslin, Scott, (2007)

"Pricing and Hedging Volatility Risk in Fixed Income Markets."
Working Paper.
Standford University GSB.

Kim, Don H. and Jonathan H. Wright, (2005)

"An Arbitrage-Free Three-Factor Term Structure Model and the Recent Behavior of Long-Term Yields and Distant-Horizon Forward Rates."
Finance and Economics Discussion Series.
Federal Reserve Board.

Lettau, Martin and Sydney Ludvigson, (2003)

Handbook of Financial Econometrics, chapter Measuring and Modeling Variation in the Risk-Return Tradeoff.
Elsevier Science B.V., Amsterdam.
Forthcoming.

Li, Haitao and Feng Zhao, (2005)

"Unspanned Stochastic Volatility: Evidence from Hedging Interest Rate Derivatives."
Journal of Finance.

Ludvigson, Sydney C. and Serena Ng, (2006)

"Macro Factors in Bond Risk Premia."
Working Paper.
Department of Economics, New York University.

Merton, Robert C., (1976)

"Option Pricing When Underlying Stock Returns Are Discontinuous."
Journal of Financial Economics, 3, 125-144.

Pan, Jun, (2002)

"The Jump-Risk Premia Implicit in Options: Evidence from an Integrated Time-Series Study."
Journal of Financial Economics, 63, 3-50.

Roberds, William and Charlse H. Whiteman, (1999)

"Endogenous Term Premia and Anomalies in the Term Struture of Interest Rates: Explaining the Predictability Smile."
Journal of Monetary Economics, 44, 555-580.

Singleton, Kenneth J., (2006)

Empirical Dynamic Asset Pricing: Model Specification and Econometric Assessment.
Princeton University Press.

Stambaugh, Robert F., (1999)

"Predictive Regressions."
Journal of Financial Economics, 54, 375-421.

Tauchen, George and Hao Zhou, (2006)

"Realized Jumps on Financial Markets and Predicting Credit Spreads."
Working Paper.
Federal Reserve Board.

Thompson, Samuel, (2004)

"Identifying Term Structure Volatility from the LIBOR-Swap Curve."
Working Paper.
Harvard University.

Turner, Christopher M., Richard Startz, and Charles R. Nelson, (1989)

"A Markov Model of Heteroskedasticity, Risk, and Learning in the Stock Market."
Journal of Financial Economics, 25, 3-22.

Valkanov, Rossen, (2003)

"Long-Horizon Regressions: Theoretical Results and Applications."
Journal of Financial Economics, 68, 201-232.

Wachter, Jessica A_, (2006)

"A Consumption-Based Model of the Term Structure of Interest Rates."
Journal of Financial Economics, 79, 365-399.

Table 1: Summary statistics and correlation matrix for excess returns, forward rates, and jump measures
Summary statistics	$ex_{t+12}^{12,24}$	$ex_{t+12}^{12,36}$	$ex_{t+12}^{12,48}$	$ex_{t+12}^{12,60}$	$f_{t}^{12}$	$f_{t}^{36}$	$f_{t}^{60}$	$RV_{t}^{1}$	$JI_{t}^{24}$	$JM_{t}^{24}$	$JV_{t}^{24}$
Mean	0.91	1.63	2.23	2.5	4.94	6.09	6.44	11.57	0.13	0.06	0.5
Std. Dev.	1.42	2.7	3.74	4.58	2.1	1.62	1.42	5.26	0.06	0.07	0.23
Skewness	-0.09	-0.16	-0.19	-0.25	-0.16	-0.18	0.18	1.27	0.37	0.2	0.87
Kurtosis	2.17	2.36	2.46	2.58	2.33	2.43	1.92	4.69	1.79	3.09	2.2

Notes: This table summarizes the main variables used in the empirical exercise. The variable definitions are the same as given in Section 3.1: $ex_{t+n}^{m,n}$ are the excess returns on holding an -month bond over the return on holding an -month bond for a holding period of months; $f_{t}^{j}$ denotes the one-year forward rate ending months; and $RV_{t}^{1}$ , $JI_{t}^{h}$ , $JM_{t}^{h}$ and $JV_{t}^{h}$ denote the realized volatility and jump measures in rolling windows ending on the last day of month .

Table 1: Summary statistics and correlation matrix for excess returns, forward rates, and jump measures
Correlation matrix	$ex_{t+12}^{12,24}$	$ex_{t+12}^{12,36}$	$ex_{t+12}^{12,48}$	$ex_{t+12}^{12,60}$	$f_{t}^{12}$	$f_{t}^{36}$	$f_{t}^{60}$	$RV_{t}^{1}$	$JI_{t}^{24}$	$JM_{t}^{24}$	$JV_{t}^{24}$
R1	1	0.98	0.96	0.92	0.22	0.35	0.33	0.12	0.11	-0.1	0.16
R2		1	0.99	0.97	0.17	0.32	0.31	0.14	0.08	-0.13	0.2
R3			1	0.99	0.13	0.31	0.32	0.1	0.1	-0.17	0.19
R4				1	0.1	0.29	0.32	0.08	0.09	-0.2	0.2
R5					1	0.91	0.78	-0.27	0.09	0.41	-0.65
R6						1	0.94	-0.41	0.27	0.19	-0.67
R7							1	-0.48	0.44	-0.02	-0.63
R8								1	-0.37	0.29	0.63
R9									1	-0.44	-0.27
R10										1	-0.26
R11											1

Table 2: Excess returns on holding an n-month bond for a holding period of one year, n=24 (Newey-West t-statistics in parentheses)
Intercept	t-statistic	$f_{t}^{12}$	$f_{t}^{12}$ t-statistic	$f_{t}^{36}$	$f_{t}^{36}$ t-statistic	$f_{t}^{60}$	$f_{t}^{60}$ t-statistic	$RV_{t}^{1}$	$RV_{t}^{1}$ t-statistic	$JI_{t}^{24}$	$JI_{t}^{24}$ t-statistic	$JM_{t}^{24}$	$JM_{t}^{24}$ t-statistic	$JV_{t}^{24}$	$JV_{t}^{24}$ t-statistic	$R^{2}$
-1.37	(-1.00)	-0.73	(-2.89)	1.91	-3.7	-0.89	(-1.74)									0.24
-3.97	(-2.81)	-0.81	(-4.15)	1.95	-5.04	-0.65	(-1.53)	1.68	(-3.19)							0.35
-1.36	(-1.00)	-0.73	(-2.88)	1.93	-3.46	-0.93	(-1.61)			0.52	(-0.1)					0.24
-0.84	(-0.59)	-0.64	(-2.29)	1.99	-3.92	-1.09	(-2.09)					-3.47	(-0.84)			0.25
-5.82	(-3.80)	-0.58	(-2.89)	2.02	-5.67	-0.75	(-1.83)							4.25	(-4.75)	0.48

Notes: This table reports the coefficient estimates in a regression of the excess returns on a -month bond over those on a 12 month bond, with a holding period of 12 months, on the term structure of forward rates, a one-month rolling window of realized S&P500 volatility and a 24 month rolling window of S&P500 jump mean, jump intensity, and jump volatility, constructed as described in the text. Observations are at the monthly frequency (end-of-month). T-statistics are shown in parentheses and are based on Newey-West standard errors with a lag truncation parameter of 11.

Table 2: Excess returns on holding an n-month bond for a holding period of one year, n=36 (Newey-West t-statistics in parentheses)
Intercept	t-statistic	$f_{t}^{12}$	$f_{t}^{12}$ t-statistic	$f_{t}^{36}$	$f_{t}^{36}$ t-statistic	$f_{t}^{60}$	$f_{t}^{60}$ t-statistic	$RV_{t}^{1}$	$RV_{t}^{1}$ t-statistic	$JI_{t}^{24}$	$JI_{t}^{24}$ t-statistic	$JM_{t}^{24}$	$JM_{t}^{24}$ t-statistic	$JV_{t}^{24}$	$JV_{t}^{24}$ t-statistic	$R^{2}$
-2.78	(-1.16)	-1.6	(-3.19)	3.89	-3.71	-1.77	(-1.81)									0.25
-7.98	(-3.19)	-1.76	(-4.61)	3.97	-5.02	-1.29	(-1.65)	3.36	(-3.37)							0.38
-2.83	(-1.19)	-1.6	(-3.27)	3.81	-3.45	-1.63	(-1.49)			-2	(-0.22)					0.26
-1.87	(-0.77)	-1.44	(-2.66)	4.03	-3.83	-2.1	(-2.06)					-5.96	(-0.78)			0.27
-11.6	(-4.08)	-1.31	(-3.74)	4.11	-6.18	-1.48	(-1.99)							8.42	(-4.92)	0.52

Table 2: Excess returns on holding an n-month bond for a holding period of one year, n=48 (Newey-West t-statistics in parentheses)
Intercept	t-statistic	$f_{t}^{12}$	$f_{t}^{12}$ t-statistic	$f_{t}^{36}$	$f_{t}^{36}$ t-statistic	$f_{t}^{60}$	$f_{t}^{60}$ t-statistic	$RV_{t}^{1}$	$RV_{t}^{1}$ t-statistic	$JI_{t}^{24}$	$JI_{t}^{24}$ t-statistic	$JM_{t}^{24}$	$JM_{t}^{24}$ t-statistic	$JV_{t}^{24}$	$JV_{t}^{24}$ t-statistic	$R^{2}$
-4.6	(-1.53)	-2.43	(-3.71)	5.41	-3.88	-2.19	(-1.70)									0.29
-11.33	(-3.39)	-2.63	(-5.26)	5.51	-5.12	-1.58	(-1.52)	4.34	(-3.06)							0.4
-4.7	(-1.57)	-2.44	(-3.85)	5.23	-3.57	-1.92	(-1.30)			-4.04	(-0.35)					0.29
-3.4	(-1.13)	-2.22	(-3.13)	5.59	-3.94	-2.63	(-1.90)					-7.87	(-0.76)			0.3
-16.11	(-4.06)	-2.05	(-4.46)	5.69	-6.08	-1.82	(-1.79)							10.99	(-4.41)	0.52

Table 2: Excess returns on holding an n-month bond for a holding period of one year, n=60 (Newey-West t-statistics in parentheses)
Intercept	t-statistic	$f_{t}^{12}$	$f_{t}^{12}$ t-statistic	$f_{t}^{36}$	$f_{t}^{36}$ t-statistic	$f_{t}^{60}$	$f_{t}^{60}$ t-statistic	$RV_{t}^{1}$	$RV_{t}^{1}$ t-statistic	$JI_{t}^{24}$	$JI_{t}^{24}$ t-statistic	$JM_{t}^{24}$	$JM_{t}^{24}$ t-statistic	$JV_{t}^{24}$	$JV_{t}^{24}$ t-statistic	$R^{2}$
-6.2	(-1.79)	-2.96	(-3.71)	6.1	-3.56	-2.14	(-1.38)									0.28
-14	(-3.52)	-3.2	(-5.20)	6.22	-4.55	-1.43	(-1.15)	5.03	(-2.77)							0.38
-6.45	(-1.86)	-2.98	(-4.01)	5.65	-3.18	-1.45	(-0.80)			-10.2	(-0.74)					0.29
-4.84	(-1.46)	-2.73	(-3.19)	6.31	-3.58	-2.64	(-1.56)					-8.93	(-0.71)			0.29
-19.98	(-4.06)	-2.51	(-4.62)	6.43	-5.51	-1.7	(-1.37)							13.16	(-4.07)	0.51

Table 3: Excess returns on holding an n-month bond for a holding period of one year, n=24 (Newey-West t-statistics in parentheses)
Intercept	t-statistic	$RV_{t}^{1}$	$RV_{t}^{1}$ t-statistic	$JI_{t}^{24}$	$JI_{t}^{24}$ t-statistic	$JM_{t}^{24}$	$JM_{t}^{24}$ t-statistic	$JV_{t}^{24}$	$JV_{t}^{24}$ t-statistic	$R^{2}$
0.52	-0.91	0.53	-0.77							0.02
0.56	-0.74			2.62	-0.5					0.01
1.04	-2.37					-2.08	(-0.45)			0.01
0.4	-0.66							1	-0.9	0.03

Notes: As for Table 2, except that the predictors are realized volatility and jump risk measures without controlling for forward rates.

Table 3: Excess returns on holding an n-month bond for a holding period of one year, n=36 (Newey-West t-statistics in parentheses)
Intercept	t-statistic	$RV_{t}^{1}$	$RV_{t}^{1}$ t-statistic	$JI_{t}^{24}$	$JI_{t}^{24}$ t-statistic	$JM_{t}^{24}$	$JM_{t}^{24}$ t-statistic	$JV_{t}^{24}$	$JV_{t}^{24}$ t-statistic	$R^{2}$
0.81	-0.74	1.12	-0.85							0.02
1.14	-0.84			3.65	-0.39					0.01
1.94	-2.47					-5.05	(-0.60)			0.02
0.42	-0.36							2.4	-1.14	0.04

Notes: As for Table 2, except that the predictors are realized volatility and jump risk measures without controlling for forward rates.

Table 3: Excess returns on holding an n-month bond for a holding period of one year, n=48 (Newey-West t-statistics in parentheses)
Intercept	t-statistic	$RV_{t}^{1}$	$RV_{t}^{1}$ t-statistic	$JI_{t}^{24}$	$JI_{t}^{24}$ t-statistic	$JM_{t}^{24}$	$JM_{t}^{24}$ t-statistic	$JV_{t}^{24}$	$JV_{t}^{24}$ t-statistic	$R^{2}$
1.41	-0.91	1.12	-0.61							0.01
1.35	-0.77			6.53	-0.54					0.01
-2.82	-2.67					-9.45	(-0.85)			0.03
0.65	-0.41							3.13	-1.13	0.04

Notes: As for Table 2, except that the predictors are realized volatility and jump risk measures without controlling for forward rates.

Table 3: Excess returns on holding an n-month bond for a holding period of one year, n=60 (Newey-West t-statistics in parentheses)
Intercept	t-statistic	$RV_{t}^{1}$	$RV_{t}^{1}$ t-statistic	$JI_{t}^{24}$	$JI_{t}^{24}$ t-statistic	$JM_{t}^{24}$	$JM_{t}^{24}$ t-statistic	$JV_{t}^{24}$	$JV_{t}^{24}$ t-statistic	$R^{2}$
1.71	-0.91	1.08	-0.47							0.01
1.6	-0.77			6.76	-0.48					0.01
3.36	-2.85					-13.56	(-1.04)			0.04
0.5	-0.26							3.98	-1.24	0.04

Notes: As for Table 2, except that the predictors are realized volatility and jump risk measures without controlling for forward rates.

Table 4: Excess returns on holding an n-month bond for a holding period of one year with non-overlapping data, n=24 (Heteroskedasticity-robust t-statistics in parentheses)
Intercept	t-statistic	$f_{t}^{12}$	$f_{t}^{12}$ t-statistic	$f_{t}^{36}$	$f_{t}^{36}$ t-statistic	$f_{t}^{60}$	$f_{t}^{60}$ t-statistic	$RV_{t}^{1}$	$RV_{t}^{1}$ t-statistic	$JI_{t}^{24}$	$JI_{t}^{24}$ t-statistic	$JM_{t}^{24}$	$JM_{t}^{24}$ t-statistic	$JV_{t}^{24}$	$JV_{t}^{24}$ t-statistic	$R^{2}$
-1.79	(-1.03)	-0.65	(-2.29)	1.54	-1.99	-0.55	(-0.79)									0.2
-3.23	(-0.96)	-0.72	(-2.72)	1.57	-2.3	-0.42	(-0.62)	1.14	-0.6							0.24
-1.79	(-1.00)	-0.65	(-2.13)	1.54	-2.01	-0.54	(-0.68)			-0.28	(-0.04)					0.2
-1.61	(-0.73)	-0.61	(-1.75)	1.53	-2.04	-0.58	(-0.72)					-0.78	(-0.10)			0.2
-5.84	(-2.73)	-0.41	(-2.36)	1.52	-2.93	-0.39	(-0.67)							4.23	-3.09	0.42

Notes: As for Table 2, except that only end-of-year observations are used to avoid overlapping holding periods. Standard errors are heteroskedasticity-robust, but make no correction for serial correlation.

Table 4: Excess returns on holding an n-month bond for a holding period of one year with non-overlapping data, n=36 (Heteroskedasticity-robust t-statistics in parentheses)
Intercept	t-statistic	$f_{t}^{12}$	$f_{t}^{12}$ t-statistic	$f_{t}^{36}$	$f_{t}^{36}$ t-statistic	$f_{t}^{60}$	$f_{t}^{60}$ t-statistic	$RV_{t}^{1}$	$RV_{t}^{1}$ t-statistic	$JI_{t}^{24}$	$JI_{t}^{24}$ t-statistic	$JM_{t}^{24}$	$JM_{t}^{24}$ t-statistic	$JV_{t}^{24}$	$JV_{t}^{24}$ t-statistic	$R^{2}$
-4.19	(-1.28)	-1.46	(-2.43)	3.17	-1.92	-0.98	(-0.69)									0.23
-6.88	(-1.06)	-1.59	(-2.81)	3.21	-2.18	-0.75	(-0.53)	2.11	-0.57							0.26
-4.29	(-1.26)	-1.52	(-2.52)	3.16	-2.05	-0.83	(-0.53)			-4.2	(-0.29)					0.24
-3.59	(-0.85)	-1.34	(-1.91)	3.12	-1.97	-1.09	(-0.65)					-2.7	(-0.18)			0.23
-12.23	(-2.78)	-0.99	(-2.99)	3.11	-3.02	-0.67	(-0.58)							8.39	-3.07	0.45

Table 4: Excess returns on holding an n-month bond for a holding period of one year with non-overlapping data, n=48 (Heteroskedasticity-robust t-statistics in parentheses)
Intercept	t-statistic	$f_{t}^{12}$	$f_{t}^{12}$ t-statistic	$f_{t}^{36}$	$f_{t}^{36}$ t-statistic	$f_{t}^{60}$	$f_{t}^{60}$ t-statistic	$RV_{t}^{1}$	$RV_{t}^{1}$ t-statistic	$JI_{t}^{24}$	$JI_{t}^{24}$ t-statistic	$JM_{t}^{24}$	$JM_{t}^{24}$ t-statistic	$JV_{t}^{24}$	$JV_{t}^{24}$ t-statistic	$R^{2}$
-6.52	(-1.47)	-2.16	(-2.65)	4.37	-1.89	-1.13	(-0.56)									0.26
-9.83	(-1.12)	-2.34	(-2.96)	4.41	-2.11	-0.83	(-0.42)	2.61	-0.52							0.29
-6.69	(-1.45)	-2.28	(-2.81)	4.36	-2.05	-0.86	(-0.39)			-7.21	(-0.37)					0.26
-5.51	(-0.97)	-1.98	(-2.05)	4.29	-1.94	-1.31	(-0.56)					-4.51	(-0.22)			0.26
-17.13	(-2.66)	-1.56	(-3.54)	4.29	-2.94	-0.72	(-0.43)							11.07	-2.74	0.45

Table 4: Excess returns on holding an n-month bond for a holding period of one year with non-overlapping data, n=60 (Heteroskedasticity-robust t-statistics in parentheses)
Intercept	t-statistic	$f_{t}^{12}$	$f_{t}^{12}$ t-statistic	$f_{t}^{36}$	$f_{t}^{36}$ t-statistic	$f_{t}^{60}$	$f_{t}^{60}$ t-statistic	$RV_{t}^{1}$	$RV_{t}^{1}$ t-statistic	$JI_{t}^{24}$	$JI_{t}^{24}$ t-statistic	$JM_{t}^{24}$	$JM_{t}^{24}$ t-statistic	$JV_{t}^{24}$	$JV_{t}^{24}$ t-statistic	$R^{2}$
-8.77	(-1.63)	-2.51	(-2.40)	4.34	-1.48	-0.44	(-0.17)									0.25
-12.16	(-1.12)	-2.68	(-2.62)	4.39	-1.6	-0.14	(-0.05)	2.67	-0.43							0.27
-9.09	(-1.61)	-2.72	(-2.77)	4.33	-1.66	0.05	(-0.02)			-13.29	(-0.55)					0.26
-7.89	(-1.13)	-2.34	(-1.97)	4.27	-1.52	-0.6	(-0.20)					-3.93	(-0.16)			0.25
-21.21	(-2.55)	-1.79	(-2.99)	4.25	-2.21	0.03	(-0.01)							12.98	-2.44	0.42

Table 5: Excess returns on holding an n-month bond for a holding period of 3 months, n=24 (Newey-West t-statistics in parentheses)
Intercept	t-statistic	$f_{t}^{12}$	$f_{t}^{12}$ t-statistic	$f_{t}^{36}$	$f_{t}^{36}$ t-statistic	$f_{t}^{60}$	$f_{t}^{60}$ t-statistic	$RV_{t}^{1}$	$RV_{t}^{1}$ t-statistic	$JI_{t}^{24}$	$JI_{t}^{24}$ t-statistic	$JM_{t}^{24}$	$JM_{t}^{24}$ t-statistic	$JV_{t}^{24}$	$JV_{t}^{24}$ t-statistic	$R^{2}$
-0.62	(-1.34)	-0.42	(-2.48)	1.19	-3.16	-0.66	(-2.43)									0.12
-1.37	(-2.65)	-0.44	(-2.58)	1.19	-3.19	-0.6	(-2.23)	0.55	(-2.21)							0.15
-0.63	(-1.36)	-0.42	(-2.49)	1.23	-3.19	-0.72	(-2.43)			0.88	(-0.43)					0.12
-0.46	(-0.92)	-0.39	(-2.14)	1.22	-3.22	-0.73	(-2.53)					-1.21	(-0.70)			0.13
-2.29	(-3.21)	-0.35	(-1.98)	1.22	-2.93	-0.62	(-2.13)							1.71	(-2.77)	0.2

Notes: This table reports the coefficient estimates in a regression of the excess returns on a n-month bond over those on a 3 month bond, with a holding period of 3 months, on the term structure of forward rates, a one-month rolling window of realized S&P500 volatility and a 24 month rolling window of S&P500 jump mean, jump intensity, and jump volatility, constructed as described in the text. Observations are at the monthly frequency (end-of-month). T-statistics are shown in parentheses and are based on Newey-West standard errors with a lag truncation parameter of 2.

Table 5: Excess returns on holding an n-month bond for a holding period of 3 months, n=36 (Newey-West t-statistics in parentheses)
Intercept	t-statistic	$f_{t}^{12}$	$f_{t}^{12}$ t-statistic	$f_{t}^{36}$	$f_{t}^{36}$ t-statistic	$f_{t}^{60}$	$f_{t}^{60}$ t-statistic	$RV_{t}^{1}$	$RV_{t}^{1}$ t-statistic	$JI_{t}^{24}$	$JI_{t}^{24}$ t-statistic	$JM_{t}^{24}$	$JM_{t}^{24}$ t-statistic	$JV_{t}^{24}$	$JV_{t}^{24}$ t-statistic	$R^{2}$
-1.02	(-1.47)	-0.75	(-2.84)	1.99	-3.38	-1.08	(-2.54)									0.13
-2.15	(-2.62)	-0.77	(-2.93)	1.99	-3.4	-0.98	(-2.36)	0.83	(-1.99)							0.15
-1.04	(-1.49)	-0.75	(-2.84)	2.05	-3.37	-1.16	(-2.50)			1.28	(-0.41)					0.13
-0.81	(-1.08)	-0.71	(-2.49)	2.03	-3.42	-1.17	(-2.59)					-1.63	(-0.59)			0.13
-3.47	(-3.11)	-0.64	(-2.37)	2.03	-3.13	-1.02	(-2.25)							2.5	(-2.53)	0.19

Table 5: Excess returns on holding an n-month bond for a holding period of 3 months, n=48 (Newey-West t-statistics in parentheses)
Intercept	t-statistic	$f_{t}^{12}$	$f_{t}^{12}$ t-statistic	$f_{t}^{36}$	$f_{t}^{36}$ t-statistic	$f_{t}^{60}$	$f_{t}^{60}$ t-statistic	$RV_{t}^{1}$	$RV_{t}^{1}$ t-statistic	$JI_{t}^{24}$	$JI_{t}^{24}$ t-statistic	$JM_{t}^{24}$	$JM_{t}^{24}$ t-statistic	$JV_{t}^{24}$	$JV_{t}^{24}$ t-statistic	$R^{2}$
-1.44	(-1.60)	-0.99	(-2.80)	2.51	-3.19	-1.31	(-2.31)									0.13
-2.72	(-2.44)	-1.01	(-2.87)	2.51	-3.21	-1.19	(-2.16)	0.93	(-1.62)							0.14
-1.46	(-1.60)	-0.99	(-2.81)	2.57	-3.17	-1.39	(-2.25)			1.32	(-0.32)					0.13
-1.22	(-1.26)	-0.95	(-2.49)	2.55	-3.23	-1.4	(-2.35)					-1.71	(-0.47)			0.13
-4.44	(-2.99)	-0.86	(-2.38)	2.56	-2.97	-1.23	(-2.05)							3.06	(-2.31)	0.18

Table 5: Excess returns on holding an n-month bond for a holding period of 3 months, n=60 (Newey-West t-statistics in parentheses)
Intercept	t-statistic	$f_{t}^{12}$	$f_{t}^{12}$ t-statistic	$f_{t}^{36}$	$f_{t}^{36}$ t-statistic	$f_{t}^{60}$	$f_{t}^{60}$ t-statistic	$RV_{t}^{1}$	$RV_{t}^{1}$ t-statistic	$JI_{t}^{24}$	$JI_{t}^{24}$ t-statistic	$JM_{t}^{24}$	$JM_{t}^{24}$ t-statistic	$JV_{t}^{24}$	$JV_{t}^{24}$ t-statistic	$R^{2}$
-1.92	(-1.72)	-1.08	(-2.42)	2.61	-2.64	-1.25	(-1.76)									0.1
-3.39	(-2.39)	-1.11	(-2.49)	2.61	-2.64	-1.12	(-1.61)	1.07	(-1.49)							0.12
-1.93	(-1.71)	-1.08	(-2.42)	2.64	-2.57	-1.29	(-1.65)			0.6	(-0.11)					0.1
-1.73	(-1.45)	-1.04	(-2.19)	2.65	-2.66	-1.33	(-1.78)					-1.46	(-0.31)			0.11
-5.35	(-2.90)	-0.93	(-2.06)	2.67	-2.48	-1.16	(-1.54)							3.51	(-2.14)	0.15

Table 6: Excess returns on holding an n-month bond for a holding period of one year (12 month rolling jump risk estimates), n=24 , (Newey-West t-statistics in parentheses)
Intercept	t-statistic	$f_{t}^{12}$	$f_{t}^{12}$ t-statistic	$f_{t}^{36}$	$f_{t}^{36}$ t-statistic	$f_{t}^{60}$	$f_{t}^{60}$ t-statistic	$RV_{t}^{1}$	$RV_{t}^{1}$ t-statistic	$JI_{t}^{12}$	$JI_{t}^{12}$ t-statistic	$JM_{t}^{12}$	$JM_{t}^{12}$ t-statistic	$JV_{t}^{12}$	$JV_{t}^{12}$ t-statistic	$R^{2}$
-1.37	(-1.00)	-0.73	(-2.89)	1.91	-3.7	-0.89	(-1.74)									0.24
-3.97	(-2.81)	-0.81	(-4.15)	1.95	-5.04	-0.65	(-1.53)	1.68	(-3.19)							0.35
-1.36	(-1.01)	-0.73	(-2.86)	1.94	-3.39	-0.93	(-1.66)			0.56	(-0.13)					0.24
-1.27	(-0.93)	-0.71	(-2.80)	1.95	-3.69	-0.95	(-1.78)					-1	(-0.51)			0.24
-5.53	(-3.84)	-0.7	(-4.21)	1.96	-5.94	-0.61	(-1.50)							3.72	(-4.69)	0.49

Notes: As for Table 2, except that 12 month rolling windows are used to measure the jump risk measures.

Table 6: Excess returns on holding an n-month bond for a holding period of one year (12 month rolling jump risk estimates), n=36 , (Newey-West t-statistics in parentheses)
Intercept	t-statistic	$f_{t}^{12}$	$f_{t}^{12}$ t-statistic	$f_{t}^{36}$	$f_{t}^{36}$ t-statistic	$f_{t}^{60}$	$f_{t}^{60}$ t-statistic	$RV_{t}^{1}$	$RV_{t}^{1}$ t-statistic	$JI_{t}^{12}$	$JI_{t}^{12}$ t-statistic	$JM_{t}^{12}$	$JM_{t}^{12}$ t-statistic	$JV_{t}^{12}$	$JV_{t}^{12}$ t-statistic	$R^{2}$
-2.78	(-1.16)	-1.6	(-3.19)	3.89	-3.71	-1.77	(-1.81)									0.25
-7.98	(-3.19)	-1.76	(-4.61)	3.97	-5.02	-1.29	(-1.65)	3.36	(-3.37)							0.38
-2.78	(-1.19)	-1.6	(-3.19)	3.88	-3.29	-1.76	(-1.57)			-0.19	(-0.03)					0.25
-2.74	(-1.14)	-1.59	(-3.18)	3.91	-3.55	-1.79	(-1.71)					-0.37	(-0.10)			0.25
-10.65	(-4.03)	-1.55	(-5.30)	4	-6.23	-1.23	(-1.65)							7.04	(-4.64)	0.5

Notes: As for Table 2, except that 12 month rolling windows are used to measure the jump risk measures.

Table 6: Excess returns on holding an n-month bond for a holding period of one year (12 month rolling jump risk estimates), n=48 , (Newey-West t-statistics in parentheses)
Intercept	t-statistic	$f_{t}^{12}$	$f_{t}^{12}$ t-statistic	$f_{t}^{36}$	$f_{t}^{36}$ t-statistic	$f_{t}^{60}$	$f_{t}^{60}$ t-statistic	$RV_{t}^{1}$	$RV_{t}^{1}$ t-statistic	$JI_{t}^{12}$	$JI_{t}^{12}$ t-statistic	$JM_{t}^{12}$	$JM_{t}^{12}$ t-statistic	$JV_{t}^{12}$	$JV_{t}^{12}$ t-statistic	$R^{2}$
-4.6	(-1.53)	-2.43	(-3.71)	5.41	-3.88	-2.19	(-1.70)									0.29
-11.33	(-3.39)	-2.63	(-5.26)	5.51	-5.12	-1.58	(-1.52)	4.34	(-3.06)							0.4
-4.63	(-1.57)	-2.43	(-3.72)	5.36	-3.37	-2.12	(-1.38)			-1	(-0.10)					0.29
-4.68	(-1.55)	-2.44	(-3.76)	5.38	-3.63	-2.15	(-1.53)					0.73	(-0.15)			0.29
-14.61	(-3.93)	-2.37	(-6.07)	5.54	-6.03	-1.51	(-1.47)							8.95	(-4.05)	0.49

Notes: As for Table 2, except that 12 month rolling windows are used to measure the jump risk measures.

Table 6: Excess returns on holding an n-month bond for a holding period of one year (12 month rolling jump risk estimates), n=60 , (Newey-West t-statistics in parentheses)
Intercept	t-statistic	$f_{t}^{12}$	$f_{t}^{12}$ t-statistic	$f_{t}^{36}$	$f_{t}^{36}$ t-statistic	$f_{t}^{60}$	$f_{t}^{60}$ t-statistic	$RV_{t}^{1}$	$RV_{t}^{1}$ t-statistic	$JI_{t}^{12}$	$JI_{t}^{12}$ t-statistic	$JM_{t}^{12}$	$JM_{t}^{12}$ t-statistic	$JV_{t}^{12}$	$JV_{t}^{12}$ t-statistic	$R^{2}$
-6.2	(-1.79)	-2.96	(-3.71)	6.1	-3.56	-2.14	(-1.38)									0.28
-14	(-3.52)	-3.2	(-5.20)	6.22	-4.55	-1.43	(-1.15)	5.03	(-2.77)							0.38
-6.32	(-1.86)	-2.96	(-3.78)	5.86	-2.96	-1.8	(-0.94)			-4.8	(-0.40)					0.28
-6.48	(-1.85)	-3	(-3.85)	6	-3.26	-1.99	(-1.15)					2.59	(-0.43)			0.28
-17.78	(-3.84)	-2.89	(-6.10)	6.26	-5.32	-1.35	(-1.08)							10.35	(-3.63)	0.47

Notes: As for Table 2, except that 12 month rolling windows are used to measure the jump risk measures.

Table 7: Excess returns on holding an n-month bond for a holding period of one year (Treasury futures as volatility/jump measures), n=24 , (Newey-West t-statistics in parentheses)
Intercept	t-statistic	$f_{t}^{12}$	$f_{t}^{12}$ t-statistic	$f_{t}^{36}$	$f_{t}^{36}$ t-statistic	$f_{t}^{60}$	$f_{t}^{60}$ t-statistic	$RV_{t}^{1}$	$RV_{t}^{1}$ t-statistic	$JI_{t}^{24}$	$JI_{t}^{24}$ t-statistic	$JM_{t}^{24}$	$JM_{t}^{24}$ t-statistic	$JV_{t}^{24}$	$JV_{t}^{24}$ t-statistic	$R^{2}$
-1.37	( -1.00)	-0.73	( -2.89)	1.91	-3.7	-0.89	( -1.74)									0.24
-1.64	( -1.13)	-0.72	( -2.80)	1.91	-3.82	-0.9	( -1.78)	0.51	(-0.38)							0.24
-1.86	( -1.11)	-0.68	( -2.50)	1.73	-2.8	-0.76	( -1.31)			6.41	(-0.79)					0.25
-2.22	( -2.13)	-0.49	( -2.05)	1.41	-2.91	-0.45	( -1.05)					-8.9	( -4.18)			0.48
-0.16	( -0.08)	-0.69	( -2.97)	1.81	-3.97	-0.82	( -1.72)							-3.08	( -1.28)	0.26

Notes: This table reports the coefficient estimates in a regression of the excess returns on an -month bond over those on a 12 month bond, with a holding period of 12 months, on the term structure of forward rates, a one-month rolling window of realized Treasury bond futures volatility and a 24 month rolling window of Treasury bond futures jump mean, jump intensity, and jump volatility, constructed as described in the text. Observations are at the monthly frequency (end-of-month). T-statistics are shown in parentheses and are based on Newey-West standard errors with a lag truncation parameter of 11.

Table 7: Excess returns on holding an n-month bond for a holding period of one year (Treasury futures as volatility/jump measures), n=36 , (Newey-West t-statistics in parentheses)
Intercept	t-statistic	$f_{t}^{12}$	$f_{t}^{12}$ t-statistic	$f_{t}^{36}$	$f_{t}^{36}$ t-statistic	$f_{t}^{60}$	$f_{t}^{60}$ t-statistic	$RV_{t}^{1}$	$RV_{t}^{1}$ t-statistic	$JI_{t}^{24}$	$JI_{t}^{24}$ t-statistic	$JM_{t}^{24}$	$JM_{t}^{24}$ t-statistic	$JV_{t}^{24}$	$JV_{t}^{24}$ t-statistic	$R^{2}$
-2.78	( -1.16)	-1.6	( -3.19)	3.89	-3.71	-1.77	( -1.81)									0.25
-3.39	( -1.34)	-1.58	( -3.14)	3.9	-3.84	-1.79	( -1.86)	1.17	(-0.49)							0.26
-3.37	( -1.15)	-1.54	( -2.85)	3.68	-3.01	-1.61	( -1.47)			7.77	(-0.55)					0.26
-4.41	( -2.53)	-1.14	( -2.62)	2.93	-3.16	-0.92	( -1.16)					-17.2	( -4.57)			0.51
-0.78	( -0.21)	-1.54	( -3.40)	3.73	-3.93	-1.65	( -1.78)							-5.08	( -1.09)	0.27

Table 7: Excess returns on holding an n-month bond for a holding period of one year (Treasury futures as volatility/jump measures), n=48 , (Newey-West t-statistics in parentheses)
Intercept	t-statistic	$f_{t}^{12}$	$f_{t}^{12}$ t-statistic	$f_{t}^{36}$	$f_{t}^{36}$ t-statistic	$f_{t}^{60}$	$f_{t}^{60}$ t-statistic	$RV_{t}^{1}$	$RV_{t}^{1}$ t-statistic	$JI_{t}^{24}$	$JI_{t}^{24}$ t-statistic	$JM_{t}^{24}$	$JM_{t}^{24}$ t-statistic	$JV_{t}^{24}$	$JV_{t}^{24}$ t-statistic	$R^{2}$
-4.6	( -1.53)	-2.43	( -3.71)	5.41	-3.88	-2.19	( -1.70)									0.29
-5.21	( -1.62)	-2.41	( -3.65)	5.42	-3.98	-2.21	( -1.73)	1.17	(-0.36)							0.29
-5.46	( -1.50)	-2.35	( -3.29)	5.09	-3.13	-1.96	( -1.37)			11.35	(-0.62)					0.29
-6.73	( -3.06)	-1.83	( -3.25)	4.15	-3.34	-1.09	( -1.03)					-22.41	( -4.63)			0.51
-2.81	( -0.58)	-2.37	( -3.89)	5.27	-3.97	-2.09	( -1.66)							-4.55	( -0.71)	0.29

Table 7: Excess returns on holding an n-month bond for a holding period of one year (Treasury futures as volatility/jump measures), n=60 , (Newey-West t-statistics in parentheses)
Intercept	t-statistic	$f_{t}^{12}$	$f_{t}^{12}$ t-statistic	$f_{t}^{36}$	$f_{t}^{36}$ t-statistic	$f_{t}^{60}$	$f_{t}^{60}$ t-statistic	$RV_{t}^{1}$	$RV_{t}^{1}$ t-statistic	$JI_{t}^{24}$	$JI_{t}^{24}$ t-statistic	$JM_{t}^{24}$	$JM_{t}^{24}$ t-statistic	$JV_{t}^{24}$	$JV_{t}^{24}$ t-statistic	$R^{2}$
-6.2	( -1.79)	-2.96	( -3.71)	6.1	-3.56	-2.14	( -1.38)									0.28
-7.01	( -1.87)	-2.93	( -3.65)	6.11	-3.66	-2.17	( -1.41)	1.55	(-0.4)							0.28
-6.93	( -1.71)	-2.89	( -3.35)	5.83	-2.99	-1.95	( -1.16)			9.63	(-0.46)					0.28
-8.78	( -3.58)	-2.23	( -3.34)	4.58	-3.03	-0.81	( -0.64)					-27.11	( -4.71)			0.5
-5.04	( -0.86)	-2.92	( -3.80)	6.01	-3.57	-2.08	( -1.36)							-2.96	( -0.37)	0.28

Table 8: Excess returns on S&P500 market index over a 3-month bill for a holding period of 3 months (Newey-West t-statistics in parentheses)
Intercept	t-statistic	$\log(P/D)$	$\log(P/D)$ t-statistic	$RV_{t}^{1}$	$RV_{t}^{1}$ t-statistic	$JI_{t}^{24}$	$JI_{t}^{24}$ t-statistic	$JM_{t}^{24}$	$JM_{t}^{24}$ t-statistic	$JV_{t}^{24}$	$JV_{t}^{24}$ t-statistic	$R^{2}$
-0.01	(-0.64)	-0.04	(-2.04)									0.04
-0.04	(-1.35)	-0.05	(-2.41)	0.03	(-1.01)							0.05
	(-0.08)	-0.05	(-2.79)			-0.12	(-1.13)					0.05
-0.01	(-0.94)	-0.04	(-2.18)					0.07	(-0.67)			0.05
0.04	(-1.17)	-0.1	(-0.40)							-0.07	(-1.44)	0.07
0.02	(-1.46)			-0.01	(-0.29)
0.01	(-0.44)					0.06	(-0.46)
0.02	(-1.95)							0.01	(-0.11)
0.06	(-3.32)									-0.08	(-2.24)	0.07

Notes: This table reports the coefficient estimates in a regression of three-month excess returns of S&P500 market index, on log price-dividend ratio, a one-month rolling window of realized S&P500 volatility and a 24 month rolling window of S&P500 jump mean, jump intensity, and jump volatility, constructed as described in the text. Observations are at the quarterly frequency (end-of-quarter). Standard errors are heteroskedasticity-robust, but make no correction for serial correlation.

Table 9: Excess returns on holding an n-month bond for a holding period of one year--market jump volatility versus price-dividend ratio, n=24 , (Newey-West t-statistics in parentheses)
Intercept	t-statistic	$f_{t}^{12}$	$f_{t}^{12}$ t-statistic	$f_{t}^{36}$	$f_{t}^{36}$ t-statistic	$f_{t}^{60}$	$f_{t}^{60}$ t-statistic	$RV_{t}^{1}$	$RV_{t}^{1}$ t-statistic	$JI_{t}^{24}$	$JI_{t}^{24}$ t-statistic	$JM_{t}^{24}$	$JM_{t}^{24}$ t-statistic	$JV_{t}^{24}$	$JV_{t}^{24}$ t-statistic	$PD_{t}$	$PD_{t}$ t-statistic	$R^{2}$
-3.16	( -2.78)	-0.74	( -4.15)	1.56	(-3.59)		( -0.01)									2.26	(-2.51)	0.36
-4.54	( -3.51)	-0.8	( -4.85)	1.68	(-4.59)	-0.07	( -0.19)	1.2	(-2.25)							1.66	(-1.84)	0.41
-3.36	( -2.90)	-0.74	( -4.20)	1.73	(-3.8)	-0.21	( -0.47)			5.37	(-1.14)					2.67	(-2.61)	0.38
-2.48	( -2.07)	-0.56	( -2.85)	1.65	(-4.02)	-0.21	( -0.54)					-7.01	( -1.69)			2.75	(-3.21)	0.41
-5.84	( -3.97)	-0.6	( -3.06)	1.9	(-5.81)	-0.5	( -1.49)							3.76	(-3.29)	0.66	(-0.77)	0.49

Notes: This table reports the coefficient estimates in a regression of the excess returns on an n-month bond over those on a 12 month bond, with a holding period of 12 months, on the term structure of forward rates, a one-month rolling window of realized S&P500 volatility and a 24 month rolling window of S&P500 jump mean, jump intensity, and jump volatility, and the log price-dividend ratio, constructed as described in the text. Observations are at the monthly frequency (end-of-month). T-statistics are shown in parentheses and are based on Newey-West standard errors with a lag truncation parameter of 11.

Table 9: Excess returns on holding an n-month bond for a holding period of one year--market jump volatility versus price-dividend ratio, n=36 , (Newey-West t-statistics in parentheses)
Intercept	t-statistic	$f_{t}^{12}$	$f_{t}^{12}$ t-statistic	$f_{t}^{36}$	$f_{t}^{36}$ t-statistic	$f_{t}^{60}$	$f_{t}^{60}$ t-statistic	$RV_{t}^{1}$	$RV_{t}^{1}$ t-statistic	$JI_{t}^{24}$	$JI_{t}^{24}$ t-statistic	$JM_{t}^{24}$	$JM_{t}^{24}$ t-statistic	$JV_{t}^{24}$	$JV_{t}^{24}$ t-statistic	$PD_{t}$	$PD_{t}$ t-statistic	$R^{2}$
-6.59	( -3.29)	-1.63	( -5.06)	3.15	(-3.95)	0.13	(-0.18)									4.83	(-3.01)	0.41
-9.24	( -4.06)	-1.73	( -5.86)	3.38	(-4.96)		( -0.01)	2.3	(-2.33)							3.67	(-2.34)	0.46
-6.88	( -3.38)	-1.62	( -5.08)	3.4	(-4.04)	-0.17	( -0.22)			7.86	(-0.97)					5.43	(-2.95)	0.42
-5.29	( -2.65)	-1.29	( -3.66)	3.32	(-4.47)	-0.26	( -0.41)					-13.39	( -1.79)			5.75	(-3.74)	0.46
-11.64	( -4.35)	-1.37	( -4.16)	3.79	(-6.48)	-0.81	( -1.44)							7.09	(-3.34)	1.82	(-1.21)	0.54

Table 9: Excess returns on holding an n-month bond for a holding period of one year--market jump volatility versus price-dividend ratio, n=48 , (Newey-West t-statistics in parentheses)
Intercept	t-statistic	$f_{t}^{12}$	$f_{t}^{12}$ t-statistic	$f_{t}^{36}$	$f_{t}^{36}$ t-statistic	$f_{t}^{60}$	$f_{t}^{60}$ t-statistic	$RV_{t}^{1}$	$RV_{t}^{1}$ t-statistic	$JI_{t}^{24}$	$JI_{t}^{24}$ t-statistic	$JM_{t}^{24}$	$JM_{t}^{24}$ t-statistic	$JV_{t}^{24}$	$JV_{t}^{24}$ t-statistic	$PD_{t}$	$PD_{t}$ t-statistic	$R^{2}$
-9.97	( -3.84)	-2.47	( -6.21)	4.36	(-4.25)	0.48	(-0.55)									6.8	(-3.31)	0.44
-13.17	( -4.32)	-2.6	( -7.02)	4.64	(-5.15)	0.32	(-0.37)	2.78	(-2.04)							5.4	(-2.74)	0.48
-10.33	( -3.92)	-2.46	( -6.26)	4.64	(-4.3)	0.12	(-0.12)			9.65	(-0.91)					7.54	(-3.15)	0.45
-8.19	( -3.35)	-2	( -4.57)	4.64	(-4.77)	-0.05	( -0.06)					-18.29	( -1.87)			8.07	(-4.03)	0.5
-16.18	( -4.38)	-2.15	( -5.16)	4.64	(-6.3)	-0.68	( -0.89)							8.71	(-2.9)	3.1	(-1.59)	0.55

Table 9: Excess returns on holding an n-month bond for a holding period of one year--market jump volatility versus price-dividend ratio, n=60 , (Newey-West t-statistics in parentheses)
Intercept	t-statistic	$f_{t}^{12}$	$f_{t}^{12}$ t-statistic	$f_{t}^{36}$	$f_{t}^{36}$ t-statistic	$f_{t}^{60}$	$f_{t}^{60}$ t-statistic	$RV_{t}^{1}$	$RV_{t}^{1}$ t-statistic	$JI_{t}^{24}$	$JI_{t}^{24}$ t-statistic	$JM_{t}^{24}$	$JM_{t}^{24}$ t-statistic	$JV_{t}^{24}$	$JV_{t}^{24}$ t-statistic	$PD_{t}$	$PD_{t}$ t-statistic	$R^{2}$
-13.42	( -4.45)	-3.02	( -7.02)	4.69	(-3.98)	1.44	(-1.42)									9.13	(-3.82)	0.47
-16.64	( -4.63)	-3.14	( -7.74)	4.97	(-4.62)	1.28	(-1.25)	2.8	(-1.68)							7.73	(-3.41)	0.5
-13.69	( -4.51)	-3.01	( -7.01)	4.93	(-3.92)	1.16	(-1)			7.41	(-0.6)					9.7	(-3.46)	0.48
-11.21	( -4.30)	-2.43	( -5.09)	4.98	(-4.49)	0.78	(-0.86)					-22.76	( -2.03)			10.71	(-4.61)	0.53
-20.1	( -4.47)	-2.67	( -5.98)	5.54	(-5.55)	0.2	(-0.22)							9.38	(-2.51)	5.16	(-2.24)	0.55

Notes: This table reports the coefficient estimates in a regression of the excess returns on an

-month bond over those on a 12 month bond, with a holding period of 12 months, on the term structure of forward rates, a one-month rolling window of realized S&P500 volatility and a 24 month rolling window of S&P500 jump mean, jump intensity, and jump volatility, and the log price-dividend ratio, constructed as described in the text. Observations are at the monthly frequency (end-of-month). T-statistics are shown in parentheses and are based on Newey-West standard errors with a lag truncation parameter of 11.

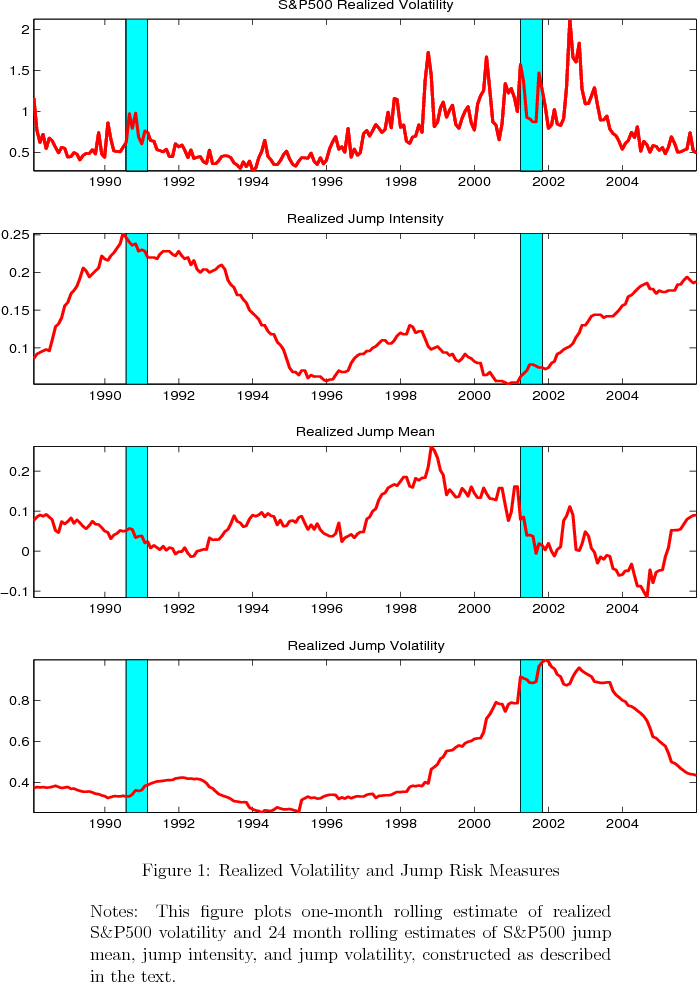
Figure 1 is a chart with four panels. The top panel shows the time series of the one-month rolling estimate of S&P500 realized volatility since 1988. NBER recessions are shaded. The realized volatility rose around the times of recessions, reaching a peak of 2 percentage points shortly after the end of the most recent recession, before falling back down. The second panel shows the time series of the two-year rolling estimate of jump intensity, with NBER recessions given by the shaded areas. This rose steeply during the recession of the early 1990s, reaching a peak of 0.25, and has been climbing again in recent years, standing just below 0.2 at the end of the sample period. The third panel shows the time series of the two-year rolling estimate of jump mean, with NBER recessions given by the shaded areas. This peaked in 1998 at over 0.2. The final panel shows the time series of the two-year rolling estimate of jump volatility, with NBER recessions given by the shaded areas. This has a notable countercyclical pattern, rising in both the recession of the early 1990s and, more sharply, during the most recent recession. It reached nearly one percentage point in 2002. At the end of the sample, it is close to its historical average of 0.4 percentage points.

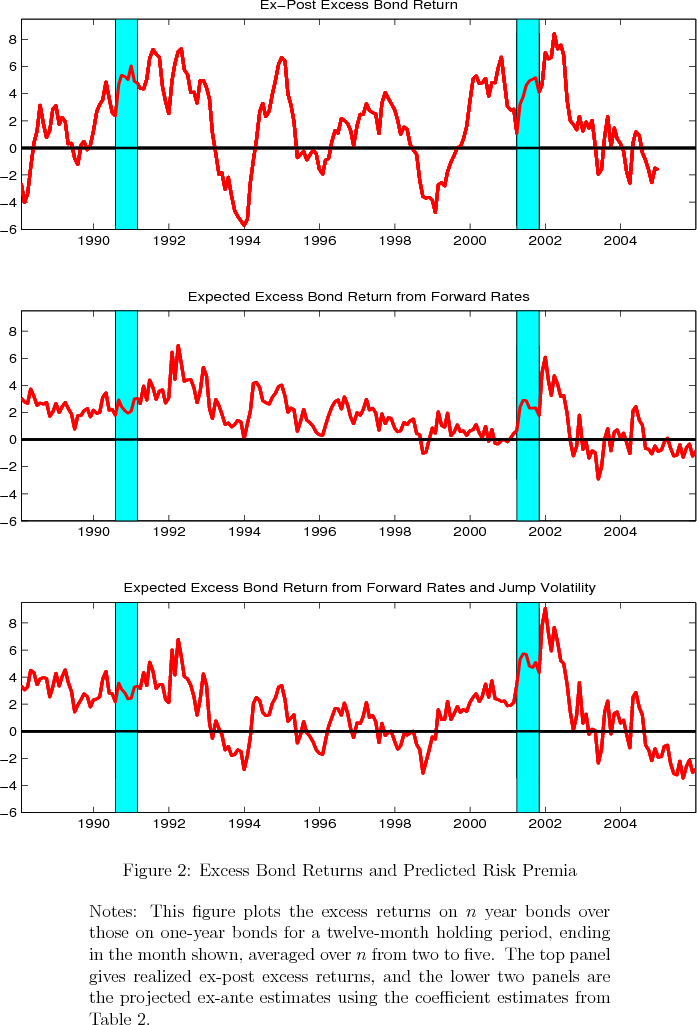
Figure 2 is a chart with three panels. The top panel plots the realized excess returns on n year bonds over those on one-year bonds for a twelve-month holding period, ending in the month shown, averaged over n from two to five. The returns are shown since 1988 and NBER recessions are shaded. Excess returns ranged from -6 to +8 percentage points. Excess returns were large and positive around the recessions. At other times, they were volatile, but were on average close to zero. The middle panel gives the projected ex-ante estimates of these excess returns using the coefficient estimates from Table 2, using the forward rates alone as predictor variables. NBER recessions are shaded. These ex-ante estimates capture a good bit of the variation in realized excess returns shown in the upper panel, but nonetheless turn out to have been too high for much of the 1990s and too low during the most recent recession. At the end of the sample, these estimates of excess returns were slightly below zero. The bottom panel gives the projected ex-ante estimates of these excess returns using the coefficient estimates from Table 2, using both the forward rates and estimated jump volatility as predictor variables, with NBER recessions shaded. These estimates track the realized excess returns in the upper panel quite closely. At the end of the sample, these estimates of excess returns fell to below -2 percentage points.

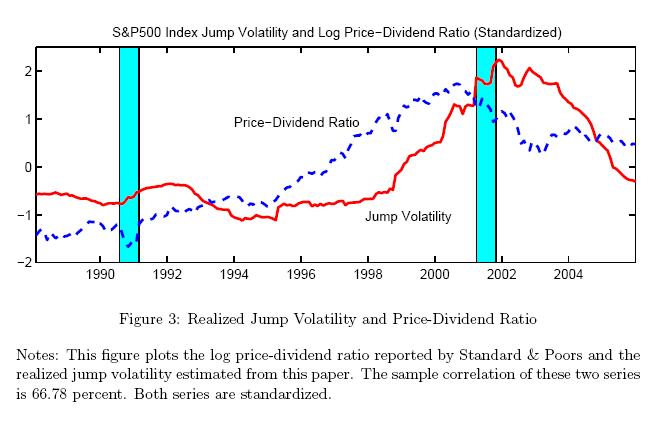
Figure 3 is a line chart that shows the time series of jump volatility and the log price-dividend ratio for the S&P 500 index. The variables are shown since 1988. NBER recessions are shaded. The two variables seem quite highly positively correlated. The sample correlation coefficient is 66.78 percent. Both rose in the 1990s, and peaked around the time of the last recession, before declining in more recent years. Both variables appear to be countercyclical. The series are both expressed in standardized units.

Footnotes

* We thank Darrell Duffie, Cam Harvey, Monika Piazzesi, and George Tauchen for helpful discussions. The views presented here are solely those of the authors and do not necessarily represent those of the Federal Reserve Board or its staff. Return to Text

* Division of Monetary Affairs, Federal Reserve Board, Mail Stop 91, Washington DC 20551 USA, E-mail [email protected], Phone 202-452-3605, Fax 202-452-2301. Return to Text

* Division of Research and Statistics, Federal Reserve Board, Mail Stop 91, Washington DC 20551 USA, E-mail [email protected], Phone 202-452-3360, Fax 202-728-5887. Return to Text

1_ Note that

is the Tri-Power Quarticity robust to jumps, and as shown by Barndorff-Nielsen and Shephard (2004),

$\displaystyle TP_t$

$\displaystyle \equiv$

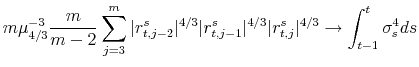$\displaystyle m \mu_{4/3}^{-3}\frac{m}{m-2} \sum_{j=3}^{m} \vert r^s_{t,j-2}\vert^{4/3} \vert r^s_{t,j-1}\vert^{4/3} \vert r^s_{t,j}\vert^{4/3} \rightarrow \int_{t-1}^{t} \sigma^4_sds$

(7)

with $\mu_{k} \equiv 2^{k/2} \Gamma((k+1)/2)/\Gamma(1/2)$ for

. Return to Text

2. Existing studies have relied heavily on complex numerical procedures or simulation methods like EMM or MCMC (see, e.g., Andersen, Benzoni, and Lund, 2002; Bates, 2000; Aït-Sahalia, 2004; Chernov, Gallant, Ghysels, and Tauchen, 2003; Pan, 2002; Eraker, Johannes, and Polson, 2003). Return to Text

3. Inference issues related to the use of highly persistent predictor variables have been studied extensively in the literature, see, e.g., Stambaugh (1999), Ferson, Sarkissian, and Simin (2003), and Campbell and Yogo (2006) and the references therein. For recent discussions of some of the difficulties associated with the use of overlapping data see, e.g., Valkanov (2003) and Boudoukh, Richardson, and Whitelaw (2006). Return to Text

4. The Fama-Bliss zero-coupon data consist of 1-, 2-, 3-, 4- and 5-year zero-coupon bonds only. To construct three-month excess returns (

), we need some yields that are not available, such as 1.75 year yields. We use the approximation $y_{t}^{n-3}\approx y_{t}^{n}$ to obtain these yields. The problem does not arise for one-year excess returns (

). Return to Text

5. There is also empirical evidence against the USV hypothesis (see, e.g., Thompson, 2004; Fan, Gupta, and Ritchken, 2003; Bikbov and Chernov, 2004). Return to Text

6_ This assumption is consistent with the affine specification as examined by Dai and Singleton (2000)_ More flexible assumptions on the market price of risk process result in the similar affine transformations between risk-neutral and objective dynamics (Duarte, 2004; Dai and Singleton, 2002; Duffee, 2002). Return to Text

^♣ This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to Text

Bond Risk Premia and Realized Jump Volatility*

Bond Risk Premia and Realized
Jump Volatility*