Skip to: [Printable Version (PDF)] [Bibliography] [Footnotes]

Finance and Economics Discussion Series: 2007-49 Screen Reader version

Operational Problems and Aggregate Uncertainty in the Federal Funds Market

Elizabeth Klee *

October 5, 2007

Keywords: Federal funds market, monetary policy implementation, payment systems

Abstract:

This paper uses operational problems at commercial banks in sending Fedwire payments as a proxy for aggregate uncertainty in end-of-day Fed account positions and then examines funds market behavior on those days. The results suggest that increased uncertainty is associated with a deviation of the federal funds rate from the FOMC's target rate, the magnitude depending on the severity of the difficulty, the payment volume of the affected participant, and the time of day. Moreover, discount window borrowing picks up on days with operational difficulties. These effects are generally transitory, and markets revert back to previous levels the next day.

The dominant factors affecting daily federal funds market conditions are, of course, the aggregate supply of and demand for Federal Reserve balances. Supply reflects actions by the trading desk at the Federal Reserve Bank of New York, which conducts daily open market operations to maintain a level of balances in the banking system, so-called "autonomous factors," which include currency in circulation and the balance in the Treasury's account at the Fed, and occasionally discount window loans, which represent balances borrowed from the Federal Reserve System. Demand for balances is determined by market conditions, which include the day of the maintenance period, and expected daily payment flows. The equilibrium of supply and demand determines the daily federal funds rate.

Factors that increase uncertainty about end-of-day balances can affect the market for balances. However, measuring uncertainty about reserve positions can be difficult. Studies have isolated factors that affect the supply of balances, such as shocks to the Treasury balance.¹ Other studies have focused on factors that affect the demand for balances, such as payment flows.² Both sets of factors increase uncertainty in reserve positions and have affects on the federal funds market. Although these factors may increase uncertainty in balance positions, some part of these flows is predictable. Less is known about the effect on the federal funds market of completely exogenous, intraday shocks to end-of-day balances at individual institutions.

In this study, we use computer problems at depository institutions as a proxy for exogenous shocks to end-of-day balances. Each day, banks send on average over $1.8 trillion in funds to each other by wire transfer using the Fedwire funds transfer service, a real-time gross settlement payment system owned and operated by the Federal Reserve. ³ Among the top 50 senders of payments over Fedwire by volume, the average rate at which payments are sent over Fedwire is approximately 1 per second. If a bank has an operational problem and cannot send funds over Fedwire, balances may become temporarily trapped in one bank's reserve account, creating aggregate uncertainty of the level of balances available in the system, and potentially affecting the federal funds market.

Based on the characteristics of normal Fedwire operations, in this paper, we employ a simple algorithm to identify outliers in payment patterns at individual depository institutions. These outliers are for the most part, simply outliers, but a subset of them may represent possible outages. After identifying days with these outliers, we examined aspects of the federal funds market on days with such possible outages. In doing so, we sought answers to the following questions, which inform researchers about banks' reaction to uncertainty in the federal funds market: Do operational difficulties have a measurable effect on the federal funds market? What are the factors that determine the magnitude of the effect? How do these effects persist?

We find that the deviation of the effective rate from the target rate is positive on days with possible operational problems and thus potentially higher aggregate uncertainty. Moreover, the magnitudes of the effects depend on the severity of the difficulty, the volume of payments made by the affected participant and the time of day at which it occurs.⁴ Perhaps as a result of the uncertainty and associated dislocations, discount window borrowing picks up on days with operational difficulties. And finally, our results show that the effect of these operational difficulties is transitory, and generally the funds rate reverts back to its previous level the next day.

To be sure, the federal funds market is a very well functioning market, and Fedwire is a well-functioning payment system. However, even in well-functioning situations problems can occur. We exploit these rare instances of difficulty to proxy for exogenous shocks to the federal funds market.

The paper proceeds as follows. Section 2 provides an example, reviews some basic facts, and discusses the data. Section 3 explores some theoretical considerations and the empirical methodology. Section 4 presents the results. Section 5 concludes.

2. Example, basic facts and data

Example: An operational outage

A simple illustrative example will guide the analysis. Suppose a bank with a significant presence in the federal funds market has a computer problem which causes it not to be able to consistently send payments from its account for lengthy periods of time. Suppose on average, this bank usually makes payments every second. If other banks can still send payments to the affected bank, but the bank cannot send out payments, its account balance will balloon. Balances will be temporarily trapped in one bank's account, and other banks will be unsure about how long the problems will persist. This leads to an increase in market uncertainty. As banks become more uncertain about end-of-day balances, they may seek to purchase funds in the market. This can result in an effective funds rate that deviates substantially from the target rate.

Before continuing into the analysis, it is important to review a few basic facts about monetary policy implementation, reserve accounting and payment systems.

Basic facts: Implementation of monetary policy, reserve accounts and payment systems

A bank's reserve requirement is applied to a two-week average level of transaction deposits, and is specified as an average level of overnight reserve balances to be maintained over a two-week reserve maintenance period. Banks may also commit to holding a level of contractual clearing balances to facilitate making payments from its Fed account. Some banks also choose to hold balances in excess of their required reserve balances and required clearing balances as a buffer stock in case of an unexpected shock to balances. However, given that banks do not currently earn interest on reserves, if a bank has funds in excess of its required balances and contractual clearing balances, it may choose to loan these funds in the federal funds market.⁵ Likewise, if a bank has fewer funds than desired, it may choose to borrow funds in the federal funds market. Trades are conducted either directly from bank to bank or through federal funds brokers. The rate at which these funds are traded is known as the federal funds rate. The Desk at the Federal Reserve Bank of New York, working with the Division of Monetary Affairs at the Board, conducts open market operations in order to provide a level of balances in the banking system such that the effective federal funds rate tends to equal the target rate set by the Federal Open Market Committee (FOMC).

Banks may borrow balances directly from the Federal Reserve through the discount window. The rate at which banks in good financial condition can borrow from the Federal Reserve is called the primary credit rate, and is currently 100 basis points above the federal funds target rate. Because discount window loans are generally more expensive than federal funds borrowed in the market, the quantity of discount window loans outstanding is generally low relative to the aggregate level of balances.

Choosing the appropriate quantities of balances to buy and sell in the federal funds market and to borrow from the discount window in order to meet overnight requirements is complicated by the fact that bank balances are not static throughout the day. Banks make and receive payments from their Federal Reserve account, at levels well in excess of the total amount of balances in the system. The average daily total value of payments in 2004 was approximately $1.9 trillion. As a point of comparison, the average daily value of Fed balances in 2004 was $23 billion. As there may be a timing mismatch between sending and receiving of funds throughout the day, many banks are overdrawn on their reserve account during the day; these are known as daylight overdrafts. The fees associated with daylight overdrafts are relatively low, particularly when contrasted with fees on overnight overdrafts. The effective annual rate for daylight overdrafts is 32.25 basis points, while that for overnight overdrafts is currently 400 basis points above the target federal funds rate.

Bank reserve managers forecast their reserve needs in order to achieve their desired levels of overnight balances to meet reserve requirements and avoid overnight overdrafts. However, uncertainty in the level of these balances may affect reserve manager decisions and thus affect the federal funds market. The example discussed above of an operational outage is one source of uncertainty about end-of-day balances. Banks expecting funds from the bank with the operational difficulty may find themselves short at the end of the day, forcing them to buy funds in the market or to take out a discount window loan in order to avoid an overnight overdraft. The results in this paper give insight into how the federal funds market is affected by this type of aggregate uncertainty shock.

It is important to realize that although we know that operational difficulties occasionally occur, there is no data series available that lists these instances with certainty. The next section describes the Fedwire data we use and our method for constructing the list of "possible outages." It also reviews the federal funds market variables used in the analysis.

Constructing the data: Fedwire and federal funds market data

The primary source of data is the Fedwire Funds service transaction data, which records transfers sent using the Fedwire Funds transfer service. These data have been used in other contexts, most notably by Furfine (1999, 2000), Whitesell (2006), and Ashcraft and Duffie (2007) to explore dynamics in the federal funds market. This paper uses the data in a different way, by taking information from the absence of payments, linking it perhaps more closely with the literature on the effect of trading stoppages on price movements as in Bhattacharya and Spiegel (1998).

We constructed our panel from those Fedwire accounts for which a significant operational difficulty could potentially impact payment system liquidity. We assume that impact can be proxied by the dollar value of payments sent from the account: higher dollar values in sent payments imply higher impact. Given this assumption, we construct the panel as follows. First, we selected the top 100 senders by dollar value in the Fedwire system in every month from January 1998 to June 2005. Then, in order to keep a roughly constant group of institutions, we narrowed this sample to include only those accounts that were included in every month, resulting in 49 accounts used in our final analysis. Approximately 60 percent of the number of Fedwire transactions and 83 percent of the value of transactions sent during June 2005 were sent by these accounts.

We looked at payment patterns for each account and identified intervals that were at least 15 minutes long during which no payments were made. We then determined whether these inactive intervals were outliers in the account's payment pattern, by taking into consideration the institution's typical payment patterns for the time of day the inactive interval occurred. Although this method identifies some outliers that might not be the result of operational problems at commercial banks, it succeeds in identifying many known disruptions. The Appendix details our method for finding outages.

Table 1 compares the distribution of intervals between payments for our entire sample, January 1998 to June 2005 - excluding the week after September 11^th - to the distribution of the outliers we identified. Over the sample period, there were approximately 437 million payments sent over Fedwire by the institutions in our sample. The median time between payments from each account is about one second. We identified 1,115 outliers, ranging from fifteen minutes - our lower bound - to over 5 $\raise.5ex\hbox{$\scriptstyle 1$}\kern-.1em/ \kern-.15em\lower.25ex\hbox{$\scriptstyle 2$}$ hours, with a median length of 43 minutes.⁶ Throughout the rest of the paper, these instances of long intervals between payments will be referred to as "possible outages."

The top part of Table 2 examines aspects of the federal funds market on days with such possible outages. Of the 1,840 days in our sample, a little more than 40 percent had at least one, and sometimes more than one, outlier that is consistent with a possible outage. On about thirty percent of the days in the whole sample the possible outage was at one of the 25 largest institutions in our sample, ranked by the number of sent payments, and on about thirty percent of the days the time between payments was longer than 30 minutes. Possible outages began in the late afternoon, between 4:00 p.m. and 6:00 p.m., on 5 percent of the operating days.

In addition to constructing our series of outages, we also constructed a series containing information on extensions to Fedwire. Fedwire participants may submit payment orders during Fedwire operating hours. Extensions to Fedwire operating hours are granted by Reserve Banks under two circumstances: if there is a failure of Reserve Bank equipments, or "there is a significant operating problem at a bank or major dealer; and, as a result the extension is deemed necessary, in the Federal Reserve Bank of New York's (or its designee's) view, to prevent a significant market disruption (i.e. the dollar value of delayed transfers exceeds $1 billion)."⁷ These extensions can be viewed as indicating operational difficulties that cause operations to deviate from normal day practices.

The variables in the Fedwire transaction data allow us to identify extensions. Fedwire has two cutoffs for transfers, third-party and settlement transactions. The cutoff for third-party transfers is at 6:00 p.m, while the cutoff for settlement transactions is 6:30 p.m. If the last third-party transfer occurred later than normal third-party transfer hours, we assumed that Fedwire was extended. Almost all settlement extensions are associated with a third-party extension, but some short third-party extensions are not associated with a settlement extension. However, because these short third-party extensions indicate an operational problem, we used extensions to third-party transfers for our analysis.

In order to see how possible outages affect the federal funds market, we paired the Fedwire data with information on federal funds market variables. Our primary variable of analysis is the daily effective federal funds rate.⁸ The daily effective federal funds rate is a volume-weighted average of rates on trades arranged by major federal funds brokers. Although the daily effective federal funds rate is close to the target rate on most days, there is deviation from the target rate throughout the day and on a day-to-day basis. This deviation from the target can be affected by uncertainty in reserve balances, the phenomenon we analyze in this paper. Thus, much of the analysis will be focused on the deviation of the effective rate from the target rate.

As shown in table 2, over the sample period, on average, the deviation of the effective federal funds rate from the target is less than a basis point. The range is considerable: from 181 basis points below the target to 156 basis points above the target. The median deviation from the target is zero basis points, and the standard deviation is 14 basis points. The distribution is skewed somewhat to the left.

The behavior of the deviation of the effective rate from the target rate changed somewhat over the period. As shown in figure 3, the deviation of the effective federal funds rate from the target rate trended down from 1998 through the beginning part of 2004, but began to pick up somewhat during the first half of 2004. Hilton (2005) provides possible causes for these trends, which include lagged reserve accounting, a low absolute funds rate through mid-2004, and a corresponding pickup with an increase in the target rate through 2005.

We also examine the effect of possible outages on federal funds market volatility, measured by the intraday standard deviation of the federal funds rate. The intraday standard deviation of the federal funds rate is a volume-weighted measure of intraday standard deviation based on total brokered funds transactions on a given day. Over the period, this measure of volatility averaged about 10 basis points, and ranged from about 1 basis point (with some frequency during the period when the target rate was at 1 percent) to a high of 341 basis points, on the June 1998 quarter end.

As our final step, we evaluate the effect of operational difficulties on discount window borrowing. During the period we study, there were two regimes of discount window borrowing: adjustment credit and primary credit. The adjustment credit period covers the first part of the sample, through to January 8, 2003. Over the period, the mean level of adjustment credit was $82 million, and the median level was $9.8 million. The values range considerably, from a low of zero to a high of $3.2 billion; the distribution is skewed to the right and exhibits heavy tails. We contrast this period to the primary credit period, which began in January 2003. Primary credit borrowing averages approximately $39.8 million an evening, and the median level is approximately $6.5 million. Like under adjustment credit, the distribution is skewed to the right and exhibits heavy tails.

With these empirical facts in mind, we turn to the theory and methodology.

3. Theory and empirical methodology

Some popular theories of daily federal funds rate behavior are based on the microstructure features of the federal funds market, including the maintenance period construct, payment flows and discount window borrowing. In this section, we review some of the established theories in the literature, sketch the theoretical model and testable empirical hypotheses, and discuss the empirical specification used in this paper.

Some established theories

A leading theoretical model of the federal funds rate posits that because balances on different days of the maintenance period are perfect substitutes for one another, the daily federal funds rate should follow a martingale process. Empirical evidence suggests otherwise, however. An early study by Roberds, Runkle and Whiteman (1993) observes that the forecasting ability of short-term rates differ according to the day of the maintenance period. Hamilton (1996) shows that the funds market tends to exhibit tightness, particularly on settlement Wednesday. Furfine (2001) finds that payment flows significantly affect the pattern of funds rate deviations from the target. Carpenter and Demiralp (2006) also find predictable behavior on days of the maintenance period other than settlement Wednesday, in addition to providing evidence of a liquidity effect in the federal funds market.

In part motivated by the empirical evidence, previous research models federal funds market microstructure that cause the funds rate process to deviate from a martingale. Ho and Saunders (1986) shows that differences in the degree of risk aversion to reserve under- or overshooting can explain why some banks are net sellers and other banks are net borrowers of funds, a characteristic that has material effects on the equilibrium federal funds rate. Hamilton (1996) provides a theoretical model that implies transaction costs cause balances not to be perfect substitutes for one another on one day of the maintenance period or another. In a similar vein, Clouse and Dow (1999) posit that the existence of a penalty for discount window borrowing can explain observed behavior in the federal funds market and the deviation from the martingale hypothesis.

As in the previously mentioned studies, this paper also finds empirical evidence rooted in market microstructure that rejects the martingale hypothesis. Previous models and empirical work do not focus on this aggregate uncertainty. Similar to the individual uncertainty case, theoretically, should an aggregate, temporary shock hit the banking system, the federal funds rate should still follow a martingale, as banks would be able to smooth perfectly any deviation the next day. These exogenous shocks should not be necessarily be associated with deviation from the target, as balances on one evening are perfect substitutes for balances on another. Again, however, empirical evidence suggests otherwise.

Sketch of a theoretical model

The observations in the previous studies lead to our theoretical model. However, a few assumptions are needed in order to control for potential biases of our estimated parameters.

Assumption 1: The operational problem creates a liquidity shock, not a credit shock.

Duffee and Singleton (2003) outline three major categories of risk: credit risk, operational risk, liquidity risk and operational risk. Credit risk is defined as "the risk of changes in value associated with unexpected changes in credit quality." In contrast, liquidity risk is defined as "the risk that the costs of adjusting financial positions will increase substantially or that a firm will lose access to financing." Operational risk, perhaps the least clearly defined of the three (and also perhaps the least understood) is "the risk of fraud, systems failures, trading errors (e.g., deal mispricing) and many other internal organizational risks."⁹ The operational difficulties we study here most likely would extend only to liquidity risks. By assuming that the operational problem is a pure liquidity shock, and not a credit shock, we can abstract from issues regarding the creditworthiness of the institution with the computer problem or its counterparties. Allowing the shock to create credit effects would be unrealistic, and would imply a more complex model of interrelated credit relationships than what is modeled here.

Assumption 2: Banks and the Desk cannot forecast the shock.

If banks could perfectly forecast that a computer problem will occur, then they would be able to smooth their reserve balances over the maintenance period. This would imply no impact on the federal funds market. Likewise, if the Desk could perfectly forecast the shock, it could provide sufficient balances so as to counteract the effect of an effective balance shortage in the system.

Assumption 3: The shock can be observed.

This assumption implies that banks monitor activity in their Fedwire accounts and react to a possible shortfall in the federal funds market at the end of the day. It is easy to imagine that banks monitor their own Fedwire accounts. However, it is difficult to see how they monitor other accounts. One way would be to check if payments that were expected from a counterparty were received. But, this would only work if the affected participant was a direct counterparty. Another way to observe an operational difficulty is by observing an extension to Fedwire, which is broadcast to major participants. Although many operational difficulties are resolved within the business day, occasionally, a difficulty may prompt an institution to request an extension to Fedwire operating hours. Fedwire extensions are broadcast electronically to all high-volume users of Fedwire. Thus, if a bank observes an extension to Fedwire, the bank can assume that an operational difficulty occurred.

With these assumptions in mind, the following is a plausible theoretical model of intraday demand for balances.

Reserve account managers forecast their needs for balances in the morning. Reserve managers monitor their account balances during the day. An operational shock to the federal funds market occurs at some point during the day. The shock increases uncertainty for reserve managers. Reserve managers may update their forecast for the level of balances in their account at the end of the day. The revision to the forecast depends on the timing of the shock, the magnitude of the shock, and the level of risk aversion of the reserve manager. If enough banks act, the revisions of the forecasts can cause dislocations in the market for balances.

Thus, let $_{T}$ denote the quantity of balances in an institution's account at the end of the day, time . Let - $\alpha$ be the time at which the reserve manager makes its forecast, with 0 $\alpha$ $< \quad T$ . A bank reserve manager forecasts its end-of-day balances as follows:

$\begin{displaymath} E_{T-\alpha } R_{T} =R_{T-\alpha } +\overline R _{T-\alpha } \end{displaymath}$

where $\overline R _{T-\alpha }$ is the expected change in balances from time T- $\alpha$ to time

. Actual balances at time

are determined by

$\begin{displaymath} R_{T} =E_{T-\alpha } R_{T} +\frac{T-\delta }{T}\gamma _{T-\delta } +\varepsilon _{T} , \end{displaymath}$

where $\gamma$ $_{T-\delta }$ is a shock that occurs due to an operational problem at time T- $\delta$ , 0

$\delta$

$\alpha$ $< \quad T$ and $\varepsilon$ $_{T}$ is a zero mean normally distributed shock occurring at time

. The expectation at time T- $\alpha$ of the shock $\gamma$ $_{T-\delta }$ equals zero, as we assumed that this shock cannot be anticipated either by institutions or the Desk. This specification takes into account the fact that although reserve managers may be able to forecast end-of-day balances more accurately towards the end of the day, the realized amount of balances will be more affected by shocks that occur towards the end of the day. Moreover, it separates out shocks over which the reserve manager can potentially alter its position versus those that it cannot. The reserve manager can adjust to the shock denoted by $\gamma$ , but not to shocks denoted by $\varepsilon$ . Whether $\gamma$ is positive or negative is an empirical question, but in this paper we assume it is negative.

Finally, depending on the magnitude and timing of the shock, bank reserve managers may update their demand. The magnitude of the deviation from the target likely depends on the parameters $\alpha$ , $\delta$ and $\gamma$ . As $\alpha$ and $\delta$ approach 0, or as $\gamma$ gets large, the dislocation in the reserve market likely increases, causing increased deviation from the target and possible discount window lending.

Empirical methodology

The assumptions and theoretical model lead to the empirical methodology. The first empirical model used to evaluate the effect of operational outages on the federal funds rate is a variant on the framework used by Hamilton (1996), Carpenter and Demiralp (2006) and Hilton (2005). These studies model the deviation from the target rate as

$\begin{displaymath} ff_{t} -tar_{t} =\xi \left( {ff_{t-1} -tar_{t-1} } \right)+\beta _{1} {\rm {\bf OUT}}_{t} +\beta _{2} ext_{t} +\beta _{3} {\rm {\bf C}}_{t} +\varepsilon _{t} \end{displaymath}$

(1)

where ff $_{t}$ represents the effective federal funds rate, tar $_{t}$ represents the target federal funds rate, OUT is a vector of outage characteristics, ext $_{t}$ is a dummy variable that indicates whether there was an extension to Fedwire, C is a vector of calendar effects, and $\varepsilon$ $_{t}$ is an error term. The vector of outage characteristics include a dummy for an outage, a dummy indicating that the outage occurred at an account ranked in the top 25 by the number of sent payments from January to June 2005, a dummy indicating that the outage lasted longer than thirty minutes and a dummy indicating that the outage occurred in the afternoon (between 4 and 6pm).

The second model tests to see if the effects of operational outages persist to the following day. We estimate (1) with lagged terms, that is

$\begin{displaymath} \begin{array}{c} (ff_{t} -tar_{t} )=\xi \left( {ff_{t-1} -tar_{t-1} } \right)+\beta _{1} {\rm {\bf OUT}}_{t} +\beta _{2} ext_{t} +\beta _{3} {\rm {\bf C}}_{t} \ +\beta ^{'}_{1} {\rm {\bf OUT}}_{\mbox{t-1}} +\beta ^{'}_{2} ext_{t-1} +\beta ^{'}_{3} {\rm {\bf C}}_{t-1} +\varepsilon _{t} \ \end{array}. \end{displaymath}$

(2)

If the coefficients on the lagged variables are statistically significantly different from zero, this provides evidence of a persistent effect. However, if they are insignificant, it illustrates that the effects of the outage are transient.

The third model investigates the effect of an outage on the probability of an extension to Fedwire. We model this as

$\begin{displaymath} \Pr (ext_{t} =1)=\Phi \left( {\gamma _{1} {\rm {\bf OUT}}_{t} +\gamma _{2} {\rm {\bf C}}_{t} } \right) \end{displaymath}$

(3)

where $\Phi$ (.) is the cumulative normal distribution. The fourth model we evaluate combines (1) and (3) into a system regression, specified as:

$\begin{displaymath} \begin{array}{c} (ff_{t} -tar_{t} )=\xi (ff_{t-1} -tar_{t-1} )+\beta _{1} ext_{t} +\beta _{2} {\rm {\bf C}}_{t} +\varepsilon _{t} \ ext_{t} =\gamma _{1} {\rm {\bf OUT}}_{t} +\gamma _{2} {\rm {\bf C}}_{t} +u_{t} \ \end{array}\end{displaymath}$

(4)

By using this specification, we address the fact that unobserved factors affecting the probability of an extension are likely correlated with the unobserved factors that affect the deviation from the target. In other words, the error terms in the two equations above are correlated. Thus, it is possible that the estimated coefficient on the extension factor is biased and inconsistent in model (1).

The fifth model investigates another federal funds market indicator and evaluates the effect of operational difficulties on the intraday standard deviation of the effective federal funds rate. Similar to the models above, the model is specified as

$\begin{displaymath} ffstddev_{t} =\xi ffstddev_{t-1} +\beta _{1} {\rm {\bf OUT}}_{t} +\beta _{2} ext_{t} +\beta _{3} {\rm {\bf C}}_{t} +\varepsilon _{t} \end{displaymath}$

(5)

Evidence of elevated intraday standard deviation on days with potential outages gives insight into some of the uncertainty created by these events and the intraday fluctuations of the funds rate.

The final model we evaluate is the following:

$\begin{displaymath} credit_{t} =\beta _{1} {\rm {\bf OUT}}_{t} +\beta _{2} ext_{t} +\beta _{3} {\rm {\bf C}}_{t} +\varepsilon _{t} \end{displaymath}$

(6)

where credit $_{t}$ is the amount of primary credit borrowed overnight on date

.¹⁰ We perform the analysis on two separate samples, the first covering the adjustment credit period and the second covering the primary credit period. We evaluate this model using a tobit correction that controls for evenings that have no discount window borrowing.

4. Empirical results

Baseline summary statistics

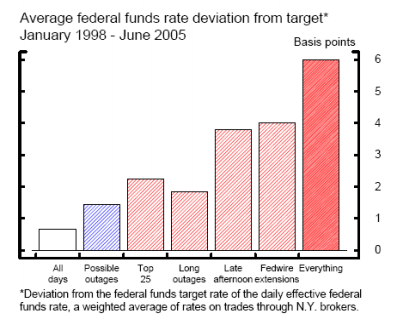
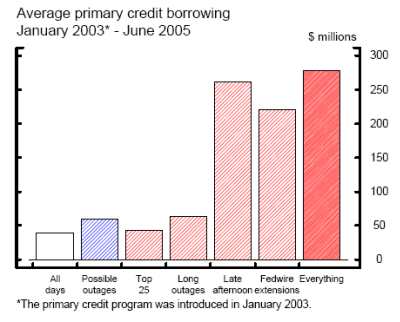
As a baseline, figures 4(a) and 4(b) show how selected federal funds market variables change with characteristics of the possible outages. The hollow bars depict the average for each variable across all days in the sample. The blue hatched bars are the averages for all days with a possible outage, the red hatched bars are the averages on days for which the possible outage has the indicated characteristic, and the solid red bars are the averages on the days where every characteristic was present.

As shown in figure 4(a), the average deviation of the effective federal funds rate from the target on all days is less than a basis point. On days with possible outages, the federal funds rate is only slightly tighter. While possible outages at the largest account holders and longer possible outages alone appear to have a moderate effect, days with possible outages that occurred in the late afternoon or were associated with Fedwire extensions led to noticeably tighter conditions in the funds market. When the possible outage had all of the characteristics, the effective federal funds rate was on average 6 basis points above the target.

Figure 4(b) shows that primary credit borrowing picks up substantially when there is a possible outage in the late afternoon or that is accompanied by a Fedwire extension. Borrowing averaged nearly $300 million on days when the possible outage had all the problematic characteristics versus a sample average of about $40 million.

The factors presented here explain only a small, but in some cases statistically significant, amount of the variation in the federal funds rate. However, further statistical tests show that these events creating aggregate uncertainty can have appreciable effects on the federal funds rate.

Model results

Table 3 presents the results from the specification in equation (1). As in previous studies, we see that the funds rate fails to follow a martingale, with persistence in deviations from the target and predictable calendar effects. As a result, we first investigated the data to determine the order of the autoregressive process, and we found that an AR(1) process fit the data relatively well.

As shown in the table, the coefficient on the lagged deviation from the target is positive and significant. The coefficients on the fifteenth of the month and the end of the month are both significantly different from zero, and indicate some predictable tightness in the funds rate.

Key results of this paper are in lines 3-7 of the table. An outage by itself does not cause significant deviation from the target, nor does an outage at an institution in the top 25 accounts of our sample. Outages that last longer than thirty minutes have a statistically significant effect at the 90 percent confidence level. However, outages that occur in the late afternoon or are accompanied by an extension both cause the effective federal funds rate to be significantly different from the target. Lines 8-11 confirm the calendar effects observed in previous studies on systematic deviations of the federal funds rate from the target rate.

As our sketch of a theoretical model predicts, outages that are longer, or occur late in the afternoon, or days with extensions are associated with a positive deviation from the target. Outages that occur earlier in the day or are shorter are not. Uncertainty associated with operational problems that can be resolved well in advance of the close of Fedwire, such that a bank would not have to take out a discount window loan or incur an overnight overdraft, on average do not result in any different behavior in the federal funds market. However, increased uncertainty at the end of the day will lead reserve managers to seek funds in the market, bidding up the target rate.

In order to investigate effects on the next day, the second column of table 3 repeats the specification in equation (1) with lagged terms. We see that operational difficulties the previous day that occur in the late afternoon do not have an appreciable effect on the deviation from the target the next day, nor do extension days. This is similar to the results with the other calendar effects, which show that lagged calendar effects do not have an appreciable effect on the target the next day.

Table 4 displays the results from estimating equation (2), and shows the effect of outages and calendar configuration on extensions. The specifications differ according to the use of calendar effects. As shown in column (1), the probability of an extension is 17.5 percentage points higher if there was an outage in the late afternoon. Other outage characteristics are not significantly correlated with the probability of an extension.

There is a distinct possibility that the probability of an extension depends on payment flows: higher payment flows suggest a greater effect of operational problems, and thus, a higher likelihood of an extension. As shown in figure 1, payment flows have cyclical patterns according to the day of the month. We control for these effects in column (2). The results strongly suggest that extensions are more likely on high payment flow days, including the mid-month date, the first of the month, and the end of a quarter. The coefficient on the late afternoon outage characteristic attenuates a bit when controlling for these other factors, however, it remains in the ballpark of the estimate in column (1) and is highly statistically significant.

In both specifications, the modest pseudo R-square statistics suggests that only a limited amount of the variation in the probability of an extension is captured by these factors. On the other hand, as shown in the lower rows of the table, the models predict the actual probability of an extension fairly well at the data means.

Table 5 presents results from the system regression of the probability of an extension in conjunction with the deviation from the target. It allows us to judge if the probability of an extension is correlated with unobserved factors that affect the deviation from the target. It also allows us to evaluate better the "treatment effect" of an extension on the deviation from the target. In the treatment equation, the dependent variable is a zero or one indicator, with a value of one indicating that an extension occurred on that business day.

As shown in Table 5, controlling for possible correlation between the error term in the treatment equation and the error term in the outcome equation increases the magnitude of the coefficient on the extension parameter from that seen in the previous specifications: the point estimate is about 4 basis points. More broadly, the results suggest that unobserved factors that affect the probability of an extension are negatively correlated with unobserved factors that affect the funds rate. Indeed, as shown by the sign and significance of the rho parameter in the lower part of the table, the correlation between the error terms of the treatment and the outcome equations indicate that there will be some attenuation bias on the extension coefficient. A counterfactual experiment suggests that if there had not been an extension requested, the effective funds rate would have been 2 basis points more firm than its actual outcome. In the theoretical model above, lengthening the day effectively increases the value of , which, in turn, suggests that there may be a diminished effect of operational outages on the federal funds rate.

Turning to another measure of price action in the funds market, table 6 summarizes information on the effect of operational outages on the intraday standard deviation of the effective federal funds rate. While an outage by itself seems to be correlated with a lower intraday standard deviation of the effective federal funds rate, outages that are longer than thirty minutes seem to increase this measure. A rise in rates above the prevailing market rate in the wake of an operational outage would cause the intraday standard deviation to increase, and it appears that this effect is more pronounced for longer outages. This phenomenon is consistent with the theoretical framework outlined above, where outages increase aggregate uncertainty and thus affect overall market functioning. However, it does not appear that other outage variables are correlated with an increase in intraday standard deviation.

The evidence presented here shows that operational difficulties can have an appreciable effect on the behavior of the effective federal funds rate. The next table also shows evidence that operational outages have effects on discount window borrowing as well. We divide the analysis into two time periods. The first period, the results shown in column (1), covers from 1998 through January 2003, the adjustment credit period. The second column shows results from the primary credit period.

Clearly, as shown in the second column, operational outages can create outsized demand for primary credit borrowing. Unlike the deviation from the target, run-of-the-mill calendar effects have no special effect on primary credit borrowing. These observations are consistent with one of the stated purposes of the primary credit facility, that is, to be a backup source of funds in case other options are not available to depository institutions.

Although there is a noticeable effect of operational problems on discount window borrowing during the primary credit period, the same is not true under the adjustment credit period. Indeed, the -statistic of the regression as a whole indicates that the hypothesis that all coefficients are equal to zero cannot be rejected. The administration of adjustment credit was quite different from the current policies under primary credit. Under adjustment credit, banks were required to have exhausted other sources of funds before turning to the discount window. Thus, even if there was an operational problem affecting the federal funds market, banks would be compelled to seek other sources of funds, and spikes above the target rate of more than 9 percentage points were not uncommon. By contrast, under current policy, banks may use primary credit as a backup source of liquidity under a "no questions asked" policy. The different policies for the administration of discount window credit could easily be driving the difference in results under the two regimes.

5. Conclusion

In sum, this paper provides a sketch of a theoretical model that explains how a bank reserve manager may react to an operational shock in the federal funds market. In addition, it offers empirical evidence that operational difficulties proxied by outliers in payment activity affect the federal funds market to varying extents, depending on the circumstances. The effects are generally more pronounced when the possible outage occurs in the late afternoon or is accompanied by an extension.

To reiterate, Fedwire is a resilient payment system, and the federal funds market is a well-functioning market. The effects of operational outages measured by the methodology in this paper are not large; that we find them to be modest is in line with our expectations. Other methodological approaches - for example, using a VaR framework to study losses to the financial system in times of financial market stress - may provide additional insight into operational risk issues by attaching a dollar amount to the effect of an operational problem. As a final point, the results in this paper point to the usefulness of central bank facilities such as the discount window and the extension of Fedwire operating hours to help to smooth market functioning in times of market stress.

Appendix: Constructing the outages

Using data from the Fedwire funds transfer service, we searched for intervals when institutions' accounts were inactive for extended periods. We examined the accounts of about fifty Fedwire participants that consistently sent the largest number of Fedwire funds payments from early 1998 to mid-2005. We identified inactive intervals that were outliers in payment patterns, taking into account the time of the day and the institution. We termed these instances of inactivity "possible outages".

Although it seems straightforward to identify gaps between payments, defining outages takes some care. As in many exchanges, the pattern of Fedwire transfers varies by the day of the month, by the time of the day and by institution.¹¹ As shown in figure 3, the number of payments made per day in the first half of 2005 ranges from a low of around 310,000 on March 25 to more than double - around 800,000 - on June 30.¹² The median number of payments per day is about 500,000 and the mean number of payments per day is approximately 480,000. The high payment flow days and maintenance period effects contribute to a relatively high variance to the distribution for the number of payments per day and a distribution skewed to the right.

As could be expected from looking at the chart, tests to see whether the monthly patterns follow a normal distribution were rejected. ¹³ However, there is some periodicity to these payment flows. Nonparametric tests of whether individual monthly distributions were equal to each other were not rejected at the 95 percent confidence level.¹⁴ The panel shows this well: Each month has approximately two maintenance periods, a few high payment flow days, and sometimes a holiday. Given that most months have these characteristics, the overall flow of payments during a month is relatively constant across months. As a result, we chose to use monthly comparisons for the basis of our analysis.

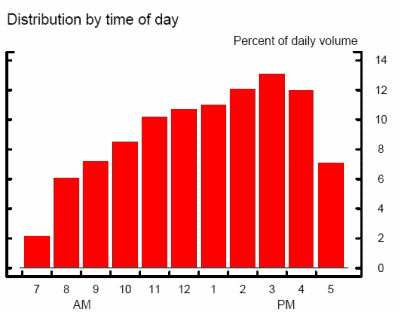
As shown in figure 2, Fedwire volume increases throughout the day, but then drops back slightly in the last two hours before the close of Fedwire.¹⁵ This increase in volume has the effect of decreasing the time between payments. As shown in table 1, during the first half of 2005, the median time between Fedwire payments was 1 second. However, the mean time between payments made between 9 and 10am is approximately 9.0 seconds, relatively more than the mean time between payments made between 5 and 6pm, 6.9 seconds. The standard deviation of the time between payments also declines as the day wanes: the standard deviation is 132.9 seconds between 9 and 10am, but only 44.0 seconds between 5 and 6pm.

Interday variability in payment patterns also depend on the time of day. The standard deviations are not constant across days; the medians of these standard deviations range from 44.0 to 149.5. Moreover, the median of the standard deviations for the time between payments is higher in the morning than in the afternoon. The interquartile ranges of these standard deviations are also wider in the morning than in the afternoon. In addition, the maximum standard deviations are also greater for the morning hours than for the afternoon hours. For these reasons, we defined outages relative to the hour in which they occurred.

Even within this special sample, the sending patterns of these institutions vary considerably. Some institutions have a distribution of sent payments that rises gradually throughout the day, while others send the majority of its payments in the morning, and then send relatively fewer payments in the afternoon.¹⁶

The above analysis suggests a methodology for identifying outages. While the relative homogeneity across months suggests examining the data on a monthly basis, the differences according to the time of day and the institution indicate that these are significant factors that should be noted when defining an outage. In addition, the heavy tails of the distributions of the time between payments implies that a nonparametric approach is likely the best methodology for identifying outliers to these distributions.¹⁷

We defined outages relative to the month, the hour of the day and the institution at which it occurred. Each outage satisfies three conditions for each month-institution-hour triple:

the outage lasted at least fifteen minutes;
the minimum number of sent payments for that hour occurred on that day; and
the maximum gap between sends on that day fell outside of the 75^th percentile plus three times the interquartile range.¹⁸

We chose fifteen minutes because extensions to Fedwire are granted in fifteen minute increments. The other two criteria are simple ways to identify outliers in a dataset, the first based on location and the second based on scale.

Bibliography

Ashcraft, Adam, and Duffie, Darrell. "Systemic Illiquidity in the Federal Funds Market," American Economic Review, vol. 97, no. 2 (May 2007), p. 221-225.

Bartolini, Leonardo, Hilton, Spence, Schwarz, Krista. 2005. "Liquidity in the Reserve Market: Evidence from broker-dealer data," mimeo, Federal Reserve Bank of New York.

Bhattacharya, Utpal and Spiegel, Matthew. 1998. "Anatomy of a Market Failure: NYSE Trading Suspensions (1974-1988)," Journal of Business and Economic Statistics, vol. 16, no. 2, p. 216-226.

Carpenter, Seth and Demiralp, Selva. " The Liquidity Effect in the Federal Funds Market: Evidence from Daily Open Market Operations " (with Selva Demiralp), Journal of Money, Credit, and Banking, vol. 38 (June 2006), p. 901-920.

Clouse, James and Dow, James P. 1999. "Fixed Costs and the Behavior of the Federal Funds Rate," Journal of Banking and Finance, vol. 23, p. 1015-1029.

Demiralp, Selva, Preslopsky, Brian, and Whitesell, William. 2006. "Overnight Interbank Loan Markets," Journal of Economics and Business, vol. 58, p. 67-83.

Duffie, Darrell and Singleton, Kenneth J. 2003. Credit Risk: Pricing, Measurement and Management. Princeton University Press.

Furfine, Craig H. 1999. "The Microstructure of the Federal Funds Market," Financial Markets, Institutions, and Instruments, vol. 8, no. 5, p. 24-44.

Furfine, Craig H. 2000. "Interbank Payments and the Daily Federal Funds Rate," Journal of Monetary Economics, October, vol. 46, no. 2, p. 535-553.

Hamilton, James. 1996. "The Daily Market for Federal Funds," Journal of Political Economy, vol. 104, no. 1, p. 26-56.

Hilton, Spence. 2005. "Trends in Federal Funds Rate Volatility," Current Issues in Economics and Finance, Federal Reserve Bank of New York, vol. 7, no. 11, July.

McAndrews, James and Rajan, Samira. 2000. "The Timing and Funding of Fedwire Funds Transfers," Economic Policy Review, Federal Reserve Bank of New York, July.

Roberds, William, Runkle, David and Whiteman, Charles H. "Resurrecting the Term Structure: A Daily View of Yield Spreads and Short-Term Interest Rate Movements," Journal of Money, Credit and Banking, vol. 28, no. 1, p. 34-53.

Taylor, John B. 2001. "Expectations, Open Market Operations, and Changes in the Federal Funds Rate," Federal Reserve Bank of St. Louis Review, July/August.

Figure 1: Daily payment volume

Figure 2: Number of payments by time of day

Figure 3: Federal funds rate deviation from the target, 1998-2005

Figure 4(a): Impact of outages on deviation from target

Figure 4(b): Impact of outages on primary credit borrowing

Table 1:Summary of payments, January 1998-June 2005

Number of payments over Fedwire
Total (mil.)	437
Median interval (sec.)	1

Possible Outages
Total	1,115
Minimum interval (min.)	15
Maximum interval (hours)	5.7
Median interval (min.)	43

Table 2: Summary Statistics

Fedwire variables
	Mean	Std. Dev	Max
Outage	0.42	0.49	1
Top 25	0.30	0.46	1
Longer than 30 minutes	0.32	0.47	1
Late afternoon	0.05	0.22	1
Extension	0.15	0.36	1

Funds market variables
	Mean	Std. Dev	Min	Median	Max
Deviation from target (bp)	0.7	141	-181	0	156
Intraday standard deviation (bp)	10	17	1	6	341

Discount window borrowing
	Mean	Std. Dev	Min	Median	Max
Adjustment credit borrowing	148.5	1645.3	0	10	45528
Primary credit borrowing	39.8	221.7	0	6.4	4151.6

Table 3: Outage and calendar effects on the effective federal funds rate
Dependent variable:ff $_{t}$ ***-tar*** $_{t}$
	(1)	(2)
Deviation from target (MU)	-0.017**	-0.016**
Deviation from target (MU) S.E.	(0.006)	(0.006)
Deviation from target (AR1,1)	0.440**	0.442**
Deviation from target (AR1,1) S.E.	(0.021)	(0.021)
Outage	-0.009	-0.009
Outage S.E.	(0.011)	(0.011)
Top 25	0.004	0.003
Top 25 S.E.	(0.009)	(0.009)
Longer than 30 minutes	0.017*	0.017**
Longer than 30 minutes S.E.	(0.009)	(0.009)
Late afternoon	0.029**	0.033**
Late afternoon S.E.	(0.012)	(0.013)
Extension	0.017**	0.017
Extension S.E.	(0.007)	(0.008)
15^th of the month	0.130**	0.126**
15^th of the month S.E.	(0.012)	(0.013)
End of month	0.106**	0.103**
End of month S.E.	(0.015)	(0.015)
First of month	0.148**	0.139**
First of month S.E.	(0.013)	(0.014)
End of quarter	-0.086**	-0.086**
End of quarter S.E.	(0.025)	(0.025)
Late afternoon (t-1)		0.011
Late afternoon (t-1) S.E.		(0.012)
Extension (t-1)		-0.001
Extension (t-1) S.E.		(0.008)
15^th of the month (t-1)		-0.008
15^th of the month (t-1) S.E.		(0.013)
First of month (t-1)		-0.006
First of month (t-1) S.E.		(0.013)
Constant estimate	-0.009	-0.009
Variance estimate	0.014	0.014
Std error estimate	0.119	0.119
AIC	-2597	-2602
SBC	-2536	-2519
Observations	1840	1839

Standard errors in parentheses.

** significant at 5 percent level.

Reported coefficients are from AR(1,1) estimation of equations (1) and (2).

Table 4: Outage and calendar effects on extensions
Dependent variable: *ext* $_{t}$
	(1)	(2)
Outage	-0.030	-0.018
Outage S.E.	(0.039)	(0.039)
Top 25	0.049	0.04
Top 25 S.E.	(0.031)	(0.030)
Longer than 30 minutes	0.046	0.037
Longer than 30 minutes S.E.	(0.033)	(0.032)
Late afternoon	0.175**	0.168**
Late afternoon S.E.	(0.050)	(0.050)
15^th of month		0.125**
15^th of month S.E.		(0.049)
End of month		0.077
End of month S.E.		(0.056)
First of month		0.115**
First of month S.E.		(0.048)
End of quarter		0.300**
End of quarter S.E.		(0.119)
Pseudo R²	0.02	0.04
Observed Pr(ext $_{t}$ )	0.155	0.155
Predicted Pr(ext $_{t}$ )	0.151	0.147
Observations	1840	1840

Robust standard errors in parentheses.

** significant at 5 percent level.

Reported coefficients are marginal effects from probit estimation of equation (3).

Table 5: Treatment effect of extensions on the effective federal funds rate
Dependent variables: (1) ff $_{t}$ ***-tar*** $_{t}$ ; (2) ***ext*** $_{1}$
	(1)	(2)
ff $_{t-1}$ -tar $_{t-1}$	0.413**
ff $_{t-1}$ -tar $_{t-1}$ S.E.	(0.077)
15th of month	0.123**	0.452**
15th of month S.E.	(0.012)	(0.151)
End of month	0.093**	0.297
End of month S.E.	(0.014)	(0.191)
First of month	0.108**	0.432**
First of month S.E.	(0.018)	(0.150)
End of quarter	-0.054	0.900**
End of quarter S.E.	(0.093)	(0.306)
Extension	0.042**
Extension S.E.	(0.013)
Outage		-0.090
Outage S.E.		(0.171)
Top 25		0.175
Top 25 S.E.		(0.122)
Longer than 30 minutes		0.174
Longer than 30 minutes S.E.		(0.133)
Late afternoon		0.603**
Late afternoon S.E.		(0.148)
Constant	-0.017**	-1.222**
Constant S.E.	(0.003)	(0.053)
Rho	-0.097**
Rho S.E.	(0.030)
Sigma	0.119**
Sigma S.E.	(0.009)
Lambda	-0.012**
Lambda S.E.	(0.003)
Observations	1839

Robust standard errors in parentheses.

** significant at 5 percent level.

Reported coefficients are from IV estimation of equation (4).

Table 6: Outage and calendar effects on the intraday standard deviation of the effective federal funds rate
Dependent variable: *ffstddev* $_{t}$
	(1)
Intraday standard deviation (MU)	0.096**
Intraday standard deviation (MU) S.E.	(0.006)
Intraday standard deviation (AR1,1)	0.382**
Intraday standard deviation (AR1,1) S.E.	(0.022)
Outage	-0.026
Outage S.E.	(0.014)
Top 25	0.002
Top 25 S.E.	(0.011)
Longer than 30 minutes	0.024**
Longer than 30 minutes S.E.	(0.012)
Late afternoon	-0.010
Late afternoon S.E.	(0.015)
Extension	0.010
Extension S.E.	0.009
15^th of the month	(0.009)
15^th of the month S.E.	(0.015)
End of month	0.030
End of month S.E.	(0.019)
First of month	0.038**
First of month S.E.	(0.016)
End of quarter	0.362**
End of quarter S.E.	(0.031)
Constant estimate	0.059
Variance estimate	0.021
Std error estimate	0.146
AIC	-1859
SBC	-1797
Observations	1840

Standard errors in parentheses.

**significant at 5 percent level.

Reported coefficients are from AR(1) estimation of equation (5).

Table 7: Outage and calendar effects on discount window borrowing
Dependent variable: *credit* $_{t}$
	Adjustment credit (1)	Primary credit (2)
Outage	-5.007	-24.347
Outage S.E.	(34.502)	(40.096)
Top 25	9.755	12.366
Top 25 S.E.	(26.346)	(30.481)
Longer than 30 minutes	-32.435	24.853
Longer than 30 minutes S.E.	(28.945)	(31.538)
Late afternoon	12.354	220.239**
Late afternoon S.E.	(37.789)	(39.386)
Extension	26.475	81.538**
Extension S.E.	(20.933)	(27.420)
15th of month	12.591	-9.171
15th of month S.E.	(36.393)	(41.111)
End of month	-59.018	-12.588
End of month S.E.	(43.701)	(50.676)
First of month	-37.86	-36.874
First of month S.E.	(36.307)	(42.392)
Quarter end	107.919	1.315
Quarter end S.E.	(74.636)	(87.797)
Constant	83.171**	8.933
Constant S.E.	(10.699)	(12.541)
Sigma	265.675	218.118
Observations	1215	625

Standard errors in parentheses

**significant at 5 percent level.

Reported coefficients are from tobit estimation of equation (6).

Footnotes

* Mail Stop 59, Board of Governors of the Federal Reserve System, 20^th and C Streets NW, Washington, DC, 20551. Tel: (202) 721-4501, Email: [email protected]. The views expressed are those of the author and not of the Board of Governors, other members of its staff or the Federal Reserve System. I thank Seth Carpenter, Jim Clouse, Doug Conover, Bill Nelson and Will Roberds for helpful comments and suggestions, and Jonathan Crane and Kristen Payne for excellent research assistance. Return to Text

1. Hamilton (1997) and Carpenter and Demiralp (2006) focus on total supply shocks. Return to Text

2. Furfine (2001), Hilton (2005). Return to Text

3. The terms "banks", "depository institutions" and "Fedwire participants" are used interchangeably in this article. Return to Text

4. Extensions are discussed in more detail below. Return to Text

5. Although contractual clearing balances do not earn explicit interest, they earn credits (up to a limit) towards priced payment services from the Federal Reserve. Return to Text

6. Extensions to Fedwire are allotted in fifteen minute increments, so we use the same increment in our analysis. Return to Text

7. Federal Reserve Bank Operating Circular 6, "Funds Transfers through the Fedwire Funds Service," effective August 1, 2004, p. 7. Return to Text

8. These data are available from the H.15 release. Return to Text

9. Duffee and Singleton (2003), p. 3-4. Return to Text

10. A constant term is included in the empirical specification. Return to Text

11. McAndrews and Rajan (2000) explore the possibility that banks coordinate their payment activity at the end of the day in order to avoid drawing down account balances or incurring overdraft fees. Return to Text

12. The analysis reflects third party transfers only. Return to Text

13. The Shapiro-Wilk test, Kolmogorov-Smirnov test, Anderson-Darling test, and Cramr-von Mises test all strongly reject the null hypothesis of payment flows following a normal distribution in a month. Return to Text

14. However, tests were rejected at the 10 percent level of significance. Return to Text

15. In contrast, the total value of transactions the percent of dollar value sent daily steadily increases throughout the day, with approximately 50 percent of the average daily dollar value sent after 5pm. Return to Text

16. Differences in sending patterns stem from posting rules and exogenous factors. Return to Text

17. We performed a Kolmogorov-Smirnov test to see whether the distribution of the gaps between sends follow a normal distribution, which was rejected. Return to Text

18. The interquartile range is the 75^th percentile minus the 25^th percentile. Return to Text

This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to Text