Skip to: [Printable Version (PDF)] [Bibliography] [Footnotes]

Finance and Economics Discussion Series: 2007-50 Screen Reader version

Choice of Mortgage Contracts: Evidence from the Survey of Consumer Finances

Brahima Coulibaly and Geng Li*

Board of Governors of the Federal Reserve System

Keywords: Mortgage contracts, risk aversion, household finance, fixed-rate, adjustable-rate

Abstract:

This study revisits the empirical question of the determinants of the choice between fixed- and adjustable-rate mortgages using more comprehensive data from the Survey of Consumer Finances (SCF) that overcome some of the data limitations in previous studies. The results from a Logit model of mortgage choice indicate that pricing variables and affordability are important considerations. We also find that factors such as mobility expectations, income volatility, and attitudes toward financial risk largely influence mortgage choice, with more risk-averse borrowers preferring fixed-rate mortgages. For households that are less risk averse, the mortgage type choice decision is less sensitive to pricing variables and income volatility, and affordability factors are not significant. These findings provide empirical support that underscore the importance of attitudes toward risks in mortgage choice.

JEL classifications: D10, G11, G21, R2

1 Introduction

Innovations in the mortgage market in the early 1980s presented homebuyers with alternative financial instruments to the traditional fixed-rate mortgage. Since then, typical borrowers have faced the choice between fixed- and adjustable-rate mortgages (FRMs and ARMs), the two dominant financial instruments in the primary market. Understanding the factors that influence the choice of one mortgage type over the other has continued to attract a significant amount of research interest in the field of household finance given the importance of real estate wealth in a typical household's portfolio.¹ There are two broad categories of factors that can influence mortgage choice: relative pricing and other terms of the contract, and borrower characteristics (affordability, mobility expectation, and demographics).

The theoretical research on the subject has generally documented the importance of both borrowers' characteristics and price factors (see, for example, Brueckner, 1986; and Alm and Follain, 1987). Alm and Follain (1984) highlight the importance of income and borrowing constraints, and Stanton and Wallace (1999) discuss the importance of interest-rate risks.² More recently, Campbell and Cocco (2003) solve a dynamic model of mortgage choice, and find that households that are borrowing-constrained with low risk aversion should prefer ARMs. They find that households that are not borrowing-constrained should also prefer ARMs when inflation risks are large relative to real interest rate risks. On the other hand, a household with a large mortgage, risky labor income, high risk aversion, a high cost of default, or a low probability of moving should prefer FRMs.

The existing empirical studies have generally documented a dominant role for pricing variables, but little or no role for borrower characteristics. In principle, if financial markets are perfect and complete, all borrower characteristics and actions would be reflected in the prices and terms of mortgage contracts. In practice, however, the presence of asymmetric information between lenders and borrowers suggests that borrower characteristics could be relevant in mortgage choice. Previous studies either used local data sets with small samples (Dhillon, Shilling, and Sirmans, 1987; Sa-Aadu and Sirmans, 1995) or national survey data with limited or no information on borrower characteristics (Brueckner and Follain, 1988; Nothaft and Wang, 1992; Boyd, 1992). The goal of this paper is to further contribute to the empirical literature by revisiting the determinants of mortgage choice while overcoming some of the data limitations in previous studies.

The Survey of Consumer Finances (SCF) has a large sample that is representative of the U.S. mortgage market. It contains comprehensive data on mortgages, as well as on broader household finances and demographics. In addition, it contains direct measures of households' attitudes toward financial risk and moving expectations, and contains data that allow us to estimate the riskiness of household income- three important borrower characteristics documented in the study by Campbell and Cocco. Data sets used in previous empirical studies contain almost no information on borrowers' attitudes toward risk and little information on mobility.³ For mobility, the existing studies have used two proxies- the number of years at current address (Dhillon, Shilling, and Sirmans, 1987; Brueckner and Follain, 1988) and indicators for whether the borrower is new to the metropolitan area (Boyd, 1992). Goodman (1982) finds that tenure at the present address is an indicator for future mobility. Using this measure in empirical studies has, however, yielded mixed results for the effect of mobility on mortgage choice, which may owe to the fact that tenure is a poor indicator for future relocation expectations as suggested by Boyd (1992). In addition to attitudes toward risk and mobility expectations, we are also able to construct a measure of riskiness of household income. To our knowledge, this is the first study to revisit mortgage choice in recentyears using such a comprehensive data set.

Results from a Logit model confirm findings in earlier studies that pricing variables and terms of the contract, namely the FRM-ARM interest rate spread, the yield curve slope, and the length of the mortgage are important considerations in mortgage choice. We find that a higher spread, a lower yield curve slope, and longer mortgages make households more likely to choose an ARM. Affordability and financial stress also play an important role, with households that are more financially constrained tending to choose ARMs. A unique finding of this paper is the importance of risk factors. Borrowers who are more risk-averse, have risky income, or that are less likely to move in the near term tend to prefer FRMs. Further, we find that when the sample is split according to attitudes toward risk, the main results are preserved for the more risk-averse sub-sample. For households that are less risk averse, we find that the mortgage type choice decision is less sensitive to pricing variables and income volatility, and affordability factors are not significant.

In the remainder of the paper, we first motivate the empirical specification using a simple conceptual framework of mortgage choice that highlights the role of borrower characteristics and pricing variables. In section 3, we describe the SCF data and sample construction methodology. In section 4, we estimate the Logit model and present the results. Section 5 concludes.

2 A Simple Conceptual Framework of Mortgage Choice

Consider a mortgage market populated with competitive borrowers and a monopolistic lender.⁴ The borrowers have heterogeneous financial states and preferences, which are summarized by a borrower characteristics vector $\theta$ . The distribution of $\theta$ is given by the cumulative density function $J(\theta)$ and the support of $\theta$ is $\Theta$ . To simplify the analysis, we assume that there are two types of mortgage contracts, a FRM and an ARM, and the lender must offer both contracts to each borrower. The two types are identical in terms of maturity, front-loaded points, prepayment options and other features, except for the interest rates in the initial periods. Let $R_{F}$ and $R_{A}$ denote the initial interest rate of the FRM and ARM contract, respectively. Typically we have $R_{F}>R_{A}$ .

Assume that the lender has perfect information on $\theta$ for each individual borrower and the cost of offering a customized mortgage contract is zero so that the lender can implement first-order price discrimination against the borrowers. For each borrower , the lender will offer a pair of $R_{F}^{i}$ and $R_{A}^{i}$ so that the borrower is indifferent between the two contracts, and indifferent between whether or not to apply for the loan. Let $V_{F}% ^{i}=V(R_{F}^{i},\;\theta^{i})$ and $V_{A}^{i}=V(R_{A}^{i},\;\theta^{i})$ be the borrower's payoff. If the corresponding FRM or ARM contract is chosen, we have

$\displaystyle V_{F}^{i} = V_{A}^{i}%$

(1)

However, in a market where the lender cannot implement first-order price discrimination either because he lacks the crucial information of $\theta$ for each individual borrower or because the cost of offering customized contracts is very high, the lender will choose to offer only limited pairs of $R_{F}$ and $R_{A}$ to maximize the total profit. In the polar case where the lender has no information about the individual borrower and, therefore, cannot price discriminate, only one pair of $R_{F}$ and $R_{A}$ is offered to the entire market. The borrowers, facing such a pair of contracts, will make a choice according to the following criteria:

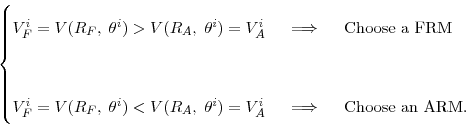
$\begin{displaymath} % latex2html id marker 1221 % \begin{cases}V_{F}^{i} = V(R_{F}, \; \theta^{i}) > V(R_{A}, \; \theta^{i}) = V_{A}^{i} \hspace{0.2in} \Longrightarrow\hspace{0.2in} \text{Choose a FRM}\\ \\ V_{F}^{i} = V(R_{F}, \; \theta^{i}) < V(R_{A}, \; \theta^{i}) = V_{A}^{i} \hspace{0.2in} \Longrightarrow\hspace{0.2in} \text{Choose an ARM}. \end{cases}\end{displaymath}$

(2)

Let $\Pi(R_{F})$ and $\Pi(R_{A})$ be the lender's profit from each contract. The lender's profit maximization problem is

$\displaystyle \max_{R_{F},\;R_{A}}\;\int_{\theta\in\Theta}\;\left[ \Pi(R_{F})\times \mathbf{1}(V_{F}^{i}>V_{A}^{i})+\Pi(R_{A})\times\mathbf{1}(V_{F}^{i}<V_{A}% ^{i})\right] ~dJ(\theta),$

(3)

where 1 $(\;\;\;)$ is the indicator function, taking on value 1 when its argument is true.

Our paper does not attempt to pin down endogenously the equilibrium $R_{F}$ and $R_{A}$ given $J(\theta)$ . Rather, we ask, given the market equilibrium interest rate for each type of mortgage contract, $R_{F}^{\ast}$ and $R_{A}^{\ast}$ , and the borrowers' characteristics: to what extent does this information help us predict the mortgage choice of each borrower? Linearizing the value function $V(R,\theta)$ , the borrower's decision problem can be rewritten as the following,

$\displaystyle \Psi^{i}=\psi(R_{F}^{\ast},R_{A}^{\ast},M^{\prime},\theta^{i})+\epsilon^{i},$

(4)

where $\epsilon^{i}$ is a stochastic error term and

is a vector of macro variables that typically include the slope of the yield curve. The borrower

chooses a ARM contract if $\Psi^{i}>0$ and an FRM contract if $\Psi^{i}\leq0$ .

3 Data Description

We use nationwide household survey data, the Survey of Consumer Finances (SCF). The SCF is a triennial cross-sectional survey conducted by the Federal Reserve Board. The main objective of the survey is to help policymakers and researchers understand households' finances. It collects extensive and high quality data on household finances and characteristics, including demographics.

In recent waves, the SCF surveyed more than 4,000 households, and has tended to oversample wealthy households. The SCF applies multiple imputations to many variables to limit missing values.⁵ The disadvantage of the multiple imputations is that it biases the standard errors in a regression analysis. We correct for this bias during estimation using the procedure provided by the SCF.⁶

The SCF collects rich data on households' mortgages, financial assets, and demographics. The survey asks homeowners whether their mortgages are ARMs. We use these self-reported data to capture the mortgage type. The SCF also collects data on other characteristics of the mortgage such as the initial mortgage year, the initial price, payments and so on.⁷ For household finances (income, debt, assets, etc...) or demographics, the survey captures these data in the year of the interview, not in the initial year of the mortgage. To remedy this deficiency, we restrict the sample to households with mortgages that have been originated within two years of the interview date. For example, if a household's mortgage was originated in 1990 and the SCF surveyed the household in the 1992 wave, we assume that data collected in 1992 should be quite close to what the household would have reported if it was surveyed in 1990.

Finally, because some key variables of interest, such as expectations about moving, are only available from the 1995 wave forward, we use only four waves of the SCF data (1995, 1998, 2001, and 2004). We obtain 17,565 observations, of which 3,636 have mortgages that are two years old or younger. Further, we exclude households that reported living on a ranch or farm, households who reported inheriting the mortgage from the previous owner, and households whose head is younger than 24 years or older than 65 years. Finally, we trim off the top one percent of the distribution of the continuous and ratio variables. After the sample selection procedure, we have 2,887 households.

4 Variables Description and Estimation Results

4.1 Variables Description

We estimate the following Logit model of mortgage type choice:

$\displaystyle L_{i}=\mathbf{1}\left( \Psi^{i}0\right)$

where

$L_{i}=$ indicator for ARM mortgage. It is 1 if borrower has an ARM and 0 otherwise.

$\begin{displaymath}\Psi^{i}=\psi\left( \begin{array}[c]{c}% {\small SPREAD,YC,SM,REFI,SUBP,OPSD,MBIR,TDIR,MOB,RISK}\ \multicolumn{1}{l}{{\small INCVOL,STOCK,EDUC,AGE,RACE,FAMSIZE,MS}}% \end{array}\right) +\epsilon^{i}\end{displaymath}$

where

SPREAD:	difference between FRM and ARM interest rates
YC:	difference between the yield on the 10-year Treasury-note and the 1-year Treasury-bill
SM:	indicator for whether the mortgage maturity is 15 years or less
REFI:	indicator for whether household is refinancing
SUBP:	indicator for whether the mortgage is subprime
OSPD:	indicator for whether households spent more than they earned in the previous year
MBIR:	ratio of the mortgage balance to household income
TDIR:	ratio of total household non-housing debt to income

MOB:	probability that the household will move in the near term
RISK :	household's attitude toward risk
INCVOL:	volatility of household income standardized by the level of income
STOCK:	indicator for financially "sophisticated" given by whether households directly hold stocks
EDUC:	indicator for college graduate
AGE:	age of the head of the household
RACE:	indicator for whether the head of the household is white
FAMSIZE:	number of family members in the household
MS:	indicator for whether household is married

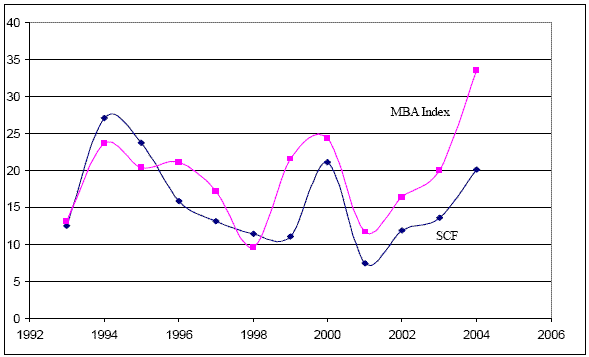
In the SCF, homeowners are asked "Is this an adjustable rate mortgage; that is, does it have an interest rate that can rise or fall from time to time?". We classify homeowners as having an ARM if the answer to this question is yes. Figure 1 depicts the evolution of the ARM origination share in the SCF in comparison to the origination share published by the Mortgage Bankers Association (MBA). As the chart shows, the dynamics of the ARM origination share in the SCF are very similar to that of the MBA.⁸

A positive and statistically significant coefficient on an independent variable indicates that a higher value of the variable makes the household more likely to choose an ARM. In the SCF data we only observe the interest rate of the contracts that homeowners chose, but not the offered interest rate of the alternative contracts. Therefore, we use the market average spread to approximate the household specific spread $\left( SPREAD\right)$ .⁹ Ceteris paribus, a wider FRM-ARM spread means that the fixed-rate mortgage is more costly, and makes homeowners more likely to choose an ARM. Therefore we expect the estimated coefficient of to be positive. The yield curve $\left( YC\right)$ is the difference between interest rates on the 10-year Treasury note and the 1-year Treasury bill. Assuming the Fisher Hypothesis holds, a steeper yield curve implies the expected future short-term interest rate will be higher than the contemporaneous short-term interest rate. Consequently, homeowners have a stronger incentive to choose a FRM to lock in the current interest rate. This suggests a negative coefficient for the yield curve $\left( YC\right)$ . Because and are economy-wide variables, including them in estimation also likely controls for part of the time series variation in ARM origination shares, and other macroeconomic factors.

The mortgage maturity is an important component of the contract. We control for it by including a dummy variable that is equal to 1 for mortgages shorter than or equal to 15 years, and zero otherwise. Anecdotal evidence suggests that a large share of ARM contracts offered are long-term, mostly 30-year, contracts. In this case, short-term mortgages would tend to be FRMs, and yield a negative coefficient on . Similarly, we also control for whether the mortgage is subprime $\left( SUBP\right)$ since more than two-thirds of subprime mortgages are ARMs. The SCF data do not report directly whether a mortgage is subprime; we approximate it using interest rate spreads. If the mortgage interest rate is more than three percentage points higher than the Treasury security of comparable maturity, we consider it subprime. By this approximation, 11.5 percent of mortgages in our sample are subprime.

Affordability and financial constraints are also expected to influence mortgage choice, as documented in some of the previous studies (e.g. Nothaft and Wang, 1992). The SCF collects comprehensive data on household finances. For example, households are asked explicitly whether total expenditures exceeded total earnings in the previous year. We include this variable to capture the household's potential financial stress around the time of the purchase. To further capture the effect of financial stress on mortgage choice, we also include the mortgage size to household income ratio $\left( MBIR\right)$ and the non-housing debt balance to household income ratio $\left( TDIR\right)$ . Our hypothesis is as follows: If a homeowner is under some financial stress, either because the mortgage is too large relative to income or because other expenditures have squeezed out too much income, the homeowner would want to lower the mortgage payment in the near term in order to deal with the financial pressure. Other factors held constant, an ARM contract would initially offer lower payments than a FRM contract. Then the homeowner would prefer an ARM to a FRM contract. Therefore the coefficients on , and tend to be positive.

Besides pricing variables and affordability, the SCF data has the unique advantage of containing direct measures of future mobility expectations and households' attitudes toward financial risk. On mobility expectation, the survey asks the following question: "We are interested in your view of the chance that you will be staying at your current address for the next two years. Using any number from zero to 100, where zero equals no chance and 100 equals absolutely certain, what do you think the chances are that you will be living at your current address two years from now?" This index measures the likelihood of staying at the same address. We subtract this index from 100 and divide the difference by 100 to normalize it to a probability measure of moving in the next two years $\left( MOB\right)$ . When a household moves, it typically has to sell the house and terminate the current mortgage. If the household expects to move within a short period of time, it would likely choose an ARM to benefit from the lower payments it offers in the initial years.

To capture attitudes toward risk, the SCF asks households if they would "take substantial financial risks expecting to earn substantial returns," "take above average financial risks expecting to earn above average returns," "take average financial risks expecting to earn average returns" or "not take any financial risks." We define a household as more risk-averse $\left( RISK\right)$ if the household reveals that it would "take average financial risks expecting to earn average returns" or "not to take any financial risks." One possible reservation about the risk attitude variable is whether it truly captures households' attitudes toward risk, and whether it matters for their financial decisions. We believe it does. Similar questions focusing on understanding households' attitude toward financial risk are also asked in the Health and Retirement Survey (HRS) and the Panel Study of Income Dynamics (PSID) data. Barsky, Juster, Kimball, and Shapiro (1997) provide a validation of the HRS financial risk attitude questions by showing significant correlation of responses to the risk question with the other types of risk taking behaviors. In a similar spirit, we find that the risk aversion variable is negatively correlated with risky financial actions such as self-employment or the holding of stocks.¹⁰ Campbell and Cocco (2003) suggest that more risk averse homeowners are more likely to choose a FRM. This prediction implies the coefficient on the risk aversion dummy to be negative.

In addition, as Campbell and Cocco (2003) point out, income volatility is an important consideration when households choose between mortgage types. Because an ARM contract induces possible changes in monthly payments, a household with volatile income is more likely to default if income declines and mortgage payments increase. To minimize the likelihood of such scenarios, homeowners with volatile income would be more inclined to choose a FRM, especially if they are risk averse. Ideally, we would like to measure the homeowner's perceived future income volatility. This information is not available in the SCF. Instead, we use the cross section income volatility to approximate the riskiness of future income. We estimate the following version of the Mincer equation by occupation using real household income data deflated by the 1982-1984 CPI and the age, education, and race of the head of household:

$\displaystyle Income = \alpha_{1} \; Age + \alpha_{2} \; Age^{2} + \alpha_{3} \; Edu + \alpha_{4} \; Race + \alpha_{5} \; YearDummies + \mu.$

(5)

We pool together the residual $\left( \mu\right)$ and calculate its standard deviation by occupation. The income volatility measure $\left( INCVOL\right)$ we use in the Logit regression is the ratio of $\mu$ to the household's real income.

Finally, we include a dummy variable for stock ownership. This is motivated by Bucks and Pence (2006) who find that many households do not recall the more complicated terms of their ARM contracts, such as their exposure to interest rate changes within the mortgage contract period. Our stock ownership dummy $\left( STOCK\right)$ helps to capture this effect under the assumption that more financially sophisticated investors understand their ARM contracts better, and therefore are more likely to choose ARMs. We present in Table 5 summary statistics for the entire sample and for the "more risk averse" and "less risk averse" sub-samples.

4.2 Estimation Results

The results of the estimation using the entire sample are reported in Table 5. We report the estimated coefficients, standard errors, and the odds ratio. For dummy variables, the odds ratio is calculated between "0" and "1". For integer variables, the odds ratio is calculated by increasing the variable by one unit, and for continuous variables, the odds ratio is calculated by increasing the variable by one standard deviation. Broadly speaking, the explanatory variables included in our model covers four categories of factors that will affect households' mortgage choice - price- and contract-related variables, affordability- and financial stress-related variables, risk factors, and demographics. The results for the entire sample are reported in columns 2-4.

We first look at the price- and contract-related factors. The FRM-ARM spread coefficient is positive and the yield curve coefficient is negative as expected. Both are statistically significant, suggesting that the price variables significantly affect mortgage type choice, and the effects are consistent with findings in previous studies. The coefficients are significant in an economic sense as well. The odds ratio estimated for suggests that an increase of one standard deviation in the spread between the FRM interest rate and the ARM interest rate will lead the homeowners to be 42 percent more likely to choose an ARM. A similar increase in the yield curve $\left( YC\right)$ slope decreases the likelihood of choosing an ARM by 28 percent. The coefficient for mortgage length dummy $\left( SM\right)$ , another important factor of mortgage contracts, is negative and highly significant, indicating that mortgages shorter than fifteen years are more likely to be FRMs. Many lenders only offer 30-year contracts for ARMs, and they offer contracts with short terms for FRMs. However, with some caveats, this result could also be viewed as supportive evidence for the affordability argument-- other things held constant, if the homeowner can afford to pay off the debt within a shorter period, he or she is less likely to encounter affordability and liquidity challenges, and hence should choose a FRM. In addition, the refinance dummy $\left( REFI\right)$ has a negative and significant coefficient, suggesting that when a homeowner refinances, he or she is more likely to refinance the existing mortgage into a FRM. This is not surprising since one important motivation of households for refinancing is to lock in attractive interest rates. Reflecting the predominance of subprime mortgages that are issued as ARMs, we find a positive and statistically significant coefficient on .

Our second category of variables focuses on the affordability, financial stress and liquidity measures (, , and ). The overspending dummy has a significant positive coefficient. The odds ratio suggests that households that spent more than they earned were 27 percent more likely to choose an ARM relative to the households that did not. Overspending households face greater financial pressure and are likely to be liquidity constrained. An ARM is attractive for these households because it provides lower payments in the initial years of the mortgage before the interest rate is adjusted. The coefficient on the balance-to-income ratio is positive and significant. We view this as the evidence of affordability concerns. The larger the mortgage balance is relative to income, the greater the financial pressure and hence the more attractive the ARM. Last, we find a positive coefficient for the total non-housing debt-to-income ratio , but the coefficient is not statistically significant. All told, the balance of the evidence suggests that households that are more financially constrained are more likely to prefer ARMs.

Turning to risk factors, the coefficient for income volatility is negative and statistically significant suggesting that households with a one standard deviation more volatile income are 36 percent less likely to choose an ARM. The moving prospect variable is positive and statistically significant, in contrast to findings in Boyd (1992) who used an indicator for whether the household is new in the metropolitan area as a proxy for mobility.¹¹ Households that are more likely to move prefer ARMs to capture the lower payments in the near term. Other variables held constant, a one standard deviation increase of the reported moving likelihood increases the likelihood of choosing an ARM by 10 percent. The coefficient on risk aversion is negative and statistically significant suggesting more risk averse households are 24 percent less likely to choose an ARM. In sum, households that are more risk averse, less likely to move, or households with more risky income prefer FRMs. These findings are consistent with the theoretical predictions in Campbell and Cocco (2003). They are also consistent with recommendations of some personal finance books. For example, Tyson and Brown (2000) recommend that households with short expected tenure should choose an ARM to take advantage of the lower interest rate it offers in the initial years of the mortgage. Similarly, Fisher and Shelly (2002) warn that ARMs are risky and recommend FRMs as safe and dependable. The results from this study suggest that borrowers consider these risk factors when making a mortgage choice.

ARM contracts tend to be more difficult to understand and this could bias households with less financial sophistication toward FRMs. To control for this type of error, we include an indicator for stock ownership and education. Presumably, households that own stocks or that are college graduates are likely to be more financially sophisticated. The results indicate that households that are more financially sophisticated or educated are about 50 percent more likely to choose ARMs. Finally, consistent with results in several previous studies, we find no evidence that standard demographic variables such as race, family size, or marital status play a role in mortgage choice.

A novel finding in this study is the effect of households' attitudes toward risk as measured by their revealed risk preferences. To further understand the effect of attitudes toward risk on mortgage choice, we split the sample by risk category. Table 5 presents the summary statistics of the more risk-averse and less risk-averse groups, respectively. About 60 percent of households in our sample are more risk-averse. As noted previously, we find that fewer households in the more risk-averse sample own stocks. In addition, the more risk-averse sample, on average, has a lower level of education, takes smaller mortgages, and tends to choose FRMs.

We run a Logit model for each sub-sample. The results are reported in columns 5-7 of Table 5 for the more risk-averse sample and in columns 8-10 of the same table for the less risk-averse sample. We find that for the more risk-averse group, most of the coefficients that are significant for the entire sample remain significant with the same sign. The exception is for moving expectation which becomes insignificant. The results for the less risk-averse group are also similar for most variables except for affordability factors, which becomes insignificant. Comparing the magnitude of the coefficients for the two risk categories, we find that the estimated coefficients for the FRM-ARM interest rate spread, income volatility, and the yield curve are smaller in magnitude for the less risk-averse sample. We interpret these findings to suggest less risk averse borrowers are less likely to be concerned with their ability to sustain their mortgage payments, and that pricing variables and income risk do not influence mortgage choice for these households as much as they do for the more risk averse borrowers.

5 Conclusion

This paper revisits the empirical evidence on the determinant of mortgage choice using more comprehensive data from the Survey of Consumer Finances (SCF). The rich nature of the survey allows us to circumvent some of the data limitations in previous studies. The results from a simple Logit model indicate that pricing variables and terms of the contract are important considerations in mortgage choice. Affordability and financial stress also play an important role. A unique finding of this paper is the importance of risk factors. Borrowers who are more risk averse, have risky income or are less likely to move in the near term tend to prefer FRMs. Further, we find that attitudes toward risk affect mortgage choice along two important dimensions: For less risk-averse borrowers, affordability factors do not significantly affect mortgage choice, and pricing variables and income volatility do not influence their mortgage choice to the same extent as that of more risk-averse borrowers. We view these results as supportive empirical evidence on the essential role of attitudes toward risk in the choice of mortgage contracts.

Bibliography

Alm James and James R. Follain, (1984).

"Alternative Mortgage Instruments, the Tilt Problem, and Consumer Welfare". Journal of Financial and Quantitative Analysis 19:1 (March), 113-26.

Alm James and James R. Follain, (1987).

"Consumer Demand for adjustable rate mortgages," Housing Finance Rev. 6, 1-16.

Barsky B., F. T. Juster, M. Kimball, and M. Shapiro, (1997).

"Preference Parameters and Behavioral Heterogeneity: An Experimental Approach in the Health and Retirement Study," Quarterly Journal of Economics (May), 537-579.

Baesel Jerome B., and Nahum Biger., (1980).

"The Allocation of Risk: Some Implications of Fixed Versus Index-Linked Mortgages," Journal of Financial and Quantitative Analysis 15 (June), 457-468.

Boyd W. James., (1992).

"Asset-Status Proxies and Consumer Preference for ARMs: An Empirical Investigation Using Probit Analysis," The Journal of Real Estate Research, Vol. 3 issue 1 (Spring).

Brueckner J., (1986).

"The pricing of interest rate caps and consumer choice in the market for adjustable-rate mortgages," Housing Finance Rev. 5, 119-136.

Brueckner J., and J.R. Follain., (1988).

"The Rise and Fall of the ARM: An Econometric Analysis of Mortgage Choice," Review of Economics and Statistics 70, 93-102.

Bucks Brian and Karen Pence., (2006).

"Do Homeowners Know Their House Values and Mortgage Terms?", Federal Reserve Board Finance and Economics Discussion Series, March.

Campbell John Y. and Joao F. Cocco., (2003).

"Household Risk Management And Optimal Mortgage Choice" The Quarterly Journal of Economics 118, 1449-1494.

Dhillon Upinder S., J.D. Shilling, and C.F. Sirmans., (1987).

"Choosing Between Fixed and Adjustable Rate Mortgages," Journal of Money, Credit, and Banking 19, 260-267.

Fisher Sarah and Susan Shelly., (2002).

The Complete Idiot's Guide to Personal Finance in Your 20's and 30's, 2nd ed., Alpha Books, Indianapolis, IN.

Goodman John L., (1982).

"Linking Local Mobility Rates: Repeat Movers and Place Effects." In Modeling Housing Market Search, edited by W.A.V. Clark. London: Croom Helm.

Nothaft E. Frank and H.K. George Wang., (1992).

"Determinants of the ARM Share of National and Regional Lending," Journal of Real Estate Finance and Economics, 5: 219-234.

Sa-aadu J., and C.F. Sirmans, (1995).

"Differentiated Contracts, Heterogeneous Borrowers, and the Mortgage Choice Decision", Journal of Money, Credit and Banking, Vol. 27, No. 2. (May), 498-510.

Smith J. Donald., (1987).

The Borrower's Choice Between Fixed and Adjustable Rate Loan Contracts. AREUEA Journal 15:2 (Summer).

Statman Meir., (1982).

"Fixed Rate or Index-Linked Mortgages from the Borrower's Point of View: A Note," Journal of Financial and Quantitative Analysis 17 (Sept.), 451-457.

Stanton Richard and Nancy Wallace., (1999).

"Anatomy of an ARM: The Interest-Rate Risk of Adjustable-Rate Mortgages," Journal of Real Estate Finance and Economics 19, 49-67.

Tyson Eric and Ray Brown., (2000).

Mortgages for Dummies, Hungry Minds Inc., New York, NY.

Figure 1: Evolution of ARM Origination Share in SCF and MBA

Table 1a: Summary Statistics of Datasets: Frequency (Percent)
Variable	Full sample	More Risk Averse	Less Risk Averse
ARM	14.6	14.1	15.6
Subprime mortgages	11.5	12.4	10.1
Overspending	12.4	12.7	11.7
Risk aversion	69.6	n.a.	n.a.
Stock Ownership	28.3	22.0	43.3
Married	76.8	76.6	77.3
College educated	48.5	42.6	61.5
White	82.0	80.1	85.0

n.a.: not available

Table 1b: Summary Statistics of Datasets: Mean
Variable	Full sample	More Risk Averse	Less Risk Averse
Age	43.5	44.4	41.4
Real initial mortgage balance $^{\ast}$	77,308	72,519	87,788
Mortgage length (years)	24.1	24.2	23.9
Mobility	15.2	14.7	16.2
Family size	3.0	3.0	3.1
Income volatility	92.8	96.0	86.0

n.a.: not available

Real values are in US dollars computed using 1982-84 prices

Table 1c: Summary Statistics of Datasets: Median
Variable	Full sample	More Risk Averse	Less Risk Averse
Initial balance-to-income ratio	159.0	164.0	146.0
Total non-housing debt-to-income ratio	12.4	12.6	12.0

n.a.: not available

Table 2: LOGIT ESTIMATES OF THE MORTGAGE CHOICE FUNCTION*
Variable	(2) Full Sample: ceof.	(3) Full Sample: ceof. St. Err	(4) More Risk Averse: Odds-ratio	(5) More Risk Averse: ceof.	(6) More Risk Averse: St. Err	(7) Less Risk averse: Odds-ratio	(8) Less Risk averse: coef.	(9) Less Risk averse: St Err.	(10) Less Risk averse: Odds-Ratio
SPREAD	0.64^**	0.12	1.42	0.80^**	0.16	1.55	0.40^**	0.2	1.25
YC	-0.33^**	0.07	0.72	-0.41^**	0.1	0.67	-0.22^**	0.12	0.8
SM	-0.83^**	0.13	0.44	-0.72^**	0.18	0.49	-0.99^**	0.21	0.37
REFI	-0.18^**	0.11	0.76	-0.22^**	0.16	0.8	-0.36^**	0.2	0.7
SUBP	2.74^**	0.16	15.51	2.58^**	0.2	13.26	3.06^**	0.28	21.29
OSPD	0.23^**	0.18	1.27	0.33^**	0.23	1.39	0.14	0.3	1.15
MBIR	0.20^**	0.05	1.28	0.25^**	0.06	1.38	0.1	0.09	1.13
TDIR	0.06	0.17	1.02	-0.08	0.25	0.98	0.29	0.26	1.1
MOB	0.36^**	0.2	1.1	0.24	0.28	1.07	0.53^**	0.3	1.15
RISK	-0.27^**	0.12	0.76
INCVOL	-0.48^**	0.12	0.64	-0.65^**	0.16	0.61	-0.56^**	0.25	0.72
STOCK	0.39^**	0.13	1.49	0.40^**	0.16	1.49	0.40^**	0.2	1.49
EDUC	0.40^**	0.14	1.5	0.34^**	0.16	1.41	0.57^**	0.25	1.77
AGE	0.01^**	0.01	1.01	0.01^**	0.01	1.01	0.01	0.01	1.01
RACE	0.22	0.17	1.25	0.18	0.21	1.2	0.31	0.32	1.36
FAMSIZE	0.01	0.05	1.01	0.04	0.06	1.04	-0.02	0.07	0.98
MS	0.18	0.18	1.2	0.21	0.24	1.24	0.14	0.28	1.15
Sample size	2,887	2,887	2,887	1,775	1,775	1,775	1,112	1,112	1,112

$^{\ast}$ and ^** indicate statistical significance at the 10 percent and 5 percent levels, respectively.
Note: We have trimmed off the top and bottom 1 percent of MBIR and TDIR to ensure that our econometric analysis is not driven by outliers or measurement errors.

Footnotes

* Coulibaly: Economist, Division of International Finance, Board of Governors of the Federal Reserve System, Washington, DC, 20551; Li: Economist, Division of Research and Statistics, Board of Governors of the Federal Reserve System, Washington, DC, 20551. We thank Karen Dynan, Catherine McDevitt, Karen Pence, Nela Richardson, Shane Sherlund, and seminar participants at Federal Reserve Board, the Midwest Economic Association Meetings, and the 2007 American Real Estate and Urban Economics Association mid-year meetings for helpful comments and discussions. The views expressed in the paper are those of the authors and do not necessarily reflect those of the Board of Governors or the Federal Reserve System. Return to Text

1. Housing wealth makes up more than 50 percent of the total wealth for U.S. households between the 40th and 80th percentiles of the national wealth distribution. See Campbell and Cocco (2003). Return to Text

2. Additional references include Baesel and Biger (1980), Smith (1987), and Statman (1982). Return to Text

3. Some studies have attempted to use family size as a proxy for risk aversion. Presumably, the presence of children in the house could be correlated with attitudes toward risks. See Brueckner and Follain (1988). Return to Text

4. A similar mortgage choice can be derived in a competitive lending market as well. Return to Text

5. The other purpose of multiple imputation is to protect the identity of the households in the sample. Return to Text

6. For details see the SCF codebook $\left( {\footnotesize http://www.federalreserve.gov/pubs/oss/oss2/2004/scf2004home.html}% \right)$ Return to Text

7. However, the survey does not collect information that would allow us to identify non-traditional mortgages such as "interest only" or " negative amortization" loans. Return to Text

8. The MBA index level is higher than the SCF level consistently after 1998, possibly reflecting conceptual differences (MBA index is application based, whereas the SCF share is transaction based) or sampling error. Return to Text

9. These data were obtained from the Mortgage Bankers Association. Return to Text

10. The correlation with self-employment and stock ownership are -0.24 and -0.13, respectively, and they are statistically significant from 0. Return to Text

11. Brueckner and Follain (1988) also used an indicator for whether the household is new in the metropolitain area. Dhillon, Shilling, and Sirmans (1987) used tenure at present address as proxy for mobility prospect. Both find results consistent with findings in this study. Return to Text

This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to Text