Imperfect Monitoring and the Discounting of Inside Money
Keywords: Inside and Outside Money, Imperfect monitoring, Gresham's law
Abstract:
JEL Classification: E40, E42.
1 Introduction
The emergence of electronic money such as stored-value and prepaid cards has renewed interest in inside (or private) money schemes. Two fundamental questions concerning inside money is whether its issuers should be regulated and how. Nineteenth century arguments, as well as more recent debates between free-banking advocates and monetarists, focus on two extremes. At one extreme is the banking school, which advocated for a relatively laizze-faire approach to private note issue. At the other extreme is the currency school, which advocated for a public monopoly on money with strict controls. More recently, the relaxation of legal restrictions on the issuance of inside money means that modern debates focus on the degree of regulation to which private issuers may be subject. This paper evaluates the efficiency of one prevalent regulatory recommendation - a requirement that private issuers redeem inside money on demand at par - in a model where inside and outside money coexist, and the issuers of inside money are imperfectly monitored. I find that for sufficiently imperfect monitoring of inside money issuers, a par redemption requirement leads to lower social welfare than if private money were redeemed at a discount.
The par redemption requirement seems common throughout recent monetary history. Such a requirement existed in most free-banking states during the Free Banking Era (1838-60) in the United States.See, for example, Rolnick-Weber (1988). More recently, the European Central Bank (1998) has established a policy on electronic money for the Eurosystem that stipulates several minimum requirements of electronic money issuers, including par redemption.Issuers are permitted to charge a small fee only to recoup costs of carrying out such a transaction. In the model of this paper, these transactions costs are assumed to be zero. Motivations for such a requirement include the safety and efficiency of the payment system. The safety argument is that par-redemption restricts the ability of inside money issuers to overissue, making an inside money scheme feasible. The efficiency argument is that currencies trading at varying exchange rates diminishes the unit-of-account function of money and so is inefficient. Implicit in this argument is the belief that inside and outside money should effectively circulate as a uniform currency, i.e. they are essentially perfect substitutes. Thus, it seems natural to ask : 1) In what settings are inside money schemes feasible? 2) In what settings are inside money and outside money not perfect substitutes? and 3) Are there any welfare implications in these settings from a par redemption requirement?
Recent research in monetary theory has shed some light on the first two questions. Cavalcanti-Wallace (1999b) provide a random-matching model of inside money (with no outside money) that is feasible because of society's ability to perfectly monitor the trading histories of the issuers.Indeed, solid and transparent legal arrangements, which define enforceable rights and obligations of participants is another regulatory requirement of electronic money schemes in the Eurosystem. This is because monitoring enables agents to punish and reward the issuers in the future for current actions. If the long-term rewards of consistent issue and redemption exceed the short-term benefits of overissuing, inside money issuers have an incentive not to overissue. In another paper, Cavalcanti-Wallace (1999a) go on to say that in an environment in which society can perfectly monitor inside money issuers, inside money is a perfect substitute for outside money, but not vice versa. Inside money can duplicate any allocation that is achievable with outside money and can also achieve even more desirable allocations because it gives private issuers access to instant liquidity which can increase trading. In such an environment, outside money is inessential, so if both types of money were to circulate, it seems optimal that they do so as a uniform currency, and a par-redemption requirement would be innocuous.
Mills (2006) generalizes the basic model in Cavalcanti-Wallace (1999a,b) by allowing (i) both inside and outside money to circulate, and (ii) monitoring of issuers to be imperfect, and overturns their result in Cavalcanti-Wallace (1999a) by showing that both inside and outside money are necessary to implement certain allocations. Such a result suggests that inside and outside money are not perfect substitutes for one another in the case of imperfect monitoring. While inside money retains the advantage it has in Cavalcanti-Wallace (1999a), imperfect monitoring implies that issuers have greater incentive to overissue, restricting its value. Outside money is not subject to such constraints and so can trade for higher levels of output. Due to the complexity of the general problem, Mills (2006) does not attempt to characterize the relative welfare of alternative monetary schemes.
The current paper, a simplified version of that in Mills (2006), provides some insight on the third question mentioned above. The model is a random-matching model of money in which some people (bankers) can be publicly monitored via a record-keeping technology while others (nonbankers) cannot be monitored at all because their trading histories are private information. I model imperfect monitoring of inside money issuers (bankers) via a lag in the record-keeping technology's updating of banker trading histories. I present numerical examples of implementable allocations for various updating lags. For lags that are neither too small nor too large, I find optimal allocations where inside money is redeemed by its issuers at a discount relative to outside money in the following sense: inside money issuers produce more to obtain outside money than they do to redeem inside money. The results are numerical because, as shown in Mills (2006), the updating lag of banker histories must be neither too short nor too long for the coexistence of both types of assets to be essential.
The results suggest that a par redemption requirement reduces welfare because it reduces the value of outside money. This intuition is straightfoward. The par requirement cannot raise the value of inside money in an environment with sufficiently imperfect monitoring because doing so would provide an incentive to overissue in the sense that inside money issuers do not wish to redeem notes. Thus, the only way to satisfy the par redemption requirement is to make inside money a perfect substitute for outside money by undoing the advantage that outside money has over inside money - namely that it can trade for higher levels of output. Such an outcome is a version of Gresham's law that bad money drives out good.
The connection between imperfect monitoring and the ability to issue inside money goes back at least to Klein (1974), who stresses the importance of reputations for private bankers to issue inside money, although in a model quite different from the one hereHis model is one of competing issuers, while mine has a great deal of cooperation in the sense that issuers redeem others' notes.. King (1983) argues that imperfect information and monitoring are central to understanding inside money. Nonetheless, recent work on the coexistence of outside and inside money by Williamson (1999), Azariadis-Bullard-Smith (2001), Bullard-Smith (2000) and Marimon-Nicolini-Teles (2003) has not focused on the challenge that imperfect history and monitoring present to the circulation of inside money. Indeed, each of these works model inside money in such a way that inside and outside money should effectively be perfect substitutes for one another. This is a direct artifact of their abstraction from imperfect monitoring.
The rest of the paper is organized as follows. Section 2 presents the environment. Section 3 describes the restricted class of mechanisms I study and the conditions for implementability. Section 4 presents the main example and results, while section 5 offers concluding remarks.
2 The Economic Environment
The background environment is the random-matching model of money from Shi (1995) and Trejos-Wright (1995). Time is discrete and the horizon is infinite. There are ![]() distinct, divisible, and
perishable types of goods at each date and there is a
distinct, divisible, and
perishable types of goods at each date and there is a ![]() continuum of each of
continuum of each of ![]() specialization types of agents, where
specialization types of agents, where ![]() An agent whose specialization type is
An agent whose specialization type is ![]() consumes only good
consumes only good ![]() and produces only good
and produces only good ![]() (modulo
(modulo ![]() ), for
), for
![]() . Each agent maximizes expected discounted utility with a discount factor
. Each agent maximizes expected discounted utility with a discount factor
![]() . Utility in a period is given by
. Utility in a period is given by ![]() where
where ![]() is the amount consumed and
is the amount consumed and ![]() is the amount produced. The function
is the amount produced. The function ![]() is defined on
is defined on
![]() , is increasing, twice differentiable, and satisfies
, is increasing, twice differentiable, and satisfies ![]() ,
,
![]() , and
, and
![]() . Moreover, there exists
. Moreover, there exists
![]() such that
such that
![]()
Agents cannot commit to future actions. This implies that those agents who produce must expect to receive something of value for doing so.
The society is able to keep a public record of the actions of a fraction ![]() of each specialization type of agent, where
of each specialization type of agent, where
![]() Agents whose histories are a part of the public record are called bankers. The fact that banker histories are part of a public record implies that
it is possible for agents to monitor their behavior. As we shall see, this implies that bankers do not need to receive something tangible to induce them to produce in a single-coincidence meeting; bankers can be rewarded and punished in the future for actions they take currently. Society has no
public record for the remaining fraction
Agents whose histories are a part of the public record are called bankers. The fact that banker histories are part of a public record implies that
it is possible for agents to monitor their behavior. As we shall see, this implies that bankers do not need to receive something tangible to induce them to produce in a single-coincidence meeting; bankers can be rewarded and punished in the future for actions they take currently. Society has no
public record for the remaining fraction ![]() of each specialization type, the nonbankers. The fact that nonbankers are anonymous implies that the society cannot
monitor their behavior. The implication is that nonbankers must receive something tangible in order to produce. We can think of
of each specialization type, the nonbankers. The fact that nonbankers are anonymous implies that the society cannot
monitor their behavior. The implication is that nonbankers must receive something tangible in order to produce. We can think of ![]() as society's capacity for keeping track of individual trading
histories.
as society's capacity for keeping track of individual trading
histories.
Public information about banker histories is not perfect because the public record is not updated immediately after every action. Specifically, there is a deterministic lag of ![]() periods,
where
periods,
where ![]() . At the beginning of each date
. At the beginning of each date ![]() , the bankers' trading histories
are known up through what they did until the beginning of date
, the bankers' trading histories
are known up through what they did until the beginning of date ![]() . For
. For ![]() ,
banker histories are unknown. Thus, if
,
banker histories are unknown. Thus, if ![]() , then banker histories are completely publicly known and society can perfectly monitor their actions. If
, then banker histories are completely publicly known and society can perfectly monitor their actions. If ![]() is sufficiently large, then banker histories are effectively unknown and society cannot monitor their actions at all. We can think of
is sufficiently large, then banker histories are effectively unknown and society cannot monitor their actions at all. We can think of ![]() as society's ability to update records.
as society's ability to update records.
In each period, nonbankers are randomly matched in pairs with either other nonbankers or with bankers. For simplicity, it is assumed that bankers never meet each other. A single-coincidence meeting is a meeting that contains a type ![]() agent (the producer) and a type
agent (the producer) and a type ![]() agent (the consumer) for some
agent (the consumer) for some ![]() . There are three basic types of single coincidence meetings: meetings between nonbankers, meetings in which a banker is a producer and a nonbanker is a consumer, and meetings in which a nonbanker is a producer and a banker is a consumer. A no-coincidence meeting is a
meeting in which neither agent produces what the other consumes. Because
. There are three basic types of single coincidence meetings: meetings between nonbankers, meetings in which a banker is a producer and a nonbanker is a consumer, and meetings in which a nonbanker is a producer and a banker is a consumer. A no-coincidence meeting is a
meeting in which neither agent produces what the other consumes. Because ![]() there are no meetings in which there is a double-coincidence of wants.
there are no meetings in which there is a double-coincidence of wants.
There are two distinct assets. These assets are indivisible and agents can carry at most one unit of one asset across dates. It is not possible for an agent to simultaneously hold a unit of both assets. Each banker has a technology that permits her to create distinct, indivisible and perfectly durable objects, called notes. Because these notes are a type of credit instrument that is issued by private individuals and may circulate as a means of payment, they may serve as inside money. The notes issued by a single banker are distinguishable from those issued by another so that counterfeiting is not a problem. Outside money, on the other hand, is neither produced nor consumed. It is indivisible and perfectly durable. Without loss of generality, refer to asset 1 as the inside money and asset 2 as the outside money.
When two agents meet, the following is common knowledge: each trading partner's specialization type, asset holdings, information type (banker or nonbanker) and the past actions of the bankers in the meeting that occurred up to ![]() periods ago.
periods ago.
3 Allocations
I shall now describe the limited class of allocations. Allocations are both stationary and symmetric. Stationarity implies that there is a steady-state distribution of assets among agents. Symmetry implies two things. First, current actions are independent of an individual's specialization type and his relative position within that type. Second, notes issued by bankers are treated symmetrically by the agents in the economy. That is to say, nonbankers treat notes issued by each banker as perfect substitutes for those issued by every other banker, and bankers redeem each others' notes.
The symmetry restriction that all bankers' notes are treated identically may seem stark, but it is not without precedent in historical inside money systems. What I have in mind is a particularly efficient but unmodeled clearinghouse mechanism of which bankers are members. Under such a mechanism, the bankers agree to redeem each others' notes at par. The Suffolk bank in New England served as such a clearinghouse during the Free Banking Era.See Rolnick-Smith-Weber (1998) for a description of the Suffolk Banking System. Regardless, the restriction that banknotes are perfect substitutes for each other makes it harder for me to show that a par-redemption requirement with outside money is inefficient because there is only one effective type of inside money to be redeemed at par.
Trade takes place only in single-coincidence meetings in which there has been no discovered defection. The make-up of a single-coincidence meeting depends on four things: the information type and asset-holding of both the producer and consumer. Let the set of information types be ![]() where
where ![]() indicates that an agent is a banker and
indicates that an agent is a banker and ![]() indicates that he is a nonbanker. I shall identify agent asset-holdings by states. Nonbankers are in one of three states in the set
indicates that he is a nonbanker. I shall identify agent asset-holdings by states. Nonbankers are in one of three states in the set
![]() . A nonbanker in state 0 has no asset-holdings. A nonbanker in state 1 has a unit of inside money and one in state 2 has a unit of outside money. Because of the symmetry imposed on banknotes, bankers do not gain from holding
other bankers' notes and so never hold a note issued by another banker. They may, however, hold outside money. Thus, a banker is in one of two states,
. A nonbanker in state 0 has no asset-holdings. A nonbanker in state 1 has a unit of inside money and one in state 2 has a unit of outside money. Because of the symmetry imposed on banknotes, bankers do not gain from holding
other bankers' notes and so never hold a note issued by another banker. They may, however, hold outside money. Thus, a banker is in one of two states, ![]() . A banker in state
. A banker in state ![]() does not have a unit of outside money and a banker in state 2 does have a unit of outside
money.
does not have a unit of outside money and a banker in state 2 does have a unit of outside
money.
If trade takes place in a single-coincidence meeting, it involves the transfer of a level of output and money-holdings. If a banker chooses not to trade, then that banker is a defector. A nonbanker does not receive such a label because a defection by him would never be discovered. A defection by
a banker is discovered ![]() periods from the date it occurred (say date
periods from the date it occurred (say date ![]() ). For the
). For the
![]() periods that follow an initial defection, a banker is an undiscovered defector. An undiscovered defector can costlessly choose to either participate in trade or to defect again. From
period
periods that follow an initial defection, a banker is an undiscovered defector. An undiscovered defector can costlessly choose to either participate in trade or to defect again. From
period ![]() on, a defecting banker is a discovered defector and is punished with autarky in all future meetings.The autarky punishment is the simplest form of punishment but is overly
draconian. It is a sufficient punishment for the inside money scheme in the model to be incentive feasible but not necessary. See Wallace (2005) for a recent contribution on a weaker form of punishment where a discovered defecting banker joins the cohort of nonbankers, and so can continue to
consume. Because weaker punishments have the effect of tighter banker incentive constraints, and it is the binding of incentive constraints that leads to the results of this paper, the qualitative results of this paper would go through with this weaker form of punishment.
on, a defecting banker is a discovered defector and is punished with autarky in all future meetings.The autarky punishment is the simplest form of punishment but is overly
draconian. It is a sufficient punishment for the inside money scheme in the model to be incentive feasible but not necessary. See Wallace (2005) for a recent contribution on a weaker form of punishment where a discovered defecting banker joins the cohort of nonbankers, and so can continue to
consume. Because weaker punishments have the effect of tighter banker incentive constraints, and it is the binding of incentive constraints that leads to the results of this paper, the qualitative results of this paper would go through with this weaker form of punishment.
There are at most 21 different single-coincidence meetings. Formally, let
![]() denote a single-coincidence meeting between a producer of information type
denote a single-coincidence meeting between a producer of information type ![]() in state
in state ![]() and a consumer of information type
and a consumer of information type ![]() in state
in state
![]() , where
, where ![]() and
and
![]() . I restrict the class of allocations further in several ways. First, I do not allow bankers to give gifts to nonbankers, even if the monitoring of bankers makes it incentive
compatible for them to do so (
. I restrict the class of allocations further in several ways. First, I do not allow bankers to give gifts to nonbankers, even if the monitoring of bankers makes it incentive
compatible for them to do so (
![]() . This assumption is meant to capture that most transactions in an economy are not based on the giving of gifts. Second, I anticipate several meetings
will have no trade because of various feasibility and incentive constraints (
. This assumption is meant to capture that most transactions in an economy are not based on the giving of gifts. Second, I anticipate several meetings
will have no trade because of various feasibility and incentive constraints (
![]() . Third, I impose no trade in meetings where agents could trade assets (
. Third, I impose no trade in meetings where agents could trade assets (
![]() . Aiyagari-Wallace-Wright (1996) has shown that the existence of two distinct assets may improve welfare in environments with the assumed
indivisibility of assets and upper-bound on money-holdings because it increases the frequency of trades by allowing agents to exchange a higher-valued asset for a lower-valued asset and production. Thus, optimal allocations in such settings suggest that two monies should trade at different levels
even when there is perfect monitoring. I do not want such an effect here because I do not want the benefit of inside money redeemed at a discount to be derived from it.The results that follow generalize for allocations that allow for the trading of assets. The interpretation, however, is less
intuitive. See the discussion following Section 4.
. Aiyagari-Wallace-Wright (1996) has shown that the existence of two distinct assets may improve welfare in environments with the assumed
indivisibility of assets and upper-bound on money-holdings because it increases the frequency of trades by allowing agents to exchange a higher-valued asset for a lower-valued asset and production. Thus, optimal allocations in such settings suggest that two monies should trade at different levels
even when there is perfect monitoring. I do not want such an effect here because I do not want the benefit of inside money redeemed at a discount to be derived from it.The results that follow generalize for allocations that allow for the trading of assets. The interpretation, however, is less
intuitive. See the discussion following Section 4.
There are four non-negative levels of output in single-coincidence meetings:
![]()
![]()
![]() and
and ![]() . The output level
. The output level ![]() is relevant in trades between nonbankers that involve inside money
is relevant in trades between nonbankers that involve inside money
![]() whereas
whereas ![]() is relevant in trades between nonbankers that
involve outside money
is relevant in trades between nonbankers that
involve outside money
![]() . In both these types of meetings, the nonbankers switch states (the producer acquires the asset while the consumer surrenders it).
. In both these types of meetings, the nonbankers switch states (the producer acquires the asset while the consumer surrenders it).
The output level ![]() is relevant in trades between nonbankers and bankers where inside money is either issued or redeemed
is relevant in trades between nonbankers and bankers where inside money is either issued or redeemed
![]() . In meetings
. In meetings
![]() inside money is issued (the nonbanker leaves the meeting in state 1, as
does the banker, who does not switch states). In meetings
inside money is issued (the nonbanker leaves the meeting in state 1, as
does the banker, who does not switch states). In meetings
![]() and
and
![]() , inside money is redeemed (the nonbanker switches to state 0 while the banker does not change states). When bankers redeem notes, they destroy them.
Bankers redeem notes issued by any banker.
, inside money is redeemed (the nonbanker switches to state 0 while the banker does not change states). When bankers redeem notes, they destroy them.
Bankers redeem notes issued by any banker.
By assuming that the level of output required when a note is issued is the same as the output required when a note is redeemed, I am assuming that banknotes do not bear "interest." While it may be optimal for these output levels to differ in a more general model, the fact that banknotes do not bear interest is consistent with historical episodes of inside money. Moreover, the symmetry of output for issue and redemption makes it harder to demonstrate that a par redemption requirement is inefficient.
Finally, the output level ![]() is relevant in trades between nonbankers and bankers that involve outside money
is relevant in trades between nonbankers and bankers that involve outside money
![]() . In each of the meetings outside money changes hands so consumers and producers switch states. This also implies that inside money is never issued nor redeemed in
such meetings. As was the case for inside money, it is assumed that the purchase or sale of goods for outside money is the same for meetings between bankers and nonbankers. This may not be optimal in a more general model, but is consistent with agents facing a uniform price for payment with outside
money regardless of type.Mills (2006) provides a more general set-up of the problem which allows for unrestricted production levels in all possible single-coincidence meetings. An advantage of the more restrictive approach here is that it is much more tractable for welfare analysis. Like the
restrictions for inside money, this restriction on outside money adds more symmetry, making it harder to demonstrate that a par redemption requirement is inefficient.
. In each of the meetings outside money changes hands so consumers and producers switch states. This also implies that inside money is never issued nor redeemed in
such meetings. As was the case for inside money, it is assumed that the purchase or sale of goods for outside money is the same for meetings between bankers and nonbankers. This may not be optimal in a more general model, but is consistent with agents facing a uniform price for payment with outside
money regardless of type.Mills (2006) provides a more general set-up of the problem which allows for unrestricted production levels in all possible single-coincidence meetings. An advantage of the more restrictive approach here is that it is much more tractable for welfare analysis. Like the
restrictions for inside money, this restriction on outside money adds more symmetry, making it harder to demonstrate that a par redemption requirement is inefficient.
The relationship of primary interest is that between ![]() and
and ![]() . If
. If
![]()
![]() then nonbanker consumers receive the same level of output from
bankers whether they redeem inside money or trade outside money. Under this relationship, I say that inside money is redeemed at par. If
then nonbanker consumers receive the same level of output from
bankers whether they redeem inside money or trade outside money. Under this relationship, I say that inside money is redeemed at par. If
![]()
![]() , then inside money is redeemed at a discount. Also of
interest is the relationship between
, then inside money is redeemed at a discount. Also of
interest is the relationship between ![]() and
and ![]() . If
. If
![]()
![]() then inside money and outside money circulate at par, whereas
if
then inside money and outside money circulate at par, whereas
if
![]()
![]() inside money circulates at a discount.
inside money circulates at a discount.
3.1 Value Functions
In this subsection, I describe the expected discounted utility for nonbankers, nondefecting bankers and undiscovered defecting bankers. These are all expressed given that no one else defects.
Let ![]() denote the fraction of each specialization type with information type
denote the fraction of each specialization type with information type ![]() in state
in state ![]() . Because each person must be in one of the states, the fractions of each specialization type in each state must satisfy
. Because each person must be in one of the states, the fractions of each specialization type in each state must satisfy
Next, let
Consider (2). With probability
The value functions for nondefecting bankers are:
For (5), with probability
![]() a banker without a unit of outside money consumes
a banker without a unit of outside money consumes ![]() and issues the nonbanker a new note. With probability
and issues the nonbanker a new note. With probability
![]() a banker without a unit of outside money produces
a banker without a unit of outside money produces ![]() and redeems a unit of inside money from the nonbanker. Finally, with probability
and redeems a unit of inside money from the nonbanker. Finally, with probability
![]() the banker produces
the banker produces ![]() and receives a unit of
outside money. Equation (6) has a similar interpretation for bankers with a unit of outside money.
and receives a unit of
outside money. Equation (6) has a similar interpretation for bankers with a unit of outside money.
I calculate recursively the initial-defector expected discounted utility, given that no one else defects. The defecting banker's payoff must include the option of disagreeing to the suggested outcome in a meeting. It must also reflect the fact that she knows with certainty that her first
defection will be discovered ![]() periods after it occurs and she will be punished with autarky from that date on. Let
periods after it occurs and she will be punished with autarky from that date on. Let
![]() denote the expected discounted utility of a defecting banker who enters the period in state
denote the expected discounted utility of a defecting banker who enters the period in state ![]() and who first defected
and who first defected ![]() periods ago. Then the value functions can be written as follows:
periods ago. Then the value functions can be written as follows:
The difference between (5)-(6) and (7)-(8) is that ![]() is replaced with
is replaced with
![]() and there are
and there are ![]() terms associated with the fact
that an undiscovered defecting banker will defect again when it is advantageous to do so. The presence of
terms associated with the fact
that an undiscovered defecting banker will defect again when it is advantageous to do so. The presence of ![]() reflects the fact that the continuation payoff of a defecting banker is
dependent on the time left before discovery. The terminal condition is
reflects the fact that the continuation payoff of a defecting banker is
dependent on the time left before discovery. The terminal condition is
for
The expected discounted utility for a banker from an initial defection given that no one else defects,
![]() , is what is relevant for the incentive constraints described below. This is obtained by solving
, is what is relevant for the incentive constraints described below. This is obtained by solving
![]() recursively from the terminal condition
recursively from the terminal condition
![]() . The terminal condition incorporates the fact that once discovered, a defecting banker is punished with autarky forever.
. The terminal condition incorporates the fact that once discovered, a defecting banker is punished with autarky forever.
3.2 Constraints
Now consider the constraints that are relevant for implementation. There are three sets of constraints: participation, free-disposal and steady-state. Participation constraints require that agents are ex-post sequentially rational. This is equivalent to the requirement that they receive non-negative gains from trade. The participation constraints can be summarized as follows:
Constraints (10)-(13) pertain to producers. For example, ![]() is produced in only one type of meeting,
is produced in only one type of meeting,
![]() . If the producer agrees to trade he gets utility
. If the producer agrees to trade he gets utility
![]() , that is, the disutility of producing now plus the expected discounted utility of having a unit of inside money at the start of the next period. If the producer
does not agree to trade, he is not discovered because he is a nonbanker, and enters next period with the expected discounted utility of a nonbanker without a unit of either money,
, that is, the disutility of producing now plus the expected discounted utility of having a unit of inside money at the start of the next period. If the producer
does not agree to trade, he is not discovered because he is a nonbanker, and enters next period with the expected discounted utility of a nonbanker without a unit of either money,
![]() . The producer agrees with the trade if constraint (10) is satisfied.
. The producer agrees with the trade if constraint (10) is satisfied.
Consider constraint (11). Output level ![]() is produced in three types of meetings,
is produced in three types of meetings,
![]() . Thus,
. Thus, ![]() must be less than the
minimum difference of the expected values of the producers in each of those meetings. In the first meeting,
must be less than the
minimum difference of the expected values of the producers in each of those meetings. In the first meeting,
![]() , the producer is a nonbanker without money and his decision is analogous to that in constraint (10). In the meeting
, the producer is a nonbanker without money and his decision is analogous to that in constraint (10). In the meeting
![]() , the producer is a banker without outside money. If she agrees she redeems a unit of inside money and receives
, the producer is a banker without outside money. If she agrees she redeems a unit of inside money and receives
![]() .
. ![]() If she disagrees, then she is an initial defector
and receives utility
If she disagrees, then she is an initial defector
and receives utility
![]() . The decision for a banker producer in a
. The decision for a banker producer in a
![]() meeting is analogous to that of a banker producer in
meeting is analogous to that of a banker producer in
![]() , but the expected discounted utilities are for a banker with a unit of outside money.
, but the expected discounted utilities are for a banker with a unit of outside money.
Constraints (12) and (13) are also derived this way. In the case of (13), it should be noted that a banker producer who defects in a meeting
![]() receives expected utility for a banker without a unit of outside money,
receives expected utility for a banker without a unit of outside money,
![]() . If she accepts, then she receives a unit of outside money and has utility
. If she accepts, then she receives a unit of outside money and has utility
![]() .
.
Constraints (14)-(17) are the participation constraints for consumers in each of the meetings and are derived in a way similar to that of the producer participation constraints.
Free-disposal constraints imply that nonbankers never dispose of either inside money or outside money and that bankers do not dispose of outside money. They are
for all
Finally, the steady-state constraints impose restrictions on state transitions. A steady-state distribution of agents over states requires that the fraction of bankers in each state and the fraction of nonbankers in each state be constant. This can be expressed by equating the inflow and outflow of each state for nonbankers and bankers. The nonbanker inflow-equal-outflow equations are
For bankers, there is one inflow-equal-outflow equation which reduces to (21).
3.3 Implementable and Optimal Allocations
This section concludes with two definitions. The first definition summarizes the set of implementable allocations as those that satisfy both incentive and feasibility constraints.
The second definition describes optimal allocations. These allocations are those that maximize a social welfare function subject to the constraint that they are implementable. The social welfare function is defined as the ex-ante utility of a representative agent.An alternative view could be to focus on the welfare of nonbankers subject to bankers receiving expected utility that is at least as large as that of the nonbankers. This has the benefit of interpreting nonbankers as households distinct from (and possibly owners of) the banking sector. In the results that follow, the banking sector is assumed to be quite small so that the social welfare defined here is drawn largely from the nonbankers and the interpretations would be similar under this alternative view of social welfare.
Absent incentive constraints (that is, absent constraints (10)-(18)), it is well-known and easy to verify that the optimal allocation is
![]() where
where ![]() is the
is the
![]() , or the level of output that maximizes joint-surplus in each of the single-coincidence meetings. This optimum, where inside money is redeemed at par with outside money, is
the benchmark allocation against which implementable allocations are compared.
, or the level of output that maximizes joint-surplus in each of the single-coincidence meetings. This optimum, where inside money is redeemed at par with outside money, is
the benchmark allocation against which implementable allocations are compared.
4 Examples
I now provide numerical examples to demonstrate that in an environment with sufficiently imperfect monitoring, the optimal allocation has inside money redeemed at a discount relative to outside money. This suggests that in some environments, a par-redemption requirement is suboptimal. The need for numerical examples stems from the complexity of an updating lag that is neither too short nor too long. If the lag is long enough, it would be optimal for an economy to circulate only outside money.
The examples take as given the parameters:
![]() , which include the number of specialization types in the economy, the fraction of each specialization type that are bankers, the discount factor, and the specification of
the period utility function. The numerical values of the parameters are:
, which include the number of specialization types in the economy, the fraction of each specialization type that are bankers, the discount factor, and the specification of
the period utility function. The numerical values of the parameters are:
In addition to the parameters above, the examples have the following distribution over states that satisfies (1) and (19)-(21):
I am now in a position to compare the optimal allocations for a variety of updating lags, ![]() . I employ standard numerical optimization methods to find the allocation
. I employ standard numerical optimization methods to find the allocation
![]() that solves the problem in Definition 2.
that solves the problem in Definition 2.
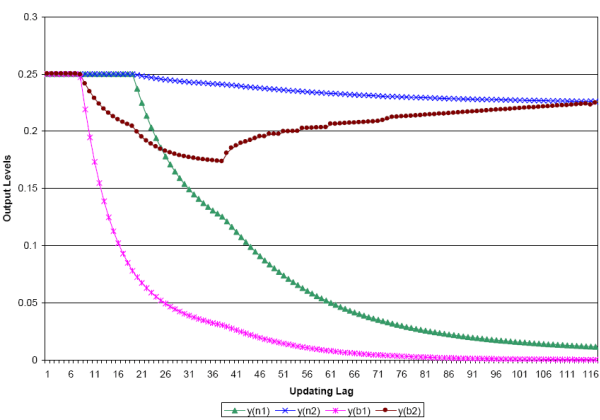
Figure 1 shows the optimal allocations without a par requirement for a variety of updating lags. Notice that for ![]() , the
optimal allocation is
, the
optimal allocation is
![]() , which is also the optimal allocation absent the incentive constraints. In this case, monitoring of bankers is perfect and none of the
banker-producer participation constraints bind. Indeed, the monitoring of bankers works well enough that, as in Cavalcanti-Wallace (1999a), outside money is inessential; social welfare would be maximized with inside money alone. Thus, with perfect monitoring and both monies circulating, the
solution has both par redemption by bankers and par trading among nonbankers.
, which is also the optimal allocation absent the incentive constraints. In this case, monitoring of bankers is perfect and none of the
banker-producer participation constraints bind. Indeed, the monitoring of bankers works well enough that, as in Cavalcanti-Wallace (1999a), outside money is inessential; social welfare would be maximized with inside money alone. Thus, with perfect monitoring and both monies circulating, the
solution has both par redemption by bankers and par trading among nonbankers.
The unconstrained optimum is implementable until ![]() . Before
. Before ![]() , although
monitoring is imperfect, it is not sufficiently imperfect to suggest an allocation where there is not par redemption. As in the case with perfect monitoring, none of the participation constraints bind. At
, although
monitoring is imperfect, it is not sufficiently imperfect to suggest an allocation where there is not par redemption. As in the case with perfect monitoring, none of the participation constraints bind. At ![]() , however, it is no longer implementable for all banker-producers to redeem inside money for
, however, it is no longer implementable for all banker-producers to redeem inside money for
![]() . In fact for any given
. In fact for any given ![]() , the optimal allocation
stipulates that
, the optimal allocation
stipulates that
![]() . A par redemption requirement would force
. A par redemption requirement would force
![]() . The only way to do this is by reducing the amount of output that can be traded for outside money, essentially undoing the advantage that outside money has over inside
money. It cannot raise the value of inside money because doing so would violate banker-producer participation constraints. Bankers would then have an incentive to overissue by issuing notes when convenient, but refusing to redeem notes. Such an outcome is a version of Gresham's law that bad money
drives out good.
. The only way to do this is by reducing the amount of output that can be traded for outside money, essentially undoing the advantage that outside money has over inside
money. It cannot raise the value of inside money because doing so would violate banker-producer participation constraints. Bankers would then have an incentive to overissue by issuing notes when convenient, but refusing to redeem notes. Such an outcome is a version of Gresham's law that bad money
drives out good.
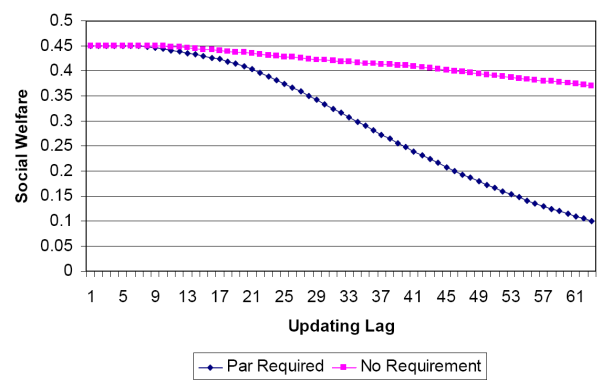
A par redemption requirement's impact on welfare, therefore, is either innocuous (for ![]() or harmful (for
or harmful (for ![]() ). Figure 2 documents this by comparing welfare results for the example both with and without the requirement under various updating lags. It is important to note that the larger the updating lag is, the greater is
the negative impact of a par redemption requirement. Thus, in the context of the model, the optimal policy when both outside and inside money circulate is to not require par redemption. Of course, if the lag gets large enough, it may be no longer optimal for inside money to circulate at all.
Indeed, in the limit, inside money would no longer be feasible because bankers would effectively be nonbankers; that is, their trading histories would be unknown.See Mills (2006) for a discussion.
). Figure 2 documents this by comparing welfare results for the example both with and without the requirement under various updating lags. It is important to note that the larger the updating lag is, the greater is
the negative impact of a par redemption requirement. Thus, in the context of the model, the optimal policy when both outside and inside money circulate is to not require par redemption. Of course, if the lag gets large enough, it may be no longer optimal for inside money to circulate at all.
Indeed, in the limit, inside money would no longer be feasible because bankers would effectively be nonbankers; that is, their trading histories would be unknown.See Mills (2006) for a discussion.
It is worth noting also, from Figure 1, that there are lags such that even though the optimum suggests nonpar redemption, par trading among nonbankers may still be optimal. In the set of examples, par trading at
![]() is sustainable until
is sustainable until ![]() . From that point on,
imperfect monitoring is sufficient enough that the use of inside money actually starts to reduce the value of outside money in nonbanker trades. Thus, there is a lag sufficiently long enough such that inside money would no longer be desirable.
. From that point on,
imperfect monitoring is sufficient enough that the use of inside money actually starts to reduce the value of outside money in nonbanker trades. Thus, there is a lag sufficiently long enough such that inside money would no longer be desirable.
On peculiar observation from Figure 1 is that ![]() is non-monotonic with an inflection point at
is non-monotonic with an inflection point at ![]() . The reason for this is the impact
. The reason for this is the impact ![]() has on discounted expected utilities of
bankers in meetings
has on discounted expected utilities of
bankers in meetings
![]() . In such a meeting, a banker produces for a unit of outside money. For
. In such a meeting, a banker produces for a unit of outside money. For ![]() , the optimal
, the optimal ![]() is such that the net gain to banker-producers in these meetings
is such that the net gain to banker-producers in these meetings
![]() is negative. Such an allocation is feasible because of the punishment to defecting is strict enough. Defection leads to expected utility
is negative. Such an allocation is feasible because of the punishment to defecting is strict enough. Defection leads to expected utility
![]() .One may be curious about the robustness of the impact of this on the par redemption requirement. Suppose the mechanism were restricted to allocations
such that bankers must have nonnegative gains to acquiring outside money,
.One may be curious about the robustness of the impact of this on the par redemption requirement. Suppose the mechanism were restricted to allocations
such that bankers must have nonnegative gains to acquiring outside money,
![]() . Such would be the case, for example, if bankers' transactions involving outside money were unobservable. This tighter constraint does bind when
. Such would be the case, for example, if bankers' transactions involving outside money were unobservable. This tighter constraint does bind when
![]() at the paper's optimal allocation of
at the paper's optimal allocation of
![]() so that it is not the optimal allocation when both types of money circulate when
so that it is not the optimal allocation when both types of money circulate when ![]() There is a different optimal allocation in this setting such that
There is a different optimal allocation in this setting such that
![]() . In fact, this spread is crucial for feasibility. So the result that optimal allocations are those in which inside money is redeemed at a discount stands up to this
weaker information structure.
. In fact, this spread is crucial for feasibility. So the result that optimal allocations are those in which inside money is redeemed at a discount stands up to this
weaker information structure.
Intuitively, the value to bankers of issuing their own notes is so high, that producing for outside money is not desirable to them. The optimal allocation must take this into account when determining the value of ![]() .
.
The net loss to bankers, however, gets smaller as ![]() gets larger and eventually becomes positive at
gets larger and eventually becomes positive at ![]() . The reason is that bankers do not get as much consumption from issuing inside money (because of tighter incentive constraints on the redemption of inside money) and so acquiring outside money becomes more attractive. Once the net gain to bankers for acquiring outside money
is positive, the optimal
. The reason is that bankers do not get as much consumption from issuing inside money (because of tighter incentive constraints on the redemption of inside money) and so acquiring outside money becomes more attractive. Once the net gain to bankers for acquiring outside money
is positive, the optimal ![]() begins to increase.
begins to increase.
The results are robust to varying levels of ![]() . The paths for each optimal level of output look like Figure 1. Higher
levels of
. The paths for each optimal level of output look like Figure 1. Higher
levels of ![]() can sustain the unconstrained optimal level of output longer. For example, for
can sustain the unconstrained optimal level of output longer. For example, for
![]() , par redemption is optimal up to
, par redemption is optimal up to ![]() , while for
, while for
![]() , par redemption is optimal for up to
, par redemption is optimal for up to ![]() . For
. For
![]() , the optimal allocation has redemption at a discount for all
, the optimal allocation has redemption at a discount for all ![]() .
.
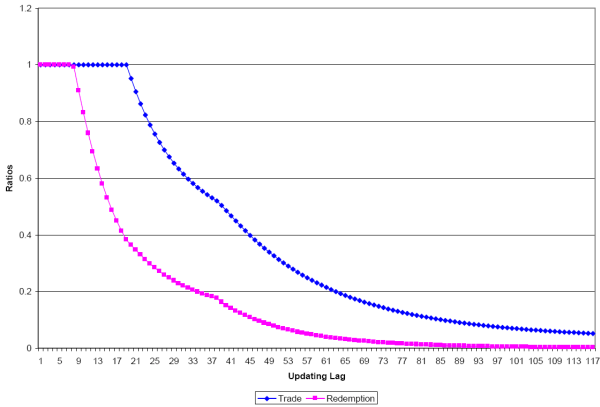
Finally, Figure 3 display trading and redemption ratios for various lags for
![]() . The trading ratio is simply
. The trading ratio is simply
![]() and the redemption ratio is
and the redemption ratio is
![]() . It is worth noting from Figure 3 that for
. It is worth noting from Figure 3 that for
![]() there are rather large drops in value for inside money quickly. Nonetheless, relatively small lags can lead to nonpar redemption with "reasonable" discounts that are around 2%.
Such discounts exist in a somewhat different context as average fees that are charged to merchants for credit and debit card transactions.
there are rather large drops in value for inside money quickly. Nonetheless, relatively small lags can lead to nonpar redemption with "reasonable" discounts that are around 2%.
Such discounts exist in a somewhat different context as average fees that are charged to merchants for credit and debit card transactions.
4.1 Discussion: Allowing Agents to Trade Assets
One of the restrictions made on allocations is that agents could not trade assets and so there is no trade in the meetings (
![]() ). However, for the meeting
). However, for the meeting
![]() , one could imagine the nonbanker producer presenting the unit of inside money for redemption by the banker consumer. The banker consumer cannot redeem the inside money with goods
production, but rather with outside money. This is a single coincidence meeting where the nonbanker could produce for the banker and may be willing to do so if holding a unit of outside money is more valuable than holding a unit of inside money.There are other meetings, particularly no-coincidence
meetings, in which a banker could redeem a unit of inside money from a nonbanker by giving that nonbanker a unit of outside money. These could only occur at par, however, because there can be no utility from the consumption of goods. For the analysis that follows, I continue to rule out asset swaps
in these types of meetings. Let
, one could imagine the nonbanker producer presenting the unit of inside money for redemption by the banker consumer. The banker consumer cannot redeem the inside money with goods
production, but rather with outside money. This is a single coincidence meeting where the nonbanker could produce for the banker and may be willing to do so if holding a unit of outside money is more valuable than holding a unit of inside money.There are other meetings, particularly no-coincidence
meetings, in which a banker could redeem a unit of inside money from a nonbanker by giving that nonbanker a unit of outside money. These could only occur at par, however, because there can be no utility from the consumption of goods. For the analysis that follows, I continue to rule out asset swaps
in these types of meetings. Let ![]() denote the amount of production in such a meeting. Thus, one may wish to interpret par redemption by bankers as swapping outside money to redeem inside
money with
denote the amount of production in such a meeting. Thus, one may wish to interpret par redemption by bankers as swapping outside money to redeem inside
money with ![]() whereas redemption at a discount would occur if
whereas redemption at a discount would occur if ![]() .
Similarly, for the meeting
.
Similarly, for the meeting
![]() we could determine whether or not inside money trades at par. Let
we could determine whether or not inside money trades at par. Let ![]() denote output in such a meeting.
denote output in such a meeting.
As stated earlier, the assumed indivisibility of assets and the upper-bound on money-holdings suggest that an optimal allocation when ![]() would have
would have ![]() so it would never be optimal to have par redemption in this sense.Again, the reader is referred to Aiyagari-Wallace-Wright (1996) for a detailed explanation. It is worth noting, however, that for the parameters of
the above example (with
so it would never be optimal to have par redemption in this sense.Again, the reader is referred to Aiyagari-Wallace-Wright (1996) for a detailed explanation. It is worth noting, however, that for the parameters of
the above example (with
![]() ) in a revised model that allows swaps in this type of meeting,
) in a revised model that allows swaps in this type of meeting,
![]() when
when ![]() and remains that way until
and remains that way until ![]() . At that point,
. At that point, ![]() begins to rise. One could interpret
begins to rise. One could interpret
![]() for
for ![]() as sufficiently large enough lags for which inside
money is redeemed at a discount relative to its perfect monitoring level.
as sufficiently large enough lags for which inside
money is redeemed at a discount relative to its perfect monitoring level.
It is also true that ![]() for
for ![]() and follows the same behavior as
and follows the same behavior as
![]() for similar
for similar ![]() . The optimal output levels
. The optimal output levels
![]() are also adjusted in order to meet incentive feasibility requirements. Specifically,
are also adjusted in order to meet incentive feasibility requirements. Specifically,
![]() and
and
![]() for all levels of
for all levels of ![]() so that par redemption and par
trading in the sense used in this paper are never optimal.
so that par redemption and par
trading in the sense used in this paper are never optimal.
5 Concluding Remarks
This paper argues that a requirement that inside money be redeemed at par with outside money may be inefficient if there is sufficiently imperfect monitoring of the issuers of inside money. In such an environment, inside and outside money are not perfect substitutes and a par-requirement forces them to circulate as if they are. The inefficiency that results is a version of Gresham's law that bad money drives out good money; satisfaction of the par redemption requirement reduces the amount of output that can be traded for outside money rather than increasing the amount of output that can be traded for inside money.
The par-redemption requirement could be one contributing factor to the relatively low number of electronic money schemes. For the issuers of electronic money, the inability of the public to perfectly monitor them may make it difficult to establish enough credibility to make it profitable for them to redeem their money at par.
In deriving the results, I make use of the assumption that agents can only hold one unit of one asset at a time. I conjecture that this assumption is not crucial. This is because what makes both types of money essential is the trade-off between outside and inside money. This trade-off would still exist if the assumption about the unit upper bound on money-holdings were dropped. The issue and redemption of inside money would still be subject to the imperfect monitoring of bankers, implying that the value of inside money is less than that of outside money. Nonetheless, the issuance of inside money would still provide bankers with liquidity that permits them to consume more frequently.
The focus on optimal steady-state allocations potentially eliminates some advantages to par redemption. For example, suppose that ![]() is constant over time but
is constant over time but ![]() can fluctuate depending on agents' speculations. This fluctuation may not be socially desirable and a par redemption requirement may improve welfare in certain situations. Take the example in
the paper when
can fluctuate depending on agents' speculations. This fluctuation may not be socially desirable and a par redemption requirement may improve welfare in certain situations. Take the example in
the paper when ![]() . There
. There
![]() is socially optimal. If agents' speculations led to an equilibrium where
is socially optimal. If agents' speculations led to an equilibrium where
![]() even though banker incentive constraints permit
even though banker incentive constraints permit
![]() , a par redemption requirement may provide benefit. An important assumption in this case is that the speculation only affects
, a par redemption requirement may provide benefit. An important assumption in this case is that the speculation only affects ![]() and not
and not ![]() . Future work could explore what such environments look like.
. Future work could explore what such environments look like.
I assume that banknotes are treated symmetrically and so serve as perfect substitutes for one another. Alternative specifications of the model could relax that assumption to investigate issues associated with competing currencies. This is direction for future work.
Finally, I model outside money as a fixed stock of objects and so abstract from any incentives for its overissue. Indeed, a government's ability to provide a sound money has been challenged by Hayek and others in the private versus public provision of money debate on the grounds that governments also have an incentive to overissue. Further, there is much work done in monetary economics in general regarding the government's incentive to overissue and how this incentive impacts a government's ability to provide sound money. This model is a useful starting point to add to these debates. Future work could incorporate a government in the model and introduce its objective and society's ability to monitor it and how these assumptions impact the incentive to overissue outside (or public) money.
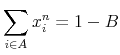 and
and 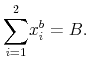
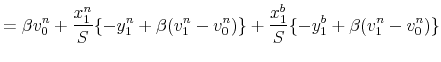
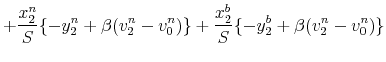
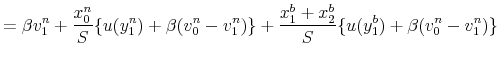
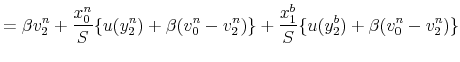
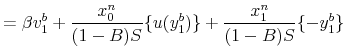
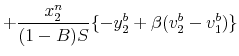
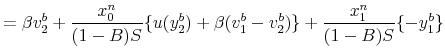
![\displaystyle =\beta\widetilde{v}_{1,\tau+1}^{b}+\frac {x_{0}^{n}}{(1-B)S}\{\max[u(y_{1}^{b}),0]\}+\frac{x_{1}^{n}}{(1-B)S}% \{\max[-y_{1}^{b},0]\}](img92.gif)
![\displaystyle +\frac{x_{2}^{n}}{(1-B)S}\{\max[-y_{2}^{b}+\beta(\widetilde{v}_{2,\tau +1}^{b}-\widetilde{v}_{1,\tau+1}^{b}),0]\}](img93.gif)
![\displaystyle =\beta\widetilde{v}_{2,\tau+1}^{b}+\frac {x_{0}^{n}}{(1-B)S}\{\max[u(y_{2}^{b})+\beta(\widetilde{v}_{1,\tau+1}% ^{b}-\widetilde{v}_{2,\tau+1}^{b}),0]\}](img95.gif)
![\displaystyle +\frac{x_{1}^{n}}{(1-B)S}\{\max[-y_{1}^{b},0]\}%](img96.gif)