
Challenges in macro-finance modeling
Keywords: Yield curve, term structure, unspanned factors, macro-finance
Abstract:
1 INTRODUCTION
In recent years there has been much interest in developing "macro-finance models", in which yields on nominal bonds are jointly modeled with one or more macroeconomic variables within a no-arbitrage framework. The need to go beyond "nominal yields only" no-arbitrage models (i.e., to include a description of the macroeconomy or other asset prices) has been felt for a long time by academic researchers and policy makers alike. Campbell, Lo, MacKinlay (1996), for example, have emphasized that, "as the term structure literature moves forward, it will be important to integrate it with the rest of the asset pricing literature." Policy makers have often used traditional theories such as the expectations hypothesis and the Fisher hypothesis to extract an approximate measure of market expectations of interest rates and macroeconomic variables like inflation, but they are also aware that risk premiums and other factors might complicate the interpretation of the information in the yield curve,1 and would welcome any progress in term structure modeling that would facilitate greater understanding of the messages in the yield curve.
Despite a lot of exciting work in macro-finance modeling of late,2 as a central bank economist who monitors markets regularly, I have found it difficult to bring current generation of models to bear on the practical analysis of bond market developments or to implement the models in real time to obtain a reliable measure of the market's expectation of key variables like inflation.3 In the academic literature there is not much evidence in this regard (either for or against macro-finance models). One exception is the recent paper of Ang, Bekaert, and Wei (2007a, henceforth ABW), which performed an extensive investigation of the out-of-sample inflation forecasting performance of various models and survey forecasts and found that the no-arbitrage models that they have used perform worse than not only survey forecasts but also other types of models.4
It thus seems useful at this juncture to review and discuss various challenges in the specification and implementation macro-finance models that might help shed light on the lack of documented practicality of macro-finance models in general and on the findings of ABW (2007a) in particular. To this end, in this paper I propose to take a closer look at what role the no-arbitrage principle is playing in macro-finance models and reconsider the assumptions that are often made in this literature. No-arbitrage itself is clearly a reasonable assumption, but the models also make additional assumptions whose validity may not have been discussed thoroughly in the existing literature. I also discuss "more advanced" issues (such as structural breaks and time-varying volatility) that require going beyond the standard affine-Gaussian framework of most macro-finance models and the challenges encountered in this regard. A big part of the challenge in macro-finance modeling is empirical, hence I shall also discuss at length the difficulties in the implementation stage (estimation and evaluation of models). Although the main focus of this paper is on the extraction of information from the yield curve (particularly inflation expectations), much of the discussion may be relevant for macro-finance models that were developed to address other issues, as they share some of the key assumptions discussed in this paper.
The state variables in the reduced-form no-arbitrage model framework (on which most macro-finance models are based) can be heuristically viewed as forming a basis onto which to project information in yields and other data. In this paper, I make a distinction between models that use (what I shall call) an "internal basis" versus models that use an "external basis". By an internal basis, I refer to a basis that is determined inside the estimation, hence unknown before the estimation. Latent factor models that describe inflation expectations and term structure jointly, such as Sangvinatsos and Wachter (2005) and D'Amico, Kim, and Wei (2007), are examples of internal basis models. By an external basis, I mean a basis that is a priori fixed completely or partially, as when a specific macroeconomic variable (such as inflation) is taken as a state variable. Note that no-arbitrage guarantees the existence of some pricing kernel, but it does not mean that the pricing kernel can be represented well by a priori selected variables. In this paper, I shall argue that external basis models involve strong assumptions, and discuss potential problems that they may give rise to in practice. All is not well with internal basis models either: the weaker assumptions of these models may come at the cost of the ability to give specific, intuitive interpretation of the yield curve movements. Most importantly, internal basis models face many empirical difficulties that are similar to those in the estimation of external basis models, in particular the overfitting and small-sample problems.
The remainder of this paper is organized as follows. Section 2 reviews the standard affine-Gaussian setup of macro-finance models, derives the affine bond pricing formula in a way that emphasizes the replicating portfolio intuition, and introduces a distinction between internal basis models and external basis models. Section 3 provides a critical examination of the assumptions in external basis models, both in the case of the "low-dimensional" and "high-dimensional" external basis models. Section 4 discusses the challenge of accommodating nonlinear/non-Gaussian effects such as structural breaks and time-varying uncertainties. Potential problems with empirical techniques commonly used in the estimation and evaluation of macro-finance models are discussed in Section 5. Section 6 comes back to ask why surveys perform better than models in inflation forecasting (as documented by ABW (2007a)), and Section 7 concludes.
2.1 Affine-Gaussian framework
Most macro-finance models in the literature are based on the "affine-Gaussian" model, given by
where
There is freedom in choosing the specific functional form of ![]() and
and
![]() and the dynamics of
and the dynamics of ![]() . Having affine forms for
. Having affine forms for ![]() and
and
![]() and the Gaussian specification (VAR(1) specification) of
and the Gaussian specification (VAR(1) specification) of ![]() constitutes the affine-Gaussian model. This form has certain limitations (discussed in Section 4), but it is still quite general and capable of encompassing many of the known models in finance and macroeconomics.
constitutes the affine-Gaussian model. This form has certain limitations (discussed in Section 4), but it is still quite general and capable of encompassing many of the known models in finance and macroeconomics.
Using the recursion relation for the price of a ![]() -period zero-coupon bond at time
-period zero-coupon bond at time ![]()
it is straightforward to show that bond prices in this model are given by
where
| 0 | 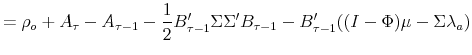 |
|
| (4) |
with boundary condition
The original "finance term structure models" such as Dai and Singleton (2000) and Duffee (2002) were written for nominal bond yields only. For example, the model (1) could be estimated with just nominal yields data, with suitable (normalization) restrictions on the
parameters ![]() ,
,![]() ,
,![]() ,... to insure that the model be econometrically identified. The state variables in this case are "latent factors" without an explicit economic meaning.
,... to insure that the model be econometrically identified. The state variables in this case are "latent factors" without an explicit economic meaning.
In a seminal paper, Ang and Piazzesi (2003, henceforth AP) proposed to combine this setup with a description of macroeconomy. Their basic insight is that the well-known Taylor-rule specification of the short rate also has an affine form:
| (5) |
where
| (6) |
one can have a system in which bond yields are linked to key macro variables. Some macroeconomic variables might not be well described by a simple VAR(1) dynamics, but this is in principle not a problem, as a higher-order VAR process (VAR(
Various macro-finance models differ by the choice of the restrictions imposed on the matrices like ![]() ,
,![]() ,..., etc. For example, AP (2003) adopt an atheoretical (statistical) approach, reminiscent of Sims (1980)'s original VAR proposal, while Hoerdahl, Tristani and Vestin (2006), henceforth HTV) imposed more structure based on a New-Keyesian model as in Clarida,
Gali, Gertler (2000) though still remaining in the reduced-form framework.
,..., etc. For example, AP (2003) adopt an atheoretical (statistical) approach, reminiscent of Sims (1980)'s original VAR proposal, while Hoerdahl, Tristani and Vestin (2006), henceforth HTV) imposed more structure based on a New-Keyesian model as in Clarida,
Gali, Gertler (2000) though still remaining in the reduced-form framework.
These are an innovation from the earlier approach of handling long-term bond yields in macroeconomic models. In fact, most macroeconomic models have not dealt with long-term bond yields at all, despite their importance for savings and investment decisions in the economy. Pre-macro-finance models like Federal Reserve's FRB/US model do contain the 5-year and 10-year nominal yields, which are specified as the expectations-hypothesis-implied yield plus a term premium (the 5-year term premium and the 10-year term premium are modeled separately),7 but the framework (1) allows not just a few selected long-term yields but the entire yield curve information to be integrated with a description of the macroeconomy.
2.2 No-arbitrage and replicating portfolios
While the derivation of the affine bond pricing equation (3) using the recursion relation involving the pricing kernel is simple and elegant, it is useful to re-derive it using the hedging (spanning) argument,8 in order to get a better sense of the role that the no-arbitrage principle is playing in macro-finance models.
Suppose there are ![]() -dimensional shocks underlying the term structure movements, denoted by a standard normal random vector
-dimensional shocks underlying the term structure movements, denoted by a standard normal random vector
![]() . The change in the value of a bond with maturity
. The change in the value of a bond with maturity ![]() can be expressed
generally as
can be expressed
generally as
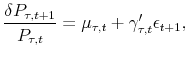 |
(7) |
where I have used the notation
Consider a portfolio formed by taking positions in ![]() bonds with maturities
bonds with maturities
![]() , with portfolio weights
, with portfolio weights
![]() . Denoting the value of this portfolio
. Denoting the value of this portfolio ![]() , the return on the
portfolio is given by
, the return on the
portfolio is given by
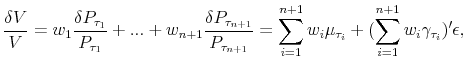 |
(8) |
where the time index
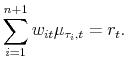 |
(9) |
Together with
![\displaystyle \left[\begin{matrix}\mu_{\tau_{1},t}-r_{t} & \cdots & \mu_{\tau_{n+1},t}-r_{t} \gamma_{\tau_{1},t} & \cdots & \gamma_{\tau_{n+1},t}\end{matrix}\right] w_{t} =0_{(n+1)\times1},](img55.gif) |
(10) |
where
where the
It is often more convenient to deal with log prices and log returns on bonds,
![]() (
(
![]() ). From the discrete-time version of the Ito's lemma,9 one has
). From the discrete-time version of the Ito's lemma,9 one has
where
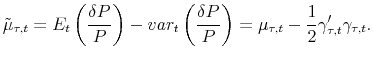 |
(13) |
Thus, eq. (11) can be also written
Note that the derivation thus far has been quite general. If the short rate and market price of risk are affine in the state variables and if the state variables follow a VAR(1) process (i.e, eq (1)), one obtains a particularly simple result. Positing that the bond prices
take the form
![]() , one has (from eq. (12))
, one has (from eq. (12))
| (15) | ||
| (16) |
Substituting these (and the expressions for
2.3 Internal basis models versus external basis models
The key formula in the above derivation of the bond pricing equation is eq. (11), or equivalently eq. (14). It states that the expected return on a bond of arbitrary maturity in excess of the short rate depends on the product of the bond-independent
market price of risk,
![]() , and the bond's sensitivity to risk,
, and the bond's sensitivity to risk,
![]() . The basic intuition underlying eq. (11) is that the yield curve is "smooth", so the risks to a bond can be hedged well by a
portfolio of (a relatively small number of) other bonds. This is well known from the factor analysis of Litterman and Scheinkman (1991) and other studies. One can also see this from the regression of the quarterly change in the 5-year yield on the changes in 6-month, 2-year, and 10-year
yields, which gives very high
. The basic intuition underlying eq. (11) is that the yield curve is "smooth", so the risks to a bond can be hedged well by a
portfolio of (a relatively small number of) other bonds. This is well known from the factor analysis of Litterman and Scheinkman (1991) and other studies. One can also see this from the regression of the quarterly change in the 5-year yield on the changes in 6-month, 2-year, and 10-year
yields, which gives very high ![]() s (e.g., 99%).
s (e.g., 99%).
Note that eq. (11) itself is silent about the structure of the
![]() vector, except for the condition that it does not depend on bond specific information (like maturity). In fact, the early generation of affine-Gaussian models assumed a constant
market price of risk vector
vector, except for the condition that it does not depend on bond specific information (like maturity). In fact, the early generation of affine-Gaussian models assumed a constant
market price of risk vector ![]() , which in effect implied a version of the expectations hypothesis. Later studies recognized that
, which in effect implied a version of the expectations hypothesis. Later studies recognized that
![]() can depend on the state of economy, thus a variable influencing the market price of risk would also influence bond prices.10 However, this creates, in a sense, too large a set of possibilities - any variable, e.g., coffee production in Brazil, could in principle enter the expression for market price of risk and, in turn, the
expression for bond yields.
can depend on the state of economy, thus a variable influencing the market price of risk would also influence bond prices.10 However, this creates, in a sense, too large a set of possibilities - any variable, e.g., coffee production in Brazil, could in principle enter the expression for market price of risk and, in turn, the
expression for bond yields.
Latent-factor models of the term structure, such as the affine-Gaussian model of Duffee (2002) (![]() model in Duffee's terminology), partly get around this problem by implicitly
defining the model in statistical terms. A "maximally flexible"
model in Duffee's terminology), partly get around this problem by implicitly
defining the model in statistical terms. A "maximally flexible" ![]() -dimensional affine-Gaussian model (1) can be viewed as an answer to the question, "what is the most
general
-dimensional affine-Gaussian model (1) can be viewed as an answer to the question, "what is the most
general ![]() -dimensional representation of the yield dynamics in which yields are Gaussian, linear in some basis, and consistent with no-arbitrage?"11 As the yield curve seems to be well described by a small number of risk sources, it stands to reason that there exists a suitable representation for a relatively small
-dimensional representation of the yield dynamics in which yields are Gaussian, linear in some basis, and consistent with no-arbitrage?"11 As the yield curve seems to be well described by a small number of risk sources, it stands to reason that there exists a suitable representation for a relatively small ![]() . Thus, the no-arbitrage principle in this setting can help describe the rich variation of the yield curve in a tractable and relatively parsimonious way, while allowing for a general pricing of risk (as
opposed to the expectations hypothesis).
. Thus, the no-arbitrage principle in this setting can help describe the rich variation of the yield curve in a tractable and relatively parsimonious way, while allowing for a general pricing of risk (as
opposed to the expectations hypothesis).
Duffee (2002)'s affine-Gaussian model describes only the nominal yield curve, but it is straightforward to write down a "joint model" of nominal yields and inflation in the same spirit by combining eq. (1) with the following specification of the inflation process,
where the one-period inflation
Such a joint model makes only fairly weak assumptions: writing the one-period inflation as the sum of expected inflation and unexpected inflation in eq. (17) is quite general, and it makes intuitive sense to have the state vector ![]() describe inflation expectations and bond yields together, as a variable that moves inflation expectation would be also expected to move nominal interest rates. At the same time, this formulation relaxes the assumptions implicit
in the two traditional theories of nominal yields: it goes beyond the expectations hypothesis, as it now allows for time-varying term premia, and the Fisher hypothesis, as it now implicitly allows for a general correlation between real rates and inflation.
describe inflation expectations and bond yields together, as a variable that moves inflation expectation would be also expected to move nominal interest rates. At the same time, this formulation relaxes the assumptions implicit
in the two traditional theories of nominal yields: it goes beyond the expectations hypothesis, as it now allows for time-varying term premia, and the Fisher hypothesis, as it now implicitly allows for a general correlation between real rates and inflation.
Note that the state vector ![]() in the joint model has more economic meaning than the nominal-yields-only model in the sense that it is now (implicitly) related to objects like inflation
expectations and inflation risk premia. However, the fact that
in the joint model has more economic meaning than the nominal-yields-only model in the sense that it is now (implicitly) related to objects like inflation
expectations and inflation risk premia. However, the fact that ![]() 's are still latent factors is potentially an unattractive feature, and makes it difficult to discuss bond market
developments in a simple manner. One would not win an "effective communication award" by telling market participants that "bond yields moved x basis points because latent factors did this and that."
's are still latent factors is potentially an unattractive feature, and makes it difficult to discuss bond market
developments in a simple manner. One would not win an "effective communication award" by telling market participants that "bond yields moved x basis points because latent factors did this and that."
Thus, many papers in the macro-finance literature take all or part of the state vector to be specific macroeconomic variables (or variables with clear macroeconomic interpretation) so as to make the connection between the yield curve and macroeconomy more explicit. These variables form an
external basis, in the sense that they are a priori fixed, partially ("mixed" models) or completely (observables-only models). Simply speaking, internal basis models try to project information in yields
![]() and "observable" macro variables
and "observable" macro variables
![]() onto the state vector
onto the state vector ![]() consisting of unobservable variables
consisting of unobservable variables
![]() , while external basis models try to project information in yields onto "observable" macro variables
, while external basis models try to project information in yields onto "observable" macro variables
![]() and latent variables (if there are any). Schematically,
and latent variables (if there are any). Schematically,
As one moves on to external basis models, one might be also moving away from the relative comfort of the original intuition behind no-arbitrage (the smoothness of the yield curve); hence a close scrutiny of additional assumptions that they involve is warranted.
3.1 Unspanned short-run inflation
One implication of having a macroeconomic variable like inflation as a state variable in the setup of eq. (1) is that short-run inflation risk can be hedged by taking positions in nominal bonds.14Many practitioners, however, would be skeptical about this claim. Policy makers are well aware of large short-run variations in price indices such as PPI and CPI that do not require a policy response, and they are careful to "smooth through the noise" in interpreting data on inflation. Blinder (1997) puts this clearly and strongly: "[The noise issue] was my principal concern as Vice-Chairman of the Federal Reserve. I think it is a principal concern of central bankers everywhere."
Market participants are also (implicitly) cognizant of these issues. One striking evidence is the bond market's reaction to the announcement of total CPI (also called "headline CPI", or simply "CPI") and core CPI. Core CPI is an inflation measure obtained by stripping out the volatile food and energy prices from total CPI. As can be seen in Figure 1a, monthly inflation based on total CPI is substantially more volatile than that of core CPI, and annual (year-on-year) inflations based on core CPI and total CPI can also differ significantly (Figure 1b). In the US, core CPI and total CPI for each month are announced in the following month (by the Bureau of Labor Statistics, typically in the second or third week). Before the release of the data, business economists partake in a survey about what the released numbers are going to be, from which "consensus expectations" are computed. The released number minus this consensus number can be viewed as a measure of the surprise component of the announcement.15
The regression of the change in the 2-year yield surrounding the data release (denoted
![]() ) on the surprise component of core CPI or total CPI (denoted
) on the surprise component of core CPI or total CPI (denoted
![]() and
and
![]() , respectively) in the 1990-2006 period gives:16
, respectively) in the 1990-2006 period gives:16
| (18) | ||
| (19) |
where the standard errors are given in parentheses. The coefficients on the surprise component in both cases are positive, in line with intuition: a positive inflation surprise leads to an upward revision in yields.
The more interesting case, however, is when both surprise components are used as regressors:
| (20) |
Note that the coefficient on
| (21) |
The coefficient on
These results do not necessarily mean that the "extra" components in the total CPI (food and energy prices) are completely irrelevant to the yield curve. They do, however, raise the question as to whether it is reasonable to treat the fluctuation in total CPI as risks that are spanned by the the yield curve factors (an implicit assumption in most external-basis macro-finance models).
In a more prosaic approach, one can also examine the spanning of short-run inflation risk by regressing the change in quarterly inflation ![]() onto the changes in 6-month, 2-year, and
10-year yields.17 This regression gives an
onto the changes in 6-month, 2-year, and
10-year yields.17 This regression gives an ![]() of at most 10% in the 1965-2006 period, in stark contrast to the aforementioned regression of the change in the 5-year yield (
of at most 10% in the 1965-2006 period, in stark contrast to the aforementioned regression of the change in the 5-year yield (![]() of 99%). Even when the lagged
inflation terms are included, as in
of 99%). Even when the lagged
inflation terms are included, as in
the
The evidence for poor spanning of short-run inflation risk raises questions as to whether external basis models are compatible with the no-arbitrage principle. Let us now address a related question -- whether external basis models can properly describe inflation expectations, which, according to the Fisher hypothesis intuition, are an important determinant of the nominal term structure.
3.2 Do macro variables form a suitable basis for representing expectations?
To those who engage in inflation forecasting extensively, the poor inflation forecast performance of macro-finance models like those of ABW (2007a) might not be a surprise: a long line of research has explored the inflation forecasting performance of the yield curve information and generally obtained disappointing results. Stock and Watson (2003) summarize the situation thus: "With some notable exceptions, the papers in this literature generally find that there is little or no marginal information content in the nominal interest rate term structure for future inflation."
One paper that does find evidence for the predictive information in the yield curve for future inflation is Mishkin (1990), so it is worth updating his results. Mishkin's regression takes the form
where
| (24) |
If the real yield were constant, subtracting this from the same equation with maturity
With yield data from 1960 to 1983, I obtain a result similar to Mishkin: for example, running the regression (23) for ![]() -year and
-year and ![]() -year gives a
-year gives a
![]() of 2.32 (with standard error 0.28), which is indeed large and significant, and in fact larger than 1 (which is also the case in Mishkin (1990) with both his "full" sample
and "pre-October 1979" sample). However, the same regression with the more recent 1984-2006 sample gives a much smaller
of 2.32 (with standard error 0.28), which is indeed large and significant, and in fact larger than 1 (which is also the case in Mishkin (1990) with both his "full" sample
and "pre-October 1979" sample). However, the same regression with the more recent 1984-2006 sample gives a much smaller
![]() of 0.17 (and standard error of 0.26). As discussed in Appendix B, the Mishkin regression coefficient probably has an upward bias, which may explain why the the coefficient in
the earlier-period sample is substantially larger than 1. But this bias also suggests that the coefficient in the 1984-2006 sample, already small, may have been overstated. In sum, even the Mishkin regression provides little support for the usefulness of the yield curve information in the more
recent sample period (which is presumably a more relevant period for current applications).
of 0.17 (and standard error of 0.26). As discussed in Appendix B, the Mishkin regression coefficient probably has an upward bias, which may explain why the the coefficient in
the earlier-period sample is substantially larger than 1. But this bias also suggests that the coefficient in the 1984-2006 sample, already small, may have been overstated. In sum, even the Mishkin regression provides little support for the usefulness of the yield curve information in the more
recent sample period (which is presumably a more relevant period for current applications).
Most of the regression-based inflation forecasting models in the literature include current and lagged inflation as regressors in order to take into account the persistence of inflation. The expected inflation over the next year in these models takes the form
where
Consider a macro-finance model (1) that has quarterly (one-period) inflation ![]() as a state variable. In other words,
as a state variable. In other words,
![]() , where
, where
![]() denotes other state variables. The expected inflation over the next year is
denotes other state variables. The expected inflation over the next year is
which is in the same form as eq. (25).19 (The case is similar with models that use annual inflation as a state variable.) As such, the difference between the macro-finance models formulated this way and the regression models is simply in the coefficients, not in the basis. There is a possibility of an "efficiency gain" with no-arbitrage models (through the imposition of useful constraints on the coefficients), but even this is not assured, if the results in ABW (2007a) are any indication. More fundamentally though, the frequently poor inflation forecast performance of regression models and macro-finance models like ABW(2007a) raises questions about the basis itself.
3.3 Lessons from simple models
Some of the key conceptual issues in the representation of the yield curve and inflation expectations may be explained through a comparison of two simple models of inflation, namely AR(1) and ARMA(1,1) models:
| (27) | ||
| (28) |
The
where the expected one-period inflation
and
The estimate of ![]() in the AR(1) model, based on US quarterly CPI inflation data from 1960Q1 to 2005Q4, is 0.785
in the AR(1) model, based on US quarterly CPI inflation data from 1960Q1 to 2005Q4, is 0.785
![]() , while the estimates of
, while the estimates of ![]() and
and ![]() in the ARMA(1,1) model are 0.935
in the ARMA(1,1) model are 0.935
![]() and 0.341
and 0.341
![]() , respectively, standard errors being in parentheses. These numbers imply fairly similar one-quarter-ahead inflation expectations, as can be seen in Figure 2a. (There is somewhat
more jaggedness in the AR(1) forecast.) The same parameter estimates, however, imply very different longer-horizon inflation expectations: the 5-year-ahead (20-quarter-ahead) inflation expectation from the AR(1) model is almost constant, while the 5-year-ahead inflation expectation from the
ARMA(1,1) model is more variable. (This reflects the difference between
, respectively, standard errors being in parentheses. These numbers imply fairly similar one-quarter-ahead inflation expectations, as can be seen in Figure 2a. (There is somewhat
more jaggedness in the AR(1) forecast.) The same parameter estimates, however, imply very different longer-horizon inflation expectations: the 5-year-ahead (20-quarter-ahead) inflation expectation from the AR(1) model is almost constant, while the 5-year-ahead inflation expectation from the
ARMA(1,1) model is more variable. (This reflects the difference between
![]() versus
versus
![]() in eq. (29).)
in eq. (29).)
An almost constant 5-year-ahead inflation expectation from the AR(1) model in the past 40 years is highly questionable. The main reason for the qualitative difference between the AR and ARMA models is that the ARMA(1,1) model tries to separate out the "unforecastable inflation" from the expected inflation, while the AR(1) model does not. This can be seen from the fact that the ARMA(1,1) model is a univariate representation of the following "two-component model":
in which
The unforecastable inflation component ![]() in eq. (32) can help explain several puzzling empirical results in the literature. Among them is the negative one-lag
autocorrelation of the changes in quarterly inflation
in eq. (32) can help explain several puzzling empirical results in the literature. Among them is the negative one-lag
autocorrelation of the changes in quarterly inflation
![]() (
(
![]() ), which, according to Rudd and Whelan (2006, Sec III.C), is an evidence against the new-Keynesian Phillips curve models (which generate positive one-lag autocorrelation).
In the case of the two-component model (32), one has
), which, according to Rudd and Whelan (2006, Sec III.C), is an evidence against the new-Keynesian Phillips curve models (which generate positive one-lag autocorrelation).
In the case of the two-component model (32), one has
| (33) |
The obviously negative first term dominates the second and third terms at appropriate parameter values, resulting in a negative
Economically, the ![]() term represents the very-short-run effects in total CPI inflation, including part of the food and energy prices that create the wedge between total CPI and core
CPI (as seen in Section 3.2), as well as the unforecastable components of the core CPI inflation and potential errors in the measurement of CPI. A large part of
term represents the very-short-run effects in total CPI inflation, including part of the food and energy prices that create the wedge between total CPI and core
CPI (as seen in Section 3.2), as well as the unforecastable components of the core CPI inflation and potential errors in the measurement of CPI. A large part of ![]() is beyond the
control of monetary policy makers (or economic agents, for that matter); thus, in some sense, the presence of a substantial amount of unforecastable inflation is a "fact of life".
is beyond the
control of monetary policy makers (or economic agents, for that matter); thus, in some sense, the presence of a substantial amount of unforecastable inflation is a "fact of life".
The importance of the ![]() -term in the two-component model (32) has a parallel implication for no-arbitrage macro-finance models: the failure to separate out the
"unspanned macro shocks" in macro-finance models may produce problems that mirror those of the AR(1) inflation model. It is worth mentioning here that Stock and Watson (2007) have also recently emphasized that separating inflation into a trend component and a serially uncorrelated shock (like
-term in the two-component model (32) has a parallel implication for no-arbitrage macro-finance models: the failure to separate out the
"unspanned macro shocks" in macro-finance models may produce problems that mirror those of the AR(1) inflation model. It is worth mentioning here that Stock and Watson (2007) have also recently emphasized that separating inflation into a trend component and a serially uncorrelated shock (like
![]() in eq. (32)) is useful for explaining key features of the US inflation dynamics,22though they do not discuss the ramifications for macro-finance (no-arbitrage) models.
in eq. (32)) is useful for explaining key features of the US inflation dynamics,22though they do not discuss the ramifications for macro-finance (no-arbitrage) models.
It is instructive to ask about the basic variable underlying the term structure of inflation expectations in the ARMA(1,1) model. As is clear from eq. (29), the basic variable is ![]() , not the realized inflation
, not the realized inflation ![]() . Note that in the case of the AR(1) model,
. Note that in the case of the AR(1) model, ![]() is
is ![]() (up to a prefactor and an intercept), as can be seen from eq. (30). This is not the case
for the ARMA(1,1) model: it is straightforward to show (by solving for
(up to a prefactor and an intercept), as can be seen from eq. (30). This is not the case
for the ARMA(1,1) model: it is straightforward to show (by solving for
![]() in eq. (28) and recursively substituting into eq. (31)) that
in eq. (28) and recursively substituting into eq. (31)) that ![]() in the ARMA(1,1) model can be expressed as
in the ARMA(1,1) model can be expressed as
This is in the exponential smoothing form, which has been familiar at least since the work of Muth (1960).
The expression (34) suggests that the connection between realized macro variables and state variables in no-arbitrage term structure models could be complicated, and that the poor inflation forecasting performance of regression models and no-arbitrage models with macro variables may be a more complex issue than being just a matter of having "efficient" coefficients (with conventional basis). To be sure, the state variables in nominal term structure models are not simply those that underlie the variation of inflation expectations. Factors that affect the real term structure and inflation risk premia should also be included in the nominal term structure model. However, it is not clear that these additional aspects would be any better described by macro variables.
Note that the expression for ![]() in eq. (34), although useful for conceptual illustration, is still deficient as a description of inflation expectations for
both subtle and fundamental reasons. The subtle reason concerns the conditioning information: if the two-component model (32) is the data generating process for inflation, the "true" inflation expectation cannot be expressed simply in terms of the past inflations (except when
in eq. (34), although useful for conceptual illustration, is still deficient as a description of inflation expectations for
both subtle and fundamental reasons. The subtle reason concerns the conditioning information: if the two-component model (32) is the data generating process for inflation, the "true" inflation expectation cannot be expressed simply in terms of the past inflations (except when
![]() in eq. (32)). Mathematically,
in eq. (32)). Mathematically,
| (35) |
In other words, the one-period inflation expectation based on the past history of inflation (as computed from the ARMA(1,1) model) is not the same as the one-period inflation expectation
More fundamentally, the ARMA model and even the two-component model are deficient, as both models imply that the one-period inflation expectation is an AR(1) process, which means that inflation expectations for all horizons are given by a single factor ![]() , with the term structure of inflation expectations monotonically sloping up when
, with the term structure of inflation expectations monotonically sloping up when ![]() is below its long-run
mean and monotonically sloping down when
is below its long-run
mean and monotonically sloping down when ![]() is above its long-run mean. This stiffness (lack of flexibility) of the model makes it difficult to describe the inflation environment of
the past decades, during which people's perception of Federal Reserve's inflation target is believed to have changed appreciably. Thus, the model's results depend materially on how long the estimation sample is. Figure 2b, based on the estimation with a "long sample" that includes the 1970s,
indicates the current (circa 2006) five-year-ahead CPI inflation expectation of about 4%, which is too high to be believed. More generally, one can view the level to which inflation mean-reverts itself as varying over time.23
is above its long-run mean. This stiffness (lack of flexibility) of the model makes it difficult to describe the inflation environment of
the past decades, during which people's perception of Federal Reserve's inflation target is believed to have changed appreciably. Thus, the model's results depend materially on how long the estimation sample is. Figure 2b, based on the estimation with a "long sample" that includes the 1970s,
indicates the current (circa 2006) five-year-ahead CPI inflation expectation of about 4%, which is too high to be believed. More generally, one can view the level to which inflation mean-reverts itself as varying over time.23
3.4 Low-dimensional external basis models
Let us now consider some specific issues that arise in external basis models with a "low-dimensional" state vector.
Suppose that one has a three-factor macro-finance model in the setup of eq. (1), with the state vector ![]() consisting of all "observable" macro variables, say, the
quarterly inflation
consisting of all "observable" macro variables, say, the
quarterly inflation ![]() , quarterly GDP growth
, quarterly GDP growth ![]() , and the effective
federal funds rate
, and the effective
federal funds rate
![]() . The inflation expectations in this model are then linear functions of contemporaneous variables
. The inflation expectations in this model are then linear functions of contemporaneous variables
![]() . (To see this, simply substitute
. (To see this, simply substitute
![]() in eq. (26).) This type of forecast (VAR(1)) has more qualitative similarity to the AR(1) model than the ARMA(1,1)
model; in particular, despite its multi-factor nature, it still mixes "signal" with "noise" and can therefore be expected to inherit many of the problems with the AR(1) model.
in eq. (26).) This type of forecast (VAR(1)) has more qualitative similarity to the AR(1) model than the ARMA(1,1)
model; in particular, despite its multi-factor nature, it still mixes "signal" with "noise" and can therefore be expected to inherit many of the problems with the AR(1) model.
Some of the macro-finance models in the literature, including Ang, Dong, and Piazzesi (2005, henceforth ADP) and ABW (2007a), remain in a relatively low-dimensional framework but use a mix of latent factors and macroeconomic variables, but these "mixed models" may still have difficulties.
Consider, for example, the ABW (2007a)'s affine model (their MDL1 model) with quarterly inflation and two latent factors, i.e.,
![]() . If the latent factors
. If the latent factors
![]() are interpreted as
are interpreted as
![]() , eq. (26) takes a form similar to the smoothing form (34). However, besides the issue that two lags might not be enough, one
may not have the freedom to interpret
, eq. (26) takes a form similar to the smoothing form (34). However, besides the issue that two lags might not be enough, one
may not have the freedom to interpret ![]() 's this way, as that would deprive the ability to describe other aspects of the nominal term structure (e.g., real interest rates, time-varying
risk premium, time-varying perceived inflation target).
's this way, as that would deprive the ability to describe other aspects of the nominal term structure (e.g., real interest rates, time-varying
risk premium, time-varying perceived inflation target).
In the mixed models, having a macro variable like ![]() as a part of the state vector may cause a distortion in the inference, as the latent factors can end up absorbing the
"unspanned" variation in
as a part of the state vector may cause a distortion in the inference, as the latent factors can end up absorbing the
"unspanned" variation in ![]() . To illustrate this schematically, suppose that the true model of the short rate is
. To illustrate this schematically, suppose that the true model of the short rate is
| (36) |
where
| (37) |
with
| (38) |
Thus the latent factor
3.5 High-dimensional external basis models
Some of the external basis macro-finance models in the literature use a fairly large number of state variables that include lagged macro variables. Many such models (including those of AP (2003) and HTV (2006)) use annual inflation
![]() (=
(=
![]() ) as a state variable instead of the one-period inflation. This may help alleviate concerns about the problem with the use of the one-period inflation, since the year-on-year
inflation partly "smooths out" the noise in quarterly inflation:
) as a state variable instead of the one-period inflation. This may help alleviate concerns about the problem with the use of the one-period inflation, since the year-on-year
inflation partly "smooths out" the noise in quarterly inflation:
![]() can be written
can be written
where the weights
Note, however, that the construction (39) automatically implies a moving average structure in
![]() , which suggests that the simple VAR(1) description would not be a good description of its dynamics. Thus, macro-finance models that use annual inflation as a state variable
typically include additional lags, e.g., AP (2003) use 12 monthly lags, in effect having a VAR(12) model. Bond yields in this case depend on a "large" set of state variables that include lagged macroeconomic variables.24
, which suggests that the simple VAR(1) description would not be a good description of its dynamics. Thus, macro-finance models that use annual inflation as a state variable
typically include additional lags, e.g., AP (2003) use 12 monthly lags, in effect having a VAR(12) model. Bond yields in this case depend on a "large" set of state variables that include lagged macroeconomic variables.24
A problem with this type of "high-dimensional" specification is that it inherits the well-known problems of the the unrestricted VAR models. In fact, AP (2003)'s inflation dynamics is a conventional VAR. They separate the vector of relevant variables into an
"observable" macro vector ![]() and an unobservable (latent) vector
and an unobservable (latent) vector ![]() , i.e.,
, i.e.,
![]() ,25 and impose the restriction that the latent factors do not affect the expectation of macroeconomic variables. Their macro vector dynamics is given by the VAR(
,25 and impose the restriction that the latent factors do not affect the expectation of macroeconomic variables. Their macro vector dynamics is given by the VAR(![]() ):
):
| (40) |
where
By having only the macro variables describe inflation dynamics, AP (2003) turned off the possibility of the yield curve saying something about future inflation. Unfortunately, it is difficult to lift that restriction. The overparametrization problem would get worse, as the full (maximally-identified) model would have an even larger number of parameters: in the specification of the state vector dynamics
![\displaystyle \left[\begin{matrix}f^{o}_{t} f^{u}_{t}\end{matrix}\right] = \left[\begin{matrix}\Phi^{o}_{1} & \Phi^{ou}_{1} \Phi^{uo}_{1} & \Phi^{u}_{1}\end{matrix}\right] \left[\begin{matrix}f^{o}_{t-1} f^{u}_{t-1}\end{matrix}\right] + \left[\begin{matrix}\Phi^{o}_{2} & \Phi^{ou}_{2} \Phi^{uo}_{2} & \Phi^{u}_{2}\end{matrix}\right] \left[\begin{matrix}f^{o}_{t-2} f^{u}_{t-2}\end{matrix}\right] + \cdots+ c+ \Sigma\epsilon_{t},](img199.gif)
|
(41) |
the matrices
Models like HTV (2006) have more structure (in the form of the new-Keynesian Phillips curve and IS equations), which may help alleviate overparametrization concerns, but at a possibly greater misspecification risk: various aspects of the new-Keynesian specification are still under debate, e.g., the presence or absence of the interest rate smoothing term (e.g., English et al (2003), Rudebusch (2006)) and the strength of the backward-looking inflation terms (e.g, Rudd and Whelan (2006)).
A common practice in the specification of external basis models that contain lags of macroeconomic variables in the state vector is to set the coefficients of the market price of risk (
![]() matrix in eq. (1)) that load on lagged macro variables to zero (e.g., AP (2003) and HTV (2006)). Even with this restriction, the number of remaining market
price risk parameters is large, and modelers often make additional ad hoc restrictions on the
matrix in eq. (1)) that load on lagged macro variables to zero (e.g., AP (2003) and HTV (2006)). Even with this restriction, the number of remaining market
price risk parameters is large, and modelers often make additional ad hoc restrictions on the
![]() matrices to reduce the number of parameters further.26 Unfortunately, the practice of setting the
matrices to reduce the number of parameters further.26 Unfortunately, the practice of setting the
![]() coefficients on lagged macro variables to zero is not as innocuous as it might appear. It implies that the expected excess return on a bond,
coefficients on lagged macro variables to zero is not as innocuous as it might appear. It implies that the expected excess return on a bond,
![]() , is completely spanned by contemporaneous macroeconomic variables (and latent factors, if there are any). Recall, from eqs. (11) and (16), that
, is completely spanned by contemporaneous macroeconomic variables (and latent factors, if there are any). Recall, from eqs. (11) and (16), that
Therefore, if
| (43) |
one cannot have
| (44) |
This asymmetry in the way yields and bond risk premia depend on lagged macro variables has nothing to do with no-arbitrage, and has little empirical basis. In other words, in order to cast the model in a "no-arbitrage" framework, many external basis macro-finance models are introducing arbitrary and nontrivial assumptions about the market price of risk. This raises the question of whether the no-arbitrage principle can play its intended role.27
3.6 Would composite factors help?
Several recent studies have explored the use of composite variables created from a large array of macroeconomic variables in modeling the term premia (e.g., Ludvigson and Ng, 2006) or the yield curve (e.g., Moench, 2006).
The composite factors may be appealing because they utilize a much bigger information set and also because they may be cross-sectionally smoothing out some of the idiosyncratic noise in quantities like CPI, hence one can expect them to reflect more of the systematic variation than the individual macro variables.
However, since these models do not address expectations concerning specific macroeconomic variables of potential interest, one cannot tackle issues such as the expectation of the CPI inflation implicit in the yield curve; thus macro-finance models based on purely composite factors would not have much to say about TIPS pricing, as TIPS are specifically indexed to the CPI.
More fundamentally, it is unclear whether composite factors can be valid state variables in no-arbitrage term structure models, as they may still face many of the aforementioned problems with external basis models. In particular, the way the composite factors in Moench (2006) and Ludvigson and
Ng (2006) are constructed is such that they are not very persistent variables.28 For example, Ludvigson and Ng (2006) report that their most persistent
factor has a monthly AR(1) coefficient of 0.77 (the half-life is less than a quarter). In order for such a variable to describe yields in the setup of (1) even just qualitatively (e.g., producing the kind of persistence that yields have), one needs long lags, which again raise
overparametrization concerns. In addition, even if principal components analysis indicates that a small number, say ![]() , of factors describe the bulk of yield curve movements, it is not clear
whether the proper truncation number for cross-sectional composite factors should be also small or is related to
, of factors describe the bulk of yield curve movements, it is not clear
whether the proper truncation number for cross-sectional composite factors should be also small or is related to ![]() .
.
4.1 Structural stability
One potential limitation of the general framework (1) is structural stability. To be sure, the debate about the structural stability of macroeconomic relationships is not new (see, e.g., Rudebusch (1998) and Sims (1998)). However, it may have different ramifications for internal basis models and external basis models, and hence merits a discussion here.
Several well-known structural instabilities are of direct relevance to macro-finance models. Many have noted that in the 1990s a large part of the term structure variation seemed to be due to the variation of real rates, while in the 1970s the variation in inflation expectations seemed to be a more dominant factor. The stark difference between the Mishkin regression coefficients in the 1960-83 and 1984-2006 periods discussed in Section 3.2 lends support to the claim of a change in the relative importance of inflation for explaining yield curve movements. Another instability is that of the Taylor rule coefficients, as argued by Clarida, Gali, and Gertler (2000) and others. Since the Taylor rule underpins the short-rate specification of many macro-finance models, this instability is a serious concern for the macro-finance models that are estimated with a "long" sample that includes the pre-Volcker disinflation period. Note also that the dynamics of many macro-finance models is similar to conventional VARs, but low-dimensional macro-VARs were often found to be unstable (e.g., Stock and Watson (1996)).
The traditional specification may also face difficulty in accommodating relatively new developments. For example, in recent years there has been an increased discussion of the effects of global forces on domestic bond markets. Increased "global liquidity" has been often cited as a potential factor pressing down inflation expectations or bond risk premia, and interest rates movements in various countries, including the United States, Euro area, and Japan, have lately become more highly correlated.29 Whether structurally stable Taylor-rule type specifications are consistent with these developments is an open question.
One may hope that concerns about structural instability would be alleviated if latent factors are also included in external basis models. For example, a macro-finance model with a Taylor-rule-like mixed specification of the short rate (similar to ADP (2005))
where
where
Furthermore, there may be instabilities other than time-varying intercept, for instance, changes in the conditional correlation of various macroeconomic variables, changes in the persistence of the macroeconomic variables, and so on. Imagine, heuristically, a situation in which the "true" model is
i.e, a Taylor-rule-like short-rate with time-varying loadings on the macroeconomic variables. In this case, the 2-factor affine model in which the state variables are
| (48) |
Again, identifying
One way to address this problem is to model these effects explicitly in non-affine/non-Gaussian models. However, these models, being richer than affine-Gaussian models, may be even more susceptible to overfitting concerns and may incur a greater risk of misspecification. The disappointing inflation forecasting performance of the vector regime-switching model and the no-arbitrage "regime-switching" model in ABW (2007a) (referred to by them as RGMVAR and MDL2, respectively) may serve as a reminder in this regard.
Alternatively, the use of an internal basis (while still remaining in the affine-Gaussian setup) may allay structural instability concerns to some extent: internal basis models are agnostic as regards the definition of the factors; thus a model that is obviously unstable from the point of view
of an external basis may not necessarily be so from the point of view of an internal basis. For example, going back to eq. (47), choosing the state variable as
![]() may be more effective than having
may be more effective than having
![]() , although there may be an even better internal basis for the problem (depending on how the rest of the model is defined).30
, although there may be an even better internal basis for the problem (depending on how the rest of the model is defined).30
Of course, no-arbitrage models with an internal basis should not be expected to answer all structural stability concerns. A strong structural instability may be difficult to capture even with an internal basis model, in which case it might be better to use a shorter, structurally more homogeneous sample.
4.2 Time-varying uncertainty
Another limitation of the affine-Gaussian models (both internal and external basis models) is that they imply homoskedastic yields, while there is copious evidence for time-varying volatility of interest rates, e.g., from interest rate derivatives as well as the stochastic-volatility models and GARCH-type models. However, it is not clear whether a no-arbitrage model that allows for time-varying volatility would produce better results. Again, the concern is that such a model may incur greater specification errors and implementation errors.
Theoretically and intuitively, one should expect a relation between term structure variables and time-varying uncertainty about interest rates: to the extent that bond market term premia arise from risk, the changing amount of interest rate risk should translate to a changing term premium. It also stands to reason that at least a part of the variation in interest rate volatility is linked to the variation in the uncertainties about key macro variables. Various studies have noted that macroeconomic uncertainties (inflation, GDP, monetary policy) have declined since the Volcker disinflation, a phenomenon often dubbed the "Great Moderation".31 One can expect this effect to be accompanied by a corresponding reduction in term premia in the bond market. Kim and Orphanides (2007) indeed report positive relationships between the term premium in the 10-year forward rate and proxies for uncertainties about monetary policy and inflation based on the dispersion of long-horizon survey forecasts.32
However, much work remains to be done to properly address the relationship between term premia and macroeconomic uncertainties, in particular inflation uncertainty. For instance, one can debate as to whether the survey dispersion measure used in Kim and Orphanides (2007) is a good proxy for uncertainty. Furthermore, their evidence is mainly about the low-frequency relation; whether there is a relation at shorter time scales remains unclear. A key difficulty addressing this question is measuring the relevant uncertainty. For example, the uncertainty measures from GARCH-type models of inflation do not seem promising for making a connection with bond market term premia, as those models imply a tight relation between short-term inflation uncertainty and long-term inflation uncertainty.33
Recall from the discussion in Section 3 that much of high-frequency variation in inflation is not spanned by interest rates. This, in turn, suggests that the changing amount of this unspanned risk might not have much connection with bond market term premia either. Furthermore, the relevant inflation uncertainty is over the life of the bond, which could be qualitatively different from short-run uncertainty about inflation.
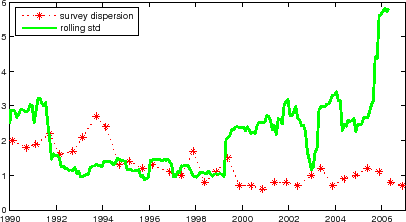 |
The increase in the volatility of monthly inflation in total CPI from about 1999 and on (which can be clearly seen in Figure 1a) is a case in point. This increase in the near-term uncertainty does not seem to have translated to an increase in the perception of longer-term uncertainty. Indeed, as shown in Figure 3, a proxy for the long-horizon inflation uncertainty based on a survey forecast dispersion has been subdued in this period, contrasting with an elevated level of one-year rolling standard derivation of monthly inflation (a simple proxy for short-run inflation uncertainty) in the same period. Even granting the imperfection of the long-horizon inflation uncertainty measure, this lack of relation bears noting.34
The complexity of inflation dynamics can thus create considerable challenge for attempts to go beyond homoskedastic models: it may be that a nonlinear model with time-varying inflation uncertainty can lead to poorer results if the model's inflation uncertainty is misspecified, as when a model that does not make a qualitative distinction between short- and long-run inflation uncertainties tries to link the rise in the volatility of short-run inflation of the recent several years (as seen in Figure 3) to bond market term premia.35
5.1 Overfitting problems
Flexibly specified no-arbitrage models tend to entail much estimation difficulty due to a large number of parameters to be estimated and due to the nonlinear relationship between the parameters and yields that necessitates a nonlinear optimization. Even if one finds the parameter vector that corresponds to the global optimum of the criterion function, not all may be fine with the resulting estimate.
The experience with the unrestricted VARs explored in the 1980s macroeconomics literature is an important reminder in this regard. Unrestricted VARs can be estimated via the OLS regression, thus the estimation itself is straightforward; however, it is well known that unrestricted VARs often lead to poor results.36The main problem is that these models get easily overparameterized, and there is little structure in the model to prevent estimations from generating unreasonable outcomes. This problem can be expected to be shared by flexibly specified macro-finance models (both internal basis models and external basis models), which are, like the unrestricted VARs, an "atheoretical" representation with a large number of parameters.
The key innovation of the macro-finance models like AP (2003), as compared to the traditional macro models, is that they link not only the short rate ![]() (
(![]() ) but also the rest of the term structure (
) but also the rest of the term structure (
![]() ) to the macroeconomy by casting the problem in the no-arbitrage framework (1), introducing the market price of risk
) to the macroeconomy by casting the problem in the no-arbitrage framework (1), introducing the market price of risk
![]() for the shocks in the model. However, it does not seem to have been seriously questioned as to whether the amount of additional information thus introduced is large enough to
compensate for the large increase in the number of parameters of the model.
for the shocks in the model. However, it does not seem to have been seriously questioned as to whether the amount of additional information thus introduced is large enough to
compensate for the large increase in the number of parameters of the model.
Note that the no-arbitrage principle tells the existence of a pricing kernel such as eq. (1), but the principle by itself does not constrain the parameters of the market price of risk (
![]() matrix). Suppose, as in AP (2003), that one has in the state vector
matrix). Suppose, as in AP (2003), that one has in the state vector ![]() observable variables, its
observable variables, its ![]() lags, and
lags, and ![]() unobservable (latent) variables, in
other words,
unobservable (latent) variables, in
other words,
| (49) |
In that case the
Empirically, yields of various maturities tend to be highly correlated, giving rise to the finding in factor analysis and principal components analysis that there is a single dominant factor. But this also means that the pure additional information in longer-term yields (beyond what is in the short rate) may be modest in amount and perhaps too delicate to capture with a specification of the market price of risk that is liable to be overfitted; the relation that one might see between yields and macro variables in macro-finance models may be more of a statement of the Taylor rule (macro description of the short rate) rather than no-arbitrage. Thus, it is not clear whether the reduced-form no-arbitrage framework (1) can do an effective job of incorporating the information in the entire yield curve.38
Though the overparametrization problem may be particularly severe with external basis models that contain lags of macroeconomic variables, internal basis models (which tend to be implemented with comparatively smaller number of factors, e.g., 3 factors) may also face serious overfitting
concerns; they may be more easily overfitted than external basis models because of the especially flexible nature (the definitional freedom) of the latent-factor models. In particular, latent factor models could fit very well data that it is asked to fit, even if the
data or the model were a poor one. For example, because yield fitting errors are minimized as a part of the estimation process, internal basis models with 3 ![]() 4 factors can fit the
cross-section of the yield curve quite well (with much smaller fitting errors than external basis models), but that by itself might not be a sufficient reason to recommend internal basis models.
4 factors can fit the
cross-section of the yield curve quite well (with much smaller fitting errors than external basis models), but that by itself might not be a sufficient reason to recommend internal basis models.
As another example, I find that estimating the 3-factor internal basis model in D'Amico et al (2007) with yields and inflation data in the 2000-2006 period and with supplementary data on the SPF survey forecast of 10-year inflation (assuming that survey expectation is the model expectation plus a measurement error whose size is also estimated) can fit very closely the survey forecast, which has hardly moved from the level of 2.5%. Such an outcome is likely due to the richness and flexibility of the model rather than a genuine feature of market expectations. The problem is that although the latent factor model is identified in principle (with suitable normalization conditions), there may be not enough discipline in the model and not enough information in other data in the sample to prevent "too close" fit of the SPF survey data.39
5.2 Small sample problems
The implementation of macro-finance models is also complicated by small sample problems that arise from the highly persistent nature of the data. Both interest rates and inflation are known to be persistent; unit-root tests often fail to reject nonstationarity (unit-root) null for them.40
In light of this, many practitioners often use nonstationary models to forecast inflation. For example, many of the inflation forecasting models used by the Federal Reserve staff impose the unit root condition.41 By the Fisher-hypothesis intuition, unit root inflation dynamics implies a unit-root interest rate dynamics.
By contrast, most of the estimated macro-finance models (or nominal term structure models) in the literature assume stationarity. This may be due in large part to tradition, but there is also an intuitive justification as well: being "rates", interest rates and inflation do not grow unboundedly, and experience tells us that these variables typically stay within the range of, say, 0% and 20%; this has been the case for modern economies (excluding special episodes like hyperinflation and deflation) as well as in ancient economies such as the Babylonian economy. The implication of unit root models that the unconditional means of inflation and interest rates are undefined and their unconditional variances are infinite is objectionable.
It thus seems more reasonable that the "true model" of yields is a stationary one, perhaps with many factors to describe the complex dynamics of yields and expectations, schematically,
In practice, however, one is forced to deal with relatively low-dimensional models, because limited amount of data make it impossible to pin down the parameters of such a model, or because one does not have enough knowledge to write down a very detailed model. In this case, it is not clear whether the "best" low-dimensional approximation
| (51) |
of the model (50) should be a stationary or nonstationary (unit-root) model.
The distinction between stationary and nonstationary models could be semantic in the sense that a stationary model that is close to the unit-root boundary is almost indistinguishable from unit-root models. But whether to assume stationarity or not can make a big difference operationally, as conventional estimations have tendency to bias down the persistence of stationary time series, the bias being stronger the smaller the sample. This makes the expectations appear converging to a long-run level faster than they actually do; thus longer-horizon expectations of inflation and interest rates in (estimated) stationary models are often artificially stable, varying little from the sample-mean of these variables.
Another manifestation of the small sample problem (besides bias) is imprecision: highly persistent interest rates effectively make the size of the sample "small"; no matter how frequently the data are sampled, some of the key aspects of the term structure model
(those pertaining to expectations in the physical measure, as opposed to the risk-neutral measure) are difficult to estimate, as stressed in Kim and Orphanides (2005). In a conventional estimation of term structure model with the last 10 ![]() 15 years' yield data, one often finds that many of the parameters of the model are estimated very imprecisely and the confidence intervals for quantities of interest like the model-implied short-rate forecast are too wide (i.e., includes almost
any scenarios).
15 years' yield data, one often finds that many of the parameters of the model are estimated very imprecisely and the confidence intervals for quantities of interest like the model-implied short-rate forecast are too wide (i.e., includes almost
any scenarios).
5.3 Are classical procedures applicable?
Most implementation of macro-finance models have relied on classical methods such as the maximum likelihood estimation (ML) and generalized method of moments (GMM), but these methods may be less effective in this context than is often presumed.
At the heart of the matter is the point that reduced-form macro-finance models are obviously an approximate representation of data, and hence not very compatible with the classical premise of having the "true model." Though it goes without saying that all models in economics and finance are approximate, this point is particularly relevant here in view of the atheoretical (statistical) nature of many of the macro-finance models and the large number of parameters. For instance, it is not clear that the ML or GMM criterion function of these models should contain a unique meaningful maximum; there might be different maxima which capture different aspects of data with differing degree of emphasis. The small sample problems discussed above adds to the difficulty, as they make asymptotic statistics a poor guide to finite sample properties.
Let us now consider specific difficulties with certain classical procedures. In some implementations the fit of certain unconditional moments are used either as an estimation condition (e.g., Brandt and Chapman (2003)) or as a diagnostic check (ABW (2007b)), for example,
and so on. As discussed above, nonstationary (unit-root) scenario cannot be dismissed easily for the "approximate model", but trying to match the moment conditions (52) in this case is pointless: the right-hand side numbers are finite, while the left-hand side numbers infinite (or indefinite). In the case of near-nonstationarity, the left-hand side numbers are finite, but the proximity to the unit root boundary means that they are likely to be very inaccurate estimates, so that "how close the unconditional moments are to sample moments" could be a poor guide to a model estimation or evaluation.42
Many of the classical estimation approaches implicitly minimize fitting errors for the one-period-ahead conditional moments. For example, the ML estimation can be viewed as minimizing the one-period prediction errors or the errors in the fit of the "likelihood score moments" (
![]() ) in a GMM framework. While in theory this could yield an asymptotically correct estimate of the true model (if the true
model exists), the inherently approximate nature of model means that fitting the one-period moments as closely as possible might come at the expense of other aspects of the model. Cochrane and Piazzesi (2006) in effect make this point when they note that conventionally estimated affine models may
have difficulty producing the kind of term premia that they find based on regressing multi-period (one-year) excess returns on a set of forward rates.
) in a GMM framework. While in theory this could yield an asymptotically correct estimate of the true model (if the true
model exists), the inherently approximate nature of model means that fitting the one-period moments as closely as possible might come at the expense of other aspects of the model. Cochrane and Piazzesi (2006) in effect make this point when they note that conventionally estimated affine models may
have difficulty producing the kind of term premia that they find based on regressing multi-period (one-year) excess returns on a set of forward rates.
In macro-finance models, the reliance on the one-period-ahead conditional moments could be further compromised by the complexity of relatively high-frequency macro data. A rather striking demonstration is provided by a comparison of the "quarterly inflation" measured in two ways: quarterly
inflation based on the CPI values in the middle month of each quarter,
![]() (e.g., log CPI difference between May and February) and in the last month of each quarter,
(e.g., log CPI difference between May and February) and in the last month of each quarter,
![]() (e.g., log CPI difference between June and March). The sample one-lag autocorrelations
(e.g., log CPI difference between June and March). The sample one-lag autocorrelations
![]() ,
,
![]() based on the 1960-2006 sample are 0.79 and 0.67, respectively. Considering that the only difference between
based on the 1960-2006 sample are 0.79 and 0.67, respectively. Considering that the only difference between
![]() and
and
![]() is the one-month shift in the definition, this is a large discrepancy. This effect is even more pronounced in the 1984-2006 sample, which gives
is the one-month shift in the definition, this is a large discrepancy. This effect is even more pronounced in the 1984-2006 sample, which gives
![]() and
and
![]() . This is largely due to a very sharp rise and reversal in the one-month total CPI inflation in 2005 (as can be seen in Figure 1a); one version of
the quarterly CPI inflation (
. This is largely due to a very sharp rise and reversal in the one-month total CPI inflation in 2005 (as can be seen in Figure 1a); one version of
the quarterly CPI inflation (
![]() ) is picking this up and the other (
) is picking this up and the other (![]() ) is not. Ang, Bekaert,
and Wei (2007b) look at lagged autocovariance terms based on
) is not. Ang, Bekaert,
and Wei (2007b) look at lagged autocovariance terms based on
![]() as a part of their diagnostic check, but nothing in theory says that
as a part of their diagnostic check, but nothing in theory says that
![]() is more valid than
is more valid than
![]() . Thus it is difficult to take either
. Thus it is difficult to take either
![]() or
or
![]() too seriously.43
too seriously.43
5.4 How can we evaluate models?
The above discussion suggests that looking at the fit of the moments that are often used in the classical estimation might not necessarily be a good criterion for model evaluation.
Some papers do look directly at practical implications of the model, such as the multi-period forecasts of inflation and interest rates. Indeed, in view of the fact that the second moment aspects of affine-Gaussian models are trivial, much attention has focused on these conditional first moments (the forecasting performance) as a part of diagnostic criteria, as in Ang and Piazzesi (2003), HTV (2006), and Moench (2006).
However, it is unclear to what extent summary measures of forecasting performance examined in these papers can help with model evaluation/selection. To be sure, looking at the forecasting performance can be useful for detecting problematic models. In Duffee (2002), for example, interest rate
forecast RMSEs that are substantially larger than the random-walk benchmark were used to highlight problems with certain stochastic-volatility no-arbitrage models (e.g., the ![]() specification). Similarly, the inflation forecast RMSEs based on ABW (2007a)'s no-arbitrage models that are substantially larger than the univariate inflation model benchmark may signal problems with the no-arbitrage models that they have used.
specification). Similarly, the inflation forecast RMSEs based on ABW (2007a)'s no-arbitrage models that are substantially larger than the univariate inflation model benchmark may signal problems with the no-arbitrage models that they have used.
Nonetheless, the RMSE measures for in-sample or out-of-sample forecasts are often ineffective in discriminating between models. For instance, ABW (2007a) obtain very similar RMSEs for the one-year out-of-sample inflation forecasts from the AR(1) and the ARMA(1,1) models, although the AR(1) model implies qualitatively quite different inflation expectations than the ARMA(1,1) model as discussed in Sec 3.3.
Furthermore, because a large part of the inflation and interest rate variations are an unforecastable variation, the RMSEs themselves may have substantial uncertainty (sampling variability).44 Thus, it may happen that the "true model" generates a RMSE that is no smaller than some other models. In this sense, it may be actually misleading to focus on the RMSE as a criterion for selecting the model that best describes the reality. In the case of in-sample forecasts, this problem is exacerbated by the possibility that RMSEs are artificially pushed down due to the use of "future information" in the generating the forecast, making interest rates and inflation look more forecastable than they actually are.
Often there are cases in which classical criteria cannot easily tell if a model's output is unreasonable, while practitioners can do so using "judgmental information." For instance, many macro-finance models estimated with data going back to 1970s generate current (circa 2006) long-horizon inflation expectation that exceeds 4%. (Recall also the AR and ARMA model outputs in Figure 2b.) Though long-horizon expectations are difficult to evaluate on purely econometric grounds as there are not many non-overlapping observations, most policy makers and market participants would immediately say that 4% long-horizon CPI inflation expectation is too high; hence models with such an output may fail the test of relevance, before any statistical tests.45
Note also that even if two models generated similar forecast RMSEs, practitioners could have a very different assessment of them, depending on the details of the forecast errors from the models (such as the direction of the errors). In the 1990s inflation data often came in on the "low" side, and it is widely believed that not all of this had been predicted by market participants, i.e., the "true" market forecast of inflation in this period likely contained a mild upward bias.46 Even if there existed a model that generated an unbiased forecast or a forecast with bias in the opposite direction (which would have forecasted inflation better), I doubt whether policy makers would view such a forecast as a realistic description of the market expectation.47
These discussions highlight the role of the larger information set of practitioners (as compared to academic researchers). Unfortunately, much of this extra information is difficult to cast in the formal language of statistical tests, and the proper evaluation of models remains a challenge for macro-finance modeling.
5.5 Would a Bayesian approach help?
The use of the Bayesian techniques to address problems with conventional (classical) estimation has a long history, but a particularly relevant early example is the Bayesian approach to the VAR forecasting. As discussed in Sections 3.5 and 5.1, unrestricted VARs share some of the key problems encountered in flexibly specified macro-finance models, in particular, the statistical (atheoretical) nature of the specification and the tendency for overparametrization. Litterman (1986) and others have documented that a Bayesian implementation with an informative prior ("random walk prior") can generate better results than the classical implementation. This gives an encouragement to take up a Bayesian strategy to address the empirical difficulties with macro-finance models.
In the macro-finance context, Ang, Dong, and Piazzesi (2005) have in fact already proposed a Bayesian approach, but it is not clear that the particular priors that they use would help overcome the problems with classical estimation discussed above. ADP state that except for the condition that the model be stationary their priors are uninformative. However, to the extent that the main problem with the classical estimation of macro-finance models is that the data by themselves are not fully informative about the model (especially as regards the overfitting and small-sample problems), it is difficult to see how uninformative priors would solve the problem. Recall that the superior performance of the Bayesian VARs (over the conventionally estimated unrestricted VARs) came from having an informative prior.
When ADP (2005) tried to estimate their model using a classical method (maximum likelihood estimation), they found that the estimated model explained most of the term structure movements in terms of the latent factor, leaving little role for macro variables to explain yield curve movements,48 an outcome that is unappealing from the viewpoint of making a connection between the macroeconomy and the yield curve. However, even granting the problems with classical methods, there may be a reason for this, namely that the estimation marginalizes the macro variables to avoid the counterfactual implication that shocks to inflation have a tight relation to the yield curve movements. This is a specification issue, i.e, one has to deal with "unspanned" variation in macro variables in the model. Addressing the problem purely as an estimation issue may lead to problems elsewhere in the model.
In my view, the main challenge for a Bayesian implementation is in coming up with suitable informative priors. This is particularly the case when there are latent factors in the model (external basis models with latent factors or internal basis models): because the economic meaning of many of the individual parameters related to the latent factors is unclear, it is difficult to provide sensible priors for them.
For illustration, consider a 3-factor internal-basis nominal-yields-only version of the affine-Gaussian model (1). This model can be normalized in different ways, as discussed in Appendix A. Suppose one has chosen certain normalization. To "simplify" the model, one could
try to impose a prior that
![]() is a diagonal matrix:
is a diagonal matrix:
where
By stating priors about the variables that have direct economic meaning, like inflation expectations, interest rate expectations, and expected bond returns, one can get around this problem of normalization dependence: surely these variables must be normalization independent. Recall also that the source of the small sample problem is the difficulty of estimating the parameters related to expectations (in the physical measure), thus imposing priors on these variables would help alleviate the problem. A prior about the 10-year inflation expectation, for example, can be expressed as
A statement like (54) can be conveniently incorporated within a Kalman-filter setting. Running a Kalman-filter-based ML estimation with with survey median (or mean) forecast (of interest rates and/or inflation) as a noisy proxy, as in D'Amico et al (2007), can be viewed as a "poor man's Bayesian" implementation, the point estimate serving as the mode of the Bayesian posterior.
6 Understanding the superior performance of survey forecast
The specification and implementation problems discussed so far may help explain why macro-finance models, which use more information than the past inflation data, could generate poorer results than simple univariate inflation models. But is the yield curve information useful at all for inflation forecasting? Why do survey forecasts perform better than univariate models (and other models)?
One reason ABW (2007a) offer for the superior performance of survey forecasts is that survey participants have more information about the economy than econometricians. This is in line with the point made in Sec 5.4 that informational differences may create a wedge between a practitioner's and an academic researcher's evaluation of a model. But it is worth exploring this issue further.
One could plausibly expect that survey forecasts may have advantages at least at short horizons, in that a potentially vast amount of information that is relevant for forecasting the near-term inflation might not be easily summarizable in terms of a small number of variables.52It may be thus instructive to examine the near-term expectations in surveys and how they are linked to longer-term expectations (i.e., the term structure of survey inflation forecasts).
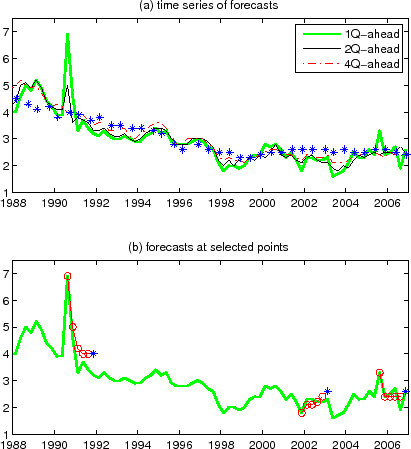 |
Fortunately, fairly detailed information about the near-term term structure of survey inflation expectations can be obtained, as survey forecasts like SPF and BCFF surveys provide CPI inflation forecasts up to the next four or more quarters. Figure 4a shows the one-quarter-ahead, two-quarters-ahead, and four-quarters-ahead CPI inflation forecasts from the Blue Chip Financial Forecasts (BCFF) survey, based on the surveys published in January, April, July, and October (taken at the end of December, March, June, and September), from 1988 to 2006. The BCFF long-horizon forecast (inflation expected between the next five to ten years), available twice a year, is also shown. It is notable that this long-horizon forecast, which can be viewed as a "quasi-long-run" mean of inflation, has moved about (shifted down) significantly. It is also notable how quickly the multi-period forecasts approach the quasi-long-run value. Not only is the 4-quarters-ahead forecast already quite similar to the long-horizon forecast, but also the 2-quarters-ahead forecast is.
Figure 4b further visualizes this point by showing the term structure of inflation expectations out to the next four quarters at several moments when the one-quarter-ahead forecasts were at their local peaks or troughs. Particularly interesting is the case of 1990Q3, when the one-quarter-ahead inflation expectation peaked. The expectations for longer horizons show that even then the survey participants expected inflation to come down quickly to the quasi-long-run level. A more recent example is 2005Q3, in which one-quarter-ahead expectation had risen amid rising oil prices and other near-term inflation pressures. Again, however, this was viewed as a temporary rise that would dissipate quickly. Thus one comes to a somewhat paradoxical conclusion that "the long-term is quite near."
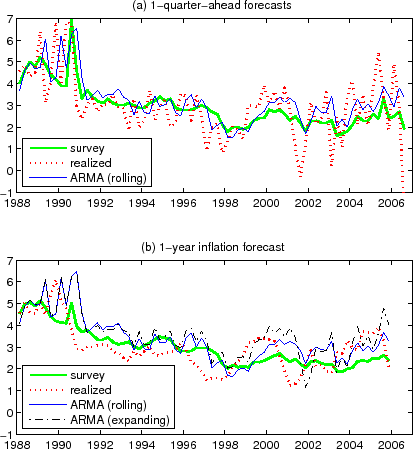 |
To get further insights into the survey forecasts, it is useful to compare them with ex post realized inflation and the real-time forecasts from the ARMA(1,1) model. Figure 5a shows the one-quarter-ahead inflation forecasts based on the BCFF
survey and the ARMA(1,1) model (20-year rolling sample forecast), as well as the realized one-quarter inflation (![]() plotted at
plotted at ![]() ). The one-quarter-ahead survey forecast is seen to be less jagged than the ARMA(1,1) forecast. The ARMA forecast's jaggedness comes from the fact that ARMA is a univariate model, thus the near-term forecast can depend substantially on the
recent realized inflation. (When the previous period's realized inflation is high, current period's inflation expectation tends to be high.) The RMSEs of the one-quarter-ahead forecast are 1.19% and 1.40% (annual percentage unit) in the 1988-2006 period for the survey forecast and the ARMA(1,1)
model, respectively; thus the survey indeed performed better. Nonetheless, much of the realized inflation is missed by the survey forecast. Granting the caveat that surveys might not necessarily be the best possible forecast, this still suggests that a substantial part of short-run inflation is
genuinely unforecastable ex ante, lending support to a formulation like the two-component model (32) in which the inflation process is separated into a trend inflation component and an unforecastable component.
). The one-quarter-ahead survey forecast is seen to be less jagged than the ARMA(1,1) forecast. The ARMA forecast's jaggedness comes from the fact that ARMA is a univariate model, thus the near-term forecast can depend substantially on the
recent realized inflation. (When the previous period's realized inflation is high, current period's inflation expectation tends to be high.) The RMSEs of the one-quarter-ahead forecast are 1.19% and 1.40% (annual percentage unit) in the 1988-2006 period for the survey forecast and the ARMA(1,1)
model, respectively; thus the survey indeed performed better. Nonetheless, much of the realized inflation is missed by the survey forecast. Granting the caveat that surveys might not necessarily be the best possible forecast, this still suggests that a substantial part of short-run inflation is
genuinely unforecastable ex ante, lending support to a formulation like the two-component model (32) in which the inflation process is separated into a trend inflation component and an unforecastable component.
Let us now examine the inflation forecast that most studies focus on, namely the one-year inflation forecast. Figure 5b shows the one-year forecasts based on the BCFF survey and the ARMA(1,1) model, along with the realized one-year inflation (
![]() plotted at
plotted at ![]() ). For reasons that will become clear soon, both the
ARMA(1,1) forecasts from an expanding sample and from a rolling sample are shown. The ARMA forecasts produce substantially larger RMSEs than the survey forecast (1.04% for the 20-year rolling sample ARMA, 1.15% for the expanding sample ARMA, 0.76% for the survey). Since one fourth of the one-year
forecast is the one-quarter-ahead forecast (i.e.,
). For reasons that will become clear soon, both the
ARMA(1,1) forecasts from an expanding sample and from a rolling sample are shown. The ARMA forecasts produce substantially larger RMSEs than the survey forecast (1.04% for the 20-year rolling sample ARMA, 1.15% for the expanding sample ARMA, 0.76% for the survey). Since one fourth of the one-year
forecast is the one-quarter-ahead forecast (i.e.,
![]() ), the superior one-quarter-ahead survey forecast explains part of this. But a still more
basic reason for the superior forecast of the survey is that the ARMA model-based forecasts substantially overpredicted inflation in the 1990s. It can be seen that the ARMA forecasts lie notably above the realized inflation (and survey forecast). This overprediction is due in large measure to the
fact that the ARMA model in real time tended to generate "too high" values of the long-run mean level (
), the superior one-quarter-ahead survey forecast explains part of this. But a still more
basic reason for the superior forecast of the survey is that the ARMA model-based forecasts substantially overpredicted inflation in the 1990s. It can be seen that the ARMA forecasts lie notably above the realized inflation (and survey forecast). This overprediction is due in large measure to the
fact that the ARMA model in real time tended to generate "too high" values of the long-run mean level (![]() in eq. (28)) to which the forecasts are converging.
in eq. (28)) to which the forecasts are converging.
This is illustrated in Figure 6, where the long-run mean parameter ![]() from the expanding sample estimation is seen to lie significantly above the long-horizon
survey forecast. Because the expanding sample includes periods of high inflation (70s and early 80s), the estimated mean does not fall quickly with declining inflation in the 80s and 90s. The use of the 20-year rolling sample produces lower
from the expanding sample estimation is seen to lie significantly above the long-horizon
survey forecast. Because the expanding sample includes periods of high inflation (70s and early 80s), the estimated mean does not fall quickly with declining inflation in the 80s and 90s. The use of the 20-year rolling sample produces lower ![]() (than the expanding sample) as the estimation sample moves away from those periods, but still the adjustment in the long-run mean is not fast enough, compared with the surveys.53
(than the expanding sample) as the estimation sample moves away from those periods, but still the adjustment in the long-run mean is not fast enough, compared with the surveys.53
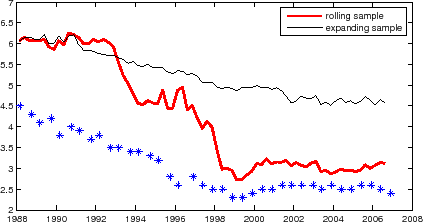 |
The key point that emerges from this discussion is that surveys produce a more successful forecast of inflation in large part because they capture the trend component of inflation better than time-series models like the ARMA(1,1) model. In stationary time series models (e.g., models in Figure 5), forecasts tend to converge to a value close to the sample mean, while nonstationary models put too much weight on recent past; thus there is scope for judgmental information to play a role, especially if trend inflation varies significantly over time. These considerations shed light on the attention that policy makers pay to long-term inflation expectations (better indicator of the trend inflation than realized inflation) and also on the use of judgmental forecasts at central banks like the Federal Reserve.
The importance of modeling the variation of long-term expectations deepens the challenge for macro-finance models: besides the specification challenge, the nearly nonstationary nature of the inflation process indicated by the substantial variability of long-term survey forecasts poses considerable empirical difficulties (discussed in Section 5). These challenges notwithstanding, the discussions in this paper can be viewed as encouraging for attempts to use term structure models to extract inflation expectations: it makes intuitive sense that the yield curve contains, at least, information about trend inflation, and the indication that the near-term informational advantage of surveys seems to wear out quickly (beyond a few quarters) gives some hope that models could capture much of the variation in inflation expectations and compete with surveys.54
7 Concluding remarks
I conclude this paper with a recapitulation of some of the key points and some remarks on how they are related to each other and to other points also made. In particular, consider the following points: (1) Not all of the variation in key macro variables is related to yield curve movements. (2) The yield curve contains useful information about the trend component of inflation. (3) The no-arbitrage principle might not be sufficient to guarantee sensible outputs from macro-finance models in practice.
As I have stressed in Section 2, the spanning argument is the basis of the no-arbitrage framework; hence the presence of a short-run inflation component that is not related to yield curve movements may undermine the validity of the models that use inflation as a state variable. Such a component may also cause difficulties in the estimation stage as well, since taking too seriously the one-period conditional moments that involve it may not be justified (Section 5.3). Furthermore, they may cause special difficulties when one tries to go beyond the affine-Gaussian setup to model time-varying uncertainties about macro variables explicitly. For example, as discussed in Section 4.2, monthly CPI inflation in recent years has been more volatile than in the 1990s, but there isn't strong evidence that this is reflected in the yield curve (e.g., as an increased term premium); an attempt to link them may thus lead to greater specification errors.
I have also argued in this paper that much of the "spanned" component of inflation (the part of inflation that is related to the yield curve) is about the trend component (whose importance was stressed in the discussion in Section 6 of why surveys perform better). This can help resolve the puzzle that the "conventional wisdom" that the change in nominal yields often reflects changes in inflation expectations dies hard, despite the poor performance of inflation forecasting models involving term structure variables. In some sense, the latent-factor models can be viewed as a way to represent market's implicit processing (filtering) of information.
No-arbitrage models of the term structure have been viewed as a promising way to go beyond the restrictive assumptions implicit in the expectations hypothesis (about how risk is incorporated in the yield curve). However, reduced-form affine-Gaussian no-arbitrage models with flexible specification of market price of risk can quickly become "too unrestrictive", with a profusion in the number of parameters of the market price of risk. In other words, the no-arbitrage principle by itself may be too weak to provide enough discipline in the model. Note also that the two technical problems with estimation discussed in Section 5 (overfitting and small sample problems) can be viewed as an extension of the specification discussion, as the main source of the problems can be viewed as there being not enough information in the data or not enough structure in the model. Coming up with an effective and non-ad hoc structure on the market price of risk and other parameters of macro-finance models thus remains an important challenge for these models.
8 DERIVATION OF THE MAXIMALLY IDENTIFIED MODELS
This Appendix shows that any ![]() -dimensional "yield-only" internal basis affine-Gaussian model (1) whose feedback matrix has all-real eigenvalues can be transformed to
the normalized form
-dimensional "yield-only" internal basis affine-Gaussian model (1) whose feedback matrix has all-real eigenvalues can be transformed to
the normalized form
written out for the case
where
| (57) |
Define an new normal random vector
| (58) |
with an orthogonal matrix
| (59) |
Thus we have
Now, define
We have
| (62) |
where
is by construction a lower triangular whose diagonal elements are 1's. We can now express the pricing kernel in terms of
where
is equivalent to the normalization in eq. (55), i.e., it can be written in the form of eq. (55) through an invariant transformation (64).
9 BIAS IN THE MISHKIN REGRESSION
This appendix presents a heuristic demonstration of a bias in the Mishkin regression. Suppose that nominal yields are entirely inflation expectations (no real yield component). Thus,
| (66) |
for general
where
| (68) |
It is well known that
| (69) |
where
| (70) |
Using eq. (67), this can be written
| (71) |
where
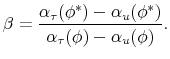 |
(72) |
It can be shown that for
Sims, C. (2002), "Comment", NBER Macroeconomics Annual 2001.
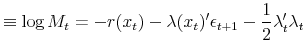
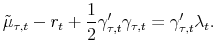
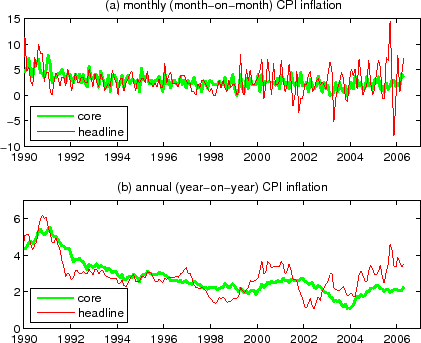
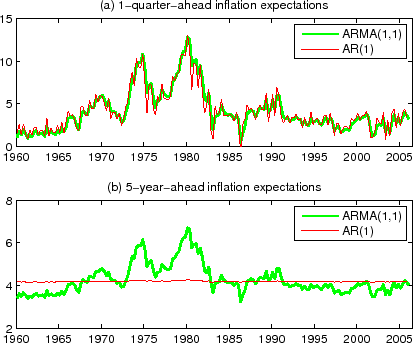
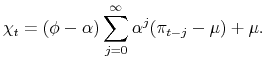
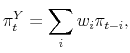
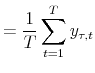
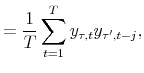
![\displaystyle \tilde{\mathcal{K}} = \left[\begin{matrix}\kappa_1 & 0 & 0 0 & \kappa_2 & 0 0 & 0 & \kappa_3 \end{matrix}\right], \tilde{\Sigma}= \left[\begin{matrix}1 & 0 & 0 \Sigma_{21} & 1 & 0 \Sigma_{31} & \Sigma_{32} &1 \end{matrix}\right], \tilde{\mu} = 0_{3\times 1}, \tilde{\rho}_o, \tilde{\rho}, \tilde{\lambda}_a, \tilde{\Lambda}_b,](img264.gif)
![\displaystyle \mathcal{K}= \left[\begin{matrix}\kappa_{11} & 0 & 0 \kappa_{21} & \kappa_{22} & 0 \kappa_{31} & \kappa_{32} & \kappa_{33} \end{matrix}\right], \Sigma= I_{3\times 3}, \mu = 0_{3\times 1}, \rho_o, \rho, \lambda_a, \Lambda_b,](img293.gif)