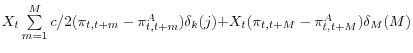The Federal Reserve Board eagle logo links to home page
Skip to: [Printable Version (PDF)] [Bibliography] [Footnotes]
Finance and Economics Discussion Series: 2008-08 Screen Reader version ♣

The "Growing Pains" of TIPS Issuance

Jennifer E. Roush1
Board of Governors of the Federal Reserve System
October 16, 2007

Keywords: Inflation risk premium, liquidity premium, treasury issuance

Abstract:

This paper provides updated calculations of the relative cost to the U.S. Treasury of previously issued TIPS by comparing the payment stream on each security to that of hypothetical nominal counterpart. While the costs of the program (so measured) are large, totaling $5 to $8 billion to date, I show that they owe largely to market illiquidity in the early years of the program. Indeed, absent these market growing pains, the program would have yielded a substantial net savings to the government as investors were willing to pay a premium to insure against inflation risk.

I. Introduction

On December 15, 2006, the BLS released the November 2006 CPI and, as a result, the payment stream on the January 15, 2007 Treasury Inflation Protected Security (henceforth TIPS) became fully known. 2 This made it possible to calculate the actual cost to the Treasury of issuing this security relative to the cost it would have incurred if it had instead issued a nominal security.

As Sack and Elsasser (2004) and Sack (2006) have shown, such relative cost calculations do not put the program in a favorable spotlight. Indeed, I update the original cost calculations by these authors and find that the TIPS program has cost the Treasury $4.5 to $7.5 billion to date. After incorporating expected future inflation payments on TIPSs that have already been issued, the estimated cost increases to between $8.5 to $16.5 billion.3

A question naturally arises: Is the TIPS program a mistake? These calculations suggest that the program has cost the tax payer billions of dollars that could have been spent on any of a number of important domestic projects. Even more important, however, for current policy makers is the question: Do these calculations imply that the TIPS program will continue to incur costs in the future?

There are a number of economic arguments that imply that the answer to both of these questions is No. The most obvious of these was made by Campbell and Shiller (1996) that relative cost calculations are in fact misleading because they involve an accounting of funds transferred between tax payers and bond holders, and therefore do not reflect any change in the welfare of the society as a whole. In addition, the TIPS program may benefit society in ways that are not captured by direct cost calculations. To name a few, TIPS provide monetary policy authorities with important real time information about inflation expectations and fiscal policy makers a direct incentive to align their spending with low inflation objectives. As discussed by Tobin (1963), inflation indexed securities also allow for a more optimal allocation of inflation risk, away from households whose savings objectives are in real terms, and toward those with an interest in acquiring such risk.

While these arguments are important to the policy debate, it is difficult to assign value to the factors involved, making it hard to know if they are sufficient to offset the measurable costs. This paper responds `No' to the same questions, but does so by staying within the original relative cost framework and digging deeper into what factors underlie the costs as measured. In the end, I find that the historical costs of the TIPS program appear to be largely due to `growing pains.' In particular, after accounting for discounts in TIPS prices that owed to illiquidity in the market in the early years of the program, cost calculations reveal that the counterfactual TIPS program would have actually saved the Treasury billions of dollars. I also show that, contrary to speculation by Sack and Elsasser (2004), the price premiums on on-the-run nominal Treasury securities during the financial turmoil of the late 1990s did not play an important role in making TIPS relatively more costly to issue during this period.

These distinctions are important because they mean that the relative cost of the TIPS program to date is essentially `water under the bridge.' Although policy makers may not have fully accounted for the costs of building a liquid TIPS market in initiating the program, these costs should not be incurred again unless there is a sizeable impingement on the liquidity of the market going forward. More than that, if history is any lesson, the results presented here provide evidence that, absent the illiquidity discounts of the past, future TIPS issuance is likely to yield a substantial net savings to the Treasury as it collects the premiums investors are willing to pay to be insured against inflation risk. Note that the outlook would not be nearly as bright if liquidity premiums in the on-the-run nominal market were the most important factor driving past costs, since the variation in these premiums is ongoing and is notoriously hard to predict.

The remainder of this paper is structured as follows. The next section provides an overview of how the relative cost of TIPS issuance is measured and updates the original calculations. Section 3 then evaluates the role of illiquidity discounts in TIPS prices, using results from D'Amico, Kim, and Wei (2007). Section 4 focuses on the role of liquidity premiums in on-the-run Treasury prices. Section 5 concludes.

II. The Relative Cost of TIPS Issuance

The relative cost of each TIPS issue can be measured by comparing the inflation payments made by the Treasury to holders of TIPS securities ( \pi _{t,t+m} ) with the breakeven inflation rate received by the Treasury at the TIPS auction (\pi _t^A ), expressed in present value terms. Sack and Elsasser assume \pi _t^A is constant over the life of the security, which allows them to estimate \pi _t^A as the implied inflation rate that equates the price of each TIPS security at auction, P_t ^{TIPS}, to a hypothetical on-the-run nominal security with the same real payment stream as the TIPS issue.4 The hypothetical security is constructed as the present discounted value of the real coupon payments on the TIPS security (c^{TIPS}) multiplied by the breakeven inflation rate, using a discount rate,\gamma _t (m), from a nominal on-the-run zero coupon yield curve, y_t^m (expressed as annual rates):

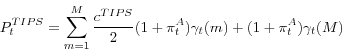
\begin{displaymath} P_t ^{TIPS}=\sum\limits_{m=1}^M {\frac{c^{TIPS}}{2}(1+\pi _t^A )\gamma _t (m)} +(1+\pi _t^A )\gamma _t (M) \end{displaymath}

with
\begin{displaymath} \gamma _t (m)=\frac{1}{(1+\frac{y_t^m }{2})^{2m}} \end{displaymath}

The choice of y_t^m is potentially important because it values the amount that the Treasury would have received with nominal issuance. Sack and Elsasser use a constant maturity on-the-run zero-coupon rate obtained from the Treasury Department. However, the fact that there are only a small number of nominal on-the-run issues makes estimation of an on-the-run yield curve imprecise at best. I avoid this problem by calculating y_t^m from an off-the-run constant maturity zero-coupon yield curve and subtracting a range of estimates for the on-the-run/off-the-run yield spread.5 The range is determined by the minimum and maximum values of the current 2, 5, 10 and 30 year on-the-run yield spread over a synthetic off-the run yield. This in turn delivers an upper and lower bound for the auction breakeven rate.6

The relative cost of each TIPS issue is then calculated as the difference between the payment streams on the hypothetical nominal and inflation indexed securities multiplied by the issuance amount:7

X_t \sum\limits_{m=1}^M {c/2(\pi _{t,t+m} -\pi _{t,t+m}^A )\delta _k (j)+} X_t (\pi _{t,t+M} -\pi _{t,t+M}^A )\delta _M (M)8

where t is the auction date and t+m is the date of the coupon payment. Here X_t is the issuance amount and the discount/compounding function, \delta _k (j)--wherej=T-(t+m), with T equal to the date of evaluation, and k=\min (T,t+m)--is determined by the term structure of nominal interest rates:

\begin{displaymath} \delta _k (j)=\frac{1}{(1+\frac{i_k^{\vert j\vert } }{2})^{2j}}\quad . \end{displaymath}

where i_k^{\vert j\vert } is the \vert j\vert -period zero-coupon nominal interest rate on date k.9

Results

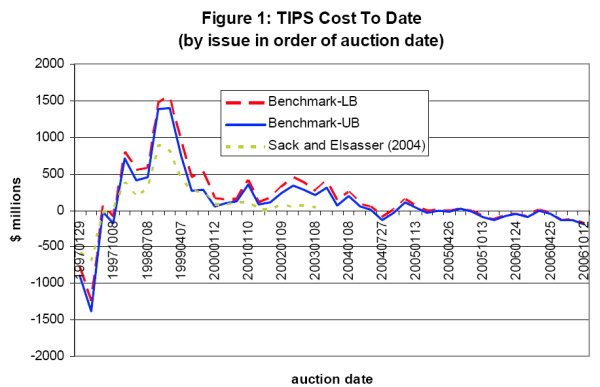
Figure 1 shows the cost of each TIPS to date, ordered by their auction date along the x-axis and with re-openings shown separate from their original issue. For the purposes of this paper, I consider TIPS securities issued through March 30, 2007, using known CPI data through February, 2007. Figure 1 below shows the costs measured only over coupon dates for which the inflation rate is known, in this case on coupon payments made through May 1, 2007.10 The lower (LB) and upper bounds (UB) of the cost for each security are shown by the dashed red and solid blue lines, respectively. The original calculations from Sack and Elsasser are shown by the dotted green line for comparison.11 The results calculated for this paper are also given in Table 1 in the Appendix.

The first few TIPS issues provided savings for the Treasury. The inaugural TIPS issue maturing in January 2007 involved savings from $782 million to $900 million, and its subsequent reopening saved the Treasury about $1.3 billion. The next issue (which matured in July 2002) approximately broke even, while its reopening saved the Treasury between $100 million and $184 million. However, all issues in the next seven years registered positive costs, with the largest costs occurring on issues auctioned in the late fall of 1998 and early 1999.12

Figure 1. Refer to Figure 1 Data link for source data.
Figure 1 Data

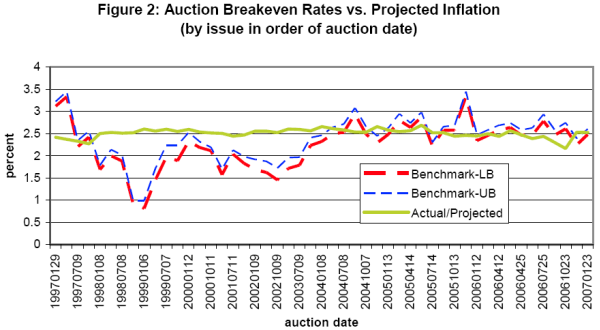
Sack and Elsasser note that this peak coincides with several financial crises in emerging markets as well as the collapse of LTCM, which were associated with heightened liquidity premiums in the on-the-run nominal market.13 They suggest that flight-to-quality flows into nominal Treasury yields may have effectively pushed auction breakeven rates well below actual inflation expectations, leading to higher relative issuance costs on these securities. In fact, auction breakeven rates were below actual/projected inflation during this period as shown in Figure 2 below.14 Of course this discrepancy could have resulted for other reasons as well: investor expectation errors in projecting inflation; or because of other risk factors such as an undervaluation of TIPS due to investor uncertainty about their ability to resell the securities into a illiquid market.

Figure 2. Refer to Figure 2 Data link for source data.
Figure 2 Data

Beginning in mid-1999, the cost of TIPS issuance declined, but remained positive, as breakeven rates at TIPS auctions began to rise back to the level of actual/projected inflation. The increase in breakeven rates is consistent with decreasing liquidity premiums in the on-the-run nominal market during this period as well as growing liquidity in the TIPS market. In addition, Kim and Wright (2005) have shown that estimates of inflation risk premia from three factor no-arbitrage models of the real and nominal term structures increased modestly over this period, implying increased attractiveness of TIPS relative to nominal issuance for the Treasury.

Since early 2004, TIPS issues have yielded a net savings for the Treasury. Since then, auction breakeven inflation rates have averaged a bit above realized inflation, implying a net savings of $308 million to $822 million. At first pass, this turn of fortune appears to bode well for future TIPS issuance. Ultimately, however, a better understanding of the factors underlying the variation in cost over time will be most helpful in projecting future costs. Note that if large liquidity premiums in the nominal Treasury market due to flight-to-quality flows were a dominant influence on previous costs, the future could easily see similar influences, making the cost of future TIPS issuance difficult to predict. All said, the primary message to take away from the results presented so far is that the total cost to date on all matured and outstanding TIPS issues is estimated at $4.5 billion to $7.5 billion.15

Total Cost Estimates

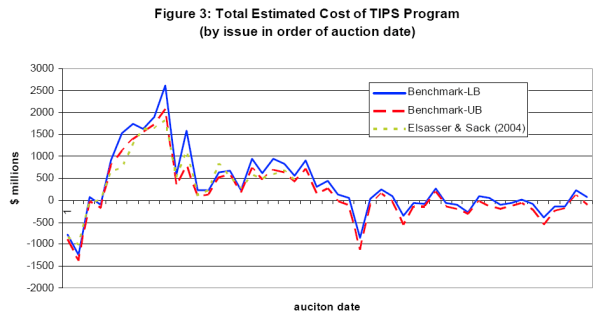
The above calculations measure the actual cost of TIPS payments in the past. However, for securities with remaining time to maturity, a potentially large portion of their eventual cost will depend on how inflation evolves relative to the breakeven rate paid to the Treasury at auction. Figure 3 presents the estimated total cost of all TIPS securities based on the assumption that headline CPI inflation will match the long-run SPF forecast of 2.5 percent over the remaining time to maturity for each issue. As above, the dashed red and blue lines present the lower and upper bounds for these costs, while the green line again presents point estimates from Sack and Elsasser for comparison. Columns 11 and 12 in Table 1 present the numbers underlying the figure.

Figure 3 also suggests that the outlook for outstanding TIPS issues has changed considerably in the last few years. TIPS issued since the beginning of 2004 are predicted to result in a net gain for the Treasury of $1.1 billion to nearly $4 billion. In these cases, the breakeven rates at auction generally exceed the predicted inflation rate based on survey data, suggesting the influence of a positive, albeit small inflation risk premium of 6 to 19 basis points, on average over this period.16 Alternatively, it could be that the survey data are a worse predictor of inflation than TIPS spreads during this period.17 If inflation turns out to be higher than 2.5 percent on average going forward, the benefit to Treasury of issuing these TIPS would erode. These caveats aside, and considering both matured and outstanding TIPS, the estimated total cost of the program is $8.5 to $16.5 billion.

Figure 3. Refer to Figure 3 Data link for source data.
Figure 3 Data

II. Accounting for TIPS Illiquidity

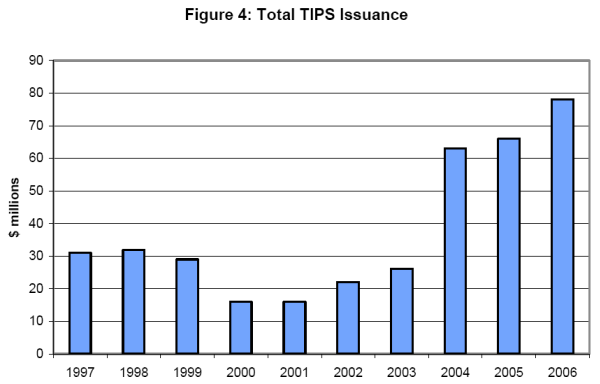
An important consideration in interpreting the cost calculations presented so far is that the TIPS market was developing throughout the period considered. For at least the first several years of the program, markets were uncertain whether the secondary market for TIPS would evolve into an active and liquid trading environment. At the time, they had good reason to be uncertain. In May 2001, the Bond Market Association recommended the termination of the TIPS program because it had "proven to be an expensive adjunct to the Treasury borrowing program."18

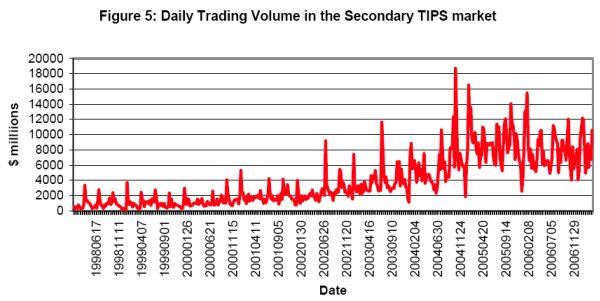
The Treasury reaffirmed its commitment to the TIPS program in its Quarterly Refunding Statement in May 2002 in an effort to reassure investors, but it wasn't until 2004 that the total quantity of TIPS issued by the Treasury substantially exceeded the amount issued in the first year of the program.19 In addition, participation in the market was likely hampered by the fact that some institutional investors are restricted from buying new asset classes. In the years since 2004, TIPS issuance has increased each year, and in 2006 it was more than two and a half times that in the first year of the program. Meanwhile, TIPS trading volumes were quite low until around mid-2002, with turnover less than 1 percent of that in the nominal Treasury market.

Figure 4. Refer to Figure 4 Data link for source data. Figure 4 Data

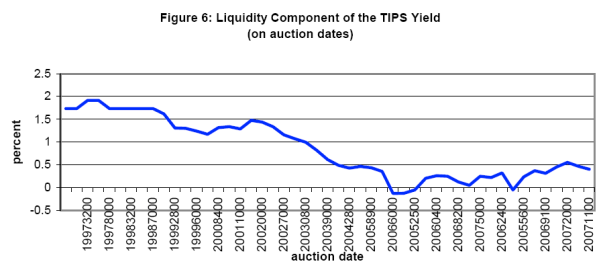
D'Amico, Kim, and Wei (2007) estimate that TIPS prices were importantly affected by an illiquidity discount during the first several years of the program. The graph below shows their estimate of TIPS yield that is attributable to this discount on auction days. To obtain these values, the authors estimate a latent, three-factor no-arbitrage affine term structure model of the TIPS and nominal yield curves, specifying the observed TIPS yield as the sum of the real yield and a liquidity component.20 Because their nominal curve is based on securities that are second-off-the run or higher, the product is essentially an estimate of the TIPS yield with the same liquidity as a nominal off-the-run security.

Figure 5. Refer to Figure 5 Data link for source data.
Figure 5 Data

Figure 6. Refer to Figure 6 Data link for source data.
Figure 6 Data

The table below reports new cost calculations using the DKW series to adjust TIPS prices to account for the illiquidity discount in TIPS prices.21 The first row repeats the net cost of the program to date and in total in the benchmark model. The second row reports what the estimated cost of TIPS issuance would have been for this period if the secondary market for TIPS market had been as liquid as it was at the end of the sample, in March 2007. Remarkably, the previously estimated cost results are now more than fully reversed: had it not had to go through the growing pains associated with developing a liquid market, the program would have resulted in an estimated net savings of $14 to $17 billion.

Table 1: Cost of TIPS Program Under Counterfactual Liquidity Assumptions


  Total Cost
($ billions ) 		Cost to Date
($ billions )
Benchmark (8.5, 16.5) (4.6, 7.6)
TIPS adj. for same liquidity as in March 2007 (-31.7, -22.5) (-17.2, -14.0)

Notes: The benchmark results are shown in the first row. The second row examines counterfactual exercises when TIPS are priced with the same liquidity as in the last month of the period, using the liquidity premium from D'Amico, Kim, Wei(2007). Negative numbers reflect net savings.

IV. Super-liquidity in the Nominal On-the-Run Treasuries Market

The on-the-run nominal U.S. Treasury market is by many measures the most liquid fixed income market in the world. As a result, investors are willing to pay a premium for on-the-run securities relative to otherwise similar securities of older issuance. This fact alone could have important consequences for the relative cost calculations because during periods when investors seek out the safety of Treasury securities in large numbers the increase in this premium may be large enough to swamp the premium investors are willing to pay for inflation protection. As already noted, if these effects are large, they would also imply that the relative cost of future TIPS issuance would be as hard to predict as the events that cause such flight-to-quality flows into the nominal market.

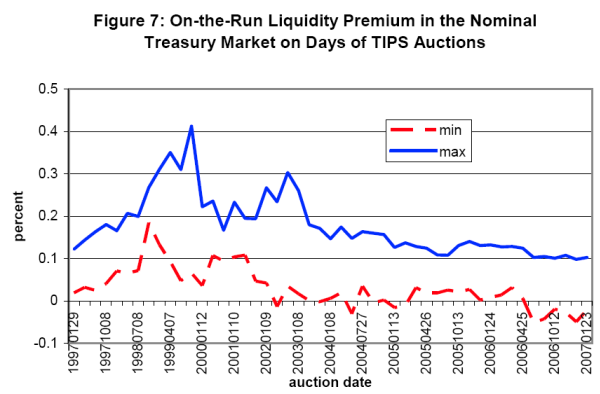
Figure 7 reports liquidity premiums in the nominal Treasury market on the days of TIPS auctions, measured as the yield spread of the off-the-run nominal Treasury security over the comparable on-the-run note.22 The maximum liquidity premium is particularly large on auction days in October 1998 and through much of 1999, suggesting that this may be an important factor in the relative cost of the TIPSs issued during this period. Over the full sample, the correlation between the cost of each TIPS issue and the nominal on-the-run liquidity premium is statistically significant at 65 percent.

To measure the effects of the liquidity preference that the nominal Treasury market has benefited from historically, I recalculate the relative cost of TIPS issuance under two counterfactual assumptions about the maximum and minimum liquidity premiums used to constitute the hypothetical on-the-run Treasury issue discussed in Section 2. First, I assume that the maximum and minimum liquidity premiums are equal to their averages during the period from September 2006 to January 2007, a period which is generally perceived to be one of relative calm in financial markets when flight-to-

Figure 7. Refer to Figure 7 Data link for source data.
Figure 7 Data

quality flows into nominal Treasury securities were not likely to have been an important driver of yields in that market, if they were present at all. Supporting this view of the

period, stock markets saw double digit gains and their daily returns were negatively correlated with bond yields; a positive correlation during stock price declines can be a signal of increased risk aversion or higher perceived risk that prompts investors to shift out of equities and into bonds. Moreover, a variety of risk spreads, including those of U.S. corporate bonds and emerging market sovereign debt, over comparable U.S. Treasury yields were at historically low levels throughout this period, as were implied volatilities derived from options, including the VIX as well as those on a variety of interest rate instruments. I also perform the cost calculations under a more extreme counterfactual assumption that the spread between the off- and on-the-run nominal Treasury security is zero.

The first column of data in Table 2 below shows the estimated total cost of TIPS under the original cost calculations, and under the first and second assumptions in rows two and three, respectively (labeled accordingly `hypothetical on-the-run nominal with no flight-to-quality' and `hypothetical off-the-run'). The cost of TIPS issuance declines about 30 percent after taking out the flight-to-quality effects and 20 to 60 percent assuming there is no liquidity premium in the on-the-run market. Nonetheless the costs are still considerable totaling between $3 to 11 billion. Thus while the super-liquidity of the on-the-run market has contributed in part to the net relative cost of TIPS, it is not a dominant driver.

Table 2: Cost of TIPS Program Under Counterfactual Assumptions about On-the-Run Nominal Treasury Premium


  Total Cost
($ billions ) 		Cost to Date
($ billions )
Benchmark (8.5, 16.5) (4.6, 7.6)
hypothetical on-the-run nominal with no flight-to-quality (6.0, 11.6) (3.3, 5.4)
hypothetical off-the-run nominal 6.7 3.6

Notes: The column labels at the left of each table refer to assumptions about hypothetical alternative nominal on-the-run Treasury issues used in determining the relative cost of the actual TIPS issues. The benchmark results consider the case when, instead of each TIPS issue, the Treasury issued a hypothetical on-the-run nominal issue with the same coupon structure. The second and third rows of the tables examine the role that the liquidity premium in the nominal Treasury market plays in determining the cost in the benchmark case.

V. Conclusion

This paper reports new calculations of the relative cost of all outstanding TIPS to date, measured as the cumulative cost of inflation compensation on coupon payments occurring before May 1, 2007. I also report new predictions for the total relative cost of TIPS, measured as the cumulative cost of inflation compensation on all coupon payments through maturity of each security, assuming future inflation follows long-run survey forecasts.

These results show that while the first two issues of TIPS resulted in savings for the Treasury, the total cost of the program to date is $5 billion to $8 billion. Including estimates of the future cost of inflation payments on all matured and outstanding TIPS implies a total cost for the TIPS program of $9 billion to $17 billion.

However, if one focuses on TIPS issued since 2004, the story is much different. The majority of these issues have yielded net savings for the Treasury. Taken together, these securities have resulted in a net savings of hundreds of millions to date, and are projected to result in a net savings of $1 to $4 billion over their full life.

What explains this change in fortune? I examine two hypotheses: that the costs in the first years of the program were due to unusual flight-to-quality flows into the on-the-run nominal Treasury market during the late 1990s which put these securities at a pricing advantage relative to TIPS at auction; and that the early costs were due to an undervaluing of TIPS due to their "newness" and the resulting uncertainty about their liquidity in the secondary market. The evidence presented here suggests that the second factor was by far the most important. In fact once I exclude these illiquidity effects, the costs calculations are more than fully reversed: the counterfactual TIPS program is estimated to have saved the Treasury $14 to $17 billion to date. While the size of these estimated savings is necessarily imprecise, they provide considerable room for optimism about future TIPS issuance.


References

Ang, Andrew, Bekaert, Geert, and Wei, Min,"Do Macro Variables, Asset Markets or Surveys Forecast Inflation Better?" Journal of Monetary Economics (forthcoming)

Campbell, John, and Shiller, Robert (1996), "A Scorecard for indexed Government Debt," National Bureau of Ecnomic Research Working Paper 5587

Capra, James R. (Chairman), and Jay, Timothy W. (Vice Chairman), "Report to the Secretary of the Treasury from the Treasury Borrowing Advisory Committee of The Bond Market Association," May 1, 2001, http://www.treas.gov/offices/domestic-finance/debt-management/adv-com/reports/rpt-2001-q2.pdf.

D'Amico, Stefania, Kim, Don, and Wei, Min (2007), "TIPS from TIPS: The Informational Content of Treasury Inflation-Portected Security Prices," Finance and Economics Discussion Series (forthcoming), Federal Reserve Board of Governors

Gurkaynak, Refet, Sack, Brian, and Wright, Jonathan (2006), The U.S. Treasury Yield Curve: 1961 to the Present," Finance and Economics Discussion Series 2006-30, Federal Reserve Board of Governors.

Gurkaynak, Refet, Sack, Brian, and Wright, Jonathan (2007)," The TIPS Yield Curve and Inflation Compensation," manuscript, Board of Governors of the Federal Reserve.

Kim, Don, and Wright, Jonathan (2005) " An Arbitrage-Free Three-Factor Term Structure Model and the Recent Behavior of Long-Term Yields and Distant Horizon Forward Rates," Finance and Economics Discussion Series 2005-33, Federal Reserve Board of Governors.

Sack, Brain and Elsasser, Robert (2004) "Treasury Inflation Indexed Debt: A review of the U.S. Experience, FRBNY Economic Policy Review, May 2004.

Sack, Brian (2006), " Treasury Saves a Billion on January 2007 TIPS," Monetary Policy Insights, Fixed Income Focus, Macroeconomic Advisors, December 15, 2006.

Tobin, James (1963), "Essays on Principles of Debt Management," in Commission on Money and Creidt, Fiscal and Debt Management Policies, Englewood Cliffs, N.J.:Prentice-Hall, Inc.


Appendix

Auction date Maturity date Coupon (percent) Par amount issued ($billions) Auction Breakeven Inflation (percent)
LB 		Auction Breakeven Inflation (percent)
UB 		Actual Inflation (to date) Projected Inflation (to maturity) Cost to Date ($millions)
LB 		Cost to Date ($millions)
UB 		Total Estimated Cost ($millions)
LB 		Total Estimated Cost ($millions)
UB
1/29/97 1/15/07 3.375 7 3.12 3.22 2.42 2.42 -782 -900 -782 -900
4/8/97 1/15/07 3.375 8 3.33 3.45 2.37 2.37 -1240 -1389 -1240 -1389
7/9/97 7/15/02 3.625 8 2.20 2.34 2.33 2.33 66 -16 66 -16
10/8/97 7/15/02 3.625 8 2.42 2.56 2.27 2.27 -100 -184 -100 -184
1/8/98 1/15/08 3.625 8 1.69 1.78 2.48 2.50 802 706 903 798
4/8/98 4/15/28 3.625 8 2.00 2.14 2.54 2.53 546 402 1517 1129
7/8/98 4/15/28 3.625 8 1.88 2.01 2.47 2.51 587 458 1738 1396
10/7/98 1/15/08 3.625 8 0.91 0.99 2.50 2.52 1463 1390 1632 1552
1/6/99 1/15/09 3.875 8 0.82 0.99 2.60 2.60 1549 1404 1896 1721
4/7/99 4/15/29 3.875 7 1.45 1.71 2.65 2.56 923 732 2603 2063
7/7/99 1/15/29 3.875 7 1.97 2.24 2.60 2.60 455 266 570 333
10/6/99 4/15/29 3.875 7 1.89 2.24 2.62 2.55 528 282 1579 788
1/12/00 1/15/10 4.25 6 2.33 2.52 2.60 2.59 164 55 223 68
7/12/00 1/15/10 4.25 5 2.18 2.31 2.52 2.53 145 89 220 139
10/11/00 4/15/29 3.875 5 2.11 2.19 2.49 2.51 154 123 628 516
1/10/01 1/15/11 3.5 6 1.57 1.70 2.47 2.50 406 348 683 591
7/11/01 1/15/11 3.5 5 2.04 2.12 2.36 2.44 104 74 224 174
10/10/01 4/15/32 3.375 5 1.83 1.98 2.33 2.47 165 115 938 729
1/9/02 1/15/12 3.375 6 1.69 1.92 2.56 2.55 318 236 610 454
7/10/02 7/15/12 3 9 1.63 1.88 2.57 2.55 450 332 940 695
10/9/02 7/15/12 3 7 1.45 1.72 2.50 2.52 384 285 831 627
1/8/03 7/15/12 3 6 1.72 1.96 2.68 2.60 272 204 567 415
7/9/03 7/15/13 1.875 11 1.79 1.97 2.69 2.59 392 314 914 715
10/9/03 7/15/13 1.875 9 2.23 2.41 2.60 2.56 133 71 314 150
1/8/04 1/15/14 2 12 2.32 2.46 2.94 2.66 255 198 438 263
4/7/04 1/15/14 2 9 2.49 2.64 2.77 2.61 90 43 123 -24
7/8/04 7/15/14 2 10 2.53 2.71 2.72 2.58 54 5 56 -128
7/27/04 1/15/25 2.375 11 2.95 3.08 2.61 2.53 -100 -140 -850 -1138
10/7/04 7/15/14 2 9 2.48 2.65 2.52 2.53 10 -31 44 -108
10/26/04 4/15/10 0.875 12 2.29 2.45 2.76 2.66 150 100 247 142
1/13/05 1/15/15 1.625 10 2.48 2.62 2.75 2.58 60 29 100 -40
1/25/05 1/15/25 2.375 8 2.79 2.94 2.74 2.54 -7 -33 -344 -567
4/14/05 1/15/15 1.625 9 2.64 2.74 2.68 2.56 10 -9 -60 -148
4/26/05 4/15/10 0.875 9 2.87 2.98 2.86 2.69 -1 -22 -82 -132
7/14/05 7/15/15 1.875 9 2.21 2.30 2.42 2.52 32 19 259 183
7/26/05 1/15/25 2.375 6 2.57 2.66 2.45 2.52 -10 -18 -54 -140
10/13/06 7/15/15 1.875 8 2.57 2.69 1.94 2.44 -79 -93 -104 -189
10/25/05 4/15/10 0.875 7 3.33 3.45 2.23 2.46 -119 -132 -275 -312
1/12/06 1/15/16 2 9 2.34 2.47 1.65 2.44 -63 -75 83 -26
1/24/06 1/15/26 2 10 2.46 2.58 2.02 2.50 -44 -57 59 -142
4/12/06 1/15/16 2 8 2.57 2.69 1.58 2.44 -81 -91 -105 -193
4/14/05 1/15/15 1.625 9 2.64 2.74 2.68 2.56 10 -9 -60 -148
4/25/06 4/15/11 2.375 11 2.46 2.58 2.13 2.47 -35 -49 7 -60
7/13/06 7/15/16 2.5 9 2.47 2.63 -0.35 2.39 -130 -137 -83 -215
7/25/06 1/15/26 2 7 2.78 2.93 -0.79 2.44 -128 -133 -393 -563
10/12/06 7/15/16 2.5 8 2.46 2.59 -1.99 2.30 -182 -187 -138 -230
10/23/06 4/15/11 2.375 7 2.61 2.74 * 2.16 0 0 -141 -183
1/11/07 1/15/17 2.375 9 2.24 2.39 * 2.53 0 0 236 116
1/23/07 1/15/27 2.375 8 2.48 2.60 * 2.53 0 0 64 -95
Total               7575 4572 16500 8489
Total Since 2004               -308 -822 -1133 -3912


Footnotes

1. Email: [email protected]; mail address: Division of Monetary Affairs, Mailstop 74, Board of Governors of the Federal Reserve System, 20th and C St. NW, Washington DC 20551. I am grateful to Jonathan Wright, Benson Durham, Jim Clouse, David Wilcox, Bill Dudley, and Michelle Steinberg for valuable comments and to Stefania D'Amico for sharing data results from D'Amico, Kim and Wei(2007). The views in this paper are solely the responsibility of the author and should not be interpreted as reflecting the views of the Board of Governors of the Federal Reserve System or of any other person associated with the Federal Reserve System. Return to Text
2. TIPS pay inflation with a two and a half month lag. For example, a coupon payment on 1/15/2007 will compensate the TIPS holder for a weighted average of the CPI for October and November 2006. Return to Text
3. In a similar spirit, Gurkaynak, Sack, and Wright (2007) show that the excess TIPS returns exceeded excess nominal returns during the period from January 1999 to June 2007, although they focus on returns from holding these securities for only one year. Return to Text
4. The calculation actually uses a "dirty price" that includes payment for accrued interest, adjusted by inflation compensation over the same period. Return to Text
5. These rates are taken from the nominal Svensson(1994) yield curve based on second off-the run securities. See Gurkaynak, Sack and Wright (2006) for description of this yield curve. Return to Text
6. This approach assumes a static nominal issuance strategy by Treasury in that it does not account for nominal issuance to cover costs incurred by a difference in realized and breakeven inflation over the life of the TIPS. Previous work on the cost of TIPS (cited above) has found calculations based on a dynamic issuance strategy to be largely similar to those assuming a static strategy in present value terms. Return to Text
7. This approach assumes a static nominal issuance strategy by Treasury in that it does not account for nominal issuance to cover costs incurred by a difference in realized and breakeven inflation over the life of the TIPS. Previous work on the cost of TIPS (cited above) has found calculations based on a dynamic issuance strategy to be largely similar to those assuming a static strategy in present value terms. Return to Text
8. Realized inflation is actually measured from headline non-seasonally adjusted CPI 2.5 months prior to the issue date to 2.5 months prior to the most recent coupon to account for the lagged indexation of TIPS securities. For clarity I suppress this detail in the notation. Return to Text
9. This calculation ignores tax effects which may matter to the total cost of TIPS in this sample. Whereas the inflation stream on TIPS is taxable (implying a receipt stream to the Treasury), only the anticipated rate of inflation imbedded in nominal yields is taxable. Over time, these effects should sum to zero if inflation forecast errors are unbiased. Return to Text
10. The difference in dates is due to the lagged indexation of TIPS. Return to Text
11. Note that the Sack and Elsasser measure cost to date on the same issues over a period ending farther in the past, and thus with a shorter sample of known inflation. Return to Text
12. The assumption that the breakeven inflation rate is constant over the life of the bond may be contributing to higher (or lower) costs. If, for example, inflation is expected to be higher (lower) over the first few years that over the full life of the bond, then due to compounding, these effects will overstated (understated) with a constant inflation rate assumption. Return to Text
13. I ran my calculations with the inflation series Sack and Elsasser had available and obtained very similar results. Return to Text
14. The actual/projected inflation series shown is the average inflation over the life of the bond to make it comparable with the auction breakeven rate. In this calculation future inflation is assumed to be equal to projections from Survey of Professional Forecasters. Return to Text
15. Gurkaynak, Sack , and Wright (2007) Return to Text
16. For a rough comparison, the estimated inflation risk premiums for a ten-year zero-coupon yield from Kim and Wright(2005) averages 40 to 60 basis points during this period. Return to Text
17. Ang, Bekaert and Wei (forthcoming, Journal of Monetary Economics) shows that the Survey of Professional Forecasters does a better job of forecasting inflation out of sample than several macro-based and term structure models. Return to Text
18. Report to the Secretary of the Treasury from the Treasury Borrowing Advisory Committee of the Bond Market Association, May 1, 2001, page 2. Return to Text
19. Outstanding TIPS securities as a percent of total marketable Treasury debt outstanding was only a few percent in the first years of the program, was about 5 percent between 2001 and 2003, and then rose to over 6 percent in 2004, and to over 9 percent by 2007. Return to Text
20. Because bond prices (either in nominal, or if inflation protected in real, terms) are not complicated by uncertain cash flows, the absence of arbitrage implies restriction on the time series and cross sectional properties of those bond prices. In addition, the model in DKW essentially prices a real bond with the same liquidity as an off-the-run nominal security. Then by comparing the corresponding yields with the actual TIPS yields, they are able to obtain a measure of the illiquidity discount embedded in TIPS yields. Return to Text
21. DKW calculate the liquidity component for five and ten year TIPS yields, which I use to adjust the auction prices of five and ten year TIPS issues. For twenty and thirty year TIPS issues, I assume that the liquidity component is equal to that for a ten year security. DKW also do not calculate liquidity yield components before 1999, because there were too few TIPS issues to construct a zero coupon yield curve until then. For auctions occurring between 1997 and 1999, I that the liquidity yield component at these auctions is equal to its value at the start of 1999. If I instead only adjust auction prices after 1999, the cost to date values are -1.4 to -4.5 billion and the total cost values are -3 billion to -12 billion. Return to Text
22. These extrema correspond to the premiums subtracted from off-the-run yields in constructing the hypothetical on-the-run nominal bonds in section 2 above. Return to Text

♣ This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to Text
Home | Economic Research and Data | Accessibility | Contact us
Last update: February 14, 2008