Skip to: [Printable Version (PDF)] [Bibliography] [Footnotes]

Finance and Economics Discussion Series: 2008-09 Screen Reader version ^♣

The Human Capital that Matters: Expected Returns and the Income of Affluent Households

Sean D. Campbell
Federal Reserve Board

George M. Korniotis
Federal Reserve Board

September 14, 2007

Keywords: Human capital, expected stock returns, affluent income

Abstract:

We implement the human capital CAPM (HCAPM) using the income growth of high income households, rather than aggregate income growth, to proxy the return to human capital (HCRT). We find that identifying the HCRT with the income growth of affluent households, those who are most likely to hold stocks, substantially improves the performance of the HCAPM. Specifically, the pricing errors, R-square's, average returns on factor mimicking portfolios, and performance relative to other macro-finance models uniformly improve as the HCRT is identified with the income growth of successively more affluent households.

* The ideas and opinions expressed are the authors' and should not be interpreted as reflecting the views of the Board of Governors of the Federal Reserve System nor its staff.

I. INTRODUCTION

An important critique of the capital asset pricing model (CAPM), first levied by Mayers (1973) and Roll (1977), is that traditional measures of the market portfolio are incomplete since they do not account for the returns to human capital. Fama and Schwert (1977), Campbell (1996), and Jagannathan and Wang (1996) address this critique by including measures of the aggregate return to human capital in empirical tests of the CAPM. In particular, Jagannathan and Wang (1996) find that the growth rate in aggregate labor income is a priced risk factor and that the resulting human capital CAPM (HCAPM) significantly improves the fit of the traditional CAPM.

At the same time, it is well-known that stocks are owned by a minority of households that are concentrated in the top of the income distribution. According to the 2004 Survey of Consumer Finances, only 21% of households directly own stocks while over 50% of households in the top income decile directly hold stocks. A substantial body of research has also shown that recognizing these participation constraints is important for understanding the link between risk and return in the stock market. Mankiw and Zeldes (1991) show that recognizing the difference in consumption between stockholders and non-stockholders improves the explanatory power of the consumption CAPM. Vissing-Jorgensesn (2002) and Brav, Constantinides and Geczy (2002) show that estimates of the elasticity of intertemporal substitution and the coefficient of relative risk aversion derived from the consumption pattern of households with considerable stockholdings are more plausible than those derived from aggregate consumption data.

In this paper we take a first step in examining the role that participation constraints play in empirical tests of the HCAPM. Specifically, we construct measures of labor income growth from households in the top percentiles of the income distribution as a proxy for the return to human capital. Since high income households are more likely to directly own stocks, their income growth rates may be a more relevant measure of the return to human capital than measures based on aggregate income growth. Of course, if the distribution of income is stable over time then income growth rates should be insensitive to whether they are calculated from the mean or from the top percentiles of the income distribution. Piketty and Saez (2003), however, document important changes in the distribution of income in the U.S. over the course of the 20^th century. Their findings suggest that the way the returns to human capital are measured may be important for empirical tests of the HCAPM.

We calculate the labor income growth rate of households in the top percentiles of the U.S. income distribution using the annual labor income data of Piketty and Saez (2003). Piketty and Saez (2003) use tax data from the Internal Revenue Service (IRS) to compute the share of labor income accruing to households (tax units) in the top 10%, 5% and 1% of the U.S. income distribution from 1913 to 2005. This data offers various advantages compared to existing datasets. First, unlike the aggregate income data provided by the Bureau of Economic Analysis (BEA), this data can be used to compute the income growth rate of high income households. Second, unlike the Current Population Survey (CPS) data, this data is not subject to top-coding and thus provides accurate estimates of the earnings of high income households.

We test whether the labor income growth rate of affluent households can price the cross-section of expected returns by following the methodology of Fama and MacBeth (1973). In the asset pricing tests, the test assets are the 25 size and book-to-market sorted portfolios in Fama and French (1993). Over the 1932 to 2005 period we find that the estimated risk price associated with the return to human capital increases and that the model's fit improves as the return to human capital is identified with the income growth of successively more affluent households. In particular, we find that the estimated price of human capital risk nearly doubles and that the empirical fit, , of the HCAPM improves by 45% when we identify the return to human capital with the income growth of those households in the top 1% of the income distribution rather than aggregate income growth. We also find that the HCAPM that identifies the return to human capital with the income growth of the top 1% of households explains the returns on the 25 size and book-to-market sorted portfolios nearly as well as the Fama-French (1993) three factor model. Further, we find that this high degree of fit is largely due to the model's ability to explain the value premium. In this sense, our results suggest that the income growth of high income, affluent households is an important indicator of "financial distress" or "bad times" for which investors are compensated.

In addition to cross-sectional asset pricing tests, we also examine the performance of factor mimicking portfolios based on different income growth measures. We find that the factor mimicking portfolio related to the income growth of high income households exhibit large and statistically significant excess returns that are similar in magnitude to those observed on the small-minus-big (SMB) factor of Fama and French (1993). In contrast, the factor mimicking portfolio constructed from average income growth exhibit small and statistically insignificant excess returns.

We also compare the performance of the HCAPM with other asset pricing models that have been recently discussed in the literature (Lettau and Ludvigson 2001b; Aït-Sahalia, Parker and Yogo 2004; Parker and Julliard 2005; Santos and Veronesi 2006; Yogo 2006). Across a variety of metrics we find that the HCAPM, defined in terms of high income households, performs as well as or better than these other models. Furthermore, we show that the information content of the return to human capital, relative to the factors proposed by these alternative models, uniformly improves as the return measure is identified with the income growth of more and more affluent households.

Our findings make several important contributions. First, our results add to the existing literature on the importance of participation constraints for empirical tests of asset pricing models. Specifically, we show that the explanatory power of the HCAPM improves as we consider the income growth of successively higher income households that are more likely to hold stocks. This finding supports the notion that the behavior of variables directly related to stockholders, rather than aggregate variables, are better suited to implementing and testing asset pricing models. Second, our results also make a contribution to the human capital literature. We find that a version of the HCAPM that employs a proxy for the return to human capital that is closely linked to those households that are most likely to own stocks explains a significant fraction of the dispersion in stock returns. In particular, we find that the explanatory power of the HCAPM is similar to that of the Fama-French (1993) three factor model and fits the data as well or better than the alternative models that we consider. Accordingly, these results indicate that human capital risk, appropriately defined, is important for understanding the link between risk and return in the stock market.

The rest of the paper is organized as follows. In Section II we discuss the human capital CAPM and its empirical implementation in this study. In Section III we describe our data paying particular attention to the data on the income of affluent households, which are used to measure the return to human capital. We discuss our main empirical results in Section IV. In Section V, we compare the HCAPM to existing macroeconomic factor models. In Section VI we present a series of robustness tests. We conclude and discuss future research in Section VII.

II. THE HUMAN CAPITAL CAPM

In the classic version of the CAPM, the expected return on a particular stock is determined by its beta with respect to the market portfolio. Early empirical work seeking to test this hypothesis identified the market portfolio with broad based stock market indexes such as the S&P 500 or the CRSP value-weighted portfolio. Mayers (1973) and Roll (1977) were among the first to point out that this interpretation of the "market portfolio" in empirical tests of the CAPM was too narrow. In particular, indexes of financial assets do not account for the return to human capital, which accounts for a large fraction of total wealth. Fama and Schwert (1977) were the first to include a proxy for the return to human capital into an empirical measure of the market portfolio. This work was followed by Campbell (1996) and Jagannathan and Wang (1996).

While the precise implementation details differ, the basic empirical strategy to incorporate human capital into the CAPM, or HCAPM, is straightforward. Consider the return to financial wealth, , and the return to non-financial (human capital) wealth, $r_t^{NF}$ . Also, let the time-invariant, aggregate share of human wealth in total wealth be denoted as $\omega$ .¹ The return on the market portfolio is simply a weighted average of the return to financial and human wealth, $r_t^M =\omega r_t^{NF} +\left( {1-\omega } \right)r_t^F$ .

The proxy for the return to financial wealth is the return on a broad stock portfolio. The return to non-financial (human capital) wealth is far more difficult to observe. In particular, there are no highly liquid, marketable securities whose value is tied to the income stream produced by a unit of human capital. As a result, an assumption must be made about how to measure $r_t^{NF}$ .

Fama and Schwert (1977) as well as Jagannathan and Wang (1996) assume that the expected return to human capital is constant. Under this assumption, the realized return is a linear function of the current growth rate of labor income, $r_t^{NF} =\left( {L_t -L_{t-1} } \right)/L_{t-1}$ . Finally, if one takes a stand on the fraction of human wealth in total wealth, $\omega$ , the return to the market portfolio, , may be constructed and asset betas may be calculated. Alternatively, one can simply use both and $r_t^{NF}$ in a two factor expected return-beta model. Using this approach the return on a particular stock, , can be expressed as a linear function of the stock's "financial" beta and "human" beta as follows,

$\begin{displaymath} \begin{array}{l} r_t^i \,\,\,\,\,\,\,\,\,\,\,=\beta _0^i +\beta _F^i r_t^F +\beta _{NF}^i r_t^{NF} +\varepsilon _t^i , \ E\left[ {r_t^i } \right]\,\,=\lambda _0 +\lambda _F \beta _F^i +\lambda _{NF} \beta _{NF}^i , \ \end{array}\end{displaymath}$

(1)

where $\lambda _F$ and $\lambda _{NF}$ are the associated "risk prices" that also reflect the composition of the market portfolio.

Shiller (1995) and Campbell (1996) use a measure of the return to human capital that allows for the possibility that expected human capital returns are time-varying. In this case, the return to human capital includes the current growth rate of income plus the present value of any forecasted changes to future income growth rates. The advantage of this dynamic approach, over the static approach adopted by Fama and Schwert (1977) and Jagannathan and Wang (1996), is that it takes into account any expected future "capital gains" from the current level of human capital.

Implementing the dynamic HCAPM, however, is complicated by the fact that an explicit forecasting model needs to specified and estimated. This is typically done by pre-estimating VAR-type models as in Campbell (1996). In this case, the revisions to future income growth rates depend on the information set used to predict the future levels of income, which implies that the inference of asset pricing tests can hinge on the state variables included in this information set.

Therefore, to side step the specification and pre-estimation issues, in the case of the dynamic HCAPM, we focus on the static HCAPM. Nevertheless, as part of our robustness tests in Section VI, we estimate Campbell's (1996) formulation. This exercise reveals that the main conclusions drawn from measuring the return to human capital with the simple growth rate of income, does not hinge on the methodology used to measure the return to human capital.

Fama and Schwert (1977), Campbell (1996) and Jagannathan and Wang (1996) use aggregate data on labor income to identify $r_t^{NF}$ . The use of aggregate data in measuring the return to human capital, however, is complicated by the fact that stock ownership is not evenly distributed across the entire population. Affluent households with high wealth and high income are more likely to hold stocks than less affluent households (Haliassos and Bertaut (1995)). Accordingly, it is not obvious how the return to human capital should be measured. In particular, should the income of households that do not own and are very unlikely to own stocks be included in the return to human capital measure?

There are two reasons to suspect that the measure of the return to human capital should be tailored towards those households that are most likely to own stocks. First, to the extent that many households do not participate in and are not marginal to the stock market, the riskiness of the return to their human capital is not relevant for pricing stocks. This point has been made in the context of consumption based models by Mankiw and Zeldes (1991), Brav, Constantinides and Geczy (2003), Vissing-Jorgensen (2003), and Aït-Sahalia, Parker and Yogo (2004). These authors show that consumption measures directly tailored to stockholders improve the predictions of consumption based asset pricing models. Second, the empirical properties of the returns to human capital differ substantially across the income spectrum. In particular, Piketty and Saez (2003) document that the share of income accruing to those households in the top 10%, 5% and 1% of the income distribution varies substantially over time. Moreover, we document that the correlation between aggregate labor income and the labor income of the highest income households is far from perfect. As a result, inferences about the importance of human capital as a risk factor in the stock market may be sensitive to how the return measure is constructed.²

III. DATA DESCRIPTION

We construct proxies for the return to human capital using the annual labor income data of Piketty and Saez (2003).³ Following Jagannathan and Wang (1996), we proxy the return to human capital with the growth rate in labor income. We compute the growth rate of real per capita labor income, as well as the growth rates of real per capita income among households in the top 1%, 5% and 10% of the income distribution.⁴ Specifically, Piketty and Saez (2003) report the share of income earned by those households in the top 10%, 5% and 1% of the U.S, income distribution, $\Theta _t^{10}$ , $\Theta _t^5$ , $\Theta _t^1$ . They also report the total amount of real income in each year, , as well as the number of households (tax units) at the aggregate level, . We use the data on income shares, total real income and the number of tax units to calculate the growth rate in per capita real income and the growth rate of per capita real income of households in the top 10%, 5% and 1% of the income distribution as follows,

$\begin{displaymath} \begin{array}{l} g_t^{agg} =\Delta y_t -\Delta n_t ,\,\,\,\,\,\,\,\,g_t^{10} =\Delta \theta _t^{10} -g_t^{agg} , \ g_t^5 =\Delta \theta _t^5 -g_t^{agg} ,\,\,\,\,\,\,\,\,\,g_t^1 =\Delta \theta _t^1 -g_t^{agg} , \ \end{array}\end{displaymath}$

(2)

where lowercase symbols represent the logarithm of their uppercase counterparts and $\Delta x_t =x_t -x_{t-1}$ .

In Figure 1 we plot the growth rate of aggregate income, $g_t^{agg}$ , as it is calculated from the Piketty and Saez (2003) data as well as the growth rate from the BEA data. The BEA data has been used in most previous studies incorporating the return to human capital in the CAPM. It is therefore important to check whether the aggregate features of the Piketty and Saez (2003) data agree with those of the BEA data. Visual inspection of Figure 1 reveals that the two series are nearly identical. The correlation between the two series is 0.99. Accordingly, the results that we find using the Piketty and Saez (2003) data can not be attributed to any discrepancies between this data and the BEA data that has been used in previous work.

In Figure 2, we plot the growth rate of per capita income among households in the top 10%, 5% and 1% of the income distribution. Periods during which an NBER recession occurred are shaded in the figure. In each plot we also include the growth rate of aggregate income for comparison. The plots in Figure 2 show a clear association between aggregate income growth and the income growth of high income households. In particular, each of these series tends to decline during recessions. There are, however, some important differences between the series. As an example, the growth rate of high income households was sharply negative in 1947 while aggregate income only experienced a modest decline. Also, all of the high income growth series become more volatile than the aggregate growth series after about 1980.

In panel A of Table 1 we report summary statistics for all four income growth series as well as the return on financial assets, proxied by the real return on the CRSP value-weighted portfolio. The CRSP return is the other factor in the HCAPM. The average growth rate of income among high income households has outpaced aggregate income growth over the 1932-2005 sample period which is consistent with the notion that income inequality has been rising in the US. The volatility of the growth rate of income is similar among the aggregate and those in the top 10% and top 5% of the income distribution while the growth rate of income among households in the top 1% of the income distribution is roughly 50% higher than that of aggregate income growth. Also, the income growth rate of high income households is considerably less persistent than the growth rate in aggregate income.

We report the correlation matrix between the four income growth rates and the market return in Panel B of Table 1. The correlation between aggregate income and the income growth of affluent households is lower for more affluent households. Specifically, the correlation between $g_t^{agg}$ and $g_t^{10}$ is 81%, while the correlation between $g_t^{agg}$ and is 73% and the correlation between $g_t^{agg}$ and is only 60%. This discrepancy between the aggregate return to human capital and the return to human capital among high income households is further illustrated by the pattern in correlation between the return to human capital and the market return. At the aggregate level, the return to human capital is negatively correlated with the market return. The correlation between the market return and the return to human capital among high income households, however, is positive and rises as the degree of affluence rises. The divergent behavior of the aggregate return to human capital and the return to human capital among affluent households is interesting because it suggests that equity is a riskier proposition for those households at the top of the income distribution.

Before moving on to a discussion of the rest of the data that we use in the paper we discuss some of the limitations of the Piketty and Saez (2003) income data. The income measures provided by Piketty and Saez (2003) are defined in terms of percentiles of the distribution of income rather than relative to a particular real income level, such as $100,000. As a result, the reference group being referred to changes over time with the distribution of income. In particular, the households represented in the top of the income distribution may differ over time in terms of their educational background and other characteristics that determine their level of human capital. In principle, data from the CPS can be used to construct income measures that are relative to a fixed income level, or a fixed level of human capital (education). This data, however, has several drawbacks. The CPS includes only a sample of US households while the Piketty and Saez (2003) data captures all tax filers. The CPS data also relies on self-reported measures of income and are only available since 1962. Finally, and perhaps most importantly, the CPS income data are top-coded, and the degree of top-coding is severe. In 1984, for example, the maximum income that could be recorded in the public use data set was $99,999. Accordingly, the Piketty and Saez (2003) data are particularly well suited to studying the properties of income growth among affluent households that are the most likely to hold stocks.

Another shortcoming of the Piketty and Saez (2003) data is that we can not directly identify the income of households that own stocks in the same way that Mankiw and Zeldes (1991) and Brav, Constantinides and Geczy (2002) identify the consumption of stockholders. Accordingly, our human capital measures are proxies for the return to human capital of stockholders in the sense that more affluent households are more likely to own stocks. While this feature of our data is clearly a limitation, we point out that we are not the first to employ proxies when attempting to measure variables that relate to stockholders. Aït-Sahalia, Parker and Yogo (2004), for example, use the sales of luxury goods from Tiffany department stores as a proxy for the consumption of wealthy stockholders. Therefore, while our proxy for the human capital returns of stockholders is imperfect it may still yield important insights into the link between human capital risk and stock returns.

Having described the income data, we next briefly describe the other data sources that we use. In our asset-pricing tests we use the 25 Fama and French (1993) portfolios.⁵ We also compare the HCAPM to the three-factor model of Fama and French (1993) and to existing macroeconomic factor models that have been recently proposed in the literature. Specifically, we compare the HCAPM with the conditional models of Lettau of Ludvigson (2001b) and Santos and Veronesi (2006), and the unconditional models of Aït-Sahalia, Parker and Yogo (2004), Parker and Julliard (2005), and Yogo (2006). To conduct a meaningful comparison of the HCAPM with these five alternative models we construct their alternative factors for an extended time period. More details on how we construct these alternative factors are provided in Appendix.

IV. MAIN EMPIRICAL RESULTS

In this section we present our main empirical results. First, we discuss the level and significance of the risk premiums on the various measures of the return to human capital, which are $g^{agg}$ , $g^{10}$ , $g^{5}$ , and $g^{1}$ . We then discuss the excess return of factor-mimicking portfolios related to the four proxies of the return to human capital. Finally, we compare the HCAPM to the three-factor model of Fama and French (1993), and examine the pricing errors of the HCAPM.

IV.1 Fama and MacBeth Risk Premiums

In Table II we present results from the estimated human capital CAPM (HCAPM) models. We estimate the model described by equation (1) using the two-pass Fama-MacBeth (1973) approach. As in other recent empirical studies, e.g. Lettau and Ludvigson (2001b), we estimate the Black (1972) version of this model that treats the zero beta rate as a parameter to be estimated. Specifically, the average real annual return on the 25 size and book-to-market sorted portfolios are regressed on a constant as well as the portfolio's market beta and human capital beta. We use four different proxies for the return to human capital, the growth rate in real aggregate income, $g^{agg}$ , and the growth rate in real income of those households in the top 10%, 5% and 1% of the income distribution, ${\begin{array}{*{20}c} {g^{10},} \hfill & {g^5,} \hfill & {g^1} \hfill \ \end{array} }$ , respectively. We refer to the estimated human capital models as HCAPM100, HCAPM10, HCAPM5 and HCAPM1. An estimate of the CAPM that excludes any measure of human capital is presented in the top row of Table II for comparison.

Aside from the parameter estimates, we present Fama and MacBeth (1973) t-statistics and Shanken (1992) adjusted t-statistics that account for measurement error in the first-pass beta estimates. We also present both the unadjusted and adjusted of the second-pass regression as a measure of model fit.

Looking at the estimates under the human capital return (HCRT) column of Table II reveals that the effect of human capital risk on expected returns is estimated to be larger as the measure of human capital is restricted to more and more affluent households. The estimated coefficient increases steadily from 0.03 in the case of the HCAPM100 to 0.12 in the case of the HCAPM1. In particular, note that the effect of doubling a portfolio's human capital beta on its expected return is estimated to be as important as a doubling of its market beta in the HCAPM1. In all other cases, the market risk associated with each portfolio is estimated to have a larger effect than human capital risk on expected returns.

The extent to which identifying the return to human capital with the income of affluent households improves the statistical significance of the human capital factor depends on the measure of statistical significance. In the case of the Fama-MacBeth t-statistics, the pattern is clear. The human capital factor associated with successively more affluent households has a more statistically significant effect on expected returns. The t-statistic on the human capital factor rises monotonically from 2.16 in the case of the HCAPM100 to 3.49 in the case of the HCAPM1. In the case of the Shanken adjusted t-statistics the pattern is not monotonic.⁶

The relative significance of the different human capital factors is somewhat ambiguous depending on which t-statistics one considers. However, the human capital measure that results in the largest improvement in model fit, as measured by adjusted , is unambiguous. The adjusted of the CAPM that ignores all human capital is 35% indicating that the simple CAPM explains a modest proportion of the variation in expected returns over the 1932-2005 period. The improvement in fit from adding the return to human capital increases as the return measure is based on the income growth of successively more affluent households. Looking at the fit measures in Table II reveals that the adjusted improves steadily from 41% to 78% as the measure of the return to human capital is restricted from the HCAPM100 to the HCAPM1. The improvement in fit from adding these alternative measures of the return to human capital indicates both that human capital risk is an important determinant of expected stock returns and that the choice of human capital measure matters. A measure of the return to human capital, which is more closely aligned with the income characteristics of those most likely to hold stocks, improves the performance of the HCAPM substantially over an aggregate measure of the return to human capital.

IV.2 Factor-Mimicking Portfolios

The results in Table II suggest that human capital risk is a priced risk factor and that measures of human capital relating to affluent households are more tightly linked to the expected returns on stocks. An alternative means of making this point is to examine the returns to factor mimicking portfolios constructed from each measure of the return to human capital. This approach has been used, among others, by Breeden, Gibbons, and Litzenberger (1989).

Specifically, for each measure of the return to human capital, $g^i,\,\,i=\left\{ {agg,\,\,10,\,\,5,\,\,1} \right\}$ , we regress the factor onto the excess returns of the 25 size and book-to-market sorted portfolios.⁷ The resulting coefficient estimates are used as portfolio weights to construct a zero cost portfolio. We present summary statistics regarding the portfolio returns of these human capital factor mimicking portfolios in Table III. Also, for comparison, we present summary statistics for the return on the three Fama-French factors, the market return (MKRT), the return on the high-minus-low portfolio (HML) and the return on the small-minus-big portfolio (SMB).

The excess return on the human capital factor mimicking portfolio increases steadily as the human capital return measure is restricted to the income growth of more and more affluent households. The factor mimicking portfolio based on $g^{agg}$ exhibits an annual excess return of roughly 0.6% which is not statistically significant at any conventional significance level. The factor mimicking portfolio based on $g^{10}$ exhibits an annual average excess return of 0.85% which is significant at the 1% level. The average excess returns on the factor mimicking portfolios constructed from and are roughly 1.2% and 2.2% respectively which are significant at the 1% level. More importantly, the average return on the mimicking portfolio associated with is similar to that associated with the SMB portfolio, which suggests that the return to assuming human capital risk is economically large. Overall, the pattern in results reported in Table III is strikingly similar to those reported in Table II. Importantly, the evidence in favor of human capital risk as a priced risk factor improves uniformly as we consider measures of the return to human capital that are more in line with the income characteristics of actual stockholders.

IV.3 Comparison to Fama-French Three Factor Model

We now turn to an analysis of the HCAPM relative to the Fama-French three factor model. Specifically, we include our various measures of the return to human capital with the market, HML and SMB factors to price the cross-section of the 25 size and book-to-market sorted portfolios over the 1932-2005 sample period.

The purpose of this analysis is not to determine whether the HCAPM dominates the three factor model. The measurement error inherent in our measures of the return to human capital alone implies that the return-based three factor model will likely outperform the HCAPM. Rather, we are interested in whether the human capital factor is systematically linked to either the size (SMB) or value (HML) factors. We are also interested in whether the pattern in results, as we consider human capital return measures drawn from increasingly affluent households, coincides with the patterns observed in Tables II and III.

In Table IV we present the results of a four factor model that contains the three original Fama-French factors plus the return to human capital factor. We estimate a different factor model for each measure of the return to human capital. The results of the three factor model of Fama and French (1993) are presented in the first row of Table IV for comparison.

Over the 1932-2005 sample period the three factor model fits the data well, exhibiting an adjusted of 86%. It is interesting to note, however, that the three factor model's degree of fit is only slightly stronger than the fit of the HCAPM1, with an adjustedof 78%. The estimated risk prices of the three factor model are similar to those reported elsewhere in the literature. The market factor exhibits a slightly negative and insignificant estimated risk price while the estimated risk prices on the size and value factors are both large and statistically significant.

The results of the four factor model that includes the return to human capital are presented in the next four rows of Table IV. Across each of the human capital measures the estimated risk price is positive. The estimated risk prices also increase monotonically as the human capital measure is restricted to more and more affluent households. The estimated risk price in the case of the HCAPM1 is six times greater than the risk price associated with the HCAPM100. The pattern in the degree of statistical significance follows the pattern in coefficient estimates. When the Fama-MacBeth t-statistics are used to gauge statistical significance the estimated price of human capital risk is significant at the 10% level or less in the case of the HCAPM5 and HCAPM1. When statistical significance is judged with the Shanken adjusted t-statistics none of the human capital factors are significant though the degree of significance rises uniformly as the measure of the return to human capital is restricted to more and more affluent households.

The effect of including the return to human capital on the estimated risk prices of the market, size and value factors is also interesting. The results indicate that including the return to the human capital of affluent households reduces the estimated risk price of the value factor. Specifically, including or to the three factor model reduces the estimated risk price on the value factor by 0.01 or roughly 15% while the estimated risk price on the size factor is unaffected by including or . Moreover, including $g^{agg}$ or $g^{10}$ to the three factor model has no effect on the estimated risk prices of either the size or value factors.

This finding suggests two things. First, the human capital premium appears to be correlated only with the value premium and this correlation is most evident when the return to human capital is identified with the income growth of relatively affluent households. Second, because the value premium has been previously associated with broad notions of the risk of "economic distress" (Chan and Chen (1991), Fama and French (1996)), our findings suggest that value investors are rewarded for bearing distress risk associated with downturns in the income of affluent households. As Cochrane (2006) points out, a central challenge of any asset pricing model is to identify a measure of "bad times" that can explain variation in expected stock returns. Our findings suggest that downturns in the income of the most affluent households represent a potentially useful indicator of these "bad" times that may be more informative than measures based on aggregate data.

IV.4 Pricing Error Analysis

The results in section IV.3 suggest that the HCAPM1 can capture the value effect. To further examine this observation, in Table V, we present average pricing errors for each of the estimated HCAPM specifications and the Fama-French three factor model. Rather than present pricing errors for each of the 25 portfolios we focus on the 10 aggregate size and book-to-market portfolios to investigate whether the HCAPM can explain the size and book-to-market effects. In the top panel we present pricing errors for the five book-to-market sorted portfolios. In the middle panel we present pricing errors for the five size sorted portfolios. Aside from the pricing errors we also report the value and significance level of the chi-squared test of the null hypothesis that the mean pricing error of the book-to-market and size sorted portfolios is zero.

The average pricing errors of the book-to-market sorted portfolios, reported in the top panel of the table, indicate that the pricing errors of these portfolios generally decline as the human capital return measure is restricted to more affluent households. The value of the chi-squared statistic declines monotonically as we move from the HCAPM100 to the HCAPM1. Also, looking at the pricing errors of individual portfolio groupings supports the results of the chi-squared tests. In particular, the average pricing error of each sub-group, B1-B5, is smaller when either or is used to measure the return to human capital than when $g^{agg}$ is used. When $g^{10}$ rather than $g^{agg}$ is used to measure the return to human capital, the average pricing error is smaller in four out of five sub-groups (B2 is the exception). This pattern in pricing errors further supports the notion that return to human capital among affluent households is systematically related to the value premium. Consequently, the risk associated with the income growth of affluent households may be an important source of distress risk that value investors are rewarded for assuming.

The pricing errors on the size sorted portfolios, reported in the middle panel, show a less consistent pattern. While the value of the chi-squared test typically declines as the human capital return measure is restricted to more affluent households the improvement is more modest than that observed in the top panel. Moreover, examining the size sorted sub-groups, S1-S5, does not reveal a consistent pattern of declining pricing errors as the human capital return measure becomes more restrictive. As an example, the average pricing error is actually larger in three of the sub-groups (S1, S2, S5) when rather than $g^{agg}$ is identified with the return to human capital. Accordingly, these results suggest that the improvements from considering more restrictive measures of the return to human capital are primarily due to the model's ability to explain the returns across high and low book-to-market portfolios.

V. COMPARISON TO OTHER MACROECONOMIC MODELS

Until now, we have focused on how well the HCAPM prices the returns on the 25 size and book-to-market sorted portfolios relative to the Fama-French three factor model. In general, it is difficult to meaningfully compare the performance of a return based and macroeconomic factor based pricing model. Accordingly, in this section we compare our HCAPM to existing macroeconomic factor models.

This comparison is interesting because it may help us to understand exactly how human capital risk helps to explain returns relative to other macroeconomic factor models. It may also help to put the contribution of these other models in perspective. In particular, the model we propose is the simplest extension to the traditional CAPM and it is based on two observations. It recognizes the importance of human capital in the aggregate wealth portfolio and the fact that stockholdings are concentrated by households at the top of the income and wealth distribution. Alternatively, the other models, which we consider in this sub-section, rely on economic mechanisms that are more involved than the simple risk-return mechanism underling the HCAPM. It is of interest to quantify the extent to which these more involved mechanisms help to improve our understanding of expected returns.

We focus on five models that have recently been introduced to the literature. Each of these models was introduced, at least in part, to explain or improve upon the poor performance of the traditional (non-human capital) CAPM. The alternative macroeconomic models that we consider are, Yogo's (2005) model of durable goods consumption (denoted "Yogo"), Parker and Julliard's (2005) model of ultimate consumption risk (denoted "PJ"), Lettau and Ludvigson's (2001b) scaled CCAPM (denoted "LL"), Aït-Sahalia, Parker and Yogo's (2004) model of luxury goods consumption (denoted "ASPY") and Santos and Veronesi's (2005) (aggregate) income to consumption ratio model (denoted "SV").

In all cases but one, we use the same data and methods used in the original implementation of the alternative macroeconomic models to construct their various factors over the 1932-2003 time period.⁸ In the case of Aït-Sahalia, Parker and Yogo's (2005) model of luxury goods consumption, the factor is only available over the 1961-2001 period. We construct a proxy for the luxury consumption growth factor by constructing a factor mimicking portfolio over the available sample period and then use the estimated weights to expand the sample to the entire 1932-2003 period. Precise details concerning the construction of each factor is contained in the appendix.

V.1 Pricing Errors

Each of the five macroeconomic factor models and the HCAPM models are estimated using the two-pass Fama-MacBeth methodology. We report average pricing errors and other metrics of goodness of fit in Table VI. Rather than report results for all of the HCAPM specifications we report results for the HCAPM100 and HCAPM1.

The top panel of Table VI reports the average pricing errors across the book-to-market sorted portfolios. Comparing the pricing errors of the HCAPM1 with the other factor models shows that the HCAPM1 typically exhibits the smallest pricing errors. In particular, the HCAPM1 exhibits the smallest average pricing errors across the book-to-market sorted portfolios in all but two cases (B2:PJ, B3:PJ). This is reflected in the size and significance of the chi-squared test. The chi-squared test of the HCAPM1 is the smallest (with the highest significance level) across all of the candidate models. The results of the top panel, however, also make clear that the precise measure of human capital return employed is important. In particular, the average pricing errors of the HCAPM100 most often exhibits the largest pricing errors and also exhibits the largest value of the chi-squared test with the lowest significance level (0.09). Therefore, the HCAPM employing aggregate income growth is the only model rejected in the top panel at conventional significance levels.

The middle panel of Table VI reports the average pricing errors for each of the size sorted portfolios. As was the case in Table V, the size sorted results are not overly sensitive to the precise measure of the return to human capital though the chi-squared test statistic does indicate that the HCAPM1 does exhibit a slightly better fit to the data. When compared with the other macroeconomic factor models the HCAPM1 falls roughly in the middle of the pack. Specifically, the better performing HCAPM exhibits a chi-squared test statistic with a p-value that is larger than two of the five alternative models.

Looking at the metrics of fit based on the 25 portfolios indicates that on the basis of RMSE and the HCAPM1 fits the data on average returns best. In particular, the HCAPM1 has an RMSE that is 10% smaller than the next best fitting model. This result indicates that human capital risk is an important priced risk factor. Importantly, the ability of the HCAPM1 to explain the cross section of average returns on the Fama-French 25 portfolios dominates the empirical performance of other models that have been recently proposed. These results also show, however, that the way we measure the return to human capital matters. In particular, the HCAPM100 does a poor job in pricing the 25 size and book-to-market sorted portfolios relative to the other factor models examined in Table VI. As a result it is important that the income growth being used to proxy for the return to human capital be related to the income characteristics of those households most likely to own stocks.

V.2 Unique Asset-Pricing Information

Finally, we examine the importance of the human capital factor relative to each of the five alternative factor models examined in Table VI. Specifically, we include the return to human capital as an additional factor in each of the five macroeconomic factor pricing models. We continue to estimate each model using the two-pass Fama-MacBeth approach. In Table VII we report the estimated risk price and associated t-statistics on the various human capital factors from each of the five alternative pricing models. The results in Table VII summarize the extent to which the additional human capital factors contain information about expected returns that is not captured by the original factors.

Across each of the five alternative models we find that the estimated risk price on the human capital factor increases as the human capital return is identified from the income growth of more and more affluent households. The estimated risk price typically increases by a factor of between three and five as the human capital return measure moves from aggregate income growth to the income growth rate of those in the top 1% of the income distribution.

The degree of statistical significance in the human capital factor follows a similar pattern. When either the Fama-MacBeth or Shanken adjusted t-statistics are used to judge significance, statistical significance generally rises as the human capital return measure is restricted to the income growth of successively more affluent households. In the case of the Fama-MacBeth t-statistics it is always the case the most significant human capital factor is that associated with the income growth of households in the top 1% of the income distribution, . In the case of the Shanken adjusted t-statistic the most significant human capital factor depends on the particular model. Nevertheless, in every case but one, the human capital factor associated with is more significant than that associated with aggregate income growth, $g^{agg}$ .⁹ Accordingly, these results confirm that human capital risk is most able to contribute to our understanding of expected stock returns when the return to human capital is identified with the income growth of the most affluent households.

VI. ROBUSTNESS ANALYSIS

We have shown that there is a strong link between human capital risk and expected returns. Importantly, we have argued that the strength of this link tightens as the proxy for the return to human capital focuses on the income growth of more and more affluent households. We now examine the robustness of these conclusions to several variations in important elements of the research design. In the first group of tests, we vary the estimation technique of the second-pass regression, we limit our sample to the post-War II period, and we estimate the model with excess returns. In the second group of tests, we estimate a fully dynamic version of the HCAPM following Campbell (1996).

VI.1 Baseline Robustness Tests

In Table VIII we examine the sensitivity of our main results to changes in estimation procedure, sample period and return measure. We discuss each of these variations in turn.

In Panel A, we examine the sensitivity of our results to a different estimation procedure. Rather than use OLS to estimate the model described in equation (1) we use GLS. We apply the GLS approach following Korniotis (2007). The model is estimated over the full sample period 1932-2005. The GLS results are very similar to those of the OLS estimates contained in Table II. We still continue to find that the fit of the HCAPM improves as the proxy for the return to human capital is focused on the earnings of those households in the top of the income distribution. Also, when GLS is employed we find that the statistical significance of the estimated risk price increases uniformly, whether one uses the Fama-MacBeth or Shanken standard errors, as the proxy for the return to human capital is defined with respect to successively more affluent households.

One difference between the GLS and OLS results in Table II is that the level of the GLS risk premiums on the HCRT is lower than that estimated using OLS. In unreported results we also find that the GLS risk premium on the CRSP return is lower than that estimated using OLS. Accordingly, even though the estimated risk premiums decline when GLS is employed, the relative size of the CRSP and human capital premiums are unaffected by the estimation method.

In Panel B, we examine the sensitivity of our results to a variation in the sample period. Our full sample period covers the range from 1932-2005. In many empirical studies the period immediately following the Great Depression is excluded to focus on the post World War II era, e.g. Lettau and Ludvigson (2001), Parker and Julliard (2005). We examine how our main results change when we only use post World War II data to examine the relationship between expected returns and human capital risk.

In general, human capital risk explains a smaller fraction of the cross-sectional variation in equity returns over the 1945-2005 period. Over the full sample the various HCAPM specifications explain roughly between 20% - 80% of the variation in expected returns. Over the 1945-2005 period these models explain roughly 7% - 35% of the variation in expected returns. Interestingly, however, the statistical significance of human capital risk, as measured by the t-statistics, is roughly similar across the full sample and post-war periods. Also, we continue to find that HCAPM specifications employing human capital return proxies drawn from more affluent households are more able to explain the spread in expected returns. This is the case both in terms of statistical significance and model fit.

Even if the fit of the HCAPM1 for the post War World II period is lower than the full sample approach, we find that its performance is comparable to other macro-finance models over a similar period. As in Section V, we estimate the HCAPM1 and existing macro-factor models over the 1945 to 2003 period. In unreported results, available on request, we find that the HCAPM1 has the second smallest pricing errors with respect to the five aggregate book-to-market portfolios. Parker and Julliard's (2005) model has the smallest pricing errors. Also, the chi-squared test-statistic and p-value of the test that the book-to-market pricing errors are zero are 1.60 and 0.66, respectively, for the HCAPM1. In the case of Parker and Julliard's (2005), they are 1.40 and 0.85.

In Panel C, we examine the sensitivity of our main results to the use of excess returns on the 25 size and book to market sorted portfolios rather than real returns. The results using excess returns are qualitatively and quantitatively similar to those using real returns. The fit, in terms of adjusted and unadjusted , of the HCAPM1 is roughly double that of the HCAPM100. The pattern in statistical significance also closely mirrors the pattern in significance of the main results found in Table II. Accordingly, the results of the main analysis are not sensitive to whether real or excess returns are used to measure expected returns.

VI.2 Dynamic HCAPM

We now examine the sensitivity of our results to the way in which the return to human capital, HCRT, is specified. Specifically, the factor model described in equation (1) is static in the sense that it ignores any predictability in either stock returns or the returns to human capital. Campbell (1996) formulates a dynamic version of the HCAPM that allows for predictable variation in both the return to human capital and financial wealth (equity returns). Campbell (1996) shows that accounting for predictability implies that there are three asset pricing factors. The resulting expected return-beta representation takes the following form,

$\begin{displaymath} \begin{array}{l} r_t^i \,\,\,\,\,\,\,\,\,\,\,\,\,=\beta _0^i +\beta _F^i r_t^F +\beta _{F,rev}^i \left[ {\left( {E_t -E_{t-1} } \right)\sum\limits_{j=1}^\infty {\rho ^jr_{t+j}^F } } \right]+\beta _{NF}^i \left[ {g_t +\left( {E_t -E_{t-1} } \right)\sum\limits_{j=1}^\infty {\rho ^jg_{t+j} } } \right], \ E\left[ {r_t^i } \right]\,\,\,=\lambda _0 +\lambda _F \beta _F^i +\lambda _{F,rev} \beta _{F,rev}^i +\lambda _{NF} \beta _{NF}^i , \ \end{array}\end{displaymath}$

(3)

where the parameter $\rho$ is a discounting factor that we set to 0.94 in our empirical analysis. The first factor is the contemporaneous return on financial assets,

. The second factor accounts for any revisions to expectations about the future return on financial assets, $\left( {E_t -E_{t-1} } \right)\sum\nolimits_{j=1}^\infty {\rho ^jr_{t+j}^F }$ . The third factor, the dynamic HCRT, is the contemporaneous growth rate of income,

$_{t}$ , plus the revision to expectations about future income growth rates, $\left( {E_t -E_{t-1} } \right)\sum\limits_{j=1}^\infty {\rho ^jg_{t+j} }$ .

We implement the dynamic HCAPM following Campbell (1996) by estimating a VAR(1) to obtain the revisions to the income growth rate and the CRSP return. The state variables in the VAR(1) are the CRSP return, the income growth rate, the dividend yield on the CRSP return, and Lettau and Ludvigson's (2001a, 2005) consumption-wealth ratio (cay). We include the dividend yield and cay as state variables in the VAR(1) because of the empirical evidence that these factors predict future stock returns (Fama and French (1988), Lettau and Ludvigson (2001a)).¹⁰

We estimate the VAR with OLS and we rescale the VAR residuals so that they have the same variance as the innovation to the CRSP return. The results from implementing the dynamic HCAPM using $g^{agg}$ , $g^{10}$ , $g^{5}$ , and $g^{1}$ are reported Table IX. In Panel A of Table IX we report the risk premiums on the dynamic HCRT as well as the $R^{2}$ and its adjusted version. In Panel B of Table IX, we report the pricing errors for the ten aggregated Fama and French (1993) portfolios.

In Panel A.1, we report the results when we estimate the second-pass regression with OLS over the full sample 1932 to 2005 period. We find that the fit of the dynamic version of the HCAPM100 improves relative to its static counterpart. Specifically, the model $R^{2}$ increases from 37% (reported in Table II) to 71%. Therefore, accounting for the predictability in aggregate income growth and the CRSP return improves the fit of the model with $g^{agg}$ . Moreover, in unreported results, we find that recognizing the predictability in each component contributes equally to the improvement in model fit. The fit of the HCAPM1 increases more modestly from 78% to 84%. This finding is not surprising given that the fit of the static HCAPM1 (78%) is already high and rather close to the fit of the Fama-French (1993) three factor model (86%).

Next, we implement some of the variations in the research design that were considered in Table VIII. Specifically, in Panel A.2 of Table IX we estimate the second-pass regression with GLS for the 1932 to 2005 period, and in Panel A.3, we estimate the second-pass regression with OLS for the 1945 to 2005 (post-World War II) period.

The GLS estimation of the dynamic HCAPM100 reveals that the risk premium of the dynamic HCRT is insignificant and its fit is only 48%. In contrast, the GLS estimation of the dynamic HCAPM1 reveals that the risk premium of the dynamic HCRT is significant, and its fit increases to 68%. We find similar results when we estimate the dynamic HCAPM for the post World War II period. In the case of the HCAPM100, the risk premium of the dynamic HCRT is insignificant and its fit is only 14%. On the contrary, in the case of the HCAPM1 the risk premium of the dynamic HCRT is significant, and the fit improves to 42%.

Next, we explore the ability of the various dynamic HCAPM models to explain the value and size effects. We therefore compute their pricing errors on the ten aggregated size and book-to market portfolios for the full sample period (1932-2005). We report these results in Panel B of Table IX. The pricing errors on all the book-to-market portfolios are the smallest for the dynamic HCAPM1 and they are the largest for the dynamic HCAPM100. Moreover, the dynamic HCAPM1 exhibits the smallest chi-squared test statistic (2.70) and the largest p-value (0.26). For the same test, the HCAPM100 has the largest chi-squared test statistic (6.07) and the smallest p-value (0.05). As in Table V, the pricing errors of the size portfolios indicate that the dynamic HCAPM1 is only modestly better than the dynamic HCAPM100 in capturing the size effect.

Across the findings in this section, we continue to find that human capital risk is priced. Furthermore, we show that proxies for the dynamic HCRT, drawn from more affluent households, exhibit larger estimated risk prices, fit the data more closely, and are better able to explain the value effect. Therefore, our conclusion about the importance of human capital as an asset pricing factor and the informativeness of the human capital of affluent households is not sensitive to whether we employ a static or dynamic version of the HCAPM.

VII. CONCLUSION

In this paper, we take a fresh look at the HCAPM motivated by the recent literature on limited stock market participation. This literature underscores the importance of explaining stock market phenomena by analyzing the behavior of households that are marginal to the stock market. We take this intuition and measure the return to human capital with the income growth of high income households rather than aggregate income growth. High income households are more likely to hold equity and hold the majority of equity by value. Therefore, the dynamics of their earnings may be informative about the evolution of stock returns.

We measure the return to human capital using the income data from Piketty and Saez (2003). This data set provides a long time-series on the income growth rates of the top deciles of the income distribution of U.S. households over the 1919 to 2005 period. In an ideal situation we would use the income of actual stockholders. Unfortunately, such data are not available for a sufficiently long time period and for a representative sample of U.S. households. Therefore, the Piketty and Saez (2003) data is a second-best alternative.

Our empirical analysis demonstrates that versions of the HCAPM (HCAPM10, HCAPM5, HCAPM1) that identify the return to human capital with the income growth rate of affluent households is successful in many dimensions. These versions of the HCAPM explain the returns on the 25 size and book-to-market portfolios more successfully than the HCAPM implemented with aggregate income growth (HCAPM100). Moreover, the degree of fit steadily increases as the return to human capital is identified with higher and higher income households. Considering the highest income households, the cross-sectional of the HCAPM1 is 78% over the full sample, while theof the HCAPM100 is 41% over the same period. Importantly, the fit of the HCAPM1 is nearly as impressive as that of the Fama-French (1993) three factor model (84%). We also show that average excess returns on factor mimicking portfolios steadily increase as the factor is identified with the income growth of more and more affluent households. While the average excess return of a portfolio based on aggregate income growth is small and insignificant, the average excess return on a portfolio based on the income growth of the highest income households is large, similar to the return on the SMB portfolio, and statistically significant.

We also show that identifying the return to human capital with the income growth of affluent households helps to explain the value effect. Across the board, we find that the pricing errors on the book-to-market portfolios decline as the return to human capital is identified with more affluent households. Across each of the five aggregated book-to-market portfolios we find that the pricing errors of the HCAPM5 and HCAPM1 are always smaller than those associated with the HCAPM100. This finding is interesting because it suggests that negative shocks to the income growth of high income households may be a source of "distress" for which value investors are compensated.

We also find that the empirical performance of the HCAPM, implemented with the income growth of affluent households, is competitive with other macro-finance models suggested by the recent asset-pricing literature. In particular, we find that the HCAPM1 explains expected returns as well as, and in some cases better than, the alternative models. In contrast, the HCAPM based on aggregate income growth, HCAPM100, exhibits the poorest fit across each of the models. Furthermore, in regressions that include both the alternative macroeconomic factors and the income growth of affluent households, the risk premium on the latter is always statistically significant. Therefore, the income growth of affluent households contains asset-pricing information not captured by other leading macroeconomic factors.

These results consistently show that the human capital risk of high income, affluent households is a priced risk factor that successfully explains variation in expected stock returns. Moreover, implementing the HCAPM by identifying the return to human capital with the income growth of high income households is more successful than an implementation employing aggregate income growth. Over a long sample period, using a variety of different metrics and after considering a number of robustness tests we find that examining the HCAPM through the lens of limited stock market participation improves our understanding of the empirical link between risk and return in the stock market.

APPENDIX

Data for Alternative Factor Models: 1932-2003

Lettau and Ludvigson (2001b). In Lettau and Ludvigson (2001b) the asset-pricing factors are a) the U.S. consumption growth rate and b) the product of the lagged mean-free cay series and the U.S. consumption growth rate. The cay is the cointegrating residual of log consumption ( from its long-term trend with log wealth ( and log labor income (. To use the Lettau of Ludvigson (2001b) factors for the 1932-2003 period, we first download the Lettau of Ludvigson annual dataset from the website of Sydney Ludvigson. This annual data cover the 1949-2001 period and have been used in Lettau of Ludvigson (2005). Next, we use the same data sources and definitions as in Lettau of Ludvigson (2005) and extend their annual data set by appending to it data for the 1932-1948 and 2002-2003 periods. The only discrepancy from Lettau of Ludvigson (2005) is related to the household wealth series ( for the period 1932-1944. Because the Flow of Funds data, the source for the wealth series in Lettau of Ludvigson (2005), are only available from 1945 onwards, we use the wealth data from Kopczuk and Saez (2004). This data can be downloaded from http://elsa.berkeley.edu/ $\sim$ saez/. Kopczuk and Saez (2004) use estate tax return data from the Internal Revenue Service (IRS) to back out a U.S. household wealth series for the period 1916-2002.

After extending the Lettau of Ludvigson (2005) data, we estimate the cointegrating relationship between , , and ( $_{a}$ $_{y}$ using the fully modified ordinary least squares (FMOLS) of Phillips and Hansen (1990). To implement the FMOLS, we use 10 autocovariance terms to compute the spectrum at zero. To calculate the standard errors of the estimates we apply the quadratic spectral of Andrews (1991) where the bandwidth is selected automatically as suggested by Phillips and Hansen (1990). The estimated cointegrating parameter $_{a}$ and $_{y}$ are 0.32 (t-statistic = 2.40) and 0.66 (t-statistic = 5.81) respectively. These estimates are very close to those in Lettau of Ludvigson (2005). Using the estimated $_{a}$ and $_{y}$ we calculate the cay (= $_{a}$ $_{y}$ , which is used in our asset-pricing tests.

Santos and Veronesi (2005). To compute the asset-pricing factor in Santos and Veronesi (2005), we first calculate the product of the CRSP market return and the ratio of per capita U.S. labor income to per capita U.S. consumption. Call this product the scaled market return. Like Santos and Veronesi (2005), the definition and sources for U.S. labor income and U.S. consumption are the same as in Lettau of Ludvigson (2001b). Second, we regress the scaled market return on the unscaled market return. Then, we compute the orthogonal component of the scaled market return, which is the Santos and Veronesi (2005) asset-pricing factor.

Parker and Julliard (2005). In Parker and Julliard (2005) the most successful asset-pricing factor is the three-year-ahead U.S. consumption growth rate. Like Parker and Julliard (2005), consumption is defined as the real per-capital personal consumption expenditures at the national U.S. level, which are extracted from Table 7.1 from the National Income and Product Accounts (NIPA). The annual consumption series ends at 2006, and therefore we can compute the 3-year-ahead consumption growth up to 2003.

Yogo (2005). In Yogo (2005) the asset pricing factors are the growth rate of real per-capita durable personal consumption and the growth rate of real per-capita consumption of non-durables and services. Both series are measured at the national U.S. level. Following Yogo (2005), durable consumption equals the chained quantity index for the net stock of consumer durable goods from BEA. This series is from the Fixed Assets tables. The consumption of non-durables and services is from Table 7.1 from the National Income and Product Accounts.

Aït-Sahalia, Parker and Yogo (2004). In Ait-Sahalia, Parker and Yogo (2004), the asset-pricing factor is the real per-capita growth rate of luxury goods consumption, which can be downloaded from http://finance.wharton.upenn.edu/ $\sim$ yogo/. Because the luxury goods series is available only from 1961 to 2001, we use the mimicking portfolio methodology to extend it to the 1932 to 2003 period. First, we estimate an OLS time-series regression of the growth rate of luxury goods consumption on the returns of the twenty-five Fama and French (1993) portfolios, which are the test asset in our asset-pricing tests (Breeden, Gibbons, and Litzenberger (1989)). The mimicking portfolio weights are defined as the normalized OLS coefficients of the previous regression (the results of the OLS regressions are available on request). Next, we use the mimicking portfolio weights and the returns of the twenty-five Fama and French (1993) portfolios for the 1932-2003 period, and we compute the mimicking portfolio of the luxury goods consumption growth rate. This mimicking portfolio is used in our asset-pricing tests.

References

Andrews, D., 1991, "Heteroskedasticity and Autocorrelation Consistent Covariance Matrix Estimation," Econometrica, 59, 1991, p. 817-858.

Aït-Sahalia, Y., J. A. Parker, and M. Yogo, 2004, "Luxury Goods and the Equity Premium," Journal of Finance, 59, p. 2959-3004.

Black, F., 1972, "Capital Market Equilibrium with Restricted Borrowing," Journal of Business, 45, p. 444-455.

Brav A., Constantinides G., and C. Geczy, 2002, "Asset Pricing with Heterogeneous Consumers and Limited Participation," Journal of Political Economy, 110, p. 793-824.

Breeden, D. J., M. R. Gibbons, and R. H. Litzenberger, 1989, "Empirical Tests of the Consumption-Oriented CAPM," Journal of Finance, 44, p. 231-262.

Campbell, J. Y., 1996, "Understanding Risk and Return," Journal of Political Economy, 104, p. 298-345.

Campbell, J. Y., and J. H. Cochrane, 1999, "By Force of Habit: A Consumption-Based Explanation of Aggregate Stock Market Behavior," Journal of Political Economy, 107, p. 205-251.

Campbell, J. Y., and S. Thompson, "Predicting Excess Stock Returns Out of Sample: Can Anything Beat a Historical Average?," Review of Financial Studies, forthcoming.

Chan K.C., and N. Chen, 1991, "Structural and return characteristics of small and large firms," Journal of Finance, 46, p. 1467-1484.

Cochrane J., 2006, "Financial Markets and the Real Economy," working paper, Chicago GSB.

Fama, E., and J. MacBeth, 1973, "Risk, Return and Equilibrium: Empirical Test," Journal of Political Economy, 71, p. 607-639.

Fama E., and K. French, 1988, "Dividend Yields and Expected Stock Returns," Journal of Financial Economics, 19, p. 3-29.

Fama E., and K. French, 1993, "Common Risk Factors in the Returns on Stocks and Bonds," Journal of Financial Economics, 33, p. 3-56.

Fama E., and K. French, 1996, "Multifactor Explanations of Asset Pricing Anomalies," Journal of Financial Economics, 33, p. 3-56.

Fama, E. F., and W. G. Schwert, 1977, "Human capital and capital market equilibrium," Journal of Finance, 51, p. 55-84.

Goyal A. and I. Welch, "A Comprehensive Look at the Empirical Performance of Equity Premium Prediction," Review of Financial Studies, forthcoming.

Haliassos M., and C. Bertaut, 1995, "Why Do So Few Hold Stocks?" Economic Journal, 105, p. 111-129.

Jagannathan R., and Z. Wang, 1996, "The Conditional CAPM and the Cross-Section of Expected Returns," Journal of Finance, 51, p. 3-53.

Kopczuk, W., and E. Saez, 2004, "Top Wealth Shares in the United States, 1916-2000: Evidence from Estate Tax Returns," National Tax Journal, 57, p. 445-487 .

Korniotis, G. M., 2007, "The Significance of Regional Risk for Expected Returns," Review of Financial Studies, forthcoming.

Lettau M., and S. Ludvigson, 2001a, "Consumption, Aggregate Wealth, and Expected Stock Returns," Journal of Finance, 56, p. 815-849.

Lettau M., and S. Ludvigson, 2001b, "Resurrecting the (C)CAPM: A Cross-Sectional Test When Risk Premia Are Time-Varying," Journal of Political Economy, 109, p. 1238-1286.

Lettau M., and S. Ludvigson, 2005, "Expected Returns and Expected Dividend Growth," Journal of Financial Economics, 76, p. 583-626.

Mankiw N., S. Zeldes, 1991, "The Consumption of Stockholders and Non-Stockholders," Journal of Financial Economics, 29, p. 97-112.

Mayers D., 1973, "Nonmarketable Assets and the Determination of Capital Asset Prices in the Absence of Riskless Rate," Journal of Business, 46, p. 258-267.

Mehra, R., and E.C. Prescott. 1985, "The Equity Premium: A Puzzle," Journal of Monetary Economics, 15, p. 145-161.

Palacios-Huerta, I., 2003, "The Robustness of the Conditional CAPM with Human Capital," Journal of Financial Econometrics, 1, p. 272-289.

Parker, J., and C. Julliard, 2005, "Consumption Risk and the Cross-Section of Expected Returns," Journal of Political Economy, 113, p. 185-222.

Phillips, P. C. B., and B. Hansen, 1990, "Statistical Inference in Instrumental Variables, Regression with I(1) Processes," Review of Economic Studies, 57, p. 99-125.

Roll, R., 1977, "A Critique of the Asset Pricing Theory's Tests," Journal of Financial Economics, 4, p. 129-176.

Saez E., and T. Piketty, 2003, "Income Inequality in the United States: 1913-1998," Quarterly Journal of Economics, 118, p. 1-39.

Santos, T., and P. Veronesi, 2006, "Labor Income and Predictable Stock Returns," Review of Financial Studies, 19, p. 1-44.

Shiller, R. J., 1995, "Aggregate income risks and hedging mechanisms," Quarterly Review of Economics and Finance, 35, p. 119-152.

Sims, C. A., 1980, "Macroeconomics and Reality," Econometrica, 48, p. 1-48.

Vissing-Jorgensen, A., 2002, "Limited Asset Market Participation and the Elasticity of Intertemporal Substitution," Journal of Political Economy, 110, p. 825-853.

Yogo, M., 2006, "A Consumption-Based Explanation of Expected Stock Returns," Journal of Finance, 61, p. 539-580.

Table I

Descriptive Statistics

This table includes descriptive statistics for various income growth rates and for the market return. $g^{agg}$ is the average real per-capita income growth rate. $g^{10}$ , $g^{5}$ , and $g^{1}$ represent the growth rates of per-capita real income of households in the top 10%, 5% and 1% of the income distribution, respectively. The income data are from Piketty and Saez (2003). The market return (MKRT) is the value-weighted return of all stocks listed on the CRSP database divided by one plus the inflation rate. The inflation rate represents the growth rate of the consumer price index (CPI) published by the Bureau of Labor Statistics (BLS). The time period is 1932 to 2005.


	$g^{agg}$	$g^{10}$	$g^{5}$	$g^{1}$	MKRT
Descriptive Statistics: Mean	1.78	2.19	2.33	2.62	12.70
Descriptive Statistics: Standard Deviation	4.89	4.18	4.94	7.44	18.25
Descriptive Statistics: Autocorrelation Coef.	38.40	13.12	8.19	14.15	-14.19
Correlation Matrix: $g^{agg}$	1
Correlation Matrix: $g^{10}$	0.81	1
Correlation Matrix: $g^{5}$	0.73	0.97	1
Correlation Matrix: $g^{1}$	0.60	0.88	0.92	1
Correlation Matrix: MKRT	-0.01	0.01	0.02	0.05	1

Table II

Fama and MacBeth Risk Premiums in the CAPM and HCAPM

The table includes the Fama and MacBeth (FMB) (1973) risk premiums estimated from the CAPM and four HCAPM specifications. For the CAPM the market return is the only risk factor. For the HCAPM the risk factors are the CRSP return (MKRT) and the return to human capital (HCRT). We examine four proxies for the return to human capital: the growth rate in aggregate labor earnings (HCAPM100), $g^{agg}$ , the growth rate in labor earnings among households in the top 10% of the income distribution (HCAPM10), $g^{10}$ , the growth rate of labor earnings among households in the top 5% of the income distribution (HCAPM5), $g^{5}$ , and the growth rate of labor earnings among households in the top 1% of the income distribution (HCAPM1), $g^{1}$ . The income data are from Piketty and Saez (2003). The FMB t-statistics are reported beneath the risk premiums and Shanken (1992) t-statistics are reported beneath the FMB t-statistics. The $R^{2}$ is the cross-sectional R-squared of Jagannathan and Wang (1996). The Adj R² is adjusted for the number of factors. The time period is 1932 to 2005. The test assets are the 25 Fama and French (1993) portfolios. Their annual returns are compounded from monthly ones and they are expressed in real terms. The inflation rate is related to the consumer price index (CPI) published by the Bureau of Labor Statistics (BLS).


	Intercept	MKRT	HCRT	$R^{2}$	g	Adj $R^{2}$
CAPM	0.019	0.12		0.37	3.56	0.35
CAPM: FMB t-statistic	0.53	2.82
CAPM: Shanken t-statistic	0.44	2.46
HCAPM100	0.019	0.12	0.03	0.43	11.20	0.41
HCAPM100: FMB t-statistic	0.51	2.93	2.74
HCAPM100: Shanken t-statistic	0.38	2.29	2.16
HCAPM10	0.002	0.14	0.05	0.54	12.50	0.52
HCAPM10: FMB t-statistic	0.05	3.27	3.22
HCAPM10: Shanken t-statistic	0.03	2.08	1.94
HCAPM5	0.004	0.14	0.07	0.68	11.86	0.67
HCAPM5: FMB t-statistic	0.12	3.22	3.30
HCAPM5: Shanken t-statistic	0.06	1.86	1.78
HCAPM1	0.013	0.12	0.12	0.78	9.86	0.78
HCAPM1: FMB t-statistic	0.36	2.94	3.49
HCAPM1: Shanken t-statistic	0.18	1.67	1.84

Table III

Returns of Mimicking Portfolios and Fama and French Factors

This table includes descriptive statistics for the factor mimicking portfolios constructed from the four human capital return proxies: $g^{agg}$ , $g^{10}$ , , and . In each case the mimicking portfolio is constructed by regressing the human capital return proxy onto the excess returns of the Fama-French (1993) 25 portfolio returns. The table also includes descriptive statistics for the SMB and HML factors of Fama and French (1993). The time period is 1932 to 2005. For more details on the data sources we use see the legend in Table II. Finally, the mean returns of the mimicking portfolios, which are statistically significant at the 1% level, are in bold face font.


	g	$g^{10}$	$g^{5}$	$g^{1}$	MKRT	SMB	HML
Mean	0.58	0.85	1.18	2.21	9.22	2.13	10.00
Median	0.38	0.53	1.13	2.10	10.83	-0.96	9.49
Maximum	11.59	7.55	8.81	13.00	57.22	54.98	39.82
Minimum	-14.69	-7.46	-6.74	-7.08	-35.95	-25.30	-9.72
St. Dev.	3.62	2.50	2.63	3.92	19.20	15.08	11.34

Table IV

Fama and MacBeth Risk Premiums in the HCAPM and the Fama-French Factors

The table reports the Fama and MacBeth (1973) risk premiums in bold face numbers under the columns titled Intercept, MKRT, SMB, HML, and HCRT. The Fama and MacBeth t-statistics are reported beneath the risk premiums, and the Shanken (1992) t-statistics are reported beneath the Fama and MacBeth t-statistics. The $R^{2}$ is the cross-sectional R-squared of Jagannathan and Wang (1996). The Adj R² is adjusted for the number of factors. The table presents the results for five models. The first model (3 FF Factors) is the Fama and French (1993) model. Its factors are the excess market return (MKRT), and the returns on the SMB and HML factors. The factors in the other four models are the three Fama and French factors plus one of four different proxies for the return to human capital (HCRT): the growth rate in aggregate labor earnings (HCAPM100), $g^{agg}$ , the growth rate in labor earnings among households in the top 10% of the income distribution (HCAPM10),¹⁰, the growth rate of labor earnings among households in the top 5% of the income distribution (HCAPM5), $g^{5}$ , and the growth rate of labor earnings among households in the top 1% of the income distribution (HCAPM1), $g^{1}$ . The time period is 1932 to 2005. The test assets are the 25 Fama and French (1993) portfolios. For more details on the data sources we use see the legend in Table II.


	Intercept	MKRT	SMB	HML	HCRT	$R^{2}$	Adj $R^{2}$
3 FF Factors	0.15	-0.03	0.04	0.07		0.86	0.86
3 FF Factors: FMB t-statistic	3.82	-0.59	2.36	3.78
3 FF Factors: Shanken t-statistic	3.24	-0.52	2.31	3.64
HCAPM100	0.17	-0.04	0.04	0.07	0.01	0.87	0.86
HCAPM100: FMB t-statistic	4.04	-0.85	2.34	3.78	0.86
HCAPM100: Shanken t-statistic	3.34	-0.73	2.29	3.60	0.76
HCAPM10	0.15	-0.02	0.04	0.07	0.02	0.89	0.89
HCAPM10: FMB t-statistic	3.62	-0.40	2.31	3.70	1.52
HCAPM10: Shanken t-statistic	2.90	-0.34	2.25	3.54	1.25
HCAPM5	0.15	-0.02	0.04	0.06	0.03	0.91	0.90
HCAPM5: FMB t-statistic	3.73	-0.51	2.35	3.63	1.71
HCAPM5: Shanken t-statistic	2.84	-0.41	2.29	3.47	1.33
HCAPM1	0.15	-0.02	0.04	0.06	0.06	0.92	0.91
HCAPM1: FMB t-statistic	3.63	-0.43	2.40	3.55	1.92
HCAPM1: Shanken t-statistic	2.64	-0.33	2.33	3.39	1.42

Table V

Pricing Errors of the HCAPM and Fama-French Model

The table reports the average pricing errors (PE) of the five size and five book-to-market aggregated Fama and French (1993) portfolios for five different models. The pricing errors are multiplied by a factor of 100. The average pricing error of each aggregated size and book-to-market portfolio is constructed from the five out of the 25 portfolios that belong to each size and book-to-market category. The table also reports the chi-squared test for each group of aggregated portfolios. The first four models are four specifications of the HCAPM: HCAPM100, HCAPM10, HCAPM5, and HCAPM1. The fifth model is the Fama-French (1993) three factor model, 3 FF. The time period is 1932 to 2005. For more details on the data sources we use see the legend in Table II.


	HCAPM100	HCAPM10	HCAPM5	HCAPM1	3 FF
PE of Book-to-Market Portfolios: B1	-3.72	-3.19	-2.15	-1.28	0.21
PE of Book-to-Market Portfolios: B2	-0.97	-0.99	-0.76	-0.66	-0.55
PE of Book-to-Market Portfolios: B3	0.91	0.73	0.88	0.68	0.39
PE of Book-to-Market Portfolios: B4	1.90	1.61	1.03	0.79	-0.18
PE of Book-to-Market Portfolios: B5	1.87	1.85	1.00	0.47	0.13
PE of Book-to-Market Portfolios: Chi-Squared Statistic	7.01	3.32	2.07	1.27	2.85
PE of Book-to-Market Portfolios: P-value of Chi-Sq Test	0.07	0.35	0.56	0.74	0.09
PE of Size Portfolios: S1	-0.50	0.12	0.70	1.04	-0.43
PE of Size Portfolios: S2	-0.42	-0.90	-0.96	-1.05	0.27
PE of Size Portfolios: S3	0.27	-0.11	-0.07	-0.16	0.05
PE of Size Portfolios: S4	1.27	1.36	1.00	0.82	0.26
PE of Size Portfolios: S5	-0.61	-0.47	-0.67	-0.65	-0.14
PE of Size Portfolios: Chi-Squared Statistic	4.96	4.69	3.88	3.93	0.80
PE of Size Portfolios: P-value of Chi-Sq Test	0.18	0.20	0.27	0.27	0.37

Table VI

Pricing Errors of Alternative Models

The table reports the average pricing errors (PE) of the five size and five book-to-market aggregated Fama and French (1993) portfolios for seven different models. The pricing errors are multiplied by a factor of 100. The pricing error of each aggregated size and book-to-market portfolio is the average of the pricing errors of the five out of the 25 portfolios that belong to each size and book-to-market category. The table also includes the chi-squared test for each of each group of aggregated portfolios. The last three rows report statistics calculated using the pricing errors of the 25 Fama-French (1993) portfolios. They are the root mean squared error pricing error (RMSE), the $R^{2}$ of Jagannathan and Wang (1996) and the adjusted $R^{2}$ . The first two models are the HCAPM100 and HCAPM1. The five remaining models are Yogo's (2005) durable goods model (Yogo), Parker and Julliard's (2005) model of ultimate consumption risk (PJ), Lettau and Ludvigson's (2001b) scaled CCAPM (LL), Aït-Sahalia, Parker and Yogo's (2004) luxury consumption model (ASPY), and Santos and Veronesi's (2005) model (SV). The precise details associated with each model's asset pricing factors are contained in the Appendix. The time period is 1932 to 2003. For more details on the data sources we use see the legend in Table II.


	HCAPM100	HCAPM1	Yogo	PJ	LL	ASPY	SV
PE of Book-to-Market Portfolios: B1	-3.66	-1.29	-2.87	-1.76	-1.53	-1.91	-2.48
PE of Book-to-Market Portfolios: B2	-0.98	-0.65	-0.96	-0.96	-1.68	-0.66	-1.12
PE of Book-to-Market Portfolios: B3	0.88	0.68	0.90	0.13	0.70	0.91	0.71
PE of Book-to-Market Portfolios: B4	1.93	0.78	1.12	0.54	0.68	0.58	1.38
PE of Book-to-Market Portfolios: B5	1.84	0.48	1.81	2.05	1.82	1.09	1.51
PE of Book-to-Market Portfolios: Chi-Squared Statistic	6.47	1.23	5.75	3.55	2.73	5.42	4.70
PE of Book-to-Market Portfolios: P-value of Chi-Sq Test	0.09	0.75	0.12	0.47	0.43	0.25	0.20
PE of Size Portfolios: S1	-0.42	1.02	0.01	0.66	-0.06	1.70	0.83
PE of Size Portfolios: S2	-0.49	-1.04	-0.41	-0.49	1.74	-0.29	-0.40
PE of Size Portfolios: S3	0.28	-0.17	0.49	-0.04	1.29	0.29	-0.28
PE of Size Portfolios: S4	1.20	0.84	-0.31	0.04	-1.64	-0.67	-0.13
PE of Size Portfolios: S5	-0.57	-0.66	0.22	-0.16	-1.33	-1.03	-0.03
PE of Size Portfolios: Chi-Squared Statistic	4.59	3.85	2.82	1.49	4.57	5.45	1.10
PE of Size Portfolios: P-value of Chi-Sq Test	0.20	0.28	0.42	0.83	0.21	0.24	0.78
25 Portfolios: RMSE	2.67	1.65	2.20	1.83	2.66	1.96	2.23
25 Portfolios: $R^{2}$	0.44	0.79	0.62	0.74	0.45	0.70	0.61
25 Portfolios: Adj $R^{2}$	0.42	0.78	0.61	0.73	0.42	0.69	0.60

Table VII

Unique Asset-Pricing Information

The table includes the Fama and MacBeth (1973) risk premiums (bold face numbers) of four income growth rates when they are included as an additional factor in five macroeconomic factor models. The table also includes the Fama and MacBeth t-statistics (beneath the risk premiums), and the Shanken (1992) t-statistics (beneath the Fama and MacBeth t-statistics). In applying the Fama and MacBeth methodology, we estimate both the first stage time-series regressions and the second stage cross-sectional regressions with OLS. We consider four income growth rates: $g^{agg}$ , $g^{10}$ , $g^{5}$ , and $g^{1}$ . The five macroeconomic models we consider are Yogo's (2005) durable goods model (Yogo), Parker and Julliard's (2005) model of ultimate consumption risk (PJ), Lettau and Ludvigson's (2001b) scaled CCAPM (LL), Aït-Sahalia, Parker and Yogo's (2004) luxury consumption model (ASPY), and Santos and Veronesi's (2005) model (SV). The precise details associated with each model's asset pricing factors are contained in the Appendix. In the estimation, the test assets are the 25 Fama and French (1993) portfolios. The time period is 1932 to 2003. For more details on the data sources we use see the legend in Table II.


	HCAPM100	HCAPM10	HCAMP5	HCAPM1
Yogo	0.03	0.04	0.05	0.09
Yogo: FMB t-statistic	2.48	2.44	2.69	2.90
Yogo: Shanken t-statistic	1.83	1.59	1.69	1.78
PJ	0.02	0.02	0.04	0.08
PJ: FMB t-statistic	1.93	1.63	2.21	2.43
PJ: Shanken t-statistic	1.58	1.28	1.56	1.59
LL	0.02	0.04	0.06	0.10
LL: FMB t-statistic	2.35	3.32	3.42	3.54
LL: Shanken t-statistic	1.41	1.67	1.76	1.87
ASPY	0.01	0.01	0.03	0.08
ASPY: FMB t-statistic	1.22	1.14	2.02	2.65
ASPY: Shanken t-statistic	1.08	0.98	1.58	1.77
SV	0.02	0.03	0.05	0.11
SV: FMB t-statistic	1.77	2.49	3.29	3.66
SV: Shanken t-statistic	1.44	1.84	2.08	1.99

Table VIII

Robustness Tests

The table includes the Fama and MacBeth (1973) risk premiums (bold face numbers), the Fama and MacBeth t-statistics (beneath the risk premiums), and the Shanken (1992) t-statistics (beneath the Fama and MacBeth t-statistics). The table includes the cross-sectional $R^{2}$ of Jagannathan and Wang (1996). The Adj $R^{2}$ is adjusted for the number of factors. The CRSP return (MKRT) is always one of the asset pricing factors. In the returns to human capital are four different income growth rates: $g^{agg}$ , $g^{10}$ , $g^{5}$ , and $g^{1}$ . In Panel B and C, we estimate the first and second stage regressions with OLS. In Panel A we estimate the second stage regression with GLS. In Panels A and C the time period is 1932 to 2005. In Panel B the time period is 1945 to 2005. The test assets in panels A and B are the 25 Fama and French (1993) portfolios. In the regression reported in Panel C, the real return of the 1-month Treasure bill is subtracted from the returns of the test assets. The Treasury bill return is from Ibbotson Associates and it is downloaded from the web site of Kenneth French. For more details on the data sources we use see the legend in Table II.


	Panel A: GLS, HCRT	Panel A: GLS, $R^{2}$	g	Panel A: GLS, Adj $R^{2}$	Panel B: Post-War II, HCRT	Panel B: Post-War II, $R^{2}$	Panel B: Post-War II, Adj $R^{2}$	Panel C: R - Rf, HCRT	Panel C: R - Rf, $R^{2}$	Panel C: R - Rf, Adj $R^{2}$
HCAPM100	0.01	0.23	3.76	0.20	-0.02	0.07	0.02	0.03	0.43	0.41
HCAPM100: FMB t-statistic	0.67				-1.79			2.74
HCAPM100: Shanken t-statistic	0.65				-1.51			2.16
HCAPM10	0.02	0.30	4.31	0.27	0.02	0.05	-0.00	0.05	0.54	0.52
HCAPM10: FMB t-statistic	1.55				1.38			3.22
HCAPM10: Shanken t-statistic	1.44				1.14			1.94
HCAPM5	0.03	0.42	4.22	0.39	0.06	0.19	0.15	0.07	0.68	0.67
HCAPM5: FMB t-statistic	2.30				2.63			3.30
HCAPM5: Shanken t-statistic	1.98				1.60			1.78
HCAPM1	0.06	0.56	3.48	0.54	0.14	0.35	0.32	0.12	0.78	0.78
HCAPM1: FMB t-statistic	3.10				3.35			3.49
HCAPM1: Shanken t-statistic	2.42				1.54			1.84

Table IX

Dynamic HCAPM

Panel A: Fama and MacBeth Risk Premiums

The table reports the results of Campbell's (1996) three-factor model. It includes the Fama and MacBeth (FMB) (1973) risk premiums (bold face numbers) of the dynamic HCRT. The FMB t-statistics are beneath the risk premiums, and the Shanken (1992) t-statistics are beneath the FMB t-statistics. The table also includes the cross-sectional $R^{2}$ and its adjusted version. The factors are the CRSP return and the revisions to expectations about its future evolution. The human capital factor is the dynamic HCRT (the growth rate of income plus the revisions to expectations about its future evolution). We estimate the revisions to expectations using a VAR(1) model on the income growth rate, the CRSP return, the dividend yield of the CRSP return, and the cay residual from Lettau and Ludvigson (2001a, 2001b). We use four income growth rates: $g^{agg}$ , $g^{10}$ , $g^{5}$ , and $g^{1}$ . In Panel A.1 and A.3, we estimate the first and second stage regressions with OLS. In Panel A.2 we estimate the second stage regression with GLS. In Panels A.1 and A.2 the time period is 1932 to 2005. In Panel A.3 the time period is 1945 to 2005. The test assets are the 25 Fama and French (1993) portfolios. For details on the data sources we use see the legend in Table II.


	Panel A.1 OLS: Dynamic HCRT	Panel A.1 OLS: $R^{2}$	Panel A.1 OLS: Adj $R^{2}$	Panel A.2 GLS: Dynamic HCRT	Panel A.2 GLS: $R^{2}$	Panel A.2 GLS: Adj $R^{2}$	Panel A.3 Post-War II: Dynamic HCRT	Panel A.3 Post-War II: $R^{2}$	Panel A.3 Post-War II: Adj $R^{2}$
HCAPM100	0.17	0.73	0.71	0.09	0.51	0.48	0.08	0.20	0.14
HCAPM100: FMB t-statistic	2.62			1.70			1.57
HCAPM100: Shanken t-statistic	1.68			1.50			1.11
HCAPM10	0.21	0.78	0.76	0.10	0.56	0.54	0.19	0.33	0.29
HCAPM10: FMB t-statistic	3.38			2.62			2.78
HCAPM10: Shanken t-statistic	1.80			2.12			1.58
HCAPM5	0.21	0.81	0.80	0.13	0.62	0.60	0.21	0.41	0.37
HCAPM5: FMB t-statistic	3.24			3.07			3.08
HCAPM5: Shanken t-statistic	1.83			2.37			1.70
HCAPM1	0.23	0.85	0.84	0.15	0.68	0.66	0.32	0.46	0.42
HCAPM1: FMB t-statistic	3.28			3.35			3.65
HCAPM1: Shanken t-statistic	1.84			2.46			1.75

Table IX (continued)

Dynamic HCAPM

Panel B: Pricing Errors


	HCAPM100	HCAPM10	HCAPM5	HCAPM1
PE of Book-to-Market Portfolios: B1	-2.36	-1.99	-1.56	-1.22
PE of Book-to-Market Portfolios: B2	-0.73	-0.52	-0.29	-0.19
PE of Book-to-Market Portfolios: B3	1.46	1.34	1.49	1.19
PE of Book-to-Market Portfolios: B4	0.71	0.47	0.26	0.40
PE of Book-to-Market Portfolios: B5	0.93	0.71	0.10	-0.18
PE of Book-to-Market Portfolios: Chi-Squared Statistic	6.07	3.92	4.92	2.70
PE of Book-to-Market Portfolios: P-value of Chi-Sq Test	0.05	0.14	0.09	0.26
PE of Size Portfolios: S1	0.70	0.82	0.99	1.10
PE of Size Portfolios: S2	-0.89	-1.08	-0.81	-0.83
PE of Size Portfolios: S3	0.26	0.24	0.44	0.10
PE of Size Portfolios: S4	0.40	0.35	-0.03	0.19
PE of Size Portfolios: S5	-0.47	-0.33	-0.58	-0.58
PE of Size Portfolios: Chi-Squared Statistic	3.74	3.57	3.72	2.89
PE of Size Portfolios: P-value of Chi-Sq Test	0.15	0.17	0.16	0.24

Figure 1

Aggregate Real Income Growth: BEA vs. Piketty-Saez Data

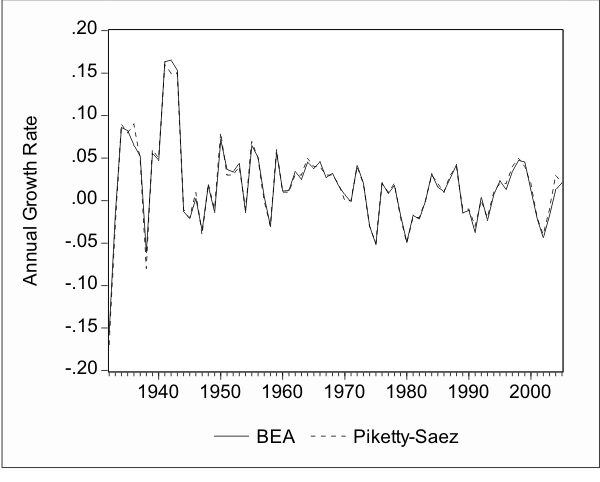
The figure above plots the annual growth rate of average income computed with data from the Bureau of Economic Analysis (BEA) in the solid line and the income tax data of Piketty and Saez (2003) in the dashed line. Both series are in real per capita terms. The time period is 1932 to 2005.

Figure 2

Income Growth of the Top 10%, 5% and 1% of the U.S. Income distribution

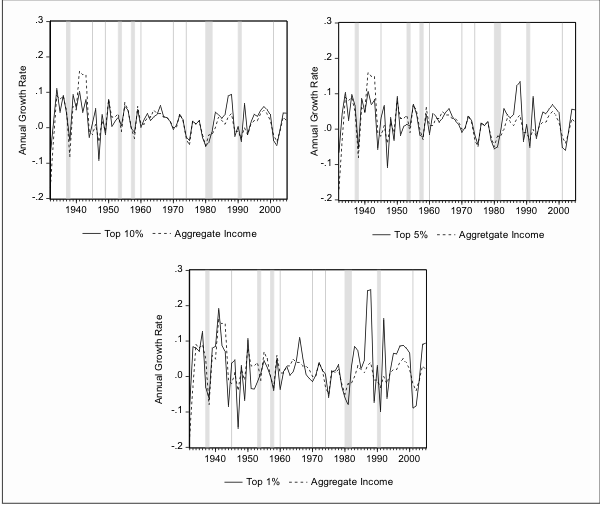
The figure above plots the annual growth rate of: aggregate income (dashed line, all sub-plots), average income among households in the top 10% of the income distribution (solid line, top left sub-plot), average income among households in the top 5% of the income distribution (solid line, top right sub-plot), and average income among households in the top 1% of the income distribution (solid line, bottom middle sub-plot). All series are in real per capita terms. The time period is 1932 to 2005. The shaded areas represent NBER recessions.

Footnotes

1. One might want to consider the fact that the share of human wealth varies over time with the return on financial and human wealth. In this paper we follow the previous literature and ignore this complication though it could, in principle, be handled by allowing $\omega$ to vary. Return to Text

2. Palacios-Huerta (2003) examines the sensitivity of the HCAPM to various measures of the return to human capital. In particular, he uses CPS data, for the period 1964-1990, to construct a measure of the return to human capital for individuals with characteristics that are indicative of stock ownership. He reports (results not shown) that this measure improves the fit of the HCAPM. In Section III, we discuss the advantages of the Piketty and Saez (2003) data to CPS data. Return to Text

3. Throughout our analysis we use income from wages and entrepreneurial activities. Wages are defined as wages and salaries and pensions (and includes bonuses, stock-option exercises, etc.). Entrepreneurial income includes profits from S-Corporations (entities not subject to corporate taxes and taxed only at the individual level), profits from partnerships, profits from sole proprietorship businesses (Schedule C income) and farm income. We exclude dividend, interest and rental income. This data can be downloaded from http://elsa.berkeley.edu/ $\sim$ saez/. Return to Text

4. Throughout we deflate nominal variables with the CPI. Return to Text

5. The portfolio returns are downloaded from http://mba.tuck.dartmouth.edu/pages/faculty/ken.french/. Return to Text

6. The non-monotonicity stems from the fact that he Shanken correction to the standard errors penalizes factors with high variance, like $g^{1}$ . See Lettau and Ludvigson (2001) for more on the behavior of the Shanken t-statistics.

Return to Text

7. For each human capital factor we have 74 annual observations. There are 25 size and book-to-market sorted portfolios. One might reasonably question whether the number of regressors is too large relative to the sample size. We have also constructed mimicking portfolios using the three Fama-French factors as base assets. The results are qualitatively and quantitatively similar. Return to Text

8. In all previous tables we have reported empirical results over the 1932-2005 period. The factor in the Parker and Julliard (2005) model is three-year-ahead consumption growth. As a result, we cut the end of the sample period to 2003 to ensure that each of the macroeconomic factors is available over the same time period. Return to Text

9. The exception to this rule is the case of the Yogo model in which the Shanken t-statistics associated with HCAPM100 and HCAPM1 are 1.83 and 1.78 respectively. Return to Text

10. It is worth noting that the predictable nature of stock returns is still a topic of considerable debate. The ability of the dividend yield, cay and other predictors has recently been debated by Goyal and Welch (2007) and Campbell and Thompson (2007). Accordingly, the results of the dynamic HCAPM should be interpreted in light of this debate. Return to Text

^♣ This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to Text