
The Trajectory of Wealth in Retirement
Keywords: Retirement wealth; mortality risk; precautionary saving; bequests; risk and uncertainty.
Abstract:
As the baby boomers begin to retire, a great deal remains unknown about the evolution of wealth toward the end of life. In this paper, we develop a new measure of household resources that converts total financial, nonfinancial, and annuitized assets into an expected annual amount of wealth per person. We use this measure, which we call "annualized comprehensive wealth," to investigate spend-down behavior among older households in the Health and Retirement Study. Our analysis indicates that, in (real) dollar terms, the median household's wealth declines more slowly than its remaining life expectancy, so that real annualized wealth actually tends to rise with age over retirement. Comparing the estimated age profiles for annualized wealth with profiles simulated from several different life cycle models, we find that a model that takes into account uncertain longevity, uncertain medical expenses, and (for higher-income retirees) intended bequests lines up best with the HRS data.
JEL classification: D91; E21; I10
1 Introduction
The adequacy of a household's wealth depends not only on the amount of total resources at the onset of retirement, but also, crucially, on how those resources are spent toward the end of the life cycle. To investigate spend-down patterns, we construct a new measure of the total resources available per expected year of life for retired households in the Health and Retirement Study (HRS), which we call "annualized comprehensive wealth." It is a comprehensive measure because in addition to net worth as it is usually defined--the sum of financial and nonfinancial wealth--it also includes the value of Social Security benefits, defined-benefit pension benefits, and, for eligible recipients, transfer payments such as Food Stamps and Supplemental Security Income. Our measure is an annualized concept in the sense that it measures wealth per expected year of remaining life per person. If this measure of total resources were either rising or falling sharply in retirement, we would probably want to know why.
By focusing on the trajectory of annualized comprehensive wealth, we are directly examining whether the total amount of resources available to fund spending in retirement tends to fall more or less quickly than life expectancy shortens. This focus provides a clearer picture of spend-down behavior than would come from looking at how the level of wealth alone changes toward the end of the life cycle. That is, the rate at which wealth balances decrease in old age is more relevant for thinking about the consumption possibilities available to older retirees than just whether balances decline at all. Annualized comprehensive wealth is a measurement concept that could help to distinguish between reductions in consumption that might result from retirees having insufficient resources to maintain a prior standard of living (a case in which we would expect both annualized wealth and consumption to be low) and the consequences of other motives, such as precautionary savings or intentional bequests (cases in which we would expect annualized wealth to exceed consumption). Whether annualized wealth rises or falls during retirement therefore provides important information about the underlying causes of spending behavior in retirement.1
The simplest life cycle model predicts that wealth balances should decline in tandem with remaining years of life, implying a roughly flat trajectory for annualized wealth. Although there are many reasons why actual behavior might differ from predictions of the simplest life cycle model, we would be inclined to interpret a sharp downward trajectory of annualized wealth as evidence that retirees were spending down their balances "too quickly" or that their initial level of resources were "too low"--particularly if the level of annualized wealth was found to reach a low level early in retirement. Using a balanced panel from 1998 to 2004, however, we find that the median value of annualized comprehensive wealth for households over 70 actually rises, from about $24,900 per person per year to about $28,100 per person per year--a net increase of 13 percent over just six years. That is, we find that at the median of the distribution, comprehensive wealth tends to fall more slowly than life expectancy. Looking at the distribution of outcomes, we estimate that more than one-third of households saw their annualized comprehensive wealth rise by more than 25 percent from 1998 through 2004, while only about one-sixth experienced a decrease of 25 percent or more. This distribution of outcomes is surprisingly similar when we look across different age groups, household compositions, and even household incomes. Indeed, even for the median low-income household in the HRS panel, we find that annualized comprehensive wealth increased slightly over the sample period (although the level of resources remained low). The top quintile of households by income, however, experienced the largest increase in annualized wealth, from $58,200 per person per year in 1998 to $69,500 per person per year in 2004. Looking across the retirement period as a whole (and holding a range of household characteristics constant), we estimate that the median value of annualized comprehensive wealth rose from about $22,000 per person per year at age 62 to about $28,000 at age 85.
Moreover, we find that the annualized values of both financial and nonfinancial assets rose over the sample period. Although some of the increase in nonfinancial wealth in retirement seems to have been accounted for by capital gains that accrued to housing between 1998 and 2004, we show that the net rise in annualized wealth over retirement persists even after controlling for capital gains.
Why might households draw down wealth slowly relative to life expectancy? To examine some likely explanations, we assume that households pursue the standard objective of maximizing expected lifetime utility, and we add to the simplest model some elements from previous studies: uncertain longevity (Yaari, 1965; Hurd, 1989; Davies, 1981; Hubbard, 1987), uncertain medical expenses (Palumbo, 1999; Anderson, French, and Lam, 2004; French and Jones, 2004a), and bequest motives (Bernheim, 1991; Laitner and Juster, 1996; Kopczuk and Lupton, 2007; Kotlikoff and Summers, 1981; Hurd, 1989,1987; Dynan, Skinner, and Zeldes, 2002; De Nardi, 2004). Our simulations indicate that models incorporating either uncertain medical expenses or bequests can generate upward-sloping profiles of annualized wealth. We obtain the closest fit with the data, however, when we incorporate both of these saving motives into the model, in combination with uncertain lifetimes. In particular, we find that the prospect of large medical expenses induces retirees to build a precautionary buffer early on, while a desire to leave a bequest leads them to maintain "excess savings" toward the end of life.
Our paper contributes to several strands of the literature on household saving and wealth. One strand, focusing on the adequacy of retirement wealth, finds that a substantial fraction of aging households are poorly positioned to finance retirement (see Mitchell and Moore, 1998; Bernheim, 1992; Munnell and Soto, 2005) and that the situation may be even worse for younger age groups (Munnell, Webb, and Delorme, 2006).2 While we find a significant share of households experiencing a decrease in annualized wealth, our results show that the median retiree seems to be building up annualized resources with age.
A related literature focuses on the optimality of observed household savings by comparing empirical data to accumulation patterns predicted by rich specifications of stochastic life cycle models (see Engen, Gale, and Uccello, 1999,2005; Scholz, Seshadri, and Khitatrakun, 2006). These papers generally find that observed behavior is in line with the predictions generated by the models. These results are also generally consistent with empirical evidence regarding observed declines in consumption at retirement (Hurd and Rohwedder, 2006). Aguiar and Hurst (2005) find, for example, that home production allows retired households to maintain standards of living while spending less, while Blau (2008) shows that an unexpected health shock could trigger an early retirement and a subsequent decline in consumption.3 Our approach is distinct from these papers in that we do not attempt to explain optimal wealth levels heading into retirement and we do not directly estimate the path of consumption after retirement. Rather, we condition on the level and composition of wealth at retirement and compare observed patterns of changes in annualized wealth in retirement to predictions from several expanded life cycle models to indirectly infer what factors are consistent with the HRS data.
2.1 Methods
We use longitudinal data from the 1998 through 2004 waves of the Health and Retirement Study (HRS). The HRS is a panel of older households that began in 1992 surveying respondents aged 51 to 61 in that year. The HRS has reinterviewed those households every two years and has added several additional cohorts along the way. In 1998, the HRS merged with a similar survey called Aging and Health Dynamics (AHEAD), which covered households aged 70 and over in 1993. The 1998 wave of the HRS also added two additional cohorts: the War Baby cohort (aged 51 to 56 in 1998) and the Children of the Depression cohort (aged 68 to 74 that year). Thus, the 1998 wave is the first to represent the full population of U.S. households aged 51 and over.
In selecting our primary data set, we begin with households aged 65 or more in the 2004 HRS survey, and we collect information for these households back to the 1998 wave.4 The advantage of using this "backward-looking" panel approach is that we condition on the survival of the household to 2004, and thus sidestep the potential for confounding survivorship bias in the 1998 cohort with household behavior.5
We begin with the RAND HRS data file, which is RAND's longitudinal file of commonly used HRS variables linked by households across time. We supplement this file with additional measures that we calculate from the HRS. Most importantly, we calculate the actuarial present value of expected flows from Social Security, defined-benefit pensions, life annuities, and transfer payments such as veterans' benefits, Food Stamps, and Supplemental Security Income. These calculations provide measures of annuity-like wealth that are often excluded from empirical analyses of portfolio and saving behavior.6 With these variables included, we can analyze a comprehensive measure of wealth in order to learn how the various components and total resources are drawn down in retirement.
2.2 Characteristics of the sample
Table 1 reports the age distribution for the sample we draw from the 2004 wave of the HRS; for couples, we report the age of the older member of the household. About half of our sample is under 75, and about half is older; married couples are much more likely to be in the younger group. Table 2 reports several other household characteristics describing our sample in 2004. Most single households are women (generally widows). Average annual income is about $44,000. Just over half of our sample have earned no more than a high school degree and fewer than one-fifth a college degree. About 1 in 10 households in our sample reports being nonwhite and about 1 in 20 being hispanic. More than a quarter of households include at least one person who perceives him or herself as being in either poor or fair health (as opposed to good or excellent health), and the average household spent about $6,700 out-of-pocket on medical care during the prior year.
2.3 The composition and level of comprehensive wealth in the HRS
Table 3 provides a breakdown of the components of comprehensive wealth for the median household aged 70 or older in 2004. The discounted present value of annuity-like benefits--Social Security, DB pensions, and other government transfers--accounted for about 44 percent of comprehensive wealth for the median household in 2004. By construction, the present value of these annuity-like streams decline as households age and their remaining life expectancies shrink. So, while we estimate a median annuity-like balance of $217,000 in 1998, by 2004 the value of this key source was just $143,000. Of course, this decline does not necessarily translate into a large drop in spendable resources per year because, as mentioned, remaining life expectancies decreased considerably over the six-year period as well.7 For the median household in 2004, net nonfinancial wealth accounted for about one-third of comprehensive wealth ($111,000), with net housing wealth (home values net of mortgage debt) constituting the lion's share of this component ($89,000). Over the period from 1998 to 2004, the median balance of nonfinancial wealth fell only slightly (in real terms), as a small increase in the median household's net housing wealth was almost as large as the decline registered for the other components.8 In 2004, just over one-fifth of the median household's comprehensive wealth was in the form of financial assets, and that year's balances were about 15 percent lower than in 1998 ($74,000 in 2004 vs. $87,000 in 1998).
Table 4 reports the evolution of comprehensive wealth from 1998 through 2004 for different types of households aged 70 and older in 2004. For the full sample, the real value of comprehensive wealth fell by 21 percent from 1998 through 2004. The rate of decline was larger for households older than age 80 (in 2004) than for those in their 70s and was much larger for single persons (around 28 percent) than for married couples (about 15 percent). In percentage terms, the net decrease in comprehensive wealth was smaller for households in the bottom quintile of the income distribution (11 percent from 1998 to 2004) and the top quintile (15 percent) than for middle-income retirees (21 percent).
3.1 Definition of annualized wealth
The significant differences in comprehensive wealth by age and marital status highlight the importance of distinguishing between wealth balances and wealth per person per expected year of life, when considering the trajectory of resources in retirement. For this reason, we construct a measure of "annualized wealth" that indicates how much a household could, in principle, afford to spend per person per year over their remaining expected lifetimes, given their total resources (including current assets and future Social Security, pension, and welfare benefits). We demonstrate below that our measure is closely related to the optimal path of consumption in a simple life-cycle model and that it can also be derived from annuity-pricing principles.
For each household, we define annualized wealth as
where
where
To develop intuition about our measure of annualized wealth, it helps to consider some extreme values of the key parameters. For example, as the real interest rate approaches zero, the annualizing factor approaches
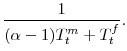 |
Thus, ignoring household economies of scale (i.e., setting
To take another extreme case, consider what happens to the annualizing factor if each member of the household were to expect to live forever. In this case,
![]() and the factor approaches
and the factor approaches
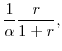 |
which implies that each year the household can afford to consume no more than its annual interest income
As we will show next, our measure of annualized wealth is closely related to two common concepts in economics--optimal consumption according to Modigliani's life cycle hypothesis and the annual payment that could be received from an actuarially fair, real, joint fixed life annuity that might be purchased (in principle) with a household's comprehensive wealth.
3.2 Annualized wealth and the Life Cycle Model
Consider the optimal consumption problem facing a representative household consisting of two members, who differ only in their probabilities of survival. Conditional on being alive in period 0, each member lives to period ![]() with cumulative probability
with cumulative probability ![]() and
and ![]() , respectively, with terminal probabilities
, respectively, with terminal probabilities
![]() . They start the period with comprehensive wealth position of
. They start the period with comprehensive wealth position of ![]() ,
which is the sum of their net worth from financial and nonfinancial assets and the present discounted value of any annuity streams (such as Social Security and DB pension benefits). According to the life cycle hypothesis, the household is assumed to maximize
,
which is the sum of their net worth from financial and nonfinancial assets and the present discounted value of any annuity streams (such as Social Security and DB pension benefits). According to the life cycle hypothesis, the household is assumed to maximize
subject to the lifetime resource constraint
where
Rearranging the resulting Euler equation for this constrained optimization problem, consumption can be shown to grow according to
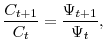 |
where
If both members of the household are alive in period 0,
Substituting this expression into the resource constraint and expanding
which we will see is identical to the formula for an actuarially-fair joint life annuity that pays
![\displaystyle C_0\frac{1+r}{r}\left[1-\left(1-\frac{1}{\alpha}\right)\frac{1}{(1+r)^{T^{m}}}-\frac{1}{(1+r)^{T^{f}}\alpha}\right]=W_0.](img41.gif) |
(6) |
Annual consumption per person,
where
The fact that our annualized wealth measure can be derived from a standard life cycle model suggests that it bears a close resemblance to the notion of permanent income that is fundamental in most analysis of consumption and savings. When we apply the measure to the data, however, we should keep
in mind that annualized wealth only equals permanent income in the special case of: (1) zero utility from bequests, (2)
![]() , and (3) log utility over annual consumption. In general, annualized wealth will not equal optimal consumption. For example, in the presence of bequests or uncertain medical
expenses, we would expect households to dissave at a slower rate than the simple life cycle model would predict. In Section 6, we investigate these issues in detail by simulating expanded life cycle models that include random medical expenses and explicit bequest motives and compare the empirical
trajectories of annualized wealth in the HRS with optimal paths from those model specifications.
, and (3) log utility over annual consumption. In general, annualized wealth will not equal optimal consumption. For example, in the presence of bequests or uncertain medical
expenses, we would expect households to dissave at a slower rate than the simple life cycle model would predict. In Section 6, we investigate these issues in detail by simulating expanded life cycle models that include random medical expenses and explicit bequest motives and compare the empirical
trajectories of annualized wealth in the HRS with optimal paths from those model specifications.
3.3 Annualized wealth and joint life annuities
We now demonstrate that our measure of annualized wealth is closely related to an actuarially fair, inflation-indexed, joint fixed life annuity that a retired household could theoretically purchase with all of its assets.11 Brown and Poterba (2000)) show that, using the "last survivor payout rule," the actuarially fair price of a fixed joint annuity paying a real amount ![]() each year that both members of a household are alive and an amount
each year that both members of a household are alive and an amount ![]() each year that only one member is alive is given
by
each year that only one member is alive is given
by
![\displaystyle p = \sum_{t=0}^{T}\left\{\frac{S_t^fS_t^m+\lambda [S_t^f(1-S_t^m)+S_t^m(1-S_t^f)]}{(1+r)^t}\right\},](img47.gif) |
where
Put another way, simple life cycle theory implies that (in the absence of bequests or precautionary saving), households would optimally fully annuitize their wealth and set annual consumption equal to the annuity receipt. However, in the expanded life cycle models we investigate in Section 6--which include explicit bequest motives and random medical expenses--full annuitization is not optimal (even if actuarially fair annuities were to exist).
3.4 Discussion of annualized wealth
We have shown that our measure of annualized wealth is closely related to optimal consumption behavior according to a stylized life cycle model, and can also be thought of as the value of an actuarially fair, real fixed annuity that a retired household could, in principle, afford to purchase with its total resources. Each angle provides a different perspective on the empirical application of our measure. What does it mean when we observe that a household in the HRS has, say, $20,000 in annualized wealth? Viewed through the lens of the life cycle model, we can say that the $20,000 corresponds loosely to each household member's permanent income, and, for certain parameterizations, to its optimal choice of consumption (per person). Viewed as an actuarially fair annuity, the measure tells us that each member of the household has enough resources to afford to purchase a real, joint life annuity that pays $20,000 per person per year, fully insulating their consumption possibilities from randomness over how long they will actually live.
3.5 Annualized wealth in the HRS
Table 6 reports the components of annualized comprehensive wealth from 1998 through 2004 for the median household aged 70 or older in 2004. At the median, annualized comprehensive wealth was $28,100 in 2004, 13 percent more than the median value in 1998 ($24,900). From 1998 to 2004, the contribution of annuity-like benefits to annualized comprehensive wealth declined slightly, from $12,800 to $12,100, likely due to the non-indexation of some DB payments. However, the decline in annuity-like wealth was more than offset by increases in the annualized value of financial assets (from $5,200 per person per expected year to $6,400) and nonfinancial wealth (from $6,900 to $9,400). Median annualized net housing wealth rose 51% from $5,100 in 1998 to $7,700 in 2004. This relatively large increase was accounted for by a net increase in actual wealth (from a balance of $84,000 in 1998 to $89,000 in 2004) combined with shorter remaining life expectancies (and, thus, smaller annualizing factors) as the median household aged. By contrast, the smaller net rise in annualized financial assets from 1998 to 2004 was accounted for by a decline in actual wealth (from $87,000 to $74,000) that was slow relative to the drop in the median household's remaining life expectancy.
That median annualized comprehensive wealth generally rose between the 1998 and 2004 waves of the HRS is one of the primary results in our paper. Clearly, part of the story for rising annualized wealth was that retirees accrued capital gains on their homes. But, retirees evidently did not offset those gains by rapidly spending down either their financial or nonfinancial assets.
Table 7 breaks down the evolution of annualized comprehensive wealth between 1998 and 2004 for the median household of different ages, family compositions, and income levels. Annualized wealth rose even faster for older retirees (aged 80-89) than younger retirees (aged 70-79). Among single retirees in 2004, annualized wealth rose in both age groups, while among married retirees in 2004, only the older cohort experienced an increase. As can be seen in the middle of the table, the time-path of annualized comprehensive wealth appears to be little affected by accounting for economies of scale in household consumption. Perhaps surprisingly, we find increases in annualized comprehensive wealth for the median household in each of the three income groups shown in the table. Among those in the bottom quintile of the income distribution in 2004, annualized comprehensive wealth increased 6 percent between 1998 and 2004. The rises were larger for middle-income retirees (13 percent) and those in the upper income quintile (19 percent).
Table 8 reports the frequency distribution of percentage changes in annualized comprehensive wealth for different types of households. Across the entire sample, the table shows that 48 percent of of retirees aged 70 and older (in 2004) experienced increases of at least 10 percent, while 30 percent experienced decreases of at least 10 percent over that time period. The table shows that the frequency distribution of changes in annualized wealth was essentially the same across age and marital status groups in 2004. We find small differences in the right tails across the three income groups--the share of households in the upper income quintile that experienced a 10 percent or larger increase is 50 percent, while the share is 46 percent among middle-income retirees and 42 percent for those in the bottom income quintile. Nonetheless, these distributions are remarkably stable across age, marital status, and income groups: In particular, in every row of Table 8, the greatest frequency of HRS households experienced an increase in annualized comprehensive wealth of 25 percent or more from 1998 through 2004.
4.1 Methodology
As a preliminary look at the evolution of resources over the course of retirement, we construct nonparametric profiles of median wealth between ages 60 and 90 years.14 To produce these profiles, we divide the sample into 3-year age bins in 1998 and calculate the median value of wealth for each bin over the following six years.15 We plot four points for each age group, corresponding to the 1998, 2000, 2002 and 2004 waves of the HRS. Arrayed by age on the horizontal axis, the series of segments trace out an empirical age profile of wealth.
Note that to interpret the resulting graph as an age profile, one must ignore the effects of cohort differences between the segments.16 In addition to cohort effects, another issue of concern is survivorship bias: since lower-wealth households are more likely to die in any given year than higher-wealth households, the slope of any given wealth segment is likely to be biased upward (i.e., more positive or less negative) relative to what would be the case without such truncation. This is an issue that we will address, at least partially, in the next section when we develop a regression-based methodology for estimating age profiles of wealth that uses the panel nature of the HRS data explicitly.
4.2 Results
Figure 1 displays median age profiles of comprehensive wealth balances (not annualized, not per person) and each of its major components (in thousands of 2004 dollars). Beginning with the top left panel, we can see that median financial wealth declines quite gradually over the retirement period--from about $70,000 at age 62 to about $20,000 by age 90 (abstracting from the relatively small cohort differences in the levels of the line segments). Nonfinancial wealth is flat at around $100,000 from age 62 until almost age 85 and it falls, on balance, at the later ages. The profile of annuity-like wealth shows a prominent peak around age 62, when Social Security benefits first come available, followed by a steady and substantial decline. This effect is more mechanical than behavioral: the present value spikes as the onset of payments approaches, then declines with life expectancy. Summing the three major components, we find that median comprehensive wealth peaks at about $500,000 around age 62 and drops to below $200,000 by the late 80s. Still, the median retiree in the HRS continues to hold a significant amount of wealth even at rather advanced ages.
The declining profiles of wealth at older ages suggests that some degree of spend-down is occurring. To learn more about the implications of this spend-down for individual resources, we turn to our concept of annualized wealth. Figure 2 shows that median annualized financial wealth is flat or rising a bit over the entire age range. This suggests that households do not appear to run down their financial wealth any more quickly than their life expectancies are shortening. We also see an increase in annualized nonfinancial wealth, suggesting that households may indeed be reluctant to fully consume their housing wealth as they age. The annualized value of annuity-like wealth is roughly flat after age 62, with perhaps a slight decline due to non-indexation of some benefits. When summed together, median annualized comprehensive wealth shows a gentle upward slope across older ages, so that, all told, the median value rises from about $17,000 per person per year at age 62 to about $30,000 per person per year at age 90.
5.1 Methodology
A natural concern regarding the nonparametric wealth profiles just discussed is that they are susceptible to survivorship bias and, in addition, make no attempt to control for the effects that a variety of observable factors have on the rate of change of household wealth in retirement. In this section, we present regression-based age profiles for comprehensive wealth that address these issues by using the full extent of the panel data in the HRS.
For each major component of comprehensive wealth, and for each income group17, we use a four-step procedure to estimate age-profiles. First, we calculate a household-level growth factor from each wave to the next (that is, three growth factors per household). Second, we pool all of the growth factors and estimate a median regression of the growth factors on a set of household characteristics, including indicators for two-year age brackets (e.g., 60-61, 62-63, etc.), survey-year dummies, and a range of other characteristics.18 Third, we use the estimated coefficients on the age indicators to calculate predicted median growth factors for each age-group and multiply these together to construct a "cumulative growth factor" across the full range of ages.19 Finally, we "connect the dots" between the predicted cumulative growth factors to form a regression-based age profile. The resulting profile will be purely relative (e.g., an index starting from one at age 60); to convert it to level terms, we benchmark the middle of each age profile so that it passes through the median level of wealth held by 75-year olds in 2004.
5.2 Results
Figure 3 shows that the regression-based age profiles are generally similar to the nonparametric profiles presented above. For retirees in the bottom income quintile, median financial wealth is essentially zero at all ages, while for those in the middle part of the income distribution, median financial wealth stays near $60,000 from age 62 to almost age 80, and then declines to about $30,000 over the next 10 years of retirement. Among upper-income households, median financial wealth stays pretty close to $250,000 from age 62 to almost age 80, and then it falls to about $125,000 by age 90.
Median nonfinancial wealth, for all three of the income groups, exhibits a slight hump shape that peaks around age 75. Thus, households in the bottom and middle quintiles of the income distribution (conditional on age and marital status) have about the same level of nonfinancial wealth in their mid-60s as they have in their mid-80s--$25,000 for the lower-income households, and $75,000 for the median income group. In the upper quintile of the income distribution, though, we estimate that despite the hump, nonfinancial wealth tends to rise a little over the course of retirement, from nearly $175,000 at the median in the mid-60s to about $200,000 by the mid-80s.
As we would expect, the present discounted value of annuity-like wealth falls steadily and substantially in retirement--for all three income groups, the median balance is about half as large around age 85 as it was around age 65. As with the nonparametric age profiles, the downward-sloping trajectory of annuity-like balances is mainly a mechanical result of shorter remaining lifespans.
Putting the major components together, the lower right panel of figure 3 shows that for retirees in all three income groups, median comprehensive wealth is fairly flat between ages 62 and 75. In the latter 70s and in the 80s, though, balances decrease more noticeably with age, particularly for households in the middle- and upper-income groups.20
Figure 4 shows the regression-based age profiles for annualized comprehensive wealth and its components. Again, these profiles are quite similar to those generated nonparametrically. It seems quite clear that households in the bottom income quintile are not relying on financial assets to finance spending in retirement--median annualized financial wealth stays at zero for this group at all ages in the HRS. However, for the middle-income retirees, median financial assets contribute about $5,000 per person per year to comprehensive wealth and, strikingly, this level does not fall over the course of retirement. Indeed, there is a very slight increase in annualized financial wealth through age 80 for the middle-income group. For households in the upper quintile of income, median annualized financial wealth shows a more pronounced increase from the early 60s (about $20,000 per person per year) through the late 70s (about $25,000); then it stays about flat for retirees in their 80s. Median nonfinancial wealth increases in annualized terms for all three income groups. While the levels are very different across the three income groups, all three groups nearly double their annualized nonfinancial wealth between the mid-60s and the mid-80s.
The median level of annualized annuity-like wealth is essentially flat for lower- and middle-income households from the mid-60s through the late-80s--at about $8,000 and $14,000 per person per year, respectively--while the upper-income quintile experiences a significant decrease over the course of retirement--from almost $20,000 per person per year in their mid-60s to about $15,000 by their late-80s. This is mainly a result of reduced wealth, in real per person terms, from private DB pension benefits as retirees age.21 Turning to the age profiles in the lower right panel, we find that, all told, between the early and the late retirement years, median annualized comprehensive wealth shows a mild net increase for lower- and middle-income households, and a pronounced rise for upper-income households.
5.3 The effect of capital gains on the estimated age profiles
How should we interpret this build-up in wealth relative to life expectancy at the end of the life cycle? Before considering explanations from the perspective of a life cycle framework, we first ask whether the upward-sloping age profiles for annualized comprehensive wealth in the HRS are simply the consequence of unexpected capital gains on housing or corporate equity over the 1998-2004 sample period. To answer this question, we re-estimate the regression-based age profiles using a counterfactual HRS dataset that holds each household's level of corporate equity and net housing wealth fixed over the sample years, letting the other components of comprehensive wealth follow their reported trajectories in the HRS.
Because equity prices gyrated markedly over the 1998-2004 period, we compute counterfactual trajectories in the HRS panel data by replacing each household's reported holdings of corporate equity in each wave with its (household-specific) average value over the six-year period.22 Similarly, because average home prices around the country climbed substantially between 1998 and 2004, we replace each household's reported housing wealth in the four waves with the level it reported in 1998 (thereby assuming no change in housing wealth over our sample period).23
Figure 5 shows that making these adjustments to the reported measures of comprehensive wealth in the HRS do not materially change our finding that, in annualized terms, median tends to rise with age during retirement for the median household in all three income groups. If anything, the profile of annualized financial wealth appears to rise slightly more after the adjustment, and both nonfinancial and comprehensive wealth continue to show clearly rising profiles. The upward sloping (regression-based) age profiles in our counterfactual measures shows that, over the sample period, other forms of financial and nonfinancial wealth (such as deposits, money market funds, mutual funds, vehicles, and business equity) increased notably in annualized terms across waves of the HRS. But more importantly, the rising slope across cohorts reflects different starting levels of wealth by age as of the base year of 1998.24 Thus, we do not think that the upward sloping age profile for annualized comprehensive wealth over retirement is being driven primarily by the effects of unanticipated capital gains on corporate equity or housing over the specific sample period that is available.
6 Predicted Age Profiles for Annualized Comprehensive Wealth from Life Cycle Model Simulations
In this section, we ask whether the pattern of rising annualized wealth at the median can be explained using fairly standard extensions to the life cycle model of consumption. In Section 3 we showed that the simplest life cycle model predicts that annualized wealth should be roughly constant in retirement. The question we turn to now is whether adding plausible bequest or precautionary motives to the life cycle model can generate upward-sloping profiles for annualized wealth that resemble those in the HRS. We adopt a modeling framework that is simple enough to illustrate the key forces that could shape the empirical patterns, but sufficiently rich to quantify realistic influences on savings behavior.25 We consider a range of fairly standard model specifications,26 but our search is by no means exhaustive.
6.1 Description of the models we consider
We consider models in which retired households maximize the expected discounted utility from consumption from their current age ![]() to a maximum age
to a maximum age ![]() subject to a budget constraint that represents a transition equation for wealth
subject to a budget constraint that represents a transition equation for wealth ![]() (more accurately, cash-on-hand) and a
non-negativity constraint for wealth at each age.27 Households are assumed to maximize lifetime utility given by
(more accurately, cash-on-hand) and a
non-negativity constraint for wealth at each age.27 Households are assumed to maximize lifetime utility given by
subject to
where
We assume utility over consumption takes the iso-elastic form,
![]() . In our framework,
. In our framework, ![]() is a state variable indicating a household's demographic structure: for couples,
is a state variable indicating a household's demographic structure: for couples, ![]() , for single men,
, for single men, ![]() , and for single women,
, and for single women, ![]() . The function
. The function
![]() is used to capture economies of scale for couples in household production (specifically,
is used to capture economies of scale for couples in household production (specifically,
![]() and
and
![]() ). In some specifications, we ignore possible economies of scale, setting
). In some specifications, we ignore possible economies of scale, setting ![]() for all
for all ![]() . In all specifications discussed in this paper, we set the preference parameter
. In all specifications discussed in this paper, we set the preference parameter ![]() to 3.28 In the transition equation for wealth, (8), we use
to 3.28 In the transition equation for wealth, (8), we use ![]() --the same value we used in our present value calculations with the HRS data. For each income group, we set
--the same value we used in our present value calculations with the HRS data. For each income group, we set ![]() to match the median level of annuity income (essentially Social Security and DB pension benefits) in the HRS. We report the full set of parameters in Table 9.
to match the median level of annuity income (essentially Social Security and DB pension benefits) in the HRS. We report the full set of parameters in Table 9.
In some versions of the life cycle model, we assume that households explicitly derive utility from leaving a bequest upon their death, according to the iso-elastic utility function:
In this set-up, the parameter
In the extended life cycle model, the variable ![]() denotes a random draw for out-of-pocket medical expenses, which will induce a precautionary motive for retirees to hold wealth
balances into old age. Our parameterization for
denotes a random draw for out-of-pocket medical expenses, which will induce a precautionary motive for retirees to hold wealth
balances into old age. Our parameterization for ![]() matches the econometric estimates that French and Jones (2004b) produced using panel data from the AHEAD
sample. In their econometric model--which is able to match many key features of the micro-data--medical expenses are assumed to have a trend component that is increasing with age (
matches the econometric estimates that French and Jones (2004b) produced using panel data from the AHEAD
sample. In their econometric model--which is able to match many key features of the micro-data--medical expenses are assumed to have a trend component that is increasing with age (![]() ) and
income (
) and
income (![]() ) and a stochastic component that is the sum of a persistent shock (AR(1)) and a transitory shock. The parameter
) and a stochastic component that is the sum of a persistent shock (AR(1)) and a transitory shock. The parameter ![]() and the non-negativity constraint (9) place a lower bound on utility in case a realization of out-of-pocket medical expenses exceeds a household's wealth.30
and the non-negativity constraint (9) place a lower bound on utility in case a realization of out-of-pocket medical expenses exceeds a household's wealth.30
Following French (2005), the natural logarithm of out-of-pocket medical expenses, ![]() , evolves according to:
, evolves according to:
where
where
Our specification of medical expenditures seems to fit the AHEAD data fairly well (see French and Jones, 2004b), but it may understate the strength of the relationship between income or wealth and medical expenses. If so, our model may attribute too much of the
observed rise in annualized resources among wealthier households to a strong bequest motive, operating through ![]() , rather than a tendency for higher-income retirees to plan to spend
significantly more on medical care in old age relative to lower-income households.
, rather than a tendency for higher-income retirees to plan to spend
significantly more on medical care in old age relative to lower-income households.
6.2 Comparison of age profiles from the HRS and the model simulations
To see how well the different model specifications stack up against the HRS data, we simulate our model for different assumptions about annuity-like income and household composition (marital status and longevity). For singles and married couples, we obtain separate decision rules for "high-," "medium-," and "low-" income households, where the income categories correspond to the HRS medians for the top quintile, middle three quintiles, and the bottom quintile of retirement income--the same categories reported above. For each income group, the simulated population is chosen to match the shares of single and married households at onset of retirement in the HRS; and, for each income group, the initial level of wealth is calibrated to match the HRS data. In the simulations, individuals survive according to probabilities in the SSA age- and sex-based life-tables, so that in each period some married households become single households, and some households (mostly singles) die.
Table 7 compares median annualized wealth at different ages in the HRS (first column) with average values for annualized wealth computed from 10,000 simulated retirement periods for each of six different model specifications (denoted Model A through Model F, described in the notes to the table). The first column shows the tendency for annualized wealth to rise markedly in the HRS between households in their late 60s to their late 70s and their late 80s. The rise occurs for single and married retirees and is true whether or not economies of scale are thought to raise "effective" levels of wealth for married retirees relative to single ones.
The second column (model A) shows that, by itself, uncertain longevity cannot explain why annualized wealth rises during retirement in the HRS. Using survival rates from the SSA life tables and our assumptions for preferences and asset returns, the simulations of model A (which do not include random medical expenses or an explicit bequest motive) imply much lower annualized wealth for the oldest retirees (aged 85 to 90 in the table) than the youngest ones (65 to 70). This means that, for the preference specifications we have considered, precautionary motives to hold wealth against the possibility of living to very advanced ages are outweighed by the high discounting implied by low survival rates in old age.
As shown in the third column (model B), adding an explicit bequest motive to the life cycle model with uncertain longevity generates an upward-sloping age profile for annualized wealth for single retirees. Married households, however, continue to show a decline, and the simulated profile for the combined simulations (labeled "full sample") is significantly flatter than the HRS profile. In all of our simulations, singles build up more annualized wealth than married households, a pattern that can be explained by noting that individuals in the model receive a boost in annualized wealth whenever a spouse dies. The inability of model B to match the annualized wealth pattern for married couples suggests that a bequest motive is not the only factor leading retirees in the HRS to build wealth in annualized terms. For a bequest function to fit the empirical age profile of median annualized wealth, it would have to be much more powerful--in particular, retirees would have to derive more utility per dollar of wealth from their bequests than from their own consumption.
The fourth column (model C) indicates that a life cycle model with random medical expenses and a relatively high consumption floor (which reduces the precautionary incentive), but without an explicit bequest motive, gets closer to matching the upward-sloping annualized wealth profile for married households. Overall, however, the match with the full HRS sample is about the same as the model with bequests and no medical expenses. While a precautionary motive and an active bequest motive seem to induce a similar slowdown in spending, neither appears sufficiently strong to explain the data patterns by itself.
Model D shows that adding the bequest function to the model with random medical expenses and a moderate consumption floor (![]() ) generates a rise in annualized wealth that is quite close
to the pattern for the full sample in the HRS. The bequest motive provides "extra" expected value from the precautionary buffer because accidental bequests (which will frequently arise when retirees die before having suffered a substantial random medical expense draw) convey utility value. The
simulated annualized wealth levels for the three age groups ($23,400, $27,000, and $29,800) are only slightly higher than those in the data ($22,500, $26,600, and $29,000). If one were to choose a specification based only on the fit with the full sample, Model D would be the obvious selection. When
we examine the results for married households, however, it is no longer clear that the model fits the best. The HRS shows a $14,000 increase in annualized wealth for married households, which is much higher than the $3,000 increase in the simulations.
) generates a rise in annualized wealth that is quite close
to the pattern for the full sample in the HRS. The bequest motive provides "extra" expected value from the precautionary buffer because accidental bequests (which will frequently arise when retirees die before having suffered a substantial random medical expense draw) convey utility value. The
simulated annualized wealth levels for the three age groups ($23,400, $27,000, and $29,800) are only slightly higher than those in the data ($22,500, $26,600, and $29,000). If one were to choose a specification based only on the fit with the full sample, Model D would be the obvious selection. When
we examine the results for married households, however, it is no longer clear that the model fits the best. The HRS shows a $14,000 increase in annualized wealth for married households, which is much higher than the $3,000 increase in the simulations.
Model E and model F are the same as model C and model D, but with a much lower consumption floor (![]() ), which significantly strengthens the precautionary motive. This specification
implies a much steeper age profile for annualized wealth for married couples, but it overshoots the annualized wealth build up for singles. For both types of households, some combination of bequests and medical expenses seems to be at work, but it is not clear which specification comes closest to
the patterns in the HRS. We can learn more about the model specifications by seeing what the simulations imply about annualized wealth for the different income categories.
), which significantly strengthens the precautionary motive. This specification
implies a much steeper age profile for annualized wealth for married couples, but it overshoots the annualized wealth build up for singles. For both types of households, some combination of bequests and medical expenses seems to be at work, but it is not clear which specification comes closest to
the patterns in the HRS. We can learn more about the model specifications by seeing what the simulations imply about annualized wealth for the different income categories.
In terms of income heterogeneity, the main feature of the HRS data our model needs to explain is the relatively flat age profiles for the lowest income category and the very steep profiles for the highest income group. Table 7 reports the simulated and actual annualized wealth levels for households in the highest, middle three, and lowest income quintiles in the HRS. The middle rows show the same numbers as the bottom rows in Table 7, so we will focus our attention on the top and bottom income groups.
Scanning across the columns of Table 7, ones can see the importance of bequests in explaining the sharp increase in annualized wealth among higher-income households. Even with a low consumption floor, the model with medical expenses and no bequests (model E) explains much less of the increase in annualized wealth than the model with only a bequest motive (model B). Model F, which introduces the largest incentive to maintain savings in old age, comes closest to matching the patterns in the HRS for high income households, but it over-predicts the rise in annualized wealth for the middle and lower income groups. Model D, which has bequests, medical expenses, and a moderate consumption floor, misses some of the build-up in annualized wealth in the highest income category, but it comes remarkably close for the other two. It captures the flat progression of annualized wealth among lower-income households, and it almost perfectly matches the increase for the medium income group. Despite its difficulty in matching the increase in annualized wealth for married and high-income households, we conclude that a specification that includes intended bequests, uncertain medical costs, and a moderate consumption floor can account for the most prominent features of spend-down patterns in the HRS.31
7 Conclusion
By introducing the concept of annualized comprehensive wealth--a measure of total resources per person per expected remaining year of retirement--our analysis brings some saving patterns into relief that would otherwise be difficult to discern. Our primary empirical finding from the HRS is that annualized comprehensive wealth tends to rise with age in retirement, reflecting the tendency for wealth balances to decrease more slowly than remaining life expectancies shorten. We find this pattern of increasing annualized wealth over retirement for most types of households and for the major components of comprehensive wealth. In addition, we estimate that a much larger share of retirees experience a considerable increase in annualized comprehensive wealth over the six years covered by our HRS sample (1998 to 2004) than experience a significant decline.
It is reasonably well known that retirees in the bottom quintile of the income distribution (conditional on their age and marital status) rely almost exclusively on DB pension benefits, Social Security benefits, and other government transfers to finance spending. Although these sources do not constitute a high level of comprehensive wealth, their annuity-like payout scheme means that they can finance a more or less constant path of outlays through retirement. While annuity-like benefits are also an important source of wealth for retirees in the middle- and upper-income groups, these retirees also tend to have significant financial and nonfinancial wealth. A new finding from our analysis is that, for the median retiree in the middle- and upper-income groups, annualized comprehensive wealth tends to rise over retirement. One might have expected wealth balances to fall roughly in line with declining longevity in retirement--after all, this is the trajectory that would be predicted by the simplest life cycle model of consumption.
To gauge what factors might lie behind the tendency for annualized comprehensive wealth to rise in retirement, we compare the empirical age profiles of annualized wealth from the HRS data with simulated profiles from life cycle models that are extended to include uncertainty about longevity, precautionary saving in light of uncertain medical expenses, and an explicit motive for retirees with greater resources to leave bequests. Within the class of models we consider, specifications that include all three of these factors seem to line up best with the rate of increase of annualized comprehensive wealth in the HRS data. In this case, saving in retirement (relative to the simplest life cycle benchmark) provides insurance against the possibility of financing consumption into advanced ages, is available to help finance possibly very large medical expenditures, and it increases the size of intended (as well as unanticipated) bequests. Quantitatively, the simulated age profiles for annualized wealth match up fairly well with the estimated profiles, although high-income households in the HRS exhibit a steeper upward trajectory for annualized wealth at older ages than the extended life cycle models predict.
Bibliography
"Consumption versus Expenditure," Journal of Political Economy, 113(5), 919-48. "You can't take it with you: Asset run-down at the end of the life cycle," Economic Perspectives, Federal Reserve Bank of Chicago, Q3, 40-54. "Differential Mortality and Wealth Accumulation," Journal of Human Resources, 35(1), 1-29. "The Rationality of Retirement Expectations and the Role of New Informaton," Review of Economics and Statistics, 87(3), 587-592. "Expectation Formation of Older Married Couples and the Rational Expectations Hypothesis," Labour Economics, 13, 191-218. "The Economic Effects of Social Security: Toward a Reconciliation of Theory and Measurement," Journal of Public Economics, 33, 273-304. "How Strong are Bequest Motives? Evidence Based on Estimates of the Demand for Life Insurance and Annuities," Journal of Political Economy, 99(5), 899-927. "Is the Baby Boom Generation Preparing Adequately for Retirement?," Discussion paper, Merrill Lynch. "Retirement and Consumption in a Life Cycle Model," Journal of Labor Economics, 26(1), 35-71. "Joint Life Annuities and Annuity Demand by Married Couples," The Journal of Risk and Insurance, 67(4), 527-553. "Wealth Accumulation Over the Life Cycle and Precautionary Savings," Journal of Business and Economic Statistics, 21(3), 339-353. "The Buffer-Stock Theory of Saving: Some Macroeconomic Evidence," Brookings Papers on Economic Activity, 1992(2), 61-156. "Buffer-Stock Saving and the Life Cycle/Permanent Income Hypothesis," The Quarterly Journal of Economics, 112(1), 1-55. "How Important is Precautionary Saving?," Review of Economics and Statistics, 80(3), 410-419. "Uncertain Lifetime, Consumption, and Dissaving in Retirement," The Journal of Political Economy, 89(3), 561-577. "The Insurance, Health, and Savings Decisions of Elderly Women Living Alone," Manuscript.Tables and Figures
| Age in 2004 | Sample Size |
Weighted Percent |
No. of Married Households |
Weighted % Married |
|---|---|---|---|---|
| 65-69 | 2,146 | 23.9 | 1,210 | 56.9 |
| 70-74 | 1,808 | 22.8 | 937 | 49.5 |
| 75-79 | 1,496 | 22.4 | 755 | 41.4 |
| 80-84 | 1,315 | 17.3 | 442 | 35.3 |
| 85-89 | 815 | 9.6 | 187 | 26.4 |
| 90 and over | 478 | 4.0 | 67 | 18.0 |
| Full Sample | 8,058 | 100.0 | 3,598 | 43.6 |
- Household observations drawn from the 2004 wave of the Health and Retirement Study (HRS).
- Throughout the paper, "age" refers to the oldest person in the household.
| Variable | Mean |
|---|---|
| Age (years) | 75.8 |
| Married (%) | 43.6 |
| Single Male (%) | 11.3 |
| Single Female (%) | 34.4 |
| Income (thous. $2004) | 43.8 |
| Have Any Children (%) | 93.5 |
| Have Only a High School Degree (%) | 53.2 |
| Have a College Degree (%) | 19.3 |
| Nonwhite (%) | 11.5 |
| Hispanic (%) | 4.9 |
| Have a Person in Fair or Poor Health (%) | 27.3 |
| OOP Medical Expense (thous. $2004) | 6.7 |
- Household observations in 2004.
- Means calculated using HRS sample weights.
| Component of Wealth | 1998 (Thousands of 2004 $) | 2000 (Thousands of 2004 $) | 2002 (Thousands of 2004 $) | 2004 (Thousands of 2004 $) | Share of Comp. Wealth in 2004 (Percent) |
|---|---|---|---|---|---|
| Financial | 87 | 90 | 77 | 74 | 22 |
| Financial: Stocks1 | 35 | 38 | 31 | 29 | 9 |
| Financial: Other2 | 51 | 52 | 47 | 45 | 14 |
| Nonfinancial | 115 | 113 | 110 | 111 | 34 |
| Nonfinancial: Housing | 84 | 84 | 87 | 89 | 27 |
| Nonfinancial: Other3 | 31 | 29 | 24 | 22 | 7 |
| Annuity-like benefits | 217 | 193 | 169 | 143 | 44 |
| Annuity-like benefits: Social Security | 140 | 126 | 110 | 95 | 29 |
| Annuity-like benefits: DB Pensions | 63 | 55 | 47 | 38 | 12 |
| Annuity-like benefits: Other4 | 14 | 12 | 11 | 10 | 3 |
| Comprehensive Wealth | 419 | 396 | 357 | 329 | 100 |
| Number of Households | 5,882 | 5,763 | 5,789 | 5,899 | -- |
- *The table reports means from subsamples selected to match the median of comprehensive wealth (CW) in the original sample, for each wave; thus, the components sum to median CW. Calculations use HRS sample weights.
- 1Includes shares held directly and indirectly through mutual funds, trusts, and retirement accounts.
- 2Includes liquid assets, bonds, and non-stock assets held in trusts and retirement accounts.
- 3Includes vehicles and businesses.
- 4Includes life annuities and government transfers.
| 1998 (Thousands of 2004 $) | 2000 (Thousands of 2004 $) | 2002 (Thousands of 2004 $) | 2004 (Thousands of 2004 $) | Cumulative Change, 1998 to 2004 |
|
|---|---|---|---|---|---|
| Full Sample | 419 | 396 | 357 | 329 | -21% |
| By Age in 2004: 70-79 | 469 | 444 | 417 | 390 | -17% |
| By Age in 2004: 80-89 | 369 | 340 | 299 | 277 | -25% |
| By Marital Status in 2004, Single: <=75 | 326 | 298 | 269 | 231 | -29% |
| By Marital Status in 2004, Single: >75 | 278 | 258 | 220 | 205 | -26% |
| By Marital Status in 2004, Married: <=75 | 768 | 741 | 715 | 651 | -15% |
| By Marital Status in 2004, Married: >75 | 598 | 562 | 576 | 525 | -12% |
| By Income in 20042: Bottom 20% | 164 | 161 | 155 | 146 | -11% |
| By Income in 20042: Middle 60% | 434 | 409 | 371 | 343 | -21% |
| By Income in 20042: Top 20% | 1018 | 978 | 887 | 863 | -15% |
- 1Comprehensive wealth is the sum of financial, nonfinancial and annuity-like wealth. Medians are computed for each age-marital status-income cell.
- 2Income categories are defined conditional on age and marital status in 1998.
| Real Interest Rate |
Real Interest Rate |
Real Interest Rate |
|
|---|---|---|---|
| 0, 1 | 100.0 | 100.0 | 100.0 |
| 0, 10 | 10.0 | 11.2 | 12.3 |
| 0, 20 | 5.0 | 6.3 | 7.6 |
| 10, 1 | 9.2 | 10.0 | 11.0 |
| 10, 10 | 5.0 | 5.6 | 6.2 |
| 10, 20 | 3.3 | 4.0 | 4.7 |
| 20, 1 | 4.8 | 5.9 | 7.1 |
| 20, 10 | 3.3 | 4.0 | 4.7 |
| 20, 20 | 2.5 | 3.1 | 3.8 |
- Annualized wealth in thousands of dollars.
 and
and 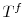 denote the expected
remaining life years for the spouses.
denote the expected
remaining life years for the spouses.
| Component of Wealth | Thousands of 2004 $ per person per year: 1998 | Thousands of 2004 $ per person per year: 2000 | Thousands of 2004 $ per person per year: 2002 | Thousands of 2004 $ per person per year: 2004 | Cumulative Change, 1998 to 2004 |
|---|---|---|---|---|---|
| Financial | 5.2 | 5.9 | 5.9 | 6.4 | 23% |
| Financial: Stocks1 | 2.1 | 2.4 | 2.3 | 2.4 | 14% |
| Financial: Other2 | 3.1 | 3.5 | 3.6 | 4.0 | 29% |
| Nonfinancial | 6.9 | 7.5 | 8.5 | 9.4 | 36% |
| Nonfinancial: Housing | 5.1 | 5.7 | 6.7 | 7.7 | 51% |
| Nonfinancial: Other3 | 1.7 | 1.8 | 1.8 | 1.7 | 0% |
| Annuity-like benefits | 12.8 | 12.6 | 12.6 | 12.3 | -4% |
| Annuity-like benefits: Social Security | 8.3 | 8.3 | 8.3 | 8.1 | -3% |
| Annuity-like benefits: DB Pensions | 3.7 | 3.5 | 3.5 | 3.3 | -11% |
| Annuity-like benefits: Other4 | 0.8 | 0.8 | 0.9 | 0.9 | 13% |
| Comprehensive Wealth | 24.9 | 25.9 | 27.0 | 28.1 | 13% |
| Number of Households | 5,882 | 5,763 | 5,789 | 5,899 | -- |
- 1Annualized wealth is wealth per person per expected year of life, in thousands of 2004 dollars (see text for details).
- 2Table reports means from subsamples selected to match median annualized comprehensive wealth (ACW) in the original sample, for each household type and each wave, so that the components sum to median ACW. Calculations use HRS sample weights.
| Classification | Thousands of 2004 $ per person per year: 1998 | Thousands of 2004 $ per person per year: 2000 | Thousands of 2004 $ per person per year: 2002 | Thousands of 2004 $ per person per year: 2004 | Cumulative Change, 1998 to 2004 |
|---|---|---|---|---|---|
| Full Sample | 24.9 | 25.9 | 27.0 | 28.1 | 13% |
| By Age in 2004: 70-79 | 23.2 | 23.9 | 24.8 | 25.4 | 9% |
| By Age in 2004: 80-89 | 27.6 | 28.3 | 30.9 | 32.6 | 18% |
| By Marital Status in 2004: <=75 | 19.8 | 20.2 | 20.5 | 21.2 | 7% |
| By Marital Status in 2004: >75 | 25.0 | 26.5 | 26.8 | 29.4 | 18% |
| By Marital Status in 2004: <=75 | 27.3 | 26.8 | 27.5 | 27.3 | 0% |
| By Marital Status in 2004: >75 | 29.0 | 29.5 | 32.1 | 32.4 | 12% |
| By Marital Status in 2004: <=75 | 32.3 | 32.2 | 33.0 | 33.2 | 3 % |
| By Marital Status in 2004: >75 | 34.0 | 34.7 | 38.5 | 39.0 | 15% |
| By Income in 20042 : Bottom 20% | 10.8 | 11.0 | 11.4 | 11.4 | 6% |
| By Income in 20042 : Middle 60% | 24.7 | 25.9 | 26.7 | 27.8 | 13% |
| By Income in 20042 : Top 20% | 58.2 | 60.4 | 64.2 | 69.5 | 19% |
- 1
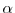 measures household economies of scale:
measures household economies of scale: 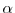 =2 implies no
scale economies, while
=2 implies no
scale economies, while 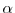 =1.67 implies a measure of scale economies sometimes used in the literature (see text for details).
=1.67 implies a measure of scale economies sometimes used in the literature (see text for details). - 2Income categories are defined conditional on age and marital status in 1998.
| Classification | Percent of Households with a Change in Annualized Comprehensive Wealth that is: <-25% |
Percent of Households with a Change in Annualized Comprehensive Wealth that is: -25% to -10% |
Percent of Households with a Change in Annualized Comprehensive Wealth that is: -10% to 10% |
Percent of Households with a Change in Annualized Comprehensive Wealth that is: 10% to 25% |
Percent of Households with a Change in Annualized Comprehensive Wealth that is: >25% |
|---|---|---|---|---|---|
| Full Sample | 17 | 13 | 22 | 13 | 35 |
| By Age in 2004: 70-79 | 17 | 14 | 23 | 14 | 33 |
| By Age in 2004: 80-89 | 17 | 11 | 22 | 11 | 38 |
| By Marital Status in 2004, Single: <=75 | 19 | 13 | 22 | 12 | 34 |
| By Marital Status in 2004, Single: >75 | 18 | 11 | 21 | 12 | 39 |
| By Marital Status in 2004, Married ( |
17 | 16 | 23 | 15 | 29 |
| By Marital Status in 2004, Married ( |
16 | 11 | 25 | 14 | 34 |
| By Marital Status in 2004, Married ( |
16 | 17 | 23 | 15 | 30 |
| By Marital Status in 2004, Married ( |
16 | 11 | 25 | 14 | 34 |
| By Income in 20042: Bottom 20% | 17 | 13 | 29 | 12 | 30 |
| By Income in 20042: Middle 60% | 17 | 13 | 23 | 13 | 33 |
| By Income in 20042: Top 20% | 19 | 13 | 18 | 12 | 38 |
- 1
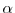 measures household economies of scale:
measures household economies of scale: 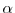 =2 implies no
scale economies, while
=2 implies no
scale economies, while 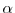 =1.67 implies a measure of scale economies sometimes used in the literature (see text for details).
=1.67 implies a measure of scale economies sometimes used in the literature (see text for details). - 2Income categories are defined conditional on age and marital status in 2004.
| Parameter | Value | Definition |
|---|---|---|
| 109 | maximum age | |
| 0.976 | discount factor | |
| 1.025 | gross real interest rate | |
| 3 | coefficient of relative risk aversion | |
| 1.67 | household equivalence scale | |
| 0.05 | bequest function parameter | |
| 5,000 | bequest function parameter | |
| 2,000-4,000 | consumption floor | |
|
|
0.909 | variance of the AR1 shock to medical costs |
|
|
1.819 | variance of the transitory shock to medical costs |
| 0.925 | correlation on the AR1 component of medical costs | |
| 0.75 | fraction of married household medical costs paid by singles | |
| 20.0, 11.5, 6.8 | income (in $1,000s) for high, medium, and low education single | |
| 35.0, 26.0, 16.0 | income (in $1,000s) for high, medium, and low education married couples | |
| 275.5, 89.2, 1.9 | initial cash on hand (in $1,000s) for high, medium, and low education single | |
| 671.4, 271.0, 71.3 | initial cash on hand (in $1,000s) for high, medium, and low education married couples |
| Age and Household Type | HRS1 | Model A2 | Model B3 | Model C4 | Model D5 | Model E6 | Model F7 |
|---|---|---|---|---|---|---|---|
| Singles: 65-70 | 19.60 | 20.92 | 21.15 | 21.30 | 21.55 | 21.84 | 21.89 |
| Singles: 75-80 | 25.20 | 22.90 | 25.23 | 25.70 | 26.75 | 29.03 | 29.85 |
| Singles: 85-90 | 27.70 | 20.17 | 27.12 | 26.36 | 29.79 | 33.45 | 36.36 |
| Married (without scales): 65-70 | 25.40 | 25.23 | 25.40 | 25.78 | 25.85 | 25.99 | 26.03 |
| Married (without scales): 75-80 | 27.90 | 23.73 | 25.09 | 27.05 | 27.55 | 28.63 | 28.93 |
| Married (without scales): 85-90 | 39.30 | 19.90 | 23.70 | 27.05 | 28.69 | 31.55 | 32.60 |
| Married (scales:
|
30.60 | 30.55 | 30.82 | 31.17 | 31.27 | 31.41 | 31.48 |
| Married (scales:
|
33.30 | 30.10 | 32.06 | 33.69 | 34.51 | 35.51 | 35.97 |
| Married (scales:
|
45.60 | 27.47 | 33.46 | 35.57 | 38.20 | 40.99 | 42.54 |
| Full sample: 65-70 | 22.50 | 22.71 | 22.93 | 23.24 | 23.35 | 23.62 | 23.64 |
| Full sample: 75-80 | 26.60 | 23.11 | 25.15 | 26.03 | 27.04 | 29.10 | 29.64 |
| Full sample: 85-90 | 29.00 | 20.18 | 26.91 | 26.34 | 29.78 | 33.48 | 35.98 |
- *Annualized wealth in thousands of 2004 dollars. See text for details. The coefficient of relative risk aversion
 , the bequest function is given by equation (10), and
, the bequest function is given by equation (10), and 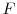 is the value of the consumption floor.
is the value of the consumption floor. - 1Median annualized wealth for pooled 1998-2004 sample in HRS.
- 2Model A: survival uncertainty with no bequests.
- 3Model B: survival uncertainty with bequest motive.
- 4Model C: medical expenses with no bequests,
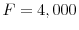 .
. - 5Model D: medical expenses with bequest motive,
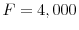 .
. - 6Model E: medical expenses with no bequests,
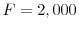 .
. - 7Model F: medical expenses with bequest motive,
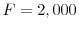 .
.
| Age and Household Type | HRS1 | Model A2 | Model B3 | Model C4 | Model D5 | Model E6 | Model F7 |
|---|---|---|---|---|---|---|---|
| Low income: 65-70 | 9.00 | 7.65 | 9.28 | 9.36 | 9.36 | 9.62 | 9.63 |
| Low income: 75-80 | 10.50 | 8.76 | 9.48 | 9.70 | 9.74 | 11.42 | 11.52 |
| Low income: 85-90 | 10.00 | 8.53 | 9.05 | 8.95 | 9.12 | 12.23 | 12.57 |
| Medium income: 65-70 | 22.50 | 22.71 | 22.93 | 23.24 | 23.35 | 23.62 | 23.64 |
| Medium income: 75-80 | 26.60 | 23.11 | 25.15 | 26.03 | 27.04 | 29.10 | 29.64 |
| Medium income: 85-90 | 28.90 | 20.18 | 26.91 | 26.34 | 29.78 | 33.48 | 35.98 |
| High income: 65-70 | 51.50 | 52.09 | 53.04 | 52.99 | 53.33 | 53.20 | 53.46 |
| High income: 75-80 | 67.60 | 55.37 | 63.08 | 61.01 | 64.93 | 62.86 | 65.49 |
| High income: 85-90 | 94.90 | 49.81 | 76.01 | 64.53 | 79.34 | 71.55 | 81.71 |
- *Annualized wealth in thousands of 2004 dollars. See text for details. The coefficient of relative risk aversion
 , the bequest function is given by equation (10), and
, the bequest function is given by equation (10), and 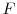 is the value of the consumption floor.
is the value of the consumption floor. - 1Median annualized wealth for pooled 1998-2004 sample in HRS.
- 2Model A: survival uncertainty with no bequests.
- 3Model B: survival uncertainty with bequest motive.
- 4Model C: medical expenses with no bequests,
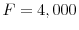 .
. - 5Model D: medical expenses with bequest motive,
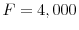 .
. - 6Model E: medical expenses with no bequests,
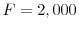 .
. - 7Model F: medical expenses with bequest motive,
 .
.
Appendix 1: Present Value Calculations for the Annuity-Like Components of Comprehensive Wealth
In this appendix, we discuss our method for computing present values of annuitized streams of payments in the HRS. The discussion closely follows material in Love, Smith, and McNair (2007) and is repeated here for convenience.
Defined Benefit Pension benefits
The HRS includes questions about both current pension benefits (for retirees) and expected future pension benefits (for those still working). Households are asked about the (current or expected) pension amount (and start date, if they have not yet begun), cost-of-living adjustments (COLAs), and survivors' benefits.32 In the case of working households, we use the expected pension at retirement; this serves to include the value of benefits not yet accrued.
We express the actuarial present value of DB payments for a plan that pays an annual amount ![]() as
as
where
The conditional survival probabilities are based on the one-year age- and sex-specific conditional death probabilities in the Social Security Administration's 2002 Period Life Table (SSA, 2006). Period life tables provide a snapshot of the mortality conditions prevailing in a single year, rather than the expected mortality experience of a given cohort over time. For young cohorts (e.g., children born in 2002), one might expect actual longevity to be significantly greater than shown in the 2002 period life table, since longevity generally improves over time. However, since our sample is of Americans aged 51 and older in 2004, we conclude that the 2002 period table (the most recent available) is a reasonable estimate of our sample's expected mortality experience.35
For DB plans with COLAs (about 40 percent of the reported plans), we use a discount factor ![]() equal to
equal to ![]() , where
, where ![]() is the real interest rate. For plans without COLAs, we set
is the real interest rate. For plans without COLAs, we set ![]() equal to
equal to ![]() , where
, where ![]() is the nominal
interest rate. The baseline results in the paper assume a nominal interest rate of 4.5 percent and a real interest rate of 2.5 percent, implying 2 percent inflation. The present-value measures are naturally sensitive to the value of
is the nominal
interest rate. The baseline results in the paper assume a nominal interest rate of 4.5 percent and a real interest rate of 2.5 percent, implying 2 percent inflation. The present-value measures are naturally sensitive to the value of ![]() . In Love, Smith, and McNair (2007), we report results using different assumptions about real rates and inflation.
. In Love, Smith, and McNair (2007), we report results using different assumptions about real rates and inflation.
The HRS collects information on multiple pension plans for respondents and their spouses. Applying equation (1), we compute present values for each of these and then sum them to arrive at our final calculation for current pensions. Some current workers report that they expect to receive lump-sum payouts from their DB plans upon retirement. To include these plans, we simply discount the lump sum back to the current age:
 |
(A-2) |
where
Social Security benefits
Computing the present value of of Social Security is quite similar to calculating DB wealth. The HRS includes questions about both current benefits for retirees and expected benefits for workers. Let
![]() and
and
![]() denote the current or expected annual social security benefits of the respondent and the spouse at ages
denote the current or expected annual social security benefits of the respondent and the spouse at ages ![]() and
and
![]() respectively. The actuarial present value of household Social Security benefits is given by
respectively. The actuarial present value of household Social Security benefits is given by
where
is the conditional probability of both household members being alive, and
is the conditional probability of exactly one household member being alive.36 The first bracketed term in equation (3) captures the fact that if both household members are alive, their total benefits will generally equal the sum of their individual amounts. The second term in the brackets reflects the rules governing survivors benefits, whereby a retirement-age widow or widower typically receives 100% of the spouse's benefits if these exceed their own benefit amount.37 Since Social Security benefits are adjusted for inflation, we discount using the real interest rate:
Respondents in the HRS are asked directly about the amount of current or expected spousal benefits. We take these amount at face value and assume that the reported benefits already reflect any adjustments due to the Social Security rules (e.g., the fact that individuals are typically entitled to the maximum of their own benefits and 50% of their spouse's).38
Annuities and welfare benefits
Our calculations of wealth from annuities and welfare payments are more straightforward. The formula for calculating the actuarial present value of annuities (![]() ) exactly parallels
equation (1), where we make similar adjustments for COLAs and survivor benefits. Our measure of expected welfare payments includes veteran's benefits, food stamps, Supplemental Security Income (SSI), and other welfare. In this calculation, we assume that individuals who are
currently receiving these payments will continue to receive the same inflation-indexed welfare payments as long as they live, and that those not currently receiving these payments never will--i.e., we do not model transitions in and out of welfare-receipt status. Since welfare benefits are
typically indexed to inflation, we discount this stream of expected welfare payments using the real interest rate and the relevant conditional survival probabilities.
) exactly parallels
equation (1), where we make similar adjustments for COLAs and survivor benefits. Our measure of expected welfare payments includes veteran's benefits, food stamps, Supplemental Security Income (SSI), and other welfare. In this calculation, we assume that individuals who are
currently receiving these payments will continue to receive the same inflation-indexed welfare payments as long as they live, and that those not currently receiving these payments never will--i.e., we do not model transitions in and out of welfare-receipt status. Since welfare benefits are
typically indexed to inflation, we discount this stream of expected welfare payments using the real interest rate and the relevant conditional survival probabilities.
Simulation Results
The solution to the model consists of a set of decision rules for consumption that depend on current assets, age, and in the case of medical expenses, the value of the current shock. With these decision rules in hand, we simulate various life histories, making different assumptions about initial assets. Where there is any uncertainty, we conduct 10,000 Monte Carlo simulations and present the resulting average profiles of consumption, financial assets, and annualized wealth. We simulate four main variations of the life-cycle model described above: (1) a baseline model with no survival uncertainty or medical expenses; (2) a model with only uncertain survival; (3) a model with uncertain survival and medical expenses; and (4) models (1) through (3) with an operative bequest motive.
Baseline life cycle model
Panel (a) in Figure A-1 shows the simulation results for the baseline life cycle model specification, in which all retirees know they will live exactly to their life expectancy, do not face random medical expense shocks, and do not value leaving bequests. One thing that stands out in that panel is the abrupt decline in income at age 82. The decline, smoother versions of which we will see in all of our simulations, is due to the fact that households receive less Social Security income when one of the members dies. Apart from income, the figure reproduces the familiar results of the standard life-cycle model. Wealth declines steadily through retirement, and consumption lies almost entirely on top of annualized wealth at all ages. This is a reflection of the central hypothesis of the standard life-cycle model: in the absence of bequests or income uncertainty, households will optimally consume their permanent income, which in this case is exactly equal to annualized wealth. In order to explain the upward-sloping annualized wealth profiles observed in the data, we will have to consider departures from the baseline model. We begin by considering the role of uncertain longevity.
Effect of uncertain longevity
Panel (b) displays average life-cycle profiles for households facing uncertain longevity. Annualized wealth and consumption now rise gradually until almost age 80 and then fall rapidly until they equal retirement income around age 95. From the value function in equation (7), we can see that survival probabilities act like the discount factor to depress the growth rate of consumption. Individuals recognize that they may not live to enjoy future consumption, so they spend more today. This discounting effect accounts for the rapid spend-down past age 80, but what, then, explains the upward sloping profiles earlier in retirement?
The increase in average consumption and annualized wealth is due to the fact that some spouses die earlier than anticipated. Early in retirement, households prepare to finance consumption for both members over their expected lifespans. Some households will live longer than expected and risk exhausting their resources. Others will experience an early death, and the surviving spouses will find themselves with a sudden increase in total resources per person, which translates into an increase in both annualized wealth and consumption. The upward-sloping portion in panel (b) reflects the tendency for this "surviving spouse" effect to dominate the discounting effect of uncertain survival. When we model only single-headed households, there is no "surviving spouse" effect, and the average profiles for consumption and annualized wealth fall throughout retirement. Even with joint households, however, the increase in annualized wealth is not nearly strong enough to match the rise in the data. We can get closer to the upward-sloping profile in the HRS data by introducing a bequest function to the model.
Effect of a bequest function
An important deviation from this simple model, and one that has received a great deal of attention in the literature, is the inclusion of an explicit bequest motive. If individuals intend to bequeath wealth to their heirs, they will naturally maintain a larger stock of financial wealth than those without a bequest motive. As these individual progress through retirement, the annualized value of this wealth will continue to rise until it reaches the value of bequests in the last period of life. To see whether bequests have the potential to explain the annualized wealth patterns in the data, we solved a life-cycle model assuming that households value bequests according to the function given by equation (10).
Adding a bequest function to the model moves us a step closer to the rising annualized wealth profiles in the data, but not all the way. Panels (c) and (d) show annualized wealth profiles for the cases of certain uncertain survival. Bequests tilt up the annualized wealth in both cases, with a marked increase toward the end of life. In the certain survival case, the sharp increase is due to the fact that the amount of wealth targeted for bequests remains constant, while the remainder of resources declines to finance consumption. When financial wealth is large, bequests have only a small effect on annualized wealth, but toward the end of life, the bequest becomes large relative to consumption needs, and annualized wealth blows up.
Effect of differential mortality by wealth
De Nardi (2006) estimate a life-cycle model populated by elderly singles and find that differential mortality (by gender, health, and earnings) plays a significant role in explaining the low rates of dissaving among the highest permanent income households. They find, for example, that median assets for individuals in the top income quintile would fall by $10,000 if they had the same survival probabilities as healthy males in the middle of the income distribution. To get a sense for whether differential mortality is likely to exert a strong enough influence on consumption behavior to explain the data, we run a simple experiment that focuses only on single males. We solve life-cycle model with three different sets of survival probabilities: a medium one that replicates the SSA life tables, a high one that one that multiplies survival rates by 1.2, and a low one that multiplies the survival rates in the life tables by 0.8.
Figure A-2 shows how the differential-mortality adjusted annualized wealth path (labeled "combined") differs from the unadjusted profiles for each of the mortality groups. We constructed the experiment so that the average value of initial wealth for all three groups is exactly equal to the initial wealth for just the medium mortality group. The medium mortality group therefore provides a baseline for the combined profile. From the figure, it appears unlikely that the magnitude of the difference between the low and high case is sufficient to explain the strongly upward sloping trend of annualized wealth observed in the data. The combined profile lies above the medium profile, but only by a slight amount, and not nearly enough to suggest a promising role for differential mortality to explain the empirical profiles. Our simulation results are not inconsistent with the findings in De Nardi (2006), as we also find that longer-lived households dissave more gradually. It is just that the effect of differential mortality alone does not appear strong enough to explain the upward-sloping annualized wealth profiles we observe in the data.
Effect of random medical expenses
Older individuals face increasing risks of poor health and large out-of-pocket medical expenses. Because Medicare provides only limited coverage for long-term care, a string of adverse health shocks can potentially wipe out a household's financial assets. At the same time, changes in health status can also alter an individual's enjoyment of consumption and leisure. Given that the incidence and severity of health shocks tends to rise with age, health may provide a key to understanding the upward sloping path of annualized wealth.
Figure A-3 displays the life-cycle profiles both with and without bequests. The left panels correspond to the specification with a high consumption floor ($4,000) and the right panels to the low floor ($2,000).39 The figures indicate that households accrue significantly more annualized resources as a precaution against out-of-pocket medical expenses that can potentially wipe out retirement wealth. Not surprisingly, the utility consequences of high medical costs depend on the size of the consumption floor. Regardless of the existence of a bequest motive, reducing the size of the consumption floor has a substantial effect on the build-up of annualized wealth.
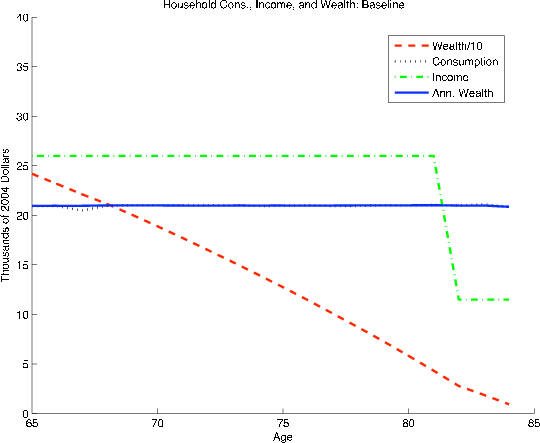 |
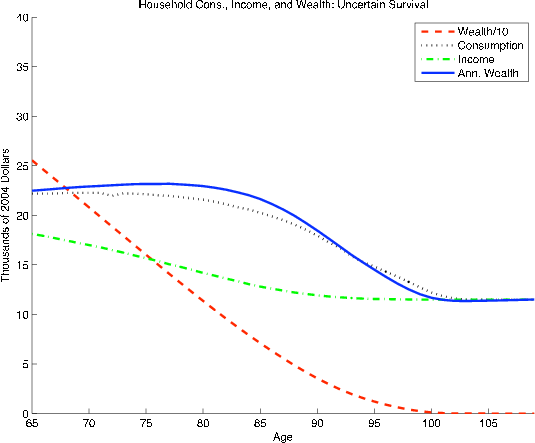 |
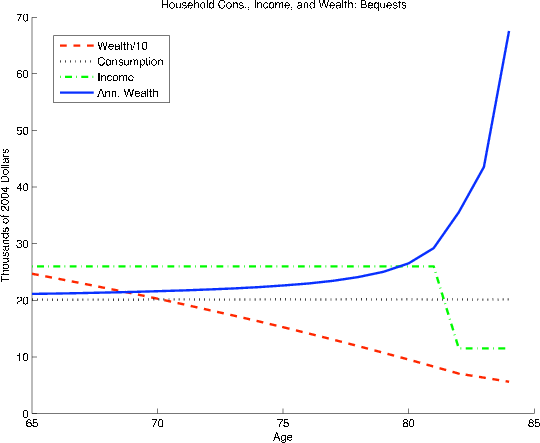 |
 |
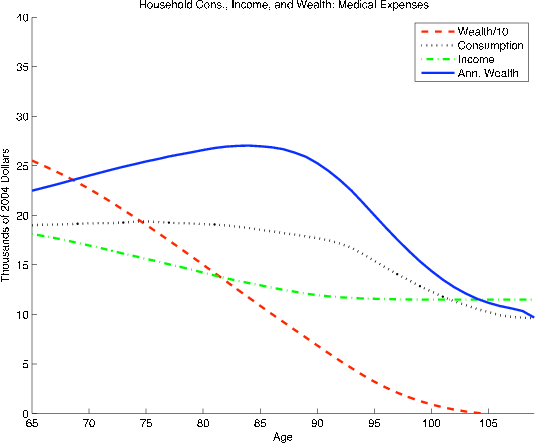 |
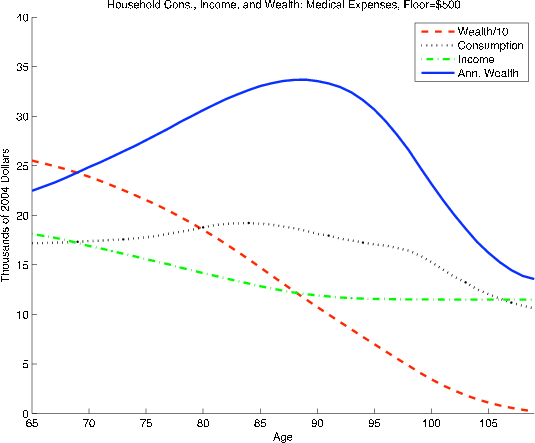 |
 |
![\displaystyle a_t=\frac{r}{1+r}\left[\alpha-(\alpha-1)\frac{1}{(1+r)^{T_t^{m}}}-\frac{1}{(1+r)^{T_t^{f}}}\right]^{-1},](img8.gif)
![\displaystyle U_0=\sum_{t=0}^T\beta^t\left\{S_t^fS_t^m\alpha u\left(\frac{C_t}{\alpha}\right)+[S_t^f(1-S_t^m)+S_t^m(1-S_t^f)]u(C_t)\right\},](img25.gif)
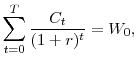
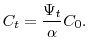
![\displaystyle C_0 \sum_{t=0}^{T}\left\{\frac{S_t^fS_t^m+\frac{1}{\alpha}[S_t^f(1-S_t^m)+S_t^m(1-S_t^f)]}{(1+r)^t}\right\}=W_0,](img36.gif)
![\displaystyle V(X_t,n_t)=\max_{C_t}\left[\alpha(n_t) U\left(C_t,\alpha(n_t)\right)+\beta \sum_{j=1}^3\psi_{t+1,j} E_tV(X_{t+1},n_j)+\beta(1-\sum_{j=1}^3\psi_{t+1,j})B(X_{t+1})\right],](img54.gif)
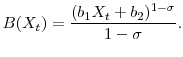

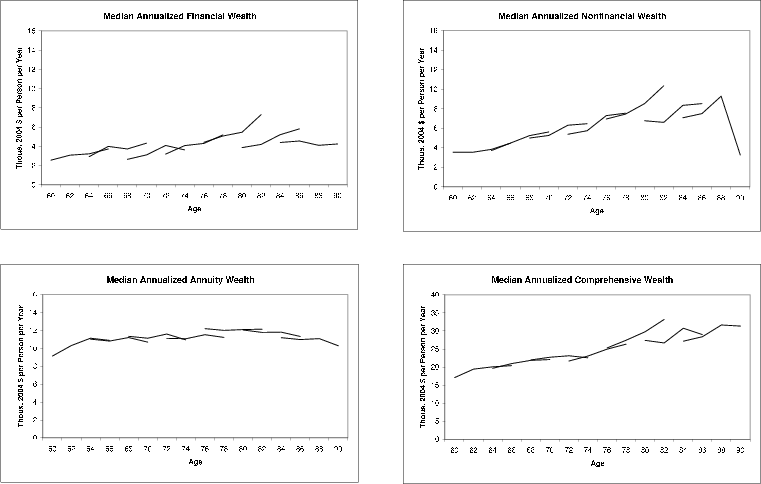
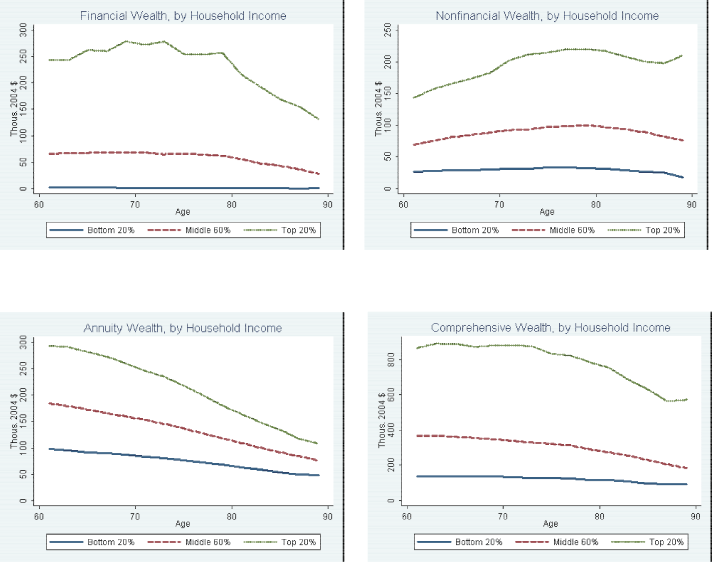
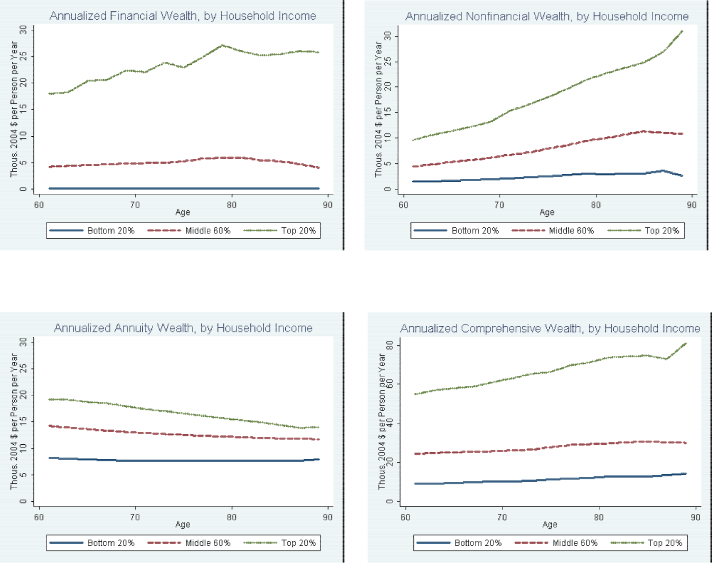
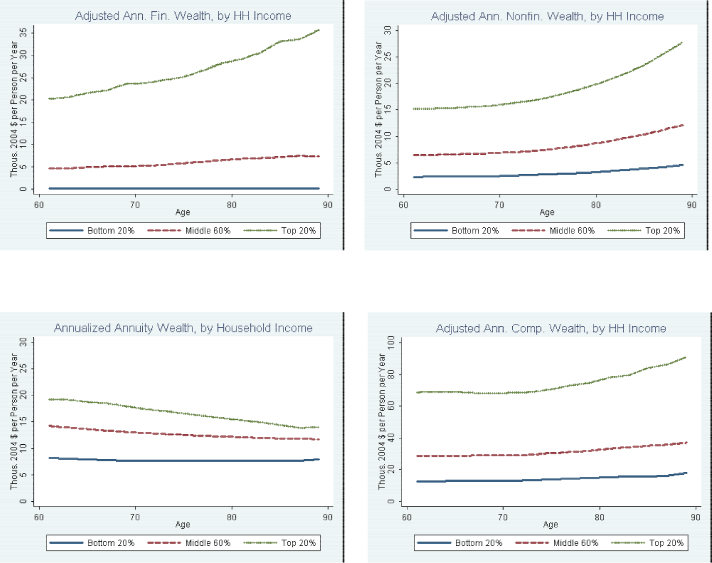
![\displaystyle DBPV=d\sum_{\tau=a_{r}}^{119}\delta^{\tau-a_{r}}\bigl\lbrace\psi^{r}(\tau,a_{r})+\theta[1-\psi^{r}(\tau,a_{r})]\psi^{s}(\tau+\Delta,a_{s})\bigr\rbrace,](img122.gif)
![\displaystyle SSPV=\sum_{\tau=a_{r}}^{119}\delta^{\tau-a_{r}}\left[\Psi_{1}(ss^{r}_{\tau}+ss^{s}_{\tau+\Delta})+\Psi_{2}\max(ss^{r}_{\tau},ss^{s}_{\tau+\Delta})\right],](img140.gif)


![a_t=\frac{r}{1+r}\left[1-\frac{1}{(1+r)^{T_t^{f}}}\right]^{-1}.](img14.gif)