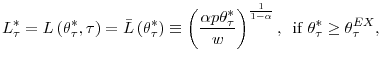Firm Dynamics with Infrequent Adjustment and Learning
Keywords: Adjustment costs, learning, young firms
Abstract:
JEL Classification: E24, L11, L16
1 Introduction
In recent years there has been renewed interest in explaining patterns of firm dynamics, with new longitudinal datasets confirming heterogeneities between firms of different size and age. In particular, small and young (surviving) firms tend to grow faster and have higher failure rates than large and old firms, so that job destruction due to plant exit and job creation due to the scaling-up of firm size decrease with age.2 Moreover, entering plants tend to be small, but survivors grow rapidly after entry and are the main factor behind the shift to the right of a cohort's size distribution.3 These patterns differ significantly across countries and sectors, suggesting that technological differences are important, but that country specific factors also matter.4
This paper proposes an explanation for the leading role of survivors' growth in post-entry firm dynamics based on the interaction between adjustment costs and a learning-about-efficiency mechanism. Following a literature that uses adjustment costs to account for some dynamic properties of firms' labor demand, such as Campbell and Fisher (2000), we show that adjustment costs can impact the lifetime dynamics of firms' labor demand in a way consistent with the data. To implement our theory, we use a standard model of firm dynamics with passive learning. In order to check the empirical fit of our model, we also assume that inefficient firms are pruned from the market, although the predictions of our theory hold even in the absence of a selection mechanism (e.g. when exit is not allowed).
Our contribution is twofold. First, we contribute to the empirical literature by introducing a decomposition of the change in a cohort's average size into a survivor component and a non-survivor component. Given the emphasis on survivors' growth, our measure allows a quick assessment of how well a particular theory matches the data in that respect. We apply our decomposition to the 1988 cohort of entrants in the Portuguese economy, using the Quadros de Pessoal dataset. Similarly to Cabral and Mata (2003), we find that growth of survivors is the main force behind the change in the cohort's average firm size. However, we also find that growth of survivors is especially intense in the initial years after entry and that there are significant cross-sector differences in terms of our decomposition. In particular, initial exit rates are smaller and the survivors' contribution to changes in size is higher in manufacturing than in services.
Second, we contribute to the theoretical literature by introducing linear adjustment costs into a model of Bayesian learning about efficiency. Our assumption of linear or proportional costs is justified by the finding of high inaction rates in employment adjustment, in varying degrees across sectors. Our model builds on Jovanovic (1982) by adding proportional costs that apply not only to regular labor adjustment, but also to job creation at entry and job destruction at exit. We show that proportional adjustment costs create incentives for firms to start smaller and, if successful, grow faster after entry. We prove this analytically in a simplified model in which there is no exit of firms. This result shows that proportional costs can generate firm growth without selection. When firms are allowed to exit, selection intensifies the effects of adjustment costs on firm growth, while costs to adjustment reduce exit rates. Therefore, adjustment costs increase the contribution of surviving firms to growth in the cohort's average size.
All that is needed for firm growth under linear adjustment costs is the existence of a learning environment that generates a stochastic process for perceived efficiency with both persistence and decreasing uncertainty in age.5 The intuition for why firms grow faster and display smaller exit rates under proportional adjustment costs is that initial uncertainty about true profitability makes entering firms prudent; that is, they enter small and "wait and see" since they want to avoid incurring superfluous entering/hiring costs and firing/shutdown costs on jobs that prove to be excessive ex post. This implies that surviving firms will grow faster, even though adjustment costs imply that there are fewer firms exiting the market and therefore less pruning of inefficient firms.
The assumption that entering firms face a Bayesian learning problem concerning their efficiency is standard in selection theories and has been advanced as an explanation for the high rates of exit, job creation, and job destruction among young firms. The initial literature on adjustment costs used a (strictly) convex specification in an attempt to explain the sluggishness in input responses to aggregate shocks. However, the assumption that costs of adjustment are linear is now standard in dynamic labor demand models, following a number of studies since the late 1980s that have documented the importance of inaction in employment adjustment at the micro level.6 Since strictly convex costs imply smooth adjustments over time, whereas linear costs imply immediate adjustment when it occurs, allowing for strictly convex costs, instead of linear costs, in the context where they also apply at entry and exit, would bias our analysis and eventually make our argument stronger. In the case of hiring/entering costs, entering firms would prefer to start smaller and adjust gradually to their optimal size, even if their perceived productivity remained unchanged or learning was absent. For firing/exiting costs, firms experiencing large declines in perceived productivity would adjust downwards in several steps, a scenario that would make firms start smaller to attenuate its effects. Therefore, by avoiding a bias towards firm growth, our decision to assume linear costs is conservative and permits a simplification of the methods employed to measure the effects of adjustment costs.7
To assess our model quantitatively, we calibrate and estimate a version of the model with finite learning horizon and positive dispersion in entry size. We conclude that linear costs are the key element to account for the high empirical contribution of survivors to changes in a cohort's average size. A calibration/estimation for the manufacturing and services cohorts also suggests that firms in manufacturing learn relatively less initially about their efficiency and are subject to substantially larger adjustment costs than firms in services.
This paper is related to the literature on both adjustment costs and firm dynamics. Within the literature on adjustment costs, the paper is associated with theories that use linear adjustment costs to explain certain aspects of the dynamic behavior of labor demand and job flows. Well-known examples are Bentolila and Bertola (1990), Hopenhayn and Rogerson (1993), and Campbell and Fisher (2000). Bentolila and Bertola (1990) and Hopenhayn and Rogerson (1993) analyze the effects of proportional firing (and hiring) costs on the dynamics of hiring and firing decisions, and on average labor demand. Both papers conclude that high firing costs make hiring and firing adjustments more sluggish, but they disagree on the implications of that for long-run employment. Campbell and Fisher (2000) use proportional costs of job creation and job destruction to explain the higher aggregate volatility of job destruction found in the U.S. manufacturing sector. These costs imply that in reaction to aggregate wage shocks employment changes at contracting firms are larger than employment changes at expanding firms. What is new in our paper is the assumption that adjustment costs apply equally to the entry/exit decisions and the hiring/firing decisions.8
Within the literature on firm dynamics the paper is connected with theories that attempt to explain the stylized facts on the lifecycle dynamics outlined above. The two main explanations for these facts are theories based on selection of firms and theories based on financing constraints.9 Selection theories stress the tendency for firms that accumulate bad realizations of productivity to exit the market and for firms that accumulate good realizations to survive and expand. This implies a composition bias towards larger and more efficient firms as smaller, inefficient, and slow-growing firms gradually exit the industry. Representative papers of selection theories are Jovanovic (1982), Hopenhayn (1992), Ericson and Pakes (1995), and Luttmer (2007). In all cases productivity realizations are exogenous, except in Ericson and Pakes (1995) where they are to some extent endogenous.
Meanwhile, theories employing financing constraints argue that some imperfection in financial markets causes young firms to have limited access to credit, forcing them to enter at a suboptimally small scale. As firms get older and survive, they establish creditworthiness and build up internal resources that enable them to expand to their optimal size. Important contributions to this literature are those of Cooley and Quadrini (2001), Albuquerque and Hopenhayn (2004), and Clementi and Hopenhayn (2006). In Cooley and Quadrini (2001) a transaction cost on equity and a default cost on debt imply that equity and debt are not perfect substitutes, so that size depends positively on the amount of equity. In Albuquerque and Hopenhayn (2004) and Clementi and Hopenhayn (2006) lenders introduce credit constraints because of limited liability of borrowers and limited enforcement of debt contracts and because of asymmetric information on the use of funds or the return on investment, respectively.
Cabral and Mata (2003) analyze whether these two theories are consistent with the evolution of a cohort's size distribution in the Portuguese manufacturing sector. They find that, as the cohort ages, the firm size distribution shifts to the right largely due to growth of surviving firms rather than exit of small firms. In addition, they find that in the first year after entry younger business owners are associated with smaller firms but that is no longer the case once the cohort gets to age seven. Assuming that age is a proxy for the entrepreneur's initial wealth, the authors conclude that the age-size effect supports the idea of financially constrained firms starting at a suboptimal size and present a model with financing constraints capturing this effect.
More recently, Angelini and Generale (forthcoming) use survey and balance sheet information for Italian manufacturing firms to analyze the impact of financing constraints on the evolution of the firm size distribution. They find that financially constrained firms tend to be small and young, although this does not have a significant effect on the overall firm size distribution. Moreover, they find that financing constraints decrease firm growth, with this effect being entirely due to small firms. In particular, being young and financially constrained does not have any additional effect. Based on these results and the fact that young firms grow faster than old firms, the authors conclude that financing constraints are not the main factor behind the evolution of the firm size distribution. In line with their argument, this paper interprets the facts presented in Cabral and Mata (2003) and other cross-sector evidence as the result of the interaction between adjustment costs and learning about efficiency.10
To our knowledge, this work is the first to suggest adjustment costs as an explanation for differences in firm dynamics by age. The paper by Cabral (1995) is nearest to this paper. In his model, firms must pay a proportional sunk cost to increase their production capacity. He argues that, in a model with Bayesian learning, a proportional capacity cost would make small entering firms grow faster than large entering firms. The reason is that small entrants are those whose initial profitability signals were not good, so their exit probabilities are higher, and therefore they choose to invest more gradually. Unlike our model, Cabral's model depends on the existence of selection. Also, by analyzing a size-growth relationship, his model is not able to explain why some large entering firms also grow substantially.
The paper is organized as follows. In section 2, we present evidence of firm dynamics for a cohort of entering firms. In section 3, we build the general model, obtain optimality conditions, and provide heuristic arguments explaining the effects of adjustment costs. In section 4, using a simplified version of the model we analytically prove the effect of linear adjustment costs on survivors' growth. In section 5, we calibrate and estimate a finite learning horizon version of the model and quantify the contribution of adjustment costs to firm dynamics. Section 6 concludes. All proofs are left for an appendix.
2 Firm Dynamics in a Cohort of Entering Firms
There is a well established literature on the identification and explanation of differences in behavior between young and old firms. In this section, we analyze firm dynamics in a cohort of entering firms. We use Quadros de Pessoal, a database containing information on all Portuguese firms with paid employees. This dataset originates from a mandatory annual survey run by the Ministry of Employment, which collects information about the firm, its establishments, and its workers. All economic sectors except public administration are included. The panel we have access to covers the period 1985-2000. Information refers to March of each year from 1985 through 1993, and to October of each year since the reformulation of the survey in 1994. On average the dataset contains 250,000 firms, 300,000 establishments, and 2,500,000 workers in each year.
The literature on firm dynamics typically finds that young firms grow faster than old firms. Using kernel density estimates of the firm size distribution in a cohort of entrants, Cabral and Mata (2003) argue graphically that the cohort's evolution is mostly due to growth of survivors rather than exit of small firms. Their analysis points to the need for a measure of the contribution of survivors versus non-survivors to the growth in a given cohort's average size. To accomplish this, we propose a decomposition of the cohort's cumulative growth that will later allow an assessment of the empirical relevance of adjustment costs. We consider the following decomposition:
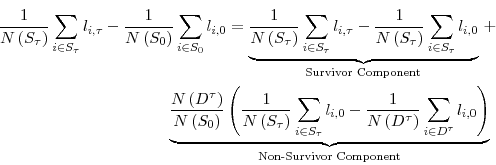
where
In general, the growth in a cohort's average size can originate from growth of survivors or from smaller initial size of non-survivors. Any theory of firm dynamics should consider both these sources of growth. Our measure allows a check on whether a particular theory can explain the key source
of growth in a cohort's average size. The survivor component compares the current average size of period ![]() survivors with their initial average size, so that it measures how much survivors
have grown. The non-survivor component compares the average initial size of period
survivors with their initial average size, so that it measures how much survivors
have grown. The non-survivor component compares the average initial size of period ![]() non-survivors with the average initial size of period
non-survivors with the average initial size of period ![]() survivors, so that it measures how relatively small non-survivors were initially.
survivors, so that it measures how relatively small non-survivors were initially.
We can obtain a similar decomposition for employment-weighted moments. The weighted decomposition contains information about the entire distribution of employment, not just its cross-sectional mean, and is affected both by within- and between-firm growth. Therefore, the weighted decomposition would be more relevant for assessing a richer model that considers the reallocation of employment shares between firms within the cohort. In the results that follow we focus on the unweighted decomposition because it analyzes within-firm growth, which in our model is the most relevant statistic to assess the effect of adjustment costs on the incentives for firms to grow.12
We can also produce a decomposition based on the cohort's annual growth instead of the cohort's cumulative growth. However, the annual version of the above decomposition is more sensitive to two aspects that would complicate the analysis in the paper. First, the annual survivor component is
significantly affected by the business cycle, especially after the first few years of life. To control for this, we would need to somehow remove the cyclical part of the survivor component. Second, as the age of the cohort increases, the annual survivor component becomes increasingly sensitive to
downsizing and exit by some survivors that become technologically outdated and consequently relatively less efficient. To fully consider this aspect of the data would force us to introduce additional parameters into the model that we present in section 3. Therefore, we believe
that by employing a decomposition based on the cohort's cumulative growth we avoid having to adjust the analysis for these two aspects, and instead focus on how intense is survivor's growth while learning-about-efficiency effects are significant.
| Year | CEx | AvEmp | CGrEmp | SComp |
|---|---|---|---|---|
| 1988 | 1.11 | |||
| 1989 | 15.6 | 1.27 | 15.2 | 69.5 |
| 1990 | 24.4 | 1.36 | 24.8 | 70.4 |
| 1991 | 30.8 | 1.43 | 31.2 | 69.7 |
| 1992 | 35.4 | 1.46 | 34.2 | 69.3 |
| 1993 | 40.0 | 1.46 | 34.6 | 68.9 |
| 1994 | 43.4 | 1.47 | 35.3 | 69.1 |
| 1995 | 46.7 | 1.48 | 36.1 | 68.7 |
| 1996 | 49.9 | 1.49 | 37.4 | 67.2 |
| 1997 | 52.7 | 1.51 | 39.6 | 68.5 |
| 1998 | 55.5 | 1.52 | 40.7 | 68.3 |
| 1999 | 58.5 | 1.54 | 43.0 | 68.9 |
Notes: CEx is the cumulative exit rate,
In table 1, we present the evolution of exit rates and the share of firm growth due to the survivor component in the 1988 cohort of entering firms for the overall economy.13 In 1988 there were ![]() entering firms. The exit rate is very high initially but tends to decrease as firms get
older.14 However, ten years after entry only
entering firms. The exit rate is very high initially but tends to decrease as firms get
older.14 However, ten years after entry only ![]() of the initial entrants remain active. There is significant growth in the cohort's average size, especially in the first few years, which is mostly due to the growth of survivors rather than to the exit of small inefficient firms: survivors' growth contributes around
of the initial entrants remain active. There is significant growth in the cohort's average size, especially in the first few years, which is mostly due to the growth of survivors rather than to the exit of small inefficient firms: survivors' growth contributes around
![]() to the growth in the cohort's average size.15
to the growth in the cohort's average size.15
Notes: ESh is the employment share of the sector in the overall economy cohort; CEx, CGrEmp, SComp are as defined in table 1.
Table 2 presents similar evidence on cohort dynamics for the manufacturing and services sectors.16 We include the employment shares
of each sector in the 1988 cohort of entering firms, which are close to shares in the overall economy. Although manufacturing has a much higher employment share than services, the number of entering firms in services surpasses that of manufacturing ( 6074 and 4834, respectively). Both sectors display a cumulative exit rate around ![]() by 1999. However, initial differences in exit rates are more significant, with manufacturing displaying the smallest values, and services displaying the highest values. In terms of initial size, manufacturing has the largest
entrants, and services the smallest. Although manufacturing has the largest entrants, it exhibits more growth in average employment and a larger contribution of survivors to that growth than services.
by 1999. However, initial differences in exit rates are more significant, with manufacturing displaying the smallest values, and services displaying the highest values. In terms of initial size, manufacturing has the largest
entrants, and services the smallest. Although manufacturing has the largest entrants, it exhibits more growth in average employment and a larger contribution of survivors to that growth than services.
We perform two robustness checks on the previous findings. First, we redo our calculations using establishments rather than firms as the unit of analysis. For the 1988 establishment cohort, we obtain similar results, although exit rates and the survivor component are higher than in the case of
firms. Second, we examine an alternative cohort to make sure our results are not driven by business cycle conditions. The Portuguese economy experienced an expansion between 1986 and 1991, a period of slow growth with a recession between 1992 and 1994, and another weaker expansion between 1995 and
2000. The growth rates of real GDP were ![]() in 1989,
in 1989, ![]() in 1992, and
in 1992, and
![]() in 1995, so that the 1991 cohort did not face as favorable a macroeconomic environment as the 1988 cohort. However, the results for the 1991 cohort are, in all dimensions, very similar
to those presented above. The results for the 1994 cohort are also very similar, but with slightly smaller values for the survivor component in the first few years after entry.17
in 1995, so that the 1991 cohort did not face as favorable a macroeconomic environment as the 1988 cohort. However, the results for the 1991 cohort are, in all dimensions, very similar
to those presented above. The results for the 1994 cohort are also very similar, but with slightly smaller values for the survivor component in the first few years after entry.17
Notes: N30 is the fraction of firms with an adjusted growth rate of employment, conditional on survival, in the interval
In table 3, we provide evidence on characteristics of labor adjustment in the 1988 cohort of entering firms. We use the distribution of the adjusted growth rate conditional on survival. Following Davis and Haltiwanger (1992), the
adjusted growth rate in period ![]() is defined as
is defined as
![]() , where
, where
![]() . The table shows that the incidence of inaction is very high, increases with age, and is higher in services than in
manufacturing. This may reflect technology-induced differences in adjustment costs, or job indivisibilities affecting to a larger extent the services sector for having a higher share of small firms. The table also shows that the large majority of firms have adjustment rates within the
. The table shows that the incidence of inaction is very high, increases with age, and is higher in services than in
manufacturing. This may reflect technology-induced differences in adjustment costs, or job indivisibilities affecting to a larger extent the services sector for having a higher share of small firms. The table also shows that the large majority of firms have adjustment rates within the
![]() interval. A high rate of inaction and small adjustment is usually considered consistent with the presence of linear or proportional adjustment costs. An additional fact is the
left skewness of the 1989 distributions, showing that survivors tend to grow initially, especially in manufacturing. This skewness is less evident in 1993, suggesting that adjustment patterns are different in initial years. The evidence on inaction justifies our assumption of linear adjustment
costs in the model that we present next.
interval. A high rate of inaction and small adjustment is usually considered consistent with the presence of linear or proportional adjustment costs. An additional fact is the
left skewness of the 1989 distributions, showing that survivors tend to grow initially, especially in manufacturing. This skewness is less evident in 1993, suggesting that adjustment patterns are different in initial years. The evidence on inaction justifies our assumption of linear adjustment
costs in the model that we present next.
3.1 Assumptions and Solution
In this section, we introduce linear adjustment costs into a model of Bayesian learning about efficiency. We derive conditions for optimal employment over time and present heuristic arguments about the effects of adjustment costs on the path of employment. Our model is based on Jovanovic (1982), adding adjustment costs and using a different specification for the idiosyncratic shock.
We assume an industry with competitive output and input markets. Current profits of a representative firm are defined by
Concerning technology we make the following assumption.
where
Part (a) basically ensures a well defined interior optimum. In some of the analyses below, we will further specialize by assuming that ![]() is Cobb-Douglas.
Meanwhile, part (b) establishes that in each period productivity is stochastic with a constant mean over the firm's lifetime. The productivity component,
is Cobb-Douglas.
Meanwhile, part (b) establishes that in each period productivity is stochastic with a constant mean over the firm's lifetime. The productivity component, ![]() , is
made of two parts:
, is
made of two parts: ![]() , which is observed before entry, and
, which is observed before entry, and ![]() , which is
never directly observed by the firm. Intuitively,
, which is
never directly observed by the firm. Intuitively, ![]() can be thought of as indexing ex ante efficiency, measuring initial technology choice, while
can be thought of as indexing ex ante efficiency, measuring initial technology choice, while ![]() indexes ex post productivity, measuring how well a firm performs within its technology choice.
indexes ex post productivity, measuring how well a firm performs within its technology choice.
The introduction of ![]() is essential to obtain a non-degenerate distribution of firms' entry size, allowing an analysis of the contribution of survivors to growth in the cohort's
average size. In contrast, the absence of
is essential to obtain a non-degenerate distribution of firms' entry size, allowing an analysis of the contribution of survivors to growth in the cohort's
average size. In contrast, the absence of ![]() in Jovanovic's (1982) model generates a degenerate distribution of firms' entry size. Under this scenario, for
any period after entry, survivors and non-survivors have the same average initial size implying a value of
in Jovanovic's (1982) model generates a degenerate distribution of firms' entry size. Under this scenario, for
any period after entry, survivors and non-survivors have the same average initial size implying a value of ![]() to our measure of the survivors' component. By assuming
to our measure of the survivors' component. By assuming
![]() , we avoid this aspect of Jovanovic's model.
, we avoid this aspect of Jovanovic's model.
Before entry the firm knows the parameters governing the stochastic process of ![]() , i.e.,
, i.e., ![]() ,
,
![]() ,
,
![]() and
and
![]() , and learns its ex ante productivity,
, and learns its ex ante productivity, ![]() , after paying a research cost,
, after paying a research cost, ![]() . After entry, the firm will learn about its specific ex post productivity,
. After entry, the firm will learn about its specific ex post productivity, ![]() , over time as it observes the realizations of productivity,
, over time as it observes the realizations of productivity, ![]() . In particular, the firm forecasts
period-
. In particular, the firm forecasts
period-![]() productivity based on the ex ante efficiency parameter
productivity based on the ex ante efficiency parameter ![]() and on the past realizations of productivity,
and on the past realizations of productivity,
![]() . Similarly to Zellner (1971), a firm with age
. Similarly to Zellner (1971), a firm with age ![]() has the following Bayesian posterior distribution for
has the following Bayesian posterior distribution for ![]() at the beginning of period
at the beginning of period ![]() :
:
In the absence of adjustment costs, while deciding whether to stay one more period or to exit, the firm compares the expected profit in case it stays, ![]() , with the opportunity cost of
doing so,
, with the opportunity cost of
doing so, ![]() , the value it would recover by selling the (exogenously determined) capital initially acquired, i.e.,
, the value it would recover by selling the (exogenously determined) capital initially acquired, i.e.,
where
At entry, we have
![]() , and in equilibrium expected profits must compensate for the cost of acquiring capital, i.e.,
, and in equilibrium expected profits must compensate for the cost of acquiring capital, i.e.,
![]() . Since markets are competitive and there is no friction in the entry and exit processes, in equilibrium the research cost equals expected gains at
the research phase, i.e.,
. Since markets are competitive and there is no friction in the entry and exit processes, in equilibrium the research cost equals expected gains at
the research phase, i.e.,
![]() . If
. If
![]() more firms will initiate research and later enter the industry, causing a decrease in output price until equality is restored. A strictly positive fixed
research cost,
more firms will initiate research and later enter the industry, causing a decrease in output price until equality is restored. A strictly positive fixed
research cost, ![]() , is essential to avoid the extreme situation where trial research is so high that only the highest productivity firms enter and survive. Because there is no reliable
capital stock variable in Quadros de Pessoal, we do not make the capital decision endogenous to the model. Instead, we assume that firms are homogeneous along the capital dimension and face the same opportunity cost of remaining in activity,
, is essential to avoid the extreme situation where trial research is so high that only the highest productivity firms enter and survive. Because there is no reliable
capital stock variable in Quadros de Pessoal, we do not make the capital decision endogenous to the model. Instead, we assume that firms are homogeneous along the capital dimension and face the same opportunity cost of remaining in activity, ![]() .
.
Up to this point, the only differences between our model and Jovanovic (1982) are that in the latter model the efficiency parameter implicitly affects the cost function and the cohort's entry size distribution is degenerate. Therefore, without adjustment costs there
would be no intertemporal linkages in our model aside from the exit decision. As in Jovanovic, because ![]() is strictly increasing in
is strictly increasing in
![]() , the exit decision is characterized by an age-dependent exit threshold. For values of
, the exit decision is characterized by an age-dependent exit threshold. For values of
![]() above or equal to that threshold, the firm would stay and choose employment to maximize current period profits. For values of
above or equal to that threshold, the firm would stay and choose employment to maximize current period profits. For values of
![]() below that threshold, the firm would leave the industry, since its expected profitability is below the opportunity cost. The increasing confidence the firm puts in
below that threshold, the firm would leave the industry, since its expected profitability is below the opportunity cost. The increasing confidence the firm puts in
![]() as it grows older implies that the exit threshold is increasing with age. This is the driving force underlying Jovanovic's result that the size distribution and the
survival probability increase with age.
as it grows older implies that the exit threshold is increasing with age. This is the driving force underlying Jovanovic's result that the size distribution and the
survival probability increase with age.
We now introduce linear adjustment costs into the model. The adjustment cost for continuing firms, ![]() , is defined as
, is defined as
With adjustment costs, the problem now becomes,
for all periods after entry (
for the entry period, where
In general, we could allow for asymmetry among the cost parameters in ![]() ,
, ![]() , and
, and ![]() . However, asymmetries between the cost of regular firing and the cost of firing at exit or between the cost of regular hiring and the cost of hiring at
entry lead to biases in entry and exit decisions. For example, if the per unit regular hiring cost is higher than the per unit entry hiring cost, then firms will hire more workers at entry in order to save on expected future higher hiring costs. Similarly, if the per unit regular firing cost is
smaller than the per unit exit firing cost, then firms facing the prospect of exit will fire workers before exiting the industry, saving on expected future higher exit firing costs. To avoid these biases, throughout the paper we assume symmetry between the parameters in
. However, asymmetries between the cost of regular firing and the cost of firing at exit or between the cost of regular hiring and the cost of hiring at
entry lead to biases in entry and exit decisions. For example, if the per unit regular hiring cost is higher than the per unit entry hiring cost, then firms will hire more workers at entry in order to save on expected future higher hiring costs. Similarly, if the per unit regular firing cost is
smaller than the per unit exit firing cost, then firms facing the prospect of exit will fire workers before exiting the industry, saving on expected future higher exit firing costs. To avoid these biases, throughout the paper we assume symmetry between the parameters in ![]() ,
, ![]() , and
, and ![]() . A more interesting distinction is between firing and hiring costs. We will see below that the conclusion of the paper is immune to asymmetries between the costs of adding and subtracting workers.
. A more interesting distinction is between firing and hiring costs. We will see below that the conclusion of the paper is immune to asymmetries between the costs of adding and subtracting workers.
In solving the firm's problem, we consider a two-step optimization procedure where the firm first chooses optimal employment in each of three possible scenarios, and then selects the scenario with the highest pay-off. More precisely,
In contrast, the non-differentiability of the objective function generates an inaction region in the employment policy, within which optimal employment does not vary with changes in productivity.
whereas if the firm adjusts downwards optimal employment satisfies
In period 0, the firm enters the industry if
![]()
Equations (6), (7) and (8) are marginal conditions, similar to the smooth pasting conditions in the (S, s) model literature, and they state that if the firm adjusts then the marginal adjustment cost must equal the expected present discounted value of the marginal revenue product for all future periods in which the firm is still in the industry, minus the increase in the exit cost when the firm decides to exit. This is the discrete-time analog of the continuous-time result present in Nickell (1986) and Bentolila and Bertola (1990), adjusted for the fact that now we also have an exit decision. Because the firm will not change employment if the marginal cost of adjustment exceeds its marginal benefit for the first unit of adjustment, proportional costs imply inaction in the employment decision of the firm.
Although the results in proposition 6 do not allow a formal proof of the effects on firm growth of adjustment costs in this general model, the following corollary of proposition 6 enables us to make qualitative heuristic statements about those effects.
Corollary #.:
where
![]()
3.2 Linear Adjustment Cost and Firm Growth
As we have seen above, in the absence of adjustment costs, optimal employment is determined solely to maximize current period profits, so that
![]() . Therefore, firms' growth is essentially a by-product of a selection mechanism: those firms that are inefficient, and therefore small, exit,
while those firms that are efficient survive and grow. There is an additional source of positive growth when the frictionless employment decision rule,
. Therefore, firms' growth is essentially a by-product of a selection mechanism: those firms that are inefficient, and therefore small, exit,
while those firms that are efficient survive and grow. There is an additional source of positive growth when the frictionless employment decision rule,
![]() , is convex in
, is convex in
![]() . Because of Jensen's inequality and because
. Because of Jensen's inequality and because
![]() is a Martingale, surviving firms will grow over time:
is a Martingale, surviving firms will grow over time:
![]() .
However,
.
However, ![]() will not be convex in
will not be convex in
![]() for general
for general
![]() .20
.20
In arguing heuristically about the impact of the proportional cost on firm growth we use the property that ![]() is weakly increasing in
is weakly increasing in
![]() , and that
, and that
![]() is locally weakly increasing in
is locally weakly increasing in
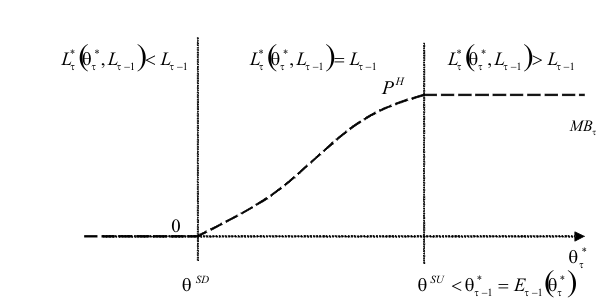
![]() . Because it is not immediately obvious why firing and hiring costs should give similar incentives for firm growth, we analyze separately these two costs.21 We present in figure 1 the case where there is a hiring cost,
. Because it is not immediately obvious why firing and hiring costs should give similar incentives for firm growth, we analyze separately these two costs.21 We present in figure 1 the case where there is a hiring cost, ![]() , and no firing cost,
, and no firing cost, ![]() . This figure assumes a given
. This figure assumes a given
![]() . For that specific value of
. For that specific value of ![]() ,
,
![]() and
and
![]() are the frontiers between non-adjustment and upward and downward adjustment, respectively. Therefore, if
are the frontiers between non-adjustment and upward and downward adjustment, respectively. Therefore, if
![]() there will be no adjustment and the marginal benefit of an additional unit of labor (represented by the dashed line) is
contained in the interval
there will be no adjustment and the marginal benefit of an additional unit of labor (represented by the dashed line) is
contained in the interval
![]() . To simplify the argument, we consider a firm whose sequence of productivity draws is such that in every period it has a perceived productivity equal to the
unconditional mean of
. To simplify the argument, we consider a firm whose sequence of productivity draws is such that in every period it has a perceived productivity equal to the
unconditional mean of
![]() , even though the firm's uncertainty over next period
, even though the firm's uncertainty over next period
![]() decreases with age.
decreases with age.
Case 1: Hiring Cost: ![]() ,
, ![]()
Because the firm starts at the hiring margin, we must have
![]() at entry, and
at entry, and
![]() , for all subsequent periods,
, for all subsequent periods,
![]() , with the two extremes of the interval representing firing and hiring of workers, respectively. Consider first a situation where exit is not allowed. Under this assumption,
(9) would become
, with the two extremes of the interval representing firing and hiring of workers, respectively. Consider first a situation where exit is not allowed. Under this assumption,
(9) would become
The Bayesian learning mechanism implies both persistence and a reduction in variance with age in the Markov process associated with
![]() . The effect of persistence, that is, the fact that
. The effect of persistence, that is, the fact that
![]() , was analyzed in the previous paragraph. The reduced uncertainty in the posterior estimate of
productivity will be reflected in a smaller inaction region as firms accumulate information on realized productivity; that is,
, was analyzed in the previous paragraph. The reduced uncertainty in the posterior estimate of
productivity will be reflected in a smaller inaction region as firms accumulate information on realized productivity; that is,
![]() decreases with
decreases with ![]() . This causes an increase in
. This causes an increase in
![]() for those firms already at the hiring margin, which must be balanced by an increase in
for those firms already at the hiring margin, which must be balanced by an increase in
![]() for the right hand side of (9) to remain equal to
for the right hand side of (9) to remain equal to ![]() . As firms become more certain about their true productivity they are more willing to adjust to their long run optimal size. Because most firms are at the hiring margin, this will cause a further increase in average size.
. As firms become more certain about their true productivity they are more willing to adjust to their long run optimal size. Because most firms are at the hiring margin, this will cause a further increase in average size.
Consider now the possibility of exit. In this case, the uncertainty reduction as the firm ages implies a decrease in the exit probability, and a further increase in the future-periods component of ![]() in (9). Consequently,
in (9). Consequently,
![]() needs to increase further in order to offset that.23 On the other hand, the smaller exit probability implies less pruning of inefficient slow-growing firms as a cohort ages, which tends to make growth in average firm size smaller. Therefore, we will have less cohort growth due to non-survivors and more cohort growth due
to survivors, so that survivors' contribution to average firm growth in the cohort should increase when exit is allowed.
needs to increase further in order to offset that.23 On the other hand, the smaller exit probability implies less pruning of inefficient slow-growing firms as a cohort ages, which tends to make growth in average firm size smaller. Therefore, we will have less cohort growth due to non-survivors and more cohort growth due
to survivors, so that survivors' contribution to average firm growth in the cohort should increase when exit is allowed.
Case 2: Firing Cost: ![]() ,
, ![]()
In this case we have ![]() ,
,
![]() ,
,
![]() . Assume first that exit is not allowed. The intuition is the same as in case 1. In comparison with
. Assume first that exit is not allowed. The intuition is the same as in case 1. In comparison with ![]() , when
, when ![]() firms start smaller and subsequently hire more frequently than they fire. As firms age, the reduction in variance of
firms start smaller and subsequently hire more frequently than they fire. As firms age, the reduction in variance of
![]() causes an increase in
causes an increase in
![]() , which must be compensated by an increase in
, which must be compensated by an increase in
![]() for firms at the hiring margin. When exit is possible, those effects become more intense, since the exit probability will decrease as firms age.
for firms at the hiring margin. When exit is possible, those effects become more intense, since the exit probability will decrease as firms age.
From the heuristic intuition we have just given it becomes clear that proportional hiring and proportional firing costs reinforce each other in creating incentives for firms to grow. In the end, our assessment of the relevance of linear adjustment costs for firm growth will depend on how well a pure selection model can fit the empirical evidence, and on how much adjustment costs improve the fit. Before we move into a quantitative assessment, we present analytical results for a simple version of the general model.
4 Model with One Period Learning Horizon and No Exit
In this section, we analyze a model where firms' efficiency is revealed after the first period of life and where firms' lifetime horizon is know with certainty at entry. We assume that firms live for ![]() periods,
periods,
![]() , and that no exit is allowed prior to age
, and that no exit is allowed prior to age ![]() . These two simplifications allow us to determine the effect of linear adjustment costs on firm growth.
. These two simplifications allow us to determine the effect of linear adjustment costs on firm growth.
The introduction of adjustment costs implies an additional expected operating cost for entering firms. Therefore, the equilibrium price must increase to generate higher expected future profits that compensate for the costs incurred while adjusting to optimal size. As a consequence, pre-entry
pruning of inefficient firms should increase while post-entry pruning should decrease. This is optimal from a social point of view, since with higher adjustment costs there should be less experimentation in order to save in unrecoverable costs. Therefore, the assumption that exit is exogenous is
not critical for the results in this section. Since adjustment costs attenuate post-entry pruning, even if exit was endogenous to the model, the relative contribution of survivors to growth in the cohort's average size would increase through this channel. By eliminating any exit prior to
![]() we focus only on the incentives for survivors to grow.
we focus only on the incentives for survivors to grow.
To formulate the problem, we use the fact that once the firm learns its true efficiency in period 2, it will adjust once and for all to its long run employment level, and it will not adjust in any of the following periods.24 Therefore, assuming that upon exit at age ![]() the firm recovers its initial investment net of exit costs, the
optimization problem in period 2 is
the firm recovers its initial investment net of exit costs, the
optimization problem in period 2 is
where
We examine the impact of adjustment costs on the log growth rate of employment, rather than the standard growth rate, in order to attenuate the effect of Jensen's inequality on firm growth.25 In this simple model, the inaction region of optimal employment can be expressed as an interval:
![]() . Therefore, the average log growth rate between period 1 and period 2, conditional on
. Therefore, the average log growth rate between period 1 and period 2, conditional on
![]() , is defined as
, is defined as
![\begin{multline*} g\left( \theta_{1}^{\ast}\right) =E\left[ \ln\left( L_{2}^{\ast}\right) -\ln\left( L_{1}^{\ast}\right) \right] =\ \int_{\nu_{1}}^{\theta^{SD}}\left\{ \ln\left( L_{2}^{\ast SD}\right) -\ln\left( L_{1}^{\ast}\right) \right\} dF_{\theta_{1}^{\ast}}\left( \theta_{2}^{\ast}\right) +\int_{\theta^{SU}}^{\nu_{2}}\left\{ \ln\left( L_{2}^{\ast SU}\right) -\ln\left( L_{1}^{\ast}\right) \right\} dF_{\theta_{1}^{\ast}}\left( \theta_{2}^{\ast}\right) \end{multline*}](img205.gif)
where
Optimal employment in period 2 is determined by
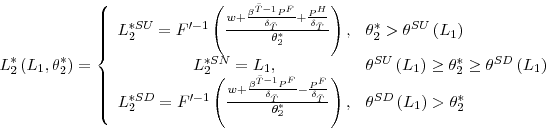
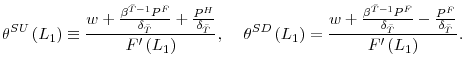
We then have the following result concerning the effects of changes in ![]() and
and ![]() on the cohort's average log growth rate of employment.
on the cohort's average log growth rate of employment.
![]()
Consider first the hiring cost. In the proof, we show that an increase in ![]() decreases both
decreases both
![]() and
and
![]() . The impact of
. The impact of ![]() on the growth rate depends on two opposing
effects. First, while in the case of
on the growth rate depends on two opposing
effects. First, while in the case of
![]() the cost of hiring can be equally spread out over
the cost of hiring can be equally spread out over ![]() periods with certainty, in the case of
periods with certainty, in the case of
![]() it will be spread out over either
it will be spread out over either ![]() periods or one period,
depending on whether the firm learns in period 2 that it has overhired. Therefore, ex ante a proportionately greater part of
periods or one period,
depending on whether the firm learns in period 2 that it has overhired. Therefore, ex ante a proportionately greater part of ![]() is attached to period 1 in the case of
is attached to period 1 in the case of
![]() than in the case of
than in the case of
![]() , affecting more
, affecting more
![]() than
than
![]() . This explains the positive effect on growth of
. This explains the positive effect on growth of ![]() for
for
![]() . Second, the hiring cost on
. Second, the hiring cost on
![]() can possibly be spread out over
can possibly be spread out over ![]() periods, while the hiring
cost on
periods, while the hiring
cost on
![]() can only be spread out over
can only be spread out over ![]() periods. This affects more
periods. This affects more
![]() than
than
![]() , and explains why the effect of
, and explains why the effect of ![]() on growth is not necessarily
positive for finite
on growth is not necessarily
positive for finite ![]() . However, as
. However, as ![]() increases the first effect
dominates so that
increases the first effect
dominates so that ![]() decreases
decreases
![]() more than
more than
![]() and growth increases.28
and growth increases.28
With respect to ![]() there is always a positive effect on growth, independently of the lifetime horizon. This occurs because an increase in
there is always a positive effect on growth, independently of the lifetime horizon. This occurs because an increase in ![]() decreases
decreases
![]() and increases
and increases
![]() . This positive effect always dominates the uncertain effect due to the fact that
. This positive effect always dominates the uncertain effect due to the fact that
![]() also decreases with
also decreases with ![]() .
.
When there are both hiring and firing costs and these costs are identical (
![]() ), then an increase in
), then an increase in ![]() has a positive effect on
has a positive effect on
![]() , for sufficiently high
, for sufficiently high ![]() , where the
required
, where the
required ![]() is lower than in item (a) of proposition 8.
is lower than in item (a) of proposition 8.
5 Calibration/Estimation Under Finite Learning Horizon
In the previous two sections, we developed heuristic and some formal arguments about the effect of adjustment costs on the incentives for firms to start smaller and grow faster after entry. In this section, we assess the contribution of adjustment costs to explain some of the basic facts on firm dynamics found in section 2, both for the overall economy and for the manufacturing and services sectors. To accomplish this, we perform a calibration/estimation of the model using computational methods.
To simulate the infinite learning horizon model we follow the suggestion of Ljungqvist and Sargent (2004) and consider an approximation where firms live forever, but learn their ex post true productivity component,
![]() , with certainty at some age
, with certainty at some age ![]() .29
.29
We assume that ![]() is Cobb-Douglas, i.e.,
is Cobb-Douglas, i.e.,
![]() ,
,
![]() . Under this assumption, when adjustment is costless, optimal employment is given by
. Under this assumption, when adjustment is costless, optimal employment is given by
where
Concerning the productivity distribution, we assume that
![]() is lognormally distributed, i.e.,
is lognormally distributed, i.e.,
![]() .30 This assumption is made for computational simplicity, and it seems reasonable on empirical grounds (see Aw et. al., 2004). In addition, this assumption is not critical as the results in section 4 suggest that the distribution of productivity mostly affects the intensity of the effect of adjustment costs on firm growth, but not the sign. In fact, proposition 8 is derived independently of the particular distribution of
.30 This assumption is made for computational simplicity, and it seems reasonable on empirical grounds (see Aw et. al., 2004). In addition, this assumption is not critical as the results in section 4 suggest that the distribution of productivity mostly affects the intensity of the effect of adjustment costs on firm growth, but not the sign. In fact, proposition 8 is derived independently of the particular distribution of
![]() . With the log-normal distribution assumption, the transition law for the
. With the log-normal distribution assumption, the transition law for the
![]() s is as follows.
s is as follows.
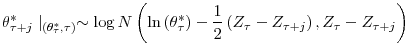 .
.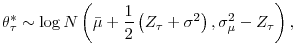
![]()
Since we assume that the firm enters the industry already knowing its ex ante productivity component ![]() (see assumption 1), we will
get a non-degenerate distribution of initial size. This occurs because
(see assumption 1), we will
get a non-degenerate distribution of initial size. This occurs because
![]() , and
, and
![]() has positive variance in the cohort's initial distribution. The next proposition analyzes the properties of the optimization problem after
has positive variance in the cohort's initial distribution. The next proposition analyzes the properties of the optimization problem after ![]() is revealed to the firm in period
is revealed to the firm in period ![]() .
.
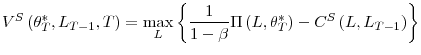 , , |
(10) |
![]()
This result enables us to simplify the computational algorithm significantly, since it implies a finite horizon dynamic programming problem. In appendix B, we present some details concerning the computational algorithm used to simulate the model. In the next subsection, we partially calibrate and estimate the learning model with costly adjustment, and in the following subsection we do a sensitivity analysis.
5.1 Calibration and Estimation of Model with Costly Adjustment
We calibrate and estimate our model to match statistics from the 1988 cohort of entering firms, both for the overall economy and the manufacturing and service sectors. We first calibrate parameters related to inputs directly from the data. We then use a form of the method of moments to estimate
the parameters associated with the learning process and the adjustment cost. These estimates are obtained so that the model generated moments match the evolution of firm size, of exit rates, and of the survivor component observed in the data. As discussed in appendix B, we find
the set of parameter values that minimize the method of moments objective function by using a simulated annealing method. This optimization method is robust to local minima, to discontinuities, and to the discretization implemented in order to simulate the model.31 A central element to our estimation strategy is a decomposition of the change in the cohort's average size into a survivor component and a non-survivor component. This decomposition
forces the model to match not only the growth in the cohort's average size but also the contribution of surviving and non-surviving firms to that growth. Similarly to section 2, with
![]() , our decomposition is defined as
, our decomposition is defined as
![\displaystyle E\left[ l_{\tau}\mid S_{\tau}\right] -E\left[ l_{0}\mid S_{0}\right] =\underset{\text{Survivor Component}}{\underbrace{E\left[ l_{\tau}-l_{0}\mid S_{\tau}\right] }}+\underset{\text{Non-Survivor Component}}{\underbrace {\Pr\left( D^{\tau}\mid S_{0}\right) \left\{ E\left[ l_{0}\mid S_{\tau }\right] -E\left[ l_{0}\mid D^{\tau}\right] \right\} }}%](img266.gif)
|
(11) |
Prior to estimation, we calibrate some parameters. The parameters ![]() and
and ![]() are calibrated with data from INE (1997) containing the Inquérito Annual às Empresas from 1990 to 1995. These data are considered reliable and cover all firms in the Portuguese economy, with sampling among firms with less than 20
workers. We measure
are calibrated with data from INE (1997) containing the Inquérito Annual às Empresas from 1990 to 1995. These data are considered reliable and cover all firms in the Portuguese economy, with sampling among firms with less than 20
workers. We measure ![]() as the 1990-1995 average of the cost share of labor in value added, and
as the 1990-1995 average of the cost share of labor in value added, and ![]() as the 1990-1995 average cost per worker. We can also obtain these values at the one-digit sectoral level. We deflate all nominal variables using the GDP sectoral price indices available in the updated version of Séries Longas para a Economia
Portuguesa in Banco de Portugal (1997). The real interest rate is calibrated as the 1990-1995 average of the implicit real interest rate on public debt transactions on the secondary market of the Lisbon Stock Exchange. The data was also taken from
Banco de Portugal (1997). We deflate the nominal interest rates using the December-to-December consumer price index from INE (1990-5). The discount rate is then obtained as
as the 1990-1995 average cost per worker. We can also obtain these values at the one-digit sectoral level. We deflate all nominal variables using the GDP sectoral price indices available in the updated version of Séries Longas para a Economia
Portuguesa in Banco de Portugal (1997). The real interest rate is calibrated as the 1990-1995 average of the implicit real interest rate on public debt transactions on the secondary market of the Lisbon Stock Exchange. The data was also taken from
Banco de Portugal (1997). We deflate the nominal interest rates using the December-to-December consumer price index from INE (1990-5). The discount rate is then obtained as
![]() , where
, where ![]() is the average real interest rate.
is the average real interest rate.
The remaining parameters, ![]() ,
,
![]() ,
,
![]() ,
, ![]() ,
, ![]() , and
, and ![]() are estimated using a method of moments estimator, which attempts to make the model match closely the evidence on cohort
dynamics presented in section 2. In particular, the estimates are selected to minimize a weighted sum of the distance between the following moments in the model and the data: (a) the time-series of the cross-sectional mean of log-employment conditional on survival,
are estimated using a method of moments estimator, which attempts to make the model match closely the evidence on cohort
dynamics presented in section 2. In particular, the estimates are selected to minimize a weighted sum of the distance between the following moments in the model and the data: (a) the time-series of the cross-sectional mean of log-employment conditional on survival,
![]() ; (b) the time-series of annual changes in the cross-sectional standard deviation of log-employment conditional on survival,
; (b) the time-series of annual changes in the cross-sectional standard deviation of log-employment conditional on survival,
![]() ; (c) the time-series of the cumulative exit rate,
; (c) the time-series of the cumulative exit rate,
![]() ; (d) and the time-series of the survivor component, as defined in (
; (d) and the time-series of the survivor component, as defined in (![]() ). In estimating the above parameters, the output price is normalized to 1, and the initial research cost,
). In estimating the above parameters, the output price is normalized to 1, and the initial research cost, ![]() , is obtained by the equilibrium condition
, is obtained by the equilibrium condition
![]() .32
.32
The decision to estimate ![]() , instead of calibrating it, deserves some discussion. First, the main purpose of this parameter is to induce endogenous exit as it represents the firm's
opportunity cost of remaining in activity. In Hopenhayn (1992), the same result is accomplished using a fixed per period operating cost. Since the per period operating cost can be seen as the periodic payment in an annuity with a present discounted value of
, instead of calibrating it, deserves some discussion. First, the main purpose of this parameter is to induce endogenous exit as it represents the firm's
opportunity cost of remaining in activity. In Hopenhayn (1992), the same result is accomplished using a fixed per period operating cost. Since the per period operating cost can be seen as the periodic payment in an annuity with a present discounted value of
![]() , the two mechanisms are equivalent. Second, because Quadros de Pessoal misses any reliable capital stock variable, we consider the capital decision to be
exogenous. A rough estimate of the magnitude of
, the two mechanisms are equivalent. Second, because Quadros de Pessoal misses any reliable capital stock variable, we consider the capital decision to be
exogenous. A rough estimate of the magnitude of ![]() is the present discounted value of an annuity with annual payments equal to the 1990-1995 average of value added minus labor costs, using the
same deflators as for
is the present discounted value of an annuity with annual payments equal to the 1990-1995 average of value added minus labor costs, using the
same deflators as for ![]() .33 Because the sample
is biased towards surviving firms, this measure overestimates the value of
.33 Because the sample
is biased towards surviving firms, this measure overestimates the value of ![]() , and we cannot use it as a reference to calibrate
, and we cannot use it as a reference to calibrate ![]() . Consequently, we estimate
. Consequently, we estimate ![]() jointly with the remaining parameters in the model.
jointly with the remaining parameters in the model.
| Parameter |
|
|
||||
|---|---|---|---|---|---|---|
| 0.56 | 0.56 | 0.57 | 0.57 | 0.73 | 0.73 | |
| 0.956 | 0.956 | 0.956 | 0.956 | 0.956 | 0.956 | |
| 11.8 | 11.8 | 13.1 | 13.1 | 7.5 | 7.5 | |
|
|
3.227 | 3.180 | 3.435 | 3.607 | 2.408 | 2.455 |
|
|
0.218 | 0.205 | 0.257 | 0.188 | 0.143 | 0.122 |
|
|
0.259 | 0.255 | 0.261 | 0.253 | 0.153 | 0.137 |
| 0.571 | 0.656 | 0.558 | 0.526 | 0.359 | 0.314 | |
| 668.4 | 775.3 | 1136.4 | 1291.1 | 179.8 | 189.0 | |
| 0 | 0.70 | 0 | 1.13 | 0 | 0.11 | |
| 122.5 | 76.5 | 180.7 | 224.1 | 22.2 | 18.6 | |
| 0.0861 | 0.0629 | 0.1727 | 0.1236 | 0.0480 | 0.0439 |
Notes: NAC refers to no-adjustment-costs case; AC refers to proportional-adjustment-costs case;
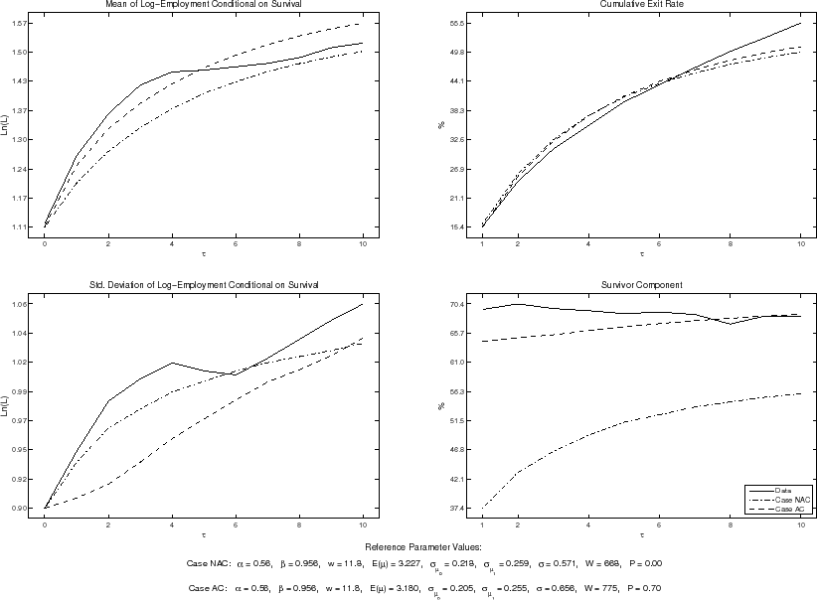
We present in table 4 the calibrated and estimated parameters for the three cohorts and the model with (AC) and without (NAC) adjustment costs, and in figure 2 we plot the overall economy data
moments and the equivalent moments in the AC and NAC models. From table 4, we verify that more information is revealed ex post
![]() , and that there is significant noise in the learning process (
, and that there is significant noise in the learning process (
![]() ,
,
![]() ). For the overall economy cohort, the AC model implies an estimate for the proportional cost of about
). For the overall economy cohort, the AC model implies an estimate for the proportional cost of about ![]() of the annual wage. As can be seen in figure 2, this proportional cost improves noticeably the fit of the survivor component.
of the annual wage. As can be seen in figure 2, this proportional cost improves noticeably the fit of the survivor component.
Figure 2 shows that although the NAC model can generate moments on firm size and exit rates that are close to equivalent empirical moments, it cannot satisfactorily match the empirical survivors' contribution. That is, the NAC model cannot explain the main source of growth in the cohort's average size, since survivors contribute much more to growth in the data than in the NAC model. This shortcoming occurs especially in the initial years after entry as the path of the survivor component is almost flat in the data, whereas it is increasing in the NAC model. The larger initial distance between the NAC model and the data in terms of the survivor component reflects the fact that, in the absence of adjustment costs, learning has a larger initial impact on the exit of small inefficient firms than on growth of survivors.
In table 4, we also calibrate/estimate the AC and NAC models for the manufacturing and services sectors, and in figure 3 we present a summary of the implied moments. In discussing the results for
the two sectors we consider the estimates for the AC model. Firms in manufacturing initially learn relatively less about their efficiency than firms in services (
![]() is smaller in manufacturing), and adjustment costs need to be relatively higher in manufacturing than in services to account for the much higher survivor
component in manufacturing (the proportional costs amount to
is smaller in manufacturing), and adjustment costs need to be relatively higher in manufacturing than in services to account for the much higher survivor
component in manufacturing (the proportional costs amount to ![]() and
and ![]() of
the annual wage, respectively). The higher adjustment costs and smaller knowledge about their efficiency at entry, implies higher incentives for manufacturing firms to start smaller and to gradually adjust to optimal size as they survive and their uncertainty is resolved. Firms in manufacturing
also pay a relatively higher initial research cost (
of
the annual wage, respectively). The higher adjustment costs and smaller knowledge about their efficiency at entry, implies higher incentives for manufacturing firms to start smaller and to gradually adjust to optimal size as they survive and their uncertainty is resolved. Firms in manufacturing
also pay a relatively higher initial research cost (![]() is higher). This, together with the smaller initial knowledge about their efficiency (
is higher). This, together with the smaller initial knowledge about their efficiency (
![]() is smaller), implies that manufacturing firms are more likely to enter the industry at the research phase (
is smaller), implies that manufacturing firms are more likely to enter the industry at the research phase (
![]() equals
equals ![]() in manufacturing and
in manufacturing and ![]() in services).
in services).
While the introduction of adjustment costs clearly improves the fit of the survivor component in the model, we cannot claim that the proportional cost explains completely the path of the survivor component in the data. In fact, in all three cohorts the initial growth of survivors seems larger
than the AC model can explain. Additionally, in the manufacturing sector, although the AC model raises noticeably the contribution of survivors relative to the NAC model, the survivor component generated by the
AC model is still somewhat below the survivor component in the data. Several factors could be behind these results. First, the introduction of a fixed entry or fixed exit cost would improve the fit of the AC model. By introducing a wedge
between the "cost" of entry and the "benefit" of exit, these fixed costs would help to control both the fraction of firms that never enter the industry,
![]() , and the amount of exit in the initial post-entry periods,
, and the amount of exit in the initial post-entry periods,
![]() . As these fixed costs increase, the first fraction increases and the second probability decreases due to a larger initial selection. Therefore, these fixed
costs would allow more freedom in adjusting
. As these fixed costs increase, the first fraction increases and the second probability decreases due to a larger initial selection. Therefore, these fixed
costs would allow more freedom in adjusting
![]() to account for the long-run survivor component, without distorting much the initial exit rates. The proportional adjustment cost would also increase,
raising the long-run value of the survivor component and making its path flatter. Second, other theories that emphasize firm growth in the first years after entry, namely those based on financing constraints, can certainly also account for the high value of the survivor component, especially in the
manufacturing sector.
to account for the long-run survivor component, without distorting much the initial exit rates. The proportional adjustment cost would also increase,
raising the long-run value of the survivor component and making its path flatter. Second, other theories that emphasize firm growth in the first years after entry, namely those based on financing constraints, can certainly also account for the high value of the survivor component, especially in the
manufacturing sector.
5.2 Sensitivity Analysis
In this subsection we explain some aspects of the calibration/estimation exercise and provide a detailed sensitivity analysis to all parameters in the model. First, we do not attempt to match the level of the cross-sectional variance of log-employment, but only its change over time. This is
because to fit the dispersion in employment, the model would require substantially larger values for both
![]() and
and
![]() . This would allow the model to match
. This would allow the model to match
![]() and
and
![]() , but would imply an excessive rate of growth in
, but would imply an excessive rate of growth in
![]() . However, this shortcoming is not a serious problem. It implies that only a fraction of the observed cohort's employment dispersion can be attributed
to a Bayesian learning process about efficiency. The remaining part could be attributed to heterogeneity in the initial choice of technology.
. However, this shortcoming is not a serious problem. It implies that only a fraction of the observed cohort's employment dispersion can be attributed
to a Bayesian learning process about efficiency. The remaining part could be attributed to heterogeneity in the initial choice of technology.
For instance, consider a model where capital is endogenous and suppose that a firm chooses its initial stock of capital, ![]() , based on the realization of a random variable indexing
technology choice. Assume further that, after selecting
, based on the realization of a random variable indexing
technology choice. Assume further that, after selecting ![]() , the firm keeps its capital stock unchanged for the remainder of its life. If the production function has constant returns to
scale, if the total opportunity cost is proportional to
, the firm keeps its capital stock unchanged for the remainder of its life. If the production function has constant returns to
scale, if the total opportunity cost is proportional to ![]() , i.e.,
, i.e.,
![]() , then we can easily prove that
, then we can easily prove that
![]() , where
, where ![]() is the value function conditional on the chosen
is the value function conditional on the chosen ![]() . Therefore, in this alternative framework, dispersion in
. Therefore, in this alternative framework, dispersion in
![]() would govern the initial dispersion in employment and only the subsequent evolution in employment dispersion would depend on the Bayesian learning process. This is the reason why we
attempt to match only the evolution of
would govern the initial dispersion in employment and only the subsequent evolution in employment dispersion would depend on the Bayesian learning process. This is the reason why we
attempt to match only the evolution of
![]() , but not its level. In the estimated models presented in table 4 only little less than
, but not its level. In the estimated models presented in table 4 only little less than ![]() of the observed dispersion in the cohort's log-employment can be attributed to the learning process.34
of the observed dispersion in the cohort's log-employment can be attributed to the learning process.34
Second, the value of
![]() affects the long-run contribution of survivors, since a relatively smaller initial dispersion would make the average size of exiting firms closer to the
average size of surviving firms in the entry period, and in this case most growth would be due to survivors. In the aforementioned extended model with an initial choice over
affects the long-run contribution of survivors, since a relatively smaller initial dispersion would make the average size of exiting firms closer to the
average size of surviving firms in the entry period, and in this case most growth would be due to survivors. In the aforementioned extended model with an initial choice over ![]() , if we had
, if we had
![]() we would have a non-degenerate initial distribution of size, entirely due to the heterogeneity in
we would have a non-degenerate initial distribution of size, entirely due to the heterogeneity in ![]() , but the survivors' component would be
, but the survivors' component would be ![]() in each period. This would occur because the distribution of initial size among exiting firms would be
equal to the distribution of initial size among surviving firms. This also explains why even with heterogeneity over
in each period. This would occur because the distribution of initial size among exiting firms would be
equal to the distribution of initial size among surviving firms. This also explains why even with heterogeneity over ![]() , we would still need to assume
, we would still need to assume
![]() in order to match the empirical facts on the importance of the survivor component.
in order to match the empirical facts on the importance of the survivor component.
While we could increase the long-run contribution of survivors by tinkering with the ratio
![]() , without adjustment costs the model cannot match the observed flatness in the path of the survivor component. For any choice of
, without adjustment costs the model cannot match the observed flatness in the path of the survivor component. For any choice of
![]() and
and
![]() , it will always be the case that the survivor component will exhibit an increasing path in the absence of adjustment costs. Note also that the ratio
, it will always be the case that the survivor component will exhibit an increasing path in the absence of adjustment costs. Note also that the ratio
![]() affects both the exit rate and the evolution of the cross-sectional firm size dispersion. If this ratio becomes too small, post-entry exit rates become
excessively high and the size dispersion increases too fast. This is the reason why in the NAC model we cannot find a value for this ratio that attains the long-run contribution of survivors found in the data, and simultaneously matches the behavior of the cumulative
exit rate and the evolution of the cross-sectional size dispersion. Therefore, the value we select for this ratio is disciplined by the exit rates and the evolution of firm size dispersion in the cohort.
affects both the exit rate and the evolution of the cross-sectional firm size dispersion. If this ratio becomes too small, post-entry exit rates become
excessively high and the size dispersion increases too fast. This is the reason why in the NAC model we cannot find a value for this ratio that attains the long-run contribution of survivors found in the data, and simultaneously matches the behavior of the cumulative
exit rate and the evolution of the cross-sectional size dispersion. Therefore, the value we select for this ratio is disciplined by the exit rates and the evolution of firm size dispersion in the cohort.
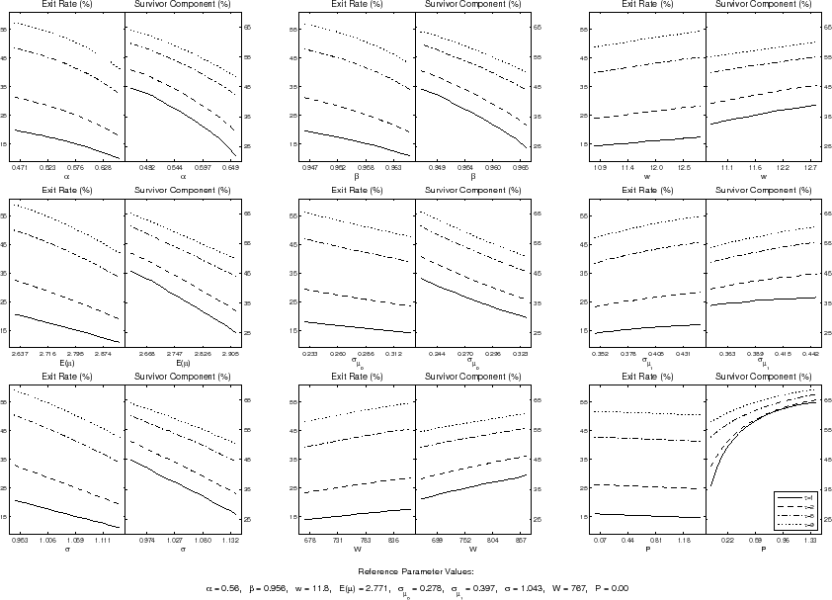
Third, to show that proportional adjustment costs are crucial for our model to fit the evidence on the survivors' contribution to growth in the cohort's average size, in figure 4 we perform a sensitivity analysis with respect to each parameter in the model. We take as benchmark the NAC model estimated for the overall economy cohort in which we do not attempt to match the evidence on the survivor component.35
From figure 4, we see that the model with costless adjustment cannot match satisfactorily the contribution of survivors to growth, even if we allow parameters (except for the proportional cost) to vary one by one from their benchmark values. In fact, no other parameter besides the proportional cost can shrink significantly the distance between the survivor component at different ages of the cohort without changing much the exit rates. The main effect of these costs is to put more emphasis on individual firm growth in the initial years of life, when exit of inefficient firms is very intense.36
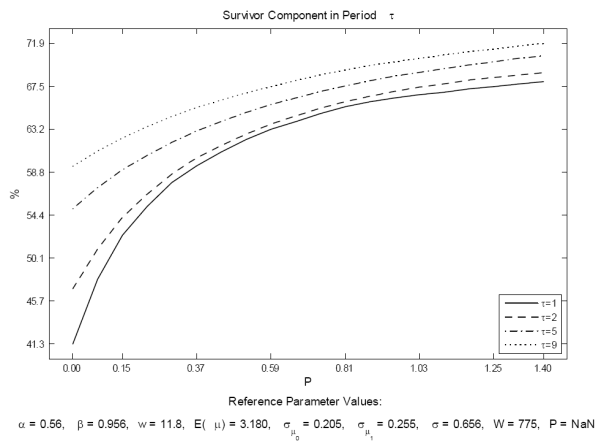
To emphasize the role of the proportional adjustment cost in replicating the evidence on the contribution of survivors, in figure 5 we present the impact of changes in ![]() on the survivor component, using as a benchmark the estimates for the AC model for the overall economy cohort in table 4. We conclude that allowing for even a small value of
on the survivor component, using as a benchmark the estimates for the AC model for the overall economy cohort in table 4. We conclude that allowing for even a small value of ![]() has a substantial impact on the survivors' contribution, with a larger effect in the initial years of life.
has a substantial impact on the survivors' contribution, with a larger effect in the initial years of life.
6 Conclusion
In this paper, we show that a model with learning about efficiency and linear adjustment costs generates incentives for entering firms to be smaller and for successful firms to expand faster after entry. We present evidence on firm dynamics for a cohort of entrant firms in the Portuguese economy. The evidence shows that growth in the cohorts' average size is driven largely by growth of survivors rather than by pruning of small inefficient firms, with rapid growth of survivors in the initial years after entry and with significant differences between manufacturing and services in the contribution of survivors. A calibration and estimation of the model reveals that the proportional adjustment cost is the key parameter to explain the high contribution of survivors to growth in the cohorts' average size. In order to explain the higher contribution of survivors in manufacturing than in services, adjustment costs need to be higher in manufacturing, both in absolute terms and in relation to the wage.
The paper proposes a channel through which linear adjustment costs to job creation and job destruction can affect firm size dynamics. Therefore, proportional costs not only make job creation and job destruction more sluggish, but also affect the lifetime dynamics of firm size. Although our theory does not provide a complete explanation for the evidence on the survivor component, the success of our model in better approximating the growth of survivors as the main source for growth suggests that adjustment costs do play a significant role in firm size adjustments after entry. From our results, we conclude that selection theories are more relevant to explain firm exit than to explain growth of survivors. Financing constraints theories should also play a role in explaining growth of survivors. Although there is not much evidence that financing constraints can explain cross-sector differences in growth of survivors, financing constraints should be especially relevant when technology requires a large startup cost, such as in manufacturing industries.
Angelini and Generale (forthcoming) argue that financing constraints are not the main determinant behind the evolution of the firm size distribution. Therefore, any government intervention to eliminate financing constraints might not change the lifetime dynamics of firm size we find in this paper. Furthermore, this paper suggests that, in sectors where adjustment costs are high and learning is important, government policies aimed at curbing financing constraints might not produce the intended results, as firms under those circumstances have incentives to start smaller and expand faster.
A. Appendix: Proofs
![\displaystyle \theta_{\tau}^{\ast}=g\left( Y_{\tau},\tau\right) =E\left( \xi\left( \eta_{\tau}\right) \mid Y_{\tau},\tau\right) =\nu_{1}+\int_{-\infty}% ^{\infty}\left[ 1-F_{\eta}\left( \eta_{\tau}\mid Y_{\tau},\tau\right) \right] d\xi\left( \eta_{\tau}\right)](img319.gif) ,
,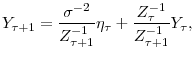
![\displaystyle F\left( \theta_{\tau+1}^{\ast}\mid\theta_{\tau}^{\ast},\tau\right) =F_{\eta }\left[ \frac{Z_{\tau+1}^{-1}}{\sigma^{-2}}g_{Y}^{-1}\left( \theta_{\tau +1}^{\ast},\tau+1\right) -\frac{Z_{\tau}^{-1}}{\sigma^{-2}}g_{Y}^{-1}\left( \theta_{\tau}^{\ast},\tau\right) \mid g_{Y}^{-1}\left( \theta_{\tau}^{\ast },\tau\right) ,\tau\right] \text{,}%](img331.gif)
![]()
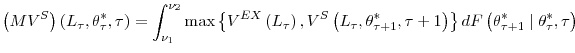 ;
;(a.i) Existence and Uniqueness: This follows from the Contraction Mapping Theorem and Blackwell's sufficient conditions (see theorems 3.2 and 3.3 in Stokey et al., 1989).
(a.ii) Continuity in
![]() : Let
: Let
![]() be the space of bounded functions on
be the space of bounded functions on ![]() which are continuous
in
which are continuous
in
![]() . This is clearly a closed subset of
. This is clearly a closed subset of
![]() , the space of bounded functions
, the space of bounded functions
![]() . Since
. Since
![]() with the sup norm
with the sup norm
![]() is a Banach space, then
is a Banach space, then
![]() is also a Banach space. Now consider
is also a Banach space. Now consider
![]() . Because
. Because
![]() is also continuous and
is also continuous and
![]() satisfies the Feller property (see lemma 2), then
satisfies the Feller property (see lemma 2), then ![]() is continuous in
is continuous in
![]() (see lemma 9.5 in Stokey et al., 1989). Since
(see lemma 9.5 in Stokey et al., 1989). Since
![]() is continuous, then
is continuous, then
![]() is continuous in
is continuous in
![]() . Therefore, applying the maximum theorem, we conclude that
. Therefore, applying the maximum theorem, we conclude that
![]() is continuous in
is continuous in
![]() . Note that the set of admissible values for employment can be made compact. First, only non-negative values are acceptable for employment.
Second, we can choose a value for
. Note that the set of admissible values for employment can be made compact. First, only non-negative values are acceptable for employment.
Second, we can choose a value for ![]() high enough, say
high enough, say ![]() , such that
, such that
![]() , for all
, for all
![]() , so that all values of interest are considered.
, so that all values of interest are considered. ![]() is
finite since
is
finite since
![]() , and
, and ![]() is bounded. Therefore,
is bounded. Therefore, ![]() as defined by (4) is continuous in
as defined by (4) is continuous in
![]() .
.
(a.iii) Strict Monotonicity in
![]() : From lemma 2 (the transition function associated with
: From lemma 2 (the transition function associated with
![]() is monotone) if
is monotone) if
![]() is weakly increasing in
is weakly increasing in
![]() , then
, then
![]() is also weakly increasing in
is also weakly increasing in
![]() . Then, because
. Then, because
![]() is strictly increasing in
is strictly increasing in
![]() (and the constraint set is not affected by
(and the constraint set is not affected by
![]() ),
),
![]() is strictly increasing in
is strictly increasing in
![]() (see theorem 9.11 in Stokey et al., 1989).
(see theorem 9.11 in Stokey et al., 1989).
(b) Exit Policy: The exit policy is determined by the condition
![]()
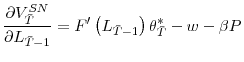 .
.Now consider a generic period
![]() , and assume that
, and assume that
![]() is continuously differentiable at
is continuously differentiable at
![]() with probability one. Because
with probability one. Because
![]() is a unique continuous function of
is a unique continuous function of ![]() ,
we can apply the dominated convergence theorem to conclude that
,
we can apply the dominated convergence theorem to conclude that
![]() is continuously differentiable at
is continuously differentiable at ![]() , for all
, for all
![]() (see theorems 3.2.16 and 3.4.3 in Swartz, 1994). Consequently, the same argument used for period
(see theorems 3.2.16 and 3.4.3 in Swartz, 1994). Consequently, the same argument used for period ![]() can be repeated here.
can be repeated here.
![]()
If it is optimal for the firm to adjust upwards, then we must solve
![\displaystyle A_{SU}=\left[ F^{\prime}\left( L_{\tau}^{\ast}\right) \theta_{\tau}^{\ast }-\left( w+P\right) \right] +\beta\frac{\partial\left( MV^{S}\right) \left( L_{\tau}^{\ast},\theta_{\tau}^{\ast},\tau\right) }{\partial L}=0\text{,}%](img412.gif)
![\displaystyle A_{SD}=\left[ F^{\prime}\left( L_{\tau}^{\ast}\right) \theta_{\tau}^{\ast }-\left( w-P\right) \right] +\beta\frac{\partial\left( MV^{S}\right) \left( L_{\tau}^{\ast},\theta_{\tau}^{\ast},\tau\right) }{\partial L}=0](img413.gif)
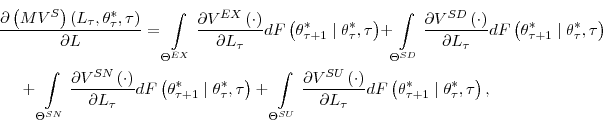
where some of the regions might be empty, and in separating the integrals we have taken into account the continuity of the integrand in
For each of the above derivatives we have
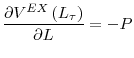 ,
,![\displaystyle \left. \frac{\partial V^{SD}\left( \cdot\right) }{\partial L}\right\vert _{\theta_{\tau+1}^{\ast}\in\Theta^{SD}\left( L_{\tau},\tau+1\right) }=-P=\left[ F^{\prime}\left( L_{\tau+1}^{\ast}\right) \theta_{\tau+1}% ^{\ast}-w\right] +\beta\frac{\partial\left( MV^{S}\right) \left( L_{\tau+1}^{\ast},\theta_{\tau+1}^{\ast},\tau+1\right) }{\partial L}\text{,}%](img416.gif)
![\displaystyle \frac{\partial V^{SN}\left( \cdot\right) }{\partial L_{\tau}}=\left[ F^{\prime}\left( L_{\tau}\right) \theta_{\tau+1}^{\ast}-w\right] +\beta\frac{\partial\left( MV^{S}\right) \left( L_{\tau},\theta_{\tau +1}^{\ast},\tau+1\right) }{\partial L}\text{,}%](img417.gif)
![\displaystyle \left. \frac{\partial V^{SU}\left( \cdot\right) }{\partial L}\right\vert _{\theta_{\tau+1}^{\ast}\in\Theta^{SU}\left( L_{\tau},\tau+1\right) }=P=\left[ F^{\prime}\left( L_{\tau+1}^{\ast}\right) \theta_{\tau+1}^{\ast }-w\right] +\beta\frac{\partial\left( MV^{S}\right) \left( L_{\tau +1}^{\ast},\theta_{\tau+1}^{\ast},\tau+1\right) }{\partial L}\text{,}%](img418.gif)
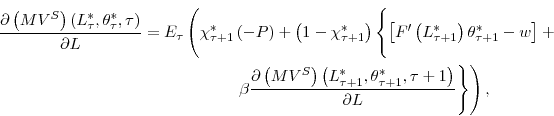
Using the law of iterated expectations, we can rewrite the above as
![\displaystyle \frac{\partial\left( MV^{S}\right) \left( L_{\tau}^{\ast},\theta_{\tau }^{\ast},\tau\right) }{\partial L}=\sum_{s=1}^{\infty}E_{\tau}\beta ^{s-1}\left\{ \tilde{\chi}_{\tau+s}^{\ast}\left( -P\right) +\hat{\chi }_{\tau+s}^{\ast}\left[ F^{\prime}\left( L_{\tau+s}^{\ast}\right) \theta_{\tau+s}^{\ast}-w\right] \right\} \text{,}%](img422.gif)
![]()
![\begin{multline*} MB_{\tau}=\left( F^{\prime}\left( L_{\tau}^{\ast}\right) \thet... ...ast}\right) \theta_{\tau+1+s}^{\ast}-w\right) \right] \right\} . \end{multline*}](img425.gif)
Taking into account that
![]()
![\begin{multline*} F^{\prime}\left( L_{1}\right) \theta_{1}^{\ast}-\left( w+P^{H}\right) +\beta\left( \int_{\nu_{1}}^{\theta^{SD}}-P^{F}dF_{\theta_{1}^{\ast}}\left( \theta_{2}^{\ast}\right) +\right. \ \left. \int_{\theta^{SD}}^{\theta^{SU}}\left\{ \delta_{\bar{T}}\left[ F^{\prime}\left( L_{1}\right) \theta_{2}^{\ast}-w\right] -\beta^{\bar{T}% -1}P^{F}\right\} dF_{\theta_{1}^{\ast}}\left( \theta_{2}^{\ast}\right) +\int_{\theta^{SU}}^{\nu_{2}}P^{H}dF_{\theta_{1}^{\ast}}\left( \theta _{2}^{\ast}\right) \right) =0 \end{multline*}](img430.gif)
(a) In the case of a proportional hiring cost, assuming
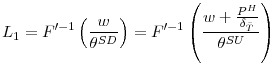 ,
, |
|
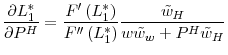 , , |
|
After some algebra we get
where
![\displaystyle \frac{\partial g}{\partial P^{H}}=\left( 1-\alpha\right) ^{-1}\left( \frac{\tilde{w}_{H}}{w\tilde{w}_{w}+P^{H}\tilde{w}_{H}}\left\{ F_{\theta _{1}^{\ast}}\left( \theta^{SD}\right) +\left[ 1-F_{\theta_{1}^{\ast}% }\left( \theta^{SU}\right) \right] \right\} -\frac{1}{w\delta\left( \bar{T}\right) +P^{H}}\left[ 1-F_{\theta_{1}^{\ast}}\left( \theta ^{SU}\right) \right] \right) \text{,}%](img439.gif)
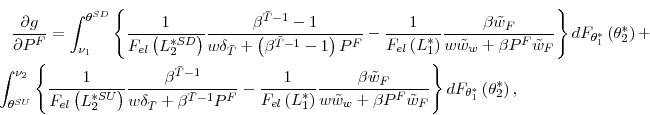
where
Under the assumption that marginal productivity is always positive, we need
![\begin{multline*} \frac{\partial g}{\partial P^{H}}=\left( 1-\alpha\right) ^{-1}... ...1-F_{\theta_{1}^{\ast}}\left( \theta^{SU}\right) \right] \right) \end{multline*}](img445.gif)
which is positive for all
![]()
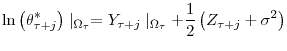 |
|
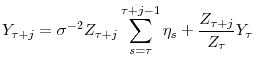 , , |
|
so that, in the end, we get
![\displaystyle E\left[ \ln\left( \theta_{\tau+j}^{\ast}\right) \mid\Omega_{\tau}\right] =Y_{\tau}+\frac{1}{2}\left( Z_{\tau+j}+\sigma^{2}\right)](img455.gif) ,
, |
|
From here the result follows by noting that
For the unconditional distribution, just note that
![]() is a sum of normal random variables, and that
is a sum of normal random variables, and that
![\displaystyle E\left[ \ln\left( \theta_{\tau}^{\ast}\right) \right] =\bar{\mu}+\frac {1}{2}\left( Z_{\tau}+\sigma^{2}\right)](img459.gif) |
|
![]()
![\begin{multline*} V^{S}\left( \theta_{T}^{\ast},L_{s-1},T\right) =\max_{L_{s}\geq0,\chi_{s}% \in\left\{ 0,1\right\} }\left\{ \left[ \Pi\left( L_{s},\theta_{T}^{\ast }\right) -C^{S}\left( L_{s},L_{s-1}\right) \right] +\right. \ \left. \beta\left\{ \chi_{s}\left[ W-C^{EX}\left( L_{\tau+s}\right) \right] +\left( 1-\chi_{s}\right) V^{S}\left( \theta_{T}^{\ast}% ,L_{s},T\right) \right\} \right\} \text{.}% \end{multline*}](img465.gif)
Consider a firm that is in the industry at time
Therefore, at time
We now prove that the firm does not exit at time ![]() after remaining in the industry at time
after remaining in the industry at time ![]() ,
, ![]() . Because the firm stays at time
. Because the firm stays at time ![]() , then
, then
![]() . Now assume that in period
. Now assume that in period ![]() the firm exits, so that
the firm exits, so that
which is a contradiction.
B. Appendix: Computational Algorithm and Estimation Method
We describe the algorithm we use to numerically simulate and estimate the finite learning horizon model in several steps.
- (i)
- Discretization and transition probability matrices associated with
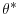 : We discretize
: We discretize
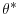 based on a uniform discrete approximation to the (cross-section) distribution of
based on a uniform discrete approximation to the (cross-section) distribution of
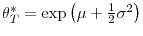 , which is
, which is
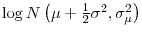 . We then employ the method of Tauchen (1986) in order to build the transition matrices associated
with this discrete approximation. We use a grid with 25 points.
. We then employ the method of Tauchen (1986) in order to build the transition matrices associated
with this discrete approximation. We use a grid with 25 points. - (ii)
- Discretization of
 We have used the decision rules for problem (12) in case of hiring and in case of firing, from which we consider
We have used the decision rules for problem (12) in case of hiring and in case of firing, from which we consider
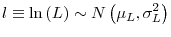 ,
,![\displaystyle \mu_{L}=\frac{1}{1-\alpha}\left\{ \bar{\mu}+\frac{1}{2}\sigma^{2}+\ln\left( \frac{\alpha p}{\sqrt{\left[ w+P^{SU}+\beta P^{EX}\right] \left[ w-\left( 1-\beta\right) P^{SD}\right] }}\right) \right\}](img484.gif) ,
,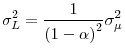 .
.
For the mean of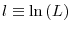 we assume that if a firm is at the upper end of the grid for
we assume that if a firm is at the upper end of the grid for 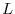 , then it should optimally decrease employment even at
, then it should optimally decrease employment even at
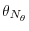 , and that if a firm is at the lower end of the grid for
, and that if a firm is at the lower end of the grid for 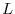 ,
then it should optimally increase employment and exit next period, even at
,
then it should optimally increase employment and exit next period, even at
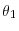 . We then find the upper and lower end of the grid for
. We then find the upper and lower end of the grid for 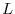 such that those
decisions occur, and use the same procedure to discretize
such that those
decisions occur, and use the same procedure to discretize 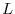 as the one used for
as the one used for 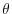 , considering 800 gridpoints.
, considering 800 gridpoints. - (iii)
- Choice for
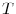 We choose
We choose 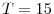 , and display results until period
, and display results until period 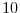 .
. - (iv)
- Model simulation For a given set of parameters we numerically compute the optimal entry, employment, and exit policy rules. In doing this, for each point in the grid for
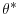 we compute the optimal employment associated with
we compute the optimal employment associated with
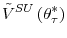
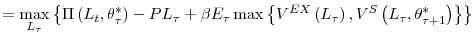
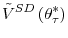
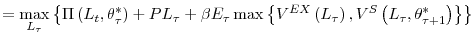
since these do not depend on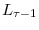 . In doing this, we first find the optimizer on the grid for
. In doing this, we first find the optimizer on the grid for 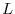 presented
in (ii). Then, we use this maximizer to implement a golden section method to find a more precise value for this maximizer.39 We
then convert these value functions into
presented
in (ii). Then, we use this maximizer to implement a golden section method to find a more precise value for this maximizer.39 We
then convert these value functions into 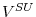 and
and 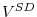 , determine the inaction
regions, and compute
, determine the inaction
regions, and compute 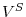 . With the optimal policy functions in hand, we generate a random sample with
. With the optimal policy functions in hand, we generate a random sample with 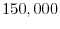 lifetime histories of
lifetime histories of
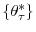 , and compute all endogenous decisions associated with each realization of a firm's lifetime history. We then use this information to compute by
simulation the relevant moments in the model.
, and compute all endogenous decisions associated with each realization of a firm's lifetime history. We then use this information to compute by
simulation the relevant moments in the model. - (v)
- Moments used in estimation We consider four sets of moments, computed among firms that actually enter the industry: (a) Exit rate: For
 , we consider
(b) Average current size conditional on survival: For
, we consider
(b) Average current size conditional on survival: For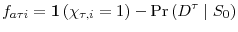
 , we consider
(c) Relative change in variance of current size conditional on survival: For
, we consider
(c) Relative change in variance of current size conditional on survival: For![\displaystyle f_{b\tau i}=l_{\tau,i}\mathbf{1}\left( \chi_{\tau,i}=0\right) -E\left[ l_{\tau}\mid S_{\tau}\right] \Pr\left( S_{\tau}\mid S_{0}\right)](img499.gif)
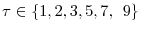 , we consider40
, we consider40
![\begin{multline*} f_{c\tau i}=\left\{ l_{\tau,i}-E\left[ l_{\tau}\mid S_{\tau}\right] \right\} ^{2}\mathbf{1}\left( \chi_{\tau,i}=0\right) -\left\{ l_{0,i}% ^{2}-E\left[ l_{0}\mid S_{0}\right] ^{2}\right\} \times\ \left\{ E[l_{\tau}^{2}\mid S_{\tau}]-E\left[ l_{\tau}\mid S_{\tau}\right] ^{2}\right\} \Pr\left( S_{t}\mid S_{0}\right) /\left\{ E[l_{0}^{2}\mid S_{0}]-E\left[ l_{0}\mid S_{0}\right] ^{2}\right\} \end{multline*}](img501.gif)
(d) Average entry size conditional on survival: For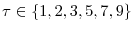 , we consider41
, we consider41
![\displaystyle f_{d\tau i}=l_{0,i}\mathbf{1}\left( \chi_{\tau,i}=0\right) -E\left[ l_{0}\mid S_{\tau}\right] \Pr\left( S_{\tau}\mid S_{0}\right)](img502.gif)
- (vi)
- Weighting matrix The weighting matrix is obtained as the inverse of the sample variance-covariance matrix of the moments in (v),
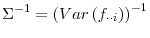 ,
, ![\displaystyle f_{\cdot\cdot i}=[f_{a\cdot i}^{\prime}~~f_{b\cdot i}^{\prime}~~f_{c\cdot i}^{\prime}~~f_{d\cdot i}^{\prime}]^{\prime}%](img504.gif)
- (vii)
- Estimation method We use a simulated annealing method to search for the set of parameter values
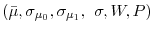 that minimizes the method of moments objective function,42
that minimizes the method of moments objective function,42
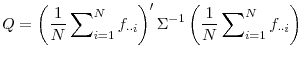
Bibliography
"Optimal Lending Contracts and Firm Dynamics," Review of Economic Studies, 71 (2), 285-315. "On The Evolution of Firm Size Distributions." American Economic Review. "Firm-Level Evidence on Productivity Differentials, Turnover, and Exports in Taiwanese Manufacturing," Journal of Development Economics, 66 (1), 51-86. Séries Longas para a Economia Portuguesa, Pós II Guerra Mundial, Vol. I and II Séries Estatísticas. Banco de PortugalFootnotes
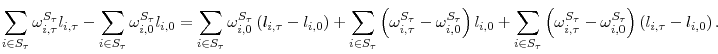
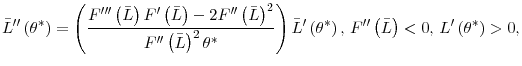
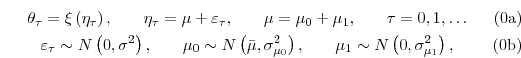
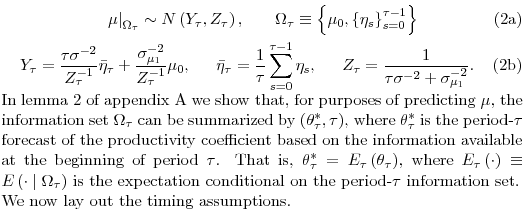
![\begin{multline} V^{S}\left( L_{\tau-1},\theta_{\tau}^{\ast},\tau\right) =\max_{L_{\tau}% }\left\{ \left[ \Pi\left( L_{\tau},\theta_{\tau}^{\ast}\right) -C^{S}\left( L_{\tau},L_{\tau-1}\right) \right] +\right. \ \left. \beta E_{\tau}\left[ \max\left\{ V^{EX}\left( L_{\tau}\right) ,V^{S}\left( L_{\tau},\theta_{\tau+1}^{\ast},\tau+1\right) \right\} \right] \right\} \text{,} % \end{multline}](img110.gif)
![\displaystyle \left[ F^{\prime}\left( L_{\tau}^{\ast}\right) \theta_{\tau}^{\ast }-w\right] +\sum_{s=1}^{\infty}E_{\tau}\beta^{s}\left\{ \tilde{\chi}% _{\tau+s}^{\ast}\left( -P\right) +\hat{\chi}_{\tau+s}^{\ast}\left[ F^{\prime}\left( L_{\tau+s}^{\ast}\right) \theta_{\tau+s}^{\ast}-w\right] \right\} =P](img133.gif) ,
,![\displaystyle \left[ F^{\prime}\left( L_{\tau}^{\ast}\right) \theta_{\tau}^{\ast }-w\right] +\sum_{s=1}^{\infty}E_{\tau}\beta^{s}\left\{ \tilde{\chi}% _{\tau+s}^{\ast}\left( -P\right) +\hat{\chi}_{\tau+s}^{\ast}\left[ F^{\prime}\left( L_{\tau+s}^{\ast}\right) \theta_{\tau+s}^{\ast}-w\right] \right\} =-P](img134.gif) ,
,![\displaystyle \left[ F^{\prime}\left( L_{0}^{\ast}\right) \theta_{0}^{\ast}-w\right] +\sum_{s=1}^{\infty}E_{0}\beta^{s}\left\{ \tilde{\chi}_{s}^{\ast}\left( -P\right) +\hat{\chi}_{s}^{\ast}\left[ F^{\prime}\left( L_{s}^{\ast }\right) \theta_{s}^{\ast}-w\right] \right\} =P](img136.gif) .
.![\begin{multline} MB\left( L_{\tau-1},\theta_{\tau}^{\ast},\tau\right) =\left( F^{\prime }\left( L_{\tau}^{\ast}\right) \theta_{\tau}^{\ast}-w\right) +\beta E_{\tau}\left[ \chi_{\tau+1}^{\ast}\left( -P\right) +\right. \ \left. \left( 1-\chi_{\tau+1}^{\ast}\right) MB\left( L_{\tau}^{\ast },\theta_{\tau+1}^{\ast},\tau+1\right) \right] % \end{multline}](img145.gif)