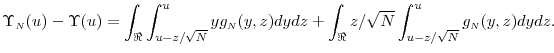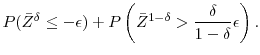Nested Simulation in Portfolio Risk Measurement*
Keywords: Nested simulation, loss distribution, value-at-risk, expected shortfall, jackknife estimator, dynamic allocation
Abstract:
Risk measurement for derivative portfolios almost invariably calls for nested simulation. In the outer step one draws realizations of all risk factors up to the horizon, and in the inner step one re-prices each instrument in the portfolio at the horizon conditional on the drawn risk factors. Practitioners may perceive the computational burden of such nested schemes to be unacceptable, and adopt a variety of second-best pricing techniques to avoid the inner simulation. In this paper, we question whether such short cuts are necessary. We show that a relatively small number of trials in the inner step can yield accurate estimates, and analyze how a fixed computational budget may be allocated to the inner and the outer step to minimize the mean square error of the resultant estimator. Finally, we introduce a jackknife procedure for bias reduction and a dynamic allocation scheme for improved efficiency.
JEL Codes: G32, C15
For a wide variety of derivative instruments, computational costs may pose a binding constraint on the choice of pricing model. The more realistic and flexible the model, the less likely that there will exist an analytical pricing formula, and so the more likely that simulation-based pricing algorithms will be required. For plain-vanilla options trading in fast-moving markets, simulation is prohibitively slow. Simple models with analytical solutions are typically employed with ad-hoc adjustments (such as local volatility surfaces) to obtain better fit to the cross-section of market prices. As such models capture underlying processes in crude fashion, they tend to require frequent recalibration and perform poorly in time-series forecasting. For path-dependent options (e.g, lookback options) and complex basket derivatives (e.g., CDO of ABS), simulation is almost unavoidable, though even here computational shortcuts may be adopted at the expense of bias.1
Risk-management applications introduce additional challenges. Time constraints are less pressing than in trading applications, but the computational task may be more formidable. When loss is measured on a mark-to-market basis, estimation via simulation of large loss probabilities or of risk-measures such as Value-at-Risk (VaR) calls for a nested procedure: In the outer step one draws realizations of all risk factors up to the horizon, and in the inner step one re-prices each position in the portfolio at the horizon conditional on the drawn risk factors. It has been widely assumed that simulation-based pricing algorithms would be infeasible in the inner step, because the inner step must be executed once for each trial in the outer step.
In this paper, we question whether inner step simulations must necessarily impose a large computational burden. We show that a relatively small number of trials in the inner step can yield accurate estimates for large loss probabilities and portfolio risk-measures such as Value-at-Risk and Expected Shortfall, particularly when the portfolio contains a large number of positions. Since an expectation is replaced by a noisy sample mean, the estimator is biased, and we are able to characterize this bias asymptotically. We analyze how a fixed and large computational budget may be allocated to the inner and the outer step to minimize the mean square error of the resultant estimator. We show how the jackknifing technique may be applied to reduce the bias in our estimator, and how this alters the optimal budget allocation. In addition, we introduce a dynamic allocation scheme for choosing the number of inner step trials as a function of the generated output. This technique can significantly reduce the computational effort to achieve a given level of accuracy.
The most studied application of nested simulation in the finance literature is the pricing of American options. An influential paper by Longstaff and Schwartz (2001) proposes a least-squares methodology in which a small number of inner step samples are used to estimate a parametric relationship between the state vector at the horizon (in this case, the stock price) and the continuation value of the option. This "LSM" estimator is applicable to a broad range of nested problems, so long as the dimension of the state vector is not too large and the relationship between state vector and continuation value is not too nonlinear. However, some care must be taken in the choice of basis functions, and in general it may be difficult to assess the associated bias (Glasserman, 2004, §8.6). Our methodology, by contrast, is well-suited to portfolios of high-dimensional and highly nonlinear instruments, can be applied to a variety of derivative types without customization, and has bias of known form.
Our optimization results for large loss probabilities and Value-at-Risk are similar to those of Lee (1998).2 Lee's analysis relies on a different and somewhat more intricate set of assumptions than ours, which are in the spirit of the sensitivity analysis of VaR by Gouriéroux et al. (2000) and the subsequent literature on "granularity adjustment" of credit VaR (Gordy, 2004; Martin and Wilde, 2002). The resulting asymptotic formulae, however, are the same.3 Our extension of this methodology to Expected Shortfall is new, as is our analysis of large portfolio asymptotics. Furthermore, so far as we are aware, we are the first to examine the performance of jackknife estimators and dynamic allocation schemes in a nested simulation setting.
In Section 1 we set out a very general modeling framework for a portfolio of financial instruments. We introduce the nested simulation methodology in Section 2. We characterize the bias in and variance of the simulation estimator, and analyze the optimal allocation of computational resources between the two stages that minimizes the mean square error of the resultant estimator. Numerical illustrations of our main results are provided in Section 3. In the last two sections, we propose some refinements to further improve computational performance of nested simulation. Simple jackknife methods for bias reduction are developed in Section 4. Our dynamic allocation scheme is introduced and examined in Section 5.
1 Model framework
Let ![]() be a vector of
be a vector of ![]() state variables that govern all prices. The vector
state variables that govern all prices. The vector
![]() might include interest rates, commodity prices, equity prices, and other underlying prices referenced by derivatives. Let
might include interest rates, commodity prices, equity prices, and other underlying prices referenced by derivatives. Let
![]() be the filtration generated by
be the filtration generated by ![]() . For use in discounting future cash
flows, we denote by
. For use in discounting future cash
flows, we denote by ![]() the value at time
the value at time ![]() of $1 invested at time
of $1 invested at time ![]() in a risk free money market account, i.e.,
in a risk free money market account, i.e.,
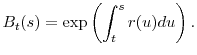
The portfolio consists of ![]() positions. The price of position
positions. The price of position ![]() at time
at time
![]() depends on
depends on ![]() ,
,
![]() , and the contractual terms of the instrument.4 Position 0 represents the sub-portfolio of instruments for which there exist analytical pricing functions. Without loss of generality, we treat this as a single composite instrument. Among the contractual terms for an instrument is its maturity. We assume maturity
, and the contractual terms of the instrument.4 Position 0 represents the sub-portfolio of instruments for which there exist analytical pricing functions. Without loss of generality, we treat this as a single composite instrument. Among the contractual terms for an instrument is its maturity. We assume maturity
![]() is finite for
is finite for
![]() . As in all risk measurement exercises, the portfolio is assumed to be held static over the model horizon.
. As in all risk measurement exercises, the portfolio is assumed to be held static over the model horizon.
Conditional on
![]() , the cashflows up to time
, the cashflows up to time ![]() are nonstochastic functions of time that
depend on the contractual terms. Let
are nonstochastic functions of time that
depend on the contractual terms. Let ![]() be the cumulative cashflow for
be the cumulative cashflow for ![]() on
on
![]() . Note that increments to
. Note that increments to ![]() can be positive or negative, and can arrive
at discrete time intervals or continuously. The market value of each position is the present discounted expected value of its cashflows under the risk-neutral measure
can be positive or negative, and can arrive
at discrete time intervals or continuously. The market value of each position is the present discounted expected value of its cashflows under the risk-neutral measure ![]() :
:
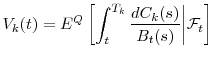
The present time is normalized to 0 and the model horizon is ![]() . "Loss" is defined as the difference between current value and discounted future value at the horizon, adjusting for
interim cashflows. Portfolio loss is
. "Loss" is defined as the difference between current value and discounted future value at the horizon, adjusting for
interim cashflows. Portfolio loss is
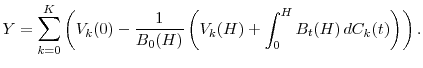
2 Simulation framework
We now develop notation related to the simulation process. The simulation is nested: There is an "outer step" in which we draw histories up to the horizon ![]() . For each trial in the outer
step, there is an "inner step" simulation needed for repricing at the horizon.
. For each trial in the outer
step, there is an "inner step" simulation needed for repricing at the horizon.
Let ![]() be the number of trials in the outer step. In each of these trials, we
be the number of trials in the outer step. In each of these trials, we
- Draw a single path
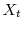 for
for ![t=(0,H]](img28.gif) under the physical measure. Let
under the physical measure. Let 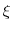 represent the filtration
represent the filtration
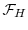 that is generated by this path.
that is generated by this path. - Evaluate the accrued value at
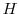 of the interim cashflows.
of the interim cashflows. - Evaluate the price of each position at
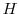 .
.
- Closed-form price for instrument 0.
- Simulation with
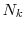 "inner step" trials for remaining positions
"inner step" trials for remaining positions
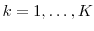 . These paths are simulated under the risk-neutral measure.
. These paths are simulated under the risk-neutral measure.
- Discount back to time 0 to get our loss
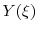 .
.
Observe that the full dependence structure across the portfolio is captured in the period up to the model horizon. Inner step simulations, in contrast, are run independently across positions. This is because the value of position ![]() at time
at time ![]() is simply a conditional expectation (given
is simply a conditional expectation (given
![]() and under the risk-neutral measure) of its own subsequent cash flows, and does not depend on future cash flows of other positions. Intuition might suggest that it would be more
efficient from a simulation perspective to run inner step simulations simultaneously across all positions in order to reduce the total number of sampled paths of
and under the risk-neutral measure) of its own subsequent cash flows, and does not depend on future cash flows of other positions. Intuition might suggest that it would be more
efficient from a simulation perspective to run inner step simulations simultaneously across all positions in order to reduce the total number of sampled paths of ![]() on
on
![]() . However, if we use the same samples of
. However, if we use the same samples of ![]() across inner step
simulations, pricing errors are no longer independent across the positions, and so do not diversify away as effectively at the portfolio level. Furthermore, when the positions are repriced independently, to reprice position
across inner step
simulations, pricing errors are no longer independent across the positions, and so do not diversify away as effectively at the portfolio level. Furthermore, when the positions are repriced independently, to reprice position ![]() we need only draw joint paths for the elements of
we need only draw joint paths for the elements of ![]() that influence that instrument. This may greatly reduce the memory footprint of the simulation, in
particular when the number of state variables (
that influence that instrument. This may greatly reduce the memory footprint of the simulation, in
particular when the number of state variables (![]() ) is large and when some of the maturities
) is large and when some of the maturities ![]() are very long relative to the horizon
are very long relative to the horizon ![]() .
.
We have assumed that initial prices ![]() are already known and can be taken as constants in our algorithm. Of course, this can be relaxed.
are already known and can be taken as constants in our algorithm. Of course, this can be relaxed.
In the following three subsections, we discuss estimation of large loss probabilities (§2.1), Value-at-Risk (§2.2), and Expected Shortfall (§2.3). For simplicity, we impose a single value of ![]() across all positions (i.e.,
across all positions (i.e., ![]() for
for ![]() ). This restriction is relaxed in Section 2.4. In Section 2.5, we consider the asymptotic behavior of the optimal allocation of computational resources as the portfolio size grows large.
Last, in Section 2.6, we elaborate on the trade-offs associated with simultaneous repricing.
). This restriction is relaxed in Section 2.4. In Section 2.5, we consider the asymptotic behavior of the optimal allocation of computational resources as the portfolio size grows large.
Last, in Section 2.6, we elaborate on the trade-offs associated with simultaneous repricing.
2.1 Estimating the probability of large losses
We first consider the problem of efficient estimation of
![]() via simulation for a given
via simulation for a given ![]() . If for each generated
. If for each generated
![]() , the mark-to-market values of each position were known, the associated
, the mark-to-market values of each position were known, the associated ![]() would be known and simulation would involve generating i.i.d. samples
would be known and simulation would involve generating i.i.d. samples
![]() and taking the average
and taking the average
![\displaystyle \frac{1}{L} \sum_{i=1}^L \ensuremath{1[Y(\xi_i)>u]}](img41.gif)
Within the inner step simulation for repricing position ![]() , each trial gives an unbiased (but very noisy) estimate of
, each trial gives an unbiased (but very noisy) estimate of ![]() . Let
. Let
![]() denote the zero-mean pricing error associated with the
denote the zero-mean pricing error associated with the
![]() such sample for position
such sample for position ![]() , let
, let ![]() denote the portfolio pricing error for the
denote the portfolio pricing error for the
![]() inner step sample, and finally let
inner step sample, and finally let
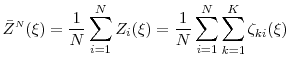
![\displaystyle \ensuremath{{\hat\alpha_\ensuremath{{\scriptscriptstyle L\negthinspace{,}\negthinspace{N}}}}}= \frac{1}{L}\sum_{\ell=1}^L \ensuremath{1[{\tilde Y}_\ell(\xi_\ell)>u]}.](img54.gif)
We now examine the mean square error of
![]() . Let
. Let
![]() denote
denote
![]() . The mean square error of the estimator
. The mean square error of the estimator
![]() separates into
separates into
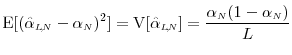
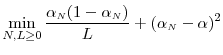 subject to subject to |
(1) |
as
Let
![]() so that
so that
![]() has a non-trivial limit as
has a non-trivial limit as
![]() . Then
. Then
![]() . Our asymptotic analysis relies on Taylor series expansion of the joint density
function
. Our asymptotic analysis relies on Taylor series expansion of the joint density
function
![]() of
of
![]() and its partial derivatives. Assumption 1 ensures that higher order terms in such expansions can be
ignored.
and its partial derivatives. Assumption 1 ensures that higher order terms in such expansions can be
ignored.
- The joint pdf
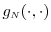 of
of 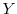 and
and
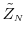 and its partial derivatives
and its partial derivatives
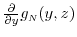 and
and
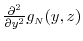 exist for each
exist for each 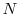 and for all
and for all 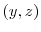 .
. - For
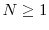 , there exist non-negative functions
, there exist non-negative functions
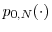 ,
,
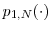 and
and
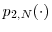 such that
such that
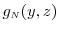
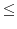
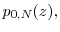
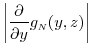
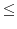
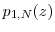
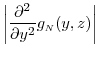
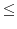
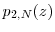
for all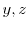 . In addition,
for
. In addition,
for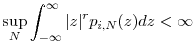
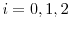 , and
, and
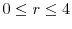 .
.
This assumption may be expected to be true in a large portfolio where there are at least a few positions that have a sufficiently smooth payoff. Alternatively, this assumption may be satisfied by perturbing ![]() and
and
![]() through adding to both of them mean zero, variance
through adding to both of them mean zero, variance ![]() independent
Gaussian random variables, also independent of
independent
Gaussian random variables, also independent of ![]() and
and
![]() . For small
. For small ![]() this has a negligible impact on the tail measures.
Then, if
this has a negligible impact on the tail measures.
Then, if
where
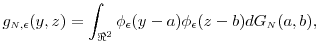
Assumption 1 is sufficient to deliver a useful convergence property. Here and henceforth, let ![]() and
and ![]() denote the density and cumulative distribution function for
denote the density and cumulative distribution function for ![]() , and let
, and let
![]() and
and
![]() denote the density and cumulative distribution function for
denote the density and cumulative distribution function for
![]() . Now let
. Now let
![]() be some sequence of real numbers that converges to a real number
be some sequence of real numbers that converges to a real number ![]() . In Appendix A.1, we prove the following lemma:
. In Appendix A.1, we prove the following lemma:
We now approximate
![]() in orders of
in orders of ![]() . We define the
function
. We define the
function
where
For the distributions and large loss levels one might expect to appear in practice, the bias will be upwards (i.e.,
![]() ). By construction, the distribution of
). By construction, the distribution of
![]() differs from the distribution of
differs from the distribution of ![]() by a mean-preserving spread, in the sense of Rothschild and Stiglitz (1970). Unless the two distributions have an infinite number of crossings, there will exist a
by a mean-preserving spread, in the sense of Rothschild and Stiglitz (1970). Unless the two distributions have an infinite number of crossings, there will exist a ![]() such that
such that
![]() for all
for all ![]() .
.
Applying Proposition 1, the objective function reduces to finding ![]() that minimizes
that minimizes
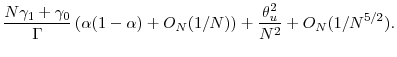
It is easy to see that an optimal ![]() for this has the form
for this has the form
Therefore optimal
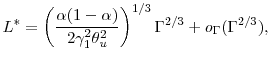 |
(5) |
and the mean square error at optimal
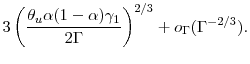
For large computational budgets, we see that ![]() grows with the square of
grows with the square of ![]() .
Thus, marginal increments to
.
Thus, marginal increments to
![]() are allocated mainly to the outer step. It is easy to intuitively see the imbalance between
are allocated mainly to the outer step. It is easy to intuitively see the imbalance between ![]() and
and ![]() . Note that when
. Note that when ![]() and
and ![]() are of the same order
are of the same order
![]() , the squared bias term contributes much less to the mean square error compared to the variance term. By increasing
, the squared bias term contributes much less to the mean square error compared to the variance term. By increasing ![]() at the expense of
at the expense of ![]() we reduce variance till it matches up in contribution to the squared bias term.
we reduce variance till it matches up in contribution to the squared bias term.
2.2 Estimating Value-at-Risk
We now consider the problem of efficient estimation of Value-at-Risk for ![]() . For a target insolvency probability
. For a target insolvency probability
![]() , VaR is the value
, VaR is the value
![]() given by
given by
Under Assumption 1, ![]() is a continuous random variable so that
is a continuous random variable so that
![]() . As before, our nested simulation generates samples
. As before, our nested simulation generates samples
![]() where
where
![]() . We sort these draws as
. We sort these draws as
![]() , so that
, so that
![]() provides an estimate of
provides an estimate of
![]() , where
, where
![]() denotes the integer ceiling of the real number
denotes the integer ceiling of the real number ![]() . Our interest is
in characterizing the mean square error
. Our interest is
in characterizing the mean square error
![]() and then minimizing it. As before, we decompose MSE into
variance and squared bias:
and then minimizing it. As before, we decompose MSE into
variance and squared bias:
To approximate bias and variance, we use the following result:
A result parallel to the bias approximation is used in the literature on "granularity adjustment" of credit VaR to adjust asymptotic approximations of VaR for undiversified idiosyncratic risk (Gordy, 2004; Martin and Wilde, 2002). To avoid lengthy technical digressions, our statement of the proposition and its derivation in Appendix A.3 abstract from certain mild but cumbersome regularity conditions; see the appendix for details.Our budget allocation problem reduces to minimizing the mean square error
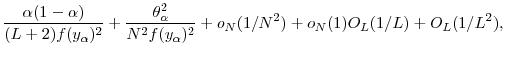
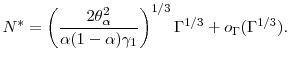
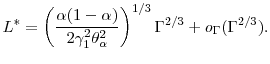
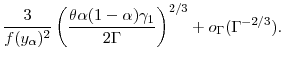
2.3 Estimating Expected Shortfall
Although Value-at-Risk is ubiquitous in industry practice, it is well understood that it has significant theoretical and practical shortcomings. It ignores the distribution of losses beyond the target quantile, so may give incentives to build portfolios that are highly sensitive to extreme tail events. More formally, Value-at-Risk fails to satisfy the sub-addivity property, so a merger of two portfolios can yield VaR greater than the sum of the two stand-alone VaRs. For this reason, Value-at-Risk is not a coherent risk-measure, in the sense of Artzner et al. (1999).
As an alternative to VaR, Acerbi and Tasche (2002) propose using generalized Expected Shortfall ("ES"), defined by
The first term is often used as the definition of Expected Shortfall for continuous variables. It is also known as "tail conditional expectations." The second term is a correction for mass at the quantile
![\displaystyle \frac{1}{\alpha}\ensuremath{{\operatorname E}\lbrack {Y}\cdot\ensuremath{1[{Y} > {y}_{\alpha}]}\rbrack}](img164.gif) |
|||
![\displaystyle \frac{1}{\alpha}\ensuremath{{\operatorname E}\lbrack {\ensuremath{{\tilde Y}}}\cdot\ensuremath{1[{\ensuremath{{\tilde Y}}} > \tilde{y}_{\alpha}]}\rbrack}](img166.gif) |
Acerbi and Tasche (2002) show that ES is coherent and equivalent to the "conditional VaR" (CVaR) measure of Rockafellar and Uryasev (2002).
We begin with the more general problem of optimally allocating a computational budget to efficiently estimate
![]() for arbitrary
for arbitrary ![]() . This is easier than the problem of estimating
. This is easier than the problem of estimating
![]() since here
since here ![]() is specified while in the latter case
is specified while in the latter case
![]() is estimated. We return later to analyze the bias associated with the estimate of
is estimated. We return later to analyze the bias associated with the estimate of
![]() .
.
Again, our sample output from the simulation to estimate
![]() equals
equals
![]() . Let
. Let
![]() denote
denote
![]() . The following proposition evaluates the bias associated with this
term.
. The following proposition evaluates the bias associated with this
term.
Using similar analysis to the proof of Proposition 3, we can establish that
Thus, analogous to Section 2.1, we consider the optimization problem
![\displaystyle \min_{N,L \geq 0} \frac{\ensuremath{{\operatorname V}\lbrack \ensuremath{{\tilde Y}}\cdot\ensuremath{1[\ensuremath{{\tilde Y}}>u]}\rbrack}}{L} + (\Upsilon_\ensuremath{{\scriptscriptstyle N}}(u)-\Upsilon(u))^2](img178.gif) subject to
subject toApplying Proposition 3 and (7), the objective function reduces to finding ![]() that minimizes
that minimizes
![\displaystyle \frac{V[Y\cdot\ensuremath{1[Y>u]}]+O_N(1/N) }{L} + \frac{\ensuremath{{(\Theta(u)-u\Theta'(u))}}^2}{N^2}+ O_{N}(1/N^{5/2}).](img179.gif)
and optimal
![\displaystyle L^* = \left( \frac{\ensuremath{{\operatorname V}\lbrack Y\cdot\ensuremath{1[Y>u]}\rbrack}} {2 \gamma_1^2 \ensuremath{{(\Theta(u)-u\Theta'(u))}}^2} \right)^{1/3}\ensuremath{\Gamma}^{2/3} +o_{\ensuremath{\Gamma}}(\ensuremath{\Gamma}^{2/3}).](img181.gif) |
(9) |
The mean square error at optimal
![\displaystyle 3 \left(\frac{\ensuremath{{(\Theta(u)-u\Theta'(u))}}\ensuremath{{\operatorname V}\lbrack Y\cdot\ensuremath{1[Y>u]}\rbrack} \gamma_1}{2 \ensuremath{\Gamma}}\right )^{2/3} + o_{\ensuremath{\Gamma}}(\ensuremath{\Gamma}^{-2/3}).](img182.gif)
We return now to the problem of the bias of
![]() . We can write the difference between the Expected Shortfall of random variables
. We can write the difference between the Expected Shortfall of random variables
![]() and
and ![]() as
as
From Proposition 3, we have
Now from the mean value theorem
where the last equality follows from Proposition 2. By substituting equations (11) and (12) into (10), we arrive at
A similar result is noted by Martin and Tasche (2007) and Gordy (2004).
2.4 Optimal allocation within the inner step
In this subsection we relax the restriction that ![]() is equal across
is equal across ![]() . We focus
on estimation of large loss probabilities. Similar analysis would allow us to vary
. We focus
on estimation of large loss probabilities. Similar analysis would allow us to vary ![]() across positions in estimating VaR and ES.
across positions in estimating VaR and ES.
We redefine ![]() as the total number of inner step simulations. This aggregate
as the total number of inner step simulations. This aggregate ![]() is to be divided up among the positions
is to be divided up among the positions
![]() by allocating
by allocating ![]() simulations for position
simulations for position ![]() where each
where each
![]() and
and
![]() . Suppose that the average effort to generate a single such inner step simulation for
. Suppose that the average effort to generate a single such inner step simulation for ![]() is
is
![]() . Then, total inner step simulation effort equals
. Then, total inner step simulation effort equals
![]() where
where
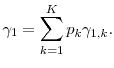
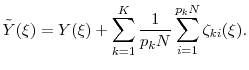
The analysis to compute the mean square error proceeds exactly as in Section 2.1. The resultant ![]() in this setting is
in this setting is
where
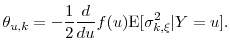
Recall from Section 2.1 that the mean square error at optimal ![]() equals
equals
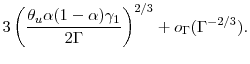
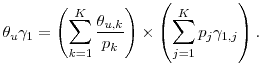
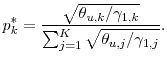
2.5 Large portfolio asymptotics
Intuition suggests that as the portfolio size increases, the optimal number of inner loops needed becomes small, even falling to ![]() for a sufficiently large portfolio. We formalize
this intuition by considering an asymptotic framework where both the portfolio size and the computational budget increases to infinity. To avoid cumbersome notation and tedious technical arguments, we focus on the case of a portfolio of exchangeable (i.e., statistically homogeneous) positions. The
arguments given are somewhat heuristic to give the flavor of analysis involved while avoiding the cumbersome and lengthy notation and assumptions needed to make it completely rigorous.
for a sufficiently large portfolio. We formalize
this intuition by considering an asymptotic framework where both the portfolio size and the computational budget increases to infinity. To avoid cumbersome notation and tedious technical arguments, we focus on the case of a portfolio of exchangeable (i.e., statistically homogeneous) positions. The
arguments given are somewhat heuristic to give the flavor of analysis involved while avoiding the cumbersome and lengthy notation and assumptions needed to make it completely rigorous.
Consider an infinite sequence of exchangeable position indexed by ![]() , and let
, and let ![]() be the loss on position
be the loss on position ![]() . Let
. Let
![]() be the average loss per position on a portfolio consisting of the first
be the average loss per position on a portfolio consisting of the first ![]() positions in the sequence, i.e.,
positions in the sequence, i.e.,
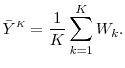
As before, instead of observing ![]() , we generate
, we generate ![]() inner step samples
inner step samples
![]() for
for
![]() , so that our simulation provides an unbiased estimator for the probability
, so that our simulation provides an unbiased estimator for the probability
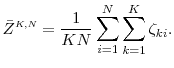
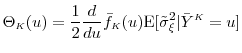
By the law of large numbers,
![]() , almost surely, so the cdf
, almost surely, so the cdf
![]() converges to a non-degenerate limiting distribution
converges to a non-degenerate limiting distribution ![]() , which is the distribution of
, which is the distribution of
![]() . Similarly,
. Similarly,
![]() converges to
converges to
![]() . Under suitable regularity conditions,
. Under suitable regularity conditions,
![]() , where
, where
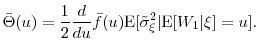
We assume that the computational budget
![]() for
for ![]() and
and
![]() . The value of
. The value of ![]() captures the size of computational budget
available relative to the time taken to generate a single inner loop sample. Note that if
captures the size of computational budget
available relative to the time taken to generate a single inner loop sample. Note that if ![]() then asymptotically even a single sample cannot be generated.
then asymptotically even a single sample cannot be generated.
Recall that ![]() denotes the number of underlying state variables that control the prices of
denotes the number of underlying state variables that control the prices of ![]() positions. Suppose that the computational effort to generate one sample of outer step simulation on average equals
positions. Suppose that the computational effort to generate one sample of outer step simulation on average equals ![]() for some function
for some function ![]() , and to generate an inner step simulation sample on the average equals
, and to generate an inner step simulation sample on the average equals
![]() for a constant
for a constant
![]() . Average effort per outer step trial then equals
. Average effort per outer step trial then equals
![]() and average effort for
and average effort for ![]() such trials equals
such trials equals
![]() . We analyze the order of magnitude of
. We analyze the order of magnitude of ![]() and
and ![]() that minimize the resultant mean square error of the estimator.
that minimize the resultant mean square error of the estimator.
The mean square error of the estimator equals
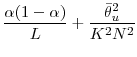
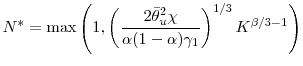
2.6 Simultaneous repricing
Up to this point, we have stipulated that the inner step samples for each position in the portfolio are generated independently (conditional on ![]() ) across positions. In application to
derivative portfolios, there may be factors common to many positions (e.g., the prices of underlying securities) and it may be computationally efficient to generate these factors once for all positions rather than generating them independently for each position. While this reduces the computational
effort required to generate a single sample of each position, it induces dependence across positions in the generated samples. If the dependence is such that the sum of the resultant noise from each position has lesser variance than if these samples were generated independently, as might be the
case when there are many offsetting positions, then the former is a preferred method. However, typically the noises generated may have positive dependence and that may enhance the variance of the resulting samples thereby increasing the total number of samples required to achieve specified
accuracy.
) across positions. In application to
derivative portfolios, there may be factors common to many positions (e.g., the prices of underlying securities) and it may be computationally efficient to generate these factors once for all positions rather than generating them independently for each position. While this reduces the computational
effort required to generate a single sample of each position, it induces dependence across positions in the generated samples. If the dependence is such that the sum of the resultant noise from each position has lesser variance than if these samples were generated independently, as might be the
case when there are many offsetting positions, then the former is a preferred method. However, typically the noises generated may have positive dependence and that may enhance the variance of the resulting samples thereby increasing the total number of samples required to achieve specified
accuracy.
We now make this idea precise in a very simple setting. Consider the case where we want to find the expectation of
![]() via simulation. Suppose that average computational effort needed to generate a sample of
via simulation. Suppose that average computational effort needed to generate a sample of
![]() by generating independent samples of
by generating independent samples of
![]() equals
equals ![]() for some constant
for some constant ![]() . Let
. Let
![]() denote the variance of these
denote the variance of these ![]() 's
(to keep the discussion simple we assume that all rv have the same variance). Then, the computational effort required to get a specified accuracy is proportional to the variance of the sample
's
(to keep the discussion simple we assume that all rv have the same variance). Then, the computational effort required to get a specified accuracy is proportional to the variance of the sample
![]() times the expected effort required to generate a single sample
times the expected effort required to generate a single sample ![]() (see Glynn and Whitt, 1992), i.e.,
(see Glynn and Whitt, 1992), i.e.,
![]() . We refer to this measure as the simulation efficiency.
. We refer to this measure as the simulation efficiency.
Now consider the case where we generate
![]() by generating dependent samples of
by generating dependent samples of
![]() . Suppose that the computational effort to generate these samples on average equals
. Suppose that the computational effort to generate these samples on average equals
![]() for some
for some ![]() . Further suppose that the correlation
between any two random variables
. Further suppose that the correlation
between any two random variables ![]() and
and ![]() for
for ![]() is
is
![]() . Then the variance of
. Then the variance of
![]() equals
equals
![]() . So the simulation efficiency equals
. So the simulation efficiency equals
![]() . We therefore prefer to draw dependent samples whenever
. We therefore prefer to draw dependent samples whenever
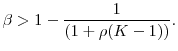
3 Numerical examples
We illustrate our results with a parametric example. Distributions for loss ![]() and the pricing errors
and the pricing errors ![]() are specified to ensure that the bias and variance of our simulation estimators are in closed-form. While the example is highly stylized, it allows us to compare our asymptotically optimal
are specified to ensure that the bias and variance of our simulation estimators are in closed-form. While the example is highly stylized, it allows us to compare our asymptotically optimal ![]() to the exact optimal solution under a finite computational budget. We have used simulation to perform similar exercises on the somewhat more realistic example of a portfolio of equity options. All our conclusions are robust.
to the exact optimal solution under a finite computational budget. We have used simulation to perform similar exercises on the somewhat more realistic example of a portfolio of equity options. All our conclusions are robust.
Consider a homogeneous portfolio of ![]() positions. Let the state variable,
positions. Let the state variable, ![]() ,
represent a single-dimensional market risk factor, and assume
,
represent a single-dimensional market risk factor, and assume
![]() . Let
. Let
![]() be the idiosyncratic component to the return on position
be the idiosyncratic component to the return on position ![]() at the
horizon, so that the loss on position
at the
horizon, so that the loss on position ![]() is
is
![]() per unit of exposure. We assume that the
per unit of exposure. We assume that the
![]() are i.i.d.
are i.i.d.
![]() . To facilitate comparative statics on
. To facilitate comparative statics on ![]() , we scale exposure sizes
by
, we scale exposure sizes
by ![]() .
.
The exact distribution for portfolio loss ![]() is
is
![]() . We assume that the position-level inner step pricing errors
. We assume that the position-level inner step pricing errors
![]() are i.i.d.
are i.i.d.
![]() per unit of exposure, so that the portfolio pricing error has variance
per unit of exposure, so that the portfolio pricing error has variance
![]() across inner step trials. This implies that the simulated loss variable
across inner step trials. This implies that the simulated loss variable
![]() is distributed
is distributed
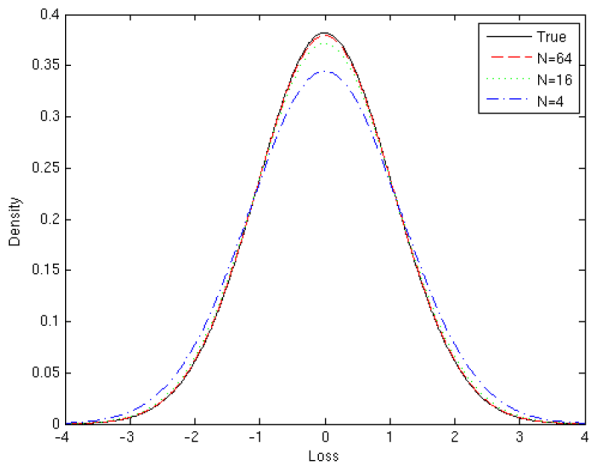
![]() . Figure 1 shows how the density of the simulated loss distribution varies with the choice of
. Figure 1 shows how the density of the simulated loss distribution varies with the choice of ![]() . For the baseline parameter values
. For the baseline parameter values ![]() ,
, ![]() and
and ![]() , we observe that the density of
, we observe that the density of
![]() for
for ![]() is a close approximation to the "true" density
for
is a close approximation to the "true" density
for ![]() . Even for
. Even for ![]() , the error due to inner step simulation appears modest.
, the error due to inner step simulation appears modest.
We consider our estimator
![]() of the large loss probability
of the large loss probability
![]() for a fixed loss level
for a fixed loss level ![]() . The expected
value of
. The expected
value of
![]() is
is
![]() . Applying Proposition 1, bias in
. Applying Proposition 1, bias in
![]() expands as
expands as
![]() where
where

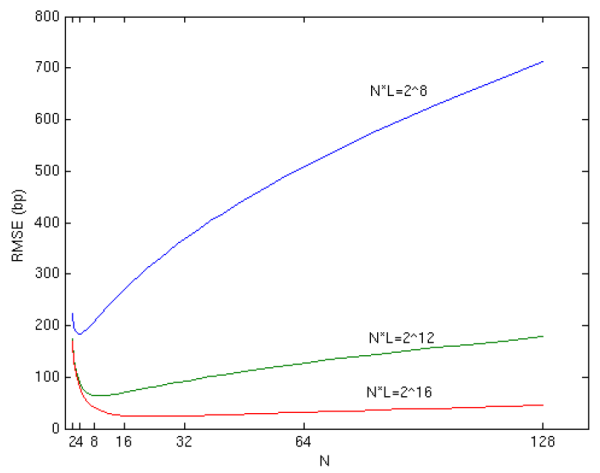
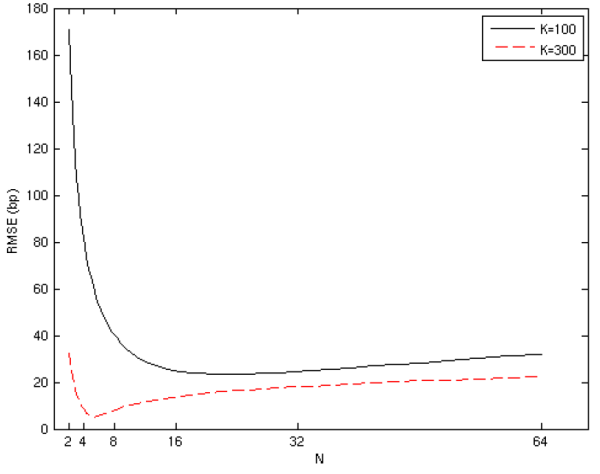
In Figure 3, we plot the exact root mean square error of
![]() as a function of
as a function of ![]() and with the computational budget held fixed. Here we make the assumption that the fixed cost of the outer step is negligible (i.e.,
and with the computational budget held fixed. Here we make the assumption that the fixed cost of the outer step is negligible (i.e.,
![]() ), so that
), so that
![]() . We observe that the optimal
. We observe that the optimal ![]() is increasing with the
budget, but remains quite modest even for the largest budget depicted (
is increasing with the
budget, but remains quite modest even for the largest budget depicted (
![]() ).
).
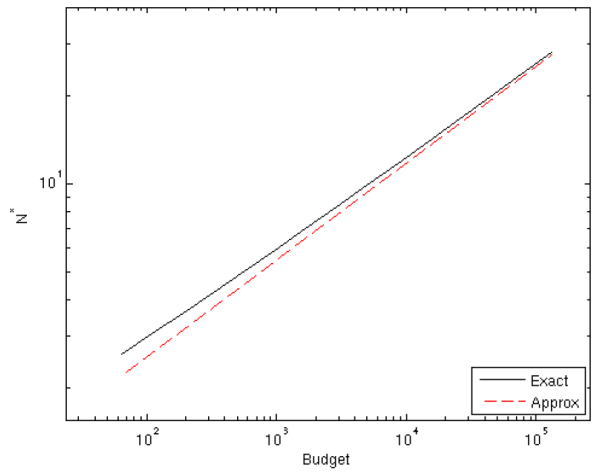
The relationship between the computational budget and optimal ![]() is explored further in Figure 4. We solve for the
is explored further in Figure 4. We solve for the ![]() that minimizes the (exact) mean square error, and plot
that minimizes the (exact) mean square error, and plot ![]() as a function of the budget
as a function of the budget
![]() . Again, we see that
. Again, we see that ![]() is much smaller than
is much smaller than ![]() and grows at a slower rate with
and grows at a slower rate with ![]() . For example, when
. For example, when
![]() , we find
, we find ![]() is under 6 and
is under 6 and ![]() is over 165. Increasing the budget by a factor of 64, we find
is over 165. Increasing the budget by a factor of 64, we find ![]() roughly quadruples while
roughly quadruples while ![]() increases by a factor of roughly 16. The figure demonstrates the accuracy of the approximation to
increases by a factor of roughly 16. The figure demonstrates the accuracy of the approximation to ![]() given by equation (4). When
given by equation (4). When
![]() , the relative error of the approximation is 8.3%. Increasing the budget to
, the relative error of the approximation is 8.3%. Increasing the budget to
![]() shrinks the relative error to under 2.5%.
shrinks the relative error to under 2.5%.
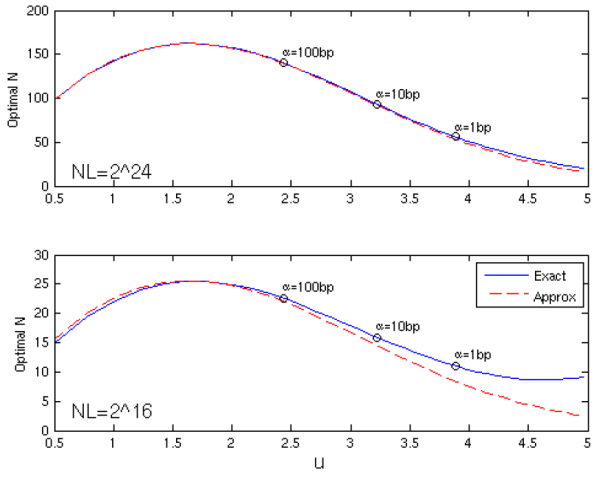
The optimal ![]() and the accuracy of its approximation may depend on the exceedance threshold
and the accuracy of its approximation may depend on the exceedance threshold ![]() , and not necessarily in a monotonic fashion. This is demonstrated in the top panel of Figure 5. The budget here is large, and we see that the approximation to
, and not necessarily in a monotonic fashion. This is demonstrated in the top panel of Figure 5. The budget here is large, and we see that the approximation to ![]() is accurate over the entire range of interest (say, for
is accurate over the entire range of interest (say, for
![]() ). When the budget is smaller (bottom panel), the accuracy of the approximation is most severely degraded in the tail.
). When the budget is smaller (bottom panel), the accuracy of the approximation is most severely degraded in the tail.
In Figure 6, we explore the relationship between portfolio size ![]() and optimal
and optimal ![]() . For simplicity, we assume here that the budget grows linearly with
. For simplicity, we assume here that the budget grows linearly with ![]() . In the baseline case of
. In the baseline case of ![]() , we find that
, we find that ![]() is roughly 23. When we triple the portfolio size (and budget), we find that
is roughly 23. When we triple the portfolio size (and budget), we find that ![]() falls to under six. If we increase the portfolio size by a factor of 10, we find that
falls to under six. If we increase the portfolio size by a factor of 10, we find that ![]() is under two. These results
suggest that the large portfolio asymptotics of section 2.5 may pertain to portfolios of realistic size.
is under two. These results
suggest that the large portfolio asymptotics of section 2.5 may pertain to portfolios of realistic size.
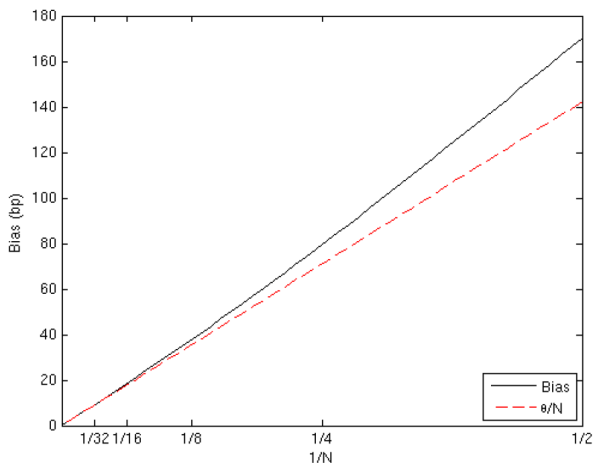
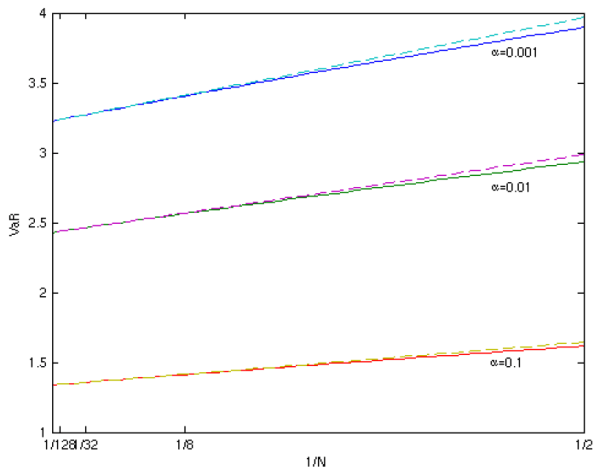
As Value-at-Risk is the risk-measure most commonly used in practice, we turn briefly to the estimation of VaR. The results of Section 2.2 show that the bias in
![]() vanishes with
vanishes with ![]() . This is
demonstrated in Figure 7 for three values of
. This is
demonstrated in Figure 7 for three values of
![]() . For each line, the y-axis intercept at
. For each line, the y-axis intercept at ![]() is the unbiased
benchmark, i.e.,
is the unbiased
benchmark, i.e.,
![]() . The distance on the y-axis between
. The distance on the y-axis between
![]() (on the solid line) for any finite
(on the solid line) for any finite ![]() and the corresponding unbiased benchmark
and the corresponding unbiased benchmark
![]() is the exact bias attributable to errors in pricing at the horizon. The dashed lines show the approximated VaR based on
is the exact bias attributable to errors in pricing at the horizon. The dashed lines show the approximated VaR based on
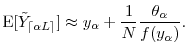
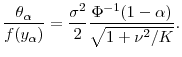
4 Jackknife estimation
Jackknife estimators, introduced over 50 years ago by Quenouille (1956), are commonly applied when bias reduction is desired. We show how jackknife methods can be applied in our setting to the estimation of large loss probabilities. Parallel methods would apply to VaR and ES.
We divide the inner loop sample of ![]() draws into
draws into ![]() non-overlapping
sections (
non-overlapping
sections (![]() and
and ![]() are selected so that
are selected so that ![]() is an integer). Section
is an integer). Section ![]() covers the
covers the ![]() draws
draws
![]() . For a single outer step trial, represented by
. For a single outer step trial, represented by ![]() , let
, let
![]() denote the sample output from the inner step
denote the sample output from the inner step
![]() as proposed in earlier sections. Let
as proposed in earlier sections. Let
![]() be the estimate of
be the estimate of ![]() that is obtained when
section
that is obtained when
section ![]() is omitted, and define
is omitted, and define
![]() similarly, e.g.,
similarly, e.g.,
![]() . Observe that the bias in
. Observe that the bias in
![]() is
is
![]() plus
plus
![]() terms, and furthermore that we can construct
terms, and furthermore that we can construct ![]() different sample
outputs this way.
different sample
outputs this way.
We now propose the jackknife inner step simulation output
The bias in

Thus, the first-order term in the bias is eliminated.
Define
![]() for
for ![]() . From the second representation of
. From the second representation of
![]() in (15), we see that the variance of the estimator
in (15), we see that the variance of the estimator
![]() is
is
where
Our jackknife estimator is the average of ![]() samples of
samples of
![]() , i.e.,
, i.e.,
![]() . The contribution of variance to its mean square error is
. The contribution of variance to its mean square error is
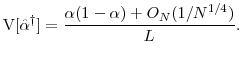
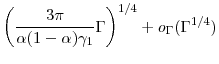 |
|||
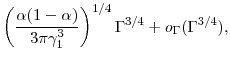 |
so even fewer inner step samples are needed for the jackknife estimator. The mean square error at optimal
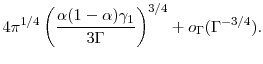
In most applications of jackknife methods, bias reduction comes at the price of increased variance. This trade-off applies here as well. To illustrate, we return to the Gaussian example of Section 3. For any parametric example, it is useful to re-write the terms in
equation (16) for the variance of
![]() as:
as:
By the symmetry of the
Similarly, we have
For the Gaussian example, let
 |
|||
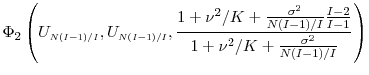 |
where
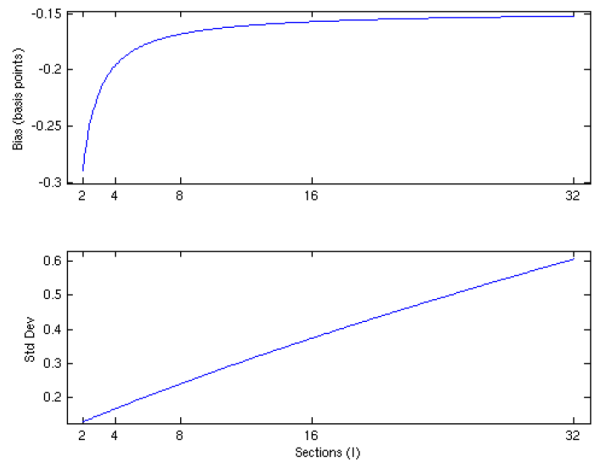
Holding fixed ![]() , we plot the bias of the jackknife estimator as a function of the number of sections (
, we plot the bias of the jackknife estimator as a function of the number of sections (![]() ) in the top panel of Figure 8. The bias is decreasing in
) in the top panel of Figure 8. The bias is decreasing in ![]() , but the sensitivity to
, but the sensitivity to ![]() is modest in both absolute terms and relative to the bias of the uncorrected estimator. The bias of the uncorrected
is modest in both absolute terms and relative to the bias of the uncorrected estimator. The bias of the uncorrected
![]() is 9.04 basis points, whereas the bias of
is 9.04 basis points, whereas the bias of
![]() is -0.29 basis points when
is -0.29 basis points when ![]() and -0.15 basis points when
and -0.15 basis points when
![]() . The standard deviation of
. The standard deviation of
![]() is plotted as a function of
is plotted as a function of ![]() in the bottom panel of the figure. We find the standard deviation increases in roughly linear fashion with
in the bottom panel of the figure. We find the standard deviation increases in roughly linear fashion with ![]() . For the uncorrected estimator, we find
. For the uncorrected estimator, we find
![]() , whereas
, whereas
![]() for
for ![]() and
and
![]() for
for ![]() .
.
The optimal choice of ![]() for minimizing mean square error will depend on
for minimizing mean square error will depend on ![]() . The
larger is
. The
larger is ![]() , the smaller the contribution of variance to MSE, so the larger the optimal
, the smaller the contribution of variance to MSE, so the larger the optimal ![]() . As a practical matter, we advocate setting
. As a practical matter, we advocate setting ![]() , which eliminates nearly all the bias at very little cost to variance. Setting
, which eliminates nearly all the bias at very little cost to variance. Setting ![]() has the further advantage of minimal memory overhead, in that one can estimate
has the further advantage of minimal memory overhead, in that one can estimate
![]() ,
,
![]() , and
, and
![]() for each outer step
for each outer step ![]() in a
single pass through the inner loop. By contrast, to implement the jackknife with
in a
single pass through the inner loop. By contrast, to implement the jackknife with ![]() sections, we need to save each of the
sections, we need to save each of the ![]() inner loop draws in order to calculate each of the
inner loop draws in order to calculate each of the ![]() estimates
estimates
![]() .
.
5 Dynamic allocation
Through dynamic allocation of workload in the inner step we can further reduce the computational effort in the inner step while increasing the bias by a negligible controlled amount or even (in many cases) decreasing the bias. Consider the estimation of large loss probabilities ![]() for a given
for a given ![]() . Bias in our estimated
. Bias in our estimated
![]() is increasing with the likelihood that the indicator
is increasing with the likelihood that the indicator
![]() obtained from the inner step simulation is not equal to the true
obtained from the inner step simulation is not equal to the true
![]() for a given realization
for a given realization ![]() of the outer step. Say we
form a preliminary estimate
of the outer step. Say we
form a preliminary estimate
![]() based on the average of a small number
based on the average of a small number ![]() of inner step
trials. If this estimate is much smaller or much larger than
of inner step
trials. If this estimate is much smaller or much larger than ![]() , it may be a waste of effort to generate many more samples in the inner simulation step. However, if this average is close to
, it may be a waste of effort to generate many more samples in the inner simulation step. However, if this average is close to
![]() , it makes sense to generate many more inner step samples in order to increase the probability that the estimated
, it makes sense to generate many more inner step samples in order to increase the probability that the estimated
![]() is equal to the true value
is equal to the true value
![]() . The variance of
. The variance of
![]() is dominated by
is dominated by
![]() , so dynamic allocation in the inner step will have little effect on the variance. As in Section 4, we develop our dynamic allocation methods
for the estimation of large loss probabilities. Similar methods would apply to VaR and ES.
, so dynamic allocation in the inner step will have little effect on the variance. As in Section 4, we develop our dynamic allocation methods
for the estimation of large loss probabilities. Similar methods would apply to VaR and ES.
Our proposed dynamic allocation (DA) scheme is very simple. For each trial ![]() of the outer step, we generate
of the outer step, we generate ![]() inner step trials (selecting
inner step trials (selecting ![]() so that
so that ![]() is an integer), and let the resulting preliminary loss estimate be denoted
is an integer), and let the resulting preliminary loss estimate be denoted
![]() . If
. If
![]() for some well-chosen
for some well-chosen
![]() then we terminate the inner step and our sample output is zero.7 Otherwise, we generate a second estimate
then we terminate the inner step and our sample output is zero.7 Otherwise, we generate a second estimate
![]() based on an additional
based on an additional
![]() conditionally independent samples. Defining
conditionally independent samples. Defining
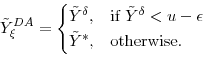
With dynamic allocation, the bias in the estimated exceedance probability is
Thus, dynamic allocation introduces a negative increment to bias, relative to the static estimator. As we have seen earlier, in typical application the static estimator has a positive bias. The joint probability
If
![]() then dynamic allocation will increase absolute bias. Even in this general case, we can derive an upper bound on
the increase in absolute bias. As shown in Appendix B, for every
then dynamic allocation will increase absolute bias. Even in this general case, we can derive an upper bound on
the increase in absolute bias. As shown in Appendix B, for every ![]() one can find an
one can find an
![]() so that the resultant increase in bias is within a specified tolerance. The issue then is to select a
so that the resultant increase in bias is within a specified tolerance. The issue then is to select a ![]() that most reduces the computational effort.
that most reduces the computational effort.
For numerical illustration, we return to our Gaussian example of Section 3. The exact expected value of
![]() in this example is
in this example is
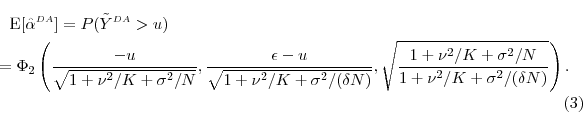
As in our baseline examples, we fix
More complex dynamic schemes are possible. For example, instead of a single stopping test at ![]() , one can have a series of
, one can have a series of ![]() stopping tests after
stopping tests after
![]() inner step trials. The bandwidths would narrow successively, i.e.,
inner step trials. The bandwidths would narrow successively, i.e.,
![]() . It may also be possible to design adaptive strategies for choosing
. It may also be possible to design adaptive strategies for choosing ![]() and
and
![]() that will converge to the optimal values as the outer step simulation progresses.
that will converge to the optimal values as the outer step simulation progresses.
6 Conclusion
We have shown that nested simulation of loss distributions poses a much less formidable computational obstacle than it might initially appear. The essential intuition is similar to the intuition for diversification in the long-established literature on portfolio choice. In the context of a large, well-diversified portfolio, risk-averse investors need not avoid high-variance investments so long as most of the variance is idiosyncratic to the position. In our risk-measurement problem, we see that large errors in pricing at the model horizon can be tolerated so long as the errors are zero mean and mainly idiosyncratic. In the aggregate, such errors have modest impact on our estimated loss distribution. More formally, we are able to quantify that impact in terms of bias and variance of the resulting estimator, and allocate workload in the simulation algorithm to minimize mean square error. Simple extensions of the basic nested algorithm can eliminate much of the bias at modest cost.
Our results suggest that current practice is misguided. In order to avoid the "inner step" simulation for repricing at the model horizon, practitioners typically rely on overly stylized pricing models with closed-form solution. Unlike the simulation pricing error in our nested approach, the pricing errors that arise due to model misspecification are difficult to quantify, need not be zero mean, and are likely to be correlated across positions in the portfolio. At the portfolio level, therefore, the error in estimates of Value-at-Risk (or other quantities of interest) cannot readily be bounded and does not vanish asymptotically. Our results imply that practitioners should retain the best pricing models that are available, regardless of their computational tractability. A single trial of a simulation algorithm for the preferred model will often be less costly than a single call to the stylized pricing function,8 so running a nested simulation with a small number of trials in the inner step may be comparable in computational burden to the traditional approach. Despite the high likelihood of grotesque pricing errors at the instrument level, the impact on estimated VaR is small. In the limit of an asymptotically large, fine-grained portfolio, even a single inner step trial per instrument is sufficient to obtain exact pricing at the portfolio level.
Our methods have application to other problems in finance. Nested simulation may arise in pricing options on complex derivatives (e.g., a European call option on a CDO tranche). When parameters in an option pricing model are estimated with uncertainty, nested simulation may also be needed to determine confidence intervals on model prices for thinly-traded complex derivatives. Similar problems arise in the rating of CDOs and other structured debt instruments when model parameters are subject to uncertainty. These applications will be developed in future work.
A. Proofs
In this section we prove Lemma 1 and Proposition 1. We then derive the expression for the mean square error of Value-at-Risk discussed in Section 2.2. We then provide a proof of Proposition 3. In our notation, we suppress the dependence on ![]() and
and ![]() wherever it is visually convenient.
wherever it is visually convenient.
A..1 Proof of Lemma 1
Note that
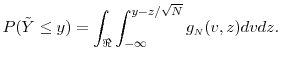
Differentiating both sides by ![]() , noting that in the RHS the interchange of integral and the derivative follows from Assumption 1 (Lang, 1968, p. 249), we get
, noting that in the RHS the interchange of integral and the derivative follows from Assumption 1 (Lang, 1968, p. 249), we get
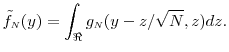
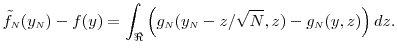
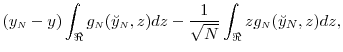
Similarly we see that
![]() as
as
![]() .
.
A..2 Proof of Proposition 1
Note that
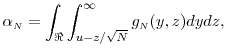
Consider the Taylor's series expansion of the pdf in (21),
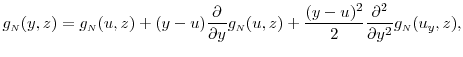
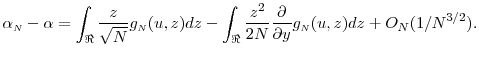
Note that the first term above equals
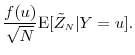
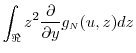 |
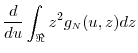 |
||
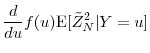 |
|||
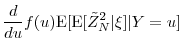 |
|||
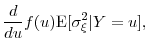 |
which completes the proof.
A..3 Mean square error for Value-at-Risk
We derive the bias and variance approximations of Proposition 2. Our treatment in places is heuristical to avoid lengthy technical issues.
We first develop an asymptotic expression for the bias
![]() . To evaluate
. To evaluate
![]() , it is useful to consider the order statistics
, it is useful to consider the order statistics
![]() of
of ![]() random variables uniformly distributed over
the unit interval. Within this appendix only, let
random variables uniformly distributed over
the unit interval. Within this appendix only, let
![]() denote the inverse of the cdf of
denote the inverse of the cdf of
![]() . Observe that
. Observe that
![]() has the same distribution as
has the same distribution as
![]() .
.
Consider the Taylor's series expansion
Taking expectations
It is well known (see, e.g., David, 1981) that
Through differentiation of the relation
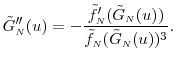
Here we omit the lengthy discussion on the technical assumptions needed to ensure that the expectation of the remainder terms in (23) has the form
Let
![]() denote the
denote the
![]() quantile corresponding to the random variable
quantile corresponding to the random variable ![]() . If
we can show that
. If
we can show that
and that
where
To see that
![]() is
is
![]() , note that due to Assumption 1,
, note that due to Assumption 1,
![]() and
and
![]() have bounded derivatives, which implies
have bounded derivatives, which implies
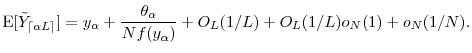
We now show (28). Using the Taylor's series expansion,
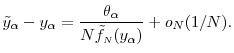
The expression for variance can be determined by subtracting (26) from (22) and squaring the difference to get
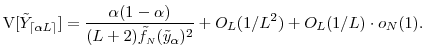
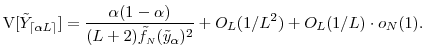
A..4 Proof of Proposition 3
The
![]() and
and
![]() can be written as
can be written as
As
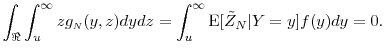
We apply a Taylor series expansion to the first term in (32):
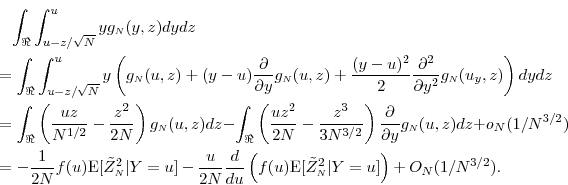
Here, in the first equality
For the second term in (32),
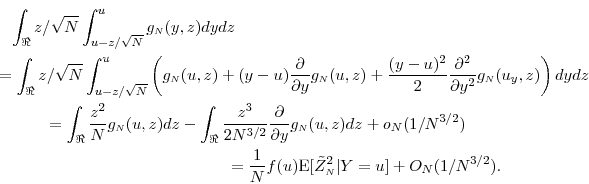
Proposition 3 follows by noting that
A..5 Proof of Proposition 4
We decompose the variance of
![]() as
as
![]() . The
expectation of
. The
expectation of
![]() is
is
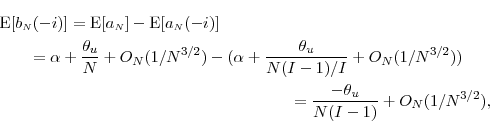
which implies that
We now argue that
![]() is
is
![]() , ignoring some minor technical issues. From expanding the square and taking expectations, observe that
, ignoring some minor technical issues. From expanding the square and taking expectations, observe that
We now show that these two probabilities are equal in their dominant term and are
![]() . Some notation is needed for this purpose. Let
. Some notation is needed for this purpose. Let
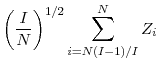 |
|||
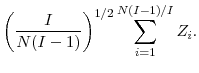 |
We assume that both
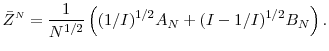
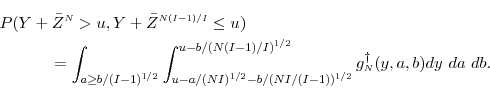
Taking a Taylor series expansion of
![\displaystyle \frac{1}{(NI)^{1/2}}f(u) \ensuremath{{\operatorname E}\lbrack (A_N- B_N/(I-1)^{1/2}) \cdot \ensuremath{1[A_N- B_N/(I-1)^{1/2}>0]}\vert Y=u\rbrack} +O_N(1/N).](img510.gif)
![\displaystyle \frac{1}{(NI)^{1/2}}f(u) \ensuremath{{\operatorname E}\lbrack (A_N- B_N/(I-1)^{1/2}) \cdot \ensuremath{1[A_N- B_N/(I-1)^{1/2}>0]}\vert Y=u\rbrack} = O_N(1/N^{1/2}).](img511.gif)
We proceed in exactly the same fashion for the second term in (33), and find that this term is also
![]() .
.
B. Bounding the bias under dynamic allocation
We can bound the absolute bias under dynamic allocation via the triangle inequality:
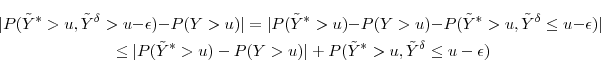
so the increase in the absolute bias is no greater than
we can upper bound each of these terms. Let
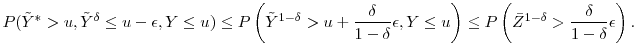
From here we can take two different approaches:
- Hoeffding's inequality (Hoeffding, 1963) can be used to develop exact bounds if the zero mean noise associated with each position is upper as well as lower bounded. This is generally true of put options, credit derivatives, and many other types of derivatives.
Let
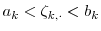 denote the bounds on position
denote the bounds on position 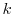 .
Then,
.
Then,
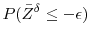
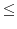
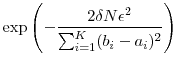
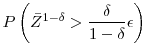
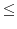
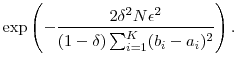
- As
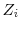 is the sum of zero mean errors from
is the sum of zero mean errors from 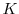 positions, we can appeal to the
central limit theorem and take each
positions, we can appeal to the
central limit theorem and take each 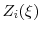 as approximately normal in distribution with mean zero and variance
as approximately normal in distribution with mean zero and variance
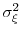 .9 Then,
.9 Then,
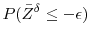
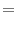
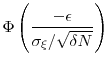
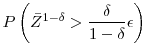
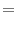
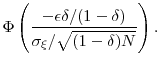
We illustrate this computation using our simple Gaussian example with baseline parameter values ![]() ,
, ![]() , and
, and ![]() . This gives us
. This gives us
![]() as the standard deviation of the
as the standard deviation of the ![]() . Let
. Let
![]() , so that
, so that
![]() . Say we fix
. Say we fix ![]() ,
,
![]() and
and
![]() . The upper bound in equation (35) for the increase in bias for
. The upper bound in equation (35) for the increase in bias for
![]() over the static estimator
over the static estimator
![]() is under
is under
![]() . The probability of stopping with the preliminary sample is
. The probability of stopping with the preliminary sample is
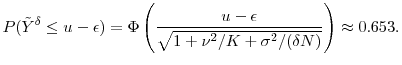
Journal of Banking and Finance, 26(7):, 1487-1503, 2002.
Mathematical Finance, 9(3):203-228, 1999.
John Wiley & Sons, second edition, 1981.
Research paper series, Algorithmics, May, 2007.
Springer-Verlag, New York, 2004.
Operations Research, 40:505-520, 1992.
In L. Felipe Perrone, Barry G. Lawson, Jason Liu, and Frederick P. Wieland, editors, Proceedings of the, 2006 Winter Simulation Conference, Piscataway, NJ, 2006. IEEE Press.
In Giorgio P. Szegö, editor, Risk Measures for the 21st Century. John Wiley & Sons, 2004.
Journal of Empirical Finance, 7:225-245, 2000.
Journal of the American Statistical Association, 58:13-30, March, 1963.
Addison-Wesley, 1968.
PhD thesis, Stanford University, October, 1998.
Review of Financial Studies, 14:113-147, 2001.
Risk, 20(2):84-89, February, 2007.
Risk, 15(11):123-128, November, 2002.
Biometrika, 43:353-360, 1956.
Journal of Banking and Finance, 26(7):, 1443-1471, 2002.
Journal of Economic Theory, 2(3):225-243, 1970.
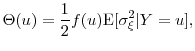
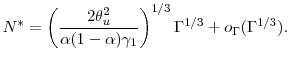
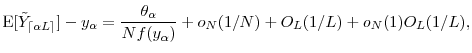
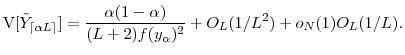
![\displaystyle N^* = \left (\frac{2 \ensuremath{{(\Theta(u)-u\Theta'(u))}}^2}{\ensuremath{{\operatorname V}\lbrack Y\cdot\ensuremath{1[Y>u]}\rbrack} \gamma_1} \right )^{1/3} \ensuremath{\Gamma}^{1/3} +o_{\ensuremath{\Gamma}}(\ensuremath{\Gamma}^{1/3}),](img180.gif)
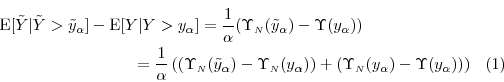
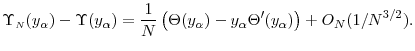
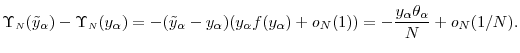
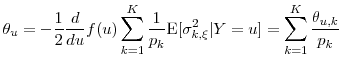
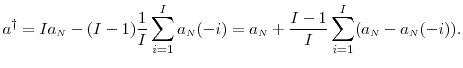
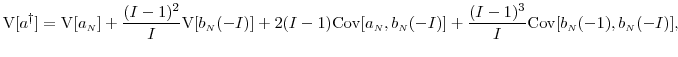
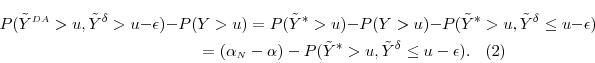
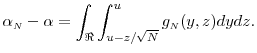
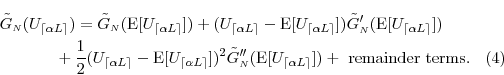
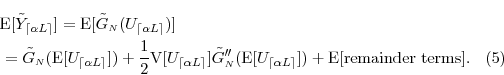
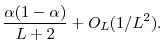
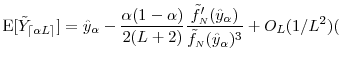 constant
constant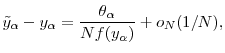
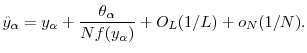
![\displaystyle \ensuremath{{\operatorname E}\lbrack \ensuremath{{\tilde Y}}\cdot\ensuremath{1[\ensuremath{{\tilde Y}}>u]}\rbrack}= \int_{\Re} \int_{u-z/\sqrt{N}}^{\infty} (y+ z/\sqrt{N})g_\ensuremath{{\scriptscriptstyle N}}(y,z) dy dz](img481.gif)
![\displaystyle \ensuremath{{\operatorname E}\lbrack Y\cdot\ensuremath{1[Y>u]}\rbrack} = \int_{\Re} \int_{u}^{\infty} y g_\ensuremath{{\scriptscriptstyle N}}(y,z) dy dz.](img483.gif)