Skip to: [Printable Version (PDF)] [Bibliography] [Footnotes]

Finance and Economics Discussion Series: 2008-25 Screen Reader version ^♣

Term Premiums and Inflation Uncertainty:
Empirical Evidence from an International Panel Dataset¹

Jonathan H. Wright^*

May 2008

Keywords: Term premiums, inflation uncertainty, inflation targeting, bond pricing

Abstract

This paper provides cross-country empirical evidence on term premia, inflation uncertainty, and their relationship. It has three components. First, I construct a panel of zero-coupon nominal government bond yields spanning ten countries and eighteen years. From these, I construct forward rates and decompose these into expected future short-term interest rates and term premiums, using both statistical methods (an affine term structure model) and using surveys. Second, I construct alternative measures of time-varying inflation uncertainty for these countries, using actual inflation data and survey expectations. I discuss some possible determinants of inflation uncertainty. Finally, I use panel data methods to investigate the relationship between term premium estimates and inflation uncertainty measures, and find a strong positive relationship. The economic determinants of term premia remain mysterious; but this evidence points to uncertainty about intermediate- to long-run inflation rates being a substantial part of the explanation for why yield curves slope up.

1. Introduction

Nominal yield curves nearly always slope up, implying that investors demand positive risk premia--or term premia--to induce them to hold long-term nominal bonds. Moreover the available evidence strongly suggests that these term premia vary over time, and have shown a secular decline since the early 1980s. Time-variation in term premia complicates the transmission mechanism of monetary policy, as it clouds the relationship between the very short-term interest rates that are controlled by central banks and longer-term interest rates that are most relevant for the decisions of households and businesses. For example, the effect of the tightening of monetary policy by the Federal Open Market Committee from 2004 to 2006 on long-term interest rates was offset by a fall in distant-horizon forward rates, that Backus and Wright (2007) argued owed mainly to a fall in term premiums. And, the effect of the recent monetary policy accommodation on long-term yields was also partly offset by a rise in long-term forward rates that could owe to a rebound in term premiums.

The term premium represents the extra expected return that risk-averse investors demand to compensate them for the possibility of a capital loss on selling a long-term bond prior to maturity. However, this statement does not constitute an explanation from a general equilibrium asset-pricing perspective, because it is not uncertainty about returns that should matter, but rather the covariance of those returns with marginal utility. The only way to rationalize positive term premia in an equilibrium asset pricing framework is that bonds must be assets that pay off most in the states of the world where investors' marginal utility is low, i.e. the covariance of bond returns with marginal utility must be negative. In a consumption-based asset pricing model, this could arise if consumption growth is negatively autocorrelated (Campbell (1986)), or it can arise in certain models with habit formation (Wachter (2006)). Alternatively, as argued by Piazzesi and Schneider (2006) and Campbell, Sunderam and Viceira (2007), it could also arise if the covariance between inflation and consumption growth is negative, so that high inflation erodes the real value of long-term nominal bonds precisely when investors' marginal utility of consumption is highest. Indeed, Piazzesi and Schneider find that in postwar U.S. data, inflation is negatively correlated with current, past and future consumption growth--exactly as needed for inflation risk to explain positive term premia. All else equal, lower inflation uncertainty should decrease the covariance between inflation and consumption growth and hence reduce the term premium.² This paper is concerned with providing empirical evidence on the relationship between inflation uncertainty and term premia. I find a strong positive relationship between longer-run inflation uncertainty and the term premiums on nominal bonds. Explanations for financial market risk premia in terms of the second moments of economic fundamentals are intuitive and appealing--and, empirically, notoriously hard to find. I do not claim that inflation uncertainty represents a complete explanation for bond risk premia; that task is far beyond the ambition of this paper. But it does suggest that inflation uncertainty is likely part of the story. Accordingly, if long-run inflation uncertainty could be eliminated, then term premiums would be lower and more stable, facilitating the monetary policy transmission mechanism.

Some papers have found empirical evidence for a relationship between inflation uncertainty and bond risk premia, including Beechey (2007) for the United Kingdom and Gürkaynak, Sack and Wright (2008) for the United States. But these papers, and the vast majority of the literature on the term structure of interest rates have used only data on a single country. This means that a rich source of information is being wasted, because there is considerable cross-country variability in the term structure of interest rates and in the macroeconomic determinants of those rates. Some authors have fitted multifactor models to the term structure of interest rates in a panel of countries, including Dungey, Martin and Pagan (2000), Brennan and Xia (2006) and Diebold, Li and Yue (2007), but these exercises are silent on the economic mechanisms that determine term premia. Ehrman, Fratzscher, Gürkaynak and Swanson (2007) studied the convergence in bond yields of euro-zone countries around the time of monetary union. That paper also compared the sensitivity of forward rates to macroeconomic news announcements across these countries. Gürkaynak, Levin and Swanson (2006), and Goldberg and Klein (2005) similarly compared the sensitivity of forward rates to news in different countries, and these papers all argue that the adoption of explicit inflation targets helps to stabilize distant-horizon forward rates. Bernanke, Laubach, Mishkin and Posen (2001) studied the behavior of foreign-U.S. interest differentials around the time that those foreign countries were adopting inflation targets. They found that countries adopting inflation targets saw a gradual reduction of their relative long-term interest rates.³

This paper expands the use of international panel data in term structure analysis. I construct a panel dataset of nominal zero-coupon government bond yields at maturities out to ten years for ten different industrialized countries with separate monetary policies: the United States, the United Kingdom, Canada, Japan, Germany, Norway, Sweden, Switzerland, Australia and New Zealand, going back to 1990, though the data start a bit later for some countries. Euro-zone countries other than Germany are omitted because their term structures have necessarily been highly correlated with those of Germany, at least since 1999. Otherwise the dataset includes all significant industrialized economies, and is to my knowledge the first paper to fit zero-coupon yield curves to all of these countries. I use these data to decompose long-term forward rates into term premiums and expected future short-term interest rates. I construct measures of inflation uncertainty, and assess the association between these measures of inflation uncertainty and term premium estimates in panel data regressions.

2. Zero-coupon yield curves

2.1 Zero-coupon yield curves

Any attempt at estimating term premia first requires zero-coupon yield curves. I obtained or constructed these data at the monthly frequency from January 1990 to December 2007 for ten industrialized countries. The data in all cases refer to the yields on the last day of each month. Table 1 lists the available maturities, sources, and sample periods of these ten different yield curves. All yields in the dataset are continuously compounded and at maturities from 3 months to 10 years, in increments of 3 months. For some countries, the data begin a bit later than January 1990. For others, the data are available even further back, but I start the sample in 1990 as a trade-off between maximizing the sample size and minimizing the likelihood of a large structural break, and also because that lines up with the available data in the survey datasets that will be used later in this paper.

Distant-horizon forward rates are useful for measuring the determinants of the yield curve other than the direct effects of the current stance of monetary policy, because these forward rates should represent the sum of long-run inflation expectations, the long-run expected real short-term interest rate and a forward term premium. Figure 1 shows the time series of nine-to-ten-year forward rates in all ten countries in the dataset. Forward rates have trended down in nearly all these countries since the early 1990s. They have also tended to converge. Whereas the range of forward rates in the early 1990s was around ten percentage points, at the end of 2007 all forward rates were between 3 and 6 percent, with the exception of Japan. Nine-to-ten-year forward rates are strongly correlated across countries; for example the decline in forward rates in 2004-2005 (the "conundrum") was evident to varying degrees in all the countries in our sample, with the sole exception of Japan. Finally, although the scale makes it a little hard to see in Figure 1, in recent years, the nine-to-ten-year forward rates in the U.S. have been towards the top of relatively narrow range across countries. In fact, in every month from 2002 to 2007, the nine-to-ten-year forward rate in the U.S. was uniformly higher than the corresponding forward rate in Germany, the U.K., Switzerland, Canada, Japan and Sweden.⁴ As a matter of accounting, this must represent higher inflation expectations in the U.S. than abroad, a higher expected real short-term interest rate (possibly reflecting faster expected productivity growth) or a higher term premium.

The international decline, and convergence, in forward rates is consistent with a reduction in long-run inflation expectations and a convergence in inflation rates. However, the magnitude of the drop in forward rates seems too big to be due to a revision to inflation expectations alone, for this would mean that inflation expectations had fallen by 5 to 10 percentage points in many industrialized countries since the early 1990s. Some light can be shed on the plausibility of this by looking at survey evidence. Professional surveys have been found by Ang, Bekaert and Wei (2007) to provide excellent forecasts of inflation, at least in the United States. Consensus Forecasts provides a range of forecasts for all the countries in the panel, as listed in Appendix A. These include, at the semiannual frequency, long-horizon forecasts: forecasts of average inflation and growth from five to ten years after the survey date. Figures 2 and 3 show the long-horizon forecasts of inflation and GDP growth. The inflation forecasts did trend downwards, but only by about a couple of percentage points; far less than the fall in forward rates. Meanwhile, there is no evident global trend in long-term growth expectations. For Japan and Germany, long-term growth expectations deteriorated markedly, but for the U.S., they improved around the turn of the century and have remained close to 3 percent, despite falling off a little in the last few years. All in all, it seems hard to account for the magnitude of the decline in forward rates in terms of revisions to inflation (or growth) expectations alone. A declining term premium seems likely to also be part of the story.

Plots of ten-over-two-year term spreads (not shown) similarly declined since the early 1990s, and converged across countries.

.

2.2 Statistical term premium estimates

I decompose five-to-ten-year forward rates into the average expected three-month interest rate from five to ten years hence and the term premium by fitting an affine term structure model of the sort considered by Dai and Singleton (2002) and others to each country separately. Because the payoffs of bonds are deterministic, the absence of arbitrage implies restrictions on the time series and cross-maturity properties of bond yields. Affine term structure models exploit these restrictions.

Specifically, I consider a homoskedastic, discrete-time affine term structure model of the sort employed by Ang and Piazzesi (2003) and Cochrane and Piazzesi (2008). Let denote the price at time of an -period zero-coupon bond, let denote its yield and be the nominal pricing kernel. The price of the bond must be . Assume that the pricing kernel is conditionally lognormal

$$M_{t+1} =\exp (-\delta _0 -{\delta }'_1 X_t -\frac{1}{2}{\lambda }'_t \Sigma \lambda _t -{\lambda }'_t \varepsilon _{t+1} )$$

where is an affine function of an x1 vector of state variables, , and is iid . Assume furthermore that the vector of state variables follows a vector autoregression (VAR)

$$X_{t+1} =\mu +\Phi X_t +\varepsilon _{t+1}$$

It then follows that

$$P_t^{(n)} =\exp (A_n +{B}'_n X_t )$$

where is a x1 vector and is an x matrix that satisfy the recursions

$$A_{n+1} =-\delta _0 +A_n +{B}'_n (\mu -\Sigma \lambda _0 )+\frac{1}{2}{B}'_n \Sigma B_n$$

$$B_{n+1} =(\Phi -\Sigma \lambda _1 )'B_n -\delta _1$$

starting from and . The state variables in could be macroeconomic variables or could simply be yield curve factors, but are assumed to be observable.

In an approach similar to that of Cochrane and Piazzesi (2008), , and can be estimated from fitting a VAR to , and the remaining parameters can be estimated by minimizing the sum of squared differences between actual and fitted yields, that is as

$$\{\hat {\lambda }_0 ,\hat {\lambda }_1 ,\hat {\delta }_0 ,\hat {\delta }_1 \}=\arg \min _{\lambda _0 ,\lambda _1 ,\delta _0 ,\delta _1 } \Sigma _t \Sigma _n (y_t (n)-\tilde {y}_t (n))^2$$

where are the model-implied yields. Having estimated the model parameters, the difference between the model-implied five-to-ten-year forward rate and the average expected three-month interest rate from five to ten years hence is the term premium, . Term premiums at other horizons can of course be computed in the same way.

Intuitively, the model is estimating the relationship between the state variables and future term structures, and using this to estimate term premiums, with all of this done within a coherent asset pricing framework. Turning to the choice of the state vector, , it is well known that yield curve measures are useful for forecasting excess bond returns; for example, when the yield curve is steep, excess returns on a long-term bond tend subsequently to be high. Empirically, yield curve variables do a better job of forecasting future excess bond returns than macroeconomic variables. Thus, using yield curve factors as the state variables seems likely to give a more robust measure of term premia than using macroeconomic variables. It also leads the model to fit better. Kim (2008)⁵ discusses robustness arguments for using yields, rather than macroeconomic series as state variables. Using yield curve factors does not preclude economic interpretation, as the resulting term premium estimates can then be regressed onto macroeconomic variables. To be sure, a complete explanation of the economic determinants of bond pricing would use macroeconomic fundamentals as state variables, but that goal is far beyond the ambition of this paper. Accordingly, I let the state vector be the first three principal components of zero-coupon yields from three months to ten years⁶.

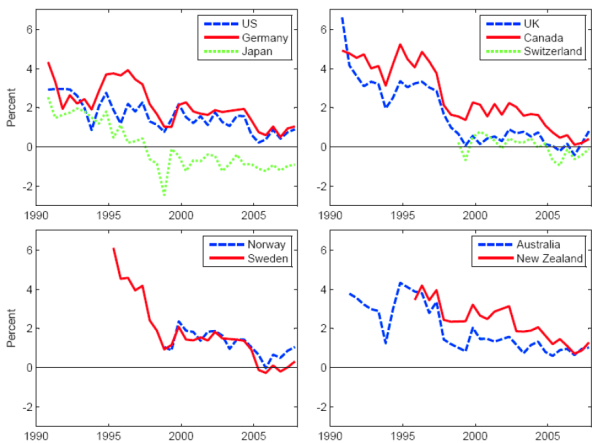
Figure 4 shows the term premium estimates for the different countries. Like the distant-horizon forward rates in Figure 1, these have generally tended to trend downwards over time and to converge. The term premium estimates are typically--but not always--positive. In the last few years, the term premium estimates for all ten countries have generally been in a range from
-1 to +2 percentage points. The term premium estimates for New Zealand have also trended down, but their level is notably lower than for the other countries, and the estimated term premium for this country is often negative.⁷ A countercyclical pattern in these term premium estimates is evident, and it is indeed a standard finding in the literature that term premiums are countercyclical (see, for example, Cochrane and Piazzesi (2005)). Term premiums seem to be highest during and immediately after recessions. For example, the U.S. term premium estimates were high during and immediately after the 1990-91 and 2001 NBER recessions. And the German, Japanese and Swiss term premium estimates were high during and immediately following the recessions that ended in those countries in April 1994, February 1994 and September 1993, respectively, judging from the Economic Cycle Research Institute (ECRI) international business cycle dates.⁸

2.3 Survey-based term premium estimates

Statistical models of the term premium are of course vulnerable to model misspecification and structural breaks. The affine term structure model in the previous subsection implies that yields at all maturities eventually revert to their long-run unconditional mean, so the possibility of a shift in long-run expectations of short-term nominal interest rates is ruled out by assumption, which is troubling since this was apparently a period of at least some decline in long-run inflation expectations.⁹ Also, the models are estimated on the whole sample period, and do not take account of any learning--a major omission (see, for example, Laubach, Tetlow and Williams (2007)).

Surveys provide an alternative, model-free, real-time, and arguably more robust way of decomposing yields into expected future short-term interest rates and term premiums. The idea is simple; if we can measure expectations of future three-month interest rates from surveys, then the term premium is just the difference between an actual yield or forward rate and the average expected future three-month interest rate over the corresponding horizon. Piazzesi and Schneider (2008) consider both term premium estimates from statistical methods (in their paper, a vector autoregression) and from surveys, calling these "objective" and "subjective" estimates respectively. This is standard terminology, though I prefer not to use it because it seems to imply that a scientific researcher should necessarily use the statistical method to measure risk premia, whereas in a world with structural breaks and learning, the survey-based measures may well be a better measure of the econometrician's conditional expectations.

Consensus Forecasts provides long-horizon forecasts for all countries in the panel twice a year. Unfortunately, these long-horizon forecasts ask respondents to predict macroeconomic aggregates, including consumer inflation and real GDP growth, but not short-term interest rates. Blue Chip is a separate survey that is very similar to Consensus Forecasts and indeed many financial and economic forecasters contribute to both surveys. But, for the United States alone, twice a year, Blue Chip provides forecasts of the average level of three-month interest rates from five to ten years hence, in addition to forecasts for consumer inflation, real GDP growth at the same horizon. Let these be, and respectively and consider the regression

$$r_t =\beta _0 +\beta _\pi \pi _t +\beta _y y_t +\varepsilon _{rt}$$ (1)

This regression can be estimated, either imposing the restriction that (corresponding to the Fisher hypothesis), or without this restriction. The coefficient estimates are shown in Table 2. I then used these coefficient estimates--imposing the Fisher hypothesis restriction--to obtain implied predictions from Consensus Forecasts of average three-month interest rates at the five- to ten-year horizon for the international data. That is, the term premium estimate is

$$TP_t^{SURVEY} =f_t^{5,10} -(\hat {\beta }_0 -\pi _t -\hat {\beta }_y y_t )$$ (2)

where denotes the five-to-ten-year forward interest rate, and the coefficient estimates are obtained from the estimation of (1) using U.S. data.¹⁰ The underlying (strong) assumption is that the relationship between equilibrium real short-term interest rates and growth is constant across countries.

The survey-based term premium estimates are shown in Figure 5. Like the affine model term premium estimates, they show a tendency of trending down, and converging over time. They are typically positive, and, with the exception of Japan, never go very negative. Given how consistently nominal yield curves slope up, this seems to be a desirable property in a reasonable term premium estimate. Negative term premiums in Japan may be rationalized by heavy demand from the especially rapidly aging population in that country for longer-term nominal bonds, as would be predicted for example by the model of Wachter (2003). The survey-based term premium estimates declined sharply during the 1990s in the U.K., Canada and Sweden around the times when the central banks in these countries were making great strides in improving the transparency and credibility of monetary policy.

3. Inflation uncertainty measures

The importance of shocks to inflation, both for bond pricing and for the inflation expectations of households and businesses, depends crucially on whether these shocks are perceived to be transitory or permanent. Permanent inflation shocks should have much larger effects on the value of long-term nominal bonds than temporary shocks to inflation. The measurement of long-run inflation uncertainty is of interest in its own right, aside from its relationship with bond risk premia. Levin and Piger (2004) fitted autoregressive models to inflation in twelve industrialized countries and found structural breaks in the autoregressive coefficients around 1990, which would be consistent with the permanent inflation shocks becoming smaller relative to temporary shocks after this time.

3.1 Unobserved component stochastic volatility model

Stock and Watson (2007) proposed an unobserved components model with stochastic volatility provides good forecasts for inflation. The model is a univariate specification that inflation is where is iid , is iid ,

and is iid . The interpretation of the model is that inflation is the sum of a stochastic trend and noise, with both the volatility of the noise (temporary shocks) and the shocks to the stochastic trend (permanent shocks) being time-varying. The model can be estimated by Markov Chain Monte Carlo methods.

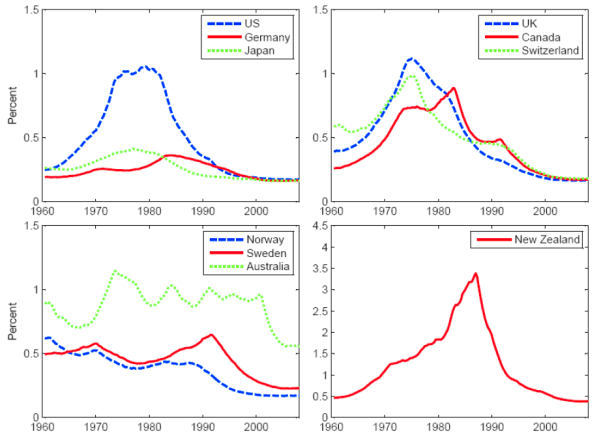
I fitted the model to quarterly consumer price inflation for the panel of countries and show the estimated time series of the standard deviation of the permanent component in Figure 6. Stock and Watson (2007) found that the standard deviation of the permanent component of inflation in the U.S. rose in the 1970s, peaked around 1980, and has come back down to a low level since then. I find this pattern as well, and find that it applies to several other countries. Germany and Japan, however, apparently did not have as much of a runup in the volatility of the permanent component of inflation. New Zealand is shown on a different scale as the peak in the volatility of the permanent component of inflation was much higher, and later (mid 1980s), than for the other industrialized countries.

3.2 Survey density forecasts

Since 1999, each January, for several countries Consensus Forecasts has asked respondents to assign probabilities to consumer price inflation falling in different buckets in that year. The predictions can then be averaged to obtain density forecasts, and the implied standard deviations can be constructed as a summary statistic. Conceptually, this is an ideal measure of agents' inflation uncertainty. Unfortunately, it has serious limitations. First, it is available only for seven countries in the panel (not for Norway, Sweden or Switzerland). Second, it is a quite short-horizon inflation uncertainty measure, as it relates to a prediction made in January for that year's inflation rate--arguably, the horizon is too short to be of much relevance for bond pricing. Third, there are only ten observations per country, as the survey is only done once a year, and only since 1999.

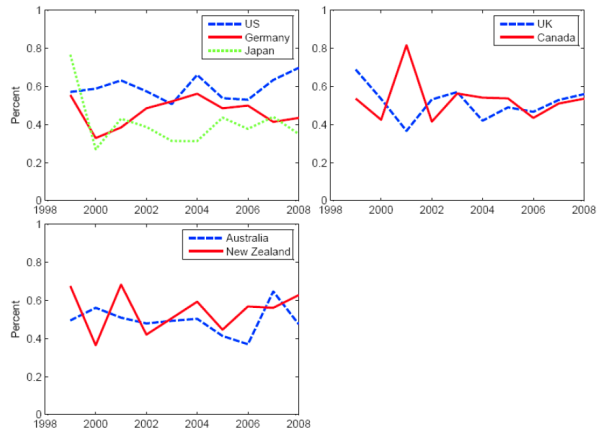
Figure 7 plots the standard deviation of survey density forecasts. They are somewhat jagged. On average, the standard deviation has been highest for the U.S. and lowest for Germany and Japan. There is little time trend over the recent period for which these data are available. However, because of the very limited availability of density forecasts, I now turn to other survey-based measures of inflation risk.

3.3 Dispersion of survey forecasts

Consensus Forecasts reports the dispersion of its forecasts for inflation in the current year and next year (the standard deviation of the responses). Dispersion of forecasts is often used as a proxy for uncertainty, though the two are distinct concepts. Cukierman and Wachtel (1979) provide a theoretical explanation for a relationship between inflation forecast uncertainty and forecast dispersion. Zarnowitz and Lambros (1987), Rich, Raymond and Butler (1992) and Rich and Tracy (2006) all assess the empirical relationship between the dispersion of survey forecasts of inflation and various measures of inflation uncertainty. They find evidence for a positive, but weak, relationship.

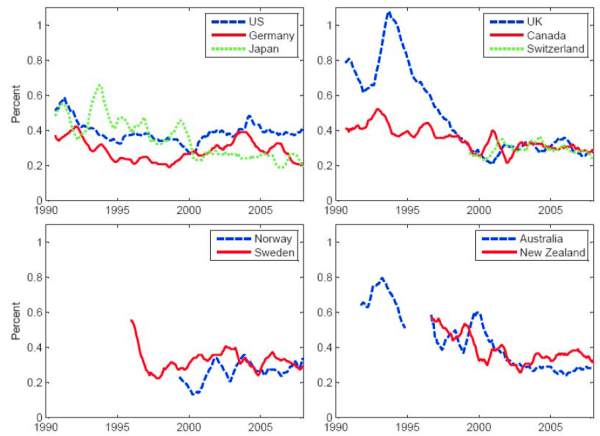
Figure 8 plots the twelve-month moving average of the dispersion of next-year inflation forecasts, which I think of as a rough measure of intermediate- to long-run inflation uncertainty. It would be preferable to have the dispersion of a longer-horizon inflation forecast, because the inflation rate for the next calendar year is surely importantly influenced by transitory factors in addition to the preferences of policymakers. But unfortunately, Consensus forecasts does not report the dispersion of inflation forecasts at longer horizons.¹¹ In any event, beliefs about intermediate- to long-term inflation should influence agents' views at the one-year horizon. The motivation for taking a twelve-month moving average is that the dispersion of the forecast for next year's inflation will tend to be higher in January than in December because the effective forecast horizon is shorter--the moving average should smooth out this seasonal pattern. As can be seen in Figure 8, dispersion has trended down in most countries since the early 1990s. The pattern is particularly stark for the United Kingdom. At one point in the early 1990s, the difference between the highest and lowest values in Consensus forecasts for U.K. year-ahead inflation exceeded 1 percentage point. Recently, this dispersion measure is about three-tenths of a percentage point in the U.K., which is roughly the same as in other countries. Dispersion of inflation beliefs was quite high in Japan during the late 1990s, at the time that deflation was taking hold. At present, the United States has a higher dispersion of year-ahead inflation beliefs than any other country considered here.

For the months and countries where both inflation dispersion and inflation density forecasts (as described in the last subsection) are available, the correlation between inflation dispersion and the standard deviation of the inflation density forecasts is 0.42. This is a moderate correlation and is entirely consistent with other work on the relationship between inflation uncertainty and dispersion.

3.4 Variability of survey forecasts

Another way of using surveys to try to proxy the uncertainty of respondents is to measure the rolling standard deviation of changes to their year-ahead mean forecasts of inflation. Although, this is again a distinct concept from inflation uncertainty, it would be natural to think of the two as being positively related. Figure 9 plots the two-year rolling standard deviation of month-to-month changes in year-ahead inflation forecasts, ending in the month shown. For example, the observation for October 1991 is the standard deviation of changes in year-ahead inflation forecasts from November 1989 to October 1991, inclusive.¹² The results are quite consistent with those in Figure 8. The variability of survey forecasts has trended down, especially for the U.K. At present, the variability of survey forecasts is highest for the United States.

The fact that all these survey-based measures of inflation uncertainty are at present highest for the U.S. may suggest that inflation expectations are relatively poorly anchored in the U.S. Other papers, using quite different methodologies, have come to the same view. In particular, Beechey, Johannsen and Levin (2007) and Gürkaynak, Levin and Swanson (2006) both show that distant-horizon forward rates are more sensitive to economic news in the United States than abroad, which they interpret as evidence that inflation expectations are relatively poorly anchored in the U.S.

3.5 The Level of Inflation Expectations and Inflation Uncertainty

Friedman (1977), Ball, Mankiw and Romer (1988) and Mankiw, Reis and Wolfers (2003) all examine the relationship between the level of actual/expected inflation and uncertainty, and conclude that there is a strong positive relationship--low inflation tends to be stable inflation. This could arise because economies with high inflation tend to get rid of nominal rigidities and so shocks fall more heavily on prices than on the output gap. Empirically, this relationship seems to show up in the data used in this paper: the inflation risk measures all trended down during the 1990s in line with survey-based inflation expectations (Figure 2). The empirical relationship between inflation expectations and inflation uncertainty could mean that a decline in inflation expectations might be accompanied by a fall in inflation uncertainty and hence in term premia, leading to a larger decrease in forward rates.

3.6 Inflation Targeting and Uncertainty

In recent years, many central banks have adopted new monetary policy strategies, including inflation targeting in which an explicit numerical goal for inflation is adopted. New Zealand was the first central bank to introduce an inflation target in 1990, and many other central banks have subsequently followed. Table 3 lists the classification that I adopt for which central banks have inflation targets and when they were adopted, that generally follows Bernanke, Mishkin, Laubach and Posen (2001). All the countries in the panel now have inflation targets, except for the United States and Japan. The dating of adoption of inflation targets is not always clear-cut. For example, the Bank of England adopted an inflation target in 1992, but did not gain operational independence until May 1997, and I accordingly classify the United Kingdom as an inflation targeter only after May 1997.

Bernanke, Mishkin, Laubach and Posen (2001) found that survey measures of inflation expectations generally tended to be lower with inflation targeting than without, although the decline in inflation expectations was gradual after the adoption of the inflation target--the announcement of the target did not generate credibility per se. Beechey, Johannsen, and Levin (2007) found that the dispersion of five-to-ten-year-ahead inflation expectations in the ECB's Survey of Professional Forecasters (SPF) has halved since 1999, when the inflation-targeting ECB was launched, and is now substantially lower than the corresponding dispersion of five-to-ten-year-ahead inflation expectations in the United States, as measured by the Federal Reserve Bank of Philadelphia's SPF.

Studying the relationship between the measures of inflation risks discussed in the previous four subsections and the presence or absence of an inflation target, one can make the following observations:

1. All three measures of inflation risks tend to be lower with an inflation target than without, but the difference is not dramatic. For example, on average the dispersion of year-ahead inflation forecasts is 0.40 for countries classified as having an explicit inflation target at that time, and 0.32 for those that are not. In the next section, I give more formal econometric evidence using panel data regressions with fixed effects.

2. The adoption of an inflation target does not cause a rapid decline in any measures of inflation risk. For example, although both survey-based inflation risk measures declined notably in the United Kingdom in the 1990s, it was a decade-long downward trend, beginning around the time that the Bank of England announced an inflation target while remaining under the control of the Treasury and continuing after the Bank was granted operational independence.

3. The direction of causality of any relationship between inflation uncertainty and the adoption of an inflation target is not clear. For example, one might argue that it was the high level and volatility of inflation in New Zealand in the 1980s that prompted that country to make radical changes in its monetary policy framework.

4. The United States--one of the two countries without an inflation target at present--seems to have the least well anchored inflation expectations, judging by the survey-based measures of inflation uncertainty.

5. On the other hand, Japan--the other country without an inflation target--at present has relatively low inflation uncertainty, showing that there is no clear-cut link between inflation targeting and these measures of inflation risks. Potentially, downward nominal rigidities and substantial resource slack may leave agents quite certain that inflation will remain close to zero over the next couple of years.

6. As the survey-based measures of inflation uncertainty that I use are at the year-ahead horizon, it could be that the differences in these measures over time and across countries represent differences in the pace at which transitory shocks to inflation are expected to die out, rather than differences in long-run inflation uncertainty. That is, it could reflect differences in the horizon over which agents expect inflation to reach its long-run expected level.

4. Term Premiums and Inflation Uncertainty

Although the estimates of bond risk premia and the measures of inflation uncertainty are of interest in their own right, the main motivation of this study is the relationship between these two. Indeed, there is good reason to think that bond risk premia could be importantly influenced by the compensation that investors demand for the risk of unexpected inflation, as argued by Piazzesi and Schneider (2006). The U.K. is unique in industrialized countries in having had a large and liquid market in index-linked government debt for several decades, and Piazzesi and Schneider found that while the U.K. nominal yield curve on average sloped up, the real yield curve on average sloped down, indicating that it is the exposure of long-term nominal bonds to unexpected inflation that makes them risky assets. Another piece of anecdotal evidence comes from looking at the nominal and real U.K. forward curves the on the day before and the day after the Bank of England was granted operational independence, shown in Figure 10. The real yield curve was little changed, but the nominal curve declined and flattened, with the ten-year nominal forward rate dropping more than half a percentage point on a single day, presumably reflecting the effect of lower inflation expectations and a lower inflation risk premium.¹³ The argument should not be overstated: real bond yields are quite volatile both in the U.S. and the U.K.--and probably too volatile to reflect shifts in expectations future real short-term interest rates alone--so term premia surely do not reflect inflation risk alone. But inflation risk seems to be an important component of the explanation, and measures of inflation uncertainty may be correlated with the inflation risk premium.

To investigate this possibility empirically, I ran panel data regressions of term premia on the different inflation risk measures. County fixed effects were included, so as to allow for the possibility that some other country-specific factors that may affect term premia are also correlated with inflation risk measures.

I considered panel regressions of the form

$$TP_{it} =\alpha _i +\beta 'x_{it} +\varepsilon _{it}$$ (3)

where denotes the term premium in country in month (with the term premium being either estimated from the affine term-structure model in subsection 2.2, or imputed from surveys as in (2)), is a vector of inflation risk measures as constructed in section 3 and/or an inflation targeting dummy that is 1 if country has an inflation target at time , and denotes a country fixed-effect. Note that this is a panel data regression in which the number of time periods is large relative to the number of cross-sectional observations.

4.1 Standard Errors

The errors in equation (3) are likely to be correlated both across countries and over time. If Australia has a positive error in a given month, it seems likely that New Zealand will as well. And if the error is positive for any given country in one month, it seems likely to be positive again the next month. Hence, ordinary standard errors in the estimation of (3) are likely to be too small.

As a potential remedy for the problem, I used the following bootstrap algorithm. In each bootstrap sample, I resampled blocks of six months of data using the same six-month windows for each country in the panel. I then used these bootstrap samples to obtain percentile-t bootstrap confidence intervals for (in the terminology of Hall (1992)). Appendix B describes the methodology in detail.

In any block bootstrap resampling scheme, the idea is that the data should be cut into blocks where the series will be dependent within the blocks, but not across the blocks. The number of such blocks has to be sufficiently large for the bootstrap to work well. The motivation of the resampling scheme devised here is that the errors are allowed to be correlated across countries, and over time, but it is hoped that the time-series dependence will be limited at horizons beyond six months.

4.2 Results

The results of the panel data regression are shown in Table 4 for the affine model term premium estimates. Point estimates are shown along with heteroskedasticity-robust standard errors and 95 percent bootstrap confidence intervals: the bootstrap intervals are used to assess statistical significance.¹⁴ In univariate regressions of the term premium on each inflation risk measure separately, the slope coefficients on the volatility of the permanent component of inflation in the UCSV model (PERM-UCSV), the dispersion of survey inflation forecasts (SURV-DISP), and the volatility of survey forecasts of inflation (SURV-VOL) are all positive and statistically significant. For example, going from a dispersion of year-ahead inflation beliefs of 1.1 percentage points to 0.3 percentage points (roughly the experience in the U.K. over the last 15 years), is estimated to lower the five-to-ten-year forward term premium by about 4 percentage points. This is a big effect, but not implausible given how far distant-horizon forward rates have fallen in the U.K. The slope coefficient on the standard deviation of survey density forecasts of inflation (SURV-DENS) is not significant, but the sample size available for this regression is especially small, with just ten time periods and seven countries. In a regression of the term premium on the inflation targeting dummy, the slope coefficient is estimated to be negative--consistent with the adoption of a numerical inflation target lowering bond risk premia--but is not statistically significant.

Table 4 also shows the results of a multivariate regression of the affine model term premium estimates on PERM-UCSV, SURV-DISP, SURV-VOL and the inflation targeting dummy. The first three are all estimated to have a positive relationship with term premia, while the coefficient estimate on the inflation targeting dummy is negative, but much smaller in absolute value in this multivariate regression than in a regression of term premia on the inflation targeting dummy alone. All coefficients in this regression are individually significant, except for SURV-VOL. As this is a panel where the number of cross-sectional observations is small relative to the number of time periods, the fixed effects are consistently estimable, and are also included in Table 4.

Table 5 turns to showing the results of regressions of survey-based term premium estimates on inflation risk measures and/or the inflation targeting dummy. In regressions of the term premium on each variable separately, PERM-UCSV, SURV-DISP, SURV-VOL all have significantly positive slope coefficients, while the inflation targeting dummy has a significantly negative coefficient and SURV-DENS is not statistically significant. The five-to-ten-year forward nominal term premium is estimated to be on average 1.6 percentage points lower for countries and time periods with inflation targets than for those without. In a joint regression of the survey term premium estimate on PERM-UCSV, SURV-DISP, SURV-VOL and the inflation targeting dummy, each coefficient is statistically significant, except for SURV-VOL. In the joint regression, the coefficient on the inflation targeting dummy is much smaller in absolute magnitude than when it is the only right-hand-side variable.

The positive relationship between term premia and inflation uncertainty suggests that the global decline in forward rates and estimates of term premiums over the past two decades owes importantly to the diminution of inflation risks. Also it suggests a possible factor contributing to the higher level of distant-horizon forward rates in the U.S. than in foreign countries (seen in Figure 1)--it could be that the relatively high level inflation uncertainty judging from surveys is driving term premiums up.¹⁵

There is a negative relationship between term premia and the inflation targeting dummy. However, this relationship becomes much weaker when measures of inflation uncertainty are controlled for. This is consistent with the view that it is inflation uncertainty rather than the existence of an explicit inflation target that influences term premia, but that the adoption of an inflation target has been helpful in reducing inflation uncertainty, at least for some countries.

4.3 Measurement Error on the left and on the right

Term premiums and inflation risk are unobservable, and the proxies used in these panel data regressions are clearly contaminated with substantial measurement error. Measurement error in the dependent variable should--as long as it is uncorrelated with the independent variable-- reduce the precision of the parameter estimates but leave them unbiased. Classical measurement error in the independent variable introduces attenuation bias in which the slope coefficients are biased towards zero. Measurement error is unavoidable in regressions of the sort considered in this paper. However, measurement error should make it harder to detect a significant relationship between inflation uncertainty and bond risk premia. As such, if we could measure these concepts perfectly, the relationship between them would be stronger still.

4.4 Some Determinants of Inflation Uncertainty

I finally turn to using panel data methods to explore the underlying determinants of inflation uncertainty a little further. As discussed earlier, inflation targeting may reduce inflation uncertainty. Another possible determinant of inflation uncertainty is the state of the business cycle. For example, one might suppose that recessions increase the odds of inflation being low (because of diminished pressures on resources), but also at the same time increase the odds of high inflation (because monetary policy accommodation may be too great, or last too long).

To investigate these hypotheses, I ran panel data regressions of the different inflation risk measures on the inflation targeting dummy and/or on recession dummy, using ECRI business cycle dates are used (NBER for the U.S.)).¹⁶ The results are shown in Table 6. The coefficients on the inflation targeting dummy and the recession dummy are both statistically significant for all the inflation risk measures, both when they are used as explanatory variables on their own, and when they are used jointly. The coefficient on the inflation targeting dummy is negative: countries with an inflation target have lower inflation uncertainty. It is also economically significant. For example, on average countries with inflation targets are estimated to have a dispersion of year-ahead inflation expectations that is nearly 20 basis points lower. That is not to say that the adoption of the inflation target results in an immediate reduction in dispersion of inflation expectations--the graphical evidence shown above would suggest that this is not the case. Meanwhile, the coefficient on the recession dummy is positive: inflation uncertainty is higher in recessions than in expansions.

5. Conclusions

Nominal yield curves nearly always slope up. A natural explanation is that long-term nominal bonds are risky assets because inflation reduces the value of long-term bonds more than short-term bonds, if inflation is positively correlated with the marginal utility of consumption. Under this story, eliminating inflation uncertainty would flatten out yield curves.

There has been little cross-country empirical evidence on the determinants of term premia, and the relationship between term premia and inflation uncertainty. This wastes a valuable source of information. Accordingly, in this paper, I have compiled a dataset of eighteen years of nominal yield curves for ten industrialized countries: which are all the major industrialized countries that have separate monetary policies at present. These can be used to construct measures of term premia.

I have also constructed measures of inflation uncertainty. These are of interest in their own right. There is, for example, some evidence that inflation uncertainty is reduced by the adoption of a numerical inflation target. However, the main goal of this paper is to study the association between bond risk premia and inflation risk measures and I have found a fairly strong positive relationship. This is not to say that inflation uncertainty comes close to representing a complete explanation for the empirical behavior of bond risk premia--if it did, then one could just use inflation risk measures as the state variables in a bond pricing model. The failure of the expectations hypothesis is overwhelming and so we know that term premia are time-varying, but the underlying causes of this time-variation in term premia remain mysterious. Indeed, it is by no means clear that it can be explained within a rational asset pricing paradigm at all. Still, it is intuitive to relate these term premia to the second moments of economic fundamentals, and it seems a useful stylized fact that both statistical and survey-based measures of term premia are quite strongly positively correlated with several different measures of inflation uncertainty. This suggests that inflation uncertainty may be an important part of the explanation for why term premiums are positive and so for why nominal yield curves slope up.

Over the past two decades, yield curves have flattened and long-term forward rates have trended down in most industrialized countries, and have converged. Although part of this surely represents a reduction in inflation expectations, the evidence presented in this paper would suggest that a larger part owes to declining term premiums. And, in turn, a likely explanation for much of the secular decline in term premiums is that greater transparency and credibility of monetary policy has reduced intermediate- to long-term inflation uncertainty.

Appendix A: Description of Consensus Forecasts

The survey dataset consists of the Consensus Forecast predictions for consumer price inflation next year, from the survey taken each month from October 1987 to January 2008, inclusive. In addition to the point forecasts, the dispersion (standard deviation) of the forecasts is also included. The following countries are included in these surveys:

1. All months: U.S., Japan, Germany, U.K., Canada.

2. From January 1996 on: Sweden.

3. From June 1998 on: Switzerland and Norway.

4. From November 1989 on: Australia (December 1994 to September 1995 are missing).

5. From October 1995 on: New Zealand.

Because the surveys are taken at the very start of each month, and the yield curve data refers to the last business day of the month, the timing convention that I adopt is to treat the survey for any given month as referring to beliefs at the end of the previous month. For example, the December 2007 observation is the survey dated January 2008.

In addition, each April and October, there is a "long-horizon" survey, asking respondents for their predictions of GDP growth and inflation from five to ten years hence. The dataset includes responses from each of these surveys from April 1990 to October 2007, inclusive. The following countries are included in these long-horizon surveys:

1. All surveys: U.S., Japan, Germany, U.K., Canada.

2. From April 1995 on: Sweden.

3. From October 1998 on: Switzerland and Norway.

4. From April 1991 on: Australia.

5. From October 1995 on: New Zealand.

Finally, each January since 1999, for all countries except Sweden, Switzerland, and New Zealand, respondents have been asked to assign odds on inflation for that country falling in different buckets in that year. Consensus averages these across respondents to obtain a density forecast, which is thus available for 7 countries in 10 years.

Since October 1995, the data have been in the publication "Consensus Forecasts for G-7 Countries and Western Europe" for all countries except Australia and New Zealand, that are instead provided in "Asia Pacific Consensus Forecasts." Prior to that, the available data were in a single publication called "Consensus Forecasts".

Appendix B: Description of bootstrap methodology.

Let and denote the parameter estimate and heteroskedasticity-robust standard error, respectively, in the original sample. The bootstrap algorithm consists of the following steps:

1. Random blocks of the data of length 6 months are drawn by resampling with replacement. Each block takes a draw for all the countries.

2. In each bootstrap sample, the parameter estimate and heteroskedasticity-robust standard error are computed as and , respectively.

3. The statistic is computed and saved.

4. Steps 1-3 are repeated 1,000 times.

5. The and percentiles of the distribution of are computed, which are referred to as and , respectively.

6. The percent percentile-t bootstrap confidence interval for is then given by .

In implementing this algorithm, I set to 5 percent, for a 95 percent confidence interval.

References

Anderson, Nicola and John Sleath (1999): New Estimates of the U.K. Real and Nominal Yield Curves, Bank of England Quarterly Bulletin, November 1999, pp.384-392.

Ang, Andrew, Geert Bekaert and Min Wei (2007): Do Macro Variables, Asset Markets or Surveys Forecast Inflation Better?, Journal of Monetary Economics, 54, pp.1163-1212.

Ang, Andrew and Monika Piazzesi (2003): A No-Arbitrage Vector Autoregression of Term Structure Dynamics with Macroeconomic and Latent Variables, Journal of Monetary Economics, 50, pp.745-787.

Bacchetta, Philippe, Elmar Mertens and Eric van Wincoop (2008): Predictability in Financial Markets: What Do Survey Expectations Tell us?, working paper.

Backus, David K. and Jonathan H. Wright (2007): Cracking the Conundrum, Brookings Papers on Economic Activity, 1, pp.293-329.

Ball, Laurence, N. Gregory Mankiw and David Romer (1988): The New Keynesian Economics and the Output-Inflation Trade-off, Brookings Papers on Economic Activity, 1, pp.1-82.

Beechey, Meredith J. (2007): Lowering the Anchor: How the Bank of England's Inflation Targeting Policies Have Shaped Inflation Expectations and Perceptions of Inflation Risk, working paper.

Beechey, Meredith J., Benjamin K. Johannsen and Andrew T. Levin (2007): Are Long-Run Inflation Expectations Anchored More Firmly in the Euro Area than in the United States?, working paper.

Bernanke, Ben S., Thomas Laubach, Frederic S. Mishkin and Adam S. Posen (2001): "Inflation Targeting: Lessons from the International Experience," Princeton University Press, Princeton, New Jersey.

Brennan, Michael J. and Yihong Xia (2006): International Capital Markets and Foreign Exchange Risk, Review of Financial Studies, 19, pp.753-795.

Campbell, John Y. (1986): Bond and Stock Returns in a Simple Exchange Economy, Quarterly Journal of Economics, 101, pp.785-804.

Campbell, John Y., Adi Sunderam and Luis M. Viceira (2007): Inflation Bets or Deflation Hedges" The Changing Risks of Nominal Bonds, working paper.

Cochrane, John H. and Monika Piazzesi (2005): Bond Risk Premia, American Economic Review, 95, pp.138-160.

Cochrane, John H. and Monika Piazzesi (2008): Decomposing the Yield Curve, working paper.

Cukierman, Alex and Paul Wachtel (1979): Differential Inflation Expectations and the Variability of the Rate of Inflation: Theory and Evidence, American Economic Review, 69, pp.595-609.

Dai, Qiang and Kenneth J. Singleton (2002): Expectation Puzzles, Time-varying Risk Premia, and Affine Models of the Term Structure, Journal of Financial Economics, 63, pp.415-441.

Diebold, Francis X., Canlin Li and Vivien Yue (2008): Global Yield Curve Dynamics and Interactions: A Generalized Nelson-Siegel Approach, Journal of Econometrics, forthcoming.

Dungey, Mardi, Vance L. Martin and Adrian R. Pagan (2000): A Multivariate Latent Factor Decomposition of International Bond Yield Spreads, Journal of Applied Econometrics, 15, pp.697-715.

Ehrman, Michael, Marcel Fratzscher, Refet S. Gürkaynak and Eric T. Swanson (2007): Convergence and Anchoring of Yield Curves in the Euro Area, European Central Bank working paper 817.

Friedman, Milton (1977): Nobel Lecture: Inflation and Unemployment, Journal of Political Economy, 85, pp.451-472.

Froot, Kenneth A. (1989): New Hope for the Expectations Hypothesis of the Term Structure of Interest Rates, Journal of Finance, 44, pp.283-305.

Goldberg, Linda S, and Michael W. Klein (2005): Establishing Credibility: Evolving Perceptions of the European Central Bank, Journal of Finance, 44, pp.283-305.

Gürkaynak, Refet S., Brian Sack and Jonathan H. Wright (2007): The U.S. Treasury Yield Curve: 1961 to the Present," Journal of Monetary Economics, 54, pp.2291-2304.

Gürkaynak, Refet S., Brian Sack and Jonathan H. Wright (2008): The TIPS Yield Curve and Inflation Compensation, Finance and Economics Discussion Series, 2008-5.

Gürkaynak, Refet S., Andrew T. Levin and Eric T. Swanson (2006): Does Inflation Targeting Anchor Long-Run Inflation Expectations? Evidence from Long-Term Bond Yields in the U.S., U.K. and Sweden, Federal Reserve Bank of San Francisco working paper 2006-9.

Hall, Peter G. (1992): "The Bootstrap and Edgeworth Expansion," Springer, New York.

Kim, Don H. (2008): Challenges in Macro-Finance Modeling, Finance and Economics Discussion Series, 2008-6.

Kozicki, Sharon and Peter A. Tinsley (2001): Shifting Endpoints in the Term Structure of Interest Rates, Journal of Monetary Economics, 47, pp.613-652.

Laubach, Thomas, Robert J. Tetlow and John C. Williams (2007): Learning and the Role of Macroeconomic Factors in the Term Structure of Interest Rates, working paper.

Levin, Andrew T. and Jeremy M. Piger (2004): Is Inflation Persistence Intrinsic in Industrial Economies?, European Central Bank working paper 334.

Levin, Andrew T. and Tack Yun (2007): The Great Moderation and the Real Yield Curve, working paper.

Mankiw, N. Gregory, Ricardo Reis and Justin Wolfers (2003): Disagreement About Inflation Expectations, NBER Macro Annual, 18, pp.209-248.

Piazzesi, Monika and Martin Schneider (2006): Equilibrium Yield Curves, NBER Macro Annual, 21, pp.389-442.

Piazzesi, Monika and Martin Schneider (2008): Bond Positions, Expectations and the Yield Curve, Federal Reserve Bank of Atlanta working paper, 2008-2.

Rich, Robert W., Jennie E. Raymond and J.S. Butler (1992): The Relationship Between Forecast Dispersion and Forecast Uncertainty: Evidence from a Survey Data-ARCH Model, Journal of Applied Econometrics, 7, pp.131-148.

Rich, Robert W and Joseph S. Tracy (2006): The Relationship Between Expected Inflation, Disagreement, and Uncertainty: Evidence from Matched Point and Density Forecasts, Federal Reserve Bank of New York Staff Reports, 253.

Stock, James H. and Mark W. Watson (2007): Why has U.S. Inflation Become Harder to Forecast?, Journal of Money, Credit and Banking, 39, pp.3-33.

Wachter, Jessica A. (2003): Risk Aversion and Allocation to Long-Term Bonds, Journal of Economic Theory, 112, pp.325-333.

Wachter, Jessica A. (2006): A Consumption-Based Model of the Term Structure of Interest Rates, Journal of Financial Economics, 79, pp.365-399.

Zarnowitz, Victor and Louis A. Lambros (1987): Consensus and Uncertainty in Economic Prediction, Journal of Political Economy, 95, pp.591-621.

Table 1: Yield Curve Data Sources

Country	Source	Start Date	Methodology
U.S.	Gürkaynak, Sack and Wright (2007)	Nov 1971	Svensson
Japan.	Datastream and author's calculations	Jan 1987	Svensson
Germany	Bundesbank and BIS database	Jan 1973	Svensson
U.K.	Anderson and Sleath (1999)	Jan 1975	Spline
Canada	Bank of Canada and BIS database	Jan 1986	Spline
Switzerland	Swiss National Bank and BIS database	Jan 1988	Svensson
Norway	Norges Bank and BIS database	Jan 1998	Svensson
Sweden	Riksbank and BIS database	Dec 1992	Svensson
Australia	Datastream and author's calculations	Feb 1987	Nelson-Siegel
New Zealand	Datastream and author's calculations	Mar 1991	Nelson-Siegel

Notes: Zero-coupon yields are available at maturities out to ten years in all cases from the start date to December 2007. Data are monthly (end-of-month). Data from before January 1990 are not used in this paper. For Japan, Australia and New Zealand, I downloaded the prices of sovereign non-callable fixed-rate government bonds from Datastream and fitted Svensson and Nelson-Siegel curves to these prices, as described for the U.S. in Gürkaynak, Sack and Wright (2007), using only dates when bonds in those countries existed at maturities out to ten years. The yield curves described in Gürkaynak, Sack and Wright and Anderson and Sleath (1999), are available on the websites of the Federal Reserve and Bank of England, respectively, and are updated regularly.

Table 2: Regression coefficients of Blue Chip Long-Horizon Three-Month Interest Rate Forecasts on corresponding Inflation and GDP Growth Forecasts

Intercept	1.98	1.56
Intercept (standard error)	(0.52)	(0.48)
Inflation	0.93	1.00 (imposed)
Inflation (standard error)	(0.07)
GDP Growth	0.10	0.17
GDP Growth (standard error)	(0.16)	(0.17)
R-squared (percent)	71.33	71.03

Notes: The first column shows the results of regressing the Blue Chip semiannual forecast of U.S. three-month average interest rates from five to ten years hence on the forecasts of U.S. GDP growth and inflation from the same surveys. The regression uses surveys from March 1987 to October 2007, for a total of 42 observations. Standard errors are shown in parentheses. The second column reports the results from the same regression, but imposing a unit coefficient on inflation (the Fisher hypothesis).

Table 3: Classification of Countries into Inflation Targeters and Others

Country	Inflation Targeter in Dec 2007	Start of Targeting Regime
U.S.	No
Japan.	No
Germany	Yes	Jan 1999
U.K.	Yes	May 1997
Canada	Yes	Feb 1991
Switzerland	Yes	Jan 2000
Norway	Yes	Mar 2001
Sweden	Yes	Jan 1993
Australia	Yes	Sep 1994
New Zealand	Yes	Mar 1990

Table 4: Slope Coefficient Estimates in Panel Data Regressions of Affine Model Term Premium on Inflation Risk Measures with fixed effects.

Regressor	(1)	(2)	(3)	(4)	(5)	(6)
PERM-UCSV	4.70				3.33
PERM-UCSV (standard error)	(0.24)				(0.43)
PERM-UCSV (confidence interval)	[3.72,5.72]				[1.23,5.53]
SURV-DISP		5.10			2.54
SURV-DISP (standard error)		(0.19)			(0.22)
SURV-DISP (confidence interval)		[4.17,6.24]			[1.53,3.61]
SURV-VOL			11.72		2.09
SURV-VOL (standard error)			(0.63)		(0.68)
SURV-VOL (confidence interval)			[8.10,14.87]		[-0.62,5.51]
Inflation Targeting Dummy				-1.37	-0.74
Inflation Targeting Dummy (standard error)				(0.07)	(0.10)
Inflation Targeting Dummy (confidence interval)				[-1.67,1.04]	[-1.24,-0.24]
SURV-DENS						0.11
SURV-DENS (standard error)						(0.87)
SURV-DENS (confidence interval)						[-2.44,2.14]
Estimated Fixed Effects: U.S.	1.79	0.76	1.53	2.78	0.81	2.13
Estimated Fixed Effects: Japan	0.56	-0.40	0.21	1.39	-0.24	0.68
Estimated Fixed Effects: Germany	1.17	0.71	1.32	2.80	1.07	1.65
Estimated Fixed Effects: U.K.	0.08	-1.40	-0.26	1.89	-0.68	0.04
Estimated Fixed Effects: Canada	1.17	0.61	1.18	3.68	1.15	1.36
Estimated Fixed Effects: Norway	-0.49	-1.02	-0.84	1.22	-0.56
Estimated Fixed Effects: Sweden	0.92	0.34	0.44	3.75	0.63
Estimated Fixed Effects: Switzerland	0.71	0.21	0.75	2.58	0.86
Estimated Fixed Effects: Australia	-2.23	-1.05	-0.35	2.64	-2.31	0.24
Estimated Fixed Effects: New Zealand	-3.55	-2.75	-2.29	0.78	-2.85	-0.86

Notes: This table reports the results of panel data regressions of the affine term premium estimates on the standard deviation of the permanent component of inflation in the UCSV model (PERM-UCSV), the dispersion of survey inflation forecasts (SURV-DENS), the volatility of survey point forecasts of inflation (SURV-VOL), the inflation targeting dummy and/or the standard deviation of survey density forecasts of inflation (SURV-DENS), with fixed effects in all cases. Entries in round brackets are heteroskedasticity-robust standard errors. Entries in square brackets are the 95 percent bootstrap confidence intervals, constructed as described in Appendix B. To conserve space, for the fixed effects, the point estimates are shown without standard errors or bootstrap confidence intervals.

Table 5: Slope Coefficient Estimates in Panel Data Regressions of Survey-Based Term Premium on Inflation Risk Measures with fixed effects.

Regressor	(1)	(2)	(3)	(4)	(5)	(6)
PERM-UCSV	9.59				5.27
PERM-UCSV (standard error)	(0.75)				(1.04)
PERM-UCSV (confidence interval)	[8.35,11.27]				[3.51,7.34]
SURV-DISP		5.49			1.69
SURV-DISP (standard error)		(0.65)			(0.60)
SURV-DISP (confidence interval)		[3.40,7.34]			[0.43,2.57]
SURV-VOL			11.08		0.54
SURV-VOL (standard error)			(0.98)		(1.36)
SURV-VOL (confidence interval)			[9.38,13.23]		[-3.54,4.16]
Inflation Targeting Dummy				-1.62	-0.81
Inflation Targeting Dummy (standard error)				(0.16)	(0.19)
Inflation Targeting Dummy (confidence interval)				[-2.08,-1.14]	[-1,26,-0.42]
SURV-DENS						-1.18
SURV-DENS (standard error)						(0.96)
SURV-DENS (confidence interval)						[-5.49,1.72]
Estimated Fixed Effects: U.S.	-0.43	-0.57	0.46	1.58	-0.26	1.76
Estimated Fixed Effects: Japan	-1.70	-1.96	-1.29	0.00	-1.69	-0.49
Estimated Fixed Effects: Germany	0.16	0.55	1.19	2.91	0.87	1.94
Estimated Fixed Effects: U.K.	-0.44	-1.03	0.26	2.61	-0.02	0.97
Estimated Fixed Effects: Canada	0.07	0.65	1.36	4.12	1.31	1.91
Estimated Fixed Effects: Norway	-0.44	-0.17	0.09	2.34	0.43
Estimated Fixed Effects: Sweden	-1.01	-0.31	-0.08	3.39	0.03
Estimated Fixed Effects: Switzerland	-1.85	-1.57	-0.91	1.29	-0.76
Estimated Fixed Effects: Australia	-5.86	-0.68	0.23	3.15	-2.71	1.74
Estimated Fixed Effects: New Zealand	-2.62	0.02	0.58	3.90	-0.38	2.46

Notes: This table reports the results of panel data regressions of the survey-based term premium estimates on the standard deviation of the permanent component of inflation in the UCSV model (PERM-UCSV), the dispersion of survey inflation forecasts (SURV-DENS), the volatility of survey point forecasts of inflation (SURV-VOL), the inflation targeting dummy and/or the standard deviation of survey density forecasts of inflation (SURV-DENS), with fixed effects in all cases. Entries in round brackets are heteroskedasticity-robust standard errors. Entries in square brackets are the 95 percent bootstrap confidence intervals, constructed as described in Appendix B. To conserve space, for the fixed effects, the point estimates are shown without standard errors or bootstrap confidence intervals.

Table 6: Slope Coefficient Estimates in Regressions of Inflation Risk Measures on Inflation Target and Business Cycle Dummies

Regressor	(1)	(2)	(3)
Dependent Variable: PERM-UCSV, Inflation Targeting Dummy	-0.16		-0.14
Dependent Variable: PERM-UCSV, Inflation Targeting Dummy (standard error)	(0.008)		(0.008)
Dependent Variable: PERM-UCSV, Inflation Targeting Dummy (confidence interval)	[-0.27,-0.12]		[-0.21,-0.10]
Dependent Variable: PERM-UCSV, ECRI Recession Dummy		0.15	0.11
Dependent Variable: PERM-UCSV, ECRI Recession Dummy (standard error)		(0.012)	(0.011)
Dependent Variable: PERM-UCSV, ECRI Recession Dummy (confidence interval)		[0.10,0.28]	[0.07,0.24]
Dependent Variable: SURV-DISP, Inflation Targeting Dummy	-0.17		-0.19
Dependent Variable: SURV-DISP, Inflation Targeting Dummy (standard error)	(0.012)		(0.012)
Dependent Variable: SURV-DISP, Inflation Targeting Dummy (confidence interval)	[-0.23,-0.11]		[-0.25,-0.14]
Dependent Variable: SURV-DISP, ECRI Recession Dummy		0.08	0.05
Dependent Variable: SURV-DISP, ECRI Recession Dummy (standard error)		(0.007)	(0.008)
Dependent Variable: SURV-DISP, ECRI Recession Dummy (confidence interval)		[0.05,0.12]	[0.03,0.07]
Dependent Variable: SURV-VOL, Inflation Targeting Dummy	-0.05		-0.05
Dependent Variable: SURV-VOL, Inflation Targeting Dummy (standard error)	(0.005)		(0.004)
Dependent Variable: SURV-VOL, Inflation Targeting Dummy (confidence interval)	[-0.09,-0.03]		[-0.06,-0.05]
Dependent Variable: SURV-VOL, ECRI Recession Dummy		0.04	0.03
Dependent Variable: SURV-VOL, ECRI Recession Dummy (standard error)		(0.005)	(0.005)
Dependent Variable: SURV-VOL, ECRI Recession Dummy (confidence interval)		[0.01,0.11]	[0.02,0.05]

Notes: This table reports the results of panel data regressions of various inflation risk measures on the dummy that is 1 if that country has an inflation target and 0 otherwise and/or a dummy that is 1 if that country is in a recession at that time, as defined by the ECRI business cycle dates (NBER for the U.S.)). The inflation risk measures are the standard deviation of the permanent component of inflation in the UCSV model (PERM-UCSV), the dispersion of survey inflation forecasts (SURV-DENS) and the volatility of survey point forecasts of inflation (SURV-VOL). Fixed effects are included, but the estimates of fixed effects are not shown. ECRI business cycle dates are available for all countries except Norway. Entries in round brackets are heteroskedasticity-robust standard errors. Entries in square brackets are the 95 percent bootstrap confidence intervals, constructed as described in Appendix B.

Figure 1: Nine-to-Ten-year Forward Rates

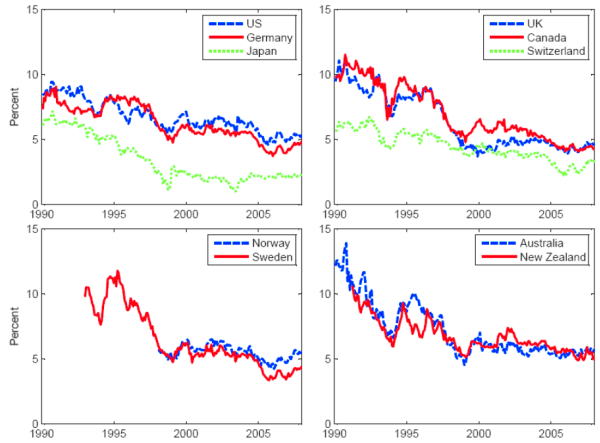
Notes: This chart shows the estimated nine-to-ten-year forward rates for the ten countries in the sample, with continuous compounding.

Figure 2: Long-Horizon Consensus Forecasts of Inflation

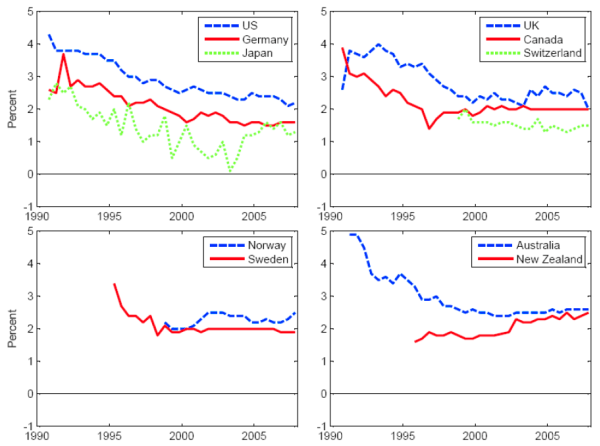
Notes: This chart plots the Consensus forecasts of average consumer price inflation from five to ten years hence against the survey date.

Figure 3: Long-Horizon Consensus Forecasts of International Growth

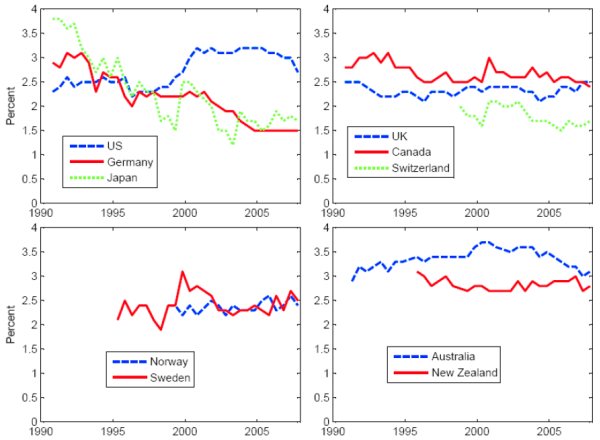
Notes: This chart plots the Consensus forecasts of average real GDP growth from five to ten years hence against the survey date.

Figure 4: Affine model Five-to-ten-year Forward Term Premium Estimates

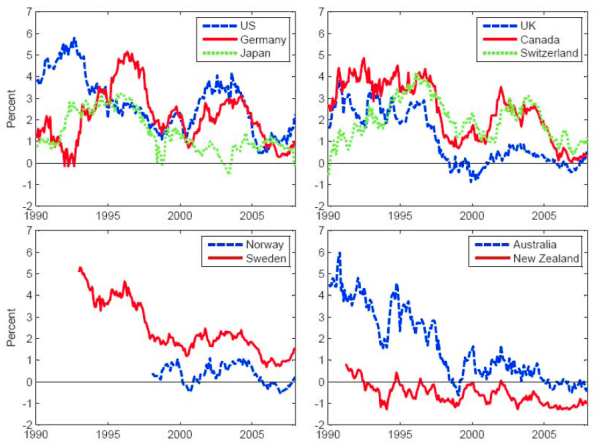
Notes: This plots the term premium component of the five-to-ten-year forward rate, as estimated from the homoskedastic exponential affine term structure model described in the text.

Figure 5: Survey-Based Five-to-ten-year Forward Term Premium Estimates

Notes: This plots the term premium component of the five-to-ten-year forward rate, as estimated from surveys, as described in the text.

Figure 6: Estimate of the Standard Deviation of the Permanent Component of Inflation

Notes: This plots the estimated permanent component of inflation, obtained from fitting UCSV models to quarterly consumer price inflation at an annualized rate (source: Main Economic Indicators) for each country separately.

Figure 7: Standard Deviation of Density forecasts for current-year inflation

Notes: This shows the standard deviation of density forecasts for current-year consumer price inflation from the Consensus survey density forecasts taken each January. Survey respondents are asked to assign probabilities on inflation falling in different buckets; Consensus reports the average probability in each bucket. The standard deviation is calculated assigning all the probability mass in each bucket to the midpoint of that bucket, and is plotted against the survey date. These survey density forecasts are available only since January 1999, and only for 7 countries.

Figure 8: Dispersion of Year-Ahead Survey Forecasts of Inflation

Notes: This shows the twelve-month moving average of the dispersion (standard deviation of point forecasts) of Consensus survey expectations of year-ahead consumer price inflation, (calendar year over calendar year percent change in prices). The dispersion is plotted against the month in which the twelve-month window ends. There is a gap for Australia because of missing data from December 1994 to September 1995 (see Appendix A).

Figure 9: Rolling Volatility of Year-Ahead Point Forecasts of Inflation

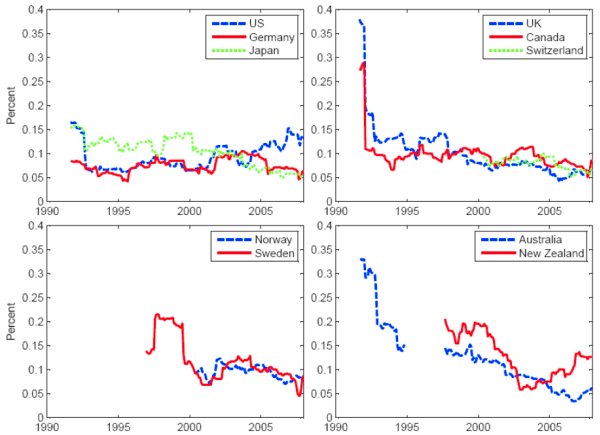
Notes: This shows the 24-month rolling standard deviation of month-to-month changes in Consensus survey expectations of year-ahead consumer price inflation, (calendar year over calendar year percent change in prices). The rolling standard deviation is plotted against the month in which the twelve-month window ends. There is a gap for Australia because of missing data from December 1994 to September 1995 (see Appendix A).

Figure 10: U.K. Nominal and Real Forward Curves Before and After Operational Independence

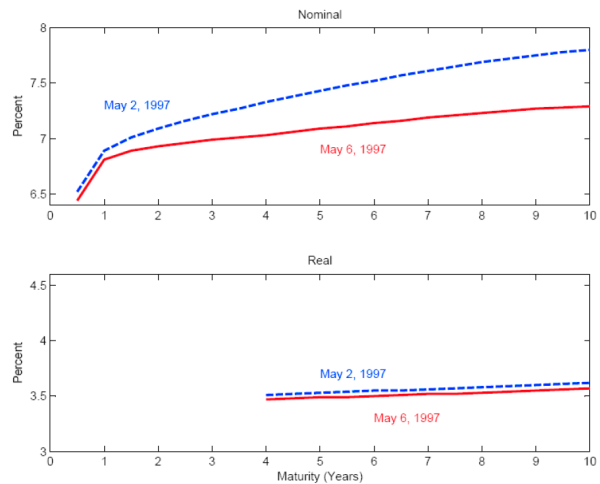
Notes: This shows the U.K. nominal and index-linked instantaneous forward real curves (source: Bank of England) on the last business day before the Bank of England was granted operational independence (Friday May 2) and the day that the announcement of independence was made (Tuesday May 6). Note that May 5 was the May Day holiday in that year.

Footnotes

1. ^* Federal Reserve Board, Washington DC 20551; [email protected]. I am grateful to Greg Duffee, Joseph Gagnon and Edith Liu for helpful discussions and to Katherine Femia and Scott Konzem for excellent research assistance. The views expressed in this paper are solely the responsibility of the author and should not be interpreted as reflecting the views of the Board of Governors of the Federal Reserve System or of any other employee of the Federal Reserve System. Return to Text

2. That is, if the correlation between inflation and consumption growth and the variance of consumption growth are both held fixed, reducing the variance of inflation must reduce the covariance between inflation and consumption growth. Return to Text

3. Focusing instead on real yields, Levin and Yun (2007) studied the relationship between consumption growth and the slope of the real yield curve, in some countries that have issued index-linked debt. Return to Text

4. The nine-to-ten-year forward rate was, on average, higher in the U.S. than in Australia and Norway over these years as well. Only New Zealand had a higher average distant-horizon forward rate. Return to Text

5. Three yield curve factors--level, slope and curvature, or some rotation thereof--provide an excellent fit to the entire term structure of nominal yields. Kim (2008) argues that if macroeconomic variables could do so as well, then it follows that one should be able to invert those macroeconomic variables from the term structure of yields. This would make the yield curve enormously useful for short-term macroeconomic forecasting. But sadly, this is not the case. Return to Text

6. Specifically, the 1, 2, 3, 4 and 6 quarter and 2, 3,....10 year zero-coupon yields. Return to Text

7. Mechanically, this is because over the available sample period, the New Zealand yield curve has on average sloped down. Return to Text

8. The ECRI creates business cycle dates for foreign countries, mirroring the methodology used by the NBER. Return to Text

9. See Kozicki and Tinsely (2001) for a discussion of term structure models in which endpoints of the short rate process are allowed to shift over time. Return to Text

10. Piazzesi and Schneider (2008) adopt a different way of estimating term premiums from surveys. The surveys that they use give a forecast of the change in ten-year yields over the next year (Consensus does so too). They then derive the implied expected excess return on holding a ten-year bond over a one-year bond for a holding period of one year and treat this as their term premium. There are three reasons why I do not adopt this approach. The first is that I only have Consensus data on forecasting changes in ten-year yields back to 1995. The second is that yield term premiums seem easier to interpret economically than holding-period expected excess returns. Finally, and most importantly, I did calculate the implied expected excess returns using the Consensus data, following Piazzesi and Schneider, and found that expected excess returns were typically negative, and below -6 percent per annum at times for some countries, which seemed to me to be outside of what could be considered reasonable. Froot (1989) and Bacchetta, Mertens and van Wincoop (2008) find that survey forecast errors for short-term predictions of expected excess bond returns are highly predictable, whereas Ang, Bekaert and Wei (2007) (and others) find that survey forecast errors for inflation are not. Perhaps survey respondents find the prediction of short-term changes in long-term bond yields to be more challenging than prediction of inflation and output growth. Return to Text

11. Consensus Forecasts does a long-horizon survey twice a year--used elsewhere in this paper--but does not report the dispersion of these forecasts. Return to Text

12. There are 22 observations in each rolling standard deviation, because there are no observations for the changes in inflation forecasts from December to January. For example, in January 1991, the year-ahead forecast was for 1992, but no forecast for 1992 was made in December 1990. Return to Text

13. If we think that agents expect inflation to reach its long-run expected value within five years (even though that long-run expectation may change from over time), then the flattening of the nominal forward curve beyond the five-year horizon shown in Figure 9 must represent, at least in part, a decline in the inflation risk premium. Return to Text

14. A coefficient is deemed significant if the 95 percent bootstrap confidence interval for that coefficient does not straddle zero. Return to Text

15. A natural corollary of any positive relationship between inflation uncertainty and term premiums is that countries with high inflation uncertainty should choose to issue shorter maturity debt. However, I do not examine the relationship between average debt maturity and inflation uncertainty in this paper. Return to Text

16. SURV-DENS was excluded because these data are only available back to 1999 and only for the U.S., Japan, Germany, the U.K., Canada, Australia and New Zealand. As none of these countries adopted an inflation target during this period, a panel data regression of SURV-DENS on the inflation targeting dummy with fixed effects would not be identified. Return to Text

^♣ This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to Text

Home | Economic Research and Data | Accessibility | Contact us
Last update: May 30, 2008