Tips from TIPS: the informational content of Treasury Inflation-Protected Security prices*
Keywords: Term structure model; Inflation expectation; Inflation risk premium; SPF; Treasury Inflation-Protected Securities (TIPS)
Abstract:
JEL Classification: G12, E31, E43
1 Introduction
Since its inception in 1997, the market for Treasury Inflation-Protected Securities (TIPS) has grown substantially and now comprises about 10% of the outstanding Treasury debt market. Almost a decade's TIPS data thus accumulated is a rich source of information to academic researchers and market participants alike. Because TIPS are securities whose coupon and principal payments are indexed to the price level, information about yields on these "real bonds" has direct implications for asset pricing models, many of which are written in terms of real consumption. Meanwhile, real-time TIPS data have attracted much attention from policy makers and market participants as a source of information about the state of economy. In particular, the differential between yields on nominal Treasury securities and on TIPS of comparable maturities, often called the "breakeven inflation (BEI) rate" or "inflation compensation", has been often used in policy circles and the financial press as a proxy for the market's inflation expectations.
However, certain complications arise in interpreting the information from TIPS yields. First, TIPS might not have been "efficiently" priced, due to their lower liquidity, the relative newness of the TIPS market, and other factors. Second, besides such institutional idiosyncrasies, the interpretation of the TIPS breakeven rate as an inflation expectation depends on the validity of the "Fisher hypothesis", which states that the nominal yield is the real yield plus expected inflation. This relation is only approximate, however, as it ignores the potential correlation between inflation and the real economy. More formally, we can define the nominal yield as the sum of the real yield, expected inflation, and the inflation risk premium. The last component may be substantial; indeed, the presence of an inflation risk premium in nominal bonds, translating to an additional financing cost for Treasury to issue nominal bonds, was one of the argument for issuing TIPS in the first place.
These issues naturally lead to the following questions: (1) Can we take TIPS yields at face value? Are they suitable for use as an input for other studies that involve ex ante real interest rates? (2) Can we take the TIPS breakeven rate as a reasonable measure of inflation expectations? Do movements in the breakeven rates reflect "fundamentals" or extraneous factors?
The purpose of our paper is to provide quantitative evidence that bears on these questions. Specifically, we model the dynamics of nominal yields, inflation, and TIPS yields in a general no-arbitrage term structure model setting, and examine the extent to which these data are consistent with each other. Furthermore, we seek to establish some basic facts about the real term structure and the inflation risk premia implicit in nominal bond yields and to obtain an estimate of the "liquidity premium" in TIPS yields.
Although there have been other studies that use a no-arbitrage framework to model the U.S. real term structure, they have not explicitly explored the efficiency of TIPS pricing or estimated a liquidity premium in TIPS yields. Also, these studies do not employ TIPS data in estimation, with the exception of Chen, Liu and Cheng (2005).1 Studies such as Ang, Bekaert and Wei (2007a), Chernov and Mueller (2007) and Buraschi and Jiltsov (2005) produce "shadow real yields" which could be compared with the TIPS yields. However, the estimates of real yields (as well as other quantities, like the inflation risk premium) from these studies differ a lot from each other, and in many cases are too much at odds with the priors of practitioners, possibly indicating problems in the specification or estimation of the model.
In view of the fact the the pricing mechanisms behind nominal and real bonds are not well understood, in this paper we take a statistical perspective, and use flexibly specified affine-Gaussian latent-factor models, which may face less misspecification concerns than some of the models in the existing literature. Also, in the estimation stage, we strive to address the small sample and overfitting problems that can lead to poor results, by utilizing additional information in survey forecasts and experimenting with different auxiliary conditions to search for robust conclusions.
Our main results can be summarized as follows. In all the cases that we have examined, estimating the model taking TIPS yields at their face value fails to produce plausible estimates of inflation expectations or inflation risk premia. The difference between the observed TIPS yields and the model-implied real yields estimated without TIPS data indicates that the "liquidity premium" was quite large in the early years of TIPS's existence, but has become smaller recently. This liquidity premium turns out to be difficult to account for within a simple rational pricing framework, suggesting that TIPS may not have been priced efficiently in their early years. Nonetheless, time variation in TIPS-based and model-implied breakeven rates are quite similar, suggesting that changes in the TIPS breakeven rates largely reflects changes in inflation expectations or in the investors' attitude toward inflation risks, rather than being random movements.
The rest of this paper is organized as follows. In Section 2, we discuss the informational content of TIPS yields in simple terms as well as the related literature. Section 3 specifies the no-arbitrage approach to modeling inflation, nominal yields, and real yields jointly. Section 4 describes the empirical strategies for estimating the model and presents the empirical results. Section 5 provides additional discussion of the model estimates and the interpretation of the TIPS information, and Section 6 concludes. Throughout the main text, we strive to keep the discussion relatively non-technical, relegating most of the technical details to the Appendices.
2.1 TIPS breakevens as measures of expected inflation
Despite potential complications associated with the inflation risk premium and the liquidity premium, TIPS breakeven rates have been frequently used as a proxy for inflation expectations by policy makers and market practitioners. The minutes of FOMC meetings often take note of changes in TIPS yields since the previous meeting,2 and it is not uncommon to see explicit references to TIPS breakeven rates in Fed officials' speeches.3 Similarly, TIPS breakeven rates are frequently cited in the financial press when discussing inflation expectations.
Such usages indicate that many practitioners find TIPS breakeven rates to be a plausible measure of market inflation expectations. Indeed, empirical evidence indicates that TIPS breakeven rates respond to news arrivals or important economic events in the "right" direction.4 It is, however, difficult to tell from such event studies whether the magnitude of the reaction is right, which is also of considerable interest. This question about the magnitude of TIPS breakeven rates' reaction to data announcements is a part of the larger discussion about whether the variability and the level of TIPS breakeven rates are reasonable, to which we now turn.
One way to examine the reasonableness of the level and the variability of TIPS breakeven rates is to compare them with another measure based on survey forecasts of inflation. There are largely two kinds of surveys available. One is the Michigan survey, which polls households (consumers), and the other, such as the Blue Chip survey or the SPF survey, polls "professionals" (business forecasters). Figure 1(a) shows the the Michigan survey of long-term inflation forecast and the 10-year SPF inflation forecast, together with the 10-year TIPS breakeven inflation rate.5 It can be seen that until recently the TIPS breakeven rate has been lower than these survey forecasts. In the case of the Michigan survey, the TIPS breakeven rate has remained substantially lower throughout the 1999-2007 period.
Note that comparing the level of TIPS breakeven rates with the Michigan survey may not be fair. An inflation measure can depend significantly on the definition of the consumption basket, how quality changes are taken into account, and other issues.6 While the TIPS breakeven rate relates to CPI inflation, the Michigan survey asks the participants for their views about the change in the "prices of things you buy" rather than inflation based on a specific price index. However, even the 10-year SPF inflation forecast, which is specifically about CPI inflation, tended to be higher than the 10-year TIPS breakeven rate until about 2004. This is surprising: one would have expected the TIPS breakevens to be higher, since it includes an inflation risk premium, which is normally believed to be positive.
One might argue that the fault lies with the survey forecast rather than with TIPS. Survey forecasts cannot be expected to be a completely reliable measure of inflation expectations. That said, a quick comparison of the 1-year ahead CPI inflation forecasting performance of the 5-year TIPS breakeven rates versus the SPF survey forecast7 for the 1999:Q1-2007:Q3 period produces the following root-mean-square errors (RMSE):
TIPS breakeven rates differ from survey forecasts not only in levels but also in variability. Figure 1(a) shows that TIPS breakeven rates exhibit greater time variation than the survey forecasts. The Michigan survey may contain a substantial amount of sampling error and other noise.8 However, once we look beyond the monthly noise and focus on the systematic movement, the long-horizon Michigan survey forecast seems to be less variable than the TIPS breakeven rate. An even greater contrast with TIPS is offered by the 10-year SPF inflation forecast, which has been pretty much immobile in the 1999-2006 period. This may appear suspicious: even if long-term inflation expectations are "well anchored", it is difficult to imagine that they have become virtually immovable as suggested by the SPF survey. Nonetheless, the qualitatively similar messages from the two surveys raise the possibility that the greater variability of TIPS breakevens may be a robust fact.
One possible explanation is that part of the TIPS breakeven rate variation is due to variations in the inflation risk premium rather than changes in inflation expectations. The difficulty with this argument is that the level consideration seems to leave little room for inflation risk premium, at least one that is positive.
3.1 Fisher hypothesis and beyond
It is useful to start with the Fisher hypothesis,
where
![\displaystyle I_{t,\tau} = E_{t}\left[ \frac{1}{\tau} \log\left( \frac{Q_{t+\tau}}{Q_{t}% }\right) \right] ,](img14.gif) |
(2) |
where
and approximate inflation expectations as
As mentioned earlier, however, the Fisher hypothesis ignores potential correlation effects. To go beyond Fisher hypothesis, one needs to model the dynamics of real rates and inflation together. For this purpose, it is convenient to utilize a no-arbitrage relation between the so-called "pricing
kernels" or "stochastic discount factors". A real (nominal) pricing kernel, ![]() (
(![]() ), has the property that it gives today's market value of a future payoff in real (nominal) terms.17 In particular, real and
nominal bond prices,
), has the property that it gives today's market value of a future payoff in real (nominal) terms.17 In particular, real and
nominal bond prices, ![]() and
and ![]() , are given by
, are given by
| (4) |
Note that in nominal terms, a real bond is an asset whose payoff is proportional to the price level. This means that the real and the nominal pricing kernels are linked by the "no-arbitrage relation"18
Using this relation, we have
Thus, by specifying the joint dynamics of
where the inflation risk premium term
It may be useful to discuss briefly the advantages and disadvantages of the no-arbitrage setup. The no-arbitrage principle is more general than the Fisher hypothesis, but in order to operationalize the no-arbitrage idea, one has to make assumptions about the dynamics of pricing kernels and the
price level, and can expect to incur some amount of specification error in the process. For example, some of the studies in the literature adopt a structural specification of the real pricing kernel, ![]() .21 While this approach has the potential benefit of making a definite connection between macroeconomic fundamentals and bond yields,
it is not clear how well the current generation of structural models can capture the mechanisms that underlie asset price variation and inflation.22
Reduced-form models are not exempt from misspecification concerns, either. One example is Richard (1978)'s model, whose potential specification problems were discussed earlier in Sec. 2.2. Note also that if a model has too small a number of factors (e.g., a
2-factor model), it may have difficulty capturing the cross-section of the nominal yield curve well, resulting in sizable fitting errors and making it difficult to discuss actual market developments based on the model.
.21 While this approach has the potential benefit of making a definite connection between macroeconomic fundamentals and bond yields,
it is not clear how well the current generation of structural models can capture the mechanisms that underlie asset price variation and inflation.22
Reduced-form models are not exempt from misspecification concerns, either. One example is Richard (1978)'s model, whose potential specification problems were discussed earlier in Sec. 2.2. Note also that if a model has too small a number of factors (e.g., a
2-factor model), it may have difficulty capturing the cross-section of the nominal yield curve well, resulting in sizable fitting errors and making it difficult to discuss actual market developments based on the model.
Although the Fisher relation in eq. (1) ignores the inflation risk premium, it leaves smaller room for cross-sectional fitting errors. Often it is unclear whether the specification errors in no-arbitrage models are any smaller than the error of ignoring the inflation risk premium. Indeed, we are not aware of any no-arbitrage model-based procedures for computing inflation expectations from bond yields that is as widely used by practitioners as the method based on the cross-sections of nominal and indexed bond yields (Fisher hypothesis). Even so, there are issues which the Fisher hypothesis simply cannot address. First, one cannot learn the dynamics of inflation expectations or the real and nominal term structures just from the cross-sectional analysis of TIPS yields and nominal yields. Second, there are periods in which the indexed bond market did not exist, such as pre-1997 in the U.S. Third, even if the indexed bond market exists, one might wish to examine whether indexed bonds are priced efficiently. To address these issues, one needs a dynamic model like the no-arbitrage model.
3.2 No-arbitrage model
In this section we provide a "big picture" description of our model, relegating technical details of the model to Appendix A.
Basically, we view our modeling problem as a statistical one: find affine functions
of an
The affine-Gaussian model of the type used here is attractive as a model for capturing the variation in term premia (departures from the expectations hypothesis); it is reasonable to expect that some of the variation in the term premium in nominal bonds reflect variations in the inflation risk premia. Furthermore, the affine-Gaussian models allow for a flexible factor correlation structure, which is important since the departure from Fisher hypothesis involves a correlation effect.
All risk factors (state variables) in our model are latent factors. This may sound unappealing as latent factors are not easy to interpret economically. While it would be desirable to be able to interpret the yield curve movements macroeconomically, in view of the fact that so little is empirically established about quantities like real yields and the inflation risk premia embedded in nominal yields (as discussed in Section 2.2), in this paper we set a more modest goal of "measuring" them. The latent factor approach seems attractive for this purpose, as it is more general than no-arbitrage models that use observed macro variables as risk factors. Kim (2007a) has argued that a substantial part of short-run inflation is unrelated to bond yields; hence the use of realized inflation as a risk factor (e.g., Ang, Bekaert and Wei (2007a) and Chernov and Mueller (2007)) involves strong assumptions.
In this paper, we focus on the three-factor (![]() ) case. Note that numerous variables could influence nominal yields, including the instantaneous inflation expectation,
) case. Note that numerous variables could influence nominal yields, including the instantaneous inflation expectation, ![]() , the real short rate,
, the real short rate, ![]() , variables that affect their future movements (such as a
time-varying perceived inflation target), variables that underlie time variation in the real term premium, the inflation risk premium, and inflation and interest rate uncertainties, among others. However, all these variables are not independent, and we can envision a relatively low-dimensional
vector of latent factors summarizing the information in these variables. We do not mean to suggest that three factors are sufficient. Nonetheless, in view of the fact that many of the nominal-yields-only models in the literature have been estimated with 3 factors (e.g., Dai and Singleton (2000),
Duffee (2002), Kim and Orphanides (2005)) and that fitting errors for nominal yields are fairly small for
, variables that affect their future movements (such as a
time-varying perceived inflation target), variables that underlie time variation in the real term premium, the inflation risk premium, and inflation and interest rate uncertainties, among others. However, all these variables are not independent, and we can envision a relatively low-dimensional
vector of latent factors summarizing the information in these variables. We do not mean to suggest that three factors are sufficient. Nonetheless, in view of the fact that many of the nominal-yields-only models in the literature have been estimated with 3 factors (e.g., Dai and Singleton (2000),
Duffee (2002), Kim and Orphanides (2005)) and that fitting errors for nominal yields are fairly small for ![]() , the three-factor case can be viewed as an important benchmark to be explored.
With fewer factors, the cross-section of yields would be fit less well, so that it might become harder to describe actual market movements. With large number of factors, on the other hand, empirical difficulties (e.g., overfitting concerns) may increase.
, the three-factor case can be viewed as an important benchmark to be explored.
With fewer factors, the cross-section of yields would be fit less well, so that it might become harder to describe actual market movements. With large number of factors, on the other hand, empirical difficulties (e.g., overfitting concerns) may increase.
Traditionally, the real term structure is often modeled as of a lower dimension than the nominal term structure.24 In this paper we let the real term structure have as many factors as the nominal term structure; if the real term structure is truly lower-dimensional than the nominal term structure, we let the data decide on that. A related point is that in a reduced-form setup like ours, one cannot make a distinction between the real and the nominal factors, as the correlation effect in a general model make such a distinction meaningless.
While the affine-Gaussian model offers a rich and flexible framework for describing inflation and the interest rates, it does have a shortcoming, namely that it implies time-invariant interest rate volatilities and inflation uncertainties. Intuitively we would expect that the term premia in nominal and real bonds, as well as the inflation risk premia, would depend not only on the price of risk but also on the quantity of risk, but affine-Gaussian models assume the latter is constant. Nonetheless, affine-Gaussian models may still provide a reasonable estimate of various quantities of economic interest as documented by Duffee (2002) and others, despite the counterfactual assumption of constant yield volatility.
It would certainly be desirable to model time-varying uncertainty explicitly, but there may be a greater risk of misspecification as well as implementation difficulties with stochastic volatility models. Furthermore, in the affine model setting, there is a trade-off between a flexible factor correlation structure and flexible stochastic volatility modeling, as discussed by Dai and Singleton (2000). Modeling of stochastic volatility is also complicated by the debates as to whether and how to incorporate unspanned stochastic volatility (USV) effects.25 Furthermore, as discussed in Kim (2007a), an explicit modeling of time-varying inflation uncertainty could be especially challenging, as the short-term and long-term inflation uncertainties may behave in a qualitative different manner. In view of these open issues with stochastic volatility models, we focus on the affine-Gaussian models in this paper, with the presumption that they would be useful benchmark results, before these "more advanced" issues are tackled.
4.1 Overall empirical strategy
Our model (sketched in Sec. 3.2 and spelled out in Appendix A) can be estimated with or without the TIPS data. If the model is estimated with the nominal yields and inflation but without the indexed-bond data, the resulting model-implied real yields can be viewed as the shadow real yield. This "hypothetical" yield can be useful in many contexts. For example, this is the relevant yield when thinking about the ex ante real interest rates implied by asset pricing models, the majority of which are written in real terms. In the case of pre-1997 U.S., indexed bonds did not exist; therefore the "hypothetical" real yields are all one can talk about.
If indexed bonds are available, as in the U.S. post-1997, one can include them in the estimation, equating the model-implied real yields with the traded indexed-bond yield up to an error term. This can potentially improve the efficiency of the estimation. On the other hand, should the model-implied real yield and the traded indexed bond yield differ for some reason, or if there is a failure of relative pricing between the indexed bonds and the nominal bonds, the inclusion of TIPS in the estimation can lead to poorer results.
The conditions that the model be (1) Gaussian, (2) linear in some basis, and (3) maximally flexible (econometrically identified), lead to an almost unique specification that we can analyze.26 However, the implementation of the model faces many challenging issues, and the estimates can depend materially on the implementation. In particular, the conventional (Kalman-filter-based) ML estimation of the model, using just nominal yields and inflation (with or without TIPS) data, leads to poor estimates which most practitioners would dismiss immediately. For example, as mentioned briefly in Sec. 2.2, one often obtains long-horizon expectations of inflation and interest rates that are too stable and fixed near the sample means of these variables. Kim and Orphanides (2005), for example, provide Monte Carlo evidence that conventional estimations tend to understate the variability of long-horizon short rate expectations and overstate the variability of term premia.
The problem is that due to the persistence of interest rates and inflation, a typical sample used in the literature (e.g., 15 years' data) is not long enough, no matter how frequently it is sampled. Basically, we have a "small-sample problem" which manifests itself in two ways: (1) a biased estimate that leads to artificially stable long-horizon expectations, and (2) a very imprecise estimate, arising from the fact that parts of the model that are important for the description of physical (real-world) dynamics of interest rates and inflation are difficult to estimate reliably. Furthermore, for a 3-factor model, the number of parameters to be estimated is already quite large, raising concerns about overfitting.27
Another difficulty is with the evaluation of the estimated model. Though in-sample and out-of-sample forecast root-mean-square errors (RMSE) can help detect problematic models, selecting a model (estimate) based on the "smallest RMSE" criterion would be inadvisable: in-sample RMSEs may have been artificially pushed down due to the use of the future information and the especially flexible nature of latent factor models, and out-of-sample RMSEs may have low statistical power especially in view of the considerable volatility of short-run inflation in the recent several years. Testing for a bias in the forecast is also ambiguous: an unbiased forecast has been traditionally regarded as desirable in the academic literature, but a mild bias may be a more realistic description of the market expectations in the sample period considered here.28
In light of these considerations, rather than relying on a single implementation, we shall explore several different implementations of the model (different options for the data and the auxiliary conditions for addressing the small-sample problems) and seek to establish relatively robust empirical conclusions, focusing on the basic question of whether disparate pieces of input data can be made consistent with reasonable priors.
4.2 Data and estimations
We use 3- and 6-month, 1-, 2-, 4-, 7-, and 10-year nominal yields and CPI-U data from January 1990 to March 2007. When TIPS yields are used, they cover a shorter period from either January 1999 or January 2005 to March 2007, and are treated as missing observations in the rest of the sample. Both the nominal and the TIPS yields are based on zero-coupon yield curves fitted at the Federal Reserve Board29 and are sampled at the weekly frequency, while CPI-U inflation is available monthly and assumed to be observed on the last Wednesday of the current month.30 Due to the complications associated with the shorter-maturity TIPS yields which are discussed in detail in Appendix B, only the 10-year (zero-coupon) TIPS yield is used in estimations with TIPS data. This focus on the 10-year TIPS yield also reflects our special interest in long-term inflation expectations; as discussed in Kim (2007a), a key information embedded in bond yields is about the "trend component" of inflation, which can be better proxied by long-term, rather than short-term, inflation expectations. Because the model we estimate does not accommodate seasonality, we use the seasonally-adjusted CPI inflation in the estimate. TIPS are indexed to non-seasonally-adjusted CPI, but our use of seasonally adjusted CPI is not expected to matter much for a relatively long maturity like 10 years.
The sample period 1990-2007 was chosen as a compromise between having more data so as to improve the efficiency of estimation, and having a more homogeneous sample so as to avoid possible structural breaks in the relation between term structure variables and inflation (e.g., the 1979-83 episode of Fed's experiment with reserve targeting). This sample period roughly spans Greenspan's tenure and a little bit of Bernanke's as well.
When TIPS data are used in the estimation, the zero-coupon TIPS yield, denoted
![]() , is taken to be
, is taken to be
where
To address the aforementioned small-sample and overfitting problems, we supplement the nominal yields, TIPS yields, and CPI data with survey data on the forecasts of future short-term (3-month) nominal rates in all estimations reported here.32 We experiment with additionally including the survey forecasts of inflation in the estimation.33 These survey-based forecasts are quite straightforward to incorporate within the Kalman-filter-based maximum-likelihood framework: they are taken as the model's forecast plus a measurement error, i.e., we assume
| (12) | ||
| (13) |
where the superscript
As in Kim and Orphanides (2005), we use the 6-month- and 12-month-ahead forecasts of the 3-month T-bill yield constructed from Blue Chip Financial Forecast that are available monthly, letting the estimation decide the size of the measurement errors
![]() . The long-horizon forecast of the 3-month T-bill yield (available twice a year) is also used, with the measurement error
. The long-horizon forecast of the 3-month T-bill yield (available twice a year) is also used, with the measurement error
![]() fixed at a fairly large value of 0.75% at an annual rate.
fixed at a fairly large value of 0.75% at an annual rate.
For estimations that also incorporate the survey inflation forecast information, we use the survey forecasts of business economists instead of the consumer survey forecasts, for reasons discussed earlier. Specifically, we use the 1- and 10-year inflation forecasts from the SPF. We could let the size of the measurement errors be free variables to be estimated. However, given that our interest is in uncovering information about inflation expectations contained in nominal and TIPS yields, we fix the measurement error variability at a large, but not irrelevant, value of 0.75% at an annual rate to avoid making the survey inflation forecast information too influential. This can be viewed in the Bayesian spirit as providing a quasi-informative prior. In sum, we perform two versions of estimation in this paper:
| (14) | ||
| (15) |
The measurement error size at
4.3 Estimation results
In the rest of the paper we examine the results from five estimation methods with different auxiliary conditions: the version I estimation without TIPS data (denoted NT-I), the version II estimation without TIPS data (denoted NT-II), the version-I estimation with 10-year TIPS yield from 1999 (denoted T99-I), and the version-II estimation with 10-year TIPS yield from 1999 (denoted T99-II). For reasons that will become clear at the end of this section and in Sec. 5, we also examine an estimation using TIPS data starting from 2005 (denoted T05-II). Table 1 provides a summary.35
The parameter estimates and the corresponding standard errors from all five estimations are given in Appendix C, while Appendix D provides some discussions on the unconditional moments of various term structure variables as implied by the model.
4.3.1 Estimations without TIPS
Let us first examine the estimations without the TIPS data (NT-I and NT-II). As can be seen from Figures 2 and 3, the results from these two estimations are broadly similar. For example, comparing the top left panels in both figures shows that the 10-year inflation expectations in both estimations trend down from about 4% in early 1990 to about 2% by mid 2005, picked up again since then and now average around 2.5%, largely in line with the SPF long-horizon inflation forecast. This might not be surprising for NT-II, as survey inflation forecasts were used in estimation, albeit with an allowance for arguably large deviations from the true forecasts. It is encouraging to see that NT-I also generates a similar downward trend rather than a flat long-term forecast; apparently the survey interest rate forecast information is helping to pin down those parameters that are relevant for describing long-horizon inflation expectations. In both NT-I and NT-II, the "term spread" between the 1-year and 10-year inflation expectations is fairly narrow, a feature that is also shared with the survey-based inflation forecasts.
The NT-I-implied inflation expectations are somewhat lower than both the model forecasts from NT-II and SPF forecasts, which in turn implies a somewhat better in-sample inflation forecasting performance by NT-I relative to that of NT-II, since realized inflation tended to be low in much of the 1990s. This does not necessarily put the NT-I results in a better light, as such a result is likely due to a look-ahead bias.36
The model-implied 10-year breakeven rates, defined as the difference between the model-implied nominal and real yields, are shown in the top right panels of Figures 2 and 3, together with the 10-year TIPS breakeven rate. Based on both NT-I and NT-II, there is a level difference between the model-implied and TIPS breakeven rates up to about 2004, with the latter being substantially lower than the former. Nonetheless, the time variation of the two are broadly similar. For example, both the model-implied and the TIPS breakeven rates peak locally at the beginning of 2000, in the middle of 2001 and 2002, and so on, and the scales of their variation are also similar. Since late 2004, the two series largely move together within 30 basis points from each other.
The bottom left panels show the inflation risk premia at the 1- and 10-year maturities. In both NT-I and NT-II, the 10-year inflation risk premium is positive and fluctuates in a range of about 50 basis points in the 1990-2007 period. It is also encouraging that for maturities of 1-year and below, the inflation risk premium is quite small.
The model-implied real yields are plotted in the bottom right panels for the 1- and 10-year maturities. A comparison across maturities reveals that the model-implied real yield is more variable at the shorter maturity, with changes in the real yield accounting for about 75 (60) percent of the variation in the nominal yield at the 1-year (10-year) maturity, which lends some support to the usual wisdom that expected inflation affects the longer-term nominal yields to a larger extent (see, for example, Fama (1975) and Mishkin (1981)). The model-implied real yield is also highly correlated with the 10-year inflation expectation.
4.3.2 Estimations with TIPS
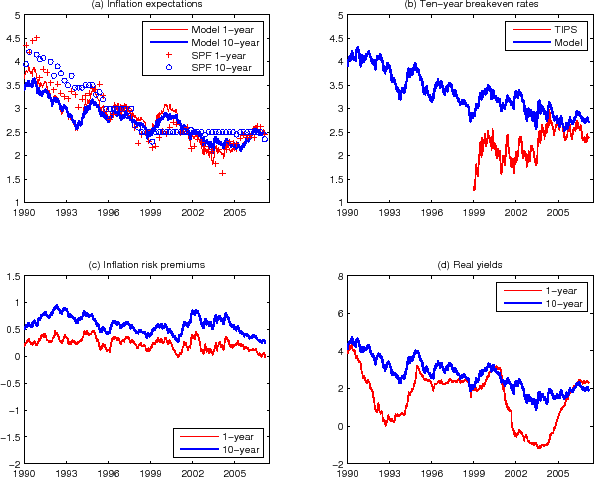
Next we look at how the model implications change when TIPS yields are used in the estimation at their face value, up to a constant liquidity premium. Figures 4 and 5 display the corresponding results from the estimation with 10-year TIPS yield data from 1999-2007, either with or without the survey inflation forecast data (T99-II and T99-I).37 The model-implied inflation expectations from the T99-I estimation, shown in the top left panel of Figure 4, are not very plausible. Few would take seriously the notion that the 10-year inflation expectation has not changed much in the past 15 years. The near constancy of model-implied long-term inflation expectation observed here arises from the tension between the upward trend in the TIPS breakeven rates, shown in the top right panel, and the downward trend in the long-term inflation expectation implied by nominal yields and interest rate forecasts, demonstrated by the NT-I estimation and shown in the top left panel of Figure 2. In addition, the variation in the 1-year inflation expectation is too large to be credible, and the level of the 1-year inflation expectation in early 1990s is too low. Comparison with the survey forecasts makes the last two points clear.
The top right panel of Figure 4 points to further problems with the T99-I estimation. While the T99-I-based breakeven rate matches the "level" of the TIPS breakeven rate better than the NT-I and NT-II estimations, it misses the short-run time variations in the TIPS breakeven rates; in fact it is almost constant over time.38 In addition, the model-implied inflation risk premium is negative and increases over the sample period. This is at odds with the general perception that the inflation risk premium has been historically positive. As discussed in Sec. 2, the inflation risk premium likely was positive and substantial in the early 1980s and probably has come down since then, whereas we observe almost the opposite behavior in the bottom right panel of Figure 4. The 95% confidence interval for the 10-year inflation risk premium in this estimation is shown in Figure A3 in Appendix C. Even allowing for sampling uncertainties, the results still appear implausible.
The results from the T99-II estimation, which uses survey inflation forecast data, are shown in Figure 5. The model-implied 1-year and 10-year inflation expectations, shown in the top left panel, are now in better accordance with survey forecasts. However, the model-implied breakeven rate, shown in the top right panel, again misses most of the short-run variability of the TIPS breakeven rate, and the inflation risk premia, shown in the bottom right panel, are even more unreasonable, implying a 10-year inflation risk premium of about -2% in 1990. Even the "short-term" (1-year) inflation risk premium departs a lot from zero, being quite negative in 1990.
We have experimented with other auxiliary estimation conditions (e.g., using the 5-year and 7-year TIPS yields in addition to the 10-year TIPS yield, using different measurement error structure for survey forecasts, etc.), but obtained similarly implausible results for inflation expectations and/or inflation risk premia. Basically, when TIPS data from 1999 to 2007 are taken at the face value up to a constant liquidity premium, it seems impossible to obtain sensible and consistent results within a 3-factor no-arbitrage model setting.39
As we can see from NT-I and NT-II estimations without TIPS data, the model-implied and TIPS breakeven rates line up reasonably well in the last several years. Thus, we also perform an estimation using the 10-year TIPS yield only from 2005 to the present (T05-II). The results from this estimation are shown in Figure 6. This shorter-sample-TIPS estimation produces more reasonable inflation risk premium estimates and agrees with the NT-I and NT-II estimation results better: The T05-II-implied 10-year breakeven rate (upper right panel of Figure 6) now shows similar variations as the TIPS breakeven rate, and contrasts sharply with those of T99-I and T99-II estimations. The 10-year inflation risk premium based on the T05-II estimation (lower left panel of Figure 6) is somewhat lower than those from NT-I and NT-II estimations, but its overall variation is similar.
5.1 Real yield and inflation risk premium
One common feature among the alternative estimation results reported in the previous section is that the model-implied 10-year real yield (long-term real yield) moves around substantially, and more specifically, it mirrors much of the movement in the 10-year nominal yield. This is the case with the 10-year TIPS yield as well. Figure 7 illustrates this point by comparing the 10-year nominal yield with the model-implied 10-year real yields from the NT-II and T05-II estimations (panel (a)) and the TIPS 10-year yield (panel (b)). The strong positive covariation between the nominal yield and the model-implied real yield (or TIPS yield) works toward reducing the variability of the breakeven inflation (the differential between the nominal yield and the real yield); even so, the breakeven inflation rate is more variable than the survey long-term inflation expectation, as we have discussed in Sec. 2.1.
Although the feature that real yields tend to track nominal yields may appear unremarkable to practitioners who largely equate the TIPS yield with the real yield, that is not the case in the extant academic literature. For example, it is harder to see a similarity between the long-term real yield and the nominal yield in Ang, Bekaert and Wei (2007a, Figures 1 and 2). Even more striking is the result of Chernov and Mueller (2007, Figure 7), in which their preferred model (Model AO) generates a 10-year real yield that stays almost constant during the entire post-1970 sample period. Note that the real yields from these studies would imply an even more variable breakeven inflation rate, which is even harder to reconcile with the survey evidence.
The term structure model allows us to decompose the real yield into a "real expectations" component and a "real term premium" component, i.e.,
where
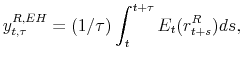 |
(17) |
while the terms inside the parentheses in eq. (16) represent deviations from the expectations hypotheses. The variance decomposition results, reported in the first two columns of Table 2, show that changes in the expected future short rates account for most of the variation in real yields at shorter maturities, while much of the variation in the 10-year real yield is due to movement in the real term premium.
Figure 8 plots the decomposition of the 10-year real yield, based on the NT-II and T05-II estimations. In both cases, the real expectations component displays a fairly "stationary" behavior, the variation being mainly the ups and downs associated with business cycles. The real term premium, on the other hand, displays a visible downward trend. This may be due in part to the gradual reduction in risk, manifested as declining uncertainty associated with key macroeconomic variables since the Volcker disinflation, a phenomenon often dubbed the "great moderation."40 The real term premium component also contains substantial short-run variation. In some sense, this is not surprising: a visual inspection of the 10-year TIPS yield and the 10-year nominal yield in the 1999-2007 period shows a lot of similar variation in them; thus, if we accept that nominal yields contains a substantial amount of term premium variation (as indicated by various expectations hypothesis tests), we can expect a similar effect for real yields as well.
Let us now turn to the inflation risk premium. It is worth noting that, although our estimates of the inflation risk premium (NT-I, NT-II, T05-II) display interesting variation over time, our inflation risk premium is a less prominent driver of the 10-year nominal yield than in some other studies. For instance, Chernov and Mueller (2007)'s results imply that most of the variation in the 10-year nominal yield is due to the variations in the inflation risk premium, because of the near-constancy of their long-term real yield estimates. Our inflation risk premium estimates also differs substantially from those in Ang, Bekaert and Wei (2007a, Figure 5). In particular, their estimates sometimes show sharp jumps even though no such changes are observed in the corresponding nominal yields (e.g., early 1987, early 1990 and late 2000).
Intuitively, the inflation risk premium can be expected to be positively linked to inflation uncertainty. We therefore correlate our inflation risk premium estimates from the NT-II and the T05-II estimations with two measures that could be viewed as proxies for such uncertainties. Our first measure of inflation uncertainty is the dispersion of long-term inflation forecasts, constructed as the distance between the average of the top ten forecasts and that of the bottom ten forecasts of CPI inflation 5 to 10 years hence from the Blue Chip Economic Indicators survey, available twice a year since 1987. As can be seen from Figure 9(b), this measure was trending lower during much of the 1990s and has been relatively stable since 2000, suggesting diminished inflation uncertainties in recent years. Inflation risk premium estimates based on the NT-II estimation are highly correlated with this measure with a correlation coefficient of 0.55. The corresponding correlation coefficient based on the T05-II estimates, however, is negative at -0.15 over the full post-1990 sample. A closer inspection reveals that the negative correlation comes primarily from the upward trend in the T05-II inflation risk premium estimates during the early sample period. Using data after 1996, the correlation coefficient becomes highly positive at 0.45.
Our next measure is the absolute implied volatility of the 10-year swaptions with an underlying swap tenor of one year (Figure 9(b)), which has been available since 2000. This variable measures long-run uncertainty associated with future nominal interest rates, and can also be viewed as a rough measure of inflation uncertainty if we are willing to assume that investors are relatively certain about future real yields. Our inflation risk premium estimates are also positively correlated with this measure with correlation coefficients of 0.63 and 0.58, based on the NT-II and T05-II estimations, respectively.
Finally, we could assess the relative contribution of each of the three components of the nominal yield in eq. (7) by decomposing the variance of the nominal yield into its covariances with the real yield, inflation expectation, and the inflation risk premium, respectively:
| var |
The last four columns of Table 2 report the results from this variance decomposition for yield maturities of 3 months, 1, 2, 5 and 10 years based on in-sample moments and the NT-II model estimates.41 Real yield movement accounts for about 3/4 of the variation at the shorter end of the yield curve. At longer maturities, real yield variation continues to play a dominant role, although changes in the inflation risk premia become more important. The contribution of expected inflation stays relatively stable at about 30 percent at all maturities.42 Note that the contribution of the inflation risk premium is modest (e.g., 6 percent for 10-year yield), consistent with our earlier remark that the inflation risk premium in our paper is a less prominent driver of nominal yields than in some other studies.
5.3 Interpreting the TIPS breakeven rates
We now revisit the question of whether TIPS breakeven rates are too variable and whether they are informative about inflation expectations of the bond market participants. Although the level of TIPS breakeven rates may have been too low in its early years due to nontrivial liquidity premium, the changes in TIPS breakeven rates at weekly or monthly frequencies may still be informative, as the adjustment of the TIPS yields to a more normal level may be a slow process.
Indeed, as discussed in Section 4, a visual inspection of the 10-year model-implied breakeven rates from the NT and the T05 estimations reveal that, apart from the different long-term trend, their time variations are quite similar to those of the 10-year TIPS breakeven rate; in this sense, TIPS breakeven rates might not be necessarily be excessively volatile. Part of this volatility in TIPS breakeven rates is due to the variation of the inflation risk premium (as seen in the bottom left panels of Figures 3 and 6), which in turn may be linked to time variation in inflation uncertainty (the changing perception of the credibility of monetary policy, the normal cyclical variation in business uncertainties, etc.) and in the price of inflation risk.
Figure 12(a) shows in blue circles a scatter plot of the weekly changes in the TIPS-based and the NT-II model-implied 10-year breakeven rates. The two breakeven rates line up closely against the 45-degree line, with a correlation coefficient of 0.76. A regression of the weekly changes in the TIPS breakeven rate onto the weekly changes in the model-implied breakeven rate produces a beta coefficient of 1.06, representing a roughly one-for-one relationship. On the other hand, the weekly changes in the breakeven rate implied by the T05-II model and those in the TIPS breakeven rate, shown in red pluses in Figure 12(a), are somewhat further away from the one-for-one relationship, with the beta coefficient in the same regression being 1.32.
It is also interesting to compare the weekly changes in the model-implied 10-year inflation expectation with the weekly changes in the 10-year TIPS breakeven rates, plotted in Figure 12(b). Both the NT-II and the T05-II estimations reveal a fairly clear positive
relation between the weekly changes in the TIPS breakeven rate and those in the model-implied inflation expectation, with the correlation in both cases being about 0.7. A regression of the weekly changes in the TIPS breakeven rate onto the weekly changes in the model-implied inflation expectation
gives a beta coefficient of 1.4 and an ![]() of 46% for NT-II, and a beta coefficient of 1.3 and an
of 46% for NT-II, and a beta coefficient of 1.3 and an ![]() of 50% for T05-II. Thus, the TIPS breakeven rates are informative about the direction of the change in inflation expectations (but somewhat overstating the magnitude), though a substantial part of the weekly changes in TIPS breakeven rates remains to be accounted for.
of 50% for T05-II. Thus, the TIPS breakeven rates are informative about the direction of the change in inflation expectations (but somewhat overstating the magnitude), though a substantial part of the weekly changes in TIPS breakeven rates remains to be accounted for.
6 Concluding remarks
In this paper we analyze the inflation-related information in nominal and TIPS yields from a "measurement perspective", i.e., using a flexibly-specified reduced-form model which has little structure beyond the no-arbitrage assumption. Our framework allows for nontrivial term premia and inflation risk premia, as opposed to the use of the expectations hypothesis and the Fisher hypothesis. We were particularly motivated by two questions: whether TIPS "breakeven rates" are informative about market inflation expectations, and whether TIPS yields are consistent with the economic fundamentals (or with no-arbitrage pricing).
We find that, at least from the viewpoint of a flexibly-specified 3-factor term structure model, we cannot reconcile TIPS data with reasonable priors about inflation expectations and inflation risk premia. TIPS yields seem to have been too high in the early years, possibly due to the newness of the security, the poor liquidity, and some degrees of mispricing. This implies that it may be problematic to use early years' TIPS data as "no-arbitrage consistent" real yields in other applications. On a more encouraging note, we find that the liquidity premium component of TIPS yields has become much smaller in recent years, suggesting that the TIPS information can be taken at its face value currently and in the future (assuming no deterioration of the TIPS market liquidity conditions going forward) more than in the past.
The answer to the question of whether the TIPS breakeven rate can be taken as inflation expectation is more complicated. We find that the weekly changes in the model-implied 10-year inflation expectation tend to line up with the weekly changes in the 10-year TIPS breakeven rate. However, we also find that time variation in the inflation risk premium and the TIPS liquidity premium, the latter of which may also include other unaccounted-for effects, are often significant enough to drive a wedge between the qualitative behavior of the breakeven rates and inflation expectations.
Our findings in this paper provide support for the use of TIPS breakeven rate information as a proxy for inflation expectations, but also provide a justification for caution. Indeed, in speeches that touch on inflation, policy makers often refer to the TIPS breakeven rate, but they also recognize that the interpretation of this measure is complicated by inflation risk premia and liquidity issues and then continue to monitor a large number of variables to gauge inflation expectations and underlying inflation pressures.51 More data and more work on TIPS modeling in the future will undoubtedly shed more light on the informational content of TIPS prices.
Appendix
A Joint no-arbitrage model of inflation and interest rates
The ![]() -dimensional vector of state variables
-dimensional vector of state variables
![]() follows a multivariate Gaussian process,
follows a multivariate Gaussian process,
where
Eq. (A-2) is a standard way of specifying the nominal pricing kernel, which describes nominal interest rates that follow diffusion processes. The nominal term structure in this paper is described by the "essentially affine" ![]() specification of Duffee (2002), i.e., the nominal short rate
specification of Duffee (2002), i.e., the nominal short rate ![]() and the market price of risk
and the market price of risk
![]() are specified to be affine functions of the state variables:
are specified to be affine functions of the state variables:
where
| (A-6) |
The "unexpected inflation" is allowed to depend on shocks that move the nominal interest rates (or expected inflation),
In some simple cases, for example, as in Campbell and Viceira (2001), the state vector ![]() can be represented intuitively:
can be represented intuitively:
![]() ,
,
![]() , etc. In general, however, the state variables
, etc. In general, however, the state variables ![]() 's are
statistical variables whose meaning of determined only implicitly by the data on yields and inflation. This is similar to "nominal yields only" model of Duffee (2002) and Dai and Singleton (2000); as we shall discuss below, some normalization restrictions have to be imposed to obtain an
econometrically identified model. By having a joint model of nominal yields and inflation (eqs. (A-2) and (A-3)), we are giving more meaning to the state variables (than the nominal-yields-only model), though they still remain "latent variables."
's are
statistical variables whose meaning of determined only implicitly by the data on yields and inflation. This is similar to "nominal yields only" model of Duffee (2002) and Dai and Singleton (2000); as we shall discuss below, some normalization restrictions have to be imposed to obtain an
econometrically identified model. By having a joint model of nominal yields and inflation (eqs. (A-2) and (A-3)), we are giving more meaning to the state variables (than the nominal-yields-only model), though they still remain "latent variables."
Applying Ito's lemma to eq. (5), we can derive the real pricing kernel process as
| (A-7) | |||
| (A-8) |
where
| (A-9) | |||
| (A-10) |
with
It is straightforward to show that in this formulation, the nominal yields, the real yields and inflation expectations all take the affine form - eq. (8) to (10), where factor loadings
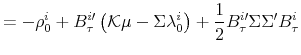 |
||
with the initial conditions
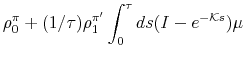 |
|||
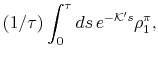 |
where
To make the model operational, we need to impose some identification restrictions (normalizations) to rule out "equivalent" models. In this paper, we impose the normalization restriction
(other parameters
However, the normalization (A-15) does cover a large set of possibilities, and is equivalent to those used in other studies such as Duffee (2002); therefore we focus on this case in this paper.55
B More on the TIPS data
This appendix is devoted to a more detailed discussion on the TIPS data. Figure A1 shows the smoothed TIPS par yield curves on June 9, 2005 in the top panel and on June 9, 1999 in the bottom panel, together with the actual traded TIPS yields that were used to create the smoothed TIPS par yield and zero coupon yield curves. The smoothing is done by assuming that the zero-coupon TIPS yield curve follows the 4-parameter Nelson-Siegel (1987) functional form up to the end of 2003 and the 6-parameter Svensson (1994) functional form thereafter,56 and minimizing the fitting error for the actual traded TIPS securities. The substantial increase in the number of points in the top panel reflects the growth of the TIPS market. Note that in 1999 there is essentially one data point on the curve between the 0 and 5 years maturity (corresponding to the 5-year TIPS issued in 1997), thus the TIPS term structure in the short-maturity region of 0-5 years cannot be determined reliably. With more points across the maturity spectrum in 2005, shorter maturity TIPS yields can be determined more reliably than in 1999.
where
C More on the Estimation and the Estimates
Here we show how to rewrite the model in a state-space form, which consists of a state equation that describes the dynamic of the state variables, and an observation equation that describes the relationship between the observable variables and the unobservable state variables.
When the time interval ![]() is small, we can discretize the continuous-time equation (A-1) as
is small, we can discretize the continuous-time equation (A-1) as
where
Define the state vector
![]() . We can write the Kalman-filter state equations in a matrix form
. We can write the Kalman-filter state equations in a matrix form
where
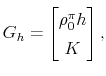 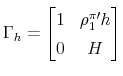 and and 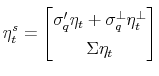 |
At each time point, we observe ![]() nominal yields and
nominal yields and ![]() TIPS yields,
both with measurement errors. We also observe the price level as well as survey forecasts of future nominal short rate or inflation, all at a lower frequency than that of the yields. We denote the vector of nominal yields as
TIPS yields,
both with measurement errors. We also observe the price level as well as survey forecasts of future nominal short rate or inflation, all at a lower frequency than that of the yields. We denote the vector of nominal yields as ![]() , the vector of TIPS yields as
, the vector of TIPS yields as
![]() , the vector of survey forecasts of the 3-month yield (the vector of
, the vector of survey forecasts of the 3-month yield (the vector of
![]() for various
for various ![]() 's) as
's) as
![]() , and the vector of survey inflation forecast as
, and the vector of survey inflation forecast as
![]() , respectively. Define the observation vector as
, respectively. Define the observation vector as
| (C-21) |
When all variables are available (at time
where
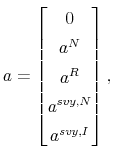 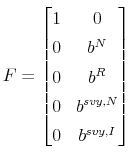 and and 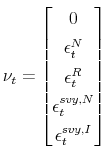 |
where
We estimate the model using the maximum likelihood method with the Kalman filter.60 Table A1 reports the parameter estimates and the corresponding standard errors for the NT-I, NT-II, T99-I, T99-II and T05-II estimations. The confidence intervals (standard errors) for quantities of economic interest, such as the inflation risk premium, can be computed using the delta method. As an example, in Figure A3 we plot the 95% confidence intervals for the 10-year inflation risk premium based the NT-I and the T99-I estimates.
Because the state variables in the model are statistical variables that are only defined up to an invariant transformation, individual parameters of the model are not easy to interpret. However, we note that in all estimations in Table A1, there is a diagonal element
(eigenvalue) of the
![]() matrix which is quite small (e.g., min(diag(
matrix which is quite small (e.g., min(diag(
![]() ))=0.0419 for NT-II); this is a necessary condition for the model to generate long-horizon expectations that have substantial variation over time. Note also that the size of the
nominal yield measurement errors (
))=0.0419 for NT-II); this is a necessary condition for the model to generate long-horizon expectations that have substantial variation over time. Note also that the size of the
nominal yield measurement errors (
![]() 's) is quite small (e.g., the 10-year nominal yield measurement error is about 5 basis points in all five estimations). In other words, the model fits the nominal yield curve
fairly well. Lastly, note that the size of the "orthogonal shock" to inflation (
's) is quite small (e.g., the 10-year nominal yield measurement error is about 5 basis points in all five estimations). In other words, the model fits the nominal yield curve
fairly well. Lastly, note that the size of the "orthogonal shock" to inflation (
![]() ) is quite large; this could lead to a material difference between the latent-factor model of the present paper and models in the literature that do not accommodate such a
shock.
) is quite large; this could lead to a material difference between the latent-factor model of the present paper and models in the literature that do not accommodate such a
shock.
D Term structure of real and nominal yields
Table A2 reports the model-implied unconditional moments for the nominal yield, the nominal term premium, the real yield, the real term premium, expected inflation and the inflation risk premium at maturities of 1 quarter, 1-, 2-, 5- and 10 years, based on the NT-II estimation.61 As can be seen from the third column, this model implies a slightly upward sloping nominal term structure, with the mean levels of yields gently rising from 4.31% at the 1-quarter maturity to 4.74% at the 10-year maturity. The model-implied real term structure is essentially flat, similar to what Ang, Bekaert and Wei (2007a) find, implying a real term premium that is close to zero at all maturities. The nominal term premium can therefore be attributed almost entirely to an upward sloping term structure of inflation risk premia, as shown in the last column, with the point estimates of the inflation risk premia ranging from 10 to 50 basis points for maturities up to ten years. The steady-state CPI inflation is estimated to be around 2.4%. After adjusting for a typical difference of around 50 basis points between the CPI and core CPI inflation measures, this estimate falls just within the 1% to 2% range for core CPI inflation commonly referred to as the Fed's "comfort zone."
We do note, however, that these results about unconditional moments should be interpreted with much caution: there is a general consensus among practitioners and policy makers that the expectations of inflation and interest rates, even at long horizons, have moved around substantially in the past few decades, which means that the data are close to the unit-root boundary (nonstationarity) where the unconditional moments are ill-defined.
Bibliography
| maturity (qtr) | real yield: real EH component | real yield: real term premium | nominal yield: real yield | nominal yield: expected inflation | nominal yield: inflation risk premium |
|---|---|---|---|---|---|
| 1 | 1.00 | 0.00 | 0.73 | 0.26 | 0.01 |
| 1 (standard error) | (0.01) | (0.01) | (0.00) | (0.02) | (0.02) |
| 4 | 0.94 | 0.06 | 0.72 | 0.26 | 0.02 |
| 4 (standard error) | (0.03) | (0.03) | (0.00) | (0.03) | (0.03) |
| 8 | 0.82 | 0.18 | 0.69 | 0.27 | 0.03 |
| 8 (standard error) | (0.05) | (0.05) | (0.00) | (0.04) | (0.04) |
| 20 | 0.49 | 0.51 | 0.62 | 0.33 | 0.04 |
| 20 (standard error) | (0.08) | (0.08) | (0.00) | (0.06) | (0.06) |
| 40 | 0.25 | 0.75 | 0.58 | 0.36 | 0.06 |
| 40 (standard error) | (0.11) | (0.11) | (0.00) | (0.11) | (0.11) |
Note: This table reports in-sample variance decompositions of real yields into the real expectations component and the real term premium component, and in-sample variance decompositions of nominal yields into the real yield, expected inflation and the inflation risk premium, all based on NT-II
model estimates. Variance decompositions of the real yields are calculated according to
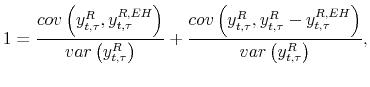 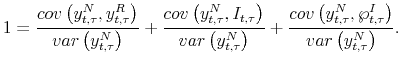 |
|---|
| NT-II | T05-II | |
|---|---|---|
| Constant | 0.74 | -0.16 |
| Constant (t-statistic) | [13.10] | [-2.81] |
| Daily Turnover | -0.45 | -0.26 |
| Daily Turnover (t-statistic) | [-28.96] | [-16.38] |
| Ten-year implied volatility | 0.07 | 0.09 |
| Ten-year implied volatility (t-statistic) | [9.03] | [11.75] |
| S&P500 implied volatility | 0.02 | 0.03 |
| S&P500 implied volatility (t-statistic) | [11.77] | [12.10] |
| Libor-FFR | 0.05 | 0.07 |
| Libor-FFR (t-statistic) | [1.42] | [1.72] |
| 0.87 | 0.81 |
| Note: This table regresses model-implied TIPS liquidity premia, |
|---|
| NT-I | NT-II | T99-I | T99-II | T05-II | |
|---|---|---|---|---|---|
| State Variables:
|
0.8597(0.5198) | 0.8169(0.4666) | 0.8630(0.1368) | 0.8433(0.1555) | 0.8720(0.4394) |
| State Variables:
|
0.0481(0.0677) | 0.0419(0.0657) | 0.0521(0.0810) | 0.0488(0.0693) | 0.0595(0.0620) |
| State Variables:
|
1.5080(0.8180) | 1.4558(0.7827) | 1.5175(0.1711) | 1.5542(0.3420) | 1.6065(0.7212) |
| State Variables:
|
-0.3216(0.3141) | -0.4376(0.3257) | -0.3385(0.2728) | -0.5437(0.2805) | -0.2812(0.2602) |
| State Variables:
|
-4.6373(9.5310) | -4.7168(9.1773) | -4.6357(1.0617) | -4.6394(2.7987) | -4.2647(6.6484) |
| State Variables:
|
-0.5415(0.2378) | -0.5558(0.2465) | -0.5649(0.2574) | -0.6195(0.2409) | -0.5114(0.2162) |
| Nominal Pricing Kernel:
|
0.0414(0.0137) | 0.0429(0.0132) | 0.0418(0.0138) | 0.0438(0.0115) | 0.0496(0.0057) |
| Nominal Pricing Kernel:
|
2.9036(5.5599) | 3.0242(5.4197) | 2.8956(0.5941) | 2.9736(1.6467) | 2.6107(3.8015) |
| Nominal Pricing Kernel:
|
0.4756(0.1130) | 0.4747(0.1160) | 0.4881(0.1246) | 0.5206(0.1144) | 0.4771(0.1024) |
| Nominal Pricing Kernel:
|
0.6183(0.0396) | 0.6216(0.0338) | 0.6135(0.0288) | 0.6095(0.0258) | 0.6090(0.0353) |
| Nominal Pricing Kernel:
|
0.4459(0.2510) | 0.3845(0.2091) | 0.4283(0.1844) | 0.3593(0.1862) | 0.3330(0.3409) |
| Nominal Pricing Kernel:
|
-0.1673(0.8515) | -0.2632(0.7712) | -0.1785(0.8719) | -0.2939(0.8008) | -0.7861(0.4900) |
| Nominal Pricing Kernel:
|
0.0656(3.4014) | -0.3082(3.2911) | -0.0031(3.4588) | -0.4506(2.9862) | -1.9781(1.3698) |
| Nominal Pricing Kernel:
|
-0.5324(1.7803) | -0.4950(1.6063) | -0.5637(0.3480) | -0.7460(0.6339) | -0.5476(1.4149) |
| Nominal Pricing Kernel:
|
1.7443(5.0050) | 1.5625(4.3385) | 1.7923(1.0253) | 2.0343(1.4944) | 1.8403(4.0156) |
| Nominal Pricing Kernel:
|
3.9083(16.7852) | 3.8860(15.8683) | 3.9766(2.1698) | 4.6583(5.8307) | 3.3807(1.5160) |
| Nominal Pricing Kernel:
|
-0.0368(0.2438) | -0.0396(0.2299) | -0.0193(0.1014) | 0.0772(0.1054) | -0.0247(0.2011) |
| Nominal Pricing Kernel:
|
-0.2734(0.1321) | -0.2499(0.1296) | -0.2886(0.1053) | -0.3761(0.0782) | -0.3128(0.1013) |
| Nominal Pricing Kernel:
|
-0.6572(0.8385) | -0.6737(0.8239) | -0.7407(0.4363) | -1.2661(0.6819) | -0.6546(0.7059) |
| Nominal Pricing Kernel:
|
-0.0684(0.3218) | -0.0662(0.2910) | -0.0777(0.0935) | -0.1527(0.0950) | -0.0858(0.2643) |
| Nominal Pricing Kernel:
|
0.6062(0.2421) | 0.5632(0.2340) | 0.6181(0.2161) | 0.7250(0.1882) | 0.7139(0.2149) |
| Nominal Pricing Kernel:
|
0.6822(2.1513) | 0.7232(2.0002) | 0.6877(0.3571) | 0.9391(0.8475) | 0.6115(1.7395) |
| Inflation:
|
0.0232(0.0096) | 0.0239(0.0108) | 0.0268(0.0048) | 0.0250(0.0078) | 0.0281(0.0059) |
| Inflation:
|
0.0764(0.6658) | 0.0993(0.5811) | -1.0700(0.5303) | -1.2517(1.1124) | -1.3801(2.7343) |
| Inflation:
|
0.2786(0.1283) | 0.3557(0.0923) | 0.1051(0.0925) | 0.2942(0.0709) | 0.4084(0.0657) |
| Inflation:
|
-0.0174(0.2035) | -0.0081(0.1702) | -0.5109(0.1582) | -0.5595(0.1642) | -0.5348(0.2232) |
| Inflation:
|
-0.1136(0.0755) | -0.1043(0.0761) | -0.1774(0.0675) | -0.1515(0.0722) | -0.1821(0.0710) |
| Inflation:
|
0.0814(0.0767) | 0.0896(0.0761) | 0.0524(0.0812) | 0.0451(0.0810) | 0.1410(0.0764) |
| Inflation:
|
0.0295(0.0619) | 0.0320(0.0589) | 0.0038(0.0549) | -0.1021(0.0503) | 0.0820(0.0591) |
| Inflation:
|
0.7144(0.0241) | 0.7168(0.0237) | 0.7545(0.0271) | 0.7661(0.0285) | 0.7368(0.0264) |
| Measurement Errors and Liquidity Premium:
|
0.1011(0.0026) | 0.1011(0.0026) | 0.1009(0.0026) | 0.1009(0.0026) | 0.1010(0.0026) |
| Measurement Errors and Liquidity Premium:
|
0.0220(0.0017) | 0.0220(0.0017) | 0.0224(0.0017) | 0.0223(0.0017) | 0.0223(0.0017) |
| Measurement Errors and Liquidity Premium:
|
0.0530(0.0016) | 0.0530(0.0016) | 0.0531(0.0017) | 0.0532(0.0017) | 0.0530(0.0017) |
| Measurement Errors and Liquidity Premium:
|
0 | 0 | 0 | 0 | 0 |
| Measurement Errors and Liquidity Premium:
|
0.0293(0.0012) | 0.0293(0.0012) | 0.0292(0.0013) | 0.0292(0.0013) | 0.0293(0.0012) |
| Measurement Errors and Liquidity Premium:
|
0 | 0 | 0 | 0 | 0 |
| Measurement Errors and Liquidity Premium:
|
0.0491(0.0019) | 0.0491(0.0019) | 0.0491(0.0019) | 0.0491(0.0019) | 0.0491(0.0019) |
| Measurement Errors and Liquidity Premium:
|
0.1757(0.0134) | 0.1756(0.0133) | 0.1757(0.0134) | 0.1761(0.0135) | 0.1763(0.0136) |
| Measurement Errors and Liquidity Premium:
|
0.2259(0.0195) | 0.2260(0.0195) | 0.2259(0.0196) | 0.2255(0.0195) | 0.2266(0.0197) |
| Measurement Errors and Liquidity Premium:
|
0.3028(0.0132) | 0.3036(0.0132) | 0.0868(0.0088) | ||
| Measurement Errors and Liquidity Premium:
|
0.0519(0.2251) | -0.1385(0.1846) | -0.1292(0.1810) |
| Note: Standard errors based on the BHHH formula are given in parentheses. |
|---|
| maturity (qtr): moment | nominal yield | nominal term premium | real yield | real premium | expected inflation | inflation risk premium |
|---|---|---|---|---|---|---|
| 1: mean | 4.31 | 0.03 | 1.84 | 0.02 | 2.39 | 0.08 |
| 1: mean (standard error) | (1.48) | (0.23) | (0.29) | (0.22) | (1.07) | (0.17) |
| 1: std. dev. | 2.03 | 0.29 | 0.89 | 0.27 | 1.32 | 0.24 |
| 1: std. dev. (standard error) | (1.23) | (0.20) | (0.14) | (0.20) | (1.00) | (0.20) |
| 4: mean | 4.33 | 0.04 | 1.83 | 0.01 | 2.39 | 0.11 |
| 4: mean (standard error) | (1.92) | (0.66) | (0.69) | (0.64) | (1.07) | (0.18) |
| 4: std. dev. | 2.52 | 0.84 | 1.11 | 0.78 | 1.30 | 0.28 |
| 4: std. dev. (standard error) | (1.67) | (0.60) | (0.48) | (0.60) | (1.02) | (0.20) |
| 8: mean | 4.32 | 0.03 | 1.78 | -0.04 | 2.39 | 0.15 |
| 8: mean (standard error) | (2.22) | (0.97) | (0.98) | (0.94) | (1.07) | (0.18) |
| 8: std. dev. | 2.86 | 1.23 | 1.36 | 1.12 | 1.28 | 0.31 |
| 8: std. dev. (standard error) | (1.98) | (0.88) | (0.80) | (0.90) | (1.03) | (0.19) |
| 20: mean | 4.38 | 0.09 | 1.72 | -0.10 | 2.39 | 0.27 |
| 20: mean (standard error) | (2.53) | (1.28) | (1.32) | (1.29) | (1.07) | (0.15) |
| 20: std. dev. | 3.20 | 1.65 | 1.69 | 1.51 | 1.21 | 0.34 |
| 20: std. dev. (standard error) | (2.32) | (1.17) | (1.18) | (1.27) | (1.08) | (0.14) |
| 40: mean | 4.74 | 0.45 | 1.88 | 0.06 | 2.39 | 0.46 |
| 40: mean (standard error) | (2.51) | (1.27) | (1.40) | (1.37) | (1.07) | (0.06) |
| 40: std. dev. | 3.16 | 1.74 | 1.76 | 1.59 | 1.09 | 0.32 |
| 40: std. dev. (standard error) | (2.32) | (1.10) | (1.28) | (1.35) | (1.12) | (0.14) |
| Note: This table reports the unconditional mean and standard deviations of nominal yields, nominal term premium, real yields, real term premia, expected inflation and inflation risk premia based on NT-II model estimates. Standard errors calculated using the delta method are reported in parentheses. |
|---|
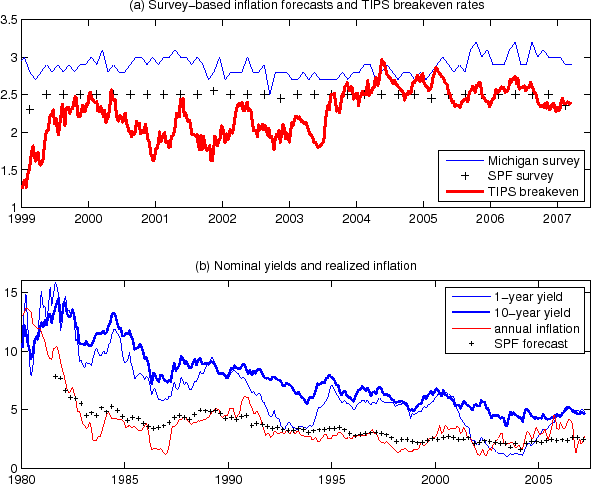 Note: The top panel plots the 10-year TIPS breakeven rate (red line), long-horizon Michigan inflation forecast (blue line), and 10-year SPF inflation forecast (black
pluses). The bottom panel plots the 1-year (thin blue line) and 10-year (thick blue line) nominal yields, together with the realized annual inflation (red line) and the corresponding SPF forecast (black pluses). Note: The top panel plots the 10-year TIPS breakeven rate (red line), long-horizon Michigan inflation forecast (blue line), and 10-year SPF inflation forecast (black
pluses). The bottom panel plots the 1-year (thin blue line) and 10-year (thick blue line) nominal yields, together with the realized annual inflation (red line) and the corresponding SPF forecast (black pluses). |
 Note: Results from the NT-I estimation: (a) Model-implied 10-year (thick blue line) and 1-year (thin red line) inflation expectation. The 10-year and 1-year
SPF survey inflation forecasts are shown in blue circles and red plus signs, respectively. (b) Model-implied 10-year breakeven rate (thin red line) and TIPS breakeven rate (thick blue line). (c) Model-implied 1-year (thin red line) and 10-year (thick blue line) inflation risk premia. (d)
Model-implied 1-year (thin red line) and 10-year (thick blue line) real yields. Note: Results from the NT-I estimation: (a) Model-implied 10-year (thick blue line) and 1-year (thin red line) inflation expectation. The 10-year and 1-year
SPF survey inflation forecasts are shown in blue circles and red plus signs, respectively. (b) Model-implied 10-year breakeven rate (thin red line) and TIPS breakeven rate (thick blue line). (c) Model-implied 1-year (thin red line) and 10-year (thick blue line) inflation risk premia. (d)
Model-implied 1-year (thin red line) and 10-year (thick blue line) real yields. |
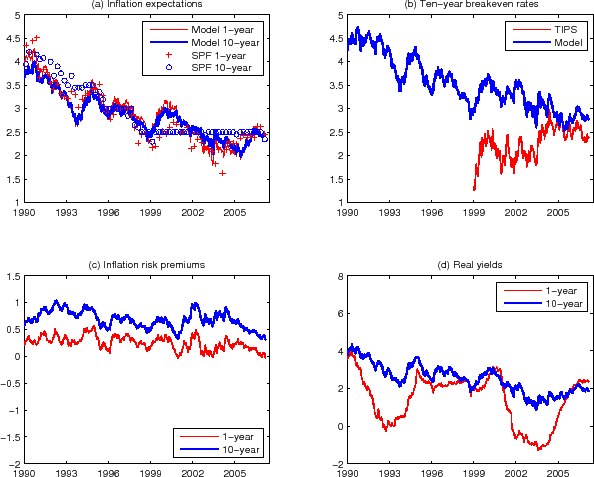 Note: Results from the NT-II estimation: (a) Model-implied 10-year (thick blue line) and 1-year (thin red line) inflation expectation. The 10-year and
1-year SPF survey inflation forecasts are shown in blue circles and red plus signs, respectively. (b) Model-implied 10-year breakeven rate (thin red line) and TIPS breakeven rate (thick blue line). (c) Model-implied 1-year (thin red line) and 10-year (thick blue line) inflation risk premia. (d)
Model-implied 1-year (thin red line) and 10-year (thick blue line) real yields. Note: Results from the NT-II estimation: (a) Model-implied 10-year (thick blue line) and 1-year (thin red line) inflation expectation. The 10-year and
1-year SPF survey inflation forecasts are shown in blue circles and red plus signs, respectively. (b) Model-implied 10-year breakeven rate (thin red line) and TIPS breakeven rate (thick blue line). (c) Model-implied 1-year (thin red line) and 10-year (thick blue line) inflation risk premia. (d)
Model-implied 1-year (thin red line) and 10-year (thick blue line) real yields. |
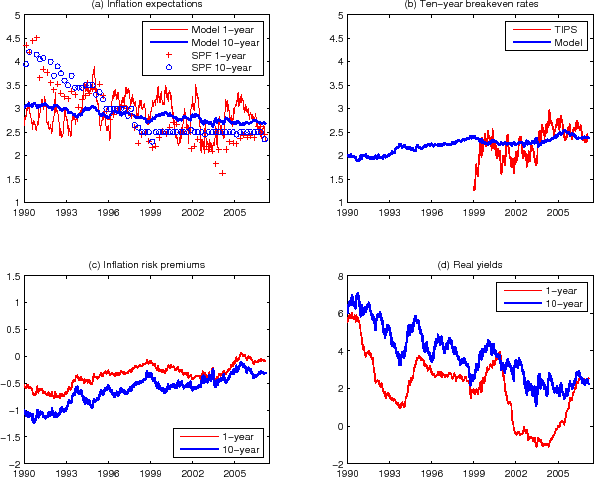 Note: Results from the T99-I estimation: (a) Model-implied 10-year (thick blue line) and 1-year (thin red line) inflation expectation. The 10-year and
1-year SPF survey inflation forecasts are shown in blue circles and red plus signs, respectively. (b) Model-implied 10-year breakeven rate (thin red line) and TIPS breakeven rate (thick blue line). (c) Model-implied 1-year (thin red line) and 10-year (thick blue line) inflation risk premia. (d)
Model-implied 1-year (thin red line) and 10-year (thick blue line) real yields. Note: Results from the T99-I estimation: (a) Model-implied 10-year (thick blue line) and 1-year (thin red line) inflation expectation. The 10-year and
1-year SPF survey inflation forecasts are shown in blue circles and red plus signs, respectively. (b) Model-implied 10-year breakeven rate (thin red line) and TIPS breakeven rate (thick blue line). (c) Model-implied 1-year (thin red line) and 10-year (thick blue line) inflation risk premia. (d)
Model-implied 1-year (thin red line) and 10-year (thick blue line) real yields. |
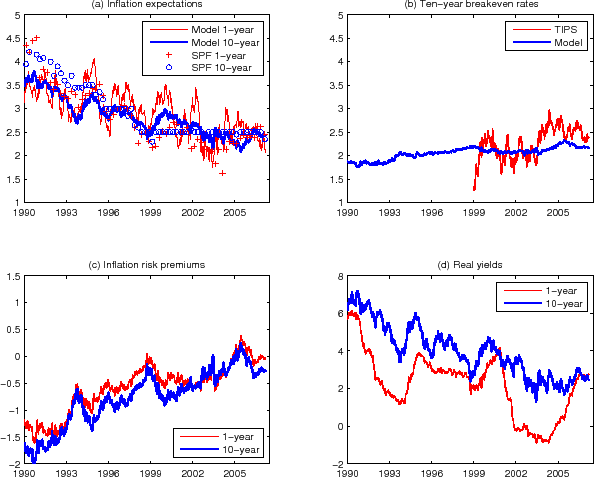 Note: Results from the T99-II estimation: (a) Model-implied 10-year (thick blue line) and 1-year (thin red line) inflation expectation. The 10-year and
1-year SPF survey inflation forecasts are shown in blue circles and red plus signs, respectively. (b) Model-implied 10-year breakeven rate (thin red line) and TIPS breakeven rate (thick blue line). (c) Model-implied 1-year (thin red line) and 10-year (thick blue line) inflation risk premia. (d)
Model-implied 1-year (thin red line) and 10-year (thick blue line) real yields. Note: Results from the T99-II estimation: (a) Model-implied 10-year (thick blue line) and 1-year (thin red line) inflation expectation. The 10-year and
1-year SPF survey inflation forecasts are shown in blue circles and red plus signs, respectively. (b) Model-implied 10-year breakeven rate (thin red line) and TIPS breakeven rate (thick blue line). (c) Model-implied 1-year (thin red line) and 10-year (thick blue line) inflation risk premia. (d)
Model-implied 1-year (thin red line) and 10-year (thick blue line) real yields. |
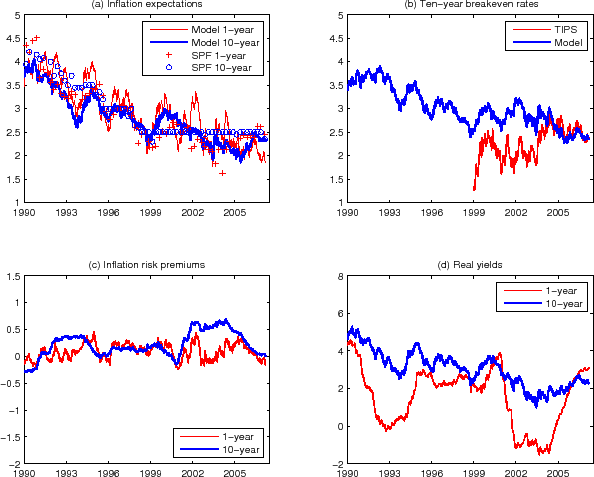 Note: Results from the T05-II estimation: (a) Model-implied 10-year (thick blue line) and 1-year (thin red line) inflation expectation. The 10-year and
1-year SPF survey inflation forecasts are shown in blue circles and red plus signs, respectively. (b) Model-implied 10-year breakeven rate (thin red line) and TIPS breakeven rate (thick blue line). (c) Model-implied 1-year (thin red line) and 10-year (thick blue line) inflation risk premia. (d)
Model-implied 1-year (thin red line) and 10-year (thick blue line) real yields. Note: Results from the T05-II estimation: (a) Model-implied 10-year (thick blue line) and 1-year (thin red line) inflation expectation. The 10-year and
1-year SPF survey inflation forecasts are shown in blue circles and red plus signs, respectively. (b) Model-implied 10-year breakeven rate (thin red line) and TIPS breakeven rate (thick blue line). (c) Model-implied 1-year (thin red line) and 10-year (thick blue line) inflation risk premia. (d)
Model-implied 1-year (thin red line) and 10-year (thick blue line) real yields. |
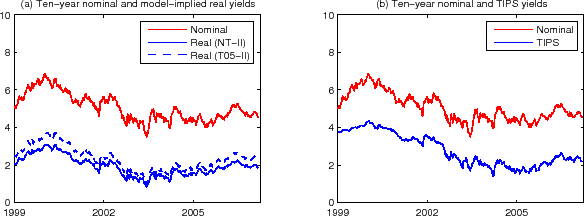 Note: (a) The red line plots the actual 10-year nominal yield, and the blue solid (dashed) line plots the implied 10-year real yield based on Model
NT-II (T05-II). (b) The red and the blue lines plot the 10-year nominal and TIPS yields, respectively. Note: (a) The red line plots the actual 10-year nominal yield, and the blue solid (dashed) line plots the implied 10-year real yield based on Model
NT-II (T05-II). (b) The red and the blue lines plot the 10-year nominal and TIPS yields, respectively. |
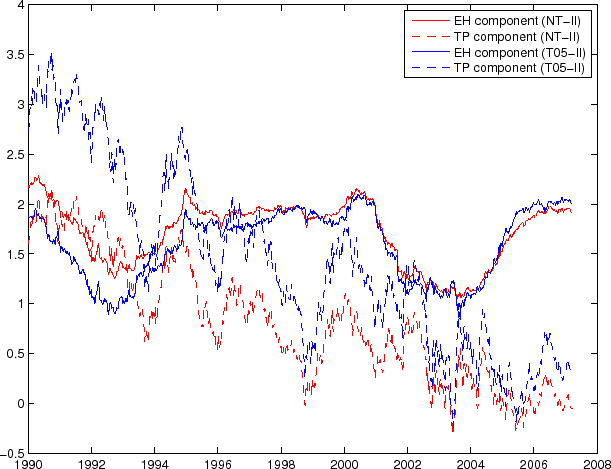 Note: Decomposition of the 10-year real yield into the real expectations component (solid lines) and the real term premium component (dashed lines). The
red lines are based on the NT-II estimation, and the blue lines are based on the T05-II estimation. Note: Decomposition of the 10-year real yield into the real expectations component (solid lines) and the real term premium component (dashed lines). The
red lines are based on the NT-II estimation, and the blue lines are based on the T05-II estimation. |
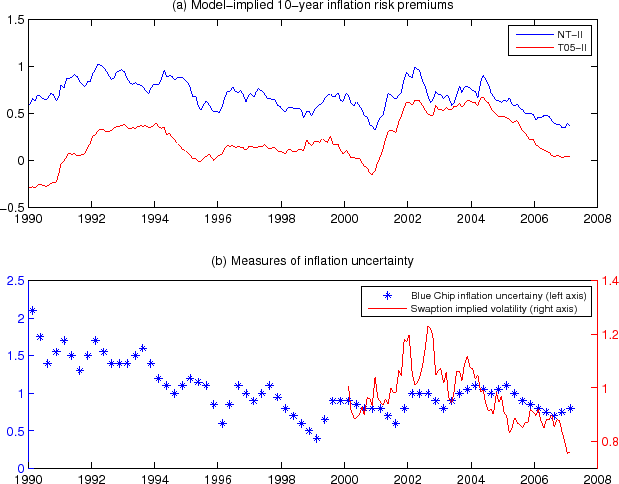 Note: (a) Model-implied 10-year inflation risk premia based on NT-II (blue line) and T05-II (red line) estimations. (b) The blue asterisks plot the
distance between the average of the top ten forecasts and that of the bottom ten forecasts of CPI inflation 5 to 10 years ahead from Blue Chip Economic Indicator survey. The red line plots the basis-point implied volatility (absolute implied volatility) from 10-year swaptions with an underlying
swap length of 1 year. Note: (a) Model-implied 10-year inflation risk premia based on NT-II (blue line) and T05-II (red line) estimations. (b) The blue asterisks plot the
distance between the average of the top ten forecasts and that of the bottom ten forecasts of CPI inflation 5 to 10 years ahead from Blue Chip Economic Indicator survey. The red line plots the basis-point implied volatility (absolute implied volatility) from 10-year swaptions with an underlying
swap length of 1 year. |
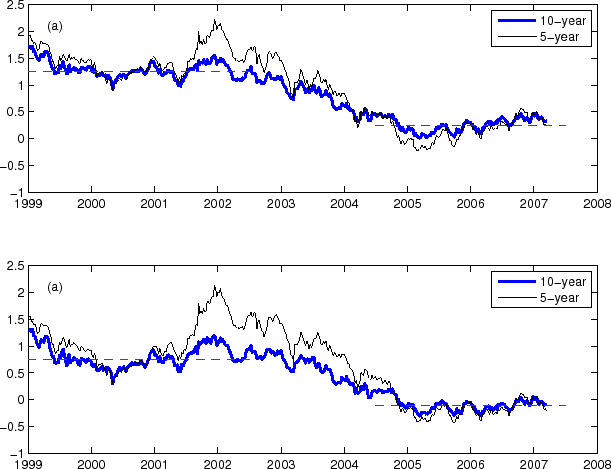 Note: (a) NT-II, (b) T05-II. The black (blue) line plots the model-implied 5-year (10-year) liquidity premium. Note: (a) NT-II, (b) T05-II. The black (blue) line plots the model-implied 5-year (10-year) liquidity premium. |
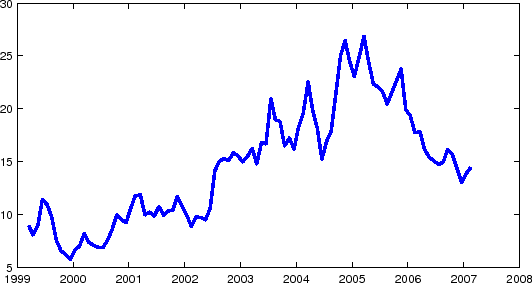 Note: in millions of dollars divided by TIPS outstanding in the corresponding month. Note: in millions of dollars divided by TIPS outstanding in the corresponding month. |
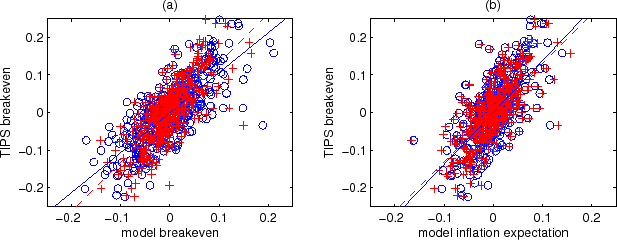 Note: (a) Scatter plots of TIPS 10-year breakeven rate against the NT-II (circles) and the T-05-II (pluses) model-implied 10-year breakeven rates. (b)
Scatter plots of TIPS 10-year breakeven rate against the NT-II (circles) and the T05-II (pluses) model-implied 10-year inflation expectations. Note: (a) Scatter plots of TIPS 10-year breakeven rate against the NT-II (circles) and the T-05-II (pluses) model-implied 10-year breakeven rates. (b)
Scatter plots of TIPS 10-year breakeven rate against the NT-II (circles) and the T05-II (pluses) model-implied 10-year inflation expectations. |
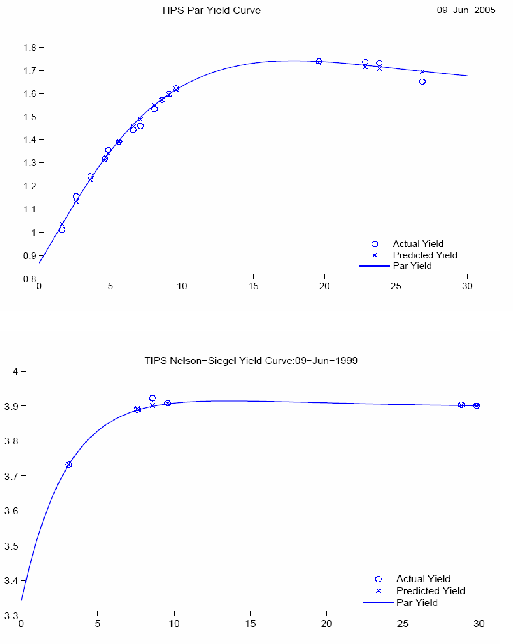 Note: The top (bottom) panel plots the fitted TIPS par yield curve together with individual TIPS yields on June 9, 2005 (June 9, 1999). Note: The top (bottom) panel plots the fitted TIPS par yield curve together with individual TIPS yields on June 9, 2005 (June 9, 1999). |
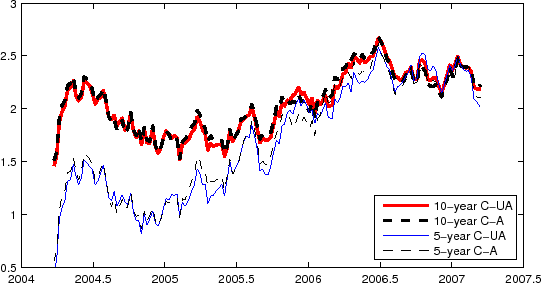 Note: This figure plots 10-year carry-unadjusted (carry-adjusted) TIPS yields in red solid (black dashed) line and 5-year carry-unadjusted (carry-adjusted) TIPS
yields in blue solid (gray dashed) line. Note: This figure plots 10-year carry-unadjusted (carry-adjusted) TIPS yields in red solid (black dashed) line and 5-year carry-unadjusted (carry-adjusted) TIPS
yields in blue solid (gray dashed) line. |
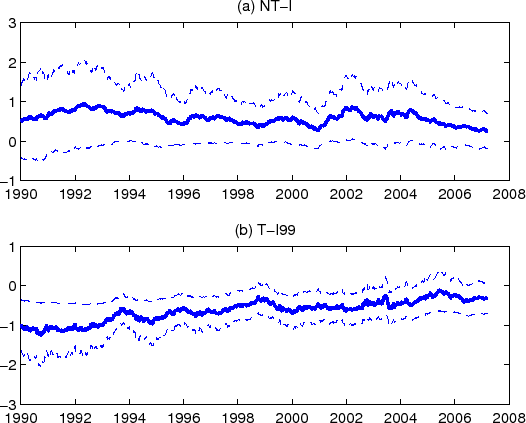 Note: The top (bottom) panel plots the 10-year inflation risk premium together with the 95% confidence bands as implied by the NT-I (T99-I) estimation. Note: The top (bottom) panel plots the 10-year inflation risk premium together with the 95% confidence bands as implied by the NT-I (T99-I) estimation. |
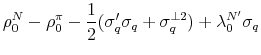
![\displaystyle \mu = 0_{3\times1}, \,\,\, \Sigma = \left[\begin{matrix}0.01 & 0 & 0 \\ \Sigma_{21} & 0.01 & 0\\ \Sigma_{31} & \Sigma_{32} & 0.01 \end{matrix}\right], \,\,\, \mathcal{K}= \left[\begin{matrix}\mathcal{K}_{11} & 0 & 0 \\ 0 & \mathcal{K}_{22} & 0\\ 0 & 0 & \mathcal{K}_{33} \end{matrix}\right],](img164.gif)
![\displaystyle \mathcal{K}= \left[\begin{matrix}\mathcal{K}_a & -\mathcal{K}_b & 0 \\ \mathcal{K}_b & \mathcal{K}_a & 0\\ 0 & 0 & \mathcal{K}_c \end{matrix}\right].](img167.gif)