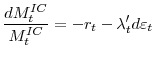Lowering the Anchor: How the Bank of England's Inflation-Targeting Policies have Shaped Inflation Expectations and Perceptions of Inflation Risk
Keywords: Inflation targeting, inflation compensation, term structure, factor model, risk premia
Abstract:
Inflation targeting as practiced by the Bank of England has undergone several changes since its adoption in 1992, including redefinition of the goal, measures to increase transparency and the granting of independence to the central bank. These changes are likely to have affected long-run inflation expectations and perceptions of future inflation risk. To that end, this paper estimates a no-arbitrage, affine, factor model of the term structure of inflation compensation in the United Kingdom. The model yields time series of expected inflation and inflation risk premia at short and long horizons estimated in a theoretically consistent manner. The results reveal that long-run inflation expectations drifted down slowly during the first five years of inflation targeting, but inflation risk premia moved down abruptly only once the Bank of England was granted independence. This event, which arguably signalled more credible commitment by the central bank to its inflation anchor, appears to have been more important in shaping inflation expectations and perceptions of inflation risk than changes in the definition of the target or measures to increase transparency.
JEL Classification: E43, E44, E52
1. Introduction
Inflation targeting conducted by the Bank of England has undergone several changes since its adoption 15 years ago. A quantitative goal for retail price inflation was first announced in October 1992 and was subsequently redefined several times, from a range to a point target, first asymmetric then symmetric. More recently the goal was lowered in tandem with the shift of the target measure to consumer price inflation. Amidst these changes, the Bank of England was granted independence to pursue its inflation goal and measures were taken to increase the Bank's transparency. These adjustments were aimed at fostering greater public understanding and credibility of the central bank's goals. How, then, have they influenced inflation expectations and perceptions of inflation risk?
This paper turns to financial market data to answer that question, taking advantage of the long history of inflation-indexed debt issued by the government in the United Kingdom to estimate a no-arbitrage, affine factor model of the inflation compensation term structure. The gap between the nominal and real term structures represents the compensation that investors receive to hold nominal rather than real government debt and is comprised of expected inflation and inflation risk premia. The term structure model returns time series of expected inflation and inflation risk premia at short and long horizons. Long-run inflation expectations inferred from the model line up closely with those from surveys of professional forecasters, but unlike surveys, the model can be fitted to high-frequency data. Risk premia are estimated in a theoretically consistent manner within the model rather than as a residual after observing expectations.
Disentangling inflation expectations from inflation risk premia matters to monetary-policy makers. Inflation expectations are an important input to the policy decision process, and financial markets provide real-time information about the expectations of a broad range of agents. As a barometer of inflation uncertainty in the broader economy, financial markets are able to quickly convey information that the central bank may need to factor into its deliberations, perhaps requiring the central bank to clarify its policy actions or reiterate its commitment to its long-run goal. Understanding when rising inflation risk premia reflect upon the credibility of the central bank or reflect broader macroeconomic sources of inflation risk matters to the conduct of policy.
The empirical results indicate that market participants' long-run expectations of retail price inflation trended down from 1992, but not until after the Bank of England was granted independence did they approach and then remain close to 2.5 percent. Inflation risk premia showed little sign of declining until 1997, when they dropped abruptly in the months following independence. This event, which arguably signalled more credible commitment of the central bank to its inflation objective, appears to have been more important in shaping inflation expectations and inflation risk than changes to the definition of the target or measures to increase transparency, such as publication of the minutes of the Monetary Policy Committee (MPC) or releasing details of internal forecasting models.
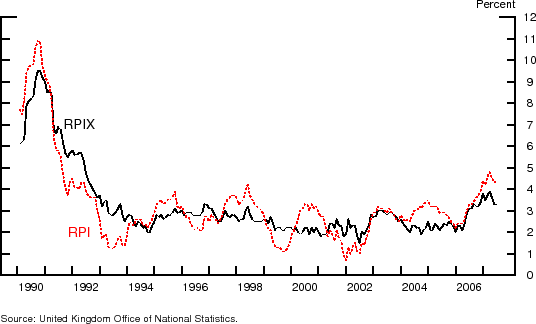
Following independence, expected future inflation and inflation risk premia remained low and fairly stable, until the inflation target measure was redefined in December 2003 from retail prices excluding mortgage interest payments (RPIX) to consumer prices (CPI). Since the announcement of the new CPI inflation target, risk premia on retail price inflation outcomes far into the future have risen 30 to 40 basis points above the range of the preceding decade. Moreover, much of the increase in inflation risk premia was concentrated in the weeks immediately following the switch to the CPI target.
Why did redefining the target raise inflation risk premia? This can be better understood by noting that inflation-indexed government debt in the United Kingdom is linked to the retail price index (RPI). In the long run, beyond the typical monetary policy cycle, forecasts of RPI and RPIX tend to coincide and their trend rates of growth are similar. But RPI and CPI outcomes are less correlated and the gap between them has been persistent at times. Disbanding the retail price inflation anchor arguably increased the compensation that investors required to hold long-run retail price inflation risk. This is not to say that the Bank of England became less credible in its commitment to controlling inflation; rather, it illustrates the role that an inflation anchor plays in moulding perceptions of future inflation risk.
The paper is structured as follows. Section 2 outlines the no-arbitrage, affine, factor model used in the paper, deriving the general asset-pricing condition and outlining the model assumptions. An overview of the data is also given. Section 3 discusses issues regarding estimation and presents the results for the sample at hand. Section 4 uses the output of the model to investigate how markets have responded to changes in the Bank of England's inflation targeting policies and Section 5 concludes.
2. A no-arbitrage factor model of inflation compensation
This paper adapts a no-arbitrage, affine, factor model to the term structure of inflation compensation, a novel application of a standard finance model. The model is based on three key assumptions: i) assets are priced by a single discount factor such that no arbitrage opportunities remain in trading inflation compensation at different maturities, ii) the dynamics of the inflation compensation term structure can be well described by three latent factors, and iii) the discount factor used to discount returns is log-normal. In other words, yields are essentially affine in the three factors.
Related research has modelled the nominal and real term structures jointly, imposing the restriction that the same three factors describe both term structures and the inflation process. (See Risa, 2001, for an application to the United Kingdom and D'Amico, Kim and Wei, 2006, and Kim and Wright, 2005 for applications to the United States.) One advantage of modelling the term structure of inflation compensation directly, as is done here, is to avoid such restrictions on the factors and instead estimate those factors and parameters that best fit the data. This does not imply that the factors underlying the inflation compensation term structure are uncorrelated with those underlying the nominal or real term structures. On the contrary, the factors may indeed covary but I do not impose restrictions about the nature of that covariance. Another reason to model inflation compensation rather than real and nominal rates (jointly or separately) is to bypass concerns about structural change in the equilibrium real interest rate.
Finally, the purely latent-factor approach to modelling the yield curve used here and elsewhere is more flexible than models that employ observable macroeconomic factors, such as ()Diebold_R_A_06 and ()Rudebusch_Wu_04. While the inclusion of observable factors lends greater interpretability to the results, it also leads to a deterioration in overall fit and greater concerns about misspecification.
2.1 Pricing of inflation-contingent assets
The model builds upon a fundamental asset-pricing condition. Begin with the familiar condition for pricing nominal bonds,
where
| (2) |
We can express equation (1) in terms of the price of a zero-coupon nominal bond that pays
Rewriting equation (3) in terms of the nominal yield,
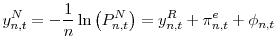 |
(4) |
where
![\displaystyle \pi_{n,t}^{e}=-\frac{1}{n}\ln\left( E_{t}\left[ \frac{Q_{t}}{Q_{t+n}% }\right] \right) .](img14.gif)
Thus we can write down a general asset pricing condition for inflation compensation. The inflation compensation yield spread,
![]() , can be viewed as the yield on a synthetic inflation bond that pays $1 at time
, can be viewed as the yield on a synthetic inflation bond that pays $1 at time ![]() . This bond will have price
. This bond will have price
![]() , where
, where
This can in turn be rewritten as a more familiar general asset pricing condition,
where
2.2 An affine factor model
The model of the term structure employed here is based upon a model proposed by ()Duffie_2002 with three latent factors, using the factor normalisation implemented by ()Kim_Orphanides_05. As stated above, it assumes that equation (6) prices all inflation compensation returns and that the time-series behaviour of the inflation compensation yield curve can be described by three underlying latent factors. The presentation of the model follows closely that found in Kim and Wright (2005).
Assume that the stochastic discount factor,
![]() , is specified as an affine function of a
, is specified as an affine function of a ![]() vector of latent
factors,
vector of latent
factors, ![]() , and evolves in a manner that mirrors equations (5) and (6):
, and evolves in a manner that mirrors equations (5) and (6):
where
The coefficient
where
The interpretation of equation (7) is that the growth rate of the stochastic discount factor reflects a risk-free inflation expectation plus an adjustment for the sources of risk in the model: the shocks,
![]() , and elements of
, and elements of
![]() , which are the time-varying market prices of those risks. In contrast to the Fisher hypothesis, which interprets the spread between nominal and real interest rates as an implied
inflation expectation, this model explicitly allows for a time-varying inflation risk premium. The inflation risk premium is comprised of term risk (the risk associated with uncertainty about future inflation rates), default risk, and liquidity risk.2 As the markets for nominal and indexed government debt in the United Kingdom are default-free and sufficiently liquid, risk due to uncertainty about future inflation rates is likely to be the
primary driver of the inflation risk premium. Other factors unrelated to inflation expectations may at times affect inflation compensation, such as changes in demand for indexed debt induced by institutional reform, tax issues or convexity. These are not identified separately and to the extent that
they do not conform to the estimated dynamics of the instantaneous inflation rate are largely attributed to the risk premium.3
, which are the time-varying market prices of those risks. In contrast to the Fisher hypothesis, which interprets the spread between nominal and real interest rates as an implied
inflation expectation, this model explicitly allows for a time-varying inflation risk premium. The inflation risk premium is comprised of term risk (the risk associated with uncertainty about future inflation rates), default risk, and liquidity risk.2 As the markets for nominal and indexed government debt in the United Kingdom are default-free and sufficiently liquid, risk due to uncertainty about future inflation rates is likely to be the
primary driver of the inflation risk premium. Other factors unrelated to inflation expectations may at times affect inflation compensation, such as changes in demand for indexed debt induced by institutional reform, tax issues or convexity. These are not identified separately and to the extent that
they do not conform to the estimated dynamics of the instantaneous inflation rate are largely attributed to the risk premium.3
The model permits tractable and nonnegative bond prices. Substituting equations (7), (8), (9) and (10) into the asset-pricing equation (6) yields
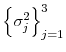 . Yields are thus affine functions of the three latent factors,
. Yields are thus affine functions of the three latent factors,
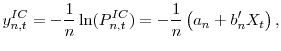
3.1 Data
I estimate the model using zero-coupon inflation compensation yields provided by the Bank of England. Inflation compensation is calculated as the spread between the nominal and real zero-coupon yield curves, smoothed using the Bank of England's preferred spline-based method and, in the case of the real yield curve, adjusted for the indexation lag on index-linked gilts; see Anderson and Sleath (2001) for details.4
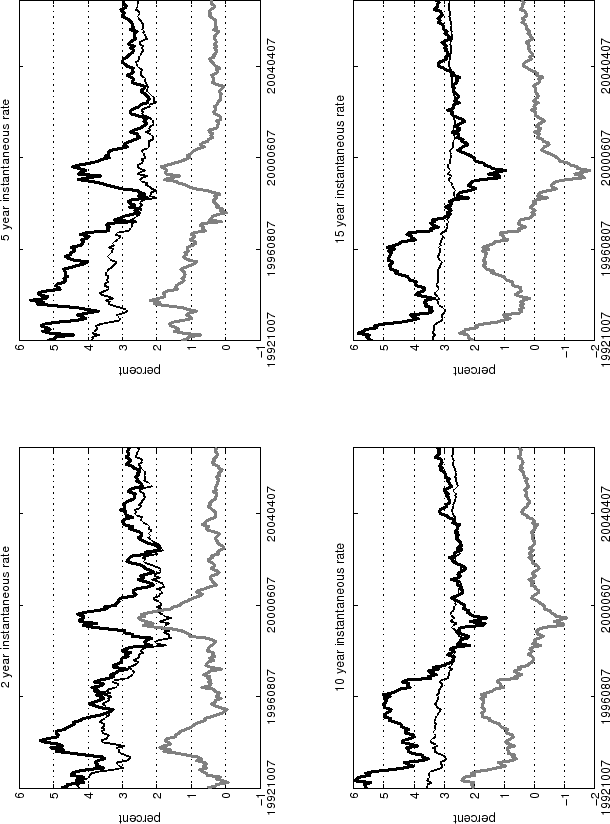
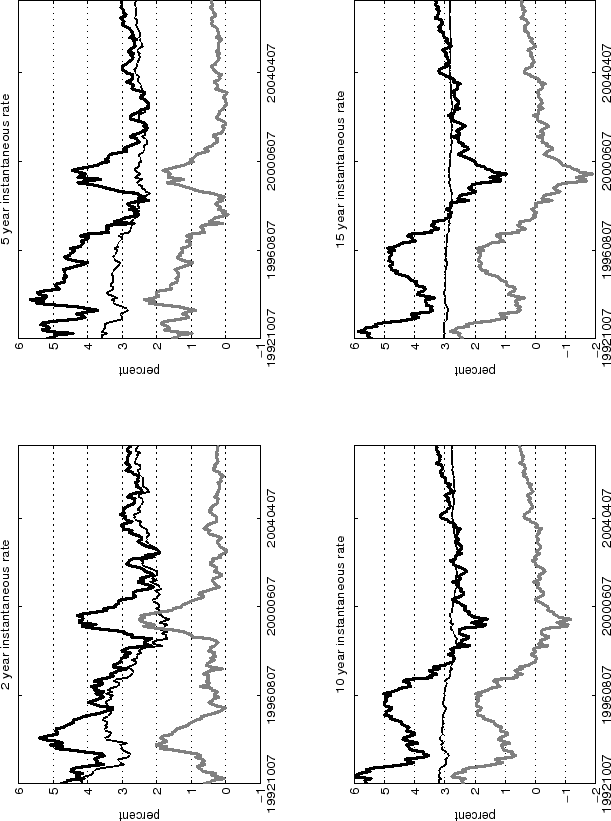
The estimation sample consists of monthly data from October 1992 to May 2007, the sample start date coinciding with the announcement of the Bank of England's first inflation target. The sample range deliberately captures the period during which the Bank of England actively pursued an inflation-targeting policy with an inflation objective at or close to 2.5 percent RPIX inflation--or its expected equivalent for CPI inflation--lessening concern about structural change in long-run policy objectives during the estimation period. The shortest-maturity yield available over the whole sample is 4 years, so the model is estimated with yields of maturity 4, 5, 6, 10 and 15 years (data shown in Figure 1). The lack of short-maturity data makes the model better suited to address questions about long-run inflation expectations and risk premia. While one can construct a fitted term structure of short-maturity yields and forward rates using the parameters estimated from longer-maturity yields, the fit is likely to be worse at short horizons. Once estimated, the parameters describing the term structure can be used to fit the model to higher-frequency data, such as daily or weekly, which will prove valuable in analysing the market reaction to changes in Bank of England policy.
Results of a two-factor model estimated over the same sample period are shown in Figure 8 at the end of the paper, but the specification is not able to meet the stylised facts of inflation expectations in the United Kingdom. Specifically, two factors are insufficient to capture the long-run dynamics of inflation compensation, with a deterioration in root mean square error particularly for long-maturity yields (see column 3 of Table 2 at the end of the paper) and overly-fast mean reversion of the most persistent factor.
3.2 Estimation
The three-factor state-space model outlined in Section 2.2 is estimated with maximum likelihood; parameter estimates and fit diagnostics are shown in Table 2 at the end of the paper. The model assumes that the latent factors are stationary processes and
accordingly, the instantaneous expected future inflation rate reverts to its long-run mean, ![]() , as maturity increases. Risk premia also revert to a stationary mean, as they are
functions of the same three latent factors, but the estimated factor loadings result in a much slower rate of mean reversion. When estimated, the most persistent factor has annual persistence of 0.853, equivalent to a half-life of about four and half years. Mean reversion of this factor is
sufficiently gradual that the model can accommodate much of the reduction in the level of inflation compensation over the sample.5 And because risk premia and
expected inflation both place some loading on this factor, they too can be far from their means for long periods.
, as maturity increases. Risk premia also revert to a stationary mean, as they are
functions of the same three latent factors, but the estimated factor loadings result in a much slower rate of mean reversion. When estimated, the most persistent factor has annual persistence of 0.853, equivalent to a half-life of about four and half years. Mean reversion of this factor is
sufficiently gradual that the model can accommodate much of the reduction in the level of inflation compensation over the sample.5 And because risk premia and
expected inflation both place some loading on this factor, they too can be far from their means for long periods.
3.2.1 A question of persistence
Estimates of persistence in time-series models are known to be biased downwards in small samples and this bias becomes more pronounced as the stationary series approaches a random walk (see Shaman and Stine, 1988, among others). Given that we have only 15 years of data with which to estimate the dynamics of the factors, it is likely that persistence, especially that of the most persistent factor, is underestimated. Such downward bias imparts too much mean reversion to long-run inflation expectations and, as a result, too much movement to far-horizon risk premia.
This small-sample estimation problem is not unique to the term-structure estimation in this paper. Kim and Orphanides (2005) address the problem by including survey data in their estimation to help pin down the dynamics of the interest-rate process of US nominal interest rates. For the United Kingdom, however, available survey forecasts pertain to RPIX, not RPI inflation, which complicates their use in estimation. An alternative is to seek an econometric solution to the estimation problem and use the survey data ex post as a cross check of the model's results.
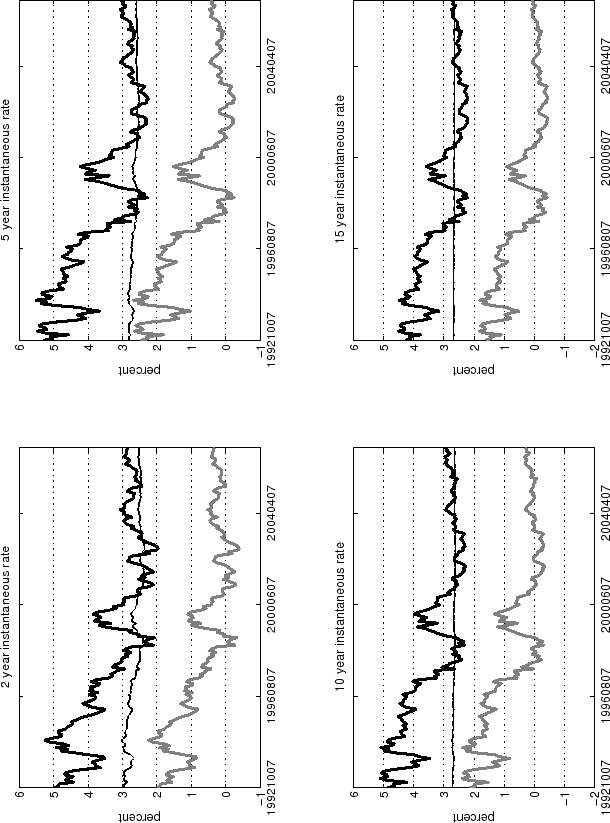
In light of the downward bias problem, I re-estimate the model restricting the persistence of the most persistent factor to its median unbiased estimate based upon Monte Carlo simulations of a first-order autoregressive process.6 Given the original estimate of annual persistence, 0.853, the median unbiased estimate is 0.913, which extends the half life of the factor to about seven and a half years. The remainder of the parameters are freely estimated and their estimates and measures of fit are shown in column 2 of Table 2 at the end of the paper. Based on the likelihood values of the restricted and unrestricted models, a likelihood ratio test with one degree of freedom cannot reject the imposed restriction. Nor is there any noticeable deterioration in fit according to the root mean square error statistics in Table 2.
Moreover, the restricted specification accords better with other macroeconomic evidence. Specifically, inflation expectations from the restricted model more closely resemble the inflation expectations of professional forecasters. To the extent that professional forecasters share similar expectations to financial market participants, survey responses are a useful cross check of the model's results.
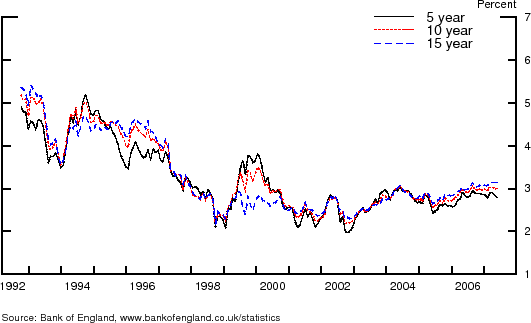
Figure 2 plots average six- to ten-year ahead RPIX inflation expectations reported by Consensus Economics each April and October against the six- to ten-year ahead instantaneous expected RPI inflation rate implied by the unrestricted and restricted specifications of the model for the same months. The figure also shows the fitted values to two out-of-sample years, 1990 and 1991. Although the model pertains to RPI inflation and survey responses to RPIX inflation, at horizons beyond the usual monetary-policy cycle, these forecasts should reasonably converge. Indeed, outcomes of both measures of inflation have averaged 3.3 percent since 1990 (see Figure 3).
Both specifications capture the disinflation of the mid 1990s, but the persistence-restricted specification does a better job of matching the high expected inflation early in the 1990s. Slower mean reversion also enables the restricted specification to track the continued decline in inflation expectations through to 2003 before rising modestly in recent years. The gap between model- and survey-based expectations in 1992 and 1993 likely reflects the prolonged period during which RPI inflation outcomes fell short of RPIX inflation, perhaps creating expectations that such a gap would persist well into the future. Ultimately, the gap between the two measures of inflation was closed by mid-1994 and model and survey expectations converge at about the same time.
Because of its coherence with survey evidence, the restricted model is preferred and will be the basis of discussion from here on. However, the two specifications tell qualitatively and, to a large extent, quantitatively similar stories about the evolution of inflation expectations and risk premia, so the choice of model does not detract from the bigger picture. Fitted decompositions from the unrestricted model are shown in Figure 6 at the end of the paper.
3.3 Expected inflation and inflation risk premia during the inflation-targeting years
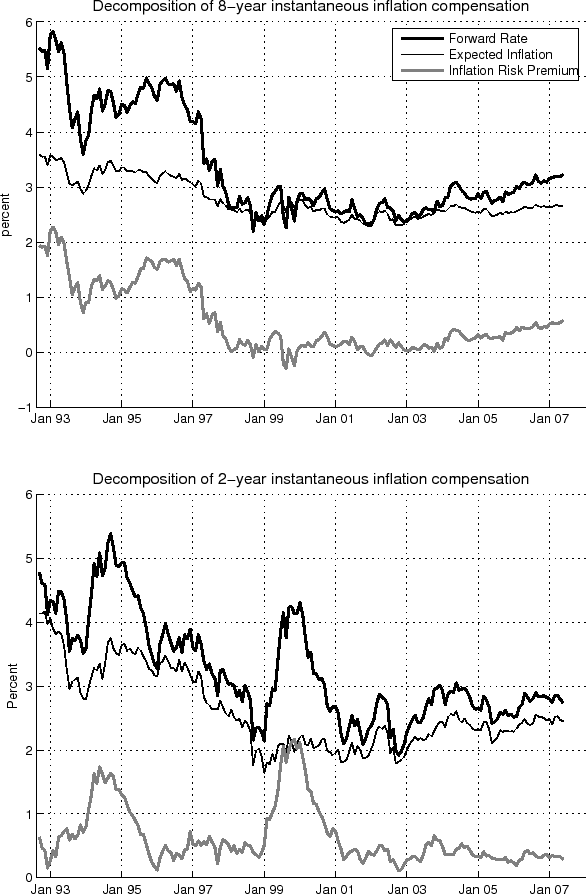
Most of the steep decline in far-forward inflation compensation between late 1992 and 1998 is attributable to a reduction in inflation risk premia. The upper panel of Figure 4 plots fitted instantaneous forward inflation compensation eight years ahead, alongside the model's decomposition into expected inflation and risk premia at that horizon. Eight-year ahead inflation expectations match closely the six-to-ten year average shown in Figure 2; forward rates at more maturities are shown in Figure 7 at the end of the paper.
During the early years of inflation targeting, far forward rates of inflation compensation declined about 3 percentage points, of which two percentage points are estimated to have been lower risk premia. The compression of risk premia during 1997 stands out, with the sharp one-day move in that year coinciding with the announcement of the Bank of England's operational independence. Through to 1998, expected inflation trended down from 3.5 percent to around 2.5 percent, which as we have already seen, matches closely the movements in private forecasters' long-run inflation expectations. After a long period of low and relatively stable far-forward rates, inflation compensation began to trend up from early 2004, a movement largely attributable to rising inflation risk premia. Indeed, by late 2006, risk premia had reached a decade high. Section 4 discusses some of the potential reasons underlying this movement.
Turning to the lower panel of Figure 4, which plots inflation compensation and its components at the two-year horizon, two features stand out. First, more of the movement in inflation compensation is attributed to expected inflation. This is intuitive given the shorter forecast horizon, where business cycle fluctuations are likely to be played out. From late 1992 to early 1998, two-year ahead inflation expectations declined by about 2 percentage points (from just under 5 percent to just under 3 percent), which accords well with the decline in near-term survey forecasts of RPIX inflation over the same period.7 The second notable feature is that short-run inflation risk premia have shown no systematic trend over the 15 years since the introduction of inflation targeting, unlike long-horizon inflation risk premia which trended down noticeably. In terms of their magnitude, long-maturity risk premia fell but it appears that as the Bank of England earned credibility in its commitment to inflation targeting, the greatest reductions in perceptions of risk concerned long-run inflation rather than the near-term outlook.
Short-maturity term premia have at times been quite variable, with the episode between January 1999 and January 2001 likely owing to the Minimum Funding Requirement for pension funds which came into effect during the late 1990s, and the threat of further reforms. Pension funds, which hold either directly or indirectly about one half of index-linked gilts, sharply increased their demand for indexed government debt at desirable maturities, raising forward inflation compensation dramatically at some horizons (and narrowing forward rates at very long horizons). Reassuringly, the model attributes very little of this movement to expected inflation, which accords well with the interpretation of developments at the time (Clews, 2002).
4. Changes in the practice of inflation targeting
Numerous researchers have argued that clarity, transparency and commitment by a central bank to its inflation objectives should help to anchor inflation expectations. Adjustments of the Bank of England's inflation-targeting policies offer natural experiments to assess these claims. The term-structure model described above--fitted to high-frequency data--makes it possible to observe how financial market participants' long-run inflation expectations and perceptions of risk responded to those adjustments. A short appendix at the end of the paper gives the chronology of refinements to the Bank of England's policies, and the following section addresses three major changes that have occurred.
1. Announcement of the inflation target and its early years
The Bank of England announced its first inflation target on ![]() October, 1992, a range target between 1 and 4 percent as measured by annual RPIX inflation. Forward rates of inflation
compensation five to ten years ahead declined about 30 basis points over the following two days, 20 basis points of which appear to have been a reduction in the inflation risk premium. However, both inflation expectations and risk premia were fairly volatile early in the sample and these moves were
quickly eroded. Over the following five years, long-run inflation expectations did drift down gradually from about 3.5 percent to 3 percent, while the inflation risk premium moved in a 1 to 2 percent band (Table 1 reports end-of-year observations and selected averages). On
October, 1992, a range target between 1 and 4 percent as measured by annual RPIX inflation. Forward rates of inflation
compensation five to ten years ahead declined about 30 basis points over the following two days, 20 basis points of which appear to have been a reduction in the inflation risk premium. However, both inflation expectations and risk premia were fairly volatile early in the sample and these moves were
quickly eroded. Over the following five years, long-run inflation expectations did drift down gradually from about 3.5 percent to 3 percent, while the inflation risk premium moved in a 1 to 2 percent band (Table 1 reports end-of-year observations and selected averages). On ![]() June, 1995, the redefinition of the target to 2.5 percent or less annual RPIX inflation elicited little market reaction on the day, although near-term inflation expectations and risk premia
appeared to decline somewhat in subsequent months.
June, 1995, the redefinition of the target to 2.5 percent or less annual RPIX inflation elicited little market reaction on the day, although near-term inflation expectations and risk premia
appeared to decline somewhat in subsequent months.
| Forward Rate | Expected Inflation | Inflation Risk Premium | |
|---|---|---|---|
| End of year: 1992 | 5.25 | 3.43 | 1.82 |
| End of year: 1993 | 3.62 | 2.90 | 0.72 |
| End of year: 1994 | 4.45 | 3.36 | 1.09 |
| End of year: 1995 | 4.59 | 3.12 | 1.48 |
| End of year: 1996 | 4.24 | 3.08 | 1.16 |
| End of year: 1997 | 3.02 | 2.69 | 0.33 |
| End of year: 1998 | 2.39 | 2.36 | 0.03 |
| End of year: 1999 | 2.48 | 2.71 | -0.23 |
| End of year: 2000 | 2.44 | 2.43 | 0.01 |
| End of year: 2001 | 2.50 | 2.43 | 0.07 |
| End of year: 2002 | 2.38 | 2.33 | 0.05 |
| End of year: 2003 | 2.70 | 2.58 | 0.12 |
| End of year: 2004 | 2.83 | 2.55 | 0.28 |
| End of year: 2005 | 2.87 | 2.54 | 0.34 |
| End of year: 2006 | 3.15 | 2.65 | 0.49 |
| 31 May 2007 | 3.24 | 2.66 | 0.58 |
| Averages: 1 Oct 1992 to 5 May 1997 | 4.66 | 3.27 | 1.39 |
| Averages: 6 May 1997 to 9 Dec 2003 | 2.63 | 2.52 | 0.11 |
| Averages: 10 Dec 2003 to 31 May 2007 | 2.96 | 2.60 | 0.36 |
Notes: Fitted model estimates of eight-year ahead instantaneous inflation compensation from the persistence-restricted specification. Numbers in the table correspond to those plotted in the upper panel of Figure 4. E
2. Independence
The announcement on ![]() May, 1997 of the granting of operational independence of the Bank of England and the creation of the MPC was met by a sharp decline in forward rates of
inflation compensation at both short and long horizons, an event also noted by ()GLS_05 and ()Geraats_Eijffinger_Cruijsen_2006 among others. Five-, eight and ten-year ahead forward rates of inflation compensation declined about 35 basis points on
the day of the announcement, cumulating to nearly 60 basis points of decline within another two days. The model allocates about one third to a decline in long-run expected inflation and about 40 basis points to lower inflation risk premia. The sharp decline was never retraced and over the following
months risk premia declined even further. Long-run expected inflation stabilised around 2.5 percent by late in the year.
May, 1997 of the granting of operational independence of the Bank of England and the creation of the MPC was met by a sharp decline in forward rates of
inflation compensation at both short and long horizons, an event also noted by ()GLS_05 and ()Geraats_Eijffinger_Cruijsen_2006 among others. Five-, eight and ten-year ahead forward rates of inflation compensation declined about 35 basis points on
the day of the announcement, cumulating to nearly 60 basis points of decline within another two days. The model allocates about one third to a decline in long-run expected inflation and about 40 basis points to lower inflation risk premia. The sharp decline was never retraced and over the following
months risk premia declined even further. Long-run expected inflation stabilised around 2.5 percent by late in the year.
The reduction in inflation risk premia during 1997 identified by the model appears consistent with declines in other measures of forecaster uncertainty. Specifically, the dispersion of point forecasts of inflation across respondents to the Bank of England's Survey of External Forecasters also started to decline from the second quarter of 1997 and leveled out from early 1999 (shown in Boero, Smith and Wallis, 2007).8 The survey question pertains to a much shorter horizon than the model-the fourth quarter of the following year-but is suggestive that perceptions of inflation risk moderated following the Bank of England's independence.
The reaction to the granting of independence has broader implications for monetary policy. Actions that enhance the perceived commitment of a central bank to its inflation goal not only align the public's inflation expectations with the central bank's target, but reduce uncertainty about future inflation outcomes. The U.K. experience also suggests that inflation targeting helps lower long-term interest rates by reducing the inflation risk premia embedded in market rates, and not just by reducing expected inflation, as argued by Geraats et al (2006). The results described above also correlate well with the findings of Gurkaynak et al (2006) that post-1997, long-horizon U.K. inflation compensation ceased to be sensitive to the surprise components of macroeconomic data releases: the reduction in inflation uncertainty seems to have gone hand-in-hand with decreased sensitivity to news.
The target was redefined a month later, on ![]() June, 1997, to a symmetric target of 2.5 percent. Much like the earlier redefinition, the change elicited little reaction in the term
structure of inflation compensation in the days following the announcement, most likely dwarfed by the changes a month earlier.
June, 1997, to a symmetric target of 2.5 percent. Much like the earlier redefinition, the change elicited little reaction in the term
structure of inflation compensation in the days following the announcement, most likely dwarfed by the changes a month earlier.
3. Redefining the target from RPIX to CPI inflation
Announced in June 2003 and implemented on ![]() December 2003, the Bank of England's inflation target was redefined from 2.5 percent measured by RPIX inflation to 2 percent measured by
annual CPI inflation. The wedge between the two reflected the expected long-run difference between the two measures arising from differences between their formulae (geometric versus arithmetic weighting), although the likely long-run difference was understood to be closer to three quarters of a
percentage point.9
December 2003, the Bank of England's inflation target was redefined from 2.5 percent measured by RPIX inflation to 2 percent measured by
annual CPI inflation. The wedge between the two reflected the expected long-run difference between the two measures arising from differences between their formulae (geometric versus arithmetic weighting), although the likely long-run difference was understood to be closer to three quarters of a
percentage point.9
Thus, in the switch to the CPI inflation target, two additional sources of risks to RPI inflation emerged. First, even were both RPIX and CPI inflation expected to return to known, respective means, the central bank had ceased to promise to address persistent deviations of RPIX inflation from its mean. Second, the expected trend rates of growth of CPI and RPIX inflation could drift apart permanently. Compositional differences could accentuate the formula effect and long-lived trends in housing-related components could drive a wedge between the two measures, greater than had previously been the case between RPI and RPIX. In other words, the new target for CPI inflation translates into an unclearly-defined goal for RPI inflation and uncertainty about the central bank's willingness to stabilise retail prices.
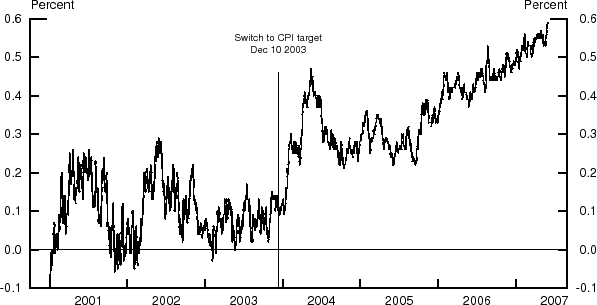
It is not altogether surprising then that the switch to the new inflation target was accompanied by an increase in long-run inflation risk premia in financial markets. Indexed debt in the United Kingdom continued to be linked to RPI after the redefinition of the target and the additional risk inherent in that measure of inflation appears to have been embedded into market-based inflation compensation. Figure 5 illustrates how abruptly that occurred. Fitted values from the model indicate that inflation risk premia rose sharply in the weeks following the adoption of the CPI inflation target to a level about 20 basis points above the average of earlier years. The model attributes no such sharp increase to inflation expectations around those weeks.
Inflation risk premia continued to rise through to mid-2004, with concerns about rapid house-price increases spilling into RPI inflation likely contributing to the rise. However, the bulk of the increase in risk premia was not retraced even after concerns about house-price appreciation had alleviated. Beginning late 2005, inflation risk premia rose further, with rising energy prices and high inflation readings during 2005 and 2006 appearing to heighten uncertainty. At short horizons, Consensus Economics survey responses indicate that in mid-2006, average RPIX inflation expectations for the coming year rose above 2.5 percent for the first time since 1998, and that CPI inflation expectations rose above 2 percent. For longer-horizon questions, survey-based RPIX and CPI inflation expectations remain close to 2.5 and 2 percent respectively. This is consistent with the model evidence that most of the recent rise in RPI-based inflation compensation owes to heightened perceptions of risk concerning long-run inflation outcomes and an increase in the compensation demanded for inflation risk.
5. Conclusion
Applying a no-arbitrage, affine factor model to the term structure of inflation compensation in the United Kingdom provides insights into how the Bank of England's policies have influenced inflation expectations. To the extent that inflation risk premia mirror perceptions of inflation risk, the model provides a way of assessing not only the level of long-run inflation expectations but also uncertainty about future inflation outcomes. It also has the advantage that it can be fitted to higher-frequency data than traditional sources of inflation expectations, namely surveys, but yields consistent results.
The model's fitted results provide insights into the effects of the Bank of England's inflation-targeting policies. Market participants' long-run expectations of retail price inflation trended down from 1992, but not until after the Bank of England was granted independence did expectations approach and remain close to 2.5 percent. In contrast, inflation risk premia showed little sign of declining until 1997, when they dropped abruptly in the months following independence. The abrupt drop suggests that independence signalled more credible commitment by the central bank to its inflation goal, bringing about a reduction in perceptions of long-horizon inflation risk. By comparison, various redefinitions of the target and measures to increase transparency, such as earlier publication of the MPC's minutes or publication of details of the Bank's forecasting model, did not have the same impact or lasting effect on expectations. The findings of this paper-that term premia were substantially lower following independence-are consistent with a long-lived reduction in long nominal term premia post independence found by ()BianchiMumtazSurico_08. Indeed, the results presented here suggest that much of the moderation in nominal term premia owed to a moderation in inflation risk.
As a final observation, long-run inflation expectations and inflation risk premia were low and fairly stable until the inflation target was redefined in December 2003 from RPIX inflation to CPI inflation. Since then, long-run RPI inflation risk premia have risen about 40 basis points, above the range established since 1997. Disbanding the RPIX inflation target has arguably increased the compensation that investors require to hold long-run retail price inflation risk, as the new target for CPI inflation translates into an unclearly-defined goal for RPI inflation and uncertainty about the central bank's willingness to stabilise retail prices. This need not reflect upon the Bank of England's credibility as an inflation targeter. To the contrary, survey-based inflation expectations do appear to be well anchored on the new CPI inflation measure and model-based RPI inflation expectations have moved relatively little. However, the experience highlights a more general point. Even in the presence of a general objective for price stability, unclear definition of and uncertain commitment to an inflation goal is likely to foster heightened perceptions of long-run inflation risk.
Bibliography
"New Estimates of the UK Real and Nominal Yield Curves," Bank of England Working Paper, No. 126.| 1992, 8 October | First inflation target, defined as a rate of 1 to 4 percent annual |
| RPIX inflation. | |
| 1994, 13 April | Minutes of the Chancellor of the Exchequer's meeting with the |
| Governor Bank of England first published. | |
| 1995, 14 June | Inflation target redefined as 2.5 percent or less annual RPIX |
| inflation. | |
| 1997, 6 May | Bank of England granted operational independence. |
| 1997, 12 June | Inflation target redefined as a symmetric target around 2.5 percent |
| annual RPIX inflation | |
| 1998, 21 October | Publication timetable for minutes of MPC meetings shortened to |
| two weeks. | |
| 2003, 9 April | Intention to switch to an inflation target measured by CPI inflation |
| announced by the Chancellor of the Exchequer. | |
| 2003, 10 December | Switch to an inflation target of 2 percent annual CPI inflation |
| announced by the Chancellor of the Exchequer. | |
| 2005, 31 January | Publication of details of the Bank of England Quarterly Model, |
| including equations, data sources and parameter values. |
| Three-factor model: Unrestricted | Three-factor model: Restricted | Two-factor model: Unrestricted | |
|---|---|---|---|
|
|
2.0695 | 0.0913* | 0.2313 |
|
|
-0.4172 | -0.7290 | -2.8732 |
|
|
-0.3318 | -0.1026 | - |
|
|
0.5990 | 1.0481 | 2.3693 |
|
|
0.3479 | -0.1393 | - |
|
|
0.1587 | 1.3183 | - |
|
|
0.0126 | 0.0026 | 0.0009 |
|
|
0.0039 | 0.0138 | 0.0154 |
|
|
0.0051 | 0.0010 | - |
|
|
0.0290 | 0.0299 | 0.0267 |
|
|
-0.3895 | -0.1988 | -0.1320 |
|
|
0.1171 | -0.3538 | -0.4484 |
|
|
-0.1494 | 0.1780 | - |
| Largest annual persistence | 0.853 | 0.913 | 0.793 |
| Log-likelihood | -37.1730 | -37.1710 | -32.3345 |
| basis points | basis points | basis points | |
|---|---|---|---|
| RMSE for zero-coupon yields: 5 year | 1.9889 | 1.9888 | 1.9144 |
| RMSE for zero-coupon yields: 10 year | 1.1477 | 1.1471 | 14.1819 |
| RMSE for zero-coupon yields: 15 year | 3.6798 | 3.6848 | 32.1835 |
* This parameter restricted to the median unbiassed estimate of the most persistent factor from the unrestricted specification. E
 |
![\displaystyle E_{t}\left[ \frac{M_{t+n}^{N}}{M_{t}^{N}}R_{n,t}^{N}\right] =1%](img1.gif)
![\displaystyle P_{n,t}^{N}=E_{t}\left[ \frac{M_{t+n}^{N}}{M_{t}^{N}}\right] =E_{t}\left[ \frac{M_{t+n}^{R}}{M_{t}^{R}}\right] E_{t}\left[ \frac{Q_{t}}{Q_{t+n}% }\right] +cov_{t}\left[ \frac{M_{t+n}^{R}}{M_{t}^{R}}\frac{Q_{t}}{Q_{t+n}% }\right] .%](img12.gif)
![\displaystyle P_{n,t}^{IC}=E_{t}\left[ \frac{M_{t+n}^{IC}}{M_{t}^{IC}}\right] %](img20.gif)