Skip to: [Printable Version (PDF)] [Bibliography] [Footnotes]

Finance and Economics Discussion Series: 2008-55 Screen Reader version ^♣

Specification Analysis of Structural Credit Risk Models*

Jing-zhi Huang

Penn State University

Hao Zhou

Federal Reserve Board

First Draft: November 2005
This Version: September 2008

Keywords: Structural credit risk models, credit default swap spreads, high frequency equity volatility, consistent specification analysis, pricing error diagnostics.

Abstract:

In this paper we conduct a specification analysis of structural credit risk models, using term structure of credit default swap (CDS) spreads and equity volatility from high-frequency return data. Our study provides consistent econometric estimation of the pricing model parameters and specification tests based on the joint behavior of time-series asset dynamics and cross-sectional pricing errors. Our empirical tests reject strongly the standard Merton (1974) model, the Black and Cox (1976) barrier model, and the Longstaff and Schwartz (1995) model with stochastic interest rates. The double exponential jump-diffusion barrier model (Huang and Huang, 2003) improves significantly over the three models. The best one among the five models considered is the stationary leverage model of Collin-Dufresne and Goldstein (2001), which we cannot reject in more than half of our sample firms. However, our empirical results document the inability of the existing structural models to capture the dynamic behavior of CDS spreads and equity volatility, especially for investment grade names. This points to a potential role of time-varying asset volatility, a feature that is missing in the standard structural models.

JEL Classification: G12, G13, C51, C52.

1 Introduction

Credit derivatives markets have been growing exponentially over the past several years. According to the most recent biennial survey by the British Bankers' Association, the global credit derivatives market is expected to exceed $8 trillion in 2006. Credit default swaps (CDS) are currently the most popular credit derivatives instrument and account for about half of the credit derivatives market. Under a CDS contract the protection seller promises to buy the reference bond at its par value when a pre-defined default event occurs. In return, the protection buyer makes periodic payments to the seller until the maturity date of the contract or until a credit event occurs. This periodic payment, usually expressed as a percentage of the notional value underlying a CDS contract, is called the CDS spread. Compared with corporate bond spreads, CDS spreads are a relatively pure pricing of default risk of the underlying entity, abstracting from numerous bond characteristics, such as seniority, coupon rates, embedded options, and guarantees. As a result, there is a growing literature on testing credit risk models using the information from the CDS market.

A widely used approach to credit risk modeling in practice is the so-called structural method, originated from Black & Scholes (1973) and Merton (1974). Whereas there have been many empirical studies of structural models, especially recently, based on corporate bond data, the empirical testing of these models using CDS spreads is quite limited. Such a testing is desirable especially given the recent empirical evidence based on the corporate bond market that existing structural models have difficulty either fitting corporate bond spreads (e.g., Jones, et al. (1984), Lyden & Saraniti (2000), Delianedis & Geske (2001), Eom, et al. (2004), Arora, et al. (2005) and Ericsson & Reneby (2005)) or explaining both spreads and default frequencies simultaneously (the so-called credit spread puzzle documented in Huang & Huang (2003)). If CDS spreads are considered to be a purer measure of credit risk than corporate bond spreads, then the existing structural models (purely default risk based) may perform better in capturing the behavior of CDS spreads than they do for corporate bond spreads. In this article we test five representative structural credit risk models using a sample of 93 single name CDS contracts during the period January 2002 - December 2004. The models we consider are the standard Merton (1974) model, the Black & Cox (1976) model with a flat barrier, the Longstaff and Schwartz (1995) model with stochastic interest rates, the Collin-Dufresne & Goldstein (2001) model with a stationary leverage, and the double exponential jump diffusion model used in Huang & Huang (2003).

More specifically, we formulate a specification test based on the pricing solutions of CDS spreads and equity volatility implied by a particular structural model. By assuming that both equity and credit markets are efficient and that the underlying structural model is correct, we obtain the identifying moment restrictions on the model parameters, such as asset volatility, the default barrier, and the speed of mean-reverting leverage. Such a GMM estimator with an ensuring -test is a consistent econometric method, for parameter estimation and specification analysis of the structural credit risk models. One advantage of such a test is that it provides us with a precise inference on whether a particular structural model is rejected or not in the data, unlike the existing studies based on calibration, rolling estimation or regression analysis. Furthermore, unlike the existing studies that focus on 5-year CDS contracts, we use the entire term structure of CDS spreads. Such a method provides us a tighter identification of structural model parameters and minimizes the effect of measurement error from using bond characteristics, and thus attributes the test results mostly to the specification error. More importantly, by focusing on the equity volatility measured with high frequency data, instead of low frequency daily data, our approach speaks directly to the recent finding that volatility dynamics has a strong potential in better explaining the credit spreads.¹

Our empirical tests reject strongly the following three standard models: the Merton (1974) model, the Black & Cox (1976) model, the Longstaff & Schwartz (1995) model. However, the double exponential jump-diffusion barrier model outperforms significantly these three models. The stationary leverage model of Collin-Dufresne & Goldstein (2001) is the best performing one among the five models examined in our analysis and more specifically, is not rejected by the GMM test for more than half of the 93 companies in our sample. In addition, the test results allow us to gain a better understanding of the structural models, which otherwise does not obtain easily from ad hoc calibrations or rolling estimation analysis. For example, when allowing the default barrier to be different from the total liabilities, we discover a negative relationship between the observed debt/asset ratio and the implied default boundary trigger. Moreover, when a dynamic leverage or a jump component is allowed for, the overall fitting of average CDS term structure is improved with a much smaller pricing error. Further more, for the best performing dynamic leverage model, the individual firms sensitivity to interest rate or varies dramatically from significant positive for investment grade names to significant negative for speculative grade names, suggesting a great deal of heterogeneity in each firm's exposure to systematic risk.

Finally, our empirical analysis sheds some light on how to improve the existing structural models in order to fit better CDS prices. One implication from our results is that a term structure model more flexible than the one-factor Vasicek (1977) model - used in Longstaff & Schwartz (1995) and Collin-Dufresne & Goldstein (2001) - may reduce the pricing error. Also judging from several pricing error diagnostics, jump augmentation seems to improve the investment grade names, while dynamic leverage seems to improve the speculative grade names. We also find that for the junk rated names, the observed spot leverage is very close to the long-run mean of the risk-neutral leverage implied by the Collin-Dufresne & Goldstein (2001) model; while for investment grades the spot leverage is much lower than the risk-neural leverages. This mirrors the recently documented low leverage puzzle for high rating firms (Chen and Zhao, 2006; Strebulaev & Yang, 2006). Our analysis also documents the inability of the standard structural models in fitting time-series of both CDS spreads and equity volatility. Given that equity volatility in structural models is time-varying, this result provides a direct evidence that a structural model with stochastic asset volatility may improve the model performance (Huang & Huang, 2003; Zhang, et al., 2006; Huang, 2005).

There are several empirical studies of structural models based on CDS data that are directly related to ours. For instance, Predescu (2005) examines the Merton (1974) model and a Black & Cox (1976) type barrier model with a rolling estimation procedure combined with the MLE approach proposed in Duan (1994). Hull, et al. (2004) study the Merton model using a calibration approach. Chen, et al. (2006) investigate the Merton, Black-Cox, and Longstaff-Schwartz models (however, their implementation of the latter model is based on an approximated solution). Examples of studies that link CDS premiums with variables from structural credit risk models using a regression analysis include Cossin & Hricko (2001); Houweling & Vorst (2005); Ericsson, et al. (2005). Our analysis differs from these studies in that we consider three more recent models (Longstaff-Schwartz, CDG, and Huang-Huang) and conduct a rigorous GMM-based specification analysis.

Structural credit risk models have also been examined empirically using information from the corporate bond market. Examples include Schaefer & Strebulaev (2004); Huang & Huang (2003); Cremers, et al. (2004); Jones, et al. (1984); Eom, et al. (2004). These studies have indicated that structural models have difficulty predicting corporate bond yield spreads accurately. One line of reasoning is that structural models may be able to do a better job in fitting CDS prices, presumably because CDS prices are a purer measure of default risk and corporate bond prices (Ericsson, et al., 2006; Longstaff, et al., 2005). One implication of our analysis is that structural models still have difficulty predicting credit spreads even if when a purer measure of credit risk is used in the empirical analysis, although a better measure of credit spread can help us rank order the extent structurally models more consistently.

Finally, notice that like many other studies such as Jones, et al. (1984), Lyden & Saraniti (2000), Delianedis & Geske (2001), Eom, et al. (2004), and Ericsson & Reneby (2005), here we examine the implications of structural models for pricing only (and ignore the implications for default probabilities under the real measure). In another word, we do not examine the credit spread puzzle here.

The rest of the paper is organized as follows. Section 2 briefly outlines the class of structural models examined in our empirical analysis. Section 3 presents our econometric method of parameter estimation and specification tests. Section 4 describes the data used in our analysis, and Section 5 reports and discusses our empirical findings. Finally, Section 6 concludes.

2 A Review of Structural Credit Risk Models

We consider five representative structural models in our empirical analysis. Specifically, they include the Merton (1974) model, the Black & Cox (1976) model, the Longstaff & Schwartz (1995) model, the Collin-Dufresne & Goldstein (2001) model, and the double exponential jump diffusion model considered in Huang & Huang (2003).² The Black and Cox model with a flat barrier examined here can be also considered to be a special case of either the exogenous-default version of Leland & Toft (1996) or the one-factor version of Longstaff & Schwartz (1995). Except for the Merton model, all other ones are barrier-type models. Among the five models, Longstaff & Schwartz (1995) and Collin-Dufresne & Goldstein (2001) are two-factor models, and the remaining three are one-factor models. For completeness, below we briefly review the five structural models to be tested in our empirical study.

Although these five models differ in certain economic assumptions, they can be embedded in the same underlying structure that includes specifications of the underlying firm's asset process, the default boundary, and the recovery rate etc. Let be the firm's asset process, the default boundary, and the default-free interest rate process. Assume that, under a risk-neutral measure,

$\displaystyle \frac{dV_t}{V_{t-}}$	$\textstyle =$	$\displaystyle ( r_t -\delta) dt + \sigma_v dW^{Q}_t + d \left[ \sum_{i=1}^{N_t^Q} \left(Z_i^Q - 1 \right)\right] - \lambda^Q \xi^Q dt,$	(1)
$\displaystyle d \ln K_t$	$\textstyle =$	$\displaystyle \kappa_\ell \ [ - \nu - \phi( r_t - \theta_\ell) - \ln (K_t/V_t) ]\, dt$	(2)
$\displaystyle d r_t$	$\textstyle =$	$\displaystyle (\alpha - \beta \, r_t) \, dt + \sigma_r \, d Z_t^Q$	(3)

where $\delta$ , $\sigma_v$ , $\kappa_\ell$ , $\theta_\ell$ , $\nu$ , $\phi$ , $\alpha$ , $\beta$ , and $\sigma_r$ are constants, and

and

are both one-dimensional standard Brownian motion under the risk-neutral measure and are assumed to have a constant correlation coefficient of $\rho$ . In Eq. (1), the process

is a Poisson process with a constant intensity $\lambda^Q > 0$ , the

's are i.i.d. random variables, and $Y^Q\equiv \ln (Z^Q_1)$ has a double-exponential distribution with a density given by

$\begin{displaymath} f_{Y^Q}(y) = p_u^Q \eta_u^Q e^{-\eta_u^Q y} {\bf 1}_{\{y\ge 0\}} + p_d^Q \eta_d^Q e^{\eta_d^Q y} {\bf 1}_{\{y < 0\}}. \end{displaymath}$

(4)

In equation (4), parameters $\eta_u^Q, \eta_d^Q>0$ and $p_u^Q, p_d^Q \ge 0$ are all constants, with

. The mean percentage jump size $\xi^Q$ is given by

$\begin{displaymath} \xi^Q = {\bf E}^Q\left[e^{Y^Q} - 1\right] = \frac{p_u^Q\eta_u^Q}{\eta_u^Q - 1} + \frac{p_d^Q\eta_d^Q}{\eta_d^Q+1} - 1. \end{displaymath}$

(5)

All five models considered in this analysis are special cases of the general specification in Eqs. (1) - (3). For instance, if the jump intensity is zero, then the asset process is a geometric Brownian motion. This specification is used in the four diffusion models, namely, the models of Merton, Black and Cox (BC), Longstaff and Schwartz (LS), and Collin-Dufresne and Goldstein (CDG). Regarding the specification of the default boundary , it is a point at the bond maturity in the Merton model. If $\kappa_\ell$ is set to be zero, then the default boundary is flat (a continuous barrier), an assumption made in Black and Cox (BC), Longstaff and Schwartz (LS), and the jump diffusion (HH) models. The mean-reverting specification in (2) is used in the Collin-Dufresne and Goldstein (CDG) model. The Vasicek model in (3) is used to describe the dynamics of the risk-free rate in the two-factor models of Longstaff and Schwartz (LS) and Collin-Dufresne and Goldstein (CDG) models. If both $\beta$ and $\sigma_r$ are zero, then the interest rate is constant, an assumption made in the three one-factor models. For simplicity and comparison with other studies, we assume a constant recovery rate.

Under each of the five structural models, we can calculate the corresponding risk-neutral default probability and then the CDS spread. Let $Q(t,\tau)$ denote the unconditional default probability over $(t,t+\tau]$ under the risk-neutral measure (or the forward measure with stochastic interest rates). Then the spread of a $\tau$ -year CDS contract is given by (under a one-factor model)

$\displaystyle \mbox{cds}(t,\tau)$	$\textstyle =$	$\displaystyle \frac{(1-R)\int_t^{t+\tau} e^{-rs} Q'(t,s) ds} {\int_t^{t+\tau} e^{-rs}[1-Q(t,s)]ds}$	(6)
	$\textstyle =$	$\displaystyle \frac{r(1-R) G(t,\tau)} {1- e^{-r\tau}[1-Q(t,\tau)] - G(t,\tau)},$	(7)

where

is the recovery,

is the interest rate, and

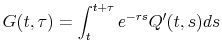$\displaystyle G(t,\tau)=\int_t^{t+\tau} e^{-rs} Q'(t,s) ds$			(8)

Eq. (7) holds for constant interest rate. As a result, the implementation of the structural models amounts to the calculation of the default probability $Q(\cdot,\cdot)$ either analytically or numerically. The default probability in the Merton (1974) and the Black and Cox (1976) models is known to have closed form solutions. The default probability in the double exponential jump diffusion model and the two-factor models do not have a known closed form solution but can be calculated using a numerical method (see, e.g., Huang and Huang (2003) for details).

3 A Specification Test of Structural Models

We use the fundamental pricing relationships implied by various credit risk models to identify structural parameters like asset volatility, default barrier, jump intensity, or dynamic leverage coefficient(s). The intuition is from Merton (1974) -- the delta function and pricing equation link equity volatility and credit spread directly to the structural variables and parameters. With these identifying restrictions, we can build an internally consistent GMM estimator (Hansen, 1982), which minimizes the fitted errors of credit spreads and equity volatility, with an appropriate weighting matrix determined by the pricing model and data sample. Along with consistent parameter estimation, we obtain an omnibus specification test, to rank order various credit risk models and to judge their pricing performance in a systematic framework. In addition, we also use the term structure and time series of CDS spreads to evaluate the economic pricing errors, which should by-and-large confirm our GMM specification test results. A structural model would be rejected by the GMM criterion function test, if the pricing errors are relatively large and exhibit systematic variations, assuming that the equity and credit markets are efficient.

The implementation of our estimation strategy has several advantages. First, we use high frequency equity returns to construct a more accurate estimate of the equity volatility, therefore minimizing the measurement error imputed into the asset volatility estimate (given any structural model for the underlying asset process), while leaving the main suspect to possible model misspecification which we really care about. Second, we use the CDS spreads as a relative purer measure of the credit risk, therefore sanitizes our approach from the specific pricing error problem associated with bond market iniquity or other non-default characteristics (Longstaff, et al., 2005). In addition, we use the term structure and time series of CDS spreads in both estimation and pricing exercise, while holding constant the model specification and parameter values, thus avoiding the rolling sample extraction approach that is inconsistent with economic assumption underlying the structural models. More importantly, by bringing in the consistency between observed equity and model implied equity, our approach has the potential to speak directly to the recent finding that time-varying equity volatility has a strong nonlinear forecasting power for credit spreads (Zhang, et al., 2006).

3.1 GMM Estimation of Structural Credit Risk Models

As described in Section 2, the CDS spread at time with maturity $\tau$ has a general pricing formula for all the structural models under consideration,

$\begin{displaymath} \mbox{cds}(t,\tau)=\frac{(1-R)\int_t^{t+\tau} e^{-rs} Q'(t,s) ds} {\int_t^{t+\tau} e^{-rs}[1-Q(t,s)]ds}, \end{displaymath}$

(9)

where

is the risk free rate,

is the recovery rate,

is the model-dependent risk-neutral default probability at time

for period

, and

is the risk-neutral default intensity. As pointed out by Merton (1974), the delta function relating the equity volatility and asset volatility is also model-dependent

$\begin{displaymath} \sigma_E (t)=\sigma_A {A_t \over E_t} {\partial E_t \over \partial A_t}, \end{displaymath}$

(10)

where the equity volatility $\sigma_E (t)$ is generally time-varying while the asset volatility $\sigma_A$ may be constant. For the jump-diffusion asset value process used by Huang & Huang (2003), the equity volatility of the continuous diffusion component satisfy Eq. (10). With observed CDS spread $\widetilde{\mbox{cds}}(t,\tau)$ and equity volatility $\widetilde{\sigma_E}(t)$ , we can specify the following overidentifying restrictions

$\begin{displaymath} f(\theta,t) = \left[ \begin{array}{c} \widetilde{\mbox{cds}}(t,\tau_1)-\mbox{cds}(t,\tau_1)\ \cdots\cdots\cdots\cdots\cdots\cdots\ \widetilde{\mbox{cds}}(t,\tau_j)-\mbox{cds}(t,\tau_j)\ \widetilde{\sigma_E}(t)-\sigma_E (t) \end{array} \right] \end{displaymath}$

(11)

where $\theta$ is the structural parameter vector for various credit risk model under consideration, e.g., asset volatility, default barrier, asset jump intensity, or dynamic leverage coefficient, etc.. The term structure of CDS spread is represented by four maturities $\tau=1,\ 3,\ 5,\ \mbox{and}\ 10$ years.

Under the null hypothesis that the model is correctly specified, we have

$\begin{displaymath} E[f(\theta,t)]=0. \end{displaymath}$

(12)

Note that both the CDS spread and the equity volatility are allowed to be observed with measurement errors. However, under the appropriately defined GMM metric, these pricing errors must be "small"; or the model specification will be rejected. The corresponding GMM estimator is given by

$\begin{displaymath} \hat \theta =\arg\min g(\theta,T)' W(T) g(\theta,T), \end{displaymath}$

(13)

where $g(\theta,T)$ refers to the sample mean of the moment conditions, $g(\theta,T) \equiv 1/T\sum_{t}^{T} f(\theta,t)$ , and

denotes the asymptotic covariance matrix of $g(\theta,T)$ (Hansen, 1982). With mild regularity conditions, the estimator of structural parameter $\theta$ is $\sqrt{T}$ -consistent and asymptotically normally distributed, under the null hypothesis. Moreover, the minimized value of the objective function multiplied by the sample size

$\begin{displaymath} J=T\min_{\theta} g(\theta,T)' W(T) g(\theta,T) \end{displaymath}$

(14)

should be asymptotically distributed as a Chi-square distribution, with the degree of freedom equal to the length of moments $f(\theta,t)$ minus the length of structural parameter $\theta$ . This allows for an omnibus test of the overidentifying restrictions. In addition, we use a heteroscedasticity robust estimator for the variance-covariance matrix

(Newey & West, 1987).

For the more general models with stochastic interest rate (Longstaff & Schwartz, 1995) or random jumps (Huang & Huang, 2003), one can expand moment restriction vector to include the pricing restrictions of interest rates and/or other maturities of CDS spreads. However, such a joint estimation scheme would be very computationally involved for a two-factor model with stochastic interest rates such as Longstaff & Schwartz (1995) and Collin-Dufresne & Goldstein (2001). This is because the default probability under the forward probability measure, $Q(t,\cdot)$ , has to be calculated with discretized numerical approximation.

To make the estimation tractable, we separately estimate the dynamic interest rate model and the firm-specific structural parameters. This is a reasonable strategy, since the interest rate parameters are common inputs in those structural credit risk models and those firm-specific parameters do not affect the interest rate process. We use the 3-month LIBOR as an proxy for the short rate and estimate the interest rate volatility $\hat \sigma_r = \mbox{VAR} (r_t)$ accordingly. Given that the one-factor Vasicek (1977) model is a very crude approximation to the observed term structure dynamics, we opt to use a nonlinear least square procedure to estimate the risk-neutral drift parameters $\alpha$ and $\beta$ month-by-month,

$\begin{displaymath}\{\hat\alpha_t,\hat\beta_t\}=\arg\min\sum_{\tau=\tau_1}^{\tau_6} \left[\hat y_{t,\tau}-y_{t,\tau}(\alpha,\beta)\right]^2\end{displaymath}$

to best match the term structure of interest swap rates $y_{t,\tau}$ with maturities of 1, 2, 3, 5, 7, and 10 years.

4 Data Description

4.1 Credit Default Swap Spreads

We choose to use the credit default swap (CDS) premium as a direct measure of credit spreads. CDS is the most popular instrument in the rapidly growing credit derivatives markets. Compared with corporate bond spreads, which were widely used in previous studies in testing structural models, CDS spreads have two important advantages. First, a CDS spread is a relatively pure pricing of default risk of the underlying entity, and the contract is typically traded on standardized terms. By contrast, bond spreads are more likely to be affected by differences in contractual arrangements, such as seniority, coupon rates, embedded options, and guarantees.³ Second, as shown by Blanco, et al. (2005) and Zhu (2006), while CDS and bond spreads are quite in line with each other in the long run, in the short run CDS spreads tend to respond more quickly to changes in credit conditions. This means that CDS market may be more efficient than bond market, therefore more appropriate for the specification tests of structural models.

Our CDS data are provided by Markit, a comprehensive data source that assembles a network of industry-leading partners who contribute information across several thousand credits on a daily basis. Based on the contributed quotes Markit creates the daily composite quote for each CDS contract; which must past the stale data test, flat curve test, and outlying data test. Together with the pricing information, the dataset also reports average recovery rates used by data contributors in pricing each CDS contract. In addition, an average of Moody's and S&P ratings is also included. In this paper we include all CDS quotes written on US entities (sovereign entities excluded) and denominated in US dollars. We eliminate the subordinated class of contracts because of their small relevance in the database and unappealing implication in credit risk pricing. We focus on CDS contracts with modified restructuring (MR) clauses, as they are the most popularly traded in the US market. We require that the CDS time series has at least 36 consecutive monthly observations to be included in the final sample. Another filter is that CDS data have to match equity price (CRSP), equity volatility (TAQ) and accounting variables (COMPUSTAT). We also exclude financial and utility sectors, following previous empirical studies on structural models. After applying these filters, we are left with 93 entities in our study. Our sample period covers January 2002 to December 2004, with maturities of 1, 2, 3, 5, 7, and 10 years.⁴ For each entity, we create the monthly CDS spread by selecting the latest composite quote in each month, and, similarly, the monthly recovery rates linked to CDS spreads.

4.2 Equity Volatility from High Frequency Data

By the theory of quadratic variation, it is possible to construct increasingly accurate measure for the model-free realized volatility or average volatility, during a fixed time interval, say a day or a month, by summing increasingly finer sampled squared high-frequency returns (Barndorff-Nielsen & Shephard, 2002; Meddahi, 2002; Andersen, et al., 2001b). The relative improvement of the high-frequency volatility estimate over the low frequency one is clearly demonstrated by Andersen & Bollerslev (1998) and Andersen, et al. (2001a), and its empirical applicability to equity return volatility has been widely accepted (see, Aït-Sahalia & Hansen, 2003, for a survey). In testing structural models, the asset return volatility is unobserved and is usually backed out from the observed equity return volatility (Eom, et al., 2004), therefore a more accurate measure of equity volatility from high-frequency data is critical in correctly estimating the asset return volatility -- the driving force behind behind the firm default risk.

Let $s_t \equiv \log S_t$ denote the day logarithmic price of the firm equity, and the intraday returns are defined as follows:

$\displaystyle r^s_{t,i} \equiv s_{t,i\cdot \Delta}-s_{t,(i-1)\cdot \Delta},$			(15)

where $r^s_{t,i}$ refers to the $i^{th}$ within-day return on day

and $\Delta$ is the sampling frequency and chosen to be 5-minute. The realized equity volatility (squared) for period

is simply given as

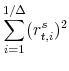$\displaystyle \widetilde{\sigma_E}(t)^2$	$\textstyle \equiv$	$\displaystyle \sum_{i=1}^{1/\Delta} (r^s_{t,i})^2$	(16)

which converges to the integrated or average variance during period

. For the double-exponential jump-diffusion model, the continuous component of equity volatility (squared) can be estimated with the so-called "bi-power variation"

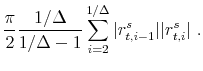$\displaystyle \widetilde{\sigma_E}(t)^2$	$\textstyle \equiv$	$\displaystyle \frac{\pi}{2}\frac{1/\Delta}{1/\Delta-1} \sum_{i=2}^{1/\Delta} \vert r^s_{t,i-1}\vert\vert r^s_{t,i}\vert\ .$	(17)

As shown by Barndorff-Nielsen & Shephard (2004), such an estimator of realized equity volatility is robust to the presence of rare and large jumps. The data are provided by the NYSE TAQ (Trade and Quote) data base, which includes intra-day (tick-by-tick) transaction data for all securities listed on NYSE, AMEX, and NASDAQ. The monthly realized variance is the sum of daily realized variances, constructed from the squares of log intra-day 5-minute returns. Then, monthly realized volatility is just the square-root of the annualized monthly realized variance.

4.3 Capital Structure and Asset Payout

Assets and liabilities are key variables in evaluating structural models of credit risk. The accounting information is obtained from Compustat on a quarterly basis and assigned to each month with the quarter. We calculate the firm asset as the sum of total liability plus market equity, where the market equity is obtained from the monthly CRSP data on shares outstanding and equity prices. Leverage ratio is estimated by the ratio of total liability to the firm asset. The asset payout ratio is proxied by the weighted average of the interest expense and dividend payout. Both ratios are reported as annualized percentages.

4.4 Risk-Free Interest Rates

To proxy the risk-free interest rates used as the benchmark in the calculation of CDS spreads, we use the 3-month LIBOR and the interest rate swaps with maturities of 1, 2, 3, 5, 7, and 10 years. These data are available from the Federal Reserve H.15 Release.

5 Empirical Results

In this section we summarize our empirical findings on testing the structural credit risk models, based on the GMM estimator defined in Section 3 with the term structure of CDS spreads and equity volatility. We also provide some diagnostics on various model specifications based on the pricing errors, and discuss some implications for future research.

5.1 Summary Statistics

In this paper, we focus on the senior unsecured CDS contracts on U.S. corporations and denominated in U.S. dollars. Subordinated class of contracts are not considered here for their small representations in the fast growing CDS market and their complicated implications in credit risk pricing. We use only the modified restructuring (MR) clauses, as they are the most popularly traded in the U.S. market. After matching with the high frequency equity volatility and firm accounting information, excluding financial and utility firms, we are left with 93 entities spanning from January 2002 to December 2004.

Table 1 provides summary statistics on CDS spreads and firm characteristics across both rating categories and sectors. As can be seen from panel A of Table 1, our sample is concentrated in the single-A and triple-B categories, which account for 75 percent of the total sample, reflecting the fact that contracts on investment-grade names dominate the CDS market. In terms of the average over both the time-series and cross-section in our sample, the 5-year CDS spread is 144 basis points, equity volatility is 38.40 percent (annualized), the leverage ratio 48.34 percent, asset payout ratio 2.14 percent, and the quoted recovery rate 40.30 percent. As expected, the CDS spread, equity volatility, and the leverage ratio all increase as rating deteriorates. However, the recovery rate essentially decreases as rating deteriorates but has low variations.

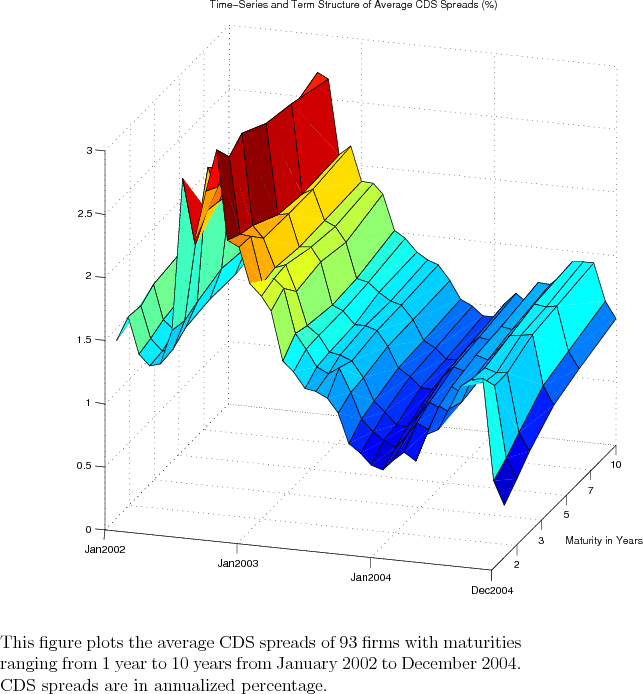
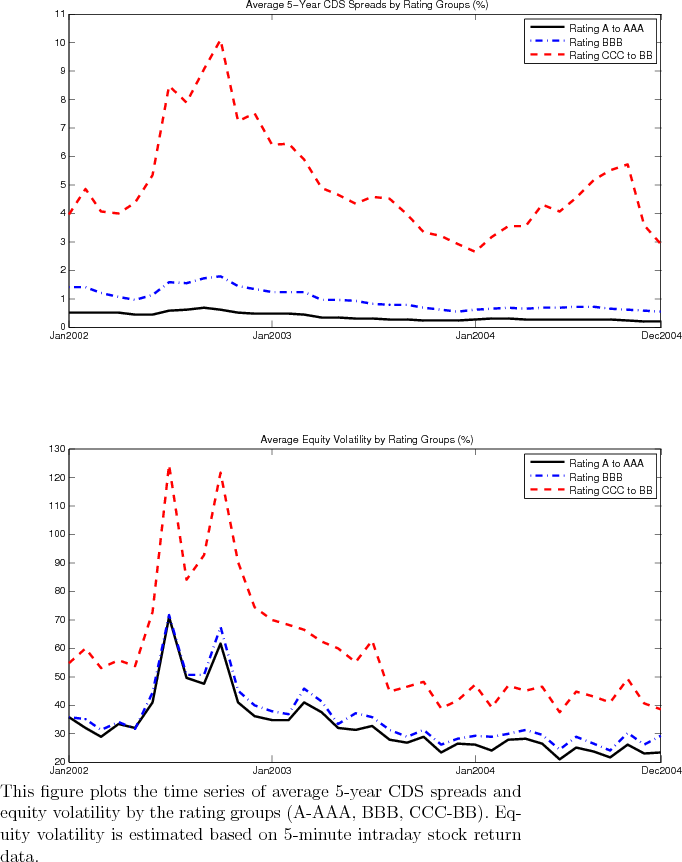
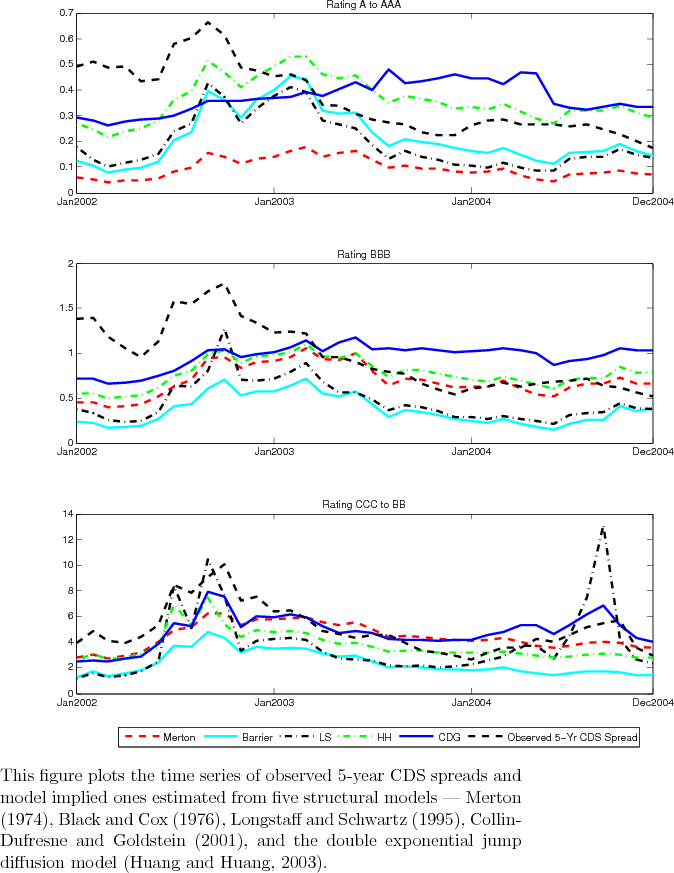
Figure 1 plots both the term structure (from 1 year to 10 years) and time evolution (over the period from January 2002 to December 2004) of the average CDS spreads. As can be seen from the figure, the average spreads show large variations and have a peak around late 2002. Figure 2 plots both the 5-year CDS spreads and equity volatility by ratings over the entire sample period. The 5-year CDS spreads clearly have a peak in late 2002 across all three rating groups although the high-yield group has another spike in late 2004. On the other hand, equity volatility is much higher in 2002 than the later part of the sample period and, in particular, has two huge spikes in 2002.

5.2 GMM Specification Test

Our econometric method is based on the model implied pricing relationship for CDS spread and equity volatility. There is clear evidence that equity volatility and credit spread are intimately related (Campbell & Taksler, 2003), and the linkage appears to be nonlinear in nature (Zhang, et al., 2006). A casual inspection of Figure 2 indicates that CDS spreads and equity volatilities appear to move together sometime during market turmoils but are only loosely related during quiet periods. A structural model with richer time-varying feature in the underlying asset may be called for to account for the observed nonlinear relationship between equity volatility and credit spread.⁵

The GMM specification test results from each of five structural credit risk models are given in Table 2. In particular, we report the percentage of firms where each of the five models is not rejected, for the whole sample as well as across both ratings and sectors. As can be seen from the table, none of the five models have a rejection rate of 100%. The existing empirical studies of the standard structural models based on corporate bond spreads have largely rejected these models as well. Our results indicates that the standard structural models are still missing something even when CDS spreads, presumably a cleaner measure of credit risk than corporate bonds spreads, are used in the empirical analysis.

Nonetheless, our empirical results provide new evidence on the relative performance of the five structural models and potential guidance on how to extend the existing models. For instance, notice that the GMM test statistics for the Merton (1974) specification are significantly higher than those for the other four extended models. (Some of the models are not nested so the -test statistics are not always directly comparable.) Whereas it is known that the Merton model underperforms the richer models, our results are the first in the literature based on a consistent econometric test that takes into account the dynamic behavior of both CDS spreads and equity volatility.

Judged by the results reported in the table on the percentage of firms where each of the five models is not rejected, the ranking of the 5 models is as follows

$\begin{displaymath} \mbox{Merton} < \mbox{Black-Cox} < \mbox{LS} < \mbox{HH} < \mbox{CDG} \end{displaymath}$

(This ranking is also consistent with results on the mean test statistic, although as cautioned earlier,

-test statistics are not always directly comparable.) In particular, the double exponential jump-diffusion model considered in Huang and Huang (2003) and especially the CDG stationary leverage model outperform significantly over the other three models, namely, Merton (1974), Black and Cox (1976), and Longstaff and Schwartz (1995). These results imply that both jumps and time varying leverage improve noticeably the model.

One finding in Eom, et al. (2004) is that the CDG model improves marginally the fitting of bond spreads over the LS model. Our results here here indicate that the CDG model's improvement over LS and other models as well is much more significant when CDS spreads are used in the analysis. Another possible reason is that the risk-neutral leverage parameters are estimated directly here, whereas they are estimated indirectly through their counter-parties in the physical measure in Eom, et al. (2004). (It is actually mentioned that in EHH that direct estimating the risk-neutral leverage parameters may improve the performance of CDG.)

Note that our empirical analysis is based on a consistent econometric method that takes the pricing models to the entire term structure of CDS spreads and equity volatility estimated using high frequency data. This is in contrast with the prevalent approach of rolling sample estimation and extraction. Of course we are aware that the GMM omnibus test may be biased toward over-rejection of the true model specification (e.g., see, Tauchen, 1986).

5.3 Parameter Estimation

In this subsection we report estimates of model parameters. First, we want to mention that we impose additional estimation restrictions to ensure proper identification of model parameters in the Longstaff-Schwartz (1995), CDG, and the jump diffusion models. For the Longstaff-Schwartz (1995) model, if the correlation coefficient $\rho$ is allowed to be free, its estimated value is around -1.2 for almost all firms in the sample. Therefore we restrict $\rho$ to be -1 in the estimation of this model. In the CDG model, the correlation coefficient $\rho$ and sensitivity coefficient $\phi$ seem difficult to be simultaneously identifiable and the correlation coefficient is not bounded between -1 and +1. As a result, we impose the restriction that $\rho=0$ . In the double-exponential jump-diffusion model, the parameters , $\eta_u^Q$ , and $\eta_d^Q$ enter the solution function multiplicatively with $\lambda^Q$ and are very difficult to identify in our GMM estimator. Currently we fix those jump parameters as follows: , $\eta_u^Q=5$ , and $\eta_d^Q=3$ , which are similar to the calibration values adopted in Huang and Huang (2003).

Table 3 reports estimates of the remaining model parameters and their standard errors across both ratings and sectors. Panel A shows the results for the asset volatility parameter $\sigma_v$ , which enters all five models. This parameter is the most accurately estimated one and significant at all conventional statistical levels. The level of the estimates is reasonable in all models.

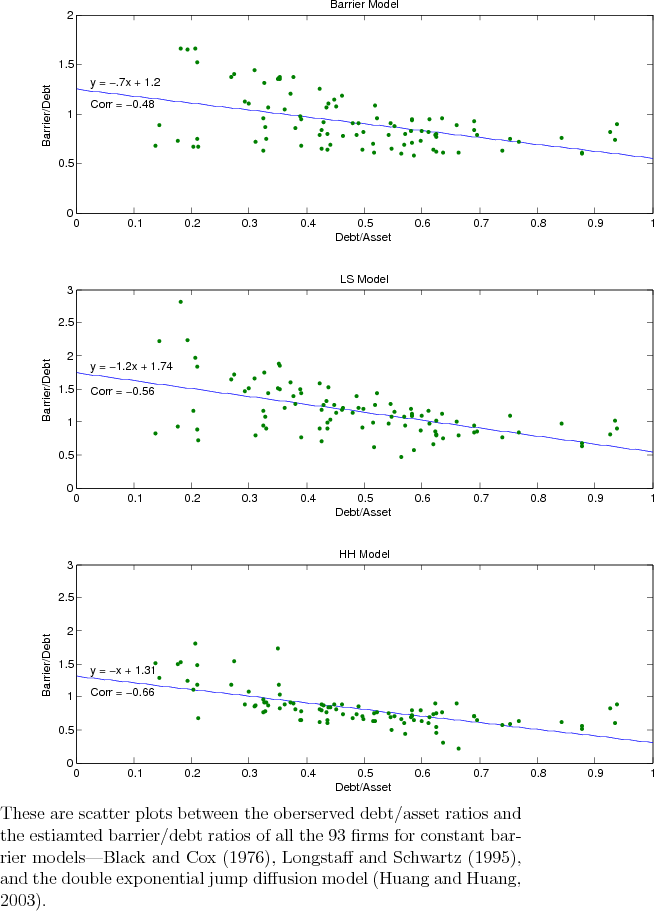
Panel B of Table 3 reports the estimated default boundary/barrier, a parameter that appears in the three models with a flat default boundary, namely, the Black and Cox (1976) barrier model, the Longstaff-Schwartz (1995) model with stochastic interest rates, and the jump model considered in Huang and Huang (2003). The default barrier scaled by the total debt, , estimated using the BC model ranges from 65% to 103%. The estimates based on LS are much higher. Results based on the jump model are largely consistent with calibration values used by Huang and Huang (2003) and the empirical estimates by Predescu (2005). Figure 3 plots the relationship between the estimated default boundary and the observed leverage ratio . As can be seen from the figure, the slope is significantly negative, indicating that a higher default boundary is implied for lower rating names. This finding is also consistent with EHH's findings based on corporate bond data.

Panel C of Table 3 reports the estimate of the jump intensity parameter in HH and the three leverage parameters in CDG. Notice that the estimated jump intensity levels for high-yield names are much higher than those for investment-grade names.

In the stationary leverage model (Collin-Dufresne & Goldstein, 2001), parameter $\kappa_{\ell}$ is the mean-reverting speed of the risk-neutral log leverage ratio $\log(K_t/V_t)$ . The mean estimated value $\hat{\kappa_\ell}$ ranges from 0.03 for the single CCC-rated name to 17.82 for AA-rated names, and is much larger than the calibrated value of 0.18 adopted by CDG and also the estimate based on regression in Frank and Goyal (2003). This is perhaps an indication that the model is missing some factor.

Parameter $\nu$ in CDG is related to $\theta_\ell$ , the long-run mean of the risk-neutral leverage ratio, as the following $\theta_\ell = {-r_t+\delta_t+\sigma_v^2/2 \over \kappa_\ell}-\nu$ . Our choice of estimating a constant $\nu$ would imply a time-varying but deterministic $\theta_\ell$ . The mean estimate $\hat \nu$ ranges from 0.11 for the single AAA-rated name to 1.00 for the single CCC-rated name, which is rather close to the calibration value of 0.60 used in CDG.

Finally the sensitivity of leverage ratio in interest rate $\phi$ in CDG seems to be critical for the model to pass the GMM specification test. More specifically, $\phi$ measures the sensitivity of the firm-specific leverage ratio dynamics to the risk-free interest rate process. This is equivalent to the risk factor loading in standard asset pricing models. As can be seen in the table, the estimate of $\phi$ varies from a large positive number of the investment grade names to a large negative number of the speculative grade names. This suggests that firms with different credit standing have very different leverage ratio dynamics as the macroeconomic risk changes over time. Such a heterogeneity of dynamics leverage ratio is the key for CDG model pass the GMM omnibus test with more than half of the sample.

5.4 Pricing Performance Evaluation

In the literature, the evaluation of structural credit risk models is generally based on comparing their pricing error on corporate bonds, although the models are typically not consistently estimated but rather judged based on ad hoc calibration or rolling sample extractions. Here we connect with the existing literature by looking at the pricing errors of candidate models, after the parameters are consistently estimated and model specification tests are conducted. If our approach is valid, then the specification test result should be consistent with the pricing errors evaluations.⁶ To be more specific, for each month and each maturity, we use the estimated structural parameters and pricing solutions to calculate the model implied CDS spreads and equity volatility. Then we compute the simple difference, absolute difference, and percentage difference between the model implied and observed ones. Finally the mean of the pooled pricing errors is reported for each name.

Table 4 reports the pricing errors on both CDS spreads and equity volatility by each rating group and sector. As can be seen from the table, in terms of average errors, the Merton (1974) model seems to over-estimate the spreads, the barrier and LS models appear to under-estimate the spreads, and the jump and leverage models are more even. The fact that combining equity price and CDS spreads would make Merton (1974) overfit is similarly found by Predescu (2005). In terms of absolute pricing performance, the barrier model (Black and Cox, 1976) always outperforms the Merton (1974) model but underperforms the Longstaff-Schwartz (1995) model. The jump model used in Huang and Huang (2003) outperforms all these three models but is dominated by the dynamic leverage model of (Collin-Dufresne & Goldstein, 2001). These results contrast the findings of (Eom, et al., 2004) based on corporate bond data that richer model specifications do not improve upon the Merton (1974) in terms of pricing errors. It is interesting that, judging from the percentage pricing errors, the jump model performs relatively better for the high rated firms, while the CDG model does better for the low rated firms.

The results from equity volatility display similar patterns as those from the CDS spreads. A noticeable difference is that the absolute pricing errors on equity volatility are generally larger than those on CDS spreads, while the percentage pricing errors are about the same order of the magnitude.

In order to pass the GMM -test, a model must perform well on both CDS spreads and equity volatility. Results based on pricing errors indicate that except for the CDG model, the others fail in either one or both dimensions.

5.5 Further Diagnostics on Model Specifications

In this subsection, we try to gain further insights on model specification errors, by examining the model-implied term structure and time series of CDS spreads, along with the model-implied equity volatility. We also discuss some implications of this analysis for improving the standard structural models.

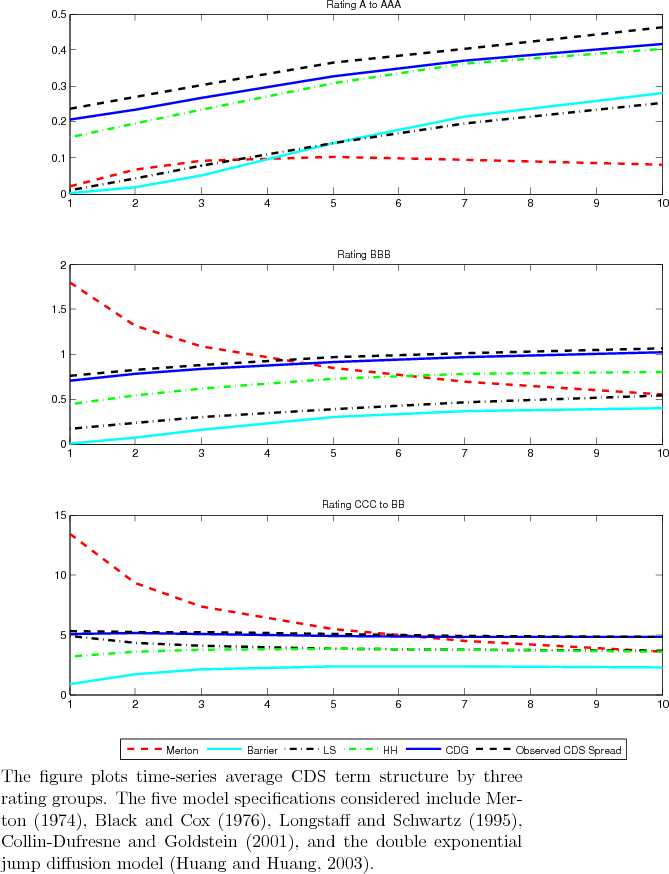
Figure 4 plots the sample average of the CDS term structure from 1 year to 10 years from both the observed data and the five candidate models. A few observations are worth mentioning here: (1) the CDG model almost completely nails the average term structure, especially for the lower rating group; (2) the Merton model clearly misses the CDS spreads, but for high grade (AAA-A) misses mostly the long maturity and for low grade (BBB-CCC) misses mostly the short maturity; (3) the Black-Cox (BC) and LS models seem to fit reasonably the lower grades (BBB-CCC), but underfit the high grades (AAA-A) especially in the short end; (4) the HH model with jumps improves upon the Merton model mostly in the short end, as jumps are sensitive for short term derivatives, although its overall performance is not very satisfying. Overall, the stationary leverage model seems to be the only one to match the curve of average term structure of CDS spread, especially for lower rated names; while the jump model seems to have potential in improving the short end of the term structure, especially for higher rated names.

Figure 5 plots the observed 5-year CDS spread against the five model implied ones. For lower ratings BB-CCC, all models seem to match the time-variations of the 5-year CDS spread well, although the CDG model is the best one. For higher ratings AAA-BBB, most models completely miss the CDS dynamics, especially for the first third of the sample, when the risk-free rate remains as low as 1%. Even CDG model can only get the average level right, but not be able to imitate the evolutions. This suggests that for higher rating firms, a time-varying factor in addition to interest rate and leverage ratio -- like stochastic asset volatility -- may be needed to fully capture the temporal changes in CDS spreads.

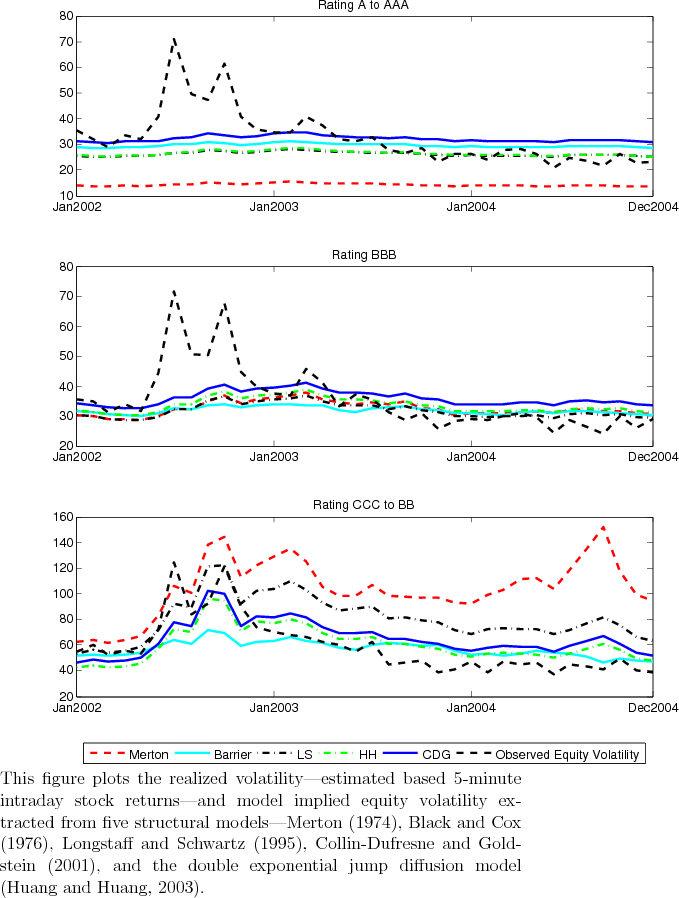
Figure 6 reports the model implied and fitted equity volatilities. Again, for lower ratings BB-CCC, the CDG model can reasonable capture the time series feature of equity volatility; while other models miss the volatility level, yet produce certain time-variations imitating the volatility dynamics. In contrast, for higher ratings AAA-BBB, all models miss completely the volatility spikes during the early sample period. The picture for AAA-A is rather bleak -- every model generates a nearly constant equity volatility but the observed one is dramatically changing over time. This evidence indicate that without time varying asset volatility, no existing model can replicate the observed equity volatility dynamics, for top investment grade names.

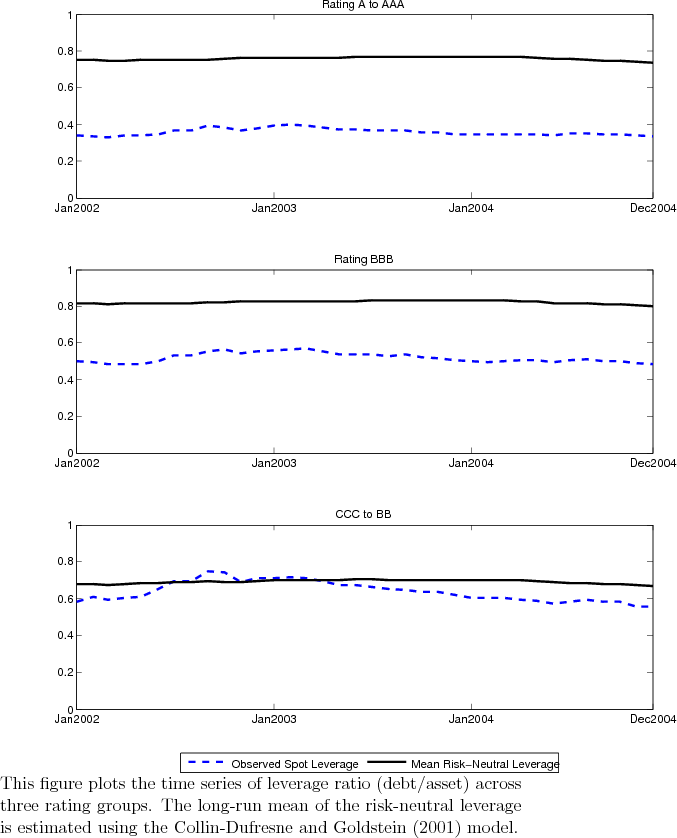
Figure 7 plots the initial spot log leverage ratio $\log(K_t/V_t)$ and the long-run mean of risk-neutral log leverage ratio. It is clear that for the speculative grade (CCC-BB) these two leverages are very closer to each other. While for low investment grade names (BBB), the observed leverage is significantly lower than the risk-neutral counterpart; and the difference becomes more dramatic for the top investment grade (AAA-A). Such a finding mirrors the recently documented evidence that highly profitable firms may opt to borrow little or no debt (Chen and Zhao, 2006; Strebulaev & Yang, 2006). Such a puzzle is worth further investigation.

In summary, dynamic leverage ratio together with stochastic interest rate seem to be crucial for a structural credit risk model to better match the CDS spread and equity volatility. In addition, incorporating jumps may help to improve the fit of the short end of CDS term structure, especially for the high investment grade names. However, something else needs to be incorporate into the existing models as they all fail to adequately capture the dynamics behavior of CDS spreads and equity volatility, especially for the high investment grade names. This suggests that incorporating a stochastic asset volatility may improve the existing structural models.

6 Conclusions

This article provides a consistent econometric specification test of five structural credit risk models using information from both the credit default swap (CDS) market and equity market. In particular, we consider the standard Merton (1974) model, the Black and Cox (1976) barrier model, the Longstaff and Schwartz (1995) model with stochastic interest rates, the stationary leverage model of Collin-Dufresne and Goldstein (2001), and the double exponential jump-diffusion barrier model studied in Huang and Huang (2003). We examine the performance of each model in capturing the behavior of CDS spreads and equity volatility both cross-sectionally and time series wise.

Existing empirical studies of structural models mainly based on corporate bond spreads and equity volatility from low frequency daily data. To our best knowledge, this study is the first direct econometric estimation and specification test of structural models using data on the term structure of CDS and equity volatility estimated with high frequency intraday data. This allows us to minimize the effects of measurement error and pricing error, and thus attribute the test results mostly to the specification error.

We find that the Merton (1974), Black and Cox (1976), and the Longstaff and Schwartz (1995) models are strongly rejected by our specification test. The jump diffusion model considered in Huang and Huang (2003) improves the performance significantly for the top investment grade names but helps the fit mainly in the short end of the CDS term structure and not much in the long end. Still, the model is rejected for more than half of our sample firms. The best of the five models is the Collin-Dufresne and Goldstein model, that cannot be rejected in more than half of our sample firms.

Nonetheless, we show that these structural models still have difficulty predicting credit spreads accurately even when CDS spreads (a purer measure of credit risk than bond spreads) are used in the analysis.

Finally, we document that the five structural models cannot capture the time-series behavior of both CDS spreads and equity volatility. Given that equity volatility in structural models is time-varying, this finding provides a direct evidence that a structural model with stochastic asset volatility (see Huang and Huang, 2003; Huang, 2005; Zhang, Zhou, and Zhu, 2006) may significantly improve the model performance, especially for the investment grade names.

Bibliography

V. Acharya & J. Carpenter (2002).

`Corporate Bond Valuation and Hedging with Stochastic Interest Rates and Endogenous Bankruptcy'.
Review of Financial Studies 15:1355-1383.

T. G. Andersen & T. Bollerslev (1998).

`Answering the Skeptics: Yes, Standard Volatility Models Do Provide Accurate Forecasts'.
International Economic Review 39:885-905.

T. G. Andersen, et al. (2003).

Handbook of Financial Econometrics, chap. Parametric and Nonparametric Volatility Measurement.
Elsevier Science B.V., Amsterdam.
forthcoming.

T. G. Andersen, et al. (2001a).

`The Distribution of Realized Stock Return Volatility'.
Journal of Financial Economics 61:43-76.

T. G. Andersen, et al. (2001b).

`The Distribution of Realized Exchange Rate Volatility'.
Journal of the American Statistical Association 96:42-55.

R. W. Anderson & S. Sundaresan (1996).

`Design and valuation of debt contracts'.
Review of Financial Studies 9(1):37-68.

N. Arora, et al. (2005).

`Reduced Form vs. Structural Models of Credit Risk: A Case Study of Three Models'.
Journal of Investment Management 3(4):43-67.

O. Barndorff-Nielsen & N. Shephard (2002).

`Estimating Quadratic Variation Using Realized Variance'.
Journal of Applied Econometrics 17:457-478.

O. Barndorff-Nielsen & N. Shephard (2004).

`Power and Bipower Variation with Stochastic Volatility and Jumps'.
Journal of Financial Econometrics 2:1-48.

F. Black & J. Cox (1976).

`Valuing Corporate Securities: Some Effects of Bond Indenture Provisions'.
Journal of Finance 31:351-367.

F. Black & M. S. Scholes (1973).

`The Pricing of Options and Corporate Liabilities'.
Journal of Political Economy 81(3):637-54.

R. Blanco, et al. (2005).

`An Empirical Analysis of the Dynamic Relationship Between Investment-Grade Bonds and Credit Default Swaps'.
Journal of Finance 60:2255-2281.

J. Campbell & G. Taksler (2003).

`Equity Volatility and Corporate Bond Yields'.
Journal of Finance 58:2321-2349.

L. Chen & X. Zhao (2006).

`Why Do more Profitable Firms Have Lower Leverage Ratios?'.
Working Paper .

R. Chen, et al. (2006).

`Sources of Credit Risk: Evidence from Credit Default Swaps'.
The Journal of Fixed Income 16(3):7-21.

P. Collin-Dufresne & R. Goldstein (2001).

`Do Credit Spreads Reflect Stationary Leverage Ratios?'.
Journal of Finance 56:1929-1957.

D. Cossin & T. Hricko (2001).

`Exploring for the Determinants of Credit Risk in Credit Default Swap Transaction Data'.
Working Paper .

M. Cremers, et al. (2004).

`Explaining the Level of Credit Spreads: Option-Implied Jump Risk Premia in a Firm Value Model'.
Working Paper Cornell University.

G. Delianedis & R. Geske (2001).

`The components of corporate credit spreads: Default, recovery, tax, jumps, liquidity, and market factors'.
working paper, UCLA.

J. Duan (1994).

`Maximum Likelihood Estimation Using Price Data Of The Derivative Contract'.
Mathematical Finance 4(2):155-167.

D. Duffie & D. Lando (2001).

`Term structures of credit spreads with incomplete accounting information'.
Econometrica 69(3):633-664.

Y. H. Eom, et al. (2004).

`Structural Models of Corporate Bond Pricing: An Empirical Analysis'.
Review of Financial Studies 17:499-544.

J. Ericsson, et al. (2005).

`The Determinants of Credit Default Swap Premia'.
Working Paper McGill University.

J. Ericsson & J. Reneby (2005).

`Estimating Structural Bond Pricing Models'.
Journal of Business 78(2):707-735.

J. Ericsson, et al. (2006).

`Can Structural Models Price Default Risk? Evidence from Bond and Credit Derivative Markets'.
Working Paper McGill University.

R. Geske (1977).

`The Valuation of Corporate Liabilities as Compound Options'.
Journal of Financial and Quantitative Analysis 12(4):541-552.

L. P. Hansen (1982).

`Large Sample Properties of Generalized Method of Moments Estimators'.
Econometrica 50(4):1029-1054.

P. Houweling & T. Vorst (2005).

`Pricing Default Swaps: Empirical Evidence'.
Journal of International Money and Finance 24:1200-1225.

J. Huang (2005).

`Affine Structural Models of Corporate Bond Pricing'.
Working Paper Penn State University.

J. Huang & M. Huang (2003).

`How Much of the Corporate-Treasury Yield Spread Is Due to Credit Risk?'.
Working Paper Penn State and Stanford.

J. Hull, et al. (2004).

`Merton's Model, Credit Risk, and Volatility Skews'.
Working Paper University of Toronto.

E. P. Jones, et al. (1984).

`Contingent Claims Analysis of Corporate Capital Structures: An Empirical Investigation'.
Journal of Finance 39:611-625.

H. E. Leland (1998).

`Agency Costs, Risk Management, and Capital Structure'.
The Journal of Finance 53(4):1213-1243.

H. E. Leland & K. B. Toft (1996).

`Optimal Capital Structure, Endogenous Bankruptcy, and the Term Structure of Credit Spreads'.
Journal of Finance 51:987-1019.

F. Longstaff & E. Schwartz (1995).

`A Simple Approach to Valuing Risky Fixed and Floating Rate Debt'.
Journal of Finance 50:789-820.

F. A. Longstaff, et al. (2005).

`Corporate Yield Spreads: Default Risk or Liquidity? New Evidence from the Credit-Default-Swap Market'.
Journal of Finance 60:2213-2253.

S. Lyden & D. Saraniti (2000).

`An Empirical Examination of the Classical Theory of Corporate Security Valuation'.
working paper, Barclays Global Investors.

N. Meddahi (2002).

`A Theoretical Comparison between Integrated and Realized Volatility'.
Journal of Applied Econometrics 17.

P. Mella-Barral & W. Perraudin (1997).

`Strategic Debt Service'.
The Journal of Finance 52(2):531-556.

R. Merton (1974).

`On the Pricing of Corporate Debt: The Risk Structure of Interest Rates'.
Journal of Finance 29:449-470.

W. K. Newey & K. D. West (1987).

`A Simple Positive Semi-Definite, Heteroskedasticity and Autocorrelation Consistent Covariance Matrix'.
Econometrica 55:703-708.

M. Predescu (2005).

`The Performance of Structural Models of Default for Firms with Liquid CDS Spreads'.
Working Paper Rotman School of Management, University of Toronto.

S. Schaefer & I. A. Strebulaev (2004).

`Structural Models of Credit Risk are Useful: Evidence from Hedge Ratios on Corporate Bonds'.
Working Paper London Business School.

I. Strebulaev & B. Yang (2006).

`The Mystery of Zero-Leverage Firms'.
Working Ppaer Standford GSB.

G. Tauchen (1986).

`Statistical Properties of Generalized Methods-of-Moments Estimators of Structural Parameters Obtained from Financial Market Data'.
Journal of Business and Economic Statistics 4(4):397-416.

O. A. Vasicek (1977).

`An Equilibrium Characterization of the Term Structure'.
Journal of Financial Economics 5:177-188.

B. Y. Zhang, et al. (2006).

`Explaining Credit Default Swap Spreads with Equity Volatility and Jump Risks of Individual Firms'.
Working Paper Federal Reserve Board.

H. Zhu (2006).

`An Empirical Comparison of Credit Spreads between the Bond Market and the Credit Default Swap Market'.
Journal of Financial Service Research 29:211-235.

This table reports summary statistics on the 93 firms, by ratings (Panel A) and sectors (Panel B), that underly the CDS contracts in the entire sample. Rating is the average of Moody's and Standard & Poor's ratings. Equity volatility is estimated using 5-minute intraday returns. Leverage ratio is the total liability divided by the total asset which is equal to total liability plus market equity. Asset payout ratio is the weighted average of dividend payout and interest expense over the total asset. Recovery rate is the quoted recovery rate accompanied with the CDS premium from the dealer-market. CDS spreads have 1-, 2-, 3-, 5-, 7-, and 10-year maturities over the period from January 2002 to December 2004.

Panel A: By Ratings (part 1)

Table 1: Summary Statistics on CDS Spreads and the Underlying Names
Rating	Firms	% of Sample	Equity Volatility (%)	Leverage Ratio (%)	Asset Payout (%)	Recovery Rate (%)
AAA	1	1.08%	36.36	63.71	2.22	40.88
AA	6	6.45%	31.50	20.92	1.53	40.92
A	25	26.88%	32.51	38.15	2.02	40.57
BBB	45	48.39%	35.54	51.84	2.26	40.73
BB	11	11.83%	47.19	57.76	2.15	39.51
B	4	4.30%	83.23	72.61	2.28	38.23
CCC	1	1.08%	81.94	93.93	2.89	26.57
Overall	93	100.00%	38.40	48.34	2.14	40.30

Table 1: Panel A: By Ratings (part 2). Maturity of CDS. Spreads Mean (%)
Rating	1-year	2-year	3-year	5-year	7-year	10-year
AAA	0.23	0.28	0.32	0.43	0.45	0.49
AA	0.12	0.13	0.15	0.20	0.23	0.28
A	0.25	0.29	0.32	0.39	0.43	0.49
BBB	0.74	0.79	0.86	0.94	0.98	1.05
BB	2.62	2.74	2.84	2.90	2.92	2.92
B	7.52	7.20	7.51	7.25	7.01	6.79
CCC	25.26	22.99	20.91	18.81	18.03	17.31
Overall	1.34	1.36	1.40	1.44	1.45	1.49

Table 1: Panel A: By Ratings (part 3). Maturity of CDS. CDS Spreads Std. Dev. (%)
AAA	0.17	0.19	0.21	0.25	0.23	0.24
AA	0.07	0.07	0.07	0.09	0.09	0.10
A	0.23	0.27	0.24	0.25	0.24	0.26
BBB	0.96	0.96	0.96	0.91	0.89	0.84
BB	2.72	2.75	2.59	2.35	2.28	2.14
B	8.67	6.19	7.61	6.12	5.90	5.25
CCC	24.96	19.40	16.48	13.65	12.68	11.81
Overall	4.434	3.775	3.615	3.177	3.036	2.854

Panel B: By Industry (part 1)

Table 1: Summary Statistics on CDS Spreads and the Underlying Names
Sector	Firms	% of Sample	Equity Volatility (%)	Leverage Ratio (%)	Asset Payout (%)	Recovery Rate (%)
Communications	6	6.45%	48.72	42.93	1.99	40.14
Consumer Cyclical	32	34.41%	38.95	48.56	2.01	40.45
Consumer Staple	14	15.05%	33.77	41.68	2.24	40.87
Energy	8	8.60%	39.93	53.89	2.47	40.05
Industrial	18	19.35%	40.24	53.90	2.01	39.90
Materials	11	11.83%	32.85	49.34	2.73	41.35
Technology	4	4.30%	45.22	40.20	1.29	38.95
Overall	93	100.00%	38.68	48.39	2.14	40.39

Table 1: Panel B: By industry (part 2). Maturity of CDS. CDS Spreads Mean (%)
Sector	1-year	2-year	3-year	5-year	7-year	10-year
Communications	2.04	1.99	2.09	2.23	2.16	2.10
Consumer Cyclical	1.57	1.58	1.58	1.61	1.62	1.66
Consumer Staple	0.74	0.81	0.86	0.92	0.94	0.98
Energy	1.58	1.38	1.53	1.43	1.47	1.48
Industrial	1.29	1.38	1.41	1.46	1.48	1.53
Materials	0.92	0.96	1.03	1.10	1.14	1.20
Technology	1.38	1.43	1.48	1.48	1.51	1.52
Overall	1.34	1.36	1.40	1.44	1.45	1.49

Table 1: Panel B: By industry (part 3). CDS Spreads Std. Dev. (%)
Communications	4.82	4.13	4.58	4.74	4.33	3.80
Consumer Cyclical	6.19	5.25	4.65	4.06	3.85	3.65
Consumer Staple	2.08	2.21	2.18	2.10	2.02	1.92
Energy	5.60	3.66	4.80	3.32	3.45	3.14
Industrial	2.36	2.54	2.34	2.16	2.09	2.07
Materials	1.46	1.42	1.43	1.39	1.38	1.34
Technology	2.20	2.17	2.12	1.82	1.74	1.59
Overall	4.43	3.78	3.62	3.18	3.04	2.85

This table reports the omnibus GMM test results of overidentifying restrictions under each of 5 structural models. The five moment conditions used in the test are constructed based on the pricing relationship for 1-, 3-, 5- and 10-year CDS spreads and for the equity volatility estimated based on 5-minute intraday data. The five model specifications considered include Merton (1974), Black and Cox (1976), Longstaff and Schwartz (1995), Collin-Dufresne and Goldstein (2001), and the double exponential jump diffusion model (Huang and Huang, 2003). Data used in the test are monthly CDS spreads and equity volatility from January 2002 to December 2004.

Table 2: Specification Test of Structural Credit Risk Models
th	5th Merton Model	50th Merton Model	95th Merton Model	5th BC Model	50th BC Model	95th BC Model	5th LS Model	50th LS Model	95th LS Model	5th HH Model	50th HH Model	95th HH Model	5th CDG Model	50th CDG Model	95th CDG Model
Percentile	12.84	17.28	18.04	10.74	15.58	17.69	7.27	15.60	17.79	3.65	10.11	15.66	0.01	2.29	16.52
Chi-Square	d.o.f = 4	d.o.f = 4	d.o.f = 4	d.o.f = 3	d.o.f = 3	d.o.f = 3	d.o.f = 3	d.o.f = 3	d.o.f = 3	d.o.f = 2	d.o.f = 2	d.o.f = 2	d.o.f = 1	d.o.f = 1	d.o.f = 1
Mean	16.70	16.70	16.70	15.26	15.26	15.26	14.65	14.65	14.65	9.95	9.95	9.95	4.18	4.18	4.18
Sig. level	0.01	0.05	0.10	0.01	0.05	0.10	0.01	0.05	0.10	0.01	0.05	0.10	0.01	0.05	0.10
Proportion Not Rejected	5/93	2/93	0/93	6/93	1/93	0/93	12/93	6/93	3/93	40/93	15/93	11/93	70/93	63/93	51/93
By Ratings: AAA	0/1	0/1	0/1	0/1	0/1	0/1	0/1	0/1	0/1	1/1	1/1	1/1	0/1	0/1	0/1
By Ratings: AA	0/6	0/6	0/6	0/6	0/6	0/6	0/6	0/6	0/6	3/6	1/6	1/6	5/6	5/6	5/6
By Ratings: A	0/25	0/25	0/25	0/25	0/25	0/25	0/25	0/25	0/25	15/25	9/25	8/25	22/25	21/25	19/25
By Ratings: BBB	2/45	0/45	0/45	2/45	0/45	0/45	6/45	2/45	2/45	17/45	3/45	1/45	36/45	31/45	23/45
By Ratings: BB	3/11	2/11	0/11	2/11	1/11	0/11	4/11	2/11	1/11	2/11	0/11	0/11	2/11	2/11	2/11
By Ratings: B	0/4	0/4	0/4	2/4	0/4	0/4	1/4	1/4	0/4	1/4	1/4	0/4	4/4	4/4	2/4
By Ratings: CCC	0/1	0/1	0/1	0/1	0/1	0/1	1/1	1/1	0/1	1/1	0/1	0/1	1/1	0/1	0/1
By Sector: Communications	1/6	0/6	0/6	2/6	0/6	0/6	1/6	0/6	0/6	4/6	0/6	0/6	5/6	5/6	4/6
By Sector: Consumer Cyclical	1/32	0/32	0/32	0/32	0/32	0/32	3/32	1/32	0/32	10/32	2/32	2/32	24/32	22/32	18/32
By Sector: Consumer Staple	0/14	0/14	0/14	0/14	0/14	0/14	0/14	0/14	0/14	9/14	3/14	2/14	11/14	9/14	8/14
By Sector: Energy	0/8	0/8	0/8	1/8	0/8	0/8	1/8	1/8	0/8	3/8	1/8	0/8	4/8	3/8	2/8
By Sector: Industrial	1/18	1/18	0/18	2/18	1/18	0/18	4/18	2/18	2/18	9/18	4/18	2/18	15/18	14/18	9/18
By Sector: Materials	1/11	0/11	0/11	0/11	0/11	0/11	2/11	1/11	0/11	5/11	5/11	5/11	9/11	8/11	8/11
By Sector: Technology	1/4	1/4	0/4	1/4	0/4	0/4	1/4	1/4	1/4	0/4	0/4	0/4	2/4	2/4	2/4

This table reports the GMM estimation results of the model parameters in each of five structural models. The five moment conditions used in the test are constructed based on the pricing relationship for 1-, 2-, 5- and 10-year CDS spreads and for the equity volatility estimated based on 5-minute intraday data. The five model specifications include Merton (1974), Black and Cox (1976), Longstaff and Schwartz (1995), Collin-Dufresne and Goldstein (2001), and the double exponential jump diffusion model (Huang and Huang, 2003). Panel A reports the asset volatility parameter estimate $\sigma_v$ in all five models, Panel B reports the default boundary estimate

in three barrier type models, and Panel C reports jump intensity estimate $\lambda^Q$ in Huang and Huang (2003) model and dynamic leverage parameters $\kappa_\ell$ , $\nu$ , $\phi$ in Collin-Dufresne and Goldstein (2001) model.

Table 3: Parameter Estimation of Structural Credit Risk Models
Panel A (part 1): Estimate of the Asset Volatility
Asset Volatility	N	Merton Model Mean	Merton Model Median	BC Model Mean	BC Model Median	LS Model Mean	LS Model Median	HH Model Mean	HH Model Median	CDG Model Mean	CDG Model Median
Whole Sample	93	0.141	0.123	0.178	0.171	0.163	0.151	0.158	0.153	0.186	0.166
Whole Sample (standard error)		(0.007)	(0.006)	(0.008)	(0.007)	(0.009)	(0.008)	(0.006)	(0.005)	(0.012)	(0.011)

Table 3: Panel A (part 2): Estimate of the Asset Volatility
Asset Volatility	N	Merton Model 5th	Merton Model 95th	BC Model 5th	BC Model 95th	LS Model 5th	LS Model 95th	HH Model 5th	HH Model 95th	CDG Model 5th	CDG Model 95th
Percentile		0.055	0.348	0.087	0.308	0.077	0.299	0.093	0.273	0.081	0.331
Percentile (standard error)		(0.002)	(0.016)	(0.003)	(0.016)	(0.003)	(0.017)	(0.003)	(0.012)	(0.004)	(0.027)

Table 3: Panel A (part 3): Estimate of the Asset Volatility
Asset Volatility: Ratings	N	Merton Model Mean	Merton Model Median	BC Model Mean	BC Model Median	LS Model Mean	LS Model Median	HH Model Mean	HH Model Median	CDG Model Mean	CDG Model Median
AAA	1	0.143	0.143	0.087	0.087	0.074	0.074	0.129	0.129	0.108	0.108
AAA (standard error)		(0.004)	(0.004)	(0.003)	(0.003)	(0.005)	(0.005)	(0.007)	(0.007)	(0.014)	(0.014)
AA	6	0.054	0.051	0.288	0.302	0.235	0.250	0.180	0.182	0.253	0.249
AA (standard error)		(0.014)	(0.014)	(0.015)	(0.015)	(0.015)	(0.015)	(0.007)	(0.006)	(0.020)	(0.020)
A	25	0.096	0.089	0.176	0.179	0.157	0.160	0.162	0.163	0.198	0.190
A (standard error)		(0.009)	(0.009)	(0.007)	(0.007)	(0.009)	(0.009)	(0.005)	(0.005)	(0.012)	(0.011)
BBB	45	0.136	0.126	0.151	0.141	0.138	0.132	0.148	0.150	0.167	0.157
BBB (standard error)		(0.005)	(0.004)	(0.007)	(0.006)	(0.007)	(0.007)	(0.006)	(0.005)	(0.011)	(0.010)
BB	11	0.210	0.212	0.220	0.211	0.221	0.195	0.183	0.141	0.212	0.165
BB (standard error)		(0.006)	(0.005)	(0.008)	(0.006)	(0.011)	(0.008)	(0.008)	(0.008)	(0.013)	(0.009)
B	4	0.363	0.378	0.245	0.250	0.252	0.246	0.179	0.183	0.200	0.180
B (standard error)		(0.010)	(0.010)	(0.009)	(0.009)	(0.010)	(0.011)	(0.010)	(0.009)	(0.011)	(0.010)
CCC	1	0.381	0.381	0.178	0.178	0.054	0.054	0.038	0.038	0.046	0.046
CCC (standard error)		(0.011)	(0.011)	(0.010)	(0.010)	(0.002)	(0.002)	(0.004)	(0.004)	(0.002)	(0.002)

Panel A (part 4): Estimate of the Asset Volatility

Table 3: Parameter Estimation of Structural Credit Risk Models
Asset Volatility: Sector	N	Merton Model Mean	Merton Model Median	BC Model Mean	BC Model Median	LS Model Mean	LS Model Median	HH Model Mean	HH Model Median	CDG Model Mean	CDG Model Median
Communications	6	0.199	0.176	0.183	0.168	0.164	0.140	0.187	0.173	0.239	0.269
Communications (standard error)		(0.006)	(0.004)	(0.007)	(0.007)	(0.010)	(0.011)	(0.007)	(0.006)	(0.020)	(0.021)
Consumer Cyclical	32	0.145	0.133	0.179	0.183	0.151	0.152	0.158	0.151	0.186	0.167
Consumer Cyclical (standard error)		(0.007)	(0.005)	(0.008)	(0.007)	(0.008)	(0.007)	(0.006)	(0.005)	(0.012)	(0.011)
Consumer Staple	14	0.103	0.079	0.193	0.188	0.178	0.165	0.148	0.148	0.175	0.161
Consumer Staple (standard error)		(0.008)	(0.008)	(0.009)	(0.008)	(0.010)	(0.009)	(0.005)	(0.005)	(0.012)	(0.011)
Energy	8	0.150	0.113	0.160	0.147	0.151	0.145	0.144	0.134	0.163	0.139
Energy (standard error)		(0.006)	(0.004)	(0.007)	(0.006)	(0.007)	(0.006)	(0.006)	(0.005)	(0.008)	(0.007)
Industrial	18	0.151	0.124	0.164	0.140	0.163	0.130	0.160	0.151	0.175	0.159
Industrial (standard error)		(0.007)	(0.006)	(0.006)	(0.006)	(0.008)	(0.007)	(0.006)	(0.005)	(0.010)	(0.009)
Materials	11	0.119	0.112	0.163	0.159	0.144	0.120	0.144	0.145	0.167	0.185
Materials (standard error)		(0.007)	(0.004)	(0.007)	(0.006)	(0.008)	(0.009)	(0.005)	(0.005)	(0.010)	(0.010)
Technology	4	0.164	0.148	0.256	0.250	0.268	0.249	0.208	0.183	0.280	0.243
Technology (standard error)		(0.007)	(0.008)	(0.009)	(0.009)	(0.017)	(0.017)	(0.009)	(0.008)	(0.024)	(0.017)

Panel B (part 1): Estimate of the Default Boundary

Table 3: Parameter Estimation of Structural Credit Risk Models
Default Barrier	N	BC Model: Mean	BC Model: Median	LS Model: Mean	LS Model: Median	HH Model: Mean	HH Model: Median
Whole Sample	93	0.911	0.827	1.163	1.093	0.824	0.761
Whole Sample (standard error)		(0.039)	(0.033)	(0.050)	(0.039)	(0.087)	(0.064)

Table 3: Panel B (part 2): Estimate of the Default Boundary
Default Barrier	N	BC Model: 5th	BC Model: 95th	LS Model: 5th	LS Model: 95th	HH Model: 5th	HH Model: 95th
Percentile		0.606	1.444	0.660	1.881	0.492	1.505
Percentile (standard error)		(0.009)	(0.086)	(0.007)	(0.117)	(0.018)	(0.259)

Table 3: Panel B (part 3): Estimate of the Default Boundary
Ratings	N	BC Model: Mean	BC Model: Median	LS Model: Mean	LS Model: Median	HH Model: Mean	HH Model: Median
AAA	1	0.959	0.959	1.115	1.115	0.759	0.759
AAA (standard error)		(0.018)	(0.018)	(0.022)	(0.022)	(0.034)	(0.034)
AA	6	0.760	0.738	1.217	1.052	1.279	1.378
AA (standard error)		(0.081)	(0.080)	(0.115)	(0.110)	(0.166)	(0.152)
A	25	1.028	0.958	1.319	1.206	0.901	0.869
A (standard error)		(0.050)	(0.046)	(0.064)	(0.060)	(0.094)	(0.067)
BBB	45	0.911	0.866	1.130	1.091	0.758	0.752
BBB (standard error)		(0.035)	(0.030)	(0.041)	(0.033)	(0.085)	(0.060)
BB	11	0.834	0.751	1.041	1.019	0.821	0.711
BB (standard error)		(0.025)	(0.022)	(0.031)	(0.036)	(0.043)	(0.032)
B	4	0.655	0.630	0.857	0.864	0.480	0.504
B (standard error)		(0.017)	(0.016)	(0.046)	(0.029)	(0.074)	(0.079)
CCC	1	0.736	0.736	1.011	1.011	0.603	0.603
CCC (standard error)		(0.011)	(0.011)	(0.001)	(0.001)	(0.105)	(0.105)

Table 3: Panel B (part 4): Estimate of the Default Boundary
Sector	N	BC Model: Mean	BC Model: Median	LS Model: Mean	LS Model: Median	HH Model: Mean	HH Model: Median
Communications	6	1.059	1.114	1.351	1.497	0.764	0.729
Communications (standard error)		(0.037)	(0.039)	(0.072)	(0.070)	(0.128)	(0.115)
Consumer Cyclical	32	0.924	0.826	1.208	1.145	0.843	0.773
Consumer Cyclical (standard error)		(0.043)	(0.037)	(0.050)	(0.038)	(0.099)	(0.061)
Consumer Staple	14	0.888	0.766	1.123	0.950	0.959	0.839
Consumer Staple (standard error)		(0.053)	(0.051)	(0.064)	(0.058)	(0.078)	(0.057)
Energy	8	0.870	0.777	1.055	0.962	0.756	0.702
Energy (standard error)		(0.031)	(0.024)	(0.042)	(0.035)	(0.062)	(0.065)
Industrial	18	0.902	0.904	1.136	1.129	0.743	0.744
Industrial (standard error)		(0.030)	(0.026)	(0.033)	(0.030)	(0.070)	(0.047)
Materials	11	0.904	0.855	1.137	1.197	0.760	0.792
Materials (standard error)		(0.038)	(0.028)	(0.053)	(0.043)	(0.097)	(0.066)
Technology	4	0.815	0.640	1.067	0.935	0.965	0.734
Technology (standard error)		(0.027)	(0.027)	(0.054)	(0.048)	(0.062)	(0.057)

Panel C (part 1): Estimates of Other Parameters in HH and CDG

Table 3: Parameter Estimation of Structural Credit Risk Models
Model / Parameter	N	HH Model: $\lambda^Q$ , Mean	HH Model: $\lambda^Q$ , Median	CDG Model: $\kappa_\ell$ , Mean	CDG Model: $\kappa_\ell$ , Median	CDG Model: $\nu$ , Mean	CDG Model: $\nu$ , Median	CDG Model: $\phi$ , Mean	CDG Model: $\phi$ , Median
Whole Sample	93	0.224	0.130	13.215	14.784	0.304	0.169	2.254	1.817
Whole Sample (standard deviation)		(0.061)	(0.037)	(0.095)	(0.048)	(0.085)	(0.011)	(0.418)	(0.145)

Table 3: Panel C (part 2): Estimates of Other Parameters in HH and CDG
Model / Percentile	N	HH Model: $\lambda^Q$ , 5th	HH Model: $\lambda^Q$ , 95th	CDG Model: $\kappa_\ell$ , 5th	CDG Model: $\kappa_\ell$ , 95th	CDG Model: $\nu$ , 5th	CDG Model: $\nu$ , 95th	CDG Model: $\phi$ , 5th	CDG Model: $\phi$ , 95th
Whole Sample		0.042	0.878	0.289	20.273	0.093	1.139	-2.609	5.008
Whole Sample (standard deviation)		(0.009)	(0.176)	(0.008)	(0.463)	(0.005)	(0.198)	(0.057)	(1.130)

Table 3: Panel C (part 3): Estimates of Other Parameters in HH and CDG
Ratings	N	HH Model: $\lambda^Q$ , 5th	HH Model: $\lambda^Q$ , 95th	CDG Model: $\kappa_\ell$ , 5th	CDG Model: $\kappa_\ell$ , 95th	CDG Model: $\nu$ , 5th	CDG Model: $\nu$ , 95th	CDG Model: $\phi$ , 5th	CDG Model: $\phi$ , 95th
AAA	1	0.051	0.051	15.044	15.044	0.106	0.106	1.183	1.183
AAA (standard error)		(0.011)	(0.011)	(0.023)	(0.023)	(0.012)	(0.012)	(0.151)	(0.151)
AA	6	0.095	0.091	17.818	19.147	0.855	0.349	13.383	3.304
AA (standard error)		(0.029)	(0.024)	(0.056)	(0.036)	(0.118)	(0.022)	(2.598)	(0.506)
A	25	0.125	0.129	16.471	16.015	0.185	0.173	2.225	1.981
A (standard error)		(0.038)	(0.027)	(0.043)	(0.026)	(0.013)	(0.011)	(0.203)	(0.157)
BBB	45	0.173	0.134	14.407	14.816	0.218	0.148	1.491	1.724
BBB (standard error)		(0.056)	(0.037)	(0.087)	(0.045)	(0.125)	(0.009)	(0.248)	(0.121)
BB	11	0.329	0.191	4.057	1.456	0.508	0.320	1.977	1.385
BB (standard error)		(0.072)	(0.059)	(0.157)	(0.100)	(0.045)	(0.024)	(0.475)	(0.312)
B	4	0.986	0.954	0.568	0.511	0.500	0.377	-3.438	-4.038
B (standard error)		(0.248)	(0.237)	(0.436)	(0.354)	(0.111)	(0.119)	(0.417)	(0.235)
CCC	1	1.788	1.788	0.026	0.026	1.001	1.001	-2.609	-2.609
CCC (standard error)		(0.286)	(0.286)	(0.007)	(0.007)	(0.252)	(0.252)	(0.065)	(0.065)

Table 3: Panel C (part 4): Estimates of Other Parameters in HH and CDG
Sector	N	Mean	Median	Mean	Median	Mean	Median	Mean	Median
Communications	6	0.285	0.164	11.802	13.594	0.278	0.239	0.333	2.377
Communications (standard error)		(0.121)	(0.080)	(0.205)	(0.162)	(0.052)	(0.028)	(0.518)	(0.253)
Consumer Cyclical	32	0.230	0.146	13.502	15.280	0.341	0.173	2.483	1.871
Consumer Cyclical (standard error)		(0.064)	(0.039)	(0.098)	(0.042)	(0.176)	(0.011)	(0.336)	(0.145)
Consumer Staple	14	0.222	0.115	15.230	15.416	0.307	0.158	3.820	1.859
Consumer Staple (standard error)		(0.033)	(0.022)	(0.052)	(0.028)	(0.052)	(0.009)	(1.128)	(0.135)
Energy	8	0.265	0.136	9.848	13.758	0.256	0.206	0.667	1.338
Energy (standard error)		(0.051)	(0.049)	(0.185)	(0.072)	(0.046)	(0.011)	(0.303)	(0.164)
Industrial	18	0.201	0.117	14.145	15.175	0.251	0.145	0.478	1.613
Industrial (standard error)		(0.065)	(0.031)	(0.054)	(0.042)	(0.025)	(0.008)	(0.117)	(0.101)
Materials	11	0.228	0.115	13.105	14.125	0.245	0.168	4.473	1.899
Materials (standard error)		(0.062)	(0.039)	(0.048)	(0.052)	(0.020)	(0.011)	(0.179)	(0.182)
Technology	4	0.119	0.138	8.836	8.960	0.523	0.380	2.871	2.564
Technology (standard error)		(0.056)	(0.047)	(0.188)	(0.087)	(0.044)	(0.023)	(0.694)	(0.618)

This table reports the pricing errors CDS Spreads and Equity Volatility under each of five structural models. The pricing errors of the CDS spreads are calculated as the average, absolute, average percentage, and absolute percentage differences between the model implied and observed spreads, across six maturities, 1, 2, 3, 5, 7, and 10 years, and monthly observations from January 2002 to December 2004. The fitted errors of equity volatility are calculated in a similar fashion. The five model specifications include Merton (1974), Black and Cox (1976), Longstaff and Schwartz (1995), Collin-Dufresne and Goldstein (2001), and the double exponential jump diffusion model (Huang and Huang, 2003).

Panel A (part 1): By Ratings

Table 4: Pricing Errors of CDS Spreads and Equity Volatility
Rating	N	Average Pricing Error: Merton	Average Pricing Error: BC	Average Pricing Error: LS	Average Pricing Error: HH	Average Pricing Error: CDG	Absolute Pricing Error: Merton	Absolute Pricing Error: BC	Absolute Pricing Error: LS	Absolute Pricing Error: HH	Absolute Pricing Error: CDG
CDS Spreads: Overall	93	0.35	-0.96	-0.52	-0.40	-0.06	1.58	1.01	1.06	0.70	0.67
CDS Spreads: AAA	1	0.23	-0.32	-0.25	-0.01	-0.11	0.39	0.32	0.26	0.19	0.20
CDS Spreads: AA	6	-0.19	-0.11	-0.16	-0.05	-0.06	0.19	0.13	0.16	0.09	0.12
CDS Spreads: A	25	-0.30	-0.24	-0.23	-0.07	-0.03	0.37	0.29	0.28	0.15	0.18
CDS Spreads: BBB	45	0.13	-0.70	-0.57	-0.27	-0.05	1.29	0.73	0.70	0.42	0.51
CDS Spreads: BB	11	-0.14	-1.43	-0.56	-0.20	-0.21	2.59	1.68	2.46	1.38	1.70
CDS Spreads: B	4	6.08	-5.18	-4.21	-3.57	-0.22	7.94	5.21	4.77	4.15	2.32
CDS Spreads: CCC	1	12.10	-13.81	7.07	-6.84	1.10	17.47	13.81	12.25	9.37	6.27
Equity Volatility: Overall	93	-0.13	-3.26	-0.42	1.33	1.02	26.53	13.36	15.05	10.89	11.37
Equity Volatility: AAA	1	-3.02	-13.89	-16.65	0.40	-7.19	12.19	14.94	16.82	11.27	11.87
Equity Volatility: AA	6	-25.15	4.22	-2.38	-6.14	0.11	25.15	11.47	11.08	8.00	8.84
Equity Volatility: A	25	-17.60	-4.58	-7.17	-2.95	-0.58	18.17	10.07	10.53	7.49	8.45
Equity Volatility: BBB	45	-3.16	-3.81	-3.90	1.69	0.22	19.08	10.85	11.98	9.53	9.82
Equity Volatility: BB	11	3.66	4.16	13.11	10.78	8.55	22.18	20.24	22.69	19.59	19.60
Equity Volatility: B	4	63.02	-10.88	41.06	6.12	-2.33	79.04	39.07	54.34	22.63	21.98
Equity Volatility: CCC	1	431.35	-31.04	38.30	14.73	21.56	431.35	39.42	47.10	31.12	36.28

Panel A (part 2): By Ratings

Table 4: Pricing Errors of CDS Spreads and Equity Volatility
CDS Spreads: Rating	N	Merton	BC	LS	HH	CDG	Merton	BC	LS	HH	CDG
CDS Spreads: Overall	93	24.36	-66.72	-36.36	-27.99	-4.11	109.94	70.70	73.77	48.50	46.91
CDS Spreads: AAA	1	62.12	-85.15	-67.79	-2.04	-30.18	106.02	85.15	70.98	50.94	53.87
CDS Spreads: AA	6	-99.91	-58.88	-84.84	-28.49	-32.19	99.91	71.03	84.89	45.87	64.31
CDS Spreads: A	25	-80.22	-65.34	-62.02	-18.14	-7.04	99.23	77.23	75.92	39.66	48.14
CDS Spreads: BBB	45	14.45	-76.20	-61.68	-28.90	-5.43	140.22	79.11	76.44	46.12	55.23
CDS Spreads: BB	11	-4.93	-49.71	-19.38	-6.96	-7.28	89.64	58.31	85.19	47.82	58.93
CDS Spreads: B	4	83.20	-70.83	-57.68	-48.80	-3.07	108.73	71.25	65.26	56.75	31.73
CDS Spreads: CCC	1	60.29	-68.80	35.22	-34.08	5.50	87.03	68.80	61.03	46.68	31.22
Equity Volatility: Rating	N	Merton	BC	LS	HH	CDG	Merton	BC	LS	HH	CDG
Equity Volatility: Overall	93	-0.34	-8.43	-1.08	3.44	2.65	68.59	34.53	38.91	28.15	29.40
Equity Volatility: AAA	1	-8.17	-37.58	-45.04	1.07	-19.46	32.98	40.42	45.50	30.50	32.13
Equity Volatility: AA	6	-79.35	13.31	-7.51	-19.39	0.36	79.35	36.20	34.96	25.24	27.89
Equity Volatility: A	25	-53.53	-13.94	-21.81	-8.96	-1.76	55.26	30.62	32.01	22.78	25.70
Equity Volatility: BBB	45	-8.84	-10.66	-10.91	4.74	0.61	53.43	30.38	33.55	26.69	27.48
Equity Volatility: BB	11	7.66	8.70	27.45	22.58	17.90	46.45	42.38	47.50	41.02	41.04
Equity Volatility: B	4	75.25	-13.00	49.04	7.31	-2.78	94.38	46.66	64.89	27.02	26.24
Equity Volatility: CCC	1	533.76	-38.41	47.40	18.22	26.68	533.76	48.78	58.28	38.51	44.89

Panel B (part 1): By Sectors

Table 4: Pricing Errors of CDS Spreads and Equity Volatility
Sector	N	Average Pricing Error: Merton	Average Pricing Error: BC	Average Pricing Error: LS	Average Pricing Error: HH	Average Pricing Error: CDG	Absolute Pricing Error: Merton	Absolute Pricing Error: BC	Absolute Pricing Error: LS	Absolute Pricing Error: HH	Absolute Pricing Error: CDG
CDS Spreads: Overall	93	0.35	-0.96	-0.52	-0.40	-0.06	1.58	1.01	1.06	0.70	0.67
CDS Spreads: Communications	6	-0.57	-1.59	-1.76	-1.49	-0.14	1.28	1.60	1.77	1.52	0.91
CDS Spreads: Consumer Cyclical	32	1.07	-1.13	-0.48	-0.46	-0.04	2.34	1.20	1.14	0.71	0.76
CDS Spreads: Consumer Staple	14	0.47	-0.68	-0.73	-0.11	-0.01	1.09	0.70	0.78	0.30	0.30
CDS Spreads: Energy	8	1.45	-1.14	-0.68	-0.68	-0.33	2.34	1.14	0.76	0.84	0.62
CDS Spreads: Industrial	18	-0.45	-0.78	-0.06	-0.34	-0.08	0.89	0.89	1.32	0.60	0.65
CDS Spreads: Materials	11	-0.34	-0.77	-0.42	-0.37	0.25	0.84	0.77	0.65	0.44	0.73
CDS Spreads: Technology	4	-1.19	-0.52	-0.34	0.92	-0.49	1.19	0.71	0.78	1.52	1.01
Equity Volatility: Sector	N	Merton	BC	LS	HH	CDG	Merton	BC	LS	HH	CDG
Overall	93	-0.13	-3.26	-0.42	1.33	1.02	26.53	13.36	15.05	10.89	11.37
Equity Volatility: Communications	6	-12.65	-15.45	-14.26	-5.74	-2.34	19.25	17.48	18.38	13.12	16.17
Equity Volatility: Consumer Cyclical	32	13.24	-2.01	-0.71	3.59	2.40	40.10	13.64	15.97	13.11	12.17
Equity Volatility: Consumer Staple	14	-5.31	2.67	6.87	-0.97	-0.60	26.05	13.03	18.68	8.39	9.16
Equity Volatility: Energy	8	6.94	-6.12	2.81	3.46	0.21	28.17	16.13	14.34	11.74	10.19
Equity Volatility: Industrial	18	-8.76	-5.81	-1.84	1.29	-0.47	13.68	11.60	12.86	9.09	9.53
Equity Volatility: Materials	11	-9.67	-1.34	-1.82	1.58	2.60	13.52	10.04	10.03	7.18	9.72
Equity Volatility: Technology	4	-19.27	-3.84	0.98	-2.76	4.72	21.01	17.53	15.12	15.12	20.73

Panel B (pat 2): By Sectors

Table 4: Pricing Errors of CDS Spreads and Equity Volatility
Sector	N	Average Pricing Error: Merton	Average Pricing Error: BC	Average Pricing Error: LS	Average Pricing Error: HH	Average Pricing Error: CDG	Absolute Pricing Error: Merton	Absolute Pricing Error: BC	Absolute Pricing Error: LS	Absolute Pricing Error: HH	Absolute Pricing Error: CDG
CDS Spreads: Sector	N	Merton	BC	LS	HH	CDG	Merton	BC	LS	HH	CDG
CDS Spreads: Overall	93	24.36	-66.72	-36.36	-27.99	-4.11	109.94	70.70	73.77	48.50	46.91
CDS Spreads: Communications	6	-26.37	-74.30	-81.99	-69.65	-6.53	59.83	74.65	82.81	71.09	42.34
CDS Spreads: Consumer Cyclical	32	66.34	-69.96	-29.66	-28.68	-2.55	144.94	74.16	70.80	44.26	46.95
CDS Spreads: Consumer Staple	14	52.73	-76.98	-82.34	-12.78	-1.04	122.89	78.94	87.97	34.36	33.93
CDS Spreads: Energy	8	96.35	-75.45	-45.42	-45.09	-21.70	155.62	75.97	50.58	55.90	40.96
CDS Spreads: Industrial	18	-30.75	-53.32	-3.78	-23.40	-5.19	60.41	60.82	90.31	40.75	44.15
CDS Spreads: Materials	11	-30.80	-70.36	-38.20	-33.74	22.90	77.16	70.67	59.74	40.31	66.60
CDS Spreads: Technology	4	-80.20	-35.09	-22.83	62.14	-32.95	80.20	48.03	52.30	102.10	68.18
Equity Volatility: Sector	N	Merton	BC	LS	HH	CDG	Merton	BC	LS	HH	CDG
Equity Volatility: Overall	93	-0.34	-8.43	-1.08	3.44	2.65	68.59	34.53	38.91	28.15	29.40
Equity Volatility: Communications	6	-25.96	-31.72	-29.26	-11.78	-4.81	39.51	35.87	37.72	26.92	33.19
Equity Volatility: Consumer Cyclical	32	33.98	-5.17	-1.82	9.21	6.17	102.94	35.01	41.00	33.67	31.25
Equity Volatility: Consumer Staple	14	-15.73	7.90	20.33	-2.88	-1.76	77.14	38.59	55.29	24.83	27.14
Equity Volatility: Energy	8	17.37	-15.34	7.04	8.67	0.53	70.55	40.40	35.91	29.40	25.52
Equity Volatility: Industrial	18	-21.77	-14.43	-4.56	3.19	-1.17	33.99	28.83	31.96	22.58	23.68
Equity Volatility: Materials	11	-29.45	-4.08	-5.55	4.82	7.92	41.16	30.56	30.52	21.85	29.60
Equity Volatility: Technology	4	-42.62	-8.48	2.16	-6.11	10.43	46.46	38.77	33.44	33.43	45.83

This appendix table reports ratings, 5-year CDS spread, equity volatility, leverage ratio, asset payout, and recovery rate, for each of the 93 firms similar as those by ratings and sectors in Table 1.

Table A1: Summary Statistics of Individual Names
Company	Last Rating	Five Yr CDS (%)	Equity Volatility (%)	Leverage Ratio (%)	Asset Payout (%)	Recovery Rate (%)
Air Prods & Chems Inc	A	0.238	28.358	33.067	2.086	40.863
Albertsons Inc	BBB	0.692	35.540	54.662	3.650	41.008
Amerada Hess Corp	BB	0.817	28.458	61.871	2.929	40.081
Anadarko Pete Corp	BBB	0.427	31.244	47.816	1.688	39.439
Arrow Electrs Inc	BBB	2.175	44.325	62.279	2.259	39.269
Autozone Inc	BBB	0.708	33.269	30.222	0.827	41.977
Avon Prods Inc	A	0.230	27.128	17.924	0.998	41.353
Baker Hughes Inc	A	0.298	39.469	20.584	1.764	40.833
Baxter Intl Inc	BBB	0.493	39.739	33.159	1.739	40.526
BellSouth Corp	A	0.550	43.254	39.213	3.308	41.848
Black & Decker Corp	BBB	0.389	29.569	45.897	1.566	42.200
Boeing Co	A	0.517	36.815	56.877	1.744	39.336
BorgWarner Inc	BBB	0.572	29.766	48.270	1.285	40.623
Bowater Inc	BB	2.751	30.755	62.578	3.583	41.287
CSX Corp	BBB	0.607	29.651	69.128	2.305	40.486
Campbell Soup Co	A	0.319	27.171	36.114	2.699	40.063
Caterpillar Inc	A	0.350	32.081	57.902	1.992	40.122
Cendant Corp	BBB	1.595	42.626	59.864	1.291	39.440
Centex Corp	BBB	0.895	41.148	69.613	2.543	40.670
Clear Channel Comms Inc	BBB	1.413	45.192	35.378	1.487	40.789
Coca Cola Entpers Inc	A	0.327	34.774	68.903	2.281	40.019
Computer Assoc Intl Inc	BB	2.889	54.727	35.045	1.044	35.840
Computer Sciences Corp	A	0.565	41.122	43.578	1.182	39.763
ConAgra Foods Inc	BBB	0.470	27.510	43.829	3.516	39.320
Corning Inc	BB	5.412	80.739	41.995	1.138	36.807
Delphi Corp	BBB	1.470	40.828	77.164	1.535	40.539
Delta Air Lines Inc	CCC	18.806	81.939	93.931	2.885	26.566
Devon Engy Corp	BBB	0.732	31.487	56.495	2.281	40.513
Diamond Offshore Drilling Inc	BBB	0.488	39.213	32.696	1.701	40.833
Dow Chem Co	A	0.817	35.536	48.723	3.166	39.775
E I du Pont de Nemours & Co	AA	0.241	30.318	37.916	2.574	41.409
Eastman Kodak Co	BBB	1.317	37.618	56.431	2.550	38.839
Eaton Corp	A	0.335	27.783	42.526	1.527	40.815
Electr Data Sys Corp	BB	2.087	51.554	50.321	2.332	40.349
Eli Lilly & Co	AA	0.219	35.486	13.956	1.898	40.494
Fedt Dept Stores Inc	BBB	0.675	38.303	54.236	1.966	41.664
Ford Mtr Co	BBB	2.977	47.060	92.612	2.769	41.849
GA Pac Corp	BB	3.824	48.523	74.892	3.547	42.054
Gen Elec Co Inc	AAA	0.427	36.356	63.713	2.223	40.883
Gen Mls Inc	BBB	0.539	24.225	44.680	3.095	41.508
Gen Mtrs Corp	BBB	2.434	35.537	94.017	2.595	41.278
Gillette Co	AA	0.147	28.421	17.574	1.672	40.977
Goodrich Corp	BBB	1.230	35.427	61.064	3.187	39.736
Goodyear Tire & Rubr Co	B	7.671	65.509	88.106	2.245	39.840
H J Heinz Co	A	0.310	23.404	39.061	3.199	41.748
Hilton Hotels Corp	BBB	2.141	36.860	51.553	2.754	41.065
Home Depot Inc	AA	0.222	39.170	14.502	0.741	42.223

Table A1: Summary Statistics of Individual Names (continued)
Company	Last Rating	Five Yr CDS (%)	Equity Volatility (%)	Leverage Ratio (%)	Asset Payout (%)	Recovery Rate (%)
IKON Office Solutions Inc	BB	3.460	48.604	73.673	1.337	38.221
Intl Business Machs Corp	A	0.381	31.166	32.683	0.578	39.991
Intl Paper Co	BBB	0.740	30.566	58.274	2.944	39.674
J C Penney Co Inc	BB	2.949	45.576	61.984	2.343	37.818
Jones Apparel Gp Inc	BBB	0.634	32.547	26.906	1.353	41.338
Kerr Mcgee Corp	BBB	0.745	26.472	59.613	3.398	41.242
Lockheed Martin Corp	BBB	0.501	32.241	44.982	1.815	41.173
Lowes Cos Inc	A	0.356	36.642	19.222	0.587	41.788
Ltd Brands Inc	BBB	0.584	44.878	21.283	3.854	41.529
Lucent Tech Inc	B	9.525	96.827	63.895	1.255	37.988
MGM MIRAGE	BB	2.167	33.197	57.910	2.675	39.764
Masco Corp	BBB	0.612	33.101	35.400	2.758	42.234
Mattel Inc	BBB	0.534	35.721	21.203	2.269	40.322
May Dept Stores Co	BBB	0.608	36.953	52.074	3.923	41.765
Maytag Corp	BBB	0.773	38.307	58.938	2.213	41.476
McDonalds Corp	A	0.322	38.651	30.956	2.107	40.051
Nordstrom Inc	BBB	0.609	40.304	43.145	1.555	41.820
Norfolk Sthn Corp	BBB	0.471	36.021	61.054	2.704	39.724
Northrop Grumman Corp	BBB	0.675	26.992	51.679	1.844	40.890
Omnicom Gp Inc	BBB	0.906	36.220	42.475	0.887	40.262
PPG Inds Inc	A	0.360	27.727	37.415	2.667	42.133
Phelps Dodge Corp	BBB	1.780	38.034	48.840	1.877	41.547
Pitney Bowes Inc	A	0.211	27.063	46.124	2.645	41.674
Praxair Inc	A	0.291	28.048	33.167	1.730	42.060
Procter & Gamble Co	AA	0.163	23.275	21.002	1.289	40.450
Rohm & Haas Co	BBB	0.353	29.283	43.281	2.241	42.235
Ryder Sys Inc	BBB	0.590	29.285	65.616	2.294	39.827
SBC Comms Inc	A	0.598	43.723	42.509	3.587	38.423
Safeway Inc	BBB	0.724	39.373	52.084	1.893	41.592
Sara Lee Corp	A	0.281	28.465	42.474	2.900	39.904
Sealed Air Corp US	BBB	2.349	35.792	44.043	1.820	37.390
Sherwin Williams Co	A	0.396	29.004	32.345	1.896	41.694
Solectron Corp	B	4.976	86.414	54.483	1.908	39.241
Southwest Airls Co	A	0.723	43.900	29.447	0.624	40.323
The Gap Inc	BB	2.889	50.769	27.086	1.429	41.034
The Kroger Co.	BBB	0.754	39.574	55.452	1.960	41.729
Tribune Co	A	0.413	25.200	34.934	1.500	41.228
Utd Tech Corp	A	0.260	30.856	37.047	1.116	39.475
V F Corp	A	0.323	25.458	31.046	2.687	38.877
Valero Engy Corp	BBB	1.075	36.741	65.574	2.174	40.715
Visteon Corp	BB	2.671	46.160	87.957	1.297	41.348
Wal Mart Stores Inc	AA	0.193	32.359	20.540	0.991	39.991
Walt Disney Co	BBB	0.714	43.767	38.906	1.644	39.191
Weyerhaeuser Co	BBB	0.753	29.759	62.255	3.509	41.164
Whirlpool Corp	BBB	0.477	31.043	58.506	2.305	40.512
Williams Cos Inc	B	6.836	84.181	83.953	3.724	35.851

Figure 1: Average CDS Spreads over the Entire Sample

Figure 2: CDS Spreads and Equity Volatility

Figure 3: Leverage Ratio and Default Boundary

Figure 4: Observed and Model Implied CDS Term Structure

Figure 5: Observed and Model 5-Year CDS Spreads

Figure 6: Observed and Model Implied Equity Volatility

Figure 7: Observed Spot Leverage and the Long-Run Mean of Risk-Neutral Leverage

Footnotes

* We would like to thank Viral Acharya, Ren-Raw Chen, Thomas Dangl, Jan Ericsson, Jean Helwege, Rangarajan Sundaram, Yi Zhou, and seminar participants at CEIBS, Cheung Kong Graduate School of Business, Lehigh, MIT, SHUFE, SWUFE, UESTC, the 2006 Econometric Society North American Winter Meeting in Boston, the 2006 Derivatives and Risk Management Conference at FDIC, the 2007 Federal Reserve Board Conference on Credit Risk and Credit Derivatives, Moody's 4th Annual Credit Risk Conference in Copenhagen, the 2007 Gutmann Center Symposium on Credit Risk and the Management of Fixed-Income Portfolios in Vienna, the 2007 CICF in Chengdu, the 2008 Mitsui Symposium at Michigan, and the 2008 Singapore International Conference on Finance for helpful comments and suggestions. Huang is at Smeal College of Business, Penn State University, University Park, PA 16802; [email protected]. Zhou is at Division of Research and Statistics, Federal Reserve Board, Washington, D.C. 20551; [email protected]. Huang acknowledges a Smeal Summer Research Grant for partial support. The views presented here are solely those of the authors and do not necessarily represent those of the Federal Reserve Board or its staff. Return to Text

1. Campbell & Taksler (2003) find that idiosyncratic equity volatility can explain a significant part of corporate bond yield spreads cross-sectionally. Huang & Huang (2003) conjecture that a structural credit risk model with stochastic asset volatility may solve the credit spread puzzle. Huang (2005) considers an affine class of structural models with both stochastic asset volatility and Lévy jumps. Based on regression analysis, Zhang, et al. (2006) provide empirical evidence that a stochastic asset volatility model may improve the model performance. Return to Text

2. Examples of other structural models include Geske (1977), Anderson & Sundaresan (1996), Mella-Barral & Perraudin (1997), Leland (1998), Duffie & Lando (2001), and Acharya & Carpenter (2002) etc. Return to Text

3. For example, Longstaff, et al. (2005) find that a large proportion of bond spreads are determined by liquidity factors, which do not necessarily reflect the default risk of the underlying asset. Return to Text

4. Additional maturities of 0.5, 15, 20, and 30 years are also available for the CDS data set. Due to the liquidity concern and missing value, we choose to focus on CDS with maturity between 1 and 10 years. Return to Text

5. In order to estimate the stochastic interest rate model of Longstaff & Schwartz (1995) and the dynamic leverage model of Collin-Dufresne & Goldstein (2001), we need to first estimate the default-free term structure model of Vasicek (1977) in Eq. (3). Parameter estimates are obtained monthly based on cross-sectional data, and not reported here for brevity. The cross-sectional pricing errors that range from 12 to 112 basis points during the sample period. Return to Text

6. In estimation we use CDS with maturities of 1, 3, 5, 10 years and equity volatility; while 2 and 7 years are too sparse to be included in estimation, they are still useful to be included in pricing error evaluation. Return to Text

^♣ This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to Text