Skip to: [Printable Version (PDF)] [Bibliography] [Footnotes]

Finance and Economics Discussion Series: 2008-56 Screen Reader version ^♣

Uncertainty and Disagreement in Economic Forecasting

Stefania D'Amico and Athanasios Orphanides
Board of Governors of the Federal Reserve System
First Version August 2006, This Version July 2008

Keywords: Survey expectations, probabilistic forecasts, inflation, uncertainty.

Abstract:

Using the probabilistic responses from the Survey of Professional Forecasters, we study the evolution of uncertainty and disagreement associated with inflation forecasts in the United States since 1968. We compare and contrast alternative measures summarizing the distributions of mean forecasts and forecast uncertainty across individuals at an approximate one-year-ahead horizon. In light of the heterogeneity in individual uncertainty reflected in the survey responses, we provide quarterly estimates for both average uncertainty and disagreement regarding uncertainty. We propose direct estimation of parametric distributions characterizing the uncertainty across individuals in a manner that mitigates errors associated with rounding and approximation of responses when individual uncertainty is small. Our results indicate that higher average expected inflation is associated with both higher average inflation uncertainty and greater disagreement about the inflation outlook. Disagreement about the mean forecast, however, may be a weak proxy for forecast uncertainty. We also examine the relationship of these measures with the term premia embedded in the term-structure of interest rates.

JEL Classification: E37, E47, C53

We would like to thank Michael McCracken, Jim Nason, Thomas Trimbur, Jonathan Wright and participants of presentations at a workshop at CIRANO, Montreal, October 14-15, 2005, and the conference in honor of Charles R. Nelson, Federal Reserve Bank of Atlanta, Atlanta, Georgia, March 31-April 1, 2006, for useful discussions and comments, and Josie Smith and Jeff Crilley for research assistance. The opinions expressed are those of the authors and do not necessarily reflect the views of the Board of Governors of the Federal Reserve System.

Correspondence: D'Amico: Federal Reserve Board, Washington, D.C. 20551, Tel.: (202) 452-2567, e-mail: Stefania.D'[email protected]. Orphanides: Federal Reserve Board, Washington, D.C. 20551, Tel.: (202) 452-2654, e-mail: [email protected].

1 Introduction

Individual decisions, aggregate economic outcomes, and asset prices are often shaped by probabilistic assessments of future events, the uncertainty surrounding them, and disagreement across individuals regarding these assessments. The roles of disagreement and uncertainty are often confounded in economic analysis, however, in large part because the observation and measurement that would be needed for such investigations is lacking. For instance, it is unclear from the available evidence whether variations over time in the risk and term premia embedded in bond and equity prices primarily reflect changes in aggregate uncertainty or swings in the degree of the consensus in beliefs about economic fundamentals.

Surveys of expectations offer one potential source for information that could be useful in addressing such questions. Unfortunately, virtually all surveys of analysts, professional forecasters, businesses, and households collect information on point predictions of future events. Aggregating information on the most likely outcome in each individual's assessment offers some indication of the degree of consensus among individuals regarding the most likely outcome. It does not, however, provide meaningful information regarding the uncertainty that each individual may attach to his or her point forecast or the evolution of the associated individual and aggregate uncertainty over time, or any disagreements regarding individual assessments of uncertainty.

The Survey of Professional Forecasters presents a useful exception to the typical survey structure. Since its inception, this quarterly survey has asked respondents to provide probabilistic assessments of the outlook for inflation and for either nominal or real output. Focusing on these probabilistic responses allows construction and limited comparisons of aggregate proxies for uncertainty and disagreement. Starting with the important study by Zarnowitz and Lambros (1988) a number of authors have suggested various approaches to measure uncertainty as reflected in these survey responses.¹In this paper, we extend earlier work and present quarterly time series of various measures of uncertainty and disagreement that correct some apparent biases due to imperfections in the survey.

We focus our attention on the probabilistic inflation forecasts that cover an almost continuous span approaching forty years, from 1968Q4 to 2006Q1. Following earlier work, our starting point is the estimation of the characteristics of the probability densities for each forecaster in each period available in the survey. An important difficulty, however, is that the design of the survey and individual respondent practices, particularly a tendency to approximate and round the probabilistic responses, induces some errors in the estimation of individual uncertainty. These errors appear especially problematic when individual uncertainty is small and can result in systematic biases in estimates of uncertainty. To arrive at an aggregate characterization of uncertainty that mitigates this problem, we propose robust estimation of a cumulative density function approximating the distribution characterizing individual uncertainty in each quarter. Doing so provides direct estimates of both the average degree of uncertainty as well as the dispersion of individual uncertainty assessments in each quarter. This allows comparing and contrasting average uncertainty not only with disagreement about the mean outlook, (the most commonly discussed form of disagreement), but also with disagreement about the uncertainty to the outlook.

As an illustration of the potential usefulness of distinguishing uncertainty from various forms of disagreement we also examine their relationship with and predictive content for the evolution of the term premia embedded in the term-structure of government securities. We show that all three measures of uncertainty and disagreement we discuss are significantly correlated with term premia. However, their comovement in the sample makes it difficult to identify their relative importance with precision.

2 Description of the Survey Data

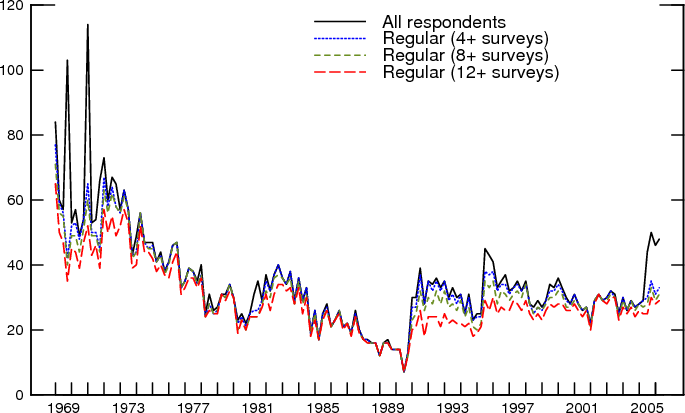
The first Survey of Professional Forecasters was conducted in November 1968 as a joint effort by the American Statistical Association and the National Bureau of Economic Research and quarterly surveys have been conducted since then. Currently, the Survey is maintained by the Federal Reserve Bank of Philadelphia that took over its administration in the summer of 1990.²The number of respondents has changed over time and, especially in its early years, fluctuated considerably. With the exception of few quarters in the late 1980s, however, the number of respondents has exceeded 20. Indeed, the survey has typically included between 20 and 40 regular respondents, that is respondents who have contributed to it numerous times over a period of one or more years.

In the following, we highlight some special features relating primarily to the density forecasts in the survey that are important for our analysis. Since the inception of the survey, respondents have been asked to provide probabilistic forecasts for inflation, as measured by the concept of aggregate output most relevant at the time of each survey (that is GNP or GDP with fixed or chain weights). A complicating factor in the design of the survey is that in each quarter respondents are asked to forecast the annual percentage changes in the average output deflator (currently the GDP price index) between the previous and current year and between the current and following year. When the survey started, there was one question referring to only one of these annual forecasts, but since the early 1980s, forecasts for both have generally been asked. Because the questions always refer to the average of the calendar year, their structure introduces a seasonal pattern in the quarterly horizons relevant for the forecast. For example, in the first quarter of the year, the current-year forecast is a 4-quarter ahead forecast, counting from the last quarter of available data (the fourth quarter of the previous year) to the last quarter of the current year. The following-year forecast reflects an 8-quarter ahead horizon, ending with the fourth quarter of the subsequent year. By contrast, in the second quarter of the year, these horizons become 3 and 7 quarters ahead, respectively. Similarly, in the third quarter the forecast horizons are 2 and 5 quarters ahead, and finally, in the fourth quarter of the year, they are down to 1 and 4 quarters ahead, respectively. As a result of this design, the underlying expected uncertainty reflected in the individual responses as well as the expected degree of disagreement have seasonal patterns. An approximate year-ahead horizon can be constructed by using a time series that concentrates on the 4-quarter ahead horizon in first quarters, the 3-quarter ahead horizon in second quarters, the 6-quarter ahead horizons in third quarters and the 5-quarter ahead in fourth quarters. Nonetheless, an element of seasonality would still remain in this quarterly series, whose importance can be examined with standard seasonal adjustment procedures.

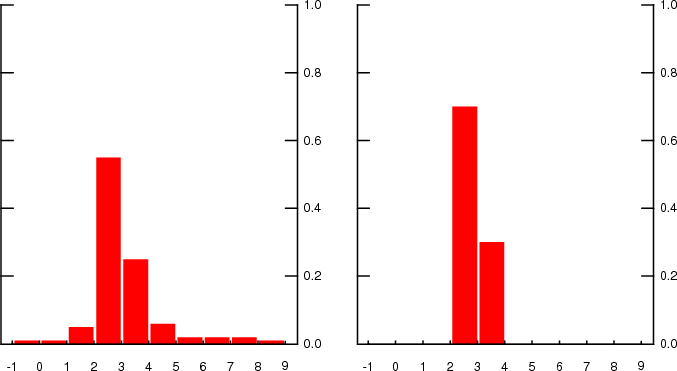
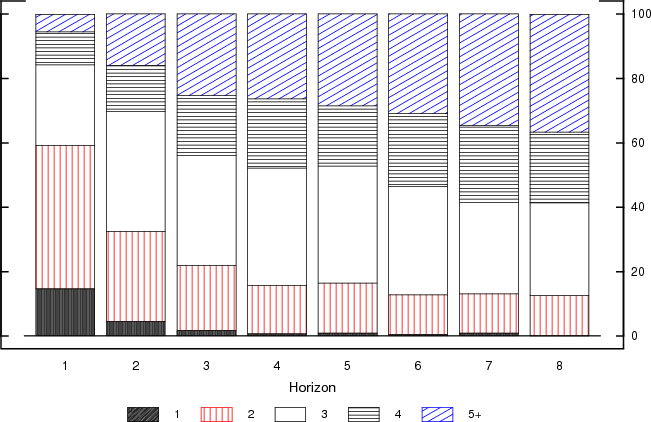
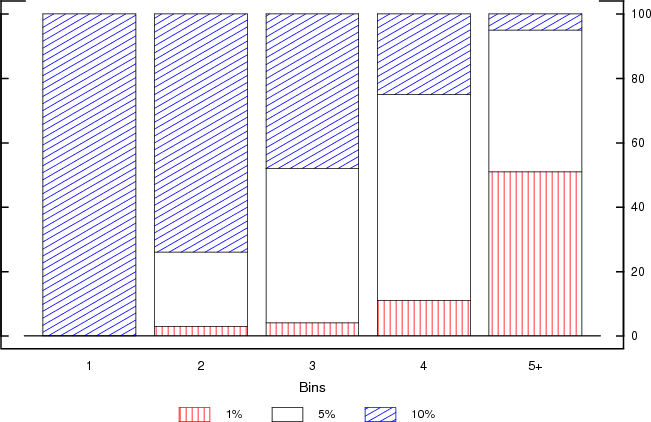
The presence of this seasonality, in conjunction with the way the questions are posed and responses presented introduces some additional complications. In each quarter, the survey presents respondents with a number of bins spanning a wide range of outcomes for the annual rate of inflation and asks them to place probabilities in those bins, summing to 100%. In recent years, the survey has included 10 bins, with width equal to one percent, except for the edges that are open ended. Figure 2 shows two examples of individual responses from this period in the form of the histogram. The example on the left shows a respondent who placed probability mass in all available bins in the questionnaire. This would be the expected outcome if the underlying distribution were continuous with wide support and the responses were provided in rather exact terms, say in multiples of 1 percent or fractions of 1 percent. This, however, is not the typical practice. Most of the time, most respondents place all their density in a few bins only. Some pertinent summary statistics for all responses since 1992 are presented in Figures 3-5. As can be seen in Figure 3, the distribution of the number of non-zero-bins depends sensitively on the forecast horizon. At one extreme, when the horizon is just one quarter, almost 60 percent of respondents place all probability mass in just one or two bins. At the other extreme, when the horizon is 8 quarters, about 60 percent of respondents use 4 or more bins in their answers.

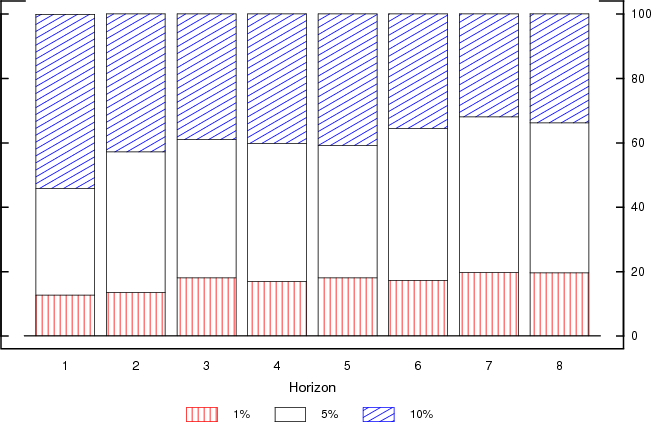
An important reason for this pattern in the number of bins employed is the manner in which respondents may be rounding the answers they provide. Examination of the individual entries reveals that quite often the probabilities in all non-zero bins are multiples of 10 percent or multiples of 5 percent. The breakdown of this practice, by horizon, is shown in Figure 4. The relationship of rounding with the number of bins employed is reported in Figure 5. In each case, responses are classified as reflecting 10% rounding if all non-zero bins are multiples of 10, 5% rounding if all non-zero bins are multiples of 5 and 1% rounding if they do not fall in either of the other two categories. As can be seen in Figure 4, almost 80 percent of two-bin responses are multiples of 10 percent, like the example on the right panel of Figure 2. By contrast, only half of responses that spread to 5 or more bins are reported in multiples of either 5 or 10 percent. This pattern suggests that answers are often provided in approximate form but also, since this approximations are more coarse when fewer bins are utilized, that it may disproportionately influence estimates of individual uncertainty when this uncertainty is relatively low.

In light of the greater prevalence of rounding and the concentration of probabilistic responses in few bins when the forecast horizon is very short, say one- or two-quarters ahead, these results suggest that it may be exceedingly difficult to obtain accurate measures of uncertainty at such horizons with this survey. At longer horizons, however, these difficulties appear to be less critical.

Some other issues also generate difficulties that need to be addressed in constructing quarterly estimates of disagreement and uncertainty that have a consistent interpretation over time. One is the changing number and width of the intervals over time. Fewer and larger bins induce greater biases. The survey initially offered 15 bins with a width of 1%. But from 1981 to 1991 only 6 bins with a width of 2% were presented to respondents. Since 1992, the probabilistic questions offer 10 bins whose width equals 1%.

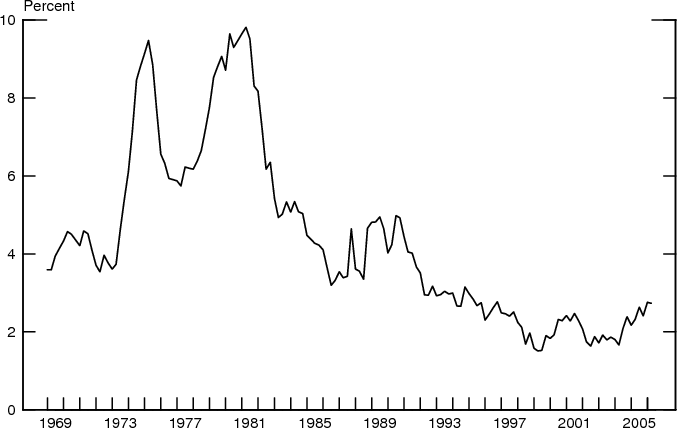
Another complication relates to changes in the number and composition of the respondents, which was shown in Figure 1. In early surveys the average number of respondents was around 60, while in recent years the average has been closer to 30. In addition, at times the turnover of the SPF forecasters has been quite high. To eliminate possible biases from these variations, attention could be restricted to a subset of "regular" forecasters who contributed consistently over a certain number of years. Zarnowitz and Lambros, for example, restricted attention to forecasters who participated in at least 12 surveys. To check the robustness of our results against such participation criteria, we computed and compared our measures using samples including only respondents who participated in at least 4, 8 and 12 surveys, in addition to the sample of all respondents.

Finally, errors in the survey introduce missing observations in some quarters. For example, there is some uncertainty about what years respondents were providing probabilistic responses in 1985:Q1 and 1986:Q1 so these two quarters are excluded from the analysis.

3 Parameter-Free Analysis of the Probabilistic Beliefs

We begin our analysis with a discussion of direct measures of uncertainty and disagreement that do not assume any specific continuous distributions for the probabilistic beliefs but are simply based on different ways of computing sample means and variances. This requires two assumptions. First, because the first and last intervals are open-ended, an assumption is needed about the range over which the individual histograms are defined. Following Zarnowitz and Lambros (1987), we assume that the first and last intervals are closed and have the same width as that of the central intervals. Results are generally not sensitive to this assumption since most of the time respondents place zero probability in the extreme intervals, but a potential bias is introduced in a few instances, when a large fraction of the probability mass is placed at the edges. The second assumption regards the concentration of the probability mass within each interval. We adopt two common alternatives, either that the probability is concentrated at the midpoint of each interval, or that the probability mass is uniformly distributed within the interval. The two imply identical estimates for the mean of the distribution but yield different estimates for the variance. If the underlying distribution is continuous, the discretization associated with providing probabilistic responses in only a few intervals introduces an approximation error. The approximation is worse when the number of intervals is small relative to the dispersion of the underlying distribution and complicates estimation of the underlying uncertainty when this is small. Estimates of the individual variances are also generally expected to have an upward bias that depends on the width of the intervals. To compensate for this bias, we apply the Sheppard correction to variance estimates from these two methods (see Kendall and Stuart (1977)). One exception is that when an individual respondent concentrates all density in just one bin, the midpoint method assigns zero variance to the underlying distribution.

To compute the mean, $\mu$ , and standard deviation, $\sigma$ , of the individual histograms for the mid-point, , and the uniform, , assumptions we apply the following formulas, respectively:

$\begin{displaymath} \mu _{i,h,t}^{M}=\mu _{i,h,t}^{U}=\sum_{j=1}^{n} \frac{(u_{j,h,t} - l_{j,h,t})}{2} \cdot p_{i,j,h,t}, \end{displaymath}$

$\begin{displaymath} \sigma_{i,h,t}^{M}= \sqrt{\left[ \sum_{j=1}^{n}\left( \frac{(u_{j,h,t} - l_{j,h,t})}{2} -\mu _{i,h,t}^{M}\right) ^{2}\cdot p_{i,j,h,t} - \frac{w_{t}^{2}}{12} \right]_+}, \end{displaymath}$

$\begin{displaymath} \sigma_{i,h,t}^{U}=\sqrt{\left[ \sum_{j=1}^{n}\frac{\left( u_{j,h,t}^{3}-l_{j,h,t}^{3}\right) }{3\left( u_{j,h,t}-l_{j,h,t}\right) }\cdot p_{i,j,h,t}-\left( \mu _{i,h,t}^{U}\right)^{2} -\frac{w_{t}^{2}}{12}\right]_+}, \end{displaymath}$

where $p_{i,j,h,t}$ is the probability that the forecaster

assigns to the

th interval in the survey conducted at time

with horizon

; $% u_{j,h,t}$ and $l_{j,h,t}$ are the upper and lower limits of the

th interval; and $w_{t}$ is the width of the central range, thus the term $\frac{% w_{t}^{2}}{12}$ represents the Sheppard's correction for the second moment.

The individual means and standard deviations across all $N_{t}$ respondents in each quarter may be used to obtain summary characteristics of their cross sectional distribution. Consider first the individual measures obtained with the midpoint method. Averaging across respondents provides aggregate measures of the mean expectation of inflation and uncertainty about inflation for a specific quarter:

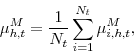
$\begin{displaymath} \mu _{h,t}^{M}=\frac{1}{N_{t}}\sum_{i=1}^{N_{t}}\mu _{i,h,t}^{M}, \end{displaymath}$

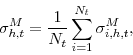
$\begin{displaymath} \sigma_{h,t}^{M}=\frac{1}{N_{t}}\sum_{i=1}^{N_{t}}\sigma_{i,h,t}^{M}, \end{displaymath}$

The cross-sectional standard deviation of the individual means provides a measure of disagreement regarding the mean forecast:

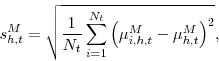
$\begin{displaymath} s_{h,t}^{M}=\sqrt{\frac{1}{N_{t}}\sum_{i=1}^{N_{t}}\left( \mu _{i,h,t}^{M}-\mu _{h,t}^{M}\right) ^{2}}, \end{displaymath}$

Further, a measure of disagreement about inflation uncertainty may be obtained from the dispersion of the second moments of the individual probabilistic beliefs:

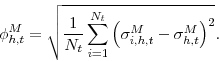
$\begin{displaymath} \phi_{h,t}^{M}=\sqrt{\frac{1}{N_{t}} \sum_{i=1}^{N_{t}} \left( \sigma_{i,h,t}^{M}-\sigma_{h,t}^{M} \right)^{2}}. \end{displaymath}$

The same formulas may be applied to the individual statistics obtained with the uniform assumption to obtain the corresponding aggregate statistics $\mu_{h,t}^U$ , $\sigma_{h,t}^U$ , $s_{h,t}^U$ and $\phi_{h,t}^U$ .

4 Parametric analysis of the probabilistic beliefs

Next we examine parametric methods for the analysis of the probabilistic beliefs. This can be divided in two parts. In the first part of the analysis we examine assumptions on the distribution of inflation faced by an individual, while in the second part we examine assumptions about the distribution of inflation uncertainty across individuals.

For the first part, we focus on the assumption that a normal distribution approximates the probabilistic beliefs of each respondent sufficiently well (Giordani and Söderlind (2003)). We also experimented with fitting alternative distributions that accommodated deviations from normality. However, we concluded that it was difficult to distinguish between true deviations from normality and apparent deviations due to the approximation and rounding of individual responses. Consequently, we decided to focus on the first two moments of the individual probabilistic distributions, and limited attention to the normal density.

For each individual probabilistic response, we fit the Normal CDF so that it matches as closely as possible the individual empirical CDF obtained by accumulating the densities in the individual bins. More precisely, we identify the mean and variance of the Normal that minimize the sum of the squared differences between the empirical CDF and the probabilities implied by the normal distribution over the same intervals. The resulting estimates of the mean and the standard deviation of the normal, , constitute the estimate of the expected inflation and of the individual uncertainty respectively, that is if

$\begin{displaymath} X_{i,h,t}\sim N\left( \mu _{i,h,t,};\sigma _{i,h,t}^{2}\right) , \end{displaymath}$

then

$\begin{displaymath} \mu _{i,h,t}^{N}=\widehat{\mu }_{i,h,t}\mbox{; }\sigma_{i,h,t}^{N}=\widehat{% \sigma }_{i,h,t}. \end{displaymath}$

If this procedure produced reliable estimates for all individuals, one could aggregate the individual results to obtain measures of the mean expected inflation and average uncertainty:

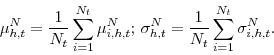
$\begin{displaymath} \mu _{h,t}^{N}=\frac{1}{N_{t}}\sum_{i=1}^{N_{t}}\mu _{i,h,t}^{N}\mbox{; }% \sigma_{h,t}^{N}=\frac{1}{N_{t}}\sum_{i=1}^{N_{t}}\sigma_{i,h,t}^{N}. \end{displaymath}$

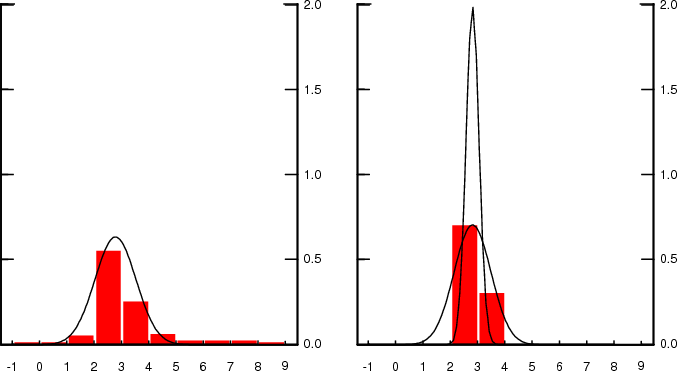
However, fitting normal densities to individual histograms as described above does not provide meaningful estimates of the underlying distribution when forecasters assign positive probabilities to fewer than 3 bins. With fewer non-zero bins, which can result from rounding when the uncertainty is small, this procedure yields biased estimates. To illustrate the difficulty encountered with fewer bins, it is instructive to compare the estimation associated with the two example empirical densities shown in Figure 6. On the left, a unique best fitting normal distribution can be identified. On the right, however, the two bins reported may reflect approximate responses that could correspond to a wide range of possible distributions. Consider the two distributions plotted with the histogram. The wider distribution could be the true underlying distribution if the zero entries in the bins from 1 to 2 and from 4 to 5 are merely the result of rounding down probabilities just under 5 percent--as would happen if the respondent rounded the entries to be multiples of 10 percent. But the narrower distribution could be correct if no such rounding took place and uncertainty was indeed so small that the true probabilities in the bins from 1 to 2 and from 4 to 5 are virtually zero. A minimization procedure that simply matches the normal CDF to the empirical CDF, cannot recognize the first possibility and its implied rounding errors. Instead, for any probabilistic forecast where all the density is concentrated in two consecutive bins, the estimation mechanically identifies the best fitting normal distribution to be the one with infinitesimal (zero) variance and a mean located at the point dividing the two consecutive bins. That is, if the approximate nature of the probabilistic responses, and associated rounding of answers, yields an entry in the survey with just 2 non-zero bins, fitting a normal density will result in a severe downward bias in the reported individual uncertainty. Using the mean of individual standard deviations computed in this manner would subsequently result in a downward bias in the estimate of average uncertainty.

This discussion suggests that when individual uncertainty is small, estimates of the variances of the underlying distributions are not trustworthy. As a result, using these individual estimates when estimating the characteristics of the distribution of uncertainty across individuals, such as the average uncertainty and the dispersion of uncertainty, could also be problematic. To mitigate this difficulty, we propose to model directly the distribution of the individual uncertainties and treat the uncertainties of forecasters that assign a positive probability only to one or two intervals as small but unobserved. Specifically, let us suppose that the individual uncertainty in quarter for horizon originates from a distribution of the individual variances, $v_{i,h,t}$ :

$\begin{displaymath}v_{i,h,t}\sim G(v, \theta_{h,t}).\end{displaymath}$

Then the characteristics of the distribution of uncertainty, including the mean of inflation uncertainty and disagreement about this uncertainty can be recovered from estimation of the parameters $\theta_{h,t}$ . To the extent this distribution could be fit by treating the variances of responses with one or two bins as small but without knowledge of their precise values, biases arising from errors in the estimation with few bins could be avoided. This can be achieved by fitting a truncated distribution to the individual variances. We implement this by fitting a distribution to the empirical CDF of the individual variances that exceed a fixed threshold, incorporating the information we have about the mass of the CDF at the threshold, but treating variances below that threshold as unobservable. An example of this fitting procedure with the Gamma distribution is presented in Figure 7. In the figure, the step function represents the empirical distribution function, plotted with observations above the threshold value which is represented by the dashed vertical line, and the smooth line shows the best fitting Gamma distribution.

More precisely, given a threshold , consider the individual variances above the threshold $v_{i,h,t}(c_{\tau })$ for all $c_{\tau }>C$ and $F(v_{i,h,t}(c_{1})),...$ $% F(v_{i,h,t}(c_{N_{c}}))$ , where $c_{1},...c_{N_{c}}$ are the right endpoints of the intervals in which the range of uncertainty values has been discretized, are the empirical CDF of $v_{i,h,t}(c_{\tau })$ defined at these endpoints. Given a candidate distribution, we can obtain the parameters $\theta$ that provide the best fit by minimizing:

$\begin{displaymath} {\min_{\theta } }\sum_{\tau =1}^{N_{c}}\left[ G\left( v_{i,h,t}(c_{\tau });\theta\right) -F(v_{i,h,t}(c_{\tau }))\right] ^{2}, \end{displaymath}$

Since uncertainty cannot take negative values, the choice of candidate models is limited to distributions with non-negative support. We examined the Gamma, Chi-square and Lognormal but in the following we concentrate our attention on the Gamma, which provided the best fit among them.

Fitting the two parameters of the Gamma, $(\alpha,~\beta)$ , in each quarter allows us to track the characteristics of the distribution of uncertainty over time. Since we are interested in average uncertainty expressed in standard deviation units, $\sigma_{i,h,t}=\sqrt{v_{i,h,t}^{~}}$ and we model the variances, $v_{i,h,t}$ , to be Gamma distributed, we apply a change in variable to recover the mean and standard deviation of $\sigma _{i,h,t}.$ If $v_{h,t}^{G}=E_{h,t}^{G}(v_{i,h,t})=% \widehat{\alpha }_{h,t}\cdot \widehat{\beta }_{h,t}$ and $Var(v_{i,h,t})=% \widehat{\alpha }_{h,t}\cdot \widehat{\beta }_{h,t}^{2},$ where $E^{G}$ indicates the expected value under the Gamma distribution, then the mean and dispersion of the cross-sectional distribution for the standard deviation may be obtained from:

$\begin{displaymath} \hat \sigma _{h,t}^{G}=E_{h,t}^{G}(\sigma _{i,h,t})=\widehat{\beta }% _{h,t}^{1/2}\cdot \frac{\Gamma (\widehat{\alpha }_{h,t}+1/2)}{\Gamma (% \widehat{\alpha }_{h,t})}, \end{displaymath}$

$\begin{displaymath} \hat \phi _{h,t}^{G}=\sqrt{E_{h,t}^{G}\left( \sigma _{i,h,t}-\sigma _{h,t}^{G}\right) ^{2}}=\sqrt{\widehat{\alpha }_{h,t}\cdot \widehat{\beta }% _{h,t}-\left( \sigma _{h,t}^{G}\right) ^{2}} \end{displaymath}$

Fitting directly the distribution of the individual uncertainties in this manner provides a way to summarize the quarterly uncertainty that improves upon taking a simple average of individual standard deviations by circumventing the problems associated with respondents with just one or two bins.

We apply this methodology to all three individual measures of uncertainty examined, that is we estimate the best fitting Gamma distributions to individual uncertainties corresponding to the uniform, midpoint, and normal assumptions described above. Using the estimated parameters we then compute the corresponding measures of average uncertainty $\sigma _{h,t}^{GU}$ , $\sigma _{h,t}^{GM}$ , $\sigma _{h,t}^{GN}$ ; and uncertainty dispersion, $\phi_{h,t}^{GU}$ , $\phi_{h,t}^{GM}$ , $\phi_{h,t}^{GN}$ .

5 Characteristics of the cross-sectional distributions over time

In this section we compare and contrast quarterly time series measuring the mean and dispersion of expected inflation and inflation uncertainty reflected in the survey data.

As already mentioned, although the survey is quarterly, its design is not conducive to the construction of exact constant-horizon quarterly time series of uncertainty and disagreement. However, an approximate one-year horizon may be obtained by combining the available 4-quarter ahead forecast available in first quarters with the 3-quarter ahead forecast available in second quarters, the 6-quarter ahead forecast available in third quarters and the 5-quarter ahead forecast available in fourth quarters.

Since the uncertainty associated with forecasting inflation likely increases with the horizon of the forecast, the approximate one-year-ahead measures we construct in this manner for uncertainty and its dispersion, $\hat \sigma$ and $\hat \phi$ , and for the dispersion of mean inflation forecasts, $\hat s$ , would be expected to have a seasonal pattern. In particular, these measures would be expected to have a seasonal low in the second quarters, and a seasonal high in the third quarters. To examine the quantitative importance of this seasonality we looked at the seasonal adjustment implied by two commonly used programs, X12 and TRAMO/SEATS. (See Findley et al (1998) and Gomez and Maravall (2000), respectively. Hood (2002) presents comparisons of the two methods.) The seasonal adjustment procedures indicated the presence of some seasonality in our approximate one-year-ahead measures but suggested that this seasonality was quite small. Consequently, in what follows we focus on the non-seasonally adjusted approximate one-year-ahead series, and present only few comparisons with their seasonally adjusted counterparts.

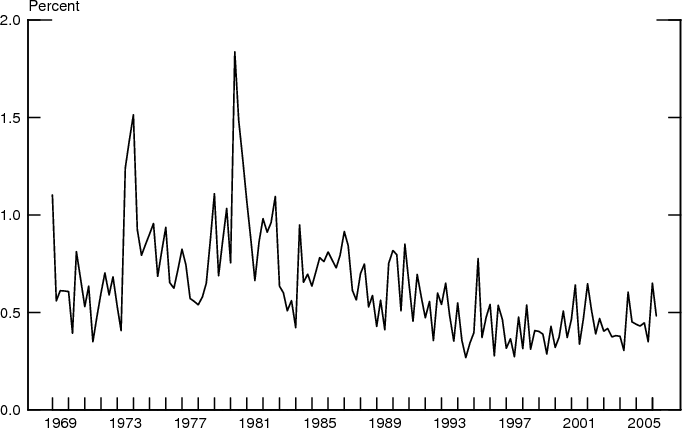
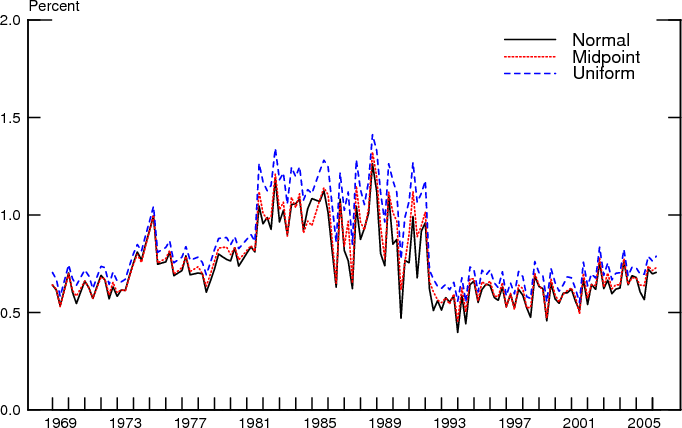
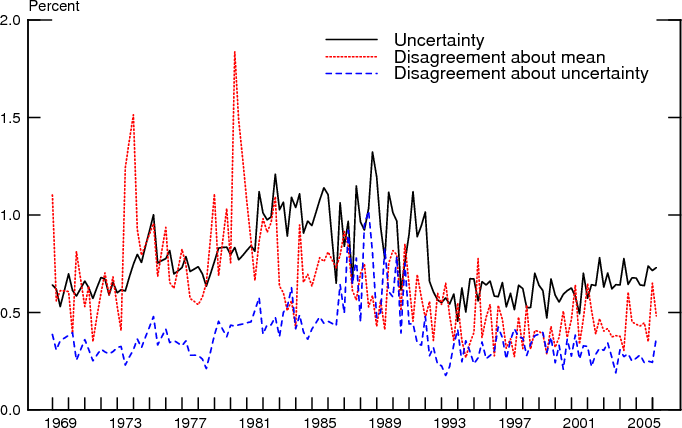
Figures 8 and 9 present the summary statistics of the distributions of the mean forecasts of inflation at the approximate year-ahead horizon obtained from the midpoint and uniform methods, which as noted before are identical. More generally, estimation of the means of the individual distributions is not very sensitive to alternative assumptions and the summary statistics based on the normal density are virtually indistinguishable from those corresponding to the non-parametric methods shown in the figures.

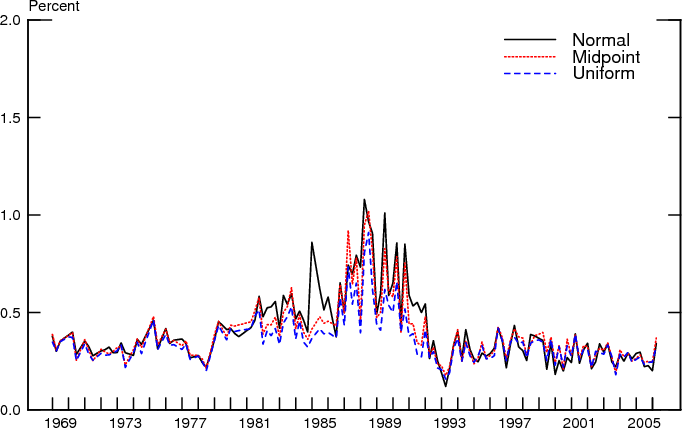
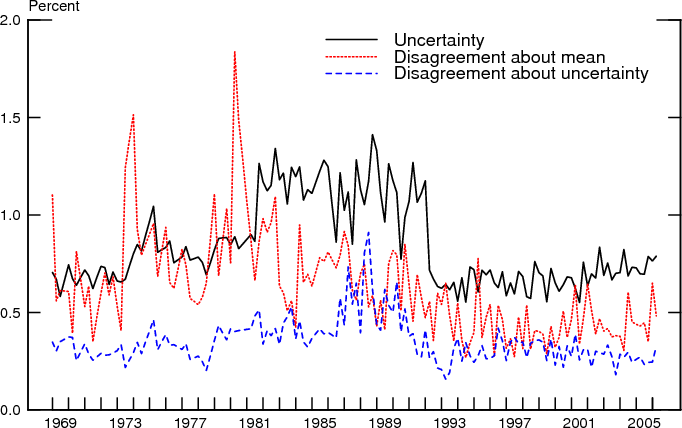
The three methods do result in somewhat different estimates of the characteristics of the distributions of uncertainty, however. Figure 10 compares the mean uncertainty at the approximate year-ahead horizon obtained by fitting the truncated Gamma distribution by quarter to each of the three alternatives. Similarly, Figure 11 compares the disagreement regarding individual uncertainty, obtained from the same fitted distributions. The mean estimates for uncertainty are generally higher for the uniform method. But the midpoint and normal methods yield very similar estimates for average uncertainty.

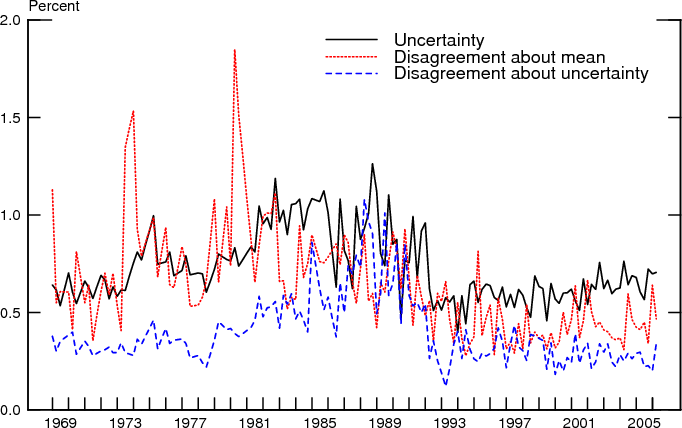
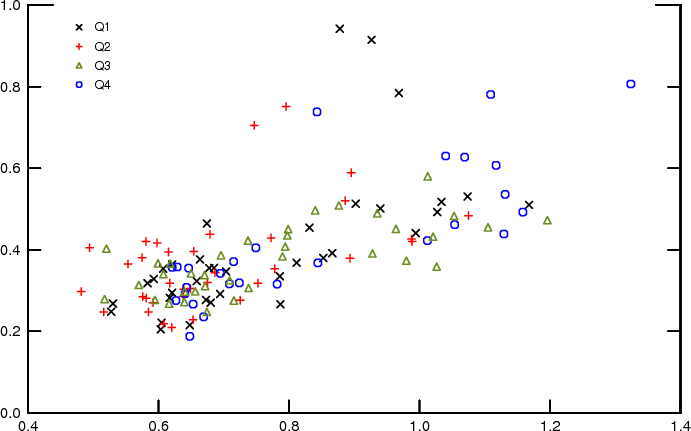
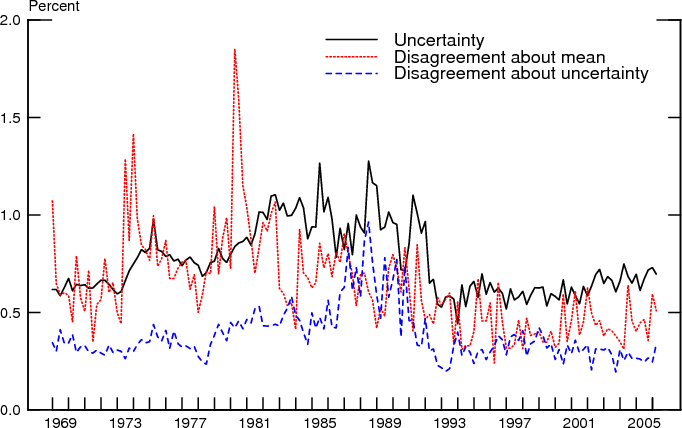
To compare the evolution of uncertainty and disagreement over time, Figures 12-14 collect the three measures corresponding to each of the three methods we used to estimate individual variances. The comovements of the three variables are essentially similar in each figure so we can focus attention on just one, the midpoint-gamma method. As can be seen, disagreement and uncertainty co-move, but their evolution differs over time. Disagreement about the mean inflation forecast rose somewhat with inflation during the 1970s but has trended downward since then and, over the past 10 or so years, has fluctuated at a level lower than before. While mean uncertainty and disagreement about uncertainty also exhibit the underlying pattern of the increase and decline in inflation over the past four decades, their levels in the last several years are similar to their levels early in the sample, unlike the pattern exhibited by disagreement about the mean outlook.

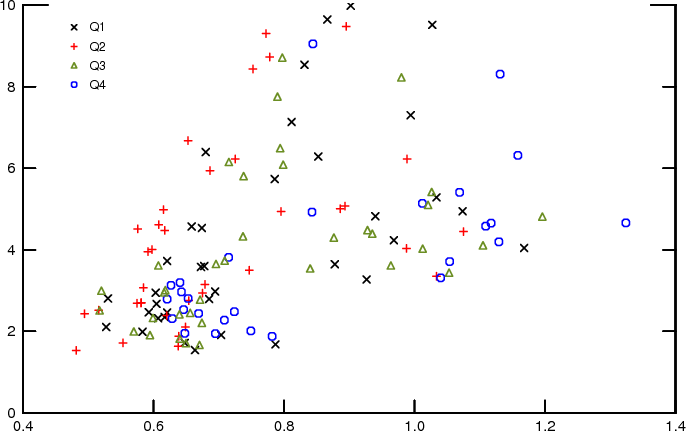
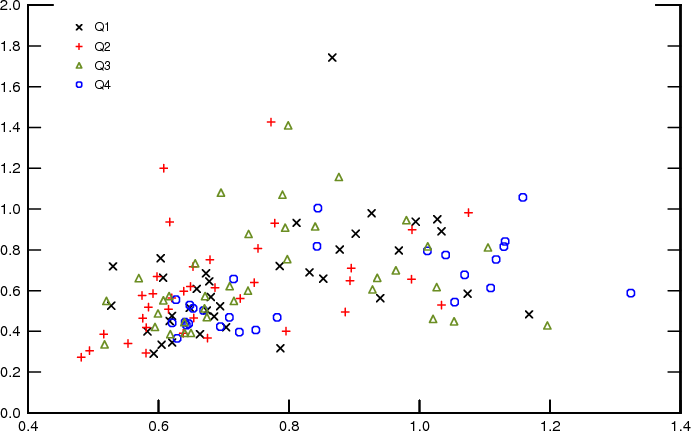
It is evident, however, that overall the means and dispersions of both the inflation outlook and the uncertainty regarding the outlook are positively correlated. Figures 15-17 present scatterplots of mean uncertainty with the mean outlook and the two measures of disagreement, presenting a visual representation of correlation of these series. The correlations are evident regardless of whether one concentrates attention on just one quarter each year (to circumvent seasonality concerns) or all quarters together. Indeed, seasonal adjustment does not change the three series very much. This can be seen, for instance, by comparing the midpoint-gamma estimates shown in Figure 13 with the same series following seasonal adjustment based on the TRAMO/SEATS procedures, which are shown in Figure 18.

Table 1 shows the correlations of the mean outlook, and the three uncertainty and disagreement measures for the midpoint-gamma estimates. The top two panels employ the approximate year-ahead forecast horizon series while the bottom two panels show the correlations based on the seasonally adjusted counterparts of these series. Within each group, we also compare results based on only regular survey respondents, who participated in at least 12 surveys, and all respondents, including irregular ones. As can be seen, the correlations with or without seasonal adjustment and based on all respondents or only regular ones are quite similar. While all correlations are positive, however, some of them are not very high. In particular, the correlation of the dispersion of the means of individual forecasts of inflation, , and mean uncertainty, $\sigma$ , is only about 0.4, suggesting that disagreement regarding the outlook may not be a very good proxy for uncertainty. In contrast, the correlation between the mean inflation outlook, $\mu$ , and its dispersion across individuals is almost 0.7, suggesting greater disagreement about the inflation outlook when inflation is expected to be high. The correlation between $\mu$ and $\sigma$ is almost 0.5, suggesting that higher inflation is also associated with a more uncertain inflation outlook. The results also indicate that disagreement about inflation uncertainty is higher when average uncertainty is higher, with a correlation between $\sigma$ and $\phi$ equal to almost 0.7.

6 Inflation and Term Premia

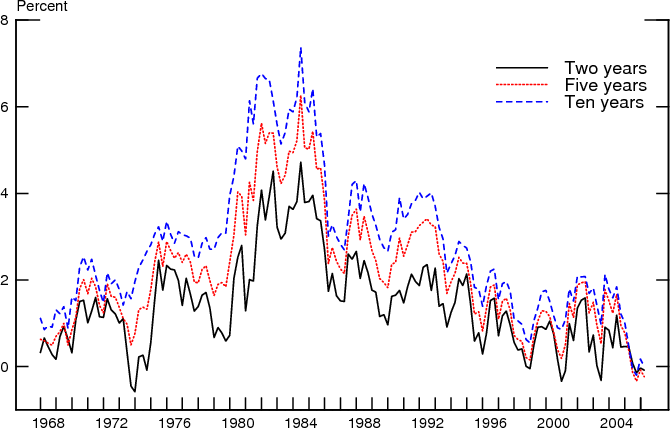
To illustrate the potential usefulness of distinguishing the various attributes of the inflation outlook, in this section we examine their relationship to term premia. As Charles Nelson noted, "isolating expectations from other factors" (1970, p. 1179) is necessary for interpreting the term structure of interest rates, so understanding how nominal term premia relate to the outlook for inflation and its uncertainty is helpful towards that end. For this analysis, we utilize estimates of the forward term premium at the 2-year, 5-year and 10-year ahead horizons obtained from an arbitrage-free three-factor model of the term structure (see Kim and Orphanides, 2005). The quarterly time-series for each premium, shown in Figure 19, selects the premium prevailing on the last business day of the middle month of the quarter, so the premia are always measured after the survey for that quarter has been conducted.

Table 2 presents the simple correlations of these three premia with the four series summarizing the distributions of the inflation outlook corresponding to the midpoint-gamma estimation. (Results from the other two methods are essentially similar.) As with Table 1, the top panels show the correlations with the approximate year-ahead horizons and the bottom panels with their seasonally adjusted counterparts. As can be seen, the term premia at all three horizons shown are positively correlated with the mean forecast for inflation as well as with mean uncertainty, and the disagreement about both the mean and the uncertainty. However, the correlation is strongest with mean uncertainty over this sample.

To gauge the statistical significance of these correlations, Table 3 presents linear regressions of the 2-year premium on each one of the various measures. The regressions allow for quarter-specific intercepts and slope coefficients to account for the seasonal nature of the inflation forecast variables. (The results are similar if we use the seasonally adjusted series without the quarter-specific coefficients.) The row noted with denotes the p-values associated with the hypothesis that all slope coefficients equal zero, (based on a HAC-robust covariance). As can be seen, each of the four attributes of the inflation forecast individually significantly correlates with the 2-year premium, but the relationship is strongest for the mean uncertainty of the forecast. The estimates are essentially similar regardless of whether the inflation forecast attributes employed are based on only regular survey respondents or all respondents, including irregular ones.

7 Concluding Remarks

In this paper we compare and contrast quarterly time series of alternative measures of uncertainty and disagreement regarding inflation expectations, based on the probabilistic responses from the Survey of Professional Forecasters. This survey covers an almost continuous span approaching forty years, from 1968Q4 to 2006Q1 and, as a result of its unique probabilistic questions, allows for direct comparison of measures of disagreement about the mean outlook across individuals and measures of uncertainty regarding the outlook.

We document imperfections in the individual probabilistic responses due to approximation and rounding of entries. This poses a challenge in estimating uncertainty, especially when this is perceived to be small. To obtain an aggregate characterization of uncertainty that mitigates biases due to these imperfections, we model and estimate directly parametric distributions of the individual uncertainties in each quarter and treat the variances of responses suggesting very small perceived uncertainty as unobservable. Our procedure yields direct estimates for average uncertainty as well as for the dispersion of individual uncertainty assessments in each quarter. This allows comparing and contrasting average uncertainty not only with disagreement about the mean outlook, but also with disagreement about the uncertainty to the outlook.

To document the potential usefulness of distinguishing uncertainty from disagreement, we examine the correlations of the various attributes of the inflation forecasts with each other and also their relationship with the term premia embedded in the term-structure of government securities. Our results indicate that disagreement about the mean inflation outlook is not a particularly good proxy for inflation uncertainty. Inflation uncertainty is more highly correlated with the mean inflation forecast rather than with the dispersion of the forecasts across individuals. Higher average uncertainty is also associated with greater disagreement about inflation uncertainty across individuals. Finally, we find that both higher expected inflation and greater average uncertainty, as well as higher disagreement about the mean outlook and its uncertainty are correlated with interest rate term premia.

References

Croushore, Dean (1993), "Introducing: The Survey of Professional Forecasters." Federal Reserve Bank of Philadelphia Business Review, November/December, 3-13.

Engelberg, Joseph, Charles F. Manski, and Jared Williams (2006), "Comparing the Point Predictions and Subjective Probability Distributions of Professional Forecasters." Working Paper Department of Economics, Northwestern University.

Findley, David, Brian C. Monsell, William R. Bell, Mark C. Otto, and Bor-Chung Chen (1998), "New Capabilities and Methods of the X-12-ARIMA Seasonal Adjustment Program." Journal of Business and Economic Statistics 16 (2), 127-77.

Giordani, Paolo, and Paul Soderlind (2003), "Inflation Forecast Uncertainty." European Economic Review, 47, 1037-1059.

Gomez, Victor and Agustin Maravall (2000), "Automatic Modeling Methods for Univariate Time Series." In A Course in Time Series. Edited by R.S. Tsay, D.Pena, and G.C. Tiao, John Wiley.

Hood, Catherine C.H.(2002). "Comparison of Time Series Characteristics for Seasonal Adjustments from SEATS and X-12-ARIMA." Proceedings of the American Statistical Association. Alexandria VA: American Statistical Association.

Kendall, Maurice and Alan Stuart (1977), The Advanced Theory of Statistics, Volume 1, 4th edition. New York: Macmillan.

Kim, Don and Athanasios Orphanides (2005), "Term Structure Estimation with Survey Data on Interest Rate Forecasts." Finance and Economics Discussion Series, 2005-48, Federal Reserve Board (October).

Lahiri, Kajal and Fushang Liu (2004), "Modeling Multi-period Inflation Uncertainty Using a Panel of Density Forecasts." Working Paper Department of Economics, State University of New York, Albany.

Nelson, Charles, R. (1970), "Testing a Model of the Term Structure of Interest Rates by Simulation of Market Forecasts." Journal of the American Statistical Association, 65(331), 1163-1179.

Rich, Robert, and Joseph Tracy (2003), "Modeling Uncertainty: Predictive Accuracy as a Proxy for Predictive Confidence." Federal Reserve Bank of New York Staff Reports, no. 161, February.

Rich, Robert, and Joseph Tracy (2006), "The Relationship between Expected Inflation, Disagreement, and Uncertainty: Evidence from Matched Point and Density Forecasts." Federal Reserve Bank of New York Staff Reports, no. 253, July.

Wallis, Kenneth F. (2005), "Combining Density and Interval Forecasts: A Modest Proposal." Oxford Bulletin of Economics and Statistics, 67, 983-994.

Zarnowitz, Victor and Louis A. Lambros (1987), "Consensus and Uncertainty in Economic Prediction." Journal of Political Economy, 95(3), 591-621.

Zarnowitz, Victor and Phillip A. Braun (1993), "Twenty-two Years of the NBER-ASA Quarterly Economic Outlook Surveys: Aspects and Comparisons of Forecasting Performance." In Business Cycles, Indicators, and Forecasting. Edited by James H. Stock and Mark W. Watson. Chicago: University of Chicago Press.

Table 1
Correlations of Attributes of Distributions of Inflation Forecasts

Midpoint-Gamma Estimates, Pooled Quarters

	$\hat \mu$	$\hat \sigma$	$\hat s$	$\hat \phi$
All respondents: $\hat \mu$	1.00
All respondents: $\hat \sigma$	0.47	1.00
All respondents: $\hat s$	0.66	0.39	1.00
All respondents: $\hat \phi$	0.25	0.65	0.25	1.00
At least 12 surveys: $\hat \mu$	1.00
At least 12 surveys: $\hat \sigma$	0.45	1.00
At least 12 surveys: $\hat s$	0.67	0.37	1.00
At least 12 surveys: $\hat \phi$	0.24	0.63	0.23	1.00

Table 1 (continued)
Correlations of Attributes of Distributions of Inflation Forecasts

Midpoint-Gamma Estimates, Seasonally Adjusted

	$\hat \mu$	$\hat \sigma$	$\hat s$	$\hat \phi$
All respondents: $\hat \mu$	1.00
All respondents: $\hat \sigma$	0.49	1.00
All respondents: $\hat s$	0.68	0.41	1.00
All respondents: $\hat \phi$	0.23	0.69	0.21	1.00
At least 12 surveys: $\hat \mu$	1.00
At least 12 surveys: $\hat \sigma$	0.46	1.00
At least 12 surveys: $\hat s$	0.69	0.40	1.00
At least 12 surveys: $\hat \phi$	0.22	0.68	0.23	1.00

Notes: $\hat \mu$ and are the mean and standard deviation of of the distribution of the individual mean forecasts. $\hat \sigma$ and $\hat \phi$ are the mean and standard deviation of the distribution of the individual standard deviations. The entries in the top panels report the correlations of the quarterly time-series obtained by pooling together the attributes of the 4-, 3-, 6-, and 5-quarter-ahead forecasts available in the first, second, third and fourth quarter, respectively. The entries in the bottom panels report correlations obtained after seasonally adjusting these series.

Table 2
Simple Correlations with Term Premia
Midpoint-Gamma Estimates, Pooled Quarters

Premium	$\hat \mu$	$\hat \sigma$	$\hat s$	$\hat \phi$
All respondents: 2-year	0.40	0.59	0.25	0.34
All respondents: 5-year	0.51	0.66	0.34	0.38
All respondents: 10-year	0.59	0.68	0.42	0.40
At least 12 surveys: 2-year	0.40	0.59	0.26	0.34
At least 12 surveys: 5-year	0.51	0.66	0.35	0.37
At least 12 surveys: 10-year	0.59	0.69	0.40	0.41

Table 2 (continued)
Simple Correlations with Term Premia
Midpoint-Gamma Estimates, Seasonally Adjusted

Premium	$\hat \mu$	$\hat \sigma$	$\hat s$	$\hat \phi$
All respondents: 2-year	0.31	0.62	0.23	0.36
All respondents: 5-year	0.44	0.69	0.32	0.40
All respondents: 10-year	0.55	0.73	0.40	0.43
At least 12 surveys: 2-year	0.31	0.63	0.25	0.37
At least 12 surveys: 5-year	0.51	0.70	0.35	0.40
At least 12 surveys: 10-year	0.54	0.72	0.43	0.44

Notes: See notes to Table 1.

Table 3
Explaining Term Premia
2-year premium,Midpoint-Gamma Estimates

Q	$\hat \mu$ (1)	$\hat \sigma$ (2)	$\hat s$ (3)	$\hat \phi$ (4)
All respondents: 1	0.16	3.23	1.34	1.63
All respondents: 2	0.17	4.65	1.07	2.32
All respondents: 3	0.39	3.93	4.24	3.56
All respondents: 4	0.22	3.64	-0.31	3.05
All respondents: $\bar R^2$	0.16	0.38	0.13	0.09
All respondents:	0.041	0.001	0.008	0.005
At least 12 surveys: 1	0.17	3.21	1.34	1.44
At least 12 surveys: 2	0.17	4.49	1.18	2.37
At least 12 surveys: 3	0.39	3.78	3.40	3.21
At least 12 surveys: 4	0.22	3.79	-0.07	4.40
$\bar R^2$	0.16	0.39	0.11	0.10
	0.041	0.001	0.028	0.011

Notes: Each column in each panel reports the slope parameters, $\gamma_{X,Q}$ of the regression:

$\begin{displaymath} \tau_t = \sum_{Q=1,4} (\gamma_{0} + \gamma_{X,Q} X_t )\cdot Q_t + \eta_t \end{displaymath}$

where $\tau$ is the two-year forward term premium, and

is the attribute of the inflation forecast shown at the top of the column. The quarter-specific constants are not reported.

denotes the p-value of the hypothesis that all the slope parameters are zero.

Figure 1: Number of Survey Respondents

Figure 1: Figure 1 displays four different time series of the number of survey respondents from 1968Q4 to 2006Q1. Time is plotted on the x-axis and the number of survey respondents, ranging from 0 to 120, is plotted on the y-axis. The time series shown include all respondents, regular respondents who completed at least four surveys, regular respondents who completed at least eight surveys, and regular respondents who completed at least twelve surveys. Except for the first two years and the last year of the sample, the four series are quite close to each other and the average number of respondents is about 30.

Figure 2: Two Examples of Individual Density Forecasts

Figure 2: Figure 2 shows two examples of individual responses to the Survey of Professional Forecasters in the form of a histogram. The x-axis displays ten bins with width equal to one percent, and the y-axis shows the probability (ranging from zero to one) of each outcome. The example on the left shows a respondent who placed probability mass in all available bins. The example on the right shows a respondent who placed probability mass in only two bins.

Figure 3: Number of Non-Zero Bins by Forecast Horizon

Figure 3: This bar chart displays the distribution of the number of non-zero-bins by forecast horizon. The horizons (x-axis) range from one to eight quarters ahead and the number of non-zero-bins range from one to five, with an open-ended edge. At the horizon of one quarter about 15% of respondents place all probability mass in one bin, about 43% place the probability mass in 2 bins, about 23% in 3 bins and the remaining percentage in 4 or more bins. When the horizon is two quarters, about 35% of respondents place the probability mass in one or two bins, about 40% in 3 bins and the remaining percentage in 4 or more bins. The number of the non-zero-bins gradually increases as the horizon increases. At the extreme, when the horizon is 8 quarters, about 60% of respondents use 4 or more bins.

Figure 4: Rounding by Forecast Horizon

Figure 4: This bar chart shows the breakdown of how responses are rounded by forecast horizon. The forecast horizons (on the x-axis) range from one to at least 5 quarters and rounding is equal to 1%, 5% and 10%. At the horizon of one quarter about 10% of responses are multiple of 1%, about 20% of responses are multiple of 5%, and about 45% are multiple of 10%. As the horizon increases the percentage of responses multiple of 1% and 5% increases and the percentage of responses multiple of 10% decreases. When the horizon is at least 5 quarters, about 20% of responses are multiple of 1%, about 42% of responses are multiple of 5%, and about 18% are multiple of 10%.

Figure 5: Rounding by Number of Non-Zero Bins

Figure 5: This bar chart shows the breakdown of how responses are rounded by the number of non-zero-bins employed. The number of non-zero-bins (x-axis) range from one to five, with an open-ended edge and rounding is at 1%, 5% and 10% intervals. In the case of one non-zero-bin, 100% of responses are multiple of 10%. In the case of two non-zero-bins, about 80% of responses are multiple of 10%. By contrast, in the case of 5 or more non-zero-bins, about 50% of responses are multiple of 1%.

Figure 6: Fitting a Normal Density: Two Examples

Figure 6: Figure 6 highlights the difficulties in fitting a continuous distribution to an individual histogram, which has few non-zero-bins. The example on the left shows a unique best-fitting normal distribution of a histogram with ten non-zero-bins (ten bins with width equal to one percent displayed on the x-axis). The example on the right shows two different distributions of an individual histogram (with only two non-zero-bins) that differs based on rounding assumptions.

Figure 7: Gamma Distribution of Individual Variances Figure 7: Figure 7 displays the gamma distribution of individual variances, using the fitting technique described on pp.9-10. It shows clearly the goodness of the fit, given that the Gamma approximates extremely closely the empirical CDF of the individual variances.

Figure 7: Figure 7 displays the gamma distribution of individual variances, using the fitting technique described on pp.9-10. It shows clearly the goodness of the fit, given that the Gamma approximates extremely closely the empirical CDF of the individual variances.

Figure 8: Inflation Outlook

Figure 8: Figure 8 presents the survey-based mean inflation outlook from 1968Q4 to 2006Q1 as a line graph. Time is plotted on the x-axis and percent (ranging from 0 to 10) is plotted on the y-axis. The time series show that inflation was around 4% from 1969 to about 1973, and then it increased very rapidly to about 10% around 1974 and around 1980. Around 1984-85 inflation was back at 4% and then starting from about 1990 inflation was fluctuating around 2.5%.

Figure 9: Disagreement Figure 9: Figure 9 displays the disagreement about the inflation outlook as a line graph from 1968Q4 to 2006Q1. Time is plotted on the x-axis and percent (ranging from 0 to 2) is plotted on the y-axis. The time series of disagreement about inflation displayed two spikes, one around 1974 at about 1.5% and one in 1980 at about 1.8%. For most of the sample, disagreement fluctuated around 0.5%.

Figure 9: Figure 9 displays the disagreement about the inflation outlook as a line graph from 1968Q4 to 2006Q1. Time is plotted on the x-axis and percent (ranging from 0 to 2) is plotted on the y-axis. The time series of disagreement about inflation displayed two spikes, one around 1974 at about 1.5% and one in 1980 at about 1.8%. For most of the sample, disagreement fluctuated around 0.5%.

Figure 10: Uncertainty

Figure 10: Figure 10 compares the mean uncertainty at the approximate one-year-ahead horizon obtained by fitting the truncated Gamma distribution to each of the three alternatives (normal, midpoint, and uniform). The figure displays these three methods from 1968Q4 to 2006Q1 as three separate time series that are all very close to each other. The three time series of uncertainty display a positive trend from 1969 to about 1981, going from 0.5% to a bit more than 1%, then they fluctuated around 1% until about 1990, and finally decreased to about 0.6% for all the nineties, increasing only slightly to about 0.7% after 2001.

Figure 11: Disagreement about uncertainty

Figure 11: Figure 11 compares the disagreement regarding individual uncertainty at the approximate one-year-ahead horizon obtained by fitting the truncated Gamma distribution to each of the three alternatives (normal, midpoint, and uniform). The figure displays these three methods from 1968Q4 to 2006Q1 as three separate time series. The three time series of the disagreement about uncertainty are extremely close to each other. They vary between 0.3% and 0.5% from 1969 to about 1981, and then they become very volatile within an interval ranging from 0.5% to about 1%, and finally after 1992 decreases to a level of about 0.25% oscillating around this level for the rest of the sample.

Figure 12: Uncertainty and Disagreement (Normal-Gamma)

Figure 12: This figure plots three different time series fitting the Gamma distribution to the Normal alternative from 1968Q4 to 2006Q1. Time is plotted on the x-axis and percent, ranging from 0 to 2 is plotted on the y-axis. The time series shown include uncertainty, disagreement about the mean, and disagreement about uncertainty. The graph shows that even if disagreement and uncertainty co-move, the disagreement time series is much more volatile than uncertainty and it starts trending down around 1982, earlier than uncertainty that starts declining only around 1992. Further, even after the decline, uncertainty stays above disagreement in the last decade of the sample. In contrast uncertainty and disagreement about uncertainty exhibit a similar pattern, but the last one is almost always below uncertainty.

Figure 13: Uncertainty and Disagreement (Midpoint-Gamma)

Figure 13: This figure is very similar to the previous figure, except that plots the three different time series from 1968Q4 to 2006Q1, fitting the Gamma to the Midpoint alternative rather than to the Normal alternative. Time is plotted on the x-axis and percent, ranging from 0 to 2 is plotted on the y-axis. The time series shown include uncertainty, disagreement about the mean, and disagreement about uncertainty.

Figure 14: Uncertainty and Disagreement (Uniform-Gamma) Figure 14: This figure plots three different time series from 1968Q4 to 2006Q1, this time fitting the Gamma to the Uniform alternative. Time is plotted on the x-axis and percent, ranging from 0 to 2 is plotted on the y-axis. The time series shown include uncertainty, disagreement about the mean, and disagreement about uncertainty, and is very similar to the previous two figures.

Figure 14: This figure plots three different time series from 1968Q4 to 2006Q1, this time fitting the Gamma to the Uniform alternative. Time is plotted on the x-axis and percent, ranging from 0 to 2 is plotted on the y-axis. The time series shown include uncertainty, disagreement about the mean, and disagreement about uncertainty, and is very similar to the previous two figures.

Figure 15: Inflation Outlook and Uncertainty Figure 15: Figure 15 presents a scatter-plot of the mean inflation outlook and uncertainty. The points are plotted by quarter (Q1, Q2, Q3, and Q4) with uncertainty on the x-axis and the mean inflation outlook on the y-axis. The graph shows a positive correlation between mean outlook and mean uncertainty independently from which quarter is under consideration.

Figure 15: Figure 15 presents a scatter-plot of the mean inflation outlook and uncertainty. The points are plotted by quarter (Q1, Q2, Q3, and Q4) with uncertainty on the x-axis and the mean inflation outlook on the y-axis. The graph shows a positive correlation between mean outlook and mean uncertainty independently from which quarter is under consideration.

Figure 16: Disagreement about Outlook and Uncertainty Figure 16: Figure 16 presents a scatter-plot of the disagreement about the mean inflation outlook and uncertainty. The points are plotted by quarter (Q1, Q2, Q3, and Q4) with uncertainty on the x-axis and the disagreement about the mean inflation outlook on the y-axis. Once more, the graph shows a positive correlation between the two series independently from which quarter is under consideration.

Figure 16: Figure 16 presents a scatter-plot of the disagreement about the mean inflation outlook and uncertainty. The points are plotted by quarter (Q1, Q2, Q3, and Q4) with uncertainty on the x-axis and the disagreement about the mean inflation outlook on the y-axis. Once more, the graph shows a positive correlation between the two series independently from which quarter is under consideration.

Figure 17: Disagreement about Uncertainty and Uncertainty Figure 17: Figure 17 presents a scatter-plot of the disagreement about uncertainty and uncertainty. The points are plotted by quarter (Q1, Q2, Q3, and Q4) with uncertainty on the x-axis and the disagreement about uncertainty on the y-axis. Once more, the graph shows a positive correlation between the two series independently from which quarter is under consideration.

Figure 17: Figure 17 presents a scatter-plot of the disagreement about uncertainty and uncertainty. The points are plotted by quarter (Q1, Q2, Q3, and Q4) with uncertainty on the x-axis and the disagreement about uncertainty on the y-axis. Once more, the graph shows a positive correlation between the two series independently from which quarter is under consideration.

Figure 18: Uncertainty and Disagreement (Midpoint-Gamma, seasonally adjusted) Figure 18: This figure plots seasonally adjusted uncertainty, disagreement about the mean, and disagreement about uncertainty fitting the Gamma distribution to the Midpoint alternative from 1968Q4 to 2006Q1. This figure is extremely similar to Figure 13, indicating that the seasonal adjustment does not cause any major change in the series.

Figure 18: This figure plots seasonally adjusted uncertainty, disagreement about the mean, and disagreement about uncertainty fitting the Gamma distribution to the Midpoint alternative from 1968Q4 to 2006Q1. This figure is extremely similar to Figure 13, indicating that the seasonal adjustment does not cause any major change in the series.

Figure 19: Term Premium

Figure 19: Figure 19 presents three quarterly term premium time series, two-, five- and ten-year ahead, from 1968Q4 to 2006Q1. Time is plotted on the x-axis and percent is plotted on the y-axis. The three series present very similar time variation, but differ in the levels. The highest level corresponds to the longer time horizon. The three time series exhibit a positive trend from 1968 to around 1984 when they reach the highest peak, at about 4.3%, 6% and 7.8% respectively for the two-, five- and ten-year term premium. After that they show a downward trend, reaching their lowest level at the end of the sample, around 0%.

Footnotes

1. Recent studies examining these density forecasts and their properties include Rich and Tracy (2003, 2006), Giordani and Soderlind (2003), Lahiri and Liu (2004), Wallis (2005), Engelberg, Manski and Williams (2006). Return to Text

2. See Zarnowitz and Braun (1987) and Croushore (1993) for useful historical descriptions and assessments of the survey. Return to Text

^♣ This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to Text