
Revisiting the Supply-Side Effects of Government Spending*
Keywords: Fiscal policy, government spending, incomplete risk sharing, entrepreneurial risk.
Abstract:
JEL codes: E13, E62.
1 Introduction
Studying the impact of government spending on macroeconomic outcomes is one of the most celebrated policy exercises within the neoclassical growth model: it is important for understanding the business-cycle implications of fiscal policy, the macroeconomic effects of wars, and the cross-section of countries. Some classics include Hall (1980), Barro (1981, 1989), Aiyagari, Christiano and Eichenbaum (1992), Baxter and King (1993), Braun and McGrattan (1993), and McGrattan and Ohanian (1999, 2006).
These studies have all maintained the convenient assumption of complete markets, abstracting from the possibility that agents' saving and investment decisions, and hence their reaction to changes in fiscal policy, may crucially depend on the extent of risk sharing within the economy. This paper contributes towards filling this gap. It revisits the macroeconomic effects of government consumption within an incomplete-markets variant of the neoclassical growth model.
The key deviation we make from the standard paradigm is the introduction of uninsurable idiosyncratic risk in production and investment. All other ingredients of our model are the same as in the canonical neoclassical growth model: firms operate neoclassical constant-returns-to-scale technologies, households have standard CRRA/CEIS preferences, and markets are competitive.
The focus on idiosyncratic production/investment risk is motivated by two considerations. First, this friction is empirically relevant. This is obvious for less developed economies. But even in the United States, privately-owned firms account for nearly half of aggregate production and employment. Furthermore, the typical investor--the median rich household--holds a very undiversified portfolio, more than one half of which is allocated to private equity.1 And second, as our paper shows, this friction upsets some key predictions of the standard neoclassical paradigm.
In the standard paradigm, the steady-state values of the capital-labor ratio, productivity (output per work hour), the wage rate, and the interest rate, are all pinned down by the equality of the marginal product of capital with the discount rate in preferences. As a result, any change in the level of government consumption, even if it is permanent, has no effect on the long-run values of these variables.2On the other hand, because higher consumption for the government means lower net-of-taxes wealth for the households, a permanent increase in government consumption raises labor supply. It follows that employment and, by implication, output and investment increase. But the long-run levels of capital intensity and productivity unchanged.
The picture is quite different once we allow for incomplete markets. The same wealth effect that, in response to an increase in government consumption, stimulates labor supply in the standard paradigm, now also discourages investment. This is simply because risk taking, and hence investment, is sensitive to wealth. We thus find very different long-run effects. First, a permanent increase in government consumption necessarily reduces the risk-free interest rate. And second, unless the elasticity of intertemporal substitution is low enough, it also reduces the capital-labor ratio, productivity, and wages.
The effect on the risk-free rate is an implication of the precautionary motive: a higher level of consumption for the government implies a lower aggregate level of wealth for the households, which is possible in steady state only with a lower interest rate. If investment was risk-free, a lower interest rate would immediately translate to a higher capital-labor ratio. But this is not the case in our model precisely because market incompleteness introduces a wedge between the risk-free rate and the marginal product of capital--this wedge is simply the risk premium on investment. Furthermore, because of diminishing absolute risk aversion, this wedge is higher the lower the wealth of the households. It follows that the negative wealth effect of higher government consumption raises the risk premium on investment and can thereby lead to a reduction in the capital-labor ratio, despite the reduction in the interest rate. We show that a sufficient condition for this to be the case is that the elasticity of intertemporal substitution is sufficiently high relative to the income share of capital--a condition easily satisfied for plausible calibrations of the model.
Turning to employment and output, there are two opposing effects. On the one hand, as with complete markets, the negative wealth effect on labor supply contributes towards higher employment and output. On the other hand, unlike complete markets, the reduction in capital intensity, productivity, and wages contributes towards lower employment and output. Depending on the income and wage elasticities of labor supply, either of the two effects can dominate.
The deviation from the standard paradigm is significant, not only qualitatively, but also quantitatively. For our preferred parametrizations of the model, the following hold. First, the elasticity of intertemporal substitution is comfortably above the critical value that suffices for an increase in government consumption to reduce the long-run levels of the capital-labor ratio, productivity, and wages. Second, a 1% increase in government spending under incomplete markets has the same impact on capital intensity and labor productivity as a 0.5%-0.6% increase in capital-income taxation under complete markets. Third, these effects mitigate, but do not fully offset, the wealth effect on labor supply. Finally, the welfare consequences are non-trivial: the welfare cost of a permanent 1% increase in government consumption is three times larger under incomplete markets than under complete markets.
The main contribution of the paper is thus to highlight how wealth effects on investment due to financial frictions can significantly modify the supply-side channel of fiscal policy. In our model, these wealth effects emerge from idiosyncratic risk along with diminishing absolute risk aversion; in other models, they could emerge from borrowing constraints. Also, such wealth effects are relevant for both neoclassical and Keynesian models. In this paper we follow the neoclassical tradition because this clarifies best our contribution: whereas wealth effects have been central to the neoclassical approach with regard to labor supply, they have been mute with regard to investment.
To the best of our knowledge, this paper is the first to study the macroeconomic effects of government consumption in an incomplete-markets version of the neoclassical growth paradigm that allows for uninsurable investment risk. A related, but different, exercise is conducted in Heathcote (2005) and Challe and Ragot (2007). These papers study deviations from Ricardian equivalence in Bewley-type models like Aiyagari's (1994), where borrowing constraints limit the ability of agents to smooth consumption intertemporally. In our paper, instead, deviations from Ricardian equivalence are not an issue: our model allows households to freely trade a riskless bond, thus ensuring that the timing of taxes and the level of debt has no effect on allocations, and instead focuses on wealth effects on investment due to incomplete risk sharing.
The particular framework we employ in this paper is a continuous-time variant of the one introduced in Angeletos (2007). That paper showed how idiosyncratic capital-income risk can be accommodated within the neoclassical growth model without loss of tractability, studied the impact of this risk on aggregate saving, and contrasted it with the impact of labor-income risk in Bewley-type models (Aiyagari, 1994; Huggett, 1997; Krusell and Smith, 1998). Other papers that introduce idiosyncratic investment or entrepreneurial risk in the neoclassical growth model include Angeletos and Calvet (2005, 2006), Buera and Shin (2007), Caggeti and De Nardi (2006), Covas (2006), and Meh and Quadrini (2006).3 The novelty of our paper is to study the implications for fiscal policy in such an environment.
Panousi (2008) studies the macroeconomic effects of capital taxation within a similar environment as ours. That paper shows that, when agents face idiosyncratic investment risk, an increase in capital taxation may paradoxically stimulate more investment in general equilibrium. This provides yet another example of how the introduction of idiosyncratic investment risk can upset some important results of the neoclassical growth model.
The rest of the paper is organized as follows. Section 2 introduces the basic model, which fixes labor supply so as to focus on the most novel results of the paper. Section 3 characterizes its equilibrium and Section 4 analyzes its steady state. Section 5 examines the steady-state effects of government consumption on the interest rate and capital accumulation. Section 6 considers three extensions that endogenize labor supply. Section 7 examines the dynamic response of the economy to a permanent change in government consumption. Section 8 concludes. All the formal results are explained in the main text; but the complete proofs are delegated to the Online Appendix.
2 The basic model
Time is continuous, indexed by
![]() . There is a continuum of infinitely-lived households, indexed by
. There is a continuum of infinitely-lived households, indexed by ![]() and distributed uniformly over
and distributed uniformly over ![]() . Each household is endowed with one unit of labor, which it supplies inelastically in a competitive labor market. Each household also owns and runs a
firm, which employs labor in the competitive labor market but can only use the capital stock invested by the particular household.4 Households cannot invest in
other households' firms and cannot otherwise diversify away from the shocks hitting their firms, but can freely trade a riskless bond. Finally, all uncertainty is purely idiosyncratic, and hence all aggregates are deterministic.
. Each household is endowed with one unit of labor, which it supplies inelastically in a competitive labor market. Each household also owns and runs a
firm, which employs labor in the competitive labor market but can only use the capital stock invested by the particular household.4 Households cannot invest in
other households' firms and cannot otherwise diversify away from the shocks hitting their firms, but can freely trade a riskless bond. Finally, all uncertainty is purely idiosyncratic, and hence all aggregates are deterministic.
2.1 Households, firms, and idiosyncratic risk
The financial wealth of household ![]() , denoted by
, denoted by ![]() , is the sum of its
holdings in private capital,
, is the sum of its
holdings in private capital, ![]() , and the riskless bond,
, and the riskless bond,
![]() :
:
The evolution of
| (2) |
where
Whereas the sequences of prices and taxes are deterministic (due to the absence of aggregate risk), firm profits, and hence household capital income, are subject to undiversified idiosyncratic risk. In particular:
| (3) |
Here,
Turning to preferences, we assume an Epstein-Zin specification with constant elasticity of intertemporal substitution (CEIS) and constant relative risk aversion (CRRA). Given a consumption process, the utility process is defined by the solution to the following integral equation:
where
Here,
Standard expected utility is nested with
![]() . We find it useful to allow
. We find it useful to allow
![]() in order to clarify that the qualitative properties of the steady state depend crucially on the elasticity of intertemporal substitution
rather than the coefficient of relative risk aversion (which in turn also guides our preferred parameterizations of the model). However, none of our results rely on allowing
in order to clarify that the qualitative properties of the steady state depend crucially on the elasticity of intertemporal substitution
rather than the coefficient of relative risk aversion (which in turn also guides our preferred parameterizations of the model). However, none of our results rely on allowing
![]() . A reader who feels uncomfortable with the Epstein-Zin specification can therefore ignore it, assume instead standard expected utility, and simply replace
. A reader who feels uncomfortable with the Epstein-Zin specification can therefore ignore it, assume instead standard expected utility, and simply replace ![]() with
with ![]() (or vice versa) in all the formulas that follow.
(or vice versa) in all the formulas that follow.
2.2 Government
The government consumes output at the rate ![]() . Government spending is deterministic, it is financed with lump-sum taxation, and it does not affect either the household's utility from
private consumption or the production of the economy. The government budget constraint is given by:
. Government spending is deterministic, it is financed with lump-sum taxation, and it does not affect either the household's utility from
private consumption or the production of the economy. The government budget constraint is given by:
| (6) |
where
2.3 Aggregates and equilibrium definition
The initial position of the economy is given by the cross-sectional distribution of
![]() . Households choose plans
. Households choose plans
![]() , contingent on the history of their idiosyncratic shocks, and given the price sequence and the government policy, so as to
maximize their lifetime utility. Idiosyncratic risk, however, washes out in the aggregate. We thus define an equilibrium as a deterministic sequence of prices
, contingent on the history of their idiosyncratic shocks, and given the price sequence and the government policy, so as to
maximize their lifetime utility. Idiosyncratic risk, however, washes out in the aggregate. We thus define an equilibrium as a deterministic sequence of prices
![]() , policies
, policies
![]() , and macroeconomic variables
, and macroeconomic variables
![]() , along with a collection of individual contingent plans
, along with a collection of individual contingent plans
![]() , such that the following conditions hold: (i) given the sequences of prices and policies, the plans are optimal
for the households; (ii) the labor market clears,
, such that the following conditions hold: (i) given the sequences of prices and policies, the plans are optimal
for the households; (ii) the labor market clears,
![]() , in all
, in all ![]() ; (iii) the bond market clears,
; (iii) the bond market clears,
![]() , in all
, in all ![]() ; (iv) the government budget is satisfied
in all
; (iv) the government budget is satisfied
in all ![]() ; and (v) the aggregates are consistent with individual behavior,
; and (v) the aggregates are consistent with individual behavior,
![]() ,
,
![]() , and
, and
![]() , in all
, in all ![]() . (Throughout, we let
. (Throughout, we let ![]() denote the mean in the cross-section of the population.)
denote the mean in the cross-section of the population.)
3 Equilibrium
In this section we characterize the equilibrium of the economy. We first solve for a household's optimal plan for given sequences of prices and policies. We then aggregate across households and derive the general-equilibrium dynamics.
3.1 Individual behavior
Since employment is chosen after the capital stock has been installed and the idiosyncratic shock has been observed, optimal employment maximizes profits state by state. By constant returns to scale, optimal firm employment and profits are linear in own capital:
| (7) |
where
Here,
The key result here is that households face risky, but linear, returns to their capital. To see how this translates to linearity of wealth in assets, let ![]() denote the present
discounted value of future labor income net of taxes, a.k.a. human wealth:
denote the present
discounted value of future labor income net of taxes, a.k.a. human wealth:
Next, define effective wealth as the sum of financial and human wealth:
It follows that the evolution of effective wealth can be described by:
The first term on the right-hand side of (10) measures the expected rate of growth in the household's effective wealth; the second term captures the impact of idiosyncratic risk.
The linearity of budgets, together with the homotheticity of preferences, ensures that, for given prices and policies, the household's consumption-saving problem reduces to a tractable homothetic problem as in Samuelson's and Merton's classic portfolio analysis. It then follows that the optimal policy rules are linear in wealth, as shown in the next proposition.
where
while
with
Condition
![]() simply says that the fraction of wealth invested in the risky asset is increasing in the risk premium
simply says that the fraction of wealth invested in the risky asset is increasing in the risk premium
![]() and decreasing in risk aversion
and decreasing in risk aversion ![]() and the
amount of risk
and the
amount of risk ![]() . Condition (13) is essentially the Euler condition: it describes the growth rate of the marginal propensity to consume as a function of
the anticipated path of risk-adjusted returns to saving. Whether higher risk-adjusted returns increase or reduce the marginal propensity to consume depends on the elasticity of intertemporal substitution. To see this more clearly, note that in steady state this condition reduces to
. Condition (13) is essentially the Euler condition: it describes the growth rate of the marginal propensity to consume as a function of
the anticipated path of risk-adjusted returns to saving. Whether higher risk-adjusted returns increase or reduce the marginal propensity to consume depends on the elasticity of intertemporal substitution. To see this more clearly, note that in steady state this condition reduces to
![]() so that higher
so that higher ![]() decreases
decreases
![]() if and only if
if and only if ![]() that is, a higher risk-adjusted return to saving
increases the fraction of savings out of effective wealth if and only if the EIS is higher than one. This is due to the familiar tension between the income and substitution effects implied by an increase in the rate of return.
that is, a higher risk-adjusted return to saving
increases the fraction of savings out of effective wealth if and only if the EIS is higher than one. This is due to the familiar tension between the income and substitution effects implied by an increase in the rate of return.
3.2 General equilibrium
Because individual consumption, saving and investment are linear in individual wealth, aggregates at any point in time do not depend on the extent of wealth inequality at that time. As a result, the aggregate equilibrium dynamics can be described with a low-dimensional recursive system.
Define
![]() as the production function in intensive form (output per work hour). From Proposition
as the production function in intensive form (output per work hour). From Proposition
![]() , the equilibrium ratio of capital to effective wealth and the equilibrium risk-adjusted return to savings are identical across
agents and can be expressed as functions of the current capital stock and risk-free rate:
, the equilibrium ratio of capital to effective wealth and the equilibrium risk-adjusted return to savings are identical across
agents and can be expressed as functions of the current capital stock and risk-free rate:
![]() and
and
![]() , where
, where
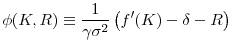 and
and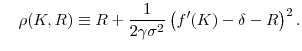
with
This system has a simple interpretation. Condition
![]() is the resource constraint of the economy; it follows from aggregating budgets across all households and the government, imposing labor- and
bond-market clearing, and using the linearity of individual firm employment to individual capital together with constant returns to scale, to get
is the resource constraint of the economy; it follows from aggregating budgets across all households and the government, imposing labor- and
bond-market clearing, and using the linearity of individual firm employment to individual capital together with constant returns to scale, to get
![]() . Condition
. Condition
![]() is the aggregate Euler condition for the economy; it follows from aggregating consumption and wealth across agents, together with the optimality
condition
is the aggregate Euler condition for the economy; it follows from aggregating consumption and wealth across agents, together with the optimality
condition
![]() for the marginal propensity to consume. Condition
for the marginal propensity to consume. Condition
![]() expresses the evolution of the present value of aggregate net-of-taxes labor income in recursive form; it follows from the definition of human
wealth combined with the intertemporal government budget, which imposes that the present value of taxes equals the present value of government consumption. Finally, condition
expresses the evolution of the present value of aggregate net-of-taxes labor income in recursive form; it follows from the definition of human
wealth combined with the intertemporal government budget, which imposes that the present value of taxes equals the present value of government consumption. Finally, condition
![]() represents market-clearig in the bond market; more precisely, it follows from aggregating bond holdings and investment across agents to get
represents market-clearig in the bond market; more precisely, it follows from aggregating bond holdings and investment across agents to get
![]() and
and
![]() , using the latter to replace
, using the latter to replace ![]() in the former, and imposing
in the former, and imposing
![]() .
.
This system characterizes the equilibrium dynamics of the economy under both complete and incomplete markets. In particular, conditions (14), (16) and (17) are exactly the same under either market structure; the key differences
between complete and incomplete markets rest in the Euler condition (15) and in the relation between the risk-adjusted return ![]() , the risk-free rate
, the risk-free rate ![]() and the marginal product of capital
and the marginal product of capital
![]() .
.
When ![]() (complete markets), arbitrage imposes that
(complete markets), arbitrage imposes that
![]() and the Euler condition reduces to its familiar complete-market version,
and the Euler condition reduces to its familiar complete-market version,
![]() . When instead
. When instead ![]() (incomplete markets), there are two important changes. First, the precautionary motive for saving introduces a positive drift in consumption growth, represented by the term
(incomplete markets), there are two important changes. First, the precautionary motive for saving introduces a positive drift in consumption growth, represented by the term
![]() in the Euler condition (15). And second, the fact that investment is subject to undiversifiable idiosyncratic risk introduces
a wedge between the risk-free rate and the marginal product of capital, so that
in the Euler condition (15). And second, the fact that investment is subject to undiversifiable idiosyncratic risk introduces
a wedge between the risk-free rate and the marginal product of capital, so that
![]() . It is worth noting here that the first effect is also shared by Aiyagari (1994) and other Bewley-type models that consider labor-income risk, whereas the second effect relies on the presence of capital-income risk.
. It is worth noting here that the first effect is also shared by Aiyagari (1994) and other Bewley-type models that consider labor-income risk, whereas the second effect relies on the presence of capital-income risk.
Finally note that condition (17) can be solved for ![]() as a function of the contemporaneous
as a function of the contemporaneous
![]() , so that the equilibrium dynamics of the economy reduce to a simple three-dimensional ODE system in
, so that the equilibrium dynamics of the economy reduce to a simple three-dimensional ODE system in
![]() Indeed, the equilibrium dynamics can be approximated with a simple shooting algorithm, similar to the one applied to the complete-markets neoclassical growth model. For
any historically given
Indeed, the equilibrium dynamics can be approximated with a simple shooting algorithm, similar to the one applied to the complete-markets neoclassical growth model. For
any historically given ![]() guess some initial values
guess some initial values
![]() and use conditions
and use conditions
![]() to compute the entire path of
to compute the entire path of
![]() for
for
![]() , for some large
, for some large ![]() then iterate on the initial guess till
then iterate on the initial guess till
![]() is close enough to its steady-state value.7 In the special case of a unit EIS (
is close enough to its steady-state value.7 In the special case of a unit EIS (![]() ), we have that
), we have that
![]() and hence
and hence
![]() for all
for all ![]() . One can then drop the Euler condition from
the dynamic system and analyze the equilibrium dynamics with a simple phase diagram in the
. One can then drop the Euler condition from
the dynamic system and analyze the equilibrium dynamics with a simple phase diagram in the ![]() space, much alike in a textbook exposition of the neoclassical growth model. Either way, this
is a significant gain in tractability relative to other incomplete-markets models, where the entire wealth distribution--an infinite dimensional object--is usually a relevant state variable for aggregate equilibrium dynamics. As in Angeletos (2007), the key is that individual policy rules are
linear in individual wealth, so that aggregate dynamics are invariant to the wealth distribution.
space, much alike in a textbook exposition of the neoclassical growth model. Either way, this
is a significant gain in tractability relative to other incomplete-markets models, where the entire wealth distribution--an infinite dimensional object--is usually a relevant state variable for aggregate equilibrium dynamics. As in Angeletos (2007), the key is that individual policy rules are
linear in individual wealth, so that aggregate dynamics are invariant to the wealth distribution.
4 Steady State
We henceforth parameterize government spending as a fraction ![]() of aggregate output to study the steady state of the economy, that is, the fixed point of the dynamic system in Proposition
2. We now show that this can be characterized as the solution to a system of two equations in
of aggregate output to study the steady state of the economy, that is, the fixed point of the dynamic system in Proposition
2. We now show that this can be characterized as the solution to a system of two equations in ![]() and
and ![]() .
.
First, note that the growth rate of consumption must be zero in steady state. Setting
![]() into the Euler condition (15) gives:
into the Euler condition (15) gives:
Using then the facts that
This condition gives the combinations of
Second, note that the growth rate of human wealth from (16) must also be zero in steady state. From this we get that:
 |
which simply states that human wealth must equal the present value of wages net of taxes. Substituting this into the bond-market clearing condition
This condition gives the combinations of
In any steady state, the capital stock and the risk-free rate must jointly solve equations
![]() and
and
![]() . In the Appendix we further show that a solution to this system exists and is unique. We thus reach the following result.
. In the Appendix we further show that a solution to this system exists and is unique. We thus reach the following result.
To understand the determination of the steady state of our model and its relation to its complete-markets counterpart, note first that condition
![]() imposes
imposes
![]() . That is, the risk-adjusted return to saving must be lower than the discount rate. In particular,
. That is, the risk-adjusted return to saving must be lower than the discount rate. In particular, ![]() must be low enough just to offset the precautionary motive for saving. If the risk-adjusted return were higher than this critical level, consumption (and wealth) would increase over time without bound, which would be a contradiction
of steady state. Conversely, if the risk-adjusted return were lower than this level, consumption (and wealth) would shrink to zero, which would once again be a contradiction of steady state. Combining this with the fact that
must be low enough just to offset the precautionary motive for saving. If the risk-adjusted return were higher than this critical level, consumption (and wealth) would increase over time without bound, which would be a contradiction
of steady state. Conversely, if the risk-adjusted return were lower than this level, consumption (and wealth) would shrink to zero, which would once again be a contradiction of steady state. Combining this with the fact that ![]() , we infer that the risk-free rate is also lower than the discount rate:
, we infer that the risk-free rate is also lower than the discount rate: ![]() . At the same time, because
. At the same time, because
![]() , it is unclear whether the marginal product of capital is higher or lower than the discount rate. Using these observations, along with the fact that the
complete-markets steady state features
, it is unclear whether the marginal product of capital is higher or lower than the discount rate. Using these observations, along with the fact that the
complete-markets steady state features
![]() , we conclude that incomplete markets necessarily reduce the risk-free rate but can have an ambiguous effect on the capital stock. In simple words, the
precautionary motive guarantees that the interest rate is lower under incomplete markets than under complete markets, but this does not necessarily translate to a higher capital stock, because investment risk introduces a wedge between the marginal product of capital and the interest rate.
, we conclude that incomplete markets necessarily reduce the risk-free rate but can have an ambiguous effect on the capital stock. In simple words, the
precautionary motive guarantees that the interest rate is lower under incomplete markets than under complete markets, but this does not necessarily translate to a higher capital stock, because investment risk introduces a wedge between the marginal product of capital and the interest rate.
A graphical representation of the steady state helps appreciate further this tension between the precautionary motive and the risk premium in our model (and will also facilitate the comparative statics of the steady state). Let ![]() and
and ![]() denote the functions defined by solving, respectively, equations
denote the functions defined by solving, respectively, equations
![]() and
and
![]() for
for ![]() as functions of
as functions of
![]() . We discuss the properties of these functions in what follows and illustrate them in Figure 1.8
. We discuss the properties of these functions in what follows and illustrate them in Figure 1.8
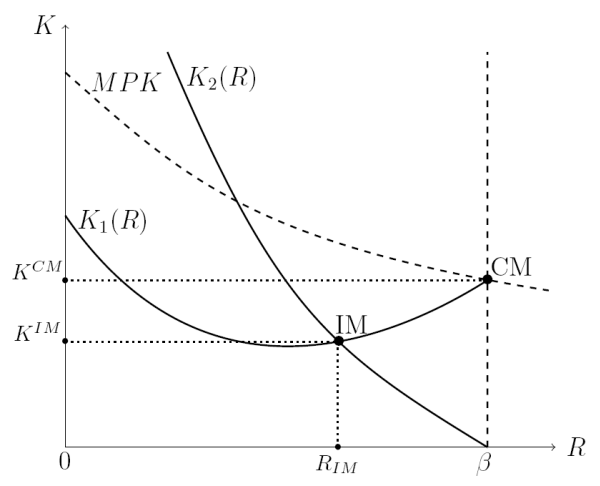
Consider first the curve ![]() . When
. When ![]() , condition
, condition
![]() reduces to
reduces to
![]() . The complete-markets counterpart of
. The complete-markets counterpart of ![]() is
therefore given by a standard curve for the marginal product of capital, represented by curve
is
therefore given by a standard curve for the marginal product of capital, represented by curve ![]() in Figure 1. The positive risk premium introduced on investment when
in Figure 1. The positive risk premium introduced on investment when ![]() implies that curve
implies that curve ![]() lies uniformly below curve
lies uniformly below curve ![]() . Indeed, the distance between the two curves measures the risk premium, as captured by the right-hand
side of
. Indeed, the distance between the two curves measures the risk premium, as captured by the right-hand
side of
![]() . Clearly, the latter is decreasing in
. Clearly, the latter is decreasing in ![]() : the higher the risk-free rate, the lower the risk premium in steady state. To understand the intuition behind this property, take for a moment the interest rate to be exogenously given. Then, an increase in
: the higher the risk-free rate, the lower the risk premium in steady state. To understand the intuition behind this property, take for a moment the interest rate to be exogenously given. Then, an increase in ![]() would lead to an increase in the steady-state level of wealth. Because of diminishing absolute risk aversion, the increase in wealth would stimulate capital accumulation. However, because of diminishing returns to capital accumulation, the ratio of capital to
wealth, i.e. the fraction
would lead to an increase in the steady-state level of wealth. Because of diminishing absolute risk aversion, the increase in wealth would stimulate capital accumulation. However, because of diminishing returns to capital accumulation, the ratio of capital to
wealth, i.e. the fraction ![]() , would fall. But then the risk premium, which is given by
, would fall. But then the risk premium, which is given by
![]() , would also fall. And because wealth explodes as
, would also fall. And because wealth explodes as
![]() , while
, while ![]() remains bounded, it follows that the risk premium must
vanish as
remains bounded, it follows that the risk premium must
vanish as
![]() . These observations explain why the distance between the two curves indeed falls monotonically with
. These observations explain why the distance between the two curves indeed falls monotonically with ![]() , and vanishes as
, and vanishes as
![]() .
.
To recap, there are two important economic effects behind curve ![]() . On the one hand, a higher
. On the one hand, a higher ![]() raises the opportunity cost of capital. This effect, which is present under both complete and incomplete markets, tends to discourage investment. On the other hand, a higher
raises the opportunity cost of capital. This effect, which is present under both complete and incomplete markets, tends to discourage investment. On the other hand, a higher ![]() is possible in steady state under incomplete markets only if aggregate wealth is higher in that steady state. This wealth effect, which is present only under incomplete markets, tends to encourage investment. Moreover, from condition
is possible in steady state under incomplete markets only if aggregate wealth is higher in that steady state. This wealth effect, which is present only under incomplete markets, tends to encourage investment. Moreover, from condition
![]() it is immediate that
it is immediate that ![]() is
U-shaped, as illustrated in Figure 1. Therefore, the opportunity-cost effect must be dominating for low
is
U-shaped, as illustrated in Figure 1. Therefore, the opportunity-cost effect must be dominating for low ![]() , while the wealth effect must be dominating for high
, while the wealth effect must be dominating for high ![]() .9
.9
Let's now turn to the curve ![]() . The complete-markets counterpart of
. The complete-markets counterpart of ![]() is the vertical line at
is the vertical line at ![]() : as
: as
![]() ,
, ![]() converges to this vertical line, whereas for any
converges to this vertical line, whereas for any
![]() ,
, ![]() lies to the left of this vertical line. In Lemma 1 in the
Appendix we show that
lies to the left of this vertical line. In Lemma 1 in the
Appendix we show that ![]() is monotonically decreasing in
is monotonically decreasing in ![]() , with
, with
![]() as
as
![]() and
and
![]() as
as
![]() .10 The intuition for the
monotonicity of
.10 The intuition for the
monotonicity of ![]() is simple. For given
is simple. For given ![]() , and hence given
, and hence given ![]() , an increase in
, an increase in ![]() reduces both
reduces both ![]() and
and
![]() and thereby necessarily reduces the right-hand side of
and thereby necessarily reduces the right-hand side of
![]() . But then, for
. But then, for
![]() to hold with the lower
to hold with the lower ![]() , it
must be that
, it
must be that ![]() also falls, which explains why
also falls, which explains why ![]() is decreasing.
is decreasing.
Since ![]() and
and ![]() are continuous in
are continuous in ![]() , and using their limiting properties from above, it is then clear that the two curves intersect at least once at some
, and using their limiting properties from above, it is then clear that the two curves intersect at least once at some
![]() . But, as already mentioned, we further show in the Appendix that this intersection is in fact unique. The incomplete-markets steady state of our model is thus represented by
point IM in Figure 1, while its complete-markets counterpart is represented by point CM. For the particular economy we have considered in this figure, the steady-state capital stock is lower
under incomplete markets than under complete markets. However, the opposite could also be true. Clearly, a sufficient condition for the steady-state capital stock to be lower than under complete markets is that the two curves intersect on the upward portion of
. But, as already mentioned, we further show in the Appendix that this intersection is in fact unique. The incomplete-markets steady state of our model is thus represented by
point IM in Figure 1, while its complete-markets counterpart is represented by point CM. For the particular economy we have considered in this figure, the steady-state capital stock is lower
under incomplete markets than under complete markets. However, the opposite could also be true. Clearly, a sufficient condition for the steady-state capital stock to be lower than under complete markets is that the two curves intersect on the upward portion of ![]() , or that the wealth effect on investment due to risk aversion dominates the usual opportunity cost effect. The following proposition identifies a condition that is both necessary and sufficient for the capital stock
to be lower than under complete markets.
, or that the wealth effect on investment due to risk aversion dominates the usual opportunity cost effect. The following proposition identifies a condition that is both necessary and sufficient for the capital stock
to be lower than under complete markets.
This result, which was first reported in Angeletos (2007), highlights how augmenting the neoclassical growth model for idiosyncratic capital-income risk can lead to lower aggregate saving, and thereby to lower aggregate output and consumption than under complete markets. This result stands in contrast to Aiyagari (1994), which documents how labor-income risk raises aggregate saving.11 We refer the interested reader to that earlier work for a more extensive discussion and quantification of this result. In the remainder of our paper, we focus on the effects of government spending, which is our main question of interest.
5 The long-run effects of government consumption
In this section we study how the steady state changes when the rate of government consumption increases. The analysis will make clear that the different impact that government spending has in our model as compared to the standard paradigm originates precisely from the wealth effects that idiosyncratic risk introduces in the demand for investment.
5.1 Characterization
To study the long-run effects of an increase in the level of government consumption, we again use a graphical representation of the steady state, namely Figure 2, which is a variant of Figure 1.
Let the initial level of government spending be ![]() and suppose that the corresponding steady state is given by point
and suppose that the corresponding steady state is given by point ![]() in Figure 2. Subsequently, let government spending increase to
in Figure 2. Subsequently, let government spending increase to
![]() . Note that condition
. Note that condition
![]() does not depend on
does not depend on ![]() , and hence
an increase in government consumption does not affect the
, and hence
an increase in government consumption does not affect the ![]() curve. Rather, it is condition
curve. Rather, it is condition
![]() , and the
, and the ![]() curve, that
depend on
curve, that
depend on ![]() . In particular, because a higher
. In particular, because a higher ![]() means lower net-of-taxes labor
income, and hence a lower
means lower net-of-taxes labor
income, and hence a lower ![]() in steady state for any given
in steady state for any given ![]() , an increase in
government consumption causes the
, an increase in
government consumption causes the ![]() curve to shift leftwards, as illustrated in Figure 2. This leftward shift is a manifestation of the negative wealth effect of higher lump-sum taxes on investment.
curve to shift leftwards, as illustrated in Figure 2. This leftward shift is a manifestation of the negative wealth effect of higher lump-sum taxes on investment.
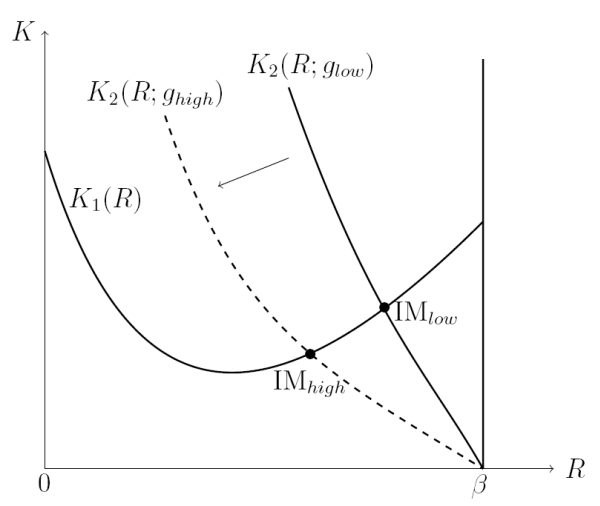
The new steady state is then represented by point ![]() . Clearly, the leftward shift in the
. Clearly, the leftward shift in the ![]() curve leads unambiguously to a decrease in
curve leads unambiguously to a decrease in ![]() . The impact on
. The impact on ![]() , on the other hand, is ambiguous. This is because, as explained in the previous section, a reduction in
, on the other hand, is ambiguous. This is because, as explained in the previous section, a reduction in ![]() entails two opposing effects on the demand for investment: the
familiar opportunity-cost channel tends to encourage investment, while the novel wealth channel of our model tends to discourage investment. As evident from the figure, if the two curves intersect on the upward portion of the
entails two opposing effects on the demand for investment: the
familiar opportunity-cost channel tends to encourage investment, while the novel wealth channel of our model tends to discourage investment. As evident from the figure, if the two curves intersect on the upward portion of the ![]() curve, that is, in the portion where the wealth effect dominates, then the increase in
curve, that is, in the portion where the wealth effect dominates, then the increase in ![]() leads to a reduction in
leads to a reduction in ![]() . In the Appendix we show that the intersection occurs in the upward portion of the
. In the Appendix we show that the intersection occurs in the upward portion of the ![]() curve if and only
if
curve if and only
if
![]() . Finally, it is easy to check that
. Finally, it is easy to check that
![]() .12 We thus reach the the
following result.
.12 We thus reach the the
following result.
This is the key theoretical result of our paper. It establishes that, as long as the EIS is sufficiently high relative to the income share of capital, a permanent increase in the rate of government consumption has a negative long-run effect on both the interest rate and the capital intensity of the economy.
It is important to appreciate how this result deviates from the standard neoclassical paradigm. With complete markets, in steady state the interest rate is equal to the discount rate
![]() , and the capital-labor ratio is determined by the equality of the marginal product of capital to the discount rate
, and the capital-labor ratio is determined by the equality of the marginal product of capital to the discount rate
![]() . It follows that, in the long run, government consumption has no effect on either
. It follows that, in the long run, government consumption has no effect on either ![]() or
or ![]()
![]()
![]() and
and ![]() This is true even when labor supply,
This is true even when labor supply, ![]() , is endogenous.13 The only difference is that, with
endogenous labor supply,
, is endogenous.13 The only difference is that, with
endogenous labor supply, ![]() changes with
changes with ![]() . In particular, when labor supply is
fixed, the increase in government consumption simply leads to a one-to-one decrease in private consumption. When instead labor supply is elastic, the increase in government consumption has a negative wealth effect, inducing agents to work more. The capital stock then increases one-to-one with labor
supply, so as to keep the the capital-labor ratio and the interest rate invariant with
. In particular, when labor supply is
fixed, the increase in government consumption simply leads to a one-to-one decrease in private consumption. When instead labor supply is elastic, the increase in government consumption has a negative wealth effect, inducing agents to work more. The capital stock then increases one-to-one with labor
supply, so as to keep the the capital-labor ratio and the interest rate invariant with ![]() .
.
In our model, instead, government consumption has non-trivial long-run effects on both the interest rate and the capital intensity of the economy. Building on the earlier discussions, we can now summarize the key mechanism in our model as follows. Because households face consumption risk, they
have a precautionary motive to save. Because preferences exhibit diminishing absolute risk aversion, this motive is stronger when the level of wealth is lower. It follows that, by reducing household wealth, higher government spending stimulates precautionary saving. But then, the risk-free rate at
which aggregate saving can be stationary has to be lower, which explains why the risk-free rate ![]() falls with
falls with ![]() At the same time, because of diminishing absolute risk aversion, the reduction in wealth tends to discourage the demand for investment. Provided that the positive effect of the lower opportunity cost of investment is not strong enough to offset this negative
wealth effect, the capital-labor ratio
At the same time, because of diminishing absolute risk aversion, the reduction in wealth tends to discourage the demand for investment. Provided that the positive effect of the lower opportunity cost of investment is not strong enough to offset this negative
wealth effect, the capital-labor ratio ![]() also falls with
also falls with ![]()
5.2 Calibration and numerical simulation
For empirically plausible calibrations of the model, the critical condition
![]() appears to be satisfied quite easily. For example, take the interest rate to be R=4% and labor income to be 65% of GDP (as in US data). This implies that H
is about 16 times GDP. With a capital-output ratio of 4 (again as in US data), this translates to an H of about 4 times K. Since in steady state
appears to be satisfied quite easily. For example, take the interest rate to be R=4% and labor income to be 65% of GDP (as in US data). This implies that H
is about 16 times GDP. With a capital-output ratio of 4 (again as in US data), this translates to an H of about 4 times K. Since in steady state
![]() this exercise gives a calibrated value for
this exercise gives a calibrated value for
![]() of about 0.25. This critical value is lower than most of the recent empirical estimates of the elasticity of intertemporal substitution, which are in most cases above
0.5 and often even above 1.14 Hence, a
negative long-run effect of government consumption on aggregate saving and productivity appears to be the most likely scenario.
of about 0.25. This critical value is lower than most of the recent empirical estimates of the elasticity of intertemporal substitution, which are in most cases above
0.5 and often even above 1.14 Hence, a
negative long-run effect of government consumption on aggregate saving and productivity appears to be the most likely scenario.
In the remainder of this section, we make a first pass at the potential quantitative importance of our results within the context of our baseline model. In the next section we then turn to an enriched version of the model that allows for endogenous labor supply, as well as a certain type of agent heterogeneity.
The economy is fully parameterized by
![]() , where
, where ![]() is the income
share of capital,
is the income
share of capital, ![]() is the discount rate,
is the discount rate, ![]() is the coefficient of
relative risk aversion,
is the coefficient of
relative risk aversion, ![]() is the (mean) depreciation rate,
is the (mean) depreciation rate, ![]() is the
elasticity of intertemporal substitution,
is the
elasticity of intertemporal substitution, ![]() is the standard deviation of the rate of return on private investment, and
is the standard deviation of the rate of return on private investment, and ![]() is the share of government consumption in aggregate output.
is the share of government consumption in aggregate output.
In our baseline parametrization, we take
![]() ,
, ![]() =0.042, and
=0.042, and ![]() =0.08; these values are standard in the literature. For risk aversion, we take
=0.08; these values are standard in the literature. For risk aversion, we take ![]() =5, a value commonly used in the
macro-finance literature to help generate plausible risk premia. For the elasticity of intertemporal substitution, we take
=5, a value commonly used in the
macro-finance literature to help generate plausible risk premia. For the elasticity of intertemporal substitution, we take ![]() =1, a value consistent with recent micro and macro
estimates.15 For the share of government, our baseline value is g=25% (as in the United States) and a higher alternative is g=40% (as in some European
countries).
=1, a value consistent with recent micro and macro
estimates.15 For the share of government, our baseline value is g=25% (as in the United States) and a higher alternative is g=40% (as in some European
countries).
What remains is ![]() . Unfortunately, there is no direct measure of the rate-of-return risk faced by the "typical" investor in the US economy. However, there are various indications
that investment risks are significant. For instance, the probability that a privately held firm survives five years after entry is less than 40%. Furthermore, even conditional on survival, the risks faced by entrepreneurs and private investors appear to be very large: as Moskowitz and
Vissing-Jørgensen (2002) document, not only is there a dramatic cross-sectional variation in the returns to private equity, but also the volatility of the book value of a (value-weighted) index of private firms is twice as large as that of the index of public firms--one more indication that
private equity is more risky than public equity. Note then that the standard deviation of annual returns is about 15% per annum for the entire pool of public firms; it is over 50% for a single public firm (which gives a measure of firm-specific risk); and it is about 40% for a portfolio of the
smallest public firms (which are likely to be similar to large private firms).
. Unfortunately, there is no direct measure of the rate-of-return risk faced by the "typical" investor in the US economy. However, there are various indications
that investment risks are significant. For instance, the probability that a privately held firm survives five years after entry is less than 40%. Furthermore, even conditional on survival, the risks faced by entrepreneurs and private investors appear to be very large: as Moskowitz and
Vissing-Jørgensen (2002) document, not only is there a dramatic cross-sectional variation in the returns to private equity, but also the volatility of the book value of a (value-weighted) index of private firms is twice as large as that of the index of public firms--one more indication that
private equity is more risky than public equity. Note then that the standard deviation of annual returns is about 15% per annum for the entire pool of public firms; it is over 50% for a single public firm (which gives a measure of firm-specific risk); and it is about 40% for a portfolio of the
smallest public firms (which are likely to be similar to large private firms).
Given this suggestive evidence, and lacking any better alternative, we let ![]() =30% for our baseline parameterization and consider
=30% for our baseline parameterization and consider ![]() =20% and
=20% and ![]() =40% for sensitivity analysis. Although these numbers are somewhat arbitrary, it is reassuring that the volatility
of individual consumption generated by our model is comparable to its empirical counterpart. For instance, using the Consumer Expenditure Survey (CEX), Malloy, Moskowitz and Vissing-Jørgensen (2006) estimate the standard deviation of consumption growth to be about 8% for stockholders (and
about 3% for non-stockholders). Similarly, using data that include consumption of luxury goods, Aït-Sahalia, Parker and Yogo (2001) get estimates between 6% and 15%. In our simulations, on the other hand, the standard deviation of individual consumption growth is less than 5% per annum (along
the steady state).
=40% for sensitivity analysis. Although these numbers are somewhat arbitrary, it is reassuring that the volatility
of individual consumption generated by our model is comparable to its empirical counterpart. For instance, using the Consumer Expenditure Survey (CEX), Malloy, Moskowitz and Vissing-Jørgensen (2006) estimate the standard deviation of consumption growth to be about 8% for stockholders (and
about 3% for non-stockholders). Similarly, using data that include consumption of luxury goods, Aït-Sahalia, Parker and Yogo (2001) get estimates between 6% and 15%. In our simulations, on the other hand, the standard deviation of individual consumption growth is less than 5% per annum (along
the steady state).
Putting aside these qualifications about the parametrization of ![]() we now examine the quantitative effects of government consumption on the steady state of the economy. Table
1 reports the per-cent reduction in the steady-state values of the capital-labor ratio
we now examine the quantitative effects of government consumption on the steady state of the economy. Table
1 reports the per-cent reduction in the steady-state values of the capital-labor ratio ![]() labor productivity
labor productivity ![]() and the saving rate
and the saving rate ![]() , relative
to what their values would have been if
, relative
to what their values would have been if ![]() were 0.16 Complete markets are indicated by CM and incomplete markets by IM.
were 0.16 Complete markets are indicated by CM and incomplete markets by IM.
|
|
|||||||
|---|---|---|---|---|---|---|---|
| baseline |
|
|
|
|
|
|
|
|
|
0 | -12.18 | 0 | -4.57 | 0 | -1.21 | 20 |
|
|
0 | -6.78 | 0 | -2.5 | 0 | -0.88 | 12 |
| 0 | -17.82 | 0 | -6.82 | 0 | -2.05 | 28 |
In our baseline parametrization, the capital-labor ratio is about 10% lower when g=25% than when ![]() Similarly, productivity is about 4% lower and the saving rate is about 1 percentage
point lower. These are significant effects. They are larger (in absolute value) than the steady-state effects of precautionary saving reported in Aiyagari (1994). They are equivalent to what would be the steady-state effects of a marginal tax on capital income equal to 17% in the complete-markets
case. (The tax rate on capital income that would generate the same effects under complete markets is given in the last column of the table, as
Similarly, productivity is about 4% lower and the saving rate is about 1 percentage
point lower. These are significant effects. They are larger (in absolute value) than the steady-state effects of precautionary saving reported in Aiyagari (1994). They are equivalent to what would be the steady-state effects of a marginal tax on capital income equal to 17% in the complete-markets
case. (The tax rate on capital income that would generate the same effects under complete markets is given in the last column of the table, as
![]() .)
.)
Not surprisingly, the effects are smaller if ![]() is lower (third row) or if
is lower (third row) or if ![]() is lower (not reported), because then risk matters less. On the other hand, the effects are larger when g=40% (final row): productivity is almost 18% lower, the saving rate is 2 percentage points lower, and the tax on capital income that would have generated the same effects under complete markets is 28%.
is lower (not reported), because then risk matters less. On the other hand, the effects are larger when g=40% (final row): productivity is almost 18% lower, the saving rate is 2 percentage points lower, and the tax on capital income that would have generated the same effects under complete markets is 28%.
Table 2 turns from level to marginal effects: it reports the change in ![]()
![]() and
and ![]() as we increase government spending by 1 percent, either
from
as we increase government spending by 1 percent, either
from ![]() to
to ![]() , or from
, or from ![]() to
to ![]() . In the first case, productivity falls by
. In the first case, productivity falls by ![]() ; in the second, by
; in the second, by ![]() . This is equivalent to what would have been, under complete markets, the effect of increasing the tax rate on capital income
by about 0.75 percentage points in the first case, and about 0.8 percentage
points in the second case.
. This is equivalent to what would have been, under complete markets, the effect of increasing the tax rate on capital income
by about 0.75 percentage points in the first case, and about 0.8 percentage
points in the second case.
|
|
|||||
|---|---|---|---|---|---|
|
|
0 | -0.52 | 0 | -0.19 | 0.75 |
|
|
0 | -0.71 | 0 | -0.26 | 0.8 |
6 Endogenous labor
In this section we endogenize labor supply in the economy. We consider three alternative specifications that achieve this goal without compromising the tractability of the model.
6.1 GHH preferences
One easy way to accommodate endogenous labor supply in the model is to assume preferences that rule out income effects on labor supply, as in Greenwood, Hercowitz and Huffman (1998). In particular, suppose that preferences are given by
![]() with
with
where
This specification highlights an important difference between complete and incomplete markets with regard to the employment impact of fiscal shocks. Under incomplete markets, an increase in government spending can have a negative general-equilibrium effect on
aggregate employment. This is never possible with complete markets, but it is possible with incomplete markets when an increase in ![]() reduces the capital-labor ratio, and thereby the wage
rate, which in turn discourages labor supply. Indeed, with GHH preferences,
reduces the capital-labor ratio, and thereby the wage
rate, which in turn discourages labor supply. Indeed, with GHH preferences,
![]() suffices for both
suffices for both ![]() and
and ![]() to fall with
to fall with ![]() in both the short run and the long run.
in both the short run and the long run.
Although it is unlikely that wealth effects on labor supply are zero in the long run, they may well be very weak in the short run. In light of our results, one may then expect that after a positive shock to government consumption both employment and investment could drop on impact under incomplete markets. Indeed, an interesting extension would be to consider a preference specification that allows for weak short-run but strong long-run wealth effects on labor supply, as in Jaimovich and Rebelo (2006).
6.2 KPR preferences
A second tractable way to accommodate endogenous labor supply is to assume that agents have homothetic preferences over consumption and leisure, as in King, Plosser, and Rebelo (1988). The specification assumed in that paper is
![]() with
with
where
The benefit of this specification is that it is standard in the literature (making our results comparable to previously reported results), while it also comes with zero cost in tractability.18 The homotheticity of the household's optimization problem is then preserved and the equilibrium analysis proceeds in a similar fashion as in the benchmark model.19 The only essential novelty is that aggregate employment is now given by
![]() , where
, where
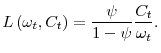 |
The neoclassical effect of wealth on labor supply is then captured by the negative relationship between
For the quantitative version of this economy, we take
![]() . This value, which is in line with King, Plosser, and Rebelo (1988) and Christiano and Eichenbaum (1992), ensures that the steady-state fraction of available time worked
approximately matches US data. The rest of the parameters are as in the baseline specification of the benchmark model.
. This value, which is in line with King, Plosser, and Rebelo (1988) and Christiano and Eichenbaum (1992), ensures that the steady-state fraction of available time worked
approximately matches US data. The rest of the parameters are as in the baseline specification of the benchmark model.
6.3 Hand-to-mouth workers
A third approach is to split the population into two groups. The first group consists of the households that have been modeled in the benchmark model; we will call this group the "investors". The second group consists of households that supply labor but do not hold any assets, and simply consume their entire labor income at each point in time; we will call this group the "hand-to-mouth workers". Their labor supply is given by
| (23) |
where
This approach could be justified on its own merit. In the United States, a significant fraction of the population holds no assets, has limited ability to borrow, and sees its consumption tracking its income almost one-to-one. This fact calls for a richer model of heterogeneity than our benchmark model. But is unclear what the "right" model for these households is. Our specification with hand-to-mouth workers is a crude way of capturing this form of heterogeneity in the model, while preserving tractability.
A side benefit of this approach is that it also gives freedom in parameterizing the wage and wealth elasticities of labor supply. Whereas the KPR preference specification imposes
![]() , the specification introduced above permits us to pick much lower elasticities, consistent with micro evidence. The point is not to argue which
parametrization of the labor-supply elasticities is more appropriate for quantitative exercises within the neoclassical growth model; this is the subject of a long debate in the literature, to which we have nothing to add. The point here is rather to cover a broader spectrum of empirically
plausible quantitative results.
, the specification introduced above permits us to pick much lower elasticities, consistent with micro evidence. The point is not to argue which
parametrization of the labor-supply elasticities is more appropriate for quantitative exercises within the neoclassical growth model; this is the subject of a long debate in the literature, to which we have nothing to add. The point here is rather to cover a broader spectrum of empirically
plausible quantitative results.
For the quantitative version of this economy, we thus take
![]() and
and
![]() , which are in the middle of most micro estimates.21 What then remains is the fraction of aggregate income absorbed by hand-to-mouth workers. As mentioned above, a significant fraction of the US population holds no assets. For example, using data from both the PSID and the SCF, Guvenen (2006) reports that the lower
, which are in the middle of most micro estimates.21 What then remains is the fraction of aggregate income absorbed by hand-to-mouth workers. As mentioned above, a significant fraction of the US population holds no assets. For example, using data from both the PSID and the SCF, Guvenen (2006) reports that the lower
![]() of the wealth distribution owns only
of the wealth distribution owns only ![]() of aggregate wealth and accounts
for about
of aggregate wealth and accounts
for about ![]() of aggregate consumption. Since some households may be able to smooth consumption even when their net worth is zero,
of aggregate consumption. Since some households may be able to smooth consumption even when their net worth is zero, ![]() is likely to be an upper bound for the fraction of aggregate consumption accounted for by hand-to-mouth agents. We thus opt to calibrate the economy so that hand-to-mouth agents account for
is likely to be an upper bound for the fraction of aggregate consumption accounted for by hand-to-mouth agents. We thus opt to calibrate the economy so that hand-to-mouth agents account for ![]() of aggregate consumption. This is also the value of the relevant parameter that one would estimate if the model were to match US aggregate consumption data--we can deduce this from Campbell and Mankiw (1989).22
of aggregate consumption. This is also the value of the relevant parameter that one would estimate if the model were to match US aggregate consumption data--we can deduce this from Campbell and Mankiw (1989).22
6.4 The long-run effects of government consumption with endogenous labor
Our main theoretical result (Proposition 5) continues to hold in all of the above variants of the benchmark model: in steady state, a higher rate ![]() of government consumption necessarily
reduces the interest rate
of government consumption necessarily
reduces the interest rate ![]() and it also reduces the capital-labor ratio
and it also reduces the capital-labor ratio ![]() labor productivity
labor productivity ![]() and the wage rate
and the wage rate ![]() if and only if the elasticity
of intertemporal substitution
if and only if the elasticity
of intertemporal substitution ![]() is higher than
is higher than
![]() .23
.23
What is not clear anymore is the effect of ![]() on
on ![]() and
and ![]() , because now
, because now ![]() is not fixed. On the one hand, the reduction in wealth stimulates labor
supply, thus contributing to an increase in
is not fixed. On the one hand, the reduction in wealth stimulates labor
supply, thus contributing to an increase in ![]() . This is the familiar neoclassical effect of government spending on labor supply. On the other hand, as long as
. This is the familiar neoclassical effect of government spending on labor supply. On the other hand, as long as
![]() , the reduction in capital intensity depresses real wages, contributing towards a reduction in
, the reduction in capital intensity depresses real wages, contributing towards a reduction in ![]() . This is the novel general-equilibrium effect due to incomplete markets. The overall effect of government spending on aggregate employment is therefore ambiguous under incomplete markets, whereas it is unambiguously positive under complete
markets.
. This is the novel general-equilibrium effect due to incomplete markets. The overall effect of government spending on aggregate employment is therefore ambiguous under incomplete markets, whereas it is unambiguously positive under complete
markets.
Other things equal, we expect the negative general-equilibrium effect to dominate, thus leading to a reduction in long-run employment after a permanent increase in government spending, if the wage elasticity of labor supply is sufficiently high relative to its income elasticity. This is clear in the GHH specification, where the wealth effect is zero. It can also be verified for the case of hand-to-mouth workers, where we have freedom in choosing these elasticities, but not in the case of KPR preferences, where both elasticities are restricted to equal one.
Given these theoretical ambiguities, we now seek to get a sense of empirically plausible quantitative effects. As already discussed, the GHH case (zero wealth effects on labor supply) is merely of pedagogical value. We thus focus on the parameterized versions of the other two cases, the economy with KPR (homothetic) preferences and the economy with hand-to-mouth workers.
Table 3 then presents the marginal effects on the steady-state levels of the capital-labor ratio, productivity, employment, and output for each of these two economies, as ![]() increases from
increases from
![]() to
to ![]() , or from
, or from ![]() to
to ![]() .24 The case of KPR preferences is indicated by KPR, while the case with hand-to-mouth workers is indicated by HTM. In either case, complete markets are indicated by CM and incomplete markets by IM.
.24 The case of KPR preferences is indicated by KPR, while the case with hand-to-mouth workers is indicated by HTM. In either case, complete markets are indicated by CM and incomplete markets by IM.
|
|
|||||||||
|---|---|---|---|---|---|---|---|---|---|
|
|
0 | -0.33 | 0 | -0.12 | 1.4 | 1.27 | 1.4 | 1.15 | 0.52 |
|
|
0 | -0.3 | 0 | -0.11 | 0.38 | 0.38 | 0.38 | 0.27 | 0.46 |
|
|
0 | -0.52 | 0 | -0.19 | 1.76 | 1.53 | 1.76 | 1.34 | 0.68 |
|
|
0 | -0.36 | 0 | -0.13 | 0.57 | 0.57 | 0.57 | 0.44 | 0.48 |
Regardless of specification, the marginal effects of higher government spending on capital intensity ![]() and labor productivity
and labor productivity ![]() are negative under incomplete markets (and are stronger the higher is
are negative under incomplete markets (and are stronger the higher is ![]() ), whereas they are zero under complete markets. As for
aggregate employment
), whereas they are zero under complete markets. As for
aggregate employment ![]() the wealth effect of higher
the wealth effect of higher ![]() turns out to dominate
the effect of lower wages under incomplete markets, so that
turns out to dominate
the effect of lower wages under incomplete markets, so that ![]() increases with higher
increases with higher ![]() under either complete or incomplete markets. However, the employment stimulus is weaker under incomplete markets, especially in the economy with hand-to-mouth workers. The same is true for aggregate output: it increases under either incomplete or complete markets, but less so under
incomplete markets. Finally, the incomplete-markets effects are on average equivalent to what would have been the effect of increasing the tax rate on capital income by about
under either complete or incomplete markets. However, the employment stimulus is weaker under incomplete markets, especially in the economy with hand-to-mouth workers. The same is true for aggregate output: it increases under either incomplete or complete markets, but less so under
incomplete markets. Finally, the incomplete-markets effects are on average equivalent to what would have been the effect of increasing the tax rate on capital income by about ![]() under
complete markets.
under
complete markets.
7 Dynamic responses
The results so far indicate that the long-run effects of government consumption can be significantly affected by incomplete risk sharing. We now examine how incomplete risk sharing affects the entire impulse response of the economy to a fiscal shock.25
Starting from the steady state with ![]() , we hit the economy with a permanent 1% increase in government spending and trace its transition to the new steady state (the one with
, we hit the economy with a permanent 1% increase in government spending and trace its transition to the new steady state (the one with
![]() ). We conduct this experiment for both the economy with KPR preferences and the economy with hand-to-mouth workers, each parameterized as in the previous section; in either case, the
transitional dynamics reduce to a simple system of two first-order ODE's in
). We conduct this experiment for both the economy with KPR preferences and the economy with hand-to-mouth workers, each parameterized as in the previous section; in either case, the
transitional dynamics reduce to a simple system of two first-order ODE's in
![]() when
when ![]() .26
.26
The results are presented in Figures 3 and 4. Time in years is on the horizontal axis, while deviations of the macro variables from their respective initial values are on the vertical axis. The interest rate and the investment rate are in simple differences, the rest of the variables are in log differences. The solid lines indicate incomplete markets, the dashed lines indicate complete markets.
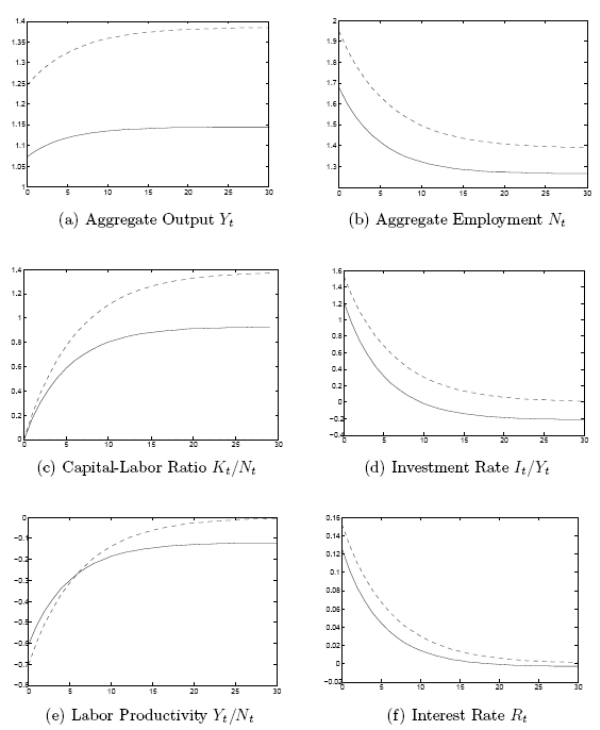
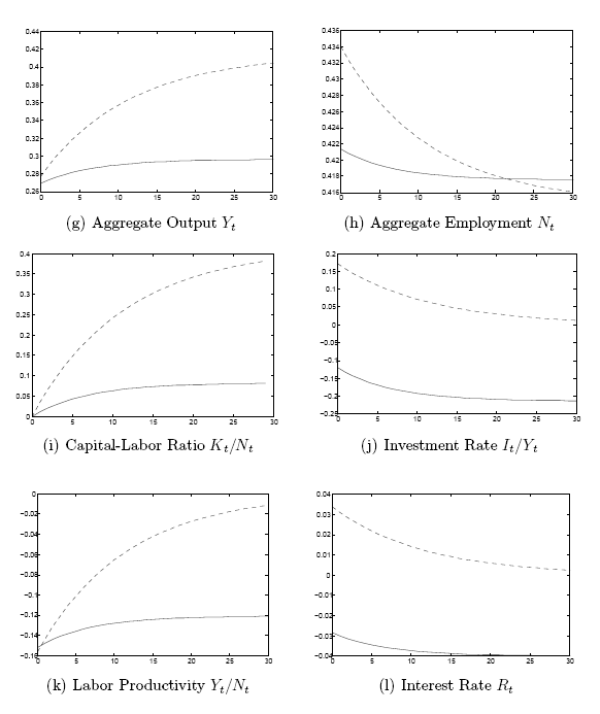
As evident in these figures, the quantitative effects of a permanent fiscal shock can be quite different between complete and incomplete markets. The overall picture that emerges is that the employment and output stimulus of a permanent increase in government spending is weaker under incomplete markets than under complete markets. And whereas we already knew this for the long-run response of the economy, now we see that the same is true for its short-run response.
This picture holds for both the economy with KPR preferences and the one with hand-to-mouth workers. But there are also some interesting differences between the two. The mitigating effect of incomplete markets on the employment and output stimulus of government spending is much stronger in the economy with hand-to-mouth workers. As a result, whereas the short-run effects of higher government spending on the investment rate and the interest are positive under complete markets in both economies, and whereas these effects remain positive under incomplete markets in the economy with KPR preferences, they turn negative under incomplete markets in the economy with hand-to-mouth workers.
To understand this result, consider for a moment the benchmark model, where there are no hand-to-mouth workers and labor supply is completely inelastic. Under complete markets, a permanent change in government spending would be absorbed one-to-one in private consumption, leaving investment and interest rates completely unaffected in both the short- and the long-run. Under incomplete markets, instead, investment and the interest rate would fall on impact, as well as in the long run. Allowing labor supply to increase in response to the fiscal shock ensures that investment and the interest rate jump upwards under complete markets. However, as long as the response of labor supply is weak enough, the response of investment and the interest rate can remain negative under incomplete markets.
As a final point of interest, we calculate the welfare cost, in terms of consumption equivalent, associated with a permanent 1% increase in government spending. Under complete markets, welfare drops by ![]() , whereas under incomplete markets it drops by
, whereas under incomplete markets it drops by ![]() . In other words, the welfare cost of an increase in government spending is three times higher under incomplete
markets than under complete markets.27
. In other words, the welfare cost of an increase in government spending is three times higher under incomplete
markets than under complete markets.27
To recap, the quantitative results indicate that a modest level of idiosyncratic investment risk can have a non-trivial impact on previously reported quantitative evaluations of fiscal policy. Note in particular that our quantitative economy with KPR preferences is directly comparable to two classics in the related literature, Aiyagari, Christiano and Eichenbaum (1992) and Baxter and King (1993). Therefore, further investigating the macroeconomic effects of fiscal shocks in richer quantitative models with financial frictions appears to be a promising direction for future research.
8 Conclusion
This paper revisited the macroeconomic effects of government consumption within a tractable incomplete-markets variant of the neoclassical growth model. Because private investment is subject to uninsurable idiosyncratic risk and because risk-taking is sensitive to wealth, the aggregate level of investment depends on the aggregate level of net-of-taxes household wealth for any given prices. It follows that an increase in government spending can crowd-out private investment simply by reducing household net worth. As a result, market incompleteness can seriously upset the supply-side effects of fiscal shocks: an increase in government consumption, even if financed with lump-sum taxation, tends to reduce capital intensity, labor productivity, and wages in both the short-run and the long-run. For plausible parameterizations of the model, these results appear to have not only qualitative, but also quantitative content.
These results might, or might not, be bad news for the ability of the neoclassical paradigm to explain the available evidence regarding the macroeconomic effects of fiscal shocks.28 However, the goal of this paper was not to study whether our model could match the data. Rather, the goal was to identify an important mechanism through which incomplete markets modify the response of the economy to fiscal shocks: wealth effects on investment.
In our model, these wealth effects originated from uninsured idiosyncratic investment risk combined with diminishing absolute risk aversion. Borrowing constraints could lead to similar sensitivity of investment to wealth (or cash flow).29 Also, this mechanism need not depend on whether prices are flexible (as in the neoclassical paradigm) or sticky (as in the Keynesian paradigm). The key insights of this paper are thus clearly more general than the specific model we employed--but the quantitative importance of these insights within richer models of the macroeconomy is, of course, a widely open question.
An important aspect left outside our analysis is the optimal financing of government expenditures. In this paper, we assumed that the increase in government spending is financed with lump-sum taxation, only because we wished to isolate wealth effects from the distortionary and redistributive effects of taxation. Suppose, however, that the government has access to two tax instruments, a lump-sun tax and a proportional income tax.30Clearly, with complete markets (and no inequality) it would be optimal to finance any exogenous increase in government spending with only lump-sum taxes. With incomplete markets, however, it is likely that an increase in government spending is financed with a mixture of both instruments: while using only the lump-sum tax would disproportionately affect the utility of poor agents, using both instruments permits the government to trade off less efficiency for more equality. Further exploring these issues, and the nature of optimal taxation for the class of economies we have studied here, is left for future research.
Bibliography
Appendix: Proofs
Proof of Proposition 1 (individual policy rules). Let ![]() denote the value function for the household's problem.
The value function depends on time
denote the value function for the household's problem.
The value function depends on time ![]() because of discounting as well as because the price sequence
because of discounting as well as because the price sequence
![]() need not be stationary. However, the value function does not depend on
need not be stationary. However, the value function does not depend on ![]() , because households have identical preferences, they have access to the same technology, and they face the same sequence of prices and the same stochastic process for idiosyncratic risk. The Bellman equation that characterizes the value function is given by:
, because households have identical preferences, they have access to the same technology, and they face the same sequence of prices and the same stochastic process for idiosyncratic risk. The Bellman equation that characterizes the value function is given by:
The first term of the Bellman equation
Because of the CRRA/CEIS specification of preferences, an educated guess is that there exists a deterministic process ![]() such that:
such that:
Because of the homogeneity of
It follows that the optimal
The first order conditions for
Substituting this into
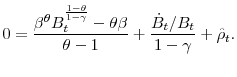 |
This ODE, together with the relevant transversality condition, determines the process for
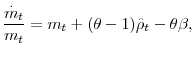 |
which is the Euler condition
Proof of Proposition 2 (equilibrium dynamics). Since aggregate labor demand is
![]() and aggregate labor supply is 1, the
labor market clears if and only if
and aggregate labor supply is 1, the
labor market clears if and only if
![]() It follows that the equilibrium wage satisfies
It follows that the equilibrium wage satisfies
![]() and, similarly, the equilibrium mean return to capital satisfies
and, similarly, the equilibrium mean return to capital satisfies
![]() The bond market, on the other hand, clears if and only if
The bond market, on the other hand, clears if and only if
![]() . Combining this with
. Combining this with
![]() gives condition (17).
gives condition (17).
Combining the intertemporal government budget with the definition of human wealth, we get
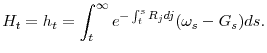 |
(30) |
Expressing this in recursive form gives condition (16).
Let
![]() denote the mean return to total saving. Aggregating the household budgets gives
denote the mean return to total saving. Aggregating the household budgets gives
![]() Combining this with (16) and with
Combining this with (16) and with
![]() , we get that
, we get that
![]() Using
Using
![]() , we get
, we get
![]() Together with the fact, in equilibrium,
Together with the fact, in equilibrium,
![]() this gives condition (14), the resource constraint.
this gives condition (14), the resource constraint.
Finally, using
![]() and therefore
and therefore
![]() together with
together with
![]() and
and
![]() , gives condition
, gives condition
![]() , the aggregate Euler condition.
, the aggregate Euler condition.
Proof of Proposition 3 (steady state). First, we derive the two equations characterizing the steady state ![]() and
and ![]() . In steady state, the Euler condition gives
. In steady state, the Euler condition gives
where
![\displaystyle \bar{\rho} =R+\frac{\left[ f^{\prime }\left( K\right)-\delta -R\right] ^{2}}{% \gamma \sigma ^{2}}\text{\ \ \ and\ \ \ }\phi =\frac{f^{\prime }\left( K\right)-\delta -R}{\gamma \sigma ^{2}} .](img353.gif) |
Combining and solving for
Next, we prove existence and uniqueness of the steady state. Let ![]() and
and
![]() denote, respectively, the risk premium and the fraction of effective wealth held in capital, when
denote, respectively, the risk premium and the fraction of effective wealth held in capital, when ![]() is given by (19):
is given by (19):
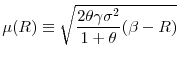 and and 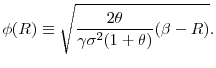 |
Note that
Finally, let
Note that we have used
Fix ![]() henceforth, and consider the limits of
henceforth, and consider the limits of ![]() as
as
![]() and
and
![]() Note that
Note that
![]() is finite and hence both
is finite and hence both ![]() and
and ![]() are finite. It follows that
are finite. It follows that
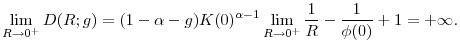 |
Furthermore,
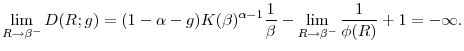 |
These properties, together with the continuity of
If we now show that
![]() is strictly decreasing in
is strictly decreasing in ![]() , then we also have uniqueness. To
show this, note that, from (32),
, then we also have uniqueness. To
show this, note that, from (32),
Now note that
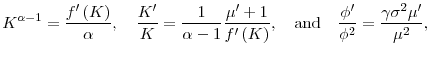 |
where we suppress the dependence of
![\displaystyle \frac{1-\alpha -g}{\alpha }\frac{f^{\prime }\left( K\right) }{R^{2}}\left[ R\frac{\mu ^{\prime }+1}{f^{\prime }\left( K\right) }-1\right] +\frac{\gamma \sigma ^{2}\mu ^{\prime }}{\mu ^{2}}=](img395.gif) |
|||
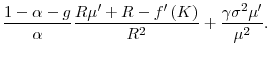 |
Since
Proof of Proposition 4 (incomplete vs complete markets). Since
![]() , wealth stationarity requires
, wealth stationarity requires
![]() . Combining this with the Euler equation
. Combining this with the Euler equation
![]() in steady state, we get
in steady state, we get
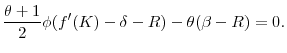 |
From this, and for steady-state capital to be lower than under complete markets, that is, for
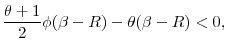 |
which, since
![]() For any
For any ![]() ,
, ![]() satisfies the following properties:
satisfies the following properties:
![]() for all
for all ![]() ;
;
![]() is decreasing in
is decreasing in ![]() and vanishes as
and vanishes as
![]() ; and, finally,
; and, finally,
![]() if and only if
if and only if
![]() which in turn is true if and only if
which in turn is true if and only if ![]() is
sufficiently high.
is
sufficiently high.
![]() For any
For any ![]() ,
,
![]() always;
always;
![]() as
as
![]() ,
,
![]() as
as
![]() .
.
![]() For any
For any
![]() as
as
![]() ,
,
![]() and
and
![]() (That is, the
(That is, the ![]() curve converges to the
curve converges to the
![]() curve, while the
curve, while the ![]() curve converges to the vertical line at
curve converges to the vertical line at
![]() .)
.)
Proof of Lemma 1.
![]() From
From
![]() it is clear that
it is clear that
![]() under complete markets, whereas
under complete markets, whereas
![]() under incomplete markets. Hence, for any given
under incomplete markets. Hence, for any given ![]() ,
steady-state
,
steady-state ![]() under incomplete markets is lower than under complete markets, which means that
under incomplete markets is lower than under complete markets, which means that ![]() lies below
lies below ![]() for every
for every ![]() . Since
. Since
![]() , it is clear that
, it is clear that ![]() , i.e. the distance between
, i.e. the distance between ![]() and
and ![]() , is
decreasing in
, is
decreasing in ![]() , and that it tends to zero as
, and that it tends to zero as
![]() . Finally, recall that
. Finally, recall that
![]() is equivalent to
is equivalent to
where
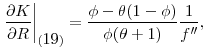 |
which proves that
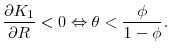 |
Since
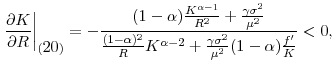
|
which proves that
Proof of Proposition 5 (steady-state impact of government spending). From (32), we have that
![]() Together with the property that
Together with the property that
![]() this implies that the steady-state
this implies that the steady-state ![]() necessarily
decreases with
necessarily
decreases with ![]() The impact of
The impact of ![]() on the steady-state
on the steady-state ![]() then follows from the fact that
then follows from the fact that
![]() defined by (19), does not depend on
defined by (19), does not depend on ![]() and is increasing in
and is increasing in ![]() if and only if
if and only if ![]() is higher than
is higher than
![]()
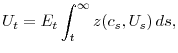
![\displaystyle z(c,U)\equiv\frac{\beta }{1-1/\theta }\left[ \frac{c^{1-1/\theta }} {((1-\gamma )U)^{\frac{-1/\theta +\gamma }{1-\gamma }}}-(1-\gamma )U \right] .](img25.gif)
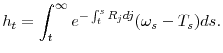
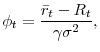
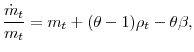
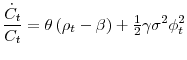
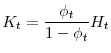
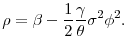
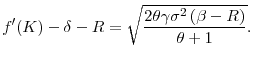
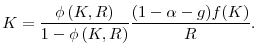
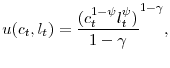
![\begin{displaymath}\begin{array}{llr} 0 &= &\max_{m,\phi }\left\{z(mw,J(w,t))+\frac{\partial J}{\partial t}(w,t)+% \frac{\partial J}{\partial w}(w,t)[\phi \bar{r}_{t}+(1-\phi )R_{t}-m]w \right. \\ & & \qquad \left. +\frac{% 1}{2}\frac{\partial ^{2}J}{\partial w^{2}}(w,t)\phi ^{2}w^{2}\sigma ^{2}\right\}. \end{array}\end{displaymath}](img315.gif)
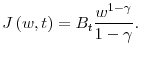
![\displaystyle 0=\max_{m,\phi }\left\{ \frac{\beta }{1-1/\theta }[B_{t}^{\frac{1/\theta -1}{% 1-\gamma }}m^{1-1/\theta }-1]+\frac{\dot{B}_{t}/B_{t}}{1-\gamma }+[\phi \bar{% r}_{t}+(1-\phi )R_{t}-m]-\frac{1}{2}\gamma \phi ^{2}\sigma ^{2}\right\} .](img325.gif)
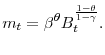
![\displaystyle K(R)=\left[ \frac{\mu (R)+\delta +R}{\alpha }\right] ^{\frac{1}{\alpha -1}}.](img366.gif)
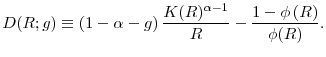
![\displaystyle \frac{\partial D}{\partial R}=(1-\alpha -g)\frac{K(R)^{\alpha -1}}{R^{2}}% \left[{(\alpha -1)R\frac{K^{\prime }(R)}{K\left( R\right) }-1}\right]+\frac{% \phi ^{\prime }(R)}{\phi \left( R\right) ^{2}} .](img389.gif)