State and Local Finances and the Macroeconomy:
The High-Employment Budget and Fiscal Impetus
Keywords: High-employment budget, fiscal impetus, net saving, fiscal policy, state and local government, budget policy
Abstract:
We examine the interplay of the economy and state and local budgets by developing and examining two measures of fiscal policy: the high-employment budget and fiscal impetus. We find that a 1 percentage point increase in cyclical GDP results in a 0.1 percentage point increase in NIPA-based net saving through the automatic response of taxes and expenditures. State and local budget policies are found to be modestly pro-cyclical. Stimulus to aggregate demand is about 0.2 percentage point less following a business cycle peak than it is during the period before the business cycle peak.
INTRODUCTION
Once again, states and localities are facing budgetary pressures and are being forced to take actions to get their fiscal houses in order. Indeed, as measured in the National Income and Product Accounts (NIPA), the sector has posted sizable deficits in its aggregate operating budget in recent quarters after having experienced a substantial improvement in budget conditions between 2002 and 2006. In this paper, we review recent developments affecting the sector and introduce some analytical tools that can help quantify the interactions between state and local budgets and the broader economy. We then use these tools to examine previous episodes of "budget repair" for insights about how the adjustment process plays out and how it affects the broader economy.
RECENT STATE AND LOCAL BUDGET DEVELOPMENTS
The fiscal condition of state and local governments lost some luster in 2007 after having improved significantly over the preceding few years; the difficulties have continued--and, in some cases, intensified in 2008. Although some governments--especially those in agricultural and energy-producing regions--continue to enjoy strong fiscal positions, others are reporting sizable shortfalls in revenues as a consequence of the macroeconomic slowdown and the downturn in real estate markets. Moreover, these difficulties have been compounded by rapid increases in energy and construction prices, along with ongoing pressure from Medicaid outlays.
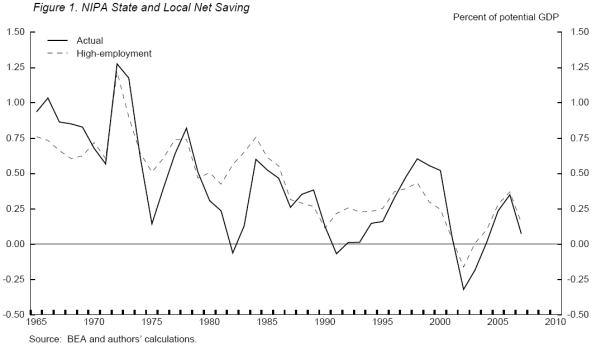
Our analysis is based on data from the NIPA. These data are aggregated across all state and local governmental units in the United States and are published on a quarterly basis by the Bureau of Economic Analysis (BEA); they are available through the second quarter of 2008 although the figures for recent years are subject to substantial revision. The key summary measure in the NIPA is net saving, which is the difference between current receipts and current expenditures and is broadly similar to the surplus or deficit in an operating budget. As Figure 1 indicates, the recent peak in net saving occurred in 2006, when it was equal to 0.4 percent of potential GDP ($46 billion)--similar to the levels reached in the late 1990s in dollar terms but somewhat smaller as a percent of GDP. However, net saving fell markedly in 2007 and turned sharply negative in the first half of 2008 as revenue increases tailed off after a period of hefty gains and as nominal expenditures--especially on energy and health care--soared.
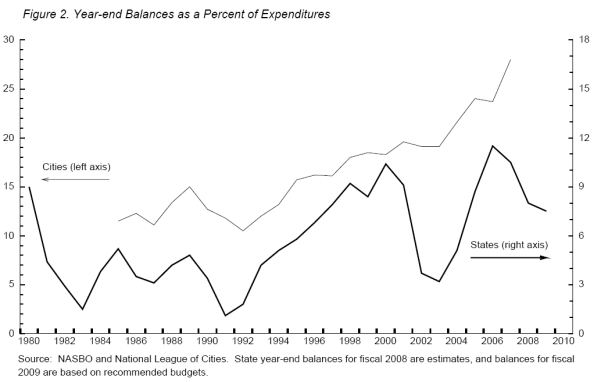
Information collected by the National Association of State Budget Officers (NASBO) is also useful in assessing the sector's fiscal condition and is presented in Figure 2.2 In the NASBO framework, the main summary indicator of the fiscal condition of the states is the aggregate balance at year-end in their general and rainy day (budget stabilization) funds. The year-end balance is a combination of stocks and flows. It captures both the flow from this year's new saving--revenues less expenditures--and the accumulated stock of savings from prior years. According to NASBO (2008), state balances at the end of fiscal 2006 were at a 30-year high (relative to expenditures) and remained elevated in fiscal 2007.3 However, tabulations of expected state budget balances as of spring 2008 point to some deterioration in fiscal 2008, and many states have reported sizable shortfalls in revenues in fiscal 2009. Data for local governments collected by the National League of Cities (2008) also point to strong budget balances in 2006 and 2007, although the organization's most recent report warned that cities' fiscal conditions have weakened dramatically since that time.
GOVERNMENT BUDGETS AND THE MACROECONOMY
State and local budgets return to the news with every cyclical downturn.4 Two questions are ever-present: (1) how much does the weakening of the economy hurt budget balances and (2) how much do actions taken to satisfy balanced budget requirements cut into overall employment and economic activity? Unfortunately, no single analytical apparatus provides satisfactory answers to both questions; thus, we rely on separate tools to answer these questions. To assess the effect of the business cycle on state and local budgets, we use a high-employment budget framework that allows us to separate NIPA net saving into its cyclical and non-cyclical components; our measure is based on the methodology developed for the federal budget by Frank de Leeuw et al (1980), refined by Cohen and Follette (2000), and subsequently applied to the state and local sector by Knight, Kusko, and Rubin (2003). To assess the effects of state and local budgetary actions on the broader economy, we adapt the "fiscal impetus" measure developed by Cohen (1987) for the federal government; this measure combines information from various sources to provide a summary indicator of the sector's discretionary budgetary actions.
High-Employment Budget
The high-employment budget methodology allows us to strip out the effects of cyclical macroeconomic developments on actual budget outcomes and thus provides an indication of the path the budget would have followed had the economy continually operated at its potential level. (Potential GDP must be estimated and is defined as the level of economic activity consistent with high and sustainable levels of resource utilization--of both labor and capital.) The high-employment cyclical adjustment reflects the automatic change in revenues and expenditures produced by cyclical swings in economic activity, i.e. deviations in actual GDP from potential GDP. By design, it is unaffected by the actions governments take to offset the automatic changes in revenue or expenditures, such as tax rate increases in response to falling receipts. Using this methodology, we can divide NIPA net saving into a "non-cyclical" component, which corresponds to the budget path associated with high-employment (or potential) GDP, and a "cyclical" component, which is the difference between actual net saving and high-employment net saving.
To construct our measure of the high-employment budget, we use the NIPA data on state and local net saving and the Congressional Budget Office's (CBO 2008a) estimates of potential GDP; we follow the procedure detailed in Cohen and Follette (2000) to adjust receipts and current expenditures to the levels they would attain if the economy were operating at its potential level. The cyclical adjustment to receipts, which accounts for the bulk of the total cyclical adjustment, depends upon three factors: the composition of receipts (Table 1), the estimated cyclicality of the base for each major tax, and the elasticity of the tax to the base. The bases for the major taxes are NIPA taxable personal income for personal taxes, NIPA corporate profits for corporate taxes, NIPA personal consumption expenditures on goods for sales taxes, and aggregate property values from the Federal Reserve's Flow of Funds accounts for property taxes.5
This is implemented through three sets of equations. Equations 1 and 2 cyclically adjust the tax bases, and equation 3 calculates the cyclical response of each component of receipts using its elasticity and the deviation of its tax base from the tax base's high-employment level.
(1) SHAREK
= SHARE
*(GDPGAP
/ GDPK
(2) BASEK = SHAREK * GDPK
(3) TAXK = TAX + TAX * ((BASEK /BASE 
- 1)*
(j,t)
For each variable, the "K" denotes the high-employment variable (potential GDP is therefore denoted as GDPK, SHARE
is the ratio of the base for the "j" th tax to GDP, GDPGAP is the difference between actual GDP and potential GDP, BASE is the relevant tax
base for the "j" th tax, TAX is tax revenue from tax "j", and (j,t) is the elasticity of tax "j" with respect to the tax base.
Following equation 1, we estimate the sensitivity of the tax bases to cyclical movements in GDP by regressing the change in the tax base (or its component parts) as a share of GDP on lags of the change in the GDP gap as a percent of potential GDP. The results are presented in Table 2, which indicates that the profit and wage shares of GDP (columns 1 and 2) are both cyclically sensitive in that, when the economy strengthens, profits rise relative to GDP and wages fall. Stated slightly differently, as GDP rises above its potential level, profits rise faster than GDP and become a larger percentage of GDP whereas wages fail to keep pace with GDP and become a smaller share of total GDP. The other income components as a share of GDP show little cyclical sensitivity. Personal consumption expenditures on goods--the base for sales taxes--as a share of GDP (column 9) also seems to show little cyclical sensitivity. We examined the cyclical sensitivity of aggregate property values somewhat differently, regressing the ratio of aggregate property values to potential GDP on the GDP gap terms (column 10), and found no statistically significant cyclical response.
The elasticities of the taxes to the tax bases are generally assumed to be 1 except for personal income taxes, corporate income taxes, and miscellaneous receipts. For personal income taxes, the estimation of the elasticity involves two steps. First, because state and local governments generally
use IRS definitions of income for their tax bases, we estimate the elasticity of the IRS measure of the personal income tax base to the NIPA-based personal income tax base. These estimates indicate that the IRS base has become quite elastic since the Tax Reform Act of 1986 (TRA-1986), increasing
from about unity before 1987 to about 1
afterwards. Second, we assume that the elasticity of state and local personal income taxes to the
IRS tax base is 1.1 because of the slightly progressive rate structure of state personal income tax schedules. Combining these two measures by multiplying them together, we estimate that the elasticity of personal income taxes to NIPA personal income was 1.1 before TRA-1986 and is now 1.5.
In contrast, we find that the elasticity of corporate income taxes with respect to the NIPA measure of the corporate tax base is less than 1. One reason is that the tax structure is essentially unit elastic for positive profits, but firms with losses pay no taxes (instead of paying negative taxes). In addition, a significant portion of corporate taxes owes to capital gains, which are not very cyclical.6 As a result of these factors, we estimate that the elasticity of corporate income subject to tax to NIPA corporate profits is about 0.8, and thus that the elasticity of corporate income taxes to NIPA corporate profits is 0.8.
For federal grants, we cyclically adjust Medicaid and AFDC grants using the procedure described below for Medicaid expenditures. For other grants, including TANF, there is no cyclical sensitivity because, in general, their levels are set through discretionary appropriations and not automatically affected by changes in economic activity. For miscellaneous taxes and fees, we estimate that the elasticity is 0.45.
On the expenditure side, we draw upon on Blank's (2001) analysis of welfare caseloads to estimate the cyclical sensitivity of Medicaid expenditures; thus, we model the cyclical portion of spending as a function of past changes in the unemployment rate.7 We use the NIPA data to generate cyclical sensitivities for all other transfer programs, but the estimated elasticities are small. Apart from transfers, we assume that the cyclical sensitivity of spending--principally on goods and services--is zero: Although governments may adjust spending in areas like education in response to changes in economic conditions, these adjustments are discretionary and thus do not qualify as the sort of automatic responses that are captured in our cyclical adjustment.
Combining our estimates of the cyclical response of revenues and expenditures, we find that each 1 percent drop in GDP reduces NIPA net saving by about 0.1 percent of GDP--equal to $13 billion in today's economy.8 Of the $13 billon hit to net saving, $11
billion comes from lower taxes and $1
billion comes from higher outlays for Medicaid (net of increased federal grants) and other transfer
payments. Most of the impact is on state governments because they rely heavily on cyclically sensitive income and sales taxes whereas local governments rely mainly on property taxes and grants from the states. Although states may transfer some of the "pain" to local governments by reducing
grants, these are policy actions--not automatic responses.
Figure 1 contains our estimates of state and local high-employment net saving as a percent of GDP. The gap between high-employment and actual net saving is closely related to the gap between potential and actual GDP and represents the cyclical component of the budget. When actual GDP is equal to
its potential level, the cyclical component is zero and actual net saving and high-employment net saving are the same. When actual GDP is below potential--as typically occurs during recessions and early expansion periods--the cyclical component of net saving is negative, and actual net saving is
lower than high-employment net saving. When actual GDP exceeds potential, the reverse is true. For example, in 2000, net saving was equal to positive $50 billion (
percent of GDP) with the cyclical component of net saving equal to $27 billion (Table 3). By 2003,
net saving had fallen to negative $20 billion, with the cyclical component equal to negative $21 billion. Accordingly, cyclical influences accounted for $48 billion--about two-thirds--of the $70 billion downswing in net saving over this period.
Once the cyclical portion of net saving has been stripped out, the remainder--that is, the "non-cyclical" portion--provides a first cut at the underlying trends in the sector's budget. It is important to realize, however, that movements in the non-cyclical budget are driven not only by legislative actions like tax cuts or changes in provisions of spending programs but also by factors like increases in health care costs or changes in the distribution of income that affect taxes and spending but are not the result of policy decisions. In addition, the cyclical adjustment--by design--does not capture all of the exogenous factors that may be associated with any particular business cycle--for example, the steep decline in capital gains taxes that accompanied the 2001 recession.9 The decline in capital gains around this period caused high-employment net saving to fall at the same time the cyclical component of net saving was also declining. Another consideration that limits the usefulness of the high-employment budget as a measure of the sector's macroeconomic impact is that it reflects only current spending and thus is unaffected by the sector's investment spending, which can have significant effects on overall GDP growth. Accordingly, to address these issues and better isolate the effects of policy actions, we developed an alternative measure, called fiscal impetus (see Cohen (1987)).
Fiscal Impetus
"Fiscal impetus" is a bottom-up approach that involves developing a measure of each major type of state or local budget action--for example, a cut in personal taxes or an increase in Medicaid reimbursement rates--and aggregating them into a single fiscal indicator that quantifies the impulse to growth in real GDP coming from state and local budget decisions. The weights used for the aggregation are based on estimates of the effects of budgetary actions on the growth of GDP. For example, the weight applied to a reduction in personal taxes is based on an estimate of the increase in aggregate consumer spending induced by the tax cut--that is, the marginal propensity to consume (MPC). Thus, fiscal impetus is model dependent. For this analysis, we use an MPC of 0.7 for changes in taxes--in other words, we assume that a tax reduction of $1 million produces $700,000 in additional consumption--and an MPC of 1.0 for changes in transfer payments; changes in purchases of goods and services also receive a weight of one. These estimates are consistent with the coefficients in the macroeconomic models used by the Federal Reserve Board staff. The higher MPC for transfers than for taxes reflects the fact that most transfers go to lower-income households, which are more likely to be liquidity constrained than the taxpaying population as a whole. Our measure is designed to quantify the first-round effects of policy changes on GDP growth. It does not take account of subsequent multiplier effects. It also does not capture the effects of cyclical movements in taxes and transfers.
Whenever possible, we use direct information to construct our estimates of state and local "policy" actions--for example, we use NASBO's figures for enacted state revenue changes to estimate changes in state tax policy. However, we have no such sources for either local taxes or for expenditures; thus, we have developed NIPA-based measures of policy change that we believe are satisfactory alternatives. With regard to local taxes, our policy indicator is the ratio of NIPA property tax receipts to nominal potential GDP, which we dub the effective property tax rate. When this effective tax rate is constant from one year to the next, policy is defined as being constant. Movements in the effective tax rate are interpreted as changes in policy; in general, they occur because localities make adjustments to their statutory tax rates or because the rate of increase in average property assessments differs from the rate of overall inflation (as measured by the GDP price index).10 Thus, when property values rise and local governments do not offset the increase with a decrease in the statutory tax rate, we score the change in revenue as a policy induced tax increase. For example, in a year when property assessments rise 20 percent, on average, overall prices rise 3 percent, and statutory tax rates are constant, on average, the effective tax rate--our policy indicator--would show an increase of 17 percent. In a scenario where localities cut the statutory tax by 5 percent in response to the run-up in assessments, the effective tax rate would rise 12 percent; this increase in the effective tax rate--not the 5 percent cut in the statutory rate--would represent the policy change.
On the expenditure side, we define constant policy for Medicaid as a constant ratio of outlays (net of federal grants) to potential GDP, and we interpret deviations in this ratio as changes in policy.11 We use a similar algorithm for other transfers. For purchases of goods and services, we include both consumption and investment expenditures and define constant policy as a constant real (i.e. inflation-adjusted) level of purchases. To measure the real demand effect of taxes and transfers, we deflate the nominal values of these items by the price index for personal consumption expenditures. After aggregating all of these effects together, we scale the result by real GDP to obtain a percentage point contribution to growth in real GDP.
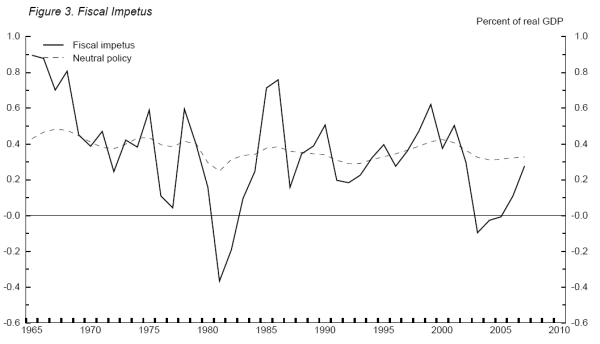
As Figure 3 indicates, state and local fiscal impetus varies a good deal from year to year. The variation was especially large in the 1980s, when fiscal impetus went from being sharply negative in the early years of the decade to quite expansionary by the middle of the decade--indeed, by
1985-86, state and local government policy actions were contributing
percentage point per year to real GDP growth. (In total, real GDP rose 4 percent in 1985 and 3
percent in 1986.) In the late 1980s and the first half of the 1990s, fiscal impetus diminished as
governments grappled with budget difficulties. However, it picked up in the late 1990s and remained elevated until budget difficulties forced another round of belt tightening in the current decade. Indeed, fiscal impetus fell to about zero during 2003-06, although it moved up in 2007 to
percent of GDP as real sector purchases rose moderately and tax and transfer policies were little
changed on net.
From a macroeconomic perspective, it is useful to examine not just whether state and local budget actions are contributing to or subtracting from GDP growth, but also whether they are helping GDP to increase above or below its potential rate. In this context, a neutral fiscal stance--represented
by the line labeled "neutral policy" on Figure 3--corresponds to the impetus to GDP growth that would emanate from the state and local sector if each component of taxes and expenditures were to grow at the rate of potential GDP. In such a case, the impetus coming from taxes and transfers would
each be zero, and the impetus from purchases would be equal to the rate of growth in real potential GDP (currently estimated by CBO to be 2
percent per year) times the share of state and local purchases in GDP (12
percent in 2007). Under a neutral fiscal stance, the share of total GDP accounted for by the state
and local sector would remain constant over time. The neutral stance fluctuates over time as a result of changes in either potential growth or in the ratio of state and local purchases to GDP and in recent years has been equal to about
percent of GDP. Thus, state and local government budget actions were consistent with GDP growing at
about its potential rate in 2007 after having been in the "below neutral" range over the preceding four years.
PRIOR BUSINESS CYCLES
Our two fiscal measures can provide useful insights on the behavior of state and local budgets around cyclical turning points.12 First, our
high-employment budget measure allows us to quantify the roles of "cyclical" and "other" factors in explaining the declines in net saving during the cyclical downturns of the past four decades (Table 4). As column 7 of the table suggests, the negative contribution to net saving from cyclical
factors was on the order of
percent of GDP (or close to it) in most of the five episodes shown. In three of the five cases,
non-cyclical factors had a neutral or small net positive effect on state and local budgets; in the remaining two cases, the budget erosion was amplified when other negative influences coincided with the cyclical downturn (column 8). For example, as noted earlier, the sharp decline in net saving
between 2000 and 2003 reflected sizable downshifts in both its cyclical and non-cyclical components; the latter occurred because the positive effects of budget tightening efforts were more than offset by the drop in capital gains realizations and other factors.
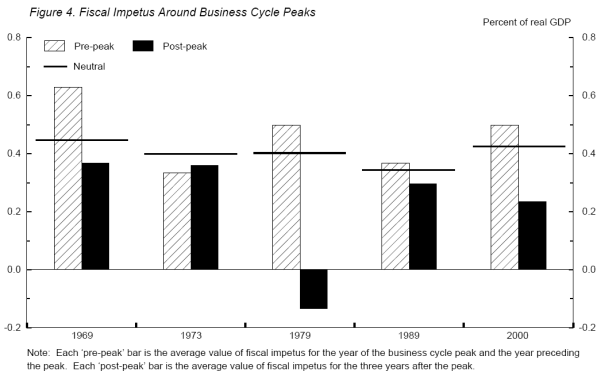
In terms of policy reactions, Figure 4 (with additional detail in Table 5) focuses on the behavior of our fiscal impetus measure around past business cycle peaks; it shows the impulse to growth in real GDP from the state and local sector during the two years up to and including the peak and during the three years after the peak. In all five episodes, policy was expansionary leading up to the peak. During the period following the peak, the amount of stimulus usually diminished and was only about half as large, on average, as it had been in period leading up to the peak; the drop-off in fiscal impetus between the two periods amounted to about 0.2 percent of GDP. The one outlier occurred after the 1973 peak, when fiscal impetus remained virtually the same as it had been preceding the peak.13 This atypical policy response may reflect the high level of net saving in 1972-73, which gave governments some scope for dissaving and stimulus. In addition, in the early 1970s, the state and local sector was expanding in many dimensions--education, welfare, environmental cleanup, etc.; these expansions were supported in part by increased federal grants, which lowered the implicit prices of some of these programs.
THE CURRENT SLOWDOWN AND LIMITATIONS OF THESE ANALYITCAL TOOLS
State and local budget positions have deteriorated sharply in recent quarters. Much of the pressure apparently has been on state budgets. State tax bases are more cyclically sensitive than those of local governments, and states are largely responsible for cyclically sensitive transfers such as Medicaid and TANF. If history is a guide, states will act to satisfy their balanced budget constraints over time and will use one-off measures to smooth the transition. However, they will likely transfer some of the pain to local governments through reductions in aid.
Will this time be different than previous slowdowns? Yes, it always is. One major consideration in applying our results to the current situation is that our analysis is geared to identifying the regular effects of the business cycle on state and local budgets and thus probably does not capture the full effects of the downturn in the housing market. These include the stresses on local budgets caused by the drop in home prices, the reduction in sales tax receipts associated with the exceptional weakness in retail sales of items related to housing, and the loss of real-estate transactions taxes and fees.14 Moreover, personal income taxes have been bolstered in recent years by strong collections of capital gains taxes. If capital gains receipts weaken in 2009--as seems likely in light of the performance of the stock market in 2008--state and local budgets could come under even more pressure than a high-employment budget analysis would suggest.
CONCLUSION
Our analysis yields two major conclusions. One is that macroeconomic developments contribute importantly to swings in state and local net saving--albeit much less than at the federal level: We estimate that, in today's economy, a 1 percent drop in GDP relative to potential--roughly equal to a
percentage point rise in the unemployment rate--would lower state and local net saving about $13
billion. If, for example, governments wanted to maintain their prior net saving positions in the face of the weaker economy, they would have to raise own-source revenues by 1 percent, cut current expenditures a comparable amount (in dollar terms), or undertake a combination of the two. Our second
conclusion is that while actions taken by state and local governments to keep budgets on track may have substantial effects on individual programs and populations, the impact of these actions on overall economic activity is relatively modest. The modest effect probably owes in part to the ability
of state and local governments to spread budget-repair efforts over a period of several years as well as the fact that balanced budget requirements help keep the sector's expenditures and revenues from getting too far off track.
We thank Eric Engen, Therese McGuire, and participants at the Spring 2008 NTA State and Local Symposium for helpful comments and suggestions. Thanks to Brian McGuire and Samuel Brown for excellent research assistance. The analysis and conclusions set forth are those of the authors and do not indicate concurrence by other members of the Federal Reserve research staff or the Board of Governors.
References
Blank, Rebecca. "What Causes Public Assistance Caseloads to Grow?" Journal of Human Resources 36 No. 1 (Winter, 2001): 85-118.
Cohen, Darrel. "Models and Measures of Fiscal Policy." Working Paper Series, Economic Activity Section No. 70. Washington D.C.: Board of Governors of the Federal Reserve System, 1987.
Cohen, Darrel and Glenn Follette. "The Automatic Fiscal Stabilizers: Quietly Doing Their Thing." Economic Policy Review 6 No. 1 (April, 2000): 35-68.
de Leeuw, Frank, Thomas Holloway, Darwin Johnson, David McClain, and Charles Waite. "The High-Employment Budget: New Estimates, 1955-1980." Survey of Current Business (November, 1980): 13-43.
Knight, Brian, Andrea Kusko and Laura Rubin. "Problems and Prospects for State and Local Governments." State Tax Notes (August 11, 2003): 427-439.
Lutz, Byron. "The Connection Between House Price Appreciation and Property Tax Revenues." National Tax Journal (September, 2008): 555-572.
National Association of State Budget Officers. The Fiscal Survey of the States. Washington D.C. June 2008.
National Conference of State Legislatures. State Budget Actions FY 2007 and FY 2008. Denver CO. April 2008.
National League of Cities. City Fiscal Conditions in 2008. Washington D.C. 2008.
Uchitelle, Louise. "Think the Economy is Bad? Wait Till the States Cut Back." New York Times (June 1, 2008).
U.S. Congressional Budget Office. The Budget and Economic Outlook: An Update. Washington D.C. 2008a.
U.S. Congressional Budget Office. The Cyclically Adjusted and Standardized Budget Measures. Washington D.C. 2008b.
| Total | State | Local | |
|---|---|---|---|
| Personal income taxes | 15.2 | 20.9 | 2.3 |
| Corporate income taxes | 3.1 | 4.2 | 0.5 |
| Sales taxes | 22.3 | 27 | 7.5 |
| Property taxes | 19.9 | 0.8 | 33.6 |
| Grants from government | 19.2 | 27.9 | 41.7 |
| Miscellaneous | 20.3 | 19.3 | 14.4 |
Source: BEA, National Income and Product Accounts (tables 3.3, 3.20, and 3.21)
Miscellaneous receipts include income receipts on assets, fees from businesses and individuals, current surplus of government enterprises, and other items.
| Independent variable | Dependent variable* #1: ( (Corporate income tax base:profits / GDP) |
Dependent variable* #2: ((Personal income tax base: wages / GDP) |
Dependent variable* #3: ((Personal income tax base: supplements / GDP) |
Dependent variable* #4: ((Personal income tax base: proprietor's income / GDP) |
Dependent variable* #5: ((Personal income tax base: rental income / GDP) |
Dependent variable* #6: ((Personal income tax base: net interest / GDP) |
Dependent variable* #7: ((Personal income tax base: other interest / GDP) |
Dependent variable* #8: ((Personal income tax base: dividends / GDP) |
Dependent variable* #9: ((Sales tax base: personal consumption of goods / GDP) |
Dependent variable* #10: ((Property tax base: Property values** / GDP) |
|---|---|---|---|---|---|---|---|---|---|---|
| gap(t) | 0.285 | -0.202 | -0.033 | -0.028 | -0.024 | -0.037 | -0.024 | -0.011 | -0.076 | 0.002 |
| gap(t) (T-statistic) | -10.628 | (-10.302) | (-4.674) | (-1.884) | (-2.587) | (-3.261) | (-3.925) | (-1.264) | (-2.547) | -1.473 |
| gap(t-1) | -0.034 | 0.112 | 0.009 | 0.002 | 0.006 | -0.007 | 0.017 | 0.009 | 0.011 | 0.002 |
| gap(t-1) (T-statistic) | (-1.164) | -5.519 | -1.259 | -0.104 | -0.593 | (-0.599) | -2.709 | -0.945 | -0.369 | -1.451 |
| gap(t-2) | -0.048 | 0.049 | -0.002 | 0.017 | -0.006 | 0.013 | 0.001 | 0.01 | 0.031 | 0.002 |
| gap(t-2) (T-statistic) | (-1.699) | -2.432 | (-0.318) | -1.121 | (-0.590) | -1.078 | -0.096 | -1.126 | -1.036 | -1.689 |
| gap(t-3) | -0.012 | 0.072 | 0.009 | 0.012 | 0.001 | 0.018 | -0.002 | -0.003 | -0.091 | 0.004 |
| gap(t-3) (T-statistic) | (-0.446) | -3.753 | -1.322 | -0.828 | -0.131 | -1.545 | (-0.364) | (-0.292) | (-3.085) | -3.233 |
| gap(t-4) | -0.107 | 0.002 | -0.006 | -0.001 | 0.003 | -0.006 | 0.003 | -0.009 | 0.031 | -0.0003 |
| gap(t-4) (T-statistic) | (-4.005) | -0.121 | (-0.960) | (-0.053) | -0.335 | (-0.551) | -0.561 | (-1.054) | -1.08 | (-0.222) |
| Adj. R2 | 0.38 | 0.411 | 0.083 | 0.006 | 0.014 | 0.051 | 0.058 | 0 | 0.044 | 0.102 |
Observations are quarterly. Sample period is 1950 to 2006. T-statistics are in parentheses.
Gap equals (actual GDP - potential GDP)/potential GDP and then first differenced.
* Dependent variable* is NIPA-based tax base divided by actual GDP and then first differenced.
** Property values are the aggregate value of household and commercial real estate as a share of potential GDP. Data on the value of real estate are from the Federal Reserve Board's Flow of Funds Accounts.
| Year | Total net saving | Non-cyclical net saving | Cyclical net saving | Cyclical own receipts: total | Cyclical own receipts: personal | Cyclical own receipts: corporate | Cyclical own receipts: sales | Cyclical own receipts: other | Cyclical expenditures net of grants: total | Cyclical expenditures net of grants: Medicaid | Cyclical expenditures net of grants: other |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2000 | 50 | 23.4 | 26.5 | 24.3 | 10.5 | 3.8 | 8 | 2 | -2.3 | -0.7 | -1.6 |
| 2003 | -20.4 | 0.8 | -21.2 | -17 | -7.2 | -2.4 | -6 | -1.4 | 4.3 | 1.7 | 2.6 |
| Change | -70.4 | -22.6 | -47.7 | -41.3 | -17.7 | -6.2 | -14 | -3.4 | 6.6 | 2.4 | 4.2 |
Source: Authors' calculations.
Note: Medicaid figures are net of federal grants. In 2003 the high level of unemployment raised total Medicaid expenditures by $4.4 billion, of which state governments paid $1.7 billion and the federal government paid $2.7 billion.
| Cycle Peak | Cycle Trough | GDP Gap (percent of potential GDP): Cycle Peak | GDP Gap (percent of potential GDP): Cycle Trough | GDP Gap (percent of potential GDP): Change | Change in Net Saving (percent of GDP): Total | Change in Net Saving (percent of GDP): Cyclical | Change in Net Saving (percent of GDP): Other |
|---|---|---|---|---|---|---|---|
| 1969 | 1971 | 2.4 | -0.9 | -3.3 | -0.24 | -0.24 | 0 |
| 1973 | 1975 | 3.5 | -4.3 | -7.8 | -0.99 | -0.65 | -0.34 |
| 1979 | 1982 | 0.5 | -6.6 | -7.1 | -0.57 | -0.71 | 0.14 |
| 1989 | 1991 | 1 | -2.8 | -3.8 | -0.45 | -0.41 | -0.04 |
| 2000 | 2003 | 2.6 | -1.7 | -4.3 | -0.69 | -0.46 | -0.23 |
Note: Estimates are for calendar years. Our cyclical dating system is based on the movements in the GDP gap (as estimated by CBO). Dates of cyclical peaks and troughs correspond to local maximum and minimum values for the GDP gap.
Source: CBO, BEA, and authors' calculations.
| Business cycle peak: 1969 | Business cycle peak: 1973 | Business cycle peak: 1979 | Business cycle peak: 1989 | Business cycle peak: 2000 | Average | |
|---|---|---|---|---|---|---|
| 1 year before | 0.81 | 0.25 | 0.6 | 0.34 | 0.62 | 0.52 |
| Year of peak | 0.45 | 0.42 | 0.4 | 0.39 | 0.38 | 0.41 |
| 1 year after | 0.39 | 0.38 | 0.16 | 0.51 | 0.5 | 0.39 |
| 2 years after | 0.47 | 0.59 | -0.37 | 0.2 | 0.3 | 0.24 |
| 3 years after | 0.25 | 0.11 | -0.19 | 0.18 | -0.1 | 0.05 |
| Average before | 0.63 | 0.34 | 0.5 | 0.37 | 0.5 | 0.47 |
| Average after | 0.37 | 0.36 | -0.13 | 0.3 | 0.23 | 0.23 |
Source: Authors' calculations.
Note: The average displayed in the final column is taken over the first 5 columns of the table.
Footnotes
The views expressed are those of the authors and do not necessarily represent those of the Board of Governors or other members of its staff. Return to Text
percent increase in welfare caseloads over eighteen months, which declines to about a 2 percent
increase after three years. In addition to welfare recipients, Medicaid covers the disabled and the poor elderly; participation by these groups is not cyclical. Return to Text percent of GDP in 2000 to 2
percent of GDP in 2002. Based on estimates from the NBER's Taxsim model, we use an average effective
tax rate for state income taxes of 5 percent. After factoring in the usual lags between liabilities and payments of capital gains taxes, this suggests that states collected about $20 billion less in capital gains taxes in 2003 than they did in 2001.