
Does Speculation Affect Spot Price Levels?
The Case of Metals with and without Futures Markets
JEL Codes: G13
1. Introduction
The role of financial speculators in the market place has been debated by academics and practitioners since the inception of futures markets. Following the seminal work of Kaldor (1939), the literature has primarily focused on whether speculative activity in the futures markets stabilizes (i.e. reduces the variance) of commodity spot prices. Part of the literature finds that the introduction of futures contracts destabilizes the spot market (Finglewski (1981), Simpson (1985), Hart and Kreps (1986), Newbury (1987), Stein (1987)). On the other extreme, Cox (1976), Turnovsky (1983), and Turnovsky and Campbell (1985) support the view that speculation is welfare improving because it reduces the variability of spot prices.
In the midst of this debate, the issue of whether speculation has a direct effect on the level of spot prices has been ignored. Recently however, commodity prices and speculative activity rose dramatically. Buyuksahin, Haigh, and Robe (2008) report that by 1999 about 5 billion dollars were invested in vehicles tracking the Standards and Poor Goldman Sachs Commodity Index (SPGSCI). By the third quarter of 2008, the investments linked to five prominent commodity indices, including the SPGSCI, rose to 140 billion. The increased participation of financial investors in the futures markets has sparked a debate on whether speculation led to the spike in commodity spot prices for some agricultural and energy products.1
Financial investors did not only seek exposure to agricultural and energy product prices because many financial investors participated in the futures markets through commodity index funds. Such funds hold futures in a variety of products because they track commodity indices like the SPGSCI.2 Therefore, if the trading activities of financial investors caused spot price appreciation, they should have affected the prices of most products in the index funds. In this study, I take up this issue and investigate the potential impact of speculation on commodity spot prices of metals, a prominent category in commodity index funds. Metals offer a unique "natural" experiment because there are metals with established futures contracts (which are included in commodity funds) and metals with no futures contracts (and thus not included in commodity funds).
My analysis offers a comparison between the spot (cash) prices across industrial metals with and without futures contracts and it is organized around two key themes. To begin with, industrial metals are primarily used in the manufacturing sector in a complementary fashion. For example, they are typically used in the form of alloys.3 Being complements to one another implies that their spot prices should be positively correlated. Therefore, if speculative activity in the futures markets were directly affecting the physical markets of the traded metals (i.e. the metals for which there are futures contracts available), then the positive correlation between the price changes of traded and non-traded commodities should weaken. Based on this prediction, the first set of empirical findings investigates the comovement between traded and non-traded metals.
I test the comovement hypothesis by studying the time patterns of metals with and without futures contracts. Over the period 1991 to 2008, I find that the correlation of metal price growth rates was consistently positive and did not decrease after 2000. I also show that the prices for metals with and without futures contracts increased substantially after 2002. The 2002 rise in prices is economically and statistically significant according to the structural break statistical tests developed by Andrews and Ploberger (1994).4
To understand the causes behind the comovement and upward shift in prices after 2002, I study the potential role of supply and demand factors in two ways. First, I use the world GDP growth rate to capture world economic activity. I find that world growth rate is positively correlated with metal price growth. Also, similar to metal price growth rates, world growth started to steadily rise after 2002. Therefore, accounting for world growth reduces the statistical significance of the structural break in metal spot prices.
Second, I study the supply and demand information that was available to the metals markets from September 1, 2003 to April 1, 2004. During this six month period all metal prices rose. I use the search engine Factiva to identify reports from industry newsletters with information on metal production, inventories, demand, etc. I use the number of reports as my information proxy. I find that for both traded and non-traded metals, the price-increasing news reports (i.e., news related to disruption of production, rising production costs, etc.), outnumber price-decreasing news reports (i.e. news related to increase in inventories, drop in consumption, etc). Thus, fundamental information about the metal markets could explain the acceleration of metal prices after 2002.
The previous findings demonstrate that the complementary relationship between traded and non-traded metal remained strong even after 2002 when speculative activity rose. Next, I study the link between speculation in futures markets and spot price appreciation more directly. For this test, I focus on the S&P Goldman-Sachs Commodity Index (SPGSCI). The SPGSCI is a weighted average of many commodity spot prices. It is tracked by many financial instruments and its returns are representative of the earrings related to investing in commodity futures contracts.
Ideally, I would like to examine if the volume in SPGSCI related instruments (measured by net open interest) had any impact on metal prices. Unfortunately, the public open interest data provided by the Commodity Futures Trading Commission (CFTC) are very limited. With this limited data, I show that the realized returns of the SPGSCI (which are available for all the years in my sample) are positively related to the net open interest of the SPGSCI contract traded on the Chicago Mercantile Exchange (CME). This is a reasonable finding because high returns from investing in the futures markets should attract more financial investors in the futures markets. Using the realized returns as a proxy for volume, I show that the SPGSCI return is unrelated to the price appreciation of metals. On the one hand, it cannot explain the shift in prices in 2002, and in general, it is not correlated to metal price growth rates.
The final test relies on implications related to no-arbitrage/storage models of commodity prices (Pindyck (2001)). In these models, speculative activity in the futures market can affect spot market price if it causes hoarding of inventories from the physical market, i.e. suppliers of commodities restrict supply to the physical markets and enter into futures contracts with speculators. In the presence of physical hoarding, contrary to standard supply and demand models, inventory formation is associated with spot price appreciation. To test the latter hypothesis, I focus on metals with futures markets. I proxy for their inventory changes with the growth of world-wide commercial stocks reported in the World Metals Statistics Yearbook. My analysis finds no evidence of physical hoarding. In particular, inventory growth is negatively correlated with price growth. Also, this negative relationship is present even after 2002.
Overall, the current paper is among the first to show that the run up in spot metal prices after 2003 is related to economic fundamentals and not to speculation by financial investors. The evidence relies on several empirical findings. First, consistent with the fact that non-precious metals are used in a complementary fashion, I find that their price growth rates are positively correlated. Their comovement is also magnified by a common structural break at the beginning of 2003. The structural break is related to supply and demand factors and it occurred around the same time as the acceleration in world economic activity. In addition, the return to the SPGSCI, a proxy for the volume in speculative activity in the futures markets, is unrelated to metal price growth rates. Finally, consistent with storage models, the negative relationship between inventory growth and price growth of trade metals has not been affected by speculation.
Beyond the contribution to the debate on speculation, the paper makes several important contributions to the literature on commodity prices. To begin with, it complements the existing studies on futures markets. It shows that speculation does not affect the level of spot prices because there is no evidence of physical hoarding. In addition, the evidence supports the predictions of various storage models. For instance, consistent with Turnovsky (1983) and Chari, Jagannathan and Jones (1990), I find that traded metals exhibit lower variability and spot price appreciation compared to non-traded metals.
The rest of the paper is organized as follows. Section 2 describes the commodity price data. Section 3 presents graphical evidence on the behavior of the spot price growth rate indices for traded and non-traded commodities. It also deals with the statistical significance of the structural break in the price growth series. Section 4 tests whether this break can be explained by economic (supply and demand) fundamentals. Section 5 looks into the relationship between metal prices, the return of the SPGSCI, and inventory growth. Finally, Section 6 provides a short literature review and Section 7 concludes the discussion.
2. Data and Methodology
My empirical analysis focuses on quarterly and annual price growth rates which are based on daily spot price data I obtained from Bloomberg. I supplement the Bloomberg data with data from the website of the U.S. Geological Survey.5 Specifically, I collect data on non-precious metals. The class of traded metals (i.e. commodities with established futures markets) includes copper, aluminum, lead, nickel, tin, and zinc. I choose the latter five commodities because they have standardized and widely traded contracts on either the Chicago Mercantile Exchange (CME) or the London Metal Exchange (LME).6 The class of non-traded commodities (i.e. commodities without any futures markets) includes steel, manganese, cadmium, cobalt, tungsten, rhodium, ruthenium, and molybdenum.7 These commodities are truly non-traded because there no futures contracts for them on the organized exchanges. Moreover, they cannot be indirectly traded because futures contracts on their alloys are also not available.8
The paper examines industrial metals because there are sufficient commodities in both the traded and non-traded classes to allow a meaningful comparison of the two commodity classes. This is not the case for other commodity classes like the agricultural products; in this instance most of them have established futures markets. Apart from data constraints, non-precious metals are typically used in tandem. Therefore, they are complementary goods and their prices should move together. I use this prediction to test whether speculation has affected this fundamental complementary relationship.
Apart from using the growth rates of individual metals, the comparison between the traded and non-traded metals uses growth rate indices. The index for each commodity class uses daily spot prices and it is calculated in three steps. First, I calculate the quarterly (annual) price at quarter
(year) ![]() of commodity
of commodity ![]() , (P
, (P![]() by a time-series average of all available daily prices in quarter (year)
by a time-series average of all available daily prices in quarter (year) ![]() . Second, I compute the quarterly (annual) price growth rate,
dP
. Second, I compute the quarterly (annual) price growth rate,
dP![]() , using the difference in natural logarithms, [ln(P
, using the difference in natural logarithms, [ln(P![]() -
ln(P
-
ln(P![]() ], which is multiplied by a 100. Third, I obtain the value of the growth rate index at
], which is multiplied by a 100. Third, I obtain the value of the growth rate index at ![]() using the simple (not weighted) cross-sectional average of dP
using the simple (not weighted) cross-sectional average of dP![]() across the commodities in either the traded and non-traded class.
across the commodities in either the traded and non-traded class.
The time period of the study is from 1991 to 2008 for the annual data. I choose this period because the daily price data for almost all non-traded commodities have many missing values prior to 1991. Because of missing values in the case of ruthenium, the quarterly data cover the 1992(Q4) to 2008(Q4) period. I do not use monthly or daily data because there are many missing values for the non-traded metals. Therefore, monthly and daily growth rates cannot be meaningfully computed.
To set the stage for the main empirical analysis, I present simple descriptive statistics for the individual metals and their indices in Table 1. I find that over the full sample period both traded and non-trade metals experienced price inflation. However, the price of non-traded ones rose substantially more. For example, the average annual growth rate for traded is 4.2% while for the non-traded is 7.2%. Moreover, the standard deviation of most non-traded metals is higher than most traded ones. These results are consistent with the model of Turnovsky (1983) and the baseline model of Chari, Jagannathan and Jones (1990).
3. Comovement across Non-Precious Metals
Using the metal price growth rates, I develop my empirical analysis around two themes. First, starting with this section, I study the comovement between traded and non-traded metals. In the second set of tests, I focus more directly on the potential link between speculation and spot prices.
3.1 Economic Intuition
In this section, I develop and test my first hypothesis, which is based on the intuition from no arbitrage/storage models. In these models, financial investors can affect spot price levels if their behavior prompts producers and storers of goods to hoard supply from the physical markets.9 Assume that rising speculative activity in the futures markets leads to an increase in today's futures contract price, ![]()
![]() , where
, where ![]() is the
delivery day. Responding to high futures prices, stores enter into futures contract with financial investors. Because storers sell their goods for futures delivery, inventory levels rise and the supply of goods to the physical markets declines. Physical hoarding then leads to higher spot prices. At
the delivery date,
is the
delivery day. Responding to high futures prices, stores enter into futures contract with financial investors. Because storers sell their goods for futures delivery, inventory levels rise and the supply of goods to the physical markets declines. Physical hoarding then leads to higher spot prices. At
the delivery date, ![]() , the futures price further increases as it converges to the new high spot price.10 Thus, physical hoarding implies a positive relationship between inventory growth and spot price inflation.11
, the futures price further increases as it converges to the new high spot price.10 Thus, physical hoarding implies a positive relationship between inventory growth and spot price inflation.11
Directly testing the above scenario is very difficult. It requires a great deal of precise trading and inventory data. Because commodity markets are international and trading takes place on regulated and unregulated markets (for example, over-the-counter markets) it is impossible to gather all the relevant data. Moreover, in the case of inventories, it is not clear what the appropriate definition of inventory is. Probably, inventory numbers should include commodities in storage and account for reserves in the ground. But the latter component cannot be measured precisely.
3.2 Traded and Non-Traded Metals
In this paper, I sidestep the aforementioned data difficulties by offering a comparison between traded and non-traded metals. To begin with, because non-precious industrial metals are complementary goods, their prices should be positively correlated. If speculative activity in the futures markets induces storers and producers to increase their inventories of traded goods, the complementary relationship between traded and non-traded industrial metals should weaken. This would imply that the positive correlation across their price growth rates should fall.
For example, take the case of the aluminum-manganese (Al-Mn) alloy.12 Assume that speculative activity in aluminum futures contracts has lead to physical hoarding of aluminum from the aluminum cash markets. The declining supply of aluminum raises the spot price of aluminum and its alloys. Because the Al-Mn alloy is now more expensive, its demand falls, which reduces the demand for manganese (the non-traded component of the alloy). Manganese becomes cheaper and, all else equal, its spot price is now negatively correlated with the spot price of aluminum.
This intuition gives rise to my first hypothesis:
Hypothesis 1:If the participation of financial investors in futures markets affects the spot market, then the complementary (positive) relationship across traded and non-traded industrial metals should weaken.
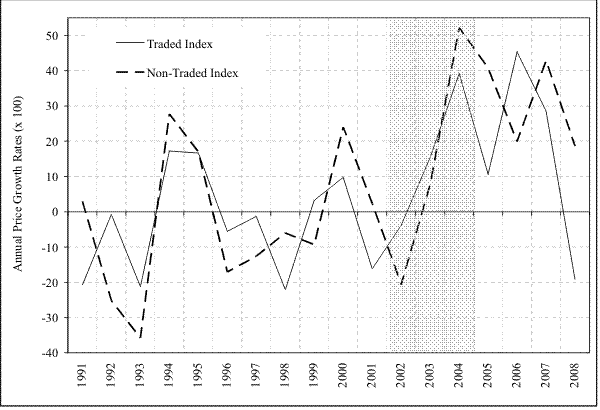
The figure depicts the time-series for the growth rates of spot price indices for traded and non-traded metals. The growth rates are calculated at the annual frequency. All growth rates are multiplied by a hundred. The shaded area highlights the period during which spot metal prices increase considerably. Figure 1 Data
3.2 Time Patterns of Traded and Non-Traded Metals
Next, I test Hypothesis 1, which implies that the correlation between traded and non-traded metals should fall due to speculative activity in the futures markets. I use graphical evidence and simple descriptive statistics. The annual and quarterly time-series of the traded and non-traded growth rate indices are presented in Figures 1 and 2 respectively. Figure 3 presents rolling correlations between the indices and the individual metals. Finally, Table 1 reports descriptive statistics for the two indices and their individual components.
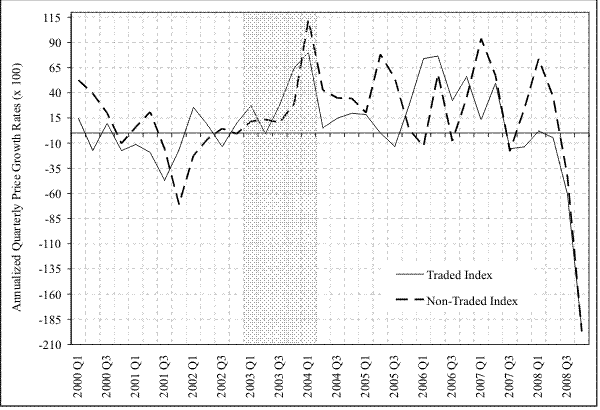
The figure depicts the time-series for the growth rates of price indices for traded and non-traded metals. The growth rates are quarterly and they are annualized (i.e. multiplied by four). All growth rates are multiplied by a hundred. The shaded area highlights the period during which spot metal prices increase considerably. Figure 2 Data
Inconsistent with Hypothesis 1, I find that traded and non-traded metals move in tandem even in recent years. For example, both traded and non-traded metals appreciated around 2003 and then depreciated in 2008. See Figures 1 and 2. Moreover, the correlation between the metal categories has been positive and stable. For example, as depicted in Figure 3, over 2000 to 2008 the annual rolling correlation between the traded and non-traded growth rate indices has been stable and always close to 0.70. Similarly, the average of the rolling correlations between each traded metal growth rate with each non-traded metal remained close to its average value of 0.30. The positive and stable correlation across the price growth rates is consistent with the fact that industrial metals are complementary goods.
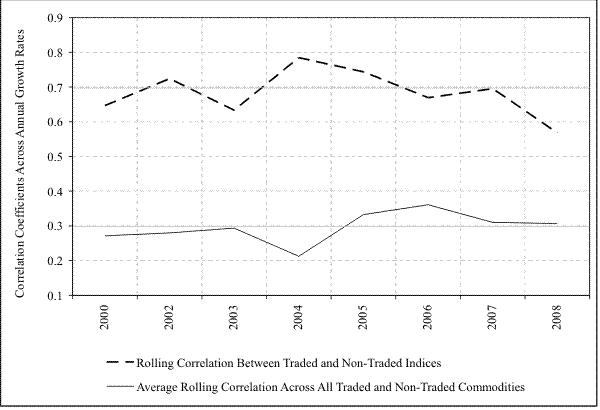
The figure depicts the time-series for the rolling correlations between the growth rates of spot price indices for traded and non-traded metals. It also includes the average of the rolling correlations between each traded metal with each non-traded metal. The growth rates are calculated at the annual frequency. The rolling correlation in year ![]() uses data from (
uses data from (![]() - 9) to
- 9) to
![]() . Figure 3 Data
. Figure 3 Data
3.2 Common Appreciation in Prices
Apart from the comovement across the price growth rates, the other salient feature in Figures 1 and 2 is that the level of the traded and non-traded indices rose significantly after 2003. For example, as shown in Table 1, over the 1991 to 2002 period the mean annual growth rate of the traded and non-traded indices was -3.7% and -4.4%, respectively. However, after 2002 the level of these mean growth rates rose dramatically. The traded index grew by 11.9% and the non-traded index grew 22.7%. See Table 1 for these descriptive statistics. Moreover, the structural break in the indices is not driven by a subset of metals as all metals exhibited a dramatic price appreciation after the end of 2002. As shown in Table 1, the shift in prices is present across all metals.
The structural break in both the traded and non-traded metals reinforces the fact that these industrial metals are complementary to one another. More importantly, their complementary relationship is strong even in recent years when financial investors have become an important investor category in commodity futures markets. It is also interesting that non-traded metals have experienced a more dramatic price appreciation compared to traded metals. By and large, the aforementioned findings do not support Hypothesis 1 and the conjecture that the participation of financial investors in the futures markets has affected the level of spot metal prices.
3.3 Formal Structural Break Tests
The previous section provided simple graphical evidence for a structural break in the growth rates of metals around the 2002 to 2003 period. In this section, I formally test the structural break using the two metal growth rate indices. First, I follow Andrews (1993) and estimate the date of the break points. Then, following Andrews and Ploberger (1994), and Hansen (1997), I test whether the break points are statistically significant. I conduct this analysis for both the annual and the quarterly growth rate indices and report the results in Table 2. Because of the dramatic drop in commodity prices in 2008, I also consider the case in which the 2008 data is excluded for the sample period.
First, in Panel A for Table 2, I report the tests with 2008 data being included in the sample. In the case of the annual data, the estimated break date is 2002 for the index of traded metals and 2003 for the index of non-traded metals. Moreover, according to the ExpF and AveF tests by Andrews and Ploberger (1994), the change in the mean of the indices on the estimated break dates are statistically significant. Specifically, their p-values, which are computed as in Hansen (1997), are always less than 0.07. In the case of the quarterly data, the estimated break date for the traded index is at the fourth quarter of 2001 and for the non-traded index is at the fourth quarter of 2002. However, only the shift in the mean value of the non-traded index is statistically significant.
The weak statistical significance of the structural break in the case of quarterly growth rates might be related to the fact that in the fourth quarter of 2008 metal prices plummeted. As depicted in Figure 2, the growth rate of the traded and non-traded index in the third quarter of 2008 was -0.61% and -0.43%, respectively. These growth rates fell dramatically in the fourth quarter of 2008; they both came very close to -2%. It is therefore possible that this decline in the growth rates is biasing the structural break tests.
Next, I exclude 2008 and re-run the structural break tests. As reported in Table 2, Panel B, the evidence in favor of a break becomes stronger and the results with annual data are now aligned with those with quarterly data. For example, in the case of the annual data, the estimated break date is again 2002 for the index of traded metals and 2003 for the index of non-traded metals. In the case of the quarterly data, the estimated break date for the traded index is fourth quarter of 2002 and for the non-traded index is third quarter of 2003. Finally, the shift in the mean value of the growth rate indices is statistically significant across both indices and data frequencies.
Overall, the formal structural break tests echo the graphical evidence in Figures 1 and 2. They show that in the beginning of 2003 metals with and without established futures market underwent a common structural break. The break roughly happened in the same period, which is consistent with the two metal classes being complementary to each other.
3.4 Panel Regression Analysis
In this Section, I further explore the structural break finding and I estimate a series of panel regressions. The panel regressions are estimated by pooling the annual and annualized quarterly spot price growth rates of the individual commodities instead of the growth rates of indices. I use the individual commodity data to exploit all their time-series and cross-sectional variation. This approach is more efficient than estimating the panel regressions with the growth rates of the indices because the indices smooth out cross-sectional differences within the traded and non-traded commodity classes.
In the case of the annual growth rates, dP![]() , I estimate two panel regressions. The regressions include a series of dummy variables, which are designed to test whether there are
differences between the levels of price growth rates before and after 2002. The regression models are:
, I estimate two panel regressions. The regressions include a series of dummy variables, which are designed to test whether there are
differences between the levels of price growth rates before and after 2002. The regression models are:
- dP
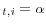
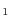 D
D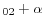
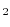 D
D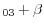
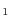 dP
dP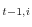 ,
,
- dP
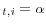
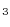 (D
(D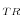
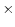 D
D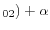
 (D
(D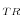
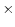 D
D
 (D
(D
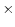 D
D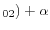
 (D
(D
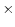 D
D
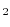 dP
dP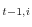 .
.
Above, D![]() is a dummy variable that takes the value of one if commodity
is a dummy variable that takes the value of one if commodity ![]() is
traded, and zero otherwise. Similarly, D
is
traded, and zero otherwise. Similarly, D![]() is a dummy variable that takes the value of one if commodity
is a dummy variable that takes the value of one if commodity ![]() is not traded, and zero otherwise. D
is not traded, and zero otherwise. D![]() (D
(D![]() is a
dummy variable that takes the value of one if year
is a
dummy variable that takes the value of one if year ![]() is prior (after) to 2003, and zero otherwise. I use the coefficient estimates from the regression models to test for the structural break in
2002. In particular, I test whether the differences (
is prior (after) to 2003, and zero otherwise. I use the coefficient estimates from the regression models to test for the structural break in
2002. In particular, I test whether the differences (![]()
![]() -
- ![]()
![]() , (
, (![]()
![]() -
- ![]()
![]() and (
and (![]()
![]() -
- ![]()
![]() are statistically different from zero.
are statistically different from zero.
In the case of quarterly data, I estimate regressions similar to regressions (a) and (b) above. However, the quarterly regressions include seasonal dummy variables for quarters 1 to 3. The time period for annual data is 1992 to 2008 and for quarterly data is 1993(Q1) to 2008(Q4).
The regressions are estimated with OLS and the estimation results are reported in Table 3. The results with annual growth rates are in columns 1 and 2, while the results with quarterly data are in columns 3 and 4. The quarterly growth rates are annualized (i.e. multiplied by four) before the estimation.
3.5 Estimation Results
In the first set of regressions, columns 1 and 3, I examine whether the mean spot price growth rates rise after the end of 2002. Consistent with the Andrews and Ploberger (1994) tests, I find that after 2002 the growth rates across all commodities increase and the difference between the
post- and pre-2003 periods are statistically significant. In particular, the difference between the coefficient estimates on the D![]() and D
and D![]() dummy variables (D
dummy variables (D![]() - D
- D![]() is 0.28 (t-statistic = 5.38) and 0.09 (t-statistic = 1.91) for annual and quarterly data, respectively. Thus, both traded and non-traded commodities underwent a structural change at the end of 2002.
is 0.28 (t-statistic = 5.38) and 0.09 (t-statistic = 1.91) for annual and quarterly data, respectively. Thus, both traded and non-traded commodities underwent a structural change at the end of 2002.
As shown in Table 1, the growth rate increase from 2003 and onwards is higher for non-traded than for traded commodities. To further examine this observation, in regression 2 and 4, I include interaction terms of the D![]() and D
and D![]() dummy variables with the structural break D
dummy variables with the structural break D![]() and D
and D![]() dummy variables.
dummy variables.
The results from regressions 2 and 4 confirm the finding from Table 1. In the case of annual growth rates, even if the difference between the interaction terms (D![]()
![]() D
D![]() and (D
and (D![]()
![]() D
D![]() is statistically significant
(difference = 0.20, t-statistic = 2.66), it is smaller in magnitude than the difference between (D
is statistically significant
(difference = 0.20, t-statistic = 2.66), it is smaller in magnitude than the difference between (D![]()
![]() D
D![]() and (D
and (D![]()
![]() D
D![]() (difference = 0.34, t-statistic = 5.01). Similarly, in the case of quarterly data, the difference between
the interaction terms (D
(difference = 0.34, t-statistic = 5.01). Similarly, in the case of quarterly data, the difference between
the interaction terms (D![]()
![]() D
D![]() and (D
and (D![]()
![]() D
D![]() is smaller (difference = 0.05, t-statistic = 0.69) than the difference between (D
is smaller (difference = 0.05, t-statistic = 0.69) than the difference between (D![]()
![]() D
D![]() and (D
and (D![]()
![]() D
D![]() (difference = 0.12, t-statistic = 1.97)
(difference = 0.12, t-statistic = 1.97)
In general, the panel regression analysis confirms that the prices of traded and non-traded metals move in tandem with both metal categories experiencing a structural break. Consequently, the participation of financial investors in the futures markets of the traded metals has not broken the complementary relationship between traded and non-traded metals. Moreover, the fact that non-traded metals experience a much higher price appreciation than traded ones after 2002 casts further doubt that speculators are the cause of the spike in commodity prices. In all, there is again no evidence to support Hypothesis 1.
4. Economic Fundamentals and Metal Prices
The previous analysis has established the comovement of metal prices. In this section, I take a closer look at metal markets and examine whether the patterns in metal price growth rates are related to economic fundamentals. I approach this question in two distinct ways. First, I account for the level of world economic activity to test Hypothesis 2:
Hypothesis 2:If supply and demand factors drive metal spot prices, world economic activity should be correlated to the price growth rate of metals.
Second, I collect news reports from industry newsletters. My goal is to compute a proxy for the fundamental information (i.e. information related to supply and demand factors) that was when metal prices started to appreciate. With the information proxy, I test the following hypothesis:
Hypothesis 3:If supply and demand factors drive metal spot prices, price increasing news should outnumber price decreasing news during the onset of the metal price inflation in 2003.
4.1 Accounting for World Economic Activity
The commodity markets are international markets and thus are affected by changes in the world economy. I proxy for world economic activity using the world per capita GDP growth published by the World Bank in the World Development Indicators (WDI).
As depicted in Figure 4, world per capita growth was about 0.6% in 2002. This percentage rose to 1.4% in 2003 and it has been about 2.3% over the 2003 to 2008 period. The rise in world economic activity in 2003 coincides with the structural break in metal spot price growth rates detected at the beginning of 2003. It is therefore very likely that the appreciation of commodity prices is related to economic fundamentals.
Next, I formally test Hypothesis 2 by adding world per capita GDP growth in the annual regressions in Table 3.13 The new regression results are reported
in Table 4 and they are divided into two groups. In the first set of regressions (1 and 2), world growth is added to the control variables to test the significance of world economic activity across the whole sample period. The second set of regressions (3 and 4) examines whether the correlation
between metal price growth rates and world economic activity changes from 2003 onwards. In particular, in regressions 3 and 4 the control variables include the interaction terms of world per capita GDP growth with the D![]() and D
and D![]() dummy variables.
dummy variables.

The figure depicts world per capita GDP growth (%). The data are from the World Bank. The growth rate for 2008 is the projection by the World Bank. The shaded area highlights the period during which spot commodity prices increase considerably. Figure 4 Data
The results from Regressions 1 and 2 demonstrate that world per capita GDP growth is an important determinant of the price growth of metals. To begin with, its coefficient estimates are significant and positive. For example, in Regression 1 the coefficient estimate and t-statistic on world
growth is 0.14 and 4.73, respectively. Moreover, in the presence of world growth the evidence for the structural break in the price growth rates weakens. In Regression 1, the estimate (t-statistic) on the D![]() dummy variable becomes negative and equal to -0.08 (0.99). In the absence of world growth, it was 0.24 and its t-statistic was 5.75. See Table 3, Regression 1. Similarly, the difference between D
dummy variable becomes negative and equal to -0.08 (0.99). In the absence of world growth, it was 0.24 and its t-statistic was 5.75. See Table 3, Regression 1. Similarly, the difference between D![]() and D
and D![]() becomes 0.15 (it is 0.28 in Table 3, Regression 1) and its t-statistic drops to 2.57 (from 5.38 in Table 3, Regression 1).
becomes 0.15 (it is 0.28 in Table 3, Regression 1) and its t-statistic drops to 2.57 (from 5.38 in Table 3, Regression 1).
The previous results provide supporting evidence for Hypothesis 2, which posits that fundamental factors drive metal prices. I further test Hypothesis 2 by testing whether the strength of the relationship changes before and after 2002, the year of the structural break. The findings in
Regressions 3 and 4 show that the coefficient estimates on the interaction terms of world growth with the D![]() and D
and D![]() dummy variables are always significant. For example, in Regression 2, the estimate (t-statistic) on the D
dummy variables are always significant. For example, in Regression 2, the estimate (t-statistic) on the D![]() interaction term is 0.12 (3.48), while
the estimate on the D
interaction term is 0.12 (3.48), while
the estimate on the D![]() interaction term is 0.24 (3.62).
interaction term is 0.24 (3.62).
Interestingly, world growth is more correlated with metal price growth rates after 2002, since the estimate on the D![]() interaction term is double the estimate on the D
interaction term is double the estimate on the D![]() interaction term. Also, when we allow for a structural break in the coefficient on world per capita GDP growth, the shift in the means of the price growth rates are no longer statistically
significant. Such a result indicates that the dramatic rise in metal prices at the end of 2002 must be related to fundamental supply and demand factors.
interaction term. Also, when we allow for a structural break in the coefficient on world per capita GDP growth, the shift in the means of the price growth rates are no longer statistically
significant. Such a result indicates that the dramatic rise in metal prices at the end of 2002 must be related to fundamental supply and demand factors.
4.2 Supply and Demand Information
The inclusion of world GDP in the panel models demonstrates that a substantial component of the variation in metal prices can be explained by world economic activity. Next, I test Hypothesis 3 and collect news reports from Factiva to compute a proxy for the type of information that was available to market participants. In particular, I focus on industry newsletters, like Platt's Metal Week, to ensure that the articles I identify provide specialized information for the metals' market. For feasibility, I focus on the period from September 01, 2003 to April 01, 2004. During this 6-month period all metal prices were rising.
For each metal, I execute two searches. The first search is designed to capture news reports that should be related to prices increasing. This search identifies reports that include phrases about a) rising demand or consumption of a metal, b) decline in inventories, or production, or reserves, or supply for a metal. For example, in the case of zinc, I search for articles that includes phrases like "disruption in production of zinc" and "inventories of zinc have been declining."
The second search is designed to capture news reports that should be related to prices declining. This search identifies reports that include phrases about a) declining demand or consumption of a metal, b) increase in inventories, or production, or reserves, or supply for a metal. For instance, in the case of tin, I search for reports including phrases like "demand for tin has been decreasing," "tin production rose."14 I conjecture that the number of news reports generated by each search is a proxy of the market perception about the state of supply/demand fundamentals.
The results of the Factiva searches are reported in Table 5. First, we see that there are more news reports for traded than for non-traded metals. Moreover, consistent with Hypothesis 3, the price increasing news reports outnumber the price decreasing ones. For example, in the case of copper, there are 32 more news report related to the price of copper rising. Overall, the Factiva news reports support Hypothesis 3 and the argument that metal prices respond to fundamental news in the metal markets.
In general, the panel regressions and the Factiva news reports indicate that the prices of traded and non-traded metals are driven by economic fundamentals. Their reliance on common supply and demand forces implies that their prices should be positively correlated. Such comovement is also consistent with the fact that industrial metals are used as complementary goods in the manufacturing sector.
5. Does Commodity Index Trading Affect Commodity Cash Prices?
The findings presented thus far support the view that the patterns in metal prices are primarily driven by economic fundamentals. In this Section, I test the potential role of speculation in futures markets on spot commodity markets more directly. This analysis is organized around three themes. First, I show that the earnings from investing in futures contracts can proxy for the volume of speculative activity in the futures markets. Second, I examine whether the volume proxy is related to metal spot prices. Finally, I focus on traded metals and test if the relationship between inventory changes and price growth rates has changed after 2002.
5.1 S&P Gold-Sachs Commodity Index
Financial investors can gain exposure to commodity price changes by investing in the futures markets. The most typical investment strategy has been to invest in products that track commodity indices like the S&P Goldman-Sachs Commodity Index (SPGSCI). The SPGSCI represents an unleveraged, long-only investment in a broad array of commodity futures. An investor can implement the index with SPGSCI instruments, like the SPGSCI futures contract traded on the Chicago Mercantile Exchange (CME).
I use the SPGSCI total return data to proxy for returns representative of investments in U.S. commodities and I test the following hypothesis:
Hypothesis 4:Speculative activity in futures markets rises when the returns from investing in futures contracts are high. Thus, if speculation in futures markets is driving commodity spot prices, there should be a positive relation between the total return of investing in futures contracts and commodity spot prices.

The figure depicts three annual rates. First, the rate of return of the SPGSCI is calculated from daily total return data from Bloomberg. Second, the excess rate of return is the difference between the SPGSCI rate of return and the CRSP value-weighted market return CRSP (FF MKT). Third, the growth in open interest spreading variable is the growth of net positions of all non-commercial traders reporting to the CFTC. This variable is only available from 1993 to 2000 and 2007 to 2008. Because the growth in open interest spreading is very volatile, for easy visualization, the first two variables are multiplied by a hundred and the last one by ten. The shaded area highlights the period during which spot metal prices increase considerably. Figure 5 Data
5.2 The Volume-Return Correlation
To test Hypothesis 4, I collect daily price data for the SPGSCI total return index from Bloomberg. I average all the price data within a year to compute an annual price index, ![]()
![]() . I calculate the annual rate of return as 100
. I calculate the annual rate of return as 100 ![]() ln(
ln(![]()
![]() /
/ ![]()
![]() . For robustness, I also calculate an excess SPGSCI return. It is given by the difference between the SPGSCI annual return and the CRSP value-weighted index of all
stocks listed on CRSP. The CRSP index is from the web site of Kenneth French.15
. For robustness, I also calculate an excess SPGSCI return. It is given by the difference between the SPGSCI annual return and the CRSP value-weighted index of all
stocks listed on CRSP. The CRSP index is from the web site of Kenneth French.15
The return data are a good proxy for the variation in financial investor participation (volume) in the futures markets. I establish the volume-return connection using open interest data for the SPGSCI futures contract traded on the Chicago Mercantile Exchange. I obtain the open interest data from the CFTC Commitments of Traders Reports.16 From these reports, I collect the variable called "non-commercial positions-spreading," which aggregates the net (long - short) positions of each non-commercial trader reporting to the CFTC. I focus on the non-commercial category because it includes financial investors like hedge funds.17
The non-commercial positions-spreading variable for the SPGSCI futures contract is only available from 1992 to 2000 and 2006 to 2008. I average the reported weekly data within each year and I compute an annual spreading variable. Then, I compute its growth rate to capture the variation in financial investor participation in the futures markets.
The open interest growth rate is depicted in Figure 5 together with the rate of return and excess return of the SPGSCI. The figure shows that there is a positive relationship between open interest growth and returns. In untabulated results, I find that the correlation between the SPGSCI total rate of return and the growth of the open interest by non-commercial traders is positive (0.43). The correlation with the excess return is also positive (0.13). Thus, the returns for the SPGSCI are a reasonable volume proxy in the futures markets.
5.3 SPGSCI Returns and Spot Metal Prices
Unfortunately, the open interest data are not available from 2001 to 2005, the period containing the structural break in metal prices. Therefore, I proxy for the volume of speculative activity in the futures markets using the SPGSCI returns.
The SPGSCI rate and excess return are plotted in Figure 5. The plot shows that the SPGCI return is highly volatile; its minimum value is -31% and its maximum value is 41%. The excess return is even more volatile; its minimum value is -56% and its maximum value is 52%. Nevertheless, the average returns between 2002 and 2007 have been high and around 10%. Gorton and Rouwenhorst (2006) also find that by 2004 an equal-weighted return index of commodity futures earned about 9% more than the respective commodity spot price index.
The graphical evidence in Figure 5 suggests that Hypothesis 4 is not supported by the data. As we see in the figure, the SPGSCI rate and excess return are not consistently rising during the period 2002 to 2004. Unlike the metal price growth rates, there does not appear to be a structural break in the two return series.
I complement the graphical evidence and formally test Hypothesis 4 by including the SPGSCI rate and excess return in the panel regressions from Section 4. The goal of the regression analysis is to test whether the SPGSCI returns can explain the structural break at the end of 2002. I report the new regressions in Table 6. Regressions 1 and 2 include SPGSCI rate of return and Regressions 3 and 4 include SPGSCI excess return over the CRSP return.
The regression results in Table 6 strongly reject Hypothesis 4. To begin with, the rate and excess return of the SPGSCI have no explanatory power for the metal price growth rates. For instance, in Regression 1 its t-statistic is only 0.85. In untabulated results, I estimate regressions in which I constrain the SPGSCI return to only affect the traded metals. I find that even in these regressions the speculative activity proxy has no impact on spot price growth rates.
Apart from being insignificant, the inclusion of the SPGSCI returns in Regressions 3 and 4 does not weaken the importance of world growth for metal prices. In the case of Regression 3, the estimate on the world growth and D![]() interaction term is positive (= 0.12) with a high t-statistic (= 3.48). Similarly, the estimate on the world growth and D
interaction term is positive (= 0.12) with a high t-statistic (= 3.48). Similarly, the estimate on the world growth and D![]() interaction term is 0.24
and its t-statistic is 3.62.
interaction term is 0.24
and its t-statistic is 3.62.
Taken together, the results in Table 6 strongly reject Hypothesis 4. They suggest that financial investor participation in the futures markets, proxied by the SPGSCI returns, is not related to the price appreciation of metals after 2002. Moreover, the failure to find supporting evidence for Hypothesis 4 reinforces the evidence for Hypotheses 2 and 3.
5.4 Inventory Formation and Price Inflation
The economic theory behind storage models suggests that the only way speculation in the futures markets can affect spot commodity prices is by leading to physical hoarding. If that were the case, inventory growth and price growth would be positively correlated. All else equal, if speculation is irrelevant these growth rates should be negatively correlated. This intuition gives rise to my final hypothesis:
Hypothesis 5:If speculative activity in futures markets affects the spot commodity prices, then the negative relationship between inventory formation and spot price changes should weaken.
The discussion in Section 3.1 argued that data limitations are a major hurdle in testing Hypothesis 5. Nevertheless, given the importance of inventory fluctuations in no-arbitrage/storage models, I use the available inventory data to test Hypothesis 5. Specifically, I focus on traded metals because data on world inventories of non-traded metals are not consistently collected. The inventory data are from the 2005 and 2008 World Metals Statistics Yearbooks published by the World Bureau of Metal Statistics. The data are annual, they cover the period from 1995 to 2007, and they refer to world total commercial stocks. With the annual growth rates of the commercial stocks, I estimate panel regressions, which I report in Table 7.
In Regressions 1 and 2, the inventory growth rate is included in the set of explanatory variables. I find that conditional on lag price growth and world per capita GDP growth, the coefficient estimates on the inventory growth rate are negative and significant. Therefore, inventory growth is
related to metal prices decreasing, a prediction of standard supply and demand models with no physical hoarding. Next, in Regressions 3 and 4, I test whether price growth responds differently to inventory growth before and after 2002. Specifically, I include in the regression interaction terms of
inventory growth with the D![]() and D
and D![]() dummy variables. The interaction terms
have negative coefficient estimates and their magnitudes are very similar. Moreover, they are statistically insignificant. Therefore, there is no supporting evidence that the relationship between inventories and metal prices has changed after 2002, the year when prices spiked.
dummy variables. The interaction terms
have negative coefficient estimates and their magnitudes are very similar. Moreover, they are statistically insignificant. Therefore, there is no supporting evidence that the relationship between inventories and metal prices has changed after 2002, the year when prices spiked.
Overall, the evidence in Table 7 does not support Hypothesis 5. My findings suggest that fluctuations in supply and demand in physical markets (as captured by inventory fluctuations) are driving the prices of traded metals. Even if the inventory data are not free of measurement errors, it is important that their growth rate is negatively correlated with the price growth rates.
6. Related Research
In this section, I survey the recent literature on speculation. Because the debate about speculation leading to spot price inflation is a recent one, there are relatively few studies on the issue. These studies nevertheless find no convincing evidence that speculation in the futures markets has led to spot price inflation. Next, I review some academic studies as well as reports from regulatory agencies.
One of the salient findings of the paper is that at the end of 2002 the prices of both traded and non-traded metals have been rising substantially. Haigh, Hranaiova, and Oswald (2005) also find that the initial appreciation in most commodity spot prices started in 2002. These authors note that spot price changes have led to changes in investor interest and not the other way around. Brunetti and Buyuksahin (2009) also show that speculative activity did not anticipate price changes. Moreover, they use detailed data on open interest and find that speculative activity in the futures market did not destabilize these markets.
My empirical results rely on long term price changes, which are captured by annual price growth rates, and show that economic fundamentals are driving these long term growth rates. Domaski and Heath (2007) argue that in the short term it is possible that financial investors can indirectly affect inventory decisions through future prices. To the extent that taking long positions in futures markets leads to higher futures prices, the value of holding inventory for future delivery increases. Under this scenario, storers might be tempted to increase inventory levels in the short term.
In the long term, however, inventory decisions should be primarily driven by factors affecting the real supply and demand of the underlying goods. Currently, there is no direct evidence that storers and producers have been ignoring supply and demand factors and have been accumulating inventories betting on the prediction that futures prices will continue to appreciate. To the contrary, the evidence in Section 5.4 suggests that storers and producers have been making inventory decisions based on supply and demand conditions in the physical commodity markets.
Even if there is no relationship between investor participation in futures markets and spot (physical) prices, Haigh, Harris, Overdahl, and Robe (2007) find that speculation has affected the futures markets themselves. In particular, they focus on the New York Mercantile Exchange's WTI sweet crude oil futures. They show that the prices of one-year and two-year futures have become cointegrated with the price of near-month futures, for the first time ever, since mid-2004.
In a related study, Buyuksahin, Haigh, and Robe (2008) investigate the comovement of commodity and equity investment returns. They use the Standard and Poor's S&P 500 return and the SPGSCI total return to proxy for the representative performance in U.S. equities and commodities. They find that the correlation between the two return indices has been very stable in the last fifteen years.
Finally, due to the public attention drawn to commodity markets, the International Organization of Securities Commissions (IOSCO) set up a Task Force to investigate the role of speculation by financial investors in the futures market. The Task Force reviewed recent reports from various international agencies. Consistent with my findings, the Final Report (March 2009) concluded that economic fundamentals, rather than speculative activity, are the most plausible cause for the recent price appreciation in commodity prices.18
One report cited by the IOSCO is a Staff report by the CFTC.19 It publishes the results of the June 2008 special call for data from over-the-counter (OTC) swap and commodity index markets. Evidence in the study shows that during December 31, 2007 to June 30, 2008, the behavior of crude oil prices and speculative activity were negatively correlated. During this period, while crude oil prices were increasing, speculative activity by commodity index traders reflected a net decline of futures equivalent contracts.
7. Conclusion
Do financial investors affect the physical commodity markets through their participation in the futures markets? To answer this question, I study industrial metals with and without futures markets. My empirical analysis evolves around two themes: comovement of metal prices and more direct tests of the impact of speculation on spot markets.
The comovement hypothesis is motivated from the fact that industrial metals are typically used by the manufacturing sector in a complementary fashion. Therefore, if supply and demand forces are the primary driver of their price changes, their long-term price patterns should move in tandem. Using annual and quarterly price growth rates for the period 1991 to 2008, I find that traded and non-traded metals are positively correlated. Moreover, both metal classes experience a structural change by the end of 2002.
The comovement across industrial metals is also supported by additional evidence. To begin with, I find that all metal prices are correlated to world per capita GDP growth, which can explain the shift in metal prices after 2002. Also, using news report, I assess the type of supply and demand information that was available about non-precious metals during the onset of metal price appreciation. I find that price increasing news reports outnumber price declining news reports.
The first set of tests suggests that fundamental information is driving metal prices. The remaining tests confirm this conclusion by finding no direct link between speculation and spot prices. First, I show that the total return of the SPGSCI, a proxy for the intensity of speculative activity in the futures markets, has no explanatory power for metal price growth rates. Finally, I search for evidence of physical hoarding by focusing on the relationship between traded metals and inventory levels. In line with my previous finding, inventory growth is negatively correlated with price growth rates suggesting that storers were not accumulating stocks due to high futures prices.
Taken together, the results indicate that in recent years the relationship between futures and physical commodity markets for industrial metals was not disturbed by financial investors. Instead, commodity spot prices changes are driven by world economy activity and financial investors are merely responding to these price changes. This conclusion is strongly confirmed by the economic developments in 2008. As shown in Figure 4, world fundamentals worsened in 2008 with world per capita GDP growth falling to 1.7%. The slow down in world economic activity reduced the demand for metals and their price plummeted. For example, the price growth rate of traded metals fell by 19.18%. See Figure 1. In response, as depicted in Figure 5, speculative activity in the futures market declined with the net open interest for the SPGSCI futures contract falling by 171%.
References
Andrews, D. W. K, 1993, "Tests of Parameter Instability and Structural Change with Unknown Change Point," Econometrica 61, 821--856.
Andrews, D. W. K. and W. Ploberger, 1994, "Optimal Tests When a Nuisance Parameter is Present Only Under the Alternative," Econometrica 62, 1383--141.
Bailey W., and K. C. Chan, 1993, "Macroeconomic Influences and the Variability of the Commodity Futures Basis," Journal of Finance 48, 555--573.
Brunetti, C., and B. Buyuksahin, 2009, "Is Speculation Destabilizing?" Working Paper.
Buyuksahin, B, M. S. Haigh, and M. A. Robe, 2008, "Commodities and Equities: A Market of One?" SSRN Working Paper, No. 1069862.
Deutsche Bank, "Commodities and the Role of Speculators," May 9, 2008, Commodities Special, Global Markets Research, Commodities Research.
Fama E. F., and K. R. French, 1988, "Business Cycles and the Behavior of Metals Prices," Journal of Finance 43, 1975--1093.
Gorton, G. and Rouwenhorst, K. G., 2006, "Facts and fantasies about commodity futures," Financial Analysts Journal 62, 47-68.
Haigh, M, J. Hranaiova, and J. Oswald, 2005, "Price dynamics, price discovery and large futures trader interactions in the energy complex", Working Paper, U.S. Commodity Futures Trading Commission.
Haigh, M. S., J. H. Harris, J. A. Overdahl, and M. A. Robe, 2007, "Market Growth, Trader Participation and Derivative Pricing, Working Paper, U.S. Commodity Futures Trading Commission.
Hansen, B. E., 1997, "Approximate Asymptotic ![]() Values for Structural-Change Tests," Journal of Business and Economic Statistics 15, 60--67.
Values for Structural-Change Tests," Journal of Business and Economic Statistics 15, 60--67.
Nielsen M. J., and E. S. Schwartz, 2004, "Theory of Storage and the Pricing of Commodity Claims," Review of Derivatives Research 7, 5--24.
Pindyck, R. S., 2001, "The Dynamics of Commodity Spot and Futures Markets: A Primer," Energy Journal, 22, 1-29.
Samuelson, P. A., 1966, "Intertemporal Price Equilibrium: A Prologue to the Theory of Speculation," in The Collected Papers of Paul A. Samuelson, Vol. II, J. E. Stiglitz, ed., Cambridge: M.I.T. Press, 946--84.
| Annual Growth Rates, 1991 - 2008 Avg | Annual Growth Rates, 1991 - 2008 STDV | Annual Growth Rates, 1991 - 2002 Avg | Annual Growth Rates, 1991-2002 STDV | Annual Growth Rates, 2003 - 2008 Avg | Annual Growth Rates, 2003 - 2008 STDV | Annualized Quarterly Growth Rates, 1992 - 2008 Avg | Annualized Quarterly Growth Rates, 1992 - 2008 STDV | Annualized Quarterly Growth Rates, 1992 - 2002 Avg | Annualized Quarterly Growth Rates, 1992 - 2002 STDV | Annualized Quarterly Growth Rates, 2003 - 2008 Avg | Annualized Quarterly Growth Rates, 2003 - 2008 STDV | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Traded: Copper | 5.3 | 0.2 | -4.5 | 0.2 | 24.9 | 0.2 | 2.8 | 0.6 | -4.6 | 0.4 | 15.5 | 0.8 |
| Traded: Aluminum | 2.5 | 0.2 | -1.6 | 0.2 | 10.7 | 0.1 | 2.1 | 0.4 | 0.4 | 0.3 | 5.1 | 0.4 |
| Traded: Lead | 5.2 | 0.3 | -4.9 | 0.2 | 25.5 | 0.3 | 4.2 | 0.5 | -3.7 | 0.3 | 17.7 | 0.7 |
| Traded: Nickel | 4.8 | 0.3 | -2.3 | 0.3 | 18.9 | 0.4 | 2.5 | 0.7 | -0.2 | 0.5 | 7.1 | 0.9 |
| Traded: Tin | 6.1 | 0.2 | -3.5 | 0.1 | 25.3 | 0.3 | 4.0 | 0.4 | -4.6 | 0.3 | 18.9 | 0.6 |
| Traded: Zinc | 1.1 | 0.3 | -5.6 | 0.2 | 14.6 | 0.5 | -0.8 | 0.5 | -5.5 | 0.4 | 7.2 | 0.7 |
| Traded Index | 4.2 | 0.2 | -3.7 | 0.1 | 20.0 | 0.2 | 2.5 | 0.4 | -3.0 | 0.3 | 11.9 | 0.6 |
| Non-Exchange Traded: Steel | 6.8 | 0.2 | -2.3 | 0.2 | 25.1 | 0.3 | 5.3 | 0.7 | 0.4 | 0.4 | 13.7 | 1.0 |
| Non-Exchange Traded: Manganese | 7.0 | 0.4 | -5.7 | 0.1 | 32.6 | 0.6 | 9.2 | 0.6 | -5.4 | 0.2 | 34.1 | 0.9 |
| Non-Exchange Traded: Cadmium | 2.4 | 0.6 | -13.1 | 0.6 | 33.4 | 0.5 | 5.4 | 1.0 | -1.8 | 1.0 | 17.7 | 1.1 |
| Non-Exchange Traded: Cobalt | 7.5 | 0.4 | -2.9 | 0.4 | 28.4 | 0.4 | 0.9 | 0.8 | -11.2 | 0.6 | 21.7 | 0.9 |
| Non-Exchange Traded: Tungsten | 7.8 | 0.3 | -1.1 | 0.3 | 25.6 | 0.4 | 9.2 | 0.6 | -0.9 | 0.5 | 26.6 | 0.7 |
| Non-Exchange Traded: Rhodium | 3.4 | 0.5 | -12.4 | 0.5 | 34.8 | 0.5 | -2.0 | 1.1 | -12.4 | 0.9 | 15.7 | 1.3 |
| Non-Exchange Traded: Ruthenium | 9.2 | 0.6 | 0.7 | 0.5 | 26.3 | 0.8 | 11.6 | 1.0 | 5.0 | 0.8 | 22.8 | 1.2 |
| Non-Exchange Traded: Molybdenum | 13.2 | 0.5 | 1.7 | 0.4 | 36.3 | 0.5 | 13.0 | 1.0 | 3.5 | 1.0 | 29.3 | 0.9 |
| Non-Traded Index | 7.2 | 0.3 | -4.4 | 0.2 | 30.3 | 0.2 | 6.6 | 0.5 | -2.8 | 0.3 | 22.7 | 0.6 |
The table reports descriptive statistics for the growth rates of spot price indices for traded and non-traded metals as well as individual metals. The sample averages are denoted by "Avg" and the sample standard deviations by "STDV". The annual data cover the 1991 to 2008 period. The quarterly data cover the 1992(Q4) to 2008(Q4) period. The quarterly growth rates are annualized (i.e., multiplied by four). All growth rates are multiplied by a hundred.
| Annual Data: Date | Annual Data: ExpF | Annual Data: AveF | Annualized Quarterly Data: Date | Annualized Quarterly Data: ExpF | Annualized Quarterly Data: AveF | |
|---|---|---|---|---|---|---|
| Index of Traded | 2002 | 1.786 | 3.105 | 2001 (Q4) | 0.582 | 1.005 |
| Index of Traded (P value) | 0.067 | 0.054 | 0.338 | 0.325 | ||
| Index Non-Traded | 2003 | 3.054 | 5.244 | 2002 (Q4) | 1.488 | 2.521 |
| Index Non-Traded (P value) | 0.014 | 0.010 | 0.095 | 0.084 |
The table reports structural break tests. The date of the break (reported underneath the column titled "Date") is the date in which the Andrews' (1993) F-test of no break is maximized. The ExpF and AveF columns report two tests of structural break following Andrews and Ploberger (1994). Underneath the test statistics (reported in smaller font) are their p-values computed as in Hansen (1997). In Panel A, the sample period includes 2008, and in Panel B, 2008 is excluded from the analysis.
| Annual Data: Date | Annual Data: ExpF | Annual Data: AveF | Annualized Quarterly Data: Date | Annualized Quarterly Data: ExpF | Annualized Quarterly Data: AveF | |
|---|---|---|---|---|---|---|
| Index of Traded | 2002 | 3.128 | 4.768 | 2002 (Q4) | 5.124 | 8.016 |
| Index of Traded (P value) | 0.013 | 0.015 | 0.001 | 0.001 | ||
| Index Non-Traded | 2003 | 2.893 | 4.622 | 2003 (Q3) | 4.946 | 7.870 |
| Index Non-Traded (P value) | 0.017 | 0.017 | 0.001 | 0.001 |
The table reports structural break tests. The date of the break (reported underneath the column titled "Date") is the date in which the Andrews' (1993) F-test of no break is maximized. The ExpF and AveF columns report two tests of structural break following Andrews and Ploberger (1994). Underneath the test statistics (reported in smaller font) are their p-values computed as in Hansen (1997). In Panel A, the sample period includes 2008, and in Panel B, 2008 is excluded from the analysis.
| Annual Regression (1) | Annual Regression (2) | Quarterly Regressions (3) | Quarterly Regressions (4) | |
|---|---|---|---|---|
| D02 | -0.04 | 0.20 | ||
| D02 (T statistic) | -1.24 | 4.10 | ||
| D03 | 0.24 | 0.29 | ||
| D03 (T statistic) | 5.76 | 5.38 | ||
| DTR x D02 | -0.02 | 0.20 | ||
| DTR x D02 (T statistic) | -0.44 | 3.42 | ||
| DTR x D03 | 0.18 | 0.25 | ||
| DTR x D03 (T statistic) | 2.99 | 3.65 | ||
| DNTR x D02 | -0.05 | 0.20 | ||
| DNTR x D02 (T statistic) | -1.26 | 3.63 | ||
| DNTR x D03 | 0.29 | 0.32 | ||
| DNTR x D03 (T statistic) | 5.28 | 5.11 | ||
| Adjusted R-squared | 0.13 | 0.13 | 0.14 | 0.14 |
The table reports OLS coefficient estimates and t-statistics (beneath the estimates and in smaller font) in Panel A. Panel B reports the difference between estimates and their t-statistics (beneath the differences and in smaller font). The sample periods are 1992 to 2008 and 1993(Q1) to 2008(Q4) for annual and quarterly data, respectively. To conserve space, I omit the coefficient estimates of the lagged spot price growth rates (included in regressions 1 to 3) and of the seasonal dummy variables (included in regressions 4 to 6). The quarterly growth rates are annualized.
| Annual Regression (1) | Annual Regression (2) | Quarterly Regressions (3) | Quarterly Regressions (4) | |
|---|---|---|---|---|
| D03 - D02 | 0.28 | 0.09 | ||
| D03 - D02 (T statistic) | 5.38 | 1.91 | ||
| (DTR x D03) - (DTR x D02) | 0.20 | 0.05 | ||
| (DTR x D03) - (DTR x D02) (T statistic) | 2.66 | 0.69 | ||
| (DNTR x D03) - (DNTR x D02) | 0.34 | 0.12 | ||
| (DNTR x D03) - (DNTR x D02) (T statistic) | 5.01 | 1.97 |
The table reports OLS coefficient estimates and t-statistics (beneath the estimates and in smaller font) in Panel A. Panel B reports the difference between estimates and their t-statistics (beneath the differences and in smaller font). The sample periods are 1992 to 2008 and 1993(Q1) to 2008(Q4) for annual and quarterly data, respectively. To conserve space, I omit the coefficient estimates of the lagged spot price growth rates (included in regressions 1 to 3) and of the seasonal dummy variables (included in regressions 4 to 6). The quarterly growth rates are annualized.
| (1) | (2) | (3) | (4) | |
|---|---|---|---|---|
| D02 | -0.22 | -0.19 | ||
| D02 (T statistic) | -4.62 | -3.65 | ||
| D03 | -0.08 | -0.30 | ||
| D03 (T statistic) | -0.99 | -1.93 | ||
| DTR x D02 | -0.21 | -0.18 | ||
| DTR x D02 (T statistic) | -3.57 | -2.85 | ||
| DTR x D03 | -0.14 | -0.36 | ||
| DTR x D03 (T statistic) | -1.52 | -2.23 | ||
| DNTR x D02 | -0.24 | -0.20 | ||
| DNTR x D02 (T statistic) | -4.38 | -3.54 | ||
| DNTR x D03 | -0.03 | -0.25 | ||
| DNTR x D03 (T statistic) | -0.40 | -1.62 | ||
| (World GDP Growth)t | 0.14 | 0.14 | ||
| (World GDP Growth)t (T statistic) | 4.73 | 4.73 | ||
| (World GDP Growth)t x D02 | 0.12 | 0.12 | ||
| (World GDP Growth)t x D02 (T statistic) | 3.48 | 3.48 | ||
| (World GDP Growth)t x D03 | 0.24 | 0.24 | ||
| (World GDP Growth)t x D03 (T statistic) | 3.62 | 3.62 | ||
| Adjusted R-squared | 0.20 | 0.20 | 0.21 | 0.21 |
The table reports OLS estimates and t-statistics (beneath the estimates and in smaller font) in Panel A. Panel B reports the difference between estimates and their t-statistics (beneath the differences and in smaller font). The time period for the regressions is 1991 to 2008. To conserve space, I omit the coefficient estimates on the lagged spot price growth. world growth is given by world per capita GDP growth published n the World Development Indicators (WDI).
| (1) | (2) | (3) | (4) | |
|---|---|---|---|---|
| D03 - D02 | 0.15 | -0.11 | ||
| D03 - D02 (T Statistic) | 2.57 | -0.66 | ||
| (DTR x D03) - (DTR x D02) | 0.07 | -0.18 | ||
| (DTR x D03) - (DTR x D02) (T Statistic) | 0.91 | -1.06 | ||
| (DNTR x D03) - (DNTR x D02) | 0.20 | -0.05 | ||
| (DNTR x D03) - (DNTR x D02) (T Statistic) | 2.90 | -0.30 |
The table reports OLS estimates and t-statistics (beneath the estimates and in smaller font) in Panel A. Panel B reports the difference between estimates and their t-statistics (beneath the differences and in smaller font). The time period for the regressions is 1991 to 2008. To conserve space, I omit the coefficient estimates on the lagged spot price growth. world growth is given by world per capita GDP growth published n the World Development Indicators (WDI).
| Price Increasing News | Price Decreasing News | Net | |
|---|---|---|---|
| Traded: Copper | 39 | 7 | 32 |
| Traded: Aluminum | 18 | 9 | 9 |
| Traded: Lead | 10 | 5 | 5 |
| Traded: Nickel | 19 | 7 | 12 |
| Traded: Tin | 18 | 5 | 13 |
| Traded: Zinc | 23 | 1 | 22 |
| Non-Exchange Traded: Steel | 17 | 5 | 12 |
| Non-Exchange Traded: Manganese | 5 | 0 | 5 |
| Non-Exchange Traded: | 3 | 2 | 1 |
| Non-Exchange Traded: Cobalt | 5 | 3 | 2 |
| Non-Exchange Traded: Tungsten | 4 | 0 | 4 |
| Non-Exchange Traded: Rhodium | 4 | 2 | 2 |
| Non-Exchange Traded: Ruthenium | 4 | 0 | 4 |
| Non-Exchange Traded: Molybdenum | 16 | 9 | 7 |
The table reports the number of news reports in industry newsletters that included news related to metal prices increasing and metal prices decreasing. The news reports are identified using the search engine Factiva over the period from September 1, 2003 to April 1, 2004. The column "Net" reports the difference between price increasing and price decreasing news.
| (1) | (2) | (3) | (4) | |
|---|---|---|---|---|
| DTR x D02 | -0.02 | -0.19 | -0.03 | -0.17 |
| DTR x D02 (T Statistic) | -0.51 | -2.78 | -0.66 | -2.83 |
| DTR x D03 | 0.17 | -0.33 | 0.18 | -0.36 |
| DTR x D03 (T Statistic) | 2.58 | -1.94 | 2.82 | -2.22 |
| DNTR x D02 | -0.05 | -0.21 | -0.06 | -0.20 |
| DNTR x D02 (T Statistic) | -1.35 | -3.39 | -1.49 | -3.52 |
| DNTR x D03 | 0.27 | -0.23 | 0.28 | -0.26 |
| DNTR x D03 (T Statistic) | 4.67 | -1.36 | 5.05 | -1.61 |
| dPt - 1, i | 0.06 | 0.06 | 0.07 | 0.05 |
| dPt - 1, i (T Statistic) | 0.96 | 0.88 | 1.09 | 0.82 |
| Rate of Return (GSCI)t | 0.12 | -0.07 | ||
| Rate of Return (GSCI)t (T Statistic) | 0.85 | -0.42 | ||
| Excess Rate of Return (GSCI)t | -0.0011 | 0.0001 | ||
| Excess Rate of Return (GSCI)t | -0.94 | 0.08 | ||
| (World GDP Growth)t x D02 | 0.13 | 0.12 | ||
| (World GDP Growth)t x D02 | 3.09 | 3.44 | ||
| (World GDP Growth)t x D03 | 0.23 | 0.24 | ||
| (World GDP Growth)t x D03 | 3.41 | 3.59 |
The table reports OLS estimates and t-statistics (beneath the estimates and in smaller font) in Panel A. Panel B reports the difference between estimates and their t-statistics (beneath the differences and in smaller font). The time period for the regressions is 1991 to 2008. To conserve space, I omit the coefficient estimates on the lagged spot price growth. The annual rate of return of the SPGSCI is calculated from the daily total return on the index obtained from Bloomberg. The excess rate of return is the difference between the SPGSCI rate of return and the CRSP value-weighted return of all stocks on CRSP. World growth is given by world per capita GDP growth published in the World Development Indicators (WDI).
| (1) | (2) | (3) | (4) | |
|---|---|---|---|---|
| (DTR x D03) - (DTR x D02) | 0.19 | -0.15 | 0.21 | -0.18 |
| (DTR x D03) - (DTR x D02) (T Statistic) | 2.44 | -0.76 | 2.70 | -1.06 |
| (DNTR x D03) - (DNTR x D02) | 0.32 | -0.02 | 0.34 | -0.05 |
| (DNTR x D03) - (DNTR x D02) (T Statistic) | 4.68 | -0.08 | 5.04 | -0.31 |
The table reports OLS estimates and t-statistics (beneath the estimates and in smaller font) in Panel A. Panel B reports the difference between estimates and their t-statistics (beneath the differences and in smaller font). The time period for the regressions is 1991 to 2008. To conserve space, I omit the coefficient estimates on the lagged spot price growth. The annual rate of return of the SPGSCI is calculated from the daily total return on the index obtained from Bloomberg. The excess rate of return is the difference between the SPGSCI rate of return and the CRSP value-weighted return of all stocks on CRSP. World growth is given by world per capita GDP growth published in the World Development Indicators (WDI).
| (1) | (2) | (3) | (4) | |
|---|---|---|---|---|
| Intercept | -0.15 | -0.15 | ||
| Intercept (T Statistic) | -2.96 | -2.76 | ||
| D02 | -0.15 | -0.15 | ||
| D02 (T Statistic) | -2.71 | -2.47 | ||
| D03 | -0.17 | -0.17 | ||
| D03 (T Statistic) | -1.23 | -1.22 | ||
| dPt - 1, i | -0.22 | -0.22 | -0.22 | -0.22 |
| dPt - 1, i (T Statistic) | -2.03 | -2.02 | -2.00 | -1.99 |
| (World GDP Growth)t x D02 | 0.07 | 0.07 | 0.07 | 0.07 |
| (World GDP Growth)t x D02 (T Statistic) | 2.34 | 2.17 | 2.18 | 1.97 |
| (World GDP Growth)t x D03 | 0.19 | 0.20 | 0.19 | 0.20 |
| (World GDP Growth)t x D03 (T Statistic) | 6.59 | 3.36 | 6.52 | 3.31 |
| (Inventory Growth)t | -0.23 | -0.23 | ||
| (Inventory Growth)t (T Statistic) | -2.19 | -2.17 | ||
| (Inventory Growth)t x D02 | -0.24 | -0.24 | ||
| (Inventory Growth)t x D02 (T Statistic) | -1.53 | -1.51 | ||
| (Inventory Growth)t x D03 | -0.22 | -0.21 | ||
| (Inventory Growth)t x D03 (T Statistic) | -1.57 | -1.54 | ||
| Adjusted R-squared | 0.58 | 0.57 | 0.57 | 0.57 |
The table reports OLS estimates and t-statistics (beneath the estimates and in smaller font). The time period for the regressions is 1997 to 2007. I only use data on metals with established futures markets. World growth is given by world per capita GDP growth published in the World Development Indicators (WDI). Inventory growth is the growth rate of total commercial stocks for the World Bureau of Metal Statistics.