A Dynamic Analysis of Consolidation in the
Broadcast Television Industry *
Keywords: Dynamic oligopoly, structural estimation, market structure
Abstract:
1 Introduction
Deregulation in 1996 and 1999 has led to substantial consolidation in the local broadcast television industry. While the consolidation has provoked considerable controversy, the forces that drive it are poorly understood. This paper exploits the exogenous change in regulation, and estimates a dynamic oligopoly model so as to separately identify the demand-side and supply-side advantages of consolidation. This is the first paper to estimate a model of consolidation in a dynamic, strategic framework.
The rapid consolidation that took place following deregulation suggests that there are competitive advantages to consolidation in the broadcast television industry. Yet the vast majority of consolidation involves stations in different local markets, which are not in direct competition with one another. These markets are often located hundreds of miles apart. Therefore it is not obvious how these firms achieve either market power or economies of scale. How, for instance, does owning an NBC-affiliated station in Hagerstown, Maryland helps Nexstar Broadcasting run its Fox-affiliated station in Fort Wayne, Indiana?1
It is possible that firms with more stations are at an advantage in negotiations with advertisers if they offer more viewers per contract. However, this only works if firms acquire portfolios of stations that are attractive to advertisers as a group. If firms are doing this, it should be reflected in higher per-station revenue for larger firms. On the other hand, it is possible that firms are able to centralize operations of stations even though they are located in separate markets, often many miles apart. If firms are doing this, it should be reflected in lower per-station costs for larger firms.
The goal of this paper is to estimate the revenue versus cost advantages of consolidation, and to identify the characteristics of a firm's portfolio of stations that enable the firm to enjoy these advantages. I consider the number of stations a firm owns, the population coverage of its stations, the average distance between its stations, the demographic heterogeneity of its viewers, and the network affiliations of its stations. These characteristics are likely to impact the attractiveness of a firm's portfolio of stations to advertisers and/or affect the ability of the firm to centralize operations of its stations.
Revenue and ownership data are available for nearly all broadcast stations since deregulation began. This permits direct observation of how the revenue generated by a firm's stations responds to changes in the firm's portfolio of stations. However, I do not observe cost, so I infer cost from patterns in how firms change their portfolios. Patterns that cannot be explained by revenue opportunities are attributed to cost savings. For example, if firms cluster their stations close together with no discernable effect on revenue, I infer that doing so reduces costs.
This method for recovering costs is complicated by the fact that a firm's portfolio decision is both dynamic and strategic. Because the buying and selling of stations involves significant sunk costs, the effects of this period's purchasing decision will likely persist through future periods. For instance, a firm must consider that the purchase of additional stations this period will increase the number of stations that it can expect to own in all future periods, so the firm must consider the effect of the purchase not only on next period's expected profits but on all future periods' expected profits. In addition, if a firm's revenue is affected by its competitors' characteristics, then a firm will consider how its own purchasing decision will affect its competitors' decisions. Suppose, for example, that a firm hesitates to acquire additional stations even though this would lower per-station costs, because doing so would prompt its competitors to do the same. I want my model to allow for this strategic behavior, so that I do not wrongly attribute it to a lack of cost savings from owning more stations.
In order to take into account both the dynamic and strategic elements of a firm's purchasing decisions, I model the decisions as a dynamic game. I estimate the dynamic game in order to recover costs. Each firm's portfolio of stations is summarized by a vector of characteristics (number of stations, population coverage, distance between stations, heterogeneity of viewers and network affiliations). In my model, a firm decides each period how to adjust these characteristics of its portfolio; this acts as an approximation of the firm's true decision about which stations to buy and sell. The firm adjusts its vector of portfolio characteristics so as to maximize the present discounted value of its expected stream of profits, basing its decision on its own current vector of portfolio characteristics, as well as those of its competitors.
The broadcast television industry is well-suited for identifying strategic behavior because firms' stations are spread across independent local markets. In a given period, different firms are present in different sets of markets, so the nature of competition that they face varies. This feature of the industry allows me to identify the effects of strategic variables on firms' payoffs, because I observe within-time variation in the values of these strategic variables.
Until recently, it was virtually impossible to estimate dynamic games such as this for computational reasons. However, several authors have recently developed methods for estimating the parameters of a dynamic game that avoid computing the equilibrium even once. I adopt the two-step method proposed by Bajari, et al. (2007) because it allows for continuous choice variables. In the first stage, I use revenue data to estimate the effects of firms' portfolio characteristics on per-station revenue. The second stage examines ownership data to estimate the strategies of firms, that is, how they adjust their portfolio characteristics each period. Given these results, I find the effects that portfolio characteristics must have on per-station costs such that the observed strategies are consistent with profit maximization. The result is a set of estimates of both the revenue and cost effects of consolidation.
This paper develops an innovative way to estimate the demand-side and supply-side advantages of consolidation in the absence of cost data. As far as I know, it is the first paper to estimate a model of merger activity in a dynamic, strategic framework. My approach allows me to isolate the relationships of interest in an industry that each year witnesses hundreds of firms considering the purchase or sale of over one thousand stations.
I find that there are both cost and revenue advantages to consolidation, but they operate through different mechanisms. Revenue advantages come through greater population coverage, which is probably attractive to advertisers who would like to reach a wider audience for each contract that they negotiate. Cost advantages come through simply owning more stations; firms appear to be able to combine operations of multiple stations so as to cut per-station costs. Cost advantages are greater when a firm's stations' viewers are more demographically homogeneous. If most of a firm's stations have the same network affiliation, the firm's per-station cost is lower, but so is its per-station revenue.
The rest of the paper proceeds as follows. Section 2 describes the relevant literature, Section 3 describes the broadcast television industry and Section 4 describes the data that I use. Section 5 describes the dynamic oligopoly model and Section 6 explains my estimation strategy in detail. Section 7 explains my results and Section 8 concludes the paper.
2 Related Literature
There is a substantial theoretical literature seeking to understand why some industries initially support many competitors but then undergo significant consolidation or "shake-outs."2 Some of these studies focus on the evolution of an industry from a highly competitive industry to an oligopoly, while others focus on the features of an industry that characterize its inherent or "natural" level of competitiveness in the long run. Because the broadcast television industry was not allowed to consolidate until the late 1990s, it is impossible to know what its natural evolution would have been. The rapid consolidation that followed deregulation suggests that there are demand-side and/or supply-side features of the industry that make it naturally concentrated rather than highly competitive. This paper takes advantage of a shake-out triggered by the exogenous deregulation in order to identify those features.
Shaked & Sutton (1987) develop the idea that certain features of an industry's production technology can lead the industry to be concentrated regardless of the size of demand. Specifically, they look at the relationship between a firm's cost and the quality of its product. My results suggest that this relationship is important in the case of the broadcast television industry. Firms with greater population coverage appear to offer advertisers an inherently higher-quality product, suggesting that consolidation changes the relationship between cost and quality for broadcasting firms.
There is relatively little empirical research on mergers and consolidation despite the obvious practical importance of the topic. A persistent problem is the difficulty of identifying the factors that drive consolidation because merger activity is endogenous. Event analysis uses the exact timing of the announcement of a merger as a source of exogeneity. Also called event studies, these look at how merger announcements affect the stock market values of the firms affected by the merger, in order to understand the effects of the merger. For instance, Knapp (1990) does an event analysis of the airline industry and concludes that mergers in this industry increase market power.
Other papers make use of exogenous sources of variation in merger activity prompted by changes in regulations. For instance, Paul (2003) and Pesendorfer (2003) both estimate the cost structure of an industry before and after consolidation, making use of revisions to merger guidelines to argue that merger activity was exogenous. Paul looks at the beef-packing industry, while Pesendorfer looks at the paper industry. Both authors conclude that consolidation alters the cost structure of firms. Kim & Singal (1993) make use of a period of time when airline mergers went uncontested, and find a positive effect of airline mergers on prices.
A few of these papers look specifically at consolidation in the broadcast television industry following deregulation. In 2006, the Federal Communications Commission (FCC) commissioned ten studies to estimate the effect of media consolidation on "diversity, competition and localism."3 Crawford (2007) considers the impact of consolidation on the quantity and quality of local television programming. Shiman (2007) studies the relationship between ownership structure and the quantity of news programming, and Hammond et al. (2007) study the relationship between consolidation and minority and female ownership of television stations. Results are largely inconclusive; they depend on the methods of measurement and estimation, and are often statistically or economically insignificant.
In all of these studies, ownership changes are treated as strictly exogenous, and the mechanisms through which they affect market outcomes are left largely unexplained. There is very little empirical work that endogenizes consolidation or firms' merger decisions. An exception is the recent literature that models mergers as matching games between firms. The approach is similar to mine in that it uses merger decisions to make inferences about the parameters of firms' payoff functions or to reveal firms' incentives. Akkus & Hortacsu (2007) model bank merger decisions to reveal what features of the merging banks enable them to create more value through merger. Park (2008) uses a matching model to analyze manager incentives in mutual fund acquisitions.4 However, matching models tend to suffer from a dimensionality problem. As far as I know, no matching model has incorporated dynamics, and even the incorporation of strategic effects has been limited. For instance, Fox (2007) suggests a way to avoid the curse of dimensionality in a matching model; the method essentially involves the assumption that a given pair of matching agents do not care about the other matches that occur in the market, so long as they prefer their own match to any other match they could have made. This assumption is reasonable in the context of, for instance, a marriage market. However, I am not willing to make this assumption, given that broadcast television firms may be directly affected by mergers between other firms in the industry. For this reason, I do not model mergers as a matching game. However, the incorporation of strategic and dynamic effects in the matching model is an interesting area for future research.
3 Broadcast Television Industry
Originally, broadcast television stations could only be viewed by those who lived within reach of the station's over-the-air signal.5They tended to be locally owned, but as major national networks emerged, the government became concerned that local programming would be dominated by national interests. The FCC put into place a number of restrictions that were meant to encourage local ownership; these are discussed in detail later. Stations were thought to be more able to respond to the needs of the local community if they were not owned by or beholden to national networks.6
The total number of stations in the country is effectively fixed over time because licenses for new stations are rarely issued, and stations virtually never give up their licenses. There are 1,251 full-power commercial stations in the country, across 210 markets.7 Many stations maintain an affiliation with a national network; the station agrees to broadcast the network's prime-time programming and advertising, usually in exchange for a fee. By maintaining affiliated stations in most markets across the country, the major networks have national coverage without violating FCC ownership rules. Four networks have essentially national coverage: ABC, CBS, Fox and NBC. The WB and UPN merged in 2006 to form CW, which has emerged as a competitor to the major four. There are also a handful of smaller networks, the most significant of which are Ion and the Spanish-language networks Univision, Telemundo and Telefutura.
The Telecommunications Act of 1996 was the first major overhaul of telecommunications policy since the Communications Act of 1934 created the FCC nearly 62 years earlier. The 1996 Act came in the wake of the breakup of AT&T, when there seemed to be some consensus among policy-makers that the telecommunications industry was over-regulated. Broadcasting companies argued that they were struggling to compete with cable television and home video, and exerted pressure on the FCC to loosen restrictions on ownership of stations. The 1996 Act removed the limit on the total number of stations that a single entity could own (previously 12) and increased from 25% to 35% the portion of the national population that a single owner's stations could cover. Further deregulation in 1999 allowed joint ownership of two stations with overlapping coverage8 (previously disallowed) as long as they were not in the same market, and allowed joint ownership of two stations in the same market (previously disallowed) as long as that left eight independent full-powered commercial stations in the market and neither of these two stations were ranked in the top four in the market in terms of viewing share.9
The industry underwent significant consolidation in the ten years following deregulation. Views on the effects of this consolidation differ dramatically. For instance, the Common Cause Education Fund argues "that profit-driven media conglomerates are investing less in news and information, and that local news in particular is failing to provide viewers with the information they need in order to participate in the democracy."10 On the other hand, the National Association of Broadcasters (NAB) maintains that "[t]he real threat today to locally-oriented services, including costly services such as local news, is not the joint ownership of broadcast stations..., but the stations' continuing challenge to maintain their economic vibrancy in the face of multichannel and other competitors that are not constrained by restrictions on local ownership structure."11 Broadcasting companies argue that ownership deregulation was necessary for the survival of broadcast television and that further deregulation is in order. Congress has explicitly allowed for this possibility; it directed the FCC to re-evaluate remaining regulations every two years to "determine whether regulation is no longer necessary in the public interest."12 Yet the debate rarely addresses the question of how station owners are helped by consolidation; in fact, this is not well understood.
This paper estimates the revenue versus cost effects of consolidation. It is generally thought that increased revenue following consolidation has negative welfare implications, while lower cost following consolidation has positive welfare implications. However, those implications do not necessarily hold in this industry. Because remaining FCC regulation prevents individual firms from dominating local markets, increased revenue following consolidation is most likely not evidence of market power. Bigger firms are able to offer advertisers more viewers per transaction. The advertiser's outside option has not changed; the bigger firm is simply offering the advertiser a more valuable product. On the other hand, it is often argued that local television programming is a public good. Thus a reduction in the costs incurred in the production of local programming may reveal under-provision of a public good. For these reasons, I hesitate to use my results to draw strong conclusions about welfare. However, as discussed in Section 2 on related literature, studies of this industry have attempted to directly measure the reduced-form effects of consolidation on particular outcomes so as to draw welfare conclusions, and have been inconclusive. It is difficult to understand the mechanisms through which consolidation affects welfare without understanding why consolidation has taken place. This paper attempts to fill that void, by identifying the demand-side and supply-side factors that have driven consolidation in this industry.
4 Data
I acquired a proprietary dataset from BIA Financial Network Inc (BIAfn), a telecommunications research firm. As far as I know, this is the first paper in economics to use this panel dataset on broadcast television stations. I observe each station's market, owner, revenue, coverage, and network affiliation annually from 1996 through 2007. Revenue is adjusted to constant 2008 dollars. Out of 1,251 full-power commercial stations, 131 stations without revenue data are dropped from my analysis, which leaves 1,120 stations. Each station is uniquely identified by its call letters. Owners do not have a unique identifier, so I look carefully at owner names in order to standardize them and create a unique identifier for each. The dataset as provided by BIAfn is at the level of the station. I construct a panel dataset at the level of the firm. There are a total of 544 firms that were active (owned at least one station) at some point between 1996 and 2007 and for which I have data.13 If a firm has exited or not yet entered, then that firm is coded as having zero stations.
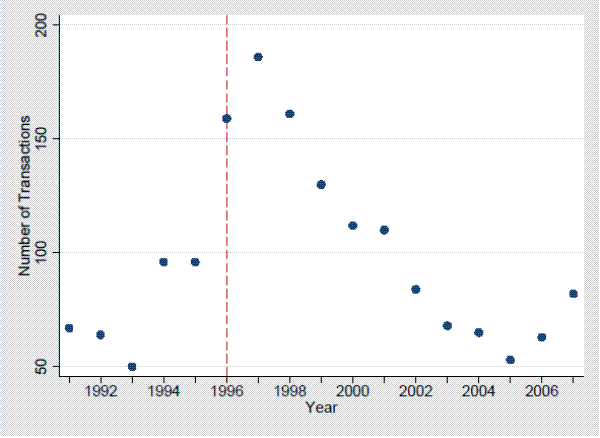
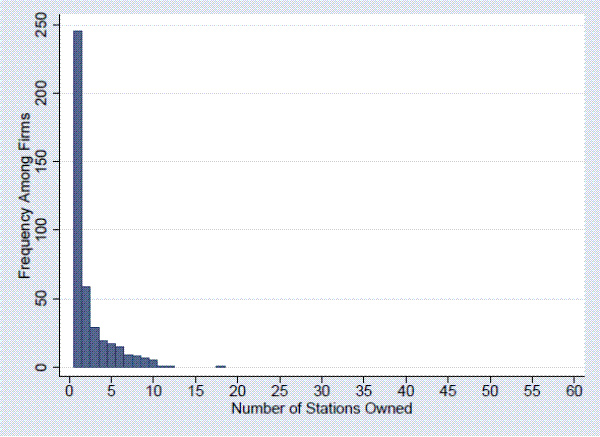
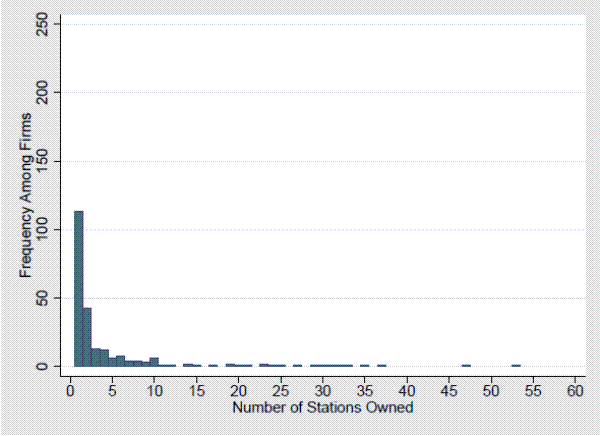
A look at the data confirms that the broadcast television industry underwent significant consolidation in the ten years following deregulation. In 1995, just before deregulation, most firms held only one station and only three firms held more than ten stations. Immediately following deregulation, stations began changing hands. Figure 1 shows the number of transactions (sales of stations) on a yearly basis before and after deregulation. Purchasing activity picked up dramatically in 1996 (the dashed line); it saw a decline following 2001, but has shown signs of picking up again in recent years. Firms that already held a relatively large number of stations tended to expand their portfolios. For instance, of the eight firms that owned ten or more stations in 1995, all but three of them owned more than twenty stations by 2007. On the other hand, individual owners tended to exit the industry. Nearly 70 percent of the firms that owned only one station in 1995 had sold their station by 2007; only one owned more than three stations by 2007. By 2007, 25 firms owned more than ten stations each, and the majority of stations were in the hands of these large owners. The greatest number of stations held by one firm in 2007 was 60. Figure 2 and Figure 3 show how the ownership structure of the industry changed over these years. The trend toward consolidation suggests that owning more stations puts firms at a competitive advantage.
For each firm in each year, I construct six variables that describe the firm's portfolio of stations. These are variables that are likely to affect the attractiveness of the stations as a group to advertisers, as well as variables that are likely to affect the extent to which the firm can centralize the operations of its stations. Note that I am trying to capture how joint ownership of these stations affects their profitability. Therefore these variables describe the firm's stations as a group, rather than characterizing the firm's stations themselves. These variables are: the number of stations owned by the firm, the total population coverage of its stations, the average distance between its stations in miles, the demographic heterogeneity of its stations' viewers, the concentration of its stations among network affiliations, and its dominance of networks. Because I have a panel of stations, I will be able to control for individual station heterogeneity.
Demographic heterogeneity is measured as the average Euclidean distance between the demographic vectors of a firms' stations. A demographic vector is defined as, among the station's viewers: {percent of households that are Caucasian; percent of households that are African-American; percent of households that are Asian; percent of households that are Hispanic}.14
The network concentration variable reflects the degree to which the firm has concentrated its stations' affiliations among just a few networks. It is the Herfindahl index as applied to the firm's concentration among eight national networks,15 divided by the expected value of this index given the number of stations held by the firm.16 The network dominance variable reflects the degree to which the firm dominates a particular network's stations. I look at each network with which the firm has at least one station affiliation, and calculate the percent of the network's stations that this firm owns. I then take the highest value among all networks to which the firm has affiliations.17
5 Model
I estimate a model in which a firm chooses each period how to adjust the characteristics of its portfolio of stations. These characteristics are as listed in the data section: number of stations, population coverage, average distance between stations, demographic heterogeneity among viewers,
network concentration and network dominance. The firm's static per-station revenue and per-station cost are functions of its own portfolio characteristics as well as those of its competitors. I assume that a firm's payoffs depend on its competitors' portfolio characteristics only through the
average values of these characteristics among all of its direct competitors. A direct competitor is defined as a firm that owns a station in one of ![]() 's markets. A firm incurs sunk costs when
it adjusts its portfolio, so the effects of this period's adjustments persist through all future periods. Therefore firms choose their portfolio each period so as to maximize the present discounted value of their expected stream of profits as a function of their own current portfolio
characteristics and their competitors' current average portfolio characteristics. This framework takes into account the strategic and dynamic elements of the firm's decision.
's markets. A firm incurs sunk costs when
it adjusts its portfolio, so the effects of this period's adjustments persist through all future periods. Therefore firms choose their portfolio each period so as to maximize the present discounted value of their expected stream of profits as a function of their own current portfolio
characteristics and their competitors' current average portfolio characteristics. This framework takes into account the strategic and dynamic elements of the firm's decision.
5.1 Revenue and Cost
Let firms be indexed by
![]() and years be indexed by
and years be indexed by
![]() . A firm's per-station revenue is a reduced-form function of its own and its competitors' portfolio characteristics:
. A firm's per-station revenue is a reduced-form function of its own and its competitors' portfolio characteristics:
where
A firm's per-station cost is a reduced-form function of its own portfolio characteristics, subject to adjustment costs:
where
The firm's static profit is:
5.2 Strategies and Equilibrium
Let ![]() be a vector consisting of
be a vector consisting of ![]() 's own portfolio characteristics and the
averages of its competitors' portfolio characteristics:
's own portfolio characteristics and the
averages of its competitors' portfolio characteristics:
The equilibrium concept is Markov-perfect Nash equilibrium; a firm's strategy depends only on its current state vector. The equilibrium can thus be defined as the strategy
![]() that satisfies:
that satisfies:
That is,
6.1 Empirical Strategy
The goal of the paper is to estimate the revenue and cost parameter vectors ![]() and
and ![]() . Because revenue is observed,
. Because revenue is observed, ![]() can be estimated by regressing per-station revenue on state variables. Costs are not observed, so I estimate the dynamic game in order to
recover the cost parameter vector
can be estimated by regressing per-station revenue on state variables. Costs are not observed, so I estimate the dynamic game in order to
recover the cost parameter vector ![]() . I use a two-step method proposed by Bajari, et al. (2007) that avoids computing the equilibrium even once and that allows for
continuous choice variables. In the first stage, I estimate the strategies governing firms' adjustments of their portfolio characteristics each period. In the second stage, value functions are estimated for the observed strategies and for randomly drawn alternative strategies; then the cost
parameters are found that minimize the sum of squared profitable deviations from the observed strategies. These are the cost parameters that "rationalize" the observed strategies given the estimated revenue parameters.
. I use a two-step method proposed by Bajari, et al. (2007) that avoids computing the equilibrium even once and that allows for
continuous choice variables. In the first stage, I estimate the strategies governing firms' adjustments of their portfolio characteristics each period. In the second stage, value functions are estimated for the observed strategies and for randomly drawn alternative strategies; then the cost
parameters are found that minimize the sum of squared profitable deviations from the observed strategies. These are the cost parameters that "rationalize" the observed strategies given the estimated revenue parameters.
6.2 Revenue Estimation
The first step is to estimate the revenue equation (1).18 The equation is at the level of the firm-year. The dependent variable is the
average revenue generated by firm ![]() 's stations in period
's stations in period ![]() . The regressors are the
characteristics of
. The regressors are the
characteristics of ![]() 's own portfolio
's own portfolio ![]() and the average characteristics among
the portfolios of
and the average characteristics among
the portfolios of ![]() 's direct competitors
's direct competitors ![]() . I also include interaction terms
between
. I also include interaction terms
between ![]() 's number of stations
's number of stations ![]() and each of the other characteristics of
and each of the other characteristics of
![]() 's portfolio (except total coverage). I have a panel of firms, so firm fixed effects are included. The firm-specific standard error of the demand shock
's portfolio (except total coverage). I have a panel of firms, so firm fixed effects are included. The firm-specific standard error of the demand shock
![]() is estimated as the standard error of the regression residual across all of firm
is estimated as the standard error of the regression residual across all of firm ![]() 's observations.
's observations.
One complication is that I am eliminating station identity from the model, yet stations are heterogeneous. Failing to take into account station heterogeneity might lead to biased coefficients on portfolio characteristics in the revenue equation, which would in turn lead to biased cost
coefficients in the second stage of estimation. This would happen if the revenue potential of a station is correlated with the characteristics of its owner's portfolio which are included in estimation.19 In order to deal with station heterogeneity, I include as a regressor in the revenue equation the average revenue generated by firm ![]() 's period-
's period-![]() stations across all years and owners. This can be thought of as the average revenue potential of
stations across all years and owners. This can be thought of as the average revenue potential of ![]() 's period-
's period-![]() stations, regardless of ownership. I also include this value in the cost equation, to allow for the (likely) possibility that
stations that generate more revenue also cost more to operate.
stations, regardless of ownership. I also include this value in the cost equation, to allow for the (likely) possibility that
stations that generate more revenue also cost more to operate.
Inclusion of the average revenue potential of firm ![]() 's stations is roughly equivalent to including station fixed effects. I also include firm and year fixed effects. Therefore I am
effectively looking at variation within the firm-station-year. Given this, the most important identification assumption is that there is no trend in a station's revenue which induces a firm with particular portfolio characteristics to purchase it (no reverse causality). Since the timing of station
purchases was largely the result of an exogenous change in regulation, this is likely to be a reasonable assumption.
's stations is roughly equivalent to including station fixed effects. I also include firm and year fixed effects. Therefore I am
effectively looking at variation within the firm-station-year. Given this, the most important identification assumption is that there is no trend in a station's revenue which induces a firm with particular portfolio characteristics to purchase it (no reverse causality). Since the timing of station
purchases was largely the result of an exogenous change in regulation, this is likely to be a reasonable assumption.
6.3 Cost Estimation
Estimation of the cost equation (2) is considerably more complicated. Costs are not observed, so I look at the strategies employed by firms - that is, their portfolio adjustments each period - in order to recover costs. If firms are acting optimally, then the ex ante value of
a state for a firm if it follows the observed strategy must be greater than it would be if it followed any other strategy. The goal is to find the cost parameter vector ![]() that makes this
true, given the estimated revenue parameter vector
that makes this
true, given the estimated revenue parameter vector ![]() and competitor strategies
and competitor strategies
![]() . Therefore, in order to recover cost estimates, I must calculate the ex ante value of being at each observed state as a function of
. Therefore, in order to recover cost estimates, I must calculate the ex ante value of being at each observed state as a function of
![]() ,
,
![]() ,
, ![]() and
and ![]() . The estimation of cost coefficients proceeds as follows: 1) Estimation of strategies 2) Estimation of the ex ante value of each observed state for the observed strategies and for alternative strategies, as a function of
. The estimation of cost coefficients proceeds as follows: 1) Estimation of strategies 2) Estimation of the ex ante value of each observed state for the observed strategies and for alternative strategies, as a function of ![]() 3) The search for
3) The search for ![]() that makes the ex ante values of states greater for the observed strategies than for the
alternative strategies.
that makes the ex ante values of states greater for the observed strategies than for the
alternative strategies.
6.3.1 Estimation of Strategies
The functions governing the evolution of ![]() 's own portfolio characteristics constitute
's own portfolio characteristics constitute ![]() 's strategy,
's strategy,
![]() . The functions governing the evolution of the average portfolio characteristics among
. The functions governing the evolution of the average portfolio characteristics among ![]() 's competitors
's competitors ![]() will act as a summary of the strategies of
will act as a summary of the strategies of ![]() 's competitors,
's competitors,
![]() . That is, the strategy of competitors is defined as
. That is, the strategy of competitors is defined as
![]() . The definition of competitors' strategies
. The definition of competitors' strategies
![]() is important when I consider alternative strategies for firm
is important when I consider alternative strategies for firm ![]() and
calculate the ex ante value of each state under these alternatives, keeping competitors' strategies
and
calculate the ex ante value of each state under these alternatives, keeping competitors' strategies
![]() fixed. By keeping fixed the evolution of the average competitors' portfolio characteristics as a function of firm
fixed. By keeping fixed the evolution of the average competitors' portfolio characteristics as a function of firm ![]() 's own portfolio characteristics, I am essentially keeping fixed firm
's own portfolio characteristics, I am essentially keeping fixed firm ![]() 's competitors' strategies. I use this technique - rather than simulating
what each of
's competitors' strategies. I use this technique - rather than simulating
what each of ![]() 's competitors do and then calculating the average portfolio characteristics among the competitors - for computational reasons.
's competitors do and then calculating the average portfolio characteristics among the competitors - for computational reasons.
Let the variables in the state vector be indexed by ![]() . I want to allow next period's state variable
. I want to allow next period's state variable ![]() to be a function of all of the variables in the state vector in this period
to be a function of all of the variables in the state vector in this period ![]() . I specify the evolution of
. I specify the evolution of ![]() as follows:
as follows:
Recall that the variables in the state vector
In (5), each state variable is subject to a time trend and a firm-specific constant. Estimation of (5) is complicated; I have a dynamic panel data model with endogenous explanatory variables, lagged dependent variables and unobserved firm heterogeneity.
In the presence of lagged dependent variables and endogenous regressors, ![]() cannot be treated as a constant to be estimated. First-differencing removes
cannot be treated as a constant to be estimated. First-differencing removes ![]() , but the endogeneity problem requires instruments. I use the estimator developed by Arellano & Bond (1991), which uses higher-order lagged differences of the regressors as
instruments. This often suffers from a weak instrument problem. Fortunately the F-statistic is greater than 10 in all of the first-stage regressions but one, when it is just under 10. A bigger problem is that the validity of the instruments requires the assumption of no serial correlation, which is
strong in this case.
, but the endogeneity problem requires instruments. I use the estimator developed by Arellano & Bond (1991), which uses higher-order lagged differences of the regressors as
instruments. This often suffers from a weak instrument problem. Fortunately the F-statistic is greater than 10 in all of the first-stage regressions but one, when it is just under 10. A bigger problem is that the validity of the instruments requires the assumption of no serial correlation, which is
strong in this case.
The following system of equations is estimated using the Arellano-Bond GMM estimator:
Equation (6) is estimated only for firms that are already active in the industry (
6.3.2 Value Function Estimation
The value function can be written:
where the expectation is over shocks to demand (
For a given state ![]() , a path of play can be simulated by using
, a path of play can be simulated by using
![]() and a set of shocks drawn from the estimated distribution of
and a set of shocks drawn from the estimated distribution of
![]() . I simulate the evolution of the state vector well into the future (100-200 periods), until the discount factor will render sufficiently small the present value of any
payoffs generated. Given a set of parameters
. I simulate the evolution of the state vector well into the future (100-200 periods), until the discount factor will render sufficiently small the present value of any
payoffs generated. Given a set of parameters ![]() and
and ![]() and draws of shocks
and draws of shocks
![]() and
and ![]() , I can calculate the present value of payoffs associated with this
path of play. Repeating this procedure numerous (1000-2000) times and averaging the present value of payoffs over all of these paths gives me an estimated ex ante value associated with this state
, I can calculate the present value of payoffs associated with this
path of play. Repeating this procedure numerous (1000-2000) times and averaging the present value of payoffs over all of these paths gives me an estimated ex ante value associated with this state ![]() .
.
6.3.3 Search for Cost Estimates
The final step is to search over possible cost parameter vectors to find ![]() which minimizes the profitable deviations generated by alternative strategies, and therefore makes
which minimizes the profitable deviations generated by alternative strategies, and therefore makes
![]() optimal given
optimal given
![]() and
and ![]() . The simulation of numerous paths of play for each
state that is observed in the data (a total of 12 years * 544 owners = 6528 states) is the computationally expensive part of the estimation process. I impose a few restrictions in order to make estimation feasible.
. The simulation of numerous paths of play for each
state that is observed in the data (a total of 12 years * 544 owners = 6528 states) is the computationally expensive part of the estimation process. I impose a few restrictions in order to make estimation feasible.
First, I impose the restriction that the firm-specific cost constant
![]() is a linear function of the firm-specific revenue constant
is a linear function of the firm-specific revenue constant
![]() . In other words, I include
. In other words, I include
![]() as a variable in the cost equation and estimate the cost coefficient on it. This is much less computationally expensive than freely estimating
as a variable in the cost equation and estimate the cost coefficient on it. This is much less computationally expensive than freely estimating
![]() , which would require the inclusion of 543 firm dummies in second-stage estimation. Effectively I am allowing for the possibility that firms that generate systematically higher
revenue incur either systematically higher or systematically lower costs. This allows for two scenarios. In one scenario, some firms are simply "better," both generating higher revenue and incurring lower costs; this would lead to a negative relationship between
, which would require the inclusion of 543 firm dummies in second-stage estimation. Effectively I am allowing for the possibility that firms that generate systematically higher
revenue incur either systematically higher or systematically lower costs. This allows for two scenarios. In one scenario, some firms are simply "better," both generating higher revenue and incurring lower costs; this would lead to a negative relationship between
![]() and
and
![]() . In another scenario, the firms that invest more in programming tend to draw in more advertising revenue, whereas firms that cut programming costs tend to take a hit to
advertising revenue; this would lead to a positive relationship between
. In another scenario, the firms that invest more in programming tend to draw in more advertising revenue, whereas firms that cut programming costs tend to take a hit to
advertising revenue; this would lead to a positive relationship between
![]() and
and
![]() . The cost coefficient on
. The cost coefficient on
![]() tells us which scenario is a better description of reality.
tells us which scenario is a better description of reality.
Another restriction is that I must write the ex ante value of a state as a linear function of the cost parameter vector ![]() :
:
where:
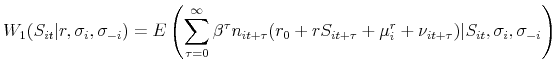
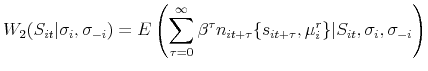
For each state observed in the data, I estimate
![]() and
and
![]() under various perturbations of the observed strategies (that is, functions governing the evolution of
under various perturbations of the observed strategies (that is, functions governing the evolution of ![]() ), keeping competitors' strategies (that is, functions governing the evolution of
), keeping competitors' strategies (that is, functions governing the evolution of ![]() ) and the revenue coefficient vector
) and the revenue coefficient vector ![]() fixed. I then find the cost coefficient vector
fixed. I then find the cost coefficient vector ![]() that must exist in order for the
observed strategies to be superior to the perturbations. The equilibrium condition (4) can be written:
that must exist in order for the
observed strategies to be superior to the perturbations. The equilibrium condition (4) can be written:
| (9) |
Let the alternative firm strategies that are considered be indexed by
| (10) |
I find
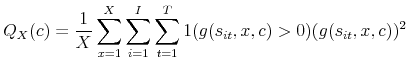 |
(11) |
That is, I find
Because the industry remains regulated, firms are not free to choose any portfolio that they want. Therefore I restrict the behavior of firms in simulated paths of play. I do not allow firms to acquire more stations than would realistically be allowed under current regulations, or to choose a
smaller average distance between stations than would be allowed. Also, I consider very small perturbations of the observed strategies as alternative strategies; these are alternatives that are presumably available to firms. A strategy perturbation consists of an increase or decrease for each
portfolio characteristic in each period of 0.5%, 1%, 1.5% or 2%, chosen randomly. For a given state, alternative strategy and portfolio characteristic, the same deviation is made in each successive period. Parameter estimates are not very sensitive to the number of alternative strategies
considered. More alternative strategies allows for more precise estimates but this comes at high computational cost. In practice I use ![]() =30.
=30.
7 Empirical Results
Revenue is observed, so the interpretation of revenue estimates is fairly straightforward. The interpretation of cost estimates is more complicated. Cost is essentially a residual, serving to explain the behavior of firms that is left unexplained by revenue. For this reason, it is unreasonable to interpret cost simply as strictly the cash that flows out of a firm in a given year; it may include the cost of raising capital, the cost of being exposed to risk, and so on. This should be kept in mind when interpreting my results.
The equilibrium condition used to recover cost assumes that the present discounted value of the expected stream of revenue from a station minus the present discounted value of the expected stream of cost of a station must be greater than zero in order for a firm to choose to own (rather than sell) the station. In reality, this value must be greater than the market value of the station, because this is what the firm must pay to own the station (or what the firm could earn by selling the station). The annual per-station cost recovered in my estimation therefore includes the annual opportunity cost of holding (not selling) the station at market value.
Suppose that the market for broadcast television stations operates perfectly, with efficient credit markets and all agents having full information. Then we would expect the market value of a station to be approximately equal to the present discounted value of the station's expected stream of profits. Therefore the annual opportunity cost of holding the station would be approximately equal to the annual profit generated by the station. In this case, recovered annual per-station cost would be close to annual per-station revenue.22 Table 1 presents summary statistics for annual per-station revenue and recovered annual per-station cost for portfolios that are observed in the data over the past ten years. The distributions of revenue and cost are highly skewed. For this reason, direct comparisons of the mean and median can be hard to interpret. However, the rough equivalence of the maximum per-station revenue and maximum recovered per-station cost shown in Table 1 is consistent with cost estimates that are relatively clean and that include opportunity cost.
It is worth thinking about how inclusion of opportunity cost in recovered cost may affect the estimated coefficients of interest, that is, the effects of a firm's portfolio characteristics on its per-station cost. As long as this opportunity cost is exogenous to the variables of interest, the estimated coefficients should not be biased. The opportunity cost of holding a station should reflect the highest value that any other firm would pay for the station. This value should not be directly affected by the portfolio characteristics of the firm in question. Therefore the coefficients of interest should not be affected.
A final point that should be kept in mind when interpreting my results is that this industry remains regulated. Therefore firms are not completely free to adjust the characteristics of their portfolios of stations. Therefore, the estimated revenue and cost effects should be interpreted as those that exist under current regulations. They do not tell us what the revenue and cost advantages of consolidation would be under an entirely different set of regulations.23
The estimated revenue coefficients ![]() and cost coefficients
and cost coefficients ![]() are
shown in Table 2. Note that the adjustment coefficients are effects on the firm's total (not per-station) cost, and that these are one-time effects that are assumed not to
persist through time. All of the other estimates are the effects of portfolio characteristics on annual per-station revenue or cost. Preliminary standard errors for cost estimates are calculated using the method described in Pakes et al. (2006); this
involves estimating the covariance matrix for the value function, taking draws from the sample distribution of the value function, and minimizing the objective function to find cost estimates for each of these draws.24 Because the units of the portfolio characteristics vary and are not necessarily intuitive, the results are easier to interpret by looking at Table 3, which shows the dollar effects of standard deviation changes in portfolio characteristics on a firm's average per-station revenue and cost, and on a firm's per-station profit (revenue less cost).
are
shown in Table 2. Note that the adjustment coefficients are effects on the firm's total (not per-station) cost, and that these are one-time effects that are assumed not to
persist through time. All of the other estimates are the effects of portfolio characteristics on annual per-station revenue or cost. Preliminary standard errors for cost estimates are calculated using the method described in Pakes et al. (2006); this
involves estimating the covariance matrix for the value function, taking draws from the sample distribution of the value function, and minimizing the objective function to find cost estimates for each of these draws.24 Because the units of the portfolio characteristics vary and are not necessarily intuitive, the results are easier to interpret by looking at Table 3, which shows the dollar effects of standard deviation changes in portfolio characteristics on a firm's average per-station revenue and cost, and on a firm's per-station profit (revenue less cost).
A standard deviation increase of 11.5 in Total Coverage in Millions (of persons) causes a $2.17 million increase in per-station revenue. That is, increasing the total population coverage of a firm's stations enables the firm to boost its per-station revenue, most likely because advertisers pay more to reach more viewers per transaction. Given that median per-station revenue is $6 million, this effect is large in magnitude.
A standard deviation change of 5 in Number of Stations owned is associated with a $1.85 million reduction in per-station cost. That is, acquiring more stations gives firms a cost advantage; firms are probably able to combine operations of multiple stations and cut costs. This effect is also quite large in magnitude.
While increasing total coverage boosts per-station revenue, it also increases per-station cost (for a given number of stations owned). A standard deviation increase of 11.5 in Total Coverage in Millions is associated with a $713,000 increase in per-station cost. However, the net effect of total coverage on per-station profit is positive and large in magnitude. A standard deviation increase of 11.5 million is associated with a $1.46 million increase in per-station profit.
Similarly, while acquiring more stations reduces per-station cost, it also reduces per-station revenue (for a given level of population coverage). A standard deviation increase in Number of Stations is associated with a $1.04 million fall in per-station revenue. It is possible that as firms acquire more stations and combine operations of their stations, the quality of programming declines, which may have a negative effect on advertising revenue. However, the net effect of owning more stations is positive. A standard deviation increase of 5 stations is associated with a $815,000 increase in per-station profit.
An increase in network concentration has opposing demand-side and supply-side effects. A standard deviation increase of 1.03 in Network Concentration reduces per-station cost by $772,500.25 An increase in network concentration achieved while acquiring additional stations further reduces per-station cost; a standard deviation increase of 20 in Network Concentration * Number of Stations reduces per-station cost by $340,000. This makes sense, because one important aspect of the management of a broadcast television station is negotiation and coordination with the national network to which the station is affiliated. Therefore operating multiple stations is probably less costly if most of the stations are affiliated with one or two networks. Yet at the same time, increased network concentration among a firm's stations hurts the revenue potential of the stations. A standard deviation increase of 20 in Network Concentration * Number of Stations lowers per-station revenue by $720,000. This is likely because an advertiser has the option of advertising through a national network rather than through the owner of network-affiliated stations. Therefore a firm's portfolio of stations is probably less attractive to an advertiser if it is essentially just a subset of the stations that are affiliated with one particular national network.
I find that the operation of multiple stations is slightly costlier if the stations' viewers are more demographically heterogeneous. A standard deviation increase of 126 in Average Demographic Heterogeneity * Number of Stations increases per-station cost by $143,640.26 I do not find any statistically significant effect of demographic heterogeneity on per-station revenue. However, existing regulation places a lower bound on this variable for firms.
I find that the average distance between a firm's stations has little effect on its per-station revenue. Again, though, existing regulation places a lower bound on this variable for firms. On the cost side, the evidence is mixed. A standard deviation decrease of 5221 in Average Distance * Number of Stations causes a $417,680 decrease in per-station cost. A simultaneous increase in number of stations and fall in average distance between stations could be achieved by acquiring an additional station that is between two stations that a firm already owns. It makes sense that this would provide cost advantages. On the other hand, a standard deviation reduction in Average Distance between Stations of 430 miles, for a given number of stations owned, actually raises per-station cost by $3 million. Firms may find that there are advantages to diversification, and spreading stations across the country may be one way of diversifying (again, given the effective lower bound on distance between stations). For instance, Sinclair Broadcast Group declares on its website that it is "one of the largest and most diversified television broadcasting companies in the country today."27 This may be attractive to investors; while few broadcasting companies are public, some such as Sinclair are and many may aspire to be.
I find that strategic effects are important in this industry; four of the six strategic variables included in estimation have large and statistically significant effects on a firm's per-station revenue. A standard deviation increase of 7.2 in Average Number among Competitors causes per-station revenue to fall by almost $1 million. This makes sense, given the finding that a firm faces lower per-station cost if it owns more stations. If a firm faces competitors with more stations, then the firm faces competitors with lower costs. Its competitors can therefore offer lower advertising prices, and draws advertisers away. A firm's per-station revenue is also lower if its competitors' stations are close together on average; a standard deviation increase of 381 in Average Distance among Competitors has a positive effect of $647,700. However, a standard deviation increase of 15.6 in Average Coverage among Competitors causes an increase in per-station revenue of $1.9 million. This means that, given the size of a firms' competitors in terms of the number of stations they own, an increase in their coverage lessens their competitive effect. A standard deviation increase of 5.7 in Average Network Domination among Competitors has a negative effect of almost $1 million on per-station revenue.
The cost coefficient on the average revenue potential of a firm's stations is 0.65. The positive sign means that stations that generate more revenue also cost more to operate. The cost coefficient on the firm's revenue fixed-effect coefficient is 0.6. The positive sign means that firms that generate higher per-station revenue also incur higher per-station cost. It appears that firms that invest more in programming (increasing costs) tend to reap higher revenue in return, while firms that cut costs tend to accept revenue losses as a result. The intuition behind the identification of this parameter is as follows: firms that earn more revenue per station are not systematically seeking out large portfolios as much as we would expect given the higher per-station revenue that they generate; this must be because they also incur higher per-station costs.
While consolidation has advantages, the process of purchasing and selling stations incurs adjustment costs. I find that purchasing a station involves a one-time cost of $1.3 million, while selling a station involves a one-time cost of $1.5 million (but the latter estimate is not statistically significant). Note that the adjustment cost is not capturing the market price of the station, which is captured in the constant term in the per-station cost equation.
I conduct a crude check of my cost numbers by calculating what they imply for the average opportunity cost of holding a station, and comparing this to typical transaction prices for stations. Based on anecdotal evidence, a typical station generates profit margins of 20%, so I roughly estimate average annual per-station operating cost as revenue divided by 1.2. The implied annual opportunity cost of holding a station is then calculated as the total per-station cost estimated by my model minus this rough estimate of per-station operating cost. The average implied annual opportunity cost of holding a station is $18 million. At an interest rate of 6%, this is consistent with an average station market value of $307 million. Given the highly skewed distribution of revenue and cost in this industry, this is likely to be much greater than the median market value. I do not have data on station sales prices, but anecdotal evidence suggests that this is reasonable.
8 Conclusion
This paper estimates the demand-side and supply-side advantages of consolidation in the broadcast television industry. The consolidation has provoked considerable controversy. However, the reasons it occurred are not well understood, because firms mainly purchase stations that are not in direct competition with one another and that are located many miles apart.
I exploit an exogenous change in regulation that led to significant consolidation in the industry. Although revenue and ownership data are available for broadcast television stations, cost data are not available. I recover costs by examining patterns in ownership changes that are left unexplained by revenue opportunities. Because the firm's purchasing decision involves dynamic and strategic elements, I model the decision as a dynamic game. The firm adjusts its portfolio characteristics each period so as to maximize the present discounted value of its expected stream of profits. My approach allows me to isolate the relationships of interest in an industry that each year witnesses hundreds of firms considering the purchase or sale of over one thousand stations. As far as I know, this paper is the first to estimate a model of merger activity in a dynamic, strategic framework.
My results suggest that consolidation in this industry offers both revenue and cost advantages, but that they operate through different mechanisms. Firms are able to generate more revenue per station if the total population coverage of their stations is greater. Advertisers are probably willing to pay more to reach more viewers per contract. On the other hand, the cost advantages of consolidation come not through wider population coverage, but through simply owning a large number of stations. The cost advantages of owning multiple stations are especially great if the firm's stations are mostly affiliated with just one or two networks and if their viewers are more demographically homogeneous. However, a lack of diversification in network affiliation hurts the revenue potential of the firm's stations. I find that strategic effects are important in this industry. A firm earns less revenue per station if its competitors own more stations on average and if its competitors' stations are located close together on average.
An interesting next step would be to use the estimated coefficients to solve the dynamic oligopoly model and conduct counterfactuals. I could determine the extent to which consolidation patterns have been driven by cost advantages, revenue advantages or strategic considerations, by simulating firms' purchasing patterns under alternative values for the revenue and cost coefficients.
Bibliography
The Review of Economic Studies 58:277-297.
Econometrica 75:1331-1370.
Federal Communications Commission Media Ownership Study No. 3.
Federal Communications Commission Media Ownership Study No. 8.
NBER Working Paper.
Econometrica 60:1127-1150.
Econometrica 50:649-670.
The American Economic Review 83(3):549-569.
The RAND Journal of Economics 33:37-61.
The RAND Journal of Economics 21:27-44.
The Journal of Political Economy 108:728-760.
The Review of Economics and Statistics 72(4):703-707.
Centre For Microdata Methods and Practices Working Paper.
Southern Economic Journal 70:110-127.
The RAND Journal of Economics 34(3):495-515.
International Economic Review 40:381-401.
Econometrica 51:1469-1483.
The Journal of Industrial Economics 36:131-146.
The RAND Journal of Economics 21:45-62.
Federal Communications Commission Media Ownership Study No. 4: News Operations.
Journal of Finance 62:2725-2762.
| Annual Per-Station Revenue† | Recovered Annual Per-Station Cost† | |
|---|---|---|
| Mean | $12.7 million | $15.0 million |
| Standard Deviation | $20.1 million | $21.1 million |
| Median | $6.0 million | $17.2 million |
| Minimum | $0.06 million | $0.01 million |
| Maximum | $169 million | $151 million |
| Effect on Per-Station Revenue † | Effect on Per-Station Cost † | |
|---|---|---|
| Number of Stations | -207* | -370* |
| Number of Stations Standard Errors | (79) | (119) |
| Squared Positive Adjustment | 1350* | |
| Squared Positive Adjustment Standard Errors | (437) | |
| Squared Negative Adjustment | 1500 | |
| Squared Negative Adjustment Standard Errors | (2712) | |
| Average Coverage Per Station in Millions | -427* | 3900* |
| Average Coverage Per Station in Millions Standard Errors | (180) | (660) |
| Total Coverage in Millions | 189* | 62* |
| Total Coverage in Millions Standard Errors | (44) | (11) |
| Avg Distance between Stations | 0.57 | -7* |
| Avg Distance between Stations Standard Errors | (0.37) | (2) |
| Avg Distance * Number of Stations | -0.04 | 0.08* |
| Avg Distance * Number of Stations Standard Errors | (0.08) | (0.036) |
| Avg Demographic Heterogeneity | -17 | 50 |
| Avg Demographic Heterogeneity Standard Errors | (14) | (68) |
| Avg Demographic Heterogeneity * Number of Stations | 6.7 | 1.14* |
| Avg Demographic Heterogeneity * Number of Stations Standard Errors | (3.7) | (0.41) |
| Network Concentration | 315 | -750* |
| Network Concentration Standard Errors | (198) | (242) |
| Network Concentration * Number of Stations | -36* | -17* |
| Network Concentration * Number of Stations Standard Errors | (10) | (4.5) |
| Network Domination | -23 | -54 |
| Network Domination Standard Errors | (39) | (31) |
| Network Domination * Number of Stations | 1.5 | 1.18 |
| Network Domination * Number of Stations Standard Errors | (1.2) | (0.57) |
| Average Revenue Potential | 1.01* | 0.65* |
| Average Revenue Potential Standard Errors | (0.02) | (0.055) |
| Average Revenue Potential * Number of Stations | -0.0057* | 0.0037* |
| Average Revenue Potential * Number of Stations Standard Errors | (0.0019) | (0.00018) |
| Avg Number among Competitors | -137* | |
| Avg Number among Competitors Standard Errors | (25) | |
| Avg Coverage in Millions among Competitors | 120* | |
| Avg Coverage in Millions among Competitors Standard Errors | (20) | |
| Avg Distance among Competitors | 1.7* | |
| Avg Distance among Competitors Standard Errors | (0.6) | |
| Average Demog Heterogeneity among Competitors | -20 | |
| Average Demog Heterogeneity among Competitors Standard Errors | (20) | |
| Average Network Concentration among Competitors | 198 | |
| Average Network Concentration among Competitors Standard Errors | (224) | |
| Average Network Domination among Competitors | -162* | |
| Average Network Domination among Competitors Standard Errors | (27) | |
| Firm Dummy Coefficient in Revenue Regression | 1 | 0.6* |
| Firm Dummy Coefficient in Revenue Regression Standard Errors | (0.3) |
| Standard Deviation | Effect on Per-Station Revenue | Effect on Per-Station Cost† | Net Effect on Per-Station Profit† | |
|---|---|---|---|---|
| Number of Stations | 4.9 | -$1,035,000* | -$1,850,000* | +$815,000 |
| Squared Positive Adjustment | 0.75 | +$1,012,000* | -$1,012,000 | |
| Squared Negative Adjustment | 1.81 | +$2,700,000* | -$2,700,000 | |
| Average Coverage Per Station in Millions | 1.78 | -$760,600 | +$6,942,000 | -$7,684,600 |
| Total Coverage in Millions | 11.5 | +$2,173,500* | +$713,000* | +$1,460,500 |
| Avg Distance between Stations | 430 | +$245,100 | -$3,010,000* | +$3,255,100 |
| Avg Distance * Number of Stations | 5221 | -$208,840 | +$417,680* | -$626,520 |
| Avg Demographic Heterogeneity | 12.1 | -$205,700 | +$605,000 | -$810,700 |
| Avg Demographic Heterogeneity * Number of Stations | 126 | +$844,000 | +$143,640* | +$700,360 |
| Network Concentration | 1.03 | +$324,450 | -$772,500* | +$1,096,950 |
| Network Concentration * Number of Stations | 20 | -$720,000* | -$340,000* | -$380,000 |
| Network Domination | 5.1 | -$117,300 | -$275,400 | +$158,100 |
| Network Domination * Number of Stations | 202 | +$303,000 | +$238,360 | +$64,640 |
| Average Revenue Potential | 15,900 | +$16,160,000* | +$10,335,000* | +$5,825,000 |
| Average Revenue Potential * Number of Stations | 197 | -$1,123* | +$729* | -$1,852 |
| Avg Number among Competitors | 7.2 | -$986,400* | -$986,400 | |
| Avg Total Coverage in Millions among Competitors | 15.6 | +$1,872,000* | +$1,872,000 | |
| Avg Distance among Competitors | 381 | +$647,700* | +$647,700 | |
| Average Demog Heterogeneity among Competitors | 10.4 | -$208,000 | -$208,000 | |
| Average Network Concentration among Competitors | 1.05 | +$207,900 | +$207,900 | |
| Average Network Domination among Competitors | 5.66 | -$916,920* | -$916,920 |
* Statistically significant at the 5% level.
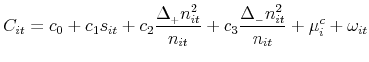
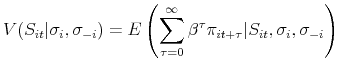
![\displaystyle E\left(\sum _{\tau =0}^{\infty }\beta ^{\tau }[n_{it+\tau }(R_{it+\tau }-C_{it+\tau })]\vert S_{it},\sigma _{i},\sigma _{-i}\right)](img51.gif)