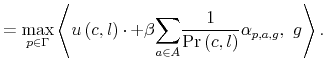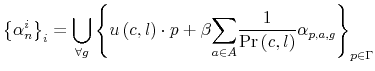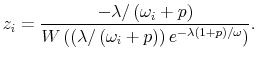The Rigidity of Labor:
Processing Savings and Work Decisions Through Shannon's Channels
Keywords: Rational inattention, savings, labor, decisionmaking
Abstract:
JEL Codes: D81, D91, E21, C63
1 Introduction
Existing macroeconomic theories have trouble fitting empirical regularities in aggregate behavior. Existing models match some U.S. business cycle facts at the expense of others. Despite the progress in the field and rich modelling tools, one peculiar dimension of the business cycle that still troubles the literature is the labor market. As a matter of theory, starting from a framework in which consumers and firm optimize, market clears and no fiscal distortion, equilibrium in the labor in equilibrium the marginal rate of substitution (MRS) between consumption and labor ought to be equal to the marginal product of labor (MPL) given by wages. As a matter of fact, the data shows a discrepancy between the two, called the labor wedge. The challenge for macroeconomic theories has been to match magnitude and volatility of such a wedge (Hall 1997).
Over the years, a number of explanations and modelling devices have been proposed to address the movement in the labor wedge over the business cycle. The principal suspects are different sorts of shocks to either the demand or the supply side of the labor market or both. Whether the shocks hit wage mark-ups,1 disutility of labor,2taxes 3 or productivity as in the search and matching literature,4 the common denominator seems to be the close connection between ad hoc modelling technologies and results. Moreover and most importantly, models based on exogenous shocks do not only fall short in micro-founded justification but also fail in providing empirically plausible predictions along other dimensions.5
This paper suggests an explanation of labor wedge and, more generally, business cycle facts, based on rational inattention.6 My choice to model people constrained by finite information processing capacity agrees with intuition and, as the paper shows, points towards the right direction to capture empirical evidence. In particular, my model is able to generate endogenously a wedge between MRS and MPL in an optimizing framework without the need of exogenous shocks.
In my model, rational households consume, work and pay attention to their wealth to maximize their lifetime utility. In the baseline model, I assume that consumers are risk adverse and have a constant disutility of labor. Under rational inattention, they cannot know the exact value of their wealth in each period due to information-processing frictions. Each period they choose information about wealth they can attend to and decide on the basis of that information how much to consume and work. Realized consumption and employment are then used to update rationally their knowledge of wealth. In my setting wages follows a Markov process and its distribution is known before consumers make their work and consumption decision. Thus, fluctuations in wealth are due to movements in labor and consumption as well as movements in wages. Consumers keep track of wealth by processing information in the limits of their Shannon capacity.
Having a bound on information processing rate suits the observation that people do not check their account on a daily basis, nor they are likely to keep track of the incidence of their expenses and hours worked on their lifetime wealth at high frequency. Using Shannon channels as modelling device has also the nice feature of providing a natural bound for information flow which depends only on the distribution of the variables that are passed through the channel, regardless of the specificity of the channel. This in turns makes the choice of this kind of information friction free from unexplained assumptions on individual characteristics.
More importantly, the predictions of the model agree with U.S. business cycle data along the dimensions analyzed. I show that even in a simple partial equilibrium with focus on the supply side of the labor market, a model in which people choose labor and consumption under information processing constraint à la Sims is able to explain several features of U.S. business cycle. In particular, my setting delivers four results: 1. ratio of standard deviation of consumption over hours worked bigger than one; 2. persistence in consumption and labor supply; 3. comovement of consumption, labor and wealth; 4. endogenously derived labor wedge with positive variance.
To understand the mechanism behind these results, consider what happens in an equivalent model with full information. When wages are deterministic and interest rates are high enough to promote savings, a consumer aware of his wealth with log utility and constant disutility of labor accumulates wealth through high labor supply which, in turns, increase period-by-period income while keeping consumption smooth. In such a context fluctuations in wealth are mostly due to fluctuations in labor supply. With information processing constraints, consumers cannot know the exact value of their wealth even with deterministic wages. They keep track of their wealth imperfectly by choosing signals as informative about wealth as channel capacity allows them to. Log utility in consumption and linear disutility of labor together with low information flow make household work hard and save at early stage of their life. With low information flow and, as a result, low informativeness of the signal each period, households keep savings and labor supply high to make sure they can sustain their consumption. As wealth accumulates, the signal on high values of wealth becomes sharper, calling for a major adjustment in behavior. The size of the adjustment is bigger the lower their processing capacity. This result is intuitive: the longer consumers wait to modify their behavior, the bigger is the variation in consumption and labor once they acknowledge the change in wealth through information processed. Furthermore, in my model, consumption is more sluggish than labor supply. The rationale for this finding lies in the preferences of consumers who dislike having to change their consumption frequently while having constant disutility of labor. Such preferences imply that when people review their consumption plan by realizing that they have saved too much or too little with respect to their lifetime possibilities, they do so by large amounts. This in turns leads to higher volatility of realized consumption with respect to labor supply and provides a rationale for the first result. The effect is stronger the lower the information flow.
The autocorrelation of consumption and employment derive from a similar logic. With signals that bring about low information, changes in behavior are slow at high frequency: the news about wealth are not enough to modify yesterday's consumption and labor supply. This implies that consumers are 'stuck' with the same choices and keep accumulating information until evidence of changes in wealth suggests otherwise.
As for the third finding, my model predicts stronger comovement of contemporaneous consumption, labor and wealth the higher the information flow. If information capacity is low, then contemporaneous consumption and labor commove strongly with lagged values of wealth. Contemporaneous consumption, labor and wealth are strongly linked via the budget constraint. Moreover, the budget constraint affects the choice of the policy function -optimal joint distribution between wealth and behavior. With high information flow, consumers' optimal policy commands to make wealth and behavior as related as possible so that the outcome from consumption and labor supply are very informative about wealth. If information flow is low, consumption and labor are strongly correlated with past values of wealth. This result is driven by the rational (Bayesian) update of consumers' information. Each period the household gets information about wealth and observes consumption and labor choices. Low information flows makes the signal on wealth imprecise forcing the household to rely mostly on the information content of his consumption and labor. This translates into periods of inertial behavior until the information collected signals enough variation in wealth to justify a change in the choices. This observation together with Bayesian updating explain why, in presence of finite rate of information, consumers delay their reaction to changes in wealth. These results are robust to higher specification of risk aversion and for the case of finite elasticity of substitution of leisure in different periods.
The last result is that my model derives endogenously a wedge between MRS and MPL. Moreover, a reasonable calibration of the model leads to magnitude and variance of this wedge in line with U.S. data 7. The key point is that people react to fluctuations of wealth according to the information they have chosen. As a result, consumption and labor are function of the optimal signal that consumers select. The lower the information flow, the less informative the signal, the more uncertain consumers are about their wealth. Consumers react to such uncertainty by modifying their consumption and labor on the basis of their perception of the wealth given the signal. This mechanism generates a discrepancy between the actual wage (MPL) and the marginal rate of substitution between consumption and labor (MRS) based on consumers' information.
Together with the contribution to the macroeconomic labor literature, this paper is closely related to the literature of rational inattention, with particular reference to Sims (2003, 2006), Tutino (2008) and Mackowiak and Wiederholt (2008a, 2008b). This paper departs from Sims (2003) and Mackowiak and Wiederholt (2008a, 2008b) since the ex-ante characterization of uncertainty is not limited to the Gaussian distribution nor the framework is constrained to be linear quadratic. Instead, as in Sims (2006) and Tutino (2008), this paper presents a fully endogenous choice of distribution of uncertainty in a dynamic context and allows for risk aversion in the specification of agents' preferences. The present framework extends Tutino (2008) by augmenting the choice space of people to consumption and labor as opposite to only consumption. This extension generates endogenously an allocation of attention, and, in turn, a different degree of persistence between consumption and labor on the basis of the stochastic properties of the joint distribution of decisions and wealth chosen by the consumers. An example might help clarifying the intuition behind this result. Suppose that a person works the same amount of hours everyday. Given this behavior, the person learns nothing about wealth through his labor supply. In this case, fluctuations of wealth are acknowledged mostly through the information content of consumption realizations and the optimal distribution of uncertainty is similar to the one derived in Tutino (2008). The household might have a better understanding of his financial possibilities by varying either consumption or leisure or both and thereby improve on both consumption and leisure. If wages are relatively stable, it might be optimal to keep labor supply fixed and offset fluctuations in wealth with changes in consumption. On the other hand, if wages change significantly, it might pay off to vary the amount of labor supply and maintain a smooth consumption profile. Amount and directions of these changes in behavior depend on the relative cost of changing consumption with respect to labor supply, the relative benefits of being better informed about wealth through either source and households' preferences implied by the curvature of the utility function. Thus, in this framework, predominance of income vs. substitution effect does not depend only on people's utility as standard macro literature delivers, but also on the relative attention people pay to current consumption and hour worked as source of information about wealth.
The rest of the paper is structured as follows: The next section presents the model and its main assumptions while section 3 illustrates the computation strategy. Section 4 is the core of the paper. It analyzes the main findings and contrasts them with US business cycle data. Section 5 provides statistics and predictions of different specifications of the model. Section 6 concludes.
2 The Model
The model is a one sector partial equilibrium discrete time problem. The economy is populated by numerous households who want to maximize the expected discounted value of their utility defined over a consumption good and leisure. I assume that the consumers have infinite elasticity of substitution between leisure in different periods.8 Their wealth evolves according to their previous period savings augmented by a fixed and exogenous interest rate and their income is given by the hours of work they decide to supply in exchange for a salary.
The households cannot process all the information available about their wealth due to limited processing capacity. Instead, they have a belief about it. The assumption that wealth is not known is meant to capture the complexity associated with mapping current value of wealth (e.g., the number that people see at the end of their personal income statement ) with their current and future possibility of consumption and leisure. The bound on information flow prevents households to perform this task immediately and with infinite precision. The model reflects households' initial uncertainty about wealth before processing any information through the assumption that people enter their life with a prior on wealth.9
Households decide which signals about wealth to choose in order to map their financial possibilities to consumption and work. They can freely choose the characteristics of their signals under the condition that the information between wealth and behavior provided by the signal flows at finite rate. I assume that the households in the economy share the same characteristics in terms of preferences, endowment and their capacity of processing information. This allows me to focus on a representative agent's economy.
2.1 Timing
Before the formal description, I provide a chronological view of the events to guide through the model. A person enters his life with a belief on wealth,
![]() . He decides on a signal that conveys information jointly on his wealth (
. He decides on a signal that conveys information jointly on his wealth (![]() ) and decision (
) and decision (
![]() ) of consumption
) of consumption
![]() and work
and work
![]() Let
Let
![]() denote the joint probability of wealth and decisions implied by the optimal choice of the signal. Note that the signal can provide information
about any dimension of behavior -
denote the joint probability of wealth and decisions implied by the optimal choice of the signal. Note that the signal can provide information
about any dimension of behavior - ![]() - and wealth -
- and wealth - ![]() - that the person wants, with
the restriction that the informativeness of the signal cannot exceed his processing capacity. Such a signal provides him with a rule of conduct for consumption and labor choices. In period
- that the person wants, with
the restriction that the informativeness of the signal cannot exceed his processing capacity. Such a signal provides him with a rule of conduct for consumption and labor choices. In period ![]() , the household draw from the optimal choice
, the household draw from the optimal choice
![]() his consumption profile (
his consumption profile (![]() ), and
labor supply (
), and
labor supply (![]() ).
).
Figure 0: A typical day of a rationally inattentive person.

Then, he observes the outcomes of his choices and use the observation to update rationally his knowledge of wealth (
![]() ). This complete his day. The day after he follows the same routine starting with
). This complete his day. The day after he follows the same routine starting with
![]() as his new prior. Figure 0 describes the events.
as his new prior. Figure 0 describes the events.
2.2 Statement and Recursive Formulation of Consumers' Problem
I discuss each element of the model in turn, starting from the constraints. First I present the budget constraint and discuss its role in updating the knowledge of wealth for an information constrained consumers. Next I turn to the information-flow constraint, key of the model. Finally I present the objective function and set up the full problem.
The structure of the economy follows closely the one of Tutino (2008) to which I refers for the mathematical details. For completeness, Appendix A proves rigorously that the problem admits a recursive formulation and that the resulting Bellman equation is a contraction.
2.2.1 Budget Constraint and Update
Consumers maximize their lifetime utility function, defined over a consumption good and leisure. Let ![]() denote the consumption good and
denote the consumption good and ![]() be labor. I collect the actions at time
be labor. I collect the actions at time ![]() in the set
in the set
![]() .
.
Consumers are limited in their choices by a budget constraint
where
Let
![]() be a particular behavior of consumer at time
be a particular behavior of consumer at time ![]() where
where ![]() is a specific outcome of the random variable
is a specific outcome of the random variable ![]() at time
at time
![]() and similarly
and similarly ![]() is a specific outcome of the random variable
is a specific outcome of the random variable ![]() . Note that
. Note that ![]() is drawn from the optimal choice
is drawn from the optimal choice
![]() .
.
The posterior of wealth conditional on observing a particular
![]() follows by Bayes' law :
follows by Bayes' law :
where
2.2.2 Choice Variable
Before processing any information about wealth (![]() ), consumption (
), consumption (![]() ) and labor
(
) and labor
(![]() ) are random variables from the perspective of the consumers. To see why, first consider that the household cannot choose
) are random variables from the perspective of the consumers. To see why, first consider that the household cannot choose ![]() and
and ![]() optimally without relating wealth and behavior (
optimally without relating wealth and behavior (![]() and
and ![]() ). Coming into the world with a probabilistic knowledge of
). Coming into the world with a probabilistic knowledge of ![]() , mapping
, mapping ![]() into
into ![]() and
and ![]() translates into finding a joint relation among wealth, consumption and labor, that makes the information about wealth as related as possible to consumption and labor. The selection of information about wealth useful to consumption
and labor, that is, the joint probability distribution of wealth, consumption and labor,
translates into finding a joint relation among wealth, consumption and labor, that makes the information about wealth as related as possible to consumption and labor. The selection of information about wealth useful to consumption
and labor, that is, the joint probability distribution of wealth, consumption and labor,
![]() , is key in the optimization of the consumers since it affects current beliefs and their updates.11
, is key in the optimization of the consumers since it affects current beliefs and their updates.11
To clarify this point, suppose that information flows at infinite rate. In this case, the optimal
![]() will be degenerate assigning to each value of
will be degenerate assigning to each value of ![]() one value for
one value for
![]() and
and
![]() . By contrast, suppose that processing information about wealth is too difficult for the consumer, then the consumer will be better off processing very limited amount
of information about wealth. This is equivalent to choosing the minimal amount of information about wealth that allow the consumer to set
. By contrast, suppose that processing information about wealth is too difficult for the consumer, then the consumer will be better off processing very limited amount
of information about wealth. This is equivalent to choosing the minimal amount of information about wealth that allow the consumer to set ![]() and
and ![]() constant for each values of
constant for each values of ![]() without breaking his budget. Such a behavior implies that consumption and labor will be almost
independent on wealth. When the information-processing effort lies in between this two extreme cases, optimizing consumers aim at setting
without breaking his budget. Such a behavior implies that consumption and labor will be almost
independent on wealth. When the information-processing effort lies in between this two extreme cases, optimizing consumers aim at setting
![]() such that the conditional probability of wealth given consumption and labor is as close to wealth as possible given the information constraint
and the preference of the consumers.
such that the conditional probability of wealth given consumption and labor is as close to wealth as possible given the information constraint
and the preference of the consumers.
To understand how consumers' preference are necessary to determine
![]() , consider a risk averse person. A risk averse individual would be more interested in knowing when his account is close to be overdrawn than a
risk-neutral one. It follows that the risk averse type wants to process more information about low values of wealth which in turns implies low values of consumption and via the effect that income has on wealth (eq.1), also about low values of labor. If the consumer finds it
extremely costly to process information, he watches out for those values of wealth, consumption and labor that reduce his utility the most by collecting information along this particular dimension. A consumer with relative better abilities of processing information can allocate his attention to
news about several combinations of wealth, consumption and labor, ranked according to his utility.12
, consider a risk averse person. A risk averse individual would be more interested in knowing when his account is close to be overdrawn than a
risk-neutral one. It follows that the risk averse type wants to process more information about low values of wealth which in turns implies low values of consumption and via the effect that income has on wealth (eq.1), also about low values of labor. If the consumer finds it
extremely costly to process information, he watches out for those values of wealth, consumption and labor that reduce his utility the most by collecting information along this particular dimension. A consumer with relative better abilities of processing information can allocate his attention to
news about several combinations of wealth, consumption and labor, ranked according to his utility.12
From the above discussion, it follows that an optimal policy function for a rationally inattentive individual involves choosing
![]() . Consumption and labor are drawn from the optimal policy
. Consumption and labor are drawn from the optimal policy
![]() .
.
2.2.3 Information Constraint
As briefly explained before, people with limited processing capacity, select optimally information about wealth and behavior within their cognitive possibilities. I model the restriction that these cognitive possibilities are finite using Shannon's mutual information (Shannon (1954), Sims (2003,
2006)) between the random variables ![]() and
and ![]() . This technology measures the maximum
reduction in uncertainty associated to a system as difference between the initial uncertainty (entropy of
. This technology measures the maximum
reduction in uncertainty associated to a system as difference between the initial uncertainty (entropy of ![]() ) and the knowledge of variable
) and the knowledge of variable ![]() provided by the observation of
provided by the observation of ![]() (conditional entropy of
(conditional entropy of ![]() given
given ![]() ). Since mutual information depends only on the joint distribution of
). Since mutual information depends only on the joint distribution of ![]() and
and ![]() for a given belief, this way of modelling residual uncertainty is applicable without additional restrictions on the nature and characteristics of
the channel. In my setting, Shannon capacity captures the ability of consumers to interpret news about their wealth, thereby regulating the speed of reaction of their behavior to these news. An intuitive analogy to Shannon capacity is the activity of a person's brain. Suppose the person reads about
the drop in prices in the housing market. According to the time he has and his knowledge of real estate, his reading of the news can lead him to make significant steps towards buying an house right away. If the person does not have enough time to absorb the information about real estate and loan
market and to map this information into his current and future net worth, he might want to push forward his decision to buy until he has figured out this link.
for a given belief, this way of modelling residual uncertainty is applicable without additional restrictions on the nature and characteristics of
the channel. In my setting, Shannon capacity captures the ability of consumers to interpret news about their wealth, thereby regulating the speed of reaction of their behavior to these news. An intuitive analogy to Shannon capacity is the activity of a person's brain. Suppose the person reads about
the drop in prices in the housing market. According to the time he has and his knowledge of real estate, his reading of the news can lead him to make significant steps towards buying an house right away. If the person does not have enough time to absorb the information about real estate and loan
market and to map this information into his current and future net worth, he might want to push forward his decision to buy until he has figured out this link.
I model people's ability to map information about wealth into consumption and labor decisions by assuming a constant and exogenous shadow cost on the information-processing constraint -mutual information between ![]() and
and ![]() -. In the model, such a cost is denoted by
-. In the model, such a cost is denoted by ![]() . This assumption has the interpretation that mapping each bit of information about wealth into consumption and labor decisions costs the same processing effort to the consumers. Different from Sims (2003) and Mackowiak and Wiederholt (2008a) where the capacity is fixed and
exhausted every period, fixing the shadow cost of processing information has the appealing property that consumers can effectively choose the amount of uncertainty they want to reduce each period according to their (perceived) financial conditions and their preferences.13 For instance, a person who finds it extremely costly to process information about wealth -i.e., high
. This assumption has the interpretation that mapping each bit of information about wealth into consumption and labor decisions costs the same processing effort to the consumers. Different from Sims (2003) and Mackowiak and Wiederholt (2008a) where the capacity is fixed and
exhausted every period, fixing the shadow cost of processing information has the appealing property that consumers can effectively choose the amount of uncertainty they want to reduce each period according to their (perceived) financial conditions and their preferences.13 For instance, a person who finds it extremely costly to process information about wealth -i.e., high ![]() -, might choose to pay attention to wealth only after he observes that his consumption/leisure profile has changed significantly over time. By contrast, a person with relative better abilities to process information -i.e., low
-, might choose to pay attention to wealth only after he observes that his consumption/leisure profile has changed significantly over time. By contrast, a person with relative better abilities to process information -i.e., low
![]() -, might find it optimal to keep close track of his wealth in order to enjoy combination of consumption and leisure that maximize his utility.
-, might find it optimal to keep close track of his wealth in order to enjoy combination of consumption and leisure that maximize his utility.
Formally, let
![]() be the mutual information implied by the choice of the joint distribution of
be the mutual information implied by the choice of the joint distribution of ![]() and
and ![]() ,
,
![]() . The constraint that limits the amount of processable information at each time
. The constraint that limits the amount of processable information at each time ![]() is given by :
is given by :
The expression in (3) says that the maximum uncertainty that the consumer can reduce about his wealth, through observation of consumption and labor supply is at most ![]() bits per unit of time. Mapping formulae into the same intuition gathered in the previous section, had the consumer had infinite processing capacity, he would be able to choose a signal which makes each of his actions informative about a particular value of wealth. This results
in a policy function for consumption, labor and wealth that depends on the -now observable- value of wealth. On the other extreme, with no processing capacity, the best one can do is to assign all the probability to a particular value of
bits per unit of time. Mapping formulae into the same intuition gathered in the previous section, had the consumer had infinite processing capacity, he would be able to choose a signal which makes each of his actions informative about a particular value of wealth. This results
in a policy function for consumption, labor and wealth that depends on the -now observable- value of wealth. On the other extreme, with no processing capacity, the best one can do is to assign all the probability to a particular value of ![]() . This makes the variables
. This makes the variables ![]() and
and ![]() independent of each other, (
independent of each other, (
![]() ). Every day, such a person spends the same amount of cash in consumption and the same amount of time working,
regardless of his financial possibilities. In the intermediate case, if the person can process a finite amount of information, he attends to information that make his saving and labor decisions as close as possible to wealth.
). Every day, such a person spends the same amount of cash in consumption and the same amount of time working,
regardless of his financial possibilities. In the intermediate case, if the person can process a finite amount of information, he attends to information that make his saving and labor decisions as close as possible to wealth.
2.2.4 Objective
Household's problem is to maximize the infinite horizon expected utility of consumption and leisure discounted at factor ![]() . Let
. Let ![]() be the (fixed and exogenous) shadow cost of processing information
be the (fixed and exogenous) shadow cost of processing information ![]() in (3) below. The control for their
maximization is a signal
in (3) below. The control for their
maximization is a signal
![]() that solves : 14
that solves : 14
subject to
and (2) and the requirement that
![]() where
where
![]() is the set of all distribution that satisfies
is the set of all distribution that satisfies
Taking first order condition with respect to
![]() results in 15
results in 15
![]()
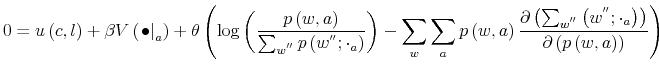
where
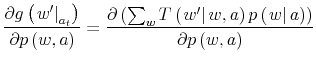
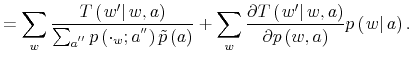
Define the solution to the optimization problem of the consumers as the distribution
![]() . Summing over all the possible realizations of
. Summing over all the possible realizations of ![]() and
and ![]() leads to the marginal distribution of labor
leads to the marginal distribution of labor
and likewise summing over
where the notation
3 Solution Strategy
To appreciate how consumers' preferences interact with the information processing constraint, I consider the following specifications for the utility function:
![\begin{displaymath} u\left( c,l\right) =\left\{ \begin{array}[c]{c}% \frac{c^{1-\gamma}}{1-\gamma}-\alpha l\ \log c-\alpha l\ \log c-\frac{\alpha}{\eta+1}l^{\eta+1}% \end{array}\right. . \end{displaymath}](img101.gif)
The computation methodology follows closely Tutino(2008) to which I refer for technical details. However, there is a computational difference that I shall highlight. The difference concerns the construction of the simplex. This paper uses a uniform random grid to generate the simplex. Such a
method is more efficient in terms of computational time than a non-uniform random grid and it requires less point to span the simplex. To sketch the methodology, we start with ![]() as the
number of possible values that
as the
number of possible values that ![]() can assume. Then, each point of the simplex,
can assume. Then, each point of the simplex, ![]() , is an
, is an ![]() array each of whose rows contains
array each of whose rows contains ![]() random values
which belong to the interval
random values
which belong to the interval
![]() and are subject to the condition that their sum is 1. The
distribution of values is uniform in the sense that it has the conditional probability distribution of a uniform distribution over the whole
and are subject to the condition that their sum is 1. The
distribution of values is uniform in the sense that it has the conditional probability distribution of a uniform distribution over the whole ![]() -cube, given that the sum per row is
1. The algorithm randomly determines the placement of random points in the
-cube, given that the sum per row is
1. The algorithm randomly determines the placement of random points in the ![]() dimensional simplexes.
dimensional simplexes.
To map the finer state space into Matlab possibilities, I interpolate the value function with the new values of (2) using a kernel regression of
![]() into
into
![]() I use an Epanechnikov kernel with smoothing parameter
I use an Epanechnikov kernel with smoothing parameter ![]() .17 Table 1 reports the benchmark parameter values and the grids.18 The value iteration converges in about 180 iterations.
.17 Table 1 reports the benchmark parameter values and the grids.18 The value iteration converges in about 180 iterations.
| Discretization | |
|---|---|
| Core State Space |
|
| Consumption Space
|
|
| Labor Space |
|
| Joint Distribution per simplex point | 100 |
| Marginal |
10 |
| Marginal |
10 |
| Marginal |
10 |
| 1.2 | |
| 0.02 | |
| 3 | |
| 0 | |
| 1.03 | |
| Discount Factor, |
0.9966 |
I shall point out another caveat for the model calibration, concerning the ratio of the interest rate, ![]() , and the inverse of the discount factor,
, and the inverse of the discount factor, ![]() . The calibration in Table 1 implies that the annualized rate of return induces consumers to save until wealth reaches its maximum. Under full information and with utility
. The calibration in Table 1 implies that the annualized rate of return induces consumers to save until wealth reaches its maximum. Under full information and with utility
![]() , such an high interest rate associated to constant disutility of labor makes the consumer accumulate wealth by varying labor supply
more than consumption. Under rational inattention, infrequency and sharpness of the adjustments of consumption and labor makes the variance of consumption higher than the one of labor. To highlight the sharp differences between full information models and rational inattention ones, I maintain the
assumption
, such an high interest rate associated to constant disutility of labor makes the consumer accumulate wealth by varying labor supply
more than consumption. Under rational inattention, infrequency and sharpness of the adjustments of consumption and labor makes the variance of consumption higher than the one of labor. To highlight the sharp differences between full information models and rational inattention ones, I maintain the
assumption ![]() throughout the numerical simulations. The parametrization of the model is summarized in Table 1.
throughout the numerical simulations. The parametrization of the model is summarized in Table 1.
4 Predictions of the Model and the Business Cycle.
The goal of this section is to provide suggestive evidence on how the model performs when compared to U.S. data. The data that I use for consumption are non durable goods from the Bureau of Economic Analysis while data for average hours worked are available from the Bureau of Labor Statistics.
All the series have quarterly frequency from 1964.I to 2007.II.. I construct figures and statistics by detrending the data with the HP filter, using a value of
![]() . I then used the detrended data to compute mean, standard deviation and the correlations. I compare the results of the model with the detrended series under the observation that
processing information through a Shannon channel filters out high frequency component of the variable(s) of interest (see Guo et al. (2005), Verdù (1996, 1999) and Sims (1998, 2003). The choice of HP filter over other filter is simply to ease the comparison with the business cycle
literature.
. I then used the detrended data to compute mean, standard deviation and the correlations. I compare the results of the model with the detrended series under the observation that
processing information through a Shannon channel filters out high frequency component of the variable(s) of interest (see Guo et al. (2005), Verdù (1996, 1999) and Sims (1998, 2003). The choice of HP filter over other filter is simply to ease the comparison with the business cycle
literature.
As for the simulated series, I define a model as a set
![]() and I compare the business cycle facts to specifications of the model that assume
and I compare the business cycle facts to specifications of the model that assume
![]()
![]() and
and ![]() . I choose three values of
. I choose three values of ![]() as a proxy for three types of individuals that face three different shadow costs of
processing information ranging from low (
as a proxy for three types of individuals that face three different shadow costs of
processing information ranging from low (
![]() ) to medium (
) to medium (
![]() ) to high (
) to high (![]() ). As for these particular numerical values, I
verify empirically that given the discretization of core states and core decisions and the baseline model with log utility of consumption and linear disutility in labor, a value of
). As for these particular numerical values, I
verify empirically that given the discretization of core states and core decisions and the baseline model with log utility of consumption and linear disutility in labor, a value of ![]() between 1 and 3 leads to the same quantitative results in terms of choice of
distribution. Thus, I pick the middle value in the set
between 1 and 3 leads to the same quantitative results in terms of choice of
distribution. Thus, I pick the middle value in the set
![]() for the high costs. The optimal choice of the joint distribution
for the high costs. The optimal choice of the joint distribution
![]() is similar for value of
is similar for value of
![]() . Again, I pick the middle value in the interval for the second choice of
. Again, I pick the middle value in the interval for the second choice of ![]() . Similar reasonings conduct to
. Similar reasonings conduct to
![]() as lower value of
as lower value of ![]() when
when ![]() takes up values in
takes up values in
![]() . Notice that for values of
. Notice that for values of ![]() above 5, households acquire very little information about wealth and set consumption and labor basically constant. Also, for values of
above 5, households acquire very little information about wealth and set consumption and labor basically constant. Also, for values of ![]() below 0.05 deliver a solution very close to the full information case.
below 0.05 deliver a solution very close to the full information case.
To get a quantitative assessment of what these costs mean, I compute the average difference in lifetime utility between the infinite capacity case and each of the ![]() -cases considered.
That is, I set
-cases considered.
That is, I set
![]() and I compute
and I compute
![]() where
where
![]() is average lifetime utility under infinite capacity case while
is average lifetime utility under infinite capacity case while
![]() is the utility under a particular value of
is the utility under a particular value of ![]() when
when ![]() takes values in
takes values in
![]() . With an average value of
. With an average value of
![]() under full information,
under full information, ![]() is associated to a loss of about
is associated to a loss of about ![]() in lifetime utility,
in lifetime utility,
![]() implies a loss of about
implies a loss of about ![]() while
while
![]() delivers a loss of about
delivers a loss of about ![]() . The values used for this computation
can be found in Table
. The values used for this computation
can be found in Table ![]() in appendix B. I assume that an economy is populated evenly by those three types. 19
in appendix B. I assume that an economy is populated evenly by those three types. 19
The computations are as follows. For each ![]() , mean, standard deviation and correlation of the simulated series are calculated after I take averages of
, mean, standard deviation and correlation of the simulated series are calculated after I take averages of ![]() Monte Carlo runs and
Monte Carlo runs and ![]() simplex points. The statistics for each of this series are in Tables
simplex points. The statistics for each of this series are in Tables
![]() . In tables
. In tables ![]() the same methodology produces the results for the
cases
the same methodology produces the results for the
cases
![]() and
and
![]() respectively. The results for the simulated series in Tables 2-4 and Table 6 are calculated by computing an arithmetic average of the series just described for
respectively. The results for the simulated series in Tables 2-4 and Table 6 are calculated by computing an arithmetic average of the series just described for
![]() . I do not filter out low frequency variations in the solution paths generated by my model since there are no exogenous shocks at high frequency. I refer to the business
cycle facts occurring between 1964.I and 2007.II as BC and to the rational inattention predictions with consumption and labor as RC which stands for Rigidity of Choice.
. I do not filter out low frequency variations in the solution paths generated by my model since there are no exogenous shocks at high frequency. I refer to the business
cycle facts occurring between 1964.I and 2007.II as BC and to the rational inattention predictions with consumption and labor as RC which stands for Rigidity of Choice.
4.1 Business Cycle Facts through Shannon's lenses.
I focus on a set of business cycle facts regarding consumption, labor and their volatility, persistence and comovement. Then I derive the labor wedge20 that the model produces. Finally I calibrate the model to match the first moment of the labor wedge from the data and see what costs of information processing it implies.
4.1.1 BC Fact 1: The ratio of standard deviations of consumption and hours 1.31
My model predicts excess volatility of consumption with respect to labor supply. This results depends on the bound of information-processing capacity and its interplay with risk aversion and disutility of labor. Consider a consumer with log utility in consumption and constant disutility of labor. Had the household had infinite capacity, he would have chosen to smooth consumption by varying labor supply. With positive and finite information-processing capacity, he does not track wealth perfectly at high frequency. He selects a signal about wealth and changes labor and consumption according to the informativeness of the signal. Willing to smooth consumption, the household rationally chooses to save and work hard while he accumulates information about his financial possibilities. Once he realizes that he is rich, he increases consumption. However, to maintain a relatively high consumption profile for prolonged time, he keeps working hard. If he has accumulated too much savings -due to low informativeness of period by period signals- when the variation in consumption occurs is sizeable. Furthermore, such variation would be bigger than the one of labor to avoid taking risks on future wealth.
Table 2 compares the model
![]() to the U.S. data. The mean of the wages is constant
throughout the simulation at 1.2.
to the U.S. data. The mean of the wages is constant
throughout the simulation at 1.2.
| Std.Dev | |
|---|---|
| Non Dur. Consumption
|
0.84 |
| Hours
|
0.64 |
| Std.Dev | |
|---|---|
| Consumption
|
1.13 |
| Labor
|
0.98 |
The explanation that my model provides to BC 1 can be summarized by the following result:
- RC Finding 1.
- For the model
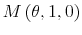 , the standard deviation of consumption over labor is 1.15. The volatility is higher the higher the information costs. For a given degree of
risk aversion, higher information costs make consumption and labor more sluggish with sudden adjustments following accumulation of wealth. This behavior of consumption and labor generates higher variance.
, the standard deviation of consumption over labor is 1.15. The volatility is higher the higher the information costs. For a given degree of
risk aversion, higher information costs make consumption and labor more sluggish with sudden adjustments following accumulation of wealth. This behavior of consumption and labor generates higher variance.
4.1.2 BC Fact 2: Non durable consumption and hours have 1st order serial correlation higher than 80%
In my model, consumption and labor are more persistent the lower the information flow. In the latter case, it occurs also that contemporaneous consumption and labor lag wealth.
Figure 1: Sample Path of Macroeconomic variables, Average across 10,000 monte Carlo, ![]()
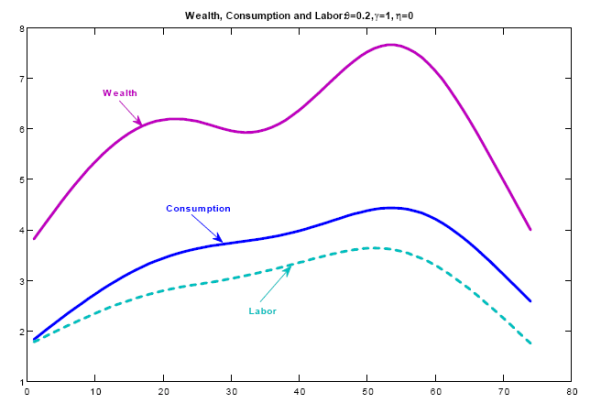
The intuition for these findings lies on the mechanism through which consumers update their knowledge of wealth, expressed in (2). Each period they choose a signal on wealth, decide consumption and labor based on the information from the signal and, given their choices, update their knowledge of wealth. The higher the processing cost, the less informative the signal. This in turn means that most of the update derives from the observations of past values of consumption and labor. As wealth accumulates, the signal consistently reports high values of wealth which trigger a reaction in behavior. This process is reflected in both delayed response to fluctuations of wealth and strong autocorrelation between current and past values of consumption and labor.
The comparison between models and findings is in Table 3.
| Std.Dev | Autocorr | |
|---|---|---|
| Non Durable Goods
|
0.84 | 93 |
| Average Hours
|
0.54 | 88 |
| Std.Dev | Autocorr | |
|---|---|---|
| Consumption
|
1.13 | 92 |
| Labor
|
0.98 | 87 |
The explanation for BC Fact 2 can be summarized as:
- RC Finding 2.
- For the model
 , the autocorrelation of consumption and labor are above 80%. Moreover, contemporaneous consumption and labor lag wealth by one
period.
, the autocorrelation of consumption and labor are above 80%. Moreover, contemporaneous consumption and labor lag wealth by one
period.
4.1.3 BC Fact 3: The contemporaneous correlation of consumption and hours is 78%.
|
|
|
|||
|---|---|---|---|---|
| 0.93 | 1 | 0.77 | 0.78 | |
| 0.66 | 0.78 | 0.88 | 1 |
My model finds a strong comovement of labor and consumption. It also predicts a strong correlation between contemporaneous consumption and wealth when information flow is high. The reason for a strong relationship among contemporaneous values of wealth, labor and consumption in my model is twofold. First, the variables are related through the budget constraint (1) which is used by the consumers to update their prior on wealth. Second, the optimal policy of the consumer is the stationary joint distribution between choices (consumption and labor) and state (wealth).
For a given shadow cost and disutility of labor, the higher the coefficient of risk aversion the higher the correlation between lagged and contemporaneous consumption and wealth. The same is true for labor and wealth. This results arises from the observation that risk averse individuals, say,
![]() pay more attention to wealth than individuals with
pay more attention to wealth than individuals with ![]() for a given
cost of processing. Controlling for the cost of information and the degree of risk aversion, people with increasing disutility of labor,
for a given
cost of processing. Controlling for the cost of information and the degree of risk aversion, people with increasing disutility of labor, ![]() , pay more attention to wealth than people with
, pay more attention to wealth than people with
![]() . However, this higher information is used to both consumption smoothing and increasing leisure. Even though the substitution effect prevails over the income effect also for
. However, this higher information is used to both consumption smoothing and increasing leisure. Even though the substitution effect prevails over the income effect also for
![]() , the resulting impact on the correlation between wealth and consumption is lower than for the case
, the resulting impact on the correlation between wealth and consumption is lower than for the case ![]() .
.
Figure 2: Consumption and wealth,
![]() . Solid line:
. Solid line: ![]() ,
, ![]() ; Dotted Line:
; Dotted Line: ![]() ,
, ![]() .
.
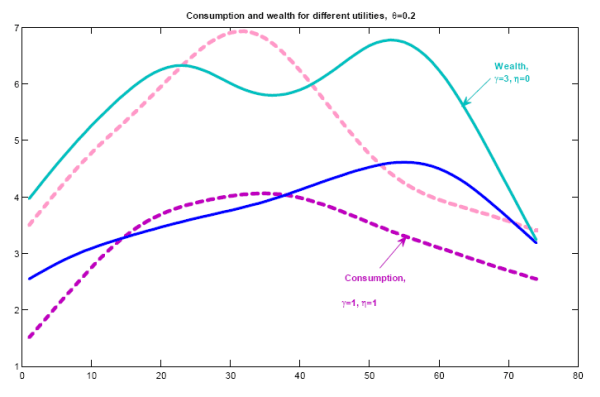
The reason why lagged value of wealth are highly correlated with contemporaneous consumption comes from the interaction between the curvature of the utility function and the information costs. High coefficient of risk aversion together with high information cost trigger a conservative consumption profile and a consistent increase in consumption when the signal conveys information about high value of wealth (cfr. RC Finding 1). With low elasticity of labor supply, the strong and positive comovement of consumption and labor (RC Finding 2) makes labor react in a way similar to consumption. When the elasticity of labor supply increases, people try to balance consumption smoothing and increase in leisure with the information available on wealth. The result is a weaker positive correlation of behavior and current and lagged values of wealth .
|
|
|
|||
|---|---|---|---|---|
| 0.90 | 1 | 0.83 | 0.90 | |
| 0.71 | 0.90 | 0.84 | 1 |
The explanation of the third business cycle fact from the model is:
- RC Finding 3.
- For the model
 the contemporaneous cross correlation between consumption and labor is 0.90%.
the contemporaneous cross correlation between consumption and labor is 0.90%.
4.1.4 BC Fact 4: U.S. labor wedge has mean 0.4 and standard deviation
 0.11
0.11
| mean | std. dev. | |
|---|---|---|
| 0.40 | 0.11 |
source: Shimer (2008)
In absence of information-processing frictions (![]() ), and assuming an household with utility
), and assuming an household with utility
![]() the labor wedge for the model is21
the labor wedge for the model is21
where the wage,
When information flows at finite rate (![]() ), consumers never observe wages directly but only through the impact wages have on signals about wealth. Thus, the MRS for
information-constrained consumers has to be equal to their perception of the wages given the signal,
), consumers never observe wages directly but only through the impact wages have on signals about wealth. Thus, the MRS for
information-constrained consumers has to be equal to their perception of the wages given the signal,
![]() . Define such perception of wages
. Define such perception of wages
![]() . Then, the wedge in my model is defined as
. Then, the wedge in my model is defined as
![]() or:
or:
which increases with
To get a sense of the magnitude involved, to obtain an average wedge
![]() , I set
, I set
![]() and
and ![]() . This specification implies the statistics in
Table 8.
. This specification implies the statistics in
Table 8.
| Mean | St.Dev |
|
|
|---|---|---|---|
| Consumption
|
3.20 | 1.08 | 0.93 |
| Labor
|
2.28 | 0.98 | 0.89 |
| Wealth
|
6.04 | 1.19 | 0.74 |
| Information Flow
|
0.93 | 0.71 |
In particular, the average consumption is
![]() and the consumption loss from not being well informed is about
and the consumption loss from not being well informed is about ![]() of households' average lifetime consumption. 22
of households' average lifetime consumption. 22
Even though the model cannot address jointly the supply and demand sides of the labor market23 and it is limited to the intensive margin, I think it offers a promising angle to explain the discrepancy between the marginal rate of substitution and the marginal product of labor. Several studies have been trying to match theory and data to explain this wedge 24: cyclical fluctuation of hours driven by variation in taxes25, time varying disutility of labor and worker's market power26 and search and matching models27.
Rather than examining the origins and bargaining of wage contracts, the suggestion of my model is to look more closely at consumers' behavior. In particular, my results show that adding a bound on information processing generates endogenously a wedge between the wage that prevails on the market
and the perception of the workers of such wages,
![]() . In my model this labor wedge
. In my model this labor wedge ![]() depends on the information-processing capacity of the consumers. Furthermore, the variance of
depends on the information-processing capacity of the consumers. Furthermore, the variance of ![]() depends
on their choice of the informativeness of the signal. To see why, suppose that a person knows that he is rich in a given period of his life. Since information-processing is costly, he may decide to care a little about his current wealth and, as a result,
depends
on their choice of the informativeness of the signal. To see why, suppose that a person knows that he is rich in a given period of his life. Since information-processing is costly, he may decide to care a little about his current wealth and, as a result, ![]() . By contrast, a person who doesn't have a lot of wealth wants to pay more attention to his financial activities which leads to a better monitoring of the wealth, or
. By contrast, a person who doesn't have a lot of wealth wants to pay more attention to his financial activities which leads to a better monitoring of the wealth, or ![]() . Note also that the choice of processing different flows of information according to consumers' needs and preferences make the variance of
. Note also that the choice of processing different flows of information according to consumers' needs and preferences make the variance of
![]() positive.
positive.
| mean | std. dev. | |
|---|---|---|
| 0.40 | 0.11 | |
| 0.40 | 0.41 |
This last result are summarized by the last findings.
- RC Finding 4.
- The labor wedge has mean 0.40 and standard deviation 0.41. The statistical properties of the wedge derive from those of the endogenously chosen distribution
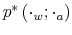 .
.
5 A closer look at Model Statistics
The results of the previous section are robust to different characterizations of
![]() . Once the value function for each model converged, I simulate the path of consumption, labor, wealth and information flow for
. Once the value function for each model converged, I simulate the path of consumption, labor, wealth and information flow for ![]() averaging the results along the dimension of the simplex as well as
averaging the results along the dimension of the simplex as well as ![]() different Monte Carlo runs.
different Monte Carlo runs.
To get a sense on how the shadow cost of information affects consumption and labor behavior, consider
![]() where
where
![]() 0.02. Table
0.02. Table ![]() shows the statistics for these and
shows the statistics for these and ![]()
![]() cases. All tables are collected in Appendix B.
cases. All tables are collected in Appendix B.
The first observation is that as the information costs increases, average consumption, labor and information flow decrease, while the standard deviations of these series increases. This is also true for wealth. These results are intuitive. Under full information, the characteristics of the
utility function
![]() command a consumption profile smooth throughout the life-cycle. Moreover, with constant disutility of labor,
command a consumption profile smooth throughout the life-cycle. Moreover, with constant disutility of labor,
![]() labor supply adjusts according to wealth fluctuations to accommodate consumption smoothing. When information flows at finite rate, rational households choose signal
about wealth with the same purpose. If processing-information has low cost,
labor supply adjusts according to wealth fluctuations to accommodate consumption smoothing. When information flows at finite rate, rational households choose signal
about wealth with the same purpose. If processing-information has low cost,
![]() , consumers can choose a signal about wealth so informative to allow them to use labor supply to smooth fluctuations in wealth and, in turn, consumption. On the other hand, if
information is costly,
, consumers can choose a signal about wealth so informative to allow them to use labor supply to smooth fluctuations in wealth and, in turn, consumption. On the other hand, if
information is costly, ![]() , consumers keep track of wealth slowly and, as a consequence, do not modify consumption and labor often. When they do change their behavior, they do so by a
significant amount. The resulting path for wealth inherits the higher variance of consumption and labor and, on average, has higher mean than in the previous case due to the increase in savings in periods of inertial behavior. A sample path of consumption under different
, consumers keep track of wealth slowly and, as a consequence, do not modify consumption and labor often. When they do change their behavior, they do so by a
significant amount. The resulting path for wealth inherits the higher variance of consumption and labor and, on average, has higher mean than in the previous case due to the increase in savings in periods of inertial behavior. A sample path of consumption under different ![]() -scenarios is in Figure 3.
-scenarios is in Figure 3.
Figure 3: Sample path of consumption for different ![]() 's. Comparing consumption for
's. Comparing consumption for
![]()
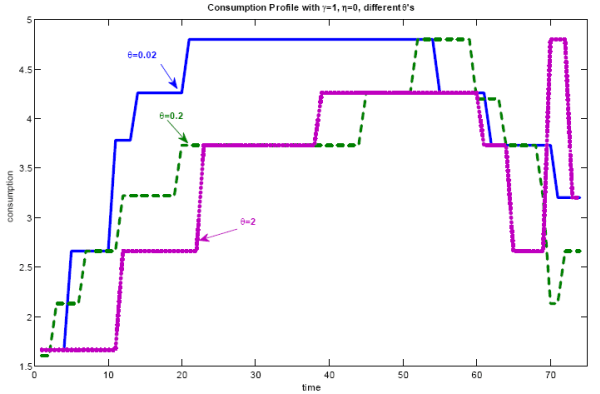
Figure 4 confirms the intuition that consumption is smoother the lower information costs. Consumers with
![]() save at the beginning of the simulated period to enjoy high level of consumption later on. By contrast, consumers with
save at the beginning of the simulated period to enjoy high level of consumption later on. By contrast, consumers with ![]() track with difficulties their wealth and this is reflected in a prolonged period of savings while processing information about wealth. This results into slow and consistent adjustments of consumption during the simulated period. One
point worth attention is the existence of precautionary savings generated by information flow constraints. Individuals with less processing capacity (
track with difficulties their wealth and this is reflected in a prolonged period of savings while processing information about wealth. This results into slow and consistent adjustments of consumption during the simulated period. One
point worth attention is the existence of precautionary savings generated by information flow constraints. Individuals with less processing capacity (![]() ) push forwards an increase in
consumption more than the other people (
) push forwards an increase in
consumption more than the other people (
![]() and
and
![]() ). Types
). Types ![]() acknowledge the accumulation of wealth due to the
additional savings later in the simulation. This forces them to increase their consumption for a short period of time at the end of the simulation period.
acknowledge the accumulation of wealth due to the
additional savings later in the simulation. This forces them to increase their consumption for a short period of time at the end of the simulation period.
Given the strong correlation between consumption and labor and the preferences of the individuals, it is not surprising that people with
![]() work harder at the beginning of the simulation to finance their good purchases, though they manage to enjoy some leisure at the end of the simulation (see Figure 5).
work harder at the beginning of the simulation to finance their good purchases, though they manage to enjoy some leisure at the end of the simulation (see Figure 5).
Figure 4: Time path consumption and labor, various ![]() . Comparing consumption and labor for
. Comparing consumption and labor for
![]()
Correlation between consumption and labor is higher the higher the information costs. The intuition for this result is that the reaction of both consumption and labor behaviors to accumulation of wealth are delayed by individual's capacity of processing information. As they have better knowledge
of how much wealth they have, they review both plans. People actions are mirrored in wealth accumulation. Individuals with
![]() build up savings at the beginning of the period to dissave gradually later on. This is akin to consumption smoothing under full information.
build up savings at the beginning of the period to dissave gradually later on. This is akin to consumption smoothing under full information.
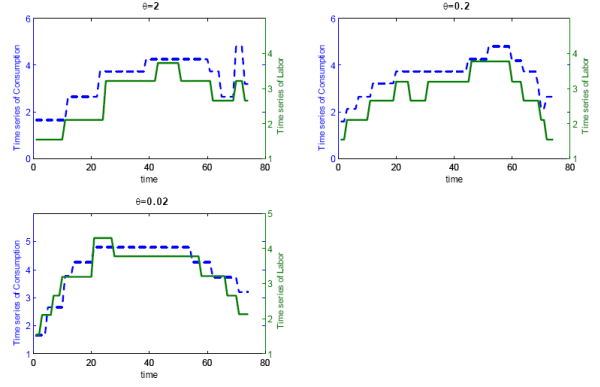
Figure 5: Time path wealth and consumption, log-lin utility, various ![]() . Comparing consumption(blue) and wealth (red) for
. Comparing consumption(blue) and wealth (red) for
![]()
People who are more constrained in their choice of the signal, adjust with delays consumption to fluctuations in wealth. Such delays smooth consumption while consumers are processing information but at the same time, calls for major adjustments afterwards.
Note also how consumption and labor lag wealth for ![]() The cross-correlation coefficients between lagged wealth and current consumption is 0.65 while the contemporaneous correlation is only 0.47. A similar result holds for labor and lagged values of wealth. This
finding is also consistent with intuition. Every period households receive little information about their wealth and rely on past values of consumption and labor to update their knowledge. While waiting, wealth accumulates and so does information until the consumers are convinced to change their
behavior. This mechanism implies that behavioral response to movement in wealth is lagged. Finally, Figures 3-5 illustrate also the high persistence of the series documented in table
The cross-correlation coefficients between lagged wealth and current consumption is 0.65 while the contemporaneous correlation is only 0.47. A similar result holds for labor and lagged values of wealth. This
finding is also consistent with intuition. Every period households receive little information about their wealth and rely on past values of consumption and labor to update their knowledge. While waiting, wealth accumulates and so does information until the consumers are convinced to change their
behavior. This mechanism implies that behavioral response to movement in wealth is lagged. Finally, Figures 3-5 illustrate also the high persistence of the series documented in table ![]() . Not surprisingly the persistence is higher the higher the information cost .
. Not surprisingly the persistence is higher the higher the information cost .
For completeness, it is worth mentioning how the model behaves with higher coefficient of risk aversion and positive and finite elasticity of substitution. Figure 6 displays the stationary marginal distribution of consumption and wealth when ![]() and
and ![]() . These marginal distributions are computed from the joint distribution to which the value iteration converges as
average over initial beliefs about wealth.
. These marginal distributions are computed from the joint distribution to which the value iteration converges as
average over initial beliefs about wealth.
For low values of ![]() , households choose to be better informed about extreme values of consumption so that they can enjoy a balanced consumption throughout their lifecycle. This is, in
essence, consumption smoothing.
, households choose to be better informed about extreme values of consumption so that they can enjoy a balanced consumption throughout their lifecycle. This is, in
essence, consumption smoothing.
Figure 6: Marginal Distribution of consumption and labor various ![]() . Comparing marginal distributions of consumption and labor
when
. Comparing marginal distributions of consumption and labor
when
![]()
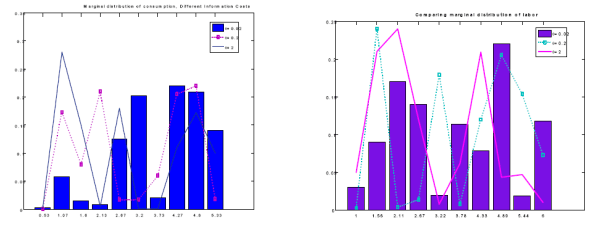
The optimal marginal probability of labor assigns high probability on low labor supply when ![]() is low: as the capacity increases, consumers wants to smooth consumption and sacrifice
their leisure to do so (recall, labor effort has constant disutility in this case,
is low: as the capacity increases, consumers wants to smooth consumption and sacrifice
their leisure to do so (recall, labor effort has constant disutility in this case, ![]() ). If information is costly to process, consumers will keep cannot process enough information, they
will keep constant their consumption and labor effort. This in turn implies working less
). If information is costly to process, consumers will keep cannot process enough information, they
will keep constant their consumption and labor effort. This in turn implies working less
When the signal about wealth is less informative on a period-by-period basis (high ![]() ), income effect takes over the substitution effect: consumers are less certain that their wealth
is high enough to enjoy leisure and as a result increase the keep constant their consumption and labor effort. The marginal probability distribution of labor reflects this pattern by allocating higher probabilities on lower values of labor (and consumption) the higher
), income effect takes over the substitution effect: consumers are less certain that their wealth
is high enough to enjoy leisure and as a result increase the keep constant their consumption and labor effort. The marginal probability distribution of labor reflects this pattern by allocating higher probabilities on lower values of labor (and consumption) the higher ![]() is.
is.
Tables ![]() show the relationship between risk aversion,
show the relationship between risk aversion, ![]() Frisch
elasticity of substitution,
Frisch
elasticity of substitution, ![]() , and shadow cost of information,
, and shadow cost of information, ![]() . For a
given
. For a
given ![]() and elasticity of substitution, the higher the coefficient of risk aversion, the higher the mean and the lower the variance of consumption. This finding makes intuitive sense
since a risk averse household would save a lot during the early stages of life to enjoy high consumption throughout later on due to the accumulated savings. Savings come from both low consumption and high labor supply at the beginning of the simulation triggered by the fear of running out of
wealth. Once consumers realize they have built a sufficient buffer to cover for consumption and leisure expenses, they increase consumption and reduce -though by a lower extent- labor supply. The peak in consumption for these types of households occur later in the simulation while labor supply is
higher at the beginning than it is later on. Thus, information costs enhance precautionary savings.
and elasticity of substitution, the higher the coefficient of risk aversion, the higher the mean and the lower the variance of consumption. This finding makes intuitive sense
since a risk averse household would save a lot during the early stages of life to enjoy high consumption throughout later on due to the accumulated savings. Savings come from both low consumption and high labor supply at the beginning of the simulation triggered by the fear of running out of
wealth. Once consumers realize they have built a sufficient buffer to cover for consumption and leisure expenses, they increase consumption and reduce -though by a lower extent- labor supply. The peak in consumption for these types of households occur later in the simulation while labor supply is
higher at the beginning than it is later on. Thus, information costs enhance precautionary savings.
Finally, for a given ![]() and
and ![]() , a lower the Frisch elasticity of
substitution (from
, a lower the Frisch elasticity of
substitution (from ![]() to
to ![]() ) generates lower mean and lower variances for
both consumption and labor. Keeping the degree of risk aversion fixed, a low elasticity of substitution for labor supply increase the income effect over the substitution effect. However, the presence of information processing constraint still favors substitution effect mitigating the income effect.
If the signal on wealth is very noisy, consumers supply more labor than they would do in case of perfect information and
) generates lower mean and lower variances for
both consumption and labor. Keeping the degree of risk aversion fixed, a low elasticity of substitution for labor supply increase the income effect over the substitution effect. However, the presence of information processing constraint still favors substitution effect mitigating the income effect.
If the signal on wealth is very noisy, consumers supply more labor than they would do in case of perfect information and ![]() , since they are not certain that their wealth is actually
decreasing. When the information collected signals that the wealth has been increased, labor supply suddenly decreased. The opposite occurs when consumers receive more and more information about a decrease in wealth.
, since they are not certain that their wealth is actually
decreasing. When the information collected signals that the wealth has been increased, labor supply suddenly decreased. The opposite occurs when consumers receive more and more information about a decrease in wealth.
6 Conclusions
I presented a model in which rational households optimize their lifetime utility under information-processing constraint à la Sims. I show that such a model, even in its simplicity, is able to replicate many empirical regularities of U.S. business cycle data: higher volatility of consumption with respect to labor, persistence and strong comovement of consumption and employment, lagged response of consumption and labor with respect to wealth and an endogenous labor wedge. In particular, the last prediction has been a challenge for macroeconomists. Existing macroeconomic theories have been explaining the labor wedge using exogenous shocks and ad-hoc market frictions, without microfounded justifications and, more importantly, without a correspondence in the data. In my setting the difference between marginal rate of substitution and marginal product of labor, i.e., wage, occurs as a result of consumers' endogenous choice of information. When households face information-processing constraints, they select signals on their wealth and make consumption and labor decisions based on those signals. Each period, wealth evolves because of savings which depends on consumption and income. The latter in turn depends on labor supply and an exogenous stochastic wage whose distribution is fixed and known. Since movements in income affect the growth of wealth and consumers keep track of it by signals, the less informative the signals, the more persistent their choices. Once wealth accumulates and households acknowledge this growth through information collected, they change their behavior consistently. This mechanisms results in a discrepancy between the marginal rate of substitution of consumption and labor and wages. Furthermore, the magnitude and the variance of the endogenous wedge are in line with the data. The same mechanism is able to capture persistence and lags of the main macroeconomic variables over U.S. business cycle. The findings of this paper suggest that making a leap to a rational inattention setting is worth the computational effort. For it gets us closer to understand and interpret empirical regularities in U.S. data than the current theoretical macro literature.
7 Appendix A: Bellman Recursion and its properties
This appendix follow closely the work of Tutino(2008). It establishes the main properties of the Bellman recursion in the discrete Rational Inattention consumption-labor model.
7.1 The Bellman Recursion is a Contraction Mapping.
- Proposition 1.
- For the discrete Rational Inattention consumption labor value recursion
 and two given functions
and two given functions  and
and  , it holds that
with
, it holds that
with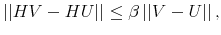
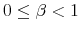 and
and
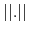 the supreme norm. That is, the value recursion
the supreme norm. That is, the value recursion 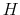 is a contraction mapping.
is a contraction mapping.
![\displaystyle H^{p}V\left( g\right) =\left[ {\displaystyle\sum\limits_{w\in W}}\left( {\displaystyle\sum\limits_{a\in A}}u\left( c,l\right) p\left( a\vert w\right) \right) g\left( w\right) -\theta\kappa+\beta{\displaystyle\sum\limits_{w\in W}\displaystyle\sum\limits_{a\in A}}\left( V\left( g_{a}^{\prime}\left( \cdot\right) \right) \right) p\left( a\vert w\right) g\left( w\right) \right] .](img227.gif)
Then it holds
![\displaystyle \beta{\displaystyle\sum\limits_{w\in W}}{\displaystyle\sum\limits_{a\in A}% }\left[ \left( V^{p_{2}}\left( g_{a}^{\prime}\left( \cdot\right) \right) \right) -\left( U^{p_{2}}\left( g_{a}^{\prime}\left( \cdot\right) \right) \right) \right] p_{2}g\left( w\right)](img247.gif) |
||
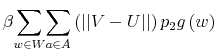 |
7.2 The Bellman Recursion is an Isotonic Mapping
- Corollary
- For the discrete Rational Inattention consumption-laving value recursion
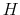 and two given functions
and two given functions 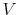 and
and 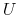 , it holds that
that is the value recursion
, it holds that
that is the value recursion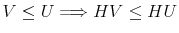
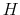 is an isotonic mapping.
is an isotonic mapping.
By definition,
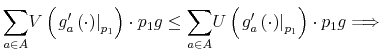
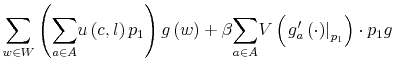 |
||
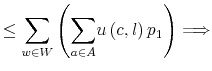 |
7.3 The Optimal Value Function is Piecewise Linear
- Proposition 2.
- If the utility is CRRA or LOG with a parameter of risk aversion
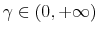 and inverse of Frisch elasticity of labor supply
and inverse of Frisch elasticity of labor supply
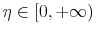 and if
and if 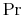
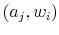 satisfies (5)-(8), then the optimal
satisfies (5)-(8), then the optimal 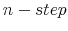 value function
value function
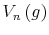 can be expressed as:
where the
can be expressed as:
where the
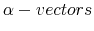 ,
,
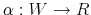 , are
, are
 dimensional hyperplanes.
dimensional hyperplanes.
and therefore if I define the vectors
I have the desired
where
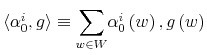 . For the general case, using equation (as in the value
function):
. For the general case, using equation (as in the value
function):
by the induction hypothesis
Plugging into the above equation (as in the Bayesian update) and by definition of
With the above:
At this point, it is possible to define
Note that these hyperplanes are independent on the prior
and define:
Note that
Now
is a finite set of linear function parametrized in the action set.
7.4 .. and Convex (PCWL)
- Proposition 3.
- Assuming the CRRA or LOG utility function and the conditions of Proposition 1, let
 be an initial value function that is piecewise
linear and convex. Then the
be an initial value function that is piecewise
linear and convex. Then the 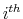 value function obtained after a finite number of update steps for a rational inattention consumption-saving problem is also
finite, piecewise linear and convex (PCWL).
value function obtained after a finite number of update steps for a rational inattention consumption-saving problem is also
finite, piecewise linear and convex (PCWL).
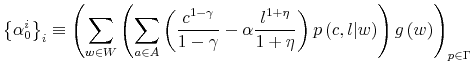
8.1 Tables
| Mean | St.Dev |
|
|
|---|---|---|---|
| Consumption
|
3.55 | 1.29 | 0.92 |
| Labor
|
2.75 | 1.12 | 0.88 |
| Wealth
|
5.73 | 2.11 | 0.94 |
| Information Flow
|
0.53 | 0.91 |
|
|
|
|
||||
|---|---|---|---|---|---|---|
|
|
0.92 | 1 | 0.86 | 0.89 | 0.75 | 0.47 |
|
|
0.88 | 0.89 | 0.88 | 1 | 0.72 | 0.41 |
|
|
0.30 | 0.47 | 0.37 | 0.41 | 0.94 | 1 |
| Mean | St.Dev |
|
|
|---|---|---|---|
| Consumption
|
4.05 | 1.11 | 0.95 |
| Labor
|
2.98 | 0.97 | 0.94 |
| Wealth
|
5.84 | 1.86 | 0.93 |
| Information Flow
|
0.98 | 0.63 |
|
|
|
|
||||
|---|---|---|---|---|---|---|
|
|
0.95 | 1 | 0.90 | 0.90 | 0.77 | 0.84 |
|
|
0.87 | 0.90 | 0.94 | 1 | 0.82 | 0.79 |
|
|
0.87 | 0.84 | 0.75 | 0.79 | 0.93 | 1 |
| Mean | St.Dev |
|
|
|---|---|---|---|
| Consumption
|
4.26 | 0.75 | 0.97 |
| Labor
|
3.76 | 0.73 | 0.77 |
| Wealth
|
6.06 | 1.21 | 0.89 |
| Information Flow
|
1.52 | 0.34 |
|
|
|
|
||||
|---|---|---|---|---|---|---|
|
|
0.97 | 1 | 0.86 | 0.94 | 0.48 | 0.88 |
|
|
0.86 | 0.94 | 0.77 | 1 | 0.76 | 0.87 |
|
|
0.88 | 0.78 | 0.77 | 0.87 | 0.89 | 1 |
| Mean | St.Dev |
|
|
|---|---|---|---|
| Consumption
|
4.11 | 1.31 | 0.93 |
| Labor
|
3.90 | 0.92 | 0.91 |
| Wealth
|
5.88 | 1.84 | 0.90 |
| Information Flow
|
1.10 | 0.45 |
|
|
|
|
||||
|---|---|---|---|---|---|---|
|
|
0.93 | 1 | 0.90 | 0.85 | 0.64 | 0.72 |
|
|
0.76 | 0.85 | 0.91 | 1 | 0.66 | 0.75 |
|
|
0.50 | 0.62 | 0.58 | 0.55 | 0.90 | 1 |
| Mean | St.Dev |
|
|
|---|---|---|---|
| Consumption
|
4.09 | 0.99 | 0.94 |
| Labor
|
2.90 | 0.74 | 0.95 |
| Wealth
|
5.07 | 1.31 | 0.97 |
| Information Flow
|
1.01 | 0.59 |
|
|
|
|
||||
|---|---|---|---|---|---|---|
|
|
0.94 | 1 | 0.88 | 0.90 | 0.73 | 0.67 |
|
|
0.95 | 0.90 | 0.95 | 1 | 0.44 | 0.54 |
|
|
0.56 | 0.67 | 0.64 | 0.64 | 0.97 | 1 |
8.2 Figures
Figure 7 Comparing consumption for different utilities,
![]() :
:
Blue: ![]() ,
, ![]() ; Green:
; Green: ![]() ,
, ![]() ; Violet:
; Violet: ![]() ,
, ![]() .
.
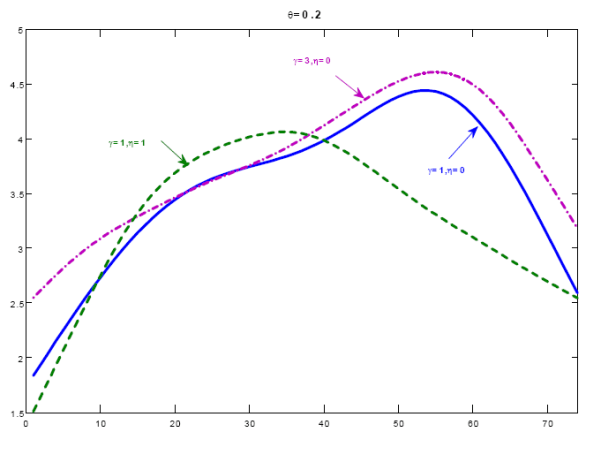
Figure 8: Comparing labor and wealth for different utilities,
![]()
Blue: ![]() ,
, ![]() ; Green:
; Green: ![]() ,
, ![]() ; Violet:
; Violet: ![]() ,
, ![]() .
.
Figure 9: Comparing savings for different utilities,
![]()
Blue: ![]() ,
, ![]() ; Green:
; Green:![]() ,
, ![]() ; Violet:
; Violet: ![]() ,
, ![]() .
.
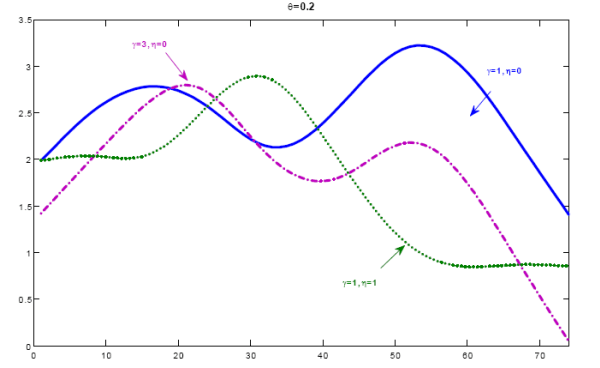
Figure 10: Comparing wealth, consumption, savings and income for different
![]() s,
s, ![]()
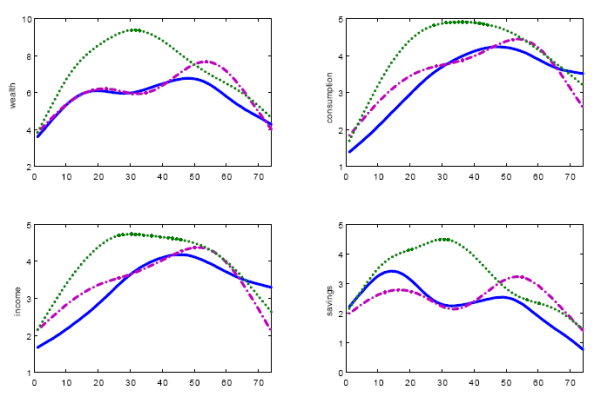
Blue: ![]() ; Violet:
; Violet:
![]() ; Green:
; Green:
![]()
9 Appendix C: Rigidity of Labor and Consumption Choices
This section builds up a low-dimension intuition for the solution strategy of the model in the section 2 before turning to the formal solution and its findings. Consider a consumer who can choose to consume a quantity in the set
![]() . Each period, he decides whether to work
. Each period, he decides whether to work
![]() in exchange for a salary
in exchange for a salary ![]() . Assume for simplicity no asset but a fixed initial endowment
. Assume for simplicity no asset but a fixed initial endowment
![]() The budget constraint is:
The budget constraint is:
where
Let
![]() denotes the utility of the consumer. Moreover, to make matters concrete, let
denotes the utility of the consumer. Moreover, to make matters concrete, let ![]() ,
,
![]() and
and
![]() and
and ![]() with probability
with probability ![]() and
and ![]() with probability
with probability
![]()
Under full information capacity and no uncertainty, the agent will work iff:
The solution for this problem is clearly
Under rational inattention, the agent can reduce his uncertainty up to an amount given by his ability of processing information. Such a constraint, expressed in terms of change in entropy is the Shannon channel. The reduction in uncertainty is obtained by choosing the distribution of a signal
informative about the underlying state (salary) as much as the Shannon channel allows it. In particular, there are 3 possible choices the consumer can make and that satisfy (26), i.e.,
![]() With the constraint
that the joint distribution
With the constraint
that the joint distribution
![]() delivers as marginal for
delivers as marginal for ![]()
![]() and
and
![]() , the joint distribution is
, the joint distribution is
The problem of the consumer is then to
s.t.
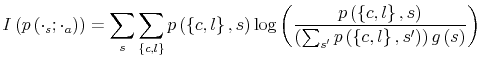
The first order condition are
![]()
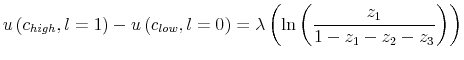
![]()
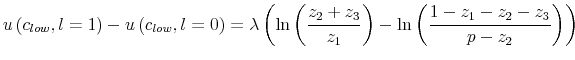
![]()
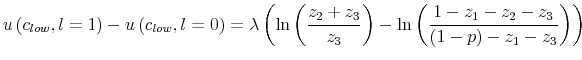
The set of first order conditions yield a system of simultaneous trascendental equations. This system of transcendental equations involving logarithms can be solved using the LambertW function., which is an inverse mapping satisfying
![]() and thus
and thus
![]() . This function has multiple branches, Branches 0 and -1 are the only ones that can take on non-complex values. Let
. This function has multiple branches, Branches 0 and -1 are the only ones that can take on non-complex values. Let ![]() . To solve the three equations, combine the last two F.O.C.'s and plug the
solution in the first using the constraints on the marginals. Let
. To solve the three equations, combine the last two F.O.C.'s and plug the
solution in the first using the constraints on the marginals. Let
![]() where
where
![]() . Then the solution for
. Then the solution for ![]() is given
by
is given
by
Figure 11 below illustrates the behavior of ![]() as function of
as function of ![]() ,
,
![]() and
and
![]() .
.
Figure 11: An analitical solution
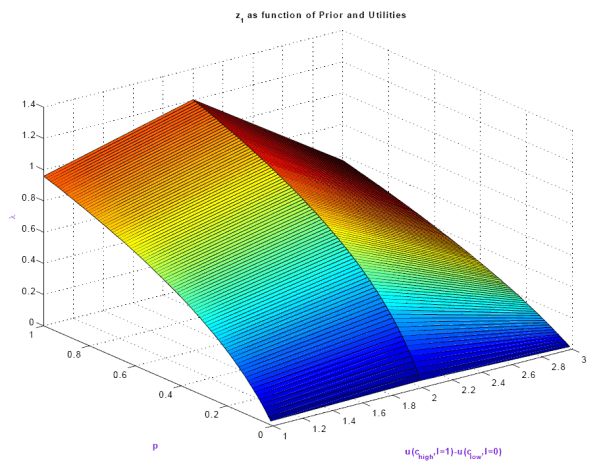
10 Appendix D
Pseudocode
Let ![]() be the shadow cost associated to
be the shadow cost associated to
![]() . Define a Model as a pair
. Define a Model as a pair
![]() . For a given specification :
. For a given specification :
- Step 1: Build the simplex. Construct a uniform grid to approximate each
 -simplex point.
-simplex point. - Step 2: For each simplex point, define
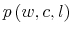 . and initialize with
. and initialize with
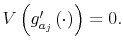
- Step 3: For each simplex point, find
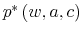 s.t.
s.t.
![]()
![]()
![\max_{_{p^{\ast}\left( w,c,l\right) }% }\left\{ {\sum\limits_{w\in W}\sum\limits_{a\in A}}\left( \frac {c_{t}^{1-\gamma}}{1-\gamma}-\alpha\frac{l^{\eta+1}}{\eta+1}\right) _{p^{\ast}\left( w,c,l\right) }-\theta\left[ \kappa\right] \right\} .](img364.gif)
- Step 4: For each simplex point, compute
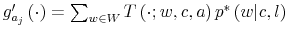 . Use a kernel regression to interpolate
. Use a kernel regression to interpolate
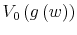 into
into
 .
. - Step 5: Optimize using csminwel and iterate on the value function up to convergence.
- Obs.
- Convergence and Computation Time vary with the specification
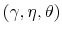 .
. -
- 120-220 iterations each taking 8min-20min
- Step 6. For each model
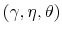 , draw from the ergodic
, draw from the ergodic
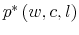 a sample
a sample
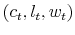 and simulate the time series of consumption, wealth, expected wealth and information flow by averaging over 1000 draws.
and simulate the time series of consumption, wealth, expected wealth and information flow by averaging over 1000 draws. - Step 7. Generate histograms of consumption and impulse response function of consumption to temporary positive and negative shocks to income.
Footnotes
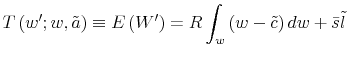
which makes the first order conditions for this case the full information solutions.
![\begin{displaymath}% \begin{array}[c]{ccc} & w_{1} & w_{2}\ \left\{ c_{1},l_{1}\right\} & p_{1} & p_{2}\ \left\{ c_{2},l_{1}\right\} & p_{3} & p_{4}\ \left\{ c_{1},l_{2}\right\} & p_{5} & p_{6}\ \left\{ c_{2},l_{2}\right\} & p_{7} & p_{8}% \end{array}. \end{displaymath}](img122.gif)
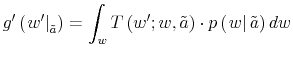
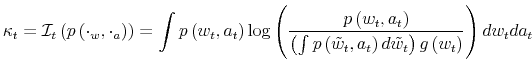
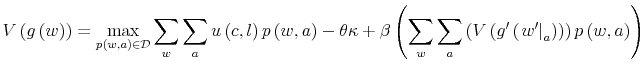
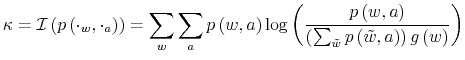
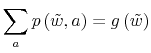
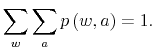
![\displaystyle +\beta\left( \sum_{w}\sum_{a}\left[ \frac{\partial\left( V\left( g^{\prime}\left( \left. w^{\prime}\right\vert _{a_{t}}\right) \right) \right) }{\partial g\left( \left. w^{\prime}\right\vert _{a_{t}}\right) }\frac{\partial g\left( \left. w^{\prime}\right\vert _{a}\right) }{\partial p\left( w,a\right) }\right] p\left( w,a\right) \right)%](img88.gif)
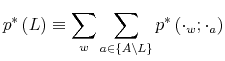
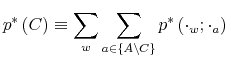
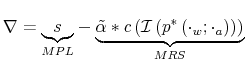
![\displaystyle V_{0}\left( g\right) =\max_{p\in\Gamma}\left[ {\displaystyle\sum \limits_{w\in W}}\left( {\displaystyle\sum\limits_{a\in A}}u\left( c,l\right) p\right) g\left( w\right) \right]%](img275.gif)
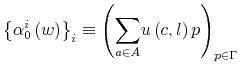
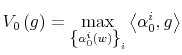
![\displaystyle V_{n}\left( g\right) =\max_{p\in\Gamma}\left[ \begin{array}[c]{c}% {\displaystyle\sum\limits_{w\in W}}\left( {\displaystyle\sum\limits_{a\in A}% }u\left( c,l\right) p\left( c,l\vert w\right) \right) g\left( w\right) +\\ +\beta{\displaystyle\sum\limits_{w\in W}}{\displaystyle\sum\limits_{a\in A}% }\left( V_{n-1}\left( g_{a}^{\prime}\left( \cdot\right) _{a}\right) \right) p\left( c,l\vert w\right) g\left( w\right) \end{array} \right]%](img280.gif)
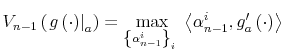
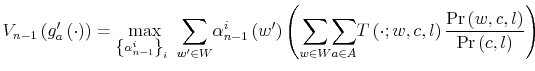
![\displaystyle =\max_{p\in\Gamma}\left[ \begin{array}[c]{c}% {\displaystyle\sum\limits_{w\in W}}\left( {\displaystyle\sum\limits_{a\in A}% }u\left( c,l\right) p\right) g\left( w\right) +\\ +\beta\max_{\left\{ \alpha_{n-1}^{i}\right\} _{i}\ }{\displaystyle\sum \limits_{w^{\prime}\in W}}\alpha_{n-1}^{i}\left( w^{\prime}\right) \left( {\displaystyle\sum\limits_{w\in W}}\left( {\displaystyle\sum\limits_{a\in A}% }\frac{T\left( \cdot;w,c,l\right) }{\Pr\left( c,l\right) }\cdot p\right) g\left( w\right) \right) \end{array} \right]](img284.gif)
![\displaystyle =\max_{p\in\Gamma}\left[ \left\langle u\left( c,l\right) \cdot p,\text{ }g\left( w\right) \right\rangle +\beta{\displaystyle\sum\limits_{a\in A}% }\frac{1}{\Pr\left( c,l\right) }\max_{\left\{ \alpha_{n-1}^{i}\right\} _{i}\ }\left\langle {\displaystyle\sum\limits_{w^{\prime}\in W}}\alpha _{n-1}^{i}\left( w^{\prime}\right) T\left( \cdot;w,c,l\right) \cdot p,\text{ }g\right\rangle \right]%](img285.gif)
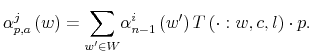
![\displaystyle V_{n}\left( g\right) =\max_{p\in\Gamma}\left[ \left\langle u\left( c,l\right) \cdot p,\text{ }g\right\rangle +\beta{\displaystyle\sum \limits_{a\in A}}\frac{1}{\Pr\left( c,l\right) }\max_{\left\{ \alpha _{p,a}^{j}\right\} _{j}\ }\left\langle \alpha_{p,a}^{j},g\right\rangle \right] ,%](img288.gif)
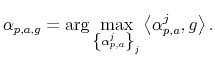
![\displaystyle =\max_{p\in\Gamma}\left[ \left\langle u\left( c,l\right) \cdot p,\text{ }g\right\rangle +\beta{\displaystyle\sum \limits_{a\in A}}\frac{1}{\Pr\left( c,l\right) }\left\langle \alpha _{p,a,g},\text{{}}g\right\rangle \right]](img292.gif)