Skip to: [Printable Version (PDF)] [Bibliography] [Footnotes]

Finance and Economics Discussion Series: 2010-05 Screen Reader version ^♣

Constant Proportion Debt Obligations:
A Post-Mortem Analysis of Rating Models*

Michael B. Gordy

Federal Reserve Board

Søren Willemann

Barclays Capital

23 September 2009

Keywords: Credit risk, securitization, structured credit, rating agencies

Abstract:

In its complexity and its vulnerability to market volatility, the CPDO might be viewed as the poster child for the excesses of financial engineering in the credit market. This paper examines the CPDO as a case study in model risk in the rating of complex structured products. We demonstrate that the models used by S&P and Moody's would have assigned very low probability to the spread levels realized in the investment grade corporate credit default swap market in late 2007, even though these spread levels were comparable to those of 2002. The spread levels realized in the first quarter of 2008 would have been assigned negligibly small probabilities. Had the models put non-negligible likelihood on attaining these high spread levels, the CPDO notes could never have achieved investment grade status. We conclude with larger lessons for the rating of complex products and for modeling credit risk in general.

JEL Codes: G24, G17

The Constant Proportion Debt Obligation (CPDO) appeared at the peak of the market for structured credit products. The first CPDO issue, ABN Amro's Surf, was arranged in the summer of 2006 and closed in November of the same year. The Surf notes were rated AAA by Standard & Poor's, yet offered a coupon 200 basis points over LIBOR. As the AAA corporate spread in this period hovered close to LIBOR, the Surf deal earned considerable attention (not all sanguine) in the financial press and industry awards such as Risk Magazine's "Deal of the Year" in February 2007.¹ When credit markets came under stress in 2007, CPDOs were among the first to unravel. The first CPDO default, on a financial-only CPDO issued by UBS, arrived in late November 2007. The defaulted notes had been rated Aaa by Moody's at issuance in March 2007.² To have met this rating standard, the modeled likelihood of default within a year must have been less than 1 in 250,000. Since 1920, no Aaa rated corporate bond has ever defaulted within a two year horizon.³ Subsequently, it appears that most CPDOs were unwound voluntarily by investors, at significant loss, or forcibly unwound. Our calculations suggest that most or all of any remaining CPDO notes would likely have defaulted by late November 2008.

In its complexity and its vulnerability to market volatility, the CPDO might be viewed as the poster child for the excesses of financial engineering in the credit market. This paper offers a case study of the CPDO. Our focus is on model risk in the methodologies used by S&P and Moody's in assigning CPDO ratings. In particular, we show that these models would have assigned very low probability to the spread levels realized in the investment grade corporate credit default swap (CDS) market in late 2007. The spread levels realized in the first quarter of 2008 would have been assigned minuscule probabilities. Had the models put non-negligible likelihood on attaining these high spread levels, the CPDO notes could never have achieved investment grade status. One can debate whether a model calibrated to available data in 2006 should have been expected to allow for the crisis conditions of 2008. However, the spread levels realized in late 2007 are qualitatively comparable to the levels seen in 2002, so ought not to have been taken as extreme events.

The academic literature on CPDOs is sparse. Cont and Jessen (2009) develop a parsimonious top-down stochastic intensity model for rating CPDOs. They show that the model-implied rating can be highly sensitive to small changes in certain parameters governing the evolution of spreads. Our study serves a complementary purpose, in that we take the agency models as given and test whether the model-implied forecast densities are consistent with the observed path of spreads prior to and during the credit crisis.

In May 2008, the Financial Times reported that Moody's CPDO ratings may have been affected by software coding errors. If it were the case that the poor performance of the agency ratings could be attributed to coding errors or subsequent model modifications, then our analyses would be of little interest. As we will describe in detail in Section 4.2, our conclusions appear to be robust. Furthermore, there have been no reports that coding errors played a significant role in S&P rating of CPDOs.⁴

We begin in Section 1 with a review of the mechanics of the CPDO strategy. In Section 2, we consider the rationale behind the strategy and summarize the risk characteristics as understood in late 2006 and early 2007. In Section 3, we document the movement of spreads in the corporate CDS market in 2007-2008 and the impact of these spread movements on CPDO performance. The models used by the rating agencies to rate CPDO are set out and evaluated in Section 4. The Discussion offers some larger lessons for the rating of complex products and for modeling credit risk in general.

1 Mechanics of the CPDO

The CPDO is a fully funded structured credit product.⁵ A special purpose vehicle (SPV) issues floating rate notes and receives par from the investors. The proceeds are held in a cash account as collateral for a long position (i.e., seller of protection) in a portfolio of CDS. For the "plain-vanilla" index CPDO, the portfolio is composed in equal shares of the CDX North American and iTraxx European investment grade five year CDS indices. This portfolio is sometimes known as the Globoxx index. The notional size of the long position is a multiple of the size of the cash account, and in this sense a CPDO is leveraged. The maturity of a CPDO is typically ten years.

Leverage is adjusted dynamically over the lifetime of the CPDO. Each day, the manager of the SPV calculates the shortfall, which is the gap between the current net asset value (NAV) of the SPV holdings (i.e., the sum of the cash account and the mark-to-market value of the CDS index portfolio) and the present value of all future contractual payments, inclusive of management fees. The target leverage is given by an increasing function of the shortfall. Details of the specification vary across issuers, but a typical formula is

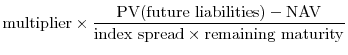
$\displaystyle {\rm multiplier}\times {{\rm PV(future\ liabilities)} - {\rm NAV} \over {{\rm index\ spread} \times {\rm remaining\ maturity}}}$

Leverage is subject to an upper bound (set at 15 in the first CPDO) and is typically at the upper bound at issuance.⁶

If the shortfall decreases to zero, the CDS portfolio is unwound and the proceeds held as cash to fund remaining contractual payments. This is referred to as a cash-in event. On the other hand, if NAV falls to a predetermined lower threshold (usually 10% of par), the CDS portfolio is unwound and remaining funds are paid out to the noteholders. This cash-out event is equivalent to a default, where the recovery rate for the noteholders is (at best) the cash-out threshold level. The CPDO contract may also impose a gap risk test to ensure that NAV can withstand a specified widening of index spreads and a specified level of default losses.⁷ If the NAV falls below the gap risk trigger, the SPV must partially unwind in order to restore compliance.

The CDS portfolio is kept in the on-the-run indices. Every six months, the CDX and iTraxx indices are refreshed. Names that have fallen below investment grade or for which CDS trading is no longer liquid are dropped from the indices and replaced with new names. On the index roll date, the SPV must purchase protection on the off-the-run index and sell protection on the on-the-run index.

Comparison and contrast with earlier forms of structured credit may provide some intuition for the essential characteristics of CPDOs. In contrast to collateralized debt obligations (CDOs), the "structuring" in a CPDO is on the asset side of the SPV balance sheet (i.e., through the use of variable leverage) and not the liability side (i.e., through tranching). All noteholders have the same priority.

The leveraged super senior CDO note is the closest direct ancestor of the CPDO. The investor in a LSS note sells leveraged protection on a super senior tranche of a CDO. For example, with note proceeds of $100 million as collateral, the LSS sells $1 billion notional of protection on a 20-100% tranche of a reference portfolio. In this case the leverage is 10. If certain predefined triggers are reached, the investor may either post additional collateral to bring the leverage down or the leveraged position in the tranche is unwound and the investor receives the posted collateral less mark-to-market losses from the unwind. The unwind triggers are based either on the level of losses due to actual defaults in the portfolio, the average spread level for the reference CDS portfolio, a combination of default losses and spread levels or actual mark-to-market. The main idea is that when the triggers are reached, if the investor does not provide additional collateral, the unwind of the tranche position is likely to have mark-to-market losses below the posted collateral. Important differences between the CPDO and LSS structures include:

Unlike the CPDO, "structuring" in the LSS note is on the asset side as well as the liability side of the SPV balance sheet.
The reference pool of the LSS note is fixed (i.e., it does not refresh to eliminate firms that have fallen below investment grade). Therefore, relative to the CPDO, the LSS note has greater exposure to the risk of defaults in the reference pool, and especially to the systematic component of default risk.
Unlike the CPDO, the leverage in the LSS structure is constant over the lifetime of the deal. The path dependence of the CPDO makes the CPDO ratings more sensitive to specification of spread processes.

CPDOs are sometimes described as a variant on credit Constant Proportion Portfolio Insurance (CPPI) deals. As explained in a Fitch report (Linden et al., 2006),

Credit CPPI notes are investments whose principal is protected by a low-risk portfolio consisting of zero-coupon bonds or a cash deposit, and whose return is increased by leveraging the exposure to a risky portfolios of CDS names. At all times, the credit CPPI is structured to ensure that investors' principal will be returned to them at maturity.

Rather than view CPDO as a variant on CPPI, it would be better to view the CPDO strategy as diametrically opposed to CPPI. When losses are incurred in a CPPI, the SPV must decrease leverage in order to protect the principal. When losses are incurred in a CPDO, the SPV must increase leverage in order to make up the increased shortfall in NAV. Return distributions are positively skewed (limited downside, unlimited upside) for CPPI, and negatively skewed for CPDO.

An obvious flaw in the first-generation CPDO design is its vulnerability to front-running. The index roll mechanism forces the CPDO SPV to purchase protection on the off-the-run index and sell protection on the on-the-run index. If CPDOs jointly account for a significant share of the CDS market, the index roll will put downward pressure on on-the-run spreads and upward pressure on off-the-run spreads. As the roll date is known in advance, other market participants can anticipate the spread changes and trade accordingly. It does not appear that the CPDO market ever grew large enough for front-running to be a significant problem in practice.⁸ The flaw was recognized early and much discussed in the practitioner literature. Among the modifications proposed and sometimes implemented:

Provide a wider window around the roll date for the manager to trade out of the off-the-run index and into the on-the-run index. Most later deals allowed for 10 days to roll the index position, and early contracts were sometimes amended along similar lines.
Allow the manager to hedge downgraded names in the indices prior to the next index roll.
Reference bespoke portfolios of CDS, rather than CDS indices. Names would be replaced upon downgrade below a pre-set threshold.⁹

CPDO deals referencing bespoke portfolios appeared by March 2007.

Relative to the first Surf issue, subsequent CPDOs issued typically sought a more conservative risk/return profile. Coupons on CPDO notes and arranger fees fell roughly by half in order to reduce the need for high leverage. Maximum leverage was sometimes reduced, say to 10.

2 Rationale and risk characteristics

The CPDO structure takes advantage of several empirical regularities in investment grade corporate credit markets. First, credit spreads appear to embed a high risk premium. Put another way, the empirical default frequency of investment grade corporate credits explains only a small fraction of the observed risk-neutral default probability embedded in market prices (e.g., Elton et al., 2001). This would suggest that an investment grade CDS portfolio could be leveraged to achieve high returns with relatively modest default risk.

Second, investment grade default intensities appear to be strongly mean-reverting in time-series.¹⁰ Consequently, CDS spreads on investment grade names tend to mean-revert. This underpins the CPDO's "double or nothing" strategy. If spreads balloon and the SPV loses value, the CPDO increases leverage. Mean-reversion implies that future spread movements are more likely to be negative than positive, and so more likely to earn gains than loses to NAV. Similarly, by decreasing leverage when spreads tighten, the CPDO avoids losses in the likely event that spreads subsequently increase.

Third, the term-structure of credit spreads is typically upward-sloping for investment grade issuers. If the index composition is unchanged, the SPV realizes a mark-to-market gain on the biannual index roll when it buys protection on the 4.5 year off-the-run index and sells protection on the new five year on-the-run index. However, if the index composition changes due to credit deterioration among some names in the off-the-run index, the roll-down benefit will be reduced or possibly negative.¹¹

Fourth, default times of investment grade names tend to be back-loaded, i.e., fixing a default probability over a given horizon, the default is more likely to occur later rather than earlier. As the CPDO mechanism trades out of names that have been downgraded, the only outright default risk being taken in the CPDO is short-term jump-to-default risk.

These arguments lend plausibility to the CPDO as a trading strategy. Many hedge funds and asset managers are active in the CDS markets, and it would not be surprising if some of these institutions were pursuing a strategy along these lines. What is less obvious is the rationale for structuring CPDO liabilities as debt rather than as equity. The sensitivity of the CPDO strategy to market volatility makes the structure inherently fragile when backed by debt. Market commentary suggests that the demand for this debt is driven by some of the same factors that drive demand for CDOs. In particular, there are pension funds and other institutions that are restricted by law or by mandate to invest primarily in investment grade debt. In the environment of tight credit spreads that prevailed until June 2007, the ability to offer 200 basis points on a AAA-rated security made for easy marketing.

Accounting treatment may also play a role. CPDO debt is primarily marketed to buy-and-hold investors who report on an accrual basis. For these investors, high mark-to-market volatility of the SPV's NAV can be ignored so long as cashflows are stable. The caveat here is that volatility in NAV ought to imply high ratings volatility, which is a problem for many buy-and-hold investors. It is not clear whether this was well-understood by investors before the credit crisis.

Relative to most other structured credit products, CPDOs offer transparency in pricing. The investors in CPDO notes hold pro-rata shares in the NAV of the SPV less the present discounted value of the management fees. The SPV is invested exclusively in liquid CDS positions and in cash, and so the NAV is easily calculated on a daily basis. A corollary of the CPDO accounting identity (i.e., that the value of liabilities must equal the NAV) is that the value of the CPDO notes at origination is below par and almost independent of the contractual coupon.¹²

In contrast to the simplicity of pricing, robust modeling of the future performance of a CPDO is far from straightforward. The dynamic leverage rule induces strong path dependency on spreads for the reference portfolio. For this reason, it is not easy to characterize in a simple manner the set of scenarios that would trigger cash-out or failure to return par at maturity. Isla et al. (2007) distill a large set of analyses into the following rules of thumb:

The lower the volatility in CDS spreads and the higher the rate of mean-reversion in spreads, the less likely is the CPDO to default on contractual payments.
The lower the coupon on the CPDO notes and the lower the arranger fees, the lower the required leverage, and so the lower the likelihood of default.
Spread-widening is generally bad news for the CPDO notes, but not necessarily. If spreads widen early in the life of the CPDO and then hold steady, the higher carry on future index positions can outweigh the initial loss of NAV. Furthermore, if spreads subsequently mean-revert, there will be a gain in NAV. However, if spreads widen late in the life of the CPDO, there is less time to make up loss before maturity. In this case, the CPDO is more likely to fail to repay full principal at maturity.
A severe spike in spreads can trigger a cash-out event. One example in the Isla et al. (2007) analysis is based on a scenario in which a steady increase in spreads from 25 basis points (bp) at inception to 75bp after 4.75 years is followed by a sudden spike to 300bp.
Default events generate large losses to NAV, and in this respect the CPDO behaves similarly to a thick equity tranche of a CDO. The index roll limits but does not eliminate the CPDO's exposure to defaults. In the downturn of 2001-02, Enron and WorldCom went from investment grade to default within six months (Linden et al., 2007).

The CPDO avoids the liability structuring that makes senior CDOs highly sensitive to correlation among the reference names, and so is regarded as less vulnerable to systematic credit risk than other structured credit products of similar rating. However, published analyses have devoted little or no attention to sensitivity to a focused sectoral credit problem. If downgrades within a major sector cause several names in the index to widen significantly and then be dropped at the next roll date, the loss in NAV could be material as the CPDO will unwind the position on the old index, thereby crystalizing mark-to-market losses. If spreads are unchanged on names outside the affected sector, the CPDO structure will not receive the benefit of higher carry to compensate. This apparent gap in the analyses is surprising because it was a focused sectoral event that caused large losses for some CDO investors in the spring of 2005.¹³ Even more obviously, the greater volatility of a single-sector portfolio increases the vulnerability of any industry-specific CPDO. The early default by a financial-only CPDO bears witness to this point.

3 Performance during the credit crisis

The great bulk of CPDO issuance took place in the fall of 2006 and spring of 2007. In this period, corporate credit spreads were at a cyclical low point and volatility in credit spreads had been subdued for nearly three years. As shown in Figure 3, the CDX was trading around 35bp during the period of issuance and had not exceeded 60bp since July 2005. The iTraxx spread was typically about 10bp lower during this period, and had not exceeded 50bp since May 2005.

Figure 1: Investment grade index spreads

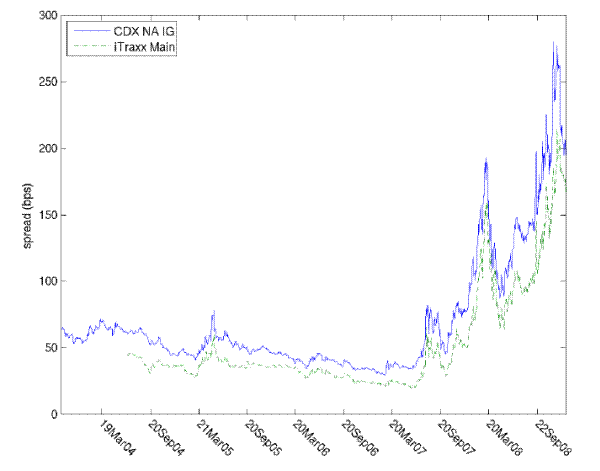
Spreads for on-the-run five year investment grade indices. CDX trading began 21 October 2003 and iTraxx trading began 22 June 2004. Biannual index roll dates are marked on the time axis. Source: MarkIt.

The first tremors of the credit crisis reached the corporate CDS market in the summer of 2007. The CDX index spiked to 81bp in early August, fell to 45bp in early October, reached 85bp in late November and thereafter increased steadily through mid March 2008, when it reached 193bp. Spreads then fell sharply to 86bp in early May, but soon were increasing again. The CDX broke 279bp on November 20, and finished the year at 195bp. The iTraxx spread followed a very similar pattern.

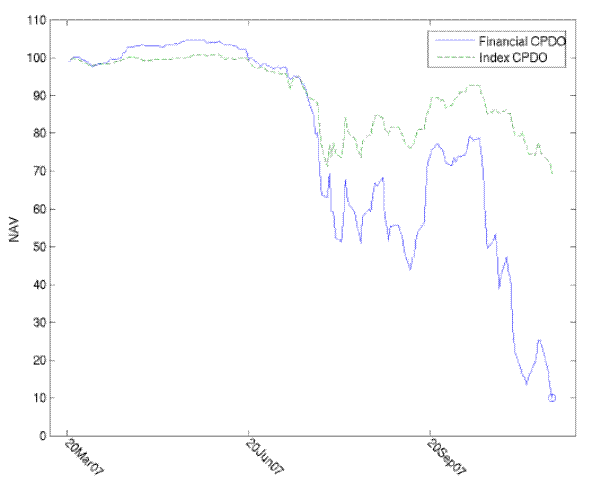
The volatility of the CDS markets induced high volatility for the NAV of CPDOs. To illustrate the effect on the performance of CPDOs, we calculate the NAV for a hypothetical CPDO that very closely emulates the first Surf note.¹⁴ Our hypothetical CPDO is issued on 25 August 2006 with a maturity of ten years. It references a 15x leveraged portfolio of the five year iTraxx Main and CDX investment grade indexes. We assume the CPDO note earns 200bp above 3-month LIBOR and the SPV pays running fees of 60bp. Arrangement fees reduce NAV at inception to 99. The cash-out barrier is 10. As depicted in Figure 3, the NAV increased steadily in the low spread period that prevailed until June 2007, and peaked at 107.5 on June 5. The NAV dropped precipitously in the first three months of 2008 and nearly triggered a cash-out event on March 14 (NAV of 14). The sharp fall in spreads over the subsequent two months brought an equally rapid recovery, and NAV reached 82.9 on May 2. The steady increase in spreads thereafter implied a steady deterioration in the NAV, and the CPDO hit its cash-out barrier on November 20, 2008.

Figure 2: NAV for a hypothetical index CPDO

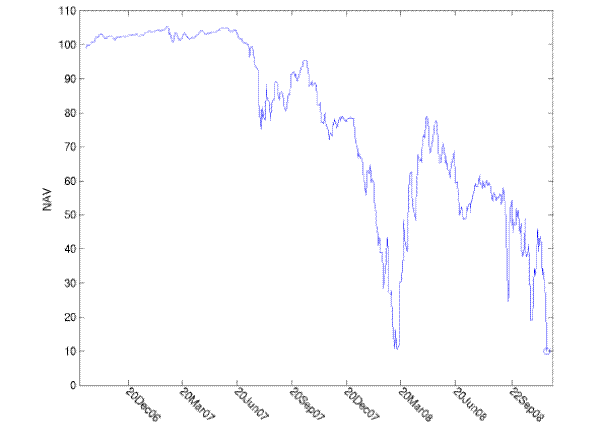
Biannual index roll dates and their midpoints are marked on the time axis. Cash-out event marked with a circle. Source: Authors' calculations.

Little of this volatility was reflected in the rating history of the Surf notes, which is shown in Table 1. The downgrade to BBB- on March 10, 2008 allowed the CPDO to retain its investment grade status (though barely, and on the watch list for downgrade). On the same date, the NAV for our proxy CPDO was 14.3, so the Surf deal must have been close to a cash-out default. The rating was withdrawn on October 23, less than one month prior to the cash-out of our proxy CPDO.

Table 1: S&P rating actions on first Surf CPDO

29-Aug-2006	AAA
20-Dec-2007	AAA/Watch Negative
20-Feb-2008	BBB+
10-Mar-2008	BBB-/Watch Negative
19-Sep-2008	B/Watch Negative
23-Oct-2008	B
23-Oct-2008	Not Rated

: S&P rating on SURF CPDO floating-rate note series 24, issued by Chess II Ltd and arranged by ABN Amro.

The credit crisis has also demonstrated the particular vulnerability of a CPDO with a more concentrated reference pool. As widely reported in the financial press, a financial-only CPDO deal arranged by UBS in March 2007 hit its cash-out trigger on November 21, 2007.¹⁵ This is the first default by a CPDO. Moody's had rated the CPDO notes Aaa at inception only eight months earlier. The UBS pool had significant concentrations of exposure to the monoline financial guarantors and mortgage issuers. Figure 3 depicts how the CDS spreads widened dramatically over the course of 2007 for four names in the pool. By year-end, their ten year CDS spreads were several times those of prevailing BBB corporate bond spreads.

Figure 3: Spreads for select financial names in 2007

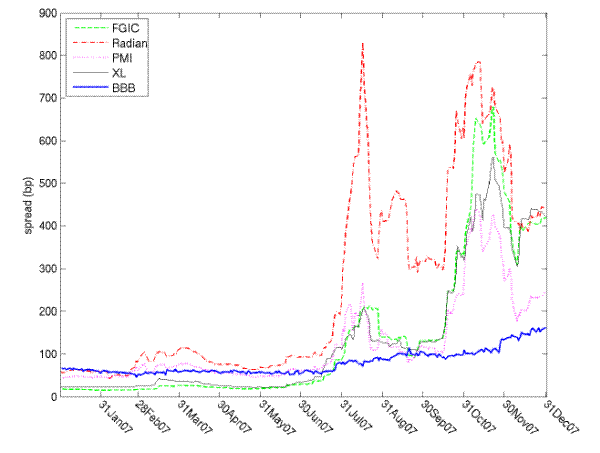
10 year CDS spreads and BBB bond spreads over 3-month LIBOR. Source: CDS data from MarkIt. BBB spread index constructed from Merrill Lynch database.

We do not have complete data on the reference portfolio for the UBS deal, but Leeming et al. (2007) study a very similar hypothetical financial-only CPDO. This hypothetical CPDO is issued on 20 March 2007 with 10 year maturity, and references a 10x leveraged bespoke portfolio of ten year CDS on 50 financial firms.¹⁶ The NAV is plotted in Figure 3. The lower leverage could not compensate for the pool's poor diversification. This hypothetical CPDO hit its cash-out trigger on the same date as did the UBS deal, and it is believed that other financial-only CPDOs of this vintage were equally vulnerable. For comparison, we also plot the NAV for a hypothetical index CPDO issued in March 2007.¹⁷ The large gap in performance demonstrates the risk inherent in taking leveraged exposure to a single sector, and especially to a volatile sector such as financials.

Figure 4: NAV for a hypothetical financial-only CPDO

Source: Leeming et al. (2007).

4 Model risk in CPDO ratings

The AAA rating assigned to the first CPDOs generated significant controversy in the financial press. Rating agencies that did not participate in the first issues published reports strongly critical of the AAA rating. Jobst et al. (2007) of DBRS find that variations in model specification, and in data source and sample period for calibration, can lead to dramatic changes in estimated rating. They demonstrate particular sensitivity to assumptions governing roll-down benefits and to assumptions on CDS market liquidity (i.e., bid-ask spreads). They acknowledge that one can justify the AAA rating on the basis of reasonable models calibrated to available data, but suggest that a BBB rating would be equally justifiable. Linden et al. (2007) of Fitch conduct similar exercises and obtain similar results. They put special emphasis on stress tests showing that the CPDO structure is less robust to extreme events than AA and AAA rated CDO tranches. They conclude, and state in blunt terms, that the first-generation CPDO notes do not achieve a rating of AA, much less AAA. As noted earlier, Cont and Jessen (2009) demonstrate that the rating of CPDOs can be highly sensitive to small changes in parameters governing the evolution of spreads.

The distress experienced in credit markets since mid-2007 provides an opportunity to evaluate ex-post the modeling assumptions that underpinned the rating of CPDOs. As we have the benefit of hindsight, our proper purpose is not to criticize rating opinions assigned ex-ante, but only to demonstrate how a model that may look reasonable at first glance can dramatically understate the risk of a complex structure such as a CPDO. In our analysis, we focus specifically on the performance of the rating agency models for credit spread dynamics.

4.1 S&P model

During the period of CPDO issuance, the S&P approach to rating index CPDOs combined a Gaussian copula model for default losses in the pool with a stochastic model for the index spread (see Wong and Chandler, 2007, for details). As the biannual index roll removes names that have drifted below investment grade, the default module simulates for the remaining life of the transaction a sequence of six month exposure to default in a pool of investment grade names.¹⁸The index spread is assumed to follow a Black-Karasinski process, which is equivalent to assuming that the log of the spread follows a Vasicek process.¹⁹ This is given by the stochastic differential equation

$\displaystyle d\,\log(S_t) = \kappa(\theta-\log(S_t))dt + \sigma dW_t$

(1)

where

is a Brownian motion, $\theta$ is the long-run mean log-spread, $\kappa$ controls the rate of mean-reversion, and $\sigma$ is the volatility parameter. Baseline parameter values for the Globoxx spread are $\kappa=0.4$ , $\sigma=0.25$ and $\theta=\log(0.004)-\sigma^2/(4\kappa)$ .

The Black-Karasinski specification has been applied to default intensity models, most notably by Pan and Singleton (2008), and Berndt (2007) shows that this specification generally outperforms CIR and jump CIR specifications for the default intensity. The distinction between credit spreads and default intensities notwithstanding, the Black-Karasinski specification would appear to be a plausible choice for this application. Even if the model is well-specified, however, its empirical performance obviously depends on parameter calibration.

Consider the rating of a CPDO on the index roll date of 20 March 2007, when the Globoxx spread was 31.6bp and the CPDO market was at its most active. Under the S&P specification, how high might spreads reasonably have been anticipated to climb? We let , and let be the maximum spread on . In Figure 4.1, we plot the upper tail of the distribution at horizons of six months and one year. Our methodology for generating a sample of is described in Appendix A. We see that $\Pr(M_{6 {\rm mo}}>70{\rm bp})$ is well below $10^{-5}$ (that is, 0.1 of one basis point). Looking to the one year horizon, we see that $\Pr(M_{1 {\rm yr}}>90{\rm bp})$ is also well below $10^{-5}$ . In 10 million simulated paths for $M_{1 {\rm yr}}$ , the model never generated a spread above 102bp. Yet the Globoxx reached 73.2bp on 30 July 2007, well within a six month horizon, and reached 144.5bp on 20 February 2008. Simply put, the model assigns very low probability to the modestly high spreads realized in the first phase of the credit crisis in the summer of 2007, and assigns effectively zero probability to the spreads realized in the spring of 2008 (which themselves were greatly surpassed by the end of 2008).

Figure 5: Tail of peak spread distribution in S&P model

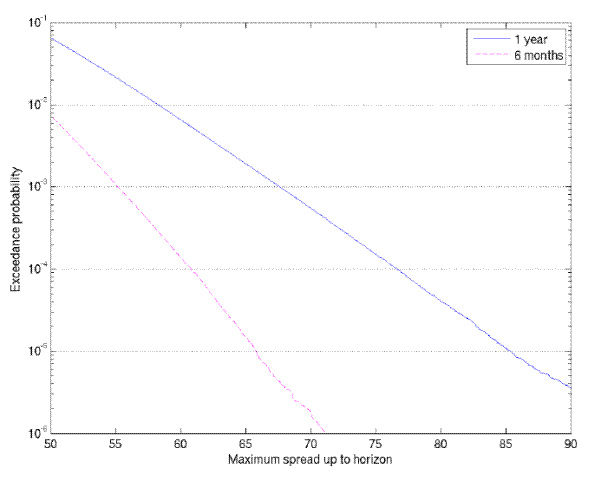
Based on 10 million paths sampled at 10000 time steps per year.

Specification tests can be applied to the S&P model using the realized path for the Globoxx. Say we observe the path at discrete intervals $t_1,\ldots,t_n$ . At each point in time, the exact transition density is Gaussian for the log spread at $t_{i+1}$ with mean $\theta(1-e^{-\kappa(t_{i+1}-t_i)}) + e^{-\kappa(t_{i+1}-t_i)}\log(S(t_i))$ and variance $\sigma^2(1-e^{-2\kappa(t_{i+1}-t_i)})/(2\kappa)$ (see Glasserman, 2004, eq. (3.46)). Therefore, we can extract standardized innovations

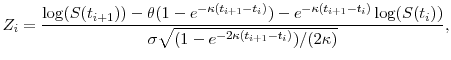
$\displaystyle Z_i = \frac{\log(S(t_{i+1})) - \theta(1-e^{-\kappa(t_{i+1}-t_i)}) - e^{-\kappa(t_{i+1}-t_i)}\log(S(t_i))} {\sigma\sqrt{(1-e^{-2\kappa(t_{i+1}-t_i)})/(2\kappa)}},$

$i=1,\ldots,n-1$ , that are iid ${\cal N}(0,1)$ if the model is specified correctly.

We examine the empirical distribution of the daily innovations for the pre-crisis period (22 June 2004 to 13 June 2007) and the crisis period (14 June 2007 to end 2008).²⁰ The breakpoint, June 14, is chosen as the date on which the troubles of two Bear Stearns hedge funds became public news. It is not obvious how index roll dates should be treated, as the jump in the spread induced by the reconstitution of the index is outside the model framework. We choose to exclude innovations for intervals containing roll dates, as this biases our analysis in favor of the S&P model. Descriptive statistics are shown in Table 2.

Table 2: Moments of the innovations $^\dagger$
Period	Days	Mean	Variance	Skewness	Kurtosis
Pre-crisis	770	-0.08	1.91 ^***	0.66	14.39 ^***
Crisis	402	0.42 ^***	11.81 ^***	-0.04	5.65 ^***

$\dagger$ :One, two and three asterisks indicate significance at 5%, 1% and 0.1% levels, respectively. Tests for mean zero, variance one and mesokurtosis are two-sided. Skewness is not tested.

In the pre-crisis period, the null hypothesis of mean zero is rejected at the 5% level in a two-sided test, but not at the 1% level. The null hypothesis of variance one is rejected even at the 0.1% level. For the crisis period, both tests reject at the 0.1% level. For the null hypothesis of mesokurtosis (i.e., kurtosis of 3), the test of Anscombe and Glynn (1983) rejects at the 0.1% level in both periods. To test the distributional assumption (standard normal), rather than just the moments, we use the Cramér-von-Mises test, and reject at the 0.1% level in each period.²¹ Excess kurtosis drives the strong rejection of normality. Say, for example, that we increase $\sigma$ in the Black-Karasinski process to 0.35. The tests of mean zero and variance one would then not reject in the pre-crisis period, but the Anscombe-Glynn and Cramér-von-Mises tests still would reject strongly for both periods.

In Figure 4.1, we plot quantiles of the innovations in these two periods against the quantiles of the normal distribution. The slopes of the dashed lines demonstrate the excess variance, whereas the departures of the marked points from the dashed lines demonstrates the excess kurtosis.

Figure 6: QQ plot for innovations in S&P model

Quantiles for the pre-crisis period are marked with blue plus signs, and quantiles for the crisis period are marked with green circles.

4.2 Moody's model

Like the S&P approach, the Moody's approach to rating CPDOs joins together a model for correlated changes in obligor status with a stochastic model for spreads. However, these component models are more elaborate than their S&P counterparts. The obligor status model captures rating migrations as well as defaults, and spreads are represented as a vector of ratings-based constant-maturity spreads with correlated innovations. Instead of modeling the spread on the pool in a top-down fashion, Moody's constructs the pool spread bottom-up from the ratings of the individual names in the pool and the spreads that correspond to those ratings. It is assumed that when an obligor changes rating grade, its CDS spread jumps to the level associated with its new grade.²²

The engine for simulating correlated migrations and defaults is a variant on the basic Gaussian copula framework, known as CDOROM, that underpins most or all of Moody's structured credit analysis. It is similar in spirit and structure to a multi-period version of the popular CreditMetrics model of portfolio credit risk.²³ Spreads are assumed to evolve over time as "constant elasticity of variance" (CEV) processes with capped variances. More precisely, the spread for grade follows the stochastic differential equation

$\displaystyle dS_{k}(t) = \kappa_k(\theta_k-S_{k}(t))dt + \min({\bar v}_k,\eta_k+\sigma_kS_k(t)^{\gamma_k}) dW_{k}(t)$

(2)

where $\theta_k$ is the long-run mean spread for the grade, $\kappa_k$ controls the rate of mean-reversion, ${\bar v}_k$ is the cap on volatility, $\eta_k$ and $\sigma_k$ are volatility parameters, and $\gamma_k$ is the CEV elasticity parameter.

is a Brownian motion, and the correlation of increments

and

for grades

is $\rho_{kj}$ . Moody's baseline parameter values for investment grade spreads are presented in Tables 3 and 4.

Table 3: Parameters for Moody's CEV spread processes
	$\theta$	$\kappa$	$\sigma$	$\gamma$	$\bar{v}$
Aaa	0.25%	8.7926	306.95%	1.1835	0.00329	0.28%
Aa	0.21%	3.3786	1822.67%	1.5831	0.00359	0.26%
A	0.33%	3.0298	220.36%	1.3376	0.00325	0.30%
Baa	1.01%	7.3130	216.67%	1.3383	0.01395	0.65%

Source: Moody's.

Table 4: Correlations for Moody's CEV spread processes
	Aaa	Aa	A	Baa
Aaa	1.0000	-0.1697	0.0953	0.2716
Aa	-0.1697	1.0000	0.0922	0.0693
A	0.0953	0.0922	1.0000	0.0763
Baa	0.2716	0.0693	0.0763	1.0000

Source: Moody's.

To permit assessment of model predictions, we construct time-series of average five-year corporate CDS spreads by rating category. Our methodology is described in Appendix B. We plot investment grade spreads for 2001-08 in Figure 4.2, and display spreads on select dates in Table 5. For the pre-crisis and crisis periods, the behavior of the rating-based spread series is similar to that of the index spreads in Figure 3. Given the composition of the Globoxx, one expects the index to be above A spreads and below Baa spreads. This is generally the case in our data except in the first half of 2007, when the Globoxx ran a few basis points higher than our Baa composite. Our sample of firms is much wider than the set of names on which the indexes are based, so the relationship between our ratings-based composites and the Globoxx is not fixed.

Figure 7: Investment grade spreads, 2001-08

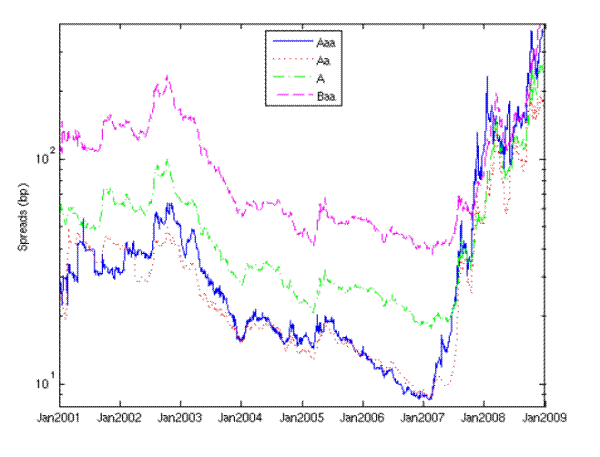
CDS spreads in basis points log-scale.

Table 5: Rating-based spreads on select dates
	Aaa	Aa	A	Baa	Globoxx
10 Oct 2002	63.8	49.3	99.2	235.88	-
20 Feb 2007	9.0	8.7	17.8	38.8	26.2
20 Mar 2007	12.3	10.9	20.3	42.6	31.6
30 July 2007	38.1	29.1	35.3	69.4	73.2
20 Nov 2007	122.5	62.5	54.2	74.9	69.3
20 Feb 2008	161.1	94.9	112.7	151.9	144.5
20 Mar 2008	137.1	122.4	139.7	178.5	145.7
15 Dec 2008	360.3	186.9	265.6	429.5	235.3

A clear feature of the data is high variability in Aaa spreads. Before the crisis, the Aaa spread would often exceed the Aa spread. During the crisis, the Aaa spread would sometimes exceed even the Baa spread. This can be seen in Figure 4.2, which restricts the window to the crisis period. The Aaa spread is based on a much smaller sample of firms than the other rating composite spreads (typically less than 40 firms for Aaa against 150-900 for the other grades), and the Aaa category is dominated by financial firms (such as monoline insurers) that were in many cases severely affected by the crisis. To avoid issues with data quality, we omit the Aaa category from our analyses below. This biases our analysis in favor of the Moody's model.

Figure 8: Investment grade spreads in the crisis period

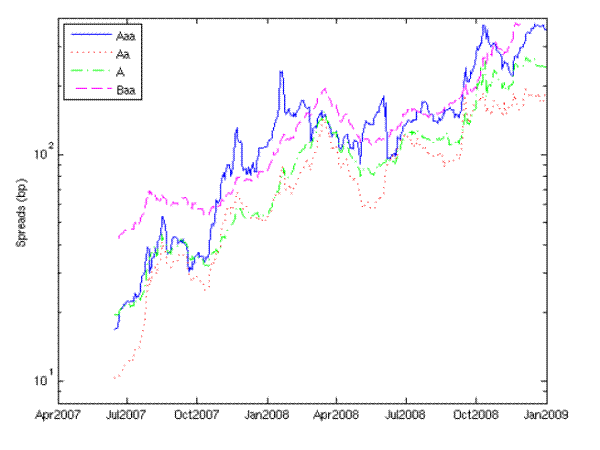
CDS spreads in basis points on log-scale. Crisis period defined as 14 June 2007 to end 2008.

Comparing the spreads of the crisis period to spreads during the previous recession, we see that the period of late 2007 to early 2008 appears roughly similar to that of October 2002. The earlier peak was less severe for the highest grades, more severe for Baa. Only in March 2008 and again in late 2008 do prevailing spreads appear to surpass clearly the earlier peak. Volatility, however, is unambiguously higher in the crisis period than in the earlier recession.

Our analysis begins with experiments similar in spirit to the assessment of the peak spread distribution in the S&P model. We fix an inception date of 20 March 2007 (an index roll date), and calculate the probability of reaching within eight months the spread levels seen on 20 November 2007 (the date of the cash-out of the UBS financial-only CPDO). We also calculate the probability of reaching within one year the spread levels of 20 March 2008, and of reaching within two years the spread levels of 15 December 2008. These spreads are given in Table 5.

We calculate the probabilities, both univariate (for each grade) and joint, by simulating the spread processes as specified by Moody's using an Euler scheme, i.e.,

$\displaystyle \Delta S_{k}(t) = \kappa_k(\theta_k-S_{k}(t)) {\delta} + \min({\bar v}_k,\eta_k+\sigma_kS_k(t)^{\gamma_k}) \sqrt{\delta} Z_k(t)$

(3)

at time intervals $t=\delta, 2\delta, \ldots$ . The innovations

are iid ${\cal N}(0,R)$ , where the correlations in matrix

are taken from Table 4. We fix $\delta$ to 1/1000 of a year.

Results are shown in Panel A of Table 6. For example, starting at 10.9bp, the probability that the Aa spread would break above 62.5bp within eight months is less than $2\times10^{-5}$ (that is, 0.2bp). The corresponding probability for the A spread is 2.4bp. In contrast, we see that Baa broke its eight month target barrier in each of the 20 million simulated paths. This is because the crisis initially had a modest effect on grades Baa and below, so the barrier for this exercise was well below the long-run mean $\theta_{Baa}$ . In none of the simulated paths did we observe the joint event, i.e., that all three spread processes simultaneously exceed barrier levels on a date within the eight month horizon. Results for the 12 month and 24 month horizon tests are even more striking. In no simulated path did the Aa spread or A spread reach its barrier at either horizon. Even for the relatively modest 12 month barrier of 178.5bp for Baa, the exceedance probability was only 10.2bp. In summary, the model did not assign any significant probability to the spread levels attained early in the crisis period, and assigned essentially zero probability to the spread levels reached in the midst of the crisis.²⁴

Table 6: Exceedance probabilities for Moody's CEV spread processes. Panel A: Original specification
Test	Aa	A	Baa
8 month	0.2	2.4	10000
12 month	0	0	10.2
24 month	0	0	0

Table 6: Exceedance probabilities for Moody's CEV spread processes. Panel B: Remove volatility caps
8 month	0.4	2.4	10000	0
12 month	0.03	0	10.2	0
24 month	0.08	0	0	0

Table 6: Exceedance probabilities for Moody's CEV spread processes. Panel C: Remove volatility caps and set $\rho =0.6$
8 month	0.4	2.4	10000	0
12 month	0.04	0	10.2	0
24 month	0.09	0	0	0

Table 6: Exceedance probabilities for Moody's CEV spread processes. Panel D: Remove volatility caps and reduce $\kappa$
8 month	0.4	1.5	7915	0
12 month	0.3	0	72.1	0
24 month	4.8	0	2.1	0

Table 6: Exceedance probabilities for Moody's CEV spread processes. Panel E: Remove volatility caps, set $\rho =0.6$ , and reduce $\kappa$
8 month	0.3	1.5	7914	0
12 month	0.3	0	71.9	0
24 month	4.8	0	2.0	0

Probabilities in basis points. Based on 20 million simulated paths with 1000 timesteps per year. Reduced $\kappa$ values equal to baseline values divided by five.

In a series of articles beginning on May 21, 2008, the Financial Times blog "FT Alphaville" (hereafter simply "FT") reports that internal documents leaked from Moody's show senior staff at the rating agency learned in early 2007 of a coding error in the implementation of the model used to rated CPDOs. FT reports that had the error been corrected, the Aaa rated notes would have been rated up to four notches lower. Even so, FT reports that CPDOs rated after the discovery of the bug still achieved the Aaa rating because Moody's, while correcting the error, made two offsetting modifications to the rating methodology.²⁵ Of the two, the most "notable" (in the phrase of the FT article) was the imposition of volatility caps in the spread processes.

While we cannot identify the model modifications with precision or confidence, it is nonetheless important to assess the potential impact of possible modifications on our test results. Removing the volatility caps has a very modest effect on the estimated exceedance probabilities, as seen in Panel B. This is largely because the volatility caps were not binding for Baa in the eight month and 12 month tests and were not binding for A spreads in the eight month test.²⁶

In order to generate large changes in the Globoxx, there must be large simultaneous changes in the Aa, A and Baa spreads. As will be discussed below, the assumed correlations in Table 4 appear distinctly lower than can be justified empirically. Therefore, assuming that FT allegations are correct, it is reasonable to suppose that the correlation assumptions were the second "fix" to the model. We report in Panel C an experiment in which we remove volatility caps and set cross-grade correlations to $\rho =0.6$ . Marginal distributions are unaffected (relative to the experiment in Panel B) by changes in the correlations. As before, at all three horizons, barriers were never jointly breached in any simulated path.

A plausible alternative is to suppose that the second fix to the model affected the mean-reversion parameters. A lower speed of mean-reversion increases the likelihood of extreme excursions away from long-run mean spreads. In Panel D, we report an experiment in which we remove volatility caps and set each $\kappa_k$ to one-fifth of its baseline value. The experiment reported in Panel E combines all three modifications. There is a modest effect on exceedance probabilities for the Aa and Baa paths. As before, however, barriers were never jointly breached in our simulations.²⁷

Specification tests can be constructed as in our analysis of the S&P model. Using equation (3), we extract the implied vector of innovations $(Z_{Aa,t},Z_{A,t},Z_{Baa,t})$ from the observed spread changes at times $t_1,\ldots,t_n$ . If the model is correctly specified, this vector is distributed standard multivariate normal with correlation matrix given by Table 4. For ease of comparison against our results for S&P, we divide our longer sample into three periods: an "early" period (1 January 2001 to 31 December 2003), a pre-crisis period (1 January 2004 to 13 June 2007), and a crisis period (14 June 2007 to end 2008).

Univariate descriptive statistics for the innovations are shown in Table 7. In all three periods and for all three rating grades, the null hypotheses of mean zero and variance one are each rejected in two sided tests at the 5% level (in nearly all cases, the rejection is at the 0.1% level). The Anscombe and Glynn (1983) test for mesokurtosis is rejected at the 1% level (one sided) for Baa spreads in the crisis period, and at the 0.1% level in all other cases. The Cramér-von-Mises tests reject in all cases at the 0.1% level.

Table 7: Moments of the innovations $^\dagger$
Rating	Mean	Variance	Skewness	Kurtosis	CvM
Early period ( observations)
Early period: Aa	0.09	1.57 ^***	17.72	412.39 ^***	19.46 ^***
Early period: A	0.13 ^***	0.38 ^***	0.71	7.11 ^***	11.79 ^***
Early period: Baa	0.09 ^**	0.46 ^***	2.01	20.55 ^***	11.22 ^***
Pre-crisis period ( observations)
Pre-crisis period: Aa	-0.35 ^***	0.36 ^***	0.47	8.52 ^***	27.58 ^***
Pre-crisis period: A	-0.25 ^***	0.34 ^***	1.40	17.01 ^***	21.15 ^***
Pre-crisis period: Baa	-1.26 ^***	0.49 ^***	0.26	6.36 ^***	141.84 ^***
Crisis period ( observations)
Crisis period: Aa	0.67 ^***	6.56 ^***	0.76	11.69 ^***	9.37 ^***
Crisis period: A	0.79 ^***	13.61 ^***	-4.51	67.04 ^***	11.98 ^***
Crisis period: Baa	0.18 ^***	1.19 ^*	-0.01	3.69 ^*	1.58 ^***

$\dagger$ : One, two and three asterisks indicate significance at 5%, 1% and 0.1% levels, respectively. Tests for mean zero, variance one and mesokurtosis are two-sided. The Cramér-von-Mises test is one-sided. Skewness is not tested.

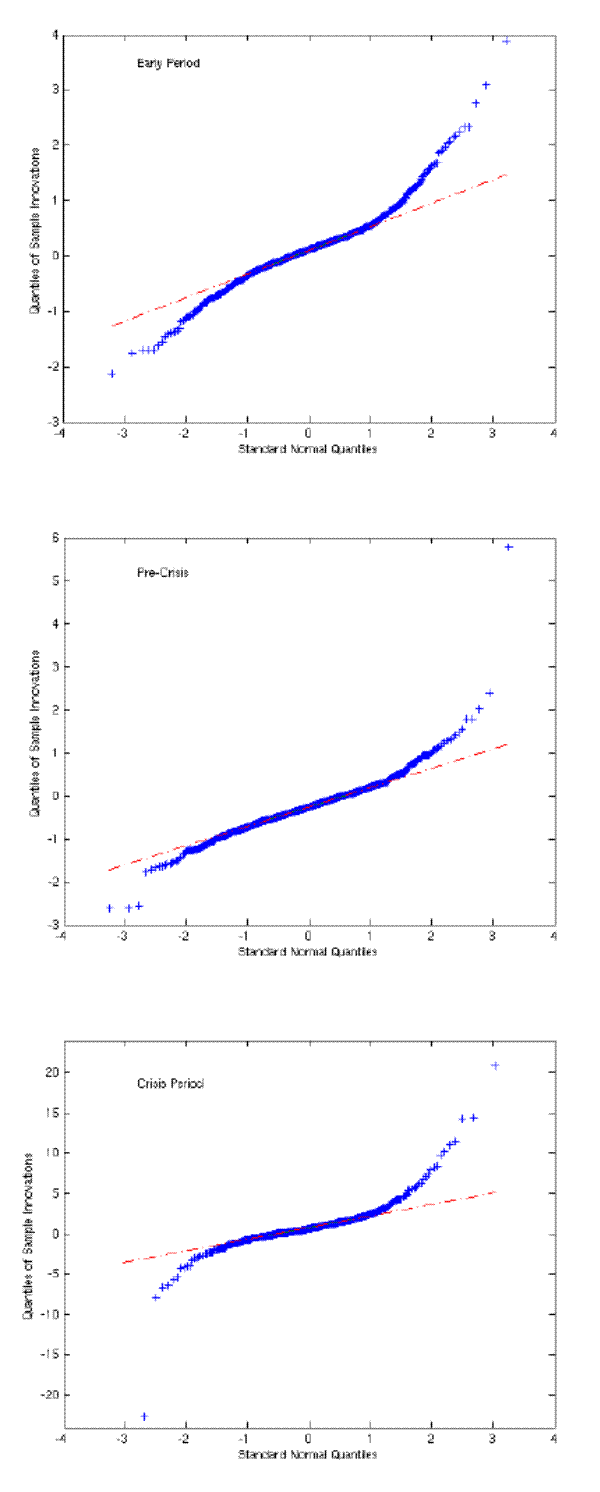
A rejection of the mean and variance tests is not necessarily undesirable from the perspective of the rating agencies, so long as the direction of the misestimation leads to a more conservative rating. In the pre-crisis period, the mean innovation is negative and the variance of the innovations too small, which suggests a conservative parameterization. However, the excess kurtosis undoes the conservative bias in the model-implied mean and variance, because the rating ultimately rests only on the "bad tail" of the distribution. The QQ plot in Figure 4.2 shows how the tails of the distribution of innovations in the A spread process depart from normality in all three periods. QQ plots for the Aa and Baa spreads are qualitatively similar.

Figure 9: QQ plots for innovations in Moody's model, grade A spreads

Bivariate correlations between spread process innovations are presented in Table 8. In the early period, correlations between Aa and A and between Aa and Baa were relatively modest, though still larger than the corresponding correlations in Moody's calibration, as shown in Table 4. The correlation between A and Baa spreads in this period is nearly 40%, and over five times as large as the assumed correlation. Due to the predominance of A and Baa issuers in the Globoxx, this has the largest impact of the three correlation parameters. In the pre-crisis and crisis periods, all estimated correlations are above 50%. Thus, even if the univariate processes had been well-specified and calibrated, the model would have dramatically understated the probability of joint exceedances under the baseline calibration. Joint tests of model fit can be constructed. Under the null hypothesis, the quadratic form $\ensuremath{Q}_t\equiv Z_tR^{-1}Z_t'$ is distributed $\chi^2(3)$ . Cramér-von-Mises tests (not reported) reject the null hypothesis at the 0.1% level in each of the three periods.

Table 8: Empirical correlations
Period	Aa/A	Aa/Baa	A/Baa
Early	0.15	0.13	0.39
Pre-crisis	0.55	0.56	0.66
Crisis	0.54	0.53	0.50

The rejections of Moody's specification cannot be satisfactorily attributed to the parameter "fixes" suggested by the FT report. Lifting the volatility caps reduces the variance of innovations in the crisis period to 1.01, 2.07 and 1.01 for the Aa, A and Baa spreads, respectively. If the speed of mean-reversion is reduced as well, the mean innovation in the crisis period is greatly reduced (though the tests of mean zero still reject at high levels of significance). However, even if we change correlations to $\rho =0.6$ , the Cramér-von-Mises tests for the quadratic form $\ensuremath{Q}_t$ continue to reject. Most importantly, excessive kurtosis is entirely robust to these parameter changes. Thus, even under the most conservative alternative specification (i.e., that of Panel E in Table 7), the model would still have understated the probability of large shocks to the spread processes both before and during the crisis.

Finally, from the perspective of Moody's model, another anomaly of 2007 is the sectoral variation in ratings-based spreads. Sectoral concentration in the Moody's model is addressed via the ratings migration correlation structure of the CDOROM/LSS module. That is, there may be sectoral risk in ratings migration but, conditional on the realized ratings of the obligors, there is no sectoral or idiosyncratic risk in spread movements. For financial obligors in 2007, this stylized characterization of risk proved inadequate. Of the four identifiable obligors included in the failed UBS financial-only CPDO, none suffered any downgrade up to the unwind date, and all remained A-rated or better. However, as demonstrated in Figure 3, the market assessment of these obligors differed sharply from that of the rating agencies.

5 Discussion

For both S&P and Moody's, the rating of CPDOs was driven by models that assigned effectively zero probability (of order $10^{-7}$ or less) to reaching the levels of spreads actually realized in the CDS markets in late 2008. This spike in spreads would, to the best of our knowledge, have triggered default and large losses for every CPDO note that had managed to survive to that point. All the issues in question had been rated AAA at origination in late 2006 or early 2007.

Perhaps more importantly, we find that the agency models failed under more mundane conditions. The models assigned very small probabilities (well under one basis point) to reaching the spread levels seen in the second half of 2007. Credit market conditions at the time were qualitatively comparable to those of the previous downturn (2001-03), and therefore should not have been relegated to the extreme tail of possible outcomes. Even during the quiet pre-crisis period, the models significantly understated kurtosis. Thus, even if the crisis is viewed as an unforeseeable regime shift, the model underpredicted the likelihood of realizing high spreads within the pre-crisis regime.

It seems highly doubtful that there will be any new issuance of CPDO in the foreseeable future. Ratings presumably would be based on less sanguine assumptions, and this would greatly reduce the maximal coupons consistent with an investment grade rating.²⁸ The CPDO is implicitly an arbitrage of rating-based investment mandates. As it merely repackages existing instruments and provides no structuring of liabilities, its raison d'être is to accommodate fixed-income investors who seek higher yield but are constrained by limits on non-investment grade holdings. If CPDO notes cannot offer a substantial yield premium over comparably-rated debt, the costs of the arbitrage (i.e., the management fees) cannot be covered. As the CPDO itself may no longer be viable, the proper aim of this case study is to extract larger lessons for the rating of complex products and for modeling credit risk in general.

We identify three broad lessons from the CPDO experience. First, stochastic volatility appears to be a salient characteristic of credit spreads, at least under the physical measure. Stochastic volatility is the most natural way to capture the excess kurtosis observed within the pre-crisis period, and to allow for the dramatic increase in volatility at the onset of the crisis. We have long had empirical evidence on the ubiquity of stochastic volatility in financial markets (see Bollerslev et al., 1992, for a survey of the early literature), so this is not surprising. Exploration of stochastic volatility in the credit risk literature has gained momentum only recently (Zhang et al., forthcoming; Jacobs and Li, 2008; Fouque et al., 2006; Gouriéroux, 2006).

Second, model implementation should not be neglected as a form of model risk. Complex products demand complex software. Unless model specifications and calibrations and pool compositions are disclosed in full detail, which heretofore has not been the case, it is impossible for third parties to verify independently the results of model simulations. Software issues seem to have affected the rating efforts of both agencies. Our results suggest that the bugs and Moody's ex-post model modifications (as reported by the Financial Times) did not play a fundamental role in the failure of the agency rating of CPDOs. Nonetheless, the episode underscores the possibility that misrating of other complex instruments could arise due to software errors.

Finally, it should be recognized that specification and calibration of a tractable yet robust process for market spreads is far from trivial. It is an adage among quants that all models break down under severe distress in the markets, so a test rooted in the experience of late 2008 might seem unfair. However, the AAA rating is intended to imply annual default probabilities under one basis point, and so is inextricably linked to extreme situations.²⁹ Indeed, in contrast to the pricing purposes for which most quant models are constructed, capturing the dynamics under "once per millenium" distress situations is more important for a rating model than fidelity to market behavior under normal conditions. The manifest difficulty of the task suggests that model risk may pose an insurmountable barrier to reliable rating of complex and market-sensitive instruments.

A. Simulation of historical maximum for a Vasicek process

Recall that the S&P model assumes that the log of the spread follows a Vasicek process. In the stationary case, tail probabilities for the maximum of a Vasicek process can be obtained analytically (Azaïs et al., 2002). When the starting value is fixed, however, we must resort to simulation.

We wish to simulate paths for the historical maximum spread on up to one year. Let denote the spread at time and let

$\displaystyle M_t = \sup_{0\leq s\leq t} S_t.$

Discrete-time paths for $\log(S_t)$ are generated using the algorithm given by Glasserman (2004, §3.3.1). This algorithm is based on the exact transition density for the Vasicek process, so the sampled

have the correct conditional and unconditional distribution at times $t=\delta,2\delta,3\delta,\ldots,1$ , where $\delta$ is the time step (in fractions of a year). We set ${\hat M}^\delta_0=S_0$ and take ${\hat M}^\delta_t$ as $\max\{{\hat M}^\delta_{t-\delta},S_t\}$ .

Our ${\hat M}^\delta_t$ is downward biased as an estimate of the "true" continuous path associated with , because we miss peaks that occur within the time step intervals. The bias is proportional to $\sqrt{\delta}$ , and can be corrected using a scheme in Glasserman (2004, §6.4). When $\delta$ is small, we find that the correction is extremely small both in absolute and relative magnitude. Furthermore, the empirical time-series is itself sampled discretely, say at intervals of $\hat\delta$ . So long as $\delta<{\hat\delta}$ , our simulated peak spread paths are biased upwards relative to the discrete empirical process ${\hat M}_t$ . In the exercise portrayed in Figure 4.1, we set $\delta=1/1000$ , which is indeed smaller than the daily intervals of the observed time-series.

B. Construction of rating-based composite spreads

Moody's documentation does not discuss the empirical construction of the rating-based composite spreads that underpin the Moody's model. Lacking such guidance, we try to construct spreads that are representative of the universe from which a corporate CDPO pool might sample. For each grade, we construct an index of dollar-denominated (USD) spreads and an index of euro-denominated (EUR) spreads, and then take an equal-weighted average of the two indexes.

To construct the USD spread on a given date for, say, Baa, we select all Baa-rated names in the Markit database on that date with a traded five-year CDS referencing senior unsecured debt under modified restructuring (MR). The CDS must be dollar-denominated. Sovereigns are excluded. We weight each firm equally in forming the composite spread.

EUR spreads are constructed similarly, except that CDS under modified-modified restructuring (MM) are included in the sample from January 2004 onwards. MM did not trade often before 2004, but eventually became the most-used standard in Europe later in the sample.

Bibliography

F.J. Anscombe and William J. Glynn.

Distribution of the kurtosis statistic

for normal samples.
Biometrika, 70(1):227-234, April, 1983.

Jean-Marc Azaïs, Jean-Marc Bardet, and Mario Wschebor.

On the tails of the distribution of the maximum of a smooth stationary Gaussian process.
ESAIM: Probability and Statistics, 6:177-184, August , 2002.

Antje Berndt.

Specification analysis of reduced-form credit risk models.April, 2007.

Tim Bollerslev, Ray Y. Chou, and Kenneth F. Kroner.

ARCH modeling in finance. Journal of Econometrics, 52:5-59, 1992.

Pierre Collin-Dufresne and Robert S. Goldstein.

Do credit spreads reflect stationary leverage ratios? Journal of Finance, 56(5):, 1929-1957, October 2001.

Rama Cont and Cathrine Jessen.

Constant Proportion Debt Obligations (CPDOs): Modeling and risk analysis. Financial Engineering Report, 2009-01, Center for Financial Engineering, Columbia University, 2009.

Sandor Csörg ${\H{o\/}}\kern.05em$ and Julian J. Faraway.

The exact and asymptotic distributions of Cramer-von Mises statistics. Journal of the Royal Statistical Society Series B, 58(1):221-234, 1996.

Jón Daníelsson.

Blame the models. Journal of Financial Stability, 4(4):321-328, December, 2008.

Dmitry Davydov and Vadim Linetsky.

Pricing and hedging path-dependent options under the CEV process. Management Science, 47(7):949-965, July , 1992.

Edwin J. Elton, Martin J. Gruber, Deepak Agrawal, and Christopher Mann.

Explaining the rate spread on corporate bonds. Journal of Finance, LVI(1):247-277, February, 2001.

Kenneth Emery, Sharon Ou, and Jennifer Tennant.

Corporate default and recovery rates, 1920-2007. Technical report, Moody's Investor Services, Global Credit Research, February 2008.

Christopher C. Finger.

A comparison of stochastic default rate models. RiskMetrics Journal, pages 49-73, November, 2000.

Jean-Pierre Fouque, Ronnie Sircar, and Knut Sølna.

Stochastic volatility effects on defaultable bonds. Applied Mathematical Finance, 13(3):215-244, September, 2006.

Paul Glasserman.

Monte Carlo Methods in Financial Engineering. Springer-Verlag, New York, 2004.

Jonny Goulden and Yasemin Saltuk.

CPDO gap risk triggers breached: A downward spiral. Europe Credit Research, JP Morgan, 20 February, 2008.

Christian Gouriéroux.

Continuous time Wishart process for stochastic risk. Econometric Reviews, 25(2-3):177-217, , 2006.

Jing-zhi Huang and Hao Zhou.

Specification analysis of structural credit risk models. FEDS, 2008-55, Federal Reserve Board, September 2008.

Lorenzo Isla, Søren Willemann, and Anre Soulier.

Understanding index CPDOs. Structured Credit Strategist, Barclays Capital, 20 April, 2007.

Kris Jacobs and Xiaofei Li.

Modeling the dynamics of credit spreads with stochastic volatility. Management Science, 54(6):, 1176-1188, June 2008.

Norbert Jobst, Yang Xuan, Sergey Zarya, Niclas Sandstrom, and Kai Gilkes.

CPDOs laid bare: Structure, risk and rating sensitivity. Commentary, DBRS, April, 2007.

Matthew Leeming, Jeff Meli, Batur Bicer, Madhur Duggar, Shobhit Gupta, Rob Hagemans, Arne Soulier, and Søren Willemann.

The first CPDO default - Background and implications. European Alpha Anticipator, Barclays Capital, 30 November, 2007.

Alexandre Linden, Charles-Henry Lecointe, and Henning Segger.

Rating credit CPPI and CPDO. CDO/Global Criteria Report, Derivative Fitch, 19 October , 2006.

Alexandre Linden, Matthias Neugebauer, and Stefan Bund.

First generation CPDO: Case study on performance and ratings. Structured Credit/Global Special Report, Derivative Fitch, 18 April, 2007.

Douglas J. Lucas, Laurie S. Goodman, and Frank J. Fabozzi.

A primer on constant Proportion Debt Obligations. Journal of Structured Finance, 13(3):72-80, Fall, 2007.

Beryl Marjolin and Olivier Toutain.

A description of Moodyâ€™s tools for monitoring CPDO transactions. Rating methodology, Moody's Investor Services, 23 July, 2008.

Jun Pan and Kenneth J. Singleton.

Default and recovery implicit in the term structure of sovereign CDS spreads. Journal of Finance, 63(5), October, 2008.

Vladislav M. Peretyatkin and William Perraudin.

Expected loss and probability of default approaches to rating collateralised debt obligations and the scope for "ratings shopping". In Michael K. Ong, editor, Credit Ratings: Methodologies, Rationale and Default Risk. Risk Books, London, 2002.

Yasemin Saltuk, Dirk Muench, and Jonny Goulden.

Understanding CPDOs. European Credit Derivatives Research, JP Morgan, 8 December , 2006.

Elwyn Wong and Cian Chandler.

CDO spotlight: Quantitative modeling approach to rating index CPDO structures. Structured Finance Criteria, Standard & Poor's, 2007.

Benjamin Yibin Zhang, Hao Zhou, and Haibin Zhu.

Explaining credit default swap spreads with the equity volatility and jump risks of individual firms.
Review of Financial Studies, forthcoming.

Footnotes

* The opinions expressed here are our own, and do not reflect the views of the Board of Governors or its staff or of Barclays Capital. This article is academic research; it is not investment advice or an invitation to make an investment. We are grateful to Anne Le Henaff, Mehdi Kheloufi-Trabaud and Michael Mueller-Heumann of Moody's and to William Morokoff and Cristina Polizu of Standard and Poor's for providing model details. We benefitted as well from helpful discussion with Michael Gibson, David Jones, David Lynch, Pat Parkinson, Yasemin Saltuk, and Mark Van Der Weide. Paul Reverdy provided outstanding research assistance. Email: $\langle$ [email protected] $\rangle$ and $\langle$ [email protected] $\rangle$ . Return to Text

1. The Surf deal also won the "Innovation of the Year" at the 2006 International Financing Review (IFR) Awards, and was featured as one of six "Deals of the Year 2006" in Euromoney, February 2007. Return to Text

2. S&P and Moody's use slightly different nomenclature for their ratings. Despite some important differences in methodology (Peretyatkin and Perraudin, 2002), investors typically view the rating scales as parallel and interchangeable. We will use Moody's notation (Aaa, Aa, A, Baa, etc.) when specifically discussing Moody's ratings or spreads tied to Moody's ratings. Otherwise, we will follow the S&P convention (AAA, AA, A, BBB, etc.). Return to Text

3. See Emery et al. (2008, Exhibit 26). Return to Text

4. On 13 June 2008, S&P reported the discovery of one error in a trial version of one of its CPDO-related models, but stated that the correction of the error did not alter the rating of the affected CPDOs. Return to Text

5. More expansive reviews of CPDO mechanics are provided by Saltuk et al. (2006) and Lucas et al. (2007). Return to Text

6. To minimize trading expenses, the SPV trades only if the difference between the target leverage and actual leverage exceeds some minimum threshold. Return to Text

7. A typical test requires that NAV be sufficient to cover a 30% widening in the indices as well as 1.4% default losses (Goulden and Saltuk, 2008). Return to Text

8. Sources at CreditFlux reported roughly 5.2 billion of CPDOs outstanding as of the index roll on 20 March 2007. Hard information on issuance is scant and perhaps unreliable. For example, Jobst et al. (2007) report under USD 2 billion of issuance by March 2007. As of February 2008, the total notional volume of CPDOs rated by Moody's was roughly 2.6 billion. Return to Text

9. There is an important trade-off here: a higher rating threshold reduces default risk, but also reduces the opportunity to profit from mean-reversion. Return to Text

10. Pan and Singleton (2008) estimate positive mean-reversion in default intensities under the physical measure for all three sovereign issuers they examine. Berndt (2007) obtains similar results using a variety of reduced-form specifications and CDS data for a large sample of corporate issuers. Huang and Zhou (2008) provide evidence of mean-reversion in corporate leverage ratios in support of the Collin-Dufresne and Goldstein (2001) structural model. Return to Text

11. Roll-down benefit will also be reduced if the term structure of CDS spreads flattens (or inverts). Isla et al. (2007) show that flattening of the spread curve can have significant implications for performance of the CPDO. Return to Text

12. The contractual coupon affects the probability of a cash-out event, and so affects the present discounted value of the management fees. Return to Text

13. Several hedge funds and investment banks at the time were selling protection in equity tranches of CDOs and buying protection in mezzanine tranches. This was seen as an attractive trade since it earned a positive carry while being hedged against general spread changes. The only caveat of this trade was a significant exposure to default risk. When the auto sector came under distress and the downgrades of Ford and GM were announced, investors feared actual defaults and hence significant losses in the equity tranche. As some hedge funds tried to unwind, the equity tranche spread widened significantly, while the mezzanine tranche spread tightened. The end result was that the hedge did not work and many investors faced significant losses. Large trading losses as a result of increases in sectoral risk was thus not new to structured credit. Return to Text

14. Specifically, we emulate the SURF CPDO floating-rate note series 24, issued by Chess II Ltd and arranged by ABN Amro. Return to Text

15. Specifically, the defaulted notes were the ELM B.V. - Series 103 - Financial Basket TYGER Notes 2017. Return to Text

16. The hypothetical CPDO contains the four names that were mentioned in Moody's rating announcements on the defaulted CPDO. These were FGIC, Radian, PMI, and XL Capital Assurance. Return to Text

17. The hypothetical index CPDO takes a 15x leveraged exposure to a portfolio of iTraxx and CDX 5 year indices. It assumes 10 year maturity, a coupon paid to the investor of 200bp, 60bp of running fees and an initial NAV of 99 net of arrangement fees. Return to Text

18. The default module is built on the "CDO Evaluator" tool that S&P uses for rating corporate CDOs. Return to Text

19. For bespoke pools, the model allows for a jump component in spreads and for multiple factors. Return to Text

20. In the results reported below, we follow calendar time in defining $t_{i+1}-t_i$ . Results are qualitatively robust to treating trading days as equally-spaced and to sampling at weekly (rather than daily) intervals. Return to Text

21. The Cramér-von-Mises $\omega^2$ statistic is 1.57 in the pre-crisis period, 9.90 in the crisis period. Exact percentiles for the statistic under the null are given by Csörg and Faraway (1996, Table 1). Return to Text

22. Recognizing the greater flexibility and internal consistency of a bottom-up approach, S&P adopted a similar CPDO model late in 2008. By that time, of course, issuance had ceased. Return to Text

23. The main CDOROM is a time-to-default copula model that is similar to standard models for CDO pricing. This model does not capture ratings migration short of default, so would be poorly suited to rating LSS and CPDO instruments. The LSS module, in contrast, simulates iterated one-year correlated migrations over the remaining maturity of the instrument. This module is not covered in publicly available documentation on CDOROM. See Finger (2000) for a comparative study of iterated CreditMetrics and Gaussian copula models. Return to Text

24. As discussed in Appendix A, there is discretization bias in using simulation to estimate exceedance probabilities. Sampling at a frequency of $\delta=1/1000$ gives us exceedance probabilities that are upward biased when our empirical sample is based on daily observations. Return to Text

25. As reported by FT, the leaked documents say of the methodology changes that "the impact of our code issue after these improvements is then reduced." According to the FT, a third methodological change was proposed but not implemented as, according to leaked documents, it "did not help the rating." On September 4, 2008, Moody's reported the discovery of one more (unspecified) error in the implementation of their CPDO rating model. The correction of the error, according to Bloomberg News, would likely result in a downgrade of the affected CPDOs by one or two notches. Return to Text

26. The volatility caps ( $\bar v$ ) for the Aa, A and Baa processes bind at spread levels of 45.6bp, 76.4bp and 230.5bp, respectively. Return to Text

27. We have not explored the sensitivity of the Moody's model to the elasticity parameter $\gamma$ . Davydov and Linetsky (1992) show that CEV option pricing models are not terribly sensitive to this parameter for vanilla options, but for barrier options the sensitivity can be quite material. Return to Text

28. Rating agency treatment of CPDOs has already become more conservative, as well as less model-driven (Marjolin and Toutain, 2008). Return to Text

29. Daníelsson (2008) builds upon this observation to argue that model-based risk management cannot be a robust foundation for macroprudential regulation. Return to Text

^♣ This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to Text

Constant Proportion Debt Obligations: A Post-Mortem Analysis of Rating Models*