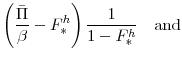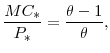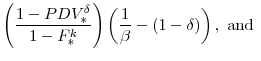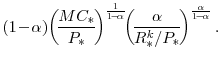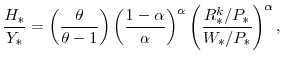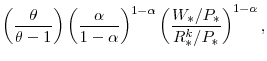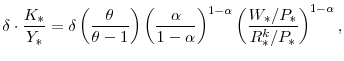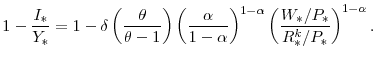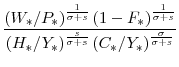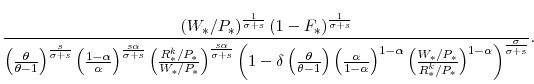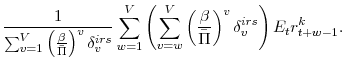General-Equilibrium Effects of
Investment Tax Incentives
Keywords: New-Keynesian model; business equipment investment; nominal depreciation allowances; partial-expensing allowances; bonus-depreciation allowances
Abstract:
JEL Classification: E10; E17; E22; E63; H25.
1 Introduction
The past two U.S. recessions have seen the enactment of sizeable fiscal stimulus packages. In each case, these packages have included significant provisions for temporary partial expensing allowances on business equipment investment.1 Specifically, the 2002 Job Creation and Worker Assistance Act, which went into effect after the 2001 recession, contained a provision for a 30 percent expensing allowance for investment undertaken between September 11, 2001 and September 10, 2004. In the 2003 Jobs and Growth Tax Relief Reconciliation Act, the allowance was raised to 50 percent and extended to December 31, 2004. Similarly, in the most recent recession the 2008 Economic Stimulus Act provided for a 50 percent expensing allowance for investment spending undertaken during the 2008 calendar year. This allowance was extended to the end of 2009 in the 2009 American Recovery and Reinvestment Act.
Despite the increased reliance on temporary expensing allowances as an instrument of countercyclical fiscal policy, to date essentially no attempt has been made to assess the impact of these provisions in a fully specified structural forward-looking general-equilibrium model--particularly the new-Keynesian framework that now serves as the workhorse specification for analyzing macroeconomic stabilization policies. This is somewhat ironic when we consider that one of the earliest calls for a structural approach to policy modelling--Lucas's 1976 paper "Econometric Policy Evaluation: A Critique"--specifically invoked the example of an investment tax incentive to make its point. It is also somewhat surprising given that an analysis of a temporary expensing allowance would seem to provide an excellent candidate for this kind of approach: There is significant scope for the general-equilibrium effects of these policies to differ from what a partial-equilibrium analysis would predict; moreover, the fact that these tax changes are temporary requires us to explicitly consider how agents' behavior today is affected by their expectations of future events.2
In this paper, we incorporate a tax system with nominal depreciation allowances into an otherwise-standard new-Keynesian model, and use the resulting setup to analyze the effect of a temporary partial expensing allowance on investment and real activity. We find that the new-Keynesian features of the model have an important influence on the magnitude of the economy's response to a temporary investment incentive; in particular, with sticky prices and wages and nominal depreciation allowances it is possible for the effects of a temporary expensing allowance on investment to be larger in general equilibrium than they are in partial equilibrium. This result contradicts the conventional view, advanced by Auerbach and Summers (1979) and Judd (1985), that partial-equilibrium calculations overstate the effect that temporary tax incentives will have on investment (a view that has largely been informed by analyses that employ neoclassical models).
We then use our model to explore two practical policy questions associated with partial expensing allowances. First, we examine a claim made by Auerbach and Summers (1979) and analyzed by Christiano (1984) that the use of temporary tax incentives on investment can be destabilizing. The intuition behind this argument is that if agents come to expect that such incentives will be put into place whenever the economy enters a recession, they will postpone their capital expenditures when a negative shock hits the economy (thereby weakening the economy further) until the incentives are actually enacted. We find that this result hinges crucially on how the model is specified--in particular, on the form that capital and/or investment adjustment costs take. Next, we look at the relative effects of two types of tax-based investment incentives: temporary partial expensing allowances, and temporary reductions in the capital tax rate. Consistent with previous research, we find that temporary partial expensing allowances provide more stimulus to investment and real activity than do temporary capital tax cuts (when both policies are set so as to have the same effect on government revenues). We also find that interestingly, the relative stimulus to investment and real activity from temporary partial expensing is greater in a model where both sticky prices and sticky wages are present.
An important incidental contribution of our analysis is the insight that it gives into how the canonical new-Keynesian model responds to an important class of fiscal policies. Previous research has provided us with a relatively broad understanding of the model's strengths and shortcomings as a tool for monetary policy evaluation. However, the model's successes (or failures) in illuminating monetary policy issues need not translate to a corresponding degree of success in the fiscal policy context. In particular, this focus on monetary policy (as well as these models' inherent complexity) has often led researchers to place less emphasis on capturing features of the economy--such as the capital-formation process--that are likely to matter much more when fiscal policy concerns are paramount. We therefore provide a relatively detailed description of how the model responds to the particular fiscal policy changes we consider, and identify those components of the model's structure that most profoundly influence our results.
The balance of the paper is organized as follows. Section 2 derives the model used in the paper, which--outside of its treatment of investment and the tax system--is similar to other new-Keynesian specifications. Section 3 uses the model to study the effects of a partial expensing allowance on capital expenditures and the macroeconomy. Section 4 examines whether the consistent use of a temporary partial expensing allowance as a countercyclical stabilization tool can itself be destabilizing, while section 5 compares the relative "bang-for-the-buck" of partial expensing allowances versus reductions in the capital tax rate. Finally, section 6 concludes.
2 A New-Keynesian Model with Nominal Taxation
Our model economy is characterized by three sets of agents: households, firms, and the government. A continuum of households consume output, supply labor (over which they have monopolistically competitive wage-setting power), and purchase goods that are then transformed into capital and rented to firms. There are two classes of firms: a continuum of intermediate-good producers, each of whom hires capital and all differentiated types of labor to produce a differentiated good (over which they have monopolistically competitive price-setting power), and a single final-good producer who aggregates the intermediate goods to produce output for final demand. Finally, the government consists of a fiscal authority, who levies taxes that are rebated to households as lump-sum transfers, and a monetary authority who sets interest rates according to a Taylor rule.
With the exception of our treatment of taxation and investment, our theoretical setup is quite similar to the sticky-price and sticky-wage monetary business cycle models used by Woodford (2003) and others to analyze monetary policy. We therefore devote most of this section to a detailed examination of those features of the model that are affected by the introduction of a nominal tax system.
2.1 Households
The preferences of household ![]() (where
(where ![]() ) are represented by the utility
function
) are represented by the utility
function
The household's budget constraint--which reflects its role in accumulating physical capital--is given by
where
The variable
All of the other variables in equations (2) and (3) are associated with the model's fiscal elements. The model's fiscal system taxes all forms of nominal personal income (that is, income from financial assets, dividends, and labor) at the rate
![]() , and taxes capital income at the rate
, and taxes capital income at the rate ![]() .3 Hence, households receive an after-tax return
.3 Hence, households receive an after-tax return ![]() on their financial assets
that is given by equation (3).4 In addition, two types of deductions are permitted against capital income: depreciation charges and
expensing allowances. Depreciation allowances reflects the fiscal authority's recognition that part of the payment capital owners receive from renting out their capital stock merely reflects compensation for the depreciation of the stock from its use in production. An expensing allowance,
meanwhile, represents a (partial) rebate of the purchase price of a new capital good. Unlike a pure subsidy or credit, however, future depreciation of the portion of the new investment good that is expensed may not later be deducted from taxable income. Thus, an expensing allowance can be loosely
thought of as a completely "front-loaded" depreciation allowance.
on their financial assets
that is given by equation (3).4 In addition, two types of deductions are permitted against capital income: depreciation charges and
expensing allowances. Depreciation allowances reflects the fiscal authority's recognition that part of the payment capital owners receive from renting out their capital stock merely reflects compensation for the depreciation of the stock from its use in production. An expensing allowance,
meanwhile, represents a (partial) rebate of the purchase price of a new capital good. Unlike a pure subsidy or credit, however, future depreciation of the portion of the new investment good that is expensed may not later be deducted from taxable income. Thus, an expensing allowance can be loosely
thought of as a completely "front-loaded" depreciation allowance.
We make the standard simplifying assumption that households directly own all capital in the economy and rent it out to firms.5 This implies that tax
provisions on investment are directly reflected in the budget constraint (2), as follows. First, an expensing allowance ![]() is applied to household
is applied to household ![]() 's time-
's time-![]() nominal expenditure on new capital goods,
nominal expenditure on new capital goods, ![]() . Second, the dollar value of depreciation at time-
. Second, the dollar value of depreciation at time-![]() from all previous purchases of capital is given as
from all previous purchases of capital is given as
![]() . However, because previously expensed capital may not receive a depreciation allowance, each term
. However, because previously expensed capital may not receive a depreciation allowance, each term
![]() in the sum in equation (2) is multiplied by
in the sum in equation (2) is multiplied by ![]() . In addition, under the U.S. tax code depreciation is computed using historical cost; as a result, the investment price in the depreciation term is written with a
. In addition, under the U.S. tax code depreciation is computed using historical cost; as a result, the investment price in the depreciation term is written with a ![]() subscript.6
subscript.6
In practice, depreciation allowances are based on a legislated schedule of depreciation rates, not the true (economic) depreciation rate ![]() . In our model, using legislated depreciation
rates to compute depreciation allowances would merely involve replacing
. In our model, using legislated depreciation
rates to compute depreciation allowances would merely involve replacing
![]() in equation (2) with
in equation (2) with
![]() , where
, where ![]() denotes the tax-life of
the capital stock--which averages around 5-
denotes the tax-life of
the capital stock--which averages around 5-![]() years (22 quarters) for equipment investment--and
years (22 quarters) for equipment investment--and
![]() denotes the rate of depreciation for tax purposes (specified by the tax code) in the
denotes the rate of depreciation for tax purposes (specified by the tax code) in the ![]() th period of the capital stock's life. However, this extension significantly increases the number of state variables in the model, and complicates our interpretation of the resulting first-order conditions for investment. In addition, it turns out that few of the model's
qualitative results are affected by our equating tax depreciation with economic depreciation.7 We therefore assume that
th period of the capital stock's life. However, this extension significantly increases the number of state variables in the model, and complicates our interpretation of the resulting first-order conditions for investment. In addition, it turns out that few of the model's
qualitative results are affected by our equating tax depreciation with economic depreciation.7 We therefore assume that
![]() throughout.
throughout.
In the absence of any adjustment costs on capital or investment spending, the capital accumulation process is given by
where the parameter
where the parameter
Finally, we bring sticky wages into the model by assuming that households are Calvo wage-setters: In any period, a fraction ![]() of households can reset their wage, while the
remaining fraction
of households can reset their wage, while the
remaining fraction ![]() are constrained to charge their existing wage (which is indexed to the steady-state rate of nominal wage growth).
are constrained to charge their existing wage (which is indexed to the steady-state rate of nominal wage growth).
In the baseline model, then, the household takes as given its initial bond stock ![]() , the expected path of the gross nominal interest rate
, the expected path of the gross nominal interest rate ![]() , the price level
, the price level ![]() , the rental rate
, the rental rate ![]() , profits income, and the legislated personal income tax rates and expensing allowances (
, profits income, and the legislated personal income tax rates and expensing allowances (![]() ,
, ![]() , and
, and ![]() ), and chooses
), and chooses
![]() so as to maximize equation (1) subject to the budget constraint
(equation 2), the demand schedule that they face for their labor (discussed below), and the capital evolution process (either equation 5 or equation 6).
so as to maximize equation (1) subject to the budget constraint
(equation 2), the demand schedule that they face for their labor (discussed below), and the capital evolution process (either equation 5 or equation 6).
2.2 Intermediate- and Final-Good Producers
The monopolistically competitive intermediate-good producer ![]() chooses each type of differentiated labor
chooses each type of differentiated labor ![]() and capital
and capital ![]() to minimize its cost of producing output
to minimize its cost of producing output ![]() , taking as given the wage rates set by each household
, taking as given the wage rates set by each household
![]() , the rental rate
, the rental rate ![]() , and the production
function. Specifically, firm
, and the production
function. Specifically, firm ![]() solves:
solves:
where
We also assume a representative final-good producing firm who takes as given the prices
![]() that are set by each intermediate-good producer, and chooses intermediate inputs
that are set by each intermediate-good producer, and chooses intermediate inputs
![]() to minimize its cost of producing aggregate output
to minimize its cost of producing aggregate output ![]() subject to a Dixit-Stiglitz production function:
subject to a Dixit-Stiglitz production function:
2.3 The Monetary Authority
The central bank sets the nominal interest rate according to a Taylor-style feedback rule. Specifically, the target nominal interest rate ![]() is assumed to respond to deviations of
output and the (gross) inflation rate from their respective target levels
is assumed to respond to deviations of
output and the (gross) inflation rate from their respective target levels ![]() and
and ![]() :
:
where
2.4 The Fiscal Authority
To keep the number of fiscal distortions in the model to a minimum, we assume a role for government that is as simple as possible; namely, one in which the fiscal authority merely raises revenues via taxation and then rebates these revenues as lump-sum transfers ![]() to households. Hence, the government faces the following budget constraint:
to households. Hence, the government faces the following budget constraint:
The government's depreciation allowance liability to household
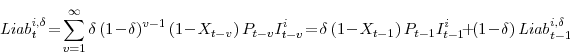
under our assumption that depreciation allowances equal true economic depreciation.8 Note that if the net stock of bonds in the economy is zero (as it will be when all bonds are domestic and privately issued), then the first term in the second line of equation (11) drops out.
An additional variable that we define here (since it will prove useful when we attempt to score different tax policies) is the discounted present value of revenues. This is given as:
where the dependence on the marginal utility of consumption,
Finally, we note in passing that changes in tax policy in our framework can be equated with shocks to suitably specified exogenous processes for the fiscal variables. For example, the introduction of a permanent partial expensing allowance is captured by a one-time
shock to ![]() , where the expensing allowance is assumed to follow an
, where the expensing allowance is assumed to follow an ![]() process
with a unit autoregressive root:
process
with a unit autoregressive root:
Shocks to other fiscal variables (such as
2.5 The Model's First-Order Conditions
We only consider the first-order conditions that are directly affected by the presence of nominal taxation.
The household's utility-maximization problem yields an intertemporal Euler equation along with a supply schedule for labor:
The solution to the household's maximization problem also yields a capital supply condition; however, when adjustment costs are present, this expression is relatively complicated. We therefore instead give here the capital supply equation that obtains when there are no adjustment costs for capital or investment, namely:
where the variable
where we again use a stochastic discount factor to value future income streams.9
In addition, factor demand schedules (in which labor and capital demand is expressed as a function of output and factor-price ratios) are obtained from the intermediate-good producers' problem, while the final-good producer's problem yields demand functions for intermediate goods and an expression for the aggregate price level. Finally, the economy faces the usual market-clearing condition.
2.6 The Log-Linearized Model Equations
We obtain a linear model by log-linearizing the model equations about a deterministic steady state. Again, we mainly focus on describing and interpreting those equations that are directly affected by the presence of a nominal tax system.
The household's Euler equation (15) becomes
| (19) |
where an asterisk in lieu of a time subscript denotes a variable's steady-state value. Finally, the household's labor supply condition log-linearizes to
where
When capital adjustment costs are present, the capital supply condition yields the following log-linear expression for the user cost:
with
When investment adjustment costs are present, the capital supply condition yields the following log-linear expression for the user cost:
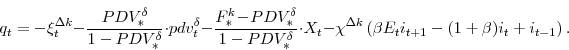
As can be seen from these equations, there are two ways in which the presence of a nominal tax system affects aggregate demand determination. First, consumption growth and the user cost are functions of the real posttax interest rate, which will not move one-for-one with changes in the nominal interest rate when income taxes are nonzero. Second, because depreciation allowances are valued at historic cost, they are worth less in current-dollar terms when inflation is positive--put differently, the nominal nature of depreciation allowances implies that nominal interest rates determine their discounted present value. Hence, an increase in nominal interest rates raises the user cost in two ways: first by raising the posttax real interest rate, and second by lowering the expected present value of depreciation allowances.10
The other components of the log-linearized model are quite standard. Capital and labor demand are given by
The log-linearized monetary policy rule, which combines equations (9) and (10), is
2.7 Calibration
The structural parameter values that we use to calibrate the baseline model are summarized in the table below. The values for ![]() ,
, ![]() , and
, and ![]() are set to match Kimball's (1995) preferred calibration;
are set to match Kimball's (1995) preferred calibration; ![]() is taken from Clarida, Galí, and Gertler (2000); and
is taken from Clarida, Galí, and Gertler (2000); and ![]() is computed from the depreciation rates and nominal
capital stocks in Katz and Herman (1997). None of these values is particularly controversial.11
is computed from the depreciation rates and nominal
capital stocks in Katz and Herman (1997). None of these values is particularly controversial.11
For ![]() , we choose a value that gives our capital adjustment cost function the same curvature properties as Kimball's specification; more concretely, the adjustment costs under this
calibration are such that, following a permanent shock (and in partial equilibrium), the capital stock adjusts 30 percent of the way to its desired level after one year.12 For investment adjustment costs, our assumed value of
, we choose a value that gives our capital adjustment cost function the same curvature properties as Kimball's specification; more concretely, the adjustment costs under this
calibration are such that, following a permanent shock (and in partial equilibrium), the capital stock adjusts 30 percent of the way to its desired level after one year.12 For investment adjustment costs, our assumed value of ![]() is set to yield a capital stock response in the
flexible-price model that is broadly similar to the response that obtains under capital adjustment costs. Finally, our assumed values for
is set to yield a capital stock response in the
flexible-price model that is broadly similar to the response that obtains under capital adjustment costs. Finally, our assumed values for ![]() and
and ![]() imply that prices and wages are fixed for one year on average, which is again standard; conditional on the value for
imply that prices and wages are fixed for one year on average, which is again standard; conditional on the value for ![]() , our assumed (inverse) labor supply elasticity
, our assumed (inverse) labor supply elasticity ![]() is then chosen so as to yield an elasticity of inflation with respect to output that is similar to what
Clarida, et al. employ in their work.13
is then chosen so as to yield an elasticity of inflation with respect to output that is similar to what
Clarida, et al. employ in their work.13
For the policy-related parameters, the values for ![]() and
and ![]() that we assume are intended to capture the average marginal tax rates on noncapital and capital income that are implied by the current U.S. tax code; a detailed description of how these values were chosen (together with a discussion of how sensitive our results are to different assumptions about
that we assume are intended to capture the average marginal tax rates on noncapital and capital income that are implied by the current U.S. tax code; a detailed description of how these values were chosen (together with a discussion of how sensitive our results are to different assumptions about
![]() and
and ![]() ) is provided in the Appendix. The
) is provided in the Appendix. The ![]() value we specify implies an inflation target of zero--which is the assumed steady-state value of inflation in the model--while the parameter values we set in our Taylor rule are
value we specify implies an inflation target of zero--which is the assumed steady-state value of inflation in the model--while the parameter values we set in our Taylor rule are
![]() ,
,
![]() , and
, and ![]() , which are the post-1979 values estimated by
Orphanides (2001) using real-time data.
, which are the post-1979 values estimated by
Orphanides (2001) using real-time data.
| Parameter | Description | Value |
|---|---|---|
| Elasticity of output with respect to capital | 0.30 | |
| Intertemporal elasticity of substitution | 0.20 | |
| Elasticity of substitution of labor | 11 | |
| Elasticity of substitution of intermediates | 11 | |
| Depreciation rate | 0.034 | |
| Households' discount factor | 0.99 | |
| Curvature param. in capital adj. cost function | 170 | |
| Curvature param. in investment adj. cost function | 4.2 | |
| Probability household can reset wage | 0.25 | |
| Probability firm can reset price | 0.25 | |
| Inverse labor supply elasticity | 2.75 | |
| Steady-state tax rate on noncapital income | 0.30 | |
| Steady-state tax rate on capital income | 0.48 | |
| Inflation target | 1.00 |
3 Effects of Partial Expensing Allowances
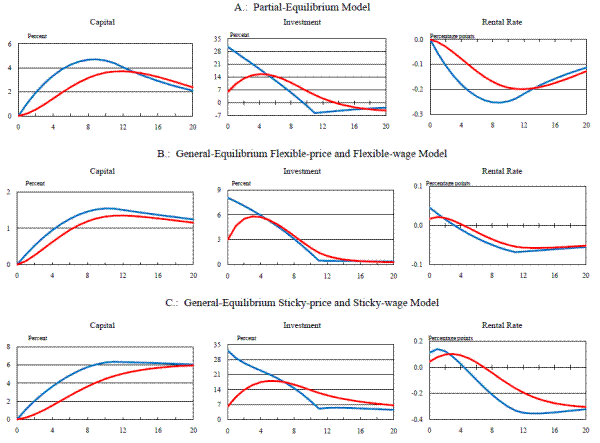
In this section, we use the baseline model to examine the effects of permanent and temporary changes in the expensing allowance on capital investment. To provide a useful benchmark, we first present results from a partial-equilibrium model that uses the same neoclassical investment specification that underpins the general-equilibrium model.14 Hence, any difference in results that obtains under the general-equilibrium framework arises because of the effects that changes in investment demand have on output, real interest rates, and consumption demand. In addition, when we compare the results from our general-equilibrium setup to those that obtain in a partial-equilibrium analysis, we first use a version of the baseline model in which prices and wages are assumed to be fully flexible (since aggregate nominal rigidities are irrelevant when output is exogenous). Later, this will permit us to separately identify the role played by sticky prices and wages in our framework.
3.1 Effect of a Permanent Partial Expensing Allowance
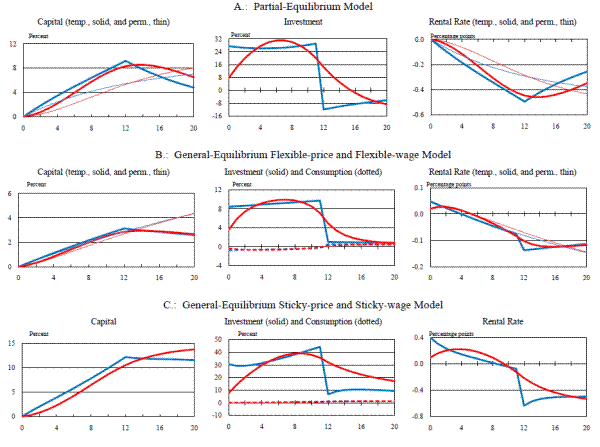
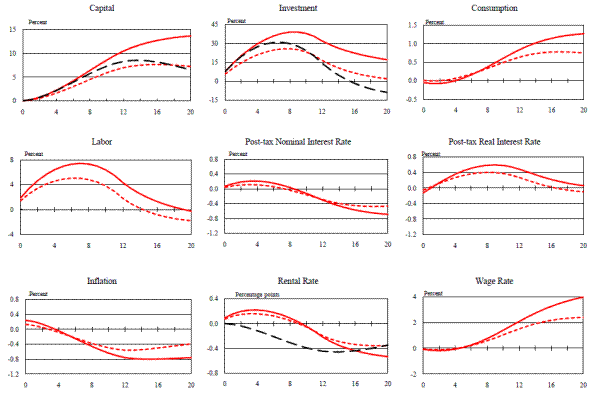
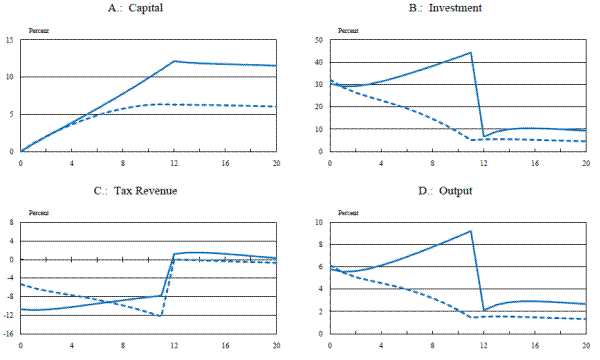
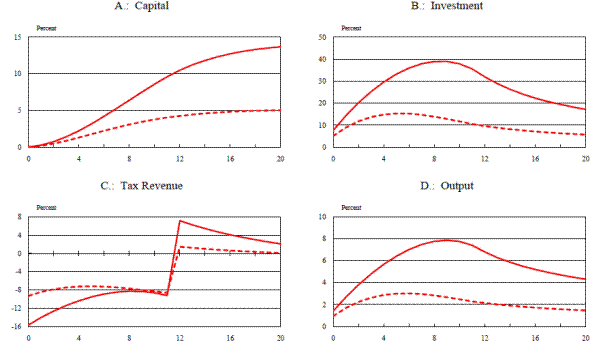
We first consider the effects of a permanent 50 percent expensing allowance.15 Figure 1 shows the predicted responses of the capital stock, gross investment, and the real rental rate from the partial-equilibrium model, while Figure 2 gives the corresponding responses from the flexible-price and flexible-wage version of the baseline model. (As consumption is an endogenous variable in the general-equilibrium model, we also plot its response in Figure 2.)16 Results from the models with capital adjustment costs are plotted in blue, while results from models that assume investment adjustment costs are plotted in red.
In both the partial- and general-equilibrium frameworks, the introduction of the permanent expensing allowance ultimately lowers the rental rate of capital by about 0.45 percentage point. This decline, however, does not take place immediately. In the partial-equilibrium model (Figure 1) the decline is restrained by the fact that any reduction in the rental rate is met with an increase in demand for capital, which, because of adjustment costs, induces an immediate jump in the price of installed capital relative to uninstalled capital. Since this relative price increase is anticipated to decline this creates an expected capital loss, which raises the rental rate of capital and offsets part of the reduction that results from the expensing allowance. As capital is installed, this offsetting effect becomes smaller and ultimately--when the capital stock is at its new long-run level and the prices of installed and uninstalled capital are equated (so that no further capital losses are anticipated)--the rental rate reaches its new long-run level. Naturally, the gradual decline in the rental rate also slows down the rate at which the capital stock and the level of investment increase. Finally (and unsurprisingly) the initial increase in the capital stock and investment is more delayed under investment adjustment costs.
In the general-equilibrium model (Figure 2) the decline in the rental rate of capital is even more gradual than in the partial-equilibrium model; this is because an endogenous increase in real interest rates now occurs (in addition to adjustment costs being present). In the general-equilibrium model, additional capital spending can only occur if more output is produced and/or a greater share of output is devoted to investment. Here, this process is mediated by higher real interest rates (not shown), which induce households both to give up some of their consumption and to supply more labor (thus raising output).17 Due to the more gradual decline in the rental rate in the general-equilibrium model, the capital stock and the level of investment increase to their new long-run levels more slowly than in the partial-equilibrium model. Indeed, while investment spending overshoots its long-run level in the partial-equilibrium model, in the general-equilibrium model the level of investment rises monotonically.
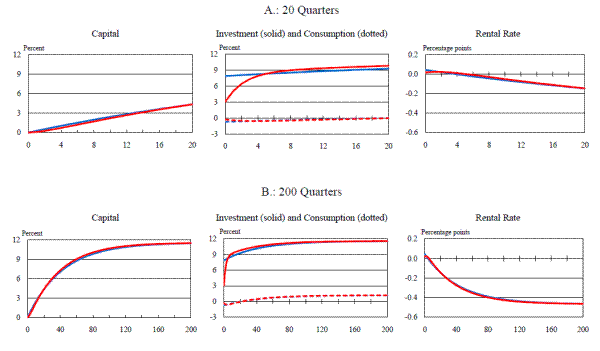
It is interesting to note just how importantly the endogenous reactions of the other variables in the general-equilibrium model--in particular, the real interest rate--contribute to the sluggish response of the capital stock. This can be most clearly seen by comparing the paths of the capital-output ratio in the baseline general-equilibrium models to its path in a third version of the model in which adjustment costs are completely absent (Figure 3). As is evident from this figure, capital or investment adjustment costs have a relatively small incremental effect on the path of the capital-output ratio that obtains in the general-equilibrium model. This point can also be illustrated by noting that the capital-output ratio eventually rises about eight percent above its baseline level as a result of the expensing allowance. In the partial-equilibrium model, therefore (in which output remains constant), the capital stock has moved roughly three-fourths of the way to its long-run value after twenty quarters. In the general-equilibrium setup, however, the capital-output ratio has moved about a third of the way to its long-run level after the same period of time has elapsed.18
3.2 Effect of a Temporary Partial Expensing Allowance
We now examine the effect of a partial expensing allowance that is put into place for a limited period of time. This adds an important forward-looking element to the model, since firms' current behavior will reflect the anticipated future change in tax policy. As a result, the model's dynamic responses are richer, and further highlight how the general-equilibrium nature of the analysis influences the results.
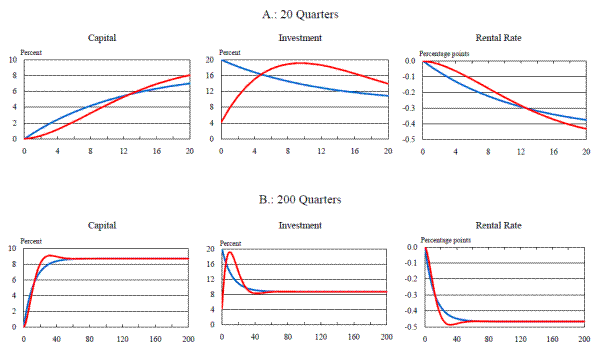
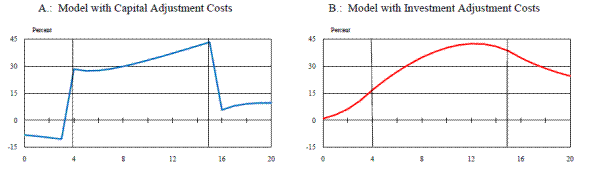
The specific experiment we consider is the introduction of a 50 percent expensing allowance that lasts for three years; all agents are assumed to fully understand and believe the temporary nature of the allowance. Panel A of Figure 4 plots the predicted responses of capital, investment, and the rental rate from the partial-equilibrium model (with capital adjustment costs--the blue lines--or investment adjustment costs--the red lines) following the introduction of the temporary expensing allowance. As before, the new allowance reduces the rental rate on capital (albeit gradually due to the presence of either capital or investment adjustment costs) and this reduction in the rental rate increases the capital stock and the level of investment spending. Interestingly, however, in this case the temporary nature of the allowance induces firms to "pull forward" their investment spending: As can be seen from the figure, the path of the capital stock following a permanent increase in the expensing allowance--plotted here as a thin line--lies below the response from the temporary-allowance case for the first four years.19 When the expensing allowance expires, the capital stock lies above its steady-state level. Disinvestment is costly, however (because there are adjustment costs), and so takes place over an extended period. When capital adjustment costs are assumed, this results in a persistent investment "pothole," as the level of investment falls below its steady-state level in order to return the capital stock to its steady-state level. When investment adjustment costs are assumed, the response of investment is smoother and shows a more pronounced hump (with the peak of the hump occurring about a year before the expensing allowance expires). In addition, the decline in investment that occurs immediately after the expiration of the expensing allowance is not as sharp and is spread over a longer period of time.
The responses of these variables (and consumption) in the flexible-price general-equilibrium model are plotted in panel B of Figure 4. As is apparent from a comparison with the partial-equilibrium case, the responses of capital and investment are smaller in the general-equilibrium model (note the differences in scales across the two panels); in addition, there is no longer an investment pothole in the model with capital adjustment costs, inasmuch as investment remains above its steady-state level even after the expensing allowance comes off (though we still obtain a sharp drop in the level of investment--and thus a reduction in its growth rate--in the period that the allowance expires). Once again, the source of this more muted response of investment is the endogenous response of real interest rates and consumption to changes in investment demand.20 In general equilibrium, higher aggregate demand pushes up real interest rates (this is needed to call forth more saving) and thus attenuates the increase in investment and the capital stock. Then, when the expensing allowance comes off, the resulting decline in aggregate demand is partly buffered by a reduction in real rates (which is reflected in the discrete drop in the rental rate that period). Both of these factors imply that in the general-equilibrium model the resulting overcapacity (and desire to disinvest) is not as severe.
It is worth noting that very little investment is pulled forward under a temporary allowance in the general-equilibrium case (this can be seen from a comparison of the leftmost plots in panels A and B of Figure 4). Put differently, the usual conclusion that a temporary investment tax incentive will have a greater (short-term) effect on investment than a permanent tax change--an insight that is readily drawn from the partial-equilibrium framework--need not be correct once general-equilibrium considerations are taken into account.21
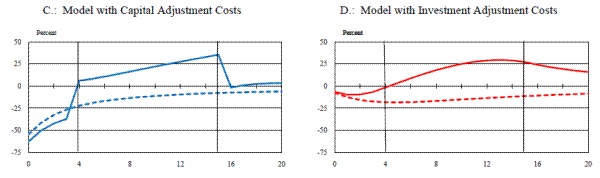
3.3 Expensing Allowances When Prices and Wages are Sticky
Up to this point, we have examined versions of the general-equilibrium model in which prices and wages were assumed to be fully flexible (this was done to permit a direct comparison with the partial-equilibrium setup). We now assume that prices and wages are sticky by incorporating the log-linearized aggregate supply relation (equation 26) and labor supply condition (equation 16) into the model.
Panel C of Figure 4 plots the responses of capital, consumption and investment, and the real rental rate from this model following the introduction of a three-year, 50 percent expensing allowance. Comparison with panel B of the figure reveals that adding nominal rigidities to the general-equilibrium model yields an investment response that is much greater than in the flexible-price case (again, note the difference in scales across the two sets of charts). The intuition for this finding is relatively straightforward. Under sticky prices, firms commit to meeting all demand for their output at their fixed, posted price. Since output is partly demand-determined, there is less need for consumption to be crowded out through an increase in real interest rates, since a positive aggregate demand shock is partly met by increased supply (this is further assisted by the presence of sticky wages, which yields a larger increase in labor input). In addition, sticky prices make firms more concerned with their capacity (now and in the future), since an increase in demand will cause a rise in their real marginal costs--and, hence, a decline in their real profits--unless they increase their capital stock. The subsequent reduction in the capital stock when the expensing allowance expires is quite sluggish in the sticky-price/sticky-wage model, which is an issue that will be returned to later. Finally, the movements in the rental rate for capital reflect the interaction of the swings in capital demand with the currently available capital supply.22
The result that the response of investment in the general-equilibrium model with sticky prices and wages is actually larger than the response that obtains in the partial-equilibrium model seems somewhat surprising at first. Moreover, it stands in marked contrast to the existing literature on tax-based investment incentives (most notably Auerbach and Summers, 1979, and Judd, 1985), which invariably finds that introducing general-equilibrium elements--specifically, the endogenous response of real interest rates that mediates the clearing of the goods market--significantly attenuates the response of investment and output relative to the partial-equilibrium case. If in rough terms we think of the results from the partial-equilibrium model as being similar to what would obtain under a horizontal aggregate supply curve and the flexible-price general-equilibrium model's results as what we might expect from a model with a vertical aggregate supply schedule, it is not unreasonable to expect that adding sticky prices and/or wages would result in a larger general-equilibrium response than a flexible-price model. But this does not explain why the model with nominal rigidities yields a larger response than the partial-equilibrium model.
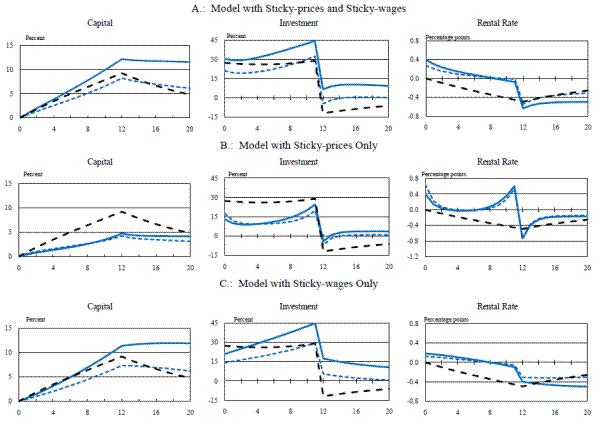
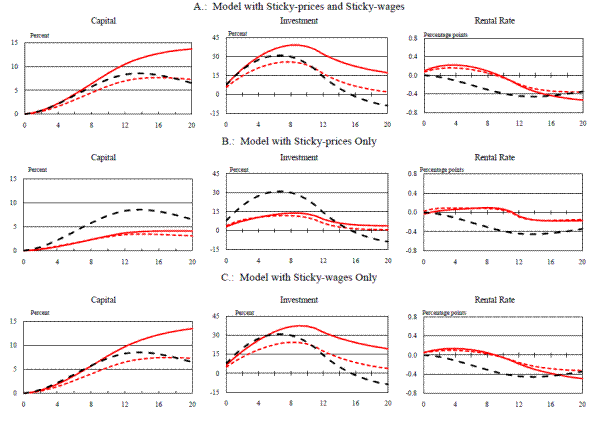
To explore this finding further, we consider an additional set of results (summarized in Figures 5 and 6) that compare the responses of the capital stock, investment, and the rental rate under various types of nominal rigidities and under alternative assumptions regarding the type of nominal distortions that are present in the tax system. (The results in Figure 5 are from the model with capital adjustment costs; for completeness, Figure 6 gives results for the model with investment adjustment costs.) We present results for a model with sticky prices and sticky wages (the baseline case--panel A), a model with sticky prices only (panel B), and a model with sticky wages only (panel C); these responses (the solid blue or red lines) are plotted against the corresponding response from the partial-equilibrium model (the dashed black line). In each case, we compute the model's responses under the "unindexed" tax system that we have been assuming up to this point (the term "unindexed" is used to highlight the fact that depreciation allowances in this case are computed using the historical cost of investment). We also examine an alternative, "indexed" system in which depreciation allowances are calculated using current costs (these responses are given by the dotted blue or red lines); although this system does not reflect the actual way that allowances are computed in the U.S. tax code, it is useful in that it permits us to isolate the implications of nominal taxation.
From these results, it is apparent that the assumption of sticky wages and the presence of an unindexed nominal tax system are together responsible for pushing the investment responses of the fully specified general-equilibrium model above the partial-equilibrium model's responses. If we begin
by comparing panels B and C, which obtain from a model with sticky prices only (panel B) or sticky wages only (panel C), we see that the investment response is larger for the sticky-wage model. This stems from the well-documented fact that the aggregate supply schedule in a
sticky-wage model with a given contract length will be much flatter than the AS curve from a model with sticky prices (and the same contract length).23
This can also be seen by considering the new-Keynesian Phillips curves that obtain under sticky wages and sticky prices (equations 21 and 26); while the two AS relations take very similar forms, there is an additional term in the wage Phillips
curve (the
![]() term) that reduces the effect of the driving process on wage inflation. Indeed, if we were to force this term to equal one, the responses from the sticky-wage and
sticky-wage/sticky-price models would be very close in magnitude to the model with sticky prices only.24
term) that reduces the effect of the driving process on wage inflation. Indeed, if we were to force this term to equal one, the responses from the sticky-wage and
sticky-wage/sticky-price models would be very close in magnitude to the model with sticky prices only.24
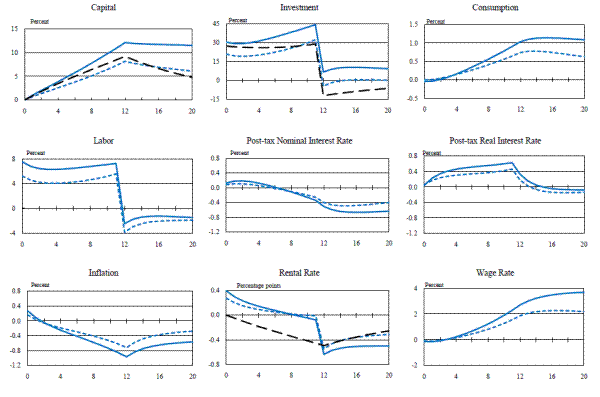
We next assess the effect that unindexed depreciation allowances ha on the model's responses. (Again, in Figures 5 and 6 the solid blue or red lines give the results for an unindexed tax system, while the dotted blue or red lines give the results for an indexed tax code.) Comparing the two sets of responses reveals that the presence of an unindexed tax system makes an important contribution to pushing the investment responses from the sticky-wage and sticky-wage/sticky-price models above the responses from the partial-equilibrium model. To determine what feature of the unindexed system is responsible for amplifying the response of spending to a temporary partial expensing allowance, we plot the responses of a number of additional variables from the sticky-wage/sticky-price model in Figure 7 (for the version of the model with capital adjustment costs) and Figure 8 (for the version with investment adjustment costs).
Consider in Figures 7 and 8 the response of investment after the expensing allowance is removed. In the models with an indexed tax system, investment is only slightly above its steady-state level once the allowance has come off; with an unindexed system, investment over this period is considerably higher. In the indexed model, investment is boosted after the allowance has come off by a slightly lower real interest rate. This in turn arises because of monetary policy: Inflation is below its steady-state level, which allows the central bank to ease (despite output's being above its steady state as well). In an unindexed model, however, investment is also a function of nominal interest rates (recall that the present value of depreciation allowances--which enters the user cost expression--depends on nominal interest rates, since depreciation allowances are computed using historical investment prices under an unindexed tax code). Hence, the lower inflation rate further stimulates investment by resulting in lower nominal interest rates. In addition, the investment responses are reinforced in the following way: If the capital stock remains elevated above its steady-state level, then the rental rate of capital will be held down, thereby driving inflation lower. This then lowers nominal interest rates, which further stimulates investment and props up the capital stock.
What about the periods before the expensing allowance comes off? Here, the investment response is boosted because the level of the capital stock is higher than it otherwise would be once the allowances expire. The presence of adjustment costs damps the response of the capital stock and investment to an expensing allowance; in particular, because investors will want to reduce their holdings of capital after the allowances expire--and because making changes to the capital stock or investment plan is costly--investment does not increase by as much as it otherwise would. But if investors know that the capital stock will remain higher after the allowances come off (as it will under a nominal tax system), then they are willing to add to the capital stock more aggressively when the allowances are in place.
The results in this subsection leave us with two conclusions. First, the nominal nature of the tax system (specifically, the use of historical costs in calculating depreciation charges against current income) has an important influence on the response of investment to a temporary partial expensing allowance. Indeed, in a fully specified model with nominal depreciation allowances, it is even possible for the responses in a general-equilibrium framework to exceed those found in a partial-equilibrium setup. Second, and more tentatively, it is not necessarily the case that expansionary fiscal policy will be inflationary: Under the calibration we assume, inflation can be pushed below its steady-state level for a prolonged period despite levels of investment, consumption, and output that exceed their steady-state values.25
3.4 Robustness Checks
A number of features of our model can conceivably affect the predicted response of investment to a change in tax policy. For example, the responses of saving and hours worked to changes in the real interest rate will obviously influence the response of investment spending to a tax shock; similarly, the independent role of the nominal interest rate on capital demand (which arises as a result of the nominal character of depreciation allowances) yields an additional way in which our characterization of the model economy's aggregate supply relation affects the model's predicted responses. Finally, a less-obvious aspect of the model's specification that turns out to have an interesting effect on our results is our implicit assumption that labor and capital can be used to produce either consumption or investment goods (which in turn reflects the single-good nature of final output in our baseline theoretical framework). We therefore briefly consider how our results are affected by employing alternative specifications for household consumption and aggregate supply, and also extend the model to incorporate sector-specific factor inputs.26
Modelling habit persistence in consumption: We added "external" habit persistence to our model by making household ![]() 's utility depend on
's utility depend on
![]() (where
(where ![]() denotes aggregate consumption). We set
denotes aggregate consumption). We set
![]() equal to 0.8, which implies a relatively large degree of habit persistence. This extension has almost no effect on the response of investment relative to the baseline model: While habit
persistence results in an aggregate log-linearized labor supply curve that now contains an additional term in
equal to 0.8, which implies a relatively large degree of habit persistence. This extension has almost no effect on the response of investment relative to the baseline model: While habit
persistence results in an aggregate log-linearized labor supply curve that now contains an additional term in ![]() , the smoothness of consumption in the baseline model is sufficiently
high that
, the smoothness of consumption in the baseline model is sufficiently
high that ![]() makes a negligible contribution.
makes a negligible contribution.
More inertial price and wage setting: We assume "hybrid" new-Keynesian price and wage equations (due to Christiano, Eichenbaum, and Evans, 2005) in which inflation is partially indexed to its own lag. In broad terms, the predicted response for investment is quite similar to the baseline specification: Although the hybrid inflation equation does in fact yield a smaller initial response of inflation, after a few quarters the path of the inflation rate is similar to what is obtained in the baseline model (in addition, because we assume that the monetary authority tries to smooth its policy rate, the path of nominal interest rates is also quite similar across the two models). However, because the hybrid Phillips curve imparts more inertia to price setting, the path of inflation (and nominal interest rates) remains higher over a longer period in the alternative model. As a result, the response of investment is attenuated slightly relative to the baseline case.
Putty-clay capital adjustment: Assume a specification in which it is costly to adjust the capital-labor ratio as well as the capital stock (this can be thought of as a convex approximation to a putty-clay investment technology).27 This additional source of inflexibility implies that there is now less benefit from adjusting the capital stock independently; as a result, the investment response in this version of the model is more muted than what obtains for the baseline model. That said, we do see a much larger swing in the rental rate for capital: Previously, firms facing changes in demand for their output were able to change their production by altering the amount of labor they hired; here this avenue is partly closed off, as it is now also costly to adjust labor inputs. The result is a more pronounced swing in demand for installed capital, which shows up as a relatively larger change in the rental rate.28
Multisector production with limited factor mobility: Our baseline model assumes a one-sector production structure in which labor and (existing) capital can be instantaneously and costlessly allocated to the production of either consumption or capital goods. As a result, a large portion of any increase in investment demand in our baseline model is accommodated by an increase in output, as households supply more hours to the economy's single production sector. A more realistic production structure would involve separate sectors for the production of consumption and investment goods and would take into account the fact that capital and labor inputs tend to be sector specific (particularly over short horizons). In such an economy, it will be more difficult to rapidly increase production in a given sector; in particular, we would expect the rise in investment demand that results from the introduction of a temporary expensing allowance to be only partially met. As a result, we will tend to see a slower response of aggregate investment to a change in tax policy.
We model sector-specific labor inputs by assuming that households incur a (convex) adjustment cost whenever they change the number of hours that they supply to the consumption or investment sector. We then allow for sector-specific capital by assuming distinct accumulation processes for the capital stocks employed in the consumption- and investment-goods sectors. We find that the presence of sector-specific factor supplies yields an investment response to a temporary expensing allowance that is roughly three-fourths as large as the baseline model, but does not change the qualitative features of the response.
4 Is Countercyclical Fiscal Policy Destabilizing?
We now turn to two policy-related questions that can be addressed in our model. The first concerns whether repeated use of temporary partial expensing allowances to smooth cyclical fluctuations in the economy can actually be destabilizing. As Auerbach and Summers (1979) and Christiano (1984) have argued, this comes about because agents begin to expect that a partial expensing allowance will be enacted when the economy is hit by a sufficiently large negative shock. They therefore postpone capital spending in anticipation of the policy, thereby further weakening the economy in the runup to the enactment of the expensing allowance. This has arguably become a more realistic concern in the current policy environment, since the last two recessions have seen the passage of significant fiscal stimulus packages that have each included provisions for temporary partial expensing of investment.
The presence of fiscal policy lags suggests that agents would expect any allowance to come into effect in some future period following an adverse shock to the economy. We therefore first consider the effect of an anticipated change in policy; to be concrete, we will look at a temporary partial expensing allowance that is expected to come into effect in a year, and that is then expected to be in effect for 12 quarters.29 Panels A and B of Figure 9 gives the implied response of investment in this case, with either capital or investment adjustment costs. In the case of capital adjustment costs, the level of investment spending drops when agents first learn that a partial expensing allowance will be put into place in the future. Just as there is a "pull-forward effect" when a temporary expensing allowance is in place (recall subsection 3.2), when an expensing allowance is expected in the future there is a "push-backward effect" that represents the postponement of investment expenditures to when the expensing allowance is in place and leads to a reduction in current investment. This desire to postpone spending is, however, partly offset by a competing desire to avoid large swings in the capital stock or investment spending (depending on the nature of the adjustment costs faced by investors). Hence, the initial dropoff in investment is smaller the larger is the predicted response of investment over the period that the temporary expensing allowance is in place and the larger are the adjustment costs present in capital formation or investment-outlay changes. Indeed, under the baseline model's wage and price rigidity and investment adjustment cost assumptions, there is no decline in investment spending prior to the expensing allowance coming into effect.30
With this in hand, we can now look at what happens if a temporary partial expensing allowance is systematically triggered by a deterioration in macroeconomic conditions. The particular shock that we consider is an adverse shock to "investment efficiency," which is the variable
![]() in the various capital evolution expressions we assume (equations 4 through 6).31 While any negative (non-policy) shock would do for our purposes, it seems plausible that the use of temporary partial expensing allowances as a policy instrument would most naturally arise
in an economy where adverse shocks to investment are a common cause of economic downturns.
in the various capital evolution expressions we assume (equations 4 through 6).31 While any negative (non-policy) shock would do for our purposes, it seems plausible that the use of temporary partial expensing allowances as a policy instrument would most naturally arise
in an economy where adverse shocks to investment are a common cause of economic downturns.
The dotted lines in panels C and D of Figure 9 give the predicted response of investment spending to a negative investment efficiency shock (once again, blue lines are used for the results from the models with capital adjustment costs, while the red lines are used for the results from the models with investment adjustment costs). The size of the shock is calibrated so that the 20 percent decline in the level of investment spending (relative to the model's baseline) over the first four quarters following the shock in the model with investment adjustment costs broadly resembles the decline in the level of real equipment investment (relative to trend) that was seen over the four quarters that followed the start of the 2001 recession.
How could we calibrate the likely policy response to such a shock? In the 2001 recession, a 50 percent partial expensing allowance went into effect (over two stages); this was also the size of the allowance included in the 2008 and 2009 stimulus bills. We therefore model the expensing allowances with a process like equation (14), where the size of the "innovation" to the expensing rate is related to the size of the shock to investment (that is, the process is specified so that the shock to investment results in a 50 percent expensing allowance being enacted after one year).
The solid lines in panels C and D of Figure 9 give the response of investment to an adverse investment efficiency shock when a temporary partial expensing allowance is anticipated.32 When capital adjustment costs are present, the expected use of partial expensing as a countercyclical stabilization tool results in an initial reduction in the level of investment (and output, not shown) relative to what it would be absent such a policy (the solid lines lie below the dotted lines). But this result is sensitive to the type of adjustment costs that is assumed and with investment adjustment costs capital spending receives a boost from an anticipated expensing allowance. Hence, the Auerbach-Summers and Christiano argument receives some support from our results, although it does not hold in all cases.33
5 Partial Expensing versus Capital Income Tax Cuts
An alternative policy that is often suggested as a means of stimulating investment spending involves reducing the tax rate on capital income. We next examine the effect of this policy on investment and output, and compare it with the effect of an expensing allowance that has the same impact on government revenues.
Model responses: Figure 10 plots the usual set of model responses from the partial-equilibrium model (panel A), the general-equilibrium flexible-price/flexible-wage model (panel B), and the general-equilibrium sticky-price/sticky-wage model (panel C) under our
two adjustment-cost specifications, following a three-year, 30 percentage point reduction in the capital tax rate ![]() . Qualitatively, a temporary cut in the capital tax rate yields a
path for investment spending that is much more front-loaded than the path that obtains under an expensing allowance (this is most obvious for the model with capital adjustment costs, though it can also be seen for the model with investment adjustment costs by noting that the peak investment
response occurs about one year earlier under a capital tax cut). The reason is that the benefits from a reduction in capital taxes are received for as long as the policy is in place; as a result, purchasing and holding a unit of capital for the full three-year period yields the greatest gains. By
contrast, an expensing allowance represents a one-time boon (in the quarter that the capital is purchased) that is worth roughly as much at the start of the three-year period as it is toward the end. Note also that the relative magnitudes of the response of investment to
a capital tax rate cut in the three different models are for the most part quite similar to the relative responses to a expensing allowance shown in Figure 4. That is, the investment response from the partial-equilibrium model is larger than that from the general-equilibrium
flexible-price/flexible-wage model, while the investment response from the sticky-price/sticky-wage model is larger than those of the two other models. That said, the response of investment to a temporary tax cut in the sticky-price/sticky-wage model is only slightly larger than the response in the
partial-equilibrium model, while in the response to an expensing allowance in the sticky-price/sticky-wage model is notably larger than its counterpart from the partial-equilibrium model. This difference stems from the fact that while the same mechanism described in subsection 3.3 still acts
to boost the investment response in the sticky-price/sticky-wage model above that of the partial-equilibrium model, its effect is less powerful. This is because a critical element of this mechanism is the offset it provides to the damping influence that capital/investment adjustment costs have on
the stimulative effects of the policy; this offset is less important when the largest effects of the policy occur toward the start of the period that the policy is in place, rather than toward the date when the policy expires.
. Qualitatively, a temporary cut in the capital tax rate yields a
path for investment spending that is much more front-loaded than the path that obtains under an expensing allowance (this is most obvious for the model with capital adjustment costs, though it can also be seen for the model with investment adjustment costs by noting that the peak investment
response occurs about one year earlier under a capital tax cut). The reason is that the benefits from a reduction in capital taxes are received for as long as the policy is in place; as a result, purchasing and holding a unit of capital for the full three-year period yields the greatest gains. By
contrast, an expensing allowance represents a one-time boon (in the quarter that the capital is purchased) that is worth roughly as much at the start of the three-year period as it is toward the end. Note also that the relative magnitudes of the response of investment to
a capital tax rate cut in the three different models are for the most part quite similar to the relative responses to a expensing allowance shown in Figure 4. That is, the investment response from the partial-equilibrium model is larger than that from the general-equilibrium
flexible-price/flexible-wage model, while the investment response from the sticky-price/sticky-wage model is larger than those of the two other models. That said, the response of investment to a temporary tax cut in the sticky-price/sticky-wage model is only slightly larger than the response in the
partial-equilibrium model, while in the response to an expensing allowance in the sticky-price/sticky-wage model is notably larger than its counterpart from the partial-equilibrium model. This difference stems from the fact that while the same mechanism described in subsection 3.3 still acts
to boost the investment response in the sticky-price/sticky-wage model above that of the partial-equilibrium model, its effect is less powerful. This is because a critical element of this mechanism is the offset it provides to the damping influence that capital/investment adjustment costs have on
the stimulative effects of the policy; this offset is less important when the largest effects of the policy occur toward the start of the period that the policy is in place, rather than toward the date when the policy expires.
Revenue Impact of Alternative Tax Policies: One of the most useful features of our model is its ability to assess the revenue consequences of alternative tax policies--in particular, we can compare the investment responses induced by a capital tax cut and an expensing allowance, where each policy is constrained to have an identical impact on government revenue.
In Figures 11 and 12 we compare the effect of a temporary capital tax cut with that of a temporary expensing allowance, where each policy is set so as to yield the same change in the present value of government revenues. The present value is computed over a five-year (or 20-quarter)
period--this corresponds to the width of the "budget window" that is typically used to score the revenue effects of Federal fiscal policy changes in the U.S.--using the following expression:
As can be seen from the figures, the expensing allowance typically yields a higher response of investment and output. Intuitively, since a capital tax applies to the income from all capital while an expensing allowance applies to expenditures on new capital only, the former represents a relatively expensive way to call forth additional investment spending.34 As is evident from Table 2, the relative responses of investment under the two policies are similar across the various models shown in Figure 10, although expensing allowances provide even greater "bang for the buck" relative to capital tax-rate cuts in the sticky-price/sticky-wage model. Again, this reflects that fact that the response of investment to a temporary expensing allowance in the sticky-price/sticky-wage model is notably larger than the corresponding response from the partial-equilibrium model, while the investment response to a temporary tax cut in the sticky-price/sticky-wage model is only slightly larger than that obtained in the partial-equilibrium model.
| Model | Adjustment Cost Assumption |
Equi-revenue Capital Tax Rate Cut |
Avg. Investment Response (periods 0-11) |
|---|---|---|---|
| Partial equilibrium | Capital | 38.6 | 0.63 |
| Partial equilibrium | Investment | 38.9 | 0.60 |
| Gen. equilibrium with flexible prices & wages | Capital | 36.7 | 0.63 |
| Gen. equilibrium with flexible prices & wages | Investment | 36.4 | 0.60 |
| Gen. equilibrium with sticky prices & wages | Capital | 32.4 | 0.56 |
| Gen. equilibrium with sticky prices & wages | Investment | 25.4 | 0.42 |
6 Conclusions and Directions for Future Work
This paper has analyzed tax-based investment incentives in the context of a fully specified general-equilibrium model. Our analysis uncovered three noteworthy results. First, our findings highlight the need to pay explicit attention to nominal rigidities. Because nominal depreciation allowances imply that investment spending and aggregate demand will depend on nominal interest rates, the evolution of inflation has a significant effect on the predicted response of investment and output. Indeed, the presence of nominal rigidities generated results that in some cases contradicted the conventional view that the general-equilibrium effects of a tax-based investment incentive are invariably smaller than the policy's partial-equilibrium effects. Second, our results provide partial confirmation of the idea that systematic reliance on temporary investment incentives as an instrument of countercyclical stabilization policy can actually be destabilizing. Finally, our analysis gives additional and even stronger support for the result--previously only considered in a partial-equilibrium setup--that, for policies with equal revenue effects, a change in the rate of capital taxation typically represents a relatively less efficacious way of stimulating investment than does a change in the expensing rate for newly purchased capital.
A natural next step is to refine the framework developed here into one that can be used for quantitative simulations. Achieving this goal would require advancing our analysis along at least three fronts. First, any serious quantitative assessment of expensing allowances must recognize the fact that these tax provisions pertain to equipment investment only. Constructing a fully specified model in which different types of capital are used in production would require making difficult decisions about the degree of substitutability across capital types. However, for the purposes of a short-term analysis, it might be sufficient to consider a model in which the stock of structures is assumed to be fixed; this would permit the model to generate more realistic predicted responses of output to tax-induced changes in equipment capital without requiring us to explicitly model the investment decision for structures.
Extending the baseline model to an open-economy setting would also represent an important refinement. With no external sector, the endogenous response of the real interest rate is larger following a tax-induced change in investment, since only domestically produced output can be used to meet the additional demand for physical capital. For the U.S. economy, this might be a reasonable first approximation (though see Auerbach, 1989, for a contrary view), as only about a third of the equipment purchased for investment in the U.S. is produced abroad. Nevertheless, an explicit treatment of external considerations in this context would yield a framework with even greater practical relevance.
More fundamentally, any model that purports to inform real-world decisionmaking should be able to demonstrate a reasonable degree of empirical validity. For the application considered here, formal empirical justification is likely to be made more difficult by the fact that the effect of tax changes on investment--let alone on interest rates, consumption, and inflation--is probably very hard to parse out; moreover, relatively few historical examples of these sorts of tax changes exist. This suggests that considering tax changes alone will not allow us to identify all of the model's parameters (though it might be possible to estimate these parameters by examining the model's predicted response to other shocks). In addition, the recent U.S. experience with partial expensing allowances suggests that numerous complicating factors--such as whether state and local governments follow the federal government in enacting parallel provisions in their own tax codes, or whether firms have taxable income to offset when the expensing allowances are in effect--will influence the real-world impact of these policies.35
Finally, an additional extension would involve constructing an apparatus that would permit the assessment of uncertain future policies. In practice, the likelihood and duration of proposed tax policies are not known with certainty, and this should attenuate the response to announced policy changes. Whether the effects of such uncertainty could be quantified in a linear framework is, however, far from clear.
 Solid line: 50 percent partial expensing allowance
Dotted line: 32.4 percentage point cut in the capital tax rate
Solid line: 50 percent partial expensing allowance
Dotted line: 32.4 percentage point cut in the capital tax rate
 Solid line: 50 percent partial expensing allowance
Dotted line: 25.4 percentage point cut in the capital tax rate
Solid line: 50 percent partial expensing allowance
Dotted line: 25.4 percentage point cut in the capital tax rate
"General-Equilibrium Effects of Investment Tax Incentives"
This appendix details the non-linear and log-linearized first-order conditions for the models presented in the February 23, 2010 draft of "General-Equilibrium Effects of Investment Tax Incentives." The appendix also provides details on the calibration of the model's effective tax rates on income.
A. Detailed Model Derivations
This section of the Appendix gathers together the first-order conditions from the baseline model of section 2 (and its later versions) that are not discussed in the text, and explicitly describes the model's equilibrium and steady-state solution.
A.1 Omitted First-Order Conditions
The intermediate-good producers' cost-minimization problem (7) yields factor demand schedules for each firm; these have the form:
where
In addition, this problem implies a marginal cost function (which is identical for all firms) that is given by:
An intermediate-good producing firm that is able to reset its price in period ![]() takes as given its nominal marginal cost
takes as given its nominal marginal cost ![]() , the aggregate price level
, the aggregate price level ![]() , and aggregate output
, and aggregate output ![]() and solves:
and solves:
![\begin{displaymath} \max_{\left\{ P^{j}_{t}\right\}} \sum_{k=0}^{\infty}\!\eta^{k} E_{t} \!\left[ \frac{\delta^{k} MU_{t+k}/P_{t+k}}{MU_{t}/P_{t}} \left( \left( P^{j}_{t} - MC^{j}_{t+k} \right) Y^{j}_{t+k} - P_{t} FC \right) \right] \end{displaymath}](img163.gif) |
(34) |
where
The final-good producing firm's cost-minimization problem (equation 8) yields a demand function for each of the intermediate goods:
The economy's goods-market clearing condition implies that
![]() , where
, where ![]() denotes actual spending on capital goods.
denotes actual spending on capital goods.
The first-order condition for capital supply for the model with capital adjustment costs is given by:
where
![\begin{displaymath} \frac{Q_{t}}{P_{t}} =\exp\!\left[-\xi^{\Delta k}_{t}+\frac{\chi^{k}}{2}\!\left(\frac{K_{t+1}}{K_{t}}\!-\!1\right)^{\!2}\right] \left(1\!-\!F^{k}_{t}X_{t}\!-\!PDV^{\delta}_{t} \left(1-X_{t} \right) \right).\end{displaymath}](img174.gif)
while the corresponding expression for capital supply under investment adjustment costs is given by:
![\begin{displaymath} E_{t}\!\left[\frac{R^{k}_{t+1} (1\!-\!F^{k}_{t+1})}{P_{t+1}}\right] = E_{t}\left[\frac{R^{f}_{t}}{\Pi_{t+1}} \cdot \frac{Q_{t}}{P_{t}} \right] - E_{t}\left[\frac{Q_{t+1}}{P_{t+1}} \left(1\!-\!\delta\right) \right] \nonumber \end{displaymath}](img175.gif) |
![\displaystyle E_{t}\!\left[\frac{Q_{t+1}}{P_{t+1}}\cdot \exp \left[\xi^{\Delta k}_{t+1}-\frac{\chi^{\Delta k}}{2}\left(\frac{I_{t+1}}{I_{t}}-1 \right)^{2} \right] \chi^{\Delta k} \left(\frac{I_{t+1}}{I_{t}}\right)^{2} \left(\frac{I_{t+1}}{I_{t}}-1\right) \right]](img176.gif) |
|||
|---|---|---|---|
![\displaystyle = E_{t}\left[\frac{R^{f}_{t}}{\Pi_{t+1}} \left(1\!-\!F^{k}_{t}X_{t}\!-\!(1-X_{t})PDV^{\delta}_{t}\!-\!\frac{Q_{t}}{P_{t}}\cdot \exp \left[\xi^{\Delta k}_{t}-\frac{\chi^{\Delta k}}{2} \left(\frac{I_{t}}{I_{t-1}}-1 \right)^{2} \right] \right. \right.](img177.gif) |
|||
![\displaystyle \left. \left. \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \times\!\left(1-\chi^{\Delta k} \left(\frac{I_{t}}{I_{t-1}}\right) \left(\frac{I_{t}}{I_{t-1}}-1\right)\!\right)\!\right)\!\right].](img178.gif) |
A.2 Steady-State Equilibrium
In deriving the model's steady-state equilibrium, we first note that the steady-state value of the inflation rate, ![]() , is assumed to equal the central bank's inflation target,
, is assumed to equal the central bank's inflation target,
![]() . The steady-state values of all other variables in the model are functions of the model's parameters as well as of the steady-state inflation rate and the steady-state value of the
tax variables (
. The steady-state values of all other variables in the model are functions of the model's parameters as well as of the steady-state inflation rate and the steady-state value of the
tax variables (![]() ,
, ![]() , and
, and ![]() ).
).
From equations (3) and (15), the steady-state pretax and posttax nominal interest rates are given by:
The steady-state value of real marginal cost is given by the inverse of the markup, while equations (17) and (33) imply that the steady-state values of the factor prices are given by:
The variable
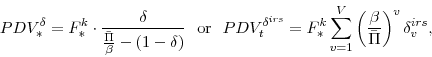
depending on whether we use economic depreciation or the legislated tax schedule for depreciation allowances. Implicit in the definition of
The steady-state ratios
![]() ,
,
![]() ,
,
![]() , and
, and
![]() can be derived from equations (4), (30), (31), and the market-clearing condition. This yields:
can be derived from equations (4), (30), (31), and the market-clearing condition. This yields:
Equations (46) and (49), together with the steady-state version of equation (16), yield the steady-state solution for real output:
Together with equations (46) through (49), equation (51) yields solutions for the steady-state values of
Finally, in the steady state real revenue is:
| (50) |
| (51) |
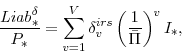 |
(52) |
A.3 Omitted Log-Linearized Model Equations
The log-linear expression for economy-wide marginal cost is
The log-linear government revenue expression is given by
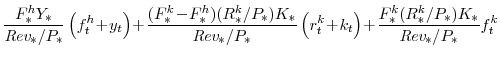
|
|||
|---|---|---|---|
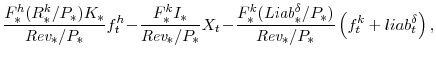
|
where

for the case where economic depreciation is used to compute firms' depreciation allowances, and
 |
|||
|---|---|---|---|
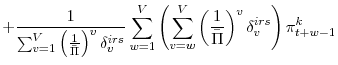 |
(54) |
for the case where legislated depreciation rates are used. We can then log-linearize equation (12), which yields:
| (55) |
In addition, note that if depreciation rates for tax purposes are given by a legislated schedule (and, so, not equivalent to economic depreciation), then the expression for the log-linearized present value of depreciation allowances (equation 23) becomes
B. Calibrating the Steady-State Tax Rates
This Appendix describes how the effective tax rates on income are calibrated, and discusses how our main results are affected by different assumed values for the capital tax rate.
B..1 Calibration of 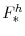
We use tabulations from the Statistics of Income (Table 3.4) to compute average marginal Federal tax rates on earned income. For 2001 (the most recent year for which these data are available), we obtain an average marginal rate that is a little more than 25 percent. We then adjust this figure to reflect income taxation by state and local governments; specifically, data from the National Income and Product Accounts (NIPAs) indicate that state and local personal income taxes represented about 2-1/2 percent of overall personal income in 2001. As this is an average (not marginal) rate, we double it to capture the progressive nature of most state and local tax systems. The sum of these two rates yields the 30 percent average marginal tax rate that we assume.
B.2 Calibration of 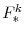
We require an estimate of the average marginal tax rate on capital income. Excluding depreciation, net capital income can be divided into three categories: dividends, retained earnings, and interest payments. If the corporate income tax rate is given by ![]() , and if dividends (and capital gains) are taxed at the rate
, and if dividends (and capital gains) are taxed at the rate ![]() , then the effective tax rate on capital
income
, then the effective tax rate on capital
income ![]() is implicitly defined by
is implicitly defined by
The preceding assumes that the double taxation of dividends (at the corporate and personal level) matters in determining the cost of capital. Under the so-called "new view" of dividend taxation, however, the taxation of dividend income at the personal level is immaterial as far as the cost of capital is concerned.36 In this case, the first tax term in parentheses on the right-hand side of equation (59) equals one, implying that the effective tax rate on capital income is 38 percent.
Finally, the simplest possible case arises when firms are financed exclusively through debt (in which case taxable corporate income is zero). This implies that all capital income is taxed at the personal tax rate, or that
![]() .
.
To assess how sensitive our results are to alternative assumptions about ![]() , the table below gives the long-run change in the real rental rate of capital (expressed as a percent
deviation from its steady-state level) following a permanent 30 percent expensing allowance for various assumed values of
, the table below gives the long-run change in the real rental rate of capital (expressed as a percent
deviation from its steady-state level) following a permanent 30 percent expensing allowance for various assumed values of ![]() .37 Based on the figures in the table (and given the log-linear structure of the model), assuming a value of
.37 Based on the figures in the table (and given the log-linear structure of the model), assuming a value of ![]() consistent with dividend taxation's having no effect on the cost of capital would reduce the model's responses by about a third, while assuming that firms are purely debt-financed would scale them down by about a half.
consistent with dividend taxation's having no effect on the cost of capital would reduce the model's responses by about a third, while assuming that firms are purely debt-financed would scale them down by about a half.
| Tax rate |
Description | Change |
|---|---|---|
| 48 percent | Baseline assumption | -5.21 |
| 38 percent | "New view" of dividend taxation | -3.68 |
| 30 percent | Fully debt-financed firms | -2.67 |
![\begin{displaymath} U_{0}=E_{0}\left\{ \sum_{t=0}^{\infty}\beta^{t} \left[\frac{1}{1-\sigma} \left(C^{i}_{t}\right)^{1-\sigma} - \frac{1}{1+s} \left( H^{i}_{t} \right)^{1+s} \right] \right\}, \end{displaymath}](img5.gif)
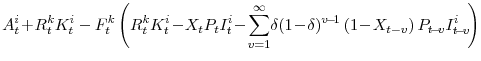
![\begin{displaymath} K^{i}_{t+1}=(1-\delta)K^{i}_{t}+I^{i}_{t}\exp\left[\xi^{\Delta k}_{t} -\frac{\chi^{k}}{2} \left(\frac{K^{i}_{t+1}}{K^{i}_{t}}-1\right)^{2}\right], \end{displaymath}](img47.gif)
![\begin{displaymath} K^{i}_{t+1}=(1-\delta)K^{i}_{t}+I^{i}_{t}\exp\left[\xi^{\Delta k}_{t} -\frac{\chi^{\Delta k}}{2} \left(\frac{I^{i}_{t}}{I^{i}_{t-1}}-1\right)^{2}\right], \end{displaymath}](img49.gif)
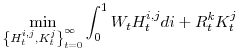
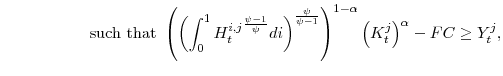
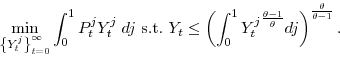
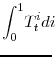
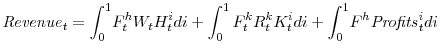
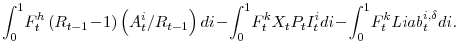
![\displaystyle {\mathit{PDV}}^{rev}_{t} =E_{t}\left[\sum_{v=0}^{\infty} \frac{\beta^{v} MU_{t+v}/P_{t+v}}{MU_{t}/P_{t}} {\mathit{Rev}}_{t+v} \right] ={\mathit{Rev}}_{t}+E_{t}\left[\frac{\beta MU_{t+1}/P_{t+v}}{MU_{t}/P_{t}} {\mathit{PDV}}^{rev}_{t+1}\right]](img97.gif)
![\begin{displaymath} \frac{1}{C^{\sigma}_{t}P_{t}} =\beta E_{t}\left[ \frac{R^{f}_{t}}{C^{\sigma}_{t+1}P_{t+1}} \right] \end{displaymath}](img105.gif)
![\begin{displaymath} W^{i}_{t}\!=\! \frac{\sum_{k=0}^{\infty} \gamma^{k} E_{t}\left[((\beta^{k} MU_{t+k}/P_{t+k})/(MU_{t}/P_{t}))\left(\!H^{i}_{t+k}\!\right)^{s} \left(\!C^{i}_{t+k}\!\right)^{\sigma}\psi H_{t+k}\right]} {\sum_{k=0}^{\infty} \gamma^{k} E_{t}\left[((\beta^{k} MU_{t+k}/P_{t+k})/(MU_{t}/P_{t}))\left((1\!-\!F^{h}_{t})/P_{t}\right) \left(\psi\!-\!1\right) H_{t+k}\right]}. \end{displaymath}](img106.gif)
![\displaystyle E_{t}\!\left[\frac{R^{k}_{t+1}(1\!-\!F^{k}_{t+1})}{P_{t+1}}\right]](img107.gif)
![\displaystyle E_{t}\left[\frac{R^{f}_{t}}{\Pi_{t+1}} \left(1\!-\!F^{k}_{t}X_{t}-PDV^{\delta}_{t} \left(1-X_{t} \right) \right) \right]](img109.gif)
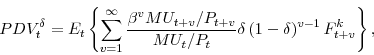

![\begin{displaymath} \pi^{w}_{t}=\beta E_{t}\pi^{w}_{t+1}+\frac{(1-\gamma)(1-\gamma\beta)}{\gamma}\cdot\frac{1}{1+\psi\!\cdot\!s} \left[\frac{F^{h}_{\ast}}{1-F^{h}_{\ast}}\cdot f^{h}_{t} + \sigma\!\cdot\!c_{t}+s\!\cdot\!h_{t}-w_{t}\right]\!, \end{displaymath}](img120.gif)
![\displaystyle E_{t}r^{k}_{t+1} \!=\! \left[\frac{F^{k}_{\ast}}{1-F^{k}_{\ast}}\right]\!f^{k}_{t+1} \!\!\!\!](img122.gif)
![\displaystyle \left[\frac{1}{1-\beta\left(1-\delta\right)}\right]\! \left(\left(r^{f}_{t}\!\!-\!E_{t}\pi_{t+1}\right) \!+\!\left(q_{t}\!-\!\beta (1-\delta) E_{t} q_{t+1}\right)\right)](img123.gif)
![\displaystyle \left[\frac{\chi^{k} \cdot \delta}{1-\beta\left(1-\delta\right)} \right] \left(\beta E_{t}k_{t+2}-\left(1+\!\beta \right)k_{t+1}\!+\!k_{t} \right),](img125.gif)
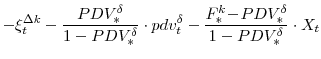
![\begin{displaymath} E_{t}r^{k}_{t+1} \!=\! \left[\frac{F^{k}_{\ast}}{1\!-\!F^{k}_{\ast}}\right]\!f^{k}_{t+1} \!+\!\left[\frac{1}{1\!-\!\beta\left(1\!-\!\delta\right)}\right]\! \left(\left(r^{f}_{t}\!\!-\!E_{t}\pi_{t+1}\right) \!+\! \left(q_{t}\!-\!\beta (1-\delta) E_{t} q_{t+1} \right)\right) \end{displaymath}](img130.gif)
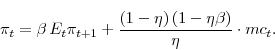
![\begin{displaymath} {\mathit{pdv}}^{\mathit{rev}}(5)_{t}=\left( \frac{1-\beta}{1-\beta^{20}} \right) E_t \left[{\mathit{rev}}_{t}-\sum_{v=1}^{19} \beta^v \left(\mathit{rev}_{t+v} - \sum_{j=0}^{v-1} (r^f_{t+j}-\pi_{t+1+j}) \right) \right], \end{displaymath}](img152.gif)
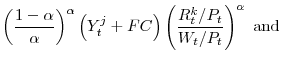
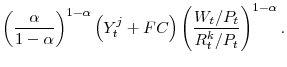
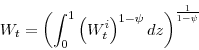
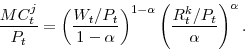
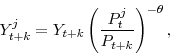
![\begin{displaymath} P^{j}_{t}= \frac{\sum_{k=0}^{\infty} \eta^{k} E_{t}\left[((\delta^{k} MU_{t+k}/P_{t+k})/(MU_{t}/P_{t}))MC^{j}_{t+k}\theta Y_{t+k}\right]} {\sum_{k=0}^{\infty} \eta^{k} E_{t}\left[((\delta^{k} MU_{t+k}/P_{t+k})/(MU_{t}/P_{t}))\left(\theta-1\right) Y_{t+k}\right]}. \end{displaymath}](img167.gif)
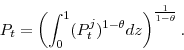
![\displaystyle = E_{t}\left[\frac{R^{f}_{t}}{\Pi_{t+1}}\cdot\frac{Q_{t}}{P_{t}} \left(1+\exp\!\left[\xi^{\Delta k}_{t}-\frac{\chi^{k}}{2}\!\left(\frac{K_{t+1}} {K_{t}}\!-\!1\right)^{\!2}\right] \chi^{k}\cdot\frac{I_{t}}{K_{t}}\left(\frac{K_{t+1}}{K_{t}}-1 \right)\!\right)\!\right]](img172.gif)
![\displaystyle - E_{t}\left[\frac{Q_{t+1}}{P_{t+1}} \left(\!(1-\delta)+\exp\!\left[\xi^{\Delta k}_{t}-\frac{\chi^{k}}{2}\!\left(\frac{K_{t+2}} {K_{t+1}}\!-\!1\right)^{\!2}\right] \chi^{k}\cdot\frac{I_{t+1}}{K_{t+1}}\left(\frac{K_{t+2}}{K_{t+1}}-1 \right)\frac{K_{t+2}}{K_{t+1}}\!\right)\!\right],](img173.gif)