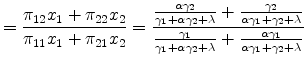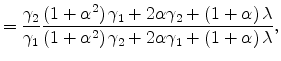Skip to: [Printable Version (PDF)] [Bibliography] [Footnotes]

Finance and Economics Discussion Series: 2010-30 Screen Reader version ^♣

An Alternative Theory of the Plant Size Distribution With an Application to Trade

Thomas J. Holmes and John J. Stevens*

Keywords: Plant size, productivity, trade, geographic concentration

Abstract:

There is wide variation in the sizes of manufacturing plants, even within the most narrowly defined industry classifications used by statistical agencies. Standard theories attribute all such size differences to productivity differences. This paper develops an alternative theory in which industries are made up of large plants producing standardized goods and small plants making custom or specialty goods. It uses confidential Census data to estimate the parameters of the model, including estimates of plant counts in the standardized and specialty segments by industry. The estimated model fits the data relatively well compared with estimates based on standard approaches. In particular, the predictions of the model for the impacts of a surge in imports from China are consistent with what happened to U.S. manufacturing industries that experienced such a surge over the period 1997-2007. Large-scale standardized plants were decimated, while small-scale specialty plants were relatively less impacted.

JEL Classification: F10, L11, L25, R12

1 Introduction

The sizes of manufacturing plants exhibit wide variation, even within the most narrowly defined industry classifications used by statistical agencies. For example, in the wood furniture industry in the United States (NAICS industry code 337122), one can find plants with over a thousand employees and other plants with as few as one or two employees. The dominant theory of such within-industry plant-size differentials models plants as varying in terms of productivity. (See Lucas (1978), Jovanovic (1982), and Hopenhayn (1992).) In this theory, some plants are lucky and draw high productivity at start-up, whereas others are unlucky and draw low productivity. The size distribution is driven entirely by the productivity distribution.

The approach has been extremely influential. It underpins recent developments in the international trade literature. Melitz (2003) and Bernard, Eaton, Jensen, and Kortum (2003, hereafter BEJK) use the approach to explain plant-level trade facts. In Melitz, plants with higher productivity draws have large domestic sales and also have the incentive to pay fixed costs to enter export markets. In this way, the Melitz model explains the fact--documented by Bernard and Jensen (1995)--that large plants within narrowly defined industries are more likely to be exporters than small plants. Relatedly, in BEJK, more productive plants have wider trade areas. Both the Melitz and the BEJK theories have a sharp implication about the impact of increased exposure to import competition on a domestic industry: the smaller plants in the industry--which are also the low productivity plants in the industry under these theories--are the first to exit.

In our view, the dominant approach to modeling plant-size differentials goes too far in attributing all variation in plant size within narrowly defined census industries to differences in productivity. It is likely that plants that are dramatically different in size are performing different functions, even if the Census Bureau happens to classify them in the same industry. Moreover, these differences in function may be systematic and may very well be directly related to how increased import competition would affect the plants.

Take wood furniture as an example. The large plants in this industry with more than a thousand employees are concentrated in North Carolina, particularly in a place called High Point. These plants make the stock bedroom and dining room furniture pieces found at traditional furniture stores. Also included in the Census classification are small facilities making custom pieces to order, such as small shops employing skilled Amish craftsmen. Let us apply the standard theory of the size distribution to this industry. Entrepreneurs that enter and draw high productivity parameters would likely open up megaplants in High Point, North Carolina; those that get low draws might open Amish shops in other locations. The Melitz model and the BEJK model both predict that the large North Carolina plants will have large market areas, while the small plants will tend to ship locally. So far so good, because this result is consistent with the data, as we will show. But what happens when China enters the wood furniture market in a dramatic fashion, as has occurred over the past 10 years? While all of the U.S. industry will be hurt, the Melitz and BEJK theories predict that the North Carolina industry will be relatively less affected because it is home to the large, productive plants. In fact, the opposite turns out to be true in the data.

To address this shortcoming, our theory takes into account that most industries have some segment that provides specialty goods, often custom-made goods, the provision of which is facilitated by face-to-face contact between buyers and sellers. This specialty segment is the province of small plants. Large plants tend to make standardized products. Here we follow the ideas of Piore and Sable (1984) and a subsequent literature distinguishing between the mass production of standardized products taking place in large plants and the craft production of specialty products taking place in small plants. When China enters the wood furniture market, naturally it follows its comparative advantage and enters the standardized segment of the market, making products similar to the stock furniture pieces produced in North Carolina. Thus, in our theory, the North Carolina industry is hurt the most by China's entry into the industry, as actually happened.

Our starting point is the Eaton and Kortum (2002) model of geography and trade as further developed in BEJK. In its basic form, plants in this model vary in productivity and location but are otherwise symmetric in terms of transportation costs and underlying consumer demand. We take this model "off the shelf" as our model of the standardized segment of an industry, and we fold in a simple model of a specialty segment. We explore two issues in the model. First, how is the size distribution of plants connected to the geographic distribution of plants (call this the plant size/geographic concentration relationship)? Second, if there is a surge in imports, what is the relative impact of the trade shock across locations that vary by geographic concentration and mean plant size?

We estimate the model separately for individual industries, using Census data that include survey information from the Commodity Flow Survey on the origins and destinations of shipments. The shipment information is critical for our analysis because it enables us to recover parameters related to the transportation cost structure in the BEJK framework.

We obtain four main empirical results. First, we estimate that in most industries, more than half of the plants in an industry can be classified as being in the specialty segment; the specialty segment dominates plant counts. Second, the pure BEJK model fails to quantitatively match the plant size/geographic concentration relationship, whereas the general model that includes the specialty segment fits this relationship well. For example, in High Point where the wood furniture industry concentrates, average plant size (as measured by sales revenue) is 6.6 times the national average. The pure BEJK model predicts a difference of only a factor 1.6, but the general model comes in quite close with a factor 6.9. The third empirical result concerns industries negatively affected by a surge of imports from China. We examine the period between the 1997 and 2007 Economic Census years. Our estimated pure BEJK model predicts that those locations with high industry concentration and high average plant size should have experienced a small increase in relative share of the domestic industry; e.g., High Point's market share in wood furniture should have risen relative to the rest of the country. Instead these areas experienced sharp declines over the period, consistent with our hypothesis. Indeed, we show that the High Point region went from having 14 wood furniture plants with more than 500 employees to only 3 plants. For our fourth empirical result, we use our general model and estimate the distribution of plant counts by standardized and specialty segments for 1997 and 2007 and analyze the changes over time. Consistent with our hypothesis, we find that those industries facing a surge of imports from China experienced a dramatic decline in the number of standardized plants. In these industries, standardized plants in 2007 numbered only about one-third of their 1997 level. In contrast, changes in counts of specialty segment plants were much less pronounced.

We find it particularly revealing to analyze what has happened in large metropolitan areas. Generally speaking, in recent decades large cities have not been home to huge manufacturing plants in the kinds of industries, like furniture and clothing, that China now dominates. In the United States, large plants in these industries have been concentrated in smaller, manufacturing-oriented areas like High Point. We show that over the period 1997 to 2007, in industries where exports from China have surged, the domestic industry has shifted toward large metropolitan areas, places where average plant size has typically been small. These are places where we expect to see a large demand for specialty and custom goods. And we also expect to find there a large supply of inputs suited for specialty and niche products. These are different from the low-skill inputs used in mass production of standardized products in large plants--inputs readily available in China and places like High Point. Our theory with a specialized-good sector can account for how import pressure from China shifts industries from places like High Point to places like New York City. Without the specialized-good segment in the model, the shift goes the other way. An interesting analogue to recent experience is found in an early case study of the garment industry circa 1960 (Hall, 1959). That study explained how large plants in places like North Carolina tended to mass-produce standardized garments like nurses' uniforms, while the small plants in New York City tended to produce fashion items. The new development is that China has entered to play the role of North Carolina, while New York still plays New York (albeit in a relative sense, given the overall decline of manufacturing as a share of the domestic economy).

There is an emerging new literature that allows for richer forms of heterogeneity across plants than the first generation of trade models with heterogeneous firms found in Melitz (2003) and BEJK. Hallak and Sivadasan (2009) allow plants to differ in the standard way regarding cost structure, but also along a second dimension in terms of a plant's ability to provide quality. Their theory can explain why smaller plants sometimes export more than larger plants. (This outcome can happen in their model if the smaller plant has sufficiently higher quality.) Bernard, Redding, and Schott (2010) develop a multi-product model of a firm with differences not only in overall firm productivity levels but also in the heterogeneity of product-specific attributes. Our paper is in the spirit of these papers in that it allows for richer heterogeneity. One difference is that we are adding heterogeneity within narrowly defined industries in the extent to which the goods being produced are tradable, with customized versions of goods being more difficult to trade. Holmes and Stevens (2004a) include a margin like this in a regional model linking plant size and geographic concentration. This paper is different from our earlier paper because it (1) uses BEJK to develop an entirely different modeling structure, (2) takes the model to the data and estimates its parameters, and (3) examines the impact of a trade shock.

The theory developed here is consistent with a variety of empirical findings in the literature. First, there is conflicting evidence in the trade literature on how tariff reductions affect domestic plant sizes. (See Head and Ries (1999).) When we take into account that plants vary in productivity as well as in function (with small plants specializing in specialty goods), we cannot tell a priori whether a given large plant will be more likely to survive a trade onslaught than a small plant. Second, the theory provides a new explanation for the well-known findings discussed earlier that exporters tend to be larger than other plants in the same narrowly defined industry. Third, the theory is consistent with the well-known fact that the size distribution of plants is highly skewed--there are many more small plants than large plants. The most prominent explanation in the literature for this skewness is the random growth theory. See Luttmer (2007) for a recent treatment. In this literature, a big plant is a lucky one that gets, say, "heads" 50 times in a row in a series of coin flips. This event is unlikely, of course, so big plants are rare. In our theory, the little plants are doing different things than the big plants. In particular, in providing a custom service that is hard to trade, there will need to be many such plants diffused across all local markets.¹

The paper is related to the macroeconomics literature on quantitative dynamic models incorporating plant heterogeneity. This literature makes heavy use of the standard theory where size differences are driven entirely by productivity differences. Given a monotonic relationship between plant size and productivity, it is possible to invert the relationship and read off the distribution of plant productivities from the distribution of plant sizes. Hopenhayn and Rogerson (1993) is an early example, Alessandria and Choi (2007) a recent example. To the extent plants of different sizes are doing different things, this strategy overstates productivity differences. The paper is also related to Buera and Kaboski (2008), which emphasizes how structural change impacts average plant size.

2 Theory

The first part of this section presents the model. The second part derives the analytic results.

2.1 Model

There is a fixed set of locations, indexed by $\ell$ . Each location typically produces goods in a variety of industries. When we go to the data, we will take into account that industries differ in their model parameters. Here we describe the model in terms of a particular industry and leave implicit the industry index.

Consumers have Cobb-Douglas utility for industry composites. Assume $\xi$ is the spending share on the particular industry we are looking at. For this industry, let $p_{\ell}$ be the composite industry price index and $q_{\ell}$ be the composite industry quantity, at location $\ell$ . Given the Cobb-Douglas assumption, spending $x_{\ell}=p_{\ell}q_{\ell}$ on the industry at the location equals

$\displaystyle x_{\ell}=\xi I_{\ell}$ ,

given income $I_{\ell}.$

The industry has two segments, the standardized segment indexed by and the specialty segment indexed by (where can be remembered as "boutique"). The industry composite $q_{\ell}$ is made up of a standardized segment $q_{\ell}^{s\text{ }}$ composite and a specialty (or boutique) segment composite $q_{\ell }^{b\text{ }}$ in the usual CES way,

$\displaystyle q_{\ell}=\left( \zeta^{s}\left( q_{\ell}^{s}\right) ^{\frac{\rho-1}{\rho} }+\zeta^{b}\left( q_{\ell}^{b}\right) ^{\frac{\rho-1}{\rho}}\right) ^{\frac{\rho}{\rho-1}}$ ,

(1)

where $\rho$ is the elasticity of substitution between the two segments and the segment weights sum to one, $\zeta^{s}+\zeta^{b}=1$ . We next describe each segment in turn.

2.1.1 The Standardized Segment

We use the BEJK model as our model of the standardized segment. There is a continuum of differentiated standard goods indexed by $j\in\lbrack0,1]$ . For example, if the industry is the wood furniture industry, then specifies a particular kind of wood furniture, such as a kitchen table of a particular size, finish, shape, and kind of wood. The different standardized goods are aggregated to obtain the standardized segment composite $q_{\ell}^{s\text{ }}$ in the usual CES way. Let $\sigma$ be the elasticity of substitution, and let $P_{\ell}(j)$ be the price of good at location $\ell$ . (For simplicity we leave the superscript implicit here, as the index only refers to tradable goods.) Then the expenditure at location $\ell$ for good equals

$\displaystyle X_{\ell}(j)=x_{\ell}^{s}\left( \frac{P_{\ell}(j)}{p_{\ell}^{s}}\right) ^{1-\sigma},$

where $x_{\ell}^{s}$ is spending on the standardized segment composite at location $\ell$ and $p_{\ell}^{s}$ is the price index,

$\displaystyle p_{\ell}^{s}=\left[ \int_{0}^{1}P_{\ell}(j)^{1-\sigma}dj\right] ^{\frac {1}{1-\sigma}}\text{.}$

As in BEJK, there are potential producers at each location with varying levels of technical efficiency. Let $Z_{ki}(j)$ index the efficiency of the th most efficient producer of good located at . This index represents the amount of good made by this producer, per unit of input.

There is an "iceberg" cost to ship tradable segment goods across locations. Let $d_{\ell i}$ be the amount of good that must be shipped to location $\ell$ from location in order to deliver one unit. There is no transportation cost for delivering to the location where the good is produced, i.e., $d_{ii}=1$ . Otherwise, $d_{\ell i}\geq1$ , for $\ell\neq i$ . Assume that the triangle inequality $d_{\ell i}\leq d_{\ell k}d_{ki}$ holds.

The distribution of efficiencies is determined as follows. Let $T_{\ell}$ denote a parameter governing the distribution of efficiency of the standard segment at location $\ell$ . Suppose the maximum efficiency $Z_{1i}$ is drawn according to

$\displaystyle F_{i}(z)=e^{-T_{i}z^{-\theta}}$ .

The parameter $\theta$ governs the variance of productivity draws.

Eaton and Kortum (2002) show that for a given standard segment good , the probability that location is the lowest-cost producer to location $\ell$ is

$\displaystyle \pi_{\ell i}=\frac{\gamma_{i}a_{\ell i}}{\sum_{k=1}^{L}\gamma_{k}a_{\ell k} }$ ,

(2)

for

$\displaystyle \gamma_{i}$	$\displaystyle \equiv T_{i}w_{i}^{-\theta}$	(3)
$\displaystyle a_{\ell i}$	$\displaystyle =\left( d_{\ell i}\right) ^{-\theta}$ ,

where $w_{i}$ is the cost of inputs at location

We refer to $\gamma_{i}$ as the cost efficiency index for location

and $a_{\ell i}$ as the distance adjustment between $\ell$ and

. Let $\Gamma=(\gamma _{1},\gamma_{2},...,\gamma_{L})$ be the cost efficiency vector and

(with elements $a_{\ell i}$ ) be the distance adjustment matrix. We can think of $\gamma_{i}a_{\ell i}$ as an index of the competitiveness of origin

at destination $\ell$ . It starts with location

's overall cost efficiency and adjusts for distance to $\ell$ . Location

's probability $\pi_{\ell i}$ of getting the sale at $\ell$ equals its own competitiveness at $\ell$ relative to the sum of all the other locations' indexes of competitiveness at $\ell$ .

BEJK consider a rich structure with multiple potential producers at each location who each get their own productivity draws. Then firms engage in Bertrand competition for consumers at each location. The equilibrium may feature limit pricing, where the lowest-cost producer matches the second-lowest-cost producer. Or the lowest cost may be so low relative to rivals' costs that the price is determined by the inverse elasticity rule for the optimal monopoly price. The very useful result of BEJK is that allowing for all of this does not matter. Conditional on a location landing a sale at $\ell$ (i.e., that location is the lowest-cost producer for $\ell$ ), the distribution of prices to $\ell$ is the same for all originations . This implies that the sales revenues from $\ell$ are allocated according to $\pi_{\ell i}$ . That is, total sales revenue of origin to destination $\ell$ is

$\displaystyle y_{\ell i}^{s}=\pi_{\ell i}x_{\ell}^{s}$ .

Total sales revenues on standardized-segment goods originating in

across all destinations is

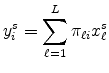$\displaystyle y_{i}^{s}=\sum_{\ell=1}^{L}\pi_{\ell i}x_{\ell}^{s}$ .

Like BEJK, we associate a plant with a particular good produced at . The measure of standardized-segment goods produced at equals $\pi_{ii}$ , the measure of goods location sells to itself.² We allow for a scaling factor $\nu^{s}$ , so that the number of standardized-segment plants at location is

$\displaystyle n_{i}^{s}=\nu^{s}\pi_{ii}.$

(4)

2.1.2 The Specialty Segment

We offer two ways to model the specialty segment. Conceptually, the two cases are very different. Yet for much of what we do in this paper, the results for the two cases are similar.

Our first case is the specialty-segment-as-nontradable-goods model. As an example of this case, consider the wood furniture industry. This industry includes plants that look like retail stores in a shopping center. A consumer can go into such an establishment and meet face-to-face with designers to come up with a design for a custom piece. When the furniture is actually made on the premises, the Census Bureau classifies the establishment as being a wood furniture manufacturer. This kind of specialty establishment is aimed at a local market, as consumers do not want to drive long distances to meet with a designer. For simplicity, we assume for this case that the transportation cost across locations is infinitely high precluding trade. For this first model, then, total sales by specialty-segment plants (also called boutique plants) at equal expenditure at ,

$\displaystyle y_{i}^{b}=x_{i}^{b}$ .

Next we simplify by assuming that average plant size in terms of revenue volume is constant across locations and equals $\bar{r}^{b}$ . Define $\nu ^{b}\equiv1/\bar{r}^{b}$ as inverse size. The number of specialty plants at

equals

$\displaystyle n_{i}^{b}=\frac{y_{i}^{b}}{\bar{r}^{b}}=\nu^{b}x_{i}^{b}$ .

(5)

The idea here is that there tends to be some efficient size of retail-like specialty establishments. If the specialty-good expenditure doubles at a location, all expansion of the industry at the location occurs on the extensive margin of a doubling of the number of establishments, rather than any increase in size of establishments. Implicitly, there are diseconomies of scale when plants get too big. This modeling assumption is plausible for retail-like custom operations.

Our second case is the specialty-segment-as-high-end-niche model. For this, we go to the other extreme and treat the specialty goods as being perfectly tradable. The products have high value-to-weight ratios and--if face-to-face contact between buyer and seller is not important--transportation costs are then immaterial. The price $p^{b\text{ } }$ for these goods is the same at all locations . The amount of high-end niche activity at a location depends on the supply of factors specific to the segment at the location. We think of this as creative talent or artisanship that is likely unrelated to the factor $T_{i}$ determining suitability for standardized goods. The total value of production $y_{i}^{b}$ at depends implicitly on the supply of creativity. Again, assume that average plant revenue volume is constant at $\bar{r}^{b}$ across locations with inverse $\nu ^{b}\equiv1/\bar{r}^{b}$ . The number of specialty plants at origin then equals

$\displaystyle n_{i}^{b}=\nu^{b}y_{i}^{b}$ .

(6)

This high-end-niche model of the specialty segment can be regarded as the limiting case of the BEJK model, where transportation cost is zero (or $d_{\ell i}^{b}=1$ ). As we will see below, average plant size is constant across locations in this limiting case of BEJK. In particular, as comparative advantage increases, the resulting expansion of output is met entirely on the extensive margin of more plants.³

We limit ourselves to these two extreme cases for technical tractability. We expect that in many cases the specialty-good sector will be some combination of these two extreme cases. That is, it will have a hard-to-trade element (because face-to-face contact between the buyer and the producer is desirable) and a high-end fashion element (because comparative advantage for the segment depends upon supply factors such as creative talent, which is different from the supply factors used to produce standardized goods).

2.2 Results

This subsection uses the model to examine two issues. First, how is average plant size at a location related to the concentration of industry at a location? Second, what is the effect of an import surge on the distribution of domestic production? We begin the analysis by discussing what happens with only standardized goods. Then we discuss how adding the specialty segment affects the results.

2.2.1 The Plant Size/Geographic Concentration Relationship

To relate average size to industry concentration, we use the location quotient at to measure industry concentration at . Recall that $y_{i}$ is the total sales revenue of producers located at and $x_{i}$ is the total expenditure of consumers located at . Letting and be the aggregate totals, the revenue location quotient $Q_{i}^{rev}$ is a location's share of sales revenue (i.e., production) over its share of expenditure (i.e., consumption),

$\displaystyle Q_{i}^{rev}\equiv\frac{y_{i}/y}{x_{i}/x}$ .

(7)

If the distribution of production exactly follows expenditure, it equals one everywhere and no locations specialize in the industry. Otherwise, if there are locations where this is greater than one, we say the location specializes in the industry and is a net exporter.

Following Holmes and Stevens (2002), we can think of a location as having two margins over which it can specialize in an industry: the extensive margin of more plants and the intensive margin of higher average plant size. To highlight these two margins, we decompose the revenue location quotient as the product of a count quotient and a size quotient,

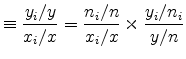$\displaystyle Q_{i}^{rev}$	$\displaystyle \equiv\frac{y_{i}/y}{x_{i}/x}=\frac{n_{i}/n}{x_{i}/x} \times\frac{y_{i}/n_{i}}{y/n}$	(8)
	$\displaystyle =Q_{i}^{count}\times Q_{i}^{size}$ ,	(9)

recalling that $n_{i}$ is the plant count at

and letting

be the aggregate plant count. The count quotient is a location's share of plant counts relative to its expenditure share. The size quotient is a location's average plant size (in sales revenue) relative to the aggregate average plant size.

For now, suppose there is only a standardized-good segment so the model reduces to an off-the-shelf BEJK model. For the benchmark case with no transportation costs we have the following proposition.

Proposition 1. With only standardized goods and no transportation costs ( $d_{\ell i}=1$ all $\ell\neq i$ ), then $Q_{i}^{size}=1$ for all so average plant size (in sales volume) is identical at all locations. All variation in $Q_{i}^{rev}$ is through the extensive margin $Q_{i}^{count}$ .

Proof. With $d_{\ell i}=1$ for all $\ell\neq i$ , the probability that serves $\ell$ in (2) reduces to

$\displaystyle \pi_{\ell i}=\frac{\gamma_{i}}{\sum_{k}\gamma_{k}},$

which is independent of destination $\ell$ . From BEJK this also equals the sales share at each location. So average plant size (in sales revenue) at each location is

$\displaystyle \bar{r}_{i}=\frac{\sum_{\ell}\pi_{\ell i}x_{\ell}}{n_{i}}=\frac{\sum_{\ell} \pi_{\ell i}x_{\ell}}{\nu^{s}\pi_{ii}}=\frac{\sum_{\ell}x_{\ell}}{\nu^{s}},$

(10)

which is constant across locations. Q.E.D.

Following the intuition about the Eaton-Kortum setup in Alvarez and Lucas (2007), the productivity at a location has an interpretation of being a function of the first-order statistic of draws from the exponential distribution. A location with productivity $T_{i}$ twice as high as another location can be interpreted as having twice as many underlying draws. With zero transportation costs, it is intuitive that a location with twice as many underlying draws will produce twice as many products.

When transportation cost is positive, the BEJK model delivers differences in average plant size across locations. Analytical results are difficult to come by, but some basic patterns can be readily discerned with numerical examples. Table 1 illustrates a numerical example with two locations. For all the parameters considered, $Q_{2}^{rev}$ is a factor four times larger than $Q_{1}^{rev}$ , so location 2 specializes in the industry to a substantial degree. We consider three possibilities for the expenditure distribution: in the first, expenditure is equal across the two locations; in the second it is three times higher in location 2; in the third it is three times higher in location 1. We also vary the distance adjustment parameter $a_{12}=\left( d_{12}\right) ^{-\theta}$ . For different levels of $a_{12}$ , we back out what the ratio $\gamma_{2}/\gamma_{1}$ must be that would result in the given values of $Q_{1}^{rev}$ and $Q_{2}^{rev}$ , and then calculate the corresponding $Q_{2}^{count}$ and $Q_{2}^{size}$ .

We start by discussing the equal expenditure case and for this case the targets are $Q_{2}^{rev}=1.60$ and $Q_{1}^{rev}=.40$ . As $a_{12}$ is decreased as we move down the table (so the distance adjustment becomes more important), the productivity advantage of location 2 must be increased to hold constant the net trade between the two locations (i.e. to keep $Q_{2}^{rev}=1.60$ ). At the limiting case where , average size is the same in both places, $Q_{2}^{size}=1$ , consistent with Proposition 1. For this limiting case, the expansion in revenue at location 2 comes entirely through the count margin, $Q_{2}^{rev}=Q_{2}^{count}=1.60$ . As $a_{12}$ is decreased, average size in location 2 increases, so both the size margin and the count margin play a role. But even as shrinks to extreme levels (and the implied $\gamma_{2}/\gamma_{1}$ goes to extreme levels), the establishment count margin is always greater than the size margin. This result holds more generally in other numerical examples with $x_{1}=x_{2}$ . This discussion gives a sense of how the BEJK model has trouble accounting for large differences in average plant size across locations, particularly if transportation costs are relatively small.

If expenditure is larger in location 2 and if trade is sufficiently difficult, the size margin will be significant. It is intuitive that when trade is difficult in the BEJK model, plants in locations with high local expenditure will tend to be big, as most sales are local. As we discuss below, high local demand will not be a relevant explanation for the large average size plants to be found in industrial centers like High Point, North Carolina. These places are relatively small cities with low local demand.

2.2.2 Response to an External Trade Shock

We next examine the impact of a trade surge in the standardized segment on the distribution of the production of standardized goods across locations. We model trade in a simple fashion. As above, suppose there are two domestic locations. Now add a third location that we call location (China). We assume location does not have any expenditure, $x_{C}=0$ . Assume the transportation cost is the same from location to both domestic locations, $d_{1C}=d_{2C}=d_{C}>1$ and let $a_{C}=d_{C}^{-\theta}$ . Let $\lambda\equiv a_{C}\gamma_{C}$ be the China surge parameter. It is 's competitiveness index (which is the same at locations 1 and 2). Finally, we allow for there to be a general equilibrium impact of China on the input prices at each location. Let $w_{i}(\lambda)$ be the input price at location given China surge $\lambda$ , and let $\gamma_{i}(\lambda)=T_{i} w_{i}(\lambda)^{-\theta}$ be the cost efficiency parameter at as a function of $\lambda$ .

Assumption 1. Assume the wage ratio $w_{2}(\lambda)/w_{1}(\lambda)$ weakly decreases in $\lambda$ and that the ratio $\lambda/\gamma_{1}(\lambda)$ strictly increases in $\lambda$ .

This assumption is sensible because the industry is disproportionately represented at location 2, so any impact on wages from the imports should disproportionately affect location 2. (And $\lambda/\gamma_{1}(\lambda)$ increasing just means that China is becoming relatively more competitive than location 1 as $\lambda$ increases.)

Using (3) and (2), we can write the probability that location 2 sells at 1 as

$\displaystyle \pi_{12}=\frac{a_{12}\gamma_{2}(\lambda)}{\gamma_{1}(\lambda)+a_{12}\gamma _{2}(\lambda)+\lambda}$

(11)

and the general formula for $\pi_{i\ell}$ is analogous. In the location quotients below, only domestic sales are used to calculate sales share (the aggregate

excludes sales from

Proposition 2. Suppose: (a) there are only standardized goods (the pure BEJK model); (b) the parameters are such that location 2 is the high concentration location (formally, $\gamma_{2}>\gamma_{1}$ so $Q_{2}^{rev}>1>Q_{1}^{rev}$ ); (c) there is symmetric distance adjustment between locations 1 and 2 ( $a_{12}=a_{21}<1$ ); and (d) Assumption 1 holds. Then (i) plant size is bigger at the high concentration location ( $Q_{2}^{size}>1>Q_{1}^{size}$ ); and (ii) the revenue location quotient $Q_{2}^{rev}$ of the high concentration location strictly increases in the China surge parameter $\lambda$ .

Proof. See Appendix A.

The expansion of the foreign location hurts sales at both locations. But in the BEJK model, it hurts sales relatively less in location 2, where the industry is concentrated. Note that taking into account general equilibrium effects through Assumption 1 makes the result stronger. Any relative input price decline at location 2 increases its domestic share.

2.2.3 How Introducing the Specialty Segment Changes the Results

It is straightforward to see how introducing the specialty segment changes the results. Consider first the average plant size at a location. Average plant size equals the weighted average of the mean plant size in the standardized segment and specialty segments:

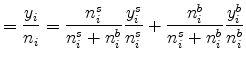$\displaystyle \bar{r}_{i}$	$\displaystyle =\frac{y_{i}}{n_{i}}=\frac{n_{i}^{s}}{n_{i}^{s}+n_{i}^{b} }\frac{y_{i}^{s}}{n_{i}^{s}}+\frac{n_{i}^{b}}{n_{i}^{s}+n_{i}^{b}}\frac {y_{i}^{b}}{n_{i}^{b}}$
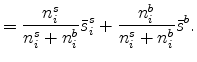	$\displaystyle =\frac{n_{i}^{s}}{n_{i}^{s}+n_{i}^{b}}\bar{s}_{i}^{s}+\frac{n_{i}^{b} }{n_{i}^{s}+n_{i}^{b}}\bar{s}^{b}.$

It is plausible that the average size of standardized plants $\bar{r}_{i}^{s}$ is typically much larger than the average size $\bar{r}^{b}$ of specialty plants. So differences in mean plant size across locations can be driven by differences in the composition of types of plants. High Point can have a large average plant size if it has a large share of standardized plants.

Next consider the impact of the trade shock. For simplicity, assume the elasticity of substitution $\rho$ between the two segments equals one (Cobb-Douglas), fixing the spending shares on the two segments.⁴ To discuss the impact of the shock, we need to distinguish between the two models of the specialty segment offered above. We begin with the nontradable case. The emergence of the new foreign location is irrelevant for the nontradable specialty sector because the infinite transportation precludes imports from location . Suppose there are two domestic locations as in Proposition 2 and the standardized segment lies completely within location 2. The nontradable segment is distributed across the two locations following expenditure. Assume the Census combines the standardized and specialty segments into one industry. Then location 2 will be measured as specializing in the overall industry. If the average plant size of standardized plants is greater than specialty plants, then location 2 will have larger plants than the domestic average. So part (i) of Proposition 2 continues to hold. But now consider an increase in the China surge parameter for standardized goods. This displaces sales of standardized goods at location 2 but has no impact on sales of specialty goods at location 1 (the only type of products produced at 1). Location 2 with high industry concentration and the large plants loses share relative to location 1 on account of the surge from location . This is the opposite of the result for the pure BEJK model (i.e., part (ii) of Proposition 2).

In the alternative model where the specialty goods are high-end niche goods but very tradable, the outcome depends upon the emerging trade partner's ability to compete in the specialty segment as well as in the standardized segment. It is likely that the circumstances that make location a strong competitor in the standardized segment (e.g., an abundance of unskilled labor) are unrelated to its competitiveness in the specialty segment. If that is the case, the specialty segment is not affected and part (ii) of Proposition 2 will not hold in this case either.

3 The Data and Some Descriptive Results

The first part of this section discusses data sources and industry and geographic classifications. The second part provides some initial descriptive results.

3.1 The Data

We analyze the confidential micro data for two programs of the U.S. Census Bureau. In the first, the 1997 Census of Manufactures (CM), the data are collected at the plant level, e.g., at a particular plant location, as opposed to being aggregated up to the firm level. For each plant, the file contains information about employment, sales revenue, location, and industry classification.

The second data file is the 1997 Commodity Flow Survey (CFS). The CFS is a survey of the shipments that leave manufacturing plants.⁵ Respondents are required to take a sample of their shipments (e.g., every 10 shipments) and specify the destination, the product classification, the weight, and the value of the shipment at origin. On the basis of this probability-weighted survey, the Census tabulates estimates of figures such as the total ton-miles shipped of particular products. There are approximately 30,000 manufacturing plants with shipments in the survey.

While we have access to the raw confidential Census data, in some instances, we report estimates based partially on publicly disclosed information rather than entirely on the confidential data. These are cases where we want to report information about narrowly defined geographic areas, but strict procedures relating to the disclosure process for the micro-data-based results get in our way. In these cases, we make partial use of the detailed public information that is made available about each plant in the Census of Manufactures. Specifically, the Census publishes the cell counts in such a way that for each plant, we can identify its six-digit NAICS industry, its location, and its detailed employment size class (e.g., 1-4 employees, 5-9 employees, 10-19 employees, etc.). We use this and other information to derive sales and employment estimates for narrowly defined geographic areas. The data appendix (Appendix B) provides details.

Plants are classified into industries according to the North American Industry Classification System, or NAICS. The finest level of plant classification in this system is the six-digit level, and there are 473 different manufacturing industries at this level. When we estimate the model, we focus on a more narrow set of 172 manufacturing industries. These are industries with diffuse demand that approximately follows the distribution of population, which allows us to use population to proxy demand when we estimate the model. Specifically, through use of the input-output tables, we selected industries that are final goods for consumers. In addition, we included intermediate products used in things like construction and health services that have diffuse demand. We excluded intermediate products used downstream for further manufacturing processing. See the data appendix for additional details.

We use Economic Areas (EAs) as defined by the Bureau of Economic Analysis (BEA) as our underlying geographic unit.⁶ There are 177 EAs that form a partition of the contiguous United States. (We exclude Alaska and Hawaii throughout the analysis.) The BEA defines EAs to construct meaningful economic geographic units, using counties as building blocks. There are 3,110 counties in the contiguous United States that are aggregated to construct the EAs. A metropolitan statistical area (MSA) is typically an EA. In addition, rural areas not part of MSAs get grouped into an EA. As an example, the EA containing the center of the wood furniture industry in North Carolina consists of 22 counties and is called the "Greensboro-Winston-Salem-High Point, NC Economic Area." For ease of exposition, in the discussion in the text we will simply refer to this as "High Point." Finally, to calculate distances between EAs, we take the population centroids of each EA and use the great circle formula.

4 Some Descriptive Results

This subsection presents descriptive evidence that sheds light on the plausibility of our thesis. We begin by looking at a selected set of seven industries for which we are able to exploit additional information about what the plants do beyond the NAICS code. We then discuss evidence for a broader set of industries.

In 1997, the Census changed its industry classification from the SIC system to the NAICS system. Seven NAICS manufacturing industries were redefined to include plants that had previously been classified as retail under SIC. For example, under the SIC system, establishments that manufactured chocolate on the premises for direct sale to consumers were classified as retail. Think here of a fancy chocolate shop making premium chocolate by hand. These were moved into NAICS 311330, "Confectionery Manufacturing from Purchased Chocolate." This industry also includes candy bar factories with more than a thousand employees. This situation--where retail candy operations are lumped into the same industry as mass-production factories making standardized goods--epitomizes what we are trying to capture in our model. Analogous to chocolate, facilities making custom furniture and custom curtains in storefront settings were moved from retail under SIC to manufacturing under NAICS. The logic underlying these reclassifications was an attempt under the NAICS system to use a "production-oriented economic concept" (Office of Management and Budget, 1994) as the basis of industry classification. The concept is that plants that use the same production technology should be grouped together in the same industry. The previous SIC system sometimes followed this logic but was inconsistent in its application.

Table 2 shows the seven NAICS manufacturing industries that were affected this way. We will refer to these industries as the 1997 Reclassification Industries and sometimes as the Seven Industry Sample. All are consumer goods industries, producing some kind of candy, textiles, or furniture. We do not regard these reclassifications in 1997 as a "mistake" by the statistical authority or any kind of deviation from normal philosophy about how to aggregate plants into industries. It is infeasible for the Census to define industry boundaries at extremely narrow detail because otherwise cells become so thin in tabulations that disclosure issues preclude publication. The Census must aggregate in some way, and its general procedure is to group standardized versions and specialty versions of the same product into the same industry.

The reclassification of these plants is fortunate for our purposes as it yields additional information that can be exploited. The data for 1997 contain a plant's SIC code in addition to its NAICS code because tabulations were published both ways for this switchover year. We refer to the plants that are in retail under SIC as SIC/Retail plants and the remaining plants as SIC/Man.

The first thing to note in Table 2 is that the SIC/Retail plants are significantly smaller than the SIC/Man plants. Next look at exports by type. A well-known result due to Bernard and Jensen (1995) is that large plants are relatively likely to export compared with small plants. The consistent pattern is that the SIC/Man plants (which are large on average) have a 3 percent export share, whereas the SIC/Retail plants (which are small) don't export at all. Furthermore, we can think of retail status as an extreme form of non-exporter status; retailers (typically) do not sell to domestic destinations outside their own immediate vicinity, let alone foreign destinations. So the connection reported here between plant size, export status, and retail status can be interpreted as a variant of a well-known empirical pattern.

Suppose we take the specialty-segment-as-nontradable-good variant of our model and use SIC/Retail status as a proxy indicator for our specialty nontradable good. An immediate implication of the model is that the geographic distribution of the SIC/Retail segment will closely track the distribution of demand. The last column of Table 2 provides evidence consistent with this pattern. It reports a measure of the distribution of industry sales which shows that plants in the SIC/Retail segment tend to closely follow population (as retail does more generally), whereas plants in the SIC/Man segment tend to be geographically concentrated.

To explain the measure, recall the definition of the location quotient $Q_{i}^{rev}$ (7) at location for a given industry, but now use population share to approximate expenditure share in the denominator. Analogous to Holmes and Stevens (2004b), for each industry we sort locations (economic areas) by the location quotient from lowest to highest and then aggregate locations into 10 approximately equal-sized population-decile classes. This aggregation helps smooth the data. Let $Q_{d}^{rev}$ be the location quotient of decile . By definition, $Q_{d}^{rev}\leq Q_{d+1}^{rev}$ . If all sales are concentrated in the top decile, then $Q_{10}^{rev}=10$ , as 100 percent of the industry is concentrated among 10 percent of the population.

We are interested in comparing the geographic dispersion of different groups of plants within the same industry. Let index a particular group of plants. (For example, for what we do in Table 2, the index signifies whether a plant is SIC/Retail or SIC/Man.) Suppose plants located in decile of type are indexed by , and let $y_{d,g,k}$ be the sales of plant of type at decile . Let $\bar{Q}^{rev}$ be the sales-weighted overall mean location quotient across plants from all locations of all types. Then

$\displaystyle \bar{Q}^{rev}\equiv\frac{\sum_{d}\sum_{g}\sum_{k}y_{d,g,k}Q_{d}^{rev}} {\sum_{d}\sum_{g}\sum_{k}y_{d,g,k}}=\frac{\sum_{d}y_{d}\frac{\frac{y_{d}}{y} }{\frac{1}{10}}}{y}=10\left[ \sum_{d=1}^{10}\left( \frac{y_{d}}{y}\right) ^{2}\right] \text{.}$

Hence, the mean location quotient $\bar{Q}^{rev}$ is exactly the standard Herfindahl index of concentration, times a factor of 10. If the entire industry is concentrated in the top decile, then $\bar{Q}^{rev}=10$ . If it is spread equally across the 10 deciles, then $\bar{Q}^{rev}=1$ . The main interest for this subsection is the conditional mean location quotient of plants of type

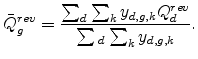
$\displaystyle \bar{Q}_{g}^{rev}=\frac{\sum_{d}\sum_{k}y_{d,g,k}Q_{d}^{rev}}{\sum{}_{d} \sum_{k}y_{d,g,k}}\text{.}$

Note that conditioning on type

enters only through the weights; plants of all types in decile

are used to define the $Q_{d}^{rev}$ associated with a sale.⁷ Conceptually, we are taking each dollar of sales in the data and associating it with the location quotient of its origin and taking means.

The last column of Table 2 presents the mean location quotients conditional on SIC/Retail or SIC/Man status. There is a clear pattern in the table that the SIC/Man segments tend to have significantly higher geographic concentration than the corresponding SIC/Retail segments. Moreover, the measures for the SIC/Retail segments are close to one. For example, in the wood furniture industry, the mean is 1.17 for SIC/Retail and 4.42 for SIC/Man.

The SIC/Retail plants in these industries are clearly what we have in mind by specialty plants. But what about the many small plants in the SIC/Man segment in these industries? We address this issue for the furniture plants by exploiting unique information available for these plants. The Census of Manufactures asks a sample of plants to itemize their shipments in various product categories. In most cases, the product definitions are unrelated to the specialty product versus standardized product distinction that would be useful for our paper. However, for the furniture industries, new product definitions were created as part of the 1997 reclassification that get directly at what we want. Specifically, across all the various furniture products, a distinction is made between products that are custom made and those not custom made, and custom products are an example of what we have in mind for specialty products.⁸ For each plant with the requisite data, we define the custom share for the plant to be the share of product shipments in the custom category. (Not all small plants are required to fill out the detailed survey of shipments and we throw out imputed values, so our data here are for a sample of plants rather than for the universe.) Table 3 reports unweighted means of this variable for the three furniture industries from Table 2 together, and with Kitchen Cabinets separated out from Household Furniture (where Household Furniture combines Wood and Upholstered).

The first thing to note at the top of the table, where the three industries are grouped together, is that plants in the SIC/Retail category on average have a significantly higher custom share than plants in the SIC/Man category, .82 versus .42. Second, within plants classified as SIC/Man, the share falls sharply with plant size, from .59 to .30 to .09 across the three size categories.

Third, looking at the breakdown where Kitchen Cabinets are separated out, we see that Kitchen Cabinets are much more likely to be custom made than Household Furniture. This is not surprising, since a kitchen cabinet is built in and has to fit a particular spot in a kitchen. In contrast, a wood bureau or dresser can be pushed up against a bedroom wall. Note from Table 2 that Kitchen Cabinet plants tend to be smaller than Household Furniture plants. Hence, when we look at the top of the table with all the industries combined, we can see that part of the reason for the sharp decline in custom share with plant size is the industry composition effect that kitchen cabinet plants make up a disproportionate fraction of the small plants. But a key point to note is that the size relationship in the custom share persists even after controlling for industry at a narrow level. Within SIC/Man plants making kitchen cabinets, the share falls sharply from .70 to .56 to .28 across the size classes. Within SIC/Man plants making household furniture, it falls from .08 to .05 to .03.

Naturally, our interest extends beyond the seven reclassification industries in Table 2. Outside these seven industries, we do not have useful product and SIC code distinctions to work with. We do have plant size for each establishment, and our last descriptive exercise makes use of it, extending earlier results in Holmes and Stevens (2002). We break plants down into four employment size categories and calculate the conditional mean location quotient $\bar{Q}_{g}^{rev}$ for each size category . These values are in the column labeled "Raw" in Table 4. Next we add six-digit NAICS fixed effects and report how the fitted values vary with plant size, holding industry effects fixed (at the mean level).⁹ These go in the column labeled "NAICS Fixed Effect."

As a reference point, we begin with the seven reclassification industries. The results are in the top panel of Table 4. In the column labeled "Raw," we see that the mean location quotient is only 1.36 in the smallest size category and rises all the way to 6.13 for the largest category. We expect that part of this relationship stems from the fact that some industries (like Kitchen Cabinets) tend to have small plants and be geographically disperse. While the inclusion of six-digit NAICS fixed effects does attenuate the relationship, it remains quite large, going from 2.46 in the smallest plant size category to 5.83 at the top. This pattern is consistent with that established in Table 2 for these industries. There, the category with large plants on average (SIC/Man) is more geographically concentrated than the category with small plants (SIC/Retail).

In the second panel we do the same exercise for the 165 other industries with diffuse demand for which we will estimate the model. The same pattern holds. Using fixed effects, the mean location quotient increases from 3.72 in the smallest plant size category to 5.41 in the largest category. The spread found here, 3.72 to 5.41 (a difference of 1.69), is half the spread of 2.46 to 5.83 (3.37) found with the seven reclassification industries. The attenuation of the effect is not surprising, as the seven are a selected sample that exemplifies the factors we are highlighting. However, the very same qualitative relationship that holds in our selected sample of seven industries also holds in the broad sample. We obtain similar results in the bottom panel for the remaining 301 industries that do not have diffuse demand.

We conclude by noting related results in Holmes and Stevens (2010b). Using CFS data and the same plant size categories as in Table 4, we show that small plants within the United States ship shorter distances than large plants. In summary, small plants tend to be more geographically diffuse, they tend to not export, and they tend to ship short distances within the United States, compared with their large plant counterparts.

5 Estimation of the Model

This section estimates the model. The first subsection considers a constrained version of the model where the standardized-goods segment is the entire industry. This subsection serves the role of providing first-stage estimates that are used later. The next subsection brings the specialty-goods segment into the analysis.

5.1 First-Stage Estimates: The Constrained Model with Only Standardized Goods

In what we call the first-stage estimates, the model is estimated under the assumption that each six-digit NAICS is a distinct standardized-product industry, i.e., each industry has its own BEJK model parameters. This procedure pins down distance adjustment parameters that will be used throughout the paper.

For each industry , the data-generating process for the industry is summarized by a vector $\Gamma^{h}=(\gamma_{1}^{h},\gamma_{2}^{h} ,...,\gamma_{L}^{h})$ that parameterizes the relative cost efficiencies of the various locations and an $L\times L$ matrix $A^{h}$ , with elements $a_{\ell i}^{h}$ , that parameterize the distance adjustments in (3). We normalize so the $\gamma_{i}^{h}$ sum to one across locations .

Assume the distance adjustment for industry takes the form

$\displaystyle a_{\ell i}^{h}=a^{h}($ dist $\displaystyle _{\ell i})=\exp(-\eta_{1} ^{h}$ dist $\displaystyle _{\ell i}-\eta_{2}^{h}$ dist $\displaystyle _{\ell i}^{2})$

(12)

so that $\ln a_{\ell i}^{h}$ is quadratic. If $\eta_{2}^{h}=0$ , then $\eta _{1}^{h}$ can be interpreted as the decay rate per mile for industry

We have restricted attention to the 172 industries for which demand is diffuse, approximately following population. For simplicity, we assume this is exactly true, so that expenditure $x_{i}^{h}$ at location in industry is proportional to population and normalize so $\sum_{i}x_{i}^{h}=1$ . The Census of Manufactures (CM) covers the universe of all plants in the United States. Subtracting out the exports of each plant, we can aggregate the plant-level sales revenue data to get $y_{i}^{h}$ , the value of domestic shipments originating at location in industry .

Other than export information, there is no destination information in the CM. However, the CFS provides survey information on shipments and their destinations that we can link to plants (and thereby determine industry). A concern we have with the CFS data is that local shipments may be overrepresented in the data. These seem too high, more than can be absorbed by local demand. We expect that sometimes shipments intended for faraway destinations get there by way of a local warehouse In cases like these, the destination found in the CFS may be the local warehouse rather than the ultimate destination. Appendix B discusses this issue further and provides some evidence on the importance of wholesaling for the manufacturing industries in our sample.

The form of our data leads us to the following strategy for estimating $\eta^{h}=\left( \eta_{1}^{h},\eta_{2}^{h}\right)$ and the productivity vector $\Gamma^{h}$ for each industry. We pick $(\eta^{h},\Gamma^{h})$ that perfectly match the distribution of sales at originating locations, as we directly observe the universe of sales at each location. Because of our concern about excessive local shipments, we throw out all local shipments in the CFS that are less than 100 miles and fit the conditional distribution of the longer shipments. Formally, set $\overline{\emph{dist}}=100$ and let $B(i,\overline{\emph{dist}})$ be the set of all destinations at least $\overline{\emph{dist}}$ from an originating location . The conditional probability that an industry shipment originating in location goes to a particular destination $\ell\in B(i,\overline{\emph{dist}})$ equals

$\displaystyle p_{\ell i}^{h,cond}=\frac{y_{\ell i}^{h}}{\sum_{\ell^{\prime}\in B(i,\overline{\emph{dist}})}y_{\ell^{\prime}i}^{h}}\text{.}$

For each value of $\eta^{h}$ , we solve for the vector $\Gamma^{h}$ such that the predicted total sales of the industry at a given location equals total sales in the CM data. Appendix C outlines our algorithm for finding a solution $\Gamma^{h}(\eta^{h})$ to the 177 nonlinear equations for the 177 locations. We can then write the conditional probability above as a function of $\eta^{h}$ . We pick $\eta^{h}$ to maximize the conditional likelihood of the destinations observed in the shipment sample.¹⁰

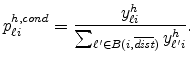
Table 5 reports estimates of $\hat{\eta}_{1}^{h}$ and $\hat{\eta}_{2}^{h}$ for several selected industries and summary statistics of the estimated parameters across the entire set of 172 industries. (See the web document, Holmes and Stevens (2010a), for detailed estimates by industry.) The reported industries are those at the 25th percentile in the distribution of the implied value of , the distance adjustment at 100 miles. The bottom industry in this dimension is "Ready-Mix Concrete," a well-known example of manufacturing industry for which shipments are overwhelmingly local. (See Syverson (2004).) For this industry and four other industries where shipments are overwhelmingly local (such as "Ice" and "Concrete Blocks"), we included shipments less than 100 miles in the estimation.¹¹ We see in Table 5 that the estimate of for Ready-Mix Concrete is .01. For Ice (not shown in the table), and for Asphalt Paving (not shown) it equals . These industries are essentially nontradable beyond 100 miles. Butter is the 25th percentile industry. For this industry there is a high degree of tradability at 100 miles ( ), but tradability drops off steeply at 500 miles ( ). The highest-ranked tradability industry is "Other Hosiery & Sock Mills." We truncate the function at one in a few industries like this where the unconstrained value exceeds one. Imposing this constraint makes little difference; unconstrained, the distance adjustment for "Other Hosiery & Sock Mills" at 100 miles is

Table 5 also reports the mean values of the parameter estimates across all industries. On average, $\eta_{1}=.003,$ meaning that if we look only at the linear component of (12), the average drop-off in is .3 percent per mile. The fact that the coefficient $\eta_{2}$ on the quadratic term is negative adds a convexity element to the relationship; the drop-off decreases with distance at a decreasing rate.

We have also reestimated the model using the data from the 1992 Census of Manufactures. We call this the 1992 SIC sample because industry classification was based on SIC that year. We use the same selection criterion to identify industries with diffuse demand and arrive at 175 industries. The mean values of the estimates are similar to the baseline 1997 NAICS case. For those industries with no change in definition between the 1992 SIC and 1997 NAICS, there is a very high correlation in the implied values of . The CFS survey for the earlier period was a larger, better-funded survey, with many more observations. In particular, the average number of shipments used to estimate the parameters of each industry is 8,500 for the earlier period and about 4,000 in the later period. Thus, estimates for the 1992 SIC sample are more precise.

Table 5 also shows what happens to the estimates when the distance threshold for including shipments in the analysis is varied. As discussed above, CFS manufacturing shipments may overstate local shipments, as some local shipments may end up in the wholesale sector to be ultimately shipped to faroff destinations. When we set $\overline{\emph{dist}}=0$ so that no observations are excluded, the average value of falls from the baseline level of .80 to . 71. With local shipments included, the model is accounting for the high relative likelihood of local sales by making transportation costs higher. If we go in the other direction and raise the cutoff to $\overline {\emph{dist}}=200$ , the average value of rises from .80 to .85.

The last topic of this subsection is goodness of fit. Recall that by construction, the total shipments originating in each location in the estimated model perfectly fit the data. For a notion of goodness of fit, we look at the distance pattern of shipments. We break the shipments above 100 miles into three distance categories, (1) 100 to 500 miles, (2) 500 to 1,000 miles, and (3) over 1,000 miles. For industry , let $share_{c}^{h}$ be the share of the shipments above 100 miles that are in distance category $c\in\{1,2,3\}$ in the data. Let $share_{c}^{h}$ be the fitted value in the estimated model. Table 6 presents descriptive statistics. In the data, on average across the industries, a share .44 of the 100-mile-plus shipments are in the 100- to 500-mile category. This figure compares to an average share of .38 in the estimated model. The model has a tendency to somewhat understate the shortest distance category and somewhat overstate the two longer distance categories. By construction, the destination of shipments in the model exactly follows the distribution of population. So locations far away from any producers will nevertheless be required in the model to receive their share of shipments. The last part of Table 6 shows that the fitted values of the model do a very good job in accounting for the cross-industry variation in the distance distribution. 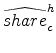The slope of $share_{c}^{h}$ in a regression on $\widehat{share}_{c}^{h}$ is approximately one for all three categories.

5.2 Second-Stage Estimates: The General Model with Specialty Goods

We now consider the general model that includes the specialty segment. Our estimation strategy focuses on determining the specialty-segment share of plant counts in an industry, rather than the specialty-segment share of revenue. Both targets are interesting, but the first target is easier to get at, so that is where we aim for a first paper.

Specialty plants are small compared to standardized plants. Thus, the count share of the specialty segment is large compared with the revenue share. To explain our procedure, it is easiest to begin by outlining how it works in a limiting case, when the revenue share of the specialty segment is zero.¹² Next we explain what we actually do, in allowing for a positive specialty-segment revenue share.

In the limiting case where the specialty-segment revenue share is zero, the first-stage procedure explained above delivers the correct estimates of the productivity vector $\Gamma$ of the standardized segment. (At this point, leaving out the superscript for industry is convenient.) This holds because the industry revenue used to construct the estimates exactly equals standard-segment revenue, for this limiting case. With estimates of $\eta$ and $\Gamma$ from the first stage, we can determine the plant counts for the standardized segment, subject to the scaling normalization $\nu^{s}$ . Recall from (4) that standardized-segment plant counts equal $n_{i} ^{s}=\nu^{s}\pi_{ii}(\eta,\Gamma)$ . Next consider plant counts for the specialty segment. In the nontradable case, using equation (5), specialty plant counts equal $n_{i}^{b}=\nu^{b}x_{i}$ . In the high-end niche case, counts depend on the supply of specialty-specific factors through (6). As a first cut, assume supply is proportional to population. This delivers $n_{i}^{b}=\nu^{b}x_{i}$ for this case as well. So for either case, the total number of plants in the given industry--standardized plus specialty--equals

$\displaystyle n_{i}=\nu^{s}\pi_{ii}(\eta,\Gamma)+\nu^{b}x_{i}$ .

(13)

To take (13) to the data, we introduce an error term. Suppose the observed total number of plants in the given industry at location equals the above expression plus an error term $\lambda+\varepsilon_{i}$ ,

$\displaystyle \tilde{n}_{i}=\nu^{s}\pi_{ii}(\eta,\Gamma)+\nu^{b}x_{i}+\lambda+\varepsilon _{i}$ ,

(14)

where the error term has variance proportional to location

's population $x_{i}$ . We use weighted least squares to construct estimates of the slopes $\hat{\nu}^{s}$ and $\hat{\nu}^{b}$ and the constant $\hat{\lambda}$ for each industry. (Given the results of the first stage, $\pi_{ii}(\eta,\Gamma)$ is data for the industry at this point.)

We now explain the modification of the above procedure to allow for positive specialty-segment revenues. Take as given a value $\bar{r}^{b}$ of specialty revenue per plant for the industry. Use $\bar{r}^{b}$ , along with the estimate $\hat{\nu}^{b}$ from above, to construct an estimate of specialty-segment revenues at location ,

$\displaystyle \hat{y}_{i}^{b}=\bar{r}^{b}\hat{\nu}^{b}x_{i}$ ,

and from this construct an estimate of standardized-segment sales at

$\displaystyle \hat{y}_{i}^{s}=\max\{\hat{y}_{i}-\hat{y}_{i}^{b},0\}$ .

Go back to the first stage to solve for a new productivity vector $\Gamma^{\prime}$ that exactly fits the new estimate of the standardized-segment sales distribution $\hat{y}_{i}^{s}$ across locations

.¹³ Using the new value of $\Gamma^{\prime}$ , run the weighted least squares regression above to produce new estimates $\hat{\nu }^{s\prime}$ and $\hat{\nu}^{b\prime}$ of the slopes. Iterate until convergence on estimates $\hat{\nu}^{s,h}$ and $\hat{\nu}^{b,h}$ on the plant count coefficients for the two segments for industry

. (Again, keeping track of the

superscript is convenient.) It remains for us to specify the choice of average specialty-plant sales revenue $\bar{r}^{b,h}$ . For each industry

, we set $\bar{r}^{b,h}$ equal to the average sales size of plants in the one to four employees category. We have experimented with alternative values for $\bar{r}^{b,h}$ , and it makes little difference for the estimates of $\hat{\nu}^{s,h}$ and $\hat{\nu}^{b,h}$ .¹⁴

Table 7 presents the results. The individual estimates are reported for the seven reclassification industries from Table 2; summary statistics are reported for the broader set of industries. We first note that allowing for the constant term $\lambda^{h}$ makes little difference; when we reestimate (14) without an intercept, we get similar results. Next note that the coefficient estimate $\hat{\nu}^{b,h}$ for specialty goods tends to be quite large. Given the scaling that the $x_{i}$ sum to one, $\hat{\nu}^{b,h}$ is an estimate of the total count of specialty plants in the industry.

Define the implied specialty count share to be

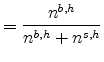Specialty count share for industry $\displaystyle h$	$\displaystyle =\frac{n^{b,h} }{n^{b,h}+n^{s,h}}$
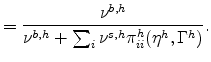	$\displaystyle =\frac{\nu^{b,h}}{\nu^{b,h}+\sum_{i}\nu^{s,h}\pi_{ii}^{h}(\eta^{h} ,\Gamma^{h})}.$

This model statistic is reported in the last column of Table 7. It averages 75.8 percent across the seven reclassification industries and 66.0 percent across the remaining 165 diffuse demand industries.

Table 8 provides more details about the distribution of the specialty count share by dividing the 172 industries into quartiles based on the specialty count share. There is no mechanical reason why the estimated coefficient $\nu^{b}$ for the regression (14) is necessarily positive. In fact, we can see in Table 8 that one industry comes in with a negative count share equal to -3.7 percent. There is also a second industry with a negative share equal to -3.0 percent. Aside from these two exceptions (which are approximately zero in any case), the other 170 industries all have strictly positive estimates of the specialty count share. Moreover, we can see in the table that the 25th percentile equals 57 percent; i.e., three-quarters of the industries have a specialty count share that exceeds this level. Thus, the estimates reveal that for the vast majority of industries, specialty plants make up the majority of plant counts.

The last column of Table 8 connects the estimates of specialty count shares in the model to shares of plants that are small in the data. In the data, a small plant is defined as a plant with 1 to 19 employees. We do not expect an exact correspondence between specialty plants in the model and small plants in the data; a small plant in the data could be a specialty plant, but it could also be a standardized plant with a low productivity draw. While there is not an exact correspondence, we expect that the specialty share in the model would likely move together with the small plant share in the data; Table 8 confirms this expectation. In particular, in the bottom quartile of industry specialty shares, the mean small plant share averages 48 percent, and this average increases monotonically across the quartiles to 67 percent for the top quartile.

6 Analysis of the Estimates

We use the estimated model to analyze two issues. The first is the plant size/geographic concentration relationship. The second is the impact of the recent surge in imports from China.

6.1 The Plant Size/Geographic Concentration Relationship

Define a high-concentration industry location to be one where the revenue location quotient is above 2 and where the location has at least 5 percent of the industry's revenues. Across the 7 reclassification industries, there are 23 different high-concentration industry locations. These locations are listed in Table 9, sorted for each industry by descending sales quotient. The breakdown into the count and size quotient is also reported. (Recall $Q_{i}^{rev}=Q_{i}^{count}\times Q_{i}^{size}$ .) It is clear from inspection of the data that the size margin plays an important role in contributing to how an industry expands at a location. Consider the wood furniture industry in the High Point area, where the revenue quotient is 27.7. The breakdown is $27.7=4.2~\times~6.6$ . Thus, average plant size in the area is 6.6 times the national average. A high contribution from the size margin holds for virtually all of the 23 individual industry locations listed in Table 8. Over these 23 cases, the size quotient on average is 5.4, compared with an average count quotient of 4.3.

The last two columns contain fitted values of the size quotient for the constrained model with only a standardized segment (the BEJK model) and the full model that includes the specialty segment.¹⁵ From the theoretical discussion in Section 2, we know that when transportation costs are not zero (and making further assumptions about the distribution of demand), the BEJK model implies that average plant size is bigger in locations that specialize in an industry. With only three exceptions, we see in Table 9 that this qualitative pattern holds for the fitted BEJK model. However, the BEJK model fails quantitatively, as the predicted size differences are small. The count margin is doing the main work of driving variations in $Q_{i}^{rev}$ , just like in the numerical examples of the BEJK model in Table 1. When we turn to the full model and allow for the specialty segment, the predicted size quotients are much larger and close to what they are in the data (though still smaller). The average size quotient in the full model equals 4.0, compared with an average of only 1.3 in the constrained model. These differences between the full and the constrained model are driven by compositional differences across locations between standardized and specialty goods in the full model. In fact, if we look only at the standardized segment in the full model, the size distribution is virtually identical to what it is in the constrained model.

Next consider the broader set of industries (the 165 remaining diffuse demand industries). We see in Table 9 that the same pattern holds with these industries as holds with the 7 reclassification industries. The mean size quotient is 5.3, so the size margin plays a big role in how locations specialize in an industry. The mean fitted value of the BEJK model of 1.3 is way off. The corresponding mean in the full model, at 3.3, is still too small but gets much of the way there. The industry-location level observations in Table 9 suggest some skewness in the distribution of the size quotients, so it is of interest to also look at the median. The median size quotient in the full model of 2.5 is close to the median of 2.6 in the data.

6.2 Impact of the China Surge

Imports from China have surged in a number of manufacturing industries in recent years. This subsection identifies a set of "China surge" industries.¹⁶ For this set of industries, the subsection examines how the geographic distribution of production in the United States has shifted in response. It compares the results to the prediction of the constrained model that does not allow for the specialty segment (i.e., the pure BEJK model). The constrained model is inconsistent with what actually happened. In contrast, the full model with the specialty segment fits the data. The last part of the subsection uses the full model to estimate the specialty count share in 2007 and compares the estimates to 2007. In the China surge industries, there is a dramatic decline in standardized segment plant counts.

We classify an industry as having a China import surge if the industry experienced a 25 percentage point increase in overall imports as a share of shipments over the period 1997 to 2007 and if China's share of total imports in the industry as of 2007 exceeds 40 percent.¹⁷ Of the 172 industries for which we have model estimates, there are 17 China surge industries, and they are listed in Table 10. The overall import share of these 17 industries rose on average from 34 percent in 1997 to 70 percent in 2007. The share of imports from China increased from 26 to 61 percent over this same period. Employment declined 66 percent on average over the period. In the infant apparel industry, employment declined an astonishing 97 percent.

It is useful to have a comparison group of industries that (1) unlike the China surge industries have not been negatively affected by imports but (2) are similar to the China surge industries in being tradable within the United States. We use food (NAICS = 311) and beverage (NAICS = 312) industries for this purpose. As shown in the bottom row of Table 9, imports in these industries are relatively small. On average, employment increased by 5 percent for these industries over the time period.

The last two columns of Table 10 report mean plant-level employment by industry for each year. Mean plant employment fell dramatically. On average across all the China surge industries, it fell from 63 to 30 employees per plant. In infant apparel, it fell from 178 to 11. A decrease in average plant size from an import surge is consistent with our theory, which emphasizes the displacement of large mass-production plants by Chinese imports. The pattern is also consistent with the standard theory. The efficient plants--which would have been large without the China surge--survive the China surge but at a smaller output level. (Inefficient plants that would have been small without the surge shut down.) To evaluate what our theory adds to the analysis, we need to look at more detailed implications.

We take our first-stage model estimates for 1997 of the pure BEJK model of the standardized sector for each of these industries and simulate the impact of a large import shock on the distribution of domestic production in 2007. As discussed in the theory section, the transportation cost from China is assumed to be the same to all domestic locations. For each industry , we set the China surge parameter for 1997 and 2007 to $\lambda_{C,1997}^{h}=0$ and

$\displaystyle \lambda_{C,2007}^{h}=\frac{\sum_{\ell=1}^{177}\left( \sum_{k=1}^{177} \gamma_{k}^{h}a_{\ell k}^{h}\right) }{177}$ .

(15)

The term in parentheses is the denominator of (2), the sum of competitiveness across originations. On account of this change in China's delivered productivity, China's share goes from zero to about half of the market. In the exercises that we do, the results are not sensitive to alternative values of (15) that we considered, e.g., half the value of (15). The reason is that we are looking at the relative impact on the distribution of production of the shock rather than the absolute impact.¹⁸ Finally, we take into account that the distribution of demand differs across time periods, by using population estimates for 1997 and 2007 when calculating the quotients for each year (this, however, makes little difference).

For the sake of illustration, it is useful to start with a detailed discussion of the wood furniture industry in High Point. Recall from above that in 1997, the sales revenue location quotient equaled $Q_{1997}^{rev}=27.7$ in High Point. Using the estimates of the BEJK model from stage 1 for 1997, to simulate the impact of a China surge equal to (15), and plugging in 2007 population values, results in a predicted value of $\hat {Q}_{2007}^{rev}=28.4$ for 2007 at High Point. This predicted increase in our estimated model with 177 locations goes the same way as the theoretical result in Proposition 2 for the special case with only two domestic locations. The pure BEJK model is predicting that locations with large plants and large domestic market share increase domestic share after a shock. The opposite actually happened. The revenue quotient for High Point fell from 28.4 to 12.8, meaning High Point's share of the domestic market fell by more than half. Panel A of Table 11 provides cell counts by plant size for the wood furniture industry that gives more details about the collapse between 1997 and 2007. The table makes clear that the collapse of the industry is at the high end of the size distribution. Looking at the United States as a whole, we see that 48 plants in 1997 have more than 500 employees, and that number falls to only 20 for 2007. In contrast, for the smallest size category, there is virtually no change. Now look the counts for just High Point to get a sense of the disproportionate way that, in the 1997 data, large plants are concentrated in High Point. In particular, 14 out of 48 U.S. plants with 500 or more employees are in High Point for 1997, but only 51 out of 3,091 plants with less than 20 employees. Finally, observe the huge losses in large plants at High Point from 1997 to 2007.

To examine the broader set of China surge industries, we find the equivalent of High Point for these other industries. Define the 1997 Primary Location to be the location with the highest 1997 location sales quotient, of those locations with at least 5 percent of 1997 sales. Table 12 restates the variables just discussed for wood furniture and then presents the summary statistics about these same variables for the other industries. For the China surge industries, simulating the BEJK model for 2007 leads to a predicted increase on average of the revenue quotient $Q^{rev}$ from 26.9 to 29.4. (If we look at the 17 individual industries, there are only 2 exceptions going the other way.) What actually happened is that the sales revenue location quotients fell dramatically, on average, from 26.9 to 12.2. (If we look at the industries individually, there is only one exception to this pattern.) When we look at the detailed size distribution information for all the China surge industries in Panel B of Table 11, we see the same thing is true with the broader set of industries as holds for just wood furniture. The big plants are collapsing and the primary locations are bearing the brunt of this collapse. Note in particular that the primary locations had 33 plants with more than 500 employees in 1997, but by 2007 this count had plunged to only 3 plants.

We address an issue regarding the definition of the primary location. It is defined as the location of first rank in its relative market share $Q^{rev}$ as of 1997. A number one location can only go down in the ranking. In particular, we expect the well-understood mechanism of "regression to the mean" to play some role, given the normal ebb and flow of market shares across locations. To gain some perspective on its contribution, we similarly define primary locations in the food and beverage comparison industries. Just as is the case for the China surge industries, average plant size is quite high for the food and beverage industries at the primary locations. Also, the average sales revenue quotient is similarly quite high (37.4 in the food and beverage industries, 26.9 in the China surge industries). Even though these industries were not actually affected by imports, we can use the estimated model to simulate a hypothetical China surge. For these industries, the predicted BEJK sales revenue quotients indeed increase on average at the primary locations, just as they do for the China surge industries. As we would expect from regression to the mean, in the data there is actually a decline, from 37.4 to 31.6. The decline is relatively small, only 16 percent, compared with the average 59 percent decline for the China surge industries. We get the same conclusion if we look at the median instead of the mean. We conclude that the sharp observed fall at the primary locations of the China surge industries extends substantially beyond anything we would expect to see from regression to the mean, in the normal ebb and flow of market shares.

We next look at what happens in big cities. Big cities are interesting to look at because in recent decades, in a relative sense, they have not been the home of large mass-production factories (which have instead concentrated in small factory towns like High Point). Given the demand for specialty goods in large cities and given the supply of unique skills in big cities that can serve as inputs for specialty goods, a priori we expect that as China knocks out standardized goods in places like High Point, the industry will shift toward specialty goods made in big cities. To examine this issue, we combine the 20 largest economic areas by population into one group and calculate the various quotients for the group as a whole. (We get similar results for other groupings of large cities.) Table 13 is the analogue of Table 12, with the big city aggregate serving as the location of interest instead of the primary location. Note that big city plants do indeed tend to be small, with $Q_{1997}^{size}=.78$ , on average across the industries. As of 1997, sales were slightly underrepresented in big cities, $Q_{1997}^{rev}=.97$ . The BEJK model predicts no change going into 2007. What actually happened is that the sales quotient increased in the big city aggregate, rising to $Q_{2007} ^{rev}=1.08$ , to become over-represented. (Looking at the individual industries, we can see that there are only 3 exceptions to this pattern of the 17 industries.) By contrast, in the food/beverage comparison group, nothing is happening.

Thus, the predictions of the pure BEJK model for changes in sales share are inconsistent with the data. Turning now to predictions of the general model that allows for the specialty segment, we first reiterate that we have not estimated a model of the division of revenue between the two segments. Rather, our estimated model is one of plant counts for the two segments. We will use the estimated model to examine predictions about changes in plant counts from a China surge. Before doing that, we note that our general model with specialty goods is consistent with the qualitative patterns about changes in sales revenues across locations just documented. Primary industry locations with large plants like High Point are in decline in terms of sales share because these locations specialize in the standardized goods that China sells. Locations with small plants, including large cities, are in relative ascent because these locations specialize in specialty goods that are poor substitutes for what China is selling.

Table 14 reports our results, comparing the predictive power for plant counts of the pure BEJK model and our general model. As in Tables 12 and 13, to calculate the fitted values for 2007, we take the estimated models for 1997 and plug in the China surge (15) as well as the 2007 population values. Panel A looks at the primary locations. Analogous to what happens in Table 12 with sales revenue shares, the pure BEJK model fails with plant counts as well. The model predicts too many plants at the primary locations (i.e., plants are too small), but in addition predicts the count shares at these locations will increase from the China surge, while in actuality they decreased significantly. The predictions of the general model are roughly in line with what happened. Across the China surge industries, the count quotients decrease on average from 6.8 to 5.5 (a decline of 1.3 points), while in the data the decrease is from 5.8 to 3.9 (a decline of 1.9 points). Panel B considers a prediction exercise that looks at all 177 Economic Areas together. For each industry, we regress the change in count quotient $\Delta Q_{i}^{count}=Q_{2007}^{count}-Q_{1997}^{count}$ for location on the predicted changes $\Delta\hat{Q}_{i}^{count}=\hat{Q}_{2007} ^{count}-\hat{Q}_{1997}^{count}$ for both models. For the pure BEJK model, the slope in the regression is actually slightly negative as changes tend to go in the opposite direction from what the pure BEJK model predicts. In contrast, for the general model the slope is close to one. (It equals .93 for wood furniture and averages .89 across all 17 industries.) This is what we get when we do this exercise on the industries actually experiencing a China surge. For the food and beverage industries, which didn't actually experience such a surge, we get a range of noisy values that on average are relatively close to zero.

Taking the results of Table 14 as a validation of our general model, our final exercise uses 2007 data to estimate specialty and standardized plant counts for that year and compares these with the 1997 estimates. The results are in Table 15.¹⁹ We begin as before with a discussion of wood furniture. For 1997, we estimate there are 697 and 3,150 plants in the standardized and specialty segments of this industry, or shares of 18.1 and 81.9 percent, respectively. For 2007, the respective counts are 213 and 3,215, or 6.2 and 93.8 percent. Thus, according to these estimates, the standardized segment collapsed to about a third of its initial plant counts, while the specialized segment remained relatively stable. This finding is consistent with the hypothesis of this paper.

For the China surge industries overall (Panel B of Table 15), there is a collapse of the standardized segment to about one-third of its prior level, similar to the wood furniture case. The specialty segment also decreases, but at a much lower rate than the standardized segment. The situation is quite different with the food and beverage industries, which has experienced little in the way of import competition. The standardized segment has actually increased somewhat in plant counts. Finally, when we look at the remaining industries, there is a downward trend in standardized plant count share. But the impact is small compared with what is happening to the China surge industries.

7 Conclusion

This paper develops a model in which industries are made up of mass-production factories making standardized goods and specialty plants making custom or niche goods. The paper uses a combination of confidential and public Census data to estimate parameters of the model and, in particular, produces estimates of plant counts in the specialty and standardized segments by industry. The estimated model fits the observed plant size/geographic concentration relationship relatively well. The estimates reveal that, for those industries that have been heavily affected by a surge of imports from China, there has been a dramatic decline in plant counts for the standardized segment, while the specialty segments have been relatively stable. The paper also shows that for the China surge industries, locations with large concentrations of the industry and large plants, like High Point, North Carolina, have declined relative to the rest of the country. These results are consistent with the hypothesis that products made in China are close substitutes to the products of big plants (like those in High Point), and not so close substitutes to the products of the small plants that are diffuse throughout the country. The results are inconsistent with standard theories that assert that small plants are just like large plants, except for having a low productivity draw.

In our theory, if a plant in the United States is huge, it is a signal that the plant is potentially vulnerable to competition from China. A huge plant is likely making something that can be traded across space--something that can be put in a container and shipped--as a local market would not likely be able to absorb all the output of a given huge plant.

To make progress, the paper proceeds under the abstraction that each plant is in one of two discrete categories: standardized or specialty. To illustrate these categories, the paper gives the example of a furniture factory with more than a thousand employees and an Amish shop employing a few skilled craftsmen. In future work, allowing for a continuum of possibilities in between the limiting two-type case would be useful. The logic of our ideas, which is put in sharp relief with our focus on the limiting case, should extend to more general approaches. That is, a comparison of a megafactory with a tiny Amish shop highlights forces that in principle are operative--albeit at a reduced extent--in a comparison of a 200-employee plant with a 50-employee plant.

Appendix A: Proof of Proposition 2

For now assume $w_{2}(\lambda)/w_{1}(\lambda)$ is constant, so $\gamma _{2}(\lambda)/\gamma_{1}(\lambda)$ is constant. Since $\lambda/\gamma_{1}(\lambda)$ strictly increases and since a proportionate change in $\gamma_{1}$ , $\gamma_{2}$ , and $\lambda$ leaves the $\pi_{\ell i}$ the same, without loss of generality assume $\gamma_{1}$ is constant in $\lambda$ .

Letting $\alpha=a_{12}=a_{21}$ , for this special case we can write the probability that location sells to location $\ell$ as

$\displaystyle \pi_{11}$	$\displaystyle =\frac{\gamma_{1}}{\gamma_{1}+\alpha\gamma_{2}+\lambda}$
$\displaystyle \pi_{12}$	$\displaystyle =\frac{\alpha\gamma_{2}}{\gamma_{1}+\alpha\gamma_{2}+\lambda }$ ,

where the expressions for $\pi_{21}$ and $\pi_{22}$ are analogous. Since $\gamma_{2}>\gamma_{1}$ , it follows that $\pi_{22}>\pi_{11}$ . The ratio of sales between the two locations is

$\displaystyle \frac{y_{2}}{y_{1}}$	$\displaystyle =\frac{\pi_{12}x_{1}+\pi_{22}x_{2}}{\pi_{11}x_{1} +\pi_{21}x_{2}}=\frac{\frac{\alpha\gamma_{2}}{\gamma_{1}+\alpha\gamma _{2}+\lambda}+\frac{\gamma_{2}}{\alpha\gamma_{1}+\gamma_{2}+\lambda}} {\frac{\gamma_{1}}{\gamma_{1}+\alpha\gamma_{2}+\lambda}+\frac{\alpha\gamma _{1}}{\alpha\gamma_{1}+\gamma_{2}+\lambda}}$	(16)
	$\displaystyle =\frac{\gamma_{2}}{\gamma_{1}}\frac{\left( 1+\alpha^{2}\right) \gamma _{1}+2\alpha\gamma_{2}+\left( 1+\alpha\right) \lambda}{\left( 1+\alpha ^{2}\right) \gamma_{2}+2\alpha\gamma_{1}+\left( 1+\alpha\right) \lambda },$

where the second line follows from straightforward manipulations. The ratio of plant counts is

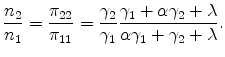
$\displaystyle \frac{n_{2}}{n_{1}}=\frac{\pi_{22}}{\pi_{11}}=\frac{\gamma_{2}}{\gamma_{1} }\frac{\gamma_{1}+\alpha\gamma_{2}+\lambda}{\alpha\gamma_{1}+\gamma _{2}+\lambda}\text{.}$

To prove part (i) of the result that $Q_{2}^{size}>1>Q_{1}^{size}$ , we must show that $\frac{y_{2}}{y_{1}}>\frac{n_{2}}{n_{1}}$ . This follows from straightforward calculations using the formulas above and $\alpha<1$ .

To prove part (ii), we need to show the ratio $\frac{y_{2}}{y_{1}}$ is increasing in $\lambda$ , for fixed $\gamma_{1}$ and $\gamma_{2}$ . From inspection of (16), this holds if

$\displaystyle \left( 1+\alpha^{2}\right) \gamma_{1}+2\alpha\gamma_{2}<\left( 1+\alpha ^{2}\right) \gamma_{2}+2\alpha\gamma_{1}$

$\displaystyle 0<\left( \gamma_{2}-\gamma_{1}\right) \left( 1-2\alpha+\alpha^{2}\right) ,$

which holds since $\alpha<1$ and $\gamma_{2}>\gamma_{1}$ .

The last step of the proof is to take into account that the relative wage $w_{2}(\lambda)/w_{1}(\lambda)$ is weakly decreasing in $\lambda$ . This implies that $\gamma _{2}(\lambda)/\gamma_{1}(\lambda)$ is weakly increasing in $\lambda$ . Since without loss of generality, we can assume $\gamma _{1}(\lambda)$ is constant in $\lambda$ , and since we have proven $\frac{y_{2}}{y_{1}}$ in (16) is increasing in $\lambda$ for fixed $\gamma_{1}$ and $\gamma_{2}$ , it is sufficient to show $\frac{y_{2}}{y_{1}}$ in (16) is increasing in $\gamma_{2}$ for fixed $\lambda$ and $\gamma_{1}$ . This follows from straightforward calculations. Q.E.D.

Appendix B: Data

This section of the appendix discusses various topics regarding the data. We have posted on the web a supplementary document, Holmes and Stevens (2010a), that contains links to data sets and supplementary tables. In particular, we post the first-stage and second-stage model estimates for all 172 NAICS industries for which we have estimated the model.

A. Joint Use of Confidential and Public Data

The Census cannot disclose results that could potentially compromise the confidentiality of the Census data. In particular, statistics at a high level of geographic and industry detail are problematic for getting through the disclosure process.

It is useful to be able to simulate the estimated model outside a secure Census facility. This makes it possible to easily replicate findings of the paper. It also makes it possible to make tables of the predictions of the model at narrow geographic and industry detail. To accomplish this goal, we made joint use of confidential and publicly available data. First, we used the confidential micro CFS data to estimate the parameters $\eta^{h}=(\eta _{1}^{h},\eta_{2}^{h})$ of the distance adjustment function $a^{h}(dist)$ for each industry . The release of these aggregate industry variables posed no disclosure risk. Second, we used publicly available data to estimate the distribution of industry revenue across locations and then used these revenue estimates to estimate the productivity vector $\Gamma^{h}$ for each industry.

To construct public revenue estimates by location, we begin with the 1997 Location of Manufacturing plants (LM) data series. The LM data are public data of cell counts by industry, county, and narrowly defined employment size categories (1-4, 5-9, 10-19, 20-49, 50-99, 100-249, 250-499, 500-999, 1,000-2,499, 2,500 and above). This is file E9731e2 from the 1997 Economic Census CD (U.S. Bureau of the Census (2001)). These cell counts are not considered a disclosure, and no information is held back. Thus, for each of the 362,829 plants in the Census of Manufactures, we have as public data the plant's county, industry, and detailed employment size category. We produce an estimate of average sales revenue conditioned on industry and employment size, and assign this to each plant as an estimate of its sales.²⁰ We then aggregate up the plant-level sales estimates to the BEA Economic Area level for each industry to obtain estimates of the location-level data needed to implement the second stage of our procedure. We found that in running the second-stage procedure, it made little difference when we used the estimated revenue data instead of the actual revenue data. For 2007, we use the analogous cell count data from County Business Patterns, and we use the same mapping between sales estimate and employment size category that we use for 1997.

B. Choice of Diffuse Demand Industries

We use the U.S. Benchmark Input-Output Accounts for 2002 (Stewart, Stone, and
Streitwieser (2007)) to classify industries. We first define a set of downstream demand (or "use") of goods that we categorize at "local demand." These are all uses in the following categories: structures, transportation, retail trade, information (publishing), finance, insurance, real estate, services, personal consumption expenditures, fixed private investment, and government services. Then for each commodity, we determine which of these deliver 75 percent or more of their sales to the local demand categories. We define these to be the diffuse demand industries. We also include borderline cases of Surgical and Dental Equipment (NAICS 339112) and Dental Equipment (NAICS 339114).

C. More Information about Data Sources Used in the Tables

Table 2. The cell counts that cross-classify the 1997 Census plants by NAICS and SIC use public data files E97B1 and E97B2 distributed at the Census web site. These files report employment by SIC and NAICS, from which mean plant size by SIC/NAICS was derived. The confidential micro data were used to calculate export shares and mean plant sales location quotients in the table.

Tables 3 through 6. These tables use the confidential micro data at the Census. Population at the EA level was calculated using Census county-level estimates for 1992 and 1997 (and below for 2007) and aggregating up to the EA level.

Tables 7 through 9 and 11 through 15 use publicly available data as discussed in Part A above.

Table 10 uses import information posted by the U.S. International Trade Commission at its web site. (For two furniture industries, NAICS 337122 and 337125, we used revised figures reported at the web site of the International Trade Administration.) Imports are "Customs Value of U.S. Imports for Consumption." The variables are reported at the six-digit NAICS level, though in some cases the five-digit level is used. Imports are reported as a share of the domestic shipments plus imports, where domestic shipments equal the product shipments in the given six-digit NAICS product for the given Economic Census year (1997 or 2007).

D. Local Shipments and Wholesaling

When estimating the model in the first stage, we condition on sales being greater than 100 miles. Here we discuss the issue of "excess local shipments" in a little more detail. Table A1 reports the distribution of shipment shares by distance category, both in the data and in the estimated models, conditioned on shipments above 100 miles. It is like Table 6 before, except it includes a breakdown by industries according to the estimated distance adjustment, i.e., $a^{h}(100)$ for industry .²¹ We see in the conditional distribution a tendency for the model to overstate distance shipped, compared with the data. However, for the most part, the discrepancy is moderate.

Table A2 uses the same estimated model (the model optimized to fit the conditional distribution) and reports how things look in the unconditional distribution. A large discrepancy in the under 100 miles category is readily apparent. In particular, consider the highest $a^{h}(100)$ industries, the ones that are most tradable. In the fitted model, local shipments less than 100 miles are predicted to be only 5 percent of sales, but in fact make up 19 percent of sales, a difference of almost a factor of four. In the limiting case where there is no discount adjustment (i.e., $a^{h}=1$ at all distances), a plant's shipments to a particular location should be proportionate to the location's population. That is, the share of shipments going less than 100 miles should equal the share of the U.S. population within 100 miles. Many of the high $a^{h}$ industries, like clothing, tend to be outside the major population centers, and that is why predicted shipments within 100 miles is so low for these industries.

In working with the CFS data, Hillberry and Hummels (2008) observe the prevalence of local shipments and, as an explanation, emphasize the role that intermediate goods might play. For some immediate goods, it may be efficient to ship to nearby downstream manufacturing plants for further processing. In our case, we have selected out--through our use of the input-output tables--those manufacturing industries that tend to ship downstream to other manufacturing plants. So the point about intermediate goods has less relevance for us than it would be without that selection.

We believe the wholesaling sector plays some role in the story. Shipments leaving plants may make stops at nearby warehouses before arriving to their ultimate destination, which may be thousands of miles away. In such a case, the shipment distance is recorded at less than 100 miles, rather than the true distance.

Table A3 provides evidence on the relevance of the wholesale sector, for our sample of manufacturing industries. The CFS is a sample of shipments leaving both manufacturing plants and wholesale plants. To link manufacturing shipments with wholesale shipments, we exploit the product-level information available in the CFS. Each shipment in the 1997 CFS is classified by SCTG product code.²² Define the ton-miles of a shipment to be the shipment's weight times its distance. For each SCTG product, we estimate the share of ton-miles originating out of wholesale plants rather than manufacturing plants. Next, for each NAICS industry, we use the manufacturing plants in the CFS to estimate the revenue share across different SCTGs. Finally, we use the SCTG sales shares to weight the SCTG-level ton-mile shares, to produce a NAICS-level Ton-Mile Wholesale Share. On average across the sample industries, about a quarter of ton-miles go through the wholesale sector. When we repeat the exercise for the 1992 SIC sample industries, the results are virtually the same.²³ We conclude that for our sample industries, the wholesale sector plays a large enough quantitative role for it to potentially be a factor in accounting for why there are more local shipments than are predicted by the model.

Appendix C: First-Stage Estimation Algorithm

We provide a detail about the first-stage estimation algorithm. As explained in the text, conditioned on the parameters $\eta$ of the distance discount, we solve for a vector of cost efficiencies to exactly match the distribution of sales revenues across locations. From the equations derived earlier, total sales revenue at location equals

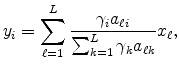
$\displaystyle y_{i}=\sum_{\ell=1}^{L}\frac{\gamma_{i}a_{\ell i}}{\sum_{k=1}^{L}\gamma _{k}a_{\ell k}}x_{\ell},$

where the $a_{\ell i}$ depend upon $\eta,$ held fixed here. Given the $y_{i}$ , $x_{\ell}$ , $a_{\ell i}$ , we need to find a vector $\Gamma=(\gamma _{1},\gamma_{2},...,\gamma_{177})$ , with the normalization $\gamma_{1}=1$ , that solves these equations.

Define $\omega_{i}$ by $\omega_{i}\equiv\frac{1}{\gamma_{i}}$ and $\omega=(1,\omega_{2},\omega_{3},...,\omega_{L})$ . Define the mapping

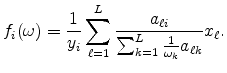
$\displaystyle f_{i}(\omega)=\frac{1}{y_{i}}\sum_{\ell=1}^{L}\frac{a_{\ell i}}{\sum_{k=1} ^{L}\frac{1}{\omega_{k}}a_{\ell k}}x_{\ell}\text{.}$

If we find a $\omega$ such that $f_{i}(\omega)=\omega_{i}$ for all $i\geq2$ , then the output equations all hold.

Note first that $f_{i}(\omega)$ is strictly increasing. Note second that $f_{i}(\omega)$ is bounded above by

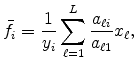
$\displaystyle \bar{f}_{i}=\frac{1}{y_{i}}\sum_{\ell=1}^{L}\frac{a_{\ell i}}{a_{\ell1} }x_{\ell}\text{,}$

which is the limit of $f_{i}(\omega)$ as $\omega$ goes to infinity. Suppose we have a point $\omega^{\circ}>f(\omega^{\circ})$ . Define the sequence $\{\omega_{0},\omega_{1},\omega_{2}...\}$ by $\omega_{0}=\omega^{\circ}$ , and $\omega_{t}=f(\omega_{t})$ . Since $f(\cdot)$ is monotonically increasing and is bounded from above, this sequence converges to a solution.

To run the algorithm, we need a starting point $\omega^{\circ}>f(\omega^{\circ})$ . In our estimation, the following procedure worked for finding a starting value. Without loss of generality, we label locations for a particular industry so that location 1 has the maximum sales revenue share, $y_{1}=\max\left\{ y_{1},y_{2},...,y_{177}\right\}$ . Then we set $\omega_{i}^{\circ}=\frac{1}{y_{i}}\lambda$ for some small $\lambda$ .

If $f(\omega)$ is convex, then any solution $\omega=f(\omega)$ is unique. We have shown that $f(\omega)$ is convex for or locations.

References

Alessandria, George, and Horag Choi. 2007. "Establishment Heterogeneity, Exporter Dynamics, and the Effects of Trade Liberalization." Working paper, Federal Reserve Bank of Philadelphia.

Alvarez, Fernando, and Robert E. Lucas, Jr. 2007. "General Equilibrium Analysis of the Eaton-Kortum Model of International Trade." Journal of Monetary Economics 54(6), 1726-68.

Bernard, Andrew B., Jonathan Eaton, J. Bradford Jensen, and Samuel Kortum. 2003. "Plants and Productivity in International Trade." American Economic Review 93(4), 1268-90.

Bernard, Andrew B., and J. Bradford Jensen. 1995. "Exporters, Jobs, and Wages in U.S. Manufacturing, 1976-1987." Brookings Papers on Economic Activity: Microeconomics, 67-119.

Bernard, Andrew B., J. Bradford Jensen, and Peter K. Schott. 2006. "Survival of the Best Fit: Exposure to Low-Wage Countries and the (Uneven) Growth of U.S. Manufacturing Plants." Journal of International Economics 68(1), 219-37.

Bernard, Andrew, Stephen Redding, and Peter Schott. 2010. "Multi-Product Firms and Product Switching." American Economic Review 100(1), 70-97.

Buera, Francisco J., and Joseph P. Kaboski. 2008. "Scale and the Origins of Structural Change." Working paper, Northwestern University.

Eaton, Jonathan, and Samuel Kortum. 2002. "Technology, Geography, and Trade." Econometrica 70(5), 1741-79.

Hallak, Juan Carlos, and Jagadeesh Sivadasan. 2009. "Firms' Exporting Behavior under Quality Constraints." Working Paper no. 14928, National Bureau of Economic Research, April.

Hall, Max, ed. 1959. Made in New York: Case Studies in Metropolitan Manufacturing. Cambridge, MA: Harvard University Press.

Head, Keith, and John Ries. 1999. "Rationalization Effects of Tariff Reductions." Journal of International Economics 47(2), 295-320.

Hillberry, Russell, and David Hummels. 2003. "Intranational Home Bias: Some Explanations." Review of Economics and Statistics 85(4), 1089-92.

Hillberry, Russell, and David Hummels. 2008. "Trade Responses to Geographic Frictions: A Decomposition Using Micro-Data." European Economic Review 52(3), 527-50.

Holmes, Thomas J., and John J. Stevens. 2002. "Geographic Concentration and Establishment Scale." Review of Economics and Statistics 84(4), 682-90.

Holmes, Thomas J., and John J. Stevens. 2004a. "Geographic Concentration and Establishment Size: Analysis in an Alternative Economic Geography Model." Journal of Economic Geography 4(3), 227-50.

Holmes, Thomas J., and John J. Stevens. 2004b. "Spatial Distribution of Economic Activities in North America." In Handbook of Regional and Urban Economics, vol. 4, Cities and Geography, ed. J. Vernon Henderson and Jacques-François Thisse, 2797-843. Amsterdam: North-Holland.

Holmes, Thomas J., and John J. Stevens. 2010a. "Web Appendix for `An Alternative Theory of the Size Distribution with an Application to Trade' with Data and Programs." Available at http://www.econ.umn.edu/~holmes/data/plantsize.

Holmes, Thomas J., and John J. Stevens. 2010b. "Exports, Borders, Distance, and Plant Size." Manuscript, University of Minnesota.

Hopenhayn, Hugo. 1992. "Entry, Exit, and Firm Dynamics in Long Run Equilibrium." Econometrica 60(5), 1127-50.

Hopenhayn, Hugo, and Richard Rogerson. 1993. "Job Turnover and Policy Evaluation: A General Equilibrium Analysis." Journal of Political Economy 101(5), 915-38.

Hsu, Wen-Tai. 2008. "Central Place Theory and Zipf's Law." Manuscript, Chinese University of Hong Kong.

Johnson, Kenneth P., and John R. Kort. 2004. "2004 Redefinition of the BEA Economic Areas." Survey of Current Business 84(11), 68-75.

Jovanovic, Boyan. 1982. "Selection and the Evolution of Industry." Econometrica 50(3), 649-70.

Lucas, Robert. 1978. "On the Size Distribution of Business Firms." Bell Journal of Economics 9(2), 508-23.

Luttmer, Erzo G. J. 2007. "Selection, Growth, and the Size Distribution of Firms." Quarterly Journal of Economics 122(3), 1103-44.

Melitz, Marc J. 2003. "The Impact of Trade on Intra-Industry Reallocations and Aggregate Industry Productivity." Econometrica 71(6), 1695-725.

Office of Management and Budget. 1994. "Economic Classification Policy Committee: Standard Industrial Classification Replacement." Federal Register 59(142), July 26.

Piore, Michael J., and Charles F. Sabel. 1984. The Second Industrial Divide. New York: Basic Books.

Stewart, Ricky L., Jessica Brede Stone, and Mary L. Streitwieser. 2007. "U.S. Benchmark Input-Output Accounts, 2002." Survey of Current Business 87(10), 19-48.

Syverson, Chad. 2004. "Market Structure and Productivity: A Concrete Example." Journal of Political Economy 112(6), 1181-222.

U.S. Bureau of the Census. 1999. 1997 Commodity Flow Survey, EC97TCF-US.

U.S. Bureau of the Census. 2001. 1997 Economic Census. CD-ROM. Washington, DC: U.S. Department of Commerce.

U.S. Bureau of the Census. 2007. County Business Patterns (CBP). www.census.gov/econ/
cbp/.

Table 1

Breakdown of $Q_2^{rev}$ into $Q_2^{count}$ and $Q_2^{size}$ for Various Parameters

Distance Adjustment: $a_{12}$	Equal Size Locations ( $x_{1}=x_{2})$ ( $Q_1^{rev}$ =.40 and $Q_2^{rev}$ =1.60): $\gamma _{2}/ \quad \gamma _{1}$	Equal Size Locations ( $x_{1}=x_{2})$ ( $Q_1^{rev}$ =.40 and $Q_2^{rev}$ =1.60): $Q_2^{count}$	Equal Size Locations ( $x_{1}=x_{2})$ ( $Q_1^{rev}$ =.40 and $Q_2^{rev}$ =1.60): $Q_2^{size}$	Location 2 Larger (3 $x_{1}=x_{2})$ ( $Q_1^{rev}$ =.31 and $Q_2^{rev}$ =1.23): $\gamma _{2}/ \quad \gamma _{1}$	Location 2 Larger (3 $x_{1}=x_{2})$ ( $Q_1^{rev}$ =.31 and $Q_2^{rev}$ =1.23): $Q_2^{count}$	Location 2 Larger (3 $x_{1}=x_{2})$ ( $Q_1^{rev}$ =.31 and $Q_2^{rev}$ =1.23): $Q_2^{size}$	Location 1 Larger ( $x_{1}$ = 3 $x_{2})$ ( $Q_1^{rev}$ =.57 and $Q_2^{rev}$ =2.29): $\gamma _{2}/ \quad \gamma _{1}$	Location 1 Larger ( $x_{1}$ = 3 $x_{2})$ ( $Q_1^{rev}$ =.57 and $Q_2^{rev}$ =2.29): $Q_2^{count}$	Location 1 Larger ( $x_{1}$ = 3 $x_{2})$ ( $Q_1^{rev}$ =.57 and $Q_2^{rev}$ =2.29): $Q_2^{size}$
1.000	4.00	1.60	1.00	12.00	1.23	1.00	1.33	2.29	1.00
0.990	4.00	1.60	1.00	11.94	1.23	1.00	1.34	2.29	1.00
0.950	4.00	1.59	1.01	11.71	1.22	1.01	1.37	2.30	0.99
0.900	4.01	1.58	1.01	11.43	1.22	1.01	1.41	2.32	0.99
0.800	4.06	1.56	1.03	10.91	1.20	1.02	1.50	2.35	0.97
0.600	4.32	1.52	1.05	10.18	1.16	1.06	1.76	2.42	0.94
0.500	4.62	1.50	1.07	10.07	1.14	1.08	1.97	2.45	0.93
0.200	8.28	1.44	1.11	13.87	1.05	1.17	4.00	2.53	0.90
0.100	15.41	1.43	1.12	23.88	1.03	1.20	7.63	2.54	0.90
0.010	150.05	1.43	1.12	225.22	1.02	1.21	75.01	2.55	0.90
0.001	1501.20	1.43	1.12	2257.89	1.02	1.21	750.11	2.55	0.90

Table 2

Descriptive Statistics for the 1997 Reclassification Industries

by SIC/Retail and SIC/Man Status

NAICS Industry Classification	Classification Based on SIC	Number of Plants	Mean Plant Employ.	Export Share	Mean Location Quotient
Chocolate Candy	SIC/Retail	440	8	.00	1.01
Chocolate Candy (NAICS 311330)	SIC/Man	421	70	.03	4.87
Nonchocolate Candy	SIC/Retail	349	4	.00	1.01
Nonchocolate Candy (NAICS 311340)	SIC/Man	276	88	.03	4.61
Curtains	SIC/Retail	1,085	4	.00	1.54
Curtains (NAICS 312121)	SIC/Man	999	21	.03	3.22
Other Apparel	SIC/Retail	724	3	.00	1.71
Other Apparel (NAICS 315999)	SIC/Man	966	25	.03	2.67
Kitchen Cabinets	SIC/Retail	2,055	5	.00	1.25
Kitchen Cabinets (NAICS 337110)	SIC/Man	5,908	15	.01	2.14
Upholstered Household Furniture	SIC/Retail	576	5	.00	1.52
Upholstered Household Furniture (NAICS 337121)	SIC/Man	1,130	77	.03	7.20
Wood Household Furniture	SIC/Retail	815	6	.00	1.17
(NAICS 337122)	SIC/Man	3,035	41	.03	4.42

Source: Authors' calculations with confidential Census data and public Census tabulations.

Table 3 (Part 1 of 3)

Mean Custom Share across Sample Plants in the Furniture Industry

by SIC/Retail and SIC/Man Status and within SIC/Man by Employment Size

Industry Grouping: Kitchen Cabinets and Household Furniture

(NAICS 337110, 337121, 337122)

Classification	Number of Sample Plants	Mean Custom Share
SIC/Retail	102	.82
SIC/Man	2,944	.42
Within SIC/Man by Emp. Size: 1-19	1,628	.59
Within SIC/Man by Emp. Size: 20-99	877	.30
Within SIC/Man by Emp. Size: 100 and above	437	.09

Table 3 (Part 2 of 3)

Mean Custom Share across Sample Plants in the Furniture Industry

by SIC/Retail and SIC/Man Status and within SIC/Man by Employment Size

Industry Grouping: Kitchen Cabinets

(NAICS 337110)

Classification	Number of Sample Plants	Mean Custom Share
SIC/Retail	48	.87
SIC/Man	1,854	.64
Within SIC/Man by Emp. Size: 1-19	1331	.70
Within SIC/Man by Emp. Size: 20-99	426	.56
Within SIC/Man by Emp. Size: 100 and above	97	.28

Table 3 (Part 3 of 3)

Mean Custom Share across Sample Plants in the Furniture Industry

by SIC/Retail and SIC/Man Status and within SIC/Man by Employment Size

Industry Grouping: Household Furniture

(NAICS 337121, 337122)

Classification	Number of Sample Plants	Mean Custom Share
SIC/Retail	54	.78
SIC/Man	1,090	.05
Within SIC/Man by Emp. Size: 1-19	297	.08
Within SIC/Man by Emp. Size: 20-99	451	.05
Within SIC/Man by Emp. Size: 100 and above	340	.03

Source: Authors' calculations with confidential Census data.

Table 4 (Part 1 of 3)

Mean Location Quotient by Plant Size for Three Groups of Industries

Reclassification Industry Sample: (7 Industries)

Plant Size Category	Number of Establishments	Mean Location Quotient: Raw	Mean Location Quotient: NAICS Fixed Effect
All	18,585	4.32	4.32
1-19	15,687	1.36	2.46
20-99	2,073	2.62	3.03
100-499	690	4.18	3.97
500+	135	6.13	5.83

Table 4 (Part 2 of 3)

Mean Location Quotient by Plant Size for Three Groups of Industries

Other Diffuse Demand Industries: (165 Industries)

Plant Size Category	Number of Establishments	Mean Location Quotient: Raw	Mean Location Quotient: NAICS Fixed Effect
All	130,986	4.86	4.86
1-19	91,608	1.73	3.72
20-99	28,291	2.37	4.01
100-499	9,533	3.75	4.60
500+	1,554	6.68	5.41

Table 4 (Part 3 of 3)

Mean Location Quotient by Plant Size for Three Groups of Industries

Remaining Manufacturing Industries: (301 Industries)

Plant Size Category	Number of Establishments	Mean Location Quotient: Raw	Mean Location Quotient: NAICS Fixed Effect
All	211,945	5.13	5.13
1-19	134,044	1.86	3.67
20-99	54,705	2.79	4.14
100-499	20,101	4.38	4.91
500+	3,095	6.92	5.82

Source: Authors' calculations with confidential Census data.

Table 5 (Part A)

Model Estimates from Stage 1

Baseline 1997 NAICS Estimates using $\overline {dist} =100$

Selected Industries by percentile of implied value of

(100):

	Parameter Estimates (s.e. in Parentheses): $\eta_{1}$	Parameter Estimates (s.e. in Parentheses): $\eta_{2}$	Implied Value of (dist) by dist: 100 miles	Implied Value of (dist) by dist: 500 miles	Implied Value of (dist) by dist: 1,000 miles	No. of CFS Shipments Used for Estimate
Ready-Mix Concrete (Minimum)	.0523 (.0004)	0 $^{\ast }$	.01	.00	.00	37,875
Creamery Butter (25 $^{th}$ percentile)	.0030 (.0003)	-8.0E-07 (1.1E-07)	.74	.27	.11	586
Wood Television Cabinets (50 $^{th}$ percentile)	.0019 (.0003)	-6.4E-07 (1.6E-07)	.83	.45	.28	546
Surgical Appliance & Supplies (75 $^{th}$ percentile)	.0008 (.0001)	-1.8E-07 (0.3E-07)	.92	.69	.52	11,670
Other Hosiery & Sock Mills (Maximum)	0 $^{\ast \ast }$	0 $^{\ast \ast }$	1.00 $^{\ast \ast }$	1.00 $^{\ast \ast }$	1.00 $^{\ast \ast }$	2,967
Baseline Estimates (Mean over 172 Industries)	.0030 (.0002)	-5.0E-07 (0.7E-07)	.80	.48	.33	3,968

$^{\ast }$ The constraint $\eta$ $_{2 }$ = 0 is imposed for this industry.

$^{\ast \ast }$ This estimate is at the constraint that (dist) $\le$ 1.

Table 5 (Part B)

Model Estimates from Stage 1

Alternative Estimates (Means across industries)

	Parameter Estimates (s.e. in Parentheses): $\eta_{1}$	Parameter Estimates (s.e. in Parentheses): $\eta_{2}$	Implied Value of (dist) by dist: 100 miles	Implied Value of (dist) by dist: 500 miles	Implied Value of (dist) by dist: 1,000 miles	No. of CFS Shipments Used for Estimate
1992 SIC (175 Industries) with $\overline {dist} =100$	.0030 (.0001)	-5.9E-07 (0.4E-07)	.78	.43	.28	8,500
1997 NAICS (172 Industries) $^{\ast \ast \ast }$ with $\overline {dist} =0$			.71	.30	.16
1997 NAICS (172 Industries) $_{\ast \ast \ast }$ with $\overline {dist} =200$			.85	.57	.42

$^{\ast \ast \ast }$ For these alternative specifications that vary $\overline {dist}$ , we did not run the individual industry estimates through the Census disclosure process. Rather, we took only the means of (100), (500), and (1000) through the disclosure process.

Table 6

Model's Goodness of Fit of the Distance Distribution of Shipments

Conditioned upon Shipments Being at Least 100 miles

Statistic Reported:	Category 1 100 $\le$ distance500	Category 2 500 $\le$ distance1,000	Category 3 1,000 $\le$ distance
Mean across industries (data)	.44	.30	.25
Mean $\widehat{share}_c^h$ across industries (model)	.38	.33	.30
Regression of (data) on $\widehat{share}_c^h$ (model): Intercept	.05 (.02)	-.03 (.02)	-.03 (.01)
Regression of (data) on $\widehat{share}_c^h$ (model): Slope	1.04 (.04)	.99 (.07)	.96 (.03)
Regression of (data) on $\widehat{share}_c^h$ (model): $R^{2}$	.81	.55	.83
Number of Observations	167	167	167

Table 7

Second-Stage Estimates of the Plant Count Parameters and Related Model and Data Statistics

	Regression Results (s.e. in Parentheses): Constant $\lambda$	Regression Results (s.e. in Parentheses): Slope (spec) $\nu$ $^{b}$	Regression Results (s.e. in Parentheses): Slope (stan) $\nu$ $^{s}$	Regression Results (s.e. in Parentheses): $R^{2}$	Estimated Specialty Count Share (Percent)
Reclassification Industries: Chocolate Candy (NAICS 311330)	.4 (.2)	621.6 (52.3)	76.7 (13.0)	.69	80.9
Reclassification Industries: Nonchocolate Candy (NAICS 311340)	.1 (.1)	487.7 (31.2)	61.3 (7.7)	.79	80.3
Reclassification Industries: Curtains (NAICS 312121)	-.9 (.3)	2184.4 (56.5)	20.0 (7.7)	.92	97.0
Reclassification Industries: Other Apparel (NAICS 315999)	-1.8 (.4)	1302.6 (114.4)	266.1 (19.9)	.89	62.9
Reclassification Industries: Kitchen Cabinets (NAICS 337110)	1.4 (1.2)	5939.6 (231.2)	185.5 (19.1)	.89	78.2
Reclassification Industries: Upholstered Household Furn. (NAICS 337121)	-1.4 (.5)	980.0 (96.6)	247.2 (8.0)	.88	49.4
Reclassification Industries: Wood Household Furn. (NAICS 337122)	-1.2 (.8)	3355.9 (138.8)	254.8 (23.1)	.85	81.9
Means of 7 Reclassification Industries	-.5 (.5)	2124.5 (103.0)	158.8 (14.1)	.85	75.8
Means of 165 Remaining Diffuse Demand Industries	-.3 (.2)	636.6 (40.3)	86.7 (6.8)	.71	66.0

Table 8

Estimated Specialty Count Share

by Quartiles of 172 Diffuse Demand Industries

Quartile	Model Summary Statistics of Specialty Count Share: Minimum	Model Summary Statistics of Specialty Count Share: Maximum	Model Summary Statistics of Specialty Count Share: Mean	Data Mean Small Plant Count Share in Percent (Small Plants Have 19 Employees or Less)
1	-3.7	57.2	35.7	47.7
2	58.2	72.0	64.8	53.8
3	72.0	81.9	77.6	63.0
4	81.9	101.2	87.6	67.0

Table 9 (Part A)

Sales, Count and Size Quotients in Data, Size Quotients for Both Models

in High Concentration Industry Locations

Industry: BEA Economic Area	Revenue Share	Data: $Q^{rev}$	Data: $Q^{count}$	Data: $Q^{size}$	BEKJ Only Model $Q^{size}$	Full Model $Q^{size}$
Chocolate Candy (NAICS 311330): Harrisburg, PA	.07	9.2	1.4	6.4	1.3	4.2
Chocolate Candy (NAICS 311330): Nashville, TN	.06	6.6	.8	7.9	1.4	3.8
Chocolate Candy (NAICS 311330): Chicago, IL	.15	4.1	1.2	3.6	1.4	3.0
Chocolate Candy (NAICS 311330): Philadelphia, PA	.08	3.3	2.1	1.6	1.2	2.5
Chocolate Candy (NAICS 311330): San Francisco, CA	.08	2.3	1.5	1.6	0.4	1.3
Nonchocolate Candy (NAICS 311340): Grand Rapids, MI	.07	11.2	1.2	9.2	1.3	4.5
Nonchocolate Candy (NAICS 311340): Chicago, IL	.24	6.8	1.5	4.6	1.4	3.8
Nonchocolate Candy (NAICS 311340): Atlanta, GA	.07	3.5	.8	4.5	1.2	2.5
Curtains (NAICS 312121): San Antonio, TX	.07	10.3	.6	16.8	0.6	7.0
Curtains (NAICS 312121): Raleigh-Durham, NC	.09	10.1	1.1	8.9	1.3	8.3
Curtains (NAICS 312121): Charlotte, NC	.06	7.6	1.7	4.5	1.3	6.7
Curtains (NAICS 312121): Boston, MA	.07	2.5	1.4	1.8	1.0	2.4
Other Apparel (NAICS 315999): New York, NY	.28	3.5	2.6	1.4	1.4	2.3
Other Apparel (NAICS 315999): Los Angeles, CA	.16	2.5	2.1	1.2	0.9	1.5
Kitchen Cabinets (NAICS 337110): Harrisburg, PA	.05	7.4	1.7	4.4	2.9	5.5
Kitchen Cabinets (NAICS 337110): Dallas, TX	.05	2.4	1.0	2.4	1.0	1.8
Upholstered Household Furn. (NAICS 337121): Tupelo, MS	.21	107.4	43.4	2.5	1.5	2.9
Upholstered Household Furn. (NAICS 337121): Charlotte, NC	.19	23.2	11.3	2.1	1.8	3.3
Upholstered Household Furn. (NAICS 337121): Knoxville, TN	.09	22.2	2.6	8.6	1.7	3.1
Upholstered Household Furn. (NAICS 337121): High Point, NC	.12	19.2	11.0	1.8	1.7	3.2
Wood Household Furn. (NAICS 337122): High Point, NC	.17	27.7	4.2	6.6	1.6	6.9
Wood Household Furn. (NAICS 337122): Charlotte, NC	.13	15.5	2.9	5.4	1.5	5.8
Wood Household Furn. (NAICS 337122): Toledo, OH	.05	13.5	.8	17.5	1.2	4.8

Table 9 (Part B)

Sales, Count and Size Quotients in Data, Size Quotients for Both Models

in High Concentration Industry Locations

Summary Statistics: 7 Reclassification Industries: = 23 Industry Locations: Mean	.11	14.0	4.3	5.4	1.3	4.0
Summary Statistics : 7 Reclassification Industries: = 23 Industry Locations: Median	.08	7.6	1.5	4.5	1.3	3.2
Summary Statistics: 165 Remaining Diffuse Demand: = 566 Industry Locations: Mean	.11	18.3	5.9	5.3	1.2	3.3
Summary Statistics: 165 Remaining Diffuse Demand: = 566 Industry Locations: Median	.09	9.3	2.9	2.6	1.1	2.5

Note: BEA Economic Areas are a combination of several nearby locations. For simplicity, we pick just one city to serve as the label. For example, the area labeled "Chicago, IL" in the table is actually labeled "Chicago-Naperville-Michigan City, IL-IN-WI" in the Economic Area data set.

Table 10

List of Industries Classified as Having a Surge of Imports from China

(Some Descriptive Statistics)

	Import Share of Shipments (Percent): 1997	Import Share of Shipments (Percent): 2007	China Share of Imports (Percent): 1997	China Share of Imports (Percent): 2007	Employment Growth 1997-2007 (Percent)	Mean Plant Employment: 1997	Mean Plant Employment: 2007
Industry: Curtains	8	56	38	65	-47	12	9
Industry: Other Household Textile Prod.	22	68	25	49	-51	64	36
Industry: Women's Cut & Sew Dress	29	67	21	55	-71	37	22
Industry: Women's Cut & Sew Suit	48	92	19	49	-91	46	17
Industry: Infants' Cut & Sew Apparel	60	99	08	62	-97	178	11
Industry: Hat, Cap, & Millinery	44	80	26	67	-74	44	30
Industry: Glove & Mitten	58	88	50	63	-78	49	26
Industry: Men's & Boys' Neckwear	25	56	02	59	-67	40	37
Industry: Other Apparel	39	80	35	64	-75	14	12
Industry: Blankbook, Loose-leaf Binder	18	47	43	52	-51	59	42
Industry: Power-Driven Handtool	28	56	18	46	-56	77	48
Industry: Electronic Computer	12	49	00	56	-68	179	75
Industry: Electric Housewares & Fans	52	78	48	76	-54	124	77
Industry: Wood Household Furniture	29	62	18	46	-51	33	18
Industry: Metal Household Furniture	29	55	37	85	-48	54	36
Industry: Silverware & Plated Ware	44	91	31	73	-82	39	11
Industry: Costume Jewelry & Novelty	31	68	31	67	-63	16	10
Industry: Mean of China Surge Industries ( = 17)	34	70	26	61	-66	63	30
Industry: Mean of Food/Beverage Comparison Group Industries ( = 35)	8	11	02	7	5	84	81

Sources: See Data Appendix.

Table 11

Plant Size Distribution of China Surge Industries in 1997 and 2007

for the United States Overall and for Plants in the Primary Location of Each Industry

for the Wood Furniture Industry and for All 17 China Surge Industries

Panel A: Wood Household Furniture Industry

Employment Size Class	Plant Size Cell Counts in United States: 1997	Plant Size Cell Counts in United States: 2007	Plant Size Cell Counts in Primary Location (High Point): 1997	Plant Size Cell Counts in Primary Location (High Point): 2007
1 to 19	3,091	3,079	51	29
20 to 49	323	278	9	6
50 to 99	165	95	6	5
100 to 249	130	68	8	3
250 to 499	78	28	13	7
500 to 999	36	15	9	3
1,000 and above	12	5	5	0

Table 11, Panel B: All 17 China Surge Industries

Employment Size Class
1 to 19
20 to 49
50 to 99
100 to 249
250 to 499
500 to 999
1,000 and above

Source: The cell counts are based on public tabulations from the Census discussed in Appendix B. The High Point, NC Area consists of the BEA Economic Area containing High Point, NC (consisting of 22 counties). For each industry, the Primary Location is the Economic Area with the highest sales revenue location quotient, among locations with at least 5 percent of U.S. sales.

Table 12: Summary Statistics for 1997 Primary Industry Location

Data and Fitted Values in BEJK Model after China Surge

Industry or Industry Group	1997 Data: $Q_{1997}^{size}$	1997 Data: $Q_{1997}^{rev}$	2007: BEJK China Surge $\hat {Q}_{2007}^{rev}$	2007: Data $Q_{2007}^{rev}$
Wood Furniture in High Point, NC	6.6	27.7	28.4	12.8
China Surge Industries ( = 17): Mean	7.9	26.9	29.4	12.2
China Surge Industries ( = 17): Medan	3.8	19.6	21.7	5.3
Food/Beverage Comparison Group ( = 34): Mean	5.9	35.3	36.7	29.8
Food/Beverage Comparison Group ( = 34): Median	3.3	19.0	21.1	12.3

Note: 1997 primary industry location is location with highest $Q_{1997}^{rev}$ of those locations with at least 5 percent of industry sales.

Table 13: Summary Statistics of 20 Largest Economic Areas by Population

Data and Fitted Values in BEJK Model after China Surge

Industry or Industry Group	1997 Data: $Q_{1997}^{size}$	1997 Data: $Q_{1997}^{rev}$	2007: BEJK China Surge $\hat {Q}_{2007}^{rev}$	2007: Data $Q_{2007}^{rev}$
Wood Furniture	.45	.44	.42	.57
China Surge Industries ( = 17): Mean	.78	.97	.97	1.08
China Surge Industries ( = 17): Median	.79	.87	.87	1.06
Food/Beverage Comparison Group ( = 35): Mean	.94	.91	.90	.90
Food/Beverage Comparison Group ( = 35): Median	.93	.89	.89	.90

Note: The 20 largest economic areas by population are grouped into one aggregate big city area. The statistics reported in the table are calculated for the big city area being treated as a single location.

Table 14A

Actual and Fitted Values of Count Quotients, 1997 and 2007

Fitted Values for BEJK Model and General Model with Specialty Segment

2007 Values Simulate China Surge using 1997

Panel A: Summary Statistics for Count Quotients of Primary Location of Industry

Industry or Industry Group	Data $Q_{\begin{array}{l} \ \ \end{array}}^{count} _{:\quad }1997$	Data $Q_{\begin{array}{l} \ \ \end{array}}^{count} _{:\quad }2007$	Pure BEJK Model $\hat {Q}_{\begin{array}{l} \ \ \end{array}}^{count} _{:\quad }1997$	Pure BEJK Model $\hat {Q}_{\begin{array}{l} \ \ \end{array}}^{count} _{:\quad }2007$	General Model with Specialty Segment $\hat {Q}_{\begin{array}{l} \ \ \end{array}}^{count} _{:\quad }1997$	General Model with Specialty Segment $\hat {Q}_{\begin{array}{l} \ \ \end{array}}^{count} _{:\quad }2007$
Wood Furniture in High Point ( = 1)	4.2	2.3	17.7	22.0	4.0	3.0
China Surge Industries ( = 17): Mean	5.8	3.9	24.5	28.6	6.8	5.5
China Surge Industries ( = 17): Median	4.2	2.9	17.0	17.5	4.8	3.5
Food/Beverage Comparison Group ( = 34): Mean	10.6	10.7	30.0	34.8	13.4	10.9
Food/Beverage Comparison Group ( = 34): Median	4.8	4.2	15.4	17.7	5.3	3.8

Table 14B

Panel B: Prediction Regression Results, $\Delta Q_^{count}$ on $\Delta \hat {Q}_^{count} _{, }$ for the Two Models

Industry or Industry Group	Mean Slope (Mean std. err.)	Mean $R^{2}$
Wood Furniture ( = 1): Pure BEJK Model	-.27 (.06)	.096
Wood Furniture ( = 1): General Model with Specialty Segment	.93 (.17)	.140
China Surge Industries ( = 17): Pure BEJK Model	-.06 (.18)	.036
China Surge Industries ( = 17): General Model with Specialty Segment	.89 (.32)	.084
Food/Beverage Comparison Group ( = 35): Pure BEJK Model	.17 (.15)	.043
Food/Beverage Comparison Group ( = 35): General Model with Spec. Seg.	.33 (.32)	.046

Note: Each regression used to construct results in Panel B has 177 Economic Area observations. Observations are weighted by 1997 population. The table reports means across the industries for each group of industries.

Table 15A

Estimates of Standardized Segment and Specialized Segment Plant Counts

by Industry Grouping for 1997 and 2007

Panel A: Wood Household Furniture (1 Industry)

	Plant Counts (Number): 1997	Plant Counts (Number): 2007	Shares (Percent): 1997	Shares (Percent): 2007
Standardized	697	213	18.1	6.2
Specialty	3,150	3,215	81.9	93.8
Total	3,847	3,428	100.0	100.0

Table 15B

Panel B: All China Surge Industries (17 Industries)

	Plant Counts (Number): 1997	Plant Counts (Number): 2007	Shares (Percent): 1997	Shares (Percent): 2007
Standardized	3,783	1,371	29.1	15.7
Specialty	9,207	7,380	70.9	84.3
Total	12,990	8,751	100.0	100.0

Table 15C

Panel C: Food and Beverage Industries (35 Industries)

	Plant Counts (Number): 1997	Plant Counts (Number): 2007	Shares (Percent): 1997	Shares (Percent): 2007
Standardized	4,234	5,390	27.4	32.7
Specialty	11,216	11,092	72.6	67.3
Total	15,450	16,482	100.0	100.0

Table 15D

Panel D: Remaining Diffuse Demand Industries (120 Industries)

	Plant Counts (Number): 1997	Plant Counts (Number): 2007	Shares (Percent): 1997	Shares (Percent): 2007
Standardized	31,969	26,568	26.1	23.5
Specialty	90,388	86,432	73.9	76.5
Total	122,357	113,000	100.0	100.0

Appendix Table A1

Mean Share of Shipments in Data and Model

Conditioned on Distance Shipped over 100 Miles

Averages across Sample Industries and by Industry Distance Adjustment

	Number of Industries	Distance Shipped: 100 to 500	Distance Shipped: 500 to 1,000	Distance Shipped: Over 1,000
Industry Grouping: Data, All Sample Industries	172	0.43	0.30	0.26
Industry Grouping: Model, All Sample Industries	172	0.38	0.33	0.30
Industry Grouping: Data, (100).5	15	0.89	0.09	0.03
Industry Grouping: Model, (100).5	15	0.77	0.17	0.06
Industry Grouping: Data, .5 $\le \quad a$ (100) .75	31	0.57	0.27	0.16
Industry Grouping: Model, .5 $\le \quad a$ (100) .75	31	0.48	0.31	0.20
Industry Grouping: Data, .75 $\le \quad a$ (100) .9	73	0.41	0.32	0.27
Industry Grouping: Model, .75 $\le < \quad a$ (100) .9	73	0.35	0.34	0.31
Industry Grouping: Data, .9 $\le \quad a$ (100)	53	0.34	0.32	0.34
Industry Grouping: Model, .9 $< \quad a$ (100)	53	0.28	0.34	0.38

Appendix Table A2

Unconditioned upon Shipments above 100 Miles

	Number of Industries	Distance Shipped: Under 100	Distance Shipped: 100 to 500	Distance Shipped: 500 to 1,000	Distance Shipped: Over 1,000
Industry Grouping: Data, All Sample Industries	172	0.27	0.32	0.22	0.19
Industry Grouping: Model, All Sample Industries	172	0.11	0.34	0.29	0.27
Industry Grouping: Data, (100).5	15	0.65	0.31	0.03	0.01
Industry Grouping: Model, (100).5	15	0.39	0.47	0.10	0.04
Industry Grouping: Data, .5 $\le \quad a$ (100) .75	31	0.33	0.39	0.18	0.11
Industry Grouping: Model, .5 $\le \quad a$ (100) .75	31	0.14	0.42	0.27	0.18
Industry Grouping: Data, .75 $\le \quad a$ (100) .9	73	0.22	0.32	0.25	0.21
Industry Grouping: Model, .75 $\le < \quad a$ (100) .9	73	0.08	0.33	0.32	0.28
Industry Grouping: Data, .9 $\le \quad a$ (100)	53	0.19	0.28	0.26	0.28
Industry Grouping: Model, .9 $< \quad a$ (100)	53	0.05	0.26	0.33	0.36

Appendix Table A3

Estimates of Ton-Mile Wholesale Share

Averages across Sample Industries and by Industry Distance Adjustment

Industry Grouping	1997 NAICS Industry Sample: Number of Industries	1997 NAICS Industry Sample: Mean of Ton-Mile Wholesale Share (Percent out of 100)	1992 SIC Industry Sample: Number of Industries	1992 SIC Industry Sample: Mean of Ton-Mile Wholesale Share (Percent out of 100)
All Sample Industries	172	24.4	175	24.2
By value of (100) for industry: Below .50	15	15.6	14	11.4
By value of (100) for industry: From .50 to .75	31	15.0	35	18.2
By value of (100) for industry: From .75 to .90	73	27.1	88	27.3
By value of (100) for industry: Above .90	53	28.7	38	27.3

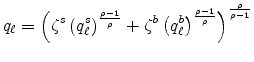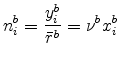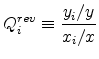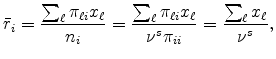
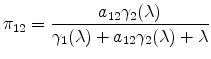
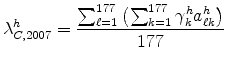Footnotes

* Holmes: University of Minnesota, Federal Reserve Bank of Minneapolis, and NBER. Stevens: The Board of Governors of the Federal Reserve System. The research presented here was funded by the National Science Foundation under Grant SES 0551062. We thank Brian Adams, Steve Schmeiser, and Julia Thornton Snider for their research assistance on this project. We have benefited from working at the Center for Economic Studies at the Census Bureau, and particularly thank Shawn Klimek, Arnie Reznek, and Lynn Riggs. The statistics reported in this paper that were derived from Census Bureau micro data were screened to ensure that they do not disclose confidential information. The views expressed herein are those of the authors and not necessarily those of the Federal Reserve Bank of Minneapolis, the Federal Reserve Board, the Federal Reserve System, or the U.S. Bureau of the Census. Return to Text

1. See Hsu (2008) for related ideas regarding the city size distribution. Return to Text

2. On account of the triangle inequality $d_{\ell i}\leq d_{\ell k}d_{ki}$ , if a particular plant is the most efficient producer at any location, it is also the most efficient producer at its own location. Return to Text

3. It is worth noting that the specialty-segment-as-nontradable-goods model is not a limiting case of the BEJK model with no transportation costs. In that limiting case, as local demand expands, sales volume expands on the intensive margin of larger average-size plants. In our model of the nontradable segment, an expansion of demand is met on the extensive margin of more plants. Return to Text

4. It is possible to generalize the argument to allow standardized goods to substitute for specialty goods. But then assumptions have to be added to make standardized goods better substitutes for each other than they are for specialty goods. Return to Text

5. Hillberry and Hummels (2003, 2008) are the first economics papers to use this confidential micro data. See U.S. Bureau of the Census (1999) for public tabulations. Return to Text

6. We use the 2004 definition; see Johnson and Kort (2004). Return to Text

7. In Holmes and Stevens (2002) we calculate an analogous measure that for each plant excludes the plant's own contribution to the location quotient and only uses the neighboring plants. This correction makes little difference in what we do here. Return to Text

8. The distinction is made in the text defining the product category. For example, product code 3371107121 is defined as "Wood vanities and other cabinetwork, custom." This is distinguished from another product where "stock line" is used in place of "custom." Return to Text

9. We regress plant location quotients on the size categories and industry fixed effects, weighting by sales. We then construct fitted values by plant size category evaluated at the mean fixed effects. Return to Text

10. The sample of plants selected for the CFS is stratified. We use the establishment sampling weights to reweight the cell count realizations and follow a pseudo-maximum likelihood approach. In writing down the likelihood, we condition on the origination of a given shipment. Return to Text

11. If, after excluding shipments below 100 miles, the implied value of

turned out to satisfy $a(100)\leq.2$ , we reestimated the model with all the shipments and used this estimate instead. For the five industries affected this way, we constrained $\eta_{2}=0$ and just allowed for the linear term $\eta_{1}$ . Return to Text

12. That is, when the standard-segment weight $\zeta^{s,h}$ and specialty-segment weight $\zeta^{b,h}$ in utility (1) go to their limits of $\zeta^{s,h}=1$ and $\zeta^{b,h}=0$ . Return to Text

13. We hold fixed $\eta$ , the parameters of the distance discount $a(\cdot)$ , throughout the procedure at the initial first-stage estimate. First, it makes little difference to allow $\eta$ to vary, since the specialty segment has a small revenue share. Second, to estimate $\eta$ , we need the confidential data. But conditioned on $\eta$ , we don't need the confidential data, as discussed in Appendix B. This makes it possible to replicate the results outside a secure Census facility, and simplifies the disclosure process. Return to Text

14. Doubling $\bar{s}^{b}$ relative to the baseline, or setting it to zero, makes virtually no difference in the results. Return to Text

15. In the constrained model, plant counts are proportional to $\pi_{ii}^{h}(\eta^{h},\Gamma^{h})$ . Return to Text

16. Our focus on the source of the imports is in the spirit of Bernard, Jensen, and Schott (2006), which focuses on exposure to low-wage countries. Return to Text

17. Imports as a share of shipments has in the denominator imports of the product plus all shipments of the product originating from domestic manufacturing plants. Return to Text

18. We did not take into account the import surge on relative input prices across locations. Given the role played by Assumption 1 in Proposition 2, we expect that taking any input price change effects into account would only make our point stronger. Return to Text

19. We hold fixed the $\eta$ estimate from 1997 and otherwise run the second-stage estimation for 2007 the same way we did for 1997. The 2007 CFS data were not available, so we could not use those data to create a 2007 specific estimate. We think it is sensible to treat the underlying transportation structure governing the $\eta$ parameter as relatively constant over the period 1997-2007. This justifies our use of the 1997 estimate for $\eta$ . Return to Text

20. We used public data on sales by size category to estimate a regression model of log sales, with employment size dummies and industry dummies. (This is file E9731g4 from the above-mentioned 1997 Economic Census CD.) We pooled the data across industries because the sales revenue data for some cells are held back due to disclosure issues. We scaled the fitted values so the aggregate totals matched published aggregates. Return to Text

21. Specifically, Table A1 is calculated from Table A2, i.e., we take the averages across industries in A2 and then calculate the conditional shares (as opposed to calculating the conditional share for each industry first and then taking averages). Return to Text

22. This is the Standard Classification of Transported Goods code. Return to Text

23. The 1992 CFS uses the Standard Transportation Commodity Codes (STCC) for product codes rather than the SCTG product codes. Despite this difference, we get no change in results. Return to Text

^♣ This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to Text