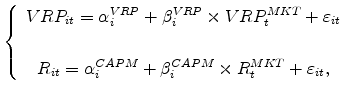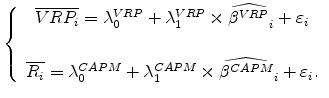Credit Default Swap Spreads and Variance Risk Premia*
Keywords: Variance risk premia, credit default swap spreads, option-implied variance, expected variance, realized variance.
Abstract:
We find that firm-level variance risk premium, estimated as the difference between option-implied and expected variances, has a prominent explanatory power for credit spreads in the presence of market- and firm-level risk control variables identified in the existing literature. Such a predictability complements that of the leading state variable--leverage ratio--and strengthens significantly with lower firm credit rating, longer credit contract maturity, and model-free implied variance. We provide further evidence that: (1) variance risk premium has a cleaner systematic component and Granger-causes implied and expected variances, (2) the cross-section of firms' variance risk premia seem to price the market variance risk correctly, and (3) a structural model with stochastic volatility can reproduce the predictability pattern of variance risk premia for credit spreads.
JEL Classification: G12, G13, G14.
1 Introduction
It has been long recognized in literature that a critical component of systematic economic risk may be missing in credit risk modeling (Jones, Mason, and Rosenfeld, 1984; Huang and Huang, 2003; Collin-Dufresne, Goldstein, and Martin, 2001; Elton, Gruber, Agrawal, and Mann, 2001), which is the main cause of the so-called credit spread puzzle. The relatively larger spikes of high investment-grade credit spreads than speculative-grade during recent financial crisis highlight a possible systematic shock that tends to explain the low frequency cyclical movements of credit spreads. In this paper, we try to explain individual firms' credit spreads by variance risk premium (VRP, hereafter) and relate the VRP component of credit spread to the exposure to systematic variance or economic uncertainty risk (Bollerslev, Tauchen, and Zhou, 2009; Drechsler and Yaron, 2009).
VRP is defined in asset pricing theories as the difference between the expected variance under the risk-neutral measure and the expected variance under the objective measure (see, Jiang and Tian, 2005; Carr and Wu, 2008b; Britten-Jones and Neuberger, 2000 , among others). Theoretically, variance risk premium isolates only firms' exposure to systematic variance risk that must be priced in all risky assets since, by construction, the risk neutral and objective expectations of firms' idiosyncratic variance risk cancel out with each other. Empirically, we estimate VRP as the difference between model-free option-implied variance and expected variance based on the realized measures estimated from high-frequency equity return data.
We present robust evidence that firm-level VRP is the most prominent predictor for credit spread variations relative to the other macroeconomic and firm specific credit risk determinants identified in the existing literature. This finding echoes the recent studies that recognize the linkage among macroeconomic condition, equity risk premium, and credit risk pricing (see, e.g., Bhamra, Kuhn, and Strebulaev, 2009; David, 2008; Chen, 2009; Chen, Collin-Dufresne, and Goldstein, 2009), but focuses on providing cross-sectional evidence of individual firms. We also find that VRP complements leverage ratio, which has been shown as a leading explanatory variable for credit spreads (Collin-Dufresne and Goldstein, 2001). Importantly, this firm-level VRP measure crowds out the popular market VRP (and VIX) that has been shown as a strong predictor for aggregate credit spread indices (Zhou, 2009; Buraschi, Trojani, and Vedolin, 2009). Such a predictive power turns out to be greater for speculative-grade credit spreads, longer CDS contract maturities, and VRP constructed from model-free option-implied variances.
Previous research seems to suggest that implied variance is informatively more efficient than realized variance in predicting credit spreads (Berndt, Lookman, and
Obreja, 2006; Carr and Wu, 2008a; Cao, Yu, and Zhong, 2008). However, by
decomposing the implied variance into VRP and expected variance, we find that VRP can substitute most of the explaining power of implied variance, especially for lower frequencies of monthly and quarterly relative to weekly. We also present evidence that the first principle component of VRP across
all firms explains 78 percent of the total variation, while that of implied variance only explains 54 percent and expected variance only 57 percent. Finally we show that, at aggregate level, VRP Granger causes implied and expected variances, but not ![]()
![]() . These additional findings imply that VRP may be an ideal measure of firms' exposures
to a systematic variance risk factor, and the economic interpretation of implied variance in explaining credit spread could largely reside on VRPs that are exposed to such a macroeconomic uncertainty risk.
. These additional findings imply that VRP may be an ideal measure of firms' exposures
to a systematic variance risk factor, and the economic interpretation of implied variance in explaining credit spread could largely reside on VRPs that are exposed to such a macroeconomic uncertainty risk.
To further corroborate the interpretation that firm VRPs are exposures to systematic uncertainty risk, we provide two additional justifications. In the first exercise, we run a two-pass regression of individual firms' VRP on the market VRP. The second stage cross-sectional regression obtains an
![]() of 14 percent and the estimated market VRP is 1.17 compared to the observed one of 1.20. In contrast, a similar exercise with firm equity returns obtains an
of 14 percent and the estimated market VRP is 1.17 compared to the observed one of 1.20. In contrast, a similar exercise with firm equity returns obtains an ![]() of 0.00 and estimated market return of 0.03 compared to observed one of 0.46. This result suggests that the cross-section of individual firms' VRPs may correctly price a systematic variance or economic uncertainty risk
factor. In another exercise, we simulate from a structural model with stochastic volatility, and find that VRP can indeed provide additional explaining power for a representative firm's credit spreads, even with the control of true leverage ratio. On the contrary, the Merton model without
stochastic volatility cannot reproduce such a stylized pattern found in our empirical exercise.
of 0.00 and estimated market return of 0.03 compared to observed one of 0.46. This result suggests that the cross-section of individual firms' VRPs may correctly price a systematic variance or economic uncertainty risk
factor. In another exercise, we simulate from a structural model with stochastic volatility, and find that VRP can indeed provide additional explaining power for a representative firm's credit spreads, even with the control of true leverage ratio. On the contrary, the Merton model without
stochastic volatility cannot reproduce such a stylized pattern found in our empirical exercise.
Our work is related to the recent effort on explaining individual firms' credit spreads from several innovative angles. Campbell and Taksler (2003) find that the increases in bond spreads can be explained by the upward trend in idiosyncratic equity volatility. Cremers, Driessen, Maenhout, and Weinbaum (2008) rely on option-implied jump risk measure to interpret the cross-sectional variations in default risk premia. Ericsson, Jacobs, and Oviedo (2004); Ericsson, Reneby, and Wang (2006) exploit credit derivatives in explaining credit spreads and evaluating structural models. Our study shares with the same spirit in terms of risk-based explanations but emphasizes on using VRP as a novel tool to isolate the firm's exposure to systematic variance risk from its idiosyncratic counterpart. This provides an economic interpretation for the superior predictive power of implied variance on credit spreads, and point to a clear direction for improving the structural credit risk modeling--by incorporating a systematic variance risk factor.
The rest of the paper will be organized as the following: Section 2 introduces the variance risk premium measure and our empirical methodology; followed by a description of data sources and summary statistics in Section 3; then Section 4 presents empirical findings of variance risk premium with respect to predicting credit spreads and discusses some economic interpretations; and Section 5 concludes.
2 Variance Risk Premia and Empirical Methodology
In this section, we introduce the concept of variance risk premium (VRP) for individual firms, following the recent literature in defining the market VRP as a difference between the model-free implied variance and forecasted realized variance. Then we outline our empirical strategy for explaining the credit default swap (CDS) spreads of individual firms, using such a firm specific VRP variable, together with other established market and firm control variables--noticeably the firm leverage ratio and risk-free rate.
2.1 Constructing the VRP Measure for Individual Firms
To construct the benchmark measure of firm VRP, we compute the model-free implied variances from the OptionMetrics data of the individual firms' equity option prices and the forecasted realized variances from high-frequency stock returns of individual companies.
Following Britten-Jones and Neuberger (2000), we apply Cox, Ross, and Rubinstein (1979) or CRR binomial lattice model to translate the OptionMetrics prices of American call options of different maturities and moneyness into implied volatilities. By
fitting a smooth cubic splines function to the implied volatilities, we compute the term structure of implied volatilities at various strikes for call options of ![]() -maturity. Then the term
structure of implied volatilities are translated back into the term structure of call prices at various strikes using the CRR model. Note that such a procedure is not model-dependent, as the CRR model serves merely as a mapping device between option prices and implied volatilities (Jiang and Tian, 2005).
-maturity. Then the term
structure of implied volatilities are translated back into the term structure of call prices at various strikes using the CRR model. Note that such a procedure is not model-dependent, as the CRR model serves merely as a mapping device between option prices and implied volatilities (Jiang and Tian, 2005).
With the term structure of call option prices, we compute risk-neutral or model-free implied variance by summing the following functional form over a spectrum of densely populated strike prices:
| (1) | |||
![\displaystyle 2\int_{0}^{\infty } \frac{C_{i}(t+T,K)/B(t,t+T)-\max[% 0,S_{i,t}/B(t,t+T)-K]}{K^{2}}dK](img12.gif) |
(2) |
where
In order to define the realized variance that we use in estimating the expected variance, let ![]() denote the logarithmic stock price of firm
denote the logarithmic stock price of firm ![]() . The realized variance over the
. The realized variance over the ![]() time interval may be measured as:
time interval may be measured as:
where the convergence relies on
For a monthly horizon and monthly data frequency, where ![]() is the end-of-month risk-neutral expected variance for firm
is the end-of-month risk-neutral expected variance for firm ![]() of the next month, and
of the next month, and ![]() is the realized variance of the current month, we adopt a linear forecast of the objective or statistical
expectation of the return variance as
is the realized variance of the current month, we adopt a linear forecast of the objective or statistical
expectation of the return variance as
![]() and the expected variance is simply the time
and the expected variance is simply the time ![]() forecast of realized variance from
forecast of realized variance from ![]() to
to ![]() based on estimated coefficients
based on estimated coefficients
![]() and
and
![]() in the linear regression,
in the linear regression,
| (4) |
where
We use this particular projection, because the model-free implied variance from options market is an informationally more efficient forecast for future realized variance than the past realized variance (see, e.g., Jiang and Tian, 2005 ); while realized variance based on high-frequency data
also provides additional power in forecasting future realized variance (Andersen, Bollerslev, Diebold, and Labys, 2001b). Therefore, a joint forecast model with one lag of implied variance and one lag of realized variance seems to capture the most forecasting power from the
time-![]() available information (Drechsler and Yaron, 2009).
available information (Drechsler and Yaron, 2009).
The variance risk premium of an individual firm, or ![]() , underlying our key empirical findings is defined as the difference between the ex-ante risk-neutral expectation and the
objective expectation of future return variation over the
, underlying our key empirical findings is defined as the difference between the ex-ante risk-neutral expectation and the
objective expectation of future return variation over the ![]() time interval,
time interval,
Such a construct at the market level has been shown to possess remarkable capability in forecasting the aggregate credit spread indices (Zhou, 2009 ). Here we investigate in detail how the VRP of individual firms can help us to understand the cross-section of individual firms' CDS spreads.
2.2 Empirical Implementation Strategy
We examine the relationship between credit default swap (CDS) spreads and variance risk premia (VRP) in the presence of market- and firm-level credit risk determinants suggested by theory and empirical evidence. We focus on monthly data to avoid picking up the market microstructure noise induced
by high frequency comovements between option and credit markets. For spreads and implied variance, they are just the matched last available end-of-month (daily) observations. Because missing dates and stale quotes signify that daily or even weekly data quality is not reliable, and if we just ignore
the daily missing values, we will introduce serial dependent error structure in the independent variable--CDS spread, which may artificially increase the prediction ![]() or significance.
Monthly data will give us more conservative but reliable estimate and is typically the shortest horizon--compared to quarterly or annual data--for picking up the low frequency risk premium movement.
or significance.
Monthly data will give us more conservative but reliable estimate and is typically the shortest horizon--compared to quarterly or annual data--for picking up the low frequency risk premium movement.
CDS spreads should also be influenced by the leverage ratio of the underlying firm and the risk-free spot rate. As suggested by the structural form credit risk models (Merton, 1974, and henceforth), leverage is the most important credit risk determinant--all else being
equal, a firm with higher leverage has a higher likelihood of default (Collin-Dufresne and Goldstein, 2001). The leverage ratio, denoted by ![]() , is computed as the
book value of debt over the sum of the book value of debt and market value of equity. Moreover, structural models predict that risk-free interest rates negatively influence the credit spread (Longstaff and Schwartz, 1995)--when the risk-free rate is increasing, it typically
signifies an improving economic environment with better earning growth opportunity for the firms, therefore lower default risk premium. Alternatively when short rate is rising, inflation risk is also increasing, nominal asset debt becomes less valuable compared to real asset equity (Zhang, Zhou, and Zhu, 2009). We define the risk-free rate variable to be the one-year swap yield, denoted by
, is computed as the
book value of debt over the sum of the book value of debt and market value of equity. Moreover, structural models predict that risk-free interest rates negatively influence the credit spread (Longstaff and Schwartz, 1995)--when the risk-free rate is increasing, it typically
signifies an improving economic environment with better earning growth opportunity for the firms, therefore lower default risk premium. Alternatively when short rate is rising, inflation risk is also increasing, nominal asset debt becomes less valuable compared to real asset equity (Zhang, Zhou, and Zhu, 2009). We define the risk-free rate variable to be the one-year swap yield, denoted by ![]() .
.
Empirical research also shows that in practice, CDS spreads contain compensation for non-default risks as well as risk premia which may be difficult to identify without the aggregate macro variables. Henceforth, we will not limit our analysis to the traditional theoretically motivated regressors
but augment our set of variables by the following market variables: (1) the market variance risk premium based on the S&P 500 denoted by ![]() to measure systemic variance or
macroeconomic uncertainty risk--all else equal, high market VRP leads to high credit spreads (Zhou, 2009);3 (2) the S&P 500
return, denoted by
to measure systemic variance or
macroeconomic uncertainty risk--all else equal, high market VRP leads to high credit spreads (Zhou, 2009);3 (2) the S&P 500
return, denoted by ![]() to proxy for the overall state of the economy--when economy is improving the credit spread should be lower as profit is rising (Zhang, Zhou,
and Zhu, 2009); (3) Moody's default premium slope, denoted by
to proxy for the overall state of the economy--when economy is improving the credit spread should be lower as profit is rising (Zhang, Zhou,
and Zhu, 2009); (3) Moody's default premium slope, denoted by ![]() , is computed as
, is computed as ![]() yield spread minus
yield spread minus ![]() yield spread to capture the default risk premium in the corporate bond market--the coefficient of the default premium slope should be positive,
consistent to the notion that CDS and corporate bond markets are cointegrated (Ericsson, Jacobs, and Oviedo, 2004; Zhu, 2006; Blanco, Brennan, and Marsh, 2005); and (4) the difference of five-year swap rate and five-year Treasury rate,
denoted by
yield spread to capture the default risk premium in the corporate bond market--the coefficient of the default premium slope should be positive,
consistent to the notion that CDS and corporate bond markets are cointegrated (Ericsson, Jacobs, and Oviedo, 2004; Zhu, 2006; Blanco, Brennan, and Marsh, 2005); and (4) the difference of five-year swap rate and five-year Treasury rate,
denoted by ![]() , as a proxy for fixed income market illiquidity--which is expected to move positively with CDS spreads (Tang and Yan, 2008).
, as a proxy for fixed income market illiquidity--which is expected to move positively with CDS spreads (Tang and Yan, 2008).
For firm characteristic variables, besides leverage ratio, we include the following controls: (1) asset turnover, denoted by ![]() , is computed as sales divided by total assets; (2)
price-earnings ratio denoted by
, is computed as sales divided by total assets; (2)
price-earnings ratio denoted by
![]() ; (3) market-to-book ratio, denoted by
; (3) market-to-book ratio, denoted by ![]() ; (4) return on assets,
denoted by
; (4) return on assets,
denoted by ![]() , computed as earnings divided by total assets; (5) the natural logarithm of sales, denoted by
, computed as earnings divided by total assets; (5) the natural logarithm of sales, denoted by
![]() . As a proxy for firm size,
. As a proxy for firm size,
![]() should influence CDS spread negatively--as a larger and more mature firm tend to be investment grade in our sample, all else being equal. Firm asset turnover, market-book ratio,
and return on assets are all expected to be negatively related to CDS spreads, because firms of high profitability and future growth tend to have lower credit risk. Price-earnings ratio may have two opposite effects on CDS spreads: on the one hand, high price-earnings ratio implies high future
asset growth reducing the likelihood of financial distress and credit risk; on the other hand, high growth firms tend to have high return volatilities that increase credit risk. These hypothesized signs of impact coefficients are consistent with the basic Merton (1974) model's implications and are
largely confirmed by the empirical literature (e.g., see Collin-Dufresne, Goldstein, and Martin, 2001).
should influence CDS spread negatively--as a larger and more mature firm tend to be investment grade in our sample, all else being equal. Firm asset turnover, market-book ratio,
and return on assets are all expected to be negatively related to CDS spreads, because firms of high profitability and future growth tend to have lower credit risk. Price-earnings ratio may have two opposite effects on CDS spreads: on the one hand, high price-earnings ratio implies high future
asset growth reducing the likelihood of financial distress and credit risk; on the other hand, high growth firms tend to have high return volatilities that increase credit risk. These hypothesized signs of impact coefficients are consistent with the basic Merton (1974) model's implications and are
largely confirmed by the empirical literature (e.g., see Collin-Dufresne, Goldstein, and Martin, 2001).
Given the nature of our cross-sectional and time-series data, we adopt the robust standard error approach of Petersen (2009) to account for both firm and time effects in large panel data sets. Therefore, the above discussions suggest the following regression
equation
and our focus is the relation between a firm's CDS spread and its variance risk premium (VRP).
3 Data Description and Summary Statistics
To conduct the empirical study, we collect data on credit default swap (CDS) spreads, equity option prices, macroeconomic variables, firm equity and balance sheet information from various sources. The summary statistics of CDS spreads, variance risk premia (VRP), and other market wide or firm-specific controls, are discussed here to set the background for examining the critical link between CDS spread and VRP.
3.1 Data Sources
Under a CDS contract, the protection seller promises to buy the reference bond at its par value when a predefined default event occurs. In return, the protection buyer makes periodic payments to the seller until the maturity date of the contract or until a credit event occurs. This periodic payment, which is usually expressed as a percentage (in basis points) of the bonds' notional value, is called the CDS spread. By definition, credit spread provides a pure measure of the default risk of the reference entity. We use CDS spreads as a direct measure of credit spreads. Compared to corporate bond yield spreads, CDS spreads are not subject to the specification of benchmark risk-free yield curve and less contaminated by non-default risk components (Longstaff, Mithal, and Neis, 2005; Ericsson, Reneby, and Wang, 2006).
Our single-name CDS spreads are obtained from a database compiled by the Markit group. The data set also reports average recovery rates, used by data contributors in pricing each CDS contract, which center around 0.4 without much variations. The sample period covers January 2001 to September 2008. We restrict our sample to US dollar denominated CDS written on US entities that are not in the government, financial, or utility sectors. We further eliminate the subordinated class of contracts because of its small relevance in the database and its unappealing implications for credit risk pricing. The maturities of Markit CDS contracts range between 6 months and 30 years. We focus on the most popular and liquid 5-year CDS contracts with modified restructuring clauses in our benchmark analysis. CDS spreads of other contract maturities ranging between 1- and 10-year are relatively liquid and are used for robustness checks. After cleaning and matching the CDS data with reliable option, equity and balance sheet information, we are left with more than 22,000 monthly observations of 382 entities in our study. For each entity, the monthly CDS spreads are matched with the monthly VRPs.
The option data is obtained from Ivy DB OptionMetrics. We keep only the options whose last trade dates match the record dates and whose option price dates match the underlying security price dates. We further eliminate the option prices that violate arbitrage boundaries (
![]() ). Stock dividend information is acquired from CRSP and taken into account when applying the CRR model to extract the implied volatility surface.
). Stock dividend information is acquired from CRSP and taken into account when applying the CRR model to extract the implied volatility surface.
We compute high-frequency realized variances using information in TAQ database that contains the intraday equity trading data spaced by 15 minutes during trading hours. Following the method outlined in previous section, we first calculate the daily variance based on the high-frequency data, then aggregate it to construct monthly realized variance. Next we estimate expected variance that is of the same maturity as the implied variance. All types of VRPs are then matched with CDS spreads on a firm-month basis.
For market and firm control variables, they are most recently available monthly or quarterly variables. Firm quarterly balance-sheet data is acquired from COMPUSTAT. For market variables, the swap rates, constant maturity Treasury yields and Moody's ![]() and
and ![]() yields are acquired from the Federal Reserve Board public website. S&P 500 index returns come from CRSP. The
market VRP is from Zhou (2009).
yields are acquired from the Federal Reserve Board public website. S&P 500 index returns come from CRSP. The
market VRP is from Zhou (2009).
3.2 Summary Statistics
Table 5 presents the summary statistics--average across the 382 firms--of the five-year CDS spreads and our benchmark VRP measure (Panel A), model-free implied variances and expected variances (Panel B). The average Moody's and S&P ratings of the CDS reference
entities range between AAA and CCC. A majority of the CDS ratings are A, BBB and BB (![]() ,
, ![]() and
and ![]() respectively, in total 81%). The average of CDS spreads in our sample is 151 basis points. They increase monotonically from 17 to 603
basis points as the credit ratings of the CDS reference entities deteriorate from AAA to CCC. The difference between the average CDS spreads for AAA grade and AA grade is 4 basis points,
whereas the difference between those for CCC grade and B grade is 235 basis points. The CDS spreads display positive skewness of around 1 and leptokurtosis of 4.44.
respectively, in total 81%). The average of CDS spreads in our sample is 151 basis points. They increase monotonically from 17 to 603
basis points as the credit ratings of the CDS reference entities deteriorate from AAA to CCC. The difference between the average CDS spreads for AAA grade and AA grade is 4 basis points,
whereas the difference between those for CCC grade and B grade is 235 basis points. The CDS spreads display positive skewness of around 1 and leptokurtosis of 4.44.
Similar to the CDS spreads, VRP displays significant variations across rating groups. The average of the benchmark VRP measure for the full sample is 33 (monthly percentage squared), increasing from 7 to 82 as CDS reference entities' credit ratings drop from AAA to CCC. High credit risk entities tend to be associated with high VRPs. The variance risk premia display positive skewness of 1.2 and leptokurtosis of 5.2.
As shown in Panel B of Table 1, the means and standard deviations of model-free implied variances are much higher than those of expected variances, but the skewness and kurtosis are similar. It suggests that implied variance could contain a larger idiosyncratic component than expected variance. The AR(1) coefficients for VRP, model-free implied and expected variances are 0.38, 0.57 and 0.45 respectively, suggesting that VRP is less persistent compared to model-free implied variances and expected variances.
We group our sample into three sub-samples by CDS ratings. The first group contains CDS of AAA, AA and A grades, the second group contains CDS of BBB grade, and the third group contains CDS of speculative grades ranging between BB and CCC. The three sub-samples contain ![]() ,
, ![]() and
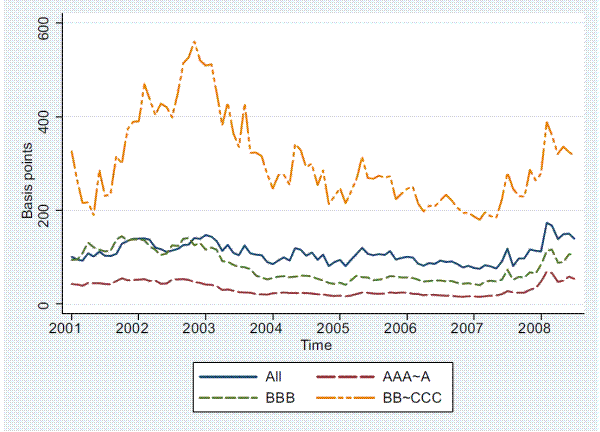
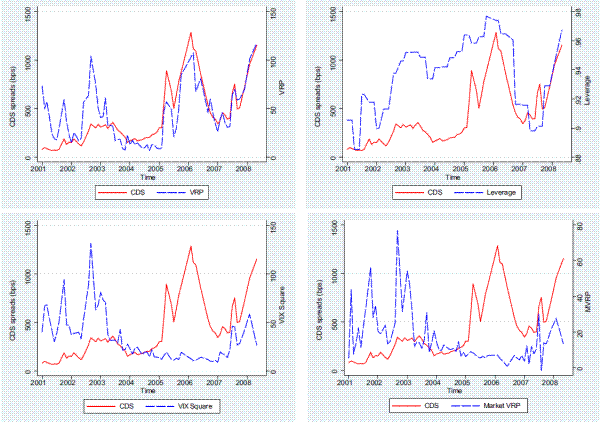
and ![]() firm-month observations respectively. Figure 1 plots the time-series of the five-year CDS spreads of whole sample and three sub-groups. The CDS spreads decrease gradually from the peaks in late 2002, then increase again as the financial crisis approaches in
mid 2007. The spreads of investment grade CDS in year 2008 are higher than those in year 2002, whereas the spreads of speculative grade CDS are lower than their 2002 level. That highlights the nature of the recent financial crisis, which is mainly fueled by the heightening of systematic risk or
economic uncertainty and affects disproportionately the high investment grade credit spreads. The difference between the investment grade and speculative grade CDS spreads, however, becomes widened during 2007-2008, potentially due to the " fly-to-quality" effect during the financial crisis that
drives up the compensation for credit risk.
firm-month observations respectively. Figure 1 plots the time-series of the five-year CDS spreads of whole sample and three sub-groups. The CDS spreads decrease gradually from the peaks in late 2002, then increase again as the financial crisis approaches in
mid 2007. The spreads of investment grade CDS in year 2008 are higher than those in year 2002, whereas the spreads of speculative grade CDS are lower than their 2002 level. That highlights the nature of the recent financial crisis, which is mainly fueled by the heightening of systematic risk or
economic uncertainty and affects disproportionately the high investment grade credit spreads. The difference between the investment grade and speculative grade CDS spreads, however, becomes widened during 2007-2008, potentially due to the " fly-to-quality" effect during the financial crisis that
drives up the compensation for credit risk.
Figure 2 further illustrates the dynamic relationships among CDS spreads, VRP, market VRP and leverage ratio for a representative firm in our sample: General Motor (GM). The CDS spread line and VRP line resemble each other closely over time. In particular, the two lines move closely during GM downgrading in year 2005 and in the recent financial crisis. In addition, the CDS spreads tend to comove with the firm's leverage ratio. A visual examination of the relationship between CDS spreads and market VRP suggests that market risk premium, market VRP in particular, may not provide powerful prediction on GM's credit spreads. For instance, the two lines move in exactly opposite direction during the period from 2004 to 2006. The market VRP line closely resembles the VIX line.
Table 2 reports the descriptive statistics for our market- and firm-level control variables--average across 382 entities the latter. The average monthly market VRP
is 22.82 (percentage-squared). The average of one-year swap rate is ![]() . The
firms in our sample have an average leverage ratio of
. The
firms in our sample have an average leverage ratio of ![]() with a standard deviation of
with a standard deviation of ![]() . For simplicity, we omit the discussion of other control variables, given that they are similar to those reported in literature.
. For simplicity, we omit the discussion of other control variables, given that they are similar to those reported in literature.
Table 3 reports the univariate correlations of the regression variables. It is shown that CDS spread is positively correlated to VRP, IV and EV. Both VRP and EV are significantly correlated to IV (0.90 and 0.95), whereas VRP and EV are much less correlated (0.73). This suggests that VRP and EV may capture different risk components embedded in IV. Among credit risk determinants, VRP and leverage have high correlations with CDS spreads, whereas other variables exhibit lower correlations, suggesting that the two variables may possess significant explanatory power for credit risk. CDS spreads are positively correlated with market VRP's (0.05), but the coefficients of market VRP turn out to be negative in the presence of firm-level VRP in the multivariate regressions in the next section. The low correlations among firm-level control variables suggest that the selected covariates well complement each other without causing serious multicollinearity.
4 Empirical Results and Analysis
In this section, we show that firm-level variance risk premia (VRP) displays a significant predictive power for CDS spreads in the presence of all other credit risk determinants. In particular, it complements the firm leverage ratio that has been shown as the leading explanatory variable for credit spreads by Collin-Dufresne and Goldstein (2001) within the Merton (1974) framework. VRP crowds out the market-level variation risk measure--market VRP--in capturing the systematic variance risk embedded in CDS spreads. The predictive power of VRP for CDS spreads increases as firm credit quality deteriorates. Model-free VRP performs better than the VRP implied from call or put options of different moneyness.
Further robustness suggests that VRP and expected variance are two indispensable components of the option-implied variance in predicting the individual firms' credit spreads. In addition, VRP seems to possess more forecasting power at monthly and quarter horizons while implied variance more at weekly horizon, and in aggregate the market VRP Granger-causes implied and expected variances. Finally, firm-level VRP measure contains a systematic variance risk exposure that is priced in the cross-section of VRPs, and our result seems to be qualitatively justifiable by simulation evidence from a structural model with stochastic asset variance risk.
4.1 The Benchmark Regressions
Table 4 reports the regression results of the relationship between five-year CDS spreads and benchmark VRP computed with model-free implied variance minus expected variance estimated from lagged implied and realized variances (see
Section 2). Regression 1 reports that CDS spreads are positively related to VRP in the univariate regression. The ![]() -statistic is a significant 10.03. In terms of economic significance, one standard deviation increase in VRP ( 21.57) will increase CDS spreads by 60 basis points, which translates into $90,000 on a CDS contract with a notional amount of $15 million.
-statistic is a significant 10.03. In terms of economic significance, one standard deviation increase in VRP ( 21.57) will increase CDS spreads by 60 basis points, which translates into $90,000 on a CDS contract with a notional amount of $15 million.
Regression 2 shows that including leverage ratio, as the leading determinant of credit spread levels and changes (Collin-Dufresne, Goldstein, and Martin, 2001; Collin-Dufresne and Goldstein, 2001), preserves the high significance of the VRP measure. As argued in theory (Merton, 1974), when default risk increases via the leverage channel, CDS spreads increase as well. Regression 3 shows that the relationship between CDS spreads and VRP remains intact in the presence of market VRP. More importantly, the sign of market VRP is driven to be negative, suggesting firm VRP subsumes market VRP in capturing systematic variance risk in predicting CDS spreads. This fact remains true with the control of leverage ratio (regression 4). As indicated in Zhou (2009), market VRP predicts a significant positive risk premium in market credit spreads, which is consistent with our firm level evidence here.
Regression 5 reports the full-scale regression results after including all control variables. The coefficient of VRP decreases slightly from 2.78 in the univariate regression to 2.29 but remains statistically significant at 1 percent level with a robust ![]() -statistic of 9.21. All the market level control variables are statistically insignificant, except
for the swap rate with a marginal
-statistic of 9.21. All the market level control variables are statistically insignificant, except
for the swap rate with a marginal ![]() -statistic of 1.70--when the short rate is increasing in an inflationary setting, nominal corporate debt would be less valuable, hence the credit spread is
higher. For firm-level controls, only the negative coefficients of market-book ratio and log sales are statistically significant at 1 percent level. The results support the intuition behind the structural-form credit risk models in that firms with higher profitability and growth opportunity tend to
have relatively smaller chance of default hence a lower credit risk premium.
-statistic of 1.70--when the short rate is increasing in an inflationary setting, nominal corporate debt would be less valuable, hence the credit spread is
higher. For firm-level controls, only the negative coefficients of market-book ratio and log sales are statistically significant at 1 percent level. The results support the intuition behind the structural-form credit risk models in that firms with higher profitability and growth opportunity tend to
have relatively smaller chance of default hence a lower credit risk premium.
The adjusted ![]() for the univariate regression indicates that 34 percent of the variation in the CDS spreads could be accounted for by the firm specific VRP that captures firm's exposure
to systematic uncertainty risk. Adding market VRP to the regression has very little impact on the adjusted
for the univariate regression indicates that 34 percent of the variation in the CDS spreads could be accounted for by the firm specific VRP that captures firm's exposure
to systematic uncertainty risk. Adding market VRP to the regression has very little impact on the adjusted ![]() , which merely increases to 0.35. It suggests that firm-level variation risk measure has much stronger explanatory power for individual firm's CDS spreads compared to the well-documented market-level variation risk measure. Including leverage ratio in the regression
increases the adjusted
, which merely increases to 0.35. It suggests that firm-level variation risk measure has much stronger explanatory power for individual firm's CDS spreads compared to the well-documented market-level variation risk measure. Including leverage ratio in the regression
increases the adjusted ![]() to 0.47, possibly capturing the firm-specific default
risk on top of systematic risk in the spirit of Merton (1974). Further adding all other control variables increases the adjusted
to 0.47, possibly capturing the firm-specific default
risk on top of systematic risk in the spirit of Merton (1974). Further adding all other control variables increases the adjusted ![]() sightly to
sightly to ![]() . It appears that, among all variables, firm level VRP and leverage ratio are the two most powerful explanatory variables affecting CDS spreads.
. It appears that, among all variables, firm level VRP and leverage ratio are the two most powerful explanatory variables affecting CDS spreads.
4.2 Robustness Checks
It is an important finding that variance risk premium (VRP) explains a significant portion of credit risk premium, which may be orthogonal to the asset return risk that is already being captured by the leverage ratio. In this section, we conduct a series of robustness checks that such a finding is reliable if we consider different credit rating entities and is robust to different CDS contract maturities, implied variances constructed from different options and moneyness, and substituting market VRP control with the popular VIX index.
The credit spreads of low quality issuers are supposed to respond more to underlying variance risk shocks captured by VRP. Therefore, we regress 5-year CDS spreads on VRP for three sub-samples respectively: AAA-A (high investment grade), BBB (low investment grade), and BB-CCC (speculative grade), based on the average CDS ratings of Moody's and S&P. We present in Table 5 both the bivariate regression results on firm VRP and leverage ratio and the multivariate regression results on VRP with all control variables. In both sets of regressions, the coefficients of VRP are highly significant and increase monotonically from to as the CDS ratings deteriorate. VRP exhibits much stronger predictability on the credit spreads of the CDS written on bonds issued by low credit quality entities. The coefficients of VRP for the lowest rating group BB-CCC are almost five-to-seven times larger than those for the highest rating group AAA-A and at least twice larger than those for the middle rating group BBB, confirming our prior. Consistent with the benchmark regressions, leverage ratio plays a significant role in affecting positively CDS spreads. The lower the credit quality of issuing entities, the more significant impact the leverage ratio has on the CDS spreads.
We examine the relationship between CDS spreads and VRP for different CDS maturities. Table 6 reports the regression results by CDS maturity terms: 1, 2, 3, 5, 7 and 10 years. In all of these regressions CDS spreads are correlated positively and significantly with
firm-level VRP and leveraged ratio. The ![]() -statistics confirms that the firm-level VRPs perform much better than the market-level VRPs in predicting individual firm credit spreads.4 The longer the maturity of a CDS contract, the more significant the impact of firm-level VRP on CDS spreads with larger slope coefficients and higher adjusted
-statistics confirms that the firm-level VRPs perform much better than the market-level VRPs in predicting individual firm credit spreads.4 The longer the maturity of a CDS contract, the more significant the impact of firm-level VRP on CDS spreads with larger slope coefficients and higher adjusted
![]() . It is intuitive that a CDS contract of longer maturity is relatively exposed to a larger amount of variance uncertainty risk and requires higher spread.
. It is intuitive that a CDS contract of longer maturity is relatively exposed to a larger amount of variance uncertainty risk and requires higher spread.
To check the extent to which the significance of the explanatory power of VRP on credit spreads depends on different methods of constructing VRP, we carry out regression analysis of CDS spreads on VRPs constructed with various option features. Besides the benchmark model-free implied variance,
we use implied variances computed from out-of-the-money, at-the-money and in-the-money put/call options. As reported in Table 7, all VRP measures display consistently significant predictability for CDS spreads in the presence of other credit risk predictors. Among them,
the VRPs constructed with model-free implied variance displays the strongest predicting power on CDS spreads, reflected in both higher ![]() -statistic and adjusted
-statistic and adjusted ![]() . The model-free implied variance is informatively more efficient than the implied variance from at-the-money (out-of-the-money or in-the-money) options alone as it incorporates by construction the option information
across all moneyness.
. The model-free implied variance is informatively more efficient than the implied variance from at-the-money (out-of-the-money or in-the-money) options alone as it incorporates by construction the option information
across all moneyness.
4.3 Implied Variance, Expected Variance, and VRP
Previous studies find that individual firm credit risk is strongly related to the option-implied volatilities consistent with an argument of informational efficiency (see, e.g., Cao, Yu, and Zhong, 2008, among others). However, in this subsection, we try to argue from several empirically angles that the explaining power of variance risk premium (VRP) for credit spread comes mainly from capturing a systematic risk component, tends to be long run, and Granger-causes implied variance.
To investigate this issue, we first carry out regressions in which VRP competes against implied variance and expected variance. Table 8 reports the results of regressing CDS spreads on those variables. The results of regression (1)-(3) indicate that with all control variables, VRP, implied variance, and expected variance explain 49, 52, and 48 percent of the variations in CDS spreads respectively. In regression (4) and (5), we test the predictability of VRP or expected variance on CDS spreads in the presence of implied variance. The coefficient of VRP remains positive while that of expected variance turns to be negative, both are statistically significant. In regression (6), we regress CDS spreads simultaneously on VRP and expected variance. The coefficients of both VRP and expected variance are positive and statistically significant at 1 percent level, suggesting that VRP and expected variance are two important components in implied variance that help to explain individual firm credit spreads.
If VRP better captures a systematic risk factor than implied variance, we might observe that the explanatory power of VRP on CDS spreads increases as data frequency becomes lower as systematic risk tends to be long-term. Panel A of Table 5 confirms such intuition by
showing that, in univariate regressions, the ![]() -statistics of VRP increases monotonically from 6.44 to 10.41 as the sample frequency changes from weekly to monthly then to quarterly. In the
presence of IV in the regressions, the
-statistics of VRP increases monotonically from 6.44 to 10.41 as the sample frequency changes from weekly to monthly then to quarterly. In the
presence of IV in the regressions, the ![]() -statistics of VRP increase consistently, while the
-statistics of VRP increase consistently, while the ![]() -statistics of implied variance keep decreasing as the frequency lowers. In both sets of regressions, the adjusted
-statistics of implied variance keep decreasing as the frequency lowers. In both sets of regressions, the adjusted ![]() increases for lower data frequency. Finally, at weekly
frequency implied variance improves the predictability of VRP by 12 percentage points; while for monthly and quarterly frequencies only by 5 percentage points.
increases for lower data frequency. Finally, at weekly
frequency implied variance improves the predictability of VRP by 12 percentage points; while for monthly and quarterly frequencies only by 5 percentage points.
We apply the Granger Causality tests on market-level VRP, IV, and EV as specified in the following regression5
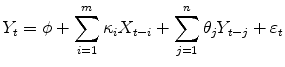 |
(9) |
and the null hypothesis is
We carry out the Principal Components Analysis on VRP, IV and EV. As reported in Table 10, the first principle component explains 78 percent of the total variation in VRP, while it only explains 54 percent in implied variance. And the first four principal components cumulatively explains 95 percent of VRP variation versus only 75 percent of implied variance. In other words, VRP is likely a cleaner measure of firms' exposure to systematic variance or economic uncertainty risk relative to the implied variance or expected variance, which is consistent with the finding that a missing systematic risk factor may hold the key for explaining the credit spread puzzle(s) (Collin-Dufresne, Goldstein, and Martin, 2001).
4.4 Cross-Sectional Validation of Market VRP
To examine to what extent firm-level VRP captures the exposure to a systematic variance risk factor, we compare the relationship between firm and market VRPs to the relationship between firm and market equity returns with the matched sample. Following the standard approach of testing CAPM (e.g.,
Lintner, 1965), we carry out two-stage regressions. In the first stage, we run time-series regressions for each firm ![]() to estimate its
to estimate its
![]() and
and
![]() , respectively:
, respectively:
We then compute each firm's average VRP,
The fundamental hypotheses being tested are
Panel A of Table 11 reports the summary statistics of
![]() and
and
![]() . As indicated by percentile, the
. As indicated by percentile, the ![]() -statistics of
-statistics of
![]() are relatively more dispersively distributed and more significant in the percentiles between 50% and 99%. In addition, the
are relatively more dispersively distributed and more significant in the percentiles between 50% and 99%. In addition, the ![]() s of the VRP regressions are generally higher than their counterparts in the CAPM regressions. The evidence suggests that VRP captures systematic risk more strongly than the well documented equity returns do. The means of the
s of the VRP regressions are generally higher than their counterparts in the CAPM regressions. The evidence suggests that VRP captures systematic risk more strongly than the well documented equity returns do. The means of the
![]() -statistics for VRP and equity return regressions are 4.29 and 3.91, respectively. The difference is on average 0.38 with a standard deviation of 0.18. Unreported mean comparison
-statistics for VRP and equity return regressions are 4.29 and 3.91, respectively. The difference is on average 0.38 with a standard deviation of 0.18. Unreported mean comparison
![]() -test shows a
-test shows a ![]() -statistic of 2.15, indicating the
-statistic of 2.15, indicating the ![]() -statistic of the VRP regressions are statistically higher than that of the equity return regressions.
-statistic of the VRP regressions are statistically higher than that of the equity return regressions.
Panel B shows that VRP is significantly related to
![]() with a
with a ![]() -statistic of 7.51, but equity return is not significantly
related to
-statistic of 7.51, but equity return is not significantly
related to
![]() . The VRP regression has an adjusted
. The VRP regression has an adjusted ![]() of 14.05 percent, compared
to an adjusted
of 14.05 percent, compared
to an adjusted ![]() of zero for the equity return regression.7 Figure 3 visualizes the fitted VRPs (equity returns) versus the observed VRPs (equity returns). We find that
of zero for the equity return regression.7 Figure 3 visualizes the fitted VRPs (equity returns) versus the observed VRPs (equity returns). We find that
![]() is 1.17 which is very close to the average market VRP of 1.20, whereas
is 1.17 which is very close to the average market VRP of 1.20, whereas
![]() is 0.03 percent which is much lower than the average monthly market equity return of 0.46 percent. The latter evidence is largely in line with the vast literature on
testing CAPM since Lintner (1965). Although both intercepts
is 0.03 percent which is much lower than the average monthly market equity return of 0.46 percent. The latter evidence is largely in line with the vast literature on
testing CAPM since Lintner (1965). Although both intercepts
![]() and
and
![]() are rejected to be zeros, we intentionally have not imposed the risk-free rate restrictions yet, so that we only focus on whether the slopes are equal to market variance
risk premium or market equity return premium. The above evidence further indicates that firm-level VRPs are able to price the systematic variance risk factor, much stronger than firm-level equity returns to price the systematic return risk factor, as advocated in standard asset pricing models.
are rejected to be zeros, we intentionally have not imposed the risk-free rate restrictions yet, so that we only focus on whether the slopes are equal to market variance
risk premium or market equity return premium. The above evidence further indicates that firm-level VRPs are able to price the systematic variance risk factor, much stronger than firm-level equity returns to price the systematic return risk factor, as advocated in standard asset pricing models.
4.5 A Structural Model with Stochastic Variance Risk
The main finding that variance risk premium (VRP) emerges as a leading explanatory variable for credit spread, suggests that there are two default risk drivers in the underlying firm asset dynamics. A structural model with stochastic volatility, as in Zhang, Zhou, and Zhu (2009), can generate the stylized fact that VRP is intimately related to credit spreads, in addition to the powerful leverage ratio (Collin-Dufresne and Goldstein, 2001).
Assume the same market conditions as in Merton (1974), and one can introduce stochastic variance into the underlying firm-value process:
where
With proper bankruptcy assumptions, we can solve the equity price, ![]() , as a European call option on firm asset
, as a European call option on firm asset ![]() with maturity
with maturity ![]() :
:
![]() with
with ![]() being the risk-free rate.
being the risk-free rate.
![]() and
and ![]() are the so-called risk-neutral probabilities. Therefore, the debt
value can be expressed as
are the so-called risk-neutral probabilities. Therefore, the debt
value can be expressed as
![]() , and its price is
, and its price is ![]() , where
, where ![]() is the face value of debt. The credit spread,
is the face value of debt. The credit spread, ![]() , is given by:
, is given by:
The structural credit risk model presented here also implies the following equity variance process,
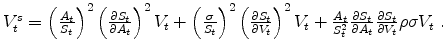 Inside simulation, we can examine the relationship between credit spread
Inside simulation, we can examine the relationship between credit spread where
Using a calibrated parameter setting for a BBB firm as in Zhang, Zhou, and Zhu (2009), we simulate 60 month of data of credit spreads, VRP, expected variance, and leverage ratio for both a Merton (1974) model and a stochastic volatility model (as above). Table 12 report the OLS regressions on explaining credit spreads with those proxies for underlying risk factors in asset value and volatility dynamics.
For the Merton (1974) model, leverage ratio will drive expected variance to be statistically insignificant, even though variance itself has a significant positive effect on credit spread. Note that for Merton model, although the asset volatility is constant, the equity volatility is time-varying; because asset value is time-varying and equity volatility is approximately leverage adjusted asset volatility. Therefore equity volatility does explain credit spread, but its effect is mostly subsumed when leverage ratio is included in the regression.
However, for the two factor stochastic volatility model, not only expected variance, VRP, and leverage ratio all have significant positive effect on credit spreads; but also any two variables combined together would both remain statistically significant with positive signs. In particular, the powerful leverage ratio cannot crowd out VRP or expected variance. This is due to the fact that both asset value and asset volatility are time-varying priced risk factors, and VRP or expected variance is not redundant to leverage ratio as in the case of one-factor Merton (1974) model. This result is qualitatively consistent with what we have discovered here for a large cross-section of individual firms' CDS spreads and VRPs.
5 Conclusions
Investors demand variance risk premium (VRP) as a compensation for firms' exposures to a systematic factor. Such a risk premium may arise from the time-varying fluctuations in the underlying cash flow or consumption volatility (Bollerslev, Tauchen, and Zhou, 2009; Bansal and Yaron, 2004). Recent studies suggest that market VRP captures the macroeconomic uncertainty or systematic variance risk that constitute a critical component in explaining the aggregate credit spread indices (Zhou, 2009; Buraschi, Trojani, and Vedolin, 2009). In this paper we carry out a comprehensive investigation on the relationship between the firm-level VRPs and credit spreads, and justify empirically that VRP provides a risk-based explanation for the credit spread variations.
We illustrate that VRPs of individual firms, estimated by the difference between model-free implied and expected variances, possess a significant explanatory power for credit default swap (CDS) spreads. Importantly, such predictability cannot be substituted for by that of market- and firm-level credit risk factors identified in previous research. In addition, firm-level VRP dominates the well-documented market-level VRP or VIX in capturing the macroeconomic uncertainty or systematic variance risk premium embedded in CDS spreads. The predictive power of VRP increases as the credit quality of CDS entities deteriorates and as the maturity of CDS contract increases. Leverage ratio and VRP emerge as two leading predictors of firms' credit spreads, pointing to asset value and stochastic volatility as two underlying risk drivers.
Empirical evidence also suggests that the superior explanatory power of VRP for CDS spreads tends to be stronger over monthly and quarterly horizons, while that of implied variance over weekly horizon. Also, the aggregate VRP seems to Granger-causes implied and expected variances, but not
![]()
![]() . A principle component analysis indicates that firms' VRPs have a much
larger systematic component relative to implied and expected variances. These additional findings imply that firms' VRP may be a good measure of exposure to a systemic variance risk or economic uncertainty factor, which is consistent with the fact that the cross-section of firm's VRPs can be used
to validate the market VRP correctly. Further more, the stylized predictability pattern of VRP for credit spread can be reproduced in simulation by a structural model with stochastic variance.
. A principle component analysis indicates that firms' VRPs have a much
larger systematic component relative to implied and expected variances. These additional findings imply that firms' VRP may be a good measure of exposure to a systemic variance risk or economic uncertainty factor, which is consistent with the fact that the cross-section of firm's VRPs can be used
to validate the market VRP correctly. Further more, the stylized predictability pattern of VRP for credit spread can be reproduced in simulation by a structural model with stochastic variance.
Bibliography
"The Distribution of Realized Stock Return Volatility," Journal of Financial Economics, vol. 61, 43-76. "The Distribution of Realized Exchange Rate Volatility," Journal of the American Statistical Association, vol. 96, 42-55. "Risks for the Long Run: A Potential Resolution of Asset Pricing Puzzles," Journal of Finance, vol. 59, 1481-1509. "Econometric Analysis of Realised Volatility and Its Use in Estimating Stochastic Volatility Models," Journal of Royal Statistical Society Series B, vol. 64, 253-280. "Default Risk Premia and Asset Returns," Carnegie Mellon University, Working Paper. "The Levered Equity Risk Premium and Credit Spreads: A United Framework," Standford University, Working Paper. "An Empirical Analysis of the Dynamic Relationship Between Investment-Grade Bonds and Credit Default Swaps," Journal of Finance, vol. 60, 2255-2281. "Expected Stock Returns and Variance Risk Premia," Review of Financial Studies," Review of Financial Studies, vol. 22, 4463-4492. "Option Prices, Implied Price Processes and Stochastic Volatility," Journal of Finance, vol. 55, 839-866. "The Joint Behavior of Credit Spreads, Stock Options and Equity Returns When Investors Disagree," Imperial College London Working Paper. "Equity Volatility and Corporate Bond Yields," Journal of Finance, vol. 58, 2321-2349. "How Important Is Option-Implied Volatility for Pricing Credit Default Swaps," Forthcoming. "Stock Options and Credit Default Swaps: A Joint Framework for Valuation and Estimation," New York University, Working Paper. "Variance Risk Premia," Review of Financial Studies, vol. 22, 1311-1341. "Macroeconomic Conditions and the Puzzles of Credit Spreads and Capital Structure," Journal of Finance, page forthcoming. "On the Relation Between the Credit Spread Puzzle and the Equity Premium Puzzle," Review of Financial Studies, vol. 22, 3367-3409. "Do Credit Spreads Reflect Stationary Leverage Ratios?" Journal of Finance, vol. 56, 1929-1957.| Rating | Firm Number | CDS Spread: Mean | CDS Spread: SD | CDS Spread: Skew. | CDS Spread: Kurt. | CDS Spread: AR(1) | VRP: Mean | VRP: SD | VRP: Skew. | VRP: Kurt. | VRP: AR(1) |
| AAA | 7 | 17.43 | 12.04 | 1.54 | 5.92 | 0.88 | 7.34 | 9.08 | 1.59 | 6.87 | 0.46 |
| AA | 17 | 20.97 | 10.29 | 0.97 | 3.62 | 0.87 | 10.16 | 11.03 | 2.00 | 9.01 | 0.40 |
| A | 101 | 33.84 | 18.18 | 1.33 | 4.98 | 0.86 | 16.97 | 15.43 | 1.46 | 5.86 | 0.52 |
| BBB | 199 | 77.07 | 39.06 | 1.10 | 4.41 | 0.84 | 23.23 | 17.81 | 1.23 | 5.25 | 0.37 |
| BB | 133 | 220.80 | 85.26 | 0.90 | 4.84 | 0.74 | 43.71 | 25.87 | 1.05 | 4.67 | 0.35 |
| B | 65 | 368.44 | 119.56 | 0.39 | 2.98 | 0.66 | 63.89 | 35.73 | 0.88 | 4.08 | 0.24 |
| CCC | 14 | 603.10 | 237.08 | 0.69 | 3.57 | 0.60 | 82.03 | 39.78 | 0.16 | 2.94 | 0.31 |
| Total | 382 | 151.18 | 58.94 | 1.01 | 4.44 | 0.80 | 32.80 | 21.57 | 1.20 | 5.20 | 0.38 |
| Rating | Implied Variance: Mean | Implied Variance: SD | Implied Variance: Skew. | Implied Variance: Kurt. | Implied Variance: AR(1) | Expected Variance: Mean | Expected Variance: SD | Expected Variance: Skew. | Expected Variance: Kurt. | Expected Variance: AR(1) |
| AAA | 40.38 | 27.39 | 1.75 | 7.23 | 0.65 | 33.04 | 18.70 | 1.10 | 6.71 | 0.65 |
| AA | 45.98 | 27.08 | 1.72 | 6.92 | 0.60 | 35.82 | 17.22 | 1.62 | 6.41 | 0.52 |
| A | 66.90 | 37.45 | 1.44 | 5.44 | 0.66 | 49.93 | 23.21 | 1.43 | 5.32 | 0.58 |
| BBB | 88.14 | 41.43 | 1.21 | 5.04 | 0.58 | 64.91 | 25.56 | 1.22 | 4.99 | 0.50 |
| BB | 144.22 | 56.45 | 1.13 | 4.86 | 0.54 | 100.51 | 33.68 | 1.12 | 4.85 | 0.32 |
| B | 193.06 | 72.30 | 1.01 | 4.23 | 0.51 | 129.17 | 41.36 | 1.00 | 4.21 | 0.28 |
| CCC | 234.52 | 69.00 | 0.53 | 3.62 | 0.41 | 152.49 | 36.33 | 0.50 | 3.62 | 0.31 |
| Total | 112.18 | 47.89 | 1.22 | 5.05 | 0.57 | 79.38 | 28.80 | 1.22 | 4.22 | 0.45 |
This table presents the summary statistics--average across the 382 firms--of the five-year CDS spreads and our benchmark Variance Risk Premium (VRP) measure (Panel A), model-free implied variances and expected variances (Panel B). The CDS spreads are in basis points. The VRP is computed as the spread between model-free implied variance and expected variance. The implied variance is the model-free implied variance. The expected variance is the linear forecast of realized variance by lagged implied and realized variance. The average Moody's and S&P ratings of the CDS reference entities range between AAA and CCC. The numbers of firms in each rating category are reported in the second column in Panel A. AR(1) denotes autocorrelation with one lag.
| Variable | Mean | SD | Skewness | Kurtosis | AR(1) | |
|
Market Level: Market VRP (%) |
22.82 | 21.92 | 2.88 | 12.32 | 0.27 | |
| Market Level: S&P 500 Return (%) | -0.02 | 1.98 | -0.17 | 4.15 | -0.17 | |
| Market Level: Swap (1 year, %) | 3.37 | 1.47 | 0.06 | 1.56 | 0.98 | |
| Market Level: |
0.99 | 0.22 | 0.64 | 2.36 | 0.95 | |
| Market Level: Swap - CMT (5 year, %) | 0.54 | 0.16 | 0.85 | 2.68 | 0.90 | |
|
Firm Level: Leverage Ratio |
0.40 | 0.06 | 0.37 | 2.88 | 0.89 | |
| Firm Level: Asset Turnover (%) | 1.09 | 0.15 | 0.09 | 3.00 | 0.79 | |
| Firm Level: Price-earnings Ratio | 16.26 | 53.55 | 0.23 | 8.06 | 0.76 | |
| Firm Level: Market/Book Ratio | 2.12 | 10.42 | 0.27 | 3.57 | 0.85 | |
| Firm Level: Return on Assets (%) | 5.69 | 6.51 | -0.67 | 7.89 | 0.69 | |
| Firm Level: Annualized Sales ($ billion) | 14.30 | 3.16 | 0.25 | 2.74 | 0.87 | |
| Firm Level: Firm Assets ($ billion) | 16.15 | 3.28 | 0.17 | 2.85 | 0.94 |
This table reports the descriptive statistics of the market- and firm-level control variables. For firm characteristics, we report the averages of the statistics across 382 firms. The market VRP is the difference between implied variance and expected variance of the S&P 500 index as in Bollerslev, Tauchen and Zhou (2009). The S&P 500 return, is the proxy for the overall state of the economy. The one year swap rate is the proxy for the risk-free interest rate. The Moody's default premium slope, defined as
| 1.00 | |||||||||||||||
| 0.58 | 1.00 | ||||||||||||||
| 0.62 | 0.90 | 1.00 | |||||||||||||
| 0.57 | 0.73 | 0.95 | 1.00 | ||||||||||||
| 0.05 | 0.26 | 0.29 | 0.28 | 1.00 | |||||||||||
| -0.02 | -0.02 | -0.02 | -0.02 | 0.17 | 1.00 | ||||||||||
| -0.08 | -0.18 | -0.17 | -0.14 | -0.32 | -0.06 | 1.00 | |||||||||
| 0.11 | 0.23 | 0.28 | 0.29 | 0.35 | -0.10 | -0.33 | 1.00 | ||||||||
| 0.07 | 0.18 | 0.26 | 0.28 | 0.27 | -0.14 | 0.15 | 0.50 | 1.00 | |||||||
| 0.52 | 0.29 | 0.32 | 0.30 | 0.05 | 0.00 | -0.09 | 0.06 | 0.02 | 1.00 | ||||||
| -0.06 | -0.03 | -0.01 | 0.01 | -0.01 | -0.01 | 0.02 | -0.00 | 0.01 | -0.05 | 1.00 | |||||
| -0.03 | -0.03 | -0.04 | -0.04 | -0.01 | 0.01 | 0.01 | -0.01 | -0.00 | -0.03 | 0.00 | 1.00 | ||||
| -0.02 | 0.00 | -0.01 | -0.01 | 0.00 | -0.00 | -0.02 | 0.00 | -0.00 | -0.02 | -0.00 | 0.00 | 1.00 | |||
| -0.28 | -0.22 | -0.23 | -0.20 | -0.04 | -0.02 | 0.06 | -0.03 | -0.01 | -0.42 | 0.10 | 0.03 | 0.02 | 1.00 | ||
| -0.17 | -0.18 | -0.20 | -0.19 | 0.04 | 0.00 | -0.01 | 0.04 | 0.06 | 0.01 | 0.38 | -0.01 | 0.01 | 0.09 | 1.00 |
This table reports the univariate correlations of the regression variables.
| Independent Variable | Regression: (1) | Regression: (2) | Regression: (3) | Regression: (4) | Regression: (5) |
| VRP | 2.78 | 2.26 | 2.92 | 2.38 | 2.29 |
| VRP: t-statistic | (10.03) | (11.00) | (10.04) | (11.06) | (9.21) |
| Leverage | 3.29 | 3.27 | 3.27 | ||
| Leverage: t-statistic | (8.89) | (9.05) | (8.60) | ||
| Market VRP | -1.12 | -1.03 | -0.94 | ||
| Market VRP: t-statistic | ( -4.38) | ( -4.48) | ( -4.34) | ||
| S&P 500 Return | 0.57 | ||||
| S&P 500 Return: t-statistic | (0.48) | ||||
| Swap Rate (1 Year) | 2.69 | ||||
| Swap Rate (1 Year): t-statistic | (1.70) | ||||
| 17.04 | |||||
| (1.09) | |||||
| Swap Rate - CMT (5 Year) | -9.62 | ||||
| Swap Rate - CMT (5 Year): t-statistic | ( -0.43) | ||||
| Asset Turnover Ratio | 3.09 | ||||
| Asset Turnover Ratio: t-statistic | (0.59) | ||||
| Price-earnings Ratio | -0.01 | ||||
| Price-earnings Ratio: t-statistic | ( -1.05) | ||||
| Market/Book Ratio | -0.02 | ||||
| Market/Book Rati: t-statistic o | ( -2.79) | ||||
| Return on Assets | -23.56 | ||||
| Return on Assets: t-statistic | ( -0.92) | ||||
| Log Sales | -12.23 | ||||
| Log Sales: t-statistic | ( -3.06) | ||||
| Constant | 28.00 | -84.68 | 41.20 | -71.82 | -0.31 |
| Constant: t-statistic | (5.89) | ( -5.67) | (10.46) | ( -5.52) | ( -0.01) |
| Adjusted |
0.34 | 0.47 | 0.35 | 0.48 | 0.49 |
This table reports the regression results of five-year CDS spreads on the VRP computed with model free implied variance
| Independent Variable | AAA-A | BBB | BB-CCC | AAA-A | BBB | BB-CCC |
| VRP | 0.48 | 1.06 | 2.20 | 0.29 | 0.81 | 2.12 |
| VRP: t-statistic | (9.58) | (10.30) | (9.46) | (8.02) | (7.34) | (7.71) |
| Leverage | 0.44 | 1.19 | 5.84 | 0.40 | 1.10 | 5.76 |
| Leverage: t-statistic | (5.33) | (6.37) | (6.47) | (5.71) | (5.38) | (6.62) |
| Market VRP | -0.01 | 0.12 | -0.60 | |||
| Market VRP: t-statistic | ( -0.28) | (1.26) | (1.13) | |||
| S&P 500 Return | -0.01 | -0.10 | 0.22 | |||
| S&P 500 Return: t-statistic | ( -0.04) | ( -0.15) | (0.09) | |||
| Swap Rate (1 Year) | -2.35 | -2.79 | -5.62 | |||
| Swap Rate (1 Year): t-statistic | ( -5.33) | ( -2.86) | ( -1.38) | |||
| 20.48 | 34.40 | 70.29 | ||||
| (6.33) | (3.72) | (1.57) | ||||
| Swap Rate - CMT (5 Year) | 39.26 | 30.29 | -51.11 | |||
| Swap Rate - CMT (5 Year): t-statistic | (6.51) | (2.07) | ( -1.02) | |||
| Asset Turnover Ratio | 3.05 | 6.00 | -36.62 | |||
| Asset Turnover Ratio: t-statistic | (2.82) | (1.63) | ( -2.26) | |||
| Price-earnings Ratio | -0.00 | -0.00 | -0.01 | |||
| Price-earnings Ratio: t-statistic | ( -1.56) | ( -0.14) | ( -0.54) | |||
| Market/Book Ratio | -0.00 | -0.17 | -0.02 | |||
| Market/Book Ratio: t-statistic | ( -0.35) | (1.07) | ( -4.29) | |||
| Return on Assets | -13.42 | -57.29 | -9.18 | |||
| Return on Assets: t-statistic | ( -1.33) | ( -2.85) | ( -0.28) | |||
| Log Sales | -4.29 | -6.14 | 8.01 | |||
| Log Sales: t-statistic | ( -6.00) | ( -1.82) | (0.85) | |||
| Constant | 10.12 | -0.38 | -137.35 | 15.11 | 11.00 | -166.68 |
| Constant: t-statistic | (4.62) | ( -0.05) | ( -2.94) | (2.50) | (0.49) | (0.02) |
| Adjusted |
0.30 | 0.30 | 0.46 | 0.50 | 0.35 | 0.47 |
This table reports the regression results of CDS spreads on VRP for three sub-samples: AAA-A, BBB, BB-CCC. The ratings are the average of Moody's and S&P ratings. Two-dimensional (firm and time) clustered standard errors in the regressions are adjusted as in Petersen (2009). The group AAA-A has 7315 observations. The group BBB has 9582 observations. The group BB-CCC has 5107 observations. The first three regressions are the regressions of VRPs and leverage. The second three regressions are the multivariate regressions with all the control variables. The numbers in the brackets are
| Independent Variable | 1-year | 2-year | 3-year | 5-year | 7-year | 10-year |
| VRP | 1.92 | 2.14 | 2.28 | 2.29 | 2.32 | 2.34 |
| VRP: t-statistic | (7.55) | (7.39) | (8.55) | (9.21) | (9.16) | (9.25) |
| Leverage | 2.08 | 2.44 | 2.81 | 3.27 | 3.27 | 3.34 |
| Leverage: t-statistic | (6.09) | (6.13) | (7.18) | (8.60) | (8.75) | (9.11) |
| Market VRP | -0.56 | -0.78 | -0.85 | -0.94 | -0.96 | -0.91 |
| Market VRP: t-statistic | ( -3.01) | ( -3.56) | ( -3.88) | ( -4.34) | ( -4.18) | ( -3.82) |
| S&P 500 Return | 0.68 | 0.76 | 0.79 | 0.57 | 0.44 | 0.31 |
| S&P 500 Return: t-statistic | (0.88) | (0.80) | (0.77) | (0.48) | (0.34) | (0.23) |
| Swap Rate (1 Year) | -7.89 | -4.69 | -2.71 | 2.69 | 6.92 | 9.89 |
| Swap Rate (1 Year): t-statistic | ( -6.03) | ( -3.36) | ( -1.89) | (1.70) | (3.96) | (5.37) |
| 12.27 | 12.36 | 15.10 | 17.04 | 15.50 | 8.53 | |
| (0.82) | (0.75) | (0.98) | (1.09) | (0.95) | (0.51) | |
| Swap Rate - CMT (5 Year) | -44.49 | -31.33 | -24.29 | -9.62 | -3.07 | 2.63 |
| Swap Rate - CMT (5 Year): t-statistic | ( -2.74) | ( -1.58) | ( -1.23) | ( -0.43) | ( -0.14) | (0.11) |
| Asset Turnover Ratio | -2.87 | -3.61 | -1.01 | 3.10 | 3.40 | 4.50 |
| Asset Turnover Ratio: t-statistic | ( -0.69) | ( -0.74) | ( -0.20) | (0.59) | (0.63) | (0.84) |
| Price-earnings Ratio | -0.00 | -0.00 | -0.01 | -0.01 | -0.01 | -0.00 |
| Price-earnings Ratio: t-statistic | ( -0.14) | ( -0.27) | ( -0.67) | ( -1.05) | ( -0.99) | ( -0.66) |
| Market/Book Ratio | -0.01 | -0.01 | -0.01 | -0.02 | -0.02 | -0.03 |
| Market/Book Ratio: t-statistic | ( -1.42) | ( -2.62) | ( -2.26) | (2.79) | ( -3.30) | ( -3.38) |
| Return on Assets | -7.75 | -15.25 | -16.24 | -23.56 | -30.56 | -33.55 |
| Return on Assets: t-statistic | ( -0.35) | ( -0.57) | ( -0.61) | ( -0.92) | ( -1.22) | ( -1.37) |
| Log Sales | -2.59 | -3.33 | -6.51 | -12.23 | -12.68 | -14.59 |
| Log Sales: t-statistic | ( -0.76) | ( -0.88) | ( -1.63) | ( -3.06) | ( -3.13) | ( -3.64) |
| Constant | -1.92 | -18.96 | -14.66 | -0.31 | -6.59 | 6.38 |
| Constant: t-statistic | ( -0.07) | ( -0.66) | ( -0.48) | ( -0.01) | ( -0.21) | (0.20) |
| Adjusted |
0.40 | 0.41 | 0.46 | 0.49 | 0.50 | 0.51 |
This table reports the regression results of CDS spreads of all maturities on the VRP computed with model free implied variance
| Independent Variable | VRP constructed with implied variance from: Model-Free | OTM, ATM, VRP constructed with implied variance from: Put Option | ATM, VRP constructed with implied variance from: Put Option | ITM, VRP constructed with implied variance from: Put Option | OTM, VRP constructed with implied variance from: Call Option | ATM, VRP constructed with implied variance from: Call Option | ITM, VRP constructed with implied variance from: Call Option |
| VRP | 2.29 | 1.56 | 2.62 | 1.22 | 1.44 | 2.53 | 1.49 |
| VRP: t-statistic | (9.21) | (7.72) | (7.50) | (6.70) | (7.21) | (7.74) | (7.46) |
| Leverage | 3.27 | 3.62 | 3.46 | 3.89 | 3.71 | 3.61 | 3.64 |
| Leverage: t-statistic | (8.60) | (8.78) | (9.47) | (8.16) | (7.75) | (9.01) | (8.72) |
| Market VRP | -0.94 | -1.04 | -1.03 | -0.50 | -0.91 | -0.97 | |
| Market VRP: t-statistic | (-4.34) | (-4.37) | (-4.19) | (-3.05) | (-3.07) | (-4.26) | (-4.18) |
| S&P 500 Return | 0.57 | 0.94 | 0.14 | -0.87 | 0.23 | 0.97 | 1.21 |
| S&P 500 Return: t-statistic | (0.48) | (0.74) | (0.10) | (-0.89) | (0.26) | (0.81) | (0.98) |
| Swap Rate (1 Year) | 2.69 | 2.65 | 1.24 | -1.94 | 0.02 | 1.04 | 2.55 |
| Swap Rate (1 Year): t-statistic | (1.70) | (1.64) | (0.79) | (-1.42) | (0.01) | (0.69) | (1.61) |
| 17.04 | 3.12 | 15.82 | 37.44 | 40.29 | 16.41 | 5.04 | |
| (1.09) | (0.18) | (0.98) | (3.00) | (3.32) | (1.05) | (0.30) | |
| Swap Rate - CMT (5 Year) | -9.62 | 15.24 | 5.66 | 18.27 | 32.76 | 14.81 | 14.96 |
| Swap Rate - CMT (5 Year): t-statistic | (-0.43) | (0.69) | (0.25) | (1.01) | (1.92) | (0.69) | (0.69) |
| Asset Turnover Ratio | 3.09 | 6.15 | 6.67 | 10.30 | 6.26 | 7.82 | 6.08 |
| Asset Turnover Ratio: t-statistic | (0.59) | (1.13) | (1.29) | (1.76) | (1.06) | (1.47) | (1.10) |
| Price-earnings Ratio | -0.01 | -0.01 | -0.01 | -0.02 | -0.02 | -0.01 | -0.01 |
| Price-earnings Ratio: t-statistic | (-1.05) | (-1.31) | (-1.38) | (-1.62) | ( |
(-1.39) | (-1.30) |
| Market/Book Ratio | -0.02 | -0.02 | -0.02 | -0.01 | -0.01 | -0.02 | -0.02 |
| Market/Book Ratio: t-statistic | (-2.79) | (-4.30) | (-2.87) | (-2.68) | ( |
(-2.75) | (-4.21) |
| Return on Assets | -23.56 | -46.95 | -34.92 | -67.76 | -76.59 | -41.86 | -50.54 |
| Return on Assets: t-statistic | (-0.92) | (-1.80) | (-1.41) | (-2.46) | ( |
(-1.62) | (-1.92) |
| Log Sales | -12.23 | -19.88 | -17.33 | -22.03 | -16.20 | -19.11 | -20.06 |
| Log Sales: t-statistic | (-3.06) | (-5.14) | (-4.54) | (-5.53) | (- 3.83) | (-5.03) | (-5.18) |
| Constant | -0.31 | -19.88 | 34.08 | 55.99 | 3.62 | 42.76 | 50.47 |
| Constant: t-statistic | (-0.01) | (-5.14) | (1.18) | (1.77) | (0.10) | (1.45) | (1.68) |
| Adjusted |
0.49 | 0.44 | 0.48 | 0.38 | 0.37 | 0.45 | 0.43 |
This table reports the regression results of CDS spreads on VRPs computed from different measures of implied variances. Besides the benchmark VRP computed from model-free implied variance, we use VRP constructed from implied variances of out-of-the-money (OTM), at-the-money (ATM) and in-the-money (ITM) put options, together with those of out-of-the-money (OTM), at-the-money (ATM) and in-the-money (ITM) call options. We adjust two-dimensional (firm and time) clustered standard errors in the regressions as in Petersen (2009). The numbers in the brackets are
| Independent Variable | (1) | (2) | (3) | (4) | (5) | (6) |
| VRP | 2.29 | 0.51 | 1.46 | |||
| VRP t-statistic | (9.21) | (2.67) | (8.36) | |||
| Model-free IV | 1.16 | 0.95 | 1.46 | |||
| Model-free IV t-statistic | (9.24) | (6.70) | (8.36) | |||
| EV | 1.65 | -0.51 | 0.95 | |||
| EV t-statistic | (8.10) | (-2.67) | (6.70) | |||
| Market VRP | -0.94 | -1.12 | -0.95 | -1.13 | -1.13 | -1.13 |
| Market VRP t-statistic | (-4.34) | (-4.52) | (-4.08) | (-4.56) | (-4.56) | (-4.56) |
| Leverage | 3.27 | 2.99 | 3.15 | 3.00 | 3.00 | 3.00 |
| Leverage t-statistic | (8.60) | (8.56) | (8.19) | (8.62) | (8.62) | (8.62) |
| S&P 500 Return | 0.57 | 0.43 | 0.00 | 0.51 | 0.51 | 0.51 |
| S&P 500 Return t-statistic | (0.48) | (0.34) | (0.00) | (0.40) | (0.40) | (0.40) |
| Swap Rate (1 Year) | 2.69 | 2.15 | 0.32 | 2.48 | 2.48 | 2.48 |
| Swap Rate (1 Year) t-statistic | (1.70) | (1.26) | (0.20) | (1.46) | (1.46) | (1.46) |
| 17.04 | 3.41 | 3.89 | 4.99 | 4.99 | 4.99 | |
| (1.09) | (0.20) | (0.23) | (0.29) | (0.29) | (0.29) | |
| Swap Rate - CMT (5 Year) | -9.62 | -50.50 | -50.11 | -45.60 | -45.60 | -45.60 |
| Swap Rate - CMT (5 Year) t-statistic | (-0.43) | (-2.02) | (-2.08) | (-1.80) | (-1.80) | (-1.80) |
| Asset Turnover Ratio | 3.09 | -2.99 | -3.39 | -2.19 | -2.19 | -2.19 |
| Asset Turnover Ratio t-statistic | (0.59) | (-0.54) | (-0.56) | (-0.40) | (-0.40) | (-0.40) |
| Price-earnings Ratio | -0.01 | -0.00 | -0.01 | -0.00 | -0.00 | -0.00 |
| Price-earnings Ratio t-statistic | (-1.05) | (-0.58) | (-0.66) | (-0.63) | (-0.63) | (-0.63) |
| Market/Book Ratio | -0.02 | -0.01 | -0.01 | -0.02 | -0.02 | -0.02 |
| Market/Book Ratio t-statistic | (-2.79) | (-2.49) | (-2.22) | (-2.56) | (-2.56) | (-2.56) |
| Return on Assets | -23.56 | -22.78 | -45.42 | -19.65 | -19.65 | -19.65 |
| Return on Assets t-statistic | (-0.92) | (-0.89) | (-1.73) | (-0.77) | (-0.77) | (-0.77) |
| Log Sales | -12.23 | -7.27 | -9.30 | -7.58 | -7.58 | -7.58 |
| Log Sales t-statistic | (-3.06) | (-1.72) | (-2.12) | (-1.82) | (-1.82) | (-1.82) |
| Constant | -0.31 | -26.87 | -13.34 | -25.59 | -25.59 | -25.59 |
| Constant t-statistic | (-0.01) | (-0.83) | (-0.40) | (-0.80) | (-0.80) | (-0.80) |
| Adjusted |
0.49 | 0.52 | 0.48 | 0.52 | 0.52 | 0.52 |
This table compares the predictability of VRP on CDS spreads to that of model-free implied and expected variances for 5-year maturity CDS spreads. Regression (1) to (3) report the multivariate regression results for VRP, implied and expected variances, along with all control variables. Regression (4) to (6) report the regression results of CDS spreads on each pairs of VRP, implied and expected variances respectively, along with all control variables. We adjust two-dimensional (firm and time) clustered standard errors in the regressions as in Petersen (2009). The numbers in the brackets are
| Independent Variable | Frequency Weekly | Frequency Weekly | Frequency Monthly | Frequency Monthly | Frequency Quarterly | Frequency Quarterly |
| VRP | 1.39 | -0.24 | 2.78 | 0.06 | 2.57 | 0.68 |
| VRP t-statistic | (6.44) | (-1.43) | (10.03) | (2.41) | (10.14) | (3.00) |
| IV | 0.10 | 1.08 | 0.95 | |||
| IV t-statistic | (10.71) | (7.46) | (6.41) | |||
| Constant | 70.49 | 0.24 | 28.00 | -13.20 | 29.71 | -7.14 |
| Constant t-statistic | (9.24) | (0.03) | (5.89) | (-1.63) | (6.83) | (-0.95) |
| Adjusted
|
0.14 | 0.26 | 0.34 | 0.39 | 0.35 | 0.40 |
| Dependent Independent | Independent Variable
|
Independent Variable
|
Independent Variable
|
Independent Variable
|
Independent Variable
|
Independent Variable
|
Independent Variable
|
Independent Variable |
|
|
6.33 | -0.17 | -0.29 | 0.06 | 0.94 | 0.03 | 0.01 | 0.74 |
|
|
(2.49) | (-1.36) | (-2.42) | (0.48) | (7.47) | (0.17) | (0.08) | |
|
|
|
|
|
|
|
|
||
|
|
2.98 | 0.10 | 0.23 | 0.02 | -0.04 | -0.09 | 0.11 | 0.31 |
|
|
(1.20) | (0.79) | (1.45) | (0.12) | (-0.28) | (-0.79) | (0.93) | |
|
|
|
|
|
|
|
|
||
|
|
3.36 | 0.71 | -0.40 | -0.06 | 0.84 | -0.20 | -0.01 | 0.58 |
|
|
(1.32) | (5.40) | (-2.56) | (-0.44) | (6.65) | (-1.24) | (-0.04) |
This table reports the results of different data frequency analysis and Granger Causality tests. Panel A shows the regression results of CDS on VRP, in the absence/presence of IV for weekly, monthly and quarterly data frequency. Panel B reports the Granger Causality tests result. We use three lags in the regressions as
|
Component |
CDS Spreads E. % | CDS Spreads C. % | VRP E. % | VRP C. % | IV E. % | IV C. % | EV E. % | EV C. % |
| 1 | 60.36 | 60.36 | 77.93 | 77.93 | 53.67 | 53.67 | 64.03 | 64.03 |
| 2 | 13.44 | 73.80 | 9.97 | 87.90 | 10.79 | 64.47 | 11.78 | 75.81 |
| 3 | 6.10 | 79.90 | 3.72 | 91.62 | 5.58 | 70.05 | 4.45 | 80.26 |
| 4 | 4.21 | 84.11 | 2.20 | 93.82 | 3.55 | 73.60 | 2.66 | 82.92 |
| 5 | 3.42 | 87.52 | 1.76 | 95.58 | 3.22 | 76.82 | 2.36 | 85.28 |
| 6 | 2.93 | 90.45 | 0.78 | 96.37 | 2.25 | 79.07 | 1.50 | 86.78 |
| 7 | 1.74 | 92.20 | 0.73 | 97.10 | 1.96 | 81.03 | 1.27 | 88.05 |
| 8 | 1.35 | 93.54 | 0.48 | 97.57 | 1.76 | 82.79 | 1.09 | 89.14 |
| 9 | 1.17 | 94.72 | 0.38 | 97.95 | 1.65 | 84.45 | 0.93 | 90.07 |
| 10 | 1.16 | 95.88 | 0.30 | 98.25 | 1.46 | 85.90 | 0.88 | 90.95 |
This table reports the principal component analysis of CDS spreads, VRP, implied and expected variances. We select firms with 48 monthly observations starting in January 2004. The sample contains 194 firms. VRP is explained mostly by first three components (91.62% cumulatively), whereas IV and EV are driven marginally by several components. Robustness checks with various samples show that sample selection does not change the results qualitatively. E: Explained. C: Cumulative.
| Percentile | VRP Regressions
|
VRP Regressions |
VRP Regressions |
CAPM Regressions
|
CAPM Regressions |
CAPM Regressions |
| 1 | -7.56 | -1.17 | -0.03 | 0.15 | 0.07 | -0.02 |
| 5 | 0.42 | 0.19 | -0.01 | 0.42 | 1.13 | 0.01 |
| 10 | 1.55 | 0.99 | 0.00 | 0.60 | 1.62 | 0.03 |
| 25 | 3.25 | 2.34 | 0.09 | 0.65 | 2.70 | 0.10 |
| 50 | 3.72 | 4.01 | 0.21 | 0.93 | 3.75 | 0.18 |
| 75 | 6.83 | 6.51 | 0.35 | 1.23 | 5.01 | 0.28 |
| 90 | 11.53 | 7.91 | 0.45 | 1.71 | 6.35 | 0.39 |
| 95 | 17.86 | 8.89 | 0.50 | 2.01 | 7.27 | 0.44 |
| 99 | 27.62 | 10.14 | 0.56 | 2.56 | 9.08 | 0.53 |
This table reports the results of comparing the relationship between firm and market VRPs to the relationship between firm and market equity returns with matched sample. Two-stage regressions are carried out, following the standard approach of testing CAPM. In the first stage, time-series regressions for each firm
| Independent | Merton Model (1) | Merton Model (2) | Merton Model (3) | Stochastic Volatility Model (4) | Stochastic Volatility Model (5) | Stochastic Volatility Model (6) | Stochastic Volatility Model (7) | Stochastic Volatility Model (8) | Stochastic Volatility Model (9) |
| EV | 6.84 | 0.64 | 2.29 | 1.53 | 0.65 | ||||
| EV t-statistic | (3.27) | (0.76) | (7.66) | (5.27) | (3.29) | ||||
| VRP | 1.45 | 0.73 | 0.46 | ||||||
| VRP t-statistic | (7.39) | (3.44) | (2.89) | ||||||
| LEV | 16.18 | 15.59 | 7.84 | 6.29 | 6.39 | ||||
| LEV t-statistic | (7.32) | (7.89) | (11.9) | (9.61) | (10.8) | ||||
| Constant | -567.2 | -407.9 | -455.7 | -143.1 | -120.6 | -255.0 | -170.8 | -252.2 | -257.3 |
| Constant t-statistic | (2.62) | (5.46) | (3.96) | (5.39) | (4.74) | (9.32) | (8.12) | (10.3) | (12.0) |
| Adjusted |
0.31 | 0.77 | 0.77 | 0.63 | 0.56 | 0.81 | 0.71 | 0.83 | 0.84 |
This table reports the OLS regression result using simulated ten years of monthly data from a Merton (1974) model and a stochastic volatility model (Zhang, Zhou, and Zhu, 2009) for a representative BBB rating firm. The dependent variable is five-year credit spread, and explanatory variables are expected variance (EV) estimated by annual historical variance, variance risk premium (VRP) estimated based on monthly realized variance, and market leverage ratio (LEV) only observable inside the simulation. Numbers in parentheses are
Figure 1: The time series of the five-year CDS spreads
This figure plots the five-year CDS spreads of full sample and three sub-samples. We group the CDS spreads into three sub-samples by CDS ratings. The first group contains CDS of AAA, AA and A grades. The second group contains CDS of BBB grade. The third group contains CDS of speculative grades ranging between BB and CCC. The three sub-samples contain 7,315, 9,582 and 5,107 observations respectively. The CDS spreads decrease gradually from the peaks in late 2002, then increase again as the financial crisis approaches in year 2007. The spreads of investment grade CDS in year 2008 are higher than those in year 2002, whereas the spreads of speculative grade CDS are lower than their 2002 level. That highlights the nature of the recent financial crisis which was fueled mostly by the financial distress of highly rated credit products. The difference between the CDS spreads for investment grade and speculative group CDS however becomes widen potentially due to the "fly-to-quality" effect during the financial crisis, driving up compensation for credit risk.Figure 2: The time series of CDS spreads, VRP, Leverage ratio, MVRP and VIX for General Motor Ltd.
This figure illustrates the dynamic relationships between CDS spreads and VRP, market VRP, VIX and leverage ratio for a representative firm in our sample: General Motor (GM). The CDS spread line and VRP line resemble each other closely over time. In particular, the two lines move closely during GM downgrading in year 2005 and in the recent financial crisis. The CDS spreads tend to co-move with the firm's leverage ratio. A visual examination of the relationship between CDS spreads and VIX suggests that the option-implied market volatility measure may not provide powerful prediction on GM's credit spreads. For instance, the two lines move in exactly opposite direction during the period between year 2004 and 2006. The MVRP line closely resembles the VIX line.Figure 3: Fitted VRPs/Equity Returns versus observed VRPs/Equity Returns
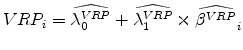 (
(
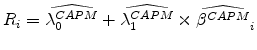 ), where the
), where the
Footnotes
*Hao Wang- Tsinghua University, School of Economics and Management, 318 Weilun Building, Beijing 100084, China, E-mail: [email protected]nghua.edu.cn, Tel: 86 10-62797482.
*Corresponding Author: Hao Zhao- Federal Reserve Board, Risk Analysis Section, Washington, DC 20551, USA, E-mail: [email protected], Tel: 1 202-452-3360.
*Yi Zhou- University of Oklahoma, Michael F. Price College of Business, Finance Division, 307 West Brooks Street, Adams Hall 250, Norman, OK 73069, USA, E-mail: [email protected], Tel: 1 405-325-1135. Return to Text
![\displaystyle RV_{i,t}\equiv \sum_{j=1}^{n}\left[ s_{i,t-1+{\frac{j}{n}}}-s_{i,t-1+{\frac{% j-1}{n}}}\right] ^{2}\longrightarrow \mbox{Variance}_{i}(t-1,t),](img23.gif)