
The Expected Real Return to Equity
Keywords: Expected returns, production-based models
Abstract:
1 Introduction
The expected return to the aggregate stock market is a key variable in the decisions of both individual investors and corporations, as emphasized by Merton (1980). A sample average of realized returns provides the simplest, and most widely used, estimate of expected returns. However, as noted by the above ubiquitous quote, future returns may differ from past values. A recent literature examines this possibility by constructing forward-looking measures of expected returns based primarily on analysts forecasts or investor surveys.1
However, as Easton and Sommers (2007) argue, analysts forecasts have an upward bias that can significantly affect estimates of expected returns based on their forecasts. Findings from surveys capture the views of only one segment of the market and, in addition, survey-based methods can suffer from many statistical biases (see Foreman (1991)). Motivated by these observations, this study presents a novel model-based estimation of the expected return to equity that relies only on observed data on aggregate dividends, earnings, investment, and valuations.
The intuition underlying the estimation is that the expected return links earnings, dividends, and investment to market values through a present value relationship. Holding all else constant, a higher expected return translates to a lower market value. Thus, one could use data on the dividends, earnings, and valuations of the US stock market to infer the expected return to equity given a model that captures the dynamics of these variables.
The model underlying the estimation is a variant of the standard production-based asset pricing model employed by Cochrane (1991), Cochrane (1996), Jermann (1998), Gomes, Kogan, and Zhang (2003), Kogan (2004), Zhang (2005), Gomes, Yaron, and Zhang (2006), Liu, Whited, and Zhang (2009) and others. The model prices an aggregate equity claim, compared to the per-share claim typically priced in the literature.2 The aggregate firm uses its assets and labor to produce output and earn profits. The firm finances interest payments and taxes from its profits and selects investment and dividends to maximize shareholder value. The model thus incorporates both taxes and leverage into the relation that maps dividends and earnings onto market values. Growth opportunities arise in the model as the firm varies its optimal scale following persistent shocks to profitability.
There are many benefits to taking a model-based approach to estimating expected returns. Such an approach avoids potential biases associated with analysts forecasts (see Easton and Sommers (2007)). The estimation uses data for the aggregate market, thus taking into account the expectations of all market participants as opposed to only analysts or survey participants. The model captures the endogeneity of dividends, which is treated as exogenous in methods based on the Gordon growth model (see Gordon (1959)). And the underlying model incorporates growth opportunities from changing investment in response to temporary shocks, which is not captured in a forecast-based approach. On the other hand, a model-based approach is necessarily predicated on a particular model of equity values. As such, I investigate the robustness of the findings to modest changes to the underlying model.
I estimate the parameters of this model using data on a U.S. representative firm constructed by aggregating firm level data from the CRSP/Compustat merged data set.3 I perform the analysis on two samples: the first uses annual data from 1966 to 2009; the second uses quarterly data from 1984:Q1 to 2009:Q4. Data availability on dividends and stockholders' equity constrain the start dates of the two samples, respectively. Both samples exclude financial firms and regulated utilities.
The parameter estimates from the annual data imply a mean expected annual real return to equity of about 4.7% to 5.3% over the period from 1966 to 2009. These estimates are within the range of values for expected returns obtained by Fama and French (2002), and Graham and Harvey (2005).4 The findings also support the decision in the limited participation literature to use a lower return to equity than would be indicated by historical returns (see Gomes and Michaelides (2005), Polkovnichenko (2007), and Gust and Lopez-Salido (2009)).
Separating the sample into two, I find that average expected returns to equity decline sharply from about 6.5% in the period from 1966 to 1987 to about 4.4% in the period from 1988 to 2009. This decline arises due to the fact that, while earnings and dividends are lower in the latter periods, valuations are higher. The model reconciles this apparent discrepancy with a lower expected return, which raises valuations by lowering the discount rate applied to future dividends. Repeating the estimation using the quarterly data from 1984:Q1 to 2009:Q4 generates an average return to equity of 4.0%, roughly similar to that obtained using the annual data from 1988 to 2009. The results suggest that mean expected returns to the aggregate stock market over the past twenty-five years have been lower than historical returns, as argued by Lettau, Ludvigson, and Wachter (2008) and Cogley and Sargent (2008).
The method yields a fairly precise estimate of the expected return to equity. The precision of the estimate arises from the sensitivity of the optimal policies and the value function to changes in mean expected returns. A small reduction in expected returns increases the present value of all future dividends. This translates to a substantial impact on firm value. Changes in expected returns also impact investment and dividend policies in the model.
The model performs fairly well on a range of diagnostic tests. The estimated standard deviation of returns equals 12%, compared to about 17% in the data. In addition, the model generates plausible time-variation in expected returns, with expected returns above 10 percent during the recessions of 1982, 1991, and 2001. Somewhat surprisingly, expected returns as measured by the annual model do not jump as much during the recent recession, as annual earnings of the corporate sector did not decline as sharply compared to prior recessions.5 In contrast, expected returns decline to a bit below zero during periods of strong earnings. One failure of the model is that it also generates a relatively high risk-free rate. As I argue below, this reflects a broader problem with production-based models with time-separable utility, as these models cannot generate risk-free rates below the economic growth rate. This problem, however, does not invalidate using the model to estimate the expected real return to equity.
The findings have sharp implications for the investment decisions of both individual and institutional investors. Current asset allocation advice is mostly based on properties of historical returns. A lower expected return to equity implies that individuals need to save more to fund retirement expenses. They may also need to reduce their allocation to equities in their portfolios. A lower expected return also impacts the actuarial calculation of pension funds and insurance firms, who base their decisions on annual expected nominal returns of 6% to 10%. In particular, a lower expected return would further exacerbate the under-funding problems of state pension funds, as discussed by Novy-Marx and Rauh (2009).
The development of the model employed in the estimation also yields a theoretical result on translating models with growth into stationary models without growth. A growing literature uses production based models to study asset prices. Many of these studies employ stationary models without growth and assume that their results map directly onto the observed data.6 However, I prove that the return to equity in the stationary model without growth equals the return in the model with growth minus the growth rate. The intuition for this result is quite simple: the return to equity in the model with growth includes a component that reflects economic growth that would be absent in the stationary model without growth. This implies that the correctly calibrated stationary model should have a return to equity equal to the observed data value minus the growth rate. The difference is economically quite substantial. A calibration targeting a mean annual return to equity of 6.5% in a model without growth yields an actual return of 8.6% when translated to an economy with a 2% growth rate. A similar argument applies for the calibration of the risk-free rate. However, this adjustment has no impact on return differences across asset classes.
This study is organized as follows. Section 2 presents the model relating earnings, dividends, and valuations. Section 3 discusses the data used in the estimation and the identification of the model parameters. Section 4 presents the results. Section 5 examines other implications of the model and Section 6 concludes.
2 Model
Consider a representative agent economy with a representative firm that employs capital and labor to produce output. The representative agent has a time-separable utility function. The agent provides a fixed supply of labor at a wage rate determined by market clearing conditions in the labor market. The agent invests in the representative firm.
The representative firm produces output using a Cobb-Douglas production function that uses assets and labor as inputs. The firm faces a downward sloping demanding curve. Let ![]() denote the
level of labor augmenting technology that grows at a constant rate
denote the
level of labor augmenting technology that grows at a constant rate ![]() . This drives all economic growth in the model. Given these assumptions, Appendix A derives the profit function of the
firm,
. This drives all economic growth in the model. Given these assumptions, Appendix A derives the profit function of the
firm,
![]() , under balanced growth conditions.
, under balanced growth conditions.
| (1) |
where
The productivity term, ![]() , measures deviations from trend growth levels and is assumed to follow an auto-regressive process with
, measures deviations from trend growth levels and is assumed to follow an auto-regressive process with
where
The firm is financed through debt and equity. Denote the level of debt by ![]() . The main purpose of including debt in the model is to incorporate leverage into the relationship between the
earning and valuation processes of the firm. For simplicity, the debt is assumed to be riskless with an interest rate of
. The main purpose of including debt in the model is to incorporate leverage into the relationship between the
earning and valuation processes of the firm. For simplicity, the debt is assumed to be riskless with an interest rate of ![]() . In unreported results, I examine the effect of allowing the
interest rate to vary with aggregate earnings, and find that this has very little effect.
. In unreported results, I examine the effect of allowing the
interest rate to vary with aggregate earnings, and find that this has very little effect.
The firm funds physical investment from its cash flow. Denote investment in physical capital by ![]() . The capital accumulation equation is given by
. The capital accumulation equation is given by
The firm uses its cash flow to fund investment, pay interest to creditors, pay taxes to the government, and pay dividends to shareholders. The taxes are paid on income adjusted for depreciation and interest expenses, as in the tax code. I consider a linear tax rate and calibrate the tax rate,
![]() , using data on aggregate taxes and aggregate pre-tax income accruing to shareholders. Given these assumptions, the dividend payout of the firm,
, using data on aggregate taxes and aggregate pre-tax income accruing to shareholders. Given these assumptions, the dividend payout of the firm,
![]() , is given by
, is given by
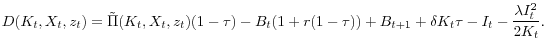 |
(3) |
Let ![]() denote the pricing kernel of the economy, which we will subsequently parametrize. The value of the firm,
denote the pricing kernel of the economy, which we will subsequently parametrize. The value of the firm,
![]() , can be expressed as the solution to the following Bellman equation:
, can be expressed as the solution to the following Bellman equation:
| (4) | |||
In effect, the aggregate firm chooses the optimal dividend and investment policies to maximize firm value. The value of the aggregate firm depends on the endogenous dividend process, which itself is influenced by the pricing kernel,
Note that ![]() denotes the current technology level, which grows over time at a steady rate. One can then map the above value function onto an economy without growth by dividing by
denotes the current technology level, which grows over time at a steady rate. One can then map the above value function onto an economy without growth by dividing by
![]() . This detrends the value function and translates it into one obtained from a stationary economy. This translation is necessary to simulate from the model in the subsequent estimation.
. This detrends the value function and translates it into one obtained from a stationary economy. This translation is necessary to simulate from the model in the subsequent estimation.
Denote the detrended variables by lowercase letters. Thus,

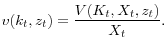
Observe that the terms involving
2.1 Estimation of the expected real return to equity
The above model can be employed to provide an estimate of the expected real return to equity. Fundamentally, we can employ data on income accruing to shareholders, dividends, investment and firm value to estimate the structural parameters of the above model given a parametrization of the pricing kernel. The expected return to equity can be derived from the estimated parameters for the pricing kernel. Appendices C and D detail the simulated method of moments estimator used to obtain the parameter estimates.9 The intuition behind the estimation is that the expected return maps earnings data onto valuation data. Therefore, given data on earnings and valuations, we can infer the expected return over the sample period. The sensitivity of the aggregate firm's policies and valuations to changes in expected returns helps generate a fairly precise estimate.
This analysis provides an alternate, forward looking perspective on the expected real return to equity that may differ from results based on historical data. Fama and French (2002) present the results of a related analysis that argues dividend growth models suggest that the expected real return to equities may be lower than historical values. Claus and Thomas (2001) use analysts forecasts to argue that the equity premium is much lower than historical values. While the hypothesis that future returns should simply reflect past returns is a compelling null hypothesis, there are robust arguments to the contrary. Stock market participation has increased steadily over the past century. Cogley and Sargent (2008) argue that the Great Depression lead to an increase in the market price of risk that has slowly dissipated over time. Lettau, Ludvigson, and Wachter (2008) argue that declining macroeconomic risk has lead to a decline in the expected equity premium. These arguments motivate using the above model to provide a forward looking estimate of the expected return to equity.
That said, the recent recession may have lead to a reexamination of the riskiness of equities with an associated change in expected returns. Unfortunately, the approach in this study cannot examine this question without data on a sufficient number of periods following the recession. However, much of the recent market turmoil was driven mainly by financial firms, and it is not necessarily given that this turmoil would have affected expected returns to nonfinancial firms, the focus of this study. As I subsequently show, these firms exhibit a quick rebound in earnings from 2009:Q2 onwards.
2.2 Mapping models without economic growth to data
The above analysis also enables the derivation of a theoretical result mapping returns in the stationary economy to those in the economy with growth, which corresponds to the observed data. Let
![]() and
and![]() denote the return to the firm in the growth economy and detrended
economy, respectively. Thus,
denote the return to the firm in the growth economy and detrended
economy, respectively. Thus,
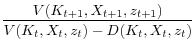 |
(6) | ||
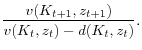 |
Now, we can establish the following:
 |
|||
As the growth rate is quite small, one could also approximate the
![]() term with
term with ![]() . The above proof employs the derivation of the value
function of the firm, which may be restrictive. Appendix B demonstrates the same result in a more general manner using the representative agent's budget constraint.
. The above proof employs the derivation of the value
function of the firm, which may be restrictive. Appendix B demonstrates the same result in a more general manner using the representative agent's budget constraint.
The above analysis demonstrates the need for adjusting the returns obtained in stationary economies for economic growth when we wish to map them onto data. The intuition for this result is quite simple: the realized returns in an economy with growth include a component that arises from the presence of growth; returns in a corresponding economy without growth equal the true returns minus a term that adjusts for the impact of growth. While this result is not fundamentally new, it has been ignored by many studies that have employed stationary economies.
Ignoring economic growth can have substantial consequences for asset pricing models. Assume that the mean annual log real return to equity equals 6.5% and that the economic growth rate equals 2%. Adjusting for growth implies that a stationary model with a mean return to equity of 6.5% corresponds to an economy with a mean return of 8.63% (=1.065*1.02-1), substantially greater than the observed rate of return in the data. Thus, the return to equity in the stationary model economy should be the desired value minus the correction for growth. This indicates that the stationary models in the literature that match the observed return to equity actually correspond to real economies with much higher returns.
This argument also applies to the risk-free rate. The production-based asset pricing models such as Gomes and Schmid (2010) and Livdan, Sapriza, and Zhang (2009) will have more difficulty generating a low risk-free rate once they incorporate
economic growth. This arises due to the fact that the pricing kernel times
![]() enters into the contraction mapping of the Bellman equation. Thus, convergence of the value function requires that the average of the above term be below one, placing an implicit
upper bound of the risk-free rate close to the growth rate. The degree of this difficulty depends on whether the target risk-free rate equals the long-term average of 1.8% reported in Campbell, Lo, and MacKinlay (1997) or the lower risk-free rate observed in more recent
data.
enters into the contraction mapping of the Bellman equation. Thus, convergence of the value function requires that the average of the above term be below one, placing an implicit
upper bound of the risk-free rate close to the growth rate. The degree of this difficulty depends on whether the target risk-free rate equals the long-term average of 1.8% reported in Campbell, Lo, and MacKinlay (1997) or the lower risk-free rate observed in more recent
data.
The analysis does not, however, imply that the focus of most studies - excess returns such as the equity premium or value premium - require an adjustment for economic growth. This arises due to the fact that the growth adjustment is necessary for all asset returns and, as such, differences in asset returns remain unchanged when stationary economies are mapped to economies with growth.
3 Data
The data for the estimation is obtained from the CRSP/Compustat merged data set. I estimate the model on both an annual data set and a quarterly data set. The sample periods for the annual and quarterly data sets extend from 1966 to 2009 and 1984:Q1 to 2009:Q4, respectively. The start dates are constrained by the lack of data on shareholders equity and dividends prior to the start dates for the annual and quarterly data sets, respectively. The sample excludes financial firms and regulated utilities as the model would not be appropriate to use for such firms. The data sets for the representative firm are constructed by aggregating firm level data on total assets, capital expenditures, common dividends, income accruing to shareholders, total liabilities, corporate taxes and the book and market values of equity from the samples. Any firm with missing values for the market value of equity is excluded from the aggregation.
Table 1 reports the summary statistics of interest for the aggregate firm; Panels A and B, respectively, report values at the annual and quarterly frequencies. All variables except the market-to-book ratio, leverage, and interest expenses are constructed after scaling by lagged total assets. The market-to-book ratio equals the market value of common equity dividend by book equity. The mean value of earnings, measured as income accruing to shareholders indicates that the aggregate earnings of nonfinancial firms are noticeably higher over the annual data period than over the quarterly data period. Aggregate dividends exhibit a similar pattern. In contrast, the aggregate valuation of nonfinancial companies is lower over the annual data period than over the quarterly data period. A way in which one could reconcile higher valuations with lower dividends and earnings would be to have a lower expected return, which, ceteris paribus, increases firm value by lowering the discount rate applied to future cash flows.
Aggregate investment and depreciation is also lower over the quarterly sample period than over the annual period, consistent with the increased importance of service and high-tech firms in the economy. About 2/3rds of the total assets of the aggregate firm are financed through debt, indicating the importance of leverage in understanding equity returns, as highlighted by Gomes and Schmid (2010).
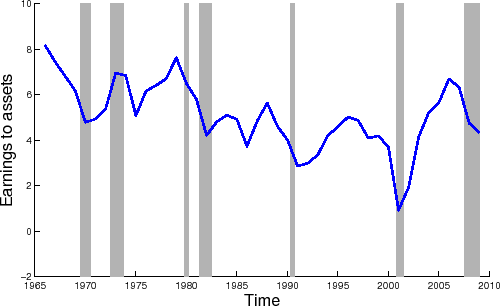
Figure 1 plots the earnings of the aggregate firm over time. Panel A plots the earnings to total assets ratio over time using the annual data; Panel B plots this series using the quarterly data. As can be seen from Panel A, the aggregate earnings to asset ratio is lower over the second half of the sample period than in the first. This demonstrates that the decline in the mean earnings noted above does not arise from any outliers, and likely reflects an important change in the performance of nonfinancial firms.
3.1 Calibrated parameters
The above model includes many auxiliary parameters, such as the corporate tax rate. One approach would be to include relevant information and estimate all of these parameters. Another approach would be to calibrate some of the model parameters to match the data, and estimate the rest. This has the benefit of focusing the estimation on the parameters of interest, and improves their identification.
Table 2 reports the calibrated values for the auxiliary parameters at the annual and quarterly frequencies. The depreciation rate is set equal to the mean ratio of aggregate depreciation to total assets over time. This is lower than the depreciation rate obtained as a ratio of the capital stock, as the total assets of firms are more than twice the total physical capital stock. The interest rate equals the mean ratio of interest payable to total liabilities. The linear tax rate is equal to mean aggregate taxes to taxable income. The calibrated tax rate is close to the federal tax rate of 35% plus the average state tax rate of 4%. There is no optimal leverage in the model as firms do not face a trade-off in selecting their debt level.10 Therefore, I calibrate total debt using the mean of the book value of leverage. Finally, the fixed cost of operations equals the ratio of selling, general, and administration expenses to total assets.
This study also highlights the importance of incorporating growth in production-based asset pricing models. As such, I report results from the estimation assuming annual growth rates of 2% and 3%, respectively. The growth rate of 2% roughly corresponds to the mean per capita real GDP growth rate over the sample period. The higher growth rate of 3.0% reflects real GDP growth over the same period. The quarterly estimates assume a quarterly growth rate of 0.5%.
3.2 Identification of model parameters
The simulated method of moments estimation involves matching moments from the data to those obtained by simulating the model given in equation (5). The matched moments include the means, variances, and autocorrelations of income and dividends plus the mean of the market-to-book ratio and the variance of investment.11 Given the black box nature of the estimation, it is helpful to provide some intuition as to which moment helps identify which parameter.
The average earnings level helps pin down the curvature of the profit function, ![]() . This reflects the link between
. This reflects the link between ![]() and the markup charged by the firm. The autocorrelation of dividends and earnings helps pin down the autocorrelation parameter,
and the markup charged by the firm. The autocorrelation of dividends and earnings helps pin down the autocorrelation parameter, ![]() . Similarly,
the variances of earnings and dividends inform the volatility of the profitability shock process,
. Similarly,
the variances of earnings and dividends inform the volatility of the profitability shock process, ![]() . This leads to some tension in the estimation as it cannot simultaneous match both
earnings and dividend variances, particularly with the quarterly data. Due to the non-linearity of the value function, the volatility of the profitability measure also influences the mean market-to-book ratio. The mean dividend level helps pin down the adjustment cost parameter,
. This leads to some tension in the estimation as it cannot simultaneous match both
earnings and dividend variances, particularly with the quarterly data. Due to the non-linearity of the value function, the volatility of the profitability measure also influences the mean market-to-book ratio. The mean dividend level helps pin down the adjustment cost parameter, ![]() . The resource constraint for the firm implies that dividends equals earnings minus the cost of investment. Given levels of earnings and investment, an increase in adjustment costs lower the
dividend payout.
. The resource constraint for the firm implies that dividends equals earnings minus the cost of investment. Given levels of earnings and investment, an increase in adjustment costs lower the
dividend payout.
Once the model has pinned down the above parameters, the average market-to-book ratio helps pin down the mean pricing kernel. Effectively, given earnings and dividends, a lower market-to-book ratio requires a lower mean pricing kernel. The volatility of investment helps identify variation within the pricing kernel as the first order condition relates investment to conditional expectations of future firm values. Finally, the expected return to equity equals the average realized return obtained from simulating the model given the estimated parameter values. The expected return is reported after transforming back into the economy with trend growth, so as to be comparable with actual data.
Although the above discussion focuses on one-to-one mappings between the moments and the parameters, the estimation employs data on all the moments to pin down all the parameters. In the model simulations, a parameter change will directly or indirectly affect all the moments. For example, an
increase in ![]() leads to a higher average market-to-book ratio and a higher investment volatility, in addition to its direct effect on the autocorrelation moments.
leads to a higher average market-to-book ratio and a higher investment volatility, in addition to its direct effect on the autocorrelation moments.
4 Results
This section presents the results from estimating the model given in (5). The first subsection estimates the model using annual data assuming a constant pricing kernel. The next three subsections estimate the model using annual data with a time-varying pricing kernel; this includes a split sample estimation. The subsequent subsection estimates the model using quarterly data, also with a time-varying pricing kernel.
4.1 Constant pricing kernel
Classic valuation studies (Samuelson (1965), Samuelson (1973) and Shiller (1981)) have argued in favor of assuming a constant pricing kernel. Further, estimating the model with a constant pricing kernel can help build
intuition. Thus, I first present results obtained by assuming that
![]() , and subsequently examine the impact of allowing the pricing kernel to vary with
, and subsequently examine the impact of allowing the pricing kernel to vary with ![]() .
.
Panel A of Table 3 presents the parameter estimates from this estimation. The expected mean return to equity from the estimation equals 4.7%, lower than the historical average real return of 6.5% used in the literature. The intuition for the estimate is that it equals the expected return at which data on earnings, dividends, and associated growth options are best reconciled with data on valuations. A higher expected return would lower the discounted present value of future dividend streams, resulting in a smaller aggregate market-to-book ratio. The precision of the estimate arises from the sensitivity of the model to changes in the expected return. Thus, the method employed in the study helps filter some of the noise in observed returns.
The point estimate for ![]() indicates some role for capital augmenting technological change or some flexibility in the aggregate supply of labor. The estimates for
indicates some role for capital augmenting technological change or some flexibility in the aggregate supply of labor. The estimates for ![]() and
and ![]() are mainly determined by the data on the income process, while the estimate for
are mainly determined by the data on the income process, while the estimate for
![]() enables the model to match the data on dividends. Note that the investment adjustment cost is the only friction in the model, and the estimate reflects the gap between income,
dividends, and investment observed in the data.
enables the model to match the data on dividends. Note that the investment adjustment cost is the only friction in the model, and the estimate reflects the gap between income,
dividends, and investment observed in the data.
Panel B of Table 3 presents the moments used in the estimation. The model moments are constructed using the parameter values reported in Panel A. The model successfully matches the first moments of income, dividends, and the market-to-book ratio in the data. However, the
model fails to generate the observed variability in each of the series.12 This arises partly as a result of all variation in the model being driven by a
single shock process. The failure of the model to match the variances also drives up the goodness-of-fit statistic
![]() .
.
Although estimating the model assuming a constant pricing kernel helps build intuition, it is clearly a restrictive assumption. As such, the next sections estimate the model under the assumption of a time-varying pricing kernel.13
4.2 Time varying pricing kernel
I parameterize the log pricing kernel as a log-linear function of current and future aggregate profitability:
where
Panels A and B of Table 4 reports the estimated parameter values and the matched moments, respectively.14 The estimates imply a
mean annual expected real return to equity of ![]() , somewhat higher than estimate obtained with the constant pricing kernel. On the other hand, the estimated value is a bit higher than the
realized mean return for the thirty five year period from 1969 to 2003 reported by Cogley and Sargent (2008). The estimates indicate that the expected return to equity is lower than historical values, consistent with the findings of Fama and French
(2002), Siegel (1999), Claus and Thomas (2001) and Jagannathan, McGrattan, and Scherbina (2001). These authors argue that historical realized returns are likely to be higher than expected returns in the future. This
could be due to either decreasing macroeconomic risk (see Lettau, Ludvigson, and Wachter (2008)), decreased market price of risk (see Cogley and Sargent (2008)) or changes in taxes (see McGrattan and Prescott (2005)).
Although it is possible that expected returns to equity may have increased following the recent financial crisis, some investors have argued that the U.S. may be heading for a period of sustained low returns.
, somewhat higher than estimate obtained with the constant pricing kernel. On the other hand, the estimated value is a bit higher than the
realized mean return for the thirty five year period from 1969 to 2003 reported by Cogley and Sargent (2008). The estimates indicate that the expected return to equity is lower than historical values, consistent with the findings of Fama and French
(2002), Siegel (1999), Claus and Thomas (2001) and Jagannathan, McGrattan, and Scherbina (2001). These authors argue that historical realized returns are likely to be higher than expected returns in the future. This
could be due to either decreasing macroeconomic risk (see Lettau, Ludvigson, and Wachter (2008)), decreased market price of risk (see Cogley and Sargent (2008)) or changes in taxes (see McGrattan and Prescott (2005)).
Although it is possible that expected returns to equity may have increased following the recent financial crisis, some investors have argued that the U.S. may be heading for a period of sustained low returns.
Incorporating time variation in expected returns also improves the fit of the model with regards to the volatility of dividends, earnings, and investment. The expected return to equity rises when aggregate profitability is low, leading to a much sharper drop in investment than would be observed if expected returns were constant. An increase in investment volatility also drives up dividend volatility. As before, the result indicates that the expected real return to equity over the sample period is lower than the historical average of the realized return.
The other parameter values are mostly similar to those obtained with a constant ![]() . The estimated value for
. The estimated value for ![]() remains somewhat higher than the values obtained from firm level estimations, partly due to its role as the sole friction in the model. The mean expected return estimate has a small standard error, even though not all components of the pricing kernel are
precisely estimated. This arises due to the fact that the pricing kernel is a non-linear transformation of
remains somewhat higher than the values obtained from firm level estimations, partly due to its role as the sole friction in the model. The mean expected return estimate has a small standard error, even though not all components of the pricing kernel are
precisely estimated. This arises due to the fact that the pricing kernel is a non-linear transformation of
![]() and
and ![]() .
.
4.3 A higher growth rate
The previous results assume an annual economic growth rate of ![]() . However, one can argue that the appropriate growth rate in the model corresponds to the growth rate of the economy, not
the per capita growth rate used before. This subsection reports the results obtained by estimating the model with an annual growth rate of
. However, one can argue that the appropriate growth rate in the model corresponds to the growth rate of the economy, not
the per capita growth rate used before. This subsection reports the results obtained by estimating the model with an annual growth rate of ![]() . The pricing kernel varies with aggregate
conditions and has the same parametrization as above.
. The pricing kernel varies with aggregate
conditions and has the same parametrization as above.
Panels A and B of Table 5 reports estimated parameter values and the moments employed in the estimation, respectively, assuming a growth rate of
![]() . The estimates for the pricing kernel parameters imply a mean annual expected real return to equity of
. The estimates for the pricing kernel parameters imply a mean annual expected real return to equity of ![]() , higher than the estimate obtained with the lower growth rate.15 The resulting estimate is similar to the values
employed in the literature. The intuition for the increase in the estimated expected return is that, ceteris paribus, a higher growth rate increases the current value of the aggregate firm. An increase in expected returns counteracts this by decreasing the value of future dividend payments. The
difference in the estimates highlights the sensitivity of the estimated expected return to assumptions about the long-run growth rate. In that regard, the results reflect the intuition of the long-run risk model of Bansal and Yaron (2004).
, higher than the estimate obtained with the lower growth rate.15 The resulting estimate is similar to the values
employed in the literature. The intuition for the increase in the estimated expected return is that, ceteris paribus, a higher growth rate increases the current value of the aggregate firm. An increase in expected returns counteracts this by decreasing the value of future dividend payments. The
difference in the estimates highlights the sensitivity of the estimated expected return to assumptions about the long-run growth rate. In that regard, the results reflect the intuition of the long-run risk model of Bansal and Yaron (2004).
The estimates for the other parameters remain similar to those obtained above, except for the adjustment cost parameter. The decrease in ![]() arises from the increase in the steady
state investment level - which equals
arises from the increase in the steady
state investment level - which equals
![]() - as a result of the higher growth rate. As the estimation algorithm aims to fit both dividends and earnings data, the investment friction decreases in order to offset the
higher investment levels.
- as a result of the higher growth rate. As the estimation algorithm aims to fit both dividends and earnings data, the investment friction decreases in order to offset the
higher investment levels.
4.4 Split sample
Estimating the model after separating the sample into two periods enables one to test whether the expected real return to equity has declined. Table 6 presents the results from estimating the model after splitting the annual sample at its midpoint, 1987. Panel A reports the parameter estimates from the two samples, and Panel B reports the matched moments. The assumed growth rate equals 2.0%, as in the baseline results.
The split sample results provide clear evidence of a decline in the expected real return to equity, which declines from 6.5% in the twenty years from 1966-87 to 4.4% from 1988-2009. The estimated decline in the expected return to equity is economically and statistically significant. This indicates that the decline in average earnings and the increase in valuations documented in Table 1 translates to a noticeable decline in the expected return to equity.
The gap between the estimated expected return to equity and realized returns may reflect a structural break in the economy or a slow moving change in expected returns.16 Lettau, Ludvigson, and Wachter (2008) argue that the decline in equity premium arose from a reduction in macroeconomic volatility. Cogley and Sargent (2008) attribute the decline in the equity premium to slow moving changes in the market price of risk following the Great Depression. Bansal and Yaron (2004) argue that slow moving changes in consumption growth drives asset prices. Panageas and Yu (2006) present a model in which technological change drives slow moving changes in expected returns over long horizons. Increased participation in the stock market may also lower the expected returns to equity. In contrast, Pastor and Veronesi (2009) provide an alternate view that the increase in equity values was a temporary phenomenon associated with the introduction and adoption of the Internet. In a related study, Pastor and Veronesi (2006) argue that the high observed valuations for the NASDAQ could be rationalized given uncertainty about future profitability. Ritter and Warr (2002) argue that the bull market in the 1990s may have been partly due to a decrease in inflation. While the results in this study cannot distinguish between these explanations, it suggests that investors should not simply rely on historical returns to equity in forming portfolio and savings choices.
The parameter estimates from the split samples are comparable to those obtained with the full sample. The model manages to fit the chosen moments quite well over the first period. It's less successful at matching all the moments over the second period, partly due to the fact that while earnings have become more volatile, dividends have become less volatile over this period.
4.5 Quarterly data
The previous analysis suggests that expected returns to equity have declined about 2 percentage points over the past forty years. Another way to verify this result would be to examine whether the model estimated using quarterly data, which are available only from 1984:Q1, generates similar results to that obtained with annual data over the later sample period.
Panels A and B of Table 7 present the estimated parameter values and the matched moments, respectively, from the estimation of the model using quarterly data from 1984:Q1 to 2009:Q4. The assumed quarterly economic growth rate equals 0.5%. The estimated expected real return to equity equals 4.0%, a bit lower than the estimate obtained using the annual data for the period from 1988 onwards. The finding provides further evidence in favor of a decline in average expected returns to equity.
The estimates for the other parameters are driven by the matched moments and are, for the most part, comparable to the annual estimates. The estimate for the adjustment cost parameter, ![]() , jumps, mainly as a result of the quadratic specification. That is,
, jumps, mainly as a result of the quadratic specification. That is, ![]() has to be much higher in order to generate the same resource cost of investment with much
lower average investment rates, since investment is now measured quarterly, not annually. As before, the mean expected return is fairly precisely estimated, while the model has difficulty pinning down some of the pricing kernel parameters. As with the estimates obtained using the annual data over
the later sample period, the model has some difficulty in matching the volatilities of dividends, earnings, and investment.
has to be much higher in order to generate the same resource cost of investment with much
lower average investment rates, since investment is now measured quarterly, not annually. As before, the mean expected return is fairly precisely estimated, while the model has difficulty pinning down some of the pricing kernel parameters. As with the estimates obtained using the annual data over
the later sample period, the model has some difficulty in matching the volatilities of dividends, earnings, and investment.
4.6 Robustness of the estimates
The previous sections present a range of estimates for the expected return to equity. Additional robustness checks on allowing a non-linear tax rule, assuming leverage varies with lagged profitability, and incorporating a time-varying interest rate lead to similar estimates of the expected return to equity for both the annual and quarterly data sets.
One area in which the model fails to match the data is the variance of the market-to-book ratio. Including this as an additional moment condition has little impact on the results, as the estimation mostly ignores this moment. This reflects the difficulty of matching variances of different orders of magnitude using a single shock process.
Overall, the estimation pins down the expected return to equity quite precisely in the range of 4% to 5.5%.17 These findings support other evidence indicating that expected returns to equity have declined and suggest that investors should not necessarily expect future returns to equity to be similar to historical returns.
5 Model implications
This section evaluates the model along some dimensions not used in the estimation, presents the conditional expected returns implied by the model, and examines the implications of the findings for investors' portfolio choice decisions.
5.1 Model evaluation
The model presented in this study is primarily aimed towards estimating the expected return to equity. The reader may be interested in understanding how the model fares with regards to features of asset prices that were not employed in the estimation.18 Such a comparison serves as an out-of-sample evaluation of the model. It also helps highlight some strengths and weaknesses of it.
Table 8 presents some statistics of interest obtained from the data and the model simulations. Panel A presents the results using the estimates obtained with the annual data reported in Table 4 and Panel B presents the results using the estimated obtained with the quarterly data reported in Table 7. The data statistics are obtained from the corresponding data sets used in the estimations. The reported statistics relate to the key variables employed in the estimation: aggregate dividends, earnings, investment, and market value.
The models generate an annualized equity return volatility of 12.3% and 14.5%, fairly close to the value observed in the data. This indicates that although the model has trouble matching all the volatilities in the data, it has some success generating a high equity return volatility.
The valuation ratios derived from the model correspond to those of the aggregate equity market. The asset pricing literature typically focuses on the valuation ratio per share outstanding. As Bansal and Yaron (2007) demonstrate, these valuation ratios may differ when the number of shares in the economy varies over time. They argue that the log aggregate market value to aggregate dividends series provides helpful information that is not captured by the per share price-dividend ratio.
The log market value to dividend ratio from the model matches the data well with the annual estimates, but is less volatile than the data for the quarterly estimates. On the other hand, the model comes close to capturing the autocorrelation of the log market value to dividend ratio at both frequencies. As Bansal and Yaron (2007) find, the log value to dividend ratio exhibits less persistence than the per share price-dividend ratio.
The quarterly dividend growth volatility from the model roughly matches the data over both periods. The model has mixed success at matching the correlation between dividends, earnings, and investment. While the model implies a very low correlation between these values with the annual data, the estimates obtained using the quarterly data imply the opposite. This divergence reflects the investment volatility in the two models. With the annual data, the model implies that investment declines sharply when earnings are low, offsetting the effect of low earnings of dividends. However, with the quarterly data, investment is much less volatile, and periods of low earnings are associated with low dividends.
One dimension along which the model fails to match the data is the risk-free rate. The estimated risk-free rates are always above the assumed economic growth rates. As discussed in Section 2.2, production-based models with time-separable utility functions cannot generate low risk-free rates once one accounts for economic growth.
5.2 Time variation in expected returns
The previous discussion has focused on the mean expected return to equity. However, the model also implies that expected returns vary with the aggregate earnings of the corporate sector.19 An examination of the model-implied conditional expected return provides another criterion for evaluating the model.
Figure 2 plots the model-implied conditional expected return to equity. Panel A plots the series constructed using the split sample estimates from the annual data reported in Table 6; Panel B plots the series constructed using the estimates from the quarterly data reported in Table 7. I construct the expected return to equity for each of the earnings grid values used in the estimation. Interpolating the observed earnings data onto the conditional expected returns to equity at these grid points generates the model-implied expected return at each data point. For the annual series, I splice together the implied expected return from the sample from 1966 to 1987 with that from the sample from 1988 to 2009.20
The figure demonstrates that the model generates noticeable variation in expected returns. Consistent with economic reasoning, the model-implied conditional expected returns reach their peak values during the recessions. Conditional expected returns reach their peak value during the recession of 2001, reflecting the sharp decline in earnings during that period. The quarterly estimates show a sharp rise in conditional expected returns during two quarters of the 2008 recession. However, expected returns decline sharply, reflecting the quick pickup in corporate earnings. Expected returns reach their lowest values around 2006, a period of robust earnings. The range of values for expected returns are generally plausible, and in particular, takes mostly positive values as emphasized by Campbell and Thompson (2008). These results indicate that the model is fairly successful at capturing time variation in expected returns.
5.3 Implications for portfolio choice
This section examines the portfolio choice implications of the estimated real return to equity. Holding all else constant, it compares the optimal equity weight obtained using the estimated expected returns to equity with the optimal equity weight obtained using a historical average for equity returns.21
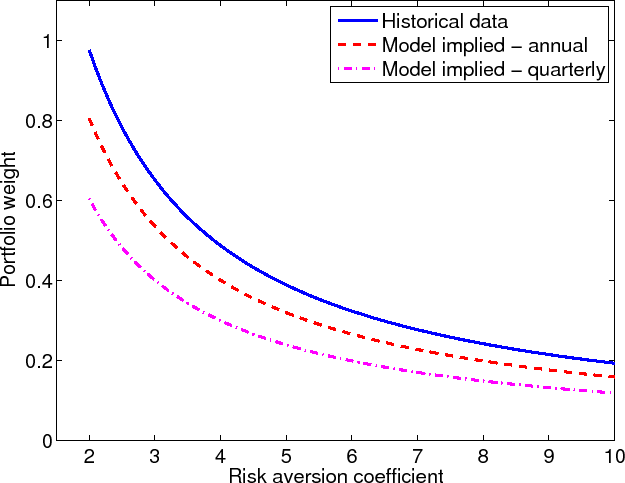
Figure 3 plots the optimal allocation to equity for a CRRA investor as a function of his risk aversion coefficient. The investor has a one year holding period. The portfolio weight using historical data was constructed assuming an annual real return to equity of 6.5% and a risk-free return of 0.5%. The excess return of 6% reflected the post-war excess return to equity. The expected volatility of the stock return was set equal to its sample average of 18.3%. The red dashed line represents the optimal equity holding for an investor who forms his decisions based on the estimated real return to equity of 5.4% reported in Table 4. The pink dashed-dot line assumes an expected return to equity of 4.0%, as reported in Table 7. In both cases, the investor uses the same values for the risk-free rate and the volatility of equity returns as the data-based investor.
Portfolio allocations based on the estimated expected return generate a lower exposure to the stock market. The gap between the two portfolios is particularly pronounced for low levels of risk-aversion. An investor with a relative risk aversion coefficient of 4 would hold 40% of his wealth in equities given an expected return of 5.4%, compared to about 50% of his wealth in equities with an expected return of 6.5%. This gap becomes even larger when one assumes the lower expected return obtained using the more recent data. Increased risk aversion reduces the gap as the investor becomes less willing to hold equities. This analysis demonstrates that the finding of a lower expected real return to equity has sharp implications for the portfolio choice decisions of an investor.
6 Conclusion
This study estimates the expected real return to equity using a production-based asset pricing approach. The intuition underlying the approach is that the expected return provides a mapping from data on earnings, dividends, and investment onto the valuation of firms. Given data on these variables and a dynamic model for their evolution over time, one can estimate the expected return to equity that generates the best fit for the model.
Using this approach, I obtain estimates for the expected real return to equity in the range of 4.0% to 6.5%, depending on the sample period and the assumed economic growth rate. These results are, for the most part, lower than mean historical returns to equity, indicating that investors expect future returns to equity to be lower than past returns. The findings are consistent with other studies in the literature that have argued that the equity premium has declined over time.
The findings have clear practical relevance as the expected return to equity has a big impact on investors' portfolio decisions. The estimated expected returns imply a substantially smaller portfolio allocation to equities than would be obtained using historical averages. The estimates also translate to lower expected portfolio returns, indicating that investors may need to increase their savings rate in order to finance retirement expenses. In addition, the results suggests that pension plans that use a high expected return to equity may overstate the adequacy of their current funding levels, lending further support to the finding of Novy-Marx and Rauh (2009) of funding shortfalls in state-sponsored pension plans.
One interesting question that this study cannot answer is whether the decline in expected returns reflects a permanent change or a temporary regime shift as in Lettau, Ludvigson, and Wachter (2008). It is quite plausible that, in light of the recent financial crisis, expected returns to equity have increased again as investors revise upward their views on the riskiness of equities. The method in this study cannot evaluate this question without data on a sufficient sample period following the crisis.
A The representative firm model
The output produced by the representative firm is given by a Cobb-Douglas specification with capital share ![]() :
:
A balanced growth path is one in which capital, output, profits, and wages grow at constant, possibly different, rates. A balanced growth is necessary in order to translate this model into a stationary economy. However, this imposes an additional requirement:
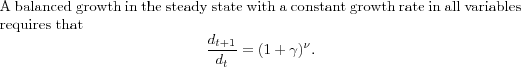
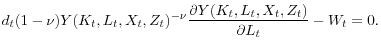
In order for
The growth in the demand shift parameter ensures that wages and sales grow at a constant rate. Such a relationship would arise in a model where the representative firm was obtained by aggregating firms that produced differentiate goods which combined to form a Dixit-Stiglitz consumption aggregator.
Corollary #.:
| (A.2) |
B Asset returns in models with and without growth
This subsection presents an alternate proof of Proposition 2.2 using only the representative consumer's budget constraint, as opposed to the firm value based proof presented in the main text.
where
The first order conditions for asset returns in the economy with growth is given by
Now consider the budget constraints in the detrended economy without growth.
where the asset holding,
Note that one cannot simply replace the consumption term in Eq. (A.4) with the detrended term to obtain (A.7). This arises from the fact that the anticipated growth in consumption arising from technological progress impacts the agent's utility. The first order conditions using the detrended problem imply that
Given that
C Simulated method of moments
The simulated method of moments estimator of Lee and Ingram (1991) and Duffie and Singleton (1993) obtains parameter estimates by matching a set of selected moments from the data to those obtained by simulation. Denote the true values of the
structural parameters by ![]() . The matched moments can be written as a solution to a minimization problem
. The matched moments can be written as a solution to a minimization problem ![]() , where
, where ![]() denotes the data and
denotes the data and ![]() the
moments to be matched. The data moments are given by
the
moments to be matched. The data moments are given by
| (A.9) |
where
| (A.10) |
This study picks
The structural parameters are obtained by minimizing a quadratic form of the distance between the data and simulated moments.
| (A.11) |
where
| (A.12) |
The above covariance matrix is calculated with the actual data set using the influence function method of Erickson and Whited (2000). The estimator is asymptotically normal for fixed
| (A.13) | |||
![\displaystyle (1 + \frac{1}{S}) \left[\frac{\partial^2{Q}}{\partial{\Psi}\partial{M}'} \left(\frac{\partial{Q}}{\partial{M}}\frac{\partial{Q}}{\partial{M}}'\right)^{-1} \frac{\partial^2{Q}}{\partial{M}\partial{\Psi}'}\right]^{-1}.](img142.gif) |
While
D Numerical solution
The simulations require a numerical solution of the value function for the aggregate firm. The capital grid has 150 points and the profitability grid has 10 points. The capital grid is centered around an approximation of the median size of the firm given the parameters. The approximate value of
the steady state capital stock ![]() for the case of the constant pricing kernel is given by the following:
for the case of the constant pricing kernel is given by the following:
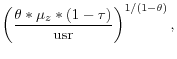 |
|||
| usr |
where
The simulated sample is generated using the value and policy functions for the aggregate firm. The law of motion for profitability is generated directly using the transition equations (2). The simulation is run for 20,000 years, with the initial 10,000 discarded as a burn-in sample. The value of the quadratic form of the distance between the data moments and the simulated moments is computed for each simulation. The program searches for the parameters that minimize this distance using the simulated annealing algorithm. Each estimation involved evaluating more than 10,000 candidate parameter sets and took about a week of computing time.
References
The table reports the summary statistics for the aggregate firm constructed by aggregating firm level data from the CRSP/Compustat merged data set at annual and quarterly frequencies. The sample periods for the annual and quarterly date are from 1966 to 2009 and 1984:Q1 to 2009:Q4, respectively. `St. dev.' denotes standard deviation. The earnings variable measures income accruing to common shareholders scaled by lagged total assets. Market-to-book equals the aggregate market value of equity scaled by the book value of equity. Leverage equals total liabilities divided by total book assets. Earnings, dividends, investment, interest costs, corporate taxes, and depreciation are all scaled by lagged total assets and reported as percentages.
| Variable | Annual data: Mean | Annual data: St. dev. | Quarterly data: Mean | Quarterly data: St. dev. |
| Earnings | 5.08 | 1.82 | 1.01 | 0.47 |
| Market-to-book | 2.19 | 0.82 | 2.87 | 0.89 |
| Dividends | 2.32 | 0.61 | 0.47 | 0.10 |
| Investment | 8.79 | 2.03 | 1.73 | 0.36 |
| Leverage | 0.59 | 0.07 | 0.64 | 0.03 |
| Interest costs | 4.03 | 1.02 | 0.86 | 0.23 |
| Corporate taxes | 4.05 | 1.65 | 0.70 | 0.19 |
| Depreciation | 5.38 | 0.39 | 1.19 | 0.09 |
The table reports the parameters that are calibrated in the estimations with annual and quarterly data sets, respectively. The calibrated parameter values differ by the sample, and are set to match the corresponding moments for each data set. Section 3.1 details the calibration of each parameter.
Panel A reports the parameters values obtained from estimating the model on the aggregate firm under the assumption of a constant pricing kernel. Panel B reports the corresponding moment values from the data and the model. The data moments are obtained using data on the aggregate firm constructed by summing the variables across all firms in a given year. Earnings, dividends, and investment are all reported as percentages. The sample period is from 1966 to 2009.denotes a goodness-of-fit measure. The annual economic growth rate,
, is assumed to be
. The pricing kernel is assumed to be a constant:
The applicable pricing kernel for the detrended model equalstimes
, in order to adjust for the impact of growth. The annualized expected real return to equity,
, equals the average equity return in the simulated data set constructed using the estimated parameter values. The standard error for the annualized expected real return to equity is computed using the delta method.
| Parameter |
|
||||||
| Estimate | 0.51 | 0.71 | 0.015 | 4.87 | 0.9634 | 4.72 | 59.83 |
| Standard error | (0.01) | (0.06) | (0.003) | (0.34) | (0.0018) | (0.20) |
| Moment | Data | Model |
| First moment of earnings | 5.08 | 5.08 |
| Variance of earnings | 2.17 | 0.20 |
| First moment of market-to-book | 2.19 | 2.34 |
| First moment of dividends | 2.32 | 2.39 |
| Variance of dividends | 0.37 | 0.19 |
| Variance of investment | 4.04 | 0.00 |
| Autocorrelation of earnings | 0.73 | 0.72 |
| Autocorrelation of dividends | 0.83 | 0.71 |
Panel A reports the parameters values obtained from estimating the model on the aggregate firm using annual data under the assumption of a time varying pricing kernel. Panel B reports the corresponding moment values from the data and the model. The data moments are obtained using data on the aggregate firm constructed by summing the variables across all firms in a given year. Earnings, dividends, and investment are all reported as percentages. The sample period is from 1966 to 2009.denotes a goodness-of-fit measure. The annual economic growth rate,
, is assumed to be
. The pricing kernel is parameterized as
wheredenotes the mean of
. The applicable pricing kernel for the detrended model equals
times
, in order to adjust for the impact of growth. The expected real return to equity,
, equals the average equity return in the simulated data set constructed using the estimated parameter values. The standard error for the annualized expected real return to equity is computed using the delta method.
| Parameter |
|
||||||||
| Estimate | 0.51 | 0.68 | 0.044 | 4.58 | 0.95 | -0.40 | -0.25 | 5.35 | 21.92 |
| Standard error | (0.01) | (0.07) | (0.005) | (0.31) | (0.11) | (0.91) | (0.30) | (0.35) |
| Moment | Data | Model |
| First moment of earnings | 5.08 | 5.06 |
| Variance of earnings | 2.17 | 1.51 |
| First moment of market-to-book | 2.19 | 2.45 |
| First moment of dividends | 2.32 | 2.41 |
| Variance of dividends | 0.37 | 0.40 |
| Variance of investment | 4.04 | 2.83 |
| Autocorrelation of earnings | 0.73 | 0.68 |
| Autocorrelation of dividends | 0.83 | 0.87 |
Panel A reports the parameters values obtained from estimating the model on the aggregate firm under the assumption of a time varying pricing kernel. Panel B reports the corresponding moment values from the data and the model. The data moments are obtained using data on the aggregate firm constructed by summing the variables across all firms in a given year. Earnings, dividends, and investment are all reported as percentages. The sample period is from 1966 to 2009.denotes a goodness-of-fit measure. The annual economic growth rate,
, is assumed to be
. The pricing kernel is parameterized as
wheredenotes the mean of
. The applicable pricing kernel for the detrended model equals
times
, in order to adjust for the impact of growth. The expected real return to equity,
, equals the average equity return in the simulated data set constructed using the estimated parameter values. The standard error for the annualized expected real return to equity is computed using the delta method.
| Parameter |
|
||||||||
| Estimate | 0.51 | 0.62 | 0.047 | 3.07 | 0.49 | -0.48 | -0.19 | 6.48 | 4.50 |
| Standard error | (0.01) | (0.07) | (0.007) | (0.33) | (0.36) | (7.14) | (2.89) | (0.56) |
| Moment | Data | Model |
| First moment of earnings | 5.08 | 5.11 |
| Variance of earnings | 2.17 | 1.48 |
| First moment of market-to-book | 2.19 | 2.27 |
| First moment of dividends | 2.32 | 2.34 |
| Variance of dividends | 0.37 | 0.40 |
| Variance of investment | 4.04 | 3.74 |
| Autocorrelation of earnings | 0.73 | 0.61 |
| Autocorrelation of dividends | 0.83 | 0.84 |
Panel A reports the parameters values obtained from estimating the model on the aggregate firm for two annual sub-samples. The pricing kernel varies with the current and next period aggregate state. Panel B reports the corresponding moment values from the data and the model. The data moments are obtained using data on the aggregate firm constructed by summing the variables across all firms in a given year. Earnings, dividends, and investment are all reported as percentages. The sub-sample periods are from 1966 to 1987 and 1988 to 2009, respectively.denotes a goodness-of-fit measure. The annual economic growth rate,
, is assumed to be
. The pricing kernel is parameterized as
wheredenotes the mean of
. The applicable pricing kernel for the detrended model equals
times
, in order to adjust for the impact of growth. The expected real return to equity,
, equals the average equity return in the simulated data set constructed using the estimated parameter values. The standard error for the expected real return to equity is computed using the delta method.
| Sample | Parameter |
|
||||||||
| 1966 - 1987 | Estimate | 0.58 | 0.55 | 0.037 | 3.24 | 1.30 | -0.17 | -0.30 | 6.50 | 1.07 |
| Standard error | (0.10) | (0.11) | (0.010) | (0.24) | (0.20) | (0.55) | (0.50) | (0.67) | ||
| 1988 - 2009 | Estimate | 0.47 | 0.62 | 0.020 | 4.87 | 0.66 | -0.85 | -0.27 | 4.44 | 16.23 |
| Standard error | (0.02) | (0.11) | (0.005) | (0.83) | (0.08) | (1.83) | (0.67) | (0.20) |
| 1966 - 1987 | 1988 - 2009 | |||
| Moment | Data | Model | Data | Model |
| First moment of earnings | 6.14 | 6.20 | 3.99 | 3.92 |
| Variance of earnings | 1.34 | 1.24 | 1.70 | 0.19 |
| First moment of market-to-book | 1.58 | 1.58 | 2.79 | 2.77 |
| First moment of dividends | 2.71 | 2.73 | 1.93 | 1.95 |
| Variance of dividends | 0.31 | 0.31 | 0.12 | 0.08 |
| Variance of investment | 1.70 | 1.82 | 1.00 | 0.81 |
| Autocorrelation of earnings | 0.60 | 0.56 | 0.68 | 0.61 |
| Autocorrelation of dividends | 0.78 | 0.81 | 0.70 | 0.66 |
Panel A reports the parameters values obtained from estimating the model on the aggregate firm under the assumption of a time varying pricing kernel using quarterly data. Panel B reports the corresponding moment values from the data and the model. The data moments are obtained using data on the aggregate firm constructed by summing the variables across all firms in a given quarter. Earnings, dividends, and investment are all reported as percentages. The sample period is from 1984:Q1 to 2009:Q4.denotes a goodness-of-fit measure. The quarterly economic growth rate,
, is assumed to be
. The pricing kernel is parameterized as
wheredenotes the mean of
. The applicable pricing kernel for the detrended model equals
times
, in order to adjust for the impact of growth. The expected real return to equity,
, equals the average equity return in the simulated data set constructed using the estimated parameter values. The standard error for the expected real return to equity is computed using the delta method.
| Parameter |
|
||||||||
| Estimate | 0.46 | 0.81 | 0.028 | 24.46 | 0.59 | -0.32 | -0.07 | 4.01 | 65.35 |
| Standard error | (0.01) | (0.07) | (0.008) | (2.03) | (0.18) | (1.34) | (0.55) | (0.49) |
| Moment | Data | Model |
| First moment of earnings | 1.01 | 1.03 |
| Variance of earnings | 0.12 | 0.04 |
| First moment of market-to-book | 2.87 | 3.09 |
| First moment of dividends | 0.47 | 0.48 |
| Variance of dividends | 0.01 | 0.01 |
| Variance of investment | 0.13 | 0.02 |
| Autocorrelation of earnings | 0.80 | 0.81 |
| Autocorrelation of dividends | 0.64 | 0.89 |
The table reports statistics of interest from the data and the model simulations. Panel A reports values from the estimation using annual data from 1966 to 2009 reported in Table 4. Panel B reports values from the estimation using quarterly data from 1984:Q1 to 2009:Q4 reported in Table 7. The data values represent the corresponding statistics from the actual data sets, while the model values are obtained from the simulated data sets given the estimated parameter values. The value-dividend ratio equals the log of the aggregate market value divided by aggregate dividends. The correlation between dividends, earnings, and investment are reported after scaling by total assets to induce stationarity.
| Statistic | Data | Model |
| Standard deviation of market return | 18.3 | 12.3 |
| Standard deviation of value-dividend ratio | 0.43 | 0.37 |
| Autocorrelation of value-dividend ratio | 0.91 | 0.71 |
| Standard deviation of dividend growth | 0.08 | 0.20 |
| Autocorrelation of dividend growth | 0.10 | -0.20 |
| Correlation between dividends and earnings | 0.75 | -0.44 |
| Correlation between dividends and investment | 0.75 | 0.03 |
| Statistic | Data | Model |
| Standard deviation of market return | 17.5 | 14.5 |
| Standard deviation of value-dividend ratio | 0.45 | 0.19 |
| Autocorrelation of value-dividend ratio | 0.91 | 0.88 |
| Standard deviation of dividend growth | 0.17 | 0.12 |
| Autocorrelation of dividend growth | -0.50 | -0.15 |
| Correlation between dividends and earnings | 0.42 | 0.87 |
| Correlation between dividends and investment | 0.39 | 0.59 |
|
Panel A: Annual data
The figure plots the aggregate earnings of nonfinancial corporations as constructed from the CRSP/Compustat merged data set. Earnings are measured as aggregate income accruing to shareholders divided by aggregate lagged total assets. Panel A reports aggregate earnings using annual data from 1966 to
2009, and Panel B reports the aggregate earnings using data from 1984:Q1 to 2009:Q4. The quarterly earnings series is annualized by multiplying by 4. The shaded areas correspond to NBER recession periods.
 Panel B: Quarterly data 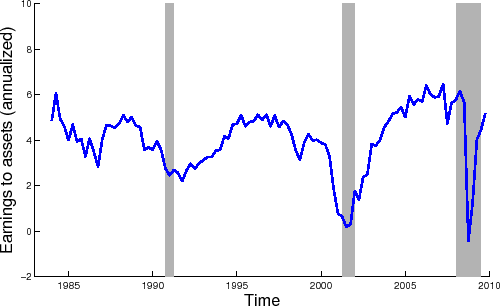 |
| Accessible Version |
|
Panel A: Annual data
The figure plots the model-implied annualized conditional expected return to equity. Panel A plots the expected return from the estimates obtained using annual data over the two sample periods reported in Table 6. The resulting model implied conditional expected return
series for the two periods are combined together to construct the series over the entire time period. Panel B plots the expected return from the estimates obtained using quarterly data reported in Table 7. The expected return to equity varies with the current value for
income accruing to shareholders scaled by lagged total assets. The shaded areas correspond to NBER recession periods.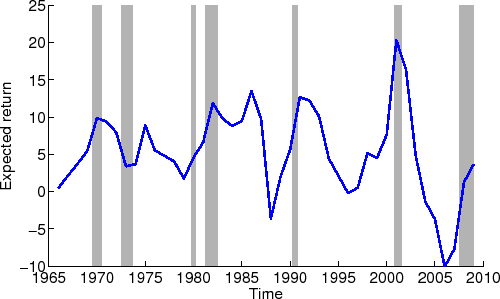 Panel B: Quarterly data 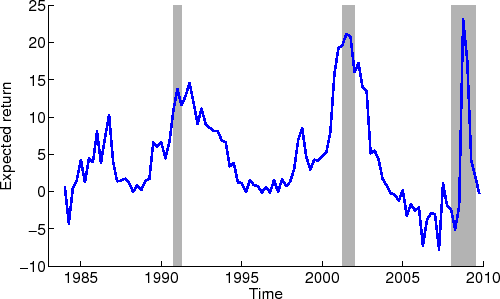 |
| Accessible Version |
 |
| Accessible Version |
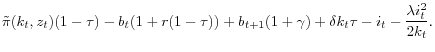
![\displaystyle \max E\left[\sum_{t=0}^{t=\infty} b^t U(C_t) \right].](img114.gif)
![\displaystyle 1 = E\left[b \frac{U_c(C_{t+1})}{U_c(C_t)} R_{t,t+1} \right].](img115.gif)
![\displaystyle \max E\left[\sum_{t=0}^{t=\infty} b^t U(c_tX_t) \right].](img118.gif)
![\displaystyle 1 = E\left[b \frac{U_c(c_{t+1}X_{t+1})X_{t+1}}{U_c(c_tX_t)X_t} \tilde{R}_{t,t+1} \right].](img119.gif)