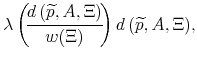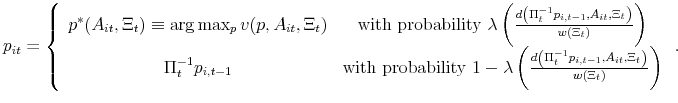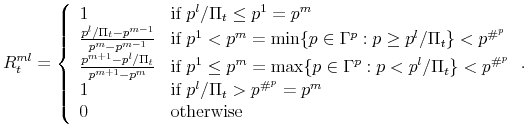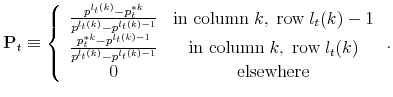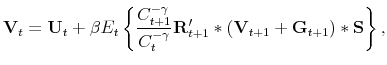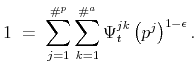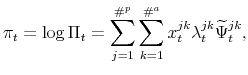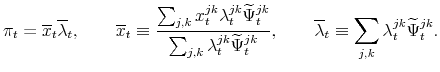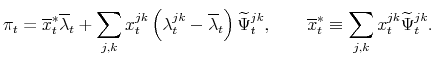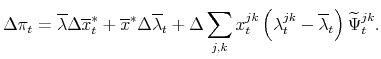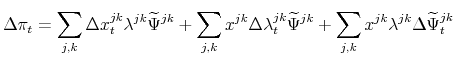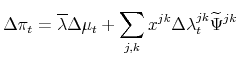Distributional Dynamics Under Smoothly State-Dependent Pricing
Keywords: Nominal rigidity, state-dependent pricing, menu costs, heterogeneity, Taylor rule
Abstract:
1 Introduction
Sticky prices are an important ingredient in modern dynamic general equilibrium models, including those used by central banks for policy analysis. But how best to model price stickiness, and to what extent stickiness of individual prices implies rigidity of the aggregate price level, remains controversial. Calvo's (1983) assumption of a constant adjustment probability is popular for its analytical tractability, and implies that monetary shocks have large and persistent real effects. However, Golosov and Lucas (2007, henceforth GL07) have argued that microfounding price rigidity on a fixed "menu cost"and calibrating to microdata implies that monetary shocks are almost neutral.
This paper calibrates and simulates a general model of state-dependent pricing that nests the Calvo (1983) and fixed menu cost (FMC) models as two opposite limiting cases, with a continuum of smooth intermediate cases lying in between. As in Dotsey, King, and Wolman (1999) and Caballero and Engel (2007), the setup rests on one fundamental property: firms are more likely to adjust their prices when doing so is more valuable. Implementing this assumption requires the selection of a parameterized family of functions to describe the adjustment hazard; the exercise is disciplined by fitting the model to the size distribution of price changes found in recent US retail microdata (Klenow and Kryvtsov 2008; Midrigan 2011; Nakamura and Steinsson 2008).1One of the calibrated parameters controls the degree of state dependence; matching the smooth distribution of price changes seen in microdata requires rather low state dependence. Therefore, impulse responses reveal substantial monetary nonneutrality, with real effects only slightly weaker than the Calvo model implies.
The impulse response analysis considers a number of issues unaddressed by previous work on state-dependent pricing. GL07 restricted attention to iid money growth shocks; this paper also considers the autocorrelated case, and shows that the shape and persistence of responses is primarily determined by the degree of state dependence, not by the autocorrelation of the driving process. Moreover, this paper also studies monetary policy governed by a Taylor rule, as opposed to an exogenous money growth process, which reinforces the conclusion that a calibrated model of state-dependent pricing implies nontrivial real effects. This paper also decomposes inflation into an "intensive margin" relating to the average desired price change, an "extensive margin" relating to
the fraction of firms adjusting, and a "selection effect" relating to
which firms adjust. This decomposition corroborates the claim of GL07, which was challenged by Caballero and Engel (2007), that the selection effect is crucial for the behavior of the FMC model. A fourth contribution of this paper is to argue that prices respond slowly to sector-specific as well as aggregate shocks, despite some recent empirical claims to the contrary. The paper also implements an algorithm for computing heterogeneous-agent economies which is well-suited to modeling state-dependent pricing but has not yet been applied in this context.
1.1 Relation to previous literature
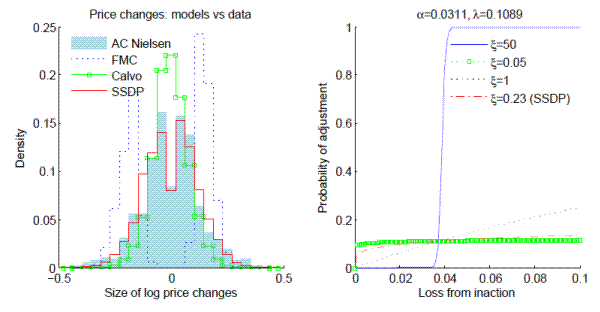
Most previous work on state-dependent pricing has obtained solutions by limiting the analysis, either focusing on partial equilibrium (e.g. Caballero and Engel, 1993, 2007; Klenow and Kryvtsov, 2008), or assuming firms face aggregate shocks only (e.g. Dotsey et al., 1999), or making strong assumptions about the distribution of idiosyncratic shocks (e.g. Caplin and Spulber, 1987; Gertler and Leahy, 2005). But Klenow and Kryvtsov (2008) argue convincingly that firms are often hit by large idiosyncratic shocks. And while heterogeneity may average out in many macroeconomic contexts, it is hard to ignore in the debate over nominal rigidities, because firm-level shocks could greatly alter firms' incentives to adjust prices. GL07 were the first to confront these issues directly, by studying a menu cost model in general equilibrium with idiosyncratic productivity shocks. They obtained a striking near-neutrality result. However, their model's fit to price data is questionable, as our Figure 1 shows. A histogram of retail microdata displays a wide range of price adjustments, whereas their FMC model generates two sharp spikes of price increases and decreases occurring near the (S,s) bounds.
Other micro facts have been addressed in more recent papers on state-dependent pricing. Eichenbaum, Jaimovich, and Rebelo (2011) and Kehoe and Midrigan (2010) modeled "temporary" price changes (sales), assuming that these adjustments are cheaper than other price changes. However, they ultimately conclude that the possibility of sales has little relevance for monetary transmission, which depends instead on the frequency of regular non-sale price changes. Guimaraes and Sheedy's (2011) model of sales as stochastic price discrimination has the same implication. Thus, since the model developed in this paper has no natural motive for sales, it will be compared to a dataset of "regular" price changes from which apparent sales have been removed. In another branch of the literature, Boivin, Giannoni, and Mihov (2009) and Mackowiak, Moench, and Wiederholt (2009) estimate that prices respond much more quickly to sectoral shocks than to aggregate shocks. However, the present paper performs a Monte Carlo exercise that shows that this finding should be treated with caution. Remarkably, even when the true response to a sector-specific shock is lagged and transitory, the estimation routine of Mackowiak et al. can erroneously conclude that sector-specific shocks have an immediate, permanent impact on prices.
Our need to allow for firm-specific shocks complicates computation, because it implies that the distribution of prices and productivities across firms is a relevant state variable.
This paper shows how to compute a dynamic general equilibrium with state-dependent pricing via the two-step algorithm of Reiter (2009), which calculates steady-state equilibrium using backwards induction on a grid, and then linearizes the equations at every grid point to calculate the dynamics.
This approach avoids some complications (and simplifying assumptions) required by other methods. In contrast to GL07, it is not necessary to assume that aggregate output stays constant after a money shock. In contrast to Dotsey, King, and Wolman (2008), it more fully exploits the recursive structure of the model, tracking the price distribution without needing to know who adjusted when. In contrast to the method of Krusell and Smith (1998), used by Midrigan (2011), there is no need to find an adequate summary statistic for the distribution. In contrast to Den Haan (1997), there is no need to impose a specific distributional form. The nonlinear, nonparametric treatment of firm-level heterogeneity in Reiter's algorithm makes it straightforward to calculate the time path of cross-sectional statistics, like our inflation decomposition; the linearization of aggregate dynamics makes it just as easy to analyze a variety of monetary policy rules or shock processes as it would be in a standard, low-dimensional DSGE model.
Several closely related papers have also remarked that FMCs imply a counterfactual distribution of price adjustments, in which small changes never occur. They proposed some more complex pricing models to fix this problem, including sectoral heterogeneity in menu costs (Klenow and Kryvtsov, 2008), multiple products on the same " menu" combined with leptokurtic technology shocks (Midrigan, 2011), or a mix of flexible- and sticky-price firms plus a mix of two distributions of productivity shocks (Dotsey et al., 2008). This paper proposes a simpler approach: we just assume the probability of price adjustment increases with the value of adjustment, and treat the hazard function as a primitive of the model. A family of hazard functions with just three parameters suffices to match the distribution of price changes at least as well as the aforementioned papers do. Our setup can be interpreted as a stochastic menu cost (SMC) model, like Dotsey et al. (1999) or Caballero and Engel (1999); under this interpretation the hazard function corresponds to the c.d.f. of the menu cost.2 Alternatively, our setup can be seen as a near-rational model, like Akerlof and Yellen (1985), in which firms are more likely to make mistakes when they are not very costly; in this case the hazard function corresponds to the distribution of error values.3 Under either interpretation, the key point is that the adjustment hazard increases smoothly with the value of adjusting, in contrast with the discontinuous jump in probability implied by the FMC model. An appropriate calibration of the smoothness of the hazard function yields a smooth histogram of price changes consistent with microdata; this smoothness is the same property that eliminates the strong selection effect found by GL07. Thus, none of the additions Dotsey et al. and Midrigan make to the FMC framework are crucial for their most important finding: a state-dependent pricing model consistent with observed price changes implies nontrivial real effects of monetary shocks, similar to those found under the Calvo framework.
2 Model
This discrete-time model embeds state-dependent pricing by firms in an otherwise-standard New Keynesian general equilibrium framework based on GL07. Besides the firms, there is a representative household and a monetary authority that either implements a Taylor rule or follows an exogenous growth process for nominal money balances.
The aggregate state of the economy at time ![]() , which will be specified in Section 2.3, is called
, which will be specified in Section 2.3, is called
![]() . Time subscripts on aggregate variables will indicate dependence, in equilibrium, on aggregate conditions
. Time subscripts on aggregate variables will indicate dependence, in equilibrium, on aggregate conditions
![]() . For example, consumption is denoted by
. For example, consumption is denoted by
![]() .
.
2.1 Household
The household's period utility function is
![]() , where
, where ![]() is consumption,
is consumption, ![]() is labor supply, and
is labor supply, and
![]() is real money balances. Utility is discounted by factor
is real money balances. Utility is discounted by factor ![]() per
period. Consumption is a CES aggregate of differentiated products
per
period. Consumption is a CES aggregate of differentiated products ![]() , with elasticity of substitution
, with elasticity of substitution ![]() :
:
The household's nominal period budget constraint is
where
Households choose
![]() to maximize expected discounted utility, subject to the budget constraint (2). Optimal consumption across the
differentiated goods implies
to maximize expected discounted utility, subject to the budget constraint (2). Optimal consumption across the
differentiated goods implies
where
so total nominal spending can be written as
Optimal labor supply, consumption, and money use imply the following first-order conditions:
2.2 Monopolistic firms
Each firm ![]() produces output
produces output ![]() using labor
using labor ![]() as its only input, under a constant returns technology:
as its only input, under a constant returns technology:
![]() .
. ![]() is an idiosyncratic productivity process that is AR(1)
in logs:
is an idiosyncratic productivity process that is AR(1)
in logs:
where
per period. Firms are owned by the household, so they discount nominal income between times
Let
![]() denote the nominal value of a firm at time
denote the nominal value of a firm at time ![]() that
produces with productivity
that
produces with productivity ![]() and sells at nominal price
and sells at nominal price ![]() . Prices are
sticky, so
. Prices are
sticky, so ![]() may or may not be optimal. However, we assume that whenever a firm adjusts its price, it chooses the optimal price conditional on its current productivity, keeping in mind
that it will sometimes be unable to adjust in the future. Hence, the value function of an adjusting firm, after netting out any costs that may be required to make the adjustment, is
may or may not be optimal. However, we assume that whenever a firm adjusts its price, it chooses the optimal price conditional on its current productivity, keeping in mind
that it will sometimes be unable to adjust in the future. Hence, the value function of an adjusting firm, after netting out any costs that may be required to make the adjustment, is
![]() . For clarity, it helps to distinguish the firm's beginning-of-period price,
. For clarity, it helps to distinguish the firm's beginning-of-period price,
![]() , from the end-of-period price at which it sells at time
, from the end-of-period price at which it sells at time ![]() ,
, ![]() , which may or may not be the same. The distributions of prices and productivities across firms at the beginning and end of
, which may or may not be the same. The distributions of prices and productivities across firms at the beginning and end of ![]() will be denoted
will be denoted
![]() and
and
![]() , respectively.
, respectively.
The gain from adjusting at the beginning of ![]() is:
is:
The main assumption of our framework is that the probability of price adjustment increases with the gain from adjustment. The weakly increasing function
The value of selling at any given price equals current profits plus the expected value of future production, which may or may not be sold at a new, adjusted price. Given the firm's idiosyncratic state variables ![]() and the aggregate state
and the aggregate state ![]() , and denoting next period's variables with primes, the Bellman equation under the near-rational interpretation of the
model is
, and denoting next period's variables with primes, the Bellman equation under the near-rational interpretation of the
model is
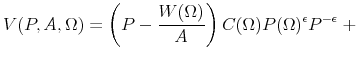 |
(11) |
Here the expectation refers to the distribution of
The right-hand side of the Bellman equation can be simplified by using the notation from (9), and the rearrangement
![]() :
:
where
The terms inside the expectation in the Bellman equation represent the value
Equation (14) is written with time subscripts for additional clarity.
2.2.1 Alternative sticky price frameworks
Our assumptions require the function ![]() to be weakly increasing and to lie between zero and one. The paper focuses primarily on the following functional form:
to be weakly increasing and to lie between zero and one. The paper focuses primarily on the following functional form:
with
In the limit ![]() , (15) nests Calvo (1983), with
, (15) nests Calvo (1983), with
![]() , making the adjustment hazard literally independent of the relevant state variable, which is
, making the adjustment hazard literally independent of the relevant state variable, which is ![]() . At the opposite extreme, as
. At the opposite extreme, as
![]() ,
,
![]() becomes the indicator
becomes the indicator
![]() , which equals 1 whenever
, which equals 1 whenever
![]() and is zero otherwise. This implies very strong state dependence, in the sense that the adjustment probability jumps from 0 to 1 when the state
and is zero otherwise. This implies very strong state dependence, in the sense that the adjustment probability jumps from 0 to 1 when the state ![]() passes the threshold level
passes the threshold level ![]() . For all intermediate values
. For all intermediate values
![]() , the hazard increases smoothly with the state
, the hazard increases smoothly with the state ![]() . In this
sense, choosing
. In this
sense, choosing ![]() to match microdata means finding the degree of state dependence most consistent with firms' observed pricing behavior.
to match microdata means finding the degree of state dependence most consistent with firms' observed pricing behavior.
The combination of Bellman equation (12) with (13) is based on a near-rational interpretation of our setup; for
![]() this version of the model will be called " SSDP", for "smoothly state-dependent pricing". However, as Table 1 shows, (12) nests several other
models under appropriate choices of the gains function
this version of the model will be called " SSDP", for "smoothly state-dependent pricing". However, as Table 1 shows, (12) nests several other
models under appropriate choices of the gains function ![]() and the hazard function
and the hazard function ![]() . Subtracting a flow of menu costs
. Subtracting a flow of menu costs
![]() out of the gains
out of the gains ![]() converts the SSDP model into the SMC model. The FMC model sets the adjustment probability to a step function, subtracting a constant menu cost
converts the SSDP model into the SMC model. The FMC model sets the adjustment probability to a step function, subtracting a constant menu cost ![]() out of
out of ![]() ; it is the limit of the SMC model as
; it is the limit of the SMC model as
![]() . The Calvo model is derived both from SSDP and from SMC as
. The Calvo model is derived both from SSDP and from SMC as
![]() .4 An alternative hazard function
derived from Woodford (2009) is also considered.
.4 An alternative hazard function
derived from Woodford (2009) is also considered.
2.3 Monetary policy and aggregate consistency
Two specifications for monetary policy are compared: a money growth rule and a Taylor rule. In both cases the systematic component of monetary policy is perturbed by an AR(1) process ![]() ,
,
where
Alternatively, under a Taylor interest rate rule, which is a better approximation to actual monetary policy, the nominal interest rate follows
where
Seigniorage revenues are paid to the household as a lump-sum transfer, and the government budget is balanced each period. Therefore total nominal transfers to the household, including dividend payments, are
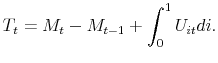 |
(19) |
Bond market clearing is simply
Equation (20) also defines a measure of price dispersion,
At this point, all equilibrium conditions have been spelled out, so an appropriate aggregate state variable
![]() can be identified. At time
can be identified. At time ![]() , the lagged distribution of transaction
prices
, the lagged distribution of transaction
prices
![]() is predetermined. Knowing
is predetermined. Knowing
![]() , the lagged price level can be substituted out of the Taylor rule, using
, the lagged price level can be substituted out of the Taylor rule, using
![]() . It can thus be seen that
. It can thus be seen that
![]() suffices to define the aggregate state. Given
suffices to define the aggregate state. Given
![]() , equations (4), (5), (6), (8), (9), (10), (12), (13), (14), (16), (18), and (20) together give enough conditions to determine the distributions
, equations (4), (5), (6), (8), (9), (10), (12), (13), (14), (16), (18), and (20) together give enough conditions to determine the distributions
![]() and
and ![]() , the price level
, the price level ![]() , the functions
, the functions
![]() ,
,
![]() ,
,
![]() , and
, and
![]() , and the variables
, and the variables ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() . Thus they determine the next state,
. Thus they determine the next state,
![]() .
.
Under a money growth rule, the time ![]() state can instead be defined as
state can instead be defined as
![]() . Substituting (7) for (6) and (17) for (18), knowing
. Substituting (7) for (6) and (17) for (18), knowing
![]() suffices to determine
suffices to determine
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() , and
, and
![]() , as well as
, as well as ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() . Thus the next state,
. Thus the next state,
![]() , can be calculated.
, can be calculated.
3 Computation
The fact that this model's state variable includes the distribution ![]() , an infinite-dimensional object, makes computing equilibrium a challenge. The popularity of the Calvo model
reflects its implication that general equilibrium can be solved up to a first-order approximation by keeping track of the average price only. Unfortunately, this result typically fails to hold if pricing is state-dependent; instead, computation requires tracking the whole distribution
, an infinite-dimensional object, makes computing equilibrium a challenge. The popularity of the Calvo model
reflects its implication that general equilibrium can be solved up to a first-order approximation by keeping track of the average price only. Unfortunately, this result typically fails to hold if pricing is state-dependent; instead, computation requires tracking the whole distribution ![]() .
.
Equilibrium will be computed here following the two-step algorithm of Reiter (2009), which is intended for contexts, like this model, with relatively large idiosyncratic shocks and also relatively small aggregate shocks. In the first step, the aggregate steady state of the model is computed on a finite grid, using backwards induction.5Second, the stochastic aggregate dynamics are computed by linearization, grid point by grid point. In other words, the Bellman equation is treated as a large system of expectational difference equations, instead of as a functional equation.
3.1 Detrending
Calculating a steady state requires detrending to make the economy stationary. Here it suffices to scale all nominal variables by the aggregate price level, defining the real wage and money supply
![]() and
and
![]() , and the real prices at the beginning and end of
, and the real prices at the beginning and end of ![]() ,
,
![]() and
and
![]() . The beginning-of-
. The beginning-of-![]() and end-of-
and end-of-![]() price distributions will be written as
price distributions will be written as
![]() and
and
![]() , respectively. At the end of
, respectively. At the end of ![]() , when goods are sold,
the real price level is one by definition:
, when goods are sold,
the real price level is one by definition:
For this detrending to make sense, the nominal price level ![]() must be irrelevant for real quantities, which must instead be functions of a real state variable
must be irrelevant for real quantities, which must instead be functions of a real state variable ![]() that is independent of nominal prices and the nominal money supply. A time subscript on any aggregate variable must now denote dependence on the real state, implying
for example
that is independent of nominal prices and the nominal money supply. A time subscript on any aggregate variable must now denote dependence on the real state, implying
for example
![]() and
and
![]() . While the price level will cancel out, inflation
. While the price level will cancel out, inflation
![]() will still appear in the model. It must be determined by real variables, satisfying
will still appear in the model. It must be determined by real variables, satisfying
![]() .
.
A similar property applies to the value function and profits, which must be homogeneous of degree one in prices. Thus, define real profits ![]() and real value
and real value ![]() as follows:
as follows:
To verify homogeneity, divide through the nominal Bellman equation (12) by
using the definitions
which satisfy
To see that these definitions of real quantities suffice to detrend the model, define the real state as
![]() . Knowing
. Knowing ![]() , in the case
of a Taylor rule, equations (5), (6), (8), (16), (18), (20), (21), (22), (24), (25), (26), and (27), with substitutions of real for nominal variables where necessary, suffice to determine the distributions
, in the case
of a Taylor rule, equations (5), (6), (8), (16), (18), (20), (21), (22), (24), (25), (26), and (27), with substitutions of real for nominal variables where necessary, suffice to determine the distributions
![]() and
and ![]() , inflation
, inflation ![]() , the functions
, the functions
![]() ,
,
![]() ,
,
![]() , and
, and
![]() , and the variables
, and the variables ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() . For a money growth rule, the real state can be defined as
. For a money growth rule, the real state can be defined as
![]() , and equation (18) is replaced by (7) and by
, and equation (18) is replaced by (7) and by
which together determine
3.2 Discretization
Price process (27) is defined over a continuum of possible values, but to solve the model numerically, the idiosyncratic states must be restricted to a finite-dimensional support. Hence, the continuous model will be approximated on a two-dimensional grid
![]() , where
, where
![]() and
and
![]() are logarithmically-spaced grids of possible values of of
are logarithmically-spaced grids of possible values of of ![]() and
and ![]() . Thus the time-varying distributions will be treated as matrices
. Thus the time-varying distributions will be treated as matrices
![]() and
and
![]() of size
of size
![]() , in which the row
, in which the row ![]() , column
, column ![]() elements, called
elements, called
![]() and
and
![]() , represent the fraction of firms in state
, represent the fraction of firms in state
![]() before and after price adjustments in period
before and after price adjustments in period ![]() , respectively. From
here on, bold face is used to identify matrices and superscripts are used to identify notation related to grids.
, respectively. From
here on, bold face is used to identify matrices and superscripts are used to identify notation related to grids.
Similarly, the value function is written as a
![]() matrix
matrix
![]() of values
of values
![]() associated with the prices and productivities
associated with the prices and productivities
![]() . The time subscript indicates the fact that the value function shifts due to changes in the aggregate state
. The time subscript indicates the fact that the value function shifts due to changes in the aggregate state ![]() . When necessary, the value is evaluated using splines at points
. When necessary, the value is evaluated using splines at points
![]() off the price grid. In particular, the policy function
off the price grid. In particular, the policy function
is selected from the reals (
Given this discrete representation, the distributional dynamics can be written in a more explicit way. First, to keep productivity ![]() on the grid
on the grid ![]() , it is assumed to follow a Markov chain defined by a matrix
, it is assumed to follow a Markov chain defined by a matrix
![]() of size
of size
![]() . The row
. The row ![]() , column
, column ![]() element of
element of
![]() represents the probability
represents the probability
| (33) |
Also, beginning-of-
| (34) |
When the deflated price
Combining the adjustments of prices and productivities, the beginning-of-![]() distribution
distribution
![]() can be calculated from the lagged distribution
can be calculated from the lagged distribution
![]() as follows:
as follows:
where the operator
Next, a firm with beginning-of-![]() state
state
![]() will adjust its price to
will adjust its price to
![]() with probability
with probability
![]() , and otherwise leave it unchanged. If adjustment occurs, prices are kept on the grid by rounding
, and otherwise leave it unchanged. If adjustment occurs, prices are kept on the grid by rounding
![]() up or down stochastically to the nearest grid points, without changing the mean. To be precise, let
up or down stochastically to the nearest grid points, without changing the mean. To be precise, let
![]() be wide enough so that
be wide enough so that
![]() for all
for all
![]() . For each
. For each ![]() , define
, define ![]() so that
so that
![]() . Then the following
. Then the following
![]() matrix governs the rounding:
matrix governs the rounding:
Now let
The same transition matrices show up when the Bellman equation is written in matrix form. Let
![]() be the
be the
![]() matrix of current profits, with elements
matrix of current profits, with elements
for
where
3.3 Computation: steady state
In an aggregate steady state, policy shocks ![]() are zero, and transaction prices converge to an ergodic distribution
are zero, and transaction prices converge to an ergodic distribution
![]() , so the aggregate state of the economy is constant:
, so the aggregate state of the economy is constant:
![]() under the Taylor rule, or
under the Taylor rule, or
![]() under a money growth rule. The steady state of any aggregate equilibrium object is indicated by dropping the
subscript
under a money growth rule. The steady state of any aggregate equilibrium object is indicated by dropping the
subscript ![]() .
.
The steady-state calculation nests the firm's backwards induction problem inside a loop that determines the steady-state real wage ![]() . Note first that
. Note first that
![]() in steady state; hence the matrix
in steady state; hence the matrix
![]() is known. Then, given
is known. Then, given ![]() , (5) determines
, (5) determines
![]() , so all elements
, so all elements ![]() of
of
![]() can be calculated from (39). Then, backwards induction on the grid
can be calculated from (39). Then, backwards induction on the grid ![]() can solve the Bellman equation
can solve the Bellman equation
Solving (41) involves finding the matrices
If (42) holds at the ergodic distribution
3.4 Computation: dynamics
Bellman equation (40) and distribution dynamics (36)-(38) are usually viewed as functional equations. However, under the discretization of Sec. 3.2, they can also be seen as two long lists of difference equations describing the values and probabilities at all grid points. Thus, Reiter (2009) proposes linearizing these equations around their steady state, calculated in Sec. 3.3. To do so, it first helps to reduce the number of variables by eliminating simple intratemporal relationships. Under a money growth rule, the model can be described by the following vector of endogenous variables:
Vector
where
where
The virtue of Reiter's method is that it combines linearity and nonlinearity in a way appropriate for the context of price adjustment, where idiosyncratic shocks are larger and more economically important to individual firms than aggregate shocks. To deal with large idiosyncratic shocks, it
treats functions of idiosyncratic states nonlinearly (calculating them on a grid). But in linearizing each equation at each grid point, it recognizes that aggregate changes (policy shocks ![]() ,
or shifts of the distribution
,
or shifts of the distribution
![]() ) are unlikely to affect individual value functions in a strongly nonlinear way. On the other hand, it makes no assumption of approximate aggregation like that of Krusell and
Smith (1998).
) are unlikely to affect individual value functions in a strongly nonlinear way. On the other hand, it makes no assumption of approximate aggregation like that of Krusell and
Smith (1998).
4.1 Parameterization
Our calibration seeks price adjustment and productivity processes consistent with microdata on price changes, like those in Klenow and Kryvtsov (2008), Nakamura and Steinsson (2008), and Midrigan (2011). Since utility parameters are not the main focus, these are set to the values used by GL07.
The discount factor is set to
![]() per year; the coefficient of relative risk aversion of consumption is set at
per year; the coefficient of relative risk aversion of consumption is set at ![]() . The coefficients on labor disutility and the utility of money are
. The coefficients on labor disutility and the utility of money are ![]() and
and ![]() , respectively, and the elasticity of substitution in the consumption aggregator is
, respectively, and the elasticity of substitution in the consumption aggregator is
![]() .
.
The main price data that will serve as an empirical benchmark are the monthly AC Nielsen data reported by Midrigan (2011).9 Therefore, the model will be
simulated at monthly frequency, with a zero steady state money growth rate, consistent with the zero average price change in that dataset. Midrigan reports the data after removing price changes attributable to temporary "sales", so our simulation results should be interpreted as a model of "
regular" price changes unrelated to sales. Conditional on these specification choices, the adjustment parameters (
![]()
![]() and
and ![]() ) and productivity parameters (
) and productivity parameters (![]() and
and
![]() ) are chosen to minimize a distance criterion between the data and the model's steady state.10 The criterion sums two terms, scaled for comparability: the first is the absolute difference between the adjustment frequencies in the data and the simulation, while the second is the Euclidean distance between
the frequency vectors associated with the histograms of nonzero price adjustments in the data and the simulation.
) are chosen to minimize a distance criterion between the data and the model's steady state.10 The criterion sums two terms, scaled for comparability: the first is the absolute difference between the adjustment frequencies in the data and the simulation, while the second is the Euclidean distance between
the frequency vectors associated with the histograms of nonzero price adjustments in the data and the simulation.
Table 2 summarizes the steady-state behavior of the model under the estimated parameters, together with evidence from four empirical studies. The baseline specification, in which
![]() ,
, ![]() , and
, and ![]() are all estimated, is labelled SSDP. The table also reports Calvo (
are all estimated, is labelled SSDP. The table also reports Calvo (
![]() estimated,
estimated,
![]() , and
, and ![]() undefined) and FMC specifications (
undefined) and FMC specifications (![]() estimated,
estimated,
![]() , and
, and
![]() undefined), as well as a version based on Woodford's (2009) adjustment function and an SMC specification. All versions of the model match the target adjustment frequency
of 10% per month. But the extreme cases of the model (Calvo and FMC) are less successful in fitting the size distribution of price adjustments than are the intermediate cases; the Calvo model understates the average size and standard deviation of price adjustments, whereas the FMC model overstates
both.
undefined), as well as a version based on Woodford's (2009) adjustment function and an SMC specification. All versions of the model match the target adjustment frequency
of 10% per month. But the extreme cases of the model (Calvo and FMC) are less successful in fitting the size distribution of price adjustments than are the intermediate cases; the Calvo model understates the average size and standard deviation of price adjustments, whereas the FMC model overstates
both.
The trouble with the FMC model, as Fig. 1 shows, is that it only produces price changes lying just outside the (S,s) bands, whereas the adjustments observed in the data are very diverse.11 Thus the FMC model that best fits the data produces adjustments that are too large on average; no adjustments in the model are less than 5%, whereas one quarter of all adjustments are below the 5% threshold in the AC Nielsen data. The Calvo model errs in the opposite direction, with too many small price adjustments, though its fit statistics are better than those of the FMC model. In contrast, all three specifications with a smoothly increasing adjustment hazard (SSDP, SMC, and Woodford) match the data well, since they permit large and small price adjustments to coexist. In fact, there is so little difference between these models that only SSDP will be discussed from here on.12
Our estimates imply fairly strong frictions impeding price adjustment. The estimated function ![]() (see Fig. 1, right panel) rises quickly at zero but is thereafter very flat. It
equals 10% per month at a loss of
(see Fig. 1, right panel) rises quickly at zero but is thereafter very flat. It
equals 10% per month at a loss of
![]() (6% of monthly labor input) and only reaches 30% per month at the highest loss that occurs with nonzero probability in the steady state equilibrium, which is
(6% of monthly labor input) and only reaches 30% per month at the highest loss that occurs with nonzero probability in the steady state equilibrium, which is ![]() , roughly 21 months' worth of labor input. Of course, the
, roughly 21 months' worth of labor input. Of course, the ![]() function is flat in
the Calvo model by construction. Our estimate of Woodford's specification implies
function is flat in
the Calvo model by construction. Our estimate of Woodford's specification implies
![]() at the most extreme losses that occur in equilibrium, but it is also very flat over the range of losses that occur frequently. For example, the cross-sectional standard
deviation of
at the most extreme losses that occur in equilibrium, but it is also very flat over the range of losses that occur frequently. For example, the cross-sectional standard
deviation of ![]() is roughly
is roughly ![]() in SSDP and
in SSDP and ![]() in the Woodford setup, whereas it is
in the Woodford setup, whereas it is ![]() in the FMC model.
in the FMC model.
Thus, in the models considered, firms do not adjust instantly even when faced with very large losses. Nonetheless, typical losses in equilibrium are more moderate, since firms usually adjust before reaching extreme situations. Across specifications, the decrease in average profits due to price stickiness (see Table 2) ranges from 1.5% of average revenues in the FMC case to 5.3% of average revenues in the Woodford specification. (The differences look larger when expressed as a fraction of average profits, since profits are a small fraction of revenues.) Clearly, these estimated adjustment frictions are nontrivial; whether they seem unrealistically large may depend on whether they are conceived literally as "menu costs" or as costs of managerial decision making, along the lines of Zbaracki et al. (2004).
4.2 Effects of monetary policy shocks
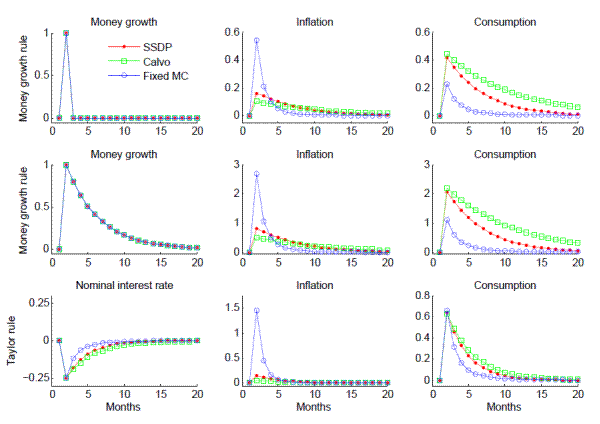
Since all specifications are calibrated to the same observed adjustment frequency, the fact that only large, valuable price changes occur in the FMC model, whereas some changes in the SSDP and Calvo frameworks are trivial, has important implications for monetary transmission. Fig. 2 compares
responses to several types of monetary shocks across these three adjustment specifications. All simulations assume the same utility parameters, and zero baseline inflation, and are calculated starting from the steady-state distribution associated with the corresponding specification. The first two
rows show impulse responses to one percentage point money growth shocks, comparing the i.i.d. case with that of monthly autocorrelation
![]() . The third row shows the responses to an i.i.d. interest rate shock under a Taylor rule.
. The third row shows the responses to an i.i.d. interest rate shock under a Taylor rule.
In all three models, an increase in money growth stimulates consumption. The fact that some prices fail to adjust immediately means expected inflation rises, decreasing the ex ante real interest rate; it also means households' real money balances increase; both of these effects raise consumption demand. However, as GL07 emphasized, the average price level adjusts rapidly in the FMC specification (lines with circles), with a large, short-lived spike in inflation. This makes changes in real variables small and transitory, approaching the monetary neutrality associated with full price flexibility. At the opposite extreme, prices adjust gradually in the Calvo specification (lines with squares), leading to a large, persistent increase in output. The response of the SSDP model (lines with dots) mostly lies between the other two, but is generally closer to that of the Calvo model.
Comparing the first and second rows of Fig. 2 shows that while the shape of the inflation and output responses differs substantially across models, it is qualitatively similar under iid and autocorrelated money growth processes. In the FMC model inflation spikes immediately regardless of the persistence of money growth. However, with autocorrelated money growth the initial spike exceeds 1% as firms anticipate that money growth will remain positive for some time. The rise in inflation is smaller but more persistent in the SSDP and Calvo cases. Note that the persistence of inflation does not differ noticeably depending on the autocorrelation of money growth, but instead appears to be determined primarily by the degree of state dependence. Thus the big difference between the impulse responses in the first and second rows is one of size, not of shape.
The third row of Fig. 2 shows responses under a Taylor rule, assuming that the underlying shock ![]() is i.i.d., and that the rule has inflation and output
coefficients
is i.i.d., and that the rule has inflation and output
coefficients
![]() and
and
![]() , and smoothing coefficient
, and smoothing coefficient
![]() . While money growth shocks are small, incremental changes to the level of the nominal money supply, Taylor rule shocks involve large fluctuations in
the level of nominal money. Nonetheless, the two types of monetary-policy shocks have similar real effects, and moreover, the finding that a micro-calibrated model of state-dependent pricing implies substantial monetary nonneutrality is strengthened in several ways by considering a Taylor rule.
First, under the Taylor rule, the SSDP and Calvo impulse responses of inflation and consumption are even closer together than they were under the money growth rule. In fact, for consumption, both SSDP and FMC imply virtually the same effect on impact as that occurring in
the Calvo model, though the effect is less persistent in the FMC case.
. While money growth shocks are small, incremental changes to the level of the nominal money supply, Taylor rule shocks involve large fluctuations in
the level of nominal money. Nonetheless, the two types of monetary-policy shocks have similar real effects, and moreover, the finding that a micro-calibrated model of state-dependent pricing implies substantial monetary nonneutrality is strengthened in several ways by considering a Taylor rule.
First, under the Taylor rule, the SSDP and Calvo impulse responses of inflation and consumption are even closer together than they were under the money growth rule. In fact, for consumption, both SSDP and FMC imply virtually the same effect on impact as that occurring in
the Calvo model, though the effect is less persistent in the FMC case.
Recall, though, that the Taylor rule responses in Fig. 2 suppose an initial drop in the nominal interest rate of 25 basis points. Since the interest rate is endogenous, the required underlying shock
![]() varies across models, and it is particularly large in the FMC case. Therefore, it is useful to consider additional ways of comparing the degree of monetary nonneutrality across
models. Thus, Table 3 compares monetary policies that imply the same inflation variability, as in Sec. VI of GL07. The calculation asks the following question: if monetary-policy shocks were the only source of observed US inflation volatility, how much output variation would they cause? Under the
SSDP specification, money growth shocks alone would explain 65% of observed output fluctuations; the figure rises to 116% under the Calvo specification, and falls to 15% in the FMC case.13 Assuming a Taylor rule, the differences across models are even stronger, and the monetary nonneutrality of the SSDP and Calvo specifications is even greater. Taylor rule shocks alone would explain 110% of US output fluctuation
under the SSDP specification, rising to 306% in the Calvo case.
varies across models, and it is particularly large in the FMC case. Therefore, it is useful to consider additional ways of comparing the degree of monetary nonneutrality across
models. Thus, Table 3 compares monetary policies that imply the same inflation variability, as in Sec. VI of GL07. The calculation asks the following question: if monetary-policy shocks were the only source of observed US inflation volatility, how much output variation would they cause? Under the
SSDP specification, money growth shocks alone would explain 65% of observed output fluctuations; the figure rises to 116% under the Calvo specification, and falls to 15% in the FMC case.13 Assuming a Taylor rule, the differences across models are even stronger, and the monetary nonneutrality of the SSDP and Calvo specifications is even greater. Taylor rule shocks alone would explain 110% of US output fluctuation
under the SSDP specification, rising to 306% in the Calvo case.
The table also reports a "Phillips curve" coefficient, calculated by regressing log output on inflation, instrumented by the exogenous monetary policy shock. The conclusions are similar: the SSDP model implies large real effects of monetary shocks, closer to the Calvo specification than to the FMC specification, and the differences across models are larger under a Taylor rule than they are under a money growth rule.
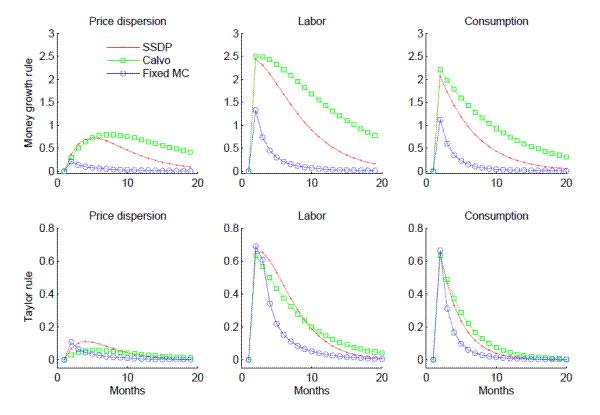
Next, Fig. 3 plots the response of price dispersion,
![]() , defined in (20). In our model, one reason prices vary is that firms face different productivities. But additional price dispersion, caused by failure
to adjust when necessary, implies inefficient variation in demand across goods that implies a decrease in aggregate productivity:
, defined in (20). In our model, one reason prices vary is that firms face different productivities. But additional price dispersion, caused by failure
to adjust when necessary, implies inefficient variation in demand across goods that implies a decrease in aggregate productivity:
![]() . In a representative agent model near a zero-inflation steady state,
. In a representative agent model near a zero-inflation steady state,
![]() is negligible because it is roughly proportional to the cross-sectional variance of prices, a quantity of second order in the inflation rate.14 But cross-sectional price variance is not second order when large idiosyncratic shocks are present, so the dispersion wedge
is negligible because it is roughly proportional to the cross-sectional variance of prices, a quantity of second order in the inflation rate.14 But cross-sectional price variance is not second order when large idiosyncratic shocks are present, so the dispersion wedge
![]() may be quantitatively important, especially since
may be quantitatively important, especially since
![]() magnifies variations in the ratio
magnifies variations in the ratio
![]() . The first row of Fig. 3 shows that for SSDP and Calvo, increased money growth throws firms' prices further out of line with fundamentals, increasing dispersion; raising
consumption therefore requires a larger increase in labor in these specifications. In contrast, the variation in
. The first row of Fig. 3 shows that for SSDP and Calvo, increased money growth throws firms' prices further out of line with fundamentals, increasing dispersion; raising
consumption therefore requires a larger increase in labor in these specifications. In contrast, the variation in
![]() is smaller in the FMC case, because all firms with severe price misalignments do in fact adjust. Interestingly, since the Taylor rule leans against inflationary shocks, there
is much less variation in the price level for the SSDP and Calvo cases in our Taylor rule simulation than there is under autocorrelated money growth. Thus, in all three specifications, a Taylor rule shock causes little variation in
is smaller in the FMC case, because all firms with severe price misalignments do in fact adjust. Interestingly, since the Taylor rule leans against inflationary shocks, there
is much less variation in the price level for the SSDP and Calvo cases in our Taylor rule simulation than there is under autocorrelated money growth. Thus, in all three specifications, a Taylor rule shock causes little variation in
![]() .
.
4.3 Inflation decompositions
Several decompositions can help illustrate the inflation dynamics implied by this model. To a first-order approximation, inflation can be calculated as an average of log nominal price changes. Using our grid-based notation, and starting from the beginning-of-period distribution
![]() ,
,
where
Dropping higher-order terms, this implies the following inflation decomposition:
where variables without time subscripts represent steady states, and
Unfortunately, this decomposition does not reveal whether a rise in the average log price adjustment
![]() is caused by a rise in all firms' desired adjustments, or by a reallocation of adjustment opportunities from firms desiring small or negative price changes to others wanting
large price increases. That is,
is caused by a rise in all firms' desired adjustments, or by a reallocation of adjustment opportunities from firms desiring small or negative price changes to others wanting
large price increases. That is,
![]() mixes changes in desired adjustments (the only relevant changes in the Calvo model) with the "selection effect" emphasized by GL07. To
distinguish between these last two effects, inflation can instead be broken into three terms: an intensive margin capturing changes in the average desired log price change, an extensive margin capturing changes in how many firms adjust, and a
selection effect capturing changes in who adjusts. These three effects are distinguished by rewriting (46) as
mixes changes in desired adjustments (the only relevant changes in the Calvo model) with the "selection effect" emphasized by GL07. To
distinguish between these last two effects, inflation can instead be broken into three terms: an intensive margin capturing changes in the average desired log price change, an extensive margin capturing changes in how many firms adjust, and a
selection effect capturing changes in who adjusts. These three effects are distinguished by rewriting (46) as
Note that in (49),
Equation (49) leads to the following inflation decomposition:
Our intensive margin effect,
An alternative decomposition, proposed by Caballero and Engel (2007), also differences (46):
They further simplify this to
under the assumption that all desired price adjustments change by
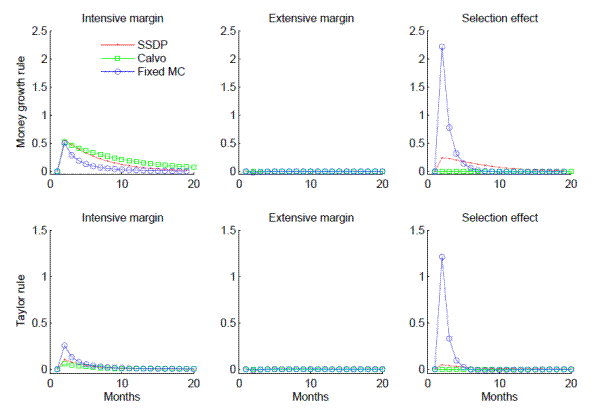
The importance of identifying the selection effect separately becomes clear in Fig. 4, which illustrates our decomposition of the inflation impulse response to monetary shocks. The three components of inflation,
![]() ,
,
![]() , and
, and
![]() , are shown to the same scale for better comparison. The graphs demonstrate (in contrast to Caballero and Engel's claim) that the short, sharp rise in inflation observed in
the FMC specification results from the selection effect. This is true both under Taylor rule shocks, where inflation spikes to 1.5% on impact, of which 1.25% is the selection component, and under (autocorrelated) money growth shocks, where inflation spikes to 2.8%, with 2.25% due to selection. In
contrast, inflation in the Calvo model is caused by the intensive margin only; in SSDP there is a nontrivial selection effect but it still only accounts for around one-third of the inflation response.
, are shown to the same scale for better comparison. The graphs demonstrate (in contrast to Caballero and Engel's claim) that the short, sharp rise in inflation observed in
the FMC specification results from the selection effect. This is true both under Taylor rule shocks, where inflation spikes to 1.5% on impact, of which 1.25% is the selection component, and under (autocorrelated) money growth shocks, where inflation spikes to 2.8%, with 2.25% due to selection. In
contrast, inflation in the Calvo model is caused by the intensive margin only; in SSDP there is a nontrivial selection effect but it still only accounts for around one-third of the inflation response.
On the other hand, the extensive margin
![]() plays a negligible role in the inflation response. This makes sense, because the simulation assumes a steady state
with zero inflation, so steady state price adjustments are responses to idiosyncratic shocks only, and the average desired adjustment
plays a negligible role in the inflation response. This makes sense, because the simulation assumes a steady state
with zero inflation, so steady state price adjustments are responses to idiosyncratic shocks only, and the average desired adjustment
![]() is very close to zero. Therefore
is very close to zero. Therefore
![]() is negligible even though the adjustment frequency
is negligible even though the adjustment frequency
![]() itself does vary.17
The extensive margin only becomes important when there is high trend inflation, so that the average desired adjustment
itself does vary.17
The extensive margin only becomes important when there is high trend inflation, so that the average desired adjustment
![]() is large and positive.
is large and positive.
As for the intensive margin, its initial effect after a money growth shock is similar across all adjustment specifications, but it is more persistent in the Calvo and SSDP cases than in the FMC case. The scale of the intensive margin depends on the autocorrelation of money growth: the mean
desired price change rises roughly one-for-one after an i.i.d. money growth shock (not shown), and rises by roughly five percentage points when money growth has autocorrelation
![]() (first row of Fig. 4). Thus, in the autocorrelated case, the intensive margin is initially
(first row of Fig. 4). Thus, in the autocorrelated case, the intensive margin is initially
![]() . In other words, firms wish to " frontload" price adjustment by approximately the same amount in all
three specifications; but many of these changes occur immediately in the FMC case (showing up as a redistribution of adjustment opportunities, i.e., a selection effect), whereas they are realized gradually in the other specifications. Under a Taylor rule, the intuition
is similar, bearing in mind that Fig. 4 is scaled to give an initial decline of 25 basis points in the nominal interest rate. This requires a larger underlying shock
. In other words, firms wish to " frontload" price adjustment by approximately the same amount in all
three specifications; but many of these changes occur immediately in the FMC case (showing up as a redistribution of adjustment opportunities, i.e., a selection effect), whereas they are realized gradually in the other specifications. Under a Taylor rule, the intuition
is similar, bearing in mind that Fig. 4 is scaled to give an initial decline of 25 basis points in the nominal interest rate. This requires a larger underlying shock ![]() in the FMC
specification than in the other cases; thus the effect on the intensive margin is larger (but less persistent) for FMC than it is for Calvo and SSDP.
in the FMC
specification than in the other cases; thus the effect on the intensive margin is larger (but less persistent) for FMC than it is for Calvo and SSDP.
4.4 Comparing effects of sector-specific and aggregate shocks
Another issue of intererest in recent empirical literature is how prices respond to sector-specific shocks. In particular, Boivin, Giannoni, and Mihov (2007) and Mackowiak, Moench, and Wiederholt (2009, henceforth MMW09) present evidence that sector-specific prices respond much more quickly to sector-specific shocks than they do to aggregate shocks. This is important, since it suggests that a Calvo model with a single adjustment rate may be inappropriate. Indeed, it might be interpreted as evidence for state dependence, and it suggests that the present model might be tested by assessing its ability to reproduce these empirical observations.
To address these questions, this section investigates "sector-specific" shocks in our model, applying the estimation routines of MMW09 to artificial panel data produced by simulating the SSDP calibration under a Taylor rule. The data cover the price levels in 79 sectors over 245 months, as in
the dataset of MMW09. Of course, the model defined here does not actually have a sectoral structure. Nonetheless, for a fixed integer ![]() , one can simulate a panel of
, one can simulate a panel of
![]() firms (each producing one specialized product), and call each block of
firms (each producing one specialized product), and call each block of ![]() consecutive firms a "sector". Productivity innovations remain i.i.d. across firms, as they are elsewhere in the paper. However, since the number of firms per sector is finite, sampling error will cause average productivity to differ across
sectors at each time. An innovation to average productivity in any artificially-defined sector can thus be regarded as a sector-specific shock. Two questions are then relevant. First, can empirical findings like those of MMW09 be reproduced by applying their methods to the model-generated data?
Second, do their estimation methods correctly identify the effects of sector-specific shocks? The answers are yes and no, respectively.
consecutive firms a "sector". Productivity innovations remain i.i.d. across firms, as they are elsewhere in the paper. However, since the number of firms per sector is finite, sampling error will cause average productivity to differ across
sectors at each time. An innovation to average productivity in any artificially-defined sector can thus be regarded as a sector-specific shock. Two questions are then relevant. First, can empirical findings like those of MMW09 be reproduced by applying their methods to the model-generated data?
Second, do their estimation methods correctly identify the effects of sector-specific shocks? The answers are yes and no, respectively.
The MMW09 statistical framework breaks inflation into aggregate and sector-specific components:
where
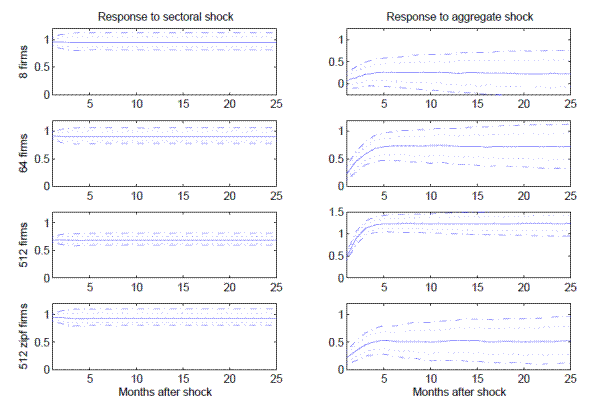
MMW09 also find that the impact of an sectoral shock on sectoral inflation is almost one-for-one, and that sectoral shocks account for around 90% of sectoral inflation variance. Fig. 5 shows that if simulated sectors are small (8 or 64 equally-weighted products), then the impact of a sectoral shock is indeed almost one-for-one; moreover, in these cases sectoral shocks explain 80% to 90% of sectoral inflation (see Fig. 6). However, if sectors consist of 512 equally-weighted products, then a one-standard deviation sectoral shock creates only 0.7 standard deviations of inflation, and sectoral shocks explain less than half of sectoral inflation variance. This is a consequence of the law of large numbers: with more firms per sector, sector-specific inflation stays closer to its conditional expectation, so aggregate shocks must explain a larger part of sectoral inflation (see the right-hand column of Fig. 5). Typical observations of sectoral inflation in MMW09's CPI data involve several hundred individual price quotes, so sectors with 8 or 64 products are unrealistically small.18 But on the other hand, CPI weights vary greatly across products in each sector (Leaver and Folk, 2004). Therefore the fourth row of the figure reports a simulation with 512 products per sector, in which the CPI weights on the products are distributed according to Zipf's law.19 This increases the importance of the highest-weighted goods, so 512 products with heterogeneous weights act like a much smaller number of equally-weighted products, with a contribution of sectoral shocks to sectoral inflation variance exceeding 85% (see Fig. 6.)
Thus, running the estimation programs of MMW09 on simulated data from our model with 512 firms of heterogeneous size largely reproduces their empirical findings.20 However, this is rather puzzling, because the estimation results are inconsistent with the known properties of the simulated model. In the model, prices only adjust once in ten months on average, and the degree of
state-dependence is low, so the true response of prices to any idiosyncratic or aggregate shock must be fairly slow. Moreover, all sector-specific behavior in the model is mean-reverting, whereas the estimates in Fig. 5 show a permanent effect of a sector-specific shock on prices. To demonstrate
these facts numerically, we consider the sector-specific shock
![]() , defined as the weighted average of firm-specific productivity shocks
, defined as the weighted average of firm-specific productivity shocks
![]() across firms in sector
across firms in sector ![]() . We assume inflation can be written as
a moving average of these sectoral shocks and the aggregate monetary shock
. We assume inflation can be written as
a moving average of these sectoral shocks and the aggregate monetary shock
![]() :
:
| (54) |
The notation is the same here as in (53). However, sector-specific inflation will not generally equal its predicted value conditional on the underlying shocks, so this specification must allow for a sector-specific inflation residual
Fig. 7 reports the responses to the sector-specific shock
![]() (left column) and the aggregate shock
(left column) and the aggregate shock
![]() , using the same simulated datasets analyzed in Fig. 5 (for accuracy, the length of each dataset is extended to 5400 months.) Responses are estimated by OLS on a
sector-by-sector basis; all sectoral estimates are shown in the same graph. For all four datasets, responses to sector-specific and aggregate shocks occur with a lag. The peak response to a sector-specific shock occurs five to ten months after the time of the shock; the sectoral price level
thereafter reverts to steady state. The time of reaction to an aggregate shock is similar, but the effects are permanent. The only effect of increasing the number of firms per sector is that aggregate shocks become more important for sectoral inflation, relative to sectoral shocks, for the reasons
discussed previously.
, using the same simulated datasets analyzed in Fig. 5 (for accuracy, the length of each dataset is extended to 5400 months.) Responses are estimated by OLS on a
sector-by-sector basis; all sectoral estimates are shown in the same graph. For all four datasets, responses to sector-specific and aggregate shocks occur with a lag. The peak response to a sector-specific shock occurs five to ten months after the time of the shock; the sectoral price level
thereafter reverts to steady state. The time of reaction to an aggregate shock is similar, but the effects are permanent. The only effect of increasing the number of firms per sector is that aggregate shocks become more important for sectoral inflation, relative to sectoral shocks, for the reasons
discussed previously.
Why does the MMW09 estimation routine find effects of sectoral shocks so different from the response to the true sectoral shock, shown in Fig. 7? The problem is that true shocks in microdata are unknown to an econometrician, so Mackowiak et al. must identify sectoral
shocks as residual price increases not explained by aggregate shocks. In the SSDP model, individual prices typically respond with a lag to true productivity shocks, so sectoral price levels do too. But in the MMW09 decomposition, the moment of the shock corresponds by
assumption to the moment of the price increase, so the response is estimated to be immediate. Mean reversion occurs by individual stochastic price jumps in the model, whereas MMW09 assumes past shocks decay deterministically (component ![]() in their eq. 1). Hence their method interprets price movements back to the mean as a sequence of new sectoral shocks that happen to go in the opposite direction (which is why the initial shock is interpreted as permanent). Thus, results
from their procedure (or others that identify sectoral shocks as inflation residuals, e.g. Boivin et al., 2007) should be treated with caution. Our Monte Carlo exercise shows that, at least in some cases, the procedure may exaggerate the speed
of response to sectoral shocks, suggesting stronger state dependence than the data actually warrant.
in their eq. 1). Hence their method interprets price movements back to the mean as a sequence of new sectoral shocks that happen to go in the opposite direction (which is why the initial shock is interpreted as permanent). Thus, results
from their procedure (or others that identify sectoral shocks as inflation residuals, e.g. Boivin et al., 2007) should be treated with caution. Our Monte Carlo exercise shows that, at least in some cases, the procedure may exaggerate the speed
of response to sectoral shocks, suggesting stronger state dependence than the data actually warrant.
5 Conclusions
This paper has computed the impact of monetary policy shocks in a quantitative macroeconomic model of state-dependent pricing. It has calibrated the model for consistency with microeconomic data on firms' pricing behavior, estimating how the probability of price adjustment depends on the value of adjustment. Given the estimated adjustment function, the paper has characterized the dynamics of the distribution of prices and productivities in general equilibrium.
The calibrated model implies that prices rise gradually after a monetary stimulus, causing a large, persistent rise in consumption and labor. Looking across specifications, the main factor determining how monetary shocks propagate through the economy is the degree of state dependence. That is, raising the autocorrelation of money growth shocks just makes their effects proportionally larger, without any notable change in the shape or persistence of the impulse responses. In contrast, decreasing state dependence from the extreme of fixed menu costs (FMC) to the opposite Calvo (1983) extreme strongly damps the initial inflation spike caused by a money shock and increases its effect on real variables. The parameterization most consistent with microdata (labelled "SSDP" throughout the paper) is fairly close to the Calvo model in terms of its quantitative effects. The conclusions are similar if the monetary authority follows a Taylor rule instead of a money growth rule, except that the degree of monetary nonneutrality differs more across adjustment specifications; in particular, the nonneutrality of the SSDP specification is increased.
This paper also decomposes the impulse response of inflation into an intensive margin effect relating to the average desired price change, an extensive margin effect relating to the number of firms adjusting, and a selection effect relating to the relative frequencies of small and large or negative and positive adjustments. Under the preferred (SSDP) calibration, about two-thirds of the effect of a monetary shock comes through the intensive margin, and most of the rest through the selection effect. The extensive margin is negligible unless the economy starts from a high baseline inflation rate. Under the FMC specification, a monetary shock instead causes a quick increase in inflation, driven by the selection effect, which eliminates most of its effects on real variables.
Since the selection effect represents changes in the adjustment probability across firms, its strength depends directly on the degree of state dependence. We say that state dependence is strong in the FMC model because it makes ![]() a step function: at the threshold, a tiny increase in the value of adjustment raises the adjustment probability from 0 to 1. Therefore the histogram of price changes consists of two spikes: there are no small changes, and firms change their
prices as soon as they pass the adjustment thresholds. Hence, in steady state, those firms that might react to monetary policy are all near the two thresholds; a monetary stimulus decreases
a step function: at the threshold, a tiny increase in the value of adjustment raises the adjustment probability from 0 to 1. Therefore the histogram of price changes consists of two spikes: there are no small changes, and firms change their
prices as soon as they pass the adjustment thresholds. Hence, in steady state, those firms that might react to monetary policy are all near the two thresholds; a monetary stimulus decreases ![]() from 1 to 0 for some firms desiring a price decrease, while increasing
from 1 to 0 for some firms desiring a price decrease, while increasing ![]() from 0 to 1 for others preferring an increase, making the inflation response quick and
intense. That is, the same property that makes money nearly neutral in the FMC model is the one which makes that model inconsistent with price microdata. A model in which adjustment depends more smoothly on the value of adjusting fits microdata better and yields larger real effects of monetary
policy. Our two other smooth specifications (SMC, and Woodford's hazard function) yield results similar to the SSDP setup that was our main focus.
from 0 to 1 for others preferring an increase, making the inflation response quick and
intense. That is, the same property that makes money nearly neutral in the FMC model is the one which makes that model inconsistent with price microdata. A model in which adjustment depends more smoothly on the value of adjusting fits microdata better and yields larger real effects of monetary
policy. Our two other smooth specifications (SMC, and Woodford's hazard function) yield results similar to the SSDP setup that was our main focus.
Low state dependence might seem inconsistent, at first, with recent empirical claims that prices react more quickly to sectoral shocks than to aggregate shocks. Indeed, our calibrated model implies that prices react only gradually to sectoral shocks. However, this paper demonstrates that the empirical methods of Mackowiak et al. (2009) may attribute an immediate, permanent impact to sectoral shocks even in a dataset where the true sectoral shocks have a lagged, temporary effect. The problem is that by treating any sector-specific change in inflation as a sectoral shock, they may confound sampling error in the timing of price adjustments with fundamental shocks. Applying the MMW09 estimation routines to simulated data from our model suggests that this problem may suffice to explain their empirical results, calling into question the evidence for price flexibility at the sectoral level.
6 Appendix: Notation
Table N1: Exogenous parameters
| Symbol | Definition | Where |
| Preferences of household: |
Utility discount factor | Sec. 2.1 |
| Preferences of household: |
Coefficient of relative risk aversion | Sec. 2.1 |
| Preferences of household: |
Disutility of labor | Sec. 2.1 |
| Preferences of household: |
Coefficient on utility of money | Sec. 2.1 |
| Preferences of household: |
Elasticity of substitution across differentiated goods | Sec. 2.1 |
| Technology of firms: |
Persistence of firm-specific productivity | Sec. 2.2 |
| Technology of firms:
|
Variance of firm-specific productivity shock | Sec. 2.2 |
| Technology of firms:
|
Adjustment probability parameter | Sec. 2.2.1 |
| Technology of firms: |
Adjustment probability parameter | Sec. 2.2.1 |
| Technology of firms: |
Adjustment probability parameter | Sec. 2.2.1 |
| Monetary policy: |
Persistence of monetary policy process | Sec. 2.3 |
| Monetary policy:
|
Variance of monetary policy shock | Sec. 2.3 |
| Monetary policy: |
Money growth target | Sec. 2.3 |
| Monetary policy: |
Inflation target in Taylor rule | Sec. 2.3 |
| Monetary policy: |
Output target in Taylor rule | Sec. 2.3 |
| Monetary policy: |
Interest rate target in Taylor rule | Sec. 2.3 |
| Monetary policy |
Interest smoothing parameter in Taylor rule | Sec. 2.3 |
| Monetary policy:
|
Inflation weighting parameter in Taylor rule | Sec. 2.3 |
| Monetary policy: |
Output weighting parameter in Taylor rule | Sec. 2.3 |
| Symbol | Definition | Where |
| Aggregate state:
|
Nominal aggregate state (In the nominal representation, any aggregate variable indexed by |
Sec. 2.1 and 2.3 |
| Variables appearing in household's problem: |
Real household consumption | Sec. 2.1 |
| Variables appearing in household's problem: |
Labor supply | Sec. 2.1 |
| Variables appearing in household's problem: |
Nominal money supply | Sec. 2.1 |
| Variables appearing in household's problem: |
Nominal price level | Sec. 2.1 |
| Variables appearing in household's problem: |
Nominal wage | Sec. 2.1 |
| Variables appearing in household's problem: |
Nominal interest factor from |
Sec. 2.1 |
| Variables appearing in household's problem: |
Nominal bonds held at |
Sec. 2.1 |
| Variables appearing in household's problem: |
Nominal lump sum transfer to household at time |
Sec. 2.1 |
| Variables appearing in household's problem: |
Consumption of good produced by firm |
Sec. 2.1 |
| Variables appearing in household's problem: |
Price of good produced by firm |
Sec. 2.1 |
| Other aggregate variables:
|
Distribution of productivities and nominal prices at beginning of |
Sec. 2.2 |
| Other aggregate variables:
|
Distribution of productivities and nominal prices at end of |
Sec. 2.2 |
| Other aggregate variables: |
Stochastic process driving monetary policy | Sec. 2.3 |
| Other aggregate variables:
|
Monetary policy shock | Sec. 2.3 |
| Other aggregate variables: |
Monetary growth factor from |
Sec. 2.3 |
| Other aggregate variables:
|
Price dispersion statistic | Sec. 2.3 |
| Symbol | Definition | Where |
| Real output of firm |
Sec. 2.2 | |
| Productivity of firm |
Sec. 2.2 | |
|
|
Productivity shock to firm |
Sec. 2.2 |
| Labor input to firm |
Sec. 2.2 | |
| Nominal profits of firm |
Sec. 2.2 | |
|
|
Nominal price of output of firm |
Sec. 2.2 |
| Symbol | Definition | Where |
|
|
Nominal profits of firm with productivity |
Sec. 2.2 |
|
|
Nominal value of firm with productivity |
Sec. 2.2 |
|
|
Optimal value of firm with productivity |
Sec. 2.2 |
|
|
Optimal nominal price of firm with productivity |
Sec. 2.2 |
|
|
Nominal gain from adjusting, given beginning-of-period nominal price
|
Sec. 2.2 |
|
|
Real gain from adjusting, given beginning-of-period nominal price
|
Sec. 2.2 |
|
|
Probability of price adjustment, given real gain |
Sec. 2.2 |
|
|
Expected nominal gains from stochastic adjustment in current period | Sec. 2.2 |
| Symbol | Definition | Where |
| Aggregate state: |
Real aggregate state | Sec. 3.1 |
| Aggregate variables: |
Real money supply | Sec. 3.1 |
| Aggregate variables: |
Real wage | Sec. 3.1 |
| Aggregate variables: |
Inflation factor from |
Sec. 3.1 |
| Aggregate variables:
|
Distribution of productivities and real prices at beginning of |
Sec. 3.1 |
| Aggregate variables: |
Distribution of productivities and real prices at end of |
Sec. 3.1 |
| Variables specific to firm: |
Real price of firm |
Sec. 3.1 |
| Variables specific to firm: |
Real price of firm |
Sec. 3.1 |
| Symbol | Definition | Where |
|
|
Real profits of firm with productivity |
Sec. 3.1 |
|
|
Real value of firm with productivity |
Sec. 3.1 |
|
|
Optimal real price of firm with productivity |
Sec. 3.1 |
|
|
Real gain from adjusting, given beginning-of-period real price
|
Sec. 3.1 |
|
|
Expected real gains from stochastic adjustment in current period | Sec. 3.1 |
|
|
The real numbers | Sec. 3.2 Symbol |
| Finite grid of possible values of productivity | Sec. 3.2 | |
| Element |
Sec. 3.2 | |
| Number of elements of grid |
Sec. 3.2 | |
| Finite grid of possible values of real price | Sec. 3.2 | |
| Element |
Sec. 3.2 | |
| Number of elements of grid |
Sec. 3.2 | |
| Two dimensional grid of prices and productivities,
|
Sec. 3.2 |
| Symbol | Definition | Where |
|
|
Profits matrix, with elements
|
Sec. 3.2 |
|
|
Value matrix, with elements
|
Sec. 3.2 |
|
|
Policy vector, with elements
|
Sec. 3.2 |
|
|
Adjustment gains matrix, with elements
|
Sec. 3.2 |
|
|
Adjustment probabilities matrix, with elements
|
Sec. 3.2 |
|
|
Matrix of expected gains from adjustment, with elements
|
Sec. 3.2 |
| Symbol | Definition | Where |
|
|
Beginning-of-period distribution matrix, with elements
|
Sec. 3.2 |
|
|
End-of-period distribution matrix, with elements
|
Sec. 3.2 |
|
|
Matrices of ones, of sizes
|
Sec. 3.2 |
|
|
Markov productivity matrix, with elements
|
Sec. 3.2 |
|
|
Markov matrix for inflation adjustment and stochastic rounding to grid |
Sec. 3.2 |
| Index of least grid element above preferred real price:
|
Sec. 3.2 | |
|
|
Matrix allocating newly adjusted prices to optimum value
|
Sec. 3.2 |
| Symbol | Definition | Where |
|
|
Vector of variables in dynamic computation | Sec. 3.4 |
|
|
Equation system linearized for dynamic computation | Sec. 3.4 |
|
|
Jacobian matrices appearing in linearized equation system | Sec. 3.4 |
| Symbol | Definition | Where |
| Inflation rate:
|
Sec. 4.3 | |
|
|
Fraction of firms adjusting prices at time |
Sec. 4.3 |
| Desired log price adjustment, given real price |
Sec. 4.3 | |
|
|
Average desired log price adjustment at time |
Sec. 4.3 |
|
|
Average log price adjustment at time |
Sec. 4.3 |
|
|
Intensive, extensive, and selection margins of inflation deviation | Sec. 4.3 |
|
|
Intensive and extensive margins (Klenow and Kryvstov definition) | Sec. 4.3 |
|
|
Intensive and extensive margins (Caballero and Engel definition) | Sec. 4.3 |
| Symbol | Definition | Where |
| Inflation rate in sector |
Sec. 4.4 | |
| Sector-specific mean inflation | Sec. 4.4 | |
| Sector-specific lag polynomial on aggregate shocks | Sec. 4.4 | |
| Sector-specific lag polynomial on sectoral shocks | Sec. 4.4 | |
| Aggregate inflation shock identified by MMW09 methodology | Sec. 4.4 | |
| Aggregate inflation shock identified by MMW09 methodology | Sec. 4.4 | |
|
|
True shock to Taylor rule | Sec. 2.3 |
| Shock to average productivity in sector |
Sec. 4.4 | |
|
|
Unexplained residual inflation in sector |
Sec. 4.4 |
Figure 6: Inflation variance contribution of sector-specific shocks identified from model-generated data. Estimated importance of sectoral shocks: contribution to sectoral inflation variance (%)
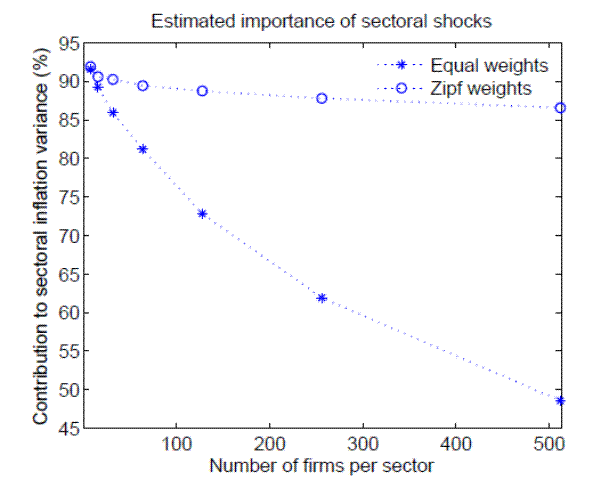 Figure 6 Data
Figure 6 Data
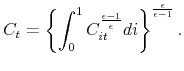
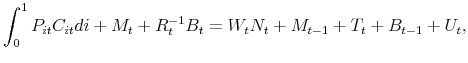
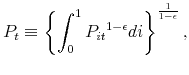
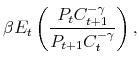
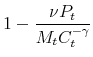
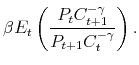
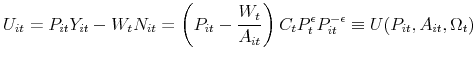
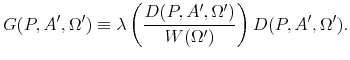
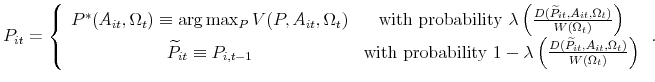
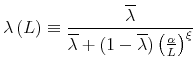
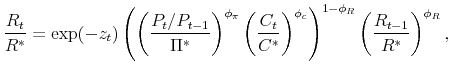
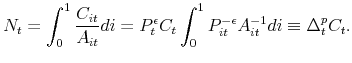
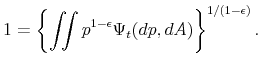
![\displaystyle v(p,A,\Xi )=u(p,A,\Xi )+\beta E\left\{ \left. \hspace{-2mm}\frac{{C(\Xi ^{\prime })^{-\gamma }}}{{C(\Xi )^{-\gamma }}}\hspace{-2mm}\left[ v\left( \frac{p}{\Pi (\Xi ,\Xi ^{\prime })},A^{\prime },\Xi ^{\prime }\right) +g\left( \frac{p}{\Pi (\Xi ,\Xi ^{\prime })},A^{\prime },\Xi ^{\prime }\right) \right] \right\vert A,\Xi \right\} ,](img154.gif)