Determining the Motives for a Positive Optimal Tax on Capital
Keywords: Optimal taxation, capital taxation
Abstract:
1 Introduction
Receipts from taxes on individuals' capital income (capital gains and dividends) in 2005 were approximately 140 billion dollars, or 15 percent of total personal income tax receipts.2 Based on the sizable tax receipts from capital income in the U.S. economy and savings disincentives created by a capital tax, considerable research has been devoted to determining whether a non-zero tax on capital income is
optimal.3 In the seminal works on this topic, Chamley (1986) and Judd (1985) conclude that it is not optimal to tax
capital in a model with infinitely lived agents who face no idiosyncratic risk. Atkeson et al. (1999) show that the optimal tax on capital is still zero in a two-period overlapping generations model when the government is allowed to condition the labor income tax on age.
Other works, such as Aiyagari (1995), Hubbard and Judd (1986), ![]() mrohoro
mrohoro![]() lu (1998), Erosa and Gervais (2002), Conesa et al. (2009), Garriga (2001), Jones et al. (1997) and Correia (1996), identify theoretical conditions
under which it is optimal to tax capital.
lu (1998), Erosa and Gervais (2002), Conesa et al. (2009), Garriga (2001), Jones et al. (1997) and Correia (1996), identify theoretical conditions
under which it is optimal to tax capital.
When determining the optimal tax on capital, the policymaker must weigh the relevant benefits versus the distortions imposed by the tax. Since a tax on capital discourages saving it is important to analyze the tax in an overlapping generations (OLG) model that includes the life cycle factors
that motivate saving. One such study, Conesa et al. (2009) uses a calibrated life cycle model and finds that the optimal tax policy consists of flat tax rates on capital and labor income of 34 percent and 14 percent, respectively.4 Additional studies such as Gervais (2010), Garriga (2001), Peterman (2010), Smyth (2006), and ![]() mrohoro
mrohoro![]() lu (1998) find a non-zero tax on capital is optimal in an OLG model. Given the computational complexities of these OLG models, it is helpful to determine the
economic factors driving these results. Studies that quantify the optimal tax on capital weigh the trade-off between realism and computational intensity when choosing simplifying assumptions. This paper quantifies the relative importance of two of the key modelling assumptions that motivate a
positive tax on capital in a canonical OLG model. Understanding the impact of these assumptions is relevant in order to more accurately determine the optimal tax on capital.
lu (1998) find a non-zero tax on capital is optimal in an OLG model. Given the computational complexities of these OLG models, it is helpful to determine the
economic factors driving these results. Studies that quantify the optimal tax on capital weigh the trade-off between realism and computational intensity when choosing simplifying assumptions. This paper quantifies the relative importance of two of the key modelling assumptions that motivate a
positive tax on capital in a canonical OLG model. Understanding the impact of these assumptions is relevant in order to more accurately determine the optimal tax on capital.
I start by solving for optimal tax policy in a benchmark model similar to the model in Conesa et al. (2009). Next, in order to measure their effect on optimal tax policy, I solve for the optimal tax policy in altered model in which I eliminate two commonly adopted assumptions that generate a non-zero tax on capital. The first assumption I eliminate is that the Frisch elasticity varies over the life cycle.5 The second assumption I change is that I relax several restrictions in the benchmark model with regards to how the government is allowed to tax accidental bequests. I test the impact of a varying Frisch elasticity since there is limited empirical evidence on whether the Frisch labor supply elasticity varies over the lifetime.6 Therefore, it is important to understand the impact of this assumption on optimal tax policy. The restrictions with regards to taxing accidental bequests are used to make the model more tractable, but these restrictions confound a motive for taxing ordinary capital with a motive to tax accidental bequests, and are not consistent with actual policy.
The main finding of this paper is that these two assumptions are responsible for almost half of the positive optimal tax on capital in the benchmark OLG model. When these two assumptions are removed from the model the optimal tax on capital is reduced from approximately 30 percent to 16 percent. Additionally, I find that there are welfare losses equivalent to 0.35 percent of total consumption if I implement the optimal tax policy from the benchmark model in the altered model. Altering just one of either two assumptions causes the optimal tax on capital to drop by approximately a third. Therefore, the simplifying restrictions on the tax function with regards to accidental bequests should not be included when determining optimal tax policy. Additionally, these results indicate that in order to more precisely determine the optimal tax on capital, one needs to empirical determine if the Frisch elasticity varies over the life cycle.
A varying Frisch elasticity over the life cycle motivates a positive optimal tax on capital because it causes the government to want to condition labor income taxes on age. If the government is disallowed from using age-dependent taxes, then a non-zero tax on capital can be used to mimic age-dependent taxes since a capital tax implicitly taxes younger labor income at a relatively higher rate. In a related work, Gervais (2010) demonstrates that a progressive labor income tax can also be used in tandem with a tax on capital to mimic an age-dependent tax policy.7 The benchmark utility function in Conesa et al. (2009) is non-homothetic in labor, which implies that the Frisch elasticity varies over the life cycle with hours worked.8 Therefore, in order to test the impact of this assumption, I determine the impact on optimal tax policy of changin the utility function such that it is homothetic in labor which implies that the Frisch elasticity does not vary.9
Restricting how the government can tax accidental bequests confounds a motive for a non-zero tax on ordinary capital income. In the benchmark model it is assumed that the government cannot distinguish accidental bequests from ordinary capital which implies that the government has to tax the returns from both sources at the same rate. Additionally, the government is restricted to taxing only the return on the accidental bequests and not the principle. Since accidental bequests are inelastic income, the government would like to fully tax them. If they cannot distinguish between the two incomes, the optimal tax on capital is an average between the optimal tax on ordinary capital income and the optimal tax on accidental bequests. I test the impact of relaxing these tax restrictions by allowing the government to separately tax accidental bequests and ordinary capital income.
Given that these two assumption motivate approximately half of the optimal tax on capital in the benchmark model, it becomes relevant to quantify the individual impact of all the modelling features that could motivate a non-zero tax on capital within a common framework. There are four common features in an OLG model that motivate a non-zero optimal tax on capital.10 These features are: (i) a varying lifetime Frisch labor supply elasticity, (ii) restrictions on how the government can tax accidental bequests, (iii) the inability of individuals to borrow, and (iv) the inability of the government to facilitate a social security program. I solve for the optimal tax policy in four other models with one of the four features that motivate a non-zero optimal tax on capital changed in order to determine the impact of each feature. Additionally, I solve for the optimal tax policy with an exogenously determined level of government debt or savings in order to ascertain its effect on optimal tax policy.11
In addition to the the non-constant Frisch elasticity and the government not being able to separately tax accidental bequests, I find that individual liquidity constraints also motivates a positive tax on capital but to a lesser extent. I find assuming the government holds savings or debts has a dramatic impact on the optimal tax on capital. When I assume that the government holds savings (debt) the optimal tax on capital decreases (increases) a significant amount. There are only small changes to the optimal tax policy when I exclude the reduced form social security program from the benchmark model, however, the life cycle profiles look less realistic. I find that the welfare cost of implementing the benchmark model's optimal tax policy in each of these alternative models ranges from .08 percent to 2.53 percent of total lifetime consumption. These results demonstrate that for some models there are large welfare consequences from using the optimal tax policy from a different model. Finally, this paper analyzes how the impact of the features change when the model is calibrated to match different targets for the Frisch elasticity since there is a large variance in the empirical estimates of this value. Generally, I find that these five features have a larger effect on the optimal tax on capital when the model is calibrated to match a medium or low Frisch elasticity as opposed to a high value.
This exercise is related to Conesa et al. (2009). However there are three important differences. First, I exclude inter-cohort heterogeneity as a possible motive for a positive tax on capital. I abstract from this type of heterogeneity because Conesa et al. (2009) demonstrate that it does not affect the level of the optimal tax on capital.12 Second, I examine how relaxing the restrictions on taxing accidental bequest affects optimal tax policy. The effects of these restrictions are not studied in Conesa et al. (2009). Third, I take an alternative approach to discern the effect of a varying Frisch elasticity. Similar to my benchmark model, Conesa et al. (2009) use a utility specification in which the agent's Frisch labor supply elasticity is negatively related to hours worked. In order to determine the impact of a varying Frisch elasticity on optimal tax policy, the authors eliminate the variance by holding the labor supply exogenously constant. Using this approach eliminates any general equilibrium effects of endogenously determined labor supply on optimal tax policy. Instead, in this paper, I eliminate the variation in the Frisch elasticity by using a utility specification that implies the Frisch labor supply elasticity is constant.13 The advantage of this approach is that it isolates the effect while including general equilibrium effects from endogenously determined labor supply. In another related exercise, Garriga (2001) examines the effect on optimal tax policy when government's discount rate is not the same as the private discount rate. He finds that as the government decreases their discount rate the optimal tax on capital increases.14 With regards to the social discount rate, this paper takes a similar approach to Conesa et al. (2009) and sets the public and private discount rate equal. Therefore, this paper focuses on the relative effect of the five other common features on optimal tax policy holding the social discount rate constant.
This paper is organized as follows: Section 2 examines a simplified version of the model in order to provide analytical insights into the effect of the two channels eliminated in the alternative specification. I introduce the computational model, and present the competitive equilibrium in section 3. Section 4 describes the functional forms and calibration parameters. Section 5 sets up the computational experiment and section 6 reports the results of the computational experiment. Section 7 examines the sensitivity of the results with respect to the target that the Frisch elasticity is calibrated to match. Finally, section 8 summarizes the papers findings.
2 Analytical Model
In this section I demonstrate the intuition in an analytically tractable model for why the two assumption changed in the alternative specification motivate a non-zero optimal tax on capital. The two assumptions I examine are a non-constant Frisch elasticity when the government cannot condition labor income taxes on age and the government not being able to distinguish between accidental bequests and ordinary capital.15 In the analytically tractable model I abstract from retirement, population growth, and progressive tax policies. Additionally, I assume that the marginal products of capital and labor are constant. This assumption permits me to focus on the life cycle elements of the model, in that changes to the tax system do not affect the pre-tax wage or rate of return. Since the factor prices do not vary, I suppress their time subscripts in this section. All of these assumptions are relaxed in the computational model. Using the primal approach, I solve for the optimal tax policies in several versions of the simplified model in order to isolate the effect of the two different assumptions.
2.1 Agent's Problem
The analytical model is a simplified model where agents live for two periods and their preferences over consumption and leisure are given by
where
and
where
A common treatment of these accidental bequests in OLG models is that when individuals die their assets are redistributed to all living agents (see Conesa et al. (2009) for an example). The living agents receive both the original assets (principle) and also the capital returns on these assets. One tractable assumption that has been employed is to restrict the tax policy such that the government cannot distinguish between accidental bequests and ordinary capital nor can they tax the principle of the accidental bequests. Additionally, the government is forced to tax the return on both ordinary capital and accidental bequests at the same rate. In section 2.4 I examine the effect of these restrictions. I assume that the tax rate on labor income can be conditioned on age in some of the models; however, the tax rate on capital income cannot.17 I combine equations 2 and 3 to form a joint intertemporal budget constraint, which is necessary for the primal approach,
The agent's problem is to maximize equation 1 subject to 4. The agent's first order conditions are
and
where
2.2 Primal Approach
In order to determine the optimal tax policy, I use the primal approach. In the primal approach the benevolent government maximizes directly over allocations, discounting future generations with social discount factor ![]() , subject to the implementability constraint. The optimal tax policy is reversed engineered from the optimal allocations. The implementability constraint is the agent's intertemporal budget constraint with the prices and taxes replaced by his first order
conditions (equations 5, 6, and 7). Including this constraint ensure that any allocation the government chooses can be supported by a competitive equilibrium.18
, subject to the implementability constraint. The optimal tax policy is reversed engineered from the optimal allocations. The implementability constraint is the agent's intertemporal budget constraint with the prices and taxes replaced by his first order
conditions (equations 5, 6, and 7). Including this constraint ensure that any allocation the government chooses can be supported by a competitive equilibrium.18
Formally, the government maximizes the objective function,
![\displaystyle [U(c_{2,0},1-h_{2,0})/\theta]+\sum_{t=0}^{\infty}\theta^{t}[U(c_{1,t},1-h_{1,t})+\beta U(c_{2,t+1},1-h_{2,t+1})],](img33.gif) |
(8) |
with respect to the implementability constraint,
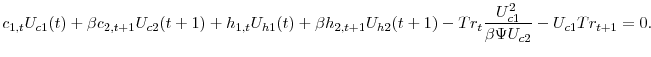 |
(9) |
and the resource constraint,
In section 2.3.2 I restrict the government from conditioning labor income taxes on age. In such a model the following constraint must be included,
I use
2.3 Impact of Non-Homothetic Utility Function
Garriga (2001) and Erosa and Gervais (2002) demonstrate that if the government cannot condition taxes on age, then in order for the optimal tax on capital to be zero the utility function must be separable and homothetic in both consumption and labor. An implication of a non-homothetic utility function is the Frisch elasticity is not constant over the lifetime. Although the violation of the primal assumptions that motivates a non-zero tax on capital is a non-homothetic utility function, I refer to the modelling assumption as a non-constant Frisch elasticity since the intuition for the result comes from this variation. In this section, I demonstrate the intuition for why a varying Frish elasticity coupled with the government's inability to condition labor income taxes on age motivates a positive optimal tax on capital.
In order to demonstrate the intuition, I consider the optimal tax policy in a world where agents live with certainty for two periods (![]() , and
, and ![]() ) under two different utility functions:
) under two different utility functions:
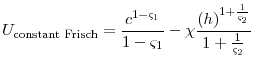 |
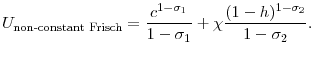 |
The first utility function is homothetic in both consumption and hours worked and the Frisch labor supply elasticity,
2.3.1 Non-constant Frisch Utility
I start by solving for the model with the non-constant Frisch utility function where the government can condition labor income taxes on age. The formulation of the government's problem, resulting first order conditions, and derivations of the optimal tax policy can be found in appendix B.1.
Conesa et al. (2009), Atkeson et al. (1999), Erosa and Gervais (2002), and Garriga (2001) demonstrate with this type of utility function and age-dependent taxes that the optimal tax policy includes no tax on capital and different tax rates on different aged labor income. Combining the agent's and government's first order conditions simplifies to the following expression for optimal labor income taxes,
Equation 12 confirms that in a model with the non-constant Frisch utility function, the optimal tax on labor income varies by age as long as
Furthermore, Conesa et al. (2009), Atkeson et al. (1999), Erosa and Gervais (2002), and Garriga (2001) demonstrate that in a similar set up if the government cannot use age-dependent taxes then the optimal tax on capital is no longer zero. The Lagrangian and first order conditions for this model where the government cannot use age-dependent taxes are in appendix B.2. Combining the governments first order conditions with respect to capital and consumption leads to the following expression
In contrast, applying the non-constant Frisch utility function to equation 7 provides the following relationship
Equations 14 and 13 demonstrate that generally for the government to ensure the agent chooses the optimal allocation, the tax on capital is not zero. In the absence of the ability to condition labor income taxes on age, the government chooses to tax capital in order to mimic an age-dependent tax on labor income.
Examining the Euler equation provies the intuition for why a tax on capital mimics an age-dependent tax on labor,
Equation 15 demonstrates that a tax on capital imperfectly mimics an age-dependent tax on labor income by creating a similar wedge on the marginal rate of substitution.20 Specifically, a positive tax on capital mimics a relatively higher tax rate on young labor income since it creates a similar impact on the left hand side of equation 15.
2.3.2 Constant Frisch Utility and Age-dependent Taxes
Next, I examine the optimal tax policy in a model with the constant Frisch utility function where the government is allowed to condition labor income taxes on age. Comparing the resulting optimal tax policy with the policy in section 2.3.1 isolates the effect of a varying Frisch elasticity on optimal tax policy. The formulation of the government's problem and their first order conditions for this model can be found in appendix B.3
Combining the agent's and government's first order equations generates the following expression for the optimal labor taxes
Equation 16 demonstrates that even if the government could condition taxes on age then they would tax labor income for different aged individuals at the same rate. Under the constant Frisch utility specification, it is not optimal to vary the labor income tax rate based on age since the Frisch elasticity is constant. Therefore, using this utility function eliminates the motive of taxing capital in order to mimic an age-dependent tax when the age-de3pendent tax is unavailable.21
2.4 Impact of Incomplete Set of Tax Instruments on Accidental Bequests
In this section I demonstrate the intuition why the assumption that the government cannot distinguish between accidental bequests and ordinary capital leads to a positive optimal tax on capital. In all of the models in this section (2.4) I use the constant Frisch utility function and allow for age-dependent taxes on labor income which eliminates all of the motives for a non-zero tax on capital discussed in section 2.3. In this section, the models include lifetime length uncertainty so some agents die with positive levels of savings. These accidental bequests are transfered to living individuals. The assumption that the government cannot distinguish between ordinary capital and accidental bequests implies two restrictions. First, the government is restricted to only taxing the return on the accidental bequests and not the principle. Second, they are forced to tax the returns on accidental bequests at the same rate as the returns on ordinary capital. In order to demonstrate the intuition why these restrictions motivates a positive tax on capital I start by solving for the optimal tax policy in an unrestricted model. I then examine the change to the optimal tax policies when I incrementally add the two restrictions to the tax policy.
2.4.1 No Restrictions on Accidental Bequest Tax Policy
I start by solving for the optimal tax policy in a simple model without restrictions on the accidental bequest tax policy. Specifically, the government taxes ordinary capital income, ![]() ,
at a rate of
,
at a rate of ![]() , and accidental bequests,
, and accidental bequests, ![]() , at a rate of
, at a rate of ![]() . The intertemporal budget constraint, equation 4, becomes:
. The intertemporal budget constraint, equation 4, becomes:
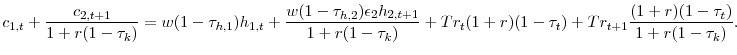 |
(17) |
The formulation of the government's problem and first order conditions can be found in appendix B.4. Combining the government's first order conditions for consumption and saving yields the following expression,
Combining the government's first order conditions for labor and savings yields the following expression for the optimal taxes on labor,
Examining equation 18, if the government fully taxes the principle on accidental bequests (
![]() ) the equation simplifies to the same as equation 14 and the optimal tax on capital is zero. Additionally, if
) the equation simplifies to the same as equation 14 and the optimal tax on capital is zero. Additionally, if
![]() then the right hand side of the equation 19 simplifies to one and it is not optimal for the government to condition labor income taxes on age. Since
accidental bequests are inelastic income it is optimal for the government to fully tax these before using other forms of taxation that are distortionary. Therefore, if the government can tax the principle and return of the accidental bequests at a separate rate from ordinary capital income then the
optimal tax policy is similar to the policy in section 2.3.2; they do not include a tax on ordinary capital income nor age-dependent taxes on labor income.
then the right hand side of the equation 19 simplifies to one and it is not optimal for the government to condition labor income taxes on age. Since
accidental bequests are inelastic income it is optimal for the government to fully tax these before using other forms of taxation that are distortionary. Therefore, if the government can tax the principle and return of the accidental bequests at a separate rate from ordinary capital income then the
optimal tax policy is similar to the policy in section 2.3.2; they do not include a tax on ordinary capital income nor age-dependent taxes on labor income.
2.4.2 Restricted Tax Policy: Cannot Tax Principle of Accidental Bequests
In this section I solve for the optimal tax policy when the government can no longer tax the principle of accidental bequests. However, I still allow the government to set separate tax rates for the returns on accidental bequests (![]() ) and ordinary capital (
) and ordinary capital (![]() ). The intertemporal budget constraint in this model is,
). The intertemporal budget constraint in this model is,
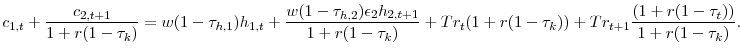 |
(20) |
The formulation of the government's problem and first order conditions can be found in appendix B.5.
Combining the government's first order conditions for consumption and savings yields the following expression,
Examining equation 21 and equation 14, demonstrates that generally the optimal tax on capital is no longer zero. Even if
Equation 22 is an expression for the optimal tax on labor income,
When the government is restricted from taxing the principle of accidental bequests, it now wants to condition labor income taxes on age. When the government taxes the return on ordinary capital they create a wedge on the marginal rate of substitution. The government would like to condition labor income taxes on age in order to unwind that wedge. Combining equations 21, 43, and 22 yields the following ratio,
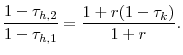 |
(23) |
This expression demonstrates that the ratio of the wedges created by the labor taxes and the tax on capital are equal. As the tax on capital income increases, it is optimal to also decrease the relative tax on young labor income to unwind this wedge because the tax on capital is like a relatively larger tax on young labor.
2.4.3 Restricted Tax Policy: Cannot Observe Accidental Bequests
I finish by exploring the optimal tax policy in a model where the government cannot distinguish between income from ordinary capital and accidental bequests. This assumption implies that the government only observes the overall returns, ![]() , and it is restricted to tax all the returns at the same rate,
, and it is restricted to tax all the returns at the same rate, ![]() . This treatment of accidental bequests is similar to
Conesa et al. (2009). The agent's intertemporal budget constraint is the same as equation 4. The formulation of the government's problem and first order conditions can be found in appendix B.6
. This treatment of accidental bequests is similar to
Conesa et al. (2009). The agent's intertemporal budget constraint is the same as equation 4. The formulation of the government's problem and first order conditions can be found in appendix B.6
Utilizing the first order conditions from the Lagrangian with respect to capital and consumption leads to the following equation,
Comparing equations 24 and 14, generally the optimal tax on capital will not be zero. Additionally, assuming
2.5 Summary of analytic results
In this section I demonstrated that with a non-constant Frisch elasticity profile, it is optimal to condition labor income taxes on age. Furthermore, if the government cannot use age-dependent taxes then it is optimal to tax capital to mimic an age-dependent labor income tax. This motive for a non-zero tax on capital is eliminated in a model that uses the constant Frisch utility function. I also demonstrated that restricting the government from setting separate tax rates on ordinary capital and accidental bequests or disallowing them from taxing the principle of the accidental bequests leads to a non-zero optimal tax on capital.
3 Computational Model
To examine the relevant magnitude of the motives for a non-zero tax on capital I examine a less parsimonious calibrated overlapping generations model that must be solved computationally. In this section, I describe the computational model (focusing on the benchmark model) and the definition of a stationary competitive equilibrium.
3.1 Demographics
In the computational model, time is assumed to be discrete and there are J overlapping generations. ![]() is the probability of an agent living to age
is the probability of an agent living to age ![]() conditional on being alive at age
conditional on being alive at age ![]() . All agents who live to an age of
. All agents who live to an age of ![]() die the next period. Agents are forced to retire at an exogenously set age
die the next period. Agents are forced to retire at an exogenously set age ![]() .
.
In each period a continuum of new agents is born. The population of new agents born each period grows at rate ![]() . Given the population growth rate and conditional survival probabilities,
the time invariant cohort shares,
. Given the population growth rate and conditional survival probabilities,
the time invariant cohort shares,
![]() , are given by
, are given by
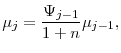 for for |
(25) |
where
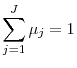 |
(26) |
If agents die before ![]() , these assets are treated as accidental bequests. In the benchmark model, the government is restricted to taxing just the returns on accidental bequests and at the
same rate that it taxes returns on ordinary capital income. In order to test the strength of the motive for a non-zero tax on capital described in section 2.4 I also use a second treatment. In the second treatment, I allow the government to consume these assets removing
this motive for a positive tax on capital.
, these assets are treated as accidental bequests. In the benchmark model, the government is restricted to taxing just the returns on accidental bequests and at the
same rate that it taxes returns on ordinary capital income. In order to test the strength of the motive for a non-zero tax on capital described in section 2.4 I also use a second treatment. In the second treatment, I allow the government to consume these assets removing
this motive for a positive tax on capital.
3.2 Individual
An individual is endowed with one unit of productive time per period which he splits between providing labor services and leisure in order to maximize his lifetime utility
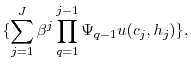 |
(27) |
where
An agent's age-specific human capital is
![]() so he receives labor income of
so he receives labor income of
![]() . Agents split their labor income between consumption and saving. An agent can save by purchasing a risk free asset. An agent's level of assets are denoted by
. Agents split their labor income between consumption and saving. An agent can save by purchasing a risk free asset. An agent's level of assets are denoted by
![]() and he receives a pre-tax net return of
and he receives a pre-tax net return of ![]() on the assets per period.
Agents being liquidity constrained early in their life is another potential motive for a positive tax on capital. In some of the iterations, I test this motive's strength by allowing agents to borrow. In these iterations of the model, agents pay the actuarially fair interest rate of
on the assets per period.
Agents being liquidity constrained early in their life is another potential motive for a positive tax on capital. In some of the iterations, I test this motive's strength by allowing agents to borrow. In these iterations of the model, agents pay the actuarially fair interest rate of
![]() to borrow.
to borrow.
3.3 Firm
Firms are perfectly competitive with constant returns to scale production technology. Aggregate technology is represented by a Cobb-Douglas production function. The aggregate resource constraint is,
| (28) |
where
3.4 Government Policy
The government consumes resources in an unproductive sector, ![]() .23 The government has two fiscal instruments to finance their consumption in the benchmark model (
.23 The government has two fiscal instruments to finance their consumption in the benchmark model (
![]() ). First, the government taxes capital income,
). First, the government taxes capital income, ![]() , according to a capital income tax schedule
, according to a capital income tax schedule
![]() . In the benchmark
. In the benchmark
![]() . In other version when the government can distinguish accidental bequests
. In other version when the government can distinguish accidental bequests
![]() . Second, the government taxes each individual's taxable labor income. Part of the pre-tax labor income is accounted for by the employer's contributions to social
security, which is not taxable under current U.S. tax law. Therefore, the taxable labor income is
. Second, the government taxes each individual's taxable labor income. Part of the pre-tax labor income is accounted for by the employer's contributions to social
security, which is not taxable under current U.S. tax law. Therefore, the taxable labor income is
![]() , which is taxed according to a labor income tax schedule
, which is taxed according to a labor income tax schedule
![]() . I impose two restrictions on the labor and capital income tax policies. First, I assume anonymity of the tax code so the rates cannot be personalized, nor can they be
age-dependent. Second, both of the taxes are functions only of the individual's relevant taxable income in the current period.
. I impose two restrictions on the labor and capital income tax policies. First, I assume anonymity of the tax code so the rates cannot be personalized, nor can they be
age-dependent. Second, both of the taxes are functions only of the individual's relevant taxable income in the current period.
In some iterations of the model I force the government to borrow or save in order to quantify its impact on optimal tax policy. I solve for the optimal tax policies under a steady state equilibrium so the government's level of savings or debt cannot change over time. Therefore, in these iterations the government holds a fixed level of savings or debt but is still not allowed to run a deficit or surplus. When the government holds savings the return on its capital is used to offset government consumption and when the government is in debt it pays the interest on its debt by reducing government consumption. This assumption implies that the government is collecting the same amount of tax revenue regardless of the level of government savings or debt.
In addition to taxing income in order to finance ![]() , the government runs a pay-as-you-go social security system in the benchmark model. The government pays
, the government runs a pay-as-you-go social security system in the benchmark model. The government pays ![]() to all individuals that are retired. Social security benefits are such that retired agents receive an exogenously determined fraction,
to all individuals that are retired. Social security benefits are such that retired agents receive an exogenously determined fraction, ![]() , of the average income of all working individuals. An agent's social security benefits are independent of his personal earnings history. Social security is financed by taxing labor income at a flat rate,
, of the average income of all working individuals. An agent's social security benefits are independent of his personal earnings history. Social security is financed by taxing labor income at a flat rate,
![]() . The payroll tax rate
. The payroll tax rate
![]() is set to ensure the social security system has a balanced budget each period. The social security system is not considered part of the tax policy that the government optimizes.
In other iterations of the model, I eliminate the social security program in order to determine its effect on the optimal tax policy.
is set to ensure the social security system has a balanced budget each period. The social security system is not considered part of the tax policy that the government optimizes.
In other iterations of the model, I eliminate the social security program in order to determine its effect on the optimal tax policy.
3.5 Definition of Stationary Competitive Equilibrium
In this section I define the competitive equilibria for the benchmark model. I do not present the definition of a competitive equilibrium for the other iterations of the model since they are similar to that of the benchmark model.
Given a social security replacement rate ![]() , government expenditures
, government expenditures ![]() , and a
sequence of population shares
, and a
sequence of population shares
![]() , a stationary competitive equilibrium is a sequence of agent allocations,
, a stationary competitive equilibrium is a sequence of agent allocations,
![]() , a production plan for the firm
, a production plan for the firm ![]() , a government labor
tax function
, a government labor
tax function
![]() , a government capital tax function
, a government capital tax function
![]() , a social security tax rate
, a social security tax rate ![]() , a utility function
, a utility function
![]() , social security benefits
, social security benefits ![]() , prices
, prices ![]() , and transfers
, and transfers ![]() such that:
such that:
- Given prices, policies, transfers, and benefits the agent maximizes the following
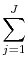 Max
Max![\displaystyle _{c_{j},h_{j},a_{j+1}}\beta^{j-1}[\prod_{q=0}^{j-1}\Psi_{q}]u(c_{j},h_{j})](img115.gif)
subject to![\displaystyle c_{j}+a_{j+1}=w\epsilon_{j}h_{j}-\tau_{ss}ws_{j}h_{j},+(1+r)(a_{j}+Tr)-T^{l}[w\epsilon_{j}h_{j}(1-.5\tau_{ss})] -T^{k}[r(a_{j}+Tr)]](img116.gif) for
for 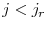 ,
,
![\displaystyle c_{j}+a_{j+1}=SS+(1+r)(a_{j}+Tr)-T^{k}[r(a_{j}+Tr_{t})],](img118.gif) for
for
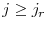
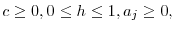 and
and 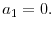
- Prices
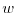 and
and 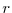 satisfy:
satisfy:
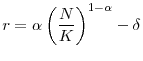 and
and 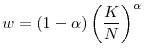
- The social security policies satisfy:
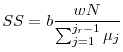 and
and 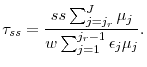
- Transfers are given by:
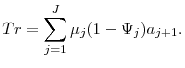
- Government budget balance:
![\displaystyle G=\sum_{j=1}^{J}\mu_{j} T^{k}[r(a_{j}+Tr)] + \sum_{j=1}^{j_{r}-1} \mu_{j}T^{l}[w\epsilon_{j}h_{j}(1-.5\tau_{ss})].](img129.gif)
- Market clearing:
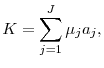
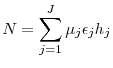 and
and
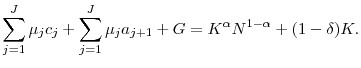
4 Calibration
In this section, I describe the the functional forms and calibration. Calibration involves two steps. The first step is choosing parameter values for which there are direct estimates in the data. Second, in order to calibrate the remaining parameters, I choose values such that under the baseline-fitted U.S. tax policy certain target values are the same in the models and the U.S. economy. I calibrate these parameters separately in the different iterations of the model.24 Table 1 lists the different models and their features. Table 2 lists all the parameter values that are the same in the models. Table 3 lists the values for the parameters that are calibrated separately in each model.
| Parameter | Value | Target |
| Demographics: Retire Age: |
65 | By Assumption |
| Demographics: Max Age: |
100 | By Assumption |
| Demographics: Surv. Prob: |
Bell and Miller (2002) | Data |
| Demographics: Pop. Growth: |
Data | |
| Preferences:Risk aversion:
|
2 | Conesa et al. (2009) |
| Technology: Capital Share: |
.36 | Data |
| Technology: Depreciation: |
8.33% |
|
| Technology: Productivity: A | 1 | Normalization |
| Government: Tax Function:
|
.258 | Gouveia and Strauss (1994) |
| Government: Tax Function:
|
.768 | Gouveia and Strauss (1994) |
| Model | Conditional Discount: |
Frisch Elasticity:
|
Disutility to Labor: |
Govt Spending: G |
|---|---|---|---|---|
| Target |
|
Frisch= 2/3 | Avg. H = 1/3 | |
| A0 (Benchmark) | 0.993 | 3 | 1.9 | 0.137 |
| B0 (Alt. Specification) | 0.994 | 2/3 | 39.8 | 0.162 |
| A1 (Constant Frisch) | 0.993 | 2/3 | 35 | 0.136 |
| A2 (Gov't Consumes Tr) | 0.994 | 3 | 2.2 | 0.164 |
| A3 (Ind. Borrowing) | 0.993 | 3 | 1.9 | 0.137 |
| A4 (Gov't Saves) | 0.986 | 3 | 2.07 | 0.137 |
| A5 (Gov't Borrows) | 0.998 | 3 | 1.81 | 0.136 |
| A6 (No SS): | 0.969 | 3 | 1.86 | 0.139 |
4.1 Demographics
In the model, agents are born at a real world age of twenty which corresponds to a model age of one. Agents are exogenously forced to retire at a real world age of 65. If an individual survives until 100 (model age 80) then he dies the next period. I use Bell and Miller (2002) to determine the conditional survival probabilities. I assume a population growth rate of 1.1 percent.
4.2 Individual
As a benchmark specification I use the non-constant Frisch utility function. In order to determine the impact on optimal tax policy of the desire to mimic an age-dependent tax that arises because of a varying Frisch elasticity, I also find the optimal tax policy using the constant Frisch utility function.
I determine ![]() such that the capital-to-output ratio matches U.S. data of 2.7 in the benchmark model.25 I determine
such that the capital-to-output ratio matches U.S. data of 2.7 in the benchmark model.25 I determine ![]() such that under the baseline-fitted U.S. tax policy agents work on average one third of their time endowment in the benchmark model. Following Conesa et al. (2009) I set
such that under the baseline-fitted U.S. tax policy agents work on average one third of their time endowment in the benchmark model. Following Conesa et al. (2009) I set
![]() which controls the relative risk aversion. I set
which controls the relative risk aversion. I set
![]() for the non-constant Frisch utility function which implies a Frisch labor supply elasticity of
2/3 when agents are working a third of their time endowment. Under the constant Frisch utility function, I set
for the non-constant Frisch utility function which implies a Frisch labor supply elasticity of
2/3 when agents are working a third of their time endowment. Under the constant Frisch utility function, I set
![]() which also implies a Frisch elasticity of two thirds. Past micro-econometric studies estimate the Frisch elasticity between 0 and
which also implies a Frisch elasticity of two thirds. Past micro-econometric studies estimate the Frisch elasticity between 0 and ![]() . For examples see Altonji (1986), MaCurdy (1981) and Domeij and Flodén (2006). However, more recent research has suggested
that these estimates may be biased downward. Some of the reasons for the bias are: utilizing weak instruments, not accounting for borrowing constraints, disregarding the life cycle impact of endogenous-age specific human capital and omitting correlated variables such as wage uncertainty. Some of
these studies include Imai and Keane (2004), Wallenius (2011), Domeij and Flodén (2006), Pistaferri (2003), and Contreras and Sinclair (2008). Rogerson and Wallenius (2009) show that because individuals choose their labor supply on both the intensive and extensive margin "micro and macro elasticities need not be the same, and that macro elasticities can be significantly larger." Furthermore, Chetty (2009) shows that small frictions in the labor market can lead the observed Frisch elasticity to be much smaller. Since there is some uncertainty about this value, I test the sensitivity of the results with regards to this parameter in section 7. I
calibrate
. For examples see Altonji (1986), MaCurdy (1981) and Domeij and Flodén (2006). However, more recent research has suggested
that these estimates may be biased downward. Some of the reasons for the bias are: utilizing weak instruments, not accounting for borrowing constraints, disregarding the life cycle impact of endogenous-age specific human capital and omitting correlated variables such as wage uncertainty. Some of
these studies include Imai and Keane (2004), Wallenius (2011), Domeij and Flodén (2006), Pistaferri (2003), and Contreras and Sinclair (2008). Rogerson and Wallenius (2009) show that because individuals choose their labor supply on both the intensive and extensive margin "micro and macro elasticities need not be the same, and that macro elasticities can be significantly larger." Furthermore, Chetty (2009) shows that small frictions in the labor market can lead the observed Frisch elasticity to be much smaller. Since there is some uncertainty about this value, I test the sensitivity of the results with regards to this parameter in section 7. I
calibrate
![]() such that the sequence matches a smoothed version of the relative hourly earnings estimated by age in Hansen (1993).
such that the sequence matches a smoothed version of the relative hourly earnings estimated by age in Hansen (1993).
I focus on the impact of a varying Frisch elasticity since there is limited empirical evidence on whether the Frisch labor supply elasticity varies over the lifetime. Two exceptions are French (2005) and Clark and Summers (1981). French (2005) estimate that the labor supply elasticity is more than three times larger for sixty year old individuals than forty year old individuals. However, the author notes that social security and pension incentives are responsible for this change. Therefore, the change in elasticity results from changes on the extensive margin and not the intensive margin. The focus of this study is changes in labor supply on the intensive margin since retirement is considered exogenous in the model. Clark and Summers (1981) suggest that teenagers may be more elastic than prime aged workers. However, teenage workers are outside the scope of this study since agents enter the model once they are in their twenties.
4.3 Firm
I assume the capital share parameter, ![]() , is .36. The depreciation rate is
set to target the observed investment-output ratio of 25.5 percent.
, is .36. The depreciation rate is
set to target the observed investment-output ratio of 25.5 percent.
4.4 Government Policy
In order to calibrate the parameters, I need a benchmark tax function to use when matching the targets in the models to the values in the data. I calibrate the model under a baseline tax function that mimics the U.S. tax code. I refer to this tax function as the baseline-fitted U.S. tax policy. I use the estimates from Gouveia and Strauss (1994) to determine the baseline-fitted U.S. tax policy. The authors match the U.S. tax code to the data using a three parameter functional form,
where
Gouveia and Strauss (1994) estimate values of
![]() and
and
![]() from the U.S. data. The authors do not fit separate tax functions for labor and capital income. Therefore, I use the same values on both sources of income for the
baseline-fitted U.S. tax policy. I calibrate government consumption,
from the U.S. data. The authors do not fit separate tax functions for labor and capital income. Therefore, I use the same values on both sources of income for the
baseline-fitted U.S. tax policy. I calibrate government consumption, ![]() , such that it equals a percentage of output under the baseline-fitted U.S. tax policy, as observed in the U.S.
data.26 Therefore, I set
, such that it equals a percentage of output under the baseline-fitted U.S. tax policy, as observed in the U.S.
data.26 Therefore, I set
![]() (for both sources of income) at the value that clears the government's budget constraint.
(for both sources of income) at the value that clears the government's budget constraint.
I calibrate the benchmark model such that ![]() is 17 percent of output. In the
model without the restrictions on taxing accidental bequests, the government raises more money from taxing accidental bequests because they fully confiscate them instead of only taxing the return on the bequests. In order to make these models comparable to the others, I adjust the government budget
constraint such that the distortionary taxes on ordinary capital and labor income are the same percent of output in both the models. This budget constraint implies that the government will raise more revenue in the models where they consume accidental bequests, however, the part from distortionary
taxes will be the same in all models. Additionally, in the models where the government holds debt (savings), I assume that the interest payments (income) offsets government consumption. Therefore, traditional government consumption not including debt services is smaller (larger) in the model with
government debt (savings) compared to the benchmark.
is 17 percent of output. In the
model without the restrictions on taxing accidental bequests, the government raises more money from taxing accidental bequests because they fully confiscate them instead of only taxing the return on the bequests. In order to make these models comparable to the others, I adjust the government budget
constraint such that the distortionary taxes on ordinary capital and labor income are the same percent of output in both the models. This budget constraint implies that the government will raise more revenue in the models where they consume accidental bequests, however, the part from distortionary
taxes will be the same in all models. Additionally, in the models where the government holds debt (savings), I assume that the interest payments (income) offsets government consumption. Therefore, traditional government consumption not including debt services is smaller (larger) in the model with
government debt (savings) compared to the benchmark.
When determining the optimal tax policy, I restrict my attention to revenue neutral changes to the tax policy where the optimal tax policy is a separate flat tax rate on capital income and on labor income (![]() and
and ![]() ). When searching for the optimal tax policy, I limit my attention to flat taxes instead of searching over progressive tax policies. Conesa et al. (2009) and Peterman (2010) solve for the optimal tax policies in a model similar to the benchmark model. They both find that the optimal tax policies are flat taxes in models that do not include within cohort heterogeneity. Therefore, I
restrict my attention to flat taxes because all the agents within a cohort are homogenous. This experiment implies that, within a model, the government consumption it is equal under the baseline-fitted U.S. tax policy and the optimal tax policies.
). When searching for the optimal tax policy, I limit my attention to flat taxes instead of searching over progressive tax policies. Conesa et al. (2009) and Peterman (2010) solve for the optimal tax policies in a model similar to the benchmark model. They both find that the optimal tax policies are flat taxes in models that do not include within cohort heterogeneity. Therefore, I
restrict my attention to flat taxes because all the agents within a cohort are homogenous. This experiment implies that, within a model, the government consumption it is equal under the baseline-fitted U.S. tax policy and the optimal tax policies.
In the benchmark model, the social security system is chosen so that the replacement rate, ![]() , is 50 percent.27 The payroll tax,
, is 50 percent.27 The payroll tax, ![]() , is determined such that the social security system contains a balanced-budget each period.
, is determined such that the social security system contains a balanced-budget each period.
5 Computational Experiment
The computational experiment begins by solving for the optimal tax policy in my benchmark model. Next, I solve for the optimal tax policy in a model that has a utility function that implies a constant Frisch elasticity and allows the government to consume accidental bequests. I choose to examine these two features because the first confounds a motive for a positive tax on capital with the desire of the government to consume accidental bequests and the second has only limited empirical motivation.
Finally, I examine the strength of each of the other motives by eliminating each of them from the benchmark model. The aspects of the benchmark model that I change are: a varying Frisch labor supply elasticity profile, no separate tax rates on accidental bequests and ordinary capital income, individual borrowing constraints, excluding exogenously determined government savings or debt, and including a reduced form social security program. I solve for the optimal tax policy in a total of eight different iterations of the model. Table 1 list the features in each iteration of the model.
To quantify the optimal tax policy, I need a social welfare function. Following Conesa et al. (2009) I choose a social welfare function that corresponds to a Rawlsian veil of ignorance (Rawls (1971)). Because in a stationary equilibrium, living agents face no earnings uncertainty the social welfare is equal to the expected lifetime utility of a newborn,
![\displaystyle SWF(\tau_{h}, \tau_{k})=\sum_{j=1}^{J}\beta^{j-1}\bigg[\prod_{q=0}^{j-1}\Psi_{q}\bigg]u(c_{j},h_{j})](img163.gif) |
(30) |
where
6 Results
In this section, I start by solving for the optimal tax policies in the benchmark model (A0) and the alternative specification (B0) in order to test the effect of the varying Frisch elasticity and accidental bequests assumptions on the optimal tax policy. Next, I change one of the features of the benchmark model and solve for the optimal tax policy (models A1, A2, A3, A4, A5, and A6) in order to determine each feature's individual effect on optimal tax policy.
6.1.1 Optimal Policies
The first two columns of table 4 list the the optimal tax policies from the benchmark model and the alternative specification model and the third column lists the ratio between the optimal tax on capital and labor income. I find that when I change the utility specification and allow the government to consume transfers the optimal tax on capital drops by almost half. Although the tax on capital remains positive, it is no longer large. Therefore, two assumptions, the first which has limited empirical motivation, and the second that confounds a motive for a positive tax on capital with the governments desire to tax accidental bequests are jointly responsible for approximately half of the large optimal tax on capital.
| Model |
|
CEV (baseline) | CEV (A0) | ||
| A0 (Benchmark): | 29.3% | 21.3% | 1.4 | 0.73% | n/a |
|---|---|---|---|---|---|
| B0 (Alternative Specification): | 16.6% | 23.7% | 0.7 | 0.95% | 0.35% |
The fourth column of table 4 lists the consumption equivalent variations based off the fitted U.S. tax policy (CEV (Baseline)). The CEV (baseline) is the uniform increase in an agent's lifetime consumption that is necessary to make him indifferent between being born
under the baseline-fitted U.S. tax policy and the optimal tax policy. I find that the CEV (baseline) is 0.73 percent and 0.95 percent in the benchmark and alternative specification models, respectively. Total consumption for all individuals in the U.S. was approximately
![]() billion in 2010, so the CEV (baseline) represents approximately
billion in 2010, so the CEV (baseline) represents approximately ![]() billion and
billion and ![]() billion dollars in the benchmark and alternative specification models, respectively.29 Next, I assess how much welfare would be lost by using the optimal tax policy from the wrong model. Specifically, I impose the optimal tax policy from A0 in model B0 and determine the increase in consumption required to return an
individual to the same level of utility as under the optimal tax policy in B0.30 I refer to this welfare measure as CEV (A0) since it measures the welfare
impact of the optimal tax policy from A0 in other models. I find that the CEV (A0) for model B0 is 0.35 percent or approximately a third of the size of CEV (baseline).
billion dollars in the benchmark and alternative specification models, respectively.29 Next, I assess how much welfare would be lost by using the optimal tax policy from the wrong model. Specifically, I impose the optimal tax policy from A0 in model B0 and determine the increase in consumption required to return an
individual to the same level of utility as under the optimal tax policy in B0.30 I refer to this welfare measure as CEV (A0) since it measures the welfare
impact of the optimal tax policy from A0 in other models. I find that the CEV (A0) for model B0 is 0.35 percent or approximately a third of the size of CEV (baseline).
6.1.2 Transition
When examining the welfare impacts of adopting the optimal tax policy it is useful to analyze the transition from the steady state under the current tax policy to the steady state under the optimal tax policy. In order to assess the transition path it is necessary to take a stand on how the tax policy adjusts as the economy moves towards the new steady state. I assume that the economy starts at the steady state under the baseline-fitted U.S. tax policy. In the first period of the analysis, the government imposes the optimal labor income tax rate. In each period the government adjusts the tax on capital in order to fulfill their budget constraint. Over time the economy converges to its new steady state which is the one computed under the optimal tax policy. I analyze the transitions in both the benchmark and alternative specification models.
Starting with the benchmark model (A0), figure 1 plots the capital and labor tax rates during the transition. The upper left and right panels of figure 1 plot the tax rate for capital and labor income, respectively. The circles represent the average marginal tax rates under the baseline-fitted U.S. tax policy and the lines are the marginal tax rate throughout the transition.31 The bottom panel of figure 1 excludes the baseline-fitted U.S. tax policy rate so that one can focus on the movement of the tax on capital throughout the transition. Under the baseline-fitted U.S. tax policy, the average marginal tax rate on labor and capital income are approximately 25.5 percent and 19.3 percent, respectively. In the first period of the transition the tax rate on labor income drops to 21.3 percent and the tax on capital income increases to approximately 29.5 percent. After the first period, the tax on labor is constant, while over time, the tax rate on capital falls a small amount before it stabilizes at its new steady state value of 29.3 percent.
Note: The circles are the tax rates in the steady state under the baseline-fitted U.S. tax policy.Figure 2 plots the evolution of the aggregate economic variables in the benchmark model during the transition. After the initial large increase in the tax on capital, agents save less and capital falls. Because of the change in the tax on labor, agents gradually increase the amount they work throughout the transition. Additionally, total consumption increases while aggregate savings decreases. Over time, as capital levels out, so does consumption to its new level which is approximately 1 percent higher than under the baseline-fitted U.S. tax policy. The decrease in capital and increase in labor over time causes wages to decline and the rental rate to increase.
Note: The figures are the percent change from the steady state under the baseline-fitted U.S. tax policy.Welfare in the transition needs to be examined for two separate groups. The first group is those that are alive at the time of the tax policy change and the second group is those that are born during the transition. The left panel of figure 3 plots the CEV (baseline) for all living individuals at the time the tax change is enacted (the first group). The x-axis for this plot is the age of the cohort when the tax change is enacted. Within the living individuals, the channels by which the tax change effects welfare differ between retired and working individuals. During the transition, there are two counteracting effects on the previously retired generation's welfare. First, the tax on capital increases which reduces the after tax return to their savings. However, since the new steady state level of capital is lower, agents increase consume in order to deplete their savings throughout the transition. The increase in consumption increase their utility.32 For the younger retired generations who live for more periods, the decrease in the value of savings dominates and their welfare drops. Conversely, for the older retired generations, the increase in consumption dominates and their welfare increases.
The working generations that are alive at the time of the tax change also experiences two counteracting forces on their utility. First, the tax on labor decreases which increases the value of the individuals time endowment. However, the increase in the tax on capital decreases the value of their savings. For younger working individuals who have not saved much, the increase in the value of their time endowment dominates and they experience a welfare increase. The older working individuals do not have as many period to work so the increase in the value of their time endowment is less important. Therefore, the decrease in the value of the older working individuals savings dominates and they experience a decline in their welfare during the transition.
Overall, I find that approximately 36 percent of the living population experiences an increase in welfare during the transition compared to the baseline steady state. The population weighted average CEV (baseline) for the living individuals at the time the new tax policy is enacted is -0.36 percent. While the new steady state welfare will be higher in model A0, these results demonstrate that during the transition generally individuals will suffer welfare loses. The right panel of figure 3 plots the welfare effects on individuals who are born during the transition. The x-axis of this plot is the number of years after the tax policy was enacted when the cohort is born. Specifically, the figure plots the CEV (baseline) for each cohort born after the new tax policy is enacted. In contrast to the individuals born prior to the policy change, I find that all these cohorts born later benefit from the tax policy change.
Note: The left panel is the CEV for all living individuals at the time of the tax change. The right panel is the CEV for all newborns after the tax change is enacted. The x-axis for the left panel is the age the cohort is when the tax policy change is enacted. The x-axis for the right panel is the number of years after the tax policy was enacted that the cohort is born.Next, turning to the alternative model (B0), figure 4 plots the capital and labor tax rates during the transition. The upper left and right panels plot the tax rate for capital and labor income, respectively. The circles represent the average marginal tax rates under the baseline-fitted U.S. tax policy and the lines are the marginal tax rates after the tax policy is adjusted. The lower panel of figure 4, excludes the average marginal tax rates under the baseline so that one can focus on the changes in the marginal tax on capital over the transition. The average marginal tax rates on both labor and capital under the baseline tax policy are higher than under the optimal tax policy. It is possible to have a revenue neutral change in the tax policy that consists of a decrease in the average marginal rates on both sources of income for two reasons. First, the baseline-fitted U.S. tax policy is progressive while the optimal tax policy consists of flat taxes. Second, the economy is larger under the optimal tax policy so total income is also larger. After the marginal tax on capital falls in the first period, it continues to fall over the transition until it levels out at the new steady state value of just below 17 percent.
Note: The circles are the tax rates in the steady state under the baseline-fitted U.S. tax policy.Figure 5 plots the evolution of the aggregate economic variables in the alternative model during the transition. During the transition, I find that capital rises at an decreasing rate in response to the decreasing tax rate on capital. Additionally, labor rises over 1.5 percent in the first period after the marginal tax rate on labor decreases. However, over the rest of the transition, total labor supply reverts towards its new steady state level which is approximately 0.8 percent higher than under the baseline-fitted U.S. tax policy. Overall, since both labor and capital increase, the size of the economy increases during the transition. These changes cause the rental (wage) rate to jump up (down) immediately after the change in tax policy but then to fall (rise) to its new level.
Note: The figures are the percent change from the steady state under the baseline-fitted U.S. tax policy.Unlike in model A0, I find that welfare improves for all living individuals when the tax policy is enacted (see left panel of figure 6). Overall, the average CEV (baseline) for living individuals is 0.71 percent indicating that the welfare increase during the transition is similar to the welfare increase in the new steady state after the tax policy change ( 0.71 percent is similar to the transitionless steady state welfare change of 0.95 percent). Additionally, I find that as the economy transitions towards the new steady state, the welfare of new cohorts born increases (see right panel of figure 6) compared to those born at the time the new policy is enacted. These two panels indicate that old individuals at the time of the policy change, and individuals born after the policy change are the groups that experience the greatest gain in welfare. The older individuals who are already retired at the time that the tax policy changes benefit from the initial large increase in the after-tax rental rate on capital. The individuals born later in the transition benefit from higher wages resulting from the larger capital stock. These results indicate that the welfare improvements from the optimal tax policy in the alternative model are similar in the new steady state and over the transition. However, the welfare effects of the new tax policy during the transition are different in model A0 and B0. The next section documents the individual impact of all the model features on optimal tax policy and the economy.
Note: The left panel is the CEV for all living individuals at the time of the tax change. The right panel is the CEV for all newborns after the tax change is enacted.6.2 Determining Individual Impact of Each Assumption
Table 5 describes the optimal tax policies and the aggregate economic variables in the seven iterations of the model that test each feature individually. Column three and four focus on the welfare impacts of the optimal tax policies. Column three, CEV (baseline), is the uniform increase in consumption necessary to make an agent indifferent between the baseline-fitted U.S. tax policy and the optimal tax policy. Within the specific model, column four, CEV (A0), is the percent increase in consumption needed to make an individual indifferent between the inferior optimal tax policy for A0 and the optimal tax policy for that model. Table 6 reports, for each model, what the percent differences in the aggregate economic variables compared to model A0 under the optimal tax policies. In this section I examine the effect of each feature on the optimal tax policy, the aggregate economic variables and life cycle profiles.
| Notes: Each row is the percent change from the benchmark model (A0). For example, A1 is the percent change between A0 and A1. |
6.2.1 Desire to mimic age-dependent tax
The first assumption I alter is changing the utility function such that the Frisch elasticity is constant. I demonstrated in section 2.3.2 that utilizing the constant Frisch utility function instead of the non-constant Frisch utility function eliminates the government's desire to condition taxes on age. Models A0 and A1 are identical except A0 uses the non-constant Frisch utility function and A1 uses the constant Frisch utility function. I find that eliminating this channel reduces the optimal tax on capital by almost 10 percentage points (see table 5).
The different optimal tax policies leads to a lower level of aggregate labor and higher capital stock in model A1 than A0. The different levels of capital and labor translate into a higher wage rate and a lower pre-tax return to capital in A1. The welfare gain from adopting the optimal tax policy is larger in A1 compared to A0. In model A1, the CEV (baseline) is 0.95 percent and CEV (A0) is 0.6 percent.
Figure 7 plots the life cycle profiles for labor supply, consumption and savings in the benchmark model (A0) and the model that eliminates the desire to condition taxes on age (A1). Generally, the life cycle profiles in the two models look similar. In the benchmark model, an agent's Frisch labor supply elasticity is negatively related to the hours they work. Therefore, in the benchmark model, agents become more elastic towards the end of their life when their hours decrease. In model A1, an agent's Frisch labor supply elasticity is constant. Therefore, agents tend to be relatively more elastic in their middle years and less elastic in their later years in model A1 compared to in model A0. Since an agent's wage drop with his human capital late in his working life, agents work fewer hours in their middle years and more hours in their later working years in model A1 (see upper left panel of figure 7).
The change in the marginal after-tax return in A1 affects the shape of the lifetime consumption profile. The intertemporal Euler equation controls the slope of consumption profile over an agent's lifetime. The relationship is,
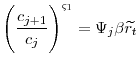 |
(31) |
where
6.2.2 Government consumption of accidental bequests
Next, I examine the effect of relaxing the assumption that the government taxes accidental bequests, at the same rate as ordinary capital income and that the government is not allowed to tax the principal of the bequests. I demonstrated in section 2.4 why these restrictions cause the optimal tax on capital to be non-zero. In model A2, I allow the government to tax these incomes at different rates. In model A2, the government fully consumes these accidental bequests as opposed to redistributing them to living agents. In this model the government raises more revenue than in A0 because they consume accidental bequests instead of only taxing the return on the bequests. In order to make the models comparable, I adjust the government budget constraint in A2 such that the distortionary taxes on ordinary capital and labor income are the same percent of output as in A0. This budget constraint implies that the government will raise more revenue in model A2, however, the part from distortionary taxes will be the same.
Comparing line one and three in table 5 shows that eliminating this motive for a positive tax on capital causes the optimal tax on capital income to drop by approximately ten percentage points. Similar to model A1, the tax on labor income increases. Even in this model, where I include a varying Frisch elasticity the optimal tax on capital drop by over a third. Therefore, the large optimal tax on capital result is not robust to allowing the government a richer policy set.33
Examining tables 5 and 6, the smaller optimal tax on capital and larger optimal tax on labor in model A2 cause agents to save more and work slightly less so aggregate output is slightly larger than in model A0. The larger capital stock and smaller amount of labor causes the pre-tax return on capital to be smaller and the wage rate to be larger. Since agent's have higher levels of savings, their accidental bequests also larger. The CEV (baseline) from adopting the optimal tax policies are similar in A0 and A2. CEV (A0) in A2 is approximately a third as large as CEV (baseline).
Figure 8 plots the life cycle profiles in model A0 and A2. The lower optimal tax on capital in A2 implies that the tax on young labor income is relatively lower. Therefore, the agents work more hours earlier in their life. In A2 there is a larger overall tax burden since the government confiscates accidental bequests. The increase in government consumption causes the consumption profile to be lower in A2. Agents compensate for the lack of income from transfers by accumulating more assets in A2.
6.2.3 Individual Liquidity Constraints
There are two forces that affect the optimal tax on capital in opposite directions when I change the model to allow individual's to borrow. First, agents prefer to smooth their consumption. Therefore, when an agent faces a hump-shaped lifetime earnings profile he would prefer to smooth his consumption by borrowing against earnings from later years to facilitate consumption in earlier years. Borrowing constraints hinder an agent's ability to shift consumption, creating a role for tax policy to help facilitate this shift. Since an individual typically accumulates more assets later in their life, increasing the tax on capital income and decreasing the tax on labor income will allocate more of the lifetime tax burden to an individual's later years, which facilitates consumption smoothing. Therefore, restricting agents from borrowing can motivate a positive tax on capital. However, second, when agents are allowed to borrow I find that agents decrease their labor supply early in their life because they are able to utilize borrowing (see the upper left panel of figure 9). This shift in hours affects the labor supply elasticity in model A3, causing young agents to supply labor more elastically than in model A0. This change in relative elasticity leads to a decrease in the desire to mimic an age-dependent tax on labor income and in turn a decrease in the optimal tax on capital. In order to determine the overall affect, I compare the optimal tax policies in a model where agents are not able to borrow (A0) and one where agents can borrow at the actuarially fair rate (A3). I find that when I eliminate individual liquidity constraints the optimal tax on capital falls nearly 7 percentage points.
The competing effects on the optimal tax policy also mean that the aggregate economic variables are similar in A3 to those in A0. Overall, the optimal tax policy in A3 looks similar to A1 so the aggregate economic variables are also similar. CEV (baseline) is similar in A0 and A3. CEV (A0) is small in model A3 since the optimal tax policies in A0 and A3 are similar.
The lower panel of figure 9 demonstrates that an agent's borrowing constraint is only binding in the first few years of their life. Therefore, eliminating borrowing constraints alters an agents hours and consumption decisions in the first few years of their life (see the upper left panel of 9). After the first five years, the life cycle profiles in model A0 and A3 look similar.
6.2.4 Government Savings and Debt
Assuming that the government has an exogenously set level of savings or debt also alters the optimal tax on capital (see Conesa et al. (2009) for an analytical derivation). In order to quantify the strength of this motive, I examine the optimal tax policy when the government has savings (A4) or debt (A5). I examine the model when government savings or debt equals 550 percent of their annual consumption. I use this number because the relative government debt to government expenditures (less defense consumption) was approximately 550 percent in 2008.34 I assume that the government borrows or saves in the form of productive capital.35 Additionally, I assume that the amount the government raises from distortionary taxes is unaffected by the debt (savings) and only government consumption is affected by the interest payments (rebates).
6.2.4.1 Savings
Comparing models A0 and A4, it is clear that this level of government savings has a large impact on optimal tax policy. Including government savings causes over a 45 percentage point drop in the optimal tax on capital and a 8 percentage point increase in the optimal tax on labor income (see table 5). The aggregate capital stock is over 17 percent larger in A4 because the government now holds capital in addition to private agents (see table 6). The higher tax rate on labor income reduces aggregate labor supply by almost 3 percent. Due to the larger capital stock, output is almost 4 percent larger in A4 compared to A0. Since the capital-labor ratio in A4 is higher wages are approximately 6.5 percent larger and the pre-tax return to capital is almost 30 percent smaller. The smaller tax on capital and lower rental rate on capital have opposing affects on the after-tax return. However, overall the after-tax return to capital is larger in A4. Although total output is larger in A4, the amount devoted to private saving is smaller by approximately 19 percent. The lower level of private savings causes a lower level of bequests. Compared to the baseline-fitted U.S. tax policy, the optimal tax in A4 is much different so the CEV (baseline) is almost two and a half times as large as in A0. Additionally, CEV (A0) is larger than CEV (baseline).
Examining the upper right and bottom panels of figure 10, it is clear that the lower private saving in A4 causes the consumption and asset accumulation profiles to be lower. Overall, the after-tax return to labor is lower in A4 which translates into the labor supply profile being lower.
6.2.4.2 Debt
Including government debt in the model causes an opposite reaction in the aggregate economic variables compared to when the government holds savings. The tax on capital increases over 24 percentage points and the lax on labor decreases by approximately 12 percentage points (see table 5) in model A5. Comparing the fourth and fifth line of table 6, it is clear that adding government debt causes the economic aggregate variables to have an opposite reaction (generally with a similar magnitude) compared to the model with government holding savings. Once again, the optimal tax policy in model A5 is much different than the baseline-fitted U.S. tax policy compared to the optimal tax policy in A0, so the CEV (basline) is almost four times as large in A4. CEV (A0) is also larger in this model.
The impact of the government holding debt on the life cycle profiles under the optimal tax policy is also opposite to the effect when the government holds savings (compare figures 10 and 11). The government holding debt causes an increase in the amount of private saving so both the consumption and asset profiles are higher in A5 compared to A0. The hours profiles look almost identical in A0 and A5.
6.3 Social Security Program
Model A6 examines the impact of the social security program on the optimal tax policy by eliminating it from model A0. Eliminating the social security program has a small impact on the optimal tax policy. When the program is excluded, the optimal tax on capital increases approximately 1.5 percent. With the exception of transfers, the aggregate economic variables look similar in A0 and A5. Since agents no longer receive social security benefits, they need to increase their level of saving in order to finance consumption once they retire. Therefore, agents hold substantially more savings after they retire to finance their consumption. Additionally, the larger savings causes an increase in accidental bequests. CEV (baseline) in model A6 is similar to in model A0. CEV (A0) is small ( 0.08 percent) since the optimal tax policies in A0 and A6 are so similar.
Without a social security program, the government would like to decrease the tax on capital (or provide a rebate on capital income) in order to mimic the welfare improving social security program. However, the motives for a positive tax on capital demonstrated in A2 and A3 are enhanced in this model and overall cause the optimal tax on capital to increase. Accidental bequests are higher in this model so the motive for a positive tax on capital demonstrated in A2 is enhanced. Also, agents must finance their own retirement with personal savings so the agents have more incentive to save. However, I recalibrate the model such that capital to output is consistent across all the models under the baseline-fitted U.S. tax policy. In order to induce a similar level of capital, the discount rate falls in model A6 (see table 3). The change in the discount rate coupled with the increased need for savings late in an agent's life causes the life cycle savings profile to shift to the right (see the lower box in figure 12). This shift means that agents face binding liquidity constraints for more years and the motive for a positive tax on capital demonstrated in model A3 is also enhanced. Overall, these three motives generally cancel each other out.
Excluding the social security program causes the life cycle consumption and savings profiles to have less realistic shapes. The upper left and right panel in figure 12 demonstrate that without a social security program the labor profile and consumption profile
are flatter when agents are working. The profiles are flatter because of the decrease in ![]() . Since agents face lifetime uncertainty and finance their own retirement consumption in model
A6, their consumption falls much more dramatically towards the end of their life. Additionally, agents accumulate more assets to finance retirement so their lifetime savings profile shifts to the right in model A6.
. Since agents face lifetime uncertainty and finance their own retirement consumption in model
A6, their consumption falls much more dramatically towards the end of their life. Additionally, agents accumulate more assets to finance retirement so their lifetime savings profile shifts to the right in model A6.
6.4 Summary of Results
Overall, I find that assuming the Frisch elasticity is non-constant, and that the government cannot distinguish accidental bequests are significant motives for a positive tax on capital. Including individual budget constraints also motivate a positive tax on capital but to a lesser extent. Including exogenously determined levels of government savings (borrowing) causes the optimal tax on capital to decrease (increase). Additionally, including a reduced form social security program is important because it causes the life cycle profiles to be more realistic.
7 Sensitivity Analysis
Next, I check the sensitivity of the results with respect to the parameter value that governs the Frisch labor supply elasticity. I choose to examine the sensitivity of the results with respect to this parameter because there is some uncertainty about the actual value of the Frisch elasticity.
In this section I test how using different Frisch elasticity parameters affects the optimal tax policy in the benchmark model and the impact of each of the model features on optimal tax policy. I solve for the optimal tax policy in model A0 with three different value of
![]() of 6, 3 and 2. These values imply a Frisch elasticity of
1/3,
2/3 and 1, respectively, if an agent works a third of their time endowment. I also solve for models A1-A6 with the different values.36 Prior to solving the models, I calibrate the models with the three different targets for the Frisch elasticity. Tables 7 and 8 lists these parameters. Generally, I find that a lower elasticity target implies a higher discount rate parameter and lower disutility to labor parameter.
of 6, 3 and 2. These values imply a Frisch elasticity of
1/3,
2/3 and 1, respectively, if an agent works a third of their time endowment. I also solve for models A1-A6 with the different values.36 Prior to solving the models, I calibrate the models with the three different targets for the Frisch elasticity. Tables 7 and 8 lists these parameters. Generally, I find that a lower elasticity target implies a higher discount rate parameter and lower disutility to labor parameter.
7.1 Effect on Optimal Tax Policies in Benchmark Models
Table 9 presents the optimal tax policies in the benchmark model calibrated to target the three different Frisch elasticities. I find that the optimal tax on capital is larger when the model is calibrated to a higher Frisch elasticity. There are two reasons that the optimal tax on capital increases. When the government is deciding between taxing capital and labor income, they are weighing the relative distortions that each tax induces on the economy. An agent will be more sensitive to a tax on labor income when the Frisch elasticity is higher. Therefore, the government prefers to reduce the tax on labor income and increase the tax on capital under the two calibrations that target a higher Frisch elasticity.
| Tax Rates | Frisch
|
Frisch
|
Frisch |
| 22.5% | 29.3% | 30.5% | |
| 22.8% | 21.3% | 20.9% |
The second reason that the optimal tax on capital increases is that the higher Frisch elasticities enhances the motive for an age-dependent tax on labor income. Figure 13 plots the life cycle profiles for the three different calibrations. The upper left panel of the figure demonstrates that as the model is calibrated to match a higher Frisch elasticities the relative change between the hours he works when he is young and old increases. A larger drop in hours enhances the motive for an age-dependent tax on labor income. Since the government cannot condition labor income taxes on ages, they increase the tax on capital.
7.2 Frisch Elasticity effect on Channels' Impact
In order to determine how changing the Frisch elasticity alters the impact on optimal tax policy of each of the channels I solve for models A0, A1, A2, A3, A4, A5 and A6 under the three different Frisch elasticity targets. Table 10 describes the optimal tax policies in the six models under the three different calibrations. Table 11 presents the percentage changes in the optimal tax policies between the benchmark model (A0) and the various models (A1-A6) under all three calibrations. Generally as the model is calibrated to match a lower Frisch elasticity, each of the channels have a larger impact on the optimal tax policy.
| Notes: Each row is the optimal tax policy for a model similar to the benchmark model with one channel removed. Low is calibrated with a target Frisch elasticity of 1/3, medium it calibrated with a target Frisch elasticity of 2/3 and high is calibrated with a target Frisch elasticity of 1. |
| Notes: Each row is the percentage change form the benchmark model. For example, A1 is the percentage change in the optimal tax policy between A0 and A1. |
The optimal tax on capital decreases in models A1, A2, A3, and A4 for all the calibrations. The optimal tax on capital increases in model A5 for all the calibrations. The optimal tax on capital increases in A6 for the low and medium calibrations and decreases for the high calibration. When the social security program is removed, the motives for a positive tax on capital from the non-constant Frisch elasticity profile and restrictions on taxing capital are enhanced (see section 6.3). However, the government also wants to mimic a welfare improving social security program by reducing the tax on capital. These three motives have competing effects on the optimal tax on capital. In the models calibrated to match the high target the desire to mimic the social security program dominates and the optimal tax on capital drops. When the models are calibrated to match the low and medium targets the effect of the non-constant Frisch elasticity profile and the restrictions on how the government can tax accidental bequests dominate so the optimal tax on capital increases.
8 Conclusion
Through an analysis of the optimal tax on capital in a standard life cycle model, this paper concludes that if one alters the utility function such that the Frisch elasticity profile is constant and allows the government to tax accidental bequests at a separate rate from ordinary capital income
then the optimal tax on capital falls from 29.3 percent to 16.4 percent. It is
important to quantify the impact of these two model features because there is not a consensus on whether the labor supply elasticity profile is upward sloping and prohibiting the government from taxing accidental bequests at a different rate from ordinary capital income confounds the government's
desire to confiscate the bequests with a positive optimal tax on capital. Although the optimal tax on capital is not zero in the model without these features, it is no longer large. Comparing steady states under the baseline-fitted U.S. tax policy and the optimal tax policy, the CEV is ![]() percent and 0.95 percent for the benchmark and alternative models, respectively. In the
case of the benchmark model, over the transition, I find that adopting the optimal tax policy causes welfare to decrease for agents who are already living at the time of the tax policy change. In contrast, I find that in the alternative specification adopting the new tax policy increases the
welfare of living individuals.
percent and 0.95 percent for the benchmark and alternative models, respectively. In the
case of the benchmark model, over the transition, I find that adopting the optimal tax policy causes welfare to decrease for agents who are already living at the time of the tax policy change. In contrast, I find that in the alternative specification adopting the new tax policy increases the
welfare of living individuals.
I also find that if the government holds savings (debt) then the optimal tax on capital decreases (increases). Removing individual liquidity constraints cause the optimal tax on capital to fall. I show that it is important to include at least a reduced form social security program in a life cycle analysis of optimal tax policy otherwise the life cycle profiles will be unrealistic. Overall, I find that in the various models, the welfare loss from adopting the optimal tax policy determined in the benchmark model as opposed to the actual optimal tax policy for that specific model range from .08 percent to 2.53 percent of total lifetime consumption. Finally, I find that generally as the models are calibrated to match a lower Frisch elasticity the effect of changing the various features is larger.
When modelling certain aspects of the economy, economists try to balance realism and tractability. I demonstrate that some of these simplifying assumptions have a sizable impact on optimal tax policy. For example assuming that the government cannot distinguish between ordinary capital and accidental bequests has large implications for optimal tax policy. Therefore, further research should focus on modelling this feature more realistically. Additionally, the shape of the Frisch labor supply elasticity profile has a large impact on the optimal tax policy. Since there is little existing empirical evidence addressing whether the Frisch elasticity varies, it is an important question for economists to examine.
A. Computational Algorithm
In order to determine the competitive equilibrium for each set of tax parameters I use a modified algorithm based on Heer and Maussner's algorithm to compute a stationary equilibrium for the overlapping generation model.37 The algorithm consists of the following steps:
- Make initial guesses of the steady state values of the aggregate capital stock, labor, transfers and social security benefits.
- Make initial guess for tax rate.
- Solve for the prices and social security tax rate.
- Compute the optimal path for consumption, savings, and employment for the new-born generation by backward induction given the initial capital stock is zero.38
- Compute the tax rate that clear the markets and compare to initial guesses. If change of tax rate is not within the tolerance then return to step 4.39
- Update the aggregate capital stock and labor and return to step 3 until convergence.
In order to determine the optimal tax policy, I solve each model's steady state in Matlab. I use a grid search method in order to determine the optimal tax policy. The models are solved with Matlab using a grid search to determine the optimal tax on policy.
B.1 Benchmark Simple Model
The Lagrangian for the benchmark simple model is
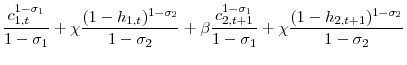 |
(32) | |
The first order conditions with respect to
and
Combining the first order equations for the government's problem with respect to consumption (equations 36 and 37) yields
Further, combining the agent's first order conditions, equations 5, and 6, under the non-constant Frisch utility specification yields
Combining equation 39 and 38 gives
Next, I combine the first order conditions for the government with respect to young and old hours,
Therefore, equation 40 and equation 41 simplify to
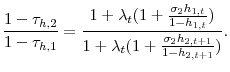 |
(42) |
Utilizing the first order conditions from the Lagrangian with respect to capital and consumption leads to the following equation,
Applying the non-constant Frisch utility function to equation 7 provides the following relationship
Equations 43 and 44 demonstrate that for the agent to choose the optimal allocation determined from the primal approach the tax on capital must equal zero. Therefore, if the government can condition labor income taxes on age, then the optimal tax on capital is zero for the non-constant Frisch utility specification.
B.2 No Age Conditional Labor Income Taxes
When the government cannot condition labor income taxes on age, the equation 11 must be included as a constraint in the Lagrangian. The Lagrangian for this model is,
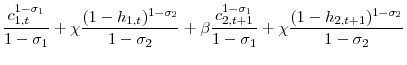 |
(45) | |
| (46) |
The first order conditions with respect to
and
Combining equations 49, 50, and 51 yields,
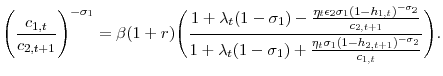 |
(52) |
B.3 Constant Frisch Utility Function
The Lagrangian for this specification is
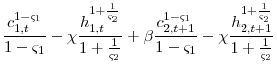 |
(53) | |
 |
The first order conditions with respect to labor, capital and consumption are
and
Combining the first order equations for the governments problem with consumption (equations 57 and 58) yields
Taking the ratio of the agent's first order conditions, equations 5 and 6, under the constant Frisch utility specification gives
Combining equation 59 and 60 yields
The ratio of first order equations for the government with respect to young and old hours is
Combining equation 62 and 61 generates the following expression for the optimal labor taxes
 |
(63) |
B.4 Unrestricted Tax Policy with Accidental Bequests
The Lagrangian for this specification is
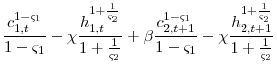 |
(64) | |
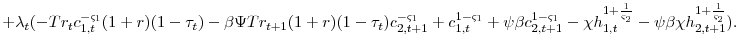
|
The first order conditions with respect to labor, capital and consumption are
and
Combining the first order equations for the governments problem with consumption (equations 68 and 69) yields
Combining the government's first order conditions with respect to labor yields,
Taking the ratio of the agent's first order conditions, equations 5 and 6, under the constant Frisch utility specification gives
Combining equations 70, 71, and 72 yields the following expression for the optimal labor income taxes,
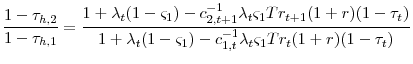 |
(73) |
B.5 Restricted to Taxing Only Return on Accidental Bequests
The Lagrangian for this specification is
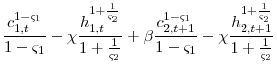 |
(74) | |
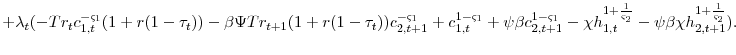
|
The first order conditions with respect to labor, capital and consumption are
and
Combining the first order equations for the governments problem with consumption (equations 78 and 79) yields
Combining the government's first order conditions with respect to labor yields,
Taking the ratio of the agent's first order conditions, equations 5 and 6, under the constant Frisch utility specification gives
Combining equations 80, 81, and 82 yields the following expression for the optimal labor income taxes,
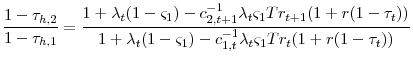 |
(83) |
B.6 One Rate on All Returns
The Lagrangian for this specification is
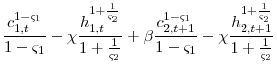 |
(84) | |
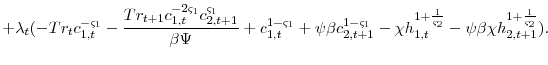
|
The first order conditions with respect to labor, capital and consumption are
and
Combining the first order equations for the governments problem with consumption (equations 88 and 89) yields
![\displaystyle \Big(\frac{c_{1,t}}{c_{2,t+1}}\Big)^{-\varsigma_{1}}=\Psi\beta(1+r)\Bigg[ \frac{1+\lambda_{t}(1-\varsigma_{1})- \frac{Tr_{t+1}\lambda_{t}\varsigma_{1}}{\beta\Psi}^{-2}c_{2,t+1}^{-1}c_{1,t}^{-2\varsigma_{1}}} {1+\lambda_{t}(1-\varsigma_{1})+\lambda_{t}\varsigma_{1}(Tr_{t}c_{1,t}^{-1} + \frac{Tr_{t+1} 2c_{2,t+1}^{\varsigma_{1}}c_{1,t}^{-1-\varsigma_{1}}}{\beta\Psi}} \Bigg]](img240.gif)
|
(90) |
Bibliography
Carnegie-Rochester Conference Series on Public Policy: Advances in Dynamic Public Finance April 20-21, 2007.
Dynamic General Equilibrium.
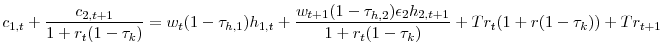
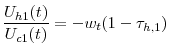
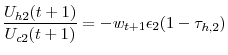
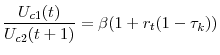
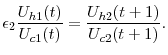
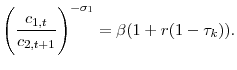
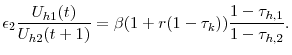
![\displaystyle \Big(\frac{c_{1,t}}{c_{2,t+1}}\Big)^{-\varsigma_{1}}=\Psi\beta(1+r)\Bigg[ \frac{1+\lambda_{t}(1-\varsigma_{1})- c_{2,t+1}^{-1}\lambda_{t}\varsigma_{1}Tr_{t+1}(1+r)(1-\tau_{t})}{1+\lambda_{t}(1-\varsigma_{1})- c_{1,t}^{-1}\lambda_{t}\varsigma_{1}Tr_{t}(1+r)(1-\tau_{t})}\Bigg].](img58.gif)
![\displaystyle \Big(\frac{c_{1,t}}{c_{2,t+1}}\Big)^{-\varsigma_{1}}=\Psi\beta(1+r)\Bigg[ \frac{1+\lambda_{t}(1-\varsigma_{1})- c_{2,t+1}^{-1}\lambda_{t}\varsigma_{1}Tr_{t+1}(1+r(1-\tau_{t}))}{1+\lambda_{t}(1-\varsigma_{1})- c_{1,t}^{-1}\lambda_{t}\varsigma_{1}Tr_{t}(1+r(1-\tau_{t}))}\Bigg].](img62.gif)
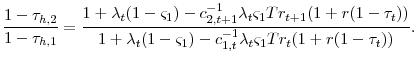
![\displaystyle \Big(\frac{c_{1,t}}{c_{2,t+1}}\Big)^{-\varsigma_{1}}=\Psi\beta(1+r)\Bigg[ \frac{1+\lambda_{t}(1-\varsigma_{1})- \frac{Tr_{t+1}\lambda_{t}\varsigma_{1}}{\beta\Psi}^{-2}c_{2,t+1}^{-1}c_{1,t}^{-2\varsigma_{1}}} {1+\lambda_{t}(1-\varsigma_{1})+\lambda_{t}\varsigma_{1}(Tr_{t}c_{1,t}^{-1} + \frac{Tr_{t+1} 2c_{2,t+1}^{\varsigma_{1}}c_{1,t}^{-1-\varsigma_{1}}}{\beta\Psi})} \Bigg].](img66.gif)
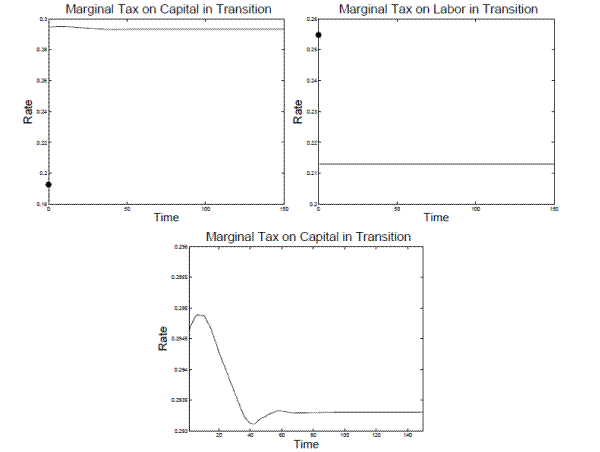
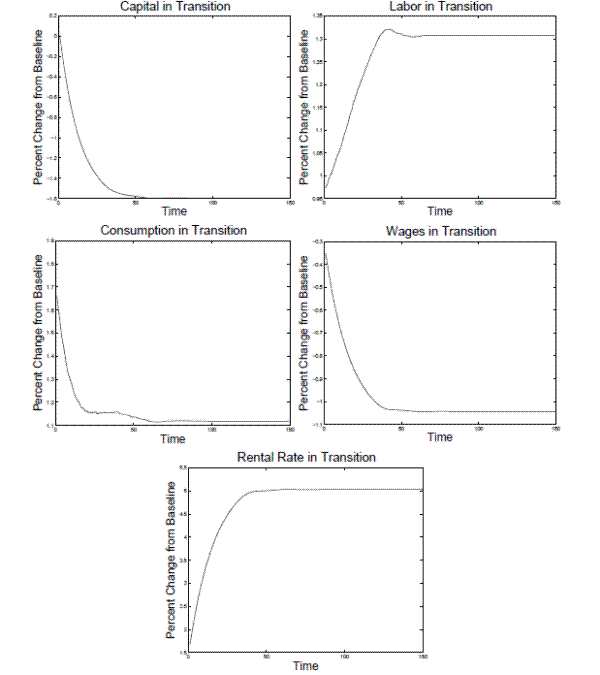

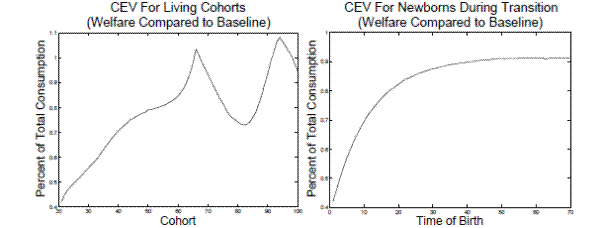
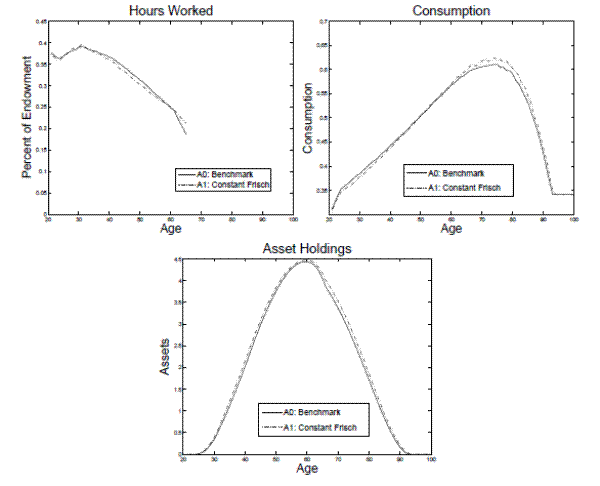
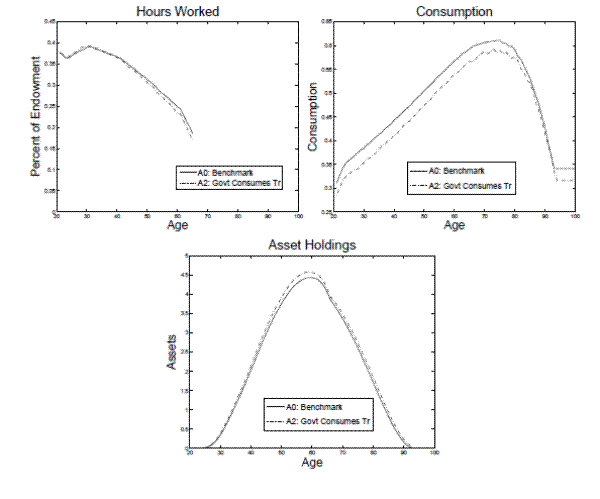
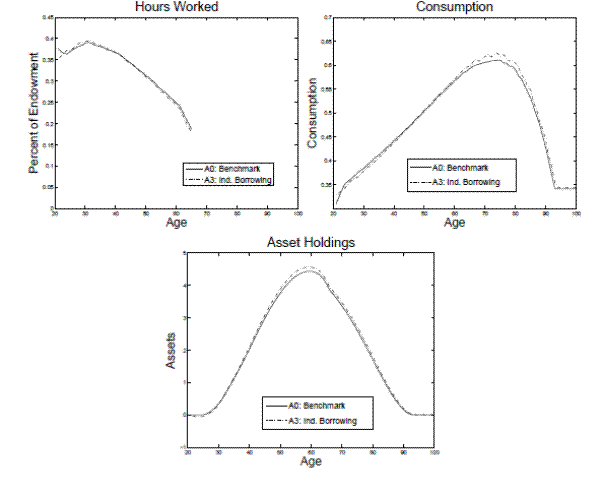
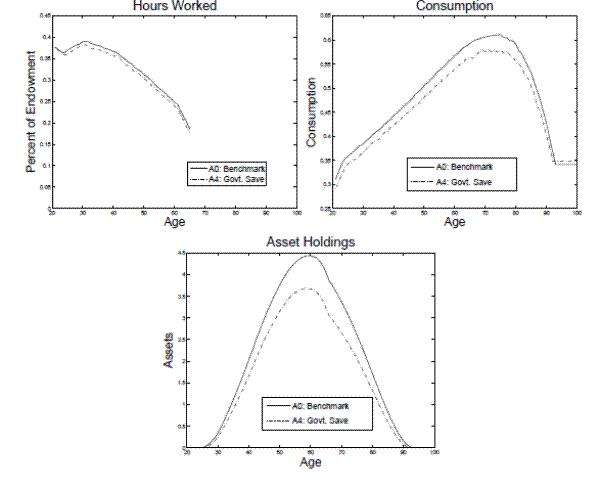
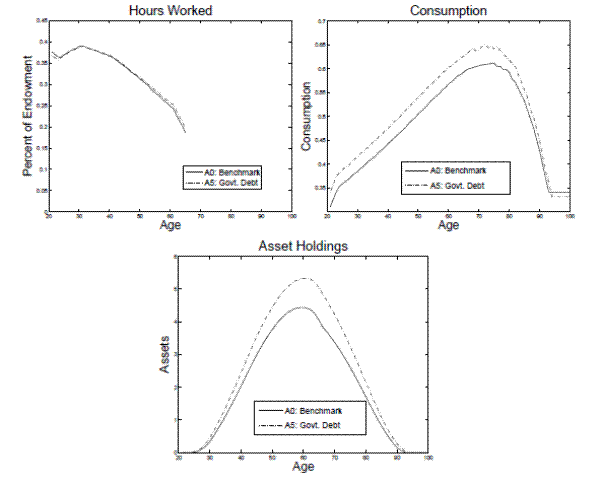
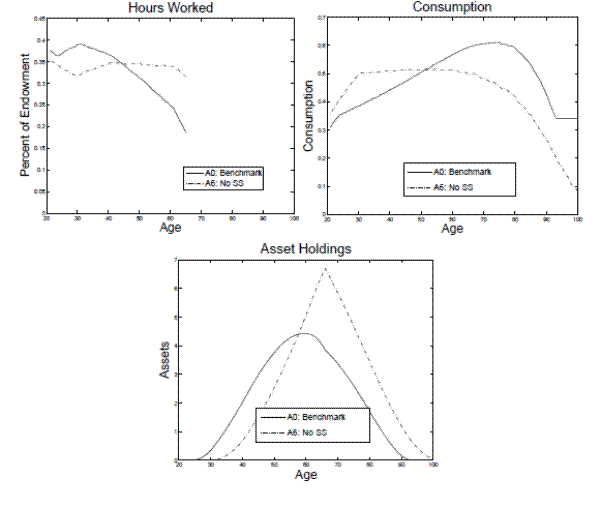
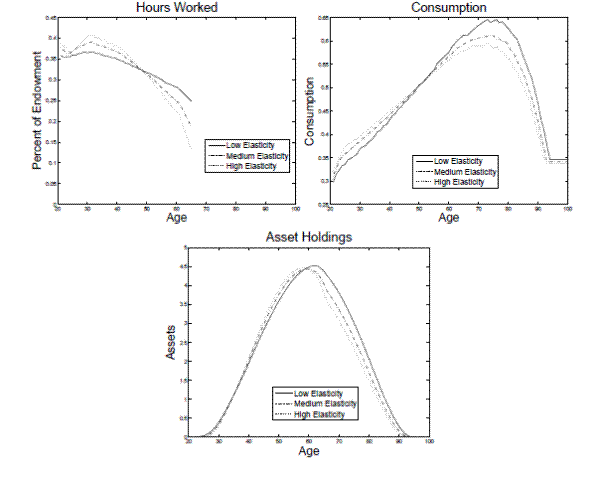
![\displaystyle \rho_{t}=\chi(1-h_{1,t})^{-\sigma_{2}}\Bigg[1+\lambda_{t}\bigg(1+\frac{\sigma_{2}h_{1,t}}{(1-h_{1,t})}\bigg)\Bigg],](img201.gif)
![\displaystyle \rho_{t+1}\theta=\chi(1-h_{2,t+1})^{-\sigma_{2}}\frac{\beta}{\epsilon_{2}}\Bigg[1+\lambda_{t}\bigg(1+\frac{\sigma_{2}h_{2,t+1}}{(1-h_{2,t+1})}\bigg)\Bigg],](img202.gif)

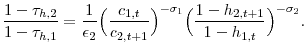
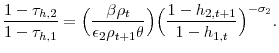
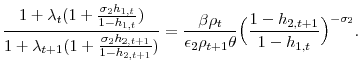
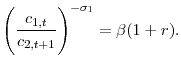
![\displaystyle \rho_{t}=\chi(1-h_{1,t})^{-\sigma_{2}}\Bigg[1-\eta_{t}\epsilon_{2}\sigma_{2}\frac{c_{2,t+1}^{-\sigma_{1}}}{(1-h_{1,t})} +\lambda_{t}(1+\frac{\sigma_{2}h_{1,t}}{(1-h_{1,t})})\Bigg],](img213.gif)
![\displaystyle \rho_{t+1}\theta\epsilon_{2}= \chi(1-h_{2,t+1})^{-\sigma_{2}}\beta\Bigg[1+\eta_{t}\sigma_{2}\frac{c_{1,t}^{-\sigma_{1}}}{(1-h_{2,t+1})} + \lambda_{t} (1+\frac{\sigma_{2}h_{2,t+1}}{(1-h_{2,t+1})})\Bigg],](img214.gif)
![\displaystyle \rho_{t}=c_{1,t}^{-\sigma_{1}}\Bigg[1+\lambda_{t}(1-\sigma_{1})+\frac{\eta_{t}\sigma_{1}(1-h_{2,t+1})^{-\sigma_{2}}}{c_{1,t}}\Bigg],](img216.gif)
![\displaystyle \theta\rho_{t+1}=\beta c_{2,t+1}^{-\sigma_{1}}\Bigg[1+\lambda_{t}(1-\sigma_{1})-\frac{\eta_{t}\epsilon_{2}\sigma_{1}(1-h_{1,t})^{-\sigma_{2}}}{c_{2,t+1}}\Bigg].](img217.gif)
![\displaystyle \rho_{t}=\chi h_{1,t}^{\frac{1}{\varsigma_{2}}}\Bigg[1+\lambda_{t}(1+\frac{1}{\varsigma_{2}})\Bigg]](img220.gif)
![\displaystyle \rho_{t+1}\theta\epsilon_{2}=\beta\chi h_{2,t+1}^{\frac{1}{\varsigma_{2}}}\Bigg[1+\lambda_{t}(1+\frac{1}{\varsigma_{2}})\Bigg],](img221.gif)
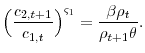
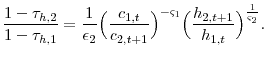
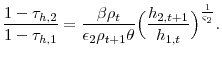
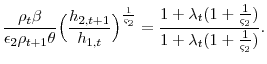
![\displaystyle \rho_{t+1}\theta\epsilon_{2}=\beta\Psi \chi h_{2,t+1}^{\frac{1}{\varsigma_{2}}} \Bigg[1+\lambda_{t}(1+\frac{1}{\varsigma_{2}})\Bigg],](img229.gif)