Commodity Index Trading and Hedging Costs1
Keywords: Commodity index traders, hedging costs, volatility
Abstract:
Trading by commodity index traders (CITs) has become an important aspect of financial markets over the past 10 years. We develop an equilibrium model of trader behavior that relates uninformed CIT trading to futures prices. The model predicts that CIT trading reduces the cost of hedging. We test the model using a unique non-public dataset which precisely identifies trader positions. We find evidence, consistent with the model, that index traders have become an important supply of price risk insurance.
JEL: G13, C32
I. Introduction
In recent years, futures contracts in commodities have increasingly become integrated into investment portfolios (Büyüksahin, Haigh, Harris, Overdahl, and Robe 2009). The amount of money invested globally in commodity indices has grown more than 10 fold between 2003 and 2008 (CFTC, 2008). Commodity index traders (CITs), which have been the main vehicle for investing in commodities, represent a new type of player in these markets (Stoll and Whaley 2010). Because index traders now represent a large portion of the futures trading, questions have arisen regarding the effect they have on financial markets. For example, the impact of index trading on the cost of diversifying (hedging) is an important policy issue, since diversification is a critical function of futures markets. Masters (2008), Singleton (2011) and others have expressed concerns that index trading leads to distortions in pricing, which can affect hedging costs. The goal of this paper is to study the effect of commodity index trading on financial markets. In this regard the paper provides several contributions to the existing literature.
First, we empirically analyze the effect of the increased market participation of commodity index traders on the cost of hedging. Using a unique proprietary dataset that precisely identifies the daily trading activity of commodity index traders, we find evidence that the presence of CITs reduces hedging costs.5 While most of the literature on the role of CITs in futures markets concentrates on its price effect,6 we believe that the cost of hedging should play a central role in the analysis.
Second, we generalize Grossman and Miller (1989) to develop an equilibrium model of trader behavior that relates uninformed CIT trading to futures prices. Theoretical models, dating back to Keynes (1930) and Hicks (1939) have focused on the role of futures markets in allowing firms to hedge their positions in the physical commodity; in particular, agents with inherent long positions in the physical product, such as raw material producers, reduce the riskiness of their portfolios by taking short positions in the futures market. The long side of these trades is taken by speculators, who are willing to hold these futures positions in exchange for positive expected returns. Hence, these models imply that, even absent superior information about futures price movement, speculators will earn positive returns.7 These positive returns come about through a futures price which is below the expected spot price at contract expiration - or what is termed backwardation. More formal models, such as Hirshleifer (1988) or Etula (2010), show that this conclusion remains, even in a model with many risky assets and opportunities for diversification. None of these models, however, studies commodity index trading. Instead, these models are based upon the dichotomy between hedgers and speculators, with variations that include noise traders, herding behavior, and other anomalies.8 CITs behave differently. Like speculators in these models (and unlike hedgers), CITs have no fundamental exposure in the underlying commodity. Unlike speculators, CITs seem to follow simple rules that are unrelated to information. That is, as Stoll and Whaley (2010) note, CITs primarily buy and hold a long position in the closest-to-maturity (nearby) contract, which entails their rolling this position from one maturity to the next, as the nearby contract nears expiration. The premise that their trading is not motivated by superior information is evidenced by their trading rules which are determined and publically disseminated well prior to the trades being executed.9
Our model analyzes how these traders interact with traditional hedgers and speculators.
The direct implication of our model is that the cost of hedging falls as CIT positions increase. The intuition behind our theoretical result comes from the fact that CITs are essentially willing to take the opposite position from hedgers at lower prices than are traditional speculators. More subtle implications of our model relate to the effect of commodity index traders on inter-maturity spreads. As noted, a key characteristic of CITs is that they primarily hold positions in the nearby contract, which usually is the most liquid contract, and periodically roll these positions to the next maturity (first deferred) contract. This exogenous movement of positions between maturities provides a natural experiment with which to examine whether inter-contract spreads vary in the manner implied by the model. In particular, our model implies that the spread between the first deferred and the nearby contract depends on both the relative sizes of CIT positions in the two maturities, and on the aggregate size of CIT positions, albeit in a way that varies across the contract cycle.10 More generally, since contract prices of different maturities are not perfectly correlated (and hence are not perfect substitutes from hedgers' perspectives) CITs' choices of which contracts to invest in will differentially impact prices along the term structure. In addition, the model implies that the size of the effect of CITs on the spread varies with the product cycle; for example, for agricultural commodities, the effect is larger just prior to the harvest, because the correlation between the return on the hedger's position and the nearby futures market is higher. Similarly, in non-agricultural markets, the effect is larger for maturities that expire just prior to seasonal demand peaks, due to higher hedging demand. Finally, the model shows that the spread varies with the size of the cash market position of hedgers.
The last contribution of our paper is to test the hypotheses generated by the model using the highly disaggregated data on trader positions provided by the Commodity Futures Trading Commission. Our findings generally support the premise that commodity index traders earn returns by taking on risk that would otherwise either remain with hedgers, or be taken on by speculators at higher prices. In particular, we find that hedging costs are positive, and that the price of hedging is increasing in the cash market position of hedgers, and decreasing in the positions of index traders. In addition, as implied by the model, the inter-maturity spread increases with the percentage of CIT holdings in the first deferred contract, and this effect is particularly large later in the harvest cycle or, more generally, when seasonal demand peaks.
As Hirshleifer (1988) shows, changes in hedging demand can only have price effects when supply is less than perfectly elastic. Our finding that the relative prices of different maturities vary predictably with CIT positions is consistent with the premise that liquidity providers have less-than-perfectly-elastic supply curves.
Although our analysis concentrates on commodity futures markets, this finding can shed light on issues relevant to equities and, in particular, to equity indices. Just as commodity index funds change their portfolios as contract expiration nears, equity index funds change their portfolios in response to publicly observable events. In particular, there is a considerable literature showing that the addition of a stock to a major index increases its share price - see e.g., Shleifer (1986) Harris and Gruel (1986), Greenwood (2005). One interpretation of this phenomenon, which is consistent with the model developed here, is that the redefinition of the index leads to an increase in the demand for that stock, as some mutual funds are contractually obligated to have a portfolio that is representative of a specific index. Thus, the increased share price results from a liquidity effect: i.e. the interaction of this higher demand with a less-than-perfectly elastic supply of existing shares of individual stocks.11 An alternative explanation is that the addition of the firm to the index represents real information about the long-term prospects of the stocks (Jain 1987) - e.g., stocks added to the index are, ceteris paribus, less likely to face bankruptcy, or will have lower spreads due to increased liquidity (see, e.g., Dhillon and Johnson 1991). In the case of commodity index funds, there is no parallel to this latter interpretation. As noted above, the timing of the roll by major CITs is announced well in advance. Hence, it would seem that there is no information content in these trades, and any price change can only be attributed to a liquidity effect.
We proceed as follows. Section II describes the Large Trader Reporting System which is used to collect data on trader positions. In Section III we empirically test whether the size of CIT positions affects hedging costs, and find that larger CIT positions does reduce hedging costs. This finding motivates the development of a model of uninformed trading and price behavior in Section IV. We test the model in Section V and conclude in Section VI.
II. Trader Positions
The position data used in this study comes from the US Commodity Futures Trading Commission's (CFTC) Large Trader Reporting System (LTRS). This non-public database contains end-of-day positions for each large trader, where large is defined as having a position greater than some threshold number of contracts, with the threshold differing across contracts.12 Large traders typically represent about 70-75 percent of the open interest in the contracts evaluated in this study. The LTRS reports the long and short positions of each large trader in each maturity futures contract, including the delta-adjusted options positions. We examine data for the period July, 2003 through December 2008.
The data used here have several advantages over the more aggregate data that is publicly-available, and has been used elsewhere (see e.g., Stoll and Whaley 2010). Specifically, we use daily data, while the publicly-available data refers to weekly observations. Second, our data is disaggregated by maturity. In combination, these features allow us to more accurately measure movements of individual trader's (or groups of traders) positions between maturities, and hence estimate the effect of hedger and CIT positions in specific maturities on prices and inter-month spreads.. Finally, our data is available at the individual trader level, which, as discussed below, allows us to measure CITs over a longer period of time.
In addition to reporting their futures and options positions, traders self-report their lines of business. Table 1 lists the nine trader categories that are important in agricultural products, along with the average number of traders and average net positions of all large traders (summed across maturities) in each category for the three most actively-traded field crops. Large traders in the first five categories are involved in some aspect of the grain industry (and are denoted commercial traders), and it is likely that their positions primarily reflect a desire to reduce their inherent risk, i.e. they are hedgers. For example, owners of grain storage facilities (category AD, whom we refer to as agricultural distributors), typically acquire long positions in physical grain, and therefore take short positions in futures markets to hedge their price exposure. Hence, to some extent, trader positions in these futures markets are natural reflections of their underlying business. As indicated in Table 1, short futures positions by distributors represent about 31 percent of open interest in wheat and corn, and about 23 percent in soybeans.13 Other commercial traders likewise tend to take short futures positions, especially in soybeans and wheat.
There are other participants in futures markets who have no fundamental exposure in the physical commodity and are referred to as non-commercials (speculators). The non-commercial category Floor Brokers and Traders (FBT) consists of traders who have no physical presence in the industry, but instead take long or short positions in order to take advantage of what they view as favorable prices (these traders are sometimes referred to as locals). They typically make bids and offers on the same day, serving as market makers by effectively providing liquidity to other market participants. Two other categories of non-commercial traders, MMT and NRP, are firms that manage investment portfolios, often referred to as hedge funds.14
Like other non-commercial traders, CITs have no physical presence in these agricultural markets. This category is different from the other categories in that it is not a self-reported category. Instead, it reflects an effort by the CFTC to develop statistics to monitor an important change in agricultural futures markets. Specifically, as commodity index traders began to hold a larger portion of open interest, the CFTC as well as many industry participants, became interested in enhanced tracking of the positions of these traders. Accordingly, in 2006, the CFTC reclassified some traders into this new category for 12 agricultural products. There was no corresponding reclassification in other futures markets, such as energy or financial futures. Hence, the clearest picture of the effect of CIT trading occurs on agricultural markets, and consequently, we focus on the three largest agricultural markets. However, our model and empirical methodology are general and apply to other markets as well.
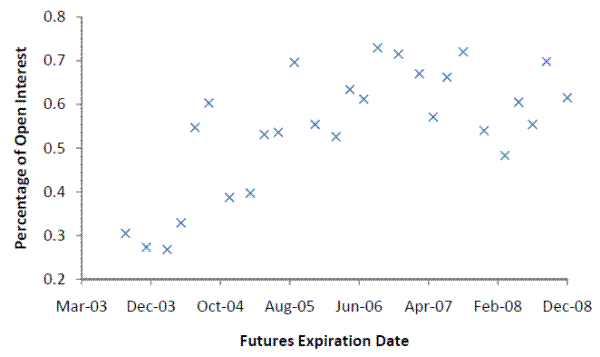
The determination as to which traders constitute CITs is based on identifying all traders with large long positions in agricultural futures contracts and evaluating whether the trades made by those firms were consistent with index trading, as well as a series of interviews with the traders (CFTC 2006). In this study, we categorize firms as CITs throughout the sample if they met the CIT criteria as of 2006 (as discussed below, the evidence suggests this treatment is appropriate). Once CITs are identified, we can track their positions back to dates prior to 2006. This allows us to have a longer time series of observations on CIT behavior. Figure 1 presents some evidence on the relative importance of CITs in the corn market. The vertical axis represents the largest end-of-day position held by CITs in each nearby contract, as a percentage of total open interest on that date. CIT's long position in the nearby corn futures contract represented about 25 to 30 percent of the total open interest in 2003. The percentage grew fairly consistently through late 2006, and fell somewhat over the last two years of the sample. One noteworthy aspect of this pattern is that it does not appear that 2006 represents a structural break in the series; instead, CIT's aggregate position in 2006 seems to be a continuation of the previous trend. The history of CIT positions in soybeans and wheat is quite similar.
III. The Price of Hedging
The traditional view of futures markets is that they allow traders with innately risky positions to hedge that risk. The canonical example is a grower who owns crops that will mature at some future date, and consequently, faces price risk until the crop is sold. By taking a short position in the futures market in that commodity, this grower is able to essentially sell the crop earlier in the season, and thereby reduce her exposure to price risk. Her counterparties on the futures market may also be reducing their risk. That is, by taking a long position in the futures market, a firm that plans to buy the crop after it matures (like a flour mill) can likewise reduce its exposure to price risk by buying the crop in advance. If these two kinds of hedgers are the only traders, then the futures price of the crop would reflect the relative demands of the two groups. However, the price that clears the market when only hedgers are present may be sufficiently high or low (relative to expected spot prices) that traders with no innate interest in the commodity may find it profitable to trade on one side of the market. The premise of the theory of normal backwardation, advanced by Keynes (1930) and Hicks (1939) is that the relative demands of long and short hedgers are such that futures price will be below the corresponding expected future spot price (i.e. short hedging demand exceeds long hedging demand). More recent work, such as Hirshleifer (1988) and Etula (2010), extends their framework to consider a broader set of portfolio options for speculators.15 The basic conclusion remains that assets (such as futures) that have a positive correlation with the innate risk held by firms will have a positive return to long positions.
While the sign of the net position of all hedgers could conceivably vary across markets, the evidence is that for most commodities, hedgers are net short in the futures market. For agricultural commodities, the largest group of hedgers is distributors, who have innate long positions in physical agricultural products. In fact, these distributors hold a much larger absolute share of open interest than any other group, as shown in Table 1. Their physical market positions typically consist of forward agreements with growers to buy crops at set prices, as well as crop inventories. Evidence on cash market positions in agricultural commodities also suggests that traders with long physical market positions hedge, by taking a short positions in the futures contract, much more often than traders with a short physical position.16 More generally, hedgers tend to be short in most commodity futures markets. Then, it follows that speculators would primarily take the long side, as implied by the backwardation model.
Put differently, one can think of the cost of hedging as the equilibrium discount (from expected spot prices) hedgers accept in order to avoid price risk. If the discount is positive, then the party who is short in the futures contract loses money, on average, on the futures contract. However, for an agent who has a pre-existing long position in the physical product (and therefore hedges in the futures market by taking a short position), that cost can be justified by the reduction in the variability of returns. In this sense, hedging is a form of insurance.
The price of this insurance can then be modeled in terms of demand and supply. In Acharya, Lochstoer and Ramadorai (2010), demand for hedging is modeled as reflecting the risk aversion of producers (who hedge), while supply is modeled as reflecting the financing constraints on speculators. While the extent of risk aversion affects the price of hedging in the model we present in Section 3 as well, we focus on changes in the hedgers' fundamental exposure in the underlying as a cause of demand shifts. The key point of departure, however, is our focus on changes in CIT positions as a source of supply shocks.17 In either case, however, the less-than-perfectly elastic supply (limit to arbitrage) means that demand changes lead to price changes. As Hirshleifer (1988) emphasizes, different assumptions about the elasticity of supply of insurance yield different implications regarding the relationship between hedger characteristics and the cost of insurance. In line with Acharya et al. (2010) our findings suggest that hedging supply is less than completely elastic.
Our measure of the cost of hedging at time t is
for each of the 27 contracts (i) for each of the three commodities (j) in our sample, during the period in which each contracts is the nearby. The left-hand side variable in equation (1) is
where
We estimate equation (1) using OLS, with Newey-West standard errors, for the 27 maturities of each of the three commodities.20 The
results (available from the authors upon request) for the
![]() and
and![]() are consistent with
our expectation; the hedging discount is increasing in both r and
are consistent with
our expectation; the hedging discount is increasing in both r and ![]() , and in the interaction term. The coefficients are
statistically significant at the 5 percent level in about 95 percent of cases. Moreover, the average R
, and in the interaction term. The coefficients are
statistically significant at the 5 percent level in about 95 percent of cases. Moreover, the average R![]() is slightly over 50 percent, indicating that the regressions are explaining most
of the variation in the cost of hedging. Overall, standard test-statistics indicate that the regressions in the first step are well-behaved.
is slightly over 50 percent, indicating that the regressions are explaining most
of the variation in the cost of hedging. Overall, standard test-statistics indicate that the regressions in the first step are well-behaved.
Table 2 presents our estimates of the regressions in equations (2) and (3). Standard errors are bootstrapped (see, e.g., Varian 2005). In our estimates for equation (2), for all three commodities, the average cost of hedging, ![]() , is increasing in
, is increasing in ![]() , and decreasing in I, as suggested by the backwardation model. In both the corn and wheat regressions, all of the coefficients have p-values of less than 5 percent (each regression has only 27 observations). More generally, this rather parsimonious model does a reasonable job in explaining changes in
average hedging costs for these two products. The lower explanatory power for the soy market could reflect the fact that futures markets exist for the two value-added soy products, soy bean meal and soy oil, so that traders may employ more complex hedging strategies (thereby reducing the accuracy
of
, and decreasing in I, as suggested by the backwardation model. In both the corn and wheat regressions, all of the coefficients have p-values of less than 5 percent (each regression has only 27 observations). More generally, this rather parsimonious model does a reasonable job in explaining changes in
average hedging costs for these two products. The lower explanatory power for the soy market could reflect the fact that futures markets exist for the two value-added soy products, soy bean meal and soy oil, so that traders may employ more complex hedging strategies (thereby reducing the accuracy
of ![]() in measuring cash positions, among other things). To interpret the coefficients, consider the effect of a one standard deviation increase in I. For
wheat, a one standard-deviation increase in CIT positions represents a change of about 50 thousand contracts, which the model implies will reduce hedging costs by 2 basis points, or about 1/3 of the mean.
in measuring cash positions, among other things). To interpret the coefficients, consider the effect of a one standard deviation increase in I. For
wheat, a one standard-deviation increase in CIT positions represents a change of about 50 thousand contracts, which the model implies will reduce hedging costs by 2 basis points, or about 1/3 of the mean.
Estimation results for equation (3) suggest that the variance of hedging costs is increasing in ![]() and decreasing in I, with
and decreasing in I, with
![]() in the corn regression and I in the soy regression having the greatest statistical significance. The R
in the corn regression and I in the soy regression having the greatest statistical significance. The R![]() s are considerably higher than in our estimations of equation (2).21
s are considerably higher than in our estimations of equation (2).21
These results suggest that index traders provide insurance for hedgers in agricultural markets, thereby reducing hedging costs, relative to a market in which index traders are absent. Although ![]() and I seem to explain some portion of variation in the mean and in the variance of hedging costs, the underlying economics suggests that there is likely to be considerable measurement error associated with our hedging cost variables. In particular,
and I seem to explain some portion of variation in the mean and in the variance of hedging costs, the underlying economics suggests that there is likely to be considerable measurement error associated with our hedging cost variables. In particular,
![]() (
(![]() ) may be a noisy estimate of
) may be a noisy estimate of ![]() (
(![]() ). Moreover,
). Moreover, ![]() (
(![]() ) will reflect information that is revealed between t and T (e.g., crop forecasts). To address the issue of measurement and estimation error and to better understand the role of CITs in futures markets, we formally model the market price for risk insurance, and derive implications for inter-month price
spread, as well as hedging costs. The advantage of analyzing inter-month spreads is that changes in market fundamentals will likely be reflected in the prices of all maturities of the commodities, and hence likely not have a large impact on price differences. The next Section first presents some
evidence on traders' behavior in the markets we study, and then presents a formal model in which we incorporate these features to derive implications concerning the relationship between trader behavior and both hedging costs and inter-month spreads.
) will reflect information that is revealed between t and T (e.g., crop forecasts). To address the issue of measurement and estimation error and to better understand the role of CITs in futures markets, we formally model the market price for risk insurance, and derive implications for inter-month price
spread, as well as hedging costs. The advantage of analyzing inter-month spreads is that changes in market fundamentals will likely be reflected in the prices of all maturities of the commodities, and hence likely not have a large impact on price differences. The next Section first presents some
evidence on traders' behavior in the markets we study, and then presents a formal model in which we incorporate these features to derive implications concerning the relationship between trader behavior and both hedging costs and inter-month spreads.
IV. The Effect of CIT Trading on Pricing
In this Section, we present a model of equilibrium in futures markets in which CITs participate. The model incorporates several salient features of commodity markets. The first important feature is that contracts of different maturities trade simultaneously. At any point in time, eight or more contracts of different maturities are trading in each product. Second, hedgers are net long in the physical product, hence their hedging consists of short futures positions. Importantly, the hedgers' risk primarily pertains to price changes between the trade date and the date at which the harvested crop can be bought or sold. As shown below, this implies that most hedgers will take large short positions in the first post-harvest futures contract each year.22
A. Empirical Regularities
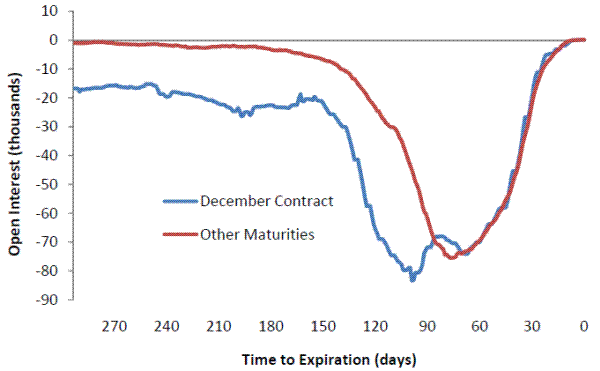
Figure 2 presents some evidence in support of this premise that hedgers take particularly large positions in the post-harvest contract. It shows that during the six plus years in our sample, the most important group of hedgers, distributors, have on average, established short positions of nearly 20,000 contracts in each year's December wheat contract by mid March (270 days before expiration of the December contract), and retained positions of about that magnitude until the December contract became the closest-to-maturity (nearby). In contrast, for other maturity months, their typical short positions are less than 5,000 contracts until the contract becomes the nearby. Similar patterns exist for corn and soybeans.
The other relevant institutional feature is that the leading CIT traders largely establish their trading positions independent of contemporaneous price. As Stoll and Whaley (2010) note, commodity index traders typically have simple buy-and-hold strategies, which allow them to take advantage of the diversification these assets provide. The two largest index funds (the GSCI and the DJ-AIG23), which together represent about 1/3 of CIT positions during our sample, announce the bulk of their annual futures market trading decisions prior to the first trading day of the year.24 In particular, they announce the percentage of their assets that will be allocated to each futures contract, which maturities of those commodity contracts they will hold, and the dates they will move positions between maturities.25
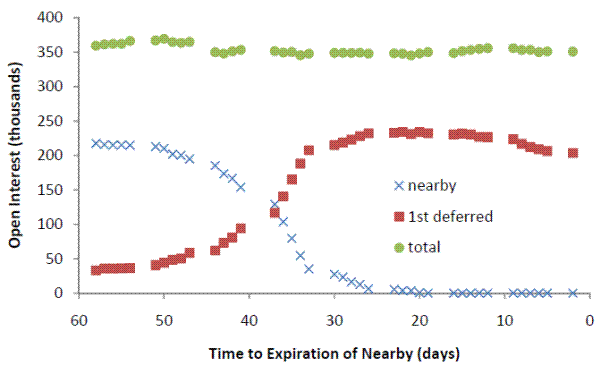
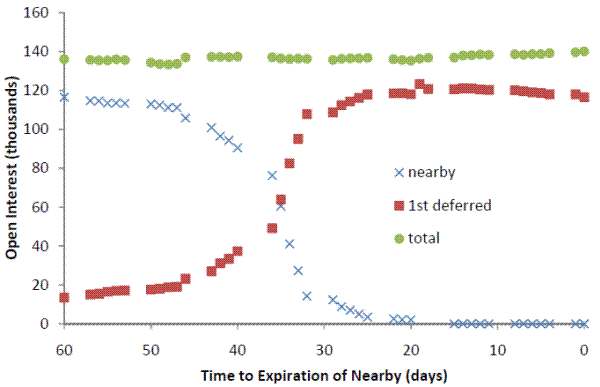
One common feature of CITs is that they primarily take positions in the nearby contract, which requires them to move their positions from the soon-to-expire nearby contract to the succeeding maturity contract.26 Figure 3 shows CIT position in the nearby and the first deferred contracts for the three commodities, as functions of the number of days until the nearby contract reaches its expiration, for a typical month (May 2007).27 The Figure shows that while CIT's overall position do not vary much over the course of a contract, their positions in individual maturities vary dramatically over this cycle. Specifically, for all three commodities, CITs' position in the first deferred contract is small compared to their position in the nearby contract at a point two months prior to expiration. Over the succeeding month or so, they move their positions from the nearby to the first deferred contract. Most of this roll takes place between 30 and 40 days prior to contract expiration.
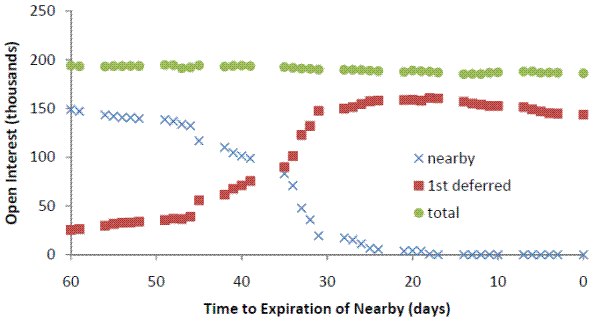
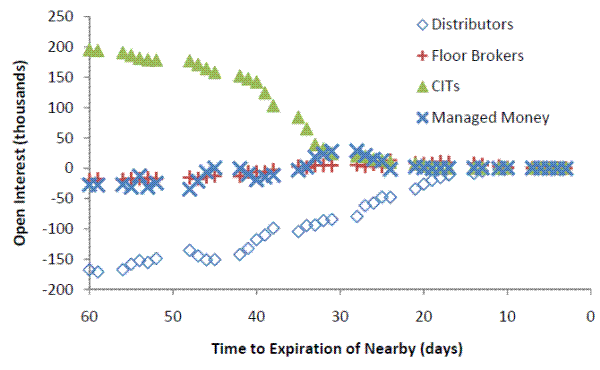
Of course, when CITs acquire a long position in a contract, there must be counterparties with corresponding short positions in that contract. Figure 4 displays the average positions of four groups of traders in the nearby corn contract, as it moves towards expiration. Market makers (floor brokers), hedge funds (managed money), and agricultural distributors (hedgers) hold positions that are in aggregate about the same size as CIT positions. Market makers' overall position looks quite different, however. Figure 5 shows the pattern of market maker positions in the wheat market. Market makers hold long positions in deferred wheat contracts that are nearly equal in size to their short positions in the nearby contract. As we show below, this pattern is consistent with rational behavior by market makers, given the strategies of CITs and agricultural distributors (hedgers).
To summarize, as an empirical regularity, we see that CITs primarily take long positions in the nearby contract, and their counter-parties in that contract consist of distributors, market makers and hedge funds. These latter two groups appear to hedge their short positions in the nearby by taking long positions in deferred contracts. CITs move positions from the nearby to the first deferred contract in a predictable manner, as the nearby moves towards expiration. Finally, hedgers take especially large short positions in the post-harvest contract each year.
B. Modeling Trader Behavior
To reflect these empirical regularities, we consider a model with three maturities of contracts in a single commodity each year, and three trader types; short hedgers (distributors), index traders (CIT), and speculators (specifically market makers and investment managers).28 Each contract is the nearby for a T-day period, and we refer to period i as the T days in which maturity i is the nearby. We characterize each kind of agent in a way that is broadly consistent with their observed trading patterns.
Index Traders
: Index trader positions are taken as exogenous; during the period in which contract i is the nearby, CITs have an initial long position of size I in contract i, and roll into maturity i+1 over the course of the T-day period (consistent with the pattern shown in Figure 3). We letOther Traders
:Other trader groups optimally allocate their portfolios, anticipating CIT behavior, and viewing the trading activity of CITs as not being information-based. Hence, we assume that hedgers and speculators take utility-maximizing positions in the various maturity futures contracts that are traded each day, and have symmetric knowledge of market fundamentals. Traders in these groups differ only in regard to their endowments; hedgers have positions in the underlying that essentially result in their being long in the physical commodity. Importantly, these "physical" positions cannot be sold at t=0 (very much in the spirit of Grossman and Miller 1989). Specifically, we assume that hedgers (distributors) have cash market positions of sizeC. Period 1 Equilibrium
In contrast to CITs, hedgers (distributors) and speculators choose utility-maximizing positions, given prices. To make the problem tractable, we assume consumption only takes place in period 3, and follow convention and assume that both distributors and speculators all have the same exponential utility functions (which imply that utility is function of mean and variance only).
Consider equilibrium at date zero. There are three futures contracts traded on that date, and they have expiration dates T, 2T and 3T days in the futures. Given an exponential utility function, both hedgers and speculators take position in the three contracts to maximize period 3 utility30
The optimum allocation at t = 0 for both hedgers and speculators is to take positions to satisfy
where X is the vector of positions in the product at three different future dates, as of date 0,
Define ![]() and
and ![]() as the number of hedgers and the number of speculators, respectively. Given the speculator and hedger decisions in (4) and the exogenous CIT behavior described above, market clearing for the maturity 1 futures market implies,
as the number of hedgers and the number of speculators, respectively. Given the speculator and hedger decisions in (4) and the exogenous CIT behavior described above, market clearing for the maturity 1 futures market implies,
on each date in period 1. Similarly, the contract 2 market must clear, so that
where I is the total CIT positions and
The market clearing conditions for maturity 3 contracts at time 0 differ in two ways from those for maturities 1 and 2. First, hedgers have innate cash positions that mature before date 3T![]() (which could be forward contracts or crops in the field) and sum to size
(which could be forward contracts or crops in the field) and sum to size ![]() . Hence
if X
. Hence
if X![]() is their optimal position in all maturity 3 claims (futures plus cash), then their future market position is
is their optimal position in all maturity 3 claims (futures plus cash), then their future market position is
![]() . Second, index traders do not (during period 1) hold positions in maturity 3 contracts. As such, market-clearing for maturity 3 at each date in period 1 implies that
. Second, index traders do not (during period 1) hold positions in maturity 3 contracts. As such, market-clearing for maturity 3 at each date in period 1 implies that
![]() or
or
It follows from equations (4) - (7) that
and similarly,
where
Note that the model predicts that speculators will take calendar spread positions. Specifically, it predicts that they will be short in the nearby and long in other maturity contracts, whenever CITs are long in the nearby. As CITs move into the first deferred, speculators will likewise take a larger short (or smaller long) position in the first deferred.
These predictions are consistent with observed trading patterns (see Figure 5). As shown in Figure 4, the position of speculators is the mirror image of CIT positions in the nearby contract, especially between 60 and 15 days prior to expiration. However, their positions aggregated across all maturities are quite different; the net positions of traders in each of these two speculator categories, aggregated across all maturities, is very close to zero, and changes very little as the nearby reaches maturity. These patterns suggest that speculators are serving as counter-parties to CITs in the nearby, and to hedgers in more distant maturities.
D. Periods 2 and 3 Equilibria
We next consider equilibrium in the two contracts trading in period 2. During period 2, CITs hold their positions in a combination of maturity 2 and maturity 3 contracts. While X![]() is characterized by an equation identical to equation (5) (save for a change in subscripts), market-clearing implies that the total positions of non-CITs in contract 3 during period 2 is
is characterized by an equation identical to equation (5) (save for a change in subscripts), market-clearing implies that the total positions of non-CITs in contract 3 during period 2 is
And solving for prices using this market clearing condition, we obtain
and,
Equations (11) and (12) characterize the cost of hedging for every t in period 2 (
![]() .
.
In period 3, the only remaining contract that affects current-year utility is the maturity 3 contract. Here, traders' optimal positions in maturity 3 claims are
![\displaystyle X_3=\frac{\left[C^{curr}-\gamma I\right]}{N_H+N_S}.](img68.gif)
This implies that at every t during period 3,
In mapping our formal model to the empirical environment of commodity futures markets, several additional aspects of the market are relevant to period 3 trading. Most importantly, the cycle of planning the following year's activity begins during the post-harvest period (period 3). This leads some traders to take positions in contracts that mature in period 6 (when next year's post-harvest contract is the nearby) during period 3, which can affect the price of the period 4 contract. The price of maturity 4 contracts is also affected by the long position that index traders take in that contract as the maturity 3 contract moves towards expiration. Thus, in period 3, traders are solving a maximization analogous to equation (1), and find optimal positions in the following year's contracts. This optimization, along with the condition that the maturity 4 contract clears implies that
Where ![]()
![]() refers to the cash (or forward) position that will be
realized in next year's post-harvest contract (period 6).
refers to the cash (or forward) position that will be
realized in next year's post-harvest contract (period 6).
E. Comparative Statics
Consistent with our informal discussion in Section II, the model presented above predicts that the presence of CITs increases futures prices, except at contract expiration. The model formalizes this premise and, importantly, yields specific predictions about relative prices. Specifically, since
CITs primarily take positions in only one or two maturities at a time, CIT trading will affect the inter-month spread ![]()
![]() . Using equations (8) and (9) or (12) and (13), we see that
. Using equations (8) and (9) or (12) and (13), we see that ![]() varies inversely with
varies inversely with ![]() (the CIT positions in the nearby contract) in
periods 1 and 2;
(the CIT positions in the nearby contract) in
periods 1 and 2;
![\displaystyle \frac{\partial S^2_i}{\partial \gamma \partial I}=\frac{\alpha }{N_H+N_S}\left[2{\sigma }^2_{i,i+1}{-\sigma }^2_i-{\sigma }^2_{i+1}\right]<0](img79.gif)
The effect of changes in the cash position, ![]() , on the spread is somewhat ambiguous when neither the nearby nor the first deferred contract are the first post-harvest contract (e.g.,
contract 3 at date 0)
, on the spread is somewhat ambiguous when neither the nearby nor the first deferred contract are the first post-harvest contract (e.g.,
contract 3 at date 0)
When contract 2 is the nearby (i.e., for
![]() ), using equations (11) and (12), we obtain
), using equations (11) and (12), we obtain
Finally, during period 3, inter-month spreads will depend on hedger's cash positions in both the current and future year's crops. From (13) and (14) we know that S![]() (the spread between the second post-harvest contract and the first post-harvest contract) will be increasing in
(the spread between the second post-harvest contract and the first post-harvest contract) will be increasing in ![]() (the size of hedgers' position in the current year crop)
(the size of hedgers' position in the current year crop)
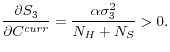
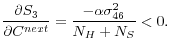
As is the case during periods 1 and 2, the inter-month spread will vary predictably with CIT behavior in period 3 as well. The same general conclusions follow, but as shown below, some magnitudes may differ. Using equations (13) and (14), we have the following comparative static result
The difference between the expression here and that in period 1 is that the covariance between maturities does not affect the spread in period 3. But, in both cases, as the index traders (in aggregate) roll their positions (![]() falls), the spread between the futures prices of the 1
falls), the spread between the futures prices of the 1![]() deferred and nearby contracts rises. Spreads will also vary with the aggregate size of
CIT positions
deferred and nearby contracts rises. Spreads will also vary with the aggregate size of
CIT positions
![\displaystyle \frac{\partial S^2_3}{\partial \gamma \partial I}=\frac{\alpha }{N_H+N_S}\left[{-\sigma }^2_3-{\sigma }^2_4\right]<0](img91.gif)
Another implication of this model is that the price of hedging - which is really the reciprocal of the return to holding a long position - should be correlated across commodities, at least for those commodities within the typical fund's holdings. That is, since index funds tend to hold a fixed portion of their portfolios in each of many commodities, changes in CIT positions will be highly correlated across the commodities that CITs buy and hold. Since changes in CIT positions will change futures returns in the same direction for all of these commodities, we would anticipate that the presence of CITs should increase the correlation of futures returns across contracts in which CIT take positions, even those unrelated in demand and supply. Indeed, Tang and Xiong (2010) find that the correlations of returns for contracts for which CITs take positions are higher than those for contracts in which CIT do not invest.
V. Empirical Implementation and Results
The model outlined in Section 3 yields predictions about the relationship between prices and trader positions (specifically, I, ![]() and
and ![]() ). Because we have daily observations on CIT and hedger positions in each maturity, we can directly test these hypotheses. We measure prices by the daily closing (settlement) prices on the
Chicago Mercantile Exchange. As discussed above, price levels are more likely affected by changes in fundamentals than are price differences. Hence, the primary variable of interest in testing our model is the difference between the daily settlement prices of the first deferred contract and the
nearby contract, which we refer to as the spread.33
). Because we have daily observations on CIT and hedger positions in each maturity, we can directly test these hypotheses. We measure prices by the daily closing (settlement) prices on the
Chicago Mercantile Exchange. As discussed above, price levels are more likely affected by changes in fundamentals than are price differences. Hence, the primary variable of interest in testing our model is the difference between the daily settlement prices of the first deferred contract and the
nearby contract, which we refer to as the spread.33
The trader position variables are constructed from the daily position data in the CFTC Large Traders Reporting System database. The empirical counterpart of I is the maximum observed end-of-day position of CITs in each maturity contract. The maximum is typically
reached 50-60 days before contract expiration. ![]() is the ratio of the end of day CIT position in the nearby to I. The empirical counterpart of
is the ratio of the end of day CIT position in the nearby to I. The empirical counterpart of ![]() , the number of traders in category k for each maturity, is the maximum number of traders in category k for each
maturity.34
, the number of traders in category k for each maturity, is the maximum number of traders in category k for each
maturity.34
In the model, ![]() represents the physical quantity that hedgers will possess at some future date in the current year. As such, in the agricultural context, it is most appropriate to
think of
represents the physical quantity that hedgers will possess at some future date in the current year. As such, in the agricultural context, it is most appropriate to
think of ![]() as the post-harvest, cash-market long positions of these traders. Although commercial traders in several of the LTRS categories include short hedgers, we focus on the
futures positions of the largest such category, agricultural distributors. These traders are particularly relevant to our analysis, not only because they represent the largest category of commercial trader, but also because as a group, they are consistently short in the futures market - both over
time and between commodities.35
as the post-harvest, cash-market long positions of these traders. Although commercial traders in several of the LTRS categories include short hedgers, we focus on the
futures positions of the largest such category, agricultural distributors. These traders are particularly relevant to our analysis, not only because they represent the largest category of commercial trader, but also because as a group, they are consistently short in the futures market - both over
time and between commodities.35
As a result, our estimates of ![]() are based on the observable futures positions of agricultural distributors, which by (7), bears a relationship to
are based on the observable futures positions of agricultural distributors, which by (7), bears a relationship to ![]() . Specifically, from equation (7), and the relationship between
. Specifically, from equation (7), and the relationship between ![]() and
and ![]() we have
we have
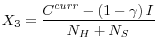

Finally, when the first post-harvest contract (e.g., December for corn and wheat) is the nearby, similar analysis shows that
In addition to CIT and hedger (distributor) positions, we would anticipate that spreads would also be affected by the period of time until expiration of the nearby contract (![]() ).
Finally, we would also like to test whether, holding the level of positions constant, the rate of change in CIT positions in the nearby (the roll) affects spreads. We measure the roll as the absolute value of the daily change in commodity index trader positions in the
nearby contract.
).
Finally, we would also like to test whether, holding the level of positions constant, the rate of change in CIT positions in the nearby (the roll) affects spreads. We measure the roll as the absolute value of the daily change in commodity index trader positions in the
nearby contract.
Before describing the details of how we estimate the model, we provide some discussion of the data.
A. Summary Statistics
Our data cover the period July 2003 until December 2008 and refer to daily observations. Table 4 reports descriptive statistics of the data; corn in panel I, soy in panel II and wheat in panel III. The three products are similar in most respects. For example, our tests show that none of the variables have Gaussian distributions, although all are stationary. Average spreads are more than 10 cents for all three products, indicating that the term structure of futures prices is typically upward sloping in our sample. All three spreads are also highly autocorrelated (the least autocorrelated is wheat, with a first-order autocorrelation of 0.83). Soybean spreads are much more volatile than the other two products.
As discussed above, a key determinant of hedging costs is the relative size of I, CITs' long futures market position, and ![]() =
= ![]() +
+ ![]() , the physical (cash) positions held by hedgers. These two variables are of
similar magnitude for corn, but I is about 3 times larger than
, the physical (cash) positions held by hedgers. These two variables are of
similar magnitude for corn, but I is about 3 times larger than ![]() for soybeans and wheat.36 We also note that
for soybeans and wheat.36 We also note that ![]() is more volatile than I for corn, but the reverse
holds for the other two products. I and
is more volatile than I for corn, but the reverse
holds for the other two products. I and ![]() are highly autocorrelated.
are highly autocorrelated.
The mean of ![]() is about 0.5 for all three products, indicating that, on average, CITs hold roughly half their positions in the nearby contract. This in turn suggests that the roll
occurs roughly symmetrically around the middle of the period in which each maturity of each contract is the nearby. Finally, the last column of Table 4 reports summary statistics for the ratio of
is about 0.5 for all three products, indicating that, on average, CITs hold roughly half their positions in the nearby contract. This in turn suggests that the roll
occurs roughly symmetrically around the middle of the period in which each maturity of each contract is the nearby. Finally, the last column of Table 4 reports summary statistics for the ratio of ![]() to
to ![]() which represents the percentage of total hedger cash position in the current year crop. It averages between 0.4 and 0.5 for the three products. That is,
more than half of hedger cash positions are in the following year's harvest well before the current year's post-harvest contract reaches expiration.
which represents the percentage of total hedger cash position in the current year crop. It averages between 0.4 and 0.5 for the three products. That is,
more than half of hedger cash positions are in the following year's harvest well before the current year's post-harvest contract reaches expiration.
B. Estimation Technique
The spread exhibits serial correlation and heteroskedasticity. To mitigate the effect of these factors and to fully capture the dynamics of both the conditional mean and the conditional variance, we adopt the GARCH(1,1) model. This model is very flexible and is widely used for describing the evolution of financial variables.37 More specifically, we estimate GARCH models with variance targeting (where the unconditional variance of the GARCH model is restricted to be equal to the sample unconditional variance). Francq, Horvath and Zakoïan (2009) show that when the model is misspecified, GARCH estimates with variance targeting are superior to unrestricted GARCH estimates.38 We estimate the following model for the spread for each commodity j
The estimation technique requires us to choose a distribution for ![]() . Most GARCH models are estimated using a normal distribution. Unfortunately, the spreads here are highly
non-normal with negative skewness and high kurtosis. The markets we analyze are typically characterized by spreads that are positive almost all the time (the spread is negative only 1.5 percent of the time for corn and wheat and 6.2 percent for soy). We, therefore, chose the generalized error
distribution, which was introduced in the GARCH literature by Nelson (1991), since it accommodates the behavior of the spread in the tails.39
. Most GARCH models are estimated using a normal distribution. Unfortunately, the spreads here are highly
non-normal with negative skewness and high kurtosis. The markets we analyze are typically characterized by spreads that are positive almost all the time (the spread is negative only 1.5 percent of the time for corn and wheat and 6.2 percent for soy). We, therefore, chose the generalized error
distribution, which was introduced in the GARCH literature by Nelson (1991), since it accommodates the behavior of the spread in the tails.39
The theoretical model in the previous Section makes a number of predictions about the parameter values. One prediction is that
![]()
![]() 0 for
0 for ![]() = 0 and
= 0 and
![]()
![]() 0 for
0 for ![]() = 1. This implies that
= 1. This implies that
![]() 0, and
0, and
![]() 0, such that
0, such that
![]()
![]()
![]() 0. Moreover, our model predicts a negative value for
0. Moreover, our model predicts a negative value for
![]() as long as
as long as
![]() for months in which the post-harvest contract is neither the nearby or the first deferred. When the last pre-harvest contract is the nearby, we would expect
a larger (in absolute value) negative value for the coefficient on
for months in which the post-harvest contract is neither the nearby or the first deferred. When the last pre-harvest contract is the nearby, we would expect
a larger (in absolute value) negative value for the coefficient on ![]() , so that
, so that
![]()
![]() 0. For the post-harvest contract, we would expect
0. For the post-harvest contract, we would expect
![]()
![]() 0, so that
0, so that
![]()
![]() 0 and
0 and
![]()
![]() 0. Conversely, in the post-harvest period, we
expect
0. Conversely, in the post-harvest period, we
expect
![]() , so that
, so that
![]() . These predictions are summarized in Table 3, while Table 5 reports estimation results.
. These predictions are summarized in Table 3, while Table 5 reports estimation results.
For all commodities the signs of the estimated parameters in the spread equation are generally in line with the model's predictions, and are statistically significant. For example, the negative signs on
![]() in the three regressions mean that the spread falls as CITs move their positions from the nearby to the first deferred.40 Similarly, the negative signs on
in the three regressions mean that the spread falls as CITs move their positions from the nearby to the first deferred.40 Similarly, the negative signs on
![]() and
and
![]() and the positive sign on
and the positive sign on
![]() mean that the greater the extent to which hedgers seek to buy insurance (hedge their risks), the higher is the price they have to pay. The negative sign on
mean that the greater the extent to which hedgers seek to buy insurance (hedge their risks), the higher is the price they have to pay. The negative sign on
![]() means that, consistent with the model, this effect is (absolutely) larger when the last pre-harvest contract is the nearby, since the correlations between the nearby futures
contract and the hedgers' underlying positions are higher. This finding suggests that it is not trading per se that affects futures prices, but rather the size of hedger and CIT positions, as implied by the model. To get an idea of the magnitude of these effects, we note
that a one standard deviation increase in the current-year cash position of hedgers (distributors) in soybeans leads to a decrease in the spread of nearly 1 cent if the nearby is the January, March, or May contracts, and close to a 3 cent decrease if the nearby is the July contract. Overall, the
pattern of coefficients suggests that the model correctly interprets market behaviors.
means that, consistent with the model, this effect is (absolutely) larger when the last pre-harvest contract is the nearby, since the correlations between the nearby futures
contract and the hedgers' underlying positions are higher. This finding suggests that it is not trading per se that affects futures prices, but rather the size of hedger and CIT positions, as implied by the model. To get an idea of the magnitude of these effects, we note
that a one standard deviation increase in the current-year cash position of hedgers (distributors) in soybeans leads to a decrease in the spread of nearly 1 cent if the nearby is the January, March, or May contracts, and close to a 3 cent decrease if the nearby is the July contract. Overall, the
pattern of coefficients suggests that the model correctly interprets market behaviors.
Our model implies that the level of CIT position in individual maturities should affect the price of that maturity, and that the level of trading activity on a trading day would only affect prices if they introduced new information. In fact, the roll-over strategies of CITs is announced well in
advance and should not introduce any additional information to the market. Hence, we would expect
![]() , the coefficient of
, the coefficient of ![]() , not to be statistically significant.
For both soy and wheat, however, the rolling activity appears to increase the spread; the greater the daily increase in CITs' positions in the first deferred position, the bigger is the spread. As such, the data suggests that trading activity does affect prices in these two markets. One possible
explanation of this finding is that some of the roll may not be completely predictable (i.e., the rolling by CITs other than the major funds). Moreover, rolling strategies may reflect information about the desired CIT position in the first deferred contract (which may also change between
maturities). These effects may be exacerbated in less liquid markets. This might explain why the effects are more significant in wheat and soybeans than in corn (which is the most liquid of the three).
, not to be statistically significant.
For both soy and wheat, however, the rolling activity appears to increase the spread; the greater the daily increase in CITs' positions in the first deferred position, the bigger is the spread. As such, the data suggests that trading activity does affect prices in these two markets. One possible
explanation of this finding is that some of the roll may not be completely predictable (i.e., the rolling by CITs other than the major funds). Moreover, rolling strategies may reflect information about the desired CIT position in the first deferred contract (which may also change between
maturities). These effects may be exacerbated in less liquid markets. This might explain why the effects are more significant in wheat and soybeans than in corn (which is the most liquid of the three).
There are also two cross-parameter restrictions implied by the theory:
![]() and
and
![]() . We fail to reject the latter restriction at the 5 percent significance level for wheat and soy, but reject for corn. That is, for wheat and soy, the evidence
supports the model's premise that when the first post-harvest contract is the nearby, the spread (that is, the price of the second post-harvest contract minus the price of the first post-harvest contract) increases with the size of hedger positions in the current-year crop. The evidence is less
favorable for the first restriction.
. We fail to reject the latter restriction at the 5 percent significance level for wheat and soy, but reject for corn. That is, for wheat and soy, the evidence
supports the model's premise that when the first post-harvest contract is the nearby, the spread (that is, the price of the second post-harvest contract minus the price of the first post-harvest contract) increases with the size of hedger positions in the current-year crop. The evidence is less
favorable for the first restriction.
The conditional variance equation is well-specified and stable with the sum of
![]() and
and
![]() less than unity. The parameter
less than unity. The parameter
![]() is significant, indicating that there is seasonality in the second moment due to the life cycle of futures contracts. Although
is significant, indicating that there is seasonality in the second moment due to the life cycle of futures contracts. Although
![]() is negative, the conditional variance is always positive. In line with the summary statistics in Table 4, the GED parameter is less than 2 for all commodities, implying that the
spread has fat tails. Finally the R
is negative, the conditional variance is always positive. In line with the summary statistics in Table 4, the GED parameter is less than 2 for all commodities, implying that the
spread has fat tails. Finally the R![]() indicates that the model well describes the evolution of the spread. This is particularly true for corn. Perhaps the
lower R
indicates that the model well describes the evolution of the spread. This is particularly true for corn. Perhaps the
lower R![]() for soybeans reflects the fact that soy traders have a broader set of instruments to use for hedging their risk, since futures and options markets
also exist for soy meal and soy oil.41
for soybeans reflects the fact that soy traders have a broader set of instruments to use for hedging their risk, since futures and options markets
also exist for soy meal and soy oil.41
VI. Conclusion
This paper analyzes the role of index traders in financial markets. Our perspective is that CITs fill the gap between short-hedge and long-hedge demand. That is, the prices that would have resulted from the trading of hedgers alone allowed index traders to profitably take long futures positions. Consistent with this premise, we find that hedging costs fell as CITs positions grew.
Within this overall framework, there appeared to be additional opportunities for profitable trading due to the temporal mismatch between the contract maturities in which CITs are taking long positions, and the maturities in which hedgers take short positions. The evidence suggests that other market participants are able to profitably accommodate both of these groups by taking spread positions (short in the nearby, long in deferred contracts).
We show that a sizable portion of the inter-month spread can be explained by the sizes of the positions of CITs and hedgers. In particular, consistent with our theoretical model, increases in the size of hedgers' cash positions lead to lower spreads (at least in the early portions of the harvest cycle). This reflects the idea that the price of assets that are highly correlated with hedgers' cash market positions more closely track changes in those positions. In addition, we find that CITs relative positions in different maturities affect the relative prices of those maturities in predictable ways. As such, the findings suggest that our model explains important aspects of the trading behavior of various agents in the market, and how their trading has reacted to changes in the size of CIT positions in futures markets.
Underlying the premise of our model is the more general notion that traders are willing to take on additional risk only in exchange for higher compensation. By tracking the behavior of groups of similarly-situated traders, we document that traders behave consistent with these models of finite liquidity. That is, it appears that, observed price effects from changes in the demand and supply for insurance against price risk can be explained by the higher cost (in terms of portfolio risk) incurred by speculators. This in turn implies that observed changes in spreads are not necessarily opportunities for arbitrage profits.
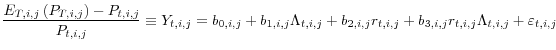
![\displaystyle E_t\left(P^{1\cdot T}\right)-P^t_1=-\frac{\alpha \left[{\sigma }^2_1\gamma I+{\sigma }^2_{12}\left(1-\gamma \right)I-{\sigma }^2_{13}C^{curr}\right]}{N_H+N_S}](img57.gif)
![\displaystyle E_t\left(P^{2\cdot T}\right)-P^t_2=-\frac{\alpha \left[{\sigma }^2_{12}\gamma I+{\sigma }^2_2\left(1-\gamma \right)I-{\sigma }^2_{23}C^{curr}\right]}{N_H+N_S}](img58.gif)
![\displaystyle X_3=\frac{\left[C^{curr}-\left(1-\gamma \right)I\right]}{N_H+N_S}.](img63.gif)
![\displaystyle E_t\left(P^{2\cdot T}\right)-P^t_2=\frac{-\alpha \left[{ -\sigma }^2_{23}(C^{curr}-\left(1-\gamma \right)I)+{\sigma }^2_2\gamma I\right]}{N_H+N_S}](img64.gif)
![\displaystyle E_t\left(P^{3\cdot T}\right)-P^t_3=\frac{-\alpha [{\sigma }^2_{32}\gamma I-{\sigma }^2_3\left(C^{curr}-\left(1-\gamma \right)I\right)]}{N_H+N_S}.](img65.gif)

![\displaystyle E_t\left(P^{4\cdot T}\right)-P^t_4=\frac{\alpha \left[{-\sigma }^2_4\left(1-\gamma \right)I+{\sigma }^2_{46}C^{next}\right]}{N_H+N_S}](img70.gif)