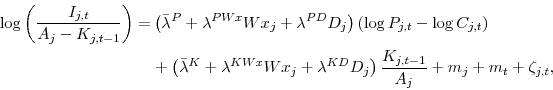Supply Constraints and Housing Market Dynamics*
Keywords: House prices, volatility, housing supply, regulation
Abstract:
Although the volatility of house prices is often ascribed to demand-side factors, constraints on housing supply have important and little-studied implications for housing dynamics. I illustrate the strong relationship in city-level data between the volatility of house prices and the regulation of new housing supply. I then employ a dynamic structural model of housing investment to estimate the effect of supply constraints on both the level of new construction and the responsiveness of investment to house prices. I find that supply constraints increase volatility through two channels: First, regulation lowers the elasticity of new housing supply by increasing lags in the permit process and adding to the cost of supplying new houses on the margin. Second, geographic limitations on the area available for building houses, such as steep slopes and water bodies, lead to less investment on average relative to the size of the existing housing stock, leaving less scope for the supply response to attenuate the effects of a demand shock. My estimates and simulations confirm that regulation and geographic constraints play critical and complementary roles in decreasing the responsiveness of investment to demand shocks, which in turn amplifies house price volatility.
1 Introduction
Recent experience in the United States has made painfully clear the importance of housing market volatility. Housing spending constitutes about 25 percent of the median household's total income, and housing wealth makes up 55 percent of the median household's net worth.1 Large swings in the price of housing thus have important microeconomic effects: Increases benefit homeowners through expansion of paper wealth and relaxed borrowing constraints, while declines tighten those constraints and may leave households "underwater" on their mortgages and unable or unwilling to move. The macro implications of housing dynamics, meanwhile, are more important today than ever, following the largest residential real estate boom and bust in at least half a century, as well as the subsequent recession.
As in most fields of economics, understanding the housing market means understanding both demand and supply. While the literature on housing demand is voluminous, progress in understanding the supply side has been much slower (DiPasquale, 1999). But recent contributions to the literature on housing supply have emphasized the importance of construction costs, particularly the costs of complying with zoning and other regulatory constraints, and the degree to which investment in the housing stock responds to house prices.
In this paper I expand on the existing literature by focusing on the role of regulation and other supply constraints in amplifying house price volatility, as well as raising price levels. Intuitively, when supply is unable to keep pace with demand shocks quickly and cheaply, more of the shocks carry through into prices. In contrast with previous work, I explicitly trace out the channels by which supply constraints affect the housing market and employ a dynamic structural model to estimate the effect of regulation and land availability on costs. I find that permitting lags and marginal costs -- costs that rise with each additional house built in a given year -- explain much of the observable differences in elasticity across markets. Differences in price volatility, in turn, depend on both the elasticity of new housing supply as well as the average level of new supply relative to the size of the existing capital stock, which is determined in part by the quantity of land available for development.
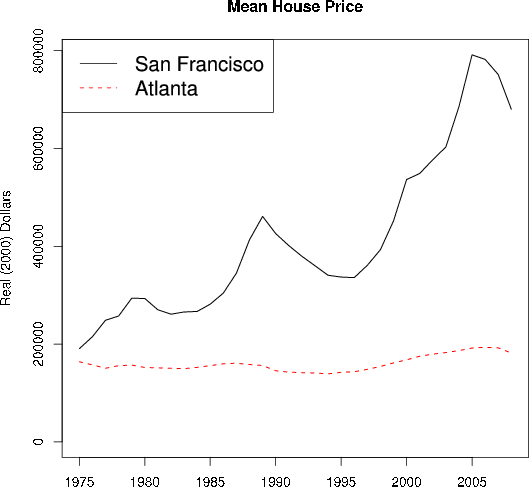
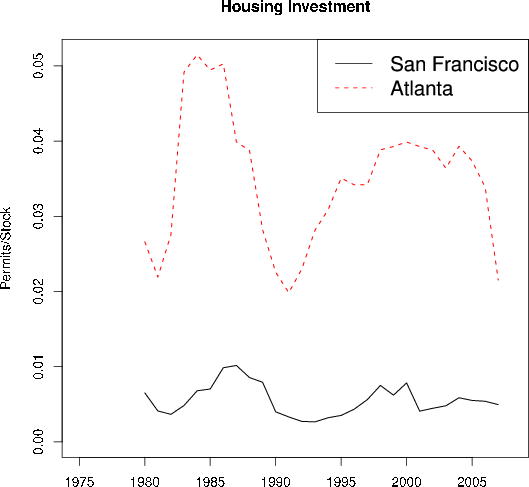
Such differences in volatility can be stark, as may be seen in figures 1 and 2: The mean price of a home in the San Francisco area was about three times as high as in Atlanta between 1984 and 2008. Yet the housing stock of San Francisco grew by an average of just 0.5 percentage point per year, while that of Atlanta grew by 3.5 percentage points per year. Moreover, price volatility in San Francisco was far greater than in Atlanta: Even apart from the trend, the standard deviation of house prices was about twice as high relative to the mean in San Francisco. Homeowners who purchased in San Francisco thus not only paid more on average, they faced far greater uncertainty about the capital gain (or loss) they could expect to realize when they moved to a new house or new city.
Several papers have argued that observed differences in construction and house price levels across metropolitan areas are due to differences in regulation and community opposition to new construction, rather than shortages of land or higher building costs (Mayer and Somerville, 2000; Glaeser et al., 2005a; Quigley and Raphael, 2005). Areas with strong demand and tightly constrained supply experience rising prices and incomes but little construction, becoming "superstar cities" like San Francisco and Boston (Gyourko et al., 2006). Other cities, such as Atlanta and Phoenix, are also in high demand but impose comparatively few regulations on supply, resulting in substantial expansion of the housing stock and (until recently) muted price changes. Geographic constraints, particularly the presence of steep hills and water, also play a key role in determining housing supply (Saiz, 2010).
In contrast with most earlier work, I focus on the relationship between supply constraints and house price volatility, rather than price or investment levels. The strong statistical association between regulation and volatility is easy to see in the data. Figure 3 shows a scatter plot and smoothing spline of within-city house price volatility against the Wharton Residential Land Use Regulatory Index (WRLURI), with each dot representing a single metropolitan statistical area (MSA).2 A simple regression of price volatility on the regulation measure indicates that a 1 standard deviation increase in regulation across cities is associated with about a 30 percent increase in volatility.
This paper explores the causal mechanisms underlying this empirical relationship.3 While the empirical literature has convincingly demonstrated that housing supply conditions can vary widely across regions, housing supply models have remained mostly ad hoc. Econometric models relating supply to prices and other fundamentals have imposed no theoretical structure on these relationships, leading to confusion even over relatively simple questions such as whether investment should relate to price levels or changes (Mayer and Somerville, 2000). Through the careful application of theory and econometrics to data on a panel of cities, I make a series of contributions.
Building on preexisting models of investment in durable goods, I develop a dynamic theory of housing supply that is grounded in the optimization problem of owners of undeveloped land. These owners must decide when to build new houses, taking into account currently available information and their rational expectations about future prices. Fluctuations in prices are driven by demand shocks, such as changes in wages or immigration patterns. The effect of these shocks on both prices and investment differs depending on the supply environment, such as the amount of land available, the differential costs of building, and the amount of time needed to build.
The model is explicitly designed so that the parameters can be estimated, and my primary contribution is empirical. I estimate the structural parameters of the model at the level of metropolitan areas, using data on house prices and construction. These cost parameters vary with observed levels of housing regulation, particularly regulatory permitting and construction lags, as well as the quantity of available land. In doing so, I deal with a series of empirical challenges. First, by starting with a microeconomic optimization problem, I am able to properly specify an estimating equation that relates prices, new housing investment, and expectations about the future. Because development lags vary across the cities in my sample, I have to carefully model the role of expectations and their effect on my estimates. Finally, I use demand-side variables that are plausibly uncorrelated with supply shocks and forecast errors to identify the supply-side parameters.
I find that regulatory costs of all kinds can add tens of thousands of dollars to the cost of building an additional house on the margin in more regulated cities relative to less regulated ones. Importantly, while regulations that raise the average cost of new housing or reduce the amount of available land can lead to higher house prices, it is marginal costs -- which rise with each additional house built in a given year -- and construction lags that affect the elasticity of supply.4 Regulatory-induced lags have particularly large effects, both by adding costs on the margin and by forcing landowners and developers to forecast further into the future when planning new development, thus lowering the correlation between actual prices and new supply.
The elasticity of supply, by definition, relates percentage changes in investment to percentage changes in price. I show that the mean level of investment also matters for volatility, since even large changes in new construction cannot relieve shocks to demand if there is little construction relative to the size of the existing capital stock of homes. The level of investment is determined in part by the availability of land, after accounting for geographic constraints.
Using the estimated cost parameters, I solve and simulate the model to explore the importance of various constraints. I find that both more regulation and less available land substantially increase the variance of house prices. The model predicts sizable differences in volatility across metropolitan areas, such as between San Francisco, a highly regulated city that is surrounded by mountains and ocean, and Atlanta, which is both comparatively lightly regulated and surrounded by flat land.
In the next section, I discuss the basics of supply and demand in the housing market before laying out my dynamic model of housing supply. In section 4 I describe the data used for estimation, including the exogenous demand shifters used to identify the supply side. Sections 5 through 7 detail the precise estimation techniques, use reduced-form regressions to illustrate the patterns in the data, and then present the structural estimates. In section 8, I use simulations to show how the estimated supply parameters carry through into volatility. The final section discusses caveats and concludes.
2 The Basics of Housing Supply and Demand
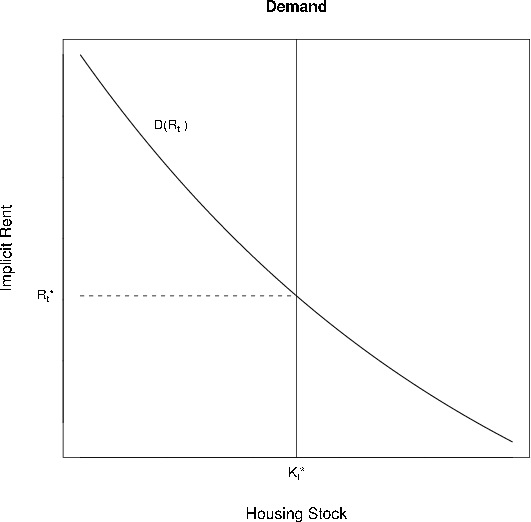
Before introducing any notation, it is worth establishing the basics of an equilibrium model of the housing market via a simple graphical representation. Figures 5 and 6 show the demand and supply sides, respectively. In figure 5, a downward-sloping demand curve relates the implicit rental cost of owning a house in a given period to the quantity of housing demanded at that rent. In the short run, the housing capital stock is fixed and is thus represented by a vertical line in the figure.
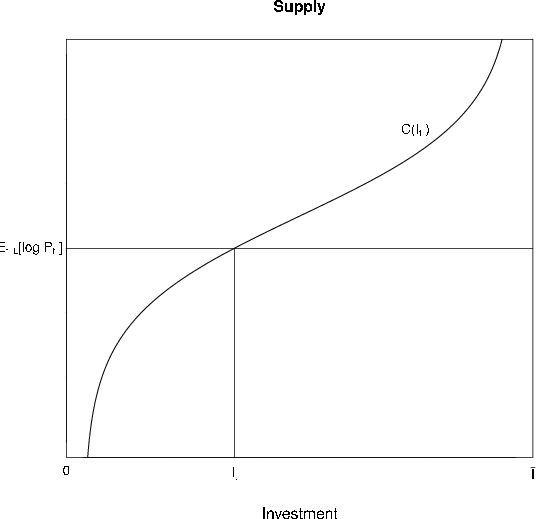
Moving to the supply side in figure 6, we see an upward sloping supply curve relating the expectation of the next period's price to the investment that will come online in that period, under the maintained assumption that it takes one period to build houses. On the margin,
the cost of building an additional house (
![]() ) must be equal to the expected price. As the expected future price rises, investment rises in step. The model is closed by positing a user cost relation -- including interest
rates, depreciation, and the full path of expected future rents -- between housing rents and prices, as well as a transition equation for the capital stock.
) must be equal to the expected price. As the expected future price rises, investment rises in step. The model is closed by positing a user cost relation -- including interest
rates, depreciation, and the full path of expected future rents -- between housing rents and prices, as well as a transition equation for the capital stock.
An unexpected and permanent increase in demand in period ![]() is represented by an upward shift in the demand curve. In the short run, supply is fixed, so the implicit rental cost of housing
rises. The expected future price increases relative to the cost of construction, generating additional investment until the price falls back and the system returns to its steady state. When marginal costs are higher or delays longer, the supply curve is more steeply sloped, so the investment
response is lessened and the return to steady state takes longer. This process underpins my results.
is represented by an upward shift in the demand curve. In the short run, supply is fixed, so the implicit rental cost of housing
rises. The expected future price increases relative to the cost of construction, generating additional investment until the price falls back and the system returns to its steady state. When marginal costs are higher or delays longer, the supply curve is more steeply sloped, so the investment
response is lessened and the return to steady state takes longer. This process underpins my results.
Price volatility in this model will depend both on the slope of the supply curve, which is the reciprocal of the elasticity, and the magnitude of investment relative to the capital stock. Because implicit rent is determined by the overall size of the capital stock, even large percent changes in investment in response to changes in price will do little to damp demand shocks if the level of investment is small relative to the capital stock. Consequently, costs that do not vary with the level of investment (fixed costs), which determine the height of the supply curve, also matter for volatility.
Although there is a time lag in the model, the supply side is myopic in the sense that the expectation of the next period's price translates directly into a level of investment, with no comparison by landowners of expected prices in different periods. Generalizing this world to a fully dynamic one with forward-looking agents requires explicitly modeling the choice of when to develop, which I take up in the next section.
3 A Dynamic Structural Model of Housing Markets
In formulating a model of housing supply, it is valuable to consider some of the special features of housing that differentiate the housing market from that of other goods or services. First, a house is not merely durable but extremely so. Although millions of new houses are built in a typical year, excepting the current bust, the median age of housing units in the United States is about 35 years.5 Thanks to this durability, housing both provides a flow of services and serves as a long-term investment, making forward-looking behavior imperative for homebuyers.
Second, the major input into housing is the land on which it is built, which is in fixed supply within a radius around a given location. This is not to say that there is a shortage of land in the world. But empty land, frequently on the outskirts of major cities, is poorly substitutable for land in desirable locations. Landowners thus have some market power, unlike purveyors of reproducible widgets, and can time their decision to sell or develop the land. This timing decision forms the core of my dynamic model of housing supply, and it differentiates my model from most previous approaches in the literature.6
Since I employ data on house prices and investment at the metropolitan level, my model focuses on cities, indexed by ![]() , which I define as infinitely divisible areas of measure
, which I define as infinitely divisible areas of measure ![]() . The capital stock of housing in
. The capital stock of housing in ![]() at time
at time ![]() is denoted
is denoted ![]() , and new investment is
, and new investment is ![]() , with each period's capital stock equal to the depreciated last period capital stock plus investment:
, with each period's capital stock equal to the depreciated last period capital stock plus investment:
3.1 Demand
Since I focus primarily on modeling and estimating the responses of cities with different supply constraints to demand shocks, I keep the demand side of the model relatively simple, in line with the graphical version discussed above and displayed in figure 5. The inverse
demand for housing in city ![]() at time
at time ![]() is given by
is given by
where
The price of a house is equal to the present value of current and expected future rent. Taking into account property taxes (
![]() ), the mortgage interest rate (
), the mortgage interest rate (![]() ) and their deductibility from income
taxes (
) and their deductibility from income
taxes (
![]() ), as well as a risk premium
), as well as a risk premium ![]() and depreciation
and depreciation ![]() , we are left with a standard formula for the user cost of housing (Himmelberg et al.,
2005; Poterba, 1984):8
, we are left with a standard formula for the user cost of housing (Himmelberg et al.,
2005; Poterba, 1984):8
Here
3.2 Supply
Owners of undeveloped land, whom I index by ![]() , choose whether or not to develop their land in each period.9 I avoid explicitly modeling the market for land or the production function for structures by assuming that the construction industry is perfectly competitive, so that development risk is borne by the landowner/developer, who also
receives any economic profits. In practice, housing developers buy or option land and undertake much of the risk involved in the process, but I elide the distinction between developers and original landowners because my data do not allow me to distinguish between them empirically.
, choose whether or not to develop their land in each period.9 I avoid explicitly modeling the market for land or the production function for structures by assuming that the construction industry is perfectly competitive, so that development risk is borne by the landowner/developer, who also
receives any economic profits. In practice, housing developers buy or option land and undertake much of the risk involved in the process, but I elide the distinction between developers and original landowners because my data do not allow me to distinguish between them empirically.
The development and construction of a house in ![]() started at
started at ![]() takes
takes
![]() periods and is irreversible once begun. A building permit must be acquired one year before the house is finished; this is approximately the amount of time that a single-family building
project takes to go from permit to start to completion, according to data from the Census Bureau. Upon completion, the landowner/developer sells it and receives the price of housing at that time (
periods and is irreversible once begun. A building permit must be acquired one year before the house is finished; this is approximately the amount of time that a single-family building
project takes to go from permit to start to completion, according to data from the Census Bureau. Upon completion, the landowner/developer sells it and receives the price of housing at that time (![]() ) less the fixed labor, materials, and regulatory costs associated with building the structure (
) less the fixed labor, materials, and regulatory costs associated with building the structure (![]() ). I assume all fixed per unit costs of construction are paid on
completion but are known with certainty at the time the decision is made.
). I assume all fixed per unit costs of construction are paid on
completion but are known with certainty at the time the decision is made.
In addition to the fixed costs, a coherent model requires costs in a given area to increase on the margin as more investment is undertaken in any period; otherwise all parcel owners would want to develop at the same time. Along with lags in the permitting process, which I discuss below, the
marginal cost of constructing an additional unit is one of the two primary channels by which regulation can affect dynamics. I incorporate increasing marginal costs by attributing to each landowner ![]() a random shock to the cost of building
a random shock to the cost of building
![]() . Since this is the only parcel-level heterogeneity in the model, I can sort the landowners according to this shock without loss of generality. Within a given city and time
period, these cost shocks follow a mean-zero cumulative distribution
. Since this is the only parcel-level heterogeneity in the model, I can sort the landowners according to this shock without loss of generality. Within a given city and time
period, these cost shocks follow a mean-zero cumulative distribution
![]() plus an overall mean cost shifter
plus an overall mean cost shifter
![]() . The scale parameter of this distribution
. The scale parameter of this distribution
![]() varies across cities, allowing different regulatory regimes to have disparate effects on the cost of building on the margin. The mean cost
varies across cities, allowing different regulatory regimes to have disparate effects on the cost of building on the margin. The mean cost
![]() affects all landowners in
affects all landowners in ![]() equally and serves as a city-level
supply shock.
equally and serves as a city-level
supply shock.
The cost of construction may also vary with the amount of undeveloped land that remains available in the city. Costs are likely to increase as the city's best land is developed, and the gradient may vary across cities either due to regulatory or geographic constraints (Saiz,
2010). Let
![]() denote a cost function that depends on the level of the capital stock relative to the total land area of the city that is not covered by water or too steeply
sloped to build on.10
denote a cost function that depends on the level of the capital stock relative to the total land area of the city that is not covered by water or too steeply
sloped to build on.10
Since construction always takes at least one period, landowners must form expectations about the path of house prices in order to decide whether to develop a given parcel now or wait. If a landowner chooses not to build on a given parcel at ![]() , she will face precisely the same choice one period in the future, after receiving any income from the current use of the land (
, she will face precisely the same choice one period in the future, after receiving any income from the current use of the land (
![]() ), such as farming or the operation of a parking lot.
), such as farming or the operation of a parking lot.
The state space (![]() ) comprises all information known at
) comprises all information known at ![]() , including the
evolution of the demand shocks up to
, including the
evolution of the demand shocks up to ![]() and the capital stock
and the capital stock ![]() periods in the
future. The future capital stock up to that point is known with certainty because the investment decisions have already been made in periods prior to
periods in the
future. The future capital stock up to that point is known with certainty because the investment decisions have already been made in periods prior to ![]() . In the simplest case, in which the
demand and supply shocks follow first-order Markov processes, the state space contains the capital stock and current shock realizations:
. In the simplest case, in which the
demand and supply shocks follow first-order Markov processes, the state space contains the capital stock and current shock realizations:
Using the above notation, a landowner's expected time ![]() value from building on parcel
value from building on parcel ![]() is
is
![\begin{displaymath}\begin{split} V^B_{j,t}\left(S_{j,t-L_j}\right) - \chi_{i,j,t-L_j} =& \beta^{L_j} \left( E \left[\log P_{j,t} \vert S_{j,t-L_j}\right] - \log C_{j,t} \right) - \eta_j\left(K_{j,t-1},A_j\right) \ &- \epsilon^S_{j,t-L_j} - \chi_{i,j,t-L_j}. \end{split}\end{displaymath}](img36.gif)
Alternatively, the flow value from not building plus the expected value of the option to build (or not) tomorrow is
Since
![]() follows a continuous probability distribution with full support over the real line and the total land area is divided among infinitely many small parcels, some parcels will
be developed in every city and period. That is, investment
follows a continuous probability distribution with full support over the real line and the total land area is divided among infinitely many small parcels, some parcels will
be developed in every city and period. That is, investment ![]() must be strictly positive, so that
must be strictly positive, so that
where
3.3 Empirical Implementation
My approach to estimating the supply side of the housing market follows the basic insight of Hansen and Singleton (1982), who point out that it is possible to estimate an equation involving (rational) expectations without fully solving the model to find a representation of
endogenous variables -- in my case, house prices -- in terms of lagged endogenous variables and contemporaneous and lagged exogenous variables. To estimate equation 3 using a standard panel of MSA-level house prices and investment -- described in detail below -- I make a
series of additional simplifying assumptions, some of which can be relaxed later. First, the discount factor ![]() is known to the econometrician a priori. Second,
the supply shocks
is known to the econometrician a priori. Second,
the supply shocks
![]() are serially uncorrelated, an assumption that can be tested. Finally,
are serially uncorrelated, an assumption that can be tested. Finally,
![]() and
and
![]() have known functional forms. Specifically, I assume that
have known functional forms. Specifically, I assume that
![]() , which is essentially the density of housing over a fixed area, and that
, which is essentially the density of housing over a fixed area, and that
![]() , which means
, which means
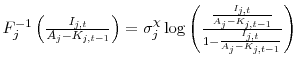 . Given these assumptions, I can
rewrite equation 3 as follows:
. Given these assumptions, I can
rewrite equation 3 as follows:
where the last term applies the fact that
To deal with the unobservable value function
![]() on the right-hand side of equation 4, I employ the representation theorem of Hotz and Miller (1993), who show that value
functions can often be rewritten as functions of conditional choice probabilities (CCPs), defined as the probabilities that a given alternative is chosen given the state of the world.13 Applying the logistic distribution function, we can write the CCP of building next period as
on the right-hand side of equation 4, I employ the representation theorem of Hotz and Miller (1993), who show that value
functions can often be rewritten as functions of conditional choice probabilities (CCPs), defined as the probabilities that a given alternative is chosen given the state of the world.13 Applying the logistic distribution function, we can write the CCP of building next period as
![\displaystyle Pr\left[B\vert S_{j,t-L_j+1}\right] = \frac{\exp\left(V^B_{i,j,t+1}/\sigma^\chi_j\right)}{\exp\left(V^B_{i,j,t+1}/\sigma^\chi_j\right) + \exp\left(V^N_{i,j,t+1}/\sigma^\chi_j\right)}.](img54.gif)
Thanks to the assumption that each city has a continuum of identical small landowners, this probability of building is precisely equal to
![]() , the ratio of parcels actually developed to the amount of available land. Substituting this into the previous expression, rearranging and taking the logarithm,
we have
, the ratio of parcels actually developed to the amount of available land. Substituting this into the previous expression, rearranging and taking the logarithm,
we have
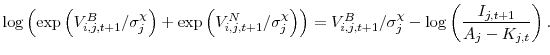
where the future supply shock disappears because I assume that the shocks are serially uncorrelated. A close analogue to this relation would result from writing the problem of a single utility-maximizing agent for each MSA and deriving an Euler equation.14 Intuitively, this similarity exists because there are no cross-parcel spillovers, so maximizing the total utility of all parcel owners gives the same result as maximizing utility individually, apart from some minor technical considerations.
There are two remaining complications that prevent estimation of equation 4. The first is the presence of unobservable expectations, specifically
![]() . Although I observe the realized prices, I cannot relate realizations and expectations without making further assumptions.
Following much of the literature on estimating dynamic models such as this one, I assume that agents form expectations rationally, so that the equation
. Although I observe the realized prices, I cannot relate realizations and expectations without making further assumptions.
Following much of the literature on estimating dynamic models such as this one, I assume that agents form expectations rationally, so that the equation
![]() defines a mean-zero forecast error.15 That is, the subjective expectations of landowners are equal to the conditional expectations.
defines a mean-zero forecast error.15 That is, the subjective expectations of landowners are equal to the conditional expectations.
Applying this definition of
![]() to equation 5, we get
to equation 5, we get
Since the outside value of land is not observed, I have folded
There are at least three possible sources of endogeneity in equation 6: First, the unobserved supply shock
![]() will in general be correlated with realized prices in city
will in general be correlated with realized prices in city ![]() at
time
at
time ![]() , since prices are determined in equilibrium. Second, the forecast error
, since prices are determined in equilibrium. Second, the forecast error
![]() is correlated with the realized value
is correlated with the realized value
![]() by construction, since the forecast error is defined to be mean independent of the expectations. Third, the housing stock in period
by construction, since the forecast error is defined to be mean independent of the expectations. Third, the housing stock in period ![]() includes investment that comes online in
includes investment that comes online in ![]() , leading mechanically to endogeneity of the housing
density term.
, leading mechanically to endogeneity of the housing
density term.
Dealing with endogeneity requires a set of exogenous demand shifters that are correlated with the relevant observables but uncorrelated with both the supply shock
![]() and the forecast error
and the forecast error
![]() . I discuss my identification strategy after first detailing my data.
. I discuss my identification strategy after first detailing my data.
4 Data
Housing markets within the United States are substantially heterogeneous, and supply-side factors like regulation and geography differ widely across metropolitan areas. This heterogeneity allows us to examine the effect of these factors on market dynamics. Essentially, each city is a separate laboratory experiment with different supply and demand conditions.
Table 1 summarizes the data used in this paper. I calculate the house price series using repeat-sales indices from the Federal Housing Finance Agency (FHFA) deflated by the Consumer Price Index and pegged to the mean house price in each city from the 2000 Census. This calculation provides a dollar-valued measure of prices that controls as best as possible for changes in the types of houses that transact in any given period.17
I specify new housing investment in each MSA and year using a weighted average of the number of housing permits issued in that area in the previous year and the current year. I calculate the weights using Census Bureau data on the time builders take to complete a house after receiving a building permit. I use permits data rather than starts or completions because the Census Bureau has a detailed inventory of permits that is finely geographically disaggregated. Although it is possible to abandon permits before starting, and even to abandon units under construction before completion, Census Bureau estimates indicate that only around 2 percent of permitted structures are not built, which is not surprising given the substantial costs involved in preparing for and acquiring a permit. I also use the permits data to calculate the total stock of housing in each MSA and year by interpolating from decennial census figures.
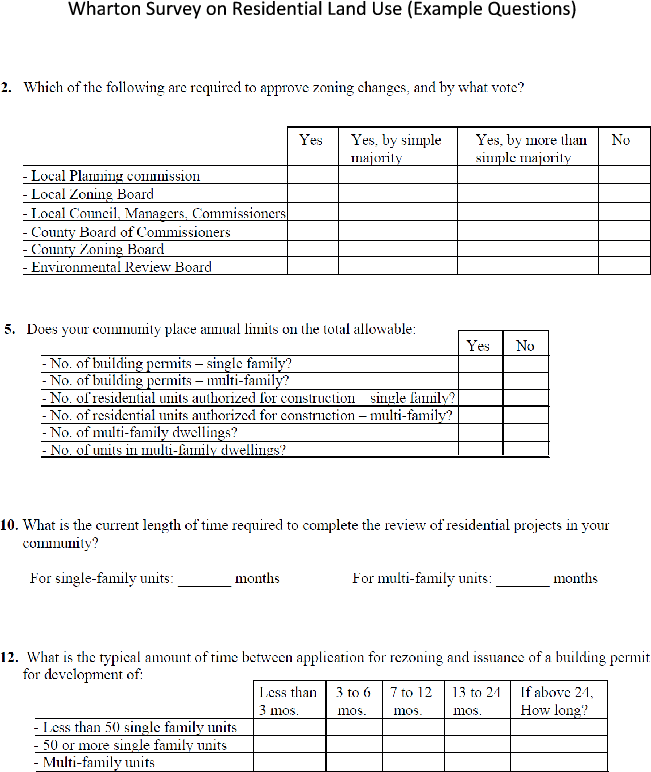
I focus on the role of three variables that capture supply constraints. The first is the Wharton Residential Land Use Regulatory Index (WRLURI), which is a measure of local regulatory constraints compiled from a 2005 survey of municipal officials (Gyourko et al., 2008). Figure 7 presents example questions from the survey, such as "What is the current length of time required to complete the review of residential projects in your community?"18 WRLURI is derived from sub-indices that cover a variety of different regulatory constraints, from financial exactions to zoning restrictions to delays in the approval process. In the context of the model, WRLURI can be interpreted as affecting lags, construction cost, and the amount of available land. That said, Gyourko et al. (2008) note that the overall index is most highly correlated with the sub-index related to average delays, which should capture some or all of the regulatory-induced construction lags. In the empirical work below, I specifically examine the role of the Approval Delay Index (ADI), which tries to measure the total delay that regulation imposes on the acquirement of a permit.19 To complement the ADI, I use a version of WRLURI that strips out the ADI as a measure of other sorts of regulation that directly affect costs and land use.
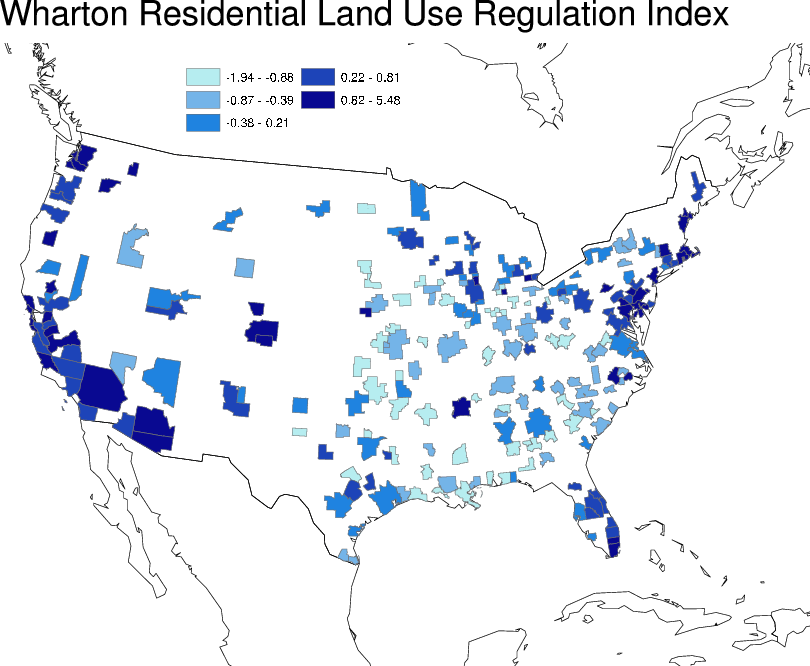
Figure 4 shows a map of every MSA in my sample, with each color representing one quintile of WRLURI. Table 2 shows the WRLURI and ADI values for the top 10 MSAs by average population over the period from 1984 to 2008, as well as San Francisco, with both regulation variables standardized to have zero mean and a standard deviation of 1. The coloration of the map and most of the values displayed in the table match the standard intuition for which markets are heavily regulated: Coastal cities (San Francisco, New York) generally display very high levels of regulation by both measures, while interior cities (Atlanta, Chicago) are typically much less regulated.
The second supply-side variable is a measure of the amount of land in each metropolitan area that is not available for development because it is steeply sloped, with a gradient greater than 15 percent.20 I calculate the amount of developable land in an MSA by subtracting this measure from the total land area in square miles of each MSA's component counties. I further scale this measure by the number of units per square mile in Manhattan, a particularly densely settled area. This ratio of the housing stock to this measure of developable "slots", which I refer to as the density of housing, can be thought of as the degree to which an MSA is currently developed relative to Manhattan.21 If costs rise as metropolitan areas "fill up", perhaps because the available land is more expensive to build on or because the outside option for the land is more valuable, the density should capture this effect.
The last measure is an estimate from the RS Means Company of the real cost of constructing a 2000-square-foot house of average quality, including labor and materials but excluding land and regulatory costs (Gyourko and Saiz, 2006). The RS Means measure should translate into
an increase in fixed construction costs in the model (![]() ). The RS Means data are available in a panel by MSA and year, but WRLURI is observed only once for each MSA -- in 2005, when the
survey was conducted -- while the Saiz measure is essentially time-invariant.
). The RS Means data are available in a panel by MSA and year, but WRLURI is observed only once for each MSA -- in 2005, when the
survey was conducted -- while the Saiz measure is essentially time-invariant.
4.1 Demand Shifters
As in any model of market equilibrium, the quasi-differenced price term in equation 6 is likely to be correlated with the supply shocks precisely because prices are set in equilibrium. Consistently estimating the supply equation requires one or more variables that are
correlated with house prices and uncorrelated with supply shocks. Given that I allow the supply parameters to differ across MSAs, these exogenous variables must also provide variation across both the time ![]() and MSA
and MSA ![]() dimensions.
dimensions.
To get variation in annual housing demand at the MSA level, I rely on two plausibly exogenous variables. The first (
![]() ) follows Bartik (1991) in imputing shifts in local labor demand by interacting national-level shifts in industry-specific employment with the average
shares (across time) of employment or compensation that those industries have in particular cities.22 For example, when auto industry employment and/or
compensation decreases nationwide due to a systemic negative demand shock, the city of Detroit and its surrounding MSA should be particularly negatively affected. I use annual MSA by industry employment data from the Census Bureau's County Business Patterns (CBP) to form this variable. To ensure
that local conditions in particular MSAs with sizable shares of total national employment in a given industry do not feed back into
) follows Bartik (1991) in imputing shifts in local labor demand by interacting national-level shifts in industry-specific employment with the average
shares (across time) of employment or compensation that those industries have in particular cities.22 For example, when auto industry employment and/or
compensation decreases nationwide due to a systemic negative demand shock, the city of Detroit and its surrounding MSA should be particularly negatively affected. I use annual MSA by industry employment data from the Census Bureau's County Business Patterns (CBP) to form this variable. To ensure
that local conditions in particular MSAs with sizable shares of total national employment in a given industry do not feed back into
![]() , I omit city
, I omit city ![]() from the "national" shift in employment when
calculating the variable for city
from the "national" shift in employment when
calculating the variable for city ![]() .
.
To provide a useful check on the employment shift-share variable, which is quite popular in the literature, I also employ county-level migration data from the IRS,
![]() .23 The idea is similar in spirit
to that behind
.23 The idea is similar in spirit
to that behind
![]() : While inflows and outflows of migrants from MSA
: While inflows and outflows of migrants from MSA ![]() are likely
endogenous with respect to local supply shocks, we can impute overall inflows for MSA
are likely
endogenous with respect to local supply shocks, we can impute overall inflows for MSA ![]() using the other outflows from MSAs that typically send many migrants to
using the other outflows from MSAs that typically send many migrants to ![]() . For example, outflows from New York to Philadelphia, Washington, Los Angeles, and other cities change in response to New York-specific shocks. The sum of these outflows can be used (along with similar sums from other
cities) to impute in-migration to Boston, because Boston typically receives a large share of its in-migrants from New York.
. For example, outflows from New York to Philadelphia, Washington, Los Angeles, and other cities change in response to New York-specific shocks. The sum of these outflows can be used (along with similar sums from other
cities) to impute in-migration to Boston, because Boston typically receives a large share of its in-migrants from New York.
Both variables are exogenous to local supply shocks under reasonable but non-verifiable conditions. The
![]() requires that a city's housing supply shocks are not systematically correlated with national industry shocks that differentially affect that city. Similarly,
requires that a city's housing supply shocks are not systematically correlated with national industry shocks that differentially affect that city. Similarly,
![]() will be exogenous provided that supply shocks in a given city are not correlated with out-migration from other cities that usually send lots of migrants to the first
city.24
will be exogenous provided that supply shocks in a given city are not correlated with out-migration from other cities that usually send lots of migrants to the first
city.24
5 Estimation Strategy
As noted above, least squares estimation of equation 6 would yield inconsistent estimates for at least three reasons: The market price of housing is determined in equilibrium and is therefore endogenous, the forecast error ![]() will be correlated with time
will be correlated with time ![]() realizations, and the lagged housing density in
realizations, and the lagged housing density in ![]() is mechanically correlated with shocks to new investment in
is mechanically correlated with shocks to new investment in ![]() .
.
The first and third endogeneity concerns can be addressed in a straightforward manner: I use the employment and migration variables detailed in the previous section to instrument for the house price term, and I use the first lag of of the quasi-differenced density to instrument for the
contemporaneous value.25 The set of underlying instruments for ![]() at
at ![]() , which I denote
, which I denote ![]() , is thus
, is thus

The relationship between the forecast error and endogeneity is more complicated to address. The standard approach in rational expectations models is to use variables dated at or before the time the expectations are formed; under the rational expectations assumption anything in the information
set of the agents must be orthogonal to the future forecast errors. It is neither easy nor desirable to do that in this case, because the true forecast lag ![]() differs across cities and may
not be perfectly observable, since the Approval Delay Index (ADI) component of WRLURI likely only captures differentials in lags caused by regulation, rather than the overall size of the time needed to plan before building.26 Moreover, the effect of the forecast error resulting from regulation is not a nuisance in this case but something I am particularly interested in estimating.
differs across cities and may
not be perfectly observable, since the Approval Delay Index (ADI) component of WRLURI likely only captures differentials in lags caused by regulation, rather than the overall size of the time needed to plan before building.26 Moreover, the effect of the forecast error resulting from regulation is not a nuisance in this case but something I am particularly interested in estimating.
Instead, I adopt a hybrid approach, using ![]() for prices and investment at period
for prices and investment at period ![]() . This one-year lag roughly corresponds with the time at which permits are issued, and it is the minimum amount of time needed for the entire process. Importantly, however, under the rational expectations assumption these instruments will still be correlated with the forecast error
between
. This one-year lag roughly corresponds with the time at which permits are issued, and it is the minimum amount of time needed for the entire process. Importantly, however, under the rational expectations assumption these instruments will still be correlated with the forecast error
between ![]() and
and ![]() . To simplify the notation, let
. To simplify the notation, let
![]() . Consider the forecast error
. Consider the forecast error
![]() , which is defined as above by
, which is defined as above by
![\begin{displaymath}\begin{split} \nu_{j,t-L_j} &= \dot{P}_{j,t} - E_{t-L_j}\left[\dot{P}_{j,t} \right] \ &= \left(\dot{P}_{j,t} - E_{t-1}\left[\dot{P}_{j,t}\right]\right) - \left(E_{t-L_j}\left[\dot{P}_{j,t}\right] - E_{t-1}\left[\dot{P}_{j,t}\right]\right). \end{split}\end{displaymath}](img77.gif)
Rather than making the somewhat implausible assumption that the ADI exactly measures the total lag, I make the less stringent assumption that
where
I allow the parameters with ![]() subscripts in equation 3,
subscripts in equation 3,
![]() and
and
![]() , to vary by MSA by interacting the primary observables with WRLURI and its sub-indices. Importantly, I take regulation as exogenously given, rather than allowing it to respond
to conditions in the housing market or even vary over time. This seems reasonable given that I estimate the model over a relatively short time span, and levels of regulation likely change slowly over time.27 This simplification is also necessary, both for data reasons -- my measure of regulation is observed only once for each city -- and to keep the model tractable.28 I do, however, use preliminary data from a new round of the Wharton survey as a robustness check; the results are similar to my preferred estimates.
, to vary by MSA by interacting the primary observables with WRLURI and its sub-indices. Importantly, I take regulation as exogenously given, rather than allowing it to respond
to conditions in the housing market or even vary over time. This seems reasonable given that I estimate the model over a relatively short time span, and levels of regulation likely change slowly over time.27 This simplification is also necessary, both for data reasons -- my measure of regulation is observed only once for each city -- and to keep the model tractable.28 I do, however, use preliminary data from a new round of the Wharton survey as a robustness check; the results are similar to my preferred estimates.
Since I am trying to identify both the main effects and interactions with the WRLURI indices, I must specify what functions of the exogenous ![]() and WRLURI I use as the actual
instrument set
and WRLURI I use as the actual
instrument set
![]() . Following a common practice in the econometric literature, I run regressions to get
. Following a common practice in the econometric literature, I run regressions to get
![]() and
and
![]() , the linear projections of the quasi-differenced log price and housing density onto the
fixed effects and the exogenous industry employment, migration, and lagged density variables. Since the very nature of the model implies that even identical demand shocks should affect prices in each MSA differently, I use a separate linear projection for each MSA, which allows the coefficients on
the demand shifters to vary. I then multiply these projections by the relevant components of WRLURI for the specification in question and use the projections and the interactions as the instruments in a second-step IV procedure.29
, the linear projections of the quasi-differenced log price and housing density onto the
fixed effects and the exogenous industry employment, migration, and lagged density variables. Since the very nature of the model implies that even identical demand shocks should affect prices in each MSA differently, I use a separate linear projection for each MSA, which allows the coefficients on
the demand shifters to vary. I then multiply these projections by the relevant components of WRLURI for the specification in question and use the projections and the interactions as the instruments in a second-step IV procedure.29
The advantage of this approach is that that it is likely to be more efficient than using an arbitrary set of functions of ![]() and WRLURI as instruments, since it directly imposes the
interaction in the instrument set. The disadvantage is that, with exactly as many instruments as endogenous variables, I cannot directly test the overidentifying restrictions that implicitly underlie the estimates.
and WRLURI as instruments, since it directly imposes the
interaction in the instrument set. The disadvantage is that, with exactly as many instruments as endogenous variables, I cannot directly test the overidentifying restrictions that implicitly underlie the estimates.
Finally, to estimate equation 6 I must either specify or estimate the discount factor ![]() . Identifying the discount rate has proven to be extremely
challenging for other researchers, so I follow much of the literature and simply assume that
. Identifying the discount rate has proven to be extremely
challenging for other researchers, so I follow much of the literature and simply assume that
![]() , a commonly accepted value.30 Even
after assuming a value for
, a commonly accepted value.30 Even
after assuming a value for ![]() , I must still choose how to deal with the compound discount factor
, I must still choose how to deal with the compound discount factor
![]() , since I cannot simultaneously identify it with
, since I cannot simultaneously identify it with
![]() ,
,
![]() , and the variance of the error term. As I have already argued, assuming values for the construction lag
, and the variance of the error term. As I have already argued, assuming values for the construction lag ![]() , such as the ADI, is not particularly attractive given that the true magnitude of the lag may be larger than what is reported, even if the ADI appropriately captures differences in the lag. Moreover, one of the points of this paper is to study the effects of
increasing the lag. While I must do so indirectly, I certainly do not want to assume away an empirical question of interest. Instead, I let
, such as the ADI, is not particularly attractive given that the true magnitude of the lag may be larger than what is reported, even if the ADI appropriately captures differences in the lag. Moreover, one of the points of this paper is to study the effects of
increasing the lag. While I must do so indirectly, I certainly do not want to assume away an empirical question of interest. Instead, I let
![]() , where
, where
![]() is a increasing function relating the ADI to the actual lag. I then divide the entire equation through by
is a increasing function relating the ADI to the actual lag. I then divide the entire equation through by
![]() and estimate the normalized equation.
and estimate the normalized equation.
Applying this normalization and equation 7 to equation 6, specifying the interactions using WRLURI excluding the ADI (![]() ) and the ADI
(
) and the ADI
(![]() ), and taking the expectation with respect to
), and taking the expectation with respect to
![]() and the fixed effects yields
and the fixed effects yields
This moment condition could form the basis of an exactly identified nonlinear Generalized Method of Moments (GMM) estimator with fixed effects. To simplify estimation a bit, take the partial derivative of the coefficient on the investment term with respect to ![]() ,
,
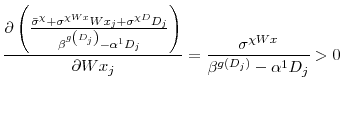
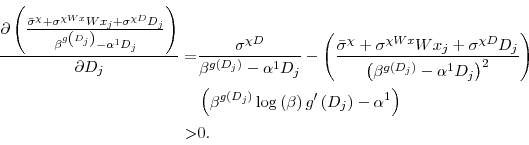
I use this moment condition as the basis for a linear-in-parameters IV estimator.
6 Reduced-Form/Myopic Model Estimates
Before presenting estimates from the full model, I provide some basic regression and IV results that generally follow equation 9 but ignore forward-looking behavior on the part of landowners. These results illustrate the patterns in the data in a transparent way and mimic typical approaches from the existing literature that can be compared with my structural estimates. They can also be interpreted as a reduced form of the structural model, although they are misspecified in that they ignore forward-looking behavior.
To specify these regressions, I start with moment condition 9 and make several simplifications. First, and most importantly, I assume that agents are myopic and do not take into account future prices or investment, which means setting all the one-period-ahead terms
(
![]() , e.g.) to zero. Second, I use the fact that
, e.g.) to zero. Second, I use the fact that
![]() for small
for small ![]() to simplify
the investment term, since the probability of investment for any slot is never more than 0.002 in my data. Third, I isolate the investment term on the left-hand side and linearize the resulting price coefficient so as to parallel typical regression models relating investment and price. These
changes yield the equation
to simplify
the investment term, since the probability of investment for any slot is never more than 0.002 in my data. Third, I isolate the investment term on the left-hand side and linearize the resulting price coefficient so as to parallel typical regression models relating investment and price. These
changes yield the equation
in which I have appended
Ignoring any endogeneity concerns about
![]() for the moment, I estimate several versions of equation 10 using ordinary least squares; the results are presented in table 3.
In the first column, I regress the log investment probability on log price and the housing density, with no interactions, while including MSA and year fixed effects to pick up persistent differences in MSA supply-side conditions or nationwide year-specific shocks. The fixed effects allow me to
focus on the effects of transitory city-specific shocks.
for the moment, I estimate several versions of equation 10 using ordinary least squares; the results are presented in table 3.
In the first column, I regress the log investment probability on log price and the housing density, with no interactions, while including MSA and year fixed effects to pick up persistent differences in MSA supply-side conditions or nationwide year-specific shocks. The fixed effects allow me to
focus on the effects of transitory city-specific shocks.
On average across years and MSAs, I find that a 1 percent increase in price is associated with a 1.35 percent increase in investment, with a standard error of just 0.04 percent. Meanwhile, a 1 percentage point higher density is associated with 1.77 percent less investment. Since the stock is less than 5 percent of developable area in almost all MSAs and shifts quite gradually within a given MSA, most of the rapid changes in investment are attributable to changes in price rather than in density.
In principle, I would like to take advantage of the RS Means construction cost data in both these reduced-form estimates and the structural model. Column (2) in table 3 shows the results of including log construction costs as a covariate; unsurprisingly, higher construction costs reduce investment, all else being equal. The coefficients on construction costs and price are quite similar, as the model suggests is appropriate. The downside of the RS Means data is that they are only available for a subset of MSAs -- less than half the sample of MSA years that are otherwise available. Since including construction costs in the regression leaves the coefficients nearly unchanged from an unreported version of column (1) that uses the same sample as column (2), I omit them from subsequent regressions.
The final two columns in the table break apart the supply elasticity and density coefficient and examine how they vary across cities. In column (3) I interact both log price and the density with the top-line WRLURI ("Regulation"), which I standardize so that it has a mean of zero and standard deviation of 1 across MSAs. The first line of column (3) indicates that a city with an average level of regulation has an elasticity of 1.69, while each 1 standard deviation increase in regulation reduces the elasticity by 0.46. The interaction of regulation with the density is also highly statistically significant and very large relative to the mean effect of -0.46, indicating that more regulation may cause cities to "fill up" more quickly. Even without a direct structural interpretation or clear identification, the sheer size of the effect of regulation on these estimates is noteworthy.
Finally, column (4) repeats the regression from column (3) but separately interacts log price with the Approval Delay Index ("Delays") and a version of WRLURI that excludes the ADI ("Regulation excl. Delays"). While the two sub-indices are highly correlated, the first should correspond to an
increase in the amount of time it takes to prepare for and acquire a building permit, while the second should capture all other cost-shifting regulations imposed by local governments, such as density restrictions, open space requirements, and so forth. Delays are likely to affect the supply
elasticity by increasing the forecast error and thus lowering the correlation between
![]() and
and
![]() , while the "everything else" measure works by raising costs faster in regulated areas as investment increases.32
, while the "everything else" measure works by raising costs faster in regulated areas as investment increases.32
Both measures have a substantial effect on the estimated supply elasticity. A city with average delays and average other regulation has an estimated elasticity of 1.72, while 1 additional standard deviation of delay reduces the elasticity by 0.37 and a 1 standard deviation increase in other regulation reduces the elasticity by 0.15. These estimates suggest that delays may be a particularly important component of regulation, at least with respect to supply elasticity. Interestingly, the magnitude of the density coefficient is decreasing in delays but much more sharply increasing in other forms of regulation. Cities seem to be "filling up" more quickly when there is more regulation, but not when there are more delays alone. This result is comforting, since it suggests that the "everything else" measure of regulation may in fact be picking up density limitations or other related factors.
6.1 IV
While enlightening, these parameter estimates are potentially inconsistent -- even ignoring dynamic considerations -- for two reasons: First, as noted above, unobserved supply shocks will be correlated with realized prices, which are determined in equilibrium. Second, the error in the forecast
of
![]() is correlated with that term by construction, since it must be mean independent of the expectation under the rational expectations assumption.
is correlated with that term by construction, since it must be mean independent of the expectation under the rational expectations assumption.
To deal with these issues, I employ
![]() and
and
![]() , as discussed in section 5 above. I project
, as discussed in section 5 above. I project
![]() onto these two variables separately for each MSA and then interact the projection with WRLURI and its sub-indices as needed to identify the interaction terms. Table 4 uses this IV method to re-estimate the specifications from table 3. The elasticity estimates in the first line are smaller in magnitude than those from the previous table, while the effects of rising density are similar.33
onto these two variables separately for each MSA and then interact the projection with WRLURI and its sub-indices as needed to identify the interaction terms. Table 4 uses this IV method to re-estimate the specifications from table 3. The elasticity estimates in the first line are smaller in magnitude than those from the previous table, while the effects of rising density are similar.33
The pattern of the interaction terms in columns (3) and (4) are essentially the same as in table 3. While the coefficients are somewhat smaller in magnitude, they are larger relative to the main effect of log price, that is, the elasticity of a city with average regulation. These estimates thus suggest, if anything, an even larger role for regulation in determining relative elasticities. In addition, non-delay regulation continues to have a very large effect on the stock/area coefficient, while the ADI interaction is positive, again suggesting that delays affect the elasticity of supply with respect to price, while other forms of regulation lead to higher prices as cities use up available land.
With or without IV, the coefficients estimated in this section are economically sizable. An elasticity of about 1 means that a typical change in log investment of 0.19 must drive up costs on the margin by 19 percent for the housing market to be in equilibrium in a given year.34 At the mean house price in my sample of about $140,000, that price increase is $26,600. For a city like San Francisco, which has an approval delay six months above the mean -- about 2.2 standard deviations -- the predicted supply elasticity using column (4) is about 0.25. This corresponds to an increase in marginal costs of more than 75 log points, which would more than double the price level, for each 0.19 increase in log investment. In equilibrium, households are unwilling, even in San Francisco, to pay such high prices, which means that actual investment tends to be much lower than the national average.
These results are informative but only suggestive of the true cost parameters and elasticities because they do not take dynamics into account. A priori, we should expect the true elasticities -- the response of supply to a one-time increase in price -- to be substantially higher than these myopic estimates, since price changes are positively autocorrelated (Glaeser and Gyourko, 2007). That is, a price increase in a given city today is likely to be followed by another increase tomorrow, so what appears to be a small response of investment to a large increase in price may simply be a rational response to price dynamics. This effect is precisely what I find in my empirical results, as I discuss in the next section.
7 Structural Model Estimates
Having established the basic correlations in the data, I now turn to estimating the structural parameters of the dynamic supply model. Table 5 shows estimates for several variants of equation 9.35 Column (1) is a baseline specification that does not allow for any MSA-level heterogeneity, so the reported parameter values are averages across high- and low-regulation cities.
The value for the parameter
![]() on the first line of the table can be interpreted as the percentage increase in the cost of constructing a single house, on the margin, that results from a 1 percent
increase in investment in a given MSA and year. Increasing investment by 1 percent leads to 0.42 percent higher costs. We can take the reciprocal of this figure to get a supply elasticity of about 2.4. Holding other factors fixed, increasing log investment by 0.19, which is the mean across MSAs and
years of the absolute change in log investment, increases costs on the margin by about 8 percent. For an average home in my sample, which is worth about $140,000, that corresponds to an increase in price of more than $11,000.
on the first line of the table can be interpreted as the percentage increase in the cost of constructing a single house, on the margin, that results from a 1 percent
increase in investment in a given MSA and year. Increasing investment by 1 percent leads to 0.42 percent higher costs. We can take the reciprocal of this figure to get a supply elasticity of about 2.4. Holding other factors fixed, increasing log investment by 0.19, which is the mean across MSAs and
years of the absolute change in log investment, increases costs on the margin by about 8 percent. For an average home in my sample, which is worth about $140,000, that corresponds to an increase in price of more than $11,000.
The effect of using up land -- that is, increasing the capital stock relative to the developable land area in a city -- is less important for annual investment, but still relevant over the long run. The estimated value of
![]() in column (1) indicates that a 1 percentage point increase in the housing density increases costs by about 337 log points. While this parameter is superficially larger than
the marginal cost parameter, it can only be interpreted once we note that the overall housing stock changes quite slowly. Even booming cities like Las Vegas and Phoenix in the mid-2000s add only a couple hundredths of a percentage point to their densities in a given year. The mean absolute change
in density across all MSAs and years is about 0.006, and a shift of that magnitude changes costs by 2 percent, or about $3,000 for the average home.36
in column (1) indicates that a 1 percentage point increase in the housing density increases costs by about 337 log points. While this parameter is superficially larger than
the marginal cost parameter, it can only be interpreted once we note that the overall housing stock changes quite slowly. Even booming cities like Las Vegas and Phoenix in the mid-2000s add only a couple hundredths of a percentage point to their densities in a given year. The mean absolute change
in density across all MSAs and years is about 0.006, and a shift of that magnitude changes costs by 2 percent, or about $3,000 for the average home.36
Column (2) shows that the estimated parameter values are similar when the RS Means construction cost is included in quasi-differenced form, as in equation 9.37 The coefficient on the cost term is small and statistically indistinguishable from zero, despite the fact that our null, based on the theory, should be a coefficient of 1. The likely explanation for this result is that the construction cost measure is highly smoothed relative to reality, so that the quasi-differencing and inclusion of fixed effects remove nearly all of the relevant variation.
Regulation plays a more interesting and important role. In column (3) I interact the marginal cost and density parameters with the top-line WRLURI measure of regulation. As in the reduced-form/myopic estimates, we can see a strong effect of regulation, raising marginal costs -- including via delays and the forecast error -- and by extension reducing the price elasticity of supply. Since the regulation measure is standardized to have mean zero, the first line of the column indicates that an MSA with an average level of regulation has a marginal cost increase of 0.40 percent for each 1 percent increase in investment.
For a city with regulation 1 standard deviation above the mean, this figure rises to 0.49 percent. Multiplying this by 0.19, which is a typical change in log investment, and the average price of housing in my sample yields an increase of $13,000 per house on the margin. For a very regulated and expensive city like Boston, with a standardized WRLURI value of about 2 and average house price of $250,000, the same increase in investment would increase costs by $28,000, more than a tenth the price of the house.38
In column (4) I break apart regulation into its two subcomponents, delays and the "everything else" measure that comprises all the WRLURI sub-indices except the ADI. For a city with average delays and average "other" regulation, a 1 percent increase in investment raises the marginal
per-house cost of construction by 0.34 percent. Approval delays of 1 standard deviation more than the mean city increase this effect by 0.07, with a standard error of 0.01.39 A single standard deviation in other regulation (
![]() ) has a smaller effect on marginal costs, 0.03.
) has a smaller effect on marginal costs, 0.03.
The density parameters for an average regulation city in columns (3) and (4) are larger than the un-interacted parameter in column (1), though the standard errors are larger as well. I find a negative effect of regulation in column (3), but the standard error is large enough that I cannot draw any meaningful conclusions. In column (4) I find a fairly sizable negative relationship between the ADI and density-related costs, along with a significant positive effect of regulation excluding delays. This pattern is similar to the one found in tables 3 and 4, although the surprising negative effect of delays on costs now outweighs the positive effect from other regulation. Importantly, we can still conclude that cities have higher costs, and thus lower investment, when they have larger housing stocks relative to their land areas.
In table 6, I show how marginal costs vary across cities with different measured levels of regulation. I use the estimated parameter values for the marginal cost of investment in column (4) of table 5 and the regulation levels reported in table 2 to impute the marginal cost of investment in each city. The first column shows the approximate percentage effect on marginal costs of a 19 log point increase in investment, which is a good yardstick because it is the average absolute change in investment across all MSAs and years in my sample. The second column multiplies this percentage by the average real house price in each city over the period from 1984 to 2008.
Cities with substantial levels of regulation, either via approval delays (the ADI) or other components of WRLURI, have much higher marginal costs of investment. For example, the effect of the 19 log point change in investment is substantially higher in New York and San Francisco (both about 11 percent) than in Atlanta (less than 8 percent) and Houston (less than 7 percent). When translated into dollar terms, these differences are much more sizable, since average prices are higher in regulated coastal cities than in relatively unregulated cities in the interior. Prices in Atlanta would rise by just $13,000 in response to a 19 point baseline change in investment, while in New York they would shift more than twice as much and in San Francisco nearly four times as much.
The response of landowners and builders to these higher marginal costs is to reduce their increases in investment in response to demand-driven price increases. As a result, price elasticities are lower on the coasts than in the interior. For example, I estimate that the price elasticity of supply in both New York and San Francisco is about 1.7, while the elasticity in Atlanta is 2.4 and in Houston 2.8. These elasticity estimates are larger than have been previously estimated in the literature because they explicitly account for dynamics, as discussed at the end of the previous section.
7.1 Robustness Checks
In estimating the structural model, I make a series of sometimes restrictive assumptions. In this section, I check the robustness of my results to alternative specifications, which are shown in table 8. Each column is a re-estimate of column (3) from table 5 -- the model with WRLURI interacted with the marginal cost and density parameters -- using a different specification.
Arguably the most important assumption underlying the estimates is the exogeneity of regulation, in particular WRLURI and its subcomponents. I rely in particular on the notion that regulation is constant over time, or at least that it does not shift in response to house price volatility or supply elasticities over the relatively short horizon of my data.40 Although I cannot directly test this assumption without better data and substantially complicating the model, I am able to provide suggestive evidence using preliminary data from a new version of the Wharton survey.41
Using the raw data from the new survey, I compute versions of WRLURI and the ADI following as closely as possible the original methodology.42 I find that the 2010 WRLURI and ADI are highly correlated with the 2005 versions, with correlation coefficients at the MSA level of about 0.7 and 0.6 respectively. This is despite the fact that there are likely to be some errors in the preliminary new data that have not yet been corrected and despite different samples of responding jurisdictions within the MSAs.
To further examine the importance of possible changes in regulation over time, we can turn to column (1) of table 8, which replaces my standard (2005) regulation measure with the one derived from the 2010 survey. The results are quite similar to those in column (3) of table 5. For a city with average regulation, a 1 percent increase in investment raises costs on the margin by 0.38 percent, essentially the same as previously estimated. More importantly, the interaction effect with WRLURI is still 0.09. The effect of increasing density on costs is now even larger than in table 5, although there is a counterintuitive negative effect of regulation on density-related fixed costs.43
Since it is this
![]() term that is vital in explaining differences in elasticities across housing markets, it is greatly comforting that the estimate is similar using the new round of the survey.
While this is not definitive proof that regulation has not endogenously changed over the sample period, it goes some way toward easing these concerns.
term that is vital in explaining differences in elasticities across housing markets, it is greatly comforting that the estimate is similar using the new round of the survey.
While this is not definitive proof that regulation has not endogenously changed over the sample period, it goes some way toward easing these concerns.
In column (2) I estimate the model including the RS Means construction cost data in the price term, essentially normalizing the coefficient on costs to be one, as theory suggests. This has minimal effects on the estimates. The final three columns examine the possibility that particular forms of
within-sample correlation in supply shocks render one or more of the instruments endogenous. For example, if the supply shocks
![]() follow a first-order autoregression over time, then I cannot use the first lag of the quasi-differenced density term as an exogenous shifter of the contemporaneous
value.44 In column (3) I instead use the second lag,
follow a first-order autoregression over time, then I cannot use the first lag of the quasi-differenced density term as an exogenous shifter of the contemporaneous
value.44 In column (3) I instead use the second lag,
![]() , as part of
, as part of ![]() . The
results are also similar to those in column (3) of table 5, although the main effect of density is larger and the interaction with regulation is negative.
. The
results are also similar to those in column (3) of table 5, although the main effect of density is larger and the interaction with regulation is negative.
Alternatively, supply shocks could be spatially rather than temporally correlated. This could render my migration-based demand shifter endogenous, since it relies on the assumption that supply shocks in a given city are uncorrelated with outflows from other cities, which are presumably affected
by their own supply shocks. In column (4) I drop
![]() entirely and rely solely on the
entirely and rely solely on the
![]() to get exogenous variation in house prices. In column (5), I use an alternative version of the migration variable in which, for the calculation of the value for MSA
to get exogenous variation in house prices. In column (5), I use an alternative version of the migration variable in which, for the calculation of the value for MSA
![]() , I exclude MSAs that are less than 100 miles away from
, I exclude MSAs that are less than 100 miles away from ![]() . In both cases, I find
estimates very similar to column (3) of table 5, which should alleviate concerns that the variable could be correlated with local supply shocks that are spatially autocorrelated at relatively close distances.
. In both cases, I find
estimates very similar to column (3) of table 5, which should alleviate concerns that the variable could be correlated with local supply shocks that are spatially autocorrelated at relatively close distances.
8 Model Simulations
Although the estimated parameters are interesting in themselves, one of the most valuable parts of estimating a structural model is the ability to perform simulations of various scenarios, including counterfactuals. In this section I show the results of a series of simulations, first varying parameters one at a time to demonstrate the effect and then showing how the estimated parameters for two cities -- San Francisco and Atlanta -- imply substantially different amounts of volatility, even given the exact same demand shocks.45 Although it is quite likely that the volatility of shocks also varies across cities, this approach allows me to isolate the role of supply constraints.
One way of showing how cities with different supply constraints respond to demand shocks is to plot their impulse response functions. In figure 8 I plot the normalized impulse responses of San Francisco and Atlanta to a one-time demand shock of about 3 percent, which is the average standard deviation of the demand innovations in the MSA vector autoregressions estimated above. Since the demand shock follows an AR(1) process with a coefficient of 0.8, the shock decays relatively slowly over time. In addition, a follow-on direct effect on house prices results from the effect of the demand shock on the future user cost shock.
Although the shocks in each city are identical, the resulting rent and price processes are very different.46 By construction, rents in both cities jump by the same amount, but they drop back much more quickly in Atlanta. Meanwhile, house prices in Atlanta jump by less than in San Francisco and are back to baseline 10 years after the shock. In San Francisco, prices take 20 years to return to baseline.
The explanation for this difference is evident in the bottom two panels: In equilibrium, the initial investment response in percentage terms appears much the same in the two cities, but because average investment is so much higher in Atlanta, the same percent increase means a much larger increase in the size of the capital stock. Consequently, by year 10 the stock in Atlanta has increased by about 0.4 percentage points, compared with 0.1 percentage points in San Francisco. This difference explains why rents return to baseline faster and why prices never jump as much in the first place, since the supply response is built into expectations.
An alternative way to examine dynamics is to repeatedly simulate the model with randomly drawn house price shocks and examine the moments of the resulting price and investment paths. The first four lines of table 9 present basic results for a series of simulations with
different elasticities but identical demand-side conditions. As a baseline I use a one-year lag and the marginal cost of investment (
![]() from equation 6) implied for a city with regulation at the MSA median by the results in column (4) from table 5. The second
line ("Low Regulation") uses the fixed and marginal costs implied for cities at the 10th percentile of delays and the all-else regulation measure, while the third line ("High Regulation") uses the costs implied for cities at the 90th percentile of those measures. The fourth line uses a two-year
lag but no direct changes in marginal costs. In each case I simulate the model using the same 100 randomly chosen 25-year paths for the demand shock and then average the relevant moment across the simulations.47
from equation 6) implied for a city with regulation at the MSA median by the results in column (4) from table 5. The second
line ("Low Regulation") uses the fixed and marginal costs implied for cities at the 10th percentile of delays and the all-else regulation measure, while the third line ("High Regulation") uses the costs implied for cities at the 90th percentile of those measures. The fourth line uses a two-year
lag but no direct changes in marginal costs. In each case I simulate the model using the same 100 randomly chosen 25-year paths for the demand shock and then average the relevant moment across the simulations.47
Comparing the first and second lines of the table, we can see that lowering regulation reduces the standard deviation of log prices relative to the baseline.48 Volatility by this measure is about 0.003 lower, or one-tenth of baseline volatility. Since the demand shocks are identical in each case, these differences must result from differences in investment. The standard deviation of log investment is appreciably higher when regulation is lower because the elasticity is higher: Landowners and builders are able to respond to demand shocks by increasing investment and the capital stock when demand is high, thus attenuating the effect of the shocks on price.
The converse is true when regulation is higher. Comparing the third line with the second, we can see that going from the 90th percentile of regulation to the 10th percentile reduces the volatility of prices by 20 percent, because it decreases the volatility of investment by about 30 percent. Moving from a one-year lag to a two-year lag, in the fourth line, has similarly sized effects on price and investment volatility. I find these sizable differences despite conservatively choosing parameters such as the elasticity of demand and the persistence of demand shocks.
The next two lines of the table emphasize that the level of new investment also matters for volatility, even keeping marginal costs the same. To do this, I vary the amount of available land while holding constant all other parameters, including the steady-state capital stock. In the "More Land" line, I change fixed costs in the supply equation consistent with a city having 10 percent more developable land, and thus a lower density. My estimates imply that this has a dramatic effect on the level of new investment, which doubles relative to the baseline. As a result, even though the elasticity of supply is only slightly lower, volatility is nearly 10 percent less than in the baseline. Conversely, when there is 10 percent less land area (the "Less Land" line) than the baseline, investment is much lower and volatility is as high as when marginal costs are high or the lag is longer.
The last two lines of the table show how real-world differences in regulation can can dramatically affect housing markets. I simulate the model using the supply parameters estimated for San Francisco and Atlanta, relying on their differing values of the ADI and the other components of WRLURI, as well as their quite different densities. The model matches the price and investment levels almost perfectly, thanks to the fixed effects. The effects on volatility are more interesting.
The highly regulated and geographically constrained city (San Francisco) has much higher and more volatile prices than the less regulated and constrained city (Atlanta). In relative terms, investment is actually more volatile in San Francisco, precisely because prices are also more volatile, but because average investment is so low relative to the capital stock, even large changes in investment have a minimal feedback effect on price. This reemphasizes the point that both the elasticity -- in percentage terms -- and the average level of new investment matter for volatility.
Since I completely shut down migration by holding the steady-state capital shocks constant and use identical demand shocks, rather than allowing different demand shock variances across cities, these results are not fully realistic, but the implications are striking and well in accord with the patterns that we observe empirically. In terms of volatility, the standard deviation of log house prices in Atlanta from 1984 to 2008, after regressing out the time trend, was about 0.08. The comparable figure for San Francisco was 0.16, twice as large. Looking back at table 9, we see that even this limited simulation can explain a percentage difference in volatility of about 45 percent. The fact that the model does a very poor job of replicating the level of price volatility on average across cities is quite interesting. It may relate to the puzzle, noted above, that house price volatility is much greater than rent volatility. Nevertheless, it is the relative values that matter for my purposes, and the simulations confirm that the model predicts wide disparities in volatility in markets with different supply-side parameters.
9 Conclusion
After the experience of recent years, the importance of volatility in house prices and housing investment is abundantly clear. Understanding the factors that govern differences in volatility requires knowledge of both the demand and supply sides of the housing market. Although we have learned a great deal about the importance of the supply side in recent years, much more research is needed.
This paper makes several contributions to our knowledge of housing supply and the role it plays in determining house price volatility. Building on previous work, I develop a dynamic structural model of housing supply that is grounded in a basic microeconomic optimization problem. I then use the model to carefully identify key structural supply-side parameters and show how they vary across metropolitan areas with observed levels of regulation. I find that regulation of all kinds causes delays and adds tens of thousands of dollars to the cost of a house on the margin in a more regulated city relative to a less regulated one. I also find that geographic constraints on land availability, which increase the effective density of cities when holding the capital stock constant, increase costs substantially and lower average investment.
In contrast with the existing literature, I am able to use the theory and data to explore the mechanisms by which these constraints affect volatility. Delays and higher marginal costs reduce supply elasticities and, as a consequence, amplify the volatility of house prices. My simulations suggest that, even in a model with no inter-metropolitan migration and identical demand shocks, observed regulation can explain a large fraction of the difference in volatility of house prices between a highly regulated city like San Francisco and a relatively unregulated one like Atlanta. Although housing regulation has deep and complex roots, this conclusion has important policy implications, both for local governments and for private groups such as homeowners' associations that often oppose new construction.
One caveat to my conclusions is that I do not study the benefits of housing supply regulation to any of the involved parties. Homeowners have a strong incentive to protect their property values, both by limiting the exposure of their homes to potentially noxious adjacent uses -- the traditional justification for zoning -- and by preventing nearby new construction that could, in effect, compete with their own homes and drive down prices when they look to sell in the future. The effect of regulation on price levels can thus be seen as a transfer to current homeowners from prospective future home buyers, who face higher prices, and some current landowners, who may be prevented from fully developing their land and selling at the market price. Although we have started to get a handle on the costs of regulation, future research should focus on quantifying the benefits, without which it is difficult to evaluate the welfare effects.
That said, what is striking about volatility is that it negatively affects current owners as well as prospective future ones. This volatility particularly hurts homeowners looking to cash out -- often, the old -- and younger, less wealthy buyers seeking their first homes. Other owners may be at least partially hedged, to the extent that the price of their current home covaries with the price of their desired future one (Paciorek and Sinai, 2010; Sinai and Souleles, 2005), but even hedged owners face problems if they end up "underwater" on their mortgages (Ferreira et al., 2010). Thus, one important implication of this paper is that future work on the distributional effects of housing supply regulation should concentrate not only on its effects on price levels but also on volatility.
Bibliography
A.1 Solution Method
The use of conditional choice probabilities enables me to consistently estimate the dynamic model of housing supply without fully solving it. But I must solve the model to simulate the behavior of housing markets under different policy regimes. The model can be numerically solved for a given set
of parameters in one of two ways: perturbation around a deterministic steady state, or fixed point iteration on the marginal condition, equation 3. Perturbation allows for rapid solution and can be implemented using standard software, but it may introduce substantial
approximation error. Conversely, fixed point iteration is very slow but can approximate the solution of the model arbitrarily well (Aruoba et al., 2006). I solve the model numerically using fixed point iteration over a finite grid covering ![]() and then interpolate between grid points using splines. I calculate expectations by integrating over the relevant distributions using quadrature methods.
and then interpolate between grid points using splines. I calculate expectations by integrating over the relevant distributions using quadrature methods.
The solution algorithm works as follows: Given a guess of investment
![]() at each grid point and a spline interpolation between them, solve for the
at each grid point and a spline interpolation between them, solve for the
![]() at each grid point that satisfies the rational expectations assumption and the marginal condition. That is, find the level of investment that implies a next-period
capital stock consistent with prices that justify that amount of investment, and repeat until convergence. Given a fine enough grid and a flexible enough interpolation, we can approximate the true
at each grid point that satisfies the rational expectations assumption and the marginal condition. That is, find the level of investment that implies a next-period
capital stock consistent with prices that justify that amount of investment, and repeat until convergence. Given a fine enough grid and a flexible enough interpolation, we can approximate the true ![]() function arbitrarily well. In practice, I can solve the model in a reasonable amount of time with a state space of no more than two or three dimensions. In the simulations presented here, I include in the state space only the capital stock, a demand shock and a shock to the user
cost of housing. This allows me to highlight the feedback effects of supply that serve to dampen the effect of demand shocks on prices.
function arbitrarily well. In practice, I can solve the model in a reasonable amount of time with a state space of no more than two or three dimensions. In the simulations presented here, I include in the state space only the capital stock, a demand shock and a shock to the user
cost of housing. This allows me to highlight the feedback effects of supply that serve to dampen the effect of demand shocks on prices.
A..2 Demand Estimation
Before I can actually perform any simulations using the supply side parameters I estimated above, I must first estimate the demand-side relationship between the capital stock and rents, as well as estimating a parsimonious time-series relationship for the demand shocks. Estimating the theoretical demand curve, which relates spot housing rents to the capital stock as in equation 1, is not a trivial endeavor for at least two reasons. First, as noted by Topel and Rosen (1988), demand shocks likely drive much of the high-frequency variation in investment. Finding variation in the housing stock that is orthogonal to these demand shocks is thus quite difficult. Second, all of the available data on rents are for apartments and cover only a relatively small subset of metropolitan areas.
I have tried various approaches to estimating the underlying demand curve using data on apartment rents from REIS, a firm that tracks the commercial real estate sector, as well as tenants' and owners' equivalent rent data from the Consumer Price Index, which are available for an even smaller subset of MSAs. In all cases I find substantially higher price volatility than rent volatility, a similar phenomenon to that discovered by Shiller (1981) for stock prices. I also find lower inverse elasticities of demand with respect to rent than with respect to prices. That is, prices are more responsive to changes in the capital stock than rents. This is hard to square with the usual user cost equation, as in equation 2, since a transitorily low capital stock (and corresponding high rents and prices) should induce more construction and lower rents in the future. Prices should thus increase less in response to a low capital stock than spot rents.
This phenomenon could simply be a result of using inconsistent rent and house price data, or it could be a sign that this model of housing demand is overly simplistic. Regardless, to match the observed data as well as possible I relate prices to the size of the capital stock in two steps. First I estimate an inverse demand curve following equation 1 by using lags of the capital stock to instrument for the current capital stock, under the assumption that the time dependence of the demand shocks is limited. I include the log wage, along with MSA and year fixed effects and MSA-specific time trends, to soak up as much variation as possible in the demand shocks.
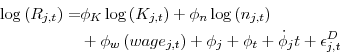
I start with a least squares regression of this equation and then instrument for the capital stock at ![]() with its first, second and third lags in turn. Using the first lag as an instrument
is valid if the demand shocks are serially uncorrelated, while the second lag is a valid instrument if the dependence of the shocks lasts no more than one period, and so forth. Since the correlation of the time
with its first, second and third lags in turn. Using the first lag as an instrument
is valid if the demand shocks are serially uncorrelated, while the second lag is a valid instrument if the dependence of the shocks lasts no more than one period, and so forth. Since the correlation of the time ![]() stock with its own lag is smaller as the length of the lag increases the estimates become increasingly noisy, although the first stage remains quite strong, with an F statistic well over 10 in all cases. I constrain
stock with its own lag is smaller as the length of the lag increases the estimates become increasingly noisy, although the first stage remains quite strong, with an F statistic well over 10 in all cases. I constrain
![]() for the purposes of recovering parameters for simulation, since the population-to-stock ratio is nearly constant over time within each MSA, as we should expect if household
sizes have been roughly constant within each MSA over the last 30 years.
for the purposes of recovering parameters for simulation, since the population-to-stock ratio is nearly constant over time within each MSA, as we should expect if household
sizes have been roughly constant within each MSA over the last 30 years.
Table 10 shows the estimates of equation 1. I find inverse elasticities of demand in the range of -1.7 to -3.0, which implies rent elasticities of demand of -0.33 to -0.60. These figures are in line with other estimates in the literature, many of which take quite different approaches to estimation.49 Using the one-lag IV inverse elasticity estimate of -2.18, I back out a value for the intercept of 1 that corresponds roughly to the average MSA in my sample.
The second step is to use the user cost relation in equation 2 to translate movements in rents into prices. For the remaining variables in equation 2 -- interest rate ![]() , income tax rate
, income tax rate
![]() , property tax rate
, property tax rate
![]() -- I use the ex post real interest rate on a conventional 30-year fixed rate mortgage; state and federal tax rates from the NBER's TAXSIM database; and property tax data from
Emrath (2002) and the Significant Features of Fiscal Federalism series.50 For
-- I use the ex post real interest rate on a conventional 30-year fixed rate mortgage; state and federal tax rates from the NBER's TAXSIM database; and property tax data from
Emrath (2002) and the Significant Features of Fiscal Federalism series.50 For
![]() , the risk premium of owner-occupied housing, I use the Flavin and Yamashita (2002) estimate of 2.0 percent. To calculate MSA-specific depreciation rates, I
subtract the population growth rate in each MSA from the ratio of investment to the capital stock and take the average. Under the assumption that the average population-to-stock ratio is constant over time in each MSA, any additional average growth in the capital stock must be going to replace
units lost to depreciation.
, the risk premium of owner-occupied housing, I use the Flavin and Yamashita (2002) estimate of 2.0 percent. To calculate MSA-specific depreciation rates, I
subtract the population growth rate in each MSA from the ratio of investment to the capital stock and take the average. Under the assumption that the average population-to-stock ratio is constant over time in each MSA, any additional average growth in the capital stock must be going to replace
units lost to depreciation.
Rather than explicitly allow these values to vary in simulation, I instead use the average values for each MSA and hold them constant over time. For each MSA and year, I then calculate the log rent implied by (time-varying) house prices and the constant user cost terms. By regressing this log
implicit rent (
![]() ) on actual log rent, log population and the log housing stock, I am able to estimate the direct effect of changes in the capital
stock on log prices, apart from the indirect effect implied by changes in rent.51 This direct effect could be due to endogenous changes in the risk premium
or some effect on expected capital gains outside the relatively simple framework I impose here. Regardless, the residuals from this regression serve as a "user cost shock" that incorporates changes in interest rates, risk premia, and taxes in a single variable.
) on actual log rent, log population and the log housing stock, I am able to estimate the direct effect of changes in the capital
stock on log prices, apart from the indirect effect implied by changes in rent.51 This direct effect could be due to endogenous changes in the risk premium
or some effect on expected capital gains outside the relatively simple framework I impose here. Regardless, the residuals from this regression serve as a "user cost shock" that incorporates changes in interest rates, risk premia, and taxes in a single variable.
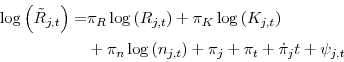
My estimates of the preceding equation are shown in table 11. As in the inverse demand estimates, I use various lags of the capital stock to instrument for the current capital stock. I also include fixed effects and time trends, as well as constraining
![]() to ensure stationarity. Depending on the specification, I find a range of estimates of this direct effect of the capital stock on house prices. The OLS estimate of the
price-stock elasticity in the first column is downward biased because the capital stock at time
to ensure stationarity. Depending on the specification, I find a range of estimates of this direct effect of the capital stock on house prices. The OLS estimate of the
price-stock elasticity in the first column is downward biased because the capital stock at time ![]() includes contemporaneous new investment, which depends on prices. For simulation purposes I
use -2.27, which is the estimate using the first lag of the capital stock as an instrument. This is the most conservative choice, apart from the clearly biased OLS estimate, since the more negative estimates in subsequent columns imply a larger feedback effect of investment into prices.
includes contemporaneous new investment, which depends on prices. For simulation purposes I
use -2.27, which is the estimate using the first lag of the capital stock as an instrument. This is the most conservative choice, apart from the clearly biased OLS estimate, since the more negative estimates in subsequent columns imply a larger feedback effect of investment into prices.
Finally, using my estimates of the last two equations, I calculate the demand and user cost residuals and estimate MSA by MSA first-order vector autoregressions to capture the interdependence of these shocks over time. I find no strong effects of the lagged user cost shock on the current demand shock, but I do find large positive effects for the remaining three coefficients. I use the average VAR coefficients of about 0.8 (demand shock on lagged demand shock), 0.8 (user cost shock on lagged user cost shock), and 0.5 (user cost shock on lagged demand shock) to parameterize the demand-side processes.
 Solid curve is a penalized regression spline relating standard deviation of detrended log house prices in each MSA to measured regulation. WRLURI standardized to have mean zero and standard deviation one. Dashed curves show +/- two standard errors. |
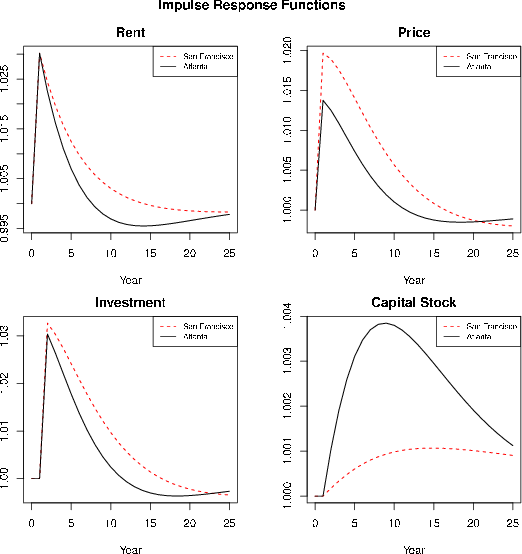 Impulse response functions for San Francisco and Atlanta, relative to mean values, in response to a 1 standard deviation demand-driven house price shock. |
| Variable | Number of MSAs | Time Period |
| Real dollar-valued house price index (FHFA, Census, CPI) | 381 | 1975-2010 (in part) |
| Total housing permits (Census) | 381 | 1981-2010 |
| Wharton Residential Land Use Regulation Index (WRLURI) | 253 | Observed once |
| Share of land within 50 km unavailable for development (Saiz 2010) | 379 | Constant |
| Real physical construction cost, avg. quality 2000 s.f. house (RS Means) | 174 | 1982-2008 |
| Demand side: Average real wage (BEA, CPI) | 382 | 1975-2009 (in part) |
| Demand side: Population (Census) | 380 | 1980-2010 |
| Instruments: Bartik employment (County Business Patterns) | 381 | 1977-2009 |
| Instruments: Migration (IRS) | 381 | 1983-2008 |
| MSA( |
WRLURI( |
ADI( |
WRLURI excl. ADI( |
Mean House Price(1984-2008) |
| New York | 0.94 | 2.54 | 0.13 | $306,000 |
| Los Angeles | 0.78 | 1.24 | 0.48 | $329,000 |
| Chicago | 0.22 | 0.74 | -0.09 | $194,000 |
| Houston | -0.27 | -0.92 | 0.08 | $119,000 |
| Atlanta | 0.19 | -0.04 | 0.26 | $161,000 |
| Philadelphia | 1.41 | 1.47 | 1.18 | $169,000 |
| Washington | 0.60 | 1.23 | 0.27 | $244,000 |
| Dallas | -0.27 | -0.36 | -0.21 | $146,000 |
| Riverside | 0.86 | 0.75 | 0.81 | $183,000 |
| Phoenix | 1.02 | 0.87 | 0.95 | $160,000 |
| San Francisco | 1.21 | 2.20 | 0.63 | $467,000 |
WRLURI (
| (1) | (2) | (3) | (4) | |
| Log Price | 1.35 | 1.41 | 1.69 | 1.72 |
| Log Price Standard Error | (0.04) | (0.06) | (0.05) | (0.06) |
| Log Price incl. Regulation | -0.46 | |||
| Log Price incl. Regulation Standard Error | (0.04) | |||
| Log Price incl. Delays | -0.37 | |||
| Log Price incl. Delays Standard Error | (0.04) | |||
| Log Price incl. Regulation excl. Delays | -0.15 | |||
| Log Price incl. Regulation excl. Delays Standard Error | (0.04) | |||
| Density | -1.77(0.11) | -1.62(0.17) | -0.98(0.14) | -1.31(0.12) |
| Density incl. Regulation | -0.46 | |||
| Density incl. Regulation Standard Error | (0.08) | |||
| Density incl. Delays | 0.39 | |||
| Density incl. Delays Standard Error | (0.07) | |||
| Density incl. Regulation excl. Delays | -0.97 | |||
| Density incl. Regulation excl. Delays Standard Error | (0.10) | |||
| Log Construction Costs | -1.49 | |||
| Log Construction Costs Standard Error | (0.19) | |||
| N | 10107 | 4470 | 6920 | 6920 |
| MSA/Year FE | Yes | Yes | Yes | Yes |
| Instrumented | No | No | No | No |
Dependent variable is the log ratio of permits to available construction "slots", as defined in the text. Density is lagged by one period and multiplied by 100. Heteroskedasticity-robust standard errors in parentheses. Regulation, Delays, and Regulation excl. Delays standardized to have mean zero and standard deviation one.
| (1) | (2) | (3) | (4) | |
| Log Price | 0.68 | 0.53 | 0.84 | 0.87 |
| Log Price Standard Error | (0.07) | (0.10) | (0.10) | (0.10) |
| Log Price incl. Regulation | -0.32 | |||
| Log Price incl. Regulation Standard Error | (0.05) | |||
| Log Price incl. Delays | -0.26 | |||
| Log Price incl. Delays Standard Error | (0.05) | |||
| Log Price incl. Regulation excl. Delays | -0.09 | |||
| Log Price incl. Regulation excl. Delays Standard Error | (0.05) | |||
| Density | -1.66 | -1.21 | -0.7 | -1.13 |
| Density Standard Error | (0.13) | (0.19) | (0.18) | (0.15) |
| Density incl. Regulation | -0.50 | |||
| Density incl. Regulation Standard Error | (0.10) | |||
| Density incl. Delays | 0.40 | |||
| Density incl. Delays Standard Error | (0.10) | |||
| Density incl. Regulation excl. Delays | -1.03 | |||
| Density incl. Regulation excl. Delays Standard Error | (0.13) | |||
| Log Construction Costs | -1.53 | |||
| Log Construction Costs Standard Error | (0.22) | |||
| N | 8831 | 4218 | 6090 | 6090 |
| MSA/Year FE | Yes | Yes | Yes | Yes |
| Instrumented | Yes | Yes | Yes | Yes |
Dependent variable is the log ratio of permits to available construction "slots". IV using MSA-level linear projections of log price onto
| Description | Parameter | (1) | (2) | (3) | (4) |
| Marginal cost of investment |
|
0.42 | 0.40 | 0.40 | 0.41 |
| Marginal cost of investment Standard Error |
|
(0.02) | (0.03) | (0.03) | (0.03) |
| Marginal cost of investment incl. Regulation |
|
0.09 | |||
| Marginal cost of investment incl. Regulation Standard Error |
|
(0.01) | |||
| Marginal cost of investment incl. Delays |
|
0.07 | |||
| Marginal cost of investment incl. Delays Standard Error |
|
(0.01) | |||
| Marginal cost of investment incl. Regulation excl. Delays |
|
0.03 | |||
| Marginal cost of investment incl. Regulation excl. Delays Standard Error |
|
(0.01) | |||
| Density |
|
3.37 | 4.20 | 4.34 | 5.32 |
| Density Standard Error |
|
(0.32) | (0.45) | (0.54) | (0.67) |
| Density incl. Regulation |
|
-0.35 | |||
| Density incl. Regulation Standard Error |
|
(0.24) | |||
| Density incl. Delays |
|
-1.64 | |||
| Density incl. Delays Standard Error |
|
(0.43) | |||
| Density incl. Regulation excl. Delays |
|
0.63 | |||
| Density incl. Regulation excl. Delays Standard Error |
|
(0.19) | |||
| Construction costs | 0.05 | ||||
| Construction costs Standard Error | (0.07) | ||||
| N | 8831 | 4044 | 6090 | 6090 | |
| MSA/Year FE | Yes | Yes | Yes | Yes | |
| Instrumented | Yes | Yes | Yes | Yes |
IV estimates of variants of Equation 9 using MSA-level linear projections onto
| MSA | Marginal Cost of Investment: Percent | Marginal Cost of Investment: Dollars | Elasticity |
| New York | 11.10 | $34,000 | 1.71 |
| Los Angeles | 9.69 | $32,000 | 1.96 |
| Chicago | 8.68 | $17,000 | 2.19 |
| Houston | 6.71 | $8,000 | 2.83 |
| Atlanta | 7.93 | $13,000 | 2.39 |
| Philadelphia | 10.43 | $18,000 | 1.82 |
| Washington | 9.54 | $23,000 | 1.99 |
| Dallas | 7.23 | $11,000 | 2.63 |
| Riverside | 9.28 | $17,000 | 2.05 |
| Phoenix | 9.53 | $15,000 | 1.99 |
| San Francisco | 10.99 | $51,000 | 1.73 |
Increase in cost of a house on the margin after an increase in log investment of 19 log points, which is the average absolute change in log investment across all MSAs and years. Calculated using parameters shown in column (4) of Table 5. See text for details.
| (1) | (2) | |
| Regulation | 0.75 | |
| Regulation Standard Error | (0.05) | |
| Delays | 0.72 | |
| Delays Standard Error | (0.05) | |
| Regulation excl. Delays | 0.23 | |
| Regulation excl. Delays Standard Error | (0.05) | |
| (Intercept) | -0.18 | -0.23 |
| (Intercept) Standard Error | (0.05) | (0.04) |
| N | 168 | 168 |
| 0.58 | 0.75 |
Regression of standardized fixed costs from model in column (4) of Table 5 on WRLURI measures of regulation, as described in text. Standard errors in parentheses. Dependent variable, Regulation, Delays, and Regulation excl. Delays standardized to have mean zero and standard deviation one.
| Description | Parameter | (1) | (2) | (3) | (4) | (5) |
| Marginal cost of investment |
|
0.38 | 0.36 | 0.40 | 0.33 | 0.41 |
| Marginal cost of investment Standard Error |
|
(0.03) | (0.03) | (0.03) | (0.03) | (0.03) |
| Marginal cost of investment incl. Regulation |
|
0.09 | 0.09 | 0.09 | 0.08 | 0.09 |
| Marginal cost of investment incl. Regulation Standard Error |
|
(0.01) | (0.02) | (0.01) | (0.01) | (0.01) |
| Density |
|
5.13 | 4.77 | 5.57 | 2.94 | 4.48 |
| Density Standard Error |
|
(0.67) | (0.67) | (0.81) | (0.55) | (0.51) |
| Density incl. Regulation |
|
-1.72 | -0.79 | -0.80 | 0.01 | -0.36 |
| Density incl. Regulation Standard Error |
|
(0.47) | (0.45) | -(0.32) | (0.21) | (0.24) |
| N | 4911 | 3426 | 6090 | 6374 | 6090 | |
| MSA/Year FE | Yes | Yes | Yes | Yes | Yes | |
| Instrumented | Yes | Yes | Yes | Yes | Yes |
IV estimates of variants of Equation 9 using MSA-level linear projections onto
| Price: Mean | Price: Std. Dev. of Log | Investment Mean | Investment: Std. Dev. of Log | Elasticity | |
| Baseline | $186,000 | 0.034 | 12,000 | 0.068 | 1.46 |
| Low Regulation | $181,000 | 0.031 | 14,400 | 0.082 | 1.91 |
| High Regulation | $190,000 | 0.037 | 10,200 | 0.057 | 1.17 |
| Two-Year Lag | $186,000 | 0.037 | 12,000 | 0.061 | 0.90 |
| More Land | $166,000 | 0.032 | 23,600 | 0.060 | 1.37 |
| Less Land | $206,000 | 0.037 | 4,900 | 0.075 | 1.53 |
| San Francisco | $447,000 | 0.040 | 3,700 | 0.061 | 1.15 |
| San Francisco (actual) | $473,000 | 0.159 | 3,900 | 0.373 | |
| Atlanta | $162,000 | 0.028 | 50,700 | 0.055 | 1.41 |
| Atlanta (actual) | $162,000 | 0.077 | 51,800 | 0.286 |
Average results from 25-year simulations using the same set of 100 randomly drawn demand shock paths in each row. Rows for Low Regulation and High Regulation impute marginal costs for cities at the 10th and 90th percentiles of regulation, respectively. Rows for San Francisco and Atlanta are simulations using the same demand shock paths and the estimated supply- and demand-side parameters of those cities. See text for further details.
| Description | Parameter | OLS | IV (Lag 1) | IV (Lag 2) | IV (Lag 3) |
| Log Pop.; -Log Stock | 1.73 | 2.18 | 2.65 | 3.03 | |
| Log Pop.; -Log Stock Standard Error | (0.11) | (0.13) | (0.19) | (0.32) | |
| Log Wage | 1.28 | 1.30 | 1.33 | 1.35 | |
| Log Wage Standard Error | (0.07) | (0.06) | (0.06) | (0.07) | |
| N | 1150 | 1150 | 1150 | 1150 | |
| MSA/Year FE | Yes | Yes | Yes | Yes | |
| MSA time trends | Yes | Yes | Yes | Yes | |
| Instrumented | No | Yes | Yes | Yes |
Dependent variable is log rent. Heteroskedasticity-robust standard errors in parentheses. The second column uses first lag of log stock as an instrument for log stock, the third column uses the second lag, and so forth. Log population and log capital stock coefficients are constrained to be equal and opposite in sign, as discussed in text.
| Description | Parameter | OLS | IV (Lag 1) | IV (Lag 2) | IV (Lag 3) |
| Log Rent | 1.02 | 0.88 | 0.64 | 0.13 | |
| Log Rent Standard Error | (0.05) | (0.05) | (0.07) | (0.15) | |
| Log Pop.; -Log Stock | 0.40 | 2.27 | 5.40 | 12.16 | |
| Log Pop.; -Log Stock Standard Error | (0.23) | (0.28) | (0.51) | (1.59) | |
| N | 1150 | 1150 | 1150 | 1150 | |
| MSA/Year FE | Yes | Yes | Yes | Yes | |
| MSA time trends | Yes | Yes | Yes | Yes | |
| Instrumented | No | Yes | Yes | Yes |
Dependent variable is log implicit rent, as definied in text. Heteroskedasticity-robust standard errors in parentheses. The second column uses first lag of log stock as an instrument for log stock, the third column uses the second lag, and so forth. Log population and log capital stock coefficients are constrained to be equal and opposite in sign, as discussed in text.
![\begin{displaymath}\begin{split}\beta^{L_j} &\left( E \left[\log P_{j,t} \vert S_{j,t-L_j}\right] - \log C_{j,t} \right) - \eta_j\left(K_{j,t-1},A_j\right) - \chi_{i,j,t-L_j} - \epsilon^S_{j,t-L_j} \\ &= \beta^{L_j} \bar{U}_{j,t} + \beta E\left[ \max \left\{V^B_{j,t+1} - \chi_{i,j,t+1}, V^N_{j,t+1}\right\} \vert S_{j,t-L_j}\right], \end{split}\end{displaymath}](img45.gif)
![\begin{displaymath}\begin{split}\beta^{L_j} &\left( E \left[\log P_{j,t} \vert S_{j,t-L_j}\right] - \log C_{j,t} \right) - \sigma^\eta_j \frac{K_{j,t}}{A_j} - \sigma^\chi_j \log\left(\frac{\frac{I_{j,t}}{A_j-K_{j,t-1}}}{1 - \frac{I_{j,t}}{A_j-K_{j,t-1}}}\right) - \epsilon^S_{j,t-L_j} \\ &= \beta^{L_j} \bar{U}_{j,t} + \beta E\left[ \sigma^\chi_j \log\left(\exp\left(V^B_{i,j,t+1}/\sigma^\chi_j\right) + \exp\left(V^N_{i,j,t+1}\sigma^\chi_j\right)\right) \vert S_{j,t-L_j}\right], \end{split}\end{displaymath}](img51.gif)
![\begin{displaymath}\begin{split}\beta^{L_j}&\left( E\left[\log P_{j,t}- \beta \log P_{j,t+1} \vert S_{j,t-L_j}\right] - \left(\log C_{j,t} - \beta \log C_{j,t+1}\right) \right) \\ &- \sigma^\eta_j \left(\frac{K_{j,t-1}}{A_j} - \beta\frac{K_{j,t}}{A_j}\right) \\ &- \sigma^\chi_j \left( \log\left(\frac{\frac{I_{j,t}}{A_j-K_{j,t-1}}}{1 - \frac{I_{j,t}}{A_j-K_{j,t-1}}}\right) - \beta E\left[ \log\left(\frac{I_{j,t+1}}{A_j - K_{j,t}}\right) \vert S_{j,t-L_j}\right] \right) \\ =& \beta^{L_j} \bar{U}_{j,t} + \epsilon^S_{j,t-L_j}, \end{split}\end{displaymath}](img58.gif)
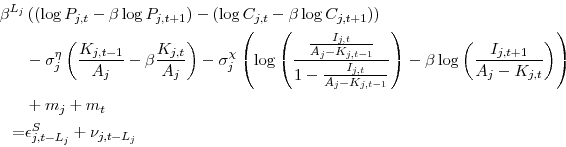
![\begin{displaymath}\begin{split}E&\left[E_{t-L_j}\left[\dot{P}_{j,t}\right] - E_{t-1}\left[\dot{P}_{j,t}\right] \vert m_j,m_t,Z_{j,t-1}, D_j \right] \\ &= \alpha^0_j + \alpha^1 D_j E\left[\dot{P}_{j,t} \vert m_j,m_t,Z_{j,t-1}, D_j \right], \end{split}\end{displaymath}](img79.gif)
![\begin{displaymath}\begin{split}E&\left[ \left( \log P_{j,t} - \beta \log P_{j,t... ... + m_t \vert \hat{Z}_{j,t},m_j,m_t \right] \\ =& 0. \end{split}\end{displaymath}](img92.gif)