
The Analytics of SVARs: A Unified Framework to Measure Fiscal Multipliers
Keywords: Fiscal policy, identification, vector autoregressions
Abstract:
Governments often use fiscal policy to stabilize economic fluctuations. For example, during the recent recession, the United States Congress approved the American Recovery and Reinvestment Act, which introduced increases in public spending and cuts in taxes by approximately 6% of GDP (CBO, 2010). The rationale for such fiscal stimulus rests on the assumption that fiscal interventions do affect economic activity. Yet, the size of fiscal multipliers, defined as the dollar response of output to an exogenous dollar spending increase or tax cut, is the subject of a long-standing debate in academia. As (Perotti, 2008) observes in his survey of the literature: "... perfectly reasonable economists can and do disagree on the basic theoretical effects of fiscal policy and on the interpretation of existing empirical evidence".
The presence of competing economic theories has motivated a large body of empirical investigations that measure the size of these fiscal multipliers. An important share of the literature relies on structural vector autoregressions (SVARs). Prominent examples include (Blanchard & Perotti, 2002), and (Mountford & Uhlig, 2009). The appeal of SVARs is that they control for endogenous movements in fiscal policies by imposing only a minimal set of assumptions, known as identification schemes. An alternative methodology identifies exogenous changes in taxation (Romer & Romer, 2010; Mertens & Ravn, 2011b) and public spending (Eichenbaum & Fisher, 2005; Ramey, 2011; Ramey & Shapiro, 1998) from narrative records, and studies their effects using VARs. Yet, despite their simple structure and the use of similar data, studies employing SVARs and narrative records report fiscal multipliers that are spread over a broad range of values. The lack of consensus prevents the profession from providing clear guidance on important policy choices, such as the size and composition of fiscal interventions.
Motivated by this knowledge gap, our paper asks two questions. Why do SVARs provide different measures of fiscal multipliers? Can we construct robust measures of fiscal multipliers using SVARs?
We answer the first question by deriving a unified analytical framework to compare competing identification schemes. We then apply this analysis to a fiscal VAR for the United States for the period 1947-2006. We show that existing identification schemes imply different restrictions on the output elasticity of tax revenue and government spending, which measure the endogenous response of tax and spending policies to economic activity.
We illustrate the framework for comparing different identification schemes with a tax policy example. Assume that only two shocks explain contemporaneous co-movements between output and tax revenue: a tax shock and a non-policy shock. The object of interest is the response of output to the tax shock. The non-policy shock controls for co-movements in the two variables due to automatic movements of tax revenue over the business cycle. In this setting, the identification of tax and non-policy shocks depends only on the restriction on one structural coefficient: the output elasticity of tax revenue.
The (Blanchard & Perotti, 2002) and the (Mountford & Uhlig, 2009) identification schemes imply output elasticities of tax revenue equal to 1.7 and 3.0, respectively. Standard sign restrictions on impulse response functions imply output elasticities of tax revenue between zero and infinity. Narrative
identification of tax shocks imply an output elasticity of tax revenue above 3. Different restrictions on the output elasticity of tax revenue generate a large dispersion in the estimates of
tax multipliers. For instance, we find that the impact tax multiplier is 0.17 dollars for an output elasticity of tax revenue equal to 1.7, whereas it is more than five times as large - at 0.93 dollars - for an output elasticity of tax revenue equal to ![]() . The impact tax multiplier is negative for all output elasticities of tax revenue smaller than 1.5. More in general, thanks to the analytical relations, we can readily map beliefs of policy-makers and economists about plausible values of the output elasticity of tax revenue into tax multipliers.
. The impact tax multiplier is negative for all output elasticities of tax revenue smaller than 1.5. More in general, thanks to the analytical relations, we can readily map beliefs of policy-makers and economists about plausible values of the output elasticity of tax revenue into tax multipliers.
These findings lead to the second question. We propose to measure fiscal multipliers more robustly by imposing restrictions on the output elasticities of fiscal variables in the form of probability distributions. In contrast to the existing literature, we impose distributions that encompass the existing empirical evidence on elasticities. The distribution of the output elasticity of tax revenue that we obtain ranges between 1.7 and 3. The distribution of the output elasticity of government spending ranges between -0.1 and 0.1. These restrictions are robust because they are generated by different approaches and empirical strategies and, hence, are less likely to be affected by particular assumptions or observations.
We apply this robust identification scheme to measure tax and spending multipliers associated with unexpected fiscal shocks.1 We document three findings. First, the median tax multiplier is 0.65 on impact, and it becomes larger than 1 five quarters after the policy intervention. Second, the median spending multiplier is larger than 1 at all horizons. Third, the probability that the tax multiplier is larger than the spending multiplier is below 0.5 at all horizons.
We also document a high probability that private consumption increases following a spending shock. Competing macroeconomic theories have different theoretical predictions regarding the effects of government spending shocks on private consumption. The standard neoclassical and New Keynesian models predict a decline in consumption (Linnemann & Schabert, 2003; Baxter & King, 1993). A recent branch of the literature (Ravn et al., 2006; Galí et al., 2007) proposes models that generate an increase in private consumption. The evidence is in line with the latter class of models.
The focus on the identification problem, as opposed to the estimation and specification of the reduced-form VAR model, is based on evidence provided by (Chahrour et al., forthcoming) and (Caldara & Kamps, 2008). (Chahrour et al., forthcoming) employ a DSGE-model approach to reject the hypothesis that the different tax multipliers estimated by the SVAR and narrative approaches are due to differences in the assumed reduced-form transmission mechanisms. (Caldara & Kamps, 2008) find that, controlling for the specification of the reduced-form VAR model, different identification schemes provide different estimates of tax and spending multipliers.
The remainder of the paper is organized as follows. Section I derives the analytical relation between output elasticities of fiscal variables and impulse response functions. It also characterizes theoretical properties of such relations. Section II reinterprets five alternative identification schemes used in the literature as restrictions on the output elasticities of fiscal variables. Section III analyses the implications of alternative priors on elasticities for fiscal multipliers. Section IV reviews the existing empirical evidence on elasticities and reports evidence on fiscal multipliers based on prior distributions that encompass the full range of elasticity estimates documented in the literature. Section V sheds light on two debates in the literature on the effects of government spending shocks: the response of private consumption and the role of fiscal foresight. Section VI concludes.
1 The Analytics of SVARs
Consider the reduced-form VAR model:
where
The reduced-form disturbances will in general be correlated with each other and consequently do not have any economic interpretation. It is thus necessary to model the contemporaneous relation between reduced-from disturbances ![]() to identify structural shocks
to identify structural shocks ![]() with an economic interpretation:
with an economic interpretation:
where
Numerical results presented in the paper are based on the estimation of an 8-equation VAR model in the logarithm of output, tax revenue, government spending (sum of government consumption and investment), private consumption, private non-residential investment (all in real, per-capita terms), CPI inflation, the 3-month T-bill rate, and a measure of stock prices. We use quarterly data for the United States from 1947 to 2006.2 To illustrate our main results on identification uncertainty, we abstract from sampling uncertainty and present results based on OLS point estimates; the evidence on fiscal multipliers reported later in the paper accounting both for identification and sampling uncertainty instead relies on Bayesian estimates.3
The estimation strategy addresses the well-known misspecification problem of SVARs in the presence of anticipated fiscal shocks (Leeper et al., 2008). Variables such as consumption, investment, and prices react to signals about future policies. Lagged values of these variables predict future policy actions and, consequently, help to identify truly unexpected fiscal shocks (Forni & Gambetti, 2010; Giannone & Reichlin, 2006).4 By including these variables in our reduced-form VAR model, we ensure that measures of anticipated fiscal shocks derived from narrative records (see (Ramey, 2011) for measures of anticipated government spending shocks, and (Mertens & Ravn, 2011b) for measures of anticipated tax shocks) do not Granger-cause the fiscal shocks identified by our SVAR models (see Appendix A).
1.1 Deriving the Analytical Relationship Between Output Elasticities of Fiscal Variables and Fiscal Multipliers
To understand how the choice of identifying restrictions affects inference, we consider a simplified example. We assume that the model consists of a non-policy variable and of a policy variable. The non-policy variable is output (![]() ). The policy variable, denoted by
). The policy variable, denoted by ![]() is either tax revenue (
is either tax revenue (![]() ), or government spending (
), or government spending (![]() ).
).
The relation between reduced-form disturbances ![]() and structural shocks
and structural shocks ![]() can be written as:
can be written as:
where
Equation (3) states that unexpected movements in output are due to either unexpected movements in the policy variable (
![]() ) or sources of business cycle fluctuations unrelated to the policy under investigation (
) or sources of business cycle fluctuations unrelated to the policy under investigation (![]() ). Equation (4) states that unexpected changes in the policy variable are either endogenous to the business cycle (
). Equation (4) states that unexpected changes in the policy variable are either endogenous to the business cycle (
![]() ) or exogenous to the business cycle and uncorrelated with non-policy sources of fluctuations (
) or exogenous to the business cycle and uncorrelated with non-policy sources of fluctuations (![]() ). Endogeneity of policy can arise either because policy-makers react to contemporaneous developments in economic activity, or because of automatic feedback from activity to tax revenue and government spending. We follow (Blanchard
& Perotti, 2002), B&P henceforth, and assume that the first channel is eliminated by the use of quarterly data. This is plausible due to information lags, legislative lags, and implementation lags faced by policy makers. Consequently, the coefficient
). Endogeneity of policy can arise either because policy-makers react to contemporaneous developments in economic activity, or because of automatic feedback from activity to tax revenue and government spending. We follow (Blanchard
& Perotti, 2002), B&P henceforth, and assume that the first channel is eliminated by the use of quarterly data. This is plausible due to information lags, legislative lags, and implementation lags faced by policy makers. Consequently, the coefficient ![]() captures the automatic response of fiscal variables to changes in economic activity, measured as the output elasticity of tax revenue (
captures the automatic response of fiscal variables to changes in economic activity, measured as the output elasticity of tax revenue (
![]() ) and the output elasticity of government spending (
) and the output elasticity of government spending (
![]() ), respectively.
), respectively.
In the bivariate case, we need to impose one identification restriction to identify the SVAR model: here this boils down to a restriction on ![]() .5 To highlight the restricted coefficient, we denote throughout the paper
.5 To highlight the restricted coefficient, we denote throughout the paper ![]() as
as
![]() . In the public finance literature, there is a long tradition of measurement of the output elasticity of fiscal variables in the context of the cyclical adjustment of budget
balances. The output elasticity of tax revenue
. In the public finance literature, there is a long tradition of measurement of the output elasticity of fiscal variables in the context of the cyclical adjustment of budget
balances. The output elasticity of tax revenue
![]() is the most familiar measure of sensitivity of taxes to income changes. This elasticity serves as an indicator of the tax system's overall progressivity. A proportional income tax
has an elasticity of 1.0. Progressive tax systems, for which tax-to-income ratios all other things equal increase with income, have an elasticity larger than 1.0. As far as the output elasticity of government spending
is the most familiar measure of sensitivity of taxes to income changes. This elasticity serves as an indicator of the tax system's overall progressivity. A proportional income tax
has an elasticity of 1.0. Progressive tax systems, for which tax-to-income ratios all other things equal increase with income, have an elasticity larger than 1.0. As far as the output elasticity of government spending
![]() is concerned, most studies - including B&P - assume its value to be zero, based on the observation that government consumption and investment have at most weak cyclical
components.
is concerned, most studies - including B&P - assume its value to be zero, based on the observation that government consumption and investment have at most weak cyclical
components.
We view numerical restrictions as priors of the economist regarding a plausible value, or a set of plausible values, for the elasticities. As we describe in Section 2, in the literature economists have formed and implemented priors on
![]() using a variety of methods.
using a variety of methods.
The system described by Equations (3) and (4) can be written in terms of impulse vectors as:
The object of interest is the contemporaneous response of output to a policy shock:6
The denominator of this expression measures the strength of macroeconomic feedback. In the special cases in which either one of ![]() or
or
![]() is zero there is no feedback.
is zero there is no feedback.
What we are interested in is to know how the output response to a policy shock depends on the prior of the econometrician about
![]() . In the bivariate model, there exists a simple-closed form solution.7 The contemporaneous response of output to a policy shock can be rewritten as:8
. In the bivariate model, there exists a simple-closed form solution.7 The contemporaneous response of output to a policy shock can be rewritten as:8
Equation (7) reveals that for a given reduced-form model (i.e. given
1.2 An Illustration of the Analytical Relationship Between Output Elasticities of Fiscal Variables and Fiscal Multipliers
To facilitate the comparison between tax multipliers and spending multipliers, we compare shocks that are intended to stimulate output, i.e. we analyze the effects of structural spending increases but structural tax cuts. Figure 1 plots the impact fiscal multiplier as a function of the output elasticity of the respective fiscal variable, evaluating the covariance matrix
![]() at the OLS estimates of the tax and spending model, respectively.
at the OLS estimates of the tax and spending model, respectively.
Figure 1 highlights two important properties of expression (7). First, the set of output responses to a policy shock is bounded, and bounds have opposite signs. An important implication is that if the econometrician does not have any information to
limit the set of plausible values for the output elasticity, the sign of the output response cannot be determined. Second, the output response to a policy shock is zero if and only if
![]() . Hence
. Hence
![]() is the threshold elasticity to determine the sign of the output response to a policy shock.
is the threshold elasticity to determine the sign of the output response to a policy shock.
The top panel of Figure 1 shows that, if the econometrician takes an agnostic view of plausible values for the output elasticity of taxes, the impact tax multiplier lies within a range between -1.07 and 1.07 dollars. However, typically at least some extra-model information may be available to narrow down the set of plausible assumptions about the output elasticity of
taxes. For example, it appears implausible to assume that the business cycle has a negative effect on tax revenue. Yet excluding negatives values of
![]() would still be insufficient to pin down the sign - let alone the size - of the impact tax multiplier. Indeed, ruling out
would still be insufficient to pin down the sign - let alone the size - of the impact tax multiplier. Indeed, ruling out
![]() , the impact tax multiplier lies within a range between -0.92 and
1.07 dollars. Furthermore, even excluding
, the impact tax multiplier lies within a range between -0.92 and
1.07 dollars. Furthermore, even excluding
![]() , i.e. assuming that the tax system is at least proportional, is insufficient to pin down the sign of the impact tax multiplier. In this case, the impact tax multiplier lies
within a range between -0.39 and
, i.e. assuming that the tax system is at least proportional, is insufficient to pin down the sign of the impact tax multiplier. In this case, the impact tax multiplier lies
within a range between -0.39 and ![]() dollars. To ensure that the impact tax (cut)
multiplier is non-negative the econometrician has to assume
dollars. To ensure that the impact tax (cut)
multiplier is non-negative the econometrician has to assume
![]() . In our application, the output elasticity of taxes has to be at least 1.5.
. In our application, the output elasticity of taxes has to be at least 1.5.
Turning to spending shocks, the bottom panel of Figure 1 shows that - again, if the econometrician takes an agnostic view of plausible values for the output elasticity of government spending - the impact spending multiplier lies within a range between 2.26 and -2.26 dollars. However, negative spending multipliers only occur if government spending is procyclical (
![]() ), given that in empirical applications the correlation between output and government spending residuals
), given that in empirical applications the correlation between output and government spending residuals
![]() is positive in general. In our application, for all values of the output elasticity of government spending smaller than 0.38 the impact spending multiplier is positive.
is positive in general. In our application, for all values of the output elasticity of government spending smaller than 0.38 the impact spending multiplier is positive.
Summing up, we have shown that the sign and size of spending and tax multipliers depend on the choice of the output elasticity of tax revenue and government spending. We have also characterized analytically the identification problem. In the next section, we show how the alternative identification schemes used in the existing literature can be mapped into priors of economists regarding the output elasticities of fiscal variables.
2 Identification Restrictions as Priors on Elasticities
In this section, we use analytical results to reinterpret identification schemes as priors on output elasticities of fiscal variables. We show that these priors are different enough to produce widely divergent fiscal multipliers. We examine five identification schemes used in the literature: the recursive approach, the traditional SVAR analysis implemented by B&P, the "pure" sign restriction approach, the penalty function approach to sign restrictions, and the narrative approach.
2.1 The Recursive Approach
We first analyze the recursive approach, proposed by (Sims, 1980). The recursive approach imposes a dogmatic prior either on the impact multiplier (tax policy) or on the output elasticity of government spending (spending policy). In the recursive approach the ordering of
the variables in the reduced-form VAR model determines the contemporaneous effects of shocks: the variable ordered first in the VAR system is only affected contemporaneously by the first shock but not by the second shock, whereas the variable ordered second is contemporaneously affected by both
shocks. The recursive VAR approach is applied via the lower-triangular Cholesky decomposition of the covariance matrix
![]() .
.
Tax Shocks. In our implementation of the recursive approach, we order output first and tax revenue second in the VAR system.10 On the one hand, assuming a zero contemporaneous response of output to a tax shock is restrictive. On the other hand, the alternative ordering, equivalent to assuming that tax revenue does not react at all contemporaneously to the business cycle, would be even more
implausible. For the chosen order, the second property of the impact multiplier mentioned in Section 1 gives the result: the impact tax multiplier is zero if and only
if the output elasticity of taxes is equal to
![]() .11 In our VAR,
.11 In our VAR,
![]() is 1.5, a value which, as we discuss in Section 4, lies within the range of empirically plausible
elasticities. This is the point denoted `CHOL' in the top panel of Figure 1. This point is a useful reference point: the impact tax (cut) multiplier will be positive if and only if
is 1.5, a value which, as we discuss in Section 4, lies within the range of empirically plausible
elasticities. This is the point denoted `CHOL' in the top panel of Figure 1. This point is a useful reference point: the impact tax (cut) multiplier will be positive if and only if
![]() .
.
Spending Shocks. We order government spending first and output second. That is, we assume that government spending is acyclical, i.e.
![]() . As discussed in Section 4, this assumption is in line with the consensus view that in the U.S. the
contemporaneous output elasticity of government spending is zero. The point denoted `BP-CHOL' in the bottom panel of Figure 1 shows that the impact spending multiplier amounts to 1.25 dollars
for this value of the elasticity. The label `BP-CHOL' reveals that in the case of the spending model this recursive formulation is equivalent to the B&P approach, to which we turn next.
. As discussed in Section 4, this assumption is in line with the consensus view that in the U.S. the
contemporaneous output elasticity of government spending is zero. The point denoted `BP-CHOL' in the bottom panel of Figure 1 shows that the impact spending multiplier amounts to 1.25 dollars
for this value of the elasticity. The label `BP-CHOL' reveals that in the case of the spending model this recursive formulation is equivalent to the B&P approach, to which we turn next.
2.2 The Blanchard-Perotti Approach
The B&P approach relies on institutional information about the tax and transfer systems and about the timing of tax collections in order to form a dogmatic prior about plausible out elasticities of fiscal variables. We provide a detailed analysis of the B&P methodology to calculate elasticities in Section 4.
Tax Shocks. The point denoted `BP' in the top panel of Figure 1 gives the value of the impact tax multiplier for the point estimate of the output elasticity of taxes constructed according to the B&P methodology (
![]() ). For this value of the output elasticity of taxes the impact tax multiplier amounts to 0.17 dollars. Notice that in our sample, the B&P elasticity is only slightly larger than the elasticity implied by the recursive approach, with the implication that the B&P tax multiplier is only slightly larger than zero.
). For this value of the output elasticity of taxes the impact tax multiplier amounts to 0.17 dollars. Notice that in our sample, the B&P elasticity is only slightly larger than the elasticity implied by the recursive approach, with the implication that the B&P tax multiplier is only slightly larger than zero.
Spending Shocks. As discussed in the previous subsection, B&P assume that government spending is acyclical, i.e.
![]() , which is equivalent to the lower-triangular Cholesky decomposition with government spending ordered first. Accordingly, the B&P and recursive approaches provide
identical estimates of spending multipliers ( 1.25 dollars on impact).
, which is equivalent to the lower-triangular Cholesky decomposition with government spending ordered first. Accordingly, the B&P and recursive approaches provide
identical estimates of spending multipliers ( 1.25 dollars on impact).
2.3 The Pure Sign Restriction Approach
An alternative approach to identification is to impose sign restrictions on impulse responses. We base the discussion of this approach on the work by M&U. M&U impose sign restrictions on impulse responses in combination with a criterion function, discussed in the next subsection. The exercise in this subsection unveils what the inference on fiscal multipliers in M&U without penalty function would have been. Other studies identifying fiscal shocks using the pure sign-restriction approach include (Canova & Pappa, 2007) and (Pappa, 2009). For the sake of simplicity, we only impose sign restrictions on impact responses.12 We continue to focus the theoretical discussion on a bivariate model, while presenting numerical results for a multivariate model. We provide intuition for the generalization of the theoretical results to multivariate models (see the appendix for details).
We follow Uhlig's suggestion to decompose the factor matrix ![]() into the lower- triangular Cholesky factor of the reduced-form covariance matrix, denoted
into the lower- triangular Cholesky factor of the reduced-form covariance matrix, denoted ![]() , and an orthogonal matrix, denoted
, and an orthogonal matrix, denoted ![]() with
with
![]() . That is, for the pure sign restriction approach we have
. That is, for the pure sign restriction approach we have ![]() .
.
The system describing the relationship between reduced-form disturbances and structural shocks can be written in compact form as
![]() . As shown in the appendix, this system - using the analytical solution for the Cholesky factorization - can be expressed as follows:
. As shown in the appendix, this system - using the analytical solution for the Cholesky factorization - can be expressed as follows:
where
Contrary to the B&P and the recursive identification strategies, the pure sign-restriction approach does not impose a dogmatic prior on the output elasticities or the impact multipliers. Instead, it places restrictions on the sign of impulse responses to the shock(s) of interest. These
restrictions translate into restrictions on the set of admissible rotation angles ![]() 14 In general, there are (infinitely) many structural models satisfying the sign restrictions, each of which has the same likelihood.
14 In general, there are (infinitely) many structural models satisfying the sign restrictions, each of which has the same likelihood.
To map the factorization of the covariance matrix
![]() described in (8) into the identification framework described in Section 1, we map restrictions on the rotation angle
described in (8) into the identification framework described in Section 1, we map restrictions on the rotation angle ![]() into restrictions on the output elasticity of the policy variable:
into restrictions on the output elasticity of the policy variable:
Tax Shocks. We apply the basic assumptions of M&U who identify a non-policy shock - labelled `business cycle shock' - and a tax shock. They assume that the business cycle shock drives up both output and tax revenue and that the tax shock is orthogonal to the
business cycle shock. M&U leave the response of output to a tax shock (the object of interest) unrestricted. In our framework, these assumptions imply the following restrictions on the elements of the factor matrix ![]() :15
:15
![\displaystyle F^{SR}=\left[ \begin{array}{cc} + & ? \\ + & +% \end{array}% \right]](img94.gif) |
Using the analytical expression for ![]() , Proposition 2 in the appendix characterizes the set of all output elasticities of tax revenue that satisfy
this sign pattern. We show in particular that all elasticities
, Proposition 2 in the appendix characterizes the set of all output elasticities of tax revenue that satisfy
this sign pattern. We show in particular that all elasticities
![]() between zero and plus infinity satisfy the above sign restrictions. Hence, in the top panel of Figure 1 all points on the line segment with
non-negative values of the output elasticity of tax revenue are elements of the set of pure sign restriction solutions.
between zero and plus infinity satisfy the above sign restrictions. Hence, in the top panel of Figure 1 all points on the line segment with
non-negative values of the output elasticity of tax revenue are elements of the set of pure sign restriction solutions.
Is this large set of pure sign restriction solutions an artefact of our dataset and reduced-form VAR model? This is very unlikely. It is generally accepted that output can be viewed as a proxy for the tax base. When the tax base expands, so does tax revenue (for constant tax rates). This is why empirically the correlation coefficient between output and tax residuals is positive (very often, strongly positive). In this case, sign restrictions alone are insufficient to pin down the sign of the tax multiplier.
The sign restrictions given above pose a challenge in the bivariate context. For all values of the elasticity between 0 and
![]() , we obtain two shocks with identical sign pattern, which puts in question identification unless additional restrictions are imposed. The above result, however, is
useful in that so far it has been hard to understand the implications of such sign restrictions for the sign of the response of output to a tax shock. For example, it would have been reasonable to assume that the sign restrictions on the business cycle shock and the orthogonality assumption are
sufficient conditions to rule out negative impact tax cut multipliers (Mountford and Uhlig, 2009: 965).
, we obtain two shocks with identical sign pattern, which puts in question identification unless additional restrictions are imposed. The above result, however, is
useful in that so far it has been hard to understand the implications of such sign restrictions for the sign of the response of output to a tax shock. For example, it would have been reasonable to assume that the sign restrictions on the business cycle shock and the orthogonality assumption are
sufficient conditions to rule out negative impact tax cut multipliers (Mountford and Uhlig, 2009: 965).
Figure 2: Kernel densities of the output elasticity of tax revenue and impact tax multiplier satisfying sign restrictions evaluated at OLS estimates.
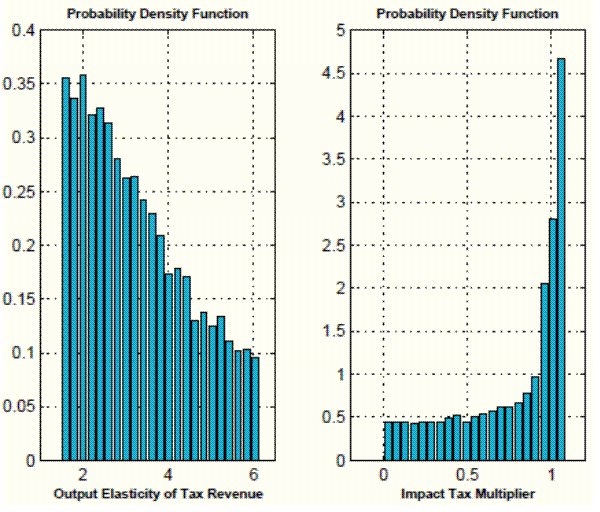
To rule out the subset of pure sign restriction solutions with negative impact tax cut multipliers, at least one additional assumption is needed. In the next subsection, we discuss the M&U approach, which adds a criterion function to the pure sign-restriction approach. In a second approach, discussed below, we impose an additional sign restriction on the response of output to a tax shock:
![\displaystyle F^{SR}=\left[ \begin{array}{cc} + & - \\ + & +% \end{array}% \right]](img97.gif) |
Proposition 4 in the appendix characterizes the set of all output elasticities of tax revenue that satisfy this sign pattern. With the additional sign restriction on the response of output to a tax shock all output elasticities of taxes between
![]() , i.e. the elasticity implied by the Cholesky factorization, and
, i.e. the elasticity implied by the Cholesky factorization, and
![]() satisfy the sign restrictions.
satisfy the sign restrictions.
Figure 2 plots the empirical distributions of the output elasticity of tax revenue and of the tax multiplier over the set of sign restriction solutions evaluated at the OLS estimate, assuming - as it is common practice in the literature - that the rotation angle is uniformly distributed over the
range satisfying the sign restrictions. Imposing this additional sign restriction "reduces" the set of admissible elasticities to all elasticities between 1.5 and ![]() , and the set of admissible multipliers to
, and the set of admissible multipliers to ![]() dollars. Of course, a drawback of the
additional assumption is that in principle we would like to leave open the sign of the response of output to a tax shock.
dollars. Of course, a drawback of the
additional assumption is that in principle we would like to leave open the sign of the response of output to a tax shock.
Finally, we can ask how the above results are affected if we move beyond the bivariate setting and impose restrictions on additional variables. For example, M&U identify the business cycle shock assuming that such shock increases not only output and taxes but also private consumption and non-residential investment. Would these additional assumptions restrict the set of admissible elasticities? Would it make the additional assumption on the output response to a tax shock redundant?
In general, the answers to these questions depend on the correlation structure between the sign-restricted variables (see the appendix for details). In our application, at the OLS estimates, all output elasticities of taxes between 0 and 73 remain admissible. In other words, the additional assumptions have only a minor effect on the set of pure sign restriction solutions identified in the bivariate case. The intuition is that consumption and investment are positively correlated with output and tax revenue. Hence, business cycle shocks that drive up output and tax revenue are very likely to also drive up consumption and investment.16 Turning to the second question, our application reveals that the lower bound of the set of admissible elasticities remains unaffected by the additional sign restrictions on the responses to a business cycle shock. These additional restrictions are, thus, by themselves insufficient to rule out negative tax cut multipliers.
Spending shocks. Similar to the identification of the tax shock, M&U identify the spending shock as a shock that increases spending and that is orthogonal to the business cycle shock. The M&U tax and spending models differ in one crucial dimension: there is no sign restriction on the response of government spending to the non-policy shock.17
The implication of the lack of restriction on the spending response to a business cycle shock is that government spending can be pro-cyclical, a-cyclical, or counter-cyclical. In fact, all output elasticities of government spending ranging between minus and plus infinity satisfy these loose restrictions.18 As can be seen in Figure 1, in our empirical application, the impact spending multiplier can range anywhere between 2.26 and -2.26 dollars, because all points on the line are elements of the set of pure sign-restriction solutions.
This minimal set of assumptions therefore does not rule out solutions for which the responses to the two shocks follow the same sign pattern. To rule out those solutions implying the same sign pattern for the two shocks, it is necessary to restrict the set of admissible output elasticities to the range between minus infinity and zero. For this range, the impact spending multiplier is positive.
Summing up, the sets of pure sign restriction solutions are very large in fiscal VAR models. Standard sign restrictions applied in the literature are insufficient to pin down the sign, let alone the size, of impact tax and spending multipliers. To pin down the sign of the impact multiplier, it is necessary either to directly restrict the object of interest (the multiplier) or to augment the pure sign restriction approach with a selection criterion, such as the one embodied in the penalty function approach to which we turn next.
2.4 Penalty Function Approach to Sign Restrictions
Pure sign restrictions alone are insufficient to pin down the sign of the multiplier. To address this limitation, M&U augment the pure sign restriction approach with a penalty function, as proposed by (Uhlig, 2005).
Tax Shocks. In a bivariate model, the M&U penalty function translates into the following objective function, maximized with respect to ![]() :
:
Proposition 4 in the appendix provides the analytical solution for this maximization problem. Importantly, we prove that the impact tax cut multiplier, evaluated at the penalty function solution, is positive for all admissible values of the correlation coefficient between output and tax residuals. An important implication is that the application of the M&U penalty function is equivalent to imposing the restriction that the output response to a tax increase is negative, as discussed in the previous subsection.
The penalty function solution in the bivariate setup maximizes the fraction of covariance between the output and tax disturbances explained by the business cycle shock. Such penalty function summarizes the belief of M&U, well grounded in the evidence provided by the DSGE literature, that fiscal shocks do not contribute substantially to business cycle fluctuations. Consequently, the role of the business cycle shock is to explain as much variability as possible in the restricted variables, letting fiscal shocks explain the residual variance. In comparison, the Cholesky factorization with output ordered first maximizes the fraction of output variance explained by the business cycle shock, explaining 100% of both the output variance and the covariance on impact. Recall that for this Cholesky factorization the impact tax multiplier is zero. For the impact multiplier to be positive, the business cycle shock has to explain more than 100% of the covariance. When this condition is fulfilled, the conditional covariance generated by the tax shock has to be negative, which is only possible if output declines in response to a tax shock meant to increase tax revenue. The penalty function in our setup selects a business cycle shock that explains 151% of the contemporaneous covariance between output and tax disturbances, while the tax shock explains -51%. Hence the penalty function, which maximizes the covariance between output and tax revenue explained by the business cycle shock, favors large positive tax cut multipliers.
In the top panel of Figure 1, the penalty function sign restriction solution is denoted `MU'. In our example, this point - compared to the B&P and recursive approaches - corresponds to a large value of the output elasticity of tax revenue (
![]() ) and to a value of the impact tax cut multiplier of 0.93 dollars. Note that the penalty function solution satisfies any additional sign restrictions on the impact responses of private consumption and investment to a business cycle shock (see appendix for details).
) and to a value of the impact tax cut multiplier of 0.93 dollars. Note that the penalty function solution satisfies any additional sign restrictions on the impact responses of private consumption and investment to a business cycle shock (see appendix for details).
Spending Shocks. To explain the identification of government spending shocks in the bivariate setting, we assume - consistent with the subsection on the pure sign restriction approach - that the business cycle shock drives up output only (leaving the response of
government spending unrestricted) and that the government spending shock is orthogonal to the business cycle shock. Trivially, the solution to the penalty function associated to these restrictions is the Cholesky factorization with output ordered first and government spending ordered second. For
this Cholesky factorization, government spending is procyclical; in our example,
![]() , and the impact spending multiplier is zero, compared to 1.25 dollars for the B&P approach.
, and the impact spending multiplier is zero, compared to 1.25 dollars for the B&P approach.
What would happen if, following M&U, we identify a business cycle shock imposing restrictions on output and tax revenue, while keeping the response of government spending unrestricted? As we show in the appendix the penalty function solution under these assumptions implies a zero impact spending multiplier (while the penalty function solution picks the same - large - impact tax cut multiplier as in the bivariate tax model). In addition, the penalty function solution selects a positive value of the output elasticity of spending (in our application the output elasticity of government spending goes down slightly compared to the one obtained for the Cholesky decomposition, to 0.36).
Summing up, the penalty-function approach to sign restrictions can be interpreted as an additional identifying assumption beyond pure sign restrictions. Moreover, in fiscal VAR models, the penalty function as specified by M&U picks a solution favoring large tax multipliers and low spending multipliers. This explains the main result of M&U, namely that tax cuts are more effective than spending increases.
2.5 Narrative Approach
An alternative methodology for estimating the effects of fiscal policy shocks using VARs is the narrative approach. Prominent examples are (Romer & Romer, 2010), who identify tax shocks studying narrative records of tax policy decisions, and (Ramey, 2011), who identifies government spending shocks using changes in military spending associated with wars. Multipliers estimated using SVAR models are different from multipliers estimated using the narrative approach. Differences are in part due to the fact that most studies using the narrative approach identify anticipated fiscal shocks. Yet, (Mertens & Ravn, 2011b) construct a series of unanticipated tax shocks based on (Romer & Romer, 2010) narrative records, and find larger multipliers than SVARs. To understand what drives such differences, we conduct the following exercise:
- We regress the reduced-form VAR residuals on the (Mertens & Ravn, 2011b) narrative series of unanticipated tax shocks, which we denote by
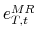 :
:
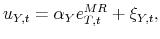
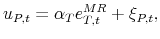
where
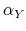 is the contemporaneous response of output to a narrative tax shock of size one standard deviation. This step follows the empirical specification for estimating tax multipliers
using narrative measures of tax shocks proposed by (Favero & Giavazzi, forthcoming).19
is the contemporaneous response of output to a narrative tax shock of size one standard deviation. This step follows the empirical specification for estimating tax multipliers
using narrative measures of tax shocks proposed by (Favero & Giavazzi, forthcoming).19 - We compute the response of output to a
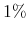 increase in tax revenue,
increase in tax revenue,
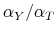 . This coefficient is equivalent to
. This coefficient is equivalent to 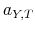 in equation
(3).
in equation
(3). - We invert the analytical function
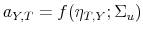 to obtain the output elasticity of tax revenue consistent with the narrative measure of the effects of tax policy on output, which we denote by
to obtain the output elasticity of tax revenue consistent with the narrative measure of the effects of tax policy on output, which we denote by
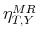 .20
.20
In our VAR model,
![]() , a value remarkably close to the elasticity associated to the M&U penalty function approach to sign restrictions.21 The associated impact tax multiplier is 0.95 dollars. In Figures 1 and 2 the
results for our application of the narrative approach are denoted `NARR'.
, a value remarkably close to the elasticity associated to the M&U penalty function approach to sign restrictions.21 The associated impact tax multiplier is 0.95 dollars. In Figures 1 and 2 the
results for our application of the narrative approach are denoted `NARR'.
The narrative tax multipliers presented in this paper are considerably smaller than the estimates reported by (Romer & Romer, 2010) and (Mertens & Ravn, 2011b). This is due to differences in the scaling of shocks. Narrative studies
consider tax shocks that increase tax revenue by ![]() . SVARs instead consider
. SVARs instead consider ![]() tax shocks that increase tax revenue by
tax shocks that increase tax revenue by
![]() i.e. SVARs account for macroeconomic feedback: if exogenous tax increases depress output, tax revenue will increase by less than one-for-one. To compare the
SVAR and narrative approaches, all shocks are rescaled following the SVAR convention.22
i.e. SVARs account for macroeconomic feedback: if exogenous tax increases depress output, tax revenue will increase by less than one-for-one. To compare the
SVAR and narrative approaches, all shocks are rescaled following the SVAR convention.22
3 Implications of Different Priors on Elasticities
In the previous section, we have concentrated on identification uncertainty to clarify the main properties of the alternative identification approaches. We now broaden the analysis, accounting also for sampling uncertainty and looking at dynamic multipliers beyond the impact period.
We start with the implications of sampling uncertainty on estimates of elasticities and impact multipliers. Figure 3 plots kernel densities of output elasticities and fiscal multipliers. The B&P and recursive approaches provide lower estimates of the output elasticity of tax revenue, and consequently of the impact tax multiplier, than the M&U and narrative approaches. The B&P and recursive approaches also provide lower estimates of the output elasticity of government spending than the M&U approach. This translates into a larger impact spending multiplier for the B&P and recursive approaches. All the identification approaches are dogmatic as regards structural uncertainty, i.e. for a given reduced-form estimate, they imply a single elasticity as well as multiplier. Distributions of elasticities and impact multipliers are uniquely due to sampling uncertainty.
Figure 4: Responses of output, tax revenue, government spending, and private consumption to a 1 dollar tax cut.
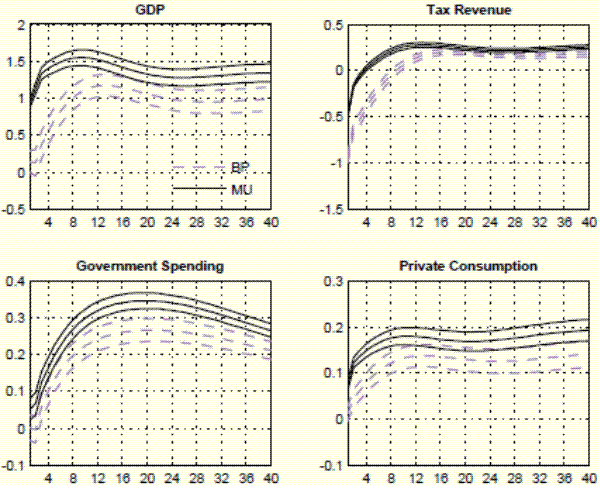
Figures 4 and 5 plot dynamic tax and spending multipliers for the B&P and M&U approaches.23 Focusing on the output multiplier, differences across approaches are substantial up to three years after the policy intervention, although differences across approaches diminish in the long-run, despite being very persistent. The top-right and bottom-left panel of Figure 4 plot the response of taxes and spending to a tax shock. For up to the three years after the policy intervention, the B&P approach predicts a larger effect of a tax cut on the deficit than does the M&U approach. The reason is that tax cuts identified with the M&U approach are partly self-financing, as they boost GDP and consequently the tax base.24 The opposite holds for the response of the deficit to spending shocks. As shown in Figure 5, the spending shock associated to the B&P approach is partly self-financing, due to the boost in tax revenue associated to the increase in GDP.
The bottom-right panel of Figure 5 plots the response of consumption to a spending shock. For the B&P approach, the response is positive at all horizons. For the M&U approach, the response is not significant for the first five quarters, and turns positive thereafter. We provide a detailed analysis of the response of consumption to a spending shock in Section 5.
Figure 5: Responses of output, tax revenue, government spending, and private consumption to a 1 dollar spending increase.
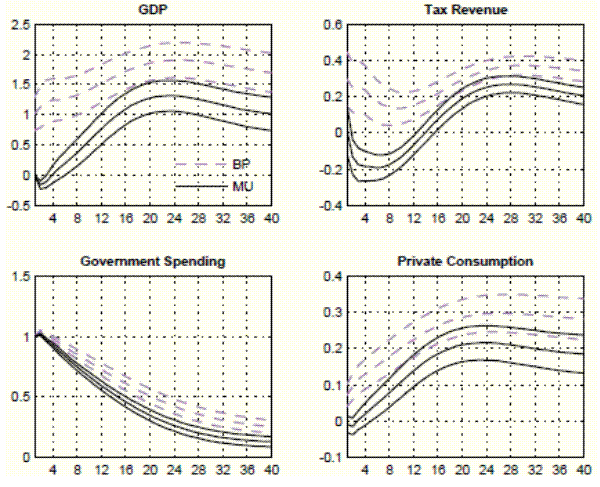
Figure 6 plots the probability of the tax multiplier being larger than the spending multiplier for all four SVAR-based approaches.25 The policy implication is very different: according to the B&P and the recursive approaches, tax multipliers are very likely to be smaller than spending multipliers for the entire forecast horizon. This probability reaches at most 0.2 two years after the policy intervention, and falls thereafter. The M&U approach instead finds that tax multipliers are very likely to be larger than spending multipliers. The probability is 1 for the first two years after the policy intervention. It declines to 0.45 after 5 years, and increases again thereafter. The pure sign restriction approach finds probabilities close to 0.5, reflecting the large structural uncertainty associated with this approach.
4 Robust Fiscal Multipliers
In the previous sections, we have shown that differences in priors on elasticities implicit in alternative identification schemes translate into large differences in fiscal multipliers. Some of the identification schemes appear very dogmatic, selecting a single value of the relevant output elasticity. Others appear quite loose, imposing almost no restriction on the relevant elasticity. In this section we strike a balance between these two extremes, surveying the existing literature on automatic stabilizers to derive distributions on elasticities that encompass the existing empirical evidence. Then we estimate fiscal multipliers based on these prior distributions.
Output elasticity of tax revenue. The size of automatic stabilizers is the subject of many empirical studies in the macro public finance literature. Several international organizations and national agencies estimate the output elasticity of tax revenue for different
tax categories, using these elasticities to construct cyclically-adjusted measures of the budget balance. Results for the B&P approach presented in this paper are based on elasticity estimates provided by (Follette & Lutz, 2010).26 These authors estimate the output elasticity of tax revenue using micro data for four different tax categories: personal income tax, social security contributions, corporate income tax,
and indirect taxes. We aggregate these elasticities to obtain a point estimate for the output elasticity
![]() according to the following aggregator:
according to the following aggregator:
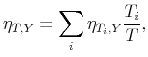 |
(11) |
where ![]() denotes the tax category,
denotes the tax category, ![]() denotes the level of tax revenue,
denotes the level of tax revenue,
![]() denotes total tax revenue, and
denotes total tax revenue, and
![]() denotes the output elasticity of tax category
denotes the output elasticity of tax category ![]() . Following
B&P, we evaluate
. Following
B&P, we evaluate ![]() and
and ![]() at their sample mean. The point estimate for the
period 1947-2006 is 1.71. (Caldara, 2011) shows that sampling uncertainty around the point estimate is small and can be safely neglected.
at their sample mean. The point estimate for the
period 1947-2006 is 1.71. (Caldara, 2011) shows that sampling uncertainty around the point estimate is small and can be safely neglected.
The NBER also estimates the output elasticity of personal income taxes and social security contributions using the TAXSIM model (Feenberg & Coutts, 1993). This model implements a micro-simulation of the U.S. federal income tax system. The model is based on a large sample of actual tax returns prepared by the Statistics of Income Division of the Internal Revenue Service. The average elasticity of personal income taxes and social security contributions estimated using TAXSIM is 1.65, which would increase the estimate for the overall elasticity to 1.8. The OECD27 also estimates the output elasticity of tax revenue for the United States. Following the OECD methodology, the aggregate elasticity is 1.2.
All these estimates of the output elasticity of taxes are lower than the value of 2.08 reported by B&P for their sample period 1947-1997. This difference is mainly due to differences in the definition of tax aggregates considered. In line with the literature cited above we use total tax revenue as tax variable. B&P instead use a concept of net taxes, subtracting transfers and net interest payments from tax revenue. This procedure mechanically increases the output elasticity of (net) taxes. The reason is that subtracting transfers and net interest payments - whose elasticity B&P set to -0.1 and 0, respectively - increases the weight associated to the other sub-elasticities28, in turn implying that the output elasticity of net taxes is much larger than the output elasticity of total tax revenue. Considering only genuine tax revenue, i.e. the four tax categories mentioned above, the B&P elasticity of taxes amounts to 1.5 for their sample period and their assumptions about sub-elasticities. This latter figure is in line with the evidence reported in the cyclical-adjustment literature cited above.
Elasticity estimates taken from this cyclical-adjustment literature are often used in DSGE modeling when authors want to move beyond the simplistic assumption of a proportional tax system (output elasticity of taxes equal to 1.0). A prominent example for the United States is (Leeper et al., 2010) who rely on elasticity estimates from B&P and the OECD to calibrate or set priors on the output elasticity of different tax categories.29
In an independent study, (Mertens & Ravn, 2011a) argue in favor of values of the output elasticity of tax revenue around 3. Their estimates are based on narrative measures of tax shocks. They make three arguments to support their finding. First, elasticity estimates from public finance studies are based on regressions that, although based on micro data, might be subject to a simultaneity bias. The narrative measure of tax shocks is exogenous to the state of the economy, and hence is not subject to such bias. Second, conditional on observing output, an SVAR identified assuming an output elasticity of tax revenue of 3 has greater explanatory power for the dynamics of tax revenues than an SVAR identified assuming a smaller value of the elasticity. Third, an elasticity of 3 generates an endogenous drop in tax revenue in 2008-2009 consistent with the drop observed in the data.
All in all, the macro public finance literature consistently documents output elasticities of tax revenue ranging from 1.2 to 1.8. Studies based on narrative measures of tax shocks find elasticities around 3. To encompass this empirical evidence, we draw the output elasticity of tax revenue from two normal distributions centered at the B&P and M&U narrative elasticity estimates of 1.7 and 3. Both distributions have a standard deviation of 1 to ensure a wide coverage around their mean.30 The top panel of Figure 7 shows that for this prior distribution the median tax multiplier is 0.65 dollars on impact. It starts to exceed one dollar five quarters after the policy intervention.
Output elasticity of government spending. Most authors in the VAR literature assume that the output elasticity of government consumption and investment is zero. In a similar vein, the cyclical-adjustment literature - e.g. the OECD - shares this assumption and does not attempt to estimate this elasticity.
There are some studies in the political-economy literature that estimate the output elasticity of government spending to assess whether fiscal policymakers behave pro-cyclically. Examples include (Lane, 2003) and (Rodden & Wibbels, 2010). Aggregate elasticities are not statistically significant in general. Yet, these papers document that some components of government consumption, such as public wages or state and local spending, are mildly pro-cyclical. Furthermore, international evidence on spending elasticities suggests that in some countries government spending is pro-cyclical. Finally, (Leeper et al., 2010) model government consumption and investment as mildly counter-cyclical.
The existing evidence tends to support the B&P assumption that in the U.S. the output elasticity of government spending is zero. However, it can also not be ruled out that government spending is mildly cyclical. Therefore, we implement a prior on the output elasticity of government spending centered at zero. We set the standard deviation to 0.1 to allow for some uncertainty. The middle panel of Figure 7 shows that for this prior distribution the median spending multiplier is 1 dollar on impact and stays above 1 dollar over the entire horizon.
The bottom panel of Figure 7 shows that the probability of the tax multiplier being larger than the spending multiplier remains below 0.5 at all horizons. Hence, for these prior distributions on the output elasticity of fiscal variables, there is no evidence to support the view that tax policy provides a larger stimulus to output than spending policy.
5 Shedding Light on Two Debates on the Effects of Spending Shocks
The analytical results presented in the previous sections can help shed light on two ongoing debates in the literature on the effects of spending shocks: the response of private consumption and the role of fiscal foresight.
5.1 On the Effects of Spending Shocks on Private Consumption
Standard RBC and New Keynesian models predict that, due to a negative wealth effect, consumption falls after a spending shock (Linnemann & Schabert, 2003;
Baxter & King, 1993). Yet, SVARs model consistently find that consumption increases.31 Assuming that government spending is acyclical (
![]() , the impact consumption multiplier is:
, the impact consumption multiplier is:
The response of consumption is positive as long as
5.2 The Role of Anticipation
What is the effect of fiscal foresight on the estimated response of output and consumption to a spending shock? Similarly to equation (12), we can write the response of output to a spending shock as:
Let us assume that, due to fiscal foresight, the reduced-form residual
This prediction is satisfied for our VAR model. The impact spending multiplier estimated using a 3-equation VAR in output, tax revenue, and government spending is 1.09 dollars, instead of
1.25 dollars in the full 8-equation VAR model including additional variables likely to capture foresight. Similarly, the impact response of consumption in a 4-equation VAR is ![]() dollars, compared to 0.09 dollars in the 8-equation VAR model.32
dollars, compared to 0.09 dollars in the 8-equation VAR model.32
6 Conclusions
We provide comprehensive evidence on fiscal multipliers for the U.S. based on data for the period 1947-2006. Our novel analytical framework allows us to reveal the core properties of the alternative identification schemes used in the fiscal VAR literature. We show that differences in estimates of fiscal multipliers documented in the literature by (Blanchard & Perotti, 2002), (Mountford & Uhlig, 2009) and (Romer & Romer, 2010) are due mostly to different restrictions on the output elasticities of tax revenue and government spending. We use extra-model information to narrow the set of empirically plausible values of the elasticities, which in turn allows us to sharpen the inference on fiscal multipliers. Our results suggest that spending multipliers tend to be larger than tax multipliers.
The analytical framework developed in this paper can be applied to study identification problems in a large class of time-series models, including VARs with time-varying reduced-form coefficients, regime-switching VARs and factor models. The use of such models can help unveil whether the transmission of fiscal policy shocks has changed over time33 or depends on the state of the economy (Auerbach & Gorodnichenko, forthcoming). Finally, the analytical framework developed here can be easily adapted to the study of other topics in empirical macroeconomics, such as the identification of monetary policy shocks.
Bibliography
Quarterly Journal of Economics 117(4):1329-68.
Appendix
A. Data and Estimation
We estimate the VAR model using Bayesian techniques. In particular, we impose prior distributions on the reduced-form coefficients
![]() and
and
![]() following the methodology discussed in (Del Negro & Schorfheide, 2011). We implement this prior, which is a variant of the well-known
Minnesota prior, through dummy observations. The hyper-parameters are chosen to impose a fairly loose prior, so that the comparison to the existing literature does not depend on the choice of the prior. Following the notation in (Del Negro & Schorfheide, 2011),
the hyper-parameters are:
following the methodology discussed in (Del Negro & Schorfheide, 2011). We implement this prior, which is a variant of the well-known
Minnesota prior, through dummy observations. The hyper-parameters are chosen to impose a fairly loose prior, so that the comparison to the existing literature does not depend on the choice of the prior. Following the notation in (Del Negro & Schorfheide, 2011),
the hyper-parameters are:
![]()
![]()
![]()
![]()
All components of national income are taken from the NIPA Tables published by the U.S. Bureau of Economic Analysis. They are in real per capita terms and are transformed from the nominal values by dividing them by the GDP deflator (NIPA Table 1.1.4, Line 1) and the population measure (NIPA Table 2.1, Line 38). The remaining series are downloaded from Federal Reserve Bank of St. Louis FRED database. The table and row numbers given below refer to the organization of the data by the BEA. Data are at a quarterly frequency from 1947I to 2006IV. We use the logarithm of all national income variables.
- GDP: Gross Domestic Product (NIPA Table 1.1.5, Line 1).
- Government Spending: Government consumption (NIPA Table 3.1, Line 16) expenditures and gross investment (NIPA Table 3.1. Line 35).
- Tax Revenue: Government current receipts (NIPA Table 3.1, Line 1).
- Private Consumption: Personal consumption expenditures (NIPA Table 1.1.5, Line 2).
- Non-Residential Investment: Private fixed investment - non-residential (NIPA Table 1.1.5, Line 9).
- CPI (Fred Series ID: CPIAUCSL): Consumer Price Index For All Urban Consumers (All Items).
- Stock Market Index: S&P 500 Composite w/GFD extension.
- Interest Rate (Fred Series ID: TB3MS): 3-Month Treasury Bill: Secondary Market Rate.
A.1 Granger-Causality Tests
Following (Ramey, 2011) we run the following Granger Causality tests:
- Do war dates Granger cause VAR shocks?
- Do Defense news Granger cause VAR spending shocks?
- Do 1-quarter ahead professional forecasts Granger cause VAR spending shocks?
- Do 4-quarter ahead professional forecasts Granger cause VAR spending shocks?
- Do Mertens and Ravn anticipated tax shocks Granger cause VAR tax shocks?
We run the following regression:
where tax and spending shocks are identified by the B&P approach at the OLS estimates. The following table reports the F-test for the null hypothesis
![]() .
.
|
B. Details of Analytical Results in Section I
The relation between reduced-form residuals ![]() and structural shocks
and structural shocks ![]() presented in (2) can also be written as:
presented in (2) can also be written as:
where
Pre-multiplying equation (1) by matrix ![]() gives the structural form of the VAR model:
gives the structural form of the VAR model:
Finally, the relation between structural coefficients
![]() and reduced-form coefficients
and reduced-form coefficients
![]() is given by:
is given by:
which describes a system of
![]() independent non-linear equations.
independent non-linear equations.
B.1 Bivariate Models
In the bivariate model, we solve a system of three equations (as many as the distinct elements of
![]() ) in three unknowns
) in three unknowns
![]() :
:
where
![\displaystyle \left[\begin{array}{cc} 1 & -a_{Y,P}\ -\eta_{P,Y} & 1\end{array}\right],](img179.gif) |
The solution of this system is:
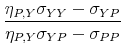 |
|||
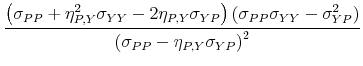 |
|||
Substituting the analytical solution for ![]() in matrix
in matrix ![]() ,we obtain the
following analytical expression for the impact impulse responses:
,we obtain the
following analytical expression for the impact impulse responses:
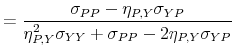 |
![\displaystyle \left[\begin{array}{cc} 1 & \frac{\sigma_{YP}-\eta_{P,Y}\sigma_{YY}}{\sigma_{PP}-\eta_{P,Y}\sigma_{YP}}\ \eta_{P,Y} & 1\end{array}\right].](img189.gif) |
The assumption that
![]() is positive definite ensures that the denominator of all impact responses is strictly larger than zero. This guarantees that impulse response functions are defined for all output
elasticities
is positive definite ensures that the denominator of all impact responses is strictly larger than zero. This guarantees that impulse response functions are defined for all output
elasticities
![]() .34
.34
B.2 Multivariate Models
In the bivariate model, we can rewrite the element i of the impulse vector associated with the policy shock ![]() as:
as:
for ![]() .
.
Let us introduce a third variable into the system:
In a three-equation VAR model, we need three restrictions to identify the system (B.1). Without loss of generality, we assume that restrictions are imposed on
![]() and
and ![]() . In the interest of space, we do not report the
solution to the three-equation system.35 The element
. In the interest of space, we do not report the
solution to the three-equation system.35 The element ![]() of the impulse vector associated with the policy shock
of the impulse vector associated with the policy shock ![]()
can be written as:
Notice that the impulse vector is independent of the restriction on
If ![]() , the solution for the impulse vector (B.3) collapses to expression (B.2), the solution for the impulse vector found in the bivariate
model. This result generalizes to VAR models of dimension
, the solution for the impulse vector (B.3) collapses to expression (B.2), the solution for the impulse vector found in the bivariate
model. This result generalizes to VAR models of dimension ![]() under the following assumptions:
under the following assumptions:
- If, without loss of generality, the policy variable is ordered first in the system, matrix
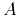 is block recursive:
where Block 2 is an
is block recursive:
where Block 2 is an![\displaystyle A=\left[\begin{array}{ccc} 1 & -\eta_{P,Y} & \mathbf{0}\ --- & --- & ---\ Block\mbox{ 2}\end{array}\right],](img208.gif)
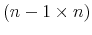 submatrix of structural coefficients for output and the additional
submatrix of structural coefficients for output and the additional 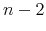 variables in the VAR, and
variables in the VAR, and
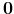 is an
is an
 vector of zeros.
vector of zeros. - The contemporaneous response of all variables to the policy shock is left unrestricted.
Under these assumptions, expression (B.2) describes the impact response of variable ![]() to a policy shock, for
to a policy shock, for
![]() . The intuition is simple: what matters for the identification of the policy shock is the output elasticity of the policy variable
. The intuition is simple: what matters for the identification of the policy shock is the output elasticity of the policy variable
![]() and the reduced-form residual
and the reduced-form residual ![]() How the remaining
How the remaining ![]() structural shocks generate fluctuations in
structural shocks generate fluctuations in ![]() is irrelevant for the identification of
is irrelevant for the identification of
![]() This is the same argument that explains why in a Cholesky decomposition, impulse responses associated to the shock ordered first do not depend on the identification of the remaining
This is the same argument that explains why in a Cholesky decomposition, impulse responses associated to the shock ordered first do not depend on the identification of the remaining
![]() shocks, ie on the ordering of the remaining
shocks, ie on the ordering of the remaining ![]() variables.
variables.
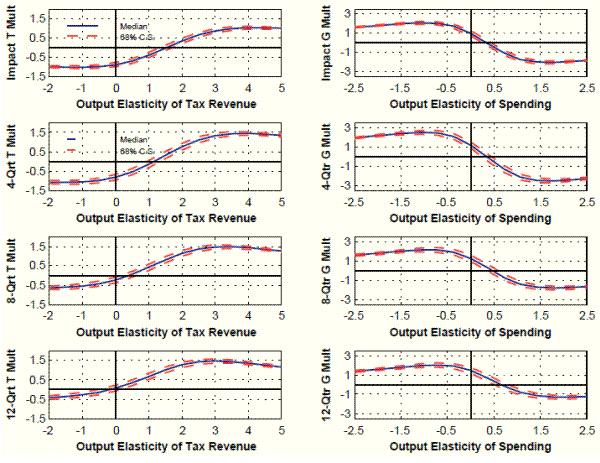
Figure 8: Tax and spending multipliers at different horizons as function of the output elasticity of tax revenue and spending.
To derive analytical expressions for impulse responses at longer horizon we start from the Moving Average (MA) representation of the SVAR model:
where
![]()
![]() . The elements of matrices
. The elements of matrices ![]() 's are functions of
the autoregressive coefficients contained in the lag polynomial
's are functions of
the autoregressive coefficients contained in the lag polynomial
![]() . 36 The matrix
. 36 The matrix
![]() contains impulse responses
contains impulse responses ![]() quarters after the shock, which are linear
combination of impact responses B.2. We do not inspect the analytical expression for impulse responses at horizon
quarters after the shock, which are linear
combination of impact responses B.2. We do not inspect the analytical expression for impulse responses at horizon ![]() . The above assumptions ensures that, for given
. The above assumptions ensures that, for given
![]() and
and
![]() , impulse responses to a policy shock
, impulse responses to a policy shock ![]() only depend on the output
elasticity of the policy variable at any horizon. Hence we can plot impulse responses as non-linear functions of the elasticities for any value of the elasticities, as we did for the impact responses.37 For instance, Figure 8 plots the tax and spending multiplier 4, 8, and 12 quarters after the shock.
only depend on the output
elasticity of the policy variable at any horizon. Hence we can plot impulse responses as non-linear functions of the elasticities for any value of the elasticities, as we did for the impact responses.37 For instance, Figure 8 plots the tax and spending multiplier 4, 8, and 12 quarters after the shock.
The output response to a policy shock (7) has the following properties:
- It has a global minimum and a global maximum such that:
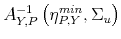
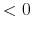
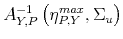
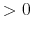
where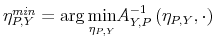 ,
,
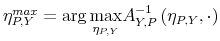 , and
, and
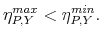
- It equals zero if and only if
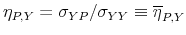 .
. - It is strictly decreasing for
![\eta_{P,Y}\in\left[\eta_{P,Y}^{max},\mbox{ }\eta_{P,Y}^{min}\right]](img233.gif) , and strictly increasing for
, and strictly increasing for
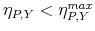 or
or
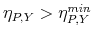 .
.
Proof of Proposition 1. First, we prove existence of a global minimum and maximum of
![]() . Note that
. Note that
![]() belongs to the family of rational functions, which are continuous and differentiable. So in order to find the global extrema of
belongs to the family of rational functions, which are continuous and differentiable. So in order to find the global extrema of
![]() we have to investigate its first and second derivatives. With some abuse of notation, denote
we have to investigate its first and second derivatives. With some abuse of notation, denote
![]() by
by
![]() . Equating the first derivative to zero we obtain two points that satisfy the necessary conditions for an extremum of
. Equating the first derivative to zero we obtain two points that satisfy the necessary conditions for an extremum of
![]() :
:
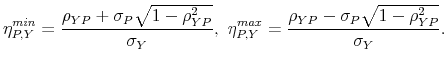 |
It is immediate to see that
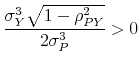 |
|||
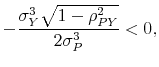 |
provided that
Finally, the global minimum and maximum of
![]() are:
are:
The second statement in Proposition 1 can be easily proved using the definition of
The third statement in Proposition 1 states that
C. Analytical Results for the Sign Restriction Approach
This part of the Appendix provides formal derivations of the results for the pure sign restriction approach and the penalty function approach to sign restrictions cited in the main text of the paper. We start with the analytical solution to the Cholesky decomposition of the covariance matrix, which will prove useful in the derivation of the analytical results for the sign restriction approach.
C.1 The Symbolic Cholesky Decomposition
We assume that the prediction error covariance matrix
![]() is a real symmetric positive definite matrix. The positive definiteness of
is a real symmetric positive definite matrix. The positive definiteness of
![]() implies
implies
![]() for all
for all ![]() and
and
![]() or, equivalently,
or, equivalently,
![]() for
for ![]() . This assumption guarantees
that the Cholesky factorization of the covariance matrix exists, i.e. a unique lower triangular matrix
. This assumption guarantees
that the Cholesky factorization of the covariance matrix exists, i.e. a unique lower triangular matrix
![]() with positive elements on the principal diagonal exists such that
with positive elements on the principal diagonal exists such that
![]() ((Golub & van Loan, 1996), Theorem 4.2.5, p. 143). We write the individual elements of the covariance matrix in terms of standard
deviations and correlation coefficients, which is useful for the presentation of the analytical results in the paper:
((Golub & van Loan, 1996), Theorem 4.2.5, p. 143). We write the individual elements of the covariance matrix in terms of standard
deviations and correlation coefficients, which is useful for the presentation of the analytical results in the paper:
The key to our analytical approach is the existence of an analytical expression for the lower-triangular Cholesky decomposition of the covariance matrix
![]() . The Cholesky decomposition has a recursive structure, which greatly simplifies the derivation of the individual elements of the Cholesky factor matrix. Denoting the Cholesky
factor of
. The Cholesky decomposition has a recursive structure, which greatly simplifies the derivation of the individual elements of the Cholesky factor matrix. Denoting the Cholesky
factor of
![]() by
by
![]() the algorithm for the computation of its individual elements can be expressed as follows:
the algorithm for the computation of its individual elements can be expressed as follows:
The computation starts from the upper left corner of ![]() and proceeds to calculate the matrix either row by row (Cholesky-Banachiewicz algorithm) or column by column (Cholesky-Crout
algorithm). The lower-triangular Cholesky decomposition of the covariance matrix
and proceeds to calculate the matrix either row by row (Cholesky-Banachiewicz algorithm) or column by column (Cholesky-Crout
algorithm). The lower-triangular Cholesky decomposition of the covariance matrix
![]() yields the following expression for the Cholesky factor
yields the following expression for the Cholesky factor ![]() , where to
save space we report only the elements of the first and second columns expressed as
, where to
save space we report only the elements of the first and second columns expressed as ![]() and
and ![]() , respectively:
, respectively:
We use the Cholesky decomposition because this allows for the derivation of simple analytical expressions. Note, however, that the inference does not depend on the use of this particular decomposition. Any other exact factorization of
C.2.1 Deriving Equation (8)
We start with the derivation of Equation (8) in the main text, which gives the factor matrix for the pure sign restriction approach. Recall that the system can be written
![]() in compact form. For the bivariate system the Cholesky factor, with output ordered first and the policy variable ordered second, can be expressed as follows:
in compact form. For the bivariate system the Cholesky factor, with output ordered first and the policy variable ordered second, can be expressed as follows:
![\displaystyle P=\left[ \begin{array}{cc} \sigma _{Y} & 0 \\ \sigma _{P}\rho _{YP} & \sigma _{P}\sqrt{1-\rho _{YP}^{2}}% \end{array}% \right] =\left[ \begin{array}{cc} \sigma _{Y} & 0 \\ \sigma _{P}\cos \varphi _{YP} & \sigma _{P}\sin \varphi _{YP}% \end{array}% \right] ,](img265.gif) |
where, to facilitate the derivation of analytical results, without loss of generality, we express the error correlation coefficient
The orthogonal matrix ![]() can be expressed as follows in the bivariate case:
can be expressed as follows in the bivariate case:
![\displaystyle Q=\left[ \begin{array}{cc} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{array}% \right] ,](img280.gif) |
where
![\displaystyle F^{SR}=\left[ \begin{array}{cc} \sigma _{Y}\cos \theta & -\sigma _{Y}\sin \theta \\ \sigma _{P}(\cos \varphi _{YP}\cos \theta +\sin \varphi _{YP}\sin \theta ) & -\sigma _{P}(\cos \varphi _{YP}\sin \theta -\sin \varphi _{YP}\cos \theta )% \end{array}% \right] .](img281.gif) |
Using basic trigonometric identities this expression can be further simplified to yield Equation (8) in the main text39:
![\displaystyle F^{SR}=\left[ \begin{array}{cc} \sigma _{Y}\cos \theta & -\sigma _{Y}\sin \theta \\ \sigma _{P}\cos (\theta -\varphi _{YP}) & -\sigma _{P}\sin (\theta -\varphi _{YP})% \end{array}% \right] .](img286.gif) |
C.2.2 The set of pure sign restriction solutions for the standard (loose) set of restrictions
We next characterize the set of pure sign restriction solutions under the baseline assumptions given in the main text (for the sake of brevity we concentrate on the more interesting case of the identification of tax shocks):
This set is non-empty for all
Proof. Abstracting from the sign restrictions, note that the interval
![]() describes the set of all possible rotation angles, with angles measured in radians. The angle
describes the set of all possible rotation angles, with angles measured in radians. The angle
![]() corresponds to a clockwise rotation by
corresponds to a clockwise rotation by
![]() , while the angle
, while the angle
![]() corresponds to a counterclockwise rotation by
corresponds to a counterclockwise rotation by
![]() . In other words, the interval describes the unit circle. Within these limits, the sign restrictions further restrict the set of admissible rotation angles:
. In other words, the interval describes the unit circle. Within these limits, the sign restrictions further restrict the set of admissible rotation angles:
This on its own would suggest that the set of pure sign restriction solutions is
First, note that the inclusion of reflections means that the sign restriction on
![]() can be disregarded as it will be satisfied, after sign-flipping where needed for all
can be disregarded as it will be satisfied, after sign-flipping where needed for all
![]() . Disregarding the sign restriction on
. Disregarding the sign restriction on
![]() implies that the set of pure sign restriction solutions grows to
implies that the set of pure sign restriction solutions grows to
![]() .
.
Second, consider the first shock for which the inclusion of reflections leads to the following conditions:
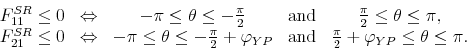
|
Note, however, that these conditions do not add solutions to the sign restriction set, once the sign-flipping is taken into consideration. The reason is that the sign-flipping can be implemented through a phase shift by
![]() (
(![]() . Shifting the subsets satisfying
. Shifting the subsets satisfying
![]() by
by ![]() (adding
(adding ![]() to
to
![]() gives the subset
gives the subset
![]() or by
or by ![]() (substracting
(substracting
![]() from
from
![]() gives the subset
gives the subset
![]() , respectively, and taking the union of the two resulting subsets gives the same set as the one satisfying
, respectively, and taking the union of the two resulting subsets gives the same set as the one satisfying
![]() . The same holds for the sign-flipping of the solutions satisfying
. The same holds for the sign-flipping of the solutions satisfying
![]() : shifting the subsets satisfying
: shifting the subsets satisfying
![]() by
by ![]() (adding
(adding ![]() to
to
![]() gives the subset
gives the subset
![]() or by
or by ![]() (substracting
(substracting ![]() from
from
![]() gives the subset
gives the subset
![]() , respectively, and taking the union of the two resulting subsets gives the same set as the one satisfying
, respectively, and taking the union of the two resulting subsets gives the same set as the one satisfying
![]() .
.
Taken together the set of all pure sign restriction solutions is given by ![]() . This set is non-empty for all admissible values of the error correlation coefficient as
. This set is non-empty for all admissible values of the error correlation coefficient as
![]() for all
for all
![]() . This completes the proof of Proposition 2.
. This completes the proof of Proposition 2.
It is worthwhile to quickly review the implications of Proposition 2 for our application. First, for the sign restrictions given by (C.4) the set will be the larger the smaller the value of
![]() , i.e. the larger the value of the correlation coefficient between reduced-form output and policy-variable disturbances.40 In our application - but also in the VARs estimated by B&P and M&U - the correlation coefficient is positive and large: for our VAR - evaluated at the OLS estimate -
, i.e. the larger the value of the correlation coefficient between reduced-form output and policy-variable disturbances.40 In our application - but also in the VARs estimated by B&P and M&U - the correlation coefficient is positive and large: for our VAR - evaluated at the OLS estimate -
![]() (and
(and
![]() ). This implies that the set
). This implies that the set ![]() is very large in
terms of the range of admissible
is very large in
terms of the range of admissible ![]() . However, regardless of the size of
. However, regardless of the size of ![]() , it
is always true that all output elasticities of taxes
, it
is always true that all output elasticities of taxes
![]() between zero and plus infinity will satisfy the sign restrictions given by (C.4). To see this recall the definition of
between zero and plus infinity will satisfy the sign restrictions given by (C.4). To see this recall the definition of
![]() given by Equation (9) in the main text:
given by Equation (9) in the main text:
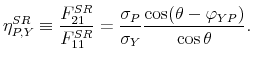 |
For the lower bound of ![]() (
(
![]() ) the elasticity is zero because the numerator
) the elasticity is zero because the numerator
![]() while the denominator
while the denominator
![]() for all
for all
![]() . For the upper bound of
. For the upper bound of ![]() (
(
![]() ) the elasticity goes to plus infinity because the denominator
) the elasticity goes to plus infinity because the denominator
![]() while the numerator
while the numerator
![]() for all
for all
![]() . In addition,
. In addition,
![]() is strictly increasing in
is strictly increasing in ![]() over
over ![]() . To see this note that the expression for the elasticity can be transformed as follows (yielding the expression shown in Equation (9) in the main text):
. To see this note that the expression for the elasticity can be transformed as follows (yielding the expression shown in Equation (9) in the main text):
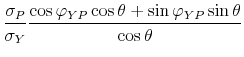 |
|||
To show that
![]() is strictly increasing in
is strictly increasing in ![]() over
over ![]() it is sufficient to show that the first derivative of
it is sufficient to show that the first derivative of
![]() with respect to
with respect to ![]() is positive for all
is positive for all ![]() , because
, because
![]() in any case. Now, the first derivative of
in any case. Now, the first derivative of
![]() with respect to
with respect to ![]() is
is
![]() , which is positive for all
, which is positive for all ![]() .
.
Note also that the expression for the impact tax cut multiplier for the sign restriction approach can be derived in analogy to Equation (6) in Section ![]() of the main text:
of the main text:
 |
|||
 |
|||
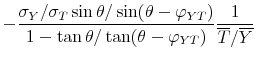 |
|||
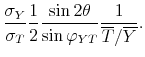 |
The main properties of the impact tax cut multiplier for the pure sign restriction approach and for the sign restrictions given by (C.4) can be summarized as follows:
- The impact multiplier is negative for
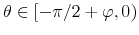 . The reason is that
. The reason is that
 for this range of
for this range of 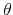 . This subset is empty if and only
if output and tax disturbances are negatively correlated (
. This subset is empty if and only
if output and tax disturbances are negatively correlated (
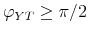 ). This subset implies
). This subset implies
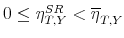 ; in our application
; in our application
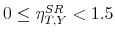 .
. - The impact multiplier is zero for
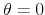 (the Cholesky factorization with output ordered first). The Cholesky factor is a particular pure sign restriction solution as long as the
correlation between output and tax disturbances is non-negative (
(the Cholesky factorization with output ordered first). The Cholesky factor is a particular pure sign restriction solution as long as the
correlation between output and tax disturbances is non-negative (
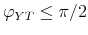 ). This Cholesky factorization implies
). This Cholesky factorization implies
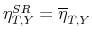 (
(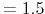 in our application).
in our application). - The impact multiplier is positive for
![\theta \in (0,\pi /2]](img364.gif) . The reason is that
. The reason is that
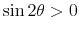 for this range of
for this range of 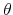 . This subset is non-empty for all
admissible values of the correlation coefficient between output and tax disturbances (
. This subset is non-empty for all
admissible values of the correlation coefficient between output and tax disturbances (
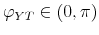 , i.e.
, i.e.
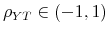 ). This subset implies
). This subset implies
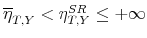 ; in our application
; in our application
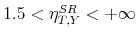 .
. - The impact multiplier reaches its maximum over
 for
for
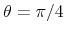 .41 The impact tax cut
multiplier, evaluated at
.41 The impact tax cut
multiplier, evaluated at
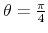 , is
, is
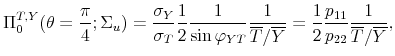
and the output elasticity of taxes, evaluated at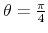 , is
, is
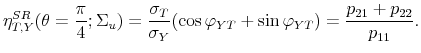
Note the simplicity of these expressions: all that it is needed for the calculation of the maximum impact multiplier and the associated elasticity is knowledge of the elements of the Cholesky factorization. In our application - with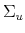 evaluated at the OLS estimate - the maximum impact tax cut multiplier is equal to 1.07 dollars and the associated output elasticity of taxes is equal to 4.15.
evaluated at the OLS estimate - the maximum impact tax cut multiplier is equal to 1.07 dollars and the associated output elasticity of taxes is equal to 4.15.
C.2.3 The set of pure sign restriction solutions for the alternative (more restrictive) set of restrictions
We next turn to the set of pure sign restriction solutions under the alternative assumptions given in the main text (again we concentrate on the more interesting case of the identification of tax shocks) under which we restrict the object of interest (the output response to a tax shock) to be negative in order to rule out negative impact tax cut multipliers:
This set is non-empty for all
Proof. Considering rotations first, note that the sign restrictions restrict the set of admissible angles to:
The intersection of the subsets satisfying the individual sign restrictions gives the set
The additional consideration of reflections does not affect this subset. To see this consider the following two subcases:
First, the subcase in which
![]() and
and
![]() but
but
![]() and
and
![]() . The individual restrictions are satisfied for the following angles:
. The individual restrictions are satisfied for the following angles:
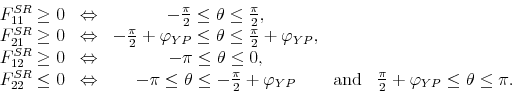
|
Taking the intersection of the subsets satisfying the individual restrictions gives the set
Second, consider the subcase in which
![]() and
and
![]() but
but
![]() and
and
![]() . These restrictions individually are satisfied for the following angles:
. These restrictions individually are satisfied for the following angles:
|
The intersection of the subsets satisfying these individual restrictions is an empty set.
Taken together the set of all pure sign restriction solutions is given by ![]() . For
. For
![]() , i.e. for
, i.e. for
![]() , the set is given by
, the set is given by
![]() ; this set is non-empty for all admissible values of the error correlation coefficient as
; this set is non-empty for all admissible values of the error correlation coefficient as
![]() for all
for all
![]() . For
. For
![]() , i.e. for
, i.e. for
![]() , the set is given by
, the set is given by
![]() ; this set is also non-empty for all admissible values of the error correlation coefficient as
; this set is also non-empty for all admissible values of the error correlation coefficient as
![]() for all
for all
![]() . This completes the proof of Proposition 3.
. This completes the proof of Proposition 3.
It is worthwhile to quickly review the implications of Proposition 3 for our application. First, for the sign restrictions given by (C.5) the set is largest for
![]() , i.e. for
, i.e. for
![]() , and shrinks as the (absolute) value of the correlation coefficient between output and policy disturbances increases. In our application
, and shrinks as the (absolute) value of the correlation coefficient between output and policy disturbances increases. In our application
![]() , i.e. the set of pure sign restriction solutions satisfying the restrictions (C.5) is given by
, i.e. the set of pure sign restriction solutions satisfying the restrictions (C.5) is given by
![]() . The lower bound of this interval corresponds to the Cholesky factorization with output ordered first, for which as shown above the impact tax cut
multiplier is zero and the output elasticity of taxes is equal to 1.5. At the upper bound of this interval the output elasticity of taxes is
. The lower bound of this interval corresponds to the Cholesky factorization with output ordered first, for which as shown above the impact tax cut
multiplier is zero and the output elasticity of taxes is equal to 1.5. At the upper bound of this interval the output elasticity of taxes is
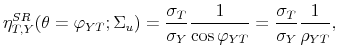 |
which in our application - evaluated at the OLS estimate - yields a value of the output elasticity of taxes of 6.15. The impact tax multiplier at the upper bound of this interval is
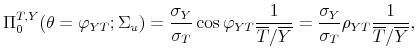 |
which in our application - evaluated at the OLS estimate - yields a value of the impact tax cut multiplier of
C.3 The Penalty Function Approach to Sign Restrictions: Bivariate Model
As an alternative to the pure sign restriction approach, the literature has used the penalty function approach to select one particular solution out of the set of pure sign restriction solutions (see e.g. (Faust, 1998), (Uhlig, 2005) and (Mountford & Uhlig, 2009)). More generally, the penalty function approach is used to numerically solve constrained nonlinear optimization problems for which closed-form analytical solutions may be hard to obtain or may not exist at all (see (Judd, 1998), pp. 123-25). The idea is to replace the constraints - here: the sign restrictions - with a continuous penalty function that permits but (heavily) penalizes choices that violate the constraints. As a result, the constrained problem is replaced with an unconstrained one.
We show here that it is possible to analytically solve the nonlinear optimization problem underlying the sign-restriction penalty function approach for the bivariate case. In particular, we show that the standard penalty function used in the literature implies that the optimum is an element of the subset ruling out negative impact tax cut multipliers that obtains when adding a sign restriction on the object of interest (the output response to a tax shock) as in (C.5). This shows what should be intuitively clear: the standard penalty function is an identifying assumption.
The standard penalty function has the sum of some or all impact impulse responses to a given shock as its arguments, where in general the impulse response of variable ![]() to shock
to shock
![]() is scaled by the standard deviation of this variable's one-step-ahead prediction error,
is scaled by the standard deviation of this variable's one-step-ahead prediction error,
![]() .42 In our notation, the individual
arguments of the penalty function can thus be written as
.42 In our notation, the individual
arguments of the penalty function can thus be written as
![]() . This expression is equivalent to the square root of the fraction of variable
. This expression is equivalent to the square root of the fraction of variable ![]() 's one-step-ahead forecast error variance explained by shock
's one-step-ahead forecast error variance explained by shock ![]() .
.
The literature, in general, proceeds as follows: first, numerically minimize a penalty function having some or all impulse responses to the first shock as its arguments. Second, if a second shock has to be identified, minimize a penalty function having some impulse responses to the second shock as arguments, imposing the further constraint that the second shock is orthogonal to the first shock. The identification of further shocks proceeds analogously.
In the bivariate case, the problem simplifies as there is a maximum of two shocks. There can be only one penalty function as the second shock imperatively has to explain all fluctuation not explained by the first shock. In line with M&U we assume that the penalty function has the impulse responses to the first shock of the sign-restricted variables as its arguments. We here again focus on the more interesting case of the identification of the tax shock. In this case the penalty function has the impulse responses of output and taxes to the business cycle shock as its arguments. This yields the following objective function (10) given in the main text:
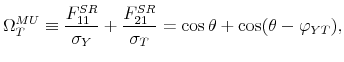 |
which is to be maximized with respect to
Expressing the problem in terms of trigonometric functions greatly facilitates the analytical solution to this optimization problem. First, the orthonormality restriction on the rotation matrix ![]() is automatically satisfied because
is automatically satisfied because
![]() holds for any
holds for any
![]() . Second, since we can analytically characterize the set of all pure-sign restriction solutions,
. Second, since we can analytically characterize the set of all pure-sign restriction solutions, ![]() (see Proposition 2), we know that the domain of
(see Proposition 2), we know that the domain of
![]() is a closed and bounded interval on
is a closed and bounded interval on
![]() . Third, as we show in the proof to the following proposition, since
. Third, as we show in the proof to the following proposition, since
![]() is a continuous and concave function on
is a continuous and concave function on ![]() , we have by
Weierstrass's theorem that
, we have by
Weierstrass's theorem that
![]() achieves its global maximum on its domain. Furthermore, this global maximum is unique. In sum, we neither have to explicitly account for the equality constraint implied by
the orthonormality assumption, nor for the inequality constraints associated with the sign restrictions. Both sets of constraints will be automatically satisfied.
achieves its global maximum on its domain. Furthermore, this global maximum is unique. In sum, we neither have to explicitly account for the equality constraint implied by
the orthonormality assumption, nor for the inequality constraints associated with the sign restrictions. Both sets of constraints will be automatically satisfied.
The following proposition gives the analytical solution to the optimization problem underlying the penalty function approach:
The global maximizer is the mid-point of the set of all pure sign restriction solutions
Proof. First, we prove that the maximum is unique and global. Since we can analytically characterize the set of all pure-sign restriction solutions, ![]() (see
Proposition 2), we know that the domain of
(see
Proposition 2), we know that the domain of
![]() is a closed and bounded interval on
is a closed and bounded interval on
![]() . Moreover,
. Moreover,
![]() is a continuous and concave function on
is a continuous and concave function on ![]() . The cosine function
is continuous for all real numbers. To show that
. The cosine function
is continuous for all real numbers. To show that
![]() is concave on
is concave on ![]() it is sufficient to show that
it is sufficient to show that
![]() and
and
![]() are both concave on
are both concave on ![]() (see (Simon & Blume, 1994), Theorem 21.8, p. 519). Using the second-derivative test it is straightforward to show that
(see (Simon & Blume, 1994), Theorem 21.8, p. 519). Using the second-derivative test it is straightforward to show that
![]() is concave on the interval
is concave on the interval
![]() and
and
![]() is concave on the interval
is concave on the interval
![]() . The set of all pure sign-restriction solutions
. The set of all pure sign-restriction solutions ![]() is a subset of both intervals for all
is a subset of both intervals for all
![]() . Then, by Weierstrass's theorem
. Then, by Weierstrass's theorem
![]() achieves its global maximum on its domain. To establish uniqueness we need to show that
achieves its global maximum on its domain. To establish uniqueness we need to show that
![]() is strictly concave
is strictly concave
![]() on its entire domain. Note, first, that
on its entire domain. Note, first, that
![]() and
and
![]() have continuous derivatives with respect to
have continuous derivatives with respect to ![]() of every order, implying that
of every order, implying that
![]() is also infinitely continuously differentiable. Concavity implies that
is also infinitely continuously differentiable. Concavity implies that
![]() on
on ![]() and
and
![]() on
on ![]() for all
for all
![]() . Furthermore,
. Furthermore,
![]() for identical angle of rotation
for identical angle of rotation
![]() if and only if
if and only if
![]() (perfect negative correlation), which is ruled out by assumption. Thus,
(perfect negative correlation), which is ruled out by assumption. Thus,
![]() is strictly concave on
is strictly concave on ![]() for all
for all
![]() , ensuring uniqueness of its global maximum.
, ensuring uniqueness of its global maximum.
Second, we prove that
![]() is the maximizer of
is the maximizer of
![]() on
on ![]() . The first-order condition for a maximum is
. The first-order condition for a maximum is
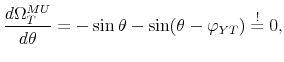 |
which after some simple derivations yields
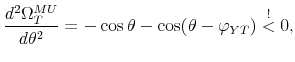 |
which evaluated at
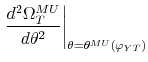 |
|||
| 0 for all |
Third, we prove that
![]() is the mid-point of both the set
is the mid-point of both the set ![]() and the subset
and the subset
![]() . First, recall that the set
. First, recall that the set ![]() of all solutions satisfying the sign
restrictions (C.4) is given by
of all solutions satisfying the sign
restrictions (C.4) is given by
![]() . The mid-point of this set is equal to half the sum of the lower and upper bound of
. The mid-point of this set is equal to half the sum of the lower and upper bound of ![]() , i.e.
, i.e.
![]() . Second, recall that the subset
. Second, recall that the subset ![]() of all solutions satisfying the more restrictive sign restrictions (C.5) is given by
of all solutions satisfying the more restrictive sign restrictions (C.5) is given by
![]() . For
. For
![]() , i.e. for non-negative error correlation, this subset is given by
, i.e. for non-negative error correlation, this subset is given by
![]() . It is easy to see that the mid-point of this interval is
. It is easy to see that the mid-point of this interval is
![]() . For
. For
![]() , i.e. for non-positive error correlation, this subset is given by
, i.e. for non-positive error correlation, this subset is given by
![]() , i.e. it is identical to
, i.e. it is identical to ![]() , for which we already showed that its mid-point is equal to
, for which we already showed that its mid-point is equal to
![]() .
.
Finally, we prove that
![]() maximizes the fraction of one-step ahead forecast error covariance explained by the first shock if the error correlation is positive and minimizes it if the error
correlation is negative. The fraction of covariance explained by the first shock is given by
maximizes the fraction of one-step ahead forecast error covariance explained by the first shock if the error correlation is positive and minimizes it if the error
correlation is negative. The fraction of covariance explained by the first shock is given by
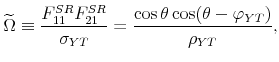 |
which is to be maximized with respect to
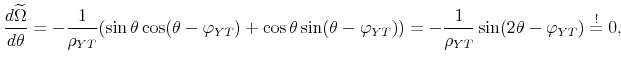 |
which has
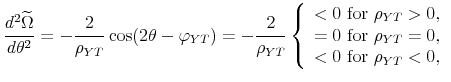 |
confirming that
It is worthwhile to quickly review the implications of Proposition 4 for our application.
- The most interesting finding is certainly that even though the objective function is maximized over the set of pure sign restriction solutions (C.4) leaving open the sign of the response of output to a tax shock (the object of interest), the solution to this maximization problem always satisfies the additional sign restriction implied by (C.5).
- The output elasticity of taxes evaluated at
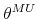 is
is
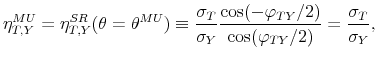
which is larger than the output elasticity of taxes evaluated at (the Cholesky factorization), given by
(the Cholesky factorization), given by
 , for all admissible values of
, for all admissible values of
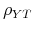 . The difference between these elasticites is the larger the lower the value of the correlation coefficient
. The difference between these elasticites is the larger the lower the value of the correlation coefficient
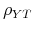 . In our application, evaluated at the OLS estimate, the elasticity
. In our application, evaluated at the OLS estimate, the elasticity
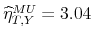 is roughly twice as large as the elasticity obtaining for the Cholesky factorization.
is roughly twice as large as the elasticity obtaining for the Cholesky factorization. - The impact tax cut multiplier, evaluated at
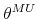 , is positive for all admissible values of
, is positive for all admissible values of
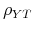 . In fact, it does not depend on
. In fact, it does not depend on
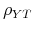 :
:
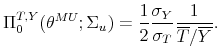
The impact tax cut multiplier is the larger the larger the standard deviation of the output error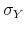 and the lower the standard deviation of the tax error
and the lower the standard deviation of the tax error
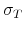 . In our application, evaluated at the OLS estimate, the impact tax cut multiplier for the penalty function solution is 0.93 dollars.
. In our application, evaluated at the OLS estimate, the impact tax cut multiplier for the penalty function solution is 0.93 dollars. - The degree of self-financing of a tax cut is 50% on impact for the penalty function solution. To see this note that from Equation (5) in Section 1 the response of taxes to a one unit tax shock is given by
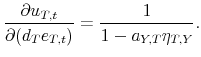
At the penalty function solution we have
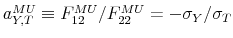 and
and
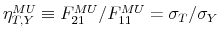 , which gives
, which gives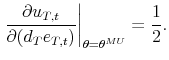
C.3.1 A brief summary of results for the spending model
We close the bivariate section with a summary of results for the spending model, which in the bivariate context is trivial. Recall that M&U do not sign restrict the response of government spending to a business cycle shock, which implies the following sign pattern
![\displaystyle F^{SR}=\left[ \begin{array}{cc} + & ? \\ ? & +% \end{array}% \right] .](img474.gif) |
For these restrictions the set of pure sign restriction solutions is simply the entire interval of admissible rotation angles
![]() .
.
The objective function for the spending model is
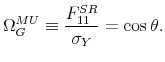 |
It is easy to see that the solution is
![]() , i.e. the penalty function solution is nothing else than the Cholesky factorization with output ordered first. For this solution the impact spending multiplier is zero.
The output elasticity of government spending implied by the penalty function solution is given by:
, i.e. the penalty function solution is nothing else than the Cholesky factorization with output ordered first. For this solution the impact spending multiplier is zero.
The output elasticity of government spending implied by the penalty function solution is given by:
In our application, as is true also for other VAR studies in this literature, the output and government spending residuals are strongly positively correlated (
![]() . For the penalty function solution - and the Cholesky factorization with output ordered first - 100% of the correlation between one step-ahead output and
government spending errors is explained by the business cycle shock, implying strongly procyclical government spending (
. For the penalty function solution - and the Cholesky factorization with output ordered first - 100% of the correlation between one step-ahead output and
government spending errors is explained by the business cycle shock, implying strongly procyclical government spending (
![]() ).43
).43
C.4 Multivariate extensions
We extend the analysis to a three-variable system with output, taxes and a third variable. The third variable, denoted ![]() , will be private consumption, denoted
, will be private consumption, denoted ![]() , private investment, denoted
, private investment, denoted ![]() , or government spending,
, or government spending, ![]() , depending on the object of interest. We restrict attention to the set of pure sign restriction solutions
, depending on the object of interest. We restrict attention to the set of pure sign restriction solutions ![]() derived for the bivariate tax model. In particular, we answer the following questions:
derived for the bivariate tax model. In particular, we answer the following questions:
- How does an additional sign restriction on the response of a third variable to the business cycle shock affect the set
 derived in the bivariate tax model? M&U, for example,
restrict the responses of consumption and investment to a business cycle shock to be positive. Does this strongly affect the set
derived in the bivariate tax model? M&U, for example,
restrict the responses of consumption and investment to a business cycle shock to be positive. Does this strongly affect the set  ?
? - Under which conditions does the penalty function solution
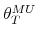 derived for the bivariate tax model satisfy the additional restriction on a third variable?
derived for the bivariate tax model satisfy the additional restriction on a third variable? - What is the impact spending multiplier implied by the set
 when the model is extended to include
when the model is extended to include  as third variable?
as third variable?
We should clarify that in this section we look at a subspace of the set of all solutions in the multivariate context. However, as we will see this is a very interesting subset, clarifying that the wide range of possible results that we derived for the bivariate context persists even if we don't look at the entire space of solutions in the multivariate context.
In the trivariate context, the orthogonal matrix ![]() can be written as the product of three Givens matrices
can be written as the product of three Givens matrices ![]() ,
, ![]() and
and ![]() , each rotating a
different pair of columns of the matrix to be transformed:
, each rotating a
different pair of columns of the matrix to be transformed:
![\displaystyle Q=\left[ \begin{array}{ccc} \cos \theta _{12} & -\sin \theta _{12} & 0 \\ \sin \theta _{12} & \cos \theta _{12} & 0 \\ 0 & 0 & 1\end{array}% \right] \left[ \begin{array}{ccc} \cos \theta _{13} & 0 & -\sin \theta _{13} \\ 0 & 1 & 0 \\ \sin \theta _{13} & 0 & \cos \theta _{13}% \end{array}% \right] \left[ \begin{array}{ccc} 1 & 0 & 0 \\ 0 & \cos \theta _{23} & -\sin \theta _{23} \\ 0 & \sin \theta _{23} & \cos \theta _{23}% \end{array}% \right] .](img489.gif)
|
In the following we focus attention on those sign restriction solutions that obtain when setting
![]() , in which case
, in which case
![]() and
and ![]() .
.
C.4.1 The effect of additional sign restrictions on third variables
We consider the following sign restrictions on the factor matrix ![]() :
:
![\displaystyle F^{SR}=\left[ \begin{array}{ccc} + & ? & ? \\ + & + & ? \\ + & ? & +% \end{array}% \right] .](img493.gif) |
These restrictions are comparable to the restrictions imposed by M&U: in the tax model we require the responses of output, taxes and the third variable (either ![]() or
or ![]() ) to be positive, whereas for the tax shock (second shock) we require the response of taxes to be positive and orthogonality to the business cycle shock.
) to be positive, whereas for the tax shock (second shock) we require the response of taxes to be positive and orthogonality to the business cycle shock.
We extend the bivariate system given by Equation (8) to a trivariate system, where
![]() denotes the residual of the third variable:
denotes the residual of the third variable:
where
We are going to assume in the following that the cross-correlations between the three residuals are all positive, i.e.
![]() . This assumption facilitates the exposition of the results but is not very restrictive as it is in line with the evidence for the fiscal VAR models
used in the literature. In these models all candidate third variables (private consumption, private investment and government spending) are robustly positively correlated with output and taxes. It can easily be shown that for this assumption all elements of the Cholesky factor except for
. This assumption facilitates the exposition of the results but is not very restrictive as it is in line with the evidence for the fiscal VAR models
used in the literature. In these models all candidate third variables (private consumption, private investment and government spending) are robustly positively correlated with output and taxes. It can easily be shown that for this assumption all elements of the Cholesky factor except for
![]() are non-negative (see Equation C.3) and the sign of
are non-negative (see Equation C.3) and the sign of ![]() is equal to the sign of
is equal to the sign of
![]() . Depending on the sign of
. Depending on the sign of ![]() the set of
pure sign restriction solutions becomes
the set of
pure sign restriction solutions becomes
We can check the implications of this condition for our empirical application.
Consider first the case in which private consumption is the third variable. In this case, - with the covariance matrix
![]() evaluated at the OLS estimate - the
evaluated at the OLS estimate - the ![]() element of the Cholesky
factor is negative, i.e. the first case in (C.7) applies. This implies that the additional restriction on the sign of the consumption response shrinks the set of pure sign restriction solutions. How large is this effect? In our empirical application the set
still covers all empirically plausible models: at the upper bound of the sign restriction set (
element of the Cholesky
factor is negative, i.e. the first case in (C.7) applies. This implies that the additional restriction on the sign of the consumption response shrinks the set of pure sign restriction solutions. How large is this effect? In our empirical application the set
still covers all empirically plausible models: at the upper bound of the sign restriction set (
![]() ) the output elasticity of taxes is equal to 73.2. In other words, the additional sign restriction on the consumption response has only a very minor effect on the set of pure sign restriction solutions derived for the bivariate model.
) the output elasticity of taxes is equal to 73.2. In other words, the additional sign restriction on the consumption response has only a very minor effect on the set of pure sign restriction solutions derived for the bivariate model.
Consider next the case in which private investment is the fourth variable. In this case, - with the covariance matrix
![]() evaluated at the OLS estimate -, the
evaluated at the OLS estimate -, the ![]() element of the Cholesky
factor is positive, i.e. the third case in (C.7) applies. To know whether the additional restriction on the investment response shrinks the set
element of the Cholesky
factor is positive, i.e. the third case in (C.7) applies. To know whether the additional restriction on the investment response shrinks the set ![]() we need
to very whether
we need
to very whether
![]() . In our application this condition is not fulfilled, i.e. the sign restriction set
. In our application this condition is not fulfilled, i.e. the sign restriction set ![]() is not affected at all by the additional sign restriction.
is not affected at all by the additional sign restriction.
Note also that the above results do not depend on the analysis of a trivariate model. If instead we look at a four-variable model with output, taxes, consumption and investment, the same results hold, with the sign restriction on the consumption response being the binding restriction in our empirical application. This is because the contemporaneous responses of consumption and investment to a business cycle shock do not depend on which one is ordered third or fourth in the system
Finally, we can ask whether the penalty function solution derived for the bivariate model,
![]() satisfies the additional sign restriction on the third variable:
satisfies the additional sign restriction on the third variable:
Note that we have ![]() by assumption and
by assumption and
![]() and
and
![]() for all
for all
![]() . If
. If
![]() then the sign restriction solution for the bivariate model automatically satisfies the sign restriction on the third variable. If
then the sign restriction solution for the bivariate model automatically satisfies the sign restriction on the third variable. If ![]() (which holds for
(which holds for
![]() ) the penalty function solution needs to satisfy the condition that
) the penalty function solution needs to satisfy the condition that
![]()
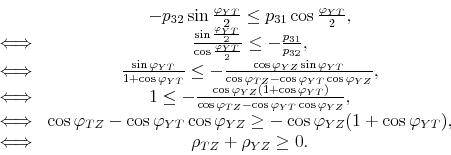 |
This condition is satisfied under the assumption of positive cross-correlation between the reduced-form errors. As we have argued above this assumption is empirically plausible. For all VAR models we are aware of output, taxes, private consumption and investment are robustly positively cross-correlated.
C.4.2 The trivariate model with government spending
We last turn to the triviate model with government spending, for which - in line with M&U - we do not sign restrict the response of government spending to a business cycle shock which gives the following sign restrictions on the factor matrix ![]() :
:
![\displaystyle F^{SR}=\left[ \begin{array}{ccc} + & ? & ? \\ + & + & ? \\ ? & ? & +% \end{array}% \right] .](img517.gif) |
In this case all pure sign restrictions solutions derived for the bivariate model remain sign restrictions in the trivariate model. The sign restriction on the spending shock is automatically satisfied because postmultiplying the Cholesky factor ![]() by
by ![]() leaves the third column of
leaves the third column of ![]() unchanged and
unchanged and ![]() for positive definite
for positive definite
![]() . This latter property has an important implication:
. This latter property has an important implication:
![]() for all
for all
![]() , i.e. the output response to a government spending shock is zero. Of course, this result would not hold if we broadened the analysis to include rotations beyond the
output-tax subspace.
, i.e. the output response to a government spending shock is zero. Of course, this result would not hold if we broadened the analysis to include rotations beyond the
output-tax subspace.
But this result is important because it also holds for the M&U penalty function if - in accordance with the assumptions made by M&U - only those responses to a business cycle shock that are sign restricted enter as arguments in the objective function to be maximized. Under this
assumption the objective function to be maximized with respect to
![]() is still the one given by (10) and the maximum still obtains for
is still the one given by (10) and the maximum still obtains for
![]() .44
.44
The output elasticity of government spending implied by this solution is
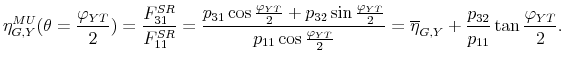 |
The output elasticity of government spending, evaluated at
![]() , will be larger than
, will be larger than
![]() for
for
![]() and smaller than
and smaller than
![]() for
for ![]() , recalling that
, recalling that
![]() for
for
![]() . In our application - evaluated at the OLS estimate -
. In our application - evaluated at the OLS estimate - ![]() but the deviation from
but the deviation from
![]() is small. The output elasticity for the penalty function solution is 0.36, compared to 0.38 for the Cholesky decomposition. But most importantly, the penalty function solution for standard sign restrictions implies a zero impact spending
multiplier.
is small. The output elasticity for the penalty function solution is 0.36, compared to 0.38 for the Cholesky decomposition. But most importantly, the penalty function solution for standard sign restrictions implies a zero impact spending
multiplier.
Footnotes
 , which is satisfied only for
, which is satisfied only for
![\displaystyle \left[ \begin{array}{c} u_{Y,t} \\ u_{P,t}% \end{array}% \right] =\frac{1}{1-a_{Y,P}\eta _{P,Y}}\left[ \begin{array}{cc} 1 & a_{Y,P} \\ \eta _{P,Y} & 1\end{array}% \right] \left[ \begin{array}{cc} d_{Y} & 0 \\ 0 & d_{P}% \end{array}% \right] \left[ \begin{array}{c} e_{Y,t} \\ e_{P,t}% \end{array}% \right] .](img49.gif)
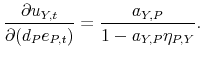
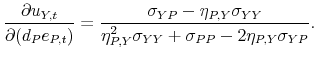
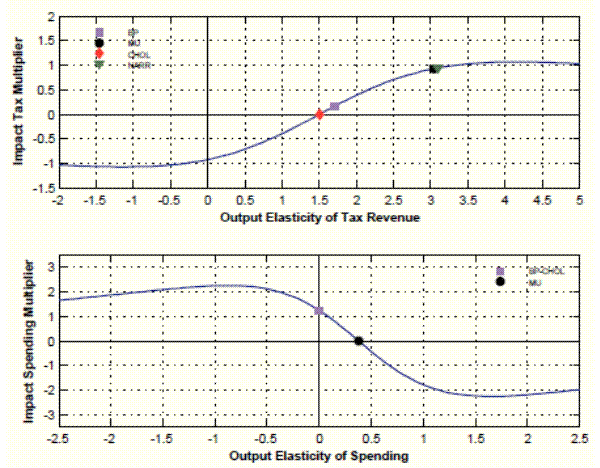
![\displaystyle \left[ \begin{array}{c} u_{Y,t} \\ u_{P,t}% \end{array}% \right] =\left[ \begin{array}{cc} \sigma _{Y}\cos \theta & -\sigma _{Y}\sin \theta \\ \sigma _{P}\cos (\theta -\varphi _{YP}) & -\sigma _{P}\sin (\theta -\varphi _{YP})% \end{array}% \right] \left[ \begin{array}{c} e_{Y,t} \\ e_{P,t}% \end{array}% \right] ,](img85.gif)
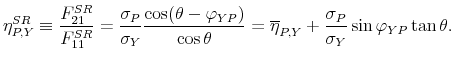
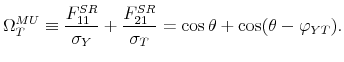
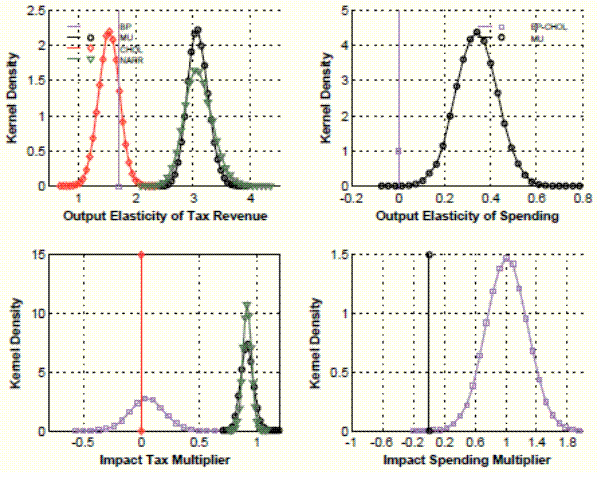
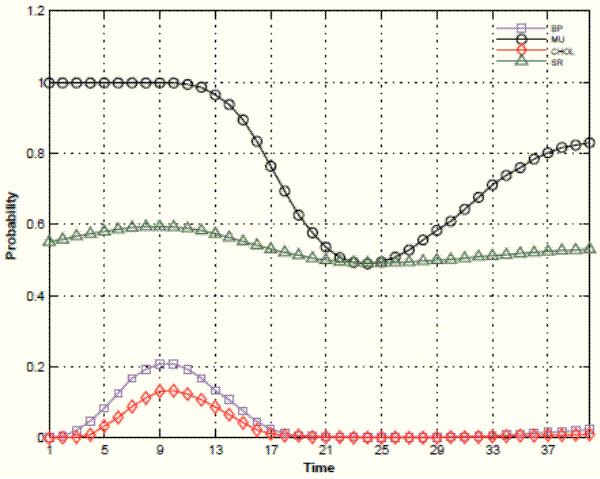
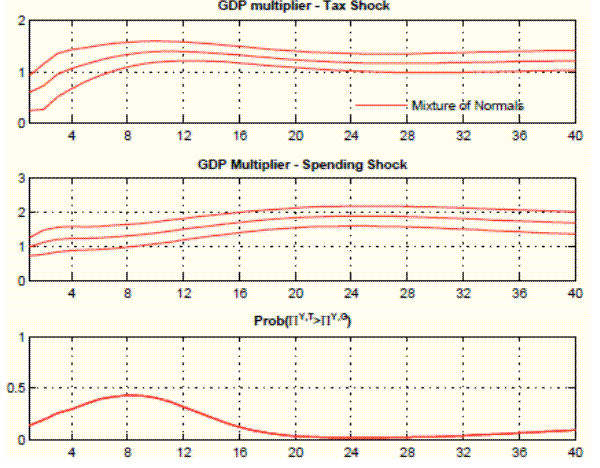
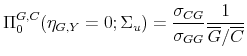 .
.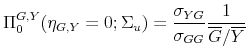 .
.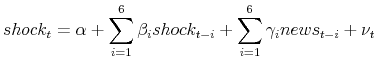
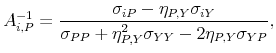
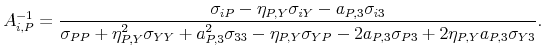
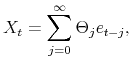
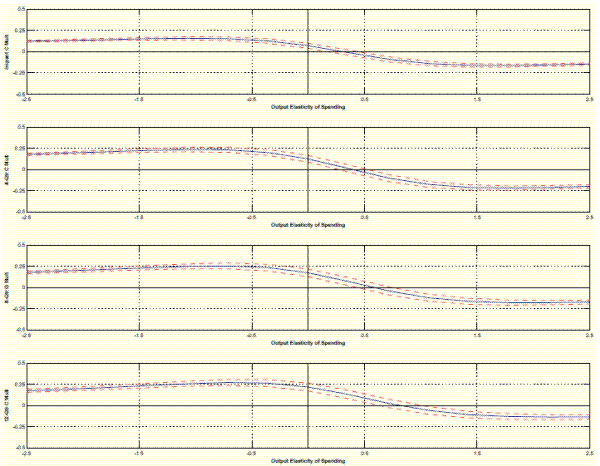
![\begin{displaymath}\begin{array}{c} \\ \Sigma _{u} \\ \left( n\times n\right)% \end{array}% =\left[ \begin{array}{ccccc} \sigma _{11} & \ldots & \sigma _{1}\sigma _{j}\rho _{1j} & \ldots & \sigma _{1}\sigma _{n}\rho _{1n} \\ \vdots & \ddots & \vdots & & \vdots \\ \sigma _{1}\sigma _{j}\rho _{1j} & \ldots & \sigma _{ii} & \ldots & \sigma _{j}\sigma _{n}\rho _{nj} \\ \vdots & & \vdots & \ddots & \vdots \\ \sigma _{1}\sigma _{n}\rho _{1n} & \ldots & \sigma _{j}\sigma _{n}\rho _{nj} & \ldots & \sigma _{nn}% \end{array}% \right] .\end{displaymath}](img259.gif)
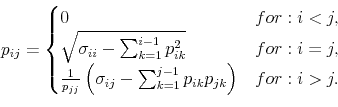
![\displaystyle \left[ \begin{array}{cc} p^{(1)} & p^{(2)}% \end{array}% \right] =\left[ \begin{array}{cc} \sigma _{1} & 0 \\ \sigma _{2}\rho _{12} & \sigma _{2}\sqrt{1-\rho _{12}^{2}} \\ \vdots & \vdots \\ \sigma _{j}\rho _{1j} & \sigma _{j}\frac{\rho _{2j}-\rho _{1j}\rho _{12}}{% \sqrt{1-\rho _{12}^{2}}} \\ \vdots & \vdots \\ \sigma _{n}\rho _{1n} & \sigma _{n}\frac{\rho _{2n}-\rho _{1n}\rho _{12}}{% \sqrt{1-\rho _{12}^{2}}}% \end{array}% \right] .](img264.gif)
![\displaystyle F^{SR}=\left[ \begin{array}{cc} + & ? \\ + & +% \end{array}% \right] .](img287.gif)
![\displaystyle F^{SR}=\left[ \begin{array}{cc} + & - \\ + & +% \end{array}% \right] .](img387.gif)
![\displaystyle \left[ \begin{array}{c} u_{Y,t} \\ u_{T,t} \\ u_{Z,t}% \end{array}% \right] =\left[ \begin{array}{ccc} p_{11} & 0 & 0 \\ p_{21} & p_{22} & 0 \\ p_{31} & p_{32} & p_{33}% \end{array}% \right] \left[ \begin{array}{ccc} \cos \theta _{12} & -\sin \theta _{12} & 0 \\ \sin \theta _{12} & \cos \theta _{12} & 0 \\ 0 & 0 & 1\end{array}% \right] \left[ \begin{array}{c} e_{Y,t} \\ e_{T,t} \\ e_{Z,t}% \end{array}% \right] ,](img495.gif)
![\displaystyle \theta _{12}\in \left\{ \begin{array}{ll} \lbrack -\frac{\pi }{2}+\varphi _{YT},\arctan (-\frac{p_{31}}{p_{32}})] & \text{if }p_{32}<0, \\ \lbrack -\frac{\pi }{2}+\varphi _{YT},\frac{\pi }{2}] & \text{if }p_{32}=0, \\ \lbrack \max (-\frac{\pi }{2}+\varphi _{YT};\arctan (-\frac{p_{31}}{p_{32}}% )),\frac{\pi }{2}] & \text{if }p_{32}>0.% \end{array}% \right.](img503.gif)