Is the Consumer Expenditure Survey Representative by Income?*
Keywords: Consumer Expenditure Survey, sampling
Abstract:
Aggregate under-reporting of household spending in the Consumer Expenditure Survey (CE) can result from two fundamental types of measurement errors: higher-income households (who presumably spend more than average) are under-represented in the CE estimation sample, or there is systematic under-reporting of spending by at least some CE survey respondents. Using a new data set linking CE units to zip-code level average Adjusted Gross Income (AGI), we show that the very highest-income households are less likely to respond to the survey when they are sampled, but unit non-response rates are not associated with income over most of the income distribution. Although increasing representation at the high end of the income distribution could in principle significantly raise aggregate CE spending, the low reported average propensity to spend for higher-income respondent households could account for at least as much of the aggregate shortfall in total spending.
1 Introduction
Aggregate spending in the Consumer Expenditure Survey (CE) is well below comparable Personal Consumption Expenditures (PCE) in the National Income and Product Accounts (NIPA), and the ratio of spending in the CE to spending in the NIPA has fallen from where it was two decades ago.8 Assuming NIPA values are a good benchmark, two potential reasons for the aggregate spending difference are that higher-income families (who presumably spend more than average) are under-represented in the CE estimation sample, or there is systematic under-reporting of spending by at least some CE survey respondents.9 Resolving why the aggregate shortfall occurs is important for weighting the Consumer Price Index (CPI) and for various research questions that involve the joint distribution of spending and income, including measuring inequality, studying savings behavior, and evaluating the distributional burden of consumption taxes.
Establishing the basic facts about the accuracy of aggregate CE spending is straight-forward in principle, but complicated in practice because the CE and PCE differ in terms of both spending concepts and population coverage.10 However, piecing together the latest Bureau of Labor Statistics (BLS) estimates with the results of a study by Garner, McClelland, and Passero (2009) provides a compelling story (Table 1). There are systematic differences across types of spending at any point in time, and there is also a general decline in the ratio of CE to PCE by about 10 percentage points between 1992 and the early 2000s. However, since 2003, the CE-to-PCE ratio has been relatively stable, both overall and within broad categories of spending.
On net, the CE now appears to be capturing 78 percent of comparable PCE. The CE is lower in most categories, but rental equivalence of owned housing is a rare exception where the CE is higher than the PCE.
11 If it is omitted, the CE's estimates of comparable spending are generally about one-third lower than the PCE. In particular, the
ratios for durables, non-durables, and non-housing services are 60, 64, and 72 percent respectively.12
Although CE is fundamentally designed to collect expenditure data, not income data, a failure to reflect the income distribution accurately could suggest that inaccuracies occur in the spending distribution as well. There is evidence that the CE does not capture as much income as in other surveys, and the missing income seems to be at the top of the income distribution. Passero (2009) shows that the CE aggregate income is only 94 percent of Current Population Survey (CPS) aggregate income.13 Evidence that the missing CE income occurs at the very highest income levels comes from comparing CE against other data sets. A comparison of the CE income distribution to the CPS, Survey of Consumer Finances (SCF), and tax return-based Statistics of Income (SOI) data sets suggests significant under-representation of the $100,000 or more income group in the CE. The CE finds fewer households in that income range, and average incomes for households that are above $100,000 are below the averages in the other data sets.
It may be that higher-income CE households are simply less likely to accurately report their incomes, but there are also good reasons to suspect that the households at the very top of the income distribution are under-represented in the CE. The first type of evidence comes from a new approach to this question developed for this paper. The approach involves linking all CE sampled households (both respondents and non-respondents) to the average Adjusted Gross Income (AGI) in their five-digit zip-code area.14 For most of the AGI distribution there is little or no association between unit non-response and zip-code level AGI, but at the very top of the income distribution the unit response rate and the ratio of average CE income to mean zip code-level AGI are both lower. That is, in the top few percentiles of households sorted by zip-code level AGI, households are less likely to participate in the CE, and those households that do participate are more likely to have incomes below the average in their zip-code.
This difference in participation suggests that high income households are under-represented in the CE; however, under-reporting of spending for at least some respondents is also quite likely. CE tabulations (reproduced in this paper) show that CE expenditures are lower than income, which suggests unusually high savings rates (even after accounting for measurement differences in income and spending). In addition, CE data show that the ratio of spending to after-tax income falls with income, suggesting very high savings rates at the top of the income distribution. Comparison of CE incomes to other data sources suggests that as much as 25 or even 50 percent of income is missing in the $100,000 or more income group. As a result, if this income under-reporting is simply due to under-reporting for high-income households, this would imply even larger discrepancies in average savings rates between those implied in the CE data and other data sources (e.g., SCF).
Why is it important to distinguish between the possible explanations for under-reporting of aggregate CE spending? The difference in CE to PCE aggregates across the broad categories in Table 1 highlights one key reason-weighting the CPI. If there are systematic differences in how well the CE survey captures aggregate expenditures across categories, the CPI weights will be biased, and the overall index will be inappropriately affected by changes in the prices of over- or under-represented categories.15 Given the plutocratic nature of the CPI, the relationship of income and spending on different types of categories suggests that under-representation of high-income families in the CE could be biasing the CPI.
In addition to weighting the CPI, however, there are also several research areas where the ratio of expenditures to income across income groups is the crucial input, and thus distinguishing between under-representation of high-income families versus under-reported expenditures for at least some respondents is crucial. CE data have been used in several studies to measure differences between consumption-expenditure and income inequality, with consumption-expenditure inequality shown to be consistently and dramatically lower.16 Bosworth, Burtless, and Sabelhaus (1991) used CE data to track changes in household saving across groups and time, and the estimated patterns of low-income dissaving and high-income saving are dramatic in every period. Finally, CE data are regularly used by government agencies and other groups to measure the distributional burden of consumption taxes. Consumption taxes appear very regressive, because the ratio of spending to income falls dramatically with income.
If the source of the aggregate CE shortfall is simply under-representation of the highest-income households, then the inequality, saving, and tax distribution studies described above may be incomplete, but they are not necessarily biased for the range of the income distribution they represent. Even though the very highest-income households are under-represented in the CE, Sabelhaus and Groen (2000) demonstrate that the overall under-reporting of spending is partially attributable to under-reporting of expenditures by at least some CE respondents.17 If expenditure under-reporting is indeed worse for higher-income households, then the results of the CE-based inequality, saving, and tax-distribution research should be revisited.
2 How Does the CE Income Distribution Compare to Other Data Sources?
Although the CE estimation sample reflects the actual distribution of households by income over most ranges, comparisons between the CE and other household surveys suggest that the very highest income families are under-represented. In this section weighted counts of CE units and average incomes are compared against three other data sources - the Current Population Survey (CPS), the Survey of Consumer Finances (SCF), and the IRS tax-return based Statistics of Income (SOI). The comparisons include one data set (CPS) that is similar to the CE in sampling strategy, but more focused on income, one that is purely administrative (SOI), and one that employs differential sampling for high-wealth households in order to capture the top of the wealth distribution (SCF). To enhance comparability for this study, CPS and SOI incomes do not include the value of capital gains since the CE income does not include gains in income.
The overall count of sampled units in the CE, CPS, and SCF are similar. Although the CE samples "consumer units," the CPS samples "households," and the SCF samples "primary economic units," the overall counts for any given year are within 2 or 3 percent (Table 2, last column). The count of units for the SOI is very different from the other surveys, because dependent filers-usually children living in their parents' home-may have to file their own tax returns. There are also differences in the income concept in the SOI, because non-taxable forms of income (mostly transfers) are not included in adjusted gross income (AGI). After adjusting for those differences, though, the four data sets are broadly consistent across the income categories.
The well-known skewness of the U.S. income distribution shows up clearly in the CE as one moves from less than $50,000 of income (65.1 million consumer units), to between $50,000 and $100,000 (34.9 million), to $100,000 or more (18.9 million). The counts of units for the CPS, SCF, and SOI are shown as differences from the CE values, and the general impression one gets is that the differences are second order. All three data sets show the same basic shape. The SOI, as expected, finds many more units in the less than $50,000 group, because of dependent filers and the fact that non-taxable transfers are not being included.
The focus of the analysis here is the top of the income distribution, however, and although the counts of units are broadly similar in the $100,000 or more income category, the total income received by that group is much lower in the CE than in the other three data sets. For example, the CPS finds 22.1 percent more income for those households. Although much of that is because the CPS finds more households above the $100,000 line, there is no reason to expect any divergence at all between the CE and CPS, because the sampling approach and income concepts are similar.18
The more noticeable differences in top incomes occur when one compares CE (and CPS) to the SCF and the SOI. The SCF uses an income concept that generally matches the CE, but employs a different sampling strategy in order to capture the top of the wealth distribution.19 The SCF finds nearly 60 percent more income in the $100,000 or more income range. To put those numbers in perspective, the nearly $2 trillion of additional income that the SCF finds at the very top is similar in magnitude to the aggregate spending mismatch that motivates this study.
The conceptual differences between CE and the SOI make direct comparisons more problematic. Using an AGI income concept with the CE data will yield an even lower estimate of income. However, the SOI still finds over 30 percent more income in the $100,000 or more range even though there are fewer tax filers in that AGI range because of the differences between AGI and the more generalized income concept used in the other surveys. Thus, on net, comparing the CE to both the SOI and SCF data suggests that the very highest income households are under-represented in the CE (and in the CPS, though to a lesser extent).
3 Why Does the CE Under-Represent the Very Highest Income Households?
The CE is designed to collect expenditure data and related demographic characteristics from a sample that is representative of the U.S. civilian non-institutional population; the weighting procedures to ensure this representativeness do not account for income. However, if the variables used to produce representative expenditure estimates are highly correlated with income, then the CE random sampling approach should still generate an unbiased representation of the true population income distribution. However, two problems associated with sampling could lead to the under-representation of very high income households.
The first potential problem is sampling variability, because income is highly concentrated at (and even within) the top percentiles, as indicated in both tax data and targeted surveys like the SCF. Sampling variability implies that the estimated aggregates will be very dependent on whether those probabilistically-rare households are chosen to participate in the survey. The fact that CE incomes are systematically lower at the top end-and not just extremely volatile at the top end-implies that sampling variability is not the problem.
The second possible problem is differential unit non-response.20 The concern here is that the highest income households are less likely to participate in the survey when they are selected. The fact that incomes are systematically lower at the top end of the income distribution in the CE suggests that differential unit non-response among very high income households is an explanation worth exploring, and that is the focus of this section.
There is no direct way to assess whether or not the very highest income families are less likely to participate in the CE when they are chosen, because we do not observe the actual incomes of non-participants. However, it is possible to make indirect inferences about survey participation using a new data set that links sampled CE units to the average Adjusted Gross Income (AGI) in their five digit zip-code area. The average AGI values linked to sampled CE units are produced by the IRS Statistics of Income Division, and are available for public use.21
The data set built for this analysis starts with all consumer units selected for the CE for calendar years 2007 and 2008.22 There are 104,830 units selected for participation, and 74 percent of those participated in the survey. However, the BLS excludes the first (or "bounding") interview when publishing expenditure estimates for publication, and that approach is followed here. Thus, the final data set includes 61,546 interviewed respondents out of 83,366 in-scope sampled units, which is an overall response rate of 74 percent.
The analysis here is based on sorting the sampled CE households into income groups using the average AGI for their zip code. This makes it possible to sort both respondents and non-respondents using the same income measure, and to test for differences in response rates across AGI percentiles. Basically, the first step uses the average response rates for the CE sample in each of the 100 AGI percentile-income groups. The second step is to compare the average incomes of respondents to the average AGI for their zip code, again, by AGI percentile. Note that in both steps the percentile-cell calculations all involve several hundred observations being averaged to create the estimated response rates or the ratio of average CE income to average AGI.
Using Zip-Code Level AGI to Sort Households
Using zip-code level AGI to proxy "true" income of non-respondents does raise a few concerns. First, the AGI concept itself is an imperfect measure of income, because it excludes non-taxable transfers along with other tax-free income such as municipal bond interest. The idea of non-taxable transfers usually evokes images of food stamps and other income maintenance programs, but it is probably more salient to note that for most Social Security recipients most or all of their Social Security is excluded from AGI. Thus, a retiree with $20,000 in taxable pensions and $20,000 in Social Security will show up with an AGI of $20,000, even though the CE would identify them as having $40,000 of income.
The second problem with using zip code-level mean AGI is the presence of dependent filers. As noted in the discussion of Table 2 in the previous section, the count of SOI "units" is much higher than CE consumer units or CPS households, because dependent children with income may file separate returns. Although the CE income calculations have been adjusted to more closely resemble the AGI income,23 both of these problems with using AGI-that AGI excludes non-taxable income and the averages include dependent filers-imply that average AGI for the zip code is a downward biased estimate of average household income. In the first case AGI income may exclude some income components, and in the second we are splitting the household-level income across too many units. As Figure 2 illustrates, the overall mean of CE income is about 14 percent higher than the mean of zip-code level AGI for the same zip-code areas.
The third problem with using zip-code level AGI is that it excludes non-filers, but in this case there is no obvious bias in average AGI. Households who receive only non-taxable transfers will not even show up in the SOI zip-code level data file, because they are not required to file tax returns. Their exclusion from the zip-code file would reduce the total number of units, but would likely not change the income ranking of the zip-codes. That is, if a $20,000 per year Social Security recipient lives in the same zip code as a $20,000 per year wage earner, we would only observe the wage earner in the zip code AGI file, but the $20,000 AGI would still be a good estimate of income for both households in the zip code. Even if this is not an accurate assumption (see the next paragraph), the exclusion of non-filers is unlikely to affect the highest income zip-code areas, which are of most interest here.
The final problem with using zip-code level AGI is that zip-code may not be a narrow enough geographic classifier from a socioeconomic perspective, meaning there is significant income variation within zip codes. This potential problem motivates the second step of the approach implemented here, because in addition to looking for differences in response rates by AGI percentile, we also consider the ratio of CE respondent-reported incomes to average AGI. This second step is designed to capture differences in response by income within zip codes, and thus control for variations in within zip code incomes, especially at the top of the distribution where our attention is focused.
Response Rates by AGI Percentiles
The first question addressed using the new zip-code linked data set is whether the probability of responding to the survey, when sampled, varies systematically with income.24 All sampled CE units are assigned the average AGI for their zip-code, and the entire data set is sorted into 100 percentile groups (0th-1st, 1st-2nd, ..., 99th-100th). Although in principle this is a simple calculation, because response is a binary outcome, the analysis is complicated to some extent because it requires acknowledging the potential effects of existing BLS post-stratification (weighting) adjustments.
The simplest calculation involves the inverse of the raw sampling probability, which BLS refers to as BASEWT. The values for BASEWT in the CE are typically around 10,000, which means that a consumer unit in the sample represents 10,000 consumer units in the U.S. civilian non-institutional population-itself plus 9,999 other consumer units that were not selected for the sample.25 Using BASEWT, the simplest calculation of response by AGI involves taking the ratio of respondents (weighted by BASEWT) to sampled units (also weighted by BASEWT) within each AGI percentile (Figure 1, lowest set of markers).
The overall response rate across AGI percentiles is 74 percent for 2007 and 2008.26 Figure 1 shows that the response rate for most AGI deciles is between
70 and 80 percent for most of the AGI distribution. Although the numbers exhibit a fair amount of variability, there is no clear pattern between (roughly) the 10
and 90 percentiles. The data do show lower response for the highest AGI percentiles, which confirms the hypothesized higher unit non-response for very-high income families. Overall, the response rate for
the top five percentiles is 66 percent, and the top one percent by AGI has a response rate of 65 percent.
Interestingly, the response rates by AGI are higher than average at the bottom of the AGI distribution. The overall response rate based on BASEWT is 80 percent for the bottom five percentiles and 84 percent in the first percentile. Given the very large sample sizes involved in these calculations-over 800 sampled units in each AGI percentile-these higher response rates for lower income zip codes are noteworthy. Although we do not pursue an explanation for higher unit non-response by lower income households here, it is certainly an interesting area for further research.
Although the unadjusted response rates (based on BASEWT) suggest that higher income households are indeed under-represented in the CE respondent sample, there are two subsequent stages of BLS post-stratification that could remedy this under-representation.27 The first-step involves the "non-interview" adjustment factor which involves applying differential adjustments based on estimated non-response patterns (this adjustment creates what BLS calls STAGE1WT). Specifically, this factor adjusts for interviews that cannot be conducted in occupied housing units due to a consumer unit's refusal to participate in the survey or the inability to contact anyone at the sample unit in spite of repeated attempts. This adjustment is performed separately for each month and "rotation group" (interview number) and yields 64 cells or factors based on region of the country, household tenure (owner or renter), household size, and race of the reference person.
If income is correlated with these 64 factors that affect unit non-response, then applying the non-interview adjustment factor could remedy the differential in response rates at very high (and very low) incomes. However, the correlation between zip-code level AGI and the BLS non-interview adjustment factor appears to be weak as shown in Figure 1 (middle set of markers). The adjustment factor raises response rates approximately uniformly across AGI percentiles. The overall adjustment factors are calibrated such that the adjusted overall response rate is basically 100 percent, meaning the new weights will sum to the count of originally sampled units, but nearly the same curvature in response rates at very high and very low percentiles is observed. Hence, households in the top five percentiles are about 10 percent less likely to participate in the survey than households in the middle ninety percentiles, and the difference is the same regardless of whether BASEWT or STAGE1WT is used to weight the data. This suggests that the CE's non-interview adjustment is not accounting for the different response rates observed at different income levels.
Finally, BLS applies a "calibration factor" that adjusts the weights to 24 "known" population counts to account for frame under-coverage. These "known" population counts are for age, race, household tenure (owner or renter), region, and urban or rural. The population counts are updated quarterly. Each consumer unit is given a calibration factor based on which of the 24 distinct groups they are in (this last adjustment creates FINLWT21, the weight that CE micro data users are most familiar with).28 Similar to the above shift shown in Figure 1 between using BASEWT and STAGE1WT, the calibration-adjusted (using FINLWT21) response rates are shifted up again (Figure 1, top set of markers). However, there is no qualitative change in the pattern. As with BASEWT and STAGE1WT, households in the top five percentiles are about 10 percent less likely to participate in the survey than households in the middle ninety percentiles.
Probit Analysis
An alternative approach to exploring the relationship between income and unit non-response involves estimating a binomial probit model, in which zip-code level AGI is included as a determinant of response status along with the 64-way matrix of stratifying variables used by the BLS in the
weighting adjustment for non-response that creates STAGE1WT. Specifically, NR (in equation (1) below) is a binary variable that is equal to zero for responding CUs and one for those that did not participate in the survey. The regression also includes 63 dummy variables corresponding to all but one
of the region-family size-race-housing tenure strata used for the non-response weighting adjustment in the CE. A fifth-order polynomial function in AGI is included using five variables: AGI,
,
,
, and
.29 The equation below is
estimated using the same sample of 61,546 responding and 21,820 non-responding CUs described above, and observations are weighted by BASEWT.
Each of the five AGI variables was asymptotically significant at the 0.01 percent significance level, even with all the stratifying variables held constant. A likelihood ratio test of the significance of the five AGI variables yielded a chi-square value of 180 with five degrees of freedom, which easily surpasses any usual significance level. The probit results of interest are:
- Probit (NR) = [stratification dummy terms] + 0.0104 AGI - 0.1133
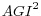/1000
+ 0.6373
- 0.1605
+ 0.0140
This equation implies a positive impact of zip code-level AGI on the nonresponse probability, with the second derivative negative, until the highest observed values of AGI. All five AGI coefficients were significant at the one percent level in a two-tailed test.
The probit approach is indicative of how one might begin to think about creating an alternative to the BLS stage-one adjustments (STAGE1WT) using AGI along with the existing BLS stratifying variables. With the probit-based noninterview adjustments, the average adjusted response rate in the top five AGI percentiles is only about three percent below that of the sample as a whole, compared to about nine percent using the BLS STAGE1WT adjustments and 10 percent using the FINLWT21 adjustments. By giving higher weights to CUs in higher-AGI areas, the probit approach does indeed imply higher aggregate weighted average CE incomes and expenditures, but the effects are modest.30
Using a revised weight based on the probit adjustment using AGI as an explanatory variable yields average income that is only about 0.37 percent higher and average spending that is about 0.19 percent higher than those using the BLS STAGE1WT. Hence, this probit analysis is able to capture the pattern shown in Figure 1, but adjusting the weights cannot account for all of the income under-reporting.
CE Incomes Relative to Average AGI
The previous analysis demonstrated that there is a differential non-response in the very-high income AGI zip-code areas. Although the CE income appears to be associated with zip-code level AGI, it is difficult to map these outcomes back to the univariate income distributions shown earlier (Table 2) because CE households are being sorted by zip-code level AGI, not their own household income (which we cannot observe for non-respondents). The next part of the analysis provides more support for the proposition that the very highest income households are under-represented in the CE.31 In this second step, we compare average CE income to average AGI within each AGI percentile, and show that the ratio generally falls with income, and is dramatically lower at the top of the AGI distribution.
Across all AGI percentiles in the linked data set, mean CE income for respondents (based on FINLWT21) is about 14 percent higher than mean AGI for all sampled units (based on BASEWT, though the exact weight chosen does not affect this answer). However, there is a distinct downward pattern across AGI percentiles (Figure 2). The ratio of mean CE income to mean AGI is about 140 percent at the bottom of the income distribution, and falls steadily as AGI increases, before plummeting to below 74 percent for the top two percentiles of AGI. Thus, Figure 2 complements Figure 1 in the following sense. Figure 1 shows that households in the top AGI percentile zip-codes are 10 percent less likely to participate than the rest of the sample, and Figure 2 suggests that the households within the top AGI percentiles that do participate are more likely to have lower incomes than the households in that zip-code who did not participate. Further, this pattern of high income areas having lower reported income may be common to many household surveys. Figure 3 illustrates a similar pattern using the CPS data and the AGI data by zip-code. Similar to Figure 2, Figure 3 is based on an analysis using calendar year 2008 CPS income data that are comparable to the AGI income concept and the same SOI file by zip-code used in CE analysis. Given these lower survey response rate among very high income households observed in the CE and CPS, it may be that a targeted over-sampling strategy such as the one used by the SCF is the only way to get accurate representation at the top of the income distribution.
Although there are conceptual differences between AGI and CE income that make direct inferences difficult, it is worth noting that the combined insights from Figure 1 and Figure 2 probably go a long way towards explaining the income distribution differences presented in Table 2. For example, the CE finds about 7 percent fewer households above $100,000 than the SCF, which is similar in magnitude to the roughly 10 percent response differentials for the top five percentiles shown in Figure 1. Also, the ratio of average income in the CE to average income in the SCF for households above $100,000 is 68 percent, which is in the same ballpark as the CE income to AGI ratios at the highest AGI percentiles. Although a direct mapping from the zip-code level AGI percentile analysis to univariate income distributions requires more research, the results here suggest that differential unit non-response probably goes a long way toward explaining the shortfalls. To fully incorporate the effects of differential unit non-response into formal post-stratification adjustments requires comparable income measures. A more complete analysis involves more fully reconciling the CE income and AGI concepts, which is a topic for future research. See the earlier discussion in the text about why AGI and CE income concepts diverge.
4 Why is Aggregate Consumer Expenditure Survey Spending So Low?
If PCE in the National Income and Product Accounts (NIPA) are viewed as the truth about what consumers actually spend in a given time period, there are two possible high-level explanations for why aggregated spending in the CE is below the corresponding PCE totals. The evidence above provides some support for the first reason, which is that the very highest income households are under-represented. However, the observed under-representation of very high-income households cannot fully explain the aggregate CE spending shortfall. The most extreme estimate of the aggregate CE income shortfall above $100,000 comes from comparing the CE to the SCF. The SCF finds about $1.7 trillion more income above $100,000 than the CE, but if one applies the BLS-reported ratio of expenditures to gross income for that group (61 percent) that implies total spending would rise by 16 percent, which explains perhaps half of the overall shortfall relative to PCE totals (as shown in Table 1).
Overall, published CE expenditures are lower than published CE after-tax incomes. For example, the ratio of published total expenditures to published after-tax income for CE respondents was 83 percent in 2006.32 Given the relationship between aggregate spending and disposable income in the NIPA data, that ratio probably should have been much higher.33 Based on that aggregate perspective and the conclusion that misrepresented high income households only explains at most half of aggregate under-reporting; at least some of the shortfall in aggregate CE spending seems attributable to under-reporting of spending (given income) by at least some CE respondents.
Knowing that the overall spending-to-income ratio seems too low for the CE survey (based on comparisons to PCE) is a starting point, but it does not help with the distributional question of whether the propensity to under-report spending varies with income itself. Researchers interested in using the CE for distributional analysis of questions about topics like consumption-expenditure versus income inequality, saving rates, or the distributional burden of consumption taxes, rely completely on the empirical joint distribution of expenditures and income. If the problem is proportional under-reporting of expenditures for all CE respondents, then the simple solution is to scale up spending for all households (perhaps by type of spending) before undertaking any distributional analysis (see Slesnick (2001) and Meyer and Sullivan (2011) for a similar approach). However, if the propensity to under-report rises with spending (and thus with income) then some sort of differential adjustments are warranted.
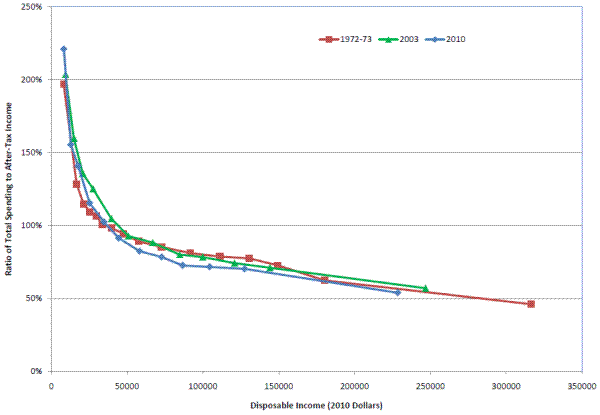
The estimated pattern of spending-to-income ratios by income in the CE may have flaws, but if it does, those flaws are not a new phenomenon. A comparison of published BLS data for 1972-73, 2003, and 2010 in Figure 4 shows that the ratio of spending to unadjusted after-tax income at any given level of income has not changed much in 40 years.34 Overall, the ratio of spending to after-tax income fell from 89 percent in 1972-73 to 84 percent in 2003 and 79 percent in 2010. While the overall spending-to-income ratios fell between 1972-73 and 2010, the ratio across income groups remained fairly constant. This occurs because of the increase in households at the higher end of the income distribution, who have lower spending-to-income ratios. Based on aggregate trends in savings rates (which are decreasing during this period), the overall spending-to-income ratio should have been higher in the last two periods than in the first. However, Figure 4 suggests that the differences in spending-to-income ratios occur across income groups at each point in time, and have not changed over time.35
The ratios of total expenditure to after-tax incomes by income shown in Figure 4 exhibit a dramatic pattern, and although there are some conceptual issues and systematic reporting errors with income taxes in the BLS tabulations, those sorts of corrections do not fundamentally change that pattern. The ratio of spending to income at low income levels seems implausibly high, and the ratio of spending to income at the top seems implausibly low. There are most likely problems with both income and expenditure reporting, and sorting households by income simply highlights those errors.
In any household survey there will be measurement error, and, given that the CE is focused on spending rather than income, it is not surprising that income may be poorly reported for some households.36 The bottom of the income distribution includes many households who under-report income (e.g., the self-employed), and hence, the high ratios of expenditure to income at low incomes can be partially explained by the presence of these households. The argument that income is missing at the bottom is reinforced by a pragmatic view of lower-income households. It is impossible to spend twice your income (Figure 4) if you have no assets to draw down and no access to credit, which is the basic conclusion one takes away from wealth surveys like the SCF or Panel Survey of Income Dynamics (PSID). Thus, except for students, households with temporary business losses, and retirees drawing down assets, the high rates of implied dissaving by lower income households in the CE are already implausible, and proportional scaling up of spending would only increase these, already implausibly high, spending-to-income ratios.
It is also unrealistic to think that families above $100,000, on average, save the fraction of their disposable income implied by Figure 4, using it for purchasing stocks, bonds, and other investments that are not captured by the CE. Such behavior would yield average wealth to income ratios for higher income households that are much different than what we observe in wealth surveys (e.g., PSID and SCF).37
5 Conclusions
Only the very highest income households seem to be under-represented in the CE Survey, but the overall under-reported spending in the CE cannot be fully explained by that shortcoming. At least some of the shortfall in aggregate CE spending seems attributable to under-reported spending by at least some CE respondents, and that has implications for research that relies on the relationship between spending and income in micro data. The observation that spending-to-income ratios fall with reported income in the CE implies that consumption-expenditure inequality will be less than income inequality, and the extent to which this ratio falls with income (and changes over time) has a dramatic impact on the estimated relationship between consumption-expenditure and income inequality. Also, if this pattern in the spending-to-income ratios is partially due to measurement of total spending, then the amount of dissaving at low incomes and saving at high incomes will both be exaggerated, and consumption taxes will appear (perhaps wrongly) to be highly regressive alternatives to income taxes.
Resolving whether expenditures are proportionally under-reported for all CE respondents or disproportionately for higher income (and thus higher spending) respondents is a crucial task facing the current multi-year CE redesign effort (called Gemini). The mission of the Gemini project is to redesign the CE in order to improve data quality through a verifiable reduction in measurement error, with a particular focus on under-reporting.38
Future research to examine this under-reporting includes a joint effort by BLS and the Census Bureau is to examine additional variables, including income, in CE's nonresponse and calibration adjustment processes. This research will address a number of questions, such as what variables are available for every household in the CE survey, both respondents and nonrespondents; what qualities characterize "good" variables for these procedures; and what variables other surveys use. An oversampling strategy such as that employed by the SCF may also be worth considering. Implementation of oversampling could be expensive, and it would not by itself address a bias problem, but if combined with revised methods for nonresponse adjustment it could be a valuable improvement. Finally, it may be the case that the demands placed on respondents in the current CE are simply too daunting, because respondents are asked to remember several hundred spending items for each month in a three-month recall period. Hence, a third approach to reconciling the difference between incomes and spending across income groups might involve streamlining the collection of spending totals, so that even high spenders will have a better chance to accurately estimate and report their total spending.39 It is hoped that the results presented in this paper will constitute a further contribution to the CE redesign program.
6 References
Aguiar, Mark A., and Mark Bils. 2011. "Has Consumption Inequality Mirrored Income Inequality?" National Bureau of Economic Research, Inc, NBER Working Papers: 16807. (February)
Attanasio, Orazio, Gabriella Berloffa, Richard Blundell, and Ian Preston. 2002. "From Earnings Inequality to Consumption Inequality," Economic Journal, 112(478): 52-59. (March)
Bee, Adam, Bruce D. Meyer, and James X. Sullivan. 2012. "Micro and Macro Validation of the Consumer Expenditure Survey." Paper presented at the conference on Improving the Measurement of Consumer Expenditures, Washington, DC, December 2-3.
Blair, Caitlin. 2011. "Constructing a PCE-Weighted Consumer Price Index," Paper presented at the conference on Improving the Measurement of Consumer Expenditures, Washington, DC, December 2-3.
Bosworth, Barry, Gary Burtless, and John Sabelhaus. 1991. "The Decline in Saving: Evidence from Household Surveys," Brookings Papers on Economic Activity, 1991(1):183-241.
Browning, Martin, and Thomas Crossley. 2009. "Are Two, Cheap Noisy Measures Better Than One Expensive, Accurate One?" American Economic Review, 99(2):99-103. (May)
Bucks, Brian K., Arthur B. Kennickell, Traci L. Mach, and Kevin B. Moore. 2009. "Changes in U.S. Family Finances from 2004 to 2007: Evidence from the Survey of Consumer Finances," Federal Reserve Bulletin, 1st Quarter 2009, 95:A1-55.
Burkhauser, Richard V, Shuaizhang Feng, Stephen P. Jenkins, and Jeff Larrimore. 2009. "Recent Trends in Top Income Shares in the USA: Reconciling Estimates from March CPS and IRS Tax Return Data." National Bureau of Economic Research, Inc, NBER Working Papers: 15320. (September)
Crossley, Thomas F. 2009. "Measuring Consumption and Saving: Introduction," Fiscal Studies, 30(3-4): 303-07. (September-December)
Garner, Thesia I., and Kathleen Short. 2009. "Accounting for Owner-Occupied Dwelling Services: Aggregates and Distributions," Journal of Housing Economics, 18(3):233-48. (September)
Garner, Thesia I., George Janini, William Passero, Laura Paszkiewicz, and Mark Vendemia. 2006. "The CE and the PCE: A Comparison," Monthly Labor Review, 129(9):20-46. (September)
Garner, Thesia I., Robert McClelland, and William Passero. 2009. "Strengths and Weaknesses of the Consumer Expenditure Survey from a BLS Perspective," paper prepared for CRIW/NBER summer institute (July, 2009)
Groves, Robert M, 2006. "Nonresponse Rates and Nonresponse Bias in Households Surveys," Public Opinion Quarterly, 70:5, pp. 646-675 (December).
Heathcote, Jonathan, Fabrizio Perri, and Giovanni L. Violante. 2010. "Unequal We Stand: An Empirical Analysis of Economic Inequality in the United States, 1967-2006," Review of Economic Dynamics, 13(1):15-51. (January)
Johnson, David, and Stephanie Shipp. 1997. "Trends in Inequality Using Consumption-Expenditures: The U.S. from 1960 to 1993," Review of Income and Wealth, 43(2):133-52. (June)
Kennickell, Arthur B., and Louise R. Woodburn. 1999. "Consistent Weight Design for the 1989, 1992 and 1995 SCFs, and the Distribution of Wealth," Review of Income and Wealth, 45(2):193-215. (June)
Kennickell, Arthur B. 2009. "Ponds and Streams: Wealth and Income in the U.S., 1989 to 2007," Board of Governors of the Federal Reserve System, Finance and Economics Discussion Series: 2009-13.
King, Susan L., Boriana Chopva, Jennifer Edgar, Jeffrey M. Gonzales, Dave E. McGrath, and Lucilla Tan. 2009. "Assessing Nonresponse Bias in the Consumer Expenditure Interview Survey," Section on Survey Research Methods, Joint Program on Survey Methods Annual Conference, 1808-1816.
Krueger, Dirk, Fabrizio Perri, Luigi Pistaferri, and Giovanni L. Violante. 2010. "Cross-Sectional Facts for Macroeconomists," Review of Economic Dynamics, 13(1): 1-14. (January)
Krueger, Dirk, and Fabrizio Perri. 2006. "Does Income Inequality Lead to Consumption Inequality? Evidence and Theory," Review of Economic Studies, 73(1):163-93. (January)
Meyer, Bruce D., Wallace K.C. Mok, and James X. Sullivan, 2009. "The Under-Reporting of Transfers in Household Surveys: Its Nature and Consequences." National Bureau of Economic Research, Inc, NBER Working Papers: 15181, originally published September 2006, revised July 2009.
Meyer, Bruce D. and James X. Sullivan, 2011. "The Material Well-Being of the Poor and the Middle Class Since 1980," American Enterprise Institute Working Paper #2011-44.
McCully, Clinton P., Brian C. Moyer, and Kenneth J. Stewart. 2007. "Comparing the Consumer Price Index and the Personal Consumption Expenditures Price Index," Survey of Current Business. (November)
Passero, William, Thesia I. Garner, Clinton McCully, and Caitlin Blair. 2011. "Understanding the Relationship: CE Survey, the CPI, and PCE." Paper presented at the conference on Improving the Measurement of Consumer Expenditures, Washington, DC, December 2-3.
Passero, William. 2009. "The Impact of Income Imputation in the Consumer Expenditure Survey," Monthly Labor Review, 132(8):25-42. (August)
Paulin, Geoffrey D., and David L. Ferraro. 1996. "Do Expenditures Explain Income? A Study of Variables for Income Imputation," Journal of Economic and Social Measurement, 22(2):103-28.
Sabelhaus, John, and Jeffrey A. Groen. 2000. "Can Permanent-Income Theory Explain Cross-sectional Consumption Patterns?" Review of Economics and Statistics, 82(3):431-38. (August)
Short, Kathleen_et al. 1998. "Poverty-Measurement Research Using the Consumer Expenditure Survey and the Survey of Income and Program Participation," American Economic Review, 88(2):352-56. (May)
Slesnick, Daniel, 2001 Consumption and Social Welfare, Cambridge: Cambridge University Press.
U.S. Department of Labor, Bureau of Labor Statistics. Handbook of Methods. Available on-line at www.bls.gov/opub/hom/.
| Year | All Goods and Services | Durable Goods | Non-Durable Goods | Owned Housing | Other Services |
|---|---|---|---|---|---|
| Garner, McClelland, and Passero (2009) 1992 | 0.88 | 0.88 | 0.69 | 1.23 | 0.90 |
| Garner, McClelland, and Passero (2009) 1997 | 0.88 | 0.80 | 0.67 | 1.26 | 0.86 |
| Garner, McClelland, and Passero (2009) 2002 | 0.84 | 0.75 | 0.63 | 1.25 | 0.82 |
| Garner, McClelland, and Passero (2009) 2003 | 0.82 | 0.79 | 0.61 | 1.26 | 0.80 |
| Garner, McClelland, and Passero (2009) 2005 | 0.83 | 0.75 | 0.63 | 1.26 | 0.81 |
| Garner, McClelland, and Passero (2009) 2007 | 0.81 | 0.69 | 0.61 | 1.30 | 0.81 |
| BLS Published Estimates Based on Latest NIPA Crosswalk 2003 | 0.77 | 0.68 | 0.62 | 1.18 | 0.70 |
| BLS Published Estimates Based on Latest NIPA Crosswalk 2005 | 0.79 | 0.68 | 0.64 | 1.16 | 0.73 |
| BLS Published Estimates Based on Latest NIPA Crosswalk 2007 | 0.78 | 0.61 | 0.63 | 1.22 | 0.71 |
| BLS Published Estimates Based on Latest NIPA Crosswalk 2009 | 0.78 | 0.60 | 0.64 | 1.11 | 0.72 |
Table 2a. Income Distribution in the Consumer Expenditure Survey, 2006
| Income: Less than $50,000 | Income: $50,000 to $99,999 | Income: $100,000 or More | All Incomes | |
|---|---|---|---|---|
| Consumer Expenditure Survey: Number of Units (Millions) | 65.1 | 34.9 | 18.9 | 118.8 |
| Consumer Expenditure Survey: Total Income (Billions) | $1,589 | $2,472 | $3,111 | $7,172 |
Table 2b. Income Distribution in three other Data Sets (Data is the Difference between the Consumer Expenditure Survey) 2006
| Income: Less than $50,000 | Income: $50,000 to $99,999 | Income: $100,000 or More | All Incomes | |
|---|---|---|---|---|
| Current Population Survey: Number of Units (Millions) | -5.5 | -0.6 | 3.2 | -2.8 |
| Current Population Survey: Total Income (Billions) | -$85 | -$51 | $688 | $551 |
| Current Population Survey: Total Income (Percent) | -5.3% | -2.1% | 22.1% | 7.7% |
| Survey of Consumer Finances: Number of Units (Millions) | -1.6 | -2.7 | 1.5 | -2.7 |
| Survey of Consumer Finances: Total Income (Billions) | $11 | -$166 | $1,832 | $1,677 |
| Survey of Consumer Finances: Total Income (Percent) | 0.7% | -6.7% | 58.9% | 23.4% |
| Statistics of Income: Number of Units (Millions) | 27.2 | -4.9 | -2.8 | 19.6 |
| Statistics of Income: Total Income (Billions) | $210 | -$353 | $1,002 | $859 |
| Statistics of Income: Total Income (Percent) | 13.2% | -14.3% | 32.2% | 12.0% |
Figure 1: Consumer Expenditure Survey (CE) Response Rates by Zip-Code Level Adjusted Gross Income (AGI) Percentile
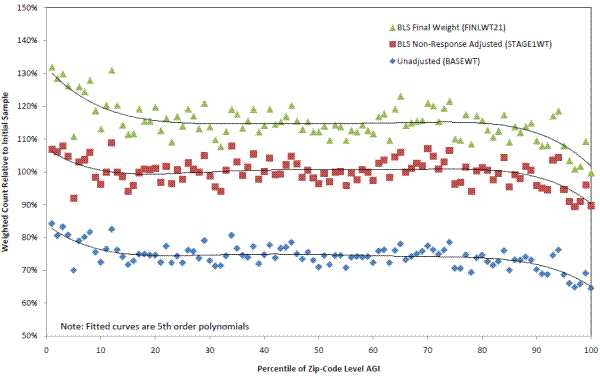Figure 1 Data
Figure 2: Ratio of Mean Consumer Expenditure Survey (CE) Income to Adjusted Gross Income (AGI) by Zip-Code Level AGI Percentile
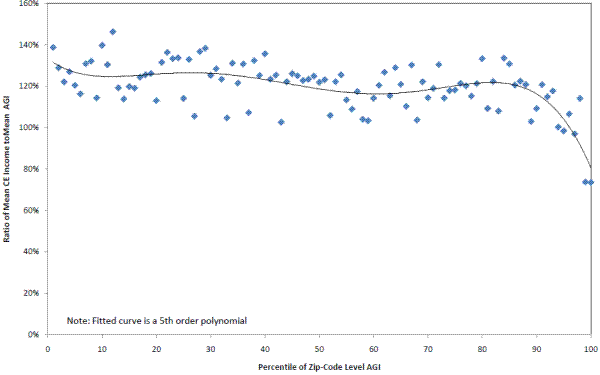Figure 2 Data
Figure 3: Ratio of Mean CPS Adjusted Gross Income (AGI) to SOI AGI by Zip-Code Level SOI AGI Percentile
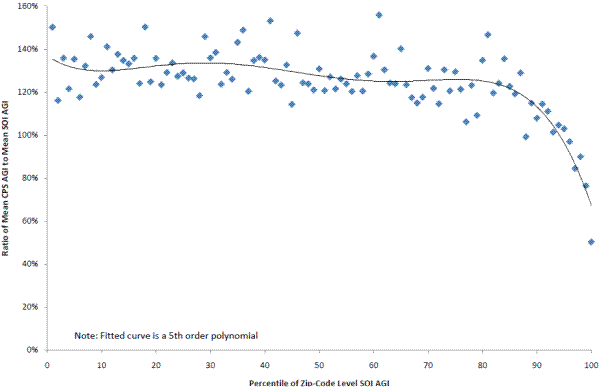Figure 3 Data
