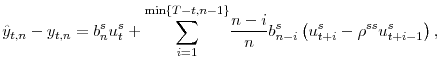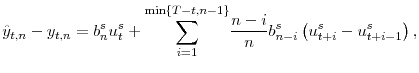Term Structure Modelling with Supply Factors and the Federal Reserve's Large Scale Asset Purchase Programs*
Keywords: Yield curve, preferred habitat, supply effects, factor models; state-space models; large-scale asset purchases (LSAP)
Abstract:
1 Introduction
Do changes in the supply of Treasury securities and other fixed-income assets affect nominal Treasury yields? This question has received renewed attention as the FOMC adopted large-scale asset purchases (LSAPs) as an alternative monetary policy tool to stimulate the economy, after the federal funds rate reached the zero lower bound during the most recent financial crisis. The answer to this question, however, is still subject to considerable uncertainty. On the one hand, the now-standard no-arbitrage term structure literature leaves little scope for the relative supply of deeply liquid financial assets, such as nominal Treasuries, to influence their prices because they can easily replicated or substituted by other similar assets. On the other hand, there is empirical evidence suggesting supply effects might exist in the Treasury market. For example, event studies typically show that the Federal Reserve's LSAP announcements had nontrivial effects on Treasury yields. More generally, Krishnamurthy and Vissing-Jorgensen (2008) and Laubach (2009) show that the total supply of Treasury debt have explanatory power for Treasury yield variations beyond that of standard yield curve factors, while Hamilton and Wu (Forthcoming) and Greenwood and Vayanos (2010b,a) provide similar evidence for the maturity structure of Treasury debt outstanding. One possible explanation for the existence of supply effect in Treasury market is offered by the preferred-habitat model of interest rates, which assumes imperfect substitutability between securities with similar maturities.
The preferred-habit literature, which features early contributions by Modigliani and Sutch (1966,1967), resorts to the assumption that there exist "preferred-habitat" investors, who demonstrate preferences for specific maturities, and that interest rate for a given maturity is only influenced by demand and supply shocks specific to that maturity. Real-world examples of such preferred-habitat investors include long-term investors, such as pension funds and insurance companies, that prefer to hold long-term bonds to match their long-duration liabilities, and short-term investors, such as money market mutual funds and foreign reserve managers, that prefer to hold Treasury bills and short-dated notes to maintain a high degree of liquidity in their portfolio. The preferred-habitat approach provides a rationale for supply effects in the government bond markets, as a shock to the stock of privately-held bonds of a particular maturity creates a shortage of those assets that cannot be wholly relieved, at existing asset prices, by substitution into other securities.
This approach of modeling interest rates has been largely abandoned in today's term structure literature, as it implies that yields at different maturities are disconnected from each other, which is at odds with the continuous yield curve one typically observes. In contrast, in the now-standard arbitrage-free term structure models of Vasicek (1977) and Cox, Jonathan E. Ingersoll, and Ross (1985), long-term interest rates differ from the expected average future short rate because investors in long-term bonds demand excess returns for bearing interest rate risks. The existence of arbitrageurs in the economy ensures that the same stochastic discount factor prices interest risks consistently across the yield curve. It also implies that any changes in the supply of Treasury securities, if unrelated to the economic fundamentals, should not have significant effect on yields.
More recently, the preferred-habit literature was revitalized in the seminar work of Vayanos and Vila (2009), who recast Treasury supply and demand shocks in an arbitrage-free framework. In their model, the existence of preferred-habitat investors provides a channel for demand and supply factors to influence Treasury yields, while the existence of risk-averse arbitrageurs, who have no maturity preference but actively trade to take advantage of arbitrage opportunities, ensures that supply shocks are transmitted smoothly across the yield curve. Vayanos and Vila (2009) show that, under certain parameterizations, the yield impact of variations in relative supplies depends on the dollar duration of the supply shocks absorbed by the arbitrageurs, which implies a direct relationship between the term premium and the total duration risks faced by private investors.
Despite the theoretical advances, empirical studies of preferred-habitat term structure models are nearly non-existent, hampered by the lack of detailed data on Treasury holdings across investors and by the complexity of the Vayanos and Vila (2009) model. In this paper, we try to fill this gap by estimating and testing a no-arbitrage term structure model with supply factors. We adopt several simplifying assumptions: first, we assume observable supply factors and measure them using data on private holdings of Treasury debt and agency mortgage backed securities (MBS). Second, we assume that supply factors influence Treasury yields predominantly through the term premium channel. Supply affects future short rates only indirectly through current and future term premiums. Finally, we adopt a two-step estimation approach where factor dynamics are estimated in the first step while bond risk premium parameters are estimated in the second step.
We also use this model to evaluate the three LSAP programs announced by the Federal Reserve. Most empirical analysis of the LSAPs are based on either event studies (e.g. Gagnon, Raskin, Remache, and Sack (2011), Swanson (2011); Krishnamurthy and Vissing-Jorgensen (2011)) or time series regressions of Treasury yields and/or Treasury term premiums on supply variables (e.g. Gagnon, Raskin, Remache, and Sack (2011); Greenwood and Vayanos (2010a); Krishnamurthy and Vissing-Jorgensen (2011); Hamilton and Wu (Forthcoming)). To our knowledge, this paper is the first to use an arbitrage-free term structure model to evaluate the effects of LSAPs. Results based on event studies are known to be sensitive to the selection of event windows. Time series regressions used in these studies, on the other hand, are likely susceptible to small-sample bias, given the highly persistence of supply variables, and endogeneity problems, as changes in Treasury supply are likely correlated with other factors driving the yield curve. Neither approach can be used to answer the question of how supply changes affect yields that are not directly used in the study. By contrast, the no-arbitrage term structure approach in this paper offers a way to consistently summarize information from the entire yield curve and allows inference across maturities.
Our estimates show that the first and the second large-scale asset purchase programs and the Maturity Extension program have a combined effect of about 100 basis points on the ten-year Treasury yield.
While the current paper emphasizes the interest risk premium channel through which LSAP works to reduce longer term Treasury yields, other channels have been suggested in the literature. For example, Krishnamurthy and Vissing-Jorgensen (2011) offer evidence that significant clientele demand exists for long-term "safe" (i.e., nearly default-free) assets, such as Treasury and agency MBS. These investors are willing to pay a premium--the "safety premium"--for holding those safe assets. A reduction in the supply of "safe" assets would raise the safety premium and lower the yields on those assets. Another example is D'Amico and King (2010), who emphasize the scarcity channel, i.e. a localized effect of supply shocks on yields of nearby maturities. They use CUSIP-level data to show the Federal Reserve's purchases have significant yield effects on both purchased securities and those at nearby maturities.
The remainder of the paper is organized as follows. Section 2 describes the data and documents the relationship between Treasury term premiums and Treasury and agency MBS supply. Section 3 reviews existing literature on the supply effects in the Treasury market, while Section 4 summarizes recent studies evaluating the effects of LSAPs on long-term Treasury yields. Section 5 describes the term structure model with supply factors. Section 6 discusses the estimation methodology and presents the empirical results. Section 7 concludes.
2 Data and Motivation
This section presents some preliminary evidence suggesting there exists a link between the supply of government securities and Treasury term premiums.3 In particular, we run monthly regressions of the form
over the sample period of March 1994 to July 2007, where
We obtain nominal Treasury yields with maturities of 3, 6, 12, 24, 60, 84, and 120 months from the Svensson (1995) zero-coupon yield curve maintained by staff at the Federal Reserve Board .4 In this explorative exercise, we use ten-year term premium estimates from a three-latent-factor Gaussian term structure model developed by Kim and Orphanides (2012), which was estimated using Treasury yields described above and Blue Chip survey forecasts of 3-month Treasury bill yields over the next two years and the next five to ten years.5 As discussed in Kim and Orphanides (2012) and Kim and Wright (2005), incorporating survey forecasts of future short rates helps alleviate the small sample problem commonly encountered when fitting term structure models to highly persistent yields.
For reasons that will be discussed later, we include in ![]() both Treasury and MBS supply variables as follows.
both Treasury and MBS supply variables as follows.
- Treasury supply variables, including
- Treasury Par-to-GDP ratio, defined as the par amount of privately-held Treasury securities as a percentage of nominal GDP, where quarterly data on nominal GDP is taken from the NIPA account and linearly interpolated to monthly frequency.
- Par-weighted average maturity of privately-held Treasury debt;
- Treasury Ten-year equivalents-to-GDP ratio, defined as the amount of privately-held Treasury securities (measured in term of ten-year equivalents6) as a percentage of nominal GDP;
- MBS supply variables, including
- MBS par-to-GDP ratio, defined as the par amount of privately-held agency MBS as a percentage of nominal GDP;
- Par-weighted average duration of privately-held agency MBS;
For each Treasury cusip, the total par amount outstanding as well as the maturity and coupon rate information are obtained from the Treasury's Monthly Statement of the Public Debt (MSPD), while the amount held in the Federal Reserve's System of Open Market Account (SOMA) is obtained from the weekly releases by the FRBNY.7The difference between total debt outstanding and SOMA holdings gives us the par amount held by private investors for each security. For each Treasury cusip, we also calculate the average duration and the ten-year equivalents using the same quotes used in constructing the Svensson yield curve as described above. We then sum over all cusips to calculate the total par amount and the total ten-year equivalents of private Treasury holdings and average across cusips to calculate the par amount-weighted average maturity and duration. We exclude Treasury bills and any previous-issued notes and bonds with remaining maturities below one year, as commonly done in the literature. For agency MBS, the par amount and average duration of privately-held agency MBS are taken from Barclays as reported for their MBS index, which includes mortgage-backed passthrough securities of Ginnie Mae (GNMA), Fannie Mae (FNMA), and Freddie Mac (FHLMC).
We control for other economic and market factors, ![]() , that can be expected to affect term premiums, including:
, that can be expected to affect term premiums, including:
- Economic fundamentals, including monthly data on capacity utilization from the Federal Reserve's G.17 release and one-year-ahead CPI inflation forecast from Blue Chip Economic Indicators survey.
- Market volatilities, including implied volatilities from options on ten-year Treasury note futures and implied volatilities from options on S&P 100 index, both from Bloomberg.
- Foreign demand for Treasury securities, measured by custody holdings of Treasury securities at the FRBNY on behalf of foreign official and international accounts as a ratio of total Treasury securities outstanding. Data on foreign custody holdings is from the Federal Reserve's H.4.1 release.8
Table 1 reports results from three variations of Regression (1), where the supply variables are the Treasury ten-year equivalents-to-GDP ratio (Reg. A), the Treasury par-to-GDP ratio and the average maturity (Reg. B), and the Treasury par-to-GDP ratio, the average Treasury maturity, the MBS par-to-GDP ratio, and the average MBS duration (Reg. C), respectively. Overall, these results suggest that term premiums are significantly and positively related to the supply variables after controlling for other economic factors. In the next section, we try to incorporate these supply variables into a standard no-arbitrage term structure model.
| 2-year Reg A | 2-year Reg B | 2-year Reg C | 5-year Reg A | 5-year Reg B | 5-year Reg C | 10-year Reg A | 10-year Reg B | 10-year Reg C | |
| Constant | -3.357*** | -6.119*** | -4.172** | -2.264 | -5.235*** | -5.354** | 1.198 | -0.860 | -4.844** |
| Constant (Standard Error) | (1.197) | (1.195) | (1.820) | (1.521) | (1.547) | (2.250) | (1.536) | (1.599) | (2.260) |
| Ten-year Treasury implied volatility | 0.056*** | 0.062*** | 0.005 | 0.101*** | 0.103*** | 0.015 | 0.144*** | 0.138*** | 0.029 |
| Ten-year Treasury implied volatility (Standard Error) | (0.021) | (0.019) | (0.016) | (0.027) | (0.025) | (0.020) | (0.027) | (0.026) | (0.020) |
| S&P 100 implied volatility | -0.007** | -0.016*** | 0.001 | -0.009** | -0.019*** | 0.003 | -0.009** | -0.016*** | 0.004 |
| S&P 100 implied volatility (Standard Error) | (0.003) | (0.003) | (0.003) | (0.004) | (0.004) | (0.003) | (0.004) | (0.004) | (0.003) |
| Foreign Treasury holdings ratio | -0.062*** | 0.038** | 0.010 | -0.073*** | 0.044 * | 0.007 | -0.058 *** | 0.039 | 0.000 |
| Foreign Treasury holdings ratio (Standard Error) | (0.015) | (0.018) | (0.013) | (0.019) | (0.024) | (0.016) | (0.020) | (0.025) | (0.016) |
| Capacity Utilization | 0.063*** | 0.015 | -0.025* | 0.047** | -0.014 | -0.056*** | -0.007 | -0.065*** | -0.093*** |
| Capacity Utilization (Standard Error) | (0.016) | (0.016) | (0.013) | (0.021) | (0.021) | (0.016) | (0.021) | (0.022) | (0.017) |
| Blue Chip CPI forecast | 0.147 | 0.352*** | 0.127* | 0.258** | 0.470*** | 0.182** | 0.348*** | 0.474*** | 0.194** |
| Blue Chip CPI forecast (Standard Error) | (0.100) | (0.091) | (0.065) | (0.127) | (0.118) | (0.080) | (0.129) | (0.122) | (0.081) |
| Treasury TYE-to-GDP ratio (%) | -0.047** | -0.039 | -0.001 | ||||||
| Treasury TYE-to-GDP ratio (%) (Standard Error) | (0.023) | (0.029) | (0.030) | ||||||
| Treasury par-to-GDP ratio (%) | 0.029 ** | 0.063 *** | 0.045*** | 0.105*** | 0.058*** | 0.140 *** | |||
| Treasury par-to-GDP ratio (%) (Standard Error) | (0.012) | (0.012) | (0.016) | (0.015) | (0.016) | (0.015) | |||
| Treasury average maturity | 0.533*** | 0.418*** | 0.639*** | 0.589*** | 0.563*** | 0.660*** | |||
| Treasury average maturity (Standard Error) | (0.092) | (0.089) | (0.119) | (0.110) | (0.123) | (0.110) | |||
| MBS par-to-GDP ratio (%) | 0.060** | 0.130*** | 0.204*** | ||||||
| MBS par-to-GDP ratio (%) (Standard Error) | (0.030) | (0.037) | (0.037) | ||||||
| MBS average duration | 0.252*** | 0.329*** | 0.328*** | ||||||
| MBS average duration (Standard Error) | (0.020) | (0.024) | (0.024) | ||||||
| R-squared | 0.67 | 0.74 | 0.88 | 0.68 | 0.73 | 0.89 | 0.69 | 0.73 | 0.89 |
| R-squared (cont'd) | 0.66 | 0.72 | 0.87 | 0.66 | 0.72 | 0.88 | 0.68 | 0.71 | 0.88 |
3.1 A Standard Gaussian Term Structure Model
We start from a standard Gaussian term structure model, where we assume yields are driven by a number of state variables, ![]() , which follows a first-order vector autoregressive
process:
, which follows a first-order vector autoregressive
process:
We further assume that there exists a stochastic discount factor of the form:
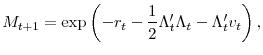
Following Duffie and Kan (1996) and Dai and Singleton (2000), the price of a ![]() -period zero-coupon bond,
-period zero-coupon bond, ![]() , can be derived by iterating on the no-arbitrage bond pricing equation
, can be derived by iterating on the no-arbitrage bond pricing equation
where
with initial conditions
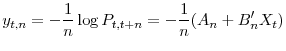
The model can therefore be conveniently represented in a state-space form as follows,
with Equation (8) being the measurement equation and Equation (9) being the state equation.
We consider the risk-neutral measure, under which the state variables![]() follow the process
follow the process
The pricing iterations (6) and (7) can therefore be restated in terms of the risk-neutral VAR parameters as
while the market price of risk,
When implementing the model, we directly estimate the physical and risk-neutral VAR parameters, which jointly decides the market prices of risk.
It is well known at least since Litterman and Scheinkman (1991) that an overwhelming portion of Treasury yield variations can be summarized by three principal components, frequently termed the level, the slope and the curvature. In our sample, more than 99% of the yield variations can be explained by the first two factors, which is the number of yield factors we use in our empirical analysis. To avoid the difficulty frequently encountered when estimating latent-factor term structure models, in all our models we assume that these two yield factors are observable and measure them using the ten-year yield and the spread between the ten-year and the three-month Treasury yields, respectively.
3.2 Term Structure Model with a Treasury Supply Factor
We assume that the state variables, ![]() , consist of both yield and supply factors, denoted
, consist of both yield and supply factors, denoted ![]() and
and ![]() , respectively. The yield factors include the level and slope factors described above. In the first model we consider, we assume there is only one supply factor,
the Treasury ten-year equivalents-to-GDP ratio.
, respectively. The yield factors include the level and slope factors described above. In the first model we consider, we assume there is only one supply factor,
the Treasury ten-year equivalents-to-GDP ratio.
As in Vayanos and Vila (2009), we motivate our model by assuming the existence of two types of private participants in the Treasury market: preferred-habitat investors, who hold only a particular maturity segment of the Treasury yield curve, and risk averse arbitrageurs, who trade to take advantage of arbitrage opportunities. There are also government agencies, like the Treasury and the Federal Reserve, which are modeled as risk-neutral participants in the Treasury market. Vayanos and Vila (2009) show that in how government bond holdings of the arbitragers affect the equilibrium bond risk premiums. For simplicity, we do not impose specific functional forms on the demand functions of preferred-habitat investors or the utility function of the arbitrageurs, which Vayanos and Vila (2009) use to derive analytical solutions linking bond risk premiums to the arbitragers' bond holdings. Instead, we simply take their conclusion and assume supply factors affect bond risk premiums, which is in the same spirit as how macro yield factors are motivated in the macro-finance term structure models (e.g. Ang and Piazzesi (2003)).
We assume that yield and supply factors only load on their own lags:
![\displaystyle \Phi=\left[ \begin{array}[c]{ccc}% \Phi_{11} & \Phi_{12} & 0\\ \Phi_{21} & \Phi_{22} & 0\\ 0 & 0 & \Phi_{33}% \end{array} \right] .](img47.gif) |
(15) |
The assumption that yield factors do not load on past supply factors may appear inconsistent with regression results reported earlier or our stated objective of assessing how supply changes affect term premium and yields. This assumption is nonetheless imposed to ensure that any evidence we shall find in support of the supply effects is driven by the data rather than by assumptions. To ensure that this condition holds empirically, we measure yield factors as residuals from a regression of the level and the slope of the yield curve on supply factors plus a constant, and order them first in the VAR. The restriction that supply factors do not load on past yield factors reflects the Treasury's stated policy that it "does not `time the market'--or seek to take advantage of low interest rates--when it issues securities. Instead, Treasury strives to lower its borrowing costs over time by relying on a regular preannounced schedule of auctions."9
We identify supply shocks by imposing a lower-diagonal structure on the volatility matrix:
![\begin{displaymath} \Omega=\left[ \begin{array}[c]{ccc}% \Omega_{11} & 0 & 0\ \Omega_{21} & \Omega_{22} & 0\ \Omega_{31} & \Omega_{32} & \Omega_{33}% \end{array}\right] , \end{displaymath}](img48.gif)
We impose the restriction that the short-term rate loads only on the two yield factors, so that shocks to supply factors do not affect interest rate expectations but can affect bond yields through the term premium channel only.
| (16) |
We also impose the restriction that the supply factors do not carry their own risk premiums but can affect term premiums by changing the risk premiums on the yield factors.
| (17) | ||
![\displaystyle =\left[ \begin{array}[c]{ccc}% \lambda_{1,11} & \lambda_{1,12} & \lambda_{1,13}\\ \lambda_{1,21} & \lambda_{1,22} & \lambda_{1,23}\\ 0 & 0 & 0 \end{array} \right] .](img56.gif) |
(18) |
The first assumption captures the fact that the supply of Treasury securities is not an important consideration when the Fed determines the short-term interest rate, while the second assumption reflects our prior that Treasury supply is unlikely to be a source of undiversifiable risk that should be priced on its own. Imposing these restrictions help reduce the number of parameters that needs to estimated and avoid the overfitting problem. Under these two assumptions, the supply factors follow the same dynamics under the physical and the risk-neutral measures:
| (19) | ||
| (20) |
where
3.3 Extending the Model to Include MBS Supply Factors
Treasury yields might also be affected by the supply of agency MBS, which are viewed by many market participants as "safe" assets and close substitutes for Treasury debt due to their implicit or explicit government guarantee. Agency MBS and Treasury securities also share two features that set them apart from other privately-issued debt. First, the net issuance of both Treasury securities and of agency MBS does not react strongly to interest rates in the short run.10Their issuance is largely determined by the federal budget deficit and housing demand, respectively, which co-vary with interest rates mainly at the business-cycle frequency. In contrast, corporate bond issuance responds more opportunistically to the level of interest rates and this response can be significant even at the weekly frequency. The fact that the net supply of Treasury securities and agency MBS is relatively inelastic in the short run is one reason why investors need to take them into consideration when pricing those assets. Second, Treasury securities, agency MBS, and corporate debt can be viewed as ultimately transferring interest risks from tax payers, mortgage borrowers, and bond-issuing corporations, respectively, to bond investors. Both tax payers and mortgage borrowers are arguably sufficiently removed from investment decisions driving high-frequency asset price variations, so that their interest rate exposure may not be fully reflected in Treasury or agency MBS prices. As a result, investor holdings of these assets may still affect their prices, even though the net supply of such assets is zero when all players in the economy are taken into account. The same argument cannot be made for bond-issuing companies, especially financial corporations.
We therefore extend the model to include two additional supply factors, the par amount (normalized by nominal GDP) and the average duration of private MBS holdings, which are appended to the list of state variables. Specifying the model dynamics is however complicated by the fact that, unlike the duration of Treasury securities or the par supply of Treasury or agency MBS, the duration of agency MBS responds strongly to the level of interest rates; a lower interest rate will prompt more mortgage borrowers to prepay and the duration of agency MBS to shorten, and vice versa. As a result, we can no longer assume that all supply variables evolve independently of the yield factors; instead we need to allow MBS duration and the level of yields to be jointly determined within the model. MBS prepayment behavior is notoriously hard to model and depends on house prices, demographics, and many other non-interest rate factors. A fully-specified MBS prepayment model is beyond the scope of this paper; such a model is also not necessary for our purposes as we only need to capture the partial effect of MBS prepayments on MBS duration arising from interest rate changes. In the empirical analysis, we therefore model the average duration of privately-held agency MBS as a linear function of its own lag and the lagged yield curve level factor, while the Treasury supply factor and the par MBS-to-GDP ratio both follow AR(1) processes.
![\displaystyle \Phi=\left[ \begin{array}[c]{ccccc}% \Phi_{11} & \Phi_{12} & 0 & 0 & 0\\ \Phi_{21} & \Phi_{22} & 0 & 0 & 0\\ 0 & 0 & \Phi_{33} & 0 & 0\\ 0 & 0 & 0 & \Phi_{44} & 0\\ \Phi_{51} & 0 & 0 & 0 & \Phi_{55}% \end{array} \right] .](img65.gif)
|
(21) |
We maintain earlier restrictions that the short-term rate loads only on the two yield factors,
| (22) |
and that all supply factors carry zero risk premiums11:
| (23) | ||
![\displaystyle =\left[ \begin{array}[c]{ccccc}% \lambda_{1,11} & \lambda_{1,12} & \lambda_{1,13} & \lambda_{1,14} & \lambda_{1,15}\\ \lambda_{1,21} & \lambda_{1,22} & \lambda_{1,23} & \lambda_{1,24} & \lambda_{1,25}\\ 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 \end{array} \right] .](img68.gif)
|
(24) |
Under these two assumptions on the short rate and the risk premiums, the supply factors follow the same dynamics under the physical and the risk-neutral measures:
| (25) | ||
| (26) |
for
4 Model Estimation and Empirical Results
We estimate the model using monthly data on Treasury yields and private holdings of Treasury and Agency MBS from March 1994 to July 2007. We assume the short rate is represented by the one-month yield, the level factor is represented by the five-year yield, and the slope factor is represented by the spread between the five-year yield and the one-month yield. Because our primary purpose is to identify the possible effect of supply factors on Treasury yield term premium, we take a two-step approach to estimate the model parameters as in Ang and Piazzesi (2003). In the first step, we estimate the factor dynamics equation (9) and the short rate equation (3) by ordinary least squares. In the second step, we estimate the remaining risk premium parameters by minimizing the average difference between observed yields and the term premium estimates described in Section 2, on the one hand, and model-implied yields and term premiums, on the other, over maturities of six months and one, two, seven, and ten years, while at the same time holding fixed all pre-estimated parameters. This two-step approach avoids the difficulties of estimating a model with many factors using the one-step maximum likelihood when yields and factors are highly persistent.
4.1 Estimation Results
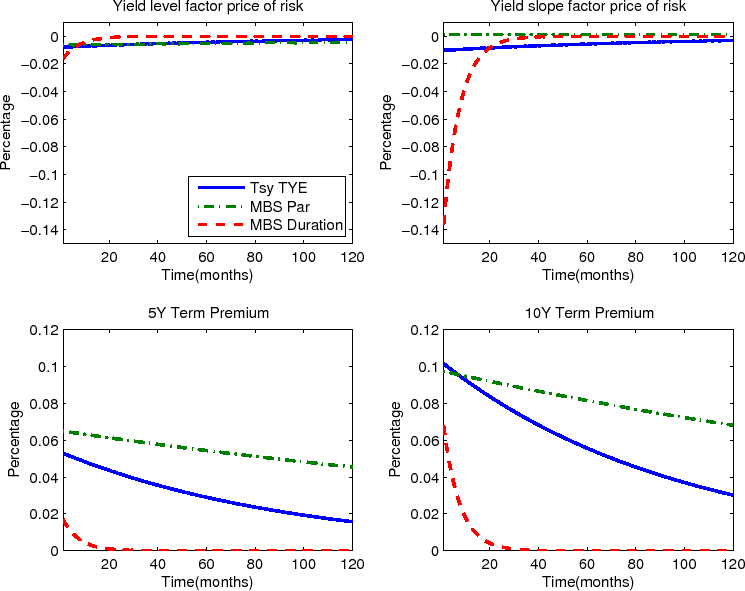
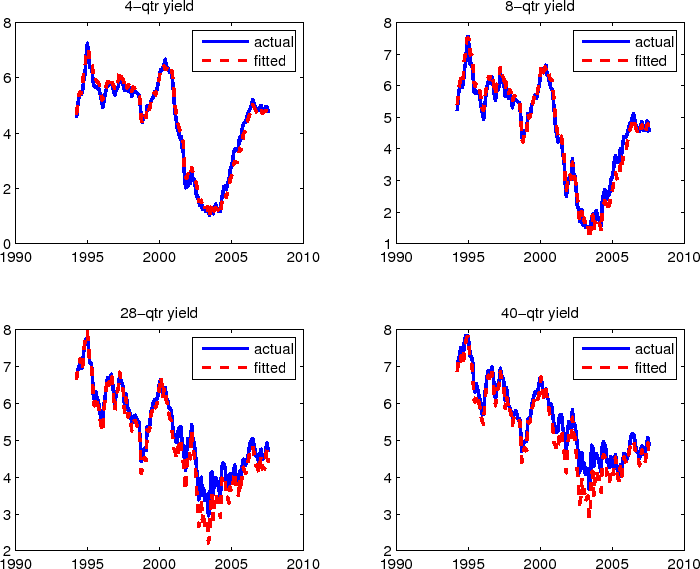
Table 2 presents the model parameter estimates and Figures (1) and 2 show the fit of the model. The risk premiums on yield level risk carry the same sign of loadings on the three supply factors as on the level factor itself, which suggests that the three supply factors carry positive interest rate level risk premium as one would expect. Similarly the risk premiums on the yield slope risk carry the same sign of loadings on two supply factors (Treasury supply factor and MBS duration factor) as on the slope factor itself, which implies these two supply factors carry positive interest rates slope risk premium. The fit of the model is also reasonably good as evidenced in the two figures.
|
|
|
|
|
|
|
|
| 0.970 | -0.010 | 0.148 | ||||
| -0.052 | 0.938 | 0.298 | ||||
| 0.990 | 0.082 | |||||
|
|
0.997 | 34.540 | ||||
|
|
0.238 | 0.860 | 2.074 |
|
|
|
|
|
|
|
|
| 0.992 | 0.019 | 0.002 | 0.002 | 0.005 | 0.969 | |
| -0.098 | 0.961 | 0.003 | -0.000 | 0.040 | 1.160 |
|
|
|
|
|
|
|
| 0.284 | |||||
| 0.296 | |||||
| 0.274 | |||||
|
|
0.142 | ||||
|
|
0.312 | 0.258 |
|
|
|
|
|
|
|
|
| -0.077 | -0.102 | -0.008 | -0.006 | -0.016 | -2.887 | |
| 0.152 | -0.080 | -0.010 | 0.002 | -0.136 | -2.908 |
| Maturity (Years) |
|
|
|
||
| 0.5 | 1.18 | -0.86 | -0.08 | 0.59 | -6.65 |
| 1 | 1.29 | -0.70 | 0.13 | 1.36 | -9.50 |
| 2 | 1.34 | -0.44 | 1.13 | 2.89 | -8.14 |
| 5 | 1.17 | -0.02 | 5.29 | 6.49 | 1.70 |
| 7 | 1.04 | 0.09 | 7.70 | 8.11 | 5.01 |
| 10 | 0.86 | 0.15 | 10.16 | 9.73 | 6.79 |
| Note: This table reports model-implied loadings of term premiums on the factors. |
As summarized in Table 3, this model suggests that a one-percentage-point decline in the Treasury ten-year equivalent to-GDP ratio or the MBS par-to-GDP ratio would reduce the ten-year Treasury yield by about 10 basis points, while a one-year shortening of the average effective duration of private MBS holdings would lower the ten-year Treasury yield by about 7 basis points.
4.2 Impulse Response and Variance Decomposition
Next we examine the impulse responses of term premiums to supply shocks. We define the bond risk premium or term premium as the difference between the actual yield ![]() and the average
future short rate,
and the average
future short rate,
![]() :
:
where the price loadings also follow a recursive relation:
with the initial conditions
Recall there are only two risk factors in this model, i.e., only the first two elements in the price of risk vector,
![]() , are non-zeros. The top panel of Figure 3 plots the impulse responses of these two elements, which represent the market price of
yield curve level and slope risks, respectively, to one unit of shock to each supply factor. The market price of yield slope risk seems to react more strongly to MBS duration shocks than the price of level risk, while the responses to Treasury and MBS par supply factors are comparable across the
two prices of risk.
, are non-zeros. The top panel of Figure 3 plots the impulse responses of these two elements, which represent the market price of
yield curve level and slope risks, respectively, to one unit of shock to each supply factor. The market price of yield slope risk seems to react more strongly to MBS duration shocks than the price of level risk, while the responses to Treasury and MBS par supply factors are comparable across the
two prices of risk.
Turning to term premiums, the bottom panel of Figure 3 plots impulse responses of 5-year and 10-year term premiums to one unit of shock to each supply factor as implied by Equations (2) and (27). MBS duration shocks seem to have smaller and more transitory effects on yields than the other two shocks, while the effects of Treasury and MBS par supply factors are both long-lasting and rising with bond maturities.
We can also use Equations (2) and (27) to decompose the conditional variance
![]() at horizon
at horizon ![]() and maturity
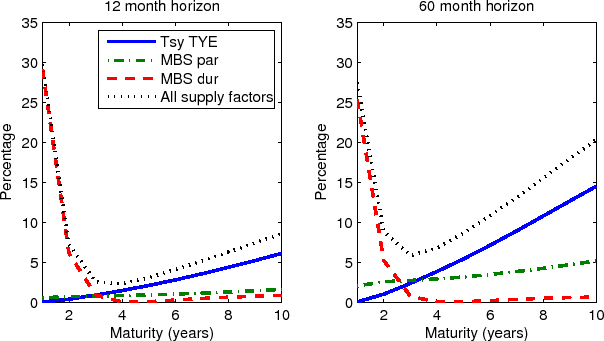
and maturity ![]() as explained by each factor. The results for maturities of 1, 5, 10 years and horizons of 12 and 60 months are reported in Figure 4 and Table 4. As expected, the Treasury and
MBS par supply factors explain very little of term premium variations at short maturities and short horizons, because short-term yields are primarily driven by interest rate expectations, which by construction are not affected by supply factors; in addition, supply factors are highly persistent and
show little variations over short horizons. As the maturity rises, however, changes in term premiums explain a larger portion of yield variations. As the forecasts horizon increases, supply factors also exhibit more notable variations. Taken together, these two observations suggest that the effect
of supply factors on term premiums should become more important at longer maturities and horizons, which is what we observe in the data. More specifically, about
as explained by each factor. The results for maturities of 1, 5, 10 years and horizons of 12 and 60 months are reported in Figure 4 and Table 4. As expected, the Treasury and
MBS par supply factors explain very little of term premium variations at short maturities and short horizons, because short-term yields are primarily driven by interest rate expectations, which by construction are not affected by supply factors; in addition, supply factors are highly persistent and
show little variations over short horizons. As the maturity rises, however, changes in term premiums explain a larger portion of yield variations. As the forecasts horizon increases, supply factors also exhibit more notable variations. Taken together, these two observations suggest that the effect
of supply factors on term premiums should become more important at longer maturities and horizons, which is what we observe in the data. More specifically, about ![]() and
and ![]() of the conditional variance of 5- and 10-year term premiums, respectively, are attributable to shocks to the supply factors. Moreover, the Treasury supply factor accounts for most of the
contributions of supply factors to term premium variations.
of the conditional variance of 5- and 10-year term premiums, respectively, are attributable to shocks to the supply factors. Moreover, the Treasury supply factor accounts for most of the
contributions of supply factors to term premium variations.
| Maturity (years) | Horizon (months) | Yield factors Level | Supply factors Slope | Supply factors Treasury | Supply factors MBS Par | Supply factors MBS Dur | Supply factors All |
| 1 | 1 | 52 | 19 | 0 | 0 | 29 | 29 |
| 1 | 12 | 38 | 61 | 1 | 0 | 0 | 2 |
| 1 | 60 | 35 | 59 | 4 | 1 | 1 | 6 |
| 5 | 1 | 44 | 26 | 0 | 1 | 29 | 30 |
| 5 | 12 | 34 | 63 | 2 | 1 | 0 | 3 |
| 5 | 60 | 33 | 58 | 6 | 2 | 1 | 9 |
| 10 | 1 | 46 | 27 | 0 | 2 | 25 | 27 |
| 10 | 12 | 29 | 62 | 5 | 3 | 0 | 9 |
| 10 | 60 | 28 | 52 | 15 | 5 | 1 | 20 |
| Note: This table reports variance decompositions of yield risk premiums. |
5 Evaluating the Federal Reserve's Asset Purchase Programs
This section uses our term structure model with supply factors to evaluate the Federal Reserve's previous asset purchase programs--LSAP1, LSAP2, and MEP, which provide natural experiments for assessing the effects of exogenous shocks to the supply of Treasury securities and their close substitutes on Treasury yields. For reference, the details of these programs are described briefly below.12
- LSAP1: On November 25, 2008, the FOMC announced the first LSAP program (LSAP1) consisting of $100 billion of purchases of agency debt and up to $500 billion of purchases of agency MBS. In March 2009, the FOMC expanded the LSAP1 program to include an additional $750 billion purchase of agency securities and $300 billion purchase of longer-term Treasury securities. The program was completed in March 2010, with a total purchase of $1.25 trillion of agency MBS, about $170 billion of agency debt, and $300 billion of Treasury securities.
- LSAP2: On November 3, 2010, the FOMC announced it would purchase $600 billion of longer-term Treasury securities over an 8-month period through June 2011 (LSAP2). LSAP2 was completed as announced, with the bulk of purchases concentrated in nominal Treasury securities with 2- to 10-year maturities.
- MEP: On September 21, 2011, the FOMC announced the Maturity Extension Program (MEP), under which the FOMC will purchase, by the end of June 2012, $400 billion of Treasury securities with remaining maturities of 6 to 30 years while simultaneously selling an equal amount of Treasuries with remaining maturities of 3 years or less. Staff estimates suggest that both the LSAP2 program and the MEP would remove about $400 billion of 10-year equivalents of private Treasury holdings from the market.
5.1 Previous empirical studies
A growing empirical literature tries to assess the effects of these asset purchase programs, which are summarized in Table 5 and described in more details below.
| Event studies | Time series regressions | Panel regressions | Estimated decline in ten-year Treasury yield (basis points) | |
| LSAP1 Gagnon, Raskin, Remache, and Sack (2011) |
|
|
91 (Event studies); 36 to 82 (Regressions) | |
| LSAP1 Krishnamurthy and Vissing-Jorgensen (2011) |
|
100 | ||
| LSAP1 D'Amico and King (2010) |
|
20-30 (Treasury purchases only) | ||
| LSAP1 D'Amico, English, López-Salido, and Nelson (2011) |
|
35 (Treasury purchases only) | ||
| LSAP2 Krishnamurthy and Vissing-Jorgensen (2011) |
|
25 | ||
| LSAP2 D'Amico, English, López-Salido, and Nelson (2011) |
|
55 | ||
| LSAP2 Meaning and Zhu (2011) |
|
21 | ||
| LSAP2 Swanson (2011) |
|
15 | ||
| MEP Hamilton and Wu (Forthcoming) |
|
22 | ||
| MEP Meaning and Zhu (2011) |
|
17 |
| Note: This table summarizes previous studies of the Federal Reserve's three asset purchase programs. |
LSAP1
- Gagnon, Raskin, Remache, and Sack (2011) using one-day window around 8 baseline events from November 25, 2008 to November 4, 2009, find that the 2-year Treasury yield declined 34bps , the ten-year Treasury yield declined 91bps, the ten-year agency debt yield declined 156bps, the current-coupon 30-year MBS yield declined 113bps, the ten-year SWAP rate 101bps, and the Baa corporate bond index yield declined 67 bps. Gagnon, Raskin, Remache, and Sack (2011) also use several regression models on a sample from January 1985 to June 2008, to estimate the effect of changes in the stock of privately-held longer-term debt (normalized by nominal GDP) on the term premium, after controlling for other factors related to business cycles, and uncertainties about economic fundamentals. From those regression models they estimate the term premium effects of the first LSAP are 36 to 82bps.
- D'Amico and King (2010), which focuses only on Treasury LSAPs, using a panel of CUSIP-level data (where they regress the cumulative change in each security price on the total amount purchased of that security and its close substitutes) find that at the end of the first LSAP, Treasury yields with remaining maturity between 5 to 15 years were 20 to 30 basis points lower than what they would otherwise have been. The largest effects are at horizons of about 6 to 8 years and 11 to 14 years, consistent with the relatively high proportion of securities purchased in these sectors.
- D'Amico, English, López-Salido, and Nelson (2011) provide empirical estimates of the effect on longer-term U.S. Treasury yields of LSAP-style operations focusing on two channels: (i) scarcity (available local supply) and (ii) duration. According to these estimates the total impact from the first Treasury LSAP program is about 35 basis points: the scarcity effect accounts for 23 basis points and the duration effect for 12 basis points. The estimates indicate that: both proxies for scarcity and duration are positively and significantly related to longer-term Treasury yields and term premiums; a sizable portion of the impact on longer-term Treasury yields has been transmitted via the nominal term-premium component; within the overall term premium, it is the real term premium component that exhibits the greatest response to these two variables; and the inflation risk premium's response, in contrast, is quite small and is not uniformly statistically significant across different specifications.
- Krishnamurthy and Vissing-Jorgensen (2011) using one-day window around 6 baseline events from November 25, 2008 to March 18, 2009, find that the ten-year Treasury yield declined 100bps, the ten-year agency debt yield declined 164bps, the
current-coupon 30-year MBS yield declined 116bps, and the Baa corporate bond index yield declined 68bps.
Overall, the above mentioned studies imply that the first round of Treasury LSAPs had an impact that ranges between 15 and 35 basis points.
LSAP2
- Krishnamurthy and Vissing-Jorgensen (2011) using an event-study approach that analyzes the period from August 26, 2010 (day before the Chairman Bernanke's Jackson Hole speech) to November 2, 2010 (day before the LSAP2 announcement), find that the ten-year Treasury yield declined 25bps, the ten-year agency debt yield declined 27bps, and the Baa corporate bond index yield declined 17bps. In addition, their regression approach predicts that LSAP2 should result in a 26.5 basis-point decline in Treasury yields, which is quite aligned with the event-study results.
- D'Amico, English, López-Salido, and Nelson (2011) results suggest that the scarcity effect from the second LSAP program is about 45 basis points and the duration effect is about 10 basis points. Thus, the total effect of the second LSAP is estimated to be about 55 basis points.
- Meaning and Zhu (2011) applying the methodology developed by D'Amico and King (2010) estimate that LSAP2 on average lowered the yield curve by 21 basis points, with a maximum impact of 108 basis point for some securities with remaining maturity of about 20 years.
- Swanson (2011) also employs an event-study approach to measure the impact of Operation Twist (1961) that is extrapolated to quantify the effect of LSAP2, based on similarities between the two programs. The size of Operation Twist accounted for 4.5% of U.S. Treasury-guaranteed debt and it appeared to have reduced short- and long-term rates by 13bps. The size of LSAP2 was very similar to Operation Twist as percentage of Treasury debt, and it is estimated to have reduced long-term rates by 15bps.
MEP
- Meaning and Zhu (2011) simulations suggest that on average, yields may drop 22 basis points for securities with a remaining maturity over 8 years.
- Hamilton and Wu (Forthcoming), using regression on a sample from 1990 to 2007, estimate the effect of variations in the average maturity of privately-held Treasury debt on the term structure of interest rates, after controlling for level, slope and curvature of the yield curve. Using the estimated coefficients they evaluate a swap experiment where the Fed sells $400bn of short-term securities and buys $400bn of long-term securities. The results indicate that yields with maturity longer than 2 year fall about 17 basis points, while short-term yields increase of a similar amount.
5.2 LSAPs as One-Period Supply Shocks
Most studies mentioned above treated these asset purchase programs as causing instant shocks to the supply variables. Following the same approach, we consider the $300 billion of Treasury security purchase in LSAP1 as roughly corresponding to a $169 billion shock to private Treasury holdings in terms of ten-year equivalents (Gagnon, Raskin, Remache, and Sack (2011), footnote 47), or a 1.2 percent shock to the Treasury supply factor when normalized by the 2009Q4 nominal GDP of $14.1 trillion. Similarly, the $1.25 trillion purchases of Agency MBS under the LSAP1 program roughly translates into a 8.9 percent shock to the MBS par supply factor. By comparison, both the $600 billion of Treasury Purchase under the LSAP2 program and the $400 billion simultaneous purchases of Treasury security with maturities longer than 6 years and sales of Treasury securities with maturity less than 3 years under the MEP are estimated to have removed about $400 billion 10-equivalents from the market, or about 2.6 percent and 2.5 percent shocks to the Treasury supply factor when normalized by the 2010Q4 and the 2011Q4 nominal GDP of $14.7 trillion and $15.3 trillion, respectively.
We use the estimated factor loadings in Table 3 to estimate the term premium effects of such supply shocks and summarize the results in Table 6. We estimate that the LSAP1 program lowered the ten-year Treasury yield by about 100 basis points, the five-year yield by about 65 basis points, and the two-year yield by about 25 basis points in the near term. By comparison, the other two programs (the LSAP2 program and the MEP) are both estimated to have lowered the ten-year Treasury yield by about 25 basis points and the five-year yield by 10 to 15 basis points, but have almost no effect on the two-year Treasury yield.
| Program | Shocks
|
Shocks
|
Shocks
|
Term Premium Effect (bps) 2-year | Term Premium Effect (bps) 5-year | Term Premium Effect (bps) 10-year |
| LSAP1 | -1.2 | -8.9 | -27 | -64 | -99 | |
| LSAP2 | -2.7 | -3 | -14 | -26 | ||
| MEP | -2.6 | -3 | -13 | -25 |
| Note: This table reports model estimates of various asset purchase programs assuming one-period shocks. |
5.3 LSAPs as a Sequence of Supply Shocks
The above analysis implicitly assumes that these asset purchase programs can be considered as one-time supply shocks that would dissipate over time following the historical dynamics of the supply variables. In reality, these programs are implemented according to pre-determined time tables and
are widely expected by market participants to be gradually unwound in the future to return the SOMA portfolio to its historical level and composition, causing changes to not only the level but also the dynamics of the supply factors during and after the purchases. As a result, the term premium
effect estimates in Table 3 may overstate or understate the true effect by ignoring the fact the the persistence of LSAP-induced supply shocks could deviate from its historical norm. To capture this divergence, we model those programs as generating a sequence of
shocks to the Treasury and agency MBS supply factors, ![]() , which become known to the investors once the programs are announced:
, which become known to the investors once the programs are announced:
| (30) | ||
| (31) |
As shown in the appendix, the time-
where
To understand the intuition in this formula, assume ![]() to be equal to an identity matrix because the supply factors are typically highly persistence as evidenced by the estimates
in Table 2. Equation 32 then simplifies to
to be equal to an identity matrix because the supply factors are typically highly persistence as evidenced by the estimates
in Table 2. Equation 32 then simplifies to
The above formula states that the Term Premium Effect (TPE) at time ![]() of any program is equal to the sum of discounted expected yield impacts from the future incremental supply shocks
generated by such a program (i.e. the total stock TPE is equal to the sum of flow TPE).14 More specifically, recall that the supply shocks generated by each
program
of any program is equal to the sum of discounted expected yield impacts from the future incremental supply shocks
generated by such a program (i.e. the total stock TPE is equal to the sum of flow TPE).14 More specifically, recall that the supply shocks generated by each
program ![]() represent changes to private holdings from the baseline scenario with no purchase program in each period.15 Therefore, the holdings difference between the current and the previous period,
represent changes to private holdings from the baseline scenario with no purchase program in each period.15 Therefore, the holdings difference between the current and the previous period,
![]() , represents the net changes (positive for asset sales and negative for asset purchase) to the private holdings in that period from the program,16 and the entire term following the summation sign represents discounted future yield responses, with
, represents the net changes (positive for asset sales and negative for asset purchase) to the private holdings in that period from the program,16 and the entire term following the summation sign represents discounted future yield responses, with ![]() representing yield responses per unit of supply shocks and
representing yield responses per unit of supply shocks and
![]() representing the discounting factor. The formula can be used to evaluate effects from both past programs and new program. For past purchase programs, the first supply shock
would be the programs' cumulative purchases by that period. For a new program that yet to be started, the first term is the new program's projected net purchase in that period.
representing the discounting factor. The formula can be used to evaluate effects from both past programs and new program. For past purchase programs, the first supply shock
would be the programs' cumulative purchases by that period. For a new program that yet to be started, the first term is the new program's projected net purchase in that period.
There are several important implications from the formula:
- A program's TPE depends on both purchase amount and investors' expectation of timing and pace of future exit sales.
- Similarly, a program's TPE is not fixed number. It can change over time depending on investors' changing expectation of timing and pace of future exit sales. For example, extending federal funds liftoff date also has important implication for program TPEs if asset sales dates are expected to be tied to federal funds liftoff dates as outlined by the FOMC in its June 2011 meeting minutes .
- The further away and the slower future exit sales, the bigger the TPE (there is less offsetting effect from those future sales due to more discounting).
- TPE of asset purchases and sales are not symmetric; yields would increase faster during asset sales than their declines during purchases (there are no offsetting terms in the TPE formula during asset sales).
To use the above TPE formula to evaluate the Fed's LSAP1, LSAP2 and MEP, we start by forming projections for SOMA Treasury and MBS holdings both under a baseline scenario with no such program and under each purchase program. We assume that the purchase proceeds at a constant speed such that the supply shocks reported in Table 6 are spread out evenly over the life span of each program. Compared with the baseline scenario, the Federal Reserve's purchases will create initial large negative shocks to the supply variables, which starts to shrink as SOMA holdings under the purchase program and under the baseline scenario start to converge when the Federal Reserve begins unwinding these programs. For illustrative purposes, we assume that investors expect the Fed to begin selling securities 2 years after the end of each program and to finish the sales 5 years after the end of the program. The results based on these assumptions are reported in Table 7, which is based on applying equation (32) to the series of supply shocks under each program (For the LSAP1 program, the duration of the Treasury purchase part is only 8 months and we ignore MBS runoff due to principal prepayment). These new estimates suggest that the LSAP1 program lowered the ten-year Treasury yield by about 60 basis points, the five-year yield by about 50 basis points, and the two-year yield by about 15 basis points in the near term. By comparison, the other two programs (the LSAP2 program and the MEP) are estimated to have lowered the ten-year Treasury yield by about 20 basis points and the five-year yield by 10 to 15 basis points, and to have almost no effect on the two-year Treasury yield. These results on LSAP1 and LSAP2 are similar to those reported in Chung, Laforte, Reifschneider, and Williams (Forthcoming).
| Program | Durations (months) | Shocks per month
|
Shocks per month
|
Shocks per month
|
Term Premium Effect (bps) 2-year | Term Premium Effect (bps) 5-year | Term Premium Effect (bps) 10-year |
| LSAP1 | 15 | -0.120 | -0.593 | -16 | -52 | -60 | |
| LSAP2 | 8 | -0.338 | -2 | -13 | -19 | ||
| MEP | 9 | -0.289 | -2 | -13 | -19 |
| Note: This table reports model estimates of various asset purchase programs using assumptions on the time paths of the purchase programs. |
6 Conclusions
In this paper, we provide evidence that private holdings of Treasury securities and agency MBS have explanatory power for variations in Treasury yields above and beyond that of standard yield curve factors.
Based on this observation, we extend the standard Gaussian essentially affine no-arbitrage term structure model to allow Treasury and MBS supply variables to affect Treasury term premiums. The model is fitted to historical data on Treasury yields as well as the supply and the maturity characteristics of private Treasury and MBS holdings. The estimation results suggest that a one-percentage-point decline in the Treasury ten-year equivalent to GDP ratio or the MBS par-to-GDP ratio would reduce the ten-year Treasury yield by about 10 basis points, while a one-year shortening of the average effective duration of private MBS holdings would lower the ten-year Treasury yield by about 7 basis points.
We then apply this model to evaluating the Federal Reserve's various asset purchase programs. Our estimates show that the first and the second large-scale asset purchase programs and the Maturity Extension program have a combined effect of about 100 basis points on the ten-year Treasury yield.
Appendix: LSAPs as a Sequence of Supply Shocks
This appendix derives the model-implied effect of a pre-announced asset purchase program by the Federal Reserve on the ![]() -period yield. Partition the state variables into yield factors
(level and slope) and supply factors (average maturity and par debt/GDP ratio) and denote by `y' and `s' respectively.
-period yield. Partition the state variables into yield factors
(level and slope) and supply factors (average maturity and par debt/GDP ratio) and denote by `y' and `s' respectively.
![\begin{displaymath}\left[ \begin{array}[c]{cc}% \rho^{yy} & \rho^{ys}\ \rho^{sy} & \rho^{ss}% \end{array}\right] .\end{displaymath}](img160.gif) We model Federal Reserve operations as inducing deterministic shocks
to
We model Federal Reserve operations as inducing deterministic shocks
to ![\begin{displaymath} \hat{X}_{t}=X_{t}+\left[ \begin{array}[c]{c}% 0\ u_{t}^{s}% \end{array}\right] \end{displaymath}](img162.gif)
We assume that once the program is announced, bond prices become affine functions of
![\displaystyle =E_{t}\left[ \exp\left( -r_{t}-\frac{1}{2}\lambda_{t}^{^{\prime}}% \lambda_{t}-\lambda_{t}^{\prime}\varepsilon_{t+1}+\hat{A}_{n-1,t}% +\hat{B}_{n-1,t}\hat{X}_{t+1}\right) \right]](img179.gif) |
||
 |
||
![\displaystyle \left. \left. \text{ }+\hat{A}_{n-1,t+1}+\hat{B}% _{n-1,t+1}\left( c+\rho\left( \hat{X}_{t}-\left[ \begin{array}[c]{c}% 0\\ u_{t}^{s}% \end{array} \right] \right) +\Sigma\varepsilon_{t+1}+\left[ \begin{array}[c]{c}% 0\\ u_{t+1}^{s}% \end{array} \right] \right) \right) \right]](img181.gif) |
||
Matching terms yields
Taking the difference between recursions (37) and (35) and iterating give
![\displaystyle =\left\{ \begin{array}[c]{cc}% \left( \hat{B}_{n-\left( T-t\right) ,T}-B_{n-\left( T-t\right) }\right) \left( \rho-\Sigma\Lambda\right) ^{T-t} & if\text{ }t+n>T\\ \left( \hat{B}_{0,t+n}-B_{0}\right) \left( \rho-\Sigma\Lambda\right) ^{n} & if\text{ }t+n\leq T \end{array} \right.](img191.gif)
|
||
since
 |
In yield terms
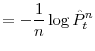 |
||
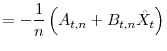 |
||
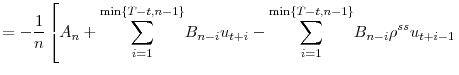 |
||
![\displaystyle \left. \text{ \ \ \ \ \ \ \ \ }+B_{n}\left( X_{t}+\left[ \begin{array}[c]{c}% 0\\ u_{t}^{s}% \end{array} \right] \right) \right]](img203.gif) |
||
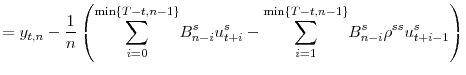 |
||
![\displaystyle =y_{t,n}-\frac{1}{n}\left[ B_{n}^{s}u_{t}^{s}+% {\displaystyle\sum\limits_{i=1}^{\min\left\{ T-t,n-1\right\} }} B_{n-i}^{s}\left( u_{t+i}^{s}-\rho^{ss}u_{t+i-1}^{s}\right) \right]](img205.gif) |
||
![\displaystyle =y_{t,n}+\left[ b_{n}^{s}u_{t}^{s}+% {\displaystyle\sum\limits_{i=1}^{\min\left\{ T-t,n-1\right\} }} \frac{n-i}{n}b_{n-i}^{s}\left( u_{t+i}^{s}-\rho^{ss}u_{t+i-1}^{s}\right) \right]](img206.gif) |
where

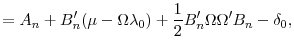
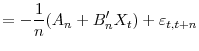
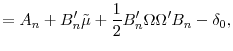

![\displaystyle =-\frac{1}{n}\left[ \left( A_{n}-A_{n}^{eh}\right) +\left( B_{n}% -B_{n}^{eh}\right) ^{\prime}X_{t}\right]%](img127.gif)