Learning from Experience in the Stock Market*
Keywords: Learning from experience, OLG, asset pricing, bubbles, heterogeneous agents
Abstract:
JEL Classification: G12, D83, D84
1 Introduction
The crucial role of expectations about the future is well understood in economics. The rational expectations hypothesis (REH) has been an important step forward allowing rigorous formalization of the process of expectations formation. Yet it has been often criticized for endowing people with "too much" knowledge about their environment.1 Empirical research studying how individuals form expectations about aggregate economic variables does not, in general, corroborate the REH. In particular, Malmendier and Nagel (2009, 2011) find evidence that, contrary to the REH, people "learn from experience," meaning that individuals are more strongly influenced by data realized during their own lifetimes than by earlier historical data. More specifically, Malmendier and Nagel (2011) find that individuals who experienced low stock market returns during their lives are less likely to participate in the stock market, invest a lower fraction of their liquid assets in stocks, and are more pessimistic about future stock returns. In addition, Malmendier and Nagel (2009) find that young individuals place more weight on recently experienced inflation than older individuals do. The upshot is that learning dynamics may be perpetual if history "gets lost" as new generations replace older ones.
In this paper, we explore how replacing the REH with " learning from experience" modifies the results of a simple general equilibrium model of the stock market. We are interested in the dynamics of heterogeneous beliefs and in the feedback loop that arises when individuals learn about variables that are the result of their collective decisions given their beliefs, a type of self-referentiality emphasized by Eusepi and Preston (2011). To this end, we extend the asset pricing model of Adam and Marcet (2011) to a stochastic overlapping generations (OLG) setup in which individuals learn the parameters of the endogenous evolution of the stock price as well as the exogenous process for dividends.
Specifically, we assume that a small random fraction of individuals exit the stock market every period with a given probability ![]() , and an equal measure of new individuals enter the
market. As in Brown and Rogers (2009), each new entrant inherits the assets but does not inherit the accumulated knowledge of his parent about the economy. Instead, children learn from their own experience, updating their beliefs in a Bayesian way with information about stock prices and dividends
which they observe during their own lifetimes. This is our main difference with Adam and Marcet's (2001) model which has infinitely-lived individuals. Our main difference with Brown and Rogers (2009) is that the mapping between dividend growth and the stock price is not known to the individuals in
our model.
, and an equal measure of new individuals enter the
market. As in Brown and Rogers (2009), each new entrant inherits the assets but does not inherit the accumulated knowledge of his parent about the economy. Instead, children learn from their own experience, updating their beliefs in a Bayesian way with information about stock prices and dividends
which they observe during their own lifetimes. This is our main difference with Adam and Marcet's (2001) model which has infinitely-lived individuals. Our main difference with Brown and Rogers (2009) is that the mapping between dividend growth and the stock price is not known to the individuals in
our model.
We find that, even if the retirement rate ![]() is quite low, so that in any given period only a small fraction of individuals are novice, the asset price fails to converge to the
rational expectations equilibrium (REE). Instead, a chaotic equilibrium emerges in which the stock price exhibits stochastic cycles (around the REE price), the frequency of which is positively related to the rate of retirement. Two forces create the oscillating dynamics. On the one hand, there is
" momentum" rooted in the continuous entry of new individuals. At any given date, a fraction of young individuals discount the experience of their parents and pay more attention to the most recent stock price developments. The latter biases the young's beliefs about the future course of dividends
and stock prices toward simple extrapolation of the recent past, and their trading activities push the asset price away from the fundamental. On the other hand, there is a force of reversal toward the REE trend. When the stock price rises too far above the fundamental value, individual leverage
constraints begin to bind. Because any given individual (including the optimistic types) can afford to buy less of the stock, the asset price must decline to the valuation of less optimistic individuals for the market to clear. The same reflecting force works also " from below", when the stock
price falls far below the fundamental value. The combination of these two factors - momentum and trend reversion - results in boom-and-bust cycles, which are only loosely related to dividends and are mainly due to speculation about the future course of the stock price, in the spirit of Harrison and
Kreps (1978).
is quite low, so that in any given period only a small fraction of individuals are novice, the asset price fails to converge to the
rational expectations equilibrium (REE). Instead, a chaotic equilibrium emerges in which the stock price exhibits stochastic cycles (around the REE price), the frequency of which is positively related to the rate of retirement. Two forces create the oscillating dynamics. On the one hand, there is
" momentum" rooted in the continuous entry of new individuals. At any given date, a fraction of young individuals discount the experience of their parents and pay more attention to the most recent stock price developments. The latter biases the young's beliefs about the future course of dividends
and stock prices toward simple extrapolation of the recent past, and their trading activities push the asset price away from the fundamental. On the other hand, there is a force of reversal toward the REE trend. When the stock price rises too far above the fundamental value, individual leverage
constraints begin to bind. Because any given individual (including the optimistic types) can afford to buy less of the stock, the asset price must decline to the valuation of less optimistic individuals for the market to clear. The same reflecting force works also " from below", when the stock
price falls far below the fundamental value. The combination of these two factors - momentum and trend reversion - results in boom-and-bust cycles, which are only loosely related to dividends and are mainly due to speculation about the future course of the stock price, in the spirit of Harrison and
Kreps (1978).
A key finding is that the heterogeneous-beliefs economy can be approximated reasonably well by an economy with a representative agent who updates his beliefs with a constant-gain learning (CGL) scheme. The approximation takes two steps. In a first step, we show that the evolution of the stock
price can be approximated using the evolution of the average (rather than the marginal) beliefs of the population. In a second step, we show that the dynamics of average beliefs can be approximated by a CGL scheme in which the gain parameter
is a function of the survival rate ![]() . This approximation implies that memories of the distant past are lost with the passage of time as a result of population turnover combined with
"learning from experience."
. This approximation implies that memories of the distant past are lost with the passage of time as a result of population turnover combined with
"learning from experience."
CGL is usually motivated based on its ability to produce realistic model features, such as amplification of the persistence of macro variables in response to aggregate shocks.2 Rarely is there a discussion of the reasons why all agents should learn in the same suboptimal way. The value of the gain parameter typically is estimated or calibrated to yield the smallest possible mean-squared forecasting error. Our contribution is to provide an alternative justification for using CGL in a representative-agent context. Namely, we see it as a useful shortcut to approximating the aggregate dynamics of an economy populated by many Bayesian learners, each of them using a decreasing gain sequence, under the assumption that they "learn from experience."
Finally, we analyze the asymptotic behavior of our economy in the limit with infinitely lived agents (taking the limit as
![]() ). We show analytically that, in this case, even if traders do not know anything about each other, endowing them with long histories of dividend and stock price
realizations is sufficient for their beliefs to eventually converge to the REE. We study the properties of the convergence, such as the speed and the shape of the transition path. We find that, if new dividend information arrives monthly, it can take several centuries before the asset price comes
close to the REE. In the baseline calibration, after a full one century of trading and learning, the median simulated stock price is still 20 percent higher than its REE counterpart.
). We show analytically that, in this case, even if traders do not know anything about each other, endowing them with long histories of dividend and stock price
realizations is sufficient for their beliefs to eventually converge to the REE. We study the properties of the convergence, such as the speed and the shape of the transition path. We find that, if new dividend information arrives monthly, it can take several centuries before the asset price comes
close to the REE. In the baseline calibration, after a full one century of trading and learning, the median simulated stock price is still 20 percent higher than its REE counterpart.
Our setup rules out the possibility of a rational bubble, defined as a gap between the stock price and the REE price that grows unboundedly in expectations. We preclude bubbles by assuming that individuals face constraints on their maximum exposure to the stock. Specifically, we cap individual leverage, defined as the multiple of the current dividend that an individual is allowed to maintain invested in the form of stock holdings. In our environment leverage is an important factor affecting the properties of convergence to the REE. In particular, the higher the degree of permissible leverage, the slower is the rate of convergence.
Our paper is related to several strands of the literature. First, it relates to the emerging literature on learning with heterogeneous agents, such as Giannitsarou (2003), Branch and McGough (2004), Branch and Evans (2006), Honkapohja and Mitra (2006), or Graham (2011). In contrast to these papers, individuals in our economy use the same Bayesian learning scheme, have the same preferences, and observe the same public variables (prices and dividends). The only source of heterogeneity is in the individual information sets used to update beliefs, with younger individuals focusing on a subset of the observations used by older ones.
Second, a related body of literature analyzes the dynamics of asset prices under Bayesian learning by a representative agent. Timmermann (1994), Weitzman (2007), and Cogley and Sargent (2008), among others, offer an explanation for some interesting asset pricing phenomena based on rational learning by a representative agent. Unlike our setup, individuals in their models use all available past information and know ex ante the correct mapping between asset prices and fundamentals; hence, they only need to learn about the latter in order to achieve convergence to the REE.
Third, following Radner (1979) and Lucas (1972), a large body of literature studies rational expectations equilibria in economies with asymmetric information. Vives (1993), in particular, analyzes the speed of convergence to REE in a model of rational learning in which the market price is
informative about an unknown parameter only through the actions of agents. Vives finds that whenever the average precision of private information is finite, convergence to the REE is slow, at the rate
![]() , where
, where ![]() is the number of trading periods.
is the number of trading periods.
Fourth, recent literature focuses on the role of higher-order expectations for asset prices. For example, Allen, Morris, and Shin (2006) analyze a linear model with asymmetric information. They find that, in the absence of common knowledge about higher-order beliefs, asset prices generally will depart from the market consensus of the expected fundamental value, typically reacting more sluggishly to changes in fundamentals.
The rest of our paper is organized as follows. In section 2, we recast the model of Adam and Marcet (2011) in an OLG setting. In section 3, we calibrate the model and analyze the properties of "learning from experience." In section 4, we show how the model can be approximated by a representative agent with CGL. Section 5 explores the case in which the survival probability approaches one, and section 6 concludes.
2 The model
In this section, we recast the model of Adam and Marcet (2011) in an OLG setup. We make some additional changes to their model as follows. First, we assume Bayesian learning of the means and the variances of the stock price and dividends.3 Second, we specify a particular market arrangement (a centralized auction), which ensures that information about the current dividend is incorporated into the contemporaneous stock price. We are also explicit about the way the market arrives at the equilibrium asset price. Third, we replace Adam and Marcet's investment constraints on the number of shares an agent can hold with constraints on individual exposure in the stock. More precisely, we assume that there is a ceiling for the maximum value an individual can invest in the stock, preventing him from going arbitrarily long in the asset. Likewise, we assume that there is a floor for an individual's position in the stock, preventing him from engaging in unlimited shorting. These value limits, which can be rationalized by underlying credit constraints, are sufficient to rule out rational bubbles without reliance on a " projection facility."4
Adam and Marcet's model is interesting to us for three reasons. First, it introduces a meaningful distinction between "internal rationality" and "external rationality." Internally rational individuals maximize expected utility given consistent beliefs about the future. Externally rational individuals are endowed, in addition, with common knowledge of each other's preferences and beliefs, for any possible path of dividends. We assume that our economy is populated by individuals who are internally rational but are not externally rational. Second, an appealing feature of the model is its simplicity, allowing us to obtain closed-form analytical expressions for the asset price dynamics. Third, despite its simplicity, the model is rich enough to be contrasted with actual data on stock prices and dividends.
The economy is populated by ![]() risk-neutral ex ante identical dynasties. Members of each dynasty have stochastic lifetimes with death (or retirement) occurring with a constant exogenous
probability,
risk-neutral ex ante identical dynasties. Members of each dynasty have stochastic lifetimes with death (or retirement) occurring with a constant exogenous
probability,
![]() . Thus, in each period, the measure of dynasts of age
. Thus, in each period, the measure of dynasts of age
![]() is constant and equal to
is constant and equal to
![]() Upon retirement, a successor inherits the assets of the former dynast but not his accumulated knowledge about the processes governing the stock price and
dividends. Instead, successors embark on their own learning experience "from scratch", starting with the identical initial belief that their predecessors had at birth, namely the belief consistent with REE.
Upon retirement, a successor inherits the assets of the former dynast but not his accumulated knowledge about the processes governing the stock price and
dividends. Instead, successors embark on their own learning experience "from scratch", starting with the identical initial belief that their predecessors had at birth, namely the belief consistent with REE.
The dynasts trade among themselves a single divisible stock, which is in fixed supply, normalized to ![]() . Each individual decides how much to invest in the asset based on inter-temporal
arbitrage. However, as emphasized by Adam and Marcet, the relevant arbitrage is not the one between selling the stock and holding it forever for its dividends. Instead, the condition that governs savings decisions is a one-period-ahead comparison between the value of the stock in the current period
and the subjective expected payoff in the following trading period.
. Each individual decides how much to invest in the asset based on inter-temporal
arbitrage. However, as emphasized by Adam and Marcet, the relevant arbitrage is not the one between selling the stock and holding it forever for its dividends. Instead, the condition that governs savings decisions is a one-period-ahead comparison between the value of the stock in the current period
and the subjective expected payoff in the following trading period.
The stock price in our model thus equals the marginal asset holder ![]() 's subjective expected present value of holding the stock for
one period, collecting the dividend
's subjective expected present value of holding the stock for
one period, collecting the dividend ![]() , and selling it in the following period at his expected price
, and selling it in the following period at his expected price
![]() . Because expectations about future prices generally would differ across individuals, the law of iterated expectations does not apply, and the pricing conditions of individuals
do not aggregate to the familiar asset pricing formula with a representative agent.
. Because expectations about future prices generally would differ across individuals, the law of iterated expectations does not apply, and the pricing conditions of individuals
do not aggregate to the familiar asset pricing formula with a representative agent.
In the following subsections we provide a sketch of the model. We provide more details in Appendix A.
2.1 Preferences and constraints
The head of dynasty
![]() receives utility from consumption
receives utility from consumption
![]() per period. He discounts future consumption by factor
per period. He discounts future consumption by factor
![]() , where
, where ![]() is a time preference parameter and
is a time preference parameter and ![]() is a constant probability of survival. The expected value of lifetime utility for dynast
is a constant probability of survival. The expected value of lifetime utility for dynast ![]() is thus
is thus
where
Individual ![]() faces the period budget constraint
faces the period budget constraint
where
In addition, the individual faces constraints on the minimum and the maximum asset exposure, defined as the maximum value in terms of consumption that he stands to lose (or gain if short-selling) if the stock price falls to zero.
Constraints (3) imply that an individual investor cannot go arbitrarily short or long in the stock. In a more detailed model, these limitations can be derived from underlying credit constraints that prevent agents from borrowing unlimited amounts of resources. Instead, we
will simply assume that ![]()
![]() and
and ![]()
![]() where parameter
where parameter
![]() (which we loosely refer to as the permissible "leverage") is the maximum multiple of the current dividend that an individual can maintain invested in the risky stock.
(which we loosely refer to as the permissible "leverage") is the maximum multiple of the current dividend that an individual can maintain invested in the risky stock.
Our exposure constraints (3) differ from the stock holding constraints used by Adam and Marcet (2011), namely
![]()
![]() , which limit the minimum and maximum
number of shares held by an individual. Their constraints suffice for the maximization problem to be well-defined at the individual level. However, they are not sufficient to prevent agents from collectively holding the entire stock at ever-rising prices.5 In contrast, our specification of the stock holding constraints puts effective bounds on the price-to-dividend ratio, without the need for a "projection facility"
that mechanically constrains beliefs to a pre-specified neighborhood.
, which limit the minimum and maximum
number of shares held by an individual. Their constraints suffice for the maximization problem to be well-defined at the individual level. However, they are not sufficient to prevent agents from collectively holding the entire stock at ever-rising prices.5 In contrast, our specification of the stock holding constraints puts effective bounds on the price-to-dividend ratio, without the need for a "projection facility"
that mechanically constrains beliefs to a pre-specified neighborhood.
Dividends follow the exogenous stochastic process
where
Given the information set available to individual ![]() , his problem is to choose consumption and equity holdings so as to maximize lifetime utility (1), subject to the
budget constraint (2), and the exposure constraints (3).
, his problem is to choose consumption and equity holdings so as to maximize lifetime utility (1), subject to the
budget constraint (2), and the exposure constraints (3).
The first-order conditions for an individual are
where
2.2 Learning from experience
Individuals are assumed to "learn from experience," that is, the information set
![]() of agent
of agent ![]() of age
of age ![]() consists of the realizations of stock prices and dividends observed during his lifetime,
consists of the realizations of stock prices and dividends observed during his lifetime,
Dynasts update their beliefs about the mean growth rate of the stock price and dividends,
![]() , as well as the covariance matrix of their innovations,
, as well as the covariance matrix of their innovations,
![]() . Given
. Given ![]() and
and ![]() individual
individual ![]() 's perceived law of motion is
's perceived law of motion is
This specification allows for beliefs about the growth rates in the share price and dividends to take on different values and their innovations to be imperfectly correlated. Individuals' prior beliefs about these parameters are of the Normal-Wishart conjugate form,
where the Wishart distribution
Individuals are assumed to be born with identical prior beliefs, centered on the REE outcome in which the asset price grows in lockstep with dividends,
The joint distribution of the stock price and dividends is computed as the posterior of
![]() conditional on information
conditional on information
![]() available up to period
available up to period ![]() . The posterior distribution is also a
Normal-Wishart with location parameters
. The posterior distribution is also a
Normal-Wishart with location parameters
![]() Defining the one-step-ahead forecast error as
Defining the one-step-ahead forecast error as
it follows from DeGroot (1970, ch. 9) that the recursive Bayesian updating scheme is given by
2.3 Timeline of events and market arrangement
Events unfold as follows. At the beginning of period ![]() individuals update their beliefs about
individuals update their beliefs about
![]() based on the stock price and dividends observed in period
based on the stock price and dividends observed in period ![]() using the recursive Bayesian updating scheme (9)-(10). Each individual's expectations about the future stock price and dividends are obtained by projecting his latest estimate of the growth rates of the stock price and
dividends into period
using the recursive Bayesian updating scheme (9)-(10). Each individual's expectations about the future stock price and dividends are obtained by projecting his latest estimate of the growth rates of the stock price and
dividends into period ![]() Given these expectations, individual
Given these expectations, individual ![]() computes his
reservation price as6
computes his
reservation price as6
The stock is traded on a multiple-round, sealed-bid, centralized auction where actual exchange occurs only in the very last round. The market-clearing price is established as follows. In the first round, each individual sends his initial sealed bid ![]() given by (11). An auctioneer sorts all the bids from highest to lowest in an order book, and notionally allocates the asset, starting from the top bidder and moving down the order
book until the entire stock is allocated.7 The auctioneer then announces publicly the time
given by (11). An auctioneer sorts all the bids from highest to lowest in an order book, and notionally allocates the asset, starting from the top bidder and moving down the order
book until the entire stock is allocated.7 The auctioneer then announces publicly the time ![]() , round 1, preliminary asset price,
, round 1, preliminary asset price, ![]() , as the bid of the marginal investor who would just be willing to hold the asset if that were the final price. Thus, price
, as the bid of the marginal investor who would just be willing to hold the asset if that were the final price. Thus, price ![]() would clear the market if trade were allowed at that point and no new information had become available.
would clear the market if trade were allowed at that point and no new information had become available.
We assume, however, that at the end of the first round the actual dividend for time ![]() becomes publicly known. Hence, in subsequent rounds of the auction, investors revise their bids based
on the preliminary price announced by the auctioneer in the preceding round
becomes publicly known. Hence, in subsequent rounds of the auction, investors revise their bids based
on the preliminary price announced by the auctioneer in the preceding round ![]() and on the time
and on the time ![]() dividend,
dividend,
Bids are collected again, and the asset is notionally allocated to the highest bidders, determining the new preliminary price of round ![]() as the price offered by
the marginal potential buyer. This process is repeated for a large number of rounds until convergence of the price
as the price offered by
the marginal potential buyer. This process is repeated for a large number of rounds until convergence of the price ![]() .8 This limiting-round price is the actual clearing price in period
.8 This limiting-round price is the actual clearing price in period ![]() at which trade occurs.9 At the end of period
at which trade occurs.9 At the end of period ![]() , owners of the asset receive the
dividend and the clearing price, and the successful bidders receive the stock. In equilibrium, individuals collectively hold the entire stock of the asset, so
, owners of the asset receive the
dividend and the clearing price, and the successful bidders receive the stock. In equilibrium, individuals collectively hold the entire stock of the asset, so
where recall that
3 Heterogeneous beliefs and speculative bubbles
In this section, we explore the implications of heterogeneity due to agents being born at different dates and focusing on data realizations from their own lifetimes, rather than on all historical data.
3.1 Calibration
The model's parameters are calibrated to match the U.S. stock market evidence as documented by Shiller (2005). We assume that each period in the model is a month, which represents a compromise: dividends typically are announced quarterly, whereas stock prices are available at a much higher frequency.
Dynasts discount future consumption by the factor
![]() , where
, where ![]() is a time preference parameter and where
is a time preference parameter and where ![]() is the probability of survival. The survival rate is set equal to
is the probability of survival. The survival rate is set equal to
![]() implying an "average life on the market" of about 20 years. We use
Shiller's (2005) stock market dataset covering the S&P index from January 1871 to June 2011 to calibrate our model. In particular, consistent with Shiller's data, we set the mean growth rate of dividends to
implying an "average life on the market" of about 20 years. We use
Shiller's (2005) stock market dataset covering the S&P index from January 1871 to June 2011 to calibrate our model. In particular, consistent with Shiller's data, we set the mean growth rate of dividends to
![]() per month, and its standard deviation to
per month, and its standard deviation to
![]() . We set the time preference parameter to
. We set the time preference parameter to
![]() consistent with an average price-to-(monthly)-dividend ratio of around 300, close to Shiller's number of 320. The leverage ceiling parameter is set to
consistent with an average price-to-(monthly)-dividend ratio of around 300, close to Shiller's number of 320. The leverage ceiling parameter is set to
![]() Note that, by imposing a limit on each individual's investment in the stock,
Note that, by imposing a limit on each individual's investment in the stock, ![]() affects the measure of households who hold the asset. Setting
affects the measure of households who hold the asset. Setting
![]() is consistent with an average stock market participation rate of around 60 percent, which is the estimate reported by Poterba et. al. (1995) for U.S. households with income over
is consistent with an average stock market participation rate of around 60 percent, which is the estimate reported by Poterba et. al. (1995) for U.S. households with income over
![]() . Prior uncertainty (or " confidence") is parameterized by setting
. Prior uncertainty (or " confidence") is parameterized by setting ![]() equivalent to four years (the duration of an undergraduate economics degree) of stock price and dividend observations. For our numerical simulations, we set the number of agents to
equivalent to four years (the duration of an undergraduate economics degree) of stock price and dividend observations. For our numerical simulations, we set the number of agents to ![]() and the number of auction rounds per period to
and the number of auction rounds per period to ![]() .10 We perform 1000 Monte Carlo simulations of 5000 months each, equivalent to more than four centuries of trading.
.10 We perform 1000 Monte Carlo simulations of 5000 months each, equivalent to more than four centuries of trading.
3.2 Simulation results
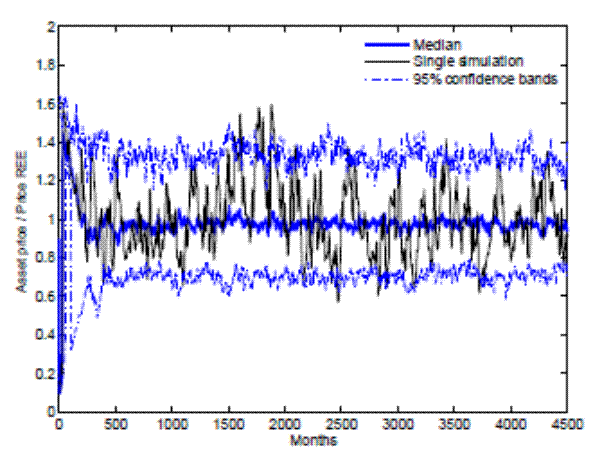
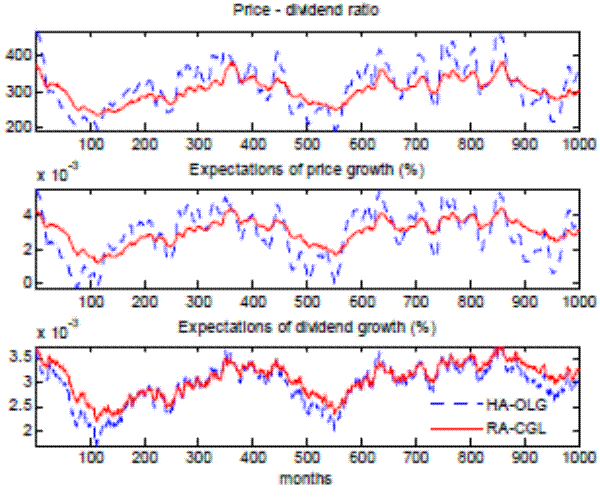
Figure 1 illustrates the behavior of the asset price according to the model. The thin solid line plots one particular simulated path of the ratio of the stock price in the OLG economy to the REE price. Notice that the ratio oscillates within a 95 percent confidence interval between 0.5 and 1.5, that is, stock price fluctuations are strongly amplified in the OLG model. Second, the median stock price in the OLG model does fairly quickly converge to the REE. In that sense, the REE asset price is a relevant statistic for the OLG model. Third, the 95 percent confidence band does not shrink over time, indicating the lack of asymptotic convergence of individual price histories.
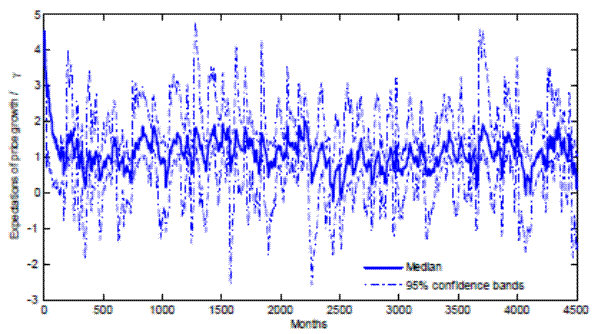
The stochastic oscillations of the stock price around the REE are related to the dynamics of learning. To see this, Figure 2 plots the evolution of price growth beliefs held by the cross-section of households relative to the REE belief ![]() . We plot the median belief, and a 95% confidence interval at each point in time. Notice that individuals' beliefs regarding the growth rate of the stock price do not converge to
. We plot the median belief, and a 95% confidence interval at each point in time. Notice that individuals' beliefs regarding the growth rate of the stock price do not converge to ![]() ; instead, they go through successive waves of optimism and pessimism vis-a-vis
; instead, they go through successive waves of optimism and pessimism vis-a-vis ![]() .
.
Two elements of our model are responsible for the oscillating dynamics. On the one hand, there is a force of momentum, which is rooted in the infrequent resetting of the learning schemes of successive cohorts of individuals. Namely, at any given date, a fraction of young individuals enters the market whose learning path initially is strongly influenced by the most recent stock price and dividend realizations. The young's forecasts inform their trading activities, and, through trade, affect the realized stock price, pulling the beliefs of older generations toward the more recent price change realizations. On the other hand, there is a force of trend-reversion, emanating from the constraints on individual risky asset exposure. Namely, as the stock price rises far above the REE, the upper bound in (3) implies that optimistic investors can buy less shares for any given dividend realization. Because, in equilibrium, all shares must be held by someone, the stock price has to fall to the valuation of less optimistic investors. The same reflecting force operates "from below", when the stock price falls too far beneath the REE.11 The combination of the two factors - momentum and trend reversion - results in boom-and-bust cycles that are only loosely related to dividends.
Indeed, similar to Harrison and Kreps (1978), asset price cycles in our model are primarily the result of speculation about the future course of the asset price. To see that, we simulated again our economy under a constant realization of the dividend growth process,
setting all dividend growth innovations to zero. We found that, even in this case, disagreement necessarily arises in investors' beliefs. In particular, over time, investors' assessments of the variance of asset price growth begin to differ because the prior confidence ![]() of a random fraction
of a random fraction ![]() of investors is reset from
of investors is reset from
![]() down to
down to
![]() in the updating scheme(10). This, together with the direct effect of
in the updating scheme(10). This, together with the direct effect of ![]() on expected future prices in (12), necessarily creates dispersion of beliefs and bid prices, which translates into cycles even in the absence of dividend shocks.
on expected future prices in (12), necessarily creates dispersion of beliefs and bid prices, which translates into cycles even in the absence of dividend shocks.
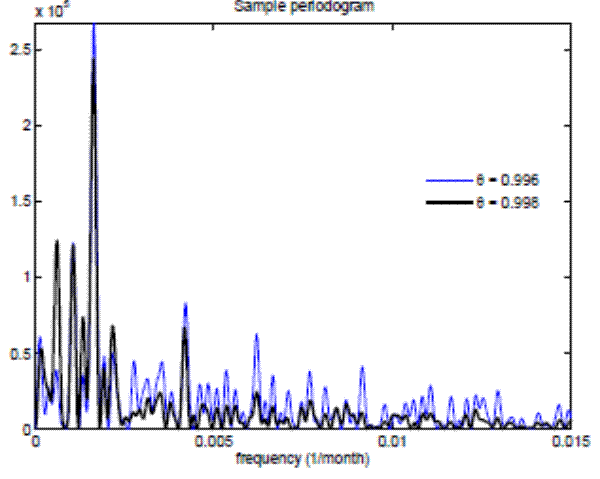
Figure 3 shows the sample periodogram and the time series of the price-dividend ratio in the absence of dividend shocks for two economies: one with N=100 traders and another with N=1000 traders. In the upper panel, the sample periodogram suggests that the economy with more agents displays more frequent price-dividend fluctuations. In the lower panel, the economy with more agents exhibits a smaller amplitude of stock price fluctuations.
In turn, Figure 4 shows the sample periodogram of the price-dividend ratio as a function of the survival rate ![]() . In the benchmark case with
. In the benchmark case with
![]() , the periodogram indicates a series of local maxima at periods of 8 to 16 years. With a higher survival rate of
, the periodogram indicates a series of local maxima at periods of 8 to 16 years. With a higher survival rate of
![]() , the peak periodicity corresponds to around 33 years. While not shown here, the amplitude of the cycles also depends on the survival rate. Namely, stock price cycles have a
smaller amplitude with a higher survival rate.
, the peak periodicity corresponds to around 33 years. While not shown here, the amplitude of the cycles also depends on the survival rate. Namely, stock price cycles have a
smaller amplitude with a higher survival rate.
Naturally, shocks to dividends do have an influence on the stock price, although the link is not nearly as direct as in the case of REE. Recall that in the REE model, stock price changes track one-to-one changes in dividends, inheriting the persistence of dividend growth (zero by assumption). In contrast, in the OLG model with "learning from experience," a sequence of positive dividend surprises has an escalating effect on asset price changes. This amplification occurs because, through trade, the young's overreaction to current information affects the stock price and, progressively, the beliefs of older generations, creating a non-linear feedback, which reinforces the effects of dividend shocks on the stock price.
4 Approximate aggregate dynamics
This section explores the possibility of analyzing the approximate aggregate dynamics of our economy without having to deal with the entire distribution of beliefs across agents. The approximation involves two parts. One part is to approximate the stock price dynamics for a given evolution of average beliefs; the second part is to approximate the evolution of average beliefs. We discuss each of these parts in turn and then combine them to arrive at a stand-alone representative-agent model that approximates the behavior of the heterogeneous-agents economy.
4.1 Price dynamics
The equilibrium price is obtained by iterating on (12) as
![]() and can be written as
and can be written as
A first-order approximation to the above expression is
Taking the average across all age groups yields
with
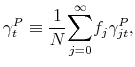 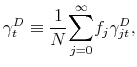 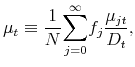 |
where
In principle, the average Lagrange multiplier should be a function of the price-dividend ratio. When the price-dividend ratio is close to the maximum leverage ![]() , the multiplier
, the multiplier
![]() should turn negative. This sign of the multiplier reflects the fact that most individuals are constrained, and hence the marginal trader is more pessimistic about the future price
than the average one. And when the price-dividend ratio is sufficiently low,
should turn negative. This sign of the multiplier reflects the fact that most individuals are constrained, and hence the marginal trader is more pessimistic about the future price
than the average one. And when the price-dividend ratio is sufficiently low, ![]() should turn positive as the marginal trader is more optimistic than average. To verify this relationship
between the price-dividend ratio and the average Lagrange multiplier, Figure 5 shows a cross-plot of the two variables from data generated by our benchmark model. The negative, quasi-linear, relationship can be approximated well by the linear function
should turn positive as the marginal trader is more optimistic than average. To verify this relationship
between the price-dividend ratio and the average Lagrange multiplier, Figure 5 shows a cross-plot of the two variables from data generated by our benchmark model. The negative, quasi-linear, relationship can be approximated well by the linear function
describing the behavior of
Using (16), the dynamics of the price-dividend ratio can be approximated as
which depends only on the average expectations about the growth rates of prices and dividends, and on the parameters
In the upper half of Table 2, we evaluate the quality of the approximation implied by equations (15) and (17). In the first two lines under the line "Price approximation," we take the actual average beliefs
![]() and
and
![]() given by the benchmark heterogeneous-agents model. In line "actual
given by the benchmark heterogeneous-agents model. In line "actual ![]() ," we also take as given the actual value of the average multiplier
," we also take as given the actual value of the average multiplier ![]() ; whereas, in line "approx.
; whereas, in line "approx. ![]() ," we use the approximate
," we use the approximate ![]() given by the law of motion (16). We consider two metrics of similarity: the
correlation between the price-dividend ratio in the heterogeneous-agents model and the approximate model; and the
given by the law of motion (16). We consider two metrics of similarity: the
correlation between the price-dividend ratio in the heterogeneous-agents model and the approximate model; and the ![]() , defined as one minus the ratio of the variance of the approximation
error to the variance of the
, defined as one minus the ratio of the variance of the approximation
error to the variance of the
![]() ratio in the benchmark model.13
We find that in both cases the approximation is reasonable. For example, when using the approximate multiplier and 1,000 agents, the correlation between approximate and actual
ratio in the benchmark model.13
We find that in both cases the approximation is reasonable. For example, when using the approximate multiplier and 1,000 agents, the correlation between approximate and actual
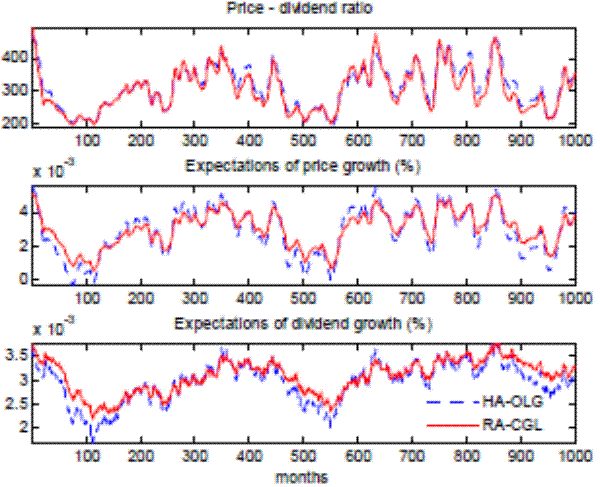
![]() ratio is 0.96. The adequacy of the approximation can also be verified visually in the upper panel of Figure 6, which plots the price-dividend ratio from the benchmark model along
with the approximation using (16) and (17).
ratio is 0.96. The adequacy of the approximation can also be verified visually in the upper panel of Figure 6, which plots the price-dividend ratio from the benchmark model along
with the approximation using (16) and (17).
4.2 Average learning dynamics
Equation (17) links the evolution of the stock price to the average market beliefs about the growth rate of the stock price and dividends. For a complete stand-alone approximation, we need to approximate the evolution of average beliefs. We begin with the evolution of the average price growth expectation, which is given by
![\displaystyle \gamma _{t}^{P}=\frac{1}{N}\overset{\infty }{\underset{j=0}{\sum }}% f_{j}\gamma _{jt}^{P}=\frac{f_{0}\gamma }{N}+\frac{1}{N}\overset{\infty }{% \underset{j=1}{\sum }}f_{j}\left[ \gamma _{j-1t-1}^{P}+\frac{1}{n_{jt}}% \left( \log \left( P_{t-1}/P_{t-2}\right) -\gamma _{j-1t-1}^{P}\right) % \right] ,](img138.gif)
|
where the prior confidence,
Assuming that individual expectations are uncorrelated with age, we obtain14
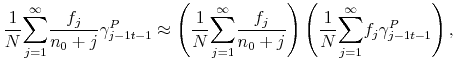
|
where the second product on the right-hand side equals
Proposition 1 In the limit as
![]()
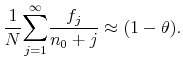 |
Proof See the Appendix.
Therefore, for ![]() close to 1, we have
close to 1, we have
that is, average beliefs about price growth are updated approximately according to a CGL scheme. CGL can thus be viewed as an approximate aggregation of the learning of individuals who update their beliefs by Bayes' rule, using data realized in their lifetimes. Notice that the CGL algorithm differs from the actual learning scheme of any of the individual agents because individual learning happens with a decreasing gain, as shown in (18). The population as a whole, however, learns approximately with a constant gain.
The evolution of average dividend expectations as
![]() can be derived symmetrically as
can be derived symmetrically as
Note that the value of the gain parameter, which appears in the approximation, equals the retirement probability (1 minus the survival rate). In our baseline calibration, this is equal to 0.004, corresponding to an expected life on the market of 20 years. In quarterly terms, the retirement probability is 0.012, which is quite close to existing estimates of the constant-gain parameter from macro time series data; for example, Milani (2007) estimates the constant-gain parameter to be 0.018 in U.S. data.
In the upper half of Table 2, the line "Price learning" and the line "Dividend learning" evaluate the adequacy of the assumption that individual expectations are uncorrelated with age. In this exercise, we take the actual price and dividend sequences from the benchmark heterogeneous-agents
model and construct series for stock price and dividend growth expectations using the approximations in (19) and (20). The table shows the two metrics of similarity: the correlation of the approximate with the true average growth expectations, as
well as the ![]() defined in sec. 4.1. By these measures, the approximation of both stock price and dividend learning dynamics are reasonably accurate. The middle and the lower panels of
Figure 6 confirm this result visually.
defined in sec. 4.1. By these measures, the approximation of both stock price and dividend learning dynamics are reasonably accurate. The middle and the lower panels of
Figure 6 confirm this result visually.
4.3 Representative-agent approximation
We now analyze the quality of the two approximations - of the stock price and of the average learning dynamics - as a unit. Namely, we consider the stand-alone representative-agent model in which the stock price is given by equation (17), with parameters ![]() and
and ![]() from Table 1 (first column), and in which average beliefs follow (19) and (20). This model can be simulated independently for any given evolution of dividends. The line "Price approximation" in the lower half of Table 2 reports the
from Table 1 (first column), and in which average beliefs follow (19) and (20). This model can be simulated independently for any given evolution of dividends. The line "Price approximation" in the lower half of Table 2 reports the ![]() and correlation with the evolution of the stock price in the benchmark heterogeneous-agents model. As can be expected, the overall approximation deteriorates because approximation errors in the stock price are compounded with errors in the average expectation
dynamics. Nevertheless, Figure 7 shows that the overall approximation is still decent; it definitely approximates the benchmark model much better than the rational expectations model (REM) does.
and correlation with the evolution of the stock price in the benchmark heterogeneous-agents model. As can be expected, the overall approximation deteriorates because approximation errors in the stock price are compounded with errors in the average expectation
dynamics. Nevertheless, Figure 7 shows that the overall approximation is still decent; it definitely approximates the benchmark model much better than the rational expectations model (REM) does.
Table 3 evaluates how well the simulated price-dividend ratio matches with the evidence documented by Shiller (2005). The model fits quite well with the observed autocorrelation of the price-dividend ratio by explaining it as a consequence of the dynamic coordination of heterogeneous beliefs. The representative agent constant-gain learning (RA-CGL) approximation produces a smoother price-dividend ratio than the benchmark heterogeneous-agents model.
Finally, Table 4 compares the one-step-ahead forecast errors (9) generated by the heterogeneous agents overlapping-generations (HA-OLG) model, the RA-CGL approximation, and the REM. The distribution of forecast errors is quite similar between the HA-OLG and the RA-CGL models.15 In particular, the forecast errors for the stock price are unbiased in the HA-OLG and the RA-CGL models but, in both cases, are more dispersed than in the REM. In addition, in the case of the HA-OLG and RA-CGL models, the distribution of price forecast errors displays more leptokurtosis than the REM.
Thus, the HA-OLG and RA-CGL models provide an unbiased average forecast of the evolution of stock prices and dividends, but the uncertainty about the future evolution of prices is larger than that of dividends. This outcome occurs because the stock price depends on market expectations, creating self-referential dynamics as emphasized in Eusepi and Preston (2011). In contrast, in the REM, the uncertainty about prices and dividends is essentially the same because agents coordinate ex ante onto the right model for asset pricing.
5 The case with infinitely lived individuals
In this section, we analyze the limiting case in which the probability of survival is
![]() We demonstrate the asymptotic convergence of the model to rational expectations despite the fact that individuals do not know anything about each other. We then analyze two
properties of the convergence process: its speed and the shape of the convergence path.
We demonstrate the asymptotic convergence of the model to rational expectations despite the fact that individuals do not know anything about each other. We then analyze two
properties of the convergence process: its speed and the shape of the convergence path.
5.1 Convergence to rational expectations
The proof of convergence consists of two steps.16 In the first step, we establish a contemporaneous relationship between the stock price and the
dividend, which depends on the current state of beliefs. In the second step, we take the limit as
![]() to establish the asymptotic convergence. The two steps are summarized by the following two propositions, the proofs of which are in Appendix C.
to establish the asymptotic convergence. The two steps are summarized by the following two propositions, the proofs of which are in Appendix C.
Proposition 2 The market-clearing stock price ![]() is given by
is given by
where
Proof See the Appendix.
Proposition 3 The stock price
![]()
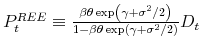 .
.
Proof See the Appendix.
5.2 Speed and shape of the convergence path
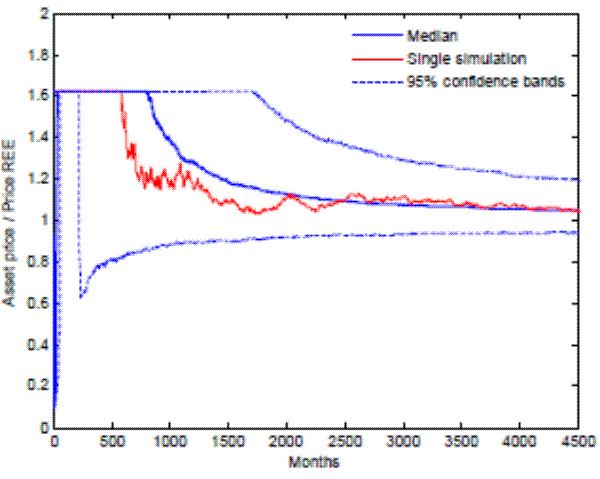
Having established asymptotic convergence, it is useful to know how long it takes for the stock price to converge to the REE.17 Figure 7 plots one randomly drawn path of the ratio of the stock price to its REE counterpart, the median across simulations, and the 95 percent confidence band.18 Remarkably, after 100 years of trading, the median stock price is still about 30 percent above the REE price. That is, even though there is asymptotic convergence, it takes a very long time for the rational expectations model to become a good approximation to the short-run dynamics generated by our model.
The convergence path is characterized by an initial " overshooting" of the stock price above the REE. Because individual learning begins with the REE as a prior belief, initially agents overestimate the growth rate of the stock price. This overestimation occurs because individuals observe
greater stock price volatility than their prior belief suggests. Thus, the initial rise in the price-dividend ratio is self-fulfilling: The stock price rises because agents expect it to rise, which generates an further increase in the stock price until the constraint
![]() is reached. The stock price remains at this level for some time, as agents progressively revise down their beliefs, eventually pulling the price back toward the
REE.
is reached. The stock price remains at this level for some time, as agents progressively revise down their beliefs, eventually pulling the price back toward the
REE.
The individual exposure constraints (3) are therefore central for the convergence process. They amount to a practical implementation of the standard transversality condition, which rules out asset price bubbles in infinite horizon models. The looser the constraint is (the
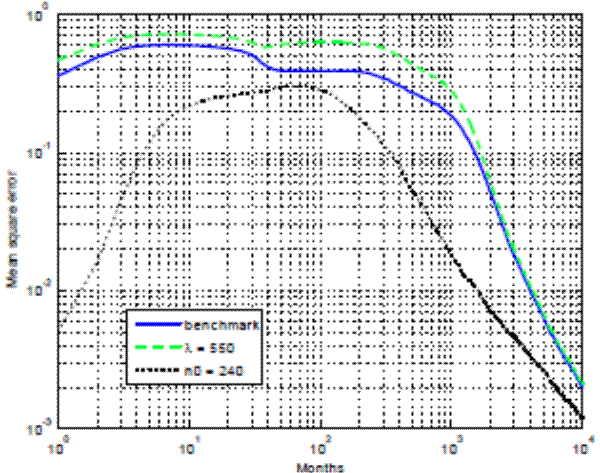
larger is ![]() ), the larger the initial overshooting and the longer it takes for the market to converge back to the REE. Another way to see this outcome is illustrated in Figure 9,
which plots the convergence in mean squared error (MSE) of the ratio of the stock price to the REE price over time. MSE is consistently higher than in the baseline calibration when the exposure constraint is relaxed by 10 percent (
), the larger the initial overshooting and the longer it takes for the market to converge back to the REE. Another way to see this outcome is illustrated in Figure 9,
which plots the convergence in mean squared error (MSE) of the ratio of the stock price to the REE price over time. MSE is consistently higher than in the baseline calibration when the exposure constraint is relaxed by 10 percent (
![]() ).
).
Figure 9 also illustrates how prior uncertainty affects the convergence. In particular, we set the confidence parameter to
![]() equivalent to 20 years of prior observations of the REE outcome. Qualitatively, the convergence is similar to the baseline calibration with
equivalent to 20 years of prior observations of the REE outcome. Qualitatively, the convergence is similar to the baseline calibration with ![]() , with initial price overshooting followed by progressive convergence to the REE price. However, the convergence is now faster so that after 40 years, the median stock price is less than 10 percent away from the
REE.19
, with initial price overshooting followed by progressive convergence to the REE price. However, the convergence is now faster so that after 40 years, the median stock price is less than 10 percent away from the
REE.19
6 Conclusions
In order to coordinate a priori to a REE, individuals must be endowed with incredible amounts of information not only about the structure of the economy and the exogenous shocks but also about the higher-order beliefs of all other market participants. If individuals lack this information, the law of iterated expectations is no longer valid and "beauty contest" dynamics may emerge as individuals embark on speculative trading as in Harrison and Kreps (1978). In particular, empirical research by Malmendier and Nagel (2009, 2011) suggests that expectations are not "externally rational" in the sense of Adam and Marcet (2011); rather, they find evidence that people "learn from experience," giving more weight to data realized during their own lifetimes than to earlier historical information.
We extend the model of Adam and Marcet to a stochastic OLG setup and analyze the effects of "learning from experience."The fact that different generations of individuals hold different beliefs leads to boom-and-bust cycles of the stock price around the REE. Even a tiny degree of "learning from experience" is sufficient to generate chaotic dynamics, which roughly resemble what we find in the data.
We show that the aggregate market dynamics can be approximated by a representative-agent model with CGL. Despite the fact that individuals learn with decreasing gain, learning by the population as a whole can be approximated by a constant gain. To a first-order approximation the gain parameter equals the survival rate, reflecting the fact that historical data is lost when successive generations "learn from experience."This result provides a plausible justification for the use of CGL algorithms in macroeconomic models instead of the more widely used rational expectations. Besides achieving more realism in modeling the expectations formation process, our approach provides needed discipline by tying the gain parameter to the survival rate.
Finally, we show that in the limiting case with infinitely lived agents, individuals can coordinate through a centralized market, and, eventually, achieve convergence to the REE. The only requirement for the equilibrium to be stationary are bounds on asset exposure that prevent coordination to an explosive path. This requirement is akin to the way transversality conditions are imposed in standard representative-agent models. We show that, for a plausible parameterization, the market converges very slowly to rational expectations. Moreover, the speed of convergence is strongly affected not only by the prior beliefs but also by the tightness of the exposure constraints.
Stock holding decision
The first-order optimality conditions of the individual's problem are:
![]() and
and
![]() , where
, where
is individual
Because the objective function is linear and the feasible set is closed, a maximum exists (and generally is a corner solution).
Symmetric rational expectations equilibrium
If individuals were identical, and this fact were common knowledge, they would be able to compute the equilibrium asset price by deduction. Namely, dividing (24) by the current dividend, dropping the ![]() subscript, and iterating the resulting equation forward while applying the law of iterated expectations and taking into account the known process for dividends (4), yields:
subscript, and iterating the resulting equation forward while applying the law of iterated expectations and taking into account the known process for dividends (4), yields:
Given that the sum of stock holdings must equal the fixed supply of the stock ![]() , it follows from (3) that the price-dividend ratio is bounded above by
, it follows from (3) that the price-dividend ratio is bounded above by ![]() ,
,
Hence the last term in (25) is zero, and therefore the equilibrium asset price is given by
where dividends follow the exogenous stochastic process defined in (4). We further impose the parameter restrictions,
which ensure that the price-dividend ratio is finite and that it is not a corner solution due to binding leverage constraints (26).
Informational limitations
We depart from REE by assuming that individuals have only limited information about the world they live in. In particular, they do not know anything about other market participants' preferences or constraints. However, they do know their own objectives and constraints and have a prior belief
about parameters ![]() and
and
![]() governing the dividend process (4). In the absence of common knowledge, from an individual's perspective, the price of the asset
itself is a stochastic process affecting optimal savings decisions much like dividends do. Hence individuals try to forecast both the dividend and the stock price, conditioning their forecasts on the history of past dividends and stock price realizations.
governing the dividend process (4). In the absence of common knowledge, from an individual's perspective, the price of the asset
itself is a stochastic process affecting optimal savings decisions much like dividends do. Hence individuals try to forecast both the dividend and the stock price, conditioning their forecasts on the history of past dividends and stock price realizations.
Formally, following Adam and Marcet (2011), denote by the operator ![]() investor
investor ![]() 's subjective expectation defined in a probability space
's subjective expectation defined in a probability space
![]() , where
, where ![]() is the space of
realizations,
is the space of
realizations, ![]() the corresponding
the corresponding ![]() -algebra, and
-algebra, and ![]() is a subjective probability measure over
is a subjective probability measure over
![]() . Denote by
. Denote by
![]() the set of histories during the lifetime of agent
the set of histories during the lifetime of agent ![]() up to period
up to period ![]() , and let
, and let
![]() When investor
When investor ![]() chooses his stock holding in
period
chooses his stock holding in
period ![]() , he takes as given
, he takes as given ![]() and his choice is contingent on
and his choice is contingent on
![]() . The space of realizations is
. The space of realizations is
where
Appendix B: Simulation algorithm
We briefly sketch the algorithm used to perform a single Monte Carlo simulation of the model:
- Generate an exogenous series for dividends
 following (4) and assuming that
following (4) and assuming that  Set
Set
 and
and
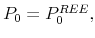 where
where
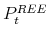 is given by (27).
is given by (27). - Initialize the prior beliefs,
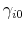 ,
,
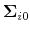 , and
, and 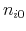 , for all agents following (7) and (8).
, for all agents following (7) and (8). - Main loop. At each point in time
 , for all
, for all  agents:
agents:
- Compute the one-step-ahead forecast errors e
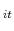 using (9)
using (9) - Draw a vector of random numbers from a uniform distribution between 0 and 1. For values greater than
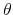 , the agent retires; otherwise he survives to the following period (the case of
infinitely lived agents is nested by setting
, the agent retires; otherwise he survives to the following period (the case of
infinitely lived agents is nested by setting
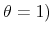 .
. - If an agent survives, update his beliefs,
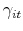 ,
,
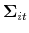 , and
, and 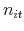 , using (10). If he
retires (he is replaced by a new agent), set
, using (10). If he
retires (he is replaced by a new agent), set
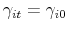 ,
,
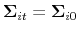 , and
, and
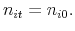
- Set the initial auction price to
- Compute the reservation price for each agent in auction round zero
 using (11).
using (11). - Auction. For each auction round
- Sort the reservation prices
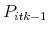 in decreasing order and notionally allocate the amount
in decreasing order and notionally allocate the amount
 to each agent until the entire stock
to each agent until the entire stock  of
the asset gets allocated. To ensure that the total does not exceed
of
the asset gets allocated. To ensure that the total does not exceed  , the marginal agent to receive a share of the asset may receive
, the marginal agent to receive a share of the asset may receive
 . The reservation price of the marginal agent is denoted as
. The reservation price of the marginal agent is denoted as
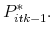
- If
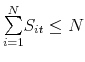 , then set
, then set
 Otherwise, set
Otherwise, set
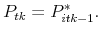
- The reservation price of each agent in round
 is computed using
(12).
is computed using
(12).
- Sort the reservation prices
- The auction is over in round
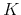 , and the stock price in period
, and the stock price in period 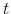 is
is
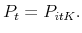
- Compute the one-step-ahead forecast errors e
- Repeat the main loop (3) for periods
 .
.
Appendix C: Proofs
Proposition 1. In the limit as
![]()
 |
Proof First we compute the series
 |
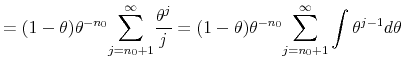 |
|
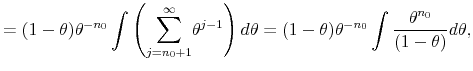 |
as
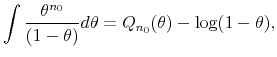 |
where
![\displaystyle \underset{\theta \rightarrow 1}{\lim }\overset{\infty }{\underset{j=1}{\sum }% }\frac{(1-\theta )\theta ^{j}}{n_{0}+j}=\underset{\theta \rightarrow 1}{\lim }\left[ (1-\theta )\theta ^{-n_{0}}\right] \left[ Q_{n_{0}}(\theta )-\log (1-\theta )\right] ,](img235.gif) |
which can be solved by applying L'Hôpital's rule,
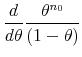 |
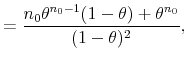 |
|
![\displaystyle \frac{d}{d\theta }\left[ Q_{n_{0}}(\theta )-\log (1-\theta )\right]](img238.gif) |
![\displaystyle =\left[ Q_{n_{0}}^{^{\prime }}(\theta )+\frac{1}{1-\theta }\right] ,](img239.gif) |
where
![\displaystyle \underset{\theta \rightarrow 1}{\lim }\left[ (1-\theta )\theta ^{-n_{0}}% \right] \left[ Q_{n_{0}}(\theta )-\log (1-\theta )\right] =\underset{\theta \rightarrow 1}{\lim }\frac{(1-\theta )^{2}\left[ Q_{n_{0}}^{^{\prime }}(\theta )+\frac{1}{1-\theta }\right] }{n_{0}\theta ^{n_{0}-1}(1-\theta )+\theta ^{n_{0}}}=\underset{\theta \rightarrow 1}{\lim }\frac{1-\theta }{% n_{0}\theta ^{n_{0}-1}(1-\theta )+\theta ^{n_{0}}}.](img241.gif)
|
Proposition 2. The stock price that clears the market at time ![]() is given by
is given by
 |
||
| (30) |
where
Proof Because individuals are identical we can drop index ![]() . In the initial round of the auction at time
. In the initial round of the auction at time ![]() , then, the price is given by
, then, the price is given by
| (32) |
where (31) holds. In the subsequent rounds, the price evolves as
If
![]() , then as
, then as
![]()
![]() would grow unboundedly were it not for constraint
(3) that prevents explosive beliefs by effectively setting an upper (and a lower) limit on the price-to-dividend ratio, and hence
would grow unboundedly were it not for constraint
(3) that prevents explosive beliefs by effectively setting an upper (and a lower) limit on the price-to-dividend ratio, and hence
![]() If
If
![]() then in the limit as
then in the limit as
![]() the first term in equation (33) tends to zero and the price for period
the first term in equation (33) tends to zero and the price for period ![]() is
is
Proposition 3. The economy converges to the REE with stock price
![]() defined in (
defined in (
![]() ).
).
Proof First, because dividends follow an exogenous process, the Bayesian learning algorithm for dividends must converge asymptotically to the true value of the parameters
Second, given the equilibrium price (21), the value of
![]() is bounded as
is bounded as
![]() Therefore, given the Bayesian updating scheme,
Therefore, given the Bayesian updating scheme,
![]() must converge ,
must converge ,
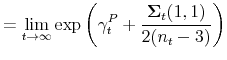 |
||
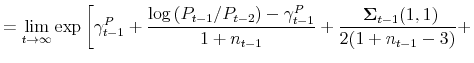 |
||
![\displaystyle \left. +\frac{n_{t-1}\left( \log \left( P_{t-1}/P_{t-2}\right) -\gamma _{t-1}^{P}\right) ^{2}}{2(1+n_{t-1}-3)\left( 1+n_{t-1}\right) }\right]](img260.gif) |
||
| (36) |
Third, the limit ![]() must satisfy
must satisfy
This last point can be proved by contradiction: suppose
by
Finally, by taking the log-difference of (34),
Together, (35) and (37) imply that the first term in the brackets on the right-hand side of (38) converges to zero, and hence the learning parameters for the stock price must also converge to the asymptotic values of the REE,
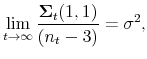 and and |
(39) |
Substituting the above in equation (34) we obtain
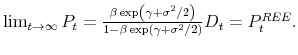
Appendix D. Tables and figures
Table 1. Average Lagrange multiplier
| Coeff. | 1000 agents | 100 agents |
| 0.9367 | 0.9221 | |
| s.e. | (0.009) | (0.010) |
| -0.0035 | -0.0033 | |
| s.e. | (0.0001) | (0.0001) |
| 0.83 | 0.77 | |
| Obs. | 3000 | 3000 |
Table 2. Approximation accuracy under different assumptions
| Single approximation step | 1000 agents |
1000 agents Correl. | 100 agents |
100 agents Correl. |
| Price approximation with actual |
0.76 | 0.89 | 0.86 | 0.95 |
| Price approximation with approx. |
0.92 | 0.96 | 0.91 | 0.96 |
| Price learning | 0.88 | 0.94 | 0.88 | 0.94 |
| Dividend learning | 0.88 | 0.94 | 0.89 | 0.94 |
| Complete RA-CGL model Price approximation | 0.67 | 0.83 | 0.59 | 0.80 |
| Complete RA-CGL model Price learning | 0.58 | 0.75 | 0.51 | 0.72 |
| Complete RA-CGL model Dividend learning | 0.88 | 0.94 | 0.88 | 0.94 |
Table 3. Moments of the price-dividend ratio
| Data | REM | HA-OLG | RA-CGL | |
| Mean | 320.3 | 307.6 | 316.8 | 309.5 |
| Standard deviation | 166.1 | 0 | 65.4 | 56.9 |
| Autocorrelation | 0.996 | - | 0.995 | 0.989 |
Table 4. Moments of the forecast errors
| Mean | Std. Dev. | Skewness | Kurtosis | |
| Price forecast errors REM |
|
0.0114 | 3.0753 | |
| Price forecast errors HA-OLG |
|
0.0207 | 3.4809 | |
| Price forecast errors RA-CGL |
|
0.0208 | 3.4934 | |
| Dividend forecast errors REM |
|
0.0114 | 3.0753 | |
| Dividend forecast errors HA-OLG |
|
0.0114 | 3.0605 | |
| Dividend forecast errors RA-CGL |
|
0.0114 | 3.0640 |
Figure 3: Price-divident ratio fluctuations in the absence of dividend shocks as a function of the number of traders
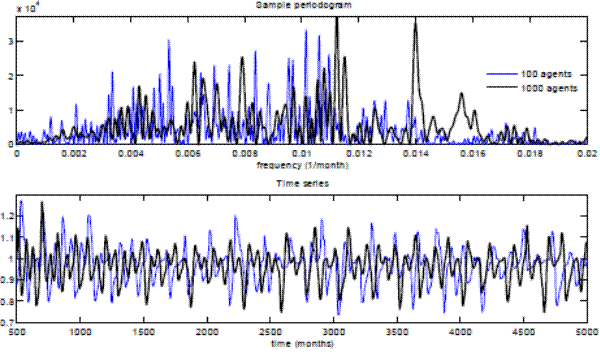 Figure 3 Data
Figure 3 Data
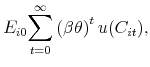
![\displaystyle \left[ \begin{array}{c} \log \left( P_{t}/P_{t-1}\right) \\ \log \left( D_{t}/D_{t-1}\right)% \end{array} \right] =\left[ \begin{array}{c} \varepsilon _{it}^{P} \\ \varepsilon _{it}^{D}% \end{array} \right] \sim N(\mathbf{\gamma }_{i},\Sigma _{i}),](img50.gif)
![\displaystyle \mathbf{\gamma } _{i}=\left[ \begin{array}{c} \gamma _{i}^{P} \\ \gamma _{i}^{D}% \end{array} \right] ,](img51.gif)
![\displaystyle \Sigma _{i}=\left[ \begin{array}{cc} \sigma _{iP}^{2} & \sigma _{iPD}^{2} \\ \sigma _{iDP}^{2} & \sigma _{iD}^{2}% \end{array}% \right] .](img52.gif)
![\displaystyle \mathbf{\Sigma }_{0}=\sigma ^{2}\left[ \begin{array}{cc} 1 & \delta \\ \delta & 1\end{array}% \right] \left( n_{0}-3\right) ,](img62.gif) where
where ![\displaystyle \mathbf{e}_{it}=\left[ \begin{array}{c} \log \left( P_{t}/P_{t-1}\right) -\gamma _{it}^{P} \\ \log \left( D_{t}/D_{t-1}\right) -\gamma _{it}^{D}% \end{array}% \right] ,](img68.gif)
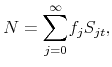
![\displaystyle P_{t\infty }=\beta \theta \left\{ \exp \left[ \gamma _{jt}^{P}+\frac{\mathbf{% \Sigma }_{jt}(1,1)}{(2j-6)}\right] P_{t\infty }+\exp \left[ \gamma _{jt}^{D}+% \frac{\mathbf{\Sigma }_{jt}(2,2)}{\left( 2j-6\right) }\right] D_{t}\right\} +\mu _{jt}.](img120.gif)
![\displaystyle \frac{1}{N}\overset{\infty }{\underset{j=0}{\sum }}f_{j}P_{t}=\frac{% 1}{N}\overset{\infty }{\underset{i=0}{\sum }}f_{j}\left[ \beta \theta \left( \left( 1+\gamma _{jt}^{P}\right) P_{t}+\left( 1+\gamma _{jt}^{D}\right) D_{t}\right) +\mu _{jt}\right]](img123.gif)
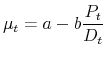
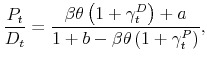
![\displaystyle \gamma _{t}^{D}=\frac{1}{N}\overset{\infty }{\underset{i=0}{\sum }}% f_{i}\gamma _{it}^{D}\approx \gamma _{t-1}^{D}+(1-\theta )\left[ \log \left( D_{t-1}/D_{t-2}\right) -\gamma _{t-1}^{D}\right] .](img148.gif)
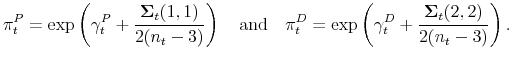
![\displaystyle \frac{P_{t}}{D_{t}}=\beta \theta E_{t}\left[ \frac{D_{t+1}}{D_{t}}\left( 1+% \frac{P_{t+1}}{D_{t+1}}\right) \right] =\overset{\infty }{\underset{j=1}{% \sum }}\left( \beta \theta \right) ^{j}e^{j\left( \gamma +\sigma ^{2}/2\right) }+\lim_{T\rightarrow \infty }E_{t}\left( \left( \beta \theta \right) ^{T}\frac{D_{t+T}}{D_{t+T-1}}\frac{P_{t+T}}{D_{t+T}}\right) .](img178.gif)
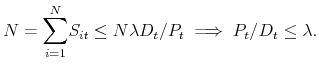
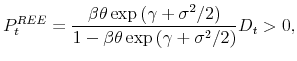
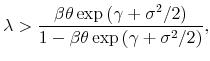
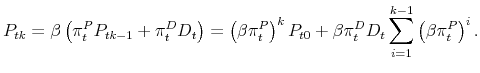
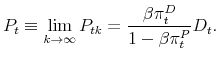
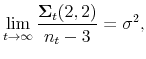 and
and ![\displaystyle \lim_{t\rightarrow \infty }\log \left( P_{t}/P_{t-1}\right) =\lim_{t\rightarrow \infty }\left\{ \log \left[ \frac{\pi _{t}^{D}\left( 1-\beta \pi _{t-1}^{P}\right) }{\pi _{t-1}^{D}\left( 1-\beta \pi _{t}^{P}\right) }\right] +\log \left( D_{t}/D_{t-1}\right) \right\} .](img270.gif)