Skip to: [Printable Version (PDF)] [Bibliography] [Footnotes]

Finance and Economics Discussion Series: 2012-46 Screen Reader version ^♣

Monetary Policy and Long-Term Real Rates¹

Samuel G. Hanson

Harvard University

Jeremy C. Stein

Federal Reserve Board

First draft: July 2012

Keywords: Monetary policy, real interest rates, term premia

Abstract:

Changes in monetary policy have surprisingly strong effects on forward real rates in the distant future. A 100 basis-point increase in the 2-year nominal yield on an FOMC announcement day is associated with a 42 basis-point increase in the 10-year forward real rate. This finding is at odds with standard macro models based on sticky nominal prices, which imply that monetary policy cannot move real rates over a horizon longer than that over which all prices in the economy can readjust. Rather, the responsiveness of long-term real rates to monetary shocks appears to reflect changes in term premia. One mechanism that may generate such variation in term premia is based on demand effects coming from "yield-oriented" investors. We find some evidence supportive of this channel.

JEL Classification: E43, E52

1 Introduction

In this paper, we document that changes in the stance of monetary policy have surprisingly strong effects on very distant forward real interest rates. Concretely, we show that a 100 basis-point (bp) increase in the 2-year nominal yield on a Federal Open Markets Committee (FOMC) announcement day-which we use as a proxy for changes in expectations regarding the path of the federal funds rate over the following several quarters-is associated with a 42 bp increase in the 10-year forward overnight real rate, extracted from the yield curve for Treasury Inflation Protected Securities (TIPS).

Our findings can be illustrated with the FOMC's much-discussed announcement on January 25, 2012. On that date the FOMC significantly changed its forward guidance, indicating that it expected to hold the federal funds rate near zero "through late 2014" whereas it had previously only stated that it expected to do so "through mid-2013."² In response to this announcement, the expected path of short-term nominal rates fell significantly from two to five years out, with the 2-year nominal yield dropping by 5 bps and the 5-year nominal yield by 14 bps. More strikingly, 10-year and 20-year real forward rates declined by 5 bps and 9 bps respectively. In other words, distant real forward rates appeared to react strongly to news about the future stance of monetary policy.

This finding is at odds with standard New-Keynesian macro models, in which the central bank's ability to influence real variables stems from that fact that goods prices are sticky in nominal terms. In such models, a change in monetary policy should have no impact on forward real interest rates at a horizon longer than that over which all nominal prices can readjust, and it seems implausible to think that this horizon could be anything close to ten years.³

So how does one make sense of our finding? One possibility is that the results are simply wrong in some sense-i.e., they are either not robust or non-causal. On the robustness front, one limitation of our analysis is that there is a relatively brief sample period in the US over which we can study real rates-TIPS were introduced in 1997 and reliable data only become available in 1999. In an effort to address this concern, we replicate our analysis on UK data over this same period and find broadly similar results.

With respect to causality, a worry is that movements in short-term nominal rates on FOMC announcement days may not reflect innovations to Fed policy per se, but rather just the response of the Fed to information about the future evolution of the economy. For example, suppose there is news suggesting a permanent positive productivity shock. It is possible that this shock both raises the natural (flexible-price) real interest rate in the economy forever, and at the same time leads the Fed to tighten in the short run. If so, it would be a mistake to conclude that the increase in distant forward real rates was caused by an autonomous change in Fed policy.

Although it is difficult to completely rule out this possibility, we can make some progress by comparing the results we get for FOMC announcement days to the analogous results for non-FOMC days. The idea is that non-FOMC days also have their fair share of macro news, but are less likely to be informative about shifts in the Fed's reaction function. Thus, if the elasticity of long-term real rates to short-term nominal rates is driven by macro news, this elasticity should be stronger on non-FOMC days, which arguably have a greater relative proportion of macro news and less reaction-function news. However, this prediction is not borne out in the data. If anything, we find the reverse: distant forward real rates react more strongly to changes in short-term nominal rates on FOMC days than on non-FOMC days. Although not a definitive test, this provides some support for thinking about the FOMC-announcement-day results as reflecting the causal consequences of changes in the stance of monetary policy.

Assuming that the results can be given a causal interpretation, what economic mechanism do they reflect? It is helpful to begin by noting that a movement in the 10-year forward real rate can always be decomposed into a change in the expected real rate that will prevail in 10 years, plus a change in the 10-year real term premium. A movement in the real term premium is equivalent to saying that when the Fed raises short-term nominal rates, this increases the expected return on a carry-trade strategy that borrows short-term and buys long-term real bonds.⁴

This decomposition suggests two broad economic channels that could be at work. The first involves monetary policy somehow moving expected future real rates at very distant horizons. If this channel were operative, it would be a form of long-run monetary non-neutrality that runs directly counter to the rational-expectations spirit of New-Keynesian models. In other words, it is hard to see how this channel could be squared with the bedrock assumption in these models, namely that nominal prices are set in a rational, forward-looking manner.

The alternative possibility is that monetary policy does not move expected future real rates far out into the future, but rather that it changes the term premia on long-term bonds. This implies that the effects on forward rates that we document should be expected to mean revert over time. To test this hypothesis, we proceed as follows. At any point in time t, we cumulate the changes in long-term forward rates that occurred solely on FOMC announcement days over the preceding three months. We then use these FOMC-announcement-day changes to forecast changes in forward rates over the subsequent twelve months. It turns out that when long-term forward rates rise on an FOMC announcement day, this portends a reversal of forward rates over the next twelve months. The evidence is thus consistent with the proposition that monetary policy shocks induce time-variation in real term premia.⁵

This then raises the question of why monetary policy might be influencing real term premia. In traditional representative-agent asset pricing models, term premia are pinned down by the covariance between real bond returns and investors' marginal utility. It is difficult to see why monetary shocks would change this covariance in the required direction, so we focus instead on an alternative class of supply-and-demand-based mechanisms. One specific explanation that we flesh out in detail has to do with a set of "yield-oriented" investors. We assume that these investors allocate their portfolios between short and long-term bonds, and in doing so, put some weight in their objective functions not just on expected holding-period returns, but also on current income or yield. This could be because of agency or accounting considerations that lead them to care about short-term measures of reported performance.

A reduction in short-term nominal rates leads these investors to rebalance their portfolios towards longer-term bonds, in an effort to keep their overall portfolio yield from declining too much. This in turn creates buying pressure that raises the price of the long-term bonds, and hence lowers long-term real yields and forward rates. Note that this price pressure is independent of expectations about the actual path of future short rates-it is a pure term-premium effect. And interestingly, according to this hypothesis, conventional monetary policy moves long-term real rates in much the same way as some of the Fed's recent unconventional policy measures, such as its quantitative-easing purchases of long-term Treasuries. These too are presumed to operate through a supply-and-demand effect on term premia as opposed to by changing expectations about the future path of rates.

We go on to provide some evidence that is consistent with our hypothesis about the role of yield-oriented investors. We do so by looking at the maturity of securities held by commercial banks. Banks fit with our conception of yield-oriented investors to the extent that they care about their reported earnings-which, given bank accounting rules, are based on current income from securities holdings and not mark-to-market changes in value. And indeed, we find that when the yield curve steepens, banks increase the maturity of their securities holdings. Moreover, the magnitudes of these portfolio shifts are large in the aggregate, so that if they had to be absorbed by other, less yield-oriented investors (e.g., broker-dealers or hedge funds) they could plausibly drive changes in market-wide term premia. We also find that primary dealers in the Treasury market-who, unlike banks, must mark their securities holdings to market-take the other side of the trade, reducing the maturity of their Treasury holdings when the yield curve steepens.

The ideas in this paper connect to several strands of prior research. There is a large literature which examines the impact of monetary policy surprises on long-term nominal interest rates. For example, Cochrane and Piazzesi (2002) find that a 100 bp increase in the one-month Eurodollar rate around the time of a fed-funds target change is associated with a 52 bp increase in 10-year nominal Treasury yields. They too cast this as something of a puzzle, remarking that: "the size of the coefficients is particularly startling" (page 92). In a similar vein, Gürkaynak, Sack, and Swanson (2005a) show that distant nominal forward rates respond strongly to a variety of macroeconomic news releases, including FOMC announcements.⁶

We sharpen the puzzle by focusing on real forward rates instead of nominal yields or nominal forward rates, which puts the long-run non-neutrality issue front-and-center. By contrast, Gürkaynak, Sack, and Swanson (2005a) argue that their results are consistent with a model in which long-run inflation expectations are not well anchored and are revised in light of incoming news. According to this explanation, monetary shocks might alter long-run inflation expectations, but would have no impact on long-run real rates.

The yield-oriented investors that drive term premia in our model are reminiscent of Rajan's (2005) account of investor behavior in a low-interest-rate environment. And the idea that supply-and-demand effects can have important consequences in the Treasury market is central to a number of recent papers, including Gagnon et al (2010), Greenwood and Vayanos (2010a, 2010b), Krishnamurthy and Vissing-Jorgensen (2011, 2012), and Vayanos and Vila (2009). An important antecedent to this work is Modigliani and Sutch (1966).

The remainder of the paper is organized as follows. In Section II, we document the strong sensitivity of long-term real forward rates to monetary policy news, and argue that this relationship is likely to be causal. In Section III, we make the case that movements in long-term forward rates around monetary policy announcements reflect changes in term premia. In Section IV, we investigate the mechanism behind these changing term premia. Section V concludes.

2 The Sensitivity of Long-Term Real Forward Rates to Monetary Policy News

2.1 Measuring Monetary Policy News

To get started, we need a measure of monetary policy news. There is a growing consensus that changes in the policy outlook are the primary form of monetary policy news on FOMC announcement days. Thus, building on Gürkaynak, Sack, and Swanson (2005b) and Campell, Evans, Fisher, and Justiniano (2012), our measurement strategy is based on the premise that, at least since 1994, a significant portion of the news contained in FOMC announcements is about the expected path of the federal funds rates over the next several quarters, as opposed to surprise changes in the current funds rate.⁷

In order to capture revisions to the full expected path of the funds rate over the coming quarters in a simple and transparent manner, we use the change in the 2-year nominal Treasury yield on FOMC announcement dates as our proxy for monetary policy news. However, as described in our robustness tests below, we obtain similar results with a variety of related variables that capture revisions in expected short rates over the following several quarters. The key is that these variables capture news about the expected medium-term path of interest rates-as opposed to only news about rates over the coming month or two.

In our baseline specification, for an FOMC meeting on day t, we compute changes from t-1 to t+1 in order to capture the full market response to the announcement. We focus on 2-day changes because Gürkaynak, Sack, and Swanson (2005b) present intra-day evidence which suggests that the market takes time to process the information contained in FOMC statements about the likely path of the funds rate. Moreover, one might expect a slightly more gradual adjustment process to the extent that some of the reaction of long-term rates is quantity-mediated-i.e., involves portfolio rebalancing by some investors-as opposed to reflecting a pure shift in the expectations of all investors. Nevertheless, our results our qualitatively similar, albeit somewhat smaller in magnitude, if we instead measure changes over the 1-day interval from day t-1 to t.

We use data from Gürkaynak, Sack, and Wright (2007, 2010) on the nominal Treasury yield curve and the real (TIPS) Treasury yield curve as updated regularly by the Federal Reserve Board. Each day they estimate the 6-parameter model of the instantaneous forward curve proposed by Svensson (1994). Zero coupon yields are then obtained by integrating along the estimated forward curve

$\displaystyle y_{t}^{(n)} =n^{-1} \int _{0}^{n}f_{t}^{(m)} dm.$

(1)

The parameters are estimated each day by minimizing a weighted sum of pricing errors. Estimates of the nominal yield curve are based on a sample of nominal Treasuries that includes almost all off-the-run notes and bonds with more than three months to maturity. Estimates of the real yield curve are based on all TIPS with a remaining maturity longer than 18 months.⁸

We can decompose the n-year nominal forward rate $f_{t}^{\$ (n)}$ into the sum of the forward real rate $f_{t}^{TIPS(n)}$ and the forward break-even inflation rate $f_{t}^{\pi (n)}$ ,

$\displaystyle f_{t}^{\$ (n)} =f_{t}^{TIPS(n)} +f_{t}^{\pi (n)} .$

(2)

The n-year nominal zero-coupon yield can be decomposed analogously

$\displaystyle y_{t}^{\$ (n)} =y_{t}^{TIPS(n)} +y_{t}^{\pi (n)} .$

(3)

2.2 Baseline Results for the US

In our baseline specifications, we regress changes in forward nominal rates, forward real rates, and forward break-even inflation rates on changes in 2-year nominal yields

$\displaystyle \Delta f_{t}^{\$ (n)}$	$\displaystyle = a_{\$} (n)+b_{\$} (n)\cdot \Delta y_{t}^{\$(2)} +\Delta \varepsilon _{t}^{\$(n)}$	(4a)
$\displaystyle \par \Delta f_{t}^{TIPS(n)}$	$\displaystyle = a_{TIPS} (n)+b_{TIPS} (n)\cdot \Delta y_{t}^{\$(2)} +\Delta \varepsilon _{t}^{TIPS(n)}$	(4b)
$\displaystyle \par \Delta f_{t}^{\pi (n)}$	$\displaystyle = a_{\pi } (n)+b_{\pi } (n)\cdot \Delta y_{t}^{\$(2)} +\Delta \varepsilon _{t}^{\pi (n)}$	(4c)

We focus on FOMC announcement dates from 1999-present. However, we exclude five FOMC announcement dates that contained significant news about the Fed's Large Scale Asset Purchases (sometimes referred to as "QE1", "QE2" and "Operation Twist").⁹ We do so because the mechanism underlying long-term rate movements on these dates is potentially different from that driving market reactions to more conventional FOMC announcements.

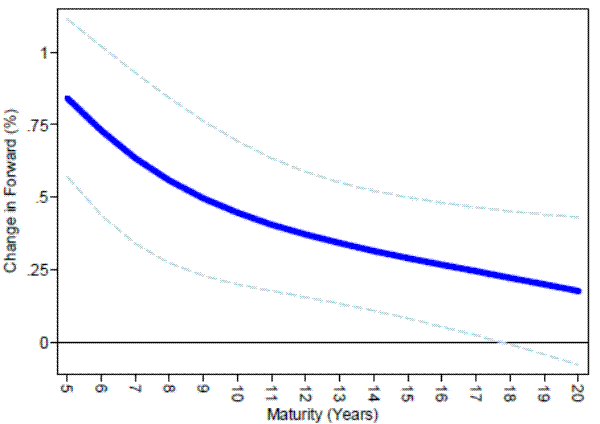
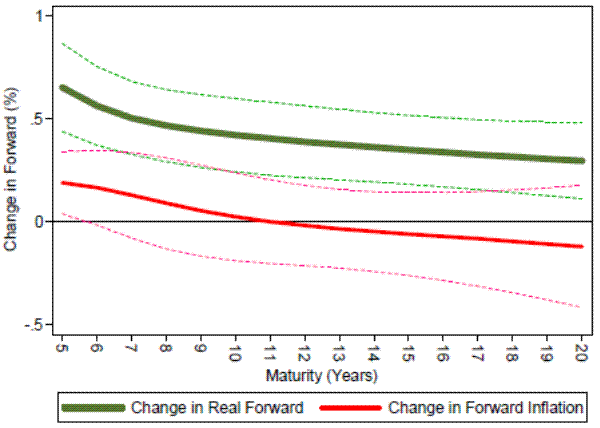
Table 1 and Figure 1 present the basic results. Panel A of Figure 1 shows how the nominal forward curve responds to a 100 basis-point shock to short-term nominal rates. Specifically, Figure 1A plots the coefficients from regression (4a) for maturities n = 5, ..., 20 along with 95% confidence intervals. Panel B of Figure 1 decomposes the response of nominal forwards into a change in real forwards and forward breakeven inflation, plotting the coefficients from regressions (4b) and (4c). By construction, the sum of the two coefficients shown in Panel B equals the coefficient in Panel A. Table 1 lists all the regression coefficients.

Table 1 and Figure 1 show that distant nominal forwards respond significantly to changes in short-term nominal rates on FOMC days. And, surprisingly, this response is driven almost exclusively by movements in real forwards. A 100 bps shock to the 2-year nominal rate on an FOMC announcement date is associated with a 45 bps increase in 10-year nominal forwards (t = 3.54). And this 45 bps increase can be decomposed into a 42 bps rise in real forwards (t = 4.63) and a 3 bps rise in forward break-even inflation (t = 0.23). This pattern holds even as we consider more distant forwards. A 100 bps shock to 2-year nominal rates is associated with an 18 bps increase in 20-year nominal forwards (t = 1.32), which reflects a 30 bps rise in real forwards (t = 3.15) and a 12 bps decline in forward break-evens (t = -0.79).

Table 2 conducts a variety of robustness exercises. First, we vary the event window. In our baseline results, we use a 2-day window from day t-1 to day t+1. In Table 2, we report comparable results where we use a 1-day window from t-1 to t. As noted above, our results are somewhat smaller in magnitude with the 2-day window. Next we try a using a variety of alternative measures of short-run nominal rates in place of 2-year Treasury yields. These include: 1-year Treasury yields; the overnight index swap (OIS) linked to the federal funds rate; fed funds futures; and Eurodollar futures contracts. The basic take-away is that everything works similarly with any variable that captures news about the medium-term path of rates, as opposed to one that only captures what the target will be in the next few weeks. This is shown explicitly where construct the "future path of policy" news factor as in Gürkaynak, Sack, and Swanson (2005b). Finally, we vary the sample. For example, we add QE dates or the dates on which FOMC minutes are released. This has little impact on the results.

2.3 Parallel Results for the UK

To further investigate the robustness of our results, we run the analogous set of regressions using UK data. To do so, we rely on the yield curve estimates published by the Bank of England (BOE) which employ the spline-based techniques described in Andersen and Sleath (2001). As above, we estimate regressions (4a), (4b), and (4c) on all dates when the BOE's Monetary Policy Committee (MPC) has met since 1999.¹⁰ Our proxy for news on MPC dates is the change in the 2-year nominal yield. And, as above, we compute changes from t-1 to t+1 for meetings on day t. And we drop six MPC dates from 2009 to 2011 when there was significant news about the BOE's quantitative easing operations.¹¹

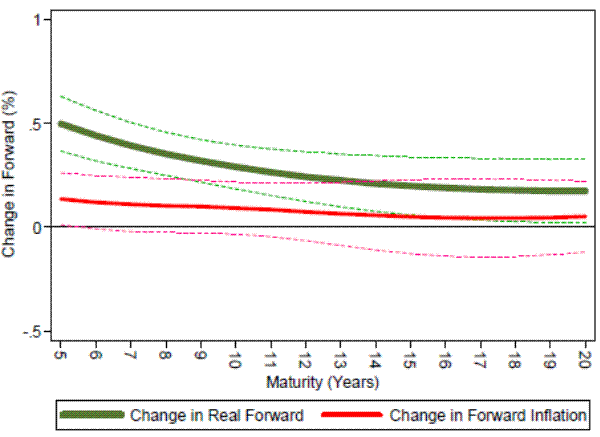
Table 3 and Figure 2 present the basic results for the UK. The estimates are generally similar to those from the US, although the magnitude of the effect is slightly smaller in the UK In particular, for the 10-year forward real rate, the coefficient on the two-year nominal yield is 0.291 in the UK as compared to 0.421 in the US.

2.4 Do Monetary Shocks Cause the Movements in Distant Real Forward Rates?

In spite of our focus on FOMC announcement days, it could be argued that the above results may not reflect a causal impact of monetary policy innovations on long-term real rates. Rather, it could be that the Fed's policy announcement is simply a response to its private information about the future evolution of the economy, and it is the release of the Fed's private information-as opposed to news about its reaction function-that moves long-term real rates.

For example, suppose the Fed has private information to the effect that the economy's long-run growth potential is weaker than previously believed. This might cause the Fed to ease policy, reducing the expected path of nominal rates over the next several quarters. And once disclosed, the same information might also lead investors to expect the long-run natural real rate to decline. However, the movement in long-term real rates would not be a causal consequence of monetary policy in this case, as it would have happened even had the Fed chosen not to ease.

This reverse-causality story is already somewhat suspect on an a priori basis, because it presumes that the Fed has material private information about the very long-run evolution of the economy. And a variety of studies have shown that the Fed does not have any forecasting advantage relative to private analysts more than a few quarters into the future.¹²

Nevertheless, we take a crude stab at testing the reverse-causality hypothesis. To do so, we compare our results above to those on all non-FOMC-announcement days. The intuition for this experiment is as follows. Non-FOMC days see the release of a variety of fundamental macro news items-the same kind of macro news that the Fed is ostensibly revealing with its FOMC announcements in the private-information story-but are less likely to bring news about the Fed's reaction function. Thus if the elasticity of long-term real rates to short-term nominal rates is simply driven by macro news, as is posited in reverse-causality hypothesis, this elasticity should be stronger on non-FOMC days, which arguably have a greater relative proportion of macro news as compared to reaction-function news.

To implement the test, we estimate

$\displaystyle \Delta f_{t}^{TIPS(n)} =a+b\cdot \Delta y_{t}^{\$ (2)} +c\cdot FOMC_{t} +d\cdot \Delta y_{t}^{\$ (2)} \times FOMC_{t} +\varepsilon _{t}^{TIPS(n)} ,$

(5)

for n = 5, 10, and 20 using all days in the sample. The results are displayed in Table 4. The key coefficient of interest is that on the interaction term, d, which captures how the elasticity of long-term real forward rates to short-term nominal rates on FOMC days differs from that on non-FOMC days. According to the reverse-causality hypothesis, we would expect this coefficient to be negative. In fact, it is generally positive, although only marginally significant. The point estimates for 10-year real forwards suggest that the elasticity on non-FOMC days is 0.268, as compared to a value of 0.421 on FOMC days.

Thus the results in Table 4 fail to support the reverse-causality hypothesis.¹³ Of course, this is not the same thing as having a clean instrument for exogenous shocks to the Fed's reaction function. So while we believe the balance of the evidence favors a causal interpretation of the role of monetary policy on long-term real forwards, the identification is admittedly not airtight.

3 Changes in Expected Future Rates vs. Changes in Term Premia

If one accepts the premise that monetary policy does indeed have an important causal impact on long-term real forward rates, the natural next question to ask is whether this reflects changes in expected future real rates or changes in term premia. If it is the former, this would represent a direct challenge to the notion that monetary policy is neutral in the long run, since the implication would be that a change in policy today has a large effect on the expected level of the real rate 10 years or more into the future. If it is the latter, this opens the door to a novel monetary transmission channel. And one would then want to understand the strength and persistence of this term premium effect, as well as the economic mechanisms that give rise to it.

3.1 Forecasting Regressions

As a matter of bond accounting, a change in the n-year forward real rate can always be decomposed into a change in the expected real rate that will prevail in n-1 years, plus a change in the n-year real term premium.¹⁴ Letting $f_{t}^{(n)}$ be the n-year forward rate at time t, $r_{t+1}^{(n)}$ the realized return on an n-period zero-coupon bond from t to t+1, and $y_{t}^{(1)}$ the yield on a one-period bond at time t (i.e., the short rate), it is straightforward to show that, for changes in distant forward rates over a short horizon, we have

$\displaystyle \Delta f_{t}^{(n)} =\overbrace{\Delta E_{t} [y_{t+n-1}^{(1)} ]}^{{\rm News about future short rates}}+\overbrace{\Delta E_{t} [\sum _{j=1}^{n-1}(r_{t+j}^{(n+1-j)} -r_{t+j}^{(n-j)} )]}^{{\rm News about future term premia}}.$

(6)

In other words, unexpected changes in long-dated forward rates must either reflect (i) news about expected short rates in the distant future or (ii) news about future term premia. This is similar to Campbell's (1991) observation that unexpected stock returns must either be due to cash-flow news or discount-rate news.

To test whether movements in distant forward rates reflect news about future short rates or news about future term premia, we run regressions in which we use 3-month changes in the forward rate, $f_{t}^{(n)} -f_{t-1/4}^{(n)}$ , to forecast subsequent changes in forward rates over a 12-month horizon, $f_{t+1}^{(n-1)} -f_{t}^{(n)}$ . Since $f_{t+1}^{(n-1)} -f_{t}^{(n)} =-(r_{t+1}^{(n)} -r_{t+1}^{(n-1)} )$ , this is directly equivalent to a test of equation (6). That is, if movements in forward rates were only informative about future short rates, and not about excess bond returns, there would be no predictable mean reversion in forward rates. Conversely, if we do find evidence of mean reversion in forward rates, this maps into a particular trading strategy that earns excess returns. For example, if the 10-year forward rate jumps up today and is expected to fall back over the next year, this is the same as saying that 10-year bonds are expected to outperform 9-year bonds over the next year.

We face an important data limitation in this forecasting exercise. Ideally, we would like to do everything in real terms, since our focus thus far has been on real rates. However, given the short span of the TIPS data and the fact that we are we are working with 12-month returns, this leaves us with only dozen fully independent observations. So we worry about relying solely on TIPS forecasting regressions from 1999-2011.

Instead we first focus on the nominal data, which allow us to consider a longer sample. We restrict attention to the 1987-present (post-Volcker) period in which inflation expectations have been relatively well-anchored in the US. It seems plausible to use the nominal data as a proxy for the missing real data over this period. In particular, our key independent variable is the change in the 10-year forward rate on FOMC announcement days. For the post-1999 period for which we have data on both, the correlation between the real and the nominal versions of this variable is 0.77. And the correlation between the nominal and real versions of our dependent variable-the change in forwards over 12-month intervals-is 0.82. This suggests that using nominal data in place of real data to extend the sample is a reasonable way to proceed.

Panel A of Table 5 presents these forecasting results. In column (1), we begin by estimating the following univariate regression

$\displaystyle f_{t+1}^{\$ (9)} -f_{t}^{\$ (10)} =a+b\cdot (f_{t}^{\$ (10)} -f_{t-1/4}^{\$ (10)} )+\varepsilon _{t+1}^{\$ (10)} .$

(7)

That is, we use the change in the 10-year nominal forward rate over the prior quarter to predict the change in forward rates over the following 12 months.¹⁵ Again, as a benchmark, one would expect b = 0 under the log expectations hypothesis. (Since $f_{t}^{\$ (10)} =E_{t} [f_{t+1}^{\$ (9)} ]$ under the expectations hypothesis, it should be impossible to forecast $f_{t+1}^{\$ (9)} -f_{t}^{\$ (10)} =f_{t+1}^{\$ (9)} -E_{t} [f_{t+1}^{\$ (9)} ]$ ). We obtain b = -0.343 (t = -3.21), implying that a 100 bps rise in the nominal forward rate in a given quarter is associated with a 34 bps decline over the following 12 months.

In column (2) we present instrumental variables (IV) estimates of equation (7) using $y_{t}^{\$ (2)} -y_{t-1/4}^{\$ (2)}$ as an instrument for $f_{t}^{\$ (10)} -f_{t-1/4}^{\$ (10)}$ . These IV estimates enable us to examine the reversion following movements in forward rates that are themselves a response to changes in short rates. The large IV estimates suggest that the response of forwards to changes in short rates is quickly reverted away. Indeed the IV estimate of b = -1.078 (t = -2.13) implies that the initial response is completely reversed within 12 months. Thus, the IV estimates are consistent with the idea that the response of distant forwards to short rates primarily reflects movements in term premia as opposed to changes in expected short rates.

Columns (3) and (4) show that similar results hold when we control for the forward rate spread $f_{t}^{\$ (10)} -y_{t}^{\$ (1)}$ -i.e., the difference between the 10-year forward rate and the short rate-as in Fama and Bliss (1987). Our results also hold up if we control for other bond forecasting variables, including the term spread as in Campbell and Shiller (1989) or linear combinations of forward rates as in Cochrane and Piazzesi (2005) and Cieslak and Pavlova (2011).

In column (5) we break the change in the 10-year forward rate into the component that occurs on FOMC days and the component that occurs on other non-FOMC days, and use these separately as predictive variables

$\displaystyle f_{t}^{\$ (10)} -f_{t+1}^{\$ (9)} =a+b\cdot (f_{t}^{\$ (10)} -f_{t-1/4}^{\$ (10)} )_{FOMC} +c\cdot (f_{t}^{\$ (10)} -f_{t-1/4}^{\$ (10)} )_{NONFOMC} +\varepsilon _{t+1}^{\$ (10)} .$

(8)

This approach is more tightly connected to our earlier findings, as it allows us to focus on those changes in forward rates that are associated with monetary-policy announcements. The cost is that it sacrifices considerable statistical power, given the small number of FOMC days.

As shown in column (5), the coefficient on the FOMC-days part of the forward rate change (b = -0.564, with a t-statistic of -1.69) is somewhat larger than its counterpart for non-FOMC days (c = -0.321, with a t-statistic of -2.86). The IV estimates, where we instrument for $(f_{t}^{\$ (10)} -f_{t-1/4}^{\$ (10)} )_{FOMC}$ and $(f_{t}^{\$ (10)} -f_{t-1/4}^{\$ (10)} )_{NONFOMC}$ with $(y_{t}^{\$ (2)} -y_{t-1/4}^{\$ (2)} )_{FOMC}$ and $(y_{t}^{\$ (2)} -y_{t-1/4}^{\$ (2)} )_{NONFOMC}$ respectively, also result in a larger coefficient for the FOMC-days piece than the non-FOMC-days piece. Although the statistical significance of the FOMC-days piece is marginal, the point estimates suggest that movements in forward rates on FOMC days contain just as much-and perhaps even slightly more-discount rate news as those on non-FOMC days.

Panel B of Table 5 presents the real analogs to equations (7) and (8) for the 1999-present period. Reassuringly, we obtain similar point estimates using the TIPS data over this shorter sample period.¹⁶ For example, the coefficient on the change in the real forward rate on FOMC announcement days from the OLS regression in column (5) is -0.567 (t = -2.05), as compared to a value of -0.564 in the nominal data using data back to 1987.

Of course, whether the sample period is 1987-present or 1999-present, any attempt to forecast annual bond returns with a relatively small number of independent observations should be viewed with a healthy dose of skepticism. At the same time, it is important to be clear on the competing theories that are at play in this case and how they might shape one's priors. Often when one is trying to predict asset returns, the null of no predictability has a strong ex ante theoretical standing, and so it may make sense to set a high bar for rejecting the null. But in this case, recall that a null of no predictability is equivalent to the proposition that monetary policy shocks have a powerful effect on expected real rates 10 years into the future-in other words, that monetary policy is non-neutral over very long horizons. For somebody who finds such a proposition hard to swallow, our forecasting results offer an alternative interpretation that may be more palatable, even if the statistical significance of these results is not overwhelming.

3.2 Impulse Response Functions

Another way to illustrate the mean reversion of forward rates is to examine their impulse response to an initial shock to short rates. To do this, we again work with daily data and the 10-year instantaneous forward rate. We begin by separately estimating

$\displaystyle f_{t+k}^{\$ (10)} -f_{t-1}^{\$ (10)} =a_{\$ } (k)+b_{\$ } (k)\cdot (y_{t+1}^{\$ (2)} -y_{t-1}^{\$ (2)} )+\Delta \varepsilon _{t+k}^{\$ (10)} ,$

(9)

for k = 1, ..., 250 using all days in the sample. That is, we regress the cumulative change in 10-year nominal forwards from day t-1 to day t+k on the change in short-term nominal rates from t-1 to t+1. These 250 regressions differ only in terms of the left-hand-side variable, namely the horizon over which we compute the cumulative subsequent change in 10-year forwards.

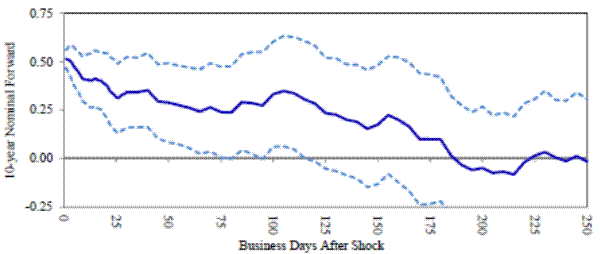
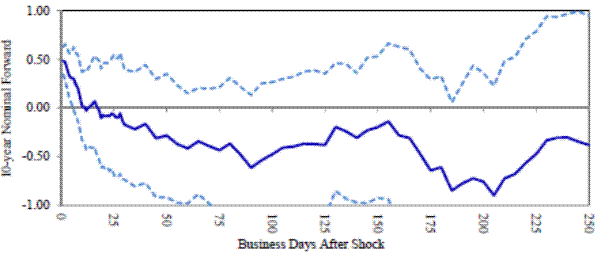
Panel A of Figure 3 plots the coefficient b ${}_{\$}$ (k) from estimating equation (9) on all days (i.e., FOMC and non-FOMC) from 1987-present.¹⁷ The graph shows that a 100 bps shock to short-term nominal rates generates a 51 bps impulse to 10-year nominal forwards upon impact-i.e., for k = 1. This effect is then gradually reverted away over the following 9 months, consistent with the idea that the initial response reflects a change in the term premium as opposed to news about short rates. Panel B repeats the same exercise, restricting attention to only FOMC dates. Consistent with our prior findings, the picture suggests that an FOMC-day impulse to forward rates dissipates especially rapidly. However, as shown by the wide confidence intervals in Panel B, the standard errors increase by a factor of three or four when we focus on just FOMC days, so any inferences about the exact timing of the mean reversion are necessarily tentative in this case.

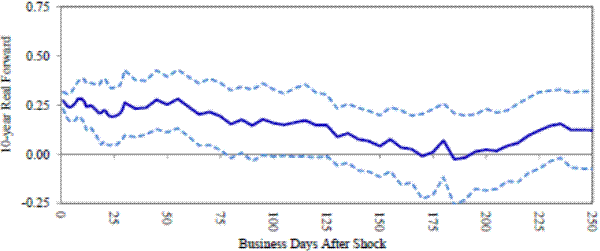
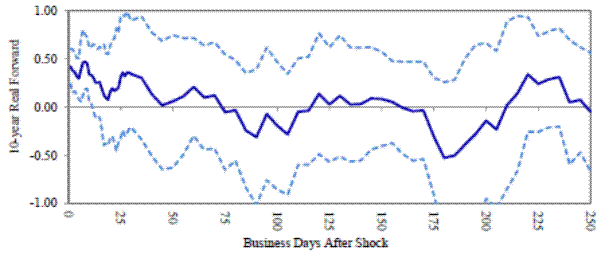
We next turn to the TIPS data from 1999-present and estimate

$\displaystyle f_{t+k}^{TIPS(10)} -f_{t-1}^{TIPS(10)} =a_{TIPS} (k)+b_{TIPS} (k)\cdot (y_{t+1}^{\$ (2)} -y_{t-1}^{\$ (2)} )+\Delta \varepsilon _{t+k}^{TIPS(10)} .$

(10)

Panel C plots the coefficient b ${}_{TIPS}$ (k) from estimating equation (10) on all days from 1999-present. The results in Panel C show that, averaging across all days, a 100 bps shock to nominal short rates is associated with a 27 bps increase in the 10-year real forward upon impact, which gradually dissipates over the following 9 months. Finally, Panel D does the same thing, but focusing only on FOMC dates. The initial impulse upon impact is 42 bps-by construction, the same as our baseline estimate from Table 2. As in Panel B, the point estimates make it appear that this effect is largely reverted away in just a few months, but again, the large standard errors associated with restricting attention to just FOMC days preclude precise inferences.

In summary, both the forecasting regressions and the impulse response functions suggest that the response of distant real forwards to nominal short rates reflects variation in term premia as opposed to news about short-term real rates far into the future. Moreover, it looks like these changes in term premia are relatively short-lived, with most of the mean reversion in forward rates occurring within a one-year horizon.

4 Why Does Monetary Policy Move Real Term Premia?

Let us review the narrative to this point. We began by documenting that monetary policy shocks are associated with large changes in distant real forward rates, and by arguing that this association is likely to be causal in nature. Next, we showed that these changes in distant forward rates appear to reflect variation in term premia as opposed to changes in expected future short rates. This leaves us with a fundamental question: what is the economic mechanism by which innovations to monetary policy influence real term premia?

Broadly speaking, there are two types of stories that one can tell. The first appeals to the standard consumption-based asset-pricing model in which the real term premium is pinned down by the covariance between real bond returns and the marginal utility of the representative investor. We discuss this theory below and argue that it is unlikely to explain our results.

An alternative class of models is one in which markets are partially segmented, and term premia are determined by supply-and-demand effects. This is how most observers have thought about the effects of the Fed's quantitative-easing policies, for example. These models are somewhat institutional by nature, so one can imagine many variations on the basic theme. For concreteness, we develop a particular supply-and-demand story based on a set of investors who care about the current yield on their portfolios. When short-term rates are low, these investors reach for yield by purchasing long-term bonds, which pushes down long-term real forward rates and lowers the term premium. We then provide some evidence that is consistent with the existence of this reaching-for-yield channel.

4.1 Real Term Premia in a Consumption-Based Asset Pricing Model

According to the standard consumption-based asset pricing model, the expected excess return on long-term real bonds at time t is given by

$\displaystyle E_{t} [R_{L,t+1} - R_{F,t} ]{\rm }=\frac{Cov_{t} [R_{L,t+1} ,- M_{t+1} ]}{E_{t} [M_{t+1} ]} =Corr_{t} [R_{L,t+1} ,- M_{t+1}]\sigma _{t} [R_{L,t+1}]\frac{\sigma_{t} [M_{t+1} ]}{E_{t} [M_{t+1}]} ,$

(11)

where the real stochastic discount factor (SDF), $M{}_{t+1}$ , depends on the marginal utility of a diversified representative investor. In light of equation (11), there are three ways to explain the finding that the real term premium falls when the Fed eases.

First, it is possible that unexpected shifts in monetary policy could affect the volatility of bond returns ${s}_{t}$ [ ${R}_{L,t+1}$ ]. However, to explain our results using this mechanism, one would further need to argue that a surprise easing meaningfully lowers conditional volatility whereas a surprise tightening raises conditional volatility. Such an asymmetry seems difficult to motivate a priori and there is little evidence for it in the data.¹⁸

Second, shifts in monetary policy could impact ${Corr}_{t}$ [ ${R}_{L,t+1}$ ,- ${M}_{t+1}$ ]. On the nominal side, Campbell, Sunderam, and Viceira (2012) argue that the correlation between inflation and the real SDF may vary over time, so this term could play a role in explaining time-variation in the inflation risk premium. It is less clear why the correlation between real bond returns and the real SDF would vary and, particularly, why it would vary meaningfully at high frequencies in response to FOMC announcements.

Finally, consider explanations that involve changes in ${s}_{t}$ [ ${M}_{t+1}$ ]-the mechanism that generates time-varying risk premia in most modern consumption-based models. These models, including habit formation (Campbell and Cochrane (1999)), long-run risks (Bansal and Yaron (2004)), or time-varying disaster risk (Gabaix (2011)), share a common reduced form: ${s}_{t}$ [ ${M}_{t+1}$ ] is high during bad economic times and low during good times. However, in order for them to be relevant for our purposes, one would have to believe that changes in the stance of monetary policy actively cause-rather than simply respond to-changes in things like long-run disaster probabilities. This seems like something of a stretch.

4.2 A Supply-and-Demand Model with Yield-Oriented Investors

An alternative explanation for why monetary policy can move term premia is based on supply-and-demand effects that operate in partially segmented bond markets.We illustrate this point with a simple model featuring a set of investors who care about the current yield on their portfolios. The key assumptions of the model are as follows. There are two dates, 1 and 2. The real log short rate at time 1, ${r}_{1}$ , is set by the central bank. The real log short rate at time 2, ${r}_{2}$ , is initially uncertain. Moreover, monetary policy is assumed to be neutral in the long run. Thus, both E[ ${r}_{2}$ ] and Var ${r}_{2}$ ] are outside of the time-1 control of the central bank and should be thought of as pinned down by long-run macroeconomic fundamentals. The only endogenous variable is ${y}_{2}$ , the time-1 log yield on real long-term (i.e., 2-period) bonds, and our interest is in seeing how ${y}_{2}$ varies with the stance of monetary policy as summarized by ${r}_{1}$ .

A fraction a of investors are "yield-oriented" with non-standard preferences described below, while a fraction (1 - a) are "expected-return-oriented" with conventional mean-variance preferences. Both investor types have unit risk tolerance.

Expected-return-oriented investors have zero initial wealth and construct long-short positions to maximize E[w ${}_{R}$ ] - Var[w ${}_{R}$ ]/2, where w ${}_{R}$ is their future wealth. If they purchase b ${}_{R}$ units of long-term bonds and finance this position by rolling over short-term borrowing, their future wealth is $w_{R} =b_{R} \cdot (2y_{2} -r_{1} -r_{2} )$ .¹⁹ Thus, expected-return-oriented investors solve

$\displaystyle \max _{b_{R} } \left\{b_{R} \cdot (2y_{2} -r_{1} -E[r_{2} ])-b_{R}^{2} \cdot Var[r_{2} ]/2\right\},$

(12)

and their demand for long-term bonds is

$\displaystyle b_{R} (y_{2} )=(Var[r_{2} ])^{-1} (2y_{2} -r_{1} -E[r_{2} ]).$

(13)

By contrast, yield-oriented investors pick their holdings of long-term bonds b ${}_{Y}$ , to solve

$\displaystyle \max _{_{b_{Y} } } \left\{b_{Y} \cdot (2y_{2} -2r_{1} )-b_{Y}^{2} \cdot Var[r_{2} ]/2\right\}.$

(14)

The only difference between equations (14) and (12) is that in (14) we have replaced E[r ${}_{2}$ ] in the first term with r ${}_{1}$ . The interpretation is that yield-oriented investors care about the spread in current yield between long- and short-term bonds (as captured by $2y_{2} -2r_{1}$ ), as opposed to the spread in expected returns (as captured by $2y_{2} -r_{1} -E[r_{2} ]$ ). Said differently, if the yield curve is upward sloping simply because E[r ${}_{2}$ ] exceeds r ${}_{1}$ , this will make long-term bonds more attractive to the yield-oriented investors, but not to the expected-return-oriented investors. Thus, the demand for long-term bonds from yield-oriented investors depends on the difference in current income from owning long- versus short-term bond

$\displaystyle b_{Y} (y_{2} )=(Var[r_{2} ])^{-1} (2y_{2} -2r_{1} ).$

(15)

We assume there is a fixed supply Q of long-term real bonds. The market clearing condition for long-term bonds is $Q=\alpha \cdot b_{Y} (y_{2}^{*} )+(1-\alpha )\cdot b_{R} (y_{2}^{*} )$ which implies that the equilibrium long-term forward rate is

$\displaystyle {\rm }\overbrace{2y_{2}^{*} -r_{1} }^{{\rm Forward rate}}=\overbrace{E[r_{2} ]}^{{\rm Expected short rate}}+\overbrace{Q\cdot Var[r_{2} ]-\alpha \cdot (E[r_{2} ]-r_{1} )}^{{\rm Term premium}}.$

(16)

Similarly, the expected excess return on long-term bonds is

$$\displaystyle 2y_{2}^{*} -E[r_{2} ]-r_{1} =\overbrace{Q\cdot Var[r_{2} ]}^{{\rm$

(17)

Equations (16) and (17) show that the term premium has two components. There is a traditional component, $Q\cdot Var[r_{2} ]$ , that depends on bond supply and fundamental uncertainty, and a reaching-for-yield component, $-\alpha (E[r_{2} ]-r_{1} )$ , that depends on the fraction of yield-oriented investors and the level of short-term interest rates.

The reaching-for-yield term in (16) and (17) is what enables the model to rationalize our prior findings, namely that an easing of monetary policy is associated with a decline in distant real forwards and a decline in the real term premium. When the central bank cuts the short rate, $E[r_{2} ]-r_{1}$ rises and the term premium falls. Intuitively, this is because yield-oriented investors are hungrier for current income when $r_{1}$ is low. As a result, they are willing to take on more duration risk by purchasing higher-yielding long-term bonds. And due to the limited risk tolerance of investors on the other side of the trade, this shift in demand lowers the term premium on these long-term bonds. Note that this explanation draws no distinction between movements in rates on FOMC versus non-FOMC days-it doesn't matter whether rates move due to news about the Fed's reaction function or news about macroeconomic fundamentals. Yield-oriented investors care about the differential carry from holding long-term bonds irrespective of its root cause.

Why, according to this view, would one expect this lower term premia to accrue largely over the following 12 months? There are a few possibilities. A first is that a decline in short rates only temporarily boosts demand for long-term Treasuries from yield-oriented investors. Perhaps some yield-oriented investors initially respond to a drop in short rates by taking on more duration risk, but over time they instead shift towards taking on more credit risk. Alternatively, if arbitrage capital moves slowly in response to changes in risk-adjusted returns, the demand shock from yield-oriented investors may be met with increased arbitrageur capital over time. Or, following Greenwood, Hanson, and Stein (2010), the increased demand for long-term bonds may be gradually accommodated by non-financial firms who adjust their debt maturity in response to shifts in investor demand. We attempt to shed some light on these issues below.

4.3 Evidence on the Behavior of Yield-Oriented Investors

In addition to rationalizing the movements in real forward rates and term premia documented in Sections II and III, the model offers an additional set of predictions. Specifically, if we can identify a priori those investors who are most prone to be yield-oriented, their holdings of long-term bonds should be increasing in the yield spread. This follows immediately from equation (15), which says that the demand of yield-oriented investors is a function of $(y_{2} -r_{1} )$ .

Of course, the holdings of the investing public as a whole must equal the fixed supply of long-term bonds, so there must be other investors (e.g., broker-dealers or hedge funds) who care less about current yield differentials and more about expected returns, and who take the other side of the trade. In what follows, we use commercial banks as a proxy for yield-oriented investors and primary dealers as a proxy for expected-return-oriented investors. As explained below, the logic of this split is based on existing accounting conventions, which arguably should have the effect of making banks more concerned with current yield than dealers.

4.3.1 Commercial Banks

We use quarterly Call Report data on the duration of commercial bank security portfolios to test the hypothesis that banks act like the yield-oriented investors in our model. Several factors suggest that commercial banks may be prone to behave in a yield-oriented fashion. First, the vast majority of commercial banks (weighted by market value) are publicly traded, so bank managers with short horizons may be tempted to take actions that boost current reported earnings at the expense of longer-term earnings (see e.g., Stein (1989)). Second, due to GAAP accounting conventions, a bank can typically boost near-term accounting earnings simply by replacing low-yielding securities in its non-trading accounts with higher-yielding securities.²⁰ This is because interest income on non-trading-account securities flows through the income statement, but unrealized gains and losses on such securities do not flow through net income. Thus, a desire to boost current reported profits could lead bank managers to invest more aggressively in long-term securities when the yield curve is steep. Finally, because GAAP earnings also drive changes in regulatory capital, a bank may be able to boost its capital ratios and generate regulatory slack in the near-term by engaging in a larger carry-trade when the curve is steep.

Given the coarse disclosure available in the Call reports, we focus on a crude measure of securities portfolio duration: the aggregate fraction of non-trading-account securities with a current remaining maturity (for fixed-rate securities) or next re-pricing date (for floating-rate securities) of one year or longer: $({SEC}_{LT}/{SEC})$ . This measure is available beginning in 1988. Using quarterly data, we estimate specifications of the form

$\displaystyle \Delta (SEC_{LT} /SEC)_{t} =a+b\cdot \Delta (y_{t}^{\$ (10)} -y_{t}^{\$ (1)} )+\Delta u_{t} ,$

(18)

where $({y}^{\$(10)} - {y}^{\$(1)})$ is the yield spread, measured as the difference in current yield between 10- and 1-year nominal Treasuries. A finding that b

0 would suggest that banks reach for yield, buying more long-term bonds when the yield curve steepens.

Table 6 presents the results from this exercise. Column (1) shows that there is a strong positive relationship between $\Delta({SEC}_{LT}/{SEC})$ and $\Delta({y}^{\$(10)}- {y}^{\$(1)})$ .²¹ In terms of dollar magnitudes, the coefficient in column (1) suggests that a 100 basis-point decline in the short rate, holding fixed the long rate, leads to a 1.06 percentage-point increase in the share of bank securities that are long term. Bank securities have averaged roughly 18.5% of total bank assets since 1988. As of 2010:Q4, commercial bank assets were $11,728 billion, so this means that a 100-bp increase in the yield spread raises bank demand for long-term securities by $23 billion = 1.06% $\times$ 18.5% $\times$ $11,728. So a 300-bp swing in the yield spread-roughly the range over a full easing cycle-would boost demand by $69 billion. Of course, the less-than-1-year versus longer-than-1-year margin is potentially only part of the overall portfolio adjustment process-banks might also be extending their duration within the longer-than-1-year bucket-and banks are just one set of investors who may care about current income. Thus, the results in Table 6 suggest that the induced shift in total demand from all yield-oriented investors could be quite substantial.

The remaining columns of Table 6 test another implication of the reaching-for-yield story. Specifically, if reaching for yield is partially driven by a desire to manage reported earnings, then this tendency should be more pronounced for publicly-traded banks than for privately-held banks. Of course, if reaching for yield is driven solely by a desire to boost capital ratios and maintain regulatory slack, then one would not expect to see much of a difference between public and private banks. To investigate this issue, we construct two versions of ${SEC}_{LT}/SEC$ , one for public banks and another for private banks.²² As shown in column (2), the results for public banks are similar to those for all banks. This true almost by construction since a large majority of aggregate commercial banking assets are held by public banks. Consistent with the earnings-management hypothesis, column (3) shows that yield-chasing behavior is less pronounced amongst private banks. The coefficient of 0.674 on $(\Delta{y}^{\$(10)}$ - ${y}^{\$(1)})$ for private banks in column (3) is only half of the corresponding coefficient for public banks in column (2). However, as shown in column (4), we cannot reject the hypothesis that the coefficient for public banks is the same that for private banks. Thus, the split between public and private banks goes in the direction predicted by the earnings-management story, but the evidence on this front is statistically weak. Moreover, the positive, albeit only marginally significant, coefficient for private banks suggests that a desire to maintain regulatory slack might also play some role.

Another question has to do with the persistence of the shifts in banks' demands for long-term bonds. We find some tentative evidence (not reported) suggesting that these demand shocks are gradually reversed over roughly the following 8 quarters. One way to see this is to add lagged values of $(\Delta{y}^{\$(10)} - {y}^{\$(1)})$ to equation (18) and then examine the cumulative sum of coefficients on contemporaneous and lagged changes in the yield spread.

4.3.2 Primary Dealers

Next we examine the Treasury holdings of primary dealers. We think of primary dealers as a natural proxy for the expected-return-oriented investors in our model, the arbitrageurs who accommodate demand shocks coming from yield-oriented investors. Importantly, primary dealer activities are either housed within broker-dealers or in commercial bank trading departments. As a result, unlike banks' non-trading accounts, primary dealers operate entirely on mark-to-market accounting. So even if they wanted to manage their earnings, playing the term spread would be less of a sure thing for them.

We work with data from the Federal Reserve Bank of New York on the aggregate holdings of primary dealers. A key advantage of this data is that we have high frequency observations of dealer holdings by maturity. Specifically, each week from July 2001-present, we have data on the aggregate net (long minus short) dealer holdings of Treasury bills (all of which mature in less than one year) and nominal coupon-bearing Treasuries broken into four buckets by remaining maturity: shorter than 3 years, 3 to 6 years, 6 to 11 years, and longer than 11 years.²³

Measuring the net duration of primary dealer positions is a bit tricky since dealers can be net short Treasuries, both in a given maturity bucket as well as overall. To deal with this complication, we compute

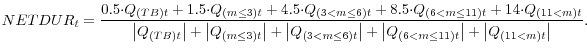
$\displaystyle NETDUR_{t} =\frac{{\rm0.5\cdot }Q_{(TB)t} +1{\rm .5\cdot }Q_{(m\le 3)t} +4{\rm .5\cdot }Q_{(3<m\le 6)t} +8{\rm .5\cdot }Q_{(6<m\le 11)t} +14{\rm\cdot }Q_{(11<m)t} }{\left\vert Q_{(TB)t} \right\vert+\left\vert Q_{(m\le 3)t} \right\vert+\left\vert Q_{(3<m\le 6)t} \right\vert+\left\vert Q_{(6<m\le 11)t} \right\vert+\left\vert Q_{(11<m)t} \right\vert} .$

(19)

The numerator is proxy for the net dollar duration of dealers' Treasury holdings. Then, to scale this variable, we divide it by the sum of the absolute positions in each maturity bucket. Thus, the scaled variable is like $(DUR_{t}^{LONG} \cdot LONG_{t} -DUR_{t}^{SHORT} \cdot SHORT_{t} )/(LONG_{t} +SHORT_{t} )$ .²⁴

Obviously, a variety of factors besides those in our model might impact the duration of dealers' Treasury holdings. In an attempt to control for some of these, we include proxies for the weekly change in the scale of dealers' net positions in Treasuries, as well as the change in their net positions across all other reportable fixed income asset classes. A related concern is that high-frequency variation in the maturity structure of dealer positions may be driven by seasonal patterns of Treasury issuance-e.g., due to seasonal fluctuations in T-bill supply or the large offerings of longer-term notes and bonds in February, May, August, and November. To deal with this, we include a full set of week-of-year dummies in order to soak up any seasonal fluctuations in Treasury supply.

Using weekly data, we then estimate specifications of the form

$\displaystyle \Delta NETDUR_{t} =a+b\cdot \Delta (y_{t}^{\$ (10)} -y_{t}^{\$ (1)} )+c'x_{t} +\Delta u_{t} .$

(20)

If dealers function as the expected-return oriented investors in our model, we would expect to find b

0. Table 7 presents the results from this exercise. Column (1) shows that there is a strong negative relationship between $\Delta{NETDUR}_{t}$ and $\Delta({y}^{\$(10)}- {y}^{\$(1)})$ . Column (2) adds the various controls, including the week-of-year dummies. While the controls substantially increase the overall explanatory power of the regression, they have little impact on the coefficient of interest. Columns (3) and (4) repeat these exercises using a more comprehensive duration measure based on dealers' holdings of both Treasuries and Agency debentures, since the latter are seen as a close substitute for Treasuries by many investors. This yields broadly similar conclusions.

Finally, we examine the dynamics of ${NETDUR}_{t}$ following a shock to the yield spread. Specifically, we separately estimate

$\displaystyle NETDUR{}_{t+k} -NETDUR{}_{t-1} =a(k)+b(k)\cdot [(y_{t}^{\$ (10)} -y_{t}^{\$ (1)} )-(y_{t-1}^{\$ (10)} -y_{t-1}^{\$ (1)} )]+\Delta \varepsilon _{t+k}^{} ,$

(21)

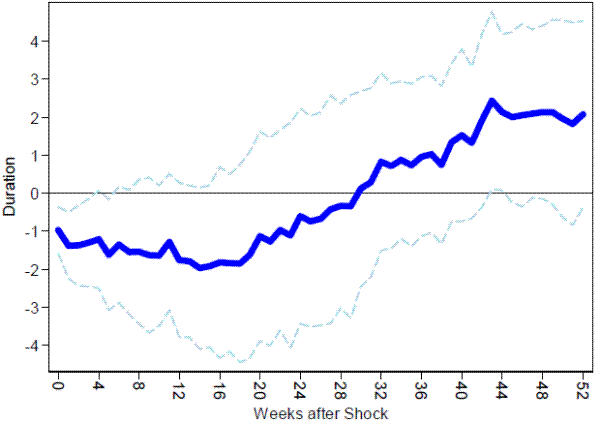
for k = 0, 1, ..., 52. Thus, as above, these regressions differ solely in terms of the differencing horizon on the left-hand-side (the estimate for k = 0 corresponds to the estimates in column (1) of Table 7). Figure 4 plots the coefficients, b(k), versus horizon k. The point estimates suggest that the initial impulse to the duration of dealers' Treasury holdings persists for roughly 5 months, but then largely vanishes within 9 months. Interestingly, this roughly matches the horizon over which the impulse from short-term nominal rates to distant real forwards is reverted away in Figure 3. One possible interpretation-in the spirit of Grossman and Miller (1988)-is that primary dealers function as front-line arbitrageurs in response to a demand shock, but over time, more arbitrage capital enters the market, allowing the dealers to unwind their positions and reversing the initial price impact. Of course, the wide confidence intervals in Figure 4 underscore that our estimates of the timing of dealers' unwind are quite imprecise, so this interpretation is necessarily somewhat speculative.

4.4 Other Supply-and-Demand Channels

Our theory of yield-oriented investors is one specific example of a supply-and-demand channel that connects monetary policy shocks to real term premia. However, one can tell other stories in a similar spirit. Hanson (2012) emphasizes time-variation in the aggregate supply of duration. Specifically, due to the negative convexity of mortgage-backed securities, the total quantity of duration risk that bond investors must bear increases when rates rise. If fixed-income markets are partially segmented from other asset markets, then this variation in aggregate duration could raise the term premium via a conditional-CAPM channel as in Vayanos and Vila (2009). The intuition is straightforward: if the supply of a given risk factor rises, the risk premium needs to rise in order to induce investors to hold the new supply. Hanson (2012) tests this alternative by using measures of aggregate fixed income duration to forecast bond returns.²⁵ He finds that this duration-risk-premium channel appears to soak up some, but not all, of the explanatory power of recent changes in forward rates for future bond returns.

5 Conclusions

Changes in the stance of monetary policy have a surprisingly strong impact on distant forward real interest rates. These movements in forward rates appear to reflect changes in term premia, which largely accrue over the next year, as opposed to varying expectations about future real rates. Moreover, our evidence suggests that the driving force behind time-varying term premia is the behavior of yield-oriented investors, who react to a cut in short rates by increasing their demand for longer-term bonds, thereby putting downward pressure on long-term rates.

Our work raises, but does not answer, a series of questions about the ultimate economic importance of this monetary transmission channel. In particular, suppose that a monetary easing lowers long-term real rates through the mechanism we have described. What might the resulting impact on corporate investment be? On the one hand, the fact that the effect of monetary policy on long-term real rates is transitory (i.e., it is reversed after about a year) might seem to imply that it would matter less for corporate capital budgeting decisions. On the other hand, some firms may view the temporarily lower long-term rates as a market-timing opportunity, i.e., a window during which it is particularly attractive to issue long-term debt. This in turn could serve to stimulate their investment.²⁶

While we have focused narrowly on term premia in the Treasury market, the idea that monetary policy can influence bond-market risk premia has potentially broader implications. Indeed, much recent work has been motivated by the hypothesis that accommodative monetary policy can reduce credit-risk premia.²⁷ It seems like a promising avenue for future work would be to study these two channels of monetary transmission in a unified setting. For example, in the context of our model, one could allow yield-oriented investors to choose among not only short-term and long-term Treasuries, but defaultable credit instruments (corporate loans, mortgages, etc.) as well. This would presumably yield a set of predictions about the co-movement of term premia and credit-risk premia in response to changes in monetary policy, and could be the basis for a wider-ranging and more integrated empirical investigation of these phenomena.

References

Adrian, Tobias and Hyun Song Shin (2010), "Financial Intermediaries and Monetary Economics," Federal Reserve Bank of New York Staff Report No. 398

Anderson, Nicola and John Sleath (2001), "New Estimates of the UK Real and Nominal Yield Curves," Bank of England working paper No. 126.

Baker, Malcolm, Jeffrey Wurgler and Jeremy C. Stein (2003), "When Does the Market Matter? Stock Prices and the Investment of Equity-Dependent Firms," Quarterly Journal of Economics Vol. 118, pp. 969-1005.

Bansal, Ravi and Amir Yaron (2004), "Risks for the Long Run: A Potential Resolution of Asset Pricing Puzzles," Journal of Finance, Vol. 59, pp. 1481-1509.

Borio, Caludio and Haibin Zu (2008), "Capital Regulation, Risk-taking and Monetary Policy: A Missing Link in the Transmission Mechanism?" BIS Working paper No. 268.

Campbell, Jeffrey R., Charles L. Evans, Jonas D.M. Fisher, and Alejandro Justiniano (2012), "Macroeconomic Effects of FOMC Forward Guidance," forthcoming Brookings Papers on Economic Activity, Spring 2012.

Campbell, John Y. (1991), "A Variance Decomposition for Stock Returns," Economic Journal Vol. 101, pp. 157-179.

Campbell, John Y., and John H. Cochrane (1999), "By Force of Habit: A Consumption-based Explanation of Aggregate Stock Market Behavior," Journal of Political Economy Vol. 107, pp. 205-251.

Campbell, John and Robert Shiller (1991), "Yield Spreads and Interest Rate Movements: A Bird's Eye View," Review of Economic Studies, Vol. 58, pp. 495-514.

Campbell, John Y., Aditya Vikram Sunderam, and Luis M. Viceira (2012), "Inflation Bets or Deflation Hedges? The Changing Risks of Nominal Bonds," Harvard University working paper.

Cieslak, Anna and Povol Povala (2011), "Understanding Bond Risk Premia," Northwestern University working paper.

Clarida, Richard, Jordi Gali, and Mark Gertler (1999), "The Science of Monetary Policy: A New Keynesian Perspective," Journal of Economic Literature, Vol. 37, pp. 1661-1707.

Cochrane, John H. and Monika Piazzesi (2002), "The Fed and Interest Rates-A High-Frequency Identification," American Economic Review: Papers and Proceedings, Vol. 92, No. 2, pp. 90-95.

Cochrane, John H. and Monika Piazzesi (2005), "Bond Risk Premia," American Economic Review, Vol. 95, No. 1, pp. 138-160.

Cook, Timothy and Hahn, Thomas (1989), "The Effect of Changes in the Federal Funds Rate Target on Market Interest Rates in the 1970s," Journal of Monetary Economics, Vol. 24 No. 3, pp. 331-51.

Evans, Charles and Marshall, David (1998), "Monetary Policy and the Term Structure of Nominal Interest Rates: Evidence and Theory," Carnegie-Rochester Conference on Public Policy, Fall 1998, No. 49, pp. 53-111.

Fama, Eugene F. and Robert R. Bliss (1987), "The Information on Long-Maturity Forward Rates," American Economic Review, Vol. 77, No.4, pp. 680-692.

Faust, Jon, Eric T. Swanson, Jonathan H. Wright (2004), "Do Federal Reserve Policy Surprises Reveal Superior Information about the Economy," Contributions to Macroeconomics Vol. 4, Iss. 1.

Gagnon, Joseph, Matthew Raskin, Julie Remache, and Brian Sack (2010), "Large-Scale Asset Purchases by the Federal Reserve: Did They Work?" Federal Reserve Bank of New York, Staff Report No. 441.

Gabaix, Xavier (2011), "Variable Rare Disasters: An Exactly Solved Framework for Ten Puzzles in Macro-Finance," forthcoming Quarterly Journal of Economics.

Gali, Jordi (2008), Monetary Policy, Inflation, and the Business Cycle, Princeton University Press, Princeton, NJ.

Greenwood, Robin, and Samuel Hanson (2012), "Issuer Quality and the Credit Cycle," NBER Working Paper No. 17197.

Greenwood, Robin, Samuel Hanson, and Jeremy Stein (2010), "A Gap-Filling Theory of Corporate Debt Maturity Choice," Journal of Finance Vol. 65, No. 3, pp. 993-1028.

Greenwood, Robin, and Dimitri Vayanos (2010a), Bond Supply and Excess Bond Returns, NBER Working Paper No.13806.

Greenwood, Robin, and Dimitri Vayanos (2010b), "Price Pressure in the Government Bond Market," American Economic Review: Papers and Proceedings, Vol. 100, No. 2, pp. 585-590.

Grossman, Sanford J. and Merton H. Miller (1988), "Liquidity and Market Structure," Journal of Finance Vol. 53, No. 3, pp. 617-633.

Gürkaynak, Refet S., Brian Sack, and Eric T. Swanson (2005a), "The Sensitivity of Long-Term Interest Rates to Economic News: Evidence and Implications for Macroeconomic Models," American Economic Review Vol. 95, No. 1, pp. 425-436.

Gürkaynak, Refet S., Brian Sack, and Eric T. Swanson (2005b), "Do Actions Speak Louder Than Words? The Response of Asset Prices to Monetary Policy Actions and Statements," International Journal of Central Banking, Vol. 1, No. 1, pp. 55-93

Gürkaynak, Refet S., Brian Sack, and Jonathan H. Wright (2007), "The US Treasury Yield Curve: 1961 to the Present," Journal of Monetary Economics, Vol. 54, No. 8, pp. 2291-2304.

Gürkaynak, Refet S., Brian Sack, and Jonathan H. Wright (2010), "The TIPS Yield Curve and Inflation Compensation," American Economic Journal: Macroeconomics, Vol. 2, No. 1, pp. 70-92.

Hanson, Samuel G. (2012) "Mortgage Convexity and Bond Risk Premia," mimeograph.

Jiménez, Gabriel, Steven Ongena, José-Luis Peydró, and Jesús Saurina (2011), "Hazardous Times for Monetary Policy: What do 23 Million Loans Say About the Impact of Monetary Policy on Credit Risk-Taking?" Bank of Spain Working Paper.

Joyce, Michael, Matthew Tong and Robert Wood (2011), "The United Kingdom's Quantitative Easing policy: Design, Operation and Impact," Bank of England Quarterly Bulletin 2011 Q3.

Krishnamurthy, Arvind, and Annette Vissing-Jorgensen (2011), "The Effects of Quantitative Easing on Interest Rates: Channels and Implications for Policy," Brookings Papers on Economic Activity, Fall 2011, pp. 215-265.

Krishnamurthy, Arvind, and Annette Vissing-Jorgensen (2012), "The Aggregate Demand for Treasury Debt," forthcoming Journal of Political Economy.

Kuttner, Kenneth N. (2001), "Monetary Policy Surprises and Interest Rates: Evidence from the Fed Funds Futures Market," Journal of Monetary Economics, Vol. 47 No. 3, pp. 523-544.

Landier, Augustin, David Sraer, and David Thesmar (2011), "The Risk-Shifting Hypothesis: Evidence from Subprime Mortgage Originations," Princeton University working paper.

Lee, Jim (2002), "Federal Funds Rate Target Changes and Interest Rate Volatility," Journal of Economics and Business Vol. 54, pp. 159-191.

Modigliani, Franco, and Richard Sutch (1966), "Debt Management and the Term Structure of Interest Rates: An Empirical Analysis of Recent Experience," Journal of Political Economy, Vol. 75, pp. 569-589.

Newey, Whitney K., and Kenneth D. West (1987), "A Simple, Positive Semi-definite, Heteroskedasticity and Autocorrelation Consistent Covariance Matrix," Econometrica,Vol. 55, 703-708.

Pflueger, Carolin E. and Luis M. Viciera (2011), "Inflation-Indexed Bonds and the Expectations Hypothesis," Annual Review of Financial Economics, Vol. 3, pp. 139-158.

Rajan, Raghuram G. (2005), "Has Financial Development Made the World Riskier?" Federal Reserve Bank of Kansas City, 2005 Economic Symposium, "The Greenspan Era: Lessons for the Future," pp. 313-369.

Romer, Christina D. and David H. Romer (2000), "Federal Reserve Information and the Behavior of Interest Rates," American Economic Review Vol. 90, No. 3, pp. 429-457.

Stein, Jeremy C. (1989), "Efficient Capital Markets, Inefficient Firms: A Model of Myopic Corporate Behavior," Quarterly Journal of Economics Vol. 104, 655-669.

Stein, Jeremy C. (1996), "Rational Capital Budgeting in an Irrational World," Journal of Business Vol. 69, pp. 429-455.

Svensson, Lars E. O. (1994), "Estimating and Interpreting Forward Rates: Sweden 1992-1994," NBER Working Paper No. 4871.

Vayanos, Dimitri and Jean-Luc Vila (2009), "A Preferred-Habitat Model of the Term Structure of Interest Rates," London School of Economics working paper.

Figure 1: Response of US forwards to monetary policy news on FOMC days. Panel A plots the coefficient ${b}_{\$}$ (n) from estimating equation (4a) on FOMC announcement dates from 1999 through February 2012 (which refer to as the "present" throughout the paper)

$\displaystyle \Delta f_{t}^{\$ (n)} =a_{\$ } (n)+b_{\$ } (n)\cdot \Delta y_{t}^{\$ (2)} +\Delta \varepsilon _{t}^{\$ (n)} .$

Panel B plots the coefficients ${b}_{TIPS}$ (n) and ${b}_{p}$ (n) from estimating equations (4b) and (4c) on FOMC announcement dates from 1999-present

$\displaystyle \Delta f_{t}^{TIPS(n)} =a_{TIPS} (n)+b_{TIPS} (n)\cdot \Delta y_{t}^{\$ (2)} +\Delta \varepsilon _{t}^{TIPS(n)} {\rm and }\Delta f_{t}^{\pi (n)} =a_{\pi } (n)+b_{\pi } (n)\cdot \Delta y_{t}^{\$ (2)} _{t} +\Delta \varepsilon _{t}^{\pi (n)} .$

Confidence intervals, based on robust standard errors, are shown as dashed lines. We exclude five FOMC announcements dates from 2009 to 2011 when there was significant news about the Federal Reserve's Large Scale Asset Purchase (LSAP) programs.

Panel A: Response of nominal forwards by maturity

Panel B: Response of real and break-even inflations forwards by maturity

Figure 2: Response of UK forwards to monetary policy news on BOE days. Panel A plots the coefficient ${b}_{\$}$ (n) from estimating equation (4a) on BOE MPC announcement dates from 1999-present

$\displaystyle \Delta f_{t}^{\$ (n)} =a_{\$ } (n)+b_{\$ } (n)\cdot \Delta y_{t}^{\$ (2)} +\Delta \varepsilon _{t}^{\$ (n)} .$

Panel B plots the coefficients ${b}_{TIPS}$ (n) and ${b}_{p}$ (n) from estimating equations (4b) and (4c) on BOE MPC announcement dates from 1999-present

Confidence intervals, based on robust standard errors, are shown as dashed lines. We exclude six MPC announcements dates when there was significant news about the BOE's quantitative easing operations which involved purchases of long-dated Gilts.

Panel A: Response of nominal forwards by maturity

Panel B: Response of real and break-even inflations forwards by maturity

Figure 3: Impulse response of 10-year US forwards to short-term nominal rates. Panel A plots the coefficient b ${}_{\$}$ (k) from estimating equation (9) using all days from 1987-present

$\displaystyle f_{t+k}^{\$ (10)} -f_{t-1}^{\$ (10)} =a_{\$ } (k)+b_{\$ } (k)\cdot (y_{t+1}^{\$ (2)} -y_{t-1}^{\$ (2)} )+\Delta \varepsilon _{t+k}^{\$ (10)} ,$

for horizons k = 1, ..., 250 days. Panel B plots repeats the same exercise, restricting attention to only FOMC dates from 1987-present. Panel C plots the coefficient b ${}_{TIPS}$ (k) from estimating equation (10) on all days from 1999-present

$\displaystyle f_{t+k}^{TIPS(10)} -f_{t-1}^{TIPS(10)} =a_{TIPS} (k)+b_{TIPS} (k)\cdot (y_{t+1}^{\$ (2)} -y_{t-1}^{\$ (2)} )+\Delta \varepsilon _{t+k}^{TIPS(10)} .$

Panel D plots repeats this exercise, restricting attention to only FOMC dates from 1999-present. Confidence intervals, based on Newey-West (1987) standard errors to account for the overlapping nature of the variables, are shown as dashed lines. In Panels A and C we allow for serial correlation at up to 1.5 $\times$ k lags (to the nearest integer). In Panels B and D, we allow for serial correlation between FOMC meetings at up to 1.5 $\times$ (k/25) lags, since FOMC meetings occur roughly every 25 business days on average.

Panel A:Nominal forwards, 1987-present, All days

Panel B:Nominal forwards, 1987-present, FOMC only

Panel C:Real forwards, 1999-present, All days

Panel D:Real forwards, 1999-present, FOMC only

Figure 4: Impulse response of primary dealer NETDUR to the yield spread. The figure plots the coefficient b(k) from estimating the following regressions using weekly data from July 2001- present

$\displaystyle NETDUR{}_{t+k} -NETDUR{}_{t-1} =a(k)+b(k)\cdot [(y_{t}^{\$ (10)} -y_{t}^{\$ (1)} )-(y_{t-1}^{\$ (10)} -y_{t-1}^{\$ (1)} )]+\Delta \varepsilon _{t+k}^{} ,$

for horizons k = 0, 1, ..., 52 weeks. Confidence intervals, based on Newey-West (1987) standard errors to account for the overlapping nature of the variables, are shown as dashed lines. Specifically, we allow for serial correlation at up to 1.5 $\times$ k lags (to the nearest integer).

Figure 4: Impulse response of primary dealer NETDUR to the yield spread. The figure plots the coefficient b(k>) from estimating the following regressions using weekly data from July 2001- present. This is a line graph with the x-axis labeled as Weeks After Shock with range from 0 to 52, and the y-axes labeled as Duration with range from -4 to 4. A small blue line begins at about -1, declines slightly to -2 by week 16, then steadily increases to 2 by week 52. The line exhibits marginal volatility. Two dashed lines surround the solid line on the top and bottom and mirror its shape, beginning about 0.5 over and under the solid line, before getting farther away to be about 2 over and under the solid line by week 52.

Table 1: Response of US Treasury forward rates to monetary policy news. Regressions of changes in nominal, real, and breakeven inflation instantaneous forward rates (X = $, TIPS, and p) on changes in the 2-year nominal yield on FOMC announcement days from 1999 through February 2012 (which refer to as the "present" throughout the paper)

$\displaystyle \Delta f_{t}^{X(n)} =a_{X} (n)+b_{X} (n)\cdot \Delta y_{t}^{\$ (2)} +\Delta \varepsilon _{t}^{X(n)} .$

We estimate these regressions for maturities of n = 5, ..., 20. For an announcement on day t, we compute the 2-day change from t-1 to t+1. t-statistics, based on robust standard errors, are shown in brackets. We exclude five FOMC announcements dates from 2009 to 2011 when there was significant news about the Federal Reserve's Large Scale Asset Purchase (LSAP) programs. Daily estimates of nominal forward rates, real forward rates, and breakeven-inflation forward rates are based on Gürkaynak, Sack, and Wright (2007 and 2010). The data, updated regularly by Federal Reserve Board staff, is available at

http://www.federalreserve.gov/pubs/feds/2006/200628/200628abs.html and http://www.federalreserve.gov/pubs/feds/2008/200805/200805abs.html .

n	${b}_{\$}$ (n)	[t]	${R}^{2}$	${b}_{TIPS}$ (n)	[t]	${R}^{2}$	${b}_{p}$ (n)	[t]	${R}^{2}$
5	0.843	[6.07]	0.30	0.653	[5.98]	0.24	0.190	[2.46]	0.05
6	0.729	[4.90]	0.21	0.563	[5.77]	0.20	0.166	[1.80]	0.04
7	0.634	[4.22]	0.16	0.505	[5.58]	0.18	0.129	[1.22]	0.02
8	0.557	[3.84]	0.13	0.467	[5.24]	0.17	0.090	[0.80]	0.01
9	0.496	[3.64]	0.11	0.441	[4.88]	0.17	0.055	[0.48]	0.00
10	0.446	[3.54]	0.09	0.421	[4.63]	0.18	0.025	[0.23]	0.00
11	0.405	[3.47]	0.09	0.405	[4.47]	0.18	0.001	[0.01]	0.00
12	0.371	[3.37]	0.08	0.390	[4.37]	0.18	-0.018	[-0.18]	0.00
13	0.342	[3.21]	0.07	0.376	[4.29]	0.17	-0.034	[-0.35]	0.00
14	0.315	[2.99]	0.07	0.362	[4.21]	0.17	-0.047	[-0.48]	0.00
15	0.291	[2.73]	0.06	0.350	[4.10]	0.15	-0.059	[-0.58]	0.00
16	0.267	[2.45]	0.06	0.338	[3.95]	0.14	-0.071	[-0.65]	0.01
17	0.244	[2.17]	0.05	0.327	[3.76]	0.13	-0.083	[-0.70]	0.01
18	0.222	[1.89]	0.04	0.316	[3.56]	0.12	-0.094	[-0.74]	0.01
19	0.199	[1.62]	0.04	0.306	[3.36]	0.11	-0.107	[-0.77]	0.01
20	0.176	[1.36]	0.03	0.296	[3.15]	0.09	-0.120	[-0.79]	0.01

Table 2: Robustness checks for US. Regressions of changes in nominal, real, and breakeven inflation instantaneous forward rates (X = $, TIPS, and p) on changes in various short rates on FOMC announcement days

$\displaystyle \Delta f_{t}^{X(n)} =a_{X} (n)+b_{X} (n)\cdot \Delta MP_{t} +\Delta \varepsilon _{t}^{X(n)} .$

t-statistics, based on robust standard errors, are shown in brackets. We first vary the window (1-day versus 2-day changes) used to compute changes in long-term forwards and short-term rates. We next use a variety of different proxies for monetary policy news on FOMC announcement dates, including the "future path of policy" news factor as in Gürkaynak, Sack, and Swanson (2005b). Finally, we vary the sample. Data on Fed Funds futures, Eurodollar futures and Overnight Index Swap rates is from Bloomberg.

	# Obs.	${b}_{\$}$ (10)	[t]	${R}^{2}$	${b}_{TIPS}$ (10)	[t]	${R}^{2}$	${b}_{p}$ (10)	[t]	${R}^{2}$
*Baseline:* 2-year UST	107	0.446	[3.54]	0.09	0.421	[4.63]	0.18	0.025	[0.23]	0.00
*Vary proxy for MP news:* 2-year UST, 1-day change	107	0.245	[2.98]	0.08	0.215	[2.90]	0.13	0.021	[0.30]	0.00
*Vary proxy for MP news:* 1-year UST	107	0.186	[1.30]	0.01	0.287	[2.60]	0.07	-0.100	[-0.89]	0.01
*Vary proxy for MP news:* 1-year UST, 1-year forward	107	0.505	[5.13]	0.17	0.408	[5.42]	0.24	0.097	[1.14]	0.02
*Vary proxy for MP news:* 3-quarter forward Eurodollar	107	0.239	[2.39]	0.07	0.286	[4.43]	0.20	-0.046	[-0.66]	0.01
*Vary proxy for MP news:* 6-quarter forward Eurodollar	107	0.398	[4.23]	0.23	0.326	[6.33]	0.33	0.072	[0.95]	0.02
*Vary proxy for MP news:* 9-month forward Fed funds	89	0.258	[1.85]	0.03	0.354	[3.72]	0.11	-0.096	[-0.82]	0.01
*Vary proxy for MP news:* 12-month forward Fed funds	74	0.308	[1.90]	0.04	0.401	[3.42]	0.14	-0.093	[-0.75]	0.01
*Vary proxy for MP news:* 1-year OIS	81	0.172	[0.84]	0.01	0.334	[2.15]	0.07	-0.162	[-1.07]	0.02
*Vary proxy for MP news:* 2-year OIS	80	0.571	[3.53]	0.12	0.595	[5.24]	0.25	-0.024	[-0.19]	0.00
*Vary proxy for MP news:* 1-year OIS, 1-year forward	80	0.570	[5.48]	0.21	0.517	[7.32]	0.33	0.052	[0.60]	0.01
*Vary proxy for MP news:* GSS (2005b) "path" factor	107	0.274	[2.43]	0.10	0.279	[3.75]	0.23	-0.005	[-0.07]	0.00
*Vary sample* Add 5 QE dates	112	0.504	[3.30]	0.10	0.455	[4.97]	0.18	0.049	[0.40]	0.00
*Vary sample* Regular meeting	100	0.452	[4.16]	0.09	0.383	[4.04]	0.14	0.069	[0.73]	0.01
*Vary sample* Unscheduled meeting	7	0.565	[2.62]	0.38	0.668	[3.66]	0.67	-0.103	[-0.38]	0.02
*Vary sample* Add minutes dates	212	0.528	[5.85]	0.17	0.312	[4.76]	0.14	0.203	[2.04]	0.04

Table 3: Response of UK gilt forward rates to monetary policy news. Regressions of changes in nominal, real, and breakeven inflation instantaneous forward rates (X = $, TIPS, and p) on changes in the 2-year nominal gilt yield on MPC announcement days from 1999-present

$\displaystyle \Delta f_{t}^{X(n)} =a_{X} (n)+b_{X} (n)\cdot \Delta y_{t}^{\$ (2)} +\Delta \varepsilon _{t}^{X(n)} .$

We estimate these regressions for maturities of n = 5, ..., 20. For an MPC announcement on day t, we compute the 2-day change from t-1 to t+1. t-statistics, based on robust standard errors, are shown in brackets. We exclude six MPC announcements dates when there was significant news about the BOE's quantitative easing operations which involved purchases of long-dated Gilts. The UK yield curve data is based on the methodology described in Andersen and Sleath (1999). The data is available at http://www.bankofengland.co.uk/statistics/Pages/yieldcurve/default.aspx.

n	${b}_{\$}$ (n)	[t]	${R}^{2}$	${b}_{TIPS}$ (n)	[t]	${R}^{2}$	${b}_{p}$ (n)	[t]	${R}^{2}$
5	0.636	[7.22]	0.35	0.499	[7.45]	0.37	0.137	[2.14]	0.04
6	0.562	[6.00]	0.27	0.441	[7.13]	0.34	0.120	[1.84]	0.03
7	0.504	[5.41]	0.23	0.394	[6.98]	0.32	0.110	[1.65]	0.02
8	0.459	[5.20]	0.20	0.354	[6.68]	0.29	0.104	[1.58]	0.02
39	0.420	[5.20]	0.19	0.320	[6.13]	0.26	0.100	[1.54]	0.02
10	0.384	[5.24]	0.18	0.291	[5.40]	0.22	0.093	[1.45]	0.02
11	0.351	[5.11]	0.17	0.266	[4.65]	0.18	0.085	[1.28]	0.02
12	0.319	[4.69]	0.14	0.244	[4.00]	0.15	0.075	[1.06]	0.01
13	0.292	[4.09]	0.11	0.226	[3.48]	0.12	0.065	[0.84]	0.01
14	0.268	[3.52]	0.09	0.211	[3.08]	0.10	0.057	[0.67]	0.01
15	0.250	[3.09]	0.07	0.199	[2.78]	0.09	0.051	[0.56]	0.00
16	0.236	[2.82]	0.06	0.190	[2.56]	0.08	0.047	[0.49]	0.00
17	0.228	[2.68]	0.06	0.183	[2.41]	0.07	0.045	[0.47]	0.00
18	0.224	[2.67]	0.06	0.179	[2.32]	0.06	0.045	[0.47]	0.00
19	0.224	[2.75]	0.06	0.176	[2.26]	0.06	0.047	[0.52]	0.00
20	0.227	[2.92]	0.07	0.175	[2.24]	0.06	0.052	[0.59]	0.01

Table 4: Response of US long-term forward rates to changes in short-term rates. Regressions of changes real instantaneous forward rates on changes in short-term nominal rates on all days, allowing for a differential response on FOMC announcement dates (excluding any QE dates)

$\displaystyle \Delta f_{t}^{TIPS(n)} =a+b\cdot \Delta y_{t}^{\$ (2)} _{t} +c\cdot FOMC_{t} +d\cdot \Delta y_{t}^{\$ (2)} \times FOMC_{t} +\varepsilon _{t}^{X(n)} .$

We estimate these regressions for 5-, 10-, and 20-year forwards using daily data from 1999 through February 2012. Standard errors are based on Newey-West standard errors allowing for serial correlation at up to 2 lags.

	5-year	10-year	20-year
$\Delta{y}^{\$(2)}$	0.493	0.268	0.240
$\Delta{y}^{\$(2)}$ [Standard Error]	[15.90]	[12.30]	[9.32]
FOMC	-0.003	-0.005	-0.010
FOMC [Standard Error]	[-0.26]	[-0.58]	[-1.20]
$\Delta{y}^{\$(2)}$ $\times$ FOMC	0.160	0.153	0.057
$\Delta{y}^{\$(2)}$ $\times$ FOMC[Standard Error]	[1.47]	[1.69]	[0.60]
Constant	-0.001	-0.001	-0.000
Constant [Standard Error]	[-0.61]	[-0.38]	[-0.23]
Observations	3,283	3,283	3,283
${R}^{2}$	0.22	0.11	0.05

Table 5: Mean reversion in forward rates. This table forecasts 12-month changes in forward rates using changes in forward rates over the past 3 months

$\displaystyle f_{t+1}^{X(9)} -f_{t}^{X(10)} =a+b\cdot (f_{t}^{X(10)} -f_{t-1/4}^{X(10)} )+c'x_{t} +\varepsilon _{t+1}^{X(10)} ,$

for X = $ and TIPS. The regressions are estimated with monthly data. To deal with the overlapping nature of the 12-month returns t-statistics are based on Newey-West (1987) standard errors allowing for serial correlation at up to 18 lags. We estimate these regressions with and without controlling for forward rate spread, ${(f}^{X(10)}_t-{yt}X\left(1\right))$ . The table shows OLS and IV estimates. In the IV specifications we instrument for ( $f^{X\left(10\right)}_t-f^{X\left(10\right)}_{t-1/4}$ ) using the change in nominal short rates over the past 3 months, ( $y^{\$\left(2\right)}_t-y^{\$\left(2\right)}_{t-1/4}$ ). We then decompose the change in 10-year forwards into components that occurred on FOMC days and on all other days: ( $f^{X\left(10\right)}_t-f^{X\left(10\right)}_{t-1/4}$ ) = $(f^{X\left(10\right)}_t-f^{X\left(10\right)}_{t-1/4})_{FOMC}$ + $(f^{X\left(10\right)}_t-f^{X\left(10\right)}_{t-1/4})_{NONFOMC}$ . In IV versions of these regressions, we instrument for ( $f^{X\left(10\right)}_t-f^{X\left(10\right)}_{t-1/4})_{FOMC}$ and ( $f^{X\left(10\right)}_t-f^{X\left(10\right)}_{t-1/4})_{NONFOMC}$ with $(y^{\$\left(2\right)}_t-y^{\$\left(2\right)}_{t-1/4})_{FOMC}$ and $(y^{\$\left(2\right)}_t-y^{\$\left(2\right)}_{t-1/4})_{NONFOMC}$ . Panel A shows nominal forecasting results from 1987-present. Panel B shows real forecasting results from 1999-present.

Panel A: Forecasting changes in nominal forward rates, 1987-present

	(1) OLS	(2) IV	(3) OLS	(4) IV	(5) OLS	(6) IV	(7) OLS	(8) IV
$f^{\$\left(10\right)}_t-f^{\$\left(10\right)}_{t-1/4}$	-0.343	-1.078	-0.284	-1.228
$f^{\$\left(10\right)}_t-f^{\$\left(10\right)}_{t-1/4}$ [Standard Error]	[-3.21]	[-2.13]	[-2.47]	[-2.53]
${\left(f^{\$\left(10\right)}_t-f^{\$\left(10\right)}_{t-1/4}\right)}_{FOMC}$					-0.564	-1.369	-0.561	-1.774
${\left(f^{\$\left(10\right)}_t-f^{\$\left(10\right)}_{t-1/4}\right)}_{FOMC}$ [Standard Error]					[-1.69]	[-0.79]	[-1.64]	[-1.17]
${\left(f^{\$\left(10\right)}_t-f^{\$\left(10\right)}_{t-1/4}\right)}_{NONFOMC}$					-0.321	-1.084	-0.256	-1.238
${\left(f^{\$\left(10\right)}_t-f^{\$\left(10\right)}_{t-1/4}\right)}_{NONFOMC}$ [Standard Error]					[-2.86]	[-2.04]	[-2.10]	[-2.39]
$f^{\$(10)}_t-y^{\$(1)}_t$			-0.137	-0.112			-0.138	-0.112
$f^{\$(10)}_t-y^{\$(1)}_t$ [Standard Error]			[-3.15]	[-2.12]			[-3.21]	[-2.10]
Constant	-0.281	-0.304	0.054	-0.037	-0.283	-0.308	0.055	-0.042
Constant [Standard Error]	[-2.76]	[-2.59]	[0.37]	[-0.19]	[-2.78]	[-2.61]	[0.37]	[-0.21]
Observations	289	289	289	289	289	289	289	289
${R}^{2}$	0.04		0.13		0.04		0.14

Panel B: Forecasting changes in real forward rates, 1999-present

	(1) OLS	(2) IV	(3) OLS	(4) IV	(5) OLS	(6) IV	(7) OLS	(8) IV
$f^{TIPS(10)}_t-f^{TIPS(10)}_{t-1/4}$	-0.514	-0.728	-0.522	-0.811
$f^{TIPS(10)}_t-f^{TIPS(10)}_{t-1/4}$ [Standard Error]	[-3.99]	[-1.27]	[-5.21]	[-1.88]
${\left(f^{TIPS\left(10\right)}_t-f^{TIPS\left(10\right)}_{t-1/4}\right)}_{FOMC}$					-0.567	-1.081	-0.533	-0.590
${\left(f^{TIPS\left(10\right)}_t-f^{TIPS\left(10\right)}_{t-1/4}\right)}_{FOMC}$ [Standard Error]					[-2.05]	[-1.75]	[-2.03]	[-1.11]
${\left(f^{TIPS\left(10\right)}_t-f^{TIPS\left(10\right)}_{t-1/4}\right)}_{NONFOMC}$					-0.498	-0.759	-0.519	-0.792
${\left(f^{TIPS\left(10\right)}_t-f^{TIPS\left(10\right)}_{t-1/4}\right)}_{NONFOMC}$ [Standard Error]					[-3.23]	[-1.38]	[-4.00]	[-1.95]
$f^{TIPS(10)}_t-y^{TIPS(1)}_t$			-0.159	-0.159			-0.159	-0.160
$f^{TIPS(10)}_t-y^{TIPS(1)}_t$ [Standard Error]			[-3.75]	[-3.75]			[-3.68]	[-3.70]
Constant	-0.228	-0.234	0.164	0.158	-0.229	-0.240	0.164	0.163
Constant [Standard Error]	[-2.85]	[-2.70]	[1.54]	[1.44]	[-2.88]	[-2.70]	[1.49]	[1.39]
Observations	142	142	142	142	142	142	142	142
${R}^{2}$	0.12		0.37		0.12		0.37

Table 6: Duration of commercial bank securities portfolios and the yield spread, 1988-2010. Regressions of quarterly changes in the aggregate duration of bank securities portfolios on quarterly changes in the yield spread

$\displaystyle \Delta (SEC_{LT} /SEC)_{t} =a+b\cdot \Delta (y_{t}^{\$ (10)} -y_{t}^{\$ (1)} )+\Delta u_{t} .$

t-statistics, based on robust standard errors, are shown in brackets. SEC ${}_{LT}$ /SEC is the fraction of non-trading account securities with a remaining maturity (for fixed rate securities) or next re-pricing date (for floating rate securities) of 1 year or more. Column (1) shows the result for all banks. Columns (2) and (3) show results for publicly-traded banks and for private banks, respectively. Finally, column (4) shows the difference between public and private banks. Thus, the t-statistics in column (4) enables one to test the hypothesis that the coefficients for public and private banks are equal. We classify a commercial bank as publicly traded if its parent Bank Holding Company has a valid CRSP link in the table maintained by researchers at the Federal Reserve Bank of New York. This linking table is available online at http://www.newyorkfed.org/research/banking_research/datasets.html.

	All Banks (1)	Public Banks (2)	Private Banks (3)	Difference:Public - Private (4)
$\Delta({y}^{(\$(10))} - {y}^{(\$(1))})$	1.060	1.229	0.674	0.555
$\Delta({y}^{(\$(10))} - {y}^{(\$(1))})$ [Standard Error]	[3.76]	[3.07]	[1.33]	[0.75]
Constant	0.009	0.003	-0.009	0.012
Constant [Standard Error]	[0.08]	[0.02]	[-0.07]	[0.07]
Observations	91	91	91	91
R-squared	0.13	0.11	0.04	0.01

Table 7: Duration of primary dealer Treasury holdings and the yield spread, 2001-present. Regressions of weekly changes in the aggregate duration primary dealer Treasury holdings on weekly changes in the yield spread

$\displaystyle \Delta NETDUR_{t} =a+b\cdot \Delta (y_{t}^{\$ (10)} -y_{t}^{\$ (1)} )+\Delta u_{t} .$

${NETDUR}_{t}$ is defined in equation (19). The even numbered columns include controls for the weekly change in the scale of dealers' net position in Treasuries and all other reportable fixed income asset classes as well as a full set of week-of-year dummies. t-statistics, based on robust standard errors, are shown in brackets. Columns (1) and (2) show this exercise for our baseline measure of the duration of dealers' Treasury holdings. Columns (3) and (4) repeat this exercise using a more comprehensive duration measure based on dealers' holdings of both Treasuries and Agency debentures. The primary dealer data is available on-line at http://www.newyorkfed.org/markets/gsds/search.cfm.

	Treasury Holdings (1)	Treasury Holdings (2)	Treasury plus Agency Holdings (3)	Treasury plus Agency Holdings (4)
$\Delta({y}^{(\$(10))} - {y}^{(\$(1))})$	-0.973	-0.884	-0.451	-0.401
$\Delta({y}^{(\$(10))} - {y}^{(\$(1))})$ [Standard Error]	[-3.12]	[-3.00]	[-3.85]	[-3.53]
Constant	0.004	-0.355	0.002	-0.118
Constant [Standard Error]	[0.12]	[-0.94]	[0.17]	[-0.84]
Controls	No	Yes	No	Yes
Observations	555	555	555	555
R-squared	0.03	0.15	0.04	0.20

Footnotes

1. We thank John Campbell, Gene Fama, Emmanuel Farhi, Robin Greenwood, Anil Kashyap, David Scharfstein, Larry Summers, Adi Sunderam, Paul Tucker, Luis Viceira, and seminar participants at Harvard University for helpful comments. The analysis and conclusions set forth are those of the authors and do not indicate concurrence by other members of the Board of Governors. Return to Text

2. Specifically, the FOMC replaced a key sentence in the December 13, 2011 statement-that it anticipated that economic conditions "are likely to warrant exceptionally low levels for the federal funds rate at least through mid-2013"-with "are likely to warrant exceptionally low levels for the federal funds rate at least through late 2014." Return to Text

3. See Clarida, Gali, and Gertler (1999) for an introduction to the New-Keynesian literature and Gali (2008) for a more detailed treatment. Return to Text

4. For those more comfortable thinking in terms of stock prices: when a company's stock price goes up, one can always decompose this into news about either its expected future earnings (the analog to news about the expected future real rate here) or about its discount rate (the analog to the term premium on a carry-trade strategy). Return to Text

5. To be clear, none of our evidence directly refutes the long-run non-neutrality hypothesis, namely that monetary policy is somehow able to move expected real rates far out into future. It is quite possible that both effects are simultaneously at work. Return to Text

6. Other papers in this tradition include Cook and Hahn (1989), Evans and Marshall (1998), and Kuttner (2001). Return to Text

7. In 1994, the FOMC began issuing a press release with the current federal funds target after every meeting and also began releasing announcements discussing the economic and policy outlook. Prior to 1994, the FOMC implicitly announced the change in its target via the size and type of the next open market operation following a policy change (typically the day after the FOMC meeting). From 1994 to mid-1999 the FOMC only released a statement when it changed the policy target. However, since mid-1999, the FOMC has released a statement following each meeting. Return to Text

8. Treasuries with less than 3 months remaining to maturity, T-bills, and on-the-run notes and bonds are omitted from the nominal sample because they often embed liquidity or convenience premia relative to other Treasuries. Short-term TIPS are omitted because lags in inflation indexation make the behavior of their yields somewhat erratic. Return to Text

9. The five FOMC announcement dates that we exclude are 3/18/09 (QE1: increased size of the LSAP from $600 billion to $1.75 trillion); 10/10/2010 (QE2: FOMC Will reinvest coupon/principal from LSAP to maintain constant portfolio); 9/21/2010 (QE2: FOMC maintains its existing policy of reinvesting principal payments); 11/03/2010 (QE2: Will purchase additional $600B of USTs); and 9/21/2011 (Operation Twist: Fed announces the Maturity Extension program, a plan to sell $400 billion of short-term USTs and buy $400 billion of long-term USTs by June 2012). Our results are robust both to including these dates, as well as to excluding a couple of others (12/16/2008 and 01/28/2009) that arguably also contained some information about the LSAPs. Return to Text

10. Although the UK has issued inflation-linked bonds since 1985, we focus on the more recent period since their monetary regime changed significantly in June 1997 when the Bank of England was granted formal independence from the UK Treasury. We begin in 1999 in order to maintain comparability with our results for the US. However, the UK results are unchanged if we consider all MPC announcements from June 1997 to present. Return to Text

11. The list is based on Table A in Joyce, Tong, and Woods (2011). The dates are 03/05/2009 (decision to purchase £75B Gilts), 05/07/2009 (decision to purchase an additional £50B Gilts), 08/06/2009 (decision to purchase an additional £50B Gilts), 11/05/2009 (decision to purchase an additional £25B Gilts), 02/04/2010 (total asset purchases will be maintained at £200B), and 10/06/2011 (decision to purchase an additional £75B Gilts). Return to Text

12. Romer and Romer (2000) argue that Fed inflation forecasts for the coming quarters outperformed those of private forecasters from the late 1960s to the early 1990s. By contrast, Faust, Swanson, and Wright (2004) argue that FOMC policy surprises contain little information that could be used to improve macroeconomic forecasts and that private forecasters do not appear to revise their forecasts in response to policy surprises. Regardless, there is no argument in the literature that the Fed has a significant forecasting advantage at anything close to a 10-year horizon. Return to Text

13. In untabulated regressions, we have redone the exercise in Table 4 with the UK data. The results are qualitatively similar. In particular, the elasticity of long-term real forward rates to short-term nominal rates is slightly higher on BOE announcement days than on non-announcement days, although the difference is not statistically significant. Return to Text

14. We work with 1-year forward rates in this section as opposed to the instantaneous forward rates used above. We do this to exploit the simple decompositions for 1-year forward rates, but this choice only has a trivial impact on the estimates. Note too that equation (6) is strictly true only over short intervals where expected excess returns are near zero. More generally, only unexpected changes in forwards-equivalently, unexpected bond returns-contain news. Return to Text

15. The regressions are estimated with monthly data, so each month we are forecasting the excess return over the following 12 months. To deal with the overlapping nature of returns, t-statistics are based on Newey-West (1987) standard errors allowing for serial correlation at up to 18 lags. Return to Text

16. One wrinkle is that we do not observe the short-term real rate, which is needed to compute the forward rate spread for long-term real bonds. Following Pflueger and Viceira (2011), we estimate the short-term real rate as the fitted value from a regression of the realized real bill return on a number of covariates. Return to Text

17. Confidence intervals are based on Newey-West (1987) standard errors to properly account for the overlapping nature of the dependent variable in regression (9). Return to Text

18. For instance, Lee (2002) estimates GARCH models which enable him to separately estimate the impact of a surprise FOMC easing versus a surprise tightening on conditional interest rate volatility. While a surprise tightening has a larger impact on interest rate volatility than a surprise easing, the evidence suggests that both positive and negative surprises raise conditional volatility. Return to Text

19. We work with log returns to facilitate the exposition. This can be viewed as a linear approximation to a model based on simple returns. Return to Text

20. Almost all non-trading-account securities are treated as "available-for-sale" under US GAAP. Although these securities are marked to market, unrealized gains/losses do not flow through the income statement (as do changes in the value of trading account securities). Instead, mark-to-market gains/losses flow through "other comprehensive income" and are accumulated on the balance sheet until realized. By contrast, interest income on these securities flows directly through the income statement. Thus, a bank can boost its near-term reported earnings by substituting high-yielding for low-yielding securities. A similar effect obtains for the small fraction of non-trading securities that are carried on the balance sheet on a historical cost basis (a.k.a., "held-to-maturity" securities). Return to Text

21. We have also tried regressing $\Delta \left(SEC_{LT} /SEC\right)$ on both and $\Delta{y}^{\$\left(10\right)}$ and $\Delta{y}^{\$\left(1\right)}$ separately. The coefficient on $\Delta{y}^{\left(10\right)}$ is positive and significant, while the coefficient on $\Delta{y}^{\left(1\right)}$ is negative and significant. And the absolute magnitudes of the two coefficients are similar, consistent with the logic of equation (15). Return to Text

22. We classify a commercial bank as publicly traded if its parent Bank Holding Company has a valid CRSP link in the linking table maintained by researchers at the Federal Reserve Bank of New York (see http://www.newyorkfed.org/research/banking_research/datasets.html). Return to Text

23. While primary dealers also report their holdings of TIPS, these are not broken out by maturity and so we do not use them to compute our measure of the maturity structure of dealers' holdings. However, dealers' holdings of TIPS are small relative to their overall Treasury holdings, so this choice has little impact on the resulting measure. Return to Text

24. Alternate approaches are to work directly with the numerator of $NETDUR_{t}$ or to scale the numerator by the amount of outstanding Treasuries. These approaches are less desirable because the resulting measures are impacted by variation in the scale of brokers' holdings relative to market as a whole and, thus, are no longer pure maturity measures. Nevertheless, we have experimented with these constructions and generally obtain similar results. Return to Text

25. One might ask why, according to this theory, the current shape of the yield curve is not a sufficient statistic for forecasting excess bond returns. Greenwood and Vayanos (2010a) provide an explanation: the yield curve contains information about both the expected path of future short rates and term premia, both of which vary over time. Measures of the quantity of aggregate duration pertain solely to the latter and, thus, can improve the forecasting power of regressions that include only the yield spread. Return to Text

26. Similar issues arise when a firm makes investment and financing decisions in the face of a transitory equity mispricing. Stein (1996) and Baker, Stein and Wurgler (2003) argue that the investment of financially-constrained firms is most sensitive to equity mispricing. One might conjecture that the same would be true here: constrained firms may be most likely to adjust investment in response to policy-induced changes in term premia. At the same time, the financing (i.e., debt maturity) decisions of unconstrained firms may adjust more as in Greenwood, Hanson, and Stein (2010). However, unlike constrained firms, this would not have a large impact on their investment. Return to Text

27. See, e.g., Rajan (2005), Borio and Zhu (2008), Greenwood and Hanson (2012), Jiménez et al (2011), Adrian and Shin (2010) and Landier, Sraer and Thesmar (2011). Return to Text

^♣ This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to Text

Monetary Policy and Long-Term Real Rates1

Monetary Policy and Long-Term Real Rates¹