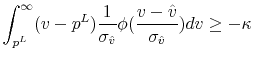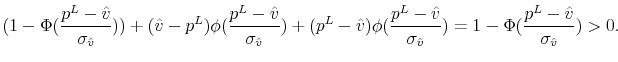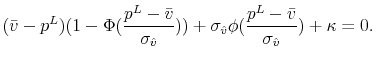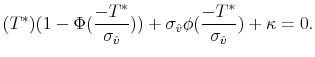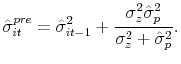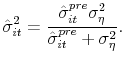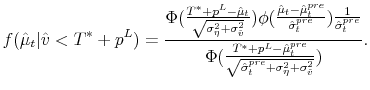Information Frictions and Housing Market Dynamics*
Keywords: Learning, housing search
Abstract:
1 Introduction
Since the seminal work of Stigler (1961), economists have long recognized the importance of imperfect information in explaining the workings of a variety of markets. Surprisingly, given its importance to the macro economy, little work has focused on the effects of imperfect information in the housing market.2 The housing market is a classic example of a market affected by imperfect information. Each house is a unique, differentiated asset; trading volume of comparable homes tends to be thin due to high transaction costs; and market conditions are highly volatile over time. These features of the housing market make it difficult for sellers to determine their home values at any point in time.
In this paper I model the effect of this type of seller uncertainty on the housing market. The model adds a framework for seller uncertainty and Bayesian learning in the spirit of Lazear (1986) to the typical features of the dynamic micro search models in the housing literature (Carrillo (2010), Horowitz (1992), Salant (1991)). I estimate the model and use it to test whether uncertainty is important for explaining several key stylized facts about housing market dynamics that have attracted much attention in the literature, in part because they are inconsistent with the predictions of standard asset pricing models.
The first fact is that price appreciation rates display predictability in the short-run. In their seminal papers, Case & Shiller (1989) and Cutler et al. (1991) find that a 1 percent increase in real annual house prices is associated with a .2 percent increase the next year, adjusting for changes in the nominal interest rate. Numerous other studies have also documented this persistence, and it has led some to question the efficiency of the housing market because it cannot be explained by fundamentals.3 Thus, an important question is whether the amount of short-run momentum found in the data is consistent with a rational model of the housing market.
Another key feature of housing markets is that sales volume and marketing time are positively and negatively correlated with sales price changes, respectively. The existing literature has convincingly emphasized the importance of search frictions and credit constraints as explanations.4 Here, I investigate whether imperfect information is an additional friction that causes housing markets to display these unusual time series properties.
At a more micro level, the literature has also documented a set of stylized facts about the behavior of individual sellers (Merlo & Ortalo-Magne (2004)). For example, sellers tend to adjust their list prices downwards, even when market conditions do not change, and sales prices for observationally equivalent homes depend on time on market (TOM). These empirical patterns are inconsistent with the predictions of existing search, matching and bargaining theories of housing transactions, which do not accommodate duration dependence in seller behavior.5 In addition to explaining the macro stylized facts discussed above, I will show that uncertainty and the gradual acquisition of information during the listing period is an explanation for these and many other dynamic features of the micro data.
I motivate the model with reduced form evidence that lack of information does affect selling behavior. While several studies show that homeowners misestimate their home values at various points during their ownership tenure6, I am not aware of other studies that investigate the information set of sellers when the home is on the market for sale. Since most sellers hire a realtor when they are ready to sell their homes, this is potentially an important distinction. The reduced form evidence comes from a new micro dataset that I compile from two independent sources. For a large sample of single family homes listed for sale with a realtor in the two major California metropolitan areas from 2007-2009, the combined dataset describes the precise location of each listing, list prices each week that the home is listed for sale, TOM, and sales prices.
I exploit cross-sectional variation in the heterogeneity of the housing bust across neighborhoods to test whether sellers price their homes using the most up to date information about local market conditions. I find that they do not; initial list prices are overly sensitive to lagged market
information. The regression results show that for two comparable homes in a given time period, the home in the neighborhood that experienced the greater amount of price depreciation in the previous four months will be listed at a ![]() price on average. Neighborhood price levels from longer than four months ago do not provide any additional explanatory power for initial list prices. This finding is consistent with anecdotal evidence that sellers, with the help of realtors, look to
previous sales of similar houses when pricing their homes, presumably because comparable sales volume can be thin and sales prices become publicly available with a lag. Evidently, realtors do not fully adjust for the downward trend in prices during my sample period.
price on average. Neighborhood price levels from longer than four months ago do not provide any additional explanatory power for initial list prices. This finding is consistent with anecdotal evidence that sellers, with the help of realtors, look to
previous sales of similar houses when pricing their homes, presumably because comparable sales volume can be thin and sales prices become publicly available with a lag. Evidently, realtors do not fully adjust for the downward trend in prices during my sample period.
Using list prices to infer seller beliefs is complicated by the fact that many unobservables affect list prices, and some of them may be correlated with lagged market information. However, the correlation between ![]() prices and lagged neighborhood price depreciation confirms that expectation bias is indeed the explanation for the inflated list prices. In particular, I find that for the same homes that have higher list prices because of high lagged neighborhood price
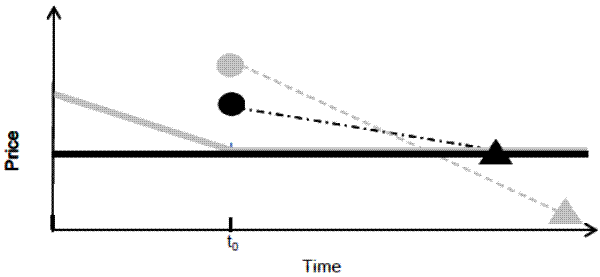
depreciation, sales prices are lower. Theoretically, higher list and lower sales prices can arise when sellers overstate their home value, but this crossing pattern, which is shown in Figure 1, cannot easily be explained by many alternative explanations for the high list prices including loss
aversion (Genesove & Mayer (2001), Anenberg (2011a)), equity constraints (Stein (1995),Genesove & Mayer (1997), Anenberg (2011a)), high unobserved
home quality, or low unobserved motivation to sell, among others. In other words, unobservables that increase list prices should also increase sales prices.7
This simple identification strategy for expectation bias could be useful in other settings where list prices or reserve prices are observed in addition to selling prices.
prices and lagged neighborhood price depreciation confirms that expectation bias is indeed the explanation for the inflated list prices. In particular, I find that for the same homes that have higher list prices because of high lagged neighborhood price
depreciation, sales prices are lower. Theoretically, higher list and lower sales prices can arise when sellers overstate their home value, but this crossing pattern, which is shown in Figure 1, cannot easily be explained by many alternative explanations for the high list prices including loss
aversion (Genesove & Mayer (2001), Anenberg (2011a)), equity constraints (Stein (1995),Genesove & Mayer (1997), Anenberg (2011a)), high unobserved
home quality, or low unobserved motivation to sell, among others. In other words, unobservables that increase list prices should also increase sales prices.7
This simple identification strategy for expectation bias could be useful in other settings where list prices or reserve prices are observed in addition to selling prices.
Having established this new evidence that information frictions are an important part of the home selling process, I incorporate them into a single-agent dynamic micro model of the home selling problem. I model seller uncertainty as a prior on the mean of the distribution of buyer valuations for their home, and this prior may be biased depending on the information available. Sellers set list prices to balance a trade-off: a high list price strengthens their bargaining position if a buyer arrives, while a low list price attracts more offers and increases the pace of learning. Conditional on the list price, buyers with idiosyncratic valuations arrive randomly. The house sells if the buyer's valuation is above the seller's reservation price, which depends on the value of declining the offer and continuing the dynamic process. Sellers in the model behave rationally and optimally given the available information.
I estimate the parameters of the model using simulated method of moments.8 The parameter estimates themselves are informative about the amount of information that sellers have and the pace of learning. I find that the standard deviation of the typical seller's prior about their home value is $38,000, which is about 7 percent of the average sales price. Learning over the course of the marketing period decreases this standard deviation by 37 percent by the time of sale, on average.
Simulations of the estimated model show that annual aggregate sales price appreciation rates persist even when changes in the market fundamentals do not. The model can account for over half of the persistence typically found in the data. To see the intuition behind this result, suppose that
there is uncertainty about demand at time ![]() , the expected value of demand is
, the expected value of demand is ![]() at time
at time ![]() , and the realization of a permanent demand shock is higher than expected at
, and the realization of a permanent demand shock is higher than expected at
![]() . Even if every seller receives an idiosyncratic signal at time
. Even if every seller receives an idiosyncratic signal at time ![]() that
demand is high, in the absence of a mechanism (either formal or informal as in Grossman & Stiglitz (1976)) that publicizes private information, the reservation price of the average Bayesian updating seller will not fully adjust to the shock at time
that
demand is high, in the absence of a mechanism (either formal or informal as in Grossman & Stiglitz (1976)) that publicizes private information, the reservation price of the average Bayesian updating seller will not fully adjust to the shock at time ![]() . In subsequent periods, after more information about the positive shock becomes available, reservation prices, and thus sales prices, will fully adjust. It is this lag in the flow of information that
gives rise to serial correlation in price changes.
. In subsequent periods, after more information about the positive shock becomes available, reservation prices, and thus sales prices, will fully adjust. It is this lag in the flow of information that
gives rise to serial correlation in price changes.
The same lag in the updating of reservation prices to demand shocks generates a positive (negative) correlation between price changes and sales volume (TOM). For example, when there is a positive demand shock, reservation prices are too low relative to the fundamentals, which leads to higher sales volume and quicker sales. The model predicts that a 1 percent increase in quarterly prices leads to a 4.8 percent increase in volume and a 7.2 percent decrease in TOM. These predicted co-movements are comparable to what is observed in the data. Thus, uncertainty does appear to be important in explaining variation in transaction rates over the housing cycle as well.9
A related paper by Head et al. (2011), written recently and independently of this one, also explores the serial correlation of house price changes. Under some calibrations and functional form assumptions, their macro model, which is one of complete information, is also able to generate some, but not all, of the momentum observed in the data. Their model, like mine, does not rely on inefficiency or irrationality of the market. Matching frictions in the spirit of Mortensen & Pissarides (1994) and Pissarides (2000) interact with a lagged housing supply response to cause market tightness (i.e. the ratio of buyers to sellers), and thus prices, to gradually rise in response to an income shock. Future efforts to explain even more of the momentum in housing market conditions could try incorporating information frictions into this type of search and matching framework.
This paper proceeds as follow. Section 2 introduces the data. Section 3 motivates the model with reduced form evidence that information frictions are an important part of the home selling problem. To investigate the broader implications of seller bias and uncertainty for housing market dynamics, Section 4 develops a model where the flow of information has an endogenous effect on selling behavior. Section 5 and 6 discuss estimation details. Section 7 simulates the model to highlight the importance of information frictions in explaining the stylized facts discussed above. Section 8 discusses the robustness of the results to certain stylized features of the model and section 9 concludes the paper.
2 Data
I use home sale and listing data for the core counties of the San Francisco Bay Area and Los Angeles. These counties include Alameda, Contra Costa, Marin, San Francisco, San Mateo, and Santa Clara in San Francisco; and Los Angeles, Orange, Riverside, San Bernardino, and Ventura counties in the Los Angeles area.
The listing data come from Altos Research, which provides information on single-family homes listed for sale on the Multiple Listing Service (MLS) from January 2007 - June 2009. Altos Research does not collect MLS data prior to 2006. Since a seller must use a licensed real estate agent to gain access to the MLS, my sample only contains selling outcomes for sellers who use realtors.10 Every Friday, Altos Research records the address, mls id, list price, and some characteristics of the house (e.g. square feet, lot size, etc.) for all houses listed for sale. From this information, it is easy to infer the date of initial listing and the date of delisting for each property. A property is delisted when there is a sale agreement or when the seller withdraws the home from the market. Properties are also sometimes delisted and then relisted in order to strategically reset the TOM field in the MLS. I consider a listing as new only if there was at least a 180 day window since the address last appeared in the listing data.
The MLS data alone does not provide information on which listings result in a sale, and what the sales price is if a sale occurs. To obtain this information, I supplement the MLS data with a transactions dataset from Dataquick that contains information about the universe of housing transactions from 1988-2009. In this dataset, the variables that are central to this analysis are the address of the property, the date of the transaction, and the sales price.
Using the address, I attempt to merge each listing to a transaction record that is within 1 year of the date of delisting from the MLS.11 I also attempt to merge each listing to a previous sale in the transaction dataset. The latter merge acquires information on the purchase price of each home, which I use to construct a predicted log selling price for each house:
I calculate these prices by applying a zip code price change index to the previous log sales price. The price index is calculated using a repeat sales analysis following Shiller (1991). I let the price index vary by zip code and month. The predicted price measures what
the economist expects house ![]() to sell for in time
to sell for in time ![]() , and it controls for
time-invariant unobserved home quality and differences in neighborhood price appreciation rates. Appendix A.2 describes how I calculate these prices from the data in more detail.
, and it controls for
time-invariant unobserved home quality and differences in neighborhood price appreciation rates. Appendix A.2 describes how I calculate these prices from the data in more detail.
Appendix A.1 describes more details of the data building process, including minor restrictions to the estimation sample (e.g. exclude listings where the ratio of the minimum list price to the maximum list price is less than the first percentile). I exclude listings where the initial listing date equals the first week of the sample and listings where the final listing data equals the last week of the sample to avoid censoring issues. I also drop all listings that do not merge to a previous transaction.12
2.1 Summary Statistics
Figure 2 shows the Case-Shiller home price index for Los Angeles and San Francisco from 2007 - 2009. During the years where the MLS and transactions data overlap, both cities experienced comparable and significant price declines. In Los Angeles, the market peaked in September 2006, and fell 37.5 percent in nominal terms through December 2009. The San Francisco market peaked in May 2006, and also fell by 37.5 percent by the end of 2009. The prolonged episode of falling prices, low sales volume, and long marketing time that my sample period covers is not an isolated event; Burnside et al. (2011) show that sustained booms and busts occur throughout housing markets around the world. For example, in real terms, Los Angeles experienced a comparable price decline during the housing bust of the early 90's.13 Thus, my sample and my results like characterize market dynamics during cold housing markets more generally.
Table 1 presents summary statistics for the listings that sell. The median time to sale is about 3 months, and there is a lot of variation. Twenty five percent of listings sell in less than 5 weeks and 25 percent take more than 25 weeks to sell. Most sellers adjust their list price at least once before they sell. These list price changes tend to be decreases: only 6 percent of list price changes are increases.14 Table 2 shows that list price changes occur throughout the selling horizon, and many occur in the first few weeks after listing. These stylized facts about list price changes seem challenging for models with complete information to explain.15 Since some sellers will quickly adjust their beliefs in response to new information, the learning model that I present below will also predict changing list prices in the first few weeks and some list price changes that are increases.
Few studies have had access to such a large dataset on home listings that includes the full history of list prices for each listing.16This feature of the data will be important for identifying the parameters of the non-stationary model of selling behavior presented below.
3 Motivating Empirical Facts
I begin by presenting strong evidence, which does not rely on my modeling assumptions below, that imperfect information does affect the home selling process. This is important because even though many features of the data are consistent with a model with uncertainty and learning as I show below and as documented in Knight (1996), alternative models may be able to explain these features as well.
3.1 Expectation Bias and List Prices
I test whether the initial list price choices of sellers reflect the most up to date market information, or whether they place undue weight on lagged information. Outdated information may affect list prices because the thinness of the market and the lag in which sales data become public make it difficult to assess current market conditions.17 Conversations with a realtor suggest that lagged comparable sales are often used as a proxy for the current market value.18
I implement this test by regressing the log list price in the initial week of listing, normalized by the log predicted sales price, on lagged price changes according to:
where the 0 subscript denotes that it is
Column 1 of Table 3 reports the results. Standard errors are clustered at the zip code level. A 1 percent increase in the price depreciation rate leads to a 0.57 percent increase in the list price, all else equal. That this estimate is less than one suggests that realtors have some information,
just not perfect information, that market conditions have deteriorated. In Columns 2-5, I continue to add lagged neighborhood price changes as regressors until the estimated coefficient becomes insignificant. One month price changes immediately before listing have the biggest effect on list price
premiums, and the effect of 1 month price changes diminish as they occur further before the month of listing. A price change between month ![]() and
and ![]() does not affect the list price premium. It makes sense that the most recent price changes are the least capitalized into list prices because the least information is available about these changes.19
does not affect the list price premium. It makes sense that the most recent price changes are the least capitalized into list prices because the least information is available about these changes.19
In Table 4, I test how the list price premium varies over the entire distribution of lagged depreciation. The regression specification is
where
| (3) |
is the local price change over the four months prior to initial listing,
3.2 Expectation Bias and Selling Outcomes
The previous section showed evidence that sellers set higher list prices when their local market is declining at a faster than average rate. I interpret this as expectation bias. In this section, I test whether market deterioration affects other variables such as the sales price and marketing time. Here, I find patterns that are consistent with expectation bias, but not with other plausible explanations for the list price results.
Columns 3 and 4 of Table 4 substitute ![]() as the dependent variable in equation (2) using the full sample and the sample of only sales, respectively.
as the dependent variable in equation (2) using the full sample and the sample of only sales, respectively. ![]() is increasing in
is increasing in ![]() , although the extreme decile of the price change distribution
appears to be an outlier. Column 5 shows that the propensity to withdraw is also increasing in
, although the extreme decile of the price change distribution
appears to be an outlier. Column 5 shows that the propensity to withdraw is also increasing in ![]() , and monotonic over the entire
, and monotonic over the entire ![]() distribution. In this specification, I include in
distribution. In this specification, I include in ![]() an additional control for the change in price level during the marketing
period,
an additional control for the change in price level during the marketing
period,
![]() , where
, where ![]() denotes the time period that the house
sells or is withdrawn.
denotes the time period that the house
sells or is withdrawn.
Column 6 reports results where the dependent variable is the log sales price normalized by the predicted log sales price in the month of sale, i.e.
![]() . Sales prices are significantly decreasing in the lower deciles of
. Sales prices are significantly decreasing in the lower deciles of ![]() , but are flat or slightly increasing in the higher deciles.
, but are flat or slightly increasing in the higher deciles.
3.3 Discussion
That higher lagged depreciation leads to longer marketing time and a higher propensity to withdraw is consistent with the expectation bias interpretation. Biased beliefs lead to higher reservation prices, which should increase marketing time in a standard search model. Biased beliefs may also draw sellers into the market, only to withdraw later once they realize that their home will not sell for what they initially expected.
The theoretical effect of inflated beliefs on sales price is ambiguous. For example, a high reservation price could cause sellers to stay on the market for longer, which allows them to sample more offers and ultimately receive a higher price at the expense of a longer time to sale. Inflated beliefs can also decrease sales prices if, for example, motivation to sell increases over time (e.g. there is a finite selling horizon). In this case, the seller is pricing too high, and potentially turning off potential buyers, exactly when he is most likely to accept higher offers.
For this reason, the sales price results alone do not tell us much about the existence of expectation bias. However, the fact that for some regions of the price decline distribution, list prices are significantly increasing while sales prices are significantly decreasing is an unusual pattern
that is consistent with expectation bias but inconsistent with alternative explanations for the list price, TOM and withdrawal results. A stylized case of this crossing property is illustrated in Figure 1. Finding a reasonable model where an omitted variable from equation (2)
increases list prices above what is expected while decreasing sales price below what is expected is a challenge. In fact, finding a model where a variable increases list prices and leads to no change in sales price, which is the case for much of the ![]() distribution, is also difficult. For example, standard models of the home selling problem, including the model we present below, predict that unobservables such as high home quality, low motivation to sell, loss aversion, and
equity constraints should all lead to higher list and higher sales prices.22 Appendix A.3 presents additional results that are consistent with the
conclusions established in this Section.
distribution, is also difficult. For example, standard models of the home selling problem, including the model we present below, predict that unobservables such as high home quality, low motivation to sell, loss aversion, and
equity constraints should all lead to higher list and higher sales prices.22 Appendix A.3 presents additional results that are consistent with the
conclusions established in this Section.
4.1 Overview and Comparison with Related Literature
The heart of my model is similar to Carrillo (2010), Horowitz (1992), Salant (1991). The seller's decision to list the home and sell it is taken as given, and the seller's objective is to maximize the selling price of the house less the holding costs of keeping the home on the market. My main contribution is to introduce uncertainty and Bayesian learning into this framework. This makes the home selling problem nonstationary; unlike in Carrillo (2010) and Horowitz (1992), sellers in my model will adjust their list prices over time and the hazard rate of selling varies over time as learning occurs.23 I endogenize the effect of information on market dynamics while 1) only introducing parameters that are identified given the dataset described in Section 2 and 2) capturing the key features of the home selling process including search, a posting price mechanism, preference heterogeneity, and duration dependence in optimal seller behavior. I discuss extensions to the model and their implications for my conclusions in Section 8.
The way that I model uncertainty and learning is similar to the existing empirical learning models (see cites in footnote 7)), but my model is unique in two ways. First, I allow the parameter, ![]() , that agents are learning about to change over time. Second, agents in my model receive direct signals about the unknown parameter (i.e.
, that agents are learning about to change over time. Second, agents in my model receive direct signals about the unknown parameter (i.e. ![]() + noise) as in the existing
studies, but also receive signals (when buyers do not inspect their house) that the unknown parameter is below a known threshold (i.e.
+ noise) as in the existing
studies, but also receive signals (when buyers do not inspect their house) that the unknown parameter is below a known threshold (i.e. ![]() + noise
+ noise ![]() T). The latter innovation introduces some new computational challenges that I discuss in Section 4.5.
T). The latter innovation introduces some new computational challenges that I discuss in Section 4.5.
4.2 Offer Process and Buyer Behavior
At the beginning of each week ![]() that the house is for sale, seller/house combination
that the house is for sale, seller/house combination ![]() selects an optimal list price,
selects an optimal list price, ![]() . This list price and a subset of the characteristics of the house are advertised to a single risk-neutral potential buyer. From now
on, I refer to these potential buyers as simply buyers. The logarithm of each buyer
. This list price and a subset of the characteristics of the house are advertised to a single risk-neutral potential buyer. From now
on, I refer to these potential buyers as simply buyers. The logarithm of each buyer ![]() 's willingness to pay (or valuation)
's willingness to pay (or valuation) ![]() is parameterized as
is parameterized as
where
I assume that
| (5) |
That is,
The advertisement only provides the buyer with a signal of their valuation. From the advertisement, the buyer forms beliefs about ![]() that are assumed
that are assumed
where
![]() is drawn from
is drawn from
![]() . Thus, buyers get an unbiased signal of their true valuation from the advertisement.24
. Thus, buyers get an unbiased signal of their true valuation from the advertisement.24
After observing
![]() , the buyer decides whether to inspect the house at some cost,
, the buyer decides whether to inspect the house at some cost, ![]() .25 If the buyer inspects, then
.25 If the buyer inspects, then ![]() is revealed to both the buyer and the seller. If
is revealed to both the buyer and the seller. If ![]() , the seller has all the bargaining power and has the right to make a 'take it or leave it' offer to the buyer at a
price equal to
, the seller has all the bargaining power and has the right to make a 'take it or leave it' offer to the buyer at a
price equal to ![]() (which I assume the buyer will accept). If
(which I assume the buyer will accept). If ![]() , then the
buyer receives some surplus: the buyer has the right to purchase the house at a price equal to the list price. If the buyer chooses not to inspect or if the buyer's valuation lies below the seller's continuation value of remaining on the market, then the buyer departs forever and the seller moves
onto the next period with her house for sale.
, then the
buyer receives some surplus: the buyer has the right to purchase the house at a price equal to the list price. If the buyer chooses not to inspect or if the buyer's valuation lies below the seller's continuation value of remaining on the market, then the buyer departs forever and the seller moves
onto the next period with her house for sale.
The proof of the following theorem, which characterizes the buyer's optimal behavior, appears in Appendix A.4.
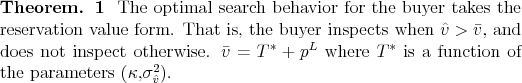
This price determination mechanism delivers a closed form relationship between ![]() and the list price, which is necessary to keep estimation tractable given that the list price choice
will be endogenous. Since the buyer receives no surplus when
and the list price, which is necessary to keep estimation tractable given that the list price choice
will be endogenous. Since the buyer receives no surplus when ![]() ,
, ![]() does not depend on the seller's reservation price or any other variable (like TOM) that provides a signal about the seller's reservation price.
does not depend on the seller's reservation price or any other variable (like TOM) that provides a signal about the seller's reservation price.
This simple model of buyer behavior endogenizes the list price and leads to a trade-off (from the seller's perspective) when setting the list price between sales price and TOM.26 The model also generates a mass point at the list price in the sales price distribution. These predicts are consistent with the empirical evidence, and with the theoretical literature on the role of asking prices as a commitment device.27
4.3 The  process
process
The underlying valuation process, ![]() , is exogenous to the model. It is not affected by the individual decisions of the buyers and sellers that I model.28 I assume that it follows a random walk with drift, so that there is no predictability in changes in housing market fundamentals. In other words, in a frictionless environment, there
should be no predictable returns to owning a house. The particular parametrization I use in estimation is
, is exogenous to the model. It is not affected by the individual decisions of the buyers and sellers that I model.28 I assume that it follows a random walk with drift, so that there is no predictability in changes in housing market fundamentals. In other words, in a frictionless environment, there
should be no predictable returns to owning a house. The particular parametrization I use in estimation is
where
4.4 Structure of Information
I assume that the seller knows all of the parameters that characterize the search problem except for the mean of the valuation distribution, ![]() . When sellers receive an offer, they
cannot separately identify
. When sellers receive an offer, they
cannot separately identify ![]() from
from ![]() . That is, sellers have difficulty
distinguishing a high offer due to high average demand from a high offer due to a strong idiosyncratic taste for the house.
. That is, sellers have difficulty
distinguishing a high offer due to high average demand from a high offer due to a strong idiosyncratic taste for the house.
Sellers have rational expectations about the ![]() process in (7). Sellers do not observe the realizations of
process in (7). Sellers do not observe the realizations of ![]() , but they observe an unbiased signal
, but they observe an unbiased signal ![]() parameterized as
parameterized as
The source of this signal is exogenous to the model, but we can think about it as idiosyncratic information about real-time market conditions that realtors can collect as professional observers of the market.
To summarize, there are three sources of information that sellers receive during the selling horizon. Sellers observe whether or not a buyer inspects. This reveals whether or not a noisy signal of a buyer's valuation exceeds a known threshold. Secondly, sellers observe the buyer's valuation if the buyer inspects. Thus, inspections are more informative to the seller than non-inspections. Since the choice of list price affects whether or not a buyer inspects, the list price has an endogenous effect on the flow of information. I am not aware of other models where the optimal list price will depend on the amount of information that the buyer response to the price is likely to provide. Finally, each period sellers observe the exogenous signal about changes in the valuation process.
Appendix A.5 shows how sellers update their beliefs with this information using Bayes' rule. The final piece of the information environment is the seller's initial prior, which is assumed to be:
The mean of the prior is given by
where
| (11) |
The parameters ![]() allow the initial beliefs to be sensitive to market conditions from the previous 4 months, as the evidence in Section 3 suggests. If
allow the initial beliefs to be sensitive to market conditions from the previous 4 months, as the evidence in Section 3 suggests. If
![]() for
for ![]() , then the average seller will have unbiased initial
beliefs, although there will still be heterogeneity due to
, then the average seller will have unbiased initial
beliefs, although there will still be heterogeneity due to ![]() . Although I do not explicitly model how this initial prior is generated, I show in Appendix A.7 that if a similar Bayesian
learning framework applies prior to the beginning of the selling horizon, then initial priors will depend on lagged information.
. Although I do not explicitly model how this initial prior is generated, I show in Appendix A.7 that if a similar Bayesian
learning framework applies prior to the beginning of the selling horizon, then initial priors will depend on lagged information.
4.5 Seller's Optimization Problem
The timing of the model is summarized in Figure 3. Each period begins with the realization of ![]() . The seller updates his beliefs, and then chooses an optimal list price. The list price is
set to balance the tradeoffs that emerge from Theorem 1. Once the list price is advertised, the buyer decides whether to inspect, the seller updates the reservation price with the information from buyer behavior, and then the seller chooses to either sell the house (if an offer is made) and receive
a terminal utility equal to the log sales price or to move onto the next period with the house for sale. Each period that the home does not sell, the seller incurs a cost
. The seller updates his beliefs, and then chooses an optimal list price. The list price is
set to balance the tradeoffs that emerge from Theorem 1. Once the list price is advertised, the buyer decides whether to inspect, the seller updates the reservation price with the information from buyer behavior, and then the seller chooses to either sell the house (if an offer is made) and receive
a terminal utility equal to the log sales price or to move onto the next period with the house for sale. Each period that the home does not sell, the seller incurs a cost ![]() , which reflects
discounting and the costs of keeping the home presentable to show to prospective buyers. I impose a finite selling horizon of 80 weeks.
, which reflects
discounting and the costs of keeping the home presentable to show to prospective buyers. I impose a finite selling horizon of 80 weeks.
The following Bellman's equation, which characterizes selling behavior at the third hash mark on the timeline in Figure 3, summarizes the seller's optimization problem:
where
5 Estimation and Identification
Table 5 summarizes the notation of all of the model parameters. I estimate the parameters using simulated method of moments. That is, I minimize a weighted average distance between sample moments and simulated moments with respect to the model's parameters. The weights are the inverses of the estimated variance of the moments. The target moments are listed in Table 6. I calculate the empirical moments using the subset of listings that sell (which introduces potential sample selection issues that I discuss in Section 8). I describe the dynamic programming techniques used to estimate the model in Appendix A.6.
The parameters that are not estimated are the time invariant holding cost (![]() ) and the buyer's inspection cost (
) and the buyer's inspection cost (
![]() or .5 percent of the list price). The conclusions that follow are related to the parameters that dictate the flow of information, and so I find that my results are not sensitive
to the choices for these parameters. I calibrate the mean (
or .5 percent of the list price). The conclusions that follow are related to the parameters that dictate the flow of information, and so I find that my results are not sensitive
to the choices for these parameters. I calibrate the mean (
![]() or .33 percent) of the
or .33 percent) of the ![]() process using the average monthly change
in the Case-Shiller index for San Francisco and Los Angeles during my sample period. I set
process using the average monthly change
in the Case-Shiller index for San Francisco and Los Angeles during my sample period. I set ![]() ,
,![]() ,
,![]() ,
,![]() equal to the coefficients on lagged
depreciation estimated in Column 4 of Table 3. Since
equal to the coefficients on lagged
depreciation estimated in Column 4 of Table 3. Since
![]() in the model (proof not reported), this implies that the initial list price will display the same level of sensitivity to lagged market conditions as
found in the data.
in the model (proof not reported), this implies that the initial list price will display the same level of sensitivity to lagged market conditions as
found in the data.
The variance of the offer distribution,
![]() , is identified by the distribution of sales prices relative to the list price. The level of initial uncertainty,
, is identified by the distribution of sales prices relative to the list price. The level of initial uncertainty,
![]() , is identified by the size of list price changes, especially in the first couple weeks after listing before depreciation in
, is identified by the size of list price changes, especially in the first couple weeks after listing before depreciation in ![]() increases the variance in list price changes. Both variances also have different predictions for TOM. More variance in the offer distribution increases TOM because the higher incidence of very good offers increases the value of
searching. More uncertainty distorts the choice of list price and reservation price, which decreases the returns to staying on the market. The average premium of the list price relative to the sales price helps to identify
increases the variance in list price changes. Both variances also have different predictions for TOM. More variance in the offer distribution increases TOM because the higher incidence of very good offers increases the value of
searching. More uncertainty distorts the choice of list price and reservation price, which decreases the returns to staying on the market. The average premium of the list price relative to the sales price helps to identify
![]() , as does the propensity for prices to occur at the list price. For example, if buyers have a lot of information about their valuation prior to inspection (low
, as does the propensity for prices to occur at the list price. For example, if buyers have a lot of information about their valuation prior to inspection (low
![]() ), sellers need to set low list prices to induce inspections.
), sellers need to set low list prices to induce inspections.
![]() is identified by the correlation between list price changes and changes in
is identified by the correlation between list price changes and changes in ![]() . A high correlation suggests that
. A high correlation suggests that
![]() is low because sellers can quickly and fully internalize changes in market conditions into their list price decisions.30 The variance of the
is low because sellers can quickly and fully internalize changes in market conditions into their list price decisions.30 The variance of the ![]() process,
process,
![]() , is identified by the variance of changes in average prices over time. In the data, I calculate this moment by taking the standard deviation of monthly price changes in
the Case-Shiller index for San Francisco and Los Angeles during my sample period.
, is identified by the variance of changes in average prices over time. In the data, I calculate this moment by taking the standard deviation of monthly price changes in
the Case-Shiller index for San Francisco and Los Angeles during my sample period.
6 Estimation Results and Model Fit
The learning model matches the data well (see Table 6 for the simulated moments at the estimated parameter vector). Even when agents have rational expectations about the severe market decline during my sample period, the model matches the lengthy TOM observed in the data. At the estimated
parameters, more uncertainty raises the list price because sellers want to test demand before dropping the price, which will attract more buyers but will also transfer more of the bargaining power to the buyer. Since uncertainty decreases over the selling horizon, the model generates declining list
prices, and would do so even if market conditions (i.e. the ![]() process) were constant. However, as in the data, a minority of list price changes are increases (6 percent in the data versus 4
percent in the model). The fraction of list price changes that are increases is not a moment that I directly target in estimation. In the model, list price increases primarily occur from sellers with low draws of
process) were constant. However, as in the data, a minority of list price changes are increases (6 percent in the data versus 4
percent in the model). The fraction of list price changes that are increases is not a moment that I directly target in estimation. In the model, list price increases primarily occur from sellers with low draws of ![]() in equation (10).
in equation (10).
Interestingly, the model fits the fact that list to sales price premiums increase with TOM. This is true even though list prices are increasing in the level of uncertainty, and the level of uncertainty decreases over the selling horizon. The reason for the increasing wedge between list and sales prices is selection: sellers with low reservation prices tend to sell quickly and post lower list prices. The model overpredicts the average list price change at delisting relative to listing. This is partly because I do not model menu costs. In Section 8 I discuss the robustness of my results to this and other simplifications.
Table 5 reports the parameter estimates and their standard errors.31 The results suggest that sellers typically accept offers that are 12 percent above the mean of the valuation distribution, which is the 92nd percentile. Given that the average sales price is $ 628,000, this implies that the mean of the offer distribution is about $ 561,000 (628000/1.12) for the typical house. Thus, the standard deviation of the seller's prior for the typical house is about $ 38,000 and the standard deviation of the offer distribution is about $47,000. I calculate that Bayesian learning reduces the standard deviation (variance) of the seller's initial prior by 37 percent (60 percent) over the course of the selling horizon.
I also relate the predictions of the model to the reduced form results presented in Section 3. As mentioned above, the specification of the initial prior in equation (10) ensures that the model replicates the correlation between lagged price depreciation and list
prices observed in the data. The model also predicts that lagged price depreciation is positively correlated with TOM.32 The stronger is perceived demand,
the higher is the reservation price, which increases TOM, all else equal. The model predicts a small effect of lagged price depreciation on sales price.33
Just as in the data, for some parts of the distribution of initial bias, more bias leads to lower sales prices. The model predicts that two alternative explanations for the high list prices found in Section 3 - high unobserved home quality (a higher ![]() ) and low unobserved motivation to sell (a higher
) and low unobserved motivation to sell (a higher ![]() ) - lead to unambiguously
) - lead to unambiguously ![]() sales prices as well higher list prices (proof not reported). Thus, the model illustrates how these explanations are inconsistent with the evidence from Section 3.
sales prices as well higher list prices (proof not reported). Thus, the model illustrates how these explanations are inconsistent with the evidence from Section 3.
7.1 Price Dynamics
It has been well documented that house price appreciation rates are persistent in the short-run. An important question is whether this predictability can be supported in an equilibrium where market participants are behaving optimally. My model of rational behavior conditional on an exogenous
level of information suggests that it can. I show this by simulating average weekly sales prices using the model for ![]() and
and ![]() new listings each week. The parameters of the model are set at their estimated values. Following the literature, I run the following regression on the simulated price series
new listings each week. The parameters of the model are set at their estimated values. Following the literature, I run the following regression on the simulated price series
| (13) |
where ![]() is the log average price over all simulated sales in week
is the log average price over all simulated sales in week ![]() .34
.34
Table 7 shows the results. The level of sales price persistence generated by the model is .124. The information frictions are completely responsible for the persistence. Column 1 shows that when the average seller has unbiased beliefs at the time of initial listing and when
![]() ,
, ![]() .35 The third and fourth columns show results when I aggregate weekly prices to the quarterly level. In this case, the dependent variable is
.35 The third and fourth columns show results when I aggregate weekly prices to the quarterly level. In this case, the dependent variable is
![]() where
where ![]() is a quarter and
is a quarter and ![]() is the simple average of all sales in quarter
is the simple average of all sales in quarter ![]() . I present these results because in practice sales do not occur frequently
enough to compute price indexes at the weekly level. Case & Shiller (1989) and Cutler et al. (1991), for example, run their regressions at the quarterly level. The aggregation alone introduces persistence, and the AR(1)
coefficient rises to .152.
. I present these results because in practice sales do not occur frequently
enough to compute price indexes at the weekly level. Case & Shiller (1989) and Cutler et al. (1991), for example, run their regressions at the quarterly level. The aggregation alone introduces persistence, and the AR(1)
coefficient rises to .152.
7.1.1 Discussion, Robustness, and Further Results
At the parameter estimates, the model generates persistence that is over half the level typically found in the data. The intuition for the result is as follows. Sellers do not fully adjust their beliefs in time ![]() to a shock to
to a shock to ![]() in time
in time ![]() , on average. The optimal
Bayesian weighting places some weight on the signal about the shock and some weight on the seller's prior expectation. Then, for example, when there is a positive shock, the average reservation price in the population rises, but is too low relative to the perfect information case. As time
progresses, however, learning from buyer behavior provides more information about the shock, and reservation prices eventually fully adjust. The same intuition holds for a negative demand shock. Thus, serial correlation in price changes arises because 1) persistent demand shocks are not immediately
capitalized into reservation prices and 2) there exists a mechanism through which additional information about these shocks arrives with a lag.
, on average. The optimal
Bayesian weighting places some weight on the signal about the shock and some weight on the seller's prior expectation. Then, for example, when there is a positive shock, the average reservation price in the population rises, but is too low relative to the perfect information case. As time
progresses, however, learning from buyer behavior provides more information about the shock, and reservation prices eventually fully adjust. The same intuition holds for a negative demand shock. Thus, serial correlation in price changes arises because 1) persistent demand shocks are not immediately
capitalized into reservation prices and 2) there exists a mechanism through which additional information about these shocks arrives with a lag.
Over shorter frequencies, the persistence is even higher, as shown in the right-most columns of Table 7. We can see this through the equation for the OLS estimate of ![]() :
:
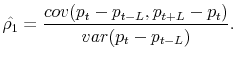 |
(14) |
As the lag length, ![]() , gets smaller, the numerator stays approximately the same and the denominator gets smaller because there are fewer shocks between time
, gets smaller, the numerator stays approximately the same and the denominator gets smaller because there are fewer shocks between time ![]() and
and ![]() . By the same logic, the persistence dies out as
. By the same logic, the persistence dies out as ![]() increases. Thus, the short-run persistence generated here does not preclude long-run mean reversion in price changes, which is an additional stylized fact about house price dynamics. The model can generate long-run mean reversion with the
addition of a mean reverting shock to the
increases. Thus, the short-run persistence generated here does not preclude long-run mean reversion in price changes, which is an additional stylized fact about house price dynamics. The model can generate long-run mean reversion with the
addition of a mean reverting shock to the ![]() process.36
process.36
The persistence generated by the model could be arbitraged away if some traders have superior access to information about the current period fundamentals. However, given that realtors already provide the typical seller with information based on their professional insights and access to data in the MLS, this seems like a difficult arbitrage. In addition, the difficulty in taking short positions and the large transaction costs involved in trading homes complicates any potential trading strategy (Meese & Wallace (1994)).
![]() potentially plays a large role in determining the amount of persistence because it affects how much of a demand shock is immediately capitalized into reservation prices. When
potentially plays a large role in determining the amount of persistence because it affects how much of a demand shock is immediately capitalized into reservation prices. When
![]() is high, there is a lot of scope for persistence because most of the information about the demand shock will arrive with a lag. To test the sensitivity of the results in Table 7 to
the point estimate of
is high, there is a lot of scope for persistence because most of the information about the demand shock will arrive with a lag. To test the sensitivity of the results in Table 7 to
the point estimate of
![]() , I re-simulate the model at the upper and lower limits of the 95 percent confidence interval for the estimate of
, I re-simulate the model at the upper and lower limits of the 95 percent confidence interval for the estimate of ![]() . The annual persistence (weekly prices) always lies between 0.12 and 0.13. Given that
. The annual persistence (weekly prices) always lies between 0.12 and 0.13. Given that
![]() (1.8 percent) at the lower end of the confidence the interval, the model does not require much signal noise at all to generate a significant amount of persistence.
(1.8 percent) at the lower end of the confidence the interval, the model does not require much signal noise at all to generate a significant amount of persistence.
I also test the sensitivity of the results to the assumption that the mean of the valuation distribution, ![]() , changes each period (i.e. each week). I simulate a version of the model
where
, changes each period (i.e. each week). I simulate a version of the model
where ![]() only changes every four periods; I multiply
only changes every four periods; I multiply
![]() by four so that the variance of
by four so that the variance of
![]() is the same as in the baseline model. In this version of the model, the annual persistence is slightly higher at .131 for weekly prices and .162 for quarterly prices.
is the same as in the baseline model. In this version of the model, the annual persistence is slightly higher at .131 for weekly prices and .162 for quarterly prices.
7.2 Sales Volume and TOM Dynamics
The existing literature has identified frictions related to search and credit constraints as explanations for the positive price-volume correlation in the housing market. In this section, I show that an information friction is an additional contributor to this correlation.
Table 8 shows the results when I regress
![]() and
and ![]() on quarterly price changes using data simulated from
the model at the estimated parameters. Column 1 shows that a 1 percent increase in quarterly prices leads to a 6.7 percent increase in sales volume. The estimate from running the same specification on the actual data for Los Angeles and San Francisco is 5 percent, which is close to the estimate
reported in Stein (1995) who uses data from the entire US housing market.37 Column 2 shows that absent the information friction,
the model does not predict a relationship between price changes and volume.
on quarterly price changes using data simulated from
the model at the estimated parameters. Column 1 shows that a 1 percent increase in quarterly prices leads to a 6.7 percent increase in sales volume. The estimate from running the same specification on the actual data for Los Angeles and San Francisco is 5 percent, which is close to the estimate
reported in Stein (1995) who uses data from the entire US housing market.37 Column 2 shows that absent the information friction,
the model does not predict a relationship between price changes and volume.
When the dependent variable is ![]() , the model generates a
, the model generates a
![]() : a 1 percent increase in quarterly prices leads to a 7.6 percent decline in TOM.38 To compare this prediction to the data, I collect a TOM time-series from the Annual Historical Data Summary produced by the California Association of Realtors. The TOM data reflects averages for the entire state of California,
while the quality adjusted price data I have is from Los Angeles and San Francisco so the comparison is quite rough. The estimate of
: a 1 percent increase in quarterly prices leads to a 7.6 percent decline in TOM.38 To compare this prediction to the data, I collect a TOM time-series from the Annual Historical Data Summary produced by the California Association of Realtors. The TOM data reflects averages for the entire state of California,
while the quality adjusted price data I have is from Los Angeles and San Francisco so the comparison is quite rough. The estimate of ![]() is -5.6 percent using LA prices and -4.1 percent
using SF prices, suggesting that the model is generating predictions that are of the same order of magnitude as the empirical price-TOM relationship.
is -5.6 percent using LA prices and -4.1 percent
using SF prices, suggesting that the model is generating predictions that are of the same order of magnitude as the empirical price-TOM relationship.
The results suggest that information frictions are important for explaining variation in transaction rates over the housing cycle. The intuition for these results is that positive shocks to home values are accompanied by reservation prices that are too low relative to the perfect information case. Lower reservation prices relative to the fundamentals leads to more and quicker transactions.
8 Discussion of Model Assumptions
In this section, I discuss the robustness of the results to a few stylized features of the model.
8.1 No Buyer Learning
In the model, changes in the offer, or willingness to pay, distribution are exogenous. A model that endogenizes buyer willingness to pay from the fundamental demand and supply conditions in the economy could also include a dynamic learning process, as the thinness and volatility of the market probably make it difficult for buyers to observe market conditions as well. We do not model such a dynamic process because it would be difficult to identify without data on buyer behavior and it would significantly complicate the seller's problem. However, I suspect that including a buyer learning process would increase the level of price persistence. In the current setup, reservation prices adjust to market shocks with a lag, but offers adjust immediately. If offers adjust with a lag as well, then the adjustment of prices to market shocks would be even slower. The correlations between volume and TOM with price changes, however, may be attenuated because sluggish reservation prices are met with sluggish demand.
8.2 Abstraction from Features of the Micro Data
The model presented above is the simplest version of an empirical model needed to highlight the effects of information frictions on market dynamics. As a result, the current version of the model does not explain some features of the micro data such as withdrawals, sales prices above list prices, and sticky list prices.39 In a working paper version of the paper Anenberg (2011b), I experimented with more detailed versions of the model to address each of these features. The main conclusions are unchanged. In this section, I summarize these adjustments to the model.
To accommodate withdrawals, I allow sellers to withdraw at any time and receive an exogenous and heterogenous termination utility, ![]() . The parameter estimates from that model suggest
that there is a group of motivated sellers, with very low
. The parameter estimates from that model suggest
that there is a group of motivated sellers, with very low ![]() as modeled above, and a group of unmotivated sellers with high
as modeled above, and a group of unmotivated sellers with high ![]() . Hardly any of the unmotivated sellers end up selling given the decline in the market. Thus, the predictions of the model with respect to sales price and volume dynamics are similar.40 This version of the model requires positive holding costs,
. Hardly any of the unmotivated sellers end up selling given the decline in the market. Thus, the predictions of the model with respect to sales price and volume dynamics are similar.40 This version of the model requires positive holding costs, ![]() , to explain why sellers do not stay on the
market indefinitely. The estimated holding costs are small.
, to explain why sellers do not stay on the
market indefinitely. The estimated holding costs are small.
To accommodate sales prices above the list price, I assume that when ![]() , there is some exogenous probability that the price gets driven up above
, there is some exogenous probability that the price gets driven up above ![]() . This addition to the model does not affect the main parameter estimates or conclusions.
. This addition to the model does not affect the main parameter estimates or conclusions.
The current model predicts that sellers should adjust their list price, oftentimes by an ![]() amount, each period. This is one reason that the model overpredicts the average list price
change at delisting relative to listing. In practice, list prices are sticky, presumably due to menu costs. In the working paper version of this paper, I show that very small menu costs can rationalize sticky list prices. Thus, I do not expect the addition of a menu cost, which would significantly
increase the computational burden, to affect the conclusions.
amount, each period. This is one reason that the model overpredicts the average list price
change at delisting relative to listing. In practice, list prices are sticky, presumably due to menu costs. In the working paper version of this paper, I show that very small menu costs can rationalize sticky list prices. Thus, I do not expect the addition of a menu cost, which would significantly
increase the computational burden, to affect the conclusions.
8.3 One Offer per Period
In the model I assume that the expected amount of information that the seller receives does not vary much over the selling horizon. In practice, the arrival of buyers may be especially strong in the first several periods while the listing is fresh. Thus, learning in the initial weeks may be
higher than the model allows for. Modeling multiple offers significantly complicates estimation, and it is not clear how the arrival rate would be identified without information on buyer behavior. Instead, I test the robustness of my results to stronger learning in the initial weeks by allowing
sellers to observe an additional draw from the offer distribution, ![]() , during each period in the first month after listing. The annual price persistence declines from .124 to .092. The
effect of price change on volume decreases from 6.7 percent to 3.3 percent, and the effect of price change on TOM increases from -7.6 percent to -5.8 percent.
, during each period in the first month after listing. The annual price persistence declines from .124 to .092. The
effect of price change on volume decreases from 6.7 percent to 3.3 percent, and the effect of price change on TOM increases from -7.6 percent to -5.8 percent.
9 Conclusion
This paper shows that information frictions play an important role in the workings of the housing market. Using a novel and robust identification strategy for expectation bias, I find direct evidence that imperfect information affects the micro decisions of individual sellers. Then, I show that a search model with uncertainty and Bayesian learning fits the key features of the micro data remarkably well, suggesting that information frictions are important in explaining the distribution of marketing times, the role of the list price, and the microstructure of the market more generally. I also use the model to highlight how micro-level decision making in the presence of imperfect information affects aggregate market dynamics. Most notably, I find a significant microfounded momentum effect in short-run aggregate price appreciation rates.
The analysis here raises several interesting directions for future research. Given the sample period that I have access to, I have argued that my results likely characterize market dynamics during cold housing markets. Since the basic mechanisms generating the main results do not depend on the market being in decline, I suspect that my model, estimated using a sample with rising prices, would be successful in explaining momentum and correlations between price, volume, and marketing time in rising markets as well. However, the magnitude of the results may differ as the pace of learning may change over the housing cycle. This paper does not discuss the welfare implications of uncertainty. In a working paper version, I use a similar model to show that the value of information to sellers is large, which helps to explain the demand for realtors that typically charge 3 percent of the sales price. On the modeling side, extending micro models of the home selling problem to the multi-agent setting, so that the pricing and selling outcomes of neighboring listings has an endogenous effect on the flow of information, is an interesting direction for future research.
Bibliography
International Economic Review 44(3):1007-1040.
Regional Science and Urban Economics 41(1):67 - 76.
mimeo Duke University .
European Journal of Operational Research 182(1):256 - 281.
Real Estate Economics 24(4):421-440.
Working Paper 16734, National Bureau of Economic Research.
American Economic Review .
forthcoming International Economic Review .
The American Economic Review 79(1):125-137.
International Economic Review 37(1):129-155.
Journal of Housing Research 7(2):145-172.
Econometrica 73(4):1137-1173.
The Review of Economic Studies 58(3):pp. 529-546.
CEPR Discussion Paper .
Marketing Science 15(1):pp. 1-20.
The Quarterly Journal of Economics 116(4):1233-1260.
The American Economic Review 87(3):255-269.
Working Paper 12787, National Bureau of Economic Research.
Real Estate Economics 26(4):719-740.
Journal of Housing Economics 2(4):339 - 357.
The American Economic Review 66(2):pp. 246-253.
mimeo Queens University .
Marketing Science 25(1):25-50.
Journal of Applied Econometrics 7(2):115-129.
The Review of Economics and Statistics 76(4):648-672.
Real Estate Economics 27(2):263-298.
Real Estate Economics 30(2):213-237.
Journal of Urban Economics 49(1):32 - 53.
The American Economic Review 76(1):14-32.
Review of Economics and Statistics 90(4):599-611.
Journal of Urban Economics 35(3):245 - 266.
Journal of Urban Economics 56(2):192-216.
The Review of Economic Studies 61(3):397-415.
Quantitative Marketing and Economics 5:1-34.
mimeo London School of Economics .
Real Estate Economics 37(1):1-22.
Review of Economic Studies 73(2):459-485.
MIT Press .
The Journal of Real Estate Finance and Economics 4:157-173.
Journal of Housing Economics 1(1):110-126.
The Quarterly Journal of Economics 110(2):379-406.
Journal of Political Economy 69(3):pp. 213-225.
Review of Economic Studies 66(3):555-78.
A.1 Data Appendix
I first describe how I combine the listing data from Altos Research with the transaction data from Dataquick. I begin by cleaning up the address variables in the listing data. The address variables in the transaction data are clean and standardized because they come from county assessor files.
The listing data contains separate variables for the street address, city, and zip code. I ignore the city variable since street address and zip code uniquely characterize houses. The zip code variable does not need any cleaning. In a large majority of cases, the address variable contains the house number, the street name, the street suffix, and the condo unit number (if applicable) in that order. We alter the street suffixes to make them consistent with the street suffixes in the transaction data (e.g. change "road" to "rd", "avenue" to "ave", etc). In some cases, the same house is listed under 2 slightly different addresses (e.g. "123 Main" and "123 Main St") with the same MLSIDs. We combine listings where the address is different, but the city and zip are the same, the MLSids are the same, the difference in dates between the two listings is less than 3 weeks, and at least one of the follow conditions applies:
- The listings have the same year built and the ratio of the list prices is greater than 0.9 and less than 1.1.
- The listings have the same square feet and the ratio of the list prices is greater than 0.9 and less than 1.1.
- The listings have the same lotsize and the ratio of the list prices is greater than 0.9 and less than 1.1.
- The first five characters of the address are the same.
We merge the listing data and the transaction data together using the address. If we get a match, we keep the match and treat it as a sale if the difference in dates between the transaction data (the closing date) and the date the listing no longer appears in the MLS data (the agreement date) is
greater than zero and less than 365 days. If the match does not satisfy this timing criteria, we keep the most recent transaction to record the previous selling price. Before we do the merge, we flag properties that sold more than once during a 1.5 year span during our sample period. To avoid
confusion during the merge that can arise from multiple sales occurring close together, we drop any listings that merge to one of these flagged properties (![]() 1 percent of listings).
1 percent of listings).
I drop listings where the ratio of the minimum list price to the maximum list price is less than the first percentile. I drop listings where the TOM is greater than the 99th percentile. I drop listings where the list to predicted price ratio is less than the 1st or greater than the 99th percentile. I drop listings where the predicted price is less than the 1st or greater than the 99th percentile. I drop listings where the sales to predicted price ratio is less than the 1st or greater than the 99th percentile.
A.2 Detail on Calculation of Predicted Prices
![]() is the log expected sales price for house
is the log expected sales price for house ![]() in month
in month ![]() . This expected price is simply equal to the previous log price paid for the house plus some neighborhood (zip code in this analysis) level of appreciation or depreciation. To calculate the level of
appreciation, I follow Shiller (1991), who estimates the following model
. This expected price is simply equal to the previous log price paid for the house plus some neighborhood (zip code in this analysis) level of appreciation or depreciation. To calculate the level of
appreciation, I follow Shiller (1991), who estimates the following model
where
![\displaystyle W_{i(j)} = \left[\frac{1}{h}\phi (\frac{dist_{ij}}{h*std(dist_{ij})})\right]^{1/2}](img119.gif) |
(16) |
where
A.3 Further Results on Expectation Bias
Appendix Table 1 presents additional results that are consistent with the conclusions established Section 3. I test whether sellers in neighborhoods where there have been a lot of recent sales are better able to detect recent price trends. In the context of the model, we could think of these
sellers as receiving signals, ![]() , with a tighter variance because there is more information about recent price trends. We run the following variation of specification (2)
, with a tighter variance because there is more information about recent price trends. We run the following variation of specification (2)
where
Column (5) shows that the effects of
![]() on list prices diminish as we move later in the sample period. The time series of prices in Figure 2 provides a likely explanation. As the housing decline deepened and sellers
learned that prices were depreciating rapidly, they did a better job of adjusting the prices of recent comparable sales for the downward trend.
on list prices diminish as we move later in the sample period. The time series of prices in Figure 2 provides a likely explanation. As the housing decline deepened and sellers
learned that prices were depreciating rapidly, they did a better job of adjusting the prices of recent comparable sales for the downward trend.
A.4 Proof of Theorem 1
Buyers will inspect house ![]() when the expected surplus from visiting exceeds the expected cost, i.e. when
when the expected surplus from visiting exceeds the expected cost, i.e. when
where
To show that the optimal buyer behavior takes the reservation value form, it is sufficient to show that the term in the integral in equation (18) is increasing in ![]() . Using properties of the truncated normal distribution, we rewrite the integral as
. Using properties of the truncated normal distribution, we rewrite the integral as
Taking the derivative of this expression with respect to ![]() gives
gives
To show the particular form of ![]() , using properties of the truncated normal distribution, we rewrite equation (18) for
, using properties of the truncated normal distribution, we rewrite equation (18) for
![]() as
as
Let
Given values for
A.5 Model Details on Learning
In this section, we detail how sellers update their beliefs in response to information that arrives during the selling horizon.
Define the following means and variances of seller beliefs over ![]() :
:
Suppose that
![]() and
and
![]() are the mean and variance of a normal distribution at any time
are the mean and variance of a normal distribution at any time ![]() . Given the assumptions made in the model, I show below that this will be the case. Then, Bayes' rule implies that the posterior after processing
. Given the assumptions made in the model, I show below that this will be the case. Then, Bayes' rule implies that the posterior after processing ![]() is also normal where
is also normal where
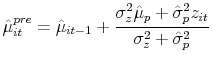 |
The best case scenario for the seller is that
![]() ; in this case, weekly changes to the mean of the valuation distribution do not increase uncertainty.
; in this case, weekly changes to the mean of the valuation distribution do not increase uncertainty.
The source of learning that decreases uncertainty in week ![]() is buyer behavior. If a buyer arrives, recall that the seller observes
is buyer behavior. If a buyer arrives, recall that the seller observes ![]() , which is a noisy signal of
, which is a noisy signal of ![]() . The posterior distribution of
. The posterior distribution of ![]() after the seller processes the information in
after the seller processes the information in ![]() remains normal with mean and variance at time
remains normal with mean and variance at time ![]() given respectively by:
given respectively by:
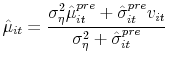 |
The initial conditions are given in equation (9).
If a buyer does not arrive, the seller observes that
![]() and the density function of the posterior is
and the density function of the posterior is
This is not a normal distribution because of the
![]() term in the normal
term in the normal ![]() in the numerator. A statistics paper by
Berk et al. (2007) shows that a normal distribution with mean and variance equal to the mean and variance of the distribution in equation (25) is a good approximation for the true posterior when demand is censored in exactly this way. I use this
approximation method here, noting that simulations show this approximation to work extremely well for my application. Then, when a buyer does not arrive, the posterior distribution after processing that
in the numerator. A statistics paper by
Berk et al. (2007) shows that a normal distribution with mean and variance equal to the mean and variance of the distribution in equation (25) is a good approximation for the true posterior when demand is censored in exactly this way. I use this
approximation method here, noting that simulations show this approximation to work extremely well for my application. Then, when a buyer does not arrive, the posterior distribution after processing that
![]() is normal with mean and variance at given respectively by:
is normal with mean and variance at given respectively by:
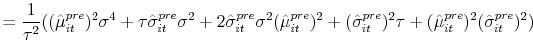 |
||
| (26) |
where
![]() ,
,
![]() , and
, and ![]() is the hazard rate
corresponding to the normal distribution with mean
is the hazard rate
corresponding to the normal distribution with mean
![]() and variance
and variance ![]() .
.
A.6 Dynamic Programming Methods
I assume a finite horizon of 80 weeks for the selling horizon. It is well known that in these types of dynamic programming problems, ![]() from equation (12) needs
to be calculated for each point in the state space. I calculate
from equation (12) needs
to be calculated for each point in the state space. I calculate ![]() for a discrete number of points and use linear (in parameters) interpolation to fill in the values for the remainder of the
state space.
for a discrete number of points and use linear (in parameters) interpolation to fill in the values for the remainder of the
state space.
The integrals in equation (12) have a closed form. No simulation is required. This avoids a source of bias that often arises in practice when the number of simulations required to preserve consistency is not feasible to implement. See Keane
& Wolpin (1994) for a more detailed discussion. The closed form arises due to the normal approximation for the pdf, ![]() , described in Berk et al. (2007),
properties of the truncated normal distribution, the absence of idiosyncratic choice specific errors from the model, linearity in equations (23) and (24), and linearity in the interpolating function.
, described in Berk et al. (2007),
properties of the truncated normal distribution, the absence of idiosyncratic choice specific errors from the model, linearity in equations (23) and (24), and linearity in the interpolating function.
The optimal list price, however, does not have a closed form. For each point in the discretized state space, I solve for the optimal list price using a minimization routine. The optimal list price also needs to be calculated when simulating selling outcomes for each seller. I approximate the list price policy function using linear (in parameters) interpolation. This is done using the discrete points used to approximate the value function.
A.7 Bayesian Learning Prior to Listing
In this section, I show that if a similar Bayesian learning framework applies prior to the beginning of the selling horizon, the initial priors will depend on lagged information. To see how, consider a simplified information structure where ![]() follows a random walk with a drift equal to zero (and normally distributed shocks). Furthermore, assume that
follows a random walk with a drift equal to zero (and normally distributed shocks). Furthermore, assume that
![]() is observable, but the seller only gets a signal
is observable, but the seller only gets a signal ![]() about
about
![]() . Then, the seller's beliefs about
. Then, the seller's beliefs about ![]() will be
will be
| (27) |
where
Table I : Summary Statistics
| List Price - Predicted Price (%) | Square Feet | Year Built | Time on Market (Weeks) | Change in List Price over Selling Horizon | Sales Price | |
|---|---|---|---|---|---|---|
| Sell Mean | 0.0778707 | 1683.398 | 1961.319 | 17.60084 | -0.1006903 | 628372.2 |
| Sell p25 | -0.0519389 | 1188 | 1950 | 5 | -0.1361322 | 360000 |
| Sell p50 | 0.0573411 | 1513 | 1960 | 12 | -0.0246967 | 530000 |
| Sell p75 | 0.1768229 | 1999 | 1980 | 25 | 0 | 765000 |
| Withdraw Mean | 0.1665035 | 1672.831 | 1959.513 | 19.58707 | -0.0711837 | |
| Withdraw p25 | 0.0152484 | 1156 | 1949 | 8 | -0.0923087 | |
| Withdraw p50 | 0.1355506 | 1495 | 1958 | 16 | -0.0128856 | |
| Withdraw p75 | 0.2783186 | 2032 | 1979 | 26 | 0 | |
| Total Mean | 0.1222327 | 1678.109 | 1960.415 | 18.59497 | -0.0859218 | 628372.2 |
| Total p25 | -0.0226412 | 1172 | 1949 | 6 | -0.1109531 | 360000 |
| Total p50 | 0.0942379 | 1504 | 1959 | 14 | -0.018519 | 530000 |
| Total p75 | 0.2294272 | 2014 | 1979 | 26 | 0 | 765000 |
Table 2: Percent of Sellers on Market that Adjust List Price by Week Since Initial Listing
| Weeks Since Listing | % Adjusting List Price |
|---|---|
| 1 | 4.47% |
| 2 | 7.72% |
| 3 | 9.91% |
| 4 | 11.21% |
| 5 | 11.42% |
| 6 | 10.82% |
| 7 | 10.20% |
| 8 | 10.27% |
| 9 | 10.47% |
| 10 | 10.26% |
| 11 | 10.04% |
| 12 | 9.78% |
| 13 | 9.88% |
| 14 | 9.86% |
| 15 | 8.91% |
| 16 | 8.97% |
| 17 | 8.95% |
| 18 | 9.24% |
| 19 | 8.99% |
| 20 | 8.92% |
| 21 | 8.83% |
| 22 | 8.69% |
| 23 | 8.68% |
| >=24 | 9.54% |
Table 3: Effects of Lagged Market Conditions on List Price
| Dependent Variable | (1) Log List Price- Log Predicted Price | (2) Log List Price- Log Predicted Price | (3) Log List Price- Log Predicted Price | (4) Log List Price- Log Predicted Price | (5) Log List Price- Log Predicted Price |
|---|---|---|---|---|---|
| Log Predicted Pricet-1 - Log Predicted Pricet | 0.5631*** | 0.7052*** | 0.7298*** | 0.7439*** | 0.7475*** |
| Log Predicted Pricet-1 - Log Predicted Pricet (Standard Error) | (0.0266) | (0.0327) | (0.0347) | (0.0367) | (0.0381) |
| Log Predicted Pricet-2 - Log Predicted Pricet-1 | 0.3933*** | 0.4858*** | 0.5167*** | 0.5298*** | |
| Log Predicted Pricet-2 - Log Predicted Pricet-1 (Standard Error) | (0.0321) | (0.0415) | (0.0473) | (0.0534) | |
| Log Predicted Pricet-3 - Log Predicted Pricet-2 | 0.2262*** | 0.3071*** | 0.3238*** | ||
| Log Predicted Pricet-3 - Log Predicted Pricet-2 (Standard Error) | (0.0366) | (0.0548) | (0.0644) | ||
| Log Predicted Pricet-4 - Log Predicted Pricet-3 | 0.1583*** | 0.1999*** | |||
| Log Predicted Pricet-4 - Log Predicted Pricet-3 (Standard Error) | (0.0478) | (0.0741) | |||
| Log Predicted Pricet-5 - Log Predicted Pricet-4 | 0.0771 | ||||
| Log Predicted Pricet-5 - Log Predicted Pricet-4 (Standard Error) | (0.0570) | ||||
| Month fixed effects | X | X | X | X | X |
| Zip code fixed effects | X | X | X | X | X |
| Observations | 175939 | 175939 | 175939 | 175939 | 175939 |
| Adjusted R-squared | 0.111 | 0.113 | 0.113 | 0.114 | 0.114 |
Notes: The Predicted Price is calculated by applying a neighborhood level of sales price appreciation to the previous log selling price. The t in the subscript of the explanatory variables denotes the month of initial listing. Regressions also include a Real Estate Owned dummy. Standard errors clustered at the zip code level are in parentheses.
Table 4: Effects of Lagged Market Conditions on Selling Outcomes
| Dependent Variable | (1) Log List Price-Log Predicted Price | (2) Log List Price-Log Predicted Price | (3) TOM | (4) TOM | (5) Withdraw | (6) Log List Price-Log Predicted Price |
|---|---|---|---|---|---|---|
| Distribution of Price Depreciation Rates: 2nd decile | 0.0196*** | 0.0111** | 2.8823*** | 3.0797*** | 0.0499*** | -0.0171*** |
| Distribution of Price Depreciation Rates: 2nd decile (Standard Error) | (0.0048) | (0.0047) | (0.3819) | (0.4404) | (0.0099) | (0.0033) |
| Distribution: 3rd decile | 0.0226*** | 0.0121** | 3.7888*** | 3.9170*** | 0.0828*** | -0.0245*** |
| Distribution: 3rd decile (Standard Error) | (0.0046) | (0.0049) | (0.4001) | (0.4555) | (0.0109) | (0.0034) |
| Distribution: 4th decile | 0.0279*** | 0.0132*** | 3.9401*** | 4.4235*** | 0.0983*** | -0.0291*** |
| Distribution: 4th decile (Standard Error) | (0.0048) | (0.0051) | (0.4131) | (0.4910) | (0.0111) | (0.0034) |
| Distribution: 5th decile | 0.0447*** | 0.0308*** | 4.5446*** | 5.4883*** | 0.1151*** | -0.0227*** |
| Distribution: 5th decile (Standard Error) | (0.0052) | (0.0054) | (0.4038) | (0.4982) | (0.0104) | (0.0035) |
| Distribution: 6th decile | 0.0490*** | 0.0371*** | 4.7441*** | 5.5356*** | 0.1199*** | -0.0197*** |
| Distribution: 6th decile (Standard Error) | (0.0054) | (0.0059) | (0.4716) | (0.6070) | (0.0112) | (0.0036) |
| Distribution: 7th decile | 0.0474*** | 0.0364*** | 4.6186*** | 5.7616*** | 0.1250*** | -0.0224*** |
| Distribution: 7th decile (Standard Error) | (0.0056) | (0.0059) | (0.5134) | (0.6659) | (0.0119) | (0.0037) |
| Distribution: 8th decile | 0.0588*** | 0.0474*** | 4.4823*** | 4.7369*** | 0.1505*** | -0.0172*** |
| Distribution: 8th decile (Standard Error) | (0.0057) | (0.0061) | (0.5507) | (0.6548) | (0.0118) | (0.0038) |
| Distribution: 9th decile | 0.0657*** | 0.0553*** | 4.9347*** | 5.2629*** | 0.1621*** | -0.0157*** |
| Distribution: 9th decile (Standard Error) | (0.0063) | (0.0065) | (0.5504) | (0.6645) | (0.0124) | (0.0040) |
| Distribution:10th decile | 0.0927*** | 0.0815*** | 3.5064*** | 2.9475*** | 0.1672*** | 0.0088** |
| Distribution:10th decile (Standard Error) | (0.0087) | (0.0091) | (0.5506) | (0.6505) | (0.0135) | (0.0042) |
| Change in Predicted Price over Selling Horizon | -0.5106*** | |||||
| Change in Predicted Price over Selling Horizon (Standard Error) | (0.0369) | |||||
| Month fixed effects | X | X | x | x | x | x |
| Zip code fixed effects | X | X | ||||
| Only Listings that Sell | x | x | x | |||
| Observations | 175939 | 87879 | 175939 | 87879 | 175939 | 87879 |
| Adjusted R-squared | 0.111 | 0.104 | 0.100 | 0.127 | 0.207 | 0.101 |
Notes: The price depreciation rate is the the predicted price from 4 months prior to the initial listing date minus the predicted price at the initial listing date. d1 is the excluded group. TOM is measured in weeks. Withdraw is a dummy variable equal to one if the listing is ultimately withdrawn. Regressions also include a Real Estate Owned dummy. Coefficients in bold denote cases where the difference in the coefficient relative to the coefficient in the decile immediately below is statistically significant at the 10 percent level. Standard errors clustered at the zip code level in parentheses. In specification 6, robust standard errors are reported.
Table 5: Parameter Estimates of the Structural Model
| Variable | Description | Estimate | Std. error |
|---|---|---|---|
| ϑ | St. dev. of Initial Prior | 0.0679 | 0.0054 |
| ϑη | St. dev. of buyer valuations | 0.0841 | 0.0022 |
| ϑv | St. dev. of buyer uncertainty over their valuation prior to inspection | 0.0606 | 0.0016 |
| ϑz | St. dev. of signal about weekly decline in mean valuations. | 0.0322 | 0.0073 |
| ϑε | St. dev. of Belief about weekly decline in mean valuations. | 0.0094 | 0.0007 |
| κ | Buyer inspection cost. | -0.005 | -- |
| c | Weekly holding cost. | 0 | -- |
| γ0 | Mean of Belief about weekly decline in mean valuations. | -0.0033 | -- |
Table 6: Moments Used in Estimation
| Moment | Simulated Moment | ||
|---|---|---|---|
| 1 | % of homes that sell 5 weeks after initial listing | 0.043 | 0.0465 |
| 2 | % of homes that sell 10 weeks after initial listing | 0.033 | 0.0389 |
| 3 | % of homes that sell 15 weeks after initial listing | 0.022 | 0.0292 |
| 4 | % of homes that sell 20 weeks after initial listing | 0.0155 | 0.0223 |
| 5 | Median Time on Market | 12 | 12 |
| 6 | 25th pctile of List Price - Sales Price | 0 | 0 |
| 7 | 50th pctile of List Price - Sales Price | 0.019 | 0.0286 |
| 8 | 75th pctile of List Price - Sales Price | 0.054 | 0.0542 |
| 9 | Corr(Change in List Price Change in Predicted Price) | 0.76 | 0.7601 |
| 10 | 5th percentile of list price change in week 3 | -0.044 | -0.0332 |
| 11 | Average Change in List Price | -0.1 | -0.1223 |
| 12 | Median (List Price - Sales Price in Week 10 - (List Price - Sales Price in Week 5)) | 0.0095 | 0.0002 |
| 13 | Median (List Price - Sales Price in Week 15 - (List Price - Sales Price in Week 10)) | 0.0042 | 0.0013 |
| 14 | Stdev. of Monthly Price Changes | 0.012 | 0.0067 |
Table 7: Sales Price Dynamics from the Simulated Model
| Dependent Variable | Annual Price Change | Annual Price Change | Annual Price Change Prices Aggregated | Annual Price Change Prices Aggregated | Semi-Annual Price Change | Semi-Annual Price Change | Prices Aggregated | Prices Aggregated |
|---|---|---|---|---|---|---|---|---|
| OLS Estimates of AR(1) Coefficient | -0.0025 | 0.1241 | 0.0402 | 0.152 | -0.0133 | 0.2789 | 0.0786 | 0.3455 |
| Assumptions: Uncertainty Over Changes in Market Conditions | x | x | x | x |
Table 8: Volume and Time-on-Market Dynamics from the Simulated Model
| Dependent Variable | Log(Sales Volume) | Log(Sales Volume) | Log(TOM) | Log(TOM) |
|---|---|---|---|---|
| Quarterly Change in Price | -0.0004 | 6.7322 | 0.0001 | -7.633 |
| Assumptions: Uncertainty Over Changes in Market Conditions | x | x |
Appendix Table 1: Robustness Specifications
| Dependent Variable | (1) List Price | (2) TOM | (3) Withdraw | (4) Sales Price | (5) List Price |
|---|---|---|---|---|---|
| Lagged Depreciation | 0.6022*** | 21.6028*** | 0.7018*** | 0.1370*** | 0.7818*** |
| Lagged Depreciation (Standard Error) | (0.0482) | (1.0780) | (0.0315) | (0.0247) | (0.1185) |
| Lagged Depreciation*Lagged Num. Sales | -0.0018*** | -0.0590*** | 0.0002 | 0.0000 | |
| Lagged Depreciation*Lagged Num. Sales (Standard Error) | (0.0003) | (0.0062) | (0.0002) | (0.0002) | |
| Lagged Num. Sales | -0.0055*** | -0.0000 | -0.0001*** | ||
| Lagged Num. Sales (Standard Error) | (0.0009) | (0.0000) | (0.0000) | ||
| Change in Expected Price over Selling Horizon | -0.5124*** | ||||
| Change in Expected Price over Selling Horizon (Standard Error) | (0.0096) | ||||
| Lagged Depreciation*Months Since Beginning of Sample Period | -0.0187** | ||||
| Lagged Depreciation*Months Since Beginning of Sample Period (Standard Error) | (0.0078) | ||||
| REO Dummy | -0.1130*** | 5.0374*** | -0.6379*** | -0.1467*** | -0.1142*** |
| REO Dummy (Standard Error) | (0.0034) | (0.1322) | (0.0017) | (0.0018) | (0.0033) |
| Month fixed effects | X | X | x | x | x |
| Zip code fixed effects | X | ||||
| Observations | 171066 | 171066 | 171066 | 85603 | 172460 |
| Adjusted R-squared | 0.111 | 0.096 | 0.202 | 0.100 | 0.112 |
![\displaystyle p^L_{i,j,t_0} - \hat{p}_{i,j,t_{0}} = \alpha_j + \gamma_t + \sum_{k=2}^{10}\alpha_k I[\Delta^4_{ijt}<d_k] + \beta_2 X_{i,j,t}+\epsilon_{i,j,t}](img17.gif)
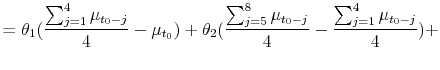
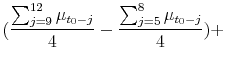
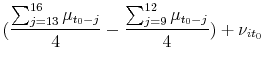
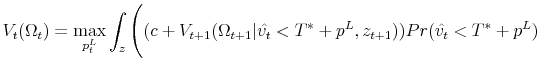
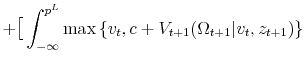
![\displaystyle + \int_{p^L}^{\infty} p^{L}_{t} \big] Pr(\hat{v_{t}}>T^*+p^L)g(v_{t}\vert\hat{v_{t}}>T^*+p^L) dv_t \Bigg) f(z_{t+1})dz_{t+1}](img68.gif)