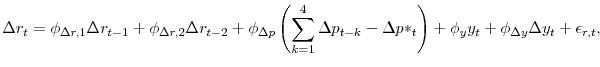The Aggregate Demand Effects of Short- and Long-Term Interest Rates
Keywords: IS curve, long-term interest rates
Abstract:
JEL Classification: E43, E44, E50.
1 Introduction
The dominant modeling paradigm in macroeconomic models used for monetary policy analysis within the academic community ascribes a central role in aggregate demand determination to the expected path of short-term interest rates, with essentially no direct role for long-term interest rates (e.g., Woodford (2003)). Dynamic-stochastic-general-equilibrium (DSGE) models employed by many central banks around the world build on this structure and also often fail to distinguish between expected short-term interest rates and long-term interest rates (e.g., the discussion in Boivin, Kiley, and Mishkin (2010)). In contrast, older large-scale macroeconomic models, such as the Federal Reserve's FRB/US model (Reifschneider, Tetlow, and Williams (1999)) and models used in the private sector (e.g., Macroeconomic Advisers (2006) and Moody's Economy.com (2006)), assume that long-term interest rates, reflecting both expected short-term interest rates and term/risk premiums (e.g., deviations from the Expectations Hypothesis), directly affect overall financial conditions and aggregate demand. Because of this assumption, analyses using such models suggest that movements in long-term interest rates induced by shifts in the expected path of short-term interest rates or by changes in term/risk premiums affect real economic activity in much the same way. Indeed, this rough correspondence influences the estimates from such research of the effects on economic activity from policy actions designed to lower term premiums (e.g., Chung et al (2011) and Fuhrer and Olivei (2011)) or the policy prescriptions offered by such analyses (e.g., Gagnon (2011)).
A long literature begins with the presumption that short- and long-term assets are imperfect substitutes (e.g., Tobin (1961), Tobin (1963), Modigliani and Sutch (1966), Modigliani and Sutch (1967), and Vayanos and Vila (2009)). Such approaches, suitably modified to include the possibility that imperfect substitutability of financial assets influences the spending of some agents, allow for potentially important roles for both short- and long-term interest rates in spending decisions.
Moreover, in such a framework, the short-term interest rate may have a larger influence on economic activity, through its impact on the entire term structure, than term and risk premiums (for equal-sized movements in long-term interest rates). Informally, such a larger effect is likely to arise because some agents may finance spending by borrowing short (and rolling over such borrowing), implying a role of expected short-term interest rates, whereas other agents may finance spending by borrowing long, implying a link between long-term rates (inclusive of both expected short rates and term/risk premiua) and spending; as spending is influenced by expected short rates under both strategies, whereas term/risk premia only affect spending for those agents financing long-term, expected short rates are likely a more powerful determinant of aggregate spending than term/risk premia, for equal-sized movements in long-term interest rates. The models developed herein formalize this intuition.
Specifically, models are presented and used to gauge the relative importance of short- and long-term interest rates, or the relative importance of the sequence of expected short-term interest rates and other components (term/risk premiums) of long-term yields, in aggregate demand determination. One model includes optimizing behavior, allows for the possibility that some agents cannot borrow/lend using both short- and long-term securities, and includes frictions that generate deviations of long-term interest rates from the Expectations Hypothesis; this model is based on Andres, Lopez-Salido, and Nelson (2004) - a framework also used in a larger dynamic stochastic general equilibrium model by Chen, Curdia, and Ferrero (2011). The second model is more loosely connected to a specific set of assumptions regarding optimizing behavior: In this alternative model, aggregate demand is assumed to be determined by the expected path of short-term interest rates and by term/risk premiums - with possibly different sensitivities of aggregate spending to each of these determinants. In broad terms, this approach builds on that of Fuhrer and Moore (1995) and Fuhrer and Rudebusch (2004), with the main addition to their analyses being the inclusion of possible roles for term/risk premiums (which are assumed to have no effect on economic activity and inflation in these earlier models). The empirical analysis will demonstrate that results are robust across the optimization-based and alternative models.
The models are estimated using data for the United States on real GDP, inflation and expected inflation, the short-term interest (federal funds) rate, and long-term interest rates (i.e, yields on Treasury securities or private (corporate) bonds). Each model fits the data similarly along many dimensions. In addition, the estimation results clearly suggest that both short- and long-term interest rates affect spending; the role of short-term interest rates (current and expected) in aggregate demand determination is larger than that of long-term rates, implying that shifts in term/risk premiums have smaller effects on spending that shifts in short-term interest rates for equal-sized movements in long-term interest rates. These results have a similar flavor to those of Andres, Lopez-Salido, and Nelson (2004) and Chen, Curdia, and Ferrero (2011), but move beyond their analysis in several ways. First, these previous analyses focused on Treasury yields, and our analysis finds some differences across results, most especially in a restricted optimization-based framework similar to Andres, Lopez-Salido, and Nelson (2004) or Chen, Curdia, and Ferrero (2011) when considering, alternatively, Treasury and private bond yields. Second, the models considered allow comparison of models strictly derived from optimization-based behavior with a model designed to match the data well, thereby illustrating robustness (in contrast to the more limited explorations of Andres, Lopez-Salido, and Nelson (2004) and Chen, Curdia, and Ferrero (2011)). Finally, our presentation focuses on the impact on output of alternative paths for long-term interest rates associated with movements in short-term interest rates or term/risk premiums, thereby addressing policy issues confronted in Chung et al (2011), Fuhrer and Olivei (2011), and Gagnon (2011).
Before turning to the analysis, two other strands of literature are relevant when thinking about the approach herein. First, purely reduced-form empirical studies have examined the link between activity, the expectations component of long rates, and the term premium component of long rates (Hamilton and Kim (2002), Wright (2006), and Rudebusch, Sack, and Swanson (2007)). Such reduced-form correlations obviously cannot address the strength of the negative relationship between spending and interest rates envisaged in IS-curve relationships. The investigation herein, by focusing on specifications suggested by economic theory, is able to identify plausible estimates of the negative relationship between interest rates and economic activity along the lines suggested by textbook analyses.
In addition, a large number of recent studies have examined the degree to which quantitative easing may affect term premiums (e.g., D'Amico and King (2010), D'Amico et al (2011), Gagnon et al (2011), Gagnon (2011), Hamilton and Wu (2011), Krishnamurthy and Vissing-Jorgensen (2011), and Swanson (2011)). The range of results across these studies suggests considerable uncertainty regarding the effects of quantitative easing on asset prices. In this study, the links between long-term interest rates and real activity are examined using data that pre-dates the recent quantitative easing policies that have motivated studies examining the impact of quantitative easing on term premiums. Nonetheless, the findings herein suggesting that term premiums may affect real activity by less than expected short-term interest rates, in conjunction with the (somewhat unsettled) conclusion from D'Amico et al (2011) and Gagnon (2011) that much of the effect of quantitative easing on long-term interest rates has operated through term premiums or other deviations from the Expectations Hypothesis, suggest that estimates of the impact of quantitative easing on real economic activity such as those of Chung et al (2011) and Fuhrer and Olivei (2011) may overstate the impetus to aggregate spending from such policy actions.1
Chen, Curdia, and Ferrero (2011) independently explored the separate roles of short- and long-term interest rates concurrently with early versions of this analysis. Their work differs along many dimensions. Chen, Curdia, and Ferrero (2011) consider a large DSGE model like those discussed in Boivin, Kiley, and Mishkin (2010), whereas the focus herein is on a smaller model. (It is unclear whether a larger or smaller model is more robust to potential mis-specification). Chen, Curdia, and Ferrero (2011) assume that Treasury yields accurately measure the role of long-term assets/liabilities in the spending decisions of private agents, whereas we consider the role of Treasury and private bond yields. Chen, Curdia, and Ferrero (2011) estimate their model through recent data, including the zero-lower bound period, whereas the analysis herein stops before that period in part because it is likely that the binding zero-lower bound on nominal interest rates implies that the linear rational expectations structure of the model, which is important in the full system estimation approach used herein and in Chen, Curdia, and Ferrero (2011), may be problematic. Finally, Chen, Curdia, and Ferrero (2011) use Bayesian methods, whereas we use maximum likelihood. As we will discuss, the Bayesian approach attributes a larger role to Treasury yields in aggregate demand determination than does maximum likelihood because of the role of prior assumptions. Despite all of these differences, one key conclusion is very similar herein and in Chen, Curdia, and Ferrero (2011): Short-term interest rates have more powerful effects on aggregate demand than long-term interest rates in both studies.
The next section presents two specifications of aggregate demand determination, both of which allow for independent influences of expected short-term interest rates and long-term interest rates on aggregate demand. The third section presents estimation results for both models and explores the plausibility of the empirical estimates. The fourth section considers the implications of the estimation results for the effects of shifts in short-term interest rates and long-term interest rates on economic activity, with a comparison to other estimates. The final section concludes.
2 The Models
In order to capture the potential importance of financial factors other than the expected path of short-term interest rates, (at least) two features are important. First, as recognized long ago (e.g., Tobin (1961), Tobin (1963)), financial assets, such as short- and long-term bonds, must be imperfect substitutes in financial portfolios: Such frictions between assets (and/or liabilities), stemming, for example, from differences in preferences over alternative assets or market structures that result in segmentation, imply that the prices of assets reflect factors other than the expected path of short-term interest rates (and payouts at each date). Second, as emphasized in Andres, Lopez-Salido, and Nelson (2004) (among others), some fraction of households or firms must be restricted from trading in the full set of available financial assets, so that the differences in asset prices associated with imperfect substitutability in portfolio choice influence spending decisions for some agents.
The next subsection reviews the model of aggregate demand (or more specifically an IS-curve equation) presented in Andres, Lopez-Salido, and Nelson (2004) to capture these features. A second specification of the "IS curve" relaxes the tight theoretical restrictions on dynamics imposed by the optimization-based model while preserving its intuitive aspects. Each specification of aggregate demand (and portfolio choices) is then combined with specifications for monetary policy behavior and inflation dynamics to deliver small structural models of macroeconomic dynamics.
2.1 Optimization-Based IS Curve
We assume that the economy consists of continuums of two types of agents, similar to Andres, Lopez-Salido, and Nelson (2004).
The first type, a fraction ![]() of the population called unconstrained agents, can trade in any financial asset, including short- and long-term nominal bonds,
subject to a (time-varying, exogenous) transaction cost on long-term bonds. This transaction cost will create deviations of long-term interest rates from those implied by the Expectations Hypothesis. The second type of agent, a fraction
of the population called unconstrained agents, can trade in any financial asset, including short- and long-term nominal bonds,
subject to a (time-varying, exogenous) transaction cost on long-term bonds. This transaction cost will create deviations of long-term interest rates from those implied by the Expectations Hypothesis. The second type of agent, a fraction ![]() of the population called constrained agents, have limited financial options: They can trade in long-term nominal bonds, but have access to no other financial assets.
of the population called constrained agents, have limited financial options: They can trade in long-term nominal bonds, but have access to no other financial assets.
A brief motivation for these assumptions is in order. Unconstrained agents trading long-term bonds face a transaction cost ![]() (a "term" premium) that is not incurred when trading
short-term bonds. This exogenous factor should be interpreted as reflecting variations in asset prices due to shifts in the liquidity or risk characteristics associated with these assets. In order for the yield on long-term bonds, inclusive of the "term/risk" premium, to have real effects on
spending, it is necessary that unconstrained agents face the transaction cost, while constrained agents do not: Absent this asymmetry, the yield on long-term bonds available to constrained agents would carry the same information as the sequence of expected short-term
rates (plus transaction costs) that determine unconstrained agents willingness to hold the long-term bond, which would thereby (indirectly) make unconstrained agents spending depend on expected short-term interest rates without the effect of the "term/risk" premium/transaction cost, as emphasized
in Andres, Lopez-Salido, and Nelson (2004). Indeed, the asymmetry in costs is exactly what allows this simple model to capture the imperfect substitutability of financial assets (as suggested by Tobin (1961)) and the impact of this imperfect substitutability
on aggregate demand determination. Andres, Lopez-Salido, and Nelson (2004) discuss these conditions in detail.
(a "term" premium) that is not incurred when trading
short-term bonds. This exogenous factor should be interpreted as reflecting variations in asset prices due to shifts in the liquidity or risk characteristics associated with these assets. In order for the yield on long-term bonds, inclusive of the "term/risk" premium, to have real effects on
spending, it is necessary that unconstrained agents face the transaction cost, while constrained agents do not: Absent this asymmetry, the yield on long-term bonds available to constrained agents would carry the same information as the sequence of expected short-term
rates (plus transaction costs) that determine unconstrained agents willingness to hold the long-term bond, which would thereby (indirectly) make unconstrained agents spending depend on expected short-term interest rates without the effect of the "term/risk" premium/transaction cost, as emphasized
in Andres, Lopez-Salido, and Nelson (2004). Indeed, the asymmetry in costs is exactly what allows this simple model to capture the imperfect substitutability of financial assets (as suggested by Tobin (1961)) and the impact of this imperfect substitutability
on aggregate demand determination. Andres, Lopez-Salido, and Nelson (2004) discuss these conditions in detail.
Turning to equations, the ith unconstrained (denoted by superscript ![]() ) agent faces a budget constraint that includes short-term bonds and a set of long-term
perpetuities that pay an exponentially decaying coupon
) agent faces a budget constraint that includes short-term bonds and a set of long-term
perpetuities that pay an exponentially decaying coupon ![]() (
(![]() ) in period
) in period
![]() , as in Woodford (2001) and Chen, Curdia, and Ferrero (2011):
, as in Woodford (2001) and Chen, Curdia, and Ferrero (2011):
Preferences over consumptions and work hours for unconstrained agents are given by
where
The budget constraint and preferences for unconstrained agents imply the following three optimality conditions for bond-holdings and consumption choices:
It is straightforward to see, on examination of equation 4, that
Taking a log-linear approximation to equations (3) and (4) (using the approximation
![]() and lower case to denote logs) yields the equation for the term-structure of bond yields:
and lower case to denote logs) yields the equation for the term-structure of bond yields:
where
Note that the rate on long-term bonds reflects, in addition to the expected path of short-term interest rates, the "term/risk premium"
![]() . This structure, which captures the intuition of bond pricing underling many discussions, was the motivation for the structure of transaction costs introduced earlier. More
structural examinations of term/risk premiums should be a priority (e.g., see the discussion in Rudebusch (2010) or Gurkaynak and Wright (2012)).
. This structure, which captures the intuition of bond pricing underling many discussions, was the motivation for the structure of transaction costs introduced earlier. More
structural examinations of term/risk premiums should be a priority (e.g., see the discussion in Rudebusch (2010) or Gurkaynak and Wright (2012)).
For the ith constrained (denoted by superscript ![]() ) agent, the budget constraint is given by
) agent, the budget constraint is given by
Note that unconstrained agents, which only participate in the long-term bond market, do not face the transaction costs
Preferences over consumptions and work hours for unconstrained agents are given by
The budget constraint and preferences for constrained agents imply the following two optimality conditions for bond-holdings and consumption choices:
Given these equations, an IS-curve linking aggregate consumption expenditure to expected short- and long-term interest rates can be derived. Define (log) aggregate consumption as
![]() and the aggregate (log) marginal utility of consumption as
and the aggregate (log) marginal utility of consumption as
![]() . From (3) and (9), the aggregate Lagrange multiplier satisfies (ignoring
constant terms)
. From (3) and (9), the aggregate Lagrange multiplier satisfies (ignoring
constant terms)
When bringing this model to the data, these equations are used as a specification for all of aggregate demand, and consumption (
where
Several features of the optimization-based IS curve deserve highlighting. First, expected short-term interest rates should be expected to have a larger effect on output than term premiums, according to (14), because expected short-term rates
directly affect spending for unconstrained agents, who have access to the short-term bond market, and indirectly affect spending for constrained agents, through the term structure equation (6) and the dependence of constrained agents on the private long-term bond for
saving/borrowing. The only case in which the coefficient on the term premium approaches that of expected short-term interest rates is the limiting one in which the share of unconstrained agents ![]() approaches zero. Second (as emphasized by Andres, Lopez-Salido, and Nelson (2004)), the assumption that constrained agents do not pay the transaction costs on long-term bonds is crucial: This assumption ensures that arbitrage does
not make long-term yields redundant for spending decisions; this can be seen by comparing equations 3, 4, and 9 and noting that inclusion of the transaction cost
approaches zero. Second (as emphasized by Andres, Lopez-Salido, and Nelson (2004)), the assumption that constrained agents do not pay the transaction costs on long-term bonds is crucial: This assumption ensures that arbitrage does
not make long-term yields redundant for spending decisions; this can be seen by comparing equations 3, 4, and 9 and noting that inclusion of the transaction cost
![]() in 9 would imply (through 3 and 4) that short-term rates were sufficient statistics for the spending
of all agents.
in 9 would imply (through 3 and 4) that short-term rates were sufficient statistics for the spending
of all agents.
The larger role for the sequences of expected short-term interest rates in aggregate demand determination is intuitive. Recent discussions have often emphasized how deviations from the Expectations Hypothesis can arise because long-term bonds have liquidity or other special characteristics (e.g., a maturity matching long-term obligations such as pensions) which imply that their price (and hence their yield) reflects the value of such characteristics (in addition to the sequence of expected short-term interest rates). The value of these additional characteristics should not necessarily affect how future cash flows associated with, for example, consumption outlays or consumer durable purchases or investments in productive capital are valued, and hence need not influence spending decisions in a manner similar to the effect of short-term interest rates. The current model provides an example, but the underlying economic intuition is more general. (With that said, specific results herein, as always, are linked to the structure assumed.)
Finally, some readers may be familiar with the form of the IS-curve from Andres, Lopez-Salido, and Nelson (2004), which is presented differently from equation 11. Andres, Lopez-Salido, and Nelson (2004) assume that the central long-term security is a zero-coupon bond of maturity L and derive the following IS-curve
Equation 11 is equivalent to equation 15 for
2.2 A Semi-Structural IS Curve
The optimization-based model of the IS curve imposes a fair amount of structure, and various researchers have espoused an approach less tightly linked to a specific model of optimization. For example, such approaches might be justified by a view that a model designed to capture consumption dynamics is insufficient to model output; alternatively, some economists may prefer to see an equation loosely tied to an underlying theory, but with more ad hoc dynamics, in order to consider the robustness of any conclusions to assumptions regarding the dynamic implications of cross-equation restrictions and rational expectations.
For these reasons, a semi-structural IS curve is also considered. This approach is largely based on the work of Fuhrer and Moore (1995) and Fuhrer and Rudebusch (2004); the latter reference suggests that relaxation of the
restrictions implied by an optimization-based IS curve (albeit one without a role for long-term interest rates) is preferred by the data. Specifically, these authors suggest an IS curve for output (![]() ) such as
) such as
Our semi-structural IS curve (equation (17)) adds a term for the the term/risk premium:
This specification is an obvious generalization of 16 that includes a role for components of long-term interest rates other than expected short rates as in the optimization-based IS curve 14. This specification can be used to assess the robustness of conclusions drawn from the optimization-based specification.
2.3 Closing the models
Given a specification for the IS curve, the macroeconomic model is closed through specifications of the exogenous processes for the term premium, an equation for the inflation process, and a set of equations governing monetary policy actions (and hence the course of the short-term interest rate).
With regard to the term premium, the models assume an exogenous autoregressive processes (with one lag)
where
Inflation dynamics are governed by a "New-Keynesian Phillips curve", with a role for the lag and lead of inflation
where
The analysis will use data for 10-year inflation expectations (
![]() ), whose equation is
), whose equation is
Monetary policy is specified via a standard reaction function for the short-term interest rate (![]() ). For this analysis, the specification of Fuhrer and Moore (1995) is
used, with the addition of a persistent shock representing a time-varying (persistent) inflation target (
). For this analysis, the specification of Fuhrer and Moore (1995) is
used, with the addition of a persistent shock representing a time-varying (persistent) inflation target (![]() ).
).
where
2.4 Summary of Alternative Model Specifications
To summarize, the two models considered are given by
- The Optimization-based IS curve model 1 consists of
equations (13), (14), (6), (18), (19), (20), (21), and (22). - The semi-structural IS curve model consists of
equations (17), (6), (18),, (19), (20), (21), and (22). - In estimation, the observable variables for each model will be output, inflation, long-term expected inflation, the nominal federal funds rate, and a long-term bond yield (either that on the 10-yr Treasury or a composite of Moody's BBB-rated bonds).
- Along with the five observables, there are five exogenous shocks as outlined above-
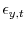 ,
,
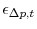 ,
,
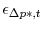 ,
,
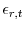 , and
, and
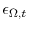 .
.
3 Estimation Results
The two models are estimated using data for the United States covering the period from the first quarter of 1964 to the fourth quarter of 2007 (before the period when the zero-lower bound on nominal interest rates became binding for the nominal federal funds rate). The models are estimated using maximum likelihood.2
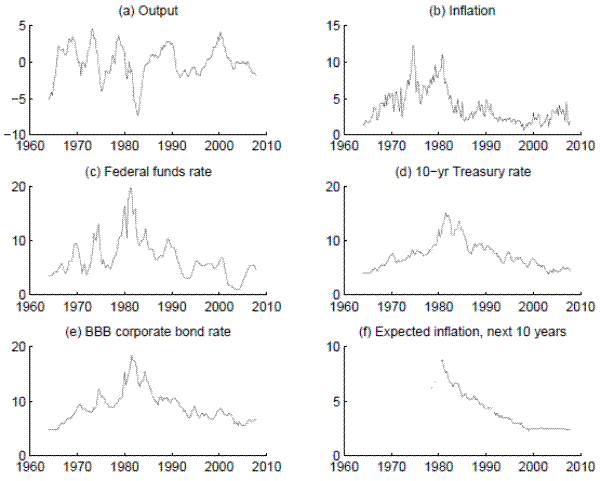
The data used are presented in figure 1.3 The data for output is given by detrended real GDP, where the trend is removed through a Hodrick-Prescott filter with a large smoothing parameter of 128,000; as shown in the upper left panel, this procedure captures common views of cyclical dynamics such as that found in the Congressional Budget Office's measure of the output gap.4Inflation is measured by the percent change in the GDP price index; the short-term interest rate is the nominal federal funds rate; the long-term risk-free rate is either the yield on a 10-year U.S. Treasury security or on a composite long-term corporate bond index, corresponding to bonds rated by Moody's as BBB and with duration of 10 years (constructed for use in the Federal Reserve's FRB/US model); and long-term inflation expectations (available sporadically prior to late 1980) are measured by splicing together the data on inflation expected over the next 10 years from the Barclays de Zoete survey from over the 1980s and early 1990s with the data from the Survey of Professional Forecasters.5Figure 1 plots the inflation and interest rate series for the 1964Q1 to 2007Q4 period.6| Parameter | Optimization Based | Semi Structural |
| Phillips-Curve |
0.58 | 0.58 |
| Phillips-Curve |
(0.014) | (0.014) |
| Phillips-Curve |
0.005 | .001 |
| Phillips-Curve |
(0.007) | (.003) |
| Phillips-Curve
|
0.64 | 0.64 |
| Phillips-Curve
|
(0.039) | (0.039) |
| Monetary Policy
|
0.09 | 0.11 |
| Monetary Policy
|
(0.064) | (0.064) |
| Monetary Policy
|
-0.18 | -0.17 |
| Monetary Policy
|
(0.068) | (0.068) |
| Monetary Policy
|
0.12 | 0.13 |
| Monetary Policy
|
(0.043) | (0.044) |
| Monetary Policy |
0.14 | 0.10 |
| Monetary Policy |
(0.041) | (0.035) |
| Monetary Policy
|
0.47 | 0.52 |
| Monetary Policy
|
(0.100) | (0.101) |
| Monetary Policy
|
1.02 | 1.03 |
| Monetary Policy
|
(0.056) | (0.057) |
| Monetary Policy
|
0.20 | 0.20 |
| Monetary Policy
|
(0.014) | (0.014) |
| Log-Likelihood | -775.4 | -771.4 |
| Parameter | Optimization Based | Semi Structural |
| Phillips-Curve |
0.58 | 0.58 |
| Phillips-Curve |
(0.013) | (0.013) |
| Phillips-Curve |
0.002 | .000 |
| Phillips-Curve |
(0.004) | (.000) |
| Phillips-Curve
|
0.64 | 0.64 |
| Phillips-Curve
|
(0.038) | (0.038) |
| Monetary Policy
|
0.06 | 0.08 |
| Monetary Policy
|
(0.064) | (0.065) |
| Monetary Policy
|
-0.19 | -0.19 |
| Monetary Policy
|
(0.068) | (0.069) |
| Monetary Policy
|
0.11 | 0.13 |
| Monetary Policy
|
(0.043) | (0.046) |
| Monetary Policy |
0.12 | 0.11 |
| Monetary Policy |
(0.037) | (0.038) |
| Monetary Policy
|
0.47 | 0.49 |
| Monetary Policy
|
(0.099) | (0.104) |
| Monetary Policy
|
1.02 | 1.03 |
| Monetary Policy
|
(0.056) | (0.057) |
| Monetary Policy
|
0.20 | 0.20 |
| Monetary Policy
|
(0.014) | (0.014) |
| Log-Likelihood | -806.7 | -802.1 |
Both the optimization-based model and the semi-structural model share coefficients for the Phillips curve and the monetary policy reaction function. Estimates of these parameters for each model, along with the standard errors, are reported in tables 1 (corresponding to estimates obtained when long-term interest rates are measured using yields on Treasury securities) and 2 (corresponding to estimates obtained when long-term interest rates are measured using yields on Corporate Bonds) . In all cases, the common parameters are very similar across the two models. With regard to the Phillips curve, the weight (
| Parameter | Optimization Based | Semi Structural |
| 40 | 40 | |
| (NA) | (NA) | |
| Treasury Yields:
|
0.97 | 1.00 |
| Treasury Yields:
|
(0.020) | (NA) |
| Treasury Yields:
|
0.86 | 0.63 |
| Treasury Yields:
|
(0.357) | (0.317) |
| Corporate Bond Yields:
|
0.97 | 1.00 |
| Corporate Bond Yields:
|
(0.049) | (NA) |
| Corporate Bond Yields:
|
1.44 | 0.88 |
| Corporate Bond Yields:
|
(1.007) | (0.292) |
| Parameter | Optimization-based Treasury Yields | Corporate Bond Yields | Semi-Structural Treasury Yields | Corporate Bond Yields |
| 0.94 | 0.91 | |||
| (0.033) | (0.031) | |||
|
|
24.0 | 39.5 | ||
|
|
(7.76) | (13.4) | ||
| 1.08 | 0.56 | |||
| (0.300) | (0.273) | |||
| 0.85 | 0.81 | |||
| (0.055) | (0.063) | |||
| 0.32 | 0.35 | |||
| (0.096) | (0.110) | |||
| 1.30 | 0.95 | |||
| (0.393) | (0.287) | |||
|
|
0.58 | 0.58 | ||
|
|
(0.489) | (0.216) | ||
|
|
20.4 | 31.5 | 0.79 | 0.77 |
|
|
(6.25) | (10.5) | (0.044) | (0.043) |
Table 3 reports the coefficients associated with the term/risk premium processes. Long-term bonds are assumed to have an duration of 10 years (
Table 4 reports the coefficients associated with the optimization-based and semi-structural IS curves. With regard to the optimization-based IS curve, aggregate demand is persistent, as indicated by the habit persistence parameter ![]() estimated to exceed 0.9. The adjusted coefficient of relative risk aversion (
estimated to exceed 0.9. The adjusted coefficient of relative risk aversion (
![]() ) (whose inverse determines interest sensitivity), is reasonably high, indicating limited short-run interest sensitivity. Most important for the questions considered herein, in
economic terms, is the share of aggregate demand linked to long-term interest rates: This share (
) (whose inverse determines interest sensitivity), is reasonably high, indicating limited short-run interest sensitivity. Most important for the questions considered herein, in
economic terms, is the share of aggregate demand linked to long-term interest rates: This share (![]() ), at about 0.4 using corporate bond yields or, more dramatically, at (less than, but insignificantly different from) 0 using Treasury yields, suggests a limited role for components of long-term interest rates other than expected short-term interest
rates. This issue will be explored in more detail in the next section.
), at about 0.4 using corporate bond yields or, more dramatically, at (less than, but insignificantly different from) 0 using Treasury yields, suggests a limited role for components of long-term interest rates other than expected short-term interest
rates. This issue will be explored in more detail in the next section.
With regard to the coefficients associated with the semi-structural IS curve, aggregate demand is persistent (with the sum of ![]() and
and ![]() above 1). Expected short-term interest rates exert a sizable effect on output (
above 1). Expected short-term interest rates exert a sizable effect on output (![]() equal a value near or in excess of
1). Term/risk premiums have a smaller effect on output (
equal a value near or in excess of
1). Term/risk premiums have a smaller effect on output (
![]() equal to 0.6). As in the optimization-based model, these results
suggest that there are sizable differences between the effect of expected short-term interest rates on output and those of term premiums on output.
equal to 0.6). As in the optimization-based model, these results
suggest that there are sizable differences between the effect of expected short-term interest rates on output and those of term premiums on output.
Before turning to that issue in more detail, several properties of the estimated models are presented. First, the (log) likelihoods (reported in the last column of table 1 and 2) favor somewhat the semi-structural models (even if one were to adjust for the number of parameters via and information criterion; this finding is similar to that of Fuhrer and Rudebusch (2004), who only consider the effect of expected short-term interest rates on output).
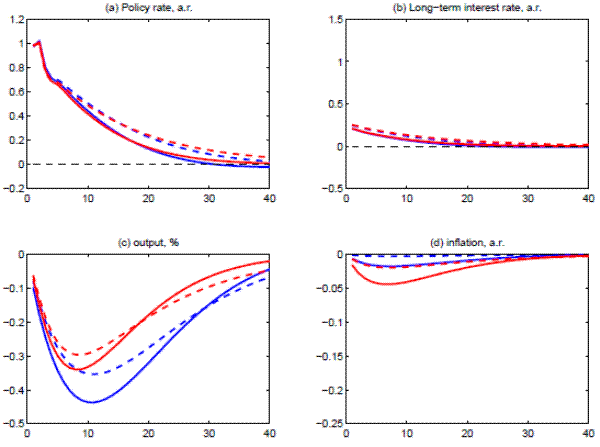 Figure 2 Data
Figure 2 Data
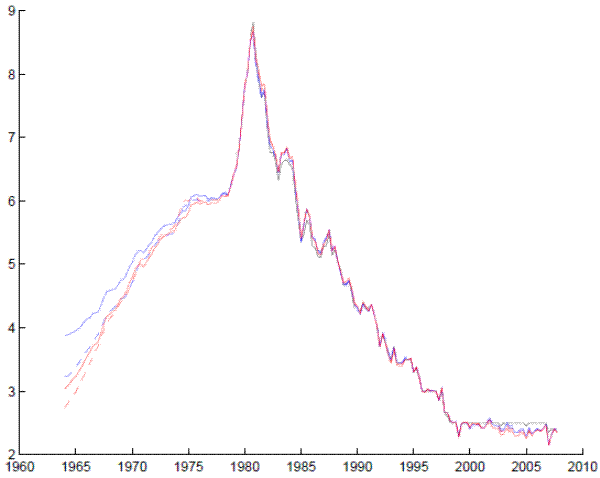 Figure 3 Data
Figure 3 Data
Second, the models ascribe a primarily role to persistent shifts in the desired rate of inflation (![]() ) in the determination of long-run inflation expectations and long-term interest
rates (a finding related to that of Kozicki and Tinsley (2001)). Figure 3 reports the survey measure of expected inflation over the next ten years along with the estimated level of
) in the determination of long-run inflation expectations and long-term interest
rates (a finding related to that of Kozicki and Tinsley (2001)). Figure 3 reports the survey measure of expected inflation over the next ten years along with the estimated level of ![]() ; the series move closely together, as should be expected, in both models and using either measure of yields on long-term bonds.
; the series move closely together, as should be expected, in both models and using either measure of yields on long-term bonds.
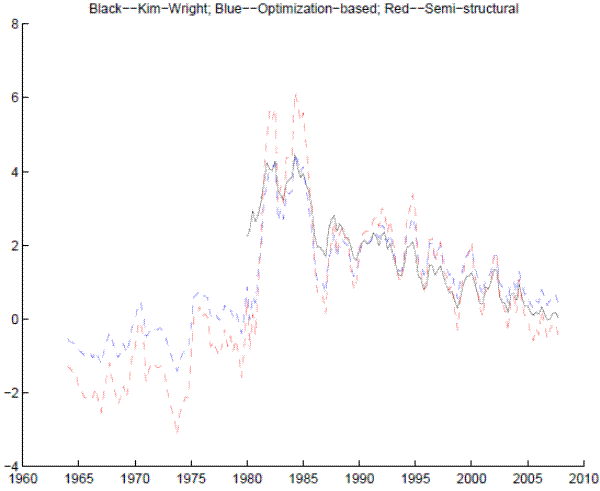
Finally, each model (estimated using Treasury yields) provides an estimate of the term premium on the 10-year Treasury bond. The estimated term premiums behave very similarly to that from standard term-structure models used in the finance literature, such as that of Kim and Wright (2005). Figure 4 reports the term premium from each model of the IS-curve and the term premium on a 10-year zero coupon Treasury security from the model of Kim and Wright (2005): The series move closely together, with a simple correlation exceeding 0.85 since 1980.7 The similarity across the series of term premiums derived from the models herein and that in other research provides some comfort that the estimation results regarding the effects of term premiums on real activity may not be solely the result of idiosyncratic modeling choices.
4 The Effects of Short- and Long-Term Interest Rates
The estimated parameters highlight a larger role for short-term interest rates than for term premiums in the determination of aggregate demand, as can be seen by the estimated value of ![]() for the model with the optimization-based IS curve and the values of
for the model with the optimization-based IS curve and the values of ![]() and
and
![]() for the semi-structural IS curve. However, it is not entirely straightforward to see the implications of alternative paths of long-term interest rates, driven by either short-term
rates or term premiums, from these coefficients, as the dynamics are complex and depend on expectations (most especially in the case of the optimization-based IS curve). To illustrate these links more clearly, the impact on output and inflation of paths for short-term interest rates or long-term
interest rates are shown for two cases that lower long-term interest rates by 100 basis points in the initial year: In the first, the shift in long-term interest rates is caused by a gradual lowering (and then return to baseline at an exponential decay rate of 0.9) of the federal funds rate by 400
basis points; in the second, an identical path of the long-term interest rate is caused by a lower term premium, holding short-term interest rates constant. In both cases, the simulations assume perfect foresight on the part of agents regarding the paths of interest rates. In these calculations,
results using the parameters estimated for the case in which long-term yields are measured by corporate bonds are presented, as these results show a larger role for term/risk premiums.
for the semi-structural IS curve. However, it is not entirely straightforward to see the implications of alternative paths of long-term interest rates, driven by either short-term
rates or term premiums, from these coefficients, as the dynamics are complex and depend on expectations (most especially in the case of the optimization-based IS curve). To illustrate these links more clearly, the impact on output and inflation of paths for short-term interest rates or long-term
interest rates are shown for two cases that lower long-term interest rates by 100 basis points in the initial year: In the first, the shift in long-term interest rates is caused by a gradual lowering (and then return to baseline at an exponential decay rate of 0.9) of the federal funds rate by 400
basis points; in the second, an identical path of the long-term interest rate is caused by a lower term premium, holding short-term interest rates constant. In both cases, the simulations assume perfect foresight on the part of agents regarding the paths of interest rates. In these calculations,
results using the parameters estimated for the case in which long-term yields are measured by corporate bonds are presented, as these results show a larger role for term/risk premiums.
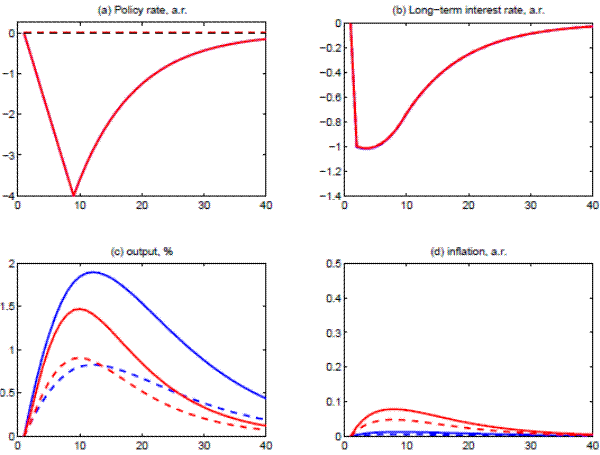 Figure 5 Data
Figure 5 Data
Figure 5 reports the results. The blue lines report the results for the model with the optimization-based IS curve, and the red lines report the results for the model with the semi-structural IS curve. For both models, the solid line reports the results for the shift
in short-term interest rates, and the dashed line reports the results for the shift in the term premium. The upper two panels prsent the paths for for short- and long-term interest rates; the long-term interest rate is about 100 basis points lower for approximately two years. When the change in
interest rates is induced by a shift in the short-term rate, the effect on output is sizable: Activity increases by 2 percent in the optimization-based IS-curve model and by ![]() percent in the semi-structural IS-curve model; in both cases, the impact peaks in the third year. The effects are more muted when the shift in long-term interest rates arises because of a decline
in the term premium: In this case, activity increases by between
percent in the semi-structural IS-curve model; in both cases, the impact peaks in the third year. The effects are more muted when the shift in long-term interest rates arises because of a decline
in the term premium: In this case, activity increases by between ![]() and 1 percent
in both the optimization-based IS-curve model and the semi-structural IS-curve model. These simulations show that, according to these models, a sustained decline in long-term interest rates brought about by a decline in the term premium has about
and 1 percent
in both the optimization-based IS-curve model and the semi-structural IS-curve model. These simulations show that, according to these models, a sustained decline in long-term interest rates brought about by a decline in the term premium has about ![]() the effect of a similar decline in long-term interest rates brought about through a decline in short-term interest rates. 8
the effect of a similar decline in long-term interest rates brought about through a decline in short-term interest rates. 8
A smaller impact of movements in term premiums, relative to that of short-term interest rates, is plausible. As highlighted in section 2, movements in long-term interest rates induced by shifts in term premiums may reflect changes in the desirability of holding financial assets of different types without affecting the demand for goods directly, and any direct effects rely on imperfections in financial markets that prevent some households or firms from accessing financial instruments of different maturities. Such imperfections are plausible-for example, many households are likely constrained to borrow for home purchases within a narrow set of mortgage choices linked to government and other institutional support for 30-year fixed rate mortgages-but presumably not universal (as highlighted by the presence of mortgages of many different terms and with fixed and adjustable rates).
These results are similar to those of Chen, Curdia, and Ferrero (2011), who explored similar issues concurrently, on several dimensions. A few points of difference are important, however. First, Chen, Curdia, and Ferrero (2011) only considered Treasury
yields; in our results, estimates were somewhat different across cases in which long-term yields were measured by those on Treasury securities and those on corporate bonds, especially within the optimization-based model similar to that of Chen, Curdia, and Ferrero (2011). This
is important because Chen, Curdia, and Ferrero (2011) use Bayesian methods which constrain the share of agents who are constrained to use long-term assets/liabilities to lie within the unit interval, and their priors over this parameter push estimates of this share toward
![]() ; our results suggest this procedure may be quantitatively important-although our qualitative results are quite similar. Second, both optimization-based and more loosely-motivated
specifications were considered herein, with broadly similar results; this suggests that the results are robust to relaxation of the tight restrictions of the optimization-based model used herein and by Chen, Curdia, and Ferrero (2011). Finally, our presentation, focusing on
sustained declines in long-term interest rates associated with either lower short-term interest rates or lower term/risk premiums, ties somewhat more closely to some policy discussions (e.g., Chung et al (2011) and Gagnon (2011)). Despite all of these
advantages, the approach of Chen, Curdia, and Ferrero (2011) also has advantages relative to the analysis herein. For example, their Bayesian approach allows a full consideration of the uncertainty regarding estimates and implications. In addition, their use of a complete DSGE
model, while potentially subject to mis-specification, provides a more complete description of macroeconomic dynamics. Overall, the results herein and in Chen, Curdia, and Ferrero (2011) are complementary.
; our results suggest this procedure may be quantitatively important-although our qualitative results are quite similar. Second, both optimization-based and more loosely-motivated
specifications were considered herein, with broadly similar results; this suggests that the results are robust to relaxation of the tight restrictions of the optimization-based model used herein and by Chen, Curdia, and Ferrero (2011). Finally, our presentation, focusing on
sustained declines in long-term interest rates associated with either lower short-term interest rates or lower term/risk premiums, ties somewhat more closely to some policy discussions (e.g., Chung et al (2011) and Gagnon (2011)). Despite all of these
advantages, the approach of Chen, Curdia, and Ferrero (2011) also has advantages relative to the analysis herein. For example, their Bayesian approach allows a full consideration of the uncertainty regarding estimates and implications. In addition, their use of a complete DSGE
model, while potentially subject to mis-specification, provides a more complete description of macroeconomic dynamics. Overall, the results herein and in Chen, Curdia, and Ferrero (2011) are complementary.
5 Conclusion
Both short- and long-term interest rates are key determinants of spending decisions. This analysis has presented two models of aggregate demand determination that distinguish between the effect on spending of expected short-term interest rates and other determinants of long-term interest rates such as term and risk premiums. In contrast to the simple models that dominate the academic literature (e.g., Woodford (2003)), long-term interest rates clearly influence aggregate demand beyond the effect of the expected path of short-term interest rates. However, consistent with a model of imperfect substitutability of financial instruments and the associated implications for aggregate demand (as in Tobin (1961), Tobin (1963), and Andres, Lopez-Salido, and Nelson (2004)), expected short-term interest rates exert a larger effect on aggregate demand than that exerted by term premiums.
Previous discussions of the potential effect of quantitative easing on long-term interest rates and aggregate demand have not drawn sharp distinctions regarding the impact on output of shifts in short-term interest rates or term premiums (e.g., Chung et al (2011), Fuhrer and Olivei (2011), and Gagnon (2011)). The results of this empirical analysis suggest that it is important to differentiate between the effects on spending of different components of long-term interest rates. The empirical findings herein would suggest that movements in term premiums have smaller effects on real activity than movements in expected short-term interest rates, for equal-sized movements in long-term interest rates.
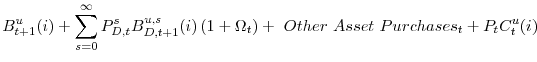
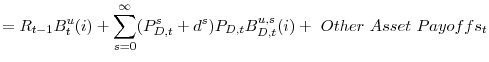
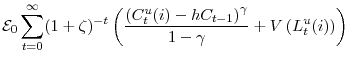
![\displaystyle \mathcal{E}_{t} \left[ P_{D,t}^{s}\Lambda_{t}^{u} \right] = \mathcal{E}_{t}\left[ (1+\zeta)^{-1} \frac{(P_{D,t+1}^{s}+d^{s})}{1+\Omega_{t}}\Lambda_{t+1}^{u} \right]](img28.gif)
![\displaystyle \mathcal{E}_{t} \left[ \Lambda_{t}^{u} \right] = \mathcal{E}_{t}\frac{\left( C_{t}^{u}(i) - hC_{t-1} \right)^{-\gamma} }{P_{t}}](img29.gif)
![\displaystyle \mathcal{E}_{t} \left[-Dp_{D,t}^{0} \right] = \mathcal{E}_{t}\left[ D \sum_{j=0}^{\infty} (1-D)^{j} \left( r_{t+j} + \Omega_{t+j} \right) \right],](img32.gif)
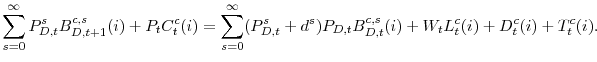
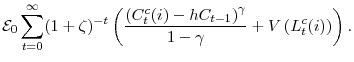
![\displaystyle \mathcal{E}_{t} \left[ \Lambda_{t}^{c} \right] = \mathcal{E}_{t}\frac{\left( C_{t}^{c}(i) - hC_{t-1} \right)^{-\gamma} }{P_{t}}](img40.gif)
![\displaystyle \lambda_{t} = \mathcal{E}_{t} \left[ \alpha \sum_{j=1}^{L}r_{t+j+L} + \left( 1- \alpha \right) L r_{t}^{L} + + \lambda_{t+1+L} \right]](img51.gif)
![\displaystyle r_{t}^{L} = \frac{1}{L}\left[ \sum_{j=1}^{L}r_{t+j+L} + \Omega_{t}^{*} \right].](img52.gif)
![\displaystyle y_{t} = (\eta_{1}+\eta_{2}) y_{t-1} - \eta_{1}\eta_{2} y_{t-2} - \mathcal{E}_{t} \left[ D \sum_{j=0}^{\infty} \left( 1-D \right)^{j} \left[ a_{r} \left( r_{t+j} - \Delta p_{t+1+j} \right) \right] \right] + \epsilon_{y,t}](img56.gif)
![\displaystyle y_{t} = (\eta_{1}+\eta_{2}) y_{t-1} - \eta_{1}\eta_{2} y_{t-2} - \mathcal{E}_{t} \left[ D \sum_{j=0}^{\infty} \left( 1-D \right)^{j} \left[ a_{r} \left( r_{t+j} - \Delta p_{t+1+j} \right) + a_{\Omega} \Omega_{t+j} \right] \right] + \epsilon_{y,t}](img57.gif)
![\displaystyle \Delta p_{L,t} = \mathcal{E}_{t} \sum_{j=1}^{40} \left[\Delta p_{t+j-1} \right].](img65.gif)