Skip to: [Printable Version (PDF)] [Bibliography] [Footnotes]

Finance and Economics Discussion Series: 2012-74 Screen Reader version ^♣

Dollar Funding and the Lending Behavior of Global Banks

Victoria Ivashina

Harvard University and NBER

David S. Scharfstein

Harvard University and NBER

Jeremy C. Stein*

Federal Reserve Board

October 2012

Keywords: Violations of covered interest parity, dollar funding pressures facing non-U.S. banks

Abstract:

A large share of dollar-denominated lending is done by non-U.S. banks, particularly European banks. We present a model in which such banks cut dollar lending more than euro lending in response to a shock to their credit quality. Because these banks rely on wholesale dollar funding, while raising more of their euro funding through insured retail deposits, the shock leads to a greater withdrawal of dollar funding. Banks can borrow in euros and swap into dollars to make up for the dollar shortfall, but this may lead to violations of covered interest parity (CIP) when there is limited capital to take the other side of the swap trade. In this case, synthetic dollar borrowing becomes expensive, which causes cuts in dollar lending. We test the model in the context of the Eurozone sovereign crisis, which escalated in the second half of 2011 and resulted in U.S. money-market funds sharply reducing the funding provided to European banks. Coincident with the contraction in dollar funding, there were significant violations of euro-dollar CIP. Moreover, dollar lending by Eurozone banks fell relative to their euro lending in both the U.S. and Europe; this was not the case for U.S. global banks. Finally, European banks that were more reliant on money funds experienced bigger declines in dollar lending.

JEL Classification: G01, G14, G15, G21

1 Introduction

A striking fact about international financial markets is the large share of dollar-denominated intermediation done by non-U.S. banks. This point is illustrated in Figure 1. Drawing on data from the Bank for International Settlements (BIS), the figure shows that both the dollar assets and the dollar liabilities of foreign banking entities have grown rapidly in the last two decades, and currently are on the order of $10 trillion, which puts them roughly on a par with U.S. banks (see also Shin, 2012). A significant part of this activity by foreign banks represents interactions with customers located outside of the United States. However, foreign banks also play a major role in domestic U.S. markets. As we discuss in more detail below, European banks alone accounted for approximately 28% of the U.S. syndicated loan market over the period 2005-2007.

[Figure 1]

The large footprint of global banks in dollar funding and lending markets raises a number of questions. Some of these have to do with the dollar's role as a favored currency for transactions by non-U.S. residents and firms-e.g., why is it that a Brazilian manufacturer might prefer to borrow in dollars as opposed to in reals? Others have to do with understanding the comparative advantage of foreign banks in lending to U.S. firms-e.g., why might an American manufacturer end up borrowing from, say, Credit Agricole as opposed to J.P. Morgan? ${}^{ }$

In this paper, we take the presence of global banks in dollar loan markets as a given, and focus on exploring the consequences of this arrangement for cyclical variation in credit supply across countries. In particular, we ask how shocks to the ability of a foreign bank to raise dollar funding translate into changes in its lending behavior, both in the U.S., and in its home market. This question is especially important in light of the observation that many foreign banks operate in the U.S. with a largely "wholesale" funding model. In other words, rather than relying in part on sticky insured deposits-as do domestic U.S. banks-foreign banks raise the majority of their short-term dollar financing from uninsured institutional sources, such as commercial paper purchased by U.S. money-market funds.¹ This makes the cost and availability of such dollar funding highly sensitive to changing perceptions of their creditworthiness.

To understand how such shocks might affect lending activity, we build a simple model, which can be described as follows. Imagine a global bank based in France that lends in euros to European firms, and in dollars to American firms. The bank has a fixed amount of equity capital that it can use to support all of its lending.² To finance the euro-denominated lending, it funds itself by issuing insured euro deposits to its local retail deposit base. By contrast, to finance the dollar-denominated lending, it funds itself by issuing uninsured commercial paper to a set of U.S. money-market funds. Initially, the bank is viewed as having near-zero credit risk, so its lack of insurance in the U.S. market does not have a material impact on its dollar funding costs.

Now suppose that there is an adverse shock to the bank's perceived creditworthiness. Given the wholesale nature of its dollar liabilities (i.e., the lack of insurance), this leads to a spike in its dollar funding costs, as the money-market funds rationally seek to cut their exposure to the bank. At the same time, the cost to the bank of funding in euros is unchanged, given the deposit insurance in that market. Said differently, as the bank becomes increasingly risky, the advantage of funding in euros relative to dollars goes up, since the former enjoys an increasing subsidy from the deposit insurance fund.

So we might expect the bank to shift its funding away from the U.S. commercial paper market and back towards the European deposit market. But does this have any implications for the geographic distribution of its lending? At first glance, one might think that there would be none. After all, if it wants to maintain the volume of its dollar-based U.S. lending, the bank can always tap its insured deposit base to raise more euros, use the proceeds to buy dollars, make the same dollar loans as before, and hedge out the foreign exchange (FX) risk using the forward market, by buying euros on a forward basis.³

This logic is correct, so long as FX forward prices are pinned down by the usual covered-interest-parity (CIP) relationship. In this case, a shock of the sort described above alters the funding mix of the global bank, but leaves its lending behavior entirely unchanged. However, if the induced funding realignment is big enough, we demonstrate that it begins to put pressure on the CIP relationship. In other words, a large surge in the demand by the global bank for FX forwards, combined with limited capacity on the part of arbitrageurs, endogenously leads to a CIP violation such that synthetic dollar funding-composed of euro-based borrowing plus a currency swap-also becomes more expensive. Indeed, in an interior equilibrium with a high level of swap activity, synthetic dollar funding and direct dollar funding wind up being equally costly to the bank, and both more expensive than direct euro borrowing.

Once this is the case, implications for the geographic pattern of lending follow immediately. Given the increased marginal cost of funding dollar loans, the bank cuts back on these. And since it has a fixed capital base, this frees up capacity to expand its now relatively more cost-efficient euro-based lending. So one distinctive and non-obvious conclusion from the model is that, in the presence of limited arbitrage and an endogenous CIP violation, an adverse shock to the global bank's perceived creditworthiness leads to a drop in its dollar-denominated lending relative to its euro-denominated lending.

We then go on to test the model's key implications. To do so, we focus on events that unfolded in the second half of 2011, a period that captures well the sort of shock to global-bank creditworthiness envisioned in our model. During this period, the credit quality of a number of large Eurozone banks began to be a source of concern, with Moody's putting the French banks BNP Paribas, Credit Agricole and Societe Generale on notice for possible downgrades on June 15, 2011. In the face of these concerns, U.S. prime money-market funds sharply reduced their funding to Eurozone banks. Some of this reduction was likely spurred by investor redemptions from money funds over the second half of 2011, but much of it appeared to preemptive on the part of the money funds. Chernenko and Sunderam (2012) document that total money-fund holdings of Eurozone bank liabilities declined by 37%, from $453 billion to $287 billion, between May and August of 2011. Fitch reports further declines through the end of 2011.⁴

Coincident with this contraction in dollar funding, there was a pronounced disruption in the dollar-euro CIP relationship, in the direction predicted by our theory. The "euro basis"-i.e., the deviation (relative to CIP) in the forward price of euros in terms of dollars, and hence in the cost of synthetic dollar borrowing-rose from a value of essentially zero at the beginning of May 2011, to over 70 bps in August, and continued to go up until reaching a peak of 150 bps in November 2011. According to BIS, between the second and fourth quarters of 2011, despite a contraction in dollar assets, Eurozone banks' net dollar position (dollar assets minus dollar liabilities) increased by $178 billion. The heightened currency mismatch suggests a greater demand for FX swaps to hedge the risk. This is consistent with a key element of our model-that strong demand for swaps from foreign banks puts pressure on the arbitrage mechanism and thereby increases the euro basis.

Using data on international syndicated lending activity from Thompson Reuters' DealScan, we show that dollar lending by Eurozone banks fell relative to their euro lending, while this was not the case for U.S. banks. As a control against possible confounding shocks, we show that dollar lending to European firms by Eurozone banks also declined relative to their euro lending. In other words, even holding fixed the nationality of the borrower, it appears that during this period of dollar funding strain, Eurozone banks were shifting strongly away from dollar-denominated lending. In addition, as a more general control for potential differences in the composition of borrowers from Eurozone and non-Eurozone banks, we construct a panel that allows us to incorporate borrower fixed effects. In particular, we are able to show that, during the period of dollar funding strain, syndicates formed to make dollar-denominated loans to a given firm were comprised of fewer Eurozone banks, while the same was not true of euro-denominated loans. Thus, the same firms that borrowed in dollars from a syndicate comprised largely of Eurozone banks were less likely to do so once these banks faced dollar funding problems.

In an effort to further isolate the mechanism in our model, we exploit the fact that Eurozone banks differ in the extent of their reliance on money-market funds. We document that in a cross-section of Eurozone banks, a greater reliance on money-market funds (defined as liabilities held by money funds divided by total short-term debt plus deposits) is associated with larger cuts in dollar-denominated loans relative to euro-denominated loans. As before, this pattern holds regardless of whether one looks at dollar loans in the U.S. or restricts the sample to loans in Europe. In essence, the unconditional patterns that we find for lending during this period of stress are more pronounced for the most money-fund-reliant Eurozone banks.

The bottom line of our analysis can be summarized as follows: Given limited arbitrage in FX forward markets, the wholesale dollar funding model typically employed by foreign banks-whereby they rely heavily on short-term uninsured sources of dollar finance-exposes their mix of lending activity to changes in perceived creditworthiness. In particular, adverse shocks to creditworthiness lead them to curtail their supply of dollar loans, relative to their supply of loans in their domestic currency. It is worth emphasizing that this is quite a different mechanism than the more familiar capital-crunch channel (as in Peek and Rosengren 1997, 2000), according to which a global bank hit with a negative shock to its capital base might be expected to cut back on lending across the board, irrespective of the currency in which the lending takes place.

This paper fits into a large literature that studies how financing frictions shape bank lending behavior. A subset of this research focuses, as we do, on multinational banks and the role they play in transmitting various kinds of shocks across borders. In addition to the important early contributions by Peek and Rosengren (1997, 2000), more recent papers include Acharya and Schnabl (2010), Chava and Purnanandam (2011), Schnabl (2012), and Cetorelli and Goldberg (2011, 2012a, 2012b). Perhaps most closely related to our work is that of Acharya, Afonso and Kovner (2012), who investigate the differential effects of the 2007 collapse of the asset-backed commercial paper market on U.S. and foreign banks.

There is also a set of papers analyzing the strikingly large CIP violations that have cropped up intermittently since the onset of the crisis, most notably in the aftermath of the bankruptcy of Lehman Brothers. These include Baba, Packer, and Nagano (2008), Coffey, Hrung, and Sarkar (2009), Griffoli and Ranaldo (2010), and more recently Levich (2012). These papers discuss the frictions that can prevent arbitrage from eliminating a CIP deviation once it emerges, but have less to say about what determines the direction and magnitude of the deviation in the first place. By contrast, in our model the CIP violation is an equilibrium outcome, and we show how it depends not only on the capital of arbitrageurs, but also on global banks' funding opportunities across dollar and non-dollar markets, and on the marginal product of their lending in each currency. That is, we connect CIP violations to the real side of the economy.

The remainder of the paper is organized as follows. Section 2 presents the model. Section 3 discusses our data sources and provides background information on the three critical components or our analysis: the role of Eurozone banks in syndicated lending in the U.S.; the dependence of Eurozone banks on dollar financing from U.S. money-market funds along with the decline in money fund assets in the second half of 2011; and the violation of covered interest parity during that same period. Section 4 establishes our key empirical results, documenting both the direct effects of Eurozone bank dollar funding difficulties on their dollar lending, and the fact that these effects are larger for more money-fund dependent banks. Section 5 concludes.

2 Model

2.1 Basic Assumptions

Our model considers a global bank B that has lending opportunities in both the U.S. and Europe. If it lends an amount L ${}^{D}$ in dollars in the U.S. at time 0, it earns an expected gross return of g(L ${}^{D}$ ) at time 1, where g( ) is a concave function. Similarly, if the bank lends an amount L ${}^{E}$ in euros in Europe at time 0, it earns an expected gross return of h(L ${}^{E}$ ) at time 1, where again, h( ) is a concave function. To keep the notation simple, we assume that riskless rates in the U.S. and Europe are both equal to r, and that the spot dollar/euro exchange rate, X ${}^{S}$ , is equal to one.

The bank faces an overall capital constraint on lending, such that aggregate lending is capped by: L ${}^{D}$ + L ${}^{E}$ $\le$ K. This constraint can be thought of as reflecting the combination of a regulatory capital regime, along with frictional costs to the bank of raising external equity finance (Myers and Majluf, 1984). We further assume that if the bank wishes to lend in dollars, it must effectively fund in dollars, and analogously for euro lending-i.e., it cannot take on any unhedged FX risk. We take this restriction as exogenous here, but it could easily be endogenized by appealing to the real-world fact that if a bank were to take on FX risk in this way, it would face an additional regulatory capital charge.⁵ Given that the capital constraint is assumed to be binding in equilibrium, if the shadow value of the constraint is high enough, it will be optimal for the bank to conserve its scarce capital by avoiding any FX exposure.

The bank has a probability p of default. We assume that if the bank defaults, all of its loans in both the U.S. and Europe turn out to be worthless, and it has no resources to pay to any of its debts. Note therefore that if the bank earns an expected gross return of g(L ${}^{D}$ ) on its dollar lending, it must be that the return accrues entirely in the non-default state. So it is more precise to say the bank earns a gross return of g(L ${}^{D}$ )/(1-p)with probability (1-p), and zero otherwise. The same applies to its returns on euro lending.

If the bank borrows from European depositors and it defaults, these depositors are made whole by the government. Hence the rate that the bank pays on European borrowing r ${}_{B}$ ${}^{E}$ , is the riskless rate: r ${}_{B}$ ${}^{E}$ ${}^{ }$ = r. Said differently, there is a government subsidy associated with European-sourced euro borrowing, and this subsidy is an increasing function of the default probability p. By contrast, if the bank borrows in the U.S. market, its creditors are only partially insured. Specifically, we assume that in expectation, U.S.-based lenders to the bank are only bailed out on a fraction (1 - $\alpha$ ) of their losses in the default state. As a result, the rate that the bank pays on U.S. borrowing, r ${}_{B}$ ${}^{D}$ , is approximated by: r ${}_{B}$ ${}^{D}$ ${}^{ }$ = r + $\alpha$ p. A literal interpretation of the parameter $\alpha$ is that it reflects the fraction of the bank's dollar financing that comes from, say, uninsured commercial paper, as opposed to deposits that are either explicitly insured, or that benefit from some perception of implicit insurance.

A less literal interpretation, but one that motivates our empirical work below, is that even among different providers of uninsured finance, some may be structurally "flightier" than others, and hence more sensitive to changes in bank creditworthiness. Money-market funds would seem to fit this description, given the run-like incentives created by their policy of allowing investors to redeem shares at a fixed value. We rely on this idea when we construct bank-level measures of $\alpha$ , associating higher values of $\alpha$ with those banks that raise more of their short-term funding from money-market funds.

Because it enjoys a bigger subsidy when borrowing in Europe, the bank would ideally like to raise all of its funding there, and then enter into an FX swap to cover the dollar-denominated portion of its lending. And indeed, this is what happens in the case where the FX swap market is frictionless-i.e., when CIP holds. In this case, the bank's funding and lending decisions decouple from one another. Funding is done entirely in euros, while lending activity in the two countries is pinned down by equating the marginal product of dollar lending to the marginal product of euro lending. And swap activity fills in the gap, by converting the appropriate amount of euro funding into synthetic dollar borrowing.

2.2 Limited Arbitrage and Deviations from CIP

Things are more complicated, however, when there are deviations from CIP. As we demonstrate, these deviations arise when the bank's swap counterparties have limited capital, and are required to use this capital to post margin in their swap transactions. As a benchmark, note that with interest rates being equal in the two countries, and with the spot exchange rate normalized to one, a simplified version of the CIP relationship-which would always hold with capital-unconstrained parties on both sides of the trade-is that the forward exchange rate must be equal to one as well. In other words, denoting the dollar/euro forward rate for a transaction in a frictionless world by X ${}_{S}$ ${}^{F}$ , we have that X ${}_{S}$ ${}^{F}$ ${}^{ }$ = 1.

Now consider the case where the counterparty is a capital-constrained arbitrageur. Let be X ${}_{B}$ ${}^{F}$ the forward price paid by the bank in this case. To pin down this price, we make two further assumptions. First, the arbitrageur has to set aside a haircut H when it enters the swap transaction; this can be thought of as the initial margin required as collateral for its position.⁶ To keep things simple, we follow Garleanu and Pedersen (2011) and assume that this haircut is proportional to the size S of the swap position. So the haircut is given by H = $\gamma$ S. Second, when the arbitrageur sets aside H for swap trading, he has to take it away from another productive activity-e.g., lending, or another arbitrage trade. This other productive activity has a net return given by f(I), where I is the amount invested. The arbitrageur has wealth of W, so his budget constraint is that I = W - H, or I = W - $\gamma$ S.

It follows that in an interior optimum where the arbitrageur is doing both activities, an equilibrium condition is that the expected excess return per unit earned on doing the swap, denoted $\Delta$ , must satisfy: $\Delta$ = $\gamma$ f'(W- $\gamma$ S). A convenient simple case is where f(I) = $\theta$ log(I) - I, in which case we have that:

$\Delta$ = $\gamma$ [( $\theta$ /(W- $\gamma$ S) - 1] (1)

In order to ensure that $\Delta$ is always non-negative, we assume that the net returns on the alternative investment are non-negative even when the level of swap activity S is zero, or that $\theta$ = W.

The forward price paid by the bank is now given by:

$\displaystyle X^F_B\approx 1+\triangle =1+\gamma \left[\frac{\theta }{\left(W-\gamma S\right)}-1\right]$ (2)

Looking at equations (1) and (2), we can see the fundamental tension facing the bank. As its creditworthiness declines-i.e., as p goes up-it would like to increasingly fund its dollar lending with synthetic dollar borrowing, that is, by borrowing in euros and pairing this with an FX swap. However as the magnitude of its swap position S grows, this puts increasing strain on the capital of the arbitrageurs who must take the other side of the trade, and hence creates a CIP deviation in which synthetic dollar borrowing becomes more expensive-as reflected in the higher forward price that the bank must pay to buy back euros with dollars when its dollar loans mature at time 1.

2.3 The Bank's Optimization Problem

We are now ready to write down the bank's optimization problem. Denote the bank's direct dollar-based borrowing as B ${}^{D}$ , and the amount of euro borrowing that it swaps into dollars as S. Note that this implies that its total dollar lending, L ${}^{D}$ , is given by L ${}^{D}$ = B ${}^{D}$ +S. The bank's optimization problem can then be written as follows:

max{L ${}^{D}$ ,S}: g(L ${}^{D}$ ) - L ${}^{D}$ (1+r) + h(L ${}^{E}$ ) - L ${}^{E}$ (1+r) - $\alpha$ pB ${}^{D}$ - S $\Delta$ (3)

subject to the constraint that L ${}^{D}$ + L ${}^{E}$ $\le$ K.

The first four terms in (3), g(L ${}^{D}$ ) - L ${}^{D}$ (1+r) + h(L ${}^{E}$ ) - L ${}^{E}$ (1+r), capture the net value created by the bank's lending in a frictionless world. The latter two terms embody the two key frictions in the model. The - $\alpha$ pB ${}^{D}$ term reflects the fact that the bank views dollar funding as more expensive than euro funding, because it carries less of an insurance subsidy. And the - S $\Delta$ term captures the economic cost to the bank of engaging in swap transactions with arbitrageurs who charge a capital-scarcity premium.

The bank's problem can be solved by taking first-order conditions with respect to L ${}^{D}$ and S. Note that in doing so, the bank takes the frictional cost of doing the swap $\Delta$ as given, even though in equilibrium $\Delta$ depends on S. That is, the bank is a price-taker in the swap market.

The following proposition characterizes the bank's behavior in equilibrium:

Proposition 1: The bank's behavior differs across two regions of the parameter space. In an interior swap equilibrium, the bank funds some of its dollar lending directly in the dollar market, and some via swaps, i.e., L ${}^{D}$ S In this equilibrium, the bank's lending is pinned down by g'(L ${}^{D}$ ) = h'(L ${}^{E}$ ) + $\alpha$ p, and its swap activity by $\Delta$ = $\alpha$ p. In a corner equilibrium, the bank does not borrow in dollars, and obtains all of its dollar funding synthetically, via swaps, so that L ${}^{D}$ =S. In this case, the bank's lending is pinned down by g'(L ${}^{D}$ ) = h'(L ${}^{E}$ ) + $\Delta$ (L ${}^{D}$ ), where $\Delta$ (L ${}^{D}$ ) is the value of the swap premium when L ${}^{D}$ =S. That is, $\Delta$ (L ${}^{D}$ )= $\gamma$ [( $\theta$ /(W- $\gamma$ L ${}^{D}$ ) - 1]. The corner equilibrium obtains when $\alpha$ p is relatively high, or when the frictions associated with arbitrage in the swap market are relatively low, i.e., when either the haircut $\gamma$ is small or arbitrageur wealth W is high. Specifically, let L ${}^{D*}$ be the solution to g'(L ${}^{D}$ ) = h'(L ${}^{E}$ ) + $\Delta$ (L ${}^{D}$ ). The corner equilibrium obtains if $\alpha$ p $\Delta$ L ${}^{D*}$ , and the interior equilibrium obtains otherwise.

Figure 2 illustrates the proposition. Suppose we start at the point where the bank's default risk p is zero. As long as we remain in an interior equilibrium, increases in p are accompanied by: i) reductions in dollar funding; ii) increases in swap activity; iii) increases in the CIP violation; iv) reductions in dollar lending; and v) increases in euro lending. Eventually, we hit the corner, where the bank is doing no dollar funding at all, and swap activity is maxed out. From this point on, further increases in p have no effect on dollar lending.

[Figure 2]

When arbitrage frictions are reduced (either because the haircut $\gamma$ is smaller or arbitrageur wealth W is higher), we hit the corner sooner, for a lower value of p. In other words, in response to a decline in its creditworthiness, the bank shifts its funding mix away from direct dollar borrowing more rapidly, because it finds it less costly to use synthetic dollars as a substitute. As a consequence, the effects on its lending are muted. In the limiting case where arbitrage is frictionless, we are always at the corner for any non-zero value of p. Thus, as soon as dollar borrowing becomes a tiny bit costly, the bank shifts all of its funding to the European market, and leaves its lending completely unchanged. Said differently, with perfect arbitrage, we have a sharp decoupling result: the model predicts very pronounced changes in funding behavior in response to small shocks, but has nothing to say about lending or CIP violations.

In our empirical work, we test the above comparative-statics implications from the interior equilibrium, using the money-market-fund episode from the second half of 2011 as a proxy for an aggregate shock to the value of p for all European banks Moreover, in addition to focusing on this time-series variation in p, we also consider a set of cross-sectional tests. The cross-sectional implications of the model arise from the fact that all the effects of interest are driven by the interaction term $\alpha$ p. If we think of two different banks as having different values of $\alpha$ -say because one is more reliant on money-market funds than the other-then the above predictions for lending should hold more strongly for the more money-fund-dependent bank. To be precise, if p jumps from zero to a positive value, the model implies that the quantitative impact on lending is greater for a bank with a higher value of $\alpha$ .

2.4 An Alternative Version of the Model

The model described above predicts that, in the presence of a CIP violation, euro-denominated lending actually increases in response to heightened concerns about bank solvency. This follows directly from the assumption of a binding capital constraint, which in turn implies that total lending is constant; if dollar lending falls it must therefore be that euro lending increases. Now we briefly sketch an alternative-and arguably more realistic-version of the model, which makes the more moderate prediction that a bank decreases its lending in both currencies, but cuts back by relatively more on its dollar lending.

Consider a setting in which there is no aggregate capital constraint, but where the bank faces increasing, convex costs of raising external funding in both dollars and euros. Suppose further that there is a shock that shifts out the cost curve for funding in dollars. This shock will lead the bank to shift its funding towards euros and to swap these euros into dollars to make up for some of the reduction in dollar funding. But as euro-denominated borrowing increases, the marginal cost of this form of borrowing also rises, leading the bank to cut its euro lending in addition to its dollar lending.

Now, in the frictionless-market case where there is no CIP violation, the bank equates the marginal value of lending across currencies, so there is no reason to expect lending in dollars to fall by more than lending in euros. By contrast, when there is a CIP violation, there is an extra cost of lending in dollars, which, just as in the baseline version of the model above, is equal to the premium paid when swapping euros into dollars. In this case, the shock to dollar funding has a larger impact on dollar lending than on euro lending, even though both decline in equilibrium.

The bottom line is that across both variants of the model, the robust prediction is that the combination of a dollar funding shock and a CIP violation leads to a decline in dollar lending relative to euro lending. By contrast, the prediction that euro lending actually goes up in absolute terms is more dependent on the specific formulation of the model-i.e. on whether or not there is a binding capital constraint. Accordingly, we focus attention on the former relative-lending hypothesis in our empirical specifications.

3 Description of the Data and Background Facts

This section describes our data sources and provides some background that will be useful for our empirical analysis. In particular, we discuss the syndicated loan market in the U.S. and Europe, and the important role that Eurozone banks play in the U.S. We also present data on Eurozone bank reliance on U.S. money-market funds, and note the problems they faced in tapping this financing source in the second half of 2011. Finally, we document that during this period there was a significant violation of covered interest parity. As the model shows, it is the combination of wholesale dollar funding difficulties and violations of covered interest parity that gives rise to a decline in dollar lending relative to euro lending.

3.1 The Role of Eurozone Banks in the U.S. Syndicated Loan Market

The loan data for our analysis come from Thompson Reuters' DealScan database of loan origination. Almost all these loans are syndicated, i.e., originated by one or more "lead" banks and funded by a syndicate of banks and other investors. Throughout the empirical analysis we measure a bank's lending activity by the amount of syndicated loans it originates. Often there are multiple lead banks originating a loan, and in those cases we prorate the loan amount by the number of lead banks in the syndicate.⁷ The country of the borrower and lender are based on the location of their headquarters as reported in DealScan.

Table I shows that European banks have a large presence in the U.S. syndicated loan market. During 2005-2007, the top European banks originated almost 25% of syndicated loans in the U.S., with about 11% coming from Eurozone banks. (The shares are not changed much if we base our lending numbers on participation in syndicated loans, not just origination.) Most of the Eurozone banks that were active in the U.S. are headquartered in France and Germany, each with about a 5% market share. Banks headquartered in countries with sovereign debt problems- Greece, Ireland, Italy, Portugal and Spain (GIIPS)-had a less than 2% share of the U.S. market. Almost 14% of U.S. syndicated loans were originated by non-Eurozone European banks-mainly those located in the U.K. and Switzerland. These banks also do a lot of Eurozone lending and raise some of their deposits in euros.⁸ Given this exposure to the euro, there is a case for including these banks in our analysis, but we take the more conservative approach of reporting the results only for Eurozone banks. However, our results are robust to including European banks outside the Eurozone.

[Table I]

Table II highlights the fact that the syndicated loan market is global in nature; Eurozone and U.S. banks lend not just in their home regions, but throughout the world. The table also makes clear the importance of dollar lending. Indeed, outside of Europe, Eurozone banks do almost all of their lending in dollars. Even within Europe, Eurozone banks do a significant fraction of their lending in dollars-almost 9% in the Eurozone and 30% in the rest of Europe. Overall, 43% of Eurozone bank lending is in dollars. Given that most of their retail deposits are in euros, this creates a currency mismatch between their assets and retail deposits. The same is not true of U.S. banks, which do 89% of their syndicated lending in dollars.

[Table II]

3.2 Eurozone Bank Reliance on U.S. Money-Market Funds and the Run in 2011

In May 2011, financial markets became increasingly concerned about the exposure of European banks to Greek sovereign debt, amidst growing worries about the country's solvency. Leading banks in France, Germany and Belgium were identified as having several billion euros of Greek sovereign bonds on their books.⁹ In response, investors began withdrawing money from U.S. prime money-market funds (MMFs), which, according to the SEC, had about one quarter of their assets invested in paper issued by Eurozone banks. The withdrawals were greater from those funds that had more exposure to Eurozone banks (Chernenko and Sunderam, 2012). This in turn led MMFs to reduce their holdings of instruments issued by Eurozone banks. According to Fitch, between May and December 2011, the 10 largest U.S. MMFs had reduced their exposure to Eurozone banks from 50% to 10% of their total assets. French banks, which were top lenders to U.S. firms, lost 94% of their funding from U.S. MMFs.¹⁰

This was an important shock to the ability of Eurozone banks to fund themselves in dollars. To measure the size of this shock for particular banks, we calculate the share of a bank's short-term funding that comes from U.S. MMFs as of the end of April 2011. This calculation is based on MMF security-level holdings compiled by Crane Data LLC from data provided by fund sponsors either on their websites or directly to Crane Data. These data cover roughly 85% of the universe of MMF holdings (with some smaller funds missing from the sample).

Our measure of MMF reliance is the sum of MMF holdings of certificates of deposit (CDs), commercial paper (CP), asset-backed CP, repurchase agreements, and other short-term bank notes and deposits scaled by the sum of banks' deposits and short-term debt. Data on a bank's short-term liabilities are taken from Capital IQ and are measured as of the end of 2010. We should emphasize that we are not scaling by banks' short-term dollar funding as that information is not available. Thus, our measure does not capture-and may greatly understate-the extent to which a bank relies on U.S. MMFs for its dollar funding.

Ideally, we would also want to distinguish between insured and uninsured dollar funding. But there is very limited information on insured deposits, and almost none on insured deposits by currency. However, it is likely that the insured dollar deposits of Eurozone banks are limited. Only five of the large Eurozone banks operate in the U.S. through subsidiaries and, with some limited exceptions, only deposits of subsidiaries are eligible for FDIC insurance. On average, deposits reported to the FDIC by these five banks are roughly 82% of their MMF funding. For Deutsche Bank, deposits reported to the FDIC are only 43% of its MMF funding.

Table III reports MMF funding reliance for the 11 Eurozone banks that were among the top fifty lenders in the U.S. syndicated loan market between 2005 and 2007. We also include MMF data for those European banks outside the Eurozone that were among the top 50 lenders. As can be seen, MMFs were an important source of short-term funding for these banks. For Deutsche Bank, the fifth-largest lender in the U.S., with 4.5% of syndicated origination volume, 7.7% of its short-term funding came from U.S. MMFs. The French banks-Societe Generale, Credit Agricole, BNP Paribas and Natixis-on average, received 5% of their short term funding from U.S. MMFs. These banks collectively represented nearly 4% of the origination volume in the U.S. market.

[Table III]

As noted above, these calculations understate the significance of MMFs as a source of dollar funding because they normalize by all short-term funding, including deposits. While no systematic data are reported on funding currencies, information provided by Credit Agricole in a presentation to analysts can give a better sense of the share of dollar funding share of U.S. MMFs.¹¹ The bank reported that in June 2011, 44% of its short-term debt was in dollars. Based on data we have on Credit Agricole's short-term debt and MMF funding in April 2011, this implies that approximately 30% of the bank's short-term dollar funding came from U.S. MMFs.

3.3 Breakdown of Covered Interest Parity in 2011

Foreign exchange swaps are the primary means through which global banks manage the currency mismatch between their assets and liabilities (e.g., Fender and McGuire, 2010). A swap contract enables a bank to exchange local currency for U.S. dollars at the current exchange rate, while agreeing to reverse the transaction-i.e., exchange U.S. dollars back to local currency-at the forward exchange rate. The typical maturity of a FX swap is three months, but as an over-the-counter instrument its maturity can be extended to several years. Counterparties typically post collateral, which is adjusted depending on movements in currencies.

In the absence of market frictions, the cost of an FX swap is pinned down by the differences in interest rates in the two currencies that are being swapped. Specifically, covered interest rate parity (CIP) implies that the differential in interest rates between two countries should be equal to the differential between the forward and the spot exchange rates. In other words, any profits that one could make by borrowing in one currency and lending in other should be erased by the cost of converting interest back to the currency in which the bank borrows.¹² A deviation from CIP, however, offers a profit opportunity and, in principal, should be driven away by arbitrageurs. So, if arbitrage is frictionless, the U.S. dollar premium (or "basis")-defined as the difference between the CIP-implied interest rate and the current unsecured U.S. interest rate-should be zero. A positive basis implies that investors can make a profit by borrowing funds in euros, converting them to dollars, investing at the existing dollar rate and converting the dollars back to euros at the end of the investment period. If investors rush to do so, the spot exchange rate will rise and the forward exchange rate will fall, which should drive down the profits from this strategy.

Given this seemingly riskless arbitrage, CIP deviations are rare (Taylor, 1987; Akram, Dagfinn and Sarno, 2008). However there have been repeated breakdowns in CIP since the beginning of the financial crisis in August of 2007. Coffey, Hrung and Sarkar (2009) document that in September of 2008 the U.S. dollar basis with respect to euro ("euro basis") shot up to over 200 basis points. Although in 2009 the euro basis declined substantially, the violation of CIP persisted. What is important for our study is that the euro basis again rose dramatically in the second half of 2011, the period characterized by the money-fund pullback from paper issued by European financial institutions.¹³

Panel A of Figure 3 shows the evolution of the euro basis for daily euro-USD exchange rate data. To construct this series we use daily quotes for 3-month euro and U.S. dollar LIBOR compiled by the British Bankers' Association and downloaded from Bloomberg, and 3-month daily spot and forward rates compiled by WM/Reuters and downloaded from Datastream.

Our estimates for 2008 closely track Coffey, Hrung and Sarkar (2009). Their results are robust to reporting frequency (daily vs. hourly) of the exchange rate data, so our use of daily rates should not be a concern. Like Coffey, Hrung and Sarkar (2009), the CIP deviation shown in Figure 3 is robust to alternative reference dollar rates. Similar patterns emerge if we use the New York Funding Rate or the Treasury bill rate. Another noteworthy observation, depicted in Panel B of Figure 3, is that CIP violation in 2011 shows up first, and is most acute, in the dollar-euro exchange rate. This observation is consistent with the implication of our model, namely that the increase in swap demand by Eurozone financial institutions is what drives the deviation in CIP.

[Figure 3]

4 Lending Behavior Following the Shock to Money-Market Funds

In this section, we examine bank lending behavior around the MMF shock. We first show that Eurozone banks reduced their dollar-denominated loans relative to euro-denominated loans. We then show that those Eurozone banks that were more MMF-dependent in their financing reduced their lending by more than other Eurozone banks.

4.1 Direct Effects of MMF Shock on Bank Lending

To examine the behavior of Eurozone banks around the MMF shock we construct a panel data set of bank-month observations from 2005-2011. Our focus is on the effect of the MMF shock on DOLLAR LOAN SHARE, the ratio of a bank's dollar-denominated loans to all its dollar- and euro-denominated loans (excluding all other currencies). The exact specification is explained in the captions to each table.

The first column of Table IV reports the results of regressing the dollar loan share on POST, a dummy variable that takes the value one if the loan occurs between May and December 2011, the period during which Eurozone banks experienced the funding shock. Only the 11 Eurozone banks are included in this specification. As in all regressions in the table, we also include bank fixed effects since there is likely to be variation across banks in the extent to which they lend in dollars and euros.

As expected, the coefficient of POST is negative and statistically significant. Standard errors are calculated to allow for correlation of the error term across an individual bank's observations within the pre-funding shock period and within the post-funding shock period. The coefficient implies that banks reduce their dollar loan share by 3.3 percentage points relative to their pre-shock average. Given that the dollar loan share has a sample mean of 16.8%, this is a fairly sizeable effect.

In calculating the dollar loan share, we convert the value of euro-denominated loans into dollars, using the spot exchange rate at loan issuance, so these loans can be compared directly to dollar-denominated loans. This raises the concern that an appreciation of the euro, as happened in the POST period, could mechanically lead to a decline in our DOLLAR LOAN SHARE variable, even if the nominal volume of loan issuance in each currency was unchanged. This mechanical effect could then potentially bias our inferences. To control for this possibility, in columns (2) and (4) of Table IV we add a control for the euro/dollar exchange rate. Interestingly, the coefficient on this variable is significantly negative-the opposite of what one would expect if there was a purely mechanical effect at work-and including it in the regression actually leads the coefficient on POST to increase somewhat.

Why might a stronger euro lead to an increase in the share of dollar lending by Eurozone banks? One hypothesis is as follows. If a Eurozone bank holds predominantly euro-denominated assets, then an increase in the value of the euro strengthens its economic capital relative to that of its U.S. counterparts. This in turns enables it to gain market share in those dollar-based loan markets where it is most likely to be in direct competition with U.S. banks. By contrast, in euro-based loan markets, where its competitors are more likely to be other European banks, a movement in the exchange rate confers less of an advantage. The net result is an increase in the share of activity the European bank does in dollar markets.¹⁴

The leading alternative explanation for the drop in the dollar lending share of Eurozone banks is that these banks experienced not so much a funding shock as a decline in dollar loan demand relative to euro loan demand. On its face, this alternative hypothesis is somewhat implausible given that the source of the shock in the first place was the Eurozone. So, if anything, one would think that there would be more of a decline in the demand for euro-denominated loans. Nevertheless, we explore this alternative hypothesis in a number of ways.

First, we examine whether the decline in the dollar loan share is observed in U.S. banks, which did not suffer from a funding shock given their limited exposure to Eurozone sovereign debt. This is effectively a difference-in-difference specification. The third column of Table IV reports the results from a regression that adds to the sample seven U.S. banks that are active in syndicated lending in the Eurozone. The variable EUROBANK*POST is an interaction between the POST dummy and a Eurozone bank dummy. Our funding-shock hypothesis implies that we should expect to see a negative coefficient. And indeed, the coefficient is negative and statistically significant. The magnitude of the coefficient implies that there is no change in the currency composition of Eurozone lending by U.S. banks in the POST period; the effect is specific to the Eurozone banks, which are the ones that suffered from the dollar funding shock.

One might be concerned that these findings are driven less by dollar funding difficulties of Eurozone banks and more by their preference to lend in Europe in response to the crisis. For example, Eurozone banks may have longer-term relationships with European borrowers and may give them priority in the allocation of scarce resources. To explore this alternative interpretation we restrict the sample to loans made in the Eurozone.¹⁵ Despite being originated in the Eurozone, a significant fraction of these loans are dollar-denominated (Table II). As the second column of the table shows, the dollar share of Eurozone loans falls in the POST period.

[Table IV]

Going further, another concern could be that the kinds of European firms that borrow in dollars from Eurozone banks are somehow different from those that borrow in euros. To investigate this possibility, in Table V we examine lending behavior at the loan level rather than at the bank level. This allows us control for unobservable, time-invariant firm characteristics because we observe multiple instances in which the same firm taps the syndicated loan market, both before and after the shock.

We run regressions for the period 2000 - 2011. Here the unit of observation is a loan and the dependent variable is EUROBANK SHARE, the fraction of banks in the loan origination syndicate that are from the Eurozone. We look at a longer period so there are more repeated transactions per borrower. We include firm fixed effects and month-year fixed effects in the regression. Our hypothesis is that EUROBANK SHARE will fall more after the MMF shock for dollar loans than for euro loans. This can be seen in the first column of Table V where the key variable of interest is the interaction of DOLLAR LOAN, a dummy variable for whether the loan is in dollars, and POST. As predicted, this coefficient is negative and statistically significant. In other words, in the wake of the dollar funding shock, the Eurozone bank share of dollar loan syndications falls more than the Eurozone bank share of euro loan syndications.

[Table V]

This result is not surprising given that Eurozone banks cut their overall dollar lending more than their euro lending. But the finding confirms our interpretation that the reduction in dollar lending by Eurozone banks is not driven by unobservable, time-invariant differences in borrower characteristics. Indeed, our procedure may make it more difficult to find an effect. The analysis is Table V is implicitly conditional on the set of firms that receive a loan following the shock. These firms are likely to be the most creditworthy firms, which may be more prone to borrow from Eurozone banks.

Table VI provides more qualitative evidence that differences in borrower types between Eurozone and non-Eurozone banks are unlikely to explain the relative decline in dollar lending by Eurozone banks. Panel A of the table lists twenty randomly selected borrowers from Eurozone banks in the U.S. in 2006. Using Capital IQ we look up the headquarters, business description, and public or private status of the firms. They are all U.S. firms, not foreign firms or their subsidiaries. On the flip side, as shown in Panel B, Eurozone borrowers of U.S. banks are all Eurozone companies, not subsidiaries of U.S. firms that want to raise capital in the Eurozone.

Panel A of Table VII provides additional evidence that a drop in dollar loan demand is unlikely to explain our findings. The table reports loan characteristics for the January, 2005-April, 20011 period (pre-shock period). The average U.S. borrower from a Eurozone bank is larger, and less leveraged than the average U.S. borrower from a U.S. bank. Just the opposite is true of European borrowers; if they borrow from Eurozone banks, they tend to be smaller, and more leveraged. Thus, banks tend to lend to riskier firms in their home markets. The implication for our study is that if one thinks that loan demand falls in response to the European debt crisis, one would think that the effect would be larger among the smaller, riskier firms; these are the types of firms that usually experience the sharpest drop in borrowing during recessions (e.g., Kashyap, Lamont and Stein, 1994). If loan demand were driving our results, we would expect to see a drop in euro loans by Eurozone banks relative to their dollar loans. We see just the opposite, which again cuts against a loan-demand story.

[Tables VI & VII]

4.2 Cross-Sectional Effects on Bank Lending

The model of Section 3 makes the cross-sectional prediction that those Eurozone banks that are the most money-fund-dependent will cut their dollar lending (relative to their euro lending) by more in response to the MMF shock. We examine this prediction by measuring money-fund dependence as the fraction of short-term funding that comes from U.S. money funds, as reported in Table III and discussed above. Recall that this measure, MMFSHARE, normalizes by all short-term debt, both dollar- and euro-denominated.

To start, for each of the 11 Eurozone banks in the sample we calculate their average U.S. quarterly dollar loan origination for two periods: (i) the period between May 2010 and April 2011 (the one year before the shock); and (ii) May 2011 through December 2011 (after the shock). The average change in dollar lending across these two periods is -3.9%. Panel A of Figure 4 then plots this change variable versus MMFSHARE at the bank level. The figure reveals a negative relationship between the two, suggesting that more MMF-dependent banks cut their dollar lending in the U.S. by more. Just the opposite is true of their euro lending in Europe as shown in Panel B of Figure 4. While, on average, banks increase their European euro lending by 22.8%, more MMF-dependent banks increase their euro lending by more. Importantly, Panel C shows that this is not the case for Eurozone banks' dollar-denominated lending in Europe. On average, banks cut their dollar Eurozone lending by 28.7%; as predicted, more MMF-dependent banks cut their dollar lending in the Eurozone by more.

To see whether these visual results are statistically significant, we return to the same structure as the regressions in Table IV. The dependent variable is DOLLAR LOAN SHARE, the fraction of a bank's loans that are in dollars. The data are monthly observations for the 11 Eurozone banks from 2005-2011, and we include both bank fixed effects and month-year fixed effects. To see whether those Eurozone banks that are most MMF-dependent cut their lending by more, we include an interaction term MMFSHARE $\times$ POST.

[Figure 4 & Table VIII]

The first column of Table VIII, which includes lending in both the U.S. and Europe, shows that the coefficient on MMFSHARE $\times$ POST is negative and statistically significant. The coefficient implies that for a bank at the 25 ${}^{th}$ percentile of MMFSHARE (1.25%), the drop in lending following the MMF shock was 1.3 percentage points (8% of the sample mean), whereas for a bank at the 75 ${}^{th}$ percentile of MMFSHARE (6.25%) the drop over the same period was 6.6 percentage points (39% of the sample mean). These differences would seem to be quite economically meaningful.

The second column of Table VIII restricts attention to dollar lending within the Eurozone. The results are very similar, indicating that the decline in MMF funding had an adverse effect on dollar lending by European banks to Eurozone firms, not just on their dollar lending to U.S. firms.

5 Conclusions

In this paper, we have shown that one of the consequences of the European sovereign debt crisis was that Eurozone banks cut their dollar-denominated lending. This is not surprising in itself; one would expect these banks to cut lending in the face of capital and liquidity constraints stemming from losses on their portfolios of sovereign bonds. More interestingly, however, we show that Eurozone banks shifted the composition of their dollar and euro lending, cutting their dollar lending by more, despite the fact that European economies were more threatened by the debt crisis.

We argue that this is a consequence of two features of the markets in which European banks fund themselves. First, European banks rely on less stable wholesale dollar funding sources to finance their dollar lending whereas a good deal of their euro lending is financed with stickier euro deposits. Second, frictions in the foreign exchange swap market limit the extent to which Eurozone banks can use euro deposits to fund their dollar lending. As swap demand from Eurozone banks rises, there is only limited arbitrage capital available to take the other side of the trade, which increases the cost of engaging in this synthetic dollar borrowing. Thus Eurozone banks adjust to strains in wholesale dollar funding markets by borrowing more in euros, but also by cutting back their dollar lending relative to euro lending.

One issue that we have not addressed is the extent to which the reduction in dollar lending by Eurozone banks created an overall tightening in credit supply to U.S. firms, and thereby exerted a contractionary effect on the U.S. economy. To some extent other banks-either U.S. or non-European banks-may have stepped in to fill the hole left by the retrenchment of the Eurozone banks. Indeed, there is evidence that Japanese banks have increased their presence in dollar loan markets (Fitch, 2012). And U.S. firms may also have turned to the bond market, as suggested by the recent work of Becker and Ivashina (2012). Since European banks tend to lend to large, highly-rated U.S. borrowers, one suspects that such substitution might be smoother than it would be with a different population of borrowers.

Thus, the ultimate cost of Eurozone bank retrenchment on dollar borrowers is difficult to assess at this point. To address this issue we will need more analysis of the borrowing behavior of firms that previously relied on the Eurozone banks for dollar funding. Nevertheless, this paper identifies a channel through which shocks outside the U.S. can affect the ability of U.S. firms to borrow. Although dollar lending by foreign banks increases the supply of credit to U.S. firms during normal times, it may also prove to be a more fragile source of funding that transmits overseas shocks to the U.S. economy.

References

Acharya, V., G. Alonso, and A. Kovner, 2012. "How do Global Banks Scramble for Liquidity? Evidence from the Asset-Backed Commercial Paper Freeze of 2007," Working Paper.

Acharya, V., and P. Schnabl, 2010. "Do Global Banks Spread Global Imbalances? Asset-

Backed Commercial Paper during the Financial Crisis of 2007-09," IMF Economic Review 58, 37-73.

Akram , F., R., Dagfinn, and L., Sarno, 2008, "Arbitrage in the Foreign Exchange Market: Turning on the Microscope," Journal of International Economics 76 (2), 237-253.

Baba, N., F. Packer, and T. Nagano, 2008, "The Spillover of Money Market Turbulence to FX

Swap and Cross-Currency Swap Markets," BIS Quarterly Review, 73-86.

Becker, B., and V. Ivashina, 2012, "Cyclicality of Credit Supply: Firm Level Evidence." Working paper.

Chernenko, S., and A. Sunderam, 2012, "The Quiet Run of 2011: Money Market Funds and the European Debt Crisis," Working paper.

Cetorelli, N., and L. Goldberg, 2011, "Global Banks and International Shock Transmission: Evidence from the Crisis," IMF Economic Review 59, 41-76.

Cetorelli, N., and L. Goldberg, 2012. "Follow the Money: Quantifying Domestic Effects of Foreign Bank Shocks in the Great Recession," American Economic Review: Papers and Proceedings 102(3), 213-218.

Cetorelli, N., and L. Goldberg, 2012. "Liquidity Management of U.S. Global Banks:

Internal Capital Markets in the Great Recession," Journal of International Economics, forthcoming.

Chava, S., and A. Purnanandam, 2011, "The Effect of Banking Crisis on Bank-Dependent Borrowers", Journal of Financial Economics 99, 116-135.

Coffey, N., W. Hrung and A. Sarkar, 2009, "Capital Constraints, Counterparty Risk, and Deviations from Covered Interest Rate Parity," Staff Report 393, Federal Reserve Bank of New York.

Fender, I., and P. McGuire, 2010, "Bank Structure, Funding Risk and the Transmission of Shocks across Countries: Concepts and Measurements," BIS Quarterly Review, 63-79.

Froot, K., and J. Stein, 1991, "Exchange Rates and Foreign Direct Investments: An Imperfect Capital Market Approach," Quarterly Journal of Economics, 1191-1217.

Garleanu N., and L. Pedersen, 2011, "Margin-Based Asset Pricing and Deviations from the Law of One Price," Review of Financial Studies 24(6), 1980-2022.

Griffolli, T., and A. Ranaldo, 2010, "Limits to Arbitrage during the Crisis: Funding Liquidity Constraints and Covered Interest Parity," Swiss National Bank Working Paper.

Kashyap, A., O. Lamont, and J. Stein, 1994, "Credit Conditions and the Cyclical Behavior of Inventories," Quarterly Journal of Economics 109, 565-592.

Levich, R., 2012, "FX Counterparty Risk and Trading Activity in Currency Forward and Future Markets," NBER Working Paper 18256.

Myers, S., and N. Majluf, "Corporate Financing and Investment Decisions When Firms Have Information that Investors Do Not Have," Journal of Financial Economics 13, 187-221.

Peek, J., and E. Rosengren, 1997, "The International Transmission of Financial Shocks: The Case of Japan," American Economic Review 87(4), 495-505.

Peek, J., and E. Rosengren, 2000, "Collateral Damage: Effects of the Japanese Bank Crisis on Real Activity in the United States," American Economic Review 90(1), 30-45.

Schnabl, P., 2012, "The International Transmission of Bank Liquidity Shocks: Evidence from an Emerging Market," Journal of Finance 67(3), 897-932.

Shin, H., 2012, "Global Banking Glut and Loan Risk Premium," IMF Economic Review 60, 155-192.

Taylor, A., and A. Sanson, 2007, "The Handbook of Loan Syndication and Trading," The McGraw-Hill Companies.

Taylor, M., 1987, "Covered Interest Parity: A High-Frequency, High-Quality Data Study," Economica 54, 429-438.

Figure 1

Dollar assets and liabilities of foreign banks

Compiled from Bank of International Settlement locational banking statistics, July 2012.

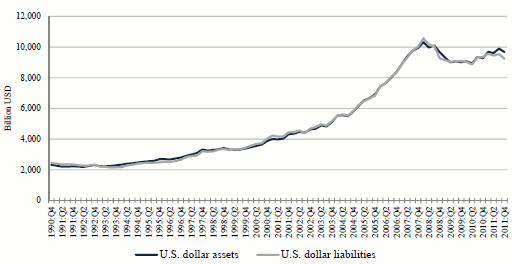
Figure 2

Equilibrium as a function of ${\mathbf \alpha }{\mathbf p}$

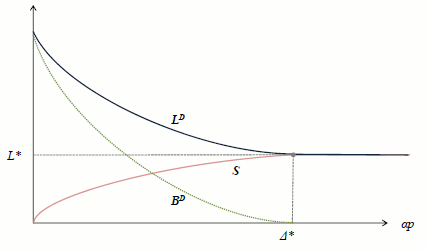
$Figure 2: Equilibrium as a function of \alpha p. This is a line graph with a horizontal dotted line extending from y=L* and a vertical dotted line extending from x=\delta*. A line labeled Ld starts above L* and decreases to L* at x=\delta*. A line labeled Bd starts at the same place as Ld above L* and decreases to 0 at x=\delta*. A line labeled S starts at 0 and increases to L* at x=\delta*.$

Figure 3

Deviations from Covered Interest Parity

Daily quotes for 3-month LIBOR are compiled by the British Bankers Association and downloaded from Bloomberg, and 3-month daily spot and forward rates are compiled by WM/Reuters and downloaded from Datastream.

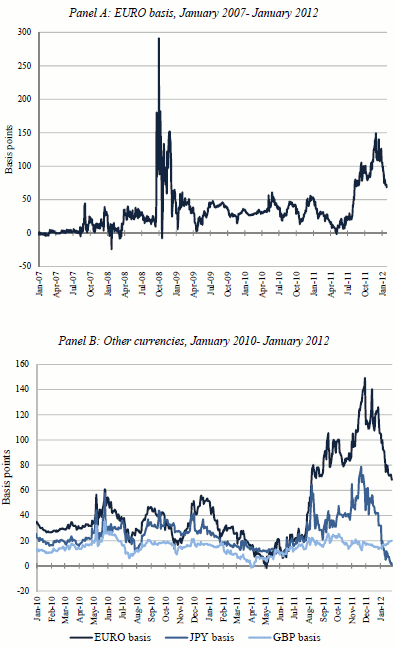
Figure 4

Change in lending and money-market fund reliance

MMF reliance is defined as MMF holdings as of April 2011scaled by (Deposits + Short Term Debt) as of the end of 2010. Change in lending is calculated at the change between: (i) the period from May 2010 to April 2011 (one year before the MMF shock) and (ii) May 2011 to December 2011 (after the MMF shock).

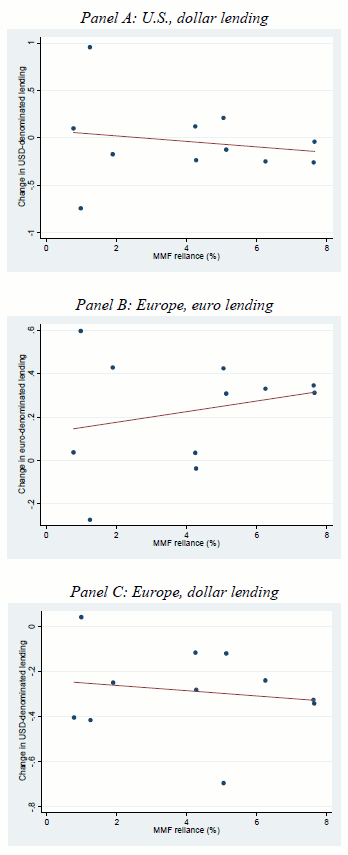
Table 1: Market share, largest lenders in Eurozone, 2005-2007

Loan amount is prorated based on the number of the lead banks ("Lead") or based on the total number of syndicate participants ("All lenders"). Lead bank is identified based on whether the lender designated as "Lead Arranger" or "Agent" in the league tables as reported in DealScan. The table reports the top 50 lenders in the Eurozone; Banesto's share is aggregated together with Santander's share. Note that Lehman Brothers went bankrupt in 2008, and Fortis was acquired by BNP Paribas in 2009.

	Market:	Share of Eurozone lending Lead	Share of Eurozone lending All lenders	Market share U.S. Lead	Market share U.S. All lenders
GIIPS: UniCredit	Italy	3.02	3.21	0.05	0.31
GIIPS: Banco Bilbao Vizcaya Argentaria	Spain	2.33	2.23	0.06	0.43
GIIPS: Intesa Sanpaolo	Italy	1.91	2.14	0.04	0.26
GIIPS: Banco Santander	Spain	2.37	2.32	0.10	0.44
GIIPS: Mediobanca	Italy	0.99	1.07	-	-
GIIPS: Banco Financiero y de Ahorros	Spain	0.90	1.00	0.01	0.04
GIIPS: La Caja de Barcelona	Spain	0.78	0.77	-	-
GIIPS: Banco de Sabadell	Spain	0.32	0.35	-	-
GIIPS: Bank of Ireland Group	Ireland	0.30	0.45	0.05	0.24
GIIPS: ICO [Instituto de Credito Oficial]	Spain	0.23	0.26	-	-
France: BNP Paribas	France	6.70	5.07	2.31	2.36
France: Credit Agricole	France	4.91	4.29	1.03	1.25
France: Societe Generale	France	4.57	3.64	0.48	1.02
France: Natixis SA	France	3.01	3.22	0.09	0.47
France: CM-CIC	France	1.32	1.72	0.00	0.06
BeNeLux: ING Group	Netherlands	2.72	2.47	0.33	0.81
BeNeLux: Fortis Bank	Belgium	1.71	1.89	0.38	0.66
BeNeLux: Rabobank	Netherlands	0.78	0.96	0.30	0.41
BeNeLux: KBC Group	Belgium	0.47	0.74	0.02	0.28
BeNeLux: Dexia Bank	Belgium	0.46	0.65	0.02	0.06
Rest of Eurozone: Commerzbank	Germany	4.92	4.74	0.50	0.90
Rest of Eurozone: Deutsche Bank	Germany	4.74	3.50	4.47	3.25
Rest of Eurozone: WestLB	Germany	1.32	1.41	0.14	0.29
Rest of Eurozone: BayernLB	Germany	1.13	1.22	0.07	0.23
Rest of Eurozone: Landesbank Baden-Wurttemberg	Germany	0.98	1.14	0.01	0.04
Rest of Eurozone: Landesbank Hessen-Thuringen [Helaba]	Germany	0.42	0.62	0.04	0.08
Rest of Eurozone: DZ Bank	Germany	0.42	0.56	0.01	0.10
Rest of Eurozone: KfW Bankengruppe	Germany	0.41	0.68	0.00	0.01
Rest of Eurozone: HSH Nordbank	Germany	0.38	0.38	0.06	0.09
Rest of Eurozone: NordLB Group	Germany	0.24	0.31	0.03	0.08
Rest of Eurozone: Svenska Handelsbanken	Sweden	0.31	0.26	-	-
Rest of Eurozone: SEB Merchant Banking	Sweden	0.29	0.40	-	0.04
Rest of Eurozone: Nordea Bank AB	Sweden	0.45	0.46	0.03	0.09
Total Eurozone:		55.82	54.11	10.65	14.28
Rest of Europe: Credit Suisse	Switzerland	1.60	1.64	3.76	0.09
Rest of Europe: UBS	Switzerland	1.26	1.23	1.73	3.37
Rest of Europe: Royal Bank of Scotland	UK	9.21	7.71	3.87	2.01
Rest of Europe: Barclays Bank	UK	3.16	2.87	2.27	3.77
Rest of Europe: HSBC	UK	3.08	2.87	1.18	2.07
Rest of Europe: Lloyds Banking Group	UK	1.01	1.33	0.39	1.57
Total Europe:		75.14	71.75	23.86	27.68
US: Citi	USA	5.66	4.03	11.45	6.70
US: JP Morgan	USA	3.75	3.13	17.08	10.13
US: Bank of America Merrill Lynch	USA	1.86	1.94	16.15	9.83
US: Goldman Sachs	USA	1.68	1.79	2.55	2.71
US: Morgan Stanley	USA	1.32	1.43	1.68	2.16
US: Lehman Brothers	USA	0.52	0.60	2.26	2.18
US: GE Capital	USA	0.52	0.56	2.36	2.29
Total U.S.:		15.29	13.49	53.53	36.00
Other: Mitsubishi UFJ Financial Group	Japan	2.27	2.47	1.85	2.45
Other: Mizuho Financial Group	Japan	0.96	1.08	0.56	1.35
Other: Sumitomo Mitsui Financial Group	Japan	0.41	0.61	0.37	0.98
Total other:		3.64	4.15	2.78	4.77

Table II

Syndicated lending around the world by currency, 2005-2007

Loan amount is prorated based on the number lead banks receiving league table credit.

	Lending in the region	% of Total lending	Lending in Euro (billion USD)	Lending in USD (billion USD)	Lending in Euro (%)	Lending in USD (%)
Eurozone banks: Eurozone	1,036.15	45.5%	941.64	89.11	90.9%	8.6%
Eurozone banks: Rest of Europe	420.64	18.5%	124.04	127.12	29.5%	30.2%
Eurozone banks: U.S.	495.52	21.8%	4.30	490.53	0.9%	99.0%
Eurozone banks: Rest of North America	17.89	0.8%	0.00	14.47	0.0%	80.9%
Eurozone banks: Asia	139.44	6.1%	10.06	102.92	7.2%	73.8%
Eurozone banks: Latin America	81.09	3.6%	2.27	78.81	2.8%	97.2%
Eurozone banks: Middle East	63.25	2.8%	3.40	59.78	5.4%	94.5%
Eurozone banks: Africa	21.27	0.9%	1.74	17.65	8.2%	83.0%
Eurozone banks Total:	2,275.25		1,087.46	980.39	47.8%	43.1%
U.S. banks: Eurozone	313.96	7.8%	252.06	60.53	80.3%	19.3%
U.S. banks: Rest of Europe	234.74	5.8%	41.48	75.46	17.7%	32.1%
U.S. banks: U.S.	3,269.47	80.8%	7.82	3,255.99	0.2%	99.6%
U.S. banks: Rest of North America	56.83	1.4%	0.12	47.79	0.2%	84.1%
U.S. banks: Asia	89.91	2.2%	5.56	60.11	6.2%	66.9%
U.S. banks: Latin America	56.79	1.4%	0.41	56.38	0.7%	99.3%
U.S. banks: Middle East	15.54	0.4%	0.16	15.38	1.0%	99.0%
U.S. banks: Africa	10.24	0.3%	0.32	8.69	3.1%	84.9%
U.S. banks Total:	4,047.48		307.93	3,580.33	7.6%	88.5%

Table III

U.S. prime money-market funds as a funding source

This table reports money-market-funds (MMF) funding reliance for the 11 Eurozone banks that were among the top fifty lenders in the U.S. syndicated loan market between 2005 and 2007. We also include MMF data for those European banks outside the Eurozone that were among the top 50 lenders in the U.S.. Note that MMF reliance=MMF holdings as of April 2011/(Deposits + Short Term Debt) as of the end of 2010.

Bank	Country	MMF reliance as of April 2011
Eurozone: Deutsche Bank	Germany	7.65
Eurozone: Rabobank	Netherlands	7.63
Eurozone: Societe Generale	France	6.25
Eurozone: ING Bank	Netherlands	5.14
Eurozone: Natixis	France	5.06
Eurozone: Credit Agricole	France	4.28
Eurozone: BNP Paribas	France	4.25
Eurozone: Commerzbank	Germany	1.90
Eurozone: Banco Bilbao Vizcaya Argentaria	Spain	1.25
Eurozone: UniCredit	Italy	0.99
Eurozone: Banco Santander	Spain	0.78
Rest of Europe: Credit Suisse	Switzerland	4.92
Rest of Europe: Barclays Bank	UK	4.37
Rest of Europe: Lloyds TSB Bank	UK	3.97
Rest of Europe: UBS	Switzerland	3.32
Rest of Europe: RBS	UK	2.29
Rest of Europe: HSBC	UK	1.49

Table IV

Share of dollar lending

The dependent variable is the fraction of loans originated by bank i in month t that is denominated in U.S. dollars(S ${}_{it}$ ). The sample includes all loans originated between 2005 and 2011that are denominated in U.S. dollars or euro; all other currencies are excluded from the sample. In specifications (1) through (4) we look at Eurozone banks only, specifications (5) through (7) look at U.S. and Eurozone banks. Specifications (3) and (4) look at lending in the European market only; the rest of the specifications look at lending in U.S. and European markets. Specifications (1) though (4) correspond to:

S ${}_{it}$ =D ${}_{i}$ + $\beta$ POST.

D ${}_{i}$ ${}_{ }$ is an originating bank fixed effect and POST is a dummy variable equal to 1 for the May 2011-December 2011 period and 0 otherwise. Specification (7) includes month fixed effects and corresponds to:

S ${}_{it}$ =D ${}_{i}$ + D ${}_{t }$ + $\beta$ EUROBANK ${}_{i}$ *POST.

EUROBANK is a dummy variable equal to 1 if bank's headquarters are located in the Eurozone and 0 otherwise. Standard errors, reported in brackets, are clustered by bank interacted with pre and post period; there are twice as many clusters as there are banks in the sample. *** p0.01, ** p0.05, * p0.10.

Banks: Market	Eurozone banks: Europe and U.S. (1)	Eurozone banks: Europe and U.S. (2)	Eurozone banks: Europe (3)	Eurozone banks: Europe (4)	Eurozone and U.S. banks (diff-in-diff): Europe and U.S. (5)	Eurozone and U.S. banks (diff-in-diff): Europe and U.S. (6)	Eurozone and U.S. banks (diff-in-diff): Europe and U.S. (7)
POST (05/2011-12/2011)	-0.0333**	-0.0422***	-0.0348***	-0.0438***	-0.0017	-0.0093	-
POST (05/2011-12/2011) [standard error]	[0.0124]	[0.0128]	[0.0123]	[0.0127]	[0.0124]	[0.0126]
EUROBANK*POST	-	-	-	-	-0.0316*	-0.0316*	-0.0316*
EUROBANK*POST [standard error]					[0.0174]	[0.0174]	[0.0180]
USD/Euro spot exchange rate	-	0.1995***	-	0.2034***	-	0.1713**	-
USD/Euro spot exchange rate [standard error]	-	[0.0523]		[0.0532]		[0.0430]
Fixed effects: Bank (D ${}_{i}$ )	Yes	Yes	Yes	Yes	Yes	Yes	Yes
Fixed effects: Month (D ${}_{t }$ )	No	No	No	No	No	No	Yes
Obs.	924	924	924	924	1,428	1,428	1,428
Clusters	22	22	22	22	34	34	34
Adj. R-squared	0.05	0.06	0.05	0.06	0.81	0.81	0.83

Table V

Choice of lender (Eurozone vs. U.S.) for dollar-denominated loans

Each observation used for the analysis reported in this table is a separate loan (l). The dependent variable is EUROBANK SHARE ${}_{l}$ , a variable between 0 and 1 equal to fraction of lead banks on the loan headquartered in the Eurozone. The benchmark specification-columns (1) and (3)-corresponds to:

EUROBANK SHARE ${}_{l}$ = D ${}_{j}$ + D ${}_{t }$ + DOLLAR LOAN ${}_{l}$ + $\beta$ DOLLAR LOAN ${}_{l}$ *POST,

where D ${}_{j}$ ${}_{ }$ is borrower fixed effects and D ${}_{t }$ is month fixed effects. DOLLAR LOAN ${}_{l}$ is a dummy for the loan being denominated in U.S. dollars. POST is a dummy variable equal to 1 for May, 2011-December, 2011 period and 0 otherwise. Specifications (3) and (4) control for the loan size, because number of lead lenders depends on the loan size. The coefficient of interest, $\beta$ , is identified off the repeated loans by the same borrower. We use loans issued over 2000-2011 period to assure that there are enough repeated loans in our sample. Standard errors, reported in brackets, are clustered by borrower interacted with pre and post period; there are twice as many clusters as there are borrowers in the sample. *** p0.01, ** p0.05, * p0.10.

Market:	Europe and U.S. (1)	Europe and U.S. (2)	Europe (3)	Europe (4)
DOLLAR LOAN	-0.0581*	-0.0548*	-0.0166	-0.0236
DOLLAR LOAN [standard error]	[0.031]	[0.030]	[0.033]	[0.031]
DOLLAR LOAN*POST	-0.0655***	-0.0651***	-0.0956**	-0.1055**
DOLLAR LOAN*POST [standard error]	[0.018]	[0.018]	[0.047]	[0.048]
Ln(Loan amount)	-	-0.0043	-	-0.0484***
Ln(Loan amount) [standard error]		[0.003]		[0.009]
Fixed effects: Borrower(D ${}_{j}$ )	Yes	Yes	Yes	Yes
Fixed effects: Month (D ${}_{t }$ )	Yes	Yes	Yes	Yes
Obs.	34,107	34,088	5,859	5,842
Clusters	13,728	13,719	2,916	2,908
Adj. R-squared	0.84	0.84	0.78	0.79

Table VI

Examples of loans

This table illustrates who are the U.S. clients of European banks (Panel A) and the Eurozone clients of U.S. banks (Panel B). The table shows twenty random loans, sorted alphabetically, issued in 2006. For each of these loans, the lending bank received Thompson Reuters league-table credit as lead arranger or lead agent. The only other filter on the sample is the borrower's country (as identified in DealScan). There is no filter on the currency; also, firms are not consolidated by parent. If there are any significant misclassifications, they should show up in this sample. Headquarters location, business description and public/private status are from Capital IQ.

Panel A: U.S. loans issues by Eurozone banks

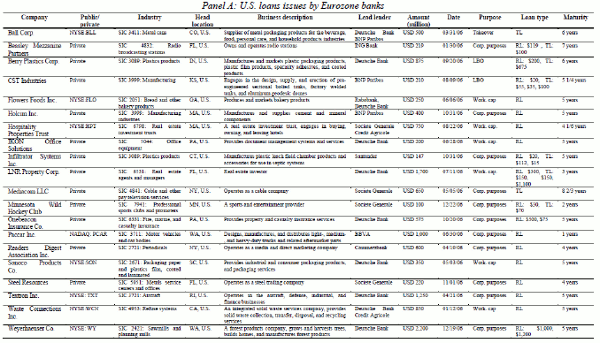
Panel B: Eurozone loans issued by U.S. banks

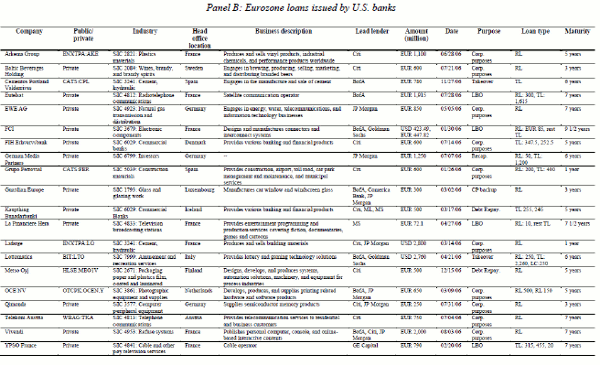
Table VII

Comparison of lending by Eurozone and U.S. banks

This table compares loan issued by U.S. and Eurozone banks during the pre-shock period January, 2005 to April, 2011. Loans are sorted using Thompson Reuters' DealScan categorizations. "Middle market" is a category specific to the U.S. lending market and refers to loans issued to firms with revenues below $1 billion. "Investment grade" refers to loans rated by S&P BBB or above. It also includes loans that are considered to be low risk, as determined by DealScan. "Leveraged" refers to loans taken by firms that have leverage above a threshold determined by DealScan. Loan amount is prorated based on the number of lead banks in the syndicate. The column labeled Diff takes the difference between the value for Eurozone and U.S. banks. *** indicates statistical significance of the difference with a p-value 0.01.

	Distribution of deals by credit quality -Equally weighted -Eurozone banks	Distribution of deals by credit quality -Equally weighted -U.S. banks	Distribution of deals by credit quality -Value weighted -Eurozone banks	Distribution of deals by credit quality -Value weighted -U.S. banks
U.S. Market: Middle market	29.57%	39.49%	9.14%	13.49%
U.S. Market: Investment grade	46.46%	41.58%	61.38%	57.52%
U.S. Market: Leveraged	23.96%	18.93%	29.49%	28.99%
European Market: Investment grade	65.26%	72.95%	65.40%	75.21%
European Market: Leveraged	34.74%	27.05%	34.60%	24.79%

	Statistic	Average loan size (million USD) - Eurozone banks	Average loan size (million USD) - U.S. banks	Average loan size (million USD) - Diff.	Average maturity (years) - Eurozone banks	Average maturity (years) - U.S. banks	Average maturity (years) - Diff.
U.S. Market: Middle market	Mean	197.37	124.69	72.68***	4.59	4.17	0.42***
U.S. Market: Middle market	Median	155.00	86.00	69.00***	5.00	4.99	0.01
U.S. Market: Middle market	Std. Dev.	158.25	123.04		2.01	1.87
U.S. Market: Investment grade	Mean	843.73	505.01	338.73***	4.18	3.50	0.68***
U.S. Market: Investment grade	Median	500.00	220.50	279.50***	4.78	3.00	1.78***
U.S. Market: Investment grade	Std. Dev.	875.35	724.41		2.74	11.76
U.S. Market: Leveraged	Mean	786.01	559.13	226.87***	5.04	4.61	0.44***
U.S. Market: Leveraged	Median	555.00	302.00	253.00***	5.00	5.00	0.00
U.S. Market: Leveraged	Std. Dev.	816.40	680.74		1.92	2.22
European Market: Investment grade	Mean	728.54	1,529.64	-801.10***	6.73	4.58	2.15***
European Market: Investment grade	Median	360.97	1,266.70	-905.73***	5.00	5.00	0.00
European Market: Investment grade	Std. Dev.	908.03	1,190.99		5.97	2.58
European Market: Leveraged	Mean	723.97	1,359.55	-635.58***	6.64	6.67	-0.03
European Market: Leveraged	Median	357.37	981.39	-624.02***	7.00	7.00	0.00
European Market: Leveraged	Std. Dev.	932.48	1214.39		2.92	2.92

Table VIII

Share of dollar lending: Money-market-fund reliance

As in Table IV, the dependent variable is the fraction of loans originated by bank i in month t that is denominated in dollars(S ${}_{it}$ ). We count all loans originated between 2005 and 2011that are denominated in dollars or euros. All specifications look at Eurozone banks only. Specification (1) looks at Eurozone banks' U.S. and European lending; specification (2) looks at European lending only. POST is a dummy variable equal to one for the May 2011-December 2011 period, and zero otherwise. The focus is on the interaction term between MMF, a continuous variable measuring bank i's reliance on the U.S. money-market funds as a fraction of total short term funding (deposits plus short-term debt), and POST. The exact specification is:

S ${}_{it}$ = D ${}_{i}$ + D ${}_{t }$ + $\beta$ MMF ${}_{i}$ *POST,

where D ${}_{i}$ ${}_{ }$ are bank fixed effects and D ${}_{t }$ are month fixed effects. Standard errors, reported in brackets, are clustered by bank interacted with pre and post period; there are twice as many clusters as there are banks in the sample. *** p0.01, ** p0.05, * p0.10.

Banks:	Eurozone banks	Eurozone banks
Market:	Europe and U.S. (1)	Europe (2)
MMF*POST	-0.0105*	-0.0101**
MMF*POST [standard error]	[0.0039]	[0.0039]
Fixed effects: Bank (D ${}_{i}$ )	Yes	Yes
Fixed effects: Month (D ${}_{t }$ )	Yes	Yes
Obs.	924	924
Clusters	22	22
Adj. R-squared	0.15	0.15

Footnotes

* We are grateful for helpful comments from Michael Palumbo, and from seminar participants at Northwestern University (Kellogg), the Banque de France/OSEO Conference, and the 4 ${}^{th}$ Paris Spring Corporate Finance Conference. We thank Peter Crane from Crane Data LLC for sharing money-market-fund data with us, Toomas Laarits and Chris Allen for research assistance, and the Division of Research at Harvard Business School for research support. The analysis and conclusions set forth are those of the authors and do not indicate concurrence by other members of the Board of Governors. Return to Text

1. When, as is often the case, foreign banks operate in the U.S. via a branch-as opposed to a separately capitalized subsidiary-they are legally precluded from raising FDIC-insured deposits. Return to Text

2. This could be because the bank finds it costly to raise new equity in the short run, and because capital regulation puts an upper bound on the ratio of total loans to book equity. Return to Text

3. We are implicitly assuming that the bank is prohibited from taking on naked exchange-rate exposure, i.e. from borrowing in euros, and lending in dollars without a hedge. We discuss this assumption in more detail below. Return to Text

4. "U.S. Money Fund Exposure and European Banks: Euro Zone Diverging,"

, January 26, 2012. Return to Text

5. Under the current regulatory framework, increased exposure to FX risk is costly to the bank. This treatment of FX risk dates back to Basel I. In a study conducted in the context of the Basel I discussion, FX risk was identified as one the fundamental risks: "There are many activities of banks which involve risk-taking, but there are few in which a bank may so quickly incur large losses as in foreign exchange transactions." (www.bis.org/publ/bcbs00e.htm.) Return to Text

6. We do not explicitly analyze the collateral posted by the bank, as opposed to by the arbitrageur. Instead, we just assume that the bank never defaults on its obligations under the swap contract, even if it does default on its short-term debt obligations. However, none of our main results are changed if there is a risk of default on the swap by the bank. This is because what matters for the bank in deciding how much swap activity to do is the premium it pays relative to the default-risk-adjusted actuarial value. Since this premium is a function of the arbitrageur's collateral constraint, and not the bank's, we focus on the former for the sake of clarity. Return to Text

7. We consider a lead bank to be one that is designated as a "Lead Arranger" or "Agent" in the DealScan database. Return to Text

8. Notoriously, the largest Icelandic banks had over two-third of their deposits in foreign currencies, most of it in euros. See "The Collapse of Iceland's Cross-Border Banks: Some Lessons for Deposits Insurance and Resolution Policies," presentation made by Mar Gudmundsson, Governor of the Central Bank of Iceland, in the BIS conference held in Basel on June 9, 2011. Return to Text

9. E.g., see "Investors Count Cost to Banks of Greek Default,"

, May 10, 2011 or "EU Banks' Risks from Greece Default Exceed Their Direct Exposures,"

, May 15, 2011. Return to Text

10. "U.S. Money Fund Exposure and European Banks: Euro Zone Diverging,"

, January 26, 2012. Return to Text

11. "Credit Agricole: Adapting to the New Environment" presentation made by Jean-Paul Chifflet, Chief Executive Officer in the Cheuvreux conference held in Paris on September 28, 2011. Return to Text

12. Specifically, in our context, CIP implies that $\left(1+r_E\right)\frac{X^F}{X^S}=(1+r_D)$ where

is the euro interest rate,

is the dollar interest rate,

is the forward exchange rate, and

is the spot exchange rate (where exchange rates are expressed as euros per dollar). The CIP-implied dollar interest rate is the value of

that solves this equation. Return to Text

13. "Euro-Dollar Basis Swap Cost at 2008 Crisis Levels," Wall Street Journal, November 16, 2011. Return to Text

14. This logic is similar to that of Froot and Stein (1991), who argue that in an imperfect capital market, a depreciation of the dollar increases inward foreign direct investment into the U.S., by raising the relative wealth of foreign investors who bid for U.S.-based assets. Return to Text

15. As before, we only look at the euro and dollar denominated loans. Return to Text

^♣ This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to Text