
Optimal CEO Incentives
and Industry Dynamics
Keywords: CEO compensation, product market structure
Abstract:
1 Introduction
There are large differences in executive pay practices among firms (see Murphy (1999) for a comprehensive discussion of this fact). This paper argues, both theoretically and empirically, that dynamic competition - i.e., competition for industry leadership - can help us to make progress on the question of which fundamental economic forces drive these differences. To this end, we develop and test the cross-sectional implications of an industry equilibrium model of optimal CEO incentives. In a large sample of U.S. CEOs and other top executives between 1993 and 2004, we find strong evidence in support of our theory, in that we document a robust negative relation between pay-performance sensitivity and, (i) across industries, the degree of heterogeneity of industry structure; (ii) within industries, firm position with respect to its peers.
The incentive structure of CEO compensation is a controversial topic that attracts attention of both academic researchers and popular press. The classical view of CEO pay as an agency problem (Holmstrom (1979), Holmstrom and Milgrom (1987)) emphasizes the trade-off between incentives and insurance. According to this view, shareholders can ensure that CEOs take optimal actions by tying CEO pay to the performance of their firms, that is, by providing high-powered incentives for CEOs to maximize the returns to shareholders.
However, the empirical literature has found a puzzling lack of evidence of high-powered incentives, which is typically interpreted to imply that CEOs are not given strong enough incentives to maximize the returns to shareholders (see Bebchuk and Fried (2004) for a forceful statement of this view). While recent studies (e.g., Hall and Liebman (1998)) document a general upward trend in high-powered incentives over the 1990s, compensation specialists and boards of directors remain vocal in decrying the weak link between executive pay and firm performance in U.S. corporations.
We argue that this "pay without performance" interpretation of the evidence is not granted. In particular, we propose an equilibrium interpretation of the observed differences in CEO incentive pay across firms. We propose that CEO compensation contracts are endogenously determined by the contracting environment, which likely differs across firms and industries. We show that relatively low pay-performance sensitivities emerge as the optimal incentive arrangement whenever returns to CEO effort are low. By emphasizing that the value of CEO effort is determined endogenously in industry equilibrium, we do not deny the importance of agency problems between stockholders and managers. Rather, our study complements the agency perspective by studying the role of equilibrium factors in shaping the contracting environment across firms.
Our model formalizes the link between CEO pay and industry structure. We introduce a standard optimal CEO compensation problem (Holmstrom (1979), Holmstrom and Milgrom (1987)) into a dynamic industry equilibrium model with differentiated Bertrand competition (e.g., Ericson and Pakes (1995), Maskin and Tirole (2000)). Shareholders choose CEO pay, while CEOs make product market and effort choices. The key innovation of our analysis is that we use a structural model with heterogeneous firms, which differ in the quality of their products.
By working harder, CEOs can improve product quality (slowly) over time. The resulting competition is dynamic since CEOs of firms that are at early stages of product development must first catch-up with the leading edge CEOs before battling for leadership in the future. Our focus is on characterizing the way the dynamic interaction between competitors affects shareholders' optimal choice of CEO compensation contracts. Since industry structure ultimately results from this dynamic interaction between competitors, the model allows for the simultaneous determination of CEO pay and industry structure.
The key cross-sectional prediction of the model is an inverse relation between the magnitude of the performance-based component of optimal CEO contracts and firm competitive position within its industry. In particular, we predict that industry leaders have lower pay-performance sensitivity than laggards. To see the intuition for this result, consider that we depart from the common assumption of exogenous returns to CEO effort. In our model, shareholders value CEO effort since it increases expected future returns - i.e., it enables firms to grow. As firms climb the product quality-ladder over time, the value of growth opportunities falls. Consequently, leading edge CEOs are optimally given weaker incentives. By contrast, laggards with low quality products value growth opportunities the most and, thus, give stronger incentives to their CEOs.
A second important prediction of the model is an inverse relation between the magnitude of the performance-based component of optimal CEO pay and the degree of heterogeneity of industry structure. In particular, we predict that pay-performance sensitivity will be lower in more heterogeneous industries, i.e. industries characterized by a fringe and dominant firms. To see the intuition for this result contrast the following two scenarios (which result as equilibrium outcomes of our model): first, an asymmetric industry, where a dominant firm enjoys a local monopoly power; second, a symmetric industry, where rivals engage in a neck-and-neck battle for leadership. It is exactly in the latter scenario that CEO effort is most valuable, since by growing faster firms can pull ahead of their rivals. Consequently, optimal pay-performance sensitivity is higher in symmetric industries. Finally, since an equilibrium outcome of our model is that symmetric industries tend to exhibit higher rates of growth, we can use the model to derive a final dynamic prediction: pay-performance sensitivity is higher in growing industries.
We test these predictions empirically in a large panel of U.S. CEOs and other top executives between 1993 and 2005. We link two standard sources of data. Our compensation data is from ExecuComp and our firm data is from Compustat. We build indicators of firm position within its industry based on the ratio of firm sales to median industry sales. We define as leaders firms that are in the highest quartile of the distribution of the ratio, and laggards firms that are in the lowest quartile of the distribution of the ratio. Finally, we construct measures of industry turbulence and heterogeneity based on average job turnover within in industry and average distance of firm sales from median industry sales. These measures have been previously employed, although with a different motivation, respectively in job turnover (see Davis, Haltiwanger, and Schuh (1996)) and capital structure studies (see Titman (1984), MacKay and Phillips (2005)).
Consistent with our industry model of optimal CEO pay, we find strong evidence of an inverse relationship between pay-performance sensitivity and, (i) across industries, the degree of heterogeneity of industry structure; (ii) within industries, firm position with respect to its peers. These findings are robust to controlling for industry fixed effects and other variables, such as firm size and industry concentration, that have been found to affect CEO incentives in previous studies (respectively, Schaefer (1998) and Baker and Hall (2004) for firm size and Aggarwal and Samwick (1999) for concentration).
Importantly, the findings are robust to using measures of incentives based on either flow compensation or the CEO's portfolio price sensitivity (PPS). This is important since it is well-known that the bulk of incentives comes from appreciation or depreciation in the value of outstanding grants (Hall and Liebman (1998)). As it is standard in the literature, we define this measure as the change in the value of the CEO's stock and option portfolio due to a 1% increase in the price of the firm's common stock. Because details on the exercise prices and maturities of CEO options are not fully disclosed in annual statements, we follow Core and Guay's (2002) approximation method. Finally, we find reliable evidence supporting the finer prediction of the model that the effect of industry heterogeneity and turbulence on pay-performance sensitivity is stronger for industry laggards than for leaders.
While our study of the link between CEO incentives and industry structure within an explicit dynamic equilibrium setting is, to the best of our knowledge, novel to corporate finance, there are various important literatures related to our work. We detail our contribution to these literatures in turn. First, we establish an equilibrium rationale for high-powered incentives and show that dynamic interaction between competitors enriches the set of cross-sectional determinants of CEO pay. By doing so, we contribute to the large literature that seeks to understand why pay-performance sensitivity and, in general, incentive pay practices, differ across firms (Jensen and Murphy (1990), and Gibbons and Murphy (1990) are seminal contributions, Hall and Liebman (1998) is a more recent important study, and Murphy (1999) is a comprehensive survey). At the theoretical level, our study extends optimal contracting models to an industry equilibrium setting (see Bernardo and Chowdhry (2002), Maksimovic and Zechner (1991) and Gomes and Livdan (2004) for other dynamic industry equilibrium models in corporate finance), hence advancing our understanding of the role of equilibrium factors in shaping the contracting environment across firms.
Second, our study contributes to the literature on CEO incentives and product market competition (see Fershtman and Judd (1987), Sklivas (1987), Scharfstein (1988), Schmidt (1997), and Raith (2003) for theoretical contributions, and Aggarwal and Samwick (1999), and Kedia (2003) for empirical work) by bringing this class of models closer to the data. Theoretical work in this area has traditionally taken a static approach and empirical tests have been hampered by the notorious difficulty to find empirical proxies for the intensity of competition. The novelty of our approach is to use a structural model of dynamic competition among heterogeneous firms, which enables us to tightly link pay-performance sensitivity to a rich set of observable industry and firm characteristics, such as, for example, position within the industry.
Third, we contribute to the recent literature in industrial organization (e.g. Ericson and Pakes (1995), Pakes and McGuire (1994, 2001), Doraszelski and Satterthwaite (2003), and Besanko and Doraszelski (2004)) that uses dynamic oligopoly models to study the evolution of industry structure. This literature abstracts from corporate control issues and assumes no separation of ownership and control. In contrast, we explicitly model such separation of ownership and control, which enables us to study the effects of CEO incentives on the evolution of industry structure.
Finally, our paper joins a small, but growing literature in corporate finance that studies simulated panels based on structural models (Gomes and Livdan (2004), Hennessy and Whited (2005, 2006) and Strebulaev (2006)). The structural approach provides a useful solution to the endogeneity problems embedded within most empirical studies, which, as shown by Coles, Lemmon, and Meschke (2003), are difficult to correct by using the standard econometric methods. This literature assumes perfect competition among firms, thus ruling out the possibility of strategic interaction among firms. Our contribution to the literature is to allow for strategic interaction and pursue a computational approach to the Markov-perfect Nash industry equilibrium (see Maskin and Tirole (1988, 2000) for a theoretical treatment of this solution concept, and Grenadier (2002) and Novy-Marx (2007) for applications in finance).
The remainder of the paper is organized as follows. Section 2 outlines our industry equilibrium model of optimal CEO incentives. Section 3 develops the key cross-sectional implications of the model. Section 4 introduces our data and tests the model's predictions. Section 5 concludes. Proofs and details on the computation of industry equilibrium are contained in Appendix A and Appendix B, respectively.
2 An Industry Model of Optimal CEO Pay
To formalize the link between CEO incentive pay and industry characteristics we introduce an optimal compensation problem along the lines of Holmstrom (1979) and Holmstrom and Milgrom (1987) into a dynamic industry equilibrium model with differentiated Bertrand competition. This section outlines the model. To ease exposition, we consider an industry without entry and exit (Appendix B outlines the more general model with endogenous entry and exit we study through numeric simulations in Section 3).
The distinguishing feature of our approach with respect to the prior literature (see Murphy (1999) for a comprehensive survey) is that our framework is consistent with the empirical evidence of substantial firm heterogeneity across a number of characteristics such as size and growth, as well as inventive pay practices. In other words, our model is structural in that we can produce a well-defined cross-sectional distribution of firms and test whether it provides a reasonable description of the data.
Our theoretical approach is based on an industry equilibrium environment with heterogeneous firms, along the lines of Ericson and Pakes (1995) and Besanko and Doraszelski (2004). Our model is an infinite-horizon dynamic game in an industry that comprises two firms, indexed by
![]() Each firm consists of a risk-neutral shareholder and a risk-neutral CEO. The shareholder can influence firm profitability only through his choice of CEO compensation, as product
market and effort decisions are delegated to the CEO. The discount rate is
Each firm consists of a risk-neutral shareholder and a risk-neutral CEO. The shareholder can influence firm profitability only through his choice of CEO compensation, as product
market and effort decisions are delegated to the CEO. The discount rate is
![]()
2.0.0.1 Timing and Demand
We consider an empirically plausible source of firm heterogeneity: in our model firms differ in the quality of their products, indexed by
![]() and
and
![]() Technically,
Technically,
![]() represents the firm's individual state. The distribution of product qualities,
represents the firm's individual state. The distribution of product qualities,
![]() fully describes the industry at each point of time. A convenient feature of our setup is that firms' individual states lend themselves to a
particularly straightforward interpretation: whenever
fully describes the industry at each point of time. A convenient feature of our setup is that firms' individual states lend themselves to a
particularly straightforward interpretation: whenever
![]() firm
firm ![]() is the current industry leader and firm
is the current industry leader and firm
![]() is the laggard.
is the laggard.
The model's primitives, as well as the firm's own state,
![]() and the state of the industry,
and the state of the industry, ![]() are common knowledge. At the
beginning of each period, firms learn about the current state,
are common knowledge. At the
beginning of each period, firms learn about the current state, ![]() . Once the state is realized, shareholders choose executive compensation and, given compensation, managers choose effort,
. Once the state is realized, shareholders choose executive compensation and, given compensation, managers choose effort,
![]() and compete in the product market, with realized profits
and compete in the product market, with realized profits ![]()
Product market profits, ![]() are the outcome if a standard differentiated Bertrand duopoly. There are
are the outcome if a standard differentiated Bertrand duopoly. There are ![]() consumers. Consumer
consumers. Consumer ![]() who chooses good
who chooses good ![]() obtains utility
obtains utility
![]() where
where
![]() indexes product quality,
indexes product quality,
![]() is the mean utility of consumers choosing good
is the mean utility of consumers choosing good ![]()
![]() is its price, and
is its price, and
![]() is consumer
is consumer ![]() 's income. Each consumer makes the choice that
maximizes his utility. As shown in Pakes and McGuire (1994), the expected fraction of consumers who choose good
's income. Each consumer makes the choice that
maximizes his utility. As shown in Pakes and McGuire (1994), the expected fraction of consumers who choose good ![]()
![]() , is given by
, is given by
![]() Hence, with constant marginal cost,
Hence, with constant marginal cost, ![]() , firm
, firm ![]() profits are given by
profits are given by
![]() Every period, managers optimally choose the price,
Every period, managers optimally choose the price, ![]() , to maximize profits. Figure 1 summarizes the timing of events within each period.
, to maximize profits. Figure 1 summarizes the timing of events within each period.
2.0.0.2 CEOs and Effort
By working harder, CEOs in our model can improve the quality of their products. However, consistent with a well documented empirical property of product improvement (see, for example, Hall et al. (1986) and Lach and Schankerman (1988), and Cohen (1995) for a survey), CEOs in our model face substantial uncertainty over the outcome of their effort. Thus, we assume that product quality is stochastically increasing in CEO effort, in the sense that although higher effort increases the chances of success, it does not guarantee success.
Technically, the evolution of product quality for firm ![]() is governed by the following law of motion
is governed by the following law of motion
where
Denoting total CEO compensation by ![]() , CEO's preferences are given by a standard additively separable utility function
, CEO's preferences are given by a standard additively separable utility function
where
2.0.0.3 Shareholders and Incentive Pay
Following Grossman and Hart (1986) and Hart and Moore (1990) we assume that CEO effort is not contractible. Thus, the central problem for shareholders is to design a compensation package to motivate the CEO to exert effort. As is standard in the theoretical literature on executive compensation (e.g. Holmstrom and Milgrom (1987), Hellwig and Schmidt (2002)), in our baseline model we study linear CEO compensation contracts and later (Section 2.2) generalize the model to a broader set of realistic non-linear contracts such as, for example, stock options. Thus, we consider "share"-contracts that specify the CEO claim as a linear function of the stock-market value of the firm:
where
Given the probability distribution of ![]() , shareholders choose CEO compensation (through the board of directors, or the compensation committee) to maximize their expected profits net
of payments to the CEO subject to satisfying the CEO participation and incentive constraints. CEO compensation decisions are rational in the sense that shareholders correctly anticipate the ensuing product market equilibrium. Formally, shareholders' problem is given by:
, shareholders choose CEO compensation (through the board of directors, or the compensation committee) to maximize their expected profits net
of payments to the CEO subject to satisfying the CEO participation and incentive constraints. CEO compensation decisions are rational in the sense that shareholders correctly anticipate the ensuing product market equilibrium. Formally, shareholders' problem is given by:
There are several noteworthy features of our model. First, our chosen specification of CEO compensation structure is entirely standard in corporate finance since the seminal contribution of Holmstrom and Milgrom (1987). Further, it is worth emphasizing that although we study CEO compensation in an industry setting, we willingly abstract from issues of strategic provision of incentives such as studied in Fershtman and Judd (1987) and Sklivas (1987).
Second, our CEO compensation framework is in line with the recent optimal delegation literature that studies the optimal degree of delegation in organizations (see, for example, Dessein (2002)) and the optimal separation of ownership and control (see, for example, Burkart, Gromb and Panunzi (1997), Gomes and Novaes (2004)).
Finally, pay-performance sensitivity choices, ![]() measure the extent to which shareholders induce the CEO to exert effort. In our setting, this standard incentive provision problem
gains a dynamic component which is novel to the literature. More concretely, as it will become clear from our equilibrium analysis, in our model shareholders value CEO effort most when it allows them to gain a competitive hedge, i.e. to catch up with or pull ahead of their industry rivals.
measure the extent to which shareholders induce the CEO to exert effort. In our setting, this standard incentive provision problem
gains a dynamic component which is novel to the literature. More concretely, as it will become clear from our equilibrium analysis, in our model shareholders value CEO effort most when it allows them to gain a competitive hedge, i.e. to catch up with or pull ahead of their industry rivals.
2.1 Industry Equilibrium
At every point of time, industry structure is fully summarized by the current state of the industry, i.e. the distribution of product qualities,
![]() which essentially determine which firms are relatively ahead and which firms are relatively behind with respect to their rivals. The evolution of the state of
the industry is driven by CEO effort, given the stochastic transition rule (1) . We solve for equilibrium in two steps: first, for any given market structure,
which essentially determine which firms are relatively ahead and which firms are relatively behind with respect to their rivals. The evolution of the state of
the industry is driven by CEO effort, given the stochastic transition rule (1) . We solve for equilibrium in two steps: first, for any given market structure,
![]() we solve for the unique CEO effort and pricing choices,
we solve for the unique CEO effort and pricing choices,
![]() and
and
![]() and the resulting profits,
and the resulting profits,
![]() ; second, we employ the equilibrium profits obtained in the first step to solve for shareholders' optimal compensation choices and the resulting
equilibrium industry structure, i.e. the constellation of Markov Perfect equilibrium (MPE) long-run states of the industry.
; second, we employ the equilibrium profits obtained in the first step to solve for shareholders' optimal compensation choices and the resulting
equilibrium industry structure, i.e. the constellation of Markov Perfect equilibrium (MPE) long-run states of the industry.
We start with a characterization of the equilibrium CEO effort and pricing choices. In the product market stage subgame, the Bertrand-Nash equilibrium in CEO pricing strategies is characterized by the set of first-order conditions
![]()
![]() For any given state of the industry,
For any given state of the industry,
![]() equilibrium profits are
equilibrium profits are
![]() Given profits, CEOs choose effort to maximize their expected utility, i.e.
Given profits, CEOs choose effort to maximize their expected utility, i.e.
![]() It is straightforward to show that the set of first-order condition characterizing CEOs' choice of effort,
It is straightforward to show that the set of first-order condition characterizing CEOs' choice of effort,
![]() for any given compensation,
for any given compensation,
![]() is
is
![]()
Shareholders choose CEO compensation optimally based on (2) . Shareholders' maximization problem can be conveniently written in recursive form using the stock market value of the firm or value function,
![]() , which is defined by the following Bellman equation
, which is defined by the following Bellman equation
where
Equilibrium industry structure is determined jointly by shareholders' choice of CEO compensation and by CEO pricing and effort strategies. Our solution concept for industry structure is Markov perfect equilibrium (MPE). This is subgame perfect equilibrium in Markov strategies, i.e. strategies
that depend only on the "payoff-relevant" (Maskin and Tirole (1988, 1995)) state of the game,
![]() . Further, our model implies a symmetric profit function, i.e.,
. Further, our model implies a symmetric profit function, i.e.,
![]() and
and
![]() , we can restrict attention to symmetric MPE. This implies symmetry in value functions,
, we can restrict attention to symmetric MPE. This implies symmetry in value functions,
![]() and
and
![]() and in policy functions,
and in policy functions,
![]() and
and
![]() Formally, we define an MPE as follows
Formally, we define an MPE as follows
Definition 1 A vector of strategies,
![]() is an MPE if for any firm
is an MPE if for any firm ![]() , any state
, any state ![]() and any shareholder's compensation strategy
and any shareholder's compensation strategy
![]()
![]()
In words, an MPE is simply a vector of shareholder's compensation strategies such that each strategy is optimal given the rival's strategy, starting from any state. Appendix A shows our model satisfies the boundedness, continuity, and uniqueness requirements in Proposition 4 in Doraszelski and Satterthwaite (2003), which allows us to establish the following:
Theorem 1 There exists a unique symmetric MPE in pure CEO compensation strategies to the game satisfying (3) with the following properties:
where
![]()
Proof See Appendix A.
The left hand side of equation (5) represents the marginal cost of high-power incentives for shareholders: stronger reliance on incentive pay, i.e. higher pay-performance sensitivity,
![]() increases the cost of CEO effort and CEO outside option.
increases the cost of CEO effort and CEO outside option.
These costs, however, are traded-off against expected productivity gains, as represented by the right hand side of equation (5) . The key contribution of our dynamic model is to highlight a novel source of benefit of high-power incentives: shareholders incentivize CEOs to
induce them to pursue growth strategies, i.e. to increase future profitability,
![]() , through product improvements.
, through product improvements.
It is immediate from (5) and CEO first-order conditions that
Corollary 2
![]() the piece-rate,
the piece-rate,
![]() given by the optimal CEO contract is:
given by the optimal CEO contract is:
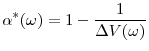 |
where
![]() and
and
![]()
There are several noteworthy features of this result. First, there is a feedback effect of industry structure, ![]() on optimal incentives. In other words, incentives depend both on own
and rival's competitive position. Second, we can take our model to the data since it allows us to sign the feedback effect. In particular, the model predicts that shareholders should rely more heavily on performance-based pay whenever growth opportunities are more valuable.
on optimal incentives. In other words, incentives depend both on own
and rival's competitive position. Second, we can take our model to the data since it allows us to sign the feedback effect. In particular, the model predicts that shareholders should rely more heavily on performance-based pay whenever growth opportunities are more valuable.
Second, and importantly, our model fully recognizes that the value of growth opportunities in turn depends on own and rival's CEO compensation strategies. Thus, in the next section we need to solve for
![]() and
and
![]() and
and
![]() jointly and analyze the link between
jointly and analyze the link between
![]() and the industry structure,
and the industry structure, ![]() that emerges in
equilibrium. This enables us to make testable predictions about which firm in which industries value growth the most, and, thus, link observable firm and industry characteristics to CEO incentives.
that emerges in
equilibrium. This enables us to make testable predictions about which firm in which industries value growth the most, and, thus, link observable firm and industry characteristics to CEO incentives.
Third, although
![]() depends on industry structure, realized CEO compensation is not indexed to the market and CEOs may end up being rewarded for luck. Thus, the well documented
evidence that this is actually the case in the data (see, for example, Bertrand and Mullainathan (2001)), while puzzling for standard agency models, is fully consistent with the optimal compensation contract that emerges from our model.
depends on industry structure, realized CEO compensation is not indexed to the market and CEOs may end up being rewarded for luck. Thus, the well documented
evidence that this is actually the case in the data (see, for example, Bertrand and Mullainathan (2001)), while puzzling for standard agency models, is fully consistent with the optimal compensation contract that emerges from our model.
2.2 Extensions
In the baseline model we have consider so far, incentive contracts are limited to stock grants. This section show that it is straightforward to generalize our framework to a broader set of observed incentive contracts, with a specific focus on stock options. To this end, we need to modify our baseline contract to specify the CEO's claim as:
where
3 Comparative Dynamics and Empirical Implications
In this section we develop several empirical implications of our model. To derive testable cross-sectional predictions about the performance-based component of optimal CEO compensation contracts, we solve numerically for industry equilibrium and study compensation and product qualities that emerge as joint outcomes of the equilibrium of the industry. We incorporate entry and exit into the basic model presented in Section 2 (details on the full mode with entry and exit are in Appendix B) so as to allow for an endogenous determination of industry structure.
Solving for equilibrium effort, compensation, pricing, and entry and exit functions numerically allows us to compute the Markov process that determines equilibrium industry structure, i.e. the distribution of firms over industry states in the long-run implied by (2.1). To compute the symmetric MPE, we use a variant of the iterative algorithm of Pakes and McGuire (1994) which we detail in Appendix B. We then use the equilibrium distributions to simulate the model for 10,000 periods. This allows us to derive a synthetic panel whose key unconditional moments we can match to our empirical sample in order to discipline our choice of parameter values.
Finally, we show that under reasonable parametric choices several novel cross-sectional relations between pay-performance sensitivity and the characteristics of firm competitive environment emerge as an equilibrium outcome of our industry. In particular, our model predicts an inverse relation between the magnitude of the performance-based component of CEO pay and, (i) across industries, the degree of heterogeneity of industry structure; (ii) within industries, firm position with respect to its peers.
3.1 Calibration
Since our data is at an annual frequency, we assume that a time period in the model corresponds to 1 year. The model primitives we need to parametrize are ![]()
![]()
![]()
![]() and
and ![]() i.e. the discount rate, demand, and technological opportunities. We choose
i.e. the discount rate, demand, and technological opportunities. We choose ![]() to match an annual interest rate of
to match an annual interest rate of ![]() . The remaining four parameters are chosen so that the model is able to
approximate the unconditional moments of our empirical panel, which essentially comprises S&P 1500 firms from ExecuComp (see next section for a detailed description of the data).
. The remaining four parameters are chosen so that the model is able to
approximate the unconditional moments of our empirical panel, which essentially comprises S&P 1500 firms from ExecuComp (see next section for a detailed description of the data).
Demand determines the profit function,
![]() We choose the market size parameter,
We choose the market size parameter, ![]() so as to have on average
six active firms, since six is the median number of firms per industry (at the four-digit SIC level) in our empirical panel To allow for entry, we set the maximum number of active firms in the industry,
so as to have on average
six active firms, since six is the median number of firms per industry (at the four-digit SIC level) in our empirical panel To allow for entry, we set the maximum number of active firms in the industry, ![]() to seven.2
to seven.2
Technological opportunities are fully described by the properties of the stochastic process that governs the law of motion between states, ![]() together with the scrap value,
together with the scrap value,
![]() and the sunk entry cost,
and the sunk entry cost, ![]() We choose the transition probability
parameter,
We choose the transition probability
parameter, ![]() to match the unconditional average of industry concentration in the empirical panel. Sunk entry cost and scrap value are chosen to match median firm life-cycle (age) and
its standard deviation in the empirical panel.
to match the unconditional average of industry concentration in the empirical panel. Sunk entry cost and scrap value are chosen to match median firm life-cycle (age) and
its standard deviation in the empirical panel.
Table 1 contains a summary of parameter values and compares the key summary statistics generated by the stationary equilibrium of the model, i.e. our artificial panel, with those of our empirical panel.
3.2 Cross-Sectional Results
Our model's most direct predictions are about the link between optimal CEO incentive pay, ![]() and industry structure. Empirically
and industry structure. Empirically ![]() measures dollar-dollar sensitivity of CEO pay to firm performance in the sense of changes of dollar pay for changes in dollar firm value, a measure commonly employed in the empirical literature at least since Jensen and Murphy (1990).
Thus, the predictions we derive in this section focus on dollar-dollar sensitivity. Importantly, our model makes predictions also for an alternative measure of sensitivity, dollar-log, which looks at changes of dollar pay for percentage changes in firm value (Hall and Liebman (1998)). At the end of
the section, we discuss preliminary results involving this alternative empirical measure of sensitivity.
measures dollar-dollar sensitivity of CEO pay to firm performance in the sense of changes of dollar pay for changes in dollar firm value, a measure commonly employed in the empirical literature at least since Jensen and Murphy (1990).
Thus, the predictions we derive in this section focus on dollar-dollar sensitivity. Importantly, our model makes predictions also for an alternative measure of sensitivity, dollar-log, which looks at changes of dollar pay for percentage changes in firm value (Hall and Liebman (1998)). At the end of
the section, we discuss preliminary results involving this alternative empirical measure of sensitivity.
Our first result is about variation in pay-performance sensitivity across-firms. It can be summarized as follows:
Result 1 (Position Effect) Industry leaders have lower pay-performance sensitivity than laggards, i.e. in all asymmetric states such that
![]() then
then
![]() with
with ![]() .
.
Panel A of Figure 2 illustrates the result by plotting, for the case when there are two firms active in the industry, the optimal pay-performance sensitivity implied by the model,
![]() as a function of own
as a function of own
![]() and rival
and rival
![]() states. Our model implies strong variation in sensitivity across different firms. In particular, moving upward from state 1 to state 19 for any given state of the rival
(States S1-S19) corresponds to upward movements in the product-quality ladder. Thus, in our model entrants produce at relatively low qualities and over time can climb the quality-ladder and improve quality through CEO effort.
states. Our model implies strong variation in sensitivity across different firms. In particular, moving upward from state 1 to state 19 for any given state of the rival
(States S1-S19) corresponds to upward movements in the product-quality ladder. Thus, in our model entrants produce at relatively low qualities and over time can climb the quality-ladder and improve quality through CEO effort.
It is apparent from Panel A of Figure 2 that the optimal pay-performance sensitivity,
![]() , is a decreasing function of own state. However, the key prediction of our model is that not only own, but also rivals' states matter. In fact,
pay-performance sensitivities are relatively higher for states above the diagonal, i.e. for laggards who produce lower quality products than their rivals, compared to states below the diagonal, i.e. for leaders who produce higher quality products than their rivals.
, is a decreasing function of own state. However, the key prediction of our model is that not only own, but also rivals' states matter. In fact,
pay-performance sensitivities are relatively higher for states above the diagonal, i.e. for laggards who produce lower quality products than their rivals, compared to states below the diagonal, i.e. for leaders who produce higher quality products than their rivals.
Panel B of Figure 2 provides further insight into the result by plotting the stock market value of the firm (left panel) and the equilibrium structure of the industry (right panel) implied by the model. Recall form Corollary 2 that, loosely speaking, optimal incentives in our model reflect the slope of the value of growth opportunities, i.e. of the maximized net present value of profits. Intuitively, incentives are high when the value of the growth opportunity associated with product improvement is high.
Thus, the importance of Result 1 is that it allows us to identify laggards and close neck-to-neck competitors as exactly the firms that value growth strategies the most and, thus, optimally choose to give stronger incentives to their CEOs. Since in industry equilibrium relatively asymmetric states do emerge, in a cross-section of firms we expect to see higher pay-performance sensitivity among laggards vis a vis leaders.
Our model also has testable implications for the variation of pay-performance sensitivity across industries. We derive these implications by performing comparative dynamics exercises, i.e. by computing industry equilibria under different values of key parameters. In particular, we predict that:
Result 2 (Symmetry and Growth Effects) Homogenous industries have higher pay-performance sensitivity than heterogeneous industries. Growth industries have higher pay-performance sensitivity than declining industries.
Panel A of Table 1.2 documents this important equilibrium implication of our model by reporting the result of a simple comparative dynamics exercise. The idea of the exercise is to vary the parameter ![]() which measures the likelihood of adverse industry-wide shocks: higher values of
which measures the likelihood of adverse industry-wide shocks: higher values of ![]() correspond to relatively harsher industry conditions, i.e. to industries where
adverse shocks are more likely. The frequency distribution of symmetric industry states and the growth rate of industry output for different values of
correspond to relatively harsher industry conditions, i.e. to industries where
adverse shocks are more likely. The frequency distribution of symmetric industry states and the growth rate of industry output for different values of ![]() reported in Panel A of Table
1.2 show that in our model these industries tend to be relatively more heterogeneous in the sense of having the mass of the probability distribution of equilibrium industry states concentrated around states where firms are neck-to-neck competitors. In addition, these industries tend to be more fast
gorwing. The last column of Panel A shows that there is a negative relation between industry heterogeneity and CEO incentives since industries that in equilibrium are more heterogeneous tend to have lower pay-performance sensitivity. In addition, there is a positive relation between industry growth
and CEO incentives since industries that in equilibrium grow at a faster rate tend to have higher pay-performance sensitivity.
reported in Panel A of Table
1.2 show that in our model these industries tend to be relatively more heterogeneous in the sense of having the mass of the probability distribution of equilibrium industry states concentrated around states where firms are neck-to-neck competitors. In addition, these industries tend to be more fast
gorwing. The last column of Panel A shows that there is a negative relation between industry heterogeneity and CEO incentives since industries that in equilibrium are more heterogeneous tend to have lower pay-performance sensitivity. In addition, there is a positive relation between industry growth
and CEO incentives since industries that in equilibrium grow at a faster rate tend to have higher pay-performance sensitivity.
The intuition for this result highlights the central mechanism at work in our model, which is in essence a selection effect. Harsher industry conditions intensify competition particularly among neck-to-neck rivals since they make exit more likely for firms that fall behind. As shown in Panel B of Figure 3, the selection effect is that, in equilibrium, heightened competition among close competitors makes heterogeneous states - i.e., states away from the diagonal - more likely. Since, as shown in Panel A of Figure 3, in such states optimal incentives are lower on average, our result obtains.
An analogous selection effect is at play for the next prediction:
Result 3 (Turbulence Effect) High turnover industries have higher pay-performance sensitivity than low turnover industries.
Panel B of Table 1.2 documents the result by again reporting the result of a simple comparative dynamics exercise. The parameter we now vary is the sunk entry cost, ![]() ,3 and higher values of
,3 and higher values of ![]() correspond to relatively less
turbulent industries, i.e. to industries where entry is more costly and, thus, in equilibrium we observe lower turnover rates. The last column of Panel B shows that there is a positive relation between turnover and CEO incentives since industries that in equilibrium display higher turnover rates
tend to have higher pay-performance sensitivity.
correspond to relatively less
turbulent industries, i.e. to industries where entry is more costly and, thus, in equilibrium we observe lower turnover rates. The last column of Panel B shows that there is a positive relation between turnover and CEO incentives since industries that in equilibrium display higher turnover rates
tend to have higher pay-performance sensitivity.
The intuition for this result again highlights the central selection effect at work in our model. If entry is more costly, in equilibrium entry only happens if also incumbents are at relatively low levels of their quality-ladder. Thus, higher entry costs make competition among neck-to-neck rivals more intense. The selection effect is now that, in equilibrium, there is tougher competition among close competitors, which makes heterogeneous states - i.e., states away from the diagonal - more likely. Since, as shown in Panel A of Figure 3, in such states optimal incentives are lower on average, our result obtains.
So far, we have derived predictions about the variation in CEO incentives either across firms (Result 1) or across industries (Results 2-3). Our model also makes a finer conditional prediction about the firms among which we expect our industry effect to be stronger:
Result 4 (Interaction Effects) Symmetry and turbulence effects are stronger for industry laggards than for leaders.
Table 1.3 reports summary statistics for this implication of our model by essentially replicating the simple comparative dynamics exercises in Table 1.2 by subsamples -i.e., looking at averages conditional on firms being industry leaders or laggards. Again, we vary
the parameter the likelihood of adverse industry-wide shocks (![]() , Panel A) and the sunk entry cost (
, Panel A) and the sunk entry cost (![]() Panel B) In both panels, the last column shows that CEO incentives vary with industry conditions both for leaders and laggards. However, the bulk of variation is among laggards.
Panel B) In both panels, the last column shows that CEO incentives vary with industry conditions both for leaders and laggards. However, the bulk of variation is among laggards.
Again, the selection effect is at work here. Changes in industry structure - i.e. shifts in the mass of the equilibrium probability distribution of industry states clearly affect both leaders and laggards. However, as Panel A of Figure 2 shows, optimal incentives as a function of the state,
![]() , are much steeper for laggards than for leaders. Thus, any change in industry states is likely to have a larger quantitative effect on the pay-performance
sensitivity of laggards, as our result states.
, are much steeper for laggards than for leaders. Thus, any change in industry states is likely to have a larger quantitative effect on the pay-performance
sensitivity of laggards, as our result states.
4 Data and Empirical Results
In this section we implement empirical tests of our model. In particular, after describing our panel data set, we specify an empirical model relating pay-performance sensitivity to the firm and industry characteristics that, based on our model, we expect to be important determinants of incentive pay. We experiment with a number of specifications and include a variety of controls for other effects that are recognized in the empirical literature (see Murphy (1999) for a comprehensive survey). In a large panel of U.S. CEOs and other top executives between 1993 and 2004, we find strong support for our model.
4.1 Data
We combine data from two separate sources. Our data on CEO and other top executive compensation are drawn from the ExecuComp database. Our data on product markets are mainly drawn from the Censuses of Manufacturers conducted by the Commerce department. This section describes each of these data sources in turn.
4.1.1 Compensation Data
Our executive compensation data is from the ExecuComp dataset compiled by Standard and Poors. This dataset includes data on total compensation for the top five executives (ranked annually by salary and bonus) at each of the firms in the S&P 500, S&P Midcap 400, and S&P SmallCap 600. In addition to measures of short-term compensation such as salary and bonus, ExecuComp contains data on components of long-term compensation such as long-term incentive plans, restricted stock, and stock appreciation rights. We use available data from 1993 to 2004. Relative to the datasets used in the studies by Jensen and Murphy (1990) and Gibbons and Murphy (1990), the advantages of the ExecuComp data are that its sample encompasses the largest 1500 firms each year and is not restricted to just chief executive officers.
Table 2 presents descriptive statistics on the components of executive compensation for all executives in the ExecuComp sample between 1993 and 2004 for whom complete data on total compensation is available. The top panel of the table pertains to the 8,320 executives who are identified as the chief executive officer of the firm. The bottom panel describes the other 38,544 executives in the sample. Our measure of total compensation can be divided into short-term compensation and long-term compensation as standard in the literature (see, for example, Gibbons and Murphy (1990) and Aggarwal and Samwick (1999)). Short-term compensation consists of salary, bonus, and other annual payments (e.g., gross-ups for tax liabilities, perquisites, preferential discounts on stock purchases). Annual short-term compensation averages $1,217,000 for the CEOs and $490,000 for the Non-CEOs. Long-term compensation includes the value of restricted stock granted, stock options granted, payouts from long-term incentive plans, and all other compensation (e.g., contributions to benefit plans, severance payments). The sample averages of long-term compensation are $3,097,000 for CEOs and $922,000 for Non-CEOs. Stock options granted are by far the most important component of long-term compensation, accounting for a sample average value of $2,508,000 for CEOs and $727,000 for Non-CEOs.
In additional to these measures of flow compensation, we also consider a measure of incentives based on the CEO's portfolio price sensitivity (PPS), in order to take into account the well-known argument that the bulk of incentives comes from appreciation or depreciation in the value of outstanding grants (Hall and Liebman (1998)). As it is standard in the literature, we define this measure as the change in the value of the CEO's stock and option portfolio due to a 1% increase in the price of the firm's common stock. Because details on the exercise prices and maturities of CEO options are not fully disclosed in annual statements, we follow Core and Guay's (2002) approximation method. Details of the computation are in Appendix C. As shown in Table 2, the median CEO PPS in our sample is about 1.4, while the average PPS is 4.2, suggesting that the measure has a significant right skew.
4.1.2 Firm Data
We include in our panel controls for firm characteristics whose relationship wit pay-performance sensitivity has been documented in previous studies. Firm characteristics are from the Compustat. Outliers are removed by winsorizing the extreme observations in the 1% left or right tail of the
distribution. We measure capital as property, plants, and equipment (item 8). Tobin's Q is the ratio of market value of assets to book value of assets. Market value of assets is defined as total assets (item6) plus market equity minus book equity. Market equity is defined as common shares
outstanding (item 25) times fiscal-year closing price (item 199). Book equity is calculated as stockholders equity (item 216) [or the first available of common equity (item 60) plus preferred stock par value (item 130) or total assets (item 6) minus total liabilities (item 181)] minus preferred
stock liquidating value (item 10) [or the first available of redemption value (item 56) or par value (item 130)] plus balance sheet deferred taxes and investment tax credit (item 35) when available minus post retirement assets (item 336) when available. Book value of assets is total assets (item
6). We measure return on equity (ROE) as the ratio of earnings to average equity for the prior fiscal year (item 20/(item 60+ item 60![]() )).
)).
4.1.3 Industry Data
We use several sources for industry data. For comparability with previous studies We limit our sample to the manufacturing sector, which contains twenty 2-digit standard industrial classification (SIC) codes from 20 to 39, and, within these 2-digit SICs, 458 separate four-digit SICs (ranging from 2001 to 3999). Financing firms (SICs 6000-6999), and regulated utilities (SICs 4900-4999) are excluded. We use four-digit SIC classifications to define industry membership. In unreported tables we replicate our findings at the three-digit level with no qualitatively different results.
To proxy for industry turbulence and firm heterogeneity within an industry we use average job turnover within in industry and average distance of firms from median industry sales. These measures have been previously employed, although with a different motivation, respectively in job turnover (see Davis, Haltiwanger, and Schuh (1996)) and capital structure studies (see Titman (1984), MacKay and Phillips (2005)). This measure allows us to proxy for the intensity of managerial effort directed toward product improvement.
To control for standard measures of product market competition used in previous studies, we include in our panel concentration ratios from the Census of Manufactures, conducted by the Bureau of the Census as part of the quinquennial Economic Censuses. Our measure of concentration is the ratio of the sales of the top four firms in the industry to total industry sales.
4.2 Empirical Specification and Results
To test the empirical predictions of our industry equilibrium model of CEO pay, we extend the standard econometric framework that estimates the sensitivity of pay to performance (see Murphy (1999) for a careful description of this approach) by allowing pay-performance sensitivity to vary in proportion to our measures of product differentiation. Accordingly, for flow measures of compensation we estimate the following equation:
where the executive ![]() works at firm
works at firm ![]() in year
in year ![]() . The dependent variable,
. The dependent variable, ![]() is dollar compensation, and the independent variables are dollar firm
performance,
is dollar compensation, and the independent variables are dollar firm
performance,
![]() alone and interacted with our measures of competitive position (Result 1), industry symmetry (Result 2) and turbulence (Result 3),
alone and interacted with our measures of competitive position (Result 1), industry symmetry (Result 2) and turbulence (Result 3), ![]() . We also include as controls
. We also include as controls ![]() itself and other variables, such as firm size and industry concentration, that control
for effects found in previous studies (respectively, Schaefer (1998) and Baker and Hall (2004) for firm size and Aggarwal and Samwick (1999) for concentration).
itself and other variables, such as firm size and industry concentration, that control
for effects found in previous studies (respectively, Schaefer (1998) and Baker and Hall (2004) for firm size and Aggarwal and Samwick (1999) for concentration).
We follow Jensen and Murphy (1990) and use as our measure of firm performance,
![]() the total dollar returns to shareholders including capital gains and dividends but net of inflation on their holdings at the beginning of the period. We emphasize that this choice
is motivated by the fact that dollar-dollar sensitivity is the relevant measure with respect to which our empirical predictions where derived.
the total dollar returns to shareholders including capital gains and dividends but net of inflation on their holdings at the beginning of the period. We emphasize that this choice
is motivated by the fact that dollar-dollar sensitivity is the relevant measure with respect to which our empirical predictions where derived.
Finally, we include year- and 2-digit SIC industry-fixed effects. The inclusion of these industry fixed-effect ensures that it is not the variation in the average pay-performance sensitivities between 2-digit industry groups but the variation in the pay-performance sensitivity within those
groups that identifies the estimated coefficient. Including the industry effects also controls for any other factor such as a macroeconomic shock that varies across broad industry groups but not within the narrow industries that comprise them. The null hypothesis is that
![]() , the coefficient on the interaction of performance and product differentiation, is equal to zero.
, the coefficient on the interaction of performance and product differentiation, is equal to zero.
We also report results using the stock measure of compensation, CEO's portfolio price sensitivity (PPS), in which case the above specification simplifies to the following:
![]()
4.2.1 Regression Results
Figure 4 shows graphically that the data lines up with comfortably with our Result 1. In particular, we estimate equation (6) with total CEO compensation (Panel A) and CEO wealth deltas (Panel B) as dependent variables separately within subsample splits based on a measure of
firm position within its industry. We measure competitive position as the ratio of the firm sales to industry median sales in the beginning of the year. Consistent with our position effect, as we move toward higher competitive position deciles - i.e., for firms that are relatively ahead in their
industry - the estimates of pay-performance sensitivity fall by an order of magnitude. These results are confirmed by Table 3, where we estimate equation (6) using competitive position as our key explanatory variable, ![]() Clearly, firms that are relatively more ahead in their industry tend to have lower equity incentives, a result which is robust to measuring incentives based on either flow comepnsation or CEO's portfolio price sensitivity (PPS).
Clearly, firms that are relatively more ahead in their industry tend to have lower equity incentives, a result which is robust to measuring incentives based on either flow comepnsation or CEO's portfolio price sensitivity (PPS).
4.2.1.1 Symmetry Effect and Interaction
To test Result 2, the left panel of Table 4 presents the estimates of equation (6) with total compensation (Panel A) and CEO wealth deltas (Panel B) as dependent variables and a measure of industry-wide heterogeneity built along the lines of MacKay and Phillips (2005). In particular, since our model links the degree of within industry firm heterogeneity to pay-performance sensitivity, we construct a measure of industry "Symmetry," defined as the average proximity of firm sales to median industry sales. Technically, our Symmetry variable is the inverse of the average distance of firm sales from industry median sales in the beginning of the year. Based on Result 2, we predict a positive relation between Symmetry and pay-performance sensitivity.
In all specifications, executive compensation is denominated in thousands and firm performance is denominated in millions of dollars. We report results for three baseline regressions: (1) with no additional controls, then (2) including industry-fixed effects, and finally (3) including industry-fixed effects as well as controls. In all specifications, consistent with Result 2, we find a positive and highly significant coefficient on the interaction of industry homogeneity and firm performance: industries with more homogeneous firm sale distribution have higher pay-performance sensitivity than industries with a more skewed firm sale distribution. Columns (2)-(3) of Table 4 show that the result is robust to adding fixed effects and controlling for firm size and industry concentration.
To test Result 4, we re-estimate equation (6) with total compensation as the dependent variable and the sample now split based on firm position within its industry. Again, we measure firm competitive position as the ratio of the firm sales to industry median sales in the beginning of the year. We define as Leaders the firms that are in the highest quartile of the distribution of the ratio, and Laggards the firms that are in the lowest quartile of the distribution of the ratio.
The center panel of Table 4 reports the results. Consistent with Result 4, the effect of industry symmetry on pay-performance sensitivity depends on firm competitive position within its (4-digit SIC) industry. In fact, Column 5 shows that for industry laggards, total executive compensation increases by up to about 31 cents for every thousand dollars of incremental shareholder wealth per year in heterogeneous industries - i.e., industries in which our Symmetry measure is close to zero. Column 4 contrasts this estimate with the case of industry leaders: now the pay-performance sensitivity is about 23 cents per thousand. Again, consistent with Result 4, the Symmetry effect is much stronger for laggards than for leaders as pay-performance sensitivity depends on Symmetry for laggards, but not for leaders.
The right panel of Table 4 presents the estimates of equation (6) using short-term compensation as the dependent variable. The results are qualitatively very similar to those in the left panel, although magnitudes are much smaller. This is to be expected given the well-documented fact that short-term incentives, such as, for example, bonuses, have much lower power than long-term incentives.
In Table 4 we have constrained pay-performance sensitivity to be equal for CEOs and non-CEOs. In Table 5 we relax this arguably questionable assumption and re-estimate the same set of regressions based on equation (6) restricting the sample to only CEOs. Panel A reports results for flow measures of comepnsation, while Panel B reports results for CEO's portfolio price sensitivity (PPS). As expected, the magnitude of all pay-performance sensitivity coefficients is much larger, which is consistent with the fact that CEOs bear more responsibility for decisions that affect profits. Qualitatively, however, our results are unchanged. Finally, the results are robust to measuring incentives based on either flow comepnsation or CEO's portfolio price sensitivity (PPS).
4.2.1.2 Turbulence Effect and Interaction
To test Result 3, the left panel of Table 6 presents the estimates of equation (6) with total compensation as dependent variables and a measure of industry turbulence, gross job turnover, based on Davis, Haltiwanger, and Schuh (1996). In particular, we measure turbulence as industry gross job turnover. Based on Result 3, we predict a positive relation between turnover and pay-performance sensitivity.
Again, executive compensation is denominated in thousands, firm performance is denominated in millions of dollars, and we report results for three baseline regressions: (1) with no additional controls, then (2) including industry-fixed effects, and finally (3) including industry-fixed effects as well as controls. In all specifications, consistent with Result 3, we find a positive and highly significant coefficient on the interaction of turnover and firm performance. Columns (2)-(3) of Table 6 show that the result is robust to adding fixed effects and controlling for firm size and industry concentration.
The center panel of Table 6 reports the results of our test of Result 4. As we did for Symmetry, we re-estimate equation (6) with total compensation as the dependent variable and the sample now split based on firm position within its industry. Again, we measure firm competitive position as the ratio of the firm sales to industry median sales in the beginning of the year. We define as Leaders the firms that are in the highest quartile of the distribution of the ratio, and Laggards the firms that are in the lowest quartile of the distribution of the ratio.
Consistent with Result 4, the effect of industry turnover on pay-performance sensitivity depends on firm competitive position within its (4-digit SIC) industry. In fact, Column 5 shows that for industry laggards, total executive compensation increases by up to about 39 cents for every thousand dollars of incremental shareholder wealth per year in heterogeneous industries - i.e., industries in which our Turnover measure is close to zero. Column 4 contrasts this estimate with the case of industry leaders: now the pay-performance sensitivity is about 22 cents per thousand. Again, consistent with Result 4, the Turnover effect is much stronger for laggards than for leaders as pay-performance sensitivity depends strongly on Turnover for laggards, but only weakly for leaders.
The right panel of Table 6 presents the estimates of equation (6) using short-term compensation as the dependent variable. The results are qualitatively very similar to those in the left panel, although magnitudes are much smaller. This is to be expected given the well-documented fact that short-term incentives, such as, for example, bonuses, have much lower power than long-term incentives.
Table 7 shows that when we estimate the same set of regressions only for CEOs, the results are qualitatively the same as in the full sample of executives, with larger magnitudes on all the coefficients.
4.2.1.3 Industry Dynamics Effect and Interaction
Table 8 presents the estimates of equation (6) with total compensation (Panel A) and CEO wealth deltas (Panel B) as dependent variables and a measure of industry growth as the main explanatory variable. In particular, we measure growh as average change in industry output in the sample period. Based on Result 2, we predict a positive relation between industry growth and pay-performance sensitivity.
Again, executive compensation is denominated in thousands, firm performance is denominated in millions of dollars, and we report results for three baseline regressions: (1) with no additional controls, then (2) including industry-fixed effects, and finally (3) including industry-fixed effects as well as controls. In all specifications, consistent with Result 2, we find a positive and highly significant coefficient on the interaction of growth and firm performance. In addition, we have a reliably negative coefficient on the interaction of a dummy for industry decline. This dummy takes the value of one for industries in the bottom quartile of output growth. Columns (2)-(3) of Table 8 show that the result is robust to adding fixed effects and controlling for firm size and industry concentration.
Panel B of Table 8 reports results for CEO's portfolio price sensitivity (PPS). Clearly, the results are robust to measuring incentives based on either flow comepnsation or CEO's portfolio price sensitivity (PPS).
4.2.1.4 Robustness
Throughout the paper, we have limited our measure of total compensation to the annual flow of resources that the shareholders could have kept for themselves had they not used it to compensate the executive. In practice, an executive also receives incentives from the effect of her actions on the value of her stock holdings. If an executive owns stock in her firm, then the total increment in her wealth due to the performance of her firm will include not only the extra pay she receives as part of the pay-performance sensitivity built into her compensation but the appreciation on her personal stock holdings. Recognizing this, the shareholders of her firm will incorporate a lower pay-performance sensitivity into her contract. Hence, the optimal compensation contract becomes a function of both industry structure and executives' stock holdings. Conditional on a particular allocation of the executives personal wealth, however, the relationship between industry structure and pay-performance sensitivity is unchanged.
To check for robustness of our results to the incentives provided by inside ownership, in Table 9 we control for the executives holdings of her firm. Column 1 reports estimates of equation (6) using total compensation as the dependent variable. Although the estimated coefficient of insider ownership is negative and significant, all our previous findings stand.
5 Conclusion
This paper develops an industry equilibrium model of optimal CEO incentives. We tested the key predictions of the model empirically in a large panel of U.S. executives between 1993 and 2004 and, consistent with the model, found strong evidence of an inverse relationship between pay-performance sensitivity and, (i) across industries, the degree of heterogeneity of industry structure; (ii) within industries, firm position with respect to its peers. In particular, we found strong evidence that firm competitive position is an important determinant of CEO incentives, in that industry leaders have reliably weaker pay-performance sensitivity than laggards.
Agency models of CEO pay emphasize the trade-off between incentives and insurance but are silent on the sources of value of CEO effort, thus leaving the important question of the link between economic fundamentals and CEO incentives essentially unanswered. Our model and empirical tests emphasize the importance of economic fundamentals for CEO incentives. Moreover, they provide a novel product market rationale for the otherwise puzzling infrequent use of high-powered incentives.
Appendix A. Proofs
Proof of Theorem (2.1) We first prove existence of a symmetric, pure strategy MPE by verifying that our model (3) satisfies the conditions of Proposition 4 in Doraszelski and Satterthwaite (2005) (DS).
Proposition 1 [Doraszelski and Satterthwaite (2005)] Assume that
- (i) The state space is finite, i.e.
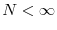 and
and
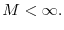 (ii) Profits are bounded, i.e. there exists
(ii) Profits are bounded, i.e. there exists
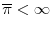 s.t.
s.t.
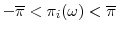 for all
for all 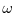 and all
and all 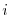 . (iii) Investments is bounded, i.e.,
. (iii) Investments is bounded, i.e.,
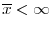 and
and
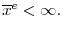 (iv) The distributions of scrap values
(iv) The distributions of scrap values
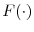 and setup costs
and setup costs
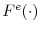 have continuous and positive densities and bounded supports, i.e. there exist
have continuous and positive densities and bounded supports, i.e. there exist
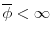 and
and
 s.t. the supports of
s.t. the supports of
 and
and
 are contained in the interval
are contained in the interval
![[ -\overline{\phi },\overline{\phi }]](img160.gif) and
and
![[ -\overline{\phi }^{e},\overline{\phi }^{e}] ,](img161.gif) respectively. (v) Firms discount future payoffs, i.e.,
respectively. (v) Firms discount future payoffs, i.e.,
-
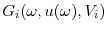 is a continuous function of
is a continuous function of
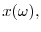
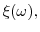 and
and 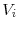 for all
for all  and all
and all  where
where
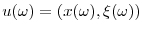 is the vector of firms' effort and cutoff entry/exit strategies.
is the vector of firms' effort and cutoff entry/exit strategies. - Transition function
 is UIC admissible and
is UIC admissible and
 is finite and larger than
is finite and larger than
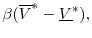 with
with
![V_{i}\in [ \underline{V}^{\ast },% \overline{V}^{\ast }] ^{\vert S\vert }.](img169.gif)
- The local income functions are symmetric and exchangeable, i.e.
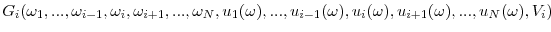
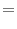
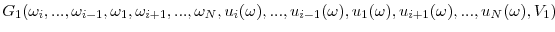
for all symmetric functions and all and
and
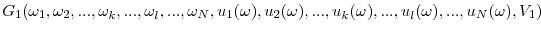
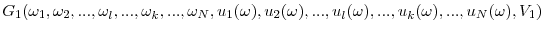
for all exchangeable functions, and all
and all 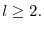
Under assumptions ![]() and 3, an equilibrium exists in cutoff entry/exit and
pure investment strategies. If, in addition assumption 4 holds, then a symmetric and anonymous equilibrium exists in cutoff entry/exit and pure investment strategies.
and 3, an equilibrium exists in cutoff entry/exit and
pure investment strategies. If, in addition assumption 4 holds, then a symmetric and anonymous equilibrium exists in cutoff entry/exit and pure investment strategies.
Lemma 1 There exists a symmetric MPE in pure strategies to the game that satisfies (4) - (5).
Proof. It suffices to verify that the game satisfies assumptions 1-4 in Prop A-0. Note that for the basic model in Section 2 without entry and exit we only need to provide arguments for existence and uniqueness of compensation strategies.
- Our model has
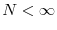 firms with states
firms with states
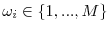 and
and
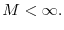 Firms discount future payoffs using
Firms discount future payoffs using
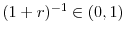 , and we assume that compensation expenditures are bounded (
, and we assume that compensation expenditures are bounded (
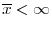 ). Boundedness of cost function (assumed functional form for costs implies that
). Boundedness of cost function (assumed functional form for costs implies that
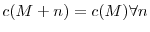 ) implies that the profit function
) implies that the profit function
 is bounded. These boundedness conditions satisfy assumption 1 in (DS).
is bounded. These boundedness conditions satisfy assumption 1 in (DS). 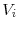 enters
enters
 only through the expected value of firm
only through the expected value of firm  's future cash flows,
ensuring continuity of
's future cash flows,
ensuring continuity of
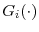 in
in 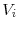 for all
for all  and all
and all 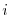 . Moreover, current profit is additively separable from investment and the transition probability function
. Moreover, current profit is additively separable from investment and the transition probability function
 is continuous, which implies that
is continuous, which implies that
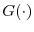 is a continuous function of
is a continuous function of
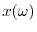 for all
for all  and
and  Continuity of
Continuity of
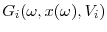 in
in
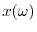 and
and 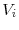 satisfies assumption 2 in (DS).
satisfies assumption 2 in (DS).- Our transition probability function
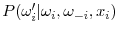 satisfies the unique investment choice (UIC) admissibility condition in (DS). We assume, in addition, that
satisfies the unique investment choice (UIC) admissibility condition in (DS). We assume, in addition, that
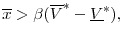 with
with
![V_{i}\in [ \underline{V}^{\ast },\overline{V}^{\ast }] ^{\vert S\vert },](img192.gif) which ensures that assumption 4 in (DS) holds.
which ensures that assumption 4 in (DS) holds. - Our model of product market competition gives rise to symmetric profit functions, i.e.
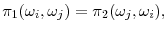 which, together with the fact that
which, together with the fact that
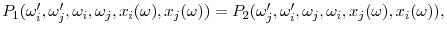 ensures that the local income functions
ensures that the local income functions
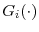 are symmetric and exchangeable, and, thus, satisfy assumption 5 in
(DS).
are symmetric and exchangeable, and, thus, satisfy assumption 5 in
(DS).
Appendix B. Details of Computation
This appendix describes the approach used to solve the full model with entry and exit numerically once the parameters of the model are set. Every period there are ![]() heterogeneous
firms active and
heterogeneous
firms active and ![]() potential entrants. To enter from state
potential entrants. To enter from state
![]() shareholders must pay a random sunk cost of
shareholders must pay a random sunk cost of ![]() drawn from a
distribution
drawn from a
distribution
![]() independently and identically distributed across firms and periods with
independently and identically distributed across firms and periods with
![]() . Setup costs are private information. We let
. Setup costs are private information. We let
![]() indicate stay out or entry respectively. If a string of unsuccessful outcomes occurs, shareholders may find it optimal to exit and
liquidate the firm, in which case they get a sell-off value of
indicate stay out or entry respectively. If a string of unsuccessful outcomes occurs, shareholders may find it optimal to exit and
liquidate the firm, in which case they get a sell-off value of ![]() dollars, exit in the next period and never re-enter again. Following Doraszelski and Satterthwaite (2003), we assume
that scrap values are randomly drawn from a distribution
dollars, exit in the next period and never re-enter again. Following Doraszelski and Satterthwaite (2003), we assume
that scrap values are randomly drawn from a distribution
![]() with
with
![]() independently and identically distributed across firms and periods, and privately observed prior to making exit and effort decisions. We let
independently and identically distributed across firms and periods, and privately observed prior to making exit and effort decisions. We let
![]() indicate exit or continuation respectively. With respect to our earlier definition in Section 2, the symmetric MPE now comprises also an
operating probability, which for an incumbent is given by
indicate exit or continuation respectively. With respect to our earlier definition in Section 2, the symmetric MPE now comprises also an
operating probability, which for an incumbent is given by
![]() and represents the probability that incumbent
and represents the probability that incumbent ![]() remains in the industry
remains in the industry![]() while for a potential entrant is
while for a potential entrant is
![]() and represents the probability that potential entrant
and represents the probability that potential entrant ![]() enters the industry.
enters the industry.
The solution to the problem of the firm is found using value and policy function iteration method along the lines of Pakes and McGuire (1994). It exploits the computational simplification entailed by the Markov Perfect assumption combined with the recursivity of the optimization problem. The
algorithm iterates on the vector containing value functions, ![]() , and the vector of policies,
, and the vector of policies, ![]() , (one for each state
, (one for each state ![]() ), until the maximum of the element-by-element difference between successive iterations in these vectors is below a pre-specified tolerance level.
All computations are carried out in Gauss 3.0.
), until the maximum of the element-by-element difference between successive iterations in these vectors is below a pre-specified tolerance level.
All computations are carried out in Gauss 3.0.
The algorithm iterates on the ![]() and
and ![]() matrices until the maximum of the
element-by-element difference between successive iterations in these matrices is below a pre-specified tolerance level. The calculations in each iteration are performed separately for each row (industry structure) using only the old values of the matrices
matrices until the maximum of the
element-by-element difference between successive iterations in these matrices is below a pre-specified tolerance level. The calculations in each iteration are performed separately for each row (industry structure) using only the old values of the matrices ![]() and
and ![]() If each element of
If each element of ![]() and
and ![]() has converged, then we are assured of having computed a MPNE of the dynamic game.
has converged, then we are assured of having computed a MPNE of the dynamic game.
We describe the process that provides us with new ![]() and
and ![]() matrices at every
iteration. The computation is done separately for each element of
matrices at every
iteration. The computation is done separately for each element of ![]() and
and ![]() Thus
we describe what the algorithm does to
Thus
we describe what the algorithm does to
![]() and
and
![]() , where
, where ![]() is the industry vector, and
is the industry vector, and ![]() stands for
stands for
![]() for every
for every
![]() Although we illustrate the updating process for the typical element
Although we illustrate the updating process for the typical element
![]() this process is done to all possible states
this process is done to all possible states
![]() .
.
For a given
![]() , the values of
, the values of
![]() and
and
![]() at each new iteration are calculated as follows:
at each new iteration are calculated as follows:
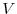 : the value function at the
: the value function at the 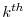 iteration is written as
iteration is written as
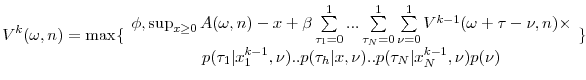
Denote the firm's expected discounted value for each of the two possible realizations of its state process,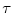 , as
, as
![\displaystyle CV( z,n) =\beta [ \begin{array}{c} \sum\limits_{\tau _{1}=0}^{1}...\sum\limits_{\tau _{h-1}=0}^{1}\sum\limits_{\tau _{h+1}=0}^{1}...\sum\limits_{\tau _{N}=0}^{1}\sum\limits_{\nu =0}^{1}V^{k-1}( z-\nu ,n) p( \nu ) \times \\ p( \tau _{1}\vert x_{1}^{k-1},\nu ) ..p( \tau _{h-1}\vert x_{h-1}^{k-1},\nu ) p( \tau _{h+1}\vert x_{h+1}^{k-1},\nu ) ..p( \tau _{N}\vert x_{N}^{k-1},\nu )% \end{array}% ]](img225.gif)
That is,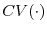 sums over the probability weighted average of the possible states of the future competitors, but not over the investing firm's own future states. Hence, we can rewrite
sums over the probability weighted average of the possible states of the future competitors, but not over the investing firm's own future states. Hence, we can rewrite
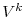 as
as
where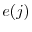 is a vector of zeros except for the
is a vector of zeros except for the 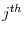 element which is one.
Then, whenever
element which is one.
Then, whenever
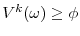
![\displaystyle V^{k}( \omega ,n) =\sup_{x\geq 0}[ A( \omega ,n) -x+\beta \frac{ax}{1+ax}CV( \omega +e( n) ,n) +\beta \frac{1}{1+ax}CV( \omega ,n) ]](img232.gif)
 : denote by
: denote by
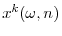 the level that solves (7), and by
the level that solves (7), and by  the
derivative with respect to
the
derivative with respect to 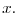 Assuming that the firm remains active, the optimal
Assuming that the firm remains active, the optimal
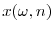 solves
solves
![\displaystyle =\beta [ D_{x}( \frac{ax}{1+ax}) CV( \omega +e( n) ,n) +D_{x}( \frac{1}{1+ax}) CV( \omega ,n) ]](img238.gif)
![\displaystyle =\beta [ D_{x}( \frac{ax}{1+ax}) v1-D_{x}( \frac{ax}{% 1+ax}) v2]](img239.gif)
and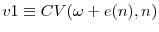 and
and
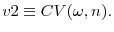 Note that
Note that
![\displaystyle D_{x}( \frac{1}{1+ax}) =\frac{a}{( 1+ax) ^{2}}=a[ 1-p( x) ] ^{2}](img242.gif)
when (and, hence,
(and, hence,
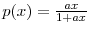 ). Thus,
). Thus,
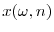 solves
solves
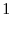
![\displaystyle =\beta [ a[ 1-p( x) ] ^{2}v1-a[ 1-p( x) ] ^{2}v2]](img246.gif)
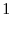
![\displaystyle =\beta a[ 1-p( x) ] ^{2}( v1-v2)](img247.gif)
![\displaystyle [ 1-p( x) ] ^{2}](img248.gif)
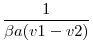
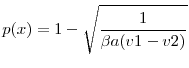
Taking the inverse of implies
implies
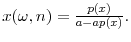
- Finally, we can use the derived formula to update the value function
![\displaystyle V^{k}( \omega ,n) =\max \{ \phi ,\sup_{x\geq 0}[ \begin{array}{c} A( \omega ,n) -x( \omega ,n) +\beta \frac{ax( \omega ,n) }{1+ax( \omega ,n) }CV( \omega +e( n) ,n) \\ +\beta \frac{1}{1+ax( \omega ,n) }CV( \omega ,n)% \end{array}% ] \}](img254.gif)
Note that if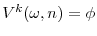 , then
, then  is 0 with probability
one. Hence, the actual
is 0 with probability
one. Hence, the actual  level is
level is
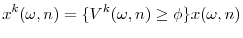
where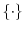 is the indicator function which takes the value of one when condition inside is satisfied, and zero otherwise.
is the indicator function which takes the value of one when condition inside is satisfied, and zero otherwise.
Appendix C. Details of Computation of CEO Portfolio Sensitivities (Core and Guay (2002))
We define the CEO's portfolio price sensitivity (PPS) as the change in the value of the CEO's stock and option portfolio due to a 1% increase in the price of the firm's common stock. Partial derivatives of the option price with respect to stock price (delta) are based on the Black-Scholes (1973)
option-pricing model adjusted for dividends by Merton (1973), with the following standard parameters: N is the cumulative probability function for the normal distribution; S is the price of the underlying stock; X is the exercise price of the option; ![]() is the expected stock return volatility over the life of the option; r is the risk-free interest rate; T is the time to maturity of the option in years; and d is the expected dividend yield over the life of the option. The six
variables necessary to compute the delta and vega of an option are the exercise price, time to maturity, volatility, risk-free rate, dividend yield, and stock price. All of these input variables are either directly observable or can be accurately estimated.
is the expected stock return volatility over the life of the option; r is the risk-free interest rate; T is the time to maturity of the option in years; and d is the expected dividend yield over the life of the option. The six
variables necessary to compute the delta and vega of an option are the exercise price, time to maturity, volatility, risk-free rate, dividend yield, and stock price. All of these input variables are either directly observable or can be accurately estimated.
Because details on the exercise prices and maturities of CEO options are not fully disclosed in annual statements, we follow Core and Guay's (2002) approximation method. They show that their method explains 99% of the actual variation in option portfolio values and sensitivities. We partition the CEO's option portfolio into three parts: (1) options from new grants, (2) exercisable options from previous grants, and (3) non-exercisable options from previous grants. ExecuComp provides full information on exercise prices (item EXPRIC in ExecuComp) and times to maturity for new grants (item EXDATE in ExecuComp ), which makes the computation of option delta fairly straightforward. However, for previously granted options, no data are available on exercise prices and times to maturity. To estimate the average exercise price for previously granted options, we use the "realizable values" as in Core and Guay (2002). The realizable value is the immediate exercise value of the CEO's options. We divide the realizable value of previously granted options by the number of options to find how much, on average, the stock price is above the exercise price. Subtracting this figure from the stock price yields the exercise price.
We follow Core and Guay (2002) when estimating times to maturity for previously granted options (unexercisable and exercisable). First, we assume that the time to maturity of an unexercisable option is one year less than that of a new grant. This assumption is consistent with evidence in Kole
(1997) that vesting periods are narrowly bounded between 20 and 28 months, with an average of 24 months. Second, we assume that the time to maturity of an exercisable option is three years less than that of an unexercisable option. Consequently, we set the maturity of an unexercisable (exercisable)
option to the new grant's maturity minus one (four). If no options are granted in the current year, we set the time to maturity of an exercisable (unexercisable) option to six (nine) years. Once the delta (![]() ) of each option partition are determined, we calculate the CEO's portfolio price sensitivity (PPS) as follows:
) of each option partition are determined, we calculate the CEO's portfolio price sensitivity (PPS) as follows:
 |
where S and N. denote the stock price and the number of options/stocks in hundreds of thousands. The subscripts NG, PGEX, PGUNEX, and STOCK stand for new grants, previously granted exercisable options, previously granted non-exercisable options, and stock holdings, respectively.
Appendix D. Figures and Tables

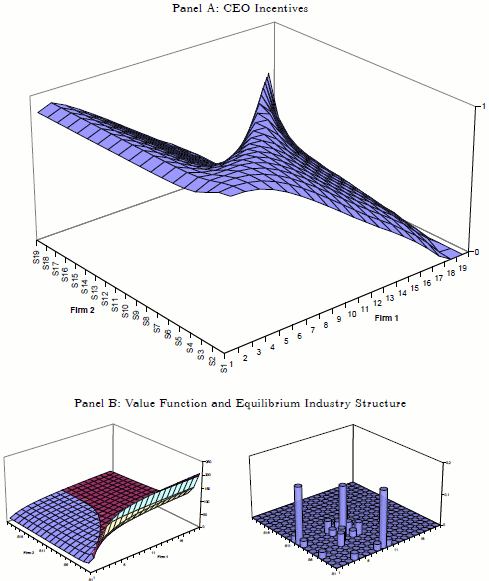
Panel A plots optimal CEO incentives of Firm 1,
![]() as a function of the state of the industry,
as a function of the state of the industry, ![]() , for two firms and a given state of the other active firms. Panel B plots the value function of Firm 1,
, for two firms and a given state of the other active firms. Panel B plots the value function of Firm 1,
![]() as a function of the state of the industry,
as a function of the state of the industry, ![]() (left
panel); and the ergodic distribution (frequency) of Markov-Perfect equilibrium industry states
(left
panel); and the ergodic distribution (frequency) of Markov-Perfect equilibrium industry states ![]() (right panel). Higher states correspond to higher quality.
(right panel). Higher states correspond to higher quality.
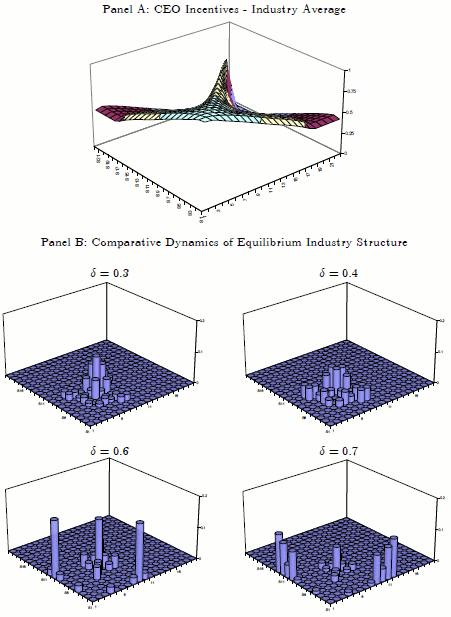
Panel A plots the average optimal CEO incentives of Firm 1 and Firm 2,
![]() , as a function of the state of the industry,
, as a function of the state of the industry, ![]() , for a given state of the other active firms. Panel B plots, for a range of aggregate shock parameters
, for a given state of the other active firms. Panel B plots, for a range of aggregate shock parameters ![]() , the ergodic distribution (frequency)
of Markov-Perfect equilibrium industry states
, the ergodic distribution (frequency)
of Markov-Perfect equilibrium industry states ![]() . Higher states correspond to higher quality.
. Higher states correspond to higher quality.
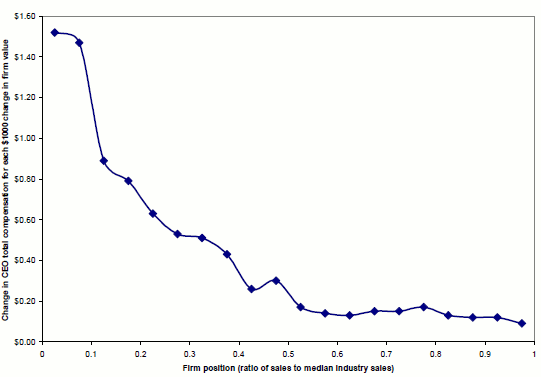
This figure plots estimated pay-performance sensitivities for CEOs of firms in different position deciles. Pay-performance sensitivity is estimated with pooled OLS regressions. The dependent variable is a measure of executive compensation in a particular firm year. The measure of total CEO compensation consists of short-term compensation and long-term compensation. Short-term compensation consists of salary, bonus, and other annual payments (e.g., gross-ups for tax liabilities, perquisites, preferential discounts on stock purchases). Long-term compensation includes the value of restricted stock granted, stock options granted, payouts from long-term incentive plans, and all other compensation (e.g., contributions to benefit plans, severance payments). Performance is defined as the product of the total inflation-adjusted return to shareholders and the beginning of period market value of the firm (Jensen and Murphy (1990)). Industry is defined by four-digit SIC code. Position is the ratio of the firm's sales to industry median sales in the beginning of the year, winsorized at 1%. Data is annual for 1993-2004, with only manufacturing (SIC 2000-3999) firms included.
| Parameter | Description | Benchmark Value |
| demand | 15 | |
| aggregate shock | 0.6 | |
| scrap value | 0.1 | |
| entry cost | 0.2 | |
| discount rate | 0.96 |
| Statistics | Panel Data | Model |
| Number of firms | 6 | 6 |
| Industry concentration | 0.37 | 0.43 |
| Median firm age | 30 | 36 |
| Standard deviation of firm age | 21 | 18 |
Summary statistics for the model are computed over 15 year periods, starting at random draws from the ergodic distribution of states, repeating the procedure 1000 times. Industry concentration is defined as the market share of the four largest firms in the industry. Age is the number of periods since the firm first appeared in the artificial panel. In the panel data, age is from Jovanovic and Rousseau (2001).
| Parameter | Frequency of Symmetric States | CEO Incentives |
|
|
64.7% | 0.76 |
|
|
50.8% | 0.62 |
|
|
50.0% | 0.60 |
|
|
32.5% | 0.47 |
|
|
25.7% | 0.32 |
|
|
11.7% | 0.15 |
| Parameter | Turnover Rate | CEO Incentives |
|
|
29.5% | 0.54 |
| 20.9% | 0.49 | |
| 15.6% | 0.47 | |
| 7.8% | 0.32 | |
| 2.3% | 0.20 |
Panel A reports, for a range of aggregate shock parameters ![]() , the incidence of symmetric states and average CEO incentives in the Markov-Perfect industry equilibrium. Incidence of
symmetric states is computed as percentage of states such that
, the incidence of symmetric states and average CEO incentives in the Markov-Perfect industry equilibrium. Incidence of
symmetric states is computed as percentage of states such that
![]() for all
for all ![]() =1,...,7, and
=1,...,7, and ![]() =2. Average CEO incentives is computed as the arithmetic average of optimal CEO incentives,
=2. Average CEO incentives is computed as the arithmetic average of optimal CEO incentives,
![]() , across all firms. Panel B reports, for a range of entry costs
, across all firms. Panel B reports, for a range of entry costs ![]() , the average turnover rate and average CEO incentives in the Markov-Perfect industry equilibrium. Average turnover rate is computed as as {probability of entry+probability of exit-probability of entry and exit}. Average CEO incentives is computed as the arithmetic average of
optimal CEO incentives,
, the average turnover rate and average CEO incentives in the Markov-Perfect industry equilibrium. Average turnover rate is computed as as {probability of entry+probability of exit-probability of entry and exit}. Average CEO incentives is computed as the arithmetic average of
optimal CEO incentives,
![]() , across all firms.
, across all firms.
| Parameter | Leader | Laggard |
|
|
0.17 | 0.95 |
|
|
0.17 | 0.83 |
|
|
0.15 | 0.72 |
|
|
0.14 | 0.57 |
|
|
0.11 | 0.41 |
|
|
0.08 | 0.21 |
| Parameter | Leader | Laggard |
|
|
0.18 | 0.68 |
| 0.16 | 0.62 | |
| 0.14 | 0.57 | |
| 0.14 | 0.39 | |
| 0.13 | 0.26 |
This table reports, for a range of aggregate shock parameters ![]() (Panel A) and for a range of entry costs
(Panel A) and for a range of entry costs ![]() (Panel B), the average CEO incentives of leaders and laggards in the Markov-Perfect industry equilibrium. Average CEO incentives is computed as the arithmetic average of optimal CEO incentives,
(Panel B), the average CEO incentives of leaders and laggards in the Markov-Perfect industry equilibrium. Average CEO incentives is computed as the arithmetic average of optimal CEO incentives,
![]() , across all firms. For any industry state, each firm's position is calculated as the ratio of its sales to industry median sales. Leaders are firms in the highest quartile of
the ratio, laggards are firms in the lowest quartile of the ratio.
, across all firms. For any industry state, each firm's position is calculated as the ratio of its sales to industry median sales. Leaders are firms in the highest quartile of
the ratio, laggards are firms in the lowest quartile of the ratio.
This Table presents descriptive statistics on the components of executive compensation for all executives in the ExecuComp sample for years 1993-2004 for whom complete data on total compensation is available. The top panel of the table pertains to the executives who are identified as the chief executive officer of the firm. The bottom panel describes the other executives in the sample. The measure of total compensation can be divided into short-term compensation and long-term compensation. Short-term compensation consists of salary, bonus, and other annual payments (e.g., gross-ups for tax liabilities, perquisites, preferential discounts on stock purchases). Long-term compensation includes the value of restricted stock granted, stock options granted, payouts from long-term incentive plans, and all other compensation (e.g., contributions to benefit plans, severance payments). Long-term share is the average share of compensation that is long-term, at the individual level. Portfolio wealth delta is the price sensitivity of the CEO's option portfolio calculated as in Core and Guay (2002).
| Payment Category (Thousands of Dollars) | Mean | Median | Standard Deviation |
| CEOs (N=8320) Total Compensation | 4315 | 2051 | 12677 |
| CEOs (N=8320) Short Term Compensation | 1217 | 893 | 1180 |
| CEOs (N=8320) Salary | 599 | 544 | 325 |
| CEOs (N=8320) Bonus | 569 | 322 | 937 |
| CEOs (N=8320) Other Annual | 49 | 0 | 250 |
| CEOs (N=8320) Long Term Compensation | 3097 | 1011 | 12405 |
| CEOs (N=8320) Restricted Stock Granted | 283 | 0 | 1633 |
| CEOs (N=8320) Stock Options Granted | 2508 | 703 | 12078 |
| CEOs (N=8320) LT Incentive Plan Payout | 166 | 0 | 813 |
| CEOs (N=8320) All Other | 138 | 20 | 845 |
| CEOs (N=8320) Long-Term Share of Total | 0.484 | 0.427 | 0.264 |
| CEOs (N=8320) Portfolio Wealth Delta | 4.25 | 1.41 | 7.79 |
| Non-CEOs (N=38544) Total Compensation | 1442 | 746 | 2844 |
| Non-CEOs (N=38544) Short Term Compensation | 490 | 365 | 830 |
| Non-CEOs (N=38544) Salary | 281 | 244 | 164 |
| Non-CEOs (N=38544) Bonus | 191 | 105 | 752 |
| Non-CEOs (N=38544) Other Annual | 19 | 0 | 185 |
| Non-CEOs (N=38544) Long Term Compensation | 922 | 310 | 2516 |
| Non-CEOs (N=38544) Restricted Stock Granted | 80 | 0 | 554 |
| Non-CEOs (N=38544) Stock Options Granted | 727 | 209 | 2191 |
| Non-CEOs (N=38544) LT Incentive Plan Payout | 50 | 0 | 263 |
| Non-CEOs (N=38544) All Other | 52 | 9 | 490 |
| Non-CEOs (N=38544) Long-Term Share of Total | 0.423 | 0.444 | 0.270 |
This table reports pooled OLS regressions of pay-performance sensitivity. The dependent variable is a measure of executive compensation in a particular firm year. The measure of total compensation consists of short-term compensation and long-term compensation. Short-term compensation consists of salary, bonus, and other annual payments. Long-term compensation includes the value of restricted stock granted, stock options granted, payouts from long-term incentive plans, and all other compensation. Portfolio wealth delta is the price sensitivity of the CEO's option portfolio calculated as in Core and Guay (2002). Performance is defined as the product of the total inflation-adjusted return to shareholders and the beginning of period market value of the firm divided by 100 (Jensen and Murphy (1990)). Position within industry is determined by the ratio of the firm's sales to industry median sales in the beginning of the year, winsorized at 1%. Industry is defined by four-digit SIC code.. Data is annual for 1993-2004, with only manufacturing (SIC 2000-3999) firms included. All regressions include year and industry fixed effects. Industry fixed effects are at the 2-digit SIC level. Standard errors are robust to heteroskedasticity and arbitrary serial correlation within industry-year cells. Levels of significance are indicated by *, **, and *** for 10%, 5%, and 1% respectively.
| Panel A: Annual Compensation | All Firms |
| Performance | 0.337
|
| Performance (Standard Error) | (0.131) |
| Position | 437.402
|
| Position (Standard Error) | (168.611) |
| Performance*Position | -0.329
|
| Performance* Position (Standard Error) | (0.122) |
| Performance*Size | -0.223
|
| Performance*Size (Standard Error) | (0.030) |
| Observations | 13080 |
| Firms | 449 |
| Adjusted R2 | 0.23 |
| Panel B: CEO Portfolio Wealth Delta | All Firms |
|---|---|
| Position | -0.307
|
| Position (Standard Error) | (0.060) |
| Observations | 5698 |
| Firms | 423 |
| Adjusted R2 | 0.14 |
| Industry fixed effects | Yes |
| Year fixed effects | Yes |
This table reports pooled OLS regressions of pay-performance sensitivity. The dependent variable is a measure of executive compensation in a particular firm year. The measure of total compensation can be divided into short-term compensation and long-term compensation. Short-term compensation consists of salary, bonus, and other annual payments (e.g., gross-ups for tax liabilities, perquisites, preferential discounts on stock purchases). Long-term compensation includes the value of restricted stock granted, stock options granted, payouts from long-term incentive plans, and all other compensation (e.g., contributions to benefit plans, severance payments). Performance is defined as the product of the total inflation-adjusted return to shareholders and the beginning of period market value of the firm (Jensen and Murphy (1990)). Industry is defined by four-digit SIC code. Symmetry is industry-year average proximity to median sales in the industry. Position within industry is determined by the ratio of the firm's sales to industry median sales in the beginning of the year, winsorized at 1%: leaders are firms in the highest quartile of the ratio, laggards are firms in the lowest quartile of the ratio. The regressions with controls include industry concentration, measured as domestic four-firm concentration ratio, and firm size, measured as assets at the beginning of the year and winsorized at 1%, and their respective interactions with performance. These coefficients are omitted from the table for brevity, and are available upon request. Industry fixed effects are at the 2-digit SIC level. Data is annual for 1993-2004, with only manufacturing (SIC 2000-3999) firms included. Standard errors are robust to heteroskedasticity and arbitrary serial correlation within industry-year cells. Levels of significance are indicated by *, **, and *** for 10%, 5%, and 1% respectively.
| (1) All Firms no fixed effects, no controls | (2) All Firms fixed effects, no controls | (3) All Firms fixed effects, controls | (4) By Position: Leader fixed effects, controls | (5) By Position: Laggard fixed effects, controls | (6) Short Term Compensation fixed effects, controls | |
| Performance | 0.062
|
0.117
|
0.344
|
0.234
|
0.313
|
0.001 |
| Performance (Standard Error) | (0.003) | (0.007) | (0.017) | (0.031) | (0.113) | (0.003) |
| Symmetry | -366.031
|
-449.727
|
46.555 | 267.468 |
38.481 | -8.244 |
| Symmetry (Standard Error) | (47.498) | (49.078) | (48.918) | (157.382) | (66.983) | (9.884) |
| Performance*Symmetry | 0.027
|
0.025
|
0.020
|
-0.001 | 0.205
|
0.001
|
| Performance*Symmetry (Standard Error) | (0.003) | (0.004) | (0.003) | (0.006) | (0.076) | (0.001) |
| Industry fixed effects | No | Yes | Yes | Yes | Yes | Yes |
| Year fixed effects | Yes | Yes | Yes | Yes | Yes | Yes |
| Observations | 30326 | 30326 | 30216 | 8670 | 8300 | 30326 |
| Firms | 449 | 449 | 449 | 114 | 112 | 449 |
| Adjusted R2 | 0.29 | 0.36 | 0.37 | 0.32 | 0.25 | 0.35 |
This table reports pooled OLS regressions of pay-performance sensitivity. The dependent variable is a measure of executive compensation in a particular firm year. The measure of total compensation can be divided into short-term compensation and long-term compensation. Short-term compensation consists of salary, bonus, and other annual payments (e.g., gross-ups for tax liabilities, perquisites, preferential discounts on stock purchases). Long-term compensation includes the value of restricted stock granted, stock options granted, payouts from long-term incentive plans, and all other compensation (e.g., contributions to benefit plans, severance payments). Portfolio wealth delta is the price sensitivity of the CEO's option portfolio calculated as in Core and Guay (2002). Performance is defined as the product of the total inflation-adjusted return to shareholders and the beginning of period market value of the firm (Jensen and Murphy (1990)). Industry is defined by four-digit SIC code. Symmetry is industry-year average proximity to median sales in the industry. Position within industry is determined by the ratio of the firm's sales to industry median sales in the beginning of the year, winsorized at 1%: leaders are firms in the highest quartile of the ratio, laggards are firms in the lowest quartile of the ratio. The regressions with controls include industry concentration, measured as domestic four-firm concentration ratio, and firm size, measured as assets at the beginning of the year and winsorized at 1%, and their respective interactions with performance. These coefficients are omitted from the table for brevity, and are available upon request. Industry fixed effects are at the 2-digit SIC level. Data is annual for 1993-2004, with only manufacturing (SIC 2000-3999) firms included. Standard errors are robust to heteroskedasticity and arbitrary serial correlation within industry-year cells. Levels of significance are indicated by *, **, and *** for 10%, 5%, and 1% respectively.
| (1) All Firms no fixed effects, no controls | (2) All Firms fixed effects, no controls | (3) All Firms fixed effects, controls | (4) By Position: Leader fixed effects, controls | (5) By Position: Laggard fixed effects, controls | |
| Performance (Annual Compensation) | 0.116
|
0.113
|
0.608
|
0.385
|
0.703
|
| Performance (Annual Compensation) (Standard Error) | (0.011) | (0.011) | (0.025) | (0.047) | (0.252) |
| Symmetry (Annual Compensation) | -925.050
|
-1202.607 | -125.116
|
-234.478 | 317.852 |
| Symmetry (Annual Compensation) (Standard Error) | (153.185) | (157.654) | (78.382) | (246.646) | (160.425) |
| Performance*Symmetry (Annual Compensation) | 0.025
|
0.022
|
0.021
|
0.006 | 0.588
|
| Performance*Symmetry (Annual Compensation) (Standard Error) | (0.010) | (0.011) | (0.005) | (0.010) | (0.186) |
| Observations (Annual Compensation) | 5805 | 5805 | 5783 | 1462 | 1445 |
| Firms (Annual Compensation) | 449 | 449 | 449 | 114 | 112 |
| Adjusted R2 (Annual Compensation) | 0.38 | 0.39 | 0.35 | 0.38 | 0.47 |
| Symmetry (CEO Portfolio Wealth Delta) | 2.553
|
2.490
|
2.391
|
1.474 | 4.463
|
| Symmetry (CEO Portfolio Wealth Delta) (Standard Error) | (1.016) | (1.002) | (1.011) | (0.926) | (1.868) |
| Observations (CEO Portfolio Wealth Delta) | 5702 | 5702 | 5702 | 1435 | 1420 |
| Firms (CEO Portfolio Wealth Delta) | 423 | 423 | 423 | 109 | 106 |
| Adjusted R2 (CEO Portfolio Wealth Delta) | 0.11 | 0.14 | 0.22 | 0.18 | 0.25 |
| Industry fixed effects | No | Yes | Yes | Yes | Yes |
| Year fixed effects | Yes | Yes | Yes | Yes | Yes |
This table reports pooled OLS regressions of pay-performance sensitivity. The dependent variable is a measure of executive compensation in a particular firm year. The measure of total compensation can be divided into short-term compensation and long-term compensation. Short-term compensation consists of salary, bonus, and other annual payments (e.g., gross-ups for tax liabilities, perquisites, preferential discounts on stock purchases). Long-term compensation includes the value of restricted stock granted, stock options granted, payouts from long-term incentive plans, and all other compensation (e.g., contributions to benefit plans, severance payments). Performance is defined as the product of the total inflation-adjusted return to shareholders and the beginning of period market value of the firm (Jensen and Murphy (1990)). Industry is defined by four-digit SIC code. Turnover is industry average annualized job creation and destruction (Davis, Haltiwanger, and Schuh (1998)). Position within industry is determined by the ratio of the firm's sales to industry median sales in the beginning of the year, winsorized at 1%: leaders are firms in the highest quartile of the ratio, laggards are firms in the lowest quartile of the ratio. The regressions with controls include industry concentration, measured as domestic four-firm concentration ratio, and firm size, measured as assets at the beginning of the year and winsorized at 1%, and their respective interactions with performance. These coefficients are omitted from the table for brevity, and are available upon request. Industry fixed effects are at the 2-digit SIC level. Data is annual for 1993-2004, with only manufacturing (SIC 2000-3999) firms included. Standard errors are robust to heteroskedasticity and arbitrary serial correlation within industry-year cells. Levels of significance are indicated by *, **, and *** for 10%, 5%, and 1% respectively.
| (1) All Firms no fixed effects, no controls | (2) All Firms fixed effects, no controls | (3) All Firms fixed effects, controls | (4) By Position: Leader fixed effects, controls | (5) By Position: Laggard fixed effects, controls | (6) Short Term Compensation fixed effects, controls | |
| Performance | 0.051
|
0.049
|
0.327
|
0.219
|
0.393
|
0.010
|
| Performanceb (Standard Error) | (0.002) | (0.002) | (0.018) | (0.032) | (0.100) | (0.004) |
| Turnover | -27.816 | 14.646 | -87.192 | -240.589 | -149.056 | -0.725 |
| Turnover (Standard Error) | (18.996) | (20.059) | (55.453) | (185.810) | (72.472) | (11.213) |
| Performance*Turnover | 0.010
|
0.011
|
0.035
|
0.020
|
0.226
|
0.005
|
| Performance*Turnover (Standard Error) | (0.001) | (0.001) | (0.006) | (0.011) | (0.088) | (0.001) |
| Industry fixed effects | No | Yes | Yes | Yes | Yes | Yes |
| Year fixed effects | Yes | Yes | Yes | Yes | Yes | Yes |
| Observations | 29606 | 29606 | 29596 | 8526 | 8245 | 29606 |
| Firms | 449 | 449 | 449 | 114 | 112 | 449 |
| Adjusted R2 | 0.18 | 0.18 | 0.36 | 0.31 | 0.24 | 0.34 |
This table reports pooled OLS regressions of pay-performance sensitivity. The dependent variable is a measure of executive compensation in a particular firm year. The measure of total compensation can be divided into short-term compensation and long-term compensation. Short-term compensation consists of salary, bonus, and other annual payments (e.g., gross-ups for tax liabilities, perquisites, preferential discounts on stock purchases). Long-term compensation includes the value of restricted stock granted, stock options granted, payouts from long-term incentive plans, and all other compensation (e.g., contributions to benefit plans, severance payments). Performance is defined as the product of the total inflation-adjusted return to shareholders and the beginning of period market value of the firm (Jensen and Murphy (1990)). Industry is defined by four-digit SIC code. Turnover is industry average annualized job creation and destruction (Davis, Haltiwanger, and Schuh (1998)). Position within industry is determined by the ratio of the firm's sales to industry median sales in the beginning of the year, winsorized at 1%: leaders are firms in the highest quartile of the ratio, laggards are firms in the lowest quartile of the ratio. The regressions with controls include industry concentration, measured as domestic four-firm concentration ratio, and firm size, measured as assets at the beginning of the year and winsorized at 1%, and their respective interactions with performance. These coefficients are omitted from the table for brevity, and are available upon request. Industry fixed effects are at the 2-digit SIC level. Data is annual for 1993-2004, with only manufacturing (SIC 2000-3999) firms included. Standard errors are robust to heteroskedasticity and arbitrary serial correlation within industry-year cells. Levels of significance are indicated by *, **, and *** for 10%, 5%, and 1% respectively.
| (1) All Firms no fixed effects, no controls | (2) All Firms fixed effects, no controls | (3) All Firms fixed effects, controls | (4) By Position: Leader fixed effects, controls | (5) By Position: Laggard fixed effects, controls | (6) Short Term Compensation fixed effects, controls | |
| Performance | 0.108
|
0.225
|
0.658
|
0.555
|
0.710
|
0.045
|
| Performance (Standard Error) | (0.012) | (0.025) | (0.051) | (0.083) | (0.331) | (0.010) |
| Turnover | -48.854 | 428.279 | -99.542 | -41.221 | -331.054 | 28.306 |
| Turnover (Standard Error) | (165.951) | (181.388) | (164.047) | (495.688) | (217.116) | (36.673) |
| Performance*Turnover | -0.010 | 0.004 | 0.052
|
0.038 | 0.522
|
0.021
|
| Performance*Turnover (Standard Error) | (0.011) | (0.020) | (0.018) | (0.029) | (0.113) | (0.004) |
| Industry fixed effects | No | Yes | Yes | Yes | Yes | Yes |
| Year fixed effects | Yes | Yes | Yes | Yes | Yes | Yes |
| Observations | 5651 | 5651 | 5651 | 1462 | 1445 | 5651 |
| Firms | 449 | 449 | 449 | 114 | 112 | 449 |
| Adjusted R2 | 0.38 | 0.43 | 0.54 | 0.53 | 0.41 | 0.54 |
This table reports pooled OLS regressions of pay-performance sensitivity. The dependent variable is a measure of executive compensation in a particular firm year. The measure of total compensation consists of short-term compensation and long-term compensation. Short-term compensation consists of salary, bonus, and other annual payments. Long-term compensation includes the value of restricted stock granted, stock options granted, payouts from long-term incentive plans, and all other compensation. Portfolio wealth delta is the price sensitivity of the CEO's option portfolio calculated as in Core and Guay (2002). Performance is defined as the product of the total inflation-adjusted return to shareholders and the beginning of period market value of the firm divided by 100 (Jensen and Murphy (1990)). Position within industry is determined by the ratio of the firm's sales to industry median sales in the beginning of the year, winsorized at 1%. Industry is defined by four-digit SIC code.. Data is annual for 1993-2004, with only manufacturing (SIC 2000-3999) firms included. All regressions include year and industry fixed effects. Industry fixed effects are at the 2-digit SIC level. Standard errors are robust to heteroskedasticity and arbitrary serial correlation within industry-year cells. Levels of significance are indicated by *, **, and *** for 10%, 5%, and 1% respectively.
| Panel A: Annual Compensation | All Firms |
|---|---|
| Performance | 0.110
|
| Performance (Standard Error) | (0.015) |
| Growing Industry | 1222.526
|
| Growing Industry (Standard Error) | (318.296) |
| Performance*Growing Industry | 0.041
|
| Performance*Growing Industry (Standard Error) | (0.015) |
| Declining Industry | -642.385
|
| Declining Industry (Standard Error) | (300.251) |
| Performance*Declining Industry | -0.013 |
| Performance*Declining Industry (Standard Error) | (0.020) |
| Observations | 13080 |
| Firms | 449 |
| Adjusted R2 | 0.12 |
| Panel B: CEO Portfolio Wealth Delta | All Firms |
|---|---|
| Growing Industry | 2.220
|
| Growing Industry (Standard Error) | (0.220) |
| Declining Industry | -1.086
|
| Declining Industry (Standard Error) | (0.225) |
| Observations | 5698 |
| Firms | 423 |
| Adjusted R2 | 0.06 |
| Industry fixed effects | No |
| Year fixed effects | Yes |
This table reports pooled OLS regressions of pay-performance sensitivity. The dependent variable is a measure of executive compensation in a particular firm year. The measure of total compensation can be divided into short-term compensation and long-term compensation. Short-term compensation consists of salary, bonus, and other annual payments (e.g., gross-ups for tax liabilities, perquisites, preferential discounts on stock purchases). Long-term compensation includes the value of restricted stock granted, stock options granted, payouts from long-term incentive plans, and all other compensation (e.g., contributions to benefit plans, severance payments). Performance is defined as the product of the total inflation-adjusted return to shareholders and the beginning of period market value of the firm (Jensen and Murphy (1990)). Percentage Owned is the percentage of common equity held by the executive through stocks and options. Industry is defined by four-digit SIC code. Symmetry is industry-year average proximity to median sales in the industry. Turnover is industry average annualized job creation and destruction (Davis, Haltiwanger, and Schuh (1998)). Position within industry is determined by the ratio of the firm's sales to industry median sales in the beginning of the year, winsorized at 1%: leaders are firms in the highest quartile of the ratio, laggards are firms in the lowest quartile of the ratio. The regressions with controls include industry concentration, measured as domestic four-firm concentration ratio, and firm size, measured as assets at the beginning of the year and winsorized at 1%, and their respective interactions with performance. These coefficients are omitted from the table for brevity, and are available upon request. Industry fixed effects are at the 2-digit SIC level. Data is annual for 1993-2004, with only manufacturing (SIC 2000-3999) firms included. Standard errors are robust to heteroskedasticity and arbitrary serial correlation within industry-year cells. Levels of significance are indicated by *, **, and *** for 10%, 5%, and 1% respectively.
| (1) All Executives robustness (ownership) | (2) All Executives leader summary | (3) All Executives laggard summary | (4) CEO Only robustness (ownership) | (5) CEO Only leader summary | (6) CEO Only laggard summary | |
| Performance | 0.723
|
0.072 | 0.578
|
1.827
|
0.477
|
1.505
|
| Performance (Standard Error) | (0.059) | (0.055) | (0.206) | (0.214) | (0.133) | (0.686) |
| Percentage Owned | 41.647 | 544.921 |
||||
| Percentage Owned (Standard Error) | (88.739) | (318.458) | ||||
| Performance*Percentage Owned | -0.578
|
-1.135
|
||||
| Performance*Percentage Owned (Standard Error) | (0.027) | (0.117) | ||||
| Performance*Turnover | 0.181
|
0.026 | 0.261
|
0.416
|
0.009 | 1.149
|
| Performance*Turnover (Standard Error) | (0.038) | (0.035) | (0.134) | (0.132) | (0.081) | (0.468) |
| Performance*Symmetry | 0.305
|
0.002 | 0.152
|
0.287
|
0.005 | 0.846
|
| Performance*Symmetry (Standard Error) | (0.029) | (0.007) | (0.071) | (0.102) | (0.018) | (0.388) |
| Observations | 1848 | 4712 | 4185 | 1143 | 903 | 844 |
| Firms | 449 | 114 | 112 | 449 | 114 | 112 |
| Adjusted R2 | 0.21 | 0.38 | 0.26 | 0.40 | 0.63 | 0.48 |
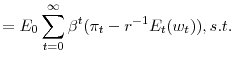
![\displaystyle \frac{\partial }{\partial \alpha }[ x( \alpha ^{\ast }( \omega ) ) +r^{-1}E_{x}O^{\prime }] =r^{-1}\frac{\partial }{\partial \alpha }E_{x}V( \omega ^{\prime })](img96.gif)
![\displaystyle V^{k}( \omega ,n) =\max \{ \phi ,\sup_{x\geq 0}[ \begin{array}{c} A( \omega ,n) -x+\beta \frac{ax}{1+ax}CV( \omega +e( n) ,n) \\ +\beta \frac{1}{1+ax}CV( \omega ,n)% \end{array}% ] \}](img228.gif)