
Real-Time Properties of the Federal Reserve's Output Gap
Keywords: Output gap, potential output, real-time data, inflation forecasting
Abstract:
1 Introduction
In a 2002 paper, Orphanides and van Norden contend that it is not possible to obtain reliable estimates of the output gap in real time. As they demonstrate, standard detrending procedures yield gap measures that are subject to large subsequent revisions, primarily because trend extraction becomes quite difficult at the endpoint of a given sample. In addition, based on data available for the 1980s and early 1990s, Orphanides (1998) concludes that Federal Reserve staff estimates of the output gap are similarly unreliable.
The purpose of this note is to consider whether these conclusions obtain for more recent vintages of the output gap estimates produced by the Federal Reserve staff. Narrative evidence suggests that the Federal Reserve's ability to recognize and quantify the mid-1990s acceleration in trend productivity in a reasonably timely manner was an important contributor to the successful conduct of monetary policy over that period.2 This points to an improved ability to estimate the gap, which should in turn be evident in the data.
A related issue concerns the usefulness of real-time estimates of the output gap for inflation forecasting. In companion work, Orphanides and van Norden (2005) find that over the post-1983 period, inflation forecasting models that use real-time estimates of the output gap typically perform worse than models that condition on final estimates of the gap. We therefore also examine whether the Federal Reserve staff estimates of the GDP gap provide a useful predictor of future inflation movements in real time.
2 Real-Time Estimates of the Federal Reserve Board Output Gap
Before each meeting of the Federal Open Market Committee (FOMC), the Federal Reserve Board's staff produce a detailed projection of various U.S. economic aggregates. This projection, which is known as the Greenbook forecast, is judgemental in the sense that it is not explicitly derived from a single model of the economy.3 In particular, the staff's estimates of potential GDP pool and judgementally weight the results from a number of estimation techniques, including statistical filters and more structural model-based procedures.4
Our set of real-time output gap estimates starts with the June 1996 Greenbook forecast; these estimates extend back to 1975:Q1 for every vintage of the forecast. The Greenbook projection is only made public with a five-year lag; hence, the most recent estimate of the gap in our dataset comes from the December 2006 Greenbook. Because the Greenbook is produced eight times a year, there will be eight sets of output gap estimates for each year (typically two per quarter).
Define the December 2006 estimates of the gap to be the gap's "final" value. We then define the corresponding real-time estimate of the quarter-![]() gap to be
the estimate of the gap from the forecast round whose closing date falls in quarter
gap to be
the estimate of the gap from the forecast round whose closing date falls in quarter ![]() . (Obtaining the period-
. (Obtaining the period-![]() gap estimate from a Greenbook in the following quarter ensures that in most cases an advance estimate of GDP--or a relatively full set of monthly indicators--would have been available for estimating the quarter-
gap estimate from a Greenbook in the following quarter ensures that in most cases an advance estimate of GDP--or a relatively full set of monthly indicators--would have been available for estimating the quarter-![]() gap.) For example, the June 1997 Greenbook forecast was completed in 1997:Q2. We therefore call the 1997:Q1 value of the gap from the June 1997 round the real-time estimate of the gap in that quarter. This means, of course, that there
can be multiple real-time observations for a given quarter; for instance, we will obtain real-time estimates of the 1997:Q1 gap from both the May 1997 and June 1997 Greenbook forecasts. We ignore the informational asymmetry generated by these timing definitions--specifically, we ignore
the fact that rounds that occur later in a given quarter will enjoy an informational advantage over those that occur earlier--as such asymmetries will be roughly constant across years. (As we document in the next section, our main conclusions are robust to alternative assumptions regarding
timing.)
gap.) For example, the June 1997 Greenbook forecast was completed in 1997:Q2. We therefore call the 1997:Q1 value of the gap from the June 1997 round the real-time estimate of the gap in that quarter. This means, of course, that there
can be multiple real-time observations for a given quarter; for instance, we will obtain real-time estimates of the 1997:Q1 gap from both the May 1997 and June 1997 Greenbook forecasts. We ignore the informational asymmetry generated by these timing definitions--specifically, we ignore
the fact that rounds that occur later in a given quarter will enjoy an informational advantage over those that occur earlier--as such asymmetries will be roughly constant across years. (As we document in the next section, our main conclusions are robust to alternative assumptions regarding
timing.)
3 The Magnitude of Revisions to the Federal Reserve's Gap Estimates
We define the gap revision as the difference between the final and real-time gap estimates. Lines 1 and 2 of Table 1 give the mean, standard deviation, and root-mean-square error (RMSE) for these revisions, together with two measures of the noise-to-signal ratio: the ratio of either the standard deviation or the RMSE of the gap revisions to the standard error of the final estimate of the gap.5 As can be seen from the table, the mean error over the full sample is small (less than a tenth of a percentage point). The standard deviation (and RMSE) of the revisions is around 0.7 percentage point; while this is large in absolute terms, it is only about half the size of the corresponding standard deviation of the final estimate of the gap.6
These standard deviation and RMSE values are also small relative to the corresponding estimates found by Orphanides (1998) in his analysis of the Greenbook output gap: Over the 1980-1992 period, Orphanides reports a RMSE of 2.8 percentage points for revisions to the Greenbook's real-time output gap estimates, which is actually greater than the 2.4 percentage point standard deviation of his "final" (end-of-1994) gap estimate. Part of this difference no doubt reflects our use of a different sample period: Relative to the 1980s, GDP in our sample period is less volatile. However, this explanation is tempered somewhat by the observation that the Federal Reserve appears to have had greater difficulty forecasting real GDP movements in recent decades (see Tulip, 2005).
Of course, another explanation for the observed reduction in the size of gap revisions is simply that the Federal Reserve staff's ability to estimate the GDP gap in real time has improved relative to the period that Orphanides examined. To assess this possibility, we used real-time GDP data to examine whether purely statistical methods for estimating the output gap yield a decline in the size of gap revisions that is comparable to what we find for the Greenbook output gap. In particular, we produced real-time estimates of the output gap using each of the six univariate detrending procedures considered by Orphanides and van Norden (2002). These procedures include three deterministic approaches (fitting a linear trend, a broken-linear trend, and a quadratic trend to log real GDP) and three unobserved-components approaches (the Hodrick-Prescott filter and the trend GDP models of Watson, 1986 and of Harvey, 1985 and Clark, 1987). The noise-to-signal ratios that obtain for these various gap estimates--which are shown in the upper panel of Table 2--imply that for all but one of the six detrending methods, the size of the real-time gap revisions relative to the volatility of the gap itself either remains about unchanged or increases somewhat from 1980-1992 to 1992-2006. Hence, these purely statistical procedures do not yield an improvement in the reliability of real-time gap estimates that is similar to what we observe for the Federal Reserve's measure, which in turn suggests that some element particular to the the Fed's estimation procedure--such as the use of judgement or the pooling of results from multiple sources--is responsible.7
In line with Orphanides (1998), however, we find that the autocorrelation of the Greenbook gap revisions is quite high: about 0.91 over the period we consider.8 It turns out that part of the autocorrelation over our sample period is attributable to a persistent string of negative errors (that diminish in magnitude) up until around 1998. Very likely, this string of errors reflects slow learning about the 1990s speedup in trend productivity growth; dropping the pre-1999 observations from the sample reduces the estimated autocorrelation coefficient to 0.70. Interestingly--and as shown in Table 3--when we compute real-time gap estimates using the univariate approaches in Orphanides and van Norden (2002), we find that the gap revision is as highly autocorrelated over the 1996-2006 period (line 2) as it is over the 1980-1992 period (line 1), with autocorrelation coefficients on the order of 0.9. For these gap measures, however, dropping the pre-1999 observations from the latter period (line 3) reduces the estimated autocorrelation coefficient for only two of the six methods (the linear and piecewise-linear detrending procedures).
As was noted above, the publication of two Greenbook forecasts per quarter implies that we will have multiple gap estimates in each quarter. In addition, even though we have obtained each time-![]() gap estimate from a Greenbook published in period
gap estimate from a Greenbook published in period ![]() , there will be occasions where an advance estimate of GDP will not have been available to produce the gap estimate
for a given quarter.9 We therefore considered two modifications to our timing assumptions. First, we recomputed the statistics in Table 1 using the
time-
, there will be occasions where an advance estimate of GDP will not have been available to produce the gap estimate
for a given quarter.9 We therefore considered two modifications to our timing assumptions. First, we recomputed the statistics in Table 1 using the
time-![]() gap estimate from the time-
gap estimate from the time-![]() Greenbook; this ensures that a complete set of
GDP data for quarter
Greenbook; this ensures that a complete set of
GDP data for quarter ![]() would have been available for producing the Greenbook estimate. Unsurprisingly, doing this (not shown) lowers the mean, standard deviation, and RMSE of the gap
revisions, but only by a very small amount (on the order of 0.02 or 0.03 percentage point in each case). Next, we recomputed the statistics in Table 1 using only the gap estimate from the second Greenbook in each quarter. Once again, the mean,
standard deviation, and RMSE of the gap revisions are little changed by this modification (not shown). However, the autocorrelation of the revisions declines slightly (to 0.84), and is considerably lower (only 0.41) if the pre-1999 revisions are excluded.
would have been available for producing the Greenbook estimate. Unsurprisingly, doing this (not shown) lowers the mean, standard deviation, and RMSE of the gap
revisions, but only by a very small amount (on the order of 0.02 or 0.03 percentage point in each case). Next, we recomputed the statistics in Table 1 using only the gap estimate from the second Greenbook in each quarter. Once again, the mean,
standard deviation, and RMSE of the gap revisions are little changed by this modification (not shown). However, the autocorrelation of the revisions declines slightly (to 0.84), and is considerably lower (only 0.41) if the pre-1999 revisions are excluded.
Finally, we also examined whether our results are affected by using a shorter period to compute the summary statistics for the gap revisions. Our set of real-time estimates ends with the October 2006 Greenbook, while our "final" gap estimate is taken from the December 2006 Greenbook. To the extent that potential GDP growth is relatively slow-moving, it seems plausible to expect little scope for revisions to the output gap in periods near the end of our sample. We therefore compute a second set of summary statistics that only use data through the December 2004 Greenbook; using this date ensures that at least two NIPA annual revisions separate the real-time gap estimates in the latter portion of the sample from the final gap estimates. These statistics are shown in Table 1 in line 2 (for the real-time gaps) and line 4 (for the final gap estimates); as can be seen, the change in the mean and variability of the gap revisions that results from shortening the sample in this manner is extremely small.10
4 Using Real-Time Gap Estimates for Inflation Forecasting
We now consider whether the uncertainty associated with current and future values of the Greenbook output gap affects its usefulness as a predictor of inflation. Specifically, we fit Phillips curve models that relate core PCE price inflation (expressed at an annual rate) to six of its own lags (with the lag coefficients constrained to sum to one, but not otherwise restricted) and to the contemporaneous and once-lagged value of share-weighted relative core import price inflation.11 In contrast to many commonly used empirical Phillips curve specifications, we do not include the relative rates of food and energy price inflation in our model.12
The starting date for the estimation is 1975:Q1 (this is dictated by the availability of historical data on the real-time output gap). For a real-time gap estimate from a Greenbook forecast in quarter ![]() , we estimate the model through quarter
, we estimate the model through quarter ![]() and then compute dynamic out-of-sample simulations at various horizons using the projected path of the gap from that vintage
of the Greenbook. Note, however, that we use the most recent vintages of core PCE and import prices in the regression; implicitly, we seek to assess how well the Federal Reserve's output gap estimates predict the economy's "true" rate of core inflation, where we assume
that the true inflation rate is captured by the most recent vintage of NIPA data. We present results for three forecast horizons: two quarters ahead, four quarters ahead, and six quarters ahead; in addition, we use the simulated values to compute the average inflation rate over the
next four quarters.
and then compute dynamic out-of-sample simulations at various horizons using the projected path of the gap from that vintage
of the Greenbook. Note, however, that we use the most recent vintages of core PCE and import prices in the regression; implicitly, we seek to assess how well the Federal Reserve's output gap estimates predict the economy's "true" rate of core inflation, where we assume
that the true inflation rate is captured by the most recent vintage of NIPA data. We present results for three forecast horizons: two quarters ahead, four quarters ahead, and six quarters ahead; in addition, we use the simulated values to compute the average inflation rate over the
next four quarters.
The forecasts from our baseline Phillips curve model (using a real-time output gap) are then compared to corresponding out-of-sample projections from four other models:
- An identical Phillips curve specification that uses the "final" estimate of the GDP gap (that is, the GDP gap from the December 2006 Greenbook) and that therefore assumes that the future path of the gap is available for constructing the model forecasts of inflation;
- A specification that omits the GDP gap but is otherwise identical to the baseline model (with six lags of inflation whose coefficients are constrained to sum to unity and the current and once-lagged value of the relative core import term);
- A univariate
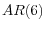 specification in which core PCE price inflation is related to six of its lags, with the sum of the coefficients on lagged inflation constrained to equal one; and,
specification in which core PCE price inflation is related to six of its lags, with the sum of the coefficients on lagged inflation constrained to equal one; and, - A univariate
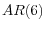 specification in which the sum of the inflation lags is unrestricted.13
specification in which the sum of the inflation lags is unrestricted.13
Table 4 gives the RMSE for each model over the various projection horizons. Comparing the top two rows of each panel reveals that using the real-time estimates and forecasts of the GDP gap in lieu of the final estimate has almost no effect on forecast accuracy. That said, models that
condition on a measure of the GDP gap improve only slightly on the unconstrained univariate model of inflation (note that even the final estimate of the gap only contributes about a percentage point to the equation's ![]() value in the full sample). We would emphasize that we attribute no significance to the fact that the Phillips curve models do slightly better than the unrestricted autoregressive model: Because we treat the path of import prices as known over the forecast period, we
are providing these models with an important informational advantage. Rather, the result that we would highlight here is that there is essentially no reduction in forecasting performance from using the real-time gap measure in the Phillips curve model as opposed to the final gap estimate, as can be
seen from a comparison of lines one and two of Table 4. (By contrast, Orphanides and van Norden, 2005, find that real-time estimates of the statistical gap measures that they consider do significantly less well in predicting inflation than do the corresponding final or
"ex post" gap estimates.)
value in the full sample). We would emphasize that we attribute no significance to the fact that the Phillips curve models do slightly better than the unrestricted autoregressive model: Because we treat the path of import prices as known over the forecast period, we
are providing these models with an important informational advantage. Rather, the result that we would highlight here is that there is essentially no reduction in forecasting performance from using the real-time gap measure in the Phillips curve model as opposed to the final gap estimate, as can be
seen from a comparison of lines one and two of Table 4. (By contrast, Orphanides and van Norden, 2005, find that real-time estimates of the statistical gap measures that they consider do significantly less well in predicting inflation than do the corresponding final or
"ex post" gap estimates.)
These results also reveal an interesting relationship among the variables in the model. As can be seen from Table 4, merely omitting the gap yields a noticeable deterioration in forecast performance. Likewise, omitting import prices but keeping either the final or real-time gap (not shown)
results in a large increase in the forecast RMSE. In addition, imposing that the sum of the coefficients on lagged inflation equals one in the univariate model also acts to reduce its forecast accuracy. The sensitivity of the model's forecasting performance to these modifications is somewhat
surprising given that jointly these three elements of the specification--imposition of a unit coefficient sum and inclusion of an output gap together with an import price term--appear to contribute very little to the overall model's forecasting performance (the RMSEs
from the full model using the final estimate of the output gap are quite close to those from the unconstrained univariate ![]() model).
model).
5 Conclusions
The results presented in Section III suggest that the conclusions found in Orphanides (1998) and Orphanides and van Norden (2002) regarding the reliability of output gap measures in real time are too pessimistic along at least one dimension. Over a nearly decade-long period, staff at the Federal Reserve Board produced estimates of the output gap whose revision properties were considerably better than those found by Orphanides and van Norden for the statistical gap measures that they considered, as well as being considerably better than the earlier Federal Reserve output gap estimates that Orphanides examined. Importantly, these more-recent estimates were constructed during a period in which the Federal Reserve staff were attempting to identify and incorporate the effects of a perceived shift in trend productivity growth; in addition, the improvement that we observe for the Greenbook output gap estimates is not shared by gap measures obtained under alternative, purely statistical detrending methods. Hence, our finding provides circumstantial evidence of an improvement in the procedures used by the Fed to estimate potential output and the GDP gap.
Our results regarding the usefulness of gap estimates for inflation forecasting are in closer agreement with Orphanides and van Norden (2005), in that we find that it is not really possible to improve on the forecasting performance of a simple univariate model with a gap-based model. However, in contrast to these authors' findings, our result does not appear to stem from difficulties associated with measuring the output gap in real time: Phillips curve models based on real-time gap measures perform about as well as models based on a full-sample gap. Instead, we view our result as reflecting the general decline in the forecastability of inflation in recent decades (particularly by gap-based models) that has been documented by Stock and Watson (2007, 2009).
On balance, our results suggest that the output gap can serve as a useful input to the policy process. Although the gap measures we consider cannot be used to improve inflation forecasts, real-time estimates of the gap appear to provide a reasonable characterization of the current state of real activity in the economy. Such a gauge is necessary for a central bank like the Federal Reserve, whose statutory mandate requires it to aim for maximum sustainable output growth and employment as well as stable prices; similarly, some sort of output gap measure is also necessary for any central bank that seeks to implement a Taylor-type monetary policy rule.
Of course, it remains to be seen whether the improvement in output gap estimation that we document will prove to be a durable phenomenon. The U.S. economy has recently undergone a once-in-a-generation upheaval that caught many analysts by surprise and whose longer-term effects--if any--are still unknown. As additional real-time estimates of the Federal Reserve Board's output gap become publicly available, it will be interesting to see whether the reliability of these gap estimates will be maintained.
6 References
Clark, Peter K., "The Cyclical Component of U.S. Economic Activity," Quarterly Journal of Economics 102 (1987), 797-814.
Harvey, A. C., "Trends and Cycles in Macroeconomic Time Series," Journal of Business and Economic Statistics 3 (1985), 216-227.
Hooker, Mark A., "Are Oil Shocks Inflationary? Asymmetric and Nonlinear Specifications versus Changes in Regime," Journal of Money, Credit, and Banking 34 (2002), 540-561.
Meyer, Laurence H., A Term at the Fed: An Insider's View (New York: Harper Business, 2004).
Mishkin, Frederic S., "Estimating Potential Output," presentation at the Conference on Price Measurement for Monetary Policy (May 24, 2007); available at
http://www.federalreserve.gov/newsevents/speech/mishkin20070524a.htm.
Orphanides, Athanasios, "Monetary Policy Evaluation with Noisy Information," Federal Reserve Board Finance and Economics Discussion Series no. 1998-50 (1998).
Orphanides, Athanasios and Simon van Norden, "The Unreliability of Output-Gap Estimates in Real Time," Review of Economics and Statistics 84 (2002), 569-583.
Orphanides, Athanasios and Simon van Norden, "The Reliability of Inflation Forecasts Based on Output Gap Estimates in Real Time," Journal of Money, Credit, and Banking 37 (2005), 583-601.
Solow, Robert M., "Where Have All the Flowers Gone? Economic Growth in the 1960s" in Joseph A. Pechman and N. J. Simler (Eds.), Economics in the Public Service: Papers in Honor of Walter W. Heller (New York: W. W. Norton, 1982).
Stock, James H., and Mark W. Watson, "Why Has U.S. Inflation Become Harder to Forecast?," Journal of Money, Credit, and Banking 39(S1) (2007), 3-33.
Stock, James H., and Mark W. Watson, "Phillips Curve Inflation Forecasts" in Jeff Fuhrer, Yolanda K. Kodrzycki, Jane Sneddon Little, and Giovanni P. Olivei (Eds.), Understanding Inflation and the Implications for Monetary Policy: A Phillips Curve Retrospective (Cambridge, MA: MIT Press, 2009)
Tulip, Peter, "Has Output Become More Predictable? Changes in Greenbook Forecast Accuracy," Federal Reserve Board Finance and Economics Discussion Series no. 2005-31 (2005).
Watson, Mark W., "Univariate Detrending Methods with Stochastic Trends," Journal of Monetary Economics 18 (1986), 49-75.
| Mean | Std. dev. | RMSE | Noise-signal ratios Std. dev. | Noise-signal ratios RMSE | |
| Greenbook output gap revisions 1. Full sample, 1996-2006 | -0.04 | 0.71 | 0.71 | 0.47 | 0.47 |
|---|---|---|---|---|---|
| Greenbook output gap revisions 2. Through Dec. 2004 GB | -0.15 | 0.73 | 0.74 | 0.45 | 0.45 |
| Memo: "Final" gap estimates 3. Full sample, 1996-2006 | 0.25 | 1.50 | |||
| Memo: "Final" gap estimates 4. Through Dec. 2004 GB | 0.29 | 1.64 |
Note: "Final" estimates replicate observations in individual quarters for comparability with real-time estimates (see text for details). Full sample contains 84 observations; sample through December 2004 Greenbook contains 69 observations.
| Hodric-Prescott | Broken Trend | Quadratic Trend | Linear Trend | Watson | Harvey-Clark | |
| 1. 1980-1992 (A. Based on standard deviation of revisions) | 1.10 | 0.62 | 0.40. 0.72 | 0.77 | 0.78 | |
| 2. 1996-2006 (A. Based on standard deviation of revisions) | 1.03 | 1.11 | 0.61 | 1.17 | 0.59 | 0.71 |
| 3. 1980-1992 (B. Based on RMSE of revisions) | 1.10 | 1.13 | 0.47 | 1.15 | 1.26 | 0.77 |
| 4. 1996-2006 (B. Based on RMSE of revisions) | 1.03 | 1.45 | 1.58 | 1.43 | 0.77 | 0.70 |
| Hodric-Prescott | Broken Trend | Quadratic Trend | Linear Trend | Watson | Harvey-Clark | |
| 1. 1980-1992 (A. Based on standard deviation of revisions) | 1.08 | 0.52 | 0.47 | 0.67 | 0.75 | 0.76 |
| 2. 1996-2006 (A. Based on standard deviation of revisions) | 1.01 | 1.04 | 0.43 | 1.13 | 0.52 | 0.70 |
| 3. 1980-1992 (B. Based on RMSE of revisions) | 1.08 | 1.53 | 0.60 | 1.49 | 1.25 | 0.75 |
| 4. 1996-2006 (B. Based on RMSE of revisions) | 1.00 | 1.57 | 1.60 | 1.56 | 0.79 | 0.69 |
| Hodric-Prescott | Broken Trend | Quadratic Trend | Linear Trend | Watson | Harvey-Clark | |
| 1. 1980-1992 | 0.92 | 0.95 | 0.83 | 0.93 | 0.93 | 0.87 |
| 2. 1996-2006 | 0.92 | 0.94 | 0.93 | 0.94 | 0.93 | 0.88 |
| 3. 1999-2006 | 0.93 | 0.68 | 0.89 | 0.63 | 0.89 | 0.90 |
| 2Q ahead | 4Q ahead | 4Q ave. | 6Q ahead | |
| Model with final gap | 0.47 | 0.47 | 0.30 | 0.49 |
| Model with real-time gap | 0.48 | 0.48 | 0.32 | 0.49 |
| Model excluding gap | 0.60 | 0.67 | 0.50 | 0.78 |
| 0.59 | 0.68 | 0.48 | 0.81 | |
| Unconstrained |
0.53 | 0.53 | 0.37 | 0.57 |
| Memo:Number of observations | 81 | 77 | 77 | 73 |
|---|