Skip to: [Printable Version (PDF)] [Bibliography] [Footnotes]

Finance and Economics Discussion Series: 2013-05 Screen Reader version ^♣

Government Debt and Macroeconomic Activity: A Predictive Analysis for Advanced Economies*

Deniz Baglan¹

Emre Yoldas²

December 2012

Keywords: Government debt, GDP growth, fixed effects estimator, recursive demeaning, near unit-root process, threshold, subsampling.

Abstract:

This paper explores the empirical relationship between government debt and future macroeconomic activity using data on twenty advanced economies throughout the post-war era. We use robust inference techniques to deal with the bias arising from the persistent nature of debt to GDP ratio as an endogenous predictor of GDP growth. Our results show that statistical significance of the csoefficient on the debt ratio in predictive regressions changes considerably with the use of robust inference techniques. For countries with relatively low average debt ratios we find a negative threshold effect as their debt ratios increase toward moderate levels. For countries with chronically high debt ratios, GDP growth slows as relative government debt increases, but we find no significant threshold effect.

JEL Classification: C32, C51, E62.

1 Introduction

In the aftermath of the recent global financial crisis, government debt in most advanced economies surged due to high levels of stimulus spending and costs of stabilizing the financial system. Aging populations and the associated social insurance costs create further pressure on public debt levels relative to total income in these economies, e.g. (Cecchetti et al., 2010).

Public debt can facilitate intergenerational transfers that allow consumption smoothing, e.g. (Cukierman & Meltzer, 1989), or provide liquidity services that can ease credit conditions for private agents, e.g. (Woodford, 1990). However, higher public debt may result in weaker economic performance due to crowding out, limitations on government services, and lower investment and hiring through real option effects due to increased uncertainty associated with high debt levels, e.g. (Baker et al., 2012).³ Moreover, as argued by (Cecchetti et al., 2011), we do not have a fully satisfactory theoretical framework to quantitatively evaluate effects of public debt accumulation, so empirical evidence is crucial to guide policy makers.

There is a growing empirical literature that evaluates effects of government debt on economic activity. (Reinhart & Rogoff, 2010) construct a historical multi-country data set and provide a comprehensive descriptive analysis of debt-growth and debt-inflation relationships. They find that a debt to GDP ratio higher than 90% is associated with considerably lower average real GDP growth rates. (Reinhart et al., 2012) identify episodes of public debt overhang in advanced economies and discuss the subsequent growth experience in detail. (Cecchetti et al., 2011), (Cecherita & Rother, 2010), and (Kumar & Woo, 2010) investigate the relationship between government debt and real activity by estimating growth regressions. These studies provide mixed evidence regarding the direction and significance of the relationship and potential nonlinearities.

We contribute to the empirical literature on the relationship between government debt and economic activity by putting the (Reinhart & Rogoff, 2010) data set for the post-war period in a formal statistical context. We aim to determine whether a higher level of debt to GDP ratio predicts slower GDP growth in the medium term, as opposed to investigating the steady state relationship between growth in per capita income and public debt, which is the focus of the aforementioned studies. Endogeneity and high persistence of debt to GDP ratio causes finite sample bias in a standard panel data setting, which we deal with using robust statistical inference techniques. We also investigate the possibility that there is a certain tipping point for debt to GDP above which further debt accumulation starts to have negative effects on output growth or already negative effects are amplified. We use subsampling methods for inference in the context of a tipping point as standard inference techniques are not applicable due to the presence of nuisance parameters under the null of a linear relationship.

Our findings can be summarized as follows. In a linear framework, higher government debt relative to GDP is not a statistically significant predictor of subsequent GDP growth when all 20 advanced economies are considered together. There is an economically significant negative threshold effect when debt to GDP ratio is close to 20%, but the threshold estimate is subject to considerable uncertainty. Data indicates considerable heterogeneity with respect to average debt ratios, so we split countries into two groups accordingly. We find that the aforementioned threshold effect is mainly driven by the countries that experienced relatively low average debt to GDP levels over the sample period. Moreover, there is a significant negative linear predictive relationship between debt to GDP and GDP growth for countries with chronivally high debt to GDP ratios but we do not find evidence for a debt tipping point for such countries.

The rest of the paper is organized as follows. We provide a detailed discussion of methodological issues in Section 2. We present and discuss the empirical results in Section 3 and conclude in Section 4.

2 Methodology

Let $y_{i,t}$ and $x_{i,t}$ denote GDP growth and debt to GDP ratio respectively for the th country in the sample for $i=1,\ldots ,N$ , and $t=1,\ldots,T$ . We are interested in the following simple predictive regression⁴

$\displaystyle y_{i,t} = \alpha _{i} + \beta x_{i,t-1} + u_{i,t}$

(1)

where $\alpha_i$ represent country fixed-effects and $u_{i,t}$ are country specific innovations that are assumed to be martingale difference with finite fourth moments.⁵ As debt to GDP ratio is endogenous, we assume $Corr(x_{i,t}, u_{i,t}) \neq 0$ . The panel regression framework allows us to incorporate heterogeneity through country fixed effects and obtain a more precise estimate of the slope coefficient compared to individual time series regressions, which may deliver noisy and mixed results. Moreover, even if slope parameters are different across individual countries, the pooled estimator from panel regression converges to a well defined average, which is robust to heterogeneity in slope coefficients.

The standard fixed effects (FE) estimator in this framework is given by

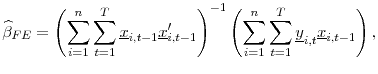$\displaystyle \widehat{\beta }_{FE}=\left( \sum_{i=1}^{n} \sum_{t=1}^{T} \underline{x}_{i,t-1} \underline{x}_{i,t-1}^{\prime} \right) ^{-1} \left( \sum_{i=1}^{n} \sum_{t=1}^{T} \underline{y}_{i,t} \underline{x}_{i,t-1} \right),$

(2)

where $\underline{x}_{i,t}=x_{i,t}-\frac{1}{T} \sum_{t=1}^{T}x_{i,t}$ and $\underline{y}_{i,t}=y_{i,t}-\frac{1}{T}\sum_{t=1}^{T}y_{i,t}$ . Endogeneity of $x_{it}$ and time-series demeaning of the data creates a correlation between the innovation process $u_{i,t}$ and the demeaned regressors $\underline{x}_{i,t-1}$ . As a result, the FE estimator is consistent as

tends to infinity, but it has a second-order asymptotic bias, which is amplified in the presence of a persistent predictor.⁶ Because debt to GDP ratio is typically very persistent, this bias will likely affect the point estimates as well as inference in the regression given in Equation 1. We will consider two alternative approaches to deal with this bias: recursive demeaning and subsampling.

Recursive demeaning has been proposed in the literature as a solution to the aforementioned finite sample bias in a panel data setting (see (Phillips & Moon, 2000)). Following (Hjalmarsson, 2010) we assume that

$\displaystyle x_{i,t} = A_{i} x_{i,t-1} + v_{i,t}$

(3)

where $A_{i}=I+C_{i}/T$ , and

is the identity matrix. In this setup,

characterizes local-to-unity behavior. The near unit-root construction can be best thought of as a tool to capture high persistence of the data in the asymptotic distribution results. If the roots are equal to unity, unit-root asymptotics apply to the model, but this would not be an economically plausible assumption in our case as government debt cannot grow indefinitely relative to total output. Assuming strict stationarity is not desirable either since debt to GDP ratio is typically extremely persistent and behaves like a unit root. Note also that the local to unity parameter matrix changes across countries, which allows individual time series to have different persistence levels. The recursive demeaning (RD) estimator is given by,

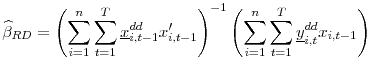$\displaystyle \widehat{\beta }_{RD}=\left( \sum_{i=1}^{n} \sum_{t=1}^{T} \underline{x}_{i,t-1}^{dd}x_{i,t-1}^{\prime }\right) ^{-1}\left( \sum_{i=1}^{n} \sum_{t=1}^{T}\underline{y}_{i,t}^{dd}x_{i,t-1}\right)$

(4)

where $\underline{y}_{i,t}^{dd}=y_{i,t}-\frac{1}{T-t+1}\sum_{s=t}^{T}y_{i,s}$ , and $\underline{x}_{i,t}^{dd}=x_{i,t}-\frac{1}{T-t+1}\sum_{s=t}^{T}x_{i,s}$ . Data dated after time

is used to construct the dependent variable $\underline{y}_{i,t}^{dd}$ , and the non-demeaned regressors, $x_{i,t-1}$ , are used as instruments. Consequently, forward demeaned innovation process $\underline{u}_{i,t}^{dd}$ and $x_{i,t-1}$ are independent of each other and $\widehat{\beta}_{RD}$ does not suffer from the aforementioned bias. (Hjalmarsson, 2010) shows that as

and

sequentially converge to infinity, $\widehat{\beta}_{RD}$ has an asymptotically normal distribution and proposes the panel equivalent of a heteroskedasticity and autocorrelation consistent estimator that calculates the long-run variance.

The second approach that we consider to deal with the finite sample bias arising due to persistent endogenous predictors is subsampling, e.g. (Wolf, 2000). This approach also allows us to investigate the possibility of a tipping point in government debt and make simultaneous inference about the predictive coefficients as well as the debt to GDP threshold. Subsampling is valid under both the local to unity structure described above in case of the RD estimator and fixed roots close to unity. To illustrate the subsampling procedure, let us consider the following nonlinear version of the model

$\displaystyle y_{i,t} = \alpha _{i} + \beta_1 \mathbf{1} \left( x_{i, t-1} < \tau \right) x_{i,t-1} + \beta_2 \mathbf{1} \left( x_{i, t-1} \geq \tau \right) x_{i, t-1} + u_{i, t},$

(5)

where $\mathbf{1}(.)$ is the standard indicator function and $\tau$ represents the threshold. The predictive coefficient of debt to GDP switches between $\beta_1$ and $\beta_2$ according to its level. We estimate $\tau$ with sequential conditional least squares by conducting a grid search over a trimmed version of the sample values of debt to GDP ratio to minimize system sum of squares.

Under the null of linearity (i.e. $H_0: \beta_1 = \beta_2$ ), $\tau$ is not identified, so standard inference methods are not applicable but subsampling is valid under relatively mild assumptions, e.g. (Gonzalo & Wolf, 2005). Subsampling is based on the idea of estimating the model on moving blocks, or subsamples, of the original data and using the resulting empirical distribution to approximate the unknown distribution of interest. Let denote the block size, such that and let $\widehat{\tau}^{b,t}$ denote the threshold estimate on the block $\{y_{t},\ldots ,y_{t+b-1}\}$ for $t=1,\ldots,T-b+1$ . Define $J_{n}(a,P)=\Pr_{P}(T\vert\widehat{\tau}-\tau\vert\leq a)$ where $\hat{\tau}$ is the full sample estimate, i.e. $\hat{\tau} \equiv \hat{\tau}^{T,1}$ , and is the probability law governing $\{y_{t}, x_{t}\}$ . The subsampling approximation to $J_{n}(a,P)$ is defined as follows

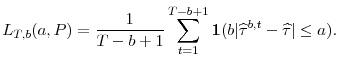$\displaystyle L_{T,b}(a,P)=\frac{1}{T-b+1} \sum_{t=1}^{T-b+1} \mathbf{1}(b\vert\widehat{\tau}^{b,t}-\widehat{\tau}\vert\leq a).$

(6)

Let $c_{T,b}(1-\alpha )$ be the $(1-\alpha)$ quantile of $L_{T,b}(a,P)$ , then the corresponding symmetric subsampling confidence interval is given by⁷

$\displaystyle SCI(\tau)=[\widehat{\tau} \mp T^{-1}c_{T,b}(1-\alpha )].$

(7)

Confidence intervals for the predictive coefficients are constructed in a similar fashion in case of both the baseline model and the nonlinear model. Finally, a specific block size is needed to make this procedure operational. To that end, we use the algorithm proposed by (Politis et al., 1999) that minimizes confidence interval volatility as a function of the block size.

3 Empirical Results

We use the post-war portion of the historical multi-country data set of (Reinhart & Rogoff, 2010) as our methods require a balanced panel and previous periods have numerous missing observations.⁸ Specifically, our annual sample runs from 1954 to 2008. The countries included in the data set are: Australia, Austria, Belgium, Canada, Denmark, Finland, France, Germany, Greece, Ireland, Italy, Japan, Netherlands, New Zealand, Norway, Portugal, Spain, Sweden, United Kingdom, and United States.

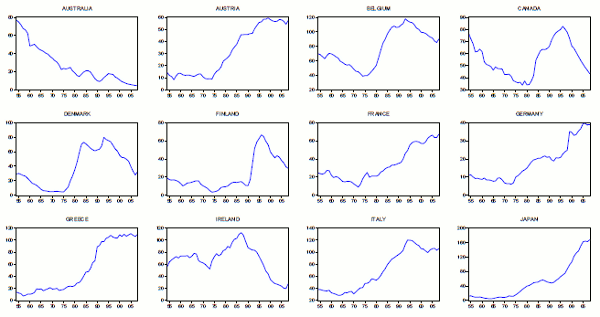
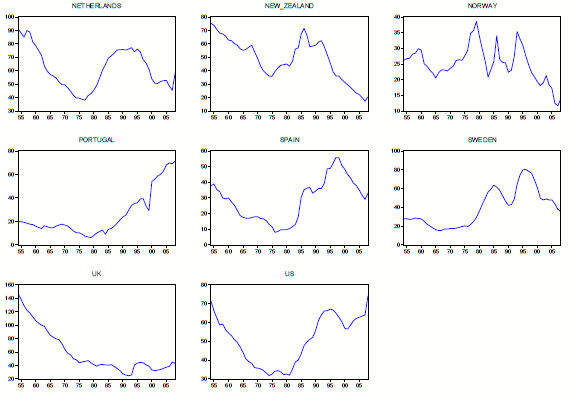
Table 1 provides summary statistics for GDP growth. The average annual GDP growth across countries is about 3.4% over the sample period. On average, GDP growth is slightly persistent and has an approximately symmetric distribution. Table 2 summarizes basic characteristics of debt to GDP ratio.⁹ Average debt to GDP across countries and over time is about 44%. The distribution of debt to GDP is right skewed for most countries in the sample. Unit root test results reflect high persistence in debt to GDP ratios. Only for two countries, Denmark and Sweden, the null of unit root can be rejected at conventional levels according to the point optimal test statistic of (Elliott et al., 1996). Debt to GDP ratios for individual countries are shown in Figures 1-2.

Table 3 summarizes results for the linear model for three, five, and ten-year horizons. We present three types of symmetric confidence intervals for the predictive coefficient: asymptotic FE, asymptotic RD, and subsampled FE. We use heteroskedasticity and autocorrelation consistent covariance standard errors for the asymptotic methods and set confidence level to 90% in all cases. The conventional method (asymptotic FE) implies a significant negative predictive relationship between debt to GDP and GDP growth. However, the two alternative procedures have quite different implications. Under the RD scheme, the point estimates become much larger in absolute value, sometimes implausibly so. The predictive coefficient is also always insignificant under this scheme. These results suggest presence of finite sample bias in the standard FE estimator and the bias-variance trade-off inherent in the RD estimator, so we conjecture that subsampled FE strikes a reasonable balance between bias and variance. The subsampled FE confidence intervals suggest no significant predictive relationship, but the width of the intervals are much smaller compared to the case of RD procedure but wider than the asymptotic FE, and on average, a notable portion of the intervals are on the negative part of the real line. The fifth percentile estimates suggest a 0.5-1.64% drag on annual GDP growth for a 10 percentage point increase in the debt to GDP ratio.

There appears to be an insignificant relationship between GDP growth and debt ratio in a linear predictive context, so we proceed to the nonlinear case to uncover the potential effects of debt intolerance at higher levels of government debt. For threshold estimation, we consider a symmetric trimming scheme that drops 15% of observations from each side of the sample distribution of debt to GDP ratios to form the search grid.¹⁰ Results are presented in Panel A of Table 4. For the three and five year horizons, point estimates of the threshold are relatively low, close to 18% while the estimate for the 10-year horizon is about 58%. In all cases, there is considerable uncertainty surrounding the point estimate of the threshold according to the subsampling confidence intervals. Interestingly , debt to GDP has a positive and significant coefficient below the threshold while it is not statistically different from zero above the threshold for three and five year horizons. Our interval estimates for the three and five year horizons imply that the expected growth differential between the two states can be as large as 3.7% per year. These estimates suggest that potential growth enhancing effects of public debt accumulation disappear at relatively low levels.

The estimated thresholds are low and the confidence intervals are fairly wide for the threshold in cases where predictive coefficients are significantly different across regimes, so we also consider a more restricted grid search to estimate the potential threshold at higher values of the debt ratio. Specifically, we extend the trimming from the left by dropping all the observations below the median and keep trimming at 15% on the right. Under this restricted scheme we find that the estimated threshold is, on average, close to 53% across all horizons considered (Table 4, Panel B). The predictive coefficient of debt to GDP is significantly negative only above the threshold for the three year horizon and both above and below the threshold for the five year horizon. However, in both cases the threshold effect is not significantly different from zero as indicated by the subsampling confidence intervals. To sum up, existence of a common debt threshold that is statistically and economically significant does not seem to be an accurate description of the nonlinear dynamics in the data when we consider all the countries jointly.

Our results so far suggest that there may be too much heterogeneity with respect to debt to GDP levels and dynamics to consider all countries jointly. For example, for seven countries in the sample debt to GDP ratio was never below 18%, the estimated threshold for three and five year horizons. Hence, we split the countries into two groups with respect to their average debt to GDP ratios over the sample and perform estimation for the low-debt and high-debt countries separately. This yields Australia, Austria, Denmark, Finland, France, Germany, Norway, Portugal, Spain, and Sweden as the low-debt group while the high-debt group is comprised of Belgium, Canada, Greece, Japan, Ireland, Italy, New Zealand, UK, and US.¹¹

Results for the linear case are presented in Table 5. The conventional interval estimates based on the FE estimator suggest significance in case of both country groups but subsampling confidence intervals indicate that debt to GDP predicts a significantly slower growth rate for high average debt countries for up to five years and the predictive coefficient is nearly significant at the 10-year horizon. For the nonlinear case we report results under symmetric trimming for both country groups in Table 6. For the three year horizon, the predictive coefficient is positive and significant below the estimated threshold of 18% and there is a significant negative threshold effect. For five and 10 year horizons, estimated thresholds are close to 30% and the predictive coefficients are not distinguishable from zero. However, a much bigger portion of the subsampling intervals lie in the positive (negative) region for $\beta_1$ ( $\beta_2-\beta_1)$ . So the threshold effect is in the expected direction but it is subject to large uncertainty for five-year and ten-year horizons. For high-debt countries, the estimated thresholds average out to about 50% across the three horizons. The predictive coefficient tends to be negative both above and below the threshold and the difference between the two regimes is not statistically distinguishable from zero. These results reinforce our previous finding that a higher debt to GDP ratio predicts a slower growth rate for high average debt countries in a linear fashion. Our subsampling based confidence intervals imply that for a 10 percentage point increase in the debt to GDP ratio, annual output growth slows between 2 and 48 basis points per year for the high average debt group.

4 Concluding Remarks

This paper contributes to the growing empirical literature on exploring implications of higher levels of government debt relative to total output for macroeconomic activity. We put the post-war portion of the (Reinhart & Rogoff, 2010) data set in a formal statistical context using estimation and inference techniques suitable to the underlying data characteristics. We find that endogeneity and persistence of government debt relative to total output causes considerable finite sample bias in a standard predictive panel data setting. We use robust inference techniques to deal with this problem. We find that higher debt relative to GDP is not a statistically significant predictor of subsequent economic growth in a linear framework. We also do not find evidence for a common debt to GDP threshold that is economically and statistically significant. However, when we split countries into two groups with respect to their average debt ratios, we find that there is a negative threshold effect for the low average debt countries and a significant negative linear predictive relationship for countries that experienced relatively higher levels of debt. We do not find evidence for increasing debt intolerance at higher levels of debt to GDP.

Bibliography

S. Baker, et al. (2012).

`Measuring Economic Policy Uncertainty'.
Stanford mimeo .

S. Cecchetti, et al. (2011).

`The Real Effects of Debt'.
Working paper .

S. Cecchetti, et al. (2010).

`The Future of Public Debt: Prospects and Implications'.
BIS Working Paper No. 300 .

C. Cecherita & P. Rother (2010).

`The Impact of High and Growing Debt on Economic Growth'.
ECB Working paper No. 1237 .

A. Cukierman & A. Meltzer (1989).

`A political theory of government debt and deficits in a neo-Ricardian framework'.
American Economic Review 79:713–732.

G. Elliott, et al. (1996).

`Efficient Tests for an Autoregressive Unit Root'.
Econometrica 64:813-836.

J. Gonzalo & M. Wolf (2005).

`Subsampling Inference in Threshold Autoregressive Models'.
Journal of Econometrics 127:201-224.

P. Hall (1988).

`On Symmetric Bootstrap Confidence Intervals'.
Journal of the Royal Statistical Society, Ser. B 50:35-45.

B. Hansen (1996).

`Inference when a Nuisance Parameter is not Identified under the Null Hypothesis'.
Econometrica 64:413-430.

E. Hjalmarsson (2010).

`Predicting Global Stock Returns'.
Journal of Financial and Quantitative Analysis 45:49-80.

R. Hodrick (1992).

`Dividend Yields and Expected Stock Returns: Alternative Procedures for Inference and Measurement'.
Review of Financial Studies 5:357-386.

M. Kumar & J. Woo (2010).

`Public Debt and Growth'.
IMF Working Paper 10/174 .

P. Phillips & H. Moon (2000).

`Nonstationary Panel Data Analysis: An Overview of some Recent Developments'.
Econometric Reviews 19:263-286.

D. Politis, et al. (1999).

Subsampling.
Springer.

C. Reinhart, et al. (2012).

`Debt Overhangs: Past and Present'.
NBER Working Paper 18015 .

C. Reinhart & K. Rogoff (2010).

`Growth in a Time of Debt'.
American Economic Review: Papers and Proceedings 100:573-578.

R. Stambaugh (1999).

`Predictive Regressions'.
Journal of Financial Economics 54:375-421.

M. Wolf (2000).

`Stock Returns and Dividend Yields Revisited: A New Way to Look at an Old Problem'.
Journal of Business & Economic Statistics 18:18-30.

M. Woodford (1990).

`Public Debt as Private Liquidity'.
American Economic Review 80:382-388.

Tables and Figures

Table 1: Descriptive Statistics for GDP Growth

Country	Mean	Std. Dev.	10th	50th	90th	ACR
Australia	3.8	1.7	1.7	3.9	6.0	0.20
Austria	3.5	2.3	0.8	3.2	6.1	$0.46^{\ast \ast \ast}$
Belgium	2.9	1.9	0.7	3.0	5.2	$0.27^{\ast \ast}$
Canada	3.5	2.3	1.1	3.3	6.3	$0.28^{\ast \ast}$
Denmark	2.6	2.2	0.1	2.5	5.8	0.09
Finland	3.4	2.9	0.4	3.3	7.0	$0.49^{\ast \ast \ast}$
France	3.2	1.9	1.1	2.7	5.6	$0.60^{\ast \ast \ast}$
Germany	2.9	2.5	0.1	2.8	6.2	$0.48^{\ast \ast \ast}$
Greece	4.1	3.0	0.4	3.8	8.1	$0.48^{\ast \ast \ast}$
Ireland	4.3	3.0	0.2	4.4	7.9	$0.44^{\ast \ast \ast}$
Italy	3.2	2.4	0.5	2.8	6.3	$0.55^{\ast \ast \ast}$
Japan	4.7	3.7	0.3	4.1	10.4	$0.75^{\ast \ast \ast}$
Netherlands	3.3	2.1	0.3	3.0	6.2	$0.35^{\ast \ast \ast}$
New Zealand	2.9	3.1	-0.3	2.8	6.2	0.00
Norway	3.4	1.7	1.0	3.6	5.2	$0.35^{\ast \ast \ast}$
Portugal	3.7	2.9	0.3	4.1	7.2	$0.42^{\ast \ast \ast}$
Spain	4.4	2.9	1.4	3.9	8.3	$0.61^{\ast \ast \ast}$
Sweden	2.7	1.9	-0.2	3.0	4.8	$0.60^{\ast \ast \ast}$
UK	2.5	1.8	0.0	2.6	4.5	$0.30^{\ast \ast}$
US	3.1	2.1	-0.1	3.3	5.8	0.06
Average	3.4	2.4	0.5	3.3	6.5	0.39

Notes: This table reports mean, 10th, 50th and 90th percentiles, and the first order autocorrelation coefficient (ACR) for GDP growth. Annual sample runs from 1954 to 2008.
$\ast$ Indicates significance at 10% level.
$\ast \ast$ Indicates significance at 5% level.
$\ast \ast \ast$ Indicates significance at 1% level.

Table 2: Descriptive Statistics and Unit Root Test Results for Debt to GDP Ratio

Country	Mean	Std. Dev.	10th	50th	90th	UR Test
Australia	27.3	19.8	7.3	20.9	57.6	486.6
Austria	31.6	19.9	10.7	26.8	57.8	70.9
Belgium	77.7	25.0	45.1	70.3	109.6	5.8
Canada	55.6	14.4	36.8	54.2	77.3	7.4
Denmark	37.3	25.5	5.1	32.4	70.6	$3.9^{\ast}$
Finland	22.9	18.2	7.7	15.0	54.1	4.2
France	33.5	18.1	14.9	26.7	61.5	30.8
Germany	18.0	10.4	7.7	16.7	35.4	60.1
Greece	51.7	40.4	11.6	28.8	108.1	51.9
Ireland	68.0	23.6	27.8	72.8	97.2	7.3
Italy	68.7	33.0	31.8	56.5	112.2	50.9
Japan	50.3	48.9	7.5	41.4	134.4	4.5
Netherlands	61.7	15.1	42.1	59.6	80.4	12.9
New Zealand	48.9	15.4	26.4	51.9	67.3	16.8
Norway	25.2	5.6	18.6	25.4	33.6	5.1
Portugal	25.6	18.8	9.5	17.3	59.6	37.9
Spain	28.7	13.6	10.9	30.0	48.6	5.9
Sweden	39.5	19.7	17.4	35.8	67.3	$2.2^{\ast \ast}$
UK	59.0	32.1	32.6	43.8	110.2	250.4
US	50.6	12.9	33.3	52.1	66.2	6.7
Average	44.1	21.5	20.2	38.9	75.4	56.1

Notes: This table reports mean, 10th, 50th, and 90th percentiles, and the point optimal unit root test statistic of (Elliott et al., 1996) (UR Test) for debt to GDP ratios. Annual sample runs from 1954 to 2008.
$\ast$ Indicates significance at 10% level.
$\ast \ast$ Indicates significance at 5% level.
$\ast \ast \ast$ Indicates significance at 1% level.

Table 3: Linear Model: All Countries

$ACI_{FE}(\beta)$	$ACI_{RD}(\beta)$	$SCI(\beta)$
[ -0.0361 -0.0113]	[ -2.3793 1.6179]	[ -0.0492 0.0021]
[ -0.0357 -0.0103]	[ -1.0554 0.5214]	[ -0.0815 0.0030]
[ -0.0300 -0.0060]	[ -0.2319 0.0159]	[ -0.1640 0.0070]

Notes: This table reports 90% symmetric confidence intervals for the predictive coefficient of debt to GDP ratio in the linear model (see Equation 1). ACI stands for asymptotic confidence interval; SCI stands for subsampling confidence interval; FE stands for fixed effects; and RD stands for recursive demeaning. Annual sample runs from 1954 to 2008. See Table 1 for a list of countries in the sample.

Table 4: Threshold Model: All Countries

	$\widehat{\tau}$	$CI(\tau)$	$CI(\beta_1)$	$CI(\beta_2)$	$CI(\beta_2-\beta_1)$
Panel A: Symmetric trimming	18.33	[8.58 28.09]	[0.0282 0.1170]	[-0.0387 0.0072]	[-0.1215 -0.0555]
Panel A: Symmetric trimming	18.80	[0.65 36.95]	[0.0215 0.1155]	[-0.0425 0.0130]	[-0.1325 -0.0340]
Panel A: Symmetric trimming	58.40	[41.17 75.63]	[-0.0970 0.0260]	[-0.0530 0.0120]	[-0.0470 0.0780]
Panel B: Asymmetric trimming	57.33	[53.36 61.31]	[-0.0849 0.0033]	[-0.0492 -0.0042]	[-0.0138 0.0414]
Panel B: Asymmetric trimming	46.60	[35.91 57.29]	[-0.0925 -0.0050]	[-0.0570 -0.0005]	[-0.0015 0.0415]
Panel B: Asymmetric trimming	58.40	[51.14 65.66]	[-0.0980 0.0260]	[-0.0630 0.0220]	[-0.0330 0.0630]

Notes: This table reports threshold estimates and 90% subsampling confidence intervals for the thresholds and predictive coefficients in the nonlinear model (see Equation 5). Symmetric trimming corresponds to the case where 15% of observations are trimmed on each side of the sample observations on debt to GDP while 50% is trimmed from the left and 15% from the right in case of asymmetric trimming. Annual sample runs from 1954 to 2008. See Table 1 for a list of countries in the sample.

Table 5: Linear Model: Country Groups

	$ACI_{FE}(\beta)$	$ACI_{RD}(\beta)$	$SCI(\beta)$
Panel A: Low-debt Countries	[ -0.0338 -0.0022]	[ -1.0652 0.4550]	[ -0.0789 0.0432]
Panel A: Low-debt Countries	[ -0.0329 -0.0041]	[ -0.6060 0.1530]	[ -0.0770 0.0400]
Panel A: Low-debt Countries	[ -0.0262 -0.0018]	[ -0.2220 -0.0040]	[ -0.0920 0.0630]
Panel B: High-debt Countries	[ -0.0411 -0.0105]	[ -6.1771 5.2153]	[ -0.0462 -0.0054]
Panel B: High-debt Countries	[ -0.0414 -0.0086]	[ -1.9693 1.3613]	[ -0.0475 -0.0025]
Panel B: High-debt Countries	[ -0.0364 -0.0036]	[ -0.2859 0.0779]	[ -0.0510 0.0120]

Notes: This table reports 90% confidence intervals for the predictive coefficient of debt to GDP ratio in the linear model (see Equation 1). ACI stands for asymptotic confidence interval; SCI stands for subsampling confidence interval; FE stands for fixed effect; and RD stands for recursive demeaning. Annual sample runs from 1954 to 2008. Low-debt countries include Germany, Finland, Norway, Portugal, Australia, Spain, Austria, France, Denmark, and Sweden. High-debt countries include New Zealand, Japan, US, Greece, Canada, UK, Netherlands, Ireland, Italy, and Belgium.

Table 6: Threshold Model: Country Groups

	$\widehat{\tau}$	$CI(\tau)$	$CI(\beta_1)$	$CI(\beta_2)$	$CI(\beta_2-\beta_1)$
Panel A: Low-debt Countries	18.00	[10.32 25.68]	[0.0312 0.1647]	[-0.0417 0.0462]	[-0.1641 -0.0273]
Panel A: Low-debt Countries	31.80	[26.89 36.71]	[-0.0325 0.1335]	[-0.0440 0.0390]	[-0.1220 0.0160]
Panel A: Low-debt Countries	28.40	[22.37 34.43]	[-0.0880 0.1430]	[-0.0860 0.0790]	[-0.1260 0.0630]
Panel B: High-debt Countries	46.00	[38.27 53.73]	[-0.1170 -0.0168]	[-0.0594 -0.0132]	[-0.0162 0.0774]
Panel B: High-debt Countries	46.40	[33.75 59.05]	[-0.1630 0.0165]	[-0.0680 -0.0075]	[-0.0770 0.1480]
Panel B: High-debt Countries	58.40	[47.77 69.03]	[-0.1470 0.0270]	[-0.0720 0.0070]	[-0.0510 0.1060]

Notes: This table reports threshold estimates and 90% subsampling confidence intervals for the thresholds and predictive coefficients in the nonlinear model (see Equation 5). For estimation of the threshold, a symmetric trimming scheme is considered where 15% of observations are trimmed on each side of the sample observations on debt to GDP. Annual sample runs from 1954 to 2008. See Table 5 for a list of countries in each group.

Figure 1: Debt to GDP Ratios Figure 1: Debt to GDP Ratios. See link below for figure data.

Figure 1 data

Figure 2: Debt to GDP Ratios (Cont'd)

Figure 2 data

Footnotes

* We would like to thank William Bassett and seminar participants at the Federal Reserve Board, the U.S. Census Bureau Center for Economic Research, and 32nd Annual International Symposium on Forecasting for useful comments. The views expressed in this paper are solely the responsibility of the authors and should not be interpreted as reflecting the views of the Board of Governors of the Federal Reserve System, or other members of its staff. Return to Text

1. Department of Economics, Howard University, E-mail: [email protected] Return to Text

2. Corresponding author. Board of Governors of the Federal Reserve System, E-mail: [email protected] Return to Text

3. See (Cecchetti et al., 2011) for a detailed discussion of pros and cons of both public and private debt. Return to Text

4. Including lagged growth rates on the right-hand side do not change our results qualitatively. We do not consider other potential predictors of output growth on the right hand side due to data limitations over the sample period. Return to Text

5. Note that for multi-period analysis, we use the reverse regression framework of (Hodrick, 1992) as it reduces noise relative to standard long-horizon regressions. In particular we run the following regression: $y_{i,t+1}=\tilde{\alpha}_i+\tilde{\beta} x_{i,t-h+1:t} + \tilde{u}_{i,t+1}$ , where

indicates that

is summed over the corresponding period. Return to Text

6. This bias is known as the (Stambaugh, 1999) bias in the finance literature, which focuses on predicting equity premium using persistent right hand side variables such as price dividend ratio. Return to Text

7. Note that we consider symmetric subsampling intervals as they are known to have better coverage properties, e.g. (Hall, 1988). Return to Text

8. Debt to GDP ratios are constructed by (Reinhart & Rogoff, 2010) and are available from Carmen Reinhart's website at http://www.carmenreinhart.com/data/. Real GDP data are taken from Angus Maddison's website available at http://www.ggdc.net/MADDISON/oriindex.htm. Return to Text

9. In this paper, debt to GDP ratio is taken as the ratio of gross central government debt to nominal GDP as in (Reinhart & Rogoff, 2010). Return to Text

10. This is common practice in threshold models, e.g. (Hansen, 1996). Note also that the results are robust to using a trimming percentage as small as 5%. Return to Text

11. Spain and Portugal recently experienced a considerable increase in their debt to GDP ratios, but the corresponding period is not covered in our sample. Return to Text

^♣ This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to Text